Elektrické přístroje. Přechodné děje při vypínání

Úlha č.2 Elektrické řístrje - cvičeí Přechdé děje ři vyíáí Zadáí: Pr vyíač a jmevité aětí = kv a jmevitý vyíací rud I k = ka vyčtěte: a) hdtu aralelíh tlumícíh dru tak, aby tlumil kmity ztaveéh aětí číaje

O Jensenově nerovnosti

O Jeseově erovosti Petr Vodstrčil petr.vodstrcil@vsb.cz Katedra aplikovaé matematiky, Fakulta elektrotechiky a iformatiky, Vysoká škola báňská Techická uiverzita Ostrava Ostrava, 28.1. 2019 (ŠKOMAM 2019)

3. Decibelové veličiny v akustice, kmitočtová pásma

3. Decibelové veličiy v akustice, kmitočtová ásma V ředchozí kaitole byly defiováy základí akustické veličiy, jako ař. akustický výko, akustický tlak a itezita zvuku. Tyto veličiy ve v raxi měí o moho

Ing. Vladimíra Michalcová, Ph.D. Katedra stavební mechaniky (228)

Stavebí statka - vyučující Dooručeá lteratura Ig. Vladmíra chalcová, h.d. Katedra stavebí mechaky (228) místost: LH 47/ tel.: (59 732) 348 e mal: vladmra.mchalcova@vsb.c www: htt://fast.vsb.c/mchalcova

Komplexní čísla. Definice komplexních čísel

Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují

elektrické filtry Jiří Petržela základní pojmy

Jiří Petržela základí ojmy základí ojmy z oblati elektrických filtrů základí ojmy elektrický filtr je lieárí dvojbra, který bez útlumu roouští je určité kmitočtové ložky, které obahuje vtuí igál rouštěé

Definice obecné mocniny

Defiice obecé mociy Zavedeí obecé mociy omocí ity číselé oslouosti lze rovést ěkolika zůsoby Níže uvedeý zůsob využívá k defiici eoeciálí fukce itu V dalším budeme otřebovat ásledující dvě erovosti: Lemma

Vícekanálové čekací systémy

Vícekaálové čekací systémy taice obsluhy sestává z ěkolika kaálů obsluhy, racujících aralelě a avzájem ezávisle. Vstuy i výstuy systému mají oissoovský charakter. Jedotky vstuující do systému obsadí ejrve

při obrábění Ing. Petra Cihlářová Odborný garant: Doc. Ing. Miroslav Píška, CSc.

Vysoké učeí tehiké v Brě Fakulta strojího ižeýrství Ústav strojíreské tehologie Odbor obráběí Téa: 5. vičeí - Výočet silové a eergetiké áročosti ři obráběí Okruhy: Výočet řezýh sil ro soustružeí a vrtáí

Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:

Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy

ASYNCHRONNÍ STROJE. Obsah

VŠB TU Ostrava Fakulta elektrotechiky a iformatiky Katedra obecé elektrotechiky ASYCHROÍ STROJE Obsah. Výzam a oužití asychroích motorů 2. rici čiosti asychroího motoru 3. Rozděleí asychroích motorů 4.

Katedra obecné elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava ENERGETIKA U ŘÍZENÝCH ELEKTRICKÝCH POHONŮ. 1.

Katedra obecé eletrotechiy Faulta eletrotechiy a iformatiy, VŠB - TU Ostrava EERGETIKA U ŘÍZEÝCH EEKTRICKÝCH POHOŮ Předmět : Rozvody eletricé eergie v dolech a lomech. Úvod: Světový tred z hledisa eletricé

8.3.1 Vklady, jednoduché a složené úrokování

8..1 Vklady, jedoduché a složeé úrokováí Předoklady: 81 Fiačí matematika se zabývá ukládáím a ůjčováím eěz, ojišťováím, odhady rizik aod. Poměrě důležitá a výosá discilía. Sořeí Při sořeí vkladatel uloží

8.2.10 Příklady z finanční matematiky I

8..10 Příklady z fiačí matematiky I Předoklady: 807 Fiačí matematika se zabývá ukládáím a ůjčováím eěz, ojišťováím, odhady rizik aod. Poměrě důležitá a výosá discilía. Sořeí Při sořeí vkladatel uloží do

Odhady parametrů 1. Odhady parametrů

Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:

Národní informační středisko pro podporu kvality

Národí iformačí středisko ro odoru kvality Testováí zůsobilosti a výkoosti výrobího rocesu RNDr. Jiří Michálek, Sc Ústav teorie iformace a automatizace AVČR UKAZATELE ZPŮSOBILOSTI 3 UKAZATELE ZPŮSOBILOSTI

CVIČENÍ Z ELEKTRONIKY

Střední růmyslová škola elektrotechnická Pardubice CVIČENÍ Z ELEKRONIKY Harmonická analýza Příjmení : Česák Číslo úlohy : Jméno : Petr Datum zadání :.1.97 Školní rok : 1997/98 Datum odevzdání : 11.1.97

HYDROMECHANICKÉ PROCESY. Doprava tekutin Čerpadla a kompresory (přednáška) Doc. Ing. Tomáš Jirout, Ph.D.

HROMECHANICKÉ PROCES orava tekti Čeradla a komresory (ředáška) oc. Ig. Tomáš Jirot, Ph.. (e-mail: Tomas.Jirot@fs.cvt.cz, tel.: 435 68) ČERPALA Základy teorie čeradel Základí rozděleí čeradel Hydrostatická

Tento materiál vznikl díky Operačnímu programu Praha Adaptabilita CZ.2.17/3.1.00/33254

Evroský sociálí od Praha & EU: Ivestujeme do vaší budoucosti eto materiál vzikl díky Oeračímu rogramu Praha Adatabilita CZ..7/3../3354 Maažerské kvatitativí metody II - ředáška č.3 - Queuig theory teorie

Obsah. 1 Mocninné řady Definice a vlastnosti mocninných řad Rozvoj funkce do mocninné řady Aplikace mocninných řad...

Obsah 1 Mocié řady 1 1.1 Defiice a vlastosti mociých řad.................... 1 1. Rozvoj fukce do mocié řady...................... 5 1.3 Aplikace mociých řad........................... 10 1 Kapitola 1

Aproximativní analytické řešení jednorozměrného proudění newtonské kapaliny

U8 Ústav rocesní a zracovatelské techniky F ČVUT v Praze Aroximativní analytické řešení jednorozměrného roudění newtonské kaaliny Některé říady jednorozměrného roudění newtonské kaaliny lze řešit řibližně

PRAVDĚPODOBNOST A STATISTIKA. Náhodný vektor nezávislost, funkce náhodného vektoru

SP Náhodý vetor ezávislost fuce NV PRAVDĚPODONOST A STATISTIKA Náhodý vetor ezávislost fuce áhodého vetoru Libor Žá Náhodý vetor stochasticá ezávislost Náhodé veličiy... defiovaé a ravděodobostím rostoru

Základní teoretický aparát a další potřebné znalosti pro úspěšné studium na strojní fakultě a k řešení technických problémů

Základí teoretický aarát a další otřebé zalosti ro úsěšé studium a strojí fakultě a k řešeí techických roblémů MATEMATIKA: logické uvažováí, matematické ástroje - elemetárí matematika (algebra, geometrie,

6.1 Systémy hromadné obsluhy

6. Systémy hromadé obsluhy Proces usoojováí áhodě i hromadě vziajících ožadavů a obsluhu se azývá roces hromadé obsluhy. Předmětem teorie hromadé obsluhy, ědy taé ozačovaé jao teorie frot (z aglicých slov

Mezní stavy konstrukcí a jejich porušov. Hru IV. Milan RůžR. zbynek.hruby.

ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém

DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ. 1) Pojem funkce, graf funkce

DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem ukce, gra ukce De: Fukcí reálé proměé azýváme pravidlo, které každému reálému číslu D přiřazuje právě jedo reálé číslo y H Toto pravidlo začíme ejčastěji

23. Mechanické vlnění

3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze

HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ

1. ZÁKLADNÍ VLASTNOSTI ASYNCHRONNÍHO MOTORU, ŠTÍTKOVÉ HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ 1. Kostrukce asychroího stroje Úkol: Sezámit se s kostrukčím uspořádáím a rozložeím viutí statoru a s možými variatami

Směrová kalibrace pětiotvorové kuželové sondy

Směrová kalibrace ětiotvorové kuželové sondy Matějka Milan Ing., Ústav mechaniky tekutin a energetiky, Fakulta strojní, ČVUT v Praze, Technická 4, 166 07 Praha 6, milan.matejka@fs.cvut.cz Abstrakt: The

BH059 Tepelná technika budov Konzultace č. 2

Vysoké učení technické v Brně Fakulta stavební Ústav ozemního stavitelství BH059 Teelná technika budov Konzultace č. 2 Zadání P6 zadáno na 2 konzultaci, P7 bude zadáno Průběh telot v konstrukci Kondenzace

BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV AUTOMATIZACE A INFORMATIKY

VYSOKÉ UČEÍ TECHICKÉ V BRĚ BRO UIVERSITY OF TECHOLOGY FAKULTA STROJÍHO IŽEÝRSTVÍ ÚSTAV AUTOMATIZACE A IFORMATIKY FACULTY OF MECHAICAL EGIEERIG ISTITUTE OF AUTOMATIO AD COMPUTER SCIECE MODELY HROMADÉ OBSLUHY

procesy II Zuzana 1 Katedra pravděpodobnosti a matematické statistiky Univerzita Karlova v Praze

limití Náhodé limití Katedra pravděpodobosti a matematické statistiky Uiverzita Karlova v Praze email: praskova@karli.mff.cui.cz 9.4.-22.4. 200 limití Outlie limití limití efiice: Řekeme, že stacioárí

1. Vztahy pro výpočet napěťových a zkratových

EE/E Eletráry ztahy pro výpočet apěťových a zratových poměrů. ztahy pro výpočet apěťových a zratových poměrů ýpočty lze provádět: ve fyziálích jedotách v poměrých jedotách v procetích jedotách Procetí

Bezpečnostní technika

Bezpečostí techika Modul pro hlídáí otáčeí a kotrolu zastaveí BH 5932 safemaster Grafické zázorěí fukce splňuje požadavky ormy EN 60204-1, kocepčí řešeí se dvěma kaály, vstupy pro iiciátory (símače) pp,

Směrnice 1/2011 Statistické vyhodnocování dat, verze 3 Verze 3 je shodná s původní Směrnicí 1/2011 verze 2, za čl. 2.3 je vložen nový odstavec

Směrice /0 Statitické vyhodocováí dat, verze 3 Verze 3 e hodá ůvodí Směricí /0 verze, za čl..3 e vlože ový odtavec. Statitické metody ro zkoušeí zůobiloti Statitická aalýza oužívaá ro aalýzu výledků zkoušky

Základní vlastnosti polovodičů

Základí vlastosti olovodičů Volé osiče áboje - elektroy -e m, - díry +e m V termodyamické rovováze latí Kocetrace osičů je možo vyjádřit omocí Fermiho eergie W F dotace doory ty N dotace akcetory ty P

zadání: Je dán stejnosměrný motor s konstantním magnetickým tokem, napájen do kotvy, indukčnost zanedbáme.

Teorie řízení 004 str. / 30 PŘÍKLAD zadání: Je dán stejnosměrný motor s konstantním magnetickým tokem, naájen do kotvy, indukčnost zanedbáme. E ce ω a) Odvoďte řenosovou funkci F(): F( ) ω( )/ u( ) b)

Iterační výpočty projekt č. 2

Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....

Interference. 15. prosince 2014

Iterferece 15. prosice 014 1 Úvod 1.1 Jev iterferece Mějme dvě postupé vly ψ 1 z,t) = A 1 cosωt kz +ϕ 1 ) a ψ z,t) = A cosωt kz +ϕ ). Uvažujme yí jejich superpozici ψ = ψ 1 +ψ a podívejme se, jaká bude

Odchylka přímek

734 Odchylka římek Předoklady: 708, 7306 Pedagogická ozámka: Pokd chcete hladký růěh začátk hodiy, je leší dořed ozorit žáky, že do otřeoat zorec ro úhel do ektorů Př : Urči úhel, který sírají ektory (

VYUŽITÍ TEORIE HROMADNÉ OBSLUHY PŘI SIMULOVÁNÍ MIMOŘÁDNÝCH UDÁLOSTÍ

16. medziárodá vedecká koerecia Riešeie krízových situácií v šeciickom rostredí, Fakulta šeciáleho ižiierstva ŽU, Žilia, 1. - 2. jú 211 VYUŽITÍ TEORIE HROMADNÉ OBSLUHY PŘI SIMULOVÁNÍ MIMOŘÁDNÝCH UDÁLOSTÍ

Reproduktor elektroakustický měnič převádějící elektrický signál na akustický signál, převážně zvukový

Měření reroduktorů Reroduktor elektroakustický měnič řevádějící elektrický signál na akustický signál, řevážně zvukový i w u Reroduktor reroduktor jako dvoubran y( t) h( t)* x( t) Y ( ω ) H ( ω ). X X

4.5.9 Vznik střídavého proudu

4.5.9 Vzik střídavého proudu Předpoklady: 4508 Miulá hodia: Pokud se v uzavřeém závitu měí magetický idukčí tok, idukuje se v ěm elektrické apětí =. Př. 1: Vodorově orietovaá smyčka se pohybuje rovoměrě

elektrické filtry Jiří Petržela pasivní filtry

Jiří Petržela výhody asivních filtrů levné a jednoduché řešení filtrace není nutné naájení aktivních rvků nevýhody asivních filtrů maximálně jednotkový řenos v roustném ásmu obtížnější kaskádní syntéza

PRAVDĚPODOBNOST A STATISTIKA. Náhodný vektor nezávislost, funkce náhodného vektoru

SP Náhodý vetor ezávislost fuce NV PRAVDĚPODONOST A STATISTIKA Náhodý vetor ezávislost fuce áhodého vetoru Libor Žá Náhodý vetor stochasticá ezávislost Náhodé veličiy... defiovaé a ravděodobostím rostoru

2. Úvod do indexní analýzy

2. Úvod do idexí aalýzy 2.. Motivace Tato kaitola se zabývá srováváím ukazatelů v datových souborech, které se liší buď časově ebo rostorově ebo věcě. Nejdůležitější je srováváí ukazatelů z časového hlediska.

Problémy hodnocení výkonnosti a způsobilosti řízení procesů v rámci nesplnění normality rozdělení dominantního znaku jakosti

Jiří Zmatlík 1, Pavel Zdvořák Problémy hodoceí výkoosti a zůsobilosti řízeí rocesů v rámci eslěí ormality rozděleí domiatího zaku jakosti Klíčová slova: eshodý rodukt, zaky jakosti měřitelé a zaky jakosti

ť ť ť ó ť Ž ť ť ó Č ň ů ť ť ť ť ů ňť ť ů ť ť ť ť ť Č Č Č Í Ý Ý ť Č Č ť Š Č ď ť Ý Ú ť ó ť ó ď ů ň Ó ť ť ó ň Ř ó Ó É ď ó Ň ň ť Č ň ó Ý Ý ť Ý Ý ó Ž Ý Č Ř Ý ť Ý ť Ň ť ť Č Á Š Č Ž Č ť ť ů Č ů Č Č ť Č Ú ď ó

Kruhový diagram. 1. Z odečtených hodnot pro jmenovité primární napětí nakreslete kruhový diagram. Asynchronní motor. P n =2kW n =905ot/min

TO - VŠB FE Datum měřeí E L E K T R C K É Kruhový diagram S T R O J E říjmeí Jméo Supia (hodoceí). Z odečteých hodot pro jmeovité primárí apětí areslete ruhový diagram.. Schéma zapojeí ;~;5Hz;x/4V L L

2.3.6 Práce plynu. Předpoklady: 2305

.3.6 Práce lynu Předoklady: 305 Děje v lynech nejčastěji zobrazujeme omocí diagramů grafů závislosti tlaku na objemu. Na x-ovou osu vynášíme objem a na y-ovou osu tlak. Př. : Na obrázku je nakreslen diagram

12. N á h o d n ý v ý b ě r

12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých

Závislost slovních znaků

Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví

NÁVRH A OVĚŘENÍ BETONOVÉ OPŘENÉ PILOTY ZATÍŽENÉ V HLAVĚ KOMBINACÍ SIL

NÁVRH A OVĚŘENÍ BETONOVÉ OPŘENÉ PILOTY ZATÍŽENÉ V HLAVĚ KOMBINACÍ SIL 1. ZADÁNÍ Navrhněte růměr a výztuž vrtané iloty délky L neosuvně ořené o skalní odloží zatížené v hlavě zadanými vnitřními silami (viz

Elektrotechnické materiály a výrobní procesy Příklady z části Materiály v elektrotechnice

Útav elektotechologie FEKT VT v Bě Akademický ok 004/005 Bakalářký tudijí ogam,. očík Elektotechické mateiály a výobí ocey Příklady z čáti Mateiály v elektotechice A. Vybaé kotaty c,998.0 8 m. - ychlot

Úloha č. 4 Kapacitní posouzení neřízené průsečné úrovňové křižovatky

Úloha č. 4 Kaacitní osouzení neřízené růsečné úrovňové křižovatky Pro zjednodušení budeme v úloze očítat s narosto symetrickým zatížením křižovatky, které by v raxi nastalo zřídka. Jelikož zatížení je

c) Pomocí Liouvillovy věty dokažte, že Liouvillovo číslo je transcendentí. xp 1 (p 1)! (x 1)p (x 2) p... (x d) p e x t f(t) d t = F (0)e x F (x),

a) Vyslovte a dokažte Liouvillovu větu o šaté aroximovatelosti algebraického čísla řádu d b) Defiujte Liouvillovo číslo c) Pomocí Liouvillovy věty dokažte, že Liouvillovo číslo je trascedetí 2 a) Defiujte

Geometrická optika. Zákon odrazu a lomu světla

Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost

Náhodný výběr 1. Náhodný výběr

Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti

Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový

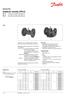Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou

OVMT Přesnost měření a teorie chyb

Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.

Petr Šedivý Šedivá matematika

LIMITA POSLOUPNOSTI Úvod: Kapitola, kde poprvé arazíme a ekoečo. Argumety posloupostí rostou ade všechy meze a zkoumáme, jak vypadají hodoty poslouposti. V kapitole se sezámíte se základími typy it a početími

UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ

3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,

7 Obyčejné diferenciální rovnice

- 9 - Občejé difereciálí rovice 7 Občejé difereciálí rovice 7 Základí ojm Difereciálí rovice Defiice Občejou difereciálí rovicí -tého řádu rozumíme rovici F(,,,, ( ) ) ebo, je-li takzvaě rozřešea vzhledem

Obr. V1.1: Schéma přenosu výkonu hnacího vozidla.

říklad 1 ro dvounáravové hnací kolejové vozidlo motorové trakce s mechanickým řenosem výkonu určené následujícími arametry určete moment hnacích nárav, tažnou sílu na obvodu kol F O. a rychlost ři maximálním

B. MECHANICKÉ KMITÁNÍ A VLNĚNÍ

B. MECHANICKÉ KMITÁNÍ A VLNĚNÍ I. MECHANICKÉ KMITÁNÍ 8.1 Kmitavý pohyb a) mechanické kmitání (kmitavý pohyb) pohyb, při kterém kmitající těleso zůstává stále v okolí určitého bodu tzv. rovnovážné polohy

Základní princip regulace U v ES si ukážeme na definici statických charakteristik zátěže

Regulace apětí v ES Základí pricip regulace v ES si ukážeme a defiici statických charakteristik zátěže Je zřejmé, že výko odebíraý spotřebitelem je závislý a frekveci a apětí a přípojicích spotřebitelů.

ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ

VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ 10. týden doc. Ing. Renata WAGNEROVÁ, Ph.D. Ostrava 2013 doc. Ing. Renata WAGNEROVÁ, Ph.D. Vysoká škola báňská

Regulační ventily (PN 16) VF 2 2-cestné, přírubové VF 3 3-cestné, přírubové

Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a

Téma: 11) Dynamika stavebních konstrukcí

Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí

MĚŘENÍ PARAMETRŮ OSVĚTLOVACÍCH SOUSTAV VEŘEJNÉHO OSVĚTLENÍ NAPÁJENÝCH Z REGULÁTORU E15

VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.

veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou

1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i

V. Normální rozdělení

V. Normálí rozděleí 1. Náhodá veličia X má ormovaé ormálí rozděleí N(0; 1). Určete: a) P (X < 1, 5); P (X > 0, 3); P ( 1, 135 < x ); P (X < 3X + ). c) číslo ε takové, že P ( X < ε) = 0,

13 Měření na sériovém rezonančním obvodu

13 13.1 Zadání 1) Změřte hodnotu indukčnosti cívky a kapacity kondenzátoru RC můstkem, z naměřených hodnot vypočítej rezonanční kmitočet. 2) Generátorem nastavujte frekvenci v rozsahu od 0,1 * f REZ do

A U. kde A je zesílení zesilovače, U 2 je výstupní napětí zesilovače a U 1 je vstupní napětí na zesilovači. Zisk po té můžeme vypočítat podle vztahu:

RIEDL 4.EB 6 /8.ZDÁNÍ a) Na předložeém ízkofrekvečím zesilovači změřte vstupí impedaci b) Změřte zesíleí a zisk pro výko 50% c) Změřte útlumovou charakteristiku Měřeí proveďte při cc =0V a maximálě 50%

Směrnice 1/2011 Statistické vyhodnocování dat, verze 4 Verze 4 je shodná se Směrnicí 1/2011 verze 3, pouze byla rozšířena o robustní analýzu

Směrce /0 Stattcké vyhodocováí dat, verze 4 Verze 4 e hodá e Směrcí /0 verze 3, ouze byla rozšířea o robutí aalýzu. Stattcké metody ro zkoušeí zůoblot Cílem tattcké aalýzy výledků zkoušek ř zkouškách zůoblot

5.5. KOMPLEXNÍ ODMOCNINA A ŘEŠENÍ KVADRATICKÝCH A BINOMICKÝCH ROVNIC

5.5. KOMPLEXNÍ ODMOCNINA A ŘEŠENÍ KVADRATICKÝCH A BINOMICKÝCH ROVNIC V této kaptole se dozvíte: jak je defováa fukce přrozeá odmoca v kompleím oboru a jaké má vlastost včetě odlšostí od odmocy v reálém

1 VÝPOČTOVÉ ZATÍŽENÍ. 1.1 Součinitel náročnosti ( 1 ) β = ( 2 ) ( 3 )

1 VÝOČOVÉ ZAÍŽENÍ Výočtové zatížeí a z ěho určeý výočtový roud sou základím velčam otřebým ro dmezováí rvků rozvodého zařízeí v ormálích rovozích stavech. ro eho staoveí e ezbyté zát stalovaý výko sotřebčů

Obvodové rovnice v časové oblasti a v operátorovém (i frekvenčním) tvaru

Obvodové rovnice v časové oblasti a v oerátorovém (i frekvenčním) tvaru EO Přednáška 5 Pavel Máša - 5. řednáška ÚVODEM V ředchozím semestru jsme se seznámili s obvodovými rovnicemi v SUS a HUS Jak se liší,

Protokol o provedeném měření

Fyzikální laboratoře FLM Protokol o rovedeném měření Název úlohy: Studium harmonického ohybu na ružině Číslo úlohy: A Datum měření: 8. 3. 2010 Jméno a říjmení: Viktor Dlouhý Fakulta mechatroniky TU, I.

7.2.4 Násobení vektoru číslem

7..4 Násobeí vektor číslem Předpoklady: 703 Tetokrát začeme hed defiicí. Násobek lového vektor číslem k je lový vektor. Násobek elového vektor = B Ačíslem k je vektor C A, přičemž C je bod, pro který platí:

SA4. Popis konstrukce a funkce STAVEBNICE HYDRAULICKÝCH HC 7100 11/98. pmax 31 MPa Q 0,5-42 dm 3. min -1 Nahrazuje HC 7100 5/95

STAVEBNICE HYDRAULICKÝCH AGREGÁTŮ ŘADY SA4 HC 7100 11/98 max 31 MPa Q 0,5-42 dm 3. mi -1 Nahrazuje HC 7100 5/95 Sestaveí hydraulického agregátu zákazickým zůsobem z tyizovaých odskui Objemy ádrží 10 až

( + ) ( ) ( ) ( ) ( ) Derivace elementárních funkcí II. Předpoklady: Př. 1: Urči derivaci funkce y = x ; n N.

.. Derivace elemetárích fukcí II Předpoklady: Př. : Urči derivaci fukce y ; N. Budeme postupovat stejě jako předtím dosazeím do vzorce: f ( + ) f ( ) f f ( + ) + + + +... + (biomická věta) + + +... + f

REE 11/12Z - Elektromechanická přeměna energie. Stud. skupina: 2E/95 Hodnocení: FSI, ÚMTMB - ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY

Předmět: REE /Z - Elektromechanická řeměna energie Jméno: Ročník: Měřeno dne: 5.0.0 Stud. kuina: E/95 Hodnocení: Útav: FSI, ÚMTMB - ÚSTAV MECHAIKY TĚLES, MECHATROIKY A BIOMECHAIKY Soluracovali: ázev úlohy:

V následující tabulce jsou uvedeny jednotky pro objemový a hmotnostní průtok.

8. Měření růtoků V následující tabulce jsou uvedeny jednotky ro objemový a hmotnostní růtok. Základní vztahy ro stacionární růtok Q M V t S w M V QV ρ ρ S w ρ t t kde V [ m 3 ] - objem t ( s ] - čas, S

Přednáška č. 10 Analýza rozptylu při jednoduchém třídění

Předáška č. 0 Aalýza roztylu ř jedoduchém tříděí Aalýza roztylu je statstcká metoda, kterou se osuzuje romělvost oakovaých realzací áhodého okusu tj. romělvost áhodé velčy. Náhodá velča vzká za relatvě

Geometrická optika. Vznikají tak dva paprsky odražený a lomený - které spolu s kolmicí v místě dopadu leží v jedné rovině a platí:

Geometrická optika Je auka o optickém zobrazováí. Byla vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým ejsou potřeba zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost

Termodynamika ideálního plynu

Přednáška 5 Termodynamika ideálního lynu 5.1 Základní vztahy ro ideální lyn 5.1.1 nitřní energie ideálního lynu Alikujme nyní oznatky získané v ředchozím textu na nejjednodužší termodynamickou soustavu

ADC (ADS) AIR DATA COMPUTER ( AIR DATA SYSTEM ) Aerometrický počítač, Aerometrický systém. V současné době se používá DADC Digital Air data computer

ADC (ADS) AIR DATA COPUTER ( AIR DATA SYSTE ) Aerometrický očítač, Aerometrický systém V současné době se oužívá DADC Digital Air data comuter Slouží ke snímání a komlexnímu zracování aerometrických a

PRAVDĚPODOBNOST ... m n

RVDĚODONOST - matematická discilía, která se zabývá studiem zákoitostí, jimiž se řídí hromadé áhodé jevy - vytváří ravděodobostí modely, omocí ichž se saží ostihout rocesy, ovlivěé áhodou. Náhodé okusy:

10.3 GEOMERTICKÝ PRŮMĚR

Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo

P. Girg. 23. listopadu 2012

Řešeé úlohy z MS - díl prví P. Girg 2. listopadu 202 Výpočet ity poslouposti reálých čísel Věta. O algebře it kovergetích posloupostí.) Necht {a } a {b } jsou kovergetí poslouposti reálých čísel a echt

PRAVDĚPODOBNOST A STATISTIKA. Náhodná proměnná vybraná rozdělení

S1P áhodá roměá vybraá rozděleí PRAVDĚPODOBOST A STATISTIKA áhodá roměá vybraá rozděleí S1P áhodá roměá vybraá rozděleí Vybraá rozděleí diskrétí P Degeerovaé rozděleí D( ) áhodá veličia X s degeerovaým

NMAF063 Matematika pro fyziky III Zkoušková písemná práce 17. ledna 2019

Jméo: Příklad 2 3 Celkem bodů Bodů 0 8 2 30 Získáo 0 Uvažujte posloupost distribucí {f } + = D (R defiovaou jako f (x = ( δ x m, kde δ ( x m začí Diracovu distribuci v bodě m Najděte limitu f = lim + f

Cvičení 3 - teorie. Teorie pravděpodobnosti vychází ze studia náhodných pokusů.

Cvičeí 3 - teorie Téma: Teorie pravděpodobosti Teorie pravděpodobosti vychází ze studia áhodých pokusů. Náhodý pokus Proces, který při opakováí dává ze stejých podmíek rozdílé výsledky. Výsledek pokusu

je vstupní kvantovaný signál. Průběh kvantizační chyby e { x ( t )}

ČÍSLICOVÉ ZPRACOVÁNÍ ZVUKOVÝCH SIGNÁLŮ Z HLEDISKA PSYCHOAKUSTIKY Fratišek Kadlec ČVUT, fakulta elektrotechická, katedra radioelektroiky, Techická 2, 66 27 Praha 6 Úvod Při číslicovém zpracováí zvukových

Laplaceova transformace.

Lalaceova transformace - studijní text ro cvičení v ředmětu Matematika -. Studijní materiál byl řiraven racovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za odory grantu IG ČVUT č. 300043 a v rámci

Oddělení technické elektrochemie, A037. LABORATORNÍ PRÁCE č.9 CYKLICKÁ VOLTAMETRIE

ÚSTV NORGNIKÉ THNOLOGI Oddělení technické elektrochemie, 037 LBORTORNÍ PRÁ č.9 YKLIKÁ VOLTMTRI yklická voltametrie yklická voltametrie atří do skuiny otenciodynamických exerimentálních metod. Ty doznaly

Intervalové odhady parametrů

Itervalové odhady parametrů Petr Pošík Části dokumetu jsou převzaty (i doslově) z Mirko Navara: Pravděpodobost a matematická statistika, https://cw.felk.cvut.cz/lib/ee/fetch.php/courses/a6m33ssl/pms_prit.pdf

1 Základy Z-transformace. pro aplikace v oblasti

Základy Z-trasformace pro aplikace v oblasti číslicového zpracováí sigálů Petr Pollák 9. říja 29 Základy Z-trasformace Teto stručý text slouží k připomeutí základích vlastostí Z-trasformace s jejími aplikacemi

VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ

VYSOÉ UČENÍ TECHNICÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAULTA ELETROTECHNIY A OMUNIAČNÍCH TECHNOLOGIÍ ÚSTAV VÝONOVÉ ELETROTECHNIY A ELETRONIY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT