2. KINETICKÁ ANALÝZA HOMOGENNÍCH REAKCÍ
|
|
|
- Jan Slavík
- před 5 lety
- Počet zobrazení:
Transkript
1 2. KINETICKÁ ANALÝZA HOMOGENNÍCH REAKCÍ Úloha 2-1 Řád reakce a rychlostní konstanta integrální metodou stupeň přeměny... 2 Úloha 2-2 Řád reakce a rychlostní konstanta integrální metodou... 2 Úloha 2-3 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku... 2 Úloha 2-4 Řád reakce a rychlostní konstanta integrální metodou měření vodivosti... 2 Úloha 2-5 Řád reakce a rychlostní konstanta integrální metodou... 3 Úloha 2-6 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku... 3 Úloha 2-7 Řád reakce a rychlostní konstanta integrální metodou měření odporu... 3 Úloha 2-8 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku... 3 Úloha 2-9 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku... 4 Úloha 2-10 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku... 4 Úloha 2-11 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku... 4 Úloha 2-12 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku... 5 Úloha 2-13 Řád reakce a rychlostní konstanta integrální metodou měření odporu... 5 Úloha 2-14 Řád reakce a rychlostní konstanta metodou poločasů... 5 Úloha 2-15 Řád reakce a rychlostní konstanta metodou poločasů... 5 Úloha 2-16 Řád reakce a rychlostní konstanta metodou poločasů... 6 Úloha 2-17 Řád reakce a rychlostní konstanta metodou poločasů... 6 Úloha 2-18 Řád reakce a rychlostní konstanta metodou zlomkových časů... 6 Úloha 2-19 Řád reakce metodou zlomkových časů z integrální křivky... 6 Úloha 2-20 Dílčí řády reakce, izolační metoda... 6 Úloha 2-21 Dílčí řády reakce... 7 Úloha 2-22 Dílčí řády reakce obecná diferenciální metoda... 7 Úloha 2-23 Řád reakce a rychlostní konstanta diferenciální metodou... 7 Úloha 2-24 Stanovení řádu reakce a rychlostní konstanty diferenciální metodou... 8 Úloha 2-25 Stanovení řádu reakce a rychlostní konstanty diferenciální metodou... 8 Úloha 2-26 Van't Hoffova diferenciální metoda... 8 Úloha 2-27 Diferenciální metoda počátečních rychlostí... 9 Úloha 2-28 Diferenciální metoda počátečních rychlostí... 9 Úloha 2-29 Stanovení dílčích řádů reakce... 9 Úloha 2-30 Stanovení dílčích řádů reakce Kinetická analýza 1
2 Úloha 2-1 Řád reakce a rychlostní konstanta integrální metodou stupeň přeměny Stanovte rychlostní konstantu a řád reakce pro tepelný rozklad oxidu dusného na zlatě při teplotě 990 C a počátečním tlaku 26,7 kpa. Při konstantním objemu byla naměřena tato data (nádoba obsahovala na počátku čistý N 2 O): Výsledek: n = 1 ; k = 1, min 1 Úloha 2-2 Řád reakce a rychlostní konstanta integrální metodou Plynná látka se rozkládá podle rovnice AB 3 (g) = 1/2 A 2 (g) + 3/2 B 2 (g). Rozklad je nevratný. V tabulce je uvedena závislost parciálního tlaku AB 3 na čase pro případ, kdy výchozí složkou je pouze AB 3. Určete celkový řád reakce (je celistvý) a hodnotu rychlostní konstanty. Výsledek: n = 2 ; k = 2, kpa 1 h 1 τ /min α 12,5 0, , , , , ,73 τ /h p AB3 /kpa Úloha 2-3 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku Oxid dusičný se rozkládá v kapalném tetrachlormethanu za uvolňování kyslíku: N 2 O 5 (v kapalném CCl 4 ) = N 2 O 4 (v kapalném CCl 4 ) + O 2 (g) Průběh reakce byl sledován při teplotě 45 C měřením celkového tlaku reagujícího systému. Tlak na počátku není nulový, je roven tlaku páry CCl 4. Byla naměřena data uvedená v tabulce. Stanovte (a) řád reakce, (b) rychlostní konstantu, (c) tlak v systému na počátku reakce (předpokládejte ideální chování plynné fáze) Výsledek: (a) n = 1, (b) k 1 = 2,028 h 1, (c) p 0 = 66,14 kpa τ /h p/kpa 0,126 84,5 0,266 99,7 0, ,7 0, ,4 0, ,8 0, ,7 146,7 Úloha 2-4 Řád reakce a rychlostní konstanta integrální metodou měření vodivosti Reakce ethyloctanu s hydroxidem sodným, CH 3 COOC 2 H 5 + NaOH = CH 3 COONa + C 2 H 5 OH byla sledována pomocí měření vodivosti reagujícího systému. Na počátku, kdy koncentrace obou výchozích složek byly stejné, 0,01 mol dm 3, byla měrná vodivost κ 0. V závislosti na čase byla měřena hodnota poměru κ/κ 0. Naměřené hodnoty jsou uvedeny v tabulce. Po dokončení reakce byla zjištěna hodnota x /x 0 = 0,359. Určete řád reakce a hodnotu rychlostní konstanty. Výsledek: n = 2; k c = 6,52 dm 3 mol 1 min 1 τ /min κ/κ 0 5 0, , , , , , Kinetická analýza 2
3 Úloha 2-5 Řád reakce a rychlostní konstanta integrální metodou Zjistěte, jakého řádu je hydrolýza ethylnitrobenzoátu (E) hydroxylovými ionty, NO 2 C 6 H 4 COOC 2 H 5 + OH = NO 2 C 6 H 4 COOH + C 2 H 5 OH pro níž byla při teplotě 15 C a stejných počátečních koncentracích reagujících látek, 0,05 mol dm 3, naměřena časová závislost množství zhydrolyzovaného esteru (viz tabulka). Jaká je hodnota rychlostní konstanty sledované reakce? Výsledek: n = 2; k c = 0,0814 dm 3 mol 1 s 1 τ /s % hydrolyzovaného E , , , , , ,35 Úloha 2-6 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku Určete rychlostní konstantu a řád reakce pro tepelný rozklad dimethyletheru na methan, vodík a oxid uhelnatý, který probíhá v plynné fázi (předpokládejte ideální chování) (CH 3 ) 2 O (g) = CH 4 (g) + H 2 (g) + CO (g) při 540 C a konstantním objemu z dat uvedených v tabulce (reaktor obsahoval na počátku pouze dimethyether). Výsledek: n =1, k c = 4, s 1 Úloha 2-7 Řád reakce a rychlostní konstanta integrální metodou měření odporu Ve vodném roztoku probíhá iontová reakce, kterou je možno schematicky zapsat 3 A + B = R + S 2 + D Kinetika reakce je sledována měřením odporu vodivostní nádobky, v níž reakce probíhá, v závislosti na reakční době. Počáteční koncentrace složek jsou (c A- ) 0 = 0,018; c B0 = 0,006 mol dm 3. Naměřené hodnoty jsou uvedeny v tabulce. Rozhodněte, zda reakce je (a) čtvrtého řádu, tj. prvého vzhledem k B a třetího vzhledem k A, (b) druhého řádu (prvého vzhledem k A, prvého vzhledem k B). Určete hodnoty rychlostních konstant k cb a k ca. Výsledek: n = 2; α = 1; β = 1; k cb = 10,772 dm 3 mol 1 min 1 ; k ca = 3 k cb = 32,316 dm 3 mol 1 min 1 Úloha 2-8 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku Sloučenina XY 3 se v toluenu rozkládá podle rovnice XY 3 (l) = 1/2 X 2 Y(l) + 5/4 Y2(g) Pruběh reakce při 30 C byl sledován měřením celkového tlaku systému v závislosti na čase (tlak v čase τ = 0 je roven tlaku páry rozpouštědla, který má při 30 C hodnotu 4,9 kpa). Stanovte řád reakce a rychlostní konstantu. Výsledek: n = 2; k c = 3, kpa 1 min 1 τ /s p AB3 /kpa 0 41, , , , ,9 τ /min R /Ω τ p /kpa 30 s 63,5 1 min 79,3 2 min 90,8 6 min 100,8 0,2 h 103,6 0,35 h 104,9 106,65 2-Kinetická analýza 3
4 Úloha 2-9 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku V uzavřené nádobě konstantního objemu probíhá jednosměrný rozklad A(g) = ν R R(g) Při konstantní teplotě 350 K byla naměřena časová závislost celkového tlaku p v nádobě, která na počátku reakce obsahovala pouze látku A. Po dokončení rozkladu má tlak v reaktoru hodnotu 177,4 kpa. Za předpokladu, že všechny plynné složky se chovají jako ideální plyny, určete: (a) stechiometrii reakce (ν R ), (b) řád reakce (je celistvý) a rychlostní konstantu, (c) poločas reakce. Výsledek: (a) ν R = 3; (b) n =1; k = 1, min 1 ; (c) τ 1/2 = 42,83 min τ /min p /kpa 0 59, , , , ,6 Úloha 2-10 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku Rozklad fosfanu probíhá při teplotě 950 C podle rovnice 4 PH 3 (g) = P 4 (g) + 6 H 2 (g) Při konstantním objemu byla tato reakce sledována měřením celkového tlaku v reakční nádobě, která na počátku obsahovala směs fosfanu a inertního plynu o molárním zlomku inertního plynu 0,1305. Z experimentální závislosti celkového tlaku na čase stanovte řád reakce a rychlostní konstantu. Předpokládejte ideální chování plynné fáze. Výsledek: n =1; k = 0,0275 min 1 Úloha 2-11 Reakce Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku C 2 H 5 NH 2 (g) = C 2 H 4 (g) + NH 3 (g), probíhající při teplotě 300 C v plynné fázi, byla sledována měřením závislosti celkového tlaku na čase s těmito výsledky: (a) Rozhodněte, zda reakce probíhá kinetikou prvého nebo druhého řádu a stanovte rychlostní konstantu (v jednotkách SI soustavy). (b) Při následujícím pokusu při stejné teplotě obsahoval reaktor na počátku kromě ethylaminu také amoniak o parciálním tlaku 10 Torr. Po jisté době, kdy bylo možno předpokládat, že veškerý ethylamin je již rozložen, byl naměřen celkový tlak 154 Torr. Určete, kolik procent původně přítomného ethylaminu se rozložilo za 15 minut od počátku reakce. Jaké jsou parciální tlaky ethylaminu, ethylenu a amoniaku v tomto okamžiku? Předpokládejte ideální chování plynné fáze. Výsledek: (a) n =1; k = 0,0931 min 1 ; (b) 75,5%; p(c 2 H 5 NH 2 ) = 2,376 kpa ; p(nh 3 ) = 8,558 kpa; p(c 2 H 4 ) = 7,224 kpa τ /min p /kpa ,30 19, , , , , ,19 τ /min p /Torr ,5 2-Kinetická analýza 4
5 Úloha 2-12 Řád reakce a rychlostní konstanta integrální metodou měření celkového tlaku Průběh rozkladu kyseliny malonové (A) CH 2 (COOH) 2 (g) = CH 4 (g) + 2 CO 2 (g) byl sledován měřením časové závislosti celkového tlaku za konstantního objemu. Získaná data jsou uvedena v přiložené tabulce. Na základě těchto dat rozhodněte, je-li sledovaná reakce prvého nebo druhého řádu, vypočítejte hodnotu rychlostní konstanty (v jednotkách SI soustavy) a rychlost reakce v okamžiku τ = 1200 s od počátku reakce. Výsledek: n =1; k = 2, s 1 ; dp(ch 2 (COOH) 2 )/dτ = 3, kpa s 1 Úloha 2-13 Řád reakce a rychlostní konstanta integrální metodou měření odporu Reakce fenacetylbromidu s pyridinem v methanolu, C 6 H 5 COCH 2 Br + C 5 H 5 N = C 6 H 5 COCH 2 C 5 H 5 N + + Br byla při 35 C sledována měřením odporu reagující směsi. Počáteční koncentrace obou složek byly stejné, 0,0285 mol dm 3. Stanovte řád reakce a rychlostní konstantu reakce. Výsledek: n = 2; k c = 0,0548 dm 3 mol 1 min 1 Úloha 2-14 Řád reakce a rychlostní konstanta metodou poločasů τ /s p /Torr τ /min R /Ω τ /min R /Ω Tepelný rozklad uhlovodíku při teplotě 500 C v nádobě objemu 101,5 dm 3, která na počátku obsahuje 1,2 molu uhlovodíku, má poločas 2 min. Když byl počáteční tlak snížen na 7,6 kpa, vzrostl poločas na 1200 s. Stanovte řád reakce a hodnotu rychlostní konstanty. Výsledek: n = 2; k p = 6, kpa 1 min 1 Úloha 2-15 Řád reakce a rychlostní konstanta metodou poločasů Při teplotě 540 K probíhá v reaktoru o objemu 5 dm 3 reakce A(g) = 2 R(g) + 1/2 S(g) Byl měřen poločas při dvou různých počátečních koncentracích látky A. Při prvém pokusu byly do reaktoru uvedeny 2 moly čisté složky A. Po 18 minutách klesla koncentrace A v reakční směsi na hodnotu 0,2 mol dm 3. Při druhém pokusu byl reaktor při teplotě 540 K naplněn čistou látkou A na tlak 5,387 MPa. Za 2 minuty bylo zjištěno, že parciální tlak složky A má poloviční hodnotu. Vypočítejte řád reakce a hodnotu rychlostní konstanty při uvedené teplotě. Uvažujte ideální chování plynné fáze. Výsledek: n = 3; k p = 0,02584 MPa 1 min 1 2-Kinetická analýza 5
6 Úloha 2-16 Řád reakce a rychlostní konstanta metodou poločasů Rozpad látky A 3 v methanolovém roztoku, A 3 = 3 A, byl sledován při teplotě 20 C měřením poločasu v závislosti na počáteční koncentraci A 3 s těmito výsledky: (a) Stanovte řád reakce a rychlostní konstantu při 20 C. (b) Je-li aktivační energie uvedené reakce 13,7 kcal mol 1, vypočítejte koncentrace A 3 a A po 10 minutách, provádíme-li reakci při teplotě 35 C a vycházíme-li z roztoku čisté A 3 o koncentraci 0,27 mol dm 3. (c A3 ) 0 τ 1/2 mol dm 3 min 0,1 21,83 0,2 15,44 0,3 12,6 0,4 10,9 Výsledek: (a) n = 1,5 ; k c = 0,12 (mol dm 3 ) 0,5 min 1 ; (b) c A3 = 0,0689 mol dm 3 ; c A = 0,6033 mol dm 3 Úloha 2-17 Řád reakce a rychlostní konstanta metodou poločasů Rozklad oxidu dusného v plynné fázi při teplotě 1030 K je reakce necelistvého řádu. V reaktoru o konstantním objemu byly naměřeny hodnoty poločasu rozkladu při různých počátečních koncentracích, které jsou uvedeny v tabulce. Najděte celkový řád reakce a vypočtěte rychlostní konstantu. Výsledek: n = 1,75; k p = 2, kpa 0,75 s 1 Úloha 2-18 Řád reakce a rychlostní konstanta metodou zlomkových časů Organická kyselina RCOOH se v plynné fázi rozkládá podle rovnice RCOOH(g) = RH(g) + CO 2 (g) Při různých počátečních tlacích byla měřena doba potřebná ke zreagování jedné třetiny původně přítomné kyseliny. Určete řád reakce a rychlostní konstantu. Výsledek: n = 2; k p = 2, kpa 1 s 1 p 0 /kpa τ 1/2 /s , ,7 212 p 0 /kpa τ 1/3 /s 2 95,7 4 47,8 6 31, ,2 12,5 15, ,9 17,5 10,9 20 9,58 Úloha 2-19 Řád reakce metodou zlomkových časů z integrální křivky Rozklad látky A probíhá jako reakce necelistvého řádu. Bylo zjištěno, že stupně přeměny α = 0,2 bylo dosaženo po 168 s, stupně přeměny α = 0,6 po 20,8 minutách od počátku reakce. Metodou zlomkových časů najděte řád této reakce. Výsledek: n = 2,5 Úloha 2-20 Dílčí řády reakce, izolační metoda Reakce X(g) + Y(g) = ν R R(g) probíhá v ideálním plynném systému. Z výsledků experimentů za konstantní teploty a objemu, uvedených v následující tabulce, určete řády reakce vzhledem k jednotlivým složkám, napište rychlostní rovnici a vypočítejte hodnotu rychlostní konstanty. 2-Kinetická analýza 6
7 p X0 = 16 kpa p Y0 = 130 kpa p Y0 /Pa τ l/2 /s p X0 /Pa τ l/2 /s , , dp dp dp 1,5 0, Výsledek: X Y R = = = kp px py ; kp = 1,8 10 Pa s dτ dτ νr dτ Úloha 2-21 Dílčí řády reakce O reakci ν A A + ν B B = ν R R je známo, že řád reakce vzhledem ke složce A je n A = 0,5. Systém, v němž byla tato reakce sledována, sestával z nasyceného roztoku A, v němž bylo rozpuštěno malé množství B a z tuhé látky A. Rozpustnost A při teplotě pokusu je 1,42 mol dm 3. Byl zjišťován čas, potřebný ke zreagování 1/4 původně přítomného množství látky B. Při počáteční koncentraci B 0,025 mol dm 3 bylo naměřeno τ l/4 = 32 min, při koncentraci c B0 = 0,04 mol dm 3 bylo τ l/4 = 20 min. Jaký je řád reakce vzhledem k B a jaká je hodnota rychlostní konstanty k cb? Napište rychlostní rovnici platnou pro tento případ. Výsledek: β = 2; k cb = 0,35 (mol dm 3 ) 1,5 min 1 dcb 0,5 ; = k 2 cb ca cb dτ Úloha 2-22 Dílčí řády reakce obecná diferenciální metoda Iontová reakce A(l) + 2 D (l) = S ( l) + N ( l) + B(l) je prvého řádu vzhledem k A. Při počátečních koncentracích c A0 = 5, mol dm 3 a c D0 = 3, mol dm 3 byla naměřena závislost rychlosti změny odporu reagujícího systému na stupni přeměny klíčové složky: Zjistěte řád reakce vzhledem k D. Výsledek: δ = d(1/r)/dτ (S min 1 ) α 1,24 0,10 1,09 0,15 0,94 0,20 0,822 0,25 0,705 0,30 0,603 0,35 Úloha 2-23 Řád reakce a rychlostní konstanta diferenciální metodou Stanovte řád reakce a hodnotu rychlostní konstanty pro reakci acetanhydridu (A) s isobutanolem (B) (CH 3 CO) 2 O + i-c 4 H 9 OH = CH 3 COOC 4 H 9 + CH 3 COOH, probíhající v benzenovém roztoku, pro níž byla při 100 C a stejných počátečních koncentracích obou složek, c A0 = c B0 = 0,3 mol dm 3, získána tato data: c A 10 6 ( dc A /dτ) c A 10 6 ( dc A /dτ) mol dm 3 mol dm 3 s 1 mol dm 3 mol dm 3 s 1 0,261 0, ,101 0,071 22,5 10,7 0, ,046 4,7 0, ,033 2,5 Výsledek: n = 2 ; k c = 2, (mol dm 3 ) 1 s 1 2-Kinetická analýza 7
8 Úloha 2-24 Stanovení řádu reakce a rychlostní konstanty diferenciální metodou Stanovte řád a hodnotu rychlostní konstanty řídícího děje při pyrolýze plynného diboranu, při 100 C z těchto experimentálních dat: Výsledek: n = 1,5 ; k p = 4, Pa 0,5 h 1 Úloha 2-25 B 2 H 6 (g) = 2 BH 3 (g) koncentrace B 2 H 6 časová změna celkového tlaku soustavy mol dm 3 kpa h 1 2, , , , Stanovení řádu reakce a rychlostní konstanty diferenciální metodou Rychlost změny koncentrace ethylalkoholu v průběhu reakce acetanhydrihu (A) s ethylalkoholem (E) (CH 3 CO) 2 O + C 2 H 5 OH = CH 3 COOC 2 H 5 + CH 3 COOH (A) (E) (HAc) v prostředí tetrachlormethanu při 70,6 C v závislosti na okamžité koncentraci vznikající kyseliny octové (HAc) při stejných počátečních koncentracích acetanhydridu a ethylalkoholu, c A0 = c E0 = 0,15 mol dm 3, je uvedena v následující tabulce: c HAc 10 6 ( dc E /dτ) c HAc 10 6 ( dc E /dτ) mol dm 3 mol dm 3 s 1 mol dm 3 mol dm 3 s 1 0, ,4 0,0660 8,04 0, ,6 0,0825 5,19 0, ,2 0,0930 3,70 0,0570 9,86 0,1020 2,63 Stanovte celkový řád reakce a rychlostní konstantu. Výsledek: n = 2; k c = 1, dm 3 mol 1 s 1 Úloha 2-26 Van't Hoffova diferenciální metoda Rozklad jisté látky (M = 575 g/mol) v organickém rozpouštědle je reakce necelistvého řádu. Na počátku reakce bylo ve 250 cm 3 rozpouštědla rozpuštěno 0,92 g látky A. Z experimentální křivky c A τ byly vyhodnoceny okamžité rychlosti změny koncentrace A, uvedené v tabulce. Stanovte řád reakce a rychlostní konstantu van't Hoffovou diferenciální metodou. Výsledek: n = 2,7 ; k c = 0,0418 (mol dm 3 ) 1,7 s 1 c A ( dc A /dτ) mol dm 3 mol cm 3 s 1 0,0062 4,62 0,0058 3,82 0,0053 3,00 0,0045 1,91 0,0037 1,10 0,0025 0,40 2-Kinetická analýza 8
9 Úloha 2-27 Diferenciální metoda počátečních rychlostí Při sledování kinetiky rozkladu kyseliny dusité (A), 3 HNO 2 (aq) = H + (aq) + NO 3 (aq) + 2 NO(g) + H2 O(l), byla naměřena závislost okamžité koncentrace kyseliny dusité (v mol dm 3 ) na čase (v min) při dvou počátečních koncentracích. Počáteční části těchto experimentálních křivek byly aproximovány polynomy: 1. c A0 = 0,075 mol dm 3 : c A = 0,075 2, τ + 6, τ 2 2. c A0 = 0,100 mol dm 3 : c A = 0,100 6, τ + 2, τ 2 Diferenciální metodou počátečních rychlostí najděte řád reakce a hodnotu rychlostní konstanty. Výsledek: n = 3,5 ; k c = 0,65 (mol dm 3 ) 2,5 min 1 Úloha 2-28 Diferenciální metoda počátečních rychlostí Pro kinetiku polymerizace vinylchloridu (V), n CH 2 =CHCl (CH 2 CHCl) n při teplotě 50 C byla získána data uvedená v tabulce. Reakce byla iniciována tepelným rozkladem benzoylperoxidu (1,1 hm.%). Byla prováděna v oddělených zkumavkách a sledována vážením polymeru po odpaření monomeru a rozpouštědla (benzoylperoxid byl odečten). Stanovte řád reakce a její rychlostní konstantu. Výsledek: n = 1,5 ; k c = (mol dm 3 ) 0,5 s 1 c V ( dc V /dτ) 0 mol dm 3 mol dm 3 s 1 0,061 4,5 0,085 7,5 0,098 9,2 0,128 14,0 0,143 16,0 0,165 20,1 Úloha 2-29 Stanovení dílčích řádů reakce Při redukci látky A, probíhající podle stechiometrické rovnice 2 A(g) + 2 H 2 (g) = R(g) + 2 H 2 O(g), byl při konstantním objemu sledován celkový tlak v závislosti na čase. Při teplotě 950 K byla získána tato data: 1. p A0 = 53,3 kpa 2. (p H2 ) 0 = 43,9 kpa (p H2 ) 0 ( dp/dτ) 0 p A0 ( dp/dτ) 0 kpa kpa s 1 kpa kpa s 1 38,6 1,3 47,98 1,2 18,7 0,63 19,59 0,2 Určete řády reakce vzhledem k jednotlivým složkám, celkový řád reakce a rychlostní konstanty pro rychlostní rovnici ( dc A /dτ ) = k cα c β 2 a pro rychlostní rovnici ( dp A /dτ ) = k pα p β 2. ca A H Výsledek: α = 2; β = 1; n = 3 ; k pa = 2, kpa 2 s 1 ; k ca = 1, (mol m 3 ) 2 s 1 pa A H 2-Kinetická analýza 9
10 Úloha 2-30 Stanovení dílčích řádů reakce Při vyhodnocování časové závislosti koncentrace bromu, získané sledováním bromace jistého uhlovodíku, RH + Br 2 = RBr + HBr byly pro různé koncentrace bromu odečteny hodnoty rychlosti, uvedené v tabulce. Uhlovodík RH byl přítomen ve velkém přebytku, takže bylo možno předpokládat, že úbytek koncentrace uhlovodíku RH během reakce je zanedbatelný. Stanovte řád reakce vzhledem k bromu. Výsledek: β = 1,5 c Br ( dc Br 2 /dτ) mol dm 3 mol dm 3 min 1 0,55 7,17 0,50 6,40 0,45 5,77 0,40 5,06 0,35 3,85 0,30 3,26 0,25 2,18 0,20 1,70 2-Kinetická analýza 10
kde k c(no 2) = 2, m 6 mol 2 s 1. Jaká je hodnota rychlostní konstanty v rychlostní rovnici ? V [k = 1, m 6 mol 2 s 1 ]
![kde k c(no 2) = 2, m 6 mol 2 s 1. Jaká je hodnota rychlostní konstanty v rychlostní rovnici ? V [k = 1, m 6 mol 2 s 1 ] kde k c(no 2) = 2, m 6 mol 2 s 1. Jaká je hodnota rychlostní konstanty v rychlostní rovnici ? V [k = 1, m 6 mol 2 s 1 ]](/thumbs/98/135866737.jpg) KINETIKA JEDNODUCHÝCH REAKCÍ Různé vyjádření reakční rychlosti a rychlostní konstanty 1 Rychlost reakce, rychlosti přírůstku a úbytku jednotlivých složek Rozklad kyseliny dusité je popsán stechiometrickou
KINETIKA JEDNODUCHÝCH REAKCÍ Různé vyjádření reakční rychlosti a rychlostní konstanty 1 Rychlost reakce, rychlosti přírůstku a úbytku jednotlivých složek Rozklad kyseliny dusité je popsán stechiometrickou
Úloha 1-39 Teplotní závislost rychlostní konstanty, reakce druhého řádu... 11
 1. ZÁKLADNÍ POJMY Úloha 1-1 Různé vyjádření reakční rychlosti rychlosti přírůstku a úbytku jednotlivých složek... 2 Úloha 1-2 Různé vyjádření reakční rychlosti změna celkového látkového množství... 2 Úloha
1. ZÁKLADNÍ POJMY Úloha 1-1 Různé vyjádření reakční rychlosti rychlosti přírůstku a úbytku jednotlivých složek... 2 Úloha 1-2 Různé vyjádření reakční rychlosti změna celkového látkového množství... 2 Úloha
Úloha 3-15 Protisměrné reakce, relaxační kinetika... 5. Úloha 3-18 Protisměrné reakce, relaxační kinetika... 6
 3. SIMULTÁNNÍ REAKCE Úloha 3-1 Protisměrné reakce oboustranně prvého řádu, výpočet přeměny... 2 Úloha 3-2 Protisměrné reakce oboustranně prvého řádu, výpočet času... 2 Úloha 3-3 Protisměrné reakce oboustranně
3. SIMULTÁNNÍ REAKCE Úloha 3-1 Protisměrné reakce oboustranně prvého řádu, výpočet přeměny... 2 Úloha 3-2 Protisměrné reakce oboustranně prvého řádu, výpočet času... 2 Úloha 3-3 Protisměrné reakce oboustranně
5. PRŮTOČNÉ HOMOGENNÍ REAKTORY
 5. PRŮTOČNÉ HOMOGENNÍ REAKTORY Úloha 5-1 Diskontinuální a průtočný reaktor s pístovým tokem... 2 Úloha 5-2 Protisměrné reakce oboustranně prvého řádu, výpočet přeměny... 2 Úloha 5-3 Protisměrné reakce
5. PRŮTOČNÉ HOMOGENNÍ REAKTORY Úloha 5-1 Diskontinuální a průtočný reaktor s pístovým tokem... 2 Úloha 5-2 Protisměrné reakce oboustranně prvého řádu, výpočet přeměny... 2 Úloha 5-3 Protisměrné reakce
Ú L O H Y. kde r je rychlost reakce vyjádřená úbytkem látkového množství kyslíku v molech v objemu 1 m
 Ú L O H Y 1. Různé vyjádření reakční rychlosti; Př. 9.1 Určete, jaké vztahy platí mezi rychlostmi vzniku a ubývání jednotlivých složek reakce 4 NH 3 (g) + 5 O (g) = 4 NO(g) + 6 H O(g). Různé vyjádření
Ú L O H Y 1. Různé vyjádření reakční rychlosti; Př. 9.1 Určete, jaké vztahy platí mezi rychlostmi vzniku a ubývání jednotlivých složek reakce 4 NH 3 (g) + 5 O (g) = 4 NO(g) + 6 H O(g). Různé vyjádření
Kolik energie by se uvolnilo, kdyby spalování ethanolu probíhalo při teplotě o 20 vyšší? Je tato energie menší nebo větší než při teplotě 37 C?
 TERMOCHEMIE Reakční entalpie při izotermním průběhu reakce, rozsah reakce 1 Kolik tepla se uvolní (nebo spotřebuje) při výrobě 2,2 kg acetaldehydu C 2 H 5 OH(g) = CH 3 CHO(g) + H 2 (g) (a) při teplotě
TERMOCHEMIE Reakční entalpie při izotermním průběhu reakce, rozsah reakce 1 Kolik tepla se uvolní (nebo spotřebuje) při výrobě 2,2 kg acetaldehydu C 2 H 5 OH(g) = CH 3 CHO(g) + H 2 (g) (a) při teplotě
Úlohy: 1) Vypočítejte tepelné zabarvení dané reakce z následujících dat: C 2 H 4(g) + H 2(g) C 2 H 6(g)
 Úlohy: 1) Vypočítejte tepelné zabarvení dané reakce z následujících dat: C 2 H 4(g) + H 2(g) C 2 H 6(g) C 2 H 4(g) + 3O 2(g ) 2CO 2(g) +2H 2 O (l) H 0 298,15 = -1410,9kJ.mol -1 2C 2 H 6(g) + 7O 2(g) 4CO
Úlohy: 1) Vypočítejte tepelné zabarvení dané reakce z následujících dat: C 2 H 4(g) + H 2(g) C 2 H 6(g) C 2 H 4(g) + 3O 2(g ) 2CO 2(g) +2H 2 O (l) H 0 298,15 = -1410,9kJ.mol -1 2C 2 H 6(g) + 7O 2(g) 4CO
Termochemie. Verze VG
 Termochemie Verze VG Termochemie Termochemie je oblast termodynamiky zabývající se studiem tepelného zabarvení chemických reakcí. Reakce, při kterých se teplo uvolňuje = exotermní. Reakce, při kterých
Termochemie Verze VG Termochemie Termochemie je oblast termodynamiky zabývající se studiem tepelného zabarvení chemických reakcí. Reakce, při kterých se teplo uvolňuje = exotermní. Reakce, při kterých
2.4 Stavové chování směsí plynů Ideální směs Ideální směs reálných plynů Stavové rovnice pro plynné směsi
 1. ZÁKLADNÍ POJMY 1.1 Systém a okolí 1.2 Vlastnosti systému 1.3 Vybrané základní veličiny 1.3.1 Množství 1.3.2 Délka 1.3.2 Délka 1.4 Vybrané odvozené veličiny 1.4.1 Objem 1.4.2 Hustota 1.4.3 Tlak 1.4.4
1. ZÁKLADNÍ POJMY 1.1 Systém a okolí 1.2 Vlastnosti systému 1.3 Vybrané základní veličiny 1.3.1 Množství 1.3.2 Délka 1.3.2 Délka 1.4 Vybrané odvozené veličiny 1.4.1 Objem 1.4.2 Hustota 1.4.3 Tlak 1.4.4
= 2,5R 1,5R =1,667 T 2 =T 1. W =c vm W = ,5R =400,23K. V 1 =p 2. p 1 V 2. =p 2 R T. p 2 p 1 1 T 1 =p 2 1 T 2. =p 1 T 1,667 = ,23
 15-17 Jeden mol argonu, o kterém budeme předpokládat, že se chová jako ideální plyn, byl adiabaticky vratně stlačen z tlaku 100 kpa na tlak p 2. Počáteční teplota byla = 300 K. Kompresní práce činila W
15-17 Jeden mol argonu, o kterém budeme předpokládat, že se chová jako ideální plyn, byl adiabaticky vratně stlačen z tlaku 100 kpa na tlak p 2. Počáteční teplota byla = 300 K. Kompresní práce činila W
c A = c A0 a k c ln c A A0
 řád n 2.řád.řád 0.řád. KINETIK JEDNODUCHÝCH REKCÍ 0 Ryhlost reae, ryhlosti přírůstu a úbytu jednotlivýh slože... 2 02 Ryhlost reae, ryhlosti přírůstu a úbytu jednotlivýh slože... 2 03 Ryhlost reae, ryhlosti
řád n 2.řád.řád 0.řád. KINETIK JEDNODUCHÝCH REKCÍ 0 Ryhlost reae, ryhlosti přírůstu a úbytu jednotlivýh slože... 2 02 Ryhlost reae, ryhlosti přírůstu a úbytu jednotlivýh slože... 2 03 Ryhlost reae, ryhlosti
Zadání příkladů řešených na výpočetních cvičeních z Fyzikální chemie I, obor CHTP. Termodynamika. Příklad 10
 Zadání příkladů řešených na výpočetních cvičeních z Fyzikální chemie I, obor CHTP Termodynamika Příklad 1 Stláčením ideálního plynu na 2/3 původního objemu vzrostl při stálé teplotě jeho tlak na 15 kpa.
Zadání příkladů řešených na výpočetních cvičeních z Fyzikální chemie I, obor CHTP Termodynamika Příklad 1 Stláčením ideálního plynu na 2/3 původního objemu vzrostl při stálé teplotě jeho tlak na 15 kpa.
1. Termochemie - příklady 1. ročník
 1. Termochemie - příklady 1. ročník 1.1. Urči reakční teplo reakce: C (g) + 1/2 O 2 (g) -> CO (g), ΔH 1 =?, známe-li C (g) + O 2 (g) -> CO 2 (g) ΔH 2 = -393,7 kj/mol CO (g) + 1/2 O 2 -> CO 2 (g) ΔH 3 =
1. Termochemie - příklady 1. ročník 1.1. Urči reakční teplo reakce: C (g) + 1/2 O 2 (g) -> CO (g), ΔH 1 =?, známe-li C (g) + O 2 (g) -> CO 2 (g) ΔH 2 = -393,7 kj/mol CO (g) + 1/2 O 2 -> CO 2 (g) ΔH 3 =
Úloha 1 Stavová rovnice ideálního plynu. p V = n R T. Látkové množství [mol]
![Úloha 1 Stavová rovnice ideálního plynu. p V = n R T. Látkové množství [mol] Úloha 1 Stavová rovnice ideálního plynu. p V = n R T. Látkové množství [mol]](/thumbs/50/27137182.jpg) TEORETICKÁ ČÁST (60 BODŮ) Úloha 1 Stavová rovnice ideálního plynu 1 bodů 1. Objem [m ] Univerzální plynová konstanta 8,145 J K 1 mol 1 p V n R T Tlak [Pa] Látkové množství [mol] Termodynamická teplota
TEORETICKÁ ČÁST (60 BODŮ) Úloha 1 Stavová rovnice ideálního plynu 1 bodů 1. Objem [m ] Univerzální plynová konstanta 8,145 J K 1 mol 1 p V n R T Tlak [Pa] Látkové množství [mol] Termodynamická teplota
Chemické výpočty 11. Stechiometrické výpočty (včetně reakcí s ideálními plyny); reakce s přebytkem výchozí látky
 Chemické výpočty 11 Stechiometrické výpočty (včetně reakcí s ideálními plyny); reakce s přebytkem výchozí látky Ing. Martin Pižl Skupina koordinační chemie místnost A213 E-mail: martin.pizl@vscht.cz Web:
Chemické výpočty 11 Stechiometrické výpočty (včetně reakcí s ideálními plyny); reakce s přebytkem výchozí látky Ing. Martin Pižl Skupina koordinační chemie místnost A213 E-mail: martin.pizl@vscht.cz Web:
4.10 ; ; 8.10 mol dm min d d d dpa dp -1 1
 verze 5.4.017 1.-4. cvičení Téma: Chemická kinetika K čemu je to dobré: - popis časového průběhů dějů ve všech oblastech chemie 1. Určete, jaké vztahy platí mezi rychlostmi vzniku a ubývání jednotlivých
verze 5.4.017 1.-4. cvičení Téma: Chemická kinetika K čemu je to dobré: - popis časového průběhů dějů ve všech oblastech chemie 1. Určete, jaké vztahy platí mezi rychlostmi vzniku a ubývání jednotlivých
N A = 6,023 10 23 mol -1
 Pro vyjadřování množství látky se v chemii zavádí veličina látkové množství. Značí se n, jednotkou je 1 mol. Látkové množství je jednou ze základních veličin soustavy SI. Jeden mol je takové množství látky,
Pro vyjadřování množství látky se v chemii zavádí veličina látkové množství. Značí se n, jednotkou je 1 mol. Látkové množství je jednou ze základních veličin soustavy SI. Jeden mol je takové množství látky,
ZÁKLADNÍ CHEMICKÉ POJMY A ZÁKONY
 ZÁKLADNÍ CHEMICKÉ POJMY A ZÁKONY Klíčová slova: relativní atomová hmotnost (A r ), relativní molekulová hmotnost (M r ), Avogadrova konstanta (N A ), látkové množství (n, mol), molární hmotnost (M, g/mol),
ZÁKLADNÍ CHEMICKÉ POJMY A ZÁKONY Klíčová slova: relativní atomová hmotnost (A r ), relativní molekulová hmotnost (M r ), Avogadrova konstanta (N A ), látkové množství (n, mol), molární hmotnost (M, g/mol),
CHEMICKÉ VÝPOČTY I. ČÁST LÁTKOVÉ MNOŽSTVÍ. HMOTNOSTI ATOMŮ A MOLEKUL.
 CHEMICKÉ VÝPOČTY I. ČÁST LÁTKOVÉ MNOŽSTVÍ. HMOTNOSTI ATOMŮ A MOLEKUL. Látkové množství Značka: n Jednotka: mol Definice: Jeden mol je množina, která má stejný počet prvků, jako je atomů ve 12 g nuklidu
CHEMICKÉ VÝPOČTY I. ČÁST LÁTKOVÉ MNOŽSTVÍ. HMOTNOSTI ATOMŮ A MOLEKUL. Látkové množství Značka: n Jednotka: mol Definice: Jeden mol je množina, která má stejný počet prvků, jako je atomů ve 12 g nuklidu
Energie v chemických reakcích
 Energie v chemických reakcích Energetická bilance reakce CH 4 + Cl 2 = CH 3 Cl + HCl rozštěpení vazeb vznik nových vazeb V chemických reakcích dochází ke změně vazeb mezi atomy. Vazebná energie uvolnění
Energie v chemických reakcích Energetická bilance reakce CH 4 + Cl 2 = CH 3 Cl + HCl rozštěpení vazeb vznik nových vazeb V chemických reakcích dochází ke změně vazeb mezi atomy. Vazebná energie uvolnění
Rychlost chemické reakce A B. time. rychlost = - [A] t. [B] t. rychlost = Reakční rychlost a stechiometrie A + B C; R C = R A = R B A + 2B 3C;
![Rychlost chemické reakce A B. time. rychlost = - [A] t. [B] t. rychlost = Reakční rychlost a stechiometrie A + B C; R C = R A = R B A + 2B 3C; Rychlost chemické reakce A B. time. rychlost = - [A] t. [B] t. rychlost = Reakční rychlost a stechiometrie A + B C; R C = R A = R B A + 2B 3C;](/thumbs/56/39180690.jpg) Rychlost chemické reakce A B time rychlost = - [A] t rychlost = [B] t Reakční rychlost a stechiometrie A + B C; R C = R A = R B A + 2B 3C; 1 1 R A = RB = R 2 3 C Př.: Určete rychlost rozkladu HI v následující
Rychlost chemické reakce A B time rychlost = - [A] t rychlost = [B] t Reakční rychlost a stechiometrie A + B C; R C = R A = R B A + 2B 3C; 1 1 R A = RB = R 2 3 C Př.: Určete rychlost rozkladu HI v následující
Bilan a ce c zák á l k ad a ní pojm j y m aplikace zákonů o zachování čehokoli 10.10.2008 3
 Výpočtový seminář z Procesního inženýrství podzim 2008 Bilance Materiálové a látkové 10.10.2008 1 Tématické okruhy bilance - základní pojmy bilanční schéma způsoby vyjadřování koncentrací a přepočtové
Výpočtový seminář z Procesního inženýrství podzim 2008 Bilance Materiálové a látkové 10.10.2008 1 Tématické okruhy bilance - základní pojmy bilanční schéma způsoby vyjadřování koncentrací a přepočtové
ZÁKLADNÍ CHEMICKÉ VÝPOČTY
 ZÁKLADNÍ CHEMICKÉ VÝPOČTY Látkové množství - vyjadřování množství: jablka pivo chleba uhlí - (téměř každá míra má svojí jednotku) v chemii existuje univerzální veličina pro vyjádření množství látky LÁTKOVÉ
ZÁKLADNÍ CHEMICKÉ VÝPOČTY Látkové množství - vyjadřování množství: jablka pivo chleba uhlí - (téměř každá míra má svojí jednotku) v chemii existuje univerzální veličina pro vyjádření množství látky LÁTKOVÉ
Složení soustav (roztoky, koncentrace látkového množství)
 VZOROVÉ PŘÍKLADY Z CHEMIE A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava Doporučená literatura z chemie: Prakticky jakákoliv celostátní učebnice
VZOROVÉ PŘÍKLADY Z CHEMIE A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava Doporučená literatura z chemie: Prakticky jakákoliv celostátní učebnice
Chemické výpočty II. Vladimíra Kvasnicová
 Chemické výpočty II Vladimíra Kvasnicová Převod jednotek pmol/l nmol/l µmol/l mmol/l mol/l 10-12 10-9 10-6 10-3 mol/l µg mg g 10-6 10-3 g µl ml dl L 10-6 10-3 10-1 L Cvičení 12) cholesterol (MW=386,7g/mol):
Chemické výpočty II Vladimíra Kvasnicová Převod jednotek pmol/l nmol/l µmol/l mmol/l mol/l 10-12 10-9 10-6 10-3 mol/l µg mg g 10-6 10-3 g µl ml dl L 10-6 10-3 10-1 L Cvičení 12) cholesterol (MW=386,7g/mol):
 OBECNÁ CHEMIE František Zachoval CHEMICKÉ ROVNOVÁHY 1. Rovnovážný stav, rovnovážná konstanta a její odvození Dlouhou dobu se chemici domnívali, že jakákoliv chem.
OBECNÁ CHEMIE František Zachoval CHEMICKÉ ROVNOVÁHY 1. Rovnovážný stav, rovnovážná konstanta a její odvození Dlouhou dobu se chemici domnívali, že jakákoliv chem.
TERMOCHEMIE. Entalpie H = Údaj o celkové... látky, není možné ji změřit, ale můžeme měřit... entalpie: H
 Entalpie = Údaj o celkové... látky, není možné ji změřit, ale můžeme měřit... entalpie: Změna entalpie = Změna energie v reakci, k níž dochází při konstantních..., reaktanty a produkty jsou stejné... (energie
Entalpie = Údaj o celkové... látky, není možné ji změřit, ale můžeme měřit... entalpie: Změna entalpie = Změna energie v reakci, k níž dochází při konstantních..., reaktanty a produkty jsou stejné... (energie
p st plyny 1 čistétuhél.akap.
 bak-08=1/1 R=8.314 = 8.314JK 1 mol 1 Reakce v ideální plynné fázi ( K=exp rg ) m = RT i a ν i i a i = { pi p st = y ip p st plyny 1 čistétuhél.akap. y i = n i n (g) n (g) = i {plyny} Pozn.:Součetpřesplynyjevč.inertů!Čistékapalinyatuhélátkymají
bak-08=1/1 R=8.314 = 8.314JK 1 mol 1 Reakce v ideální plynné fázi ( K=exp rg ) m = RT i a ν i i a i = { pi p st = y ip p st plyny 1 čistétuhél.akap. y i = n i n (g) n (g) = i {plyny} Pozn.:Součetpřesplynyjevč.inertů!Čistékapalinyatuhélátkymají
Inovace bakalářského studijního oboru Aplikovaná chemie CZ.1.07/2.2.00/ Výpočty z chemických vzorců
 Výpočty z chemických vzorců 1. Hmotnost kyslíku je 80 g. Vypočítejte : a) počet atomů kyslíku ( 3,011 10 atomů) b) počet molů kyslíku (2,5 mol) c) počet molekul kyslíku (1,505 10 24 molekul) d) objem (dm
Výpočty z chemických vzorců 1. Hmotnost kyslíku je 80 g. Vypočítejte : a) počet atomů kyslíku ( 3,011 10 atomů) b) počet molů kyslíku (2,5 mol) c) počet molekul kyslíku (1,505 10 24 molekul) d) objem (dm
Termochemie se zabývá tepelným zabarvením chemických reakcí Vychází z 1. termodynamického zákona. U změna vnitřní energie Q teplo W práce
 Termochemie Termochemie se zabývá tepelným zabarvením chemických reakcí Vychází z 1. termodynamického zákona U = Q + W U změna vnitřní energie Q teplo W práce Teplo a práce dodané soustavě zvyšují její
Termochemie Termochemie se zabývá tepelným zabarvením chemických reakcí Vychází z 1. termodynamického zákona U = Q + W U změna vnitřní energie Q teplo W práce Teplo a práce dodané soustavě zvyšují její
Ústřední komise Chemické olympiády. 42. ročník. KRAJSKÉ KOLO Kategorie D. SOUTĚŽNÍ ÚLOHY TEORETICKÉ ČÁSTI Časová náročnost: 60 minut
 Ústřední komise Chemické olympiády 42. ročník 2005 2006 KRAJSKÉ KOLO Kategorie D SOUTĚŽNÍ ÚLOHY TEORETICKÉ ČÁSTI Časová náročnost: 60 minut Institut dětí a mládeže Ministerstva školství, mládeže a tělovýchovy
Ústřední komise Chemické olympiády 42. ročník 2005 2006 KRAJSKÉ KOLO Kategorie D SOUTĚŽNÍ ÚLOHY TEORETICKÉ ČÁSTI Časová náročnost: 60 minut Institut dětí a mládeže Ministerstva školství, mládeže a tělovýchovy
Laboratorní cvičení z kinetiky chemických reakcí
 Laboratorní cvičení z kinetiky chemických reakcí LABORATORNÍ CVIČENÍ 1. Téma: Ovlivňování průběhu reakce změnou koncentrace látek. podmínek průběhu reakce. Jednou z nich je změna koncentrace výchozích
Laboratorní cvičení z kinetiky chemických reakcí LABORATORNÍ CVIČENÍ 1. Téma: Ovlivňování průběhu reakce změnou koncentrace látek. podmínek průběhu reakce. Jednou z nich je změna koncentrace výchozích
[ ] d[ Y] rychlost REAKČNÍ KINETIKA X Y
![[ ] d[ Y] rychlost REAKČNÍ KINETIKA X Y [ ] d[ Y] rychlost REAKČNÍ KINETIKA X Y](/thumbs/78/77051926.jpg) REAKČNÍ KINETIKA Faktory ovlivňující rychlost chemických reakcí Chemická povaha reaktantů - reaktivita Fyzikální stav reaktantů homogenní vs. heterogenní reakce Teplota 10 C zvýšení rychlosti 2x 3x zýšení
REAKČNÍ KINETIKA Faktory ovlivňující rychlost chemických reakcí Chemická povaha reaktantů - reaktivita Fyzikální stav reaktantů homogenní vs. heterogenní reakce Teplota 10 C zvýšení rychlosti 2x 3x zýšení
Ch - Chemické reakce a jejich zápis
 Ch - Chemické reakce a jejich zápis Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE Tento dokument byl
Ch - Chemické reakce a jejich zápis Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE Tento dokument byl
Dynamická podstata chemické rovnováhy
 Dynamická podstata chemické rovnováhy Ve směsi reaktantů a produktů probíhá chemická reakce dokud není dosaženo rovnovážného stavu. Chemická rovnováha má dynamický charakter protože produkty stále vznikají
Dynamická podstata chemické rovnováhy Ve směsi reaktantů a produktů probíhá chemická reakce dokud není dosaženo rovnovážného stavu. Chemická rovnováha má dynamický charakter protože produkty stále vznikají
Acidobazické děje - maturitní otázka z chemie
 Otázka: Acidobazické děje Předmět: Chemie Přidal(a): Žaneta Teorie kyselin a zásad: Arrhemiova teorie (1887) Kyseliny jsou látky, které odštěpují ve vodném roztoku proton vodíku H+ HA -> H+ + A- Zásady
Otázka: Acidobazické děje Předmět: Chemie Přidal(a): Žaneta Teorie kyselin a zásad: Arrhemiova teorie (1887) Kyseliny jsou látky, které odštěpují ve vodném roztoku proton vodíku H+ HA -> H+ + A- Zásady
VYPRACOVAT NEJPOZDĚJI DO 16. 12. 2015
 Máte před sebou pracovní list. Téma : CHEMICKÝ DĚJ Jestliže ho zpracujete, máte možnost získat známku, která má nejvyšší hodnotu v elektronické žákovské knížce. Ovšem je nezbytné splnit následující podmínky:
Máte před sebou pracovní list. Téma : CHEMICKÝ DĚJ Jestliže ho zpracujete, máte možnost získat známku, která má nejvyšší hodnotu v elektronické žákovské knížce. Ovšem je nezbytné splnit následující podmínky:
Chemická kinetika. Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky)
 Chemická kinetika Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky) Rychlé reakce výbuch, neutralizace H + +OH Pomalé reakce rezivění železa Časová závislost průběhu
Chemická kinetika Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky) Rychlé reakce výbuch, neutralizace H + +OH Pomalé reakce rezivění železa Časová závislost průběhu
Hmotnost. Výpočty z chemie. m(x) Ar(X) = Atomová relativní hmotnost: m(y) Mr(Y) = Molekulová relativní hmotnost: Mr(AB)= Ar(A)+Ar(B)
 Hmotnostní jednotka: Atomová relativní hmotnost: Molekulová relativní hmotnost: Molární hmotnost: Hmotnost u = 1,66057.10-27 kg X) Ar(X) = m u Y) Mr(Y) = m u Mr(AB)= Ar(A)+Ar(B) m M(Y) = ; [g/mol] n M(Y)
Hmotnostní jednotka: Atomová relativní hmotnost: Molekulová relativní hmotnost: Molární hmotnost: Hmotnost u = 1,66057.10-27 kg X) Ar(X) = m u Y) Mr(Y) = m u Mr(AB)= Ar(A)+Ar(B) m M(Y) = ; [g/mol] n M(Y)
3 Acidobazické reakce
 3 Acidobazické reakce Brønstedova teorie 1. Uveďte explicitní definice podle Brønstedovy teorie. Kyselina je... Báze je... Konjugovaný pár je... 2. Doplňte tabulku a pojmenujte všechny sloučeniny. Kyselina
3 Acidobazické reakce Brønstedova teorie 1. Uveďte explicitní definice podle Brønstedovy teorie. Kyselina je... Báze je... Konjugovaný pár je... 2. Doplňte tabulku a pojmenujte všechny sloučeniny. Kyselina
Autor: Tomáš Galbička www.nasprtej.cz Téma: Roztoky Ročník: 2.
 Roztoky směsi dvou a více látek jsou homogenní (= nepoznáte jednotlivé částečky roztoku - částice jsou menší než 10-9 m) nejčastěji se rozpouští pevná látka v kapalné látce jedna složka = rozpouštědlo
Roztoky směsi dvou a více látek jsou homogenní (= nepoznáte jednotlivé částečky roztoku - částice jsou menší než 10-9 m) nejčastěji se rozpouští pevná látka v kapalné látce jedna složka = rozpouštědlo
Sada 7 Název souboru Ročník Předmět Formát Název výukového materiálu Anotace
 Sada 7 Název souboru Ročník Předmět Formát Název výukového materiálu Anotace VY_52_INOVACE_737 8. Chemie notebook Směsi Materiál slouží k vyvození a objasnění pojmů (klíčová slova - chemická látka, směs,
Sada 7 Název souboru Ročník Předmět Formát Název výukového materiálu Anotace VY_52_INOVACE_737 8. Chemie notebook Směsi Materiál slouží k vyvození a objasnění pojmů (klíčová slova - chemická látka, směs,
TERMOCHEMIE, TERMOCHEMICKÉ ZÁKONY, TERMODYNAMIKA, ENTROPIE
 TERMOCHEMIE, TERMOCHEMICKÉ ZÁKONY, TERMODYNAMIKA, ENTROPIE Chemická reakce: Jestliže se za vhodných podmínek vyskytnou 2 látky schopné spolu reagovat, nastane chemická reakce. Při ní z výchozích látek
TERMOCHEMIE, TERMOCHEMICKÉ ZÁKONY, TERMODYNAMIKA, ENTROPIE Chemická reakce: Jestliže se za vhodných podmínek vyskytnou 2 látky schopné spolu reagovat, nastane chemická reakce. Při ní z výchozích látek
VI. VÝPOČET Z CHEMICKÉ ROVNICE
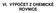 VI. VÝPOČET Z CHEMICKÉ ROVNICE ZÁKLADNÍ POJMY : Chemická rovnice (např. hoření zemního plynu): CH 4 + 2 O 2 CO 2 + 2 H 2 O CH 4, O 2 jsou reaktanty; CO 2, H 2 O jsou produkty; čísla 2 jsou stechiometrické
VI. VÝPOČET Z CHEMICKÉ ROVNICE ZÁKLADNÍ POJMY : Chemická rovnice (např. hoření zemního plynu): CH 4 + 2 O 2 CO 2 + 2 H 2 O CH 4, O 2 jsou reaktanty; CO 2, H 2 O jsou produkty; čísla 2 jsou stechiometrické
3 Acidobazické reakce
 3 Acidobazické reakce Brønstedova teorie 1. Uveďte explicitní definice podle Brønstedovy teorie. Kyselina je... Báze je... Konjugovaný pár je... 2. Doplňte tabulku a pojmenujte všechny sloučeniny. Kyselina
3 Acidobazické reakce Brønstedova teorie 1. Uveďte explicitní definice podle Brønstedovy teorie. Kyselina je... Báze je... Konjugovaný pár je... 2. Doplňte tabulku a pojmenujte všechny sloučeniny. Kyselina
Hydrochemie koncentrace látek (výpočty)
 1 Atomová hmotnostní konstanta/jednotka m u Relativní atomová hmotnost Relativní molekulová hmotnost Látkové množství (mol) 1 mol je takové množství látky, které obsahuje tolik částic, kolik je atomů ve
1 Atomová hmotnostní konstanta/jednotka m u Relativní atomová hmotnost Relativní molekulová hmotnost Látkové množství (mol) 1 mol je takové množství látky, které obsahuje tolik částic, kolik je atomů ve
DOUČOVÁNÍ KVINTA CHEMIE
 1. ÚVOD DO STUDIA CHEMIE 1) Co studuje chemie? 2) Rozděl chemii na tři důležité obory. DOUČOVÁNÍ KVINTA CHEMIE 2. NÁZVOSLOVÍ ANORGANICKÝCH SLOUČENIN 1) Pojmenuj: BaO, N 2 0, P 4 O 10, H 2 SO 4, HMnO 4,
1. ÚVOD DO STUDIA CHEMIE 1) Co studuje chemie? 2) Rozděl chemii na tři důležité obory. DOUČOVÁNÍ KVINTA CHEMIE 2. NÁZVOSLOVÍ ANORGANICKÝCH SLOUČENIN 1) Pojmenuj: BaO, N 2 0, P 4 O 10, H 2 SO 4, HMnO 4,
Chemické veličiny, vztahy mezi nimi a chemické výpočty
 SBÍRKA ŘEŠENÝCH PŘÍKLADŮ PRO PROJEKT PŘÍRODNÍ VĚDY AKTIVNĚ A INTERAKTIVNĚ CZ.1.07/1.1.24/01.0040 Chemické veličiny, vztahy mezi nimi a chemické výpočty Mgr. Jana Žůrková, 2013, 20 stran Obsah 1. Veličiny
SBÍRKA ŘEŠENÝCH PŘÍKLADŮ PRO PROJEKT PŘÍRODNÍ VĚDY AKTIVNĚ A INTERAKTIVNĚ CZ.1.07/1.1.24/01.0040 Chemické veličiny, vztahy mezi nimi a chemické výpočty Mgr. Jana Žůrková, 2013, 20 stran Obsah 1. Veličiny
SBÍRKA ÚLOH CHEMICKÝCH VÝPOČTŮ
 SBÍRKA ÚLOH CHEMICKÝCH VÝPOČTŮ ALEŠ KAJZAR BRNO 2015 Obsah 1 Hmotnostní zlomek 1 1.1 Řešené příklady......................... 1 1.2 Příklady k procvičení...................... 6 2 Objemový zlomek 8 2.1
SBÍRKA ÚLOH CHEMICKÝCH VÝPOČTŮ ALEŠ KAJZAR BRNO 2015 Obsah 1 Hmotnostní zlomek 1 1.1 Řešené příklady......................... 1 1.2 Příklady k procvičení...................... 6 2 Objemový zlomek 8 2.1
4. MECHANISMY A TEORIE CHEMICKÉ KINETIKY
 4. MECHANISMY A TEORIE CHEMICKÉ KINETIKY Úloha 4-1 Řešení reačních schémat... Úloha 4- Řešení reačních schémat... Úloha 4-3 Řešení reačních schémat... Úloha 4-4 Řešení reačních schémat... 3 Úloha 4-5 Řešení
4. MECHANISMY A TEORIE CHEMICKÉ KINETIKY Úloha 4-1 Řešení reačních schémat... Úloha 4- Řešení reačních schémat... Úloha 4-3 Řešení reačních schémat... Úloha 4-4 Řešení reačních schémat... 3 Úloha 4-5 Řešení
Do známky zkoušky rovnocenným podílem započítávají získané body ze zápočtového testu.
 Podmínky pro získání zápočtu a zkoušky z předmětu Chemicko-inženýrská termodynamika pro zpracování ropy Zápočet je udělen, pokud student splní zápočtový test alespoň na 50 %. Zápočtový test obsahuje 3
Podmínky pro získání zápočtu a zkoušky z předmětu Chemicko-inženýrská termodynamika pro zpracování ropy Zápočet je udělen, pokud student splní zápočtový test alespoň na 50 %. Zápočtový test obsahuje 3
Výzkum vlivu přenosových jevů na chování reaktoru se zkrápěným ložem katalyzátoru. Petr Svačina
 Výzkum vlivu přenosových jevů na chování reaktoru se zkrápěným ložem katalyzátoru Petr Svačina I. Vliv difuze vodíku tekoucím filmem kapaliny na průběh katalytické hydrogenace ve zkrápěných reaktorech
Výzkum vlivu přenosových jevů na chování reaktoru se zkrápěným ložem katalyzátoru Petr Svačina I. Vliv difuze vodíku tekoucím filmem kapaliny na průběh katalytické hydrogenace ve zkrápěných reaktorech
Rozpustnost s. Rozpouštění = opakem krystalizace Veličina udávající hmotnost rozpuštěné látky v daném objemu popř. v hmotnosti nasyceného roztoku.
 Rozpustnost 1 Rozpustnost s Rozpouštění = opakem krystalizace Veličina udávající hmotnost rozpuštěné látky v daném objemu popř. v hmotnosti nasyceného roztoku. NASYCENÝ = při určité t a p se již více látky
Rozpustnost 1 Rozpustnost s Rozpouštění = opakem krystalizace Veličina udávající hmotnost rozpuštěné látky v daném objemu popř. v hmotnosti nasyceného roztoku. NASYCENÝ = při určité t a p se již více látky
Teorie transportu plynů a par polymerními membránami. Doc. Ing. Milan Šípek, CSc. Ústav fyzikální chemie VŠCHT Praha
 Teorie transportu plynů a par polymerními membránami Doc. Ing. Milan Šípek, CSc. Ústav fyzikální chemie VŠCHT Praha Úvod Teorie transportu Difuze v polymerních membránách Propustnost polymerních membrán
Teorie transportu plynů a par polymerními membránami Doc. Ing. Milan Šípek, CSc. Ústav fyzikální chemie VŠCHT Praha Úvod Teorie transportu Difuze v polymerních membránách Propustnost polymerních membrán
Sbírka příkladů z teoretických základů analytické chemie Tomáš Křížek Karel Nesměrák
 UNIVERZITA KARLOVA Přírodovědecká fakulta Katedra analytické chemie Sbírka příkladů z teoretických základů analytické chemie Tomáš Křížek Karel Nesměrák Praha 2016 1 Protolytické rovnováhy 1.1 Vypočítejte
UNIVERZITA KARLOVA Přírodovědecká fakulta Katedra analytické chemie Sbírka příkladů z teoretických základů analytické chemie Tomáš Křížek Karel Nesměrák Praha 2016 1 Protolytické rovnováhy 1.1 Vypočítejte
CHEMICKÉ REAKCE A HMOTNOSTI A OBJEMY REAGUJÍCÍCH LÁTEK
 CHEMICKÉ REAKCE A HMOTNOSTI A OBJEMY REAGUJÍCÍCH LÁTEK Význam stechiometrických koeficientů 2 H 2 (g) + O 2 (g) 2 H 2 O(l) Počet reagujících částic 2 molekuly vodíku reagují s 1 molekulou kyslíku za vzniku
CHEMICKÉ REAKCE A HMOTNOSTI A OBJEMY REAGUJÍCÍCH LÁTEK Význam stechiometrických koeficientů 2 H 2 (g) + O 2 (g) 2 H 2 O(l) Počet reagujících částic 2 molekuly vodíku reagují s 1 molekulou kyslíku za vzniku
5. CHEMICKÉ REAKTORY
 5. CHEMICÉ REAORY 5.1 IZOERMNÍ REAORY... 5.1.1 Diskontinuální reaktory... 5.1. Průtočné reaktory... 5.1..1 Průtočné reaktory s pístovým tokem... 5.1.. Průtočné reaktory s dokonale promíchávaným obsahem...4
5. CHEMICÉ REAORY 5.1 IZOERMNÍ REAORY... 5.1.1 Diskontinuální reaktory... 5.1. Průtočné reaktory... 5.1..1 Průtočné reaktory s pístovým tokem... 5.1.. Průtočné reaktory s dokonale promíchávaným obsahem...4
Chemická kinetika Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky)
 Chemická kinetika Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky) Rychlé reakce výbuch H + O, neutralizace H + +OH Pomalé reakce rezivění železa Časová závislost
Chemická kinetika Chemická kinetika studuje Rychlost chemických reakcí Mechanismus reakcí (reakční kroky) Rychlé reakce výbuch H + O, neutralizace H + +OH Pomalé reakce rezivění železa Časová závislost
Inovace profesní přípravy budoucích učitelů chemie
 Inovace profesní přípravy budoucích učitelů chemie I n v e s t i c e d o r o z v o j e v z d ě l á v á n í CZ.1.07/2.2.00/15.0324 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem
Inovace profesní přípravy budoucích učitelů chemie I n v e s t i c e d o r o z v o j e v z d ě l á v á n í CZ.1.07/2.2.00/15.0324 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem
Obsah Chemická reakce... 2 PL:
 Obsah Chemická reakce... 2 PL: Vyčíslení chemické rovnice - řešení... 3 Tepelný průběh chemické reakce... 4 Rychlost chemických reakcí... 4 Rozdělení chemických reakcí... 4 1 Chemická reakce děj, při němž
Obsah Chemická reakce... 2 PL: Vyčíslení chemické rovnice - řešení... 3 Tepelný průběh chemické reakce... 4 Rychlost chemických reakcí... 4 Rozdělení chemických reakcí... 4 1 Chemická reakce děj, při němž
9. Chemické reakce Kinetika
 Základní pojmy Kinetické rovnice pro celistvé řády Katalýza Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti reakční mechanismus elementární reakce a molekularita reakce reakční rychlost
Základní pojmy Kinetické rovnice pro celistvé řády Katalýza Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti reakční mechanismus elementární reakce a molekularita reakce reakční rychlost
Roztok je homogenní (stejnorodá) směs dvou a více látek. Částice, které tvoří roztok, jsou dokonale rozptýleny a vzájemně nereagují.
 ROZTOKY Roztok je homogenní (stejnorodá) směs dvou a více látek. Částice, které tvoří roztok, jsou dokonale rozptýleny a vzájemně nereagují. Roztoky podle skupenství dělíme na: a) plynné (čistý vzduch)
ROZTOKY Roztok je homogenní (stejnorodá) směs dvou a více látek. Částice, které tvoří roztok, jsou dokonale rozptýleny a vzájemně nereagují. Roztoky podle skupenství dělíme na: a) plynné (čistý vzduch)
ANODA KATODA elektrolyt:
 Ukázky z pracovních listů 1) Naznač pomocí šipek, které částice putují k anodě a které ke katodě. Co je elektrolytem? ANODA KATODA elektrolyt: Zn 2+ Cl - Zn 2+ Zn 2+ Cl - Cl - Cl - Cl - Cl - Zn 2+ Cl -
Ukázky z pracovních listů 1) Naznač pomocí šipek, které částice putují k anodě a které ke katodě. Co je elektrolytem? ANODA KATODA elektrolyt: Zn 2+ Cl - Zn 2+ Zn 2+ Cl - Cl - Cl - Cl - Cl - Zn 2+ Cl -
Fázové heterogenní rovnováhy Fáze = homogenní část soustavy, oddělná fyzickým rozhraním, na rozhraní se vlastnosti mění skokem
 Fázové heterogenní rovnováhy Fáze = homogenní část soustavy, oddělná fyzickým rozhraním, na rozhraní se vlastnosti mění skokem Rovnováha Tepelná - T všude stejná Mechanická - p všude stejný Chemická -
Fázové heterogenní rovnováhy Fáze = homogenní část soustavy, oddělná fyzickým rozhraním, na rozhraní se vlastnosti mění skokem Rovnováha Tepelná - T všude stejná Mechanická - p všude stejný Chemická -
Relativní atomová hmotnost
 Relativní atomová hmotnost 1. Jak se značí relativní atomová hmotnost? 2. Jaké jsou jednotky Ar? 3. Zpaměti urči a) Ar(N) b) Ar (C) 4. Bez kalkulačky urči, kolika atomy kyslíku bychom vyvážili jeden atom
Relativní atomová hmotnost 1. Jak se značí relativní atomová hmotnost? 2. Jaké jsou jednotky Ar? 3. Zpaměti urči a) Ar(N) b) Ar (C) 4. Bez kalkulačky urči, kolika atomy kyslíku bychom vyvážili jeden atom
Učební osnovy Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Chemický kroužek ročník 6.-9.
 Učební osnovy Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Chemický kroužek ročník 6.-9. Školní rok 0/03, 03/04 Kapitola Téma (Učivo) Znalosti a dovednosti (výstup) Počet hodin pro kapitolu Úvod
Učební osnovy Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Chemický kroužek ročník 6.-9. Školní rok 0/03, 03/04 Kapitola Téma (Učivo) Znalosti a dovednosti (výstup) Počet hodin pro kapitolu Úvod
Laboratorní práce č. 8: Elektrochemické metody stanovení korozní rychlosti
 Laboratorní práce č. 8: Elektrochemické metody stanovení korozní rychlosti Cíl práce: Cílem laboratorní úlohy Elektrochemické metody stanovení korozní rychlosti je stanovení korozní rychlosti oceli v prostředí
Laboratorní práce č. 8: Elektrochemické metody stanovení korozní rychlosti Cíl práce: Cílem laboratorní úlohy Elektrochemické metody stanovení korozní rychlosti je stanovení korozní rychlosti oceli v prostředí
ŘEŠENÍ KONTROLNÍHO TESTU ŠKOLNÍHO KOLA
 Ústřední komise Chemické olympiády 48. ročník 2011/2012 ŠKOLNÍ KOLO kategorie C ŘEŠENÍ KONTROLNÍHO TESTU ŠKOLNÍHO KOLA KONTROLNÍ TEST ŠKOLNÍHO KOLA (60 BODŮ) Úloha 1 Neznámý nerost 21 bodů 1. Barva plamene:
Ústřední komise Chemické olympiády 48. ročník 2011/2012 ŠKOLNÍ KOLO kategorie C ŘEŠENÍ KONTROLNÍHO TESTU ŠKOLNÍHO KOLA KONTROLNÍ TEST ŠKOLNÍHO KOLA (60 BODŮ) Úloha 1 Neznámý nerost 21 bodů 1. Barva plamene:
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto
 Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Výpočty ph roztoků kyselin a zásad ph silných jednosytných kyselin a zásad. Pro výpočty se uvažuje, že silné kyseliny a zásady jsou úplně disociovány.
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Výpočty ph roztoků kyselin a zásad ph silných jednosytných kyselin a zásad. Pro výpočty se uvažuje, že silné kyseliny a zásady jsou úplně disociovány.
Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115
 Číslo projektu: Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo šablony: 31 Název materiálu: Ročník: Identifikace materiálu: Jméno autora: Předmět: Tématický celek: Anotace: CZ.1.07/1.5.00/3.0
Číslo projektu: Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo šablony: 31 Název materiálu: Ročník: Identifikace materiálu: Jméno autora: Předmět: Tématický celek: Anotace: CZ.1.07/1.5.00/3.0
Roztok. Homogenní směs molekul, které mohou být v pevném, kapalném nebo plynném stavu. Pravé roztoky
 Roztok Homogenní směs molekul, které mohou být v pevném, kapalném nebo plynném stavu Pravé roztoky Micelární a koloidní roztoky (suspenze): částice velké 1 nm 10 µm Tyndallův jev 1 Druhy roztoků Složka
Roztok Homogenní směs molekul, které mohou být v pevném, kapalném nebo plynném stavu Pravé roztoky Micelární a koloidní roztoky (suspenze): částice velké 1 nm 10 µm Tyndallův jev 1 Druhy roztoků Složka
Soli. ph roztoků solí - hydrolýza
 Soli Soli jsou iontové sloučeniny vzniklé neutralizační reakcí. Např. NaCl je sůl vzniklá reakcí kyseliny HCl a zásady NaOH. Př.: Napište neutralizační reakce jejichž produktem jsou CH 3 COONa, NaCN, NH
Soli Soli jsou iontové sloučeniny vzniklé neutralizační reakcí. Např. NaCl je sůl vzniklá reakcí kyseliny HCl a zásady NaOH. Př.: Napište neutralizační reakce jejichž produktem jsou CH 3 COONa, NaCN, NH
Stanovení izoelektrického bodu kaseinu
 Stanovení izoelektrického bodu kaseinu Shlukování koloidních částic do větších celků makroskopických rozměrů nazýváme koagulací. Ke koagulaci koloidních roztoků bílkovin dochází porušením solvatačního
Stanovení izoelektrického bodu kaseinu Shlukování koloidních částic do větších celků makroskopických rozměrů nazýváme koagulací. Ke koagulaci koloidních roztoků bílkovin dochází porušením solvatačního
Pozn.: Pokud není řečeno jinak jsou pod pojmem procenta míněna vždy procenta hmotnostní.
 Sebrané úlohy ze základních chemických výpočtů Tento soubor byl sestaven pro potřeby studentů prvního ročníku chemie a příbuzných předmětů a nebyl nikterak revidován. Prosím omluvte případné chyby, překlepy
Sebrané úlohy ze základních chemických výpočtů Tento soubor byl sestaven pro potřeby studentů prvního ročníku chemie a příbuzných předmětů a nebyl nikterak revidován. Prosím omluvte případné chyby, překlepy
Hydrochemie koncentrace látek (výpočty)
 Atomová hmotnostní konstanta/jednotka m u Relativní atomová hmotnost Relativní molekulová hmotnost Látkové množství (mol) mol je takové množství látky, které obsahuje tolik částic, kolik je atomů ve 2
Atomová hmotnostní konstanta/jednotka m u Relativní atomová hmotnost Relativní molekulová hmotnost Látkové množství (mol) mol je takové množství látky, které obsahuje tolik částic, kolik je atomů ve 2
Ú L O H Y
 Ú L O H Y 1. Vylučování kovů - Faradayův zákon; Př. 8.1 Stejný náboj, 5789 C, projde při elektrolýze každým z roztoků těchto solí: (a) AgNO 3, (b) CuSO 4, (c) Na 2 SO 4, (d) Al(NO 3 ) 3, (e) Al 2 (SO 4
Ú L O H Y 1. Vylučování kovů - Faradayův zákon; Př. 8.1 Stejný náboj, 5789 C, projde při elektrolýze každým z roztoků těchto solí: (a) AgNO 3, (b) CuSO 4, (c) Na 2 SO 4, (d) Al(NO 3 ) 3, (e) Al 2 (SO 4
Cvičení z termomechaniky Cvičení 2. Stanovte objem nádoby, ve které je uzavřený dusík o hmotnosti 20 [kg], teplotě 15 [ C] a tlaku 10 [MPa].
![Cvičení z termomechaniky Cvičení 2. Stanovte objem nádoby, ve které je uzavřený dusík o hmotnosti 20 [kg], teplotě 15 [ C] a tlaku 10 [MPa]. Cvičení z termomechaniky Cvičení 2. Stanovte objem nádoby, ve které je uzavřený dusík o hmotnosti 20 [kg], teplotě 15 [ C] a tlaku 10 [MPa].](/thumbs/25/6795424.jpg) Příklad 1 Stanovte objem nádoby, ve které je uzavřený dusík o hmotnosti 20 [kg], teplotě 15 [ C] a tlaku 10 [MPa]. m 20[kg], t 15 [ C] 288.15 [K], p 10 [MPa] 10.10 6 [Pa], R 8314 [J. kmol 1. K 1 ] 8,314
Příklad 1 Stanovte objem nádoby, ve které je uzavřený dusík o hmotnosti 20 [kg], teplotě 15 [ C] a tlaku 10 [MPa]. m 20[kg], t 15 [ C] 288.15 [K], p 10 [MPa] 10.10 6 [Pa], R 8314 [J. kmol 1. K 1 ] 8,314
Teoretický protokol ze cvičení 6. 12. 2010 Josef Bušta, skupina: 1, obor: fytotechnika
 Úloha: Karboxylové kyseliny, č. 3 Úkoly: Příprava kys. mravenčí z chloroformu Rozklad kys. mravenčí Esterifikace Rozklad kys. šťavelové Příprava kys. benzoové oxidací toluenu Reakce kys. benzoové a salicylové
Úloha: Karboxylové kyseliny, č. 3 Úkoly: Příprava kys. mravenčí z chloroformu Rozklad kys. mravenčí Esterifikace Rozklad kys. šťavelové Příprava kys. benzoové oxidací toluenu Reakce kys. benzoové a salicylové
Úlohy z fyzikální chemie
 Úlohy z fyzikální chemie Bakalářský kurz Kolektiv ústavu fyzikální chemie Doc. Ing. Lidmila Bartovská, CSc., Ing. Michal Bureš, CSc., Doc. Ing. Ivan Cibulka, CSc., Doc. Ing. Vladimír Dohnal, CSc., Doc.
Úlohy z fyzikální chemie Bakalářský kurz Kolektiv ústavu fyzikální chemie Doc. Ing. Lidmila Bartovská, CSc., Ing. Michal Bureš, CSc., Doc. Ing. Ivan Cibulka, CSc., Doc. Ing. Vladimír Dohnal, CSc., Doc.
Úvod do koroze. (kapitola, která bude společná všem korozním laboratorním pracím a kterou studenti musí znát bez ohledu na to, jakou práci dělají)
 Úvod do koroze (kapitola, která bude společná všem korozním laboratorním pracím a kterou studenti musí znát bez ohledu na to, jakou práci dělají) Koroze je proces degradace kovu nebo slitiny kovů působením
Úvod do koroze (kapitola, která bude společná všem korozním laboratorním pracím a kterou studenti musí znát bez ohledu na to, jakou práci dělají) Koroze je proces degradace kovu nebo slitiny kovů působením
ANODA KATODA elektrolyt:
 Ukázky z pracovnívh listů 1) Naznač pomocí šipek, které částice putují k anodě a které ke katodě. Co je elektrolytem? ANODA KATODA elektrolyt: Zn 2+ Cl - Zn 2+ Zn 2+ Cl - Cl - Cl - Cl - Cl - Zn 2+ Cl -
Ukázky z pracovnívh listů 1) Naznač pomocí šipek, které částice putují k anodě a které ke katodě. Co je elektrolytem? ANODA KATODA elektrolyt: Zn 2+ Cl - Zn 2+ Zn 2+ Cl - Cl - Cl - Cl - Cl - Zn 2+ Cl -
SHRNUTÍ A ZÁKLADNÍ POJMY chemie 8.ročník ZŠ
 SHRNUTÍ A ZÁKLADNÍ POJMY chemie 8.ročník ZŠ 1. ČÍM SE ZABÝVÁ CHEMIE VLASTNOSTI LÁTEK, POKUSY - chemie přírodní věda, která studuje vlastnosti a přeměny látek pomocí pozorování, měření a pokusu - látka
SHRNUTÍ A ZÁKLADNÍ POJMY chemie 8.ročník ZŠ 1. ČÍM SE ZABÝVÁ CHEMIE VLASTNOSTI LÁTEK, POKUSY - chemie přírodní věda, která studuje vlastnosti a přeměny látek pomocí pozorování, měření a pokusu - látka
CHEMIE. Pracovní list č. 4 - žákovská verze Téma: Tepelné zabarvení chemických reakcí. Mgr. Kateřina Dlouhá. Student a konkurenceschopnost
 www.projektsako.cz CHEMIE Pracovní list č. 4 - žákovská verze Téma: Tepelné zabarvení chemických reakcí Lektor: Projekt: Reg. číslo: Mgr. Kateřina Dlouhá Student a konkurenceschopnost CZ.1.07/1.1.07/03.0075
www.projektsako.cz CHEMIE Pracovní list č. 4 - žákovská verze Téma: Tepelné zabarvení chemických reakcí Lektor: Projekt: Reg. číslo: Mgr. Kateřina Dlouhá Student a konkurenceschopnost CZ.1.07/1.1.07/03.0075
Vyjadřuje poměr hmotnosti rozpuštěné látky k hmotnosti celého roztoku.
 Koncentrace roztoků Hmotnostní zlomek w Vyjadřuje poměr hmotnosti rozpuštěné látky k hmotnosti celého roztoku. w= m A m s m s...hmotnost celého roztoku, m A... hmotnost rozpuštěné látky Hmotnost roztoku
Koncentrace roztoků Hmotnostní zlomek w Vyjadřuje poměr hmotnosti rozpuštěné látky k hmotnosti celého roztoku. w= m A m s m s...hmotnost celého roztoku, m A... hmotnost rozpuštěné látky Hmotnost roztoku
Inovace studia molekulární a buněčné biologie reg. č. CZ.1.07/2.2.00/07.0354
 Inovace studia molekulární a buněčné biologie reg. č. CZ.1.07/2.2.00/07.0354 LRR/CHPB2 Chemie pro biology 2 Karboxylové kyseliny Lucie Szüčová Osnova: fyzikální vlastnosti karboxylových kyselin, základní
Inovace studia molekulární a buněčné biologie reg. č. CZ.1.07/2.2.00/07.0354 LRR/CHPB2 Chemie pro biology 2 Karboxylové kyseliny Lucie Szüčová Osnova: fyzikální vlastnosti karboxylových kyselin, základní
Gymnázium, Milevsko, Masarykova 183 Školní vzdělávací program (ŠVP) pro vyšší stupeň osmiletého studia a čtyřleté studium 4.
 Vyučovací předmět - Chemie Vzdělávací obor - Člověk a příroda Gymnázium, Milevsko, Masarykova 183 Školní vzdělávací program (ŠVP) pro vyšší stupeň osmiletého studia a čtyřleté studium 4. ročník - seminář
Vyučovací předmět - Chemie Vzdělávací obor - Člověk a příroda Gymnázium, Milevsko, Masarykova 183 Školní vzdělávací program (ŠVP) pro vyšší stupeň osmiletého studia a čtyřleté studium 4. ročník - seminář
3 Acidobazické reakce
 3 Acidobazické reakce Brønstedova teorie 1. Uveďte explicitní definice podle Brønstedovy teorie. Kyselina je... Báze je... Konjugovaný pár je... 2. Doplňte tabulku a pojmenujte všechny sloučeniny. Kyselina
3 Acidobazické reakce Brønstedova teorie 1. Uveďte explicitní definice podle Brønstedovy teorie. Kyselina je... Báze je... Konjugovaný pár je... 2. Doplňte tabulku a pojmenujte všechny sloučeniny. Kyselina
CH 2 = CH 2 ethen systematický název propen CH 2 = CH CH 3 but-1-en CH 2 = CH CH 2 CH 3 but-2-en CH 3 CH = CH CH 3 buta-1,3-dien CH 2 = CH CH = CH 2
 Základní názvy organických látek alifatické nasycené alkany (příklady s nerozvětvenými řetězci) methan CH 4 ethan CH 3 CH 3 propan CH 3 CH 2 CH 3 butan CH 3 CH 2 CH 2 CH 3 pentan CH 3 CH 2 CH 2 CH 2 CH
Základní názvy organických látek alifatické nasycené alkany (příklady s nerozvětvenými řetězci) methan CH 4 ethan CH 3 CH 3 propan CH 3 CH 2 CH 3 butan CH 3 CH 2 CH 2 CH 3 pentan CH 3 CH 2 CH 2 CH 2 CH
CHE NÁRODNÍ SROVNÁVACÍ ZKOUŠKY BŘEZNA Datum konání zkoušky: 30. března Max. možné skóre: 30 Počet řešitelů testu: 176
 NÁRODNÍ SROVNÁVACÍ ZKOUŠKY CHE T BŘEZNA 2019 Datum konání zkoušky: 30. března 2019 Max. možné skóre: 30 Počet řešitelů testu: 176 Max. dosažené skóre: 28,7 Počet úloh: 30 Min. možné skóre: -1 0,0 Průměrná
NÁRODNÍ SROVNÁVACÍ ZKOUŠKY CHE T BŘEZNA 2019 Datum konání zkoušky: 30. března 2019 Max. možné skóre: 30 Počet řešitelů testu: 176 Max. dosažené skóre: 28,7 Počet úloh: 30 Min. možné skóre: -1 0,0 Průměrná
CHEMICKÁ ROVNOVÁHA PRINCIP MOBILNÍ (DYNAMICKÉ) ROVNOVÁHY
 CHEMICKÁ ROVNOVÁHA PRINCIP MOBILNÍ (DYNAMICKÉ) ROVNOVÁHY V reakční kinetice jsme si ukázali, že zvratné reakce jsou charakterizovány tím, že probíhají současně oběma směry, tj. od výchozích látek k produktům
CHEMICKÁ ROVNOVÁHA PRINCIP MOBILNÍ (DYNAMICKÉ) ROVNOVÁHY V reakční kinetice jsme si ukázali, že zvratné reakce jsou charakterizovány tím, že probíhají současně oběma směry, tj. od výchozích látek k produktům
1/6. 2. Stavová rovnice, plynová konstanta, Avogadrův zákon, kilomol plynu
 1/6 2. Stavová rovnice, plynová konstanta, Avogadrův zákon, kilomol plynu Příklad: 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 2.10, 2.11, 2.12, 2.13, 2.14, 2.15, 2.16, 2.17, 2.18, 2.19, 2.20, 2.21, 2.22,
1/6 2. Stavová rovnice, plynová konstanta, Avogadrův zákon, kilomol plynu Příklad: 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 2.10, 2.11, 2.12, 2.13, 2.14, 2.15, 2.16, 2.17, 2.18, 2.19, 2.20, 2.21, 2.22,
Rovnováha Tepelná - T všude stejná
 Fázové heterogenní rovnováhy Fáze = homogenní část soustavy, oddělná fyzickým rozhraním, na rozhraní se vlastnosti mění skokem Rovnováha Tepelná - T všude stejná Mechanická - p všude stejný Chemická -
Fázové heterogenní rovnováhy Fáze = homogenní část soustavy, oddělná fyzickým rozhraním, na rozhraní se vlastnosti mění skokem Rovnováha Tepelná - T všude stejná Mechanická - p všude stejný Chemická -
Ukázky z pracovních listů B
 Ukázky z pracovních listů B 1) Označ každou z uvedených rovnic správným názvem z nabídky. nabídka: termochemická, kinetická, termodynamická, Arrheniova, 2 HgO(s) 2Hg(g) + O 2 (g) H = 18,9kJ/mol v = k.
Ukázky z pracovních listů B 1) Označ každou z uvedených rovnic správným názvem z nabídky. nabídka: termochemická, kinetická, termodynamická, Arrheniova, 2 HgO(s) 2Hg(g) + O 2 (g) H = 18,9kJ/mol v = k.
Jana Fauknerová Matějčková
 Jana Fauknerová Matějčková převody jednotek výpočet ph ph vodných roztoků ph silných kyselin a zásad ph slabých kyselin a zásad, disociační konstanta, pk ph pufrů koncentace 1000mg př. g/dl mg/l = = *10000
Jana Fauknerová Matějčková převody jednotek výpočet ph ph vodných roztoků ph silných kyselin a zásad ph slabých kyselin a zásad, disociační konstanta, pk ph pufrů koncentace 1000mg př. g/dl mg/l = = *10000
CHO cvičení, FSv, ČVUT v Praze
 2. Chemické rovnice Chemická rovnice je schématický zápis chemického děje (reakce), který nás informuje o reaktantech (výchozích látkách), produktech, dále o stechiometrii reakce tzn. o vzájemném poměru
2. Chemické rovnice Chemická rovnice je schématický zápis chemického děje (reakce), který nás informuje o reaktantech (výchozích látkách), produktech, dále o stechiometrii reakce tzn. o vzájemném poměru
9 Charakter proudění v zařízeních
 9 Charakter proudění v zařízeních Egon Eckert, Miloš Marek, Lubomír Neužil, Jiří Vlček A Výpočtové vztahy Jedním ze způsobů, který nám v praxi umožňuje získat alespoň omezené informace o charakteru proudění
9 Charakter proudění v zařízeních Egon Eckert, Miloš Marek, Lubomír Neužil, Jiří Vlček A Výpočtové vztahy Jedním ze způsobů, který nám v praxi umožňuje získat alespoň omezené informace o charakteru proudění
2 Cu + S Cu 2 S n(cu)=2mol n(cu 2 S)=1mol M(Cu)=63,5 g mol M(Cu 2 S)=159 g mol
 n... látkové množství látky (mol) M... molární hmotnost látky (g/mol) m... hmotnost látky (m) III. Výpočty z chemických rovnic chemické rovnice umožňují vypočítat množství jednotlivých látek, které se
n... látkové množství látky (mol) M... molární hmotnost látky (g/mol) m... hmotnost látky (m) III. Výpočty z chemických rovnic chemické rovnice umožňují vypočítat množství jednotlivých látek, které se
KONTROLNÍ TEST ŠKOLNÍHO KOLA (70 BODŮ)
 KONTROLNÍ TEST ŠKOLNÍHO KOLA (70 BODŮ) Úloha 1 Ic), IIa), IIId), IVb) za každé správné přiřazení po 1 bodu; celkem Úloha 2 8 bodů 1. Sodík reaguje s vodou za vzniku hydroxidu sodného a dalšího produktu.
KONTROLNÍ TEST ŠKOLNÍHO KOLA (70 BODŮ) Úloha 1 Ic), IIa), IIId), IVb) za každé správné přiřazení po 1 bodu; celkem Úloha 2 8 bodů 1. Sodík reaguje s vodou za vzniku hydroxidu sodného a dalšího produktu.
Hmotnost atomů a molekul 6 Látkové množství 11. Rozdělení směsí 16 Separační metody 20. Hustota, hmotnostní a objemový zlomek 25.
 Obsah Obecná chemie II. 1. Látkové množství Hmotnost atomů a molekul 6 Látkové množství 11 2. Směsi Rozdělení směsí 16 Separační metody 20 3. Chemické výpočty Hustota, hmotnostní a objemový zlomek 25 Koncentrace
Obsah Obecná chemie II. 1. Látkové množství Hmotnost atomů a molekul 6 Látkové množství 11 2. Směsi Rozdělení směsí 16 Separační metody 20 3. Chemické výpočty Hustota, hmotnostní a objemový zlomek 25 Koncentrace
