POHYB BODU V CENTRÁLNÍM POLI SIL
|
|
|
- Jindřiška Julie Hrušková
- před 5 lety
- Počet zobrazení:
Transkript
1 POHYB BODU V CENTRÁLNÍM POLI SIL SPECIFIKCE PROBLÉMU Centální siloé pole je takoé pole sil, kdy liboolném bodě postou nositelka síly působící na pohybující se bod pochází peným bodem postou (tz centem siloého pole) Poznámka: Známou aplikací tohoto duhu pohybu je pohyb planet kolem Slunce esp dužice kolem Země Střed elmi hmotného tělesa (Slunce případě planet, esp Země případě dužic) je centem e smyslu předchozí definice, kteým stále pochází nositelka gaitační síly na bod působící Velikost gaitační síly F je podle Newtonoa gaitačního zákona Mm ona F κ, kde M je hmotnost centa, m hmotnost bodu a zdálenost bodu od středu 3 κ 6,67 m kg s je uniezální gaitační konstanta centa Veličina [ ] ŘEŠENÍ Duhá impulzoá ěta tdí, že časoá deiace momentu hybnosti pohybujícího se bodu k penému počátku je ona momentu ýslednice sil na bod působících k témuž počátku Jestliže za pený počátek beeme centum centálního pole sil, je moment ýslednice k němu nuloý Podle impulzoé ěty musí moment hybnosti k němu být konstantní Vekto momentu hybnosti je kolmý na oinu učenou polohoým ektoem a ektoem ychlosti bodu Tato oina tedy musí být stálá (ona oině učené naáděcí polohou a ychlostí bodu) Pohyb centálním poli sil je poto oinným pohybem Zaeďme do této oiny pohybu polání souřadnice se středem centu siloého pole a s hlaním směem e směu k bodu naedení (polohoá počáteční podmínka) Pohyboá onice bodu e ektooém tau má obecně ta m a i F i () tans smě ad smě Vzhledem k definici centálního pole a k zaedení poláních souřadnic do tansezálního směu žádná síla nepůsobí Poto () má ta ma t Potože m dostááme zhledem k yjádření tansezální složky zychlení ýaz d d ϕ + () Potože d d + d ϕ d d ϕ +, (3)
2 je podle () paá stana (3) nuloá Výaz je poto konstantní Veličina w (4) w se nazýá plošná ychlost (zhledem k centu) Její definice je d Oud ztah (4) ihned plyne Poznámka: d w [ m / s], kde d je plocha opsaná půodičem bodu L za čas Tuto plochu lze počítat (až na difeenciálně malou eličinu duhého řádu) jako plochu tojúhelníka CLM, jenž má jednu oděsnu délky a duhou délky d ϕ (jako kuhoý oblouček na poloměu příslušející k úhlu d ϕ ) Plochu d učíme jako plochu tohoto tojúhelníka, tedy ) Z řešení pohyboé onice bodu () tansezálním směu byla odozena poučka: Plošná ychlost bodu při pohybu centálním poli sil je konstantní Tento fakt je znám jako duhý Kepleů zákon ) Všimněme si, že po odození tohoto zákona nebylo potřeba znát konkétní ta funkce elikosti síly na zdálenosti od centa Tento zákon by platil po jakoukoli záislost Fomulujme nyní pohyboou onici () do adiálního směu Zde ( záponě oientoaném adiálním směu) působí Newtonoa gaitační síla Po dosazení z gaitačního zákona a ze ztahu po adiální složku zychlení dostaneme po zkácení hmotností difeenciální onici tau Po kadát plošné ychlosti zřejmě platí d M κ (5) w 4 4 Duhý sčítanec leé stany (5) lze přepsat jako 3 a pohyboou onici pak na ta d (6) 3 Zaeďme noou funkci u, kteou budeme chápat jako funkci nezáisle poměnné ϕ (duhá polání souřadnice), jež je sama funkcí času Bude tedy zaedeno
3 Deiujme tuto onici podle času d () t u( ϕ() t ) (7) du du du w (8) u Deiujme tuto onici poduhé s yužitím ztahu w konst w le Poto Dosazením do (6) získáme d d u w d d u u (9) d u Potože podle (7) u, získáme kácením 3 u u κ M u d u κ + u u onici M w 4 konst To je lineání difeenciální onice II řádu s konstantními koeficienty (dokonce bez členu s pní deiací) s konstantní stanou po neznámou funkci u ( ϕ) Obecné řešení homogenní onice je zřejmě u H ( ϕ) C cosϕ + C sinϕ (kořeny chaakteistické onice λ, ± i ) a patikulání řešení u P ( p) Obecné řešení () je poto () u ( ϕ) + C cosϕ + C sin ϕ, () kde integační konstanty C a C učíme z počátečních podmínek (bodu a ychlosti naedení na dáhu centálním poli) Je třeba učit du u ϕ a ϕ, jestliže klasické počáteční podmínky po onici (6) funkci ( t) jsou t (zdálenost bodu naedení od d centa) a t (ekto ychlosti naedení) Potože hlaní smě poláních souřadnic byl olen na naáděcí bod L, jsou ekialentní tyto polohoé počáteční podmínky:
4 t u ϕ () Rychlostní počáteční podmínku učíme z ýazů po adiální a tansezální složku ychlosti, kteé platí i po počáteční čas (a úhel ϕ ) Přitom podle obázku zřejmě cosβ t t sin β Poto platí t a d t cosβ, (3) t t t sin β, (4) t t kde je elikost naádění ychlosti a β naáděcí úhel (iz obázek) Podle (8) ošem (3) přepíšeme jako a podle ztahu po plošnou ychlost (4) zase přepíšeme na d du cos β t w ϕ (5) w sin β t (6) Podělením onic (5) a (6) ( tomto pořadí) získáme konečně odkud cot du d du β, g ϕ cotg β ϕ ϕ (7) Počáteční podmínky () a (7) aplikujeme na řešení () a jeho deiaci Dosazením t do () získáme s ohledem na () Dosazením t do (8) získáme s ohledem na (7) du C sin ϕ + C cosϕ (8) u( ) + C C (9) du cotgβ ( ) C () Dosazením konstant (9), () do () máme konkétní řešení pohyboé onice e tau κm cotgβ u( ϕ) + cosϕ sin ϕ () ( ϕ) Poeďme nyní tansfomaci lineání kombinace sinů a kosinů na kosinus fázoě posunutý Zaedeme-li konstanty a γ jako
5 dostaneme podle () cotg β + ; cotgβ cosγ ; sin γ () ( ϕ) κm + cos( ϕ + 4 γ) w + cos( ϕ + γ) κm To je polání ohniskoá onice kuželosečky o paametu numeické ýstřednosti p, (3) cotg β ε + p (4) a peicentem (bodem nejbližším k centu) úhloé odchylce -γ od směu bodu naedení Podle (6) naíc je Dosazením do (3) a (4) dostaneme po úpaě sin β (5) sin β p, sin β ε + (6) Z počátečních podmínek,, β a hmotnosti M centa učíme typ kuželosečky ( ε kužnice, ε (,) elipsa, ε paabola, ε > ěte hypeboly) i její ozměy Po kužnici je p R (polomě kužnice), po paabolu je její paamet učující eličinou Po elipsu a b e a mb hypebolu platí p, ε, kde a, b jsou poloosy, e délkoá ýstřednost a a a Honí znaménko platí po elipsu, spodní po hypebolu Oud p a, ± ( ε ) p b, (7) ± ( ε ) kde honí znaménko opět platí po elipsu a spodní po hypebolu
6 Uažujme nyní smě naedení kolmo k půodiči naáděcího bodu, tedy úhel naedení π β Z (4) a (5) dostaneme po tento případ cotg π ε, γ nebo π (7a) Po danou naáděcí zdálenost je ε (po > ) ostoucí funkcí naáděcí ychlosti Učíme, po jakou ychlost je ε (kužnice) a po jakou je ε (paabola) Zřejmě ε I, ε I II (8) Naáděcí ychlosti I (8) říkáme pní kosmická ychlost (příslušející k centu M a naáděcí zdálenosti ) Rychlosti II I říkáme duhá kosmická ychlost π Při naáděcím úhlu β (tz odooný h) je po I tajektoie kuhoá, po ( I, II ) tajektoie eliptická s bodem naedení peicentu, po II je tajektoie paabolická a po > II je dahou ěte hypeboly (bližní k centu) Po ε (, ), čemuž odpoídá (, I ), je dahou oněž elipsa s bodem naedení apocentu (nejzdálenější bod od centa) Poznámky: ) Rychlost I lze také chápat jako ychlost onoměně se pohybujícího bodu po kuhoé dáze kolem středu centa hmotnosti M Na bod působí pouze Newtonoa gaitační síla Pohyboá onice ozepsaná do nomáloého směu je m a n κ m M Po nomáloé zychlení při kuhoém pohybu zřejmě platí a n Poto Pohyboá onice do směu tečny má tiiální ta ) Rychlost II lze oněž chápat jako ychlost sislého hu e zdálenosti od středu centa nutnou k dosažení (bez přísunu enegie při zanedbání působení ostatních kosmických těles) teoeticky nekonečné zdálenosti Použijeme ětu o změně kinetické enegie mezi statem (poloha ychlost ) a nekonečnou I II
7 zdáleností (ychlost nuloá) V půběhu pohybu působí na bod pouze Newtonoa gaitační síla mířící e směu záponého příůstku dáhy (páci spotřeboáá) Věta o změně E tedy dáá k odkud mm m II κ dy y dy κ M II y y 3) Po eliptickou (nebo kuhoou) dáhu má smysl hoořit o době oběhu T centa Potože plošná ychlost je konstantní, platí wt, kde je plocha opsaná půodičem bodu za čas t Po t T je π a b (plocha celé elipsy) Tedy wt π a b (9) Podle (3) platí po paamet elipsy b p (3) a Z (3) a b w Dosazením do (9) po zkácení w Umocněním oud a T π a 3 a T 4π T 4π konst 3 a Tento ýsledek je znám jako III Kepleů zákon Po dě tělesa obíhající kolem téhož centa tak platí T T a konst 3 3 a T a T a Kadáty dob oběhu dou těles kolem téhož centa se k sobě mají jako třetí mocniny elkých poloos jejich eliptických dah 4) Při kantitatiním yčíslení např tajektoií dužic Země je třeba znáti hmotnost Země Učíme ji pomocí znalosti poloměu Země R a pochoého gaitačního zychlení g Tíha mg bodu na zemském pochu je Newtonoa přitažliá síla na zdálenosti R Poto platí M m m g κ odkud R
8 Po Zemi ychází M Země 4 5,983 kg g R M κ g 9,8m/ s ; R 6,378 6 m; κ 3 6,67 m kg s, takže PŘÍKLD Uažujme dužici Země naedenou na dáhu e zdálenosti km od středu Země (tedy 56 km nad hladinou moří) statoací ychlostí 6 km / s pod naáděcím úhlem o ( ) β ad 57,3 Učete ta dáhy a případě její eliptičnosti její poloosy, dobu oběhu a ychlosti dužice peigeu a apogeu Řešení: Z (5) po plošnou ychlost máme w sin β, což po dosazení dáá o w 393km / s Dosazením do () získáme γ,376 ad 5 49 Úhel o γ π γ 4,6943ad je pak úhel, jenž síá smě na peigeum dáhy se směem na bod naedení (z pólu poláních souřadnic, jenž jest e středu Země) Dosazením 3 4 κ 6,67 m kg s, M 5,983 kg získáme po numeickou ýstřednost do (4) ( ) dáhy ε, Dahou je tedy elipsa Její paamet má podle (3) hodnotu p 998km Podle (7) pak (honí znaménka) po poloosy elipsy dostááme a 379 km, b 968km Délkoá ýstřednost dáhy je podle sé definice e a ε 75km Podle obázku se zakeslenými ýznamnými body elipsy (S - střed, C ohnisko střed Země, P peigum, apogeum) a důležitými zdálenostmi ( P zdálenost peigea, zdálenost apogea od středu Země) dostááme P a e 5954 km; a + e 4 km Potože polomě Země je z 6378 km, znamená to, že peigeum leží pod pochem Země Dahou tedy bude pouze eliptický oblouk mezi bodem naedení a pním kontaktem se π ab zemským pochem Po dobu oběhu (fiktiní) by podle (9) platilo T 4878 sec w 4 hod 7 min 58 sec Podle (5) aplikoané na peigeum a apogeum (to jest hlaní choly π P P dáhy, kdy β ) dostááme w, kde P je ychlost peigeu a w apogeu Oud x ( x P, ), takže číselně ychází P,7 km/ s, x 3, km / s
9 Poznámka: Podle (8) je e statoací poloze pní kosmická ychlost duhá kosmická ychlost 8,6 km/ s 5,77 km/ s a PŘÍKLD Uažujme opět tělesa naedená gaitačním poli Země odooným hem π β e zdálenosti km od středu Země na kuželosečkoé dáhy postupně naáděcími ychlostmi 3; 5; 5,77; 7; 8,6; km / s Popište pohyb těles e šech šesti uedených případech Řešení: Podle (7a) je po danou statoací polohu numeická ýstřednost dáhy ona 8 ε 3,7 Dosazením zadaných statoacích ychlostí získáme ýsledky obsažené následující tabulce: Číslo případu [ km s] / 3 5 5,77 7 8,6 ε -,79 -,48,,473,,7 Z ýsledků plyne, že pní da případy ykazují ε < Jedná se tedy o eliptickou dáhu s bodem naedení apogeu Třetí případ byl olen tak, aby naáděcí ychlost byla na 3 platné cify ychlostí pní kosmickou Dáha by měla být kuhoá Ve skutečnosti ε ychází malé kladné (nepatně eliptická dáha s bodem naedení peigeu) Čttý případ dáá ε ( ; ), tedy klasickou elipsu s bodem naedení peigeu Pátý případ byl olen tak, aby naáděcí ychlost byla na 3 platné cify ychlostí duhou kosmickou Dáha by měla býti paabolická Ve skutečnosti ychází ε o tochu ětší, takže dahou je ěte hypeboly od paaboly se málo lišící Šestý případ dáá ε >, takže dahou je klasická ěte hypeboly Podle (3) a (5) učíme plošné ychlosti dužice a paamety p její dáhy po jednotlié případy Podle (7) dále učíme délky poloos dah (po hypeboly je poloosa b fiktiní) Délkoou ýstřednost učíme z ýazu e a ε Z ýazů a e a a + e učíme po eliptické dáhy p zdálenost peigea a apogea od středu Země Potože hypebola je neuzařená křika, není po ni definoána a p (zdálenost naedení)po pní případ je p < z (polomě Země), takže po naedení touto ychlostí dané poloze dojde ke kontaktu s pochem Země a dahou je lastně jen eliptický oblouk Po eliptické dáhy učíme naíc plochu elipsy P π ab, dobu oběhu Země podle (9) a ze ztahu w P P naíc učíme ychlost obou hlaních cholech eliptické dáhy Po hypebolické dáhy zřejmě platí P a není definoána Doba peiody T i ychlost peigeu P po případ jsou hypotetické hodnoty, potože těleso této polohy nedosáhne Číselné ýsledky jsou shnuty následující tabulce:
10 Číslo případu [ km s] / p [ Mm] 3,48 9,,3 7,68 4,7 36,84 a [ Mm] 6,939 9,63,3, ,67,96 b [ Mm] 4,747 9,33,3,73 358,55,736 e [ Mm] 5,6,386,3, ,67 3,96 P [ Mm],878 7,7,,,, [ Mm],,,7 33, [ Mm ] P 3,5 8,3 453,4 437, - - T [ s] [ h m s] T,, h 35m 49 s [ km s] h 36 m 5 s 3h 38m 7s 9h 3m 8s - - P / 9,7 8,3 5,77 7, 8,6, [ km s] / 3, 5, 5,76,5 - -
I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í
 GRAVITAČNÍ POLE I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í 1. Newtonů aitační zákon (1687 Newton díle Mateatické pincipy příodní filozofie) aždá dě hotná tělesa na sebe nazáje působí stejně
GRAVITAČNÍ POLE I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í 1. Newtonů aitační zákon (1687 Newton díle Mateatické pincipy příodní filozofie) aždá dě hotná tělesa na sebe nazáje působí stejně
Gravitační pole. a nepřímo úměrná čtverci vzdáleností r. r r
 Newtonův avitační zákon: Gavitační pole ezi dvěa tělesy o hotnostech 1 a, kteé jsou od sebe vzdáleny o, působí stejně velké síly vzájené přitažlivosti, jejichž velikost je přío úěná součinu hotností 1
Newtonův avitační zákon: Gavitační pole ezi dvěa tělesy o hotnostech 1 a, kteé jsou od sebe vzdáleny o, působí stejně velké síly vzájené přitažlivosti, jejichž velikost je přío úěná součinu hotností 1
Newtonův gravitační zákon
 Gavitační pole FyzikaII základní definice Gavitační pole je posto, ve kteém působí gavitační síly. Zdojem gavitačního pole jsou všechny hmotné objekty. Každá dvě tělesa jsou k sobě přitahována gavitační
Gavitační pole FyzikaII základní definice Gavitační pole je posto, ve kteém působí gavitační síly. Zdojem gavitačního pole jsou všechny hmotné objekty. Každá dvě tělesa jsou k sobě přitahována gavitační
Reakce v jednotlivých úložných bodech t les soustavy zatížené n kolika silami jsou dány geometrickým sou tem reakcí v p íslušných bodech, zp
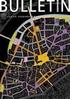 Ob.78. Podobně jako předcházejících příkladech přeedeme soustau těles a 3 na statickou soustau tříklouboého nosníku, zobazenou paé části obázku. Tuto soustau nemůžeme řešit přímo se šemi působícími silami
Ob.78. Podobně jako předcházejících příkladech přeedeme soustau těles a 3 na statickou soustau tříklouboého nosníku, zobazenou paé části obázku. Tuto soustau nemůžeme řešit přímo se šemi působícími silami
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 F8 KEPLEOVY ZÁKONY Evopský sociální fond Paha & EU: Investujeme do vaší udoucnosti F8 KEPLEOVY ZÁKONY Kepleovy zákony po planetání pohy zfomuloval Johannes Keple (1571 1630) na základě měření Tychona Baheho
F8 KEPLEOVY ZÁKONY Evopský sociální fond Paha & EU: Investujeme do vaší udoucnosti F8 KEPLEOVY ZÁKONY Kepleovy zákony po planetání pohy zfomuloval Johannes Keple (1571 1630) na základě měření Tychona Baheho
Hlavní body. Keplerovy zákony Newtonův gravitační zákon. Konzervativní pole. Gravitační pole v blízkosti Země Planetární pohyby
 Úvod do gavitace Hlavní body Kepleovy zákony Newtonův gavitační zákon Gavitační pole v blízkosti Země Planetání pohyby Konzevativní pole Potenciál a potenciální enegie Vztah intenzity a potenciálu Úvod
Úvod do gavitace Hlavní body Kepleovy zákony Newtonův gavitační zákon Gavitační pole v blízkosti Země Planetání pohyby Konzevativní pole Potenciál a potenciální enegie Vztah intenzity a potenciálu Úvod
v 1 = at 1, (1) t 1 = v 1
 Příklad Statující tyskové letadlo musí mít před vzlétnutím ychlost nejméně 360 km/h. S jakým nejmenším konstantním zychlením může statovat na ozjezdové dáze dlouhé,8 km? Po ychlost v ovnoměně zychleného
Příklad Statující tyskové letadlo musí mít před vzlétnutím ychlost nejméně 360 km/h. S jakým nejmenším konstantním zychlením může statovat na ozjezdové dáze dlouhé,8 km? Po ychlost v ovnoměně zychleného
Newtonův gravitační zákon Gravitační a tíhové zrychlení při povrchu Země Pohyby těles Gravitační pole Slunce
 Gavitační pole Newtonův gavitační zákon Gavitační a tíhové zychlení při povchu Země Pohyby těles Gavitační pole Slunce Úvod V okolí Země existuje gavitační pole. Země působí na každé těleso ve svém okolí
Gavitační pole Newtonův gavitační zákon Gavitační a tíhové zychlení při povchu Země Pohyby těles Gavitační pole Slunce Úvod V okolí Země existuje gavitační pole. Země působí na každé těleso ve svém okolí
2. ZÁKLADY KINEMATIKY
 . ZÁKLDY KINEMTIKY Kinemaika se zabýá popisem pohbu čásice nebo ělesa, aniž sleduje příčinné souislosi. Jedním ze základních lasnosí pohbu je, že jeho popis záleží na olbě zažného ělesa ( souřadnicoého
. ZÁKLDY KINEMTIKY Kinemaika se zabýá popisem pohbu čásice nebo ělesa, aniž sleduje příčinné souislosi. Jedním ze základních lasnosí pohbu je, že jeho popis záleží na olbě zažného ělesa ( souřadnicoého
29. OBJEMY A POVRCHY TĚLES
 9. OBJEMY A POVRCHY TĚLES 9.. Vypočítejte poch kádu ABCDEFGH, jestliže ) AB =, BC = b, BH = u b) AB =, BH = u, odchylk AG EH je ϕ H G Poch kádu učíme podle zoce: S = b + c + bc ( ) c E F D b C ) A B u
9. OBJEMY A POVRCHY TĚLES 9.. Vypočítejte poch kádu ABCDEFGH, jestliže ) AB =, BC = b, BH = u b) AB =, BH = u, odchylk AG EH je ϕ H G Poch kádu učíme podle zoce: S = b + c + bc ( ) c E F D b C ) A B u
Dráhy planet. 28. července 2015
 Dáhy plnet Pet Šlecht 28. čevence 205 Výpočet N střední škole se zpvidl učí, že dáhy plnet jsou elipsy se Sluncem v ohnisku. Tké se učí, že tento fkt je možné dokázt z Newtonov gvitčního zákon. Příslušný
Dáhy plnet Pet Šlecht 28. čevence 205 Výpočet N střední škole se zpvidl učí, že dáhy plnet jsou elipsy se Sluncem v ohnisku. Tké se učí, že tento fkt je možné dokázt z Newtonov gvitčního zákon. Příslušný
F5 JEDNODUCHÁ KONZERVATIVNÍ POLE
 F5 JEDNODUCHÁ KONZERVATIVNÍ POLE Evopský sociální fond Paha & EU: Investujeme do vaší budoucnosti F5 JEDNODUCHÁ KONZERVATIVNÍ POLE Asi nejznámějším konzevativním polem je gavitační silové pole Ke gavitační
F5 JEDNODUCHÁ KONZERVATIVNÍ POLE Evopský sociální fond Paha & EU: Investujeme do vaší budoucnosti F5 JEDNODUCHÁ KONZERVATIVNÍ POLE Asi nejznámějším konzevativním polem je gavitační silové pole Ke gavitační
I. MECHANIKA 4. Soustava hmotných bodů II
 I. CHIK 4. Soustaa hmotných bodů II 1 Obsah Spojté ozložení hmotnost. Počet stupňů olnost. Knematka tuhého tělesa. Zjednodušení popsu otace kolem osy a peného bodu. Chaslesoa ěta. Dynamka tuhého tělesa.
I. CHIK 4. Soustaa hmotných bodů II 1 Obsah Spojté ozložení hmotnost. Počet stupňů olnost. Knematka tuhého tělesa. Zjednodušení popsu otace kolem osy a peného bodu. Chaslesoa ěta. Dynamka tuhého tělesa.
K přednášce NUFY080 Fyzika I prozatímní učební materiál, verze 01 Keplerova úloha Leoš Dvořák, MFF UK Praha, Keplerova úloha
 K řednášce NUFY080 Fyzika I ozatímní učební mateiál, veze 01 Keleova úloha eoš Dvořák, MFF UK Paha, 014 Keleova úloha Chceme sočítat, jak se ohybuje hmotný bod gavitačně řitahovaný nehybným silovým centem.
K řednášce NUFY080 Fyzika I ozatímní učební mateiál, veze 01 Keleova úloha eoš Dvořák, MFF UK Paha, 014 Keleova úloha Chceme sočítat, jak se ohybuje hmotný bod gavitačně řitahovaný nehybným silovým centem.
( ) Kinematika a dynamika bodu. s( t) ( )
 Kineika a ynamika bou Kineika bou Bo se pohybuje posou po křice, keá se nazýá ajekoie nebo áha bou. Tajekoie je učena půoičem (polohoým ekoem), keý je funkcí času ( ) V záislosi na ypu ajekoie ozlišujeme:
Kineika a ynamika bou Kineika bou Bo se pohybuje posou po křice, keá se nazýá ajekoie nebo áha bou. Tajekoie je učena půoičem (polohoým ekoem), keý je funkcí času ( ) V záislosi na ypu ajekoie ozlišujeme:
Kinematika hmotného bodu. Petr Šidlof
 et Šilof Úo Kinemtik popis pohybu (nezkoumá příčiny pohybu) Šiší souislosti: mechnik tuhých těles sttik kinemtik ynmik Mechnik mechnik poných těles sttik kinemtik ynmik mechnik tekutin hyosttik ynmik tekutin
et Šilof Úo Kinemtik popis pohybu (nezkoumá příčiny pohybu) Šiší souislosti: mechnik tuhých těles sttik kinemtik ynmik Mechnik mechnik poných těles sttik kinemtik ynmik mechnik tekutin hyosttik ynmik tekutin
Kinematika tuhého tělesa
 Kinematika tuhého tělesa Pet Šidlof TECHNICKÁ UNIVERZITA V LIERCI Fakulta mechatoniky, infomatiky a mezioboových studií Tento mateiál vznikl v ámci pojektu ESF CZ.1.07/2.2.00/07.0247 Reflexe požadavků
Kinematika tuhého tělesa Pet Šidlof TECHNICKÁ UNIVERZITA V LIERCI Fakulta mechatoniky, infomatiky a mezioboových studií Tento mateiál vznikl v ámci pojektu ESF CZ.1.07/2.2.00/07.0247 Reflexe požadavků
e en loh 1. kola 44. ro n ku fyzik ln olympi dy. Kategorie D Auto i loh: I. Volf (1), epl (2), J. J r (3 a 7) 1. Cel okruh rozd l me na p t sek podle
 e en loh. kola 44. o n ku fyzik ln olymi dy. Kategoie D Auto i loh: I. Volf (), el (), J. J (3 a 7). Cel okuh ozd l me na t sek odle chaakteu ohybu motocyklisty. Zaedeme ozna en : t = s, t = 40 s, t 3
e en loh. kola 44. o n ku fyzik ln olymi dy. Kategoie D Auto i loh: I. Volf (), el (), J. J (3 a 7). Cel okuh ozd l me na t sek odle chaakteu ohybu motocyklisty. Zaedeme ozna en : t = s, t = 40 s, t 3
7. Gravitační pole a pohyb těles v něm
 7. Gravitační pole a pohyb těles v něm Gravitační pole - existuje v okolí každého hmotného tělesa - představuje formu hmoty - zprostředkovává vzájemné silové působení mezi tělesy Newtonův gravitační zákon:
7. Gravitační pole a pohyb těles v něm Gravitační pole - existuje v okolí každého hmotného tělesa - představuje formu hmoty - zprostředkovává vzájemné silové působení mezi tělesy Newtonův gravitační zákon:
1.3.7 Rovnoměrný pohyb po kružnici II
 ..7 Ronoměný pohyb po kužnici II Předpoklady: 6 Pedagogická poznámka: Obsah hodiny je hodně nadnesený. Pokud necháte žáky počítat samostatně, yjde na dě hodiny. Úodní ozbo nedopoučuji příliš uychloat.
..7 Ronoměný pohyb po kužnici II Předpoklady: 6 Pedagogická poznámka: Obsah hodiny je hodně nadnesený. Pokud necháte žáky počítat samostatně, yjde na dě hodiny. Úodní ozbo nedopoučuji příliš uychloat.
1.6.8 Pohyby v centrálním gravitačním poli Země
 1.6.8 Pohyby centrálním graitačním poli emě Předpoklady: 160 Pedagogická poznámka: Pokud necháte experimentoat s modelem studenty, i případě, že už program odellus znají, stráíte touto hodinou dě yučoací
1.6.8 Pohyby centrálním graitačním poli emě Předpoklady: 160 Pedagogická poznámka: Pokud necháte experimentoat s modelem studenty, i případě, že už program odellus znají, stráíte touto hodinou dě yučoací
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Spojité rozložení náboje
 EEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Spojité ozložení náboje Pete Doumashkin MIT 006, překlad: Jan Pacák (007) Obsah. SPOJITÉ OZOŽENÍ NÁBOJE.1 ÚKOY. AGOITMY PO ŘEŠENÍ POBÉMU ÚOHA 1: SPOJITÉ OZOŽENÍ
EEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Spojité ozložení náboje Pete Doumashkin MIT 006, překlad: Jan Pacák (007) Obsah. SPOJITÉ OZOŽENÍ NÁBOJE.1 ÚKOY. AGOITMY PO ŘEŠENÍ POBÉMU ÚOHA 1: SPOJITÉ OZOŽENÍ
Kinematika. Hmotný bod. Poloha bodu
 Kinematika Pohyb objektů (kámen, automobil, střela) je samozřejmou součástí každodenního života. Pojem pohybu byl poto známý už ve staověku. Modení studium pohybu začalo v 16. století a je spojeno se jmény
Kinematika Pohyb objektů (kámen, automobil, střela) je samozřejmou součástí každodenního života. Pojem pohybu byl poto známý už ve staověku. Modení studium pohybu začalo v 16. století a je spojeno se jmény
Lineární algebra. 1) Vektor, lineární závislost a nezávislost. Def.: Číselným vektorem n-rozměrného prostoru nazýváme uspořádanou množinu n čísel
 Lineání lge ) Vekto, lineání záislost nezáislost Def: Číselným ektoem n-ozměného postou nzýáme uspořádnou množinu n čísel,, ) ( n Čísl,, n nzýáme souřdnice ektou, číslo n dimenzí neo ozměem ektou Opece
Lineání lge ) Vekto, lineání záislost nezáislost Def: Číselným ektoem n-ozměného postou nzýáme uspořádnou množinu n čísel,, ) ( n Čísl,, n nzýáme souřdnice ektou, číslo n dimenzí neo ozměem ektou Opece
Keplerova úloha. Abstrakt: Článek řeší problém pohybu planety (Země) kolem Slunce.
 Kepleova úloha Keple-2c.TEX jan.obzalek@mff.cuni.cz Abstakt: Článek řeší poblém pohybu planety (Země) kolem Slunce. Úplná úloha: co zanebáme Chceme vyšetřit pohyb planety, např. Země, v naší sluneční soustavě.
Kepleova úloha Keple-2c.TEX jan.obzalek@mff.cuni.cz Abstakt: Článek řeší poblém pohybu planety (Země) kolem Slunce. Úplná úloha: co zanebáme Chceme vyšetřit pohyb planety, např. Země, v naší sluneční soustavě.
Obecný rovinný pohyb. teorie současných pohybů, Coriolisovo zrychlení dynamika obecného rovinného pohybu,
 Obecný oinný pohyb ynik, 7. přednášk Obsh přednášky : teoie součsných pohybů, Coiolisoo zychlení dynik obecného oinného pohybu, ob studi : si 1,5 hodiny Cíl přednášky : seznáit studenty se zákldy teoie
Obecný oinný pohyb ynik, 7. přednášk Obsh přednášky : teoie součsných pohybů, Coiolisoo zychlení dynik obecného oinného pohybu, ob studi : si 1,5 hodiny Cíl přednášky : seznáit studenty se zákldy teoie
Kinamatika mechanismů
 Kinamatika mechanismů Obsah přednášk : přeod mechanismu, alié soukolí, ozubené soukolí, předlohoé a planetoé soukolí, kladkostoje a aiáto; mechanism s poměnným přeodem. Přeod mechanismu analtické řešení
Kinamatika mechanismů Obsah přednášk : přeod mechanismu, alié soukolí, ozubené soukolí, předlohoé a planetoé soukolí, kladkostoje a aiáto; mechanism s poměnným přeodem. Přeod mechanismu analtické řešení
Řešení úloh krajského kola 58. ročníku fyzikální olympiády Kategorie B Autor úloh: J. Thomas
 Řešení úlo kajskéo kola 58 očníku fyzikální olympiády Kategoie B Auto úlo: J Tomas a) Doba letu střely od okamžiku výstřelu do zásau označíme t V okamžiku výstřelu se usa nacází ve vzdálenosti s měřené
Řešení úlo kajskéo kola 58 očníku fyzikální olympiády Kategoie B Auto úlo: J Tomas a) Doba letu střely od okamžiku výstřelu do zásau označíme t V okamžiku výstřelu se usa nacází ve vzdálenosti s měřené
2.1 Shrnutí základních poznatků
 .1 Shnutí základních poznatků S plnostěnnými otujícími kotouči se setkáváme hlavně u paních a spalovacích tubín a tubokompesoů. Matematický model otujících kotoučů můžeme s úspěchem využít např. i při
.1 Shnutí základních poznatků S plnostěnnými otujícími kotouči se setkáváme hlavně u paních a spalovacích tubín a tubokompesoů. Matematický model otujících kotoučů můžeme s úspěchem využít např. i při
1.3.6 Dynamika pohybu po kružnici II
 .3.6 Dynamika ohybu o kužnici II Pedaoická oznámka: Sočítat šechny uedené říklady jedné hodině není eálné. Př. : Vysětli, oč se čloěk ři jízdě na kole (motocyklu) musí ři ůjezdu zatáčkou naklonit. Podobná
.3.6 Dynamika ohybu o kužnici II Pedaoická oznámka: Sočítat šechny uedené říklady jedné hodině není eálné. Př. : Vysětli, oč se čloěk ři jízdě na kole (motocyklu) musí ři ůjezdu zatáčkou naklonit. Podobná
FYZIKA I. Gravitační pole. Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERITA OSTRAVA FAKULTA STROJNÍ FYIKA I Gravitační pole Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art. Dagmar Mádrová
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERITA OSTRAVA FAKULTA STROJNÍ FYIKA I Gravitační pole Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art. Dagmar Mádrová
Fyzika. Fyzikální veličina - je mírou fyzikální vlastnosti, kterou na základě měření vyjadřujeme ve zvolených jednotkách
 Fyzika Studuje objekty neživé příody a vztahy mezi nimi Na základě pozoování a pokusů studuje obecné vlastnosti látek a polí, indukcí dospívá k obecným kvantitativním zákonům a uvádí je v logickou soustavu
Fyzika Studuje objekty neživé příody a vztahy mezi nimi Na základě pozoování a pokusů studuje obecné vlastnosti látek a polí, indukcí dospívá k obecným kvantitativním zákonům a uvádí je v logickou soustavu
vzdálenost těžiště (myslí se tím těžiště celého tělesa a ne jeho jednotlivých částí) od osy rotace
 Přehled příkladů 1) Valiý pohyb, zákon zachoání energie ) Těžiště tělesa nebo moment setračnosti ýpočet integrací - iz http://kf.upce.cz/dfjp/momenty_setracnosti.pdf Nejčastější chyby: záměna momentu setračnosti
Přehled příkladů 1) Valiý pohyb, zákon zachoání energie ) Těžiště tělesa nebo moment setračnosti ýpočet integrací - iz http://kf.upce.cz/dfjp/momenty_setracnosti.pdf Nejčastější chyby: záměna momentu setračnosti
Kapitola 5. Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které
 Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
Harmonický pohyb, výchylka, rychlost a zrychlení
 Střední půmyslová škola a Vyšší odboná škola technická Bno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky postřednictvím ICT Název: Téma: Auto: Číslo: Anotace: Mechanika, kinematika Hamonický pohyb,
Střední půmyslová škola a Vyšší odboná škola technická Bno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky postřednictvím ICT Název: Téma: Auto: Číslo: Anotace: Mechanika, kinematika Hamonický pohyb,
Gravitace. Kapitola 8. 8.1 Gravitační zákon. 8.1.1 Isaac Newton a objev gravitačního zákona
 Kapitola 8 Gavitace 8.1 Gavitační zákon 8.1.1 Isaac Newton a objev gavitačního zákona Keple objevil své evoluční zákony o pohybu planet v oce 1609 a 1619. Dlouho však byly jeho výsledky přijímány s nedůvěou.
Kapitola 8 Gavitace 8.1 Gavitační zákon 8.1.1 Isaac Newton a objev gavitačního zákona Keple objevil své evoluční zákony o pohybu planet v oce 1609 a 1619. Dlouho však byly jeho výsledky přijímány s nedůvěou.
MAGNETICKÉ POLE ELEKTRICKÉHO PROUDU. r je vyjádřen vztahem
 MAGNETICKÉ POLE ELEKTRICKÉHO PROUDU udeme se zabývat výpočtem magnetického pole vytvořeného danou konfiguací elektických poudů (podobně jako učení elektického pole vytvořeného daným ozložením elektických
MAGNETICKÉ POLE ELEKTRICKÉHO PROUDU udeme se zabývat výpočtem magnetického pole vytvořeného danou konfiguací elektických poudů (podobně jako učení elektického pole vytvořeného daným ozložením elektických
Učební text k přednášce UFY102
 Matematický popis vlnění vlna - ozuch šířící se postředím zachovávající svůj tva (pofil) Po jednoduchost začneme s jednodimenzionální vlnou potože ozuch se pohybuje ychlostí v, musí být funkcí jak polohy
Matematický popis vlnění vlna - ozuch šířící se postředím zachovávající svůj tva (pofil) Po jednoduchost začneme s jednodimenzionální vlnou potože ozuch se pohybuje ychlostí v, musí být funkcí jak polohy
Elektrické a magnetické pole zdroje polí
 Elektické a magnetické pole zdoje polí Co je podstatou elektomagnetických jevů Co jsou elektické náboje a jaké mají vlastnosti Co je elementání náboj a bodový elektický náboj Jak veliká je elektická síla
Elektické a magnetické pole zdoje polí Co je podstatou elektomagnetických jevů Co jsou elektické náboje a jaké mají vlastnosti Co je elementání náboj a bodový elektický náboj Jak veliká je elektická síla
Obsah. Obsah. 2.3 Pohyby v radiálním poli Doplňky 16. F g = κ m 1m 2 r 2 Konstantu κ nazýváme gravitační konstantou.
 Obsah Obsah 1 Newtonův gravitační zákon 1 2 Gravitační pole 3 2.1 Tíhové pole............................ 5 2.2 Radiální gravitační pole..................... 8 2.3..................... 11 3 Doplňky 16
Obsah Obsah 1 Newtonův gravitační zákon 1 2 Gravitační pole 3 2.1 Tíhové pole............................ 5 2.2 Radiální gravitační pole..................... 8 2.3..................... 11 3 Doplňky 16
KLASICKÁ MECHANIKA. Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny.
 MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
Diferenciální operátory vektorové analýzy verze 1.1
 Úvod Difeenciální opeátoy vektoové analýzy veze. Následující text popisuje difeenciální opeátoy vektoové analýzy. Měl by sloužit především studentům předmětu MATEMAT na Univezitě Hadec Kálové k přípavě
Úvod Difeenciální opeátoy vektoové analýzy veze. Následující text popisuje difeenciální opeátoy vektoové analýzy. Měl by sloužit především studentům předmětu MATEMAT na Univezitě Hadec Kálové k přípavě
1. Dvě stejné malé kuličky o hmotnosti m, jež jsou souhlasně nabité nábojem Q, jsou 3
 lektostatické pole Dvě stejné malé kuličk o hmotnosti m jež jsou souhlasně nabité nábojem jsou pověšen na tenkých nitích stejné délk v kapalině s hustotou 8 g/cm Vpočtěte jakou hustotu ρ musí mít mateiál
lektostatické pole Dvě stejné malé kuličk o hmotnosti m jež jsou souhlasně nabité nábojem jsou pověšen na tenkých nitích stejné délk v kapalině s hustotou 8 g/cm Vpočtěte jakou hustotu ρ musí mít mateiál
POHYBY V GRAVITAČNÍM POLI ZEMĚ POHYBY TĚLES V HOMOGENNÍM TÍHOVÉM POLI ZEMĚ
 Předmět: Ročník: Vytořil: Datum: FYZIKA PRVNÍ MGR. JÜTTNEROVÁ 9. 9. 01 Náze zpracoaného celku: POHYBY V GRAVITAČNÍM POLI ZEMĚ POHYBY TĚLES V HOMOGENNÍM TÍHOVÉM POLI ZEMĚ Jde o pohyby těles blízkosti porchu
Předmět: Ročník: Vytořil: Datum: FYZIKA PRVNÍ MGR. JÜTTNEROVÁ 9. 9. 01 Náze zpracoaného celku: POHYBY V GRAVITAČNÍM POLI ZEMĚ POHYBY TĚLES V HOMOGENNÍM TÍHOVÉM POLI ZEMĚ Jde o pohyby těles blízkosti porchu
Geometrie. RNDr. Yvetta Bartáková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Geometie RND. Yett Btákoá Gymnázium, OŠ VOŠ Ledeč nd ázou Objemy pochy těles komolá těles VY INOVACE_05 9_M Gymnázium, OŠ VOŠ Ledeč nd ázou Objemy pochy těles A) Komolý jehln - je těleso, kteé znikne půnikem
Geometie RND. Yett Btákoá Gymnázium, OŠ VOŠ Ledeč nd ázou Objemy pochy těles komolá těles VY INOVACE_05 9_M Gymnázium, OŠ VOŠ Ledeč nd ázou Objemy pochy těles A) Komolý jehln - je těleso, kteé znikne půnikem
[GRAVITAČNÍ POLE] Gravitace Gravitace je všeobecná vlastnost těles.
![[GRAVITAČNÍ POLE] Gravitace Gravitace je všeobecná vlastnost těles. [GRAVITAČNÍ POLE] Gravitace Gravitace je všeobecná vlastnost těles.](/thumbs/54/34794266.jpg) 5. GRAVITAČNÍ POLE 5.1. NEWTONŮV GRAVITAČNÍ ZÁKON Gravitace Gravitace je všeobecná vlastnost těles. Newtonův gravitační zákon Znění: Dva hmotné body se navzájem přitahují stejně velkými gravitačními silami
5. GRAVITAČNÍ POLE 5.1. NEWTONŮV GRAVITAČNÍ ZÁKON Gravitace Gravitace je všeobecná vlastnost těles. Newtonův gravitační zákon Znění: Dva hmotné body se navzájem přitahují stejně velkými gravitačními silami
3. Vlny. 3.1 Úvod. 3.2 Rovnice postupné vlny v bodové řadě a v prostoru
 3. Vlny 3. Úod Vlnění můžeme pozoroat například na odní hladině, hodíme-li do ody kámen. Mechanické lnění je děj, při kterém se kmitání šíří látkoým prostředím. To znamená, že například zuk, který je mechanickým
3. Vlny 3. Úod Vlnění můžeme pozoroat například na odní hladině, hodíme-li do ody kámen. Mechanické lnění je děj, při kterém se kmitání šíří látkoým prostředím. To znamená, že například zuk, který je mechanickým
GEOMETRICKÉ APLIKACE INTEGRÁLNÍHO POČTU
 Integální počet funkcí jedné eálné poměnné - 4. - GEOMETRICKÉ APLIKACE INTEGRÁLNÍHO POČTU PŘÍKLAD Učete plochu pod gfem funkce f ( x) = sinx n intevlu,. Ploch pod gfem nezáponé funkce f(x) se n intevlu,
Integální počet funkcí jedné eálné poměnné - 4. - GEOMETRICKÉ APLIKACE INTEGRÁLNÍHO POČTU PŘÍKLAD Učete plochu pod gfem funkce f ( x) = sinx n intevlu,. Ploch pod gfem nezáponé funkce f(x) se n intevlu,
1.7.2 Moment síly vzhledem k ose otáčení
 .7. oment síly vzhledem k ose otáčení Předpoklady 70 Pedagogická poznámka Situaci tochu komplikuje skutečnost, že žáci si ze základní školy pamatují součin a mají pocit, že se pouze opakuje notoicky známá
.7. oment síly vzhledem k ose otáčení Předpoklady 70 Pedagogická poznámka Situaci tochu komplikuje skutečnost, že žáci si ze základní školy pamatují součin a mají pocit, že se pouze opakuje notoicky známá
POVRCH A OBJEM KOULE A JEJÍCH ČÁSTÍ
 Pojekt ŠABLONY NA GVM Gymnázium Velké Meziříčí egistační číslo pojektu: CZ..07/.5.00/4.0948 IV- Inoace a zkalitnění ýuky směřující k ozoji matematické gamotnosti žáků středníc škol POVRCH A OBJEM KOULE
Pojekt ŠABLONY NA GVM Gymnázium Velké Meziříčí egistační číslo pojektu: CZ..07/.5.00/4.0948 IV- Inoace a zkalitnění ýuky směřující k ozoji matematické gamotnosti žáků středníc škol POVRCH A OBJEM KOULE
SMR 1. Pavel Padevět
 SMR Pavel Padevět Oganzace předmětu Přednášející Pavel Padevět, K 3, D 09 e-mal: pavel.padevet@fsv.cvut.cz Infomace k předmětu: https://mech.fsv.cvut.cz/student SMR Heslo: odné číslo bez lomítka (případně
SMR Pavel Padevět Oganzace předmětu Přednášející Pavel Padevět, K 3, D 09 e-mal: pavel.padevet@fsv.cvut.cz Infomace k předmětu: https://mech.fsv.cvut.cz/student SMR Heslo: odné číslo bez lomítka (případně
3.3. Operace s vektory. Definice
 Operace s ektory.. Operace s ektory Výklad Definice... Nechť ϕ je úhel do nenloých ektorů, (obr. ). Skalárním sočinem ektorů, rozmíme číslo, které bdeme označoat. (někdy strčně ) a které definjeme roností.
Operace s ektory.. Operace s ektory Výklad Definice... Nechť ϕ je úhel do nenloých ektorů, (obr. ). Skalárním sočinem ektorů, rozmíme číslo, které bdeme označoat. (někdy strčně ) a které definjeme roností.
4. konference o matematice a fyzice na VŠT Brno, Fraktály ve fyzice. Oldřich Zmeškal
 4. konfeence o matematice a fyzice na VŠT Bno, 15. 9. 25 Faktály ve fyzice Oldřich Zmeškal Ústav fyzikální a spotřební chemie, Fakulta chemická, Vysoké učení technické, Pukyňova 118, 612 Bno, Česká epublika
4. konfeence o matematice a fyzice na VŠT Bno, 15. 9. 25 Faktály ve fyzice Oldřich Zmeškal Ústav fyzikální a spotřební chemie, Fakulta chemická, Vysoké učení technické, Pukyňova 118, 612 Bno, Česká epublika
ε ε [ 8, N, 3, N ]
![ε ε [ 8, N, 3, N ] ε ε [ 8, N, 3, N ]](/thumbs/92/110750106.jpg) 1. Vzdálenost mezi elektonem a potonem v atomu vodíku je přibližně 0,53.10-10 m. Jaká je velikost sil mezi uvedenými částicemi a) elektostatické b) gavitační Je-li gavitační konstanta G = 6,7.10-11 N.m
1. Vzdálenost mezi elektonem a potonem v atomu vodíku je přibližně 0,53.10-10 m. Jaká je velikost sil mezi uvedenými částicemi a) elektostatické b) gavitační Je-li gavitační konstanta G = 6,7.10-11 N.m
Příklad 1 (25 bodů) Částice nesoucí náboj q vletěla do magnetického pole o magnetické indukci B ( 0,0, B)
 Přijímací zkouška na naazující magisterské studium - 05 Studijní program Fyzika - šechny obory kromě Učitelstí fyziky-matematiky pro střední školy, Varianta A Příklad Částice nesoucí náboj q letěla do
Přijímací zkouška na naazující magisterské studium - 05 Studijní program Fyzika - šechny obory kromě Učitelstí fyziky-matematiky pro střední školy, Varianta A Příklad Částice nesoucí náboj q letěla do
Duktilní deformace, část 1
 uktilní defomace, část uktilní (plastická) defomace je taková defomace, při níž se mateiál defomuje bez přeušení koheze (soudžnosti). Plasticita mateiálu záleží na tzv. mezi plasticity (yield stess) -
uktilní defomace, část uktilní (plastická) defomace je taková defomace, při níž se mateiál defomuje bez přeušení koheze (soudžnosti). Plasticita mateiálu záleží na tzv. mezi plasticity (yield stess) -
Cavendishův pokus: Určení gravitační konstanty,,vážení Země
 Cavendishův pokus: Učení gavitační konstanty,,vážení Země Jiří Kist - Mendlovo gymnázium, Opava, SO@seznam.cz Teeza Steinhatová - gymnázium J. K. Tyla Hadec Kálové, SteinT@seznam.cz 1. Úvod Abstakt: Cílem
Cavendishův pokus: Učení gavitační konstanty,,vážení Země Jiří Kist - Mendlovo gymnázium, Opava, SO@seznam.cz Teeza Steinhatová - gymnázium J. K. Tyla Hadec Kálové, SteinT@seznam.cz 1. Úvod Abstakt: Cílem
FYZIKA I. Mechanická energie. Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Mechanická enegie Pof. RND. Vilém Mád, CSc. Pof. Ing. Libo Hlaváč, Ph.D. Doc. Ing. Iena Hlaváčová, Ph.D. Mg. At. Dagma Mádová Ostava
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Mechanická enegie Pof. RND. Vilém Mád, CSc. Pof. Ing. Libo Hlaváč, Ph.D. Doc. Ing. Iena Hlaváčová, Ph.D. Mg. At. Dagma Mádová Ostava
F1040 Mechanika a molekulová fyzika
 4 Mechnik molekuloá fzik Pe Šfřík 4 Přednášk 4 Mechnik molekuloá fzik Tped b Pe Šfřík 4 Mechnik molekuloá fzik... Zchlení:... 3 Pohb po kužnici... 4 Pohb z hledisk ůzných pozooelů... 6 Pohboé onice hmoného
4 Mechnik molekuloá fzik Pe Šfřík 4 Přednášk 4 Mechnik molekuloá fzik Tped b Pe Šfřík 4 Mechnik molekuloá fzik... Zchlení:... 3 Pohb po kužnici... 4 Pohb z hledisk ůzných pozooelů... 6 Pohboé onice hmoného
Cvičení z termomechaniky Cvičení 6.
 Příklad 1: Pacovní látkou v poovnávacím smíšeném oběhu spalovacího motou je vzduch o hmotnosti 1 [kg]. Počáteční tlak je 0,981.10 5 [Pa] při teplotě 30 [ C]. Kompesní pomě je 7, stupeň zvýšení tlaku 2
Příklad 1: Pacovní látkou v poovnávacím smíšeném oběhu spalovacího motou je vzduch o hmotnosti 1 [kg]. Počáteční tlak je 0,981.10 5 [Pa] při teplotě 30 [ C]. Kompesní pomě je 7, stupeň zvýšení tlaku 2
Řešení úloh 1. kola 52. ročníku fyzikální olympiády. Kategorie B Autořiúloh:M.Jarešová(5),P.Šedivý(1,4),J.Thomas(2,3,7), K.RauneraP.Šedivý(6).
 Řešení úloh 1. kola 52. očníku fyzikální olympiády. Kategoie B Autořiúloh:M.Jaešová(5),P.Šedivý(1,4),J.Thomas(2,3,7), K.auneaP.Šedivý(6). 1.a) Potože se tyč otáčí velmi pomalu, můžeme každou její polohu
Řešení úloh 1. kola 52. očníku fyzikální olympiády. Kategoie B Autořiúloh:M.Jaešová(5),P.Šedivý(1,4),J.Thomas(2,3,7), K.auneaP.Šedivý(6). 1.a) Potože se tyč otáčí velmi pomalu, můžeme každou její polohu
Základní pojmy Rovnoměrný přímočarý pohyb Rovnoměrně zrychlený přímočarý pohyb Rovnoměrný pohyb po kružnici
 Kinemaika Základní pojmy Ronoměný přímočaý pohyb Ronoměně zychlený přímočaý pohyb Ronoměný pohyb po kužnici Základní pojmy Kinemaika - popiuje pohyb ělea, neuduje jeho příčiny Klid (pohyb) - učujeme zhledem
Kinemaika Základní pojmy Ronoměný přímočaý pohyb Ronoměně zychlený přímočaý pohyb Ronoměný pohyb po kužnici Základní pojmy Kinemaika - popiuje pohyb ělea, neuduje jeho příčiny Klid (pohyb) - učujeme zhledem
Trivium z optiky Vlnění
 Tivium z optiky 7 1 Vlnění V této kapitole shnujeme základní pojmy a poznatky o vlnění na přímce a v postou Odvolávat se na ně budeme často v kapitolách následujících věnujte poto vyložené látce náležitou
Tivium z optiky 7 1 Vlnění V této kapitole shnujeme základní pojmy a poznatky o vlnění na přímce a v postou Odvolávat se na ně budeme často v kapitolách následujících věnujte poto vyložené látce náležitou
V soustavě N hmotných bodů působí síly. vnější. vnitřní jsou svázány principem akce a reakce
 3.3. naka sousta hotnýh bodů (HB) Soustaa hotnýh bodů toří nejobenější těleso ehank. a odíl od tuhého tělesa se ůže taoě ěnt. V soustaě hotnýh bodů působí síl F nější (,,... ) ntřní jsou sáán pnpe ake
3.3. naka sousta hotnýh bodů (HB) Soustaa hotnýh bodů toří nejobenější těleso ehank. a odíl od tuhého tělesa se ůže taoě ěnt. V soustaě hotnýh bodů působí síl F nější (,,... ) ntřní jsou sáán pnpe ake
Modelové úlohy přijímacího testu z matematiky
 PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY KARLOVY V PRAZE Modelové úlohy přijímacího testu z matematiky r + s r s r s r + s 1 r2 + s 2 r 2 s 2 ( ) ( ) 1 a 2a 1 + a 3 1 + 2a + 1 ( a b 2 + ab 2 ) ( a + b + b b a
PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY KARLOVY V PRAZE Modelové úlohy přijímacího testu z matematiky r + s r s r s r + s 1 r2 + s 2 r 2 s 2 ( ) ( ) 1 a 2a 1 + a 3 1 + 2a + 1 ( a b 2 + ab 2 ) ( a + b + b b a
Na obrázku je nakreslen vlak, který se pohybuje po přímé trati, nakresli k němu vhodnou souřadnou soustavu. v
 ..7 Znaménka Předpoklad: 4 Opakoání: Veličin s elikostí a směrem = ektoroé eličin. Vektor je určen také sým koncoým bodem (pokud začíná počátku) polohu bodu můžeme určit pomocí ektoru, který začíná počátku
..7 Znaménka Předpoklad: 4 Opakoání: Veličin s elikostí a směrem = ektoroé eličin. Vektor je určen také sým koncoým bodem (pokud začíná počátku) polohu bodu můžeme určit pomocí ektoru, který začíná počátku
ELEKTŘINA A MAGNETIZMUS
 ELEKTŘIN MGNETIZMUS III Elektický potenciál Obsah 3 ELEKTRICKÝ POTENCIÁL 31 POTENCIÁL POTENCIÁLNÍ ENERGIE 3 ELEKTRICKÝ POTENCIÁL V HOMOGENNÍM POLI 4 33 ELEKTRICKÝ POTENCIÁL ZPŮSOENÝ ODOVÝMI NÁOJI 5 331
ELEKTŘIN MGNETIZMUS III Elektický potenciál Obsah 3 ELEKTRICKÝ POTENCIÁL 31 POTENCIÁL POTENCIÁLNÍ ENERGIE 3 ELEKTRICKÝ POTENCIÁL V HOMOGENNÍM POLI 4 33 ELEKTRICKÝ POTENCIÁL ZPŮSOENÝ ODOVÝMI NÁOJI 5 331
Vnitřní energie ideálního plynu podle kinetické teorie
 Vnitřní energie ideálního plynu podle kinetické teorie Kinetická teorie plynu, která prní poloině 9.století dokázala úspěšně spojit klasickou fenoenologickou terodynaiku s echanikou, poažuje plyn za soustau
Vnitřní energie ideálního plynu podle kinetické teorie Kinetická teorie plynu, která prní poloině 9.století dokázala úspěšně spojit klasickou fenoenologickou terodynaiku s echanikou, poažuje plyn za soustau
MASARYKOVA UNIVERZITA PEDAGOGICKÁ FAKULTA KATEDRA GEOGRAFIE. Planetární geografie seminář
 MASARYKOA UNIERZITA PEDAGOGICKÁ FAKULTA KATEDRA GEOGRAFIE květen 2008 I Měření vzdáleností ve vesmíru 1) ýpočet hodnoty pc a ly ze známé AU a převod těchto hodnot. 1 AU = 150 10 6 km Z definice paralaxy
MASARYKOA UNIERZITA PEDAGOGICKÁ FAKULTA KATEDRA GEOGRAFIE květen 2008 I Měření vzdáleností ve vesmíru 1) ýpočet hodnoty pc a ly ze známé AU a převod těchto hodnot. 1 AU = 150 10 6 km Z definice paralaxy
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT
 Střední půmyslová škola a Vyšší odboná škola technická Bno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky postřednictvím ICT Název: Téma: Auto: Číslo: Anotace: Mechanika, dynamika Pohybová ovnice po
Střední půmyslová škola a Vyšší odboná škola technická Bno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky postřednictvím ICT Název: Téma: Auto: Číslo: Anotace: Mechanika, dynamika Pohybová ovnice po
Přijímací zkouška na navazující magisterské studium 2015
 Přijímací zkouška na navazující magisterské studium 205 Studijní program: Studijní obory: Fyzika FFUM Varianta A Řešení příkladů pečlivě odůvodněte. Příklad (25 bodů) Pro funkci f(x) := e x 2. Určete definiční
Přijímací zkouška na navazující magisterské studium 205 Studijní program: Studijní obory: Fyzika FFUM Varianta A Řešení příkladů pečlivě odůvodněte. Příklad (25 bodů) Pro funkci f(x) := e x 2. Určete definiční
Obsah dnešní přednášky : Obecný rovinný pohyb tělesa. Teorie současných pohybů, Coriolisovo zrychlení, dynamika obecného rovinného pohybu.
 Obsh dnešní řednášky : Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. osu osu = A otce = A otce A A A A efeenční bod sueosice
Obsh dnešní řednášky : Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. osu osu = A otce = A otce A A A A efeenční bod sueosice
ELEKTRICKÝ NÁBOJ COULOMBŮV ZÁKON INTENZITA ELEKTRICKÉHO POLE
 ELEKTRICKÝ NÁBOJ COULOMBŮV ZÁKON INTENZITA ELEKTRICKÉHO POLE 1 ELEKTRICKÝ NÁBOJ Elektický náboj základní vlastnost někteých elementáních částic (pvní elektické jevy pozoovány již ve staověku janta (řecky
ELEKTRICKÝ NÁBOJ COULOMBŮV ZÁKON INTENZITA ELEKTRICKÉHO POLE 1 ELEKTRICKÝ NÁBOJ Elektický náboj základní vlastnost někteých elementáních částic (pvní elektické jevy pozoovány již ve staověku janta (řecky
Ekvivalentní vztahy a veličiny v elektromagnetickém poli. Elektrostatické a stacionární magnetické pole
 Ekiaentní ztahy a eičiny eektomagnetickém poi Eektické a magnetické poe má z hediska budících zdojů zcea odišnou poahu. Eektické poe pomysně ytéká z kadných nábojů a téká do záponých. Zdojem magnetického
Ekiaentní ztahy a eičiny eektomagnetickém poi Eektické a magnetické poe má z hediska budících zdojů zcea odišnou poahu. Eektické poe pomysně ytéká z kadných nábojů a téká do záponých. Zdojem magnetického
FYZIKA I. Rovnoměrný, rovnoměrně zrychlený a nerovnoměrně zrychlený translační pohyb
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Ronoměrný, ronoměrně zrychlený neronoměrně zrychlený trnslční pohyb Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hláč, Ph.D. Doc.
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Ronoměrný, ronoměrně zrychlený neronoměrně zrychlený trnslční pohyb Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hláč, Ph.D. Doc.
cos cos φ ω Převod mechanismu Aplikovaná mechanika, 9. přednáška analytické řešení mechanismu s pravoúhlou kulisou ω, ε φ převod derivace převodu
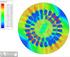 Přeod mechnismu nlytické řešení mechnismu s oúhlou kulisou, ε, y y sin y& & cos && y && cos & & && ε cos y& && y ε cos mechnismus s oměnným řeodem ( ) likoná mechnik, 9. řednášk f řeod sin sin deice řeodu
Přeod mechnismu nlytické řešení mechnismu s oúhlou kulisou, ε, y y sin y& & cos && y && cos & & && ε cos y& && y ε cos mechnismus s oměnným řeodem ( ) likoná mechnik, 9. řednášk f řeod sin sin deice řeodu
Na obrázku je nakreslený vlak, který se pohybuje po přímé trati, nakresli k němu vhodnou souřadnou soustavu. v
 ..6 Znaménka Předpoklad: 3, 5 Opakoání: Veličin s elikostí a směrem = ektoroé eličin Vektor je určen také sým koncoým bodem (pokud začíná počátku) polohu bodu můžeme určit pomocí ektoru, který začíná počátku
..6 Znaménka Předpoklad: 3, 5 Opakoání: Veličin s elikostí a směrem = ektoroé eličin Vektor je určen také sým koncoým bodem (pokud začíná počátku) polohu bodu můžeme určit pomocí ektoru, který začíná počátku
1.3.8 Rovnoměrně zrychlený pohyb po kružnici I
 1.3.8 Rovnoměně zychlený pohyb po kužnici I Předpoklady: 137 Opakování: K veličinám popisujícím posuvný pohyb existují analogické veličiny popisující pohyb po kužnici: ovnoměný pohyb pojítko ovnoměný pohyb
1.3.8 Rovnoměně zychlený pohyb po kužnici I Předpoklady: 137 Opakování: K veličinám popisujícím posuvný pohyb existují analogické veličiny popisující pohyb po kužnici: ovnoměný pohyb pojítko ovnoměný pohyb
Teorie současných pohybů, Coriolisovo zrychlení, dynamika obecného rovinného pohybu.
 Obsh dnešní řednášky : Alikoná echnik, 4. řednášk Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. Alikoná echnik, 4. řednášk
Obsh dnešní řednášky : Alikoná echnik, 4. řednášk Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. Alikoná echnik, 4. řednášk
Modelové úlohy přijímacího testu z matematiky
 PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY KARLOVY V PRAZE Modelové úlohy přijímacího testu z matematiky r + s r s r s r + s 1 r2 + s 2 r 2 s 2 ( ) ( ) 1 a 2a 1 + a 3 1 + 2a + 1 ( a b 2 + ab 2 ) ( a + b + b b a
PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY KARLOVY V PRAZE Modelové úlohy přijímacího testu z matematiky r + s r s r s r + s 1 r2 + s 2 r 2 s 2 ( ) ( ) 1 a 2a 1 + a 3 1 + 2a + 1 ( a b 2 + ab 2 ) ( a + b + b b a
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C)
 VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
Vlastní čísla a vlastní vektory
 5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
6 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ
 6 6 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Pohyblivost mechanické soustavy charakterizujeme počtem stupňů volnosti. Je to číslo, které udává, kolika nezávislými parametry je určena poloha jednotlivých členů soustavy
6 6 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Pohyblivost mechanické soustavy charakterizujeme počtem stupňů volnosti. Je to číslo, které udává, kolika nezávislými parametry je určena poloha jednotlivých členů soustavy
R2.213 Tíhová síla působící na tělesa je mnohem větší než gravitační síla vzájemného přitahování těles.
 2.4 Gravitační pole R2.211 m 1 = m 2 = 10 g = 0,01 kg, r = 10 cm = 0,1 m, = 6,67 10 11 N m 2 kg 2 ; F g =? R2.212 F g = 4 mn = 0,004 N, a) r 1 = 2r; F g1 =?, b) r 2 = r/2; F g2 =?, c) r 3 = r/3; F g3 =?
2.4 Gravitační pole R2.211 m 1 = m 2 = 10 g = 0,01 kg, r = 10 cm = 0,1 m, = 6,67 10 11 N m 2 kg 2 ; F g =? R2.212 F g = 4 mn = 0,004 N, a) r 1 = 2r; F g1 =?, b) r 2 = r/2; F g2 =?, c) r 3 = r/3; F g3 =?
Mechanická silová pole
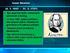 Mechanická siloá pole siloé pole mechanice je ekooé pole chaakeizoané z. inenziou siloého pole (inenziou síly): E m [ms ] inenzia je oožná se zychlením, keé siloé pole aném mísě uělí liboolnému ělesu Siloé
Mechanická siloá pole siloé pole mechanice je ekooé pole chaakeizoané z. inenziou siloého pole (inenziou síly): E m [ms ] inenzia je oožná se zychlením, keé siloé pole aném mísě uělí liboolnému ělesu Siloé
Sluneční plachetnice. 1. Trocha historieequation Chapter 1 Section 1. 2. Pohyb v gravitačním poli
 Sluneční plachetnice 1. Tocha histoieequation Chapte 1 Section 1 O plachetnici poháněné tlakem slunečního záření, kteá letí napříč sluneční soustavou, snily desítky spisovatelů a fyziků. Mezi nejznámějšími
Sluneční plachetnice 1. Tocha histoieequation Chapte 1 Section 1 O plachetnici poháněné tlakem slunečního záření, kteá letí napříč sluneční soustavou, snily desítky spisovatelů a fyziků. Mezi nejznámějšími
Kartézská soustava souřadnic
 Katézská soustava souřadnic Pavotočivá Levotočivá jednotkové vekto ve směu souřadnicových os Katézská soustava souřadnic otonomální báze z,, z Katézská soustava souřadnic polohový (adius) vekto z,, z velikost
Katézská soustava souřadnic Pavotočivá Levotočivá jednotkové vekto ve směu souřadnicových os Katézská soustava souřadnic otonomální báze z,, z Katézská soustava souřadnic polohový (adius) vekto z,, z velikost
3. VEKTOROVÝ POČET A ANALYTICKÁ GEOMETRIE
 Euklidoský prostor. VEKTOROVÝ POČET A ANALYTICKÁ GEOMETRIE Průodce studiem Geometrii lze budoat metodou syntetickou nebo metodou analytickou. Při syntetické metodě pracujeme přímo s geometrickými objekty.
Euklidoský prostor. VEKTOROVÝ POČET A ANALYTICKÁ GEOMETRIE Průodce studiem Geometrii lze budoat metodou syntetickou nebo metodou analytickou. Při syntetické metodě pracujeme přímo s geometrickými objekty.
Úvod do nebeské mechaniky
 OPT/AST L09 Úvod do nebeské mechaniky pohyby astronomických těles ve společném gravitačním poli obecně: chaotický systém nestabilní numerické řešení speciální případ: problém dvou těles analytické řešení
OPT/AST L09 Úvod do nebeské mechaniky pohyby astronomických těles ve společném gravitačním poli obecně: chaotický systém nestabilní numerické řešení speciální případ: problém dvou těles analytické řešení
Fyzika 1 - rámcové příklady Kinematika a dynamika hmotného bodu, gravitační pole
 Fyzika 1 - rámcové příklady Kinematika a dynamika hmotného bodu, gravitační pole 1. Určete skalární a vektorový součin dvou obecných vektorů AA a BB a popište, jak závisí výsledky těchto součinů na úhlu
Fyzika 1 - rámcové příklady Kinematika a dynamika hmotného bodu, gravitační pole 1. Určete skalární a vektorový součin dvou obecných vektorů AA a BB a popište, jak závisí výsledky těchto součinů na úhlu
Zobrazení kružnice v pravoúhlé axonometrii. osy, která je normálou roviny dané kružnice; délka hlavní poloosy je rovna poloměru
 Geometie Zoazovací metody Zoazení kužnice v pavoúhlé axonometii Zoazení kužnice ležící v souřadnicové ovině Výklad v pavoúhlé axonometii lze poměně snadno sestojit půmět kužnice dané středem a poloměem,
Geometie Zoazovací metody Zoazení kužnice v pavoúhlé axonometii Zoazení kužnice ležící v souřadnicové ovině Výklad v pavoúhlé axonometii lze poměně snadno sestojit půmět kužnice dané středem a poloměem,
OBJEMY A POVRCHY TĚLES
 OBJEMY A POVRCHY TĚLES Metodický mteiál do semináře MA SDM Růžen Blžkoá, Ien Budínoá KOMOLÝ JEHLAN Ojem komolého jehlnu Po zjednodušení ododíme zthy po komolý jehln, jehož podstmi jsou čtece. Oznčení:
OBJEMY A POVRCHY TĚLES Metodický mteiál do semináře MA SDM Růžen Blžkoá, Ien Budínoá KOMOLÝ JEHLAN Ojem komolého jehlnu Po zjednodušení ododíme zthy po komolý jehln, jehož podstmi jsou čtece. Oznčení:
MATEMATIKA III. π π π. Program - Dvojný integrál. 1. Vypočtěte dvojrozměrné integrály v obdélníku D: ( ), (, ): 0,1, 0,3, (2 4 ), (, ) : 1,3, 1,1,
 MATEMATIKA III Program - vojný integrál. Vpočtěte dvojrozměrné integrál v obdélníku : + dd = { < > < > } ( 3), (, ) : 0,, 0,, dd = { < > < > } ( 4 ), (, ) :,3,,, + dd = { < > < > } ( ), (, ):,0,,, + dd=
MATEMATIKA III Program - vojný integrál. Vpočtěte dvojrozměrné integrál v obdélníku : + dd = { < > < > } ( 3), (, ) : 0,, 0,, dd = { < > < > } ( 4 ), (, ) :,3,,, + dd = { < > < > } ( ), (, ):,0,,, + dd=
3.7. Magnetické pole elektrického proudu
 3.7. Magnetické pole elektického poudu 1. Znát Biotův-Savatův zákon a umět jej použít k výpočtu magnetické indukce v jednoduchých případech (okolí přímého vodiče, ve středu oblouku apod.).. Pochopit význam
3.7. Magnetické pole elektického poudu 1. Znát Biotův-Savatův zákon a umět jej použít k výpočtu magnetické indukce v jednoduchých případech (okolí přímého vodiče, ve středu oblouku apod.).. Pochopit význam
1 vod V nebesk mechanice asto studujeme pohyby elativn mal ch t les v adi- ln m gavita n m poli osamocen ho t lesa s mnohon sobn v t hmotnost. Nejv t
 POHYB T LESA PO ELIPTICK TRAJEKTORII V RADI LN M GRAVITA N M POLI Obsah Studijn text po e itele FO a ostatn z jemce o fyziku P emysl ediv a Ivo Volf { VFO Hadec K lov 1 vod 2 2 Geometie elipsy 4 3 Kepleovy
POHYB T LESA PO ELIPTICK TRAJEKTORII V RADI LN M GRAVITA N M POLI Obsah Studijn text po e itele FO a ostatn z jemce o fyziku P emysl ediv a Ivo Volf { VFO Hadec K lov 1 vod 2 2 Geometie elipsy 4 3 Kepleovy
b) Maximální velikost zrychlení automobilu, nemají-li kola prokluzovat, je a = f g. Automobil se bude rozjíždět po dobu t = v 0 fg = mfgv 0
 Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
1.8.10 Proudění reálné tekutiny
 .8.0 Proudění reálné tekutiny Předpoklady: 809 Ideální kapalina: nestlačitelná, dokonale tekutá, bez nitřního tření. Reálná kapalina: zájemné posouání částic brzdí síly nitřního tření. Jaké mají tyto rozdíly
.8.0 Proudění reálné tekutiny Předpoklady: 809 Ideální kapalina: nestlačitelná, dokonale tekutá, bez nitřního tření. Reálná kapalina: zájemné posouání částic brzdí síly nitřního tření. Jaké mají tyto rozdíly
S S obsahy podstav S obsah pláště
 Předmět: Ročník: ytořil: Datum: MATEMATIKA DRUHÝ MGR. JÜTTNEROÁ 7.. 04 Náze zpacoaného celku: PORCHY A OBJEMY KOMOLÝCH TĚLE, KOULE A JEJÍCH ČÁTÍ PORCH A OBJEM KOMOLÉHO JEHLANU Komolý jehlan: má dě podstay,
Předmět: Ročník: ytořil: Datum: MATEMATIKA DRUHÝ MGR. JÜTTNEROÁ 7.. 04 Náze zpacoaného celku: PORCHY A OBJEMY KOMOLÝCH TĚLE, KOULE A JEJÍCH ČÁTÍ PORCH A OBJEM KOMOLÉHO JEHLANU Komolý jehlan: má dě podstay,
Digitální učební materiál. III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Příjemce podpory Gymnázium, Jevíčko, A. K.
 Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím

 DYNAMIKA HMOTNÉHO BODU Součást Newtonovské klasická mechanika (v
DYNAMIKA HMOTNÉHO BODU Součást Newtonovské klasická mechanika (v