Matematická logika. Miroslav Kolařík
|
|
|
- Miloslav Kryštof Beran
- před 5 lety
- Počet zobrazení:
Transkript
1 Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika pro informatiky II, Olomouc 2006.
2 Obsah 1 Sémantika PL
3 Jazyk PL je určen svými relačními a funkčními symboly spolu s definicí jejich arity. Z těchto symbolů spolu se symboly proměnných, logických spojek, kvantifikátorů a pomocných symbolů se skládají termy a formule daného jazyka. Samotné termy a formule jsou syntaktické pojmy a nemají žádný význam (tj. term sám o sobě nemá žádnou hodnotu, formule sama o sobě nemá žádnou pravdivostní hodnotu). To je například dobře patrné u termu x + 0: abychom mohli uvažovat hodnotu tohoto termu, musí mít přiřazenu nějakou hodnotu proměnná x a dále musíme interpretovat symboly + a 0. Interpretací funkčních a relačních symbolů se zabývá sémantika PL (ta přiřazuje význam funkčním a relačním symbolům). Poznamenejme ještě, že interpretaci proměnných definuje tzv. ohodnocení proměnných (viz dále).
4 Struktura pro jazyk Intuitivní pojem interpretace jazyka nyní přesně zavedeme: Definice Struktura pro jazyk typu R,F,σ je trojice M = M,R M,F M, která sestává z neprázdné množiny M a dále z množin R M = {r M M n r R,σ(r) = n}, F M = {f M : M n M f F,σ(f ) = n}. Pokud R, pak interpretujeme vždy relací identity, tj. M = ω M = { u,u u M}.
5 Jinými slovy, struktura M pro jazyk typu R,F,σ je systém relací a funkcí na jisté množině M, přitom ke každému n-árnímu relačnímu symbolu r R je ve struktuře M odpovídající n-ární relace r M R M na M a ke každému n-árnímu funkčnímu symbolu f F je ve struktuře M odpovídající n-ární funkce f M F M v M. Nehrozí-li nebezpečí nedorozumění, budeme někdy vynechávat horní indexy a místo r M a f M budeme psát jen r a f.
6 Příklad Uvažujme jazyk typu R,F,σ, kde R = {p, }, F = {c, }, c je nulární, p je unární, a jsou binární. Necht M = Z. Definujme relace p M (unární, tj. podmnožina M), M a funkce c M (nulární, tj. vybraný prvek z M) a M následovně: p M = {m M m je větší nebo rovno nule}, M = { m 1,m 2 M M m 1 je menší nebo rovno m 2 }, c M = 0, m 1 M m 2 = m 1 + m 2, tj. c M je číslo nula a M je operace sčítání celých čísel. Jinou strukturu pro stejný jazyk dostaneme, pokud změníme výše uvedenou strukturu tak, že c M = 1, případně ještě definujeme m 1 M m 2 = m 1 m 2 (násobení celých čísel). Další strukturou (opět) pro stejný jazyk je struktura s nosičem M = {a,b}, p M = {a,b}, M = { a,a, b,b, b,a }, c M = b a M a b s operací M definovanou tabulkou: a a b. b a a
7 Jak tedy vidíme, k danému jazyku PL existuje nekonečně mnoho struktur. Variabilita je dána jednak nosičem M, který může mít libovolný (nenulový) počet prvků, dále každý relační symbol r může být interpretován libovolnou relací r M příslušné arity a konečně každý funkční symbol f může být interpretován libovolnou funkcí f M příslušné arity. Necht M je struktura pro jazyk typu R,F,σ. M-ohodnocení proměnných (krátce jen M-ohodnocení, popř. jen ohodnocení) je zobrazení v přiřazující každé proměnné x prvek v(x) M. Jsou-li v a v ohodnocení a x je proměnná, píšeme v = x v pokud pro každou proměnnou y x je v(y) = v (y), tj. v a v se liší nejvýše v tom, jakou hodnotu přiřazují proměnné x.
8 Definice Necht v je M-ohodnocení. Hodnota t M,v termu t v M při v je definována { v(x), je-li t proměnná x t M,v = f M ( t 1 M,v,..., t k M,v ), je-li t tvaru f (t 1,...,t k ). Uvědomme si, že při dané struktuře M a při daném M-ohodnocení v je každému termu t přiřazena právě jedna hodnota t M,v z univerza M. Dále je patrné, že hodnota t M,v nezávisí na hodnotách přiřazených ohodnocením v těm proměnným, které se v t nevyskytují (lze dokázat jednoduše strukturální indukcí).
9 Příklad Uvažujme jazyk typu {p, },{c, },σ, kde σ(c) = 0, σ(p) = 1, σ( ) = σ( ) = 2. Necht M = Z. Definujme relace p M, M a funkce c M a M následovně: p M = {m M m je větší nebo rovno nule}, M = { m 1,m 2 M M m 1 je menší nebo rovno m 2 }, c M = 0, m 1 M m 2 = m 1 + m 2. Vezmeme-li v této struktuře term (x (c y)) x, pak při ohodnocení v, kde v(x) = 10, v(y) = 50 máme (x (c y)) x M,v = x (c y) M,v + x M,v = = ( x M,v + c y M,v )+ x M,v = = ( x M,v +( c M,v + y M,v ))+ x M,v = = (v(x) + (c M + v(y))) + v(x) = (10 + (0 + 50)) + 10 = 70. Dále definujeme pravdivostní hodnotu formule ve struktuře při daném ohodnocení.
10 Definice Pravdivostní hodnota ϕ M,v formule ϕ při M-ohodnocení v je definována následovně: (i) pro atomické formule { 1, je-li t1 r(t 1,...,t n ) M,v = M,v,..., t n M,v r M 0, jinak (ii) pro formule{ ϕ ve tvaru α a α β 1, pokud α M,v = 0 α M,v = 0, pokud α M,v = 1 1, pokud α M,v = 0 nebo α β M,v = β M,v = 1 0, jinak (iii) pro kvantifikovanou formuli ϕ 1, pokud pro každé v takové, že ( x)ϕ M,v = v = x v je ϕ M,v = 1 0, jinak. Je-li ϕ M,v = 1 ( ϕ M,v = 0), říkáme, že formule ϕ je pravdivá (nepravdivá) ve struktuře M při ohodnocení v.
11 Stejně jako u ohodnocení termů je (při daných M a v) každé formuli ϕ přiřazena právě jedna hodnota ϕ M,v. Strukturální indukcí lze jednoduše dokázat, že hodnota ϕ M,v nezávisí na hodnotách přiřazených ohodnocením v proměnným, které se ve ϕ nevyskytují. Uvědomme si, že říct: "formule ϕ je pravdivá" nemá smysl, protože pravdivost ϕ vztahujeme vždy k nějaké struktuře při některém ohodnocení proměnných. Běžně sice říkáme např. "formule ( x)( y)x x + abs(y) je pravdivá", ale to je způsobeno tím, že implicitně nějakou strukturu předpokládáme dle kontextu, ve kterém formuli uvažujeme. Např. v matematické analýze jde většinou o číselné struktury, např. reálná čísla s běžnými relacemi ("menší nebo rovno") a operacemi ("sčítání reálných čísel", "absolutní hodnota").
12 Nyní budeme zkoumat platnost formulí ve struktuře "přes všechna ohodnocení" a platnost formulí "přes všechny struktury". Definice Formule ϕ se nazývá tautologie ve struktuře (pravdivá ve struktuře) M, jestliže ϕ M,v = 1 pro každé M-ohodnocení v. Formule ϕ se nazývá tautologie, jestliže je ϕ tautologie v každé struktuře M. Formule ϕ je tedy tautologie, jestliže pro libovolnou strukturu M a libovolné ohodnocení v je ϕ M,v = 1. Definice Teorie v jazyku PL typu R,F,σ je libovolná množina T formulí jazyka tohoto typu. Struktura M jazyka typu R,F,σ se nazývá model teorie T (píšeme M = T, popř. T M = 1), jestliže každá formule z T je pravdivá v M.
13 Poznámka: Teorie formalizuje soubor předpokladů. Pojem teorie je zcela přirozený. Běžně se říká "S tvojí teorií nesouhlasím." apod. Přitom teorií rozumíme soubor tvrzení, které daná osoba zastává. Soubor tvrzení v PL představuje množina formulí. Též pojem model je přirozený a vyskytuje se v běžné komunikaci. Například obratem "Představme si modelovou situaci, kdy... " chceme vyjádřit, abychom se soustředili na nějaký konkrétní model jisté teorie. Příklad Uvažujme jazyk J typu R,F,σ, kde R = {r}, F = /0 a σ(r) = 2. Struktury pro J jsou M = M,{r M }, /0, kde r M je binární relace na M (tedy struktury jsou vlastně binární relace na M). Struktura M je modelem teorie T = {( x)r(x,x),( x,y,z)((r(x,y) r(y,z)) r(x,z))}, právě když je relace r M reflexivní a tranzitivní.
14 Poznámka: Některé teorie nemají model. Příklad Mějme jazyk typu R,F,σ, kde R = {r}, F = /0 a r je unární. Teorie T = {( x)r(x),( x) r(x)} zřejmě nemá žádný model. Nyní zavedeme sémantické vyplývání v PL. Definice Množina S formulí sémanticky plyne z množiny T formulí (píšeme T = S; píšeme také T = ϕ, jestliže S = {ϕ}, podobně když T = {ψ}), jestliže každý model T je modelem S. Tedy T = S, právě když v každé struktuře, ve které jsou pravdivé všechny formule z T, jsou také pravdivé všechny formule z S.
15 Všimněme si, že pojem sémantického vyplývání je zaveden analogicky jako v případě VL, jen místo "pravdivostních ohodnocení" používáme z pochopitelných důvodů pojem model. Dále platí, že ϕ je tautologie, právě když = ϕ. Vidíme i jak prokázat, že daná formule ϕ sémanticky neplyne z teorie T. Stačí najít jediný model M = T a M-ohodnocení v takové, že ϕ M,v = 0 (což nemusí být vůbec jednoduché). Podotkněme ještě, že daleko větším problémem je ověření, zda-li ϕ z T sémanticky plyne. Příklad Formule ϕ = ( x,y,z,w)((r(x,y) r(y,z) r(z,w)) r(x,w)) sémanticky plyne z formule ψ = ( x,y,z)((r(x,y) r(y,z)) r(x,z)), tj. ψ = ϕ. Obrácené vyplývání, tj. ϕ = ψ, neplatí.
16 Příklad Následující tautologie vyjadřují záměnu pořadí kvantifikátorů: = ( x)( y)ϕ ( y)( x)ϕ, = ( x)( y)ϕ ( y)( x)ϕ, = ( x)( y)ϕ ( y)( x)ϕ. Ukažme, že implikaci ve 3. tautologii nelze obrátit. Uvažujme jazyk typu R, /0,σ, kde R = {r}, σ(r) = 2 a strukturu tohoto jazyka M = M,{r M }, /0, kde M = {a,b} a relace r M je definována r M = { a,b, b,a }. Ve struktuře M máme ( y)( x)r(x,y) M,v = 1 při libovolném ohodnocení v. Na druhou stranu však ( x)( y)r(x,y) M,v = 0, tj. máme model, ve kterém není ( y)( x)ϕ ( x)( y)ϕ pravdivá.
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Predikátová logika. Teoretická informatika Tomáš Foltýnek
 Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška pátá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Úvod do informatiky přednáška pátá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška třetí Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška třetí Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
1 Pravdivost formulí v interpretaci a daném ohodnocení
 1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
Výroková a predikátová logika - VI
 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Základní pojmy matematické logiky
 KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
Místo pojmu výroková formule budeme používat zkráceně jen formule. Při jejich zápisu
 VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
Pro každé formule α, β, γ, δ platí: Pro každé formule α, β, γ platí: Poznámka: Platí právě tehdy, když je tautologie.
 Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
2.2 Sémantika predikátové logiky
 14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
Predik atov a logika - pˇredn aˇska () Predik atov a logika - pˇredn aˇska / 16
 Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Sémantika predikátové logiky
 Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Úvod do predikátové logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
 Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Logické programy Deklarativní interpretace
 Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Další (neklasické) logiky. Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20
 Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
KMA/MDS Matematické důkazy a jejich struktura
 Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
teorie logických spojek chápaných jako pravdivostní funkce
 Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Predikátová logika dokončení
 Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Základy logiky a teorie množin
 Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Logika Libor Barto. Výroková logika
 Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Rezoluční kalkulus pro logiku prvního řádu
 AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
Úvod do informatiky. Miroslav Kolařík. Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008.
 Úvod do informatiky přednáška čtvrtá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Pojem relace 2 Vztahy a operace s (binárními) relacemi
Úvod do informatiky přednáška čtvrtá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Pojem relace 2 Vztahy a operace s (binárními) relacemi
Modely Herbrandovské interpretace
 Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Výroková logika - opakování
 - opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
- opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
Predikátová logika. prvního řádu
 Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Matematická logika. Rostislav Horčík. horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Predikátová logika Motivace Výroková
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Sémantika výrokové logiky. Alena Gollová Výroková logika 1/23
 Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Lineární algebra Kapitola 1 - Základní matematické pojmy
 Lineární algebra Kapitola 1 - Základní matematické pojmy 1.1 Relace a funkce V celém textu budeme používat následující označení pro číselné množiny: N množina všech přirozených čísel bez nuly, N={1, 2,
Lineární algebra Kapitola 1 - Základní matematické pojmy 1.1 Relace a funkce V celém textu budeme používat následující označení pro číselné množiny: N množina všech přirozených čísel bez nuly, N={1, 2,
Klasická predikátová logika
 Klasická predikátová logika Matematická logika, LS 2012/13, závěrečná přednáška Libor Běhounek www.cs.cas.cz/behounek/teaching/malog12 PřF OU, 6. 5. 2013 Symboly klasické predikátové logiky Poznámky Motivace
Klasická predikátová logika Matematická logika, LS 2012/13, závěrečná přednáška Libor Běhounek www.cs.cas.cz/behounek/teaching/malog12 PřF OU, 6. 5. 2013 Symboly klasické predikátové logiky Poznámky Motivace
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
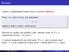 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Matematická analýza 1
 Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Teorie množin. Čekají nás základní množinové operace kartézské součiny, relace zobrazení, operace. Teoretické základy informatiky.
 Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
Množiny, relace, zobrazení
 Množiny, relace, zobrazení Množiny Množinou rozumíme každý soubor určitých objektů shrnutých v jeden celek. Zmíněné objekty pak nazýváme prvky dané množiny. Pojem množina je tedy synonymem pojmů typu soubor,
Množiny, relace, zobrazení Množiny Množinou rozumíme každý soubor určitých objektů shrnutých v jeden celek. Zmíněné objekty pak nazýváme prvky dané množiny. Pojem množina je tedy synonymem pojmů typu soubor,
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
1 Predikátová logika. 1.1 Syntax. jaký mohou mít formule význam (sémantiku). 1. Logických symbolů: 2. Speciálních (mimologických) symbolů:
 1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace
 RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
RELACE Pojem binární relace patří mezi nejzákladnější matematické pojmy. Binární relace slouží k vyjádření vztahů mezi prvky nějakých množin. Vztahy mohou být různé povahy. Patří sem vztah býti potomkem,
Úvod do informatiky. Miroslav Kolařík. Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008.
 Úvod do informatiky přednáška třetí Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Množiny, relace a funkce úvod Množiny, relace a funkce
Úvod do informatiky přednáška třetí Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Množiny, relace a funkce úvod Množiny, relace a funkce
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška sedmá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Čísla a číselné obory 2 Princip indukce 3 Vybrané
Úvod do informatiky přednáška sedmá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Čísla a číselné obory 2 Princip indukce 3 Vybrané
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška šestá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Úvod do informatiky přednáška šestá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Základy matematické logiky
 OBSAH 1 Základy matematické logiky Obsah 1 Úvod 2 1.1 Předmět matematiky.......................... 2 1.2 Nástin historie.............................. 2 1.3 Axiomatická výstavba matematických teorií.............
OBSAH 1 Základy matematické logiky Obsah 1 Úvod 2 1.1 Předmět matematiky.......................... 2 1.2 Nástin historie.............................. 2 1.3 Axiomatická výstavba matematických teorií.............
0. ÚVOD - matematické symboly, značení,
 0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Úvod do logiky (PL): sémantika predikátové logiky
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sémantika predikátové logiky doc. PhDr. Jiří
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sémantika predikátové logiky doc. PhDr. Jiří
Formální systém výrokové logiky
 Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Výroková logika. Sémantika výrokové logiky
 Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
15. Moduly. a platí (p + q)(x) = p(x) + q(x), 1(X) = id. Vzniká tak struktura P [x]-modulu na V.
![15. Moduly. a platí (p + q)(x) = p(x) + q(x), 1(X) = id. Vzniká tak struktura P [x]-modulu na V. 15. Moduly. a platí (p + q)(x) = p(x) + q(x), 1(X) = id. Vzniká tak struktura P [x]-modulu na V.](/thumbs/17/161542.jpg) Učební texty k přednášce ALGEBRAICKÉ STRUKTURY Michal Marvan, Matematický ústav Slezská univerzita v Opavě 15. Moduly Definice. Bud R okruh, bud M množina na níž jsou zadány binární operace + : M M M,
Učební texty k přednášce ALGEBRAICKÉ STRUKTURY Michal Marvan, Matematický ústav Slezská univerzita v Opavě 15. Moduly Definice. Bud R okruh, bud M množina na níž jsou zadány binární operace + : M M M,
UDL 2004/2005 Cvičení č.6 řešení Strana 1/5
 UDL 2004/2005 Cvičení č.6 řešení Strana 1/5 Opakování pojmů relace a funkce Relace R nad množinami A, B je podmnožina kartézského součinu: R A B Kartézský součin množin A = {a 1, a 2,, a 4 }, B = {b 1,
UDL 2004/2005 Cvičení č.6 řešení Strana 1/5 Opakování pojmů relace a funkce Relace R nad množinami A, B je podmnožina kartézského součinu: R A B Kartézský součin množin A = {a 1, a 2,, a 4 }, B = {b 1,
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
1 Výroková logika 1. 2 Predikátová logika 3. 3 Důkazy matematických vět 4. 4 Doporučená literatura 7
 1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
Matematika I. Přednášky: Mgr. Radek Výrut, Zkouška:
 Přednášky: Mgr. Radek Výrut, Matematika I katedra matematiky, UL-605, rvyrut@kma.zcu.cz tel.: 377 63 2658 Zkouška: Písemná část zkoušky - příklady v rozsahu zápočtových prací Ústní část zkoušky - základní
Přednášky: Mgr. Radek Výrut, Matematika I katedra matematiky, UL-605, rvyrut@kma.zcu.cz tel.: 377 63 2658 Zkouška: Písemná část zkoušky - příklady v rozsahu zápočtových prací Ústní část zkoušky - základní
Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka
 Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška desátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. Obsah 1 Úvod do modální logiky 2 Logické programování a Prolog 3
Matematická logika přednáška desátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. Obsah 1 Úvod do modální logiky 2 Logické programování a Prolog 3
prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. BI-ZMA ZS 2009/2010
 Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Abstrakt Text je určen jako doplňkový k přednášce Matematická logika a Paradigmata programování 4.
 Abstrakt Text je určen jako doplňkový k přednášce Matematická logika a Paradigmata programování 4. 1 Matematická logika - poznámky k přednáškám Radim Bělohlávek 29. května 2003 1 Co je (matematická) logika?
Abstrakt Text je určen jako doplňkový k přednášce Matematická logika a Paradigmata programování 4. 1 Matematická logika - poznámky k přednáškám Radim Bělohlávek 29. května 2003 1 Co je (matematická) logika?
Predikátová logika [Predicate logic]
![Predikátová logika [Predicate logic] Predikátová logika [Predicate logic]](/thumbs/74/70612837.jpg) Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony.
 Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce
 Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Matematická indukce, sumy a produkty, matematická logika
 Matematická indukce, sumy a produkty, matematická logika 8.9. -.0.009 Matematická indukce Jde o následující vlastnost přirozených čísel: Předpokládejme:. Nějaké tvrzení platí pro.. Platí-li tvrzení pro
Matematická indukce, sumy a produkty, matematická logika 8.9. -.0.009 Matematická indukce Jde o následující vlastnost přirozených čísel: Předpokládejme:. Nějaké tvrzení platí pro.. Platí-li tvrzení pro
Poznámka. Je-li f zobrazení, ve kterém potřebujeme zdůraznit proměnnou, píšeme f(x) (resp. f(y), resp. f(t)) je zobrazení místo f je zobrazení.
 2. ZOBRAZENÍ A FUNKCE 2.1 Zobrazení 2. 1. 1 Definice: Nechť A a B jsou množiny. Řekneme že f je zobrazení množiny A do množiny B jestliže (i) f A B (ii) ke každému z množiny A eistuje právě jedno y z množiny
2. ZOBRAZENÍ A FUNKCE 2.1 Zobrazení 2. 1. 1 Definice: Nechť A a B jsou množiny. Řekneme že f je zobrazení množiny A do množiny B jestliže (i) f A B (ii) ke každému z množiny A eistuje právě jedno y z množiny
1 Základní pojmy. 1.1 Množiny
 1 Základní pojmy V této kapitole si stručně připomeneme základní pojmy, bez jejichž znalostí bychom se v dalším studiu neobešli. Nejprve to budou poznatky z logiky a teorie množin. Dále se budeme věnovat
1 Základní pojmy V této kapitole si stručně připomeneme základní pojmy, bez jejichž znalostí bychom se v dalším studiu neobešli. Nejprve to budou poznatky z logiky a teorie množin. Dále se budeme věnovat
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška devátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. Obsah 1 Úvod do fuzzy logiky 2 Úvod do aplikací fuzzy logiky 3 Výroková
Matematická logika přednáška devátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. Obsah 1 Úvod do fuzzy logiky 2 Úvod do aplikací fuzzy logiky 3 Výroková
α β ) právě tehdy, když pro jednotlivé hodnoty platí β1 αn βn. Danou relaci nazýváme relace
 Monotónní a Lineární Funkce 1. Relace předcházení a to Uvažujme dva vektory hodnot proměnných α = α,, 1 αn ( ) a β = ( β β ) 1,, n x,, 1 xn. Říkáme, že vekto r hodnot α předchází vektor hodnot β (značíme
Monotónní a Lineární Funkce 1. Relace předcházení a to Uvažujme dva vektory hodnot proměnných α = α,, 1 αn ( ) a β = ( β β ) 1,, n x,, 1 xn. Říkáme, že vekto r hodnot α předchází vektor hodnot β (značíme
Logika. 6. Axiomatický systém výrokové logiky
 Logika 6. Axiomatický systém výrokové logiky RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Logika 6. Axiomatický systém výrokové logiky RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Výroková a predikátová logika - IV
 Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Lineární algebra : Lineární prostor
 Lineární algebra : Lineární prostor (3. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 17. dubna 2014, 14:43 1 2 3.1 Aximotické zavedení lineárního prostoru Číselné těleso Celou lineární
Lineární algebra : Lineární prostor (3. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 17. dubna 2014, 14:43 1 2 3.1 Aximotické zavedení lineárního prostoru Číselné těleso Celou lineární
KATEDRA INFORMATIKY UNIVERZITA PALACKÉHO ÚVOD DO INFORMATIKY VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN
 KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO ÚVOD DO INFORMATIKY RADIM BĚLOHLÁVEK VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ
KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO ÚVOD DO INFORMATIKY RADIM BĚLOHLÁVEK VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ
Výroková logika dokazatelnost
 Výroková logika dokazatelnost Ke zjištění, zda formule sémanticky plyne z dané teorie (množiny formulí), máme k dispozici tabulkovou metodu. Velikost tabulky však roste exponenciálně vzhledem k počtu výrokových
Výroková logika dokazatelnost Ke zjištění, zda formule sémanticky plyne z dané teorie (množiny formulí), máme k dispozici tabulkovou metodu. Velikost tabulky však roste exponenciálně vzhledem k počtu výrokových
Úvod do teoretické informatiky(2017/2018) cvičení 6 1
 Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Matematická logika. Lekce 1: Motivace a seznámení s klasickou výrokovou logikou. Petr Cintula. Ústav informatiky Akademie věd České republiky
 Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují
 Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují 1. u + v = v + u, u, v V 2. (u + v) + w = u + (v + w),
Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují 1. u + v = v + u, u, v V 2. (u + v) + w = u + (v + w),
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - XI
 Výroková a predikátová logika - XI Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XI ZS 2014/2015 1 / 21 Další dokazovací systémy PL Hilbertovský kalkul
Výroková a predikátová logika - XI Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XI ZS 2014/2015 1 / 21 Další dokazovací systémy PL Hilbertovský kalkul
I) Příklady (převeďte následující věty do formulí PL1 a ověřte jejich ekvivalenci pomocí de Morganových zákonů):
 I) Příklady (převeďte následující věty do formulí PL1 a ověřte jejich ekvivalenci pomocí de Morganových zákonů): 1. Všechna prvočísla větší než 2 jsou lichá. Je-li prvočíslo větší než 2, pak je liché.
I) Příklady (převeďte následující věty do formulí PL1 a ověřte jejich ekvivalenci pomocí de Morganových zákonů): 1. Všechna prvočísla větší než 2 jsou lichá. Je-li prvočíslo větší než 2, pak je liché.
Co je to univerzální algebra?
 Co je to univerzální algebra? Při studiu řadu algebraických struktur (grupoidy, pologrupy, grupy, komutativní grupy, okruhy, obory integrity, tělesa, polosvazy, svazy, Booleovy algebry) se často některé
Co je to univerzální algebra? Při studiu řadu algebraických struktur (grupoidy, pologrupy, grupy, komutativní grupy, okruhy, obory integrity, tělesa, polosvazy, svazy, Booleovy algebry) se často některé
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice
 Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Okruh č.9: sémantické metody dokazování v PL1 model formule Tradiční Aristotelova logika kategorický sylogismus subjekt predikátové výroky
 Okruh č.9: sémantické metody dokazování v PL1 Pomocí metody Vennových diagramů a relačních struktur vytváříme grafický model situace, která je úsudkem vyjádřena. Ověřujeme, zda náš graficky znázorněný
Okruh č.9: sémantické metody dokazování v PL1 Pomocí metody Vennových diagramů a relačních struktur vytváříme grafický model situace, která je úsudkem vyjádřena. Ověřujeme, zda náš graficky znázorněný
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Základní pojmy teorie množin Vektorové prostory
 Základní pojmy teorie množin Přednáška MATEMATIKA č. 1 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz 7. 10. 2010 Základní pojmy teorie množin Základní pojmy
Základní pojmy teorie množin Přednáška MATEMATIKA č. 1 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz 7. 10. 2010 Základní pojmy teorie množin Základní pojmy
Logika. 2. Výroková logika. RNDr. Luděk Cienciala, Ph. D.
 Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Pravděpodobnost a statistika
 Pravděpodobnost a statistika 1 Náhodné pokusy a náhodné jevy Činnostem, jejichž výsledek není jednoznačně určen podmínkami, za kterých probíhají, a které jsou (alespoň teoreticky) neomezeně opakovatelné,
Pravděpodobnost a statistika 1 Náhodné pokusy a náhodné jevy Činnostem, jejichž výsledek není jednoznačně určen podmínkami, za kterých probíhají, a které jsou (alespoň teoreticky) neomezeně opakovatelné,
Přednáška 2: Formalizace v jazyce logiky.
 Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Predikátová logika. Z minula: 1. jazyk logiky 1. řádu. 2. term a formule. 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy
 1 Predikátová logika Z minula: 1. jazyk logiky 1. řádu 2. term a formule 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy 5. vázané a volné výskyty proměnných ve formuli 6. otevřené
1 Predikátová logika Z minula: 1. jazyk logiky 1. řádu 2. term a formule 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy 5. vázané a volné výskyty proměnných ve formuli 6. otevřené
