Fyzikální korespondenční seminář UK MFF III. E
|
|
|
- Emilie Černá
- před 8 lety
- Počet zobrazení:
Transkript
1 21. ročník, úloha III. E... zkoumáme pohyb Slunce (8 bodů; průměr 2,88; řešilo 16 studentů) Změřte co nejpřesněji výšku Slunce nad obzorem v pravé poledne a dobu od východu středu slunečního disku do jeho západu. Odvážlivci se mohou pokusit vypočítat teoretickou délku dne a hodnoty srovnat a okomentovat případný nesoulad. Experimentální úlohu navrhl Pavel Brom. Experimentální úloha se zabývá zdánlivým pohybem Slunce po obloze. Zkusme se nejprve zamyslet, jak by se teoreticky mělo Slunce pohybovat, a pak vypočítat časy jeho východu a západu. Budeme k tomu potřebovat zadefinovat několik základních astronomických pojmů. Teorie Ekvatoreální souřadnice jsou polární souřadný systém na nebeské sféře (podobně jako ze měpisná šířka a délka na zemském povrchu) tvořený souřadnicemi rektascenze α a deklinace δ. Množina bodů s nulovou deklinací tvoří tzv. nebeský rovník, což je v podstatě průmět zem ského rovníku na nekonečně vzdálenou nebeskou sféru se středem v centru Země. Rektascenzi měříme podél nebeského rovníku proti směru otáčení Země od tzv. jarního bodu. Udáváme ji buď ve stupních, nebo v hodinách a minutách od 0 do 24 hodin. Deklinace je úhlová vzdá lenost bodu na nebeské sféře od nebeského rovníku, měřená směrem k severnímu světovému pólu kladně a na jih záporně. Ekliptika je velká kružnice na nebeské sféře tvořená množinou bodů do kterých se může v průběhu roku zdánlivě promítat Slunce v důsledku oběhu Země kolem Slunce. Jarní bod je jeden z průsečíků ekliptiky a nebeského rovníku. Slunce se promítá do jarního bodu každý rok na pravé poledne světového času v den jarní rovnodennosti. Podobně jako ekvatoreální souřadnice můžeme zavést i ekliptikální souřadnice: ekliptikální šířku a délku λ. Sklon roviny světového rovníku k rovině ekliptiky budeme značit ε. Místní hvězdný čas t s je v podstatě rektascenze bodu daného průsečíkem průmětu místního poledníku na nebeskou sféru a nebeského rovníku měřená v hodinách a minutách. Můžeme jej vypočítat jako čas uplynulý od 12:00 UT poslední jarní rovnodennosti t s = 24 + doba otočení Země! zeměpisná délka + hodin. 15 Rozdíl rektascenze nějakého bodu na nebeské sféře a místního hvězdného času ϑ = t s α se nazývá hodinový úhel toho bodu. Nakonec azimutální souřadnice jsou také polární souřadnice na nebeské sféře, které jsou však vztaženy na konkrétního pozorovatele, resp. pozorovací stanoviště. Azimut A se určuje podobně jako v zeměpisu, avšak směru s azimutem A = 0 odpovídá směr na jih (oproti zeměpisnému směru na sever). Druhou souřadnicí je pak výška nad místním matematickým - 1 -
2 horizontem h (horizont je přesně vodorovným směrem). severní světový pól severní světový pól ekliptika δ α jarní bod nebeský rovník nebeský rovník Slunce α δ λ jarní bod Obr. 1. Ekvatoreální souřadnice Obr. 2. Ekliptikální souřadnice Na zdánlivý pohyb Slunce po obloze mají vliv především rotace Země kolem své osy jednou za 23 hodin 56 minut a 4,09 vteřiny a oběh Země kolem Slunce jednou za rok (365,2524 stř. slunečního dne). Za jedno otočení Země kolem své osy se Země zároveň posune asi o 1/365 své cesty po oběžné dráze stejným směrem, jako se sama točí, takže na obloze Slunce uteče přibližně o 1. Země se proto musí mezi dvěma východy Slunce (anebo dvěma přechody místním poledníkem na pravé poledne) otočit asi o 361 a sluneční den tak trvá právě 24 hodin. Země obíhá kolem Slunce po elipse s těžištěm soustavy v jejím ohnisku. Rychlost oběhu se v průběhu roku mění čím blíž ke Slunci, tím rychlejší je oběh. Průměrnou úhlovou rychlost oběhu vypočítáme snadno jako ω = 360 /rok. A dále můžeme vypočítat jakýsi přibližný směr ke Slunci, neboli jakousi jeho střední polohu na ekliptice (ekliptikální délku středního Slunce), ze vztahu λ s = ωt r + λ 0, kde T r je čas od posledního průchodu Země periheliem a λ 0 jeho ekliptikální délka v tomto čase (Země v periheliu 3. ledna řekněme o půlnoci, λ 0 = 281,92 ). Díky nerovnoměrnému oběhu Země kolem Slunce skutečné Slunce na obloze střední Slunce někdy předbíhá a někdy za ním zaostává. To má mimo jiné za následek také skutečnost, že pravé poledne nenastává přesně ve 12:00 místního středního slunečního času (pásmový čas s korekcí na zeměpisnou délku oproti po ledníku, na kterém je pásmový čas počítaný). Rozdíl pravého slunečního času a středního slunečního času udává tzv. časová rovnice. Maximální časový rozdíl průchodu středního a sku - 2 -
3 tečného Slunce rovinou místního poledníku je kolem 18 minut to je také maximální chyba vhodně postavených slunečních hodin 1. skutečná Země střední Země M E střední Slunce skutečné Slunce Obr. 3. Pravá (E) a střední (M) anomálie Střední a skutečné Slunce se setkávají v den jarní rovnodennosti o 12:00 UT (λ = 0 ). Vztah mezi ekliptikální délkou středního Slunce a skutečnou ekliptikální délkou λ je dán Keplerovou rovnicí M = E e sin E, kde M = λ s λ 0 π je tzv. střední anomálie, E = λ λ 0 π tzv. pravá anomálie a e je excentricita zemské dráhy. Střední a pravá anomálie jsou směry od Slunce k tzv. střední Zemi (pohybující se rychlostí ω po kruhové dráze kolem Slunce) a skutečné Zemi. Zajímavou vlastností této rovnice je, že ji nelze vyřešit analyticky. I přesto však existuje mnoho způsobů, jak najít E s dostatečnou přesností. Můžeme použít třeba iterativní metodu E 0 = 0, E i+1 = M + e sin E i. Pro i = 10 už dává táto metoda docela přesné výsledky (i přitom můžeme libovolně zvyšovat, dokud E i 1 E i není menší než maximální požadovaná chyba). S pomocí výše uvedených vztahů můžeme v každém okamžiku vypočítat souřadnice Slunce na nebeské sféře. Známe ekliptikální délku λ a ekliptikální šířka je vždy nulová. Zbytek výpočtu je už pouze o transformaci souřadnic z jedné souřadné soustavy do druhé. Nejdříve provedeme transformaci z ekliptikálních do ekvatoreálních souřadnic, pak spočítáme místní hvězdný čas a hodinový úhel a nakonec dostaneme vztahy pro azimut a výšku Slunce pro místního pozo rovatele. Známe-li, v jaké úhlové výšce h o se nachází místní fyzický obzor v bodě, ve kterém Slunce vychází, resp. zapadá, můžeme z těchto vztahů zpětně vyjádřit časy východu a západu Slunce. Veličinu h o už samozřejmě určíme měřením. Tím se vyhneme také všem zbytečným 1) Z dob, kdy si mechanické hodiny mohli dovolit pouze bohatí profesoři a chudí studenti byli odkázáni na sluneční hodiny na náměstí, pochází také společensky zavedená maximální doba čekání na schůzku známá též jako akademická čtvrthodinka
4 komplikacím se zakřivením Země, nadmořskou výškou atp., které někteří z vás v řešení uva žovali. A můžeme také měřit třeba východ Slunce nad střechu sousedova domu o deváté ráno místo skutečného času. z z ekliptika y α λ δ Slunce y jarní bod x x Obr. 4. Konverze z ekvatoreálních do ekliptických souřadnic přes kartézské Podrobně předvedeme pouze prvou transformaci souřadnic. Zbylé se provádějí zcela analo gicky. Chceme transformovat úhly λ a 0 udávající směr na jiné dva úhly α a δ. Všimneme si, že soustava ekvatoreálních souřadnic je oproti ekliptikálním souřadnicím pouze otočená o úhel ε kolem přímky dané spojnicí jarního a podzimního bodu (druhý průsečík rovníku a ekliptiky). Ze směrů nejprve uděláme vektory v kartézském souřadném systému. Přidáme třetí souřad nici r a pro jednoduchost ji položíme rovnou 1. Vektor zadaný trojicí r, λ a ekliptikální šířkou v sobě obsahuje směr ke Slunci. Pak polární souřadnice převedeme na pravoúhlé kartézské. Osa z bude směřovat od pozorovatele k severnímu pólu ekliptiky, z-ová složka vektoru tedy bude r sin 0 = 0. Položíme-li osu x od pozorovatele směrem k jarnímu bodu a osu y kolmo na předchozí dvě, bude transformace zbylých souřadnic snadná: x = cos λ a y = sin λ. Otočíme teď vektor daný kartézskými souřadnicemi x, y a z v rovině (y, z) o úhel ε x = x, y = y cos( ε) z sin( ε), z = y sin( ε) + z cos( ε). Zbývá už jen převést vektor [x, y, z ] zpátky do polárních souřadnic α = arctg y x, - 4 -
5 δ = arctg z p x 2 + y 2. Při konverzi z ekvatoreálních do azimutálních souřadnic budeme potřebovat znát hodinový úhel ϑ a zeměpisnou šířku ϕ pozorovacího stanoviště. Rovina nebeského rovníku je oproti rovině horizontu skloněná o 90 ϕ (anebo pro pozorovatele na některém zeměpisném pólu splývá rovina rovníku s horizontem). Otáčet budeme tentokrát kolem osy směrující od západního k východnímu bodu o zmíněný úhel. Osa otáčení bude totožná s jednou z kartézských souřadnic. Zbylé dvě budou směrovat nejprve k světovému pólu a směrem s hodinovým úhlem 12 hodin v rovině rovníku a po otočení do zenitu a směrem k jižnímu bodu. Po provedení výše zmíněných operací dostaneme následující vztah pro výšku Slunce nad obzorem cos ϑ sin(ϕ 90 ) + sin δ cos(ϕ 90 ) h = arctg p sin 2 ϑ + (cos ϑ cos(ϕ 90 ) sin δ sin(ϕ 90 )). 2 Postup měření S tímto teoretickým podkladem můžeme přejít k samotnému měření. Na měření výšky Slunce nad obzorem jsme ze dvou disků CD, jednoho obalu na CD, pár kapek vteřinového lepidla a malého binokuláru zhotovili jednoduchý přístroj známý už několik století všem ná mořníkům pod jménem sextant 2. dalekohled vodní hladina Obr. 5. Měření výšky Slunce pomocí sextantu Naše verze přístroje byla o něco jednodušší. Ve vektorovém grafickém editoru jsme si na kreslili vlastní stupnici s poněkud realističtějším rozlišením, namísto polopropustného zrcátka jsme použili pouze zrcátko (vystřižené z druhého CD) s poloviční šířkou a obě zrcátka byla přidělaná přímo k otočnému CD se stupnicí, resp. k obalu. Nejtěžší část byla nastavit zrcátka přesně paralelně tak, aby při výchylce stupnice 0 byl pohled dalekohledem umístěným vedle obalu rozdělený na dvě vzájemně neposunuté půlky (odraz v zrcátku a přímý pohled). Po hled do dalekohledu (s objektivovým slunečním filtrem samozřejmě) při správné výchylce na sextantu vypadal tak, že půlka Slunce byla vidět v zrcátku a druhá neposunutá půlka přímo. 2) Podrobný návod, jak takové zařízení postavit, najdete např. na adrese nav/cdsextantproject.htm
6 Normální použití sextantu počítá s využitím viditelné mořské hladiny. Moře v Praze bohužel není, takže jsme museli improvizovat. Vyrobili jsme si klidnou vodní hladinu a pak jsme měřili úhlovou vzdálenost Slunce od jeho odrazu na ní. Výška nad obzorem byla polovina tohoto úhlu. Výchylku jsme mohli pak odečíst na stupnici s vernierem, kterou jsme si vytiskli na dobré laserové tiskárně s přesností kolem 3. Skutečnou chybu měření odhadujeme asi na třetinu šířky slunečního disku, tj. asi na 10. Použití vodní hladiny jako reference vodorovného směru se příliš nehodilo pro měření výšky při východu, resp. západu Slunce. V těchto případech jsme proto měřili výšku Slunce přímo nad rovným horizontem. Obr. 6. Konstrukce sextantu ze dvou CD Výsledky měření Dne jsme z Kolejí 17. listopadu (50 7 s.z.š, v.z.d.) pozorovali východ Slunce nad místní horizont v 7:32 místního pásmového času a západ Slunce v 16:59. Pozorovaná délka dne tedy byla 9 h 27 m. Časy východu a západu Slunce vypočtené výše uvedeným po stupem byly 7:26, resp. 17:07. Rozdíl teoretické a pozorované délky dne byl tudíž asi 14 minut, hlavně díky nerovnému horizontu. V čase, kdy jsme pozorovali východ Slunce, se už mělo. nacházet ve výšce h o = 0,9. To nám dává první odhad na výšku východního horizontu. Tento odhad pro tak malou výšku je však zkreslený. Chybu má na svědomí jev nazývaný atmosférická refrakce. Vypočtené hodnoty totiž nebraly v úvahu zemskou atmosféru. Světlo ne beských těles při své cestě k pozorovateli prochází vrstvou atmosféry s nenulovým a proměnným indexem lomu. Vrstva atmosféry je pro malé h velice tlustá, proto je i refrakce v této oblasti největší. Refrakci můžeme vypočítat např. pomocí tohoto přibližného empirického vzorce (dává výsledek v úhlových vteřinách) 1,02 R = tg h + 10,3 h+5,11 P 1010 hpa T, kde P je tlak, T teplota a h vypočtená výška nad obzorem. Objekt pak pozorujeme ve výšce o hodnotu R větší než vypočtená. V následující tabulce je orientačně uvedená hodnota refrakce - 6 -
7 pro různé pozorované h při normálních podmínkách. h [ ] 0 0, R [ ] ,5 1,5 0,5 Průměr Slunce je asi 32. Jelikož velikost refrakce v nulové výšce nad obzorem je větší než tato hodnota, můžeme na velmi rovném horizontu pozorovat východ celého Slunce nad horizont dříve, než je jednoduše předpovězený čas. Sluneční den by takto měl trvat o pár minut déle. Jak je však vidět z pozorování, je tato odchylka prakticky zanedbatelná vůči ostatním vlivům. Dne jsme ze stejného pozorovacího stanoviště provedli následující sérii měření výšky Slunce nad místním horizontem. t 7:17 7:20 7:24 7:26 7:32 7:35 7:40 7:46 h [ ] 0 0,25 1 1,5 2 2,5 3 3,7 Použijeme-li první odhad výšky horizontu na určení skutečné výšky nad obzorem (h obs = h + h o) a porovnáme pozorovanou a vypočtenou výšku, najdeme závislost vynesenou v grafu h obs h t refrakce 0.6 h [ ] h t [ ] Obr. 7. Porovnání rozdílu pozorované a vypočtené výšky Slunce s refrakcí Jelikož pozorované rozdíly jsou příliš malé v porovnání s chybou, nedají se z těchto pozoro vání vyvodit jednoznačné závěry. Avšak posloupnost hodnot dává tušit pokles rozdílu teoretické a pozorované výšky Slunce, který odpovídá průběhu refrakce. Měření výšky Slunce kolem poledne počasí v době psaní tohoto textu příliš nepřálo. Čas, kdy výška Slunce dosahuje maxima, teoreticky spočítáme tak, že výšku h(t) derivujeme podle času a položíme rovnou nule. Výšku Slunce nad obzorem ale můžeme jednodušeji určit podle přibližného vzorce h max = 90 ϕ + δ, (1) - 7 -
8 kde δ je deklinace Slunce v daný den a ϕ zeměpisná šířka. Uskutečnili jsme pouze jedno krátké měření dne ve 12:20. Vypočtený čas kulmi nace pro dané datum byl t max = 12:13 SEČ. Naměřená výška h = ±10 byla ve výborné shodě s vypočtenou h t = Refrakce ve výškách kolem 30 je už hluboko pod chybou měření a výška Slunce se kolem poledne mění velice pomalu, takže na těch pár minutách také nesešlo. Poznámky k došlým řešením Závěrem ještě pár slov k došlým řešením. Co se teoretické části týče, jen málo z vás se zamyslelo nad tím, jak to s pohybem Slunce po obloze vlastně je. Světlou výjimkou byla např. Zuzana Dočekalová. Tereza Jeřábková a Veronika Paštyková se pokusily navrhnout jed nodušší metodu na výpočet délky dne. To lze učinit, pokud budeme pokládat deklinaci Slunce v průběhu dne za konstantní a zastavíme Zemi na její dráze v jednom bodě. Odchylka oproti přesnému výpočtu by byla při správném provedení docela malá. Celkem zdařilá řešení došla také od Karla Koláře či Petra Vanyu. Mnoho řešitelů spoléhalo na udávané časy východu či západu Slunce z předpovědi počasí. Často však bez toho, aby si uvědomili, jak tento čas opravit na geografickou polohu svého sta noviště. Vzhledem k tomu, že tyto časy jsou v ČR nejčastěji udávané pro polohu Prahy, mohou se místní časy lišit až o téměř 20 minut (na stejné zeměpisné šířce vyjde Slunce o 4 minuty dřív na každý stupeň délky směrem na východ). Už jednoduché použití vzorce (1) pro výpočet maximální úhlové výšky Slunce bylo hodnoceno 2 body. Naopak neuvedení základních údajů, jako jsou poloha pozorovacího stanoviště, či dokonce ani datum pozorování, se odrazilo na bodovém počtu negativně. V praktické části této úlohy řešitelé také projevili až překvapivě málo fantazie. Téměř výlučně používané metody na měření výšky Slunce byly měření délky stínu anebo ukazovátko přidělané na úhloměru. I při nejlepší vůli není přesnost všech popsaných pokusů lepší než asi jeden až dva stupně 3. To je ovšem na většinu praktických aplikací žalostně málo. Asi nejjednodušší možné měření by bylo měření částmi ruky. Když člověk natáhne ruku před sebe a roztáhne prsty, tak vzdálenost od konce palce po konec malíčku je Šířka sevřené pěsti je asi 10 a šířka palce přibližně 2. Změřit úhlovou vzdálenost Slunce od obzoru touto metodou by možná bylo v některých případech přesnější (než došlé výsledky). Peter Greškovič grepe@fykos.mff.cuni.cz Fyzikální korespondenční seminář je organizován studenty UK MFF. Je zastřešen Oddělením pro vnější vztahy a propagaci UK MFF a podporován Ústavem teoretické fyziky UK MFF, jeho zaměstnanci a Jednotou českých matematiků a fyziků. 3) S tím také souvisí jedna často opakovaná nepřesnost když je chyba 2, neudáváme výsledek na tři desetinná místa! - 8 -
Obr. 4 Změna deklinace a vzdálenosti Země od Slunce v průběhu roku
 4 ZÁKLADY SFÉRICKÉ ASTRONOMIE K posouzení proslunění budovy nebo oslunění pozemku je vždy nutné stanovit polohu slunce na obloze. K tomu slouží vztahy sférické astronomie slunce. Pro sledování změn slunečního
4 ZÁKLADY SFÉRICKÉ ASTRONOMIE K posouzení proslunění budovy nebo oslunění pozemku je vždy nutné stanovit polohu slunce na obloze. K tomu slouží vztahy sférické astronomie slunce. Pro sledování změn slunečního
Filip Hroch. Astronomické pozorování. Filip Hroch. Výpočet polohy planety. Drahové elementy. Soustava souřadnic. Pohyb po elipse
 ÚTFA,Přírodovědecká fakulta MU, Brno, CZ březen 2005 březnového tématu Březnové téma je věnováno klasické sférické astronomii. Úkol se skládá z měření, výpočtu a porovnání výsledků získaných v obou částech.
ÚTFA,Přírodovědecká fakulta MU, Brno, CZ březen 2005 březnového tématu Březnové téma je věnováno klasické sférické astronomii. Úkol se skládá z měření, výpočtu a porovnání výsledků získaných v obou částech.
Sférická trigonometrie v matematické geografii a astronomii
 Sférická trigonometrie v matematické geografii a astronomii Mgr. Hana Lakomá, Ph.D., Mgr. Veronika Douchová 00 Tento učební materiál vznikl v rámci grantu FRVŠ F1 066. 1 Základní pojmy sférické trigonometrie
Sférická trigonometrie v matematické geografii a astronomii Mgr. Hana Lakomá, Ph.D., Mgr. Veronika Douchová 00 Tento učební materiál vznikl v rámci grantu FRVŠ F1 066. 1 Základní pojmy sférické trigonometrie
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Geodetická astronomie 3/6 Aplikace keplerovského pohybu
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Geodetická astronomie 3/6 Aplikace keplerovského pohybu
Seriál VII.IV Astronomické souřadnice
 Výfučtení: Astronomické souřadnice Představme si naši oblíbenou hvězdu, kterou chceme ukázat našemu kamarádovi. Kamarád je ale zrovna na dovolené, a tak mu ji nemůžeme ukázat přímo. Rádi bychom mu tedy
Výfučtení: Astronomické souřadnice Představme si naši oblíbenou hvězdu, kterou chceme ukázat našemu kamarádovi. Kamarád je ale zrovna na dovolené, a tak mu ji nemůžeme ukázat přímo. Rádi bychom mu tedy
Astronomická pozorování
 KLASICKÁ ASTRONOMIE Astronomická pozorování Základní úloha při pozorování nějakého děje, zejména pohybu těles je stanovení jeho polohy (rychlosti) v daném okamžiku Astronomie a poziční astronomie Souřadnicové
KLASICKÁ ASTRONOMIE Astronomická pozorování Základní úloha při pozorování nějakého děje, zejména pohybu těles je stanovení jeho polohy (rychlosti) v daném okamžiku Astronomie a poziční astronomie Souřadnicové
Astronomická refrakce
 Astronomická refrakce Co mají společného zamilované páry, které v láskyplném objetí nedočkavě čekají na západ slunce a parta podivně vyhlížejících mladých lidí, kteří s teodolitem pobíhají po parku a hledají
Astronomická refrakce Co mají společného zamilované páry, které v láskyplném objetí nedočkavě čekají na západ slunce a parta podivně vyhlížejících mladých lidí, kteří s teodolitem pobíhají po parku a hledají
Vzdálenosti ve sluneční soustavě: paralaxy a Keplerovy zákony
 Vzdálenosti ve sluneční soustavě: paralaxy a Keplerovy zákony Astronomové při sledování oblohy zaznamenávají především úhly a pozorují něco, co se nazývá nebeská sféra. Nicméně, hvězdy nejsou od Země vždy
Vzdálenosti ve sluneční soustavě: paralaxy a Keplerovy zákony Astronomové při sledování oblohy zaznamenávají především úhly a pozorují něco, co se nazývá nebeská sféra. Nicméně, hvězdy nejsou od Země vždy
Základní jednotky v astronomii
 v01.00 Základní jednotky v astronomii Ing. Neliba Vlastimil AK Kladno 2005 Délka - l Slouží pro určení vzdáleností ve vesmíru Základní jednotkou je metr metr je definován jako délka, jež urazí světlo ve
v01.00 Základní jednotky v astronomii Ing. Neliba Vlastimil AK Kladno 2005 Délka - l Slouží pro určení vzdáleností ve vesmíru Základní jednotkou je metr metr je definován jako délka, jež urazí světlo ve
Vzdálenosti a východ Slunce
 Vzdálenosti a východ Slunce Zdeněk Halas KDM MFF UK, 2011 Aplikace matem. pro učitele Zdeněk Halas (KDM MFF UK, 2011) Vzdálenosti a východ Slunce Aplikace matem. pro učitele 1 / 8 Osnova Zdeněk Halas (KDM
Vzdálenosti a východ Slunce Zdeněk Halas KDM MFF UK, 2011 Aplikace matem. pro učitele Zdeněk Halas (KDM MFF UK, 2011) Vzdálenosti a východ Slunce Aplikace matem. pro učitele 1 / 8 Osnova Zdeněk Halas (KDM
základy astronomie 1 praktikum 3. Astronomické souřadnice
 základy astronomie 1 praktikum 3. Astronomické souřadnice 1 Úvod Znalost a správné používání astronomických souřadnic patří k základní výbavě astronoma. Bez nich se prostě neobejdete. Nejde ale jen o znalost
základy astronomie 1 praktikum 3. Astronomické souřadnice 1 Úvod Znalost a správné používání astronomických souřadnic patří k základní výbavě astronoma. Bez nich se prostě neobejdete. Nejde ale jen o znalost
1.2 Sluneční hodiny. 100+1 příklad z techniky prostředí
 1.2 Sluneční hodiny Sluneční hodiny udávají pravý sluneční čas, který se od našeho běžného času liší. Zejména tím, že pohyb Slunce během roku je nepravidelný (to postihuje časová rovnice) a také tím, že
1.2 Sluneční hodiny Sluneční hodiny udávají pravý sluneční čas, který se od našeho běžného času liší. Zejména tím, že pohyb Slunce během roku je nepravidelný (to postihuje časová rovnice) a také tím, že
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
Měření vzdáleností, určování azimutu, práce s buzolou.
 Měření vzdáleností, určování azimutu, práce s buzolou. Měření vzdáleností Odhadem Vzdálenost lze odhadnout pomocí rozlišení detailů na pozorovaných objektech. Přesnost odhadu závisí na viditelnosti předmětu
Měření vzdáleností, určování azimutu, práce s buzolou. Měření vzdáleností Odhadem Vzdálenost lze odhadnout pomocí rozlišení detailů na pozorovaných objektech. Přesnost odhadu závisí na viditelnosti předmětu
MAPY VELKÉHO A STŘEDNÍHO MĚŘÍTKA
 MAPA A GLÓBUS Tento nadpis bude stejně velký jako nadpis Planeta Země. Můžeš ho napsat přes půl nebo klidně i přes celou stranu. GLÓBUS Glóbus - zmenšený model Země - nezkresluje tvary pevnin a oceánů
MAPA A GLÓBUS Tento nadpis bude stejně velký jako nadpis Planeta Země. Můžeš ho napsat přes půl nebo klidně i přes celou stranu. GLÓBUS Glóbus - zmenšený model Země - nezkresluje tvary pevnin a oceánů
Astronavigace. Zdeněk Halas KDM MFF UK, Aplikace matem. pro učitele
 Základní princip Zdeněk Halas KDM MFF UK, 2011 Aplikace matem. pro učitele Zdeněk Halas (KDM MFF UK, 2011) Aplikace matem. pro učitele 1 / 13 Tradiční metody Tradiční navigační metody byly v nedávné době
Základní princip Zdeněk Halas KDM MFF UK, 2011 Aplikace matem. pro učitele Zdeněk Halas (KDM MFF UK, 2011) Aplikace matem. pro učitele 1 / 13 Tradiční metody Tradiční navigační metody byly v nedávné době
Soutěžní úlohy části A a B (12. 6. 2012)
 Soutěžní úlohy části A a B (1. 6. 01) Pokyny k úlohám: Řešení úlohy musí obsahovat rozbor problému (náčrtek dané situace), základní vztahy (vzorce) použité v řešení a přesný postup (stačí heslovitě). Nestačí
Soutěžní úlohy části A a B (1. 6. 01) Pokyny k úlohám: Řešení úlohy musí obsahovat rozbor problému (náčrtek dané situace), základní vztahy (vzorce) použité v řešení a přesný postup (stačí heslovitě). Nestačí
ANALYTICKÁ GEOMETRIE V ROVINĚ
 ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
Interpretace pozorování planet na obloze a hvězdné obloze
 Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
5a. Globální referenční systémy Parametry orientace Země (EOP) Aleš Bezděk
 5a. Globální referenční systémy Parametry orientace Země (EOP) Aleš Bezděk Teoretická geodézie 4 FSV ČVUT 2017/2018 LS 1 Celková orientace zemského tělesa, tj. precese-nutace+pohyb pólu+vlastní rotace,
5a. Globální referenční systémy Parametry orientace Země (EOP) Aleš Bezděk Teoretická geodézie 4 FSV ČVUT 2017/2018 LS 1 Celková orientace zemského tělesa, tj. precese-nutace+pohyb pólu+vlastní rotace,
pohyb hvězdy ve vesmírném prostoru vlastní pohyb hvězdy pohyb, změna, souřadné soustavy vzhledem ke stálicím precese,
 Změny souřadnic nebeských těles pohyb hvězdy ve vesmírném prostoru vlastní pohyb hvězdy vlastní pohyb max. 10 /rok, v průměru 0.013 /rok pohyb, změna, souřadné soustavy vzhledem ke stálicím precese, nutace,
Změny souřadnic nebeských těles pohyb hvězdy ve vesmírném prostoru vlastní pohyb hvězdy vlastní pohyb max. 10 /rok, v průměru 0.013 /rok pohyb, změna, souřadné soustavy vzhledem ke stálicím precese, nutace,
Seriál II.II Vektory. Výfučtení: Vektory
 Výfučtení: Vektory Abychom zcela vyjádřili veličiny jako hmotnost, teplo či náboj, stačí nám k tomu jediné číslo (s příslušnou jednotkou). Říkáme jim skalární veličiny. Běžně se však setkáváme i s veličinami,
Výfučtení: Vektory Abychom zcela vyjádřili veličiny jako hmotnost, teplo či náboj, stačí nám k tomu jediné číslo (s příslušnou jednotkou). Říkáme jim skalární veličiny. Běžně se však setkáváme i s veličinami,
Interpretace pozorování planet na obloze a hvězdné obloze
 Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
Interpretace pozorování planet na obloze a hvězdné obloze
 Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Kosmická geodézie 1/99 Výpočet zeměpisné šířky z měřených
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Kosmická geodézie 1/99 Výpočet zeměpisné šířky z měřených
Orientace v terénu bez mapy
 Písemná příprava na zaměstnání Terén Orientace v terénu bez mapy Zpracoval: por. Tomáš Diblík Pracoviště: OVIÚ Osnova přednášky Určování světových stran Určování směrů Určování č vzdáleností Určení č polohy
Písemná příprava na zaměstnání Terén Orientace v terénu bez mapy Zpracoval: por. Tomáš Diblík Pracoviště: OVIÚ Osnova přednášky Určování světových stran Určování směrů Určování č vzdáleností Určení č polohy
1.1 Oslunění vnitřního prostoru
 1.1 Oslunění vnitřního prostoru Úloha 1.1.1 Zadání V rodném městě X slavného fyzika Y má být zřízeno muzeum, připomínající jeho dílo. Na určeném místě v galerii bude umístěna deska s jeho obrazem. V den
1.1 Oslunění vnitřního prostoru Úloha 1.1.1 Zadání V rodném městě X slavného fyzika Y má být zřízeno muzeum, připomínající jeho dílo. Na určeném místě v galerii bude umístěna deska s jeho obrazem. V den
Korekce souřadnic. 2s [ rad] R. malé změny souřadnic, které je nutno uvažovat při stanovení polohy astronomických objektů. výška pozorovatele
![Korekce souřadnic. 2s [ rad] R. malé změny souřadnic, které je nutno uvažovat při stanovení polohy astronomických objektů. výška pozorovatele Korekce souřadnic. 2s [ rad] R. malé změny souřadnic, které je nutno uvažovat při stanovení polohy astronomických objektů. výška pozorovatele](/thumbs/51/28250241.jpg) OPT/AST L07 Korekce souřadnic malé změny souřadnic, které je nutno uvažovat při stanovení polohy astronomických objektů výška pozorovatele konečný poloměr země R výška h objektu závisí na výšce s stanoviště
OPT/AST L07 Korekce souřadnic malé změny souřadnic, které je nutno uvažovat při stanovení polohy astronomických objektů výška pozorovatele konečný poloměr země R výška h objektu závisí na výšce s stanoviště
Eudoxovy modely. Apollónios (225 př. Kr.) ukázal, že oba přístupy jsou při aplikaci na Slunce ekvivalentní. Deferent, epicykl a excentr
 Počátek goniometrie Eudoxovy modely Deferent, epicykl a excentr Apollónios (225 př Kr) ukázal, že oba přístupy jsou při aplikaci na Slunce ekvivalentní Zdeněk Halas (KDM MFF UK) Goniometrie v antice 25
Počátek goniometrie Eudoxovy modely Deferent, epicykl a excentr Apollónios (225 př Kr) ukázal, že oba přístupy jsou při aplikaci na Slunce ekvivalentní Zdeněk Halas (KDM MFF UK) Goniometrie v antice 25
Měření tíhového zrychlení reverzním kyvadlem
 43 Kapitola 7 Měření tíhového zrychlení reverzním kyvadlem 7.1 Úvod Tíhové zrychlení je zrychlení volného pádu ve vakuu. Závisí na zeměpisné šířce a nadmořské výšce. Jako normální tíhové zrychlení g n
43 Kapitola 7 Měření tíhového zrychlení reverzním kyvadlem 7.1 Úvod Tíhové zrychlení je zrychlení volného pádu ve vakuu. Závisí na zeměpisné šířce a nadmořské výšce. Jako normální tíhové zrychlení g n
b) Maximální velikost zrychlení automobilu, nemají-li kola prokluzovat, je a = f g. Automobil se bude rozjíždět po dobu t = v 0 fg = mfgv 0
 Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Obsah. 1 Sférická astronomie Základní problémy sférické astronomie... 8
 Obsah 1 Sférická astronomie 3 1.1 Základní pojmy sférické astronomie................. 3 1.2 Souřadnicové soustavy........................ 5 1.2.1 Azimutální souřadnicový systém............... 6 1.2.2 Ekvatoreální
Obsah 1 Sférická astronomie 3 1.1 Základní pojmy sférické astronomie................. 3 1.2 Souřadnicové soustavy........................ 5 1.2.1 Azimutální souřadnicový systém............... 6 1.2.2 Ekvatoreální
Rovinné přetvoření. Posunutí (translace) TEORIE K M2A+ULA
 Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Rychlost, zrychlení, tíhové zrychlení
 Úloha č. 3 Rychlost, zrychlení, tíhové zrychlení Úkoly měření: 1. Sestavte nakloněnou rovinu a změřte její sklon.. Změřte závislost polohy tělesa na čase a stanovte jeho rychlost a zrychlení. 3. Určete
Úloha č. 3 Rychlost, zrychlení, tíhové zrychlení Úkoly měření: 1. Sestavte nakloněnou rovinu a změřte její sklon.. Změřte závislost polohy tělesa na čase a stanovte jeho rychlost a zrychlení. 3. Určete
X = A + tu. Obr x = a 1 + tu 1 y = a 2 + tu 2, t R, y = kx + q, k, q R (6.1)
 .6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
.6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 2/3 GPS - Výpočet drah družic školní rok
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 2/3 GPS - Výpočet drah družic školní rok
Identifikace práce. B III: (max. 18b)
 vyplňuje žák čitelně tiskacím písmem. Identifikace práce Žák identifikátor / jméno příjmení rok narození* (*nehodící se škrtni, identifikační číslo obdržíš po vyřešení části online) Pokud jsi část řešil(a)
vyplňuje žák čitelně tiskacím písmem. Identifikace práce Žák identifikátor / jméno příjmení rok narození* (*nehodící se škrtni, identifikační číslo obdržíš po vyřešení části online) Pokud jsi část řešil(a)
Výpočet vzdálenosti Země Slunce pozorováním přechodu Venuše před Sluncem
 Výpočet vzdálenosti Země Slunce pozorováním přechodu Venuše před Sluncem Podle mateiálu ESO přeložil Rostislav Halaš Úkol: Změřit vzdálenost Země Slunce (tzv. astronomickou jednotku AU) pozorováním přechodu
Výpočet vzdálenosti Země Slunce pozorováním přechodu Venuše před Sluncem Podle mateiálu ESO přeložil Rostislav Halaš Úkol: Změřit vzdálenost Země Slunce (tzv. astronomickou jednotku AU) pozorováním přechodu
Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice
 Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice Kartografie přednáška 5 Referenční plochy souřadnicových soustav slouží k lokalizaci bodů, objektů
Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice Kartografie přednáška 5 Referenční plochy souřadnicových soustav slouží k lokalizaci bodů, objektů
4. Matematická kartografie
 4. Země má nepravidelný tvar, který je dán půsoením mnoha sil, zejména gravitační a odstředivé (vzhledem k rotaci Země). Odstředivá síla způsouje, že tvar Země je zploštělý, tj. zemský rovník je dále od
4. Země má nepravidelný tvar, který je dán půsoením mnoha sil, zejména gravitační a odstředivé (vzhledem k rotaci Země). Odstředivá síla způsouje, že tvar Země je zploštělý, tj. zemský rovník je dále od
REKONSTRUKCE ASTROLÁBU POMOCÍ STEREOGRAFICKÉ PROJEKCE
 REKONTRUKCE ATROLÁBU POMOCÍ TEREOGRAFICKÉ PROJEKCE Václav Jára 1 1 tereografická projekce a její vlastnosti tereografická projekce kulové plochy je středové promítání z bodu této kulové plochy do tečné
REKONTRUKCE ATROLÁBU POMOCÍ TEREOGRAFICKÉ PROJEKCE Václav Jára 1 1 tereografická projekce a její vlastnosti tereografická projekce kulové plochy je středové promítání z bodu této kulové plochy do tečné
PLANETA ZEMĚ A JEJÍ POHYBY. Maturitní otázka č. 1
 PLANETA ZEMĚ A JEJÍ POHYBY Maturitní otázka č. 1 TVAR ZEMĚ Geoid = skutečný tvar Země Nelze vyjádřit matematicky Rotační elipsoid rovníkový poloměr = 6 378 km vzdálenost od středu Země k pólu = 6 358 km
PLANETA ZEMĚ A JEJÍ POHYBY Maturitní otázka č. 1 TVAR ZEMĚ Geoid = skutečný tvar Země Nelze vyjádřit matematicky Rotační elipsoid rovníkový poloměr = 6 378 km vzdálenost od středu Země k pólu = 6 358 km
Základní škola, Ostrava-Poruba, I. Sekaniny 1804, příspěvková organizace
 Základní škola, Ostrava-Poruba, I. Sekaniny 1804, příspěvková organizace Název projektu Zkvalitnění vzdělávání na ZŠ I.Sekaniny - Škola pro 21. století Registrační číslo projektu CZ.1.07/1.4.00/21.1475
Základní škola, Ostrava-Poruba, I. Sekaniny 1804, příspěvková organizace Název projektu Zkvalitnění vzdělávání na ZŠ I.Sekaniny - Škola pro 21. století Registrační číslo projektu CZ.1.07/1.4.00/21.1475
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 4/3 GPS - oskulační elementy dráhy družice
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 1 4/3 GPS - oskulační elementy dráhy družice
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C)
 VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
Odchylka ekliptiky od roviny Galaxie
 Jiří Kapr 1, Jakub Fuis 2, Tomáš Bárta 3 1 Gymnázium Plasy, Plasy 2 Gymnázium Botičská, Praha 3 Gymnázium Nad Štolou, Praha Týden Vědy, 2010 Jiří Kapr 1, Jakub Fuis 2, Tomáš Bárta 3 1 Gymnázium Plasy,
Jiří Kapr 1, Jakub Fuis 2, Tomáš Bárta 3 1 Gymnázium Plasy, Plasy 2 Gymnázium Botičská, Praha 3 Gymnázium Nad Štolou, Praha Týden Vědy, 2010 Jiří Kapr 1, Jakub Fuis 2, Tomáš Bárta 3 1 Gymnázium Plasy,
Planeta Země. Pohyby Země a jejich důsledky
 Planeta Země Pohyby Země a jejich důsledky Pohyby Země Planeta Země je jednou z osmi planet Sluneční soustavy. Vzhledem k okolnímu vesmíru je v neustálém pohybu. Úkol 1: Které pohyby naše planeta ve Sluneční
Planeta Země Pohyby Země a jejich důsledky Pohyby Země Planeta Země je jednou z osmi planet Sluneční soustavy. Vzhledem k okolnímu vesmíru je v neustálém pohybu. Úkol 1: Které pohyby naše planeta ve Sluneční
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD. 9, m s.
 TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
Měření tíhového zrychlení matematickým a reverzním kyvadlem
 Úloha č. 3 Měření tíhového zrychlení matematickým a reverzním kyvadlem Úkoly měření: 1. Určete tíhové zrychlení pomocí reverzního a matematického kyvadla. Pro stanovení tíhového zrychlení, viz bod 1, měřte
Úloha č. 3 Měření tíhového zrychlení matematickým a reverzním kyvadlem Úkoly měření: 1. Určete tíhové zrychlení pomocí reverzního a matematického kyvadla. Pro stanovení tíhového zrychlení, viz bod 1, měřte
ČAS. Anotace: Materiál je určen k výuce zeměpisu v 6. ročníku základní školy. Seznamuje žáky s pohyby Země, počítáním času a časovými pásmy.
 ČAS Anotace: Materiál je určen k výuce zeměpisu v 6. ročníku základní školy. Seznamuje žáky s pohyby Země, počítáním času a časovými pásmy. Pohyby Země v minulosti si lidé mysleli, že je Země centrem Sluneční
ČAS Anotace: Materiál je určen k výuce zeměpisu v 6. ročníku základní školy. Seznamuje žáky s pohyby Země, počítáním času a časovými pásmy. Pohyby Země v minulosti si lidé mysleli, že je Země centrem Sluneční
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 6: Geometrická optika Datum měření: 8. 4. 2016 Doba vypracovávání: 10 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
Fyzikální praktikum FJFI ČVUT v Praze Úloha 6: Geometrická optika Datum měření: 8. 4. 2016 Doba vypracovávání: 10 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klasifikace: 1 Zadání 1. DÚ: V přípravě
CZECH REPUBLIC. Pravidla soutěže týmů
 Pravidla soutěže týmů 1. Soutěže týmů se mohou účastnit týmy tří a více studentů. 2. Tým dostane sadu 5 úloh, na jejichž řešení má 60 minut. 3. O výsledku týmů rozhoduje celkový součet bodů za všech 5
Pravidla soutěže týmů 1. Soutěže týmů se mohou účastnit týmy tří a více studentů. 2. Tým dostane sadu 5 úloh, na jejichž řešení má 60 minut. 3. O výsledku týmů rozhoduje celkový součet bodů za všech 5
Praktikum z astronomie 0. Měření refrakce. Zadání
 20. února 2007 Praktikum z astronomie 0 Zadání Astronomická refrakce Úkolem je určit polohu zapadajícího nebo vycházejícího nebeského tělesa měřením a výpočtem. str. 48 Teodolitem změřte polohu známého
20. února 2007 Praktikum z astronomie 0 Zadání Astronomická refrakce Úkolem je určit polohu zapadajícího nebo vycházejícího nebeského tělesa měřením a výpočtem. str. 48 Teodolitem změřte polohu známého
Matematika 1 MA1. 1 Analytická geometrie v prostoru - základní pojmy. 4 Vzdálenosti. 12. přednáška ( ) Matematika 1 1 / 32
 Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1
 SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1 (Souřadnicové výpočty 4, Orientace osnovy vodorovných směrů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec
SYLABUS PŘEDNÁŠKY 10 Z GEODÉZIE 1 (Souřadnicové výpočty 4, Orientace osnovy vodorovných směrů) 1. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec
37. PARABOLA V ANALYTICKÉ GEOMETRII
 37.. Napiš rovnici paraboly, která má osu rovnoběžnou s osou y a prochází body A 0; 60, B 4; 8, C 8;36. 0m p60n 4m p8n 8m p36n m p pn 0 6 8 6 mm p pn 64 6 7 3 mm p pn 6 8m64 p 3 64 6m9 p Je-li osa rovnoběžná
37.. Napiš rovnici paraboly, která má osu rovnoběžnou s osou y a prochází body A 0; 60, B 4; 8, C 8;36. 0m p60n 4m p8n 8m p36n m p pn 0 6 8 6 mm p pn 64 6 7 3 mm p pn 6 8m64 p 3 64 6m9 p Je-li osa rovnoběžná
ZÁKLADY FYZIKÁLNÍCH MĚŘENÍ FJFI ČVUT V PRAZE. Úloha 5: Měření tíhového zrychlení
 ZÁKLADY FYZIKÁLNÍCH MĚŘENÍ FJFI ČVUT V PRAZE Datum měření: číslo skupiny: Spolupracovali: 1 Úvod 1.1 Pracovní úkoly [1] Úloha 5: Měření tíhového zrychlení Jméno: Ročník, kruh: Klasifikace: 1. V domácí
ZÁKLADY FYZIKÁLNÍCH MĚŘENÍ FJFI ČVUT V PRAZE Datum měření: číslo skupiny: Spolupracovali: 1 Úvod 1.1 Pracovní úkoly [1] Úloha 5: Měření tíhového zrychlení Jméno: Ročník, kruh: Klasifikace: 1. V domácí
Definice Tečna paraboly je přímka, která má s parabolou jediný společný bod,
 5.4 Parabola Parabola je křivka, která vznikne řezem rotační kuželové plochy rovinou, jestliže odchylka roviny řezu od osy kuželové plochy je stejná jako odchylka povrchových přímek plochy a rovina řezu
5.4 Parabola Parabola je křivka, která vznikne řezem rotační kuželové plochy rovinou, jestliže odchylka roviny řezu od osy kuželové plochy je stejná jako odchylka povrchových přímek plochy a rovina řezu
Měření teploty a tlaku. Tematický celek: Termodynamika. Úkol:
 Název: Měření teploty a tlaku. Tematický celek: Termodynamika. Úkol: 1. Zopakujte si, co víte o teplotě a jejím měření. 2. Zopakujte si, co víte o atmosférickém tlaku. 3. Navrhněte robota, který bude po
Název: Měření teploty a tlaku. Tematický celek: Termodynamika. Úkol: 1. Zopakujte si, co víte o teplotě a jejím měření. 2. Zopakujte si, co víte o atmosférickém tlaku. 3. Navrhněte robota, který bude po
2. Kinematika bodu a tělesa
 2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
Hvězdářský zeměpis Obloha a hvězdná obloha
 Hvězdářský zeměpis Obloha a hvězdná obloha směr = polopřímka, spojující oči, kterými sledujeme svět kolem sebe, s daným objektem obzor = krajina, kterou obzíráme, v našem dohledu (budovy, stromy, kopce)
Hvězdářský zeměpis Obloha a hvězdná obloha směr = polopřímka, spojující oči, kterými sledujeme svět kolem sebe, s daným objektem obzor = krajina, kterou obzíráme, v našem dohledu (budovy, stromy, kopce)
A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz
![A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz](/thumbs/47/23721460.jpg) 1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
základy astronomie 1 praktikum 6. Pozorování dalekohledem
 základy astronomie 1 praktikum 6. Pozorování dalekohledem 1 Úvod Oko bylo základním přístrojem astronoma, základním detektorem světla po dlouhá staletí ba tisíciletí, a zůstalo jím dokonce i tři století
základy astronomie 1 praktikum 6. Pozorování dalekohledem 1 Úvod Oko bylo základním přístrojem astronoma, základním detektorem světla po dlouhá staletí ba tisíciletí, a zůstalo jím dokonce i tři století
Měření horizontálních a vertikálních úhlů Úhloměrné přístroje a jejich konstrukce Horizontace a centrace Přesnost a chyby v měření úhlů.
 Měření horizontálních a vertikálních úhlů Úhloměrné přístroje a jejich konstrukce Horizontace a centrace Přesnost a chyby v měření úhlů Kartografie přednáška 10 Měření úhlů prostorovou polohu směru, vycházejícího
Měření horizontálních a vertikálních úhlů Úhloměrné přístroje a jejich konstrukce Horizontace a centrace Přesnost a chyby v měření úhlů Kartografie přednáška 10 Měření úhlů prostorovou polohu směru, vycházejícího
Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky
 Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky Úkol : 1. Určete mřížkovou konstantu d optické mřížky a porovnejte s hodnotou udávanou výrobcem. 2. Určete vlnovou délku λ jednotlivých
Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky Úkol : 1. Určete mřížkovou konstantu d optické mřížky a porovnejte s hodnotou udávanou výrobcem. 2. Určete vlnovou délku λ jednotlivých
ČAS, KALENDÁŘ A ASTRONOMIE
 ČAS, KALENDÁŘ A ASTRONOMIE Čas Založen na základě praktických zkušeností s následností dějů Je vzájemně vázán s existencí hmoty a prostoru, umožňuje rozhodnout o následnosti dějů, neexistuje možnost zpětné
ČAS, KALENDÁŘ A ASTRONOMIE Čas Založen na základě praktických zkušeností s následností dějů Je vzájemně vázán s existencí hmoty a prostoru, umožňuje rozhodnout o následnosti dějů, neexistuje možnost zpětné
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Kosmická geodézie 5/ Určování astronomických zeměpisných
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Kosmická geodézie 5/ Určování astronomických zeměpisných
Rozvoj vzdělávání žáků karvinských základních škol v oblasti cizích jazyků Registrační číslo projektu: CZ.1.07/1.1.07/02.0162
 ZŠ Určeno pro Sekce Předmět Rozvoj vzdělávání žáků karvinských základních škol v oblasti cizích jazyků Registrační číslo projektu: CZ.1.07/1.1.07/02.0162 Téma / kapitola ZŠ Dělnická žáky 6. a 7. ročníků
ZŠ Určeno pro Sekce Předmět Rozvoj vzdělávání žáků karvinských základních škol v oblasti cizích jazyků Registrační číslo projektu: CZ.1.07/1.1.07/02.0162 Téma / kapitola ZŠ Dělnická žáky 6. a 7. ročníků
Astronomie jednoduchými prostředky. Miroslav Jagelka
 Astronomie jednoduchými prostředky Miroslav Jagelka 20.10.2016 Když si vystačíte s kameny... Stonehenge (1600-3100 BC) Pyramidy v Gize (2550 BC) El Castilllo (1000 BC) ... nebo s hůlkou Gnomón (5000 BC)
Astronomie jednoduchými prostředky Miroslav Jagelka 20.10.2016 Když si vystačíte s kameny... Stonehenge (1600-3100 BC) Pyramidy v Gize (2550 BC) El Castilllo (1000 BC) ... nebo s hůlkou Gnomón (5000 BC)
Zavedeme-li souřadnicový systém {0, x, y, z}, pak můžeme křivku definovat pomocí vektorové funkce.
 KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
STANOVENÍ TÍHOVÉHO ZRYCHLENÍ REVERZNÍM KYVADLEM A STUDIUM GRAVITAČNÍHO POLE
 DANIEL TUREČEK 2005 / 2006 1. 412 5. 14.3.2006 28.3.2006 5. STANOVENÍ TÍHOVÉHO ZRYCHLENÍ REVERZNÍM KYVADLEM A STUDIUM GRAVITAČNÍHO POLE 1. Úkol měření 1. Určete velikost tíhového zrychlení pro Prahu reverzním
DANIEL TUREČEK 2005 / 2006 1. 412 5. 14.3.2006 28.3.2006 5. STANOVENÍ TÍHOVÉHO ZRYCHLENÍ REVERZNÍM KYVADLEM A STUDIUM GRAVITAČNÍHO POLE 1. Úkol měření 1. Určete velikost tíhového zrychlení pro Prahu reverzním
Orbit TM Tellerium Kat. číslo 113.4000
 Orbit TM Tellerium Kat. číslo 113.4000 Orbit TM Tellerium s velkým glóbusem Země pro demonstrování ročních období, stínů a dne a noci Orbit TM Tellerium s malou Zemí pro demonstrování fází Měsíce a zatmění
Orbit TM Tellerium Kat. číslo 113.4000 Orbit TM Tellerium s velkým glóbusem Země pro demonstrování ročních období, stínů a dne a noci Orbit TM Tellerium s malou Zemí pro demonstrování fází Měsíce a zatmění
MASARYKOVA UNIVERZITA PEDAGOGICKÁ FAKULTA KATEDRA GEOGRAFIE. Planetární geografie seminář
 MASARYKOA UNIERZITA PEDAGOGICKÁ FAKULTA KATEDRA GEOGRAFIE květen 2008 I Měření vzdáleností ve vesmíru 1) ýpočet hodnoty pc a ly ze známé AU a převod těchto hodnot. 1 AU = 150 10 6 km Z definice paralaxy
MASARYKOA UNIERZITA PEDAGOGICKÁ FAKULTA KATEDRA GEOGRAFIE květen 2008 I Měření vzdáleností ve vesmíru 1) ýpočet hodnoty pc a ly ze známé AU a převod těchto hodnot. 1 AU = 150 10 6 km Z definice paralaxy
SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE
 SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Řešení kruţnicových oblouků v souřadnicích) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec 2015
SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Řešení kruţnicových oblouků v souřadnicích) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec 2015
3. Vypočítejte chybu, které se dopouštíte idealizací reálného kyvadla v rámci modelu kyvadla matematického.
 Pracovní úkoly. Změřte místní tíhové zrychlení g metodou reverzního kyvadla. 2. Změřte místní tíhové zrychlení g metodou matematického kyvadla. 3. Vypočítejte chybu, které se dopouštíte idealizací reálného
Pracovní úkoly. Změřte místní tíhové zrychlení g metodou reverzního kyvadla. 2. Změřte místní tíhové zrychlení g metodou matematického kyvadla. 3. Vypočítejte chybu, které se dopouštíte idealizací reálného
Pravoúhlá axonometrie
 Pravoúhlá axonometrie bod, přímka, rovina, bod v rovině, trojúhelník v rovině, průsečnice rovin, průsečík přímky s rovinou, čtverec v půdorysně, kružnice v půdorysně V Rhinu vypneme osy mřížky (tj. červenou
Pravoúhlá axonometrie bod, přímka, rovina, bod v rovině, trojúhelník v rovině, průsečnice rovin, průsečík přímky s rovinou, čtverec v půdorysně, kružnice v půdorysně V Rhinu vypneme osy mřížky (tj. červenou
Identifikace práce prosíme vyplnit čitelně tiskacím písmem
 Identifikace práce prosíme vyplnit čitelně tiskacím písmem Žák/yně jméno příjmení identifikátor Identifikátor zjistíš po přihlášení na http://olympiada.astro.cz/korespondencni. Jeho vyplnění je nutné.
Identifikace práce prosíme vyplnit čitelně tiskacím písmem Žák/yně jméno příjmení identifikátor Identifikátor zjistíš po přihlášení na http://olympiada.astro.cz/korespondencni. Jeho vyplnění je nutné.
Skládání různoběžných kmitů. Skládání kolmých kmitů. 1) harmonické kmity stejné frekvence :
 Skládání různoběžných kmitů Uvědomme si principiální bod tohoto problému : na jediný hmotný bod působí dvě nezávislé pružné síl ve dvou různých směrech. Jednotlivé mechanické pohb, které se budou skládat,
Skládání různoběžných kmitů Uvědomme si principiální bod tohoto problému : na jediný hmotný bod působí dvě nezávislé pružné síl ve dvou různých směrech. Jednotlivé mechanické pohb, které se budou skládat,
ORLÍ PERO. Sluneční hodiny
 ORLÍ PERO Sluneční hodiny Vyrob sám pěkné a přesné sluneční hodiny, zdůvodni přesný úhel rafije, prokaž znalosti o pohybu slunce po obloze vysvětli pojmy : ekliptika, nebeský (světový) rovník, kdy slunce
ORLÍ PERO Sluneční hodiny Vyrob sám pěkné a přesné sluneční hodiny, zdůvodni přesný úhel rafije, prokaž znalosti o pohybu slunce po obloze vysvětli pojmy : ekliptika, nebeský (světový) rovník, kdy slunce
Management rekreace a sportu. 10. Derivace
 Derivace Derivace Před mnoha lety se matematici snažily o obecné vyřešení úlohy, jak sestrojit tečnu k dané křivce a také yzici zápolili s problémem určení rychlosti nerovnoměrného pohybu K zásadnímu obratu
Derivace Derivace Před mnoha lety se matematici snažily o obecné vyřešení úlohy, jak sestrojit tečnu k dané křivce a také yzici zápolili s problémem určení rychlosti nerovnoměrného pohybu K zásadnímu obratu
1 Analytická geometrie
 1 Analytická geometrie 11 Přímky Necht A E 3 a v R 3 je nenulový Pak p = A + v = {X E 3 X = A + tv, t R}, je přímka procházející bodem A se směrovým vektorem v Rovnici X = A + tv, t R, říkáme bodová rovnice
1 Analytická geometrie 11 Přímky Necht A E 3 a v R 3 je nenulový Pak p = A + v = {X E 3 X = A + tv, t R}, je přímka procházející bodem A se směrovým vektorem v Rovnici X = A + tv, t R, říkáme bodová rovnice
Čas a kalendář. RNDr. Aleš Ruda, Ph.D.
 Čas a kalendář RNDr. Aleš Ruda, Ph.D. Obsah přednášky 1) Čas a způsoby jeho 2) Místní a pásmový čas 3) Datová hranice 4) Kalendář 1. Čas a způsoby jeho podstata určování času rotace Země - druhy časů:
Čas a kalendář RNDr. Aleš Ruda, Ph.D. Obsah přednášky 1) Čas a způsoby jeho 2) Místní a pásmový čas 3) Datová hranice 4) Kalendář 1. Čas a způsoby jeho podstata určování času rotace Země - druhy časů:
VEKTOR. Vymyslete alespoň tři příklady vektorových a skalárních fyzikálních veličin. vektorové: 1. skalární
 VEKTOR Úvod Vektor je abstraktní pojem sloužící k vyjádření jistého směru a velikosti. S vektorovými veličinami se setkáváme například ve fyzice. Jde o veličiny, u nichž je rozhodující nejen velikost,
VEKTOR Úvod Vektor je abstraktní pojem sloužící k vyjádření jistého směru a velikosti. S vektorovými veličinami se setkáváme například ve fyzice. Jde o veličiny, u nichž je rozhodující nejen velikost,
Země třetí planetou vhodné podmínky pro život kosmického prachu a plynu Měsíc
 ZEMĚ V POHYBU Anotace: Materiál je určen k výuce přírodovědy v 5. ročníku ZŠ. Seznamuje žáky se základními informacemi o Zemi, jejích pohybech a o historii výzkumu vesmíru. Země Země je třetí planetou
ZEMĚ V POHYBU Anotace: Materiál je určen k výuce přírodovědy v 5. ročníku ZŠ. Seznamuje žáky se základními informacemi o Zemi, jejích pohybech a o historii výzkumu vesmíru. Země Země je třetí planetou
Lingebraické kapitolky - Analytická geometrie
 Lingebraické kapitolky - Analytická geometrie Jaroslav Horáček KAM MFF UK 2013 Co je to vektor? Šipička na tabuli? Ehm? Množina orientovaných úseček majících stejný směr. Prvek vektorového prostoru. V
Lingebraické kapitolky - Analytická geometrie Jaroslav Horáček KAM MFF UK 2013 Co je to vektor? Šipička na tabuli? Ehm? Množina orientovaných úseček majících stejný směr. Prvek vektorového prostoru. V
Matematická kartografie. Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT. Referenční plochy
 Matematická kartografie Buchar.: Matematická kartografie 10, ČVUT; Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT Referenční plochy referenční elipsoid (sféroid) zploštělý rotační elipsoid Besselův
Matematická kartografie Buchar.: Matematická kartografie 10, ČVUT; Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT Referenční plochy referenční elipsoid (sféroid) zploštělý rotační elipsoid Besselův
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: graf funkce, derivace funkce a její
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: graf funkce, derivace funkce a její
PRAKTIKUM I Mechanika a molekulová fyzika
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I Mechanika a molekulová fyzika Úloha č. XXI Název: Měření tíhového zrychlení Pracoval: Jiří Vackář stud. skup. 11 dne 10..
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I Mechanika a molekulová fyzika Úloha č. XXI Název: Měření tíhového zrychlení Pracoval: Jiří Vackář stud. skup. 11 dne 10..
Přednášející: Ing. M. Čábelka Katedra aplikované geoinformatiky a kartografie PřF UK v Praze
 Seminář z geoinformatiky Úvod do geodézie Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Úvod do geodézie
Seminář z geoinformatiky Úvod do geodézie Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Úvod do geodézie
Obsah. Obsah. 2.3 Pohyby v radiálním poli Doplňky 16. F g = κ m 1m 2 r 2 Konstantu κ nazýváme gravitační konstantou.
 Obsah Obsah 1 Newtonův gravitační zákon 1 2 Gravitační pole 3 2.1 Tíhové pole............................ 5 2.2 Radiální gravitační pole..................... 8 2.3..................... 11 3 Doplňky 16
Obsah Obsah 1 Newtonův gravitační zákon 1 2 Gravitační pole 3 2.1 Tíhové pole............................ 5 2.2 Radiální gravitační pole..................... 8 2.3..................... 11 3 Doplňky 16
100 1500 1200 1000 875 750 675 600 550 500 - - 775 650 550 500 450 400 350 325 - -
 Prostý kružnicový oblouk Prostý kružnicový oblouk se používá buď jako samostatné řešení změny směru osy nebo nám slouží jako součást směrové změny v kombinaci s přechodnicemi nebo složenými oblouky. Nejmenší
Prostý kružnicový oblouk Prostý kružnicový oblouk se používá buď jako samostatné řešení změny směru osy nebo nám slouží jako součást směrové změny v kombinaci s přechodnicemi nebo složenými oblouky. Nejmenší
KLASICKÁ MECHANIKA. Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny.
 MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
R2.213 Tíhová síla působící na tělesa je mnohem větší než gravitační síla vzájemného přitahování těles.
 2.4 Gravitační pole R2.211 m 1 = m 2 = 10 g = 0,01 kg, r = 10 cm = 0,1 m, = 6,67 10 11 N m 2 kg 2 ; F g =? R2.212 F g = 4 mn = 0,004 N, a) r 1 = 2r; F g1 =?, b) r 2 = r/2; F g2 =?, c) r 3 = r/3; F g3 =?
2.4 Gravitační pole R2.211 m 1 = m 2 = 10 g = 0,01 kg, r = 10 cm = 0,1 m, = 6,67 10 11 N m 2 kg 2 ; F g =? R2.212 F g = 4 mn = 0,004 N, a) r 1 = 2r; F g1 =?, b) r 2 = r/2; F g2 =?, c) r 3 = r/3; F g3 =?
základy astronomie 2 praktikum 5 Dynamická paralaxa hvězd
 základy astronomie praktikum Dynamická paralaxa hvězd 1 Úvod Dvojhvězdy jsou nenahraditelným zdrojem informací ze světa hvězd. Nejvýznamnější jsou z tohoto pohledu zákrytové dvojhvězdy, tedy soustavy,
základy astronomie praktikum Dynamická paralaxa hvězd 1 Úvod Dvojhvězdy jsou nenahraditelným zdrojem informací ze světa hvězd. Nejvýznamnější jsou z tohoto pohledu zákrytové dvojhvězdy, tedy soustavy,
Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].
![Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y]. Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].](/thumbs/91/104981778.jpg) Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
DUM č. 20 v sadě. 12. Fy-3 Průvodce učitele fyziky pro 4. ročník
 projekt GML Brno Docens DUM č. 20 v sadě 12. Fy-3 Průvodce učitele fyziky pro 4. ročník Autor: Miroslav Kubera Datum: 21.06.2014 Ročník: 4B Anotace DUMu: Prezentace je zaměřena na základní popis a charakteristiky
projekt GML Brno Docens DUM č. 20 v sadě 12. Fy-3 Průvodce učitele fyziky pro 4. ročník Autor: Miroslav Kubera Datum: 21.06.2014 Ročník: 4B Anotace DUMu: Prezentace je zaměřena na základní popis a charakteristiky
Čas a kalendář. důležitá aplikace astronomie udržování časomíry a kalendáře
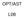 OPT/AST L08 Čas a kalendář důležitá aplikace astronomie udržování časomíry a kalendáře čas synchronizace s rotací Země vzhledem k jarnímu bodu vzhledem ke Slunci hvězdný čas definován jako hodinový úhel
OPT/AST L08 Čas a kalendář důležitá aplikace astronomie udržování časomíry a kalendáře čas synchronizace s rotací Země vzhledem k jarnímu bodu vzhledem ke Slunci hvězdný čas definován jako hodinový úhel
Optika pro mikroskopii materiálů I
 Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
KINEMATIKA HMOTNÉHO BODU. Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník
 KINEMATIKA HMOTNÉHO BODU Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník Kinematika hmotného bodu Kinematika = obor fyziky zabývající se pohybem bez ohledu na jeho příčiny Hmotný bod - zastupuje
KINEMATIKA HMOTNÉHO BODU Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník Kinematika hmotného bodu Kinematika = obor fyziky zabývající se pohybem bez ohledu na jeho příčiny Hmotný bod - zastupuje
May 31, Rovnice elipsy.notebook. Elipsa 2. rovnice elipsy. SOŠ InterDact Most, Mgr.Petra Mikolášková
 Elipsa 2 rovnice elipsy SOŠ InterDact Most, Mgr.Petra Mikolášková 1 Název školy Autor Název šablony Číslo projektu Předmět SOŠ InterDACT s.r.o. Most Mgr. Petra Mikolášková III/2_Inovace a zkvalitnění výuky
Elipsa 2 rovnice elipsy SOŠ InterDact Most, Mgr.Petra Mikolášková 1 Název školy Autor Název šablony Číslo projektu Předmět SOŠ InterDACT s.r.o. Most Mgr. Petra Mikolášková III/2_Inovace a zkvalitnění výuky
