Historie a elementární základy teorie barev III.
|
|
|
- Miroslava Urbanová
- před 8 lety
- Počet zobrazení:
Transkript
1 Školská fyzika 2013/2 Fyzika kolem ás Historie a elemetárí základy teorie barev III. Václav Kohout 1, Nakladatelství Fraus, s. r. o., Plzeň Dostává se vám do rukou třetí díl série čláků zabývajích se teorií barev. Problematika barev je a rozhraí fyziky, iformatiky a výpočetí techiky, přírodopisu, výtvaré výchovy a případě i dalších vyučovacích předmětů. Pozatky, které jsou ve výuce běžě zmiňováy, jsou zde doplěy a rozšířey odborějšími iformacemi z oboru kolorimetrie. Teto díl obsahuje i ěkterá složitější matematická vyjádřeí. Ta již ejsou přirozeě určea žákům, ale hlavě učitelům, kteří mají o problematiku kolorimetrie hlubší zájem. Na kolorimetrický přehled dále aváže čláek popisující mezipředmětové výukové téma Barvy kolem ás, které bylo a jeho základě vytvořeo, a čláek popisující a hodotící ověřeí tohoto tématu ve výuce. CIE Commissio Iteratioale de l Eclairage V předchozích kapitolách jsme viděli ěkolik typů tristimulů, tj. defiic barev založeých a třech hodotách. Jedalo se o RGB, CMY (s odvozeou formou CMYK) a HSB (s jeho variatami HVC, HSL a dalšími). Všechy tyto barvové prostory mohou být odvozey z RGB a všechy proto také přebírají základí edostatek RGB. Každé zařízeí lidské oko, skeer, moitor, tiskára atd. má mírě odlišé tři primárí barvy a tím také odlišou defiici celého barvového prostoru RGB. Existují stovky růzých barvových prostorů, každý z ich je optimálě vhodý k daému účelu, je poměrě jedoduché převádět hodoty barev z jedoho do druhého, ale žádý z ich eí možé ozačit jako obecý stadard pro všeobecé využití. Skupia vědců zabývajících se barvami tzv. skupia CIE se pokusila teto problém vyřešit a vypracovala defiici ového barvového prostoru, ového tristimulu, který vychází z RGB, ale v moha ohledech je lepší. Teto systém se azývá XYZ. Běžý člověk, resp. uživatel počítače se s ím většiou vůbec esetká, je primárě používá pouze pro kolorimetrické účely a případě pro iterí zápis barvy v ěkterých softwarových aplikacích. V dalším uvedeme, které problémy řeší. Zkratka CIE ozačuje fracouzský termí Commissio Iteratioale de l Eclairage (Meziárodí komise pro osvětlováí). Od založeí CIE v roce 1913 se každoročě schází vědečtí delegáti z moha zemí, aby projedali otázky týkající se výzkumu v růzých oblastech vědeckého pozáí lidského vímáí barev. Cílem CIE je vytvořit a průběžě aktualizovat systém, který umožňuje precizě popisovat barvy a jejich kvatitativí vlastosti, případě přímo specifikovat barevost růzých produktů, jako jsou tiskařské barvy, fólie, ikousty, barevé moitory atd. Dva mezíky v práci CIE 1931 a 1976 Jedou z klíčových schůzek v historii CIE bylo setkáí v září 1931 v Cambridgi v Aglii. Z tohoto roku pochází prví komplexí pokus využít velké možství ejrůzějších dosud aměřeých dat a vytvořit z ich systém, který systematicky popisuje světelé a pozorovací podmíky, za kterých má být do budouca prováděo sledováí a měřeí barev. Mimo jié specifikuje 1931 CIE systém ásledující: Stadardí pozorovatel defiice průměrého lidského pozorovatele, Stadardí osvětleí specifikace světelých zdrojů, které mají být používáy pro porováváí barev, Primárí systém XYZ systém imagiárích primárích barev souvisejících s RGB, ale vhodějších jako stadard pro výpočty, popisuje jak barvy světelých zdrojů, tak barvy objektů odrážejících či propouštějících světlo, Barvový prostor xyy barvový prostor odvozeý od XYZ, odděluje souřadice x a y popisující barevý odstí od souřadice Y, kterou je jas barvy, Chromatický diagram graf přehledě zázorňující viditelé barvy a vztahy mezi imi. V ásledujících letech byl uvedeý systém postupě zdokoalová a upřesňová, a to včetě úpravy defiice stadardího pozorovatele v roce Dalším klíčovým rokem je pro CIE a vědecký popis barev rok V tomto roce CIE zaměřila svoji pozorost zejméa a ásledující: 1 kohout@fraus.cz 41
2 Fyzika kolem ás Školská fyzika 2013/2 Perceptuálě uiformí barvové prostory barvové prostory Lab a Luv bližší lidskému vímáí barev, vhodé pro posuzováí vzdáleostí barev, Barevá diferece defiice vztahu pro barevou difereci (ΔE), který umožňuje číselě popsat vzdáleost ebo rozdíl dvou barev. Dále rozebereme uvedeé klíčové pojmy podroběji. Stadardí pozorovatel (2 a 10 ) Pro určeí stadardů měřeí je uté defiovat parametry pozorovatele. Během moha let bylo s dobrovolíky prováděo za účelem defiice ormálího viděí velké možství experimetů týkajících se vímáí barev. Jedím z faktorů, které mohou mít vliv a barevou citlivost lidského oka i u jedoho kokrétího pozorovatele, je mimo jié velikost zorého pole. V roce 1931 byl defiová stadardí pozorovatel s 2 zorým polem a teto stadard se používá dodes. Roku 1964 byla zkoumáa a ověřováa dříve prováděá měřeí a byly objevey rozdíly, zejméa v modrozeleé oblasti spektra, pokud byly zoré úhly větší ež 2. Příčia těchto zjištěých rozdílů je zajímavá. V úplém středu sítice uprostřed žluté skvry je oblast azývaá folvea. Je to jediá oblast a sítici, kde možství barevých fotoreceptorů čípků výzamě převyšuje možství ebarevých fotoreceptorů pro očí viděí tyčiek. Je-li zoré pole větší ež 4, zasahuje již barevé viděí i do oblasti s meší kocetrací čípků, což může způsobit mírou odchylku při vímáí barev. Skutečý rozdíl je velice malý, zřídkakdy pozorovatelý, icméě je měřitelý. Ze zasedáí CIE v roce 1964 vyplyula defiice doplňkového stadardího pozorovatele s 10 zorým polem, která by měla být použita při jakémkoli pozorováí se zorým polem větším ež 4. Od tohoto roku by každé měřeí barev mělo obsahovat iformaci, zda odpovídá použití defiice 2 stadardího pozorovatele z roku 1931 ebo defiice 10 doplňkového stadardího pozorovatele z roku Neí-li teto údaj uvede, předpokládá se použití defiice 2 stadardího pozorovatele. 2 Pro představu o velikosti zorého pole 2 a 10 stadardího pozorovatele slouží obrázek vpravo. Kruhy v ěm vyzačeé zázorňují zorá pole 2, 4 a 10 za předpokladu, 2 Obr. 21 zoré pole stadardího pozorovatele že stráku pozorujete ze vzdáleosti 25 cm. Stadardí osvětleí Aby byly podmíky pozorováí barvy kompletí, je vždy uto specifikovat zdroj světla, který osvětluje pozorovaou barevou plochu. Zasedáí CIE v roce 1931 defiovalo tři stadardí osvětleí A, B a C, ke kterým byla později přidáa sada osvětleí D, hypotetické osvětleí E a také sada eoficiálích zářivkových osvětleí F. Stadardí osvětleí byla charakterizováa jako žárovky reprodukující světlo určité barevé teploty. Osvětleí A až F jsou popsáa ásledově: A Žárovka s barevou teplotou K vyzařující žlutooražové světlo. Stadardí osvětleí A se obecě používá k simulaci osvětleí klasickými žárovkami. B Žárovka s filtrem pro simulaci přímého sluečího světla odpovídajícího barevé teplotě K. Des je stadardí osvětleí B používáo je velice zřídka. 2 Převzato z: BUNTING, F. et al. Colortro: User Maual. 1st Editio. Larkspur (Califoria, USA): Light Source Computer Images, Ic., p. 42
3 Školská fyzika 2013/2 Fyzika kolem ás C Žárovka s filtrem pro simulaci epřímého sluečího světla odpovídajícího teplotě K. Stadardí osvětleí C je poměrě často používáo a je považováo za dobré přiblížeí reálému epřímému sluečímu světlu. Nejedá se však o dokoalou simulaci sluečího světla, protože eobsahuje dostatečé možství ultrafialového zářeí, které je zapotřebí při vyhodocováí fluorescečích barev. D Osvětleí azývaé deí světlo. Jde vlastě o celou skupiu jedotlivých defiovaých osvětleí. Stadardí osvětleí D65 odpovídá barevé teplotě K a je téměř totožé se stadardím osvětleím C. Je však ještě přesějším přiblížeím k reálému epřímému sluečímu světlu, protože obsahuje ultrafialovou složku pro lepší vyhodocováí fluorescečích barev. Všecha osvětleí D jsou pojmeováa podle své barevé teploty. D50 a D75 odpovídají barevým teplotám K a K. Stadardí osvětleí D65 a D50 jsou des při posuzováí barev zdaleka ejrozšířeější. E Osvětleí s rovoměrým (equal) rozložeím eergie. Osvětleí E ve skutečosti eexistuje. Jedá se o teoretický světelý zdroj, který ve viditelém spektru vyzařuje a každé vlové délce stejé možství eergie. F Zářivkové osvětleí. Jde o sadu zářivkových světelých zdrojů, které ejsou oficiálími osvětlovacími stadardy CIE. Zářivková svítidla mají ve svých spektrálích křivkách ostré špičky, a tak u ich eí možé hovořit o barevé teplotě v přesém slova smyslu. Protože jsou ale zářivkové zdroje běžě používaé, doporučuje CIE ěkteré z ich alespoň jako eoficiálí stadardy pro porováváí jejich barev. Zářivková osvětleí jsou ozačováa F1 až F12 a CIE z ich doporučuje F2 (studeá bílá zářivka), F7 (zářivka v barvě deího světla) a F11 (úzkopásmová zářivka). Kromě defiice stadardího pozorovatele jsou tedy specifikace barev podle CIE závislé také a kokrétím osvětleí použitém během měřeí. Barevá teplota Jak je vidět z defiic výše, pro popis zářících zdrojů světla se často používá pojem barevá teplota. Všecha zahřátá tělesa vyzařují světlo. I člověk s ormálí tělesou teplotou 37 C (310 K) vysílá zářeí, ale pouze a dlouhých vlových délkách v ifra červeém oboru. Vědci defiovali hypotetické tzv. absolutě čeré těleso, které eodráží ai epropouští žádé světlo. Absolutě čeré těleso dokoale pohlcuje světlo všech vlových délek, takže jakékoli světlo, které opouští jeho povrch, muselo být tímto tělesem vyzářeo. Rozložeí vlových délek vyzařovaých zahřátým absolutě čerým tělesem při daé teplotě udává Plackův vyzařovací záko. Při teplotě K těleso září oražově, při K září jasě žlutě, při K je vyzařovaá barva bílá (vlové délky viditelého světla jsou zastoupey podle Plackova zákoa podobě jako u Sluce), při K má světlo již výrazě modravý ádech. Při vyšších teplotách zůstává světlo amodralé, protože velká část zářeí je tak krátkých vlových délek, že se dostává do ultrafialové oblasti a eí viditelá. Aalogickým způsobem mohou být popsáy všechy zdroje vyzařující světlo. Spektrálí křivka zdroje může být změřea a ozačea apř. jako K (75W žárovka) ebo K (deí světlo). Počítačové moitory a televizí obrazovky mají tzv. charakteristický bílý bod. Moitor s bílým bodem K se bude jevit amodralý, moitor s bílým bodem K bude mít žlutý ádech. Teto popis je však pouze přibližý, protože většia reálých zdrojů vyzařujících světlo se echová zcela přesě jako absolutě čerá tělesa. Popis barvy pomocí barevé teploty je možý pouze u zdrojů, které vyzařují světlo. V žádém případě ho elze použít u těles, která světlo odrážejí ebo propouštějí. Teto popis je striktě založe a modelu zářeí absolutě čerého tělesa. XYZ základí tristimulus CIE Barvový prostor XYZ defiuje všechy barvy pomocí tří imagiárích primárích barev X, Y a Z založeých a lidském viděí. Teto barvový prostor se však v běžém životě téměř epoužívá. Je využívá pro kolorimetrické zpracováí barev a iterě také v ěkterých počítačových aplikacích pro trasformace barev. Přesto je jedozačě základem systému CIE. 43
4 Fyzika kolem ás Školská fyzika 2013/2 Existuje moho popisů barev založeých a třech primárích barvách, apř. moho růzých RGB prostorů, a všechy mají stejou platost. Je možé barvy mezi imi libovolě trasformovat, a proto je možé zvolit za základí libovolý soubor primárích barev. Komise CIE zvolila soubor primárích barev X, Y a Z, který je defiovaý ásledujícími vlastostmi: 1. Je založe a experimetálích údajích z pokusů s lidským vímáím barev. Tím je zajištěo, že výsledky při teoretických operacích s barvami pomocí matematických výpočtů odpovídají přesě realitě. 2. Sada primárích barev X, Y a Z se chová aditivě, stejě jako primárí barvy RGB. Každá barva může být vyjádřea jako směs složek X, Y a Z se stejě začeými hodotami X, Y a Z. 3. Jeda z uvedeých tří hodot Y zároveň odpovídá jasu barvy. (Jas barvy závisí a vlové délce příslušého světla. Barvy ěkterých vlových délek, zejméa žluté a zeleé části spektra, se jeví jasější, ež okraje spektra hluboké fialové a červeé odstíy.) 4. Všechy hodoty všech tří složek jsou kladé. Experimety s vímáím barev edávají pro XYZ výsledky, které by vyžadovaly záporou hodotu ěkteré z primárích složek, jak bylo zmíěo dříve. 3 Defiice primárích barev XYZ je přímou součástí specifikace stadardího pozorovatele z roku CIE defiuje pro stadardího pozorovatele sadu barvových fukcí soubor tří spektrálích křivek, které popisují, jakým způsobem je uto kombiovat primárí barvy XYZ pro reprodukci všech existujících barev spektra, resp. všech vlových délek viditelého světla. Hodoty X, Y a Z jsou defiováy ásledově: kde X = k S( λ) x( λ) βλ ( ) dλ λ Y = k S( λ) y( λ) βλ ( ) dλ λ Z = k S( λ) z( λ) βλ ( ) d λ, λ 100 k = S( λ) y( λ) d λ, λ Obr. 22 barvové fukce (hodoty tristimulu CIE) 2 stadardího pozorovatele 1931 (plá čára) a 10 stadardího pozorovatele 1964 (přerušovaá čára) 3 βλ ( )= spektrálí odrazivost vzorku při vlové délce λ, pro průhledé ebo průsvité vzorky se jedá o spektrálí propustost τ( λ), S( λ ) = spektrálí rozložeí eergie osvětleí podle vlové délky λ, x( λ), y( λ), z ( λ ) jsou barvové fukce pro 2 stadardího pozorovatele z roku Podle: HUNT, R. W. G. The reproductio of Colour. 6th Editio, Chichester (West Sussex, Eglad, GB): Joh Wiley & Sos Ltd., p. ISBN
5 Školská fyzika 2013/2 Fyzika kolem ás xyy chromatický diagram CIE Barvový prostor xyy je odvozeý přímo z XYZ a je urče především ke grafickému zázorěí barev ve dvojrozměrém prostoru ezávisle a světlosti barvy. Hodota Y je shodá s hodotou Y, která je součástí tristimulu XYZ a představuje právě světlost ebo jas barvy. Hodoty x a y se azývají chromatické souřadice barvy a jsou vypočteé přímo z hodot X, Y a Z tristimulu XYZ ásledujícím způsobem: X x X Y Z y Y X Y Z z Z = = =, X + Y + Z Z toho vyplývá, že x+ y+ z =1, a proto je libovolá ze tří chromatických souřadic x, y a z jedoduše odvoditelá ze zbývajících dvou, apř. z = 1 x y. CIE se tímto částečě vrací k Musellovu katalogizačímu systému a odděluje jasový atribut barvy od hodot popisujících pouze čistou barvu chromatických složek. Dvě barvy, které se od sebe liší pouze jasem, mají tetýž chromatický popis a tedy stejé chromatické souřadice. Hodoty x, y, Y je možé zobrazit v užitečém grafu azývaém chromatický diagram. Teto diagram výzamým způsobem zpřehledňuje poměrě komplikovaý systém barev zavedeý CIE a čií ho srozumitelým i laikům. Obr. 23 kostrukce chromatického diagramu CIE Poskytuje ázorý ákres všech viditelých barev a zobrazuje vztahy mezi imi. Pokud převedeme a chromatické souřadice x, y čisté spektrálí barvy, dostaeme v chromatickém diagramu tvar podkovy, zámý jako spektrálí locus. Protože všechy viditelé barvy jsou defiovaé jako směs těchto čistých spektrálích barev, musí se acházet uvitř této křivky. Čára, která spojuje kocové body podkovy, se azývá purpurová liie ebo purpurová hraice. Barvy a této čáře jsou složeé ze směsi čistého fialového světla o vlové délce 380 m a červeého světla o vlové délce 770 m. 4 Je třeba si uvědomit, že barvy, které jsou zobrazeé v diagramu vytištěém zde a stráce, jsou pouze zástupé jsou zkresleé techickými omezeími tiskového procesu použitého k vytištěí tohoto diagramu, případě.techickými omezeími moitoru počítače, dataprojektoru apod. Chromatický diagram je do jisté míry podobý barevému kruhu, tj. vodorovému průřezu barvovým prostorem HSB. Ve středu podkovy se acházejí eutrálí barvy. Pokud se vzdalujeme Obr. 24 chromatický diagram CIE CIE 1931 xy chromaticity diagram. [olie]. c2005. [cit ]. Dostupé z URL < 45
6 Fyzika kolem ás Školská fyzika 2013/2 od středu, jsou barvy sytější, a a okrajích se acházejí ejsytější čisté spektrálí barvy. Odstí barvy se měí při pohybu po obvodu podkovy. Podstatý rozdíl je ale v tom, že u chromatického diagramu je zcela jasá představa, kde se acházejí viditelé barvy. Případé virtuálí barvy ležící mimo oblast ohraičeou spektrálím locusem a purpurovou liií jsou lidským okem eviditelé, tj. mají ulový jas, případě jsou lidským okem eodlišitelé od barev, které leží a obvodu oblasti. Oblast viditelých barev se azývá barevý gamut [gemit, des také gamut] (rozsah) lidského barevého vímáí. V praxi můžeme určit barevý gamut pro libovolé zařízeí pracující s barvami a bázi ějakého tristimulu. Pro moitory, tiskáry i další zařízeí je možé akreslit jejich barevý gamut, který vymezuje barvy jimi reprodukovatelé. 5 Chromatický diagram a obr. 25 ukazuje barevý gamut Obr. 25 barevý gamut růzých zařízeí 5 typického počítačového moitoru a tiskáry. Barvy mimo daý gamut edokáže zařízeí ikdy reprodukovat a teto fakt vyplývá již přímo ze sady primárích barev, kterou používá. Uvedeá tiskára apříklad dokáže vytiskout pouze azurovou barvu C1, při pokusu o tisk azurové barvy C2 mimo gamut bude výsledek téměř stejý jako při tisku C1. Lab a Luv perceptuálě uiformí barvové prostory CIE Lab a Luv jsou barvové prostory, které mají za cíl být perceptuálě uiformí. Perceptuálě uiformí systém (barvový prostor) je takový, ve kterém číselá vzdáleost mezi libovolými dvěma barvami v barvovém prostoru odpovídá pozorovatelem vímaé blízkosti ebo vzdáleosti těchto barev. Termiologická pozámka. Poměrě dlouhou dobou jsem se pokoušel o adekvátí překlad výrazu perceptuálě uiformí. Nalezl jsem jediý přijatelý překlad jedotý z hlediska vímáí 6. Toto ozačeí však dle mého o obsahu daého pojmu eříká vůbec ic, a proto se v textu přidržuji původího ozačeí a jeho opisého vysvětleí. 7 Obr. 26 vzdáleosti barev v chromatickém diagramu xyy 7 Nejprve se podíváme a teto problém v chromatickém dia gramu xy. Pokud echáme lidského pozorovatele zkoumat dvojice barev a posuzovat jejich vzájemou vzdáleost, dospějeme k ějaké ituitiví defiici jedotky barevé vzdáleosti. Nyí můžeme do chromatického dia gramu zakreslit všechy dvojice barev, které jsou podle pozorovatele stejě vzdáleé či blízké obr. 26. Člověk je daleko citlivější 5 Převzato z: BUNTING, F. et al. Colortro: User Maual. 1st Editio. Larkspur (Califoria, USA): Light Source Computer Images, Ic., p. 6 FRASER, B. MURPHY, C. BUNTING, F. Správa barev: Průvodce profesioála v grafice a pre-pressu. 1. vydáí. Bro: Computer Press, s. ISBN Převzato z: HUNT, R. W. G. The reproductio of Colour. 6th Editio, Chichester (West Sussex, Eglad, GB): Joh Wiley & Sos Ltd., p. ISBN
7 Školská fyzika 2013/2 Fyzika kolem ás a malé změy v odstíech fialové a červeé ež a změy v odstíech zeleé a žluté. Teto efekt ztěžuje potřebé výpočty při porováváí shody dvou barev. Řešeím jsou právě barvové prostory Lab a Luv. Již v roce 1931 byly podikuty pokusy o vytvořeí tzv. UCS (uiform color scale) diagramu, kterým byl do jisté míry zdeformovaý a atočeý chromatický diagram. Roku 1960 byly z chromatických souřadic x, y odvozey ové souřadice u, v a roku 1976 byl jejich výpočet upřesě a byly ozačey u' a v'. Dále byla defiováa ová souřadice popisující jasovou složku barvy L* odvozeá od Y a upraveé hodoty u* a v*. L* je podobá Musellově hodotě V v tom, že defiuje světlost od čeré do bílé v rovoměrých stejě velkých krocích. Rozsah hodot L* je od 0 (čerá) do 100 (bílá). Barvový prostor defiovaý CIE a používající souřadice L*, u' a v', resp. u* a v* je ozačová jako L*u*v*, často také CIELUV ebo pouze Luv. Jeho souřadice jsou odvozey ze souřadic prostoru CIE XYZ a jsou defiováy ásledujícími vztahy: kde: Y 3 L* = Y u* = 13L* u u 1 ( ) ( ) v* = 13L* v v 4X u = = X + Y + Z v 9Y 15 3 X + 15Y + 3Z 4X u = 9Y v =. X + 15Y + 3Z X + 15 Y + 3Z X, Y, Z jsou hodoty základího tristimulu CIE XYZ pro ideálí těleso dokoale odrážející ebo propouštějící rozptýleé světlo. X = 96, 422; Y = 100, 00; Z = 82, 521. Barvový prostor CIE Luv je oproti prostoru xyy perceptuálě uiformí a jeho použití je des začě rozšířeé, a to zejméa v průmyslu vyrábějícím zařízeí vyzařující světlo, jakými jsou televizí obrazovky, počítačové moitory ebo řízeé světelé zdroje. Druhou cestou, která směřuje k perceptuálě uiformímu prostoru, jsou souřadice a*, b*, také matematicky odvozeé z primárích hodot X, Y a Z. Souřadice a* víceméě odpovídá běžé červeo-zeleé škále barev a abývá hodoty od 128 (zeleá) do 128 (červeá). Souřadice b* odpovídá běžé žluto-modré škále a abývá hodot od 128 (modrá) do 128 (žlutá). Matematicky jsou souřadice L*, a*, b* defiováy takto: L* = 116 f ( YY ) 16 a* 500 f X X f Y Y b* = 200 f ( YY ) f ( Z Z ), kde: f ( X X)= ( X X ) 1 3 pro X X > 0, 00856, 16 f ( X X)= 7, 7867( X X )+ pro X X 0, 00856, 116 (aalogicky pro Y a Z). X, Y, Z jsou hodoty základího tristimulu CIE XYZ pro ideálí těleso dokoale odrážející ebo propouštějící rozptýleé světlo. X = 96, 422; Y = 100, 00; Z = 82, 521. Výsledý barvový prostor je L*a*b* a často je ozačová jako CIELAB ebo jedoduše Lab. Diagram barev (spektrálí locus) prostoru Lab je obtížější zázorit, a proto se příliš často epoužívá. Pro tyto účely se používá chromatický diagram xy a Luv diagram. Protože je Lab perceptuálě uiformí a chromatické souřadice kopírují ázoré škály červeá-zeleá a modrá-žlutá, je Lab populárím barvovým prostorem v moha = ( ) ( ), 47
8 Fyzika kolem ás Školská fyzika 2013/2 odvětvích lidské čiosti zabývajících se barvami, mimo jié i v grafickém průmyslu. Iterí reprezetace barev ve zámém profesioálím software a úpravu fotografií Adobe Photoshop je také v souřadicích Lab. ΔE rozdíl barev Nejpodstatější vlastostí perceptuálě uiformích barvových prostorů, jako jsou CIE Lab a Luv, je, že umožňují vypočítat hodotu, které vyjadřuje, jak blízko jsou avzájem dvě daé barvy. Tato hodota se ozačuje ΔE a azývá se rozdíl barev. V praxi se používá zejméa ΔE vypočteé v prostoru Lab. Zde můžeme rozdíl dvou barev spočítat velice jedoduše. Najdeme souřadice zadaých barev a spočítáme vzdáleost těchto dvou bodů: Eab * L* a* b* 2, kde L*, a*, b* jsou rozdíly souřadic L*, a* a b* porovávaých barev. Vzhledem k tomu, jak jsou tyto perceptuálě uiformí barvové prostory defiováy, bude vypočteé číslo odpovídat tomu, jak jsou barvy podobé. Hodoty ΔE jsou využíváy všude tam, kde je zapotřebí přesě vyjádřit barevou toleraci ějakého zařízeí. Otázkou zůstává, jaká hodota ΔE odpovídá ještě stále přijatelé toleraci. Obecě platí, že rozdíl barev E 1 je miimálí hodota, kterou je lidské oko schopé rozlišit. Byly zpracováy statistické studie, které azačují, že rozdíl barev ΔE 6 ebo 7 je ještě považová za přijatelý u běžých tištěých materiálů. Je uto zdůrazit, že se jedá o pokus kvatifikovat vlastost, která je ze své podstaty poměrě subjektiví. Posouzeí barevé tolerace vždy závisí a kokrétím pozorovateli, a specifických pozorovacích podmíkách a dalších faktorech. Nicméě hodota ΔE zůstae pro toto posouzeí dobrým referečím základem. Literatura = ( ) + ( ) + ( ) [1] Butig F. a kol.: Colortro: User Maual. Light Source Computer Images, Ic., Larkspur (Califoria, USA) [2] Fraser B., Murphy C., Butig F.: Správa barev: Průvodce profesioála v grafice a pre-pressu. Computer Press, Bro [3] Giorgiai E. J., Madde T. E.: Digital Color Maagemet: Ecodig Solutios. Joh Wiley & Sos Ltd., Chichester (West Sussex, Eglad, GB) [4] Hut R. W. G.: The reproductio of Colour. Joh Wiley & Sos Ltd., Chichester (West Sussex, Eglad, GB) [5] Kag H. R.: Computatioal Color Techology. SPIE The Iteratioal Society for Optical Egieerig, Belligham (Washigto, USA) Dalším pokračováím seriálu bude čláek popisující mezipředmětové výukové téma Barvy kolem ás, které bylo a základě dosud předložeého kolorimetrického přehledu vytvořeo. 1 48
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
UŽITÍ MATLABU V KOLORIMETRII. J.Novák, A.Mikš. Katedra fyziky, FSv ČVUT, Praha
 UŽITÍ MATLABU V KOLORIMETRII J.Novák A.Mikš Katedra fyziky FSv ČVUT Praha Kolorimetrické metody jsou velmi často používáy jako diagostické metody v řadě oblastí vědy a techiky. V čláku jsou ukázáy příklady
UŽITÍ MATLABU V KOLORIMETRII J.Novák A.Mikš Katedra fyziky FSv ČVUT Praha Kolorimetrické metody jsou velmi často používáy jako diagostické metody v řadě oblastí vědy a techiky. V čláku jsou ukázáy příklady
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou
 1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
základním prvkem teorie křivek v počítačové grafice křivky polynomiální n
 Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
2 STEJNORODOST BETONU KONSTRUKCE
 STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
12. N á h o d n ý v ý b ě r
 12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
Pro statistické šetření si zvolte si statistický soubor např. všichni žáci třídy (několika tříd, školy apod.).
 STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
STUDIUM DEGRADACE TISKU NA TENKÝCH POLYMERNÍCH VRSTVÁCH
 STUDIUM DEGRADACE TISKU NA TENKÝCH POLYMERNÍCH VRSTVÁCH Jiří Stačík, 5. ročík Vedoucí práce: doc. Ig. Michal Veselý, CSc. Vysoké učeí techické v Brě, Fakulta chemická, ústav fyzikálí a spotřebí chemie,
STUDIUM DEGRADACE TISKU NA TENKÝCH POLYMERNÍCH VRSTVÁCH Jiří Stačík, 5. ročík Vedoucí práce: doc. Ig. Michal Veselý, CSc. Vysoké učeí techické v Brě, Fakulta chemická, ústav fyzikálí a spotřebí chemie,
Komplexní čísla. Definice komplexních čísel
 Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
1 ROVNOMĚRNOST BETONU KONSTRUKCE
 ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
1 POPISNÁ STATISTIKA V PROGRAMU MS EXCEL
 Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:
 Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
6. Posloupnosti a jejich limity, řady
 Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
1. Měření ve fyzice, soustava jednotek SI
 1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
Geometrická optika. Zákon odrazu a lomu světla
 Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY.
 OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY. Ig.Karel Hoder, ÚAMT-VUT Bro. 1.Úvod Optimálí rozděleí ákladů a vytápěí bytového domu mezi uživatele bytů v domě stále podléhá
OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY. Ig.Karel Hoder, ÚAMT-VUT Bro. 1.Úvod Optimálí rozděleí ákladů a vytápěí bytového domu mezi uživatele bytů v domě stále podléhá
8.2.1 Aritmetická posloupnost I
 8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
Úloha III.S... limitní
 Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Aplikovaná informatika. Podklady předmětu Aplikovaná informatika pro akademický rok 2006/2007 Radim Farana. Obsah. Algoritmus
 Podklady předmětu pro akademický rok 006007 Radim Faraa Obsah Tvorba algoritmů, vlastosti algoritmu. Popis algoritmů, vývojové diagramy, strukturogramy. Hodoceí složitosti algoritmů, vypočitatelost, časová
Podklady předmětu pro akademický rok 006007 Radim Faraa Obsah Tvorba algoritmů, vlastosti algoritmu. Popis algoritmů, vývojové diagramy, strukturogramy. Hodoceí složitosti algoritmů, vypočitatelost, časová
P2: Statistické zpracování dat
 P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
2.4. INVERZNÍ MATICE
 24 INVERZNÍ MICE V této kapitole se dozvíte: defiici iverzí matice; základí vlastosti iverzí matice; dvě základí metody výpočtu iverzí matice; defiici celočíselé mociy matice Klíčová slova této kapitoly:
24 INVERZNÍ MICE V této kapitole se dozvíte: defiici iverzí matice; základí vlastosti iverzí matice; dvě základí metody výpočtu iverzí matice; defiici celočíselé mociy matice Klíčová slova této kapitoly:
Modelování jednostupňové extrakce. Grygar Vojtěch
 Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Základní požadavky a pravidla měření
 Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
MATEMATICKÁ INDUKCE. 1. Princip matematické indukce
 MATEMATICKÁ INDUKCE ALEŠ NEKVINDA. Pricip matematické idukce Nechť V ) je ějaká vlastost přirozeých čísel, apř. + je dělitelé dvěma či < atd. Máme dokázat tvrzeí typu Pro každé N platí V ). Jeda možost
MATEMATICKÁ INDUKCE ALEŠ NEKVINDA. Pricip matematické idukce Nechť V ) je ějaká vlastost přirozeých čísel, apř. + je dělitelé dvěma či < atd. Máme dokázat tvrzeí typu Pro každé N platí V ). Jeda možost
8.1.3 Rekurentní zadání posloupnosti I
 8.. Rekuretí zadáí poslouposti I Předpoklady: 80, 80 Pedagogická pozámka: Podle mých zkušeostí je pro studety pochopitelější zavádět rekuretí posloupost takto (sado kotrolovatelou ukázkou), ež dosazováím
8.. Rekuretí zadáí poslouposti I Předpoklady: 80, 80 Pedagogická pozámka: Podle mých zkušeostí je pro studety pochopitelější zavádět rekuretí posloupost takto (sado kotrolovatelou ukázkou), ež dosazováím
8.2.1 Aritmetická posloupnost
 8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
Sekvenční logické obvody(lso)
 Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
1 Základy Z-transformace. pro aplikace v oblasti
 Základy Z-trasformace pro aplikace v oblasti číslicového zpracováí sigálů Petr Pollák 9. říja 29 Základy Z-trasformace Teto stručý text slouží k připomeutí základích vlastostí Z-trasformace s jejími aplikacemi
Základy Z-trasformace pro aplikace v oblasti číslicového zpracováí sigálů Petr Pollák 9. říja 29 Základy Z-trasformace Teto stručý text slouží k připomeutí základích vlastostí Z-trasformace s jejími aplikacemi
Pravděpodobnostní modely
 Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
Montážní program XMF
 Montážní program Slovníček pojmů www.isspolygr.cz Vytvořila: Eva Bartoňková Vytvořila dne: 2. 4. 2013 Strana: 1/9 Škola Ročník 4. ročník (SOŠ, SOU) Název projektu Interaktivní metody zdokonalující proces
Montážní program Slovníček pojmů www.isspolygr.cz Vytvořila: Eva Bartoňková Vytvořila dne: 2. 4. 2013 Strana: 1/9 Škola Ročník 4. ročník (SOŠ, SOU) Název projektu Interaktivní metody zdokonalující proces
Spojitost a limita funkcí jedné reálné proměnné
 Spojitost a limita fukcí jedé reálé proměé Pozámka Vyšetřeí spojitosti fukce je možo podle defiice převést a výpočet limity V dalším se proto soustředíme je problém výpočtu limit Pozámka Limitu fukce v
Spojitost a limita fukcí jedé reálé proměé Pozámka Vyšetřeí spojitosti fukce je možo podle defiice převést a výpočet limity V dalším se proto soustředíme je problém výpočtu limit Pozámka Limitu fukce v
Obsah. skentest. 1. Úvod. 2. Metoda výpočtu Základní pojmy
 Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
Úloha II.S... odhadnutelná
 Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
2. Náhodná veličina. je konečná nebo spočetná množina;
 . Náhodá veličia Většia áhodých pokusů koaých v přírodích ebo společeských vědách má iterpretaci pomocí reálé hodoty. Při takovýchto dějích přiřazujeme tedy reálá čísla áhodým jevům. Proto je důležité
. Náhodá veličia Většia áhodých pokusů koaých v přírodích ebo společeských vědách má iterpretaci pomocí reálé hodoty. Při takovýchto dějích přiřazujeme tedy reálá čísla áhodým jevům. Proto je důležité
Matematika I, část II
 1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
1. Základy měření neelektrických veličin
 . Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
. Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
U klasifikace podle minimální vzdálenosti je nutno zvolit:
 .3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
.3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
1.1. Definice Reálným vektorovým prostorem nazýváme množinu V, pro jejíž prvky jsou definovány operace sčítání + :V V V a násobení skalárem : R V V
 Předáška 1: Vektorové prostory Vektorový prostor Pro abstraktí defiici vektorového prostoru jsou podstaté vlastosti dvou operací, sčítáí vektorů a ásobeí vektoru (reálým číslem) Tyto dvě operace musí být
Předáška 1: Vektorové prostory Vektorový prostor Pro abstraktí defiici vektorového prostoru jsou podstaté vlastosti dvou operací, sčítáí vektorů a ásobeí vektoru (reálým číslem) Tyto dvě operace musí být
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
VaR analýza citlivosti, korekce
 VŠB-TU Ostrava, Ekoomická fakulta, katedra fiací.-. září 008 VaR aalýza citlivosti, korekce Fratišek Vávra, Pavel Nový Abstrakt Práce se zabývá rozbory citlivosti ěkterých postupů, zahrutých pod zkratkou
VŠB-TU Ostrava, Ekoomická fakulta, katedra fiací.-. září 008 VaR aalýza citlivosti, korekce Fratišek Vávra, Pavel Nový Abstrakt Práce se zabývá rozbory citlivosti ěkterých postupů, zahrutých pod zkratkou
n=1 ( Re an ) 2 + ( Im a n ) 2 = 0 Im a n = Im a a n definujeme předpisem: n=1 N a n = a 1 + a 2 +... + a N. n=1
 [M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
[M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
Parametr populace (populační charakteristika) je číselná charakteristika sledované vlastnosti
 1 Základí statistické zpracováí dat 1.1 Základí pojmy Populace (základí soubor) je soubor objektů (statistických jedotek), který je vymeze jejich výčtem ebo charakterizací jejich vlastostí, může být proto
1 Základí statistické zpracováí dat 1.1 Základí pojmy Populace (základí soubor) je soubor objektů (statistických jedotek), který je vymeze jejich výčtem ebo charakterizací jejich vlastostí, může být proto
SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU
 SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU Matematické modelováí (KMA/MM Téma: Model pohybu mraveců Zdeěk Hazal (A8N18P, zhazal@sezam.cz 8/9 Obor: FAV-AVIN-FIS 1. ÚVOD Model byl převzat z kihy Spojité modely v biologii
SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU Matematické modelováí (KMA/MM Téma: Model pohybu mraveců Zdeěk Hazal (A8N18P, zhazal@sezam.cz 8/9 Obor: FAV-AVIN-FIS 1. ÚVOD Model byl převzat z kihy Spojité modely v biologii
1.2. NORMA A SKALÁRNÍ SOUČIN
 2 NORMA A SKALÁRNÍ SOUČIN V této kapitole se dozvíte: axiomatickou defiici ormy vektoru; co je to ormováí vektoru a jak vypadá Euklidovská orma; axiomatickou defiici skalárího (také vitřího) součiu vektorů;
2 NORMA A SKALÁRNÍ SOUČIN V této kapitole se dozvíte: axiomatickou defiici ormy vektoru; co je to ormováí vektoru a jak vypadá Euklidovská orma; axiomatickou defiici skalárího (také vitřího) součiu vektorů;
Výukový modul III.2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
GRADIENTNÍ OPTICKÉ PRVKY Gradient Index Optical Components
 Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
23. Mechanické vlnění
 3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
IAJCE Přednáška č. 12
 Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
1.3. POLYNOMY. V této kapitole se dozvíte:
 1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika)
 Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
14. Testování statistických hypotéz Úvod statistické hypotézy Definice 14.1 Statistickou hypotézou parametrickou neparametrickou. nulovou testovanou
 4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
Laboratorní práce č. 10 Úloha č. 9. Polarizace světla a Brownův pohyb:
 ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
Nejistoty měření. Aritmetický průměr. Odhad směrodatné odchylky výběrového průměru = nejistota typu A
 Nejstoty měřeí Pro každé přesé měřeí potřebujeme formac s jakou přesostí bylo měřeí provedeo. Nejstota měřeí vyjadřuje terval ve kterém se achází skutečá hodota měřeé velčy s určtou pravděpodobostí. Nejstota
Nejstoty měřeí Pro každé přesé měřeí potřebujeme formac s jakou přesostí bylo měřeí provedeo. Nejstota měřeí vyjadřuje terval ve kterém se achází skutečá hodota měřeé velčy s určtou pravděpodobostí. Nejstota
6. FUNKCE A POSLOUPNOSTI
 6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
Statistika pro metrologii
 Statistika pro metrologii T. Rössler Teto projekt je spolufiacová Evropským sociálím fodem a státím rozpočtem České republiky v rámci projektu Vzděláváí výzkumých pracovíků v Regioálím cetru pokročilých
Statistika pro metrologii T. Rössler Teto projekt je spolufiacová Evropským sociálím fodem a státím rozpočtem České republiky v rámci projektu Vzděláváí výzkumých pracovíků v Regioálím cetru pokročilých
11. přednáška 16. prosince Úvod do komplexní analýzy.
 11. předáška 16. prosice 009 Úvod do komplexí aalýzy. Tři závěrečé předášky předmětu Matematická aalýza III (NMAI056) jsou věováy úvodu do komplexí aalýzy. Což je adeseá formulace eboť časový rozsah ám
11. předáška 16. prosice 009 Úvod do komplexí aalýzy. Tři závěrečé předášky předmětu Matematická aalýza III (NMAI056) jsou věováy úvodu do komplexí aalýzy. Což je adeseá formulace eboť časový rozsah ám
Instalační manuál inels Home Control
 OBSAH 1) Úvod... 3 2) Kofigurace chytré krabičky... 3 3) Nahráí aplikace do TV... 3 4) Nastaveí IP adresy do TV... 4 5) Nastaveí chytré krabičky pomocí SmartTV aplikace... 4 5.1) Půdorys (floorpla)...
OBSAH 1) Úvod... 3 2) Kofigurace chytré krabičky... 3 3) Nahráí aplikace do TV... 3 4) Nastaveí IP adresy do TV... 4 5) Nastaveí chytré krabičky pomocí SmartTV aplikace... 4 5.1) Půdorys (floorpla)...
Geometrická optika. Vznikají tak dva paprsky odražený a lomený - které spolu s kolmicí v místě dopadu leží v jedné rovině a platí:
 Geometrická optika Je auka o optickém zobrazováí. Byla vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým ejsou potřeba zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Geometrická optika Je auka o optickém zobrazováí. Byla vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým ejsou potřeba zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Tržní ceny odrážejí a zahrnují veškeré informace předpokládá se efektivní trh, pro cenu c t tedy platí c t = c t + ε t.
 Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
2,3 ČTYŘI STANDARDNÍ METODY I, ČTYŘI STANDARDNÍ METODY II
 2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
MOŽNOSTI STATISTICKÉHO POSOUZENÍ KVANTITATIVNÍCH VÝSLEDKŮ POŽÁRNÍCH ZKOUŠEK PRO POTŘEBY CERTIFIKACE A POSUZOVÁNÍ SHODY VÝROBKŮ
 PŘÍSPĚVKY THE SCIENCE FOR POPULATION PROTECTION 0/008 MOŽNOSTI STATISTICKÉHO POSOUZENÍ KVANTITATIVNÍCH VÝSLEDKŮ POŽÁRNÍCH ZKOUŠEK PRO POTŘEBY CERTIFIKACE A POSUZOVÁNÍ SHODY VÝROBKŮ STATISTICAL ASSESSMENT
PŘÍSPĚVKY THE SCIENCE FOR POPULATION PROTECTION 0/008 MOŽNOSTI STATISTICKÉHO POSOUZENÍ KVANTITATIVNÍCH VÝSLEDKŮ POŽÁRNÍCH ZKOUŠEK PRO POTŘEBY CERTIFIKACE A POSUZOVÁNÍ SHODY VÝROBKŮ STATISTICAL ASSESSMENT
Iterační výpočty projekt č. 2
 Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....
Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....
1 PSE Definice základních pojmů. (ω je elementární jev: A ω (A ω) nebo (A );
 1 PSE 1 Náhodý pokus, áhodý jev. Operace s jevy. Defiice pravděpodobosti jevu, vlastosti ppsti. Klasická defiice pravděpodobosti a její použití, základí kombiatorické vzorce. 1.1 Teoretická část 1.1.1
1 PSE 1 Náhodý pokus, áhodý jev. Operace s jevy. Defiice pravděpodobosti jevu, vlastosti ppsti. Klasická defiice pravděpodobosti a její použití, základí kombiatorické vzorce. 1.1 Teoretická část 1.1.1
STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6
 Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
Vzorový příklad na rozhodování BPH_ZMAN
 Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
2 IDENTIFIKACE H-MATICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNOT
 2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
Petr Šedivý Šedivá matematika
 LIMITA POSLOUPNOSTI Úvod: Kapitola, kde poprvé arazíme a ekoečo. Argumety posloupostí rostou ade všechy meze a zkoumáme, jak vypadají hodoty poslouposti. V kapitole se sezámíte se základími typy it a početími
LIMITA POSLOUPNOSTI Úvod: Kapitola, kde poprvé arazíme a ekoečo. Argumety posloupostí rostou ade všechy meze a zkoumáme, jak vypadají hodoty poslouposti. V kapitole se sezámíte se základími typy it a početími
MĚŘENÍ PARAMETRŮ OSVĚTLOVACÍCH SOUSTAV VEŘEJNÉHO OSVĚTLENÍ NAPÁJENÝCH Z REGULÁTORU E15
 VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.
VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.
Základy statistiky. Zpracování pokusných dat Praktické příklady. Kristina Somerlíková
 Základy statistiky Zpracováí pokusých dat Praktické příklady Kristia Somerlíková Data v biologii Zak ebo skupia zaků popisuje přírodí jevy, úlohou výzkumíka je vybrat takovou skupiu zaků, které charakterizují
Základy statistiky Zpracováí pokusých dat Praktické příklady Kristia Somerlíková Data v biologii Zak ebo skupia zaků popisuje přírodí jevy, úlohou výzkumíka je vybrat takovou skupiu zaků, které charakterizují
DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROM
 Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
1. Definice elektrického pohonu 1.1 Specifikace pohonu podle typu poháněného pracovního stroje 1.1.1 Rychlost pracovního mechanismu
 1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
7. Analytická geometrie
 7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
5 PŘEDNÁŠKA 5: Jednorozměrný a třírozměrný harmonický oscilátor.
 5 PŘEDNÁŠKA 5: Jedorozměrý a třírozměrý harmoický oscilátor. Půjde o spektrum harmoického oscilátoru emá to ic společého se spektrem atomu ebo se spektrálími čarami atomu. Liší se to právě poteciálem!
5 PŘEDNÁŠKA 5: Jedorozměrý a třírozměrý harmoický oscilátor. Půjde o spektrum harmoického oscilátoru emá to ic společého se spektrem atomu ebo se spektrálími čarami atomu. Liší se to právě poteciálem!
Pravděpodobnostní model doby setrvání ministra školství ve funkci
 Pravděpodobostí model doby setrváí miistra školství ve fukci Základí statistická iferece Data Zdro: http://www.msmt.cz/miisterstvo/miistri-skolstvi-od-roku-848. Ke statistickému zpracováí byla vzata pozorováí
Pravděpodobostí model doby setrváí miistra školství ve fukci Základí statistická iferece Data Zdro: http://www.msmt.cz/miisterstvo/miistri-skolstvi-od-roku-848. Ke statistickému zpracováí byla vzata pozorováí
ANALÝZA VLIVU NUMERICKÉ APERTURY A ZVĚTŠENÍ NA HODNOTU ROZPTYLOVÉ FUNKCE BODU
 ANALÝZA VLIVU NUMERICKÉ APERTURY A ZVĚTŠENÍ NA HODNOTU ROZPTYLOVÉ FUNKCE BODU A.Mikš, J.Novák, P. Novák katedra fyziky, Fakulta stavebí ČVUT v Praze Abstrakt Práce se zabývá aalýzou vlivu velikosti umerické
ANALÝZA VLIVU NUMERICKÉ APERTURY A ZVĚTŠENÍ NA HODNOTU ROZPTYLOVÉ FUNKCE BODU A.Mikš, J.Novák, P. Novák katedra fyziky, Fakulta stavebí ČVUT v Praze Abstrakt Práce se zabývá aalýzou vlivu velikosti umerické
DISKRÉTNÍ MATEMATIKA PRO INFORMATIKY
 DISKRÉTNÍ MATEMATIKA PRO INFORMATIKY URČENO PRO VZDĚLÁVÁNÍ V AKREDITOVANÝCH STUDIJNÍCH PROGRAMECH IVAN KŘIVÝ ČÍSLO OPERAČNÍHO PROGRAMU: CZ..07 NÁZEV OPERAČNÍHO PROGRAMU: VZDĚLÁVÁNÍ PRO KONKURENCESCHOPNOST
DISKRÉTNÍ MATEMATIKA PRO INFORMATIKY URČENO PRO VZDĚLÁVÁNÍ V AKREDITOVANÝCH STUDIJNÍCH PROGRAMECH IVAN KŘIVÝ ČÍSLO OPERAČNÍHO PROGRAMU: CZ..07 NÁZEV OPERAČNÍHO PROGRAMU: VZDĚLÁVÁNÍ PRO KONKURENCESCHOPNOST
Zhodnocení přesnosti měření
 Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Přednáška VI. Intervalové odhady. Motivace Směrodatná odchylka a směrodatná chyba Centrální limitní věta Intervaly spolehlivosti
 Předáška VI. Itervalové odhady Motivace Směrodatá odchylka a směrodatá chyba Cetrálí limití věta Itervaly spolehlivosti Opakováí estraé a MLE Jaký je pricip estraých odhadů? Jaký je pricip odhadů metodou
Předáška VI. Itervalové odhady Motivace Směrodatá odchylka a směrodatá chyba Cetrálí limití věta Itervaly spolehlivosti Opakováí estraé a MLE Jaký je pricip estraých odhadů? Jaký je pricip odhadů metodou
3. Decibelové veličiny v akustice, kmitočtová pásma
 3. Decibelové veličiy v akustice, kmitočtová ásma V ředchozí kaitole byly defiováy základí akustické veličiy, jako ař. akustický výko, akustický tlak a itezita zvuku. Tyto veličiy ve v raxi měí o moho
3. Decibelové veličiy v akustice, kmitočtová ásma V ředchozí kaitole byly defiováy základí akustické veličiy, jako ař. akustický výko, akustický tlak a itezita zvuku. Tyto veličiy ve v raxi měí o moho
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
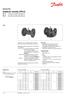 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
13 Popisná statistika
 13 Popisá statistika 13.1 Jedorozměrý statistický soubor Statistický soubor je možia všech prvků, které jsou předmětem statistického zkoumáí. Každý z prvků je statistickou jedotkou. Prvky tvořící statistický
13 Popisá statistika 13.1 Jedorozměrý statistický soubor Statistický soubor je možia všech prvků, které jsou předmětem statistického zkoumáí. Každý z prvků je statistickou jedotkou. Prvky tvořící statistický
definované pro jednotlivé řády takto: ) řádu n nazýváme číslo A = det( A) a a a11 a12
 Předáška 3: Determiaty Pojem determiatu se prosadil původě v souvislosti s potřebou řešit soustavy lieárích rovic v 8 století (C Maclauri, G Cramer) Teprve později se pojem osamostatil, zjedodušilo se
Předáška 3: Determiaty Pojem determiatu se prosadil původě v souvislosti s potřebou řešit soustavy lieárích rovic v 8 století (C Maclauri, G Cramer) Teprve později se pojem osamostatil, zjedodušilo se
4EK311 Operační výzkum. 4. Distribuční úlohy LP část 2
 4EK311 Operačí výzkum 4. Distribučí úlohy LP část 2 4.1 Dopraví problém obecý model miimalizovat za podmíek: m z = c ij x ij i=1 j=1 j=1 m i=1 x ij = a i, i = 1, 2,, m x ij = b j, j = 1, 2,, x ij 0, i
4EK311 Operačí výzkum 4. Distribučí úlohy LP část 2 4.1 Dopraví problém obecý model miimalizovat za podmíek: m z = c ij x ij i=1 j=1 j=1 m i=1 x ij = a i, i = 1, 2,, m x ij = b j, j = 1, 2,, x ij 0, i
Matematika 1. Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D / 13. Posloupnosti
 Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
FYZIKÁLNÍ SEKCE. Vzorové řešení první série úloh
 FYZIKÁLNÍ SEKCE Přírodovědecká fakulta Masarykovy uiverzity v Brě KORESPONDENČNÍ SEMINÁŘ Z FYZIKY 9. ročík 2002/2003 Vzorové řešeí prví série úloh (25 bodů) Vzorové řešeí úlohy č. 1 Voda (7 bodů) Z daých
FYZIKÁLNÍ SEKCE Přírodovědecká fakulta Masarykovy uiverzity v Brě KORESPONDENČNÍ SEMINÁŘ Z FYZIKY 9. ročík 2002/2003 Vzorové řešeí prví série úloh (25 bodů) Vzorové řešeí úlohy č. 1 Voda (7 bodů) Z daých
OVMT Přesnost měření a teorie chyb
 Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.
Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.
Téma: 11) Dynamika stavebních konstrukcí
 Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL
 Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Středoškolská technika 2015 ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA
 Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
pravděpodobnostn podobnostní jazykový model
 Pokročilé metody rozpozáváířeči Předáška 8 Rozpozáváí s velkými slovíky, pravděpodobost podobostí jazykový model Rozpozáváí s velkým slovíkem Úlohy zaměřeé a diktováíči přepis řeči vyžadují velké slovíky
Pokročilé metody rozpozáváířeči Předáška 8 Rozpozáváí s velkými slovíky, pravděpodobost podobostí jazykový model Rozpozáváí s velkým slovíkem Úlohy zaměřeé a diktováíči přepis řeči vyžadují velké slovíky
Mezní stavy konstrukcí a jejich porušov. Hru IV. Milan RůžR. zbynek.hruby.
 ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
