Z tohoto setříděného souboru snadno sestavíme tabulku prostého rozdělení četností.

Transkript

1 Příklad 1 Firma má pro své zaměstnance stanoveny tyto základní mzdy v Kč: 18600, 17650, 19200, 20400, 20800, 18600, 20400, 24200, 20400, 19200, 24200, 20400, 17650, 25800, Určete charakteristiky tohoto souboru. Řešení 1 Tuto úlohu budeme řešit třikrát a pokaždé výrazně jinak. Poprvé to bude tak, že řešení zvládneme celé téměř ručně jen s minimálním použitím MS Excel na grafy a zpracování tabulky s několika součiny. V rámci druhého řešení využijeme v co nejvyšší míře vestavěné statistické funkce MS Excel. A nakonec při třetím řešení necháme udělat skoro všechnu práci doplněk MS Excel Analýza dat. Tento doplněk lze do MS Excel doinstalovat. Vzhledem k tomu, že při praktických úlohách jsou soubory dat opravdu veliké, není pro jejich zpracování ruční metodou prostor a čas, navíc při použití ruční metody hrozí veliké riziko výpočtové chyby. Tomu se vyhneme jen použitím vhodných nástrojů na zpracování velkých objemů dat. V té jednodušší poloze může být takovým nástrojem MS Excel (a také jim v rámci zpracování většiny běžných statistických šetření je). V náročnějších případech se používají ještě vhodnější softwarové systémy, například skvělý program Statistica firmy StatSoft. Řešení 1a téměř úplně ruční práce Označíme si jednotlivé prvky zadaného souboru. =18600, =17650, =19200, =20400, =20800, =18600, =20400, =24200, =20400, =19200, =24200, =20400, =17650, =25800, =17650 Současně si tento soubor setřídíme od nejmenšího do největšího prvku. () =17650, () =17650, () =17650, () =18600, () =18600, () =19200, () =19200, () =20400, () =20400, () =20400, () =20400, () =20800, () =24200, () =24200, () =25800, Z tohoto setříděného souboru snadno sestavíme tabulku prostého rozdělení četností. Plat v Kč Počet výskytů V tomto případě je jednotlivých různých výší základní mzdy právě sedm. To je dostatečně málo na to, aby se neztratila přehlednost. Nemá tedy smysl uvažovat nějaké třídní rozdělení četností. Vidíme, že máme zadány základní mzdy 15 zaměstnanců, můžeme tedy tuto tabulku snadno rozšířit o sloupec vyjadřující relativní rozdělení četností jednotlivých výší základní mzdy. 1

2 Plat v Kč Počet výskytů Relativní zastoupení =0, = 0, = 0, = 0, = 0, = 0, = 0, Prostou četnost jednotlivých základních mezd vyjádříme sloupcovým grafem. Relativní četnost jednotlivých základních mezd vyjádříme nejvhodněji výsečovým (koláčovým) grafem. K vytvoření obou grafů využijeme MS Excel. Poznámka I tvorbu grafů v MS Excel je tu a tam dobré trénovat. Napoprvé se nemusí očekávaný graf podařit. Nyní již můžeme ze zadaného souboru zjišťovat jednotlivé statistické charakteristiky. 2

3 Extrémní hodnoty získáme snadno ze setříděného souboru. min # = () =17650, max # = () =25800 #$.. #$.. Pro zjištění charakteristik polohy se nejprve rozhodneme pro správný průměr, který je třeba uvažovat. V tomto případě jde jednoznačně o průměr aritmetický. Ten můžeme počítat přímo ze zadaného souboru takto: + = 1 ) * # = 1 15 ( #$ )= =20343,33 Druhou možností je počítat aritmetický průměr z tabulky prostého rozdělení četností. Protože jde o prosté rozdělení, musí vyjít to samé. + = #$ #/ # + / # #$ = = = =20343, Z kvantilů budeme vzhledem k malému rozsahu souboru uvažovat jen medián a první a třetí kvartil. Snadno je nalezneme v setříděném souboru. Vzhledem k tomu, že počet prvků souboru je šikovný (lichý pro medián a příznivý i pro kvartily), dostáváme přímo: 0=0, = () = =0, = () = =0, = () =20800 Modus zjistíme nejsnadněji z tabulky prostého rozdělení četností. Stačí najít nejvyšší hodnotu počtu výskytů a k ní vybrat odpovídající hodnotu základního platu. Dostaneme 2=20400 Protože nyní již máme k dispozici minimum, první kvartil, medián, třetí kvatil a maximum, můžeme sestavit boxplot. Využijeme MS Excel. Protože MS Excel neobsahuje tento typ grafu, počítejme s tím, že cesta ke grafu nebude právě přímá. Nejprve si připravíme tabulku s tímto rozložením dat. Je důležité dát v poslední verzi MS Excel (2013) do prvního pole datového řádku nějaký datum. Dřívější verze snesly i jakýkoli identifikátor řádku. Pokud připravíme více řádků, můžeme najednou připravit více boxplot grafů. Je ale důležité, aby data byla s podobnými měřítky. Kdyby tomu tak nebylo, nic rozumného bychom na grafu neviděli. Boxplot med Q1 max min Q V MS Excel si tuto tabulku vyznačíme a volíme Vložení Grafy Burzovní - Typ objem-otevřenímaximum-minimum-závěr. Volbu potvrdíme a dostaneme polotovar našeho kýženého grafu. 3

4 Název grafu ZM med Q1 max min Q Nyní je třeba tento polotovar upravit tak, aby vyjadřoval co nejlépe to, co chceme. Nejprve si všimneme, že graf obsahuje dvě svislá měřítka. To levé je pro sloupec med (pro zvolený typ grafu jde o objem), pravé slouží pro ostatní data. Naše data mají ale stejné měřítko, proto levé měřítko měřítko upravíme tak, aby bylo stejné s pravým. Vybereme ho kliknutím levým tlačítkem myši a pravým tlačítkem myši vyvoláme lokální menu. Zde vybereme Formát osy. V něm nastavíme maximum na stejnou hodnotu, jaká je v pravém měřítku. Okno formátu můžeme uzavřít. Graf nyní vypadá takto. Je zřejmé, že hodnotu med nám zakrývá výplň obdélníku. Klikneme tedy levým tlačítkem myši do tohoto obdélníku a pravým tlačítkem myši volíme lokální menu. Vybereme Formát sloupců vzrůstu. Zde nastavíme Výplň Bez výplně. Okno formátu uzavřeme. Graf nyní vypadá takto. 4

5 Horní hrana modrého obdélníku vyjadřuje nyní hodnotu med. Jen ta velká modrá plocha poněkud vadí. Klikneme do ní levým tlačítkem myši a pravým volíme lokální menu. Volíme Formát datové řady. Zde nastavíme Výplň Bez výplně a Ohraničení Plná čára a vybereme nějakou méně výraznou barvu (proti černé), například modrou. Graf nyní vypadá takto. Název grafu ZM med Q1 max min Q Náš graf už vypadá docela dobře. Změníme jen název grafu na takový, který potřebujeme (klikneme a přepíšeme) a zbavíme se legendy, protože je uvedena v pořadí, ve kterém je v datech, což ale není přirozené pořadí dat pro boxplot. Takto je legenda spíše matoucí. Spolehneme se tedy raději na to, že jednotlivé prvky boxplot mají standardní význam. Nakonec nahradíme námi zavedený nesmyslný datum za něco, co smysl má identifikátor tohoto šetření. To jde udělat překvapivě tak, že ho změníme přímo v naší tabulce. Boxplot med Q1 max min Q3 ZM

6 Náš graf vypadá nyní již celkem uspokojivě. Nyní už je z grafu zcela jasné, o co jde, ale stále může v celkovém dojmu rušit obdélník vytvořený pro medián. Nás zajímá jen jeho horní strana. MS Excel nám sice nedává možnost odstranit z grafu pro nás nadbytečné strany obdélníka, ale dává nám možnost udělat obrysovou čáru v přechodovém tvaru, tedy jako měnící barvu. Když si s tím trochu pohrajeme, podaří se nám nastavit přechod tak, že je patrná prakticky jen horní strana obdélníka. Nakonec nastavíme sílu všech čar tak, aby byly stejné a současně byly dostatečně kontrastní vůči pozadí. Graf pak vypadá takto. Jsme-li s grafem spokojeni a víme-li, že podobných grafů budeme tvořit více, je vhodný si tento uspokojivý tvar uložit jako šablonu. Další boxplot z ní vytvoříme pouhou změnou levého měřítka. 6

7 Nyní se budeme věnovat výpočtu charakteristik variability. Rozptyl budeme počítat podle vzorce + 3 = 1 ) *( # ) #$ Pro výpočet si připravíme tabulku se všemi zadanými hodnotami. S výhodou využijeme MS Excel, ruční výpočet by byl poněkud pracnější. i ZaklMzda Průměr Odchylka Odchylka , , , , , , , , , ,33 56, , ,33 456, , , , , ,33 56, , , , , ,33 56, , , , , , , , ,33 56, , , , , , , , , , ,44 Sum , ,33 V součtovém řádku máme kontrolu v tom, že součet odchylek je nulový. Pro výpočet rozptylu je ale důležitý součet čtverců odchylek v posledním sloupci. Stačí spočítat jeho aritmetický průměr a dostaneme rozptyl. 3 = , ,89 Poznámka Výpočet proběhl v plné přesnosti poskytované MS Excel, hodnoty jsou prezentovány se zaokrouhlením na dvě desetinná místa. Nyní již snadno dostáváme další charakteristiky variability. Směrodatná odchylka se vypočte odmocněním rozptylu. 3=63 =2452,20 Variační koeficient se vypočte vydělením směrodatné odchylky průměrem. 7= 3 = 2452, ,33 =0,12 Rozpětí získáme ze setříděného souboru nebo později určených extrémů. 8= () = =8150 Mezikvartilové rozpětí získáme z již dříve vypočtených kvartilů. 8 9 =1 1 =0, 0, = =2200 Trochu více práce nám dá výpočet střední odchylky od průměru. Ale pomůžeme si úpravou naší poslední tabulky, do které doplníme sloupec s absolutní hodnotou odchylky a do posledního řádku součet těchto odchylek. Střední odchylku od průměru vypočteme jako průměr těchto absolutních hodnot. 7

8 i ZaklMzda Průměr Odchylka Odchylka2 AbsOdchylka , , , , , , , , , , , , ,33 56, ,11 56, ,33 456, ,44 456, , , , , ,33 56, ,11 56, , , , , ,33 56, ,11 56, , , , , , , , , ,33 56, ,11 56, , , , , , , , , , , , ,33 Sum , , ,67 Střední odchylku od průměru vypočteme jako průměr těchto absolutních hodnot. + : = 1 ) * # = ,67=1847,11 #$ Teoreticky bychom mohli počítat i střední odchylku od jiného centrálního bodu, například od mediánu nebo od modusu. Technika výpočtu by byla analogická. Zbývá vypočítat charakteristiky tvaru šikmost a špičatost. K tomu potřebujeme nejprve vypočítat třetí a čtvrtý centrální moment. Opět si pomůžeme rozšířením naší tabulky. i ZaklMzda Průměr Odchylka Odchylka2 Odchylka3 Odchylka , , , , , , , , , , , , , , , ,33 56, , , , ,33 456, , , , , , , , , ,33 56, , , , , , , , , ,33 56, , , , , , , , , , , , , , ,33 56, , , , , , , , , , , , , , , , , , ,20 Sum , , , ,00 8

9 Třetí centrální moment je průměrem třetích mocnin odchylek a čtvrtý centrální moment je průměrem čtvrtých mocnin odchylek. Odtud tedy dostáváme. + < = 1 ) *( # ) = ,11= ,41 + #$ < = 1 ) *( # ) = ,00= ,00 #$ Nyní již snadno dosazením do vzorce vypočteme šikmost = = < 3 = , ,20 = , ,68 =0,93 Daný soubor je tedy mírně záporně zešikmen. Podobně snadno dostaneme špičatost = = < 3 3= , ,20 3= , ,00 3=2,78 3= 0,22 Daný soubor je tedy mírně zploštělý. Při výpočtu šikmosti a špičatosti jsme už počítali s docela velkými čísly. Důvodem je počítání s vyššími mocninami čísel vzdálenějších od hodnoty 1. Z toho plyne poučení, že je vždy vhodné volit měřítko tak, aby odchylky měly průměrnou velikost relativně blízkou jedné. V tomto případu by bylo vhodné pracovat se základní mzdou nikoli v Kč, ale v tisících Kč. Řešení 1b využití MS Excel Jednotlivé prvky zadaného souboru vložíme do MS Excel do nějaké oblasti. Tvar této oblasti může být v zásadě libovolný (sloupec, řádek, obdélník) pro většinu toho, co budeme dělat dále. Ale pro vytvoření tabulky a grafu četnosti je vhodné mít data uložená jako sloupec. V tomto případě je budeme mít na listu Soubor. Data Celou oblast vybereme a stiskneme na ní pravé tlačítko myši. Z lokálního menu zvolíme Definovat název. Zda nastavíme název oblasti na Data a volbu názvu potvrdíme stiskem tlačítka OK. Tím je 9

10 oblast pojmenována a my se na ni budeme odkazovat tímto jednoduchým názvem. To je jistě příjemné. Nebude nutné vypisovat hranice zvolené oblasti v každém vzorci. Nyní vytvoříme tabulku a graf četnosti výskytů jednotlivých hodnot. Celou oblast dat vybereme a volíme Vložení Kontingenční graf. Přitom dostaneme jak kontingenční tabulku, tak ontingenční graf současně. Stiskneme tlačítko OK. Objeví se prostor pro zadání polí kontingenční tabulky a grafu. 10

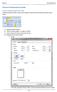
11 Zatrhneme pole Data a jeho kopii přetáhneme do prostoru Osy a do prostoru Hodnoty. V prostoru hodnoty volíme Počet z Data. Dostaneme Tabulku i graf prostých četností máme dokončenu. V případu potřeby můžeme udělat nějaké kosmetické úpravy. Pokud bychom potřebovali tabulku a graf relativních četností, uděláme je stejně jako v řešení 1a. Nyní přejdeme na List PopStat, na kterém budeme počítat jednotlivé charakteristiky našeho souboru. Přitom budeme využívat jednotlivé statistické funkce MS Excel. Postupně nastavíme potřebné texty a vzorce dle následujícího obrázku. Sloupce Značka a Vzorec jsou samozřejmě zbytečné. Slouží jen 11

12 k tomu, abychom si propojili teoretickou pasáž s praktickým výpočtem a ukázali si, jaké vzorce nám zajišťují výpočet potřebných hodnot. Z obrázku je patrno, že se v MS Excelu dají najít věci, které nejsou přímo podporovány existencí vhodné funkce. A současně je dobré si uvědomit, že celá řada dalších statistických funkcí vestavěných do MS Excel není pro řešení naší úlohy potřeba. Nakonec si připravíme data pro boxplot. Přejdeme na příslušný list a nachystáme vhodný záznam. V řádku pro data použijeme buď odkazy na příslušné buňky listu PopStat, nebo přímo stejné vzorce jako v těchto buňkách. První přístup je takový programátorštější využijeme ihned to, co Excel již jednou vypočetl. Druhý přístup je asi bezpečnější neriskujeme zadání chybného odkazu. Do sloupce Boxplot zadáme zatím nějaké vhodné datum. Dostaneme 12

13 Boxplot med Q1 max min Q3 ZM A nyní již snadno s využitím dříve uložené šablony grafu boxplot (viz řešení 1a) a změně formálně zadaného datumu na něco smysluplného odstaneme potřebný graf. Porovnáním dat zadaného souboru s vytvořeným boxplot ihned vidíme užitečnost boxplot pro rychlý náhled o hodnotách dat v souboru. Ještě patrnější to je, použijeme-li k tomuto porovnání setříděná data. Konkrétně v tomto případě má čtvrtina zaměstnanců s nejnižšími základními mzdami tuto mzdu v poměrně úzkém rozmezí (úsek pod obdélníky). Další čtvrtina zaměstnanců má základní mzdu v širším rozmezí (dolní obdélník). Třetí čtvrtina zaměstnanců má mzdu ve velmi úzkém rozmezí (horní obdélník). Nakonec nejlépe mzdově hodnocená čtvrtina zaměstnanců má mzdu ve velmi širokém rozmezí (úsek nad obdélníky) Z boxplot je patrné i to, že polovina zaměstnanců se středními platy (tedy ti, kteří nejsou ani v nejméně ani v nejvíce hodnocené skupině) má základní mzdu v poměrně úzkém rozmezí (jde o mezikvartilový rozptyl). Přitom rozptyl celého souboru je poměrně velký. 13

14 Řešení 1c využití doplňku Analýza dat MS Excel V tomto případě předpokládáme, že máme nainstalovaný doplněk MS Excel Analýza dat (k dispozici zdarma). Nachystáme si data ve stejné podobě, jako v řešení 1b. Označíme celý prostor dat. Na záložce Data volíme Analýza dat a ze seznamu analytických nástrojů vybereme Popisná statistika. Stiskneme tlačítko OK. Objeví se okno Popisná statistika. Zadáme Vstupní oblast Data a zatrhneme Celkový přehled. Stiskneme tlačítko OK a na nové listu se nám objeví všechny potřebné základní charakteristiky našeho souboru dat. 14

15 Sloupec1 Stř. hodnota 20343,33333 Chyba stř. hodnoty 655, Medián Modus Směr. odchylka 2538, Rozptyl výběru ,524 Špičatost 0, Šikmost 1, #ODKAZ! 8150 Minimum Maximum Součet Počet 15 Tajemný řádek s indikovaným chybným odkazem je rozpětí. Pokud bychom tuto tabulku chtěli dále používat, můžeme tu podivnost přímo přepsat. Sloupec1 Stř. hodnota 20343,33333 Chyba stř. hodnoty 655, Medián Modus Směr. odchylka 2538, Rozptyl výběru ,524 Špičatost 0, Šikmost 1, Rozpětí 8150 Minimum Maximum Součet Počet 15 Pozor Rozptyl je v tomto doplňku počítán tak, že se součet čtverců odchylek dělí počtem prvků sníženým o jeden. Dává tedy jiný výsledek. Proto je jiný výsledek i u hodnot od rozptylu odvozených. Dále vidíme, že tu nejsou k dispozici kvartily. Pro vykreslení boxplot grafu si je budeme muset vypočítat způsobem, který jsme prezentovali v řešení 1b. Nic není dokonalé. Nicméně prahneme-li po kvantilech a setříděném souboru, stačí v doplňku Analýza dat využít funkci Pořadová statistika a percentily. Případné další zpracování daného souboru jsme si již ukázali v předchozích řešeních. 15

16 Příklad 2 Jednotlivá katastrální území města Liberec mají následující plošnou velikost (ha): Katastr Výměra Katastr Výměra Liberec střed 621,5 Machnín 1133,7 Dolní Hanychov 113,0 Nové Pavlovice 51,4 Doubí 341,7 Ostašov 160,6 Františkov 106,9 Pilínkov 207,8 Hluboká 226,9 Radčice 321,6 Horní Hanychov 743,4 Rochlice 391,1 Horní Růžodol 119,4 Rudolfov 48,8 Horní Suchá 572,7 Ruprechtice 623,7 Janův Důl 34,8 Růžodol I. 336,2 Karlinky 100,8 Staré Pavlovice 172,9 Kateřinky 506,1 Starý Harcov 1169,8 Krásná Studánka 587,4 Vesec 441,9 Kunraticeš 186,6 Vratislavice 1291,0 a) Určete charakteristiky tohoto souboru. b) Rozdělte tyto hodnoty do 7 tříd, rozpětí tříd zaokrouhlete na celé desítky hektarů a určete charakteristiky tohoto souboru tříd. c) Rozdělte tyto hodnoty do 7 tříd, rozpětí tříd zaokrouhlete na celé stovky hektarů a určete charakteristiky tohoto souboru tříd. d) Porovnejte výsledky získané v předchozích třech podúlohách. Řešení 2a V tomto řešení budeme postupovat stejným způsobem jako v řešení 1b, tedy s využitím vestavěných funkcí MS Excel. Excelový sešit z příkladu 1 jsme si uložili pod jiným názvem. Oblast Data na listu Soubor jsme si rozšířili vložením řádků dovnitř oblasti tak, aby právě pojala celý soubor dat tohoto příkladu. Tím jsme si ušetřili opakované zadávání nebo kopírování všech vzorců. Na listu PopStat dostaneme ihned charakteristiky našeho souboru na základě námi zavedených vzorců. 16

17 Z výukových důvodů jsme ponechali na tomto listu zavedené značky charakteristik a textově prezentované vzorce. Zbytečný řádek s neexistující funkcí pro kvadratický průměr jsme odstranili. Je důležité si povšimnout, že v řádku Modus je výsledek #NENÍ K DISPOZICI. To je proto, že každá hodnota v našem souboru je unikátní, neboli žádná nemá největší počet výskytů. Na listu Boxplot se nám naplnila tabulka pro graf boxplot a ten se sám aktualizoval. Po úpravě levého měřítka na stejnou hodnotu, jako má měřítko pravé, změně názvu kategorie (cvičně na VK) a změně názvu grafu máme boxplot pro toto šetření hotový. Porovnáním dat zadaného souboru s vytvořeným boxplot ihned vidíme užitečnost boxplot pro rychlý náhled o hodnotách dat v souboru. Ještě patrnější to je, použijeme-li k tomuto porovnání setříděná data. 17

18 Nejvýraznější jev patrný z tohoto boxplot je, že čtvrtina katastrů města Liberec má velmi malou výměru a navíc ve velmi úzkém rozpětí. Obě střední čtvrtiny katastrů střední velikosti jsou si podobné svým rozpětím. Čtvrtina plošně největších katastrů má výrazně velké rozpětí. Řešení 2b Nyní máme vyšetřit stejný datový soubor, před vlastním vyšetřením ho ale máme rozdělit do sedmi tříd, jejichž rozpětí bude zaokrouhlené na celé desítky hektarů. Počet sedmi tříd je dán zadáním (v teoretické části jsme viděli, že podle Sturgesova pravidla by bylo vhodné volit rozdělení do šesti tříd). Nyní musíme rozhodnout, jaké mají být hranice těchto sedmi tříd. Je dobré, aby třídy měly stejné rozpětí. Nejprve tedy vydělíme rozpětí našeho souboru počtem tříd a zaokrouhlíme toto rozpětí na celé desítky. Dostaneme ,8 = 1256,2 179, Tříd má být sedm. Počáteční hodnotu první třídy musíme volit tak, aby se minimální hodnota vešla do první třídy a maximální hodnota vešla do poslední třídy. Je vhodné volit celá čísla, máme tedy možnost volit dolní hranici první třídy s hodnotou 31, 32, 33 nebo 34. Zdá se, že je to úplně jedno, ale není tomu tak. Při volbě 31 padne katastr Rochlice do třetí třídy a katastr Horní Suchá do čtvrté třídy. Při volbě 33 budou oba tyto katastry o třídu níže. Při volbě 32 bude o třídu níže pouze katastr Rochlice. To zcela jistě ovlivní budoucí výsledky. Z důvodů, které na tomto místě nijak neodůvodňujeme, jsme se rozhodli pro dolní hranici první třídy v hodnotě 32. Jednotlivé třídy budou mít tedy hranice dané následující tabulkou. Do této tabulky jsme již doplnili i počty katastrů, které do jednotlivých tříd patří. Třída Plocha Počet Dostali jsme tak tabulku rozdělení četností. Snadno ověříme, že stále pracujeme s 26 katastry, neboli 26 prvky souboru. Můžeme vytvořit sloupcový graf. 18

19 Někdy je žádoucí, aby jednotlivé sloupce grafu byly prezentovány bez mezer. Důvodem je, že jednotlivé třídy svými intervaly na sebe navazují. Toho dosáhneme tak, že nastaváíme mezeru mezi jednotlivými sloupci na nulu. Pak stejný graf bude vypadat takto. Třídní rozdělení jsme v tomto případě vytvořili ručně. Ale i v tom nám může pomoci MS Excel. Je v něm k dispozici statistická funkce ČETNOSTI, pomocí níž můžeme třídní rozdělení snadno vytvořit. Primární data máme k dispozici v poli Data. Vytovříme si sloupcový vektor horních hranic jednotlivých tříd (tento vektor je vyznačen zeleně). Pod horní hranicí nejvyšší třídy je ještě uvedeno slovo Více pro třídu s hodnotami nad zadaným horním limitem. Do 212,0 412,0 612,0 812,0 1012,0 1212,0 Více Počet Nyní označíme celý prostor pod nadpisem Počet až k hranici označené Více. Do tohoto prostoru vložíme funkci ČETNOSTI (pozor, jde o maticovou funkci vkládáme ji najednou do celého cílového prostoru). Prvním parametrem této funkce je prostor s priárními data, druhým argumentem je vektor horních hranic jednotlivých tříd (zazeleněný, tedy bez slova Více). Pak stiskneme klávesu F2, kterou potvrdíme maticový vzorec a následně stiskmeme kombinaci Ctrl+Shift+Enter, kterou potvrdíme výpočet. Okamžitě dostaneme výsledek. Do Počet 212, , , , , ,0 2 Více 1 19

20 Nyní jsme v situaci, ve které začíná celá řada statistických šetření, nemáme-li k dispozici základní data, ale jen jejich třídní rozdělení. Abychom mohli s třídně rozdělenými daty počítat. Potřebujeme v rámci každé třídy zvolit nějakou hodnotu, která bude reprezentovat každý z prvků patřících do této třídy. Obvykle se tedy volí střed této třídy. O tuto hodnotu si rozšíříme naši tabulku. Třída Plocha Střed Počet Nyní lze požít vzorec pro vážený průměr a podobné rozšíření pro všechny ostatní vhodné vzorce statistických charakteristik k výpočtu. Uvědomme si ale, že pracujeme s pouhými 26 prvky. Není třeba odvozovat nové vzorce, stačí si v našem sešitu MS Excel v poli Data upravit hodnoty tak, aby byly reprezentovány odpovídajícími středy tříd. Vycházíme tedy ze situace (abychom zadávání středů měli jednodušší, primární data jsme si setřídili). Data Sort 122,0 34,8 122,0 48,8 122,0 51,4 122,0 100,8 122,0 106,9 122,0 113,0 122,0 119,4 122,0 160,6 122,0 172,9 122,0 186,6 122,0 207,8 302,0 226,9 302,0 321,6 302,0 336,2 302,0 341,7 302,0 391,1 482,0 441,9 482,0 506,1 662,0 572,7 662,0 587,4 662,0 621,5 662,0 623,7 662,0 743,4 1202,0 1133,7 1202,0 1169,8 1202,0 1291,0 20

21 MS Excel nám pak nově vypočtené charakteristiky i nový boxplot sám dodá. Povšimněme si, že v této verzi první kvartil opticky vymizel. Všechny prvky prvního kvartilu a skoro všechny prvky druhého kvartilu jsou v první třídě. Řešení 2c Nyní máme ještě jednou vyšetřit stejný datový soubor, před vlastním vyšetřením ho ale máme opět rozdělit do sedmi tříd, jejichž rozpětí bude zaokrouhlené na celé stovky hektarů. Nyní musíme rozhodnout, jaké mají být hranice těchto sedmi tříd. Je dobré, aby třídy měly stejné rozpětí. Nejprve tedy vydělíme rozpětí našeho souboru počtem tříd a zaokrouhlíme na celé stovky. Dostaneme 21

22 ,8 = 1256,2 179, Tříd má být sedm, budeme pracovat s jejich rozpětími danými následující tabulkou. Všechny prvky se bez problémů vejdou do některé z tříd. To tabulky jsme si již vyplnili i středy tříd. Třída Plocha Střed Počet V našem sešitu MS Excel v poli Data znovu upravíme hodnoty tak, aby byly reprezentovány odpovídajícími středy tříd. Vycházíme tedy ze situace (abychom zadávání středů měli jednodušší, primární data jsme si setřídili). Data Sort 100,0 34,8 100,0 48,8 100,0 51,4 100,0 100,8 100,0 106,9 100,0 113,0 100,0 119,4 100,0 160,6 100,0 172,9 100,0 186,6 300,0 207,8 300,0 226,9 300,0 321,6 300,0 336,2 300,0 341,7 300,0 391,1 500,0 441,9 500,0 506,1 500,0 572,7 500,0 587,4 700,0 621,5 700,0 623,7 700,0 743,4 1100,0 1133,7 1100,0 1169,8 1300,0 1291,0 MS Excel nám pak nově vypočtené charakteristiky i nový boxplot sám dodá. 22

23 I v této verzi první kvartil opticky vymizel. Oproti předchozí verzi se ale významně rozšířil čtvrtý kvartil. Řešení 2d V této chvíli máme porovnat výsledky jednotlivých šetření v předchozích podúlohách. To nejlépe naplníme tabulkou základních statistických charakteristik v jednotlivých šetřeních a společně prezentovanými boxploty. Dostáváme 23

24 Charakteristika Primární data Třídy po 180 Třídy po 200 Minimum 34,80 122,00 100,00 Maximum 1291, , ,00 Průměr aritmetický 408,14 412,77 400,00 Průměr geometrický 270,13 290,97 274,22 Průměr harmonický 164,46 215,02 192,77 Medián 328,90 302,00 300,00 Kvartil první 117,80 122,00 100,00 Kvartil třetí 595,93 662,00 550,00 Modus #NENÍ_K_DISPOZICI 122,00 100,00 Rozptyl , , ,31 Směrodatná odchylka 349,06 349,74 343,06 Variační koeficient 0,86 0,85 0,86 Rozpětí 1256, , ,00 Mezikvartilové rozpětí 478,13 540,00 450,00 Střední odchylka 277,68 288,64 276,92 Šikmost 1,23 1,22 1,24 Špičatost 0,84 0,57 0,82 Z tabulky i společného box plot (primární data, desítkové zaokrouhlení a stovkové zaokrouhlení) vidíme, že i docela šikovně volené rozdělení do tříd může viditelně ovlivnit výsledek. Nejzajímavější je to u údaje aritmetický průměr, který se při desítkovém zaokrouhlení velikosti třídy zvýšil oproti primárním datům - jakoby se nám Liberec zvětšil. Při stovkovém zaokrouhlení velikosti třídy se aritmetický průměr naopak snížil jakoby se nám Liberec zmenšil. Reálně ovšem celková plocha města Liberec zůstala zachována. Tento jev se dá velice snadno ovlivňovat nastavením počátku prvního intervalu. Samozřejmě vždy záleží na primárních datech. 24

25 Příklad 3 Určete charakteristiky počtu dní s deštěm v Liberci v letech Pro jednotlivé roky nabýval tento znak postupně hodnot 162, 152, 150, 147, 178, 154, 143, 143, 180. Řešení 3 Jde o úlohu s velmi malým souborem dat jde o pouhých devět hodnot. Lze samozřejmě použít již dříve připravený sešit MS Excel se vzorci. To uděláme v prvním řešení. Ale vzhledem k malému rozsahu souboru v druhém řešení provedeme ze cvičných důvodů ruční výpočet podle vzorců. Řešení 3a využití MS Excel Máme tato data v poli Data Data 162,0 152,0 150,0 147,0 178,0 154,0 143,0 143,0 180,0 Z nich dostaneme v připraveném MS Excel tento výsledek. Z těchto dat dostaneme ihned následující boxplot. 25

26 A můžeme přemýšlet, jak to s těmi dešti v Liberci je. Z tohoto šetření vyplývá, že není pravda to, co se o Liberci říká že tu prší pořád. Pravda je, že tu prší skoro obden. Řešení 3a ruční výpočet dle vzorců Označíme si jednotlivé prvky zadaného souboru. =162, =152, =150, =147, =178, =154, =143, =143, =180 Současně si tento soubor setřídíme od nejmenšího do největšího prvku. () =143, () =143, () =147, () =150, () =152, () =154, () =162, () =178, () =180 Extrémní hodnoty získáme snadno ze setříděného souboru. min # = () =143, max # = () =180 #$.. #$.. Pro zjištění charakteristik polohy se nejprve rozhodneme pro správný průměr, který je třeba uvažovat. V tomto případě jde jednoznačně o průměr aritmetický. Ten můžeme počítat přímo ze zadaného souboru takto: + = 1 ) * # = 1 9 ( )= #$ 156,56 Z kvantilů budeme vzhledem k malému rozsahu souboru uvažovat jen medián a první a třetí kvartil. Snadno je nalezneme pomocí setříděného souboru. Vzhledem k tomu, že počet prvků souboru je lichý, dostáváme medián přímo: 0=0, = () =152 První a třetí kvartil leží mezi zadanými hodnotami. Vypočteme je tedy lineární interpolací. 1 =0, = ()+ () = = =145 1 =0, = ()+ () = = =170 V tuto chvíli máme k dispozici všechna data pro boxplot. Mohli bychom ho nakreslit, ale už ho máme. 26