5.7 Vlhkost vzduchu Absolutní vlhkost Poměrná vlhkost Rosný bod Složení vzduchu Měření vlhkosti vzduchu
|
|
|
- Přemysl Liška
- před 8 lety
- Počet zobrazení:
Transkript
1 Fázové přechody Fáze Fázové rozhraní Gibbsovo pravidlo fází Fázový přechod Fázový přechod prvního druhu Fázový přechod druhého druhu Clausiova-Clapeyronova rovnice Skupenství Skupenské teplo Měrné skupenské teplo Molární skupenské teplo Tání Tání krystalických látek Tání amorfních látek Skupenské teplo tání Anomálie vody Tuhnutí Tuhnutí chemicky čistých krystalických látek Skupenské teplo tuhnutí Tuhnutí kovů Vypařování Skupenské teplo vypařování Pára Odpařování Kondenzace Skupenské teplo kondenzace Sublimace Skupenské teplo sublimační Desublimace Fázový diagram Fázový diagram p-t Křivky chladnutí Termická analýza Slitina Vlastnosti slitin Binární soustava Pevné roztoky Eutektikum Ternární soustava Kritický stav 5.7 Vlhkost vzduchu Absolutní vlhkost Poměrná vlhkost Rosný bod Složení vzduchu Měření vlhkosti vzduchu
2 Fázové přechody Fáze je část termodynamické soustavy, která je fyzikálně i chemicky homogenní a od ostatní části soustavy je oddělena ostrým fázovým rozhraním za předpokladu, že nepůsobí vnější síly. Například voda v uzavřené láhvi tvoří jednu fázi, její hladina tvoří ostré rozhraní se vzduchem, který je v láhvi uzavřen. Pro rovnováhu fází ve vícefázové soustavě platí Gibbsovo pravidlo fází. Přeměnu jedné fáze v jinou fázi, například led ve vodu, nazýváme fázový přechod. Rozlišujeme fázové přechody prvního a druhého druhu na základě určitých charakteristik těchto přechodů. Budeme se v této části zabývat pouze přechody prvního druhu, které nazýváme změny skupenství. Pro fázové přechody prvního druhu platí obecně Clausiova-Clapeyronova rovnice. Při změně skupenství látka přijímá nebo odevzdává okolí skupenské teplo. Známe tyto změny skupenství: tání a tuhnutí, vypařování, var a kondenzace, sublimace a desublimace. Fázový diagram je grafické vyjádření závislosti mezi proměnnými určujícími rovnovážný stav soustavy, tj. mezi termodynamickou teplotou T, tlakem p, koncentrací, entropií S. Plošné fázové diagramy obsahují křivky rovnováhy dvou fází. Trojrozměrné fázové diagramy obsahují plochy rovnováhy dvou fází. Nejčastěji je používán fázový diagram p-t, který obsahuje tři křivky rovnováhy: křivku syté páry, křivku tání a sublimační křivku. Společným bodem těchto křivek je trojný bod; je to bod, v němž látka současně existuje ve všech třech skupenstvích. Křivka syté páry končí kritickým bodem, v němž mizí rozdíl mezi kapalinou a její parou. Při teplotě vyšší než je kritická teplota, existuje daná látka pouze v plynném stavu. V historii hrála nízká kritická teplota některých látek velkou překážku při jejich zkapalňování, například při postupném zkapalňování vzduchu, hélia. Fáze Fáze je část termodynamické soustavy, která, nepůsobí-li vnější síly, je fyzikálně i chemicky homogenní a od ostatních částí soustavy je oddělena ostrým fázovým rozhraním. Například fázemi vody jsou krystalická modifikace ledu, voda jako kapalinaa vodní pára. Vodný roztok kuchyňské soli tvoří jednu fázi (ale o dvou složkách), olej ve vodě tvoří dvě fáze. Viz fázový diagram, fázový přechod, skupenství látky. Fázové rozhraní
3 Fázové rozhraní je myšlená plocha oddělující dvě fáze, např. dvě kapaliny, kapalinu a pevnou látku, dvě různé krystalické struktury téže látky atd. Gibbsovo pravidlo fází Gibbsovo pravidlo fází též Gibbsův zákon fází (Gibbsovo fázové pravidlo) je kritérium, které platí pro termodynamickou rovnováhu fází ve vícefázové soustavě. Je vyjádřeno vztahem mezi počtem termodynamických stupňů volnosti soustavy v, počtem fází f a počtem nezávislých složek s v rovnovážné heterogenní soustavě, na kterou z vnějších faktorů působí jen tlak a teplota: v = s - f + 2. Počet (termodynamických) stupňů volnosti soustavy v je dán nejmenším počtem nezávislých parametrů, jimiž je jednoznačně určen stav soustavy, tj. počtem proměnných intenzivních veličin. Složkami soustavy rozumíme chemicky čisté látky, z nichž lze danou soustavu fází složit. Např. soustava složená z vody a její syté páry je jednosložková soustava o dvou fázích. Jestliže jeden z parametrů je konstantní, např. tlak, pak v = s - f + 1. Podle počtu stupňů volnosti v, tj. počtu nezávisle proměnných intenzivních veličin určujících rovnovážný stav soustavy, rozeznáváme soustavu: invariantní v = 0, univariantní (monovariantní) v = 1, bivariantní v = 2, atd. Příklady: Uzavřená nádoba částečně naplněná vodou je soustavou o jedné složce s =1 a dvou fázích f = 2 (plynné a kapalné). Soustava je univariantní, neboť podle Gibbsova pravidla fází v = = 1, tedy určité teplotě odpovídá právě jeden určitý tlak. Voda ve všech třech skupenstvích (pevném, plynném a kapalném) může současně existovat jen v tzv. trojném bodě, kdy soustava je invariantní v = 0. Tomuto stavu odpovídá jediná hodnota teploty a tlaku, trojný bod vody je určen tlakem 611 Pa a teplotou 273,16 K. Viz fázový přechod, skupenství látky. Fázový přechod Fázový přechod též fázová přeměna je přeměna jedné fáze v jinou, např. pevné fáze v kapalnou, kapalné v plynnou, aby nastal stav termodynamické rovnováhy, která byla porušena vlivem vnějších sil. Fázový přechod jednosložkových soustav (viz složka) dělíme podle Ehrenfesta na fázový přechodprvního druhu a druhého druhu (řádu). Pro fázový přechod platí, že při dané teplotě a tlaku a stejné hmotnosti látky jsou si volné entalpie obou fází rovny:
4 G1( p, T) = G2( p, T), tj. volná entalpie soustavy jako celku se při přeměně látky z jedné fáze do druhé (při fázovém přechodu) nezmění. Fázový přechod prvního druhu Pro fázový přechod prvního druhu se první derivace volné entalpie pro obě fáze liší: G T G p p T = S, = V. Fázový přechod prvního druhu je charakterizován tím, že se při teplotě fázového přechodu skokem mění vnitřní energie U látky a měrný objem v (tj. i hustota ρ, v = 1/ρ), dochází při něm k přijímání nebo odevzdání tepla fázového přechodu (viz skupenské teplo). Tyto přechody se nazývají změny skupenství, např. tání, vypařování atd. Fázový přechod druhého druhu V případě, že je první derivace volné entalpie pro obě fáze nulová, jedná se o fázový přechod druhého druhu. Při tomto přechodu se nemění měrný objem látky, látka nepřijímá ani neodevzdává teplo fázového přechodu. Mění se při něm skokem charakteristické veličiny dané látky, např. součinitel teplotní objemové roztažnosti, měrná tepelná kapacita při stálém tlaku nebo stlačitelnost apod. Příkladem je přechod pevné feromagnetické látky v paramagnetickoulátku při Curiově teplotě nebo přechod některých látek za nízké teploty do stavu elektrické supravodivosti nebo přechod do supratekutého stavu. Skupenství Skupenství, též skupenství látky, je základní charakteristika stavu látky související se stupněm uspořádanosti částic (molekul, atomů, iontů). Skupenství látky závisí na vztahu mezi kinetickou energií částic a energií jejich vzájemného působení (viz mezimolekulové síly). Rozlišujeme skupenství: plynné, kapalné, pevné a plazma. Skupenství látky, v němž je celková kinetická energie částic větší než celková energie jejich vzájemného působení, je plynné skupenství. Látka v plynném skupenství se nazývá plyn. Skupenství látky, v němž je celková kinetická energie částic srovnatelná s celkovou energií jejich vzájemného působení, je kapalné skupenství. Částice se v něm uspořádají krátkodobě, řádově na nanosekundy. Jedná se o krátkodosahové uspořádání, to znamená, že při něm na
5 sebe vzájemně působí pouze nejbližší částice. Tyto shluky atomů, molekul nebo iontů se mohou vzájemně pohybovat. Látka v kapalném skupenství látky se nazývá kapalina. Skupenství látky, v němž je celková kinetická energie částic menší než celková energie jejich vzájemného působení, je pevné skupenství. Částice jsou v něm uspořádány dlouhodobě a jedná se buď o dalekodosahové uspořádání (krystalické látky), nebo krátkodosahové (amorfní látky). Částice kmitají kolem pevných rovnovážných poloh. Látka v pevném skupenství se nazývá pevná látka. Přechod látky z jednoho skupenství do jiného skupenství se nazývá změna skupenství, též skupenská změna. Známe tyto změny skupenství: tání, tuhnutí, vypařování, var, kondenzace, sublimace a desublimace. Látka při změně skupenství přijímá nebo odevzdává skupenské teplo okolí. Viz fázový přechod prvního druhu. Skupenské teplo Skupenské teplo, značka Q, je teplo přijaté nebo odevzdané soustavou při izotermické změně skupenství za stálého tlaku. Jednotkou SI skupenského tepla je joule, značka J. V minulosti byl pro skupenské teplo používán termín latentní teplo a značka L. Skupenské teplo můžeme vyjádřit jako změnu vhodných termodynamických funkcí, např. T S, kde T je termodynamická teplota a S je změna entropie, nebo H, změna entalpie. Jedná se tedy o teplo, které přijme nebo odevzdá homogenní těleso určitého skupenství při změně skupenství za stálé teploty a tlaku. Těleso při změně skupenství přijímá nebo odevzdává skupenské teplo okolí. Těleso přijímá skupenské teplo od okolí při tání, vypařování, varu a sublimaci. Okolí tělesa při uvedených změnách skupenství se ochlazuje. Těleso Látka odevzdává skupenské teplo do okolí při tuhnutí, kondenzaci a desublimaci. Okolí tělesa při uvedených změnách ohřívá. Podle druhu fázové přeměny 1. druhu rozlišujeme skupenské teplo tání, skupenské teplo tuhnutí,
6 skupenské teplo vypařování, skupenské teplo vypařování při teplotě varu se nazývá skupenské teplo varu. skupenské teplo kondenzace, skupenské teplo sublimační a skupenské teplo desublimační. Měrné skupenské teplo Teplo přijaté nebo odevzdané látkou o jednotkové hmotnosti při izotermické změně skupenství za stálého tlaku je měrné skupenské teplo, značka l. Pro měrné skupenské teplo platí vztah Q l =, m kde Q je celkové přijaté nebo odevzdané teplo tělesem z dané látky při izotermické změně a m je hmotnost tělesa. Jednotkou SI měrného skupenského tepla je joule na kilogram, značka J/kg. Viz měrné skupenské teplo tání, měrné skupenské teplo vypařování, měrné skupenské teplo varu, měrné skupenské teplo sublimační. Molární skupenské teplo Teplo přijaté nebo odevzdané látkou o jednotkovém látkovém množství (molem) při izotermické změně skupenství za stálého tlaku se nazývá molární skupenské teplo, značka Q, (L). Jednotkou SI molárního skupenského tepla je joule na mol, značka J/mol. Tání Tání, též tavení, je změna skupenství pevné látky v kapalnou, která nastává při určité teplotě za daného vnějšího tlaku, přijímá-li látka teplo. Tání krystalických látek U krystalických látek tání nastává tehdy, když je narušena krystalová mřížka, tj. když amplituda kmitání částic krystalové mřížky je srovnatelná se vzdáleností mezi částicemi. Tehdy energie kmitání vzroste na hodnotu vazebné energie krystalu, vazba se rozruší a krystal přejde do kapalné fáze. Protože všechny vazby v daném krystalu jsou stejně silné, probíhá narušení vazeb při tání při určité teplotě, která se během fázového přechodu nemění. Tání chemicky čisté krystalické látky nastává při daném tlaku a teplotě zvané teplota tání, značka T t. Ta je stálá, pokud jsou obě fáze, pevná a kapalná, ve vzájemné termodynamické rovnováze, a závisí obvykle nepatrně jen na vnějším tlaku (viz křivka tání). Stálost teploty
7 tání je důležitou kontrolou čistoty látek. Nečisté látky (směsi několika látek) při zahřívání nejdříve měknou a přecházejí spojitě v kapalinu za stálého růstu teploty. Jestliže se jedná o tání krystalické látky za normálního tlaku, potom tuto teplotu nazýváme o normální teplota tání. Například normální teplota tání ledu je 0 C. Zvýší-li se tlak nad pevnou látkou o dp, potom se teplota tání dané pevné látky buď sníží o dt (např. voda v krystalickém stavu - led), nebo zvýší o dt (platí pro většinu pevných látek), viz Clausiova- Clapeyronova rovnice. Přehřátá pevná látka je pevná látka při teplotě vyšší, než je teplota tání při daném tlaku. o Příkladem je naftalen C 10 H 8 přehřátý nad asi 80 C za normálního tlaku. Tento stav je metastabilní, snadno se naruší a látka taje při nižší normální teplotě tání. Tání amorfních látek Amorfní látka nemá určitou teplotu tání, protože vazby mezi jejími částicemi jsou různě silné. U amorfní látky existuje interval měknutí. Skupenské teplo tání Při tání látka přijímá z okolí teplo zvané skupenské teplo tání. Jednotkou SI skupenského teplo je joule, značka J. Měrné skupenské teplo tání, značka l t, je teplo, které přijme homogenní pevné těleso o hmotnosti jeden kilogram zahřáté na teplotu tání při daném tlaku, aby změnilo skupenství za téže teploty a tlaku. Jednotkou SI měrného skupenského tepla taní je joule na kilogram, značka J/kg. Viz též tuhnutí. Anomálie vody Anomálie vody je odlišná závislost hustoty vody na teplotě v porovnání s ostatními kapalinami. Zatímco se u většiny kapalin hustota s rostoucí teplotou zmenšuje, hustota vody se od o postupně zvětšuje až do teploty 3, 98 C. Potom s rostoucí teplotou hustota vody postupně klesá, jako u jiných kapalin. Příklad: Tato zvláštní vlastnost vody umožňuje život vodním živočichům v jezerech a rybnících i za mrazů. Jestliže je hladina rybníku zamrzlá, potom pod vrstvou ledu o teplotě 0 o C je voda téže teploty. Směrem ke dnu však teplota jednotlivých vrstev vody o stoupá až do teploty 3, 98 C. Voda o této teplotě má největší hustotu. Kromě toho má voda ještě jiné zajímavé vlastnosti, např. relativně velkou měrnou tepelnou kapacitu. 0 o C
8 Tuhnutí Tuhnutí je změna skupenství kapalné látky v pevnou, opačný děj je tání. V případě chemicky čistých látek se místo tání užívá pojem krystalizace. Tuhnutí nastává, odevzdává-li kapalina teplo za daného vnějšího tlaku při určité teplotě zvané teplota tuhnutí, značka T t. Tuhnutí chemicky čistých krystalických látek Chemicky čisté krystalické látky mají teplotu tuhnutí při stejném tlaku rovnou teplotě tání. Při krystalizaci se uspořádává pohyb molekul, který se postupně mění v tepelné kmity kolem určitých středních poloh, takže se vytváří krystalová mřížka. Pro libovolnou chemicky čistou kapalinu tento proces probíhá při konstantní teplotě krystalizace. Krystalizace kapaliny začíná v blízkosti krystalizačních jader, kterými jsou příměsi, prachové částice, místní (lokální) poruchy homogenity kapaliny apod. V těchto místech se začíná projevovat určitá uspořádanost v rozmístění částic, což vede k vytváření krystalové mřížky. V nepřítomnosti krystalizačních jader může být kapalina ochlazena na teplotu nižší než je teplota tuhnutí za daného tlaku. Taková kapalina se nazývá přechlazená kapalina; je to kapalina při teplotě nižší, než je její teplota tuhnutí při daném tlaku. Například vodu zbavenou vzduchu (po dlouhém varu) lze běžně za normálního tlaku při rovnoměrném a pomalém odevzdávání tepla přechladit pod teplotu tuhnutí o 10 kelvinů i více. Přechlazená kapalina je v metastabilním stavu, který se snadno naruší a látka tuhne při své původní teplotě tuhnutí. To znamená, že při narušení metastabilního stavu zvýší svou teplotu na teplotu tuhnutí při daném tlaku. Skupenské teplo tuhnutí Při tuhnutí látka odevzdává okolí teplo zvané skupenské teplo tuhnutí. Měrné skupenské teplo tuhnutí, značka l t, je teplo, které odevzdá pevná látka o hmotnosti jeden kilogram ochlazená na teplotu tuhnutí při daném tlaku a změní se přitom v kapalinu téže teploty a tlaku. Měrné skupenské teplo tuhnutí dané krystalické látky má stejnou hodnotu jako měrné skupenské teplo tání téže látky při dané teplotě a tlaku, ale má opačné znaménko (látka je přijímá z okolí). Jednotkou SI měrného skupenského tepla tuhnutí je joule na kilogram, značka J/kg. Tuhnutí kovů V technické praxi je známo tuhnutí kovů, což je fázový přechod roztaveného kovu do stavu pevného, který je způsoben ochlazováním. Při ochlazování kovu na teplotu tuhnutí, která se u čistých kovů shoduje s jejich teplotou tání, dochází ke krystalizaci kovu pokračující až do úplného ztuhnutí taveniny - tzv. primární krystalizace. Ve ztuhlém kovu probíhá obvykle ještě krystalizace sekundární. Počátek tuhnutí kovu se zjistí prodlevami na křivkách chladnutí (v. obr. 5.14), které ukážou na různé přeměny probíhající během tuhnutí v kovu. Kromě změn
9 strukturálních dochází i k elektrickým změnám, popřípadě ke změnám magnetických vlastností kovu. Viz též tání, Clausiova-Clapeyronova rovnice. Vypařování Vypařování je změna skupenství kapalné látky v plynnou látku (v páru) při teplotě nižší, než je teplota varu při daném tlaku. Nastává na volném povrchu kapaliny při každé teplotě. Při vypařování přijímá kapalina teplo z okolí. Na povrchu kapaliny, která je ve styku se vzduchem nebo s jiným plynem, se vytvoří tenká vrstva syté páry, která difunduje do vzduchu, a to tím pomaleji, čím více se tlak syté páry příslušný dané teplotě liší od tlaku vzduchu nebo okolního plynu. Tlak syté páry při vypařování je totiž vždy nižší než tlak okolního plynu. Protože změna skupenství probíhá jen na povrchu kapaliny, je vypařování za obvyklých poměrů jen pozvolné. Vypařování přejde ve var při zvýšení teploty kapaliny na takovou hodnotu, až se tlak její syté páry rovná právě tlaku plynu nad volným povrchem kapaliny (při zanedbání kapilárního tlaku a hydrostatického tlaku kapaliny) a vznikající sytá pára se přitom může volně rozpínat. Při varu se kapalina vypařuje nejen na svém volném povrchu, jako u vypařování, ale i uvnitř. Bubliny syté páry, které přitom uvnitř kapaliny vznikají, stoupají na povrch kapaliny. Teplota, při které var za daného tlaku nastává, se nazývá teplota varu, značka T v. Teplota varu kapaliny se mění s tlakem, kterému je kapalina a její pára vystavena, například tlaku vzduchu. Jestliže se jedná o var kapaliny za normálního tlaku, potom tuto teplotu nazýváme o normální teplota varu, značka T vn. Například normální teplota varu vody je asi 100 C, ale přesně podle ITC-90 normální teplota varu vody je 99,97 C. Zvýší-li se tlak nad kapalinou o dp, potom se zvýší i teplota varu dané kapaliny o dt (viz Clausiova-Clapeyronova rovnice). Skupenské teplo vypařování Při změně skupenství vypařováním nebo varem přijímá kapalina skupenské teplo vypařování nebo skupenské teplo varu. Jednotkou SI je joule, značka J. Měrné skupenské teplo vypařování (měrné skupenské teplo výparné), značka l v, je teplo přijaté látkou o hmotnosti jeden kilogramem při izotermické změně skupenství kapalného v plynné za téhož tlaku. Jeho hodnota s rostoucí teplotou klesá, při kritické teplotě je nulová. Jedná-li se o var, potom příslušné teplo je měrné skupenské teplo varu, což je teplo, které přijme kapalina o hmotnosti jeden kilogram při své teplotě varu za daného tlaku a změní se přitom při dané teplotě a tlaku v sytou páru. Jednotkou SI měrného skupenského tepla vypařování (varu) je joule na kilogram, značka J/kg. o Pára
10 Pára je plynné skupenství látky při teplotách nižších, než je kritická teplota. Páru lze zkapalnit pouhým zvýšením tlaku bez jejího ochlazování. Sytá pára je pára., která je v termodynamické rovnováze s kapalnou nebo pevnou látkou. Její tlak je určen teplotou, nikoli jejím objemem (viz též vypařování, sublimace). Zmenšuje-li se objem syté páry při stálé teplotě a tlaku, sytá pára kapalní (kondenzuje), až zbude jen kapalná fáze. Naopak při zvětšování objemu kapaliny o stálé hmotnostise kapalina vypařuje, až zůstane v nádobě jen sytá pára. Při dalším zvětšování objemu není již pára kapalinou sycena a stává se přehřátou parou. Při stlačování, respektive ochlazování syté páry může pára v případě, že neobsahuje kondenzační jádra (prachové částice nebo částice s nábojem), dosáhnout vyššího tlaku, respektive nižší teploty, než odpovídá syté páře. Vzniká podchlazená pára. Podchlazená pára, též přesycená pára, je pára., která má vyšší tlak a hustotu než sytá pára téže teploty. Stav je nestabilní. Směs syté páry a drobných volně vznášejících se kapiček kapaliny (mlha) se nazývá mokrá pára, což je termín používaný v technice. Přehřátá pára je pára, která má nižší tlak a hustotu než sytá pára téže teploty. Chová se podobně jako ideální plyn a to tím lépe, čím je její teplota větší než je kritická teplota. Přehřátá pára nemůže rovnovážně koexistovat s kapalnou fází (na rozdíl od syté páry). Viz též stavová rovnice, van der Waalsova rovnice, zkapalňování plynů. Odpařování Odpařování kapaliny, zpravidla odpařování vody, je fázový přechod 1. druhu nevroucí vody v sytou páru u hladiny (povrchu) vody, a to při teplotě, která je nižší než teplota varu vody za daného atmosférického tlaku. Odpařování se liší od vypařování tím, že teplo potřebné k odpařování přijímá povrchová vrstva vody pouze z celé hmotnost vody, čímž se voda ochlazuje. Odpařování je nejrozšířenější jev v přírodě kolem nás: odpařování vody na povrchu moře, řek, rybníků, po dešti atd., odpařování potu na lidské pokožce (odvádí přebytečné teplo a dosahuje se chladícího účinku), sušení mokrého prádla atd. Voda se může odpařovat jak ve stavu kapalném, tak ve stavu pevném (viz sublimace). Rychlost odpařování kapaliny nebo pevné látky z plošné jednotky jejího povrchu při teplotě T je dána vztahem dm M = α p, dt 2πRT kde p je tlak syté páry molární hmotnosti M, R je plynová konstanta a α p je součinitel vypařování, který je vždy menší než jedna. Můžeme jej zjistit z naměřené rychlosti vypařování v tom případě, kdy známe teplotu a tlak syté páry. V přírodě se většinou
11 experimentálně měří na daném místě ze vzorku kapaliny nebo pevné látky za daných podmínek. Kondenzace Kondenzace, též kapalnění, je změna skupenství plynného v kapalné, která je možná jen při teplotě nižší, než je kritická teplota Tk příslušné kapaliny. Při teplotách T > Tk není možné uskutečnit změnu skupenství i při velmi vysokých tlacích, tj. změnit plyn v kapalinu při dané teplotě. Při nadkritických teplotách již může látka existovat pouze v plynném skupenství. Kondenzace je opačný proces k vypařování. Skupenské teplo kondenzace Skupenské teplo kondenzace je teplo, které odevzdává plyn svému okolí při kondenzaci v kapalinu. Viz skupenské teplo. Měrné skupenské teplo kondenzace dané látky má stejnou hodnotu jako měrné skupenské teplo vypařování téže látky za dané teploty a tlaku, ale má opačné znaménko (látka měrné skupenské teplo kondenzace odevzdává okolí). Částice, na kterých začíná kondenzace, se nazývají kondenzační jádra, též kondenzační centra. Stejně jako u varu touto částicí může být prach nebo částice s nábojem. Kondenzace na částici s nábojem probíhá rychleji než na téže částici bez náboje. Příkladem je rychlá kondenzace vodních kapek v bouřkových oblacích. Sublimace Sublimace je změna skupenství pevné látky v plynnou. Při sublimaci nastává vypařování částic (molekul, iontů, atomů) pevné látky (odlučování částic) z povrchu pevné látky a jejich přechod do plynného skupenství. Skupenské teplo sublimační Aby mohly částice pevné látky opustit její povrch, je nutno vynaložit práci na překonání mezimolekulových sil a na odtržení částic od povrchu pevné látky. Při sublimaci látka přijímá z okolí teplo zvané skupenské teplo sublimační. Viz skupenské teplo. Měrné skupenské teplo sublimační, značka l s, je teplo, které přijme pevná látka o hmotnosti jeden kilogram při dané teplotě a tlaku a změní se přitom izotermicky v jeden kilogram syté páry. Tlak syté páry nad sublimující pevnou látkou je vždy nižší než tlak syté páry nad kapalným povrchem téže látky. Jako příklad může být nízká relativní vlhkost vzduchu za mrazivých dní. (Srovnej fázový diagram.)
12 Měrné skupenské teplo sublimační je vždy větší než měrné skupenské teplo vypařování. V trojném bodě dané látky pro měrná skupenská tepla platí: l = l + l s t v, kde ls je měrné skupenské teplo sublimační, lt je měrné skupenské teplo tání a lv je měrné skupenské teplo vypařování. Desublimace Desublimace je změna skupenství látky přímo z plynného v pevné skupenství. Desublimace je opačný proces k sublimaci. Měrné skupenské teplo desublimační určité krystalické látky má stejnou hodnotu jako měrné skupenské teplo sublimační při dané teplotě a tlaku, ale má opačné znaménko. Látka toto měrné skupenské teplo odevzdává okolí. Fázový diagram Fázový diagram, též rovnovážný diagram, stavový diagram, je grafické vyjádření závislosti mezi proměnnými určujícími rovnovážný stav soustavy (termodynamická teplota T, tlak p, složení, entropie). Podle počtu stupňů volnosti soustavy jsou fázové diagramy plošné (rovinné) nebo prostorové. V případě jednosložkové soustavy (viz složka), která má maximálně dva stupně volnosti (viz Gibbsovo pravidlo fází), lze rovnovážné podmínky znázornit pomocí dvourozměrného fázového diagramu, pro nějž je nejvýhodnější zvolit jako proměnné p a T. Pokud bychom chtěli znázornit také objemové změny v soustavě, museli bychom sestrojit trojrozměrný model plochy p-v-t, jejíž každý bod znázorňuje svými souřadnicemi jednu trojici rovnovážných hodnot p, V, T. Na osu objemu vynášíme obvykle molární objem V m nebo měrný objem v. Trojrozměrný model plochy p-v-t zachycuje i objemové změny. Na obrázku p-v-t diagram je tento model pro oxid uhličitý, což je látka, která při tuhnutí zmenšuje svůj objem. Pro látku, která při tuhnutí svůj objem zvětšuje (jako např. voda), by ta část plochy p-v-t, která je na obrázku označena slovy pevná látka - kapalina, měla opačný sklon. Obr. (F_5_8_5_b) p-v-t diagram + ;obr ve Slovníku
13 Na dalších obrázcích p-v diagram a p-t diagram je ukázka projekce plochy p-v-t do rovin p-v a p-t. Projekce p-t se obvykle používá jako tzv. fázový diagram, i když ve skutečnosti jsou fázovými diagramy všechny uvedené. V p-t diagramu jsou stavy, ve kterých existují současně (koexistují) dvě fáze v rovnováze, vyznačeny body ležícími na křivkách, které nazýváme fázové křivky nebo křivky rovnováhy dvou fází (viz fázový diagram p-t). Naproti tomu ve V-T diagramu nebo p-v diagramu jsou takové stavy vyznačeny body vyplňujícími plošné oblasti diagramu. Obr. (F_5_8_5_c) p-v diagram + ; obr ve Slovníku Obr. (F_5_8_5_c) p-t diagram + ;obr ve Slovníku Fázové diagramy pro vícesložkové soustavy jsou v částech termická analýza, binární soustava a ternární soustava. Fázový diagram p-t Fázový diagram p-t jednosložkové soustavy obsahuje tři křivky, které vyjadřují vždy termodynamickou rovnováhu dvou fází.
14 Obrázek Fázový diagram p-t vody je příkladem fázového diagramu jednosložkové soustavy. V diagramu p je tlak, t Celsiova teplota. Obr. (F_5_8_?) Fázový diagram p-t vody + ;obr ve Slovníku Fázový diagram obsahuje tyto tři křivky termodynamické rovnováhy vždy dvou fází: Křivka syté páry, též křivka vypařování je křivka, která ve fázovém diagramu. znázorňuje rovnovážný stav kapalného a plynného skupenství téže látky. Na obrázku Fázový diagram p-t vody je v - křivka vypařování (viz též vypařování, kondenzace). Křivka syté páry začíná trojným bodem A a končí kritickým bodem K. Křivka tání je křivka, která ve fázovém diagramu znázorňuje rovnovážný stav kapalné a pevné fáze téže látky. Na obrázku Fázový diagram p-t vody je t křivka tání (viz též tání, tuhnutí). Křivka tání začíná trojným bodem A, pravděpodobně však nemá ukončení konkrétním bodem. Pro vodu má křivka tání v každém bodě zápornou směrnici, protože teplota tání vody s rostoucím tlakem klesá (srovnej fázový diagram oxidu uhličitého, Clausiova-Clapeyronova rovnice). Sublimační křivka je křivka, která ve fázovém diagramu znázorňuje rovnovážný stav pevného a plynného skupenství téže látky. V obrázku Fázový diagram p-t vody je s sublimační křivka (viz též sublimace, desublimace). Křivka končí trojným bodem A. Společným bodem křivky syté páry, křivky tání a sublimační křivky ve fázovém diagramu je trojný bod, což je bod, který znázorňuje rovnovážný stav pevného, kapalného a plynného skupenství téže látky. Na obrázku Fázový diagram p-t vody je označen A. Charakterizuje stav čisté látky, který je určen tlakem a teplotou, v němž tři skupenství (např. led, voda a vodní pára) jsou v termodynamické rovnováze a mohou vedle sebe nezměněně existovat. o Trojný bod vody je určen tlakem 611 Pa a teplotou 273,16 K, tj. 0, 01 C. Jeho název vyplývá z toho, že ve fázovém diagramu z trojného bodu vycházejí tři křivky pro rovnovážné stavy vždy dvou fází. Viz též fázový přechod. Křivky chladnutí
15 Křivky chladnutí jsou křivky, které zaznamenávají teplotu při chladnutí v závislosti na čase při přechodu z kapalného skupenství do pevného skupenství a dále na normální teplotu okolí. Obr. (F_5_8_5_2_a Křivky chladnutí + ;obr ve Slovníku Na obrázku Křivky chladnutí jsou schematicky zakresleny tři křivky chladnutí čistého kovu, slitiny a polymorfní taveniny: U čistých kovů teplota přechodu z kapalné do pevné fáze se projeví vodorovným úsekem na křivce chladnutí tak zvaná prodleva. Délka vodorovného úseku odpovídá době potřebné ke ztuhnutí veškerého čistého kovu (viz krystalizace). Teplota zde neklesá, protože látka odevzdává skupenské teplo, které předtím přijala při přechodu z pevného skupenství do kapalného při stejné teplotě. U slitin se objeví na křivce chladnutí šikmá prodleva udávající počátek a konec tuhnutí slitiny (viz teplota tání směsí). U polymorfního kovu na křivce chladnutí se za překrystalizačních teplot objevují pod prodlevou odpovídající teplotě tavení další vodorovné prodlevy, během nichž dochází za konstantní teploty k překrystalizaci za současného uvolňování překrystalizačního tepla. Sestavením křivek chladnutí v závislosti na složení slitiny dostaneme rovnovážný diagram zkoumané slitiny. Viz též tuhnutí. Termická analýza Termická analýza je způsob určování rovnovážných stavů mezi kapalnou a pevnou fází z křivek závislosti mezi dobou chladnutí a teplotou soustavy. Vylučování pevné fáze z taveniny se projeví zlomem nebo prodlevou na křivce (viz křivky chladnutí). Vylučování pevné látky z taveniny se provede pro různá složení a sestaví se fázový diagram (někdy i pomocí jiných metod). Slitina
16 Slitina je látka složená z několika kovů nebo z kovů a nekovových prvků, které jsou v kapalné fázi rozpustné a které tvoří v pevné fázi soudržný celek. Od chemických sloučenin se liší tím, že vznikají ve vzájemných poměrech nezávislých na atomových hmotnostech, od mechanických směsí tím, že lze jejich složky oddělit jen chemicky. Vlastnosti slitin Slitiny mají obvykle lepší vlastnosti než čisté kovy, z nichž byly vyrobeny. Proto mají větší technický význam, než tyto čisté kovy. Vlastnosti slitin lze do značné míry měnit změnou jejich složení: Hustota slitiny bývá větší, než by odpovídalo hustotě jednotlivých složek. Pevnost a tvrdost slitiny je větší než u základního kovu, tj. kovu, který ve slitině převládá. Houževnatost a tvárnost bývá menší. Teplota tání slitiny je obvykle nižší než u jednotlivých složek. Elektrická vodivost i tepelná vodivost slitin je menší než u čistých kovů. Slitiny se většinou vyrábějí míšením tekutých kovů (tavením), přičemž se do základního kovu přidávají vedlejší kovy jako legury. Binární soustava Binární soustava, též dvousložková soustava, je soustava o dvou složkách. Příklady binárních soustav: plynná směs dusíku a kyslíku, směs methanolu ethanolu, slitina bismutu a kadmia. Je-li binární soustava tvořena jedinou fází, pak může být podle Gibbsova pravidla fází binární soustava nejvýše trivariantní. Z toho plyne, že chování binární soustavy je možno znázornit v trojrozměrném diagramu (proměnnými jsou teplota, tlak a složení). V praxi se používají plošné diagramy, když jedna z veličin je konstantní. Například: pro konstantní teplotu diagramy tlak - složení (izotermní diagramy) nebo pro konstantní tlak diagramy teplota - složení (izobarické diagramy). V kondenzované binární soustavě je nejvyšší počet stupňů volnosti soustavy pro rovnovážný stav roven dvěma. Proto ke grafickému znázornění stačí plošné izobarické diagramy typu teplota-složení. Pevné roztoky Látky, které jsou v kapalné fázi dokonale mísitelné, tvoří roztok, který je homogenní. U řady z nich je úplná nebo částečná mísitelnost zachována i po ztuhnutí v pevné fázi. Vznikají takto samostatné strukturní fáze - pevné roztoky. Jako příklad uvádíme dva izobarické rovnovážné diagramy binárních soustav a vznik pevných roztoků:
17 Příklad na vznik pevného roztoku: Rovnovážný izobarický diagram pro tání a tuhnutí v případě neomezené rozpustnosti složek v kapalné a v pevné fázi je na obrázku Rovnovážný diagram neomezená rozpustnost v pevné fázi. Jedná se o vznik pevného roztoku (slitiny) Cu-Ni. Obr. (F_5_8_5_3_b) Rovnovážný diagram - neomezená rozpustnost v pevné fázi + ;obr 5.15 ve Slovníku Diagram má dvě křivky jdoucí od teploty tání jednoho čistého kovu ke druhému. Horní křivka (likvidus) vyjadřuje složení kapalného roztoku (taveniny), který je v rovnováze s vyloučenými krystaly v závislosti na teplotě. Spodní křivka (solidus) udává složení vylučujících se krystalů pevného roztoku. Nad křivkou likvidu je termodynamicky stabilní homogenní roztok (nebo tavenina), v oblasti mezi křivkou likvidu a solidu existují vedle sebe dvě fáze- krystaly pevného roztoku a kapalný roztok, pod křivkou solidu je stabilní pevná fáze - pevný roztok. Na obrázku Vznik pevného roztoku neomezená rozpustnost můžeme sledovat tuhnutí binární slitiny M např. o složení c 0. Krystalizace začne při dosažení teploty T vyloučením prvních krystalů pevného roztoku o koncentraci 1. Při poklesu teploty na T 1 c 2 krystalizují z taveniny další krystaly. Složení krystalů bude 3 a taveniny c Při dalším poklesu teploty roste postupně množství krystalů a zmenšuje se množství taveniny. Přitom složení krystalů se postupně mění v rozmezí koncentrací až c a taveniny v rozmezí koncentrací c až 4. Při teplotě T je krystalizace ukončena. Slitina je tvořena jen krystaly 0 c 3 pevného roztoku o průměrném složení během krystalizace vyrovnávat difuzí. Druhý příklad na vznik pevného roztoku: c 2. c1 0 c 0. Rozdíly ve složení krystalů i taveniny se musejí Rovnovážný izobarický diagram pro tání a tuhnutí binární soustavy v případě, že složky v kapalné fázi se spolu mísí neomezeně a v pevné fázi se prakticky nemísí je v části eutektikum. Eutektikum Rovnovážný izobarický diagram pro tání a tuhnutí binární soustavy v případě, že složky v kapalné fázi se spolu mísí neomezeně a v pevné fázi se prakticky nemísí je na obrázku Rovnovážný diagram složky v pevné fázi se nemísí. Obr. (F_5_8_5_3_1_a) Rovnovážný diagram složky v pevné fázi se nemísí + ;obr ve Slovníku
18 V rovnovážném diagramu jsou A, B jsou složky roztoku, x B je molární zlomek složky B (na vodorovnou osu jsou vyneseny molární zlomky složky A a složky B, každý z nich je jiný, jejich součet v daném bodě je roven jedné). Při ochlazování roztoku podél úsečky XX se po snížení teploty začne z daného roztoku vylučovat čistá pevná složka A, jejíž koncentrace T t,a v roztoku při dalším ochlazování začne klesat. Čistá pevná látka B se začne z roztoku vylučovat až při poklesu teploty na T t,b. V bodě E se rovnovážné křivky obou látek protínají při složení roztoku x E, což je eutektické složení. Uvedený diagram je eutektický diagram, teplota T E je eutektická teplota. Roztok nebo tavenina, má-li vysokou teplotu při složení x 1 bude tuhnout při teplotě tuhnutí T 1, s dalším ochlazením se objeví čistá pevná látka A. Délky úseků l1 a l 2 v diagramu jsou v tomtéž poměru, v jakém jsou molární zlomky látky A a látky B při dané teplotě (tzv. pákové pravidlo). Když roztok dosáhne složení x E a trvale odevzdává teplo okolí, potom se z roztoku současně vylučují čistá pevná látka A i B, přičemž poměr složek v této směsi bude dán bodem E, zvaným eutektický bod. Termín eutektický bod se používá pro slitiny, zatímco pro vodné roztoky je používán termín kryohydratický bod. Eutektická pevná látka, též eutektikum, má trvale stejné složení dané bodem E, přičemž to není sloučenina, protože její složení se mění např. s tlakem. Vzájemné uspořádání složek v tomto binárním eutektiku může být lamelární, tyčinovité, globulární (zrnité) nebo degenerované. V rovnovážných diagramech binárních slitin se zpravidla vynáší závislost teploty na hmotnostním složení slitiny v procentech. Eutektikum je směs dvou látek, které při ochlazování tuhnou jako celek, ne postupně při různých teplotách (viz křivky chladnutí). Srovnejte s ternární soustavou. Ternární soustava
19 Ternární soustava je soustava složená se tří složek. V ternární soustavě je počet stupňů volnosti v pro rovnovážný stav určen vztahem v = 5 - f, kde f je počet fází (viz Gibbsovo pravidlo fází). Je-li v ternární soustavě přítomna pouze jedna fáze, je v = 4, tzn. že ke grafickému znázornění chování ternární soustavy by bylo třeba čtyřrozměrných diagramů. Prakticky se však používají plošné rovnovážné diagramy, které jsou sestrojeny obvykle pro konstantní teplotu a tlak v pravoúhlém nebo rovnostranném trojúhelníku. Využívá se skutečnosti, že jen dvě ze tří koncentrací jsou nezávisle proměnné. Uvedené diagramy se nazývají ternární diagramy. Koncentrace ternární soustavy se znázorňují v rovnostranném trojúhelníku, kde každý vrchol odpovídá jedné ze složek A, B, C. o Je to v podstatě znázorňování v soustavě souřadnic, jejichž osy X a Y svírají spolu úhel 60, viz obrázek Koncentrační trojúhelník. Každý bod ležící na jedné ze stran tohoto trojúhelníka AB, BC, CA odpovídá určitému hmotnostnímu zlomku nebo koncentraci příslušných dvou složek (lze zde odečíst složení binárních soustav A-B, B-C, C-A). Každý bod ležící uvnitř trojúhelníka odpovídá ternární soustavě složené ze všech tří složek A, B, C. Složení libovolné ternární soustavy dané bodem ležícím v koncentračním trojúhelníku se určuje z vlastností rovnostranného trojúhelníka na základě věty: Součet délek kolmic spuštěných z libovolného bodu uvnitř rovnostranného trojúhelníka na jeho strany se rovná výšce trojúhelníka. Potom délka každé kolmice je mírou látkového množství (koncentrace) příslušné složky, např. ve slitině. Když výšce trojúhelníka přiřadíme hodnotu 100 %, potom délky kolmic určují přímo v procentech složení ternární soustavy. Například délky kolmic bodu X vyjadřují procenta složek, které leží na protilehlých vrcholech trojúhelníka, přičemž platí h= h h + h (viz obrázek). Konkrétně v uvedeném případě složce A odpovídá h 1 %, složce B odpovídá h 2 % a složce C odpovídá h 3 %. Obr. (F_5_8_5_4_b) Koncentrační trojúhelník + ;obr ve Slovníku Srovnej s binární soustavou. Kritický stav
20 Kritický stav je stav látky, ve které mizí rozdíl mezi kapalným skupenstvím a plynným skupenstvím. Kritický stav je charakterizován kritickou teplotou T k, kritickým tlakem p k a kritickým molárním objemem Vmk nebo kritickou hustotou ρ. k Pojem kritického stavu se často zobecňuje i na případy, kdy roli různých skupenství představují různé modifikace látek. Bod K znázorňující kritický stav, viz obrázek Fázový diagram vody, se nazývá kritický bod. Tímto bodem končí křivka vypařování, tj. křivka znázorňující rovnováhu mezi kapalným a plynným skupenstvím. Kritický bod pro vodu má tyto hodnoty: kritická teplota T k = 647,3 K, kritický tlak p k = 22,13 MPa, 3 kritická hustota ρ k = 328 kg/m. Viz též van der Waalsova stavová rovnice, izotermy reálných plynů. Izotermy reálných plynů Izotermy reálných plynů jsou křivky závislosti tlaku reálného plynu na jeho molárním objemu při izotermickém ději. Rozlišujeme experimentální izotermy reálného plynu, jejichž jednotlivé body vycházejí z měření molárního objemu a tlaku daného plynu při dané teplotě, teoretické izotermy reálného plynu, též van der Waalsovy izotermy, které jsou zkonstruovány podle van der Waalsovy stavové rovnice pro 1 mol reálného plynu pro různé teploty. Experimentální izotermy reálného plynu Na obrázku Experimentální izotermy oxidu uhličitého jsou izotermy pro teploty T < T < T < T < T < T 4 Pro teploty T < T k, kde T je kritická teplota, obsahuje každá 1 2 k 3. izoterma plynulý přechod látky z plynného skupenství do kapalného. Pro T > T k je látka v plynném skupenství. Na izotermě odpovídající teplotě T představuje bod A přehřátou páru (plyn). Stlačením této přehřáté páry při T = k onst. se pára stane sytou párou (bod B), která je v termodynamické rovnováze se svou kapalinou. Tlak p B syté páry závisí pouze na teplotě a na chemickém složení páry, přičemž tlak syté páry roste s rostoucí teplotou. Teplota přehřáté páry je vždy vyšší než teplota syté páry za téhož tlaku. Dalším stlačením se sytá pára stane mokrou párou, tedy látkou o dvou fázích kapaliny a její syté páry. Dalším stlačením postupně sytá pára kapalní, bod C představuje pouze kapalinu. k Obr. (F_5_8_7_b1_1.tif) Experimentální izotermy oxidu uhličitého {#5_8_7_a;} + ; obr ve Slovníku základní
Kontrolní otázky k 1. přednášce z TM
 Kontrolní otázky k 1. přednášce z TM 1. Jak závisí hodnota izobarického součinitele objemové roztažnosti ideálního plynu na teplotě a jak na tlaku? Odvoďte. 2. Jak závisí hodnota izochorického součinitele
Kontrolní otázky k 1. přednášce z TM 1. Jak závisí hodnota izobarického součinitele objemové roztažnosti ideálního plynu na teplotě a jak na tlaku? Odvoďte. 2. Jak závisí hodnota izochorického součinitele
Tepelná vodivost. střední rychlost. T 1 > T 2 z. teplo přenesené za čas dt: T 1 T 2. tepelný tok střední volná dráha. součinitel tepelné vodivosti
 Tepelná vodivost teplo přenesené za čas dt: T 1 > T z T 1 S tepelný tok střední volná dráha T součinitel tepelné vodivosti střední rychlost Tepelná vodivost součinitel tepelné vodivosti při T = 300 K součinitel
Tepelná vodivost teplo přenesené za čas dt: T 1 > T z T 1 S tepelný tok střední volná dráha T součinitel tepelné vodivosti střední rychlost Tepelná vodivost součinitel tepelné vodivosti při T = 300 K součinitel
Termika. Nauka o teple se zabývá měřením teploty, tepla a tepelnými ději.
 Termika Nauka o teple se zabývá měřením teploty, tepla a tepelnými ději. 1. Vnitřní energie Brownův pohyb a difúze látek prokazují, že částice látek jsou v neustálém neuspořádaném pohybu. Proto mají kinetickou
Termika Nauka o teple se zabývá měřením teploty, tepla a tepelnými ději. 1. Vnitřní energie Brownův pohyb a difúze látek prokazují, že částice látek jsou v neustálém neuspořádaném pohybu. Proto mají kinetickou
Fyzikální chemie VŠCHT PRAHA. bakalářský kurz. Prof. Ing. Josef Novák, CSc. a kolektiv. (2. listopadu 2008)
 Fyzikální chemie bakalářský kurz Prof. Ing. Josef Novák, CSc. a kolektiv (2. listopadu 2008) VŠCHT PRAHA Tato skripta jsou určena pro posluchače bakalářského kurzu Fyzikální chemie na VŠCHT v Praze. Obsahují
Fyzikální chemie bakalářský kurz Prof. Ing. Josef Novák, CSc. a kolektiv (2. listopadu 2008) VŠCHT PRAHA Tato skripta jsou určena pro posluchače bakalářského kurzu Fyzikální chemie na VŠCHT v Praze. Obsahují
II. VNITŘNÍ ENERGIE, PRÁCE A TEPLO
 II. VNITŘNÍ ENERGIE, PRÁCE A TEPLO 2.1 Vnitřní energie tělesa a) celková energie (termodynamické) soustavy E tvořena kinetickou energií E k jejího makroskopického pohybu jako celku potenciální energií
II. VNITŘNÍ ENERGIE, PRÁCE A TEPLO 2.1 Vnitřní energie tělesa a) celková energie (termodynamické) soustavy E tvořena kinetickou energií E k jejího makroskopického pohybu jako celku potenciální energií
1 ZÁKLADNÍ VLASTNOSTI TECHNICKÝCH MATERIÁLŮ Vlastnosti kovů a jejich slitin jsou dány především jejich chemickým složením a strukturou.
 1 ZÁKLADNÍ VLASTNOSTI TECHNICKÝCH MATERIÁLŮ Vlastnosti kovů a jejich slitin jsou dány především jejich chemickým složením a strukturou. Z hlediska použitelnosti kovů v technické praxi je obvyklé dělení
1 ZÁKLADNÍ VLASTNOSTI TECHNICKÝCH MATERIÁLŮ Vlastnosti kovů a jejich slitin jsou dány především jejich chemickým složením a strukturou. Z hlediska použitelnosti kovů v technické praxi je obvyklé dělení
Veličiny- základní N A. Látkové množství je dáno podílem N částic v systému a Avogadrovy konstanty NA
 YCHS, XCHS I. Úvod: plán přednášek a cvičení, podmínky udělení zápočtu a zkoušky. Základní pojmy: jednotky a veličiny, základy chemie. Stavba atomu a chemická vazba. Skupenství látek, chemické reakce,
YCHS, XCHS I. Úvod: plán přednášek a cvičení, podmínky udělení zápočtu a zkoušky. Základní pojmy: jednotky a veličiny, základy chemie. Stavba atomu a chemická vazba. Skupenství látek, chemické reakce,
Metalografie ocelí a litin
 Metalografie ocelí a litin Metalografie se zabývá pozorováním a zkoumáním vnitřní stavby neboli struktury kovů a slitin. Dále také stanoví, jak tato struktura souvisí s chemickým složením, teplotou a tepelným
Metalografie ocelí a litin Metalografie se zabývá pozorováním a zkoumáním vnitřní stavby neboli struktury kovů a slitin. Dále také stanoví, jak tato struktura souvisí s chemickým složením, teplotou a tepelným
CHEMICKÁ ENERGETIKA. Celá termodynamika je logicky odvozena ze tří základních principů, které mají axiomatický charakter.
 CHEMICKÁ ENERGETIKA Energetickou stránkou soustav a změnami v těchto soustavách se zabývá fyzikální disciplína termodynamika. Z široké oblasti obecné termodynamiky se chemická termodynamika zajímá o chemické
CHEMICKÁ ENERGETIKA Energetickou stránkou soustav a změnami v těchto soustavách se zabývá fyzikální disciplína termodynamika. Z široké oblasti obecné termodynamiky se chemická termodynamika zajímá o chemické
Nauka o materiálu. Přednáška č.10 Difuze v tuhých látkách, fáze a fázové přeměny
 Nauka o materiálu Přednáška č.10 Difuze v tuhých látkách, fáze a fázové přeměny Difuze v tuhých látkách Difuzí nazýváme přesun atomů nebo iontů na vzdálenost větší než je meziatomová vzdálenost. Hnací
Nauka o materiálu Přednáška č.10 Difuze v tuhých látkách, fáze a fázové přeměny Difuze v tuhých látkách Difuzí nazýváme přesun atomů nebo iontů na vzdálenost větší než je meziatomová vzdálenost. Hnací
2.4 Stavové chování směsí plynů Ideální směs Ideální směs reálných plynů Stavové rovnice pro plynné směsi
 1. ZÁKLADNÍ POJMY 1.1 Systém a okolí 1.2 Vlastnosti systému 1.3 Vybrané základní veličiny 1.3.1 Množství 1.3.2 Délka 1.3.2 Délka 1.4 Vybrané odvozené veličiny 1.4.1 Objem 1.4.2 Hustota 1.4.3 Tlak 1.4.4
1. ZÁKLADNÍ POJMY 1.1 Systém a okolí 1.2 Vlastnosti systému 1.3 Vybrané základní veličiny 1.3.1 Množství 1.3.2 Délka 1.3.2 Délka 1.4 Vybrané odvozené veličiny 1.4.1 Objem 1.4.2 Hustota 1.4.3 Tlak 1.4.4
Fázové heterogenní rovnováhy Fáze = homogenní část soustavy, oddělná fyzickým rozhraním, na rozhraní se vlastnosti mění skokem
 Fázové heterogenní rovnováhy Fáze = homogenní část soustavy, oddělná fyzickým rozhraním, na rozhraní se vlastnosti mění skokem Rovnováha Tepelná - T všude stejná Mechanická - p všude stejný Chemická -
Fázové heterogenní rovnováhy Fáze = homogenní část soustavy, oddělná fyzickým rozhraním, na rozhraní se vlastnosti mění skokem Rovnováha Tepelná - T všude stejná Mechanická - p všude stejný Chemická -
Rovnováha Tepelná - T všude stejná
 Fázové heterogenní rovnováhy Fáze = homogenní část soustavy, oddělná fyzickým rozhraním, na rozhraní se vlastnosti mění skokem Rovnováha Tepelná - T všude stejná Mechanická - p všude stejný Chemická -
Fázové heterogenní rovnováhy Fáze = homogenní část soustavy, oddělná fyzickým rozhraním, na rozhraní se vlastnosti mění skokem Rovnováha Tepelná - T všude stejná Mechanická - p všude stejný Chemická -
ZMĚNY SKUPENSTVÍ LÁTEK ČÁST 01
 ZMĚNY SKUPENSTVÍ LÁTEK ČÁST 01 A) Výklad: Změny skupenství látky Látka se může vyskytovat ve třech různých skupenstvích PEVNÉM, KAPALNÉM nebo PLYNNÉM. Např. voda (H 2 O)- může se vyskytovat jako krystalický
ZMĚNY SKUPENSTVÍ LÁTEK ČÁST 01 A) Výklad: Změny skupenství látky Látka se může vyskytovat ve třech různých skupenstvích PEVNÉM, KAPALNÉM nebo PLYNNÉM. Např. voda (H 2 O)- může se vyskytovat jako krystalický
CHEMICKY ČISTÁ LÁTKA A SMĚS
 CHEMICKY ČISTÁ LÁTKA A SMĚS Látka = forma hmoty, která se skládá z velkého množství základních stavebních částic: atomů, iontů a... Látky se liší podle druhu částic, ze kterých se skládají. Druh částic
CHEMICKY ČISTÁ LÁTKA A SMĚS Látka = forma hmoty, která se skládá z velkého množství základních stavebních částic: atomů, iontů a... Látky se liší podle druhu částic, ze kterých se skládají. Druh částic
Mol. fyz. a termodynamika
 Molekulová fyzika pracuje na základě kinetické teorie látek a statistiky Termodynamika zkoumání tepelných jevů a strojů nezajímají nás jednotlivé částice Molekulová fyzika základem jsou: Látka kteréhokoli
Molekulová fyzika pracuje na základě kinetické teorie látek a statistiky Termodynamika zkoumání tepelných jevů a strojů nezajímají nás jednotlivé částice Molekulová fyzika základem jsou: Látka kteréhokoli
I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í
 CHEMICKY ČISTÉ LÁTKY A SMĚSI Látka = forma hmoty, která se skládá z velkého množství základních částic: atomů, iontů a... 1. Přiřaďte látky: glukóza, sůl, vodík a helium k níže zobrazeným typům částic.
CHEMICKY ČISTÉ LÁTKY A SMĚSI Látka = forma hmoty, která se skládá z velkého množství základních částic: atomů, iontů a... 1. Přiřaďte látky: glukóza, sůl, vodík a helium k níže zobrazeným typům částic.
TEPELNÉ JEVY. Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie
 TEPELNÉ JEVY Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie Vnitřní energie tělesa Každé těleso se skládá z látek. Látky se skládají z částic. neustálý neuspořádaný pohyb kinetická energie vzájemné působení
TEPELNÉ JEVY Mgr. Jan Ptáčník - GJVJ - Fyzika - Tercie Vnitřní energie tělesa Každé těleso se skládá z látek. Látky se skládají z částic. neustálý neuspořádaný pohyb kinetická energie vzájemné působení
Základem molekulové fyziky je kinetická teorie látek. Vychází ze tří pouček:
 Molekulová fyzika zkoumá vlastnosti látek na základě jejich vnitřní struktury, pohybu a vzájemného působení částic, ze kterých se látky skládají. Termodynamika se zabývá zákony přeměny různých forem energie
Molekulová fyzika zkoumá vlastnosti látek na základě jejich vnitřní struktury, pohybu a vzájemného působení částic, ze kterých se látky skládají. Termodynamika se zabývá zákony přeměny různých forem energie
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny
 Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
Transportní jevy v plynech Reálné plyny Fázové přechody Kapaliny Hustota toku Zatím jsme studovali pouze soustavy, které byly v rovnovážném stavu není-li soustava v silovém poli, je hustota částic stejná
Zadání příkladů řešených na výpočetních cvičeních z Fyzikální chemie I, obor CHTP. Termodynamika. Příklad 10
 Zadání příkladů řešených na výpočetních cvičeních z Fyzikální chemie I, obor CHTP Termodynamika Příklad 1 Stláčením ideálního plynu na 2/3 původního objemu vzrostl při stálé teplotě jeho tlak na 15 kpa.
Zadání příkladů řešených na výpočetních cvičeních z Fyzikální chemie I, obor CHTP Termodynamika Příklad 1 Stláčením ideálního plynu na 2/3 původního objemu vzrostl při stálé teplotě jeho tlak na 15 kpa.
Krása fázových diagramů jak je sestrojit a číst Silvie Mašková
 Krása fázových diagramů jak je sestrojit a číst Silvie Mašková Katedra fyziky kondenzovaných látek Matematicko-fyzikální fakulta Univerzita Karlova Praha Pár základích pojmů na začátek Co jsou fázové diagramy?
Krása fázových diagramů jak je sestrojit a číst Silvie Mašková Katedra fyziky kondenzovaných látek Matematicko-fyzikální fakulta Univerzita Karlova Praha Pár základích pojmů na začátek Co jsou fázové diagramy?
FYZIKÁLNA PODSTATA A MECHANIZMUS PLASTICKEJ DEFORMÁCIE
 FYZIKÁLNA PODSTATA A MECHANIZMUS PLASTICKEJ DEFORMÁCIE Vysoká škola technická a ekonomická v Českých Budějovicích Institute of Technology And Business In České Budějovice Tento učební materiál vznikl v
FYZIKÁLNA PODSTATA A MECHANIZMUS PLASTICKEJ DEFORMÁCIE Vysoká škola technická a ekonomická v Českých Budějovicích Institute of Technology And Business In České Budějovice Tento učební materiál vznikl v
Fyzikální chemie. Magda Škvorová KFCH CN463 magda.skvorova@ujep.cz, tel. 3302. 14. února 2013
 Fyzikální chemie Magda Škvorová KFCH CN463 magda.skvorova@ujep.cz, tel. 3302 14. února 2013 Co je fyzikální chemie? Co je fyzikální chemie? makroskopický přístup: (klasická) termodynamika nerovnovážná
Fyzikální chemie Magda Škvorová KFCH CN463 magda.skvorova@ujep.cz, tel. 3302 14. února 2013 Co je fyzikální chemie? Co je fyzikální chemie? makroskopický přístup: (klasická) termodynamika nerovnovážná
p V = n R T Při stlačování vkládáme do systému práci a tím se podle 1. věty termodynamické zvyšuje vnitřní energie systému U = q + w
 3. DOPRAVA PLYNŮ Ve výrobních procesech se často dopravují a zpracovávají plyny za tlaků odlišných od tlaku atmosférického. Podle poměru stlačení, tj. poměru tlaků před a po kompresi, jsou stroje na dopravu
3. DOPRAVA PLYNŮ Ve výrobních procesech se často dopravují a zpracovávají plyny za tlaků odlišných od tlaku atmosférického. Podle poměru stlačení, tj. poměru tlaků před a po kompresi, jsou stroje na dopravu
Doprovodné otázky pro studenty, kvízy, úkoly aj.
 Doprovodné otázky pro studenty, kvízy, úkoly aj. Otázky: 1. Jak se projeví menší hustota ledu v porovnání s vodou při zamrzání vodních nádrží a toků? 2. Jaký jev se nazývá anomálie vody? 3. Vysvětlete
Doprovodné otázky pro studenty, kvízy, úkoly aj. Otázky: 1. Jak se projeví menší hustota ledu v porovnání s vodou při zamrzání vodních nádrží a toků? 2. Jaký jev se nazývá anomálie vody? 3. Vysvětlete
Tepelně vlhkostní mikroklima. Vlhkost v budovách
 Tepelně vlhkostní mikroklima Vlhkost v budovách Zdroje vodní páry stavební vlhkost - vodní pára vázaná v materiálech v důsledku mokrých technologických procesů (chemicky nebo fyzikálně vázaná) zemní vlhkost
Tepelně vlhkostní mikroklima Vlhkost v budovách Zdroje vodní páry stavební vlhkost - vodní pára vázaná v materiálech v důsledku mokrých technologických procesů (chemicky nebo fyzikálně vázaná) zemní vlhkost
Výměna tepla může probíhat vedením (kondukcí), prouděním (konvekcí) nebo sáláním (zářením).
 10. VÝMĚNÍKY TEPLA Výměníky tepla jsou zařízení, ve kterých se jeden proud ohřívá a druhý ochlazuje sdílením tepla. Nezáleží přitom na konečném cíli operace, tj. zda chceme proud ochladit nebo ohřát, ani
10. VÝMĚNÍKY TEPLA Výměníky tepla jsou zařízení, ve kterých se jeden proud ohřívá a druhý ochlazuje sdílením tepla. Nezáleží přitom na konečném cíli operace, tj. zda chceme proud ochladit nebo ohřát, ani
ZÁKLADNÍ ŠKOLA KOLÍN II., KMOCHOVA 943 škola s rozšířenou výukou matematiky a přírodovědných předmětů
 ZÁKLADNÍ ŠKOLA KOLÍN II., KMOCHOVA 943 škola s rozšířenou výukou matematiky a přírodovědných předmětů Autor Číslo materiálu Mgr. Vladimír Hradecký 8_F_1_13 Datum vytvoření 2. 11. 2011 Druh učebního materiálu
ZÁKLADNÍ ŠKOLA KOLÍN II., KMOCHOVA 943 škola s rozšířenou výukou matematiky a přírodovědných předmětů Autor Číslo materiálu Mgr. Vladimír Hradecký 8_F_1_13 Datum vytvoření 2. 11. 2011 Druh učebního materiálu
Chemie = přírodní věda zkoumající složení a strukturu látek a jejich přeměny v látky jiné
 Otázka: Obecná chemie Předmět: Chemie Přidal(a): ZuzilQa Základní pojmy v chemii, periodická soustava prvků Chemie = přírodní věda zkoumající složení a strukturu látek a jejich přeměny v látky jiné -setkáváme
Otázka: Obecná chemie Předmět: Chemie Přidal(a): ZuzilQa Základní pojmy v chemii, periodická soustava prvků Chemie = přírodní věda zkoumající složení a strukturu látek a jejich přeměny v látky jiné -setkáváme
Stavové neboli fázové diagramy jednosložkových a dvousložkových systémů. Doc. Ing. Jiří Vondrák, DrSc
 Stavové neboli fázové diagramy jednosložkových a dvousložkových systémů Doc. Ing. Jiří Vondrák, DrSc 1. Obecný úvod Tato stať se zabývá stavem látek, a to ve skupenství kapalném či tuhém, a přechody mezi
Stavové neboli fázové diagramy jednosložkových a dvousložkových systémů Doc. Ing. Jiří Vondrák, DrSc 1. Obecný úvod Tato stať se zabývá stavem látek, a to ve skupenství kapalném či tuhém, a přechody mezi
Třídění látek. Chemie 1.KŠPA
 Třídění látek Chemie 1.KŠPA Systém (soustava) Vymezím si kus prostoru, látky v něm obsažené nazýváme systém soustava okolí svět Stěny soustavy Soustava může být: Izolovaná = stěny nedovolí výměnu částic
Třídění látek Chemie 1.KŠPA Systém (soustava) Vymezím si kus prostoru, látky v něm obsažené nazýváme systém soustava okolí svět Stěny soustavy Soustava může být: Izolovaná = stěny nedovolí výměnu částic
ZMĚNY SKUPENSTVÍ LÁTEK
 ZMĚNY SKUPENSTVÍ LÁTEK TÁNÍ A TUHNUTÍ - OSNOVA Kapilární jevy příklad Skupenské přeměny látek Tání a tuhnutí Teorie s video experimentem Příklad KAPILÁRNÍ JEVY - OPAKOVÁNÍ KAPILÁRNÍ JEVY - PŘÍKLAD Jak
ZMĚNY SKUPENSTVÍ LÁTEK TÁNÍ A TUHNUTÍ - OSNOVA Kapilární jevy příklad Skupenské přeměny látek Tání a tuhnutí Teorie s video experimentem Příklad KAPILÁRNÍ JEVY - OPAKOVÁNÍ KAPILÁRNÍ JEVY - PŘÍKLAD Jak
IV. Fázové rovnováhy. 4. Fázové rovnováhy Ústav procesní a zpracovatelské techniky FS ČVUT v Praze
 IV. Fázové rovnováhy 1 4. Fázové rovnováhy 4.1 Základní pojmy 4.2 Fázové rovnováhy jednosložkové soustavy 4.3 Fázové rovnováhy dvousložkových soustav 4.3.1 Soustava tuhá složka tuhá složka 4.3.2 Soustava
IV. Fázové rovnováhy 1 4. Fázové rovnováhy 4.1 Základní pojmy 4.2 Fázové rovnováhy jednosložkové soustavy 4.3 Fázové rovnováhy dvousložkových soustav 4.3.1 Soustava tuhá složka tuhá složka 4.3.2 Soustava
KINETICKÁ TEORIE STAVBY LÁTEK
 KINETICKÁ TEORIE STAVBY LÁTEK Látky kteréhokoliv skupenství se skládají z částic. Prostor, který těleso zaujímá, není částicemi beze zbytku vyplněn (diskrétní struktura látek). Rozměry částic jsou řádově
KINETICKÁ TEORIE STAVBY LÁTEK Látky kteréhokoliv skupenství se skládají z částic. Prostor, který těleso zaujímá, není částicemi beze zbytku vyplněn (diskrétní struktura látek). Rozměry částic jsou řádově
Termodynamika materiálů. Vztahy a přeměny různých druhů energie při termodynamických dějích podmínky nutné pro uskutečnění fázových přeměn
 Termodynamika materiálů Vztahy a přeměny různých druhů energie při termodynamických dějích podmínky nutné pro uskutečnění fázových přeměn Důležité konstanty Standartní podmínky Avogadrovo číslo N A = 6,023.10
Termodynamika materiálů Vztahy a přeměny různých druhů energie při termodynamických dějích podmínky nutné pro uskutečnění fázových přeměn Důležité konstanty Standartní podmínky Avogadrovo číslo N A = 6,023.10
Chemie. Mgr. Petra Drápelová Mgr. Jaroslava Vrbková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Chemie Mgr. Petra Drápelová Mgr. Jaroslava Vrbková Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou Směsi VY_32_INOVACE_03_3_01_CH Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou SMĚSI Směsi jsou složitější látky, které
Chemie Mgr. Petra Drápelová Mgr. Jaroslava Vrbková Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou Směsi VY_32_INOVACE_03_3_01_CH Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou SMĚSI Směsi jsou složitější látky, které
Vzdělávací oblast: Člověk a příroda. Vyučovací předmět: Chemie. Třída: tercie. Očekávané výstupy. Poznámky. Přesahy. Žák: Průřezová témata
 Vzdělávací oblast: Člověk a příroda Vyučovací předmět: Chemie Třída: tercie Očekávané výstupy Uvede příklady chemického děje a čím se zabývá chemie Rozliší tělesa a látky Rozpozná na příkladech fyzikální
Vzdělávací oblast: Člověk a příroda Vyučovací předmět: Chemie Třída: tercie Očekávané výstupy Uvede příklady chemického děje a čím se zabývá chemie Rozliší tělesa a látky Rozpozná na příkladech fyzikální
Stanovení křivky rozpustnosti fenol-voda. 3. laboratorní cvičení
 Stanovení křivky rozpustnosti fenol-voda 3. laboratorní cvičení Mgr. Sylvie Pavloková Letní semestr 2016/2017 Cíl pochopení základních principů fázové rovnováhy heterogenních soustav základní principy
Stanovení křivky rozpustnosti fenol-voda 3. laboratorní cvičení Mgr. Sylvie Pavloková Letní semestr 2016/2017 Cíl pochopení základních principů fázové rovnováhy heterogenních soustav základní principy
3.2 Látka a její skupenství
 3.2 Látka a její skupenství Skupenství látky a jejich změny sublimace PEVNÁ LÁTKA tání desublimace tuhnutí PLYN vy pa řo vá ní KAPALINA zka pal ňo vá ní Látka a změna vnitřní energie Změna vnitřní energie
3.2 Látka a její skupenství Skupenství látky a jejich změny sublimace PEVNÁ LÁTKA tání desublimace tuhnutí PLYN vy pa řo vá ní KAPALINA zka pal ňo vá ní Látka a změna vnitřní energie Změna vnitřní energie
FYZIKÁLNÍ CHEMIE I: 2. ČÁST
 Univerzita J. E. Purkyně v Ústí nad Labem Přírodovědecká fakulta FYZIKÁLNÍ CHEMIE I: 2. ČÁST KCH/P401 Ivo Nezbeda Ústí nad Labem 2013 1 Obor: Klíčová slova: Anotace: Toxikologie a analýza škodlivin, Chemie
Univerzita J. E. Purkyně v Ústí nad Labem Přírodovědecká fakulta FYZIKÁLNÍ CHEMIE I: 2. ČÁST KCH/P401 Ivo Nezbeda Ústí nad Labem 2013 1 Obor: Klíčová slova: Anotace: Toxikologie a analýza škodlivin, Chemie
CHEMICKÁ ROVNOVÁHA PRINCIP MOBILNÍ (DYNAMICKÉ) ROVNOVÁHY
 CHEMICKÁ ROVNOVÁHA PRINCIP MOBILNÍ (DYNAMICKÉ) ROVNOVÁHY V reakční kinetice jsme si ukázali, že zvratné reakce jsou charakterizovány tím, že probíhají současně oběma směry, tj. od výchozích látek k produktům
CHEMICKÁ ROVNOVÁHA PRINCIP MOBILNÍ (DYNAMICKÉ) ROVNOVÁHY V reakční kinetice jsme si ukázali, že zvratné reakce jsou charakterizovány tím, že probíhají současně oběma směry, tj. od výchozích látek k produktům
Termomechanika 8. přednáška Doc. Dr. RNDr. Miroslav Holeček
 Termomechanika 8. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Termomechanika 8. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Nultá věta termodynamická
 TERMODYNAMIKA Nultá věta termodynamická 2 Práce 3 Práce - příklady 4 1. věta termodynamická 5 Entalpie 6 Tepelné kapacity 7 Vnitřní energie a entalpie ideálního plynu 8 Výpočet tepla a práce 9 Adiabatický
TERMODYNAMIKA Nultá věta termodynamická 2 Práce 3 Práce - příklady 4 1. věta termodynamická 5 Entalpie 6 Tepelné kapacity 7 Vnitřní energie a entalpie ideálního plynu 8 Výpočet tepla a práce 9 Adiabatický
TÉMA: Molekulová fyzika a tepelné děje v plynech VNITŘNÍ ENERGIE TĚLESA
 U.. vnitřní energie tělesa ( termodynamické soustavy) je celková kinetická energie neuspořádaně se pohybujících částic tělesa ( molekul, atomů, iontů) a celková potenciální energie vzájemné polohy těchto
U.. vnitřní energie tělesa ( termodynamické soustavy) je celková kinetická energie neuspořádaně se pohybujících částic tělesa ( molekul, atomů, iontů) a celková potenciální energie vzájemné polohy těchto
OSTRAVSKÁ UNIVERZITA V OSTRAVĚ MOLEKULOVÁ FYZIKA 1
 OSTRAVSKÁ UNIVERZITA V OSTRAVĚ MOLEKULOVÁ FYZIKA 1 Molekulové jevy v kapalinách ERIKA MECHLOVÁ OSTRAVA 2004 Tento projekt byl spolufinancován Evropskou unií a českým státním rozpočtem Recenzent: Prof.
OSTRAVSKÁ UNIVERZITA V OSTRAVĚ MOLEKULOVÁ FYZIKA 1 Molekulové jevy v kapalinách ERIKA MECHLOVÁ OSTRAVA 2004 Tento projekt byl spolufinancován Evropskou unií a českým státním rozpočtem Recenzent: Prof.
Výroba páry - kotelna, teplárna, elektrárna Rozvod páry do místa spotřeby páry Využívání páry v místě spotřeby Vracení kondenzátu do místa výroby páry
 Úvod Znalosti - klíč k úspěchu Materiál přeložil a připravil Ing. Martin NEUŽIL, Ph.D. SPIRAX SARCO spol. s r.o. V Korytech (areál nádraží ČD) 100 00 Praha 10 - Strašnice tel.: 274 00 13 51, fax: 274 00
Úvod Znalosti - klíč k úspěchu Materiál přeložil a připravil Ing. Martin NEUŽIL, Ph.D. SPIRAX SARCO spol. s r.o. V Korytech (areál nádraží ČD) 100 00 Praha 10 - Strašnice tel.: 274 00 13 51, fax: 274 00
Do známky zkoušky rovnocenným podílem započítávají získané body ze zápočtového testu.
 Podmínky pro získání zápočtu a zkoušky z předmětu Chemicko-inženýrská termodynamika pro zpracování ropy Zápočet je udělen, pokud student splní zápočtový test alespoň na 50 %. Zápočtový test obsahuje 3
Podmínky pro získání zápočtu a zkoušky z předmětu Chemicko-inženýrská termodynamika pro zpracování ropy Zápočet je udělen, pokud student splní zápočtový test alespoň na 50 %. Zápočtový test obsahuje 3
SKUPENSKÉ PŘEMĚNY POJMY K ZOPAKOVÁNÍ. Testové úlohy varianta A
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D11_Z_OPAK_T_Skupenske_premeny_T Člověk a příroda Fyzika Skupenské přeměny Opakování
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D11_Z_OPAK_T_Skupenske_premeny_T Člověk a příroda Fyzika Skupenské přeměny Opakování
PROCESY V TECHNICE BUDOV 8
 UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY PROCESY V TECHNICE BUDOV 8 Dagmar Janáčová, Hana Charvátová Zlín 2013 Tento studijní materiál vznikl za finanční podpory Evropského sociálního
UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ FAKULTA APLIKOVANÉ INFORMATIKY PROCESY V TECHNICE BUDOV 8 Dagmar Janáčová, Hana Charvátová Zlín 2013 Tento studijní materiál vznikl za finanční podpory Evropského sociálního
Téma sady: Všeobecně o vytápění. Název prezentace: základní pojmy 1
 Téma sady: Všeobecně o vytápění. Název prezentace: základní pojmy 1 Autor prezentace: Ing. Eva Václavíková VY_32_INOVACE_1201_základní_pojmy_1_pwp Název školy: Číslo a název projektu: Číslo a název šablony
Téma sady: Všeobecně o vytápění. Název prezentace: základní pojmy 1 Autor prezentace: Ing. Eva Václavíková VY_32_INOVACE_1201_základní_pojmy_1_pwp Název školy: Číslo a název projektu: Číslo a název šablony
TERMOMECHANIKA 1. Základní pojmy
 1 FSI VUT v Brně, Energetický ústav Odbor termomechaniky a techniky prostředí prof. Ing. Milan Pavelek, CSc. TERMOMECHANIKA 1. Základní pojmy OSNOVA 1. KAPITOLY Termodynamická soustava Energie, teplo,
1 FSI VUT v Brně, Energetický ústav Odbor termomechaniky a techniky prostředí prof. Ing. Milan Pavelek, CSc. TERMOMECHANIKA 1. Základní pojmy OSNOVA 1. KAPITOLY Termodynamická soustava Energie, teplo,
F - Změny skupenství látek
 F - Změny skupenství látek Určeno jako učební text pro studenty dálkového studia a jako shrnující text pro studenty denního studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn
F - Změny skupenství látek Určeno jako učební text pro studenty dálkového studia a jako shrnující text pro studenty denního studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn
 Jiøí Vlèek ZÁKLADY STØEDOŠKOLSKÉ CHEMIE obecná chemie anorganická chemie organická chemie Obsah 1. Obecná chemie... 1 2. Anorganická chemie... 29 3. Organická chemie... 48 4. Laboratorní cvièení... 69
Jiøí Vlèek ZÁKLADY STØEDOŠKOLSKÉ CHEMIE obecná chemie anorganická chemie organická chemie Obsah 1. Obecná chemie... 1 2. Anorganická chemie... 29 3. Organická chemie... 48 4. Laboratorní cvièení... 69
Hydrochemie koncentrace látek (výpočty)
 1 Atomová hmotnostní konstanta/jednotka m u Relativní atomová hmotnost Relativní molekulová hmotnost Látkové množství (mol) 1 mol je takové množství látky, které obsahuje tolik částic, kolik je atomů ve
1 Atomová hmotnostní konstanta/jednotka m u Relativní atomová hmotnost Relativní molekulová hmotnost Látkové množství (mol) 1 mol je takové množství látky, které obsahuje tolik částic, kolik je atomů ve
6. Stavy hmoty - Plyny
 skupenství plynné plyn x pára (pod kritickou teplotou) stavové chování Ideální plyn Reálné plyny Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti skupenství plynné reálný plyn ve stavu
skupenství plynné plyn x pára (pod kritickou teplotou) stavové chování Ideální plyn Reálné plyny Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti skupenství plynné reálný plyn ve stavu
BUBEN A JEHO VESTAVBY Vývoj funkce bubnu
 BUBEN A JEHO VESTAVBY Vývoj funkce bubnu U kotlů vodotrubných ztrácí původní funkci výparné plochy Tvoří buben spojovací prvek pro varnice a spádové trubky Do bubnu se napájí Z bubnu se kotel odluhuje
BUBEN A JEHO VESTAVBY Vývoj funkce bubnu U kotlů vodotrubných ztrácí původní funkci výparné plochy Tvoří buben spojovací prvek pro varnice a spádové trubky Do bubnu se napájí Z bubnu se kotel odluhuje
Fáze a fázové přechody
 Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika) Fáze a fázové přechody Pojem fáze je zobecněním pojmu skupenství, označuje homogenní část makroskopického tělesa. Jednotlivé fáze v
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika) Fáze a fázové přechody Pojem fáze je zobecněním pojmu skupenství, označuje homogenní část makroskopického tělesa. Jednotlivé fáze v
Chemie. Charakteristika předmětu
 Vzdělávací obor : Chemie Chemie Charakteristika předmětu Chemie je zahrnuta do vzdělávací oblasti Člověk a příroda. Chemie je vyučována v 8. a 9. ročníku s hodinovou dotací 2 hodiny týdně. Převáţná část
Vzdělávací obor : Chemie Chemie Charakteristika předmětu Chemie je zahrnuta do vzdělávací oblasti Člověk a příroda. Chemie je vyučována v 8. a 9. ročníku s hodinovou dotací 2 hodiny týdně. Převáţná část
Mendelova zemědělská a lesnická univerzita v Brně
 Mendelova zemědělská a lesnická univerzita v Brně Bobtnání dřeva Fyzikální vlastnosti dřeva Protokol č.3 Vypracoval: Pavel Lauko Datum cvičení: 24.9.2002 Obor: DI Datum vyprac.: 10.12.02 Ročník: 2. Skupina:
Mendelova zemědělská a lesnická univerzita v Brně Bobtnání dřeva Fyzikální vlastnosti dřeva Protokol č.3 Vypracoval: Pavel Lauko Datum cvičení: 24.9.2002 Obor: DI Datum vyprac.: 10.12.02 Ročník: 2. Skupina:
ZÁKLADNÍ POZNATKY MOLEKULOVÉ FYZIKY A TERMIKY. Mgr. Jan Ptáčník - GJVJ - 2. ročník - Molekulová fyzika a termika
 ZÁKLADNÍ POZNATKY MOLEKULOVÉ FYZIKY A TERMIKY Mgr. Jan Ptáčník - GJVJ - 2. ročník - Molekulová fyzika a termika Částicová struktura látek Látky jakéhokoli skupenství se skládají z částic Částicemi jsou
ZÁKLADNÍ POZNATKY MOLEKULOVÉ FYZIKY A TERMIKY Mgr. Jan Ptáčník - GJVJ - 2. ročník - Molekulová fyzika a termika Částicová struktura látek Látky jakéhokoli skupenství se skládají z částic Částicemi jsou
CHEMIE POTRAVIN - cvičení ÚVOD & VODA
 CHEMIE POTRAVIN - cvičení ÚVOD & VODA ZÁPOČET Podmínka pro získání zápočtu = úspěšné zvládnutí testů TEST #1: Úvod, Voda, Minerální látky TEST #2: Aminokyseliny, Peptidy, Bílkoviny a jejich reakce TEST
CHEMIE POTRAVIN - cvičení ÚVOD & VODA ZÁPOČET Podmínka pro získání zápočtu = úspěšné zvládnutí testů TEST #1: Úvod, Voda, Minerální látky TEST #2: Aminokyseliny, Peptidy, Bílkoviny a jejich reakce TEST
215.1.9 - REKTIFIKACE DVOUSLOŽKOVÉ SMĚSI, VÝPOČET ÚČINNOSTI
 215.1.9 - REKTIFIKACE DVOUSLOŽKOVÉ SMĚSI, VÝPOČET ÚČINNOSTI ÚVOD Rektifikace je nejčastěji používaným procesem pro separaci organických látek. Je široce využívána jak v chemické laboratoři, tak i v průmyslu.
215.1.9 - REKTIFIKACE DVOUSLOŽKOVÉ SMĚSI, VÝPOČET ÚČINNOSTI ÚVOD Rektifikace je nejčastěji používaným procesem pro separaci organických látek. Je široce využívána jak v chemické laboratoři, tak i v průmyslu.
Termodynamika. T [K ]=t [ 0 C] 273,15 T [ K ]= t [ 0 C] termodynamická teplota: Stavy hmoty. jednotka: 1 K (kelvin) = 1/273,16 část termodynamické
![Termodynamika. T [K ]=t [ 0 C] 273,15 T [ K ]= t [ 0 C] termodynamická teplota: Stavy hmoty. jednotka: 1 K (kelvin) = 1/273,16 část termodynamické Termodynamika. T [K ]=t [ 0 C] 273,15 T [ K ]= t [ 0 C] termodynamická teplota: Stavy hmoty. jednotka: 1 K (kelvin) = 1/273,16 část termodynamické](/thumbs/24/2778201.jpg) Termodynamika termodynamická teplota: Stavy hmoty jednotka: 1 K (kelvin) = 1/273,16 část termodynamické teploty trojného bodu vody (273,16 K = 0,01 o C). 0 o C = 273,15 K T [K ]=t [ 0 C] 273,15 T [ K ]=
Termodynamika termodynamická teplota: Stavy hmoty jednotka: 1 K (kelvin) = 1/273,16 část termodynamické teploty trojného bodu vody (273,16 K = 0,01 o C). 0 o C = 273,15 K T [K ]=t [ 0 C] 273,15 T [ K ]=
Pracovní list: Opakování učiva 8. ročníku
 Pracovní list: Opakování učiva 8. ročníku Komentář ke hře: 1. Třída se rozdělí do čtyř skupin. Vždy spolu soupeří dvě skupiny a vítězné skupiny se pak utkají ve finále. 2. Každé z čísel skrývá otázku.
Pracovní list: Opakování učiva 8. ročníku Komentář ke hře: 1. Třída se rozdělí do čtyř skupin. Vždy spolu soupeří dvě skupiny a vítězné skupiny se pak utkají ve finále. 2. Každé z čísel skrývá otázku.
Termodynamika (td.) se obecně zabývá vzájemnými vztahy a přeměnami různých druhů
 Termodynamika (td.) se obecně zabývá vzájemnými vztahy a přeměnami různých druhů energií (mechanické, tepelné, elektrické, magnetické, chemické a jaderné) při td. dějích. Na rozdíl od td. cyklických dějů
Termodynamika (td.) se obecně zabývá vzájemnými vztahy a přeměnami různých druhů energií (mechanické, tepelné, elektrické, magnetické, chemické a jaderné) při td. dějích. Na rozdíl od td. cyklických dějů
CVIČENÍ č. 3 STATIKA TEKUTIN
 Rovnováha, Síly na rovinné stěny CVIČENÍ č. 3 STATIKA TEKUTIN Příklad č. 1: Nákladní automobil s cisternou ve tvaru kvádru o rozměrech H x L x B se pohybuje přímočarým pohybem po nakloněné rovině se zrychlením
Rovnováha, Síly na rovinné stěny CVIČENÍ č. 3 STATIKA TEKUTIN Příklad č. 1: Nákladní automobil s cisternou ve tvaru kvádru o rozměrech H x L x B se pohybuje přímočarým pohybem po nakloněné rovině se zrychlením
Metody termické analýzy. 3. Termické metody všeobecně. Uspořádání experimentů.
 3. ermické metody všeobecně. Uspořádání experimentů. 3.1. vhodné pro polymery a vlákna ermická analýza je širší pojem pro metody, při nichž se měří fyzikální a chemické vlastnosti látky nebo směsi látek
3. ermické metody všeobecně. Uspořádání experimentů. 3.1. vhodné pro polymery a vlákna ermická analýza je širší pojem pro metody, při nichž se měří fyzikální a chemické vlastnosti látky nebo směsi látek
Chemické výpočty. = 1,66057. 10-27 kg
 1. Relativní atomová hmotnost Chemické výpočty Hmotnost atomů je velice malá, řádově 10-27 kg, a proto by bylo značně nepraktické vyjadřovat ji v kg, či v jednontkách odvozených. Užitečnější je zvolit
1. Relativní atomová hmotnost Chemické výpočty Hmotnost atomů je velice malá, řádově 10-27 kg, a proto by bylo značně nepraktické vyjadřovat ji v kg, či v jednontkách odvozených. Užitečnější je zvolit
Zákony ideálního plynu
 5.2Zákony ideálního plynu 5.1.1 Ideální plyn 5.1.2 Avogadrův zákon 5.1.3 Normální podmínky 5.1.4 Boyleův-Mariottův zákon Izoterma 5.1.5 Gay-Lussacův zákon 5.1.6 Charlesův zákon 5.1.7 Poissonův zákon 5.1.8
5.2Zákony ideálního plynu 5.1.1 Ideální plyn 5.1.2 Avogadrův zákon 5.1.3 Normální podmínky 5.1.4 Boyleův-Mariottův zákon Izoterma 5.1.5 Gay-Lussacův zákon 5.1.6 Charlesův zákon 5.1.7 Poissonův zákon 5.1.8
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Seminář chemie (SCH) Náplň: Obecná chemie, anorganická chemie, chemické výpočty, základy analytické chemie Třída: 3. ročník a septima Počet hodin: 2 hodiny týdně Pomůcky: Vybavení odborné učebny,
Předmět: Seminář chemie (SCH) Náplň: Obecná chemie, anorganická chemie, chemické výpočty, základy analytické chemie Třída: 3. ročník a septima Počet hodin: 2 hodiny týdně Pomůcky: Vybavení odborné učebny,
ROZBOR METOD NÁLITKOVÁNÍ LITINOVÝCH ODLITKŮ
 RZBR ETD ÁLITKVÁÍ LITIVÝCH DLITKŮ Vondrák Vladimír, Pavelková Alena, Hampl Jiří VŠB TU strava, 17. listopadu 15, 78 33 strava 1. ÚVD Smršťování litin je průvodním jevem chladnutí, probíhajícím od počáteční
RZBR ETD ÁLITKVÁÍ LITIVÝCH DLITKŮ Vondrák Vladimír, Pavelková Alena, Hampl Jiří VŠB TU strava, 17. listopadu 15, 78 33 strava 1. ÚVD Smršťování litin je průvodním jevem chladnutí, probíhajícím od počáteční
Stanovení dělící účinnosti rektifikační kolony
 Stanovení dělící účinnosti rektifikační kolony Destilace je jedna z nejběžnějších separačních metod v chemickém průmyslu, především v odvětví organické výroby a petrochemii. Návrh či diagnostika destilačních
Stanovení dělící účinnosti rektifikační kolony Destilace je jedna z nejběžnějších separačních metod v chemickém průmyslu, především v odvětví organické výroby a petrochemii. Návrh či diagnostika destilačních
Hydrochemie koncentrace látek (výpočty)
 Atomová hmotnostní konstanta/jednotka m u Relativní atomová hmotnost Relativní molekulová hmotnost Látkové množství (mol) mol je takové množství látky, které obsahuje tolik částic, kolik je atomů ve 2
Atomová hmotnostní konstanta/jednotka m u Relativní atomová hmotnost Relativní molekulová hmotnost Látkové množství (mol) mol je takové množství látky, které obsahuje tolik částic, kolik je atomů ve 2
Fyzikální učebna vybavená audiovizuální technikou, interaktivní tabule, fyzikální pomůcky
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Fyzika (FYZ) Molekulová fyzika, termika 2. ročník, sexta 2 hodiny týdně Fyzikální učebna vybavená audiovizuální technikou, interaktivní tabule, fyzikální pomůcky
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Fyzika (FYZ) Molekulová fyzika, termika 2. ročník, sexta 2 hodiny týdně Fyzikální učebna vybavená audiovizuální technikou, interaktivní tabule, fyzikální pomůcky
Základní charakteristika výzkumné činnosti Ústavu fyzikální chemie
 Základní charakteristika výzkumné činnosti Ústavu fyzikální chemie Základním předmětem výzkumu prováděného ústavem je chemická termodynamika a její aplikace pro popis vybraných vlastností chemických systémů
Základní charakteristika výzkumné činnosti Ústavu fyzikální chemie Základním předmětem výzkumu prováděného ústavem je chemická termodynamika a její aplikace pro popis vybraných vlastností chemických systémů
III/2 Inovace a zkvalitnění výuky prostřednictvím ICT. Pracovní list č.3 k prezentaci Křivky chladnutí a ohřevu kovů
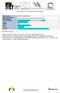 Číslo projektu CZ.1.07/1.5.00/34.0514 Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Tematická oblast Strojírenská technologie, vy_32_inovace_ma_22_06 Autor
Číslo projektu CZ.1.07/1.5.00/34.0514 Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Tematická oblast Strojírenská technologie, vy_32_inovace_ma_22_06 Autor
Název DUM: Změny skupenství v příkladech
 Základní škola národního umělce Petra Bezruče, Frýdek-Místek, tř. T. G. Masaryka 454 Zpracováno v rámci OP VK - EU peníze školám Jednička ve vzdělávání CZ.1.07/1.4.00/21.2759 Název DUM: Změny skupenství
Základní škola národního umělce Petra Bezruče, Frýdek-Místek, tř. T. G. Masaryka 454 Zpracováno v rámci OP VK - EU peníze školám Jednička ve vzdělávání CZ.1.07/1.4.00/21.2759 Název DUM: Změny skupenství
LOGO. Změny skupenství
 Změny skupenství Látka existuje ve třech skupenstvích Pevném Kapalném Plynném Látka může přecházet z jednoho skupenství do druhého. Existují tedy tyto změny skupenství: Změny skupenství plyn sublimace
Změny skupenství Látka existuje ve třech skupenstvích Pevném Kapalném Plynném Látka může přecházet z jednoho skupenství do druhého. Existují tedy tyto změny skupenství: Změny skupenství plyn sublimace
bak-06=1/1 http://www.vscht.cz/fch/cz/pomucky/kolafa/n403011p.html
 bak-06=1/1 pst=101325 = 1.013e+05 Pa R=8.314 = 8.314JK 1 mol 1 Gibbsovo fázové pravidlo v = k f + 2 C počet stupnů volnosti počet složek počet fází počet vazných podmínek 1. Gibbsovo fázové pravidlo Určete
bak-06=1/1 pst=101325 = 1.013e+05 Pa R=8.314 = 8.314JK 1 mol 1 Gibbsovo fázové pravidlo v = k f + 2 C počet stupnů volnosti počet složek počet fází počet vazných podmínek 1. Gibbsovo fázové pravidlo Určete
Měřicí a řídicí technika Bakalářské studium 2007/2008. odezva. odhad chování procesu. formální matematický vztah s neznámými parametry
 MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
12. Termomechanika par, Clausiova-Clapeyronova rovnice, parní tabulky, základni termodynamické děje v oblasti par
 1/18 12. Termomechanika par, Clausiova-Clapeyronova rovnice, parní tabulky, základni termodynamické děje v oblasti par Příklad: 12.1, 12.2, 12.3, 12.4, 12.5, 12.6, 12.7, 12.8, 12.9, 12.10, 12.11, 12.12,
1/18 12. Termomechanika par, Clausiova-Clapeyronova rovnice, parní tabulky, základni termodynamické děje v oblasti par Příklad: 12.1, 12.2, 12.3, 12.4, 12.5, 12.6, 12.7, 12.8, 12.9, 12.10, 12.11, 12.12,
IDEÁLNÍ PLYN. Stavová rovnice
 IDEÁLNÍ PLYN Stavová rovnice Ideální plyn ) rozměry molekul jsou zanedbatelné vzhledem k jejich vzdálenostem 2) molekuly plynu na sebe působí jen při vzájemných srážkách 3) všechny srážky jsou dokonale
IDEÁLNÍ PLYN Stavová rovnice Ideální plyn ) rozměry molekul jsou zanedbatelné vzhledem k jejich vzdálenostem 2) molekuly plynu na sebe působí jen při vzájemných srážkách 3) všechny srážky jsou dokonale
Fyzikální principy uplatňované v anesteziologii a IM
 Fyzikální principy uplatňované v anesteziologii a IM doc. Ing. Karel Roubík, Ph.D. ČVUT v Praze, Fakulta biomedicínského inženýrství e mail: roubik@fbmi.cvut.cz, tel.: 603 479 901 Tekutiny: plyny a kapaliny
Fyzikální principy uplatňované v anesteziologii a IM doc. Ing. Karel Roubík, Ph.D. ČVUT v Praze, Fakulta biomedicínského inženýrství e mail: roubik@fbmi.cvut.cz, tel.: 603 479 901 Tekutiny: plyny a kapaliny
Vzdělávací oblast: Člověk a příroda Vzdělávací obor (předmět): Chemie - ročník: PRIMA
 Směsi Látky a jejich vlastnosti Předmět a význam chemie Vzdělávací oblast: Člověk a příroda Vzdělávací obor (předmět): Chemie - ročník: PRIMA Téma Učivo Výstupy Kódy Dle RVP Školní (ročníkové) PT K Předmět
Směsi Látky a jejich vlastnosti Předmět a význam chemie Vzdělávací oblast: Člověk a příroda Vzdělávací obor (předmět): Chemie - ročník: PRIMA Téma Učivo Výstupy Kódy Dle RVP Školní (ročníkové) PT K Předmět
Digitální učební materiál
 Evidenční číslo materiálu: 516 Digitální učební materiál Autor: Mgr. Pavel Kleibl Datum: 22. 1. 2013 Ročník: 8. Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Fyzika Tematický okruh: Energie Téma:
Evidenční číslo materiálu: 516 Digitální učební materiál Autor: Mgr. Pavel Kleibl Datum: 22. 1. 2013 Ročník: 8. Vzdělávací oblast: Člověk a příroda Vzdělávací obor: Fyzika Tematický okruh: Energie Téma:
Ch - Chemie - úvod VARIACE
 Ch - Chemie - úvod Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně vytvořen,
Ch - Chemie - úvod Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně vytvořen,
9 FYZIKA. 9.1 Charakteristika vyučovacího předmětu. 9.2 Vzdělávací obsah
 9 FYZIKA 9.1 Charakteristika vyučovacího předmětu Obsahové vymezení Vzdělávací obsah vyučovacího předmětu je vytvořen na základě rozpracování oboru Fyzika ze vzdělávací oblasti Člověk a příroda. Vzdělávání
9 FYZIKA 9.1 Charakteristika vyučovacího předmětu Obsahové vymezení Vzdělávací obsah vyučovacího předmětu je vytvořen na základě rozpracování oboru Fyzika ze vzdělávací oblasti Člověk a příroda. Vzdělávání
Plyn. 11 plynných prvků. Vzácné plyny. He, Ne, Ar, Kr, Xe, Rn Diatomické plynné prvky H 2, N 2, O 2, F 2, Cl 2
 Plyny Plyn T v, K Vzácné plyny 11 plynných prvků He, Ne, Ar, Kr, Xe, Rn 165 Rn 211 N 2 O 2 77 F 2 90 85 Diatomické plynné prvky Cl 2 238 H 2, N 2, O 2, F 2, Cl 2 H 2 He Ne Ar Kr Xe 20 4.4 27 87 120 1 Plyn
Plyny Plyn T v, K Vzácné plyny 11 plynných prvků He, Ne, Ar, Kr, Xe, Rn 165 Rn 211 N 2 O 2 77 F 2 90 85 Diatomické plynné prvky Cl 2 238 H 2, N 2, O 2, F 2, Cl 2 H 2 He Ne Ar Kr Xe 20 4.4 27 87 120 1 Plyn
Kalibrace teploměru, skupenské teplo Abstrakt: V této úloze se studenti seznámí s metodou kalibrace teploměru a na základě svých
 Úloha 6 02PRA1 Fyzikální praktikum 1 Kalibrace teploměru, skupenské teplo Abstrakt: V této úloze se studenti seznámí s metodou kalibrace teploměru a na základě svých měření i ověří Gay-Lussacův zákon.
Úloha 6 02PRA1 Fyzikální praktikum 1 Kalibrace teploměru, skupenské teplo Abstrakt: V této úloze se studenti seznámí s metodou kalibrace teploměru a na základě svých měření i ověří Gay-Lussacův zákon.
9. Struktura a vlastnosti plynů
 9. Struktura a vlastnosti plynů Osnova: 1. Základní pojmy 2. Střední kvadratická rychlost 3. Střední kinetická energie molekuly plynu 4. Stavová rovnice ideálního plynu 5. Jednoduché děje v plynech a)
9. Struktura a vlastnosti plynů Osnova: 1. Základní pojmy 2. Střední kvadratická rychlost 3. Střední kinetická energie molekuly plynu 4. Stavová rovnice ideálního plynu 5. Jednoduché děje v plynech a)
Keramika. Technická univerzita v Liberci Nekovové materiály, 5. MI Doc. Ing. K. Daďourek 2008
 Keramika Technická univerzita v Liberci Nekovové materiály, 5. MI Doc. Ing. K. Daďourek 2008 Tuhost a váha materiálů Keramika má největší tuhost z technických materiálů Keramika je lehčí než kovy, ale
Keramika Technická univerzita v Liberci Nekovové materiály, 5. MI Doc. Ing. K. Daďourek 2008 Tuhost a váha materiálů Keramika má největší tuhost z technických materiálů Keramika je lehčí než kovy, ale
ÚSTAV ORGANICKÉ TECHNOLOGIE
 LABORATOŘ OBORU I ÚSTAV ORGANICKÉ TECHNOLOGIE () A Určování binárních difúzních koeficientů ve Stefanově trubici Vedoucí práce: Ing. Pavel Čapek, CSc. Umístění práce: laboratoř 74 Určování binárních difúzních
LABORATOŘ OBORU I ÚSTAV ORGANICKÉ TECHNOLOGIE () A Určování binárních difúzních koeficientů ve Stefanově trubici Vedoucí práce: Ing. Pavel Čapek, CSc. Umístění práce: laboratoř 74 Určování binárních difúzních
10. Energie a její transformace
 10. Energie a její transformace Energie je nejdůležitější vlastností hmoty a záření. Je obsažena v každém kousku hmoty i ve světelném paprsku. Je ve vesmíru a všude kolem nás. S energií se setkáváme na
10. Energie a její transformace Energie je nejdůležitější vlastností hmoty a záření. Je obsažena v každém kousku hmoty i ve světelném paprsku. Je ve vesmíru a všude kolem nás. S energií se setkáváme na
T0 Teplo a jeho měření
 Teplo a jeho měření 1 Teplo 2 Kalorimetrie Kalorimetr 3 Tepelná kapacita 3.1 Měrná tepelná kapacita Měrná tepelná kapacita při stálém objemu a stálém tlaku Poměr měrných tepelných kapacit 3.2 Molární tepelná
Teplo a jeho měření 1 Teplo 2 Kalorimetrie Kalorimetr 3 Tepelná kapacita 3.1 Měrná tepelná kapacita Měrná tepelná kapacita při stálém objemu a stálém tlaku Poměr měrných tepelných kapacit 3.2 Molární tepelná
STRUKTURA PEVNÝCH LÁTEK A KAPALIN
 STRUKTURA PEVNÝCH LÁTEK A KAPALIN 19. ZMĚNY SKUPENSTVÍ, FÁZOVÝ DIAGRAM Autor: Ing. Eva Jančová DESS SOŠ a SOU spol. s r. o. SKUPENSTVÍ - Skupenství neboli stav je konkrétní forma látky, charakterizovaná
STRUKTURA PEVNÝCH LÁTEK A KAPALIN 19. ZMĚNY SKUPENSTVÍ, FÁZOVÝ DIAGRAM Autor: Ing. Eva Jančová DESS SOŠ a SOU spol. s r. o. SKUPENSTVÍ - Skupenství neboli stav je konkrétní forma látky, charakterizovaná
9. MĚŘENÍ TEPELNÉ VODIVOSTI
 Měřicí potřeby 9. MĚŘENÍ TEPELNÉ VODIVOSTI 1) střídavý zdroj s regulačním autotransformátorem 2) elektromagnetická míchačka 3) skleněná kádinka s olejem 4) zařízení k měření tepelné vodivosti se třemi
Měřicí potřeby 9. MĚŘENÍ TEPELNÉ VODIVOSTI 1) střídavý zdroj s regulačním autotransformátorem 2) elektromagnetická míchačka 3) skleněná kádinka s olejem 4) zařízení k měření tepelné vodivosti se třemi
FYZIKA na LF MU cvičná. 1. Který z následujících souborů jednotek neobsahuje jen základní nebo odvozené jednotky soustavy SI?
 FYZIKA na LF MU cvičná 1. Který z následujících souborů jednotek neobsahuje jen základní nebo odvozené jednotky soustavy SI? A. kandela, sekunda, kilogram, joule B. metr, joule, kalorie, newton C. sekunda,
FYZIKA na LF MU cvičná 1. Který z následujících souborů jednotek neobsahuje jen základní nebo odvozené jednotky soustavy SI? A. kandela, sekunda, kilogram, joule B. metr, joule, kalorie, newton C. sekunda,
