ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV
|
|
|
- Vlasta Šmídová
- před 8 lety
- Počet zobrazení:
Transkript
1 ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV
2 OSNOVA PŘEDNÁŠKY Příprava dat pro numerické analýzy čištění dat, odlehlé body, transformace, standardizace, EDA Design ekologických experimentů manipulativní experimenty vs přírodní experimenty (pozorování) Typy sbíraných dat kategoriální vs kvantitativní, pokryvnosti, frekvence Ekologická podobnost indexy podobnosti a vzdálenosti mezi vzorky Klasifikace hierarchická vs nehierarchická, aglomerativní vs divisivní Ordinace lineární vs unimodální, přímá vs nepřímá Regrese zobecněné lineární modely, regresní a klasifikační stromy Ellenbergovy indikační hodnoty kalibrace Indexy druhové bohatosti alfa, beta a gamma diverzita, akumulační druhová křivka, rarefaction Případové studie na použití jednotlivých metod 2
3 LITERATURA Doporučená Lepš J. & Šmilauer P. (2001) Mnohorozměrná analýza ekologických dat v anglické verzi vyšlo v nakladatelství Cambridge v roce 2003 jako Multivariate Analysis of Ecological Data using CANOCO Herben T. & Münzbergová Z. (2003) Zpracování geobotanických dat v příkladech. Část 1. Data o druhovém složení ftp://botany.natur.cuni.cz/skripta/zpracovani_geobot_dat/multivar.pdf Pro fajnšmekry Wildi O. (2010) Data Analysis in Vegetation Ecology. Wiley-Blackwell. Gotelli N.J. & Ellison A.M. (2004) A Primer of Ecological Statistics. Sinauer Associates. Palmer M. Ordination methods for ecologists, website Oksanen J. (2004) Multivariate Analysis in Ecology, Lecture Notes. Legendre P. & Legendre L. (1998) Numerical Ecology (Second English Edition). Elsevier. 3
4 SOFTWARE CANOCO for Windows 4.5 ordinační analýzy CanoDraw for Windows 4.0 kreslení ordinačních diagramů a odpovědních křivek druhů PC-ORD 5 numerické klasifikace, ordinační analýzy, analýza odlehlých bodů STATISTICA 9.0 regrese, regresní a klasifikační stromy Kde co sehnat: CANOCO, CanoDraw a PC-ORD instalace z AVRUMELu nebo webových stránek předmětu (záložka Software) STATISTICA licenci je třeba získat po přihlášení na v sekci Nabídka software 4
5 DALŠÍ INFORMACE Webové stránky předmětu: přednášky, software, příklady ke cvičení, studijní materiály některé sekce vyžadují přihlášení Cvičení probíhat bude v Bohunicích v druhé půlce semestru a zaměřené bude na analýzu dat v programu CANOCO a jejich vizualizaci v programu CanoDraw tři čtyřhodinové bloky Zkouška vypracování závěrečné práce (pokyny viz webové stránky předmětu, sekce Závěrečná práce) vlastní zkouška představuje asi půlhodinovou diskuzi nad závěrečnou prací, doplněná o rozšiřující otázky týkající se probírané látky 5
6 TYPY SBÍRANÝCH DAT PŘÍPRAVA DAT PRO ANALÝZY
7 DATA O EKOLOGII SPOLEČENSTEV popisují společenstvo, případně i jeho prostředí společenstvo je typicky sledováno na určité ploše (v případě rostlin a některých málo mobilních živočichů) nebo např. v pastech (v případě mobilních živočichů) složení živého společenstva je popsáno přítomností jednotlivých druhů daného typu organismů, na jedné ploše (v jedné pasti) se přitom vyskytuje většinou více než jeden druh prostředí je popisováno jednou nebo více proměnnými, o kterých se předpokládá, že ovlivňují studovaný typ organismů ekologická data jsou ve své podstatě mnohorozměrná a dají se vyjádřit maticí dat (data matrix) ekologická data vždy obsahují řadu zkreslení (bias) např. sampling bias přehlédnutí některých druhů 7
8 TYPY PROMĚNNÝCH Kategoriální (kvalitativní, nominální, prezenčně-absenční) např. geologický substrát, půdní typy, binární proměnné (přítomnostabsence druhu) kategorie jsou unikátní (každý jedinec/pozorování spadá právě do jedné z nich) a nelze je smysluplně seřadit Ordinální (semikvantitativní) např. Braun-Blanquetova stupnice pro odhad pokryvnosti druhů jednotlivé stupně (kategorie) lze seřadit, rozdíly mezi stupni jsou různě velké Kvantitativní diskrétní (počty, měření s malou přesností) x kontinuální (přesná měření) poměrová stupnice (ratio scale) x rozdílová stupnice (interval scale)
9 TYPY PROMĚNNÝCH ALTERNATIVNÍ TŘÍDĚNÍ Typ proměnné binární (dvoustavový, presence-absence) mnohostavový neseřazený seřazený semikvantitativní (ordinální) kvantitativní (měření) diskontinuální (počty, diskrétní) kontinuální Příklady přítomnost nebo absence druhu geologický substrát stupnice pokryvností druhy počet jedinců teplota, hloubka půdy Legendre & Legendre
10 PRIMÁRNÍ DATA 10
11 PRIMÁRNÍ DATA 11
12 mgs/5152_tapes-small.jpg PRIMÁRNÍ DATA Zadávání primárních dat spreadsheet, metadata Uchování a zpřístupnění primárních dat problematika dlouhodobé archivace a nosičů dat zpřístupnění primárních dat Kontrola a čištění dat sloučení taxonomické nomenklatury chyby a chybějící data (možnosti nahrazení chybějících dat) analýza odlehlých bodů (outlier analysis) někdy i vyloučení vzácných druhů (odstranění šumu v datech) EDA exploratory data analysis 12
13 EDA EXPLORATORY DATA ANALYSIS obecně: metoda pro odhalení různých vlastností dat (description of pattern in data) slouží např. k vytěžování dat (data mining, data dredging moderní, ale problematická metoda zpracování dat) grafická EDA: odhalení odlehlých bodů (outlier analysis) distribuce dat (normalita) a nutnost transformace box-plot (krabicový graf) a histogram pro jednorozměrná data scatterplot (bodový graf) pro dvou a vícerozměrná data John Tukey ( ) 13
14 EDA EXPLORATORY DATA ANALYSIS ANALÝZA ODLEHLÝCH BODŮ BOX-PLOT & HISTOGRAM XERSSW Frequency Median 25%-75% Range Outliers XERSSW (head index) 14
15 EDA EXPLORATORY DATA ANALYSIS ANALÝZA ODLEHLÝCH BODŮ - SCATTERPLOT XERSSW XERSW XERSSW XERSW 15
16 DETAILY KE KRABICOVÝM GRAFŮM (BOXPLOT) Klasický boxplot (střední hodnota = medián) maximální hodnota Q3 horní kvartil Q2 - medián Q1 spodní kvartil minimální hodnota Definice odlehlých bodů a extrémů (STATISTICA) outlier 16
17 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY TRANSFORMACE Transformace dat mění relativní vzdálenosti mezi jednotlivými hodnotami a tím i tvar jejich distribuce Proč data transformovat? protože škála měření je arbitrární a nemusí odpovídat ekologickému významu proměnné deset prstů => používání desítkové soustavy protože (některé) statistické testy vyžadují, aby data byla normálně rozložená (normal distribution) měla homogenní varianci (homoskedasticita, mezi průměrem a směrodatnou odchylkou není žádný vztah) protože lineární vztahy se interpretují lépe než vztahy nelineární 17
18 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY TRANSFORMACE Na co si dát při transformaci pozor? aby transformace rozložení dat ještě nezhoršila a nevytvořila nové odlehlé body abychom při komentování výsledků používali netransformované hodnoty proměnných Typy transformace lineární přičtení konstanty nebo vynásobení konstantou nemění výsledky statistického testování nulových hypotéz např. převod teploty měřené ve stupních Celsia na stupně Fahrenheita nelineární log transformace, odmocninová transformace atd. může změnit výsledky statistického testování 18
19 ROZDĚLENÍ DAT (DATA DISTRIBUTION) symetrické (symetrical) pozitivně (doprava) zešikmené* (right skewed) negativně (doleva) zešikmené (left skewed) * ekologická data jsou často zešikmená pozitivně (doprava), protože jsou omezená nulou na začátku 19
20 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY zdroj: wikipedia.org TRANSFORMACE Logaritmická transformace (log transformation) pro data s výrazně pozitivně (doprava) šikmou distribucí (right skewed), u kterých existuje vztah mezi směrodatnou odchylkou a průměrem (lognormální rozložení) Y* = log (Y), případně Y* = log (a*y + c) na základě logaritmu nezáleží (10, 2, e) konstanta a = 1; pokud je Y z intervalu <0;1>, potom a > 1 konstanta c se přidává, pokud proměnná Y obsahuje nuly c může být např. 1, nebo arbitrárně zvolené malé číslo (0,001) na konstantě c může záležet výsledek analýz (ANOVA), a proto je dobré vybírat takové číslo, aby transformovaná proměnná byla co nejvíce symetrická 20
21 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY Odmocninová transformace (square-root transformation) vhodná pro mírně doprava zešikmená data (right skewed), např. počty druhů (Poisson distribution) Y* = Y, případně Y* = (Y + c) konstanta c se přičítá, pokud soubor obsahuje nuly c může být např. 0,5, nebo 3/8 (0,325) třetí a vyšší odmocnina je účinnější na více zešikmená data (čtvrtá odmocnina se používá pro abundance druhů s mnoha nulami a několika vysokými hodnotami) Mocninná transformace (power transformation) vhodná pro data negativně (doleva) sešikmená (left skewed) Y* = Y p TRANSFORMACE pokud p < 1 - odmocninová transformace (p = 0,5 druhá odmocnina, p = 0,25 čtvrtá odmocnina atd.) 21
22 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY TRANSFORMACE logaritmická odmocninová Legendre & Legendre (1998) 22
23 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY TRANSFORMACE 23 Münch. Med. Wschr. 124, 1982
24 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY TRANSFORMACE Transformace pomocí arcsin (angular transformation) vhodná pro procentické hodnoty (a obecně podíly) Y* = arcsin Y nebo Y* = arcsin Y použitelná pro hodnoty v intervalu <-1; 1> transformované hodnoty jsou v radiánech Reciproká transformace (reciprocal transformation) vhodná pro poměry (například výška/hmotnost, počet dětí v populaci na počet žen atd.) Y* = 1/Y 24
25 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY TRANSFORMACE Box-Cox transformace (zobecněná mocniná transformace) zobecněná parametrická transformace iterativní hledání parametru λ (lambda), pro které je rozdělení transformované proměnné nejblíže normálnímu rozdělení používá se v případě, že nemáme a priori představu, jakou transformaci použít Neparametrické metody transformace např. metoda Omnibus pro ordinální data Legendre & Legendre
26 MAJÍ DATA NORMÁLNÍ ROZDĚLENÍ? GRAFICKÁ ANALÝZA Histogram s křivkou normálního rozdělení Počet pozorování Soil depth vizuální zhodnocení normality dat možno otestovat Kolmogorov-Smirnov testem Q-Q diagram (Quantile-Quantile plot) Oček. normál. hodnoty Pozorovaný kvantil porovnání rozdělení dvou proměnných, vynáší proti sobě kvantily jednotlivých proměnných jedna proměnná může být teoretická distribuce (v tomto případě normální rozdělení, kdy se vychází z kumulativní distribuční funkce) na stejném principu pracuje Shapiro-Wilk test 26
27 Theoretical quantiles Theoretical quantiles Theoretical quantiles Frequency Frequency Frequency MAJÍ DATA NORMÁLNÍ ROZDĚLENÍ? GRAFICKÁ ANALÝZA normální rozdělení pozitivně zešikmené negativně zešikmené variable variable variable Sample quantiles Sample quantiles Sample quantiles 27
28 Soil ph Soil ph Frequency Frequency BIMODÁLNÍ DATA transformace nepomůže, možnost rozdělit na dva podsoubory Soil ph Soil ph Annual precipitation [mm] Annual precipitation [mm]
29 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY Centrování výsledná proměnná má průměr roven nule Y i * = Y i průměr (Y) Standardizace v úzkém slova smyslu STANDARDIZACE PROMĚNNÝCH výsledná proměnná má průměr roven nule a směrodatnou odchylku rovnu jedné synchronizuje proměnné měřené v různých jednotkách a na různých stupnicích Y i * = (Y i průměr (Y)) / směrodatná odchylka (Y) Změna rozsahu hodnot (ranging) výsledná proměnná je v rozsahu 0 až 1 Y i * = Y i / Y max nebo Y i * = (Y i Y min ) / (Y max Y min ) 29
30 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY STANDARDIZACE MATICE SPOLEČENSTVA Standardizace v případě matice společenstva (vzorky x druhy) standardizace po druzích (by species) dává velkou váhu vzácným druhům ne vždy smysluplná (pokud se druh vyskytuje vzácně v jednom snímku, standardizace po druzích dá tomuto snímku velkou váhu) standardizace po vzorcích (by samples) pokud je analýza zaměřená na relativní proporce mezi druhy, ne jejich absolutní abundance vhodné v případě, že výsledné abundance závisí na důkladnosti, s jakou sbíráme data (např. při odchytu živočichů doba strávená na ploše nebo počet pastí) 30
31 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY TRANSFORMACE matematická funkce, jejíž argumenty nejsou odvozené z dat, na která je transformace aplikovaná (data independent) nejčastější důvod je změnit tvar rozložení proměnné, případně zajistit homoskedasticitu STANDARDIZACE mění data pomocí statistiky, která je spočtená na datech samotných, např. průměr, součet, rozsah aj. (data dependent) nejčastější důvod použití je vyrovnat rozdíly v relativním významu (váze) jednotlivých ekologických proměnných, druhů nebo vzorků ve své podstatě je to další typ transformace 31
32 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY KÓDOVÁNÍ DAT (DATA CODING) např. nahrazení kódů u alfa-numerických stupnic, např. Braun-Blanquetovy stupnice dominance-abundance Br.-Bl.: r ordinální hodnoty: střední hodnoty procent:
33 PŘÍPRAVA DAT PRO NUMERICKÉ ANALÝZY KÓDOVÁNÍ DAT (DATA CODING) Dummy variables metoda, jak převést kvalitativní (kategoriální) proměnnou na kvantitativní (binární) proměnné použitelné v analýzách pokud má kategoriální proměnná n stavů (hodnot), pro její vyjádření stačí n-1 dummy proměnných (jedna z proměnných je vždy lineárně závislá na ostatních) hodnoty dummy proměnné KAMB LITO RANK FLUVI kambizem litozem ranker fluvizem
34 SOUBORY S VELKÝM POČTEM NUL (ANEB VÝZNAM NULY V EKOLOGII) dva možné významy nuly: 1. hodnota může být ve skutečnosti nenulová, ale díky našim možnostem měření jsme ji naměřili jako nulovou (například koncentrace látky v roztoku) 2. hodnota je skutečná nula například absence druhu data obsahující pravé nuly obsahují dva typy informace: 1. druh chybí nebo je přítomen? 2. pokud je druh přítomen, jaká je jeho abundance? v datech obsahujících velké množství pravých nul je většina informace prvního typu problém pravých nul při logaritmické transformaci soubor s velkým počtem pravých nul není vhodné logaritmicky transformovat (přičítat k nim konstantu c), ale lépe ji nahradit binární proměnnou (prezence-absence) 34
35 DESIGN EKOLOGICKÝCH EXPERIMENTŮ To call in the statistician after the experiment is done may be no more than asking him to perform a post mortem examination: he may be able to say what the experiment died of. Sir Ronald Fisher, Indian Statistical Congress, Sankhya 1939
36 ZÁKLADNÍ OTÁZKA: CO CHCI EXPERIMENTEM ZJISTIT? Jaká je variabilita proměnné Y v čase nebo prostoru? pattern description nejčastější otázka v ekologických observačních studiích Má faktor X vliv na proměnnou Y? hypothesis testing, otázka pro manipulativní experiment může platit i pro některé přírodní experimenty, ale výsledky těchto testů jsou podstatně slabší (nemáme kontrolu nad vlivem ostatních faktorů, které mohou výsledky ovlivnit) Chová se proměnná Y tak, jak předpovídá hypotéza H? klasická konfrontace mezi teorií a reálnými daty platí pro data získaná jak manipulativním tak přírodním experimentem ne vždy je snadné najít správnou hypotézu Jaký model nejlépe vystihuje vztah mezi faktorem X a proměnnou Y? experimentem sbíráme podklady pro matematické modelování 36
37 MANIPULATIVNÍ VS PŘÍRODNÍ EXPERIMENTY Manipulativní experimenty uměle manipulujeme vysvětlující proměnnou (X) a sledujeme reakci vysvětlované proměnné (Y) umožňuje přímé testování hypotéz známe směr vztahu mezi příčinou a důsledkem - kauzalita Přírodní experimenty (pozorování, observační studie) vysvětlující proměnnou manipuluje sama příroda slouží spíše ke generování než testování hypotéz neznáme směr vztahu mezi příčinou a důsledkem - korelace 37
38 MANIPULATIVNÍ VS PŘÍRODNÍ EXPERIMENTY SROVNÁNÍ TESTOVANÝCH HYPOTÉZ Příklad: na ostrovech v Karibiku sledujeme vztah mezi počtem ještěrek na určité ploše a počtem pavouků (Gotelli & Ellison 2004) Manipulativní experiment Provedení: v jednotlivých plochách (klecích) je uměle ovlivněn počet ještěrek a sledováno množství pavouků Nulová hypotéza: počet ještěrek nemá vliv na počet pavouků v klecích Alternativní hypotéza: se vzrůstající hustotou ještěrek klesá počet pavouků (ještěrky žerou pavouky) 38
39 MANIPULATIVNÍ VS PŘÍRODNÍ EXPERIMENTY Přírodní experiment (pozorování, observační studie) Provedení: SROVNÁNÍ TESTOVANÝCH HYPOTÉZ na vybraných plochách je sledován počet ještěrek a počet pavouků Možné hypotézy: 1. počet ještěrek (negativně) ovlivňuje počet pavouků (ještěrky žerou pavouky) 2. počet pavouků má vliv na počet ještěrek (draví pavouci napadají mláďata ještěrek) 3. počet ještěrek i pavouků je ovlivňován neměřeným faktorem prostředí (třeba vlhkostí) 4. některý faktor prostředí ovlivňuje sílu vztahu mezi ještěrkami a pavouky (třeba zase vlhkost) 39
40 závisle proměnná závisle proměnná MANIPULATIVNÍ EXPERIMENT PRESS VS PULSE EXPERIMENT Press experiment (experiment pod stálým tlakem ) zásah je proveden na začátku experimentu a pak znovu v pravidelných intervalech měří resistenci systému na experimentální zásah jak je systém (společenstvo) schopné odolávat, případně se přizpůsobit změnám v podmínkách prostředí Pulse experiment (pulzní experiment, jednou a dost ) zásah je proveden jen jednou, obvykle na začátku experimentu měří resilienci systému jak pružně je systém (společenstvo) schopné reagovat na experimentální zásah čas čas 40
41 PŘÍRODNÍ EXPERIMENT (POZOROVÁNÍ) SNAPSHOT VS TRAJECTORY EXPERIMENT Snapshot experiment (momentka) opakuje se v prostoru, ale ne v čase sběr vzorků provedu na několika (mnoha) lokalitách v relativně krátkém čase (týden, sezóna, dva roky sběru dat pro diplomku...) představuje většinu přírodních experimentů v ekologii zahrnuje i sukcesní studie, kdy sledujeme zároveň různá sukcesní stadia Trajectory experiment (sledujeme trajektorii procesu v čase) opakuje se v čase (a případně i v prostoru) sběr vzorků se na daných (většinou pevně vymezených plochách) opakuje několikrát za sebou sukcesní studie prováděné několik let, trvalé plochy v lesních porostech opakovaně měřené jednou za x let 41
42 MANIPULATIVNÍ EXPERIMENT ZÁKLADNÍ TYPY ROZMÍSTĚNÍ PLOCH kompletně znáhodněný design nebere v úvahu heterogenitu prostředí ne vždy je nejvhodnější znáhodněné bloky vlastní bloky jsou vnitřně homogenní (pokud možno) počet bloků = počet opakování bloky jsou umístěné podle gradientu prostředí v každém bloku je právě jedna replikace každého zásahu gradient prostředí 42
43 MANIPULATIVNÍ EXPERIMENT ZÁKLADNÍ TYPY ROZMÍSTĚNÍ PLOCH latinský čtverec předpokládá přítomnost dvou gradientů v prostředí každý sloupec a každý řádek obsahuje právě jednu variantu zásahu možno použít i několik latinských čtverců gradient 1 gradient 2 43
44 MANIPULATIVNÍ EXPERIMENT NEJČASTĚJŠÍ CHYBY pseudoreplikace testovat lze jen rozdíly v průměrech jednotlivých bloků plochy se stejným zásahem jsou umístěny blízko sebe, a mají proto větší pravděpodobnost, že si budou podobné i bez vlivu vlastního zásahu neúplně znáhodněný design v podstatě pseudoreplikace, jen méně zřejmá gradient prostředí gradient prostředí 44
45 gradient prostředí gradient prostředí gradient prostředí MANIPULATIVNÍ EXPERIMENT NEJČASTĚJŠÍ CHYBY design se znáhodněnými bloky špatná orientace bloků správně špatně špatně 45
46 MANIPULATIVNÍ EXPERIMENT S VÍCE NEŽ JEDNÍM TYPEM ZÁSAHU faktoriální design každá hladina prvního faktoru je kombinovaná s každou hladinou druhého faktoru (případně třetího atd.) například kombinace koseno vs nekoseno hnojeno vs nehnojeno jednotlivé kombinace mohou být rozmístěny v prostoru např. v rámci latinského čtverce ano ne koseno hnojeno 46
47 MANIPULATIVNÍ EXPERIMENT S VÍCE NEŽ JEDNÍM TYPEM ZÁSAHU split-plot design faktory jsou strukturovány hierarchicky (nested) například plochy hnojené různými hnojivy (C, N, P) v rámci bloků umístěných na vápenci (modrá) a žule (červená barva) N N P C C P N C P C P N P P N C C N 47
48 letecký pohled plán zásahů MANIPULATIVNÍ EXPERIMENTY PŘÍPADOVÉ STUDIE ROTHAMSTED (ENGLAND) PARK GRASSLAND EXPERIMENT (ZALOŽEN 1843) 48 Silvertown et al. (2006) J.Ecol.
49 MANIPULATIVNÍ EXPERIMENTY PŘÍPADOVÉ STUDIE ROTHAMSTED (ENGLAND) PARK GRASSLAND EXP. 49 Třídění bylinné biomasy do druhů (kolem roku 1930) (
50 MANIPULATIVNÍ EXPERIMENTY PŘÍPADOVÉ STUDIE KOMPETICE O SVĚTLO V EXPERIMENTÁLNÍM PROSTŘEDÍ Při vyšším přísunu živin rostou rostliny rychleji a začnou si konkurovat o světlo tak proč jim trochu nepřisvítit? Hautier et al. (2009) Science 324:
51 MANIPULATIVNÍ EXPERIMENTY PŘÍPADOVÉ STUDIE STANOVENÍ POTENCIÁLNÍ STANOVIŠTNÍ PRODUKTIVITY V DOUBRAVÁCH PĚSTOVÁNÍM ŘEDKVIČEK VE SKLENÍKU 51 Veselá et. al (2008): Bioassay experiment for assessment of site productivity in oak forests. - 17th International Workshop European Vegetation Survey, Brno, Czech Republic,
52 MANIPULATIVNÍ EXPERIMENTY PŘÍPADOVÉ STUDIE VLIV HERBIVORNÍCH RYB NA DRUHOVÉ SLOŽENÍ KORÁLOVÝCH ÚTESŮ hustá klec zabrání všem rybám na začátku experimentu... řídká klec zabrání jen velkým rybám... a po čtyřech měsících pod klecí Atol Agatti (Lakedivy, Indie) Autor: Nicole Černohorská (v rámci vypracování její disertační práce na zoologii) 52
53 detailní pohled na korálový útes s nárostem řas (autor: Nicole Černohorská) 53
54 PŘÍRODNÍ EXPERIMENT (OBSERVAČNÍ STUDIE) Preferenční ROZMÍSTĚNÍ VZORKOVACÍCH PLOCH 54
55 PŘÍRODNÍ EXPERIMENT (OBSERVAČNÍ STUDIE) ROZMÍSTĚNÍ VZORKOVACÍCH PLOCH Systematické rozmístění v síti (lattice) 55
56 PŘÍRODNÍ EXPERIMENT (OBSERVAČNÍ STUDIE) ROZMÍSTĚNÍ VZORKOVACÍCH PLOCH Systematické rozmístění v síti (grid) 56
57 PŘÍRODNÍ EXPERIMENT (OBSERVAČNÍ STUDIE) ROZMÍSTĚNÍ VZORKOVACÍCH PLOCH Systematické rozmístění na transektu 57
58 PŘÍRODNÍ EXPERIMENT (OBSERVAČNÍ STUDIE) ROZMÍSTĚNÍ VZORKOVACÍCH PLOCH Náhodné rozmístění 58
59 PŘÍRODNÍ EXPERIMENT (OBSERVAČNÍ STUDIE) ROZMÍSTĚNÍ VZORKOVACÍCH PLOCH Preferenční rozmístění statistické hledisko: snímky nejsou náhodným výběrem, což limituje jejich použití při statistických analýzách (Lajer 2007, Folia Geobotanica) hledisko vegetačního ekologa: popisují maximální variabilitu vegetace praktické důsledky: snímky bývají druhově bohatší, obsahují větší počet diagnostických nebo vzácných druhů Náhodné (a systematické) rozmístění statistické hledisko: snímky jsou náhodným výběrem v reálném prostoru (ne ale v ekologickém hyperprostoru) hledisko veg. ekologa: nezachytí celou variabilitu vegetace - chybí maloplošné a vzácné vegetační typy, převládají velkoplošné a běžné typy, zahrnují řadu špatně klasifikovatelných vegetačních přechodů praktické důsledky: snímky odrážejí reálnou strukturu a bohatost vegetace v krajině, ale metoda je neúměrně pracná 59
60 PŘÍRODNÍ EXPERIMENT (OBSERVAČNÍ STUDIE) ROZMÍSTĚNÍ VZORKOVACÍCH PLOCH Stratifikované náhodné rozmístění 60
61 STRATIFIKACE KRAJINY V GIS Teplota Srážky Půdní typy Stratifikované jednotky Austin et al
62 PROSTOROVÁ AUTOKORELACE bližší plochy jsou si podobnější 62
63 PROSTOROVÁ AUTOKORELACE vlastnosti určitého pozorování (vzorku) mohou být do určité míry odvozeny z pozorování v jeho okolí jednotlivá pozorování na sobě nejsou nezávislá běžná vlastnost prakticky všech reálných ekologických dat příroda se nechová podle zákonů statistiky může být pozitivní (bližší vzorky jsou si podobnější než by odpovídalo jejich náhodnému výběru) nebo negativní (sousední vzorky jsou si méně podobné než kdyby byly vybrány náhodou) Vše souvisí se vším, ale bližší věci spolu souvisejí více než ty vzdálené Waldo Tobler (1969), První zákon geografie 63
64 PROSTOROVÁ AUTOKORELACE Co způsobuje prostorovou autokorelaci biologických dat? omezené možnosti disperze, genetický tok nebo klonální růst sousedé jsou si podobnější organismy jsou omezeny ekologickými faktory (například vlhkost nebo teplota), které jsou samy o sobě prostorově autokorelovány Jak se prostorová autokorelace projevuje při analýze dat? pozitivní PA zvyšuje pravděpodobnost chyby prvního druhy (Type 1 error), totiž že zamítneme nulovou hypotézu, která platí (statistické testy vycházejí průkazněji než by měly) negativní PA způsobuje opačný efekt problém je v počtu stupňů volnosti (degrees of freedom): pokud si stupně volnosti představíme jako množství informace, kterou každý nový vzorek přináší, pak každý nový nezávislý vzorek přináší jeden stupeň volnosti, ale prostorově autokorelovaný vzorek přináší méně 64
65 PROSTOROVÁ AUTOKORELACE Příklad: Vliv nadmořské výšky na vegetaci, studovaný pomocí transektů vedených podél nadmořské výšky prostorově neautokorelované transekty (každý transekt na různé hoře) prostorově autokorelované transekty (paralelně vedle sebe na jedné hoře) 65
66 PROBLÉM PROSTOROVÉ ŠKÁLY (SCALE OF THE STUDY) zrno (grain size) velikost nejmenší studované jednotky, zpravidla vzorkované plochy rozsah (extent) velikost studovaného území interval vzdálenost mezi vzorkovanými plochami Legendre & Legendre (1998) 67
67 PROBLÉM PROSTOROVÉ ŠKÁLY (SCALE OF THE STUDY) velikost zrna (plochy, vzorku) je dána vlastnostmi a velikostí studovaných objektů různý prostorový rozsah zachycení různých ekologických procesů, vliv různých ekologických faktorů platí pravidlo, že studie malého rozsahu jsou hůře zobecnitelné Legendre & Legendre (1998) 68
68 TVAR PLOCHY čtvercová obdélníková kruhová čtverec obdélník kruh celková plocha 100 m m m 2 rozměr tvaru m 20 5 m poloměr 5,64 m obvod 40 m 50 m ~ 35 m 69
69 TVAR PLOCHY Whittaker Stohlgren Keeley & Fotheringham (2005) J.Veg.Sci. Kunin 70
70 gradient prostředí VLIV TVARU A ORIENTACE PLOCHY NA ZAZNAMENANOU DRUHOVOU BOHATOST obdélníkové plochy mohou mít vyšší druhovou bohatost než čtvercové plochy (o stejné ploše) 71 Stohlgren et al. (1995) Vegetatio 117: ; Condit et al. (1996) J.Ecol. 84: ; Keeley & Fotheringham (2005) J.Veg.Sci. 16:
71 VELIKOST PLOCHY STUDIUM VEGETACE NA VÍCE MĚŘÍTCÍCH SOUČASNĚ 72
72 VELIKOST PLOCHY STUDIUM VEGETACE NA VÍCE MĚŘÍTCÍCH SOUČASNĚ Vztah mezi velikostí snímku a počtem druhů ve snímku bělokarpatské louky ve srovnání s jinými typy travinné vegetace Jongepierová [ed.](2008): Louky Bílých Karpat. 73
73 EKOLOGICKÁ PODOBNOST (ECOLOGICAL RESEMBLANCE)
74 EKOLOGICKÁ PODOBNOST Q VS R ANALÝZA Vzorky Druhy druh 1 druh 2 druh 3 vzorek vzorek vzorek vztahy mezi vzorky Q analýza vztahy mezi druhy (nebo obecně mezi deskriptory) R analýza 76
75 PODOBNOSTI X VZDÁLENOSTI (Q ANALÝZA) Indexy podobnosti slouží k vyjádření podobnosti mezi vzorky, ne k jejich umístění do mnohorozměrného prostoru (například ordinace) nejnižší hodnota 0 vzorky nesdílejí žádný druh nejvyšší hodnota (1 nebo jiná) vzorky jsou identické Vzdálenosti mezi vzorky slouží k umístění vzorků v mnohorozměrném prostoru nejnižší hodnota 0 vzorky jsou identické (ve stejné lokaci) hodnota se zvyšuje se zvyšující se nepodobností mezi vzorky 77
76 INDEXY PODOBNOSTI kvalitativní vs kvantitativní kvalitativní pro presenčně-absenční data kvantitativní pro data vyjadřující abundance, počty aj. symetrické vs asymetrické dvojité nepřítomnosti ( double-zero ) počet druhů, které chybí zároveň v obou vzorcích, v kontrastu s počtem druhů které se vyskytují zároveň v obou vzorcích symetrické dvojité nepřítomnosti hodnotí stejně jako dvojité přítomnosti (totiž že vyjadřují podobnost mezi vzorky); v ekologii se prakticky nepoužívají asymetrické dvojité nepřítomnosti ignorují; nejčastější typ indexů podobnosti v ekologii 78
77 PROBLÉM DVOJITÝCH NEPŘÍTOMNOSTÍ (DOUBLE-ZEROS) Skutečnost, že druh chybí zároveň v obou snímcích, může znamenat, že: vzorky leží mimo ekologickou niku druhu nemůžeme ale říci, zda oba vzorky leží na stejné straně ekologického gradientu mimo niku druhu (a jsou si tedy docela podobné) nebo na stranách opačných (a jsou pak úplně odlišné) vzorky leží uvnitř ekologické niky druhy, ale druh se ve vzorku nevyskytuje, protože se tam nedostal (dispersal limitation) jsme ho přehlédli a nezaznamenali (sampling bias) nachází se právě v dormantním stadiu a není proto vidět (jednoletky, geofyty) 79
78 vlhkomilný druh 1 vlhkomilný druh 2 mezický druh 1 mezický druh 2 suchomilný druh 1 suchomilný druh 2 PROBLÉM DVOJITÝCH NEPŘÍTOMNOSTÍ (DOUBLE-ZEROS) snímek snímek snímek snímky 1 až 3 jsou seřazeny podle vlhkosti stanoviště snímek 1 je nejvlhčí, snímek 3 nejsušší snímek 1 a 3 neobsahují ani jeden mezický druh snímek 1 je pro tyto druhy příliš vlhký, snímek 3 příliš suchý symetrické indexy podobnosti: dvojitá nepřítomnost mezických druhů bude zvyšovat podobnost snímků 1 a 3 asymetrické indexy: dvojité nepřítomnosti budou ignorovány 80
79 INDEXY PODOBNOSTI PRO KVALITATIVNÍ DATA druh je ve vzorku č. 1 a počet druhů přítomných v obou vzorcích b, c počet druhů přítomných jen v jednom vzorku přítomen d počet druhů, které chybí v obou vzorcích ( double zeros ) nepřítomen ve vzorku č. 2 přítomen a b Pokud nebereme v úvahu druhy nepřítomné v obou vzorcích (d), lze zobrazit i pomocí Vennova diagramu nepřítomen c d c a b 81 vzorek č. 1 vzorek č. 2
80 INDEXY PODOBNOSTI PRO KVALITATIVNÍ DATA Jaccardův koeficient J = a / (a + b + c) Sørensenův koeficient S = 2a / (2a + b + c) přítomnosti druhu v obou vzorcích (a) přisuzuje dvojnásobnou váhu Simpsonův koeficient Si = a / [a + min (b,c)] vhodný pro vzorky velmi odlišné počtem druhů c a b 82 vzorek č. 1 vzorek č. 2
81 INDEXY PODOBNOSTI PRO KVANTITATIVNÍ DATA např. zobecněný Sørensenův koeficient (procentická podobnost, percentage similarity) PS = [2 Σ min (x i, y i )] / Σ (x i + y i ) x i, y i... kvantita i-tého druhu ve srovnávaných vzorcích má rozsah od 0 do 1 pro presenčně absenční data přechází v 2a / (2a + b + c) velmi vhodný pro ekologická data percentage dissimilarity (PD, Bray-Curtis index) = 1 PS 83
82 VZDÁLENOSTI MEZI VZORKY (DISTANCE MEASURES) všechny indexy podobnosti (kvalitativní i kvantitativní) lze převést na distance D = 1 S, nebo D = (1 S) kde D je vzdálenost (distance) a S je podobnost (similarity) odmocninový převod se používá například pro Sørensenův koeficient neplatí obráceně (ne všechny vzdálenosti se dají převést na podobnosti např. Euklidovská vzdálenost) 84
83 VZDÁLENOSTI MEZI VZORKY (DISTANCE MEASURES) Euklidovská vzdálenost (Euclidean distance) ED = Σ (x i y i ) 2 rozsah: od 0 (identické vzorky), horní mez není dána rozsah hodnot výrazně záleží na použitých jednotkách míra citlivá na odlehlé body - nevhodná pro ekologická data tětivová vzdálenost (chord distance, relativized Euclidean distance) Euklidovská vzdálenost použitá na datech standardizovaných přes vzorky (by sample norm) rozsah: od 0 (identické vzorky) do 2 (vzorky nesdílí žádný druh) Chi-kvadrát vzdálenost (chi-square distance) málokdy se používá přímo na výpočet vzdálenosti mezi vzorky vyjadřuje vzdálenost mezi vzorky v unimodálních ordinačních metodách (např. v korespondenční analýze, CA) 85
84 EUKLIDOVSKÁ VZDÁLENOST PARADOX může se stát, že dva vzorky, které sdílejí některé druhy (vzorky 1 a 3), budou mít větší vzdálenost než dva vzorky, které nesdílí ani jeden druh (vzorky 1 a 2) Vzorky Druhy druh 1 druh 2 druh 3 vzorek vzorek vzorek ,732 4,243 Eucl (vzorek 1, vzorek 2) = (0-1) 2 + (1-0) 2 + (1-0) 2 = 1,732 Eucl (vzorek 1, vzorek 3) = (0-0) 2 + (1-4) 2 + (1-4) 2 = 4,243 86
85 INDEXY PODOBNOSTI MEZI DRUHY (R ANALÝZA) V kolika vzorcích je... druh č. 1 přítomen nepřítomen druh č. 2 přítomen a b nepřítomen c d Diceův index Dice = 2a / (2a + b + c) stejný jako Sørensenův index pro podobnost mezi vzorky uveden dříve než Sørensen (Dice 1945 vs Sørensen 1948) Pearsonův korelační koeficient r není vhodný pro data s velkým počtem nul, ani po transformaci 87
86 MATICE PODOBNOSTÍ (VZDÁLENOSTÍ) MEZI VZORKY (NEBO DRUHY) je symetrická (podobnost mezi 2. a 3. snímkem = podobnost mezi 3. a 2. snímkem) diagonála obsahuje pouze nuly (matice vzdáleností) nebo pouze jedničky (matice podobností) matice Euklidovských vzdáleností mezi 10 vzorky 88
87 vzorky Zastoupení nul v matici [%] MATICE VZORKY DRUHY V EKOLOGII SPOLEČENSTEV (SPARSE MATRIX, ŘÍDKÁ MATICE) více než 90% hodnot tvoří nuly, u velkých souborů až 99% Počet vegetačních snímků v matici 89 druhy
88 NUMERICKÁ KLASIFIKACE
89 PROČ MÁ SMYSL VĚCI KLASIFIKOVAT? vlnová délka (~ ekologický gradient) 91
90 PROČ MÁ SMYSL VĚCI KLASIFIKOVAT? vlnová délka (~ ekologický gradient) 92
91 KLASIFIKACE O klasifikaci obecně platí: smyslem je najít diskontinuity v jinak kontinuální realitě, které můžeme pojmenovat například proto, abychom si usnadnili komunikaci cílem je seskupit podobné objekty (vzorky, druhy) do skupin, které jsou vnitřně homogenní, dobře popsatelné a zároveň dobře odlišitelné od ostatních skupin O klasifikaci ekologických dat platí: pokud analyzuji vzorky daná skupina obsahuje vzorky s podobným druhovým složením (např. podobná stanoviště) pokud analyzuji druhy daná skupina obsahuje druhy s podobným ekologickým chováním 93
92 VYUŽITÍ KLASIFIKACE V PRAXI KNIHY A KNIHOVNA 94
93 VYUŽITÍ KLASIFIKACE V PRAXI VYHLEDÁVAČ GOOGLE 95
94 KLASIFIKACE OBECNÉ ROZDĚLENÍ neřízená (unsupervised, bez učitele) cílem je vytvořit novou klasifikaci pomocí datového souboru výslednou klasifikaci můžeme ovlivnit pouze výběrem metody (kombinace klasifikačního algoritmu a míry podobnosti), případně požadovaného počtu shluků numerické metody klasifikace (cluster analysis, TWINSPAN) řízená (supervised, s učitelem) cílem je aplikovat již existující klasifikaci ( danou učitelem ) na datový soubor klasifikační systém musíme nejdříve naučit, jak má vypadat výsledná klasifikace (training), a systém ji pak reprodukuje na dalších vzorcích ANN artificial neural networks, klasifikační stromy, náhodné lesy (random forests), COCKTAIL 96
95 KLASIFIKACE OBECNÉ ROZDĚLENÍ subjektivní vs objektivní v době rozkvětu metod numerické klasifikace se věřilo, že numerické metody přinášejí klasifikaci založenou na objektivních kritériích, tedy tu která skutečně existuje (narozdíl od té subjektivní, která je výmyslem badatele ) všechny klasifikace jsou ale z principu subjektivní v případě, že Bůh není, pak není nikdo, kdo by řekl, která klasifikace je jediná správná neformalizovaná vs formalizovaná formalizovaná klasifikace je taková, která je provedena na základě jasných kritérií a díky tomu je možné ji znovu reprodukovat opakem je klasifikace založená na neformálních kritériích (například pocitu), kterou pak není snadné zopakovat 97
96 OTÁZKY, KTERÉ BYCH SI MĚL POLOŽIT PŘED TÍM, NEŽ ZAČNU NĚCO KLASIFIKOVAT Pro jaký účel klasifikaci dělám? chci klasifikovat můj datový soubor (srovnat knihy v mojí domácí knihovničce) chci vytvořit obecný klasifikační systém, který bude použitelný i na další soubory (vytvořit knihovnický systém kategorizace knih, používaný i v jiných knihovnách) Podle jakých kritérií budu objekty klasifikovat? kritérium, podle kterého budu posuzovat, jestli si jsou objekty více či méně podobné (knihy budu třídit podle obsahové podobnosti nebo např. podle velikosti) odpovídá výběru indexu podobnosti mezi vzorky Jak stanovím hranice mezi jednotlivými skupinami? odpovídá výběru klasifikačního algoritmu 98
97 KLASIFIKACE klasifikační metody nehierarchické (K-means clustering) divisivní hierarchické aglomerativní (klasická cluster analysis) monotetické (asociační analýza) polytetické (TWINSPAN) 99
98 KLASIFIKACE klasifikační metody nehierarchické (K-means clustering) divisivní hierarchické aglomerativní (klasická cluster analysis) monotetické (asociační analýza) polytetické (TWINSPAN) 100
99 KLASIFIKACE HIERARCHICKÁ A AGLOMERATIVNÍ Shluková analýza (cluster analysis ) hierarchická metoda shluky jsou hierarchicky uspořádány aglomerativní metoda shluky jsou tvořeny odspodu, tzn. postupným shlukováním jednotlivých vzorků do větších skupin základní volby: míra nepodobnosti mezi vzorky (distance measure) shlukovací (klastrovací) algoritmus (clustering algorithm) pozor NEJDE O OBJEKTIVNÍ metodu klasifikace (ta neexistuje), protože výsledná podoba klasifikace je ovlivněna řadou našich SUBJEKTIVNÍCH rozhodnutí 101
100 SHLUKOVÁ ANALÝZA (CLUSTER ANALYSIS) Výsledek shlukové analýzy je ovlivněn celou řadou rozhodnutí, které provádíme na různých úrovních zpracování dat sběr dat volba důležitostní hodnoty (pokryvnost, početnost) primární data transformace strandardizace míra nepodobnosti (Euklidovská, Bray-Curtis atd.) matice nepodobností výběr klastrovacího algoritmu (single linkage, complete linkage atd.) výsledná klasifikace 102
101 SHLUKOVÁ ANALÝZA (CLUSTER ANALYSIS) SHLUKOVACÍ ALGORITMY Metoda jednospojná (single linkage) páry vzorků seřazené podle podobností matice podobností Legendre & Legendre 1998 výsledný dendrogram 103
102 SHLUKOVÁ ANALÝZA (CLUSTER ANALYSIS) SHLUKOVACÍ ALGORITMY Metoda jednospojná (single linkage, nearest neighbour) vzorky se pojí ke shluku, ve kterém je jim nejpodobnější vzorek přidám se ke skupině, ve které je ten, kdo je mí nejvíc sympatický Metoda všespojná (complete linkage, farthest neighbour) vzorky se připojí ke shluku až v okamžiku, kdy shluk obsahuje všechny podobné vzorky přidám se ke skupině ve které je ten, kdo je mi nejmíň nesympatický single linkage complete linkage 104
103 distance SHLUKOVÁ ANALÝZA (CLUSTER ANALYSIS) DENDROGRAM záleží na tom, které vzorky jsou spojeny na které úrovni nezáleží na tom, který vzorek (skupina) je vpravo a který vlevo 105
104 METODA JEDNOSPOJNÁ VS VŠESPOJNÁ Bray-Curtis distance / Single linkage Bray-Curtis distance / Complete linkage metoda jednospojná se výrazně řetězí 106
105 METODA JEDNOSPOJNÁ VLIV TRANSFORMACE DRUHOVÝCH DAT Single linkage / Euclidean distance / no transformation Single linkage / Euclidean distance / LOG transformation transformace dat (např. logaritmická) může výrazně ovlivnit výsledný dendrogram v případě euklidovských vzdáleností a jednospojné metody obzvlášť 107
106 SHLUKOVÁ ANALÝZA (CLUSTER ANALYSIS) SHLUKOVACÍ ALGORITMY Average linkage (např. UPGMA) zahrnuje řadu metod, které stojí mezi single a complete linkage a v ekologii jsou smysluplnější UPGMA (unweighted pair-group method using arithmetic averages) vzorek se připojí ke shluku, ke kterému má největší (neváženou) průměrnou podobnost se všemi jeho vzorky přidám se ke skupině, ve které jsou mi všichni v průměru nejvíc sympatičtí Euclidean distance / UPGMA 108
107 SHLUKOVÁ ANALÝZA (CLUSTER ANALYSIS) SHLUKOVACÍ ALGORITMY Wardova metoda (Ward s minimum variance method) Euclidean distance / Ward's method ke shluku se připojí vzorek, jehož vzdálenost od centroidu shluku je nejmenší (počítáno přes čtverce vzdáleností mezi vzorky a centroidy shluků) neměla by se kombinovat se Sørensenovým (Bray-Curtis) indexem podobnosti 109
108 SHLUKOVÁ ANALÝZA (CLUSTER ANALYSIS) Flexible clustering (beta flexible) nastavení parametru β ovlivňuje řetězení dendrogramu nejvíc se řetězí pro β ~ 1, nejméně pro β = -1 SHLUKOVACÍ ALGORITMY optimální reprezentace vzdáleností mezi vzorky je při β = -0,25 Legendre & Legendre
109 KLASIFIKACE klasifikační metody nehierarchické (K-means clustering) divisivní hierarchické aglomerativní (klasická cluster analysis) monotetické (asociační analýza) polytetické (TWINSPAN) 111
110 KLASIFIKACE TWINSPAN (Two Way INdicator Species ANalysis) HIERARCHICKÁ A DIVISIVNÍ divisivní metoda začíná dělením celého souboru vzorků a postupuje směrem dolů polytetická metoda každé dělení závisí na několika (indikačních) druzích (x monotetická metoda dělení ovlivňuje jediný druh) metoda velmi oblíbená mezi vegetačními ekology ale algoritmus je poměrně složitý, s řadou arbitrárních kroků, a proto má také řadu zarytých odpůrců vzorky jsou uspořádány podle první osy korespondenční analýzy (CA, DCA) a podle ní jsou rozděleny do dvou shluků (vzorky s pozitivním skóre a negativním skóre) metoda ošetří vzorky, které leží blízko středu osy, a které tak mají velkou pravděpodobnost, že budou špatně klasifikovány 112
111 KLASIFIKACE TWINSPAN (Two Way INdicator Species ANalysis) HIERARCHICKÁ A DIVISIVNÍ pseudospecies metoda primárně funguje pro kvalitativní data kvantitativní informace se dodává rozdělením druhů na pseudospecies podle abundance (cut levels) výsledkem je (mimo jiné) tabulka podobná fytocenologické snímky z určitých klastrů a druhy s vysokou fidelitou k dané skupině jsou seskupeny dohromady metoda vhodná v případě, že jsou data strukturovaná podle jednoho výrazného gradientu vhodné na hledání (několika málo) ekologicky interpretovatelných skupin v datech PC-ORD, JUICE 113
112 TWINSPAN 114
113 MODIFIKOVANÝ TWINSPAN (ROLEČEK ET AL. 2009) na rozdíl od původního algoritmu (a) umožňuje modifikovaný TWINSPAN (b) dopředu stanovit cílový počet skupin algoritmus se po každém dělení na dvě skupiny rozhoduje, kterou ze skupin bude dále dělit vybere tu, která je více heterogenní na základě její betadiverzity míru betadiverzity je nutné zvolit (např. Jaccardův index podobnosti) JUICE 115
114 KLASIFIKACE klasifikační metody nehierarchické (K-means clustering) divisivní hierarchické aglomerativní (klasická cluster analysis) monotetické (asociační analýza) polytetické (TWINSPAN) 116
115 KLASIFIKACE NEHIERARCHICKÁ K-means clustering (shlukování metodou K-průměrů) nehierarchická metoda všechny shluky jsou si rovny minimalizuje sumy čtverců vzdáleností mezi vzorky uvnitř shluků na začátku uživatel zvolí počet shluků iterativní metoda, začne od náhodného přiřazení vzorků do shluků, postupně přehazuje vzorky mezi shluky a hledá optimální řešení výsledek do určité míry záleží na počátečním rozmístění shluků do vzorků a je proto dobré proces mnohokrát zopakovat (najít stabilní řešení) STATISTICA, SYN-TAX 2000 Legendre & Legendre
116 STANOVENÍ DRUHŮ TYPICKÝCH PRO JEDNOTLIVÉ SHLUKY Analýza indikačních druhů (Dufrêne & Legendre 1997) - IndVal relativní abundance a frekvence druhu uvnitř a mimo shluk možnost testování signifikance Monte-Carlo permutačním testem Fidelita (věrnost) druhu ke vzorku (Chytrý et al. 2002) Phi koeficient asociace (analogie Pearsonova korelačního koeficientu r) ϕ = (ad bc) / (a + b)(c + d)(a + c)(b + d) rozsah <-1, 1>, 0 při shodné frekvenci uvnitř a vně shluku v JUICE možnost standardizace na velikost skupiny exaktní Fisherův test pro testování signifikance Počet vzorků ve shluku A mimo shluk A obsahující daný druh a b neobsahující daný druh c d 122
117 ORDINAČNÍ ANALÝZA
118 KONCEPCE MNOHOROZMĚRNÉHO PROSTORU Prostor může být definován 1) druhy (species space ) druhy jsou osami mnohorozměrného prostoru vzorky jsou body v tomto prostoru zobrazení původní matice druhy-vzorky 2) vzorky (sample space) vzorky jsou osami mnohorozměrného prostoru druhy jsou body v tomto prostoru zobrazení původní matice druhy-vzorky 3) ekologickými gradienty (ecological space) osami jsou ekologické gradienty jako body do něj lze zobrazit druhy i vzorky Zuur et al. (2007) 134
119 ORDINACE OPODSTATNĚNÍ jeden gradient prostředí většinou ovlivňuje chování (abundanci) několika druhů najednou základní chování společenstev druhová data jsou redundantní pokud znám chování (abundanci) jednoho druhu, můžu do určité míry odhadnout chování i některých dalších druhů díky této redundanci je možné (a hlavně smysluplné) zredukovat mnohorozměrný prostor, ve kterém jsou druhy/vzorky rozmístěny (prostory 1 a 2), na několik málo dimenzí ekologického prostoru (prostor 3) pokud by chování druhů bylo na sobě úplně nezávislé, existovala by celá řada ekvivalentních možností, jak mnohorozměrný prostor zredukovat, a ani jedna by nepřinesla nic nového 135
120 ORDINACE RŮZNÉ FORMULACE PROBLÉMU 1) hledání skrytých proměnných (ordinačních os) najdi několik proměnných (ordinačních os), které nejlépe vystihují vliv všech druhů eigenvalue based methods 2) rozmístění vzorků v ordinačním prostoru najdi takové rozmístění vzorků v redukovaném ordinačním prostoru, aby vzdálenost mezi vzorky co nejvěrněji odrážela jejich nepodobnost vypočtenou z druhového složení jednotlivých vzorků distance based methods 136
121 NEPŘÍMÁ VS PŘÍMÁ ORDINACE UNCONSTRAINED VS CONSTRAINED ORD. Nepřímá ordinace vychází pouze z matice vzorky druhy hledá proměnné (ordinační osy), které nejlépe reprezentují variabilitu v druhových datech slouží k popisu mnohorozměrných dat (pattern description) a generování hypotéz, ne k testování hypotéz Přímá ordinace vychází ze dvou matic: vzorky druhy a vzorky proměnné prostředí ordinační osy představují směr největší variability v druhových datech, která může být vysvětlena na základě a priori známých proměnných prostředí slouží spíše k testování hypotéz o vlivu proměnných prostředí na druhová data, neslouží k popisu dat 137
122 abundance abundance MODELY ODPOVĚDI DRUHŮ NA GRADIENT PROSTŘEDÍ lineární unimodální gradient gradient 138
123 abundance druhu abundance druhu LINEÁRNÍ MODEL ODPOVĚDI DRUHU JEN PŘI KRÁTKÉM EKOLOGICKÉM GRADIENTU krátký ekologický gradient dlouhý ekologický gradient gradient prostředí (ph, nadm. výška) gradient prostředí (ph, nadm. výška) 139 Lepš & Šmilauer (2003) Multivariate analysis of...
124 ZÁKLADNÍ TYPY ORDINAČNÍCH TECHNIK (ZALOŽENÝCH NA VÝPOČTU EIGENVALUES) lineární odpověď druhů unimodální odpověď druhů nepřímá ordinace (unconstrained) přímá ordinace (constrained) PCA (Principal Component Analysis, analýza hlavních komponent) RDA (Redundancy Analysis, redundanční analýza) CA (Correspondence Analysis, korespondenční analýza) DCA (Detrended Correspondence analysis, detrendovaná korespondenční analýza) CCA (Canonical Correspondence Analysis, kanonická korespondenční analýza) 140
125 NEPŘÍMÁ ORDINACE PRINCIP hledání skryté proměnné (gradientu), který nejlépe reprezentuje chování všech druhů podél tohoto gradientu první ordinační osa (ordination axis) a skóre vzorků na této ordinační ose (sample scores) odhad optima (odpovědi) jednotlivých druhů na této ose (species scores) druhá a vyšší ordinační osy musejí být lineárně nezávislé na všech nižších ordinačních osách 141
126 sp2 NEPŘÍMÁ ORDINACE PRINCIP (PCA) sp1 sp2 samp1 2 1 samp4 samp2 3 4 samp3 5 0 samp4 7 6 samp5 9 2 a) rozmístění vzorků v prostoru definovaném druhy b) výpočet těžiště shluku c) centrování os d) rotace os samp2 samp1 samp3 sp1 samp5 142 Legendre & Legendre (1998)
127 NEPŘÍMÁ ORDINACE ALGORITMUS (CA) 5 výpočetních kroků 1. začni s arbitrárním (náhodným) skóre vzorků (x i ) 2. vypočti nové skóre pro jednotlivé druhy (species score, y i ) jako průměr skóre vzorků x i vážený abundancí druhu ve vzorcích 3. vypočti nové skóre pro jednotlivé vzorky (sample score, x i ) jako průměr skóre druhů y i vážený abundancí druhů ve vzorku 4. standardizuj skóre jednotlivých vzorků (natáhni osu) 5. pokud se skóre nemění, zastav, pokud ano, pokračuj krokem 2 143
128 NEPŘÍMÁ ORDINACE CA UNIMODÁLNÍ METODA 144 Lepš & Šmilauer (2003) Multivariate analysis of...
129 NEPŘÍMÁ ORDINACE CA UNIMODÁLNÍ METODA 145 Lepš & Šmilauer (2003) Multivariate analysis of...
130 NEPŘÍMÁ ORDINACE CA UNIMODÁLNÍ METODA 146 Lepš & Šmilauer (2003) Multivariate analysis of...
131 NEPŘÍMÁ ORDINACE CA UNIMODÁLNÍ METODA 147 Lepš & Šmilauer (2003) Multivariate analysis of...
132 NEPŘÍMÁ ORDINACE CA UNIMODÁLNÍ METODA 148 Lepš & Šmilauer (2003) Multivariate analysis of...
133 ORDINAČNÍ DIAGRAMY nepřímá ordinace přímá ordinace lineární metoda unimodální metoda Lepš & Šmilauer (2003) Multivariate analysis of
134 ORDINAČNÍ DIAGRAMY KONVENCE zobrazení vzorků -> body zobrazení druhů -> šipky (lineární metody) -> body, centroidy (unimodální metody) zobrazení ordinačních os vodorovná bývá osa vyššího řádu (např. první) orientace os je arbitrární zobrazení proměnných prostředí šipky (kvantitativní proměnné) centroidy (kategoriální proměnné) typ ordinačního diagramu: scatterplot - 1 typ dat (vzorky nebo druhy) biplot - 2 typy dat (např. vzorky a druhy) triplot - 3 typy dat (např. vzorky, druhy a proměnné prostředí) Lepš & Šmilauer (2003) Multivariate analysis of
135 ARTEFAKTY V ORDINACÍCH Podkova (Horseshoe effect ) PCA pořadí vzorků podél první osy neodráží jejich skutečnou nepodobnost v extrémním případě se mohou okraje přiblížit nebo dokonce překřížit Oblouk (Arch effect ) CA pořadí vzorků podél první osy stále odráží jejich nepodobnost druhá osa je nelineární kombinací první osy 151
136 ARTEFAKTY V ORDINACÍCH Podkova a oblouk (Horseshoe and arch effect) důsledek algoritmu - každá následující osa musí být lineárně nezávislá na předchozích osách, ale neuvažuje se nelineární závislost důsledek projekce - nelineární vztahy mezi druhy a gradienty prostředí se promítají do lineárního prostoru definovaného Euklidovskými vzdálenostmi 152
137 SIMULOVANÁ DATA POUZE JEDEN EKOLOGICKÝ GRADIENT simulovaný gradient dlouhý 5000 jednotek 300 druhů s unimodální odpovědí, různými šířkami nik 500 vzorků náhodně rozmístěných podél gradientu 153
138 SIMULOVANÁ DATA ARTEFAKTY PCA - podkova CA - oblouk o vzorky + druhy 154
139 ARTEFAKTY V ORDINACÍCH MOŽNOSTI ŘEŠENÍ odstranění trendu z ordinačních os (detrending) detrendovaná korespondenční analýza, Detrended Correspondence Analysis (DCA, Hill & Gauch 1980) detrending by segments (nejčastější) detrending by polynomials (pokud v analýze používám kovariáty) použití takových ordinačních technik, které umožňují ordinaci vzorků v prostoru pomocí jiných metrik než je Euklidovská distance (PCA) nebo chi-kvadrát distance (CA) analýza hlavních koordinát, Principal Coordinate Analysis (PCoA) nemetrické mnohorozměrné škálování, Non-metric Multidimensional Scaling (NMDS) 155
140 DETRENDED CORRESPONDENCE ANALYSIS PROCES ODSTRANĚNÍ TRENDU Krok 1 rozdělení první osy na několik segmentů Krok 2 vycentrování druhé osy každého segmentu kolem nuly 156
141 DETRENDED CORRESPONDENCE ANALYSIS PROCES ODSTRANĚNÍ TRENDU Krok 3 nelineární přeškálování první osy, které odstraňuje nahloučení vzorků na koncích gradientů -> výsledný ordinační diagram má osy naškálované v jednotkách směrodatné odchylky (SD) -> platí, že druhové složení se změní o polovinu na gradientu o délce 1-1,4 SD (half-change in species composition), celé druhové složení se obmění na 4 SD ter Braak (1987) 157
142 DETRENDED CORRESPONDENCE ANALYSIS VÝHODY A NEVÝHODY neelegantní metoda, která je někdy přirovnávána k použití kladiva na data (hlavně část týkající se rozdělení osy na segmenty a jejich centrování) výsledek je silně ovlivněn arbitrárním rozhodnutím o počtu segmentů (doporučuje se vyzkoušet více možností) pokud jsou v datech dva nebo více hlavních gradientů (ordinačních os), DCA si s nimi neporadí (detrending do určité míry poškodí druhou a vyšší ordinační osy) i kladivo, pokud je v rukou odborníka, může být použito efektivně - metoda často dává ekologicky dobře interpretovatelné výsledky osy DCA jsou v jednotkách SD, které umožňují zjistit, jak dlouhý gradient naše data pokrývají 158
143 SIMULOVANÁ DATA (JEDEN EKOLOGICKÝ GRADIENT) DCA o vzorky + druhy 159
144 VÝBĚR ORDINAČNÍ METODY NA ZÁKLADĚ DCA LINEÁRNÍ NEBO UNIMODÁLNÍ? lineární metody vyžadují homogenní data, unimodální jsou vhodná i pro data heterogenní kuchařka alá Lepš & Šmilauer (2003) - zjištění délky gradientu (heterogenity dat) pomocí metody DCA, detrending by segments pokud je délka 1. osy DCA menší než 3 SD použiji lineární techniku větší než 4 SD použiji unimodální techniku v rozmezí 3-4 SD obě techniky pracují rozumně alternativní doporučení (Legendre & Gallagher 2001) na data aplikovat Hellingerovu transformaci a dále je zpracovávat pomocí lineárních metod, které jsou robustnější 160
145 PCOA (PRINCIPAL COORDINATE ANALYSIS) ORDINACE ZALOŽENÁ NA DISTANCÍCH syn. MDS Metric Dimensional Scaling alternativní metoda nepřímé ordinace vstupní data matice nepodobností mezi vzorky výpočet matice nepodobností jakýkoliv index nepodobnosti pokud zvolím Euklidovskou vzdálenost -> identické s PCA pokud zvolím Chi-kvadrát vzdálenost -> obdoba CA v CANOCO se počítá programem PrCoord 161
146 NMDS (NON-METRIC MULTIDIMENSIONAL SCALING) ORDINACE ZALOŽENÁ NA DISTANCÍCH další alternativa nepřímých ordinací, nemetrická varianta PCoA vstupní data matice nepodobností mezi vzorky výpočet matice nepodobností jakýkoliv index nepodobnosti výsledek je značně ovlivněn výběrem indexu nepodobnosti iterativní algoritmus, který nemusí pokaždé dojít ke stejnému výsledku (lokální optima) na začátku je nutno určit počet dimenzí, se kterými bude metoda pracovat (obvykle k = 2 nebo 3) při větším množství dat VELMI časově náročná v CANOCO se počítá programem WinKyst, který je ke stažení zde: 162
147 NMDS NON-METRIC MULTIDIMENSIONAL SCALING náhodné rozmístění vzorků v prostoru rozmístění vzorků v prostoru respektuje jejich nepodobnost 163
148 vzdálenost mezi vzorky v ordinačním diagramu NMDS NON-METRIC MULTIDIMENSIONAL SCALING stress = 7.47 nepodobnost v druhovém složení mezi vzorky 164
149 POROVNÁNÍ METOD DCA A NMDS DCA NMDS 165 data z údolí Vltavy, klasifikace metodou TWINSPAN (Zelený & Chytrý 2007)
150 POROVNÁNÍ METOD DCA A NMDS DCA NMDS při větším počtu vzorků tvoří trojúhelník nebo pěticípou hvězdu (artefakt) má tendenci jakákoliv data zobrazit jako kouli 166
151 POROVNÁNÍ METOD DCA A NMDS SIMULOVANÁ DATA (JEDEN GRADIENT) DCA NMDS o vzorky + druhy 167
152 Gradient 2 SIMULOVANÁ DATA DVA RŮZNĚ DLOUHÉ GRADIENTY 168 Gradient 1
153 SIMULOVANÁ DATA DVA RŮZNĚ DLOUHÉ GRADIENTY 169
154 SIMULOVANÁ DATA DVA STEJNĚ DLOUHÉ GRADIENTY 170
155 SIMULOVANÁ DATA DVA RŮZNĚ DLOUHÉ GRADIENTY krátké gradienty dlouhé gradienty 171
156 POROVNÁNÍ METOD ZALOŽENÝCH NA VÝPOČTU EIGENVALUES A DISTANCÍ Eigenvalue-based ordination methods DCA, PCA a CA a jejich omezené (constrained) varianty DCCA, RDA a CCA vstupní data = matice vzorky x druhy, ze kterých se extrahují hlavní ordinační osy (eigenvectors) interpretace zaměřena na směry variability v datech, vysvětlené jednotlivými ordinačními osami Distance-based ordination methods NMDS a PCoA vstupní data = matice nepodobností interpretace zaměřena se na vzdálenosti mezi vzorky v redukovaném ordinačním prostoru 172
157 POUŽITÍ PROMĚNNÝCH PROSTŘEDÍ V ORDINACI DVA ALTERNATIVNÍ POSTUPY Y samples species matrix X samples environmental factors matrix oba přístupy jsou relevantní a navzájem se doplňují! 173 Legendre & Legendre (1998)
158 POUŽITÍ PROMĚNNÝCH PROSTŘEDÍ V ORDINACI DVA ALTERNATIVNÍ POSTUPY 1. nepřímá ordinace + korelace získám skóre vzorků na hlavních ordinačních osách skóre vzorků koreluji s jednotlivými proměnnými prostředí + určitě zachytím hlavní gradienty v druhovém složení nemusím zachytit tu část variability v druhovém složení, která je vztažená k jednotlivým proměnným prostředí 2. přímá ordinace proměnné prostředí vstupují přímo jako vysvětlující proměnné do ordinace skóre vzorků na osách je ovlivněno vztahem k těmto proměnným prostředí + určitě zachytím variabilitu v datech, která se vztahuje k jednotlivým proměnným prostředím nemusím zachytit část variability v druhových datech, která není vysvětlena žádnou proměnnou prostředí 174
159 species 1 (residual) env 1 env spe 1 spe 2 spe 3 species species 1 (predicted) spe 1 spe 2 spe spe 1 spe 2 spe 3 PŘÍMÁ ORDINAČNÍ ANALÝZA matice vzorky druhy sam 1 sam 2 sam 3 sam 4 sam 5 sam 6 regrese abundance druhu na proměnné prostředí predikované hodnoty gradient sam 1 sam 2 sam 3 sam 4 sam 5 sam 6 sam 7 sam 7 sam 1 sam 2 sam gradient residuály sam 1 sam 2 sam 3 sam 4 sam 5 sam 4 sam 6 sam 5 sam 6 sam 7 matice s vysvětlujícími proměnnými gradient sam 7
160 spe 1 spe 2 spe 3 spe 1 spe 2 spe 3 matice predikovaných hodnot ordinační osy s omezením (constrained axes) sam 1 sam 2 sam 3 sam 4 sam 5 sam 6 sam 7 ordinace počet ordinačních os s omezením = počet vysvětlujících proměnných (pokud je vysvětlující proměnná kategoriální, počet os je roven počtu kategorií minus 1) sam 1 sam 2 sam 3 ordinace sam 4 sam 5 sam 6 sam 7 matice residuálů ordinační osy bez omezení (unconstrained axes) 176
161 PŘÍMÁ ORDINACE RDA INTERPRETACE VÝSLEDKŮ CCA 177
162 PŘÍMÁ ORDINAČNÍ ANALÝZA MONTE-CARLO PERMUTAČNÍ TEST testuje nulovou hypotézu, že druhové složení je nezávislé na vysvětlující proměnné test první kanonické osy vliv jen jedné kvantitativní proměnné test všech kanonických os vliv všech proměnných, nebo vliv jedné kategoriální proměnné s více kategoriemi (počet os = počet kategorií 1) testová statistika F data (pseudo-f) P hladina signifikance n x počet permutací, kde F perm >= F data N celkový počet permutací 178
163 PŘÍMÁ ORDINAČNÍ ANALÝZA MONTE-CARLO PERMUTAČNÍ TEST 179 Herben & Münzbergová 2001
164 PŘÍMÁ ORDINAČNÍ ANALÝZA MONTE-CARLO PERMUTAČNÍ TEST randomizace ploch bez omezení (unrestricted randomization) randomizace ploch v blocích (randomization within blocks defined by covariables) 180 Herben & Münzbergová 2001
165 JAK ČÍST VÝSLEDKY ORDINAČNÍCH METOD? procento variability vysvětlené hlavními osami CANOCO: cummulative percentage variance of species data vypočte se také jako eigenvalue / total variance ukazuje, jak úspěšný byl celý proces ordinace čím více jsou jednotlivé druhy korelované, tím více variability bude vysvětleno několika málo hlavními osami má smysl srovnávat vysvětlenou variabilitu hlavních os různými ordinačními technikami na stejných datech nemá smysl srovnávat vysvětlenou variabilitu hlavních os stejnými ordinačními technikami na různých datech (eigenvalues jsou závislé na počtu hráčů ve hře druhů, vzorků) skóre (souřadnice) závisle proměnných (druhů) na osách u lineárních technik skóre = regresní koeficient, v ordinačních diagramech zobrazeny jako šipky u unimodálních technik skóre = optimum druhu, v ordinačních diagramech zobrazeny jako body 181
166 JAK ČÍST VÝSLEDKY ORDINAČNÍCH METOD? skóry vzorků (snímků) na osách v ordinačních diagramech vzorky zobrazeny jako body (lineární i unimodální techniky) vzdálenost mezi body v ordinačním prostoru odpovídá nepodobnosti mezi vzorky (ne ale nepodobnosti celého floristického složení, ale jenom té části, která je vyjádřena zobrazenými ordinačními osami) skóry nezávislých (vysvětlujících proměnných) * regresní koeficienty, důležitá jsou jejich znaménka test signifikance (Monte-Carlo permutační test) * ukazuje na statistickou významnost použitých vysvětlujících proměnných 182 * jen přímé ordinační techniky
167 JEDNOTLIVÉ PROMĚNNÉ TERMINOLOGIE vysvětlované / závislé proměnné CANOCO: druhy (species) vysvětlující / nezávislé proměnné, prediktory * CANOCO: proměnné prostředí (environmental variables) měřené nebo odhadované proměnné vzorky, objekty, případy (cases) CANOCO: snímky (samples) kovariáty, nezajímavé vysvětlující / nezávislé proměnné * CANOCO: kovariáty (covariables) proměnné, jejichž vliv nás nezajímá a chceme ho z analýzy odstranit 183 * jen přímé ordinační techniky
168 POSTUPNÝ VÝBĚR VYSVĚTLUJÍCÍCH PROMĚNNÝCH FORWARD SELECTION ze souboru vysvětlujících proměnných umožňuje vybrat jen ty, které mají průkazný vliv v každém kroku testuje zvlášť vliv jednotlivých proměnných (Monte-Carlo permutační test) vybere tu proměnnou, která vysvětlí nejvíce variability a zároveň je signifikantní; tuto proměnnou pak do modelu zahrne jako kovariátu v dalším kroku znovu testuje vliv jednotlivých proměnných na druhová data (s odstraněním vlivu kovariát) a opakuje předchozí kroky testy signifikance jsou zatíženy mnohonásobným porovnáním, a jsou proto poměrně liberální (počet signifikantních proměnných je často nerealisticky vysoký a vyžaduje např. Bonferroniho korekci) 184
169 PROBLÉM MNOHONÁSOBNÉHO POROVNÁNÍ Simulace: 25 náhodně vygenerovaných proměnných otestování průkaznosti korelace každé proměnné s každou (čtvercová matice) průkazné korelace (p < 0.05) jsou označeny červeně dohromady 300 analýz, z nich je 16 průkazných 185
170 PARCIÁLNÍ ORDINACE PARTIAL ORDINATION odstraňuje část variability vysvětlené proměnnými, které jsou pro nás nezajímavé (například vliv umístění ploch do bloků) následně se přímou nebo nepřímou ordinací analyzuje zbytková variabilita nezajímavé proměnné se definují jako kovariáty pokud následuje přímá ordinace ordinační osy představují čistý vliv ostatních vysvětlujících proměnných bez vlivu kovariát pokud následuje nepřímá ordinace ordinační osy zachycují zbytkovou variabilitu v druhových datech po odstranění vlivu kovariát 186
171 ROZKLAD VARIANCE VARIANCE PARTITIONING zbytková variabilita variabilita vysvětlená proměnnou 1 variabilita vysvětlená proměnnou 2 vysvětlená variabilita sdílená proměnnou 1 a proměnnou 2 Borcard et al. 1992, Ecology 73:
172 ROZKLAD VARIANCE vysvětlující proměnná VARIANCE PARTITIONING kovariáta vysvětlená variabilita 1 a 2 není [a]+[b]+[c] 1 není [a]+[b] 2 není [b]+[c] 1 2 [a] 2 1 [c] sdílená variabilita [b] = (([a]+[b]) + ([b]+[c]) ([a]+[b]+[c])) nevysvětlená variabilita [d] = Total inertia ([a]+[b]+[c]) [d] [a] [b] [c] proměnná 1 proměnná 2 [a]+[b] celkový (marginal) vliv proměnné 1 [a] čistý (partial, conditional) vliv proměnné 1 (bez vlivu prom. 2) 188 Borcard et al. 1992, Ecology 73:
173 vysvětlená variabilita VYSVĚTLENÁ VARIABILITA A ADJUSTOVANÝ R 2 R 2 R 2 Adj počet vysvětlujících proměnných počet vzorků v datovém souboru vysvětlená variabilita stoupá s počtem vysvětlujících proměnných (i když jsou náhodné) a klesá s počtem vzorků v datovém souboru, adjustovaný R 2 se nemění platí pro přímou (kanonickou) ordinační analýzu i mnohonásobnou regresi Peres-Neto et al. (2006) Ecology 189
174 VYSVĚTLENÁ VARIABILITA A ADJUSTOVANÝ R 2 nelze srovnávat vysvětlenou variabilitu v analýzách založených na různém počtu vzorků a druhů i náhodná proměnná vysvětlí nenulové množství variability (při následném testování signifikance ale bude neprůkazná) množství vysvětlené variability stoupá s počtem vysvětlujících proměnných (i když tyto jsou třeba úplně náhodné) nelze srovnávat variabilitu vysvětlenou modelem s různým počtem vysvětlujících proměnných (čím víc proměnných, tím víc vysvětlené variability) možné řešení použití tzv. adjustovaného R 2, tzn. vysvětlené variability ošetřené o variabilitu, kterou by vysvětlil stejný počet náhodných proměnných adjustovaný R 2 je možné spočítat pro lineární ordinační metody, pro unimodální je třeba použít metody založené na permutacích 190
175 NEVYSVĚTLENÁ VARIABILITA [d] ordinační metody jsou založené na modelu (lineární nebo unimodální) odpovědi druhu na gradient prostředí, který je velkým zjednodušením skutečnosti variance nevysvětlená modelem (složka D) ve skutečnosti obsahuje variabilitu, která by mohla být vysvětlena některou z proměnných, pokud by se data chovala podle teoretického modelu varianci nevysvětlenou modelem tedy nelze interpretovat jen jako zbytkovou variabilitu, která je dána šumem v datech a tím, že ne všechny proměnné prostředí byly měřeny Total inertia proto není měřítkem celkové variability v druhových datech, ale variability, kterou je možné zachytit pomocí zvoleného modelu (lineárního nebo unimodálního) variabilita vysvětlená danou proměnnou prostředí a vypočtená jako eigenvalue / total inertia je proto podhodnocená Økland (1999) J. Veg.Sci. 10: vedle procenta vysvětlené variability (eigenvalue / total inertia) uvádějte také relativní množství variability, kterou daná proměnná vysvětlí z celkové variability vysvětlené všemi proměnnými prostředí 191
176 MANTEL TEST KORELACE MEZI MATICEMI NEPODOBNOSTÍ 193 Legendre & Legendre 1998
177 MANTEL TEST proměnná prostředí ph D e druhová data sp1 sp (eucl.) D sp D e D sp r = p =
178 SHRNUTÍ 195 Legendre & Legendre 1998
179 PCA PŘÍKLAD TRENDY V NÁZVECH ČLÁNKŮ V EKOLOGICKÝCH ČASOPISECH 199 Nobis & Wohlgemuth (2004) Oikos
180 200 Nobis & Wohlgemuth (2004) Oikos
181 DCA PŘÍKLAD FLORISTICKÁ DATA Z NP PODYJÍ skóry pro jednotlivé kvadráty z 1. a 2. osy DCA (na základě jejich floristického složení) byly promítnuty do síťové mapy Chytrý et al. (1999) Preslia 201
182 PCA PŘÍKLAD ZMĚNY V DRUHOVÉM SLOŽENÍ PÁLAVSKÝCH DUBOHABŘIN (R. HEDL 2005, DISERTAČNÍ PRÁCE) Výrazný úbytek druhové bohatosti bylinného (E1) a keřového (E2) patra v posledních 50ti letech. Data jsou založená na zopakování fytocenologických snímků na plochách snímkovaných Jaroslavem Horákem v šedesátých letech. Změna v druhovém složení vegetace v průběhu 50ti let samovolné sukcese (PCA diagram). 202
183 NMDS PŘÍKLAD ZMĚNY V DRUHOVÉM SLOŽENÍ KORÁLOVÝCH ÚTESŮ ZASAŽENÝCH DISTURBANCÍ EL NINO 203 Anderson et al. (2011) Ecology Letters
184 RDA PŘÍKLAD VLIV ZÁSAHU NA KLÍČENÍ SEMENÁČŮ RDA: počet semenáčů jednotlivých druhů v ploškách cm jako závislá proměnná, zásah jako vysvětlující proměnná; eig. 1. osy: 0,046, eig. 4. osy: 0,331, MC test 1. osy: p < 0, Špačková et al.(1998) Folia Geobotanica
185 CCA PŘÍKLAD ROZDÍL MEZI PRADÁVNÝMI A DRUHOTNÝMI LESY Vojta (2007) Preslia 205
186 CCA PŘÍKLAD STANOVENÍ EKOLOGICKÉHO OPTIMA JEDNOTLIVÝCH DRUHŮ MĚKKÝŠŮ PODÉL EKOLOGICKÝC GRADIENTŮ 206 Horsák et al. (2007) Acta Oecologica
187 ELLENBERGOVY INDIKAČNÍ HODNOTY
188 ELLENBERGOVY INDIKAČNÍ HODNOTY (EIH) optima druhů rostlin na gradientu živin, vlhkosti, půdní reakce, kontinentality, teploty, světla a salinity (salinita se ve Střední Evropě nepoužívá) hodnoty na ordinální škále (1-9, případně 1-12 pro vlhkost) optima stanovená na základě terénních pozorování, v některých případech upřesněna experimentálně hodnoty tabelované původně pro Německo, ale používané i v okolních zemích, pro vzdálenější státy (Anglie, Itálie, Řecko) byly tyto hodnoty překalibrovány, jinde (Maďarsko, Švýcarsko) se používají alternativní hodnoty od jiných autorů (Borhidi, resp. Landolt) tabulky obsahují pouze údaje o druhových optimech, ne o šířkách druhové niky v případě, že nemám měřená data o proměnných prostředí, průměrné EIH nabízejí ekologicky intuitivní odhad stanovištních podmínek 209
189 ELLENBERGOVY INDIKAČNÍ HODNOTY (EIH) POUŽITÍ PRO KALIBRACI EIV pro půdní reakci Mycelis muralis Moehringia trinervia Mercurialis perennis Lathyrus vernus Myosotis sylvatica Milium effusum Melica nutans Melampyrum pratense Myosotis ramosissima Lychnis viscaria Melittis melissophyllum průměr 210
190 ELLENBERGOVY INDIKAČNÍ HODNOTY (EIH) POUŽITÍ PRO KALIBRACI EIV pro půdní reakci Mycelis muralis Moehringia trinervia Mercurialis perennis Lathyrus vernus Myosotis sylvatica Milium effusum Melica nutans Melampyrum pratense Myosotis ramosissima Lychnis viscaria Melittis melissophyllum průměrná hodnota:
191 PROČ SE EIH TVÁŘÍ JAKO LEPŠÍ PROMĚNNÉ NEŽ MĚŘENÉ FAKTORY PROSTŘEDÍ? díky způsobu jak jsou počítány, obsahují průměrné EIH informaci o podobnosti v druhovém složení mezi vegetačními snímky vegetační snímky s úplně stejným druhovým složením budou mít přesně stejné průměrné EIH pro měřené faktory toto ale neplatí malý rozdíl v druhovém složení mezi vegetačními snímky povede jen k malému rozdílu v jejich průměrných EIH průměrná EIH pro daný vegetační snímek obsahuje dvojí informaci: 1. ekologicky relevantní informaci o charakteru stanoviště, a to díky použití tabelovaných druhových EIH, které jsou založeny na empirických pozorování ekologických nároků druhů v terénu 2. informaci o podobnosti druhového složení daného snímku k ostatním snímkům v datovém souboru, která je v nich uložena díky způsobu, jak jsou průměrné EIH počítány měřené faktory prostředí obsahují jen informaci o ekologickém charakteru stanoviště, ne o podobnosti v druhovém složení 212
192 VÝPOČET PRŮMĚRNÝCH EIH H. Ellenberg Empirická zkušenost s ekologií druhů průměrné Ellenbergovy indikační hodnoty Data o druhovém složení průměrná EIH pro daný vegetační snímek obsahuje dvojí informaci: 1. ekologicky relevantní informaci o charakteru stanoviště, a to díky použití tabelovaných druhových EIH, které jsou založeny na empirických pozorování ekologických nároků druhů v terénu 2. informaci o podobnosti druhového složení daného snímku k ostatním snímkům v datovém souboru, která je v nich uložena díky způsobu, jak jsou průměrné EIH počítány 213
193 VÝPOČET PRŮMĚRNÝCH EIH H. Ellenberg Empirická zkušenost s ekologií druhů průměrné Ellenbergovy indikační hodnoty Data o druhovém složení díky způsobu jak jsou počítány, obsahují průměrné EIH informaci o podobnosti v druhovém složení mezi vegetačními snímky vegetační snímky s úplně stejným druhovým složením budou mít přesně stejné průměrné EIH pro měřené faktory toto ale neplatí malý rozdíl v druhovém složení mezi vegetačními snímky povede jen k malému rozdílu v jejich průměrných EIH 214
194 VÝPOČET PRŮMĚRNÝCH EIH H. Ellenberg Empirická zkušenost s ekologií druhů průměrné Ellenbergovy indikační hodnoty!! Data o druhovém složení problém nastává v okamžiku, kdy jsou průměrné EIH analyzovány současně s daty o druhovém složení, ze kterých jsou vypočteny 215
195 VYTVOŘENÍ PRŮMĚRNÝCH EIH, KTERÉ NEOBSAHUJÍ EKOLOGICKOU INFORMACI průměrné reálné EIH pro půdní reakci: průměrné znáhodněné EIH pro půdní reakci: průměrné reálné EIH obsahují ekologicky relevantní informaci a informaci o podobnosti v druhovém složení průměrné znáhodněné EIH obsahují pouze informaci o podobnosti v druhovém složení (ekologicky relevantní informace byla zničena promícháním druhových EIH mezi druhy) 216
196 KORELACE PRŮMĚRNÝCH EIH SE SKÓRY SNÍMKŮ NA OSÁCH DCA průměrná EIH bude s velkou pravděpodobností signifikantně korelovaná s DCA, i když neobsahuje ekologickou informaci! Počet signifikantních korelací mezí osami DCA a průměrnými znáhodněnými EIH (šedé sloupečky) nebo náhodnými čísly (bílé sloupečky) 1000 opakování 217
197 PRŮMĚRNÉ EIH V NEPŘÍMÉ ORDINACI DCA1 DCA2 R 2 P orig P modif Světlo 0,477 0,879 0,600 < 0,001 0,004 Teplota 0,350 0,937 0,471 < 0,001 0,011 Kontinentalita 0,726 0,688 0,148 0,004 0,452 Vlhkost -0,925 0,381 0,897 < 0,001 < 0,001 Živiny -0,998 0,066 0,831 < 0,001 < 0,001 Půdní reakce -0,653 0,757 0,429 < 0,001 0,
198 průměrná Mean EIH Ellenberg pro reaction půdní reakci vysvětlená Explained variability variabilita [%] [%] měřené ph náhodná čísla průměrné reálné EIH průměrné znáhodnéné EIH náhodná čísla POROVNÁNÍ MĚŘENÉHO PŮDNÍHO PH A VYPOČTENÉ PRŮMĚRNÉ EIH PRO PŮDNÍ REAKCI VYSVĚTLUJÍCÍ PROMĚNNÉ V CCA měřené ph Measured soil ph real ph měřené ph Ellenberg reaction EIH pro půdní reakci Průměrná EIH pro půdní reakci vysvětlí víc variability než měřené ph, i když obě proměnné jsou spolu těsně korelované 219
199 PRŮMĚRNÉ ELLENBERGOVY INDIKAČNÍ HODNOTY PRAVIDLA POUŽITÍ použití průměrných EIH v analýze spolu s jinými proměnnými vypočtenými z těchto dat může vést k závěrům, které jsou optimističtější, než by ve skutečnosti měly být pokud jsou k dispozici relevantní měřené faktory prostředí, není třeba používat zároveň i průměrné EIH jen proto, že je tak snadné je vypočíst průkaznost jejich vztahu s jinými proměnnými, které jsou odvozeny ze stejných druhových dat, by měla být testována modifikovaným permutačním testem, který bere v potaz skutečnost, že testované proměnné na sobě nejsou nezávislé průměrné EIH by neměly být bez dalšího statistického ošetření srovnávány s analogickými měřenými faktory prostředí, protože se oproti nim mohou neoprávněně jevit lepšími, než ve skutečnosti jsou (například tím, že jsou lépe korelované nebo častěji a více průkazné) 221
200 PŘÍKLADY NA POUŽÍTÍ PRŮMĚRNÝCH EIH Použití na floristická data z NP Podyjí ekologické gradienty v krajině (Chytrý et al. 1999, Preslia) 222
201 Ekologická kalibrace vegetačních jednotek v přehledu Vegetace ČR (Chytrý [ed.] 2007) 223
202 ZOBECNĚNÉ LINEÁRNÍ MODELY REGRESNÍ A KLASIFIKAČNÍ STROMY
203 REGRESE KORELACE Korelace popis závislosti mezi dvěma proměnnými, bez znalosti kauzálního vztahu počítám: korelační koeficient (r), případně signifikanci korelačního koeficientu (t-test) Regrese předpokládá kauzální vztah mezi vysvětlující (x) a vysvětlovanou (y) proměnnou jedná se o typ modelu výběr nejlepší vysvětlující proměnné, nejlepšího modelu, predikce vysvětlované proměnné počítám: regresní koeficient (b = sklon regresní přímky), koeficient determinace (R 2 ), signifikanci regrese (t-test, ANOVA, Monte-Carlo permutační test) 225
204 REGRESE KORELACE Ale: většinou platí, že i když počítám korelaci, předpokládám (možná jen podvědomě), že mezi proměnnými existuje nějaký kauzální vztah a tím se rozdíl mezi korelací a regresí stírají Dvě situace: vysvětlující proměnná (x) je měřená bez chyby (většinou proto, že je kontrolovaná experimentálním designem) použijeme regresi (korelace v tomto případě nemá smysl) obě proměnné (x a y) jsou měřené s chybou (případ jak dat z experimentů, tak z empirických pozorování) záleží na tom, co od analýzy očekáváme pokud je cílem vytvoření modelu nebo testování hypotéz, pak použijeme regresi pokud ne použijeme korelaci 226
205 LINEÁRNÍ REGRESE PŘEDPOKLADY 1. lineární model správně popisuje funkční vztah mezi vysvětlující a vysvětlovanou proměnnou pokud je vztah nelineární a nepomůže transformace, je třeba použít nelineární regresní model nebo zobecněný lineární model 2. vysvětlující proměnná je měřená přesně (bez náhodné složky) metoda nejmenších čtverců ale funguje i v případě, že vysvětlující proměnná je měřená s chybou 3. každá hodnota vysvětlované proměnné (y) je nezávislá na ostatních hodnotách y, náhodná složka vysvětlované proměnné má normální rozdělení zvláště pro data z observačních studií často neplatí pravidlo o nezávislosti (a většinou ani nevíme, jak moc toto pravidlo neplatí) 4. variance vysvětlující proměnné je konstantní podél celé regresní přímky (homoskedasticita) transformace dat málokdy řeší oba problémy najednou ztransformovaná proměnná bude mít normální rozdělení, ale ne konstantní varianci, a naopak toto řeší metoda zobecněných lineárních modelů (GLM) 227
206 REGRESE lineární model y i = β 0 + β 1 x i + ε i y i... hodnota vysvětlované (závislé) proměnné pro i-té pozorování x i... hodnota vysvětlující (nezávislé) proměnné pro i-té pozorování β 0... regresní koeficient, posun regresní přímky (intercept), udává souřadnici průsečíku regresní přímky s osou y β 1... regresní koeficient, sklon regresní přímky (slope) ε i... chyba mnohonásobná regrese regrese jedné vysvětlované proměnné na několika (j) vysvětlujících proměnných y i = β 0 + Σ j β j x ij + ε i 228
207 REGRESE ZOBECNĚNÉ LINEÁRNÍ MODELY (GLM) umožňují modelovat vysvětlované proměnné s jiným než normálním (Gaussovým) rozložením náhodné složky počty jedinců Poissonovo rozložení presence/absence binomické rozložení zavádí tzv. link-funkci (η, theta), která překládá rozsah hodnot vysvětlujících proměnných (pravá strana rovnice) na rozsah hodnot vysvětlované proměnné (levá strana rovnice) η i = b 0 + Σ j b j x ij η i... lineární prediktor y i = ŷ i + ε i ŷ i... hodnota vysvětlované proměnné y i predikovaná modelem -> platí g (ŷ i ) = η i g... link funkce Poissonovo rozložení log link: η = log (ŷ i ) Binomické rozložení logit link: η = log [ŷ i / (1 ŷ i )] Gaussovo rozložení identity link: η = ŷ i 229
208 REGRESNÍ A KLASIFIKAČNÍ STROMY REGRESSION AND CLASSIFICATION TREES, CART metoda podobná mnohonásobné regresi jedna vysvětlovaná a několik vysvětlujících proměnných má minimální předpoklady na charakter (rozložení) dat explorativní analýza slouží k popisu dat, ne k testování hypotéz vysvětlující proměnné mohou být kategoriální i kvantitativní vysvětlovaná proměnná: pokud je kategoriální klasifikační strom pokud je kvantitativní regresní strom 230
209 REGRESNÍ A KLASIFIKAČNÍ STROMY REGRESSION AND CLASSIFICATION TREES, CART FLUVISOL <> a 31.2 ; 71 obs; 35.8% COVERE32 <> ; 17 obs; 3.4% obs ELEVATION <> ; 42 obs; 5.7% obs ph.h <> ; 59 obs; 9.3% ph.h <> ; 25 obs; 2.8% 3 SURFIS <> ; 20 obs; 1.6% obs COVERE32 <> ; 17 obs; 6.5% obs obs SOILDPT <> ; 12 obs; 5.3% obs obs obs obs Total deviance explained = 70.4 % 231 data o druhové bohatosti lesů na Vltavě v závislosti na měřených faktorech prostředí (Zelený, nepubl.)
210 INDEXY DIVERZITY
211 Jurasinski et al. (2009) ALFA, BETA A GAMA DIVERZITA Alfa diverzita druhová bohatost vzorku Beta diverzita (species turnover) změna v druhovém složení mezi vzorky Gama diverzita celková druhová bohatost regionu Robert Harding Whittaker ( ) 234
EKOLOGICKÝCH EXPERIMENTŮ
 DESIGN EKOLOGICKÝCH EXPERIMENTŮ To call in the statistician after the experiment is done may be no more than asking him to perform a post mortem examination: he may be able to say what the experiment died
DESIGN EKOLOGICKÝCH EXPERIMENTŮ To call in the statistician after the experiment is done may be no more than asking him to perform a post mortem examination: he may be able to say what the experiment died
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV
 ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Typy sbíraných dat kategoriální vs kvantitativní, pokryvnosti, frekvence Příprava dat pro numerické analýzy čištění dat, odlehlé body, transformace,
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Typy sbíraných dat kategoriální vs kvantitativní, pokryvnosti, frekvence Příprava dat pro numerické analýzy čištění dat, odlehlé body, transformace,
NUMERICKÁ KLASIFIKACE. David Zelený Zpracování dat v ekologii společenstev
 NUMERICKÁ KLASIFIKACE http://wfc3.gsfc.nasa.gov PROČ MÁ SMYSL VĚCI KLASIFIKOVAT? vlnová délka (~ ekologický gradient) 172 http://wfc3.gsfc.nasa.gov PROČ MÁ SMYSL VĚCI KLASIFIKOVAT? vlnová délka (~ ekologický
NUMERICKÁ KLASIFIKACE http://wfc3.gsfc.nasa.gov PROČ MÁ SMYSL VĚCI KLASIFIKOVAT? vlnová délka (~ ekologický gradient) 172 http://wfc3.gsfc.nasa.gov PROČ MÁ SMYSL VĚCI KLASIFIKOVAT? vlnová délka (~ ekologický
EKOLOGICKÁ PODOBNOST (ECOLOGICAL RESEMBLANCE) David Zelený Zpracování dat v ekologii společenstev
 EKOLOGICKÁ PODOBNOST (ECOLOGICAL RESEMBLANCE) EKOLOGICKÁ PODOBNOST Q VS R ANALÝZA Vzorky Druhy druh 1 druh 2 druh 3 vzorek 1 0 1 1 vzorek 2 1 0 0 vzorek 3 0 4 4 vztahy mezi vzorky Q analýza vztahy mezi
EKOLOGICKÁ PODOBNOST (ECOLOGICAL RESEMBLANCE) EKOLOGICKÁ PODOBNOST Q VS R ANALÝZA Vzorky Druhy druh 1 druh 2 druh 3 vzorek 1 0 1 1 vzorek 2 1 0 0 vzorek 3 0 4 4 vztahy mezi vzorky Q analýza vztahy mezi
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV
 ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Příprava dat pro numerické analýzy čištění dat, odlehlé body, transformace, standardizace, EDA Design ekologických experimentů manipulativní experimenty
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Příprava dat pro numerické analýzy čištění dat, odlehlé body, transformace, standardizace, EDA Design ekologických experimentů manipulativní experimenty
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV
 ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Příprava dat pro numerické analýzy čištění dat, odlehlé body, transformace, standardizace, EDA Design ekologických experimentů manipulativní experimenty
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Příprava dat pro numerické analýzy čištění dat, odlehlé body, transformace, standardizace, EDA Design ekologických experimentů manipulativní experimenty
ZPRACOVÁNÍ DAT V EKOLOGII
 ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV VÍT SYROVÁTKA OSNOVA PŘEDNÁŠKY o Příprava dat pro numerické analýzy typy sbíraných dat, čištění dat, odlehlé body, transformace, standardizace, EDA o Ekologická podobnost
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV VÍT SYROVÁTKA OSNOVA PŘEDNÁŠKY o Příprava dat pro numerické analýzy typy sbíraných dat, čištění dat, odlehlé body, transformace, standardizace, EDA o Ekologická podobnost
INDEXY DIVERZITY. David Zelený Zpracování dat v ekologii společenstev
 INDEXY DIVERZITY Jurasinski et al. (2009) ALFA, BETA A GAMA DIVERZITA Alfa diverzita druhová bohatost vzorku Beta diverzita (species turnover) změna v druhovém složení mezi vzorky Gama diverzita celková
INDEXY DIVERZITY Jurasinski et al. (2009) ALFA, BETA A GAMA DIVERZITA Alfa diverzita druhová bohatost vzorku Beta diverzita (species turnover) změna v druhovém složení mezi vzorky Gama diverzita celková
ZPRACOVÁNÍ DAT V EKOLOGII
 ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV VÍT SYROVÁTKA OSNOVA PŘEDNÁŠKY o Příprava dat pro numerické analýzy typy sbíraných dat, čištění dat, odlehlé body, transformace, standardizace, EDA o Ekologická podobnost
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV VÍT SYROVÁTKA OSNOVA PŘEDNÁŠKY o Příprava dat pro numerické analýzy typy sbíraných dat, čištění dat, odlehlé body, transformace, standardizace, EDA o Ekologická podobnost
Zpracování studie týkající se průzkumu vlastností statistických proměnných a vztahů mezi nimi.
 SEMINÁRNÍ PRÁCE Zadání: Data: Statistické metody: Zpracování studie týkající se průzkumu vlastností statistických proměnných a vztahů mezi nimi. Minimálně 6 proměnných o 30 pozorováních (z toho 2 proměnné
SEMINÁRNÍ PRÁCE Zadání: Data: Statistické metody: Zpracování studie týkající se průzkumu vlastností statistických proměnných a vztahů mezi nimi. Minimálně 6 proměnných o 30 pozorováních (z toho 2 proměnné
V praxi pracujeme s daty nominálními (nabývají pouze dvou hodnot), kategoriálními (nabývají více
 9 Vícerozměrná data a jejich zpracování 9.1 Vícerozměrná data a vícerozměrná rozdělení Při zpracování vícerozměrných dat, hledáme souvislosti mezi dvěmi, případně více náhodnými veličinami. V praxi pracujeme
9 Vícerozměrná data a jejich zpracování 9.1 Vícerozměrná data a vícerozměrná rozdělení Při zpracování vícerozměrných dat, hledáme souvislosti mezi dvěmi, případně více náhodnými veličinami. V praxi pracujeme
Příklad 2: Určení cihlářských surovin na základě chemické silikátové analýzy
 Příklad 2: Určení cihlářských surovin na základě chemické silikátové analýzy Zadání: Deponie nadložních jílových sedimentů SHP byla testována za účelem využití v cihlářské výrobě. Z deponie bylo odebráno
Příklad 2: Určení cihlářských surovin na základě chemické silikátové analýzy Zadání: Deponie nadložních jílových sedimentů SHP byla testována za účelem využití v cihlářské výrobě. Z deponie bylo odebráno
STATISTICKÉ METODY; ZÍSKÁVÁNÍ INFORMACÍ Z DRUHOVÝCH A ENVIRONMENTÁLNÍCH DAT
 STATISTICKÉ METODY; ZÍSKÁVÁNÍ INFORMACÍ Z DRUHOVÝCH A ENVIRONMENTÁLNÍCH DAT (NE)VÝHODY STATISTIKY OTÁZKY si klást ještě před odběrem a podle nich naplánovat design, metodiku odběru (experimentální vs.
STATISTICKÉ METODY; ZÍSKÁVÁNÍ INFORMACÍ Z DRUHOVÝCH A ENVIRONMENTÁLNÍCH DAT (NE)VÝHODY STATISTIKY OTÁZKY si klást ještě před odběrem a podle nich naplánovat design, metodiku odběru (experimentální vs.
Vícerozměrné statistické metody
 Vícerozměrné statistické metody Shluková analýza Jiří Jarkovský, Simona Littnerová FSTA: Pokročilé statistické metody Typy shlukových analýz Shluková analýza: cíle a postupy Shluková analýza se snaží o
Vícerozměrné statistické metody Shluková analýza Jiří Jarkovský, Simona Littnerová FSTA: Pokročilé statistické metody Typy shlukových analýz Shluková analýza: cíle a postupy Shluková analýza se snaží o
Přednáška 5. Výběrová šetření, Exploratorní analýza
 Přednáška 5 Výběrová šetření, Exploratorní analýza Pravděpodobnost vs. statistika Výběrová šetření aneb jak získat výběrový soubor Exploratorní statistika aneb jak popsat výběrový soubor Typy proměnných
Přednáška 5 Výběrová šetření, Exploratorní analýza Pravděpodobnost vs. statistika Výběrová šetření aneb jak získat výběrový soubor Exploratorní statistika aneb jak popsat výběrový soubor Typy proměnných
ÚKOL 2 1886 22 5,77 5,00 5 2,531,003,056 -,869,113
 ÚKOL 2 Jméno a příjmení: UČO: Imatrik. ročník: Úkol 2.1: V souboru EVS99_cvicny.sav zjistěte, zdali rozložení názoru na to, kdo by měl být odpovědný za zajištění bydlení (proměnná q54h), je normální. Řešte
ÚKOL 2 Jméno a příjmení: UČO: Imatrik. ročník: Úkol 2.1: V souboru EVS99_cvicny.sav zjistěte, zdali rozložení názoru na to, kdo by měl být odpovědný za zajištění bydlení (proměnná q54h), je normální. Řešte
PŘÍKLADY POUŽITÍ ORDINAČNÍCH METOD
 PŘÍKLADY POUŽITÍ ORDINAČNÍCH METOD 1 PŘÍKLAD NA ROZKLAD VARIANCE SPOLEČENSTVA MĚKKÝŠŮ NA PRAMENIŠTÍCH druhové složení společenstev měkkýšů druhové složení slatiništní vegetace ph Ca cond Mg Na měřené proměnné
PŘÍKLADY POUŽITÍ ORDINAČNÍCH METOD 1 PŘÍKLAD NA ROZKLAD VARIANCE SPOLEČENSTVA MĚKKÝŠŮ NA PRAMENIŠTÍCH druhové složení společenstev měkkýšů druhové složení slatiništní vegetace ph Ca cond Mg Na měřené proměnné
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV
 ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Příprava dat pro numerické analýzy typy sbíraných dat, čištění dat, odlehlé body, transformace, standardizace, EDA Ekologická podobnost indexy podobnosti
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Příprava dat pro numerické analýzy typy sbíraných dat, čištění dat, odlehlé body, transformace, standardizace, EDA Ekologická podobnost indexy podobnosti
INDEXY DIVERZITY. David Zelený Zpracování dat v ekologii společenstev
 INDEXY DIVERZITY ALFA, BETA A GAMA DIVERZITA Alfa diverzita druhová bohatost vzorku Beta diverzita (species turnover) změna v druhovém složení mezi vzorky Gama diverzita celková druhová bohatost regionu
INDEXY DIVERZITY ALFA, BETA A GAMA DIVERZITA Alfa diverzita druhová bohatost vzorku Beta diverzita (species turnover) změna v druhovém složení mezi vzorky Gama diverzita celková druhová bohatost regionu
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV
 ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Typy sbíraných dat kategoriální vs kvantitativní, pokryvnosti, frekvence Příprava dat pro numerické analýzy čištění dat, odlehlé body, transformace,
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Typy sbíraných dat kategoriální vs kvantitativní, pokryvnosti, frekvence Příprava dat pro numerické analýzy čištění dat, odlehlé body, transformace,
REGRESE VS KALIBRACE. David Zelený Zpracování dat v ekologii společenstev
 REGRESE VS KALIBRACE David Zelený METODY GRADIENTOVÉ ANALÝZY Data, která máme: počet charakteristik prostředí počet druhů Apriorní znalost vztahů mezi druhy a prostředím? Použijeme: Dostaneme: 1, n 1 ne
REGRESE VS KALIBRACE David Zelený METODY GRADIENTOVÉ ANALÝZY Data, která máme: počet charakteristik prostředí počet druhů Apriorní znalost vztahů mezi druhy a prostředím? Použijeme: Dostaneme: 1, n 1 ne
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV
 ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Příprava dat pro numerické analýzy typy sbíraných dat, čištění dat, odlehlé body, transformace, standardizace, EDA Ekologická podobnost indexy podobnosti
ZPRACOVÁNÍ DAT V EKOLOGII SPOLEČENSTEV OSNOVA PŘEDNÁŠKY Příprava dat pro numerické analýzy typy sbíraných dat, čištění dat, odlehlé body, transformace, standardizace, EDA Ekologická podobnost indexy podobnosti
Organizační pokyny k přednášce. Matematická statistika. Přehled témat. Co je statistika?
 Organizační pokyny k přednášce Matematická statistika 2012 2013 Šárka Hudecová Katedra pravděpodobnosti a matematické statistiky Matematicko-fyzikální fakulta UK hudecova@karlin.mff.cuni.cz http://www.karlin.mff.cuni.cz/
Organizační pokyny k přednášce Matematická statistika 2012 2013 Šárka Hudecová Katedra pravděpodobnosti a matematické statistiky Matematicko-fyzikální fakulta UK hudecova@karlin.mff.cuni.cz http://www.karlin.mff.cuni.cz/
PCA BIPLOT ŠKÁLOVÁNÍ OS (1)
 PCA BIPLOT ŠKÁLOVÁNÍ OS (1) 1 (sites) o zaměření na odlišnosti mezi lokalitami zachovány euklidovské vzdálenosti mezi vzorky úhly mezi šipkami neodpovídají kovariancím (korelacím) proměnných variance skóre
PCA BIPLOT ŠKÁLOVÁNÍ OS (1) 1 (sites) o zaměření na odlišnosti mezi lokalitami zachovány euklidovské vzdálenosti mezi vzorky úhly mezi šipkami neodpovídají kovariancím (korelacím) proměnných variance skóre
Je-li rostlinné společenstvo tvořeno pouze jedinci jedné populace, mluvíme o monocenóze nebo také o čistém prostoru.
 EKOLOGIE SPOLEČENSTVA (SYNEKOLOGIE) Rostlinné společenstvo (fytocenózu) můžeme definovat jako soubor jedinců a populací rostlin rostoucích společně na určitém stanovišti, které jsou ovlivňovány svým prostředím,
EKOLOGIE SPOLEČENSTVA (SYNEKOLOGIE) Rostlinné společenstvo (fytocenózu) můžeme definovat jako soubor jedinců a populací rostlin rostoucích společně na určitém stanovišti, které jsou ovlivňovány svým prostředím,
Regresní a korelační analýza
 Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Regresní analýza Cíl regresní analýzy: stanovení formy (trendu, tvaru, průběhu)
Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Regresní analýza Cíl regresní analýzy: stanovení formy (trendu, tvaru, průběhu)
Dálkový průzkum Země. Ústav geoinformačních technologií Lesnická a dřevařská fakulta MENDELU
 Dálkový průzkum Země Ústav geoinformačních technologií Lesnická a dřevařská fakulta MENDELU Klasifikace obrazu Klasifikaci můžeme obecně definovat jako seskupování vzájemně si podobných prvků (entit) do
Dálkový průzkum Země Ústav geoinformačních technologií Lesnická a dřevařská fakulta MENDELU Klasifikace obrazu Klasifikaci můžeme obecně definovat jako seskupování vzájemně si podobných prvků (entit) do
Diverzita doubrav ve vztahu k produktivitě stanoviště. Irena Veselá
 Diverzita doubrav ve vztahu k produktivitě stanoviště Irena Veselá Proč doubravy? Omezení datového souboru: výběr ploch s dominantními druhy Quercus petraea nebo Q. robur => konstantní vliv na bylinné
Diverzita doubrav ve vztahu k produktivitě stanoviště Irena Veselá Proč doubravy? Omezení datového souboru: výběr ploch s dominantními druhy Quercus petraea nebo Q. robur => konstantní vliv na bylinné
Získávání znalostí z dat
 Získávání znalostí z dat Informační a komunikační technologie ve zdravotnictví Získávání znalostí z dat Definice: proces netriviálního získávání implicitní, dříve neznámé a potencionálně užitečné informace
Získávání znalostí z dat Informační a komunikační technologie ve zdravotnictví Získávání znalostí z dat Definice: proces netriviálního získávání implicitní, dříve neznámé a potencionálně užitečné informace
Dynamické metody pro predikci rizika
 Dynamické metody pro predikci rizika 1 Úvod do analýzy časových řad Časová řada konečná posloupnost reálných hodnot určitého sledovaného ukazatele měřeného v určitých časových intervalech okamžikové např
Dynamické metody pro predikci rizika 1 Úvod do analýzy časových řad Časová řada konečná posloupnost reálných hodnot určitého sledovaného ukazatele měřeného v určitých časových intervalech okamžikové např
DIVERZITA. David Zelený Zpracování dat v ekologii společenstev
 DIVERZITA ALFA, BETA A GAMA DIVERZITA Alfa diverzita druhová bohatost vzorku Beta diverzita (species turnover) změna v druhovém složení mezi vzorky heterogenita druhového složení Gama diverzita celková
DIVERZITA ALFA, BETA A GAMA DIVERZITA Alfa diverzita druhová bohatost vzorku Beta diverzita (species turnover) změna v druhovém složení mezi vzorky heterogenita druhového složení Gama diverzita celková
Univerzita Pardubice Fakulta chemicko technologická Katedra analytické chemie Licenční studium Management systému jakosti
 Univerzita Pardubice Fakulta chemicko technologická Katedra analytické chemie Licenční studium Management systému jakosti 2.1 Tvorba lineárních regresních modelů při analýze dat Autor práce: Přednášející:
Univerzita Pardubice Fakulta chemicko technologická Katedra analytické chemie Licenční studium Management systému jakosti 2.1 Tvorba lineárních regresních modelů při analýze dat Autor práce: Přednášející:
KGG/STG Statistika pro geografy
 KGG/STG Statistika pro geografy 10. Mgr. David Fiedor 27. dubna 2015 Nelineární závislost - korelační poměr užití v případě, kdy regresní čára není přímka, ale je vyjádřena složitější matematickou funkcí
KGG/STG Statistika pro geografy 10. Mgr. David Fiedor 27. dubna 2015 Nelineární závislost - korelační poměr užití v případě, kdy regresní čára není přímka, ale je vyjádřena složitější matematickou funkcí
David Zelený GRADIENTOVÁ ANALÝZA
 David Zelený Zpracování dat v ekologii společenstev G GRADIENTOVÁ ANALÝZA HISTORIE WHITTAKER 1956 - PŘÍMÁ GRADIENTOVÁ ANALÝZA Zpracování dat v ekologii společenstev 108 Whittaker (1956): Vegetation of
David Zelený Zpracování dat v ekologii společenstev G GRADIENTOVÁ ANALÝZA HISTORIE WHITTAKER 1956 - PŘÍMÁ GRADIENTOVÁ ANALÝZA Zpracování dat v ekologii společenstev 108 Whittaker (1956): Vegetation of
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz
 Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická
NAIL072 ROZPOZNÁVÁNÍ VZORŮ
 NAIL072 ROZPOZNÁVÁNÍ VZORŮ RNDr. Jana Štanclová, Ph.D. jana.stanclova@ruk.cuni.cz www.cuni.cz/~stancloj LS Zk 2/0 OSNOVA 1. Úvod do rozpoznávání vzorů 2. Bayesovská teorie rozpoznávání 3. Diskriminační
NAIL072 ROZPOZNÁVÁNÍ VZORŮ RNDr. Jana Štanclová, Ph.D. jana.stanclova@ruk.cuni.cz www.cuni.cz/~stancloj LS Zk 2/0 OSNOVA 1. Úvod do rozpoznávání vzorů 2. Bayesovská teorie rozpoznávání 3. Diskriminační
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc.
 Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 010 1.týden (0.09.-4.09. ) Data, typy dat, variabilita, frekvenční analýza
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 010 1.týden (0.09.-4.09. ) Data, typy dat, variabilita, frekvenční analýza
Testy nezávislosti kardinálních veličin
 Testy nezávislosti kardinálních veličin Komentované řešení pomocí programu R Ústav matematiky Fakulta chemicko inženýrská Vysoká škola chemicko-technologická v Praze Načtení vstupních dat Vstupní data
Testy nezávislosti kardinálních veličin Komentované řešení pomocí programu R Ústav matematiky Fakulta chemicko inženýrská Vysoká škola chemicko-technologická v Praze Načtení vstupních dat Vstupní data
Pro bodový odhad při základním krigování by soustava rovnic v maticovém tvaru vypadala následovně:
 KRIGING Krigování (kriging) označujeme interpolační metody, které využívají geostacionární metody odhadu. Těchto metod je celá řada, zde jsou některé příklady. Pro krigování se používá tzv. Lokální odhad.
KRIGING Krigování (kriging) označujeme interpolační metody, které využívají geostacionární metody odhadu. Těchto metod je celá řada, zde jsou některé příklady. Pro krigování se používá tzv. Lokální odhad.
Pořízení licencí statistického SW
 Pořízení licencí statistického SW Zadavatel: Česká školní inspekce, Fráni Šrámka 37, 150 21 Praha 5 IČO: 00638994 Jednající: Mgr. Tomáš Zatloukal Předpokládaná (a maximální cena): 1.200.000 vč. DPH Typ
Pořízení licencí statistického SW Zadavatel: Česká školní inspekce, Fráni Šrámka 37, 150 21 Praha 5 IČO: 00638994 Jednající: Mgr. Tomáš Zatloukal Předpokládaná (a maximální cena): 1.200.000 vč. DPH Typ
Statistika. Program R. popisná (deskriptivní) statistika popis konkrétních dat. induktivní (konfirmatorní) statistika. popisná statistika
 Statistika Cvičení z matematické statistiky na PřF Šárka Hudecová Katedra pravděpodobnosti a matematické statistiky Matematicko-fyzikální fakulta Univerzity Karlovy léto 2012 Základní dělení popisná (deskriptivní)
Statistika Cvičení z matematické statistiky na PřF Šárka Hudecová Katedra pravděpodobnosti a matematické statistiky Matematicko-fyzikální fakulta Univerzity Karlovy léto 2012 Základní dělení popisná (deskriptivní)
Matematická statistika
 Matematická statistika Daniel Husek Gymnázium Rožnov pod Radhoštěm, 8. A8 Dne 12. 12. 2010 v Rožnově pod Radhoštěm Osnova Strana 1) Úvod 3 2) Historie matematické statistiky 4 3) Základní pojmy matematické
Matematická statistika Daniel Husek Gymnázium Rožnov pod Radhoštěm, 8. A8 Dne 12. 12. 2010 v Rožnově pod Radhoštěm Osnova Strana 1) Úvod 3 2) Historie matematické statistiky 4 3) Základní pojmy matematické
Některé zákony rozdělení pravděpodobnosti. 1. Binomické rozdělení
 Přednáška 5/1 Některé zákony rozdělení pravděpodobnosti 1. Binomické rozdělení Předpoklady: (a) pst výskytu jevu A v jediném pokuse P (A) = π, (b) je uskutečněno n pokusů, (c) pokusy jsou nezávislé, tj.
Přednáška 5/1 Některé zákony rozdělení pravděpodobnosti 1. Binomické rozdělení Předpoklady: (a) pst výskytu jevu A v jediném pokuse P (A) = π, (b) je uskutečněno n pokusů, (c) pokusy jsou nezávislé, tj.
Biostatistika a matematické metody epidemiologie- stručné studijní texty
 Biostatistika a matematické metody epidemiologie- stručné studijní texty Bohumír Procházka, SZÚ Praha 1 Co můžeme sledovat Pro charakteristiku nebo vlastnost, kterou chceme sledovat zvolíme termín jev.
Biostatistika a matematické metody epidemiologie- stručné studijní texty Bohumír Procházka, SZÚ Praha 1 Co můžeme sledovat Pro charakteristiku nebo vlastnost, kterou chceme sledovat zvolíme termín jev.
Pomůcka pro cvičení: 3. semestr Bc studia
 Pomůcka pro cvičení: 3. semestr Bc studia Statistika Základní pojmy balíček: Statistics Pro veškeré výpočty je třeba načíst balíček Statistic. Při řešení můžeme použít proceduru infolevel[statistics]:=1,
Pomůcka pro cvičení: 3. semestr Bc studia Statistika Základní pojmy balíček: Statistics Pro veškeré výpočty je třeba načíst balíček Statistic. Při řešení můžeme použít proceduru infolevel[statistics]:=1,
Pokud data zadáme přes "Commands" okno: SDF1$X1<-c(1:15) //vytvoření řady čísel od 1 do 15 SDF1$Y1<-c(1.5,3,4.5,5,6,8,9,11,13,14,15,16,18.
 Regresní analýza; transformace dat Pro řešení vztahů mezi proměnnými kontinuálního typu používáme korelační a regresní analýzy. Korelace se používá pokud nelze určit "kauzalitu". Regresní analýza je určena
Regresní analýza; transformace dat Pro řešení vztahů mezi proměnnými kontinuálního typu používáme korelační a regresní analýzy. Korelace se používá pokud nelze určit "kauzalitu". Regresní analýza je určena
Uni- and multi-dimensional parametric tests for comparison of sample results
 Uni- and multi-dimensional parametric tests for comparison of sample results Jedno- a více-rozměrné parametrické testy k porovnání výsledků Prof. RNDr. Milan Meloun, DrSc. Katedra analytické chemie, Universita
Uni- and multi-dimensional parametric tests for comparison of sample results Jedno- a více-rozměrné parametrické testy k porovnání výsledků Prof. RNDr. Milan Meloun, DrSc. Katedra analytické chemie, Universita
Vícerozměrné statistické metody
 Vícerozměrné statistické metody Podobnosti a vzdálenosti ve vícerozměrném prostoru, asociační matice II Jiří Jarkovský, Simona Littnerová Vícerozměrné statistické metody Práce s asociační maticí Vzdálenosti
Vícerozměrné statistické metody Podobnosti a vzdálenosti ve vícerozměrném prostoru, asociační matice II Jiří Jarkovský, Simona Littnerová Vícerozměrné statistické metody Práce s asociační maticí Vzdálenosti
S E M E S T R Á L N Í
 Univerzita Pardubice Fakulta chemicko-technologická Katedra analytické chemie S E M E S T R Á L N Í P R Á C E Licenční studium Statistické zpracování dat při managementu jakosti Předmět ANOVA analýza rozptylu
Univerzita Pardubice Fakulta chemicko-technologická Katedra analytické chemie S E M E S T R Á L N Í P R Á C E Licenční studium Statistické zpracování dat při managementu jakosti Předmět ANOVA analýza rozptylu
Multivariátní porovnání dat - klastrová (shluková) analýza
 Multivariátní porovnání dat - klastrová (shluková) analýza - bez apriorních předpokladů Shluková analýza Shluková analýza - cluster analysis úvod - definice princip algoritmy výsledky Shluková analýza
Multivariátní porovnání dat - klastrová (shluková) analýza - bez apriorních předpokladů Shluková analýza Shluková analýza - cluster analysis úvod - definice princip algoritmy výsledky Shluková analýza
PSY117/454 Statistická analýza dat v psychologii přednáška 8. Statistické usuzování, odhady
 PSY117/454 Statistická analýza dat v psychologii přednáška 8 Statistické usuzování, odhady Výběr od deskripce k indukci Deskripce dat, odhad parametrů Usuzování = inference = indukce Počítá se s náhodným
PSY117/454 Statistická analýza dat v psychologii přednáška 8 Statistické usuzování, odhady Výběr od deskripce k indukci Deskripce dat, odhad parametrů Usuzování = inference = indukce Počítá se s náhodným
a) Základní informace o souboru Statistika: Základní statistika a tabulky: Popisné statistiky: Detaily
 Testování hypotéz Testování hypotéz jsou klasické statistické úsudky založené na nějakém apriorním předpokladu. Vyslovíme-li předpoklad o hodnotě neznámého parametru nebo o zákonu rozdělení sledované náhodné
Testování hypotéz Testování hypotéz jsou klasické statistické úsudky založené na nějakém apriorním předpokladu. Vyslovíme-li předpoklad o hodnotě neznámého parametru nebo o zákonu rozdělení sledované náhodné
Odhalení skryté struktury a vnitřních vazeb dat vícerozměrnou statistickou analýzou pitné vody
 Odhalení skryté struktury a vnitřních vazeb dat vícerozměrnou statistickou analýzou pitné vody Prof. RNDr. Milan Meloun, DrSc, Katedra analytické chemie, Univerzita Pardubice, 532 10 Pardubice, milan.
Odhalení skryté struktury a vnitřních vazeb dat vícerozměrnou statistickou analýzou pitné vody Prof. RNDr. Milan Meloun, DrSc, Katedra analytické chemie, Univerzita Pardubice, 532 10 Pardubice, milan.
Metodika. Zájmová území
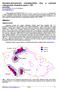 Sociálně-ekonomické charakteristiky obcí a vybraná velkoplošná chráněná území v ČR Karel Matějka IDS, Na Komořsku 2175/2a, 143 00 Praha 4 matejka@infodatasys.cz V rámci projektu GA ČR P404/11/0354 Protected
Sociálně-ekonomické charakteristiky obcí a vybraná velkoplošná chráněná území v ČR Karel Matějka IDS, Na Komořsku 2175/2a, 143 00 Praha 4 matejka@infodatasys.cz V rámci projektu GA ČR P404/11/0354 Protected
Za hranice nejistoty(2)
 Za hranice nejistoty(2) MUDr. Jaroslava Ambrožová OKB-H Nemocnice Prachatice, a.s. 19.5.2014 1 TNI 01 0115: VIM EP15-A2 User Verification of performance for Precision and Trueness C51-A Expression of measurement
Za hranice nejistoty(2) MUDr. Jaroslava Ambrožová OKB-H Nemocnice Prachatice, a.s. 19.5.2014 1 TNI 01 0115: VIM EP15-A2 User Verification of performance for Precision and Trueness C51-A Expression of measurement
Analýza dat na PC I.
 CENTRUM BIOSTATISTIKY A ANALÝZ Lékařská a Přírodovědecká fakulta, Masarykova univerzita Analýza dat na PC I. Popisná analýza v programu Statistica IBA výuka Základní popisná statistika Popisná statistika
CENTRUM BIOSTATISTIKY A ANALÝZ Lékařská a Přírodovědecká fakulta, Masarykova univerzita Analýza dat na PC I. Popisná analýza v programu Statistica IBA výuka Základní popisná statistika Popisná statistika
Bayesovská klasifikace digitálních obrazů
 Výzkumný ústav geodetický, topografický a kartografický Bayesovská klasifikace digitálních obrazů Výzkumná zpráva č. 1168/2010 Lubomír Soukup prosinec 2010 1 Úvod V průběhu nedlouhého historického vývoje
Výzkumný ústav geodetický, topografický a kartografický Bayesovská klasifikace digitálních obrazů Výzkumná zpráva č. 1168/2010 Lubomír Soukup prosinec 2010 1 Úvod V průběhu nedlouhého historického vývoje
Analýza variance (ANOVA) - jednocestná; faktor s pevným efektem; mnohonásobná srovnání
 Analýza variance (ANOVA) - jednocestná; faktor s pevným efektem; mnohonásobná srovnání 1. Analýzu variance (ANOVu) používáme při studiu problémů, kdy máme závislou proměnou spojitého typu a nezávislé proměnné
Analýza variance (ANOVA) - jednocestná; faktor s pevným efektem; mnohonásobná srovnání 1. Analýzu variance (ANOVu) používáme při studiu problémů, kdy máme závislou proměnou spojitého typu a nezávislé proměnné
Metodologie pro ISK II
 Metodologie pro ISK II Všechny hodnoty z daného intervalu Zjišťujeme: Centrální míry Variabilitu Šikmost, špičatost Percentily (decily, kvantily ) Zobrazení: histogram MODUS je hodnota, která se v datech
Metodologie pro ISK II Všechny hodnoty z daného intervalu Zjišťujeme: Centrální míry Variabilitu Šikmost, špičatost Percentily (decily, kvantily ) Zobrazení: histogram MODUS je hodnota, která se v datech
Karta předmětu prezenční studium
 Karta předmětu prezenční studium Název předmětu: Číslo předmětu: 545-0250 Garantující institut: Garant předmětu: Ekonomická statistika Institut ekonomiky a systémů řízení RNDr. Radmila Sousedíková, Ph.D.
Karta předmětu prezenční studium Název předmětu: Číslo předmětu: 545-0250 Garantující institut: Garant předmětu: Ekonomická statistika Institut ekonomiky a systémů řízení RNDr. Radmila Sousedíková, Ph.D.
Statistika. Diskrétní data. Spojitá data. Charakteristiky polohy. Charakteristiky variability
 I Přednáška Statistika Diskrétní data Spojitá data Charakteristiky polohy Charakteristiky variability Statistika deskriptivní statistika ˆ induktivní statistika populace (základní soubor) ˆ výběr parametry
I Přednáška Statistika Diskrétní data Spojitá data Charakteristiky polohy Charakteristiky variability Statistika deskriptivní statistika ˆ induktivní statistika populace (základní soubor) ˆ výběr parametry
č. 98/2011 Sb. VYHLÁŠKA ze dne 30. března 2011 o způsobu hodnocení stavu útvarů povrchových vod, způsobu hodnocení ekologického potenciálu silně
 č. 98/2011 Sb. VYHLÁŠKA ze dne 30. března 2011 o způsobu hodnocení stavu útvarů povrchových vod, způsobu hodnocení ekologického potenciálu silně ovlivněných a umělých útvarů povrchových vod a náležitostech
č. 98/2011 Sb. VYHLÁŠKA ze dne 30. března 2011 o způsobu hodnocení stavu útvarů povrchových vod, způsobu hodnocení ekologického potenciálu silně ovlivněných a umělých útvarů povrchových vod a náležitostech
Zpracování a vyhodnocování analytických dat
 Zpracování a vyhodnocování analytických dat naměřená data Zpracování a statistická analýza dat analytické výsledky Naměř ěřená data jedna hodnota 5,00 mg (bod 1D) navážka, odměřený objem řada dat 15,8;
Zpracování a vyhodnocování analytických dat naměřená data Zpracování a statistická analýza dat analytické výsledky Naměř ěřená data jedna hodnota 5,00 mg (bod 1D) navážka, odměřený objem řada dat 15,8;
5EN306 Aplikované kvantitativní metody I
 5EN306 Aplikované kvantitativní metody I Přednáška 3 Zuzana Dlouhá Předmět a struktura kurzu 1. Úvod: struktura empirických výzkumů 2. Tvorba ekonomických modelů: teorie 3. Data: zdroje a typy dat, význam
5EN306 Aplikované kvantitativní metody I Přednáška 3 Zuzana Dlouhá Předmět a struktura kurzu 1. Úvod: struktura empirických výzkumů 2. Tvorba ekonomických modelů: teorie 3. Data: zdroje a typy dat, význam
Simulace systému hromadné obsluhy Nejčastější chyby v semestrálních pracích
 Simulace systému hromadné obsluhy Nejčastější chyby v semestrálních pracích Nedostatešný popis systému a jeho modelu vstupy S výstupy Systém Část prostředí, kterou lze od jeho okolí oddělit fyzickou nebo
Simulace systému hromadné obsluhy Nejčastější chyby v semestrálních pracích Nedostatešný popis systému a jeho modelu vstupy S výstupy Systém Část prostředí, kterou lze od jeho okolí oddělit fyzickou nebo
5EN306 Aplikované kvantitativní metody I
 5EN306 Aplikované kvantitativní metody I Přednáška 3 Zuzana Dlouhá Předmět a struktura kurzu 1. Úvod: struktura empirických výzkumů 2. Tvorba ekonomických modelů: teorie 3. Data: zdroje a typy dat, význam
5EN306 Aplikované kvantitativní metody I Přednáška 3 Zuzana Dlouhá Předmět a struktura kurzu 1. Úvod: struktura empirických výzkumů 2. Tvorba ekonomických modelů: teorie 3. Data: zdroje a typy dat, význam
VÍCEROZMĚRNÝ STATISTICKÝ SOUBOR
 KORELACE A REGRESE 1 Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného základu (reg. č. CZ.1.07/..00/8.001)
KORELACE A REGRESE 1 Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného základu (reg. č. CZ.1.07/..00/8.001)
Drsná matematika IV 7. přednáška Jak na statistiku?
 Drsná matematika IV 7. přednáška Jak na statistiku? Jan Slovák Masarykova univerzita Fakulta informatiky 2. 4. 2012 Obsah přednášky 1 Literatura 2 Co je statistika? 3 Popisná statistika Míry polohy statistických
Drsná matematika IV 7. přednáška Jak na statistiku? Jan Slovák Masarykova univerzita Fakulta informatiky 2. 4. 2012 Obsah přednášky 1 Literatura 2 Co je statistika? 3 Popisná statistika Míry polohy statistických
Mgr. Jan Mládek, Ph.D. (2013)
 Ekologie zdrojů: interakce půdy, vegetace a herbivorů (EKO/EZI) Mgr. Jan Mládek, Ph.D. (2013) 7. blok 24/05/2013 Rozvoj a inovace výuky ekologických oborů formou komplementárního propojení studijních programů
Ekologie zdrojů: interakce půdy, vegetace a herbivorů (EKO/EZI) Mgr. Jan Mládek, Ph.D. (2013) 7. blok 24/05/2013 Rozvoj a inovace výuky ekologických oborů formou komplementárního propojení studijních programů
Hluboká říční údolí jako objekt pro modelování vztahů vegetace a proměnných prostředí?
 David Zelený Biologická fakulta JčU v Českých Budějovicích školitel: Milan Chytrý (PřF MU Brno) Hluboká říční údolí jako objekt pro modelování vztahů vegetace a proměnných prostředí? Vltava pod Dívčím
David Zelený Biologická fakulta JčU v Českých Budějovicích školitel: Milan Chytrý (PřF MU Brno) Hluboká říční údolí jako objekt pro modelování vztahů vegetace a proměnných prostředí? Vltava pod Dívčím
SEMESTRÁ LNÍ PRÁ CE. Licenč ní studium STATISTICKÉZPRACOVÁ NÍ DAT PŘ I KONTROLE A Ř ÍZENÍ JAKOSTI
 SEMESTRÁ LNÍ PRÁ CE Licenč ní studium STATISTICKÉZPRACOVÁ NÍ DAT PŘ I KONTROLE A Ř ÍZENÍ JAKOSTI Předmě t ANOVA A ZÁ KON PROPAGACE CHYB U JEDNOROZMĚ RNÝ CH DAT Ú stav experimentá lní biofarmacie, Hradec
SEMESTRÁ LNÍ PRÁ CE Licenč ní studium STATISTICKÉZPRACOVÁ NÍ DAT PŘ I KONTROLE A Ř ÍZENÍ JAKOSTI Předmě t ANOVA A ZÁ KON PROPAGACE CHYB U JEDNOROZMĚ RNÝ CH DAT Ú stav experimentá lní biofarmacie, Hradec
Statistická analýza dat v psychologii. Věci, které můžeme přímo pozorovat, jsou téměř vždy pouze vzorky. Alfred North Whitehead
 PSY117/454 Statistická analýza dat v psychologii Přednáška 8 Statistické usuzování, odhady Věci, které můžeme přímo pozorovat, jsou téměř vždy pouze vzorky. Alfred North Whitehead Barevná srdíčka kolegyně
PSY117/454 Statistická analýza dat v psychologii Přednáška 8 Statistické usuzování, odhady Věci, které můžeme přímo pozorovat, jsou téměř vždy pouze vzorky. Alfred North Whitehead Barevná srdíčka kolegyně
(Auto)korelační funkce. 2. 11. 2015 Statistické vyhodnocování exp. dat M. Čada www.fzu.cz/ ~ cada
 (Auto)korelační funkce 1 Náhodné procesy Korelace mezi náhodnými proměnnými má široké uplatnění v elektrotechnické praxi, kde se snažíme o porovnávání dvou signálů, které by měly být stejné. Příkladem
(Auto)korelační funkce 1 Náhodné procesy Korelace mezi náhodnými proměnnými má široké uplatnění v elektrotechnické praxi, kde se snažíme o porovnávání dvou signálů, které by měly být stejné. Příkladem
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc.
 Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 2010 1.týden (20.09.-24.09. ) Data, typy dat, variabilita, frekvenční analýza
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika 2010 1.týden (20.09.-24.09. ) Data, typy dat, variabilita, frekvenční analýza
RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr.
 Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
Poznámky k předmětu Aplikovaná statistika, 9.téma
 Poznámky k předmětu Aplikovaná statistika, 9téma Princip testování hypotéz, jednovýběrové testy V minulé hodině jsme si ukázali, jak sestavit intervalové odhady pro některé číselné charakteristiky normálního
Poznámky k předmětu Aplikovaná statistika, 9téma Princip testování hypotéz, jednovýběrové testy V minulé hodině jsme si ukázali, jak sestavit intervalové odhady pro některé číselné charakteristiky normálního
Ústav matematiky Fakulta chemicko inženýrská Vysoká škola chemicko-technologická v Praze
 Komentované řešení pomocí programu R Ústav matematiky Fakulta chemicko inženýrská Vysoká škola chemicko-technologická v Praze Popis vstupních dat Vstupní data pro úlohu (A) se nacházejí v souboru "glukoza.csv".
Komentované řešení pomocí programu R Ústav matematiky Fakulta chemicko inženýrská Vysoká škola chemicko-technologická v Praze Popis vstupních dat Vstupní data pro úlohu (A) se nacházejí v souboru "glukoza.csv".
Statistická analýza volebních výsledk
 Statistická analýza volebních výsledk Volby do PSP R 2006 Josef Myslín 1 Obsah 1 Obsah...2 2 Úvod...3 1 Zdrojová data...4 1.1 Procentuální podpora jednotlivých parlamentních stran...4 1.2 Údaje o nezamstnanosti...4
Statistická analýza volebních výsledk Volby do PSP R 2006 Josef Myslín 1 Obsah 1 Obsah...2 2 Úvod...3 1 Zdrojová data...4 1.1 Procentuální podpora jednotlivých parlamentních stran...4 1.2 Údaje o nezamstnanosti...4
Statgraphics v. 5.0 STATISTICKÁ INDUKCE PRO JEDNOROZMĚRNÁ DATA. Martina Litschmannová 1. Typ proměnné. Požadovaný typ analýzy
 Dichotomická proměnná (0-1) Spojitá proměnná STATISTICKÁ INDUKCE PRO JEDNOROZMĚRNÁ DATA Typ proměnné Požadovaný typ analýzy Ověření variability Předpoklady Testy, resp. intervalové odhad Test o rozptylu
Dichotomická proměnná (0-1) Spojitá proměnná STATISTICKÁ INDUKCE PRO JEDNOROZMĚRNÁ DATA Typ proměnné Požadovaný typ analýzy Ověření variability Předpoklady Testy, resp. intervalové odhad Test o rozptylu
1.4 ANOVA. Vliv druhu plodiny na míru napadení houbami Fusarium culmorum a Fusarium graminearum v systému ekologického hospodaření
 1.4 ANOVA Úloha 1 Jednofaktorová ANOVA Vliv druhu plodiny na míru napadení houbami Fusarium culmorum a Fusarium graminearum v systému ekologického hospodaření Bylo měřeno množství DNA hub Fusarium culmorum
1.4 ANOVA Úloha 1 Jednofaktorová ANOVA Vliv druhu plodiny na míru napadení houbami Fusarium culmorum a Fusarium graminearum v systému ekologického hospodaření Bylo měřeno množství DNA hub Fusarium culmorum
Semestrální projekt. do předmětu Statistika. Vypracoval: Adam Mlejnek 2-36. Oponenti: Patrik Novotný 2-36. Jakub Nováček 2-36. Click here to buy 2
 Semestrální projekt do předmětu Statistika Vypracoval: Adam Mlejnek 2-36 Oponenti: Patrik Novotný 2-36 Jakub Nováček 2-36 Úvod Pro vypracování projektu do předmětu statistika jsem si zvolil průzkum kvality
Semestrální projekt do předmětu Statistika Vypracoval: Adam Mlejnek 2-36 Oponenti: Patrik Novotný 2-36 Jakub Nováček 2-36 Úvod Pro vypracování projektu do předmětu statistika jsem si zvolil průzkum kvality
Členění území lokality
 Členění území lokality Předkládaný podklad pro členění území vznikl v Kanceláři metropolitního plánu a je prvním uceleným názorem na definování pražských lokalit. Podklad vznikl jako syntéza dvanácti názorů
Členění území lokality Předkládaný podklad pro členění území vznikl v Kanceláři metropolitního plánu a je prvním uceleným názorem na definování pražských lokalit. Podklad vznikl jako syntéza dvanácti názorů
Mendelova zemědělská a lesnická univerzita v Brně
 Mendelova zemědělská a lesnická univerzita v Brně Bobtnání dřeva Fyzikální vlastnosti dřeva Protokol č.3 Vypracoval: Pavel Lauko Datum cvičení: 24.9.2002 Obor: DI Datum vyprac.: 10.12.02 Ročník: 2. Skupina:
Mendelova zemědělská a lesnická univerzita v Brně Bobtnání dřeva Fyzikální vlastnosti dřeva Protokol č.3 Vypracoval: Pavel Lauko Datum cvičení: 24.9.2002 Obor: DI Datum vyprac.: 10.12.02 Ročník: 2. Skupina:
Vícerozměrné statistické metody
 Praktické řešení v software Statistica Jiří Jarkovský, Simona Littnerová Vícerozměrné metody 1. Vstupní data pro vícerozměrné analýzy 2. Metriky podobností a vzdáleností 3. Cluster Analysis 4. Principal
Praktické řešení v software Statistica Jiří Jarkovský, Simona Littnerová Vícerozměrné metody 1. Vstupní data pro vícerozměrné analýzy 2. Metriky podobností a vzdáleností 3. Cluster Analysis 4. Principal
Analýza dat z dotazníkových šetření
 Analýza dat z dotazníkových šetření Cvičení 6. Rozsah výběru Př. Určete minimální rozsah výběru pro proměnnou věk v souboru dovolena, jestliže 95% interval spolehlivost průměru proměnné nemá být širší
Analýza dat z dotazníkových šetření Cvičení 6. Rozsah výběru Př. Určete minimální rozsah výběru pro proměnnou věk v souboru dovolena, jestliže 95% interval spolehlivost průměru proměnné nemá být širší
Regresní analýza. Eva Jarošová
 Regresní analýza Eva Jarošová 1 Obsah 1. Regresní přímka 2. Možnosti zlepšení modelu 3. Testy v regresním modelu 4. Regresní diagnostika 5. Speciální využití Lineární model 2 1. Regresní přímka 3 nosnost
Regresní analýza Eva Jarošová 1 Obsah 1. Regresní přímka 2. Možnosti zlepšení modelu 3. Testy v regresním modelu 4. Regresní diagnostika 5. Speciální využití Lineární model 2 1. Regresní přímka 3 nosnost
STATISTICA Téma 8. Regresní a korelační analýza, regrese prostá
 STATISTICA Téma 8. Regresní a korelační analýza, regrese prostá 1) Lineární i nelineární regrese prostá, korelace Naeditujeme data viz obr. 1. Obr. 1 V menu Statistika zvolíme submenu Pokročilé lineární/nelineární
STATISTICA Téma 8. Regresní a korelační analýza, regrese prostá 1) Lineární i nelineární regrese prostá, korelace Naeditujeme data viz obr. 1. Obr. 1 V menu Statistika zvolíme submenu Pokročilé lineární/nelineární
Klíčová slova prediktory absolvování studia medicíny, logistická regrese, ROC křivky
 STUDIUM SOUVISLOSTÍ MEZI ÚSPĚŠNOSTÍ STUDIA MEDICÍNY, ZNÁMKAMI STUDENTŮ NA STŘEDNÍ ŠKOLE A VÝSLEDKY PŘIJÍMACÍCH ZKOUŠEK 1 Čestmír Štuka, Petr Šimeček Anotace Studie analyzuje úspěšnost studentů přijatých
STUDIUM SOUVISLOSTÍ MEZI ÚSPĚŠNOSTÍ STUDIA MEDICÍNY, ZNÁMKAMI STUDENTŮ NA STŘEDNÍ ŠKOLE A VÝSLEDKY PŘIJÍMACÍCH ZKOUŠEK 1 Čestmír Štuka, Petr Šimeček Anotace Studie analyzuje úspěšnost studentů přijatých
Analýza rozptylu. Přednáška STATISTIKA II - EKONOMETRIE. Jiří Neubauer
 ANOVA Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz ANOVA ANOVA je nástroj pro zkoumání vztahu mezi vysvětlovanými a vysvětlujícími
ANOVA Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz ANOVA ANOVA je nástroj pro zkoumání vztahu mezi vysvětlovanými a vysvětlujícími
2. Základní typy dat Spojitá a kategoriální data Základní popisné statistiky Frekvenční tabulky Grafický popis dat
 2. Základní typy dat Spojitá a kategoriální data Základní popisné statistiky Frekvenční tabulky Grafický popis dat Anotace Realitu můžeme popisovat různými typy dat, každý z nich se specifickými vlastnostmi,
2. Základní typy dat Spojitá a kategoriální data Základní popisné statistiky Frekvenční tabulky Grafický popis dat Anotace Realitu můžeme popisovat různými typy dat, každý z nich se specifickými vlastnostmi,
Rozptyl. Pozn.: rozptyl je nezávislý na posunu hustoty pravděpodobnosti na ose x, protože Var(X) mi určuje jen šířku rozdělení.
 Rozptyl Základní vlastnosti disperze Var(konst) = 0 Var(X+Y) = Var(X) + Var(Y) (nezávislé proměnné) Lineární změna jednotek Y = rx + s, například z C na F. Jak vypočítám střední hodnotu a rozptyl? Pozn.:
Rozptyl Základní vlastnosti disperze Var(konst) = 0 Var(X+Y) = Var(X) + Var(Y) (nezávislé proměnné) Lineární změna jednotek Y = rx + s, například z C na F. Jak vypočítám střední hodnotu a rozptyl? Pozn.:
Rozhodovací stromy a lesy
 Rozhodovací stromy a lesy Klára Komprdová Leden 2012 Příprava a vydání této publikace byly podporovány projektem ESF č. CZ.1.07/2.2.00/07.0318 Víceoborová inovace studia Matematické biologie a státním
Rozhodovací stromy a lesy Klára Komprdová Leden 2012 Příprava a vydání této publikace byly podporovány projektem ESF č. CZ.1.07/2.2.00/07.0318 Víceoborová inovace studia Matematické biologie a státním
Popisná statistika. Komentované řešení pomocí MS Excel
 Popisná statistika Komentované řešení pomocí MS Excel Vstupní data Máme k dispozici data o počtech bodů z 1. a 2. zápočtového testu z Matematiky I v zimním semestru 2015/2016 a to za všech 762 studentů,
Popisná statistika Komentované řešení pomocí MS Excel Vstupní data Máme k dispozici data o počtech bodů z 1. a 2. zápočtového testu z Matematiky I v zimním semestru 2015/2016 a to za všech 762 studentů,
8. Posloupnosti, vektory a matice
 . jsou užitečné matematické nástroje. V Mathcadu je často používáme například k rychlému zápisu velkého počtu vztahů s proměnnými parametry, ke zpracování naměřených hodnot, k výpočtům lineárních soustav
. jsou užitečné matematické nástroje. V Mathcadu je často používáme například k rychlému zápisu velkého počtu vztahů s proměnnými parametry, ke zpracování naměřených hodnot, k výpočtům lineárních soustav
Vyzařování černého tělesa, termoelektrický jev, závislost odporu na teplotě.
 Klíčová slova Vyzařování černého tělesa, termoelektrický jev, závislost odporu na teplotě. Princip Podle Stefanova-Boltzmannova zákona vyzařování na jednotu plochy a času černého tělesa roste se čtvrtou
Klíčová slova Vyzařování černého tělesa, termoelektrický jev, závislost odporu na teplotě. Princip Podle Stefanova-Boltzmannova zákona vyzařování na jednotu plochy a času černého tělesa roste se čtvrtou
KORELACE. Komentované řešení pomocí programu Statistica
 KORELACE Komentované řešení pomocí programu Statistica Vstupní data I Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu Popisná
KORELACE Komentované řešení pomocí programu Statistica Vstupní data I Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu Popisná
Kurz SPSS: Jednoduchá analýza dat. Jiří Šafr
 Kurz SPSS: Jednoduchá analýza dat Jiří Šafr vytvořeno 29. 6. 2009 Dva základní typy statistiky 1. Popisná statistika: metody pro zjišťování a sumarizaci informací grfy, tabulky, popisné chrakteristiky
Kurz SPSS: Jednoduchá analýza dat Jiří Šafr vytvořeno 29. 6. 2009 Dva základní typy statistiky 1. Popisná statistika: metody pro zjišťování a sumarizaci informací grfy, tabulky, popisné chrakteristiky
SYSTÉM TECHNICKO-EKONOMICKÉ ANALÝZY VÝROBY TEKUTÉHO KOVU - CESTA KE SNIŽOVÁNÍ NÁKLADŮ
 SYSTÉM TECHNICKO-EKONOMICKÉ ANALÝZY VÝROBY TEKUTÉHO KOVU - CESTA KE SNIŽOVÁNÍ NÁKLADŮ FIGALA V. a), KAFKA V. b) a) VŠB-TU Ostrava, FMMI, katedra slévárenství, 17. listopadu 15, 708 33 b) RACIO&RACIO, Vnitřní
SYSTÉM TECHNICKO-EKONOMICKÉ ANALÝZY VÝROBY TEKUTÉHO KOVU - CESTA KE SNIŽOVÁNÍ NÁKLADŮ FIGALA V. a), KAFKA V. b) a) VŠB-TU Ostrava, FMMI, katedra slévárenství, 17. listopadu 15, 708 33 b) RACIO&RACIO, Vnitřní
Teorie časových řad Test 2 Varianta A HODNOCENÍ (max. 45 bodů z 50 možných)
 Teorie časových řad Test 2 Varianta A HODNOCENÍ (max. 45 bodů z 50 možných) 1. SPECIFIKACE (12 bodů): (1) Graf průběhu proměnných (1) Obě řady se chovají stejně, lze předpokládat jejich lineární vztah
Teorie časových řad Test 2 Varianta A HODNOCENÍ (max. 45 bodů z 50 možných) 1. SPECIFIKACE (12 bodů): (1) Graf průběhu proměnných (1) Obě řady se chovají stejně, lze předpokládat jejich lineární vztah
SPECIES ATTRIBUTES IN ANALYSIS OF COMMUNITY ECOLOGY DATA
 SPECIES ATTRIBUTES IN ANALYSIS OF COMMUNITY ECOLOGY DATA HOW TO ANALYSE RELATIONSHIP BETWEEN SAMPLE ATTRIBUTES AND SPECIES ATTRIBUTES VIA SPECIES COMPOSITION? species sample attributes samples L R 222
SPECIES ATTRIBUTES IN ANALYSIS OF COMMUNITY ECOLOGY DATA HOW TO ANALYSE RELATIONSHIP BETWEEN SAMPLE ATTRIBUTES AND SPECIES ATTRIBUTES VIA SPECIES COMPOSITION? species sample attributes samples L R 222
