Na začátku rozdělíme práci a určíme, které podproblémy je potřeba vyřešit. Tyto
|
|
|
- Nikola Machová
- před 8 lety
- Počet zobrazení:
Transkript
1 Kapitola 1 Rozděl a panuj Rozděl a panuj je programovací metoda. Často se označuje latinsky Divide et Empera nebo anglicky Divide and Conquer. Vychází z toho, že umíme zadaný problém rozložit na menší podproblémy stejného typu. Na začátku rozdělíme práci a určíme, které podproblémy je potřeba vyřešit. Tyto podproblémy si necháme vyřešit rekurzivně. Složením jejich řešení dostaneme řešení původního problému. Algoritmus se volá rekurzivně tak dlouho, dokud se nedostane k problémům konstantní velikosti, které už umí hravě vyřešit. Vysvětlíme si to ještě jednou na pohádce o tom, jak si římský císař hraje na popelku. Inu i římskému císaři se někdy stane, že mu v sýpkách smíchají čočku a hrách. Jak to roztřídit? Císař přeci nemůže dělat takovou práci sám, má na to lidi. A tak si zavolá vojáky a nechá směs čočky a hrachu rozdělit na tři zhruba stejně velké hromádky. Potom zavolá své generály, každému přiřadí jednu hromádku a nechá je oddělit čočku od hrachu. Ale i takový generál se nebude dřít sám. Po vzoru císaře, rozdělí svojí hromádku na tři a rozdělí práci mezi své podřízené. Takto projde předávání práce celou hierarchií římské armády, až to skončí u otroků. Každý otrok dostane jednu misku směsi a tu roztřídí. Jeho pán si od všech svých otroků vybere zvlášť čočku a zvlášť hrách a předá je výše. Takto projde slučování hromádek zpátky až k císaři, který, ke své spokojenosti a rozmarnosti, nechá přesunout všechnu čočku zpátky do sýpky a hrách hodí sviním, aby se příště s čočkou nesmíchal. Použití metody rozděl a panuj si ukážeme v následujících úlohách. 1.1 Hanojské věže Příběh: V jednom indickém chrámu mají tři věže Věž zrození, Věž života a Věž zkázy. Uvnitř každé z nich je kůl, na kterém je navlečeno několik zlatých disků. Ve všech třech věžích je dohromady 64 disků. Každý disk je jinak široký. Disky smí být na kůlu navlečeny pouze tak, že menší a užší disk leží na širším. Jinak to prý přinese smůlu. Proto každý kůl spolu s disky vypadá jako kužel. Při stvoření chrámu byly všechny disky navlečeny na jeden kůl ve Věži stvoření. Kněží, kteří v chrámu přebývají, každý den přesunou jeden disk (víc jich přesunout nesmí) tak, aby se jim co nejdříve podařilo přesunout všechny disky na kůl ve Věži zkázy. Jinak by se zastavilo plynutí života. Stará legenda říká, že až se jim to podaří, tak nastane konec světa. 1
2 2 KAPITOLA 1. ROZDĚL A PANUJ Úkol pro Vás: Dokázali byste napsat program, který kněžím vypíše instrukce, jak mají disky přesunovat? Už jsou z toho celí zmatení a moc by jim to pomohlo. Na začátku jsou všechny disky navlečeny na první kůl a máte je přestěhovat na poslední kůl. Pokud se budeme držet zásady rozděl a panuj, tak zkusíme problém rozložit na podproblémy, jejichž vyřešení přehodíme na někoho jiného (třeba na rekurzi). Abychom mohli největší disk přesunout na správné místo, tak nejprve necháme všechny menší disky přestěhovat na třetí odkládací tyčku. Pak přesuneme největší disk. Na závěr necháme všechny odložené disky přesunout nad největší disk. 1: Hanoj(n, odkud, pres, kam) 2: if n 1 then 3: Hanoj(n 1, odkud, kam, pres) 4: Vypiš( Přeneste disk z,odkud, do, kam) 5: Hanoj(n 1, pres, odkud, kam) Jaká je časová složitost tohoto algoritmu? Ta je úměrná tomu, kolikrát budou muset kněží přenést nějaký disk. Označme celkový počet přenesení disků pomocí T (n). Z uvedeného algoritmu je vidět rekurence T (n) = 2T (n 1) + 1. Rekurenci můžeme vyřešit například postupným rozepisováním. Dostaneme T (n) = 2T (n 1) + 1 = 2(2(T (n 2) + 1) + 1 = = 2(2(2 (2T (1) + 1) + 1) + 1) + 1 = 2 n + 2 n = 2 n+1. Takže časová složitost algoritmu Hanoj je exponenciální. Legenda říká, že disků je 64. Jestliže byl chrám založen zhruba před 3000 lety, dokážete určit kdy nastane konec světa? Má smysl se toho obávat? 1.2 Mergesort Mergesort je třídící algoritmus využívající metody rozděl a panuj. Dostane vstup, například posloupnost čísel, který rozdělí na dvě skoro stejné části. Ty nechá setřídit rekurzivně. Výsledné posloupnosti slije do jedné a tu vrátí jako setříděnou posloupnost. Co znamená slít dvě setříděné posloupnosti P 1, P 2 do jedné? Cílem je vytvořit jednu posloupnost P, která obsahuje prvky obou předchozích posloupností a je setříděná. Menší prvek z počátečních (a nejmenších) prvků setříděných posloupností P 1, P 2 je určitě nejmenším prvkem výsledné posloupnosti P. Proto ho odtrhneme a přidáme na začátek P. Tím z P 1, P 2 vzniknou posloupnosti P 1, P 2. Pro ty můžeme celý postup zopakovat a tím dostaneme druhý nejmenší prvek P. Dalším opakováním postupně odtrháme všechny prvky obou setříděných posloupností P 1, P 2 a sestavujeme požadovanou posloupnost P.
3 1.2. MERGESORT 3 Slévání si můžeme představovat trochu jako zip na oblečení. Dvě ozubené části zipu (setříděné posloupnosti) přiložíme k sobě a zapneme je jezdcem. Jezdec kontroluje, že do sebe ozubené části zapadají podle velikosti. Klasická implementace Mergesortu pracuje se spojovým seznamem prvků. Pokud chceme mergesort implementovat v poli, tak se neobejdeme bez pomocného pole B[ ], kam budeme ukládat mezivýsledky. Procedura Mergesort(l, p) setřídí úsek pole A[l..p] mezi indexy l a p. Pole A[n] i pomocné pole B[n] jsou globální proměnné. 1: Mergesort(l, p) 2: if l < p then 3: stred := (l + p)/2 4: Mergesort(l, stred) 5: Mergesort(stred + 1, p) 6: Merge(l,p) Procedura Merge(l, p) slije setříděné podposloupnosti A[l..stred] a A[stred + 1..p] do jedné setříděné posloupnosti A[l..p]. Pro ukládání mezivýsledků potřebuje pomocné pole B[l..p]. Procedura Merge má časovou složitost O(m), kde m je délka výsledné posloupnosti. 1: Merge(l, p) 2: stred := (l + p)/2 3: i := l {Index na začátek první setříděné posloupnosti. } 4: j := stred + 1 {Index na začátek druhé setříděné posloupnosti.} 5: k := l {Index do pole B[ ], kam zapisujeme výsledek.} 6: while k p do 7: if i > stred then {První posloupnost došla.} 8: B[k] := A[j] 9: j := j : else if j > p then {Druhá posloupnost došla.} 11: B[k] := A[i] 12: i := i : else if A[i] < A[j] then {Žádná posloupnost nedošla.} 14: B[k] := A[i] 15: i := i : else 17: B[k] := A[j] 18: j := j : k := k : for k := l to p do {Kopírování výsledků z B[l..p] do A[l..p]} 21: A[k] := B[i] Časová složitost Mergesort je určena rekurencí T (n) = 2T (n/2) + O(n), protože dvakrát řešíme podúlohu poloviční velikosti a jednou sléváme výsledky dohromady. Následující obrázek ilustruje průběh algoritmu a slévání jednotlivých částí. Strom rekurze máme nakreslený vzhůru nohama, protože se algoritmus nejprve zanoří, co nejhlouběji to jde, a teprve při zpáteční cestě provádí slévání podposloupností (úseků pole). Pro lidi je přirozenější ta zpáteční cesta, na které se něco děje.
4 4 KAPITOLA 1. ROZDĚL A PANUJ 3. hladina hladina hladina hladina Strom rekurze má hloubku nejvýše log n, protože při každém zavolání Mergesort rozdělíme posloupnost v půlce. Na k-té hladině 1 se slévají dvě posloupnosti délky n/2 k+1 do posloupnosti délky n/2 k. Těchto slévání se na k-té hladině vykoná 2 k. Proto je celková práce na k-té hladině rovna O(n). Z toho dostáváme časovou složitost algoritmu mergesort O(n log n). Poznámka k implementaci: Na konci každého volání Merge kopírujeme výsledky z pomocného pole B[ ] do pole A[ ]. Tomu se můžeme vyhnout tak, že budeme při rekurzivním volání Mergesortu střídat význam pole A[ ] a B[ ]. Na sudých hladinách dostane Merge posloupnost v poli B[ ] a vytvoří setříděnou posloupnost do pole A[ ] a v lichých hladinách naopak. Prohazování můžeme zrealizovat tak, že funkci Merge předáme i ukazatele na tyto pole a při rekurzivním zavolání ukazatele prohodíme. Mohlo by se stát, že střídání polí po hladinách vyjde tak, že budeme v poslední hladině chtít slévat položky z B[ ] do pole A[ ]. Proto na začátku celého algoritmu nakopírujeme celý vstup z A[ ] i do pole B[ ]. 1.3 Medián posloupnosti Máme posloupnost n prvků, například čísel. Medián je takové číslo z posloupnosti čísel, že 50% čísel je větších nebo rovno mediánu, ale také 50% čísel je menších nebo rovno mediánu. Jinými slovy, když si posloupnost setřídíme, tak nazveme prvek, který leží uprostřed, mediánem. Pokud je prvků lichý počet, tak je medián ten prostřední prvek. Pokud je počet prvků sudý, tak máme mediány dva spodní a horní medián. Abychom si zjednodušili výklad, budeme za medián považovat spodní medián. 2 Medián se používá ve statistice, protože to je jedno číslo, které vypovídá něco typického o množině čísel. Podobným číslem je průměr. 3 Poznámka: Kolik informace nám přinese údaj o průměrné mzdě v Heské republice? Pro běžné lidi je to jen číslo, kvůli kterému jsou nespokojeni, že nevydělávají dost. Pokud bude 10% obyvatel vydělávat 110tis. Kč/měsíc a zbylých 90% obyvatel jen 10tis. Kč/měsíc, tak je průměrná mzda v Heské republice 20tis. Kč. Ovšem kdo ji má? Naproti tomu medián platů v Heské republice je 10tis. Kč/měsíc. To je číslo, které mnohem lépe popisuje celou situaci. 1 k-tou hladinou myslíme k-tou hladinu od kořene. Na obrázku je strom nakreslen vzhůru nohama a proto je to na obrázku k-tá hladina od zdola. 2 Běžně se za medián bere průměr spodního a horního mediánu. To je ale hodnota, ne prvek. 3 Víte o tom, že máte nadprůměrný počet očí? Tedy pokud nejste ten výjimečný případ.
5 1.3. MEDIÁN POSLOUPNOSTI 5 Úkol: Dosteneme pole obsahující n různých čísel. 4 Jak co nejrychleji najít medián? Nebo když tento problém zobecníme, jak co nejrychleji najít k-tý nejmenší prvek? 5 Řešení 1: Nejjednoduším řešením je, že si pole setřídíme a potom vypíšeme k-tý prvek. Třídění nám zabere čas O(n log n). Řešení 2: Můžeme upravit Quicksort ze strany?? tak, aby po rozdělení úseku pole A[l..p] pivotem nezpracovával levý i pravý úsek pole, ale aby už pracoval jen s úsekem, ve kterém leží k-tý nejmenší prvek. 1: QuickSelect(l, p, k) 2: if l < p then 3: pivot := A[ (l + p)/2 ] 4: q :=Partition(l, r, pivot) 5: if q k then 6: QuickSelect(l, q, k) 7: else 8: QuickSelect(q + 1, p, k) 9: else 10: Output(A[l]) Připomeňme, že funkce q :=Partition(l, p, pivot) rozdělí úsek pole A[l..p] na dva úseky A[l..q] a A[q + 1..p], kde první úsek obsahuje pouze prvky menší nebo rovny pivotu a druhý úsek pouze prvky větší než pivot. Implementace funkce je popsána u quicksortu na straně??. V ideálním případě, kdy se nám podaří vybrat všechny pivoty tak, aby se každý úsek pole rozdělil přesně napůl, bude časová složitost tohoto řešení O(n + n/2 + n/ ) = O(2n) = O(n). Ovšem pokud budeme mít smůlu a pivot bude vždy nejmenším nebo největším prvkem z aktuálního úseku, tak bude časová složitost tohoto řešení O(n + (n 1) + (n 2) + + 1) = O(n 2 ). Naštěstí, stejně jako u quicksortu, v průměrném případě nastane první varianta a časová složitost bude lineární. Řešení 3: Předchozí řešení vylepšíme tak, že si v každé iteraci vybereme dobrého pivota, který leží dostatečně daleko od okrajů aktuálního úseku. Chceme, aby v úseku pole A[l..p] délky n vždy existovalo aspoň 3n/10 prvků menších než pivot a 3n/10 prvků věších než pivot. Pivota vybereme následovně: 1. Prvky pole rozdělíme do pětic a v každé pětici nalezneme medián. 2. Vezmeme pouze mediány ze všech pětic a rekurzivně pomocí QuickSelect() na nich najdeme medián. Podívejme se na následující obrázek. V každé pětici jsou hodnoty setříděné podle velikosti a sloupce s pěticemi jsou seřazeny podle hodnot jejich mediánů. Algoritmus nepotřebuje nic třídit, pouze nalezne v každé pětici medián (znázorněn modře) a potom nalezne medián mediánů (na tomto obrázku má hodnotu 41). 4 Proč různých čísel? Pro různá čísla na vstupu nebudeme muset diskutovat okrajové případy u výpočtu mediánu přes pětice. Zjednoduší se tím výklad, ale algoritmus funguje i pro čísla, která nemusí být různá. 5 U řady problémů, které se řeší pomocí metody Rozděl a panuj, je jednodušší vyřešit zobecněný problém, než hledat přímé řešení problému.
6 6 KAPITOLA 1. ROZDĚL A PANUJ Všechny prvky, které leží v první šedé oblasti jsou menší než medián mediánů a všechny prvky ve druhé šedé oblasti jsou větší než medián mediánů. Prvků větších než medián mediánů je aspoň 3 n/10 1 3n/10 1. Podobně prvků menších než medián mediánů je aspoň 3n/10 1. (Protože n nemusí být dělitelné 5, může být v poslední pětici jen 1 prvek. Proto musíme počítat pečlivěji než podle obrázku). Analýza časové složitosti: Nechť T (n) označuje časovou složitost algoritmu Quick- Select. Nalezení mediána mediánů bude trvat O(n) + T ( n/5 ). Rekurzivní volání QuickSelect() na podúseku pole proběhne v čase O(n) + T (7n/10 + 1). Celkem dostáváme T (n) = T (7n/10 + 1) + T ( n/5 ) + O(n). Teď už stačí jen vyřešit tuto rekurenci. Zkusíme hledat řešení rekurence ve tvaru T (n) = cn, pro nějakou zatím neznámou konstantu c. Dosazením do rekurence dostaneme T (n) c(7n/10 + 1) + c( n/5 )+an c(9n/10+2)+an = cn (cn/10 2c an). Pokud bude (cn/10 2c an) 0, tak máme vyhráno. Tato podmínka je ekvivalentní s c 10a(n/(n 20)). Stačí zvolit c = 10a a pro n > 20 bude řešení T (n) = cn platit. Pro n 20 je T (n) = O(1). 1.4 Master theorem, řešení rekurencí Při určování časové složitosti algoritmu založeného na metodě Rozděl a panuj se typicky dostaneme k rekurenci, kterou potřebujeme vyřešit. Abychom ji nemuseli zdlouhavě rozepisovat a přemýšlet, jak ji vyřešit, naučíme se následující univerzální metodu. Věta 1 (Master theorem) Nechť T : N N je funkce splňující T (n) = at ( n/b ) + O(n d ) pro nějaké konstanty a > 0, b > 0 a d 0. Potom O(n d ) T (n) = O(n d log n) O(n log b a ) pokud d > log b a pokud d = log b a pokud d < log b a Důkaz: Pro jednoduchost předpokládejme, že n je mocnina b. Díky je n/b = n/b. Velikost podproblémů se při každém rekurzivním zanoření zmenší b krát. Proto se po nejvýše log b n zanořeních zmenší až na konstantu (základní případ). Z toho dostáváme, že výška stromu rekurze je nejvýše log b n.
7 1.4. MASTER THEOREM, ŘEŠENÍ REKURENCÍ 7 velikost n a = 4 velikost n/b velikost n/b 2 hloubka log b n velikost b velikost 1 šířka a log b n = n log b a Při každém rekurzivním zavolání se rozvětvíme na a podproblémů. Proto bude na k-té hladině stromu rekurze a k podproblémů, každý o velikosti n/b k. Všechna práce prováděná na k-té hladině trvá a k O(( n b k ) d) = O(n d ) ( a b d ) k. Časy strávené v hladinách 0 až log b n tvoří geometrickou posloupnost s kvocientem a/b d. Celková časová složitost T (n) = O(n d ) log b n ( a ) k. k=0 b Podle hodnoty d kvocientu nastanou následující tři případy: a/b d < 1. Posloupnost je klesající. Největší je první člen O(n d ). Součet prvních log b n členů geometrické posloupnosti je nejvýše kvocient-krát větší než první člen. Proto T (n) = O(n d ). a/b d = 1. Všechny členy posloupnosti mají stejnou velikost a to O(n d ). Proto T (n) = O(n d ) log b n. a/b d > 1. Posloupnost je rostoucí. Součet prvních log b n členů geometrické posloupnosti je nejvýše kvocient-krát větší než poslední a největší člen. Jeho hodnota je O(n ( d a/b d) log b n ). n d ( a b d ) logb n = n d Proto T (n) = O(n log ba ). ( ) a log b n (b log b n ) d = a log b n = a (log a n)(log b a) = n log b a. Tyto případy přesně odpovídají rozdělení případů z věty. Zbývá ukázat, že věta platí i pro n, které není mocninou b. Už víme, že věta platí pro n, která jsou mocninou b. Toho využijeme. Nechť n + je nejbližší mocnina b větší než n. Podívejme se na první případ, kdy má řešení rekurence tvar T (n) = O(n d ). Ostaní případy si odůvodníte analogicky. Funkce T (n) je rostoucí a proto T (n) < T (n + ). Z nerovnosti n + < bn plyne, že O(n d +) = O((bn) d ) = O(n d ). Poskládáním nerovností dostaneme T (n) < T (n + ) = O(n d +) = O(n d ). Proto T (n) = O(n d ). Jak se dá Master Theorem použít v algoritmech z předchozích sekcí knihy, u kterých už jsme časovou složitost spočítali jinak? Časová složitost binárního vyhledávání (vyhledávání půlením intervalu) je určena rekurencí T (n) = T (n/2) + O(1).
8 8 KAPITOLA 1. ROZDĚL A PANUJ Pro její vyřešení použijeme Master Theorem s konstantami a = 1, b = 2, d = 0 a dostaneme T (n) = O(log n). Časová složitost mergesortu je určena rekurencí T (n) = 2T (n/2) + O(n). Pro její vyřešení použijeme Master Theorem s konstantami a = 2, b = 2, d = 1 a dostaneme T (n) = O(n log n). Příklad: Vyřešte rekurenci T (n) = 2T ( n) + log n. Tato rekurence vypadá jako ošklivá čarodějnice, ale můžeme z ní udělat Popelku, když vhodně převlékneme proměnné. Nejprve použijeme substituci proměnné m = log n a dostaneme T (2 m ) = 2T (2 m/2 ) + m. Pak použijeme substituci funkce S(m) = T (2 m ) a dostaneme S(m) = 2S(m/2) + m. Tuhle krásku už umíme vyřešit například pomocí Master Theoremu. S(m) = O(m log m). Změnou S(m) zpět na T (n) dostaneme T (n) = T (2 m ) = S(m) = O(log n log log n). (Všechny substituce jsou korektní, protože jsme použili rostoucí funkce.) 1.5 Příklady 1. (Ruční třídění karet) Dostanete balíček zamíchaných karet. Jakým způsobem ho setřídíte? Dokážete něco říci o tomto algoritmu? Jakou bude mít časovou složitost? Jaké budou jeho nároky na prostor (paměť)? 2. (Hledání pevného bodu zobrazení) Dostaneme setříděné pole různých čísel A[1,..., n]. Chceme zjistit, jestli existuje index i, pro který A[i] = i. Pomocí metody rozděl a panuj navrhněte algoritmus běžící v čase O(log n). 3. (Většinový prvek) Dostaneme pole n prvků A[1,..., n]. Prvky nemusíme nutně umět porovnávat, 6 ale pro každé dva indexy i, j umíme zjistit, jestli A[i] = A[j]. Prvek má v poli většinu, pokud se vyskytuje na více než polovině políček. Navrhněte algoritmus, který zjistí, jestli pole obsahuje prvek mající většinu a případně ho vypíše. (a) Ukažte, jak vyřešit tento problém v čase O(n log n). Nápověda: Rozdělte pole na dvě pole poloviční velikosti a zkuste v nich najít prvek mající většinu. (b) Najděte algoritmus běžící v lineálním čase. Nápověda: Prvky libovolně spárujte. Dostanete n/2 párů. Pro každý pár zjistěte, jestli jsou prvky stejné. Pokud ano, tak nechte jeden z nich a druhý prvek smažte. Pokud jsou prvky různé, tak smažte oba. Takto získáme nejvýše n/2 prvků. Ukažte, že nově získané prvky mají většinový prvek právě tehdy, když ho má i původních n prvků. 4. (Házení vajíčka z mrakodrapu) Na návštěvě Singapuru jste dostali jako dárek na uvítanou nerozbitelné vajíčko. Tvrdí Vám, že je vyrobeno nejmodernější technologií a i když má jen tuhou skořápku, tak prý nejde rozbít. Rozhodnete se to vyzkoušet a proto budete vajíčko házet z mrakodrapu na chodník. 7 6 Prvky mohou odpovídat obrázkům či jiným souborům. Místo dlouhého souboru si stačí pamatovat hodnotu dlouhé hašovací funkce. Existují hašovací funkce (například MD5), které nám s velmi vysokou pravděpodobností zaručí, že každý obrázek dostene jinou hodnotu hašovací funkce. 7 Singapur má jedny z nejvyšších mrakodrapů světa. Než to ale budete realizovat, tak si pořádně prostudujte, co zakazují přísné singapurské zákony. Pokud byste z mrakodrapu plivali, tak vás každé plivnutí vyjde na $1000.
9 1.5. PŘÍKLADY 9 Mrakodrap má n pater. Jaké je nejnižší patro, ze kterého už se vajíčko rozbije? (Klidně se může stát, že se vajíčko nerozbije ani z n-ého patra.) Kolik nejméně pokusů budete muset provést, aby jste to zjistili? Pokusem myslíme jedno hození vajíčka na chodník. (a) Máte jen jedno vajíčko. (b) A co když budete mít dvě, naprosto stejná vajíčka? (c) Jak to zobecnit pro k vajíček? Nejprve zkuste najít co nejlepší horní odhad na počet pokusů. Teprve pak se zamyslete nad tím, jak dokázat, že to lépe nejde. Nápověda: Formulka pro počet pokusů není jednoduchá. Stačí, když ukážete, jak spočítat počet pokusů pro n-patrový mrakodrap například na počítači. 5. (Procvičení řešení rekurencí) Vyřešte následující rekurence. Řešení určete s přesností Θ-notace. (a) T (n) = 2T (n/3) + 1 (b) T (n) = 5T (n/4) + n (c) T (n) = 7T (n/7) + n (d) T (n) = 9T (n/3) + n 2 (e) T (n) = 8T (n/2) + n 3 (f) T (n) = 49T (n/25) + n 3/2 log n (g) T (n) = 2T (n/2) + n/ log n (h) T (n) = 16T (n/4) + n! (i) T (n) = T (n 1) + 2 (j) T (n) = T (n 1) + n c, kde c 1 je konstanta (k) T (n) = T (n 1) + c n, kde c > 1 je konstanta (l) T (n) = 2T (n 1) + 1 (m) T (n) = T ( n) + 1 (n) T (n) = nt ( n) + 1 Nápověda: (k předposlední rekurenci) Zkuste použít substituci S(m) = T (2 m ). Substituce je korektní, protože 2 m je rostoucí funkce.
10 10 KAPITOLA 1. ROZDĚL A PANUJ
11 Literatura 11
přirozený algoritmus seřadí prvky 1,3,2,8,9,7 a prvky 4,5,6 nechává Metody řazení se dělí:
 Metody řazení ve vnitřní a vnější paměti. Algoritmy řazení výběrem, vkládáním a zaměňováním. Heapsort, Shell-sort, Radix-sort, Quicksort. Řazení sekvenčních souborů. Řazení souborů s přímým přístupem.
Metody řazení ve vnitřní a vnější paměti. Algoritmy řazení výběrem, vkládáním a zaměňováním. Heapsort, Shell-sort, Radix-sort, Quicksort. Řazení sekvenčních souborů. Řazení souborů s přímým přístupem.
Intervalové stromy. Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme. 1. Změna jednoho čísla v posloupnosti.
 Intervalové stromy Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme průběžně provádět tyto dvě operace: 1. Změna jednoho čísla v posloupnosti. 2. Zjištění součtu čísel
Intervalové stromy Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme průběžně provádět tyto dvě operace: 1. Změna jednoho čísla v posloupnosti. 2. Zjištění součtu čísel
IB108 Sada 1, Příklad 1 Vypracovali: Tomáš Krajča (255676), Martin Milata (256615)
 IB108 Sada 1, Příklad 1 ( ) Složitost třídícího algoritmu 1/-Sort je v O n log O (n.71 ). Necht n = j i (velikost pole, které je vstupním parametrem funkce 1/-Sort). Lehce spočítáme, že velikost pole předávaná
IB108 Sada 1, Příklad 1 ( ) Složitost třídícího algoritmu 1/-Sort je v O n log O (n.71 ). Necht n = j i (velikost pole, které je vstupním parametrem funkce 1/-Sort). Lehce spočítáme, že velikost pole předávaná
Tento text je stručným shrnutím těch tvrzení Ramseyovy teorie, která zazněla
 Ramseyovy věty Martin Mareš Tento text je stručným shrnutím těch tvrzení Ramseyovy teorie, která zazněla na mé letošní přednášce z Kombinatoriky a grafů I Předpokládá, že čtenář se již seznámil se základní
Ramseyovy věty Martin Mareš Tento text je stručným shrnutím těch tvrzení Ramseyovy teorie, která zazněla na mé letošní přednášce z Kombinatoriky a grafů I Předpokládá, že čtenář se již seznámil se základní
13. Třídící algoritmy a násobení matic
 13. Třídící algoritmy a násobení matic Minulou přednášku jsme probírali QuickSort, jeden z historicky prvních třídících algoritmů, které překonaly kvadratickou složitost aspoň v průměrném případě. Proč
13. Třídící algoritmy a násobení matic Minulou přednášku jsme probírali QuickSort, jeden z historicky prvních třídících algoritmů, které překonaly kvadratickou složitost aspoň v průměrném případě. Proč
Seminář z IVT Algoritmizace. Slovanské gymnázium Olomouc Tomáš Kühr
 Seminář z IVT Algoritmizace Slovanské gymnázium Olomouc Tomáš Kühr Algoritmizace - o čem to je? Zatím jsme se zabývali především tím, jak určitý postup zapsat v konkrétním programovacím jazyce (např. C#)
Seminář z IVT Algoritmizace Slovanské gymnázium Olomouc Tomáš Kühr Algoritmizace - o čem to je? Zatím jsme se zabývali především tím, jak určitý postup zapsat v konkrétním programovacím jazyce (např. C#)
Anotace. Informace o praktiku z programování!!! Direktivy překladače Soubory (textové) Quicksort Metoda rozděl a panuj
 Anotace Informace o praktiku z programování!!! Direktivy překladače Soubory (textové) Quicksort Metoda rozděl a panuj Direktivy překladače Překladač kontroluje plno věcí, například: zda nekoukáme za konec
Anotace Informace o praktiku z programování!!! Direktivy překladače Soubory (textové) Quicksort Metoda rozděl a panuj Direktivy překladače Překladač kontroluje plno věcí, například: zda nekoukáme za konec
12. Aproximační algoritmy
 12. Aproximační algoritmy (F.Haško,J.enda,.areš, ichal Kozák, Vojta Tůma) Na minulých přednáškách jsme se zabývali různými těžkými rozhodovacími problémy. Tato se zabývá postupy, jak se v praxi vypořádat
12. Aproximační algoritmy (F.Haško,J.enda,.areš, ichal Kozák, Vojta Tůma) Na minulých přednáškách jsme se zabývali různými těžkými rozhodovacími problémy. Tato se zabývá postupy, jak se v praxi vypořádat
5 Rekurze a zásobník. Rekurzivní volání metody
 5 Rekurze a zásobník Při volání metody z metody main() se do zásobníku uloží aktivační záznam obsahující - parametry - návratovou adresu, tedy adresu, kde bude program pokračovat v metodě main () po skončení
5 Rekurze a zásobník Při volání metody z metody main() se do zásobníku uloží aktivační záznam obsahující - parametry - návratovou adresu, tedy adresu, kde bude program pokračovat v metodě main () po skončení
DYNAMICKÉ PROGRAMOVÁNÍ A PROBLÉM BATOHU
 ČVUT V PRAZE FAKULTA INFORMAČNÍCH TECHNOLOGIÍ JAN SCHMIDT A PETR FIŠER MI-PAA DYNAMICKÉ PROGRAMOVÁNÍ A PROBLÉM BATOHU EVROPSKÝ SOCIÁLNÍ FOND PRAHA A EU: INVESTUJEME DO VAŠÍ BUDOUCNOSTI Dynamické programování
ČVUT V PRAZE FAKULTA INFORMAČNÍCH TECHNOLOGIÍ JAN SCHMIDT A PETR FIŠER MI-PAA DYNAMICKÉ PROGRAMOVÁNÍ A PROBLÉM BATOHU EVROPSKÝ SOCIÁLNÍ FOND PRAHA A EU: INVESTUJEME DO VAŠÍ BUDOUCNOSTI Dynamické programování
Algoritmizace Dynamické programování. Jiří Vyskočil, Marko Genyg-Berezovskyj 2010
 Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
zejména Dijkstrův algoritmus pro hledání minimální cesty a hladový algoritmus pro hledání minimální kostry.
 Kapitola Ohodnocené grafy V praktických aplikacích teorie grafů zpravidla graf slouží jako nástroj k popisu nějaké struktury. Jednotlivé prvky této struktury mají často přiřazeny nějaké hodnoty (může jít
Kapitola Ohodnocené grafy V praktických aplikacích teorie grafů zpravidla graf slouží jako nástroj k popisu nějaké struktury. Jednotlivé prvky této struktury mají často přiřazeny nějaké hodnoty (může jít
A4B33ALG 2010/05 ALG 07. Selection sort (Select sort) Insertion sort (Insert sort) Bubble sort deprecated. Quicksort.
 A4B33ALG 2010/05 ALG 07 Selection sort (Select sort) Insertion sort (Insert sort) Bubble sort deprecated Quicksort Stabilita řazení 1 Selection sort Neseřazeno Seřazeno Start T O U B J R M A K D Z E min
A4B33ALG 2010/05 ALG 07 Selection sort (Select sort) Insertion sort (Insert sort) Bubble sort deprecated Quicksort Stabilita řazení 1 Selection sort Neseřazeno Seřazeno Start T O U B J R M A K D Z E min
PŘEDNÁŠKA 2 POSLOUPNOSTI
 PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Třídění, vyhledávání Daniela Szturcová
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Třídění, vyhledávání Daniela Szturcová
Anotace. Dynamické programování, diskrétní simulace.
 Anotace Dynamické programování, diskrétní simulace. Problémy, které byly Přednášející jde tentokrát do M1, počet platných uzávorkování pomocí n párů závorek, počet rozkladů přirozeného čísla na součet
Anotace Dynamické programování, diskrétní simulace. Problémy, které byly Přednášející jde tentokrát do M1, počet platných uzávorkování pomocí n párů závorek, počet rozkladů přirozeného čísla na součet
StatSoft Odkud tak asi je?
 StatSoft Odkud tak asi je? Ukážeme si, jak bychom mohli vypočítat pravděpodobnosti, na které jsme se ptali v minulém newsletteru Úkolem bylo zjistit, z kterého kraje nejpravděpodobněji pochází náš výherce
StatSoft Odkud tak asi je? Ukážeme si, jak bychom mohli vypočítat pravděpodobnosti, na které jsme se ptali v minulém newsletteru Úkolem bylo zjistit, z kterého kraje nejpravděpodobněji pochází náš výherce
Výhody a nevýhody jednotlivých reprezentací jsou shrnuty na konci kapitoly.
 Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
IB111 Úvod do programování skrze Python
 Vyhledávání, řazení, složitost IB111 Úvod do programování skrze Python 2012 Otrávené studny 8 studen, jedna z nich je otrávená laboratorní rozbor dokáže rozpoznat přítomnost jedu ve vodě je drahý (je časově
Vyhledávání, řazení, složitost IB111 Úvod do programování skrze Python 2012 Otrávené studny 8 studen, jedna z nich je otrávená laboratorní rozbor dokáže rozpoznat přítomnost jedu ve vodě je drahý (je časově
0. Lineární rekurence Martin Mareš, 2010-07-04
 0 Lineární rekurence Martin Mareš, 2010-07-04 V tomto krátkém textu se budeme zabývat lineárními rekurencemi, tj posloupnostmi definovanými rekurentní rovnicí typu A n+k = c 0 A n + c 1 A n+1 + + c k 1
0 Lineární rekurence Martin Mareš, 2010-07-04 V tomto krátkém textu se budeme zabývat lineárními rekurencemi, tj posloupnostmi definovanými rekurentní rovnicí typu A n+k = c 0 A n + c 1 A n+1 + + c k 1
Součin matice A a čísla α definujeme jako matici αa = (d ij ) typu m n, kde d ij = αa ij pro libovolné indexy i, j.
 Kapitola 3 Počítání s maticemi Matice stejného typu můžeme sčítat a násobit reálným číslem podobně jako vektory téže dimenze. Definice 3.1 Jsou-li A (a ij ) a B (b ij ) dvě matice stejného typu m n, pak
Kapitola 3 Počítání s maticemi Matice stejného typu můžeme sčítat a násobit reálným číslem podobně jako vektory téže dimenze. Definice 3.1 Jsou-li A (a ij ) a B (b ij ) dvě matice stejného typu m n, pak
Rekurzivní algoritmy
 Rekurzivní algoritmy prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA) ZS
Rekurzivní algoritmy prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA) ZS
Binární vyhledávací stromy pokročilé partie
 Binární vyhledávací stromy pokročilé partie KMI/ALS lekce Jan Konečný 30.9.204 Literatura Cormen Thomas H., Introduction to Algorithms, 2nd edition MIT Press, 200. ISBN 0-262-5396-8 6, 3, A Knuth Donald
Binární vyhledávací stromy pokročilé partie KMI/ALS lekce Jan Konečný 30.9.204 Literatura Cormen Thomas H., Introduction to Algorithms, 2nd edition MIT Press, 200. ISBN 0-262-5396-8 6, 3, A Knuth Donald
Kapitola 11. Vzdálenost v grafech. 11.1 Matice sousednosti a počty sledů
 Kapitola 11 Vzdálenost v grafech V každém grafu lze přirozeným způsobem definovat vzdálenost libovolné dvojice vrcholů. Hlavním výsledkem této kapitoly je překvapivé tvrzení, podle kterého lze vzdálenosti
Kapitola 11 Vzdálenost v grafech V každém grafu lze přirozeným způsobem definovat vzdálenost libovolné dvojice vrcholů. Hlavním výsledkem této kapitoly je překvapivé tvrzení, podle kterého lze vzdálenosti
V každém kroku se a + b zmenší o min(a, b), tedy vždy alespoň o 1. Jestliže jsme na začátku dostali 2
 Euklidův algoritmus Doprovodný materiál pro cvičení Programování I. NPRM044 Autor: Markéta Popelová Datum: 31.10.2010 Euklidův algoritmus verze 1.0 Zadání: Určete největšího společného dělitele dvou zadaných
Euklidův algoritmus Doprovodný materiál pro cvičení Programování I. NPRM044 Autor: Markéta Popelová Datum: 31.10.2010 Euklidův algoritmus verze 1.0 Zadání: Určete největšího společného dělitele dvou zadaných
Semestrální z předmětu MM
 Semestrální z předmětu MM práce Diferenční rovnice Jméno a příjmení: Osobní číslo: Studijní skupina: Obor: E-mail: Jan Forejt A07026 1. ročník, komb. studium Matematika forejt@cs.mfcr.cz Datum odevzdání:
Semestrální z předmětu MM práce Diferenční rovnice Jméno a příjmení: Osobní číslo: Studijní skupina: Obor: E-mail: Jan Forejt A07026 1. ročník, komb. studium Matematika forejt@cs.mfcr.cz Datum odevzdání:
Matice se v některých publikacích uvádějí v hranatých závorkách, v jiných v kulatých závorkách. My se budeme držet zápisu s kulatými závorkami.
 Maticové operace Definice Skalár Představme si nějakou množinu, jejíž prvky lze sčítat a násobit. Pěkným vzorem jsou čísla, která už známe od mala. Prvky takové množiny nazýváme skaláry. Matice Matice
Maticové operace Definice Skalár Představme si nějakou množinu, jejíž prvky lze sčítat a násobit. Pěkným vzorem jsou čísla, která už známe od mala. Prvky takové množiny nazýváme skaláry. Matice Matice
Břetislav Fajmon, UMAT FEKT, VUT Brno. Poznámka 1.1. A) první část hodiny (cca 50 minut): představení všech tří metod při řešení jednoho příkladu.
 Břetislav Fajmon, UMAT FEKT, VUT Brno Poznámka 1.1. A) první část hodiny (cca 50 minut): představení všech tří metod při řešení jednoho příkladu. Na jiných příkladech je téma podrobně zpracováno ve skriptech
Břetislav Fajmon, UMAT FEKT, VUT Brno Poznámka 1.1. A) první část hodiny (cca 50 minut): představení všech tří metod při řešení jednoho příkladu. Na jiných příkladech je téma podrobně zpracováno ve skriptech
Stromy, haldy, prioritní fronty
 Stromy, haldy, prioritní fronty prof. Ing. Pavel Tvrdík CSc. Katedra počítačů FEL České vysoké učení technické DSA, ZS 2008/9, Přednáška 6 http://service.felk.cvut.cz/courses/x36dsa/ prof. Pavel Tvrdík
Stromy, haldy, prioritní fronty prof. Ing. Pavel Tvrdík CSc. Katedra počítačů FEL České vysoké učení technické DSA, ZS 2008/9, Přednáška 6 http://service.felk.cvut.cz/courses/x36dsa/ prof. Pavel Tvrdík
1. série. Pohádky. Téma: Datumodeslání:
 Téma: Datumodeslání: º Ò ¾¼¼ 1. série Pohádky ½º ÐÓ Ó Ýµ ¾º ÐÓ Ó Ýµ Princezna si dělá pořádek ve svých truhličkách. Vysype na stůl do dvou hromádek drahokamy º ÐÓ Ó Ýµ naprvníjichje17,nadruhé10.pokaždé,kdyžnaberezjednéhromádkydorukykameny(vždy
Téma: Datumodeslání: º Ò ¾¼¼ 1. série Pohádky ½º ÐÓ Ó Ýµ ¾º ÐÓ Ó Ýµ Princezna si dělá pořádek ve svých truhličkách. Vysype na stůl do dvou hromádek drahokamy º ÐÓ Ó Ýµ naprvníjichje17,nadruhé10.pokaždé,kdyžnaberezjednéhromádkydorukykameny(vždy
Algoritmická matematika 3 Mgr. Petr Osička, Ph.D. ZS 2014. Rozděl a panuj
 Algoritmická matematika 3 KMI/ALM3 Mgr. Petr Osička, Ph.D. ZS 2014 1 Základní princip Rozděl a panuj Technika rozděl a panuj je založená na následující myšlence. Z dané vstupní instance I vygenerujeme
Algoritmická matematika 3 KMI/ALM3 Mgr. Petr Osička, Ph.D. ZS 2014 1 Základní princip Rozděl a panuj Technika rozděl a panuj je založená na následující myšlence. Z dané vstupní instance I vygenerujeme
GRAFY A GRAFOVÉ ALGORITMY
 KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO GRAFY A GRAFOVÉ ALGORITMY ARNOŠT VEČERKA VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ
KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO GRAFY A GRAFOVÉ ALGORITMY ARNOŠT VEČERKA VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ
Základní datové struktury III: Stromy, haldy
 Základní datové struktury III: Stromy, haldy prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní
Základní datové struktury III: Stromy, haldy prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní
Obecná informatika. Matematicko-fyzikální fakulta Univerzity Karlovy v Praze. Podzim 2012
 Obecná informatika Přednášející Putovních přednášek Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Podzim 2012 Přednášející Putovních přednášek (MFF UK) Obecná informatika Podzim 2012 1 / 18
Obecná informatika Přednášející Putovních přednášek Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Podzim 2012 Přednášející Putovních přednášek (MFF UK) Obecná informatika Podzim 2012 1 / 18
NPRG030 Programování I, 2018/19 1 / :03:07
 NPRG030 Programování I, 2018/19 1 / 20 3. 12. 2018 09:03:07 Vnitřní třídění Zadání: Uspořádejte pole délky N podle hodnot prvků Měřítko efektivity: * počet porovnání * počet přesunů NPRG030 Programování
NPRG030 Programování I, 2018/19 1 / 20 3. 12. 2018 09:03:07 Vnitřní třídění Zadání: Uspořádejte pole délky N podle hodnot prvků Měřítko efektivity: * počet porovnání * počet přesunů NPRG030 Programování
DobSort. Úvod do programování. DobSort Implementace 1/3. DobSort Implementace 2/3. DobSort - Příklad. DobSort Implementace 3/3
 DobSort Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 V roce 1980 navrhl Dobosiewicz variantu (tzv. DobSort),
DobSort Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 V roce 1980 navrhl Dobosiewicz variantu (tzv. DobSort),
Název: Kutálení plechovek
 Název: Kutálení plechovek Výukové materiály Téma: Elektrostatika Úroveň: 2. stupeň ZŠ, popř. i SŠ Tematický celek: Vidět a poznat neviditelné Předmět (obor): Doporučený věk žáků: Doba trvání: Specifický
Název: Kutálení plechovek Výukové materiály Téma: Elektrostatika Úroveň: 2. stupeň ZŠ, popř. i SŠ Tematický celek: Vidět a poznat neviditelné Předmět (obor): Doporučený věk žáků: Doba trvání: Specifický
Mimo samotné správnosti výsledku vypočteného zapsaným algoritmem je ještě jedno
 12 Délka výpočtu algoritmu Mimo samotné správnosti výsledku vypočteného zapsaným algoritmem je ještě jedno neméně důležité hledisko k posouzení vhodnosti algoritmu k řešení zadané úlohy. Jedná se o čas,
12 Délka výpočtu algoritmu Mimo samotné správnosti výsledku vypočteného zapsaným algoritmem je ještě jedno neméně důležité hledisko k posouzení vhodnosti algoritmu k řešení zadané úlohy. Jedná se o čas,
Algoritmus pro hledání nejkratší cesty orientovaným grafem
 1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
Cvičení Programování I. Stručné poznámky ke cvičení ze
 Cvičení Programování I Cvičící: Pavel urynek, KIM, pavel.surynek@seznam.cz emestr: Zima 2005/2006 Kroužek: Matematika/59 Rozvrh: Pátek 10:40-12:10 (učebna K2) tručné poznámky ke cvičení ze 14.10.2005 1.
Cvičení Programování I Cvičící: Pavel urynek, KIM, pavel.surynek@seznam.cz emestr: Zima 2005/2006 Kroužek: Matematika/59 Rozvrh: Pátek 10:40-12:10 (učebna K2) tručné poznámky ke cvičení ze 14.10.2005 1.
1. Minimální kostry. 1.1. Od mìsteèka ke kostøe
 . Minimální kostry Napadl sníh a přikryl peřinou celé městečko. Po ulicích lze sotva projít pěšky, natož projet autem. Které ulice prohrneme, aby šlo dojet odkudkoliv kamkoliv, a přitom nám házení sněhu
. Minimální kostry Napadl sníh a přikryl peřinou celé městečko. Po ulicích lze sotva projít pěšky, natož projet autem. Které ulice prohrneme, aby šlo dojet odkudkoliv kamkoliv, a přitom nám házení sněhu
8. Geometrie vrací úder (sepsal Pavel Klavík)
 8. Geometrie vrací úder (sepsal Pavel Klavík) Když s geometrickými problémy pořádně nezametete, ony vám to vrátí! Ale když užzametat,takurčitěnepodkoberecamístosmetákupoužijtepřímku.vtéto přednášce nás
8. Geometrie vrací úder (sepsal Pavel Klavík) Když s geometrickými problémy pořádně nezametete, ony vám to vrátí! Ale když užzametat,takurčitěnepodkoberecamístosmetákupoužijtepřímku.vtéto přednášce nás
Algoritmizace složitost rekurzivních algoritmů. Jiří Vyskočil, Marko Genyg-Berezovskyj 2010
 složitost rekurzivních algoritmů Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Vyjádřen ení složitosti rekurzivního algoritmu rekurentním m tvarem Příklad vyjádření složitosti rekurzivního algoritmu rekurencí:
složitost rekurzivních algoritmů Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Vyjádřen ení složitosti rekurzivního algoritmu rekurentním m tvarem Příklad vyjádření složitosti rekurzivního algoritmu rekurencí:
Jak pracovat s absolutními hodnotami
 Jak pracovat s absolutními hodnotami Petr Matyáš 1 Co to je absolutní hodnota Absolutní hodnota čísla a, dále ji budeme označovat výrazem a, je jeho vzdálenost od nuly na ose x, tedy je to vždy číslo kladné.
Jak pracovat s absolutními hodnotami Petr Matyáš 1 Co to je absolutní hodnota Absolutní hodnota čísla a, dále ji budeme označovat výrazem a, je jeho vzdálenost od nuly na ose x, tedy je to vždy číslo kladné.
Kategorie mladší. Řešení 1. kola VI. ročník
 Kategorie mladší Úloha 1A Korálky Řešení 1. kola Způsobů, jak korálky při splnění všech Heleniných podmínek navléci, je celá řada a dá se říci, že správné jsou všechny postupy, které nakonec vedou ke správnému
Kategorie mladší Úloha 1A Korálky Řešení 1. kola Způsobů, jak korálky při splnění všech Heleniných podmínek navléci, je celá řada a dá se říci, že správné jsou všechny postupy, které nakonec vedou ke správnému
Jedna dvě, kytka jde. Cílová skupina: 6. - 7.ročník. Potřebný čas: 90 minut (2 vyučovací hodiny s týdenním rozestupem) Trvalé porozumění:
 Jedna dvě, kytka jde Cílová skupina: 6. - 7.ročník Potřebný čas: 90 minut (2 vyučovací hodiny s týdenním rozestupem) Trvalé porozumění: Žák pochopí, že podle stavby semene se dělí krytosemenné na dvě skupiny.
Jedna dvě, kytka jde Cílová skupina: 6. - 7.ročník Potřebný čas: 90 minut (2 vyučovací hodiny s týdenním rozestupem) Trvalé porozumění: Žák pochopí, že podle stavby semene se dělí krytosemenné na dvě skupiny.
Hledání k-tého nejmenšího prvku
 ALG 14 Hledání k-tého nejmenšího prvku Randomized select CLRS varianta Partition v Quicksortu 0 Hledání k-tého nejmenšího prvku 1. 2. 3. Seřaď seznam/pole a vyber k-tý nejmenší, složitost (N*log(N)). Nevýhodou
ALG 14 Hledání k-tého nejmenšího prvku Randomized select CLRS varianta Partition v Quicksortu 0 Hledání k-tého nejmenšího prvku 1. 2. 3. Seřaď seznam/pole a vyber k-tý nejmenší, složitost (N*log(N)). Nevýhodou
Prohledávání do šířky = algoritmus vlny
 Prohledávání do šířky = algoritmus vlny - souběžně zkoušet všechny možné varianty pokračování výpočtu, dokud nenajdeme řešení úlohy průchod stromem všech možných cest výpočtu do šířky, po vrstvách (v každé
Prohledávání do šířky = algoritmus vlny - souběžně zkoušet všechny možné varianty pokračování výpočtu, dokud nenajdeme řešení úlohy průchod stromem všech možných cest výpočtu do šířky, po vrstvách (v každé
Filtrace snímků ve frekvenční oblasti. Rychlá fourierova transformace
 Filtrace snímků ve frekvenční oblasti Rychlá fourierova transformace semestrální práce z předmětu KIV/ZVI zpracoval: Jan Bařtipán A03043 bartipan@students.zcu.cz Obsah Úvod....3 Diskrétní Fourierova transformace
Filtrace snímků ve frekvenční oblasti Rychlá fourierova transformace semestrální práce z předmětu KIV/ZVI zpracoval: Jan Bařtipán A03043 bartipan@students.zcu.cz Obsah Úvod....3 Diskrétní Fourierova transformace
Anotace. pointery (pars prima). Martin Pergel,
 Anotace Základní třídicí algoritmy, jednotky oddělený překlad, pointery (pars prima). Problém třídění jednoduché třídicí algoritmy Bublinkové třídění (BubbleSort), zatřid ování alias třídění přímým vkládáním
Anotace Základní třídicí algoritmy, jednotky oddělený překlad, pointery (pars prima). Problém třídění jednoduché třídicí algoritmy Bublinkové třídění (BubbleSort), zatřid ování alias třídění přímým vkládáním
Determinant. Definice determinantu. Permutace. Permutace, vlastnosti. Definice: Necht A = (a i,j ) R n,n je čtvercová matice.
 [] Definice determinantu BI-LIN, determinant, 9, P Olšák [2] Determinant je číslo jistým způsobem charakterizující čtvercovou matici det A 0 pro singulární matici, det A 0 pro regulární matici používá
[] Definice determinantu BI-LIN, determinant, 9, P Olšák [2] Determinant je číslo jistým způsobem charakterizující čtvercovou matici det A 0 pro singulární matici, det A 0 pro regulární matici používá
Pedagog pouze kontroluje a fixuje správné držení těla a správný úchop pastelky. Individuálně napomáhá.
 VČELKY LETÍ DO ÚLU Na obrázku poletují včelky s košíčky na zádech kolem kruhového úlu. Ve skutečnosti dovnitř úlu nevidíme, proto nám ho malíř namaloval zevnitř. Tento úl má tři komůrky. Velkou, menší
VČELKY LETÍ DO ÚLU Na obrázku poletují včelky s košíčky na zádech kolem kruhového úlu. Ve skutečnosti dovnitř úlu nevidíme, proto nám ho malíř namaloval zevnitř. Tento úl má tři komůrky. Velkou, menší
NPRG030 Programování I 3/2 Z --- NPRG031 Programování II --- 2/2 Z, Zk
 NPRG030 Programování I 3/2 Z --- NPRG031 Programování II --- 2/2 Z, Zk Pavel Töpfer Katedra softwaru a výuky informatiky MFF UK MFF Malostranské nám., 4. patro, pracovna 404 pavel.topfer@mff.cuni.cz http://ksvi.mff.cuni.cz/~topfer
NPRG030 Programování I 3/2 Z --- NPRG031 Programování II --- 2/2 Z, Zk Pavel Töpfer Katedra softwaru a výuky informatiky MFF UK MFF Malostranské nám., 4. patro, pracovna 404 pavel.topfer@mff.cuni.cz http://ksvi.mff.cuni.cz/~topfer
Algoritmizace I. Ak. rok 2015/2016 vbp 1. ze 132
 Ak. rok 2015/2016 vbp 1. ze 132 Ing. Vladimír Beneš, Ph.D. vedoucí katedry Petrovický K101 katedra informatiky a kvantitativních metod E-mail: vbenes@bivs.cz Telefon: 251 114 534, 731 425 276 Konzultační
Ak. rok 2015/2016 vbp 1. ze 132 Ing. Vladimír Beneš, Ph.D. vedoucí katedry Petrovický K101 katedra informatiky a kvantitativních metod E-mail: vbenes@bivs.cz Telefon: 251 114 534, 731 425 276 Konzultační
KMA/PDB. Karel Janečka. Tvorba materiálů byla podpořena z prostředků projektu FRVŠ č. F0584/2011/F1d
 KMA/PDB Prostorové spojení Karel Janečka Tvorba materiálů byla podpořena z prostředků projektu FRVŠ č. F0584/2011/F1d Obsah Prostorové spojení pomocí hnízděných cyklů. Prostorové spojení pomocí R-stromů.
KMA/PDB Prostorové spojení Karel Janečka Tvorba materiálů byla podpořena z prostředků projektu FRVŠ č. F0584/2011/F1d Obsah Prostorové spojení pomocí hnízděných cyklů. Prostorové spojení pomocí R-stromů.
Lenka Zalabová. Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita. zima 2012
 Algebra - třetí díl Lenka Zalabová Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích zima 2012 Obsah 1 Dělitelnost 2 Grupy zbytkových tříd 3 Jedna z
Algebra - třetí díl Lenka Zalabová Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích zima 2012 Obsah 1 Dělitelnost 2 Grupy zbytkových tříd 3 Jedna z
Union-Find problém. Kapitola 1
 Kapitola 1 Union-Find problém Motivace: Po světě se toulá spousta agentů. Často se stává, že jeden agent má spoustu jmen/přezdívek, které používá například při rezervaci hotelu, restaurace, na návštěvě
Kapitola 1 Union-Find problém Motivace: Po světě se toulá spousta agentů. Často se stává, že jeden agent má spoustu jmen/přezdívek, které používá například při rezervaci hotelu, restaurace, na návštěvě
Tabulka. Datová struktura, která umožňuje vkládat a později vybírat informace podle identifikačního klíče. Mohou být:
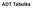 ADT Tabulka Datová struktura, která umožňuje vkládat a později vybírat informace podle identifikačního klíče. Mohou být: pevně definované (LUT Look Up Table) s proměnným počtem položek Konvence: Tabulka
ADT Tabulka Datová struktura, která umožňuje vkládat a později vybírat informace podle identifikačního klíče. Mohou být: pevně definované (LUT Look Up Table) s proměnným počtem položek Konvence: Tabulka
Umělá inteligence I. Roman Barták, KTIML. roman.bartak@mff.cuni.cz http://ktiml.mff.cuni.cz/~bartak
 Umělá inteligence I Roman Barták, KTIML roman.bartak@mff.cuni.cz http://ktiml.mff.cuni.cz/~bartak Na úvod Agent s reflexy pouze převádí současný vjem na jednu akci. Agent s cílem umí plánovat několik akcí
Umělá inteligence I Roman Barták, KTIML roman.bartak@mff.cuni.cz http://ktiml.mff.cuni.cz/~bartak Na úvod Agent s reflexy pouze převádí současný vjem na jednu akci. Agent s cílem umí plánovat několik akcí
Základy řazení. Karel Richta a kol.
 Základy řazení Karel Richta a kol. Přednášky byly připraveny s pomocí materiálů, které vyrobili Marko Berezovský, Petr Felkel, Josef Kolář, Michal Píše a Pavel Tvrdík Katedra počítačů Fakulta elektrotechnická
Základy řazení Karel Richta a kol. Přednášky byly připraveny s pomocí materiálů, které vyrobili Marko Berezovský, Petr Felkel, Josef Kolář, Michal Píše a Pavel Tvrdík Katedra počítačů Fakulta elektrotechnická
BAKALÁŘSKÁ PRÁCE. Numerické metody jednorozměrné minimalizace
 UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Numerické metody jednorozměrné minimalizace Vedoucí bakalářské práce: RNDr. Horymír
UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Numerické metody jednorozměrné minimalizace Vedoucí bakalářské práce: RNDr. Horymír
10. Editor databází dotazy a relace
 10. Editor databází dotazy a relace Dotazy Dotazy tvoří velkou samostatnou kapitolu Accessu, která je svým významem téměř stejně důležitá jako oblast návrhu a úpravy tabulek. Svým rozsahem je to ale oblast
10. Editor databází dotazy a relace Dotazy Dotazy tvoří velkou samostatnou kapitolu Accessu, která je svým významem téměř stejně důležitá jako oblast návrhu a úpravy tabulek. Svým rozsahem je to ale oblast
Standardně máme zapnutý panel nástrojů Formátování a Standardní.
 Zapnutí a vypnutí panelů nástrojů Standardně máme zapnutý panel nástrojů Formátování a Standardní. Úkol: Vyzkoušejte si zapnout a vypnout všechny panely nástrojů. Nechte zapnutý panely nástrojů Formátování
Zapnutí a vypnutí panelů nástrojů Standardně máme zapnutý panel nástrojů Formátování a Standardní. Úkol: Vyzkoušejte si zapnout a vypnout všechny panely nástrojů. Nechte zapnutý panely nástrojů Formátování
3. Matice a determinanty
 . Matice a determinanty Teorie matic a determinantů představuje úvod do lineární algebry. Nejrozsáhlejší aplikace mají matice a determinanty při řešení systémů lineárních rovnic. Pojem determinantu zavedl
. Matice a determinanty Teorie matic a determinantů představuje úvod do lineární algebry. Nejrozsáhlejší aplikace mají matice a determinanty při řešení systémů lineárních rovnic. Pojem determinantu zavedl
8. Posloupnosti, vektory a matice
 . jsou užitečné matematické nástroje. V Mathcadu je často používáme například k rychlému zápisu velkého počtu vztahů s proměnnými parametry, ke zpracování naměřených hodnot, k výpočtům lineárních soustav
. jsou užitečné matematické nástroje. V Mathcadu je často používáme například k rychlému zápisu velkého počtu vztahů s proměnnými parametry, ke zpracování naměřených hodnot, k výpočtům lineárních soustav
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 21.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Složitost a NP-úplnost
 Složitost a NP-úplnost RNDr. Ondřej Čepek, Ph.D. Do formátu TEX převedl Ladislav Strojil Připomínky, dotazy, opravy na emailu: Ladislav@Strojil.cz Verze 1.1.1 Nejnovější verze k nalezení vždy na http://ladislav.strojil.cz/np.php
Složitost a NP-úplnost RNDr. Ondřej Čepek, Ph.D. Do formátu TEX převedl Ladislav Strojil Připomínky, dotazy, opravy na emailu: Ladislav@Strojil.cz Verze 1.1.1 Nejnovější verze k nalezení vždy na http://ladislav.strojil.cz/np.php
Implementace seznamů do prostředí DELPHI pomocí lineárního seznamu
 Implementace seznamů do prostředí DELPHI pomocí lineárního seznamu Ukazatel a dynamické datové struktury v prostředí DELPHI Důležitým termínem a konstrukčním programovým prvkem je typ UKAZATEL. Je to vlastně
Implementace seznamů do prostředí DELPHI pomocí lineárního seznamu Ukazatel a dynamické datové struktury v prostředí DELPHI Důležitým termínem a konstrukčním programovým prvkem je typ UKAZATEL. Je to vlastně
Mgr. Karel Pazourek. online prostředí, Operační program Praha Adaptabilita, registrační číslo CZ.2.17/3.1.00/31165.
 Mnohočleny z různých stran Mgr. Karel Pazourek Kurz vznikl v rámci projektu Rozvoj systému vzdělávacích příležitostí pro nadané žáky a studenty v přírodních vědách a matematice s využitím online prostředí,
Mnohočleny z různých stran Mgr. Karel Pazourek Kurz vznikl v rámci projektu Rozvoj systému vzdělávacích příležitostí pro nadané žáky a studenty v přírodních vědách a matematice s využitím online prostředí,
Predispozice pro výuku IKT (2015/2016)
 Konzervatoř P. J. Vejvanovského Kroměříž Predispozice pro výuku IKT (15/16) Základní algoritmy pro počítání s celými a racionálními čísly Adam Šiška 1 Sčítání dvou kladných celých čísel Problém: Jsou dána
Konzervatoř P. J. Vejvanovského Kroměříž Predispozice pro výuku IKT (15/16) Základní algoritmy pro počítání s celými a racionálními čísly Adam Šiška 1 Sčítání dvou kladných celých čísel Problém: Jsou dána
Složitost algoritmů. Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol.
 Složitost algoritmů Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol., 2017 Datové struktury a algoritmy, B6B36DSA 02/2017, Lekce 3
Složitost algoritmů Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol., 2017 Datové struktury a algoritmy, B6B36DSA 02/2017, Lekce 3
Katedra kybernetiky skupina Inteligentní Datové Analýzy (IDA) 9. dubna 2009. Filip Železný (ČVUT) Vytěžování dat 9.
 Vytěžování dat Filip Železný Katedra kybernetiky skupina Inteligentní Datové Analýzy (IDA) 9. dubna 2009 Filip Železný (ČVUT) Vytěžování dat 9. dubna 2009 1 / 22 Rozhodovací pravidla Strom lze převést
Vytěžování dat Filip Železný Katedra kybernetiky skupina Inteligentní Datové Analýzy (IDA) 9. dubna 2009 Filip Železný (ČVUT) Vytěžování dat 9. dubna 2009 1 / 22 Rozhodovací pravidla Strom lze převést
Základy algoritmizace a programování
 Základy algoritmizace a programování Složitost algoritmů. Třídění Přednáška 8 16. listopadu 2009 Který algoritmus je "lepší"? Různé algoritmy, které řeší stejnou úlohu zbytek = p % i; zbytek = p - p/i*i;
Základy algoritmizace a programování Složitost algoritmů. Třídění Přednáška 8 16. listopadu 2009 Který algoritmus je "lepší"? Různé algoritmy, které řeší stejnou úlohu zbytek = p % i; zbytek = p - p/i*i;
Obsah přednášky. Analýza algoritmu Algoritmická složitost Návrhy algoritmů Urychlování algoritmů 1/41
 Obsah přednášky Analýza algoritmu Algoritmická složitost Návrhy algoritmů Urychlování algoritmů 1/41 Analýza algoritmu Proč vůbec dělat analýzu? pro většinu problémů existuje několik různých přístupů aby
Obsah přednášky Analýza algoritmu Algoritmická složitost Návrhy algoritmů Urychlování algoritmů 1/41 Analýza algoritmu Proč vůbec dělat analýzu? pro většinu problémů existuje několik různých přístupů aby
Použití databází. Mnoho postupů, které si ukážeme pro prací s formulářů využijeme i při návrhu tiskových sestav.
 Formuláře Formuláře se v aplikaci Access používají zejména na úpravu dat. Upravovat data přímo v tabulce není příliš komfortní a proto si ukážeme jak vytvořit zadávací formulář, pomocí kterého budeme zadávat,
Formuláře Formuláře se v aplikaci Access používají zejména na úpravu dat. Upravovat data přímo v tabulce není příliš komfortní a proto si ukážeme jak vytvořit zadávací formulář, pomocí kterého budeme zadávat,
STROMOVE ALGORITMY Prohledavani do sirky (level-order) Po vodorovnejch carach fronta
 STROMOVE ALGORITMY Prohledavani do sirky (level-order) Po vodorovnejch carach vlož do fronty kořen opakuj, dokud není fronta prázdná 1. vyber uzel z fronty a zpracuj jej 2. vlož do fronty levého následníka
STROMOVE ALGORITMY Prohledavani do sirky (level-order) Po vodorovnejch carach vlož do fronty kořen opakuj, dokud není fronta prázdná 1. vyber uzel z fronty a zpracuj jej 2. vlož do fronty levého následníka
8) Jaké jsou důvody pro použití víceprůchodového překladače Dříve hlavně kvůli úspoře paměti, dnes spíše z důvodu optimalizace
 1) Charakterizujte křížový překladač Překlad programu probíhá na jiném procesoru, než exekuce. Hlavním důvodem je náročnost překladače na cílovém stroji by ho nemuselo být možné rozběhnout. 2. Objasněte
1) Charakterizujte křížový překladač Překlad programu probíhá na jiném procesoru, než exekuce. Hlavním důvodem je náročnost překladače na cílovém stroji by ho nemuselo být možné rozběhnout. 2. Objasněte
Řešení: PŘENESVĚŽ (N, A, B, C) = přenes N disků z A na B pomocí C
 Hanojské věže - 3 kolíky A, B, C - na A je N disků různé velikosti, seřazené od největšího (dole) k nejmenšímu (nahoře) - kolíky B a C jsou prázdné - úkol: přenést všechny disky z A na B, mohou se odkládat
Hanojské věže - 3 kolíky A, B, C - na A je N disků různé velikosti, seřazené od největšího (dole) k nejmenšímu (nahoře) - kolíky B a C jsou prázdné - úkol: přenést všechny disky z A na B, mohou se odkládat
Prioritní fronta, halda
 Prioritní fronta, halda Priority queue, heap Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2018 1 / 26 Prioritní fronta Halda Heap sort 2 / 26 Prioritní fronta (priority queue) Podporuje
Prioritní fronta, halda Priority queue, heap Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2018 1 / 26 Prioritní fronta Halda Heap sort 2 / 26 Prioritní fronta (priority queue) Podporuje
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE. Optimalizace trasy při revizích elektrospotřebičů
 VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Hlavní specializace: Ekonometrie a operační výzkum Název diplomové práce Optimalizace trasy při revizích elektrospotřebičů Diplomant: Vedoucí
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Hlavní specializace: Ekonometrie a operační výzkum Název diplomové práce Optimalizace trasy při revizích elektrospotřebičů Diplomant: Vedoucí
Test prvočíselnosti. Úkol: otestovat dané číslo N, zda je prvočíslem
 Test prvočíselnosti Úkol: otestovat dané číslo N, zda je prvočíslem 1. zkusit všechny dělitele od 2 do N-1 časová složitost O(N) cca N testů 2. stačí zkoušet všechny dělitele od 2 do N/2 (větší dělitel
Test prvočíselnosti Úkol: otestovat dané číslo N, zda je prvočíslem 1. zkusit všechny dělitele od 2 do N-1 časová složitost O(N) cca N testů 2. stačí zkoušet všechny dělitele od 2 do N/2 (větší dělitel
Rozděl a panuj. Často se setkáme s úlohami, které lze snadno rozdělit na nějaké menší úlohy a z jejich
 Rozděl a panuj Často se setkáme s úlohami, které lze snadno rozdělit na nějaké menší úlohy a z jejich výsledků zase snadno složit výsledek původní velké úlohy. Přitom menší úlohy můžeme řešit opět týmž
Rozděl a panuj Často se setkáme s úlohami, které lze snadno rozdělit na nějaké menší úlohy a z jejich výsledků zase snadno složit výsledek původní velké úlohy. Přitom menší úlohy můžeme řešit opět týmž
2.4.8 Další příklady s grafy funkcí s absolutní hodnotou
 ..8 Další příklady s grafy funkcí s absolutní hodnotou Předpoklady: 0-07 Pedagogická poznámka: Následující dva příklady je většinou nutné studentům dovysvětlit. Prohlížení vlastních poznámek jim většinou
..8 Další příklady s grafy funkcí s absolutní hodnotou Předpoklady: 0-07 Pedagogická poznámka: Následující dva příklady je většinou nutné studentům dovysvětlit. Prohlížení vlastních poznámek jim většinou
Dynamické programování
 Dynamické programování prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Dynamické programování prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
2 Spojité modely rozhodování
 2 Spojité modely rozhodování Jak již víme z přednášky, diskrétní model rozhodování lze zapsat ve tvaru úlohy hodnocení variant: f(a i ) max, a i A = {a 1, a 2,... a p }, kde f je kriteriální funkce a A
2 Spojité modely rozhodování Jak již víme z přednášky, diskrétní model rozhodování lze zapsat ve tvaru úlohy hodnocení variant: f(a i ) max, a i A = {a 1, a 2,... a p }, kde f je kriteriální funkce a A
6. Lineární (ne)rovnice s odmocninou
 @06 6. Lineární (ne)rovnice s odmocninou rovnice Když se řekne s odmocninou, znamená to, že zadaná rovnice obsahuje neznámou pod odmocninou. není (ne)rovnice s odmocninou neznámá x není pod odmocninou
@06 6. Lineární (ne)rovnice s odmocninou rovnice Když se řekne s odmocninou, znamená to, že zadaná rovnice obsahuje neznámou pod odmocninou. není (ne)rovnice s odmocninou neznámá x není pod odmocninou
IB111 Úvod do programování skrze Python
 Vyhledávání, řazení, složitost IB111 Úvod do programování skrze Python 2014 1 / 48 Otrávené studny 8 studen, jedna z nich je otrávená laboratorní rozbor dokáže rozpoznat přítomnost jedu ve vodě je drahý
Vyhledávání, řazení, složitost IB111 Úvod do programování skrze Python 2014 1 / 48 Otrávené studny 8 studen, jedna z nich je otrávená laboratorní rozbor dokáže rozpoznat přítomnost jedu ve vodě je drahý
Náplň. v.0.03 16.02.2014. - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění
 Náplň v.0.03 16.02.2014 - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění Spojení dvou samostatně setříděných polí void Spoj(double apole1[], int adelka1, double
Náplň v.0.03 16.02.2014 - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění Spojení dvou samostatně setříděných polí void Spoj(double apole1[], int adelka1, double
Rozptyl. Pozn.: rozptyl je nezávislý na posunu hustoty pravděpodobnosti na ose x, protože Var(X) mi určuje jen šířku rozdělení.
 Rozptyl Základní vlastnosti disperze Var(konst) = 0 Var(X+Y) = Var(X) + Var(Y) (nezávislé proměnné) Lineární změna jednotek Y = rx + s, například z C na F. Jak vypočítám střední hodnotu a rozptyl? Pozn.:
Rozptyl Základní vlastnosti disperze Var(konst) = 0 Var(X+Y) = Var(X) + Var(Y) (nezávislé proměnné) Lineární změna jednotek Y = rx + s, například z C na F. Jak vypočítám střední hodnotu a rozptyl? Pozn.:
KATEDRA INFORMATIKY UNIVERZITA PALACKÉHO LINEÁRNÍ ALGEBRA 1 OLGA KRUPKOVÁ VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN
 KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO LINEÁRNÍ ALGEBRA 1 OLGA KRUPKOVÁ VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY
KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO LINEÁRNÍ ALGEBRA 1 OLGA KRUPKOVÁ VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY
3. Středoškolská stereometrie v anaglyfech
 3. Středoškolská stereometrie v anaglyfech V předchozích dvou kapitolách jsme zjistili, jak se zobrazují tělesa ve středovém promítání a hlavně v lineární perspektivě, a jak pomocí těchto promítání vytvořit
3. Středoškolská stereometrie v anaglyfech V předchozích dvou kapitolách jsme zjistili, jak se zobrazují tělesa ve středovém promítání a hlavně v lineární perspektivě, a jak pomocí těchto promítání vytvořit
Rozmístěte na šachovnici 6 6 čtyři tchýně 1 tak, aby se navzájem neohrožovaly a právě jedno volné pole zůstalo neohrožené.
 Úlohy na šachovnici 3. podzimní série Vzorové řešení Úloha 1. Rozmístěte na šachovnici 6 6 čtyři tchýně 1 tak, aby se navzájem neohrožovaly a právě jedno volné pole zůstalo neohrožené. (Martin Töpfer)
Úlohy na šachovnici 3. podzimní série Vzorové řešení Úloha 1. Rozmístěte na šachovnici 6 6 čtyři tchýně 1 tak, aby se navzájem neohrožovaly a právě jedno volné pole zůstalo neohrožené. (Martin Töpfer)
Název: Elektromagnetismus 3. část (Elektromagnetická indukce)
 Výukové materiály Název: Elektromagnetismus 3. část (Elektromagnetická indukce) Téma: Vznik indukovaného napětí, využití tohoto jevu v praxi Úroveň: 2. stupeň ZŠ, případně SŠ Tematický celek: Vidět a poznat
Výukové materiály Název: Elektromagnetismus 3. část (Elektromagnetická indukce) Téma: Vznik indukovaného napětí, využití tohoto jevu v praxi Úroveň: 2. stupeň ZŠ, případně SŠ Tematický celek: Vidět a poznat
Maturitní téma: Programovací jazyk JAVA
 Maturitní téma: Programovací jazyk JAVA Insert Sort (třídění vkládáním) 1. Jako setříděnou část označíme první prvek pole. Jako nesetříděnou část označíme zbytek pole. 2. Vezmeme první (libovolný) prvek
Maturitní téma: Programovací jazyk JAVA Insert Sort (třídění vkládáním) 1. Jako setříděnou část označíme první prvek pole. Jako nesetříděnou část označíme zbytek pole. 2. Vezmeme první (libovolný) prvek
Programování. Debugging a testování. Martin Urza
 Programování Debugging a testování Martin Urza Co je debugging? V počítačích nulté generace byly důvodem některých chyb zkraty, které způsoboval mimo jiné hmyz, jenž do těchto strojů zalézal. Odstraňování
Programování Debugging a testování Martin Urza Co je debugging? V počítačích nulté generace byly důvodem některých chyb zkraty, které způsoboval mimo jiné hmyz, jenž do těchto strojů zalézal. Odstraňování
Lingebraické kapitolky - Počítání s maticemi
 Lingebraické kapitolky - Počítání s maticemi Jaroslav Horáček KAM MFF UK 20 Rozehřívačka: Definice sčítání dvou matic a násobení matice skalárem, transpozice Řešení: (A + B ij A ij + B ij (αa ij α(a ij
Lingebraické kapitolky - Počítání s maticemi Jaroslav Horáček KAM MFF UK 20 Rozehřívačka: Definice sčítání dvou matic a násobení matice skalárem, transpozice Řešení: (A + B ij A ij + B ij (αa ij α(a ij
Rozklad problému na podproblémy
 Rozklad problému na podproblémy Postupný návrh programu rozkladem problému na podproblémy zadaný problém rozložíme na podproblémy pro řešení podproblémů zavedeme abstraktní příkazy s pomocí abstraktních
Rozklad problému na podproblémy Postupný návrh programu rozkladem problému na podproblémy zadaný problém rozložíme na podproblémy pro řešení podproblémů zavedeme abstraktní příkazy s pomocí abstraktních
TGH05 - Problém za milion dolarů.
 TGH05 - Problém za milion dolarů. Jan Březina Technical University of Liberec 20. března 2012 Časová složitost algoritmu Závislost doby běhu programu T na velikosti vstupních dat n. O(n) notace, standardní
TGH05 - Problém za milion dolarů. Jan Březina Technical University of Liberec 20. března 2012 Časová složitost algoritmu Závislost doby běhu programu T na velikosti vstupních dat n. O(n) notace, standardní
Lineární algebra : Násobení matic a inverzní matice
 Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
