1.2.7 Druhá odmocnina
|
|
|
- Miluše Bílková
- před 8 lety
- Počet zobrazení:
Transkript
1 ..7 Druhá odmocnina Předpoklady: umocňování čísel na druhou Pedagogická poznámka: Probrat obsah této hodiny není možné ve 4 minutách. Já osobně druhou část (usměrňování) probírám v další hodině, jejíž zbytek vyplní počítání sbírky nebo písemka. Př. : Definuj druhou odmocninu z nezáporného čísla a. Druhá odmocnina z nezáporného reálného čísla a je takové nezáporné číslo x pro které platí: x = a. Píšeme: x = a Pedagogická poznámka: Velká většina studentů s případnou malou pomocí dokáže vymyslet správnou definici založenou na umocňování na druhou. Přesto upozorňuji na fakt, že odmocnina je definována pomocí mocnění (aniž bych zmiňoval inverzní funkci), aby si studenti uvědomili svázanost těchto dvou operací. Jediné, o co je nutné prodiskutovat je požadavek na odmocninu jako na nezáporné číslo, kde studentům připomínám výhody jednoznačné definice a důvody, které v matematice vedou na požadavek na jednoznačnost (opět bez toho, abychom mluvili o odmocnině jako o funkci). Z definice vyplývá: 6 = 4 (protože ( π ) 9 nelze = 6 ) = π (protože π je číslo, které po umocnění na druhou dá π ) (nejde udělat odmocninu ze záporného čísl (sice platí 4 = 6, ale odmocnina musí být nezáporná) Podmínka, že odmocnina je nezáporné číslo je důležitá. Zajišťuje nám jednoznačnost při určování odmocniny, existuje pouze jediné číslo, které může vyjít. Př. : Odhadni s přesností na celá čísla velikost následujících odmocnin: 7 9 π < 7 <, protože 6 < 9 < 7, protože < π <, protože 4 = < 7 < 9 = 6 = 6 < 9 < 49 = 7 = < π < 4 = Pozor: 6 = 4 jediná hodnota X x x x = 6 = 4; = 4 dvě hodnoty
2 Jaké nezáporné číslo umocněné na druhou se rovná 6? Proč? ptáme se na různé věci a proto dostáváme různé odpovědi Která čísla jsou kořeny rovnice x = 6? Pravidla pro počítání s odmocninami Pro všechna nezáporná čísla a, b platí: a b = a b a b a b = a b a = a + b nedá se roztrhnout!!!!!!! b Proč jde roztrhnout odmocninu přes krát a nejde ji roztrhnout přes +? a b = ( a b ) = ( a b ) = ( a ) ( b ) = a b a + b = a + b a + b = a + a b + b = a + a b + b Můžeme si to ukázat i na konkrétních číslech = = = 4 + = 7 Pomocí pravidel je možné počítat i odmocniny na první pohled příliš těžké: 900 = 9 00 = 0 = 0 Př. : Vypočti následující odmocniny: 4400 ; 0,008 ; = = 0 = 0 0,008 = 0,000 8 = 0,0 9 = 0,09 = 9 = = Pedagogická poznámka: Pokud se objeví problémy s výpočtem 0,008 přidávám několik příkladů na odmocniny desetinných čísel. Diskutovali jsme také o tom, že stejně jako odmocnina zmenší u mocnin deseti počet nul na polovinu, zmenší na polovinu i počet desetinných míst (pokud jde v obou případech o sudou mocninu). Všechna čísla nejdou odmocnit úplně: = 4 = = částečné odmocnění Př. 4: Částečně odmocni: 0 ; 7 ; 7. 0 = = = 7 = 4 8 = 4 9 = = 6 7 = =
3 Poznámka: Při částečném odmocňování nezáleží na pořadí v jaké číslo na součin rozložíme: 0 = 0 = =. Pedagogická poznámka: Tento způsob používají studenti asi častěji a je třeba ho legitimovat. Někdy je možné zjednodušit součin: = 4 = = 6. Je zbytečné čísla strkat pod jednu odmocninu a násobit je mezi sebou = 6 = 6, u složitějších příkladů to zdržuje a zvětšuje pravděpodobnost chyby. Jindy zase podíl: 0 = = = 4 9 Př. : Zjednoduš součiny: = 6 = 4 7 = 9 = 9 9 = = = = = 4 6 = 7 Pedagogická poznámka: Poslední příklad je často řešen následovně: 8 4 = = = = 7 Odmocnin je ve výrazu tolik, že je snadné některou přehlédnout. Doporučuju upozornit na dodržování zásady KISS (keep it small and stupid) o níž se mluví v hodině 604. Jinak jde o podobný problém jako při násobení zlomků v hodině 0. Průběžně se snažím na takových příkladech upozorňovat na fakt, že nestačí pouze umět pravidla a správně je používat. Je nutné postupovat tak, aby student měl v každém okamžiku kontrolu nad příkladem a výpočet příliš nebobtnal. Př. 6: Zjednoduš podíly: = nebo také: nebo také: 7 9 nebo také: = = Usměrnění zlomku
4 Takové upravení zlomku, aby se odmocnina nevyskytovala ve jmenovateli. Historicko-estetické důvody v předkalkulačkové době bylo těžké určit hodnotu zlomku, když byla ve jmenovateli, kterým se dělí, odmocnina s nekonečným rozvojem (ono se špatně dělí už tříciferným číslem natož číslem, které má cifer nekonečně mnoho). Mám zlomek. Potřebuju vynásobit jmenovatel : nejde, změnil bych zlomek na jiné číslo, násobit můžu pouze jedničkou (ta ho nezmění) zkusím vynásobit zlomkem = = 4 = přesně to jsem potřeboval = Př. 7: Usměrni zlomky: d) 9 8 = = = = = - rozšiřuju jen, mi ve jmenovateli nevadí d) = = 8 9 rozšiřuju - nejdřív zlomek zjednoduším a pak teprve Pedagogická poznámka: Bod spočítají všichni, už v ale mají někteří problémy s v čitateli, v se zbytečně rozšiřuje i. Můžeme usměrnit i složitější zlomky, třeba Zkusíme klasiku: Další pokus:. = = - odmocnina nezmizela =, + + ( ) odmocnina stále žije a zlomek je daleko složitější V čem je problém? Jmenovatel jsem umocňoval vzorcem ( a + = a + ab + b, zkrachovalo to kvůli členu ab ( a = ) hledám vzorec, který nemá tento člen a b ( a ( a + = +. 4
5 = + + Nový pokus: a b a b a + b = a b Pedagogická poznámka: Moc bych se přimlouval, aby studenti dostali možnost zkusit usměrnění zlomku a společně nalézt správné řešení. Jde i o nácvik obecné schopnosti řešit problémy:. pokus. hledání zádrhele. odstranění zádrhele Př. 8: Usměrni zlomky: ( a ( a + = a b = = Př. 9: (BONUS) Usměrni zlomek + Odmocniny nejde odstranit najednou, zkusím to postupně. + budu brát jako jedno číslo Shrnutí: Odmocnina z a je kladné číslo, které se po umocnění druhou rovná a souvisí s umocňováním a chová se podobně.
1.2.5 Reálná čísla I. Předpoklady: 010204
 .2.5 Reálná čísla I Předpoklady: 00204 Značíme R. Reálná čísla jsou čísla, kterými se vyjadřují délky úseček, čísla jim opačná a 0. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý
.2.5 Reálná čísla I Předpoklady: 00204 Značíme R. Reálná čísla jsou čísla, kterými se vyjadřují délky úseček, čísla jim opačná a 0. Každé reálné číslo je na číselné ose znázorněno právě jedním bodem. Každý
2.2.10 Slovní úlohy vedoucí na lineární rovnice I
 Slovní úlohy vedoucí na lineární rovnice I Předpoklady: 0, 06 Pedagogická poznámka: Řešení slovních úloh představuje pro značnou část studentů nejobtížnější část matematiky Důvod je jednoduchý Po celou
Slovní úlohy vedoucí na lineární rovnice I Předpoklady: 0, 06 Pedagogická poznámka: Řešení slovních úloh představuje pro značnou část studentů nejobtížnější část matematiky Důvod je jednoduchý Po celou
Aritmetika s didaktikou II.
 Katedra matematiky PF UJEP Aritmetika s didaktikou II. KM / 0026 Přednáška 0 Desetinnáčísla O čem budeme hovořit: Budeme definovat desetinnáčísla jako speciální racionálníčísla. Naučíme se poznávat různé
Katedra matematiky PF UJEP Aritmetika s didaktikou II. KM / 0026 Přednáška 0 Desetinnáčísla O čem budeme hovořit: Budeme definovat desetinnáčísla jako speciální racionálníčísla. Naučíme se poznávat různé
Konzultace z předmětu MATEMATIKA pro první ročník dálkového studia
 - - Konzultce z předmětu MATEMATIKA pro první ročník dálkového studi ) Číselné obor ) Zákldní početní operce procentový počet ) Absolutní hodnot reálného čísl ) Intervl množinové operce ) Mocnin ) Odmocnin
- - Konzultce z předmětu MATEMATIKA pro první ročník dálkového studi ) Číselné obor ) Zákldní početní operce procentový počet ) Absolutní hodnot reálného čísl ) Intervl množinové operce ) Mocnin ) Odmocnin
M - Příprava na čtvrtletní písemnou práci
 M - Příprava na čtvrtletní písemnou práci Určeno pro třídu 1ODK. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
M - Příprava na čtvrtletní písemnou práci Určeno pro třídu 1ODK. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
10 je 0,1; nebo taky, že 256
 LIMITY POSLOUPNOSTÍ N Á V O D Á V O D : - - Co to je Posloupnost je parta očíslovaných čísel. Trabl je v tom, že aby to byla posloupnost, musí těch čísel být nekonečně mnoho. Očíslovaná čísla, to zavání
LIMITY POSLOUPNOSTÍ N Á V O D Á V O D : - - Co to je Posloupnost je parta očíslovaných čísel. Trabl je v tom, že aby to byla posloupnost, musí těch čísel být nekonečně mnoho. Očíslovaná čísla, to zavání
Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018. 3. Reálná čísla
 Moderní technologie ve studiu aplikované fyziky CZ..07/..00/07.008 3. Reálná čísla RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny. K nejvýznamnějším patří množina reálných čísel,
Moderní technologie ve studiu aplikované fyziky CZ..07/..00/07.008 3. Reálná čísla RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny. K nejvýznamnějším patří množina reálných čísel,
3. Polynomy Verze 338.
 3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
Příprava na 1. čtvrtletní písemku pro třídu 1EB
 Variace 1 Příprava na 1. čtvrtletní písemku pro třídu 1EB Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Číselné
Variace 1 Příprava na 1. čtvrtletní písemku pro třídu 1EB Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Číselné
( x ) 2 ( ) 2.5.4 Další úlohy s kvadratickými funkcemi. Předpoklady: 2501, 2502
 .5. Další úlohy s kvadratickými funkcemi Předpoklady: 50, 50 Pedagogická poznámka: Tato hodina patří mezi ty méně organizované. Společně řešíme příklad, při dalším počítání se třída rozpadá. Já řeším příklady
.5. Další úlohy s kvadratickými funkcemi Předpoklady: 50, 50 Pedagogická poznámka: Tato hodina patří mezi ty méně organizované. Společně řešíme příklad, při dalším počítání se třída rozpadá. Já řeším příklady
1 Matematické základy teorie obvodů
 Matematické základy teorie obvodů Vypracoval M. Košek Toto cvičení si klade možná přemrštěný, možná jednoduchý, cíl dosáhnout toho, aby všichní studenti znali základy matematiky (a fyziky) nutné pro pochopení
Matematické základy teorie obvodů Vypracoval M. Košek Toto cvičení si klade možná přemrštěný, možná jednoduchý, cíl dosáhnout toho, aby všichní studenti znali základy matematiky (a fyziky) nutné pro pochopení
Krize ve vztahu. Udělejte si audit partnerského vztahu
 Krize ve vztahu Krize ke vztahům neodmyslitelně patří. Mění se naše nálady, mění se naše preference, měníme se v průběhu života sami o sobě. A nyní to vynásobte dvěma. Ještě je nutné podotknout, že tyto
Krize ve vztahu Krize ke vztahům neodmyslitelně patří. Mění se naše nálady, mění se naše preference, měníme se v průběhu života sami o sobě. A nyní to vynásobte dvěma. Ještě je nutné podotknout, že tyto
2.2.2 Zlomky I. Předpoklady: 020201
 .. Zlomky I Předpoklady: 0001 Pedagogická poznámka: V hodině je třeba postupovat tak, aby se ještě před jejím koncem začala vyplňovat tabulka u posledního příkladu 9. V loňském roce jsme si zopakovali
.. Zlomky I Předpoklady: 0001 Pedagogická poznámka: V hodině je třeba postupovat tak, aby se ještě před jejím koncem začala vyplňovat tabulka u posledního příkladu 9. V loňském roce jsme si zopakovali
Stanovy horolezeckého oddílu "ROT SPORT"
 Stanovy horolezeckého oddílu "ROT SPORT" Horolezecký oddíl "ROT SPORT" je dobrovolným občanským sdružením zájemců o horolezecký sport, navazující na sportovní a duchovní hodnoty českých a saských horolezců
Stanovy horolezeckého oddílu "ROT SPORT" Horolezecký oddíl "ROT SPORT" je dobrovolným občanským sdružením zájemců o horolezecký sport, navazující na sportovní a duchovní hodnoty českých a saských horolezců
Kód uchazeče ID:... Varianta: 15
 Fakulta informačních technologií ČVUT v Praze Přijímací zkouška z matematiky 2013 Kód uchazeče ID:.................. Varianta: 15 1. V únoru byla zaměstnancům zvýšena mzda o 15 % lednové mzdy. Následně
Fakulta informačních technologií ČVUT v Praze Přijímací zkouška z matematiky 2013 Kód uchazeče ID:.................. Varianta: 15 1. V únoru byla zaměstnancům zvýšena mzda o 15 % lednové mzdy. Následně
Algoritmizace a programování
 Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů. Naučí nás rozdělit
Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů. Naučí nás rozdělit
5.6.6.3. Metody hodnocení rizik
 5.6.6.3. Metody hodnocení rizik http://www.guard7.cz/lexikon/lexikon-bozp/identifikace-nebezpeci-ahodnoceni-rizik/metody-hodnoceni-rizik Pro hodnocení a analýzu rizik se používají různé metody. Výběr metody
5.6.6.3. Metody hodnocení rizik http://www.guard7.cz/lexikon/lexikon-bozp/identifikace-nebezpeci-ahodnoceni-rizik/metody-hodnoceni-rizik Pro hodnocení a analýzu rizik se používají různé metody. Výběr metody
Zapojení horního spína e pro dlouhé doby sepnutí III
 - 1 - Zapojení horního spína e pro dlouhé doby sepnutí III (c) Ing. Ladislav Kopecký, srpen 2015 V p edchozí ásti tohoto lánku jsme dosp li k zapojení horního spína e se dv ma transformátory, které najdete
- 1 - Zapojení horního spína e pro dlouhé doby sepnutí III (c) Ing. Ladislav Kopecký, srpen 2015 V p edchozí ásti tohoto lánku jsme dosp li k zapojení horního spína e se dv ma transformátory, které najdete
ROZCVIČKY. (v nižší verzi může být posunuta grafika a špatně funkční některé odkazy).
 ROZCVIČKY Z MATEMATIKY 8. ROČ Prezentace jsou vytvořeny v MS PowerPoint 2010 (v nižší verzi může být posunuta grafika a špatně funkční některé odkazy). Anotace: Materiál slouží k procvičení základních
ROZCVIČKY Z MATEMATIKY 8. ROČ Prezentace jsou vytvořeny v MS PowerPoint 2010 (v nižší verzi může být posunuta grafika a špatně funkční některé odkazy). Anotace: Materiál slouží k procvičení základních
4. Kdy nelze práva z vadného plnění uplatnit? Práva z vadného plnění Vám nenáleží, pokud:
 Reklamační řád Tento Reklamační řád upravuje způsob a podmínky reklamace vad zboží zakoupeného prostřednictvím on-line portálu Laury Janáčkové umístěného na webovém rozhraní www.laurajanackova.cz od naší
Reklamační řád Tento Reklamační řád upravuje způsob a podmínky reklamace vad zboží zakoupeného prostřednictvím on-line portálu Laury Janáčkové umístěného na webovém rozhraní www.laurajanackova.cz od naší
Zadávací dokumentace k výběrovému řízení č. 0224002876 na: DODÁVKY KOŘENÍ. (dále jen Zadávací dokumentace )
 Zadávací dokumentace k výběrovému řízení č. 0224002876 na: DODÁVKY KOŘENÍ (dále jen Zadávací dokumentace ) Obchodní firma: Letiště Praha, a. s. se sídlem: Praha 6, K Letišti 6/1019, PSČ 160 08 zapsaná
Zadávací dokumentace k výběrovému řízení č. 0224002876 na: DODÁVKY KOŘENÍ (dále jen Zadávací dokumentace ) Obchodní firma: Letiště Praha, a. s. se sídlem: Praha 6, K Letišti 6/1019, PSČ 160 08 zapsaná
Vyhláška č. 294/2015 Sb., kterou se provádějí pravidla provozu na pozemních komunikacích
 Změny 1 vyhláška č. 294/2015 Sb. Vyhláška č. 294/2015 Sb., kterou se provádějí pravidla provozu na pozemních komunikacích a která s účinností od 1. ledna 2016 nahradí vyhlášku č. 30/2001 Sb. Umístění svislých
Změny 1 vyhláška č. 294/2015 Sb. Vyhláška č. 294/2015 Sb., kterou se provádějí pravidla provozu na pozemních komunikacích a která s účinností od 1. ledna 2016 nahradí vyhlášku č. 30/2001 Sb. Umístění svislých
VYUŽITÍ NEURONOVÝCH SÍTÍ PROSTŘEDÍ MATLAB K PREDIKCI HODNOT NÁKLADŮ PRO ELEKTRICKÉ OBLOUKOVÉ PECE
 VYUŽITÍ NEURONOVÝCH SÍTÍ PROSTŘEDÍ MATLAB K PREDIKCI HODNOT NÁKLADŮ PRO ELEKTRICKÉ OBLOUKOVÉ PECE V. Hon VŠB TU Ostrava, FEI, K455, 17. Listopadu 15, Ostrava Poruba, 70833 Abstrakt Neuronová síť (dále
VYUŽITÍ NEURONOVÝCH SÍTÍ PROSTŘEDÍ MATLAB K PREDIKCI HODNOT NÁKLADŮ PRO ELEKTRICKÉ OBLOUKOVÉ PECE V. Hon VŠB TU Ostrava, FEI, K455, 17. Listopadu 15, Ostrava Poruba, 70833 Abstrakt Neuronová síť (dále
Tabulka přípravy učební jednotky s cíli v oblasti průřezových témat a čtenářství
 Tabulka přípravy učební jednotky s cíli v oblasti průřezových témat a čtenářství Učební jednotka Příprava na vyučování Globální výchovy s cíli v oblastech EV a čtenářství Název učební jednotky (téma) Varování
Tabulka přípravy učební jednotky s cíli v oblasti průřezových témat a čtenářství Učební jednotka Příprava na vyučování Globální výchovy s cíli v oblastech EV a čtenářství Název učební jednotky (téma) Varování
Exponenciála matice a její užití. fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu
 1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
c sin Příklad 2 : v trojúhelníku ABC platí : a = 11,6 dm, c = 9 dm, α = 65 0 30. Vypočtěte stranu b a zbývající úhly.
 9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
2.5.26 Procenta pomocí trojčlenky
 2.5.26 Procenta pomocí trojčlenky Předpoklady: 020525 Pedagogická poznámka: Že procenta představují trojčlenku objeví určitě někdo už v předchozí hodině. Takový žák trojčlenku k počítání samozřejmě používat
2.5.26 Procenta pomocí trojčlenky Předpoklady: 020525 Pedagogická poznámka: Že procenta představují trojčlenku objeví určitě někdo už v předchozí hodině. Takový žák trojčlenku k počítání samozřejmě používat
1.1.11 Poměry a úměrnosti I
 1.1.11 Poměry a úměrnosti I Předpoklady: základní početní operace, 010110 Poznámka: Následující látka bohužel patří mezi ty, kde je nejvíce rozšířené používání samospasitelných postupů, které umožňují
1.1.11 Poměry a úměrnosti I Předpoklady: základní početní operace, 010110 Poznámka: Následující látka bohužel patří mezi ty, kde je nejvíce rozšířené používání samospasitelných postupů, které umožňují
Kreativní malování. s dětmi. Dana Cejpková
 Kreativní malování s dětmi Dana Cejpková Ukázka knihy z internetového knihkupectví www.kosmas.cz U k á z k a k n i h y z i n t e r n e t o v é h o k n i h k u p e c t v í w w w. k o s m a s. c z, U I D
Kreativní malování s dětmi Dana Cejpková Ukázka knihy z internetového knihkupectví www.kosmas.cz U k á z k a k n i h y z i n t e r n e t o v é h o k n i h k u p e c t v í w w w. k o s m a s. c z, U I D
Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio
 Aplikační list Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio Ref: 15032007 KM Obsah Vyvažování v jedné rovině bez měření fáze signálu...3 Nevýhody vyvažování jednoduchými přístroji...3
Aplikační list Vyvažování tuhého rotoru v jedné rovině přístrojem Adash 4900 - Vibrio Ref: 15032007 KM Obsah Vyvažování v jedné rovině bez měření fáze signálu...3 Nevýhody vyvažování jednoduchými přístroji...3
The University of Plymouth
 The University of Plymouth Jmenuji se Lukáš Widomski, je mi 19 let a tento rok jsem udělal maturitu na SPŠ EI Kratochvílova 7. Označil bych se jako průměrný, cílevědomý student, který vzal osud do svých
The University of Plymouth Jmenuji se Lukáš Widomski, je mi 19 let a tento rok jsem udělal maturitu na SPŠ EI Kratochvílova 7. Označil bych se jako průměrný, cílevědomý student, který vzal osud do svých
1.4.1 Výroky. Předpoklady: Výrok je sdělení, u něhož má smysl otázka, zda je či není pravdivé
 1.4.1 Výroky Předpoklady: Výrok je sdělení, u něhož má smysl otázka, zda je či není pradié Číslo π je iracionální. pradiý ýrok Ach jo, zase matika. není ýrok V rozrhu máme deset hodin matematiky týdně.
1.4.1 Výroky Předpoklady: Výrok je sdělení, u něhož má smysl otázka, zda je či není pradié Číslo π je iracionální. pradiý ýrok Ach jo, zase matika. není ýrok V rozrhu máme deset hodin matematiky týdně.
Příloha č. 7. ročník 9. 1h 1x za 14 dní. dotace. nepovinný. povinnost
 Příloha č. 7 Seminář z matematiky V učebním plánu 2. druhého stupně se zařazuje nepovinný předmět Seminář z matematiky. V tematickém okruhu Čísla a početní operace na prvním stupni, na který navazuje a
Příloha č. 7 Seminář z matematiky V učebním plánu 2. druhého stupně se zařazuje nepovinný předmět Seminář z matematiky. V tematickém okruhu Čísla a početní operace na prvním stupni, na který navazuje a
STANOVISKO č. STAN/1/2006 ze dne 8. 2. 2006
 STANOVISKO č. STAN/1/2006 ze dne 8. 2. 2006 Churning Churning je neetická praktika spočívající v nadměrném obchodování na účtu zákazníka obchodníka s cennými papíry. Negativní následek pro zákazníka spočívá
STANOVISKO č. STAN/1/2006 ze dne 8. 2. 2006 Churning Churning je neetická praktika spočívající v nadměrném obchodování na účtu zákazníka obchodníka s cennými papíry. Negativní následek pro zákazníka spočívá
Rozhodnutí o námitkách
 Veřejná zakázka Dodávka vozidel pro městskou policii a magistrát hlavního města Prahy Zadávaná v otevřeném řízení zahájeném dne 19. 09. 2014 ev. č. Věstníku veřejných zakázek 487282 (dále jen zakázka )
Veřejná zakázka Dodávka vozidel pro městskou policii a magistrát hlavního města Prahy Zadávaná v otevřeném řízení zahájeném dne 19. 09. 2014 ev. č. Věstníku veřejných zakázek 487282 (dále jen zakázka )
METODICKÝ POKYN - DEFINICE MALÝCH A STŘEDNÍCH PODNIKŮ
 Regionální rada regionu soudržnosti Moravskoslezsko METODICKÝ POKYN - DEFINICE MALÝCH A STŘEDNÍCH PODNIKŮ verze 1.06 Evidence změn Verze Platnost od Předmět změny Strany č. 1.01 22. 10. 2007 Sestavování
Regionální rada regionu soudržnosti Moravskoslezsko METODICKÝ POKYN - DEFINICE MALÝCH A STŘEDNÍCH PODNIKŮ verze 1.06 Evidence změn Verze Platnost od Předmět změny Strany č. 1.01 22. 10. 2007 Sestavování
Pokud máte doma dítě s atopickým ekzémem, jistě pro vás není novinkou, že tímto onemocněním trpí každé páté dítě v Evropě.
 Máme tu jaro a s ním, bohužel, zhoršení stavu většiny atopiků. Příroda se probouzí, tráva se zelená, první květiny a stromy kvetou a vzduch se alergeny jen hemží Co dělat s tím, aby to naši nejmenší přežili
Máme tu jaro a s ním, bohužel, zhoršení stavu většiny atopiků. Příroda se probouzí, tráva se zelená, první květiny a stromy kvetou a vzduch se alergeny jen hemží Co dělat s tím, aby to naši nejmenší přežili
Příklad 1.3: Mocnina matice
 Řešení stavových modelů, módy, stabilita. Toto cvičení bude věnováno hledání analytického řešení lineárního stavového modelu. V matematickém jazyce je takový model ničím jiným, než sadou lineárních diferenciálních
Řešení stavových modelů, módy, stabilita. Toto cvičení bude věnováno hledání analytického řešení lineárního stavového modelu. V matematickém jazyce je takový model ničím jiným, než sadou lineárních diferenciálních
Algoritmizace a programování
 Pátek 14. října Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů.
Pátek 14. října Algoritmizace a programování V algoritmizaci a programování je důležitá schopnost analyzovat a myslet. Všeobecně jsou odrazovým můstkem pro řešení neobvyklých, ale i každodenních problémů.
STUDNY a jejich právní náležitosti.
 STUDNY a jejich právní náležitosti. V současné době je toto téma velmi aktuální, a to na základě mediální kampaně, která však je, jako obvykle, silně poznamenána povrchními znalostmi a řadou nepřesností,
STUDNY a jejich právní náležitosti. V současné době je toto téma velmi aktuální, a to na základě mediální kampaně, která však je, jako obvykle, silně poznamenána povrchními znalostmi a řadou nepřesností,
VÝROČNÍ ZPRÁVA O ČINNOSTI DĚTI PATŘÍ DOMŮ, O.S., V ROCE 2008
 VÝROČNÍ ZPRÁVA O ČINNOSTI DĚTI PATŘÍ DOMŮ, O.S., V ROCE 2008 1. Základní údaje o sdružení Název: Děti patří domů, o.s. Sídlo: Višňovka 185, 252 03 Řitka Identifikační číslo: 22682660 Zapsáno u MV ČR pod
VÝROČNÍ ZPRÁVA O ČINNOSTI DĚTI PATŘÍ DOMŮ, O.S., V ROCE 2008 1. Základní údaje o sdružení Název: Děti patří domů, o.s. Sídlo: Višňovka 185, 252 03 Řitka Identifikační číslo: 22682660 Zapsáno u MV ČR pod
Operace nad celými tabulkami
 10 Operace nad celými tabulkami V předchozích kapitolách jsme se převážně zabývali sloupci tabulek. V této kapitole se naučíme provádět některé operace, které ovlivňují tabulky jako celek. Probereme vlastnosti
10 Operace nad celými tabulkami V předchozích kapitolách jsme se převážně zabývali sloupci tabulek. V této kapitole se naučíme provádět některé operace, které ovlivňují tabulky jako celek. Probereme vlastnosti
2.8.23 Využití Pythagorovy věty III
 .8.3 Využití Pythagorovy věty III Předpoklady: 008 Př. 1: Urči obsah rovnoramenného trojúhelníku se základnou 8 cm a rameny 5,8 cm. Pro výpočet obsahu potřebujeme znát jednu ze stran a odpovídající výšku.
.8.3 Využití Pythagorovy věty III Předpoklady: 008 Př. 1: Urči obsah rovnoramenného trojúhelníku se základnou 8 cm a rameny 5,8 cm. Pro výpočet obsahu potřebujeme znát jednu ze stran a odpovídající výšku.
PRINCIPY ŠLECHTĚNÍ KONÍ
 PRINCIPY ŠLECHTĚNÍ KONÍ Úvod Chovatelská práce u koní měla v minulosti velmi vysokou úroveň. Koně sloužili jako vzor, obecná zootechnika a řada dalších chovatelských předmětů byla vyučována právě na koních
PRINCIPY ŠLECHTĚNÍ KONÍ Úvod Chovatelská práce u koní měla v minulosti velmi vysokou úroveň. Koně sloužili jako vzor, obecná zootechnika a řada dalších chovatelských předmětů byla vyučována právě na koních
7. Odraz a lom. 7.1 Rovinná rozhraní dielektrik - základní pojmy
 Trivium z optiky 45 7 draz a lom V této kapitole se budeme zabývat průchodem (lomem) a odrazem světla od rozhraní dvou homogenních izotropních prostředí Pro jednoduchost se omezíme na rozhraní rovinná
Trivium z optiky 45 7 draz a lom V této kapitole se budeme zabývat průchodem (lomem) a odrazem světla od rozhraní dvou homogenních izotropních prostředí Pro jednoduchost se omezíme na rozhraní rovinná
Android Elizabeth. Verze: 1.3
 Android Elizabeth Program pro měření mezičasů na zařízeních s OS Android Verze: 1.3 Naposledy upraveno: 12. března 2014 alesrazym.cz Aleš Razým fb.com/androidelizabeth Historie verzí Verze Datum Popis
Android Elizabeth Program pro měření mezičasů na zařízeních s OS Android Verze: 1.3 Naposledy upraveno: 12. března 2014 alesrazym.cz Aleš Razým fb.com/androidelizabeth Historie verzí Verze Datum Popis
1. POLOVODIČOVÁ DIODA 1N4148 JAKO USMĚRŇOVAČ
 1. POLOVODIČOVÁ DIODA JAKO SMĚRŇOVAČ Zadání laboratorní úlohy a) Zaznamenejte datum a čas měření, atmosférické podmínky, při nichž dané měření probíhá (teplota, tlak, vlhkost). b) Proednictvím digitálního
1. POLOVODIČOVÁ DIODA JAKO SMĚRŇOVAČ Zadání laboratorní úlohy a) Zaznamenejte datum a čas měření, atmosférické podmínky, při nichž dané měření probíhá (teplota, tlak, vlhkost). b) Proednictvím digitálního
Marketing. Modul 3 Zásady marketingu
 Marketing Modul 3 Zásady marketingu Výukový materiál vzdělávacích kurzů v rámci projektu Zvýšení adaptability zaměstnanců organizací působících v sekci kultura Tento materiál je spolufinancován z Evropského
Marketing Modul 3 Zásady marketingu Výukový materiál vzdělávacích kurzů v rámci projektu Zvýšení adaptability zaměstnanců organizací působících v sekci kultura Tento materiál je spolufinancován z Evropského
Směrnice k Pravidlům hry ICCF Turnaje jednotlivců a družstev (platné od 1. 1. 2016)
 Směrnice k Pravidlům hry ICCF Turnaje jednotlivců a družstev (platné od 1. 1. 2016) Směrnice k Pravidlům hry ICCF Turnaje jednotlivců a družstev Klasická pošta Článek 1a Pravidla šachu FIDE se nacházejí
Směrnice k Pravidlům hry ICCF Turnaje jednotlivců a družstev (platné od 1. 1. 2016) Směrnice k Pravidlům hry ICCF Turnaje jednotlivců a družstev Klasická pošta Článek 1a Pravidla šachu FIDE se nacházejí
MONFISH Junior BOAT CUP 2016
 Muškařský klub Monfish junior, z.s. ve spolupráci se Středočeským územním svazem, MO Brandýs nad Labem-Stará Boleslav a MO Mělník pořádají dne 23. 4. 2016 MONFISH Junior BOAT CUP 2016 Místo konání: Revír:
Muškařský klub Monfish junior, z.s. ve spolupráci se Středočeským územním svazem, MO Brandýs nad Labem-Stará Boleslav a MO Mělník pořádají dne 23. 4. 2016 MONFISH Junior BOAT CUP 2016 Místo konání: Revír:
Výzva k podání nabídek
 Výzva k podání nabídek Číslo zakázky Název zakázky: Předmět zakázky Vzděláváním k vyšší adaptabilitě zaměstnanců firmy Pozemní stavitelství Zlín, a.s. jazykové vzdělávání Zakázka na nákup služeb Datum
Výzva k podání nabídek Číslo zakázky Název zakázky: Předmět zakázky Vzděláváním k vyšší adaptabilitě zaměstnanců firmy Pozemní stavitelství Zlín, a.s. jazykové vzdělávání Zakázka na nákup služeb Datum
Dodatečné informace č. 3 k zadávacím podmínkám
 Dodatečné informace č. 3 k zadávacím podmínkám Zakázka: Zadavatel: Evropské domy v krajích stavební úpravy objektu Nový Hluchák budova bez č.p. v areálu Pospíšilova 365, Hradec Králové Královéhradecký
Dodatečné informace č. 3 k zadávacím podmínkám Zakázka: Zadavatel: Evropské domy v krajích stavební úpravy objektu Nový Hluchák budova bez č.p. v areálu Pospíšilova 365, Hradec Králové Královéhradecký
Press kit Můžeme se zdravou stravou vyvarovat střevních zánětů?
 Press kit Můžeme se zdravou stravou vyvarovat střevních zánětů? 1 Chronické střevní problémy trápí stále více pacientů V posledních letech roste počet těch, kteří se potýkají s chronickými střevními záněty.
Press kit Můžeme se zdravou stravou vyvarovat střevních zánětů? 1 Chronické střevní problémy trápí stále více pacientů V posledních letech roste počet těch, kteří se potýkají s chronickými střevními záněty.
matematika vás má it naupravidl
 VÝZNAM Algebrický výrz se zvádí intuitivn bez p esn ího vmezení v kolizi s názv dvoj len, troj len, mnoho len. Stále se udr uje fle ná p edstv, e ísl ozn ují mno ství, e jsou zobecn ním vnímné skute nosti.
VÝZNAM Algebrický výrz se zvádí intuitivn bez p esn ího vmezení v kolizi s názv dvoj len, troj len, mnoho len. Stále se udr uje fle ná p edstv, e ísl ozn ují mno ství, e jsou zobecn ním vnímné skute nosti.
Územní plánování, charakter intravilánu a osídlení obce Nosislav
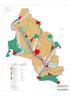 Územní plánování, charakter intravilánu a osídlení obce Nosislav 15.4.2007 Ponechal Lukáš, Hromková Lucie 1 Obec Nosislav leží v okolí řeky Svratky na hranici Ždánického lesa a Dyjskosvrateckého úvalu.
Územní plánování, charakter intravilánu a osídlení obce Nosislav 15.4.2007 Ponechal Lukáš, Hromková Lucie 1 Obec Nosislav leží v okolí řeky Svratky na hranici Ždánického lesa a Dyjskosvrateckého úvalu.
Stavební úprava závodní kuchyně
 Česká republika - MINISTERSTVO FINANCÍ Letenská 15, poštovní přihrádka 77, 118 10 Praha 1 V Praze dne 23.06.2015 Č. j.: MF 28609/2015/6602-1 Věc: Výzva více zájemcům o veřejnou zakázku malého rozsahu podle
Česká republika - MINISTERSTVO FINANCÍ Letenská 15, poštovní přihrádka 77, 118 10 Praha 1 V Praze dne 23.06.2015 Č. j.: MF 28609/2015/6602-1 Věc: Výzva více zájemcům o veřejnou zakázku malého rozsahu podle
Matematika - Sekunda Matematika sekunda Výchovné a vzdělávací strategie Učivo ŠVP výstupy
 - Sekunda Matematika Výchovné a vzdělávací strategie Kompetence k řešení problémů Kompetence komunikativní Kompetence sociální a personální Kompetence občanská Kompetence k učení Kompetence pracovní Učivo
- Sekunda Matematika Výchovné a vzdělávací strategie Kompetence k řešení problémů Kompetence komunikativní Kompetence sociální a personální Kompetence občanská Kompetence k učení Kompetence pracovní Učivo
6. DIDAKTICKÁ JEDNOTKA PREVENCE KONFLIKTŮ, KOMUNIKACE
 6. DIDAKTICKÁ JEDNOTKA PREVENCE KONFLIKTŮ, KOMUNIKACE Úvod Pro bezproblémové vztahy ve školním prostředí je třeba znát dynamiku interakcí a pravidla komunikace. Je nutné, aby všichni měli možnost se svobodně
6. DIDAKTICKÁ JEDNOTKA PREVENCE KONFLIKTŮ, KOMUNIKACE Úvod Pro bezproblémové vztahy ve školním prostředí je třeba znát dynamiku interakcí a pravidla komunikace. Je nutné, aby všichni měli možnost se svobodně
Rozšířená nastavení. Kapitola 4
 Kapitola 4 Rozšířená nastavení 4 Nástroje databáze Jak již bylo zmíněno, BCM používá jako úložiště veškerých informací databázi SQL, která běží na všech lokálních počítačích s BCM. Jeden z počítačů nebo
Kapitola 4 Rozšířená nastavení 4 Nástroje databáze Jak již bylo zmíněno, BCM používá jako úložiště veškerých informací databázi SQL, která běží na všech lokálních počítačích s BCM. Jeden z počítačů nebo
Mnohem lepšá vlastnosti mç usměrňovač dvoucestnâ
 USMĚRŇOVAČE Usměrňovače sloužá k usměrněná střádavâch proudů na proudy stejnosměrnã. K vlastnámu usměrněná se použávajá diody, ať již elektronky, či polovodičovã. Elektronkovã usměrňovače - tzv.eliminçtory-
USMĚRŇOVAČE Usměrňovače sloužá k usměrněná střádavâch proudů na proudy stejnosměrnã. K vlastnámu usměrněná se použávajá diody, ať již elektronky, či polovodičovã. Elektronkovã usměrňovače - tzv.eliminçtory-
Aktivity s GPS 3. Měření některých fyzikálních veličin
 Aktivity s GPS 3 Měření některých fyzikálních veličin Autor: L. Dvořák Cílem materiálu je pomoci vyučujícím s přípravou a následně i s provedením terénního cvičení s využitím GPS přijímačů se žáky II.
Aktivity s GPS 3 Měření některých fyzikálních veličin Autor: L. Dvořák Cílem materiálu je pomoci vyučujícím s přípravou a následně i s provedením terénního cvičení s využitím GPS přijímačů se žáky II.
VÝSTUPY Z DOTAZNÍKU SPOKOJENOSTI. Setkání zpracovatelů projektů v rámci programu KLASTRY CzechInvest, Praha, Štěpánská 15 29.
 VÝSTUPY Z DOTAZNÍKU SPOKOJENOSTI Setkání zpracovatelů projektů v rámci programu KLASTRY CzechInvest, Praha, Štěpánská 15 29. června 2006 Dotazník vyplnilo celkem 13 ze 14 účastníků setkání. Výsledné bodové
VÝSTUPY Z DOTAZNÍKU SPOKOJENOSTI Setkání zpracovatelů projektů v rámci programu KLASTRY CzechInvest, Praha, Štěpánská 15 29. června 2006 Dotazník vyplnilo celkem 13 ze 14 účastníků setkání. Výsledné bodové
4.2.16 Ohmův zákon pro uzavřený obvod
 4.2.16 Ohmův zákon pro uzavřený obvod Předpoklady: 040215 Postřeh z minulých měření: Při sestavování obvodů jsme používali stále stejnou plochou baterku. Přesto se její napětí po zapojení do obvodu měnilo.
4.2.16 Ohmův zákon pro uzavřený obvod Předpoklady: 040215 Postřeh z minulých měření: Při sestavování obvodů jsme používali stále stejnou plochou baterku. Přesto se její napětí po zapojení do obvodu měnilo.
4.5.1 Magnety, magnetické pole
 4.5.1 Magnety, magnetické pole Předpoklady: 4101 Pomůcky: magnety, kancelářské sponky, papír, dřevěná dýha, hliníková kulička, měděná kulička (drát), železné piliny, papír, jehla (špendlík), korek (kus
4.5.1 Magnety, magnetické pole Předpoklady: 4101 Pomůcky: magnety, kancelářské sponky, papír, dřevěná dýha, hliníková kulička, měděná kulička (drát), železné piliny, papír, jehla (špendlík), korek (kus
Kočí, R.: Účelové pozemní komunikace a jejich právní ochrana Leges Praha, 2011
 Kočí, R.: Účelové pozemní komunikace a jejich právní ochrana Leges Praha, 2011 Účelové komunikace jsou důležitou a rozsáhlou částí sítě pozemních komunikací v České republice. Na rozdíl od ostatních kategorií
Kočí, R.: Účelové pozemní komunikace a jejich právní ochrana Leges Praha, 2011 Účelové komunikace jsou důležitou a rozsáhlou částí sítě pozemních komunikací v České republice. Na rozdíl od ostatních kategorií
4. Připoutejte se, začínáme!
 4. Připoutejte se, začínáme! Pojďme si nyní zrekapitulovat základní principy spreadů, které jsme si vysvětlili v předcházejících kapitolách. Řekli jsme si, že klasický spreadový obchod se skládá ze dvou
4. Připoutejte se, začínáme! Pojďme si nyní zrekapitulovat základní principy spreadů, které jsme si vysvětlili v předcházejících kapitolách. Řekli jsme si, že klasický spreadový obchod se skládá ze dvou
1.7. Mechanické kmitání
 1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
se věc hodí k účelu, který pro její použití Prodávající uvádí nebo ke kterému se věc tohoto druhu obvykle používá,
 Reklamační řád Výrobní společnosti SIR JOSEPH s.r.o., se sídlem Koškova 1766, Turnov, 51101, IČ 46506152, DIČ CZ46506152, zapsané v obchodním rejstříku vedeném u Krajského soudu v Hradci Králové, oddíl
Reklamační řád Výrobní společnosti SIR JOSEPH s.r.o., se sídlem Koškova 1766, Turnov, 51101, IČ 46506152, DIČ CZ46506152, zapsané v obchodním rejstříku vedeném u Krajského soudu v Hradci Králové, oddíl
Statistika ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA DOPRAVNÍ. Jiří Volf, Adam Kratochvíl, Kateřina Žáková. Semestrální práce - 0 -
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA DOPRAVNÍ Jiří Volf, Adam Kratochvíl, Kateřina Žáková 2 34 Statistika Semestrální práce - 0 - 1. Úvod Popis úlohy: V této práci se jedná se o porovnání statistických
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA DOPRAVNÍ Jiří Volf, Adam Kratochvíl, Kateřina Žáková 2 34 Statistika Semestrální práce - 0 - 1. Úvod Popis úlohy: V této práci se jedná se o porovnání statistických
POŘÍZENÍ NÍZKOEMISNÍHO ZDROJE A ZATEPLENÍ KULTURNĚ SPOLEČENSKÉ BUDOVY DŘEŠÍNEK
 VÝZVA K PODÁNÍ NABÍDEK K VEŘEJNÉ ZAKÁZCE MALÉHO ROZSAHU POŘÍZENÍ NÍZKOEMISNÍHO ZDROJE A ZATEPLENÍ KULTURNĚ SPOLEČENSKÉ BUDOVY DŘEŠÍNEK ZADÁVANÉ DLE ZÁVAZNÝCH POKYNŮ PRO ŽADATELE A PŘÍJEMCE PODPORY V OPŽP
VÝZVA K PODÁNÍ NABÍDEK K VEŘEJNÉ ZAKÁZCE MALÉHO ROZSAHU POŘÍZENÍ NÍZKOEMISNÍHO ZDROJE A ZATEPLENÍ KULTURNĚ SPOLEČENSKÉ BUDOVY DŘEŠÍNEK ZADÁVANÉ DLE ZÁVAZNÝCH POKYNŮ PRO ŽADATELE A PŘÍJEMCE PODPORY V OPŽP
VY_32_INOVACE_OV_1AT_01_BP_NA_ELEKTRO_PRACOVISTI. Střední odborná škola a Střední odborné učiliště, Dubno
 Číslo projektu Číslo materiálu Název školy Autor CZ.1.07/1.5.00/34.0581 VY_32_INOVACE_OV_1AT_01_BP_NA_ELEKTRO_PRACOVISTI Střední odborná škola a Střední odborné učiliště, Dubno Štícha Roman Tematická oblast
Číslo projektu Číslo materiálu Název školy Autor CZ.1.07/1.5.00/34.0581 VY_32_INOVACE_OV_1AT_01_BP_NA_ELEKTRO_PRACOVISTI Střední odborná škola a Střední odborné učiliště, Dubno Štícha Roman Tematická oblast
HODNOCENÍ VÝVOJE NEHODOVOSTI V ROCE 2012 A POROVNÁNÍ SE STÁTY EU
 HODNOCENÍ VÝVOJE NEHODOVOSTI V ROCE 2012 A POROVNÁNÍ SE STÁTY EU Ing. Petr Pokorný, Mgr. Zuzana Strnadová, Centrum dopravního výzkumu, v.v.i, červen 2013 Email: petr.pokorny@cdv.cz, zuzana.strnadova@cdv.cz
HODNOCENÍ VÝVOJE NEHODOVOSTI V ROCE 2012 A POROVNÁNÍ SE STÁTY EU Ing. Petr Pokorný, Mgr. Zuzana Strnadová, Centrum dopravního výzkumu, v.v.i, červen 2013 Email: petr.pokorny@cdv.cz, zuzana.strnadova@cdv.cz
1. Základní údaje OBCHODNÍ PODMÍNKY
 OBCHODNÍ PODMÍNKY Tak jako v každém obchodě, i v tom našem se snažíme nastavit a dodržovat pravidla, která mají v první řadě chránit naše zákazníky a ujistit je, že jim vyjdeme vstříc jak jen bude v našich
OBCHODNÍ PODMÍNKY Tak jako v každém obchodě, i v tom našem se snažíme nastavit a dodržovat pravidla, která mají v první řadě chránit naše zákazníky a ujistit je, že jim vyjdeme vstříc jak jen bude v našich
VYSOKÁ ŠKOLA FINANČNÍ A SPRÁVNÍ, o.p.s. Fakulta ekonomických studií katedra řízení podniku. Předmět: ŘÍZENÍ LIDSKÝCH ZDROJŮ (B-RLZ)
 VYSOKÁ ŠKOLA FINANČNÍ A SPRÁVNÍ, o.p.s. Fakulta ekonomických studií katedra řízení podniku Předmět: ŘÍZENÍ LIDSKÝCH ZDROJŮ (B-RLZ) Téma 7: HODNOCENÍ PRACOVNÍHO VÝKONU, ODMĚŇOVÁNÍ ŘÍZENÍ PRACOVNÍHO VÝKONU
VYSOKÁ ŠKOLA FINANČNÍ A SPRÁVNÍ, o.p.s. Fakulta ekonomických studií katedra řízení podniku Předmět: ŘÍZENÍ LIDSKÝCH ZDROJŮ (B-RLZ) Téma 7: HODNOCENÍ PRACOVNÍHO VÝKONU, ODMĚŇOVÁNÍ ŘÍZENÍ PRACOVNÍHO VÝKONU
Řešení: Dejme tomu, že pan Alois to vezme popořadě od jara do zimy. Pro výběr fotky z jara má Alois dvanáct možností. Tady není co počítat.
 KOMBINATORIKA ŘEŠENÉ PŘÍKLADY Příklad 1 Pan Alois dostal od vedení NP Šumava za úkol vytvořit propagační poster se čtyřmi fotografiemi Šumavského národního parku, každou z jiného ročního období (viz obrázek).
KOMBINATORIKA ŘEŠENÉ PŘÍKLADY Příklad 1 Pan Alois dostal od vedení NP Šumava za úkol vytvořit propagační poster se čtyřmi fotografiemi Šumavského národního parku, každou z jiného ročního období (viz obrázek).
Modul Řízení objednávek. www.money.cz
 Modul Řízení objednávek www.money.cz 2 Money S5 Řízení objednávek Funkce modulu Obchodní modul Money S5 Řízení objednávek slouží k uskutečnění hromadných akcí s objednávkami, které zajistí dostatečné množství
Modul Řízení objednávek www.money.cz 2 Money S5 Řízení objednávek Funkce modulu Obchodní modul Money S5 Řízení objednávek slouží k uskutečnění hromadných akcí s objednávkami, které zajistí dostatečné množství
Zadavatel: Zadavatel ve smyslu zákona: územní samosprávný celek - 2 odst. 2 písm. c) zákona Právní forma: Název zakázky:
 Výzva k podání nabídky v souladu se zákonem č. 137/2006 Sb., o veřejných zakázkách, s Pokyny pro zadávání veřejných zakázek Regionálního operačního programu NUTS II Severovýchod a Směrnicí č.3 Rady Královéhradeckého
Výzva k podání nabídky v souladu se zákonem č. 137/2006 Sb., o veřejných zakázkách, s Pokyny pro zadávání veřejných zakázek Regionálního operačního programu NUTS II Severovýchod a Směrnicí č.3 Rady Královéhradeckého
Jak jednat. se stavebním úřadem. Michal Lalík. e s. stavebnímu zákonu z praxe
 Jak jednat se stavebním úřadem 148 Michal Lalík ne nejčastější ejčastějš jč tějš ší otázky ot ázk y a odpovědi odpově ědi ě di ke e s stavebnímu zákonu z praxe o éh ěn zd te kt u je o ro js P a o Ukazka
Jak jednat se stavebním úřadem 148 Michal Lalík ne nejčastější ejčastějš jč tějš ší otázky ot ázk y a odpovědi odpově ědi ě di ke e s stavebnímu zákonu z praxe o éh ěn zd te kt u je o ro js P a o Ukazka
Ovoce do škol Příručka pro žadatele
 Ve smečkách 33, 110 00 Praha 1 tel.: 222 871 556 fax: 296 326 111 e-mail: info@szif.cz Ovoce do škol Příručka pro žadatele OBSAH 1. Základní informace 2. Schválení pro dodávání produktů 3. Stanovení limitu
Ve smečkách 33, 110 00 Praha 1 tel.: 222 871 556 fax: 296 326 111 e-mail: info@szif.cz Ovoce do škol Příručka pro žadatele OBSAH 1. Základní informace 2. Schválení pro dodávání produktů 3. Stanovení limitu
Veřejné osvětlení v kostce
 Veřejné osvětlení v kostce Proč rekonstruovat veřejné osvětlení Bezpečnost za to stojí Veřejné osvětlení patří mezi důležité služby obyvatelstvu. Osvětlení chodníků, ulic, silnic a veřejných prostranství
Veřejné osvětlení v kostce Proč rekonstruovat veřejné osvětlení Bezpečnost za to stojí Veřejné osvětlení patří mezi důležité služby obyvatelstvu. Osvětlení chodníků, ulic, silnic a veřejných prostranství
Osvětlovací modely v počítačové grafice
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Semestrální práce z předmětu Matematické modelování Osvětlovací modely v počítačové grafice 27. ledna 2008 Martin Dohnal A07060 mdohnal@students.zcu.cz
Západočeská univerzita v Plzni Fakulta aplikovaných věd Semestrální práce z předmětu Matematické modelování Osvětlovací modely v počítačové grafice 27. ledna 2008 Martin Dohnal A07060 mdohnal@students.zcu.cz
3.1.5 Energie II. Předpoklady: 010504. Pomůcky: mosazná kulička, pingpongový míček, krabička od sirek, pružina, kolej,
 3.1.5 Energie II Předpoklady: 010504 Pomůcky: mosazná kulička, pingpongový míček, krabička od sirek, pružina, kolej, Př. 1: Při pokusu s odrazem míčku se během odrazu zdá, že se energie míčku "někam ztratila".
3.1.5 Energie II Předpoklady: 010504 Pomůcky: mosazná kulička, pingpongový míček, krabička od sirek, pružina, kolej, Př. 1: Při pokusu s odrazem míčku se během odrazu zdá, že se energie míčku "někam ztratila".
SPECIÁLNÍ PRAVIDLA SÓLOVÉ & PÁROVÉ BRUSLENÍ
 SPECIÁLNÍ PRAVIDLA SÓLOVÉ & PÁROVÉ BRUSLENÍ Pravidlo 306 Chování bruslařů, činovníků a ostatních 1. Povzbuzování a rady jakéhokoliv druhu, obzvláště napovídání ze strany činovníků a jiných osob během předvádění
SPECIÁLNÍ PRAVIDLA SÓLOVÉ & PÁROVÉ BRUSLENÍ Pravidlo 306 Chování bruslařů, činovníků a ostatních 1. Povzbuzování a rady jakéhokoliv druhu, obzvláště napovídání ze strany činovníků a jiných osob během předvádění
VÝZVA K PODÁNÍ NABÍDKY ZADÁVACÍ DOKUMENTACE
 VÝZVA K PODÁNÍ NABÍDKY ZADÁVACÍ DOKUMENTACE Věc: Veřejná zakázka malého rozsahu Název: EV. číslo: VZ/2015/2/02 1. Identifikační údaje zadavatele Název zakázky: Zadavatel: Sídlo: Uherskohradišťská nemocnice
VÝZVA K PODÁNÍ NABÍDKY ZADÁVACÍ DOKUMENTACE Věc: Veřejná zakázka malého rozsahu Název: EV. číslo: VZ/2015/2/02 1. Identifikační údaje zadavatele Název zakázky: Zadavatel: Sídlo: Uherskohradišťská nemocnice
VÝKLADOVÁ PRAVIDLA K RÁMCOVÉMU PROGRAMU PRO PODPORU TECHNOLOGICKÝCH CENTER A CENTER STRATEGICKÝCH SLUŽEB
 VÝKLADOVÁ PRAVIDLA K RÁMCOVÉMU PROGRAMU PRO PODPORU TECHNOLOGICKÝCH CENTER A CENTER STRATEGICKÝCH SLUŽEB Rámcový program pro podporu technologických center a center strategických služeb schválený vládním
VÝKLADOVÁ PRAVIDLA K RÁMCOVÉMU PROGRAMU PRO PODPORU TECHNOLOGICKÝCH CENTER A CENTER STRATEGICKÝCH SLUŽEB Rámcový program pro podporu technologických center a center strategických služeb schválený vládním
Přípravné kurzy pro zájemce o studium
 Přípravné kurzy pro zájemce o studium Brno, 2015 Obsah O přípravných kurzech... 2 Termíny... 3 Místo konání... 3 Rozpis zaměstnání... 4 Studijní předpoklady... 4 Matematika... 5 Anglický jazyk... 5 Tělesná
Přípravné kurzy pro zájemce o studium Brno, 2015 Obsah O přípravných kurzech... 2 Termíny... 3 Místo konání... 3 Rozpis zaměstnání... 4 Studijní předpoklady... 4 Matematika... 5 Anglický jazyk... 5 Tělesná
Obsah. Logická zkoumání
 Obsah Logická zkoumání O smyslu a významu 17 Výklady o smyslu a významu 43 Funkce a pojem 55 Pojem a předmět 79 Myšlenka. Logické zkoumání 95 Recenze Husserlovy Filosofie aritmetiky 123 Základy aritmetiky
Obsah Logická zkoumání O smyslu a významu 17 Výklady o smyslu a významu 43 Funkce a pojem 55 Pojem a předmět 79 Myšlenka. Logické zkoumání 95 Recenze Husserlovy Filosofie aritmetiky 123 Základy aritmetiky
SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNÍ A STAVEBNÍ TÁBOR, KOMENSKÉHO 1670 SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2 ŠKOLNÍ ROK 2014/2015 Obsah 1 Dělitelnost přirozených čísel... 3 2 Obvody a obsahy
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNÍ A STAVEBNÍ TÁBOR, KOMENSKÉHO 1670 SBÍRKA PŘÍKLADŮ PRO OPAKOVÁNÍ NA PŘIJÍMACÍ ZKOUŠKY 2 ŠKOLNÍ ROK 2014/2015 Obsah 1 Dělitelnost přirozených čísel... 3 2 Obvody a obsahy
Obsah. Trocha právničiny
 Trocha právničiny - Pokud se vám můj ebook líbí, řekněte o tom svým známým. Pošlete jim odkaz na webovou stránku, kde si jej mohou zakoupit. Ebook je mým duševním vlastnictvím a jeho tvorba mě stála spoustu
Trocha právničiny - Pokud se vám můj ebook líbí, řekněte o tom svým známým. Pošlete jim odkaz na webovou stránku, kde si jej mohou zakoupit. Ebook je mým duševním vlastnictvím a jeho tvorba mě stála spoustu
Pokyny k hodnocení úlohy 1 ZADÁNÍ. nebo NEDOSTATEČNÉ ŘEŠENÍ. nebo CHYBNÉ ŘEŠENÍ. nebo CHYBĚJÍCÍ ŘEŠENÍ 0
 PZK 9 M9-Z-D-PR_OT_ST M9PZD6CT Pokyny k hodnocení Pokyny k hodnocení úlohy BODY ZADÁNÍ Vypočtěte, kolikrát je rozdíl čísel,4 a,7 (v tomto pořadí) menší než jejich součet. (V záznamovém archu je očekáván
PZK 9 M9-Z-D-PR_OT_ST M9PZD6CT Pokyny k hodnocení Pokyny k hodnocení úlohy BODY ZADÁNÍ Vypočtěte, kolikrát je rozdíl čísel,4 a,7 (v tomto pořadí) menší než jejich součet. (V záznamovém archu je očekáván
NÁZEV/TÉMA: Období dospělosti
 NÁZEV/TÉMA: Období dospělosti Vyučovací předmět: Psychologie a komunikace Škola: SZŠ a VOŠZ Znojmo Učitel: Mgr. Olga Černá Třída + počet žáků: 2. ročník, obor ZA, 24 žáků Časová jednotka: 1 vyučovací jednotka
NÁZEV/TÉMA: Období dospělosti Vyučovací předmět: Psychologie a komunikace Škola: SZŠ a VOŠZ Znojmo Učitel: Mgr. Olga Černá Třída + počet žáků: 2. ročník, obor ZA, 24 žáků Časová jednotka: 1 vyučovací jednotka
DODATEČNÉ INFORMACE Č. 4
 DODATEČNÉ INFORMACE Č. 4 1.1. Název veřejné zakázky: Tělocvična, ZŠ Dolní Břežany 1.2. Evidenční číslo veřejné zakázky: VZ 512860 1.3. Identifikační údaje o zadavateli Název: Obec Dolní Břežany Sídlo:
DODATEČNÉ INFORMACE Č. 4 1.1. Název veřejné zakázky: Tělocvična, ZŠ Dolní Břežany 1.2. Evidenční číslo veřejné zakázky: VZ 512860 1.3. Identifikační údaje o zadavateli Název: Obec Dolní Břežany Sídlo:
VŠEOBECNÉ PODMÍNKY PLATNÉ PRO
 1 VŠEOBECNÉ PODMÍNKY PLATNÉ PRO ZASTUPOVÁNÍ V CELNÍM ŘÍZENÍ NA ZÁKLADĚ PLNÉ MOCI PELMI, spol. s r.o., obchodní společnost založená podle českého práva se sídlem Musílkova 568/35, Praha 5 - Košíře, PSČ
1 VŠEOBECNÉ PODMÍNKY PLATNÉ PRO ZASTUPOVÁNÍ V CELNÍM ŘÍZENÍ NA ZÁKLADĚ PLNÉ MOCI PELMI, spol. s r.o., obchodní společnost založená podle českého práva se sídlem Musílkova 568/35, Praha 5 - Košíře, PSČ
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ
 ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
Nabídka vzdělávacích seminářů
 Nabídka vzdělávacích seminářů Vzdělávací semináře na nabízená témata je možné si objednat přímo pro vaší organizaci. Poptávku lze zasílat na emailovou adresu vzdelavani@amalthea.cz. Seznam vzdělávacích
Nabídka vzdělávacích seminářů Vzdělávací semináře na nabízená témata je možné si objednat přímo pro vaší organizaci. Poptávku lze zasílat na emailovou adresu vzdelavani@amalthea.cz. Seznam vzdělávacích
Výzva pro předložení nabídek k veřejné zakázce malého rozsahu s názvem Výměna lina
 VÝCHOVNÝ ÚSTAV A ŠKOLNÍ JÍDELNA NOVÁ ROLE Školní 9, Nová Role, PSČ: 362 25, Tel: 353 851 179 Dodavatel: Výzva pro předložení nabídek k veřejné zakázce malého rozsahu s názvem Výměna lina 1. Zadavatel Výchovný
VÝCHOVNÝ ÚSTAV A ŠKOLNÍ JÍDELNA NOVÁ ROLE Školní 9, Nová Role, PSČ: 362 25, Tel: 353 851 179 Dodavatel: Výzva pro předložení nabídek k veřejné zakázce malého rozsahu s názvem Výměna lina 1. Zadavatel Výchovný
NEJČASTĚJI KLADENÉ DOTAZY K PUBLICITĚ PROJEKTŮ OP LZZ
 NEJČASTĚJI KLADENÉ DOTAZY K PUBLICITĚ PROJEKTŮ OP LZZ A) Povinnost příjemců zajišťovat publicitu projektů 1. Z čeho vyplývá povinnost příjemců podpory dodržovat vizuální identitu ESF/OP LZZ a zajišťovat
NEJČASTĚJI KLADENÉ DOTAZY K PUBLICITĚ PROJEKTŮ OP LZZ A) Povinnost příjemců zajišťovat publicitu projektů 1. Z čeho vyplývá povinnost příjemců podpory dodržovat vizuální identitu ESF/OP LZZ a zajišťovat
DOMOVNÍ ŘÁD BYTOVÉHO DRUŽSTVA ZÁZVORKOVA 2007, 2008, 2009
 DOMOVNÍ ŘÁD BYTOVÉHO DRUŽSTVA ZÁZVORKOVA 2007, 2008, 2009 Úvodní ustanovení 1. V návaznosti na příslušné zákony a stanovy družstva obsahuje domovní řád pravidla užívání bytů, nebytových a společných částí
DOMOVNÍ ŘÁD BYTOVÉHO DRUŽSTVA ZÁZVORKOVA 2007, 2008, 2009 Úvodní ustanovení 1. V návaznosti na příslušné zákony a stanovy družstva obsahuje domovní řád pravidla užívání bytů, nebytových a společných částí
Výstupy Učivo Téma. Čas. Základní škola a mateřská škola Hať. Školní vzdělávací program. Průřezová témata, kontexty a přesahy,další poznámky
 provádí pamětné a písemné početní Čísla přirozená Opakování září, říjen operace v oboru přirozených čísel porovnává a uspořádává čísla celá a Čísla celá, racionální racionální, provádí početní operace
provádí pamětné a písemné početní Čísla přirozená Opakování září, říjen operace v oboru přirozených čísel porovnává a uspořádává čísla celá a Čísla celá, racionální racionální, provádí početní operace
Obec Jino any : 00241342,252 25 Jino any
 Obec Jino any : 00241342,252 25 Jino any Oznámení zám ru V souladu s ust. 39 odst. 1 zákona. 128/2000 Sb. o obcích ve zn ní pozd jších p edpis oznamuje obec Jino any sv j zám r pronajmout tento nemovitý
Obec Jino any : 00241342,252 25 Jino any Oznámení zám ru V souladu s ust. 39 odst. 1 zákona. 128/2000 Sb. o obcích ve zn ní pozd jších p edpis oznamuje obec Jino any sv j zám r pronajmout tento nemovitý
