RLC obvody Jaroslav Reichl, 2006
|
|
|
- Františka Konečná
- před 8 lety
- Počet zobrazení:
Transkript
1 obvody Jaroslav eichl, 6 obvody obvody e název pro obvody, které sou pipoeny ke zdroi stídavého naptí a které sou obecn tvoeny rezistore o odporu, ideální cívkou s indukností a ideální kondenzátore s kapacitou Bude-li obvod tvoen en dvi z uvedených prvk, nebude se v ateatických vztazích popisuících chování obvodu vyskytovat len odpovídaící prvku, který v obvodu není zaazen Proto bude výklad proveden pro obecný pípad obvodu Sériový obvod Fyzikální popis Prvky obvodu (viz obr ) prochází stený proud, ale naptí na ednotlivých prvcích se liší ak hodnotou tak i vzáenou fází: naptí u na rezistoru á stenou fázi akou proud, naptí u na cívce pedbíhá proud a naptí u na kondenzátoru se za proude zpožue Stená fáze proudu a naptí na rezistoru e dána vlastností rezistoru Není žádný fyzikální dvod, pro by lo k fázovéu posunu docházet Na cívce a kondenzátoru e ale situace iná Zpoždní proudu vzhlede k naptí na cívce e zpsobeno elektroagnetickou indukcí naptí v cívce, kterou prochází stídavý proud Prchode tohoto proudu vzniká v cívce asov pronné (t nestacionární) agnetické pole, které e píinou indukce naptí v cívce Následke toho zaíná cívkou procházet proud, který á ovše ve srovnání s proude, který indukovaný proud svý agnetický pole vyvolal, opaný sr ívka si totiž snaží udržet pvodní agnetické pole, které v ní bylo pedtí, než zaalo docházet ke zná tohoto pole Práv uvedený poznatek e obsahe enzova zákona: NDKOVANÝ KTKÝ POD V ZAVNÉM OBVOD MÁ TAKOVÝ SM, Ž SVÝM MAGNTKÝM POM PSOBÍ POT ZMN MAGNTKÉHO NDK NÍHO TOK, KTÁ J JHO PÍ NO (SP KTÁ TNTO POD VYVOAA) Pedbíhání proudu vzhlede k naptí na kondenzátoru e zpsobeno periodický nabíení a vybíení kondenzátoru Ten se v první tvrtin periody stídavého naptí nabíí V okažiku, kdy dosáhne naptí na kondenzátoru axiální hodnoty, prochází kondenzátore nulový proud Pak se kondenzátor zaíná vybíet, což znaená, že postupn klesá naptí ezi eho deskai a roste proud, který í protéká Jakile proud dosáhne svého axia (v polovin periody), e kondenzátor vybit a zaíná se nabíet opan, než byl nabit pvodn Proud postupn klesá, až dosáhne opt nulové hodnoty V ten okažik e kondenzátor nabit na axiální naptí, které e ovše opané, než naptí, na které byl nabit na konci první tvrtiny periody V poslední tvrtin periody se kondenzátor opt vybíí a proud se zvtšue Práv popsaný d se periodicky opakue Vzhlede k práv popsaný fázový rozdíl ezi proude a naptí na cívce a kondenzátoru, nelze efektivní hodnotu výsledného naptí v celé obvodu získat prostý aritetický soute! obr obr Mateatický popis poocí reálných ísel S využití fázorového diagrau (viz obr ), který získáe zakreslení fázor naptí a proudu do kartézské soustavy souadnic, e ožné získat i výsledné naptí sériového zapoení rezistoru, cívky a kondezátoru Proud a naptí na rezistoru nesou fázov posunuté Vzhlede k tou, že v sériové obvodu prochází všei prvky stený proud (v obvodu nesou žádné uzly, takže se proud neá kde dlit do rzných vtví obvodu), znázorue se tento proud na vodorovnou osu fázorového diagrau Tento proud e spolený vše prvk v obvodu Na tutéž osu se nanáší i naptí na rezistoru Dvod e prostý: na rezistoru nedochází k žádnéu fázovéu posuvu, takže i fázory naptí a proudu nesou vi sob niak pootoené Naptí na cívce se nanáší na kladnou poloosu y To pln odpovídá fyzikálníu popisu chování cívky v obvodu stídavého proudu (resp stídavého naptí): naptí vrcholí (t dosahue svého axia) díve než proud, který í prochází (a který prochází celý obvode) Je nutné si uvdoit, že fázorový diagra znázorue rozložení fázor naptí a proudu en v urité asové okažiku: v ase t a pak vždy za periodu Fakt, že se okažité hodnoty proudu i naptí v obvodu ní, si lze pedstavit tak, že fázorový diagra bude rotovat kole svého poátku (kole poátku kartézské soustavy) proti sru hodinových ruiek (t
2 obvody Jaroslav eichl, 6 vlevo) Pak e asné, že naptí na cívce skuten dosahue svého axia v ase t, zatíco proud v ase t T A to e pln v souladu s fyzikální popise chování cívky pipoené ke zdroi stídavého naptí 4 Na základ podobných úvah e zeé, že naptí na kondenzátoru, které se za proude opožue (resp proud procházeící kondenzátore pedbíhá naptí), e nutné zakreslit na zápornou poloosu y Vyádit vztah ezi efektivníi hodnotai naptí, a na ednotlivých prvcích obvodu znaená vektorov (t se zapotení píslušného fázového posunu) seíst fázory odpovídaící uvedený naptí: = Poznáka: Fázory sou v textu oznaené tuný píse a na obrázcích (aby neohlo doít k zán se skalárníi veliinai) sou oznaené ako vektory Podle obr lze pro efektivní hodnotu výsledného naptí s využití Pythagorovy vty psát: Aby bylo ožné vzáen porovnat paraetry ednotlivých prvk obvodu, zavádí se i pro cívku a kondenzátor zdánlivé odpory Zdánlivý odpor cívky se nazývá induktance (induktivní reaktance) X a platí pro ni vztah: X Zdánlivý odpor kondenzátoru se nazývá kapacitance (kapacitní reaktance) X a e definována vztahe: X V obou uvedených vztazích e f, kde f e frekvence stídavého naptí resp proudu, a nazývá se úhlová frekvence Pro ednotky uvedených veliin platí: X X S využití tchto vztah lze vztah pro výsledné naptí obvodu dále rozepsat a poté upravit: X X Obvod ako celek e pak charakterizován ediný paraetre, který se nazývá ipedance Z pedance pedstavue zdánlivý odpor celého obvodu Proto pro ni platí: Z ; Z Pro fázový rozdíl naptí a proudu v obvodu pak e ožné podle obr psát:, ; Dále e ožné zavést poe reaktance X X X, která charakterizue vlastnosti té ásti obvodu stídavého proudu, v níž se elektroagnetická energie není v teplo, ale en v energii elektrického a agnetického pole eaktance tedy popisue chování cívky a kondenzátoru obr 3 obr 4
3 obvody Jaroslav eichl, 6 Zvláštní pípad nastává v obvodu v sérii, e-li pi dané frekvenci induktance obvodu stená ako eho kapacitance: X X pedance e pak dána en odpore rezistoru: Z Fázový rozdíl proudu a naptí e nulový a obvod á vlastnost rezistence (t obvod se chová ako kdyby v n byl zapoen en rezistor bez cívky a bez kondenzátoru) pedance e proto ze všech ožných stav daného obvodu neenší a proto obvode (pi dané naptí) prochází nevtší proud Tento stav se oznaue ako rezonance stídavého obvodu a píslušnou rezonanní frekvenci f lze urit z podínky, z níž vyplývá: f Skutenost, že pi rezonanci e ipedance obvodu iniální, dokuentue i obr 3, na které sou zobrazeny grafy závislosti odporu, induktance, kapacitance a ipedance na frekvenci proudu (resp naptí) Odpor rezistoru na frekvenci proudu nezávisí, induktance cívky se s rostoucí frekvencí proudu zvtšue a kapacitance kondenzátoru s rostoucí frekvencí proudu klesá pedance dosahue svého inia práv v pípad rezonance obvodu, kdy e eí hodnota totožná s odpore rezistoru a kapacitance a induktance sou stené Na obr 4 e zobrazen prbh fázového posunu proudu a naptí 3 Mateatický popis poocí koplexních ísel Peforulování ady fyzikálních problé do koplexních ísel se tyto probléy vtšinou ateaticky zednoduší S koplexníi ísly se totiž veli ednoduše pracue a pro každý typ úlohy (podle ateatického zápisu rovnic, podle povahy hledaného ešení, ) e vhodný iný zápis koplexních ísel Dležité e ovše na konci úlohy správn interpretovat získané ešení, t piadit koplexní ísl (resp eich iaginární áste) správný fyzikální sysl Na základ fyzikálního popisu obvodu (viz odstavec ), který e zobrazen na obr, e ožné zakreslit fázory proudu a naptí na ednotlivých prvcích obvodu i do Gaussovy roviny, do níž se zobrazuí koplexní ísla Z poátku bude postup stený ako v odstavci : proud procházeící obvode e na všech prvcích obvodu stený a á nulový fázový posun vi naptí na rezistoru Proto se ob tyto veliiny zobrazuí na reálnou osu (viz obr 5) Naptí na cívce, které se pedbíhá oproti proudu procházeícíu cívkou práv o 9, se zobrazue na kladnou iaginární poloosu Analogicky se naptí na kondenzátoru (které se za proude tekoucí kondenzátore o 9 opožue) obr 5 zobrazí na zápornou iaginární poloosu Grafická znázornní na obr a obr 5 sou tedy veli podobná Výpoet se ale liší Naptí na rezistoru o odporu e dáno vztahe Naptí na cívce o induknosti e dáno vztahe: kde e iaginární ednotka, pro kterou platí X, Poznáka: V ateatice se tatáž iaginární ednotka znaí sybole i Sybol e zde volen zárn, aby nedocházelo k zán s okažitou hodnotou proudu, která se znaí i Peznaení iaginární ednotky se ateatické definice a pravidla, kterýi se poítání s koplexníi ísly ídí, nezní! Analogicky lze definovat naptí na kondenzátoru vztahe X Na první pohled není asné, že naptí na kondenzátoru á fázový posun vi proudu, který á ít - t že se za proude v obvodu zpožue o tvrt periody To e ožné ukázat tak, že naptí vyádíe tak, ak se koplexní ísla bžn vyaduí, t iaginární ednotkou v itateli: Z tohoto vztahu e vidt, že naptí na kondenzátoru skuten á sysl nanášet v Gaussov rovin na zápornou iaginární poloosu Jiný zpsobe e ožné odvodit kapacitanci kondenzátoru poocí gonioetrického tvaru koplexních ísel Staí si uvdoit (a to e vysvtleno už v odstavci a zobrazeno na obr ), že naptí na kondenzátoru e vzhlede k proudu posunuto o Pak lze psát: 3
4 obvody Jaroslav eichl, 6 X cos sin Ve srovnání s popise obvodu poocí reálných ísel (viz odstavec ), se pi použití koplexních ísel zní i výpoet hodnoty celkového naptí Úvodní úvaha e stená: = Po dosazení: 4 íselná hodnota výsledného naptí e pak dána absolutní hodnotou koplexního ísla, ve které už nevystupue iaginární ednotka :, což e stený vztah ako vztah, který byl odvozen s použití reálných ísel (viz odstavec ) Pro ipedanci pak platí: Z a eí íselná hodnota e dána vztahe Z, což e opt stený vztah, který byl odvozen pi popisu poocí reálných ísel (viz odstavec ) Pro fázový rozdíl naptí a proudu v obvodu lze použít stený vztah ako v odstavci (viz obr 5):, ; Mateatický popis rezonance se neliší Pi rezonanci prochází obvode axiální proud a proto e tedy ipedance obvodu iniální To znaená, že X X, odkud pío vyplývá vztah pro rezonanní frekvenci f : f Paralelní obvod Fyzikální podstata Fyzikální podstata innosti paralelního (viz obr 6) obvodu vyplývá z chování rezistoru, cívky a kondenzátoru v obvodu stídavého proudu, které bylo popsáno v odstavci Odlišnost spoívá ve skutenosti, paraleln spoené prky obvodu aí stené naptí, ale procházeí ii rzné proudy Ty se liší se neen hodnotou, ale i fází: proud i procházeící rezistore á stenou fázi ako naptí na rezistoru, proud i procházeící cívkou se za naptí opožue o tvrtinu periody a proud i procházeící kondenzátore ho o stený fázový posun pedbíhá obr 6 obr 7 Mateatický popis poocí reálných ísel Vzhlede k rzný fází proud, není ožné získat celkový proud obvodu aritetický soute proud v ednotlivých vtvích, ale e nutné opt využít fázory: = + + kde, Pro efektivní hodnotu výsledného proudu dostanee (podle obr 7): a, sou efektivní hodnoty proud v ednotlivých vtvích obvodu Na základ skutenosti, že naptí e na všech tech prvcích obvodu stené a podle definice výpotu naptí (resp proudu) na rezistoru, cívce a kondenzátoru, lze psát: Obvod e opt charakterizován ediný paraetre - ipedancí Z, pro kterou platí:
5 obvody Jaroslav eichl, 6 Z Paralelní zapoení obvodu e vhodné popisovat poocí aditance Y, která e definovaná vztahe Y ; Y, Z z nhož po dosazení vztahu pro ipedanci dostanee Y Pro fázový rozdíl proudu a naptí lze podle obr 7 psát:, ; Záporné znaénko ped zloke e ve výrazu pro proto, aby bylo ožné vzáen srovnat fázové posunutí (viz obr 4 a obr 9) v sériové a paralelní obvodu V paralelní obvodu e totiž úhel orientován opan, než u sériového obvodu Na obr 7 e tedy tento úhel orientován od proudu k naptí u paralelního obvodu e ožné hovoit o rezonanci Ta nastává opt pi rezonanní frekvenci f, pi níž e fázový rozdíl proudu a naptí nulový - a tedy ipedance e axiální resp aditance e iniální a obvode prochází iniální proud Pro rezonanní frekvenci v to pípad platí:, odkud pro rezonanní frekvenci paralelního obvodu vyplývá stený vztah ako e ten, který popisue rezonanci sériového obvodu (viz odstavec a 3): f Závislost ipedance, kapacitance, induktance a odporu na frekvenci e zobrazena na obr 8 Poznáka: Zdánlivé odpory cívky a kondenzátoru sou v uvozovkách, že se needná o tytéž veliiny ako v pípad sériového obvodu, ale o eich pevrácené hodnoty obr 8 obr 9 3 Mateatický popis poocí koplexních ísel Popis paralelního obvodu poocí koplexních ísel e analogický popisu sériového obvodu (viz odstavec 3) Podle obr e vidt, že proud procházeící rezistore není vzhlede k naptí na rezistoru niak posunut Proto platí: Proud na cívce se zpožue za naptí, takže s využití koplexních ísel lze psát:, X obr odkud po vydlení koplexního ísla (t po rozšíení celého výrazu iaginární ednotkou ), vychází: 5
6 obvody Jaroslav eichl, 6 Pro proud na kondenzátoru, který se vzhlede naptí pedbíhá, lze analogicky psát: X Pro výsledný proud lze nyní psát: Hodnota výsledného proudu e dána absolutní hodnotou koplexního ísla: Aditanci obvodu e definovaná vztahe: Y a eí íselná hodnota e dána vztahe Y Jak e vidt, tak rovnice, které vyaduí celkový proud obvodu i eho aditanci sou totožné s ti, které byly odvozeny pi poítání s reálnýi ísly Stené výsledky lze odvodit i pro fázový posun ezi naptí a proude v obvodu a pro rezonanní frekvenci obr Píklad: rete rezonanní frekvenci obvodu, ehož schéa e na obr ešení: ešení lze provést na základ výpotu celkové aditance obvodu Ta e dána vztahe Postupnýi úpravai lze získat: Y Y Y X X X X X X Y X X X X X X ezonance obvodu nastává tehdy, když z ehož lze po úpravách postupn získat X X X X X X X X, 6
7 obvody Jaroslav eichl, 6 f 7 Ve srovnání s frekvencí sériového nebo paralelního obvodu (viz odstavce a ) e frekvence obvodu, ehož schéa e na obr, dána koplikovanší vztahe - liší se faktore, který e dán práv zapoení prvk v obvodu 3 Náhradní schéata V pedchozí textu bylo rozebíráno chování cívky a kondenzátoru ve stídavé obvodu Mlky se pedpokládalo, že de o ideální prvky To ale není ve skutenosti pravda 3 ívka ívky sou elektrotechnické souástky, které výrazný zpsobe zesiluí agnetické pole, pípadn na agnetické pole reaguí (nap indukcí naptí, ) Jsou tvoeny závity izolovaného vodie, který e navinut na ádru cívky Saotný vodi á ale sv (Ohický) odpor Proto e teba skutenou cívku chápat ako sériové spoení ideální cívky a rezistoru, který pedstavue odpor vinutí cívky obr (viz obr ) cívek, které aí podstatn vtší induktanci ve srovnání s odpore svého vinutí, e ožné odpor vinutí vi induktanci celé obr 3 cívky zanedbat Pro výslednou ipedanci takové cívky platí: Z Proud procházeící cívkou nebude posunut vi naptí o!!! Je nutné postupovat ako v obvodu ( obvod, ve které chybí kondenzátor) a poítat podle vztahu, který lze odvodit podle obr 3: Úhel se nazývá ztrátový úhel a e to doplnk fázového posunu do úhlu Hodnota se nazývá initel akosti cívky 3 Kondenzátor Kondenzátory sou souástky, které slouží pro kuulaci elektrické energie Neednodušší sou kondenzátory deskové, které sou tvoeny iniáln dvi vzáen rovnobžnýi deskai, ezi niiž e dielektriku (izolant) A práv izolant ezi deskai kondenzátoru e píinou vzniku ztrát, které ovlivuí celkovou ipedanci (už ne en kapacitanci) kondenzátoru zapoeného do obvodu stídavého proudu obr 4 obr 5 Skutený kondenzátor tedy lze nahradit paralelní zapoení ideálního kodnezátoru a rezistoru, který pedstavue ztráty v dielektriku (viz obr 4) Pro ipedanci skuteného kondenzátoru platí (podle odstavce 3): Z Je vidt, že ednodušší vztah lze získat s využití aditance:
8 obvody Jaroslav eichl, 6 Y = Z Fázový rozdíl ezi proude a naptí nebude, nebo ke kondenzátoru e paraleln pipoen rezistor Proto e teba fázový rozdíl urit na základ paralelního zapoení obvodu, ve které není zapoena cívka: Sten ako u náhradního schéatu cívky, i u kondenzátoru lze zavést ztrátový úhel tak, aby platilo Vztah definue ztrátový initel kondenzátoru 4 initel akosti obvodu initel akosti cívky, kondenzátoru a obvodu se definue vztahe Q, kde e axiální energie akuulovaná na dané prvku, ehož initel akosti e teba urit, a T e energie, která se na dané prvku pení na iné fory energie (energii agnetického pole, elektrickou energii kondenzátoru, ) V nebo obvodu e energie T dána souine prrného výkonu na rezistoru a periody T, tedy T 8 T T, f kde f e frekvence stídavého proudu V obvodu e axiální akuulovaná energie na této ásti obvodu dána energií agnetického pole cívky, tedy a proto pro initel akosti obvodu platí f Q T f V obvodu e axiální akuulovaná energie dána elektrickou energií kondenzátoru e X, na základ ehož e ožné pro initel akosti obvodu psát e f Q T f V sériové obvodu, který e v rezonanci, se akuulue konstantní nožství energie Je-li naptí na kondenzátoru axiální, neprochází cívkou proud Proto Pro initel akosti tak lze psát (s využití initele akosti pro a obvod) Q (resp Q ), protože pi rezonanci platí V paralelní obvodu, který e v rezonanci, se akuulue konstantní nožství energie Prochází-li cívkou axiální proud, e naptí na kondenzátoru nulové; obecn e
9 obvody Jaroslav eichl, 6 a tedy e Q (resp Q ) 9
FYZIKA 2. ROČNÍK. Příklady na obvody střídavého proudu. A1. Určete induktanci cívky o indukčnosti 500 mh v obvodu střídavého proudu o frekvenci 50 Hz.
 FYZKA. OČNÍK Příklady na obvody střídavého proudu A. rčete induktanci cívky o indukčnosti 500 H v obvodu střídavého proudu o frekvenci 50 Hz. = 500 0 3 H =?. = ω = π f = 57 Ω ívka á induktanci o velikosti
FYZKA. OČNÍK Příklady na obvody střídavého proudu A. rčete induktanci cívky o indukčnosti 500 H v obvodu střídavého proudu o frekvenci 50 Hz. = 500 0 3 H =?. = ω = π f = 57 Ω ívka á induktanci o velikosti
Podívejte se na časový průběh harmonického napětí
 Střídavý proud Doteď jse se zabývali pouze proude, který obvode prochází stále stejný sěre (stejnosěrný proud). V praxi se ukázalo, že tento proud je značně nevýhodný. kázalo se, že zdroje napětí ůže být
Střídavý proud Doteď jse se zabývali pouze proude, který obvode prochází stále stejný sěre (stejnosěrný proud). V praxi se ukázalo, že tento proud je značně nevýhodný. kázalo se, že zdroje napětí ůže být
Vznik střídavého proudu Obvod střídavého proudu Výkon Střídavý proud v energetice
 Střídavý proud Vznik střídavého proudu Obvod střídavého proudu Výkon Střídavý proud v energetice Vznik střídavého proudu Výroba střídavého napětí:. indukční - při otáčivé pohybu cívky v agnetické poli
Střídavý proud Vznik střídavého proudu Obvod střídavého proudu Výkon Střídavý proud v energetice Vznik střídavého proudu Výroba střídavého napětí:. indukční - při otáčivé pohybu cívky v agnetické poli
KOMPLEXNÍ DVOJBRANY - PŘENOSOVÉ VLASTNOSTI
 Koplexní dvobrany http://www.sweb.cz/oryst/elt/stranky/elt7.ht Page o 8 8. 6. 8 KOMPEXNÍ DVOJBNY - PŘENOSOVÉ VSTNOSTI Intergrační a derivační článek patří ezi koplexní dvobrany. Integrační článek á vlastnost
Koplexní dvobrany http://www.sweb.cz/oryst/elt/stranky/elt7.ht Page o 8 8. 6. 8 KOMPEXNÍ DVOJBNY - PŘENOSOVÉ VSTNOSTI Intergrační a derivační článek patří ezi koplexní dvobrany. Integrační článek á vlastnost
Fázorové diagramy pro ideální rezistor, skutečná cívka, ideální cívka, skutečný kondenzátor, ideální kondenzátor.
 FREKVENČNĚ ZÁVISLÉ OBVODY Základní pojmy: IMPEDANCE Z (Ω)- charakterizuje vlastnosti prvku pro střídavý proud. Impedance je základní vlastností, kterou potřebujeme znát pro analýzu střídavých elektrických
FREKVENČNĚ ZÁVISLÉ OBVODY Základní pojmy: IMPEDANCE Z (Ω)- charakterizuje vlastnosti prvku pro střídavý proud. Impedance je základní vlastností, kterou potřebujeme znát pro analýzu střídavých elektrických
Základy elektrotechniky
 Základy elektrotechniky 3. přednáška Řešení obvodů napájených haronický napětí v ustálené stavu ZÁKADNÍ POJMY Časový průběh haronického napětí: kde: U u U. sin( t ϕ ) - axiální hodnota [V] - úhlový kitočet
Základy elektrotechniky 3. přednáška Řešení obvodů napájených haronický napětí v ustálené stavu ZÁKADNÍ POJMY Časový průběh haronického napětí: kde: U u U. sin( t ϕ ) - axiální hodnota [V] - úhlový kitočet
Rezistor je součástka kmitočtově nezávislá, to znamená, že se chová stejně v obvodu AC i DC proudu (platí pro ideální rezistor).
 Rezistor: Pasivní elektrotechnická součástka, jejíž hlavní vlastností je schopnost bránit průchodu elektrickému proudu. Tuto vlastnost nazýváme elektrický odpor. Do obvodu se zařazuje za účelem snížení
Rezistor: Pasivní elektrotechnická součástka, jejíž hlavní vlastností je schopnost bránit průchodu elektrickému proudu. Tuto vlastnost nazýváme elektrický odpor. Do obvodu se zařazuje za účelem snížení
1 Měření paralelní kompenzace v zapojení do trojúhelníku a do hvězdy pro symetrické a nesymetrické zátěže
 1 Měření paralelní kompenzace v zapoení do troúhelníku a do hvězdy pro symetrické a nesymetrické zátěže íle úlohy: Trofázová paralelní kompenzace e v praxi honě využívaná. Úloha studenty seznámí s vlivem
1 Měření paralelní kompenzace v zapoení do troúhelníku a do hvězdy pro symetrické a nesymetrické zátěže íle úlohy: Trofázová paralelní kompenzace e v praxi honě využívaná. Úloha studenty seznámí s vlivem
VY_32_INOVACE_06_III./1._OBVOD STŘÍDAVÉHO PROUDU
 VY_32_INOVACE_06_III./1._OBVOD STŘÍDAVÉHO PROUDU Střídavý proud Vznik střídavého napětí a proudu Fyzikální veličiny popisující jevy v obvodu se střídavý proude Střídavý obvod, paraetry obvodu Střídavý
VY_32_INOVACE_06_III./1._OBVOD STŘÍDAVÉHO PROUDU Střídavý proud Vznik střídavého napětí a proudu Fyzikální veličiny popisující jevy v obvodu se střídavý proude Střídavý obvod, paraetry obvodu Střídavý
Vznik a vlastnosti střídavých proudů
 3. Střídavé proudy. Naučit se odvození vztahu pro okažitý a průěrný výkon střídavého proudu, znát fyzikální význa účiníku.. ět použít fázorový diagra na vysvětlení vztahu ezi napětí a proude u jednoduchých
3. Střídavé proudy. Naučit se odvození vztahu pro okažitý a průěrný výkon střídavého proudu, znát fyzikální význa účiníku.. ět použít fázorový diagra na vysvětlení vztahu ezi napětí a proude u jednoduchých
Vítězslav Stýskala, Jan Dudek. Určeno pro studenty komb. formy FBI předmětu / 06 Elektrotechnika
 Stýskala, 00 L e k c e z e l e k t r o t e c h n i k y Vítězslav Stýskala, Jan Dudek rčeno pro studenty komb. formy FB předmětu 45081 / 06 Elektrotechnika B. Obvody střídavé (AC) (všechny základní vztahy
Stýskala, 00 L e k c e z e l e k t r o t e c h n i k y Vítězslav Stýskala, Jan Dudek rčeno pro studenty komb. formy FB předmětu 45081 / 06 Elektrotechnika B. Obvody střídavé (AC) (všechny základní vztahy
13 Měření na sériovém rezonančním obvodu
 13 13.1 Zadání 1) Změřte hodnotu indukčnosti cívky a kapacity kondenzátoru RC můstkem, z naměřených hodnot vypočítej rezonanční kmitočet. 2) Generátorem nastavujte frekvenci v rozsahu od 0,1 * f REZ do
13 13.1 Zadání 1) Změřte hodnotu indukčnosti cívky a kapacity kondenzátoru RC můstkem, z naměřených hodnot vypočítej rezonanční kmitočet. 2) Generátorem nastavujte frekvenci v rozsahu od 0,1 * f REZ do
STŘÍDAVÝ PROUD POJMY K ZOPAKOVÁNÍ. Testové úlohy varianta A
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D17_Z_OPAK_E_Stridavy_proud_T Člověk a příroda Fyzika Střídavý proud Opakování
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Jitka Novosadová MGV_F_SS_3S3_D17_Z_OPAK_E_Stridavy_proud_T Člověk a příroda Fyzika Střídavý proud Opakování
frekvence f (Hz) perioda T = 1/f (s)
 1.) Periodický pohyb - každý pohyb, který se opakuje v pravidelných intervalech Poet Poet cykl cykl za za sekundu sekundu frekvence f (Hz) perioda T 1/f (s) Doba Doba trvání trvání jednoho jednoho cyklu
1.) Periodický pohyb - každý pohyb, který se opakuje v pravidelných intervalech Poet Poet cykl cykl za za sekundu sekundu frekvence f (Hz) perioda T 1/f (s) Doba Doba trvání trvání jednoho jednoho cyklu
Prbh funkce Jaroslav Reichl, 2006
 rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
4.6.6 Složený sériový RLC obvod střídavého proudu
 4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 4, 4605 Minulá hodina: Ohmický odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 4, 4605 Minulá hodina: Ohmický odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
( ) ( ) 2 2 B A B A ( ) ( ) ( ) B A B A B A
 Vzdálenost dvou bod, sted úseky Ž Vzdálenost dvou bod Pi vyšetování vzájemné polohy bod, pímek a rovin lze použít libovolnou vhodn zvolenou soustavu souadnic (afinní). však pi vyšetování metrických vlastností
Vzdálenost dvou bod, sted úseky Ž Vzdálenost dvou bod Pi vyšetování vzájemné polohy bod, pímek a rovin lze použít libovolnou vhodn zvolenou soustavu souadnic (afinní). však pi vyšetování metrických vlastností
6. Střídavý proud. 6. 1. Sinusových průběh
 6. Střídavý proud - je takový proud, který mění v čase svoji velikost a smysl. Nejsnáze řešitelný střídavý proud matematicky i graficky je sinusový střídavý proud, který vyplývá z konstrukce sinusovky.
6. Střídavý proud - je takový proud, který mění v čase svoji velikost a smysl. Nejsnáze řešitelný střídavý proud matematicky i graficky je sinusový střídavý proud, který vyplývá z konstrukce sinusovky.
Efektivní hodnota proudu a nap tí
 Peter Žilavý: Efektivní hodnota proudu a naptí Efektivní hodnota proudu a naptí Peter Žilavý Katedra didaktiky fyziky MFF K Praha Abstrakt Píspvek experimentáln objasuje pojem efektivní hodnota stídavého
Peter Žilavý: Efektivní hodnota proudu a naptí Efektivní hodnota proudu a naptí Peter Žilavý Katedra didaktiky fyziky MFF K Praha Abstrakt Píspvek experimentáln objasuje pojem efektivní hodnota stídavého
DIGITÁLNÍ UČEBNÍ MATERIÁL
 DIGITÁLNÍ UČEBNÍ MATERIÁL škola Střední škola F. D. Roosevelta pro tělesně postižené, Brno, Křižíkova 11 číslo projektu číslo učebního materiálu předmět, tematický celek ročník CZ.1.07/1.5.00/34.1037 VY_32_INOVACE_ZIL_VEL_123_12
DIGITÁLNÍ UČEBNÍ MATERIÁL škola Střední škola F. D. Roosevelta pro tělesně postižené, Brno, Křižíkova 11 číslo projektu číslo učebního materiálu předmět, tematický celek ročník CZ.1.07/1.5.00/34.1037 VY_32_INOVACE_ZIL_VEL_123_12
GE - Vyšší kvalita výuky CZ.1.07/1.5.00/
 Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Téma: Elektřina a magnetismus Autor: Název: Datum vytvoření: 3. 4. 2014
Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Téma: Elektřina a magnetismus Autor: Název: Datum vytvoření: 3. 4. 2014
Obvod střídavého proudu s kapacitou
 Obvod střídavého proudu s kapacitou Na obrázku můžete vidět zapojení obvodu střídavého proudu s kapacitou. Pomocí programů Nové přístroje 2012 a Dvoukanálový osciloskop pro SB Audigy 2012 proveďte daná
Obvod střídavého proudu s kapacitou Na obrázku můžete vidět zapojení obvodu střídavého proudu s kapacitou. Pomocí programů Nové přístroje 2012 a Dvoukanálový osciloskop pro SB Audigy 2012 proveďte daná
FYZIKA II. Petr Praus 9. Přednáška Elektromagnetická indukce (pokračování) Elektromagnetické kmity a střídavé proudy
 FYZIKA II Petr Praus 9. Přednáška Elektromagnetická indukce (pokračování) Elektromagnetické kmity a střídavé proudy Osnova přednášky Energie magnetického pole v cívce Vzájemná indukčnost Kvazistacionární
FYZIKA II Petr Praus 9. Přednáška Elektromagnetická indukce (pokračování) Elektromagnetické kmity a střídavé proudy Osnova přednášky Energie magnetického pole v cívce Vzájemná indukčnost Kvazistacionární
23. Mechanické vlnní. Postupné vlnní:
 3. Mechanické vlnní Mechanické vlnní je dj, pi které ástice pružného prostedí kitají kole svých rovnovážných poloh a tento kitavý pohyb se penáší postupuje) od jedné ástice k druhé vlnní že vzniknout pouze
3. Mechanické vlnní Mechanické vlnní je dj, pi které ástice pružného prostedí kitají kole svých rovnovážných poloh a tento kitavý pohyb se penáší postupuje) od jedné ástice k druhé vlnní že vzniknout pouze
1A Impedance dvojpólu
 1A pedance dvojpólu Cíl úlohy Na praktických příkladech procvičit výpočty odulů a arguentů ipedancí různých dvojpólů. Na základních typech prakticky užívaných obvodů ověřit ěření příou souvislost ezi ipedancí
1A pedance dvojpólu Cíl úlohy Na praktických příkladech procvičit výpočty odulů a arguentů ipedancí různých dvojpólů. Na základních typech prakticky užívaných obvodů ověřit ěření příou souvislost ezi ipedancí
Zadané hodnoty: R L L = 0,1 H. U = 24 V f = 50 Hz
 . STŘÍDAVÉ JEDNOFÁOVÉ OBVODY Příklad.: V elektrickém obvodě sestávajícím ze sériové kombinace rezistoru reálné cívky a kondenzátoru vypočítejte požadované veličiny určete také charakter obvodu a nakreslete
. STŘÍDAVÉ JEDNOFÁOVÉ OBVODY Příklad.: V elektrickém obvodě sestávajícím ze sériové kombinace rezistoru reálné cívky a kondenzátoru vypočítejte požadované veličiny určete také charakter obvodu a nakreslete
Paralelní kompenzace elektrického vedení (Distribuce Elektrické Energie - BDEE)
 FAKULTA ELEKTROTECHNIKY A KOMUNIKANÍCH TECHNOLOGIÍ VYSOKÉ UENÍ TECHNICKÉ V BRN Paralelní kompenzace elektrického vedení (Distribuce Elektrické Energie - BDEE) Autor textu: Ing. Martin Paar, Ph.D. Ing.
FAKULTA ELEKTROTECHNIKY A KOMUNIKANÍCH TECHNOLOGIÍ VYSOKÉ UENÍ TECHNICKÉ V BRN Paralelní kompenzace elektrického vedení (Distribuce Elektrické Energie - BDEE) Autor textu: Ing. Martin Paar, Ph.D. Ing.
Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018. 4. Komplexní čísla
 Moderní technologie ve studiu aplikované fyiky CZ.1.07/..00/07.0018 4. Komplexní čísla Matematickým důvodem pro avedení komplexních čísel ( latinského complexus složený), byla potřeba rošířit množinu (obor)
Moderní technologie ve studiu aplikované fyiky CZ.1.07/..00/07.0018 4. Komplexní čísla Matematickým důvodem pro avedení komplexních čísel ( latinského complexus složený), byla potřeba rošířit množinu (obor)
Elektromagnetický oscilátor
 Elektromagnetický oscilátor Již jsme poznali kmitání mechanického oscilátoru (závaží na pružině) - potenciální energie pružnosti se přeměňuje na kinetickou energii a naopak. T =2 m k Nejjednodušší elektromagnetický
Elektromagnetický oscilátor Již jsme poznali kmitání mechanického oscilátoru (závaží na pružině) - potenciální energie pružnosti se přeměňuje na kinetickou energii a naopak. T =2 m k Nejjednodušší elektromagnetický
Prostedky automatického ízení
 VŠB-TU Ostrava / Prostedky automatického ízení Úloha. Dvoupolohová regulace teploty Meno dne:.. Vypracoval: Petr Osadník Spolupracoval: Petr Ševík Zadání. Zapojte laboratorní úlohu dle schématu.. Zjistte
VŠB-TU Ostrava / Prostedky automatického ízení Úloha. Dvoupolohová regulace teploty Meno dne:.. Vypracoval: Petr Osadník Spolupracoval: Petr Ševík Zadání. Zapojte laboratorní úlohu dle schématu.. Zjistte
Výkon střídavého proudu, účiník
 ng. Jaromír Tyrbach Výkon střídavého proudu, účiník odle toho, kterého prvku obvodu se výkon týká, rozlišujeme u střídavých obvodů výkon činný, jalový a zdánlivý. Ve střídavých obvodech se neustále mění
ng. Jaromír Tyrbach Výkon střídavého proudu, účiník odle toho, kterého prvku obvodu se výkon týká, rozlišujeme u střídavých obvodů výkon činný, jalový a zdánlivý. Ve střídavých obvodech se neustále mění
ELEKTŘINA A MAGNETIZMUS
 EEKTŘINA A MAGNETIZMUS XII Střídavé obvody Obsah STŘÍDAÉ OBODY ZDOJE STŘÍDAÉHO NAPĚTÍ JEDNODUHÉ STŘÍDAÉ OBODY EZISTO JAKO ZÁTĚŽ 3 ÍKA JAKO ZÁTĚŽ 5 3 KONDENZÁTO JAKO ZÁTĚŽ 6 3 SÉIOÝ OBOD 7 3 IMPEDANE 3
EEKTŘINA A MAGNETIZMUS XII Střídavé obvody Obsah STŘÍDAÉ OBODY ZDOJE STŘÍDAÉHO NAPĚTÍ JEDNODUHÉ STŘÍDAÉ OBODY EZISTO JAKO ZÁTĚŽ 3 ÍKA JAKO ZÁTĚŽ 5 3 KONDENZÁTO JAKO ZÁTĚŽ 6 3 SÉIOÝ OBOD 7 3 IMPEDANE 3
3. Kmitočtové charakteristiky
 3. Kmitočtové charakteristiky Po základním seznámení s programem ATP a jeho preprocesorem ATPDraw následuje využití jednotlivých prvků v jednoduchých obvodech. Jednotlivé příklady obvodů jsou uzpůsobeny
3. Kmitočtové charakteristiky Po základním seznámení s programem ATP a jeho preprocesorem ATPDraw následuje využití jednotlivých prvků v jednoduchých obvodech. Jednotlivé příklady obvodů jsou uzpůsobeny
LABORATORNÍ CVIENÍ Stední prmyslová škola elektrotechnická
 Stední prmyslová škola elektrotechnická a Vyšší odborná škola, Pardubice, Karla IV. 13 LABORATORNÍ VIENÍ Stední prmyslová škola elektrotechnická Píjmení: Hladna íslo úlohy: 14 Jméno: Jan Datum mení: 14.
Stední prmyslová škola elektrotechnická a Vyšší odborná škola, Pardubice, Karla IV. 13 LABORATORNÍ VIENÍ Stední prmyslová škola elektrotechnická Píjmení: Hladna íslo úlohy: 14 Jméno: Jan Datum mení: 14.
Identifikátor materiálu: VY_32_INOVACE_351
 dentifikátor materiálu: VY_32_NOVACE_351 Anotace Autor Jazyk Očekávaný výstup Výuková prezentace.na jednotlivých snímcích jsou postupně odkrývány informace, které žák zapisuje či zakresluje do sešitu.
dentifikátor materiálu: VY_32_NOVACE_351 Anotace Autor Jazyk Očekávaný výstup Výuková prezentace.na jednotlivých snímcích jsou postupně odkrývány informace, které žák zapisuje či zakresluje do sešitu.
17. Elektrický proud v polovodiích, užití polovodiových souástek
 17. Elektrický proud v polovodiích, užití polovodiových souástek Polovodie se od kov liší pedevším tím, že mají vtší rezistivitu (10-2.m až 10 9.m) (kovy 10-8.m až 10-6.m). Tato rezistivita u polovodi
17. Elektrický proud v polovodiích, užití polovodiových souástek Polovodie se od kov liší pedevším tím, že mají vtší rezistivitu (10-2.m až 10 9.m) (kovy 10-8.m až 10-6.m). Tato rezistivita u polovodi
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE MASARYKŮV ÚSTAV VYŠŠÍCH STUDIÍ. Katedra inženýrské pedagogiky BAKALÁŘSKÁ PRÁCE
 ČESKÉ VYSOKÉ ČENÍ TEHNKÉ V PZE MSYKŮV ÚSTV VYŠŠÍH STDÍ Katedra inženýrské pedagogiky KÁŘSKÁ PÁE Praha 9 c. Pavel Řezníček ČESKÉ VYSOKÉ ČENÍ TEHNKÉ V PZE MSYKŮV ÚSTV VYŠŠÍH STDÍ Katedra inženýrské pedagogiky
ČESKÉ VYSOKÉ ČENÍ TEHNKÉ V PZE MSYKŮV ÚSTV VYŠŠÍH STDÍ Katedra inženýrské pedagogiky KÁŘSKÁ PÁE Praha 9 c. Pavel Řezníček ČESKÉ VYSOKÉ ČENÍ TEHNKÉ V PZE MSYKŮV ÚSTV VYŠŠÍH STDÍ Katedra inženýrské pedagogiky
Pravdpodobnost výskytu náhodné veliiny na njakém intervalu urujeme na základ tchto vztah: f(x)
 NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
3. Změřte závislost proudu a výkonu na velikosti kapacity zařazené do sériového RLC obvodu.
 Pracovní úkoly. Změřte účiník: a) rezistoru, b) kondenzátoru C = 0 µf) c) cívky. Určete chybu měření. Diskutujte shodu výsledků s teoretickými hodnotami pro ideální prvky. Pro cívku vypočtěte indukčnost
Pracovní úkoly. Změřte účiník: a) rezistoru, b) kondenzátoru C = 0 µf) c) cívky. Určete chybu měření. Diskutujte shodu výsledků s teoretickými hodnotami pro ideální prvky. Pro cívku vypočtěte indukčnost
Základy elektrotechniky
 Základy elektrotechniky 5. přednáška Elektrický výkon a energie 1 Základní pojmy Okamžitá hodnota výkonu je deinována: p = u.i [W; V, A] spotřebičová orientace - napětí i proud na impedanci Z mají souhlasný
Základy elektrotechniky 5. přednáška Elektrický výkon a energie 1 Základní pojmy Okamžitá hodnota výkonu je deinována: p = u.i [W; V, A] spotřebičová orientace - napětí i proud na impedanci Z mají souhlasný
ELEKTROMAGNETICKÉ POLE
 ELEKTROMAGNETICKÉ POLE 1. Magnetická síla působící na náboj v magnetickém poli Fyzikové Lorentz a Ampér zjistili, že silové působení magnetického pole na náboj Q, závisí na: 1. velikosti náboje Q, 2. relativní
ELEKTROMAGNETICKÉ POLE 1. Magnetická síla působící na náboj v magnetickém poli Fyzikové Lorentz a Ampér zjistili, že silové působení magnetického pole na náboj Q, závisí na: 1. velikosti náboje Q, 2. relativní
Určeno pro posluchače bakalářských studijních programů FS
 rčeno pro posluchače bakalářských studijních programů FS 3. STŘÍDAVÉ JEDNOFÁOVÉ OBVODY Příklad 3.: V obvodě sestávajícím ze sériové kombinace rezistoru, reálné cívky a kondenzátoru vypočítejte požadované
rčeno pro posluchače bakalářských studijních programů FS 3. STŘÍDAVÉ JEDNOFÁOVÉ OBVODY Příklad 3.: V obvodě sestávajícím ze sériové kombinace rezistoru, reálné cívky a kondenzátoru vypočítejte požadované
W1- Měření impedančního chování reálných elektronických součástek
 Návod na laboratorní úlohu Laboratoře oboru I W1- Měření impedančního chování reálných elektronických součástek Úloha W1 1 / 6 1. Úvod Impedance Z popisuje úhrnný "zdánlivý odpor" prvků obvodu při průchodu
Návod na laboratorní úlohu Laboratoře oboru I W1- Měření impedančního chování reálných elektronických součástek Úloha W1 1 / 6 1. Úvod Impedance Z popisuje úhrnný "zdánlivý odpor" prvků obvodu při průchodu
1.1. Základní pojmy 1.2. Jednoduché obvody se střídavým proudem
 Praktické příklady z Elektrotechniky. Střídavé obvody.. Základní pojmy.. Jednoduché obvody se střídavým proudem Příklad : Stanovte napětí na ideálním kondenzátoru s kapacitou 0 µf, kterým prochází proud
Praktické příklady z Elektrotechniky. Střídavé obvody.. Základní pojmy.. Jednoduché obvody se střídavým proudem Příklad : Stanovte napětí na ideálním kondenzátoru s kapacitou 0 µf, kterým prochází proud
TRANSFORMÁTORY Ing. Eva Navrátilová
 STŘEDNÍ ŠOLA, HAVÍŘOV-ŠUMBAR, SÝOROVA 1/613 příspěvková organizace TRANSFORMÁTORY Ing. Eva Navrátilová - 1 - Transformátor jednofázový = netočivý elektrický stroj, který využívá elektromagnetickou indukci
STŘEDNÍ ŠOLA, HAVÍŘOV-ŠUMBAR, SÝOROVA 1/613 příspěvková organizace TRANSFORMÁTORY Ing. Eva Navrátilová - 1 - Transformátor jednofázový = netočivý elektrický stroj, který využívá elektromagnetickou indukci
Přijímací zkouška na navazující magisterské studium Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy
 Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Digitální učební materiál
 Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
NEWTONOVY POHYBOVÉ ZÁKONY
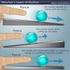 NEWTONOVY POHYBOVÉ ZÁKONY Metodika Mgr. Michal Schovánek kvten 2010 Newtonovy pohybové zákony patí mezi nejobtížnjší kapitoly stedoškolské mechaniky. Popisované situace jsou sice jednoduše demonstrovatelné,
NEWTONOVY POHYBOVÉ ZÁKONY Metodika Mgr. Michal Schovánek kvten 2010 Newtonovy pohybové zákony patí mezi nejobtížnjší kapitoly stedoškolské mechaniky. Popisované situace jsou sice jednoduše demonstrovatelné,
2. STŘÍDAVÉ JEDNOFÁZOVÉ OBVODY
 2. STŘÍDAVÉ JEDNOFÁZOVÉ OBVODY Příklad 2.1: V obvodě sestávajícím ze sériové kombinace rezistoru reálné cívky a kondenzátoru vypočítejte požadované veličiny určete také charakter obvodu a nakreslete fázorový
2. STŘÍDAVÉ JEDNOFÁZOVÉ OBVODY Příklad 2.1: V obvodě sestávajícím ze sériové kombinace rezistoru reálné cívky a kondenzátoru vypočítejte požadované veličiny určete také charakter obvodu a nakreslete fázorový
Základní otázky pro teoretickou část zkoušky.
 Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Obvodové prvky a jejich
 Obvodové prvky a jejich parametry Ing. Martin Černík, Ph.D. Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace. Elektrický obvod Uspořádaný systém elektrických prvků a vodičů sloužící
Obvodové prvky a jejich parametry Ing. Martin Černík, Ph.D. Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace. Elektrický obvod Uspořádaný systém elektrických prvků a vodičů sloužící
Kapacita, indukčnost; kapacitor-kondenzátor, induktor-cívka
 Kapacita, indukčnost; kapacitor-kondenzátor, induktor-cívka Kondenzátor je schopen uchovat energii v podobě elektrického náboje Q. Kapacita C se udává ve Faradech [F]. Kapacita je úměrná ploše elektrod
Kapacita, indukčnost; kapacitor-kondenzátor, induktor-cívka Kondenzátor je schopen uchovat energii v podobě elektrického náboje Q. Kapacita C se udává ve Faradech [F]. Kapacita je úměrná ploše elektrod
=2πf. i(t)=im.sin(ωt)
 1. b Střídavý proud, je termín označující elektrický proud, jehož směr se periodicky střídá. při běžné síťové frekvenci 50 Hz se směr proudu změní každých 10 milisekund. http://cs.wikipedia.org/wiki/st%c5%99%c3%addav%c3%bd_proud
1. b Střídavý proud, je termín označující elektrický proud, jehož směr se periodicky střídá. při běžné síťové frekvenci 50 Hz se směr proudu změní každých 10 milisekund. http://cs.wikipedia.org/wiki/st%c5%99%c3%addav%c3%bd_proud
Střední průmyslová škola elektrotechnická a informačních technologií Brno
 Střední průmyslová škola elektrotechnická a informačních technologií Brno Číslo a název projektu: CZ.1.07/1.5.00/34.0521 Investice do vzdělání nesou nejvyšší úrok Autor: Ing. Bohumír Jánoš Tématická sada:
Střední průmyslová škola elektrotechnická a informačních technologií Brno Číslo a název projektu: CZ.1.07/1.5.00/34.0521 Investice do vzdělání nesou nejvyšší úrok Autor: Ing. Bohumír Jánoš Tématická sada:
teorie elektronických obvodů Jiří Petržela analýza obvodů s regulárními prvky
 Jiří Petržela příklad pro příčkový filtr na obrázku napište aditanční atici etodou uzlových napětí zjistěte přenos filtru identifikujte tp a řád filtru Obr. : Příklad na příčkový filtr. aditanční atice
Jiří Petržela příklad pro příčkový filtr na obrázku napište aditanční atici etodou uzlových napětí zjistěte přenos filtru identifikujte tp a řád filtru Obr. : Příklad na příčkový filtr. aditanční atice
FYZIKA 3. ROČNÍK. Vlastní kmitání oscilátoru. Kmitavý pohyb. Kinematika kmitavého pohybu. y m
 Vlastní itání oscilátoru Kitavý pohb Kitání periodicý děj zařízení oná opaovaně stejný pohb a periodic se vrací do určitého stavu. oscilátor zařízení, teré ůže volně itat (závaží na pružině, vadlo) it
Vlastní itání oscilátoru Kitavý pohb Kitání periodicý děj zařízení oná opaovaně stejný pohb a periodic se vrací do určitého stavu. oscilátor zařízení, teré ůže volně itat (závaží na pružině, vadlo) it
FYZIKA II. Petr Praus 10. Přednáška Elektromagnetické kmity a střídavé proudy (pokračování)
 FYZIKA II Petr Praus 10. Přednáška Elektromagnetické kmity a střídavé proudy (pokračování) Osnova přednášky činitel jakosti, vektorové diagramy v komplexní rovině Sériový RLC obvod - fázový posuv, rezonance
FYZIKA II Petr Praus 10. Přednáška Elektromagnetické kmity a střídavé proudy (pokračování) Osnova přednášky činitel jakosti, vektorové diagramy v komplexní rovině Sériový RLC obvod - fázový posuv, rezonance
Fyzikální praktikum...
 Kabinet výuky obecné fyziky, UK MFF Fyzikální praktikum... Úloha č.... Název úlohy:... Jméno:...Datum měření:... Datum odevzdání:... Připomínky opravujícího: Možný počet bodů Udělený počet bodů Práce při
Kabinet výuky obecné fyziky, UK MFF Fyzikální praktikum... Úloha č.... Název úlohy:... Jméno:...Datum měření:... Datum odevzdání:... Připomínky opravujícího: Možný počet bodů Udělený počet bodů Práce při
Pídavný modul rozvaha lze vyvolat z hlavní nabídky po stisku tlaítka Výkazy / pídavné moduly.
 Výkaz rozvaha Pídavný modul rozvaha lze vyvolat z hlavní nabídky po stisku tlaítka Výkazy / pídavné moduly. Po spuštní modulu se zobrazí základní okno výkazu: V tabulce se zobrazují sloupce výkazu. Ve
Výkaz rozvaha Pídavný modul rozvaha lze vyvolat z hlavní nabídky po stisku tlaítka Výkazy / pídavné moduly. Po spuštní modulu se zobrazí základní okno výkazu: V tabulce se zobrazují sloupce výkazu. Ve
Integrovaná střední škola, Sokolnice 496
 Název projektu: Moderní škola Integrovaná střední škola, Sokolnice 496 Registrační číslo: CZ.1.07/1.5.00/34.0467 Název klíčové aktivity: V/2 - Inovace a zkvalitnění výuky směřující k rozvoji odborných
Název projektu: Moderní škola Integrovaná střední škola, Sokolnice 496 Registrační číslo: CZ.1.07/1.5.00/34.0467 Název klíčové aktivity: V/2 - Inovace a zkvalitnění výuky směřující k rozvoji odborných
1 Motory s permanentními magnety
 1 Motory s permanentními magnety Obr. 1 Píný ez synchronním motorem s permanentními magnety 1. kw, p=4 Motory s permanentními magnety jsou synchronní motory, které místo budicího vinutí pro vytvoení magnetického
1 Motory s permanentními magnety Obr. 1 Píný ez synchronním motorem s permanentními magnety 1. kw, p=4 Motory s permanentními magnety jsou synchronní motory, které místo budicího vinutí pro vytvoení magnetického
Identifikátor materiálu: VY_32_INOVACE_352
 dentifikátor materiálu: VY_32_NOVACE_352 Anotace Autor Jazyk Výuková prezentace.na jednotlivých snímcích jsou postupně odkrývány informace, které žák zapisuje či zakresluje do sešitu. ng. Vadim Starý Čeština
dentifikátor materiálu: VY_32_NOVACE_352 Anotace Autor Jazyk Výuková prezentace.na jednotlivých snímcích jsou postupně odkrývány informace, které žák zapisuje či zakresluje do sešitu. ng. Vadim Starý Čeština
1 Elektrotechnika 1. 11:00 hod. R. R = = = Metodou postupného zjednodušování vypočtěte proudy všech větví uvedeného obvodu. U = 60 V. Řešení.
 A : hod. Elektrotechnika Metodou postupného zjednodušování vypočtěte proudy všech větví uvedeného obvodu. R I I 3 R 3 R = 5 Ω, R = Ω, R 3 = Ω, R 4 = Ω, R 5 = Ω, = 6 V. I R I 4 I 5 R 4 R 5 R. R R = = Ω,
A : hod. Elektrotechnika Metodou postupného zjednodušování vypočtěte proudy všech větví uvedeného obvodu. R I I 3 R 3 R = 5 Ω, R = Ω, R 3 = Ω, R 4 = Ω, R 5 = Ω, = 6 V. I R I 4 I 5 R 4 R 5 R. R R = = Ω,
Czech Technical University in Prague Faculty of Electrical Engineering. Fakulta elektrotechnická. České vysoké učení technické v Praze.
 Nejprve několik fyzikálních analogií úvodem Rezonance Rezonance je fyzikálním jevem, kdy má systém tendenci kmitat s velkou amplitudou na určité frekvenci, kdy malá budící síla může vyvolat vibrace s velkou
Nejprve několik fyzikálních analogií úvodem Rezonance Rezonance je fyzikálním jevem, kdy má systém tendenci kmitat s velkou amplitudou na určité frekvenci, kdy malá budící síla může vyvolat vibrace s velkou
3.1.3 Rychlost a zrychlení harmonického pohybu
 3.1.3 Rychlost a zrychlení haronického pohybu Předpoklady: 312 Kroě dráhy (výchylky) popisujee pohyb i poocí dalších dvou veličin: rychlosti a zrychlení. Jak budou vypadat jejich rovnice? Společný graf
3.1.3 Rychlost a zrychlení haronického pohybu Předpoklady: 312 Kroě dráhy (výchylky) popisujee pohyb i poocí dalších dvou veličin: rychlosti a zrychlení. Jak budou vypadat jejich rovnice? Společný graf
Základy elektrotechniky řešení příkladů
 Název vzdělávacího programu Základy elektrotechniky řešení příkladů rčeno pro potřeby dalšího vzdělávání pedagogických pracovníků středních odborných škol Autor ng. Petr Vavřiňák Název a sídlo školy Střední
Název vzdělávacího programu Základy elektrotechniky řešení příkladů rčeno pro potřeby dalšího vzdělávání pedagogických pracovníků středních odborných škol Autor ng. Petr Vavřiňák Název a sídlo školy Střední
GE - Vyšší kvalita výuky CZ.1.07/1.5.00/
 Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Téma: Elektřina a magnetismus Autor: Název: Datum vytvoření: 25. 3. 2014
Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Téma: Elektřina a magnetismus Autor: Název: Datum vytvoření: 25. 3. 2014
STŘÍDAVÝ ELEKTRICKÝ PROUD Výkon střídavého proudu TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY.
 STŘÍDAVÝ ELEKTRKÝ PROD Výkon střídavého proudu TENTO PROJEKT JE SPOLFNANOVÁN EVROPSKÝM SOÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPBLKY. VÝKON A PRÁE STŘÍDAVÉHO PROD = L - nebo - L Pokud strany troúhelníku
STŘÍDAVÝ ELEKTRKÝ PROD Výkon střídavého proudu TENTO PROJEKT JE SPOLFNANOVÁN EVROPSKÝM SOÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPBLKY. VÝKON A PRÁE STŘÍDAVÉHO PROD = L - nebo - L Pokud strany troúhelníku
STŘÍDAVÝ ELEKTRICKÝ PROUD Trojfázová soustava TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY.
 STŘÍDAVÝ ELEKTRICKÝ PROUD Trojfázová soustava TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Vznik trojfázového napětí Průběh naznačený na obrázku je jednofázový,
STŘÍDAVÝ ELEKTRICKÝ PROUD Trojfázová soustava TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Vznik trojfázového napětí Průběh naznačený na obrázku je jednofázový,
Zbytky zákaznického materiálu
 Autoi: V Plzni 31.08.2010 Obsah ZBYTKOVÝ MATERIÁL... 3 1.1 Materiálová žádanka na peskladnní zbytk... 3 1.2 Skenování zbytk... 7 1.3 Vývozy zbytk ze skladu/makulatura... 7 2 1 Zbytkový materiál V souvislosti
Autoi: V Plzni 31.08.2010 Obsah ZBYTKOVÝ MATERIÁL... 3 1.1 Materiálová žádanka na peskladnní zbytk... 3 1.2 Skenování zbytk... 7 1.3 Vývozy zbytk ze skladu/makulatura... 7 2 1 Zbytkový materiál V souvislosti
Ele 1 elektromagnetická indukce, střídavý proud, základní veličiny, RLC v obvodu střídavého proudu
 Předmět: Ročník: Vytvořil: Datum: ELEKTROTECHNIKA PRVNÍ ZDENĚK KOVAL Název zpracovaného celku: 30. 9. 203 Ele elektromagnetická indukce, střídavý proud, základní veličiny, RLC v obvodu střídavého proudu
Předmět: Ročník: Vytvořil: Datum: ELEKTROTECHNIKA PRVNÍ ZDENĚK KOVAL Název zpracovaného celku: 30. 9. 203 Ele elektromagnetická indukce, střídavý proud, základní veličiny, RLC v obvodu střídavého proudu
Teoretické základy vakuové techniky
 Vakuová technika Teoretické základy vakuové techniky tlak plynu tepeln! pohyb molekul st"ední volná dráha molekul proud#ní plynu vakuová vodivost $erpání plyn% ze systém% S klesajícím tlakem se chování
Vakuová technika Teoretické základy vakuové techniky tlak plynu tepeln! pohyb molekul st"ední volná dráha molekul proud#ní plynu vakuová vodivost $erpání plyn% ze systém% S klesajícím tlakem se chování
3.2.2 Rovnice postupného vlnění
 3.. Rovnice postupného vlnění Předpoklady: 310, 301 Chcee najít rovnici, která bude udávat výšku vlny v libovolné okažiku i libovolné bodě (v jedno okažiku je v různých ístech různá výška vlny). Veličiny
3.. Rovnice postupného vlnění Předpoklady: 310, 301 Chcee najít rovnici, která bude udávat výšku vlny v libovolné okažiku i libovolné bodě (v jedno okažiku je v různých ístech různá výška vlny). Veličiny
3.2.2 Rovnice postupného vlnění
 3.. Rovnice postupného vlnění Předpoklady: 310, 301 Chcee najít rovnici, která bude udávat výšku vlny v libovolné okažiku i libovolné bodě (v jedno okažiku je v různých ístech různá výška vlny). Veličiny
3.. Rovnice postupného vlnění Předpoklady: 310, 301 Chcee najít rovnici, která bude udávat výšku vlny v libovolné okažiku i libovolné bodě (v jedno okažiku je v různých ístech různá výška vlny). Veličiny
ELEKTŘINA A MAGNETIZMUS kontrolní otázky a odpovědi
 ELEKTŘINA A MAGNETIZMUS kontrolní otázky a odpovědi Peter Dourmashkin MIT 26, překlad: Vladimír Scholtz (27) Obsah KONTROLNÍ OTÁZKY A ODPOVĚDI 2 OTÁZKA 61: RL OBVOD 2 OTÁZKA 62: LC OBVOD 2 OTÁZKA 63: LC
ELEKTŘINA A MAGNETIZMUS kontrolní otázky a odpovědi Peter Dourmashkin MIT 26, překlad: Vladimír Scholtz (27) Obsah KONTROLNÍ OTÁZKY A ODPOVĚDI 2 OTÁZKA 61: RL OBVOD 2 OTÁZKA 62: LC OBVOD 2 OTÁZKA 63: LC
NESTACIONÁRNÍ MAGNETICKÉ POLE. Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník
 NESTACIONÁRNÍ MAGNETICKÉ POLE Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník Nestacionární magnetické pole Vektor magnetické indukce v čase mění směr nebo velikost. a. nepohybující
NESTACIONÁRNÍ MAGNETICKÉ POLE Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník Nestacionární magnetické pole Vektor magnetické indukce v čase mění směr nebo velikost. a. nepohybující
PŘECHODOVÝ JEV V RC OBVODU
 PŘEHODOVÝ JEV V OBVOD Pracovní úkoly:. Odvoďte vztah popisující časovou závislost elektrického napětí na kondenzátoru při vybíjení. 2. Měřením určete nabíjecí a vybíjecí křivku kondenzátoru. 3. rčete nabíjecí
PŘEHODOVÝ JEV V OBVOD Pracovní úkoly:. Odvoďte vztah popisující časovou závislost elektrického napětí na kondenzátoru při vybíjení. 2. Měřením určete nabíjecí a vybíjecí křivku kondenzátoru. 3. rčete nabíjecí
Kapitola 2. o a paprsek sil lze ztotožnit s osou x (obr.2.1). sil a velikost rovnou algebraickému součtu sil podle vztahu R = F i, (2.
 Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
1. Co je elektrický proud? Elektrický proud je projev pohybu elektrického náboje. Vyjadujeme ho jako celkový náboj, který projde za jednotku asu.
 1. 1. Co je elektrický proud? Elektrický proud je projev pohybu elektrického náboje. Vyjadujeme ho jako celkový náboj, který projde za jednotku asu. Q I [A] t 2. Co ovlivuje velikost odporu? Velikost odporu
1. 1. Co je elektrický proud? Elektrický proud je projev pohybu elektrického náboje. Vyjadujeme ho jako celkový náboj, který projde za jednotku asu. Q I [A] t 2. Co ovlivuje velikost odporu? Velikost odporu
Obvody střídavého proudu: zobrazování a základní veličiny
 Název projektu: Automatizace výrobních procesů ve strojírenství a řemeslech Registrační číslo: CZ.1.07/1.1.30/01.0038 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 109 Tento projekt
Název projektu: Automatizace výrobních procesů ve strojírenství a řemeslech Registrační číslo: CZ.1.07/1.1.30/01.0038 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 109 Tento projekt
Nelineární obvody. V nelineárních obvodech však platí Kirchhoffovy zákony.
 Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
GYMNÁZIUM CHEB. SEMINÁRNÍ PRÁCE Grafy funkcí sbírka ešených úloh. Radek HÁJEK, 8.A Radka JIROUŠKOVÁ, 8.A Cheb, 2006 Petr NEJTEK, 8.
 GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE Grafy funkcí sbírka ešených úloh Radek HÁJEK, 8.A Radka JIROUŠKOVÁ, 8.A Cheb, 006 Petr NEJTEK, 8.A Prohlášení Prohlašujeme, že jsme seminární práci na téma: Grafy funkcí
GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE Grafy funkcí sbírka ešených úloh Radek HÁJEK, 8.A Radka JIROUŠKOVÁ, 8.A Cheb, 006 Petr NEJTEK, 8.A Prohlášení Prohlašujeme, že jsme seminární práci na téma: Grafy funkcí
Identifikátor materiálu: VY_32_INOVACE_355
 Identifikátor materiálu: VY_32_INOVACE_355 Anotace Autor Jazyk Očekávaný výstup Výuková prezentace.na jednotlivých snímcích jsou postupně odkrývány informace, které žák zapisuje či zakresluje do sešitu.
Identifikátor materiálu: VY_32_INOVACE_355 Anotace Autor Jazyk Očekávaný výstup Výuková prezentace.na jednotlivých snímcích jsou postupně odkrývány informace, které žák zapisuje či zakresluje do sešitu.
[Otázky Autoelektrikář + Mechanik elektronických zařízení 1.část] Na rezistoru je napětí 25 V a teče jím proud 50 ma. Rezistor má hodnotu.
![[Otázky Autoelektrikář + Mechanik elektronických zařízení 1.část] Na rezistoru je napětí 25 V a teče jím proud 50 ma. Rezistor má hodnotu. [Otázky Autoelektrikář + Mechanik elektronických zařízení 1.část] Na rezistoru je napětí 25 V a teče jím proud 50 ma. Rezistor má hodnotu.](/thumbs/73/69077176.jpg) [Otázky Autoelektrikář + Mechanik elektronických zařízení 1.část] 04.01.01 Na rezistoru je napětí 5 V a teče jím proud 25 ma. Rezistor má hodnotu. A) 100 ohmů B) 150 ohmů C) 200 ohmů 04.01.02 Na rezistoru
[Otázky Autoelektrikář + Mechanik elektronických zařízení 1.část] 04.01.01 Na rezistoru je napětí 5 V a teče jím proud 25 ma. Rezistor má hodnotu. A) 100 ohmů B) 150 ohmů C) 200 ohmů 04.01.02 Na rezistoru
Měření závislosti indukčnosti cívky (Distribuce elektrické energie - BDEE)
 FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Měření závislosti indukčnosti cívky (Distribuce elektrické energie - BDEE) Autoři textu: Ing. Jan Varmuža Květen 2013 epower
FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Měření závislosti indukčnosti cívky (Distribuce elektrické energie - BDEE) Autoři textu: Ing. Jan Varmuža Květen 2013 epower
MEG jako blokující m ni s permanentním magnetem
 1 MEG jako blokující ni s peranentní agnete (c) Ing. Ladislav Kopecký, bezen 2016 Tento lánek navazuje na lánek MEG jako dvojinný blokující ni. Pro pochopení principu je nutné chápat, jak funguje blokující
1 MEG jako blokující ni s peranentní agnete (c) Ing. Ladislav Kopecký, bezen 2016 Tento lánek navazuje na lánek MEG jako dvojinný blokující ni. Pro pochopení principu je nutné chápat, jak funguje blokující
LABORATORNÍ CVIENÍ Stední prmyslová škola elektrotechnická
 Stední prmyslová škola elektrotechnická a Vyšší odborná škola, Pardubice, Karla IV. 13 LABORATORNÍ CVIENÍ Stední prmyslová škola elektrotechnická Píjmení: Hladna íslo úlohy: 3 Jméno: Jan Datum mení: 10.
Stední prmyslová škola elektrotechnická a Vyšší odborná škola, Pardubice, Karla IV. 13 LABORATORNÍ CVIENÍ Stední prmyslová škola elektrotechnická Píjmení: Hladna íslo úlohy: 3 Jméno: Jan Datum mení: 10.
22. Mechanické a elektromagnetické kmity
 . Mechanicé a eletroagneticé ity. Mechanicé ity Oscilátor tleso, teré je schoné itat, (itání zsobuje síla ružnosti, nebo tíhová síla, i itání se eriodicy ní otenciální energie oscilátoru v energii ineticou
. Mechanicé a eletroagneticé ity. Mechanicé ity Oscilátor tleso, teré je schoné itat, (itání zsobuje síla ružnosti, nebo tíhová síla, i itání se eriodicy ní otenciální energie oscilátoru v energii ineticou
Návrh realizace transformátoru Thane C. Heinse IV.
 1 Návrh realizace transformátoru Thane C. Heinse IV. Ing. Ladislav Kopecký, ervenec 2016 Ve tvrté ásti lánku budeme navrhovat TH transformátor s topologií UUI s konkrétními typy jader UU a I, p emž použijeme
1 Návrh realizace transformátoru Thane C. Heinse IV. Ing. Ladislav Kopecký, ervenec 2016 Ve tvrté ásti lánku budeme navrhovat TH transformátor s topologií UUI s konkrétními typy jader UU a I, p emž použijeme
u = = B. l = B. l. v [V; T, m, m. s -1 ]
![u = = B. l = B. l. v [V; T, m, m. s -1 ] u = = B. l = B. l. v [V; T, m, m. s -1 ]](/thumbs/51/28180013.jpg) 5. Elektromagnetická indukce je děj, kdy ve vodiči, který se pohybuje v magnetickém poli a protíná magnetické, indukční čáry, vzniká elektrické napětí. Vodič se stává zdrojem a je to nejrozšířenější způsob
5. Elektromagnetická indukce je děj, kdy ve vodiči, který se pohybuje v magnetickém poli a protíná magnetické, indukční čáry, vzniká elektrické napětí. Vodič se stává zdrojem a je to nejrozšířenější způsob
TopoL sbr bod pro AAT
 TopoL sbr bod pro AAT technologický postup Jindich Hoda Ph.D. únor 2005 Pi práci v SW TopoL se budete pi sbru bod pro aerotriangulaci ídit následujícím pracovním postupem, viz obrázek 1. Obr. 1 pracovní
TopoL sbr bod pro AAT technologický postup Jindich Hoda Ph.D. únor 2005 Pi práci v SW TopoL se budete pi sbru bod pro aerotriangulaci ídit následujícím pracovním postupem, viz obrázek 1. Obr. 1 pracovní
TROJFÁZOVÝ OBVOD SE SPOT EBI EM ZAPOJENÝM DO HV ZDY A DO TROJÚHELNÍKU
 TROJFÁZOVÝ OBVOD E POT EBI EM ZAPOJENÝM DO HV ZDY A DO TROJÚHELNÍKU Návod do m ení Ing. Vít zslav týskala, Ing. Václav Kolá Únor 2000 poslední úprava leden 2014 1 M ení v trojázových obvodech Cíl m ení:
TROJFÁZOVÝ OBVOD E POT EBI EM ZAPOJENÝM DO HV ZDY A DO TROJÚHELNÍKU Návod do m ení Ing. Vít zslav týskala, Ing. Václav Kolá Únor 2000 poslední úprava leden 2014 1 M ení v trojázových obvodech Cíl m ení:
OBVOD S INDUKČNOSTÍ A KAPACITOU
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr.Milan Staněk MGV_F_SS_2S3_D09_Z_ELMAG_Obvod_s_indukcnosti_a_kapacit ou_pl Člověk a příroda Fyzika Netacionární
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr.Milan Staněk MGV_F_SS_2S3_D09_Z_ELMAG_Obvod_s_indukcnosti_a_kapacit ou_pl Člověk a příroda Fyzika Netacionární
Ústav fyziky a měřicí techniky Laboratoř chemických vodivostních senzorů. Měření elektrofyzikálních parametrů krystalových rezonátorů
 Ústav fyziky a měřicí techniky Laboratoř chemických vodivostních senzorů Návod na laboratorní úlohu Měření elektrofyzikálních parametrů krystalových rezonátorů . Úvod Krystalový rezonátor (krystal) je
Ústav fyziky a měřicí techniky Laboratoř chemických vodivostních senzorů Návod na laboratorní úlohu Měření elektrofyzikálních parametrů krystalových rezonátorů . Úvod Krystalový rezonátor (krystal) je
R O V N O B Ž N Í K (2 HODINY)
 R O V N O B Ž N Í K (2 HODINY)? Co to vlastn rovnobžník je? Na obrázku je dopravní znaka, která íká, že vzdálenost k železninímu pejezdu je 1 m (dva pruhy, jeden pruh pedstavuje vzdálenost 80 m): Pozorn
R O V N O B Ž N Í K (2 HODINY)? Co to vlastn rovnobžník je? Na obrázku je dopravní znaka, která íká, že vzdálenost k železninímu pejezdu je 1 m (dva pruhy, jeden pruh pedstavuje vzdálenost 80 m): Pozorn
2. Určete optimální pracovní bod a účinnost solárního článku při dané intenzitě osvětlení, stanovte R SH, R SO, FF, MPP
 FP 5 Měření paraetrů solárních článků Úkoly : 1. Naěřte a poocí počítače graficky znázorněte voltapérovou charakteristiku solárního článku. nalyzujte vliv různé intenzity osvětlení, vliv sklonu solárního
FP 5 Měření paraetrů solárních článků Úkoly : 1. Naěřte a poocí počítače graficky znázorněte voltapérovou charakteristiku solárního článku. nalyzujte vliv různé intenzity osvětlení, vliv sklonu solárního
Symbolicko - komplexní metoda II Sériové zapojení prvků R, L a C
 Symboliko - komplexní metoda Sériové zapojení prvků, a Použité zdroje: Blahove, A.: Elektrotehnika, nformatorium spol.s r.o., Praha 2005 Wojnar, J.: áklady elektrotehniky, Tribun E s.r.o., Brno 2009 http://hyperphysis.phy-astr.gsu.edu
Symboliko - komplexní metoda Sériové zapojení prvků, a Použité zdroje: Blahove, A.: Elektrotehnika, nformatorium spol.s r.o., Praha 2005 Wojnar, J.: áklady elektrotehniky, Tribun E s.r.o., Brno 2009 http://hyperphysis.phy-astr.gsu.edu
2. Posouzení efektivnosti investice do malé vtrné elektrárny
 2. Posouzení efektvnost nvestce do malé vtrné elektrárny Cíle úlohy: Posoudt ekonomckou výhodnost proektu malé vtrné elektrárny pomocí základních metod hodnocení efektvnost nvestních proekt ako sou metoda
2. Posouzení efektvnost nvestce do malé vtrné elektrárny Cíle úlohy: Posoudt ekonomckou výhodnost proektu malé vtrné elektrárny pomocí základních metod hodnocení efektvnost nvestních proekt ako sou metoda
Obvod střídavého proudu s indukčností
 Obvod střídavého proudu s indukčností Na obrázku můžete vidět zapojení obvodu střídavého proudu s indukčností. Pomocí programů Nové přístroje 2012 a Dvoukanálový osciloskop pro SB Audigy 2012 proveďte
Obvod střídavého proudu s indukčností Na obrázku můžete vidět zapojení obvodu střídavého proudu s indukčností. Pomocí programů Nové přístroje 2012 a Dvoukanálový osciloskop pro SB Audigy 2012 proveďte
Elektřina a magnetizmus závěrečný test
 DUM Základy přírodních věd DUM III/2-T3-20 Téma: závěrečný test Střední škola Rok: 2012 2013 Varianta: TEST - A Zpracoval: Mgr. Pavel Hrubý a Mgr. Josef Kormaník TEST Elektřina a magnetizmus závěrečný
DUM Základy přírodních věd DUM III/2-T3-20 Téma: závěrečný test Střední škola Rok: 2012 2013 Varianta: TEST - A Zpracoval: Mgr. Pavel Hrubý a Mgr. Josef Kormaník TEST Elektřina a magnetizmus závěrečný
