Michal Sláma. Pythagorejské trojúhelníky Pythagorean triangles
|
|
|
- Jiří Havlíček
- před 7 lety
- Počet zobrazení:
Transkript
1 Univerzita Karlova v Praze Pedagogická fakulta BAKALÁŘSKÁ PRÁCE Michal Sláma Pythagorejské trojúhelníky Pythagorean triangles Katedra matematiky a didaktiky matematiky Vedoucí bakalářské práce: RNDr. Antonín Jančařík, Ph.D. Studijní program: Specializace v pedagogice, Matematika se zaměřením na vzdělávání Informační technologie se zaměřením na vzdělávání 2015
2 Prohlašuji, že jsem bakalářskou práci na téma Pythagorejské trojúhelníky vypracoval pod vedením vedoucího bakalářské práce samostatně za použití v práci uvedených pramenů a literatury. Dále prohlašuji, že tato bakalářská práce nebyla využita k získání jiného nebo stejného titulu. V Praze dne Michal Sláma
3 Rád bych touto cestou vyjádřil poděkování RNDr. Antonínu Jančaříkovi, Ph.D., za jeho cenné rady, trpělivost při vedení mé bakalářské práce a za vstřícnost a pomoc při získání potřebných informací a podkladů. V Praze dne Michal Sláma
4 Název: Pythagorejské trojúhelníky Autor: Michal Sláma Katedra: Katedra matematiky a didaktiky matematiky Vedoucí bakalářské práce: RNDr. Antonín Jančařík, Ph.D. Abstrakt: Práce se zabývá praktickými úlohami s pythagorejskými trojúhelníky. V první části se věnuje různým druhům odvození parametrizací pythagorejských trojúhelníků. Další části se věnují odvození vlastností délek stran a poloměrů vepsaných a připsaných kružnic v nich. V závěru se pomocí Heronovských trojúhelníků a rozkladů na pythagorejské trojúhelníky částečně řeší úloha o pythagorejském nebo Heronovském trojúhelníku, kde všechny výšky jsou celá čísla. V poslední části práce jsou poskytnuty seznamy pythagorejských a Heronovskýchh trojúhelníků, které mohou být využity k tvorbě školních úloh. Klíčová slova: Pythagorejské trojúhelníky, Heronovské trojúhelníky, vepsané a připsané kružnice, celočíselné výšky
5 Title: Pythagorean triangles Author: Michal Sláma Department: Department of mathematics and mathematical education Supervisor: RNDr. Antonín Jančařík, Ph.D. Abstract: The thesis considers usable problems concerning pythagorean triangles. In the first part, there is described an expression of a parametrization of pythagorean triangles. Next parts are dedicated to an expression of properties of edges and radii of the incircle and excircles. Next chapters describe Heronian triangles and their decomposition to pythagorean triangles, as a way to solution of the problem of a Heronian triangle where all heights are integer numbers. In addition are given some examples of triangles for school practice. Keywords: Pythagorean triangles, Heronian triangles, incircle and excircles, triangle heights as integer numbers
6 Obsah Úvod 10 1 Popis a generování Základní definice Klasický zápis pythagorejského trojúhelníka Nedostatko-přebytkové značení Maticové stromy Vlastnosti stran v pythagorejských trojúhelnících Odlišná parita odvěsen Dělitelnost délek stran čtyřmi Dělitelnost délek stran třemi Dělitelnost délek stran pěti Kružnice vepsané a připsané Poloměr kružnice vepsané a kružnic připsaných Primitivní pythagorejské trojúhelníky odvozené z poloměru vepsané kružnice Generování všech trojúhelníků s daným poloměrem kružnice vepsané Poloměr vepsané kružnice ve vztahu k délce strany Obvody a obsahy Počet pythagorejských trojúhelníků se shodným obvodem Obvod pythagorejského trojúhelníka v klasickém značení Dělitelnost obsahu šesti
7 5 Počty Počet možných odvěsen Počet trojúhelníků s danou délkou odvěsny nebo přepony Trojúhelníky, kde délky obou odvěsen jsou čtverce Trojúhelníky, kde odvěsna a přepona jsou čtverce Heronovské trojúhelníky 45 7 Získané výsledky Nalezené pythagorejské trojúhelníky Nalezené Heronovské trojúhelníky Závěr 53 Literatura 53 A Pythagorejské trojúhelníky 57 B Rovnoramenné Heronovské trojúhelníky 61 C Obecné Hernovské trojúhelníky 63
8 Seznam obrázků 1.1 Grafické znázornění zápisu (1.1) Grafické znázornění nedostatko-přebytkového značení (1.5) K odvození poloměrů připsaných kružnic Zápis délek stran trojúhelníka (3.5) Rozklad Heronovského trojúhelníka na dva pythagorejské
9 Seznam příloh Pythagorejské trojúhelníky Rovnoramenné Heronovské trojúhelníky Obecné Hernovské trojúhelníky
10 Úvod Při výběru tématu a následné práci jsem vycházel ze své praxe učitele. Ačkoliv jsou pythagorejské trojúhelníky jako téma dobře prozkoumané a popsané jak z hlediska historického, tak z pohledu didaktického, často narážím na drobné nedostatky při hledání a tvorbě materiálů k přípravě hodin, kde pythagorejské trojúhelníky jsou vedlejším tématem. Cílem práce je proto zaměřit se na vlastnosti pythagorejských trojúhelníků, které mohou být užitečné pro tvorbu úloh pro druhý stupeň základní školy, at už v geometrii při rýsování výšek a výpočtu obsahů, nebo v aritmetice v úlohách souvisejících s Pythagorovou větou. Dalším cílem je vytvořit seznam trojúhelníků s celočíselnými výškami, kde by rýsování a následný počet obsahu závisel méně na přesnosti a výšce zvolené pro výpočet. V úvodní kapitole se budu zabývat možnostmi, jak pythagorejský trojúhelník popsat, parametrizovat a generovat, aby se proces hledání trojúhelníků s požadovanými vlastnostmi dal automatizovat. V kapitole 2 popíšu vlastnosti stran pythagorejského trojúhelníka, kapitola 3 se soustředí na výsledky spjaté s obvody a obsahy pythagorejských trojúhelníků. V kapitole 4 ukážu, jaký je vztah mezi pythagorejským trojúhelníkem a poloměry kružnic vepsané a připsaných. Kapitola 5 se věnuje otázce, kolik existuje pythagorejských trojúhelníků splňujících určité vlastnosti. Kapitola 6 o Heronovských trojúhelnících na pythagorejské trojúhelníky přirozeně navazuje a navrhuje, jak požadované trojúhelníky hledat. Poslední kapitola 7 potom prezentuje nalezená řešení úlohy o trojúhelníku s celočíselnými stranami a výškami, který lze narýsovat na papír rozměru A3. V přílohách jsou k nalezení tabulky s trojúhelníky použitelnými i při jiných příležitostech. 10
11 Kapitola 1 Popis a generování Studium pravoúhlých trojúhelníků a jejich vlastností se datuje již do dob starověkého Egypta nebo Číny, i když evropský náhled ovlivnila kultura starého Řecka, kde byla Pythagorova věta pravděpodobně poprvé dokázána (viz. [21]). Cílem této práce je studium pravoúhlých trojúhelníků s přirozenými délkami stran, které se nazývají pythagorejské. Základním problémem, se kterým se setkáváme, jsou metody generování těchto trojúhelníků. V této kapitole se budeme věnovat různým metodám reprezentace pythagorejských trojúhelníků, které umožňují jednodušší způsob generovaní pythagorejských trojúhelníků, a sice klasické značení, nedostatko-přebytkové značení a popis pomocí maticového stromu. Každá z předvedených možností má také výhody v přehlednosti nebo struktuře proti prostému popisu pomocí délek stran. Předložené metody zápisu v této kapitole nepředstavují kompletní výčet, ale pro účely této práce jsou postačující. 1.1 Základní definice Definice 1.1. Trojice přirozených čísel x, y a z řešící rovnici x 2 + y 2 = z 2 se nazývá pythagorejská. Pythagorejskou trojici budeme značit (x, y, z). Z definice pythagorejské trojice vyplývá, že x, y a z odpovídají délkám stran pravoúhlého trojúhelníka. Takový trojúhelník budeme 11
12 nazývat pythagorejský a vzhledem k jednoznačnosti vztahu mezi pythagorejskou trojicí a pythagorejským trojúhelníkem budeme pro oba pojmy používat totožné značení (x, y, z). Lemma 1.2. Pro každou pythagorejskou trojici (x, y, z) existuje právě jeden pravoúhlý trojúhelník, jehož délky stran jsou určeny přirozenými čísly x, y a z. Důkaz. Nejprve ověříme trojúhelníkové nerovnosti. Z přirozenosti čísel x, y a z a vztahu x 2 + y 2 = z 2 dostáváme 2xy > 0 z 2 + 2xy > z 2 x 2 + y 2 + 2xy > z 2 (x + y) 2 > z 2 x + y > z, 2x 2 +2xz > 0 2x 2 +y 2 +2xz > y 2 x 2 +z 2 +2xz > y 2 (x+z) 2 > y 2 x+z > y, 2y 2 +2yz > 0 2y 2 +x 2 +2yz > x 2 y 2 +z 2 +2yz > x 2 (y +z) 2 > x 2 y +z > x. Tím jsme dokázali, že přirozená čísla x, y, z odpovídají délkám stran trojúhelníku a podle Pythagorovy věty je tento trojúhelník pravoúhlý, nebot délky stran splňují rovnici x 2 + y 2 = z 2. V pythagorejském trojúhelníku (x, y, z) odpovídají x a y délkám odvěsen a z délce přepony. Definice 1.3. Pythagorejský trojúhelník (x, y, z), kde x a y jsou nesoudělná čísla, se nazývá primitivní. Z primitivního pythagorejského trojúhelníka (x, y, z) se dá vytvořit nekonečně mnoho trojúhelníků vynásobením všech délek stran stejnou přirozenou konstantou, ale všechny tyto trojúhelníky budou větší a podobné původnímu. Lemma 1.4. Pro každý pythagorejský trojúhelník (x, y, z) platí jedna z následujících možností: 1. (x, y, z) tvoří primitivní pythagorejský trojúhelník 2. existuje primitivní trojúhelník (x 1, y 1, z 1 ), který je trojúhelníku (x, y, z) podobný. Tedy existuje přirozené číslo d tak, že x = dx 1, y = dy 1 a z = dz 1. 12
13 Důkaz. Důkaz lze najít např. v [24, s. 2]. V případě, že jsou x a y nesoudělné, je pythagorejský trojúhelník primitivní. V opačném případě existuje přirozené číslo d > 1, které je největším společným dělitelem x a y, tj. lze psát x = d x 1 a y = d y 1, kde x 1 a y 1 jsou přirozená čísla. Potom ze vztahu x 2 + y 2 = d 2 x d 2 y1 2 = d 2 (x y1) 2 = d 2 z1 2 vyplývá, že k trojúhelníku (x, y, z) existuje menší podobný pythagorejský trojúhelník (x 1, y 1, z 1 ), který vznikl vydělením stran konstantou d. Vzhledem k tomu, že d je největším společným dělitelem x a y, jsou x 1 a y 1 nesoudělné a (x 1, y 1, z 1 ) je primitivní. 1.2 Klasický zápis pythagorejského trojúhelníka V této části zavedeme zápis trojúhelníka pomocí dvou nesoudělných přirozených čísel. Tento způsob zápisu se datuje až do časů starého Řecka a Euklida (viz. [14, Kniha X, Věta XXIX]) a v literatuře ([24, Kap. 2], [6], [12], [13]) se označuje jako klasický. Věta 1.5. Každý primitivní pythagorejský trojúhelník (x, y, z), kde y je sudé číslo, se dá zapsat ve tvaru x = m 2 n 2, y = 2mn, z = m 2 + n 2, (1.1) kde m a n jsou nesoudělná přirozená čísla, m > n. Důkaz. Z předpokladu, že (x, y, z) je primitivní a y je sudé, vyplývá, že x musí být liché (nesoudělnost s y). Odtud dále vyplývá, že z je také liché číslo. Pythagorejská rovnice se dá použitím vzorce pro rozdíl čtverců přepsat do tvaru y 2 = (z x)(z + x). (1.2) Potom čísla z x a z + x, protože jsou součtem a rozdílem lichých čísel, musejí být sudá. Označme tedy z + x = 2a, z x = 2b, (1.3) 13
14 kde a a b jsou přirozená čísla. Současně platí a > b. Následně po úpravě máme z = a + b, x = a b. Necht a i b mají společného dělitele d > 1. Potom platí, že d x a d z, a odtud již d 2 y 2. Protože (x, y, z) je primitivní trojúhelník, jsou čísla x, y a z nesoudělná; což je spor s předpokladem. Čísla a a b tudíž musí být nesoudělná. Protože y bylo zvoleno jako sudé číslo, můžeme označit y = 2c. (1.4) Potom kombinací rovností (1.2), (1.3) a (1.4) a vydělením čtyřmi získáme vztah c 2 = ab. Součin nesoudělných čísel ab tvoří druhou mocninu právě tehdy, když jsou a i b druhými mocninami. Existují tedy přirozená nesoudělná čísla m, n, kde m > n, pro která platí a = m 2, b = n 2, c = mn. Po dosazení zpět a vyjádření délek stran původního trojúhelníka dostáváme vztahy (1.1). Lemma 1.6. Mějme primitivní trojúhelník (x, y, z) v klasickém zápisu (1.1). Potom mají čísla m a n odlišnou paritu, tj. jedno je sudé a druhé je liché. Důkaz. Protože m a n jsou nesoudělná čísla, nemohou být obě sudá. Nemohou být ani obě lichá, protože by x jako rozdíl dvou lichých čísel muselo být sudé. Tento zápis délek stran pythagorejského trojúhelníku pomocí dvou nesoudělných přirozených čísel m a n, kde m > n, lze graficky znázornit pomocí obrázku 1.1. Generovat podle něj seznamy trojúhelníků je jednodušší než prostá iterace všech možných stran, takže má použití i při tvorbě tabulek a seznamů. 14
15 Obrázek 1.1: Grafické znázornění zápisu (1.1). 1.3 Nedostatko-přebytkové značení Klasické značení (1.1) je v literatuře i při praktickém generování pythagorejských trojúhelníků velmi oblíbené, i přes nemožnost vyjádřit s jeho pomocí všechny pythagorejské trojúhelníky (viz. [25]). Lze ukázat ([17]), že při odlišné reprezentaci pythagorejského trojúhelníku (x, y, z), která využívá tzv. nedostatek (anglicky height ) h = z y a přebytek (anglicky excess ) e = x + y z trojúhelníku, je možné popsat všechny pythagorejské trojúhelníky. Je evidentní, že obě čísla h a e budou kladná, a na rozdíl od klasického značení, kde m a n nemají evidentní geometrický význam, zde e vyjadřuje, o kolik je cesta z X do Y po přeponě kratší než cesta po odvěsná1ch. Grafické znázornění tohoto značení je na obrázku 1.2. V této části budeme uvažovat, že v pythagorejském trojúhelníku (x, y, z) platí x < y. V literatuře se nedostatko-přebytkový zápis tak často jako klasický zápis nevyskytuje, ale díky možnosti propojit takto zapsané pythagorejské trojúhelníky vzájemnými vztahy je užitečný pro mnoho důkazů, například týkajících se obvodu trojúhelníků a kružnice vepsané i opsané trojúhelníku. Tento typ zápisu byl užit poprvé v [25] a v různých podobách například v [16], [8] a [28]. [18] a [17] pak dokázali, že reprezentace pomocí nedostatku a přebytku umožňuje popsat všechny pythagorejské trojúhelníky. Věta 1.7 ([17]). Ke každé dvojici (k, h) přirozených čísel přiřad me pythagorejskou trojici 15
16 Obrázek 1.2: Grafické znázornění nedostatko-přebytkového značení (1.5). takovýmto způsobem: Necht h = pq 2, kde p je přirozené číslo neobsahující čtverec a q je přirozené číslo. Označme d = 2pq pro p liché, a d = pq pro p sudé a dále necht k > 2h/d. Pak trojice ( h + dk, dk + (dk) 2 /2h, h + dk + (dk) 2 /2h ) (1.5) popisuje pythagorejský trojúhelník. Toto přiřazení je jednoznačné, tj. pro každou dvojici čísel (k, h) existuje právě jeden pythagorejský trojúhelník (x, y, z) a naopak. Navíc platí, že tento trojúhelník je primitivní právě tehdy, když k a h jsou nesoudělná a h = q 2 pro q liché nebo h = 2q 2. Poznámka 1.8. Vidíme, že ve znění věty se neobjevuje parametr e, ale je nahrazen rozepsaným tvarem e = kd. Tento zápis usnadňuje důkazy. Poznámka 1.9. Řekneme, že číslo neobsahuje čtverec, pokud v jeho prvočíselném rozkladu nemá žádné prvočíslo exponent větší než jedna. Pro větší přehlednost je zde souhrn vztahů mezi parametry x, y a z a h, k, p a d. výpočet h: h = z y, určení p a q: zapsat h do tvaru h = pq 2, kde p neobsahuje čtverec, 16
17 výpočet d: výpočet k: d = 2pq pro p liché, d = pq pro p sudé, k = (x h)/d. Lemma 1.10 ([17]). K libovolnému přirozenému číslu h, zapsanému ve tvaru h = pq 2, kde p je přirozené číslo neobsahující čtverec a kde q je přirozené číslo, přiřadíme přirozené číslo d ve tvaru d = 2pq pokud p je liché a tvaru d = pq pokud p je sudé. Potom 2h d 2. Současně, pro každé přirozené D takové, že 2h D 2, platí, že d D. Důkaz. Pro liché p je d ve tvaru d = 2pq. Potom d 2 = 4p 2 q 2 = 4ph. Pro sudé p je d = pq a označme p = 2p 0. Potom d 2 = 4p 2 0q 2 = 2p 0 h. Pro obě možnosti tedy platí, že 2h d 2. Pro přirozené číslo D existuje prvočíselný rozklad ve formě D = d r 1 1 d r 2 2 d r k k a jeho druhá mocnina tedy bude mít tvar D 2 = d 2r 1 1 d 2r 2 2 d 2r k. Podle předpokladu p neobsahuje čtverec, k můžeme tedy psát p = p 1 p 2 p m a q 2 = q 2t 1 1 q 2t 2 2 q 2tn n. Z předpokladů víme, že 2h D 2, potom pro každé q i existuje nějaké d j tak, q i = d j a 2t i 2r j. Odtud plyne, že q D a D můžeme zapsat jako D = qd 1, kde D 1 = s u 1 1 s u 2 2 s u l l. Z předpokladů víme, že 2h = 2pq 2 D 2 a současně D 2 = q 2 D 2 1. Potom 2p D 2 1. Protože p ze způsobu konstrukce neobsahuje čtverec, musí i p D 1. Pro p sudé máme d = pq D. Pokud p je liché, D 2 1 obsahuje 2 2, bude i 2p D 1, a tudíž d = 2pq D. Lemma Za předpokladů Věty 1.7 existuje k N, takové, že přebytek e lze zapsat ve tvaru e = dk. Důkaz. Z (1.5) vyplývá, že e 2 = 2(z x)(z y) = 2(z x)h. Odtud vidíme, že 2h e 2 a podle předchozího Lemmatu d e. Nyní se již dostáváme k důkazu Věty 1.7. Důkaz Věty 1.7. Musíme ukázat, že trojice (1.5) tvoří pythagorejský trojúhelník (x, y, z), tedy že čísla x, y, z jsou přirozená, splňují rovnici x 2 + y 2 = z 2 a x < y. Označme x = h + dk, y = dk + (dk) 2 /2h a z = h + dk + (dk) 2 /2h. 1. V předchozím Lemmatu 1.10 jsme ukázali, že 2h d 2. Odtud a z přirozenosti h, k a d plyne, že x, y a z jsou přirozená čísla. 17
18 2. Prostým umocněním a porovnáním lze snadno ukázat, že x 2 + y 2 = z Vzhledem k požadavku na uspořádání x < y musí platit h+dk < dk +(dk) 2 /2h. To ale snadno plyne z předpokladu k > 2h/d. Vzhledem k jednoznačnému vztahu mezi stranami trojúhelníku x, y a z na jedné straně a nedostatkem h, přebytkem e, resp. k, na druhé straně, odpovídá každému trojúhelníku (x, y, z) jedna dvojice (e, h), resp. (k, h). Zbývá nám ukázat, že trojúhelník je primitivní tehdy a jen tehdy, když h a k jsou nesoudělná a h = q 2 pro q liché nebo h = 2q 2. Necht je trojúhelník (1.5) primitivní. U primitivního trojúhelníku platí, že z x a z y jsou nesoudělná čísla. Předpokládejme naopak, že mají společného dělitele r. Potom r dělí i součet (z x) 2 + (z y) 2 = (3z 2x 2y)z. Musí tedy platit, že r z nebo r (3z 2x 2y). V prvním případě by z dělitelností obou rozdílů plynulo, že r y a r x, což je ve sporu s předpokladem o nesoudělnosti x a y. V druhém případě platí, že r dělí 3z 2x 2y = 2(z x) + 2(z y) z a tudíž opět r z. V obou případech mají x, y a z společného dělitele, trojúhelník tedy není primitivní. Tím jsme dospěli ke sporu. Můžeme nadále předpokládat, že z x = k2 d 2 2h a z y = h (1.6) nemají společného dělitele. Pro liché číslo p můžeme psát k 2 d 2 /2h = 2pk 2 a h = pq 2, tudíž díky jejich nesoudělnosti musí být p = 1, q musí být liché, 2k a q musí být nesoudělná. Pro p sudé můžeme psát k 2 d 2 /2h = pk 2 /2 a h = pq 2, tudíž díky jejich nesoudělnosti musí být p = 2, a k a 2q musí být nesoudělná. Po sloučení obou případů dostáváme, že i k a h jsou nesoudělná čísla. Nyní ukážeme opačnou implikaci. Pro h ve tvaru q 2 (tj. q liché, p = 1) můžeme psát x = h + dk = q 2 + 2qk = q(q + 2k) a y = dk + d 2 k 2 /2h = 2k(q + k). Pro spor předpokládejme, že x i y mají společného dělitele r. Potom r nemůže být 2, protože x = q(q+2k) je liché. Tedy 18
19 r musí dělit q nebo q + 2k, a musí dělit k nebo q + k. Ze všech těchto čtyř možností vyplývá, že r q a r k, což je spor s předpokladem věty. Odtud již máme, že x a y nemají společného dělitele a trojúhelník (1.5) je tedy primitivní. Pro možnost, kde h bude tvaru 2q 2, dostáváme z výrazů pro x = 2q(q + k) a y = k(q + 2k) obdobnou argumentací stejný závěr. Důsledek 1.12 (Věty 1.7, [17]). Pro primitivní pythagorejský trojúhelník, kde x je sudé, jsou zápisy (k, h), (k, q) a (e, h) ekvivalentní. Důkaz. Podle Věty 1.7 je v primitivním pythagorejském trojúhelníku h ve tvaru h = q 2 pro q liché nebo h = 2q 2. V důkazu Věty 1.7 jsme ukázali, že v prvním případě je x liché a v druhém případě je x sudé. Odtud snadno plyne ekvivalence mezi zápisy (k, h) a (k, q). Mějme nyní dané (k, h). Víme, že h = 2q 2, tedy p = 2. Pro sudé p je d = 4q, což postačuje k určení e = kd. Naopak pokud máme dané (e, h), opět je d = 4q a odtud již získáme k. Důsledek 1.13 ([17]). Necht (x, y, z) je primitivní pythagorejský trojúhelník. Potom platí následující: 1. Pokud je x liché, trojúhelník se popíše pomocí dvojice (k, q 2 ), kde 2k a q jsou nesoudělná a strany se vyjádří (q 2 + 2qk, 2qk + 2k 2, q 2 + 2qk + 2k 2 ). 2. Pokud je x sudé, trojúhelník se popíše pomocí dvojice (k, 2q 2 ), kde k a 2q jsou nesoudělná a strany se vyjádří (2q 2 + 2qk, 2qk + k 2, 2q 2 + 2qk + 2k 2 ). Důkaz. Důkaz vychází z důkazu Věty Maticové stromy K jinému způsobu zápisu a generování pythagorejských trojúhelníků vede myšlenka představit si velikosti stran pythagorejského trojúhelníka jako sloupcový vektor. Poprvé se tato myšlenka objevila v [4] a později byla použita např. v [11], [15] a [20]. K lepší názornosti bude užitečné pracovat s čísly k a q z nedostatko-přebytkového značení z minulé podkapitoly. Pomocí takovéhoto zápisu lze snadno vidět názornost a vztahy mezi trojúhelníky ve stromové 19
20 struktuře. Generování pythagorejských trojúhelníků pomocí matic lze nalézt v literatuře v mnoha dalších podobách například v [1] a [27]. Označme A 1, A 2 a A 3 následující matice: A 1 = , A 2 = , A 3 = Věta 1.14 ([17]). Necht (x, y, z) je primitivní pythagorejský trojúhelník, a předpokládejme, že x je sudé. Potom každý pythagorejský primitivní trojúhelník dostaneme vynásobením trojúhelníka (4, 3, 5) jakožto sloupcového vektoru jedinečnou kombinací matic A i. Poznámka Matice A 1, A 2 a A 3 nejsou jediné, které transformují pythagorejskou trojici na jinou pythagorejskou trojici. Podrobně se tomuto tématu věnuje například [5] a [2]. V [26] je podrobné vysvětlení, jakou obecnou formu takové matice mají. Důkaz. Dle Důsledku 1.12, můžeme zapsat primitivní pythagorejský trojúhelník pomocí dvojice (k, q). Pro připomenutí, předpisy pro jednotlivé délky stran jsou x = 2q(q + k), y = k(2q + k) a z = 2q 2 + 2qk + k 2. Dále označme T (k, q) sloupcový vektor tvořený délkami stran tohoto trojúhelníku, tj. T (k, q) = 2q(q + k) k(2q + k) 2q 2 + 2qk + k 2. Snadno nahlédneme, že primitivní pythagorejský trojúhelník (4, 3, 5) odpovídá T (1, 1). Násobením například maticí A 2 vznikne nový trojúhelník (x, y, z ): A 2 T (k, q) = q(q + k) k(2q + k) = 2q 2 + 2qk + k 2 6q qk + 4k 2 8q qk + 3k 2 = 10q qk + 5k 2 x y z. 20
21 Ověření, že se jedná pythagorejský trojúhelník je snadné. Trojúhelník (x, y, z ) je v nedostatko-přebytkovém značení vyjádřen pomocí (k, h ), resp. (k, q ), kde h = z y = 2q 2 + 4qk + 2k 2 = 2(q + k) 2, q = (q + k) a d = 2(q + k). Odtud h = 2q 2 a k = x h = 6q2 + 10qk + 4k 2 2(q + k) 2 d 2(q + k) = 2q2 + 3qk + k 2 q + k = 2q + k. Obdobným způsobem získáme vztah mezi vyjádřením původního trojúhelníka a trojúhelníkem vzniklým násobením maticemi A 1 a A 3, neboli A 1 T (k, q) = T (k, q + k), A 2 T (k, q) = T (2q + k, q + k), A 3 T (k, q) = T (2q + k, q). Lze ukázat, že pro tyto trojúhelníky platí h = 2q 2, kde q = q + k v prvním a druhém případě, resp. q = q ve třetím případě. Z nesoudělnosti k a 2q (Důsledek 1.13) a vyjádření k a q snadno nahlédneme nesoudělnost k a 2q. Odtud již plyne, že po vynásobení maticemi A 1, A 2 resp. A 3 jsou nově vzniklé pythagorejské trojúhelníky opět primitivní. Můžeme si povšimnout, že při násobení A i (k, q) dostáváme tři různé trojúhelníky (k, q ), nebot k < q v prvním případě, q < k < 2q v druhém a 2q < k ve třetím. Nyní zbývá ukázat, že zadaný primitivní pythagorejský trojúhelník T (k, q), kde k > 1 nebo q > 1 a k a 2q jsou nesoudělné, lze získat z trojúhelníka T (1, 1) jedinečnou kombinací matic A 1, A 2 a A 3. Protože matice A i mají determinant roven jedné, existují k nim matice inverzní. Pokud těmito maticemi A 1 i vynásobíme trojúhelník T (k, q) dostáváme: A 1 1 T (k, q) = T (k, q k), k < q, A 1 2 T (k, q) = T (2q k, k q), q < k < 2q, A 1 3 T (k, q) = T (k 2q, q), 2q < k. 21
22 Pro trojúhelník T (k, q) platí právě jedna z možností k < q, q < k < 2q nebo 2q < k. Tyto případy jsou disjunktní. Násobením A 1 1, A 1 2, resp. A 1 3 vznikne nový primitivní pythagorejský trojúhelník T (k, q ), kde q + k < q + k. Opakováním najdeme složení inverzních matic A 1 i n... A 1 i 1, který převádí trojúhelník T (k, q) na trojúhelník T (1, 1). Opačným postupem, tj. vynásobením maticemi A i1... A in získáme z trojúhelníku T (1, 1) = (4, 3, 5) zvolený trojúhelník T (k, q). Tato cesta také bude jediná, protože kdyby v nějakém kroku platilo A i T (k, q ) = A j T (k, q ) pro i j, musely by pro výsledný trojúhelník T (k, q) platit současně dvě nerovnosti, které ale popisují disjunktní případy. Tím je tvrzení dokázáno. Poznámka Pro zobecnění postupu na všechny primitivní pythagorejské trojúhelníky vynásobíme sloupcový vektor stran maticí M, která (x, y, z) převede na (y, x, z) M = 1 0 0, Tvrzení Věty 1.14 bude platit i pro trojúhelníky s lichým x, pokud nahradíme matice A i maticemi MA i M a trojúhelník (4, 3, 5) trojúhelníkem (3, 4, 5). 22
23 Kapitola 2 Vlastnosti stran v pythagorejských trojúhelnících Pro pythagorejské trojúhelníky platí kromě samotné rovnice mnoho dalších zajímavých vlastností, mezi nimi např. dělitelnost délek stran. Znalost těchto zákonitostí usnadňuje odhalení pythagorejských trojúhelníků v úlohách bez předchozí přípravy. 2.1 Odlišná parita odvěsen Jednou ze základních vlastností primitivního pythagorejského trojúhelníku je, že má právě jednu odvěsnu lichou a právě jednu odvěsnu sudou. Lemma 2.1. Necht (x, y, z) je primitivní pythagorejský trojúhelník. Pak platí, že odvěsny mají odlišnou paritu. Důkaz. Tento důkaz lze nalézt v [24, s. 4]. Mějme primitivní pythagorejský trojúhelník (x, y, z). Z definice 1.3 jsou délky odvěsen nesoudělná čísla, a tudíž nemohou být obě sudá. Ukážeme, že délky odvěsen nemohou být současně lichá čísla. Předpokládejme pro spor, že jsou délky obou odvěsen lichá čísla. Necht x = 2k + 1, y = 2l + 1, kde k, l N. Druhou 23
24 mocninu x lze zapsat jako (2k + 1) 2 = 4k 2 + 4k + 1 = 4k(k + 1) + 1, a druhou mocninu y nápodobně. Vzhledem k tomu, že bud k nebo k + 1 je sudé číslo, zbytek x 2 při dělení osmi je jedna, tj. lze psát x 2 = 8p + 1, a y 2 = 8q + 1, kde p a q jsou lichá přirozená čísla. Odtud plyne, že x 2 + y 2 = 8(p + q) + 2. Součet druhých mocnin x a y dává tedy číslo, které je sudé, složené z násobku osmi a zbytku dva. Takové číslo ale nebude čtvercem, protože druhá mocnina přirozeného čísla musí být bud dělitelná 4 (pokud je druhou mocninou čísla sudého) nebo lichá. A tím dostáváme spor, nebot zde se jedná o číslo sudé, která má po dělení čtyřmi zbytek dva. Neexistuje tedy přirozené číslo z, které splňuje x 2 + y 2 = z Dělitelnost délek stran čtyřmi Lemma 2.2. Necht (x, y, z) je pythagorejský trojúhelník. Pak je délka alespoň jedné odvěsny dělitelná čtyřmi. Důkaz. Důkaz lze nalézt např. v [24, s. 6]. Bez újmy na obecnosti předpokládejme, že (x, y, z) je primitivní trojúhelník. Pro obecný pythagorejský trojúhelník tvrzení Věty snadno dostaneme s pomocí Lemmatu 1.4. V klasickém zápisu (1.1) primitivního trojúhelníka platí y = 2mn. Podle Lemmatu 1.6 je součin mn sudé číslo, a proto je y dělitelné čtyřmi. Důsledek 2.3. V žádném pythagorejském trojúhelníku nejsou všechny délky stran prvočísla. 24
25 2.3 Dělitelnost délek stran třemi Věta 2.4. Necht (x, y, z) je pythagorejský trojúhelník. Pak délka alespoň jedné odvěsny je dělitelná třemi. Důkaz. Důkaz lze nalézt v [24, s. 23]. Pro spor předpokládejme, že ani x ani y nejsou čísla dělitelná třemi, a jsou tedy ve tvaru x = 3k ± 1, y = 3l ± 1, pro nějaká celá čísla k a l. Pythagorejská rovnice potom dává předpis pro z 2 ve tvaru z 2 = x 2 + y 2 = 9k 2 ± 6k l 2 ± 6l + 1 = 3(3k 2 + 3l 2 ± 2k ± 2l) + 2, neboli zbytek z 2 po dělení třemi je dva. Pokud by z bylo dělitelné třemi, bude i jeho mocnina dělitelná třemi. Pokud z třemi dělitelné není, pak z identity použité pro umocnění čísel nedělitelných třemi (3t ± 1) 2 = 9t 2 ± 6t + 1 = 3(3t 2 ± 2t) + 1 ale plyne, že zbytek z 2 po dělení třemi je jedna. Ani v jednom z případů zbytek z 2 po dělení třemi není dva. Vyčerpáním všech možností se dostáváme do sporu s předpokladem, a tedy délka alespoň jedné odvěsny musí být dělitelná třemi. 2.4 Dělitelnost délek stran pěti Věta 2.5. Necht (x, y, z) je pythagorejský trojúhelník. Pak délka alespoň jedné strany je dělitelná pěti. Důkaz. Důkaz lze nalézt v [24, s. 24]. Mějme přirozené číslo n, které není dělitelné pěti, potom je ve tvaru n = 5k ± 1, nebo n = 5k ± 2, 25
26 kde k je celé číslo. Jeho druhá mocnina má tvar n 2 = 25k 2 ± 10k + 1 = 5(5k 2 ± 2k) + 1, nebo n 2 = 25k 2 ± 20k + 4 = 5(5k 2 ± 4k) + 4, neboli n 2 mod 5 = 1 nebo n 2 mod 5 = 4. Mějme tedy trojici (x, y, z), kde žádná ze stran pěti dělitelná není. Pro přehlednost rozboru případů, v jakém tvaru vychází z 2, užijeme tabulku: x 2 mod 5 y 2 mod 5 x 2 + y 2 mod První a čtvrtý případ vedou ke sporu s předpokladem, protože číslo nedělitelné pěti nemá v druhé mocnině po dělení pěti jiný zbytek než jedna, nebo čtyři. V druhém a třetím případě je z 2 dělitelné pěti, což je spor s předpokladem. V primitivním pythagorejském trojúhelníku tedy nemůže nastat situace, kdy žádná strana není dělitelná pěti. 26
27 Kapitola 3 Kružnice vepsané a připsané Konstrukce kružnice vepsané a kružnic připsaných patří mezi oblíbená cvičení na rýsování os úhlů a spouštění kolmic. Vztahy mezi délkami stran a poloměrem těchto kružnic jsou jednoduché a lze je snadno zkontrolovat a ověřit po rýsování. Vztahům mezi délkami stran a poloměry kružnic vepsaných a připsaných se věnuje např. [24], [29] a [10]. 3.1 Poloměr kružnice vepsané a kružnic připsaných Věta 3.1. Necht (x, y, z) je pythagorejský trojúhelník a označme r poloměr v něm vepsané kružnice. Pak lze r vyjádřit jako r = x + y z. 2 Odtud navíc plyne, že poloměr r je přirozené číslo. Důkaz. Důkaz lze nalézt např. v [24, s. 42]. Pro obsah pythagorejského trojúhelníka (x, y, z) platí nejen Heronův vzorec S = s(s x)(s y)(s z), kde s = (x + y + z)/2 je polovina obvodu trojúhelníka, ale i jednodušší zápis pomocí délek 27
28 odvěsen S = xy 2. (3.1) Díky vepsané kružnici lze také obsah pythagorejského trojúhelníka zapsat jako součet obsahů jednotlivých trojúhelníků, s vrcholy ve středu vepsané kružnice a s výškou r, tj. S = xr 2 + yr 2 + zr 2 = x + y + z r = sr. (3.2) 2 V dalším kroku doplníme součin xy na čtverec a odstraněním druhých mocnin užitím pythagorejské rovnice s cílem dostat součin, v němž bude jeden člen polovina obvodu, tj. (3.1) můžeme přepsat jako S = xy 2 = 2xy 4 = x2 + 2xy + y 2 z 2 = 4 = (x + y)2 z 2 (x + y + z)(x + y z) = 4 = x + y + z 2 x + y z. 2 4 = Porovnáním s (3.2) dostáváme, že r = (x +y z)/2. Z Lemmatu 2.1 plyne, že výraz x +y z je sudé číslo, a r je tedy přirozené. Poznámka 3.2. K důkaz předchozí Věty je možné využít i klasické značení (1.1) pomocí dvojice m, n přirozených nesoudělných čísel, tj. x = m 2 n 2, y = 2mn, z = m 2 + n 2. (3.3) Porovnáním (3.1) a (3.2) a dosazením z (3.3) vyjádříme poloměr vepsané kružnice jako r = xy 2 2 x + y + z = = 2mn(m2 n 2 ) 2m 2 + 2mn (m 2 n 2 )2mn m 2 n 2 + 2mn + m 2 + n 2 = = n(m n)(m + n) m + n = n(m n). Protože m i n jsou přirozená čísla, je i jejich rozdíl a součin přirozené číslo. 28
29 Pro poloměry kružnic připsaných platí podobné tvrzení. Věta 3.3. Necht (x, y, z) je pythagorejský trojúhelník a označme r x, r y a r z poloměry kružnic připsaných ke stranám x, y a z. Pak platí r x = x y + z 2, r y = y x + z 2 a odtud navíc plyne, že r x, r y a r z jsou přirozená čísla., r z = x + y + z. 2 Důkaz. Důkaz provedeme s využitím vztahů mezi pythagorejským trojúhelníkem a poloměrem kružnice připsané ke straně x, tj. r x, které jsou zřejmé z Obrázku 3.1. Označme jako T 2 bod doteku kružnice připsané ke straně x se stranou x, a dále označme u jako vzdálenost mezi body Y a T 2 a v jako vzdálenost mezi body T 2 a Z. Je evidentní, že platí x = u + v a z + u = y + v a r x = v. Odtud snadno plyne, že z + x v = y + v a r x = v = x y+z 2. Pro poloměry ostatních připsaných kružnic je důkaz obdobný. Ve všech případech je čitatel Obrázek 3.1: K odvození poloměrů připsaných kružnic. kladné sudé číslo, a proto jsou poloměry opsaných kružnic r x, r y, r z přirozená čísla. Poznámka 3.4. Jiný důkaz předchozí Věty lze najít v [3]. 29
30 3.2 Primitivní pythagorejské trojúhelníky odvozené z poloměru vepsané kružnice Ve Větě 3.1 bylo ukázáno, že poloměr r kružnice vepsané závisí na délkách stran. Nabízí se proto otázka, zda lze z daného poloměru zpětně pythagorejský trojúhelník zkonstruovat. Věta 3.5 ([24, s. 42]). Necht r je přirozené číslo. Pak trojice ( 2r + 1, 2r 2 + 2r, 2r 2 + 2r + 1 ). (3.4) tvoří primitivní pythagorejský trojúhelník a r odpovídá poloměru kružnice jemu vepsané. Důkaz. Necht x = 2r + 1, y = 2r 2 + 2r a z = 2r 2 + 2r + 1. Snadno nahlédneme, že všechna tři čísla jsou přirozená. Pro ověření, že x, y a z tvoří strany pythagorejského trojúhelníka, dokážeme rovnost x 2 + y 2 = z 2. Umocněné délky stran mají tvar x 2 + y 2 = (2r + 1) 2 + (2r 2 + 2r) 2 = 4r 2 + 4r r 4 + 8r 3 + 4r 2 = = 4r 4 + 8r 3 + 8r 2 + 4r + 1, z 2 = (2r 2 + 2r + 1) 2 = 4r 4 + 4r 3 + 2r 2 + 4r 3 + 4r 2 + 2r + 2r 2 + 2r + 1 = = 4r 4 + 8r 3 + 8r 2 + 4r + 1. Protože jsou délky odvěsen nesoudělná čísla, je získaný trojúhelník primitivní. Navíc platí, že (x + y z)/2 = r, tedy r je poloměr kružnice vepsané v trojúhelníku (3.4). Ukázali jsme, že k danému poloměru r jsme schopni nalézt primitivní pythagorejský trojúhelník. Zůstává otázkou, zda je tento trojúhelník jednoznačný, nebo existují i jiné primitivní pythagorejské trojúhelníky se stejným poloměrem vepsané kružnice. Například pro r = 3 je možno nalézt dva primitivní trojúhelníky, (7, 24, 25) a (8, 15, 17); oba jsou primitivní. Věta 3.6 ([24, s. 43]). Necht r je přirozené číslo a k 0 necht označuje počet lichých prvočíselných dělitelů r. Pak existuje právě 2 k primitivních pythagorejských trojúhelníků s vepsanou kružnicí o poloměru r. 30
31 Důkaz. Tento důkaz vychází z [22]. Necht r je přirozené číslo a k 1 je počet lichých prvočíselných dělitelů r. Uvažujme libovolný rozklad r = uv, kde u a v jsou nesoudělná přirozená čísla a u je liché. Položme m = u + v a n = v. Z nesoudělnosti čísel u a v plyne nesoudělnost čísel m a n. Vzhledem k tomu, že u je liché, musí být jedno z čísel m a n sudé (pro v liché je sudé m, pro v sudé je sudé n). Dále platí m > n, nebot jistě u + v > v. Pro každý takový rozklad r = uv tedy existuje jediný primitivní pythagorejský trojúhelník (x, y, z) s poloměrem vepsané kružnice r, kde x = m 2 n 2, y = 2mn, z = m 2 + n 2 a r = n(m n). Nyní zbývá ukázat, že pro dané r existuje 2 k možných rozkladů uv, splňující podmínky výše. Necht r > 1 je liché. Potom má r pouze liché prvočíselné dělitele a prvočíselné rozklady čísel r, u a v můžeme psát r = k i=1 p e i i, u = k i=1 p f i i a v = k i=1 p e i f i i, kde p i jsou navzájem různá lichá prvočísla a e i f i pro každé i = 1, 2,..., k. Vzhledem k nesoudělnosti čísel u a v musí být pro každé i bud e i = 0 nebo e i = f i. Pro zvolené r tedy existuje 2 k možných rozkladů. Necht je nyní r sudé. Potom má r kromě k lichých prvočíselných dělitelů ještě za dělitele číslo 2, a jeho prvočíselný rozklad můžeme psát jako r = 2 n r 1, kde n 1 a r 1 je liché (a má k lichých prvočíselných dělitelů). Pak u = 2 j u 1, v = 2 n j v 1 a u 1 v 1 = r 1. Vzhledem k nesoudělnosti u a v musí být opět j = 0 nebo j = n. V případě, že j = n, je ale u sudé, což je spor s předpokladem. Musí tedy být u = u 1 a v = 2 n v 1. Podle předchozího bodu existuje 2 k možných rozkladů čísla r 1, a tedy i čísla r. 31
32 3.3 Generování všech trojúhelníků s daným poloměrem kružnice vepsané Pokud bychom chtěli získat nejen primitivní, ale všechny trojúhelníky s daným poloměrem kružnice jemu vepsané, stačí si uvědomit, že libovolných neprimitivní trojúhelník získáme z nějakého primitivního trojúhelníku vynásobením všech stran stejným přirozeným číslem. Necht (x, y, z) je pythagorejský trojúhelník a necht d je největší společný dělitel délek jeho stran. Pak existovat primitivní pythagorejský trojúhelník (x 1, y 1, z 1 ), kde x = d x 1, y = d y 1, z = d z 1, r = x + y z 2 = d x1 + y 1 z 1, 2 neboli d dělí nejen délky všech stran, ale i poloměr vepsané kružnice. Vydělením poloměru kružnice původního trojúhelníka přirozeným číslem se dostaneme k poloměru kružnice vepsané trojúhelníku primitivnímu. Na druhou stranu, pokud máme dán poloměr r 1 kružnice vepsané primitivnímu pythagorejskému trojúhelníku (x 1, y 1, z 1 ), a d je libovolné přirozené číslo, pak r = d r 1 je poloměr kružnice vepsané pythagorejskému trojúhelníku (d x 1, d y 1, d z 1 ). Pro nalezení všech trojúhelníků s daným poloměrem kružnice vepsané r, je postačující nalézt pro každého dělitele d r všechny primitivní pythagorejské trojúhelníky s poloměrem kružnice vepsané r 1 = r/d a poté vynásobit všechny strany konstantou d. 3.4 Poloměr vepsané kružnice ve vztahu k délce strany V práci [19] je popsána metoda pro nalezení všech primitivních pythagorejských trojúhelníků, která využívá vztahu mezi délkami stran a poloměru kružnice vepsané. Tyto vztahy jsou viditelné z obrázku 3.2. Délky stran se dají zapsat pomocí poloměru vepsané kružnice a zbytku na straně x a y. Zbytek strany z je díky tečnám ke kružnici stejně veliký. x = 2r + p, y = 2r + q, z = 2r + p + q. (3.5) 32
33 Obrázek 3.2: Zápis délek stran trojúhelníka (3.5). Věta 3.7. (2r +p, 2r +q, 2r +p+q) je primitivní pythagorejský trojúhelník tehdy a jen tehdy, když p, q, r jsou přirozená čísla, splňující 2r 2 = pq a kde p a q jsou nesoudělná s odlišnou paritou. Důkaz. Důkaz vychází z [19]. Necht x = 2r + p, y = 2r + q a z = 2r + p + q. 1. Necht (x, y, z) tvoří primitivní pythagorejský trojúhelník. Ze vztahu x 2 +y 2 = z 2 plyne, že 2r 2 = pq. Dále z grafické interpretace parametrů r, p, q plyne, že r odpovídá poloměru kružnice vepsané, a podle Věty 3.1 je tento poloměr přirozené číslo. Dále p = x 2r a q = y 2r a tedy p i q jsou přirozená čísla. Předpokládejme, že p a q mají společného dělitele k, můžeme tedy psát p = k p 1 a q = k q 1. Ze vztahu 2r 2 = pq = k 2 p 1 q 1 dostáváme, že p 1 q 1 = 2(r/k) 2 a tedy r = k r 1. Odtud již dostáváme, že x, y i z mají společného dělitele k a trojúhelník tedy není primitivní. Tím jsme dospěli ke sporu a tedy p a q jsou nesoudělná. Ze vztahu 2r 2 = pq dále plyne, že p nebo q musí být sudé. Vzhledem k nesoudělnosti nemohou být obě sudá a mají tudíž opačnou paritu. 2. Necht p, q, r jsou přirozená čísla splňující 2r 2 = pq, p a q nesoudělná s odlišnou paritou. Výpočtem lze snadno ověřit, že trojice (x, y, z) splňuje pythagorejskou rovnici. Bez újmy na obecnosti předpokládejme, že p je liché. Musíme ukázat, že x a y jsou nesoudělné. Necht r = r t 1 1 r t 2 2 rn tn je prvočíselný rozklad r. Ze vztahu 2r 2 = 2r 2t 1 1 r 2t 2 2 rn 2tn 33 = pq
34 a nesoudělnosti p a q dále plyne, že každé prvočíslo r i je bud v p, nebo q. Můžeme tedy psát p = P 2 a q = 2Q 2, kde P a Q jsou nesoudělná, P je liché a platí r = P Q. Předpokládejme nyní, že x a y mají společného dělitele přirozené číslo k > 1, neboli x = kx 1, y = ky 1 a z = kz 1, pro přirozená x 1, y 1 a z 1. Z vyjádření stran (3.5) a nahrazením p = P 2, q = 2Q 2 a r = P Q dále plyne, že z 1 x 1 = 2Q 2 /k a z 1 y 1 = P 2 /k, neboli k Q a současně k P. Tím jsme dospěli ke sporu s předpokladem. Poznámka 3.8. Předchozí metoda odpovídá metodě generování pythagorejských trojúhelníků, kterou zavedl [9], a dokázána byla také např. v [23]. Parametrizace Dicksonovy metody odpovídá parametrizaci jako ve Větě 3.7, pouze se místo poloměru kružnice opsané uvažuje její průměr R = 2r. 34
35 Kapitola 4 Obvody a obsahy Zákonitosti spojující obvody a obsahy pro počet pythagorejských trojúhelníků umožňují nejen snazší tvorbu většího množství stejných úloh, ale i jednodušší ověření správných výsledků. 4.1 Počet pythagorejských trojúhelníků se shodným obvodem Věta 4.1 ([24, s. 33]). Pro každé přirozené číslo n existuje alespoň n různých pythagorejských trojúhelníků se stejným obvodem. Důkaz. Mějme n různých primitivních pythagorejských trojúhelníků (x i, y i, z i ), i = 1, 2,..., n, s obvodem o i = x i + y i + z i. Necht je o nejmenším společným násobkem obvodů o i, i = 1, 2,..., n. Potom pro každé i, i = 1, 2,..., n je trojice ( o xi o i, o y i, o z ) i o i o i pythagorejský trojúhelník s obvodem o. Přirozenost stran nahlédneme z o i o. Tyto pythagorejské trojúhelníky jsou navzájem různé, protože jsou podobné původním trojúhelníkům, které jsou z předpokladu různé. 35
36 4.2 Obvod pythagorejského trojúhelníka v klasickém značení Věta 4.2. Necht (x, y, z) je pythagorejský trojúhelník. Potom existují přirozená čísla k, m a n, kde m a n jsou nesoudělná a m > n, tak, že obvod o trojúhelníka má tvar o = 2km(m+n). Důkaz. Důkaz lze nalézt v [24, s. 34.]. Z Lemmatu 1.4 plyne, že existuje přirozené číslo k a primitivní pythagorejský trojúhelník (x 1, y 1, z 1 ) takový, že x = kx 1, y = ky 1 a z = kz 1. Předpokládejme že y 1 je sudé (pro x 1 sudé je důkaz věty obdobný). Z Věty 1.5 plyne, že existuje dvojice přirozených nesoudělných čísel m a n, m > n, popisující primitivní trojúhelník (x 1, y 1, z 1 ), kde x 1 = m 2 n 2, y 1 = 2mn a z 1 = m 2 + n 2. Pak lze obvod primitivního trojúhelníku vyjádřit jako o 1 = m 2 n 2 + 2mn + m 2 + n 2 = 2m 2 + 2mn = 2m(m + n) a pro pythagorejský trojúhelník (x, y, z) se výraz změní na o = k(m 2 n 2 ) + 2kmn + k(m 2 + n 2 ) = 2km 2 + 2kmn = 2km(m + n). 4.3 Dělitelnost obsahu šesti Věta 4.3. Obsah pythagorejského trojúhelníka (x, y, z) je dělitelný šesti. Důkaz. Můžeme předpokládat, že (x, y, z) je primitivní pythagorejský trojúhelník, obecný případ je snadným důsledkem Lemmatu 1.4. Z Vět 2.4 a 2.2 plyne, že 12 xy. Odtud již vyplývá, že obsah S = xy/2 je dělitelný šesti. Věta 4.4 ([24, s. 37]). Pro každé přirozené číslo n existuje alespoň n pythagorejských trojúhelníků (x k, y k, z k ), k = 1, 2,..., n, kde z k jsou navzájem různé a obsahy S k = x k y k /2 jsou totožné. 36
37 Důkaz. Důkaz provedeme indukcí. Pro n = 1 je tvrzení triviální. Předpokládejme, že pro n 1 tvrzení věty platí, tj. existuje n pythagorejských trojúhelníků (x k, y k, z k ), k = 1, 2,..., n s různými přeponami a stejným obsahem. Bez újmy na obecnosti předpokládejme, že přepona prvního trojúhelníka z 1 je liché číslo. Pro k = 1, 2,..., n položme x k = 2(y 2 1 x 2 1)z 1 x k, ȳ k = 2(y 2 1 x 2 1)z 1 y k, z k = 2(y 2 1 x 2 1)z 1 z k, a pro k = n + 1 položme x n+1 = (y 2 1 x 2 1) 2, ȳ n+1 = 4x 1 y 1 z 2 1, z n+1 = 4x 2 1y z 4 1. Trojúhelníky ( x k, ȳ k, z k ), k = 1, 2,..., n, jsou pythagorejské, protože délky stran jsou vynásobeny konstantou, takže stále zůstávají podobné svým původním trojúhelníkům. Trojúhelník ( x n+1, ȳ n+1, z n+1 ) není podobný žádnému z předchozích, ale jak lze výpočtem ověřit, je pythagorejský. Obsah jednotlivých odvozených trojúhelníků je shodný a sice 4(y1 2 x 2 1) 2 z1-krát 2 větší než obsah trojúhelníků původních. Spočítáním obsahu trojúhelníka ( x n+1, ȳ n+1, z n+1 ) můžeme ukázat, že i tento má stejný obsah, neboli stejný násobek obsahu trojúhelníka (x 1, y 1, z 1 ). Trojúhelníky ( x k, ȳ k, z k ), k = 1, 2,..., n, mají přepony dané sudými čísly, naproti tomu trojúhelník ( x n+1, ȳ n+1, z n+1 ) má přeponu danou číslem lichým. Ukázali jsme, že pro n+1 existuje také n + 1 pythagorejských trojúhelníků, se shodným obsahem, ale různými přeponami a právě jedna z přepon je lichá. Tím je důkaz dokončen. 37
38 Kapitola 5 Počty Tato kapitola sdružuje výsledky o počtech pythagorejských trojúhelníků splňujících určité vlastnosti. 5.1 Počet možných odvěsen Věta 5.1. Necht x je přirozené číslo. Pak existuje pythagorejský trojúhelník (x, y, z) tehdy a jen tehdy, když x > 2. Důkaz. Důkaz lze nalézt např. v [24, s. 26]. Jako první ukážeme nutnou podmínku, tj. že x > 2. Ze vzorce x 2 = z 2 y 2 = (z y)(z + y) vyplývá, že jak z y, tak z + y jsou přirozená čísla. Při minimálních hodnotách y a z musí být y 1, z y 1, z 2. Z toho dostaneme z + y = 3, tudíž x 2 3 a x 1. Pokud by navíc bylo x = 2, dostaneme 4 = (z y)(z + y), což v součinnosti s podmínkami z y 1 a z + y 3 dává hodnoty pro dvojčleny z y = 1 a z + y = 4, neboli 2z = 5. Číslo z ale musí být přirozené, tudíž x 2. Dále ukážeme postačitelnost. Necht je x > 2 liché číslo. Protože platí ( ) x x ( 1 x = 2 2 a 1 2 (x2 1) a 1 2 (x2 + 1) jsou přirozená čísla, odpovídá trojice ( x, 1 2 (x2 1), 1 2 (x2 + 1) ) pythagorejskému trojúhelníku. Pokud je x sudé číslo, pak x2 1 a x ) jsou přirozená čísla
39 a navíc platí ( ) x x ( ) x = Trojice (x, x 2 /4 1, x 2 /4 + 1) je tedy pythagorejský trojúhelník. 5.2 Počet trojúhelníků s danou délkou odvěsny nebo přepony Věta 5.2. Necht x je přirozené číslo. Pak existuje pouze konečný počet pythagorejských trojúhelníků, kde x je délka odvěsny. Důkaz. Důkaz lze nalézt např. v [24, s. 30]. Necht (x, y, z) je pythagorejský trojúhelník. Z rovnice x 2 = z 2 y 2 = (z y)(z + y) plyne, že číslo z + y dělí x 2. Odtud plyne, že z i y jsou menší než x 2, a proto je možných kombinací y a z pouze konečně mnoho. Věta 5.3. Necht n je přirozené číslo. Pak existuje alespoň n pythagorejských trojúhelníků se stejnou délkou odvěsny x, kde x je přirozené číslo. Důkaz. Důkaz lze nalézt např. v [24, s. 30]. Necht k = 0, 1,..., n 1 a označme y k = 2 k ( 2 2n 2k 1 ), a z k = 2 k ( 2 2n 2k + 1 ). Potom z k jsou různá čísla, protože po dělení číslem 2 k dávají různý zbytek, ale současně pro všechna k platí x 2 k = z 2 k y 2 k = 2 2k ( 2 2n 2k + 1 ) 2 2 2k ( 2 2n 2k 1 ) 2 = (2 n+1 ) 2, neboli druhá odvěsna x k nezávisí na k, tedy x k = x = 2 n+1 pro k = 0, 1,..., n. Tak jsme získali n různých pythagorejských trojúhelníků (x, y k, z k ) se stejnou délkou odvěsny x. Věta 5.4. Necht n je přirozené číslo. Pak existuje alespoň n pythagorejských trojúhelníků se stejnou délkou přepony z, kde z je přirozené číslo. 39
40 Důkaz. Důkaz lze nalézt např. v [24, s. 31]. Necht n je přirozené číslo, a položme z = ( )( ) [(2 + n) ] a necht pro k = 3, 4,..., n + 2 mají odvěsny délky x k = k2 1 k z, a y k = 2k k z. Protože pro všechna k = 3, 4,..., n + 2 je z/(k 2 + 1) přirozené číslo, jsou i x k přirozená čísla pro všechna k = 3, 4,..., n + 2. Je snadné ověřit, že x 2 k + y2 k = z2, tedy pro každé k = 3, 4,..., n + 2 je (x k, y k, z) pythagorejský trojúhelník. Posledním krokem je dokázat, že těchto n trojúhelníků (x k, y k, z), kde k = 3, 4,..., n + 2, není vzájemně podobných. Máme Dále platí x k = z x k y k = k2 1 k z 2k k z = (k 1)2 2 z > 0. k z, a tudíž délky jednotlivých odvěsen x k 2 +1 k jsou uspořádané, tj. a y k x 3 < x 4 < < x n < x n+1 < x n+2. Ke zvolenému n jsme tedy nalezli n různých pythagorejských trojúhelníků se stejnou délkou přepony a s rostoucím délkou delší odvěsny. 5.3 Trojúhelníky, kde délky obou odvěsen jsou čtverce Věta 5.5 ([24, s. 49]). Necht (x, y, z) je pythagorejský trojúhelník. Pak nemohou současně délky obou odvěsen být druhou mocninou přirozených čísel. Důkaz. Předpokládejme, že existují pythagorejské trojúhelníky, kde délky obou odvěsen jsou čtverce. Vezměme z nich trojúhelník (x, y, z), který má přeponu kratší nebo stejně dlouhou 40
41 než libovolný jiný. Pak existují přirozená čísla a a b taková, že x = a 2 a y = b 2. Předpokládejme, že a a b jsou soudělná čísla se společným dělitelem d, tj. a = d a 1 a b = d b 1. Pak z 2 = x 2 + y 2 = a 4 + b 4 = (da 1 ) 4 + (db 1 ) 4 = d 4 (a b 4 1), tudíž z je dělitelné d 2 a lze psát z = d 2 z 1. Odtud máme z 2 1 = a b 4 1. Tedy trojúhelník (a 2 1, b 2 1, z 1 ) je pythagorejský trojúhelník s odvěsnou z 1 < z, což je spor s předpokladem o trojúhelníku (x, y, z). Čísla a a b tedy musí být nesoudělná a trojúhelník (a 2, b 2, z) je tedy primitivní. Díky Lemmatu 2.1 můžeme bez újmy na obecnosti předpokládat, že b 2 je sudé a a 2 liché. Podle Věty 1.5 existují nesoudělná přirozená čísla m, n, m > n, že x = a 2 = m 2 n 2, y = b 2 = 2mn a z = m 2 + n 2. Ze vztahu pro a 2 plyne, že (a, n, m) je pythagorejský trojúhelník, a podle Lemmatu 2.1 nemohou být a a n současně lichá čísla. Tedy n musí být sudé. Označme n = 2k, kde k je přirozené číslo a nesoudělné s m, protože n a m jsou nesoudělná. Potom b 2 = 2mn lze přepsat jako b 2 = 2 2 mk. Označme dále b = 2l pro přirozené číslo l. Pak platí l 2 = mk, a protože m a k jsou nesoudělná čísla, musí každé z nich být čtvercem. Tedy existují nesoudělná přirozená čísla r a s, kde m = r 2, k = s 2. Z nesoudělnosti m a n plyne nesoudělnost a a n. Trojúhelník (a, n, m) je tedy primitivní a n je sudé. Existují tedy nesoudělná přirozená čísla m a n, m > n, taková, že a = m 2 n 2, n = 2 m n, m = m 2 + n 2. 41
42 Výše jsme ukázali, že n = 2s 2, tedy s 2 = m n a odtud opět plyne, že m a n jsou čtverce. Existují tedy přirozená čísla r a s, že m = r 2 a n = s 2. Dohromady tedy máme m = r 2 a současně m = m 2 + n 2 = r 4 + s 4, a proto ( r 2, s 2, r) tvoří pythagorejský trojúhelník, kde délky obou odvěsen jsou čtverce. Protože m = r 2, platí r < m; současně z = m 2 + n 2, tedy m < z a tedy také r < z. To ale spor s předpokladem, protože trojúhelník ( r 2, s 2, r) má přeponu menší než trojúhelník (a 2, b 2, z). 5.4 Trojúhelníky, kde odvěsna a přepona jsou čtverce Věta 5.6 ([24, s. 49]). Necht (x, y, z) je pythagorejský trojúhelník. Pak nemohou současně délky přepony a jedné odvěsny být druhou mocninou přirozených čísel. Důkaz. Předpokládejme, že existují pythagorejské trojúhelníky, kde délka jedné odvěsny a délka přepony jsou druhými mocninami přirozených čísel. Z nich vezměme takový trojúhelník (x, y, z), který má přeponu kratší nebo stejně dlouhou než libovolný jiný. Bez újmy na obecnosti předpokládejme, že x = a 2 a z = c 2. Pokud by x a z byla soudělná čísla, existovalo by přirozené číslo d, pro které by bylo x = a 2 = d 2 a 2 1, z = c 2 = d 2 c 2 1 a y 2 = z 2 x 2 = d 4 (c 2 1 a 2 1). Tedy d 4 y 2 a d 2 y, tedy y = d 2 y 1. Trojúhelník (a 2 1, y 1, c 2 1) má menší přeponu c 1 < z, ale to je spor s předpokladem o trojúhelníku (x, y, z). Čísla x a z jsou tudíž nesoudělná a trojúhelník (x, y, z) je primitivní a čísla a a c budou nesoudělná. Dále předpokládejme, že y je sudé. Pak dle Věty 1.5 existují nesoudělná přirozená čísla m, n, m > n, pro která platí x = a 2 = m 2 n 2, y = 2mn, z = c 2 = m 2 + n 2. Odtud odvodíme a 2 c 2 = (m 2 + n 2 )(m 2 n 2 ) = m 4 n 4, 42
43 neboli v trojúhelníku (n 2, ac, m 2 ) jsou délky jedné přepony a odvěsny čtverce, navíc je délka přepony m 2 < c 2, což je spor s předpokladem. Za y tedy musíme vzít liché číslo a x = a 2 je sudé číslo. Pythagorejská rovnice bude vzhledem k y 2 ve tvaru y 2 = c 4 a 4 = (c 2 + a 2 )(c 2 a 2 ). Jelikož v každém primitivním pythagorejském trojúhelníku je délka přepony liché číslo (viz. Lemma 2.1), je i c liché. Dále y je liché a a je sudé číslo, proto jsou obě čísla (c 2 +a 2 ), (c 2 a 2 ) lichá. Také je snadné nahlédnout, že jejich společný dělitel by musel dělit jak c 2, tak a 2, která jsou ale nesoudělná. Platí tedy, že (c 2 + a 2 ) a (c 2 a 2 ) jsou lichá nesoudělná čísla a jejich součin je čtverec. Musí proto existovat přirozená lichá nesoudělná čísla s a r, s > r, pro která je r 2 = c 2 a 2, s 2 = c 2 + a 2. Potom máme ( ) 2 ( ) 2 s + r s r + = c Obě čísla (s + r)/2, (s r)/2 jsou přirozená a nesoudělná, protože čísla r a s jsou lichá a nesoudělná. Trojúhelník ((s + r)/2, (s r)/2, c) je tedy primitivní a existují opět podle Věty 1.5 nesoudělná přirozená čísla m a n, m > n, kde bude v případě sudého čísla (s r)/2 platit s + r 2 = m 2 n 2, s r 2 = 2mn a c = m 2 + n 2, nebo s + r 2 = 2mn, s r 2 = m 2 n 2 a c = m 2 + n 2 v případě, že je (s r)/2 liché. V obou případech bude vyjádření 2x stejné, a sice 2x = 2a 2 = s 2 r 2 = 8mn(m 2 n 2 ). 43
Důkazové metody. Teoretická informatika Tomáš Foltýnek
 Důkazové metody Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Matematický důkaz Jsou dány axiomy a věta (tvrzení, teorém), o níž chceme ukázat, zda platí. Matematický důkaz je nezpochybnitelné
Důkazové metody Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Matematický důkaz Jsou dány axiomy a věta (tvrzení, teorém), o níž chceme ukázat, zda platí. Matematický důkaz je nezpochybnitelné
2.4.11 Nerovnice s absolutní hodnotou
 .. Nerovnice s absolutní hodnotou Předpoklady: 06, 09, 0 Pedagogická poznámka: Hlavním záměrem hodiny je, aby si studenti uvědomili, že se neučí nic nového. Pouze používají věci, které dávno znají, na
.. Nerovnice s absolutní hodnotou Předpoklady: 06, 09, 0 Pedagogická poznámka: Hlavním záměrem hodiny je, aby si studenti uvědomili, že se neučí nic nového. Pouze používají věci, které dávno znají, na
když n < 100, n N, pak r(n) = n,
 Zúžená aritmetika úvod Nad a Stehlíková Autorem netradiční aritmetické struktury, v rámci které se budeme nadále pohybovat, je Prof. Milan Hejný. Nejdříve si zavedeme základní pojmy. Základem zúžené aritmetiky
Zúžená aritmetika úvod Nad a Stehlíková Autorem netradiční aritmetické struktury, v rámci které se budeme nadále pohybovat, je Prof. Milan Hejný. Nejdříve si zavedeme základní pojmy. Základem zúžené aritmetiky
2.7.2 Mocninné funkce se záporným celým mocnitelem
 .7. Mocninné funkce se záporným celým mocnitelem Předpoklady: 70 Mocninné funkce se záporným celým mocnitelem: znamená? 3 y = = = = 3 y y y 3 = ; = ; = ;.... Co to Pedagogická poznámka: Nechávám studenty,
.7. Mocninné funkce se záporným celým mocnitelem Předpoklady: 70 Mocninné funkce se záporným celým mocnitelem: znamená? 3 y = = = = 3 y y y 3 = ; = ; = ;.... Co to Pedagogická poznámka: Nechávám studenty,
65. ročník matematické olympiády Řešení úloh klauzurní části školního kola kategorie B
 65. ročník matematické olympiády Řešení úloh klauzurní části školního kola kategorie B 1. Nejprve zjistíme, jak lze zapsat číslo 14 jako součet čtyř z daných čísel. Protože 4 + 3 3 < 14 < 4 4, musí takový
65. ročník matematické olympiády Řešení úloh klauzurní části školního kola kategorie B 1. Nejprve zjistíme, jak lze zapsat číslo 14 jako součet čtyř z daných čísel. Protože 4 + 3 3 < 14 < 4 4, musí takový
3.2.4 Podobnost trojúhelníků II
 3..4 odobnost trojúhelníků II ředpoklady: 33 ř. 1: Na obrázku jsou nakresleny podobné trojúhelníky. Zapiš jejich podobnost (aby bylo zřejmé, který vrchol prvního trojúhelníku odpovídá vrcholu druhého trojúhelníku).
3..4 odobnost trojúhelníků II ředpoklady: 33 ř. 1: Na obrázku jsou nakresleny podobné trojúhelníky. Zapiš jejich podobnost (aby bylo zřejmé, který vrchol prvního trojúhelníku odpovídá vrcholu druhého trojúhelníku).
Vztah mezi dvěma čísly, které se rovnají, se nazývá rovnost, jako například : ( 2) 3 = 8 4 = 2 ; 16 = 4 ; 1 = 1 a podobně. 2
 Lineární rovnice o jedné neznámé O rovnicích obecně Vztah mezi dvěma čísly, které se rovnají, se nazývá rovnost, jako například : ( ) 8 ; 6 ; a podobně. ; Na rozdíl od rovností obsahuje rovnice kromě čísel
Lineární rovnice o jedné neznámé O rovnicích obecně Vztah mezi dvěma čísly, které se rovnají, se nazývá rovnost, jako například : ( ) 8 ; 6 ; a podobně. ; Na rozdíl od rovností obsahuje rovnice kromě čísel
(a) = (a) = 0. x (a) > 0 a 2 ( pak funkce má v bodě a ostré lokální maximum, resp. ostré lokální minimum. Pokud je. x 2 (a) 2 y (a) f.
 I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
I. Funkce dvou a více reálných proměnných 5. Lokální extrémy. Budeme uvažovat funkci f = f(x 1, x 2,..., x n ), která je definovaná v otevřené množině G R n. Řekneme, že funkce f = f(x 1, x 2,..., x n
{ } 9.1.9 Kombinace II. Předpoklady: 9108. =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce.
 9.1.9 Kombinace II Předpoklady: 9108 Př. 1: Je dána pěti prvková množina: M { a; b; c; d; e} =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce. Vypisujeme
9.1.9 Kombinace II Předpoklady: 9108 Př. 1: Je dána pěti prvková množina: M { a; b; c; d; e} =. Vypiš všechny dvoučlenné kombinace sestavené z těchto pěti prvků. Urči počet kombinací pomocí vzorce. Vypisujeme
Matematika 9. ročník
 Matematika 9. ročník Náhradník NáhradníkJ evátá třída (Testovací klíč: PFFNINW) Počet správně zodpovězených otázek Počet nesprávně zodpovězených otázek 0 26 Počítání s čísly / Geometrie / Slovní úlohy
Matematika 9. ročník Náhradník NáhradníkJ evátá třída (Testovací klíč: PFFNINW) Počet správně zodpovězených otázek Počet nesprávně zodpovězených otázek 0 26 Počítání s čísly / Geometrie / Slovní úlohy
( ) 2.4.4 Kreslení grafů funkcí metodou dělení definičního oboru I. Předpoklady: 2401, 2208
 .. Kreslení grafů funkcí metodou dělení definičního oboru I Předpoklady: 01, 08 Opakování: Pokud jsme při řešení nerovnic potřebovali vynásobit nerovnici výrazem, nemohli jsme postupovat pro všechna čísla
.. Kreslení grafů funkcí metodou dělení definičního oboru I Předpoklady: 01, 08 Opakování: Pokud jsme při řešení nerovnic potřebovali vynásobit nerovnici výrazem, nemohli jsme postupovat pro všechna čísla
2.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou
 .8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 0,, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli jednotlivé kroky postupu při řešení rovnic (nerovnic)
.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 0,, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli jednotlivé kroky postupu při řešení rovnic (nerovnic)
STEREOMETRIE. Vzdálenost bodu od přímky. Mgr. Jakub Němec. VY_32_INOVACE_M3r0113
 STEREOMETRIE Vzdálenost bodu od přímky Mgr. Jakub Němec VY_32_INOVACE_M3r0113 VZDÁLENOST BODU OD PŘÍMKY V PROSTORU Při hledání vzdálenosti bodu od geometrického útvaru v prostoru je nutné si vždy úlohu
STEREOMETRIE Vzdálenost bodu od přímky Mgr. Jakub Němec VY_32_INOVACE_M3r0113 VZDÁLENOST BODU OD PŘÍMKY V PROSTORU Při hledání vzdálenosti bodu od geometrického útvaru v prostoru je nutné si vždy úlohu
Kvadratické rovnice pro učební obory
 Variace 1 Kvadratické rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jkaékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Variace 1 Kvadratické rovnice pro učební obory Autor: Mgr. Jaromír JUŘEK Kopírování a jkaékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
1. Kruh, kružnice. Mezi poloměrem a průměrem kružnice platí vztah : d = 2. r. Zapíšeme k ( S ; r ) Čteme kružnice k je určena středem S a poloměrem r.
 Kruh, kružnice, válec 1. Kruh, kružnice 1.1. Základní pojmy Kružnice je množina bodů mající od daného bodu stejnou vzdálenost. Daný bod označujeme jako střed kružnice. Stejnou vzdálenost nazýváme poloměr
Kruh, kružnice, válec 1. Kruh, kružnice 1.1. Základní pojmy Kružnice je množina bodů mající od daného bodu stejnou vzdálenost. Daný bod označujeme jako střed kružnice. Stejnou vzdálenost nazýváme poloměr
( ) 2.5.7 Neúplné kvadratické rovnice. Předpoklady: 020501
 ..7 Neúplné kvadratické rovnice Předpoklady: Pedagogická poznámka: Tato hodina patří mezi vzácné výjimky, kdy naprostá většina studentů skončí více než pět minut před zvoněním. Nechávám je dělat něco jiného
..7 Neúplné kvadratické rovnice Předpoklady: Pedagogická poznámka: Tato hodina patří mezi vzácné výjimky, kdy naprostá většina studentů skončí více než pět minut před zvoněním. Nechávám je dělat něco jiného
Svobodná chebská škola, základní škola a gymnázium s.r.o. Zlomky sčítání a odčítání. Dušan Astaloš. samostatná práce, případně skupinová práce
 METODICKÝ LIST DA2 Název tématu: Autor: Předmět: Zlomky sčítání a odčítání Dušan Astaloš Matematika Ročník:. Učebnice: Kapitola, oddíl: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný
METODICKÝ LIST DA2 Název tématu: Autor: Předmět: Zlomky sčítání a odčítání Dušan Astaloš Matematika Ročník:. Učebnice: Kapitola, oddíl: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný
Kvadratické rovnice pro studijní obory
 Variace 1 Kvadratické rovnice pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Variace 1 Kvadratické rovnice pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratické
Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana 1 (celkem 7) Číselné soustavy
 Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana (celkem 7) Polyadické - zobrazené mnohočlenem desítková soustava 3 2 532 = 5 + 3 + 2 + Číselné soustavy Číslice tvořící zápis čísla jsou vlastně
Číselné soustavy Ing. M. Kotlíková, Ing. A. Netrvalová Strana (celkem 7) Polyadické - zobrazené mnohočlenem desítková soustava 3 2 532 = 5 + 3 + 2 + Číselné soustavy Číslice tvořící zápis čísla jsou vlastně
Soustavy lineárních rovnic
 1 Soustavy lineárních rovnic Příklad: Uvažujme jednoduchý příklad soustavy dvou lineárních rovnic o dvou neznámých x, y: x + 2y = 5 4x + y = 6 Ze střední školy známe několik metod, jak takové soustavy
1 Soustavy lineárních rovnic Příklad: Uvažujme jednoduchý příklad soustavy dvou lineárních rovnic o dvou neznámých x, y: x + 2y = 5 4x + y = 6 Ze střední školy známe několik metod, jak takové soustavy
Zákonitosti, vztahy a práce s daty
 20mate matematika Jednotlivé kapitoly mají rozsah čtyř stran a každá kapitola je obohacena o rozšiřující učivo. sčítání a odčítání Zákonitosti, vztahy a práce s daty 1 Vyřeš úlohy. a) Součet všech čísel
20mate matematika Jednotlivé kapitoly mají rozsah čtyř stran a každá kapitola je obohacena o rozšiřující učivo. sčítání a odčítání Zákonitosti, vztahy a práce s daty 1 Vyřeš úlohy. a) Součet všech čísel
1.3.1 Kruhový pohyb. Předpoklady: 1105
 .. Kruhový pohyb Předpoklady: 05 Předměty kolem nás se pohybují různými způsoby. Nejde pouze o přímočaré nebo křivočaré posuvné pohyby. Velmi často se předměty otáčí (a některé se přitom pohybují zároveň
.. Kruhový pohyb Předpoklady: 05 Předměty kolem nás se pohybují různými způsoby. Nejde pouze o přímočaré nebo křivočaré posuvné pohyby. Velmi často se předměty otáčí (a některé se přitom pohybují zároveň
INŽENÝRSKÁ MATEMATIKA LOKÁLNÍ EXTRÉMY
 INŽENÝRSKÁ MATEMATIKA LOKÁLNÍ EXTRÉMY FUNKCÍ DVOU PROMĚNNÝCH Robert Mařík 2. října 2009 Obsah z = x 4 +y 4 4xy + 30..................... 3 z = x 2 y 2 x 2 y 2........................ 18 z = y ln(x 2 +y)..........................
INŽENÝRSKÁ MATEMATIKA LOKÁLNÍ EXTRÉMY FUNKCÍ DVOU PROMĚNNÝCH Robert Mařík 2. října 2009 Obsah z = x 4 +y 4 4xy + 30..................... 3 z = x 2 y 2 x 2 y 2........................ 18 z = y ln(x 2 +y)..........................
Kvantové počítače algoritmy (RSA a faktorizace čísla) http://marble.matfyz.cz
 Kvantové počítače algoritmy (RSA a faktorizace čísla) http://marble.matfyz.cz 14. 4. 2004 1. Algoritmus RSA Asymetrické šifrování. Existuje dvojice tajného a veřejného klíče, takže není nutné předat klíč
Kvantové počítače algoritmy (RSA a faktorizace čísla) http://marble.matfyz.cz 14. 4. 2004 1. Algoritmus RSA Asymetrické šifrování. Existuje dvojice tajného a veřejného klíče, takže není nutné předat klíč
Soustavy lineárních rovnic
 Soustavy lineárních rovnic Buď (T, +, ) těleso. Pak soustava rovnic a 11 x 1 + a 12 x 2 + + a 1n x n = b 1, a 21 x 1 + a 22 x 2 + + a 2n x n = b 2,................................... a m1 x 1 + a m2 x
Soustavy lineárních rovnic Buď (T, +, ) těleso. Pak soustava rovnic a 11 x 1 + a 12 x 2 + + a 1n x n = b 1, a 21 x 1 + a 22 x 2 + + a 2n x n = b 2,................................... a m1 x 1 + a m2 x
Svobodná chebská škola, základní škola a gymnázium s.r.o. pochopení pojmů a výpočtů objemů a obvodů
 METODICKÝ LIST DA46 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Obvod a obsah I. - obrazce Astaloš Dušan Matematika šestý frontální, fixační,
METODICKÝ LIST DA46 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Obvod a obsah I. - obrazce Astaloš Dušan Matematika šestý frontální, fixační,
ALGEBRA LINEÁRNÍ, KVADRATICKÉ ROVNICE
 ALGEBRA LINEÁRNÍ, KVADRATICKÉ ROVNICE A NEROVNICE, SOUSTAVY ROVNIC A NEROVNIC Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21.
ALGEBRA LINEÁRNÍ, KVADRATICKÉ ROVNICE A NEROVNICE, SOUSTAVY ROVNIC A NEROVNIC Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21.
( ) ( ) ( ) 2 ( ) 2.7.16 Rovnice s neznámou pod odmocninou II. Předpoklady: 2715
 .7.6 Rovnice s neznámou pod odmocninou II Předpoklady: 75 Př. : Vyřeš rovnici y + + y = 4 y + + y = 4 / ( y + + y ) = ( 4) y + + 4 y + y + 4 y = 6 5y + 4 y + y = 8 5y + 4 y + y = 8 - v tomto stavu nemůžeme
.7.6 Rovnice s neznámou pod odmocninou II Předpoklady: 75 Př. : Vyřeš rovnici y + + y = 4 y + + y = 4 / ( y + + y ) = ( 4) y + + 4 y + y + 4 y = 6 5y + 4 y + y = 8 5y + 4 y + y = 8 - v tomto stavu nemůžeme
9.2.5 Sčítání pravděpodobností I
 9.2.5 Sčítání pravděpodobností I Předpoklady: 9203 Pedagogická poznámka: Následující problém sice zadávám jako příklad, ale minimálně na začátku s žáky počítám na tabuli. I kvůli tomu, aby jejich úprava
9.2.5 Sčítání pravděpodobností I Předpoklady: 9203 Pedagogická poznámka: Následující problém sice zadávám jako příklad, ale minimálně na začátku s žáky počítám na tabuli. I kvůli tomu, aby jejich úprava
UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
3. Ve zbylé množině hledat prvky, které ve srovnání nikdy nejsou napravo (nevedou do nich šipky). Dát do třetí
 DMA Přednáška Speciální relace Nechť R je relace na nějaké množině A. Řekneme, že R je částečné uspořádání, jestliže je reflexivní, antisymetrická a tranzitivní. V tom případě značíme relaci a řekneme,
DMA Přednáška Speciální relace Nechť R je relace na nějaké množině A. Řekneme, že R je částečné uspořádání, jestliže je reflexivní, antisymetrická a tranzitivní. V tom případě značíme relaci a řekneme,
Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.
 Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.b Co je množinou středů všech kružnic v rovině, které prochází
Kapitola I - Množiny bodů daných vlastností I.a Co je množinou všech bodů v rovině, které mají od daných dvou různých bodů stejnou vzdálenost? I.b Co je množinou středů všech kružnic v rovině, které prochází
KONSTRUKČNÍ ÚLOHY ŘEŠENÉ UŽITÍM MNOŽIN BODŮ
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KONSTRUKČNÍ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KONSTRUKČNÍ
M - Rovnice - lineární a s absolutní hodnotou
 Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
Rovnice a jejich ekvivalentní úpravy Co je rovnice Rovnice je matematický zápis rovnosti dvou výrazů. př.: x + 5 = 7x - M - Rovnice - lineární a s absolutní hodnotou Písmeno zapsané v rovnici nazýváme
Dualita v úlohách LP Ekonomická interpretace duální úlohy. Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 6 Katedra ekonometrie FEM UO Brno Uvažujme obecnou úlohu lineárního programování, tj. úlohu nalezení takového řešení vlastních omezujících podmínek a 11 x 1 + a 1 x +... + a 1n x n = b 1 a
Přednáška č. 6 Katedra ekonometrie FEM UO Brno Uvažujme obecnou úlohu lineárního programování, tj. úlohu nalezení takového řešení vlastních omezujících podmínek a 11 x 1 + a 1 x +... + a 1n x n = b 1 a
Dopravní úloha. Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 9 Katedra ekonometrie FEM UO Brno Distribuční úlohy Budeme se zabývat 2 typy distribučních úloh dopravní úloha přiřazovací problém Dopravní úloha V dopravním problému se v typickém případě
Přednáška č. 9 Katedra ekonometrie FEM UO Brno Distribuční úlohy Budeme se zabývat 2 typy distribučních úloh dopravní úloha přiřazovací problém Dopravní úloha V dopravním problému se v typickém případě
4.6.6 Složený sériový RLC obvod střídavého proudu
 4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 41, 4605 Minulá hodina: odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
4.6.6 Složený sériový LC obvod střídavého proudu Předpoklady: 41, 4605 Minulá hodina: odpor i induktance omezují proud ve střídavém obvodu, nemůžeme je však sčítat normálně, ale musíme použít Pythagorovu
Aritmetika s didaktikou I.
 Katedra matematiky PF UJEP Aritmetika s didaktikou I. KM1 / 0001 Přednáška 03 Operace v množině, vlastnosti binárních operací O čem budeme hovořit: zavedení pojmu operace binární, unární a další operace
Katedra matematiky PF UJEP Aritmetika s didaktikou I. KM1 / 0001 Přednáška 03 Operace v množině, vlastnosti binárních operací O čem budeme hovořit: zavedení pojmu operace binární, unární a další operace
Lokální a globální extrémy funkcí jedné reálné proměnné
 Lokální etrémy Globální etrémy Použití Lokální a globální etrémy funkcí jedné reálné proměnné Nezbytnou teorii naleznete Breviáři vyšší matematiky (odstavec 1.). Postup při hledání lokálních etrémů: Lokální
Lokální etrémy Globální etrémy Použití Lokální a globální etrémy funkcí jedné reálné proměnné Nezbytnou teorii naleznete Breviáři vyšší matematiky (odstavec 1.). Postup při hledání lokálních etrémů: Lokální
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
2.7.1 Mocninné funkce s přirozeným mocnitelem
 .7. Mocninné funkce s přirozeným mocnitelem Předpoklad: 0 Pedagogická poznámka: K následujícím třem hodinám je možné přistoupit dvěma způsob. Já osobně doporučuji postupovat podle učebnice. V takovém případě
.7. Mocninné funkce s přirozeným mocnitelem Předpoklad: 0 Pedagogická poznámka: K následujícím třem hodinám je možné přistoupit dvěma způsob. Já osobně doporučuji postupovat podle učebnice. V takovém případě
Př. 3: Dláždíme čtverec 12 x 12. a) dlaždice 2 x 3 12 je dělitelné 2 i 3 čtverec 12 x 12 můžeme vydláždit dlaždicemi 2 x 3.
 1..20 Dláždění III Předpoklady: 01019 Př. 1: Najdi n ( 84,96), ( 84,96) D. 84 = 4 21 = 2 2 7 96 = 2 = 4 8 = 2 2 2 2 2 D 84,96 = 2 2 = 12 (společné části rozkladů) ( ) n ( 84,96) = 2 2 2 2 2 7 = 672 (nejmenší
1..20 Dláždění III Předpoklady: 01019 Př. 1: Najdi n ( 84,96), ( 84,96) D. 84 = 4 21 = 2 2 7 96 = 2 = 4 8 = 2 2 2 2 2 D 84,96 = 2 2 = 12 (společné části rozkladů) ( ) n ( 84,96) = 2 2 2 2 2 7 = 672 (nejmenší
Matematika - Tercie Matematika tercie Výchovné a vzdělávací strategie Učivo ŠVP výstupy
 - Tercie Matematika Výchovné a vzdělávací strategie Kompetence k řešení problémů Kompetence komunikativní Kompetence sociální a personální Kompetence občanská Kompetence k učení Kompetence pracovní Učivo
- Tercie Matematika Výchovné a vzdělávací strategie Kompetence k řešení problémů Kompetence komunikativní Kompetence sociální a personální Kompetence občanská Kompetence k učení Kompetence pracovní Učivo
Diferenciální počet funkcí jedné proměnné
 Diferenciální počet funkcí jedné proměnné 1 Diferenciální počet funkcí jedné proměnné - Úvod Diferenciální počet funkcí jedné proměnné - úvod V přírodě se neustále dějí změny. Naší snahou je nalézt příčiny
Diferenciální počet funkcí jedné proměnné 1 Diferenciální počet funkcí jedné proměnné - Úvod Diferenciální počet funkcí jedné proměnné - úvod V přírodě se neustále dějí změny. Naší snahou je nalézt příčiny
AUTORKA Barbora Sýkorová
 ČÍSLO SADY III/2 AUTORKA Barbora Sýkorová NÁZEV SADY: Číslo a proměnná číselné označení DUM NÁZEV DATUM OVĚŘENÍ DUM TŘÍDA ANOTACE PLNĚNÉ VÝSTUPY KLÍČOVÁ SLOVA FORMÁT (pdf,, ) 1 Pracovní list číselné výrazy
ČÍSLO SADY III/2 AUTORKA Barbora Sýkorová NÁZEV SADY: Číslo a proměnná číselné označení DUM NÁZEV DATUM OVĚŘENÍ DUM TŘÍDA ANOTACE PLNĚNÉ VÝSTUPY KLÍČOVÁ SLOVA FORMÁT (pdf,, ) 1 Pracovní list číselné výrazy
Úlohy krajského kola kategorie A
 65. ročník matematické olympiády Úlohy krajského kola kategorie A 1. Na tabuli jsou napsána různá přirozená čísla. Jejich aritmetický průměr je desetinné číslo, jehož desetinná část je přesně 0,2016. Jakou
65. ročník matematické olympiády Úlohy krajského kola kategorie A 1. Na tabuli jsou napsána různá přirozená čísla. Jejich aritmetický průměr je desetinné číslo, jehož desetinná část je přesně 0,2016. Jakou
Sada 2 Microsoft Word 2007
 S třední škola stavební Jihlava Sada 2 Microsoft Word 2007 04. Text v záhlaví, zápatí, číslování stránek Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
S třední škola stavební Jihlava Sada 2 Microsoft Word 2007 04. Text v záhlaví, zápatí, číslování stránek Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
Řešení 3. série. typ čtverce o kolik se zvýší počet 1 x 1 2k + 1 2 x 2 2k 1 3 x 3 2k 3. . k x k 3 (k + 1) x (k + 1) 1
 Řešení 3 série Řešení S-I-3-1 Než se pustíme o řešení úlohy s n x n čtvercovými poli, zkusme ohalit princip na šachovnici s konkrétním počtem polí Na šachovnici 1 x 1 je pouze 1 čtverec Na šachovnici 2
Řešení 3 série Řešení S-I-3-1 Než se pustíme o řešení úlohy s n x n čtvercovými poli, zkusme ohalit princip na šachovnici s konkrétním počtem polí Na šachovnici 1 x 1 je pouze 1 čtverec Na šachovnici 2
= musíme dát pozor na: jmenovatel 2a, zda je a = 0 výraz pod odmocninou, zda je > 0, < 0, = 0 (pak je jediný kořen)
 .8.7 Kvadratické rovnice s parametrem Předpoklady: 507, 803 Pedagogická poznámka: Na první pohled asi každého zarazí, že takřka celá hodina je psána jako příklady a studenti by ji měli vypracovat samostatně.
.8.7 Kvadratické rovnice s parametrem Předpoklady: 507, 803 Pedagogická poznámka: Na první pohled asi každého zarazí, že takřka celá hodina je psána jako příklady a studenti by ji měli vypracovat samostatně.
Definice 6.2.1. z = f(x,y) vázané podmínkou g(x,y) = 0 jsou z geometrického hlediska lokálními extrémy prostorové křivky k, Obr. 6.2.1. Obr. 6.2.
 Výklad Dalším typem extrémů, kterým se budeme zabývat jsou tzv. vázané extrémy. Hledáme extrémy nějaké funkce vzhledem k předem zadaným podmínkám. Definice 6.2.1. Řekneme, že funkce f : R n D f R má v
Výklad Dalším typem extrémů, kterým se budeme zabývat jsou tzv. vázané extrémy. Hledáme extrémy nějaké funkce vzhledem k předem zadaným podmínkám. Definice 6.2.1. Řekneme, že funkce f : R n D f R má v
Kapitola 7: Integrál. 1/14
 Kapitola 7: Integrál. 1/14 Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní funkcí k
Kapitola 7: Integrál. 1/14 Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní funkcí k
Funkce více proměnných
 Funkce více proměnných Funkce více proměnných Euklidův prostor Body, souřadnice, vzdálenost bodů Množina bodů, které mají od bodu A stejnou vzdálenost Uzavřený interval, otevřený interval Okolí bodu
Funkce více proměnných Funkce více proměnných Euklidův prostor Body, souřadnice, vzdálenost bodů Množina bodů, které mají od bodu A stejnou vzdálenost Uzavřený interval, otevřený interval Okolí bodu
Svobodná chebská škola, základní škola a gymnázium s.r.o.
 METODICKÝ LIST DA41 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Poměry III. postupný poměr Astaloš Dušan Matematika sedmý frontální, fixační samostatná práce upevnění znalostí
METODICKÝ LIST DA41 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Poměry III. postupný poměr Astaloš Dušan Matematika sedmý frontální, fixační samostatná práce upevnění znalostí
Věty o pravoúhlém trojúhelníku. Vztahy pro výpočet obvodu a obsahu. Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu
 Věty o pravoúhlém trojúhelníku Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu b v a obou úseků přepony: v 2 = c a c b c b c a Eukleidova věta o odvěsně A c B Druhá mocnina délky
Věty o pravoúhlém trojúhelníku Eukleidova věta o výšce. Druhá mocnina výšky k přeponě je rovna součinu b v a obou úseků přepony: v 2 = c a c b c b c a Eukleidova věta o odvěsně A c B Druhá mocnina délky
2.1.13 Funkce rostoucí, funkce klesající I
 .1.13 Funkce rostoucí, funkce klesající I Předpoklad: 111 Pedagogická poznámka: Následující příklad je dobrý na opakování. Můžete ho studentům zadat na čas a ten kdo ho nestihne nebo nedokáže vřešit, b
.1.13 Funkce rostoucí, funkce klesající I Předpoklad: 111 Pedagogická poznámka: Následující příklad je dobrý na opakování. Můžete ho studentům zadat na čas a ten kdo ho nestihne nebo nedokáže vřešit, b
KIV/ZI Základy informatiky. MS Excel maticové funkce a souhrny
 KIV/ZI Základy informatiky MS Excel maticové funkce a souhrny cvičící: Michal Nykl zimní semestr 2012 MS Excel matice (úvod) Vektor: (1D) v = [1, 2, 3, 5, 8, 13] Např.: matice sousednosti Matice: (2D)
KIV/ZI Základy informatiky MS Excel maticové funkce a souhrny cvičící: Michal Nykl zimní semestr 2012 MS Excel matice (úvod) Vektor: (1D) v = [1, 2, 3, 5, 8, 13] Např.: matice sousednosti Matice: (2D)
EXPONENCIÁLNÍ A LOGARITMICKÁ FUNKCE
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol EXPONENCIÁLNÍ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol EXPONENCIÁLNÍ
Využití EduBase ve výuce 2
 B.I.B.S., a. s. Využití EduBase ve výuce 2 Projekt Vzdělávání pedagogů v prostředí cloudu reg. č. CZ.1.07/1.3.00/51.0011 Mgr. Jitka Kominácká, Ph.D. a kol. 2015 1 Obsah 1 Obsah... 2 2 Úvod... 3 3 Aktivita:
B.I.B.S., a. s. Využití EduBase ve výuce 2 Projekt Vzdělávání pedagogů v prostředí cloudu reg. č. CZ.1.07/1.3.00/51.0011 Mgr. Jitka Kominácká, Ph.D. a kol. 2015 1 Obsah 1 Obsah... 2 2 Úvod... 3 3 Aktivita:
Druhá mocnina a odmocnina Irena Budínová PDF MU budinova@ped.muni.cz
 Druhá mocnina a odmocnina Irena Budínová PDF MU budinova@ped.muni.cz Materiál byl zpracován v rámci projektu "Systémová podpora trvalého profesního rozvoje (CPD) pedagogických pracovníků propojením pedagogické
Druhá mocnina a odmocnina Irena Budínová PDF MU budinova@ped.muni.cz Materiál byl zpracován v rámci projektu "Systémová podpora trvalého profesního rozvoje (CPD) pedagogických pracovníků propojením pedagogické
Lineární algebra. Vektorové prostory
 Lineární algebra Vektorové prostory Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu:
Lineární algebra Vektorové prostory Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu:
15 s. Analytická geometrie lineárních útvarů
 5 s Analytická geometrie lineárních útvarů ) Na přímce: a) Souřadnice bodu na přímce: Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý
5 s Analytická geometrie lineárních útvarů ) Na přímce: a) Souřadnice bodu na přímce: Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý
Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 18 TVORBA PLOCH]
![Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 18 TVORBA PLOCH] Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 18 TVORBA PLOCH]](/thumbs/41/22292385.jpg) Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Aleš Najman [ÚLOHA 18 TVORBA PLOCH] 1 ÚVOD V této kapitole je probírána tématika tvorby ploch pomocí funkcí vysunutí, rotace a tažení. V moderním světě,
Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Aleš Najman [ÚLOHA 18 TVORBA PLOCH] 1 ÚVOD V této kapitole je probírána tématika tvorby ploch pomocí funkcí vysunutí, rotace a tažení. V moderním světě,
Finanční matematika Vypracovala: Mgr. Zuzana Kopečková
 Finanční matematika Vypracovala: Mgr. Zuzana Kopečková Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace žáků ke studiu technických
Finanční matematika Vypracovala: Mgr. Zuzana Kopečková Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace žáků ke studiu technických
10. Polynomy a racionálně lomenné funkce
 10 Polynomy a racionálně lomenné funkce A Polynomy Definice 101 Reálný polynom stupně n (neboli mnohočlen) je funkce tvaru p(x) = a n x n + a n 1 x n 1 + + a 0, kde a 1,, a n R, a n 0, která každému komplexnímu
10 Polynomy a racionálně lomenné funkce A Polynomy Definice 101 Reálný polynom stupně n (neboli mnohočlen) je funkce tvaru p(x) = a n x n + a n 1 x n 1 + + a 0, kde a 1,, a n R, a n 0, která každému komplexnímu
1.1.1 Kvadratické rovnice (dosazení do vzorce) I
 .. Kvadratické rovnice (dosazení do vzorce) I Předpoklady: základní početní operace Rovnicí se nazývá vztah rovnosti mezi dvěma výrazy obsahujícími jednu nebo více neznámých. V této kapitole se budeme
.. Kvadratické rovnice (dosazení do vzorce) I Předpoklady: základní početní operace Rovnicí se nazývá vztah rovnosti mezi dvěma výrazy obsahujícími jednu nebo více neznámých. V této kapitole se budeme
Tvorba trendové funkce a extrapolace pro roční časové řady
 Tvorba trendové funkce a extrapolace pro roční časové řady Příklad: Základem pro analýzu je časová řada živě narozených mezi lety 1970 a 2005. Prvním úkolem je vybrat vhodnou trendovou funkci pro vystižení
Tvorba trendové funkce a extrapolace pro roční časové řady Příklad: Základem pro analýzu je časová řada živě narozených mezi lety 1970 a 2005. Prvním úkolem je vybrat vhodnou trendovou funkci pro vystižení
Orientovaná úseka. Vektory. Souadnice vektor
 Vektory, operace s vektory Ž3 Orientovaná úseka Mjme dvojici bod A, B (na pímce, v rovin nebo prostoru), které spojíme a vznikne tak úseka. Pokud budeme rozlišovat, zda je spojíme od A k B nebo od B k
Vektory, operace s vektory Ž3 Orientovaná úseka Mjme dvojici bod A, B (na pímce, v rovin nebo prostoru), které spojíme a vznikne tak úseka. Pokud budeme rozlišovat, zda je spojíme od A k B nebo od B k
http://www.zlinskedumy.cz
 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 2, 3 Obor Anotace CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Elektronické obvody, vy_32_inovace_ma_42_06
Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor Ročník 2, 3 Obor Anotace CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Elektronické obvody, vy_32_inovace_ma_42_06
Řešení: ( x = (1 + 2t, 2 5t, 2 + 3t, t); X = [1, 2, 2, 0] + t(2, 5, 3, 1), přímka v E 4 ; (1, 2, 2, 0), 0, 9 )
![Řešení: ( x = (1 + 2t, 2 5t, 2 + 3t, t); X = [1, 2, 2, 0] + t(2, 5, 3, 1), přímka v E 4 ; (1, 2, 2, 0), 0, 9 ) Řešení: ( x = (1 + 2t, 2 5t, 2 + 3t, t); X = [1, 2, 2, 0] + t(2, 5, 3, 1), přímka v E 4 ; (1, 2, 2, 0), 0, 9 )](/thumbs/39/20455694.jpg) . Vyjádřete koeficienty vektoru (, 8, 9) vzhledem k následující bázi vektorového prostoru V : (,, 5), (,, ), (5,, ). [,, ].. Určete všechny hodnoty parametru u, pro které vektor a patří do vektorového
. Vyjádřete koeficienty vektoru (, 8, 9) vzhledem k následující bázi vektorového prostoru V : (,, 5), (,, ), (5,, ). [,, ].. Určete všechny hodnoty parametru u, pro které vektor a patří do vektorového
Funkce. Liché a sudé funkce, periodické funkce. Mgr. Tomáš Pavlica, Ph.D. Digitální učební materiály, 2012-14. Gymnázium Uherské Hradiště
 Funkce Liché a, periodické funkce Mgr. Tomáš Pavlica, Ph.D. Gymnázium Uherské Hradiště Digitální učební materiály, 01-14 Obsah Sudé a 1 Sudé a 3 Sudé a Sudá funkce f má vzhledem k ose o y symetrický definiční
Funkce Liché a, periodické funkce Mgr. Tomáš Pavlica, Ph.D. Gymnázium Uherské Hradiště Digitální učební materiály, 01-14 Obsah Sudé a 1 Sudé a 3 Sudé a Sudá funkce f má vzhledem k ose o y symetrický definiční
Jakub Juránek. 1.64 Určete počet kvádru, jejichž velikosti hran jsou přirozená čísla nejvýše rovná deseti. Kolik je v tomto počtu krychlí?
 Jakub Juránek UČO 393110 1.64 Určete počet kvádru, jejichž velikosti hran jsou přirozená čísla nejvýše rovná deseti. Kolik je v tomto počtu krychlí? Kvádr a b c, a, b, c {1, 2,..., 10} a b c = c a b -
Jakub Juránek UČO 393110 1.64 Určete počet kvádru, jejichž velikosti hran jsou přirozená čísla nejvýše rovná deseti. Kolik je v tomto počtu krychlí? Kvádr a b c, a, b, c {1, 2,..., 10} a b c = c a b -
2.1. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné x je taková
 .. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
.. Funkce a jejich graf.. Pojem funkce a její vlastnosti. Reálná funkce f jedné reálné proměnné je taková binární relace z množin R do množin R, že pro každé R eistuje nejvýše jedno R, pro které [, ] f.
Vzdělávací oblast: Matematika a její aplikace. Obor vzdělávací oblasti: Seminář z matematiky. Ročník: 7. Poznámky
 Vzdělávací oblast: Matematika a její aplikace Obor vzdělávací oblasti: Seminář z matematiky Ročník: 7. Výstupy - kompetence Učivo Průřezová témata,přesahy, a další poznámky - převádí jednotky délky, času,
Vzdělávací oblast: Matematika a její aplikace Obor vzdělávací oblasti: Seminář z matematiky Ročník: 7. Výstupy - kompetence Učivo Průřezová témata,přesahy, a další poznámky - převádí jednotky délky, času,
Výrazy lze též zavést v nečíselných oborech, pak konstanty označuji jeden určitý prvek a obor proměnné není množina čísel.
 Výrazy. Rovnice a nerovnice. Výraz je matematický pojem používaný ve školské matematice. Prvním druhem matematických ů jsou konstanty. Konstanty označují právě jedno číslo z množiny reálných čísel. Například
Výrazy. Rovnice a nerovnice. Výraz je matematický pojem používaný ve školské matematice. Prvním druhem matematických ů jsou konstanty. Konstanty označují právě jedno číslo z množiny reálných čísel. Například
Různostranné obecné Rovnoramenné Rovnostranné. třetí, základna, je různá
 Trojúhelník Trojúhelník - AB určují tři body A, B,, které neleží na jedné přímce. Trojúhelník je rovněž možno považovat za průnik tří polorovin nebo tří konvexních úhlů. γ, γ, γ Body A, B,, se nazývají
Trojúhelník Trojúhelník - AB určují tři body A, B,, které neleží na jedné přímce. Trojúhelník je rovněž možno považovat za průnik tří polorovin nebo tří konvexních úhlů. γ, γ, γ Body A, B,, se nazývají
Dutý plastický trojúhelník by Gianelle
 Dutý plastický trojúhelník by Gianelle Připravíme si rokajl dle našeho výběru pro začátek nejlépe dvě barvy jedné velikosti Já používám korálky Miyuki Delica v tmavě červené barvě, matné s AB úpravou na
Dutý plastický trojúhelník by Gianelle Připravíme si rokajl dle našeho výběru pro začátek nejlépe dvě barvy jedné velikosti Já používám korálky Miyuki Delica v tmavě červené barvě, matné s AB úpravou na
Úlohy 22. ročníku Mezinárodní fyzikální olympiády - Havana, Cuba
 Úlohy 22. ročníku Mezinárodní fyzikální olympiády - Havana, Cuba Petr Pošta Text pro soutěžící FO a ostatní zájemce o fyziku 2 1. úloha Obrázek 1.1 ukazuje pevný, homogenní míč poloměru R. Před pádem na
Úlohy 22. ročníku Mezinárodní fyzikální olympiády - Havana, Cuba Petr Pošta Text pro soutěžící FO a ostatní zájemce o fyziku 2 1. úloha Obrázek 1.1 ukazuje pevný, homogenní míč poloměru R. Před pádem na
Pingpongový míček. Petr Školník, Michal Menkina. TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií
 Petr Školník, Michal Menkina TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinancován
Petr Školník, Michal Menkina TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinancován
4.2.7 Voltampérová charakteristika rezistoru a žárovky
 4.2.7 Voltampérová charakteristika rezistoru a žárovky Předpoklady: 4205 Pedagogická poznámka: Tuto hodinu učím jako běžnou jednohodinovku s celou třídou. Některé dvojice stihnou naměřit více odporů. Voltampérová
4.2.7 Voltampérová charakteristika rezistoru a žárovky Předpoklady: 4205 Pedagogická poznámka: Tuto hodinu učím jako běžnou jednohodinovku s celou třídou. Některé dvojice stihnou naměřit více odporů. Voltampérová
Geometrické vektory. Martina Šimůnková. Katedra aplikované matematiky. 9. března 2008
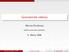 Geometrické vektory Martina Šimůnková Katedra aplikované matematiky 9. března 2008 Martina Šimůnková (KAP) Geometrické vektory 9. března 2008 1/ 27 Definice geometrického vektoru 1 Definice geometrického
Geometrické vektory Martina Šimůnková Katedra aplikované matematiky 9. března 2008 Martina Šimůnková (KAP) Geometrické vektory 9. března 2008 1/ 27 Definice geometrického vektoru 1 Definice geometrického
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
Zvyšování kvality výuky technických oborů Klíčová aktivita IV. Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma IV.. Kvadratické funkce, rovnice a nerovnice
Digitální učební materiál
 Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_2_03 ŠVP Podnikání RVP 64-41-L/51
Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_2_03 ŠVP Podnikání RVP 64-41-L/51
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto
 Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Jana
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Jana
Maturitní okruhy z matematiky školní rok 2007/2008
 Maturitní okruhy z matematiky školní rok 2007/2008 1. ALGEBRAICKÉ VÝRAZY 2 2 2 3 3 3 a ± b ; a b ; a ± b ; a ± b 1.1. rozklad výrazů na součin: vytýkání, užití vzorců: ( ) ( ) 1.2. určování definičního
Maturitní okruhy z matematiky školní rok 2007/2008 1. ALGEBRAICKÉ VÝRAZY 2 2 2 3 3 3 a ± b ; a b ; a ± b ; a ± b 1.1. rozklad výrazů na součin: vytýkání, užití vzorců: ( ) ( ) 1.2. určování definičního
Jan Březina. Technical University of Liberec. 17. března 2015
 TGH03 - stromy, ukládání grafů Jan Březina Technical University of Liberec 17. března 2015 Kružnice - C n V = {1, 2,..., n} E = {{1, 2}, {2, 3},..., {i, i + 1},..., {n 1, n}, {n, 1}} Cesta - P n V = {1,
TGH03 - stromy, ukládání grafů Jan Březina Technical University of Liberec 17. března 2015 Kružnice - C n V = {1, 2,..., n} E = {{1, 2}, {2, 3},..., {i, i + 1},..., {n 1, n}, {n, 1}} Cesta - P n V = {1,
Digitální učební materiál
 Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_1_16 ŠVP Podnikání RVP 64-41-L/51
Digitální učební materiál Projekt Šablona CZ.1.07/1.5.00/34.0415 Inovujeme, inovujeme III/2 Inovace a zkvalitnění výuky prostřednictvím ICT (DUM) DUM č. VY_32_INOVACE_CH29_1_16 ŠVP Podnikání RVP 64-41-L/51
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Informační
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Informační
Testování výškové přesnosti navigační GPS pro účely (cyklo)turistiky
 Fakulta aplikovaných věd Katedra matematiky Testování výškové přesnosti navigační GPS pro účely (cyklo)turistiky Kompletní grafické přílohy bakalářské práce Plzeň 2006 David Velhartický Seznam příloh Praktický
Fakulta aplikovaných věd Katedra matematiky Testování výškové přesnosti navigační GPS pro účely (cyklo)turistiky Kompletní grafické přílohy bakalářské práce Plzeň 2006 David Velhartický Seznam příloh Praktický
Semestrální práce NÁVRH ÚZKOPÁSMOVÉHO ZESILOVAČE. Daniel Tureček zadání číslo 18 cvičení: sudý týden 14:30
 Semestrální práce NÁVRH ÚZKOPÁSMOVÉHO ZESILOVAČE Daniel Tureček zadání číslo 18 cvičení: sudý týden 14:30 1. Ověření stability tranzistoru Při návrhu úzkopásmového zesilovače s tranzistorem je potřeba
Semestrální práce NÁVRH ÚZKOPÁSMOVÉHO ZESILOVAČE Daniel Tureček zadání číslo 18 cvičení: sudý týden 14:30 1. Ověření stability tranzistoru Při návrhu úzkopásmového zesilovače s tranzistorem je potřeba
PŘIJÍMACÍ ZKOUŠKY 2010 - I.termín
 MATEMATIKA Obor: 79-41-K/81 Součet bodů: Opravil: Kontroloval: Vítáme vás na gymnáziu Omská a přejeme úspěšné vyřešení všech úloh. Úlohy můžete řešit v libovolném pořadí. V matematice pracujeme s čísly
MATEMATIKA Obor: 79-41-K/81 Součet bodů: Opravil: Kontroloval: Vítáme vás na gymnáziu Omská a přejeme úspěšné vyřešení všech úloh. Úlohy můžete řešit v libovolném pořadí. V matematice pracujeme s čísly
Matematika ve 4. ročníku
 Matematika ve 4. ročníku září Čte a zapisuje přirozená čísla. učebnice strana 3 9 Počítá po stovkách a desítkách. chvilky strana 1 8 Čte, píše a zobrazuje čísla na číselné ose, teploměru, modelu. kalkulačka
Matematika ve 4. ročníku září Čte a zapisuje přirozená čísla. učebnice strana 3 9 Počítá po stovkách a desítkách. chvilky strana 1 8 Čte, píše a zobrazuje čísla na číselné ose, teploměru, modelu. kalkulačka
Rostislav Horčík. 13. října 2006
 3. přednáška Rostislav Horčík 13. října 2006 1 Lineární prostory Definice 1 Lineárním prostorem nazýváme každou neprázdnou množinu L, na které je definováno sčítání + : L L L a násobení reálným číslem
3. přednáška Rostislav Horčík 13. října 2006 1 Lineární prostory Definice 1 Lineárním prostorem nazýváme každou neprázdnou množinu L, na které je definováno sčítání + : L L L a násobení reálným číslem
Domácí úkol DU01_2p MAT 4AE, 4AC, 4AI
 Příklad 1: Domácí úkol DU01_p MAT 4AE, 4AC, 4AI Osm spolužáků (Adam, Bára, Cyril, Dan, Eva, Filip, Gábina a Hana) se má seřadit za sebou tak, aby Eva byly první a Dan předposlední. Příklad : V dodávce
Příklad 1: Domácí úkol DU01_p MAT 4AE, 4AC, 4AI Osm spolužáků (Adam, Bára, Cyril, Dan, Eva, Filip, Gábina a Hana) se má seřadit za sebou tak, aby Eva byly první a Dan předposlední. Příklad : V dodávce
1.2.26 Přepočet přes jednotku - podruhé II
 1.2.26 Přepočet přes jednotku - podruhé II Předpoklady: 010225 Pedagogická poznámka: První příklad nechávám řešit žáky, pak diskutujeme důvodech dělení. Př. 1: Za 0,85 hodiny zalévání spotřebovalo zavlažovací
1.2.26 Přepočet přes jednotku - podruhé II Předpoklady: 010225 Pedagogická poznámka: První příklad nechávám řešit žáky, pak diskutujeme důvodech dělení. Př. 1: Za 0,85 hodiny zalévání spotřebovalo zavlažovací
Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech.
 Kapitola 9 Skalární součin Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech. Definice 9.1 Je-li x = (x 1,..., x n ) T R n 1 reálný
Kapitola 9 Skalární součin Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech. Definice 9.1 Je-li x = (x 1,..., x n ) T R n 1 reálný
Teorie grafů. Bedřich Košata
 Teorie grafů Bedřich Košata Co je to graf Možina bodů (uzlů) spojených "vazbami" Uzel = vrchol (vertex, pl. vertices) Vazba = hrana (edge) K čemu je to dobré Obecný model pro Sítě Telekomunikační Elektrické
Teorie grafů Bedřich Košata Co je to graf Možina bodů (uzlů) spojených "vazbami" Uzel = vrchol (vertex, pl. vertices) Vazba = hrana (edge) K čemu je to dobré Obecný model pro Sítě Telekomunikační Elektrické
2.1 Pokyny k otevřeným úlohám. 2.2 Pokyny k uzavřeným úlohám TESTOVÝ SEŠIT NEOTVÍREJTE, POČKEJTE NA POKYN!
 MATEMATIKA 9 M9PZD16C0T01 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 17 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby 1 Základní informace k zadání zkoušky Časový
MATEMATIKA 9 M9PZD16C0T01 DIDAKTICKÝ TEST Jméno a příjmení Počet úloh: 17 Maximální bodové hodnocení: 50 bodů Povolené pomůcky: pouze psací a rýsovací potřeby 1 Základní informace k zadání zkoušky Časový
Escort Servis Night Prague
 Escort Servis Night Prague Escortní služby po celé Praze Vize projektu Vypracovali: Jiří Blažek, Cyril Filcík, Michal Dvořák Obsah Cíl projektu...2 Zainteresované instituce a osoby...2 Zadavatel...2 Uživatelé
Escort Servis Night Prague Escortní služby po celé Praze Vize projektu Vypracovali: Jiří Blažek, Cyril Filcík, Michal Dvořák Obsah Cíl projektu...2 Zainteresované instituce a osoby...2 Zadavatel...2 Uživatelé
2.8.10 Rovnice s neznámou pod odmocninou a parametrem
 .8.10 Rovnie s neznámou pod odmoninou a parametrem Předpoklady: 806, 808 Budeme postupovat stejně jako v předhozíh hodináh. Nejdříve si zopakujeme obený postup při řešení rovni s neznámou pod odmoninou
.8.10 Rovnie s neznámou pod odmoninou a parametrem Předpoklady: 806, 808 Budeme postupovat stejně jako v předhozíh hodináh. Nejdříve si zopakujeme obený postup při řešení rovni s neznámou pod odmoninou
4. Výčtem prvků f: {[2,0],[3,1],[4,2],[5,3]}
![4. Výčtem prvků f: {[2,0],[3,1],[4,2],[5,3]} 4. Výčtem prvků f: {[2,0],[3,1],[4,2],[5,3]}](/thumbs/41/22269260.jpg) 1/27 FUNKCE Základní pojmy: Funkce, definiční obor, obor hodnot funkce Kartézská soustava souřadnic, graf funkce Opakování: Číselné množiny, úpravy výrazů, zobrazení čísel na reálné ose Funkce: Zápis:
1/27 FUNKCE Základní pojmy: Funkce, definiční obor, obor hodnot funkce Kartézská soustava souřadnic, graf funkce Opakování: Číselné množiny, úpravy výrazů, zobrazení čísel na reálné ose Funkce: Zápis:
