ANALÝZA ROSTOUCÍHO VÝVOJE OBJEMU POSKYTNUTÝCH HYPOTEČNÍCH ÚVĚRŮ V ČESKÉ REPUBLICE
|
|
|
- Naděžda Valentová
- před 8 lety
- Počet zobrazení:
Transkript
1 ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LVII 17 Číslo 3, 2009 ANALÝZA ROSTOUCÍHO VÝVOJE OBJEMU POSKYTNUTÝCH HYPOTEČNÍCH ÚVĚRŮ V ČESKÉ REPUBLICE P. Střelcová, L. Střelec Došlo: 20. února 2009 Abstract STŘELCOVÁ, P., STŘELEC, L.: Analysis of increasing trend of mortgage volume in the Czech Republic. Acta univ. agric. et silvic. Mendel. Brun., 2009, LVII, No. 3, pp The aim of this paper is an empirical analysis of mortgage volume in the Czech Republic and factors identification of the increasing trend of the mortgage volume in the period from 2001 to Firstly, analysis of quarterly time series of mortgage volume and average mortgage rate are performed. Consequently, causality between mortgage volume and average mortgage rate is analysed. The morgage rate is the most important factor for economic subjects decision of residential investment. Afterwards, it is analysed causality between mortgage volume and selected factors via multiple regression analysis. Based on this analysis, influencing factors for multiple regression analysis describing mortgage vo lume are selected. Our empirical analysis validate the causality between mortgage volume and mortgage rate, unemployment rate and price level of real estates. Part of this paper is also economic eduction of causality and estimation of expect progress of mortgage volume especially in connection with present economic and business recession. mortgage, interest rate, average wage, unemployment, inflation, multiple regression analysis Náklady na zajištění vlastního bydlení zpravidla znamenají velkou finanční zátěž domácností jako ekonomických subjektů, neboť obvykle představují několikanásobek průměrného ročního příjmu domácnosti a jsou jedním z významných faktorů ovlivňujících rozhodování ekonomických subjektů při volbě formy bydlení. Domácnosti, které se rozhodují zajistit si vlastní bydlení koupí či stavbou domu či bytu, zpravidla nedisponují úsporami ve výši pořizovací ceny jejich nového domu či bytu. Obvykle je tak jejich jedinou možností získat chybějící finanční prostředky na finančních trzích, přičemž jedním z nejfrekventovanějších nástrojů financování bydlení je hypoteční úvěr, který mimo jiné patří k nejstarším typům úvěrů a je dnes prakticky všude na světě nejvýznamnější formou financování investic do bydlení. Hypoteční úvěr je podle obecně platné definice půjčka zajištěná zástavním právem k nemovitosti. Od klasických úvěrů se liší především svým zajištěním zástavním právem, nižším úročením (po sledovanou dobu se průměrné úrokové sazby pohybovaly v rozmezí 5,45 % a 8,23 %) a dlouhodobostí (doba splatnosti se obvykle pohybuje mezi pěti a třiceti roky). Cílem této práce je empirická analýza objemu hypotečních úvěrů poskytnutých v České republice fyzickým osobám v letech 2001 až K vlastní analýze je využito klasického regresního modelu. Dílčím cílem práce je identifikovat faktory, které vývoj objemu poskytnutých hypotečních úvěrů ovlivňují a na základě nich se pokusit o předpověď. Práce je rozdělena do čtyř hlavních částí. V první je vymezen regresní model popisující vztah objemu hypotečních úvěrů fyzickým osobám v České republice a vybraných faktorů. Ve druhé části jsou prezentovány výsledky odhadnutých regresních modelů včetně ověření jejich kvality. Ve třetí části jsou diskutovány dosažené výsledky a očekávaný vývoj v kontextu současné finanční krize. Čtvrtá část obsahuje souhrn nejdůležitějších výsledků. MATERIÁL A METODY Analyzovaným materiálem je objem hypotečních úvěrů poskytnutých fyzickým osobám v České republice za jednotlivá čtvrtletí roků 2001 až
2 154 P. Střelcová, L. Střelec Zdrojem analyzovaného materiálu je Ministerstvo pro místní rozvoj ČR ( Český statistický úřad ( a Ministerstvo práce a sociál ních věcí ČR ( Analýza objemu hypotečních úvěrů České republiky je v práci rozdělena do tří základních celků. V první fázi je sledován vývoj objemu hypotečních úvěrů a průměrná úroková sazba z hypotečních úvěrů v závislosti na čase. Ve druhé fázi je využito jednorozměrného regresního modelu, přičemž je zkoumán vliv průměrných úrokových sazeb (IR) na objem hypotečních úvěrů (OHÚ). V rámci této analýzy předpokládáme, že průměrná úroková sazba je rozhodujícím faktorem pro objem hypotečních úvěrů. V souvislosti s ekonomickou teorií tak budeme analyzovat funkční vztah: OHÚ = f(ir), přičemž předpokládáme negativní vliv úrokové sazby na objem hypotečních úvěrů, neboť očekáváme, že s rostoucí úrokovou sazbou z hypotečních úvěrů klesá poptávka po nich a následně klesá i objem poskytnutých hypotečních úvěrů a opačně, tj. očekáváme OHÚ = f(i R). Konečně ve třetí fázi je využito vícerozměrného regresního modelu, přičemž je zkoumán vliv vybraných proměnných na objem poskytnutých hypotečních úvěrů. Jako vysvětlující proměnné jsou uvažovány následující proměnné: průměrná úroková sazba z hypotečních úvěrů v daném čtvrtletí vyjádřená v procentních bodech (IR t ), průměrná měsíční nominální mzda daného čtvrtletí vyjádřená v Kč (NM t ), míra nezaměstnanosti v daném čtvrtletí vyjádřená v procentních bodech (N t ), průměrná cena nemovitostí vyjádřená v daném čtvrtletí jako tempo přírůstku vůči prvnímu sledovanému čtvrtletí, tj. vůči referenčnímu čtvrtletí I/2001 (PN t ), míra inflace vyjádřená jako tempo přírůstku indexu spotřebitelských cen vůči prvnímu sledovanému čtvrtletí, tj. vůči referenčnímu čtvrtletí I/2001 (I t ). V rámci vícerozměrného regresního modelu tak budeme analyzovat funkční vztah: OHÚ = f(ir, NM, N, PN, I), přičemž předpokládáme pozitivní vliv nominální mzdy, negativní vliv úrokové sazby a míry nezaměstnanosti a u míry inflace a cenové hladiny nemovitostí lze očekávat jak pozitivní, tak i negativní vliv, tj. očekáváme OHÚ = f( IR, NM, N, PN, I ). Pozitivní vliv nominální mzdy vychází z ekonomické logiky, kdy zvýšení příjmů domácností vede za jinak stejných podmínek ke zvýšené poptávce po vlastním bydlení a tedy i po zvýšené poptávce po hypotečních úvěrech. Negativní vliv úrokové sazby z hypotečních úvěrů vychází z teorie peněz a je dán tím, že v případě jejího zvýšení klesá poptávka po hypotečních úvěrech a klesá tak i jejich poskytnutý objem a opačně. V případě negativního vlivu míry nezaměstnanosti pak předpokládáme, že s rostoucí mírou nezaměstnanosti dochází k poklesu zájmu o hypoteční úvěry především díky finanční náročnosti, kterou si nezaměstnaný nemůže díky poklesu příjmu dovolit. Rovněž podmínky hypotečních bank obvykle zahrnují požadavek na minimální příjem domácnosti, který v případě, že nějaký její člen je nezaměstnaný, obvykle poklesne. V případě zvýšení průměrné ceny nemovitostí lze identifikovat protichůdné síly, kdy na jedné straně zvýšení průměrných cen nemovitostí vede k poklesu poptávky po nich, avšak na druhé straně lze očekávat i pozitivní vliv, kdy růst průměrné ceny nemovitostí je ovlivněn inflací a růst cenové hladiny způsobí za jinak stejných podmínek i nárůst objemu poskytnutých hypotečních úvěrů. Dalším důvodem k předpokladu pozitivního vlivu této proměnné lze najít v domněnce, že nemovitost lze považovat za jednu z forem investic, která vykazuje relativně stabilní růstový trend, a tudíž lze předpokládat, že s růstem cen nemovitostí lze očekávat i růst objemu hypotečních úvěrů, neboť potenciální investoři nemusejí disponovat dostatečnými vlastními prostředky či dokonce, i když jimi disponují, je pro ně výhodnější využít hypotečních úvěrů a výhod z nich plynoucích (např. daňové výhody, státní podpora apod.), což sníží celkové náklady na tuto investici a udrží likvidní prostředky pro jiné investice. V rámci této práce tak budeme očekávat, že pozitivní dopad této proměnné převládne, tj. že s rostoucí průměrnou cenou nemovitostí bude docházet k nárůstu objemu poskytnutých hypotečních úvěrů. Konečně v případě vlivu míry změny cenové hladiny (inflace) lze očekávat jak pozitivní, tak i negativní vliv, neboť na jedné straně lze předpokládat, že s růstem cenové hladiny jsou znehodnocovány fixní splátky hypotečních úvěrů po dobu fixace úrokové sazby a také, že růst inflace bude zahrnut do rozhodování spotřebitelů, kteří budou očekávat do budoucna díky růstu inflace růst nájemného i stavebních prací, což způsobí aktuální růst poptávky po vlastním bydlení a tedy i po hypotečních úvěrech. Na druhou stranu lze však očekávat, že podobně jako spotřebitelé budou reagovat na očekávaný růst inflace i poskytovatelé hypotečních úvěrů, kteří tento růst promítnou do úrokových sazeb, což bude mít za následek klesající poptávku po hypotečních úvěrech. Otázkou pak je, který vliv převládne. Obvykle lze za lépe informované subjekty považovat poskytovatele hypotečních úvěrů, kteří zahrnou svá očekávání do úrokových sazeb, tj. lze očekávat spíše negativní vliv růstu cenové hladiny. Pro vlastní analýzu objemu hypotečních úvěrů je využito klasické regresní analýzy. Klasický regresní model využitelný jak pro popis vývoje průřezových
3 Analýza rostoucího vývoje objemu poskytnutých hypotečních úvěrů v České republice 155 dat, tak i pro popis časových řad lze pak zapsat jako (viz Hušek, 1999) Y = xβ + ε, kde Y... náhodný vektor pozorování vysvětlované (závisle) proměnné X.. matice pozorování vysvětlujících (nezávisle) proměnných β... vektor neznámých parametrů ε... vektor náhodných veličin (chyb). Odhad vhodné regresní funkce Ŷ lze pak zapsat jako Ŷ = Xβˆ, kde βˆ... vektor odhadovaných parametrů regresní funkce. Odhady parametrů metodou nejmenších čtverců (OLS) jsou pak dány vztahem βˆ = (X T X) 1 X T Y. Mimo odhad parametru regresního modelu je v této práci rovněž testována významnost jednotlivých parametrů modelu a celková vhodnost modelu. Pro testování statistické významnosti jednotlivých parametrů regresní funkce je využito t-testů. Pro každý regresní parametr β j, kde j = 1,, k, pak formulujeme následující hypotézy H 0 : b j = 0 t j < τ H 0 : nezamítáme H 1 : b j = 0 t j τ H 1 : nezamítáme, přičemž testová statistika t má tvar βˆj βˆj t j = =, SE(βˆj) RSS hj+1, n p j+1 kde SE(βˆj)...standardní chyba odhadu RSS...reziduální součet čtverců p = k počet parametrů regresní funkce včetně konstantního členu h j+1, j+1...je j + 1-vý diagonální prvek matice H = (X T X) 1 a kde kritická hodnota je τ = t 1 α/2 (n p). Pro posouzení celkové vhodnosti, resp. průkaznosti regresního modelu je využito tzv. F-testu. Pro regresní funkci formulujeme následující hypotézy H 0 : β 0 = = β j = 0 F < F C H 0 : nezamítáme H 1 : H 0 neplatí F F C H 1 : nezamítáme, přičemž testová statistika F má tvar ESS/(p 1) F =, RSS/(n p) kde ESS...vysvětlený součet čtverců RSS...reziduální součet čtverců p = k počet parametrů regresní funkce včetně konstantního členu a kde kritická hodnota je F C = F 1 α (p 1, n p). Pro posouzení celkové vhodnosti modelu je ve vlastní práci využito rovněž tzv. indexu, resp. v případě lineární regresní funkce koeficientu, determinace, jež vychází z rozkladu čtverců, kdy pro metodu nejmenších čtverců má celková suma čtverců (TSS) dvě komponenty, a to sumu čtverců vysvětlenou regresí (ESS) a reziduální sumu čtverců (RSS). Koeficient determinace má pak tvar ESS RSS R 2 = = 1. TSS TSS Nezkreslený koeficient determinace korigující koeficient determinace o rozsah výběru a počet parametrů regresní funkce má pak tvar n 1 R 2 = 1 (1 R 2 ). n p K ověření vhodnosti modelu je mimo F-testu a koeficientu determinace využito rovněž Ramseyho RESET testu specifikace modelu (blíže viz Ramsey, 1969) a testů homoskedasticity, sériové korelace a normality chybového členu. Zvolenými testy ověřujícími homoskedasticitu chybového členu jsou Whiteův test (viz blíže např. Studenmund, 2005) a Breusch-Paganův test (viz blíže např. Greene, 1993), v jejichž případě je nulovou hypotézou H 0 : homoskedasticita a alternativní hypotézou H 1 : heteroskedasticita chybového členu. Problematika sériové korelace chybového je v práci ověřována pomocí Durbin-Watsonova testu, Breusch-Godfreyova testu, Box-Pierce testu a Ljung- Box test (vše viz blíže např. Greene, 1993), v jejichž případě je nulovou hypotézou hypotéza H 0 : sériová korelace není přítomna a alternativní hypotézou H 1 : sériová korelace chybového členu. K ověření normality chybového členu je pak využito chí-kvadrát testu normality, Shapiro-Wilkova testu a Jarque-Bera testu normality (vše viz blíže např. Thode, 2002), v jejichž případě je nulovou hypotézou H 0 : normalita a alternativní hypotézou H 1 : nenormalita chybového členu. VÝSLEDKY Obr. 1 zobrazuje vývoj objemu hypotečních úvěrů a průměrných úrokových sazeb z hypotečních úvěrů v ČR v jednotlivých čtvrtletích let 2001 až Z vývoje je patrný lineární pokles průměrných úrokových sazeb, kdy úroková sazba během sledovaných let poklesla z přibližně 8 % na aktuálních cca 5,5 %, a přibližně exponenciální růst objemu hypotečních úvěrů, kdy za první čtvrtletí 2001 byl objem hypotečních úvěrů cca 3 mld. Kč a za čtvrté čtvrtletí 2007 dokonce již cca 36 mld. Kč. Z výše uvedeného důvodu exponenciálního vývoje objemu poskytnutých hypotečních úvěrů je v následující části analyzován vývoj objemu poskytnutých hypotečních úvěrů vyjádřených jako přirozený logaritmus původních hodnot, tj. při popisu časové řady a rovněž i v regresní analýze je využito semilogaritmické (logaritmicko-lineární) funkční formy.
4 156 P. Střelcová, L. Střelec OHÚ (v mld. Kč) I II III IV I II III IV I II III IV I II III IV I II III IV I II III IV I II III IV IR (v %) Objem HÚ Úroková sazba 1: Vývoj objemu poskytnutých hypotečních úvěrů a průměrné úrokové sazby z hypotečních úvěrů v ČR v letech 2001 až 2007 Nejprve tak byla ověřena závislost sledovaných veličin (přirozeného logaritmu objemu poskytnutých hypotečních úvěrů a průměrné úrokové sazby z hypotečních úvěrů) na čase, tj. byly vypočteny OLS odhady parametrů, standardních chyb odhadů parametrů a nezkreslené (korigované) odhady indexu determinace, dále byly provedeny t-testy významnosti jednotlivých odhadů parametrů a celkový F- test vhodnosti modelu. Získané výsledky pro model závislosti přirozeného logaritmu hypotečních úvěrů na čase (období) jsou následující: ln(ohú t ) = 1, ,0940 t (0,0031) t = 30,63 n = 28 R 2 = 0,9720 F = 938,337 DW = 1,96. Získané výsledky pro model závislosti průměrné úrokové sazby z hypotečních úvěrů na čase (období) jsou pak následující: IR t = 8,1528 0,1084 t (0,0035) t = 30,57 n = 28 R 2 = 0,9719 F = 934,809 DW = 0,07. Ze statistického hlediska jsou oba modely statisticky průkazné, pouze v případě modelu závislosti průměrné úrokové sazby je patrná sériová korelace v reziduích vyjádřena velmi nízkou hodnotou Durbin-Watson statistiky. Uvedené modely však nelze považovat za vhodné, neboť nejsou podloženy ekonomickou interpretací a jsou dány pouze aktuálním vývojem sledovaných proměnných. Proto v následující části práce přistoupíme k identifikaci faktorů ovlivňujících objem poskytnutých hypotečních úvěrů. Jak již bylo uvedeno výše, jedním z nejdůležitějších faktorů při rozhodování ekonomických subjektů o financování vlastního bydlení je úroková sazba. Následující část proto obsahuje analýzu vztahu objemu poskytnutých hypotečních úvěrů (v logaritmickém vyjádření) a průměrné úrokové sazby z hypotečních úvěrů. Obr. 2 zobrazuje bodový diagram vztahu přirozeného logaritmu objemu poskytnutých hypotečních úvěrů a průměrné úrokové sazby z hypotečních úvěrů. Vývoj empirických hodnot pak potvrzuje volbu semilogaritmického (logaritmicko-lineárního) regresního modelu, neboť po zlogaritmování hodnot objemu poskytnutých hypotečních úvěrů lze vztah mezi přirozeným logaritmem objemu poskytnutých hypotečních úvěrů a průměrných úrokových sazeb popsat lineárním modelem. Pro zvolený semilogaritmický model byly následně vypočteny OLS odhady parametrů, standardních chyb odhadů parametrů a nezkreslené (korigované) odhady indexu determinace, dále byly provedeny t- testy významnosti jednotlivých odhadů parametrů a celkový F-test vhodnosti modelu. Získané výsledky pro semilogaritmický model jsou následující: ln (OHÚ t ) = 8,0926 0,8522 IR t (0,031) t = 27,538 n = 28 R 2 = 0,9656 F = 758,317 DW = 1,60.
5 Analýza rostoucího vývoje objemu poskytnutých hypotečních úvěrů v České republice 157 Ze statistického hlediska je proměnná IR u analyzovaného modelu na 1% hladině významnosti statisticky významná, F-test také signalizuje statistickou průkaznost regresního modelu. Sledovaný model byl podroben rovněž i RESET testu specifikace modelu (viz Tab. I). Pro srovnání jsou uvedeny rovněž i výsledky RESET testu pro lineární, kvadratickou a inverzní funkční formu. 4,5 4,0 3,5 3,0 ln(ohú) 2,5 2,0 1,5 1,0 0,5 0,0 5,0 5,5 6,0 6,5 7,0 7,5 8,0 8,5 IR 2: Bodový diagram přirozeného logaritmu objemu poskytnutých hypotečních úvěrů a průměrné úrokové sazby z hypotečních úvěrů v ČR v letech 2001 až 2007 I: Výsledky RESET testu Model Testová statistika F p-value Lineární 22,295 0,0000 Kvadratický 6,938 0,0044 Inverzní 15,936 0,0000 Semilogaritmický 5,071 0,0146 Z tabulky I je patrné, že pouze v případě semilogaritmické funkční formy nebyla hypotéza o správné specifikaci modelu na 1% hladině významnosti zamítnuta, tj. semilogaritmický (logaritmicko-lineární) model lze považovat za vhodný. V následující části jsou rezidua uvedeného semilogaritmického modelu podrobena další analýze, konkrétně je ověřena hypotéza o homoskedasticitě chybového členu, neautokorelovanosti chybového členu a normalitě chybového členu. V Tab. II jsou uvedeny výsledky dvou testů heteroskedasticity, a to konkrétně Whiteova testu a Breusch-Paganova testu. II: Testy heteroskedasticity chybového členu Model Testová statistika p-value Whiteův test LM = 2,3748 0,3050 Breusch-Paganův test LM = 4,1332 0,0421 Z výsledků testů heteroskedasticity je patrné, že výsledky a závěry obou testů jsou rozdílné. Zatímco Whiteův test hypotézu o homoskedasticitě chybového členu na 5% hladině významnosti nezamítá (tuto hypotézu nezamítá dokonce ani na 30% hladině významnosti), tak Breusch-Paganův test hy-
6 158 P. Střelcová, L. Střelec potézu o homoskedasticitě chybového členu na 5% hladině významnosti zamítá. Uvedený rozpor mezi výsledky tak naznačuje, že heteroskedasticita chybového členu by mohla způsobovat problémy při odhadu parametrů regresního modelu, především díky zvýšení rozptylu odhadovaných parametrů. V Tab. III jsou uvedeny výsledky čtyř testů autokorelace, a to Durbin-Watsonova testu testujícím autokorelaci prvního řádu a Breusch-Godfrey testu, Box- Pierce testu a Ljung-Box testu testující autokorelaci vyššího řádu. V případě Breusch-Godfrey testu, Box-Pierce testu a Ljung-Box testu testující autokorelaci vyššího řádu je testována autokorelace šestého řádu, neboť T = 28 = 6 (zaokrouhleno na celý řád nahoru). III: Testy autokorelace chybového členu Model Testová statistika p-value Durbin-Watsonův test DW = 1,5981 0,0966 Breusch-Godfrey test F = 1,5837 0,203 Box-Pierce test Chí-kvadrát = 9,0184 0,173 Ljung-Box test Chí-kvadrát = 6,6207 0,357 Z výsledků testů autokorelace chybového členu je patrné, že není přítomna ani autokorelace prvního řádu, ani autokorelace vyššího řádu. V Tab. IV je uveden výsledek tří testů normality chybového členu a to chí-kvadrát testu, Shapiro- Wilkova testu a Jarque-Bera testu normality. IV: Testy normality chybového členu Model Testová statistika p-value Chí-kvadrát test Chí-kvadrát = 11,2318 0,0036 Shapiro-Wilkův test SW = 0,9223 0,0394 Jarque-Bera test Chí-kvadrát = 8,7554 0,0126 Z výsledků testů normality chybového členu je patrné, že ve všech případech byla hypotéza o normalitě chybového členu na 5% hladině významnosti zamítnuta. Z uvedených testů reziduální složky (chybového členu) je patrné, že rezidua pravděpodobně vykazují heteroskedasticitu. K nápravě heteroskedasticity je využito techniky heroskedasticky korigovaných standardních chyb. Výsledkem techniky heteroskedasticky korigovaných standardních chyb je semilogaritmický (logaritmicko-lineární) model ve tvaru: ln (OHÚ t ) = 8,1194 0,8540 IR t (0,024) t = 35,14 n = 28 R 2 = 0,979 F = 1235,11 DW = 1,58. Z výsledků je patrné, že došlo ke snížení standardní chyby regresního parametru a k mírnému zvýšení korigovaného indexu determinace. Parametry regresního modelu i model jako celek je statisticky významný na 1% hladině významnosti. Analyzovaný semilogaritmický model lze na základě výsledků regresní analýzy považovat za statisticky průkazný. Z ekonomického hlediska tento regresní model vypovídá o negativním vlivu průměrné úrokové sazby z hypotečních úvěrů na objem poskytnutých hypotečních úvěrů a došlo tak k potvrzení očekávaného negativního vlivu průměrné úrokové sazby z hypotečních úvěrů na objem hypotečních úvěrů konkrétně výsledkem regresní analýzy je, že zvýšení průměrné úrokové sazby z hypotečních úvěrů o jeden procentní bod způsobí pokles přirozeného logaritmu objemu hypotečních úvěrů o 0,8540, což znamená, že zvýšení průměrné úrokové sazby z hypotečních úvěrů o jeden procentní bod způsobí pokles objemu hypotečních úvěrů o cca 85,4 %, neboť změna přirozeného logaritmu lze na základě Taylorova rozvoje charakterizovat přibližně jako relativní změna v čase t vůči času t 1 (viz Arlt, 2007). Uvedený jednorozměrný model však není z ekonomického hlediska úplný, neboť nelze uvažovat o tom, že by objem hypotečních úvěrů byl ovlivňován pouze vývojem průměrné úrokové sazby z hypotečních úvěrů (byť lze tuto proměnnou považovat za nejdůležitější z pohledu žadatelů o úvěr). Naopak lze identifikovat další proměnné, které podstatným způsobem ovlivňují objem hypotečních úvěrů v daném období. Za takové proměnné lze na základě ekonomické teorie považovat rovněž růst cen nemovitostí, míru nezaměstnanosti, míru inflace, příjmy obyvatel, úrokové sazby konkurenčních produktů
7 Analýza rostoucího vývoje objemu poskytnutých hypotečních úvěrů v České republice 159 (např. úvěrů ze stavebního spoření) apod. V následující analýze tak je sledován vztah vybraných proměnných a objemu hypotečních úvěrů a to v rámci vícenásobného regresního modelu. Objem poskytnutých hypotečních úvěrů v daném období je opět analyzován jako přirozený logaritmus původních hodnot objemu poskytnutých hypotečních úvěrů. Jako vysvětlující proměnné jsou uvažovány následující proměnné: průměrná úroková sazba z hypotečních úvěrů v daném čtvrtletí vyjádřená v procentních bodech, průměrná měsíční nominální mzda daného čtvrtletí vyjádřená v Kč, míra nezaměstnanosti v daném čtvrtletí vyjádřená v procentních bodech, průměrná cena nemovitostí vyjádřená v daném čtvrtletí jako tempo přírůstku vůči prvnímu sledovanému čtvrtletí, tj. vůči referenčnímu čtvrtletí I/2001, a míra inflace vyjádřená jako tempo přírůstku indexu spotřebitelských cen vůči prvnímu sledovanému čtvrtletí, tj. vůči referenčnímu čtvrtletí I/2001. Získané odhady parametrů včetně odhadů standardních chyb a t-statistik pro vícerozměrný regresní model jsou: ln Ŷ t = 9,8284 0,8839 IR t 0,1403 N t 0,00001 NM t + 0,0080 PN t 0,0529 I t (0,1688) (0,0692) (0,00003) (0,0033) (0,0369) t = 5,2357 2,0272 0,4119 2,3963 1,4347 n = 28 R 2 = 0,980 F = 251,6249 DW = 2,23. Uvedený model je statisticky průkazný. Z hlediska ekonomické teorie však je nutné tento model odmítnout, neboť model předpokládá, že k růstu objemu hypotečních úvěrů dojde při současném snížení průměrné nominální měsíční mzdy (i když je daný parametr velmi blízký nule a navíc je tento parametr na 5% hladině významnosti statisticky nevýznamný). Sledovaný model byl rovněž podroben RESET testu specifikace modelu (viz Tab. V). V: RESET test Model Testová statistika F p-value Semilogaritmický 0,552 0,5843 Z tabulky V je patrné, že hypotéza o správné specifikaci na 5% hladině významnosti zamítnuta nebyla. Problémem však může být multikolinearita vysvětlujících proměnných. Tab. VI tak obsahuje matici párových korelačních koeficientů mezi vysvětlujícími proměnnými a v závorkách hodnoty p-hodnoty hypotézy o nezávislosti. VI: Matice párových korelačních koeficientů IR 1 N NM PN I IR N NM PN I 0,5056 (0,0061) 0,9179 0,9053 0,9285 0,5056 (0,0061) 1 0,6652 (0,0001) 0,6458 (0,0002) 0,7567 0,9179 0,6652 (0,0001) 1 0,8917 0,9045 0,9053 0,6458 (0,0002) 0, ,9299 0,9285 0,7567 0,9045 0,9299 Pozn.: V závorkách jsou uvedeny p-hodnoty hypotézy o nezávislosti. 1 Všechny párové korelační koeficienty jsou statisticky významné na 1% hladině významnosti. Nejvyšší párový korelační koeficient v absolutní hodnotě je mezi proměnnými PN a I, IR a I, IR a NM, IR a PN a NM a I. Tyto hodnoty naznačují problém s multikolinearovanými proměnnými. Pro další analýzu byly ještě vypočteny VIF faktory (viz Tab. VII). VII: VIF vysvětlujících proměnných Proměnná VIF IR 48,6 N 12,2 NM 13,5 PN 8,8 I 55,1
8 160 P. Střelcová, L. Střelec Z Tab. VII je patrné, že hodnoty větší než 10 vykazují všechny proměnné mimo proměnné PN a lze tyto proměnné považovat za multikolinearované, což s sebou přináší problémy s kvalitou odhadů parametrů pomocí OLS metody. V další analýze je tudíž přistoupeno k úpravě modelu a k selekci proměnných za účelem vynechání multikolinearovaných proměnných. Z tohoto důvodu byla vynechána proměnná inflace (I), která je mimo problému s multikolinearitou navíc na 5% hladině významnosti statisticky nevýznamná. Rovněž z ekonomického hlediska lze o vynechání této proměnné uvažovat spíše než o vynechání proměnné průměrné úrokové sazby IR, kterou lze považovat za nejdůležitější faktor při rozhodování ekonomických subjektů o hypotečních úvěrech. Získané odhady parametrů včetně odhadů standardních chyb a t-statistik pro modifikovaný vícerozměrný regresní model jsou ln Ŷ t = 6,9275 0,6709 IR t 0,0515 N t + 0,00001 NM t + 0,0062 PN t (0,0822) (0,0317) (0,00003) (0,0032) t = 8,1640 1,6260 0,3950 1,9660 n = 28 R 2 = 0,980 F = 300,2057 DW = 2,24. Při testování významnosti regresních parametrů vícenásobného regresního modelu byla na 5% hladině významnosti prokázána statistická významnost pouze pro parametr u proměnné IR. Ostatní proměnné jsou na 5% hladině významnosti statisticky neprůkazné. Celkový F-test přesto naznačuje, že model je statisticky průkazný. Korigovaný index determinace má hodnotu 0,980. Rovněž z pohledu očekávaných znamének je model v souladu s ekonomickou teorií. Pro následující model lze uvažovat o vynechání proměnné průměrné nominální měsíční mzdy, poněvadž tato proměnná je statisticky nevýznamná a její hodnota je prakticky nulová, tudíž její vliv na hodnoty závisle proměnné není rozhodující. Získané odhady parametrů včetně odhadů standardních chyb a t-statistik pro modifikovaný vícerozměrný regresní model jsou ln Ŷ t = 7,3187 0,6930 IR t 0,0578 N t + 0,0064 PN t (0,0591) (0,0269) (0,0031) t = 11,73 2,149 2,043 n = 28 R 2 = 0,979 F = 414,8048 DW = 2,28. Při testování významnosti regresních parametrů vícenásobného regresního modelu byla na 5% hladině významnosti prokázána statistická významnost pouze pro parametry u proměnných IR a N. Proměnná PN sice není na 5% hladině významnosti statisticky průkazná, avšak p-value je 0,0522, tj. tato proměnná je průkazná na cca 5,2% hladině významnosti. Celkový F-test naznačuje, že model je statisticky průkazný. Korigovaný index determinace má hodnotu 0,979. Z hlediska ekonomické teorie i statistické významnosti modelu lze tento model považovat za vhodný, a proto je níže podroben bližší analýze a to především z hlediska multikolinearity nezávisle proměnných a testů reziduí na přítomnost heteroskedasticity, sériové korelace a nenormality rozdělení. V Tab. VIII jsou uvedeny hodnoty VIF vysvětlujících proměnných, které však nesignalizují problém s multikolinearitou vysvětlujících proměnných. VIII: VIF vysvětlujících proměnných Proměnná VIF IR 5,89 N 1,82 PN 7,52 V Tab. IX jsou uvedeny výsledky dvou testů heteroskedasticity, a to Whiteova testu a Breusch-Paganova testu. IX: Testy heteroskedasticity chybového členu Model Testová statistika p-value Whiteův test LM = 11,7395 0,2284 Breusch-Paganův test LM = 4,5049 0,2119 Z výsledků testů heteroskedasticity je patrné, že heteroskedasticita chybového členu nebyla na 5% hladině významnosti identifikována. V Tab. X jsou pak uvedeny výsledky čtyř testů autokorelace, a to Durbin-Watsonova testu testujícím autokorelaci prvního řádu a Breusch-Godfrey testu, Box-Pierce testu a Ljung-Box testu testující autokorelaci vyššího řádu. V případě Breusch-Godfrey testu, Box-Pierce testu a Ljung-Box testu testující autokorelaci vyššího řádu je testována autokorelace šestého řádu, neboť T = 28 = 6 (zaokrouhleno na celý řád nahoru). Z výsledků testů autokorelace chybového členu je patrné, že není přítomna autokorelace prvního řádu ani autokorelace vyššího řádu. V Tab. XI je uveden výsledek tří testů normality chybového členu, a to chí-kvadrát testu, Shapiro-Wilkova testu a Jarque- Bera testu normality.
9 Analýza rostoucího vývoje objemu poskytnutých hypotečních úvěrů v České republice 161 X: Testy autokorelace chybového členu Model Testová statistika p-value Durbin-Watsonův test DW = 2,2787 0,5624 Breusch-Godfrey test F = 1,0731 0,414 Box-Pierce test Chí-kvadrát = 7,3767 0,287 Ljung-Box test Chí-kvadrát = 6,0952 0,413 XI: Testy normality chybového členu Model Testová statistika p-value Chí-kvadrát test Chí-kvadrát = 1,1825 0,5536 Shapiro-Wilkův test SW = 0,9753 0,7275 Jarque-Bera test Chí-kvadrát = 1,0146 0,6021 Z výsledků testů normality chybového členu je patrné, že ve všech případech zůstává hypotéza o normalitě chybového členu na 5% hladině významnosti nezamítnuta, tj. chybový člen má normální rozdělení. Z uvedených testů reziduální složky (chybového členu) je patrné, že rezidua nevykazují ani heteroskedasticitu, ani sériovou korelaci, přičemž nebyla zamítnuta ani hypotéza o normalitě rozdělení. Chybový člen tak lze považovat za klasický normální chybový člen splňující Gauss-Markov teorém a odhadované parametry metodou OLS tak lze považovat za nejlepší nevychýlené odhady. Analyzovaný semilogaritmický model tak lze na základě výsledků regresní analýzy považovat za statisticky průkazný. Z ekonomického hlediska tento regresní model vypovídá o negativním vlivu průměrné úrokové sazby z hypotečních úvěrů a míry nezaměstnanosti na objem poskytnutých hypotečních úvěrů a o pozitivním vlivu ceny nemovitostí na objem hypotečních úvěrů. Došlo tak k potvrzení očekávaných vlivů sledovaných proměnných na objem poskytnutých hypotečních úvěrů, přičemž v případě cen nemovitostí převážil námi předpokládaný pozitivní vliv, kdy s rostoucími cenami nemovitostí roste poptávka po nich a to z důvodu předpokladu růstu nájemného a následně tedy díky rostoucí poptávce po vlastním bydlení, která převáží negativní dopad růstu ceny. Konkrétně výsledkem regresní analýzy je, že zvýšení průměrné úrokové sazby z hypotečních úvěrů o jeden procentní bod způsobí pokles přirozeného logaritmu objemu hypotečních úvěrů o 0,6930, tj. způsobí pokles objemu poskytnutých hypotečních úvěrů o 69,3 %, dále pak zvýšení míry nezaměstnanosti o jeden procentní bod způsobí pokles přirozeného logaritmu objemu hypotečních úvěrů o 0,0578, tj. způsobí pokles objemu poskytnutých hypotečních úvěrů o 5,8 % a konečně nárůst průměrné ceny nemovitostí o jeden procentní bod oproti referenčnímu období prvního čtvrtletí roku 2001 způsobí nárůst přirozeného logaritmu objemu hypotečních úvěrů o 0,0064, tj. způsobí zvýšení objemu poskytnutých hypotečních úvěrů o 0,6 % a naopak. DISKUSE Vývoj objemu poskytnutých hypotečních úvěrů prodělal za sledované období bouřlivý vývoj. Počátky hypotečního bankovnictví v České republice byly spojeny s nedůvěrou v bankovní systém a obavami o jeho další vývoj. Postupem času se však hypoteční úvěry staly jedním z nejoblíbenějších a nejpoužívanějších nástrojů financování vlastního bydlení. To dokresluje i vývoj objemu poskytnutých hypotečních úvěrů za sledované období, kdy v prvním čtvrtletí roku 2001 bylo poskytnuto hypotečních úvěrů za cca 2,79 mld. Kč, přičemž v posledním sledovaném období, tj. v posledním čtvrtletí roku 2007, bylo poskytnuto hypotečních úvěrů za cca 35,54 mld. Kč, tj. jedná se o celkový nárůst cca 1275 %. Tento bouřlivý vývoj během sledovaného období lze mimo růstu oblíbenosti hypotečních úvěrů rovněž charakterizovat rostoucí úrovní české ekonomiky, poklesu průměrných úrokových sazeb a poklesu míry nezaměstnanosti. Všechny tyto faktory měly pozitivní vliv na rostoucí trend poskytnutých hypotečních úvěrů. Tento rostoucí trend však v polovině roku 2007 ustal a došlo ke stagnaci, resp. k mírnému poklesu objemu poskytnutých úvěrů. Tento vývoj pokračoval i během roku Hlavním důvodem stagnace, resp. mírného poklesu nebyla rostoucí úroveň průměrných úrokových sazeb z hypotečních úvěrů, neboť průměrné úrokové sazby v roce 2008 v jednotlivých čtvrtletích dále klesaly (až na 5,37 % v posledním čtvrtletí roku ), avšak byl způsoben rostoucí obavou obyvatel z dalšího ekonomického vývoje a rostoucí mírou nezaměstnanosti. Rovněž lze u nově poskytnutých hypotečních úvěrů identi- 1 viz úrokové sazby hypotečních úvěrů se státní finanční podporou pro fyzické osoby
10 162 P. Střelcová, L. Střelec fikovat v posledních měsících roku 2008 nárůst úrokových sazeb a to především u hypoték s jednoletou dobou fixace, které dokonce atakovaly šestiprocentní hranici. Průměrná úroková sazba všech typů fixací měřená ukazatelem FINCENTRUM HYPO- INDEX 2 pak v prosinci 2008 meziměsíčně vzrostla o šest setin procentního bodu na úroveň 5,69 %. Podobný vývoj lze očekávat i v roce 2009, který lze charakterizovat nepříznivým vývojem české ekonomiky, rostoucí nezaměstnaností, rostoucí úrokovou sazbou z nově poskytnutých hypotečních úvěrů a stagnací či mírným poklesem cen nemovitostí. Dle některých odhadů lze očekávat až 20% pokles cen nemovitostí na úroveň jejich reálné hodnoty. Pozitivní vliv poklesu cen nemovitostí však pravděpodobně nedokáže vyvážit rostoucí nezaměstnanost a růst úrokových sazeb z hypotečních úvěrů spojených s obavou o další ekonomický vývoj země, což se pravděpodobně projeví v poklesu objemu poskytnutých hypotečních úvěrů. Autoři tak očekávají, že objem poskytnutých hypotečních úvěrů bude mírně klesat a ustálit by se měl na úrovni cca 20 až 25 mld. Kč v jednotlivých čtvrtletích roku 2009, tj. za rok 2009 v celkové hodnotě 80 až 100 mld. Kč, čímž by se celoroční objem poskytnutých hypotečních úvěrů dostal na úroveň roku 2006 z rekordních hodnot za roky 2007 (cca 142 mld. Kč) a 2008 (cca 114 mld. Kč). SOUHRN Cílem této práce je empirická analýza objemu hypotečních úvěrů poskytnutých fyzickým osobám v České republice v letech 2001 až 2007 a identifikace faktorů, které ovlivňují rostoucí trend vývoje objemu hypotečních úvěrů. Dílčím cílem práce je rovněž vyvození ekonomických souvislostí mezi analyzovanými proměnnými a odhad jejich budoucího vývoje v kontextu současné ekonomické a hospodářské krize. Vývoj objemu poskytnutých hypotečních úvěrů prodělal za sledované období bouřlivý expanzivní vývoj. To dokresluje i vývoj objemu poskytnutých hypotečních úvěrů za sledované období, kdy v prvním čtvrtletí roku 2001 bylo poskytnuto hypotečních úvěrů za cca 2,79 mld. Kč, přičemž v posledním sledovaném období, tj. v posledním čtvrtletí roku 2007 bylo poskytnuto hypotečních úvěrů za cca 35,54 mld. Kč, tj. jedná se o celkový nárůst cca 1275 %. Na základě ekonomických předpokladů byly pro vlastní analýzu vybrány hlavní ekonomické ukazatele, konkrétně průměrná úroková sazba z hypotečních úvěrů, míra nezaměstnanosti, inflace, průměrná cenová úroveň nemovitostí a průměrné nominální mzdy. Z výsledků provedené regresní analýzy vyplývá, že rostoucí trend objemu poskytnutých hypotečních úvěrů ve sledovaném období byl ovlivněn klesající průměrnou úrokovou sazbou z hypotečních úvěrů, klesající nezaměstnaností a rostoucí průměrnou cenou nemovitostí. Výsledkem regresní analýzy tak je následující model: ln Ŷ t = 7,3187 0,6930 IR t 0,0578 N t + 0,0064 PN t (0,0591) (0,0269) (0,0031) t = 11,73 2,149 2,043 n = 28 R 2 = 0,979 F = 414,8048 DW = 2,28. kde Ŷ t je objem poskytnutých hypotečních úvěrů v čase t, IR t je průměrná úroková sazba z hypotečních úvěrů v čase t, N t je míra nezaměstnanosti v čase t a PN t je změna průměrných cen nemovitostí v čase t oproti prvnímu čtvrtletí roku Analyzovaný semilogaritmický (logaritmicko-lineární) model je statisticky průkazný s hodnotou korigovaného indexu determinace 0,979. Uvedený model umožňuje popsat vývoj poskytnutých hypotečních úvěrů v čase t jako funkci úrokové sazby z hypotečních úvěrů v čase t, míry nezaměstnanosti v čase t a průměrné cenové úrovně nemovitostí v čase t oproti referenčnímu období. Na základě ekonomické teorie jsme očekávali negativní dopad úrokové sazby a míry nezaměstnanosti a pozitivní dopad změny cenové hladiny nemovitostí. Tyto předpoklady pak byly na základě regresní analýzy potvrzeny. Pro rok 2009 však lze očekávat mírný pokles objemu poskytnutých hypotečních úvěrů, který lze charakterizovat nepříznivým vývojem české ekonomiky, rostoucí nezaměstnaností, rostoucí úrokovou sazbou z hypotečních úvěrů a stagnací či mírným poklesem cen nemovitostí. Pozitivní vliv poklesu cen nemovitostí však pravděpodobně nedokáže vyvážit rostoucí obavu obyvatel z rostoucí nezaměstnanosti a rostoucích úrokových sazeb z hypotečních úvěrů, což se pravděpodobně projeví v poklesu objemu poskytnutých hypotečních úvěrů. Autoři tak očekávají, že objem poskytnutých hypotečních úvěrů bude mírně klesat a ustálit by se měl na úrovni cca 20 až 25 mld. Kč v jednotlivých čtvrtletích roku 2009, tj. za rok 2009 v celkové hodnotě 80 až 100 mld. Kč, čímž by se celoroční objem poskytnutých hypotečních úvěrů dostal na úroveň roku hypoteční úvěr, úroková sazba, průměrná nominální mzda, nezaměstnanost, inflace, vícenásobná regresní analýza 2 viz
11 Analýza rostoucího vývoje objemu poskytnutých hypotečních úvěrů v České republice 163 SUMMARY The aim of this paper is an empirical analysis of mortgage volume in the Czech Republic and factors identification of the increasing trend of the mortgage volume in the period from 2001 to Part of this paper is also economic eduction of causality and estimation of expect progress of mortgage vo lume especially in connection with present economic and business recession. Mortgage volume passed through an expansive progress. For example, in I/2001 the mortgage vo lume was only about 3 mld. CZK and in IV/2007 the mortgage volume was just 36 mld. CZK. Therefore, there is a total growth rate about 1275 %. On the basis of economic assumptions the main economic variables was chosen, namely average mortgage rate, unemployment rate, inflation, average price level of real estates and average wages. Using multiple regression analysis, increasing trend of mortgage volu me was affected by decreasing average mortgage rate, decreasing unemployment rate and increasing average price level of real estates. As a result of regression analysis is a following model ln Ŷ t = 7,3187 0,6930 IR t 0,0578 N t + 0,0064 PN t (0,0591) (0,0269) (0,0031) t = 11,73 2,149 2,043 n = 28 R 2 = 0,979 F = 414,8048 DW = 2,28 where Ŷ t is mortgage volume in time t, IR t is average mortgage rate in time t, N t is unemployment rate in time t and PN t is percent change of average price level of real estates in time t in comparison with the basic period (I/2001). This semilog model is statistical significant with R 2 = 0,979. Consequently, this model allow to describe the mortgage volume in time t as a function of mortgage rate in time t, unemployment rate in time t and percent change of average price level of real estates in time t in comparison with the basic period (I/2001). We assumed a negative impact of mortgage rate and unemployment rate and positive impact of average price level of real estates. These assumptions was verified through regression analysis. As a prediction we expect slight loss in mortgage volume. Our reasons for this assumption are following: we expect increase in unemployment rate and average mortgage rate as results of business and economic recession. Consequently, increases of interest and unemployment rates causes decrease of mortgage demand and it causes decrease of mortgage volume. We expect the mortgage volume of every quarters of 2009 will be about mld. CZK. Therefore, in 2009 we expect total mortgage vo lume about mld. CZK. LITERATURA ARLT, J., ARLTOVÁ, M., 2007: Ekonomické časové řady. Praha: Grada Publishing, 285 s. ISBN GREENE, W. H., 1993: Econometrics analysis. New Jersey, 1026 s. ISBN HUŠEK, R., 1999: Ekonometrická analýza. Praha: Ekopress. 300 s. ISBN X. RAMSEY, J. B., 1969: Test for Specification Errors in Classical Linear Squares Regression Analysis. Journal of the Royal Statistical Society. s STUDENMUND, A. H., 2005: Using econometrics. Addison Wesley, 5 edition. 656 s. ISBN THODE, H. C., 2002: Testing for normality. New York: Marcel Dekker, 368 s. ISBN Adresa Ing. Petra Střelcová, Ústav ekonomie, Ing. Luboš Střelec, Ústav statistiky a operačního výzkumu, Mendelova zemědělská a lesnická univerzita v Brně, Zemědělská 1, Brno, Česká republika, xprocha9@ node.mendelu.cz, xstrelec@node.mendelu.cz
12 164
Ilustrační příklad odhadu LRM v SW Gretl
 Ilustrační příklad odhadu LRM v SW Gretl Podkladové údaje Korelační matice Odhad lineárního regresního modelu (LRM) Verifikace modelu PEF ČZU Praha Určeno pro posluchače předmětu Ekonometrie Needitovaná
Ilustrační příklad odhadu LRM v SW Gretl Podkladové údaje Korelační matice Odhad lineárního regresního modelu (LRM) Verifikace modelu PEF ČZU Praha Určeno pro posluchače předmětu Ekonometrie Needitovaná
4EK211 Základy ekonometrie
 4EK Základy ekonometrie Odhad klasického lineárního regresního modelu II Cvičení 3 Zuzana Dlouhá Klasický lineární regresní model - zadání příkladu Soubor: CV3_PR.xls Data: y = maloobchodní obrat potřeb
4EK Základy ekonometrie Odhad klasického lineárního regresního modelu II Cvičení 3 Zuzana Dlouhá Klasický lineární regresní model - zadání příkladu Soubor: CV3_PR.xls Data: y = maloobchodní obrat potřeb
Závislost obsahu lipoproteinu v krevním séru na třech faktorech ( Lineární regresní modely )
 Úloha M608 Závislost obsahu lipoproteinu v krevním séru na třech faktorech ( Lineární regresní modely ) Zadání : Při kvantitativní analýze lidského krevního séra ovlivňují hodnotu obsahu vysokohustotního
Úloha M608 Závislost obsahu lipoproteinu v krevním séru na třech faktorech ( Lineární regresní modely ) Zadání : Při kvantitativní analýze lidského krevního séra ovlivňují hodnotu obsahu vysokohustotního
Korelační a regresní analýza
 Korelační a regresní analýza Analýza závislosti v normálním rozdělení Pearsonův (výběrový) korelační koeficient: r = s XY s X s Y, kde s XY = 1 n (x n 1 i=0 i x )(y i y ), s X (s Y ) je výběrová směrodatná
Korelační a regresní analýza Analýza závislosti v normálním rozdělení Pearsonův (výběrový) korelační koeficient: r = s XY s X s Y, kde s XY = 1 n (x n 1 i=0 i x )(y i y ), s X (s Y ) je výběrová směrodatná
EKONOMETRIE 7. přednáška Fáze ekonometrické analýzy
 EKONOMETRIE 7. přednáška Fáze ekonometrické analýzy Ekonometrická analýza proces, skládající se z následujících fází: a) specifikace b) kvantifikace c) verifikace d) aplikace Postupné zpřesňování jednotlivých
EKONOMETRIE 7. přednáška Fáze ekonometrické analýzy Ekonometrická analýza proces, skládající se z následujících fází: a) specifikace b) kvantifikace c) verifikace d) aplikace Postupné zpřesňování jednotlivých
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie ZS 2015/16 Cvičení 7: Časově řady, autokorelace LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE 1. Časové řady Data: HDP.wf1
4EK211 Základy ekonometrie ZS 2015/16 Cvičení 7: Časově řady, autokorelace LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE 1. Časové řady Data: HDP.wf1
PRAVDĚPODOBNOST A STATISTIKA
 PRAVDĚPODOBNOST A STATISTIKA Definice lineárního normálního regresního modelu Lineární normální regresní model Y β ε Matice n,k je matice realizací. Předpoklad: n > k, h() k - tj. matice je plné hodnosti
PRAVDĚPODOBNOST A STATISTIKA Definice lineárního normálního regresního modelu Lineární normální regresní model Y β ε Matice n,k je matice realizací. Předpoklad: n > k, h() k - tj. matice je plné hodnosti
ANALÝZA VÝVOJE KLESAJÍCÍ PORODNOSTI V ČESKÉ REPUBLICE
 ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LVI 15 Číslo 3, 8 ANALÝZA VÝVOJE KLESAJÍCÍ PORODNOSTI V ČESKÉ REPUBLICE
ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LVI 15 Číslo 3, 8 ANALÝZA VÝVOJE KLESAJÍCÍ PORODNOSTI V ČESKÉ REPUBLICE
PRAVDĚPODOBNOST A STATISTIKA
 PRAVDĚPODOBNOST A STATISTIKA Definice lineárního normálního regresního modelu Lineární normální regresní model Y Xβ ε Předpoklady: Matice X X n,k je matice realizací. Předpoklad: n > k, h(x) k - tj. matice
PRAVDĚPODOBNOST A STATISTIKA Definice lineárního normálního regresního modelu Lineární normální regresní model Y Xβ ε Předpoklady: Matice X X n,k je matice realizací. Předpoklad: n > k, h(x) k - tj. matice
Stanovení manganu a míry přesnosti kalibrace ( Lineární kalibrace )
 Příklad č. 1 Stanovení manganu a míry přesnosti kalibrace ( Lineární kalibrace ) Zadání : Stanovení manganu ve vodách se provádí oxidací jodistanem v kyselém prostředí až na manganistan. (1) Sestrojte
Příklad č. 1 Stanovení manganu a míry přesnosti kalibrace ( Lineární kalibrace ) Zadání : Stanovení manganu ve vodách se provádí oxidací jodistanem v kyselém prostředí až na manganistan. (1) Sestrojte
Úvodem Dříve les než stromy 3 Operace s maticemi
 Obsah 1 Úvodem 13 2 Dříve les než stromy 17 2.1 Nejednoznačnost terminologie 17 2.2 Volba metody analýzy dat 23 2.3 Přehled vybraných vícerozměrných metod 25 2.3.1 Metoda hlavních komponent 26 2.3.2 Faktorová
Obsah 1 Úvodem 13 2 Dříve les než stromy 17 2.1 Nejednoznačnost terminologie 17 2.2 Volba metody analýzy dat 23 2.3 Přehled vybraných vícerozměrných metod 25 2.3.1 Metoda hlavních komponent 26 2.3.2 Faktorová
Modelování objemu hypotečních úvěrů poskytnutých Českou spořitelnou
 Mendelova univerzita v Brně Provozně ekonomická fakulta Modelování objemu hypotečních úvěrů poskytnutých Českou spořitelnou Diplomová práce Vedoucí práce: Mgr. David Hampel, Ph.D. Bc. Tereza Jezdinská
Mendelova univerzita v Brně Provozně ekonomická fakulta Modelování objemu hypotečních úvěrů poskytnutých Českou spořitelnou Diplomová práce Vedoucí práce: Mgr. David Hampel, Ph.D. Bc. Tereza Jezdinská
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie Predikce Multikolinearita Cvičení 4 Zuzana Dlouhá Aplikace EM predikce obecně ekonomické prognózování, předpověď, předvídání hlavním cílem je odhad hodnot vysvětlované proměnné
4EK211 Základy ekonometrie Predikce Multikolinearita Cvičení 4 Zuzana Dlouhá Aplikace EM predikce obecně ekonomické prognózování, předpověď, předvídání hlavním cílem je odhad hodnot vysvětlované proměnné
4ST201 STATISTIKA CVIČENÍ Č. 10
 4ST201 STATISTIKA CVIČENÍ Č. 10 regresní analýza - vícenásobná lineární regrese korelační analýza Př. 10.1 Máte zadaný výstup regresní analýzy závislosti závisle proměnné Y na nezávisle proměnné X. Doplňte
4ST201 STATISTIKA CVIČENÍ Č. 10 regresní analýza - vícenásobná lineární regrese korelační analýza Př. 10.1 Máte zadaný výstup regresní analýzy závislosti závisle proměnné Y na nezávisle proměnné X. Doplňte
Dynamické metody pro predikci rizika
 Dynamické metody pro predikci rizika 1 Úvod do analýzy časových řad Časová řada konečná posloupnost reálných hodnot určitého sledovaného ukazatele měřeného v určitých časových intervalech okamžikové např
Dynamické metody pro predikci rizika 1 Úvod do analýzy časových řad Časová řada konečná posloupnost reálných hodnot určitého sledovaného ukazatele měřeného v určitých časových intervalech okamžikové např
18AEK Aplikovaná ekonometrie a teorie časových řad. Řešení domácích úkolů č. 1 a 2 příklad 1
 18AEK Aplikovaná ekonometrie a teorie časových řad Řešení domácích úkolů č. 1 a 2 příklad 1 Obecné pravidlo pro všechny testy Je stanovena nulová hypotéza: H 0 Je stanovena alternativní hypotéza: H A Je
18AEK Aplikovaná ekonometrie a teorie časových řad Řešení domácích úkolů č. 1 a 2 příklad 1 Obecné pravidlo pro všechny testy Je stanovena nulová hypotéza: H 0 Je stanovena alternativní hypotéza: H A Je
Regresní analýza. Eva Jarošová
 Regresní analýza Eva Jarošová 1 Obsah 1. Regresní přímka 2. Možnosti zlepšení modelu 3. Testy v regresním modelu 4. Regresní diagnostika 5. Speciální využití Lineární model 2 1. Regresní přímka 3 nosnost
Regresní analýza Eva Jarošová 1 Obsah 1. Regresní přímka 2. Možnosti zlepšení modelu 3. Testy v regresním modelu 4. Regresní diagnostika 5. Speciální využití Lineární model 2 1. Regresní přímka 3 nosnost
UPLATNĚNÍ ADITIVNÍHO INDEXOVÉHO ROZKLADU PŘI HODNOCENÍ FINANČNÍ VÝKONNOSTI ODVĚTVÍ ČESKÝCH STAVEBNÍCH SPOŘITELEN
 ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LV 9 Číslo 6, 2007 UPLATNĚNÍ ADITIVNÍHO INDEXOVÉHO ROZKLADU PŘI HODNOCENÍ
ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LV 9 Číslo 6, 2007 UPLATNĚNÍ ADITIVNÍHO INDEXOVÉHO ROZKLADU PŘI HODNOCENÍ
Teorie časových řad Test 2 Varianta A HODNOCENÍ (max. 45 bodů z 50 možných)
 Teorie časových řad Test 2 Varianta A HODNOCENÍ (max. 45 bodů z 50 možných) 1. SPECIFIKACE (12 bodů): (1) Graf průběhu proměnných (1) Obě řady se chovají stejně, lze předpokládat jejich lineární vztah
Teorie časových řad Test 2 Varianta A HODNOCENÍ (max. 45 bodů z 50 možných) 1. SPECIFIKACE (12 bodů): (1) Graf průběhu proměnných (1) Obě řady se chovají stejně, lze předpokládat jejich lineární vztah
4EK211 Základy ekonometrie
 4EK11 Základy ekonometrie Autokorelace Cvičení 5 Zuzana Dlouhá Gauss-Markovy předpoklady Náhodná složka: Gauss-Markovy předpoklady 1. E(u) = náhodné vlivy se vzájemně vynulují. E(uu T ) = σ I n konečný
4EK11 Základy ekonometrie Autokorelace Cvičení 5 Zuzana Dlouhá Gauss-Markovy předpoklady Náhodná složka: Gauss-Markovy předpoklady 1. E(u) = náhodné vlivy se vzájemně vynulují. E(uu T ) = σ I n konečný
Příloha č. 1 Grafy a protokoly výstupy z adstatu
 1 Příklad 3. Stanovení Si metodou OES Byly porovnávány naměřené hodnoty Si na automatickém analyzátoru OES s atestovanými hodnotami. Na základě testování statistické významnosti regresních parametrů (úseku
1 Příklad 3. Stanovení Si metodou OES Byly porovnávány naměřené hodnoty Si na automatickém analyzátoru OES s atestovanými hodnotami. Na základě testování statistické významnosti regresních parametrů (úseku
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie Predikce Multikolinearita Cvičení 4 Zuzana Dlouhá Aplikace EM predikce obecně ekonomické prognózování, předpověď, předvídání hlavním cílem je odhad hodnot vysvětlované proměnné
4EK211 Základy ekonometrie Predikce Multikolinearita Cvičení 4 Zuzana Dlouhá Aplikace EM predikce obecně ekonomické prognózování, předpověď, předvídání hlavním cílem je odhad hodnot vysvětlované proměnné
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Ilustrační příklad odhadu SM v SW Gretl
 Ilustrační příklad odhadu SM v SW Gretl Odhad simultánního modelu (SM) Verifikace modelu PEF ČZU Praha Určeno pro posluchače předmětu Ekonometrie Needitovaná studijní pomůcka MM2011 Úvodní obrazovka Gretlu
Ilustrační příklad odhadu SM v SW Gretl Odhad simultánního modelu (SM) Verifikace modelu PEF ČZU Praha Určeno pro posluchače předmětu Ekonometrie Needitovaná studijní pomůcka MM2011 Úvodní obrazovka Gretlu
You created this PDF from an application that is not licensed to print to novapdf printer (http://www.novapdf.com)
 Závislost náhodných veličin Úvod Předchozí přednášky: - statistické charakteristiky jednoho výběrového nebo základního souboru - vztahy mezi výběrovým a základním souborem - vztahy statistických charakteristik
Závislost náhodných veličin Úvod Předchozí přednášky: - statistické charakteristiky jednoho výběrového nebo základního souboru - vztahy mezi výběrovým a základním souborem - vztahy statistických charakteristik
Inovace bakalářského studijního oboru Aplikovaná chemie
 http://aplchem.upol.cz CZ.1.07/2.2.00/15.0247 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Regrese Závislostproměnných funkční y= f(x) regresní y= f(x)
http://aplchem.upol.cz CZ.1.07/2.2.00/15.0247 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Regrese Závislostproměnných funkční y= f(x) regresní y= f(x)
Statistika. Regresní a korelační analýza Úvod do problému. Roman Biskup
 Statistika Regresní a korelační analýza Úvod do problému Roman Biskup Jihočeská univerzita v Českých Budějovicích Ekonomická fakulta (Zemědělská fakulta) Katedra aplikované matematiky a informatiky 2008/2009
Statistika Regresní a korelační analýza Úvod do problému Roman Biskup Jihočeská univerzita v Českých Budějovicích Ekonomická fakulta (Zemědělská fakulta) Katedra aplikované matematiky a informatiky 2008/2009
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie ZS 2014/15 Cvičení 5: Vícenásobná regrese, multikolinearita LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE 1. Jednoduchá
4EK211 Základy ekonometrie ZS 2014/15 Cvičení 5: Vícenásobná regrese, multikolinearita LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE 1. Jednoduchá
POLYNOMICKÁ REGRESE. Jedná se o regresní model, který je lineární v parametrech, ale popisuje nelineární závislost mezi proměnnými.
 POLYNOMICKÁ REGRESE Jedná se o regresní model, který je lineární v parametrech, ale popisuje nelineární závislost mezi proměnnými. y = b 0 + b 1 x + b 2 x 2 + + b n x n kde b i jsou neznámé parametry,
POLYNOMICKÁ REGRESE Jedná se o regresní model, který je lineární v parametrech, ale popisuje nelineární závislost mezi proměnnými. y = b 0 + b 1 x + b 2 x 2 + + b n x n kde b i jsou neznámé parametry,
Regresní analýza 1. Regresní analýza
 Regresní analýza 1 1 Regresní funkce Regresní analýza Důležitou statistickou úlohou je hledání a zkoumání závislostí proměnných, jejichž hodnoty získáme při realizaci experimentů Vzhledem k jejich náhodnému
Regresní analýza 1 1 Regresní funkce Regresní analýza Důležitou statistickou úlohou je hledání a zkoumání závislostí proměnných, jejichž hodnoty získáme při realizaci experimentů Vzhledem k jejich náhodnému
Testování hypotéz o parametrech regresního modelu
 Testování hypotéz o parametrech regresního modelu Ekonometrie Jiří Neubauer Katedra kvantitativních metod FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Jiří Neubauer (Katedra UO
Testování hypotéz o parametrech regresního modelu Ekonometrie Jiří Neubauer Katedra kvantitativních metod FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Jiří Neubauer (Katedra UO
Testování hypotéz o parametrech regresního modelu
 Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Lineární regresní model kde Y = Xβ + e, y 1 e 1 β y 2 Y =., e = e 2 x 11 x 1 1k., X =....... β 2,
Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Lineární regresní model kde Y = Xβ + e, y 1 e 1 β y 2 Y =., e = e 2 x 11 x 1 1k., X =....... β 2,
z dat nasbíraných v letech 1959 1994. Ke zpracování dat byl použit statistický software R. Základní model poptávkové funkce, ze kterého vycházíme,
 Úloha 1: V naší studii se zabýváme poptávkovou funkcí životního pojištění, vycházíme z dat nasbíraných v letech 1959 1994. Ke zpracování dat byl použit statistický software R. Základní model poptávkové
Úloha 1: V naší studii se zabýváme poptávkovou funkcí životního pojištění, vycházíme z dat nasbíraných v letech 1959 1994. Ke zpracování dat byl použit statistický software R. Základní model poptávkové
KORELACE. Komentované řešení pomocí programu Statistica
 KORELACE Komentované řešení pomocí programu Statistica Vstupní data I Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu Popisná
KORELACE Komentované řešení pomocí programu Statistica Vstupní data I Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu Popisná
Ekonometrie. Jiří Neubauer
 Úvod do analýzy časových řad Ekonometrie Jiří Neubauer Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Jiří Neubauer (Katedra ekonometrie UO Brno) Úvod do analýzy
Úvod do analýzy časových řad Ekonometrie Jiří Neubauer Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Jiří Neubauer (Katedra ekonometrie UO Brno) Úvod do analýzy
LINEÁRNÍ REGRESE. Lineární regresní model
 LINEÁRNÍ REGRESE Chemometrie I, David MILDE Lineární regresní model 1 Typy závislosti 2 proměnných FUNKČNÍ VZTAH: 2 závisle proměnné: určité hodnotě x odpovídá jediná hodnota y. KORELACE: 2 náhodné (nezávislé)
LINEÁRNÍ REGRESE Chemometrie I, David MILDE Lineární regresní model 1 Typy závislosti 2 proměnných FUNKČNÍ VZTAH: 2 závisle proměnné: určité hodnotě x odpovídá jediná hodnota y. KORELACE: 2 náhodné (nezávislé)
AVDAT Geometrie metody nejmenších čtverců
 AVDAT Geometrie metody nejmenších čtverců Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Lineární model klasický lineární regresní model odhad parametrů MNČ y = Xβ + ε, ε
AVDAT Geometrie metody nejmenších čtverců Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Lineární model klasický lineární regresní model odhad parametrů MNČ y = Xβ + ε, ε
Statistika II. Jiří Neubauer
 Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Časová řada konečná posloupnost reálných hodnot určitého sledovaného ukazatele měřeného v určitých
Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Časová řada konečná posloupnost reálných hodnot určitého sledovaného ukazatele měřeného v určitých
VÝVOJ INDEXŮ SPOTŘEBITELSKÝCH CEN
 ČESKÁ ZEMĚDĚLSKÁ UNIVERZITA V PRAZE Fakulta provozně ekonomická Katedra statistiky Studijní obor: Veřejná správa a regionální rozvoj Teze k diplomové práci VÝVOJ INDEXŮ SPOTŘEBITELSKÝCH CEN Vypracovala:
ČESKÁ ZEMĚDĚLSKÁ UNIVERZITA V PRAZE Fakulta provozně ekonomická Katedra statistiky Studijní obor: Veřejná správa a regionální rozvoj Teze k diplomové práci VÝVOJ INDEXŮ SPOTŘEBITELSKÝCH CEN Vypracovala:
5EN306 Aplikované kvantitativní metody I
 5EN306 Aplikované kvantitativní metody I Přednáška 5 Zuzana Dlouhá Předmět a struktura kurzu 1. Úvod: struktura empirických výzkumů 2. Tvorba ekonomických modelů: teorie 3. Data: zdroje a typy dat, význam
5EN306 Aplikované kvantitativní metody I Přednáška 5 Zuzana Dlouhá Předmět a struktura kurzu 1. Úvod: struktura empirických výzkumů 2. Tvorba ekonomických modelů: teorie 3. Data: zdroje a typy dat, význam
RESEARCH TRH REZIDENČNÍCH NEMOVITOSTÍ V PRAZE ZPRÁVA O STAVU ZA ROK 2012
 RESEARCH TRH REZIDENČNÍCH NEMOVITOSTÍ V PRAZE ZPRÁVA O STAVU ZA ROK 212 25 26 27 28 29 21 211 212 213* 214* Dovolujeme si Vám nabídnout zprávu týkající se stavu na pražském rezidenčním trhu v roce 212.
RESEARCH TRH REZIDENČNÍCH NEMOVITOSTÍ V PRAZE ZPRÁVA O STAVU ZA ROK 212 25 26 27 28 29 21 211 212 213* 214* Dovolujeme si Vám nabídnout zprávu týkající se stavu na pražském rezidenčním trhu v roce 212.
Tomáš Karel LS 2012/2013
 Tomáš Karel LS 2012/2013 Doplňkový materiál ke cvičení z předmětu 4ST201. Na případné faktické chyby v této presentaci mě prosím upozorněte. Děkuji. Tyto slidy berte pouze jako doplňkový materiál není
Tomáš Karel LS 2012/2013 Doplňkový materiál ke cvičení z předmětu 4ST201. Na případné faktické chyby v této presentaci mě prosím upozorněte. Děkuji. Tyto slidy berte pouze jako doplňkový materiál není
TECHNIKA UMĚLÝCH PROMĚNNÝCH V PRŮŘEZOVÉ ANALÝZE A V MODELECH ČASOVÝCH ŘAD
 TECHNIKA UMĚLÝCH PROMĚNNÝCH V PRŮŘEZOVÉ ANALÝZE A V MODELECH ČASOVÝCH ŘAD Umělé (dummy) proměnné se používají, pokud chceme do modelu zahrnout proměnné, které mají kvalitativní či diskrétní charakter,
TECHNIKA UMĚLÝCH PROMĚNNÝCH V PRŮŘEZOVÉ ANALÝZE A V MODELECH ČASOVÝCH ŘAD Umělé (dummy) proměnné se používají, pokud chceme do modelu zahrnout proměnné, které mají kvalitativní či diskrétní charakter,
AVDAT Klasický lineární model, metoda nejmenších
 AVDAT Klasický lineární model, metoda nejmenších čtverců Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Lineární model y i = β 0 + β 1 x i1 + + β k x ik + ε i (1) kde y i
AVDAT Klasický lineární model, metoda nejmenších čtverců Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Lineární model y i = β 0 + β 1 x i1 + + β k x ik + ε i (1) kde y i
FAKTORY PŮSOBÍCÍ NA CESTUJÍCÍ V DOPRAVNÍM SYSTÉMU FACTORS WHICH HAVE EFFECT ON PASSENGERS IN TRANSPORT SYSTEM
 FAKTORY PŮSOBÍCÍ NA CESTUJÍCÍ V DOPRAVNÍM SYSTÉMU FACTORS WHICH HAVE EFFECT ON PASSENGERS IN TRANSPORT SYSTEM Kateřina Pojkarová 1 Anotace:Pro uskutečňování svých cest si lidé vybírají různé způsoby, a
FAKTORY PŮSOBÍCÍ NA CESTUJÍCÍ V DOPRAVNÍM SYSTÉMU FACTORS WHICH HAVE EFFECT ON PASSENGERS IN TRANSPORT SYSTEM Kateřina Pojkarová 1 Anotace:Pro uskutečňování svých cest si lidé vybírají různé způsoby, a
ANOVA. Semestrální práce UNIVERZITA PARDUBICE. Fakulta chemicko-technologická Katedra analytické chemie
 UNIVERZITA PARDUBICE Fakulta chemicko-technologická Katedra analytické chemie ANOVA Semestrální práce Licenční studium Galileo Interaktivní statistická analýza dat Brno 2015 Ing. Petra Hlaváčková, Ph.D.
UNIVERZITA PARDUBICE Fakulta chemicko-technologická Katedra analytické chemie ANOVA Semestrální práce Licenční studium Galileo Interaktivní statistická analýza dat Brno 2015 Ing. Petra Hlaváčková, Ph.D.
Využití regresní analýzy pro modelování státního dluhu
 Mendelova univerzita v Brně Provozně ekonomická fakulta Využití regresní analýzy pro modelování státního dluhu Bakalářská práce Vedoucí práce: Mgr. Kateřina Myšková, Ph.D. Alžběta Surovcová Brno 2012 Tímto
Mendelova univerzita v Brně Provozně ekonomická fakulta Využití regresní analýzy pro modelování státního dluhu Bakalářská práce Vedoucí práce: Mgr. Kateřina Myšková, Ph.D. Alžběta Surovcová Brno 2012 Tímto
6. Lineární regresní modely
 6. Lineární regresní modely 6.1 Jednoduchá regrese a validace 6.2 Testy hypotéz v lineární regresi 6.3 Kritika dat v regresním tripletu 6.4 Multikolinearita a polynomy 6.5 Kritika modelu v regresním tripletu
6. Lineární regresní modely 6.1 Jednoduchá regrese a validace 6.2 Testy hypotéz v lineární regresi 6.3 Kritika dat v regresním tripletu 6.4 Multikolinearita a polynomy 6.5 Kritika modelu v regresním tripletu
Matematické modelování Náhled do ekonometrie. Lukáš Frýd
 Matematické modelování Náhled do ekonometrie Lukáš Frýd Výnos akcie vs. Výnos celého trhu - CAPM model r it = r ft + β 1. (r mt r ft ) r it r ft = α 0 + β 1. (r mt r ft ) + ε it Ekonomický (finanční model)
Matematické modelování Náhled do ekonometrie Lukáš Frýd Výnos akcie vs. Výnos celého trhu - CAPM model r it = r ft + β 1. (r mt r ft ) r it r ft = α 0 + β 1. (r mt r ft ) + ε it Ekonomický (finanční model)
UNIVERZITA OBRANY Fakulta ekonomiky a managementu. Aplikace STAT1. Výsledek řešení projektu PRO HORR2011 a PRO GRAM2011 3. 11.
 UNIVERZITA OBRANY Fakulta ekonomiky a managementu Aplikace STAT1 Výsledek řešení projektu PRO HORR2011 a PRO GRAM2011 Jiří Neubauer, Marek Sedlačík, Oldřich Kříž 3. 11. 2012 Popis a návod k použití aplikace
UNIVERZITA OBRANY Fakulta ekonomiky a managementu Aplikace STAT1 Výsledek řešení projektu PRO HORR2011 a PRO GRAM2011 Jiří Neubauer, Marek Sedlačík, Oldřich Kříž 3. 11. 2012 Popis a návod k použití aplikace
Tomáš Karel LS 2012/2013
 Tomáš Karel LS 2012/2013 Doplňkový materiál ke cvičení z předmětu 4ST201. Na případné faktické chyby v této presentaci mě prosím upozorněte. Děkuji. Tyto slidy berte pouze jako doplňkový materiál není
Tomáš Karel LS 2012/2013 Doplňkový materiál ke cvičení z předmětu 4ST201. Na případné faktické chyby v této presentaci mě prosím upozorněte. Děkuji. Tyto slidy berte pouze jako doplňkový materiál není
Analýza nemovitostí. 1. února 2010. Autoři: Bc. Tomáš Tyl, Mgr. Petr Syrový. Schválil: Ing. Vladimír Fichtner
 Analýza nemovitostí 1. února 2010 Autoři: Bc. Tomáš Tyl, Mgr. Petr Syrový Schválil: Ing. Vladimír Fichtner 1 Obsah OBSAH... 2 DŮLEŽITÉ UPOZORNĚNÍ... 2 1. NAŠE DOPORUČENÍ - ZÁVĚR... 3 2. NAŠE DOPORUČENÍ
Analýza nemovitostí 1. února 2010 Autoři: Bc. Tomáš Tyl, Mgr. Petr Syrový Schválil: Ing. Vladimír Fichtner 1 Obsah OBSAH... 2 DŮLEŽITÉ UPOZORNĚNÍ... 2 1. NAŠE DOPORUČENÍ - ZÁVĚR... 3 2. NAŠE DOPORUČENÍ
Úrokové sazby dál padají
 Úrokové sazby dál padají 22.7.2014 - Hypotéky v červnu opět prudce zlevňovaly. První z bank, která v červnu měnila úrokové sazby, byla UniCredit Bank, která snížila nabídkové sazby u 3 a 5letých fixací.
Úrokové sazby dál padají 22.7.2014 - Hypotéky v červnu opět prudce zlevňovaly. První z bank, která v červnu měnila úrokové sazby, byla UniCredit Bank, která snížila nabídkové sazby u 3 a 5letých fixací.
Univerzita Pardubice SEMESTRÁLNÍ PRÁCE. Tvorba lineárních regresních modelů. 2015/2016 RNDr. Mgr. Leona Svobodová, Ph.D.
 Univerzita Pardubice SEMESTRÁLNÍ PRÁCE Tvorba lineárních regresních modelů 2015/2016 RNDr. Mgr. Leona Svobodová, Ph.D. Úloha 1 Porovnání regresních přímek u jednoduchého lineárního regresního modelu Porovnání
Univerzita Pardubice SEMESTRÁLNÍ PRÁCE Tvorba lineárních regresních modelů 2015/2016 RNDr. Mgr. Leona Svobodová, Ph.D. Úloha 1 Porovnání regresních přímek u jednoduchého lineárního regresního modelu Porovnání
STATISTIKA I Metodický list č. 1 Název tématického celku:
 STATISTIKA I Metodický list č. 1 Analýza závislostí Základním cílem tohoto tématického celku je seznámit se s pokročilejšími metodami zpracování statistických údajů.. 1. kontingenční tabulky 2. regresní
STATISTIKA I Metodický list č. 1 Analýza závislostí Základním cílem tohoto tématického celku je seznámit se s pokročilejšími metodami zpracování statistických údajů.. 1. kontingenční tabulky 2. regresní
ANALÝZA VÝVOJE TRHU STAVEBNÍHO SPOŘENÍ V ČR
 ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LIII 8 Číslo 3, 2005 ANALÝZA VÝVOJE TRHU STAVEBNÍHO SPOŘENÍ V ČR
ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LIII 8 Číslo 3, 2005 ANALÝZA VÝVOJE TRHU STAVEBNÍHO SPOŘENÍ V ČR
JEDNOVÝBĚROVÉ TESTY. Komentované řešení pomocí programu Statistica
 JEDNOVÝBĚROVÉ TESTY Komentované řešení pomocí programu Statistica Vstupní data Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu
JEDNOVÝBĚROVÉ TESTY Komentované řešení pomocí programu Statistica Vstupní data Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu
Statgraphics v. 5.0 STATISTICKÁ INDUKCE PRO JEDNOROZMĚRNÁ DATA. Martina Litschmannová 1. Typ proměnné. Požadovaný typ analýzy
 Dichotomická proměnná (0-1) Spojitá proměnná STATISTICKÁ INDUKCE PRO JEDNOROZMĚRNÁ DATA Typ proměnné Požadovaný typ analýzy Ověření variability Předpoklady Testy, resp. intervalové odhad Test o rozptylu
Dichotomická proměnná (0-1) Spojitá proměnná STATISTICKÁ INDUKCE PRO JEDNOROZMĚRNÁ DATA Typ proměnné Požadovaný typ analýzy Ověření variability Předpoklady Testy, resp. intervalové odhad Test o rozptylu
Vliv úrokové sazby na objem poskytnutých hypotečních úvěrů
 Mendelova univerzita v Brně Provozně ekonomická fakulta Vliv úrokové sazby na objem poskytnutých hypotečních úvěrů Bakalářská práce Vedoucí práce: Ing. Luboš Střelec Ph.D. Autor práce: Andrea Korbičková
Mendelova univerzita v Brně Provozně ekonomická fakulta Vliv úrokové sazby na objem poskytnutých hypotečních úvěrů Bakalářská práce Vedoucí práce: Ing. Luboš Střelec Ph.D. Autor práce: Andrea Korbičková
Korelace. Komentované řešení pomocí MS Excel
 Korelace Komentované řešení pomocí MS Excel Vstupní data Tabulka se vstupními daty je umístěna v oblasti A2:B84 (viz. obrázek) Prvotní představu o tvaru a síle závislosti docházky a počtu bodů nám poskytne
Korelace Komentované řešení pomocí MS Excel Vstupní data Tabulka se vstupními daty je umístěna v oblasti A2:B84 (viz. obrázek) Prvotní představu o tvaru a síle závislosti docházky a počtu bodů nám poskytne
{ } ( 2) Příklad: Test nezávislosti kategoriálních znaků
 Příklad: Test nezávislosti kategoriálních znaků Určete na hladině významnosti 5 % na základě dat zjištěných v rámci dotazníkového šetření ve Šluknově, zda existuje závislost mezi pohlavím respondenta a
Příklad: Test nezávislosti kategoriálních znaků Určete na hladině významnosti 5 % na základě dat zjištěných v rámci dotazníkového šetření ve Šluknově, zda existuje závislost mezi pohlavím respondenta a
MEZIREGIONÁLNÍ PŘEPRAVA NA ŽELEZNICI V ČR INTERREGINAL RAILWAY TRANSPORT IN CZECH REPUBLIC
 MEZIREGIONÁLNÍ PŘEPRAVA NA ŽELEZNICI V ČR INTERREGINAL RAILWAY TRANSPORT IN CZECH REPUBLIC Kateřina Pojkarová 1 Anotace:Článek se věnuje železniční přepravě mezi kraji v České republice, se zaměřením na
MEZIREGIONÁLNÍ PŘEPRAVA NA ŽELEZNICI V ČR INTERREGINAL RAILWAY TRANSPORT IN CZECH REPUBLIC Kateřina Pojkarová 1 Anotace:Článek se věnuje železniční přepravě mezi kraji v České republice, se zaměřením na
VZTAHY MEZI PRODUKCÍ, NÁKLADY A CENOVOU ÚROVNÍ V ZEMĚDĚLSTVÍ A NÁRODNÍM HOSPODÁŔSTVÍ
 VZTAHY MEZI PRODUKCÍ, NÁKLADY A CENOVOU ÚROVNÍ V ZEMĚDĚLSTVÍ A NÁRODNÍM HOSPODÁŔSTVÍ J. Burianová katedra ekonomických teorií, PEF Vysoká škola zemědělská, 165 21 Praha 6 - Suchdol Anotace: Příspěvek ukazuje
VZTAHY MEZI PRODUKCÍ, NÁKLADY A CENOVOU ÚROVNÍ V ZEMĚDĚLSTVÍ A NÁRODNÍM HOSPODÁŔSTVÍ J. Burianová katedra ekonomických teorií, PEF Vysoká škola zemědělská, 165 21 Praha 6 - Suchdol Anotace: Příspěvek ukazuje
ŠETŘENÍ ÚVĚROVÝCH PODMÍNEK BANK ČERVENEC
 ŠETŘENÍ ÚVĚROVÝCH PODMÍNEK BANK ČERVENEC Samostatný odbor finanční stability Sekce měnová Odbor měnové politiky a fiskálních analýz 2017 ČERVENEC 2017 1 I. ÚVOD A SHRNUTÍ Šetření úvěrových podmínek bank
ŠETŘENÍ ÚVĚROVÝCH PODMÍNEK BANK ČERVENEC Samostatný odbor finanční stability Sekce měnová Odbor měnové politiky a fiskálních analýz 2017 ČERVENEC 2017 1 I. ÚVOD A SHRNUTÍ Šetření úvěrových podmínek bank
Ekonomický a ekonometrický model. Předpoklady, formulace EKO modelu a očekávání o chování proměnných
 Exogenní (γ) Simultánní dynamický model Tento model zkoumá vzájemné závislosti vývoje tempa růstu/poklesu HDP, míry nezaměstnanosti a míry inflace v České republice v závislosti na indexu spotřebitelských
Exogenní (γ) Simultánní dynamický model Tento model zkoumá vzájemné závislosti vývoje tempa růstu/poklesu HDP, míry nezaměstnanosti a míry inflace v České republice v závislosti na indexu spotřebitelských
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
T T. Think Together 2013. Marta Gryčová THINK TOGETHER
 Česká zemědělská univerzita v Praze Provozně ekonomická fakulta Doktorská vědecká konference 4. února 2013 T T THINK TOGETHER Think Together 2013 Mzdová disparita v českém agrárním sektoru v období od
Česká zemědělská univerzita v Praze Provozně ekonomická fakulta Doktorská vědecká konference 4. února 2013 T T THINK TOGETHER Think Together 2013 Mzdová disparita v českém agrárním sektoru v období od
vzorek1 0.0033390 0.0047277 0.0062653 0.0077811 0.0090141... vzorek 30 0.0056775 0.0058778 0.0066916 0.0076192 0.0087291
 Vzorová úloha 4.16 Postup vícerozměrné kalibrace Postup vícerozměrné kalibrace ukážeme na úloze C4.10 Vícerozměrný kalibrační model kvality bezolovnatého benzinu. Dle následujících kroků na základě naměřených
Vzorová úloha 4.16 Postup vícerozměrné kalibrace Postup vícerozměrné kalibrace ukážeme na úloze C4.10 Vícerozměrný kalibrační model kvality bezolovnatého benzinu. Dle následujících kroků na základě naměřených
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Ekonomické faktory a rezidenční bydlení
 Ekonomické faktory a rezidenční bydlení Roman Hauptfleisch Relace mezi úrokovými sazbami, cenami nemovitostí a hospodářským vývojem Demografické ukazatele Nízké hypoteční úrokové sazby Nárůst objemu hypoték
Ekonomické faktory a rezidenční bydlení Roman Hauptfleisch Relace mezi úrokovými sazbami, cenami nemovitostí a hospodářským vývojem Demografické ukazatele Nízké hypoteční úrokové sazby Nárůst objemu hypoték
ZOBECNĚNÝ LINEÁRNÍ REGRESNÍ MODEL. METODA ZOBECNĚNÝCH NEJMENŠÍCH ČTVERCŮ
 ZOBECNĚNÝ LINEÁRNÍ REGRESNÍ MODEL. METODA ZOBECNĚNÝCH NEJMENŠÍCH ČTVERCŮ V následujícím textu se podíváme na to, co dělat, když jsou porušeny některé GM předpoklady. Nejprve si připomeňme, o jaké předpoklady
ZOBECNĚNÝ LINEÁRNÍ REGRESNÍ MODEL. METODA ZOBECNĚNÝCH NEJMENŠÍCH ČTVERCŮ V následujícím textu se podíváme na to, co dělat, když jsou porušeny některé GM předpoklady. Nejprve si připomeňme, o jaké předpoklady
odpovídá jedna a jen jedna hodnota jiných
 8. Regresní a korelační analýza Problém: hledání, zkoumání a hodnocení souvislostí, závislostí mezi dvěma a více statistickými znaky (veličinami). Typy závislostí: pevné a volné Pevná závislost každé hodnotě
8. Regresní a korelační analýza Problém: hledání, zkoumání a hodnocení souvislostí, závislostí mezi dvěma a více statistickými znaky (veličinami). Typy závislostí: pevné a volné Pevná závislost každé hodnotě
Úloha 1: Lineární kalibrace
 Úloha 1: Lineární kalibrace U pacientů s podezřením na rakovinu prostaty byl metodou GC/MS měřen obsah sarkosinu v moči. Pro kvantitativní stanovení bylo nutné změřit řadu kalibračních roztoků o různé
Úloha 1: Lineární kalibrace U pacientů s podezřením na rakovinu prostaty byl metodou GC/MS měřen obsah sarkosinu v moči. Pro kvantitativní stanovení bylo nutné změřit řadu kalibračních roztoků o různé
TVORBA LINEÁRNÍCH REGRESNÍCH MODELŮ PŘI ANALÝZE DAT. Semestrální práce UNIVERZITA PARDUBICE. Fakulta chemicko-technologická Katedra analytické chemie
 UNIVERZITA PARDUBICE Fakulta chemicko-technologická Katedra analytické chemie TVORBA LINEÁRNÍCH REGRESNÍCH MODELŮ PŘI ANALÝZE DAT Semestrální práce Licenční studium Galileo Interaktivní statistická analýza
UNIVERZITA PARDUBICE Fakulta chemicko-technologická Katedra analytické chemie TVORBA LINEÁRNÍCH REGRESNÍCH MODELŮ PŘI ANALÝZE DAT Semestrální práce Licenční studium Galileo Interaktivní statistická analýza
TRH REZIDENČNÍCH NEMOVITOSTÍ V PRAZE
 RESEARCH TRH REZIDENČNÍCH NEMOVITOSTÍ V PRAZE ZPRÁVA O STAVU ZA 1/H1 5 7 9 1 11 1 13 Jan 1 Feb 1 March 1 April 1 May 1 June 1 5 7 9 1 11 1 13 1* 15* 1* Tato nová zpráva Vám poskytne aktuální informace
RESEARCH TRH REZIDENČNÍCH NEMOVITOSTÍ V PRAZE ZPRÁVA O STAVU ZA 1/H1 5 7 9 1 11 1 13 Jan 1 Feb 1 March 1 April 1 May 1 June 1 5 7 9 1 11 1 13 1* 15* 1* Tato nová zpráva Vám poskytne aktuální informace
ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD. Samostatný odbor finanční stability
 ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD Samostatný odbor finanční stability 0 ZÁTĚŽOVÉ TESTY LISTOPAD 0 ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR (LISTOPAD 0) SHRNUTÍ Výsledky zátěžových testů bankovního
ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR LISTOPAD Samostatný odbor finanční stability 0 ZÁTĚŽOVÉ TESTY LISTOPAD 0 ZÁTĚŽOVÉ TESTY BANKOVNÍHO SEKTORU ČR (LISTOPAD 0) SHRNUTÍ Výsledky zátěžových testů bankovního
4EK211 Základy ekonometrie
 4EK211 Základ ekonometrie Odhad klasického lineárního regresního modelu I Cvičení 2 Zuzana Dlouhá Metodologický postup tvor EM 1. Specifikace modelu určení proměnných určení vzájemných vaze mezi proměnnými
4EK211 Základ ekonometrie Odhad klasického lineárního regresního modelu I Cvičení 2 Zuzana Dlouhá Metodologický postup tvor EM 1. Specifikace modelu určení proměnných určení vzájemných vaze mezi proměnnými
ROZBOR VÝVOJE A ROZDÍLŮ CEN VYBRANÝCH AGRÁRNÍCH KOMODIT V ČR A V NĚKTERÝCH STÁTECH EU
 ROZBOR VÝVOJE A ROZDÍLŮ CEN VYBRANÝCH AGRÁRNÍCH KOMODIT V ČR A V NĚKTERÝCH STÁTECH EU ANALYSIS OF DEVELOPMENT AND DIFFERENCES IN PRICES OF AGRICULTURAL COMMODITIES IN THE CZECH REPUBLIC AND SOME EUROPEAN
ROZBOR VÝVOJE A ROZDÍLŮ CEN VYBRANÝCH AGRÁRNÍCH KOMODIT V ČR A V NĚKTERÝCH STÁTECH EU ANALYSIS OF DEVELOPMENT AND DIFFERENCES IN PRICES OF AGRICULTURAL COMMODITIES IN THE CZECH REPUBLIC AND SOME EUROPEAN
Kalibrace a limity její přesnosti
 Univerzita Pardubice Fakulta chemicko-technologická Katedra analytické chemie Licenční studium GALILEO a limity její přesnosti Seminární práce Monika Vejpustková leden 2016 OBSAH Úloha 1. Lineární kalibrace...
Univerzita Pardubice Fakulta chemicko-technologická Katedra analytické chemie Licenční studium GALILEO a limity její přesnosti Seminární práce Monika Vejpustková leden 2016 OBSAH Úloha 1. Lineární kalibrace...
Základy ekonometrie. XI. Vektorové autoregresní modely. Základy ekonometrie (ZAEK) XI. VAR modely Podzim / 28
 Základy ekonometrie XI. Vektorové autoregresní modely Základy ekonometrie (ZAEK) XI. VAR modely Podzim 2015 1 / 28 Obsah tématu 1 Prognózování s VAR modely 2 Vektorové modely korekce chyb (VECM) 3 Impulzní
Základy ekonometrie XI. Vektorové autoregresní modely Základy ekonometrie (ZAEK) XI. VAR modely Podzim 2015 1 / 28 Obsah tématu 1 Prognózování s VAR modely 2 Vektorové modely korekce chyb (VECM) 3 Impulzní
4EK211 Základy ekonometrie
 4EK211 Základy ekonometrie Logistická křivka Umělé proměnné Cvičení 11 Zuzana Dlouhá Logistická křivka log-lineární model patří mezi poptávkové funkce, ty dělíme na: a) klasické D = f (příjem, cenový index,
4EK211 Základy ekonometrie Logistická křivka Umělé proměnné Cvičení 11 Zuzana Dlouhá Logistická křivka log-lineární model patří mezi poptávkové funkce, ty dělíme na: a) klasické D = f (příjem, cenový index,
Ověření platnosti teorie o Phillipsově křivce v ekonomice České republiky
 Mendelova univerzita v Brně Provozně ekonomická fakulta Ověření platnosti teorie o Phillipsově křivce v ekonomice České republiky Bakalářská práce Vedoucí práce Mgr. Kateřina Myšková, Ph.D. Milan Lorenz
Mendelova univerzita v Brně Provozně ekonomická fakulta Ověření platnosti teorie o Phillipsově křivce v ekonomice České republiky Bakalářská práce Vedoucí práce Mgr. Kateřina Myšková, Ph.D. Milan Lorenz
RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr.
 Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
TRH REZIDENČNÍCH NEMOVITOSTÍ V PRAZE
 RESEARCH TRH REZIDENČNÍCH NEMOVITOSTÍ V PRAZE 15/H1 5 7 8 9 1 11 1 13 1 Leden 1 Únor 1 Březen 1 Duben 1 Květen 1 Červen 1 Červenec 1 Srpen 1 Září 1 Říjen 1 Listopad 1 Prosinec 15 Leden 15 Únor 15 Březen
RESEARCH TRH REZIDENČNÍCH NEMOVITOSTÍ V PRAZE 15/H1 5 7 8 9 1 11 1 13 1 Leden 1 Únor 1 Březen 1 Duben 1 Květen 1 Červen 1 Červenec 1 Srpen 1 Září 1 Říjen 1 Listopad 1 Prosinec 15 Leden 15 Únor 15 Březen
Semestrální práce. 3.3 Tvorba nelineárních regresních modelů v analýze dat
 Semestrální práce 1 3.3 Tvorba nelineárních regresních modelů v analýze dat Ing. Ján Lengyel, CSc. Centrální analytická laboratoř Ústav jaderného výzkumu Řež, a. s. Husinec Řež 130 250 68 Řež V Řeži, únor
Semestrální práce 1 3.3 Tvorba nelineárních regresních modelů v analýze dat Ing. Ján Lengyel, CSc. Centrální analytická laboratoř Ústav jaderného výzkumu Řež, a. s. Husinec Řež 130 250 68 Řež V Řeži, únor
S E M E S T R Á L N Í
 Univerzita Pardubice Fakulta chemicko-technologická Katedra analytické chemie S E M E S T R Á L N Í P R Á C E Licenční studium Statistické zpracování dat při managementu jakosti Předmět ANOVA analýza rozptylu
Univerzita Pardubice Fakulta chemicko-technologická Katedra analytické chemie S E M E S T R Á L N Í P R Á C E Licenční studium Statistické zpracování dat při managementu jakosti Předmět ANOVA analýza rozptylu
6. Lineární regresní modely
 6. Lineární regresní modely 6.1 Jednoduchá regrese a validace 6.2 Testy hypotéz v lineární regresi 6.3 Kritika dat v regresním tripletu 6.4 Multikolinearita a polynomy 6.5 Kritika modelu v regresním tripletu
6. Lineární regresní modely 6.1 Jednoduchá regrese a validace 6.2 Testy hypotéz v lineární regresi 6.3 Kritika dat v regresním tripletu 6.4 Multikolinearita a polynomy 6.5 Kritika modelu v regresním tripletu
4EK211 Základy ekonometrie
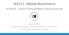 4EK211 Základy ekonometrie ZS 2014/15 Cvičení 6: Dummy proměnné, úvod do časových řad LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE 1. Multikolinearita
4EK211 Základy ekonometrie ZS 2014/15 Cvičení 6: Dummy proměnné, úvod do časových řad LENKA FIŘTOVÁ KATEDRA EKONOMETRIE, FAKULTA INFORMATIKY A STATISTIKY VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE 1. Multikolinearita
Statistická analýza jednorozměrných dat
 Statistická analýza jednorozměrných dat Prof. RNDr. Milan Meloun, DrSc. Univerzita Pardubice, Pardubice 31.ledna 2011 Tato prezentace je spolufinancována Evropským sociálním fondem a státním rozpočtem
Statistická analýza jednorozměrných dat Prof. RNDr. Milan Meloun, DrSc. Univerzita Pardubice, Pardubice 31.ledna 2011 Tato prezentace je spolufinancována Evropským sociálním fondem a státním rozpočtem
MÍRY ZÁVISLOSTI (KORELACE A REGRESE)
 zhanel@fsps.muni.cz MÍRY ZÁVISLOSTI (KORELACE A REGRESE) 2.5 MÍRY ZÁVISLOSTI 2.5.1 ZÁVISLOST PEVNÁ, VOLNÁ, STATISTICKÁ A KORELAČNÍ Jednorozměrné soubory - charakterizovány jednotlivými statistickými znaky
zhanel@fsps.muni.cz MÍRY ZÁVISLOSTI (KORELACE A REGRESE) 2.5 MÍRY ZÁVISLOSTI 2.5.1 ZÁVISLOST PEVNÁ, VOLNÁ, STATISTICKÁ A KORELAČNÍ Jednorozměrné soubory - charakterizovány jednotlivými statistickými znaky
5EN306 Aplikované kvantitativní metody I
 5EN306 Aplikované kvantitativní metody I Přednáška 3 Zuzana Dlouhá Předmět a struktura kurzu 1. Úvod: struktura empirických výzkumů 2. Tvorba ekonomických modelů: teorie 3. Data: zdroje a typy dat, význam
5EN306 Aplikované kvantitativní metody I Přednáška 3 Zuzana Dlouhá Předmět a struktura kurzu 1. Úvod: struktura empirických výzkumů 2. Tvorba ekonomických modelů: teorie 3. Data: zdroje a typy dat, význam
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz
 Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická
Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická statistika Doc. RNDr. Gejza Dohnal, CSc. dohnal@nipax.cz Pravděpodobnost a matematická
Cvičící Kuba Kubina Kubinčák Body u závěrečného testu
 1. Příklad U 12 studentů jsme sledovali počet dosažených bodů na závěrečném testu (od 0 do 60). Vždy 4 z těchto studentů chodili k jednomu ze 3 cvičících panu Kubovi, panu Kubinovi, nebo panu Kubinčákovi.
1. Příklad U 12 studentů jsme sledovali počet dosažených bodů na závěrečném testu (od 0 do 60). Vždy 4 z těchto studentů chodili k jednomu ze 3 cvičících panu Kubovi, panu Kubinovi, nebo panu Kubinčákovi.
Přílohy. Spotřeba elektřiny. Model závislosti spotřeby elektřiny
 Přílohy Spotřeba elektřiny Model závislosti spotřeby elektřiny Model 24: OLS, za použití pozorování 22-213 (T = 12) Závisle proměnná: C_ele_domkWH koeficient směr. chyba t-podíl p-hodnota ------------------------------------------------------------------
Přílohy Spotřeba elektřiny Model závislosti spotřeby elektřiny Model 24: OLS, za použití pozorování 22-213 (T = 12) Závisle proměnná: C_ele_domkWH koeficient směr. chyba t-podíl p-hodnota ------------------------------------------------------------------
(motto: An unsophisticated forecaster uses statistics as a drunken man uses lamp-posts - for support rather than for illumination.
 Neparametricke testy (motto: An unsophisticated forecaster uses statistics as a drunken man uses lamp-posts - for support rather than for illumination. Andrew Lang) 1. Příklad V následující tabulce jsou
Neparametricke testy (motto: An unsophisticated forecaster uses statistics as a drunken man uses lamp-posts - for support rather than for illumination. Andrew Lang) 1. Příklad V následující tabulce jsou
ANALÝZA DLOUHODOBÉ NEZAMĚSTNANOSTI V ZEMÍCH EU # ANALYSIS OF LONG-TERM UNEMPLOYMENT IN EU COUNTRIES. KLÍMA Jan, PALÁT Milan.
 ANALÝZA DLOUHODOBÉ NEZAMĚSTNANOSTI V ZEMÍCH EU # ANALYSIS OF LONG-TERM UNEMPLOYMENT IN EU COUNTRIES KLÍMA Jan, PALÁT Milan Abstract The paper is aimed at assessing the long-term unemployment of males,
ANALÝZA DLOUHODOBÉ NEZAMĚSTNANOSTI V ZEMÍCH EU # ANALYSIS OF LONG-TERM UNEMPLOYMENT IN EU COUNTRIES KLÍMA Jan, PALÁT Milan Abstract The paper is aimed at assessing the long-term unemployment of males,
Semestrální práce. 2. semestr
 Licenční studium č. 89002 Semestrální práce 2. semestr Tvorba lineárních regresních modelů při analýze dat Příklad 1 Porovnání dvou regresních přímek u jednoduchého lineárního regresního modelu. Počet
Licenční studium č. 89002 Semestrální práce 2. semestr Tvorba lineárních regresních modelů při analýze dat Příklad 1 Porovnání dvou regresních přímek u jednoduchého lineárního regresního modelu. Počet
4ST201 STATISTIKA CVIČENÍ Č. 7
 4ST201 STATISTIKA CVIČENÍ Č. 7 testování hypotéz parametrické testy test hypotézy o střední hodnotě test hypotézy o relativní četnosti test o shodě středních hodnot testování hypotéz v MS Excel neparametrické
4ST201 STATISTIKA CVIČENÍ Č. 7 testování hypotéz parametrické testy test hypotézy o střední hodnotě test hypotézy o relativní četnosti test o shodě středních hodnot testování hypotéz v MS Excel neparametrické
ŠETŘENÍ O VÝVOJI ÚVĚROVÝCH PODMÍNEK LEDEN
 ŠETŘENÍ O VÝVOJI ÚVĚROVÝCH PODMÍNEK LEDEN Samostatný odbor finanční stability Sekce měnová a statistiky Odbor měnové politiky a fiskálních analýz 213 LEDEN 213 1 I. ÚVOD A SHRNUTÍ Čtvrtletní šetření ČNB
ŠETŘENÍ O VÝVOJI ÚVĚROVÝCH PODMÍNEK LEDEN Samostatný odbor finanční stability Sekce měnová a statistiky Odbor měnové politiky a fiskálních analýz 213 LEDEN 213 1 I. ÚVOD A SHRNUTÍ Čtvrtletní šetření ČNB
