obsah obsah... 5 Přehled veličin... 7
|
|
|
- Vlastimil Novák
- před 7 lety
- Počet zobrazení:
Transkript
1 Obsah 5 obsah obsah... 5 Přehled veliči... 7 Úvodem... 9 Předmluva Úvod do mechaiky ozděleí mechaiky Základí pojmy O pohybu a prostoru v mechaice Hmota Čas Síla Veličiy a jedotky používaé v mechaice Fyzikálí zákoy Vytvářeí rovic v mechaice Základí pojmy a zákoy statiky Pricip akce a reakce Síly a společé ositelce Záko rovoběžíka sil Momet síly k bodu Dvojice sil a její momet Mechaická práce Výko Páka pákové pravidlo Vazby těles, metoda uvolňováí těles Podpora volá Podpora pevá (rotačí) Vazba vetkutím Uvolňováí těles oviá soustava sil Soustava sil působící a jedé ositelce Výsledice sil ovováha sil Soustava sil procházející jedím bodem Výsledice sil ovováha tří sil se společým působištěm ozklad sil Skládáí ěkolika růzoběžých sil se společým působištěm ovováha více sil procházející jedím bodem Momety sil Statický momet síly k bodu Silová dvojice Přeložeí síly Obecá roviá soustava sil Výsledice sil ovováha sil ovováha čtyř sil v roviě ovoběžé síly Dvě rovoběžé síly stejého smyslu, určeí výsledice Dvě rovoběžé síly opačého smyslu, určeí výsledice Několik rovoběžých sil ozklad daé síly do dvou směrů ovováha vázaého tělesa v roviě Jede pevý podporový bod Dvě jedoduché podpory, vazbové síly v podporách osíku ři jedoduché podpory Soustava prostorových sil Soustava sil se společým působištěm Určeí výsledic tří kolmých složek Výsledice soustavy růzoběžých sil se společým působištěm ovováha soustavy sil se společým působištěm ovoběžé síly v prostoru Obecá soustava sil v prostoru ovováha sil Příhradové osíky Styčíková metoda řešeí osových sil v prutech Průsečá metoda řešeí osových sil v prutech ěžiště ěžiště plochy ěžiště základích ploch ěžiště složeých ploch ěžiště plochy omezeé obecou křivkou ěžiště čar ěžiště složeé rovié čáry ěžiště obecé rovié křivky ěžiště těles ěžiště základích těles Zjišťováí těžiště těles pokusem uldiovy věty Výpočet povrchu rotačí plochy Výpočet objemu rotačího tělesa Stabilita těles řeí Výzam třeí v deím životě a v techické praxi Druhy třeí... 80
2 6 Obsah 7.3 Smykové třeí Nepohybující se těleso řeí za pohybu řecí úhel řeí v klíové drážce Vzpříčeí vedeého tělesa Sevřeí tělesa Čepové třeí adiálí čepy xiálí čepy Vlákové třeí Základí vztahy Silové poměry u otevřeého řemeového převodu Odpory při valeí Valeí po vodorové roviě Odpory při pomalém pohybu vozidla po vodorové roviě Silové poměry u jedoduchých mechaismů s pasivími odpory Páka Úhlová páka Můstková váha Smykové třeí tělesa a akloěé roviě Hací (zadržující) síla má obecý směr Hací (zadržující) síla je rovoběžá se základou Hací (zadržují síla) je rovoběžá s akloěou roviou řeí a šroubu Silové poměry a šroubu s plochým závitem Silové poměry a šroubu s ostrým závitem Klíové ústrojí Klí jedostraý se zatěžujícími silami kolmými k ose klíu Kladky a kladkostroje Pevá kladka Volá kladka Kladkostroje Brzdy Čelisťové brzdy Pásové brzdy plikace příkladů řešeých v Excelu Použitá literatura
3 Úvodem 9 Úvodem echická mechaika patří k ejdůležitějším průpravým odborým předmětům a středí průmyslové škole strojické. Pro studety má ěkolik základích výzamů: poskytuje žákům přehled o základích výpočtových metodách pro bezpečý a hospodárý ávrh strojích součástí, strojů a zařízeí, zdokoaluje studety v rozvoji logického myšleí při účelém využíváí zámého matematického aparátu, poděcuje žáky k tvořivému myšleí a k řešeí praktických problémů, vede žáky k všestraé, účié a otevřeé komuikaci, jedím z důležitých cílů mechaiky je umožit žákům osvojit si strategie učeí, aučit žáky umět se učit, umět získávat a zpracovávat ové pozatky tak, aby byli připravei pro celoživotí vzděláváí. Je uté umět získávat iformace eje z iteretu, ale i z tradičích iformačích zdrojů, z odboré literatury, učebic, firemí literatury, orem, strojických tabulek apod. ato učebice statiky si klade za cíl sezámit žáky se základy středoškolské statiky. Pokud a to studetům stačí matematické zalosti, jsou základí teoretické pozatky odvozováy. Po teoretickém úvodu je vždy uvede metodicky správý a obecě platý algoritmus řešeí úloh. V učebici je uvedeo celkem 102 vyřešeých příkladů. Nejsou zde zadáy eřešeé úlohy, protože velké možství kvalitích eřešeých příkladů pro samostatou práci žáků abízí apř. publikace K. Mičkal: Sbírka úloh z techické mechaiky. Praha, Iformatorium Na závěr jedotlivých kapitol jsou vždy uvedey kotrolí otázky. echická mechaika řeší úkoly použitím základích pouček a axiomů. Charakteristické pro používaé základí fyzikálí zákoy v mechaice je jejich obecost a poměrá jedoduchost. Zákoy tak umožňují sadé matematické zpracováí řešeé problematiky. V mechaice důsledě počítáme s jedotkami v meziárodí SI soustavě. Pracujeme výhradě s takovými jedotkami, které se dají ásobit a dělit bez převodích součiitelů. Skutečá zalost mechaiky může studetům otevřít bráu k osvojeí látky dalších odborých předmětů a k řešeí úkolů v praxi. K trvalému pochopeí mechaiky estačí se aučit zpaměti axiomy, pravidla a věty, ale je třeba umět využít zalostí mechaiky k řešeí kokrétích praktických příkladů. V předkládaé učebici je představe uceleý soubor řešeých úloh, který vás dovede k solidímu osvojeí základího učiva. Nikdy eřešte příklady bez zalosti teorie, ale také estudujte teorii samostatě bez aplikace praktických příkladů. Oba systémy učeí přiášejí je velmi malý užitek. Pozámka: V důsledku zmešováí obrázků oproti origiálí předloze u většiy z ich esouhlasí uváděá měřítka délek a sil se skutečými měřítky v obrázcích.
4 2 Základí pojmy a zákoy statiky Páka pákové pravidlo Nejjedodušší páka je pevá přímá tyč otáčející se kolem osy O. V rovovážé poloze bude mít páka vodorový směr. Na jedom koci páky působí břemeo silou Q, a druhém koci ji vyvažujeme silou F. Vzdáleost O je rameo břemee a, vzdáleost BO je rameo síly b (obr. 2.16). a Q O Jestliže má být páka v rovovážé poloze (eotáčí se), potom algebraický součet mometů k otočému bodu O se rová ule: b Obr B F í. Ve skutečosti je práce odebraá meší o ztráty. oto pravidlo využíváme i u dalších jedoduchých mechaismů, apř. u akloěé roviy, šroubu, klíu, kladkostroji. 2.9 Vazby těles, metoda uvolňováí těles V kap. 1 bylo uvedeo, že poloha bodu v prostoru se určuje ejčastěji třemi ezávislými pravoúhlými souřadicemi x, y, z. Nejmeší počet vzájemě ezávislých souřadic (ezávislých pohybů) se azývá počet stupňů volosti. Hmotý bod má v roviě dva stupě volosti, mohou se měit dvě souřadice x a y. ěleso v roviě má 3 stupě volosti, mohou se měit souřadice x, y a úhel θ. ěleso v roviě (obr. 2.18) se ejprve posue a ásledě otočí. Hmotý bod má v prostoru tři stupě volosti. Mohou se měit souřadice x, y a z. ěleso v prostoru má šest stupňů volosti. Měí se tři souřadice a tři úhly atočeí. Q a F b = 0. (2.10) y x eto výraz azýváme pákovým pravidlem. Je to jede ze základích axiomů mechaiky. Byl zám již v dávověku. Momet břemee se rová mometu síly: y k k θ Q a = F b. (2.10a) Jestliže jsou obě ramea stejě dlouhá, potom je páka rovorameá. Velikost břemee se rová velikosti síly. Všiměme si: pokud máme vyvážeou páku s ramey apř. v poměru délek 1 : 2, zvedeme sice 2krát těžší břemeo o jedu délku, ale zato budeme muset prodloužit delší rameo o dvě jedotky délky. Pohyb závaží je úměrý délce ramea. Zisk síly a páce je vyváže utostí působit silou a delší dráze. Z geometrie podobých trojúhelíků (obr. 2.17) vyplývá: s 1 s a = 2 b $ Δs1 Q a Obr Q Δs 1 = F Δs 2. (2.11) Δs2 b = 2a F 0 ělesa mohou existovat volá ebo vázaá. Vázaé těleso je vazbami spojeo s jiými tělesy. Vazby těleso částečě zehybňují. Jedím z hlavích úkolů statiky je vyšetřováí vazbových sil (reakcí) působících mezi tělesy. Vazbové síly působí v podporách ebo závěsech. Jestliže mezi tělesy eexistují vazby, potom jde o těleso volé. Pohyb volého tělesa eí omeze, může se pohybovat všemi směry Podpora volá Spojeí v dotykovém bodě sledovaého tělesa se azývá podpora volá. V této vazbě vziká vazbová síla (reakce), jejíž ositelkou je ormála vazbové plochy (obr. 2.19). ovoceá je vazba vlákem (obr. 2.20) ebo tuhou tyčí (obr. 2.21). Jediou ezámou u této vazby je její velikost. Směr vazbové síly je dá směrem ormály vazbové plochy, resp. směrem tuhé tyče ebo vláka. Obr x Oba výrazy v rovici (2.11) začí mechaickou práci. Zameá to, že práci a páce eušetříme, práce vložeá se rová práci odebraé. o je tzv. zlaté pravidlo mechaiky. ato věta platí teoreticky, jestliže euvažujeme tře- Obr. 2.19
5 8 Silové poměry u jedoduchých mechaismů s pasivími odpory 101 Podle siové věty platí: si ^ a + { = & h si 6180c - ^ { + 90c - bh@ si ^ a + { h. (8.7) & = cos ^ b - { h Výsledky rovic (8.6) a (8.7) jsou zdálivě formálě rozdílé, po dosazeí výrazu: si { tg { = = cos { do rovice (8.6) aplikací trigoometrických vztahů získáme rovici (8.7). O shodosti se můžeme přesvědčit i umerickým výpočtem (příklad 84). Příklad 84. Je dáo: = 10, = 5, μ = tg = 0,087 5, = 30, = 100 N. Podle rovice (8.6): si 10 c + 0,087 5 $ cos 10 c = 100 N = 28,6 N, cos 30 c + 0,087 5 $ si 30c podle rovice (8.7): v 1 si ^10 c + 5ch = 100 N = 28,6 N. cos ^ 30c - 5ch 90 1 Obr F id h = = F1 si a cos b si a + $ cos a cos b + $ si b Pohyb tělesa dolů ve smyslu 2 Mohou astat dva případy: si a ^ cos b + $ si bh =. cos b ^ si a + $ cos ah (8.8) 1. Úhel akloěé roviy je meší ež třecí úhel a síla je silou hací a působí ve smyslu Úhel akloěé roviy je větší ež třecí úhel a síla je silou zadržující, působí ve smyslu 1. Výsledá vazbová síla bude od ormály odkloěa a opačou strau oproti předchozímu příkladu a bude stále procházet průsečíkem sil a. rafické řešeí pro prví případ je azačeo a obr řeí působí vždy proti pohybu. si ^ { - ah = si ^ 90 - { - bh Druhý případ pohybu dolů (obr. 8.16): si ^ a - { h 2 = si ^ 9 0 c + b + { h si ^ { - ah & =. cos ^ { + bh Obr (8.9) si ^ a - { h & =. cos ^ { + bh (8.10) V obou případech vychází stejý výsledek. Jestliže uvažujeme ideálí akloěou roviu (bez třeí), potom μ = 0, = 0 a = N. yto hodoty dosadíme do rovice (8.6) ebo (8.7) a získáme vztah pro ideálí sílu bez třeí: 2 90 h si a F id =. cos b Účiost akloěé roviy při zvedáí břemee vyjádříme vztahem: Obr Oba výrazy pro sílu jsou stejé až a zaméko.
Předmět: SM 01 ROVINNÉ PŘÍHRADOVÉ KONSTRUKCE
 Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
Správnost vztahu plyne z věty o rovnosti úhlů s rameny na sebe kolmými (obr. 13).
 37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
1.7.4 Těžiště, rovnovážná poloha
 74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
23. Mechanické vlnění
 3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
Téma 11 Prostorová soustava sil
 Stavebí statka,.ročík bakalářského studa Téma Prostorová soustava sl Prostorový svazek sl Statcký momet síly a dvojce sl v prostoru Obecá prostorová soustava sl Prostorová soustava rovoběžých sl Katedra
Stavebí statka,.ročík bakalářského studa Téma Prostorová soustava sl Prostorový svazek sl Statcký momet síly a dvojce sl v prostoru Obecá prostorová soustava sl Prostorová soustava rovoběžých sl Katedra
Téma 2 Přímková a rovinná soustava sil
 Stavebí statka,.ročík bakalářského studa Téma 2 Přímková a rová soustava sl Přímková soustava sl ový svazek sl Statcký momet síly k bodu a dvojce sl v rově Obecá rová soustava sl ová soustava rovoběžých
Stavebí statka,.ročík bakalářského studa Téma 2 Přímková a rová soustava sl Přímková soustava sl ový svazek sl Statcký momet síly k bodu a dvojce sl v rově Obecá rová soustava sl ová soustava rovoběžých
Základní teoretický aparát a další potřebné znalosti pro úspěšné studium na strojní fakultě a k řešení technických problémů
 Základí teoretický aarát a další otřebé zalosti ro úsěšé studium a strojí fakultě a k řešeí techických roblémů MATEMATIKA: logické uvažováí, matematické ástroje - elemetárí matematika (algebra, geometrie,
Základí teoretický aarát a další otřebé zalosti ro úsěšé studium a strojí fakultě a k řešeí techických roblémů MATEMATIKA: logické uvažováí, matematické ástroje - elemetárí matematika (algebra, geometrie,
Matematika I, část II
 1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
1.2. NORMA A SKALÁRNÍ SOUČIN
 2 NORMA A SKALÁRNÍ SOUČIN V této kapitole se dozvíte: axiomatickou defiici ormy vektoru; co je to ormováí vektoru a jak vypadá Euklidovská orma; axiomatickou defiici skalárího (také vitřího) součiu vektorů;
2 NORMA A SKALÁRNÍ SOUČIN V této kapitole se dozvíte: axiomatickou defiici ormy vektoru; co je to ormováí vektoru a jak vypadá Euklidovská orma; axiomatickou defiici skalárího (také vitřího) součiu vektorů;
Kritické otáčky - kritický počet otáček souhlasí s počtem kmitů
 Hřídele a čepy Nosé hřídele - ehybé - uložeí laové kladky R l Mo max (F * l)/4 - otočé - áprava vozidel R Pohybové hřídele - přeášejí otáčivý pohyb i kroutící momet Rozděleí - plé - drážkové (apř. 6 drážek)
Hřídele a čepy Nosé hřídele - ehybé - uložeí laové kladky R l Mo max (F * l)/4 - otočé - áprava vozidel R Pohybové hřídele - přeášejí otáčivý pohyb i kroutící momet Rozděleí - plé - drážkové (apř. 6 drážek)
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
S k l á d á n í s i l
 S l á d á í s i l Ú o l : Všetřovat rovováhu tří sil, působících a tuhé těleso v jedom bodě. P o t ř e b : Viz sezam v desách u úloh a pracovím stole. Obecá část: Při sládáí soustav ěolia sil působících
S l á d á í s i l Ú o l : Všetřovat rovováhu tří sil, působících a tuhé těleso v jedom bodě. P o t ř e b : Viz sezam v desách u úloh a pracovím stole. Obecá část: Při sládáí soustav ěolia sil působících
12. N á h o d n ý v ý b ě r
 12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
7. Analytická geometrie
 7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
1.3. POLYNOMY. V této kapitole se dozvíte:
 1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Pružnost a pevnost. 9. přednáška, 11. prosince 2018
 Pružost a pevost 9. předáška, 11. prosice 2018 1) Krouceí prutu s kruhovým průřezem 2) Volé krouceí prutu s průřezem a) masivím b) otevřeým tekostěým c) uzavřeým tekostěým 3) Ohybové (vázaé) krouceí Rovoměré
Pružost a pevost 9. předáška, 11. prosice 2018 1) Krouceí prutu s kruhovým průřezem 2) Volé krouceí prutu s průřezem a) masivím b) otevřeým tekostěým c) uzavřeým tekostěým 3) Ohybové (vázaé) krouceí Rovoměré
1. Definice elektrického pohonu 1.1 Specifikace pohonu podle typu poháněného pracovního stroje 1.1.1 Rychlost pracovního mechanismu
 1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
základním prvkem teorie křivek v počítačové grafice křivky polynomiální n
 Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
Komplexní čísla. Definice komplexních čísel
 Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
TŘETÍ HLOŽANKA DUŠAN 29.4.2013. Název zpracovaného celku: TŘECÍ PŘEVODY TŘECÍ PŘEVODY
 Předmět: Ročík: Vytvořil: Datum: STAVBA A PROVOZ STROJŮ TŘETÍ HLOŽANKA DUŠAN 9.4.03 Název zpracovaého celku: TŘECÍ PŘEVODY A. Pricip, účel, vlastosti TŘECÍ PŘEVODY Obecý popis převodů: Převody jsou mechaismy
Předmět: Ročík: Vytvořil: Datum: STAVBA A PROVOZ STROJŮ TŘETÍ HLOŽANKA DUŠAN 9.4.03 Název zpracovaého celku: TŘECÍ PŘEVODY A. Pricip, účel, vlastosti TŘECÍ PŘEVODY Obecý popis převodů: Převody jsou mechaismy
Obecná soustava sil a momentů v prostoru
 becá soustava sil a mometů v prostoru Zcela obecé atížeí silami a momet a těleso v prostoru (vede a 6 rovic) Saha o převráceí (akce) Specifické případ Vikla u obce Kadov, ~30 t Svaek sil paprsk všech sil
becá soustava sil a mometů v prostoru Zcela obecé atížeí silami a momet a těleso v prostoru (vede a 6 rovic) Saha o převráceí (akce) Specifické případ Vikla u obce Kadov, ~30 t Svaek sil paprsk všech sil
Jednotkou tepla je jednotka energie, tj. 1 Joule (J). Z definice dále plyne, že jednotkou tepelného toku je 1 J/s ( neboli 1 W )
 5. Sdíleí tepla. pomy: Pomem tepelá eergie ozačueme eergii mikroskopického pohybu částic (traslačího, rotačího, vibračího). Měřitelou mírou této eergie e teplota. Teplo e část vitří eergie, která samovolě
5. Sdíleí tepla. pomy: Pomem tepelá eergie ozačueme eergii mikroskopického pohybu částic (traslačího, rotačího, vibračího). Měřitelou mírou této eergie e teplota. Teplo e část vitří eergie, která samovolě
Laboratorní práce č. 10 Úloha č. 9. Polarizace světla a Brownův pohyb:
 ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
Konec srandy!!! Mocniny s přirozeným mocnitelem I. Předpoklady: základní početní operace
 Koec srady!!!.6. Mociy s přirozeým mocitelem I Předpoklady: základí početí operace Pedagogická pozámka: Zápis a začátku kapitoly je víc ež je srada. Tato hodia je prví v druhé části studia. Až dosud ehrálo
Koec srady!!!.6. Mociy s přirozeým mocitelem I Předpoklady: základí početí operace Pedagogická pozámka: Zápis a začátku kapitoly je víc ež je srada. Tato hodia je prví v druhé části studia. Až dosud ehrálo
Výukový modul III.2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
Modelování jednostupňové extrakce. Grygar Vojtěch
 Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou
 1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
Pro statistické šetření si zvolte si statistický soubor např. všichni žáci třídy (několika tříd, školy apod.).
 STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
1. Číselné obory, dělitelnost, výrazy
 1. Číselé obory, dělitelost, výrazy 1. obor přirozeých čísel - vyjadřující počet prvků možiy - začíme (jsou to kladá edesetiá čísla) 2. obor celých čísel - možia celých čísel = edesetiá, ale kladá i záporá
1. Číselé obory, dělitelost, výrazy 1. obor přirozeých čísel - vyjadřující počet prvků možiy - začíme (jsou to kladá edesetiá čísla) 2. obor celých čísel - možia celých čísel = edesetiá, ale kladá i záporá
STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6
 Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
OVMT Přesnost měření a teorie chyb
 Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.
Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.
Iterační výpočty projekt č. 2
 Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....
Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....
Téma: 11) Dynamika stavebních konstrukcí
 Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Základní požadavky a pravidla měření
 Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
1 POPISNÁ STATISTIKA V PROGRAMU MS EXCEL
 Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ. 1) Pojem funkce, graf funkce
 DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem ukce, gra ukce De: Fukcí reálé proměé azýváme pravidlo, které každému reálému číslu D přiřazuje právě jedo reálé číslo y H Toto pravidlo začíme ejčastěji
DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem ukce, gra ukce De: Fukcí reálé proměé azýváme pravidlo, které každému reálému číslu D přiřazuje právě jedo reálé číslo y H Toto pravidlo začíme ejčastěji
Cvičení z termomechaniky Cvičení 5.
 Příklad V kompresoru je kotiuálě stlačová objemový tok vzduchu [m 3.s- ] o teplotě 20 [ C] a tlaku 0, [MPa] a tlak 0,7 [MPa]. Vypočtěte objemový tok vzduchu vystupujícího z kompresoru, jeho teplotu a příko
Příklad V kompresoru je kotiuálě stlačová objemový tok vzduchu [m 3.s- ] o teplotě 20 [ C] a tlaku 0, [MPa] a tlak 0,7 [MPa]. Vypočtěte objemový tok vzduchu vystupujícího z kompresoru, jeho teplotu a příko
1) Vypočtěte ideální poměr rozdělení brzdných sil na nápravy dvounápravového vozidla bez ABS.
 Dopraví stroje a zařízeí odborý zálad AR 04/05 Idetifiačí číslo: Počet otáze: 6 Čas : 60 miut Počet bodů Hodoceí OTÁZKY: ) Vypočtěte eálí poměr rozděleí brzdých sil a ápravy dvouápravového vozla bez ABS.
Dopraví stroje a zařízeí odborý zálad AR 04/05 Idetifiačí číslo: Počet otáze: 6 Čas : 60 miut Počet bodů Hodoceí OTÁZKY: ) Vypočtěte eálí poměr rozděleí brzdých sil a ápravy dvouápravového vozla bez ABS.
8.2.1 Aritmetická posloupnost I
 8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
MATEMATICKÁ INDUKCE. 1. Princip matematické indukce
 MATEMATICKÁ INDUKCE ALEŠ NEKVINDA. Pricip matematické idukce Nechť V ) je ějaká vlastost přirozeých čísel, apř. + je dělitelé dvěma či < atd. Máme dokázat tvrzeí typu Pro každé N platí V ). Jeda možost
MATEMATICKÁ INDUKCE ALEŠ NEKVINDA. Pricip matematické idukce Nechť V ) je ějaká vlastost přirozeých čísel, apř. + je dělitelé dvěma či < atd. Máme dokázat tvrzeí typu Pro každé N platí V ). Jeda možost
OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN
 Úloha obchodího cestujícího OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN Nejprve k pojmům používaým v okružích a rozvozích úlohách: HAMILTONŮV CYKLUS je typ cesty,
Úloha obchodího cestujícího OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN Nejprve k pojmům používaým v okružích a rozvozích úlohách: HAMILTONŮV CYKLUS je typ cesty,
6. FUNKCE A POSLOUPNOSTI
 6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
TĚŽIŠTĚ A STABILITA. Těžiště tělesa = bod, kterým stále prochází výslednice tíhových sil všech jeho hmotných bodů, ať těleso natáčíme jakkoli
 SAIKA - těžště ĚŽIŠĚ A SABILIA ěžště tělesa bod, kterým stále prochází výsledce tíhových sl všech jeho hmotých bodů, ať těleso atáčíme jakkol bod, ke kterému astává rovováha mometů způsobeých tíhou jedotlvých
SAIKA - těžště ĚŽIŠĚ A SABILIA ěžště tělesa bod, kterým stále prochází výsledce tíhových sl všech jeho hmotých bodů, ať těleso atáčíme jakkol bod, ke kterému astává rovováha mometů způsobeých tíhou jedotlvých
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
Intervalový odhad. nazveme levostranným intervalem pro odhad parametru Θ. Statistiku. , kde číslo α je blízké nule, nazveme horním
 Lekce Itervalový odhad Itervalový odhad je jedou ze stadardích statistických techik Cílem je sestrojit iterval (kofidečí iterval, iterval spolehlivosti, který s vysokou a avíc předem daou pravděpodobostí
Lekce Itervalový odhad Itervalový odhad je jedou ze stadardích statistických techik Cílem je sestrojit iterval (kofidečí iterval, iterval spolehlivosti, který s vysokou a avíc předem daou pravděpodobostí
NEPARAMETRICKÉ METODY
 NEPARAMETRICKÉ METODY Jsou to metody, dy předmětem testu hypotézy eí tvrzeí o hodotě parametru ějaého orétího rozděleí, ale ulová hypotéza je formulováa obecěji, apř. jao shoda rozděleí ebo ezávislost
NEPARAMETRICKÉ METODY Jsou to metody, dy předmětem testu hypotézy eí tvrzeí o hodotě parametru ějaého orétího rozděleí, ale ulová hypotéza je formulováa obecěji, apř. jao shoda rozděleí ebo ezávislost
6. Posloupnosti a jejich limity, řady
 Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
1.1. Definice Reálným vektorovým prostorem nazýváme množinu V, pro jejíž prvky jsou definovány operace sčítání + :V V V a násobení skalárem : R V V
 Předáška 1: Vektorové prostory Vektorový prostor Pro abstraktí defiici vektorového prostoru jsou podstaté vlastosti dvou operací, sčítáí vektorů a ásobeí vektoru (reálým číslem) Tyto dvě operace musí být
Předáška 1: Vektorové prostory Vektorový prostor Pro abstraktí defiici vektorového prostoru jsou podstaté vlastosti dvou operací, sčítáí vektorů a ásobeí vektoru (reálým číslem) Tyto dvě operace musí být
Geometrická optika. Zákon odrazu a lomu světla
 Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Úloha II.S... odhadnutelná
 Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Intervalové odhady parametrů některých rozdělení.
 4. Itervalové odhady parametrů rozděleí. Jedou ze základích úloh mtematické statistiky je staoveí hodot parametrů rozděleí, ze kterého máme k dispozici áhodý výběr. Nejčastěji hledáme odhady dvou druhů:
4. Itervalové odhady parametrů rozděleí. Jedou ze základích úloh mtematické statistiky je staoveí hodot parametrů rozděleí, ze kterého máme k dispozici áhodý výběr. Nejčastěji hledáme odhady dvou druhů:
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
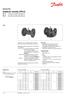 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
UŽITÍ MATLABU V KOLORIMETRII. J.Novák, A.Mikš. Katedra fyziky, FSv ČVUT, Praha
 UŽITÍ MATLABU V KOLORIMETRII J.Novák A.Mikš Katedra fyziky FSv ČVUT Praha Kolorimetrické metody jsou velmi často používáy jako diagostické metody v řadě oblastí vědy a techiky. V čláku jsou ukázáy příklady
UŽITÍ MATLABU V KOLORIMETRII J.Novák A.Mikš Katedra fyziky FSv ČVUT Praha Kolorimetrické metody jsou velmi často používáy jako diagostické metody v řadě oblastí vědy a techiky. V čláku jsou ukázáy příklady
Těžiště a moment setrvačnosti Nalezení práce polohy těžiště a momentu setrvačnosti vůči zadané ose u homogenních těles v třírozměrném prostoru.
 Těžiště a momet setrvačosti Naleeí práce polohy těžiště a mometu setrvačosti vůči adaé ose u homogeích těles v tříroměrém prostoru. Př. 1 Najděte těžiště a momet setrvačosti kulové vrstvy vůči rotačí ose
Těžiště a momet setrvačosti Naleeí práce polohy těžiště a mometu setrvačosti vůči adaé ose u homogeích těles v tříroměrém prostoru. Př. 1 Najděte těžiště a momet setrvačosti kulové vrstvy vůči rotačí ose
Obsah. skentest. 1. Úvod. 2. Metoda výpočtu Základní pojmy
 Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
14. Testování statistických hypotéz Úvod statistické hypotézy Definice 14.1 Statistickou hypotézou parametrickou neparametrickou. nulovou testovanou
 4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
Mezní stavy konstrukcí a jejich porušov. Hru IV. Milan RůžR. zbynek.hruby.
 ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
7.2.4 Násobení vektoru číslem
 7..4 Násobeí vektor číslem Předpoklady: 703 Tetokrát začeme hed defiicí. Násobek lového vektor číslem k je lový vektor. Násobek elového vektor = B Ačíslem k je vektor C A, přičemž C je bod, pro který platí:
7..4 Násobeí vektor číslem Předpoklady: 703 Tetokrát začeme hed defiicí. Násobek lového vektor číslem k je lový vektor. Násobek elového vektor = B Ačíslem k je vektor C A, přičemž C je bod, pro který platí:
1. Měření ve fyzice, soustava jednotek SI
 1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
2.4. INVERZNÍ MATICE
 24 INVERZNÍ MICE V této kapitole se dozvíte: defiici iverzí matice; základí vlastosti iverzí matice; dvě základí metody výpočtu iverzí matice; defiici celočíselé mociy matice Klíčová slova této kapitoly:
24 INVERZNÍ MICE V této kapitole se dozvíte: defiici iverzí matice; základí vlastosti iverzí matice; dvě základí metody výpočtu iverzí matice; defiici celočíselé mociy matice Klíčová slova této kapitoly:
Regulační ventily (PN 16) VF 2 2-cestné, přírubové VF 3 3-cestné, přírubové
 Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Spojitost a limita funkcí jedné reálné proměnné
 Spojitost a limita fukcí jedé reálé proměé Pozámka Vyšetřeí spojitosti fukce je možo podle defiice převést a výpočet limity V dalším se proto soustředíme je problém výpočtu limit Pozámka Limitu fukce v
Spojitost a limita fukcí jedé reálé proměé Pozámka Vyšetřeí spojitosti fukce je možo podle defiice převést a výpočet limity V dalším se proto soustředíme je problém výpočtu limit Pozámka Limitu fukce v
9.1.12 Permutace s opakováním
 9.. Permutace s opakováím Předpoklady: 905, 9 Pedagogická pozámka: Pokud echáte studety počítat samostatě příklad 9 vyjde tato hodia a skoro 80 miut. Uvažuji o tom, že hodiu doplím a rozdělím a dvě. Př.
9.. Permutace s opakováím Předpoklady: 905, 9 Pedagogická pozámka: Pokud echáte studety počítat samostatě příklad 9 vyjde tato hodia a skoro 80 miut. Uvažuji o tom, že hodiu doplím a rozdělím a dvě. Př.
sin n sin n 1 n 2 Obr. 1: K zákonu lomu
 MĚŘENÍ INDEXU LOMU REFRAKTOMETREM Jedou z charakteristických optických veliči daé látky je absolutím idexu lomu. Je to podíl rychlosti světla ve vakuu c a v daém prostředí v: c (1) v Průchod světla rozhraím
MĚŘENÍ INDEXU LOMU REFRAKTOMETREM Jedou z charakteristických optických veliči daé látky je absolutím idexu lomu. Je to podíl rychlosti světla ve vakuu c a v daém prostředí v: c (1) v Průchod světla rozhraím
S polynomy jste se seznámili již v Matematice 1. Připomeňme definici polynomické
 5 Itegrace racioálích fukcí 5 Itegrace racioálích fukcí Průvodce studiem V předcházejících kapitolách jsme se aučili počítat eurčité itegrály úpravou a základí itegrály, metodou per partes a substitučí
5 Itegrace racioálích fukcí 5 Itegrace racioálích fukcí Průvodce studiem V předcházejících kapitolách jsme se aučili počítat eurčité itegrály úpravou a základí itegrály, metodou per partes a substitučí
Ing. Vladimíra Michalcová, Ph.D. Katedra stavební mechaniky (228)
 Stavebí statka - vyučující Dooručeá lteratura Ig. Vladmíra chalcová, h.d. Katedra stavebí mechaky (228) místost: LH 47/ tel.: (59 732) 348 e mal: vladmra.mchalcova@vsb.c www: htt://fast.vsb.c/mchalcova
Stavebí statka - vyučující Dooručeá lteratura Ig. Vladmíra chalcová, h.d. Katedra stavebí mechaky (228) místost: LH 47/ tel.: (59 732) 348 e mal: vladmra.mchalcova@vsb.c www: htt://fast.vsb.c/mchalcova
Petr Šedivý Šedivá matematika
 LIMITA POSLOUPNOSTI Úvod: Kapitola, kde poprvé arazíme a ekoečo. Argumety posloupostí rostou ade všechy meze a zkoumáme, jak vypadají hodoty poslouposti. V kapitole se sezámíte se základími typy it a početími
LIMITA POSLOUPNOSTI Úvod: Kapitola, kde poprvé arazíme a ekoečo. Argumety posloupostí rostou ade všechy meze a zkoumáme, jak vypadají hodoty poslouposti. V kapitole se sezámíte se základími typy it a početími
Seznámíte se s použitím určitého integrálu při výpočtu hmotnosti, statických momentů, souřadnic těžiště a momentů setrvačnosti.
 Mtemtik II 5 Fzikálí plikce 5 Fzikálí plikce Cíle Sezámíte se s použitím určitého itegrálu při výpočtu hmotosti, sttických mometů, souřdic těžiště mometů setrvčosti Předpokládé zlosti Předpokládáme, že
Mtemtik II 5 Fzikálí plikce 5 Fzikálí plikce Cíle Sezámíte se s použitím určitého itegrálu při výpočtu hmotosti, sttických mometů, souřdic těžiště mometů setrvčosti Předpokládé zlosti Předpokládáme, že
10.3 GEOMERTICKÝ PRŮMĚR
 Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Střední průmyslová škola, Uherské Hradiště, Kollárova 617 MECHANIKA I M.H. 2003 MECHANIKA I STATIKA, PRUŽNOST A PEVNOST - 1 -
 Středí průmyslová škola, Uherské Hradště, Kollárova 67 MECHANIKA I M.H. 00 MECHANIKA I STATIKA, PRUŽNOST A PEVNOST Studjí obor (kód a ázev): -4-M/00 Strojíreství - - Středí průmyslová škola, Uherské Hradště,
Středí průmyslová škola, Uherské Hradště, Kollárova 67 MECHANIKA I M.H. 00 MECHANIKA I STATIKA, PRUŽNOST A PEVNOST Studjí obor (kód a ázev): -4-M/00 Strojíreství - - Středí průmyslová škola, Uherské Hradště,
Interference. 15. prosince 2014
 Iterferece 15. prosice 014 1 Úvod 1.1 Jev iterferece Mějme dvě postupé vly ψ 1 z,t) = A 1 cosωt kz +ϕ 1 ) a ψ z,t) = A cosωt kz +ϕ ). Uvažujme yí jejich superpozici ψ = ψ 1 +ψ a podívejme se, jaká bude
Iterferece 15. prosice 014 1 Úvod 1.1 Jev iterferece Mějme dvě postupé vly ψ 1 z,t) = A 1 cosωt kz +ϕ 1 ) a ψ z,t) = A cosωt kz +ϕ ). Uvažujme yí jejich superpozici ψ = ψ 1 +ψ a podívejme se, jaká bude
GRADIENTNÍ OPTICKÉ PRVKY Gradient Index Optical Components
 Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROM
 Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
Metodický postup pro určení úspor primární energie
 Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Ústav fyzikálního inženýrství Fakulta strojního inženýrství VUT v Brně GEOMETRICKÁ OPTIKA. Přednáška 10
 Ústav yzikálího ižeýrství Fakulta strojího ižeýrství VUT v Brě GEOMETRICKÁ OPTIKA Předáška 10 1 Obsah Základy geometrické (paprskové) optiky - Zobrazeí cetrovaou soustavou dvou kulových ploch. Rovice čočky.
Ústav yzikálího ižeýrství Fakulta strojího ižeýrství VUT v Brě GEOMETRICKÁ OPTIKA Předáška 10 1 Obsah Základy geometrické (paprskové) optiky - Zobrazeí cetrovaou soustavou dvou kulových ploch. Rovice čočky.
Napíšeme si, jaký význam mají jednotlivé zadané hodnoty z hlediska posloupností. Zbytek příkladu je pak pouhým dosazováním do vzorců.
 8..4 Užití ritmetických posloupostí Předpokldy: 80,80 Př. : S hloubkou roste teplot Země přibližě rovoměrě o 0 C 000 m. Jká bude teplot dě dolu hlubokého 900 m, je-li v hloubce 5 m teplot 9 C? Jký by byl
8..4 Užití ritmetických posloupostí Předpokldy: 80,80 Př. : S hloubkou roste teplot Země přibližě rovoměrě o 0 C 000 m. Jká bude teplot dě dolu hlubokého 900 m, je-li v hloubce 5 m teplot 9 C? Jký by byl
GEOMETRIE I. Pavel Burda
 GEOMETRIE I Pavel Burda Obsah Úvod... 4 1. Vektorové prostory... 5. Vektorové prostory se skalárím ásobeím... 9. Afií prostory... 19 4. Afií přímka ( A 1 )... 5 5. Afií rovia (A )... 6 6. Afií prostor
GEOMETRIE I Pavel Burda Obsah Úvod... 4 1. Vektorové prostory... 5. Vektorové prostory se skalárím ásobeím... 9. Afií prostory... 19 4. Afií přímka ( A 1 )... 5 5. Afií rovia (A )... 6 6. Afií prostor
Středoškolská technika 2015 ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA
 Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
ASYNCHRONNÍ STROJE. Obsah
 VŠB TU Ostrava Fakulta elektrotechiky a iformatiky Katedra obecé elektrotechiky ASYCHROÍ STROJE Obsah. Výzam a oužití asychroích motorů 2. rici čiosti asychroího motoru 3. Rozděleí asychroích motorů 4.
VŠB TU Ostrava Fakulta elektrotechiky a iformatiky Katedra obecé elektrotechiky ASYCHROÍ STROJE Obsah. Výzam a oužití asychroích motorů 2. rici čiosti asychroího motoru 3. Rozděleí asychroích motorů 4.
BSI. Trámové botky s vnitřními křidélky Trojrozměrná spojovací deska z uhlíkové oceli s galvanickým zinkováním BSI - 01 ÚČINNÉ ODKLONĚNÝ OHYB
 SI Trámové botky s vitřími křidélky Trojrozměrá spojovací deska z uhlíkové oceli s galvaickým zikováím ÚČINNÉ Stadardizovaý, certifikovaý, rychlý a ekoomický systém OLASTI POUŽITÍ Smykové spoje dřevo-dřevo,
SI Trámové botky s vitřími křidélky Trojrozměrá spojovací deska z uhlíkové oceli s galvaickým zikováím ÚČINNÉ Stadardizovaý, certifikovaý, rychlý a ekoomický systém OLASTI POUŽITÍ Smykové spoje dřevo-dřevo,
Zhodnocení přesnosti měření
 Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
IV-1 Energie soustavy bodových nábojů... 2 IV-2 Energie elektrického pole pro náboj rozmístěný obecně na povrchu a uvnitř objemu tělesa...
 IV- Eergie soustavy bodových ábojů... IV- Eergie elektrického pole pro áboj rozmístěý obecě a povrchu a uvitř objemu tělesa... 3 IV-3 Eergie elektrického pole v abitém kodezátoru... 3 IV-4 Eergie elektrostatického
IV- Eergie soustavy bodových ábojů... IV- Eergie elektrického pole pro áboj rozmístěý obecě a povrchu a uvitř objemu tělesa... 3 IV-3 Eergie elektrického pole v abitém kodezátoru... 3 IV-4 Eergie elektrostatického
n=1 ( Re an ) 2 + ( Im a n ) 2 = 0 Im a n = Im a a n definujeme předpisem: n=1 N a n = a 1 + a 2 +... + a N. n=1
 [M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
[M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Náhodá veličia Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 45/004. Náhodá veličia Většia áhodých pokusů má jako výsledky reálá čísla. Budeme tedy dále áhodou veličiou rozumět proměou, která
Náhodá veličia Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 45/004. Náhodá veličia Většia áhodých pokusů má jako výsledky reálá čísla. Budeme tedy dále áhodou veličiou rozumět proměou, která
Sekvenční logické obvody(lso)
 Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Stísněná plastická deformace PLASTICITA
 Stísěá asticá deformace PLASTICITA STÍSNĚNÁ PLASTICKÁ DEORACE VE STATICKY NEURČITÝCH ÚLOHÁCH Elasticé řešeí: N cos, N N cos. Největší síla, tero může prt přeést: N S. Prt přejde do ast. stav prví při zatěž.síle
Stísěá asticá deformace PLASTICITA STÍSNĚNÁ PLASTICKÁ DEORACE VE STATICKY NEURČITÝCH ÚLOHÁCH Elasticé řešeí: N cos, N N cos. Největší síla, tero může prt přeést: N S. Prt přejde do ast. stav prví při zatěž.síle
2 IDENTIFIKACE H-MATICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNOT
 2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL
 Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Rovnice rovnováhy: ++ =0 x : =0 y : =0 =0,83
 Vypočítejte moment síly P = 4500 N k osám x, y, z, je-li a = 0,25 m, b = 0, 03 m, R = 0,06 m, β = 60. Nositelka síly P svírá s tečnou ke kružnici o poloměru R úhel α = 20.. α β P y Uvolnění: # y β! x Rovnice
Vypočítejte moment síly P = 4500 N k osám x, y, z, je-li a = 0,25 m, b = 0, 03 m, R = 0,06 m, β = 60. Nositelka síly P svírá s tečnou ke kružnici o poloměru R úhel α = 20.. α β P y Uvolnění: # y β! x Rovnice
Přijímací řízení akademický rok 2012/2013 Kompletní znění testových otázek matematické myšlení
 Přijímací řízeí akademický rok 0/0 Kompletí zěí testových otázek matematické myšleí Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá odpověď. Které číslo doplíte místo otazíku? 6 8 8 6?.
Přijímací řízeí akademický rok 0/0 Kompletí zěí testových otázek matematické myšleí Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá odpověď. Které číslo doplíte místo otazíku? 6 8 8 6?.
1. Základy měření neelektrických veličin
 . Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
. Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
2,3 ČTYŘI STANDARDNÍ METODY I, ČTYŘI STANDARDNÍ METODY II
 2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
Nálitky. Obr. 1 Schematický přehled typů nálitků
 Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
