Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
|
|
|
- Martin Němec
- před 8 lety
- Počet zobrazení:
Transkript
1 Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální fond. Praha & EU: Investujeme do vaší budoucnosti RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 1 / 13
2 Logika X. Prenexní normální tvar. Skolemizace. Rezoluční metoda. RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 2 / 13
3 Prenexní normální tvar Definice Formule je v prenexním normální tvaru, jestliže je ve tvaru (Q 1 x 1 )...(Q n x n )A, kde A je otevřená formule, Q i jsou kvantifikátory, x i jsou proměnné. ( x)( y)( z)(y < x y ), ( k)(n = 2k) Definice Formule B je varianta formule A, jestliže se liší jen přejmenováním vázaných proměnných. ( u)( v)( w)(w < u v ), ( l)(n = 2l). Věta Je-li B varianta A, pak A B. ( x)( y)( z)(y < x y ) ( u)( v)( w)(w < u v ) (( k)(n = 2k) ( l)(n = 2l)) RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 3 / 13
4 Prenexní operace Chceme mít formule v prenexním tvaru. Víme: (( x)a ( x)b) ( x)(a B) (( x)a ( x)b) ( x)(a B) Prenexní operace 1 ( x)a ( x) A ( x)a ( x) A 2 Není-li x volná v A, pak (A ( x)b(x)) ( x)(a B(x)) (A ( x)b(x)) ( x)(a B(x)) 3 Není-li x volná v A, pak (A ( x)b(x)) ( x)(a B(x)) (A ( x)b(x)) ( x)(a B(x)) 4 Není-li x volná v B, pak (( x)a(x) B) ( x)(a(x) B) (( x)a(x) B) ( x)(a(x) B) RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 4 / 13
5 Prenexní operace - důkaz ad 2. Není-li x volná v A, pak (A ( x)b(x)) ( x)(a B(x)). Dokážeme (A ( x)b(x)) ( x)(a B(x)). Sporem. Kdyby ex. M tak, že M = (A ( x)b(x)) ( x)(a B(x)), pak M = (A ( x)b(x)) a M = ( x)( A B(x)), tedy existuje m M tak, že A B[m], ale A B[m].. Dokážeme ( x)(a B(x)) (A ( x)b(x)). Sporem. Kdyby ex. M tak, že M = ( x)(a B(x) (A ( x)b(x)), pak M = ( x)(a B(x)) a M = A a M = ( x) B(x), tedy existuje m M tak, že B[m], ale A B[m] a A.. ad 3. Není-li x volná v A, pak (A ( x)b(x)) ( A ( x)b(x)) ( x)( A B(x)) ( x)(a B(x)) ad 4. Není-li x volná v B, pak (( x)a(x) B) ( ( x)a(x) B) (( x) A(x) B) ( x)(a(x) B) RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 5 / 13
6 Prenexní normální tvar Věta Ke každé formuli existuje formule s ní ekvivalentní v prenexním normálním tvaru. Příklady: 1 ( a)( b)((a < b) ( c)(a < b < c) ( a)( b)( c)((a < b) (a < b < c) 2 ( x)(x = 0) ( x)(x = S(0)) ( x)(x = 0) ( y)(y = S(0)) ( x)( y)((x = 0) (y = S(0))) 3 ( x)(x > 0) ( y)(x + y > 0)) ( z)(z > 0) ( y)(x + y > 0)) ( z)( y)((z > 0) (x + y > 0)) ( y)( z)((z > 0) (x + y > 0)) 4 ( ɛ)((ɛ > 0) ( δ)( x)((δ > 0) ( x c < δ) ( f (x) f (c) < ɛ)) ( ɛ)( δ)( x)((ɛ > 0) ((δ > 0) ( x c < δ) ( f (x) f (c) < ɛ)) RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 6 / 13
7 Skolemizace Chceme jen obecné kvantifikátory. Definice T je konzervativní rozšíření teorie T, právě když L L a pro každou formuli jazyka L platí T = A, právě když T = A. ( x)a(x)... vybereme novou konstantu c L = L {c} T = T {( x)a(x) A(c)} ( x)( y)a(x, y)... definujeme novou funkci f (x) L = L {f (x)} T = T {( x)a(x, f (x))) ( x)( y)a(x, y)} RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 7 / 13
8 Skolemův normální tvar Věta Ke každé uzavřené formuli A existuje formule A S, která je v prenexním normální tvaru, kde všechny kvantifikátory jsou obecné, tzv. Skolemův normální tvar. Příklady: A je splnitelná, právě když A S je splnitelná. ( y)( x)(x > y)... definujeme konstantu c tak, že ( x)(x > c) ( x)( y)(x > y)... definujeme funkci f (x) tak, že ( x)(x > f (x)) ( t)( x)( y)( z)( u)( w)a(t, x, y, z, u, w)... c ( x)( y)( z)( u)( w)a(c, x, y, z, u, w)... g(x, y) ( x)( y)( u)( w)a(c, x, y, g(x, y), u, w)... h(x, y, u) ( x)( y)( u)a(c, x, y, g(x, y), u, h(x, y, u)) RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 8 / 13
9 Otevřené jádro formule Věta Nechť A je otevřená formule s volnými proměnnými x 1,..., x n. Potom pro libovolnou interpretaci M platí M = A, právě když M = ( x 1 )...( x n )A. A je tautologie ( x 1 )...( x n )A je tautologie. A se nazývá otevřené jádro formule ( x 1 )...( x n )A Příklad: ( x)( y)((x > y) (y > x)) je pravdivé v N, právě když (x > y) (y > x) je pravdivé v N A(x) je tautologie, právě když ( x)a(x) je tautologie. POZOR! A(x) ( x)a(x) není tautologie. A(x) ( x)a(x) není tautologie. ( x 1 )...( x n )A není logicky ekvivalentní s A. RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 9 / 13
10 Rezoluční metoda v predikátové logice 1 Teorie. Konjunkce formuĺı. 2 Prenexní normální tvar. 3 Skolemizace. 4 Otevřené jádro formule. 5 Klausule. 6 Resolventy formuĺı. 7 Kontradikce? Příklad: ( x)(p(x) Q(x)), ( x) P(x) = ( x)q(x)? ( x)(p(x) Q(x)) ( x) P(x) ( x)q(x) ( x)(p(x) Q(x)) ( z) P(z) ( y) Q(y) ( z)( x)( y)((p(x) Q(x)) P(z) Q(y)) ( x)( y)((p(x) Q(x)) P(c) Q(y)) (P(x) Q(x)) P(c) Q(y)) Q(c), Q(c), RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 10 / 13
11 Rezoluční metoda v predikátové logice Žádný člověk není zvíře Některé zvíře je šelma. Tudíž některá šelma není člověk. ( x)(c(x) z(x)), ( x)(z(x) s(x)) = ( x)(s(x) c(x)) ( x)( c(x) z(x)) ( x)(z(x) s(x)) ( x)(s(x) c(x)) ( x)( c(x) z(x)) ( v)(z(v) s(v)) ( u)(s(u) c(u)) ( x)( c(x) z(x)) (z(k) s(k)) ( u)(s(u) c(u)) ( x)( u)( c(x) z(x)) z(k) s(k) ( s(u) c(u)) (( c(x) z(x)) z(k) s(k) ( s(u) c(u)))... otevřená formule s(k), c(k), z(k), z(k),. RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 11 / 13
12 Příklady Každá větší ryba je rychlejší než menší ryba. Tudíž jestliže je nějaká ryba největší, pak je i nějaká ryba nejrychlejší, v(x, y), r(x, y) ( x)( y)(v(x, y) r(x, y)) = ( z)( y)v(z, y) ( z)( y)r(z, y) Sporem: ( x)( y)(v(x, y) r(x, y)) (( z)( u)v(z, u) ( z)( u)r(z, u)) ( x)( y)(v(x, y) r(x, y)) ( z)( u)v(z, u) ( s)( t)r(s, t) ( x)( y)( v(x, y) r(x, y)) ( z)( u)v(z, u) ( s)( t) r(s, t) RM: ( x)( y)( v(x, y) r(x, y)) ( u)v(c, u) ( s) r(s, f (s)) v(c, u), r(c, f (c)), v(c, f (c)), v(c, f (c)) r(c, f (c)). Spor. STROM: Tedy existuje c tak, že ( u)v(c, u). Tedy též existuje d tak, že r(c, d). Tedy i v(c, d). Ale v(c, d) r(c, d). Tedy spor. RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 12 / 13
13 Příklad Každý Cadillac je dražší než jakékoli levné vozidlo. Tudíž Cadillac není levné vozidlo, c(x), l(x) d(x, y) ( x)( y)((c(x) l(y)) d(x, y)) = ( x)(c(x) l(x)) Kdyby tomu tak nebylo, pak ( x)( y)((c(x) l(y) d(x, y))) ( x)(c(x) l(x)) Označme si toto konkrétní auto m. Platí c[m] l[m] (( c[m] l[y])) d[m, m]). Tedy d[m, m]. To je spor. RNDr. Kateřina Trlifajová PhD. (FIT ČVUT) Logika XI. BI-MLO, ZS 2011/12 13 / 13
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Sémantika predikátové logiky
 Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Logika III. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika III. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika III. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Cvičení z logiky II.
 Cvičení z logiky II. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 https://edux.fit.cvut.cz/courses/bi-mlo/lectures/
Cvičení z logiky II. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 https://edux.fit.cvut.cz/courses/bi-mlo/lectures/
Logika II. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika II. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika II. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Predikátová logika. prvního řádu
 Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
2.1 Formule predikátové logiky. větám. Použijte k tomu predikátových symbolu uvedených v textu.
 6 Kapitola 2 Příklady z predikátové logiky 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolu uvedených
6 Kapitola 2 Příklady z predikátové logiky 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolu uvedených
2016 Česká republika ŽENY (aktuální k )
 2016 Česká republika ŽENY (aktuální k 27. 11. 2017) věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002462 0.997538 100 000.00 246.23 99787 8205207 82.05 100 000.00 243.07 5 066 877.57 34 975.90 176 922
2016 Česká republika ŽENY (aktuální k 27. 11. 2017) věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002462 0.997538 100 000.00 246.23 99787 8205207 82.05 100 000.00 243.07 5 066 877.57 34 975.90 176 922
Česká republika - ŽENY
 2012 Česká republika - ŽENY věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002338 0.997662 100000 234 99804 8088058 80.88 100 000.00 229.43 4 164 194.04 22 355.11 130 483 842.84 1 731 180.86 1 0.000144
2012 Česká republika - ŽENY věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002338 0.997662 100000 234 99804 8088058 80.88 100 000.00 229.43 4 164 194.04 22 355.11 130 483 842.84 1 731 180.86 1 0.000144
Skolemizace. x(x + f(x) = 0). Interpretace f unární funkce, která pro daný
 Skolemizace převod formulí na formule bez existenčních kvantifikátorů v jazyce, který je rozšířen o tzv. Skolemovy funkce; zachovává splnitelnost idea převodu: formuli x 1... x n yp (x 1,..., x n, y) transformujeme
Skolemizace převod formulí na formule bez existenčních kvantifikátorů v jazyce, který je rozšířen o tzv. Skolemovy funkce; zachovává splnitelnost idea převodu: formuli x 1... x n yp (x 1,..., x n, y) transformujeme
Stefan Ratschan. Fakulta informačních technologíı. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Úvod do logiky (PL): negace a ekvivalence vět mimo logický
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): negace a ekvivalence vět mimo logický čtverec
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): negace a ekvivalence vět mimo logický čtverec
Převyprávění Gödelova důkazu nutné existence Boha
 Převyprávění Gödelova důkazu nutné existence Boha Technické podrobnosti Důkaz: Konečná posloupnost výrokůkorektně utvořených formulí nějakého logického kalkulu), z nichž každý jelogickým) axiomem, postulátemteorie),
Převyprávění Gödelova důkazu nutné existence Boha Technické podrobnosti Důkaz: Konečná posloupnost výrokůkorektně utvořených formulí nějakého logického kalkulu), z nichž každý jelogickým) axiomem, postulátemteorie),
Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka
 Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Logika. 8. Automatické dokazování v predikátové logice (obecná rezoluční metoda)
 Logika 8. Automatické dokazování v predikátové logice (obecná rezoluční metoda) RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním
Logika 8. Automatické dokazování v predikátové logice (obecná rezoluční metoda) RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Splnitelnost množin Definice Množina
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Splnitelnost množin Definice Množina
1 Pravdivost formulí v interpretaci a daném ohodnocení
 1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
Predikátová logika [Predicate logic]
![Predikátová logika [Predicate logic] Predikátová logika [Predicate logic]](/thumbs/74/70612837.jpg) Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Rezoluce v predikátové logice
 Rezoluce v predikátové logice Jiří Velebil: X01DML 15. října 2010: Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná
Rezoluce v predikátové logice Jiří Velebil: X01DML 15. října 2010: Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2015/2016 1 / 22 Herbrandova věta Úvod Redukce nesplnitelnosti na
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2015/2016 1 / 22 Herbrandova věta Úvod Redukce nesplnitelnosti na
Hilbertovský axiomatický systém
 Hilbertovský axiomatický systém Predikátová logika H 1 Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 24. října 2008 Specifikace H 1 Jazyk L H1 přejímáme jazyk predikátové logiky
Hilbertovský axiomatický systém Predikátová logika H 1 Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 24. října 2008 Specifikace H 1 Jazyk L H1 přejímáme jazyk predikátové logiky
1 Výroková logika 1. 2 Predikátová logika 3. 3 Důkazy matematických vět 4. 4 Doporučená literatura 7
 1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
2.5 Rezoluční metoda v predikátové logice
 2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
2.2 Sémantika predikátové logiky
 14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
Predikátová logika. Teoretická informatika Tomáš Foltýnek
 Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Rezoluce v predikátové logice
 Rezoluce v predikátové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná iff X =
Rezoluce v predikátové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná iff X =
Cvičení z logiky I. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Cvičení z logiky I. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský
Cvičení z logiky I. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský
Základní pojmy matematické logiky
 KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
Predikátová logika. Kapitola 2. 2.1 Formule predikátové logiky
 5 Kapitola 2 Predikátová logika 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolů uvedených v textu.
5 Kapitola 2 Predikátová logika 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolů uvedených v textu.
Úvod do logiky (PL): ekvivalence a negace výroků logického
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): ekvivalence a negace výroků logického čtverce
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): ekvivalence a negace výroků logického čtverce
V této výukové jednotce se student seznámí se základními pojmy z teorie predikátového počtu.
 1 Predikátová logika Základní informace V této výukové jednotce se student seznámí se základními pojmy z teorie predikátového počtu. Výstupy z výukové jednotky Student se seznámí se základními termíny
1 Predikátová logika Základní informace V této výukové jednotce se student seznámí se základními pojmy z teorie predikátového počtu. Výstupy z výukové jednotky Student se seznámí se základními termíny
IA008 Computational logic Version: 6. května Formule je v konjunktivní normální formě (CNF), pokud má tvar α 1... α n,
 1 Převody do normálních forem Příklad 1.1: Vyjádřete následující formule v DNF pomocí pravdivostní tabulky a pomocí převodu logických spojek. a) (A B) C b) (A B) C c) (A B) (C D) Formule je v disjunktivní
1 Převody do normálních forem Příklad 1.1: Vyjádřete následující formule v DNF pomocí pravdivostní tabulky a pomocí převodu logických spojek. a) (A B) C b) (A B) C c) (A B) (C D) Formule je v disjunktivní
Logika. 5. Rezoluční princip. RNDr. Luděk Cienciala, Ph. D.
 Logika 5. Rezoluční princip RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Logika 5. Rezoluční princip RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Logika I. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika I. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika I. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Místo pojmu výroková formule budeme používat zkráceně jen formule. Při jejich zápisu
 VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
Jazyk matematiky. 2.1. Matematická logika. 2.2. Množinové operace. 2.3. Zobrazení. 2.4. Rozšířená číslená osa
 2. Jazyk matematiky 2.1. Matematická logika 2.2. Množinové operace 2.3. Zobrazení 2.4. Rozšířená číslená osa 1 2.1 Matematická logika 2.1.1 Výrokový počet logická operace zapisujeme čteme česky negace
2. Jazyk matematiky 2.1. Matematická logika 2.2. Množinové operace 2.3. Zobrazení 2.4. Rozšířená číslená osa 1 2.1 Matematická logika 2.1.1 Výrokový počet logická operace zapisujeme čteme česky negace
Klínové řemeny obalované s úzkým průřezem
 profilem Řemenice a lanové kladky Spojky a křížové emeny Řetězové pohony Inteligentní nástroje Klínové ky Spojky a křížové klouby Ozubené řemeny Řetězová í nástroje Klínové řemeny a řemeny s úzkým profilem
profilem Řemenice a lanové kladky Spojky a křížové emeny Řetězové pohony Inteligentní nástroje Klínové ky Spojky a křížové klouby Ozubené řemeny Řetězová í nástroje Klínové řemeny a řemeny s úzkým profilem
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
3. Polynomy Verze 338.
 3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. BI-ZMA ZS 2009/2010
 Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Kapitola 11: Lineární diferenciální rovnice 1/15
 Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
Predikátová logika. 3.1 Formule predikátové logiky
 12 Kapitola 3 Predikátová logika 3.1 Formule predikátové logiky 3.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolů uvedených v textu.
12 Kapitola 3 Predikátová logika 3.1 Formule predikátové logiky 3.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolů uvedených v textu.
 k n ( k) n k F n N n C F n F n C F F q n N C F n k 0 C [n, k] [n, k] q C [n, k] k n C C (n k) n C u C u T = T. [n, k] C (n k) n T = k (n k). F n N u = (u 1,..., u n ) v = (v 1,..., v n ) F n d(u, v) u
k n ( k) n k F n N n C F n F n C F F q n N C F n k 0 C [n, k] [n, k] q C [n, k] k n C C (n k) n C u C u T = T. [n, k] C (n k) n T = k (n k). F n N u = (u 1,..., u n ) v = (v 1,..., v n ) F n d(u, v) u
Přednáška 3: rozhodování o platnosti úsudku
 Přednáška 3: rozhodování o platnosti úsudku Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky Úsudky Úsudek je platný, jestliže nutně, za všech okolností, tj. při všech interpretacích, ve kterých
Přednáška 3: rozhodování o platnosti úsudku Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky Úsudky Úsudek je platný, jestliže nutně, za všech okolností, tj. při všech interpretacích, ve kterých
Rezoluční kalkulus pro logiku prvního řádu
 AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
Negace bázového atomu Negace atomu s existenčním termem Negace klauzule Negace množiny klauzulí Predikát rovnosti. Klauzulární logika
 Vlastnosti klauzulí, negace Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 27. října 2008 Věta o transferu bázového atomu
Vlastnosti klauzulí, negace Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 27. října 2008 Věta o transferu bázového atomu
Další (neklasické) logiky. Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20
 Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Logika Libor Barto. Výroková logika
 Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Výroková a predikátová logika - XII
 Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Přednáška 2: Formalizace v jazyce logiky.
 Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
)(x 2 + 3x + 4),
 3 IREDUCIBILNÍ ROZKLADY POLYNOMŮ V T [X] 3 Ireducibilní rozklady polynomů v T [x] - rozklady polynomů na ireducibilní (dále nerozložitelné) prvky v oboru integrity polynomů jedné neurčité x nad tělesem
3 IREDUCIBILNÍ ROZKLADY POLYNOMŮ V T [X] 3 Ireducibilní rozklady polynomů v T [x] - rozklady polynomů na ireducibilní (dále nerozložitelné) prvky v oboru integrity polynomů jedné neurčité x nad tělesem
Výroková logika. Sémantika výrokové logiky
 Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Cyklickékódy. MI-AAK(Aritmetika a kódy)
 MI-AAK(Aritmetika a kódy) Cyklickékódy c doc. Ing. Alois Pluháček, CSc., 2011 Katedra číslicového návrhu Fakulta informačních technologií České vysoké učení technické v Praze Evropský sociální fond Praha&
MI-AAK(Aritmetika a kódy) Cyklickékódy c doc. Ing. Alois Pluháček, CSc., 2011 Katedra číslicového návrhu Fakulta informačních technologií České vysoké učení technické v Praze Evropský sociální fond Praha&
Úvod do teoretické informatiky(2017/2018) cvičení 6 1
 Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Výroková logika - opakování
 - opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
- opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
Systém přirozené dedukce výrokové logiky
 Systém přirozené dedukce výrokové logiky Korektnost, úplnost a bezespornost Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 6. října 2008 Věta o korektnosti Věta (O korektnosti Systému
Systém přirozené dedukce výrokové logiky Korektnost, úplnost a bezespornost Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 6. října 2008 Věta o korektnosti Věta (O korektnosti Systému
Logika. 2. Výroková logika. RNDr. Luděk Cienciala, Ph. D.
 Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
4. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
 FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
Matematické důkazy Struktura matematiky a typy důkazů
 Matematické důkazy Struktura matematiky a typy důkazů Petr Liška Masarykova univerzita 18.9.2014 Motto: Matematika je tvořena z 50 procent formulemi, z 50 procent důkazy a z 50 procent představivostí.
Matematické důkazy Struktura matematiky a typy důkazů Petr Liška Masarykova univerzita 18.9.2014 Motto: Matematika je tvořena z 50 procent formulemi, z 50 procent důkazy a z 50 procent představivostí.
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - XI
 Výroková a predikátová logika - XI Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XI ZS 2014/2015 1 / 21 Další dokazovací systémy PL Hilbertovský kalkul
Výroková a predikátová logika - XI Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XI ZS 2014/2015 1 / 21 Další dokazovací systémy PL Hilbertovský kalkul
Predikátová logika dokončení
 Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce
 Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Výroková a predikátová logika - XIII
 Výroková a predikátová logika - XIII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIII ZS 2013/2014 1 / 13 Úvod Algoritmická (ne)rozhodnutelnost Které
Výroková a predikátová logika - XIII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIII ZS 2013/2014 1 / 13 Úvod Algoritmická (ne)rozhodnutelnost Které
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Výroková a predikátová logika - V
 Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Řešení: Ano. Řešení: Ne.
 1 ÚLOHY Z PREDIKÁTOVÉ LOGIKY Instance, varianty. UF.1.1. Substituovatelnost. 1. Buď ϕ formule ( z)(x=z)&y < x a dále x, y, z různé proměnné, F unární funkční symbol, c konstantní symbol. Uveďte, zda je
1 ÚLOHY Z PREDIKÁTOVÉ LOGIKY Instance, varianty. UF.1.1. Substituovatelnost. 1. Buď ϕ formule ( z)(x=z)&y < x a dále x, y, z různé proměnné, F unární funkční symbol, c konstantní symbol. Uveďte, zda je
4 Počítání modulo polynom
 8 4 Počítání modulo polynom Co se vyplatilo jendou, vyplatí se i podruhé. V této kapitole zavedeme polynomy nad Z p a ukážeme, že množina všech polynomů nad Z p tvoří komutativní okruh s jednotkou. Je-li
8 4 Počítání modulo polynom Co se vyplatilo jendou, vyplatí se i podruhé. V této kapitole zavedeme polynomy nad Z p a ukážeme, že množina všech polynomů nad Z p tvoří komutativní okruh s jednotkou. Je-li
Úvod do logiky (PL): analýza vět mimo logický čtverec
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): analýza vět mimo logický čtverec doc. PhDr.
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): analýza vět mimo logický čtverec doc. PhDr.
Základy matematické logiky
 OBSAH 1 Základy matematické logiky Obsah 1 Úvod 2 1.1 Předmět matematiky.......................... 2 1.2 Nástin historie.............................. 2 1.3 Axiomatická výstavba matematických teorií.............
OBSAH 1 Základy matematické logiky Obsah 1 Úvod 2 1.1 Předmět matematiky.......................... 2 1.2 Nástin historie.............................. 2 1.3 Axiomatická výstavba matematických teorií.............
Matematická analýza ve Vesmíru. Jiří Bouchala
 Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/19 typu: m x (sin x, cos x) R(x, ax +...)dx. Matematická analýza ve Vesmíru.
Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/19 typu: m x (sin x, cos x) R(x, ax +...)dx. Matematická analýza ve Vesmíru.
Polynomy nad Z p Konstrukce faktorových okruhů modulo polynom. Alena Gollová, TIK Počítání modulo polynom 1/30
 Počítání modulo polynom 3. přednáška z algebraického kódování Alena Gollová, TIK Počítání modulo polynom 1/30 Obsah 1 Polynomy nad Zp Okruh Zp[x] a věta o dělení se zbytkem 2 Kongruence modulo polynom,
Počítání modulo polynom 3. přednáška z algebraického kódování Alena Gollová, TIK Počítání modulo polynom 1/30 Obsah 1 Polynomy nad Zp Okruh Zp[x] a věta o dělení se zbytkem 2 Kongruence modulo polynom,
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
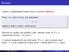 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
pouze u některých typů rovnic a v tomto textu se jím nebudeme až na
 Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Okruh č.9: sémantické metody dokazování v PL1 model formule Tradiční Aristotelova logika kategorický sylogismus subjekt predikátové výroky
 Okruh č.9: sémantické metody dokazování v PL1 Pomocí metody Vennových diagramů a relačních struktur vytváříme grafický model situace, která je úsudkem vyjádřena. Ověřujeme, zda náš graficky znázorněný
Okruh č.9: sémantické metody dokazování v PL1 Pomocí metody Vennových diagramů a relačních struktur vytváříme grafický model situace, která je úsudkem vyjádřena. Ověřujeme, zda náš graficky znázorněný
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Která tvrzení jsou pravdivá nezávisle na tom, který den v týdnu byla vyslovena? Tvrzení trosečníka Dana.
 Trosečníci Adam, Barry, Code a Dan zapoměli po čase kalendář. Začali se dohadovat, který den v týdnu vlastně je. Každý z nich řekl svůj názor: A: Dnes je úterý nebo zítra je neděle B: Dnes není úterý nebo
Trosečníci Adam, Barry, Code a Dan zapoměli po čase kalendář. Začali se dohadovat, který den v týdnu vlastně je. Každý z nich řekl svůj názor: A: Dnes je úterý nebo zítra je neděle B: Dnes není úterý nebo
Lineární algebra Kapitola 1 - Základní matematické pojmy
 Lineární algebra Kapitola 1 - Základní matematické pojmy 1.1 Relace a funkce V celém textu budeme používat následující označení pro číselné množiny: N množina všech přirozených čísel bez nuly, N={1, 2,
Lineární algebra Kapitola 1 - Základní matematické pojmy 1.1 Relace a funkce V celém textu budeme používat následující označení pro číselné množiny: N množina všech přirozených čísel bez nuly, N={1, 2,
Výroková logika syntaxe a sémantika
 syntaxe a sémantika Jiří Velebil: AD0B01LGR 2015 Handout 01: & sémantika VL 1/16 1 Proč formální jazyk? 1 Přirozené jazyky jsou složité a často nejednoznačné. 2 Komunikace s formálními nástroji musí být
syntaxe a sémantika Jiří Velebil: AD0B01LGR 2015 Handout 01: & sémantika VL 1/16 1 Proč formální jazyk? 1 Přirozené jazyky jsou složité a často nejednoznačné. 2 Komunikace s formálními nástroji musí být
Mgr. Rudolf Blažek, Ph.D. prof. RNDr. Roman Kotecký Dr.Sc.
 Náhodné veličiny III Mgr. Rudolf Blažek, Ph.D. prof. RNDr. Roman Kotecký Dr.Sc. Katedra teoretické informatiky Fakulta informačních technologií České vysoké učení technické v Praze c Rudolf Blažek, Roman
Náhodné veličiny III Mgr. Rudolf Blažek, Ph.D. prof. RNDr. Roman Kotecký Dr.Sc. Katedra teoretické informatiky Fakulta informačních technologií České vysoké učení technické v Praze c Rudolf Blažek, Roman
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
LDF MENDELU. Simona Fišnarová (MENDELU) LDR druhého řádu VMAT, IMT 1 / 22
 Lineární diferenciální rovnice druhého řádu Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
Lineární diferenciální rovnice druhého řádu Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
Matematická logika. Rostislav Horčík. horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Predikátová logika Motivace Výroková
Matematika III přednáška Aplikace vytvořujících funkcí - další úlohy
 S Matematika III - 14. přednáška Aplikace vytvořujících funkcí - další úlohy Michal Bulant Masarykova univerzita Fakulta informatiky 18. 12. 2007 Obsah přednášky Řešení rekurencí Q Exponenciální vytvořující
S Matematika III - 14. přednáška Aplikace vytvořujících funkcí - další úlohy Michal Bulant Masarykova univerzita Fakulta informatiky 18. 12. 2007 Obsah přednášky Řešení rekurencí Q Exponenciální vytvořující
KMA/MDS Matematické důkazy a jejich struktura
 Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Teoretická informatika - Úkol č.1
 Teoretická informatika - Úkol č.1 Lukáš Sztefek, xsztef01 18. října 2012 Příklad 1 (a) Gramatika G 1 je čtveřice G 1 = (N, Σ, P, S) kde, N je konečná množina nonterminálních symbolů N = {A, B, C} Σ je
Teoretická informatika - Úkol č.1 Lukáš Sztefek, xsztef01 18. října 2012 Příklad 1 (a) Gramatika G 1 je čtveřice G 1 = (N, Σ, P, S) kde, N je konečná množina nonterminálních symbolů N = {A, B, C} Σ je
Úvod do logiky (PL): logický čtverec (cvičení)
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): logický čtverec (cvičení) doc. PhDr. Jiří
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): logický čtverec (cvičení) doc. PhDr. Jiří
Kapitola 7: Neurčitý integrál. 1/14
 Kapitola 7: Neurčitý integrál. 1/14 Neurčitý integrál 2/14 Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní
Kapitola 7: Neurčitý integrál. 1/14 Neurčitý integrál 2/14 Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Rezoluce ve výrokové logice
 Rezoluce ve výrokové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce ve VL 1/13 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. 2 X nesplnitelná iff X = ff. 3 Hledání kritických důsledků X syntakticky.
Rezoluce ve výrokové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce ve VL 1/13 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. 2 X nesplnitelná iff X = ff. 3 Hledání kritických důsledků X syntakticky.
