Návody na cvičení Geodézie I

Transkript

1 Návody na cvičení Geodézie I Institut geodézie a důlního měřictví Ročník 1 Semestr: letní Cvičící: Ing. Jiří Pospíšil Forma studia a rozsah Prezenční: Zápočet a zkouška 3+3 Kombinovaná: Zápočet a zkouška 18+0 Cíle předmětu vyjádřené dosaženými dovednostmi a kompetencemi Předmět se zabývá prostředím měření geodetických veličin a základními pojmy z teorie chyb. Jsou probrány metody měření úhlů a délek a popsány příslušné geodetické přístroje a jejich podmínky správnosti. Literatura Kubečka, E. : Geodézie a důlní měřictví, skripta VŠB, Ostrava 1992 Ratiborský, J. : Geodézie,skripta ČVUT, Praha 1995 Vitásek, J. Nevosád, Z. : Geodézie I., skripta VUT Brno 1999 Hauf, M. a kol. : Geodézie ( technický průvodce ), SNTL Praha 1989 Schenk, J. Geodézie, VŠB-TU Ostrava 2005, ISBN Mikulenka, V. Základní souřadnicové úlohy, VŠB-TU Ostrava 2002, Sládková, D. Měření úhlů, směrů a rektifikace, VŠB-TU Ostrava 2002, Mazalová, J. Měření délek a komparace měřidel a dálkoměrů, VŠB-TU Ostrava 2002, Sládková, D. Měření výšek, VŠB-TU Ostrava 2002,

2 Osnova předmětu Přednášky: 1. Úvod do metodiky měření geodetických veličin, vliv prostředí na měřené veličiny, práce v souřadnicových a výškových systémech.základní pojmy z teorie měřických chyb, vyrovnání metodou nejmenších čtverců, zákon o přenášení chyb. 2. Měření vodorovných úhlů a směrů, definice úhlů a směrů. Pomůcky pro určování stálých úhlů (hranůlky) 3. Přístroje pro měření úhlů. Teodolit rozdělení podle typu, přesnosti, Popis teodolitu. 4. Podmínky správnosti teodolitu. Systematické a nahodilé chyby při měření úhlů teodolitem. 5. Metody měření úhlů vodorovných a svislých - kontrola měření mezní odchylky. 6. Měření magnetických směrů deklinace, přístroje a pomůcky. Magnetické polygonové pořady 7. Měření gyroskopických směrů, princip gyrokompasu, přístroje, metodika měření. 8. Měření délek měření měřidly (pásmy) systematické a nahodilé chyby měření. Kontrola měření - mezní odchylky. 9. Nepřímé metody měření délek optické dálkoměry, paralaktické měření délek. Kontrola měření délek mezní odchylky. 10. Elektrooptické dálkoměry, princip, systematické chyby, metody měření. Kontrola měření délek mezní odchylky. 11. Převody naměřených délek na výpočetní plochu. V různých souřadnicových systémech Cvičení: 1. Stavění stativu v terénu, centrace teodolitu pomocí mechanické a optické olovnice 2. Popis teodolitu Theo 020, Jednoduché měření úhlů ve dvou polohách dalekohledu, zpracování zápisníku. 3. Popis teodolitu Theo 010, Měření směrů v řadách a skupinách, zpracování zápisníku 4. Zaměření protínání zpět ve dvou skupinách 5. Paralaktické měření délek 6. Přesné měření délek pásmem 7. Měření délek optickým dálkoměrem nitkový (Theo 020), dvojobrazový (Brt 007) 8. Zaměření a výpočet polygonového pořadu Podmínky absolvování cvičení Cvičení z předmětu Geodézie I jsou povinná. Účastí na cvičení student má povolené 20% absence na cvičení během semestru. Přesáhne-li počet absencí stanovený limit student musí předložit potvrzení o návštěvě lékaře apod. pro všechny absence. Odevzdání vypracovaných programů ze cvičení 3 až 8. Programy musí být vypracovány bez chyb a se všemi náležitostmi. Programy budou vypracovány podle vzoru na:

3 Cvičení č.1 Stavění stativu v terénu, centrace teodolitu pomocí mechanické a optické olovnice V tomto cvičení je úkolem zvládnout centraci a horizontaci přístroje nad daný bod. Jde o to, aby osa alhidády stroje (teodolitu) probíhala daným bodem a stroj byl urovnán do vodorovné polohy. K tomuto cvičení doporučuji shlédnout video na: Pomůcky: Teodolit THEO 020 Stativ Kolík s hřebíkem Kladivo Postup: Postavení stroje na bod můžeme rozdělit do 6 fází. 1. Příprava stativu Vysuneme nohy stativu a stativ umístíme nad bod tak, aby střed hlavy stativu byl přibližně nad bodem a hlava byla co nejvíce ve vodorovná. K tomu můžeme využít olovnici zavěšené na upínacím šroubu. Hlavu stativu umístěte do takové výšky, aby měřič při měření stál ve vzpřímené poloze (nemusel se při cílení hrbit nebo stát na špičkách). Poté vyjmeme měřící přístroj z krabice a pomocí upínacího šroubu připevníme na stativ. Po vyjmutí stoje zavřete krabici. 2. Hrubá centrace Nyní máme za úkol přístroj zcentrovat nad daný bod. Toho docílíme pohybem noh stativu ve směru šipek (obr1). Pohyb přístroje na bodem sledujeme v optickém dostřeďovači. Obr.1 Hrubá centrace

4 Pohyb přístroje bude kolmo k noze kterou pohybujeme a stejným směrem jako směr pohybu nohy (obr.2). Obr. 2 Pohyb stativu a pohyb v zorném poli dostřeďovače 3. Hrubá horizontace Jde o srovnání svislé osy přístroje kolmo k vodorovné rovině. K tomuto úkonu použijeme krabicovou libelu a noh stativu. Vysouváním a zasouváním noh stativu urovnáme krabicovou libelu. Vždy pohybujeme nohou, která je v ose výchylky bubliny krabicové libely (obr.3). Postup opakujeme dokud nebude bublina ve středu krabicové libely. Obr. 3 Hrubá horizontace

5 4. Jemná centrace Opět jde o urovnání osy přístroje nad daný bod. Uvolníme upínací šroub stativu a přístrojem jemně pohneme po hlavě stativu, tak abychom viděli bod ve středu optického dostřeďovače (obr. 4). Poté upínací šroub opět utáhneme. Obr. 4 Jemná centrace 5. Jemná horizontce Nyní musíme osu přístroj přesně urovnat kolmo k vodorovné rovině. K tomu budeme používat trubicovou libelu a stavěcí šrouby na trojnožce měřícího přístroje. Alhidádu s trubicovou libelou natočíme tak, aby osa trubicové libely byla rovnoběžná se spojnicí dvou stavěcích šroubů (obr. 5 A). Oběma rukama protisměrně otáčíme šrouby tak, aby se bublina trubicové libely dostala do jejího středu. (Pravidlo levého palce Otáčíme stavěcí šroub ukazováčkem a palcem levé ruky. Směr pohybu bubliny trubicové libely bude stejný jako směr pohybu palce). Obr. 5 Jemná horizontce (šipky ukazují směr pohybu stavěcích šroubů a bubliny v libele)

6 6. Kontrola Po ukončení jemné horizontace je nutné opět zkontrolovat centraci přístroje. Došlo-li k vychýlení přístroje nad bodem musíme znovu provést centraci (odst. 4) a následně horizontaci (odst. 5). Tento postup opakujeme dokud není přístroj dokonale urovnán. Po ustavení stroje můžeme přejít k vlastnímu měření. Typy a způsoby měření jsou popsány dále v textu. Závěr Úkolem každého studenta je, alespoň 2x během cvičení ustavit teodolit nad daný bod.

7 Cvičení č. 2 a 3 Popis teodolitu THEO 020B, jednoduché měření úhlů Popis teodolitu Theo 010, měření směrů v řadách a skupinách V průběhu druhého a třetího cvičení bude probíhat praktická práce s teodolity THEO 020 a THEO 010. V rámci cvičení budou probrány jednotlivé části teodolitu a popis jejich funkcí. Dále bude probíhat měření směrů v řadách a skupinách a zpracování měření. Pomůcky: THEO 010 THEO 020 Stativ Zápisník a tužka Podložka pod zápisník Co nám říká terminologický slovník VÚGTK: Teodolit - úhloměrný přístroj s vodorovným a výškovým kruhem a dalekohledem k měření a vytyčování vodorovných a svislých úhlů. Teodolit s automatickým urovnáváním indexu - teodolit, u něhož je indexová libela nahrazena kompenzátorem. Reiterační teodolit, teodolit s kruhem na posun - teodolit, který má kromě hrubě i jemně otáčivé osy alhidády i frikčně otáčivou, ale samostatnou osu vodorovného kruhu, takže nemůže dojít k strhování kruhu alhidádou Repetiční teodolit - teodolit pro přesné měření vodorovných a svislých úhlů s otáčivou osou vodorovného kruhu i alhidády. Vernierový teodolit -teodolit, který má jako čtecí zařízení k děleným kruhům vernier doplněný lupou anebo vernierový hranolový mikroskop. Mikroskopový teodolit - theodolit, jehož skleněné dělené kruhy se čtou jedním hranolovým mikroskopem, nebo jehož kovový kruh se čte dvěma, popř. čtyřmi šroubovými mikroskopy. Minutový teodolit - teodolit, jehož dělené kruhy umožňují číst úhlové minuty. Vteřinový teodolit - teodolit, jehož dělené kruhy umožňují číst úhlové vteřiny Univerzální teodolit - teodolit s vodorovným a svislým kruhem, nitkovým dálkoměrem a nivelační libelou. Teodolit THEO 020 Tento teodolit se skládá z těchto částí: alhidáda, trojnožka (dostřeďovací podložka, centrační podložka), kolimátor, libela (krabicová, trubicová), dalekohled, svislý a vodorovný kruh (limbus), zrcátko, repetiční svora (součástí je Mahlerova páčka), stavěcí šroub, upínací šroub, pérovací (pérová) destička, hrubá ustanovka horizontální/vertikální, jemná ustanovka horizontální/vertikální, Alhidádový most (rameno), alhidádová vidlice, okulár, objektiv, odečítací mikroskop, optický centr (dostřeďovač), přepínací knoflík čtení, záměrný kříž, mechanický kompenzátor, optické čočky/hranoly/klíny, planparalelní destičky. Popis teodolitu THEO 020 je zobrazen na obrázcích č. 6 a 7.

8 Obr. 6 - Popis teodolitu THEO 020 Obr. 7 Popis teodolitu THEO 020

9 Čtení hodnot na teodolitu THEO 020 Teodolit THEO 020 je minutový teodolit (minimální hodnota pro odečtení je 0,01gonu) Nejprve je nutné osvětlit vodorovný a svislí kruh pomocí zrcátka. Zrcátko odklopíme a nastavíme tak, aby nám do teodolitu odráželo co nejvíce světla.v zorném poli mikroskopu vidíme dvě, popřípadě jednu úhloměrnou stupnici. Zobrazení stupnice pro vertikální úhly se dá vypnout/zapnout pomocí knoflíku pro přepínání čtení. Zaostření obrazu se provádí pomocí černého rýhovaného prstence na mikroskopu. Dále odečítáme jednotlivé úhlové hodnoty pro dané směry (obr. 8). Měřené hodnoty zapisujeme do zápisníku. Vertikální kruh Odečítaní hodnota 96,8950 g Horizontální kruh Odečítaní hodnota 143,7400 g Obr. 8 Čtení hodnot THEO 020 Nastavení požadovaného čtení u Theo 020 se provádí pomocí repetiční svory. Nejprve s rozepnutou svorou, přibližně otočíme alhidádu na požadované čtení na vodorovném kruhu a utáhneme hrubou ustanovku. Pomocí jemné ustanovky otočíme stoj přesně na požadované čtení. Sepneme repetiční svoru, povolíme ustanovku a zacílíme na daný cíl. Odepneme svoru a poté přečteme hodnotu na vodorovném kruhu a zapíšeme do zápisníku.

10 Teodolit THEO 010 Tento teodolit má obdobné části jako teodolit THEO 020 a dále budou popsány jen rozdíly těchto přístrojů. Základním rozdílem je přesnost a způsob odečítání hodnot na úhloměrných stupnicích a způsob jakým se pohybuje vodorovný kruh. THEO 010 je vteřinový teodolit a přesnost odečítání je 0,0001 g (při šedesátinném dělení kruhů je přesnost 1 ). Příklad odečtení je na obr.9. Je nutné, aby se vždy před odečtení hodnoty srovnaly (koincidovaly) koincidenční rysky. Koincidenci provedeme pootočením bubínku mikrometru, tak aby rysky v horní i dolní polovině koincidenční mřížky (levý dolní rámeček) byly nad sebou. Po koincidenci je možné číst úhlovou hodnotu, ta se čte zleva doprava. Odečítaná hodnota Hz = 134,3228 g Obr. 9 - Čtení hodnot THEO 010 Dalším rozdílem je způsob pohybu vodorovných kruhů. U THEO 020 se k tomuto účelů používá repetiční svora, u THEO 010 se používá pastorek. Přístroje vybavené pastorkem se také nazývají s kruhem (limbem) na postrk. Princip spočívá v tom, že pomocí pastorku lze nezávisle otáčet vodorovným kruhem. Před otáčením pastorku je nutné povolit pojistku proti svévolnému otočení. Po nastavení čtení pojistku opět sepněte. Budeme-li chtít nastavit na kruhu čtení určité hodnoty, musíme nejdříve zacílit do požadovaného směru a poté otáčíme pastorkem dokud v mikroskopu nečteme požadovanou hodnotu. V mikroskopu vždy vidíme pouze jednu stupnici a to stupnici kruhu horizontálního (modrozelené barvy), nebo kruhu vertikálního (žluté barvy). Přepínání mezi stupnicemi provádíme knoflíkem umístěným u hrubých ustanovek. Na další straně následuje obrázek (obr. 10) s popisem teodolitu THEO 010

11 Obr. 10 Teodolit THEO 010

12 Měření vodorovných úhlů Měřený směr - vodorovný úhel záměry odečtený na libovolně orientovaném úhloměrném přístroji. Měřený úhel - rozdíl dvou měřených směrů na jednom bodě včetně případných početních korekcí. Vodorovný úhel, horizontální úhel - úhel mezi pravoúhlými průměty dvou záměr do vodorovné roviny, měřený na vodorovném kruhu úhloměrného přístroje. První (druhá) poloha stroje - Poloha stroje, kdy je svislý kruh nalevo (napravo) od dalekohledu při měření směru. Měření v řadách Měření vodorovných úlu provádíme tak, že nejprve ustavíme měřící přístroj nad bodem a poté zvolíme počáteční směr. Na tento počáteční směr nastavíme hodnotu vodorovném kruhu, která je o málo větší než nula. U teodolitu THEO 020 se nastavení provede tak, že nejprve alhidádu natočíme na požadované čtení. Poté sepneme repetiční svoru a zacílíme na počáteční směr. Svoru rozepneme a přečteme počáteční čtení, které zapíšeme do zápisníku. Dále otočíme směrem doprava a zacílíme na další směr, odečteme hodnotu na horizontálním kruhu a zapíšeme do zápisníku. Měříme na požadovaný počet směrů a hodnoty zapisujeme. Nakonec je nutné opět zacílit na počáteční směr a hodnotu opět zapsat do zápisníku. Pořadí měřených směrů (obr. 10A δa, δb, δc, δd, δa ) V tuto chvíli máme změřenu I. ŘADU. I. Řada je chápana tak že se zaměří všechny směry v jedné poloze dalekohledu (obr. 11A). A I. Řada B II. Řada Obr. 11 Měření směrů v řadách

13 Měření ve skupinách Měření úhlů ve skupinách je základní metodou pro určování velikosti úhlů. Princip metody spočívá v tom, že skupina se skládá ze dvou řad. První řadu měříme dle předchozí kapitoly. Druhá řada se měří ve druhé poloze stroje. A to v opačném směru otáčení teodolitu při cílení (obr. 11B). Použijeme-li měření více než v jedné skupině na začátku každé skupina se nastavuje odlišné čtení i na počáteční směr. 2R i =, kde s je počet měřených skupin na stanovišti. s Budeme li měřit teodolitem na stanovišti ve třech skupinách bude počáteční čtení v I. skupině 0 g, ve II. skupině 67 g, a ve III. skupině 133 g. Budeme-li mít teodolit stupňový, pak počáteční hodnoty budou 0, 60 a 120. Při měření nastavujeme vždy hodnotu o málo větší než hodnotu vypočtenou (př. 0,0230 g, 67,0198 g atd.) Hodnotu o málo větší nastavujeme z důvodu čistě praktických abychom se při výpočtu zápisníku nedostali do záporných hodnot. Příklad cílení a odečítání hodnot podle obr. 11. I. řada δa, δb, δc, δd, δa II. řada δa, δd, δc, δb, δa Při měření ve více skupinách tento postup opakujeme s tím, že vždy pro čtení δa v první skupině nastavujeme požadované čtení. Vyplnění a výpočet zápisníku Výsledky měření se vyplňují do předepsaných tiskopisů (ke stažení na - formuláře). Pro různá měření může být k dispozici více typů zápisníků. Je nutné upozornit, že digitální přístroje bývají zpravidla vybaveny funkcí automatické registrace, kdy se hodnoty registrují do paměti přístroje a poté se zkopírují do počítače, kde s pomocí speciálního softwaru vyhodnotí. Zápisník se vyplňuje vždy tužkou a čitelně. V zápisníku se negumuje, chybný zápis škrtneme a pokračujeme na novém řádku. Budeme-li měřit na stanovisku směry podle obr. 11 zápisník se vyplní způsobem popsaným na obr. 12 ( modře je popsáno pořadí zapisovaných hodnot) Do sloupce Stanovisko napíšeme označení bodu kde je postavený měřící přístroj (teodolit). Do druhého sloupce Cíl napíšeme označení bodů, na které měříme směry. Třetí sloupec je předtištěný a označuje polohu dalekohledu (první nebo druhá poloha). Do sloupce Vodorovný úhel měřený vpisujeme hodnoty odečítané v mikroskopu (popřípadě hodnoty zobrazené na displeji digitálního přístroje)

14 Obr. 12 Zápis hodnot do zápisníku - I. skupina Po zapsání hodnot se provede výpočet (obr.13). Ve sloupci Vodorovný úhel - průměr se vypočtou průměry pro jednotlivé směry z I. a II. polohy stroje. Hodnota celých grádů se určí podle hodnoty v prví poloze. Sloupec Vodorovný úhel orientace na 0 se vypočte tak, že hodnota na počáteční směr je opravena na nulu. Poté se původní hodnota počátečního směru musí od dalších směrů odečíst. Sloupec Skupinový průměr je k tomu, aby se zprůměrovaly hodnoty směrů z více skupin (obr. 14). Dále je nutné provést opravu měřených směrů. Směr na cíl A by měl být stejný jako poslední směr na bod A, to se však stane jen výjimečně. Proto se musí opravit hodnota v uzávěru skupiny a to tak, aby byla rovna hodnotě směru počátečního. Hodnota se vydělí počtem měřených směrů a pak se jednotlivé hodnoty pro dané směry opraví. První směr zůstává roven nule, druhý se opraví o hodnotu O o =, n Kde o oprava, O odchylka v uzávěru skupiny, n počet měřených směrů ve skupině. Při opravách směrů musíme vždy jednotlivé opravy sčítat (první směr 3, druhý směr 3+3, třetí směr 6+3,a čtvrtý 9+3). Kdybychom opravili každý směr jen o hodnotu 0,0003 g, docílili bychom pouze toho, že by se směry natočili o 0,0003 g proti směru hodinových ručiček. Ve výsledku by byly úhly mezi směry BC, CD a AD menší o 0,0003 g a součet úhlů by byl 399,9991 g. Výsledné opravené směry napíšeme do sloupce opravené směry. Jako poslední je nutné udělat adjustaci zápisníku. Adjustace spočívá v tom, že se trvalým způsobem (nejlépe tuší) vyznačí nejdůležitější hodnoty v zápisníku. Vždy se zvýrazní Záhlaví zápisníku, stanoviště, cíl, opravené směry a červeně se vyznačí opravy směrů (na obrázku tučně zvýrazněné). Obr. 13 Výpočet zápisníku pro 1 skupinu

15 Obr. 14 Výpočet zápisníku pro 2 skupiny Měření svislých úhlů Svislý úhel, vertikální úhel - úhel ve svislé rovině mezi vodorovným nebo svislým směrem a záměrou na bod. Na svislém kruhu úhloměrného přístroje se měří výškové úhly (od vodorovného směru) nebo zenitové vzdálenosti (od svislého směru). Výškový úhel - úhel ve svislé rovině, měřený od vodorovného směru ke směru na zaměřovaný bod; je kladný směrem k zenitu, záporný k nadiru; záporný výškový úhel se někdy označuje jako hloubkový úhel. Zenitový úhel, zenitová vzdálenost - svislý úhel mezi směrem k zenitu a k zaměřovanému bodu. Měření svislých úhlů je v porovnání s měřením vodorovných úhlů jednodušší. Svislé úhly se měří pouze v obou polohách dalekohledu. Svislé úhly se odečítají pomocí odečítacích zařízení tzv. indexů na svislé kruhu teodolitu. Svislý kruh je pevně spojen s dalekohledem a otáčí se zároveň se sklápěním dalekohledu, zatím co indexy jsou pevně spojeny s konstrukcí alhidády. Svislý úhel je opět rozdílem dvou směrů a podle nastavení nulového směru můžeme rozdělit svislé úhly na úhly výškové a zenitové. Úhly zenitové (obr. 15) mají nulový směr nastaven do zenitu (nadhlavníku) v první poloze dalekohledu, úhly výškové (obr. 16) mají nulový směr nastaven ve vodorovné rovině. Výškové úhly jsou kladné (výškové) nebo záporné (hloubkové) podle směru od vodorovné osy viz. Výškový úhel. Součet svislých úhlů v první a druhé poloze musí být vždy 4R (400 g, 360 ). V případě, není-li součet roven 4R, výsledný výškový úhel se opraví o polovinu odchylky. Příklad zápisníku je na obr.17.

16 Obr. 15 Zenitové úhly Obr. 16 Výškové úhly

17 Obr. 17 Zápisník měření vodorovných a svislých úhlů

18 Závěr Po absolvování cvičení a vyhotovení programů by měl student zvládnout názvosloví částí teodolitů, měření v řadách a skupinách včetně zpracování zápisníků. Úkolem každého studenta(tky) bude vypracovat popis určitých částí teodolitu, a provést měření vodorovných a svislých úhlů ve dvou skupinách na 3 směry oběma typy teodolitů. Následně student měření zpracuje a odevzdá adjustovaný zápisník.

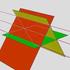
19 Cvičení č. 4 Zaměření protínání zpět ve dvou skupinách V tomto cvičení se provede zaměření protínání zpět ve dvou skupinách a následný výpočet metodou Collinsova bodu. Cvičení bude probíhat na pozorovatelně IGDM (střecha budovy A). Pomůcky THEO 010 Zápisník, tužka, podložka Postup měřických prací Cvičení může probíhat pouze za dobrých klimatických podmínek ( dobrá viditelnost), aby bylo možno měřit na trigonometrické body v okolí. Studenti se rozdělí do dvojic a každý student z dvojice provede zaměření protínání zpět ve dvou skupinách na tři směry. Následně student provede výpočet zápisníku a adjustaci. Z měřených směrů se vypočtou úhly. Metodou Collinsova bodu vypočtěte protínáním zpět souřadnice měřického stanoviště (výpočet bude proveden ručně). Souřadnice pro výpočet naleznete pomocí webové aplikace ČÚZK - databáze bodových polí ( K technické zprávě programu připojte výkres (ve vhodném měřítku na formát A4), kde budou vyneseny body použité pro výpočet protínání zpět a souřadnice stanoviska. Odevzdat : Technická zpráva (viz. vzor programů) Adjustovaný zápisník měření Výpočet protínání zpět Výkres A4 Poznámka Na obr. 18 je zobrazena situace orientací s čísly TB. Na pozorovatelně jsou umístěny tři pilíře 341, 342, 343, přičemž z pravého pilíře č.341 není viditelnost na body č. 29 a 89, z prostředního č. 342 není viditelnost na 89 a 20 a z levého č.343 není viditelnost na bod č.20. Fotodokumentace TB z pohledu měřiče je v příloze č.1. Závěr Cvičení č.4 má sloužit k procvičení měření úhlů v řadách a skupinách a opakování výpočtu protínání zpět metodou Collinsova bodu. Jako podklad použijte šablonu programů umístěnou na webových stránkách Institutu geodézie a důlního měřictví:

20 Obr. 18 Situace protínání zpět

21 Cvičení č. 5 Paralaktické měření délek Náplní cvičení bude měření délek pomocí základnové latě. U této metody se určuje paralaktický úhel s použitím základny s konstantní délkou. Paralaktické měření délek se používá pro určení vzdáleností do 100 až 120m. Paralakticky se vždy určují délky vodorovné. Určujeme-li vzdálenost mezi dvěma body, na jeden bod se postaví vteřinový teodolit (THEO 010) a na druhý se do trojnožky na stativu upne základnová lať. Základnová lať (někdy také nazývaná Bala lať) má zpravidla délku l = 2m a je opatřená na koncích a uprostřed terči. (Lať je vyrobena tak, že její délka 2m má maximální odchylku ±0,1mm.). Základnová lať se pomocí kolimátoru natočí kolmo ke spojnici stanoviska a bodu, na který se měří délka (obr. 19). Měření paralaktického úhlu se provádí jen v jedné poloze teodolitu metodou LPP L. Nejprve se zacílí na levý terč L základnové latě a odečte se. Při každém čtení se vždy provede dvojí koincidence mřížky a obě hodnoty se zapíší do zápisníku. Potom se zacílí na pravý terč P, odečte a zapíše. Zacílení se poruší jemnou horizontální ustanovkou, opět se zacílí na pravý terč P a odečte. Pokračujeme otáčením alhidády doprava a zacílíme na levý terč L. Tento postup tvoří jednu paralaktickou skupinu. Při měření ve více skupinách se počáteční čtení mění o 2 g až 3 g. Směr otáčení alhidády má být opačný než v předchozí skupině. Obr. 19 Paralaktické měření délek (jednoduchý paralaktický článek) Délka se vypočte podle vzorce l δ s = cot g, 2 2 kde l je délka základnové latě (2m) a δ je velikost paralaktického úhlu (obr. X). Po úpravě dostáváme: δ s = cot g. 2 V případě, že nejde vidět na jeden z koncových terčů latě, lze měřit na poloviční délku základnové latě. Pak by se měřil paralaktický úhle δ = δ/2 a délka základnové latě je l = l/2 (1m), pak je vzorec pro výpočet délky: l s = cot gδ. 2 Maximální měřená délka má závislost na volbě typu paralaktického článku. V předchozím textu je popsán základní paralaktický článek. Jednotlivé typy viz. přednášky, nebo jsou popsány v literatuře. Příklad zápisníku (obr. 20) pro paralaktické měření délek je na následující straně.

22 Obr. 20 Zápisník paralaktického měření úhlů (dvě skupiny) Paralaktické měření délek, paralaktická metoda - metoda, při které se určují délky nepřímo z paralaktické základny měřením paralaktického úhlu. Paralaktický článek s vodorovnou základnovou latí, paralaktický článek se základnovou latí paralaktický článek s paralaktickou latí kolmo na konci nebo uprostřed měřené délky Paralaktický článek - geometrický obrazec sloužící pro výpočet délky pomocí paralaktického úhlu a relativně velmi přesně určené základny; tvary paralaktických článků bývají různé (trojúhelník, soustava trojúhelníků) podle místních podmínek Paralaktický článek s pomocnou základnou - paralaktický článek, jehož délka se odvodí z pomocné základny; délka této základny se určí přímo paralakticky; pomocná základna se volí obvykle kolmo uprostřed nebo na konci určované délky nebo v obecné poloze Pomůcky THEO 010 Stativ 2x Základnová lať (Bala lať) Olovnice Zápisník, podložka, tužka Postup prací Měřické práce budou probíhat za budovou A, kde je vybudované cvičné bodové pole. Každá dvojice si vybere trojici bodů, přičemž musí být zaručena viditelnost z jednoho bodu na dva zbylé. Na tento bod postavíme stativ s teodolitem. Na zbylé dva body budeme určovat vzdálenost a úhel mezi nimi. Na druhý bod se postaví stativ se základnovou latí, třetí bod bude signalizován olovnicí. Paralaktickou metodou se zaměří délka ve dvou skupinách a zároveň se zaměří úhel α mezi body, také ve dvou skupinách. Vyměníme stativ se základnovou latí za olovnici a provedeme paralaktické měření délky i na druhý bod (obr. 21). Měření zpracujeme do zápisníku, zápisník adjustujeme a provedeme výpočet třetí stany s 1-2 trojúhelníku (St.,1 2).

23 Obr. 21 Příklad paralaktického měření délek Odevzdat: Technická zpráva (viz. vzor programů) Adjustovaný zápisník měření Výkres A4 Závěr: Cílem cvičení je procvičit paralaktické měření délek. Každý student zaměří dvě délky a jeden úhel tak, aby bylo možné dopočítat třetí stanu trojúhelníku. Měřené hodnoty zapište do příslušných zápisníků, zápisníky vypočtěte a adjustujte podle předchozích příkladů ( třetí stranu v měřeném trojúhelníku.

24 Cvičení č. 7 Měření délek pásmem Měření délek pásmem se řadí mezi metody přímé. Měření délek můžeme podle přesnosti rozdělit do dvou kategorií na měření délek technickými metodami a přesné měření délek pásmem. Ve cvičení použijeme obou metod. Technické metody Tyto metody se používají při měření oměrných měr, konstrukčních oměrných, ortogonální metodě atd. Koncové body měřené přímky se vždy signalizují výtyčkou ve stojánku. Při měření dálky přesahující trojnásobek kladu pásma a při měření ve velmi svažitém terénu se vytyčují mezilehlé body měřené úsečky. Ve cvičení budeme měřit délku ve svažitém terénu ve vodorovné poloze pásma. Délky budeme měřit vždy 2krát a měření budeme provádět ne směru po svahu dolů (obr.22). Bude nutné zkrátit délku kladu pásma, tak aby měřič mohl pohodlně provážit koncový bod pásma. Cvičení bude probíhat ve čtyřčlenných skupinách. Obr měření délek pásmem ve svažitém terénu Postup měření Dva měřiči obsluhují pásmo, jedem provádí zařazení do směru a jeden kontroluje vodorovnou polohu pásma. Vyznačíme v terénu měřenou úsečku její koncový a počáteční bod stabilizujeme kolíkem a signalizujeme výtyčkou. Nulu pásma přiložíme k výše položenému bodu měřené úsečky a koncový bod zařadíme do směru měřené úsečky, pásmo srovnáme do vodorovné polohy. Koncový bod pásma provážíme olovnicí na terén a bod označíme hřebem (měřickou jehlou). Tento bod nám bude sloužit jako výchozí pro další klad pásma.

25 Tento postup opakujeme a ž ke koncovému bodu. Poslední měřená část úsečka s nejvyšší pravděpodobností nevyjde na celý klad pásma. Tato část se nazývá doměrek. Do zápisníku pro měření délka pásmem zapisujeme: jména měřičů, délku kladu a číslo pásma, označení měřené úsečky, počet kladů a doměrek. Po dokončení měření délka úsečka měření opakujeme, při druhém měření použijeme jinou hodnotu pro počáteční čtení (cca 0,1-1m). Přesné měření délek pásmem Při přesném měření délek pásmem je nutné naměřené hodnoty opravit o systematické chyby a provést redukce pro zobrazení na referenční plochu: - Opravy systematických chyb (z teploty, protažení, průhybu, komparace pásma). - Redukci délky na vodorovnou. - Redukci délky do nulového horizontu. - Redukci délky do zobrazovací roviny S-JTSK. Postup prací U přesných metod měření délek musí být měřené úseky kratší než délka pásma. Délky měřte vždy minimálně 2x, přičemž se počáteční čtení vždy posune minimálně o hodnotu 0,10m. Rozdíl v měření stejné délky nesmí přesáhnout hodnotu s = 5 mm. Pro převod na vodorovnou délku zaměřte zenitové úhly a to vždy ve dvou polohách dalekohledu. Pásmo se napíná silou kterou okamžitě odečítáme na siloměru ( je vhodné délku odečítat při napínací síle která je rovna napínací síle při komparaci). Při měření je nutné měřit teplotu nutnou pro výpočet opravy z teploty. Déle budeme uvažovat že pásmo je komparované a má správnou délku, musíme také znát parametry pásma potřebné pro výpočty oprav. Na body mezi nimiž měříme délku postavíme stativy s trojnožkou, povedeme centraci a horizontaci. Po té do trojnožek upneme hroty pro měření délky. Dva měřiči napnou pásmo tak, aby hroty byly u stupnice s milimetrovým dělením, odečte se napínací síla, hodnoty pásma u obou hrotů a teplota. Tento postup opakujeme do té doby, pokud nejméně dvě měřené délky budou vyhotovovat podmínce s = 5 mm. Měřenou šikmou délku opravíme o systematické chyby. Šikmou délku přepočítáme na vodorovnou. Do výpočtu použijeme zenitový úhel měřený v terénu. Tento musí vypočten z měření v obou polohách dalekohledu.

26 Délku opravíme o redukci do nulového horizontu a o redukci do zobrazovací roviny S-JTSK. Pro přehlednost celý výpočet uspořádejte do tabulky. Pomůcky: - pásmo a siloměr - stativy - trojnožka a terč - hroty - Theo teploměr Konstanty potřebné k výpočtu o průměrná výška bodů je H = 265 m.n.m. Bpv o koeficient délkového zkreslení do zobrazovací roviny S-JTSK je m = 0,99998 o pásmo je komparované o koeficient roztažnosti oceli λ t = m.1 C -1 o teplota při komparaci pásma byla 20 C o napínací síla při komparaci byla F = 100N o Yongův modul pružnosti v tahu E = N.m -2 o průřez pásma A = m 2 o hmotnost jednoho metru pásma je m = 0,03 kg, tudíž měrná délková tíha je γ = 0,3 N.m -1 o l měřená délka o l - délka opravená o systematické chyby a redukovaná na vodorovnou o střední poloměr země R = m Oprava z teploty ot = λ t.( t t0). l Oprava z protažení ( F F0 ) o pt = l. A. E Oprava z průhybu 3 2 l. G o pr = kde: G = γ = m. g F Redukce délky na nulovou plochu o H = H. l / R Redukce do zobrazovací roviny S-JTSK o Z = l. m Odevzdat: Technická zpráva (viz. vzor programů) Zápisník měření délek pro technické metody Měřené hodnoty a tabulku oprav pro přesné metody