MODERNÍ VYUČOVÁNÍ. Moderní výuka přírodních věd. Každé dítě musí zažít radost z poznání. Téma: MATEMATIKA A PŘÍRODNÍ VĚDY
|
|
|
- Marian Kříž
- před 8 lety
- Počet zobrazení:
Transkript
1 MODERNÍ VYUČOVÁNÍ Moderní výuka přírodních věd Příprava dnešních studentů na příležitosti zítřka Téma: MATEMATIKA A PŘÍRODNÍ VĚDY květen červen / 0 Každé dítě musí zažít radost z poznání Prof. Milan Hejný o matematice, která v dětech vzbuzuje skutečný zájem Cena 9 Kč / 03/0 časopis na podporu rozvoje vzdělání a školství
2 Téma O matematice O matematice nejen v Čechách Matematika se v určitých vlnách objevuje i v zájmu českých médií, leč bohužel vždy spíše v momentech ne příliš příjemných. Velkou vlnu diskusí, které ale nevyústily do konkrétních návrhů a řešení, vzbudila PISA 009, nedávno zase rezonovala debata o státních maturitách z matematiky. Průběžně se pak ozývají hlasy firem, pro které je schopnost myšlení vybudovaná právě na základech matematiky a logiky a dostatek kvalitních absolventů v přírodovědných oborech jednou z klíčových otázek české konkurenceschopnosti. připravila Leona G. Šteigrová První velkou debatu na téma matematika v Čechách vyvolalo nejprve šetření TIMMS a poté PISA 009, přičemž oba výzkumy potvrdily to stejné že s matematikou jsme na tom hůř a hůř. V šetření PISA byl výsledek českých žáků v matematické gramotnosti sice (alespoň) průměrný (čeští žáci s výsledkem 93 bodů zůstali za průměrem zemí OECD, který je 96 bodů), nicméně alarmující bylo samo zjištění, že v období od roku 003 do roku 009 se výsledky českých žáků zhoršily nejvíce ze všech zemí, které se obou cyklů výzkumu zúčastnily. Obdobné průměrné výsledky jako ČR měly i země našeho pohabsburského dědictví, naopak daleko před námi bylo ze zemí EU Německo aj. Z výzkumu navíc vyplynulo, že dívky i chlapci měli téměř stejné výsledky a že obecně horší výsledky se týkají všech druhů škol s výjimkou škol speciálních, které zůstaly zhruba na stejné úrovni. Jak však v našem rozhovoru zdůrazňuje prof. Hejný, alarmující na obou šetřeních je skutečnost, že čeští žáci a studenti mají velkou nelibost vůči matematice. Právě tento negativní postoj vůči matematice je věc dlouhodobá, kterou nelze snadno napravit, a která bude mít vážné dopady i na budoucnost. A pokud v tomto čísle zmiňujeme i přírodní vědy, pak můžeme jedním dechem říct to stejné i o výsledcích v přírodovědné gramotnosti: výsledek průměrný, nicméně za poměrně krátké časové období od roku 006 do roku 009 doznaly výsledky českých žáků druhého nejvyššího zhoršení mezi zúčastněnými zeměmi. Ke zhoršení došlo ve všech druzích škol kromě středních odborných škol bez maturity, kde se výsledky téměř nezměnily. Zatím poslední matematickou diskusi vyvolaly státní maturity z matematiky. Jak v rozhovoru pro Hospodářské noviny připustil i dlouholetý zastánce povinné maturity z matematiky a ředitel PORG Václav Klaus ml., i on jako vystudovaný matematik počítal úlohy hodinu a padesát sedm minut, což rozhodně neodpovídá tomu, jak by měla státní maturita vypadat. Zřejmě by neměla být IQ testem, který vyplňujeme pod časovým presem, bez možnosti hlubšího přemýšlení, a může být spíše otázkou osobní psychické odolnosti, než trvalé znalosti. S Václavem Klausem lze souhlasit i v tom, že následná harmonizace ze strany Cermatu, který je odpovědný za kvalitní přípravu státních maturit (a rozhodně v tomto směru netrpí nedostatkem finančních prostředků), je spíše podvodem s výsledky s ohledem na veřejné mínění. Naopak lze v tomto ocenit přístup nového otevřeně přiznal a jménem ministerstva se maturantům omluvil. Stále více však na význam matematiky upozorňují soukromé firmy, které si uvědomují, že matematika není jen o počítání, ale o způsobu myšlení, logickém a systematickém uvažování, které se následně promítne v celé řadě dalších dovedností a znalostí. Jednou z iniciativ je Matematika s chutí, která se snaží podpořit učitele matematiky na nejnižších stupních v tom, aby se snažili děti více zaujmout, a zatraktivnit tak tento často neoblíbený předmět. Komplexní odpovědí na otázku jak matematiku zatraktivnit je však spíše ucelená a vyzkoušená metodika, podpořená již hotovou sadou učebnic, kterou se v tomto vydání rovněž zabýváme. SOUTĚŽ Otázka povinné maturity z matematiky byla již v médiích položena mnohokrát, často však na ni odpovídala široká veřejnost se svým osobním pohledem opřeným o vlastní zkušenost. Jaký je však váš názor? Znechutila by tato povinnost matematiku žákům ještě více? Nebo by byla návratem k důrazu na exaktní vědy a logické přemýšlení? Napište nám svůj názor a získejte jednu z uvedených cen: Měla by být maturita z matematiky povinná? A) Ano, určitě by byla prospěšná. B) Ne, vedlo by to jen k dalšímu biflování pro účely testu a žáci a studenti by měli matematiku ještě méně rádi než nyní. C) Asi by to bylo prospěšné, ale obával/a bych se toho, aby se matematika nezvrhla jen v přípravu na úlohy v testu. D) Mám jiný názor: myslím si, že Odpovědi nám prosím zasílejte do 30. června 0 em na adresu redakce: redakce@modernivyucovani.cz (do předmětu u uveďte slovo soutěž ). Pro tři z vás, jejichž odpovědi vylosujeme, máme připravenu:. až 5. ročník ZŠ a nové (či prodloužení stávajícího) předplatné časopisu Moderní na jeden rok. Nové předplatné rovněž můžete darovat jiné škole. 5
3 Rozhovor Prof. Milan Hejný Každé dítě musí zažít radost z poznání a pocit vlastní autenticity při řešení otázek Rozhovor s prof. Milanem Hejným o matematice, která děti baví a učí je logicky a systematicky přemýšlet připravila Leona G. Šteigrová Na matematiku existuje řada velmi rozporuplných pohledů. Jaké jsou vaše vzpomínky? Nebavila vás, báli jste se písemek, chtěli jste ji mít už za sebou, děsila vás možnost povinné maturity z matematiky? Nebo jste patřili k těm šťastnějším, kteří v ní objevili její kouzlo a význam pro budoucí život? Na řadě českých škol se již naštěstí zabydlel k výuce matematiky přístup, který klade hlavní důraz na poznání, na radost z řešení otázek, na zapojení i těch nejslabších žáků. Přístup, který v budoucnu dětem otevře dveře všude tam, kde je třeba logické a systematické myšlení. O této metodě výuky matematiky jsme si povídali s jejím tvůrcem prof. Milanem Hejným. Co vás osobně na matematice tak upoutalo, že jste se jí rozhodl celoživotně věnovat? Nemohu říct, že bych na základní škole v matematice exceloval, možná naopak. Měl jsem ale velice chytrého otce, jenž mi ukázal i jiný pohled na matematiku který byl úplně jiný než ona školská matematika. Právě díky tomuto jeho přístupu jsem ale předčil své spolužáky ve chvíli, kdy přišly na řadu zlomky či záporná čísla, kterým jsem díky tatínkově matematice rozuměl. Pak už přišly na řadu olympiády v matematice, a tak jsem šel nakonec studovat matematicko-fyzikální fakultu do Prahy. Od počátku jste se chtěl věnovat práci s dětmi didaktice matematiky? Hlavní impulz ve mně vzbudil až zážitek s mým synem, který podle mě byl na matematiku dobrý, ale jeho postupy pro řešení úloh nebyly shodné s těmi, které vyučovala a chtěla od žáků vidět paní učitelka. Jeden z nesouladů s přístupem této paní učitelky mě přivedl k tomu, abych sám začal učit. Domluvil jsem si tedy na jedné škole možnost bezplatně vyučovat jednu třídu, přičemž můj vědecký zájem se přeorientoval právě na práci s dětmi a výuku matematiky. V této činnosti se ke mně přidalo ještě několik kolegů, se kterými jsme pak své poznatky a zkušenosti shrnuli do dodnes používané publikace k metodice matematiky. V těch dobách vznikl i můj deník, kam jsem si opět na radu svého otce zapisoval vše, co mě překvapilo, čemu jsem nerozuměl. Nyní je to pro mě velmi cenný 6 materiál pro práci na didaktice a metodice matematiky. Počítal jste od počátku s tím, že z vašeho přístupu k matematice vzniknou učebnice využívané dnes na školách? Vůbec ne. Své poznatky z a vědecké práce jsem považoval spíše za teorie. s nabídkou vydat učebnice matematiky pro. až 5. ročník. Věřím, že tyto učebnice přinášející naprosto odlišný přístup jsou investicí do budoucnosti. Kudy tedy vede cesta od teorie k praktické výuce? Mně a našemu týmu pro přípravu učebnic bylo od počátku jasné, že nejdůležitější je vyzkoušet učebnice v praxi protože pokud by to děti nebraly, bylo by to k ničemu. I zde jsme však měli velké štěstí, protože u nás studovala paní Jitka Michnová, z jejíž diplomové práce bylo evidentní, že je právě tou učitelkou, kterou hledáme. Naší metodě od počátku věřila a výsledky, které ve třídě měla, byly skutečně neuvěřitelné. V médiích toho bylo o jejích výsledcích napsáno již mnoho včetně toho, kdy v soutěži Cvrček dosáhlo z více než osmi tisíc dětí Středočeského kraje plného počtu bodů jen 5 dětí, z toho pět žáků Jitky Michnové. Co je ale z mého pohledu mnohem důležitější než tyto špičkové výkony, je fakt, že její nejslabší žák, který byl v první třídě v psychologické poradně navržen do praktické školy, byl lepší než středočeský průměr. Každé dítě musí být v hodině intelektuálně přítomno Vy se tedy snažíte svým přístupem zaujmout matematikou všechny děti a nevyhledávat jen ty matematicky nadané? Přesně tak, toto není elitářská učebnice pro horních deset tisíc dětí, to je skutečně komplexní učebnice pro každého. Klíčové zde je, aby každé dítě během hodiny bylo zaměstnáno, něco dělalo, bylo intelektuálně přítomno. Poznání nepřichází zvenčí, od učitele či učebnice, dopracovat se k němu musí každý sám Co tedy ve svém přístupu považujete za nejdůležitější? Poznání žáci nedostávají ani od učitele, ani od učebnice. Poznání nepřichází zvenčí. K poznání se dopracují děti samy. Tato cesta k poznání je samozřejmě dlouhá. Tradiční učitelé mohou být iritováni tím, že celou hodinu stráví jednou úlohou, možná ji ani nedořeší. Normálně by jich vyřešili osm. Jenže on či ona si absolutně neuvědomí, že zde nejde o nácvik řešení úloh, ale především o rozvíjení myšlení. A když se děti podílejí na hledání samotného řešení, doberou se k výsledku, který není cizí, je skutečně jejich, ony na něj přišly. Navíc pečlivě pracujeme s rozdílem mezi procesem a konceptem přirozeně je nám dáno, že naše myšlení prochází procesem, aby došlo ke konceptu. Tradičně to ale ve
4 Rozhovor Prof. Milan Hejný škole činíme naopak ukážeme dětem vzoreček, tedy koncept, a pak je nutíme dosazovat do něho, aniž by prošli procesem poznáním. I nejslabší dítě musí zažít radost z poznání Lze však tento přístup aplikovat ve třídě, kde jsou různě nadaní žáci? Přirozeně. Jen musí být výuka organizována tak, aby i ti nejtalentovanější žáci, i ti nejslabší, pracovali. My jsme připravili úlohy, při nichž si každé dítě může určit tempo, jakým jde vpřed. I to nejslabší dítě ale musí zažít radost z poznání. Musí mít onu radost, že řešení vymyslelo, že není takříkajíc intelektuální příživník. Žák ví, že není tak rychlý jako někdo jiný, ale také ví, že sám na řešení přišel že ten je autentický, nikoli protetický. Nejlepší učitel dětem nic neprozrazuje, odpovědnost za chybu nechává na nich, je jim ale skutečným partnerem Co je tedy nejdůležitější vlastností učitele, aby takto děti vedl? Nic dětem neprozradit, umět se jim přizpůsobovat a být jim partnerem. Děti mohou najít nejrůznější řešení, mít řadu nápadů, ale učitel není od toho, aby jen říkal, co je dobře a co špatně. Z toho, přiznávám, má řada učitelů strach. Strach z toho být přistižen, že třeba i něco neví. Učitel nemá vstupovat do myšlenkových pochodů dětí a odpovědnost za případnou chybu má nechávat na nich. Zde totiž zcela platí, že chyba je cesta k poznání. Pokud se dítě dopustí chyby, tou nejhorší variantou je říct mu: Tady je chyba, mělo to být tak a tak. Tím ho odstavíme pouze do role konzumenta. Ideální řešení je ukázat jinou úlohu, při níž si děti samy uvědomí svou předchozí chybu. Sloupečky úloh nejsou o poznání, ale o stereotypním, nudném nácviku který nikam nevede Je tento přístup pro děti přirozenější, snazší? Samozřejmě. Své poznání nepřebírá žák od autority, od učitele, ale od svého kamaráda, jazykem jemu blízkým, velmi přirozeným způsobem. Nezahání ho to do kouta. A navíc vychází i z genetické podmíněnosti, která je patrná i v kognitivní sféře děti jsou naprogramovány na to, aby postupovaly nahoru, aby poznávaly nové věci. Pokud jim dáme sloupečky úloh, kde není poznání, ale jen stereotypní nácvik, nebaví je to, jsou tím otrávení. A nejhorší je, že ti slabší žáci, mezi které jsem patřil i já, se pak jen bojí, že se bude zase počítat, že ostatní pak učitel pochválí, jak jsou rychlí, kdežto oni budou zase ti pomalí. Suma sumárum na jedné straně frustrace, na druhé nuda. To je pravý opak toho, o co se snažíme my. Jaký pokrok děti touto metodou v matematice dělají? Obecně víme, že děti v první třídě nemají jít nad číslo dvacet, ve třetí třetí nad tisícovku. Pokud však necháváme děti v první třídě tvořit vlastní úlohy, pro spolužáky nebo pro učitele, ony samy tam použijí i milion. My dospělí se tváříme, že to nesmějí, ale oni tomu rozumějí. Zde je patrný ten obrovský intelektuální potenciál, který naše malá země má. My se jej ale jakoby snažíme nerozvíjet. Jenomže velké země si mohou dovolit vychovávat extenzivně udržovat slabší průměr a pečovat o svou špičku. Malé země, jako jsme my, si to dovolit nemohou. My nesmíme nechat promarnit talenty, které máme. Zmínil jste složitější příklady je tedy možné vaší metodou přistupovat i ke složitější matematice? I vysokoškolskou matematiku lze takto vyučovat. Já tak například vyučuji budoucí druhostupňové učitele teorii množin hlavně pomocí úloh. Bohužel studenti mají často za sebou tak dlouhé školování vzorcologie, že jsou pak nešťastní, pokud jim řeknu, aby si vzoreček objevili sami. A když už ho objeví, chtějí ode mě potvrdit správnost tohoto zjištění. To by se u dětí zvyklých na naši metodu nestalo. Jinak v tuto chvíli pracujeme na sbírkách úloh, které by byly pro 6. až 9. ročníky, nicméně podle některých učitelů jsou některé naše úlohy složité i pro maturanty. Tento váš přístup zní však spíše jako obecný princip, aplikovatelný na všechny předměty, zejména na ty méně oblíbené a pro děti neatraktivní. Nebo je skutečně jen výsadou matematiků? Matematika má v tomto výsadní postavení, protože s poměrně malou faktografickou a pojmovou výbavou lze formulovat hodně těžké úlohy a zejména jejich široké spektrum. Proto je pro tuto metodu tak vhodná. Tento postoj však významně mění i způsob myšlení, přístupu k problémům. Projevuje se to v jiných předmětech? Zkušenosti s tím mají zejména naši učitelé, nicméně pokud vím, zlepšuje se tím ruku v ruce například i čtenářská gramotnost, protože děti častěji musí vyjádřit svůj názor, vysvětlit ho, prezentovat jej. To vede k soustavné kultivaci jazyka a schopnosti porozumět a vyjadřovat se. Největším úspěchem je skutečný zájem dětí o matematiku Prof. RNDr. Milan Hejný Po absolvování Matematicko-fyzikální fakulty na Karlově univerzitě v Praze (959) působil na ČVUT v Praze, VŠD působí na Karlově univerzitě, kde v roce 993 získal titul profesora matematiky a didaktiky matematiky. Milan Hejný mnoho let učil matematiku na základních školách a od roku 976, kdy společně se svým otcem Vítem Hejným založil letní školy Pythagoras, věnuje všechny svoje síly výzkumu, přípravě budoucích učitelů a práci s učiteli nejen v ČR a SR, ale i v zahraničí (například v Montrealu vedl dvouměsíční intenzivní kvalifikační kurz učitelů Kanady). Po roce 989 krátce působil i jako náměstek ministra školství. Za svoji pedagogickou a vědeckou práci byl prof. Hejný oceněn nejvyšším vyznamenáním Jednoty českých matematiků i nejvyšším vyznamenáním Jednoty slovenských matematiků a fyziků. Prof. Hejný je světově uznávaný odborník, který přednášel na mnoha mezinárodních konferencích a dlouhodobě působil na univerzitách v USA a Kanadě. Kolik škol dosud na tuto metodu výuky matematiky přešlo? Přece jen tak hluboká změna není v učitelské praxi snadným přestupem. Máte pravdu, že přechod k této metodě je náročný. Snažíme se pořádat semináře, kde chceme učitelům s tímto přístupem pomoct. Spoléháme také na zvyšující se počet učitelů, kteří tuto metodu začali využívat, přičemž je o její účinnosti přesvědčil především obrovský zájem dětí. Zájem, se kterým se do té doby nesetkali. Ač se tedy využívání naší učebnice šíří jen postupně a někdy pomalu, objevuje se spolu s tím řada učitelů s velkým U kterým záleží na dětech, naplňuje je jejich zájem a radost z poznání, jde jim o to, že děti vidí šťastné. Co je pro učitele často největší překážkou? 7
5 Pohled nakladatele Možná pocit, že jejich znalosti jsou nedostatečné. Že na to, co děti nakonec počítají, ani nestačí. Na tom ale není nic špatného. Učitel sem nepřichází jako všeznalý mudrc, ale jako někdo, kdo přináší otázky a úlohy, povzbuzuje děti Alarmujícím sdělením mezinárodních výzkumů je zvyšující se nelibost žáků vůči matematice Myslíte si, že impulzem pro změnu našeho přístupu k matematice mohou být zhoršující se výsledky, například v PISA? Osobně považuji za nejvíce alarmující zvyšující se nelibost žáků vůči matematice. Tedy vztahovou záležitost, která má pak obrovský dopad na řadu dalších proměnných. Navíc se jedná o setrvačný, dlouhodobý problém. Pokud jde o poznatky, tam už nejsem tak negativní může to být věcí našich osnov. Vezměme například zlomky, ve kterých naši žáci dopadli špatně, protože se s nimi do páté třídy nesetkají, což je podle mě velká chyba. V našich učebnicích s nimi pracujeme již od první třídy každé dítě přece ví, co je polovina. Školy často plýtvají talentem dětí Jsou v zahraničí nějaké obdobné metody? Abych pravdu řekl, o žádných nevím. Spíše nás kontaktují z jiných zemí, ale bohužel je to více na akademické bázi. Nyní máme velmi dobrou spolupráci s Polskem, z něhož bych zmínil práci Edyty Gruszczyk-Kolczyńské, která svým testem měří matematické nadání dětí. Test na 500 dětech provedla při příchodu do první třídy, talentovaných na matematiku bylo mírně přes 50 %. Po půl roce ve škole je to již jen 0 %. To je velmi alarmující plýtvání talentem. Jaké postavení by měla mít matematika ve škole? Měla by být například povinná maturita z matematiky? Máme-li k dispozici kalkulačky, mohla by být současná matematika ve škole vlastně fakultativní. To, co by měla skutečně žákům a studentům otvírat, není jednoduché počítání, ale způsob myšlení. Myšlení, které potřebuje i archeolog či právník. Přemýšlet logicky, organizovat věci, systematicky je promýšlet. Jak by například vypadaly naše současné zákony, kdyby lidé vládli pravidly logiky? Určitě by byly bez tolika chyb a potřeb doplnění a oprav. A povinná maturita? Určitě bych byl proti, protože si jsem téměř jistý, že by vedla jen k dalšímu zbytečnému biflování bez porozumění. Hejného matematika v učebnicích Přestože netradiční metoda výuky matematiky profesora Hejného zaujala několik nakladatelů, nikdo nenašel odvahu se do vydání učebnice pustit. Rozhodný krok nakonec udělalo Naklada- Vůbec jsme neměli tušení, jak to dopadne. Vnitřně jsme cítili, že je to dobrá cesta, ale zároveň nám bylo jasné, že hodně trnitá. Velkým otazníkem pro nás bylo, zda se po ní budou chtít učitelé vydat, vzpomíná na časy rozhodování odpovědná redaktorka projektu Jana Tomšíková. Jak dále přiznává, trvalo dva roky, než se dostavily první výsledky. A byly úspěšné! Od učitelů, kteří novou metodu ověřovali přímo v prostředí výuky, jsme začali získávat první pozitivní reakce. Ty se týkaly především viditelného rozvoje matematického myšlení u žáků, jejich radosti z objevování a osvojování si nových znalostí a vědomostí, popisuje Tomšíková. Správnost rozhodnutí hledat nové cesty ve výuce matematiky pak v roce 009 ukázalo mezinárodní testování vědomostí žáků (PISA). Podle něj se patnáctiletí Češi umístili v podprůměru čtenářské gramotnosti a o mnoho lépe nedopadli ani v matematice a přírodních vědách. Právě úlohy v PISA jsou určené k testování matematické gramotnosti patnáctiletých žáků jsou vždy zasazeny do určitých reálných situací, což naše děti ve školách příliš často nevidí. Praxe v hodinách matematiky v našich školách 8 většinou vypadá tak, že učitel při převážně instruktivním zadává dětem procvičování samotných algoritmů. Hlavní myšlenka nabízené metody spočívá v poznání, že když žák sám řešením vhodných úloh matematiku objevuje, jsou jeho znalosti pevnější, hlubší a trvalejší. To však vyžaduje mít k dispozici bohaté soubory vhodných úloh, jejichž řešením třída opravdu celou matematiku prvního stupně objeví. Jsme rádi, že právě to se týmu profesora Hejného podařilo v učebnicích matematiky pro. až 5. ročník, které jsme vydali. Žáci s jejich pomocí dokážou například velice rychle vyřešit rovnice o dvou neznámých za pomoci krokování, hraním si s ikonkami zvířátek a porovnáváním jejich síly, vážením na vahách, pomocí hadů či pavučin. A navíc je to i baví, vysvětluje Jana Tomšíková. matiky ucelenou řadu těchto učebnic pro první stupeň. Všechny učebnice jsou plně interaktivní, jsou tedy obohaceny o videa, audia, další cvičení, animace a pokračujeme dál. V současné době zpracováváme rukopis Sbírky úloh pro druhý stupeň a sbírka pak projde zkušebním testováním přímo ve školách. Takže i učitelé na druhém stupni, kteří zatím učili klasickou metodou, si budou moct vyzkoušet netradiční pojetí matematiky, dodává Jana Tomšíková.
6 Rozhovor Jitka Michnová Tvořivější, nadšené a zvídavé děti i to může být matematika Rozhovor s Jitkou Michnovou, ZŠ Ing. M. Plesingera Božinova, Neratovice Již řada učitelů i novinářů se přišla podívat do třídy paní učitelky Jitky Michnové na, o kterém se toho už hodně napsalo. A každý další, kdo třídu navštíví, zažívá zřejmě stejný pocit jako jeho předchůdci že takhle by mělo vypadat, které bychom buď sami rádi ve svých školních letech zažili, nebo bychom jej chtěli dopřát svým dětem. Ani se nedivím, že občas měl někdo i pocit, že to děti s paní učitelkou jen hrají, že ostatní hodiny určitě vypadají jinak. Osobně jsem nikdy nezažila a tudíž ani nevěřila že při hodině matematiky (resp. geometrie) je na všech dětech ve třídě patrné zaujetí, každou chvilku se zvedá les rukou až dokud se nehlásí všichni, a třeťáci jako rozcvičku počítají příklady, které daly zabrat i některým dospělým. S paní učitelkou jsme si tedy povídali o tom, kde se bere ono nadšení a co je potřeba k tomu, aby se toto kouzlo ve třídě odehrálo. Kdy jste se s metodou poprvé setkala? A proč vás oslovila natolik, že jste se rozhodla svou výuku kompletně odklonit od tradičního způsobu? Myslím, že to přinesl sám život. Měla jsem osobní zkušenosti jako žák i jako rodič. Z pohledu rodiče jsem některé věci ve vzdělávání svých synů nepovažovala za nejšťastnější. Chtěla jsem, aby pocit méněcennosti či neschopnosti mí žáci neměli, nezažili. Když pan profesor Hejný mluvil o matematice již na přednáškách na vysoké škole, cítila jsem, že mi mluví z duše. Bylo to přesně to, co jsem potřebovala slyšet, co člověk cítil, že je správné, ale neexistoval odborník, který by řekl: ano, takto můžete učit. Proto jsem i po studiích zůstala v kontaktu s fakultou a s metodou začala ve svých třídách. A již od počátku, kdy jsme ve třídě využili byť jen několik experimentálních úloh, se okamžitě dostavil úspěch a pokrok. Mohla jsem se tak přesvědčit o účinnosti této metody ještě dřív, než byla v učebnicích. Hejného metoda na mě dělá dojem, že je to spíše obecný přístup, který by byl využitelný v jakýchkoli předmětech. Že to je jiná filozofie v přístupu k žákům a učení, která odstupuje od důrazu na roli učitele a proces. Lze tedy její myšlenky využít i v jiných předmětech? Učitel, který chce být úspěšný v matematice, musí splňovat dvě roviny využít geniálně zpracovanou metodu pana profesora a současně být učitelem smýšlejícím konstruktivně. Obecně u něj musí platit, že má se žákem partnerský vztah, klade otázky, vyzývá děti k diskusi, vychází z toho, co znají místo aby jim dokazoval, co nevědí nepotřebuje zadávat nadměrné množství domácí přípravy. Pokud se tyto dvě roviny sejdou, je úspěch zaručen. A přirozeně lze zmíněný konstruktivní přístup využít v jakémkoli oboru či předmětu. Děti se tak učí jinému způsobu myšlení spíše než pouze jinak počítat. Má to nějaký dopad na jejich přístup a výsledky i v jiných předmětech? Matematika je oproti jiným předmětům zejména o rozvoji myšlení. Není jen o logickém uvažování, ale také o kombinatorickém uvažování, o zdravém rozumu a to se následně promítá do dalších předmětů. Děti mají mnohem větší tendenci ptát se, chtít vědět proč, jdou po příčině problémů. A to pak platí napříč předměty. Navíc se mi vybavuje scéna s jednou paní vychovatelkou, která mi potvrdila obrovský rozdíl mezi skupinami, které se učí naší metodou, a těmi, které ne. Mí žáci, pokud od paní vychovatelky dostali například nějakou šablonku a chyběl k ní nos, se okamžitě zvedli, vzali papír a nůžky a vyrobili si ho. Ostatní seděli a čekali, až jim někdo pomůže a dá jim to, co chybí. Obecně bych tedy řekla, že jsou tvořivější a nebojí se. A to je pak patrné ve všech jejich činnostech. 9
7 Rozhovor Jitka Michnová Zůstává mezi dětmi rozdíl podle talentu na matematiku že je ve třídě pár skutečně talentovaných a ostatní víceméně s matematikou bojují? Nebo dává větší šanci i těm, řekněme, slabším? Naše matematika není určitě jen pro ty nadané, spíše naopak. Je ale pravda, že se díky ní ve třídě významně rozevírají nůžky ti talentovaní jdou neuvěřitelně dopředu. Skutečně jsem měla na konci páté třídy děti, které byly absolutně suverénně schopny řešit soustavy rovnic. Slabý žák se sice k tomuto nedobere, je pomalejší, delší dobu setrvá u některé činnosti, ale dělá také významné pokroky. Co má tedy umět páťák, to i naše slabší děti skutečně umí. Jsou pro vás výsledky dětí v olympiádách a výzkumech tou hlavní hnací silou proč v této metodě pokračovat? Nadšení dětí. To je pro mě hlavní motivací. Výsledky v soutěžích a výzkumech jsou již hmatatelné výsledky, které jsou vidět. Dokud se ale nedostaví, což trvá třeba pět let, je skutečně hnací silou a nejsilnější motivací nadšení našich dětí. Matematika se učí velmi dobře, hodiny jsou pestré, žádné stereotypy, děti to baví a baví to i mě. Předpokládala bych, že argumentem proti této metodě je názor, že je nutné stihnout všechnu látku, že není prostor si v hodině hrát Naše metoda je o tom, že děti získávají poznatek ze zkušenosti, ze své činnosti. A postupem času je z toho složitější matematika. Dokud jsme ve fázi získávání zkušenosti, jeví se celá metoda, jako že si jen hrajeme. Pravdou ale je, že děti už v této fázi sbírají hlubší poznání, které se posléze zhodnotí. V první, ve druhé třídě se tedy může zdát, že děti nedělají pokroky, ale již ve třetí třídě, když vše matematicky zapíšeme, je náhle patrné, že děti udělaly skutečně hodně a že jsou výrazně dál než jejich vrstevníci v jiných třídách. Ony už klidně násobí i v oboru velké násobilky, pracují se zápornými čísly a hlavně, není to kvůli tomu, že to po nich někdo chce, ale je to pro ně přirozené. A osobně si myslím, že od třetího ročníku jsme už významně dále než ostatní. Jak jsou vlastně děti hodnoceny? Píší se klasické písemné práce? Hodnocení naší matematiky je skutečně náročné. I zde ale děti píší prověrky nebo úlohy na známky po probrání určité látky. Cvičení na známky píšeme tak jednou za týden, někdy ani to ne. Občas dávám jen jedničky nebo nic. Jde mi o to někam dítě přivést, pomoci mu. Osobně si už ani nevzpomínám, kdy jsem naposledy dala pětku. V pilotní třídě jsme navíc k našim prověrkám psali i ty tzv. běžné prověrky. Jednak jsme chtěli vědět, zda nám někde 0 něco přece jen neuniká, a také abych mohla i rodičům dokázat, že děti vše zvládají. Jak na tento přístup reagují rodiče? Jsou metodou od počátku nadšeni? Nebo to přece jen chvíli trvá, než pochopí, že matematika se dá učit i jinak než tak, jak na to byli sami zvyklí? To je velmi důležitá otázka. Rodiče mají přirozeně obavu o své děti a často považují přístup, jakým byli ve škole vyučováni oni, za dostatečný. Já jsem vždy kladla důraz na komunikaci s rodiči a vysvětlení jim hned na počátku, jak celá koncepce naší matematiky vypadá a k čemu jejich děti přivede. Rodičům jsem na schůzkách například předkládala některé úlohy, aby pochopili matematickou hloubku, která se za nimi skrývá. Současně mám zkušenost, že od třetího ročníku se situace významně uklidňuje děti již vše převádí do matematických zápisů, které jsou rodičům blízké, a navíc přicházejí první soutěže a úspěchy, jež jsou pro rodiče silným argumentem. Obecně ale musím říct, že skutečně nelze komunikaci s rodiči podceňovat. Naše matematika je zabudována do tzv. prostředí, která nejsou pro rodiče srozumitelná. A samozřejmě, chtějí-li se rodiče s dětmi učit, tomuto přístupu nerozumí. Proto je v případě matematiky prosím, aby se s dětmi neučili a nepomáhali jim. Dětem nedávám domácí úkoly a nic navíc od nich nechci, a i přesto vše zvládají. U vás tedy neexistují domácí úkoly? Určitě ne povinné úkoly z matematiky. Máme ale série dobrovolných úkolů, kterými se děti i baví. Nicméně dostávají úkoly v jiných předmětech, například v češtině. Co myslíte, že je největší brzdou pro širší využívání této metody? Proč je stále ještě rozšířena na malém počtu škol? Myslím, že brzdou mohou být peníze. Školy často nemají prostředky na školení učitelů. My nemáme prostředky na školení lektorů, a tak dalším učitelům přednáší stále jen autorský tým, kde jsou všichni vázáni svou hlavní pedagogickou činností. Co mohu potvrdit, je však zájem o naše konference, letní školy a semináře, které jsou vždy plné. V čem je využití této metody nejnáročnější? Určitě není náročné na zázemí školy, na finanční prostředky. Na co je naopak velmi náročné, je učitel. Buď to musí být skutečně konstruktivně smýšlející učitel, nebo se tomu musí alespoň blížit. Řada učitelů to v sobě má, jen o tom nevědí nebo si sami sobě nedovolili to připustit. Když ale učitelé řadu přežívajících předsudků opustí, uvolní se a budou s dětmi přirozeně pracovat, věřím, že budou úspěšní. Jitka Michnová Vystudovala Pedagogickou fakultu Univerzity Karlovy v Praze, obor učitelství pro. stupeň základní školy. Pracovala nejprve jako učitelka v mateřské škole, rok působila jako vychovatelka na základní škole v Neratovicích, kde zůstala jako učitelka. stupně. Spolupracuje s PedfUK Praha jako externí učitel v oblasti didaktiky matematiky či na dalších projektech a DVPP. Od roku 006 je rovněž lektorkou Akademie ho vzdělávání a spoluautorkou učebnic matematiky pro. 5. ročník nakladatelství všeho druhu a čtení knížek všeho druhu. Pokud by se chtěl ředitel/učitel rozhodnout, že na tuto metodu také přistoupí, co by měl být jeho/její první krok? Vřele doporučuji vzít učitele do otevřených hodin, aby viděli děti. Je to podle mě určitě nejúčinnější, protože pokud o tom s někým jen hovořím, zní řada věcí neuvěřitelně. Současně není nejvhodnější učiteli nařídit, že musí podle této metody učit, aniž by k ní sám přilnul. Může pak totiž sklouznout k tomu, že sice vezme naše učebnice, ale dál učí instruktivně, a nedostane se tak k očekávaným výsledkům. Inspirují se u vás vaši kolegové? Ano. A už zaznamenali i své úspěchy, například výsledky v soutěži Cvrček v mé třídě se to už bere jako samozřejmost, ale úspěchy se objevují i u mých kolegů, což mě ohromně těší. Na závěr jedna aktuální otázka byla byste pro povinnou maturitu z matematiky? Trochu bych se obávala, aby se z matematiky nestalo jen učení se pro maturitu. Stereotypní dril maturitních úloh.
8 Pohled učitele Renata Mikolašová Napsali jste nám o vaší zkušenosti s matematikou Matematika je královnou věd, skrývá v sobě velké množství pojmů a pravidel připravila Mgr. Renata Mikolašová, třídní učitelka 5.A ZŠ v Komenského ulici v Bílovci Dobrý učitel si vybere cestu, která vede k rozvoji jeho žáků. Nemusím ve výuce použít jen jednu učebnici, ale jak vyplývá z názorů, počítali jsme i z jiných alternativ, využívali jsme v hodině také PC programy. Matematika dnes není jen o plus a minus, ale o aplikaci těchto znalostí v praxi. A přesně takovou změnu požadují po učitelích odborníci. Nebojte se, kolegové, a zkuste něco, co přinese do vašich hodin změnu a opravdové matematické pracovní prostředí. Volba učebnice Vzdělávání v oboru matematiky klade důraz na důkladné porozumění základním myšlenkovým postupům a pojmům a jejich vzájemným vztahům. Když jsme před pěti lety vybírali nové učebnice pro prvňáčky, naše volba padla na učebnice nakla- RVP a našemu ŠVP, měly přehledné roční plánování, ve svém obsahu neopomíjely ani průřezová témata. Učebnice i pracovní sešity byly pestré jak ve vztahu k metodám a formám práce, tak svým obsahem a náplní. A tak jsme v září 007 začali pracovat s učebnicemi, které byly pro vyučující nové a netradiční. Každá hodina předpokládala důkladnou přípravu učitele a znalost jednotlivých prostředí, které učebnice nabízejí. Metodika je zpracována velmi dobře a byla, hlavně v začátcích, velmi dobrou a důležitou podporou a vysvětlovací oporou. Ohlasy rodičů Občas jsme zaznamenali hlasy rodičů, že sami nechápou, co mají děti doma dělat, co právě procvičují a počítají. Chyběly jim klasické sloupečky s příklady. Děti ovšem většinou věděly, co mají doma procvičovat. Orientovaly se v jednotlivých prostředích, objevovaly svět matematiky zkrátka jinak než jejich rodiče doposud. Proto by měl být každý učitel komunikačně zdatný, aby dokázal ovlivnit postoj rodičů k různým metodám či vyučovacím formám. Musí umět vysvětlit, proč pracuje s dětmi tak či onak. To bývá mnohdy nejsložitější přesvědčit okolí, že tvořivost, kreativita, odvaha riskovat jsou přece vlastnosti, které táhnou výkon nahoru a nutí děti přemýšlet. Tyto učebnice jsou založeny na novém přístupu k výuce, na výchově k tvořivosti a samostatné práci. Zohledňují žáky z hlediska nadání a vlastního tempa. Podporují geometrii, která je v praxi neodmyslitelnou součástí vědění. Jsou určeny jak dětem nadaným, tak i těm, které mají s výukou z různých důvodů potíže. Děti diskutují, argumentují a přicházejí na postup řešení samy. Co na to naši žáci Ondřej: Z matematiky se mi učilo dobře, líbily se mi pyramidy, pavučiny a indické násobení. Některé příklady se mi zdály těžké, nejde mi děda Lesoň. Rodiče říkají, že máme hodně složité učebnice. Barbora: Z učebnice se mi učilo dobře, nejvíce mě bavily logické slovní úlohy, také úlohy o rodině Klosových a Malých. Moc mě nebavila zvířátka dědy Lesoně a geometrie. Nejlepší byl vždy závěr učebnice Žáci sobě. Vendula: Z této učebnice se mi učí dobře, nejvíce pak geometrie. Taky jsem v ní dokázala lépe pochopit zlomky, než mi je vysvětlovali doma rodiče. Mám ráda ještě slovní úlohy. Ondřej: Z těchto učebnic se mi učilo dobře, byly v nich záludné logické úlohy. Mohlo by jich tam být ještě víc. Názory žáků, kteří se v předešlých ročnících učili podle jiných učebnic: Barbora: Tyto učebnice jsou úplně něco jiného. Moc se mi líbí. Někdy byly příklady moc těžké a nedala jsem to. Ale jindy zase ano. Líbily se mi i obrázky. Renáta: Byl to dost velký rozdíl. Na učebnicích se mi líbí zvláštní úkoly pyramidy, pavučiny a některé slovní úkoly. Eliška: Mě překvapily pyramidy a úkoly na Pravdu a Nepravdu.
9 Matematika Ukázky úloh pro. 5. ročník ZŠ Hlubší porozumění sčítání Zpracování informace Doplň číslo Bydleli jsme v 5. podlaží. Přestěhovali jsme se o podlaží výše. Ve kterém podlaží bydlíme teď? Teď bydlíme v _ podlaží. Doplň, aby byl součet tří sousedních políček 6 0 Bus Můžeš každý nákup zaplatit pouze třemi mincemi? Koupil Za kolik jsem Kč 3 Kč 6 Kč 8 Kč Kč Platil jsem Kč Kč 5 Kč 0 Kč Vyřeš a krokuj Doplň Spoj 3 čísla a vytvoř 9 Hra 3 + = 6 + = = = = = + + Vyřeš šifru 8 5 = A + = C = J = M = R 5 3 = U 3 = S 3 7 Zapiš kolik Žlutých je o _ více / méně než zelených. Bylo by dobré, aby si žáci situaci nakreslili. Obrázek pomůže také u slovní úlohy na straně. Jeden žák zavelí: Postav se na pětku, jdi kroky vpřed, pak kroky vpřed. Teď! Žáci řeší úlohu v lavicích. Pak si zvolí žáka, který výsledek odkrokuje. Postupně tak řešíme všech 6 úloh. 3 Kolik cestujících jelo v autobusu na úseku od A do B? Kolik na úseku od B do C? Kolik na úseku od C do D? Poslední řádek si vyplní žák sám. 37. ročník. ročník. ročník 3. ročník Doplň závodník pořadí Práce se strukturovanou informací Písemné odčítání III Aritmetické algoritmy John nám předvedl, že lze jeho způsob písemného odčítání použít ve všech případech. Vypočítej stejně jako John: a) 63 8; b) 8 37; c) Za č. 5 jsou hlemýždi č.. Hned za č. 5 je č. _. Před č. jsou hlemýždi č.. Hned před č. je č. _. Za č. _ následuje č.. Před č. _ je č = = Doplň, aby byl součet tří sousedních čísel 8 Doplň tak, aby byl součet dvou čísel ve vybarvených polích Každý ze čtyř barevných útvarů rozděl na dvě části a slož z nich čtverec. Jak jsem nakupoval Koupil Za kolik jsem Kč 7 Kč Kč Kč Platil jsem Kč Kč 5 Kč 0 Kč HRA Odeber dřívka, aby zůstaly jen čtverce. Ema má 0 Kč. Má pětkrát víc než Jan. Kolik korun má Jan? Jak by se řešení změnilo, kdybychom místo součtu 8 požadovali jiný počet, např. nebo, 9 či 0? Snažíme se platit nejmenším počtem mincí. Doplníme do tabulky poslední řádek. Přeměna rovinných útvarů (rovinná chirurgie) patřila k základním geometrickým m dovednostem řeckých matematiků. Slavnou Pythagorovu větu budeme v budoucnu dokazovat at tímto nástrojem. 9
10 Matematika Ukázky úloh pro. 5. ročník ZŠ Sousedé Aritmetické vztahy Schody a rovnice Doplň tak, aby byl součet tří sousedních čísel 7. Doplň tak, aby byl součet tří sousedních čísel 0 a součet všech pěti čísel Z původních peněz nám zbylo 0 Kč. Jakou částku jsme již utratili, jestliže jsme na začátku měli: a) 0 Kč; d) 50 Kč; b) 80 Kč; e) Kč; c) 60 Kč; f) 0 Kč? 3 Doplň do tabulky indického násobení chybějící číslice. 0 Přepiš do sešitu, vypočítej a zkontroluj na kalkulačce (70 + 7) 59 (70 7) (60 + 7) 58 (60 7) ( ) 357 (50 37) (0 + 7) 56 (0 7) 3 Do čtvercové mříže narýsuj všech pět typů rovnoramenných trojúhelníků, které můžeš vymodelovat na geodesce (viz str. 8): a) Změř v milimetrech obvod každého z nich. b) Zjisti jejich obsahy Vyřeš do sešitu. Doplň do dvou žlutých polí tři, anebo čtyři šipky tak, aby byl zápis krokování na schodech správný. Šipky ve žlutých polích musejí mít stejný směr. V prvním žlutém poli musí být více, anebo stejně šipek jako ve druhém. Najdi více řešení. Pokračuj v řadě čísel, až překročíš 00: a),, 8, 5, 3 ; b), 9, 7, 5, 33 ; c), 8,, 0 5 Pokračuj v řadě čísel, až překročíš 00: a) 5,, 3, 6 ; b) 9, 30,, 5 ; c) 37, 5, 53, 6 Již před 000 lety lidé znali polovinu, třetinu, čtvrtinu, stojedenatřicetinu aj. a uměli je používat. Trvalo jim více než 000 let, než objevili takový zlomek, jako jsou např. 3/7. Proto i my náročný pojem zlomek připravujeme s velikým předstihem tak, jak tomu bylo v historii Zaokrouhlování můžeme zapsat pomocí znaku. Například: Zaokrouhli na desítky a zapiš: 8, 97, 7, 555, 6, 80,, 36, 65, 999. Kalkulačka je rychlým a výkonným řemeslníkem ve světě aritmetiky. Myslet ale nedokáže. Je chytrá jenom tak, jak chytrý a šikovný je ten, kdo ji používá. 3. ročník 3. ročník 3. ročník 5. ročník Náhodná procházka 3 Vyřeš pavučinu, ve které je osm čísel. Zjisti hodnotu žluté i modré šipky, když je: A B C D Stojím na horním poli označeném X. Po podlaze se pohybuji podle hodu mincí. Padne-li orel (o), postoupím o pole ve směru šipky o. Padneli panna (p), postoupím o pole ve směru šipky p. Při každé procházce mám 6 hodů. První procházka byla určena těmito hody: o, o, p, p, o, p. Skončil jsem na poli D. Celý postup zapíši XooppopD. Vyřeš úlohu: a) Na kterém poli skončí procházka Xpooopo? b) Najdi procházku, která skončí na poli E. Hledej více řešení. c) Uskutečni 0 procházek a do tabulky zapiš, kolikrát jsi skončil na poli A, kolikrát na B atd. Na poli A B C D E F G Skončil jsem Vyřeš algebrogramy: a) A A + AA = 6; f) JJ + K K = ; b) B B + C C = 3; g) LL + L L + L = 60; c) D D + E E = 37; h) MM + N N = 0 + P; d) F F + G G = 00; i) QQ + R R = 0 S; e) HH + H H = 30 I; j) UU = U U + U V. 3 Pokračuj v řadě, která se láme číslem 50: a) 5, 0, 35, 50, 65, 5, 30 ; c), 5, 9 ; b), 3, 5 ; d) 5, 3, Kolik let je dohromady bratrům Hančiny tety? (Viz str. 6.) O X P A B C D E F G a) F = 76, G = 5; b) E = 53, G = ; c) E = 66, H = 7; d) A = 8, H = 95; e) A = 7, D = 00; f) E + F = 8, B = 7; g) E + F = 3, B = ; h) E + F =, B = 5. * Vyřeš, když víš, že v horní pavučině se E + F = 3. Zjisti hodnotu žluté i modré šipky, když je: a) C = 8; b) C = 38; c) C = 3; d) G = 33; e) G = 9; f) G = 68; g) H = 38; h) H = 0; i) H = 83; j) D = 0; k) D = 3; l) D = Vyřeš. U prvních tří obdélníků najdi součet jeho čtyř středových čísel. U posledního obdélníku je tento součet Vyřeš hady. 7 K Výprava trvala a) 00 hodin, b) 000 hodin, c) hodin, d) hodin. Kolik je to dnů? Kolik je to měsíců? Výsledky najdi jako dělení se zbytkem a pak je zaokrouhli na celé dny a celé měsíce. Měsíc počítáme jako 30 dnů. 8 Jedno z čísel 55, 56,, 6, 65 má tu vlastnost, že při dělení kterýmkoli z čísel, 3,, 5 a 6 vyjde zbytek. Které je to číslo? 9 Číslo 69 má tu vlastnost, že při dělení kterýmkoli z čísel 6, 7 a 8 vyjde zbytek. Najdi další čtyři trojmístná čísla mající tuto vlastnost. 0 * Vyřeš algebrogramy : 8 : + 6 : a) ABC : C = CC b) ABC : C = BC c) AAB : B = CB d) ABA : A = CCA E F * G H 60 Při jedné náhodné procházce žádnou hlubší zákonitost nenajdeme. Po tisíci náhodných procházkách můžeme vyslovit závažná tvrzení. Taková tvrzení používají při své práci ekonomové, biologové, astronomové, dopravci apod. 6 ZÁKONITOSTI, VZTAHY A PRÁCE S DATY 3
11 Rozhovor Pavla Polechová o matematice v MŠ Matematika v mateřské škole? Proč ne?! připravila Leona G. Šteigrová Mateřskou školu si bezesporu málokdy spojíme s kroužkem matematiky. O tom, že na tom není nic zvláštního, že to děti baví a dokáže zaujmout i největší zlobily, jsme si povídali s Pavlou Polechovou, která se tomuto tématu věnuje a kroužky sama vede. Proč vůbec začínat s matematikou již u tak malých dětí? Nemají na čísla ještě hodně času? A jedná se vůbec o matematiku, jak si ji řada z nás představuje, nebo je to spíše o něčem jiném? Děti si s matematikou začínají samy. Tady je důležité poznamenat, že pracuji vždy paralelně s vychovatelkou a nemusím se v daný okamžik starat o všechny děti. Mohu být s několika dětmi v malé oddělené místnosti, která je používána i jinými lektorkami a nese hrdý název učebna, ale já ji vnímám jako specializovanou hernu, jejíž zaměření se mění. V úterý a v pátek mezi půl devátou a desátou je to herna zaměřená na matematiku. Možnost přijít do matematické her- RNDr. Pavla Polechová, CSc. Vystudovala Matematicko-fyzikální fakultu Univerzity Karlovy v Praze. Řadu let pracovala ve Hvězdárně a planetáriu hl. města Prahy, kde vedla kurzy a kroužky matematiky, astronomie a astrofyziky pro ZŠ a SŠ, poté přešla do Ústavu V letech působila na České školní inspekci, dalších pět let pak strávila na Ministerstvu školství, mládeže a tělovýchovy se zaměřením na koncepce a mezinárodní spolupráci. Několik let také externě spolupracovala s Výzkumným ústavem pedagogickým. Nyní působí v občanském sdružení a klubu dětí Hlásek a v komunitní škole Robinson, kde se zaměřuje právě na výchovu pro vztah k matematice. ny mají všechny děti, které v předškolním zařízení aktuálně jsou. Častěji ale rozložím hračky ve velké hlavní herně, aby se k nim mohly dostat všechny děti zcela spontánně, když je to zrovna napadne i ty, které by samy od sebe nepřišly. Pokud jde o zmíněná čísla : mluvená podoba čísla se používá běžně, tak jako v rodině, podle potřeby ( je tu ještě jedno místečko, podej mi druhou ručičku, ). Hlavní vychovatelka děti na začátku dne často nahlas počítá a děti čísla jdoucí za sebou opakují s ní. V psané či tištěné podobě ale pracujeme s čísly skutečně jen výjimečně, a to i když se sejde skupinka dětí, která je zná. Já děti čísla neučím, takže ano, myslím si, že je to o něčem jiném, než si většina lidí představuje. Když přišla dcerka hlavní vychovatelky (školačka) poprvé za maminkou, nejdřív se při zmínce o matematice skoro vyděsila. Pak viděla naše hračky a změnu postoje nebylo možné na její tváři přehlédnout. O ten jiný postoj nám právě hodně jde. Hovoříme-li o mateřské škole s jak starými dětmi lze pracovat, resp. vy osobně pracujete? Nejmladším dětem, které se o tyto činnosti zajímají, nejsou v některých případech ani tři roky. Dětem těsně před vstupem do povinného vzdělávání umožňuji pobyt v matematicky obohaceném prostředí přednostně, ale odcházejí a odpojují se samy a nikdy je ani k přechodu do malé herny nenutím. Jaké úlohy či aktivity děláte? První inspirací byly učebnice pro. třídu týmu prof. Hejného. Najdeme tam třeba rozvíjení citu pro rytmus optický i zvukový, takže u nás například používáme uvítací říkanku, při níž lze tleskat a dupat do rytmu. Pak jsou tam různá bludiště, ta děti také velmi rády řeší, což je vstup do metody pokusů a omylů včetně záznamu každého pokusu. Velmi oblíbené je u nás také třídění obrázků na kartičkách nebo dřevěných destičkách podle jejich barev a tvarů. Dále můžeme podporovat schopnost analyzovat situaci vykreslenou na obrázcích, kde jde o určování polohy, směru, porovnání velikostí vše samozřejmě formou hry a jen pokud a dokud to děti baví. Malé děti mohou hrát kvarteta ve dvou, kdy pracují s negací (musím od druhého chtít to, co nemám). Děti také baví modelovat tělesa ze špejlí a modelíny, hrát hry pracující fakticky s obvodem a obsahem pravoúhelníků Jak se k tomu děti staví? Nechtějí si raději hrát? Tyto aktivity provádějí děti zcela spontánně, samostatně a proto, že chtějí, takže ony si opravdu vlastně hrají. Jde o to, aby si matematiku mohly užívat nejen v mateřské, ale i v základní škole, neboť víme, že to je možné. Dnes jsem byla se zahraničním studentem u paní učitelky Jitky Michnové, byla to moje třetí návštěva u ní. Opět jsem viděla trvalý a jaksi samozřejmý respekt k diskusi dětí, opět jsem byla svědkem radosti při ohlášení, že následující hodinu bude matematika, viděla jsem hravost a zájem, opět došlo i na výbuch nadšení. Na konci hodiny jsem se od šťastných dětí dozvěděla, že to bylo hustý, což je projev nejvyššího uznání. Opravdu je to tak, že žádné dítě se nemusí matematiky bát, naopak si ji může užívat, protože děti experiment, objevování a tvoření milují. Jen to využít! Je mezi dětmi patrné, že některé jsou na matematiku nadané, jde jim to od ruky, a jiné spíše ne? Některé děti, dokonce i děti kolem tří let věku, mají o matematické aktivity větší zájem a dožadují se slovy já chci něco dělat nebo ještě, ještě, ale postupně se chytí všechny. Nevím, co je dřív jestli zájem, a tedy rozvoj nadání, nebo zda z nadání plyne
12 Rozhovor Pavla Polechová o matematice v MŠ zájem a k tomu bych se přikláněla jde o vzájemnou interakci obojího. Zájem se ale nedostaví, když budu dítě do něčeho nutit, stejně jako se nedostaví objev zákonitosti nebo vztahu, když ho učitel prozradí dřív, než k němu může dítě dojít samo. Umí tento přístup zaujmout i hyperaktivní zlobidla, nebo přitahuje spíš přemýšlivé děti? V Hlásku jsme měli jedno přemýšlivé zlobidlo jménem Jiřík, které bylo aktivní až hyperaktivní. Potřeboval víc pozornosti, když nebyl zlobidlem. Pak ke zlobení nedošlo. A jsou lepší kluci (jak by asi řada lidí normálně očekávala), nebo holčičky? Moje skóre při sledování nejaktivnějších holčiček a kluků je 5: ve prospěch holčiček. Podobnou zkušenost mají i jiní, kdo používají metodu prof. Hejného a mám dojem, že by to stálo za výzkum. Ve škole pozorujeme, že holčičky jsou snaživější a poslušnější, takže ochotněji sledují učitelku, která jim vysvětlí mnohé z toho, na co by bez ní přišly samy ale už nemohou, už se to dozvěděly. Kluci snahy učitelky všechno vysvětlit ignorují častěji než děvčata, takže šance na jejich vlastní matematické objevy jsou vyšší. Troufalá hypotéza, že? V čem je největší přínos tohoto přístupu? Jaký vliv má na budoucnost dětí? Mám za to, že vliv je zcela zásadní. Myslím, že tento přístup prostě otvírá, vlastně spíše udržuje a posiluje přirozenou chuť k učení jako takovému. Malé děti pořád něco zkouší neboli pořád se učí z vlastního zájmu a s plným nasazením. Jak píše John Holt, kdybychom děti učili chodit a mluvit, nikdy by se to nenaučily. Řada dětí má dnes odklad na přechod do první třídy na základní škole. Může dětem tento přístup pomoct při přechodu do první třídy? O tom jsem přesvědčena. Možná by ale dávalo smysl ptát se i obráceně: do jaké míry a za jakých okolností lze efekt tohoto přístupu při přechodu do první třídy potlačit či zlikvidovat? To mi dělá starosti. Nerada dělám něco, co má malý nebo pomíjivý efekt. Pomůže dětem účast v těchto aktivitách v budoucnosti s lepším přístupem, zájmem i výsledky jen v matematice, nebo má dopad i na další předměty? Už jsem se vlastně zmínila o podpoře kompetence k učení. Určitě také dochází ke zlepšování schopnosti logicky uvažovat a argumentovat. Zkušenosti kolegů rovněž ukazují na zlepšení porozumění mluvenému či psanému slovu, což zpětně ovlivňuje učení ve všech ostatních předmětech. Některé prvky, např. dramatizaci, lze využít v ostatních předmětech přímo. To mi připomíná, že v hlavní roli jsou děti, nikoli učitel. Lze tento přístup aplikovat v každé mateřské škole? Nebo je náročný na kapacity, čas? Problémem může být matematicky obohacené prostředí, tedy matematicky orientované a přitom poměrně jednoduché hračky. Vyrábím si je většinou sama. Jsou ale i velmi nenáročné, a přitom vděčné pomůcky, třeba papír ve tvaru čtverce a nůžky. Pokud bych se rozhodla v mateřské škole touto cestou vydat, co bych měla podniknout? Určitě by bylo inspirativní podívat se do hodiny učitele, který tuto metodu dobře používá, a to nejlépe v první třídě. Také do učebnice pro první třídu. Neméně důležité je to, co platí pro vzdělávání obecně pozorovat děti, přemýšlet o nich a nechat se jimi inspirovat. Vysvědčení vzdělávacím systémům evropských zemí Studie Klíčové údaje o vzdělávání 0 je pravidelně zpracovávána Evropskou komisí (ve spolupráci sítě Eurydice a Eurostat) k posouzení vývoje národních vzdělávacích systémů v Evropě. Publikace prostřednictvím 95 ukazatelů zachycuje oblasti, jako jsou demografická situace, struktury vzdělávacích systémů, účast na vzdělávání, finanční zdroje, učitelé a řídící pracovníci, vzdělávací procesy a úrovně dosaženého vzdělání a přechod do zaměstnání. Za pozitivní trendy napříč Evropou lze označit delší dobu účasti v povinném vzdělávání, vzrůstající autonomii škol a zejména vysokoškolských institucí, zvyšující se důležitost zabezpečení kvality vzdělávání či nárůst počtu absolventů vysokých škol a jejich rychlé uplatnění na trhu práce. Citlivějším tématem je otázka financování vzdělávání, které se v letech udrželo na stejných hodnotách, avšak na hospodářskou krizi od roku 008 zareagovala řada zemí různými kroky, často však se snahou tyto prostředky neomezovat. Obecně tak i financování v řadě zemí zůstalo stabilní. Negativním zjištěním je, že podle studie atraktivita učitelské profese klesá, a to i přesto, že řada evropských zemí zavedla podpůrná opatření pro začínající učitele a současně zvýšila učitelům platy, někde až o 0 %. Studie však současně upozorňuje na rostoucí nedostatek učitelů v některých zemích Evropy. Například Německo, Velká Británie, Itálie, Nizozemsko, Rakousko či Belgie se mohou v budoucnu potýkat s vážným nedostatkem učitelů. Věk mnohých současných učitelů se blíží věku důchodovému a současně klesá počet absolventů učitelského studia. Více informací: eurydice/documents/key_data_series/3en_hi.pdf 5
13 Téma Hejného matematika i pro druhý stupeň Matematika i pro druhý stupeň a často ještě mnohem dál připravila Pavla Polechová, koordinátorka týmu pro přípravu souborů úloh matematiky pro. stupeň Zatímco v učebnicích a pracovních listech jsou úlohy z jednotlivých prostředí promíchány, vznikají nyní Sešity pro první stupeň, v nichž budou jednotlivá prostředí pojednána jako samostatné celky. Učitelé prvního stupně uvidí, kam až jednotlivá prostředí na konci prvního stupně dosáhnou a která témata matematiky pokryjí, zatímco učitelé vyšších stupňů se dozvědí něco o znalostech a dovednostech dětí, které prošly touto metodikou. Tým profesora Hejného totiž chystá soubor i pro druhý až třetí stupeň. Úlohy nebudou uspořádány podle ročníků, ale budou gradovány podle různých parametrů obtížnosti a učitelé dostanou i určité know-how, aby mohli sami obtížnost jednotlivých úloh modifikovat a využívat proměnnou obtížnost jako odpověď na výsledek formativního hodnocení. INZERCE John F. Taylor Jak přežít s hyperaktivitou a poruchami pozornosti Rádce pro děti s ADHD a ADD Napomínají tě ve škole za to, že vyrušuješ? Nejde ti učení? Neumíš usměrnit chování? Možná máš ADD (poruchu pozornosti) nebo ADHD (poruchu pozornosti spojenou s hyperaktivitou). V této knize se dozvíš informace o těchto poruchách. Naučíš se, jak udržet na uzdě své nálady a jak překonat pocity neúspěchu a strachu. brož., 8 s., 5 Kč Žádejte v knihkupectvích nebo na adrese nakladatelství: Portál s. r. o., tel , obchod@portal.cz Knihkupectví Portál: Jindřišská 30, Praha / Klapkova, Praha 8 / Dominikánské nám. 8, Brno Provizorně tým pracuje se strukturou, kterou prof. Hejný vytvořil již před rokem. Struktura obsahuje celá čísla, racionální a reálná čísla, rovnice, práci s daty, jazyk písmen (algebru), rovinnou geometrii a prostorovou geometrii. Není pochyb o tom, že prostředí mohou pokrýt celou oblast matematiky i pro druhý a třetí stupeň včetně např. funkcí. Vše bude Naděžda Kalábová Příroda plná her Hry plné přírody Publikace představuje soubor her, činností a úkolů odehrávajících se v přírodě nebo týkajících se přírody. Aktivity nenásilně a zábavnou formou informují, poučí o zákonitostech a dějích v přírodě, lze je využít pro práci v hodinách přírodopisu, ale také českého jazyka, matematiky, pracovního, výtvarné či tělesné výchovy, úkoly totiž často pracují s poznatky a tématy různých oborů. brož., 60 s., 5 Kč prověřeno i podle RVP. Některá témata, která jsou v tradičním pojetí matematiky zařazena samostatně, jsou v metodice tématy průřezovými: např. kombinatorika, úprava výrazů. Každý sešit má dvě části: úlohy pro žáky a metodiku pro učitele s výsledky a komentáři. Sešity budou vydány v elektronické podobě, což umožní materiály v pravidelných zhruba půlročních intervalech doplňovat, opravovat i obohacovat o komentáře a nové zkušenosti. Pokud student neprošel Hejného matematikou na prvním stupni, může na tento přístup přejít zřejmě i později, nicméně problém je v tom, že na druhém stupni je zpravidla již vztah k matematice buď vytvořen, nebo poničen. Ani to ale nemusí být obecně platné, já sama jsem získala k matematice vztah až v sedmé třídě. Jeden příklad ze souborů úloh pro. stupeň Číselné vztahy, které otevírají cestu k algebře, obsahují například tuto úlohu: Z hlavy vypočítejte a výsledky si zapisujte. + 3 = = = = = = = = Vysvětlete, jak jste získali poslední výsledek. (Série dílčích výsledků, 9, 6, 5, 36, vede k poznání, že výsledek je čtverec. Přesněji: (n-) = n. Tento výsledek lze zdůvodnit graficky pomocí postupného zvětšování čtverce při ponechání jednoho pevného vrcholu, nebo dokázat matematickou indukcí.) 6
12 klíčových principů Hejného metody
 12 klíčových principů Hejného metody Hejného metoda je založena na respektování 12 základních principů, které geniálně skládá do uceleného konceptu tak, aby dítě objevovalo matematiku samo a s radostí.
12 klíčových principů Hejného metody Hejného metoda je založena na respektování 12 základních principů, které geniálně skládá do uceleného konceptu tak, aby dítě objevovalo matematiku samo a s radostí.
MATEMATIKA HEJNÉHO. S jakými jste přišli otázkami?
 MATEMATIKA HEJNÉHO S jakými jste přišli otázkami? Desatero pro rodiče Věřme tomu, že děti jsou chytré a že jsou schopny při dobrém vedení většinu matematických poznatků objevit samy. Raději nehodnoťte.
MATEMATIKA HEJNÉHO S jakými jste přišli otázkami? Desatero pro rodiče Věřme tomu, že děti jsou chytré a že jsou schopny při dobrém vedení většinu matematických poznatků objevit samy. Raději nehodnoťte.
DOTAZNÍK PRO URČENÍ UČEBNÍHO STYLU
 DOTAZNÍK PRO URČENÍ UČEBNÍHO STYLU Projekt MOTIVALUE Jméno: Třida: Pokyny Prosím vyplňte vaše celé jméno. Vaše jméno bude vytištěno na informačním listu s výsledky. U každé ze 44 otázek vyberte a nebo
DOTAZNÍK PRO URČENÍ UČEBNÍHO STYLU Projekt MOTIVALUE Jméno: Třida: Pokyny Prosím vyplňte vaše celé jméno. Vaše jméno bude vytištěno na informačním listu s výsledky. U každé ze 44 otázek vyberte a nebo
Základy Hejného metody zpracovala Ivana Čiháková Matematika dle metody VOBS.
 Základy Hejného metody zpracovala Ivana Čiháková ivana.cihakova@centrum.cz Matematika dle metody VOBS. Úlohy jsou z učebnic matematiky pro 1. 5. ročník vydané nakladatelstvím Fraus v letech 2007-2011 Autoři
Základy Hejného metody zpracovala Ivana Čiháková ivana.cihakova@centrum.cz Matematika dle metody VOBS. Úlohy jsou z učebnic matematiky pro 1. 5. ročník vydané nakladatelstvím Fraus v letech 2007-2011 Autoři
MODERNÍ VYUČOVÁNÍ. Moderní výuka přírodních věd. Každé dítě musí zažít radost z poznání. Téma: MATEMATIKA A PŘÍRODNÍ VĚDY
 MODERNÍ VYUČOVÁNÍ Moderní výuka přírodních věd Příprava dnešních studentů na příležitosti zítřka Téma: MATEMATIKA A PŘÍRODNÍ VĚDY květen červen / 2012 Každé dítě musí zažít radost z poznání Prof. Milan
MODERNÍ VYUČOVÁNÍ Moderní výuka přírodních věd Příprava dnešních studentů na příležitosti zítřka Téma: MATEMATIKA A PŘÍRODNÍ VĚDY květen červen / 2012 Každé dítě musí zažít radost z poznání Prof. Milan
Úvod do matematiky profesora Hejného. VISK Praha
 Úvod do matematiky profesora Hejného VISK Praha 6. 1. 2015 Metoda VOBS Schéma? Hejného metoda vyučování matematice Hejného metoda vyučování matematice Východiska Učebnice a autoři, působení Úzké spojení
Úvod do matematiky profesora Hejného VISK Praha 6. 1. 2015 Metoda VOBS Schéma? Hejného metoda vyučování matematice Hejného metoda vyučování matematice Východiska Učebnice a autoři, působení Úzké spojení
ZŠ KUNOVICE, U PÁLENICE
 ZŠ KUNOVICE, U PÁLENICE ŠKOLA, KDE SI SVŮJ POCIT ÚSPĚCHU ZAŽIJE KAŽDÉ DÍTĚ ŠKOLA,KDE UČITELÉ I ŽÁCI PŘEMÝŠLEJÍ NAD TÍM, CO, JAK A PROČ DĚLAJÍ CO NA ŠKOLE OCEŇUJÍ RODIČE CO NA ŠKOLE OCEŇUJÍ RODIČE Zdroj:
ZŠ KUNOVICE, U PÁLENICE ŠKOLA, KDE SI SVŮJ POCIT ÚSPĚCHU ZAŽIJE KAŽDÉ DÍTĚ ŠKOLA,KDE UČITELÉ I ŽÁCI PŘEMÝŠLEJÍ NAD TÍM, CO, JAK A PROČ DĚLAJÍ CO NA ŠKOLE OCEŇUJÍ RODIČE CO NA ŠKOLE OCEŇUJÍ RODIČE Zdroj:
MATEMATIKA - 4. ROČNÍK
 VZDĚLÁVACÍ OBLAST: VZDĚLÁVACÍ OBOR: PŘEDMĚT: MATEMATIKA A JEJÍ APLIKACE MATEMATIKA MATEMATIKA - 4. ROČNÍK Téma, učivo Rozvíjené kompetence, očekávané výstupy Mezipředmětové vztahy Poznámky Opakování ze
VZDĚLÁVACÍ OBLAST: VZDĚLÁVACÍ OBOR: PŘEDMĚT: MATEMATIKA A JEJÍ APLIKACE MATEMATIKA MATEMATIKA - 4. ROČNÍK Téma, učivo Rozvíjené kompetence, očekávané výstupy Mezipředmětové vztahy Poznámky Opakování ze
II. MATEMATIKA A JEJÍ APLIKACE
 II. MATEMATIKA A JEJÍ APLIKACE Charakteristika vzdělávací oblasti Tato oblast je v našem vzdělávání zastoupena jedním předmětem matematikou, od 1. do 9. ročníku. Podle vývoje dětské psychiky a zejména
II. MATEMATIKA A JEJÍ APLIKACE Charakteristika vzdělávací oblasti Tato oblast je v našem vzdělávání zastoupena jedním předmětem matematikou, od 1. do 9. ročníku. Podle vývoje dětské psychiky a zejména
Jméno a Příjmení. Třída. Škola
 Studentský dotazník Vážení studenti, cílem tohoto průzkumu je zjistit váš postoj k matematice a k výukovému nástroji Khan Academy. Vaše názory a odpovědi pomohou dalším studentům a učitelům při zapojování
Studentský dotazník Vážení studenti, cílem tohoto průzkumu je zjistit váš postoj k matematice a k výukovému nástroji Khan Academy. Vaše názory a odpovědi pomohou dalším studentům a učitelům při zapojování
Testy do hodin - souhrnný test - 6. ročník
 Kolik procent škol jste předstihli Škola: Název: Obec: BCEH ZŠ a MŠ, Slezská 316 Slavkov - 6. ročník ČESKÝ JAZYK Máte lepší výsledky než 7 % zúčastněných škol. MATEMATIKA Máte lepší výsledky než 7 % zúčastněných
Kolik procent škol jste předstihli Škola: Název: Obec: BCEH ZŠ a MŠ, Slezská 316 Slavkov - 6. ročník ČESKÝ JAZYK Máte lepší výsledky než 7 % zúčastněných škol. MATEMATIKA Máte lepší výsledky než 7 % zúčastněných
Časové a organizační vymezení
 Vzdělávací oblast Vzdělávací obor Vyučovací předmět Týdenní hodinové dotace Časové a organizační vymezení Matematika a její aplikace Matematika a její aplikace Matematika 1. stupeň 2. stupeň 1. ročník
Vzdělávací oblast Vzdělávací obor Vyučovací předmět Týdenní hodinové dotace Časové a organizační vymezení Matematika a její aplikace Matematika a její aplikace Matematika 1. stupeň 2. stupeň 1. ročník
Matematika s chutí Proč? S kým? A jak?
 Matematika s chutí Proč? S kým? A jak? První otázka Proč jsme se rozhodli realizovat projekt Matematika s chutí? Důvod první: Motivace a vztah k matematice Od roku 2003 (PISA věnovaná především matematice)
Matematika s chutí Proč? S kým? A jak? První otázka Proč jsme se rozhodli realizovat projekt Matematika s chutí? Důvod první: Motivace a vztah k matematice Od roku 2003 (PISA věnovaná především matematice)
Příloha č. 3 Vybrané ukazatele specifického tematického šetření
 Tabulka P8 Vybrané ukazatele specifického tematického šetření Vybrané ukazatele specifického tematického šetření k hodnocení organizace vzdělávání a dovedností dětí v oblasti matematické gramotnosti v
Tabulka P8 Vybrané ukazatele specifického tematického šetření Vybrané ukazatele specifického tematického šetření k hodnocení organizace vzdělávání a dovedností dětí v oblasti matematické gramotnosti v
Místní akční plán rozvoje vzdělávání II ORP Strakonice CZ /0.0/0.0/17_047/
 Místní akční plán rozvoje vzdělávání II ORP Strakonice CZ.02.3.68/0.0/0.0/17_047/0009074 Členové pracovní skupiny ve spolupráci s realizačním týmem identifikovali a popsali příčiny problémů ke každé prioritní
Místní akční plán rozvoje vzdělávání II ORP Strakonice CZ.02.3.68/0.0/0.0/17_047/0009074 Členové pracovní skupiny ve spolupráci s realizačním týmem identifikovali a popsali příčiny problémů ke každé prioritní
Základní škola a Mateřská škola Třešňová 99 Osoblaha Výsledky žáků ze základní školy
 Kód školy: 13017 HLAVNÍ ŠETŘENÍ PISA 2015 ŠKOLNÍ ZPRÁVA Základní škola a Mateřská škola Třešňová 99 Osoblaha Výsledky žáků ze základní školy Praha, leden 2016 Obsah 1 Úvod... 3 2 Šetření PISA... 3 3 Gramotnosti
Kód školy: 13017 HLAVNÍ ŠETŘENÍ PISA 2015 ŠKOLNÍ ZPRÁVA Základní škola a Mateřská škola Třešňová 99 Osoblaha Výsledky žáků ze základní školy Praha, leden 2016 Obsah 1 Úvod... 3 2 Šetření PISA... 3 3 Gramotnosti
HEJNÉHO METODA V MATEMATICE NA PRVNÍM STUPNI ZŠ
 HEJNÉHO METODA V MATEMATICE NA PRVNÍM STUPNI ZŠ MGR. Jana Hromasová Zasloužená radost z poznání je hlavní autorem a vedoucím autorského kolektivu, který pro Nakladatelství Fraus vytvořil učebnice matematiky
HEJNÉHO METODA V MATEMATICE NA PRVNÍM STUPNI ZŠ MGR. Jana Hromasová Zasloužená radost z poznání je hlavní autorem a vedoucím autorského kolektivu, který pro Nakladatelství Fraus vytvořil učebnice matematiky
Mezinárodní výzkum PISA 2009
 Mezinárodní výzkum PISA 2009 Zdroj informací: Palečková, J., Tomášek, V., Basl, J,: Hlavní zjištění výzkumu PISA 2009 (Umíme ještě číst?). Praha: ÚIV 2010. Palečková, J., Tomášek V. Hlavní zjištění PISA
Mezinárodní výzkum PISA 2009 Zdroj informací: Palečková, J., Tomášek, V., Basl, J,: Hlavní zjištění výzkumu PISA 2009 (Umíme ještě číst?). Praha: ÚIV 2010. Palečková, J., Tomášek V. Hlavní zjištění PISA
pracovní listy Výrazy a mnohočleny
 A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Cvičení z matematiky 3 Ročník: 8. 4 Klíčové kompetence (Dílčí kompetence) 5 Kompetence k učení vybírat a využívat pro efektivní
A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Cvičení z matematiky 3 Ročník: 8. 4 Klíčové kompetence (Dílčí kompetence) 5 Kompetence k učení vybírat a využívat pro efektivní
Výsledky dotazníkového šetření 2013 dotazník pro rodiče
 Výsledky dotazníkového šetření 2013 dotazník pro rodiče Zákonní zástupci žáků naší školy byli vyzváni k vyplnění anonymních dotazníků, týkajících se vztahů (v souvislosti se školou), výchovy a vzdělání,
Výsledky dotazníkového šetření 2013 dotazník pro rodiče Zákonní zástupci žáků naší školy byli vyzváni k vyplnění anonymních dotazníků, týkajících se vztahů (v souvislosti se školou), výchovy a vzdělání,
CLIL ZÁKLADNÍ ŠKOLA, MATICE ŠKOLSKÉ 3, ČESKÉ BUDĚJOVICE
 CLIL ZÁKLADNÍ ŠKOLA, MATICE ŠKOLSKÉ 3, ČESKÉ BUDĚJOVICE CLIL - CONTENT AND LANGUAGE INTEGRATED LEARNING PROPOJENÍ JAZYKOVÉ VÝUKY A VYUČOVACÍHO PŘEDMĚTU VÝUKA NEJAZYKOVÝCH PŘEDMĚTŮ (MATEMATIKA, VÝTVARNÁ
CLIL ZÁKLADNÍ ŠKOLA, MATICE ŠKOLSKÉ 3, ČESKÉ BUDĚJOVICE CLIL - CONTENT AND LANGUAGE INTEGRATED LEARNING PROPOJENÍ JAZYKOVÉ VÝUKY A VYUČOVACÍHO PŘEDMĚTU VÝUKA NEJAZYKOVÝCH PŘEDMĚTŮ (MATEMATIKA, VÝTVARNÁ
Škola: CEKPV Datum:
 Mapa školy Vyhodnocení projektu Mapa ScioŠkoly Souhrnný přehled - Škola: CEKPV Datum: 13. 11. 2018 Následuje výčet hodnot, které mohou, ale také musí být cílem školy. Ohodnoťte, prosím, jednotlivé položky
Mapa školy Vyhodnocení projektu Mapa ScioŠkoly Souhrnný přehled - Škola: CEKPV Datum: 13. 11. 2018 Následuje výčet hodnot, které mohou, ale také musí být cílem školy. Ohodnoťte, prosím, jednotlivé položky
Pravidla pro hodnocení žáků
 Pravidla pro hodnocení žáků Hodnocení výsledků vzdělávání žáků se řídí příslušnými paragrafy školského zákona. Podrobnosti o hodnocení výsledků žáků a jeho náležitostech stanoví ministerstvo prováděcím
Pravidla pro hodnocení žáků Hodnocení výsledků vzdělávání žáků se řídí příslušnými paragrafy školského zákona. Podrobnosti o hodnocení výsledků žáků a jeho náležitostech stanoví ministerstvo prováděcím
RNDr. Milan Šmídl, Ph.D. Co je to BOV?
 RNDr. Milan Šmídl, Ph.D Co je to BOV? BOV = Badatelsky Orientovaná Výuka Inquiry Based Science Education (IBSE) Inguiry = bádání, zkoumání, hledání pravdy cílevědomý proces formulování problémů, kritického
RNDr. Milan Šmídl, Ph.D Co je to BOV? BOV = Badatelsky Orientovaná Výuka Inquiry Based Science Education (IBSE) Inguiry = bádání, zkoumání, hledání pravdy cílevědomý proces formulování problémů, kritického
Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ ŘÍJEN LISTOPAD PROSINEC
 Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ Úvod k učivu o přirozeném čísle. Numerace do 5, čtení čísel 0-5. Vytváření souborů o daném počtu předmětů. Znaménka méně, více, rovná se, porovnávání
Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ Úvod k učivu o přirozeném čísle. Numerace do 5, čtení čísel 0-5. Vytváření souborů o daném počtu předmětů. Znaménka méně, více, rovná se, porovnávání
MATEMATIKA CHARAKTERISTIKA PŘEDMĚTU pro 1. až 5. ročník
 1. Obsahové, časové a organizační vymezení předmětu 1.1 Vzdělávací obsahy, ze kterých je vyučovací předmět utvořen MATEMATIKA CHARAKTERISTIKA PŘEDMĚTU pro 1. až 5. ročník Vzdělávání klade důraz na důkladné
1. Obsahové, časové a organizační vymezení předmětu 1.1 Vzdělávací obsahy, ze kterých je vyučovací předmět utvořen MATEMATIKA CHARAKTERISTIKA PŘEDMĚTU pro 1. až 5. ročník Vzdělávání klade důraz na důkladné
Volba střední školy jak to vidí osmáci
 Volba střední školy jak to vidí osmáci Studie občanského sdružení Než zazvoní 2. června 2014 Studie o výběru školy Tento dokument je veřejnou součástí širší dlouhodobé studie občanského sdružení Než zazvoní,
Volba střední školy jak to vidí osmáci Studie občanského sdružení Než zazvoní 2. června 2014 Studie o výběru školy Tento dokument je veřejnou součástí širší dlouhodobé studie občanského sdružení Než zazvoní,
ZÁPIS Z 2. SETKÁNÍ PRACOVNÍ SKUPINY KARIÉROVÉ PORADENSTVÍ V ZÁKLADNÍCH ŠKOLÁCH
 ZÁPIS Z 2. SETKÁNÍ PRACOVNÍ SKUPINY KARIÉROVÉ PORADENSTVÍ Datum jednání: 12.10.2016 Čas jednání: 13:00 hodin V ZÁKLADNÍCH ŠKOLÁCH Místo jednání: Kancelář MAS Lednicko-valtický areál, z.s., Lidická 3116/134,
ZÁPIS Z 2. SETKÁNÍ PRACOVNÍ SKUPINY KARIÉROVÉ PORADENSTVÍ Datum jednání: 12.10.2016 Čas jednání: 13:00 hodin V ZÁKLADNÍCH ŠKOLÁCH Místo jednání: Kancelář MAS Lednicko-valtický areál, z.s., Lidická 3116/134,
MATE MATIKA. učebnice pro 2. stupeň ZŠ a víceletá gymnázia
 MATE MATIKA učebnice pro. stupeň ZŠ a víceletá gymnázia OBSAH Zlomky 5 Rovnice Množiny 7 Jazyk písmen II 7 Rodina Mnohoúhelníky 50 Trojúhelník I Prvočísla I 5 Záporná čísla 7 Mocniny 55 Dělitelnost 0
MATE MATIKA učebnice pro. stupeň ZŠ a víceletá gymnázia OBSAH Zlomky 5 Rovnice Množiny 7 Jazyk písmen II 7 Rodina Mnohoúhelníky 50 Trojúhelník I Prvočísla I 5 Záporná čísla 7 Mocniny 55 Dělitelnost 0
INOVACE VÝUKY V ZŠ DOLNÍ BŘEŽANY
 PROJEKTOVÝ ZÁMĚR OPVK (oblast 1.4) VYKUK PATRON ZŠ A MŠ DOLNÍ BŘEŽANY INOVACE VÝUKY V ZŠ DOLNÍ BŘEŽANY Příjemce: ZŠ a MŠ Dolní Břežany 1 1) IDENTIFIKACE PŘEDKLADATELE PROJEKTU Název: ZŠ a MŠ Dolní Břežany
PROJEKTOVÝ ZÁMĚR OPVK (oblast 1.4) VYKUK PATRON ZŠ A MŠ DOLNÍ BŘEŽANY INOVACE VÝUKY V ZŠ DOLNÍ BŘEŽANY Příjemce: ZŠ a MŠ Dolní Břežany 1 1) IDENTIFIKACE PŘEDKLADATELE PROJEKTU Název: ZŠ a MŠ Dolní Břežany
Reálná čísla a výrazy. Početní operace s reálnými čísly. Složitější úlohy se závorkami. Slovní úlohy. Číselné výrazy. Výrazy a mnohočleny
 A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Cvičení z matematiky 3 Ročník: 9. 4 Klíčové kompetence (Dílčí kompetence) 5 Kompetence k učení učí se vybírat a využívat vhodné
A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Cvičení z matematiky 3 Ročník: 9. 4 Klíčové kompetence (Dílčí kompetence) 5 Kompetence k učení učí se vybírat a využívat vhodné
Dodatek č. 25 ke Školnímu vzdělávacímu programu pro základní vzdělávání Cesta k poznání a vědění k
 Dodatek č. 25 ke Školnímu vzdělávacímu programu pro základní vzdělávání Cesta k poznání a vědění k 1. 9. 2016 Dodatek je vytvořený na základě aktuálního RVP ZV, který nabývá platnosti k 1. 9. 2018 na základě
Dodatek č. 25 ke Školnímu vzdělávacímu programu pro základní vzdělávání Cesta k poznání a vědění k 1. 9. 2016 Dodatek je vytvořený na základě aktuálního RVP ZV, který nabývá platnosti k 1. 9. 2018 na základě
2. Předmětem hodnocení je osobní pokrok žáka. Učitel porovnává jeho aktuální výkon s předchozími výsledky práce.
 6.1. HODNOCENÍ ŽÁKŮ Hodnocení žáků vychází ze zákona č.561/2004 Sb., školského zákona a z vyhlášky č.48/2005 Sb., o základním vzdělávání a některých náležitostech plnění povinné školní docházky. Hodnocení
6.1. HODNOCENÍ ŽÁKŮ Hodnocení žáků vychází ze zákona č.561/2004 Sb., školského zákona a z vyhlášky č.48/2005 Sb., o základním vzdělávání a některých náležitostech plnění povinné školní docházky. Hodnocení
Učitelé matematiky a CLIL
 ŠULISTA Marek. Učitelé matematiky a CLIL. Učitel matematiky. Jednota českých matematiků a fyziků, 2014, roč. 23, č. 1, s. 45-51. ISSN 1210-9037. Učitelé matematiky a CLIL Úvod V České republice došlo v
ŠULISTA Marek. Učitelé matematiky a CLIL. Učitel matematiky. Jednota českých matematiků a fyziků, 2014, roč. 23, č. 1, s. 45-51. ISSN 1210-9037. Učitelé matematiky a CLIL Úvod V České republice došlo v
Klima školy - varianta pro rodiče
 Základní škola Roztoky, okres Rakovník, příspěvková organizace Klima školy - varianta pro rodiče výsledek dotazníkového šetření Název dotazníku: KLIMA ŠKOLY 2017 Datum: 26. 04. 2017 Graf 1: Celkový přehled
Základní škola Roztoky, okres Rakovník, příspěvková organizace Klima školy - varianta pro rodiče výsledek dotazníkového šetření Název dotazníku: KLIMA ŠKOLY 2017 Datum: 26. 04. 2017 Graf 1: Celkový přehled
Kurz č.: KV01 Karlovy Vary 12. 12. 2006 17. 4. 2007 ZÁVĚREČNÁ PRÁCE
 Kurz č.: KV01 Karlovy Vary 12. 12. 2006 17. 4. 2007 ZÁVĚREČNÁ PRÁCE Žákovský projekt v hodinách matematiky 8.ročníku základní školy na téma: Geometrie mého okolí Karlovy Vary, 2007 Mgr. Jaroslava Janáčková
Kurz č.: KV01 Karlovy Vary 12. 12. 2006 17. 4. 2007 ZÁVĚREČNÁ PRÁCE Žákovský projekt v hodinách matematiky 8.ročníku základní školy na téma: Geometrie mého okolí Karlovy Vary, 2007 Mgr. Jaroslava Janáčková
Cíl: Opakování učiva, příprava na II.čtvrtletní práci s využitím ICT ve výuce.
 Závěrečná práce kurzu počítačové gramotnosti ST06 (L. Demelová) Příprava na hodinu MATEMATIKY 4. ročník Jsme malotřídní vesnická škola se třemi třídami a 4. ročník tvoří díky vyššímu počtu žáků samostatnou
Závěrečná práce kurzu počítačové gramotnosti ST06 (L. Demelová) Příprava na hodinu MATEMATIKY 4. ročník Jsme malotřídní vesnická škola se třemi třídami a 4. ročník tvoří díky vyššímu počtu žáků samostatnou
Předmět: Logické hrátky
 Předmět: Logické hrátky Charakteristika předmětu Logické hrátky Vyučovací předmět Logické hrátky je volitelným předmětem v 6. ročníku. Rozšiřuje a prohlubuje obsah předmětu Matematika vzdělávacího oboru
Předmět: Logické hrátky Charakteristika předmětu Logické hrátky Vyučovací předmět Logické hrátky je volitelným předmětem v 6. ročníku. Rozšiřuje a prohlubuje obsah předmětu Matematika vzdělávacího oboru
CLIL - DOTAZNÍK PRO RODIČE
 CLIL - DOTAZNÍK PRO RODIČE Jméno žáka: 1. Má vaše dítě další sourozence? Kolik jim je let? 2. Jakou školku vaše dítě navštěvuje? 3. Jak se vaše dítě projevuje ve skupině vrstevníků (např. drží se spíše
CLIL - DOTAZNÍK PRO RODIČE Jméno žáka: 1. Má vaše dítě další sourozence? Kolik jim je let? 2. Jakou školku vaše dítě navštěvuje? 3. Jak se vaše dítě projevuje ve skupině vrstevníků (např. drží se spíše
Vnímání fyziky středoškolskými studenty včera, dnes a zítra
 Vnímání fyziky středoškolskými studenty včera, dnes a zítra Radko Pöschl KDF MFF UK Praha, Česká Republika TŘI užitečné ODKAZY Pöschl, R. Vnímání matematiky a fyziky středoškolskými studenty. Diplomová
Vnímání fyziky středoškolskými studenty včera, dnes a zítra Radko Pöschl KDF MFF UK Praha, Česká Republika TŘI užitečné ODKAZY Pöschl, R. Vnímání matematiky a fyziky středoškolskými studenty. Diplomová
Matematika. ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání:
 Studijní obor: Aplikovaná chemie Učební osnova předmětu Matematika Zaměření: ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání: denní Celkový počet vyučovacích hodin za
Studijní obor: Aplikovaná chemie Učební osnova předmětu Matematika Zaměření: ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání: denní Celkový počet vyučovacích hodin za
NA PRAVOU MÍRU: Článek Asistent pedagoga: Často je zaměňován s osobním asistentem dítěte. Jaká je jeho funkce ve vyučování?
 NA PRAVOU MÍRU: Článek Asistent pedagoga: Často je zaměňován s osobním asistentem dítěte. Jaká je jeho funkce ve vyučování? PODÍVEJTE SE S NÁMI, V ČEM JE ČLÁNEK NEPŘESNÝ, ZAVÁDĚJÍCÍ, NEBO INFORMAČNĚ ZASTARALÝ:
NA PRAVOU MÍRU: Článek Asistent pedagoga: Často je zaměňován s osobním asistentem dítěte. Jaká je jeho funkce ve vyučování? PODÍVEJTE SE S NÁMI, V ČEM JE ČLÁNEK NEPŘESNÝ, ZAVÁDĚJÍCÍ, NEBO INFORMAČNĚ ZASTARALÝ:
na některé otázky všichni neodpověděli Dotazník pro rodiče a) určitě ano 67,5 % b) spíše ano 30 % c) nevím, nedokážu posoudit 0 % d) spíše ne 2,5 %
 Vyhodnocení dotazníků: rozdáno 100% dotazníků, vráceno 95% dotazníků na některé otázky všichni neodpověděli Dotazník pro rodiče Je atmosféra školy, když ji navštívíte, podle vás pozitivní? a) určitě ano
Vyhodnocení dotazníků: rozdáno 100% dotazníků, vráceno 95% dotazníků na některé otázky všichni neodpověděli Dotazník pro rodiče Je atmosféra školy, když ji navštívíte, podle vás pozitivní? a) určitě ano
Organizace 6. tříd. žáci budou pokračovat ve 3 nebo 4 třídách minimálně 21/22 žáků na třídu rozdělení třídních kolektivů závisí na
 Organizace 6. tříd žáci budou pokračovat ve 3 nebo 4 třídách minimálně 21/22 žáků na třídu rozdělení třídních kolektivů závisí na přijetí žáků na jiné školy (víceletá gymnázia, sportovní třídy) počtu žáků
Organizace 6. tříd žáci budou pokračovat ve 3 nebo 4 třídách minimálně 21/22 žáků na třídu rozdělení třídních kolektivů závisí na přijetí žáků na jiné školy (víceletá gymnázia, sportovní třídy) počtu žáků
Křesťanská základní škola Jihlava, nám. Svobody 1369 / 3, 586 01 Jihlava
 Křesťanská základní škola Jihlava, nám. Svobody 1369 / 3, 586 01 Jihlava 1. 4 Zlepšení podmínek pro vzdělávání na základních školách operačního programu vzdělávání pro konkurenceschopnost Datum zahájení
Křesťanská základní škola Jihlava, nám. Svobody 1369 / 3, 586 01 Jihlava 1. 4 Zlepšení podmínek pro vzdělávání na základních školách operačního programu vzdělávání pro konkurenceschopnost Datum zahájení
Zpráva z evaluačního nástroje Dotazník strategií učení cizímu jazyku
 Zpráva z evaluačního nástroje Dotazník strategií učení cizímu jazyku Škola Testovací škola NÚOV, Praha Třída 4. A Předmět Angličtina Učitel pepa novák Vážená paní učitelko, vážený pane učiteli, v této
Zpráva z evaluačního nástroje Dotazník strategií učení cizímu jazyku Škola Testovací škola NÚOV, Praha Třída 4. A Předmět Angličtina Učitel pepa novák Vážená paní učitelko, vážený pane učiteli, v této
Itálie Dotazník pro učitele VŠ připravující budoucí učitele cizích jazyků Zpracování údajů
 Itálie Dotazník pro učitele VŠ připravující budoucí učitele cizích jazyků Zpracování údajů O Vás 1. Dotazník vyplnilo sedm vysokoškolských pedagogů připravujících budoucí učitele cizích jazyků. 2. Šest
Itálie Dotazník pro učitele VŠ připravující budoucí učitele cizích jazyků Zpracování údajů O Vás 1. Dotazník vyplnilo sedm vysokoškolských pedagogů připravujících budoucí učitele cizích jazyků. 2. Šest
2. LMP SP 3. LMP SP + 2. LMP NSP. operace. Závislosti, vztahy a práce s daty. Závislosti, vztahy a práce s daty. v prostoru
 ŠVP LMP Charakteristika vyučovacího předmětu Matematika Obsahové, časové a organizační vymezení vyučovacího předmětu Matematika Vzdělávací obsah předmětu Matematika je utvořen vzdělávacím obsahem vzdělávacího
ŠVP LMP Charakteristika vyučovacího předmětu Matematika Obsahové, časové a organizační vymezení vyučovacího předmětu Matematika Vzdělávací obsah předmětu Matematika je utvořen vzdělávacím obsahem vzdělávacího
K výuce matematiky na školách v ČR
 K výuce matematiky na školách v ČR Podklady k vystoupení členů Jednoty českých matematiků a fyziků v Poslanecké sněmovně PČR Praha 14. 3. 2018 Celkový stav výuky matematiky na našich školách není dobrý.
K výuce matematiky na školách v ČR Podklady k vystoupení členů Jednoty českých matematiků a fyziků v Poslanecké sněmovně PČR Praha 14. 3. 2018 Celkový stav výuky matematiky na našich školách není dobrý.
Římské číslice porovnávání zvířátek
 Římské číslice porovnávání zvířátek On-line diskuze k virtuální hospitaci ve vyučovací hodině v 6. ročníku Vyučující: Mgr. Bc. Miroslav Halló a Mgr. Lucie Krobová Expert: Doc. RNDr. Darina Jirotková, Ph.D.
Římské číslice porovnávání zvířátek On-line diskuze k virtuální hospitaci ve vyučovací hodině v 6. ročníku Vyučující: Mgr. Bc. Miroslav Halló a Mgr. Lucie Krobová Expert: Doc. RNDr. Darina Jirotková, Ph.D.
Charakteristika prostředí. Přínos pro rozvoj žáka. Ukázky z učebnice
 Hra simuluje cestování autobusem na pravidelné lince spojující několik zastávek. Autobus je lepenková krabice a cestující jsou plastikové lahve. Zastávky jsou jistá místa ve třídě, jako dveře, umyvadlo,
Hra simuluje cestování autobusem na pravidelné lince spojující několik zastávek. Autobus je lepenková krabice a cestující jsou plastikové lahve. Zastávky jsou jistá místa ve třídě, jako dveře, umyvadlo,
Klima školy - varianta pro rodiče
 Základní škola a Mateřská škola Neznašov Klima školy - varianta pro rodiče výsledek dotazníkového šetření Název dotazníku: Klima školy - 2015/2016 (červen) Datum: 26. 05. 2016 Graf 1: Celkový přehled školy
Základní škola a Mateřská škola Neznašov Klima školy - varianta pro rodiče výsledek dotazníkového šetření Název dotazníku: Klima školy - 2015/2016 (červen) Datum: 26. 05. 2016 Graf 1: Celkový přehled školy
Název vícedenní školy: Barrandov II. příměstská. Termín: Hodinová dotace: PhDr. Jana Slezáková, Ph.D. Mgr. Jana Hanušová, Ph.D.
 Název vícedenní školy: Barrandov II Typ: příměstská Termín: 26. 8. 29. 8. 2017 Hodinová dotace: Garanti: Otevřené skupiny: 24h PhDr. Jana Slezáková, Ph.D. Mgr. Jana Hanušová, Ph.D. ZŠ 1. stupeň začátečníci
Název vícedenní školy: Barrandov II Typ: příměstská Termín: 26. 8. 29. 8. 2017 Hodinová dotace: Garanti: Otevřené skupiny: 24h PhDr. Jana Slezáková, Ph.D. Mgr. Jana Hanušová, Ph.D. ZŠ 1. stupeň začátečníci
M A R T I N R O M A N S O U Č A S N É T R E N D Y
 M A R T I N R O M A N S O U Č A S N É T R E N D Y VE V Z D Ě L Á V Á N Í Školství ve světe se změnilo za posledních 40 let zásadně více než v ČR. V UK výsledek tlaku u zaměstnavatelů (excel, angličtina,
M A R T I N R O M A N S O U Č A S N É T R E N D Y VE V Z D Ě L Á V Á N Í Školství ve světe se změnilo za posledních 40 let zásadně více než v ČR. V UK výsledek tlaku u zaměstnavatelů (excel, angličtina,
Měsíc: učivo:. PROSINEC Numerace do 7, rozklad čísla 1 7. Sčítání a odčítání v oboru do 7, slovní úlohy.
 Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ Úvod k učivu o přirozeném čísle. Numerace do 5, čtení čísel 0-5. Vytváření souborů o daném počtu předmětů. Znaménka méně, více, rovná se, porovnávání
Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ Úvod k učivu o přirozeném čísle. Numerace do 5, čtení čísel 0-5. Vytváření souborů o daném počtu předmětů. Znaménka méně, více, rovná se, porovnávání
Revize rámcových vzdělávacích programů. Helena Marinková
 Revize rámcových vzdělávacích programů Helena Marinková 1. 6. 2017 první RVP z roku 2005 Proč? dokumenty vzdělávací politiky: Strategie vzdělávací politiky do roku 2020 Strategie digitálního vzdělávání
Revize rámcových vzdělávacích programů Helena Marinková 1. 6. 2017 první RVP z roku 2005 Proč? dokumenty vzdělávací politiky: Strategie vzdělávací politiky do roku 2020 Strategie digitálního vzdělávání
III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení šablony/označení sady VY_32_INOVACE_04_M3 M 3
 Záznamový arch Název školy: Základní škola a Mateřská škola Brno, Bosonožské nám. 44, příspěvková organizace Číslo projektu: CZ.1.07/1.4.00/21.2499 Číslo a název šablony klíčové aktivity: III/2 Inovace
Záznamový arch Název školy: Základní škola a Mateřská škola Brno, Bosonožské nám. 44, příspěvková organizace Číslo projektu: CZ.1.07/1.4.00/21.2499 Číslo a název šablony klíčové aktivity: III/2 Inovace
Pedagogika I Zimní semestr Akademický rok 2014/15
 Pedagogika I Zimní semestr Akademický rok 2014/15 Cíle výchovy a vzdělávání: Otázky spojené s konceptem klíčových kompetencí podle RVP. Učitel a cíle výuky. Pavla Zieleniecová, MFF UK 1 Obsah: 1. Tři otázky
Pedagogika I Zimní semestr Akademický rok 2014/15 Cíle výchovy a vzdělávání: Otázky spojené s konceptem klíčových kompetencí podle RVP. Učitel a cíle výuky. Pavla Zieleniecová, MFF UK 1 Obsah: 1. Tři otázky
Příloha 1: Dotazník předvýzkum
 Příloha 1: Dotazník předvýzkum Dobrý den milý ţáku, milá ţákyně základní školy! Dotazník, který se ti dostává do rukou, se skládá ze tří částí. V části A a C si prosím pozorně přečti každou otázku a odpověz
Příloha 1: Dotazník předvýzkum Dobrý den milý ţáku, milá ţákyně základní školy! Dotazník, který se ti dostává do rukou, se skládá ze tří částí. V části A a C si prosím pozorně přečti každou otázku a odpověz
4.1.2. Vzdělávací oblast : Jazyk a jazyková komunikace Vzdělávací obor: Cizí jazyk
 4.1.2. Vzdělávací oblast : Jazyk a jazyková komunikace Vzdělávací obor: Cizí jazyk Charakteristika vyučovacího předmětu Anglický jazyk 1.Obsahové vymezení vyučovacího předmětu Cílem vzdělávání předmětu
4.1.2. Vzdělávací oblast : Jazyk a jazyková komunikace Vzdělávací obor: Cizí jazyk Charakteristika vyučovacího předmětu Anglický jazyk 1.Obsahové vymezení vyučovacího předmětu Cílem vzdělávání předmětu
Závěrečná zpráva o seminářích Rozvíjíme matematickou gramotnost na základní a střední škole v roce 2015
 Závěrečná zpráva o seminářích Rozvíjíme matematickou gramotnost na základní a střední škole v roce 20. Úvod Vzhledem k závažnosti matematického vzdělávání, které provází děti a žáky od předškolního věku
Závěrečná zpráva o seminářích Rozvíjíme matematickou gramotnost na základní a střední škole v roce 20. Úvod Vzhledem k závažnosti matematického vzdělávání, které provází děti a žáky od předškolního věku
Rozvoj čtenářské a matematické gramotnosti v rámci projektu P-KAP 1. díl Čtenářská gramotnost
 Rozvoj čtenářské a matematické gramotnosti v rámci projektu 1. díl Čtenářská gramotnost Mgr. Květa Popjuková Garantka oblasti Čtenářská a matematická gramotnost Národní ústav pro vzdělávání podpora krajského
Rozvoj čtenářské a matematické gramotnosti v rámci projektu 1. díl Čtenářská gramotnost Mgr. Květa Popjuková Garantka oblasti Čtenářská a matematická gramotnost Národní ústav pro vzdělávání podpora krajského
Učební osnovy pracovní
 ZV Základní vzdělávání 5 týdně, povinný ČaPO: Sčítání a odčítání s přechodem přes desítku Žák: ČaPO: sčítá a odčítá v oboru do 20-ti s přechodem přes desítku - sčítání a odčítání v oboru přirozených čísel
ZV Základní vzdělávání 5 týdně, povinný ČaPO: Sčítání a odčítání s přechodem přes desítku Žák: ČaPO: sčítá a odčítá v oboru do 20-ti s přechodem přes desítku - sčítání a odčítání v oboru přirozených čísel
MANUÁL K DIDAKTICKÉMU TESTU Z MATEMATIKY PŘIJÍMAČKY MSK 2011
 MANUÁL K DIDAKTICKÉMU TESTU Z MATEMATIKY PŘIJÍMAČKY MSK 2011 Didaktickým testem z matematiky budou ověřovány matematické dovednosti, které nepřesahují rámec dřívějších osnov ZŠ a jsou definované v Rámcovém
MANUÁL K DIDAKTICKÉMU TESTU Z MATEMATIKY PŘIJÍMAČKY MSK 2011 Didaktickým testem z matematiky budou ověřovány matematické dovednosti, které nepřesahují rámec dřívějších osnov ZŠ a jsou definované v Rámcovém
Kategorie vytvořené na základě RVP a projektu Evaluace inf. gramotnosti žáků ZŠ.
 Specialista Profík Objevitel Průzkumník Začátečník Kategorie vytvořené na základě RVP a projektu Evaluace inf. gramotnosti žáků ZŠ. Dovednost řešit problémy žák teprve získává, zatím neumí řešit bez pomoci
Specialista Profík Objevitel Průzkumník Začátečník Kategorie vytvořené na základě RVP a projektu Evaluace inf. gramotnosti žáků ZŠ. Dovednost řešit problémy žák teprve získává, zatím neumí řešit bez pomoci
Proč děláme práci, která nás nebaví?
 Proč děláme práci, která nás nebaví? Podle průzkumů se věnuje až 70% lidí zaměstnání, které je nenaplňuje a někdy i doslova sere. V poslední době nad touto otázkou hodně přemýšlím. Sám jsem vlastně dlouho
Proč děláme práci, která nás nebaví? Podle průzkumů se věnuje až 70% lidí zaměstnání, které je nenaplňuje a někdy i doslova sere. V poslední době nad touto otázkou hodně přemýšlím. Sám jsem vlastně dlouho
MINISTERSTVO ŠKOLSTVÍ, MLÁDEŽE A TĚLOVÝCHOVY. Učební osnova předmětu MATEMATIKA. pro nástavbové studium. varianta B 6 celkových týd.
 MINISTERSTVO ŠKOLSTVÍ, MLÁDEŽE A TĚLOVÝCHOVY Učební osnova předmětu MATEMATIKA pro nástavbové studium (hodinová dotace: varianta A 4 až 5 celkových týd. hodin, varianta B 6 celkových týd. hodin) Schválilo
MINISTERSTVO ŠKOLSTVÍ, MLÁDEŽE A TĚLOVÝCHOVY Učební osnova předmětu MATEMATIKA pro nástavbové studium (hodinová dotace: varianta A 4 až 5 celkových týd. hodin, varianta B 6 celkových týd. hodin) Schválilo
A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Matematika 3 Ročník: 8. 4 Klíčové kompetence. Opakování 7.
 A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Matematika 3 Ročník: 8. 4 Klíčové kompetence Výstupy Učivo Průřezová témata Evaluace žáka Poznámky (Dílčí kompetence) 5 Kompetence
A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Matematika 3 Ročník: 8. 4 Klíčové kompetence Výstupy Učivo Průřezová témata Evaluace žáka Poznámky (Dílčí kompetence) 5 Kompetence
ZŠ 1. stupeň pokročilí 2 skupiny ZŠ 2. stupeň pokročilí 2 skupiny
 Název vícedenní školy: Luna III Typ: pobytová Termín: 7. 8. 11. 8. 2017 Hodinová dotace: Garanti: 32h Jana Hanušová Renáta Zemanová Otevřené skupiny: ZŠ 1. stupeň začátečníci 3 skupiny ZŠ 1. stupeň pokročilí
Název vícedenní školy: Luna III Typ: pobytová Termín: 7. 8. 11. 8. 2017 Hodinová dotace: Garanti: 32h Jana Hanušová Renáta Zemanová Otevřené skupiny: ZŠ 1. stupeň začátečníci 3 skupiny ZŠ 1. stupeň pokročilí
Základní škola Olomouc, příspěvková org. Gagarinova 19, Olomouc Droždín. Vyhodnocení dotazníku pro rodiče Listopad 2014
 Základní škola Olomouc, příspěvková org. Gagarinova 19, Olomouc Droždín Vyhodnocení dotazníku pro rodiče Listopad 214 Rozdaných dotazníků: 76 Odevzdaných dotazníků: 7 Z toho: Počet odevzdaných dotazníků
Základní škola Olomouc, příspěvková org. Gagarinova 19, Olomouc Droždín Vyhodnocení dotazníku pro rodiče Listopad 214 Rozdaných dotazníků: 76 Odevzdaných dotazníků: 7 Z toho: Počet odevzdaných dotazníků
Role experimentu ve vědecké metodě
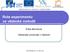 Role experimentu ve vědecké metodě Erika Mechlová Ostravská univerzita v Ostravě Obsah Úvod 1. Pozorování 2. Uvedení a formulace problému. Sbírání informací 3. Stanovení hypotéz řešení problému 4. Provedení
Role experimentu ve vědecké metodě Erika Mechlová Ostravská univerzita v Ostravě Obsah Úvod 1. Pozorování 2. Uvedení a formulace problému. Sbírání informací 3. Stanovení hypotéz řešení problému 4. Provedení
TRENDS IN INTERNATIONAL MATHEMATICS AND SCIENCE STUDY
 Identification Label TRENDS IN INTERNATIONAL MATHEMATICS AND SCIENCE STUDY Školní dotazník 4. ročník Česká školní inspekce Fráni Šrámka 37 150 21 Praha 5 IEA, 2014 Školní dotazník Vaše škola souhlasila
Identification Label TRENDS IN INTERNATIONAL MATHEMATICS AND SCIENCE STUDY Školní dotazník 4. ročník Česká školní inspekce Fráni Šrámka 37 150 21 Praha 5 IEA, 2014 Školní dotazník Vaše škola souhlasila
Zabezpečení výuky žáků se speciálními vzdělávacími potřebami
 Zabezpečení výuky žáků se speciálními vzdělávacími potřebami Charakteristika Žákem se speciálními vzdělávacími potřebami je žák, který k naplnění svých vzdělávacích potřeb nebo k uplatnění a užívání svých
Zabezpečení výuky žáků se speciálními vzdělávacími potřebami Charakteristika Žákem se speciálními vzdělávacími potřebami je žák, který k naplnění svých vzdělávacích potřeb nebo k uplatnění a užívání svých
Úvodní část: Představení se a úloha na zjištění kolik nám je let.
 Anežka Pekárková, Romana Bredová Výuka 12.10.2011, sudý týden Cíl: Procvičit sčítání a odčítání v různých prostředích Úvodní část: Představení se a úloha na zjištění kolik nám je let. ÚLOHA: Od čísla 100
Anežka Pekárková, Romana Bredová Výuka 12.10.2011, sudý týden Cíl: Procvičit sčítání a odčítání v různých prostředích Úvodní část: Představení se a úloha na zjištění kolik nám je let. ÚLOHA: Od čísla 100
Školní vzdělávací program pro základní vzdělávání, Základní škola Krásného 24
 Školní vzdělávací program pro základní vzdělávání, Základní škola Krásného 24 Obsahové, časové a organizační vymezení vyučovacího předmětu Anglický jazyk rozšířená výuka 1. stupeň Výuka je zaměřena převážně
Školní vzdělávací program pro základní vzdělávání, Základní škola Krásného 24 Obsahové, časové a organizační vymezení vyučovacího předmětu Anglický jazyk rozšířená výuka 1. stupeň Výuka je zaměřena převážně
ŠKOLA. - jaká by dnes měla být? Mgr. Marie Gottfriedová
 ŠKOLA - jaká by dnes měla být? Mgr. Marie Gottfriedová SMYSL ŠKOLY Proč máme mít školu? Co by škola měla žákům dát/nabídnout? Jaký by měl být absolvent, který školu opouští? Čím by měl být vybavený? Co
ŠKOLA - jaká by dnes měla být? Mgr. Marie Gottfriedová SMYSL ŠKOLY Proč máme mít školu? Co by škola měla žákům dát/nabídnout? Jaký by měl být absolvent, který školu opouští? Čím by měl být vybavený? Co
0,2 0,20 0, Desetinná čísla II. Předpoklady:
 1.2.2 Desetinná čísla II Předpoklady: 010201 Pedagogická poznámka: Je třeba zahájit tak, aby se stihl ještě společný začátek příkladu 7 (pokud někdo příklad 7 začne s předstihem, nevadí to, ale jde o to,
1.2.2 Desetinná čísla II Předpoklady: 010201 Pedagogická poznámka: Je třeba zahájit tak, aby se stihl ještě společný začátek příkladu 7 (pokud někdo příklad 7 začne s předstihem, nevadí to, ale jde o to,
CHARAKTERISTIKA. VZDĚLÁVACÍ OBLAST VYUČOVACÍ PŘEDMĚT ZODPOVÍDÁ VOLITELNÉ PŘEDMĚTY Seminář z matematiky Mgr. Dana Rauchová
 CHARAKTERISTIKA VZDĚLÁVACÍ OBLAST VYUČOVACÍ PŘEDMĚT ZODPOVÍDÁ VOLITELNÉ PŘEDMĚTY Seminář z matematiky Mgr. Dana Rauchová Vyučovací volitelný předmět Cvičení z matematiky je zařazen samostatně na druhém
CHARAKTERISTIKA VZDĚLÁVACÍ OBLAST VYUČOVACÍ PŘEDMĚT ZODPOVÍDÁ VOLITELNÉ PŘEDMĚTY Seminář z matematiky Mgr. Dana Rauchová Vyučovací volitelný předmět Cvičení z matematiky je zařazen samostatně na druhém
MATEMATIKA. Naučme děti myslet. Určeno pro rodiče žáků 1. stupně ZŠ s výukou matematiky podle metody prof. Hejného
 MATEMATIKA Naučme děti myslet Určeno pro rodiče žáků 1. stupně ZŠ s výukou matematiky podle metody prof. Hejného Nabídka materiálů pro výuku matematiky v 1.-5. ročníku ZŠ Plakáty ZÁBAVNÁ MATEMATIKA pro
MATEMATIKA Naučme děti myslet Určeno pro rodiče žáků 1. stupně ZŠ s výukou matematiky podle metody prof. Hejného Nabídka materiálů pro výuku matematiky v 1.-5. ročníku ZŠ Plakáty ZÁBAVNÁ MATEMATIKA pro
Tisková konference Praha 29. srpna 2012
 Tisková konference Praha 29. srpna 2012 Martin Ježek, ředitel projektu Rozumíme penězům Markéta Vaňková, CSR manažerka GE Money Bank Program 1. Vývoj projektu Rozumíme penězům 2. Výsledky průzkumu mezi
Tisková konference Praha 29. srpna 2012 Martin Ježek, ředitel projektu Rozumíme penězům Markéta Vaňková, CSR manažerka GE Money Bank Program 1. Vývoj projektu Rozumíme penězům 2. Výsledky průzkumu mezi
( ) ( ) Rozklad mnohočlenů na součin I (vytýkání) Předpoklady:
 1.8.6 Rozklad mnohočlenů na součin I (vytýkání) Předpoklady: 010805 Pedagogická poznámka: Na začátku každé rozkládací hodiny jsou přidány příklady na opakování úprav mnohočlenů. Důvod je jediný, čtyři
1.8.6 Rozklad mnohočlenů na součin I (vytýkání) Předpoklady: 010805 Pedagogická poznámka: Na začátku každé rozkládací hodiny jsou přidány příklady na opakování úprav mnohočlenů. Důvod je jediný, čtyři
VÝSLEDKY ŘÍZENÝCH ROZHOVORŮ NA ZAPOJENÝCH ŠKOLÁCH
 VÝSLEDKY ŘÍZENÝCH ROZHOVORŮ NA ZAPOJENÝCH ŠKOLÁCH Během března až května 2013 jsme postupně navštívili všechny zapojené školy. Jedním z účelů návštěvy byly rozhovory ke školním vzdělávacím programům s
VÝSLEDKY ŘÍZENÝCH ROZHOVORŮ NA ZAPOJENÝCH ŠKOLÁCH Během března až května 2013 jsme postupně navštívili všechny zapojené školy. Jedním z účelů návštěvy byly rozhovory ke školním vzdělávacím programům s
A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Matematika 3 Ročník: 8. 4 Klíčové kompetence. Opakování 7.
 A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Matematika 3 Ročník: 8. 4 Klíčové kompetence Výstupy Učivo Průřezová témata Evaluace žáka Poznámky (Dílčí kompetence) 5 Kompetence
A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Matematika 3 Ročník: 8. 4 Klíčové kompetence Výstupy Učivo Průřezová témata Evaluace žáka Poznámky (Dílčí kompetence) 5 Kompetence
MATE MATIKA. pracovní sešit pro 2. stupeň ZŠ a víceletá gymnázia
 F MATE MATIKA pracovní sešit pro 2. stupeň ZŠ a víceletá gymnázia Milí žáci, vážení učitelé, k vašim rukám se právě dostal pracovní sešit F. Tato publikace vám nabízí velké množství inspirace, námětů a
F MATE MATIKA pracovní sešit pro 2. stupeň ZŠ a víceletá gymnázia Milí žáci, vážení učitelé, k vašim rukám se právě dostal pracovní sešit F. Tato publikace vám nabízí velké množství inspirace, námětů a
Pozornost OBSAH. PhDr. Kamila Balharová, ZŠ Táborská, Praha Ilustrace: Michaela Suchoňová, ZŠ Třinec. Metodika 1. Úvod 2
 NÁPRAVNÁ CVIČNÍ PhDr. Kamila Balharová, ZŠ Táborská, Praha Ilustrace: Michaela Suchoňová, ZŠ Třinec OBSAH Metodika 1. Úvod 2 2. Metodický komentář 2 2.1 Hledej rozdíly 2. Závěr 4. Zdroje Materiál Pracovní
NÁPRAVNÁ CVIČNÍ PhDr. Kamila Balharová, ZŠ Táborská, Praha Ilustrace: Michaela Suchoňová, ZŠ Třinec OBSAH Metodika 1. Úvod 2 2. Metodický komentář 2 2.1 Hledej rozdíly 2. Závěr 4. Zdroje Materiál Pracovní
Gramatika. Minulý čas prostý. Minulý čas průběhový. Předpřítomný čas. Podmínkové věty typ I. Modální slovesa. Vyjadřování budoucnosti
 A B C D E F 1 Vzdělávací oblast: Jazyk a jazyková komunikace 2 Vzdělávací obor: Cizí jazyk 3 Vzdělávací předmět Anglický jazyk 4 Ročník: 8. 5 Klíčové kompetence Průřezová témata Výstupy Učivo (Dílčí kompetence)
A B C D E F 1 Vzdělávací oblast: Jazyk a jazyková komunikace 2 Vzdělávací obor: Cizí jazyk 3 Vzdělávací předmět Anglický jazyk 4 Ročník: 8. 5 Klíčové kompetence Průřezová témata Výstupy Učivo (Dílčí kompetence)
Vzdělávací oblast: Matematika a její aplikace Vyučovací předmět MATEMATIKA 1. OBDOBÍ Oblast:
 Vzdělávací oblast: a její aplikace Vyučovací předmět MATEMATIKA 1. OBDOBÍ Období: 1. Číslo a početní operace Používá přirozená čísla k modelování reálných situací Počítá předměty v daném souboru Vytváří
Vzdělávací oblast: a její aplikace Vyučovací předmět MATEMATIKA 1. OBDOBÍ Období: 1. Číslo a početní operace Používá přirozená čísla k modelování reálných situací Počítá předměty v daném souboru Vytváří
Učitelka nebo učitel techniky a praktických činností je...
 Učitelka nebo učitel techniky a praktických činností je... Průvodce, který uchazeče o studium jednoduše seznámí s charakteristikou studijního programu budoucnosti. Učitelka nebo učitel techniky a praktických
Učitelka nebo učitel techniky a praktických činností je... Průvodce, který uchazeče o studium jednoduše seznámí s charakteristikou studijního programu budoucnosti. Učitelka nebo učitel techniky a praktických
INSPEKČNÍ ZPRÁVA. Základní škola Benešov, Dukelská 1818. Dukelská 1818, 256 01 Benešov. Identifikátor školy: 600 041 956
 Česká školní inspekce Středočeský inspektorát INSPEKČNÍ ZPRÁVA Základní škola Benešov, Dukelská 1818 Dukelská 1818, 256 01 Benešov Identifikátor školy: 600 041 956 Termín konání inspekce: 15. červen 2006
Česká školní inspekce Středočeský inspektorát INSPEKČNÍ ZPRÁVA Základní škola Benešov, Dukelská 1818 Dukelská 1818, 256 01 Benešov Identifikátor školy: 600 041 956 Termín konání inspekce: 15. červen 2006
ZŠ 1. stupeň začátečníci 2 skupiny ZŠ 1. stupeň pokročilí 2 skupiny ZŠ 2. stupeň začátečníci 2 skupiny
 Název vícedenní školy: Luna II Typ: pobytová Termín: 18. 7. 21. 7. 2017 Hodinová dotace: Garanti: Otevřené skupiny: 24h Mgr. Et Mgr. Pavel Šalom, Mgr. Lenka Rybová (rozená Bořánková) MŠ 1 skupina ZŠ 1.
Název vícedenní školy: Luna II Typ: pobytová Termín: 18. 7. 21. 7. 2017 Hodinová dotace: Garanti: Otevřené skupiny: 24h Mgr. Et Mgr. Pavel Šalom, Mgr. Lenka Rybová (rozená Bořánková) MŠ 1 skupina ZŠ 1.
TEST CTIŽÁDOSTI. Využitelný pro měření kompetence: podnikavost, výkonnost, vedení lidí, flexibilita
 TEST CTIŽÁDOSTI Využitelný pro měření kompetence: podnikavost, výkonnost, vedení lidí, flexibilita Forma: papír - tužka Čas na administraci: max. 10 min. Časový limit: ne Vyhodnocení: ručně cca 10 minut
TEST CTIŽÁDOSTI Využitelný pro měření kompetence: podnikavost, výkonnost, vedení lidí, flexibilita Forma: papír - tužka Čas na administraci: max. 10 min. Časový limit: ne Vyhodnocení: ručně cca 10 minut
Jak vnímaj. mají fyziku studenti pražských gymnázi. Mgr. Radko Pöschl
 Jak vnímaj mají fyziku studenti pražských gymnázi zií? Mgr. Radko Pöschl TŘI užitečné ODKAZY Pöschl, R. Vnímání matematiky a fyziky středoškolskými studenty. Diplomová práce. KDF MFF UK, Praha, 2005. http://kdf.mff.cuni.cz/vyzkum/npvii/npv.php
Jak vnímaj mají fyziku studenti pražských gymnázi zií? Mgr. Radko Pöschl TŘI užitečné ODKAZY Pöschl, R. Vnímání matematiky a fyziky středoškolskými studenty. Diplomová práce. KDF MFF UK, Praha, 2005. http://kdf.mff.cuni.cz/vyzkum/npvii/npv.php
EU peníze školám. Základní škola Jablunkov, Lesní 190, příspěvková organizace. Žadatel projektu: 2 834 891Kč
 Základní škola Jablunkov, Lesní 190, příspěvková organizace P R O J E K T O V Ý Z Á M Ě R EU peníze školám Žadatel projektu: Název projektu: Název operačního programu: Prioritní osa programu: Název oblasti
Základní škola Jablunkov, Lesní 190, příspěvková organizace P R O J E K T O V Ý Z Á M Ě R EU peníze školám Žadatel projektu: Název projektu: Název operačního programu: Prioritní osa programu: Název oblasti
DIGITÁLNÍ ARCHIV VZDĚLÁVACÍCH MATERIÁLŮ
 DIGITÁLNÍ ARCHIV VZDĚLÁVACÍCH MATERIÁLŮ Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast CZ.1.07/1.5.00/34.0963 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti
DIGITÁLNÍ ARCHIV VZDĚLÁVACÍCH MATERIÁLŮ Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast CZ.1.07/1.5.00/34.0963 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti
Standard studijního programu Matematika se zaměřením na vzdělávání
 Standard studijního Matematika se zaměřením na vzdělávání A. Specifika a obsah studijního : Typ bakalářský Oblast/oblasti vzdělávání Matematika/Učitelství 60 % /40 % 1 Základní tematické okruhy algebra
Standard studijního Matematika se zaměřením na vzdělávání A. Specifika a obsah studijního : Typ bakalářský Oblast/oblasti vzdělávání Matematika/Učitelství 60 % /40 % 1 Základní tematické okruhy algebra
Název vícedenní školy: Brno. příměstská. Termín: Hodinová dotace: RNDr. Dagmar Môťovská, Mgr. Jaroslava Kloboučková
 Název vícedenní školy: Brno Typ: příměstská Termín: 31. 7. 4. 8. 2017 Hodinová dotace: Garanti: Otevřené skupiny: 32h RNDr. Dagmar Môťovská, Mgr. Jaroslava Kloboučková ZŠ 1. stupeň (1.-2.tř) začátečníci
Název vícedenní školy: Brno Typ: příměstská Termín: 31. 7. 4. 8. 2017 Hodinová dotace: Garanti: Otevřené skupiny: 32h RNDr. Dagmar Môťovská, Mgr. Jaroslava Kloboučková ZŠ 1. stupeň (1.-2.tř) začátečníci
PROBLÉM DELEGOVÁNÍ v procesu VEDENÍ LIDÍ v praxi vedoucího/řídícího pracovníka:
 VEDENÍ LIDÍ a DELEGOVÁNÍ PROBLÉM DELEGOVÁNÍ v procesu VEDENÍ LIDÍ v praxi vedoucího/řídícího pracovníka: forma ukládání úkolů PROČ zdůvodnění úkolu ztotožnění se pracovníka s úkolem přesvědčit se o tom,
VEDENÍ LIDÍ a DELEGOVÁNÍ PROBLÉM DELEGOVÁNÍ v procesu VEDENÍ LIDÍ v praxi vedoucího/řídícího pracovníka: forma ukládání úkolů PROČ zdůvodnění úkolu ztotožnění se pracovníka s úkolem přesvědčit se o tom,
Identifikace. Koncepce ZŠ - Mateřská a základní škola Raduška. Název školy: ZAČÍT SPOLU Základní škola a Mateřská škola Kadaň
 Koncepce ZŠ - Mateřská a základní škola Raduška Identifikace Název školy: ZAČÍT SPOLU Základní škola a Mateřská škola Kadaň Adresa školy: Kpt. Jaroše 612, 432 01 Kadaň Ředitelka školy: Bc. Diana Roubová
Koncepce ZŠ - Mateřská a základní škola Raduška Identifikace Název školy: ZAČÍT SPOLU Základní škola a Mateřská škola Kadaň Adresa školy: Kpt. Jaroše 612, 432 01 Kadaň Ředitelka školy: Bc. Diana Roubová
SEZNAM PŘÍLOH. Příloha č. 1 : Dotazník pro rodiče. Příloha č. 2 : Dotazník pro děti. Příloha č. 3 : Otázky k rozhovorům s dětmi
 SEZNAM PŘÍLOH Příloha č. 1 : Dotazník pro rodiče Příloha č. 2 : Dotazník pro děti Příloha č. 3 : Otázky k rozhovorům s dětmi Příloha č. 4 : Žádost o souhlas s vyplněním dotazníku Příloha č. 1 - Dotazník
SEZNAM PŘÍLOH Příloha č. 1 : Dotazník pro rodiče Příloha č. 2 : Dotazník pro děti Příloha č. 3 : Otázky k rozhovorům s dětmi Příloha č. 4 : Žádost o souhlas s vyplněním dotazníku Příloha č. 1 - Dotazník
