Roční zpráva o stavu řešení projektu
|
|
|
- Roman Ševčík
- před 8 lety
- Počet zobrazení:
Transkript
1 Projekt TE (Centrum digitální optiky) je řešen s finanční podporou TA ČR Roční zpráva o stavu řešení projektu 2012 Dílčí výstup projektu TE (Centrum digitální optiky) Pracovní balíček: Management projektu Identifikační číslo výstupu: TE DV001 Datum dosažení dílčího výstupu: Předkládá: doc. Mgr. Jaroslav Řeháček, Ph.D., řešitel projektu
2 Průběh řešení projektu v roce 2012 Projekt Centrum digitální optiky byl zahájen 1. března 2012 v souladu s návrhem projektu. Byla ustavena organizační struktury centra, nastaveny mechanizmy komunikace, vytvořeny intranetové i veřejné webové stránky, bylo zahájeno řešení projektu ve všech pěti pracovních balíčcích, byla prováděna kontrola stavu řešení 2x ročně na jednáních Řídícího výboru Centra, byl organizován Technický seminář Centra, kde byly prezentovány dosažené výsledky, byla důsledně implementována pravidla pro publicitu projektů financovaných TA ČR. Postup prací. Řešení projektu v roce 2012 probíhalo v souladu s plánem. Výsledky projektu byly prezentovány na prestižní konferenci SPIE Defense, Security, and Sensing 2012 v Baltimore. Některé výsledky dosažené nad rámec plánu byly publikovány. Týká se to zejména podpůrného teoretického a experimentálního výzkumu nových metod manipulace, detekce a zpracování optického signálu. Tyto nové ideje budou v dalších letech využity při aplikovaném výzkumu v rámci jednotlivých pracovních balíčků projektu. Výsledky jsou prezentovány v této zprávě. Podrobný popis postupu prací v roce 2012 je uveden níže v členění po jednotlivých pracovních balíčcích. Za zmínku stojí, že plnění plánu strategické výzkumné agendy pracovního balíčku Digitální zobrazování s podporou technologií PMS v roce 2012 naznačilo možnost nových technických a konstrukčních alternativ. V návrhu projektu se předpokládalo, že prostorová modulace světla bude realizována pomocí počítačem řízených optoelektronických zařízení, která využívají elektrooptického jevu v kapalných krystalech. V průběhu řešení projektu byly navrženy nové způsoby provedení PMS, které otevírají prostor pro náhradu dosud používaných modulátorů světla difraktivními prvky vyrobenými standardními technologiemi. Tato změna by měla zásadní význam pro konstrukci celého systému a kromě výrazného snížení nákladů by vedla k mnohem jednoduššímu a kompaktnějšímu technickému řešení. Pozitivní výsledek těchto aktivit nelze s dostatečnou jistotou zaručit, jejich význam je ale natolik zásadní, že bude vhodné možnost změny technologie PMS prověřit, i když tato činnost nebyla v návrhu projektu plánována. Čerpání prostředků. Plánované náklady projektu v roce 2012 byly 39 mil Kč, z toho 26 mil. Kč hrazených z veřejné podpory a 13 mil. Kč hrazených z neveřejných prostředků. V průběhu roku došlo k některým přesunům nákladů mezi pracovními balíčky a mezi jednotlivými kategoriemi nákladů v mezích povolených poskytovatelem. Tyto změny byly prováděny ve snaze využít prostředky projektu co nejúčelněji. V důsledku výše zmíněného pozdějšího než předpokládaného poskytnutí podpory došlo u některých účastníků projektu k mírnému nedočerpání prostředků. V dalších letech lze očekávat, že budou prostředky čerpány v plné výši. U účastníka Meopta-optika, s.r.o. došlo v průběhu roku ke změně druhu pořizované investice a výrazné změně pořizovací ceny investice. Tato změna neměla vliv na rozložení uznaných nákladů projektu. Změna byla oznámena poskytovateli a následně poskytovatelem schválena. Řešitelský tým. V průběhu roku nedošlo v řešitelském týmu k podstatným změnám s výjimkou změny zodpovědné osoby balíčku Multi senzorické a hyperspektrální zobrazovací systémy. Ukázalo se, že vlastní výzkumná činnost Dr. Radka Čelechovského bude úzce souviset s výzkumem prováděným v rámci balíčků Digitální ramanova spektroskopie a Ramanova optická aktivita a Digitální zobrazování s podporou technologie PMS. Dr. Čelechovský rozšíří své působení i do výzkumné a vývojové činnosti dalších dvou balíčků, čímž byla významně posílena provázanost těchto třech balíčků. Úvazek Dr. Čelechovského u společnosti Pramacom-HT, spol. s r.o. pokrývá jeho činnosti v balíčku Multi senzorické a hyperspektrální zobrazovací systémy, jak byly uvedeny v návrhu projektu, neumožňuje mu však převzít odpovědnost za celý balíček, který proniká do působení dalších pracovišť. Proto byl zodpovědnou osobou nově
3 určen Mgr. Filip Chlup, který s Dr. Čelechovským dlouhodobě spolupracuje a nadále se problematice bude věnovat plným úvazkem. Mgr. Filip Chlup pracuje ve společnosti Pramacom-HT od ukončení studia na Přírodovědecké fakultě UP v Olomouci, specializace optoelektronika v roce Věnuje se problematice optických měření v IR oblasti, optické konstrukci a rádiové komunikaci. Byl zapojen do řešení projektů TIP a POTENCIÁL, publikoval v odborných časopisech a je spoluautorem knihy Fyzikální základy radaru. Na zasedání Řídícího výboru Centra byla tato změna prodiskutována a odsouhlasena. Řídící výbor. Byl ustaven Řídící výbor Centra digitální optiky ve složení: doc. Mgr. Jaroslav Řeháček, Ph.D. (UP), řešitel manažer projektu Mgr. Petr Přikryl (Meopta optika, s.r.o.) Mgr. Jiří Oulehla (PRAMACOM-HT, spol. s r.o.) Lukáš Kapitán (ZEBR s.r.o.) prof. RNDr. Zdeněk Hradil, CSc. (UP) doc. RNDr. Radim Chmelík, Ph.D. (VUT Brno) Mgr. Roman Burianec (Meopta optika, s.r.o.) Ing. Kamil Odstrčil (Meopta optika, s.r.o.) Mgr. Filip Chlup (PRAMACOM-HT, spol. s r.o.) Mgr. Vladimír Chlup (PRAMACOM-HT, spol. s r.o.) Ing. Lubomír Husák (ZEBR s.r.o.) RNDr. Josef Kapitán, Ph.D. (UP) prof. RNDr. Zdeněk Bouchal, Dr. (UP) Ing. Martin Antoš, Ph.D. (VUT Brno) prof. RNDr. Pavel Zemánek, Ph.D. (Ústav přístrojové techniky AV ČR, v.v.i.) doc. Mgr. Kamil Postava, Dr. (VŠB-TU Ostrava) Složení Výboru a jeho status je přílohou Smlouvy o spolupráci na řešení programového projektu č. TE ze dne 20. července Účast v Řídícím výboru přijali dva externí odborníci z významných institucí podílejících se na aplikovaném výzkumu a vývoji v ČR. Pro účely interní komunikace bylo zřízeno internetové rozhraní s využitím technologie Wiki se zabezpečeným přístupem (omezeným na členy řešitelského týmu) na adrese Dále byly zřízeny internetové stránky pro veřejnost Komunikace uvnitř Centra dále probíhá prostřednictvím pravidelných jednání Řídícího výboru a písemných zápisů z těchto jednání, a prostřednictvím pravidelných technických seminářů.
4 Plnění plánu Management projektu Činnosti Ustavování organizační struktury centra, nastavování mechanizmů komunikace. Ukončeno. Průběžné řízení projektu. Probíhá. Milníky Pravidelné zasedání řídícího výboru 2x. Splněno. Pravidelný technický seminář. Splněno. Dílčí cíle Webové rozhraní Centra digitální optiky. Splněno. Dosažení deklarovaných cílů a milníků projektu pro rok Splněno. Dílčí výstupy Roční zpráva o stavu řešení projektu. Splněno Digitální Ramanova spektroskopie a Ramanova optická aktivita Činnosti Provádění analýzy komplexního optického uspořádání spektrometru. Probíhá. Volba materiálů a technologií opracování pro stavbu objektivů v UV oblasti. Probíhá. Provádění analýzy využití různých typů polohovacích zařízení pro pohyblivé části spektrometru. Probíhá. Milníky, dílčí cíle a dílčí výstupy nebyly plánovány. Multi senzorické a hyperspektrální zobrazovací systémy Činnosti Aplikovaný výzkum v oblasti analýza a syntéza optických soustav pro IR oblast. Probíhá. Aplikovaný výzkum opracování netradičních optických materiálů pro zobrazovací pásmo (1,0 μm až 15 μm). Probíhá. Aplikovaný výzkum tenkých optických vrstev pro spektrální pásma (1,0 μm až 15 μm). Probíhá. Milníky, dílčí cíle a dílčí výstupy nebyly plánovány. Digitální zobrazování s podporou technologie PMS Činnosti Teoretická analýza technik zobrazování pomocí PMS a metod digitální rekonstrukce obrazu.
5 Probíhá. Návrh metod pokročilé holografické rekonstrukce. Probíhá. Vývoj softwaru pro řízení PMS. Status: Probíhá. Návrh numerických modelů pro simulaci zobrazování pomocí PMS. Probíhá. Realizace experimentů pro ověření zobrazovacích vlastností systémů pracujících s využitím PMS. Probíhá. Návrh optimalizovaných systémů pro holografický záznam a digitální rekonstrukci obrazu. Probíhá. Milníky, dílčí cíle a dílčí výstupy nebyly plánovány. Zpracování dat S-H senzoru v metrologii a zobrazování. Činnosti Analyzování současné technologické špičky v oblasti S-H detekce po hardwarové a softwarové stránce. Ukončeno. Aplikovaný výzkum v oblasti informačních protokolů pro S-H detekci. Probíhá. Programování software pro kontrolu dat z S-H senzoru a diagnostiku intenzity a vlnoplochy. Probíhá. Aplikovaný výzkum možností měření kvality optických ploch pomocí S-H technologie. Probíhá. Milníky nebyly plánovány. Dílčí cíle Analýza současné technologické špičky v oblasti S-H detekce po hardwarové a softwarové stránce. Splněno. Dílčí výstupy Výzkumná zpráva: Analýza současné technologické špičky v oblasti S-H detekce. Splněno. Závěr: Bylo dosaženo všech plánovaných milníků, dílčích cílů a dílčích výstupů.
6 Pracovní balíček: Digitální Ramanova spektroskopie a Ramanova optická aktivita Analýza komplexního optického uspořádání spektrometru. Ramanův rozptyl je neelastický rozptyl fotonů vznikající při interakci dopadajícího záření s vibračními nebo rotačními stavy molekul. Rozptýlené záření má obecně jinou vlnovou délku než záření dopadající a na základě jeho analýzy můžeme získat velké množství informací o charakteru a struktuře studovaného systému. Ramanova optická aktivita (ROA) spočívá v měření velmi malého rozdílu v intenzitě Ramanova rozptylu z chirálních molekul odpovídající levotočivě a pravotočivě kruhově polarizovanému záření. Toto rozšíření techniky Ramanova rozptylu o citlivost k optické aktivitě molekul pak informační obsah ve spektrech ještě dále významně rozšiřuje, obzvláště o data týkající se prostorového uspořádání, konformačního chování a případně i dynamiky studovaných molekul. Ramanův rozptyl je dvoufotonový proces a je tedy možné volit vlnovou délku excitačního záření, geometrii rozptylu, tj. úhel mezi dopadajícím a rozptýleným zářením, a v případě Ramanovy optické aktivity i tzv. modulační schéma, kdy je detekován rozdíl v odezvě molekuly vůči dopadajícímu levo- a pravotočivě kruhově polarizovanému záření a/nebo se detekuje rozdíl mezi kruhově polarizovanými složkami rozptýleného záření. Obr. 1: Základní schéma Ramanova spektrometru. Spektrální analyzátor může být jak disperzní spektrograf vybavený např. difrakční mřížkou, tak i interferometr. Na UP je v rámci projektu je prováděna komplexní analýza optické soustavy Ramanova spektrometru a spektrometru pro měření ROA. Jde o komplexní proces zahrnující optiku pro přenos excitačního záření na vzorek, přenos rozptýleného záření ze vzorku na vstup spektrografu a optiku samotného spektrografu zobrazující spektrum na plošný detektor. Analýza optické soustavy Ramanova spektrometru je prováděna za účelem zjištění optimálního experimentálního uspořádání spektrometru za účelem maximalizace poměru signál/šum se zohledněním optimálního spektrálního rozlišení, maximální intenzity ozáření (W/m2) vzorku, která ještě nezpůsobí jeho degradaci, množství vzoru potřebného experiment a jeho koncentrace, možnosti měnit fyzikální parametry vzorku (teploty), možnosti minimalizovat degradaci vzorku zářením pomocí rotující nebo průtočné kyvety apod.
7 Vlnová délka excitačního záření ovlivňuje především intenzitu Ramanova rozptylu, který je nepřímo úměrný její čtvrté mocnině (v případě ROA dokonce její páté mocnině). S klesající vlnovou délkou ovšem také často výrazně roste intenzita nežádoucího fluorescenčního pozadí buď vzorku samotného nebo stopových nečistot. To představuje velký experimentální problém především díky tomu, že fluorescence má o mnoho řádů vyšší účinný průřez a často i intenzitu než Ramanův rozptyl. V případě biologicky zajímavých molekul (proteinů, nukleových kyselin, sacharidů apod.) je obvykle jako volena excitační vlnová délka záření v oblasti kolem 532 nm (historicky také 488 nebo 514 nm) jako dobrý kompromis mezi intenzitou Ramanova rozptylu a nepříliš velkou úrovní fluorescenčního pozadí. Je-li naproti tomu excitační vlnová délka záření nižší než cca 260 nm, tedy v hluboké ultrafialové spektrální oblasti (DUV), dochází k spektrálnímu oddělení fluorescence a Ramanova rozptylu a fluorescence tak přestává být experimentální omezením při záznamu spekter. Kromě vyšší intenzity Ramanova rozptylu je také velkou motivací rezonanční zesílení Ramanových spekter, ke kterému dochází v případech, kdy je energie dopadajícího záření vyšší nebo alespoň srovnatelná s rozdílem mezi elektronovými stavy molekul. Změnou excitační vlnové délky je tak možné studovat signál z vybraných částí molekuly (chromoforů). Obr. 2: Závislost Ramanových spekter myoglobinu na vlnové délce excitačního záření. Při excitační vlnové délce 415 nm dochází k rezonančnímu zesílení vibračních módů poryrinového kruhu, při vlnové délce 229 nm postranních skupin tryptofanu a při vlnové délce 206 nm peptidových vazeb (Asher et al. Chem. Rev. 2012, 112, ). Při návrhu optické sestavy Ramanova spektrometru je nutné respektovat zákon zachování optického rozsahu (étendue, Abbého invariant) s cílem optimálně využít tok záření vycházející ze vzorku. Situace je komplikovanější v tom, že záření vychází z objemu vzorku (a nikoliv plochy) odpovídajícímu např. fokusovanému Gaussovskému svazku, přičemž osa svazku není obecně paralelní se vstupní rovinou spektrografu. Intenzita Ramanova rozptylu i Ramanovy optické aktivity závisí na geometrii rozptylu, přičemž Ramanův rozptyl má největší intenzitu v pravoúhlém uspořádání. Optimální poměr signálu a šumu se u ROA naproti tomu dosahuje ve zpětném rozptylu, což je právě případ, kdy osa svazku není paralelní, ale kolmá na štěrbinu spektrografu. Svazek rozptýleného záření je v případě geometrie zpětného (popř. i přímého) rozptylu nutné transformovat tak, aby nedocházelo ke ztrátám záření na štěrbině spektrografu. Tento úkol je z optického hlediska velmi náročný, jednoduchých optických prvků (např. válcové čočky) není možné využít, neboť díky zákonu zachování étendue by došlo k nežádoucí změně výstupního úhlu záření v jednom směru a výsledný kužel záření by pak nebyl dobře navázán na spektrální analyzátor
8 (spektrograf). Obr. 3: Porovnání části optické sestavy Ramanova spektrometru v a) pravoúhlé geometrii a b) geometrii zpětného rozptylu. V druhém případě je osa svazku kolmá na vstup spektrografu. V rámci prováděné analýzy se pokoušíme vyhodnotit parametry několika řešení tohoto problému, které byly v minulosti navrženy a případně vybrat to, které by bylo nejvhodnější pro Ramanovu spektroskopii. Mezi ně patří sestavy několika multimódových optických vláken (W. Hug, J. Raman Spectrosc. 1999, 30, 841), využití sestavy úzkoprofilových zrcadel metodou krájení štěrbiny (I. S. Bowen, Astrophys. J., 1938, 88, 113) nebo pomocí kódovaných apertur (např. Hadamardovy masky, M. E. Germ, Appl. Optics, 2006, 45, 2965) a následného matematického zpracování zaznamenaného obrazu. V poslední době se také ukazuje použití speciálních interferometrů (J. Harlander et. Al, Astrophys. J., 1992, 396, 730) jako velmi zajímavé a slibné řešení spektrálních analyzátorů pro Ramanovu spektroskopii. Výsledkem prováděné analýzy bude v březnu 2013 protokol, který bude sloužit jako zadávací specifikace pro optické soustavy vyvíjené v rámci projektu. Jedním z možných spektrálních analyzátorů vhodný pro záznam Ramanových spekter v hlubohé ultrafialové oblasti spektra je spektrograf v Czerny-Turnerově uspořádání vybavený reflexní difrakční mřížkou, v němž jsou zrcadla nahrazena objektivy. V rámci analýzy optického uspořádání spektrometru bylo ve firmě Meopta, s.r.o. provedeno detailní testování již dříve vyvinutých a zhotovených UV objektivů se světelností F/2 a ohniskovou délkou 100 mm. Objektivy byly navrženy tak, aby poskytovaly rozlišení 80 čar/mm s kontrastem vyšším než 50%. Z materiálů, použitelných pro DUV a umožňující spektrální korekci objektivů, byla zvolena kombinace taveného křemene a CaF2. Nejprve bylo provedeno měření optických parametrů samostatného UV objektivu. Naměřená hodnota průměru vstupní pupily byla 53,6±0,1mm. Ohnisková vzdálenost byla měřena pro předmětový úhel 1 pro vlnové délky 234, 242, 254, 262, 266 a 270nm. Výsledky ukazují, světelnost objektivu je oproti jmenovité přibližně o 6% vyšší, což příznivě ovlivňuje energetickou bilanci. Funkce přenosu kontrastu byla měřena na optické ose objektivu pro tytéž uvedené vlnové délky. Hodnoty kontrastu pro prostorovou frekvenci 80č/mm a polohy zaostření odpovídající použitým vlnovým délkám jsou v intervalu 0,66 0,73. Protože nebylo možné provést současné měření v tangenciální a radiální orientace objektivu, bylo měření opakováno pro otočení objektivu o 90 dle optické osy se srovnatelnými naměřenými hodnotami. Dosažené výsledky dosahují dobrou stablitu pro celé sledované spektrum. Rovněž prakticky shodné výsledky pro tangenciální a radiální orientaci objektivu svědčí o výborné realizaci z hlediska dosažené centricity optiky. Výsledky měření spektrální propustnosti jsou pro celou funkční oblast nm vyšší než 70%,
9 přičemž maximální hodnota na 265nm je 88%. Pro devítičočkový netmelený objektiv vyrobený z taveného křemene (celková tloušťka 43,3mm) a CaF2 (celková tloušťka 50,2 mm) lze tento výsledek považovat za velmi dobrý. AR vrstvy byly optimalizovány pro oblast nm s požadovanou zbytkovou reflexivitou Ravg < 0.2%. Obr. 4: Naměřená spektrální propustnost UV objektivu pro osový bod. Dalším krokem bylo měření optických parametrů dvojice UV objektivů v sestavě s difrakční mřížkou s 3600 vrypy/mm (typ Richardson 53009BK01-170R). Obr. 5: a) Schéma optické soustavy spektrografu, b) sestava objektivů a difrakční mřížky použitá pro testování. Nejdříve byla proměřena účinnost difrakční mřížky pro zjištění její správné orientace. Difrakční účinnost v +1. řádu (ve směru blazovacího úhlu) byla 33%, v -1. řádu pak 9%. První difrakční řád byl proto využíván v měřících sestavách, které jsou popsány dále. Požadované spektrální rozlišení celé sestavy bylo řádově 0,045 nm. Dosažitelné spektrální rozlišení uvedené difrakční mřížky o využitém rozměru mm je řádově vyšší, kolem 0,0014 nm. Výsledné spektrální rozlišení je tedy určováno geometrickou šířkou štěrbiny a zobrazovacími parametry objektivu.
10 V první fázi určování spektrálního rozlišení sestavy byly použity dva zdroje záření: nízkotlaká argon-rtuťová výbojka poskytující intenzivní spektrální čáru kolem 265,2 nm a Nd:YAG laser s vlnovou délkou 266nm. Nízkotlakou výbojkou Hg (Ar) Oriel model 6035 byla prosvětlena štěrbina o šířce 5 um a výšce několika mm, která byla umístěna v předmětové rovině objektivu 1. Štěrbina byla nastavena tak, aby z objektivu 1 vycházel kolimovaný svazek. Tento svazek dopadal téměř kolmo na difrakční mřížku. Pomocí goniometru, na němž byla upevněna difrakční mřížka, byl do požadovaných úhlů nastaven objektiv 2, který zobrazuje svazek záření vystupující z difrakční mřížky. Obraz byl snímán za pomoci UV CCD kamery s mikroskopovým objektivem o zvětšení 15x. Pro ideální objektivy by spektrální šířka obrazu štěrbiny byla 0,014 nm, s uvážením, že přirozená spektrální šířka atomové čáry rtuti je mnohem nižší, než tato hodnota. Naměřená spektrální pološířka profilu napříč obrazem štěrbiny (tedy ve směru difrakce) byla přibližně 0,027nm. Obr. 6: a) Intenzitní profil spektrální čáry rtuti ve směru difrakce (řez kolmo na obraz štěrbiny). Pološířka profilu napříč obrazem štěrbiny (tedy ve směru difrakce) je přibližně 90pixelů, což ve skutečnosti odpovídá 0,028 mm. To dává hodnotu spektrální pološířky přibližně 0,027nm. b) Zvětšený obraz difrakcí rozšířené štěrbiny (snímáno pomocí kamery s mikroskopovým objektivem 15x ). Další měření spektrální pološířky bylo provedeno s laserovým zdrojem o střední vlnové délce 266 nm. Laserový svazek byl nejprve pomocí mikroskopového objektivu 40x0,3 zaostřen do bodu, který tvořil předmět objektivu 1 sestavy spektrografu. UV objektiv 1 byl vůči předmětu nastaven tak, aby předmět byl na optické ose objektivu a přitom z objektivu vycházel kolimovaný svazek, podobně, jako v předchozím případě. Obraz objektivu 2 byl opět sledován pomocí UV CCD kamery s mikroskopovým objektivem se zvětšením 15x. Spektrální šířka laserového zdroje byla určena jako 0,09 nm a je tedy limitujícím faktorem určujícím rozlišení. Jelikož bylo předmětem objektivu 1 fokusovaný pas laserového svazku o šířce řádově jednotek um, vertikální profil obrazu difraktovaného laserového zdroje udává prostorové rozlišení optické sestavy spektrografu ve vertikální směru. Jak měření samotného objektivu, tak měření v předpokládané tandemové sestavě s difrakční mřížkou nasvědčují, že může být dobrým základem pro stavbu Ramanova spektrometru, pracujícího v UV oblasti. V další období bude probíhat další testování optických parametrů spektrografu ve spektrální oblasti nm.
11 Obr. 7: a) Intenzitní profil laserového svazku ve směru difrakce. Pološířku svazku ve směru difrakce je přibližně 300 pixelů. Z velikosti pixelu použité kamery 4,65 um a zvětšení mikroskopu 15 vychází skutečná pološířka svazku přibližně 0,093 mm. Tento úhel odpovídá spektrální pološířce zdroje 0,09 nm. b) Obraz nasnímaný kamerou s mikroskopovým objektivem 15x zaostřeným do obrazové roviny Probíhá také patentová rešerše v oblasti aplikací optických soustav pro UV Ramanovu spektroskopii. Cílem je podání patentu, jehož součástí je vyvinutá soustava dvojice UV objektivů v uspořádání určeném pro UV Ramanovu spektroskopii. Volba materiálů a technologií opracování pro stavbu objektivů v UV oblasti. Provádění činností ve firmě Meopta-optika, s.r.o. se v rámci vývoje technologií opracování materiálů pro UV oblast prolíná s pracovním balíčkem č. 3 Multisenzorické a hyperspektrální systémy a činností Aplikovaný výzkum opracování netradičních optických materiálů pro zobrazovací pásmo (1,0um až 15um), neboť použité materiály jsou v některých případech shodné (např. fluorid vápenatý). Prvním úkolem a základem prováděných činností bylo vytipovat vhodné materiály pro UV, IR oblast pro první zkoušky technologie opracování. V roce 2012 probíhalo také řešení základního strojního vybavení pro úvodní zkoušky a testování technologií opracování neskleněných materiálů pro UV a IR oblasti. Došlo k seznámení se s materiály doporučenými pro UV a IČ oblast, při výběru materiálů byly zohledněny otázky škodlivosti materiálů pro lidské zdraví. Pro technologické zkoušky opracování byly vybrány pro UV oblast materiály fluorid vápenatý (CaF 2) a tavený křemen (fused silica), přičemž tavený křemen se v Meoptě standardně používá pro výrobu optických elementů. Technologii pro opracování CaF2 je teprve nutné v rámci řešení projektu vyvinout. Pro IČ oblast byly vybrány materiály s minimem zdravotní závadnosti CaF2, germánium (Ge), tavený křemen a ZnS.
12 Obr. 8: Křivka propustnosti desek o tloušťce 10 mm z materiálu CaF2 a tavený křemen v UV oblasti (dle katalogu firmy Linos). Křivky propustnosti výrazně 0závisí na kvalitě použitého matriálu. Obr. 9: Degradace materiálů pro UV oblast po aplikaci UV záření o vlnové dílce 193 nm a 8000 J/cm2 ( pulsů). (zdoj: katalog firmy Linos) Tavený křemen je mnohem více náchylný k degradaci než CaF2. Byly stanoveny tvary a rozměry vhodných polotovarů a jejich množství pro technologické zkoušky (byl proveden návrh na nákup 30-ti kusů kotoučků průměru = 35±0,5 mm, tloušťky 8 ± 0,5 mm od každého z materiálů, nebo jejich násobků s přídavky 3mm na prořez pily). Byla provedena poptávka polotovarů vybraných materiálů (kromě taveného křemene, který se v Meoptě standardně používá) u dodavatelských firem s ohledem na orientaci krystalů a jejich využití pro UV a IČ oblast. Materiál CaF 2 byl poptán u firmy Hellma Materials, Ge a ZnS u firmy Korth Kristalle. Byly dodány polotovary Ge (10x tyč o průměru 35mm, tloušťka 30mm, monokrystal s osou růstu v ose kotoučku), ZnS Flir Grade (10x tyč o průměru 35mm, tloušťka 30mm, monokrystal s osou růstu v ose kotoučku). Byl proveden výběr vhodných brusiv a leštiv. Vzhledem k jednoznačné výhodě při opracování rovinných ploch, rychlosti, spolehlivosti a
13 reprodukovatelnosti v tvorbě lešticích nástrojů bylo dohodnuto, že úvodní základní zkoušky a testování leštiv, podložek a metody bude probíhat na substrátech s rovinnými plochami. Proto byly v této úvodní fázi zajišťovány zvolené materiály: germanium, CaF 2, tavený křemen (fused silica), křemík (Si) a ZnS v podobě kotoučků s rovnoběžnými rovinnými plochami. Byl proveden návrh na nákup hmotného investičního majetku a dalších provozních nákladů pro Centrum digitální optiky za rok Pro provádění leštění byl vytipován v první polovině roku 2012 rovinný lešticí stroj Lapmaster 36, který by měl být zakoupen v roce Všechny důležité parametry jako je geometrická přesnost, čistota povrchů, drsnost ploch a celková propustnost včetně vrstev budou po dodání tohoto stroje a vakuové aparatury v roce 2013 prakticky vyvíjeny a testovány. Práce na opracování materiálů ale započaly již v r.2012 na provizorní technice. Pro následné zkoušky opracování (především leštění) daných materiálů byl poptán Laserový analyzátor velikosti částic FRITSCH Analysette 22- NanoTec plus, umožňující granulometrický rozbor vybraných leštiv. Druhým zařízením je Planetový kulový mlýnek p-5/2 FRITSCH pro mletí (zjemnění zrn) leštiv (v optické výrobě se zjemněná leštiva běžně používají). Pro další testy s ohledem na připravované vývoje přímo na sférických plochách byly nárokovány klasické stroje od fy. Optotech. Jsou to stroje s klasickou autorotační kývavou kinematikou umožňující v operaci broušení použití brousicích litinových nástrojů a v leštění nástrojů zejména smolné povahy, ale též použití nástrojů z moderních materiálů jako je polyuretanová lešticí fólie a též fólie typu Desmopan, Desmoflex a další. Tyto relativně jednoduché stroje Optotech jsou pod dodávány tímto výrobním označením: HM NC-P HM Lapping Machine rpm weights HM Traditional Polisher 5-50 rpm weights HM Traditional Machine with Excenter (n=150/min) HM Traditional Machine with Excenter (n=50/min) K těmto strojům byly korespondenčně získány další technické parametry a rovněž cenové nabídky. Pro leštění především CaF2 a podobných materiálů byly dále vytipovány stroje od firmy Stock Konstruktion GmbH. Vhodnost těchto strojů se dále potvrdila po návštěvě firmy Hellma Materials, které jsou zde používány. Provedli jsme dále zjištění ceny této technicky lepší techniky a zjistili, že jsou lacinější než alternativní stroje firmy Optotech. Místo strojů HM a HM firmy Opatech budou pro nákup zvoleny výhodnějších stroje NLP 220 DAS, NLP 330 DAS a NLP 400 DAHS firmy Stock Konstruktiv Gmbh. Byla uskutečněna návštěva firmy Hellma Materials, kde byly diskutovány otázky týkající se specifikace materiálu CaF2 pro UV a IČ oblast, včetně odpovídající orientace krystalu, homogenity, pnutí i laserové odolnosti. Probrána byla i technologie opracování surového ingotu pro potřeby zorientování krystalu, nařezání polotovarů a jejich měření. Dále byl předveden strojní park a poskytnuty základní informace a rady týkající se opracování tohoto materiálu (viz. Prezentace firmy Hellma Materials HMAT Meeting Meopta).
14 Obr. 10: Monokrystal CaF2. a znázornění osy (111) krystalu. Při leštění ploch orientovaných kolmo na tento směr dochází k nejlepším výsledným parametrům po opracování povrchu. Přímo na místě u firmy Hellma Materials bylo zjištěno, že v oblasti technologie opracování se firma pohybuje v základních polohách a kvalitách. Jde jim jen o to materiál uřezat, frézovat, zjemnit broušením či lapováním a zprůhlednit leštěním. Tato operace leštění je z našeho pohledu a našich potřeb bez patřičné kvality, geometrie, čistoty a drsnosti povrchu. Přesto zde byly získány cenné informace a bylo možné se fyzicky seznámit se stroji, na kterých probíhá leštění. Tyto stroje původně dodávala firma Naicotec, nyní jsou dodávány výrobcem Stock Konstruktion GmbH. Obr. 11: Zlomová struktura na leštěných rovinných plochách materiálu CaF2 s náhodnou orientací krystalu. Uskutečněná návštěva fy. Helma umožnila dále zadat správné technické specifikace a v současné době probíhá nákup materiálu CaF2 s určenou osou růstu krystalu ve směru 111. Takto orientovaný materiál umožňuje získání vyšší finální kvality z titulu geometrického tvaru a drsnosti povrchů u takto tvořené optiky.
15 Byly zahájeny zkoušky opracování materiálu Ge, CaF2 na prvních polotovarech předskokanech, které byly již dříve objednány k prvním zkouškám vrstvení. Polotovary kotoučky o průměru 20mm a tloušťce 2mm byly nakoupeny od firmy MaTecK GmbH, Ge - monokrystal s orientací (111), CaF2 - IR grade, monokrystal s náhodnou orientací. Zkoušky opracování byly započaty klasickou brousicí a lešticí technologií na smole i umělých podložkách standardními optickými leštivy. Po leštění Ge, CaF2 klasickou technologií byla dosažena drsnost a rovinnost u germánia: Sq = 1,5nm, 3/0,5(0,7) a u CaF2: Sq = 3,7nm, 3/0,5(0,1 až 1). Měřením na interferometru Zygo byla u CaF 2 odhalena zlomovitá struktura vzniklá opracováním materiálu nařezaného bez ohledu na osu (111) tedy s náhodnou orientací os krystalu Byly zahájeny zkoušky opracování Ge, CaF 2 technologií CNC na umělých podložkách. Dále byly dodány stroje Laserový analyzátor velikosti částic FRITSCH Analysette 22- NanoTec plus, planetový kulový mlýnek p-5/2 FRITSCH a bylo provedeno zaškolení obsluhy. V roce 2013 budou po obdržení konkrétní specifikace sférických čoček a výše uvedených strojů zahájeny zkoušky opracování a testování sférických ploch na žádaných materiálech. Provádění analýzy využití různých typů polohovacích zařízení pro pohyblivé části spektrometru. V rámci projektu byly testovány a porovnávány možnosti polohovacích zařízení, které jsou používány na výrobních linkách firmy ZEBR s.r.o. Díky poptávce po plně automatizovaných strojích je kladen stále větší důraz na spolehlivost, rychlost a přesnost výroby, zároveň však i na jednoduchost obsluhy a ekonomičnost provozu. Proto v rámci technického zdokonalování a nabídky lepších parametrů zařízení byly hledány varianty náhrady jednotlivých prvků dosavadního technického řešení. Zásadní vliv na přesnost a rychlost výroby mají prvky vytvářející na stroji mechanický pohyb a tím ovládající jednotlivé mechanizmy stroje. Obecně používané prvky v automatizaci vytvářející pohyb můžeme rozdělit z našeho pohledu na dvě kategorie. První kategorii tvoří prvky založené na principu energie uložené ve formě stlačeného vzduchu nebo tlaku hydraulického oleje. Celá soustava je pak tvořena vždy zdrojem natlakovaného média (kompresor případně hydraulické čerpadlo), prvky rozvádějícími médiu (hadice, trubky), řídicími a spínacími členy (ventily, senzory) a samozřejmě vlastními akčními členy, které převádí energii na lineární, rotační nebo kyvný pohyb (pneumatické a hydraulické válce, pneumotory). Druhou kategorii akčních prvků vytvářející pohyb tvoří elektrické pohony. Elektrický pohon je souhrnem zařízení, která zajišťují ovládání přeměny elektrické energie v mechanickou energii. Hlavní součástí elektrického pohonu je elektrický motor, který je však doplněn ovládacími a řídicími přístroji, které ovládají motor řiditelnými zdroji elektrické energie. Řízením elektrického pohonu rozumíme změny rychlosti, momentu, výkonu a dalších požadovaných proměnných parametrů. Automatizované stroje firmy ZEBR jsou již řadu let osazovány pneumatickými prvky renomované firmy FESTO. Díky pravidelnému školení a množství realizovaných aplikací, byla získána řada zkušeností v nasazování celé škály různých typů ovládacích ventilků a pneumatických válců, vždy specializovaná pro konkrétní úlohu. Díky požadavku zvyšování rychlosti a spolehlivosti mechanických pohybů ovládaných pneumatikou se otevřela problematika vyhodnocení a seřízení průběhu pneumatického cyklu. Porovnání jednotlivých prvků a zvolení optimální varianty je vždy vázáno na měření časových průběhů jednotlivých veličin. Zde je potřeba ale vždy převést neelektrickou veličinu
16 na elektrickou pomocí převodníků/snímačů. Byly proto pořízeny převodníky průtoku a tlaku vzduchu na elektrickou veličinu, monitorující spotřebu a časové průběhy tlaku v měřených částech pneumatického systému. Dále byla zakoupena vysokorychlostní kamera typu SBOx, která je schopna díky pořízení velkého množství snímků za sekundu zaznamenat rychlé pohyby a zpětně připojeným PC na časové ose analyzovat jednotlivé snímky průběhu. Díky tomuto vybavení byly pozorovány rozdíly rychlostí pohybu při použití různých typů pneumatických válců (průměry pístnic, typy plynulých dorazů válců), způsobu přívodu vzduchu (tloušťka hadiček, škrtící a zpětné klapky) a typů řídicích ventilů. Pro nejvíce časově náročnou aplikaci, kdy bylo potřeba pomocí pneumatiky vykonat rychlý pohyb sevření v co nejkratším čase, bylo dosaženou vhodnou volbou pneumatických prvků, reakční doby daného pohyb do 5 ms od vystavení elektrického povelu. Při takto rychlých aplikacích dochází v pneumatickém systému k jevům, které ovlivňují správnou činnost systému, snižují jeho spolehlivost pro práci ve výše uvedených krátkých časech. Tyto jevy aktuálně zkoumáme, konzultujeme s vývojovým oddělením německého výrobce pneumatických prvků, provádíme testování. Po pořízení nových měřících a testovacích zařízení jsme ovšem zjistili, že problém sestává z většího množství okolností, které činnost systému ovlivňují, všechny jevy nám zatím nejsou zcela srozumitelné. Specialisté od výrobce pneumatiky se s obdobnými aplikacemi, kde velké množství pneumatických prvků má vykonat přesnou práci v krátkém čase, ještě nesetkali a celou problematiku řešíme s výrobcem společně. Jsme na začátku cesty a následující období bude věnováno dalšímu zkoumání této problematiky. Dalším z problémů, se kterými se potýkáme, je vhodné měřící, zaznamenávací a vyhodnocovací zařízení, které dále na trhu hledáme. Doposud pořízený soubor zahrnutý do měřící stolice nedostačuje všem našim potřebám. Elektrické pohony nacházejí v automatizaci stále větší oblibu při řízení pohybů díky své komfortnosti, variabilitě, jednoduché řiditelnosti a ekonomické výhodnosti. Protože stroje firmy ZEBR jsou vybavovány asynchronními a servomotorickými pohony několika předních světových výrobců, je získávání odborných znalostí v této oblasti prioritou. Problematika elektrických pohonů se ovšem neomezuje jen na samotný výběr vhodného typu servomotoru a servozesilovače (jeho řízení), ale zahrnuje kompletní integraci do mechaniky stroje a zároveň napojení na nadřazený řídicí systém stroje (PLC - Programmable Logic Controller) s příslušným softwarovým vybavením. Právě možnosti softwaru na straně PLC i servozesilovače prochází neustálým vývojem a výrobci se snaží co nejvíce usnadňovat integraci motorických pohonů tvorbou pomocných SW nástrojů a ladících prostředků. Kromě základních funkcí servozesilovače, kdy slouží jako regulátor proudové, rychlostní a polohové smyčky se zpětnou vazbou, je trendem výrobců využít výpočetní výkon servozesilovačů na přídavné funkce, kterým může být řízení pomocí integrovaných vstupně-výstupních portů. Takto lze realizovat rychlé odezvy procesu v řádu mikrosekund v návaznosti na koordinaci s řízeným pohybem servomotoru. Pro srovnání, při řízení procesu pomocí PLC dosahujeme odezvy jen v řádech milisekund. V našich aplikacích používáme víc typů servozesilovačů, ale pro nejrychlejší polohovací úlohy byl vybrán digitální, typ AKD firmy Kollmorgen. Ten díky digitální proudové (0,67 µs), rychlostní (62,5 µs) a polohové regulační smyčce (125 µs) zajišťuje vysokou dynamiku pohonu a opakovatelnost nastavených pracovních pohybů. Zde využíváme i přídavné funkce zastavení na značku, tj. zachycení nástupné hrany digitálního vstupu a dopolohování o definovanou vzdálenost. Zde proběhl dlouhodobý vývoj SW jak na straně řídicího PLC, tak i firmwaru servozesilovače, kdy byly s výrobcem komunikovány naše návrhy pro dokonalejší funkce systému, které jsme získali důkladným zkoumáním procesů, analýzami a testováním. Tyto činnosti vedly k dosažení požadované přesnosti a opakovatelnosti. Díky tomu mohla být zvýšena nejen produktivita strojů firmy ZEBR, ale zároveň i přesnost výrobků. Do paměti servozesilovače lze jednoduchým způsobem zapsat krátký uživatelský program, který může v sobě zahrnout příkazy a parametry využívané vlastním firmwarem
17 servozesilovače. Tím se doba odezvy v řízené technologii zkracuje pod dobu 1 mikrosekundy! V minulosti se pro pohon válcovacích tratí používaly AC servomotory v kombinaci se servozesilovačem, jehož výstupní proud se pohyboval okolo 6A. Starší typy motorů díky svojí konstrukci měly velmi nízký koeficient Ke což je konstanta udávající točivý moment na hřídeli v Nm, při proudu servozesilovače 1A. Pokud tedy byl zapotřebí v aplikaci větší krouticí moment, přistupovalo se ke snižování provozní rychlosti např. z 3000 rpm na 2000 rpm i méně. Tabulka používaných typů AC motorů typ AC motoru koeficient Ke SBL ,5 Nm/A BSH ,2 Nm/A BDH ,4 Nm/A N ,6 Nm/A Max. otáčky Nmax 3000 rpm 4000 rpm 3000 rpm 3000 rpm Tyto na pohled stejné motory však dosahují při budícím proudu 6A, což je trvale možný dodávaný proud servozesilovačem, rozdílné krouticí momenty při provozních otáčkách v rozmezí od 7,2 do 9,6 Nm. Je zde větší rezerva pro špičkový krouticí moment a také energetická úspora při běžném provozu. Nejnovější typy střídavých synchronních servomotorů mají ve statoru rozložené trojfázové vinutí a permanentní magnety na rotoru. Tenká vrstva magnetů ze vzácných zemin neodym/železo/bór je umístěna na povrchu rotorové hřídele, čímž je dosažen malý moment setrvačnosti motoru. Vyšší krouticí moment, tedy i vyšší výkon motorů nové řady je dosažen zlepšením odvodu tepla ze statoru motoru do přední příruby spolu s optimalizovaným magnetickým obvodem. Zkrácení statorových svazků použitím segmentového vinutí spolu s dosažením vyššího plnění vinutí má za důsledek zkrácení délky celého motoru. Uvedené přednosti zvyšují poměr krouticího momentu k zastavěnému objemu servomotoru a rozšiřují oblasti použití z konstrukčního hlediska. Jednou z důležitých částí komplexních strojů vyráběných ve firmě Zebr jsou válcovací trati. Již z principu válcování je patrné, že u tvářeného materiálu procházejícího tratí dochází k prokluzům mezi válcovacími koly a materiálem. Vzhledem k tomu že potřebujeme válcovaný materiál polohovat s přesností do 0,2 mm na jednom metru, je nutné na polohu válcovaného materiálu navázat přesné externí odměřování. Nastává zde nárok na servozesilovač, aby jeho externí zpětná vazba mohla být dle potřeby aktivována (v provozu válcování) a deaktivována (když v trati není materiál, nebo je právě zaváděn obsluhou a externí odměřování je neaktivní). Většina výrobců servozesilovačů toto přepínání vazby neumožňuje vyžadují pouze jednu a to trvalou vazbu. Někteří dokonce neumožňují ani tuto trvalou externí zpětnou vazbu. Z tohoto důvodu nebylo možné používat servozesilovače, byť nové generace, výrobců jako je Schneider Electric nebo Beckhoff. Výrobce Kollmorgen má ve výrobním programu servozesilovače které vyhovují jak po stránce připojení odměřování, tak i po stránce doby odezvy v regulačních smyčkách. Předpokládáme proto použití těchto prvků, přičemž budeme aktivně sledovat jejich vývoj s ohledem na naše požadavky. V návaznosti na inovaci servomotorických pohonů bylo hledáno řešení k zvýšení výkonu řídicího systému, který díky své omezené rychlosti datové komunikace, takto nepřímo ovlivňuje reakční dobu celého systému. To bylo docíleno tím, že byl vytipován nový vizualizační operátorský panel, který díky svým vlastnostem ulehčí výpočetní výkon PLC, který pak může být využit více pro řízení pohonů. V rámci plánovaných činností pro rok 2013 bude firma Zebr provádět další zkoumání činnosti rychlých pneumatických systémů, vzájemné ovlivňování prvků, nežádoucí tlakové spády a další nežádoucí jevy,
18 které činí pneumatiku nespolehlivou pro rychlé a přesné polohování při použití většího množství prvků na malém prostoru. Podobná činnost bude prováděna na hydraulických systémech, kde předpokládáme zahájení činností v druhé polovině roku. Nadále budou pokračovat práce na vylepšení funkcí nových řad servozesilovačů a to jak na straně námi požadovaných úprav firmwarů výrobce, tak na straně obsluhy servozesilovače z řídicího PLC. Dosažené parametry a výsledky budou dokumentovány měřeními. V rámci inovace a zlepšení spolehlivosti strojů budou nahrazeny vytipované mechanizmy, poháněné současně pneumatikou, servomotorickými pohony. Na UP dochází v rámci prováděné činnosti k výběru vhodných motorizovaných polohovacích zařízení s ohledem na jejich využití v Ramanově spektrometru a ve spektrometru pro měření Ramanovy optické aktivity. Bylo zahájeno zjišťování dostupných možností pro provedení rotačních nebo lineárních posuvů, jejich specifických vlastností, se zaměřením na použití výsledků pro polohování komponent spektrometru. Použití motorizovaných posuvů je plánováno především pro: - polohování polarizačních komponent, - pro rotaci a/nebo lineární posuv kyvety se vzorkem (pro polohování vzorku i snížení jeho degradace intenzivním UV/VIS zářením). Obr. 12: Základní schéma spektrometru pro měření Ramanovy optické aktivity (ROA) s vyznačením motorizovaných jednotek (podklad pro obr. převzat a upraven z Disertační práce J. Haeslera, Fribourg 2006). Základem pro vývoj spektrometrů pro měření Ramanovy optické aktivity je spektrometr vyvinutý prof. Wernerem Hugem (H. Hug, Measurement of Raman optical aktivity, Comprehensive Chiroptical Spectroscopy Vol. 1, 2012, ), který je základem komerčně dostupného přístroje, v současné době vyráběném pouze jedinou firmou Biotools. Ve spektrometru se nachází motorizované jednotky
19 trojího druhu (viz obr.): 1. Kontinuálně rotující jednotky: rychlý lineární rotátor 1 a 2 (LR1, LR2) a pomalý lineární rotátor 3 (LR3). Lineární rotátor je rotující půlvlnná deska. Je-li na vstupu lineárně polarizované záření, výstupem je taktéž lineárně polarizované záření, jehož směr polarizace rotuje v závislosti na úhlu otočení motoru. Doba rotace LR1 udává časovou jednotku (TU, time unit), u komerčního přístroje je 1 TU = 4,59 ms (odpovídající rychlosti rotace asi rpm). Doba rotace LR2 je 15/16 TU a doba rotace LR3 je 16 TU, takže orientace všech rotátorů se zopakuje za 16 TU (LR1 provede 16 otáček, LR2 15 otáček a LP3 jednu otáčku). Důležitá je rovnoměrná rotace s přesně definovanou frekvencí. Není-li rotace rovnoměrná, určité polarizační stavy záření (polohy polarizačního prvku) se vyskytují s nerovnoměrnou četností a dochází k vytváření systematických chyb při měření. Přesně definovaná frekvence určuje časování ostatních událostí měřicího cyklu. 2. Jednotky pro přesné opakované polohování polarizačních optických komponent: čtvrtvlnné desky. Dopadá-li na čtvrtvlnnou desku kruhově polarizované záření, výstupem je záření lineárně polarizované. Ortogonálně lineárně polarizované záření je možné generovat otočením čtvrtvlnné desky o +/- 90. Cílem jednotky je velice přesné a co nejrychlejší polohování fázové desky pro minimalizaci nevyužitelné doby měření. 3. Jednotky zasouvající a vysouvající optické prvky do optické dráhy: cirkulární převodník 1 (CP1) a cirkulární převodník 2 (CP2). Cirkulární převodník je půlvlnná deska, která má tu vlastnost, že dopadající pravotočivě kruhově polarizované záření mění na levotočivě kruhově polarizované záření a naopak. V rámci činnosti byly provedeny přípravné práce a základní měření na motorizovaných jednotkách dostupných na katedře optiky ve všech třech uvedených kategoriích. Bylo započato testování DC motorů firmy Faulhaber s dutou hřídelí s ohledem na rovnoměrnost rotace s přesně definovanou frekvencí. Byly provedeny první testy PID řízení těchto kontinuálně rotujících jednotek. Byly provedeny první testy polohování čtvrtvlnných desek pomocí krokových motorů s dutou hřídelí o průměru 40 mm od firmy Precistep. Ovládání je prováděno pomocí jednotek (driverů) firmy Technosoft umožňující přesný, plynulý chod a provádění polohování v mikrokrocích. Řízení motorů bylo vyvinuto v jazyku C++ s využitím knihoven dodávaných firmou Technosoft. Výsledky prvních testů jsou velice slibné a toto řešení bude nadále podrobně zkoumáno a rozvíjeno. Byly provedeny testy lineární motorizované jednotky M-683 firmy Physik Instrumente založené na piezomotorech. Tyto jednotky umožňují rychlost posuvu řádově 350 mm/s a délku posuvu 50 mm. Řízení jednotek bylo vyvinuto v jazyku C++ s využitím knihoven dodávaných výrobcem lineárních piezomotorů. Tyto jednotky jsou benchmarkem pro další vývoj lineárních posuvů. V roce 2012 docházelo k pravidelným konzultacím s partnerem projektu firmou Zebr s.r.o. Zkušenosti firmy Zebr s.r.o. s použitím elektrických pohonů i jejich integrací do komplexních zařízení se ukazují jako nedocenitelné a bylo navrženo několik inovativních řešení ve zmiňovaných oblastech. Byly diskutovány možnosti synchronizace rotačních zařízení. K vzájemné úzké spolupráci bude docházet i v následujícím období, budou zkoumány další možnosti realizace jednotlivých polohovacích jednotek.
20 Pracovní balíček: Multi senzorické a hyperspektrální zobrazovací systémy Analýza a syntéza optických soustav pro IR oblast. Bylo detailněji analyzováno pět nových US patentů optických soustav, které jsou určeny pro sledovaná spektrální pásma SWIR, eswir, MWIR, LWIR, případně jejich kombinace. Konstrukční analýza probíhala pomocí software OSLO Premium. Program OSLO byl doplněn několika vlastními podprogramy, které umožní snadnější zacházení s analyzovanými daty. Konstrukční syntéza byla prováděna na základě aberační teorie prvního a třetího řádu s následným využitím řady optimalizačních algoritmů. Byly sledovány limitní možnosti dosažení fyzikálně dokonalého zobrazení soustavami pouze s refraktivními kulovými plochami a rotační symetrií. První konstrukční zkušenosti byly prováděny i s cílem budoucího využití jak refraktivních asferických ploch, tak i difraktivních ploch. Je zřejmé, že použití těchto typů ploch v optických systémech pro LWIR a MWIR je velmi efektivní a výzkum i vývoj systémů s těmito prvky uskutečňovaný v rámci tohoto projektu zreální možnosti jejich nasazení. Důležitou roli hrají dostupné refraktivní materiály pro všechny čtyři uvažované spektrální oblasti. Byla studovány odborné publikace k tomuto tématu stejně, jako příslušné materiálové listy jednotlivých výrobců a potenciálních dodavatelů. Databáze využívaného programu OSLO byla částečně doplněna o optické konstanty vztahujících se k těmto materiálům. Byly zvoleny základní materiály vhodné pro refraktivní či difraktivní zobrazovací optické IR systémy, které budou v rámci tohoto úkolu dále vyvíjeny a používány. V pásmu LWIR se analýza zaměřuje zejména na materiály: Ge, ZnSe, ZnS a chalkogenní sklo AMTIR 1, případně jeho alternativy od jiných výrobců vyráběné pod různými obchodními názvy. Úzká vazba mezi vlastním detektorem a optickým systémem vyžaduje efektivní napojení parametrů. V oblasti LWIR je vzhledem k velké vlnové délce záření nutné zajistit, aby optický systém byl fyzikálně dokonalý. Spojíme-li požadavek dokonalého zobrazení ve smyslu Rayleighova kritéria s Nyquistovou vzorkovací frekvencí, dostaneme pro oblast LWIR mezní frekvenci νr-n (bod nulového kontrastu křivky MTF), kterou musí fyzikálně dokonalý optický systém dosáhnout. Tyto hodnoty uvádíme v následující tabulce společně s údaji o některých nechlazených LWIR čipech, které jsou na trhu (regulovaném státy výrobců) k dispozici. V tabulce je také uvedeno k nim odpovídající krajní clonové číslo cr-n. Je zřejmé, že v oblasti LWIR miniaturizace velikosti pixelů dosáhla z hlediska rozlišovací schopnosti své praktické meze a další zmenšování velikosti pixelů nemá podstatný smysl. Z teoretického hlediska má mezní velikost pixelu pro střední vlnovou délku 10 μm velikost 12,5 x12,5 μm. Pro názornost uvádíme i dva příklady optimalizovaných dvou optických systémů LWIR. První příklad LWIR objektivu, znázorněný na obr. 1A představuje jednoduchý triplet se sférickými plochami, v kombinaci materiálů AMTIR1- ZnS-AMTIR1, který rámcově splňuje požadavky odpovídající prvnímu řádku v tab. 1. Opomeneme-li další důležité požadavky na konstrukci IR objektivu, jako jsou atermalizace a odstranění narcisismu, je zřejmé, že i jednoduchá stavba tripletu je schopna, na rozdíl od optických soustav určených pro VIS oblast, dosáhnout korekčního stavu, který odpovídá fyzikálně dokonalému systému a splňuje požadavky na kvalitu zobrazení celého systému. počet pixelů 320 x 240 velikost pixelu velikost senzoru úhlopříčka νr-n krajní clonové f' pro 2τ =20 [μm] [mm] [mm] [č/mm] číslo cr-n [mm] x
21 160 x ,8 x 3, , x ,6 x 7, x ,9 x4, , x x x ,9 x 8,2 13, , x ,5 x 13,1 21, ,68 62 Tab. 1: Nechlazené detektory na bázi amorfního Si a optické systémy v pásmu LWIR Obr. 1A: Objektiv LWIR 1,7/57 pro zorné pole 20 Při přechodu k vyšším světelnostem je problematika optické konstrukce složitější. Vysoké požadavky na kvalitu zobrazení a vysoké světelnosti jsou protichůdné a v případě použití jen kulových ploch vedou k mnohačlenným systémům. Použití asférických nebo difraktivních ploch jeproto téměř nezbytné pro zachování jednoduchosti systému s malým počtem ploch. Obr. 1B ukazuje alternativu dvojčlenného objektivu jen ze dvou germániových čoček, který vychází z patentu US Na první pohled jednoduchá dvojčlenná stavba je ovšem jak konstrukčně, tak i technologicky a výrobně značně sofistikovaným systémem. Každá ze čtyř ploch je rotačně symetrická asférická plocha až do stupně y12. Soustava je sice fyzikálně dokonalá, ale pro případ čipu s velikosti pixelů 17 x17 μm, který je uveden na čtvrtém řádku tabulky 1, má nízkou světelnost. V tomto případě je clonové číslo příliš nízké a bude výrazně omezovat kvalitu zobrazení celého systému. Použijeme-li čip se stejným počtem pixelů 384x288, ale s jejich větší velikostí, to je 25 x 25 μm, musíme dle tabulky 1 použít objektiv o ohniskové vzdálenosti 34mm. Výsledky pro stejnou stavbu objektivu jsou zobrazeny na obr. 1C. V tomto případě je objektiv téměř fyzikálně dokonalý a svými parametry jen mírně překračuje meze pro dosažení úrovně, kdy neomezuje rozlišení dané vzorkovací frekvencí čipu.
22 Obr. 1B: Objektiv LWIR 1,1/20 pro zorné pole 20 Obr. 1C: Objektiv LWIR 1,1/34 pro zorné pole 20 V pásmu MWIR se v optických systémech nejčastěji používají materiály: germánium, CaF2, AMTIR 3, IG5, ZnSe, ZnS v úpravě Cleratran, tavený křemen a Si. Nejčastější rozměry čipů a velikosti jejich pixelů v současnosti nabízených systémů jsou uvedeny v tab. 2 současně s mezní frekvenci ν R-N a krajním clonovým číslem cr-n. počet pixelů velikost pixelu velikost senzoru úhlopříčka νr-n krajní clonové [μm] [mm] [mm] [č/mm] číslo cr-n f' pro 2τ =20 [mm] 320 x x 12 12, x x 12,8 20, ,5 58
23 1280 x ,2 x 15,4 24, ,5 70 Tab. 2: Chlazené detektory a optické systémy v pásmu MWIR na bázi Hg-Cd-Te Příklad objektivu MWIR 3/150 s pevnou ohniskovou vzdáleností je uveden na obr. 2. Objektiv je určen pro úzké zorné pole 4,7. Je zřejmé, že z hlediska rozlišovací schopnosti splňuje požadavky uvedené v tab. 2 v prvním řádku. Významné je i to, že aperturní clona je za optickými členy v obrazovém prostoru a lze ji ztotožnit se studenou clonou, která je u MWIR objektivů většinou nutná. Oproti pásmu LWIR více jak dvakrát kratší vlnová délka neklade z hlediska kvality zobrazení na světelnost objektivu již tak velké požadavky. Pro větší zorná pole a vyšší světelnosti diktované nyní zdůrazněním požadavku na zvýšení poměru S/N začíná převažovat omezení kvality působené aberacemi optické soustavy. V pásmu SWIR (alespoň v pásmu kratšího SWIR 0,9 až 1,7 μm) lze z hlediska spektrální propustnosti použít většinu obvyklých optických skel. Negativem ovšem je, že disperzní vlastnosti mnohých skel se v pásmu SWIR poněkud unifikují a neposkytují již tak velké možnosti ke korekci barevných vad jak tomu je v pásmu VIS. Rozšířené pásmo eswir (0,9 až 2,5 μm) představuje téměř 3 oktávy spektra a barevná korekce je tak obzvlášť komplikovaná. Pro konstrukční činnost má proto velký význam krystalický CaF2. Obr. 2: Objektiv MWIR 2/150 pro zorné pole 4,7 ; studená clona v zadní části objektivu Vzhledem k následujícím milníkům s konkrétními výstupy, byla oblasti SWIR věnována největší pozornost a byly studovány možnosti dosažení širokopásmové achromatizace. V tomto bodě činnost navazuje výzkum na výsledky získané v rámci řešení projektu TIP FR-TI1/364, který byl v roce 2012 ukončen. V tabulce 3 jsou uvedeny čtyři typy detektorů InGaAS, které se uplatňují v oblasti 0,9 až 1,7 μm. V tabulce již neuvádíme údaje hodnoty pro krajní clonové číslo cr-n, ani mezní frekvenci ν R-N, protože v oblasti SWIR již většinou neurčují kvalitu zobrazení. počet pixelů velikost pixelu velikost senzoru [μm] [mm] úhlopříčka [mm] f' pro 2τ =40 [mm] f' pro 2τ =20 [mm] 320 x , x 12
24 640 x x 12,8 20, x ,8 x 9, , x ,2 x 15,4 24, Tab. 3: Nechlazené detektory a optické systémy v pásmu SWIR na bázi In-Ga-As Některé nejnovější výsledky optické konstrukce (US2012/ ) naznačují, že významným prvkem pro širokopásmové zobrazovací systémy mohou být tvarově svobodné nesymetrické odrazné plochy, které se také stávají předmětem našeho studia. Část výsledků z konstrukční analýzy optických systémů pro IR oblast byla shrnuta v příspěvku na semináři v Meoptě, jehož prezentační část je k dispozici na webu k projektu. Tam jsou také rámcově uvedeny dosažené výsledky s objektivy SWIR. Opracování netradičních optických materiálů pro zobrazovací pásmo (1,0 μm až 15 μm) V rámci řešení ve firmě Meopta-optika, s.r.o. proběhla v první fázi poptávka polotovarů vybraných optických materiálů (kromě Fused silici, která se ve společnosti Meopta-optika, s.r.o. standardně používá pro výrobu opt. elementů) u dodavatelských firem s ohledem na orientaci krystalů a jejich využití pro IČ oblast. Materiál CaF2 byl poptán u firmy Hellma, Ge a ZnS u firmy Korth Kristalle. Ve druhé fázi došlo k dodání polotovarů Ge (10x rod průměr 35mm, tloušťka 30mm, monokrystal s osou růstu v ose kotoučku), ZnS Flir Grade (10x rod průměr 35mm, tloušťka 30mm, monokrystal s osou růstu v ose kotoučku) Pro následné zkoušky opracování (především leštění) daných materiálů byl poptán LASEROVÝ ANALYZÁTOR VELIKOSTI ČÁSTIC FRITSCH Analysette 22- NanoTec plus, umožňující granulometrický rozbor vybraných leštiv. Druhým dodaným zařízením byl Planetový kulový mlýnek p5/2 FRITSCH pro mletí (zjemnění zrn) leštiv. Dále proběhly zkoušky opracování materiálu Ge, CaF2 na polotovarech tzv. předskokanech, které byly objednány RNDr. Jankujem k jeho prvním zkouškám vrstvení. Polotovary kotoučky o průměru 20 mm a tloušťce 2 mm byly nakoupeny od firmy MaTecK GmbH, Ge - monokrystal s orientací (111), CaF 2 - IR grade, monokrystal s náhodnou orientací. Zkoušky opracování byly započaty klasickou brousicí a lešticí technologií na smole i umělých podložkách standardními optickými leštivy. Proběhla návštěva firmy Hellma Materials, kde byly diskutovány otázky týkající se specifikace materiálu CaF2 pro IČ oblast, včetně odpovídající orientace krystalu, homogenity, pnutí i laserové odolnosti. Probrána byla i technologie opracování surového ingotu pro potřeby zorientování krystalu, nařezání polotovarů a jejich měření. Dále byl předveden strojní park a poskytnuty základní informace a rady týkajicí se opracování tohoto materiálu (viz. Prezentace firmy Hellma Materials HMAT Meeting Meopta). O této cestě byla pro potřeby projektu vytvořena cestovní zpráva. V následujících testech byla zvyšovaná přesnost rovinnosti pro Germánium. Kontrolní měření probíhala na interferometru Zygo. Dále bylo testováno opracování Ge technologií CNC na umělých podložkách. V závěru roku byl dodán stroj pro opracování LASEROVÝ ANALYZÁTOR VELIKOSTI ČÁSTIC FRITSCH Analysette 22- NanoTec plus.
25 Tenké optické vrstvy pro spektrální pásma (1,0 μm až 15 μm). V rámci řešení projektu zavedení IR technologii v Meoptě-optice byla v roce 2012 pozornost zaměřena zejména na specifikaci vakuové aparatury vhodné pro tuto činnost, studiu literatury k dané problematice, vytipování a nákupu potřebných napařovacích materiálů, lodiček a podložných materiálů. Přestože vakuové aparatury byla specifikovány ve spolupráci s firmami LO a Umicore byla v rámci minimalizace nákladu rozhodnuto o nákupu již použité vakuové aparatury Bak 760, která bude přestavena Vakuum servisem Rožnov za cca 3 miliony korun. Vzhledem k opožděnému finálnímu objednání vakuové aparatury z důvodu diskusí v Meoptě Přerov a nepřítomností majitele k závěrečnému souhlasu s tímto řešením se nepodařilo vakuovou aparatury zajistit do konce roku, a proto plánovaný termín dodávky do Meopty je až 3-4 měsíc roku Současně s objednávkou vakuové aparatury se řešil i problém jejího umístění a rozsah potřebných úprav nového pracoviště. Vzhledem k nedostatku řešitelských kapacit v oblasti technologií vrstvení byl v 10 měsíci uvolněn 1 pracovník z výroby, který pracoval jako obsluha obdobné vakuové aparatury Bak 760 a je postupně zaškolován jako pracovník oddělení tenkých vrstev. Po dodání nové vakuové aparatury převezme hlavní technologickou odpovědnost za její činnost.
26 Pracovní balíček: Digitální zobrazování s podporou technologie PMS Teoretické i experimentální činnosti probíhaly v koordinaci UP a VUT s aplikačním pracovištěm firmy Meopta-optika, s.r.o. Toto pracoviště rovněž provedlo rešerši přístupů k aplikaci PMS v optické metrologii a aktuální průzkum trhu. Na tomto základě vyhodnotilo vhodné přístupy k metrologické aplikaci PMS a s tím související nutné vybavení laboratoře. Bylo vytvořeno potřebné technické zázemí pro plánované činnosti. Zobrazování pomocí PMS a metod digitální rekonstrukce obrazu. Prostorová modulace světla (PMS), která představuje základní techniku pracovního balíčku, je moderní optoelektronickou technologií s širokým aplikačním potenciálem. PMS je založena na elektrooptickém jevu v kapalných krystalech, umožňujícím řízenou změnu indexu lomu jednotlivých buněk. Podle konstrukčního typu zařízení je změna indexu lomu využita k modulaci amplitudy nebo fáze dopadajícího záření. Index lomu jednotlivých buněk lze měnit pomocí vhodného softwaru téměř v reálném čase, takže metoda je z hlediska praktického využití dostatečně operativní a univerzální. Schválený program balíčku se zaměřuje na zobrazovací a metrologické aplikace PMS. V průběhu řešení projektu byla hlavní pozornost zaměřena na metody digitálního zobrazování s podporou PMS. Pracovní činnost byla rozdělena do dvou základních aktivit orientovaných na vlastní výzkum digitálního korelačního zobrazení a na systematické studium principů a vlastností metod PMS zobrazování, založené na mezinárodních odborných publikacích. Digitální korelační zobrazování s nekoherentním světlem Aktivita byla zaměřena na výzkum metody, jejíž teoretické a experimentální základy byly ve spolupráci VUT Brno a UP Olomouc vytvořeny před zahájením projektu (P. Bouchal et al, Opt. Express 19, 15603, 2011). Metoda pracuje s korelačními záznamy zobrazovaného objektu, které jsou pomocí PMS pořízeny v prostorově nekoherentním světle. Digitální 3D rekonstrukce obrazu je provedena zpracováním korelačních záznamů pomocí vhodných algoritmů. V roce 2012 byly získány výsledky, které metodu rozvíjejí jak z hlediska využívaných fyzikálních mechanismů, tak i nových experimentálních konfigurací a modifikací. Získané výsledky mají praktický význam a vedou ke zvýšení výkonu metody a rozšíření spektra možných aplikací. Prokazatelnými výstupy jsou odborné publikace, vytvořené teoretické a technické zázemí a funkční experimenty, které poskytují základ pro následující etapy řešení projektu. Hlavní výsledky teoretické analýzy lze shrnout následovně: Byl vytvořen matematický model metody, který umožňuje kompletní popis záznamu a rekonstrukce pozorovaných objektů a určení základních parametrů zobrazení. Na základě matematického modelu bylo vytvořeno zázemí pro numerické simulace používané k ověřování nových principů zobrazení a návrhů optimalizovaných experimentálních sestav. S využitím výpočetních modelů a provedených experimentů byl ověřen hybridní koherenční charakter metody. Ten kombinuje záznam objektu provedený v prostorově nekoherentním záření s jeho následnou digitální rekonstrukcí, která probíhá v plně koherentním režimu. Tento
27 mechanismus umožňuje s kvazimonochromatickými prostorově nekoherentními zdroji dosáhnout efektů, které jsou v plně optických experimentech dostupné jen s koherentním zářením. Byla navržena a experimentálně ověřena metoda, která pro rekonstrukci obrazu využívá vírových stavů světla. V realizovaných experimentech byly světelné víry implementovány opticky při záznamu hologramů pomocí PMS, nebo digitálně při rekonstrukci standardních záznamů. Vírové stavy světla umožňují dosažení izotropního i anizotropního zvýraznění hran rekonstruovaných objektů. Proti dříve známým technikám je metoda originální tím, že pracuje s nekoherentním zářením a umožňuje zvýšení kontrastu hran u 3D objektů [1]. Byly navrženy a experimentálně ověřeny modifikace sestavy zajištující maximální optický výkon z hlediska rozlišení, velikosti zorného pole [2] a spektrální odolnosti. Rešerše známých metod zobrazování s využitím PMS Součástí řešení bylo vytvoření systematického přehledu metod využívajících technologií PMS. K průniku PMS do zobrazovacích a metrologických aplikací dochází teprve v posledních letech, takže informace bylo nutné získávat z aktuálních odborných publikací v mezinárodních časopisech. Cílem rešeršní práce bylo rozšíření dosavadních poznatků o možnostech PMS a nalezení vhodných principů využitelných v oblastech digitální mikroskopie a průmyslové metrologie. S ohledem na rozsáhlost této problematiky, byla pozornost věnována zejména metodám jednocestného korelačního zobrazování a filtrace prostorového spektra, které při zachování kompaktnosti systému poskytují informaci nad rámec klasického zobrazení. Základní zobrazovací metodou aktivně rozvíjenou v průběhu řešení projektu je digitální korelační zobrazování s nekoherentním světlem. Porovnání jednotlivých metod provedené v rešerši bude využito pro další rozvoj a modifikace této metody, a to jak z hlediska využívaných principů, tak i optimální volby parametrů experimentu. V rámci metrologických aplikací je hlavní pozornost zaměřena na střihovou interferometrii realizovanou pomocí PMS. Návrhy dalších možných metod budou provedeny s ohledem na předpokládané využití pro kontrolu optických ploch. Výsledky teoretické analýzy principů zobrazování pomocí PMS, včetně poznatků provedené rešerše, budou zpracovány ve výzkumné zprávě s plánovaným termínem dokončení 03/2013. Návrh metod pokročilé holografické rekonstrukce. Při holografickém zobrazování v některých případech vznikají v rekonstruované obrazové komplexní amplitudě optické víry, tedy singularity, které se vyznačují nenulovou hodnotou fázového rozdílu na uzavřené křivce obsahující bod nulové intenzity. Tyto víry způsobují problémy při navazování fáze (odstranění skoků fáze s hodnotou 2π). Pokud je sama funkce propustnosti vzorku vírová, pak je případný vír přenesen i do zobrazení. Při zobrazení reálných vzorků, kdy fázové posuvy závisejí na rozdílu optických drah daných rozdíly v rozložení indexu lomu vzorku, však obvykle signální svazek tyto singularity neobsahuje. Případné víry v obrazové fázi pak mají původ v koherentním zobrazovacím procesu, případně vznikají při rozptylu svazku v difuzním prostředí, které může obklopovat vzorek. Cílem činnosti je vytipovat vhodné metody navazování fáze, které jsou odolné vůči přítomnosti vírů v obrazové fázi, jednak najít možnost rekonstrukce nevírové funkce propustnosti vzorku. Z testovaných známých algoritmů navazování fáze se jako nejvhodnější nyní jeví modifikovaný Goldsteinův algoritmus, který je nyní testován z hlediska maximální rychlosti a adaptován pro použití v holografické rekonstrukci. Vznik vírů během zobrazení lze objasnit a
28 simulovat pomocí teoretického popisu zobrazení v holografickém mikroskopu, který byl rozpracován [3]. Příklad vzniku vírů při zobrazení modelového vzorku s nevírovou funkcí propustnosti je na obrázku 1. Tento teoretický popis byl zobecněn také pro přítomnost difusního prostředí v zobrazovací cestě [4]. Bylo zjištěno, že vznik a vývoj optických vírů při změně parametrů simulovaného zobrazení je ve shodě se známou teorií (viz např. Allen et al. Ultramicroscopy 88 (2001) 85 97). Obr. 1: Příklad simulace vzniku optických vírů při holografickém zobrazení fázového objektu s bezvírovou funkcí propustnosti, jejíž fáze je znázorněna na obrázku a). Optické víry (vyznačeny šipkami) v obrazové fázi na obrázku b) vznikly v důsledku omezeného rozlišení optické soustavy. Činnost bude pokračovat zobecněním teoretických poznatků a ověřením vhodné metody rekonstrukce bezvírového předmětového pole na základě naměřené obrazové fáze. Za vhodný přístup považujeme korekci obrazové fáze pomocí fitování teoretických dat na výsledky experimentu. Tento přístup je aktuálně testován. Software pro řízení PMS Základem řešení je technologie prostorové modulace světla (PMS), která využívá elektrooptického jevu v kapalných krystalech. V laboratořích UP Olomouc jsou k dispozici systémy firem Hamamatsu, Boulder a Holoeye, které umožňují energeticky efektivní fázovou modulaci vstupního záření. Požadovaná změna fáze světelné vlny je určena elektrickými signály, které mění index lomu jednotlivých buněk LCD. Provedení PMS vyžaduje realizaci fázových hologramů a jejich přenos na LCD. Příprava počítačem generovaných hologramů je realizována pomocí algoritmů připravovaných v prostředí Matlab, jejich přenos na LCD byl řešen pomocí jednoduchého uživatelského softwaru. V průběhu roku 2012 probíhal podle stanoveného plánu vývoj řídícího softwaru jak na úrovni algoritmů pro přípravu hologramů, tak i automatizace jejich přenosu na LCD. V digitálním zobrazování vyvíjeném v pracovním balíčku je rekonstrukce obrazu prováděna ze tří korelačních záznamů, které vyžadují odeslání tří rozdílných fázových hologramů na LCD. Tyto operace nelze dostatečně rychle a efektivně provést pomocí standardního uživatelského softwaru. Pro řízení experimentu byl proto využit systém LabView, který je na VUT běžně užíván a na UP Olomouc byla pořízena akademická licence z prostředků projektu. V průběhu řešení projektu bylo úspěšně vyřešeno automatické odesílání počítačem generovaných hologramů na LCD a načítání korelačních záznamů ze CCD do počítače. V následném období bude řešena komunikace se softwarem pro rekonstrukci obrazu z pořízených korelačních záznamů. Řešení probíhá v souladu s původním plánem a ukončení vývoje softwaru ve stanoveném termínu je reálné.
29 Návrh numerických modelů pro simulaci zobrazování pomocí PMS. Prostorová modulace světla (PMS) je v zobrazovacích aplikacích nejčastěji využívána pro realizaci strukturovaného osvětlení, filtraci prostorového spektra, nebo dělení vlnoplochy. Korelační zobrazovací metody vyvíjené v balíčku jsou založeny na interferenci vln, které vznikají rozdělením vstupní vlny pomocí PMS. Zobrazovací systém představuje jednocestný interferometr, který může pracovat s prostorově nekoherentním zářením a pro korelační záznam využívá časovou koherenci. Zobrazení má v tomto případě část optickou, ve které je proveden záznam objektu, a část digitální, ve které jsou záznamy numericky zpracovány a následně rekonstruovány. Celý proces je závislý na velkém počtu experimentálních parametrů, jejichž vlivy je nutné vyšetřit pomocí numerických simulačních modelů. Pro návrhy a optimalizaci systémů byly v prostředí Matlab vytvořeny virtuální experimenty, které byly použity k řešení následujících problémů: Určení impulzní odezvy při záznamu a rekonstrukci bodových objektů v monochromatickém záření. Určení parametrů experimentu pro optimální rozlišení systému a kvantifikace subdifrakčního rozlišení. Subdifrakční rozlišení bylo experimentálně prokázáno a příspěvek k diskuzi překročení difrakčního limitu je v přípravě k publikaci. Analýza korelačních záznamů při použití záření s proměnnou šířkou spektra a stanovení závislosti rozlišení detailů na koherenční délce použitého zdroje. Analýza umožnila určení parametrů, se kterými byla experimentálně ověřena možnost záznamu a rekonstrukce 3D objektů v bílém světle. Výsledky jsou originální jak z hlediska základní teorie, tak i aplikací a připravují se k publikaci. Ověření rotace obrazu při diskrétní spirální filtraci prostorového spektra. Výsledky byly publikovány [5] a je zvažováno jejich další využití v metodách umožňujících přesnou lokalizaci pozorovaných objektů. Úkoly, které byly pro simulační aktivity stanoveny v původním návrhu projektu, jsou již v této fázi řešení splněny. V průběhu řešení projektu se ale objevila řada nových námětů, a je zřejmé, že optické simulace budou významnou aktivitou i po stanoveném termínu 03/2013. Jedním z důležitých podnětů je ověření možnosti realizace PMS pomocí standardních difraktivních elementů. Tuto možnost je nutné prověřit pomocí přesných virtuálních experimentů a mohla by mít zásadní význam pro další průběh řešení projektu. Nahrazení prostorových modulátorů prvky vyrobenými metodami elektronové litografie by zvýšilo kompaktnost systému a výrazně snížilo náklady konstruovaného systému. Realizace experimentů pro ověření zobrazovacích vlastností systémů pracujících s využitím PMS. Ověřovací experimenty, které byly v průběhu řešení projektu realizovány, demonstrují nestandardní vlastnosti a široký aplikační potenciál digitálních zobrazovacích metod využívajících technologie prostorové modulace světla (PMS). Návrhy ověřovacích experimentů vycházely jak z vlastních teoretických podnětů, tak i studia nových odborných publikací. Realizaci ověřovacích experimentů předcházely návrhy a optimalizace parametrů provedené v připravených simulačních modelech. Na ověření základního principu záznamu a rekonstrukce 3D objektů v kvazimonochromatickém prostorově nekoherentním záření navázaly pokročilé experimenty, které prokázaly možnost vírového záznamu a rekonstrukce obrazu, dosažení subdifrakčního rozlišení a zobrazení s využitím širokospektrálního záření. Ověřovací experimenty byly zaměřeny i na dílčí úkoly, které jsou motivované aplikacemi a návrhy výhodného konstrukčního uspořádání systému. Tyto činnosti budou pokračovat a v optimálním
30 případě by mohly vést k realizaci PMS pomocí difraktivních prvků připravených standardními technologiemi. Zvýraznění kontrastu amplitudových přechodů 3D objektů v nekoherentním světle Hybridní koherenční režim digitálního zobrazování, umožňující nekoherentní záznam a koherentní rekonstrukci objektů, se stal základem experimentů založených na využití koherentních vírových stavů světla. Vírové zobrazení je používáno v mikroskopii pro zvýšení kontrastu hran transparentních objektů. Tato metoda byla navržena v roce 2005 a její princip vyžaduje použití koherentního záření. Spirální mikroskopie využívá efektů konstruktivní a destruktivní interference, které při zobrazování s vírovou impulzní odezvou vedou ke zvýraznění gradientů amplitudy nebo fáze pozorovaných objektů. Obr. 2: Standardní a vírové digitální zobrazení USAF testu: a) standardní způsob záznamu a rekonstrukce hologramů, b) rekonstrukce hologramů zaznamenaných pomocí vírové referenční vlny, c) rekonstrukce standardních záznamů provedená pomocí digitální spirální filtrace. Obr. 3: Trojrozměrné zobrazení jehly umístěné před kruhovou clonou: a) přímý optický obraz, b) vírová rekonstrukce obrazu při zaostření na jehlu, c) vírová rekonstrukce s numerickým přeostřením na clonu. Srovnání různých režimů zobrazení blechy: d) přímý optický obraz, e) standardní rekonstrukce korelačních záznamů, f) rekonstrukce s digitální spirální filtrací. Ověřovací experimenty provedené v balíčku prokázaly možnost vytvořit vírovou impulsní odezvu i v digitálním korelačním zobrazení při použití prostorově nekoherentního světla. Pro dosažení vírového režimu zobrazení byly navrženy dvě rozdílné techniky, realizované buď v optické, nebo digitální části experimentu. Optická realizace je založena na korelačním záznamu, ve kterém je standardní referenční vlna nahrazena vírovou vlnou se šroubovitou vlnoplochou. Realizace takové referenční vlny byla provedena návrhem vhodného počítačem generovaného hologramu a jeho odesláním na LCD.
31 Hologramy objektu vytvořené pomocí vírových korelačních záznamů jsou potom rekonstruovány obvyklým způsobem. V digitální realizaci se pracuje se standardními korelačními záznamy objektu a vírová impulsní odezva je získána spirální modulací prostorového spektra, provedenou při rekonstrukci záznamů. Rekonstrukce získané diskutovanými postupy jsou uvedeny v obrázku 2. Optická i digitální alternativa vírového zobrazení byla realizována a funkčnost a použitelnost návrhu byla ověřena na rozlišovacích testech i reálných objektech. Metoda je specifická tím, že umožňuje zvýraznění amplitudových gradientů v nekoherentním světle, a jejím hlavním přínosem je možnost použití i v trojrozměrném zobrazování viz obrázek 3. Podle našich informací se jedná o první demonstraci tohoto typu zobrazení. Získané výsledky prezentované v obrázcích 2 a 3 byly publikovány v prestižním optickém časopise [1] s impaktním faktorem. Korelační holografické zobrazení v bílém světle Zobrazovací systém, který byl v průběhu řešení projektu analyzován a rozvíjen, představuje jednocestný interferometr s dělením vlnoplochy pomocí prostorové modulace světla (PMS). Tento systém poskytuje interferenční záznamy jednotlivých bodů pozorovaného objektu, které jsou vzájemně zcela nekorelované. Takový způsob záznamu nevyžaduje prostorovou koherenci použitého záření, ale pracuje s koherencí časovou. Korelační bodové záznamy mohou vzniknout pouze tehdy, když rozdíl optických drah interferujících vln nepřesáhne koherenční délku použitého záření. V základní experimentální konfiguraci byly pro záznam používány vlny vyžadující šířku spektra použitého zdroje 10 až 20 nm. V odborných publikacích zveřejněných v roce 2012 (X. Lai et al, Opt. Lett. 37, 2445, 2012) byl proveden návrh geometrie interferujících vln, která vede k výraznému zmenšení rozdílu optických drah. Na základě těchto publikačních podnětů byla v rámci řešení projektu provedena série experimentů, která prokázala možnost výrazného rozšíření spektra použitého záření. Bylo tak možné pracovat s LED o šířce spektra 60 nm bez použití spektrálních filtrů. V optimalizovaném systému byl úspěšně proveden záznam a rekonstrukce objektů v podmínkách extrémně nízké časové koherence odpovídající bílému světlu. Výsledky získané v experimentální konfiguraci poskytující nejvyšší odolnost z pohledu snížené koherence světla jsou v obrázku 4. Obr. 4: Rekonstrukce korelačních záznamů pořízených při rozdílné časové koherenci světla určené spektrálními filtry o pološířce: a) 10 nm, b) 40 nm a c) 70 nm. d) Rekonstrukce korelačních záznamů vytvořených v bílém světle halogenové žárovky.
32 Pro záznamy bylo v tomto případě použito bílé světlo halogenové žárovky v kombinaci se spektrálními filtry. Porovnání výsledků získaných při záření o spektrální šířce 10 nm a v bílém světle ukazuje zřejmý pokles rozlišení. Pro vysvětlení tohoto efektu byl navržen výpočetní model, který umožňuje najít přímou souvislost mezi koherenční délkou použitého zdroje a dosaženým rozlišením. Teoretické výsledky jsou v dobrém souladu s experimenty a jsou připraveny k publikaci. Závěry provedené analýzy jsou příslibem pro rozvoj PMS interferometrie v bílém světle a zejména pro využití vyvíjené zobrazovací metody ve fluorescenční mikroskopii. Návrh optimalizovaných systémů pro holografický záznam a digitální rekonstrukci obrazu. V průběhu řešení projektu byla realizována řada experimentů rozvíjejících digitální zobrazovací technologie s ohledem na nové netradiční principy a vlastnosti zobrazení. Na základě odborných publikací a vlastních návrhů byly ale také provedeny experimenty, jejichž cílem bylo vytvoření sestav, které budou optimální jak z hlediska optického výkonu, tak i technických a konstrukčních řešení. Byla nalezena a úspěšně experimentálně prověřena konfigurace zajištující optimální rozlišovací schopnost systému, při které je překročen difrakční limit použitého mikroskopového objektivu. Dále byl vytvořen a úspěšně experimentálně testován nový návrh sestavy zajištující úplné korelační překrytí interferujících vln, které vedlo k výraznému zvětšení využitelného zorného pole. Optimalizace systému z hlediska rozlišovací schopnosti a ověření subdifrakčního rozlišení Při standardním optickém zobrazování je rozlišení detailů omezeno difrakčním limitem, který je jednoznačně daný pracovní vlnovou délkou a numerickou aperturou systému. V digitálním zobrazování je situace složitější a dosažené rozlišení závisí nejen na parametrech použitého mikroskopového objektivu, ale také na geometrii, ve které je proveden záznam hologramů. V sestavě studované v projektu jsou klíčovými parametry ohnisková vzdálenost čočky vytvořené pomocí PMS a poloha CCD při záznamu hologramů. Souvislost mezi parametry použitého optického systému, záznamovou geometrií a dosaženým rozlišením byla podrobně studována ve vytvořených modelech a správnost výpočtů byla ověřována experimentálně. Tento postup umožnil provést optimální nastavení systému a prokázal možnost dosáhnout v předmětovém prostoru rozlišení detailů, které jsou za hranicí difrakčního limitu použitého mikroskopového objektivu. V tomto smyslu lze tedy hovořit o subdifrakčním rozlišení, které je významnou vlastností zobrazovacích systémů. Ve zkoumané metodě digitálního zobrazování plyne možnost překonání difrakčního limitu přímo z vlastností systému a lze jí dosáhnout vhodnou kombinací parametrů PMS a geometrických parametrů použitých při záznamu hologramů. Dvoustupňový proces zobrazení, který kombinuje optickou a digitální část, nemá předmětovou a obrazovou aperturu vázanou s příčným měřítkem zobrazení prostřednictvím Lagrangeova invariantu, jak je tomu v čistě optickém zobrazení. Tato vlastnost umožňuje měnit rozlišení systému volbou jeho základních parametrů a v optimálním případě překročit difrakční limit optického zobrazení vytvořeného použitým objektivem.
33 Obr. 5: Demonstrace subdifrakčního rozlišení: a) přímý difrakčně limitovaný optický obraz s rozlišením 40,3 č/mm, b) digitálně rekonstruovaný obraz s rozlišením 57 č/mm. Experimentální demonstrace subdifrakčního rozlišení v popsaném systému digitálního zobrazení je na obrázku 5. Experiment byl proveden s nízkou numerickou aperturou objektivu, při které se neprojeví optické vady a systém pracuje jako fyzikálně dokonalý. Tímto způsobem byla ověřena možnost překonání difrakčního limitu, ale pro praktické použití je nutné experiment realizovat s vyšším obrazovým výkonem. Tento úkol bude dále řešen s ohledem na technické a konstrukční problémy. Zvětšení korelačního zorného pole Velikost využitelného zorného pole a rozlišovací schopnost jsou nejdůležitějšími optickými parametry každého zobrazovacího systému. V klasických optických systémech je zorné pole vymezeno mechanicky v rovině obrazu nebo meziobrazu a jeho velikost určují rozměry účinné plochy detektoru nebo clony zorného pole. V korelačním zobrazování o velikosti oblasti, ve které je obraz úspěšně rekonstruován, navíc rozhoduje míra překrytí signálního a referenčního pole. Přestože korelační překrytí má zásadní význam, v dostupné odborné literatuře nebyla tato problematika dosud systematicky zpracována. Při řešení projektu byla pozornost zaměřena jak na teoretickou analýzu, tak i na experimentální ověření korelačně podmíněného zorného pole. Obr. 6: Demonstrace zvětšení zorného pole: a) zorné pole redukované nedostatečným korelačním překryvem ve standardní konfiguraci, b) zvětšené zorné pole v sestavě s přizpůsobovacím optickým systémem dostupné zorné pole je omezené účinnou plochou detektoru, c) rekonstrukce korelačního záznamu v plném zorném poli objektivu při použití optimalizovaného systému. Výsledky ukázaly, že ve známých konfiguracích je korelační překrytí signální a referenční vlny zajištěno jen v omezené části zorného pole použitého mikroskopového objektivu. Pro určení míry korelačního překrytí byl zaveden faktor, který umožnil jednoduchou kvantifikaci překrytí ve
34 všech používaných experimentálních konfiguracích. Analýzou bylo prokázáno, že zmenšení zorného pole mikroskopového objektivu způsobené nedostatečným korelačním překrytím se projevuje nevýrazněji při použití objektivu s velkým zvětšením a při nastavení parametrů, které vedou k optimálnímu rozlišení. V návaznosti na provedenou analýzu byla navržena modifikace systému, která zabezpečuje úplné korelační překrytí signální a referenční vlny v celém zorném poli použitého objektivu. Tohoto efektu bylo dosaženo pomocí dvoučlenného přizpůsobovacího optického systému, který byl vřazen mezi PMS a CCD. Po této úpravě bylo možné provést rekonstrukci obrazu v zorném poli, které bylo ve srovnání s dříve užívaným systémem až několikanásobně větší. Průkazné experimentální výsledky jsou demonstrovány v obrázku 6 a jsou zpracovány v publikaci, která je v recenzním řízení [2]. Literatura [1] P. Bouchal and Z. Bouchal, Selective edge enhancement in three-dimensional vortex imaging with incoherent light, Opt. Lett. 37, (2012). [2] P. Bouchal and Z. Bouchal, Wide-field common-path incoherent correlation microscopy with perfect overlaping of interfering beams, J. Europ. Opt. Soc.Rap. Public (zasláno). [3] R. Chmelík, Coherent Imaging with Incoherent Light in Digital Holographic Microscopy. Proc. SPIE (v tisku). [4] M. Henzlová, Theoretical study of coherence-controlled holographic microscopy in the presence of scattering media. Proc. SPIE (v tisku). [5] M. Baránek and Z. Bouchal, Rotating point spread function in spiral phase contrast imaging with discrete phase modulation, Proc. SPIE (v tisku).
35 Pracovní balíček: Zpracování dat S-H senzoru v metrologii a zobrazování Analyzování současné technologické špičky v oblasti S-H detekce. Tato činnost měla za úkol přehledně zmapovat technologickou úroveň nejnovějších S-H detektorů na světovém trhu a dát tak řešitelům informace o tom, jaké technologie jsou dnes komerčně dostupné, jaké možnosti tyto systémy nabízí a kde je potencionální prostor pro aplikaci nově vzniklých technologií v rámci projektu. Na trhu se vyskytují i uzavřené jednoúčelové metrologické systémy, jejichž základem je S-H detekce, ty ovšem nebyly do analýzy zahrnuty, protože v projektu jde o technologii S-H jako takovou. S-H systémy mají svou hardwarovou a softwarovou část, proto se při analyzování senzoru musí brát v potaz obě složky. Softwarová část má obecně na výkon systému větší vliv, což je dáno různou úrovní použitých algoritmů. Jelikož žádný výrobce neposkytne přímé informace o druhu jím využívaných algoritmů, byly udávané vlastnosti systémů konfrontovány se současnou odbornou literaturou a byly tak vytipovány nejpravděpodobněji využívané algoritmy. Hardwarová část S-H detektoru má dva základní prvky a to CCD kameru a mikročočkové pole. Jelikož většina výrobců S-H detektorů tyto klíčové prvky nakupuje, byly do analýzy zahrnuty i možnosti výrobců těchto jednotlivých komponent a bylo sledováno, kteří výrobci nejčastěji poskytují své komponenty pro S-H detektory. Pro přímý kontakt s výrobci byly navštíveny veletrhy v Baltimore-USA a Frankfurtu-Německo. Zejména u nějvětších výrobců S-H detektorů, což jsou Imagine Optics a Optocraft, byl zachycen trend využívání velkých CCD čipů, což umožňuje konstrukci detektorů s velkým prostorovým rozlišením. Je to dáno zejména rozvojem čipů na kinofilmový formát. Nevýhodou takovýchto čipů je velké množství přenášených dat a tím malá frekvence snímkování, velké nároky na výpočetní techniku a velká pořizovací cena. Přes tyto nevýhody bylo rozhodnutu zakoupit takovouto kameru pro potřeby projektu a sestavit tak systém s co možná nejvyšším prostorovým rozlišením. Nejlepším zdrojem informací byly získané manuály systémů firem Imagine Optics, Thorlabs a Flexible Optical. Z těchto manuálů jde vyčíst důležité informace a používaných algoritmech a toku dat v senzoru. Tyto informace jsou zvláště cenné pro sestavování Meopta software pro S-H detektor. Některé již byly v průběhu roku zapracovány, větší část bude zapracována v roce příštím v rámci činnosti Programování software pro kontrolu dat z S-H senzoru a diagnostiku intenzity a vlnoplochy. O S-H detekci je velký zájem i výzkumné sféře a tato problematika se často vyskytuje i v současné odborné literatuře. Zejména se jedná o nové typy algoritmů pro zlepšení dynamického rozsahu a citlivosti senzoru. Některé z těchto algoritmů byly vybrány a budou se realizovat v Meopta software v následujícím roce. Obecně lze říci, že úroveň současných SH systémů pro optickou metrologii se blíží úrovni dosud dominantní digitální interferometrie, což je dáno zejména rozvojem CCD prvků a velkému pokroku v digitálním zpracování obrazu v posledních letech. Z analýzy též vyplývá, že u všech systémů podstatnou část ceny tvoří vždy software. Meopta jako člen řešitelského týmu již svůj základní software vlastní, ten ovšem ještě úrovně software zavedených firem nedosahuje. Závěry učiněné při této analýze dávají jasný přehled potřebných vylepšení a lze říci, že všechny cíle jsou dosažitelné. Ze zkušeností učiněných na vlastních sestavách jsme narazili též na problém s maskováním signálu pro výpočet aberací, který ani v konkurenčních software není spolehlivě vyřešen. Významnost tohoto problému je diskutována i v literatuře. Zde se tedy nabízí možnost předstihnout konkurenci.
36 Informační protokoly pro S-H detekci. Cílem našeho snažení je prozkoumat možnosti detekce netradičního stavu světla pomocí S-H senzoru. Proces detekce je úzce spjatý s digitální rekonstrukcí stavu analyzovaného optického signálu. Výzkum na katedře optiky se zaměřil na statistickou analýzu detekovaného signálu S-H detektoru z hlediska informačních protokolů využívaných ve kvantové informatice. Bylo vyjasněno, že informace odpovídající detekci za jednotlivými ohraničenými mikročočkami odpovídá navzájem se nepřekrývajícím (ortogonálním) detekcím. Z tohoto pohledu neposkytuje měření tomograficky kompletní informaci na neomezeném prostoru signálních stavů. Byla studována otázka, za jakých dodatečných omezujících podmínek je možné získanou informaci považovat za úplnou. Tento výzkum je nezbytnou součástí pro následnou úspěšnou praktickou aplikaci tomografické rekonstrukce na reálný signál. Výzkum v oblasti nových informačních protokolů se dále zabýval otázkou výsledné meze rozlišitelnosti jednotlivých parametrů. V rámci vypsané bakalářské práce je ve zjednodušeném modelu studovaná difrakční mez S-H detekce pro úhlové rozlišení s využitím Fisherovy informace. Následné rozšíření pak povede k vyjasnění meze rozlišení pro další detekovatelné parametry, např. stupeň koherence mezi dvěma překrývajícími se rovinnými vlnami. Popis S-H detekce úzce souvisí s aperturní syntézou a proto se činnost zaměřila i na studium a modifikací metod využívaných v této oblasti. Jako základní stav optického pole pro tyto úvahy byla vybrána superpozice rovinných vln. Z fourierovského popisu optiky víme, že ze superpozice rovinných vln jde připravit jakýkoli stav pole a tyto vlny je možno navíc jednoduše připravovat laboratorně. Příkladem stavu světla, který není možné detekovat tradičními S-H metodami je částečně koherentní superpozice dvou a více vzájemně nakloněných rovinných vln. Takto připravený stav světla lze popsat pomocí koherenční matice, což je hermitovská matice, která pro výše zmíněnou superpozici d vln má hodnost d a obsahuje d(d+1)/2 nezávislých elementů. V první fázi úvah jsme zanedbali interferenci mezi jednotlivými mikročočkami. Proces měření S-H senzoru lze popsat jednoduchým vztahem, který je založený na výpočtu stopy součinu koherenční matice a matice měření. Matice měření charakterizuje proces měření intenzity na konkrétním pixelu detektoru při využití určité mikročočky. Našim cílem bylo nejprve uvážit za jakých podmínek je možné z libovolné známé superpozice nakloněných rovinných vln rekonstruovat z daného měření S-H senzoru koherenční matici a diskutovat, jak je tato rekonstrukce odolná vzhledem k případnému šumu na detektoru. Za účelem další diskuze byly odvozeny matice měření pro mikročočky s čtvercovou a kruhovou propustností. Tyto matice obsahují podle typu propustnosti sinc nebo jinc funkce doplněné o příslušné fázové faktory. Dobrou mírou odolnosti daného měření vzhledem k šumu se ukazují být tzv. singulární hodnoty matice měření. Aby bylo možné rekonstrukci provést, je nutné mít k dispozici stejný počet nenulových singulárních hodnot matice měření, jako je počet nezávislých elementů koherenční matice. Pro vyšší singulární hodnoty bude rekonstrukce odolnější. Z numerické analýzy tohoto problému vyplynula výrazná závislost singulárních hodnot na volbě konkrétní superpozice rovinných vln. Z tohoto důvodu byly numericky zjištěny singulární hodnoty
37 v závislosti na volbě daných náklonů. Grafy na obr. 1 znázorňují nejnižší singulární hodnotu v závislosti na volbě superpozice náklonů rovinných vln. Obrázek vlevo demonstruje situaci pro 2 mikročočky a 10 pixelů za každou z nich. Pro srovnání je na obrázku vpravo stejný graf pro 40 mikročoček a 15 pixelů za každou z nich. Z obou grafů je patrné výrazné zlepšení napříč celým prostorem nakloněných vln po přidání mikročoček a pixelů. Obr. 1: Singulární hodnoty matice měření pro systém rovinných vln o různém náklonu. V blízké budoucnosti bude provedena optimalizace počtu a velikosti mikročoček a velikosti pixelů s ohledem na singulární hodnoty. V současné době probíhá analýza vlivu interference mezi jednotlivými mikročočkami. Za účelem ověřování nových informačních protokolů pro SH detekci byla v laboratoři Univerzity Palackého vytvořena experimentální sestava, na které se provádí základní experimenty a současně analyzují technologické problémy vyplývající ze zcela nového pohledu na S-H detekci, viz. obr. 2. Protože obecně se bude zkoumat signál částečně koherentní, obsahuje sestava dva nezávislé laserové zdroje, které umožňují vytvářet současně nekoherentní i koherentní superpozice vln. Dále sestava obsahuje prostorový modulátor světla pro vytváření různých typů optických signálů, jako například optických vortexů. Jako S-H senzor se používá systém firmy Flexible Optical, který má hexagonální pole mikročoček a 1/2palce USB CCD. Ten bude v příštím roce řešení nahrazen vhodnějším senzorem vlastní konstrukce, kde parametry budou určeny na základě současných poznatků s novými detekčními technikami a výsledky první výzkumné zprávy balíčku. Pro matematické zpracování jsou využívány programy v systému OCTAVE. Základním kamenem nových metod po technologické stránce je věrný matematický popis měřícího zařízení, který determinuje rozlišení metody a její přesnost. Prvním poznatkem při uplatnění protokolů kvantové tomografie na reálný signál byl velký vliv šumu a vzorkování na rozlišitelnost jednotlivých stavů světla. Pro vyřešení problému šumu lze s výhodou uplatnit na signál frekvenční propusti, hrozí zde ale distorze užitečného signálu, proto jsou v současnosti studovány možnosti sofistikovanějších algoritmů. Pro problém vzorkování a také vzájemné orientace mikročoček a CCD je vyvíjena vlastní metoda kalibrace pomocí základní vlny studovaného systému. Může to být například rovinná vlna nebo základní gaussovský svazek. Při této kalibraci jsou určovány posuvy intenzitních težišť za každou mikročočkou jako při klasické rekonstrukci, mohou zde tudíž najít uplatnění existující algoritmy. Také tvar apertur jednotlivých mikročoček hraje významnou roli, proto bylo potřeba u stávající sestavy pracovat s difrakcí na hexagonální apertuře.
38 Obr. 2: Experimentální sestava pro výzkum v oblasti informačních protokolů: SM1-jednomodové vlákno s navázaným He-Ne laserem, f1- kolimační čočka, SLM- prostorový modulátor světla, 4ffiltrační 4f systém s prostorovou filtrací, BS- dělič svazku, SM2- jednomodové vlákno s navázanou laserovou diodou, f2- kolimační čočka, S-H- Shack-Hartmann detektor. Dva nezávislé zdroje umožňují vytváření částečně koherentních signálů. Aplikovaný výzkum nových informačních protokolů ve firmě Meopta-optika, s.r.o. byl zaměřen na možnost měřění paraxiálních ohnisek optických systémů pomocí S-H detektoru. Při klasickém způsobu měření ohnisek je přístupná pouze efektivní hodnota tohoto parametru, protože jsou přítomny vlnové aberace vyšších řádů. Komplexní detekce pomocí S-H senzoru může tento problém vyřešit. Metoda navíc nevyžaduje nejdražší část konvečních systémů-kolimátor. Může tak poskytnout cenově výhodné řešení. Vlastní experiment je proveden v následujícím uspořádání. Svazek laseru je navázán do optického vlákna, jehož konec slouží jako bodový zdroj sférické vlny. Tento bodový zdroj je umístěn přibližně do předmětového ohniska měřené čočky. V obrazovém prostoru v dané vzdálenosti od čočky jsou následně pomocí S-H senzoru detekovány Zernikovy koeficienty vlnoplochy. Speciálně nás zajímá Seidelův koeficient rozostření. Abychom ho určili, je nutné znát dva Zernikovy koeficienty (Z3 a Z8). Změnou vzdálenosti předmětového bodu v kombinaci se souběžným měřením koeficientů získáváme postupně závislost, kterou fitujeme teoreticky odvozeným vztahem. Ohnisko čočky měříme nepřímo, jako jeden z parametrů získaných fitováním. Aby bylo možné měření optimalizovat vzhledem k různému počtu poloh bodového zdroje a jejich vzájemným vzdálenostem, byl vytvořen numerický model v programu Mathematica popisující proces měření. Tento model je schopný pro určitou ohniskovou vzdálenost čočky odhadnout nejistotu měření ohniska. Hlavní úlohu hraje v modelu nejistota měření polohy a nejistota měření daných Zernikových koeficientů.
39 S problematikou úzce souvisí znalost základních parametrů S-H senzoru, popřípadě metody jejich zjišťování. Mezi základní parametry patří vzdálenost L matice mikročoček od detektoru, velikost pixelu a vzdálenost mikročoček. Jestliže o těchto parametrech nemáme přesnou informaci, výsledné měření ohniska bude vykazovat systematickou odchylku. Existují dvě metody, jak tyto parametry měřit. Doposud bylo provedeno měření vzdálenosti L pomocí nakloněné rovinné vlny. S-H senzor je umístěn na goniometru, který mění náklon rovinné vlny vytvořené kolimátorem. Výsledky byly zpracovány numericky v program Mathematica. V blízké době plánujeme předchozí výsledek porovnat s metodou, která využívá sférické vlny, jejíž poloměr křivosti je v průběhu měření postupně měněn. Poloměr křivosti je současně měřen na S-H senzoru a výsledná závislost fitována teoreticky odvozeným vztahem. Jestliže bodový zdroj sférické vlny neleží na ose měřené čočky, bude vlna za čočkou vykazovat určité zklenutí. Tento příspěvek je v průběhu detekce vlnoplochy započítán do Zernikova koeficientu Z3, což může negativně ovlivnit přesnost metody měření paraxiálního ohniska. V programu Oslo byly zjištěny pro zvolené čočky koeficienty vlnových aberací charakterizující zklenutí. V současnosti probíhá závěrečná fáze analýzy vlivu náklonu čočky na výpočet ohniska. Teoretické úvahy jsou doprovázeny paralelně probíhajícími experimenty, které ověřující teoreticky nabyté zkušenosti. Pro tyto účely jsme vytvořili experimentální sestavu. Z výsledků experimentů měření ohniska tří vybraných čoček jsou patrny poměrně velké systematické odchylky (půl procenta až procento) od hodnoty paraxiálního ohniska, které bylo vypočítáno v programu Oslo. Našim cílem je v nejbližší době tyto odchylky vysvětlit. Pokud by byly způsobeny zklenutím čočky, bude nutné diskutovat vhodný způsob justáže čočky do měřící sestavy. Software pro kontrolu dat z S-H senzoru a diagnostiku intenzity a vlnoplochy. Firma Meopta-optika, s.r.o. disponovala vlastním software pro vyhodnocování vlnoplochy již před začátkem projektu, jeho vlastnosti ovšem nebyly optimální a to jak v otázce použitých algoritmů, tak ve vnitřní organizační struktuře. V rámci této činnosti je proto rozvíjen zcela nový software, který bude obsahovat všechny prvky moderních konkurenčních řešení a přitom bude maximálně otevřený a modulární, tak aby ho bylo snadné využívat pro nové postupy a aplikace při řešení celého pracovního balíčku. Předně bylo rozhodnuto vytvořit celý systém jako přísně objektový, tzn. podle principů objektového programování. V tomto systému je každá část procesu zpracování dat z S-H senzoru koncipována jako samostatná jednotka a celý systém je pak kompozicí těchto základním jednotek. Po naprogramování těchto jednotek je stavba nového systému velice rychlá a je tak snadné sestavit zcela nový S-H software podle aktuálních potřeb. Při jakékoli inovaci některé části kódu je také snadné provést aktualizaci všech existujících aplikací. Třetí velkou výhodou je snadný přístup k datům v kterémkoli místě měřícího řetězce. To je důležité pro rozvoj nových detekčních postupů, což je náplní řešení pracovního balíčku v příštích letech. Během prvního roku se podařilo naprogramovat všechny základní jednotky a v současnosti je tedy možno využít všech výše uvedených výhod.
40 Obr. 3: Mapa zpracování dat v S-H senzoru.diagram zhruba odpovídá objektové struktuře problému a každá činnost znamená určitý algoritmus. Obr. 4: Vliv decentralizace masky a optického svazku obsahujícího sférickou vadu velikosti 1λ na aberační Zernikův koeficient C31. Parametr a je relativní posun masky vůči poloměru masky a C31 je v λ. Je vidět že i pro malou chybu decentralizace 2% je vygenerován chybný koeficient 0,15λ. Vzorkování svazku mikročočkami je přitom na úrovni chyby decentralizace 4-10%. Pro nalezení možných vylepšení a analyzování konkurenčního software byla sestavena mapa zpracování dat v S-H senzoru, viz. obr. 3. Řešitelský se pak zaměřil na jednotlivé kroky a snažil se nalézt v dostupné odborné literatuře současný trend řešení příslušného problému. Inspirací je též řešení daného problému komerčními výrobci. V prvním roce se pozornost zaměřila především na konec celého řetězce tj. na problémy rekonstrukce OPD, maskování a výpočet aberací. V oblasti rekonstrukce OPD byl naprogramován nový postup, tak aby bylo možno snadno využívat jak modální tak zonální rekonstrukci. V rámci výpočtu vlnových aberací byla provedena zásadní inovace. Současný systém
41 umožňuje vyčíslování Zernikových polynomů různých řazení a jejich převod na Seidlovy aberace a také umožňuje vyčíslovat Strehl koeficienty pro jednotlivé aberace. Vzhledem k neortogonalitě dat z SH senzoru je plánován přechod na SVD algoritmus, což je u komerčních systému standard, v našem software zatím chybí. Problém maskování je zvlášť zajímavý, protože není uspokojivě řešen u žádného komerčního výrobce S-H senzorů a nabízí se zde tedy možnost inovačního náskoku. Problém umísťování masky do optického svazku je u S-H senzoru velmi důležitý kvůli nízkému vzorkování a tudíž malé přesnosti tohoto úkonu. Přitom vliv na koeficienty aberací je velmi značný, jak ukazuje obr.4 na příkladu komy a svazku obsahujícího sférickou vadu. V Meoptě byl implementován postup, který umožňuje zpřesnit maskování až o jeden řád. V plánu jsou další zpřesnění tohoto postupu a pro zákazníky Meopty-optika by to měla být zvláště zajímavá součást S-H software. Měření kvality optických ploch pomocí S-H technologie. Tato činnost má podpůrný charakter pro jeden z výstupů projektu a to měřící stanice tvaru optických prvků rovinné a sférické optiky. V prvních třech letech řešení by prováděné činnosti měly dát podklad pro finální návrh, nákupy a montáž stanice. V prvním roce se řešitelé zaměřili především na vztah hardwarových parametrů senzoru a metrologických parametrů jako je dynamický rozsah, přesnost a rozlišení. Na základě těchto úvah byly navrženy první nákupy klíčových komponent- CCD kamery a mikročočkových polí. Byl proveden průzkum systémů využívajících S-H senzor pro měření optických prvků. Komerčně dostupné systémy S-H senzorů představují po softwarové stránce uzavřená řešení použitelná na omezený okruh aplikací. Jen zřídka jsou nabízena ucelená řešení pro měření optických prvků (např. Trioptics, Optocraft). Takový systém je vzhledem ke značné různorodosti měřených součástí náročný z hlediska své stavby a rozsahu dodávaného příslušenství. Je zpracován přehled porovnávající možnosti měření optických prvků interferometricky a pomocí S-H senzoru. Uvedené metody si konkurují jen částečně, v některých ohledech se doplňují. Orientační měření ukazují, že při použití S-H senzoru je důležité, aby kontrolovaná apertura byla zobrazena na vstupní otvor S-H senzoru, což u zařízení, které má pokrýt širší sortiment optických prvků, vede ke komplikovanější optické konstrukci. Byla navržena první sestava pro měření rovinných ploch do průměru 190 mm pomocí S-H senzoru. Pro tuto sestavu byly zakoupeny její základní součásti a pokračuje se v návrhu sestavy mechaniky.
42 Seznam prezentací a publikací Prezentace: 1. B. Stoklasa, J. Řeháček, Z. Hradil, Adaptive IR and VIS image fusion, SPIE Defense, Security + Sensing 2012, Baltimore, USA 2. B. Stoklasa, J. Řeháček, Z. Hradil, L.L. Sanchez-Soto, Shack-Hartmann tomography and Laguerre-Gaussian beam characterization, Fifth International Conference "Singular Optics SO'2012", Sevastopol, Ukrajina Publikace: 1. B. Stoklasa, J. Řeháček, Z. Hradil, Adaptive IR and VIS image fusion, Multisensor, multisource information fusion: Architectures, algorithms and applications 2012 Book Series: Proceedings of SPIE 8407, 84070Y (2012). 2. P. Bouchal and Z. Bouchal, Selective edge enhancement in three-dimensional vortex imaging with incoherent light, Opt. Lett. 37, (2012). 3. P. Bouchal and Z. Bouchal, Wide-field common-path incoherent correlation microscopy with perfect overlaping of interfering beams, J. Europ. Opt. Soc. Rap. Public (zasláno). 4. R. Chmelík, Coherent Imaging with Incoherent Light in Digital Holographic Microscopy, Proc. SPIE (v tisku). 5. M. Henzlová, Theoretical study of coherence-controlled holographic microscopy in the presence of scattering media, Proc. SPIE (v tisku). 6. M. Baránek and Z. Bouchal, Rotating point spread function in spiral phase contrast imaging with discrete phase modulation, Proc. SPIE (v tisku). 7. Y.S. Teo, B. Stoklasa, B.-G. Englert, et al., Incomplete quantum state estimation: A comprehensive study, Phys. Rev. A 85, (2012). 8. D. Mogilevtsev, J. Řeháček, Z. Hradil, Self-calibration for self-consistent tomography, New Journal of Physics 14, (2012). 9. D. Sych, J. Řeháček, Z. Hradil, et al., Informational completeness of continuous-variable measurements, Phys. Rev. A 86, (2012).
43
44
45
46
47
48
49
50
51
52
53 Selective edge enhancement in three-dimensional vortex imaging with incoherent light Petr Bouchal 1 and Zdeněk Bouchal 2, * July 15, 2012 / Vol. 37, No. 14 / OPTICS LETTERS Central European Institute of Technology, Brno University of Technology, Technická 10, Brno, Czech Republic 2 Department of Optics, Palacký University, 17. listopadu 1192/12, Olomouc, Czech Republic *Corresponding author: bouchal@optics.upol.cz Received March 30, 2012; revised May 27, 2012; accepted May 29, 2012; posted May 30, 2012 (Doc. ID ); published July 13, 2012 We demonstrate a new imaging method enabling a selective edge contrast enhancement of three-dimensional amplitude objects with spatially incoherent light. The imaging process is achieved in a spiral modification of Fresnel incoherent correlation holography and uses a vortex impulse response function. The correlation recordings of the object are acquired in a one-way interferometer with the wavefront division carried out by a spatial light modulator. Two different methods based on applying a helical reference wave in the hologram recording and a digital spiral phase modulation in image reconstruction are proposed for edge enhancement of amplitude objects. Results of both isotropic and anisotropic spiral imaging are demonstrated in experiments using an LED as an incoherent source of light Optical Society of America OCIS codes: , , Contrast enhancement of the edges is an operation that is often used in optical image processing. Previously, the edge contrast enhancement of amplitude objects was performed in a coherent imaging using the radial Hilbert transform to modulate the Fourier spectrum [1]. This filtering technique acts isotropically so that all the edges in a sample are highlighted independently of their local direction. The anisotropic spiral filtering resulting in an apparent shadow effect was also demonstrated [2,3]. All the methods based on a spiral filtering create the image by the convolution of a complex function representing the sample with a vortex impulse response function of the optical system. Since the edge enhancement is a consequence of constructive and destructive interference of individual vortices, the use of coherent light is required [4,5]. In this Letter, we propose and experimentally demonstrate a new imaging technique enabling the edge contrast enhancement of amplitude objects using incoherent light. Our method is based on the Fresnel incoherent correlation holography (FINCH) technique, which was modified to operate with a vortex imaging. In its basic form, FINCH includes both optical and digital steps and allows reconstruction of three-dimensional (3D) objects. This method requires quasi-monochromatic spatially incoherent light and utilizes a spatial light modulator (SLM) to perform correlation recordings of the object. The holograms are then processed and reconstructed using suitable numerical algorithms [6]. We modified the experiment to ensure that the FINCH imaging created with an incoherent light will have some benefits of the spiral contrast methods previously presented with a fully coherent light. This is possible due to special coherence properties of the FINCH configuration that result from a combination of optical and digital imaging techniques [7]. Object information is contained in optical correlation recordings that are created using an incoherent light. Subsequent digital reconstruction takes place in a fully coherent regime [7] and allows interference of vortex structures required to emphasize edges of amplitude objects [5]. We propose two different methods that allow switching from standard FINCH to the spiral contrast imaging operation. The first method relates to changes in the optical recording of the object being based on application of a helical reference wave. The second method works with standard FINCH recordings, and the vortex imaging is achieved by a digital spiral phase modulation during their processing. A basic principle of the method is shown in Fig. 1. A source emitting quasi-monochromatic spatially incoherent light illuminates the object. Its individual points represent secondary sources that emit spherical waves. These light waves are collimated by the lens CL and directed to the SLM. By the SLM operation, each incident wave is doubled and the signal and reference waves are formed. Because the waves originate from the same point, they are spatially coherent. If the optical path difference of the waves does not exceed the coherence length of the source, they can interfere. At the CCD, the complex amplitude of the light emitted by a single point of the object is given as A 0j a r exp iφ r a s exp iφ s iϑ j, j 1, 2, 3, where a s, Φ s and a r, Φ r denote amplitudes and phases of the signal and reference waves, respectively, and ϑ j are constant phase shifts imposed on the signal wave by the SLM. Intensity records I 0j ja 0j j 2 are repeated three times for different phase shifts of the signal wave allowing the elimination of the holographic twin image [6]. The basic difference between the standard FINCH and its optical spiral modification consists in preparation of the phase maps to generate the signal and reference waves. While in the Fig. 1. (Color online) Standard and spiral configurations for a correlation imaging with incoherent light /12/ $15.00/ Optical Society of America
54 2950 OPTICS LETTERS / Vol. 37, No. 14 / July 15, 2012 standard configuration Φ s and Φ r correspond to the phases of spherical and plane waves, respectively, in the optical spiral method, a helical reference wave is generated by the SLM. Its phase involves a term depending on the azimuthal angle φ and integer parameter m called the topological charge, Φ r mφ. The phase maps that drive the SLM to create the signal and reference waves are shown in the middle part of Fig. 1, where (a) and (b) correspond to the plane and helical reference waves, respectively. Intensities I 0j represent the point correlation records, and their shape is shown in the right panel of Fig. 1. The upper snapshot is obtained in the standard configuration being similar to the Fresnel zone plate. For the spiral contrast, the point correlation record has a typical shape of the spiral pattern, known from the interference of optical vortices. Before digital image reconstruction, three intensity records I 0j are processed [6], and a complex function T is created, T exp i Φ s Φ r. In[7], it was shown that T corresponds to the quadratic phase of a diffractive lens whose parameters depend on both the experiment geometry and a position of the object point. For the helical reference wave, T corresponds to the vortex diffractive lens having a spiral phase with the topological charge m. In the point imaging, the complex amplitude is obtained using the Fresnel transform, A 0 0 FrfTg. For a plane reference wave, the point spread function (PSF) with the shape of the Airy pattern is obtained. If the reconstruction is performed from the spiral correlation records, the vortex PSF with an annular shape appears in the digital image (Fig. 1). The vortex imaging can be achieved even if the reconstruction is performed using standard recordings taken with a plane reference wave. Here the reconstruction is carried out in the frequency domain and a spiral phase mask modulates the spatial spectrum of the complex function T. This effective and operational technique represents a digital analogy of the spiral contrast previously used in a coherent optical imaging [1,5]. Edge enhancement of real incoherently illuminated objects with the transmission t is possible because the image is formed in a hybrid mode of spatial coherence. As separate object points are mutually uncorrelated, the intensity records of the whole object are given by a convolution, I j t I 0j. It shows that the intensity records of individual object points I 0j are superimposed incoherently to obtain the final intensity. Before the digital image reconstruction, three intensity records of the object point are processed to create the phase function T, which represents a diffractive lens. As demonstrated in [7], its transmission, focal length, and lateral axis position carry information about the amplitude and the spatial position of the recorded point of the observed object. Information about the entire object is encoded in the coherent superposition of individual diffractive lenses [7]. This is why the resulting complex amplitude of the digitally reconstructed image A 0 is obtained in a coherent mode as a convolution A 0 t A 0 0. The complex amplitude A0 0 has a typical vortex structure with an annular amplitude and a spiral phase given by the term exp imφ. Each point of the digital image has a vortex phase so that a phase difference of mπ appears at a symmetric position in any radial line with respect to the vortex core. This Fig. 2. (Color online) Scheme of the experiment. SF, spectral filter; CL, collimating lens; D, diaphragm; P, polarizer; BS, beam splitter; SLM, spatial light modulator. property allows interference effects leading to the edge enhancement of amplitude objects [1,5]. The proposed method has been experimentally verified in the system illustrated in Fig. 2. The collimated LED (Thorlabs, 625 nm) with the spectral filter (FWHM 3 nm) was used as a light source. To create object correlation records, the achromatic lens (f 150 mm) and the SLM (Hamamatsu, pixels) were used. Two lenses (f mm and f mm) were randomly multiplexed on the SLM to realize the dual lens FINCH with spherical signal and reference waves [8,9]. The CCD (Retiga 4000 R) was placed at a distance 495 mm behind the SLM to capture holograms of the object. Results obtained using both optically and digitally implemented spiral contrast methods are shown in Fig. 3. Three intensity patterns representing correlation records of a point object I 0j are shown in the FINCH column. The image obtained by a direct reconstruction of standard records of the United States Air Force (USAF) test is in the left panel (label DR). If the spiral phase mask (m 1) is applied during processing of the standard records, the image with an apparent edge contrast enhancement is obtained (left panel, label SM). The PSF obtained by the direct and spiral reconstruction of standard records of a point object is shown at the bottom of Fig. 3. The spiral correlation records of a point object created by using a helical reference wave (m 1) are shown in the S-FINCH column. The PSF obtained by their direct reconstruction is at the bottom. The image of the USAF test obtained by a direct reconstruction of its spiral records is in the right panel. Edge enhancement is comparable with results of the digital spiral phase modulation. The anisotropic edge enhancement of a pinhole is shown in Fig. 4. The results were obtained by a sine-modulated Fig. 3. (Color online) Demonstration of the standard and spiral imaging in the FINCH configuration. Images labeled DR and SM were obtained by the direct reconstruction and the digital spiral phase modulation, respectively.
55 July 15, 2012 / Vol. 37, No. 14 / OPTICS LETTERS 2951 Fig. 4. (Color online) Demonstration of isotropic and anisotropic edge contrast enhancement: (a) standard FINCH reconstruction, (b) isotropic spiral FINCH, (c) (e) anisotropic spiral FINCH with preferred directions. Fig. 5. (Color online) Needle placed some distance in front of a pinhole: (a) optical imaging, (b) spiral reconstruction with the needle in focus, and (c) spiral reconstruction numerically refocused on the pinhole. Images of a flea: (d) optical imaging, (e) standard FINCH, and (f) isotropic spiral reconstruction. spiral modulation [3] during reconstruction of the standard FINCH records. In Fig. 5, the edge enhancement in 3D spiral imaging is demonstrated. As an object, eye of a needle placed in front of a pinhole was used. Though the needle and the pinhole are slightly longitudinally shifted, the sharp edges can be successively reconstructed from the same recordings provided that the reconstruction distances are appropriately chosen. In the top row, the optical image (a) is compared with the spiral reconstruction, where the needle (b) and the pinhole (c) are in focus. In the bottom row, three different images of a flea are shown. The optical imaging (d), the standard FINCH imaging (e), and the spiral reconstruction (f) are demonstrated there. In conclusion, we proposed and experimentally verified a vortex image reconstruction in FINCH based on a spiral modulation of light. The spiral imaging carried out optically or digitally, either in the space or frequency domain, was demonstrated. The main advantage of the method is the edge contrast enhancement of the 3D objects that can be achieved even when incoherent light is used. In experiments, both the isotropic and anisotropic edge enhancement were demonstrated. The proposed spiral modification of FINCH extends the variability and application potential of the method. The digital spiral modulation seems to be especially advantageous. It works with standard correlation FINCH recordings so that imaging conditions can be changed even during reconstruction. Though FINCH is a holographic method, the initial phase related to the refractive index of the object cannot be reconstructed. The reason is that the correlation recordings are made in a one-way interferometer so that a constant reference phase is not available. There are two ways to reconstruct the phase objects: to do a phase conjugation of the reference wave or to operate with a partial spatial correlation of light during the object reconstruction. These ideas are a challenge for the future and are subject to further research. This work was supported by the Czech Ministry of Education, project MSM , the Technology Agency of the Czech Republic, project TE , IGA project of the Palacký University PrF , and the project Central European Institute of Technology (CEITEC) CZ.1.05/1.1.00/ from European Regional Development Fund. Adrian Bradu from University of Kent is acknowledged for valuable comments on the manuscript. References 1. J. A. Davis, D. E. McNamara, D. M. Cottrell, and J. Campos, Opt. Lett. 25, 99 (2000). 2. A. Jesacher, S. Furhapter, S. Bernet, and M. Ritsch-Marte, Phys. Rev. Lett. 94, (2005). 3. M. K. Sharma, J. Joseph, and P. Senthilkumaran, Appl. Opt. 50, 5279 (2011). 4. S. Bernet, A. Jesacher, S. Furhapter, Ch. Maurer, and M. Ritsch-Marte, Opt. Express 14, 3792 (2006). 5. C. Maurer, A. Jesacher, S. Bernet, and M. Ritsch-Marte, Laser Photon. Rev. 5, 81 (2011). 6. J. Rosen and G. Brooker, Opt. Lett. 32, 912 (2007). 7. P. Bouchal, J. Kapitán, R. Chmelík, and Z. Bouchal, Opt. Express 19, (2011). 8. B. Katz, J. Rosen, R. Kelner, and G. Brooker, Opt. Express 20, 9109 (2012). 9. X. Lai, Y. Zhao, X. Lv, Z. Zhou, and S. Zeng, Opt. Lett. 37, 2445 (2012).
56 Wide-field common-path incoherent correlation microscopy with perfect overlapping of interfering beams Petr Bouchal 1 and Zdeněk Bouchal 2 1 Central European Institute of Technology, Brno University of Technology, Technická 10, Brno, Czech Republic 2 Department of Optics, Palacký University, 17. listopadu 1192/12, Olomouc, Czech Republic Corresponding author: petr.bouchal@ceitec.vutbr.cz Keywords: spatial light modulator, digital holography, optical microscopy Incoherent correlation microscopy is recently discovered technique for digital imaging of three-dimensional objects in a quasi-monochromatic spatially incoherent light. Its operation is based on wavefront division carried out by a spatial light modulator and capturing correlation recordings of the observed scene. To achieve image reconstruction, at least a partial overlapping of the signal and reference waves created by the spatial light modulator is necessary. In the known experimental configurations, the overlapping of interfering beams is strongly reduced in off-axis areas of the object and the image can be reconstructed only in a very small portion of the field of view provided by the used microscope objective lens. Here we propose and successfully demonstrate modified experimental system working with two-component relay optics inserted between the microscope objective and the spatial light modulator and providing full overlapping of correlated beams in all areas of the field of view of the objective lens. The benefits and applicability of the proposed system design are clearly demonstrated on the imaging of the USAF resolution targets. 1
57 1 Introduction Digital holographic microscopy is a powerful imaging technique suitable for both metrology and bio-photonic applications including surface analysis or marker-free dynamic live cell imaging [1, 2]. It is based on the principles of optical holography, which are advantageously combined with the recording of the holograms by a digital image sensor. The subsequent reconstruction of the holograms is performed numerically with a computer, and enables three-dimensional imaging without scanning. The digital holographic reconstruction was also used in the coherence-controlled microscope, where a quantitative phase contrast imaging and a coherence gating optical sectioning were demonstrated [3]. In recent years, the development of microscopy was favorably influenced by modern technologies enabling light shaping by a spatial light modulator (SLM). The SLM can be used in both illuminating and imaging paths of the optical microscope, where it ensures a structured specimen illumination, or amplitude and phase modulation of the spatial spectrum, respectively [4]. Using these phase modulation techniques, the spatial light interference microscopy (SLIM) [5, 6] and the spiral phase contrast imaging [7] were presented as powerful techniques capable of measuring nanoscale structures and dynamics in live cells or enhancing standard phase contrast methods. A variability of operations provided by the SLM was also used to design the universal microscope, that operatively combines the standard techniques of optical microscopy [8,9]. Light shaping by the SLM is also useful for digital microscopy. In the common-path phase-shifting lensless holographic microscopy, the SLM was used for a wave multiplexing ensuring a holographic recording and digital reconstruction of the specimen [10]. In its basic configuration, the digital holographic microscopy is limited to applications operating with coherent light needed to create holograms. Such a requirement is not necessary in the recently proposed Fresnel incoherent correlation holography that utilizes a SLM for holographic recording of observed objects illuminated by a quasi-monochromatic spatially incoherent light [11]. This technique removes many barriers for practical development of holography using incoherent light and is especially attractive for fluorescence microscopy. Recently, new modifications of the original system improving signal to noise 2
58 ratio and allowing the use of sources with a broader spectrum have emerged [12,13]. The potential of the incoherent correlation microscopy has been further demonstrated by the imaging beyond the Rayleigh diffraction limit and by the spiral recording and reconstruction of holograms resulting in selective edge contrast enhancement of three-dimensional objects [14]. The spiral edge contrast enhancement was successfully verified due to a hybrid coherence regime of the method leading to a fully coherent vortex reconstruction of the correlation records even though they were created in spatially incoherent light [15]. Although the incoherent correlation microscopy was presented in several experiments as a promising method with the wide application potential, the available field of view (FOV) of the method has not yet been investigated in any approach. In this paper, the FOV is studied in detail both theoretically and experimentally. In the investigated common-path incoherent correlation microscopy, the FOV is not directly determined by the microscope objective lens, but some restrictions due to the correlation overlapping of interfering beams must be taken into account. Here we show that a reduction of the FOV caused by the insufficient correlation overlapping becomes particularly critical when using the microscope objective with a high magnification. The overlapping coefficient was defined by ray optics calculations and used to quantify the FOV in known experimental configurations. We also showed that a significant extension of the FOV is possible in the modified system using a two-component relay optics to achieve a perfect overlapping of the correlated beams. In the improved configuration, the common-path incoherent correlation microscopy allows image reconstruction in the full FOV of the used microscope objective. Theoretical predictions were successfully verified by the experiments demonstrating image reconstruction of the USAF resolution targets illuminated by a light-emitting diode. 2 FOV in basic configurations of the common-path incoherent correlation microscopy In the correlation microscopy, the FOV is not uniquely determined by geometric conditions for the passage of light as in the direct imaging, but a correlation overlapping of the 3
59 interfering beams associated with the basic principle of the method must also be taken into consideration. A simplified scheme of the method is in Fig. 1. To explain its operation, it is reasonable to assume that the observed object is composed of an infinite number of point sources that emit mutually uncorrelated light. Light waves originating Figure 1: Demonstration of the image reconstruction in the common-path incoherent correlation microscopy. from separate object points are collimated by a microscope objective (MO) and directed towards the SLM. Each wave incident on the SLM is divided into two waves, called the signal and reference wave. These waves are spatially correlated because originate from the same object point. If their optical path difference does not exceed the coherence length of the used source, they can interfere. The interference pattern has a shape of the Fresnel zone plate and carries information about the amplitude and the three-dimensional position of the relevant object point. A final record of the observed object is created by the addition of intensities of individual interference patterns because different points of the object are mutually uncorrelated. Information about the object is extracted by the processing and reconstruction of three object recordings acquired with different phase shifts of the signal wave. Experimental setup shown in Fig. 1 allows both direct and correlation imaging. In the direct imaging, the SLM produces a quadratic phase modulation and operates as the lens with a focal length f d. The image on the CCD is then created by a two-lens system consisting of the MO and the SLM lens with the focal lengths f 0 and f d, respectively. 4
60 The FOV is determined by a ray tracing shown in Fig. 2a. Figure 2: Illustration of ray trajectories in (a) the direct imaging and the common-path incoherent correlation microscopy with (b) standard and (c) dual lens configurations. In the correlation imaging, each point of the object must be recorded as the Fresnel interference pattern. This is achieved in a common-path interferometer based on the wave splitting implemented by the SLM. Using the control software, the SLM transmission function t j = a exp(iθ r ) + b exp(iθ s + iϑ j ) is set, where a and b are coefficients providing desired power distribution between the reference and signal waves, ϑ j, j = 1, 2, 3, are constant phase shifts imposed on the signal wave, and θ r and θ s are phase functions for a wavefront transformation of the signal and reference wave. Three object recordings implemented with different phase shifts ϑ j allow to eliminate the holographic twin image [16]. The phase functions θ r and θ s enable two different modes of imaging, here called the standard and dual lens imaging. In the standard common-path correlation imaging, 5
61 θ r corresponds to a constant phase shift. For object points located near the focal plane of the MO, the reference wave corresponds to a collimated beam. The signal wave is generated by the quadratic phase function θ s that represents a lens with the focal length f d. In the dual lens imaging, both θ r and θ s are quadratic phase functions representing lenses with the focal lengths f d 1 and f d 2, respectively [12,13]. In this case, the correlation record of the object point is produced by interference of two spherical waves. In the case of the correlation imaging, the FOV must be determined with respect to the desired overlapping of the signal and reference waves. The situation is illustrated in Fig. 2b for the standard correlation imaging working with the plane reference wave and the spherical signal wave. Capturing the signal and reference waves on the CCD is not sufficient for imaging of the examined off-axis point. It can be successfully reconstructed only when the signal and reference waves are at least partially overlapped on the CCD. In the known configurations of the correlation imaging this condition can hardly be satisfied, especially if the best resolution is required. This is due to significant differences in the direction of propagation of the signal and reference waves. In the correlation imaging, the FOV is reduced in comparison with the direct imaging. This effect is remarkable when the MO with a high magnification is used. Reduction of the FOV caused by the lack of correlation overlapping is estimated for both the standard and dual lens configurations using simple ray optics calculations. Standard configuration In the standard configuration, the SLM acts as a beam splitter, which transforms the signal wave as a lens with the focal length f d, while the reference wave transmits unaffected. To estimate the degree of overlapping of interfering beams, the chief rays of the signal and reference waves must be traced and their positions on the CCD determined. The transverse coordinates of the intersections x s and x r are calculated by geometry shown in Fig. 2b and can be written as x s = x ( ) 1, x r = x ( ) 1, (1) f 0 f d 2 f 0 2 where f 0 is the focal length of the MO, 1 is the separation distance between the MO 6
62 and the SLM, 2 is a position of the CCD with respect to the SLM and 2x 0 is the FOV of the used MO. The FOV of the MO is given by the field number F and the magnification m 0, 2x 0 = F m 0. (2) A separation of the signal and reference waves on the CCD can be conveniently defined by a distance of the spot centers and can be written as x = x s x r = x f 0 f d. (3) The correlation overlapping also depends on the spot size of the detected signal and reference beams D s and D r given as D s = 2 f d f d D 0, D r = D 0, (4) where D 0 is the diameter of the exit pupil of the MO. It can be expressed by its numerical aperture NA as D 0 = 2NAf 0. If we distinguish the beam spots according to their size as D M = max{d s, D r } and D m = min{d s, D r }, a measure of the area overlapping of the interfering beams can be simply quantified by a coefficient P defined as 1, for x D, P = S/S m, for D < x < D +, 0, for x > D +, (5) where S = S j, j=m,m S m = πd2 m 4, ( S j = D2 j 4 arccos 1 2h ) ( ) j Dj D j 2 h j h j (D j h j ), j = m, M, h m = (D+ x)( x + D ) 2 x, h M = (D+ x)( x D ), 2 x D + = D M + D m 2, D = D M D m. 2 7
63 A partial overlapping of beams is determined by 0 < P < 1, whereas the limit value P = 1 stands for a full overlapping of beams and P = 0 for fully separated beams. Dual lens configuration In the dual lens configuration, the SLM splits an input wave into the signal and reference waves and transforms them as a dual lens with two different focal lengths f d 1 and f d 2, respectively. In this case, the signal and reference waves are spherical waves and the positions of their chief rays on the CCD are determined by x s = x ( ) 1, x r = x ( ) 1. (6) f 0 f d 1 2 f 0 f d 2 2 The geometrical separation of beam spots x is obvious from Fig. 2c and can be expressed as x = x f 0 f, (7) f d 1f d 2 where f = f d 1 f d 2. The spot size of the signal and reference beams is given as D s = 2 f d 1 f d 1 D 0, D r = 2 f d 2 D 0. (8) f d 2 The overlapping coefficient P can again be determined by (5) as a ratio of the overlapping area of the signal and reference beams S and the beam spot area S m. For object points close to the optical axis, the signal and reference waves have a full overlapping, P = 1. For off-axis points, the overlapping is reduced and P rapidly decreases with the distance x of the object point from the axis. A smaller beam overlapping causes a quality degradation of the correlation imaging and the image reconstruction is impossible when the signal and reference beams are completely separated, P = 0. The coefficient P can thus be used to define the usable FOV of the correlation imaging. In numerical calculations, the relative FOV x/x 0 is used, where 2x denotes the evaluated FOV in correlation microscopy and 2x 0 is the maximal FOV provided by the field number F of the MO (in our analysis F = 26.5 mm is used). With both the standard and dual lens configurations, a required beam overlapping strongly limits the FOV and the correlation imaging utilizes only a fraction of the FOV available in a direct imaging provided by the MO. In Fig. 3, the dependence of the coefficient P on 2 is illustrated for both the standard and dual lens 8
64 configurations. The distance 2 determines the position of the CCD owing to the SLM and represents an important parameter of the correlation imaging. With the positioning of the CCD, the magnification of the correlation imaging can be changed. If the observed object is placed near the focal plane of the MO with the focal length f 0, the magnification is simply given by m = 2 /f 0 [15]. The CCD position 2 also significantly affects the resolution of the correlation imaging. In the standard configuration, the best resolution is achieved with the condition 2 = 2f d, where f d is the focal length of the lens realized by the SLM. In the double lens configuration, the best resolution is achieved in the setting 2 = 2f d 1f d 2/(f d 1 + f d 2), where f d 1 and f d 2 are the focal lengths of the SLM lenses [13]. The correlation overlapping significantly changes with the CCD position 2 and reaches its minimum just in the most important positions, where the best resolution is achieved. This is clearly demonstrated for both standard Fig. 3a and double lens configuration Fig. 3b. On the plane of the best resolution, the correlation coefficient P has the same value in both configurations. For the MO with NA = 0.28 and f 0 = 20 mm its value is P 0.6 for the relative FOV x/x 0 = 0.05 and P 0.3 for x/x 0 = 0.1. For the MO with higher magnification (NA = 0.55, f 0 = 4 mm), the FOV is further reduced. For the relative FOV x/x 0 = 0.05, the coefficient P 0.15 is obtained, while for x/x 0 = 0.1 the signal and reference beams are completely separated, P = 0. If we assume with regard to the experimental experience that the overlapping P 0.3 is sufficient for reconstructing the image with acceptable quality, the FOV for the correlation imaging is approximately 10 smaller than in the direct imaging when the MO with f 0 = 20 mm is used. In the case of the MO with f 0 = 4 mm, the correlation FOV is more than 20 smaller than in the direct imaging realized by the MO. The size of the correlation FOV can be extended by shortening the distance 1 between the MO and the SLM. In Fig. 4, the dependence of P on the relative FOV is demonstrated for two different settings 1 = 150 and 250 mm. The situation is identical for both standard and dual lens configurations and corresponds to the CCD positions 2 ensuring the best resolution. In terms of theory, 1 shortening leads to a steady overlapping improvement of the interfering beams and in the limit 1 0, the full overlapping is achieved. Unfortunately, the shortening of 1 has 9
65 Figure 3: Dependence of the correlation overlapping of interfering beams on the distance 2 for different parameters of the MO (NA = 0.28, f 0 = 20 mm and NA = 0.55, f 0 = 4 mm) and different parts of the relative FOV (x/x 0 = 0.05 and x/x 0 = 0.1): (a) standard configuration with 1 = 250 mm, f d = mm, (b) dual lens configuration with 1 = 250 mm, f d 1 = 400 mm and f d 2 = 649 mm. technical limitations. In most cases, a reflective SLM is used and a sufficient distance 1 is required for an insertion of the beam splitter and the polarizer or for an implementation of angular separation of incident and reflected beams. The distance 1 used in numerical simulation corresponds to real experimental possibilities. Figure 4: Dependence of the correlation overlapping of interfering beams on the relative FOV for different parameters of the MO (NA = 0.28, f 0 = 20 mm and NA = 0.55, f 0 = 4 mm) and various settings 1. 10
66 3 FOV in the common-path incoherent correlation microscopy with relay optics As was demonstrated, the overlapping of interfering beams is negatively influenced by increasing the distance between the MO and the SLM. As is clear from (3) and (7), an ideal beam overlapping is achieved in both standard and dual lens configurations when the SLM is placed just behind the objective lens, 1 = 0. In this case, the chief rays Figure 5: Demonstration of a perfect correlation overlapping of interfering beams in the setup with two-component relay optics. of the signal and reference waves coincide so that x = 0 for all points of the FOV of the used MO. Unfortunately, this condition cannot be met neither in the standard nor dual lens configurations for technical reasons. Here we present a novel setup modification where effects requiring the setting 1 = 0 are effectively achieved using two-component relay optics. An operation of the system is obvious from the ray paths illustrated in Fig. 5. The setup is supplemented by two lens system that is placed between the MO and the SLM and ensures imaging of the exit pupil of the MO on an active area of the SLM. This is achieved when the inserted relay optics is configured as the 4F system operating with the unitary magnification. The exit pupil of the MO is then placed at the front focal plane of the lens L 1 and the SLM is positioned at the back focal plane of the lens L 2. Such a configuration is adequate to the technically unattainable setting 1 = 0 in the standard and dual lens experiments. The relay optics ensures that the chief rays of the signal and reference waves coincide and a perfect overlapping of interfering beams is achieved in the full FOV of the used MO. This modification of the system is of great practical importance, because the FOV of the correlation imaging is as large as the FOV 11
67 of the used MO regardless of the experimental parameters and the CCD positioning. The benefits of this method are evident from the experimental results. The common-path correlation microscopy is essentially a digital holography method in which the continuous spatial distribution of optically generated holograms is sampled by the discrete sensitive pixels on a CCD array. In these systems, the space-bandwidth product (SBP) is introduced as a quantity that is directly related to the information capacity of the hologram [17]. To compare the demands imposed on detection devices, the SBP was determined for standard and dual lens configurations, and consequently also for both systems supplemented by the relay optics. In accordance with the traditional definition, the SBP was calculated as SW = L x W x, where L x is the transverse size of the detector needed to capture the hologram and W x stands for the highest spatial frequency contained in the hologram. In all examined configurations, L x = max{x s, x r } was used, where x s and x r are the transverse positions of the spot centers of the signal and reference waves on the CCD. The maximal spatial frequency W x was determined by evaluating the relationship for a local frequency of the hologram. It can be written as W x = (1/2π)( Φ/ x) x=xm, where Φ is the phase difference of the signal and reference wave at the hologram plane and x m denotes the transverse coordinate where the local spatial frequency reaches its maximal value. In all examined configurations, the SBP was evaluated for the full FOV of the MO and the CCD positions for the best resolution. It was verified that the SBP becomes minimal in the dual lens configuration with the relay optics. In comparison with earlier experiments, the use of the relay system provides not only full correlation overlapping, but it also reduces the SPB at the same object size. In such a manner the relay optics reduces demands on the hologram detection. 4 Experimental results Reduction of the FOV in standard and dual lens configurations and the proposed modification for the full overlapping of interfering beams were verified experimentally in the setup illustrated in Fig. 6. The collimated LED (Thorlabs, 625nm) with the spectral filter SF (FWHM 10 nm) was used as an incoherent source of light. The FOV was examined 12
68 Figure 6: Set-up for the common-path incoherent correlation microscopy using the relay optics for a perfect correlation overlapping and an extended FOV: SF - spectral filter, MO - microscope objective, P - polarizer, L 1, L 2 - two-component relay optics, BS - beam splitter, SLM - spatial light modulator. using USAF resolution targets placed at the front focal plane of the Melles Griot MO (NA = 0.28, f 0 = 20 mm and NA = 0.55, f 0 = 4 mm). The signal and reference waves were created using the SLM (Hamamatsu, pixels) and the correlation records were captured on the CCD (Retiga 4000 R). The polarizer was used to achieve an optimal phase modulation by the SLM. In initial experiments, the setup was used without relay optics to demonstrate a reduction of the FOV of the MO due to the lack of the correlation overlapping of the signal and reference waves. Subsequently, the experimental system was supplemented by the relay optics for a perfect overlapping of interfering beams. It was composed of two identical achromatic doublets with the focal length 150 mm. As is evident from Fig. 7, the correlation recordings made in the standard setup and the modified experiment with relay lenses are fundamentally different. When using the relay optics, the defocused correlated images of the USAF target created by the signal and reference waves are in a perfect overlapping and coincide (Fig. 7a). In the standard configuration, a sufficient overlapping is reached only in the center of the FOV indicated by a dashed line in Fig. 7d. For off-axis parts of the object, the images created by the signal and reference waves are mutually shifted by a large distance x and are almost separated. The correlation recordings can not be successfully reconstructed in this part of the FOV. In the dual lens imaging, the shift of interfering waves can be positively influenced by reducing the 13
69 distance f, which is the difference of the focal lengths of the SLM lenses. This effect is evident from Figs. 7b and 7c illustrating the correlation recordings taken with f 1 = 53 mm and f 2 = 249 mm, respectively. Unfortunately, the reduction of f does not lead to an increase of the FOV, because the signal and reference waves reduce not only their lateral separation but also the areas of their spots and the overlapping area remains unchanged. The correlation recordings shown in Fig. 7 were taken by the Melles Griot Figure 7: Correlation recordings of the USAF resolution targets demonstrating various degrees of overlapping of the signal and reference waves in different experimental configurations: (a) perfect overlapping in the setup with relay optics, (b) dual lens configuration with f 1 = 53 mm and (c) f 2 = 249 mm, (d) insufficient overlapping in standard configuration. MO with NA = 0.28 and f 0 = 20 mm. The separation distance between the MO and the SLM was set to the minimal achievable value 1 = 270 mm. The best resolution of the system was ensured by the fixed position of the CCD, 2 = 495 mm, which was combined with the focal length of the SLM lens f d = mm in the standard configuration and f d1 = 470 mm and f d2 = 523 mm in the dual lens configuration. The final images of the USAF resolution targets created by the processing and reconstruction of the demonstrated correlation recordings are shown in Fig. 8. Advantages of the proposed modification of the setup are more apparent there, because the image is not reconstructed in areas with insufficient overlapping of interfering beams. The images of the groups 6 and 7 of the USAF target obtained by the reconstruction of the correlation recordings acquired in the standard and dual lens configurations are shown in Figs. 8a 14
70 and 8c, respectively. The FOV specified by the correlation overlapping is approximately 2x 0.3 mm and remains the same in both the standard and dual lens configurations. This experimental finding is consistent with the theoretical results demonstrated in Fig. 3. Significant improvement of the FOV arises in both configurations when the relay lenses are used. The reconstructed images are shown in Figs. 8b and 8d. As is obvious, the FOV completely fills a detection area of the CCD in this case. Although the benefits of the relay system are indisputably demonstrated, the images 8b and 8d still cannot demonstrate the full potential of the modified setup, because the correlation field used in the image reconstruction is not fully captured by a single CCD frame. In order to demonstrate the full FOV when using the relay system, nine records were carried out at different lateral positions of the CCD while other system settings remained unchanged. The resulting correlation record used in the image reconstruction was then created by a fusion of the partial CCD records. The obtained wide-field image is shown in Fig. 8e. Compared with the image reconstructed from a single CCD frame, the groups 4 and 5 additionally may be seen there. Thus, the correlation FOV obtained in known configurations (Figs. 8a and 8c) is only a fraction of the FOV available in the proposed system with the relay optics (Fig. 8e). To demonstrate a full functionality of the system modification in the conditions of digital microscopy, the experiment was also performed using the Melles Griot MO with higher magnification (NA = 0.55, f 0 = 4 mm). The results obtained are presented in Fig. 9. Here, the finest elements of the groups 8 and 9 of the USAF target were reconstructed in the dual lens configuration that was adjusted to achieve the best resolution. Extension of the FOV in the system using the relay optics Fig. 9b is again significant in comparison with usual arrangement Fig. 9a. Moreover, the reconstructed image 9b still does not show all the available FOV, because the correlation field exceeded a detection area of the CCD and it was not fully captured by a single CCD frame. 15
71 Figure 8: Images of the USAF resolution target reconstructed from the correlation recordings captured in different experimental configurations using the Melles Griot MO with NA=0.28 and f 0 = 20 mm: (a) standard configuration (SC), (b) SC with relay optics, (c) dual lens configuration (DLC), (d) DLC with relay optics, (e) DLC with relay optics and image reconstructed from the correlation recordings obtained by a fusion of nine partial CCD frames. 5 Conclusions In the paper, the basic configurations of incoherent correlation microscopy were examined in a connection with the available FOV. As the main result, the new modification of experiments was proposed that provides a perfect overlapping of interfering beams and allows a significant extension of the FOV. The partial results of the paper may be summarized as follows: It was first demonstrated that in the common-path incoherent correlation microscopy the image is reconstructed in the FOV determined by the conditions of 16
72 Figure 9: Images of the USAF resolution target reconstructed from the correlation recordings captured in the dual lens configuration (DLC) using the Melles Griot MO with a higher magnification (NA=0.55 and f 0 = 4 mm): (a) usual DLC and (b) DLC with the relay optics. the correlation overlapping of interfering beams. Ray optics calculations were performed allowing a simple estimation of the FOV by the conveniently defined correlation coefficient. It was shown that the correlation FOV depends on the parameters of the experiment and significantly reduces the FOV of the used MO in both the standard and dual lens configurations. We verified that the reduction of the FOV caused by the lack of the correlation overlapping occurs mostly in the settings ensuring the best resolution and when the MO with higher magnification is used. The use of relay lenses was proposed to ensure a perfect correlation overlapping of interfering beams in all known configurations of the common-path correlation microscopy regardless of used parameters of the experiment. The common-path incoherent correlation microscopy is a promising imaging technique supported by modern light shaping technologies. It allows numerical reconstruction of three-dimensional objects from the correlation recordings acquired in spatially incoherent quasi-monochromatic light. Recently, the special properties of the method including sub-diffraction resolution, improved signal to noise ratio [12], extension of the permissible spectral bandwidth of the used light sources or spiral edge enhancement [14] were successfully demonstrated and considered for application in fluorescence microscopy. The 17
73 proposed modification of the setup resulting in a full correlation overlapping and extension of the FOV considerably increases optical parameters and application potential of the method. Acknowledgment This work was supported by the Czech Ministry of Education, project No. MSM , the Technology Agency of the Czech Republic, project No. TE , the IGA project of the Palacký University PrF and the project CEITEC - Central European Institute of Technology No. CZ.1.05/1.1.00/ from European Regional Development Fund. REFERENCES [1] P. Marquet, B. Rappaz, P. J. Magistretti, E. Cuche, Y. Emery, T. Colomb, and Ch. Depeursinge, Digital holographic microscopy: a non invasive contrast imaging technique allowing quantitative visualization of living cells with sub wavelength accuracy, Opt. Lett., 30(5), (2005). [2] L. Lovicar, J. Komrska, and R. Chmelík, Quantitative-phase-contrast imaging of a two-level surface described as a 2D linear filtering process, Opt. Express 18(20), (2010) [3] P. Kolman, and R. Chmelík, Coherence-controlled holographic microscope, Opt. Express 18(21), (2010). [4] C. Maurer, A. Jesacher, S. Bernet, and M. Ritsch-Marte, What spatial light modulators can do for optical microscopy, Laser Photonics Reviews 5, (2011). [5] Z. Wang, L. Millet, M. Mir, H. Ding, S. Unarunotai, J. Rogers, M. U. Gillette, and G. Popescu, Spatial light interference microscopy (SLIM), Opt. Express 19(2), (2010). 18
74 [6] Z. Wang, I.S. Chun, X. Li, Z.Y. Ong, E. Pop, L. Millet, M. Gillette, and G. Popescu, Topography and refractometry of nanostructures using spatial light interference microscopy, Opt. Lett. 35(2), (2010). [7] S. Furhapter, A. Jesacher, S. Bernet, M. Ritsch-Marte, Spiral phase contrast imaging in microscopy, Opt. Express 13(3), (2005). [8] M.Warber, S. Zwick, T. Haist, and W. Osten, SLM-based phase-contrast filtering for single and multiple image acquisition, Optics and Photonics for Information Processing III, Proceedings of SPIE 7442, 74420E-74420E-12 (2009). [9] M. Hasler, T. Haist, W. Osten, SLM-based microscopy, Optical Micro-and Nanometrology, Proceedings of SPIE V-84300V-8 (2012). [10] V. Micó, and J. García, Common-path phase-shifting lensless holographic microscopy, Opt. Lett. 35(23) (2010). [11] J. Rosen and G. Brooker, Fluorescence incoherent color holography, Opt. Express 15(5), (2007). [12] X. Lai, Y. Zhao, X. Lv, Z. Zhou, and S. Zeng, Fluorescence holography with improved signal-to-noise ratio by near image plane recording, Opt. Lett. 37(13), (2012). [13] B. Katz, J. Rosen, R. Kelner, and G. Brooker, Enhanced resolution and throughput of Fresnel incoherent correlation holography (FINCH) using dual diffractive lenses on a spatial light modulator (SLM), Opt. Express 20(8), (2012). [14] P. Bouchal, and Z. Bouchal, Selective edge enhancement in three-dimensional vortex imaging with incoherent light Opt. Lett. 37(14), (2012). [15] P. Bouchal, J. Kapitán, R. Chmelík, and Z. Bouchal, Point spread function and twopoint resolution in Fresnel incoherent correlation holography, Opt. Express 19(16), (2011). 19
75 [16] I. Yamaguchi and T. Zhang, Phase-shifting digital holography, Opt. Lett. 22(16), (1997). [17] L. Xu, X. Peng, Z. Guo, J. Miao, and A. Asundi, Imaging analysis of digital holography, Opt. Express 13(7), (2005). 20
76 Coherent Imaging with Incoherent Light in Digital Holographic Microscopy Radim Chmelik a,b a CEITEC Central European Institute of Technology, Brno University of Technology, Technicka 10, Brno, , Czech Republic; b Institute of Physical Engineering, Faculty of Mechanical Engineering, Brno University of Technology, Technicka 2, Brno, , Czech Republic ABSTRACT Digital holographic microscope (DHM) allows for imaging with a quantitative phase contrast. In this way it becomes an important instrument, a completely non-invasive tool for a contrast intravital observation of living cells and a cell drymass density distribution measurement. A serious drawback of current DHMs is highly coherent illumination which makes the lateral resolution worse and impairs the image quality by a coherence noise and a parasitic interference. An uncompromising solution to this problem can be found in the Leith concept of incoherent holography. An off-axis hologram can be formed with arbitrary degree of light coherence in systems equipped with an achromatic interferometer and thus the resolution and the image quality typical for an incoherent-light wide-field microscopy can be achieved. In addition, advanced imaging modes based on limited coherence can be utilized. The typical example is a coherence-gating effect which provides a finite axial resolution and makes DHM image similar to that of a confocal microscope. These possibilities were described theoretically using the formalism of three-dimensional coherent transfer functions and proved experimentally by the coherence-controlled holographic microscope which is DHM based on the Leith achromatic interferometer. Quantitative-phase-contrast imaging is demonstrated with incoherent light by the living cancer cells observation and their motility evaluation. The coherence-gating effect was proved by imaging of model samples through a scattering layer and living cells inside an opalescent medium. Keywords: holographic microscopy, quantitative phase contrast, coherence of light, coherence gate, imaging in turbidmedia 1. DIGITAL HOLOGRAPHIC MICROSCOPY The reason of still growing interest in digital holographic microscopes is their quantitative-phase-contrast (QPC) imaging mode 1. Unlike standard light microscopy techniques including the Zernike phase contrast or the Nomarski DIC, the QPC image directly represents phase shifts introduced by an object. This allows for applications of a variety of advanced image-processing algorithms such as numerical focusing 1, or complex-field deconvolution 2. Digital holographic microscopes (DHM) are usually based on the classical off-axis holographic setup 1,3 following that proposed in 1966 by Van Lighten and Osterberg 4 (cf. Fig. 1). Microscope optics is built into one arm of a conventional (i.e. Mach-Zehnder or Michelson) interferometer. Advantage of this setup in comparison with phase-shifting techniques is a high frame rate especially when it is completed with the Fourier reconstruction algorithms 5. This enables a stable record even of very fast processes to carry out. DHM is applied frequently as a living-cells-observation tool providing a strong imaging contrast by a completely noninvasive intravital method 3,6-11. In addition, QPC images are interpreted as the signal proportional to the density distribution of a cell dry-mass 11,12. Living cells motility and growth can be optically measured 11 by processing of QPC signal, as well as their reactions to external stimuli 10, which makes DHM an excellent tool for cytopatogenicity and cytotoxicity tests. Digital image focusing can be accomplished using a single hologram record and cells can be thus traced in 3D by processing of holographic time-lapse series 13. Reflected-light DHMs are typically applied for surface topography measurements 1 including measurements of dynamical systems (MEMS, MOEMS) 14. Subnanometer resolution can be achieved in z-axis 8,15.
77 At present, DHM is often combined with another imaging modalities or manipulation techniques: epifluorescence microscopy 16,17, optical tweezers 18, and second-harmonic generation 19. However, the basis of the holographic optical system itself has remained in principle unchanged since M BS D O C Sp S BS M Figure 1. Typical set-up of a contemporary digital holographic microscope: S source (laser diode), BS beam splitters, M mirrors, C condenser lens, Sp specimen, O objective lens, D detector (CCD camera). This classical off-axis holographic system works properly with a coherent illumination, which brings some substantial disadvantages about: images are impaired with a coherence noise (speckles) and unintended interference patterns. Moreover, the lateral resolution for a coherent light is twice the value for an incoherent illumination (cf. Section 3 below). For this reason, partially coherent light is a preferable option for DHM imaging It is known that the reduction of spatial coherence attenuates the region of numerical refocusing 20, but, on the other hand, it suppresses the influence of scattering media surrounding an observed object, whilst simultaneous reduction of temporal coherence makes this effect stronger 21,23. For these reasons, to have an off-axis holographic system working perfectly with completely incoherent illumination is strongly desirable. 2. COHERENCE-CONTROLLED HOLOGRAPHIC MICROSCOPY The incoherent off-axis holography concept has been proposed by Leith and Upatnieks 24 in A conventional interferometer is replaced by the so-called achromatic interferometer 24,25, which exhibits also the feature of spatial invariance 26. As interference fringes are also the image of a diffraction grating, the fringe pattern is independent of inputbeam direction and wavelength. This means that incoherent off-axis holography is feasible with arbitrarily broad and broadband light sources 27. Use of this concept in microscopy promises the image quality and the resolving power typical for a wide-field microscopy with incoherent illumination. Moreover, a strong reduction of light coherence is expected to result in the coherence-gating effect. Light scattered outside the object plane is suppressed in the output image, which makes the incoherent-holography imaging process similar to that of a confocal microscope 28,29. The first off-axis DHM with the achromatic Leith interferometer was built and experimentally verified in 1999 by Chmelik and Harna for reflected light Optical sectioning with a broad source was demonstrated 30 becoming stronger with a broad and broadband source 31. DHM based on the Leith interferometer (at present called coherence-controlled holographic microscope CCHM) has been then designed and completed for transmitted-light 33. A new generation of CCHM 34 designed for the attachment of classic condenser lenses, infinity-corrected objective lenses and with multimodal imaging capability is presently developed.
78 Figure 2. Optical setup of the transmitted-light coherence-controlled holographic microscope: S...light source, L...relay lens, M...mirrors, G...diffraction grating, C...objective lenses used as condenser ones, R...reference plane, Sp...specimen, O...objective lenses, OP...output plane, OL...output lens, D...detector (CCD camera). The optical setup of the transmitted-light CCHM is explained in Fig. 2. Light beam emitted by the source S (typically a halogen lamp, with an interference filter or a stop possibly attached to) is split by the diffraction grating G to the interferometer arms. The specimen Sp and the reference object R are imaged to the output plane OP, where a highcontrast image-plane hologram is formed for both coherent and incoherent illumination. The interference pattern is recorded by a camera D and numerically processed by an attached PC. Image processing is based on the method of carrier removal in the Fourier plane 5. Image intensity and quantitative phase are on-line computed with the rate of 12 fps. The capability of a high-quality QPC imaging in CCHM has been verified on living cancer cells 10. A time-lapse study accomplished by CCHM has shown differences in dry mass dynamics between cells of diverse malignancy stressed by nutritional and energy deprivation 10. The coherence-gating effect was proved experimentally by applying a diffuser over a specimen and illumination with a broad source. Fig. 3a shows that a conventional bright-field image of a model amplitude specimen is destroyed by scattering of light within the diffuser, while CCHM intensity still clearly reveals its features 33. The coherence gating effect exhibited by CCHM allowed for QPC imaging of living cells in a medium containing active phospholipids (Fig. 3b) which caused strong scattering of light. It was experimentally proved that in the presence of this turbid medium the classic Zernike phase contrast was not applicable. Figure 3. a) Images of a Cu foil with rectangular openings covered by a diffuser demonstrate coherence-gating by CCHM: bright field (BF) image is destroyed by scattering of light within the diffuser, while CCHM intensity signal still clearly reveals the object features. Halogen-lamp illumination with a narrow-band filter at 650 nm (FWHM 10 nm), and objective lenses 10x/NA = 0.25 were used. b) Quantitative phase contrast CCHM images of living cells of human breast carcinoma, cell line G3S2 in vitro, in two moments of a time-lapse observation (the times are indicated). Halogen-lamp illumination with a narrow-band filter at 650 nm (FWHM 10 nm), and objective lenses 20x/NA = 0.40 were used. The images in Fig. 3 were formed by ballistic light separated from diffuse one by the effect of coherence gating. The diffuse light is usually assumed to be only ballast light decreasing the image contrast (cf. e.g. Ref. 35). However, CCHM allows obtaining images also by diffuse light. This light hits the image plane out of the relevant Gaussian image points
79 being deflected by a scattering medium. All the diffuse light which is laterally shifted by a certain distance in the image plane can be collected and separated from the remaining part of diffuse and ballistic light by introduction of the same lateral shift to the reference wave THEORY OF IMAGING BY CCHM 3.1 Fundamentals of 3D imaging theory, the influence of coherence on imaging The numerically reconstructed complex image signal of CCHM is described (with the help of the linear-systems theory and in the 1 st Born approximation of the scattering theory) by the inverse Fourier transform 29 u i ( i i i i i i x, y, z ) T( m, n, s) c( m, n, s)exp[2 i( mx ny sz )] dmdnds. (1) The transverse position of an image point is described by the Cartesian coordinates x i, y i of the conjugated point in the object plane, z i is the defocus of an object measured positively towards an objective lens, and m, n, s are spatial frequencies in the directions of Cartesian coordinate axes. The object is described by the Fourier transform T(m,n,s) of its three-dimensional (3D) scattering potential, c(m,n,s) is a 3D coherent transfer function (CTF), which depends 29 on the numerical apertures of objective and condenser lenses, and on the coherence properties of a source. Integrations in (1) are carried out over the interval (-, ). It is obvious from the form of (1) that imaging by CCHM is coherent for any degree of coherence of illumination. However, the range of object spatial frequencies transferred by CCHM strongly depends on the coherence of light. This dependence is demonstrated with the help of CTF supports (spatial-frequency passbands) calculated according (1) and depicted in Fig. 4. Objective and condenser lenses are assumed to be aplanatic with the same numerical aperture NA. Figure 4. Cross-sections of CCHM passbands (i.e. support of c(m,n,s), in grey), for a reflected-light set-up (a-c) and for a transmitted-light set-up (d, e), for a point monochromatic source (a, d), for a broad monochromatic source (b, e), and for a broad broadband source (c). 3D CTFs have cylindrical symmetry about the s axis; s, m are axial and transverse spatial frequencies, respectively, NA is the numerical aperture both of condenser and objective lenses, and λ v is a wavelength in vacuum. For a point monochromatic (i.e. coherent) source (Fig. 4a, d), the transverse cut-off frequency of CCHM equals to NA/λ v, where λ v is a wavelength in vacuum. As the 3D point spread function (PSF) of CCHM is the 3D Fourier transform of its
80 3D CTF and the CTF support has a zero width in the axial direction for a coherent source (see Fig. 4a, d), the axial resolution approaches infinity in this case. This means CCHM (or any other DHM) has no capability to resolve in axial direction with a coherent illumination despite of the possibility to numerically refocus. This is why coherent-light DHM imaging completed with numerical refocusing is sometimes classified not as 3D, but as 2½D imaging 37. The use of a broad monochromatic source filling the aperture of condenser lenses increases the transverse cut-off frequency to 2NA/λ v, which is twice the value for a coherent illumination (Fig. 4b, e). Moreover, the passband for a reflected-light set-up (Fig. 4b) has a non-zero width in the axial direction, which means that the axial resolution has now a finite value (the microscope is capable of optical sectioning), which can be further decreased by broadening of the source spectrum (Fig. 4c). 3.2 Fundamentals of 2D imaging theory, point spread function and two-point resolution A two-dimensional (2D) object is characterized by the function T 2D (m,n), which is the 2D Fourier transform of the object transmission function t 2D (x,y). It follows from (1) that the complex signal of CCHM for an in-focus object is then expressed by the 2D inverse Fourier transform u i ( 2D 2D i i i i x, y,0) T ( m, n) c ( m, n)exp[2 i( mx ny )] dmdn, (2) where 2D CTF c 2D (m,n) is the projection of 3D CTF c(m,n,s) along the s axis c ( m, n) c(m,n,s) ds. (3) 2D According to the convolution theorem, the signal (2) can be expressed also by the convolution u i ( 2D 2D i i i i i i x, y,0) t ( x, y ) h ( x, y ), (4) where h 2D (x i,y i ) denotes 2D PSF of CCHM, which is the 2D Fourier transform of 2D CTF c 2D (m,n). 2D PSF can be derived analytically in the paraxial approximation from 3D CTF 29. For a point monochromatic source h 2D i i 2J1( v) ( x, y ), v where NA i 2 i 2 v 2 ( x ) ( y ), (5) where NA is the numerical aperture of both condenser and objective lenses, λ v is a wavelength in vacuum, and J 1 is the Bessel function of the first kind and of the first order. For a broad monochromatic source, 2D PSF of CCHM is identical with that for incoherent (bright-field) imaging h 2D i ( x, y i 2 2J1( v) ), v where v NA i 2 i 2 v 2 ( x ) ( y ). (6) The substantial difference follows from the fact that imaging in CCHM is coherent, described by Eq. (4). This is why we have to consider possible phase shifts introduced by an object. For example, a two-point object is described by the transmission function t 2D ( v i i i i i i i x, y ) ( x ) ( y ) exp( i ) ( x x ) ( y ), (7) where δ denotes the Dirac delta function, φ is the phase shift introduced by one of the point objects, and Δx i is its transverse shift. Then, according to (4), u i ( 2D 2D i i i i i i i x, y,0) h ( x, y ) exp( i ) h ( x x, y ). (8) For a broad monochromatic source and in the paraxial approximation, 2D PSF is expressed by Eq. (6). Then, it is evident from (8) that the Rayleigh criterion is appropriate for two-point resolution assessment in the case of a zero phase shift φ. Otherwise, the resolution is better than indicated by the Rayleigh criterion. The extreme case corresponds to φ = π, when two principal maxima of u i are separated by a line of its zero value for any Δx i.
81 4. CONCLUSIONS A great potential of a digital holographic microscopy consists in the fact that imaging parameters depend considerably on the coherence of illumination. One extreme corresponds to classic coherent-illumination off-axis holography including full possibility of numerical focusing and the other to confocal-microscopy-like imaging without coherence noise and artifacts and with the quality and resolution comparable with a wide-field microscopy. The coherence can be made a free parameter controlling the nature of imaging by means of a specific DHM design based on the Leith achromatic and spatially invariant interferometer. This possibility was proved experimentally by the coherence-controlled holographic microscope (CCHM), which is DHM based on the Leith achromatic interferometer. Quantitative phase contrast provided by CCHM is a promising instrument of future evaluation of living cancer cells behavior, particularly, from the point of view of intracellular motility. Coherence gating was demonstrated by CCHM imaging of a model sample through a scattering obstacle as well as of living cells in a turbid medium. It has been proved theoretically that the overall imaging process of CCHM is coherent for any degree of coherence of illumination. 3D spatial-frequency passbands of CCHM were studied theoretically in dependence on coherence properties of a source. It is evident that lower coherence of illumination corresponds to better transverse and axial resolution of CCHM. Point spread functions (PSF) for 2D objects were derived in the paraxial approximation. For a broad monochromatic source 2D PSF of CCHM is identical with that for classic incoherent imaging. This is why the two-point resolution limit of CCHM is given by the Rayleigh criterion assuming that two point objects introduce the same phase shift. ACKNOWLEDGEMENT This work is supported by the project CEITEC Central European Institute of Technology (CZ.1.05/1.1.00/ ) from European Regional Development Fund, by MIT CR (project FR-TI4/660), and by TA CR (project TE ). REFERENCES [1] Cuche, E., Bevilacqua, F., and Depeursinge, C., Digital holography for quantitative phase-contrast imaging, Opt. Lett. 24, (1999). [2] Cotte, Y., Toy, M. F., Pavillon, N., and Depeursinge, C., Microscopy image resolution improvement by deconvolution of complex fields, Optics Express 18, (2010). [3] Cuche, E., Marquet, P., and Depeursinge, C., Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms, Appl. Opt. 38, (1999). [4] Van Lighten, R. F., Osterberg, H., Holographic Microscopy, Nature 211, 282 (1966). [5] Kreis, T., Digital holographic interference-phase measurement using the Fourier-transform method, JOSA A 3, (1986). [6] Carl, D., Kemper, B., Wernicke, G., and von Bally, G., Parameter-optimized digital holographic microscope for high-resolution living-cell analysis, Appl. Opt. 43, (2004). [7] Ikeda, T., Popescu, G., Dasari, R.R., and Feld, M. S., Hilbert phase microscopy for investigating fast dynamics in transparent systems, Opt. Lett. 30, (2005). [8] Marquet, P., Rappaz, B., Magistretti, P. J., Cuche, E., Emery, Y., Colomb, T., and Depeursinge, C., Digital holographic microscopy: a noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy, Opt. Lett. 30, (2005). [9] Kemper, B., Carl, D., Schnekenburger, J., Bredebusch, I., Schäfer, M., Domschke, W., and von Bally, G., Investigation of living pancreas tumor cells by digital holographic microscopy, J. Biomed. Opt. 11, (2006). [10] Janeckova, H., Vesely, P., and Chmelik, R., Proving Tumour Cells by Acute Nutritional/Energy Deprivation as a Survival Threat: A Task for Microscopy, Anticancer Research 29, (2009). [11] Sridharan, S., Mir, M., and Popescu, G., Simultaneous optical measurements of cell motility and growth, Biomed. Opt. Expr. 2, (2011).
82 [12] Barer, R., Interference microscopy and mass determination, Nature 169(4296), (1952). [13] Langehanenberg, P., Ivanova, L., Bernhardt, I., Ketelhut, S., Vollmer, A., Dirksen, D., Georgiev, G., von Bally, G., and Kemper, B., Automated three-dimensional tracking of living cells by digital holographic microscopy, J. Biomed. Opt. 14, (2009). [14] Emery, Y., Cuche, E., Marquet, F., Aspert, N., Marquet, P., Kühn, J., Botkine, M., Colomb, T., Montfort, F., Charrière, F., Depeursinge, C., Debergh, P., and Conde, R., Digital Holographic Microscopy (DHM) for metrology and dynamic characterization of MEMS and MOEMS, Proc. SPIE 6186, 61860N (2006). [15] Kühn, J., Charrière, F., Colomb, T., Cuche, E., Montfort, F., Emery, Y., Marquet, P., and Depeursinge, C., Axial sub-nanometer accuracy in digital holographic microscopy, Meas. Sci. Technol. 19, (2008). [16] Pavillon, N., Benke, A., Boss, D., Moratal, C., Kühn, J., Jourdain, P., Depeursinge, C., Magistretti, P. J., and Marquet, P., Cell morphology and intracellular ionic homeostasis explored with a multimodal approach combining epifluorescence and digital holographic microscopy, J. Biophoton. 3, (2010). [17] Makhlouf,H., Perronet,K., Dupuis,G., Lévêque-Fort, S., and Dubois, A., Simultaneous optically sectioned fluorescence and optical coherence microscopy with full-field illumination, Opt. Lett. 37, (2012). [18] DaneshPanah, M., Zwick, S., Schaal, F., Warber, M., Javidi, B., and Osten, W., 3D Holographic Imaging and Trapping for Non-Invasive Cell Identification and Tracking, J. Display Technol. 6, (2010). [19] Shaffer, E., Moratal, C., Magistretti, P., Marquet, P., and Depeursinge C., Label-free second-harmonic phase imaging of biological specimen by digital holographic microscopy, Opt. Lett. 35, (2010). [20] F. Dubois, L. Joannes, and J.-C. Legros, Improved three-dimensional imaging with a digital holography microscope with a source of partial spatial coherence, Appl. Opt. 38, (1999). [21] Dubois, F., Yourassowsky, C., Monnom, O., Legros, J.-C., Debeir, O., Ham, P. V., Kiss, R., and Decaestecker, C., Digital holographic microscopy for the three-dimensional dynamic analysis of in vitro cancer cell migration, J. Biomed. Opt. 11, (2006). [22] Dubois, F., Callens, N., Yourassowsky, C., Hoyos, M., Kurowski, P., and Monnom, O., Digital holographic microscopy with reduced spatial coherence for three-dimensional particle flow analysis, Appl. Opt. 45, (2006). [23] Dubois, F., Yourassowsky, C., Callens, N., Minetti, C., and Queeckers, P., Applications of digital holographic microscopes with partially spatial coherence sources, Journal of Physics: Conference Series 139, (2008). [24] Leith, E. N., and Upatnieks, J., Holography with Achromatic-Fringe Systems, JOSA 57, (1967). [25] Leith, E. N., and Swanson, G. J., Achromatic interferometers for white light optical processing and holography, Appl. Opt. 19, (1980). [26] Leith, E. N., and Chang, B. J., Space-Invariant Holography with Quasi-Coherent Light, Appl. Opt. 12, (1973). [27] Leith, E. N., Chien, W.-C., Mills, K. D., Athey, B. D., and Dilworth, D. S., Optical sectioning by holographic coherence imaging: a generalized analysis, JOSA A 20, (2003). [28] Sun, P.-C., and Leith, E. N., Broad-source image plane holography as a confocal imaging process, Appl. Opt. 33, (1994). [29] Chmelík, R., Three-dimensional scalar imaging in high-aperture low-coherence interference and holographic microscopes, J. Mod. Opt. 53, (2006). [30] Chmelík, R., and Harna, Z., Parallel mode confocal microscope, Opt. Eng. 38, (1999). [31] Chmelík, R., Holographic confocal microscopy, Proc SPIE 4356, (2000). [32] Chmelík, R., and Harna, Z., Surface profilometry by a parallel-mode confocal microscope, Opt. Eng. 41, (2002). [33] Kolman, P., and Chmelík, R., Coherence-controlled holographic microscope, Opt. Expr. 18, (2010). [34] Slabý, T., Antoš, M., Dostál, Z., and Chmelík, R., Coherence-controlled holographic microscope, Proc. SPIE 7746, 77461R R-8 (2010). [35] Kempe, M., Genack, A. Z., Rudolph, W., and Dorn, P., Ballistic and diffuse light detection in confocal and heterodyne imaging systems, JOSA A 14, (1997). [36] Lošťák, M., Kolman, P., Dostál, Z., Chmelík, R., Diffuse light imaging with a coherence controlled holographic microscope, Proc. SPIE 7746, 77461N N-9 (2011). [37] Kou, S. S., and Sheppard, C. J. R., Imaging in digital holographic microscopy, Opt. Expr (2007).
83 Theoretical study of coherence-controlled holographic microscopy in the presence of scattering media Michala Henzlová a,b, Martin Lošt ák a,b and Radim Chmelík a,b a CEITEC-Central European Institute of Technology, Brno University of Technology, Technická 10, Brno, , Czech Republic; b Institute of Physical Engineering, Faculty of Mechanical Engineering, Brno University of Technology, Technická 2, Brno, , Czech Republic ABSTRACT In this paper the theoretical description of the imaging process of a coherence-controlled holographic microscope (CCHM) is carried out for the case when the object beam is influenced by a scattering medium (a diffuser) present between an observed object and an objective lens of the microscope. The calculation is based on the decomposition of the diffuser transmission function into its frequency components. The complete holographic image is then computed as the superposition of holographic images for individual frequency components. The dependence of fundamental imaging characteristics on the coherence state of an illumination is demonstrated. Keywords: holographic microscopy, coherence gate, turbid-media imaging 1. INTRODUCTION The Coherence-Controlled Holographic Microscopy (CCHM) 1 is a novel holographic-microscopy technique for a quantitative-phase-contrast observation of living cells with the illumination of arbitrarily low coherence. In conventional digital holographic microscopes with a coherent illumination (e.g. laser-diode one), a speckle field is usually generated by the presence of any obstacle (dust particles, scratches etc.) in the optical system. In the CCHM, the generation of the coherent noise is prevented by a low-coherence illumination. In addition, a coherence gate separates a ballistic light from a diffuse one, allowing to reveal structures hidden behind a diffusive medium. A coherent transfer function (CTF), which is the function describing the transfer of spatial frequencies of an object by an optical system, has already been derived for CCHM. 2 In this paper, a similar approach is used for the calculation of CTF for CCHM with a diffuser placed in the object space. An observed object, a reference object and the diffuser are assumed to be two-dimensional planar objects. Thus, the geometric factor 2 (necessary for the calculation) C = 1 for each of these objects. 2. COHERENCE-CONTROLLED HOLOGRAPHIC MICROSCOPE The coherence-controlled holographic microscope 3 (see Fig.1) is a two beam interferometer completed with an imaging optics. It consists of two optically equivalent arms an object arm and a reference arm. The light from a source is split by a beamsplitter (BS) into these two arms. The source is imaged to the front focal planes of condenser lenses thus forming the Köhler illumination. In the object arm the light passes through a specimen (Sp) while in the reference arm it passes through a reference object (R). Both the specimen and the reference object are imaged into the output plane. The essential component of CCHM is a diffraction grating, which is placed in the reference arm and imaged also into the output plane. In this way, a contrast off-axis image-plane hologram is generated with an illumination of arbitrarily low coherence. The interference pattern of the hologram is recorded in the output plane by a CCD camera. The image intensity and phase are then obtained from the recorded image by numerical processing. 3 The object planes, the image planes and the output plane are optically conjugated planes in the both of the arms. Then, we can express the image amplitude in the output plane by the help of the object-space coordinates. Let o (r t, κ) be a complex amplitude of the object wave and r (r t, κ) a complex amplitude of the reference wave michala.henzlova@ceitec.vutbr.cz; phone
84 M C R O TL BS a Diffraction grating Light source BS Reference beam M Output lens b Output plane Lens M Object beam M Output lens M C Sp D O TL BS M Figure 1. Scheme of the transmitted-light coherence-controlled holographic microscope 3 with diffuser in the object space: (BS) beamsplitters, (M) mirrors, (C) condenser lenses, (Sp) specimen, (R) reference object, (D) diffuser or diffraction grating in the object space, (O) infinity-corrected objective lenses, (TL) tube lenses, (α, β) angles of diffraction and interference. in the output plane, where κ = (κ x, κ y, κ z ) is a reduced wavevector ( κ = 1/λ, λ is a wavelength) corresponding to a plane wave in the object space, and r = (r t, z) = (x, y, z) is a position vector in the Cartesian coordinate system in the object space with the origin at the intersection of the optical axis and the object plane. The signal resulting from the numerical reconstruction of the recorded hologram can be described by the expression 2 u (r) = o (r, κ) r (r, κ) κ z κ 3 d 3 κ, (1) where an asterisk marks a complex conjugate function in the whole text. 2.1 Imaging characteristics of CCHM In the 1st Born approximation of a scattering theory, the numerically reconstructed signal is given by the inverse Fourier transform 2 u (r) = T (µ) c (µ) exp (2πiµ r) d 3 µ, (2) where µ = (µ x, µ y, µ z ) is a vector of spatial frequencies a scattering vector, T (µ) is the Fourier transform of a scattering potential t (r) of an object and c (µ) is a 3D coherent transfer function (CTF) given by the expression 2 c (µ) = { [ i (κ) P c (κ) 2 P (κ) P (κ + µ) δ (κ z + µ z ) κ 2 (κ x + µ x ) 2 (κ y + µ y ) 2] } 1/2 κ z κ 3 d3 κ, (3) where P (κ) and P c (κ) are 3D pupil functions 2 of the objective and the condenser lenses in the κ-space, i (κ) is the spectral intensity of a source in the κ-space (κ is the reduced wavevector of a plane wave in the object space corresponding to one point and one wavelength of the source) and δ (κ z ) denotes the Dirac delta function. For a monochromatic light with a wavelenght λ 0, the projections of the supports of the 3D pupil functions P (κ), P c (κ) to the µ x -µ y plane are circles of radii NA o /λ 0, NA c /λ 0, where NA o and NA c are numerical apertures
85 of the objective and the condenser lenses, 2 respectively. As the relation (3) has the form of 3D pupil functions correlation, the projection of the support of 3D CTF to the same plane µ x -µ y (the transverse passband of CCHM, i.e. the area of transferred transverse spatial frequencies) is a circle with the radius µ t,max = (NA c + NA o ) /λ 0. See Fig. 4a for illustration. 3. THE EFFECT OF A DIFFRACTION GRATING In this section, we suppose that a diffraction grating with a single spatial frequency g = (g x, g y, 0) in its spectrum is placed between the observed object and the objective lens of the microscope, and describe its influence on the imaging process. Results are then used in the Section 4 for the calculation of CTF with the presence of a diffuser in the object space. The calculation is based on the decomposition of the diffuser transmission function into its frequency components. Also the possibility of a mutual shift of beams in the object and the reference arm is taken into account. 3.1 Scattering potential of a diffraction grating The diffraction grating located in a plane z = z g (see Fig. 2) can be described 2, 4 by the scattering potential t g (x, y, z) = exp [2πi (g x x + g y y)] δ (z z g ), (4) where g x, g y are spatial frequencies of the diffraction grating. For the following calculation it is useful to derive the Fourier transform T g ( µg ) of the function tg (r) T g ( µg ) = t g (r) exp ( 2πiµ g r ) d 3 r = δ (µ g,x g x ) δ (µ g,y g y ) exp ( 2πiµ g,z z g ), (5) where µ g = (µ g,x, µ g,y, µ g,z ) is a scattering vector corresponding to the diffraction grating. An angular spectrum U 3 (κ 3,t ) of a scattered wave can then be expressed 2 by the relation U 3 (κ 3,t ) = U 2 (κ 3,t g) exp [ 2πi (κ 3,z κ 2,z ) z g ], (6) where U 2 (κ 2,t ) is the angular spectrum of a primary wave, and κ 3,z κ 2,z = κ 3,z κ 3,z 1 + 2κ 3,t g t g t 2 κ 2 3,z. (7) Object Objective lens Condenser lens Diffraction grating Figure 2. Configuration of elements in the object space. 3.2 Approximation In the following text we will suppose Then we can approximate the expression (7) as follows g κ 3,z, κ 3,t κ 3,z. (8) κ 3,z κ 2,z κ 3,t g t κ and in this way modify the argument in the exponential function in Eq. (6). g t 2 2κ, (9)
86 3.3 Shift of the reference beam The diffraction grating in the object space causes that the rays coming from the sample are focused into different points of the output plane than undeviated rays. This suggests an assumption that a convenient transverse displacement of the reference beam in the output plane will allow interference of the reference beam with equally deviated rays of the object beam. See Fig. 3 for illustration. Object beam a) b) Image plane Image plane A o A o Object Diffuser Object Diffuser Condenser lens Objective lens Condenser lens Objective lens Reference beam Image plane A r Image plane A r Reference object A r Reference object Figure 3. Effect of the reference beam shift in the output (image) plane. For the sake of simplicity, the arms are depicted separately. a) If no shift of the reference beam is introduced, rays of the reference beam coincide with the rays of the object beam, which are undeviated by the diffraction grating (diffuser). b) If a shift r t of the reference beam (in the image plane) is introduced, rays of the reference beam coincide with the rays of the object beam, which are deviated by the diffraction grating by the same r t. Suppose the shift r t of the reference beam with respect to the object beam in the output plane. The shift is expressed in the object-space coordinate system. Now, we have to modify Eq. (1) by the substitution of the vector r t in the argument of the reference-wave complex amplitude for the vector r t r t. Then the resulting signal is expressed by the relation u (r) = o (r t, κ) r (r t r t, κ) κ z κ 3 d 3 κ. (10) 3.4 Coherent transfer function The CTF is calculated by an approach similar to that used previously for the description of CCHM imaging without a diffraction grating in the object space. 2 Scattering by the diffraction grating is described by Eq. (5) and the approximation (9) is applied. The resulting CTF is then described by the relation c g (µ, g) = exp (2πig r t ) ( exp 2πi z ) g κ µ g δ [ ( i (κ) P c (κ) 2 P (κ) P (κ + µ + g) exp 2πiκ g z g κ r t )] { [ (κ z µ z ) κ 2 (κ x + µ x + g x ) 2 (κ y + µ y + g y ) 2] } 1/2 κ z κ 3 d3 κ ; (11) the resulting signal is given by Eq. (2) with c g (µ, g) inserted instead of c (µ).
87 4. THE EFFECT OF A DIFFUSER 4.1 Diffuser as a superposition of diffraction gratings Consider a diffuser to be a random medium described by a complex transmission function a (r t ). This function is zero outside a finite diffracting aperture A and the probability density of its phase is uniform in the interval ( π, π. 5 The scattering potential of the diffuser placed in the plane z = z g is then 2 t d (r) = a (r t ) δ(z z g ), and its Fourier transform T d can be written as T d (µ d ) = exp ( 2πiµ d,z z g ) a (r t ) exp ( 2πiµ d,t r t ) d 2 r t = exp ( 2πiµ d,z z g ) A ( µ d,t ), (12) which, according to Eq. (5), we can write as the superposition of diffraction gratings with spatial frequencies g T d (µ d ) = 4.2 Coherent transfer function A (g) δ ( µ d,t g ) exp ( 2πiµ d,z z g ) d 2 g = A (g) T g (µ d ) d 2 g. (13) With respect to Eq. (13), the relation for CTF of CCHM with a defocused diffuser can be derived as c d (µ) = After the substitution of the formula (11) for c g (µ, g) to (14) we obtain c d (µ) = exp A (g) exp (2πig r t ) ( 2πi z ) { g κ µ g δ (κ z µ z ) A (g) c g (µ, g) d 2 g. (14) [ ( i (κ) P c (κ) 2 P (κ) P (κ + µ + g) exp 2πiκ g z )] g κ r t [ κ 2 (κ x + µ x + g x ) 2 (κ y + µ y + g y ) 2] 1/2 } κ z κ 3 d3 κ d 2 g. (15) The following calculations are made for a monochromatic source with a wavelength λ 0. We express its spectral intensity by the relation i (κ) i 2 (κ t ) δ (κ κ 0 ), (16) where κ 0 = 1/λ 0 and i 2 (κ t ) describes the spatial distribution of the intensity. The function i 2 (κ t ) will be specified later. Then, CTF for a monochromatic source is described by the expression c d (µ) = κ 2 0 where κ z = exp A (g) exp (2πig r t ) ( 2πi z ) { g µ g δ (κ z µ z ) κ 0 κ 2 0 κ t 2. The resulting signal is again given by Eq. (2). [ ( i 2 (κ t ) P c (κ) 2 P (κ) P (κ + µ + g) exp 2πiκ g z )] g r t κ 0 [ κ 2 0 (κ x + µ x + g x ) 2 (κ y + µ y + g y ) 2] 1/2 } d 2 κ t d 2 g, (17)
88 4.3 A point monochromatic source A point source is described by the function i 2 (κ t ) = δ (κ x /κ) δ (κ y /κ) = κ 2 δ (κ x ) δ (κ y ). (18) After the substitution of (18) for i 2 (κ t ) in the expression (17) we can integrate over the variables κ x and κ y. In this way we obtain c d (µ) = P c (κ 0 ) 2 P (κ 0 ) ( P (κ 0 + µ + g) A (g) exp (2πig r t ) exp 2πi z ) g µ g κ 0 where κ 0 = (0, 0, κ 0 ). We can modify the Dirac delta function as follows { [ δ (κ 0 + µ z ) κ 2 0 (µ x + g x ) 2 (µ y + g y ) 2] } 1/2 = = { [ δ (κ 0 + µ z ) κ 2 0 (µ x + g x ) 2 (µ y + g y ) 2] } 1/2 d 2 g, (19) κ 0 + µ ( z [g 2 (κ0 µ z + g x µ x ) (µ 2 x + µ 2 z + gx) δ y µ y + )] 2 (κ 0 µ z + g x µ x ) (µ 2 2 x + µ 2 z + gx) 2. (20) The integration over the spatial frequency g y then gives the expression c d (µ) = P c (κ 0 ) 2 P (κ 0 ) P [κ 0 + µ + f (g x, µ, κ 0 )] κ 0 + µ z 2 (κ0 µ z + g x µ x ) (µ 2 x + µ 2 z + g 2 x) [ A [f (g x, µ, κ 0 )] exp [2πif (g x, µ, κ 0 ) r t ] exp 2πi z ] g µ f (g x, µ, κ 0 ) dg x, (21) κ 0 where the vector function f (g x, µ, κ 0 ) is defined as follows ( f (g x, µ, κ 0 ) = g x, µ y + ) 2 (κ 0 µ z + g x µ x ) (µ 2 x + µ 2 z + gx) 2. (22) In Eq. (21) we shall notice the function A [f (g x, µ, κ 0 )] integrated over g x. This function is random being the Fourier transform of another random function (see Eq. (12)) and also it is a function of spatial frequencies µ. This is why the result of the integration, CTF for coherent light source, must be another complex random function. Finally, a point spread function is then given by the inverse Fourier transform of a random function so it is a random function, too. This result corresponds to the formation of a coherent noise (speckles) when a coherent light source is used. 4.4 A broad monochromatic source Start again with Eq. (17), while assuming now that the source image fills the aperture of condenser lenses with a constant intensity. Then we can set i 2 (κ t ) = const. > 0, (23) because the illumination-beam aperture is limited by the condenser-lens pupil function P c (κ) in the integrand in Eq. (17). The integration over κ t in this equation can be written as [ ( ξ (κ t ) exp 2πiκ g z )] g r t d 2 κ t, (24) κ 0
89 where ξ (κ t ) is a slowly varying function within the supports of the 3D pupil functions. This is why we suppose that this expression differs significantly from zero only for g z g κ 0 r t. (25) Then, the expression (17) can be roughly approximated by the following formula c d (µ) κ 2 0 exp A (g) exp (2πig r t ) ( 2πi z ) { g µ g δ (κ z µ z ) κ 0 ( P c (κ) 2 P (κ) P (κ + µ + g) δ g z ) g r t κ 0 [ κ 2 0 (κ x + µ x + g x ) 2 (κ y + µ y + g y ) 2] 1/2 } d 2 κ t d 2 g, (26) where a constant factor has been omitted. Finally, after the integration over g we get the formula for CTF c d (µ) 1 ( ) ( κ 0 κ 3 exp (2πiµ r t ) A r t exp 2πi κ ) 0 r t r t 0 z2 g z g z g ( ) [ ] P c (κ) 2 P κ 0 (κ) P κ + µ + r t κ 3 z zδ (κ z + µ z ) κ 20 κ t + µ t + r t κ 0 /z g 2 d 2 κ t, (27) g where κ z = κ 2 0 κ2 x κ 2 y. In the expression (27), the random function A ( r t κ 0 /z g ) plays the role of a factor independent of the spatial frequency µ. That means CTF itself is not a random function of µ. Consequently, the object structure is revealed in the CCHM image, which is in agreement with the experimental results. 6 The insertion of the relation (27) into the relation (2) for the resulting image signal makes it clear that: The resulting image is laterally shifted by r t. The linear phase term 2πir t r t κ 0 /z g is added to the image phase. The image signal is multiplied by the random factor A ( r t κ 0 /z g ), which is however a constant for a given beam shift r t. The transverse passband (area of transferred transverse spatial frequencies or the projection of the support of 3D CTF to the plane µ x -µ y ) of the microscope has the same circular form and radius as for the case without a diffuser, but it is shifted in the κ-space by µ t = r t κ 0 /z g, which means that higher spatial frequencies are transferred than in the case of the zero shift (ballistic-light imaging). This result is illustrated in Fig. 4. CONCLUSIONS In this paper we demonstrate theoretically the ability of CCHM to image a specimen through a defocused thin plane diffuser in the object space using a broad (spatially incoherent) monochromatic source. This result is in agreement with the experiment. 6 The approximate formula for the related CTF has been derived in the paraxial approximation. The transverse passband of CCHM has unchanged form in this case, but it is possibly shifted by µ t = r t κ 0 /z g, according to the vector r t of the reference-beam shift in the output plane. The imaging with the shift allows for the transfer of frequencies with the maximum value greater than in the case of imaging with the zero shift (Fig. 4). Nevertheless the possible achievement of superresolution effects by a numerical processing of images with different r t is complicated by the presence of the random factor A ( r t κ 0 /z g ) in (27). Imaging with a coherent illumination (a point monochromatic source) through a diffuser is destroyed by a coherent noise which precludes the observation of a specimen.
90 a) b) Figure 4. The transverse passband of CCHM (the projection of the support of 3D CTF to the plane µ x -µ y ) for imaging with a broad monochromatic source a) without a diffuser in the object space, b) with the diffuser and the reference beam shifted by r t. The size of the area is limited by the numerical apertures of condenser lenses (NA c) and objective lenses (NA o): µ t,max = (NA c + NA o) /λ 0 according to the section 2.1. The passband is shifted proportionally to the shift r t. ACKNOWLEDGMENTS This work is supported by MIT CR (project FR-TI4/660), by TA CR (project TE ), by the project CEITEC - Central European Institute of Technology (CZ.1.05/1.1.00/ ) from European Regional Development Fund, and by MEYS CR (project CZ.1.07/2.2.00/ ). REFERENCES 1. P. Kolman and R. Chmelík, Coherence-controlled holographic microscope, Optics Express 18(21), pp , R. Chmelik, Three-dimensional scalar imaging in high-aperture low-coherence interference and holographic microscopes, Journal of Modern Optics 53(18), pp , T. Slabý, M. Antoš, Z. Dostál, P. Kolman, and R. Chmelík, Coherence-controlled holographic microscope, in Proceedings of SPIE, 7746, p R, E. Leith and G. Swanson, Achromatic interferometers for white light optical processing and holography, Applied Optics 19, pp , J. C. Dainty, An introduction to Gaussian speckle, in Proc. Soc. Photo-Opt. Instrum. Eng, 243, pp. 2 8, M. Lošt ák, P. Kolman, Z. Dostál, and R. Chmelík, Diffuse light imaging with a coherence controlled holographic microscope, in Proceedings of SPIE, 7746, p N, 2010.
Spektrometr pro měření Ramanovy optické aktivity: proč a jak. Optická sestava a využití motorizovaných jednotek.
 Spektrometr pro měření Ramanovy optické aktivity: proč a jak. Optická sestava a využití motorizovaných jednotek. Josef Kapitán Centrum digitální optiky Digitální Ramanova spektroskopie a Ramanova optická
Spektrometr pro měření Ramanovy optické aktivity: proč a jak. Optická sestava a využití motorizovaných jednotek. Josef Kapitán Centrum digitální optiky Digitální Ramanova spektroskopie a Ramanova optická
Konstrukční varianty systému pro nekoherentní korelační zobrazení
 Konstrukční varianty systému pro nekoherentní korelační zobrazení Technický seminář Centra digitální optiky Vedoucí balíčku (PB4): prof. RNDr. Radim Chmelík, Ph.D. Zpracoval: Petr Bouchal Řešitelské organizace:
Konstrukční varianty systému pro nekoherentní korelační zobrazení Technický seminář Centra digitální optiky Vedoucí balíčku (PB4): prof. RNDr. Radim Chmelík, Ph.D. Zpracoval: Petr Bouchal Řešitelské organizace:
Veřejná soutěž ve výzkumu, vývoji a inovacích vyhlášená v roce 2011, program CK - 1. výzva, 2. stupeň veřejné soutěže. Centrum digitální optiky
 Veřejná soutěž ve výzkumu, vývoji a inovacích vyhlášená v roce 2011, program CK - 1 výzva, 2 stupeň veřejné soutěže PID: TE01020229 Centrum digitální optiky Program: TE - Program Technologické agentury
Veřejná soutěž ve výzkumu, vývoji a inovacích vyhlášená v roce 2011, program CK - 1 výzva, 2 stupeň veřejné soutěže PID: TE01020229 Centrum digitální optiky Program: TE - Program Technologické agentury
Zobrazování s využitím prostorového modulátoru světla
 Zobrazování s využitím prostorového modulátoru světla Technický seminář Centra digitální optiky vedoucí balíčku (PB4): prof. RNDr. Radim Chmelík, Ph.D. Řešitelské organizace: Pracovní balíček Zobrazování
Zobrazování s využitím prostorového modulátoru světla Technický seminář Centra digitální optiky vedoucí balíčku (PB4): prof. RNDr. Radim Chmelík, Ph.D. Řešitelské organizace: Pracovní balíček Zobrazování
Meo S-H: software pro kompletní diagnostiku intenzity a vlnoplochy
 Centrum Digitální Optiky Meo S-H: software pro kompletní diagnostiku intenzity a vlnoplochy Výzkumná zpráva projektu Identifikační čí slo výstupu: TE01020229DV003 Pracovní balíček: Zpracování dat S-H senzoru
Centrum Digitální Optiky Meo S-H: software pro kompletní diagnostiku intenzity a vlnoplochy Výzkumná zpráva projektu Identifikační čí slo výstupu: TE01020229DV003 Pracovní balíček: Zpracování dat S-H senzoru
Centrum digitální optiky (TE01020229) Jaroslav Řeháček (PřF UP) řešitel
 Centrum digitální optiky (TE01020229) Jaroslav Řeháček (PřF UP) řešitel Centrum digitální optiky idea projektu vytvoření silného konsorcia na území ČR v oblasti digitální optiky využití dlouholeté spolupráce
Centrum digitální optiky (TE01020229) Jaroslav Řeháček (PřF UP) řešitel Centrum digitální optiky idea projektu vytvoření silného konsorcia na území ČR v oblasti digitální optiky využití dlouholeté spolupráce
Společná laboratoř optiky. Skupina nelineární a kvantové optiky. Představení vypisovaných témat. bakalářských prací. prosinec 2011
 Společná laboratoř optiky Skupina nelineární a kvantové optiky Představení vypisovaných témat bakalářských prací prosinec 2011 O naší skupině... Zařazení: UP PřF Společná laboratoř optiky skupina nelin.
Společná laboratoř optiky Skupina nelineární a kvantové optiky Představení vypisovaných témat bakalářských prací prosinec 2011 O naší skupině... Zařazení: UP PřF Společná laboratoř optiky skupina nelin.
Světlo jako elektromagnetické záření
 Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
M I K R O S K O P I E
 Inovace předmětu KBB/MIK SVĚTELNÁ A ELEKTRONOVÁ M I K R O S K O P I E Rozvoj a internacionalizace chemických a biologických studijních programů na Univerzitě Palackého v Olomouci CZ.1.07/2.2.00/28.0066
Inovace předmětu KBB/MIK SVĚTELNÁ A ELEKTRONOVÁ M I K R O S K O P I E Rozvoj a internacionalizace chemických a biologických studijních programů na Univerzitě Palackého v Olomouci CZ.1.07/2.2.00/28.0066
ZÁKLADNÍ ČÁSTI SPEKTRÁLNÍCH PŘÍSTROJŮ
 ZÁKLADNÍ ČÁSTI SPEKTRÁLNÍCH PŘÍSTROJŮ (c) -2008, ACH/IM BLOKOVÉ SCHÉMA: (a) emisní metody (b) absorpční metody (c) luminiscenční metody U (b) monochromátor často umístěn před kyvetou se vzorkem. Části
ZÁKLADNÍ ČÁSTI SPEKTRÁLNÍCH PŘÍSTROJŮ (c) -2008, ACH/IM BLOKOVÉ SCHÉMA: (a) emisní metody (b) absorpční metody (c) luminiscenční metody U (b) monochromátor často umístěn před kyvetou se vzorkem. Části
- Rayleighův rozptyl turbidimetrie, nefelometrie - Ramanův rozptyl. - fluorescence - fosforescence
 ROZPTYLOVÉ a EMISNÍ metody - Rayleighův rozptyl turbidimetrie, nefelometrie - Ramanův rozptyl - fluorescence - fosforescence Ramanova spektroskopie Každá čára Ramanova spektra je svými vlastnostmi závislá
ROZPTYLOVÉ a EMISNÍ metody - Rayleighův rozptyl turbidimetrie, nefelometrie - Ramanův rozptyl - fluorescence - fosforescence Ramanova spektroskopie Každá čára Ramanova spektra je svými vlastnostmi závislá
Optika pro mikroskopii materiálů I
 Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Pozorování Slunce s vysokým rozlišením. Michal Sobotka Astronomický ústav AV ČR, Ondřejov
 Pozorování Slunce s vysokým rozlišením Michal Sobotka Astronomický ústav AV ČR, Ondřejov Úvod Na Slunci se důležité děje odehrávají na malých prostorových škálách (desítky až stovky km). Granule mají typickou
Pozorování Slunce s vysokým rozlišením Michal Sobotka Astronomický ústav AV ČR, Ondřejov Úvod Na Slunci se důležité děje odehrávají na malých prostorových škálách (desítky až stovky km). Granule mají typickou
13. Spektroskopie základní pojmy
 základní pojmy Spektroskopicky významné OPTICKÉ JEVY absorpce absorpční spektrometrie emise emisní spektrometrie rozptyl rozptylové metody Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
základní pojmy Spektroskopicky významné OPTICKÉ JEVY absorpce absorpční spektrometrie emise emisní spektrometrie rozptyl rozptylové metody Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Pokročilé cvičení z fyzikální chemie KFC/POK2 Vibrační spektroskopie
 Pokročilé cvičení z fyzikální chemie KFC/POK2 Vibrační spektroskopie Vibrace molekul mohou být měřeny buď pomocí absorpce infračerveného záření, nebo pomocí neelastického rozptylu záření, tzn. Ramanova
Pokročilé cvičení z fyzikální chemie KFC/POK2 Vibrační spektroskopie Vibrace molekul mohou být měřeny buď pomocí absorpce infračerveného záření, nebo pomocí neelastického rozptylu záření, tzn. Ramanova
C Mapy Kikuchiho linií 263. D Bodové difraktogramy 271. E Počítačové simulace pomocí programu JEMS 281. F Literatura pro další studium 289
 OBSAH Předmluva 5 1 Popis mikroskopu 13 1.1 Transmisní elektronový mikroskop 13 1.2 Rastrovací transmisní elektronový mikroskop 14 1.3 Vakuový systém 15 1.3.1 Rotační vývěvy 16 1.3.2 Difúzni vývěva 17
OBSAH Předmluva 5 1 Popis mikroskopu 13 1.1 Transmisní elektronový mikroskop 13 1.2 Rastrovací transmisní elektronový mikroskop 14 1.3 Vakuový systém 15 1.3.1 Rotační vývěvy 16 1.3.2 Difúzni vývěva 17
VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ
 VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ P. Novák, J. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán výukový software pro
VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ P. Novák, J. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán výukový software pro
Spektrální charakteristiky
 Spektrální charakteristiky Cíl cvičení: Měření spektrálních charakteristik filtrů a zdrojů osvětlení 1 Teoretický úvod Interakcí elektromagnetického vlnění s libovolnou látkou vzniká optický jev, který
Spektrální charakteristiky Cíl cvičení: Měření spektrálních charakteristik filtrů a zdrojů osvětlení 1 Teoretický úvod Interakcí elektromagnetického vlnění s libovolnou látkou vzniká optický jev, který
Základy NIR spektrometrie a její praktické využití
 Nicolet CZ s.r.o. The world leader in serving science Základy NIR spektrometrie a její praktické využití NIR praktická metoda molekulové spektroskopie, nahrazující pracnější, časově náročnější a dražší
Nicolet CZ s.r.o. The world leader in serving science Základy NIR spektrometrie a její praktické využití NIR praktická metoda molekulové spektroskopie, nahrazující pracnější, časově náročnější a dražší
Úvod. Rozdělení podle toku energie: Rozdělení podle počtu fází: Rozdělení podle konstrukce rotoru: Rozdělení podle pohybu motoru:
 Indukční stroje 1 konstrukce Úvod Indukční stroj je nejpoužívanější a nejrozšířenější elektrický točivý stroj a jeho význam neustále roste (postupná náhrada stejnosměrných strojů). Rozdělení podle toku
Indukční stroje 1 konstrukce Úvod Indukční stroj je nejpoužívanější a nejrozšířenější elektrický točivý stroj a jeho význam neustále roste (postupná náhrada stejnosměrných strojů). Rozdělení podle toku
od 70mm (měřeno od zadní desky s axiálním výstupem) interní prvky opatřeny černou antireflexní vrstvou, centrální trubice s vnitřní šroubovicí
 Model QM-1 (s válcovým tubusem) QM-1 je základním modelem řady distančních mikroskopů Questar, které jsou celosvětově oceňovanými optickými přístroji zejména z hlediska extrémně precizní optiky a mechanického
Model QM-1 (s válcovým tubusem) QM-1 je základním modelem řady distančních mikroskopů Questar, které jsou celosvětově oceňovanými optickými přístroji zejména z hlediska extrémně precizní optiky a mechanického
Návrh optické soustavy - Obecný postup
 Inovace a zvýšení atraktivity studia optiky reg. c.: CZ.1.07/2.2.00/07.0289 Přednášky - Metody Návrhu Zobrazovacích Soustav SLO/MNZS Návrh optické soustavy - Obecný postup Miroslav Palatka Tento projekt
Inovace a zvýšení atraktivity studia optiky reg. c.: CZ.1.07/2.2.00/07.0289 Přednášky - Metody Návrhu Zobrazovacích Soustav SLO/MNZS Návrh optické soustavy - Obecný postup Miroslav Palatka Tento projekt
Momentové motory. (vestavné provedení) TGQ Momentové (přímé) motory
 Momentové motory (vestavné provedení) TGQ Momentové (přímé) motory Komplexní dodávky a zprovoznění servopohonů, dodávky řídicích systémů. Česká společnost TG Drives dodává již od roku 1995 servopohony
Momentové motory (vestavné provedení) TGQ Momentové (přímé) motory Komplexní dodávky a zprovoznění servopohonů, dodávky řídicích systémů. Česká společnost TG Drives dodává již od roku 1995 servopohony
Úloha 3: Mřížkový spektrometr
 Petra Suková, 2.ročník, F-14 1 Úloha 3: Mřížkový spektrometr 1 Zadání 1. Seřiďte spektrometr pro kolmý dopad světla(rovina optické mřížky je kolmá k ose kolimátoru) pomocí bočního osvětlení nitkového kříže.
Petra Suková, 2.ročník, F-14 1 Úloha 3: Mřížkový spektrometr 1 Zadání 1. Seřiďte spektrometr pro kolmý dopad světla(rovina optické mřížky je kolmá k ose kolimátoru) pomocí bočního osvětlení nitkového kříže.
PRAKTIKUM III. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009.
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
Moderní metody rozpoznávání a zpracování obrazových informací 15
 Moderní metody rozpoznávání a zpracování obrazových informací 15 Hodnocení transparentních materiálů pomocí vizualizační techniky Vlastimil Hotař, Ondřej Matúšek Katedra sklářských strojů a robotiky Fakulta
Moderní metody rozpoznávání a zpracování obrazových informací 15 Hodnocení transparentních materiálů pomocí vizualizační techniky Vlastimil Hotař, Ondřej Matúšek Katedra sklářských strojů a robotiky Fakulta
ABSORPČNÍ A EMISNÍ SPEKTRÁLNÍ METODY
 ABSORPČNÍ A EMISNÍ SPEKTRÁLNÍ METODY 1 Fyzikální základy spektrálních metod Monochromatický zářivý tok 0 (W, rozměr m 2.kg.s -3 ): Absorbován ABS Propuštěn Odražen zpět r Rozptýlen s Bilance toků 0 = +
ABSORPČNÍ A EMISNÍ SPEKTRÁLNÍ METODY 1 Fyzikální základy spektrálních metod Monochromatický zářivý tok 0 (W, rozměr m 2.kg.s -3 ): Absorbován ABS Propuštěn Odražen zpět r Rozptýlen s Bilance toků 0 = +
Emise vyvolaná působením fotonů nebo částic
 Emise vyvolaná působením fotonů nebo částic PES (fotoelektronová spektroskopie) XPS (rentgenová fotoelektronová spektroskopie), ESCA (elektronová spektroskopie pro chemickou analýzu) UPS (ultrafialová
Emise vyvolaná působením fotonů nebo částic PES (fotoelektronová spektroskopie) XPS (rentgenová fotoelektronová spektroskopie), ESCA (elektronová spektroskopie pro chemickou analýzu) UPS (ultrafialová
Projekt FRVŠ č: 389/2007
 Závěrečné oponentní řízení 7.2.2007 Projekt FRVŠ č: 389/2007 Název: Řešitel: Spoluřešitelé: Pracoviště: TO: Laboratoř infračervené spektrometrie Doc. Ing. Milan Honner, Ph.D. Ing. Petra Vacíková, Ing.
Závěrečné oponentní řízení 7.2.2007 Projekt FRVŠ č: 389/2007 Název: Řešitel: Spoluřešitelé: Pracoviště: TO: Laboratoř infračervené spektrometrie Doc. Ing. Milan Honner, Ph.D. Ing. Petra Vacíková, Ing.
Optické spektroskopie 1 LS 2014/15
 Optické spektroskopie 1 LS 2014/15 Martin Kubala 585634179 mkubala@prfnw.upol.cz 1.Úvod Velikosti objektů v přírodě Dítě ~ 1 m (10 0 m) Prst ~ 2 cm (10-2 m) Vlas ~ 0.1 mm (10-4 m) Buňka ~ 20 m (10-5 m)
Optické spektroskopie 1 LS 2014/15 Martin Kubala 585634179 mkubala@prfnw.upol.cz 1.Úvod Velikosti objektů v přírodě Dítě ~ 1 m (10 0 m) Prst ~ 2 cm (10-2 m) Vlas ~ 0.1 mm (10-4 m) Buňka ~ 20 m (10-5 m)
Regionální centrum speciální optiky a optoelektronických systémů TOPTEC
 Ústav fyziky plazmatu AV ČR, v. v. i. Regionální centrum speciální optiky a optoelektronických systémů TOPTEC 1/15 ředitelství ÚFP TOPTEC Ústí n. Labem Praha Liberec Turnov Ostrava Plzeň České Budějovice
Ústav fyziky plazmatu AV ČR, v. v. i. Regionální centrum speciální optiky a optoelektronických systémů TOPTEC 1/15 ředitelství ÚFP TOPTEC Ústí n. Labem Praha Liberec Turnov Ostrava Plzeň České Budějovice
Rozsah průmyslového výzkumu a vývoje Etapa 9 Systém kontroly povrchových vad
 Příloha č. 1a Popis předmětu zakázky Rozsah průmyslového výzkumu a vývoje Etapa 9 Systém kontroly povrchových vad Zadání Výzkum kontrolního zařízení pro detekci povrchových vad sochoru, návrh variant systému
Příloha č. 1a Popis předmětu zakázky Rozsah průmyslového výzkumu a vývoje Etapa 9 Systém kontroly povrchových vad Zadání Výzkum kontrolního zařízení pro detekci povrchových vad sochoru, návrh variant systému
Úvod do spektrálních metod pro analýzu léčiv
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Úvod do spektrálních metod pro analýzu léčiv Pavel Matějka, Vadym Prokopec pavel.matejka@vscht.cz pavel.matejka@gmail.com Vadym.Prokopec@vscht.cz
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Úvod do spektrálních metod pro analýzu léčiv Pavel Matějka, Vadym Prokopec pavel.matejka@vscht.cz pavel.matejka@gmail.com Vadym.Prokopec@vscht.cz
Zdroje optického záření
 Metody optické spektroskopie v biofyzice Zdroje optického záření / 1 Zdroje optického záření tepelné výbojky polovodičové lasery synchrotronové záření Obvykle se charakterizují zářivostí (zářivý výkon
Metody optické spektroskopie v biofyzice Zdroje optického záření / 1 Zdroje optického záření tepelné výbojky polovodičové lasery synchrotronové záření Obvykle se charakterizují zářivostí (zářivý výkon
Měření optických vlastností materiálů
 E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
Fyzika II. Marek Procházka Vlnová optika II
 Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
CENTRUM VZDĚLÁVÁNÍ PEDAGOGŮ ODBORNÝCH ŠKOL
 Projekt: CENTRUM VZDĚLÁVÁNÍ PEDAGOGŮ ODBORNÝCH ŠKOL Kurz: Stavba a provoz strojů v praxi 1 OBSAH 1. Úvod Co je CNC obráběcí stroj. 3 2. Vlivy na vývoj CNC obráběcích strojů. 3 3. Směry vývoje CNC obráběcích
Projekt: CENTRUM VZDĚLÁVÁNÍ PEDAGOGŮ ODBORNÝCH ŠKOL Kurz: Stavba a provoz strojů v praxi 1 OBSAH 1. Úvod Co je CNC obráběcí stroj. 3 2. Vlivy na vývoj CNC obráběcích strojů. 3 3. Směry vývoje CNC obráběcích
V letošním roce je v plánu vývoj a výroba prototypu ISSR, o jejichž vlastnostech a aplikacích bych zde rád podrobněji referoval.
 Použití spektrometrů s řádkovými senzory v přírodních vědách Pavel Oupický, UFP VOD AV ČR Praha, v.v.i., Detašované pracoviště Turnov ( dále jen UFP VOD ) Úvod: Základními přístroji pro určování světelných
Použití spektrometrů s řádkovými senzory v přírodních vědách Pavel Oupický, UFP VOD AV ČR Praha, v.v.i., Detašované pracoviště Turnov ( dále jen UFP VOD ) Úvod: Základními přístroji pro určování světelných
Optická konfokální mikroskopie a mikrospektroskopie. Pavel Matějka
 Optická konfokální mikroskopie a Pavel Matějka 1. Konfokální mikroskopie 1. Princip metody - konfokalita 2. Instrumentace metody zobrazování 3. Analýza obrazu 2. Konfokální 1. Luminiscenční 2. Ramanova
Optická konfokální mikroskopie a Pavel Matějka 1. Konfokální mikroskopie 1. Princip metody - konfokalita 2. Instrumentace metody zobrazování 3. Analýza obrazu 2. Konfokální 1. Luminiscenční 2. Ramanova
Fotoelektronová spektroskopie Instrumentace. Katedra materiálů TU Liberec
 Fotoelektronová spektroskopie Instrumentace RNDr. Věra V Vodičkov ková,, PhD. Katedra materiálů TU Liberec Obecné schéma metody Dopad rtg záření emitovaného ze zdroje na vzorek průnik fotonů několik µm
Fotoelektronová spektroskopie Instrumentace RNDr. Věra V Vodičkov ková,, PhD. Katedra materiálů TU Liberec Obecné schéma metody Dopad rtg záření emitovaného ze zdroje na vzorek průnik fotonů několik µm
Měření charakteristik pevnolátkového infračerveného Er:Yag laseru
 Měření charakteristik pevnolátkového infračerveného Er:Yag laseru Ondřej Ticháček, PORG, ondrejtichacek@gmail.com Abstrakt: Úkolem bylo proměření základních charakteristik záření pevnolátkového infračerveného
Měření charakteristik pevnolátkového infračerveného Er:Yag laseru Ondřej Ticháček, PORG, ondrejtichacek@gmail.com Abstrakt: Úkolem bylo proměření základních charakteristik záření pevnolátkového infračerveného
Měření optických vlastností materiálů
 E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
HPLC - Detektory A.Braithwaite and F.J.Smith; Chromatographic Methods, Fifth edition, Blackie Academic & Professional 1996 Colin F. Poole and Salwa K.
 Vysokoúčinná kapalinová chromatografie - Detektory - I Příprava předmětu byla podpořena projektem OPPA č. CZ.2.17/3.1.00/33253 HPLC - Detektory A.Braithwaite and F.J.Smith; Chromatographic Methods, Fifth
Vysokoúčinná kapalinová chromatografie - Detektory - I Příprava předmětu byla podpořena projektem OPPA č. CZ.2.17/3.1.00/33253 HPLC - Detektory A.Braithwaite and F.J.Smith; Chromatographic Methods, Fifth
ODŮVODNĚNÍ VEŘEJNÉ ZAKÁZKY
 ODŮVODNĚNÍ VEŘEJNÉ ZAKÁZKY s názvem MIKROSKOPY PRO CEITEC MU - ČÁST 8 vyhotovené podle 156 zákona č. 137/2006 Sb., o veřejných zakázkách, 1. ODŮVODNĚNÍ ÚČELNOSTI VEŘEJNÉ ZAKÁZKY v platném znění (dále jen
ODŮVODNĚNÍ VEŘEJNÉ ZAKÁZKY s názvem MIKROSKOPY PRO CEITEC MU - ČÁST 8 vyhotovené podle 156 zákona č. 137/2006 Sb., o veřejných zakázkách, 1. ODŮVODNĚNÍ ÚČELNOSTI VEŘEJNÉ ZAKÁZKY v platném znění (dále jen
MĚŘENÍ ABSOLUTNÍ VLHKOSTI VZDUCHU NA ZÁKLADĚ SPEKTRÁLNÍ ANALÝZY Measurement of Absolute Humidity on the Basis of Spectral Analysis
 MĚŘENÍ ABSOLUTNÍ VLHKOSTI VZDUCHU NA ZÁKLADĚ SPEKTRÁLNÍ ANALÝZY Measurement of Absolute Humidity on the Basis of Spectral Analysis Ivana Krestýnová, Josef Zicha Abstrakt: Absolutní vlhkost je hmotnost
MĚŘENÍ ABSOLUTNÍ VLHKOSTI VZDUCHU NA ZÁKLADĚ SPEKTRÁLNÍ ANALÝZY Measurement of Absolute Humidity on the Basis of Spectral Analysis Ivana Krestýnová, Josef Zicha Abstrakt: Absolutní vlhkost je hmotnost
Přenos signálů, výstupy snímačů
 Přenos signálů, výstupy snímačů Topologie zařízení, typy průmyslových sběrnic, výstupní signály snímačů Přenosy signálů informací Topologie Dle rozmístění ŘS Distribuované řízení Většinou velká zařízení
Přenos signálů, výstupy snímačů Topologie zařízení, typy průmyslových sběrnic, výstupní signály snímačů Přenosy signálů informací Topologie Dle rozmístění ŘS Distribuované řízení Většinou velká zařízení
Ultrazvuková kontrola obvodových svarů potrubí
 Ultrazvuková kontrola obvodových svarů potrubí Úlohou automatického ultrazvukového zkoušení je zejména nahradit rentgenové zkoušení, protože je rychlejší, bezpečnější a podává lepší informace o velikosti
Ultrazvuková kontrola obvodových svarů potrubí Úlohou automatického ultrazvukového zkoušení je zejména nahradit rentgenové zkoušení, protože je rychlejší, bezpečnější a podává lepší informace o velikosti
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU MĚŘICKÝ SNÍMEK Základem měření je fotografický snímek, který je v ideálním případě
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník MĚŘICKÝ SNÍMEK PRVKY VNITŘNÍ A VNĚJŠÍ ORIENTACE CHYBY SNÍMKU MĚŘICKÝ SNÍMEK Základem měření je fotografický snímek, který je v ideálním případě
3. Vlastnosti skla za normální teploty (mechanické, tepelné, optické, chemické, elektrické).
 PŘEDMĚTY KE STÁTNÍM ZÁVĚREČNÝM ZKOUŠKÁM V BAKALÁŘSKÉM STUDIU SP: CHEMIE A TECHNOLOGIE MATERIÁLŮ SO: MATERIÁLOVÉ INŽENÝRSTVÍ POVINNÝ PŘEDMĚT: NAUKA O MATERIÁLECH Ing. Alena Macháčková, CSc. 1. Souvislost
PŘEDMĚTY KE STÁTNÍM ZÁVĚREČNÝM ZKOUŠKÁM V BAKALÁŘSKÉM STUDIU SP: CHEMIE A TECHNOLOGIE MATERIÁLŮ SO: MATERIÁLOVÉ INŽENÝRSTVÍ POVINNÝ PŘEDMĚT: NAUKA O MATERIÁLECH Ing. Alena Macháčková, CSc. 1. Souvislost
Ing. Petr Knap Carl Zeiss spol. s r.o., Praha
 METROTOMOGRAFIE JAKO NOVÝ NÁSTROJ ZAJIŠŤOVÁNÍ JAKOSTI VE VÝROBĚ Ing. Petr Knap Carl Zeiss spol. s r.o., Praha ÚVOD Společnost Carl Zeiss Industrielle Messtechnik GmbH již dlouhou dobu sleduje vývoj v poměrně
METROTOMOGRAFIE JAKO NOVÝ NÁSTROJ ZAJIŠŤOVÁNÍ JAKOSTI VE VÝROBĚ Ing. Petr Knap Carl Zeiss spol. s r.o., Praha ÚVOD Společnost Carl Zeiss Industrielle Messtechnik GmbH již dlouhou dobu sleduje vývoj v poměrně
PSI (Photon Systems Instruments), spol. s r.o. Ústav přístrojové techniky AV ČR, v.v.i.
 PSI (Photon Systems Instruments), spol. s r.o. Ústav přístrojové techniky AV ČR, v.v.i. Konstrukce a výroba speciálních optických dielektrických multivrstev pro systémy FluorCam Firma příjemce voucheru
PSI (Photon Systems Instruments), spol. s r.o. Ústav přístrojové techniky AV ČR, v.v.i. Konstrukce a výroba speciálních optických dielektrických multivrstev pro systémy FluorCam Firma příjemce voucheru
Laboratorní úloha č. 7 Difrakce na mikro-objektech
 Laboratorní úloha č. 7 Difrakce na mikro-objektech Úkoly měření: 1. Odhad rozměrů mikro-objektů z informací uváděných výrobcem. 2. Záznam difrakčních obrazců (difraktogramů) vzniklých interakcí laserového
Laboratorní úloha č. 7 Difrakce na mikro-objektech Úkoly měření: 1. Odhad rozměrů mikro-objektů z informací uváděných výrobcem. 2. Záznam difrakčních obrazců (difraktogramů) vzniklých interakcí laserového
VIBRAČNÍ SPEKTROMETRIE
 VIBRAČNÍ SPEKTROMETRIE (c) -2012 RAMANOVA SPEKTROMETRIE 1 PRINCIP METODY Měří se rozptýlené záření, které vzniká interakcí monochromatického záření z viditelné oblasti s molekulami vzorku za současné změny
VIBRAČNÍ SPEKTROMETRIE (c) -2012 RAMANOVA SPEKTROMETRIE 1 PRINCIP METODY Měří se rozptýlené záření, které vzniká interakcí monochromatického záření z viditelné oblasti s molekulami vzorku za současné změny
Souřadnicové měření je měření prostorových souřadnic prováděné pomocí CMM Souřadnicový měřicí stroj CMM je měřicí systém k měření prostorových souřadn
 Seminář z oboru GPS (Geometrické Specifikace Produktů) Současný stav v oblasti návaznosti souřadnicových měřicích strojů v systémech kvality Doc. Tykal Osnova: Úvod Zkoušení CMM: - typy zkoušek - podmínky
Seminář z oboru GPS (Geometrické Specifikace Produktů) Současný stav v oblasti návaznosti souřadnicových měřicích strojů v systémech kvality Doc. Tykal Osnova: Úvod Zkoušení CMM: - typy zkoušek - podmínky
CHARAKTERIZACE MATERIÁLU POMOCÍ DIFRAKČNÍ METODY DEBYEOVA-SCHERREROVA NA ZPĚTNÝ ODRAZ
 CHARAKTERIZACE MATERIÁLU POMOCÍ DIFRAKČNÍ METODY DEBYEOVA-SCHERREROVA NA ZPĚTNÝ ODRAZ Lukáš ZUZÁNEK Katedra strojírenské technologie, Fakulta strojní, TU v Liberci, Studentská 2, 461 17 Liberec 1, CZ,
CHARAKTERIZACE MATERIÁLU POMOCÍ DIFRAKČNÍ METODY DEBYEOVA-SCHERREROVA NA ZPĚTNÝ ODRAZ Lukáš ZUZÁNEK Katedra strojírenské technologie, Fakulta strojní, TU v Liberci, Studentská 2, 461 17 Liberec 1, CZ,
Optika a nanostruktury na KFE FJFI
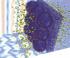 Optika a nanostruktury na KFE FJFI Marek Škereň 28. 11. 2012 www: email: marek.skeren@fjfi.cvut.cz tel: 221 912 825 mob: 608 181 116 Skupina optické fyziky Fakulta jaderná a fyzikálně inženýrská České
Optika a nanostruktury na KFE FJFI Marek Škereň 28. 11. 2012 www: email: marek.skeren@fjfi.cvut.cz tel: 221 912 825 mob: 608 181 116 Skupina optické fyziky Fakulta jaderná a fyzikálně inženýrská České
VY_32_INOVACE_FY.12 OPTIKA II
 VY_32_INOVACE_FY.12 OPTIKA II Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Optická čočka je optická soustava dvou centrovaných
VY_32_INOVACE_FY.12 OPTIKA II Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Optická čočka je optická soustava dvou centrovaných
Molekulová spektroskopie 1. Chemická vazba, UV/VIS
 Molekulová spektroskopie 1 Chemická vazba, UV/VIS 1 Chemická vazba Silová interakce mezi dvěma atomy. Chemické vazby jsou soudržné síly působící mezi jednotlivými atomy nebo ionty v molekulách. Chemická
Molekulová spektroskopie 1 Chemická vazba, UV/VIS 1 Chemická vazba Silová interakce mezi dvěma atomy. Chemické vazby jsou soudržné síly působící mezi jednotlivými atomy nebo ionty v molekulách. Chemická
Frekvenční analýza optických zobrazovacích systémů
 OPT/OZI L05 Frekvenční analýza optických zobrazovacích systémů obecný model vstupní pupila výstupní pupila v z u y z o x z i difrakčně limitovaný zobrazovací systém: rozbíhavá sférická vlna od bodového
OPT/OZI L05 Frekvenční analýza optických zobrazovacích systémů obecný model vstupní pupila výstupní pupila v z u y z o x z i difrakčně limitovaný zobrazovací systém: rozbíhavá sférická vlna od bodového
11 Manipulace s drobnými objekty
 11 Manipulace s drobnými objekty Zpracování rozměrově malých drobných objektů je zpravidla spojeno s manipulací s velkým počtem objektů, které jsou volně shromažďovány na různém stupni uspořádanosti souboru.
11 Manipulace s drobnými objekty Zpracování rozměrově malých drobných objektů je zpravidla spojeno s manipulací s velkým počtem objektů, které jsou volně shromažďovány na různém stupni uspořádanosti souboru.
Fluorescence (luminiscence)
 Fluorescence (luminiscence) Patří mezi luminiscenční metody fotoluminiscence. Luminiscence efekt, kdy excitované molekuly či atomy vyzařují světlo při přechodu z excitovaného do základního stavu. Podle
Fluorescence (luminiscence) Patří mezi luminiscenční metody fotoluminiscence. Luminiscence efekt, kdy excitované molekuly či atomy vyzařují světlo při přechodu z excitovaného do základního stavu. Podle
Snímkování termovizní kamerou
 AB Solartrip,s.r.o. Na Plavisku 1235 755 01 Vsetín www.solarniobchod.cz mobil 777 642 777, e-mail: r.ostarek@volny.cz AKCE: Termovizní diagnostika vnitřní prostory rodinného domu č. p. 197 Ústí u Vsetína
AB Solartrip,s.r.o. Na Plavisku 1235 755 01 Vsetín www.solarniobchod.cz mobil 777 642 777, e-mail: r.ostarek@volny.cz AKCE: Termovizní diagnostika vnitřní prostory rodinného domu č. p. 197 Ústí u Vsetína
FOTOAKUSTIKA. Vítězslav Otruba
 FOTOAKUSTIKA Vítězslav Otruba 2010 prof. Otruba 2 The spectrophone 1881 A.G. Bell návrh a Spektrofonu (spectrophone) pro účely posouzení absorpčního spektra subjektů v těch částech, které jsou neviditelné.
FOTOAKUSTIKA Vítězslav Otruba 2010 prof. Otruba 2 The spectrophone 1881 A.G. Bell návrh a Spektrofonu (spectrophone) pro účely posouzení absorpčního spektra subjektů v těch částech, které jsou neviditelné.
Pohony šicích strojů
 Pohony šicích strojů Obrázek 1:Motor šicího stroje Charakteristika Podle druhu použitého pohonu lze rozdělit šicí stroje na stroje a pohonem: ručním, nožním, elektrickým pohonem. Motor šicího stroje se
Pohony šicích strojů Obrázek 1:Motor šicího stroje Charakteristika Podle druhu použitého pohonu lze rozdělit šicí stroje na stroje a pohonem: ručním, nožním, elektrickým pohonem. Motor šicího stroje se
Pokročilé robotické technologie pro průmyslové aplikace
 Vize v automatizaci - Digitální továrna 4. října 2011 Výstaviště Brno Pokročilé robotické technologie pro průmyslové aplikace Aleš Pochylý, Tomáš Kubela, Vladislav Singule, Lukáš Flekal 1/18 Pokročilé
Vize v automatizaci - Digitální továrna 4. října 2011 Výstaviště Brno Pokročilé robotické technologie pro průmyslové aplikace Aleš Pochylý, Tomáš Kubela, Vladislav Singule, Lukáš Flekal 1/18 Pokročilé
Inteligentní koberec ( )
 Inteligentní koberec (10.4.2007) Řešení projektu bylo rozděleno do dvou fází. V první fázi byly hledány vhodné principy konstrukce senzorového pole. Druhá fáze se zaměřuje na praktické ověření vlastností
Inteligentní koberec (10.4.2007) Řešení projektu bylo rozděleno do dvou fází. V první fázi byly hledány vhodné principy konstrukce senzorového pole. Druhá fáze se zaměřuje na praktické ověření vlastností
METROTOMOGRAFIE JAKO NOVÝ NÁSTROJ ZAJIŠŤOVÁNÍ JAKOSTI VE VÝROBĚ
 METROTOMOGRAFIE JAKO NOVÝ NÁSTROJ ZAJIŠŤOVÁNÍ JAKOSTI VE VÝROBĚ Ing. Petr Knap Carl Zeiss spol. s r.o., Praha ÚVOD Společnost Carl Zeiss Industrielle Messtechnik GmbH již dlouhou dobu sleduje vývoj v poměrně
METROTOMOGRAFIE JAKO NOVÝ NÁSTROJ ZAJIŠŤOVÁNÍ JAKOSTI VE VÝROBĚ Ing. Petr Knap Carl Zeiss spol. s r.o., Praha ÚVOD Společnost Carl Zeiss Industrielle Messtechnik GmbH již dlouhou dobu sleduje vývoj v poměrně
Vzorkovací zesilovač základní princip všech digitálních osciloskopů, záznamníků, převodníků,
 5. října 2015 1 TYPY SIGNÁLŮ Vzorkovací zesilovač základní princip všech digitálních osciloskopů, záznamníků, převodníků, http://www.tek.com/products/oscilloscopes/dpo4000/ 5. října 2015 2 II. ÚPRAVA SIGNÁLŮ
5. října 2015 1 TYPY SIGNÁLŮ Vzorkovací zesilovač základní princip všech digitálních osciloskopů, záznamníků, převodníků, http://www.tek.com/products/oscilloscopes/dpo4000/ 5. října 2015 2 II. ÚPRAVA SIGNÁLŮ
POPIS VYNALEZU K AUTORSKÉMU OSVĚDČENÍ. obr Z ČESKOSLOVENSKA SOCIALISTICKÁ ( 19 ) G 01 F 23/28. (22) Přihlášeno 18 09 84 (21) PV 6988-84
 ČESKOSLOVENSKA SOCIALISTICKÁ R E P U B L I K A ( 19 ) POPIS VYNALEZU K AUTORSKÉMU OSVĚDČENÍ 250928 (И) (BI) (22) Přihlášeno 18 09 84 (21) PV 6988-84 (51) Int. Cl. 4 G 01 F 23/28 ÚftAD PRO VYNÁLEZY A OBJEVY
ČESKOSLOVENSKA SOCIALISTICKÁ R E P U B L I K A ( 19 ) POPIS VYNALEZU K AUTORSKÉMU OSVĚDČENÍ 250928 (И) (BI) (22) Přihlášeno 18 09 84 (21) PV 6988-84 (51) Int. Cl. 4 G 01 F 23/28 ÚftAD PRO VYNÁLEZY A OBJEVY
Technický boroskop zařízení na monitorování spalovacích procesů
 Technický boroskop zařízení na monitorování spalovacích procesů Katedra experimentální fyziky PřF UP Olomouc Doc. Ing. Luděk Bartoněk, Ph.D. Zvyšování účinnosti spalovacích procesů v různých odvětvích
Technický boroskop zařízení na monitorování spalovacích procesů Katedra experimentální fyziky PřF UP Olomouc Doc. Ing. Luděk Bartoněk, Ph.D. Zvyšování účinnosti spalovacích procesů v různých odvětvích
nano.tul.cz Inovace a rozvoj studia nanomateriálů na TUL
 Inovace a rozvoj studia nanomateriálů na TUL nano.tul.cz Tyto materiály byly vytvořeny v rámci projektu ESF OP VK: Inovace a rozvoj studia nanomateriálů na Technické univerzitě v Liberci Experimentální
Inovace a rozvoj studia nanomateriálů na TUL nano.tul.cz Tyto materiály byly vytvořeny v rámci projektu ESF OP VK: Inovace a rozvoj studia nanomateriálů na Technické univerzitě v Liberci Experimentální
Základy NIR spektrometrie a její praktické využití
 Nicolet CZ s.r.o. The world leader in serving science Základy NIR spektrometrie a její praktické využití NIR praktická metoda molekulové spektroskopie, nahrazující pracnější, časově náročnější a dražší
Nicolet CZ s.r.o. The world leader in serving science Základy NIR spektrometrie a její praktické využití NIR praktická metoda molekulové spektroskopie, nahrazující pracnější, časově náročnější a dražší
Laserové technologie v praxi I. Přednáška č.2. Základní konstrukční součásti laserů. Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011
 Laserové technologie v praxi I. Přednáška č.2 Základní konstrukční součásti laserů Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011 Konstrukce laseru 1 - Aktivní prostředí 2 - Čerpací zařízení 3 - Optický
Laserové technologie v praxi I. Přednáška č.2 Základní konstrukční součásti laserů Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011 Konstrukce laseru 1 - Aktivní prostředí 2 - Čerpací zařízení 3 - Optický
Spektroskopické metody. převážně ve viditelné, ultrafialové a blízké infračervené oblasti
 Spektroskopické metody převážně ve viditelné, ultrafialové a blízké infračervené oblasti Elektromagnetické záření Elektromagnetické záření je postupné vlnění elektromagnetického pole složeného z kombinace
Spektroskopické metody převážně ve viditelné, ultrafialové a blízké infračervené oblasti Elektromagnetické záření Elektromagnetické záření je postupné vlnění elektromagnetického pole složeného z kombinace
Novinky pro výuku vláknové optiky a optoelektroniky
 Novinky pro výuku vláknové optiky a optoelektroniky Moderní výukové soubory Praha 20. dubna 2006 MIKROKOM Praha Martin Hájek, Jan Brouček, Miroslav Švrček, Ondřej Hanzálek Výukové soubory 1. krok do vláknové
Novinky pro výuku vláknové optiky a optoelektroniky Moderní výukové soubory Praha 20. dubna 2006 MIKROKOM Praha Martin Hájek, Jan Brouček, Miroslav Švrček, Ondřej Hanzálek Výukové soubory 1. krok do vláknové
CT-prostorové rozlišení a citlivost z
 CT-prostorové rozlišení a citlivost z Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika Prostorové rozlišení a citlivost z Prostorové rozlišení význam vyjádření rozlišení měření rozlišení
CT-prostorové rozlišení a citlivost z Doc.RNDr. Roman Kubínek, CSc. Předmět: lékařská přístrojová fyzika Prostorové rozlišení a citlivost z Prostorové rozlišení význam vyjádření rozlišení měření rozlišení
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV RADIOELEKTRONIKY. OPTICKÝ SPOJ LR-830/1550 Technický popis
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV RADIOELEKTRONIKY OPTICKÝ SPOJ LR-830/1550 Technický popis BRNO, 2009 1 Návrh a konstrukce dálkového spoje 1.1 Optická
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV RADIOELEKTRONIKY OPTICKÝ SPOJ LR-830/1550 Technický popis BRNO, 2009 1 Návrh a konstrukce dálkového spoje 1.1 Optická
Praktikum z experimentálních metod biofyziky a chemické fyziky I. Vypracoval: Jana Čurdová, Martin Kříž, Vít Marek. Dne: 2.3.
 Praktikum z experimentálních metod biofyziky a chemické fyziky I. Vypracoval: Jana Čurdová, Martin Kříž, Vít Marek. Dne:.3.3 Úloha: Radiometrie ultrafialového záření z umělých a přirozených světelných
Praktikum z experimentálních metod biofyziky a chemické fyziky I. Vypracoval: Jana Čurdová, Martin Kříž, Vít Marek. Dne:.3.3 Úloha: Radiometrie ultrafialového záření z umělých a přirozených světelných
TERMOGRAFICKÉ MĚŘENÍ LOPATEK ROTAČNÍHO STROJE "FROTOR"
 TERMOMECHANIKA TECHNOLOGICKÝCH PROCESŮ VÝZKUMNÁ ZPRÁVA TERMOGRAFICKÉ MĚŘENÍ LOPATEK ROTAČNÍHO STROJE "FROTOR" Autoři: Ing. Pavel Litoš Ing. Jiří Tesař Číslo projektu: Číslo zprávy: Odpovědný pracovník
TERMOMECHANIKA TECHNOLOGICKÝCH PROCESŮ VÝZKUMNÁ ZPRÁVA TERMOGRAFICKÉ MĚŘENÍ LOPATEK ROTAČNÍHO STROJE "FROTOR" Autoři: Ing. Pavel Litoš Ing. Jiří Tesař Číslo projektu: Číslo zprávy: Odpovědný pracovník
Laserové technologie v praxi II. Cvičeníč.1
 Laserové technologie v praxi II. Cvičeníč.1 Měření ztrát na optických prvcích laseru KLS 246-2 Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011 1) Měření výkonu a energie laseru Teoretická hodnota v manuálu:
Laserové technologie v praxi II. Cvičeníč.1 Měření ztrát na optických prvcích laseru KLS 246-2 Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011 1) Měření výkonu a energie laseru Teoretická hodnota v manuálu:
EXPERIMENTÁLNÍ METODA URČENÍ ZÁKLADNÍCH PARAMETRŮ OBJEKTIVU ANALAKTICKÉHO DALEKOHLEDU. A.Mikš 1, V.Obr 2
 EXPERIMENTÁLNÍ METODA URČENÍ ZÁKLADNÍCH PARAMETRŮ OBJEKTIVU ANALAKTICKÉHO DALEKOHLEDU A.Mikš, V.Obr Katedra fyziky, Fakulta stavební ČVUT, Praha Katedra vyšší geodézie, Fakulta stavební ČVUT, Praha Abstrakt:
EXPERIMENTÁLNÍ METODA URČENÍ ZÁKLADNÍCH PARAMETRŮ OBJEKTIVU ANALAKTICKÉHO DALEKOHLEDU A.Mikš, V.Obr Katedra fyziky, Fakulta stavební ČVUT, Praha Katedra vyšší geodézie, Fakulta stavební ČVUT, Praha Abstrakt:
i β i α ERP struktury s asynchronními motory
 1. Regulace otáček asynchronního motoru - vektorové řízení Oproti skalárnímu řízení zabezpečuje vektorové řízení vysokou přesnost a dynamiku veličin v ustálených i přechodných stavech. Jeho princip vychází
1. Regulace otáček asynchronního motoru - vektorové řízení Oproti skalárnímu řízení zabezpečuje vektorové řízení vysokou přesnost a dynamiku veličin v ustálených i přechodných stavech. Jeho princip vychází
Katalog vzdělávacích programů SMC Industrial Automation CZ s.r.o.
 Katalog vzdělávacích programů SMC Industrial Automation CZ s.r.o. Strana 1 Úvod Katalog vzdělávacích programů společnosti SMC obsahuje témata pokrývající znalosti pneumatických, elektropneumatických prvků
Katalog vzdělávacích programů SMC Industrial Automation CZ s.r.o. Strana 1 Úvod Katalog vzdělávacích programů společnosti SMC obsahuje témata pokrývající znalosti pneumatických, elektropneumatických prvků
3D KAMERY A TECHNOLOGIE
 3D KAMERY A TECHNOLOGIE strojové vidění nás baví Zdeněk Šebestík, ATEsystem s.r.o., 2016 KDO JSME Vznik v roce 2013, spol. s r.o. 5 majitelů, pouze vlastní kapitál Dnes 18 zaměstnanců, 3 ext. spolupracovníci
3D KAMERY A TECHNOLOGIE strojové vidění nás baví Zdeněk Šebestík, ATEsystem s.r.o., 2016 KDO JSME Vznik v roce 2013, spol. s r.o. 5 majitelů, pouze vlastní kapitál Dnes 18 zaměstnanců, 3 ext. spolupracovníci
ANALÝZA MĚŘENÍ TVARU VLNOPLOCHY V OPTICE POMOCÍ MATLABU
 ANALÝZA MĚŘENÍ TVARU VLNOPLOCHY V OPTICE POMOCÍ MATLABU J. Novák, P. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán software pro počítačovou simulaci
ANALÝZA MĚŘENÍ TVARU VLNOPLOCHY V OPTICE POMOCÍ MATLABU J. Novák, P. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán software pro počítačovou simulaci
25 A Vypracoval : Zdeněk Žák Pyrometrie υ = -40 C.. +10000 C. Výhody termovize Senzory infračerveného záření Rozdělení tepelné senzory
 25 A Vypracoval : Zdeněk Žák Pyrometrie Bezdotykové měření Pyrometrie (obrázky viz. sešit) Bezdotykové měření teplot je měření povrchové teploty těles na základě elektromagnetického záření mezi tělesem
25 A Vypracoval : Zdeněk Žák Pyrometrie Bezdotykové měření Pyrometrie (obrázky viz. sešit) Bezdotykové měření teplot je měření povrchové teploty těles na základě elektromagnetického záření mezi tělesem
Princip rastrovacího konfokálního mikroskopu
 Konfokální mikroskop Obsah: Konfokální mikroskop... 1 Princip rastrovacího konfokálního mikroskopu... 1 Rozlišovací schopnost... 2 Pozorování povrchů ve skutečných barvách... 2 Konfokální mikroskop Olympus
Konfokální mikroskop Obsah: Konfokální mikroskop... 1 Princip rastrovacího konfokálního mikroskopu... 1 Rozlišovací schopnost... 2 Pozorování povrchů ve skutečných barvách... 2 Konfokální mikroskop Olympus
Spektrální analyzátor Ocean optics
 Anna Kapchenko, Václav Dajčar, Jan Zmelík 4.3.21 1. Zadání: Spektrální analyzátor Ocean optics Získat praktické zkušenosti s měřením spektrálních charakteristik pomocí spektrálního analyzátoru Ocean Optics
Anna Kapchenko, Václav Dajčar, Jan Zmelík 4.3.21 1. Zadání: Spektrální analyzátor Ocean optics Získat praktické zkušenosti s měřením spektrálních charakteristik pomocí spektrálního analyzátoru Ocean Optics
Metody využívající rentgenové záření. Rentgenovo záření. Vznik rentgenova záření. Metody využívající RTG záření
 Metody využívající rentgenové záření Rentgenovo záření Rentgenografie, RTG prášková difrakce 1 2 Rentgenovo záření Vznik rentgenova záření X-Ray Elektromagnetické záření Ionizující záření 10 nm 1 pm Využívá
Metody využívající rentgenové záření Rentgenovo záření Rentgenografie, RTG prášková difrakce 1 2 Rentgenovo záření Vznik rentgenova záření X-Ray Elektromagnetické záření Ionizující záření 10 nm 1 pm Využívá
Defektoskopie a defektometrie
 Defektoskopie a defektometrie Aplikace počítačového vidění Karel Horák Skupina počítačového ového vidění Ústav automatizace a měřicí techniky Fakulta elektrotechniky a komunikačních technologií Vysoké
Defektoskopie a defektometrie Aplikace počítačového vidění Karel Horák Skupina počítačového ového vidění Ústav automatizace a měřicí techniky Fakulta elektrotechniky a komunikačních technologií Vysoké
Akustooptický modulátor s postupnou a stojatou akustickou vlnou
 Úloha č. 8 pro laserová praktika (ZPLT) KFE, FJFI, ČVUT, Praha v. 2017/2018 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské
Úloha č. 8 pro laserová praktika (ZPLT) KFE, FJFI, ČVUT, Praha v. 2017/2018 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské
POHON 4x4 JAKO ZDROJ VIBRACÍ OSOBNÍHO AUTOMOBILU
 POHON 4x4 JAKO ZDROJ VIBRACÍ OSOBNÍHO AUTOMOBILU Pavel NĚMEČEK, Technická univerzita v Liberci 1 Radek KOLÍNSKÝ, Technická univerzita v Liberci 2 Anotace: Příspěvek popisuje postup identifikace zdrojů
POHON 4x4 JAKO ZDROJ VIBRACÍ OSOBNÍHO AUTOMOBILU Pavel NĚMEČEK, Technická univerzita v Liberci 1 Radek KOLÍNSKÝ, Technická univerzita v Liberci 2 Anotace: Příspěvek popisuje postup identifikace zdrojů
Ing. Jiří Fejfar, Ph.D. Dálkový průzkum Země
 Ing. Jiří Fejfar, Ph.D. Dálkový průzkum Země strana 2 Co je DPZ Dálkový průzkum je umění rozdělit svět na množství malých barevných čtverečků, se kterými si lze hrát na počítači a odhalovat jejich neuvěřitelný
Ing. Jiří Fejfar, Ph.D. Dálkový průzkum Země strana 2 Co je DPZ Dálkový průzkum je umění rozdělit svět na množství malých barevných čtverečků, se kterými si lze hrát na počítači a odhalovat jejich neuvěřitelný
Analýza optické trasy optickým reflektometrem
 Analýza optické trasy optickým reflektometrem Zadání: Pomocí optického reflektometru, zkrácené označení OTDR (Optical Time-Domain Reflectometer), proměřte trasu, která je složena z několika optických vláken.
Analýza optické trasy optickým reflektometrem Zadání: Pomocí optického reflektometru, zkrácené označení OTDR (Optical Time-Domain Reflectometer), proměřte trasu, která je složena z několika optických vláken.
Projekt Brána do vesmíru
 Projekt Brána do vesmíru Hvězdárna Valašské Meziříčí, p. o. Krajská hvezdáreň v Žiline Základy (ne)vědecké astronomické fotografie 1. Astronomický dalekohled 2. Astronomická fotografie jednoduchými prostředky
Projekt Brána do vesmíru Hvězdárna Valašské Meziříčí, p. o. Krajská hvezdáreň v Žiline Základy (ne)vědecké astronomické fotografie 1. Astronomický dalekohled 2. Astronomická fotografie jednoduchými prostředky
Třícestné regulační ventily, vyvažování portů třícestných regulačních ventilů
 Třícestné regulační ventily, vyvažování portů třícestných regulačních ventilů Vyvažování regulačních okruhů patří k základům metodiky vyvažování soustav jako takových. Cílem vyvážení regulačního okruhu
Třícestné regulační ventily, vyvažování portů třícestných regulačních ventilů Vyvažování regulačních okruhů patří k základům metodiky vyvažování soustav jako takových. Cílem vyvážení regulačního okruhu
Moderní trendy měření Radomil Sikora
 Moderní trendy měření Radomil Sikora za společnost RMT s. r. o. Členění laserových měřičů Laserové měřiče můžeme členit dle počtu os na 1D, 2D a 3D: 1D jsou tzv. dálkoměry, které měří vzdálenost pouze
Moderní trendy měření Radomil Sikora za společnost RMT s. r. o. Členění laserových měřičů Laserové měřiče můžeme členit dle počtu os na 1D, 2D a 3D: 1D jsou tzv. dálkoměry, které měří vzdálenost pouze
Výukové texty. pro předmět. Měřící technika (KKS/MT) na téma. Tvorba grafické vizualizace principu měření otáček a úhlové rychlosti
 Výukové texty pro předmět Měřící technika (KKS/MT) na téma Tvorba grafické vizualizace principu měření otáček a úhlové rychlosti Autor: Doc. Ing. Josef Formánek, Ph.D. Tvorba grafické vizualizace principu
Výukové texty pro předmět Měřící technika (KKS/MT) na téma Tvorba grafické vizualizace principu měření otáček a úhlové rychlosti Autor: Doc. Ing. Josef Formánek, Ph.D. Tvorba grafické vizualizace principu
Kvantové technologie v průmyslu a výzkumu
 Kvantové technologie v průmyslu a výzkumu Jejich budoucí význam a využití www.quantumphi.com. Kvantové technologie - přehled Kvantové technologie přinesou vylepšení mnoha stávajících zařízení napříč všemi
Kvantové technologie v průmyslu a výzkumu Jejich budoucí význam a využití www.quantumphi.com. Kvantové technologie - přehled Kvantové technologie přinesou vylepšení mnoha stávajících zařízení napříč všemi
Graf I - Závislost magnetické indukce na proudu protékajícím magnetem. naměřené hodnoty kvadratické proložení. B [m T ] I[A]
![Graf I - Závislost magnetické indukce na proudu protékajícím magnetem. naměřené hodnoty kvadratické proložení. B [m T ] I[A] Graf I - Závislost magnetické indukce na proudu protékajícím magnetem. naměřené hodnoty kvadratické proložení. B [m T ] I[A]](/thumbs/27/10456203.jpg) Pracovní úkol 1. Proměřte závislost magnetické indukce na proudu magnetu. 2. Pomocí kamery změřte ve směru kolmém k magnetickému poli rozštěpení červené spektrální čáry kadmia pro 8-10 hodnot magnetické
Pracovní úkol 1. Proměřte závislost magnetické indukce na proudu magnetu. 2. Pomocí kamery změřte ve směru kolmém k magnetickému poli rozštěpení červené spektrální čáry kadmia pro 8-10 hodnot magnetické
