PARAMETRICKÉ MODELOVÁNÍ V ARCHITEKTUŘE
|
|
|
- Miloslav Brož
- před 7 lety
- Počet zobrazení:
Transkript
1 Žilinská univerzita v Žiline Stavebná fakulta Študentská vedecká odborná činnosť Akademický rok PARAMETRICKÉ MODELOVÁNÍ V ARCHITEKTUŘE Meno a priezvisko študenta : Martin Matúšů Ročník a odbor štúdia : 5., Pozemní stavby a Architektura Vedúci práce : Ing. Jan Müller Žilina :
2 Úvod, co znamená parametrické modelování Mnohé obory lidské činnosti zaznamenaly novou vizi, která nejen znamenala rázný průlom, ale také změnila směr vývoje daného oboru na další roky. V oboru CAD (computer aided design) navrhování pomocí počítače a CADG (computer aided geometric design) počítačové geometrie, kde vznikají každý rok nové programy, se stovkami novátorských funkcí, hraje právě takovou úlohu parametrické modelování. Před dvaceti lety musel každý uživatel CAD programu při modelování svých 2D a 3D objektů počítat s tím, že bude-li nucen svůj model nebo výkres z nějakého důvodu změnit, bude třeba část nebo celou již provedenou práci smazat a začít znovu a to často několikrát než konečně dospěje k hotovému modelu nebo výkresu. Za otce myšlenky parametrického modelování je považován Samuel P. Geisberg, profesor matematiky který emigroval z Ruska do Spojených států. Jeho cílem bylo vyvinout modelovací systém který by umožňoval vytváření geometrie pomocí vlastností a parametrů, metodou která přiřadí rozměry a jiné proměnné ke geometrii takovým způsobem, že při změněně hodnoty parametru se automaticky změní i geometrie. Takto můžeme při návrhu vyzkoušet mnoho variant a změny našeho návrhu mohou být uskutečněny velmi rychle ve srovnání s ručním překreslováním, které vyžadují zastaralé CAD aplikace. Myšlenka parametrického modelování měla velký význam pro dnešní překotný vývoj softwaru pro modelování počítačové geometrie. Parametrické modelování, původně vyvinuté především pro letecký a automobilový průmysl, začíná pronikat i do architektury. V moderní architektuře, která nachází nové, často velmi složité geometrické tvary je nezbytné vytvořit celou řadu variant než lze dospět k řešení které je architektonicky kvalitní, vyhoví po stránce statiky a je ekonomické. Tvorbu těchto variant usnadňuje parametrické modelování. Budova Swiss-Re od Normana Fostera a ukázka parametrického modelu. Zdroj: Foster and Partners
3 Změna klíčových parametrů profilové křivky a pohled na stavbu. Vytvořeno pomocí skriptu v softwaru Bentley. Zdroj: Foster and Partners Řada významných současných architektů (např. Norman Foster) přiznává že je jim parametrické modelování velkým pomocníkem, umožňuje měnit jednotlivé prvky modelu přitom automaticky regeneruje celý model podobným způsobem jako tabulkový procesor přepočítá celou tabulky při změně některé vstupní hodnoty. Jako takový se parametrický model stává živým modelem, který neustále reaguje na naše změny a tak nabízí flexibilitu návrhu která dříve nebyla možná. Parametrická by měla být také racionalizace modelu, architektonického konceptu, tedy převod koncepčního modelu, často se jedná o složitou zakřivenou plochu na vyrobitelné, staticky únosné a ekonomické prvky. Obsah a cíl práce, proč vůbec programovat Podnětem pro mou práci je potřeba zjednodušit a urychlit tvorbu počítačových modelů architektury. Především při účasti na architektonických soutěžích, kdy vzniká potřeba v krátkém čase vymodelovat daný koncept, myšlenku architekta, umět tento model parametricky měnit, nejen pro účely vizualizace, ale také usnadnit tvorbu dokumentace, umět převézt model do podoby kterou vyžadují profese k posouzení návrhu. A následně upravit model podle výsledků například statického posouzení. V současnosti se nabízí široká paleta softwaru pro modelovaní i parametrické modelování, je ale těžké, snad nemožné vytvořit jeden program který by byl vhodný k modelování všech velmi různých druhů moderní architektury, uživatel je tak často nucen pracovat za pomocí funkcí, které jsou pro daný účel neefektivní a často je nucen smířit se z horším výsledkem práce než jaký by umožňoval program optimalizovaný pro danou úlohu. Snažím se vytvořit program který bude naopak umožňovat rychlé plně parametrické a přesné modelování dané úlohy. Vlastní modelování křivek a povrchů musím programovat také proto že ve stávajících aplikacích nemá uživatel přístup k rovnicím křivek a povrchů nemůžu je tedy dostatečně přesně a rychle racionalizovat, převádět na reálné vyrobitelné prvky.
4 První vytvořený program řeší parametrické modelování návrhu na trojský most v Praze zpracovaný pro ateliér Archicon, program je určen pouze pro danou úlohu a mé seznámení se s programováním. Druhý program jsem nazval FreeForm, je obecnější a na základě současné teorie počítačové geometrie, vytváří obecnější parametrické modely a převádí je na reálnou geometrii. Je založen především na dnes velmi oblíbené technice modelování pomocí křivek. Modelování pomocí křivek je jednoduchá, uživatelsky nenáročná a přitom velmi silná technika modelování. Objemy jsou definovány pomocí křivek, program je parametrický takže změnou těchto křivek dojde i k změně modelu, pokud je vybraná křivka použita v modelu. Velká pozornost je věnována převodu koncepčního modelu na reálnou geometrii, je vytvořen program pro dělení vytvořených křivek na lineární úseky, úseky mohou být stejně dlouhé, mohou být ve vzájemné posloupnosti a nebo může být několik zadaných délek řazeno za sebou v náhodném nebo určeném sledu. Dále je zpracován program na úpravu normálových vektorů křivky, za účelem větší ekonomičnosti návrhu, každá funkce bude vysvětlena a popsána. Program je zpracován v skriptovacím jazyku aplikace 3D Studio - Maxscript, při vykreslování vytvářených objektů je využito aplikace 3DS, to mi umožňuje soustředit se na programovaní modelování křivek a ploch, nemusím se zabývat algoritmy pro vykreslování. Maxscript je jazyk částečně objektově orientovaný, což výrazně zjednodušuje programování, především zprávu více objektů stejného druhu s různými parametry. Vše lze definováno jako objekt a jeho vlastnosti, takto lze jednoduše definovat parametrické změny objektů jako změny vlastností objektů. Například objekt křivka má mimo jiných vlastnost matici kontrolních body a jejich změnou dojde ke změně té části křivky kterou daný kontrolní bod ovlivňuje. Modelování křivek Při programování jsem si vyzkoušel řadu křivek které nabízí současná teorie, do programu jsem nakonec zahrnul kromě obyčejné spojité linie a základních tvarů, beziérovu křivku, b- spline křivku a catmull-rom křivku. Všechny křivky jsou po částech spojité kubické křivky. Kteroukoliv z křivek nebo linii lze editovat pomocí společných nástrojů pro vkládání, Roleta programu FreeForm
5 mazání a posun kontrolních uzlu a bodů. Za uzel je považován kontrolní bod který leží na křivce, za bod kontrolní bod neležící na křivce. Editovat lze najednou pouze jednu křivku. Vybraná křivka se zobrazuje červeně, ostatní křivky modře. Editace se provádí v reálném čase, při posunu kontrolních bodů se křivka okamžitě překresluje. Překresluje se jen ta část křivky kterou daný kontrolní bod ovlivňuje, to umožňuje vytvářet a upravovat složité křivky v reálném čase. Beziérova křivka V programu je použita kubická beziérova křivka, beziérovy křivky vyšších stupňů jsou sice hladší ale také špatně ovladatelné. Beziérova kubika je dána uzly a body. Uzly jsou označené čtvercem, leží na křivce a jsou to místa kde na sebe navazují jednotlivé kubické segmenty beziérovy křivky. Body jsou označeny křížkem, leží mimo křivku na tečně ke křivce v místě koncových bodů jednotlivých kubických úseků. Kubická beziérova křivka není ideální k určení volných tvarů, je hůře ovladatelná než ostatní uvedené křivky. Výhodou je že je jednoduchá, složená z méně segmentů než například b-spline, takže operace jako dělení na lineární úseky je rychlejší než u ostatních křivek. Beziérova kubická křivka a její kontrolní body a kontrolní polygon Posun kontrolního bodu.
6 Při posunu bodu se změní i pozice jemu odpovídajícího opačného bodu, tak je zaručena spojitost křivky. Beziérova křivka má spojitost 1.řádu. Při posunu uzlu se zároveň posunou i odpovídající body. B-spline křivka Je dána jen body, které leží mimo křivku, jde tedy o aproximační křivku. Jen první a poslední bod, v případě otevřené křivky leží na křivce. Je to opět po částech spojitá kubická křivka, ale se spojitostí 2. řádu, proto umožňuje definovat volnější, organičtější tvary než beziérova křivka. B-spline křivka a její kontrolní polygon a kontrolní body. Editace křivky se provádí opět posunem kontrolních bodů. Posunutí kontrolního bodu ovlivňuje dva segmenty na každou stranu od kontrolního bodu. První bod je označen jako uzel a v případě posunutí přes poslední bod křivky dojde k uzavření křivky. První kontrolní bod uzavřené křivky je označen křížkem v čtverečku. V případě jeho smazaní dojde k otevření křivky. V případě obecné uzavřené b-spline křivky žádný z kontrolních bodů neleží na křivce. Uzavřená B-Spline křivka
7 Chceme-li kontrolovat bod kterým obecně aproximační b-spline křivka prochází, můžeme jej získat vložením tří bodů na stejnou souřadnici, tak se ale naruší spojitost křivky. Další možnost jak kontrolovat bod kterým křivka prochází je umístěním tří bodů na stejnou přímku, k tomuto účelu je v uživatelském rozhraní funkce, bod-uzel. Uzel je pak označen jako vždy čtverečkem a při posunu jednoho z bodů na přímce jsou posunuty i ostatní takže všechny tři body leží na přímce i po transformaci. Otevření B-spline křivky. Catmull-rom křivka Křivka byla původně vyvinuta pro počítačovou animaci pro určení dráhy pohybu animovaného objektu, křivka má totiž tu vlastnost že body na křivce body které získáme dosazením do rovnice křivky mají přibližně stejnou vzdálenost. Opět se jedná o po částech spojitou kubickou křivku, jednotlivé segmenty začínají a končí v kontrolních bodech, jedná se tedy o interpolační křivku, takže vytvářená křivka prochází všemi svými kontrolními body. Díky této vlastnosti je křivka mezi uživateli velmi oblíbená, i když nedokáže vyjádřit takové množství tvarů jako b-spline křivka. Křivka je navíc poměrně špatně ovladatelná, navazování jednotlivých segmentů je totiž zajištěno shodností tečny v uzlech, směr těchto tečen ale uživatel nemůže upravovat. Křivku známe například z programu AutoCAD
8 Catmull-Rom křivka. Modelování povrchů pomocí křivek Loft (šablonování profilu po křivce) Je nejčastěji používaná technika modelování, v mém programu je povrch vytvářen tak že křivka profilu se posunuje v kolmé rovině k páteřní křivce a vytváří takto povrch. Loft povrch a křivky které jej určují.
9 Povrch je parametrický takže změna páteřní křivky nebo profilu (žebra) vede k okamžitému překreslení povrchu. Úpravy páteřní křivky. Při změně páteřní křivky se povrch zprůhlední aby uživatel mohl sledovat křivku, kterou edituje a která by jinak byla skrytá za povrchem. Křivky určující Loftový objekt mohou být otevřené i uzavřené, pokud jsou spojité vytváří spojitý povrch. Spojitý, uzavřený Loft Povrch.
10 Umístění profilu na páteřní křivce. Každý profil může mít svůj střední bod, který určuje umístění profilu na páteřní křivce, pokud není střední bod zadán profil se umístí prvním bodem na páteřní křivku. Vyjádření rotačního povrchu pomocí Loft objektu, má tu výhodu, že páteř kružnice, určuje typ objektu, otevřením nebo úpravou páteřní křivky změníme typ objektu, bez nutnosti objekt mazat a znovu vytvářet. 2-Rail Sweep (šablonování profilu po 2 křivkách) Na rozdíl od předchozího se profil transformuje mezi dvěma danými křivkami, profil se zvětší, posune a pootočí tak aby první bod profilu ležel na první křivce, poslední bod na druhé. Je nutné aby obě páteřní křivky měli stejný počet segmentů, to vždy neznamená stejný počet kontrolních bodů, pokud jsou páteřní křivky různého typu.
11 Šablonování profilu s konstantní výškou profilu. Takto lze vymodelovat celou řadu hladkých, volných tvarů, mohou a nemusí být spojité, otevřené, uzavřené Šablonování s různou výškou profilu.
12 Racionalizace křivek Kontrola vzájemných vzdáleností bodů na křivce Každá z kubických křivek v mém programu je po částech dána rovnicí: [ x( t), y( t), z( )] Q ( t) = t, kde 3 2 x ( t) = a t + b t + c t + d x 3 2 y ( t) = a t + b t + c t + d z y 3 2 z ( t) = a t + b t + c t + d beziérova, catmull-rom a b-spline křivka se vzájemně liší pouze tím jakým způsobem jsou z polohy kontrolních bodů stanoveny konstanty a d pro každou souřadnici. Vykreslit křivku můžeme mimo metod atypických pro každou křivku (např. algoritmus decasteljau pro bezierovu křivku), obecně dosazováním za parametr t, pro každý segment. Pokud se konstanty stanoví před vykreslováním, je vykreslení velmi rychlé. x y z y x z y x z Body na křivce stanovené prostým dosazováním za parametr křivky t mají různé vzájemné vzdálenosti Logickou možností jak určit stejně vzdálené body na křivce je rozdělit křivku po délce na stejně dlouhé úseky a na kraje těchto úseků vložit body.
13 Body na křivce stanovené rozdělením křivky na stejně dlouhé úseky také nejsou stejně vzdálené Program umí nalézt na jakékoliv kubické křivce stejně vzdálené body. Využívá numerické matematiky a stanoví vzdálenosti až na 7 platných míst. Přesnost lze nastavit pomocí množství iterací, které ovlivňují dobu výpočtu. Stejně vzdálené body na křivce stanovené pomocí iterační metody.
14 Jsou zadané 3 délky, které se ve vypočteném měřítku na křivce opakují v náhodném pořadí. Program na nalezení stejně vzdálených bodů nemusí hledat jen stejně dlouhé úseky, délky úseků také mohou být ve vzájemné posloupnosti a nebo může být několik zadaných délek řazeno za sebou v náhodném nebo určeném sledu. Optimalizace normálových vektorů křivek pro loft povrchy Nevhodné umístění profilu na loft objektu. Někdy nemusí být vhodné umístit profily loft objektu kolmo k páteřní křivce, profily se mohou vzájemně protínat a také vzdálenosti sobě si odpovídajících bodů jednotlivých profilů jsou různé.
15 Ukázka směrů které najde algoritmus pro kružnici a obecnou křivku.. Program umí nalézt pro křivky takové směry pro které platí, že odpovídající si body v těchto směrem mají stejné vzdálenosti. Pro kružnici program jako optimální směry nalezne normálové vektory. Pro některé složité křivky popsané směry nemusí existovat, takové křivky lze optimalizovat po částech. V tomto případě jsou žebra na páteřní křivce umístěny v optimalizovaných směrech tedy takových směrech aby vzdálenosti sobě si odpovídajících bodů jednotlivých žeber byli stejné. Délky odpovídajících si prvků jsou pak stejné.
16 Ukázka racionalizovaného modelu vloženého do software Nexis. Model je korektní, koncové body navazujících prvků jsou na stejné souřadnici. Závěr, důvody racionalizace modelu a směr dalšího vývoje Kontrola vzájemných vzdálenosti budů na volný křivkách není nutná jen z důvodů ekonomických ale i estetických. Vzdálenosti budů určených klasicky vypočtením délky křivky a dělením křivky na stejně dlouhé úseky jsou po převedení na lineární useky různě dlouhé, to není ekonomické ani estetické. Normálové vektory, které se většinou používají k určení směru profilu na křivce nejsou vhodné proto že vzájemné vzdálenosti odpovídajících si bodů jednotlivých profilů jsou různé, a to opět není ekonomické ani estetické.
17 V mém programu je například možné vymodelovat plášť nové Allianz Arény od architektů Herzoga a de Meurona Další vývoj - Přidání více základních tvarů vyjádřených pomocí křivek. - Snažit se o provázání a spolupráci s některým ze statických programů, umět na geometrii přiřadit zatížení a být tak schopen parametrickým modelářem vytvořené varianty posoudit a vybrat tu nejvhodnější. - Pro často opakované funkce např. pro transformace do používaného skriptovacího jazyku přidat nové příkazy pomocí jazyka C++ takové funkce jsou mnohem rychlejší než ty vytvořené pomocí skriptu. -Přidání dalších funkcí obvyklých v programech pro modelování pomocí křivek.
18
Jana Dannhoferová Ústav informatiky, PEF MZLU
 Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
Základní vlastnosti křivek
 křivka množina bodů v rovině nebo v prostoru lze chápat jako trajektorii pohybu v rovině či v prostoru nalezneme je také jako množiny bodů na ploše křivky jako řezy plochy rovinou, křivky jako průniky
křivka množina bodů v rovině nebo v prostoru lze chápat jako trajektorii pohybu v rovině či v prostoru nalezneme je také jako množiny bodů na ploše křivky jako řezy plochy rovinou, křivky jako průniky
Aproximační křivky. Trocha historie. geometrické modelování veliký pokrok v oblasti letectví 1944 Roy Liming
 Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
Počítačová grafika RHINOCEROS
 Počítačová grafika RHINOCEROS Ing. Zuzana Benáková Základní otázkou grafických programů je způsob zobrazení určitého tvaru. Existují dva základní způsoby prezentace 3D modelů v počítači. První využívá
Počítačová grafika RHINOCEROS Ing. Zuzana Benáková Základní otázkou grafických programů je způsob zobrazení určitého tvaru. Existují dva základní způsoby prezentace 3D modelů v počítači. První využívá
Aproximační křivky. Trocha historie. geometrické modelování veliký pokrok v oblasti letectví 1944 Roy Liming
 Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
KŘIVKY A PLOCHY. Obrázky (popř. slajdy) převzaty od
 KŘIVKY A PLOCHY JANA ŠTANCLOVÁ jana.stanclova@ruk.cuni.cz Obrázky (popř. slajdy) převzaty od RNDr. Josef Pelikán, CSc., KSVI MFF UK Obsah matematický popis křivek a ploch křivky v rovině implicitní tvar
KŘIVKY A PLOCHY JANA ŠTANCLOVÁ jana.stanclova@ruk.cuni.cz Obrázky (popř. slajdy) převzaty od RNDr. Josef Pelikán, CSc., KSVI MFF UK Obsah matematický popis křivek a ploch křivky v rovině implicitní tvar
Kristýna Bémová. 13. prosince 2007
 Křivky v počítačové grafice Kristýna Bémová Univerzita Karlova v Praze 13. prosince 2007 Kristýna Bémová (MFF UK) Křivky v počítačové grafice 13. prosince 2007 1 / 36 Pojmy - křivky a jejich parametrické
Křivky v počítačové grafice Kristýna Bémová Univerzita Karlova v Praze 13. prosince 2007 Kristýna Bémová (MFF UK) Křivky v počítačové grafice 13. prosince 2007 1 / 36 Pojmy - křivky a jejich parametrické
Základní vlastnosti ploch
 plocha zpravidla se definuje jako výsledek spojitého pohybu jisté tvořící křivky podél zadané trajektorie lze obohatit o možnost spojitých změn tvaru tvořící křivky x v průběhu pohybu podél trajektorie
plocha zpravidla se definuje jako výsledek spojitého pohybu jisté tvořící křivky podél zadané trajektorie lze obohatit o možnost spojitých změn tvaru tvořící křivky x v průběhu pohybu podél trajektorie
Křivky a plochy technické praxe
 Kapitola 7 Křivky a plochy technické praxe V technické praxi se setkáváme s tím, že potřebujeme křivky a plochy, které se dají libovolně upravovat a zároveň je jejich matematické vyjádření jednoduché.
Kapitola 7 Křivky a plochy technické praxe V technické praxi se setkáváme s tím, že potřebujeme křivky a plochy, které se dají libovolně upravovat a zároveň je jejich matematické vyjádření jednoduché.
Plochy zadané okrajovými křivkami
 Plochy zadané okrajovými křivkami Lineární plát plocha je určena dvěma okrajovými křivkami, pokud by pro tyto křivky byly intervaly, v nichž leží hodnoty parametru, různé, provedeme lineární transformaci
Plochy zadané okrajovými křivkami Lineární plát plocha je určena dvěma okrajovými křivkami, pokud by pro tyto křivky byly intervaly, v nichž leží hodnoty parametru, různé, provedeme lineární transformaci
5. Plochy v počítačové grafice. (Bézier, Coons)
 5. PLOCHY V POČÍAČOVÉ GRAFICE Cíl Po prostudování této kapitoly budete umět popsat plochy používané v počítačové grafice řešit příklady z praxe, kdy jsou použity plochy Výklad Interpolační plochy - plochy,
5. PLOCHY V POČÍAČOVÉ GRAFICE Cíl Po prostudování této kapitoly budete umět popsat plochy používané v počítačové grafice řešit příklady z praxe, kdy jsou použity plochy Výklad Interpolační plochy - plochy,
POČÍTAČOVÁ GRAFIKA - PGR 2012037 2014 2015 PROGRAM PŘEDNÁŠEK. Po 9:00-10:30, KN:A-214
 PROGRAM PŘEDNÁŠEK Po 9:00-10:30, KN:A-214 1P 16. 2. Křivky definice, analytické vyjádření. Bézierova křivka definice, vlastnosti, odvození Bernsteinových polynomů, de Castejlau algoritmus. 2P 23. 2. Spojitost
PROGRAM PŘEDNÁŠEK Po 9:00-10:30, KN:A-214 1P 16. 2. Křivky definice, analytické vyjádření. Bézierova křivka definice, vlastnosti, odvození Bernsteinových polynomů, de Castejlau algoritmus. 2P 23. 2. Spojitost
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Základy parametrického modelování Skicovací nástroje
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Základy parametrického modelování Skicovací nástroje
PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII
 PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII V úvodu analytické geometrie jsme vysvětlili, že její hlavní snahou je popsat geometrické útvary (body, vektory, přímky, kružnice,...) pomocí čísel nebo proměnných.
PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII V úvodu analytické geometrie jsme vysvětlili, že její hlavní snahou je popsat geometrické útvary (body, vektory, přímky, kružnice,...) pomocí čísel nebo proměnných.
9 Prostorová grafika a modelování těles
 9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
13 Barvy a úpravy rastrového
 13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
11 Zobrazování objektů 3D grafiky
 11 Zobrazování objektů 3D grafiky Studijní cíl Tento blok je věnován základním algoritmům zobrazení 3D grafiky. Postupně budou probrány základní metody projekce kolmé promítání, rovnoběžné promítání a
11 Zobrazování objektů 3D grafiky Studijní cíl Tento blok je věnován základním algoritmům zobrazení 3D grafiky. Postupně budou probrány základní metody projekce kolmé promítání, rovnoběžné promítání a
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ
 11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti: 1. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti: 1. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
Zobrazování těles. problematika geometrického modelování. základní typy modelů. datové reprezentace modelů základní metody geometrického modelování
 problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
Ctislav Fiala: Optimalizace a multikriteriální hodnocení funkční způsobilosti pozemních staveb
 16 Optimální hodnoty svázaných energií stropních konstrukcí (Graf. 6) zde je rozdíl materiálových konstant, tedy svázaných energií v 1 kg materiálu vložek nejmarkantnější, u polystyrénu je téměř 40krát
16 Optimální hodnoty svázaných energií stropních konstrukcí (Graf. 6) zde je rozdíl materiálových konstant, tedy svázaných energií v 1 kg materiálu vložek nejmarkantnější, u polystyrénu je téměř 40krát
Matematický ústav UK Matematicko-fyzikální fakulta
 Geometrické modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta 5. října 2016 Zbyněk Šír (MÚ UK) - Geometrické modelování 5. října 2016 1 / 14 Obsah dnešní přednášky Co je to geometrické
Geometrické modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta 5. října 2016 Zbyněk Šír (MÚ UK) - Geometrické modelování 5. října 2016 1 / 14 Obsah dnešní přednášky Co je to geometrické
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ. u. v = u v + u v. Umět ho aplikovat při
 . VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti:. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti:. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
NEXIS 32 rel. 3.50. Generátor fází výstavby TDA mikro
 SCIA CZ, s. r. o. Slavíčkova 1a 638 00 Brno tel. 545 193 526 545 193 535 fax 545 193 533 E-mail info.brno@scia.cz www.scia.cz Systém programů pro projektování prutových a stěnodeskových konstrukcí NEXIS
SCIA CZ, s. r. o. Slavíčkova 1a 638 00 Brno tel. 545 193 526 545 193 535 fax 545 193 533 E-mail info.brno@scia.cz www.scia.cz Systém programů pro projektování prutových a stěnodeskových konstrukcí NEXIS
Přehled. Motivace Úvod. Křivky a plochy počítačové grafiky. Závěr. Rozvoj počítačové grafiky Výpočetní geometrie
 Vývoj výpočetní geometrie Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz Přehled Motivace Úvod Rozvoj počítačové grafiky Výpočetní geometrie Křivky a plochy počítačové
Vývoj výpočetní geometrie Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz Přehled Motivace Úvod Rozvoj počítačové grafiky Výpočetní geometrie Křivky a plochy počítačové
Rhino - základní příkazy
 Rhino - základní příkazy Příkazy - volíme z hlavní nabídky levým tlačítkem myši - ikonou z nástrojové lišty levým (LTM)/pravým(PTM) tlačítkem myši Příkaz ukončíme pravým tlačítkem myši (Enter) nebo klávesou
Rhino - základní příkazy Příkazy - volíme z hlavní nabídky levým tlačítkem myši - ikonou z nástrojové lišty levým (LTM)/pravým(PTM) tlačítkem myši Příkaz ukončíme pravým tlačítkem myši (Enter) nebo klávesou
Výhody programu OCAD
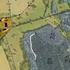 Program OCAD vektorový program pro počítačovou tvorbu map původně - mapy pro orientační běh (začátek 90. let), později zobecněn pro tvorbu různých druhů map autorem Hans Steinegger (+2004) firma OCAD AG,
Program OCAD vektorový program pro počítačovou tvorbu map původně - mapy pro orientační běh (začátek 90. let), později zobecněn pro tvorbu různých druhů map autorem Hans Steinegger (+2004) firma OCAD AG,
Matematika I, část I. Rovnici (1) nazýváme vektorovou rovnicí roviny ABC. Rovina ABC prochází bodem A a říkáme, že má zaměření u, v. X=A+r.u+s.
 3.4. Výklad Předpokládejme, že v prostoru E 3 jsou dány body A, B, C neležící na jedné přímce. Těmito body prochází jediná rovina, kterou označíme ABC. Určíme vektory u = B - A, v = C - A, které jsou zřejmě
3.4. Výklad Předpokládejme, že v prostoru E 3 jsou dány body A, B, C neležící na jedné přímce. Těmito body prochází jediná rovina, kterou označíme ABC. Určíme vektory u = B - A, v = C - A, které jsou zřejmě
Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ]
![Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ] Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ]](/thumbs/24/3705963.jpg) Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ] 1 CÍL KAPITOLY V této kapitole si představíme Nástroje kreslení pro tvorbu 2D skic v modulu Objemová součást
Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ] 1 CÍL KAPITOLY V této kapitole si představíme Nástroje kreslení pro tvorbu 2D skic v modulu Objemová součást
MATURITNÍ TÉMATA Z MATEMATIKY
 MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
0. Pak existuje n tak, že Bµ APn
 Euklidovský prostor Základní pojmy: bod, přímka rovina Základní vztahy: bod leží na přímce přímka prochází bodem bod leží v rovině rovina prochází bodem bod inciduje s přímkou přímka inciduje s bodem bod
Euklidovský prostor Základní pojmy: bod, přímka rovina Základní vztahy: bod leží na přímce přímka prochází bodem bod leží v rovině rovina prochází bodem bod inciduje s přímkou přímka inciduje s bodem bod
Bézierovy křivky Bohumír Bastl KMA/GPM Geometrické a počítačové modelování Bézierovy křivky GPM 1 / 26
 Bézierovy křivky Bohumír Bastl (bastl@kma.zcu.cz) KMA/GPM Geometrické a počítačové modelování Bézierovy křivky GPM 1 / 26 Opakování Spline křivky opakování Bézierovy křivky GPM 2 / 26 Opakování Interpolace
Bézierovy křivky Bohumír Bastl (bastl@kma.zcu.cz) KMA/GPM Geometrické a počítačové modelování Bézierovy křivky GPM 1 / 26 Opakování Spline křivky opakování Bézierovy křivky GPM 2 / 26 Opakování Interpolace
ÚLOHY S POLYGONEM. Polygon řetězec úseček, poslední bod je totožný s prvním. 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU
 ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
Singularity rotačních obalových ploch
 Singularity rotačních obalových ploch Ivana Linkeová ČVUT v Praze, Fakulta strojní, Ústav technické matematiky Karlovo nám. 13, 121 35 Praha 2 Nové Město Ivana.Linkeova@fs.cvut.cz Abstrakt. V příspěvku
Singularity rotačních obalových ploch Ivana Linkeová ČVUT v Praze, Fakulta strojní, Ústav technické matematiky Karlovo nám. 13, 121 35 Praha 2 Nové Město Ivana.Linkeova@fs.cvut.cz Abstrakt. V příspěvku
Základy 3D modelování a animace v CGI systémech Cinema 4D C4D
 EVROPSKÝ SOCIÁLNÍ FOND Základy 3D modelování a animace v CGI systémech Cinema 4D C4D PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Mgr. David Frýbert 2013 CGI systémy Computer - generated imagery - aplikace
EVROPSKÝ SOCIÁLNÍ FOND Základy 3D modelování a animace v CGI systémech Cinema 4D C4D PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI Mgr. David Frýbert 2013 CGI systémy Computer - generated imagery - aplikace
15. listopadu Matematický ústav UK Matematicko-fyzikální fakulta. Hermitovská interpolace
 Geometrické modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta Hermitovská interpolace 15. listopadu 2017 Zbyněk Šír (MÚ UK) - Geometrické modelování 15. listopadu 2017 1 / 23 Hermiteovská
Geometrické modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta Hermitovská interpolace 15. listopadu 2017 Zbyněk Šír (MÚ UK) - Geometrické modelování 15. listopadu 2017 1 / 23 Hermiteovská
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Pokročilé metody parametrického modelování Modelování
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Pokročilé metody parametrického modelování Modelování
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika analytická geometrie. Mgr. Pavel Liška
 Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
VZOROVÉ PŘÍKLADY Z MATEMATIKY A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava
 VZOROVÉ PŘÍKLADY Z MATEMATIKY A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava I Úprav algebraických výrazů zlomk, rozklad kvadratického trojčlenu,
VZOROVÉ PŘÍKLADY Z MATEMATIKY A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava I Úprav algebraických výrazů zlomk, rozklad kvadratického trojčlenu,
2. Kinematika bodu a tělesa
 2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
NURBS REPREZENTACE KŘIVEK V MAPLE
 25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Karolína Kundrátová NURBS REPREZENTACE KŘIVEK V MAPLE Abstrakt Parametrizace křivek jako NURBS (tj. neuniformní racionální B-spliny) patří k moderním postupům
25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Karolína Kundrátová NURBS REPREZENTACE KŘIVEK V MAPLE Abstrakt Parametrizace křivek jako NURBS (tj. neuniformní racionální B-spliny) patří k moderním postupům
Matematický ústav UK Matematicko-fyzikální fakulta
 Geometrické modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta 2. října 2018 Zbyněk Šír (MÚ UK) - Geometrické modelování 2. října 2018 1 / 15 Obsah dnešní přednášky Co je to geometrické
Geometrické modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta 2. října 2018 Zbyněk Šír (MÚ UK) - Geometrické modelování 2. října 2018 1 / 15 Obsah dnešní přednášky Co je to geometrické
AutoCAD výstup výkresu
 Kreslení 2D technické dokumentace AutoCAD výstup výkresu Ing. Richard Strnka, 2012 1. Výstup z AutoCADu Výklad: Výstup z programu AutoCAD je možný několika různými způsoby. Základní rozdělení je na výstup
Kreslení 2D technické dokumentace AutoCAD výstup výkresu Ing. Richard Strnka, 2012 1. Výstup z AutoCADu Výklad: Výstup z programu AutoCAD je možný několika různými způsoby. Základní rozdělení je na výstup
1.1. Spuštění ArchiCADu 16 1.2. Práce s projektem 16. 1.3. Pracovní plocha 19
 Obsah 1 Seznámení s ArchiCADem 15 1.1. Spuštění ArchiCADu 16 1.2. Práce s projektem 16 Vytvoření nového projektu 16 Vytvoření nového projektu při spuštění ArchiCADu 17 Možné způsoby nastavení nového projektu:
Obsah 1 Seznámení s ArchiCADem 15 1.1. Spuštění ArchiCADu 16 1.2. Práce s projektem 16 Vytvoření nového projektu 16 Vytvoření nového projektu při spuštění ArchiCADu 17 Možné způsoby nastavení nového projektu:
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Náplň: Cvičení z matematiky geometrie (CZMg) Systematizace a prohloubení učiva matematiky Planimetrie, Stereometrie, Analytická geometrie, Kombinatorika, Pravděpodobnost a statistika Třída: 4.
Předmět: Náplň: Cvičení z matematiky geometrie (CZMg) Systematizace a prohloubení učiva matematiky Planimetrie, Stereometrie, Analytická geometrie, Kombinatorika, Pravděpodobnost a statistika Třída: 4.
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
Rovnice přímky v prostoru
 Rovnice přímky v prostoru Každá přímka v prostoru je jednoznačně zadána dvěma body. K vyjádření všech bodů přímky lze použít parametrické rovnice. Parametrická rovnice přímky p Pokud A, B jsou dva různé
Rovnice přímky v prostoru Každá přímka v prostoru je jednoznačně zadána dvěma body. K vyjádření všech bodů přímky lze použít parametrické rovnice. Parametrická rovnice přímky p Pokud A, B jsou dva různé
Analytická geometrie (AG)
 Analytická geometrie (AG) - zkoumá geometrické útvary pomocí algebraických a analytických metod Je založena na vektorech a soustavě souřadnic, rozděluje se na AG v rovině a v prostoru. Analytická geometrie
Analytická geometrie (AG) - zkoumá geometrické útvary pomocí algebraických a analytických metod Je založena na vektorech a soustavě souřadnic, rozděluje se na AG v rovině a v prostoru. Analytická geometrie
Plochy počítačové grafiky II. Interpolační plochy Bezierovy pláty nad obdélníkovou a trojúhelníkovou sítí Recionální Bezierovy pláty B-spline NURBS
 II Interpolační plochy Bezierovy pláty nad obdélníkovou a trojúhelníkovou sítí Recionální Bezierovy pláty B-spline NURBS Konstrukce a zadání plochy hraniční křivky sítí bodů Kinematicky vytvořené křivky
II Interpolační plochy Bezierovy pláty nad obdélníkovou a trojúhelníkovou sítí Recionální Bezierovy pláty B-spline NURBS Konstrukce a zadání plochy hraniční křivky sítí bodů Kinematicky vytvořené křivky
i=1 Přímka a úsečka. Body, které leží na přímce procházející body a a b můžeme zapsat pomocí parametrické rovnice
 I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
U Úvod do modelování a simulace systémů
 U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na. x 2 x 1
 Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
CORELDRAW SEZNÁMENÍ S PROGRAMEM. Lenka Bednaříková
 CORELDRAW SEZNÁMENÍ S PROGRAMEM Lenka Bednaříková SEZNÁMENÍ S OKNEM APLIKACE Panel nabídek Panel nástrojů Panel vlastností Ukotvitelné panely Okno nástrojů Paleta barev Okno kresby Pravítko Stavový řádek
CORELDRAW SEZNÁMENÍ S PROGRAMEM Lenka Bednaříková SEZNÁMENÍ S OKNEM APLIKACE Panel nabídek Panel nástrojů Panel vlastností Ukotvitelné panely Okno nástrojů Paleta barev Okno kresby Pravítko Stavový řádek
Gymnázium Česká a Olympijských nadějí, České Budějovice, Česká 64, 37021
 Maturitní témata MATEMATIKA 1. Funkce a jejich základní vlastnosti. Definice funkce, def. obor a obor hodnot funkce, funkce sudá, lichá, monotónnost funkce, funkce omezená, lokální a globální extrémy funkce,
Maturitní témata MATEMATIKA 1. Funkce a jejich základní vlastnosti. Definice funkce, def. obor a obor hodnot funkce, funkce sudá, lichá, monotónnost funkce, funkce omezená, lokální a globální extrémy funkce,
Obsah. Co je nového v Advance CAD 2015 NOVINKY... 5 VYLEPŠENÍ... 8
 Obsah NOVINKY... 5 1: Nová ukotvitelná paleta nástrojů...5 2: Oříznutí výřezu...5 3: Různé typy licencí...5 4: Uživatelské nastavení stránky...6 5: Nastavení barev pro šrafy...7 6: Asociativita úhlových
Obsah NOVINKY... 5 1: Nová ukotvitelná paleta nástrojů...5 2: Oříznutí výřezu...5 3: Různé typy licencí...5 4: Uživatelské nastavení stránky...6 5: Nastavení barev pro šrafy...7 6: Asociativita úhlových
Modelování sestav. Autodesk INVENTOR. Ing. Richard Strnka, 2012
 Modelování sestav Autodesk INVENTOR Ing. Richard Strnka, 2012 Modelování sestavy přepínače Příprava modelování sestavy Z určeného adresáře překopírujte soubory sestavy 1-4 do vašeho pracovního adresáře.
Modelování sestav Autodesk INVENTOR Ing. Richard Strnka, 2012 Modelování sestavy přepínače Příprava modelování sestavy Z určeného adresáře překopírujte soubory sestavy 1-4 do vašeho pracovního adresáře.
Čebyševovy aproximace
 Čebyševovy aproximace Čebyševova aproximace je tzv hledání nejlepší stejnoměrné aproximace funkce v daném intervalu Hledáme funkci h x, která v intervalu a,b minimalizuje maximální absolutní hodnotu rozdílu
Čebyševovy aproximace Čebyševova aproximace je tzv hledání nejlepší stejnoměrné aproximace funkce v daném intervalu Hledáme funkci h x, která v intervalu a,b minimalizuje maximální absolutní hodnotu rozdílu
Obsah KAPITOLA 1 13 KAPITOLA 2 33
 Obsah KAPITOLA 1 13 Seznámení s programem AutoCAD 13 Úvod 13 Spuštění programu AutoCAD 13 Okno aplikace AutoCAD 16 Ovládací prvky 17 Příkazový řádek 20 Dynamická výzva 24 Vizuální nastavení 24 Práce s
Obsah KAPITOLA 1 13 Seznámení s programem AutoCAD 13 Úvod 13 Spuštění programu AutoCAD 13 Okno aplikace AutoCAD 16 Ovládací prvky 17 Příkazový řádek 20 Dynamická výzva 24 Vizuální nastavení 24 Práce s
Modelování ve Scia Engineer
 Apollo Bridge Apollo Bridge Architect: Ing. Architect: Miroslav Ing. Maťaščík Miroslav Maťaščík - Alfa 04 a.s., - Alfa Bratislava 04 a.s., Bratislava Design: DOPRAVOPROJEKT Design: Dopravoprojekt a.s.,
Apollo Bridge Apollo Bridge Architect: Ing. Architect: Miroslav Ing. Maťaščík Miroslav Maťaščík - Alfa 04 a.s., - Alfa Bratislava 04 a.s., Bratislava Design: DOPRAVOPROJEKT Design: Dopravoprojekt a.s.,
Globální matice konstrukce
 Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Nelineární problémy a MKP
 Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Obsah. Úvod do studia 11 Co byste měli předem znát 13. Úvod do obsluhy AutoCADu 23. Kapitola 1 11. Kapitola 1 23
 Předmluva 9 Komu je tato kniha určena 11 Kapitola 1 11 Úvod do studia 11 Co byste měli předem znát 13 CAD technologie 13 Product Lifecycle Management 14 AutoCAD není jenom CAD, je to vývojová platforma
Předmluva 9 Komu je tato kniha určena 11 Kapitola 1 11 Úvod do studia 11 Co byste měli předem znát 13 CAD technologie 13 Product Lifecycle Management 14 AutoCAD není jenom CAD, je to vývojová platforma
Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014. 1. Obor reálných čísel
 Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014 1. Obor reálných čísel - obor přirozených, celých, racionálních a reálných čísel - vlastnosti operací (sčítání, odčítání, násobení, dělení) -
Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014 1. Obor reálných čísel - obor přirozených, celých, racionálních a reálných čísel - vlastnosti operací (sčítání, odčítání, násobení, dělení) -
Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jana Kalinová [ÚLOHA 25 NÁSTROJE II.ČÁST]
![Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jana Kalinová [ÚLOHA 25 NÁSTROJE II.ČÁST] Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jana Kalinová [ÚLOHA 25 NÁSTROJE II.ČÁST]](/thumbs/93/114372910.jpg) Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Jana Kalinová [ÚLOHA 25 NÁSTROJE II.ČÁST] 1 CÍL KAPITOLY Úloha Nástroje II je pokračováním obšírné kapitoly v roletovém menu Nástroje, přičemž navazujeme
Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Jana Kalinová [ÚLOHA 25 NÁSTROJE II.ČÁST] 1 CÍL KAPITOLY Úloha Nástroje II je pokračováním obšírné kapitoly v roletovém menu Nástroje, přičemž navazujeme
Autodesk AutoCAD 2018
 Novinky Autodesk AutoCAD 2018 www.graitec.cz www.cadnet.cz, helpdesk.graitec.cz, www.graitec.com Novinky Autodesk AutoCAD 2018 PDF dokument obsahuje přehled novinek produktu AutoCAD 2018. AutoCAD 2018
Novinky Autodesk AutoCAD 2018 www.graitec.cz www.cadnet.cz, helpdesk.graitec.cz, www.graitec.com Novinky Autodesk AutoCAD 2018 PDF dokument obsahuje přehled novinek produktu AutoCAD 2018. AutoCAD 2018
Obecný princip 3D numerického modelování výrubu
 Obecný princip 3D numerického modelování výrubu Modelovaná situace Svislé zatížení nadloží se přenáší horninovým masivem na bok tunelu Soustava lineárních rovnic Soustavou lineárních rovnic popíšeme určované
Obecný princip 3D numerického modelování výrubu Modelovaná situace Svislé zatížení nadloží se přenáší horninovým masivem na bok tunelu Soustava lineárních rovnic Soustavou lineárních rovnic popíšeme určované
KMA/GPM Barycentrické souřadnice a
 KMA/GPM Barycentrické souřadnice a trojúhelníkové pláty František Ježek jezek@kma.zcu.cz Katedra matematiky Západočeské univerzity v Plzni, 2008 19. dubna 2009 1 Trojúhelníkové pláty obecně 2 Barycentrické
KMA/GPM Barycentrické souřadnice a trojúhelníkové pláty František Ježek jezek@kma.zcu.cz Katedra matematiky Západočeské univerzity v Plzni, 2008 19. dubna 2009 1 Trojúhelníkové pláty obecně 2 Barycentrické
Využití programu AutoCAD při vytváření geometrie konstrukce v prostředí programu ANSYS
 Využití programu AutoCAD při vytváření geometrie konstrukce v prostředí programu ANSYS Abstrakt Jan Pěnčík 1 Článek popisuje a porovnává způsoby možného vytváření geometrie konstrukce v prostředí programu
Využití programu AutoCAD při vytváření geometrie konstrukce v prostředí programu ANSYS Abstrakt Jan Pěnčík 1 Článek popisuje a porovnává způsoby možného vytváření geometrie konstrukce v prostředí programu
Předpokládané znalosti žáka 1. stupeň:
 Předpokládané znalosti žáka 1. stupeň: ČÍSLO A POČETNÍ OPERACE používá přirozená čísla k modelování reálných situací, počítá předměty v daném souboru, vytváří soubory s daným počtem prvků čte, zapisuje
Předpokládané znalosti žáka 1. stupeň: ČÍSLO A POČETNÍ OPERACE používá přirozená čísla k modelování reálných situací, počítá předměty v daném souboru, vytváří soubory s daným počtem prvků čte, zapisuje
Matematika. ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání:
 Studijní obor: Aplikovaná chemie Učební osnova předmětu Matematika Zaměření: ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání: denní Celkový počet vyučovacích hodin za
Studijní obor: Aplikovaná chemie Učební osnova předmětu Matematika Zaměření: ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání: denní Celkový počet vyučovacích hodin za
Zavedeme-li souřadnicový systém {0, x, y, z}, pak můžeme křivku definovat pomocí vektorové funkce.
 KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
Text úlohy. Která barva nepatří do základních barev prostoru RGB? Vyberte jednu z nabízených možností: a. Černá b. Červená c. Modrá d.
 Úloha 1 Která barva nepatří do základních barev prostoru RGB? a. Černá b. Červená c. Modrá d. Zelená Úloha 2 V rovině je dán NEKONVEXNÍ n-úhelník a bod A. Pokud paprsek (polopřímka) vedený z tohoto bodu
Úloha 1 Která barva nepatří do základních barev prostoru RGB? a. Černá b. Červená c. Modrá d. Zelená Úloha 2 V rovině je dán NEKONVEXNÍ n-úhelník a bod A. Pokud paprsek (polopřímka) vedený z tohoto bodu
Praktické využití Mathematica CalcCenter. Ing. Petr Kubín, Ph.D. xkubin@fel.cvut.cz www.powerwiki.cz Katedra elektroenergetiky, ČVUT v Praze, FEL
 Praktické využití Mathematica CalcCenter Ing. Petr Kubín, Ph.D. xkubin@fel.cvut.cz www.powerwiki.cz Katedra elektroenergetiky, ČVUT v Praze, FEL Obsah Popis Pojetí Vlastnosti Obecná charakteristika Ovladače
Praktické využití Mathematica CalcCenter Ing. Petr Kubín, Ph.D. xkubin@fel.cvut.cz www.powerwiki.cz Katedra elektroenergetiky, ČVUT v Praze, FEL Obsah Popis Pojetí Vlastnosti Obecná charakteristika Ovladače
ALLPLAN BRIDGE PARAMETRICKÉ NAVRHOVÁNÍ MOSTŮ. INTELIGENTNÍ A FLEXIBILNÍ PŘEJDĚTE NA NAŠE PROFESIONÁLNÍ BIM PRODUKTY PRO NÁVRH A KONSTRUKCI MOSTŮ
 ALLPLAN BRIDGE PARAMETRICKÉ NAVRHOVÁNÍ MOSTŮ. INTELIGENTNÍ A FLEXIBILNÍ PŘEJDĚTE NA NAŠE PROFESIONÁLNÍ BIM PRODUKTY PRO NÁVRH A KONSTRUKCI MOSTŮ NOVÉ! ALLPLAN BRIDGE Stáhněte si bezplatnou zkušební verzi
ALLPLAN BRIDGE PARAMETRICKÉ NAVRHOVÁNÍ MOSTŮ. INTELIGENTNÍ A FLEXIBILNÍ PŘEJDĚTE NA NAŠE PROFESIONÁLNÍ BIM PRODUKTY PRO NÁVRH A KONSTRUKCI MOSTŮ NOVÉ! ALLPLAN BRIDGE Stáhněte si bezplatnou zkušební verzi
SolidWorks. SW je parametrický 3D modelář a umožňuje. Postup práce v SW: Prostředí a ovládání
 SolidWorks Prostředí a ovládání SW je parametrický 3D modelář a umožňuje objemové a plošné modelování práci s rozsáhlými sestavami automatické generování výrobních výkresu spojení mezi modelováním dílu,
SolidWorks Prostředí a ovládání SW je parametrický 3D modelář a umožňuje objemové a plošné modelování práci s rozsáhlými sestavami automatické generování výrobních výkresu spojení mezi modelováním dílu,
NetStork 7.0 Co se změnilo od verze 6.0?
 Co se změnilo od verze 6.0? 1 Obsah 1 Nástroj pro správu vrstev (podkladových map)... 3 2 Kopírování struktury podzemní trasy... 3 3 Modelování optických rozvaděčů... 5 4 Import dat z DWG/DXF... 6 5 Export
Co se změnilo od verze 6.0? 1 Obsah 1 Nástroj pro správu vrstev (podkladových map)... 3 2 Kopírování struktury podzemní trasy... 3 3 Modelování optických rozvaděčů... 5 4 Import dat z DWG/DXF... 6 5 Export
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Cvičení z matematiky Náplň: Systematizace a prohloubení učiva matematiky Třída: 4. ročník Počet hodin: 2 Pomůcky: Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné obory
Předmět: Cvičení z matematiky Náplň: Systematizace a prohloubení učiva matematiky Třída: 4. ročník Počet hodin: 2 Pomůcky: Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné obory
Vzorce počítačové grafiky
 Vektorové operace součet vektorů rozdíl vektorů opačný vektor násobení vektoru skalárem úhel dvou vektorů velikost vektoru a vzdálenost dvojice bodů v rovině (v prostoru analogicky) u = B A= b a b a u
Vektorové operace součet vektorů rozdíl vektorů opačný vektor násobení vektoru skalárem úhel dvou vektorů velikost vektoru a vzdálenost dvojice bodů v rovině (v prostoru analogicky) u = B A= b a b a u
Obsah. Úvod do prostorového modelování 9. Prostředí AutoCADu při práci ve 3D 15 KAPITOLA 1 KAPITOLA 2
 KAPITOLA 1 Úvod do prostorového modelování 9 Produkty společnosti Autodesk 9 3D řešení 10 Vertikální řešení založené na platformě AutoCAD 10 Obecný AutoCAD 11 Obecné 2D kreslení 11 Prohlížeče a pomocné
KAPITOLA 1 Úvod do prostorového modelování 9 Produkty společnosti Autodesk 9 3D řešení 10 Vertikální řešení založené na platformě AutoCAD 10 Obecný AutoCAD 11 Obecné 2D kreslení 11 Prohlížeče a pomocné
SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE
 SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Řešení kruţnicových oblouků v souřadnicích) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec 2015
SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Řešení kruţnicových oblouků v souřadnicích) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec 2015
Obsah. Předmluva 15 KAPITOLA 1 17 KAPITOLA 2 39
 Předmluva 15 KAPITOLA 1 17 AutoCAD Tour 17 Úvod 17 Spuštění programu AutoCAD 18 Okno aplikace AutoCAD 20 Ovládací prvky 22 Příkazový řádek 25 Dynamická výzva 28 Vizuální nastavení 29 Práce s výkresovými
Předmluva 15 KAPITOLA 1 17 AutoCAD Tour 17 Úvod 17 Spuštění programu AutoCAD 18 Okno aplikace AutoCAD 20 Ovládací prvky 22 Příkazový řádek 25 Dynamická výzva 28 Vizuální nastavení 29 Práce s výkresovými
Systematizace a prohloubení učiva matematiky. Učebna s dataprojektorem, PC, grafický program, tabulkový procesor. Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky Systematizace a prohloubení učiva matematiky 4. ročník 2 hodiny Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky Systematizace a prohloubení učiva matematiky 4. ročník 2 hodiny Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné
Polygonální objekty v Rhinoceros Volné modelování
 přednáška 10 Polygonální objekty v Rhinoceros Volné modelování 10.1 Polygonální objekty v Rhinoceros Jak již bylo zmíněno v první přednášce, program Rhinoceros je plošný modelář a při popisu svých objektů
přednáška 10 Polygonální objekty v Rhinoceros Volné modelování 10.1 Polygonální objekty v Rhinoceros Jak již bylo zmíněno v první přednášce, program Rhinoceros je plošný modelář a při popisu svých objektů
ŠVP Školní očekávané výstupy. - vytváří konkrétní soubory (peníze, milimetrový papír, apod.) s daným počtem prvků do 100
 5.2 MATEMATIKA A JEJÍ APLIKACE 5.2.1 MATEMATIKA A JEJÍ APLIKACE Matematika 1. období 3. ročník RVP ZV Obsah RVP ZV Kód RVP ZV Očekávané výstupy ŠVP Školní očekávané výstupy ŠVP Učivo M3101 používá přirozená
5.2 MATEMATIKA A JEJÍ APLIKACE 5.2.1 MATEMATIKA A JEJÍ APLIKACE Matematika 1. období 3. ročník RVP ZV Obsah RVP ZV Kód RVP ZV Očekávané výstupy ŠVP Školní očekávané výstupy ŠVP Učivo M3101 používá přirozená
Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory
 Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory Zkouška ověřuje znalost základních pojmů, porozumění teorii a schopnost aplikovat teorii při
Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory Zkouška ověřuje znalost základních pojmů, porozumění teorii a schopnost aplikovat teorii při
Matematika PRŮŘEZOVÁ TÉMATA
 Matematika ročník TÉMA 1-4 Operace s čísly a - provádí aritmetické operace v množině reálných čísel - používá různé zápisy reálného čísla - používá absolutní hodnotu, zapíše a znázorní interval, provádí
Matematika ročník TÉMA 1-4 Operace s čísly a - provádí aritmetické operace v množině reálných čísel - používá různé zápisy reálného čísla - používá absolutní hodnotu, zapíše a znázorní interval, provádí
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
( ) ( ) ( ) Tečny kružnic I. Předpoklady: 4501, 4504
 7.5.5 Tečny kružnic I Předpoklady: 451, 454 Pedagogická poznámka: Následující dvě hodiny jsou na gymnázium asi početně nejnáročnější. Ačkoliv jsou příklady optimalizované na co nejmenší početní obtížnost,
7.5.5 Tečny kružnic I Předpoklady: 451, 454 Pedagogická poznámka: Následující dvě hodiny jsou na gymnázium asi početně nejnáročnější. Ačkoliv jsou příklady optimalizované na co nejmenší početní obtížnost,
PROGRAMY PRO GIS. Formovat/formulovat problém pro aplikaci v počítači. Fungování GIS programů na základní úrovni - "uvažovat" jako počítač
 PROGRAMY PRO GIS Formovat/formulovat problém pro aplikaci v počítači Fungování GIS programů na základní úrovni - "uvažovat" jako počítač Jak počítače řeší problémy procesor central processing unit - CPU
PROGRAMY PRO GIS Formovat/formulovat problém pro aplikaci v počítači Fungování GIS programů na základní úrovni - "uvažovat" jako počítač Jak počítače řeší problémy procesor central processing unit - CPU
Diplomová práce Prostředí pro programování pohybu manipulátorů
 Diplomová práce Prostředí pro programování pohybu manipulátorů Štěpán Ulman 1 Úvod Motivace: Potřeba plánovače prostorové trajektorie pro výukové účely - TeachRobot Vstup: Zadávání geometrických a kinematických
Diplomová práce Prostředí pro programování pohybu manipulátorů Štěpán Ulman 1 Úvod Motivace: Potřeba plánovače prostorové trajektorie pro výukové účely - TeachRobot Vstup: Zadávání geometrických a kinematických
KOMPLEXNÍ VZDĚLÁVÁNÍ KATEDRA STROJNÍ SPŠSE a VOŠ LIBEREC
 KOMPLEXNÍ VZDĚLÁVÁNÍ KATEDRA STROJNÍ SPŠSE a VOŠ LIBEREC CNC CAM Cíl podproduktu HSM Works Tento kurz si klade za cíl naučit uživatele ovládat program HSMWorks. Dalším cílem je naučit uživatele základním
KOMPLEXNÍ VZDĚLÁVÁNÍ KATEDRA STROJNÍ SPŠSE a VOŠ LIBEREC CNC CAM Cíl podproduktu HSM Works Tento kurz si klade za cíl naučit uživatele ovládat program HSMWorks. Dalším cílem je naučit uživatele základním
Tvorba prezentaci v Autodesk Inventoru 10
 Tvorba prezentaci v Autodesk Inventoru 10 Příprava montážní dokumentace vyžaduje věnovat zvýšenou pozornost postupu sestavování jednotlivých strojních uzlů a detailům jednotlivých komponentů. Inventoru
Tvorba prezentaci v Autodesk Inventoru 10 Příprava montážní dokumentace vyžaduje věnovat zvýšenou pozornost postupu sestavování jednotlivých strojních uzlů a detailům jednotlivých komponentů. Inventoru
Obsah. Předmluva 13 KAPITOLA 1 KAPITOLA 2
 Předmluva 13 KAPITOLA 1 AutoCAD Tour 15 Úvod 15 Spuštění programu AutoCAD 15 Okno aplikace AutoCAD 17 Ovládací prvky 19 Příkazový řádek 22 Dynamická výzva 25 Vizuální nastavení 26 Práce s výkresovými soubory
Předmluva 13 KAPITOLA 1 AutoCAD Tour 15 Úvod 15 Spuštění programu AutoCAD 15 Okno aplikace AutoCAD 17 Ovládací prvky 19 Příkazový řádek 22 Dynamická výzva 25 Vizuální nastavení 26 Práce s výkresovými soubory
Grafická data jsou u 2D vektorové grafiky uložena ve voxelech NEPRAVDA Grafická data jsou u rastrové grafiky uložena v pixelech PRAVDA Grafická data
 Grafická data jsou u 2D vektorové grafiky uložena ve voxelech Grafická data jsou u rastrové grafiky uložena v pixelech Grafická data jsou u vektorové grafiky uložena v pixelech Na rozdíl od rastrové grafiky
Grafická data jsou u 2D vektorové grafiky uložena ve voxelech Grafická data jsou u rastrové grafiky uložena v pixelech Grafická data jsou u vektorové grafiky uložena v pixelech Na rozdíl od rastrové grafiky
Vzdělávací obor matematika
 "Cesta k osobnosti" 6.ročník Hlavní okruhy Očekávané výstupy dle RVP ZV Metody práce (praktická cvičení) obor navázání na již zvládnuté ročník 1. ČÍSLO A Žák používá početní operace v oboru de- Dělitelnost
"Cesta k osobnosti" 6.ročník Hlavní okruhy Očekávané výstupy dle RVP ZV Metody práce (praktická cvičení) obor navázání na již zvládnuté ročník 1. ČÍSLO A Žák používá početní operace v oboru de- Dělitelnost
Adobe Photoshop 9. Vytváření cest nástrojem Pero
 olygr.cz XMF, montážní program 1. Seznámení s programem Adobe Photoshop 9. Vytváření cest nástrojem Pero Vytvořil: Tomáš Fab dní škola polygrafická, 110 27 00 Brno ody zdokonalující edukaci na ISŠP 34.05381
olygr.cz XMF, montážní program 1. Seznámení s programem Adobe Photoshop 9. Vytváření cest nástrojem Pero Vytvořil: Tomáš Fab dní škola polygrafická, 110 27 00 Brno ody zdokonalující edukaci na ISŠP 34.05381
volitelný předmět ročník zodpovídá CVIČENÍ Z MATEMATIKY 8. MACASOVÁ Učivo obsah
 Výstupy žáka ZŠ Chrudim, U Stadionu Učivo obsah Mezipředmětové vztahy Metody + formy práce, projekty, pomůcky a učební materiály ad. Poznámky je schopen vypočítat druhou mocninu a odmocninu nebo odhadnout
Výstupy žáka ZŠ Chrudim, U Stadionu Učivo obsah Mezipředmětové vztahy Metody + formy práce, projekty, pomůcky a učební materiály ad. Poznámky je schopen vypočítat druhou mocninu a odmocninu nebo odhadnout
Mechanika s Inventorem
 Mechanika s Inventorem 2. Základní pojmy CAD data FEM výpočty Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Optimalizace Tomáš MATOVIČ, publikace 1 Obsah přednášky: Lagrangeův
Mechanika s Inventorem 2. Základní pojmy CAD data FEM výpočty Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Optimalizace Tomáš MATOVIČ, publikace 1 Obsah přednášky: Lagrangeův
Zadejte ručně název první kapitoly. Manuál. Rozhraní pro program ETABS
 Zadejte ručně název první kapitoly Manuál Rozhraní pro program ETABS Všechny informace uvedené v tomto dokumentu mohou být změněny bez předchozího upozornění. Žádnou část tohoto dokumentu není dovoleno
Zadejte ručně název první kapitoly Manuál Rozhraní pro program ETABS Všechny informace uvedené v tomto dokumentu mohou být změněny bez předchozího upozornění. Žádnou část tohoto dokumentu není dovoleno
1. Přímka a její části
 . Přímka a její části přímka v rovině, v prostoru, přímka jako graf funkce, konstrukce přímky nebo úsečky, analytická geometrie přímky, přímka jako tečna grafu, přímka a kuželosečka Přímka v rovině a v
. Přímka a její části přímka v rovině, v prostoru, přímka jako graf funkce, konstrukce přímky nebo úsečky, analytická geometrie přímky, přímka jako tečna grafu, přímka a kuželosečka Přímka v rovině a v
Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].
![Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y]. Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].](/thumbs/91/104981778.jpg) Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
