SOUČASNÉ TRENDY V APLIKACÍCH STATISTICKÝCH A KVANTITATIVNÍCH METOD V KONTEXTU PROSTOROVÝCH ANALÝZ
|
|
|
- Tereza Kubíčková
- před 8 lety
- Počet zobrazení:
Transkript
1 Medzinárodná vedecká konferencia TRENDY V APLIKOVANÍ ŠTATISTICKÝCH METÓD PRI ZLEPŠOVANÍ KVALITY júl 2010, Malá Ida ISBN SOUČASNÉ TRENDY V APLIKACÍCH STATISTICKÝCH A KVANTITATIVNÍCH METOD V KONTEXTU PROSTOROVÝCH ANALÝZ CURRENT TRENDS IN APPLICATIONS OF STATISTICS AND QUANTITATIVE METHODS IN THE CONTEXT OF SPATIAL ANALYSIS Eva Heřmanová RNDr. Eva Heřmanová (odborná asistentka) Katedra arts managementu Podnikohospodářská fakulta Vysoké školy ekonomické v Praze, Česká republika eva.hermanova@seznam.cz Abstrakt Předkládaný příspěvek by měl velmi stručnou formou představit hlavní specifika a problémy související s používáním klasických statistických metod na prostorově definovaná data. Jedná se zejména o problém tzv. prostorové autokorelace a prostorové nestacionarity, jejichž existenci do relativně nedávné doby sociální geografové víceméně nevnímali, resp. jim nevěnovali zvláštní pozornost a v podstatě jim nepříkládali žádný význam. Kľúčové slová Prostorové analýzy, statistické a kvantitatívni metody Abstract This paper should present a very concise form the main specifics and problems associated with using traditional statistical methods for spatial data defined. These include so-called problem. Spatial autocorrelation and spatial non-stationarity, the existence of relatively recent social geographers broadly "perceive", respectively. They did not pay special attention and virtually no attach much importance to them. Key words Spatial analysis, statistical and quantitative methods 23
2 TRENDY V APLIKOVANÍ ŠTATISTICKÝCH METÓD PRI ZLEPŠOVANÍ KVALITY 2010 Úvod Předkládaný příspěvek by měl velmi stručnou formou představit hlavní specifika a problémy související s používáním klasických statistických metod na prostorově definovaná data. Jedná se zejména o problém tzv. prostorové autokorelace a prostorové nestacionarity, jejichž existenci do relativně nedávné doby sociální geografové víceméně nevnímali, resp. jim nevěnovali zvláštní pozornost a v podstatě jim nepříkládali žádný význam. Teprve se vznikem nových kvantitativních metod vyvinutých explicitně pro prostorové analýzy (např. Fotheringham, Brundson, Charlton (2000)) se zviditelňuje i nová kvantitativní geografie, která již není pouhým uživatelem zavedených statistických metod, ale zabývá se i vlastní tvorbou, specifickými aplikacemi a novými myšlenkami v kontextu možného zkvalitnění prováděných analýz prostorových dat, a to nejen na poli geografie. Velké množství problémů spojených s analýzami prostorových dat, jež však nelze vtěsnat do tohoto příspěvku, je řešeno nejen sociální geografií, ale i prostorovou statistikou, prostorovou ekonometrií či nejobecněji řečeno prostorovým modelováním sociálně ekonomických charakteristik a vztahů. K těmto účelům jsou využívány zejména regresní modely zahrnující i prostorovou dimenzi (Anselin 1988), které bývají odvozeny od regresních modeků a analýz časových řad (Hepple 1996). Terminologicky lze snad ještě předeslat (viz i Horák 2002), že pojem analýza prostorových dat nelze ztotožnit s pojmem prostorová analýza dat. V prvním případě totiž může jít o jakoukoliv popisnou či vývojovou - analýzu prostorově definovaných dat, ve druhém případě pak jde o výhradně geografický úhel pohledu, tj. o snahu o podchycení, poznání či vysvětlení prostorových zákonitostí, vztahů či územních gradientů. Ve vztahu k analýze prostorových dat je nutné zdůraznit i význam geografických informačních systémů (dále GIS), jejichž aplikace umožňuje získat nové poznatky a informace o zkoumaných jevech. Hlavní výhodou GISů je možnost zahrnutí dále popsaných metod a vizualizace výsledků prostorových analýz na libovolné hierarchické úrovni. I když použití GISů není nutnou podmínkou prostorového modelování, přináší jejich propojení se statistickými analýzami výsledky, které bychom jinak těžko získávali. Z autorů a ze základních prací, z nichž tento příspěvek přímo nebo i nepřímo, ale nejvýznamněji čerpá, resp. na něž navazuje, je třeba uvést zejména následující práce - Nezdařilová (1984b), Spurná (2006), Spurná (2008a, 2008b), Netrdová, Nosek (2009). Specifika a povaha prostorových dat Problémy spojené se statistickou analýzou geografických dat vyplývají z jejich komplexní povahy (Hampl 1971, Hampl 1983) a dále z toho, že jak jevy, tak i vztahy nelze ve zkoumaném území považovat za homogenní, neboť se mění v závislosti na umístění v prostoru, tj. v závislosti a konkrétních reálných podmínkách. Aplikaci statistických metod v geografii komplikuje samotná prostorová, tj. vzájemně závislá povaha geografických dat, čímž nebývá ve většině případů splněna podmínka nezávislosti dat, která je vyžadována v souvislosti s použitím metod regresního a korelačního počtu. Další problémy spojené s používáním standartních statistických metod souvisí s tím, že řada sociálně-ekonomických jevů a je popisujících souborů dat nevykazuje normální rozložení četností, jež je předpokládáno (viz i Korčák 1941). To má dopad zejména na veličiny popisné statistiky, např. při měření variability souborů dat aj. Jednou z dalších diskutovaných otázek spojených s analýzou prostorových dat je volba určitého typu i hierarchie územních jednotek, kdy různá vymezení sousedních prostorových jednotek mohou přispět k rozdílným výsledkům. Možnost takovéhoto zkreslení je proto potřeba si při analýzách neustále uvědomovat (podrobněji viz Spurná 2006, s ). 24
3 Eva Heřmanová Problém a metoda prostorové autokorelace Do geografické literatury zavedli pojem prostorová autokorelace Cliff, Ord (1973), když z ekonometrie převzali princip metody časové autokorelace. Základní myšlenka prostorové autokorelace nebyla nicméně ani předtím v geografii neznámá, ba právě naopak. Jednu ze stěžejních otázek geografického výzkumu totiž tvoří otázka, zda geografická prostorová data vykazují prostorovou závislost, tj. do jaké míry je výskyt určitého jevu v dané územní jednotce závislý na výskytu tohoto jevu v jednotkách sousedních. Na myšlenku, resp. existenci prostorové autokorelace však upozorňovala řada autorů již předtím, když např. uváděla, že charakteristiky určitého místa nejsou závislé jen na ostatních charakteristikách tohoto místa, ale jsou také ovlivněny vazbami k ostatním místům a jejich vlivem (Spurná 2006, s. 76). Matematicky řečeno lze prostorovou autokorelaci chápat jako pravděpodobnost jevu y v prostorové jednotce i je určitou funkcí pravděpodobností tohoto jevu v jednotkách j, které jsou prostorově blízké jednotce i. (Nezdařilová 1984a). Laičtěji řečeno, jak vyplývá i z prostého překladu tohoto pojmu, představuje prostorová autokorelace korelaci jednoho jevu se sebou samým v prostoru a projevuje se statisticky významným uspořádáním hodnot sledovaného jevu v daném území. Stejně jako v případě párové korelace neukazuje ani signifikantní prostorová autokorelace na kauzální vztah a nevypovídá nic o příčinách daného prostorového uspořádání. (Nezdařilová 1984a). Prostorová autokorelace je dnes měřena různými statistikami (Spurná 2006, s , Netrdová, Nosek 2009), které popisují míru (ne)podobnosti pozorovaných hodnot v blízkých územních jednotkách (či bodech). Pokud vysoké hodnoty dané proměnné vykazují tendenci shlukovat se v některých částech studovaného regionu a nízké hodnoty tíhnou k tomu shlukovat se v jiných oblastech, hovoříme o pozitivní prostorové autokorelaci. Analogicky i naopak, pokud se vysoké hodnoty proměnné nacházejí v těsné blízkosti s nízkými hodnotami, hovoříme o negativní prostorové autokorelaci. Pokud jsou data lokalizována tak, že neexistuje žádný vztah mezi blízkými hodnotami, hovoříme o nulové prostorové autokorelaci. Dnes je již prokázáno, že téměř všechna prostorová data vykazují nějakou formu pozitivní prostorové autokorelace, což může mít různé dopady na závěry v rámci prostorového modelování (Fotheringham a kol. 2002). Problém prostorové nestacionarity regresních modelů Pojem prostorová nestacionarita (Fotheringham a kol. 2002), se týká nestability zkoumaných často zejména sociálních - jevů a vztahů v prostoru, a to z hlediska a v závislosti na jejich umístění. Laicky řečeno, při použití klasických modelů regresní analýzy lze totiž získat jiný funkční vztah mezi dvěma proměnnými např. v jihozápadní a severovýchodní části Česka, v různě rozvinutých územích (např. v regionech rostoucích, stagnujících či zaostávajících, viz např. Lavický 2009) nebo i na různých hierarchických úrovních (obce, okresy, regiony). Pro věcně shodnou zkoumanou souvztažnost mezi proměnnými lze tedy získat vzájemně se lišící dílčí lokální regresní modely, které jsou navíc zpravidla i odlišné od modelů globálních, tj. např. za celé Česko. Problematika prostorové nestacionarity tedy velmi úzce souvisí se současným trendem a zaměřením kvantitativních metod na lokální statistiky. Ve statistické literatuře se v souvislosti se zmíněnou problematikou nestacionarity setkáváme s pojmem stabilní regresní funkce, a to ve smyslu obecně platného vztahu. Hebák, Novák (1978, s. 72) definují stabilní regresní funkce jakožto funkce, jejichž typ je v čase a v prostoru relativně neměnný a jejichž parametry jsou neměnné nebo se mění formalizovatelným způsobem. V souvislosti se stabilitou regresních funkcí je také možno diskutovat i otázku složitosti a výstižnosti regresního modelu. Je zřejmé, že se zvyšováním počtu parametrů či počtu statisticky významných proměnných v určitém regresním modelu nebo použitím vhodného složitějšího tvaru matematické funkce dochází obecně ke zvýšení 25
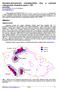
4 TRENDY V APLIKOVANÍ ŠTATISTICKÝCH METÓD PRI ZLEPŠOVANÍ KVALITY 2010 výstižnosti tohoto modelu. Zároveň však model ztrácí svoji zobecňující schopnost a v extrémním případě by se mohl stát i jen formálně přesným popisem specifických vztahů v určitém prostoru a čase (Nezdařilová 1983a). Jak k tomu dál ještě výstižně poznamenávají Hebák, Novák (1978), neustálé zlepšování modelu z hlediska kritéria založeného na shodě údajů s regresním modelem může mít za následek vzdálení se od obecných rysů zkoumané závislosti, tzn. takový výsledek, že daným údajům perfektně vyhovující funkce bude časoprostorově zcela nestabilní. Mezi hlavní důvody prostorové nestability regresních funkcí patří bezesporu pravá podstata analyzovaných vztahů či závislostí, které se za určitých okolností mohou v prostoru skutečně odlišovat. Rozdíly mohou způsobovat například odlišné lidské postoje či preference v různých oblastech, rozdílné reakce na stejné podněty může indikovat i administrativní či politické prostředí. Často se v této souvislosti hovoří o kontextuálních faktorech ovlivňujících chování jedinců. (Spurná 2006, s. 85). Myšlenka, že chování jednotlivců se může i velmi významně v prostoru odlišovat koresponduje nejen s postmoderními přístupy v geografii (zdůrazňujícími místo a lokální podmínky jako důležitý rámec pro pochopení příčin určitého chování, viz např. Holt-Jensen, 1999), ale i s řadou sociologických prací zkoumajících problematiku tzv. regionálních mentalit. Další důvod prostorové nestacionarity lze možná spatřovat i v nesprávně navrženém regresním modelu (nezahrnutí některých významných proměnných) nebo v použití nesprávného funkčního vztahu, které může vést až k přílišnému zjednodušení reality a reálné nemožnosti nalezení jakýchkoli pravidelností, byť možná existujících. Z výše uvedených důvodů je jak identifikace odchylek od globálního modelu (klasicky metodou zbytků z regrese), tak zejména identifikace odchylek lokálně či regionálně platných vztahů (dále popsaná metoda geograficky vážené regrese) velmi přínosná, neboť umoňuje lepší vhled do problematiky a nasměrování i větší efektivnost dalšího případného výzkumu. Jednoduchý a velmi názorný příklad prostorové nestacionarity zjištěných regresních vztahů si dovolím pro oživení příspěvku převzít z diplomové práce P. Spurné (Netrdové) (2006), jíž mi bylo ctí dělat oponentku. Autorka propočetla vztah mezi podílem vysokoškolsky vzdělaných osob a volební účastí sledovanou na úrovni obcí a městských částí, a to zvlášť pro okresy Blansko, Brno-město a Brno-venkov. Celkový globální výsledek za 296 územních jednotek vypovídá o mírné negativní závislosti mezi uvedenými proměnnými. Propočtou-li se však dílčí regresní modely za jednotlivé okresy, vychází každá ze závislostí výrazně odlišně, ve dvou případech (okres Brno-město a Brno-venkov) dokonce dochází k převrácení směru závislosti (viz obr. č. 1). Jak uvádí Spurná (2006), zatímco obce v okrese Blansko s obecně nižším podílem vysokoškolsky vzdělaných osob a vysokou volební účastí vykazují negativní závislost znázorněnou přímkou s větším sklonem, u dvou brněnských okresů, jejichž jednotky jsou více variabilní z hlediska zastoupení vysokoškolsky vzdělaných osob, se závislost obrací výrazným způsobem na pozitivní. Další prostorový příklad Simpsonova paradoxu u vztahu mezi cenou domu a hustotou zalidnění nalezneme ve Fotheringham a kol. (2002). Výše zmíněný jev je znám jako tzv. Simpsonův paradox (Hendl 2004) a přestože se jeho původní popsání vztahovalo na neprostorová data, platí jak je vidět níže - i pro různě agregovaná prostorová data. Při nejrůznějších geografických analýzách podobného typu tedy může dojít k tomu, že celkový výsledek za hierarchicky větší území nejen, že nebude reprezentovat skutečné vztahy mezi proměnnými, ale bude možná i pravým opakem vztahů reálných, platných na lokální úrovni. 26
5 Eva Heřmanová Obr. č. 1: Simpsonův paradox na příkladu volebního chování Zdroj: Spurná, 2006, s. 87 Výše uvedeným problémům je zejména v poslední době v české geografické literatuře věnována zvýšená pozornost a lze říci, že svým způsobem lze považovat jejich diskusi, zviditelňování a zejména snahu o řešení za impuls pro další vývoj speciálních kvantitativních metod, které lze označit za prostorové, a tedy i geografické. Jednou z nich je i metoda geograficky vážené regrese (geographically weighted regression, dále GWR). Metoda geograficky vážené regrese Metoda GWR patří do skupiny metod lokálních analýz, které zohledňují prostorové efekty na zkoumané vztahy (další, zde nejmenované metody viz Spurná 2006, s ) a výrazným způsobem tak rozšiřují možnosti statistické analýzy prostorových dat. Autory metody, která vznikla v 90. letech 20. století a kterou lze označit i jako metodu analýzy prostorově proměnlivých vztahů, jsou profesor kvantitativní geografie Fotheringham a jeho spolupracovníci Brunsdon a Charlton. Tito autoři také vyvinuli speciální software GWR (viz jehož výstupy lze propojit jak s běžnými statistickými programy (SPSS), tak i se softwarem GISů (ArcMap). Protože na tomto místě nelze plně vysvětlit matematický aparát, resp. matematický a statistický rámec metody GWR, je třeba zájemce odkázat na primární zdroj (citovanou publikaci autorů GWR a příslušné internetové stránky). Jen velmi orientačně lze snad uvést rozdíl mezi klasickým regresním modelem (spojeným s požadavkem a představou prostorové stacionarity regresních parametrů) a metodou GWR, která využívá pohyblivé, resp. proměnlivé lokální regresní koeficienty, tj. jinak řečeno, přímo předpokládá existenci odlišných prostorových vztahů dvou a více proměnných. Jestliže je klasický regresní model popsán jako y = + β x + ε, lze model geograficky vážené regrese obecně vyjádřit jako y = β ( u, v ) β ( u, v ) i i β 0 k k ik + x + 0 i i k k i i ik i, kde kde (u i,v i ) označuje souřadnice i-tého bodu v prostoru a lokální regresní koeficient β k (u i,v i ) vyjadřuje hodnotu spojité funkce β k (u,v) v bodě i. i ε 27
6 TRENDY V APLIKOVANÍ ŠTATISTICKÝCH METÓD PRI ZLEPŠOVANÍ KVALITY 2010 Mezi základní výstupy, které lze touto metodou získat, patří soubor odhadů lokálních regresních koeficientů, který je obvykle znázorňován kartograficky (jako spojitý povrch). Tyto odhady mohou být rovněž testovány z hlediska významnosti prostorových odlišností. Dále mohou být jako výstup získány a využity i lokální směrodatné odchylky a lokální verze dalších klasických regresních výstupů (lokální absolutní člen, lokální koeficient determinace). Příklady a možnosti aplikace GWR Pro ilustraci a snad i inspiraci lze dále alespoň stručně a výběrově uvést příklady aplikace metody GWR, které byly dosud publikovány. Brunsdon a kol. (1998) použili diskutovanou metodu k hledání závislostí mezi dlouhodobou nemocnosti lidí ve věku 45 až 65 let a různými socioekonomickými charakteristikami (nezaměstnanost mužů, hustota zalidnění, průměrný počer ososb připadajících na jednu místnost) v oblasti severní Anglie. Fotheringham a kol. (2001, 2002) např. zkoumali prostorovou nestacionaritu faktorů školní (ne)úspěšnosti žáků (ve standardizovaných testech z matematiky) na základních školách v severní Anglii. Mezi faktory, které do ananlýzy zahrnuli patřila např. velikost škol, nezaměstnanost ve spádové oblasti školy, podíl jednočlenných domácností či podíl černošského obyvatelstva atd. Výsledky analýz v obou případech prokázaly existenci výrazných lokální odchylky ve sledovaných vztazích. O rok později byl vytvořen model závislosti tržní ceny domu na jeho kvalitativních charakteristikách (počet koupelen, stáří domu, vzdálenost od centra), jenž byl zkoumán z hlediska jeho lokálních modifikací. Další z modelů, který uvádí i Spurná (2006), vytvořili Huang a Leung (2002) v rámci zkoumání úrovně regionální industrializace v čínské provincii Jiangsu; mezi zkoumané podmiňující faktory pak zahrnuli např. míru urbanizace a HDP na 1 obyvatele. Další model vytvořili Kyratso a Yiorgos (2004), kteří cenu půdy v měřítku domovních bloků zkoumali v metropolitní oblasti řeckého města Volos a vztahovali ji ke vzdálenosti od obchodních center, podílu zastavěnosti ploch a k dalším veličinám. V Česku je zatím asi jedinou aplikací převážně didakticky zaměřený model geograficky vážené regrese zkoumající globální a lokální podoby vztahu mezi volební účastí a podílem vysokoškolsky vzdělaného obyvatelstva (Spurná 2006). V blíže necitované zahraniční literatuře ( se však snad vyskytují i aplikace GWR, kde tato metoda byla využita k modelování vztahu mezi vývojem kruhové výčetní základny a výčetní tloušťky a k upřesnění parametrů výškových funkcí, tj. v rámci modelování specifické problematiky lesních porostů. Závěr Lze říci, že donedávna bylo používání statistických a kvantitativních metod v geografii výrazně volnější než v jiných, exaktnějších oborech. Specifická povaha geografických dat (vzájemná prostorová závislost jevů, levostranně asymetrické rozložení četností) společně se způsobem vymezení územních jednotek způsobovaly porušování řady předpokladů klasické popisné statistiky i metod regresního a korelačního počtu. Především však - z pohledu geografa neoddiskutovatelná existence prostorové nestacionarity sociálněekonomických vztahů by měla být v budoucnu reflektována jak v rámci interpretace výsledků analýz, tak v rámci nových kvantitativních metod, a to daleko více než dosud. Většina z nemnoha dosavadních uživatelů přisuzuje již dnes metodě GWR budoucí vysokou využitelnost v sociálněgeografickém výzkumu a právem ji považuje za statistickou metodu s výraznou explorační povahou a schopností odhalit prostorové odchylky v charakteru zkoumaných vztahů. Výhodou této metody je, že modelovaný vztah vždy popisuje realitu výstižněji ve srovnání s výsledky globálního modelu a že svým způsobem řeší i problém předem daného (např. administrativního) rozčlenění územních jednotek, jež zpravidla neodpovídá přirozenému prostorovému rozložení zkoumaného jevu či vztahu. Výhodou této metody je i její vysoká intuitivní srozumitelnost v kontextu celkem všeobecně známého 28
7 Eva Heřmanová konceptu regresní ananlýzy. Její budoucí pravděpodobně vysokou využitelnost lze spojovat i s neustále se zlepšujícími vizualizačními možnostmi (GIS) a rozvojem počítačové techniky i speciálních softwarů. Aplikační oblasti metody GWR lze spatřovat jak již bylo naznačeno - v prostorové analýze domovního a bytového fondu, v analýze lokálních podmíněností cen nemovitostí, v analýze sítí občanské vybavenosti, ale i sociálně-patologických jevů či lokálních podmínek v kontextu zemědělské výroby či lesnických prací. Máme-li tedy závěrem shrnout hlavní trendy využívání statistických či kvantitativních metod v rámci prostorových analýz, lze uvést zejména primární zaměření na explorační (nikoli nutně generalizující) povahu analýz, na metody lokální analýzy a na vizualizaci výstupů pomocí GISů. Literatura [1] Anselin, L. (1988): Spatial econometrics: Methods and models. Kluwer Academic Publishers, Dordrecht, 284 s. [2] Brundson, C., Fotheringham, S., Charlton, M. (1998): Geographically weighted regression modelling spatial non-stationarity. The Statistician, 47, č. 3, str [3] Cliff, A. D., Ord, J. K. (1973): Spatial autocorrelation. Pion, London, 178 s. [4] Cliff, A. D., Haggett, P., Ord, J. K., Bassett, K., Davies, R. (1975): Elements of spatial structure a quantitative approach. Cambridge University Press, Cambridge, 258 s. [5] Drápela, K.: Využití výsledků NIL ČR pomocí geograficky vážené regrese (GWR). LDF MZLU v Brně, přístup z [6] Fotheringham, A. S., Brundson, C., Charlton, M. (2000): Quantitative geography Perspectives on spatial data analysis. SAGE Publications, London, 270 s. [7] Fotheringham, A. S., Charlton, M. E., Brundson, C. (2001): Spatial variations in school performance: a local analysis using geographically weighted regression. Geographical & Environmental Modelling, 5, č. 1, str [8] Fotheringham, A. S., Brundson, C., Charlton, M. (2002): Geographically weighted regression the analysis of spatially varying relationships. John Wiley & Sons, London, 269 str. [9] Hampl, M. (1971): Teorie diferenciace a komplexity světa. Univerzita Karlova, Praha, 183 s. [10] Hampl, M. (1983): K problematice sociálněgeografických pravidelností. In: Geografický výzkum v Československé akademii věd , sborník referátů. Geografický ústav ČSAV, Liblice, str [11] Hebák, P., Novák, I. (1978): K problému stability regresních funkcí. Statistika 1978, str [12] Hendl, J. (2004): Přehled statistických metod zpracování dat analýza a metaanalýza dat. Portál, Praha, 584 s. [13] Hepple, L. W. (1996): Directions and opportunities in spatial econometrics. In: Longley, P., Batty, M. (eds): Spatial analysis: Modelling in a GIS environment. GeoInformation International, Cambridge, s [14] Heřmanová, E. (1991): Vybrané vícerozměrné statistické metody v geografii. SPN, Praha, 133 s. [15] Hindls, R., Hronová, S., Seger, J., Fischer, J. (2007): Statistika pro ekonomy. 8. vyd. Praha, Professional Publishing, 417 s., ISBN [16] Horák, J. (2002): Prostorová analýza dat. Učební text VŠB-TU Ostrava. [ [17] Holt-Jensen, A. (1999): Geography history and concepts. SAGE Publications, London, 228 s. [18] Huang, Y., Leung, Y. (2002): Analysing regional industrialisation in Jiangsu province using geographically weighted regression. Journal of Geographical Systems, 4, str [19] Korčák, J. (1941): Přírodní dualita statistického rozložení. Statistický obzor, 5 6, str
8 TRENDY V APLIKOVANÍ ŠTATISTICKÝCH METÓD PRI ZLEPŠOVANÍ KVALITY 2010 [20] Kyratso, M., Yiorgos, (2004): Defining a geographically weighted regression model of urban evolution. Application to the city of Volos, Greece. 44th European Congress of the European Regional Science Association: Regions and Fiscal Federalism, University of Porto, , přístup z [21] Lavický, M. (2009): Analýza regionální nezaměstnanosti v České republice během hospodářské recese Diplomová práce. Katedra sociální geografie a regionálního rozvoje PřF UK, Praha, 68 s., rukopis. [22] Meloun, M., Militký, J. (2002): Kompendium statistického zpracování dat. ACADEMIA, Praha, 764 s. [23] Netrdová, P., Nosek, V. (2009): Přístupy k měření významu geografického rozměru společenských nerovnoměrností. Geografie Sborník České geografické společnosti, 2009/1, roč. 114, s [24] Nezdařilová, E. (1984a): Metody kvantitativní analýzy v geografii se zaměřením na metody regrese a korelace. Diplomová práce. Katedra sociální geografie a regionálního rozvoje PřF UK, Praha, 157 s., rukopis. [25] Nezdařilová, E. (1984b): Prostorová autokorelace jako pojem a metoda geografické analýzy. Geografie Sborník ČGS, 89, č. 1, s [26] Pavlík, Z., Kűhnl, K. (1981): Úvod do kvantitativních metod pro geografy. SPN, Praha, 267 s. [27] Spurná, P. (2006): Současné trendy v kvantitativní analýze geografických dat se zaměřením na využití metody geograficky vážené regrese. Diplomová práce. Katedra sociální geografie a regionálního rozvoje PřF UK, Praha, 150 s., rukopis. [28] Spurná, P. (2008a): Prostorová autokorelace všudypřítomný jev při analýze prostorových dat? Sociologický časopis/czech Sociological Review, 2008, Vol. 44, No. 4, s [29] Spurná, P. (2008b): Geograficky vážená regrese metoda analýzy prostorové nestacionarity geografických jevů. Geografie Sborník České geografické společnosti. 113/2, s [30] Unwin, A., Unwin, D. (1998): Exploratory spatial data analysis with local statistics. The Statistician, 47, č. 3, s [31] Wei, Y. D., Yu, D. (2005): Geographically weighted regression. [ [32] Zhang, L., Shi, H. (2004): Local modeling of tree growth by geographically weighted regression. Forest Science, 50, č. 2, s [33] Oficiální stránky týkající se metody GWR. [ [34] Oficiální stránky týkající se softwaru GeoDa. [ 30
Cíl Vyhodnotit současný stav migračně prostorové diferenciace území ČR a migrační tendence na základě údajů za obce ČR
 Cíl Vyhodnotit současný stav migračně prostorové diferenciace území ČR a migrační tendence na základě údajů za obce ČR Data Obce ČR 2011 (Veřejná databáze ČSÚ) SPSS IBM, ArcGIS Proměnné: intenzita migračního
Cíl Vyhodnotit současný stav migračně prostorové diferenciace území ČR a migrační tendence na základě údajů za obce ČR Data Obce ČR 2011 (Veřejná databáze ČSÚ) SPSS IBM, ArcGIS Proměnné: intenzita migračního
Prostorová variabilita
 Prostorová variabilita prostorová závislost (autokorelace) reprezentuje korelaci mezi hodnotami určité náhodné proměnné v místě i a hodnotami téže proměnné v jiném místě j; prostorová heterogenita je strukturální
Prostorová variabilita prostorová závislost (autokorelace) reprezentuje korelaci mezi hodnotami určité náhodné proměnné v místě i a hodnotami téže proměnné v jiném místě j; prostorová heterogenita je strukturální
Karta předmětu prezenční studium
 Karta předmětu prezenční studium Název předmětu: Kvantitativní metody v geografii (KMG) Číslo předmětu: 548 Garantující institut: Garant předmětu: Institut geoinformatiky Ing. Igor Ivan, Ph.D. Kredity:
Karta předmětu prezenční studium Název předmětu: Kvantitativní metody v geografii (KMG) Číslo předmětu: 548 Garantující institut: Garant předmětu: Institut geoinformatiky Ing. Igor Ivan, Ph.D. Kredity:
REGIONÁLNÍ KONCENTRACE AKTIVIT PODNIKŮ. Příklad využití individuálních dat ve spojení s autokorelační statistikou
 REGIONÁLNÍ KONCENTRACE AKTIVIT PODNIKŮ Příklad využití individuálních dat ve spojení s autokorelační statistikou Kristýna Meislová [meislova@tc.cz] 14. dubna 2016 Co bude následovat I. Proč zkoumat prostorovou
REGIONÁLNÍ KONCENTRACE AKTIVIT PODNIKŮ Příklad využití individuálních dat ve spojení s autokorelační statistikou Kristýna Meislová [meislova@tc.cz] 14. dubna 2016 Co bude následovat I. Proč zkoumat prostorovou
3. ROZMÍSTĚNÍ OBYVATELSTVA
 3. ROZMÍSTĚNÍ OBYVATELSTVA O čem je mapový oddíl ROZMÍSTĚNÍ OBYVATELSTVA? Mapový oddíl obsahuje tři mapové listy, které se věnují základním charakteristikám vývoje počtu a rozmístění obyvatelstva v českých
3. ROZMÍSTĚNÍ OBYVATELSTVA O čem je mapový oddíl ROZMÍSTĚNÍ OBYVATELSTVA? Mapový oddíl obsahuje tři mapové listy, které se věnují základním charakteristikám vývoje počtu a rozmístění obyvatelstva v českých
GEOSTATISTIKA. Ing. Jan Popelka, Ph.D. Fakulta životního prostředí UJEP (výběr z materiálu)
 GEOSTATISTIKA Ing. Jan Popelka, Ph.D. Fakulta životního prostředí UJEP (výběr z materiálu) 1 ZÁKLADNÍ POJMY ŠIRŠÍ VYMEZENÍ GEOSTATISTIKY GEOSTATISTIKA je statistická analýza prostorově lokalizovaných dat.
GEOSTATISTIKA Ing. Jan Popelka, Ph.D. Fakulta životního prostředí UJEP (výběr z materiálu) 1 ZÁKLADNÍ POJMY ŠIRŠÍ VYMEZENÍ GEOSTATISTIKY GEOSTATISTIKA je statistická analýza prostorově lokalizovaných dat.
Prostorová autokorelace všudypřítomný jev při analýze prostorových dat?
 Prostorová autokorelace všudypřítomný jev při analýze prostorových dat? PAVLÍNA SPURNÁ* Přírodovědecká fakulta Univerzity Karlovy, Praha Spatial Autocorrelation A Pervasive Phenomenon in the Analysis of
Prostorová autokorelace všudypřítomný jev při analýze prostorových dat? PAVLÍNA SPURNÁ* Přírodovědecká fakulta Univerzity Karlovy, Praha Spatial Autocorrelation A Pervasive Phenomenon in the Analysis of
Statistická analýza jednorozměrných dat
 Statistická analýza jednorozměrných dat Prof. RNDr. Milan Meloun, DrSc. Univerzita Pardubice, Pardubice 31.ledna 2011 Tato prezentace je spolufinancována Evropským sociálním fondem a státním rozpočtem
Statistická analýza jednorozměrných dat Prof. RNDr. Milan Meloun, DrSc. Univerzita Pardubice, Pardubice 31.ledna 2011 Tato prezentace je spolufinancována Evropským sociálním fondem a státním rozpočtem
You created this PDF from an application that is not licensed to print to novapdf printer (http://www.novapdf.com)
 Závislost náhodných veličin Úvod Předchozí přednášky: - statistické charakteristiky jednoho výběrového nebo základního souboru - vztahy mezi výběrovým a základním souborem - vztahy statistických charakteristik
Závislost náhodných veličin Úvod Předchozí přednášky: - statistické charakteristiky jednoho výběrového nebo základního souboru - vztahy mezi výběrovým a základním souborem - vztahy statistických charakteristik
STATISTICKÉ PROGRAMY
 Slezská univerzita v Opavě Obchodně podnikatelská fakulta v Karviné STATISTICKÉ PROGRAMY VYUŽITÍ EXCELU A SPSS PRO VĚDECKO-VÝZKUMNOU ČINNOST Elena Mielcová, Radmila Stoklasová a Jaroslav Ramík Karviná
Slezská univerzita v Opavě Obchodně podnikatelská fakulta v Karviné STATISTICKÉ PROGRAMY VYUŽITÍ EXCELU A SPSS PRO VĚDECKO-VÝZKUMNOU ČINNOST Elena Mielcová, Radmila Stoklasová a Jaroslav Ramík Karviná
SOCIÁLNĚGEOGRAFICKÁ EXPONOVANOST OBCÍ JIHOČESKÉHO KRAJE # SOCIOGEGRAPHICAL EXPOSITION OF COMMUNITIES IN THE SOUTHBOHEMIAN REGION.
 SOCIÁLNĚGEOGRAFICKÁ EXPONOVANOST OBCÍ JIHOČESKÉHO KRAJE # SOCIOGEGRAPHICAL EXPOSITION OF COMMUNITIES IN THE SOUTHBOHEMIAN REGION KLUFOVÁ, Renata Abstract The aim of the paper is to represent a social geographic
SOCIÁLNĚGEOGRAFICKÁ EXPONOVANOST OBCÍ JIHOČESKÉHO KRAJE # SOCIOGEGRAPHICAL EXPOSITION OF COMMUNITIES IN THE SOUTHBOHEMIAN REGION KLUFOVÁ, Renata Abstract The aim of the paper is to represent a social geographic
Smíšené regresní modely a možnosti jejich využití. Karel Drápela
 Smíšené regresní modely a možnosti jejich využití Karel Drápela Regresní modely Základní úloha regresní analýzy nalezení vhodného modelu studované závislosti vyjádření reálného tvaru závislosti minimalizace
Smíšené regresní modely a možnosti jejich využití Karel Drápela Regresní modely Základní úloha regresní analýzy nalezení vhodného modelu studované závislosti vyjádření reálného tvaru závislosti minimalizace
4. ROZMÍSTĚNÍ OBYVATELSTVA
 4. ROZMÍSTĚNÍ OBYVATELSTVA O čem je mapový oddíl ROZMÍSTĚNÍ OBYVATELSTVA? Oddíl obsahuje tři mapové dvojlisty, které se věnují základním charakteristikám vývoje počtu a rozmístění obyvatelstva v českých
4. ROZMÍSTĚNÍ OBYVATELSTVA O čem je mapový oddíl ROZMÍSTĚNÍ OBYVATELSTVA? Oddíl obsahuje tři mapové dvojlisty, které se věnují základním charakteristikám vývoje počtu a rozmístění obyvatelstva v českých
KGG/STG Statistika pro geografy
 KGG/STG Statistika pro geografy 1. Úvod, základní pojmy Mgr. David Fiedor 16. února 2015 Osnova 1 Úvod - organizace výuky 2 3 Struktura přednášek Úvod, základní pojmy Popisná statistika Teoretická rozdělení
KGG/STG Statistika pro geografy 1. Úvod, základní pojmy Mgr. David Fiedor 16. února 2015 Osnova 1 Úvod - organizace výuky 2 3 Struktura přednášek Úvod, základní pojmy Popisná statistika Teoretická rozdělení
aktivita A0705 Metodická a faktografická příprava řešení regionálních disparit ve fyzické dostupnosti bydlení v ČR
 aktivita A0705 Metodická a faktografická příprava řešení regionálních disparit ve fyzické dostupnosti bydlení v ČR 1 aktivita A0705 Metodická a faktografická příprava řešení regionálních disparit ve fyzické
aktivita A0705 Metodická a faktografická příprava řešení regionálních disparit ve fyzické dostupnosti bydlení v ČR 1 aktivita A0705 Metodická a faktografická příprava řešení regionálních disparit ve fyzické
Aplikace konceptu lokalit a relačního prostoru na diferenciaci venkovského prostoru
 Aplikace konceptu lokalit a relačního prostoru na diferenciaci venkovského prostoru Vladan Hruška vladan.hruska@ujep.cz odborný asistent Katedra geografie PřF Univerzita Jana Evangelisty Purkyně v Ústí
Aplikace konceptu lokalit a relačního prostoru na diferenciaci venkovského prostoru Vladan Hruška vladan.hruska@ujep.cz odborný asistent Katedra geografie PřF Univerzita Jana Evangelisty Purkyně v Ústí
Úvodem Dříve les než stromy 3 Operace s maticemi
 Obsah 1 Úvodem 13 2 Dříve les než stromy 17 2.1 Nejednoznačnost terminologie 17 2.2 Volba metody analýzy dat 23 2.3 Přehled vybraných vícerozměrných metod 25 2.3.1 Metoda hlavních komponent 26 2.3.2 Faktorová
Obsah 1 Úvodem 13 2 Dříve les než stromy 17 2.1 Nejednoznačnost terminologie 17 2.2 Volba metody analýzy dat 23 2.3 Přehled vybraných vícerozměrných metod 25 2.3.1 Metoda hlavních komponent 26 2.3.2 Faktorová
6. Dokončená bytová výstavba v relaci s vybranými statistickými charakteristikami území správních obvodů obcí s rozšířenou působností Zlínského kraje
 6. Dokončená bytová výstavba v relaci s vybranými statistickými charakteristikami území správních obvodů obcí s rozšířenou působností Zlínského kraje Kapitola si klade za cíl posoudit případný vztah intenzity
6. Dokončená bytová výstavba v relaci s vybranými statistickými charakteristikami území správních obvodů obcí s rozšířenou působností Zlínského kraje Kapitola si klade za cíl posoudit případný vztah intenzity
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
METODOLOGIE I - METODOLOGIE KVANTITATIVNÍHO VÝZKUMU
 METODOLOGIE I - METODOLOGIE KVANTITATIVNÍHO VÝZKUMU vyučující doc. RNDr. Jiří Zháněl, Dr. M I 4 Metodologie I 7. ANALÝZA DAT (KVANTITATIVNÍ VÝZKUM) (MATEMATICKÁ) STATISTIKA DESKRIPTIVNÍ (popisná) ANALYTICKÁ
METODOLOGIE I - METODOLOGIE KVANTITATIVNÍHO VÝZKUMU vyučující doc. RNDr. Jiří Zháněl, Dr. M I 4 Metodologie I 7. ANALÝZA DAT (KVANTITATIVNÍ VÝZKUM) (MATEMATICKÁ) STATISTIKA DESKRIPTIVNÍ (popisná) ANALYTICKÁ
Karta předmětu prezenční studium
 Karta předmětu prezenční studium Název předmětu: Prostorová analýza dat (PAD) Číslo předmětu: 548-0044 Garantující institut: Garant předmětu: Institut geoinformatiky doc. Dr. Ing. Jiří Horák Kredity: 5
Karta předmětu prezenční studium Název předmětu: Prostorová analýza dat (PAD) Číslo předmětu: 548-0044 Garantující institut: Garant předmětu: Institut geoinformatiky doc. Dr. Ing. Jiří Horák Kredity: 5
Tabulka 1 Rizikové online zážitky v závislosti na místě přístupu k internetu N M SD Min Max. Přístup ve vlastním pokoji 10804 1,61 1,61 0,00 5,00
 Seminární úkol č. 4 Autoři: Klára Čapková (406803), Markéta Peschková (414906) Zdroj dat: EU Kids Online Survey Popis dat Analyzovaná data pocházejí z výzkumu online chování dětí z 25 evropských zemí.
Seminární úkol č. 4 Autoři: Klára Čapková (406803), Markéta Peschková (414906) Zdroj dat: EU Kids Online Survey Popis dat Analyzovaná data pocházejí z výzkumu online chování dětí z 25 evropských zemí.
ZX510 Pokročilé statistické metody geografického výzkumu. Téma: Měření síly asociace mezi proměnnými (korelační analýza)
 ZX510 Pokročilé statistické metody geografického výzkumu Téma: Měření síly asociace mezi proměnnými (korelační analýza) Měření síly asociace (korelace) mezi proměnnými Vztah mezi dvěma proměnnými existuje,
ZX510 Pokročilé statistické metody geografického výzkumu Téma: Měření síly asociace mezi proměnnými (korelační analýza) Měření síly asociace (korelace) mezi proměnnými Vztah mezi dvěma proměnnými existuje,
Korelace. Komentované řešení pomocí MS Excel
 Korelace Komentované řešení pomocí MS Excel Vstupní data Tabulka se vstupními daty je umístěna v oblasti A2:B84 (viz. obrázek) Prvotní představu o tvaru a síle závislosti docházky a počtu bodů nám poskytne
Korelace Komentované řešení pomocí MS Excel Vstupní data Tabulka se vstupními daty je umístěna v oblasti A2:B84 (viz. obrázek) Prvotní představu o tvaru a síle závislosti docházky a počtu bodů nám poskytne
MÍRY ZÁVISLOSTI (KORELACE A REGRESE)
 zhanel@fsps.muni.cz MÍRY ZÁVISLOSTI (KORELACE A REGRESE) 2.5 MÍRY ZÁVISLOSTI 2.5.1 ZÁVISLOST PEVNÁ, VOLNÁ, STATISTICKÁ A KORELAČNÍ Jednorozměrné soubory - charakterizovány jednotlivými statistickými znaky
zhanel@fsps.muni.cz MÍRY ZÁVISLOSTI (KORELACE A REGRESE) 2.5 MÍRY ZÁVISLOSTI 2.5.1 ZÁVISLOST PEVNÁ, VOLNÁ, STATISTICKÁ A KORELAČNÍ Jednorozměrné soubory - charakterizovány jednotlivými statistickými znaky
31. 3. 2014, Brno Hanuš Vavrčík Základy statistiky ve vědě
 31. 3. 2014, Brno Hanuš Vavrčík Základy statistiky ve vědě Motto Statistika nuda je, má však cenné údaje. strana 3 Statistické charakteristiky Charakteristiky polohy jsou kolem ní seskupeny ostatní hodnoty
31. 3. 2014, Brno Hanuš Vavrčík Základy statistiky ve vědě Motto Statistika nuda je, má však cenné údaje. strana 3 Statistické charakteristiky Charakteristiky polohy jsou kolem ní seskupeny ostatní hodnoty
ANALÝZA DLOUHODOBÉ NEZAMĚSTNANOSTI V ZEMÍCH EU # ANALYSIS OF LONG-TERM UNEMPLOYMENT IN EU COUNTRIES. KLÍMA Jan, PALÁT Milan.
 ANALÝZA DLOUHODOBÉ NEZAMĚSTNANOSTI V ZEMÍCH EU # ANALYSIS OF LONG-TERM UNEMPLOYMENT IN EU COUNTRIES KLÍMA Jan, PALÁT Milan Abstract The paper is aimed at assessing the long-term unemployment of males,
ANALÝZA DLOUHODOBÉ NEZAMĚSTNANOSTI V ZEMÍCH EU # ANALYSIS OF LONG-TERM UNEMPLOYMENT IN EU COUNTRIES KLÍMA Jan, PALÁT Milan Abstract The paper is aimed at assessing the long-term unemployment of males,
Statistika. Regresní a korelační analýza Úvod do problému. Roman Biskup
 Statistika Regresní a korelační analýza Úvod do problému Roman Biskup Jihočeská univerzita v Českých Budějovicích Ekonomická fakulta (Zemědělská fakulta) Katedra aplikované matematiky a informatiky 2008/2009
Statistika Regresní a korelační analýza Úvod do problému Roman Biskup Jihočeská univerzita v Českých Budějovicích Ekonomická fakulta (Zemědělská fakulta) Katedra aplikované matematiky a informatiky 2008/2009
Aplikace výsledků European Social Survey a Schwartzových hodnotových orientací v oblasti reklamy
 Aplikace výsledků European Social Survey a Schwartzových hodnotových orientací v oblasti reklamy Ing. Ludmila Navrátilová Vysoké učení technické v Brně, Fakulta podnikatelská, Kolejní 4, 612 00 Brno, Česká
Aplikace výsledků European Social Survey a Schwartzových hodnotových orientací v oblasti reklamy Ing. Ludmila Navrátilová Vysoké učení technické v Brně, Fakulta podnikatelská, Kolejní 4, 612 00 Brno, Česká
ANALÝZA POPULAČNÍHO VÝVOJE VE VYBRANÝCH REGIONECH ČR # POPULATION MOVEMENT ANALYSIS IN SELECTED REGIONS OF THE CZECH REPUBLIC. PALÁT, Milan.
 ANALÝZA POPULAČNÍHO VÝVOJE VE VYBRANÝCH REGIONECH ČR # POPULATION MOVEMENT ANALYSIS IN SELECTED REGIONS OF THE CZECH REPUBLIC PALÁT, Milan Abstract The paper is aimed at the presentation obtained in the
ANALÝZA POPULAČNÍHO VÝVOJE VE VYBRANÝCH REGIONECH ČR # POPULATION MOVEMENT ANALYSIS IN SELECTED REGIONS OF THE CZECH REPUBLIC PALÁT, Milan Abstract The paper is aimed at the presentation obtained in the
Algoritmy pro shlukování prostorových dat
 Algoritmy pro shlukování prostorových dat Marta Žambochová Katedra matematiky a informatiky Fakulta sociálně ekonomická Univerzita J. E. Purkyně v Ústí nad Labem ROBUST 21. 26. leden 2018 Rybník - Hostouň
Algoritmy pro shlukování prostorových dat Marta Žambochová Katedra matematiky a informatiky Fakulta sociálně ekonomická Univerzita J. E. Purkyně v Ústí nad Labem ROBUST 21. 26. leden 2018 Rybník - Hostouň
Vybrané aspekty vztahu nabídky a poptávky v lokalizačních analýzách
 Vybrané aspekty vztahu nabídky a poptávky v lokalizačních analýzách Selected aspects of the relationship of supply and demand in location analyses Tereza Beníšková, Jaroslav Urminský VYSOKÁ ŠKOLA BÁŇSKÁ
Vybrané aspekty vztahu nabídky a poptávky v lokalizačních analýzách Selected aspects of the relationship of supply and demand in location analyses Tereza Beníšková, Jaroslav Urminský VYSOKÁ ŠKOLA BÁŇSKÁ
STATISTIKA. Inovace předmětu. Obsah. 1. Inovace předmětu STATISTIKA... 2 2. Sylabus pro předmět STATISTIKA... 3 3. Pomůcky... 7
 Inovace předmětu STATISTIKA Obsah 1. Inovace předmětu STATISTIKA... 2 2. Sylabus pro předmět STATISTIKA... 3 3. Pomůcky... 7 1 1. Inovace předmětu STATISTIKA Předmět Statistika se na bakalářském oboru
Inovace předmětu STATISTIKA Obsah 1. Inovace předmětu STATISTIKA... 2 2. Sylabus pro předmět STATISTIKA... 3 3. Pomůcky... 7 1 1. Inovace předmětu STATISTIKA Předmět Statistika se na bakalářském oboru
Užití země v České republice v letech 1994 až 2012 Karel Matějka IDS, Na Komořsku 2175/2a, 143 00 Praha 4, Česká republika matejka@infodatasys.
 Užití země v České republice v letech 1994 až 2012 Karel Matějka IDS, Na Komořsku 2175/2a, 143 00 Praha 4, Česká republika matejka@infodatasys.cz Po roce 19 došlo k výrazné změně hospodářských poměrů v
Užití země v České republice v letech 1994 až 2012 Karel Matějka IDS, Na Komořsku 2175/2a, 143 00 Praha 4, Česká republika matejka@infodatasys.cz Po roce 19 došlo k výrazné změně hospodářských poměrů v
INDUKTIVNÍ STATISTIKA
 10. SEMINÁŘ INDUKTIVNÍ STATISTIKA 3. HODNOCENÍ ZÁVISLOSTÍ HODNOCENÍ ZÁVISLOSTÍ KVALITATIVNÍ VELIČINY - Vychází se z kombinační (kontingenční) tabulky, která je výsledkem třídění druhého stupně KVANTITATIVNÍ
10. SEMINÁŘ INDUKTIVNÍ STATISTIKA 3. HODNOCENÍ ZÁVISLOSTÍ HODNOCENÍ ZÁVISLOSTÍ KVALITATIVNÍ VELIČINY - Vychází se z kombinační (kontingenční) tabulky, která je výsledkem třídění druhého stupně KVANTITATIVNÍ
Grafický a číselný popis rozložení dat 3.1 Způsoby zobrazení dat Metody zobrazení kvalitativních a ordinálních dat Metody zobrazení kvan
 1 Úvod 1.1 Empirický výzkum a jeho etapy 1.2 Význam teorie pro výzkum 1.2.1 Konstrukty a jejich operacionalizace 1.2.2 Role teorie ve výzkumu 1.2.3 Proces ověření hypotéz a teorií 1.3 Etika vědecké práce
1 Úvod 1.1 Empirický výzkum a jeho etapy 1.2 Význam teorie pro výzkum 1.2.1 Konstrukty a jejich operacionalizace 1.2.2 Role teorie ve výzkumu 1.2.3 Proces ověření hypotéz a teorií 1.3 Etika vědecké práce
Testování hypotéz o parametrech regresního modelu
 Testování hypotéz o parametrech regresního modelu Ekonometrie Jiří Neubauer Katedra kvantitativních metod FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Jiří Neubauer (Katedra UO
Testování hypotéz o parametrech regresního modelu Ekonometrie Jiří Neubauer Katedra kvantitativních metod FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Jiří Neubauer (Katedra UO
DISPARITY KRAJŮ ČR. Pavla Jindrová Univerzita Pardubice, Fakulta ekonomicko-správní, Ústav matematiky
 DISPARITY KRAJŮ ČR Pavla Jindrová Univerzita Pardubice, Fakulta ekonomicko-správní, Ústav matematiky Abstract: The Czech Republic is structured among 14 regions (NUTS3). The comparison among regions of
DISPARITY KRAJŮ ČR Pavla Jindrová Univerzita Pardubice, Fakulta ekonomicko-správní, Ústav matematiky Abstract: The Czech Republic is structured among 14 regions (NUTS3). The comparison among regions of
Korelační a regresní analýza. 1. Pearsonův korelační koeficient 2. jednoduchá regresní analýza 3. vícenásobná regresní analýza
 Korelační a regresní analýza 1. Pearsonův korelační koeficient 2. jednoduchá regresní analýza 3. vícenásobná regresní analýza Pearsonův korelační koeficient u intervalových a poměrových dat můžeme jako
Korelační a regresní analýza 1. Pearsonův korelační koeficient 2. jednoduchá regresní analýza 3. vícenásobná regresní analýza Pearsonův korelační koeficient u intervalových a poměrových dat můžeme jako
PRAVDĚPODOBNOST A STATISTIKA 1
 Metodický list č 1. Název tématického celku: Vymezení role Pravděpodobnosti a Matematické Statistiky v širším celku čisté a aplikované matematiky. Základním cílem tohoto tématického celku je základní pojmy
Metodický list č 1. Název tématického celku: Vymezení role Pravděpodobnosti a Matematické Statistiky v širším celku čisté a aplikované matematiky. Základním cílem tohoto tématického celku je základní pojmy
PROSTOROVÁ STATISTIKA V MATLABU. , Liberci, Liberec
 PROSTOROVÁ STATISTIKA V MATLABU, Liberci, 461 17 Liberec Abstrakt: # prostorové kovariance$# # & ' variogramu (lokální variabilita) resp. jeho ( ) ) jazyku Matlab *,- 1. Úvod.'# ')$' ) ' &/ ' #, ),', '
PROSTOROVÁ STATISTIKA V MATLABU, Liberci, 461 17 Liberec Abstrakt: # prostorové kovariance$# # & ' variogramu (lokální variabilita) resp. jeho ( ) ) jazyku Matlab *,- 1. Úvod.'# ')$' ) ' &/ ' #, ),', '
METODOLOGICKÁ VÝCHODISKA ANALÝZ REGIONÁLNÍHO ROZVOJE METHODOLOGICAL STARTING POINTS OF REGIONAL DEVELOPMENT ANALYSES.
 METODOLOGICKÁ VÝCHODISKA ANALÝZ REGIONÁLNÍHO ROZVOJE METHODOLOGICAL STARTING POINTS OF REGIONAL DEVELOPMENT ANALYSES Libuše Svatošová Anotace: Při hodnocení regionálního rozvoje je nutné sledovat a analyzovat
METODOLOGICKÁ VÝCHODISKA ANALÝZ REGIONÁLNÍHO ROZVOJE METHODOLOGICAL STARTING POINTS OF REGIONAL DEVELOPMENT ANALYSES Libuše Svatošová Anotace: Při hodnocení regionálního rozvoje je nutné sledovat a analyzovat
STATISTIKA jako vědní obor
 STATISTIKA jako vědní obor Cílem statistického zpracování dat je podání informace o vlastnostech a zákonitostech hromadných jevů. Statistika se zabývá popisem hromadných jevů - deskriptivní, popisná statistika
STATISTIKA jako vědní obor Cílem statistického zpracování dat je podání informace o vlastnostech a zákonitostech hromadných jevů. Statistika se zabývá popisem hromadných jevů - deskriptivní, popisná statistika
SOUČASNÉ TRENDY V KVANTITATIVNÍ ANALÝZE GEOGRAFICKÝCH DAT
 Univerzita Karlova v Praze Přírodovědecká fakulta katedra sociální geografie a regionálního rozvoje Pavlína Netrdová SOUČASNÉ TRENDY V KVANTITATIVNÍ ANALÝZE GEOGRAFICKÝCH DAT MOŽNOSTI A PROBLÉMY PROSTOROVÉ
Univerzita Karlova v Praze Přírodovědecká fakulta katedra sociální geografie a regionálního rozvoje Pavlína Netrdová SOUČASNÉ TRENDY V KVANTITATIVNÍ ANALÝZE GEOGRAFICKÝCH DAT MOŽNOSTI A PROBLÉMY PROSTOROVÉ
BRNO KOMPLEXNÍ DOPRAVNÍ ANALÝZA
 MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA GEOGRAFICKÝ ÚSTAV BRNO KOMPLEXNÍ DOPRAVNÍ ANALÝZA Diplomová práce Jan Kučera Vedoucí práce: Mgr. Daniel Seidenglanz, Ph.D. Brno 2013 Bibliografický záznam Autor:
MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA GEOGRAFICKÝ ÚSTAV BRNO KOMPLEXNÍ DOPRAVNÍ ANALÝZA Diplomová práce Jan Kučera Vedoucí práce: Mgr. Daniel Seidenglanz, Ph.D. Brno 2013 Bibliografický záznam Autor:
Testování hypotéz a měření asociace mezi proměnnými
 Testování hypotéz a měření asociace mezi proměnnými Testování hypotéz Nulová a alternativní hypotéza většina statistických analýz zahrnuje různá porovnání, hledání vztahů, efektů Tvrzení, že efekt je nulový,
Testování hypotéz a měření asociace mezi proměnnými Testování hypotéz Nulová a alternativní hypotéza většina statistických analýz zahrnuje různá porovnání, hledání vztahů, efektů Tvrzení, že efekt je nulový,
Statistika. Základní pojmy a cíle statistiky. Roman Biskup. (zapálený) statistik ve výslužbě, aktuálně analytik v praxi ;-) roman.biskup(at) .
 Statistika Základní pojmy a cíle statistiky Roman Biskup (zapálený) statistik ve výslužbě, aktuálně analytik v praxi ;-) roman.biskup(at)email.cz 12. února 2012 Statistika by Birom Statistika Pojmy a cíle
Statistika Základní pojmy a cíle statistiky Roman Biskup (zapálený) statistik ve výslužbě, aktuálně analytik v praxi ;-) roman.biskup(at)email.cz 12. února 2012 Statistika by Birom Statistika Pojmy a cíle
Cíle korelační studie
 Korelační studie Cíle korelační studie cíle výzkumu v psychologii deskripce predikce explanace kontrola korelační studie popisuje vztah (ko-relaci) mezi proměnnými cíle - deskripce, příp. predikce První
Korelační studie Cíle korelační studie cíle výzkumu v psychologii deskripce predikce explanace kontrola korelační studie popisuje vztah (ko-relaci) mezi proměnnými cíle - deskripce, příp. predikce První
Testování hypotéz o parametrech regresního modelu
 Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Lineární regresní model kde Y = Xβ + e, y 1 e 1 β y 2 Y =., e = e 2 x 11 x 1 1k., X =....... β 2,
Statistika II Katedra ekonometrie FVL UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Lineární regresní model kde Y = Xβ + e, y 1 e 1 β y 2 Y =., e = e 2 x 11 x 1 1k., X =....... β 2,
Tvorba nelineárních regresních modelů v analýze dat
 Univerzita Pardubice Fakulta chemicko-technologická, Katedra analytické chemie Licenční studium GALILEO Interaktivní statistická analýza dat Semestrální práce z předmětu Tvorba nelineárních regresních
Univerzita Pardubice Fakulta chemicko-technologická, Katedra analytické chemie Licenční studium GALILEO Interaktivní statistická analýza dat Semestrální práce z předmětu Tvorba nelineárních regresních
ANALÝZA DAT V R 3. POPISNÉ STATISTIKY, NÁHODNÁ VELIČINA. Mgr. Markéta Pavlíková Katedra pravděpodobnosti a matematické statistiky MFF UK
 ANALÝZA DAT V R 3. POPISNÉ STATISTIKY, NÁHODNÁ VELIČINA Mgr. Markéta Pavlíková Katedra pravděpodobnosti a matematické statistiky MFF UK www.biostatisticka.cz POPISNÉ STATISTIKY - OPAKOVÁNÍ jedna kvalitativní
ANALÝZA DAT V R 3. POPISNÉ STATISTIKY, NÁHODNÁ VELIČINA Mgr. Markéta Pavlíková Katedra pravděpodobnosti a matematické statistiky MFF UK www.biostatisticka.cz POPISNÉ STATISTIKY - OPAKOVÁNÍ jedna kvalitativní
VYUŽITÍ SOFTWARU MATHEMATICA VE VÝUCE PŘEDMĚTU MATEMATIKA V EKONOMII 1
 VYUŽITÍ SOFTWARU MATHEMATICA VE VÝUCE PŘEDMĚTU MATEMATIKA V EKONOMII 1 Orlando Arencibia, Petr Seďa VŠB-TU Ostrava Abstrakt: Příspěvek je věnován diskusi o inovaci předmětu Matematika v ekonomii, který
VYUŽITÍ SOFTWARU MATHEMATICA VE VÝUCE PŘEDMĚTU MATEMATIKA V EKONOMII 1 Orlando Arencibia, Petr Seďa VŠB-TU Ostrava Abstrakt: Příspěvek je věnován diskusi o inovaci předmětu Matematika v ekonomii, který
Využití analýz viditelnosti v procesech veřejné správy
 Využití analýz viditelnosti v procesech veřejné správy Jan Caha jan.caha@mendelu.cz Mendelova Univerzita v Brně Geoinformace ve veřejné správě 2019 Analýzy viditelnosti analýzy viditelnosti? hodnocení
Využití analýz viditelnosti v procesech veřejné správy Jan Caha jan.caha@mendelu.cz Mendelova Univerzita v Brně Geoinformace ve veřejné správě 2019 Analýzy viditelnosti analýzy viditelnosti? hodnocení
Organizační chování. Rozvoj poznání v organizačním chování
 Organizační chování Rozvoj poznání v organizačním chování Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty vojenského leadershipu Registrační
Organizační chování Rozvoj poznání v organizačním chování Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty vojenského leadershipu Registrační
Proměny počtu žáků základních škol v souvislosti s populačním vývojem v obcích Česka
 DISKUSNÍ VEČER ČESKÉ DEMOGRAFICKÉ SPOLEČNOSTI 7. 12. 2016 Proměny počtu žáků základních škol v souvislosti s populačním vývojem v obcích Česka Mgr. Marie Kusovská, Ph.D. mariekusovska@gmail.com Osnova
DISKUSNÍ VEČER ČESKÉ DEMOGRAFICKÉ SPOLEČNOSTI 7. 12. 2016 Proměny počtu žáků základních škol v souvislosti s populačním vývojem v obcích Česka Mgr. Marie Kusovská, Ph.D. mariekusovska@gmail.com Osnova
KORELACE. Komentované řešení pomocí programu Statistica
 KORELACE Komentované řešení pomocí programu Statistica Vstupní data I Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu Popisná
KORELACE Komentované řešení pomocí programu Statistica Vstupní data I Data umístěná v excelovském souboru překopírujeme do tabulky ve Statistice a pojmenujeme proměnné, viz prezentace k tématu Popisná
Statistická analýza dat podzemních vod. Statistical analysis of ground water data. Vladimír Sosna 1
 Statistická analýza dat podzemních vod. Statistical analysis of ground water data. Vladimír Sosna 1 1 ČHMÚ, OPZV, Na Šabatce 17, 143 06 Praha 4 - Komořany sosna@chmi.cz, tel. 377 256 617 Abstrakt: Referát
Statistická analýza dat podzemních vod. Statistical analysis of ground water data. Vladimír Sosna 1 1 ČHMÚ, OPZV, Na Šabatce 17, 143 06 Praha 4 - Komořany sosna@chmi.cz, tel. 377 256 617 Abstrakt: Referát
Korelační a regresní analýza
 Korelační a regresní analýza Analýza závislosti v normálním rozdělení Pearsonův (výběrový) korelační koeficient: r = s XY s X s Y, kde s XY = 1 n (x n 1 i=0 i x )(y i y ), s X (s Y ) je výběrová směrodatná
Korelační a regresní analýza Analýza závislosti v normálním rozdělení Pearsonův (výběrový) korelační koeficient: r = s XY s X s Y, kde s XY = 1 n (x n 1 i=0 i x )(y i y ), s X (s Y ) je výběrová směrodatná
MOŽNOSTI VYUŽITÍ SHLUKOVÉ ANALÝZY V Q-METODOLOGII
 MOŽNOSTI VYUŽITÍ SHLUKOVÉ ANALÝZY V Q-METODOLOGII CHRÁSKA Miroslav, CZ Resumé Příspěvek seznamuje s možnostmi využití shlukové analýzy při zpracování výzkumu provedeného pomocí Q-metodologie. Ve výzkumu
MOŽNOSTI VYUŽITÍ SHLUKOVÉ ANALÝZY V Q-METODOLOGII CHRÁSKA Miroslav, CZ Resumé Příspěvek seznamuje s možnostmi využití shlukové analýzy při zpracování výzkumu provedeného pomocí Q-metodologie. Ve výzkumu
LIMITY APLIKACE STATISTICKÝCH TESTŮ VÝZNAMNOSTI V PEDAGOGICKÉM VÝZKUMU: SEMINÁŘ PRO NESTATISTIKY
 LIMITY APLIKACE STATISTICKÝCH TESTŮ VÝZNAMNOSTI V PEDAGOGICKÉM VÝZKUMU: SEMINÁŘ PRO NESTATISTIKY Seminář ČAPV 2018 Upozornění Prezentace obsahuje pouze doprovodný text k semináři pro doktorandy v rámci
LIMITY APLIKACE STATISTICKÝCH TESTŮ VÝZNAMNOSTI V PEDAGOGICKÉM VÝZKUMU: SEMINÁŘ PRO NESTATISTIKY Seminář ČAPV 2018 Upozornění Prezentace obsahuje pouze doprovodný text k semináři pro doktorandy v rámci
HODNOCENÍ JIHOČESKÉHO KRAJE Z HLEDISKA CEN NEMOVITOSTÍ URČENÝCH PRO BYDLENÍ V NÁVAZNOSTI NA EKONOMICKÝ RŮST REGIONU 1
 HODNOCENÍ JIHOČESKÉHO KRAJE Z HLEDISKA CEN NEMOVITOSTÍ URČENÝCH PRO BYDLENÍ V NÁVAZNOSTI NA EKONOMICKÝ RŮST REGIONU 1 Ivana Staňková, Tomáš Volek Jihočeská univerzita v Českých Budějovicích, Zemědělská
HODNOCENÍ JIHOČESKÉHO KRAJE Z HLEDISKA CEN NEMOVITOSTÍ URČENÝCH PRO BYDLENÍ V NÁVAZNOSTI NA EKONOMICKÝ RŮST REGIONU 1 Ivana Staňková, Tomáš Volek Jihočeská univerzita v Českých Budějovicích, Zemědělská
Statistické vyhodnocení průzkumu funkční gramotnosti žáků 4. ročníku ZŠ
 Statistické vyhodnocení průzkumu funkční gramotnosti žáků 4. ročníku ZŠ Ing. Dana Trávníčková, PaedDr. Jana Isteníková Funkční gramotnost je používání čtení a psaní v životních situacích. Nejde jen o elementární
Statistické vyhodnocení průzkumu funkční gramotnosti žáků 4. ročníku ZŠ Ing. Dana Trávníčková, PaedDr. Jana Isteníková Funkční gramotnost je používání čtení a psaní v životních situacích. Nejde jen o elementární
Aplikovaná statistika v R - cvičení 3
 Aplikovaná statistika v R - cvičení 3 Filip Děchtěrenko Matematicko-fyzikální fakulta filip.dechterenko@gmail.com 5.8.2014 Filip Děchtěrenko (MFF UK) Aplikovaná statistika v R 5.8.2014 1 / 10 Lineární
Aplikovaná statistika v R - cvičení 3 Filip Děchtěrenko Matematicko-fyzikální fakulta filip.dechterenko@gmail.com 5.8.2014 Filip Děchtěrenko (MFF UK) Aplikovaná statistika v R 5.8.2014 1 / 10 Lineární
6. Lineární regresní modely
 6. Lineární regresní modely 6.1 Jednoduchá regrese a validace 6.2 Testy hypotéz v lineární regresi 6.3 Kritika dat v regresním tripletu 6.4 Multikolinearita a polynomy 6.5 Kritika modelu v regresním tripletu
6. Lineární regresní modely 6.1 Jednoduchá regrese a validace 6.2 Testy hypotéz v lineární regresi 6.3 Kritika dat v regresním tripletu 6.4 Multikolinearita a polynomy 6.5 Kritika modelu v regresním tripletu
REGIONÁLNÍ DISPARITY DISPARITY V REGIONÁLNÍM ROZVOJI ZEMĚ, JEJICH POJETÍ, IDENTIFIKACE A HODNOCENÍ
 Series on Advanced Economic Issues Faculty of Economics, VŠB-TU Ostrava Alois Kutscherauer Hana Fachinelli Jan Sucháček Karel Skokan Miroslav Hučka Pavel Tuleja Petr Tománek REGIONÁLNÍ DISPARITY DISPARITY
Series on Advanced Economic Issues Faculty of Economics, VŠB-TU Ostrava Alois Kutscherauer Hana Fachinelli Jan Sucháček Karel Skokan Miroslav Hučka Pavel Tuleja Petr Tománek REGIONÁLNÍ DISPARITY DISPARITY
PRAVDĚPODOBNOST A STATISTIKA
 PRAVDĚPODOBNOST A STATISTIKA Definice lineárního normálního regresního modelu Lineární normální regresní model Y β ε Matice n,k je matice realizací. Předpoklad: n > k, h() k - tj. matice je plné hodnosti
PRAVDĚPODOBNOST A STATISTIKA Definice lineárního normálního regresního modelu Lineární normální regresní model Y β ε Matice n,k je matice realizací. Předpoklad: n > k, h() k - tj. matice je plné hodnosti
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Statistické metody - nástroj poznání a rozhodování anebo zdroj omylů a lží
 Statistické metody - nástroj poznání a rozhodování anebo zdroj omylů a lží Zdeněk Karpíšek Jsou tři druhy lží: lži, odsouzeníhodné lži a statistiky. Statistika je logická a přesná metoda, jak nepřesně
Statistické metody - nástroj poznání a rozhodování anebo zdroj omylů a lží Zdeněk Karpíšek Jsou tři druhy lží: lži, odsouzeníhodné lži a statistiky. Statistika je logická a přesná metoda, jak nepřesně
Obsah Úvod Kapitola 1 Než začneme Kapitola 2 Práce s hromadnými daty před analýzou
 Úvod.................................................................. 11 Kapitola 1 Než začneme.................................................................. 17 1.1 Logika kvantitativního výzkumu...........................................
Úvod.................................................................. 11 Kapitola 1 Než začneme.................................................................. 17 1.1 Logika kvantitativního výzkumu...........................................
VÝVOJ INDEXŮ SPOTŘEBITELSKÝCH CEN
 ČESKÁ ZEMĚDĚLSKÁ UNIVERZITA V PRAZE Fakulta provozně ekonomická Katedra statistiky Studijní obor: Veřejná správa a regionální rozvoj Teze k diplomové práci VÝVOJ INDEXŮ SPOTŘEBITELSKÝCH CEN Vypracovala:
ČESKÁ ZEMĚDĚLSKÁ UNIVERZITA V PRAZE Fakulta provozně ekonomická Katedra statistiky Studijní obor: Veřejná správa a regionální rozvoj Teze k diplomové práci VÝVOJ INDEXŮ SPOTŘEBITELSKÝCH CEN Vypracovala:
Pracovní celky 3.2, 3.3 a 3.4 Sémantická harmonizace - Srovnání a přiřazení datových modelů
 Pracovní celky 3.2, 3.3 a 3.4 Sémantická harmonizace - Srovnání a datových modelů Obsah Seznam tabulek... 1 Seznam obrázků... 1 1 Úvod... 2 2 Metody sémantické harmonizace... 2 3 Dvojjazyčné katalogy objektů
Pracovní celky 3.2, 3.3 a 3.4 Sémantická harmonizace - Srovnání a datových modelů Obsah Seznam tabulek... 1 Seznam obrázků... 1 1 Úvod... 2 2 Metody sémantické harmonizace... 2 3 Dvojjazyčné katalogy objektů
Prostorové vzorce aktivit high-tech sektoru
 Prostorové vzorce aktivit high-tech sektoru Kristýna Meislová, Technologické centrum AV ČR ÚVOD Znalost socio-ekonomických rozdílů v území a jejich prostorových vzorců je důležitým předpokladem pro hledání
Prostorové vzorce aktivit high-tech sektoru Kristýna Meislová, Technologické centrum AV ČR ÚVOD Znalost socio-ekonomických rozdílů v území a jejich prostorových vzorců je důležitým předpokladem pro hledání
HYPOTÉZY. Kvantitativní výzkum není nic jiného než testování hypotéz. (Disman 2002, s. 76) DEDUKCE (kvantitativní přístup)
 HYPOTÉZY Hypotéza není ničím jiným než podmíněným výrokem o vztazích mezi dvěma nebo více proměnnými. Na rozdíl od problému, který je formulován v podobě otázky explicitně, nebo implicitně vyjádřené, hypotéza
HYPOTÉZY Hypotéza není ničím jiným než podmíněným výrokem o vztazích mezi dvěma nebo více proměnnými. Na rozdíl od problému, který je formulován v podobě otázky explicitně, nebo implicitně vyjádřené, hypotéza
ZNALOSTI A DOVEDNOSTI ČESKÝCH MUŽŮ V OBLASTI INFORMAČNÍ BEZPEČNOSTI - VÝSLEDKY STATISTICKÉ ANALÝZY
 ZNALOSTI A DOVEDNOSTI ČESKÝCH MUŽŮ V OBLASTI INFORMAČNÍ BEZPEČNOSTI - VÝSLEDKY STATISTICKÉ ANALÝZY Knowledge and skills of Czech men in the field of information security - the results of statistical analysis
ZNALOSTI A DOVEDNOSTI ČESKÝCH MUŽŮ V OBLASTI INFORMAČNÍ BEZPEČNOSTI - VÝSLEDKY STATISTICKÉ ANALÝZY Knowledge and skills of Czech men in the field of information security - the results of statistical analysis
PRAVDĚPODOBNOST A STATISTIKA 1 Metodický list č 1.
 Metodický list č 1. Název tématického celku: Elementární statistické zpracování 1 - Kolekce a interpretace statistických dat, základní pojmy deskriptivní statistiky. Cíl: Základním cílem tohoto tematického
Metodický list č 1. Název tématického celku: Elementární statistické zpracování 1 - Kolekce a interpretace statistických dat, základní pojmy deskriptivní statistiky. Cíl: Základním cílem tohoto tematického
VÝVOJ PLODNOSTI VE STÁTECH A REGIONECH EVROPSKÉ UNIE PO ROCE 1991
 UNIVERZITA KARLOVA V PRAZE PŘÍRODOVĚDECKÁ FAKULTA KATEDRA DEMOGRAFIE A GEODEMOGRAFIE VÝVOJ PLODNOSTI VE STÁTECH A REGIONECH EVROPSKÉ UNIE PO ROCE 1991 Seminář mladých demografů Proměny demografického chování
UNIVERZITA KARLOVA V PRAZE PŘÍRODOVĚDECKÁ FAKULTA KATEDRA DEMOGRAFIE A GEODEMOGRAFIE VÝVOJ PLODNOSTI VE STÁTECH A REGIONECH EVROPSKÉ UNIE PO ROCE 1991 Seminář mladých demografů Proměny demografického chování
Základy biostatistiky II. Veřejné zdravotnictví 3.LF UK - II
 Základy biostatistiky II Veřejné zdravotnictví 3.LF UK - II Teoretické rozložení-matematické modely rozložení Naměřená data Výběrové rozložení Teoretické rozložení 1 e 2 x 2 Teoretické rozložení-matematické
Základy biostatistiky II Veřejné zdravotnictví 3.LF UK - II Teoretické rozložení-matematické modely rozložení Naměřená data Výběrové rozložení Teoretické rozložení 1 e 2 x 2 Teoretické rozložení-matematické
Aplikovaná statistika pro učitele a žáky v hodinách zeměpisu aneb jak využít MS Excel v praxi. Geografický seminář 30. března 2011 Pavel Bednář
 Aplikovaná statistika pro učitele a žáky v hodinách zeměpisu aneb jak využít MS Excel v praxi Geografický seminář 30. března 2011 Pavel Bednář Výchozí stav Sebehodnocení práce s MS Excel studujícími oboru
Aplikovaná statistika pro učitele a žáky v hodinách zeměpisu aneb jak využít MS Excel v praxi Geografický seminář 30. března 2011 Pavel Bednář Výchozí stav Sebehodnocení práce s MS Excel studujícími oboru
Vysoká škola báňská technická univerzita Ostrava. Fakulta elektrotechniky a informatiky
 Vysoká škola báňská technická univerzita Ostrava Fakulta elektrotechniky a informatiky Bankovní účty (semestrální projekt statistika) Tomáš Hejret (hej124) 18.5.2013 Úvod Cílem tohoto projektu, zadaného
Vysoká škola báňská technická univerzita Ostrava Fakulta elektrotechniky a informatiky Bankovní účty (semestrální projekt statistika) Tomáš Hejret (hej124) 18.5.2013 Úvod Cílem tohoto projektu, zadaného
MODERNÍ TRENDY V KARTOGRAFICKÉM DESIGNU Z HLEDISKA UŽIVATELSKÝCH ASPETŮ ALENA VONDRÁKOVÁ KATEDRA GEOINFORMATIKY UNIVERZITA PALACKÉHO V OLOMOUCI
 Z HLEDISKA UŽIVATELSKÝCH ASPETŮ ALENA VONDRÁKOVÁ KATEDRA GEOINFORMATIKY UNIVERZITA PALACKÉHO V OLOMOUCI DESIGN JE JAKO KOŘENÍ MŮŽE UDĚLAT VÝBORNOU SLUŽBU NEBO VŠECHNO HODNOTA UŽITEČNOST PŘÍNOSNOST - Morville,
Z HLEDISKA UŽIVATELSKÝCH ASPETŮ ALENA VONDRÁKOVÁ KATEDRA GEOINFORMATIKY UNIVERZITA PALACKÉHO V OLOMOUCI DESIGN JE JAKO KOŘENÍ MŮŽE UDĚLAT VÝBORNOU SLUŽBU NEBO VŠECHNO HODNOTA UŽITEČNOST PŘÍNOSNOST - Morville,
UKÁZKA VYUŽITÍ PROGRAMU WINQSB PŘI VÝUCE KVANTITATIVNÍCH METOD V ROZHODOVÁNÍ V DISTANČNÍ FORMĚ STUDIA
 UKÁZKA VYUŽITÍ PROGRAMU WINQSB PŘI VÝUCE KVANTITATIVNÍCH METOD V ROZHODOVÁNÍ V DISTANČNÍ FORMĚ STUDIA ALENA KOLČAVOVÁ, LENKA DRÁBKOVÁ Abstrakt: V úvodu příspěvku je nastíněna současná situace stavu připravenosti
UKÁZKA VYUŽITÍ PROGRAMU WINQSB PŘI VÝUCE KVANTITATIVNÍCH METOD V ROZHODOVÁNÍ V DISTANČNÍ FORMĚ STUDIA ALENA KOLČAVOVÁ, LENKA DRÁBKOVÁ Abstrakt: V úvodu příspěvku je nastíněna současná situace stavu připravenosti
RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr.
 Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
Analýza dat pro Neurovědy RNDr. Eva Janoušová doc. RNDr. Ladislav Dušek, Dr. Jaro 2014 Institut biostatistiky Janoušová, a analýz Dušek: Analýza dat pro neurovědy Blok 7 Jak hodnotit vztah spojitých proměnných
Metodika. Zájmová území
 Sociálně-ekonomické charakteristiky obcí a vybraná velkoplošná chráněná území v ČR Karel Matějka IDS, Na Komořsku 2175/2a, 143 00 Praha 4 matejka@infodatasys.cz V rámci projektu GA ČR P404/11/0354 Protected
Sociálně-ekonomické charakteristiky obcí a vybraná velkoplošná chráněná území v ČR Karel Matějka IDS, Na Komořsku 2175/2a, 143 00 Praha 4 matejka@infodatasys.cz V rámci projektu GA ČR P404/11/0354 Protected
VÝVOJOVÉ TENDENCE V MĚŘENÍ FINANČNÍ VÝKONNOSTI A JEJICH
 VÝVOJOVÉ TENDENCE V MĚŘENÍ FINANČNÍ VÝKONNOSTI A JEJICH REFLEXE V MANAŽERSKÉM ÚČETNICTVÍ 1 Developmental Tendencies in Financial Performance Measurements and Its Impact on Management Accounting Úvod Zbyněk
VÝVOJOVÉ TENDENCE V MĚŘENÍ FINANČNÍ VÝKONNOSTI A JEJICH REFLEXE V MANAŽERSKÉM ÚČETNICTVÍ 1 Developmental Tendencies in Financial Performance Measurements and Its Impact on Management Accounting Úvod Zbyněk
Měření závislosti statistických dat
 5.1 Měření závislosti statistických dat Každý pořádný astronom je schopen vám předpovědět, kde se bude nacházet daná hvězda půl hodiny před půlnocí. Ne každý je však téhož schopen předpovědět v případě
5.1 Měření závislosti statistických dat Každý pořádný astronom je schopen vám předpovědět, kde se bude nacházet daná hvězda půl hodiny před půlnocí. Ne každý je však téhož schopen předpovědět v případě
1. Statistická analýza dat Jak vznikají informace Rozložení dat
 1. Statistická analýza dat Jak vznikají informace Rozložení dat J. Jarkovský, L. Dušek, S. Littnerová, J. Kalina Význam statistické analýzy dat Sběr a vyhodnocování dat je způsobem k uchopení a pochopení
1. Statistická analýza dat Jak vznikají informace Rozložení dat J. Jarkovský, L. Dušek, S. Littnerová, J. Kalina Význam statistické analýzy dat Sběr a vyhodnocování dat je způsobem k uchopení a pochopení
Statistické testování hypotéz II
 PSY117/454 Statistická analýza dat v psychologii Přednáška 9 Statistické testování hypotéz II Přehled testů, rozdíly průměrů, velikost účinku, síla testu Základní výzkumné otázky/hypotézy 1. Stanovení
PSY117/454 Statistická analýza dat v psychologii Přednáška 9 Statistické testování hypotéz II Přehled testů, rozdíly průměrů, velikost účinku, síla testu Základní výzkumné otázky/hypotézy 1. Stanovení
Jana Vránová, 3. lékařská fakulta UK
 Jana Vránová, 3. lékařská fakulta UK Vznikají při zkoumání vztahů kvalitativních resp. diskrétních znaků Jedná se o analogii s korelační analýzou spojitých znaků Přitom předpokládáme, že každý prvek populace
Jana Vránová, 3. lékařská fakulta UK Vznikají při zkoumání vztahů kvalitativních resp. diskrétních znaků Jedná se o analogii s korelační analýzou spojitých znaků Přitom předpokládáme, že každý prvek populace
Úvod do problematiky měření
 1/18 Lord Kelvin: "Když to, o čem mluvíte, můžete změřit, a vyjádřit to pomocí čísel, něco o tom víte. Ale když to nemůžete vyjádřit číselně, je vaše znalost hubená a nedostatečná. Může to být začátek
1/18 Lord Kelvin: "Když to, o čem mluvíte, můžete změřit, a vyjádřit to pomocí čísel, něco o tom víte. Ale když to nemůžete vyjádřit číselně, je vaše znalost hubená a nedostatečná. Může to být začátek
9.1 BYTOVÝ FOND V ČESKU Zuzana Kopecká, Jana Jíchová
 9.1 BYTOVÝ FOND V ČESKU Zuzana Kopecká, Jana Jíchová Strukturu a kvalitu bytového fondu lze považovat za jeden z indikátorů kvality života a rozvoje regionu (Baxa 2010). Charakter a způsob bydlení (např.
9.1 BYTOVÝ FOND V ČESKU Zuzana Kopecká, Jana Jíchová Strukturu a kvalitu bytového fondu lze považovat za jeden z indikátorů kvality života a rozvoje regionu (Baxa 2010). Charakter a způsob bydlení (např.
2.3 Proměna věkové struktury
 2.3 Proměna věkové struktury Proces suburbanizace má značný vliv na proměnu věkové struktury obcí (nejen) v suburbánní zóně Prahy. Vzhledem k charakteristické věkové struktuře migrantů (stěhují se především
2.3 Proměna věkové struktury Proces suburbanizace má značný vliv na proměnu věkové struktury obcí (nejen) v suburbánní zóně Prahy. Vzhledem k charakteristické věkové struktuře migrantů (stěhují se především
Intervalový odhad. Interval spolehlivosti = intervalový odhad nějakého parametru s danou pravděpodobností = konfidenční interval pro daný parametr
 StatSoft Intervalový odhad Dnes se budeme zabývat neodmyslitelnou součástí statistiky a to intervaly v nejrůznějších podobách. Toto téma je také úzce spojeno s tématem testování hypotéz, a tedy plynule
StatSoft Intervalový odhad Dnes se budeme zabývat neodmyslitelnou součástí statistiky a to intervaly v nejrůznějších podobách. Toto téma je také úzce spojeno s tématem testování hypotéz, a tedy plynule
Současný stav likvidace dat v organizacích
 Současný stav likvidace dat v organizacích Current state of data disposing in organizations Ing. Vít Pěkný Abstrakt Článek prezentuje výsledky zjištěné dotazníkovým šetřením, které bylo realizované v roce
Současný stav likvidace dat v organizacích Current state of data disposing in organizations Ing. Vít Pěkný Abstrakt Článek prezentuje výsledky zjištěné dotazníkovým šetřením, které bylo realizované v roce
Modelování sesuvu svahu v Halenkovicích pomocí metody kriging
 Modelování sesuvu svahu v Halenkovicích pomocí metody kriging Robert Zůvala, Eva Fišerová Katedra matematické analýzy a aplikací matematiky Přírodovědecká fakulta Univerzity Palackého v Olomouci ROBUST
Modelování sesuvu svahu v Halenkovicích pomocí metody kriging Robert Zůvala, Eva Fišerová Katedra matematické analýzy a aplikací matematiky Přírodovědecká fakulta Univerzity Palackého v Olomouci ROBUST
T T. Think Together 2011. Martina Urbanová THINK TOGETHER. Jak měřit spolupráci obcí How to measure inter-municipality cooperation
 Česká zemědělská univerzita v Praze Provozně ekonomická fakulta Doktorská vědecká konference 7. února 2011 T T THINK TOGETHER Jak měřit spolupráci obcí How to measure inter-municipality cooperation Martina
Česká zemědělská univerzita v Praze Provozně ekonomická fakulta Doktorská vědecká konference 7. února 2011 T T THINK TOGETHER Jak měřit spolupráci obcí How to measure inter-municipality cooperation Martina
Č. j.: TF/5/14 V Praze dne
 Č. j.: TF/5/14 V Praze dne 5.11.2014 Pokyn děkana K realizaci Studijního a zkušebního řádu pro studium v doktorských studijních programech České zemědělské univerzity v Praze na Technické fakultě ČZU v
Č. j.: TF/5/14 V Praze dne 5.11.2014 Pokyn děkana K realizaci Studijního a zkušebního řádu pro studium v doktorských studijních programech České zemědělské univerzity v Praze na Technické fakultě ČZU v
MĚŘENÍ STATISTICKÝCH ZÁVISLOSTÍ
 MĚŘENÍ STATISTICKÝCH ZÁVISLOSTÍ v praxi u jednoho prvku souboru se často zkoumá více veličin, které mohou na sobě různě záviset jednorozměrný výběrový soubor VSS X vícerozměrným výběrovým souborem VSS
MĚŘENÍ STATISTICKÝCH ZÁVISLOSTÍ v praxi u jednoho prvku souboru se často zkoumá více veličin, které mohou na sobě různě záviset jednorozměrný výběrový soubor VSS X vícerozměrným výběrovým souborem VSS
2.1 Dlouhodobý vývoj počtu obyvatel
 2.1 Dlouhodobý vývoj počtu obyvatel 1921 2011 Jako první podklad pro vytvoření prognózy využíváme dlouhodobý vývoj počtu obyvatel obcí suburbánní zóny Prahy. Vymezení suburbánní zóny bylo provedeno s ohledem
2.1 Dlouhodobý vývoj počtu obyvatel 1921 2011 Jako první podklad pro vytvoření prognózy využíváme dlouhodobý vývoj počtu obyvatel obcí suburbánní zóny Prahy. Vymezení suburbánní zóny bylo provedeno s ohledem
Organizační chování. Vědy o organizaci (cvičení)
 Organizační chování Vědy o organizaci (cvičení) Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty vojenského leadershipu Registrační
Organizační chování Vědy o organizaci (cvičení) Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty vojenského leadershipu Registrační
Studium závislosti výpočetního času algoritmu GPC prediktivního řízení na volbě typu popisu matematického modelu v regulátoru
 1 Portál pre odborné publikovanie ISSN 1338-0087 Studium závislosti výpočetního času algoritmu GPC prediktivního řízení na volbě typu popisu matematického modelu v regulátoru Barot Tomáš Elektrotechnika
1 Portál pre odborné publikovanie ISSN 1338-0087 Studium závislosti výpočetního času algoritmu GPC prediktivního řízení na volbě typu popisu matematického modelu v regulátoru Barot Tomáš Elektrotechnika
