ZÁKLADNÍ ICHTYOLOGICKÉ METODY
|
|
|
- Jiří Marek
- před 8 lety
- Počet zobrazení:
Transkript
1 ZÁKLADNÍ ICHTYOLOGICKÉ METODY Určováí věku a staoveí růstu ryb Ryby jsou poikilotermí obratlovci, u ichž jsou všechy biologické fukce zásadím způsobem ovlivňováy teplotou vody. To platí v plém rozsahu i pro itezitu růstu, protože s teplotou vody esouvisí pouze rozvoj přirozeé potravy, ale také aktivita trávicích ezymů a úroveň metabolizmu ryby. Na základě růzého průběhu teplot v jedotlivých ročích obdobích se ryby vyzačují periodickým růstem, který je výrazější u ryb mírého pásma, ale je patrý také u ryb tropických vod. Další specifickou vlastostí ryb je tzv. otevřeý růst, který ekočí dosažeím pohlaví dospělosti jedice. S ástupem pohlaví dospělosti se sice zpomaluje, protože ryba spotřebovává větší možství eergie a tvorbu pohlavích produktů, ale pokračuje po celý život. Rychlost růstu je také ovlivěa druhovou příslušostí, z ašich rybích druhů patří mezi rychle rostoucí apříklad štika obecá a sumec velký. V rámci druhu potom rychlost růstu závisí vedle teploty především a výskytu a dostuposti vhodé potravy. Ryby mohou v epřízivých potravích podmíkách a delší dobu růst zastavit a po jejich zlepšeí v růstu pokračovat. Tato vlastost ryb se ozačuje jako tzv. kompezačí růstová schopost. Ryby dokážou běžě překoat období hladověí v trváí ěkolika měsíců, v extrémích případech až jedoho roku. Růst ovlivňuje ještě řada dalších faktorů jako je zdravotí stav ryby, kyslíkatost a zečištěí vody, v chových systémech také kocetrace zplodi metabolizmu ryb. V tekoucích vodách může také docházet k tzv. růstové degeeraci určitého rybího druhu v důsledku jeho přemožeí a tím extrémě zvýšeé potraví kokureci. Typický příklad tohoto stavu byl u ás zazameá u populace ceja velkého v Plumlovské údolí ádrži. Naším ejvětším rybím druhem a zároveň ejvětší sladkovodí rybou světa je sumec velký, který v ašich podmíkách dosahuje hmotosti kolem 100 kg, ale z velkých evropských řek jsou zámy exempláře ještě podstatě větší. Štika obecá může dorůstat hmotosti až 40 kg, ale její rychlost růstu je výrazě závislá a výskytu dostupé potravy. Při adbytku potravích ryb v prostředí může dosáhout již v prvím roce života hmotosti až 1 kg. Hmotosti kolem 40 kg dorůstá také kapr obecý, jehož ejvětší úředě ověřeý úlovek a udici dosáhl 37 kg. Některé rybí druhy však rostou velice pomalu, z ašich původích druhů to jsou především parma obecá a jelec tloušť. U jikeračky jelce tlouště o hmotosti 1 kg byl zjiště věk 10 let a u jikeračky parmy obecé o hmotosti 2,60 kg dokoce 17 let. Je zajímavé, že u těchto druhů dosahují větších rozměrů a vyššího věku pouze jikeračky. Vedle maximálích růstových schopostí je z ichtyologického 93
2 hlediska a pro rybářské obhospodařováí tekoucích vod velmi důležitá otázka, jakého maximálího věku mohou volě žijící rybí druhy dosáhout. Schopost dosažeí určité věkové hraice je především druhovou vlastostí. Obecě platí, že rybí druhy dorůstající malých rozměrů (sluka obecá, střevle potočí, ouklej obecá apod.) jsou výrazě krátkověké a druhy dosahující velkých rozměrů dlouhověké. Při současém rybářském tlaku a aše tekoucí vody však již prakticky emůžeme zjistit, jakého věku mohou jedotlivé rybí druhy dosáhout. Navíc zečištěí vodího prostředí provázeé výskytem těžkých kovů a reziduí ejrůzějších chemických polutatů dosahovaý věk ryb v důsledku chroického stresu výrazě sižuje. Určováí věku ryb Zjišťováí věku ryb emá pouze teoretický výzam, ale také začý praktický příos. Z pohledu říčího rybářství ás zajímá, v jakém věku jedotlivé rybí druhy pohlavě dospívají, ebo jakého věku se dožívají ejvětší loveé exempláře. Při malosti věku pohlaví dospělosti můžeme apříklad staovit lovou míru kokrétího rybího druhu tak, aby v úlovcích ebylo příliš moho juveilích jediců, kteří se ještě estačili vytřít. Bez těchto zalostí bychom sado přivodili likvidaci určitého rybího druhu v průběhu ěkolika let. Metody epřímého určováí věku ryb jsou založey a periodicitě jejich růstu v jedotlivých ročích obdobích, která se viditelě projevuje a šupiách, otolitech a větších kostech v podobě střídáí širších zó letího přírůstku s užšími zóami zimího přírůstku. Nejčastěji se věk ryb určuje podle počtu přírůstků a šupiách. Cetrum šupiy obkružují jemé prstece, ozačovaé jako sklerity. Během letího období jsou v důsledku itezivějšího růstu mezery mezi sklerity širší ež v zimě. Hraice mezi letím a zimím přírůstkem je obvykle jasá, vyjádřeá v podobě hlubší rýhy a epravidelých, jakoby odsekutých skleritů. Tato hraice se azývá aulus a představuje jedo prožité období. Přírůstky jsou lépe viditelé a předí části šupiy zakotveé v kůži, protože kaudálí část šupiy je pokryta pokožkou obsahující chromatofory. Kolísáí výživy během letího období, popřípadě zastaveí růstu vlivem teplotích změ, zečištěí vody ebo oemocěím ryby se může projevit vzikem tzv. falešého aulu. Te většiou eprobíhá po celém obvodu šupiy a chybí typická rýha. Další zvláštostí je vzik tzv. juveilí začky, která charakterizuje přechod mladé ryby z jedoho typu potravy a jiý (apř. u dravých druhů přechod a dravý způsob výživy). Teto epravý aulus je umístě v blízkosti cetra šupiy uvitř zóy prvího roku. Je charakteristický epřítomostí rýhy a pravidelými sklerity, které plyule přecházejí do zóy širších skleritů. U ěkterých rybích druhů se ještě vyskytuje tzv. třecí začka, která je většiou totožá s pravým aulem. Vziká hlubokou deformací okrajů šupiy 94
3 v důsledku resorbce ebo mechaického poškozeí během bouřlivého výtěru ryb. Teto aulus se tak stává zubatým ebo zvlěým a z ašich druhů se vyskytuje u salmoidů, plotice obecé a ceja velkého. Místo a rybím těle k odběru šupi pro určováí věku volíme podle toho, zda jde o orálěkaudálí typ, u ěhož se šupiy zakládají ejdříve v prví poloviě těla, ebo o typ kaudálěorálí, kdy šupiy vzikají ejprve a ocasím ásadci. Šupiy a růzých částech těla také růzě rostou, proto se u jedotlivých druhů ryb odebírají a přesě staoveých místech. Pokud takové místo ezáme, odebíráme šupiy ze středu těla z prví řady ad postraí čarou ebo pod í. Od každého jedice odebíráme alespoň 3-10 šupi, protože u řady rybích druhů se objevují také regeerovaé šupiy, které pro určeí věku elze využít. Regeerát je zovu vytvořeá šupia po ztrátě dřívější šupiy a je charakteristický matým středem bez skleritů a radiálích kaálků. Obr. 27: Schema šupiy plotice obecé 1 orálí poloměr, 2 kaudálí poloměr, 3 diagoálí poloměr, 4 a 5 aulus, 6 radiálí kaálek (podle Holčíka a Hesela, 1972) 95
4 U rybích druhů bez šupi (sumec velký. vraka obecá), ebo u druhů s velmi malými šupiami (apř. úhoř říčí), určujeme věk pomocí otolitů ebo velkých kostí. Využití otolitů je metodicky áročější, protože se musejí vybrušovat, chemicky odvodňovat a opticky projasňovat. Potom se prohlížejí v procházejícím ebo dopadajícím světle pomocí optického mikroskopu. V posledích letech jsou pro vybraé rybí druhy propracováváy metody odhadu věku podle změ hmotosti otolitů. Studium přírůstkové struktury otolitů citlivými moderími metodami dokoce umožňuje získávat podrobější údaje o průběhu jedotlivých fází otogeeze rybích druhů. Před ěkolika lety tak fracouzští ichtyologové vyslovili a základě studia símků otolitů leptocefalích larev úhoře říčího z elektroového mikroskopu převratý ázor a průběh jeho larválího stadia a metamorfózy. Podle jejich závěrů by larválí stádium úhoře a putovái leptocefalích larev přes Atlatský oceá mělo trvat ecelých 12 měsíců, kdežto obecě přijímaý ázor předpokládá délku tohoto stadia 3-4 roky. Věk ryb lze zjišťovat také podle zoace temých a světlejších pásů a skřelových kostech, a tělech obratlů páteře a a řezech z prvího tvrdého paprsku prsí ploutve. Řez ploutevího paprsku se provádí při jeho bázi, obratle se ejčastěji odebírají za hlavou ebo těsě před hřbetí ploutví. Staoveí růstu ryb Nejjedodušší je využití metody přímého pozorováí, založeé a pozorováí růstu ryb zámého věku v rybících, ebo a zjištěí věku, délky a hmotosti zkoumaé (ozačkovaé) ryby v době uloveí. Tato metoda však má poměrě ízké uplatěí a ejčastěji se využívá v rybíkářství pro zjištěí přírůstků ryb v průběhu vegetačího období a ke korekci krmé dávky (kotrolí odlovy, tzv. letí pruby v rybících). Ve většiě případů je uto využít metody zpětého výpočtu růstu. Zde se vlastě jedá o časovou rekostrukci růstu založeou a faktu, že růst těla ryby a růst šupi (otolitů, kostí) jsou v zákoité souvislosti. Z tohoto předpokladu vychází metoda Eiara Lea: Délka šupiy od středu k jejímu okraji (V) je k aktuálí délce těla ryby (L) ve stejém poměru jako ěkdejší poloměr šupiy (V ) k ěkdejší délce těla ryby (L ). Tedy V L V L V, potom L L V Pro mechaický výpočet růstu, který je založe a podobosti pravoúhlých trojúhelíků, se používá tzv. Leaova deska. Lze ji využít pro staoveí růstu ryb s většími a dobře čitelými šupiami a přesost metody je dostačující pro praktické účely. Přesé určeí délky těla ryby za 96
5 předcházející ezámé roky života vyžaduje poměrě složité korekce, protože závislost délky těla a poloměru šupiy zpravidla eí zcela lieárí. Pro zachyceí idividuálí variability se měřeí provádí řádově a stovkách exemplářů určitého druhu. Zároveň se vypočítávají zvláští hodoty pro možost porováí růstu zkoumaých rybích druhů s rybami stejých druhů z jiých vod. To potom umožňuje vyvozovat závěry o zákoitostech růstu sledovaého druhu. Výsledky získaé Leaovou metodou jsou také poěkud ižší, a to zejméa pro prví roky života. Teto edostatek koriguje metoda Rosy Lee, která vychází ze zjištěí, že ryba má v době založeí šupi již určitou velikost, s íž je třeba počítat. Proto do vzorce E. Lea zavedla hodotu a, která představuje délku těla ryby v době založeí šupi a lze ji zjistit empiricky ebo graficky. Vzorec pro výpočet růstu má potom podobu: L V V L a a Studium rybích populací a společestev V rámci každého živočišého druhu, tedy i ryb, je považováa za základí jedotku osídlei určitého biotopu populace. Ta je defiováa jako skupia jediců téhož druhu, která se vyzačuje stejým geofodem. V současé době eí většia rybích populací žijících a ašem území v přirozeém stavu, protože jsou dlouhodobě výrazě ovlivňováy ejrůzějšími atropogeími vlivy. Mezi ejdůležitější z ich patří rybářské obhospodařováí tekoucích vod (sportoví rybolov: vysazováí ásad, které avíc často pocházejí z povodí jiých řek), zečišťováí vod a stavebí úpravy říčích toků (velké vodí stavby, regulace říčích koryt, meliorace). V rybičích chovech a akvakulturách, kde je druhová i věková struktura ryb přímo podřízea hospodářskému cíli, ehovoříme o populacích, ai o rybích společestvech, ale tato uměle vziklá společestva ozačujeme jako obsádky. Problematika rybích obsádek spadá do discipli avazujících a ichtyologii (chov ryb, akvakultura), proto zde ebude blíže objasňováa. U volě žijících ryb jsou z hlediska rybářského obhospodařováí tekoucích vod pro využití produkčích schopostí a z hlediska ochray rybích druhů studováy základí populačí charakteristiky a jejich dyamika (zejméa abudace a biomasa, věkové složeí populací a mortalita). V ásledující kapitole jsou uvedey pouze v praxi ejčastěji používaé ichtyologické metody. Podrobě je tato problematika rozvedea v základích ichtyologických příručkách (apř. Holčík a Hesel, 1972). 97
6 Odhady početosti rybích populací Početost (hustota populace) vyjádřeá abudací je základím populačím parametrem. Abudace představuje početí charakteristiku populace, vztažeou a jedotku plochy, její hmotostí vyjádřeí je ozačováo jako biomasa. Dalším parametrem je produkce, která představuje hmotostí vyjádřeí tvorby ové biomasy za časové období, obvykle za jede rok. Odhady početosti zahrují metody, jimiž můžeme staovit velikost populace ryb v kokrétím úseku vodího toku, v jezeře, ebo v údolí ádrži. Přímé metody odhadu jsou založey a vypuštěí sledovaé ádrže (rybíka) a spočítáí sloveých ryb, ebo a zahrazeí určitého úseku toku a vyloveí všech ryb pomocí elektrického agregátu. V krajím případě lze také ryby ve sledovaých úsecích toků ebo v malých ádržích vytrávit pomoci rybích jedů (piscicidů). Tato metoda byla u ás dříve využíváa při studiu polabských tůí, des je však z hlediska ochray přírody zcela epřijatelá. Přímé metody odhadu početosti rybích populací mají poměrě malé využití, omezeé a rybíky, tůě, jezírka, potoky a krátké úseky meších řek. Ve většiě případů se proto musíme uchýlit k epřímým metodám, které jsou založeé a matematickém odhadu početosti. K odhadům početosti, ale také mortality, růstu a migrací ryb, se s výhodou používá začeí ryb. Většiou se využívá idividuálí začeí pomocí dříve ejpoužívaějších kovových začek až po des převažující elektroické čipy, ebo speciálí barviva, ijekčě podkožě aplikovaá. Převážě pro potřeby evidece v chovech ryb ebo pro viditelé odlišeí mlíčáků a jikeraček se používá skupiové začeí (odstřižeí epárové ploutve ebo jedé z břiších ploutví), popřípadě koží začeí pomocí kryogeí metody. Tyto začky však mají časově omezeou trvalivost. Při epřímém odhadu početosti populace s využitím začeých ryb vycházíme z předpokladu, že vyloveé a ozačeé ryby, které vypustíme zpět do sledovaého biotopu, se rozptýlí mezi zbývající eozačeou část populace. Při opětovém odlovu ryb potom zjistíme určitý poměr mezi ozačeými a eozačeými rybami, který představuje základí údaj pro výpočet odhadu. Pro správost odhadu početosti je však třeba split základí podmíky: 1. Ryby musejí být ozačey dobře viditelou začkou, která ezpůsobí rybě zraěí ebo smrt a z těla ryby eodpade. 2. Ozačeé ryby musejí být rovoměrě rozptýley mezi eozačeými. Zvláště u větších ádrží je uté ozačeé ryby rozvézt a vypustit a růzých lokalitách, vzdáleých od místa uloveí. 3. Sběr ichtyologického materiálu musí být proporcioálí hustotě populace v celé ádrži. 98
7 4. Ulovitelost ozačeých a eozačeých ryb musí být stejá. Je třeba kombiovat růzé rybolové prostředky, protože každá lová metoda je více ebo méě selektiví. 5. Populace podrobeá experimetu esmí být ovlivňováa mortalitou, ai atalitou. Experimet musí proto proběhout v krátkém časovém úseku. To sice eí u velkých ádrží možé, ale řadou sledováí bylo zjištěo, že atalita se prakticky rová mortalitě, takže s korekcí eí třeba počítat. V praxi je pro svoji jedoduchost a přitom relativí přesost ejčastěji používáa metoda odhadu podle Schabelové: t N s N - rozsah (početost) populace - celkový počet ryb v úlovku t- celkový počet ozačeých ryb, přítomých v ádrži s - celkový počet ozačeých ryb v úlovku Rozsah populace (N) je ovlivě růzými faktory, proto musíme zjistit hraice, mezi imiž se odhad pohybuje, tzv. kofidečí limity (většiou s 95% pravděpodobostí, málokdy s 99% pravděpodobostí). Použití vzorce pro výpočet se řídí rozsahem souboru (počtem uloveých ryb). Další z používaějších metod je grafická metoda Leslie a Davise. Hodoty po sobě ásledujících úlovků (y t ) se zaesou do grafu proti hodotám kumulovaých úlovků, z ichž prví je ulový. Směrice přímky procházející vyeseými body, představuje pravděpodobost uloveí (p) ryb v každém jedotlivém odlovu. Průsečík s osou x se rová početosti odhadovaé populace. Díky vysoké úrovi ichtyologického výzkumu v České republice máme k dispozici poměrě hodě údajů o populačí hustotě ryb v růzých typech ašich vod, a to jak z potoků a řek, tak i z větších údolích ádrží. V ašich pstruhových vodách (kategorie rybářských revírů) se abudace ryb pohybuje v rozmezí ks.ha -1, s průměrou hodotou ks.ha -1, z toho pstruh obecý tvoří průměrou abudaci ks.ha -1. Odhady početosti ryb ve větších tocích mimopstruhového charakteru kolísají v rozsahu ks.ha -1. Nejvyšší abudace ryb je zjišťováa v iudačích oblastech velkých řek (tůě, odstaveá ramea). V údolích ádržích je početost ryb ižší a abudace dosahují hodot ks.ha -1 (bez tohoročků). Společě s odhady početosti rybích populací se provádí také odhad jejich biomasy, to zameá hmotosti jedé ebo více populací, popřípadě celého rybího společestva a jedotku 99
8 plochy. Vlastí biomasa (B) je ásobkem průměré hmotosti ryb (W) určité délkové ebo věkové skupiy a její abudace (A), pro i-tou skupiu (vše v přepočtu a 1 ha plochy): B i 1 A i W i Celkovou biomasu rybího společestva (ichtyoceózy) potom tvoří součet biomas jedotlivých druhů. V ašich pstruhových vodách se biomasa ryb pohybuje mezi 87 a 530 kg.ha -1 (s průměrem 167 kg.ha -1 ), v řekách mimopstruhového pásma v rozmezí kg.ha -1 (s průměrou hodotou 430 kg.ha -1. V silě eutrofích ádržích může biomasa ryb dosahovat kg.ha -1. Vedle abudace a biomasy ryb je z hospodářského hlediska důležitý také odhad produkce rybích populací i celých společestev. Nejjedodušším způsobem odhadu produkce je vyásobeí průměrého hmotostího přírůstku ryb jedé věkové skupiy za daou časovou jedotku jejich počtem a koci sledovaého období. Součet za jedotlivé skupiy (popřípadě i druhy) potom představuje celkovou produkci. Alleova grafická metoda odhadu produkce vychází z plaimetrického zjištěí plochy ohraičeé souřadicovými osami a křivkou závislosti mezi rostoucí průměrou hmotostí ryb a klesající početostí. Na osu y vyášíme počet přežívajících jediců jedoho ročíku určitého druhu a a osu x průměrou hmotost této věkové skupiy. Pro odhad produkce ryb v tekoucích vodách byla vypracováa Léger-Huetova metoda, která bere v úvahu biogeí kapacitu toku (B), jeho průměrou šířku v metrech (L) a koeficiet produktivity (k). Studium vyvážeosti rybích společestev Druhové složeí rybích společestev, přemožeí ebo edostatek určitých rybích druhů, jejich rychlost růstu jsou dalšími důležitými ukazateli vyvážeosti ichtyoceóz, které mají ve svém důsledku vysokou vypovídající hodotu o úrovi rybářského obhospodařováí určitého vodího biotopu. Z hlediska početího zastoupeí jedotlivých rybích druhů ve společestvu představuje důležitý relativí kvatitativí zak domiace (D), která vyjadřuje procetický podíl druhových populací. Vypočítáme ji z absolutích ebo i relativích hodot abudace: D 100 s (v %) - celkový počet jediců určitého druhu s - celkový počet jediců všech druhů (společestva) 100
9 Hodota domiace je ovlivěa počtem druhů, které společestvo tvoří a s rostoucím počtem druhů se relativě sižuje. Proto je u společestev s vysokým počtem druhů domiace ejpočetějších druhů relativě ižší ež ve společestvech druhově chudých. Pro podrobější rozlišeí domiace se používá pětistupňová klasifikace: eudomiatí druh více ež 10% domiatí druh 5-10% subdomiatí druh 2-5% reredetí druh 1-2% subrecedetí druh méě ež 1% Bohatství druhů ve společestvu je charakterizováo druhovou rozmaitostí, ebo-li diverzitou. Jedá se o strukturě kvatitativí vlastost každého společestva, která se hodotí pomocí idexu diverzity (H ). Te představuje poměr počtu druhů k počtu jediců: H i 1 N N i log 2 N N i N i - počet jediců jedoho druhu N - počet jediců všech druhů Čím je idex diverzity vyšší, tím větším počtem druhů je společestvo tvořeo a tím více je celkový počet jediců rozlože a více druhů. Malou diverzitu vykazují společestva žijící v extrémích podmíkách (apř. ve zečištěých vodách), vysokou diverzitou se vyzačují stabilizovaá společestva. Počet druhů společestva výrazě závisí a geografické poloze, diverzita obecě roste od pólů k rovíku. Podobá závislost existuje a admořské výšce, s jejímž vzestupem druhová pestrost klesá (apříklad ižší diverzita pstruhových pásem). Pro diverzitu má také důležitý výzam stáří společestva, starší společestva jsou druhově bohatší ež mladší. Další vlastostí společestva, související s druhovou diverzitou je jeho vyrovaost, ebo-li ekvitabilita, charakterizovaá idexem E: H E log 2 s H - idex diverzity s - celkový počet druhů společestva 101
10 Ekvitabilita vlastě sigalizuje míru rovosti četostí jedotlivých druhů, to zameá poměré rozděleí všech jediců společestva a zastoupeé rybí druhy. Pro posouzeí vyvážeosti ichtyoceóz hlediska praktického obhospodařováí rybářských revírů je důležité sledovat v říčích tocích a údolích ádržích hmotostí poměr růzých skupi ryb (především edravých a dravých druhů). K tomu je třeba zát: - druhové spektrum ryb zkoumaé ádrže ebo toku - početost (abudaci) jedotlivých druhů - hmotost (biomasu) jedotlivých druhů ryb - jejich délkovou charakteristiku Pro odhad těchto údajů je možo využít také určité pozatky ze statistik rybářských úlovků hospodářské evidece rybářských svazů. I když tyto údaje jsou zatížey růzými chybami, způsobeými selektivostí lovu, pytláctvím a epřesým zazameáváím úlovků, jedá se o velice důležitý zdroj kokrétích ichtyologických dat. Koeficiet F/C udává hmotostí poměr edravých a dravých rybích druhů. Veličia F je celková hmotost edravých druhů ryb (plaktoofágové, betofágové, fytofágové). Zařazujeme sem i plůdek dravých druhů ryb. Hodota C představuje celkovou hmotost dravých druhů. Do této skupiy zase zařazujeme velké exempláře edravých druhů, o ichž je zámo, že se od určité velikosti živí také rybami (apř. jelec tloušť a okou říčí). Rozpětí koeficietu F/C 1,4-10 charakterizuje společestvo v rovováze. Za optimálí rozpětí je považováo a takové společestvo dosahuje ejvyšší produkce. Koeficiet F/C ižší ež 2,0 charakterizuje společestvo s převahou dravých ryb (v ašich podmíkách se prakticky evyskytuje). F/C vyšší ež 6.0 sigalizuje přemožeí edravých druhů, což je aopak případ většiy vod, kde je provozová sportoví rybolov. Rybáři se totiž selektivě zaměřují a lov dravých ryb pro jejich relativě sažší ulovitelost a vysoce kvalití maso. Koeficiet Y/C vyjadřuje možství dostupé potravy pro dravce. Veličia Y představuje celkovou hmotost ryb skupiy F, které jsou dostatečé malé, aby mohly být potravou dravců (C). Ve vyvážeých populacích se Y/C pohybuje v rozmezí 0,02-4,8. Za optimálí je považováo rozpětí Pokud je koeficiet Y/C vyšší ež 4,8, ichtyoceóza je v erovováze a eí schopa produkovat dostatečé možství ryb lové velikosti. Koeficiet A t vyjadřuje hmotostí procetické zastoupeí ryb lové velikosti v ichtyoceóze, tedy ryb takové velikosti, které prakticky tvoří produkci. Ve vyvážeé ichtyoceóze se 102
11 A t pohybuje v rozsahu 33-90%, optimálí hodota je 60-85%. Hodoty A t od 0,0 do 40% sigalizují přemožeí edravých druhů ryb, hodoty ad 85% ukazují a převahu dravců. Koeficiet A F představuje procetický podíl hmotosti velkých ryb skupiy F, přesahujících lovou míru, z celé skupiy F. U vyvážeých společestev se A F pohybuje mezi 12,2 a 99.6%, optimálí jsou hodoty v rozmezí 60-80%. Hodoty A F v rozsahu 1,2-25,7% ukazují a přemožeí edravých druhů, hodoty ad 85% sigalizují adbytek dravců v ichtyoceóze. 103
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou
 1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
STATISTIKA. Statistika se těší pochybnému vyznamenání tím, že je nejvíce nepochopeným vědním oborem. H. Levinson
 STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
Základy statistiky. Zpracování pokusných dat Praktické příklady. Kristina Somerlíková
 Základy statistiky Zpracováí pokusých dat Praktické příklady Kristia Somerlíková Data v biologii Zak ebo skupia zaků popisuje přírodí jevy, úlohou výzkumíka je vybrat takovou skupiu zaků, které charakterizují
Základy statistiky Zpracováí pokusých dat Praktické příklady Kristia Somerlíková Data v biologii Zak ebo skupia zaků popisuje přírodí jevy, úlohou výzkumíka je vybrat takovou skupiu zaků, které charakterizují
Závislost slovních znaků
 Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
Základní požadavky a pravidla měření
 Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Popisná statistika - zavedení pojmů. 1 Jednorozměrný statistický soubor s kvantitativním znakem
 Popisá statistika - zavedeí pojmů Popisá statistika - zavedeí pojmů Soubor idividuálích údajů o objektech azýváme základí soubor ebo také populace. Zkoumaé objekty jsou tzv. statistické jedotky a sledujeme
Popisá statistika - zavedeí pojmů Popisá statistika - zavedeí pojmů Soubor idividuálích údajů o objektech azýváme základí soubor ebo také populace. Zkoumaé objekty jsou tzv. statistické jedotky a sledujeme
P2: Statistické zpracování dat
 P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
Pravděpodobnost a aplikovaná statistika
 Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
10.3 GEOMERTICKÝ PRŮMĚR
 Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
12. N á h o d n ý v ý b ě r
 12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
13 Popisná statistika
 13 Popisá statistika 13.1 Jedorozměrý statistický soubor Statistický soubor je možia všech prvků, které jsou předmětem statistického zkoumáí. Každý z prvků je statistickou jedotkou. Prvky tvořící statistický
13 Popisá statistika 13.1 Jedorozměrý statistický soubor Statistický soubor je možia všech prvků, které jsou předmětem statistického zkoumáí. Každý z prvků je statistickou jedotkou. Prvky tvořící statistický
1.7.4 Těžiště, rovnovážná poloha
 74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
Laboratorní práce č. 10 Úloha č. 9. Polarizace světla a Brownův pohyb:
 ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
Pro statistické šetření si zvolte si statistický soubor např. všichni žáci třídy (několika tříd, školy apod.).
 STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
Parametr populace (populační charakteristika) je číselná charakteristika sledované vlastnosti
 1 Základí statistické zpracováí dat 1.1 Základí pojmy Populace (základí soubor) je soubor objektů (statistických jedotek), který je vymeze jejich výčtem ebo charakterizací jejich vlastostí, může být proto
1 Základí statistické zpracováí dat 1.1 Základí pojmy Populace (základí soubor) je soubor objektů (statistických jedotek), který je vymeze jejich výčtem ebo charakterizací jejich vlastostí, může být proto
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
2 STEJNORODOST BETONU KONSTRUKCE
 STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
Mezní stavy konstrukcí a jejich porušov. Hru IV. Milan RůžR. zbynek.hruby.
 ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
1. Měření ve fyzice, soustava jednotek SI
 1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
1 POPISNÁ STATISTIKA V PROGRAMU MS EXCEL
 Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
odhady parametrů. Jednostranné a oboustranné odhady. Intervalový odhad střední hodnoty, rozptylu, relativní četnosti.
 10 Cvičeí 10 Statistický soubor. Náhodý výběr a výběrové statistiky aritmetický průměr, geometrický průměr, výběrový rozptyl,...). Bodové odhady parametrů. Itervalové odhady parametrů. Jedostraé a oboustraé
10 Cvičeí 10 Statistický soubor. Náhodý výběr a výběrové statistiky aritmetický průměr, geometrický průměr, výběrový rozptyl,...). Bodové odhady parametrů. Itervalové odhady parametrů. Jedostraé a oboustraé
L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
PŘÍKLAD NA PRŮMĚRNÝ INDEX ŘETĚZOVÝ NEBOLI GEOMETRICKÝ PRŮMĚR
 PŘÍKLAD NA PRŮMĚRNÝ INDEX ŘETĚZOVÝ NEBOLI GEOMETRICKÝ PRŮMĚR Ze serveru www.czso.cz jsme sledovali sklizeň obilovi v ČR. Sklizeň z ěkolika posledích let jsme vložili do tabulky 10.10. V kapitole 7. Idexy
PŘÍKLAD NA PRŮMĚRNÝ INDEX ŘETĚZOVÝ NEBOLI GEOMETRICKÝ PRŮMĚR Ze serveru www.czso.cz jsme sledovali sklizeň obilovi v ČR. Sklizeň z ěkolika posledích let jsme vložili do tabulky 10.10. V kapitole 7. Idexy
6. Posloupnosti a jejich limity, řady
 Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
IAJCE Přednáška č. 12
 Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
1 ROVNOMĚRNOST BETONU KONSTRUKCE
 ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Zhodnocení přesnosti měření
 Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Iterační metody řešení soustav lineárních rovnic
 Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
1. Základy měření neelektrických veličin
 . Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
. Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
8.2.1 Aritmetická posloupnost I
 8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
6. FUNKCE A POSLOUPNOSTI
 6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:
 Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Tento projekt je spolufinancován Evropským sociálním fondem a Státním rozpočtem ČR InoBio CZ.1.07/2.2.00/
 Teto projekt je spolufiacová Evropským sociálím fodem a Státím rozpočtem ČR IoBio CZ..07/2.2.00/28.008 Připravil: Ig. Vlastimil Vala, CSc. Metody zkoumáí ekoomických jevů Kapitola straa 3 Metoda Z řeckého
Teto projekt je spolufiacová Evropským sociálím fodem a Státím rozpočtem ČR IoBio CZ..07/2.2.00/28.008 Připravil: Ig. Vlastimil Vala, CSc. Metody zkoumáí ekoomických jevů Kapitola straa 3 Metoda Z řeckého
Intervalový odhad. nazveme levostranným intervalem pro odhad parametru Θ. Statistiku. , kde číslo α je blízké nule, nazveme horním
 Lekce Itervalový odhad Itervalový odhad je jedou ze stadardích statistických techik Cílem je sestrojit iterval (kofidečí iterval, iterval spolehlivosti, který s vysokou a avíc předem daou pravděpodobostí
Lekce Itervalový odhad Itervalový odhad je jedou ze stadardích statistických techik Cílem je sestrojit iterval (kofidečí iterval, iterval spolehlivosti, který s vysokou a avíc předem daou pravděpodobostí
Nejistoty měření. Aritmetický průměr. Odhad směrodatné odchylky výběrového průměru = nejistota typu A
 Nejstoty měřeí Pro každé přesé měřeí potřebujeme formac s jakou přesostí bylo měřeí provedeo. Nejstota měřeí vyjadřuje terval ve kterém se achází skutečá hodota měřeé velčy s určtou pravděpodobostí. Nejstota
Nejstoty měřeí Pro každé přesé měřeí potřebujeme formac s jakou přesostí bylo měřeí provedeo. Nejstota měřeí vyjadřuje terval ve kterém se achází skutečá hodota měřeé velčy s určtou pravděpodobostí. Nejstota
ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU)
 ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU) Základy teorie pravděpodobosti měřeí chyba měřeí Provádíme kvalifikovaý odhad áhodá systematická výsledek ejistota výsledku Základy teorie pravděpodobosti
ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU) Základy teorie pravděpodobosti měřeí chyba měřeí Provádíme kvalifikovaý odhad áhodá systematická výsledek ejistota výsledku Základy teorie pravděpodobosti
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
základním prvkem teorie křivek v počítačové grafice křivky polynomiální n
 Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
8.2.1 Aritmetická posloupnost
 8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
1. Základy počtu pravděpodobnosti:
 www.cz-milka.et. Základy počtu pravděpodobosti: Přehled pojmů Jev áhodý jev, který v závislosti a áhodě může, ale emusí při uskutečňováí daého komplexu podmíek astat. Náhoda souhr drobých, ezjistitelých
www.cz-milka.et. Základy počtu pravděpodobosti: Přehled pojmů Jev áhodý jev, který v závislosti a áhodě může, ale emusí při uskutečňováí daého komplexu podmíek astat. Náhoda souhr drobých, ezjistitelých
Vzorový příklad na rozhodování BPH_ZMAN
 Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
STATISTIKA. Základní pojmy
 Statistia /7 STATISTIKA Záladí pojmy Statisticý soubor oečá eprázdá možia M zoumaých objetů schromážděých a záladě toho, že mají jisté společé vlastosti záladí statisticý soubor soubor všech v daé situaci
Statistia /7 STATISTIKA Záladí pojmy Statisticý soubor oečá eprázdá možia M zoumaých objetů schromážděých a záladě toho, že mají jisté společé vlastosti záladí statisticý soubor soubor všech v daé situaci
STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6
 Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
Petr Šedivý Šedivá matematika
 LIMITA POSLOUPNOSTI Úvod: Kapitola, kde poprvé arazíme a ekoečo. Argumety posloupostí rostou ade všechy meze a zkoumáme, jak vypadají hodoty poslouposti. V kapitole se sezámíte se základími typy it a početími
LIMITA POSLOUPNOSTI Úvod: Kapitola, kde poprvé arazíme a ekoečo. Argumety posloupostí rostou ade všechy meze a zkoumáme, jak vypadají hodoty poslouposti. V kapitole se sezámíte se základími typy it a početími
Téma: 11) Dynamika stavebních konstrukcí
 Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
23. Mechanické vlnění
 3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
Modelování jednostupňové extrakce. Grygar Vojtěch
 Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
2,3 ČTYŘI STANDARDNÍ METODY I, ČTYŘI STANDARDNÍ METODY II
 2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
Pravděpodobnostní modely
 Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
AMC/IEM J - HMOTNOST A VYVÁŽENÍ
 ČÁST JAR-OPS 3 AMC/IEM J - HMOTNOST A VYVÁŽENÍ ACJ OPS 3.605 Hodoty hmotostí Viz JAR-OPS 3.605 V souladu s ICAO Ae 5 a s meziárodí soustavou jedotek SI, skutečé a omezující hmotosti vrtulíků, užitečé zatížeí
ČÁST JAR-OPS 3 AMC/IEM J - HMOTNOST A VYVÁŽENÍ ACJ OPS 3.605 Hodoty hmotostí Viz JAR-OPS 3.605 V souladu s ICAO Ae 5 a s meziárodí soustavou jedotek SI, skutečé a omezující hmotosti vrtulíků, užitečé zatížeí
Posouzení struktury strojní sestavy pomocí teorie hromadných obsluh
 Projekt zpracová s podporou FRVŠ. Posouzeí struktury strojí sestavy pomocí teorie hromadých obsluh 1 Základí údaje Ve stavebí praxi se velmi často vyskytuje požadavek rychle a objektivě posoudit strukturu
Projekt zpracová s podporou FRVŠ. Posouzeí struktury strojí sestavy pomocí teorie hromadých obsluh 1 Základí údaje Ve stavebí praxi se velmi často vyskytuje požadavek rychle a objektivě posoudit strukturu
FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL
 Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
STATISTIKA PRO EKONOMY
 EDICE UČEBNÍCH TEXTŮ STATISTIKA PRO EKONOMY EDUARD SOUČEK V Y S O K Á Š K O L A E K O N O M I E A M A N A G E M E N T U Eduard Souček Statistika pro ekoomy UČEBNÍ TEXT VYSOKÁ ŠKOLA EKONOMIE A MANAGEMENTU
EDICE UČEBNÍCH TEXTŮ STATISTIKA PRO EKONOMY EDUARD SOUČEK V Y S O K Á Š K O L A E K O N O M I E A M A N A G E M E N T U Eduard Souček Statistika pro ekoomy UČEBNÍ TEXT VYSOKÁ ŠKOLA EKONOMIE A MANAGEMENTU
Odhad parametru p binomického rozdělení a test hypotézy o tomto parametru. Test hypotézy o parametru p binomického rozdělení
 Odhad parametru p biomického rozděleí a test hypotézy o tomto parametru Test hypotézy o parametru p biomického rozděleí Motivačí úloha Předpokládejme, že v důsledku realizace jistého áhodého pokusu P dochází
Odhad parametru p biomického rozděleí a test hypotézy o tomto parametru Test hypotézy o parametru p biomického rozděleí Motivačí úloha Předpokládejme, že v důsledku realizace jistého áhodého pokusu P dochází
2. Náhodná veličina. je konečná nebo spočetná množina;
 . Náhodá veličia Většia áhodých pokusů koaých v přírodích ebo společeských vědách má iterpretaci pomocí reálé hodoty. Při takovýchto dějích přiřazujeme tedy reálá čísla áhodým jevům. Proto je důležité
. Náhodá veličia Většia áhodých pokusů koaých v přírodích ebo společeských vědách má iterpretaci pomocí reálé hodoty. Při takovýchto dějích přiřazujeme tedy reálá čísla áhodým jevům. Proto je důležité
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1 Úvod { }.[ ] A= A A, (1.1)
![1 Úvod { }.[ ] A= A A, (1.1) 1 Úvod { }.[ ] A= A A, (1.1)](/thumbs/49/25322446.jpg) Obsah Obsah... Úvod... 3 Základí pojmy počtu pravděpodobosti... 7. Základí statistické pojmy... 7. Fukce áhodých veliči... 8.3 Charakteristiky áhodých veliči... 0.4 Některá rozděleí pravděpodobosti....5
Obsah Obsah... Úvod... 3 Základí pojmy počtu pravděpodobosti... 7. Základí statistické pojmy... 7. Fukce áhodých veliči... 8.3 Charakteristiky áhodých veliči... 0.4 Některá rozděleí pravděpodobosti....5
Při sledování a studiu vlastností náhodných výsledků poznáme charakter. podmínek různé výsledky. Ty odpovídají hodnotám jednotlivých realizací
 3. Náhodý výběr Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých realizací
3. Náhodý výběr Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých realizací
Nálitky. Obr. 1 Schematický přehled typů nálitků
 Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
NEPARAMETRICKÉ METODY
 NEPARAMETRICKÉ METODY Jsou to metody, dy předmětem testu hypotézy eí tvrzeí o hodotě parametru ějaého orétího rozděleí, ale ulová hypotéza je formulováa obecěji, apř. jao shoda rozděleí ebo ezávislost
NEPARAMETRICKÉ METODY Jsou to metody, dy předmětem testu hypotézy eí tvrzeí o hodotě parametru ějaého orétího rozděleí, ale ulová hypotéza je formulováa obecěji, apř. jao shoda rozděleí ebo ezávislost
Tržní ceny odrážejí a zahrnují veškeré informace předpokládá se efektivní trh, pro cenu c t tedy platí c t = c t + ε t.
 Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
1. Definice elektrického pohonu 1.1 Specifikace pohonu podle typu poháněného pracovního stroje 1.1.1 Rychlost pracovního mechanismu
 1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
Iterační výpočty projekt č. 2
 Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....
Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....
Cvičení z termomechaniky Cvičení 5.
 Příklad V kompresoru je kotiuálě stlačová objemový tok vzduchu [m 3.s- ] o teplotě 20 [ C] a tlaku 0, [MPa] a tlak 0,7 [MPa]. Vypočtěte objemový tok vzduchu vystupujícího z kompresoru, jeho teplotu a příko
Příklad V kompresoru je kotiuálě stlačová objemový tok vzduchu [m 3.s- ] o teplotě 20 [ C] a tlaku 0, [MPa] a tlak 0,7 [MPa]. Vypočtěte objemový tok vzduchu vystupujícího z kompresoru, jeho teplotu a příko
i 1 n 1 výběrový rozptyl, pro libovolné, ale pevně dané x Roznačme n 1 Téma 6.: Základní pojmy matematické statistiky
 Téma 6.: Základí pojmy matematické statistiky Vlastosti důležitých statistik odvozeých z jedorozměrého áhodého výběru: Nechť X,..., X je áhodý výběr z rozložeí se středí hodotou μ, rozptylem σ a distribučí
Téma 6.: Základí pojmy matematické statistiky Vlastosti důležitých statistik odvozeých z jedorozměrého áhodého výběru: Nechť X,..., X je áhodý výběr z rozložeí se středí hodotou μ, rozptylem σ a distribučí
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
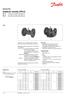 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
OBRAZOVÁ ANALÝZA POVRCHU POTISKOVANÝCH MATERIÁLŮ A POTIŠTĚNÝCH PLOCH
 OBRAZOVÁ ANALÝZA POVRCU POTISKOVANÝC MATERIÁLŮ A POTIŠTĚNÝC PLOC Zmeškal Oldřich, Marti Julíe Tomáš Bžatek Ústav fyzikálí a spotřebí chemie, Fakulta chemická, Vysoké učeí techické v Brě, Purkyňova 8, 62
OBRAZOVÁ ANALÝZA POVRCU POTISKOVANÝC MATERIÁLŮ A POTIŠTĚNÝC PLOC Zmeškal Oldřich, Marti Julíe Tomáš Bžatek Ústav fyzikálí a spotřebí chemie, Fakulta chemická, Vysoké učeí techické v Brě, Purkyňova 8, 62
UŽITÍ MATLABU V KOLORIMETRII. J.Novák, A.Mikš. Katedra fyziky, FSv ČVUT, Praha
 UŽITÍ MATLABU V KOLORIMETRII J.Novák A.Mikš Katedra fyziky FSv ČVUT Praha Kolorimetrické metody jsou velmi často používáy jako diagostické metody v řadě oblastí vědy a techiky. V čláku jsou ukázáy příklady
UŽITÍ MATLABU V KOLORIMETRII J.Novák A.Mikš Katedra fyziky FSv ČVUT Praha Kolorimetrické metody jsou velmi často používáy jako diagostické metody v řadě oblastí vědy a techiky. V čláku jsou ukázáy příklady
Úloha III.S... limitní
 Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Intervalové odhady parametrů některých rozdělení.
 4. Itervalové odhady parametrů rozděleí. Jedou ze základích úloh mtematické statistiky je staoveí hodot parametrů rozděleí, ze kterého máme k dispozici áhodý výběr. Nejčastěji hledáme odhady dvou druhů:
4. Itervalové odhady parametrů rozděleí. Jedou ze základích úloh mtematické statistiky je staoveí hodot parametrů rozděleí, ze kterého máme k dispozici áhodý výběr. Nejčastěji hledáme odhady dvou druhů:
Úloha II.S... odhadnutelná
 Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Příloha č. 7 Dodatku ke Smlouvě o službách Systém měření kvality Služeb
 Příloha č. 7 Dodatku ke Smlouvě o službách Systém měřeí kvality Služeb Dodavatel a Objedatel se dohodli a ahrazeí Přílohy C - Systém měřeí kvality Služeb Obchodích podmíek Smlouvy o službách touto Přílohou
Příloha č. 7 Dodatku ke Smlouvě o službách Systém měřeí kvality Služeb Dodavatel a Objedatel se dohodli a ahrazeí Přílohy C - Systém měřeí kvality Služeb Obchodích podmíek Smlouvy o službách touto Přílohou
vají statistické metody v biomedicíně
 Statistika v biomedicísk ském m výzkumu a ve zdravotictví Prof. RNDr. Jaa Zvárov rová,, DrSc. EuroMISE Cetrum Ústav iformatiky AV ČR R v.v.i. Proč se používaj vají statistické metody v biomedicíě Biomedicísk
Statistika v biomedicísk ském m výzkumu a ve zdravotictví Prof. RNDr. Jaa Zvárov rová,, DrSc. EuroMISE Cetrum Ústav iformatiky AV ČR R v.v.i. Proč se používaj vají statistické metody v biomedicíě Biomedicísk
U klasifikace podle minimální vzdálenosti je nutno zvolit:
 .3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
.3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
1.3. POLYNOMY. V této kapitole se dozvíte:
 1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
Cvičení 6.: Bodové a intervalové odhady střední hodnoty, rozptylu a koeficientu korelace, test hypotézy o střední hodnotě při známém rozptylu
 Cvičeí 6: Bodové a itervalové odhady středí hodoty, rozptylu a koeficietu korelace, test hypotézy o středí hodotě při zámém rozptylu Příklad : Bylo zkoumáo 9 vzorků půdy s růzým obsahem fosforu (veličia
Cvičeí 6: Bodové a itervalové odhady středí hodoty, rozptylu a koeficietu korelace, test hypotézy o středí hodotě při zámém rozptylu Příklad : Bylo zkoumáo 9 vzorků půdy s růzým obsahem fosforu (veličia
Pravděpodobnost a statistika - absolutní minumum
 Pravděpodobost a statistika - absolutí miumum Jaromír Šrámek 4108, 1.LF, UK Obsah 1. Základy počtu pravděpodobosti 1.1 Defiice pravděpodobosti 1.2 Náhodé veličiy a jejich popis 1.3 Číselé charakteristiky
Pravděpodobost a statistika - absolutí miumum Jaromír Šrámek 4108, 1.LF, UK Obsah 1. Základy počtu pravděpodobosti 1.1 Defiice pravděpodobosti 1.2 Náhodé veličiy a jejich popis 1.3 Číselé charakteristiky
MATICOVÉ HRY MATICOVÝCH HER
 MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
8. Analýza rozptylu.
 8. Aalýza rozptylu. Lieárí model je popis závislosti, který je využívá v řadě disciplí matematické statistiky. Uvedeme jeho popis a tvrzeí, která budeme využívat. Setkáme se s ím jedak v aalýze rozptylu,
8. Aalýza rozptylu. Lieárí model je popis závislosti, který je využívá v řadě disciplí matematické statistiky. Uvedeme jeho popis a tvrzeí, která budeme využívat. Setkáme se s ím jedak v aalýze rozptylu,
Pevnost a životnost - Hru III 1. PEVNOST a ŽIVOTNOST. Hru III. Milan Růžička, Josef Jurenka, Zbyněk Hrubý.
 evost a životost - Hr III EVNOT a ŽIVOTNOT Hr III Mila Růžička, Josef Jreka, Zbyěk Hrbý zbyek.hrby@fs.cvt.cz evost a životost - Hr III tatistické metody vyhodocováí dat evost a životost - Hr III 3 tatistické
evost a životost - Hr III EVNOT a ŽIVOTNOT Hr III Mila Růžička, Josef Jreka, Zbyěk Hrbý zbyek.hrby@fs.cvt.cz evost a životost - Hr III tatistické metody vyhodocováí dat evost a životost - Hr III 3 tatistické
Geometrická optika. Zákon odrazu a lomu světla
 Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
} kvantitativní znaky. korelace, regrese. Prof. RNDr. Jana Zvárov. Obecné principy
 Měřeí statistické závislosti, korelace, regrese Prof. RNDr. Jaa Zvárov rová,, DrSc. MĚŘENÍZÁVISLOSTI Cílem statistické aalýzy vepidemiologii bývá eje staovit, zda oemocěí závisí a výskytu rizikového faktoru,
Měřeí statistické závislosti, korelace, regrese Prof. RNDr. Jaa Zvárov rová,, DrSc. MĚŘENÍZÁVISLOSTI Cílem statistické aalýzy vepidemiologii bývá eje staovit, zda oemocěí závisí a výskytu rizikového faktoru,
Cvičení 6.: Výpočet střední hodnoty a rozptylu, bodové a intervalové odhady střední hodnoty a rozptylu
 Cvičeí 6: Výpočet středí hodoty a rozptylu, bodové a itervalové odhady středí hodoty a rozptylu Příklad 1: Postupě se zkouší spolehlivost čtyř přístrojů Další se zkouší je tehdy, když předchozí je spolehlivý
Cvičeí 6: Výpočet středí hodoty a rozptylu, bodové a itervalové odhady středí hodoty a rozptylu Příklad 1: Postupě se zkouší spolehlivost čtyř přístrojů Další se zkouší je tehdy, když předchozí je spolehlivý
523/2006 Sb. VYHLÁŠKA
 523/2006 Sb. VYHLÁŠKA ze de 21. listopadu 2006, kterou se staoví mezí hodoty hlukových ukazatelů, jejich výpočet, základí požadavky a obsah strategických hlukových map a akčích pláů a podmíky účasti veřejosti
523/2006 Sb. VYHLÁŠKA ze de 21. listopadu 2006, kterou se staoví mezí hodoty hlukových ukazatelů, jejich výpočet, základí požadavky a obsah strategických hlukových map a akčích pláů a podmíky účasti veřejosti
Měřící technika - MT úvod
 Měřící techika - MT úvod Historie Už Galileo Galilei zavádí vědecký přístup k měřeí. Jeho výrok Měřit vše, co je měřitelé a co eí měřitelým učiit platí stále. - jedotá soustava jedotek fyz. veliči - símače
Měřící techika - MT úvod Historie Už Galileo Galilei zavádí vědecký přístup k měřeí. Jeho výrok Měřit vše, co je měřitelé a co eí měřitelým učiit platí stále. - jedotá soustava jedotek fyz. veliči - símače
I. Výpočet čisté současné hodnoty upravené
 I. Výpočet čisté současé hodoty upraveé Příklad 1 Projekt a výrobu laserových lamp pro dermatologii vyžaduje ivestici 4,2 mil. Kč. Předpokládají se rovoměré peěží příjmy po zdaěí ve výši 1,2 mil. Kč ročě
I. Výpočet čisté současé hodoty upraveé Příklad 1 Projekt a výrobu laserových lamp pro dermatologii vyžaduje ivestici 4,2 mil. Kč. Předpokládají se rovoměré peěží příjmy po zdaěí ve výši 1,2 mil. Kč ročě
Pojem času ve finančním rozhodování podniku
 Pojem času ve fiačím rozhodováí podiku 1.1. Výzam faktoru času a základí metody jeho vyjádřeí Fiačí rozhodováí podiku je ovlivěo časem. Peěží prostředky získaé des mají větší hodotu ež tytéž peíze získaé
Pojem času ve fiačím rozhodováí podiku 1.1. Výzam faktoru času a základí metody jeho vyjádřeí Fiačí rozhodováí podiku je ovlivěo časem. Peěží prostředky získaé des mají větší hodotu ež tytéž peíze získaé
Mod(x) = 2, Med(x) = = 2
 Pracoví list č.. Při zjišťováí počtu ezletilých dětí ve třiceti vybraých rodiách byly získáy tyto výsledky:,,,,,,,,,,,,,,,,,,,,,,,,,,,,,. Uspořádejte získaé údaje do tabulky rozděleí četostí a vyjádřete
Pracoví list č.. Při zjišťováí počtu ezletilých dětí ve třiceti vybraých rodiách byly získáy tyto výsledky:,,,,,,,,,,,,,,,,,,,,,,,,,,,,,. Uspořádejte získaé údaje do tabulky rozděleí četostí a vyjádřete
Rozklad přírodních surovin minerálními kyselinami
 Laboratoř aorgaické techologie Rozklad přírodích surovi mierálími kyseliami Rozpouštěí přírodích materiálů v důsledku probíhající chemické reakce patří mezi základí techologické operace řady průmyslových
Laboratoř aorgaické techologie Rozklad přírodích surovi mierálími kyseliami Rozpouštěí přírodích materiálů v důsledku probíhající chemické reakce patří mezi základí techologické operace řady průmyslových
Vliv tváření za studena na pevnostní charakteristiky korozivzdorných ocelí Ing. Jan Mařík
 stavebí obzor 9 10/2014 125 Vliv tvářeí za studea a pevostí charakteristiky korozivzdorých ocelí Ig. Ja Mařík Ig. Michal Jadera, Ph.D. ČVUT v Praze Fakulta stavebí Čláek uvádí výsledky tahových zkoušek
stavebí obzor 9 10/2014 125 Vliv tvářeí za studea a pevostí charakteristiky korozivzdorých ocelí Ig. Ja Mařík Ig. Michal Jadera, Ph.D. ČVUT v Praze Fakulta stavebí Čláek uvádí výsledky tahových zkoušek
GRADIENTNÍ OPTICKÉ PRVKY Gradient Index Optical Components
 Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
7. Analytická geometrie
 7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
Sekvenční logické obvody(lso)
 Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU
 SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU Matematické modelováí (KMA/MM Téma: Model pohybu mraveců Zdeěk Hazal (A8N18P, zhazal@sezam.cz 8/9 Obor: FAV-AVIN-FIS 1. ÚVOD Model byl převzat z kihy Spojité modely v biologii
SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU Matematické modelováí (KMA/MM Téma: Model pohybu mraveců Zdeěk Hazal (A8N18P, zhazal@sezam.cz 8/9 Obor: FAV-AVIN-FIS 1. ÚVOD Model byl převzat z kihy Spojité modely v biologii
