Řešení diferenciálních rovnic 1. řádu
|
|
|
- Vladimíra Horáková
- před 7 lety
- Počet zobrazení:
Transkript
1 Diferenciální rovnice 1. řádu Metoda separace proměnných Lineární diferenciální rovnice1.řádu Řešení diferenciálních rovnic 1. řádu. p.1/13
2 Metoda separace proměnných Příklad Nalezněte řešení diferenciální rovnice y = xy2 x x 2 y y počáteční podmínce y( 1 2 )= 2., které vyhovuje Příklad Nalezněte obecné řešení diferenciální rovnice y =6x 2 y. Příklad Nalezněte řešení diferenciální rovnice y = počáteční podmínce y(0) = 1. x 2y +1, které vyhovuje. p.2/13
3 Příklad Nalezněte řešení diferenciální rovnice y = xy2 x x 2 y y y( 1 2 )= 2., které vyhovuje počáteční podmínce?. p.3/13
4 Příklad Nalezněte řešení diferenciální rovnice y = xy2 x x 2 y y y( 1 2 )= 2. Výsledek:, které vyhovuje počáteční podmínce y(x) = 5 4x 2, x ( 1, 1).. p.3/13
5 Příklad Nalezněte řešení diferenciální rovnice y = xy2 x x 2 y y y( 1 2 )= 2. Návod: Použijeme metodu separace proměnných., které vyhovuje počáteční podmínce. p.3/13
6 Příklad Nalezněte řešení diferenciální rovnice y = xy2 x, které vyhovuje počáteční podmínce x 2 y y y( 1 2 )= 2. Řešení: Postup rozdělíme do čtyř kroků. 1. krok: Zúpravy plyne: y = xy2 x x 2 y y g(x) = h(y) = y2 1 y y = x(y2 1) (x 2 1)y x x 2 1, x ±1,, y krok: Nalezneme všechna konstantní řešení. Hledejme kořeny rovnice h(y) =0. y 2 1 y =0 y 2 1=0 (y 1)(y +1)=0 y = ±1 Další Rovnice má konstantní řešení y(x) = 1 a y(x) =1. Ani jedno ovšem nesplňuje počáteční podmínku y( 1 2 )= 2.. p.3/13
7 Příklad Nalezněte řešení diferenciální rovnice y = xy2 x, které vyhovuje počáteční podmínce x 2 y y y( 1 2 )= 2. Řešení: 3. krok: Najdeme obdélník, kde je h(y) 0 akdeležíbod ( 1 2, 2).Tedy 1 2 ( 1, 1) a 2 (, 1).Grafhledaného řešení ležívobdélníku ( 1, 1) (, 1). Hledejme toto řešení. dy dx = x(y2 1) y (x 2 1)y y 2 1 dy = x x 2 1 dx 2y y 2 1 dy = Spočteme hodnotu integrační konstanty: 2x x 2 1 dx ln y2 1 =ln x C ln ( 2) 2 1 =ln ( 1 2 )2 1 + C ln 3 ln( 3 4 )=C C =ln4. Hledejme dál funkční předpis řešení. ln y 2 1 =ln x 2 1 +ln4 ln y 2 1 =ln4 x 2 1 y 2 1 =4 x 2 1 Pro x ( 1, 1) je x 2 1 < 0 a x 2 1 = (x 2 1).Pro y (, 1) je y 2 1 > 0 a y 2 1 = y 2 1. y 2 1= 4(x 2 1) y 2 =1 4(x 2 1) y = 5 4x 2 Další. p.3/13
8 Příklad Nalezněte řešení diferenciální rovnice y = xy2 x, které vyhovuje počáteční podmínce x 2 y y y( 1 2 )= 2. Řešení: Funkční hodnoty hledané funkce leží v intervalu (, 1),tedy y<0. Proto y(x) = 5 4x krok: Určíme definiční oborřešení. Výraz 5 4x 2 másmysl,pokud 5 4x 2 0 ( 5 2x)( 5+2x) 0. Nerovnici řeší x 5 2, 5 2 ( 1, 1).Definičním oborem řešení bude celý interval ( 1, 1), pokud pro každé x ( 1, 1) je y(x) < x 2 < 1 5 4x 2 > 1 x 2 1 < 0 Poslední nerovnost je splněna právě naintervalu ( 1, 1). Funkce y(x) = 5 4x 2, x ( 1, 1) je řešením rovnice y = xy2 x x 2 y y vyhovujícím počáteční podmínce y( 1 2 )= 2.. p.3/13
9 Příklad Nalezněte řešení diferenciální rovnice y = xy2 x, které vyhovuje počáteční podmínce x 2 y y y( 1 2 )= 2. Maple: > DR:=(diff(y(x),x)=(x*(y(x))ˆ2-x)/(xˆ2*y(x)-y(x))); > PP:=y(0.5)=-2; DR := d dx y(x) = x y(x)2 x x 2 y(x) y(x) > dsolve({dr,pp},y(x)); PP := y(0.5) = 2 y(x) = 5 4 x 2. p.3/13
10 Příklad Nalezněte řešení diferenciální rovnice y = xy2 x x 2 y y y( 1 2 )= 2. Mathematica: DR = y [x]==(x(y[x]) 2 x)/(x 2 y[x] y[x]), které vyhovuje počáteční podmínce y [x] == x+xy[x]2 y[x]+x 2 y[x] PP = y[1/2] == 2 y [ ] 1 2 == 2 DSolve[{DR, PP},y[x],x] Solve::ifun : Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information. More... Solve::ifun : Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information. More... DSolve::bvnul : For some branches of the general solution, the given boundary conditions lead to an empty solution. More... {{y[x] }} 5 4x 2. p.3/13
11 Příklad Nalezněte obecné řešení diferenciální rovnice y =6x 2 y.?. p.4/13
12 Příklad Nalezněte obecné řešení diferenciální rovnice y =6x 2 y. Výsledek: y(x) =0, x, R y K (x) = ( x 3 + K ) 2 3, K R, x ( K, ).. p.4/13
13 Příklad Nalezněte obecné řešení diferenciální rovnice y =6x 2 y. Návod: Použijeme metodu separace proměnných.. p.4/13
14 Příklad Nalezněte obecné řešení diferenciální rovnice y =6x 2 y. Řešení: Postup rozdělíme do čtyř kroků. 1. krok: g(x) =6x 2, x R, h(y) = y, y 0, ). 2. krok: Kořeny rovnice h(y) =0 odpovídají konstantním řešením. y =0 y =0 Rovnice má jedno konstantní řešení y(x) =0, x R. 3. krok: Vobdélníku (, ) (0, ) je h(y) 0.Tamležígrafyhledaných řešení. Najděme je. dy 1 dx =6x2 y dy = 6x 2 dx y 1 2 dy = 6x 2 dx y 2y 1 2 =2x 3 + C y 1 2 = x 3 + C 2 Integrační konstantu C 2 označme K.Zposlednírovnostivyjádříme y.umocnění na druhou je ekvivalentní úprava pouze tehdy, když obě strany rovnice jsou kladné nebo záporné. Protože y 1 2 > 0,musíbýt x 3 + K>0.Tedy ( y K (x) = x K), x 3 + K>0, R K. 4. krok: Řešení existujeprovšechna reálná x,prokterá x 3 + K>0,tedypro x> 3 K. Navíc musí platitnerovnost y>0 azároveň platí ( x 3 + K ) 2 > 0. Obecným řešením rovnice je množina funkcí y K (x) = ( x 3 + K ) 2, x ( 3 K, ) plus konstantní řešení y(x) =0, x R.. p.4/13
15 Příklad Nalezněte obecné řešení diferenciální rovnice y =6x 2 y. Maple: > DR:=(diff(y(x),x)=6*xˆ2*sqrt(y(x))); > dsolve(dr,y(x)); DR := d dx y(x) =6x2 y(x) y(x) x 3 C1 =0. p.4/13
16 Příklad Nalezněte obecné řešení diferenciální rovnice y =6x 2 y. Mathematica: DR = y [x] ==6x 2Sqrt[y[x]] y [x] ==6x 2 y[x] DSolve[DR,y[x],x] {{ ( y[x] 1 4 4x 6 +4x 3 C[1] + C[1] 2)}} Simplify[%] {{ y[x] 1 ( 4 2x 3 + C[1] ) }} 2 Lehce se můžete přesvědčit, že řešeníjestejnéjakovnašem výpočtu.. p.4/13
17 Příklad Nalezněte řešení diferenciální rovnice y = y(0) = 1. x 2y +1, které vyhovuje počáteční podmínce?. p.5/13
18 Příklad Nalezněte řešení diferenciální rovnice y = y(0) = 1. Výsledek: x 2y +1, které vyhovuje počáteční podmínce y(x) = 1+ 2x , x R.. p.5/13
19 Příklad Nalezněte řešení diferenciální rovnice y = y(0) = 1. Návod: Použijeme metodu separace proměnných. x 2y +1, které vyhovuje počáteční podmínce. p.5/13
20 Příklad Nalezněte řešení diferenciální rovnice y = y(0) = 1. Řešení: x 2y +1, které vyhovuje počáteční podmínce Postup rozdělíme do tří kroků. 1. krok: Pravá strana rovnice je ve tvaru g(x) h(y), kde g(x) =x, x R, h(y) = 1 2y +1, y krok: Protože vždy h(y) 0, rovnice nemá žádné konstantní řešení. 3. krok: Najdeme obdélník, kde je h(y) 0 akdeležíbod (0, 1). Protože 1 (, 1 2 ),ležígrafhledaného řešení vobdélníku (, ) (, 1 2 ). Hledejme toto řešení. dy dx = x 2y +1 (2y +1) dy = x dx y 2 + y = x2 2 + C Spočteme hodnotu integrační konstanty: ( 1) 2 1= C C =0. Další. p.5/13
21 Příklad Nalezněte řešení diferenciální rovnice y = y(0) = 1. Řešení: x 2y +1, které vyhovuje počáteční podmínce Hledejme dál funkční předpis řešení. Musíme vyřešit kvadratickou rovnici pro neznámou y. y 2 + y x2 2 =0 D =1 4 ( x2 2 ) =1+2x 2 y 1,2 = 1 ± 1+2x 2 2 Pro všechna reálná x je diskriminat kladný (D =1+2x 2 > 0 ). Otázkou zůstává, které y je řešení. Funkční hodnoty hledané funkce leží v intervalu (, 1 2 ), tedy chceme, aby y 1,2 < 1 2,tj. 1 ± 1+2x 2 2 < 1 2 ± 1+2x 2 < 0. Poslední nerovnost je splněna pouze pro znaménko mínus. Řešením je tedy funkce y(x) = 1 1+2x 2 2, x R.. p.5/13
22 Příklad Nalezněte řešení diferenciální rovnice y = y(0) = 1. Maple: x 2y +1 > DR:=(diff(y(x),x)=(x)/(2*y(x)+1)); > PP:=y(0)=-1; DR := d dx y(x) =, které vyhovuje počáteční podmínce x 2y(x) +1 > dsolve({dr,pp},y(x)); PP := y(0) = 1 y(x) = x 2 2. p.5/13
23 Příklad Nalezněte řešení diferenciální rovnice y = y(0) = 1. Mathematica: {{ y[x] 1 4 ( 2x 3 + C[1] ) 2 }} x 2y +1, které vyhovuje počáteční podmínce DR = y [x] ==x/(2y[x]+1) y [x] == x 1+2y[x] PP = y[0] == 1 y[0] == 1 DSolve[{DR, PP},y[x],x] DSolve::bvnul : For some branches of the general solution, the given boundary conditions lead to an empty solution. More... {{ y[x] 1 2 ( 1 )}} 1+2x 2. p.5/13
24 Lineární diferenciální rovnice 1. řádu Příklad Nalezněte řešení diferenciální rovnice 1 2 y xy = x, které vyhovuje počáteční podmínce y(0) = 7. Příklad Nalezněte všechna řešení diferenciální rovnice y = 2y + x Příklad Nalezněte řešení diferenciální rovnice (1 + x) y + xy =0, které vyhovuje počáteční podmínce y(0) = 10. x.. p.6/13
25 Příklad Nalezněte řešení diferenciální rovnice y(0) = y xy = x, které vyhovujepočáteční podmínce?. p.7/13
26 Příklad Nalezněte řešení diferenciální rovnice y(0) = 7. Výsledek: 1 2 y xy = x, které vyhovujepočáteční podmínce y(x) =8e x2 1, x R.. p.7/13
27 Příklad Nalezněte řešení diferenciální rovnice y(0) = 7. Návod: 1 2 y xy = x, které vyhovujepočáteční podmínce a) Řešení lineární diferenciální rovnice y + a(x)y = b(x) má tvar y(x) =y H (x) +y P (x),kde y H (x) je obecné řešení přiřazené homogenní diferenciální rovnice a y P (x) je partikulární (jedno) řešení dané rovnice. Obecné řešení y H (x) hledáme metodou separace proměnných a víme, že y H (x) =Cϕ(x),kde ϕ(x) je jedno řešení přiřazené homogenní rovnice. Partikulární řešení y P (x) hledáme ve tvaru y P (x) =C(x)ϕ(x) tzv. metodou variace konstanty. b) Vtomtopřípadě lzetaképoužít metodu separace proměnných.. p.7/13
28 Příklad Nalezněte řešení diferenciální rovnice y(0) = 7. Řešení: 1 2 y xy = x, které vyhovujepočáteční podmínce Postupujeme ve čtyřech krocích. Zadenou NLDR (Nehomogenní Lineární Diferenciální Rovnici) převedeme na tvar y 2xy =2x, knípřiřazená homogenní rovniceje y 2xy =0. 1. krok: Hledejme metodou separace proměnných ϕ(x), jedno nenulové řešenípřiřazené homogenní rovnice. dy 1 dx =2xy y dy = 2x dx ln y = x 2 y =e x2 např. y = ϕ(x) =e x2. Integrační konstantu jsme nepsali, protože hledáme jedno řešení ϕ(x).tedy y H (x) =Ce x2. 2. krok: Partikulární řešení dané nehomogenní lineární rovnice hledáme ve tvaru součinu y P (x) =C(x) ϕ(x) =C(x)e x2, kde C(x) je neznámá funkce, tj. v y H (x) nahradíme konstantu C funkcí. Hledejme ji. Chceme, aby y P (x) bylo řešení NLDR.Spočteme y P (x) : Další. p.7/13
29 Příklad Nalezněte řešení diferenciální rovnice y(0) = 7. Řešení: y P (x) =C (x)e x2 + C(x)2xe x2 1 2 y xy = x, které vyhovujepočáteční podmínce a dosadíme y (x) a y (x) do rovnice. P P y 2xy =2x C (x)e x2 + C(x)2xe x2 2xC(x)e x2 =2x C (x) =2xe x2 C(x) = 2xe x2 dx C(x) = e x2 Integrační konstantu nepíšeme, nebot hledáme jedno řešení y P (x),tedyjednu funkci C(x). Dosadíme za C(x). Partikulární řešení je y P (x) = e x2 e x2 = krok: Výsledky kroku jedna a dva dávají obecné řešení zadané rovnice y(x) =y H (x) +y P (x) =Ce x2 1. Pravá strana NLDR ( b(x) =2x ) a koeficient u y ( a(x) =2x )jsouspojité funkce na R. Tedy definiční oborřešení je R. 4. krok: Ze všech nalezených řešení (obecného řešení NLDR) vybereme jedno, které splňuje počáteční podmínku y(0) = 7. 7=Ce 0 1 C =8. Řešením dané počáteční úlohy je funkce y(x) =8e x2 1, x R.. p.7/13
30 Příklad Nalezněte řešení diferenciální rovnice 1 2 y xy = x, které vyhovujepočáteční podmínce y(0) = 7. Maple: > DR:=(0.5*diff(y(x),x)-x*y(x)=x); > PP:=y(0)=7; DR := 0.5( d dx y(x)) x y(x) =x > dsolve({dr,pp},y(x)); PP := y(0) = 7 y(x) = 1 +8e (x2 ). p.7/13
31 Příklad Nalezněte řešení diferenciální rovnice y(0) = 7. Mathematica: DR = y [x]/2 xy[x] ==x xy[x]+ y [x] 2 == x PP = y[0] == 7 y[0] == 7 DSolve[{DR, PP},y[x],x] }} x2 {{y[x] 1+8e 1 2 y xy = x, které vyhovujepočáteční podmínce. p.7/13
32 Příklad Nalezněte všechna řešení diferenciální rovnice y = 2y + x. x?. p.8/13
33 Příklad Nalezněte všechna řešení diferenciální rovnice y = 2y + x x Výsledek: y(x) = x + Cx 2,x<0 nebo y(x) = x + Cx 2,x>0, kde C je libovolná reálná konstanta... p.8/13
34 Příklad Nalezněte všechna řešení diferenciální rovnice y = 2y + x x Návod: Rovnice je lineární diferenciální rovnicetvaru y + a(x)y = b(x) ajejířešení hledáme podle návodu v předchozím příkladě... p.8/13
35 Příklad Nalezněte všechna řešení diferenciální rovnice y = 2y + x x Řešení: Postupujeme ve třech krocích. Danou NLDR převedeme na tvar. y 2 x y =1, knípřiřazená homogenní rovniceje y 2 x y =0. 1. krok: Hledejme metodou separace proměnných ϕ(x), jedno nenulové řešení přiřazené homogenní rovnice. dy dx = 2 x y 1 y dy = 2 x dx ln y =2ln x y = x 2 např. y = ϕ(x) =x 2. Integrační konstantu jsme nepsali, protože hledáme jedno řešení ϕ(x).tedy y H (x) =Cx 2. Další. p.8/13
36 Příklad Nalezněte všechna řešení diferenciální rovnice y = 2y + x x Řešení: 2. krok: Partikulární řešení dané nehomogenní lineární rovnice hledáme ve tvaru součinu y P (x) =C(x) ϕ(x) =C(x)x 2, kde C(x) je neznámá funkce, tj. v y H (x) nahradíme konstantu C funkcí. Hledejme ji. Chceme, aby y P (x) bylo řešení zadané NLDR.Spočteme y (x) : P y (x) P =C (x)x 2 + C(x)2x a dosadíme y (x) a y (x) do rovnice. P P. y 2 x y =1 C (x)x 2 + C(x)2x 2 x C(x)x2 =1 C (x) = 1 x 2 C(x) = 1 x 2 dx C(x) = 1 x Integrační konstantu nepíšeme, nebot hledáme jedno řešení y P (x),tedyjednu funkci C(x). Dosadíme za C(x). Partikulární řešení je y P (x) = 1 x x2 = x. Další. p.8/13
37 Příklad Nalezněte všechna řešení diferenciální rovnice y = 2y + x x Řešení: 3. krok: Výsledky kroku jedna a dva dávají obecné řešení zadané rovnice y(x) =y H (x) +y P (x) =Cx 2 x.. Pravá strana NLDR ( b(x) =1) a koeficient u y ( a(x) = 2 x )jsouspojitéfunkce R na \{0}. Tedy definiční oborřešení je bud interval (, 0) nebo interval (0, ).. p.8/13
38 Příklad Nalezněte všechna řešení diferenciální rovnice y = 2y + x x Maple: > DR:=(diff(y(x),x)=(2*y(x)+x)/(x));. > dsolve(dr,y(x)); DR := d dx y(x) = 2y(x) +x x y(x) = x + x 2 C1. p.8/13
39 Příklad Nalezněte všechna řešení diferenciální rovnice y = 2y + x x Mathematica: DR = y [x] ==(2y[x] +x)/x y [x] == x+2y[x] x DSolve[DR,y[x],x] {{ y[x] x + x 2 C[1] }}.. p.8/13
40 Příklad Nalezněte řešení diferenciální rovnice (1 + x) y + xy =0, které vyhovujepočáteční podmínce y(0) = 10.?. p.9/13
41 Příklad Nalezněte řešení diferenciální rovnice (1 + x) y + xy =0, které vyhovujepočáteční podmínce y(0) = 10. Výsledek: y(x) = 10(x +1)e x, x > 1.. p.9/13
42 Příklad Nalezněte řešení diferenciální rovnice (1 + x) y + xy =0, které vyhovujepočáteční podmínce y(0) = 10. Návod: Řešení homogenní lineární diferenciální rovnice a 1 (x)y + a 0 (x)y =0,kdea 1 (x) 0,má tvar y(x) =Cϕ(x), kde ϕ(x) je jedno řešení dané homogenní rovnice. Funkci ϕ(x) hledáme metodou separace proměnných.. p.9/13
43 Příklad Nalezněte řešení diferenciální rovnice (1 + x) y + xy =0, které vyhovujepočáteční podmínce y(0) = 10. Řešení: Postupujeme ve dvou krocích. 1. krok: Hledejme metodou separace proměnných ϕ(x), jedno nenulové řešenídané homogenní rovnice. y = xy 1+x dy dx = xy x +1 ( 1 y dy = 1 1 ) x +1 1 y dy = x x +1 dx dx ln y = x +ln x +1 y =e x x +1 např. y = ϕ(x) =e x (x +1). Integrační konstantu jsme nepsali, protože hledáme jedno řešení ϕ(x).tedy y(x) =C(x +1)e x. Koeficient u y ( a 1 (x) =x +1) a koeficient u y ( a 0 (x) =x )jsouspojitéfunkce R na,alea 1 (x) 0pro x 1. Tedy definiční oborřešení jeinterval(, 1) nebo interval ( 1, ). 2. krok: Ze všech nalezených řešení vybereme jedno, které splňuje počáteční podmínku y(0) = = C(0 + 1)e 0 C =10. Řešením dané počáteční úlohy je funkce y(x) = 10(x +1)e x, x ( 1, ), protože 0 ( 1, ).. p.9/13
44 Příklad Nalezněte řešení diferenciální rovnice (1 + x) y + xy =0, které vyhovujepočáteční podmínce y(0) = 10. Maple: > DR:=((x+1)*diff(y(x),x)+x*y(x)=0); > PP:=y(0)=10; DR := (x +1)( d dx y(x)) + x y(x) =0 > dsolve({dr,pp},y(x)); PP := y(0) = 10 y(x) =10e ( x) (x +1). p.9/13
45 Příklad Nalezněte řešení diferenciální rovnice (1 + x) y + xy =0, které vyhovujepočáteční podmínce y(0) = 10. Mathematica: DR =(1+x)y [x] +xy[x] ==0 xy[x] +(1+x)y [x] ==0 PP = y[0] == 10 y[0] == 10 DSolve[{DR, PP},y[x],x] {{ y[x] 10e x (1 + x) }}. p.9/13
46 Řešení diferenciálních rovnic 1. řádu Příklad Je funkce y(x) =2x +3,x R řešením diferenciální rovnice (y ) 2 + xy = y. Příklad Je funkce y(x) =e 1 x,x>0 řešením diferenciální rovnice y ln y + xy =0. Příklad Je funkce y(x) = 3x ,x R řešením diferenciální rovnice y = x2 y, které vyhovuje počáteční podmínce y(0) = p.10/13
47 Příklad Je funkce y(x) =2x +3,x R řešením diferenciální rovnice (y ) 2 + xy = y.?. p.11/13
48 Příklad Je funkce y(x) =2x +3,x R řešením diferenciální rovnice (y ) 2 + xy = y. Výsledek: Není řešením.. p.11/13
49 Příklad Je funkce y(x) =2x +3,x R řešením diferenciální rovnice (y ) 2 + xy = y. Návod: Vypočteme y (x) a do diferenciální rovnice dosadíme za y (x) a y(x).levá strana rovnice se musí rovnat pravé pro všechna reálná x.. p.11/13
50 Příklad Je funkce y(x) =2x +3,x R řešením diferenciální rovnice (y ) 2 + xy = y. Řešení: Spočteme: y (x) =2.Levá strava rovnice je L := (2) 2 + x 2=4+2x apravá strana je P := 2x +3. Tedy L P pro všechna reálná x, funkce y(x) = 2x +3 není řešením dané rovnice.. p.11/13
51 Příklad Je funkce y(x) =2x +3,x R řešením diferenciální rovnice (y ) 2 + xy = y. Maple: > res:=y(x)=2*x+3; res := y(x) =2x +3 > DR:=((diff(y(x),x))ˆ2+x*diff(y(x),x)=y(x)); DR := ( d dx y(x))2 + x ( d dx > odetest(res,dr); y(x)) = y(x) 1 Nenulový výsledek znamená, že testovaná funkce není řešením dané diferenciální rovnice.. p.11/13
52 Příklad Je funkce y(x) =2x +3,x R řešením diferenciální rovnice (y ) 2 + xy = y. Mathematica: DR =(D[y[x],x]) 2+xD[y[x],x]==y[x] xy [x] +y [x] 2 == y[x] res[x ]=2x x DR/.y res 4+2x == 3 + 2x L P, funkce není řešením diferenciální rovnice.. p.11/13
53 Příklad Je funkce y(x) =e 1 x,x>0 řešením diferenciální rovnice y ln y + xy =0.?. p.12/13
54 Příklad Je funkce y(x) =e 1 x,x>0 řešením diferenciální rovnice y ln y + xy =0. Výsledek: Je řešením.. p.12/13
55 Příklad Je funkce y(x) =e 1 x,x>0 řešením diferenciální rovnice y ln y + xy =0. Návod: Vypočteme y (x) a do diferenciální rovnice dosaíme za y (x) a y(x).levá strana rovnicesemusí rovnat nule pro x>0.. p.12/13
56 Příklad Je funkce y(x) =e 1 x,x>0 řešením diferenciální rovnice y ln y + xy =0. Řešení: ( Spočteme: y x (x) =e 1 1 x 2 ).Pravá strana rovnice je nula a levá strava rovnice je x x x L := e ln e + xe ( 1x 2 ) =e 1 x 1 x e 1 x 1 x =0 pro všechna reálná x>0, funkce y(x) =e 1 x je řešením dané diferenciální rovnice.. p.12/13
57 Příklad Je funkce y(x) =e 1 x,x>0 řešením diferenciální rovnice y ln y + xy =0. Maple: > res:=y(x)=exp(1/x); res := y(x) =e ( x 1 ) > DR:=(y(x)*ln(y(x))+x*diff(y(x),x)=0); DR := y(x)ln(y(x)) + x ( d dx y(x)) = 0 > odetest(res,dr); > simplify(%) assuming x::real; e ( 1 x ) ln(e ( 1 x ) ) e( 1 x ) 0 Výsledek 0 znamená, že testovaná funkce je řešením dané diferenciální rovnice. x. p.12/13
58 Příklad Je funkce y(x) =e 1 x,x>0 řešením diferenciální rovnice y ln y + xy =0. Mathematica: DR = y[x]log[y[x]] + xd[y[x],x]== 0 Log[y[x]]y[x] +xy [x] ==0 res[x ]=Exp[1/x] e 1 x Assuming[x >0, Simplify[DR/.y res]] True Funkce je řešením diferenciální rovnice.. p.12/13
59 Příklad Je funkce y(x) = 3x 3 +3 počáteční podmínce y(0) = 3,x R řešením diferenciální rovnice y = x y, které vyhovuje?. p.13/13
60 Příklad Je funkce y(x) = 3x 3 +3 počáteční podmínce y(0) = Výsledek: Není řešením. 3,x R řešením diferenciální rovnice y = x y, které vyhovuje. p.13/13
61 Příklad Je funkce y(x) = 3x 3 +3 počáteční podmínce y(0) = Návod: 3,x R řešením diferenciální rovnice y = x y, které vyhovuje Vypočt eme y (x) a do diferenciální rovnice dosadíme za y (x) a y(x).levá strana rovnicesemusírovnatpravéprovšechna reálná x amusíbýt splněna počáteční podmínka.. p.13/13
62 Příklad Je funkce y(x) = 3x 3 +3 počáteční podmínce y(0) = Řešení: 3,x R řešením diferenciální rovnice y = x Ověříme, zda je splněna počáteční podmínka. y, které vyhovuje y(0) = = 3 3 Dále zkoumáme, zda je daná funkce řešením příslušné rovnice. Spočteme: y (x) = 1 3 9x 2 2 3x 3 +3 = 3x 2 2 3x Levá strava rovnice je apravá strana je P := L := x 2 3x x 2 2 3x 3 +3 Tedy L P pro všechna reálná x, funkce y(x) = = 3x 2 3x x není řešením dané rovnice.. p.13/13
63 Příklad Je funkce y(x) = 3x 3 +3 počáteční podmínce y(0) = Maple: 3,x R řešením diferenciální rovnice y = x > f:=x->sqrt(3)/3*(sqrt(xˆ3+1)); y, které vyhovuje f := x x 3 +1 > f(0); 3 3 > res:=y(x)=sqrt(3)/3*(sqrt(xˆ3+1)); res := y(x) = > DR:=(diff(y(x),x)=(xˆ2)/y(x)); 3 x > odetest(res,dr); DR := d dx y(x) = x2 y(x) 3 x x p.13/13
64 Příklad Je funkce y(x) = 3x 3 +3 počáteční podmínce y(0) = Mathematica: DR = D[y[x],x]==x 2/y[x] 3,x R řešením diferenciální rovnice y = x y, které vyhovuje y [x] == x2 y[x] res[x ]=Sqrt[3x 3+3]/3 3+3x res[sqrt[3]/3] DR/.y res 2 3x 2 == 3x2 3+3x3 3+3x 3 L P, funkce není řešením diferenciálním rovnice.. p.13/13
Kapitola 10: Diferenciální rovnice 1/14
 Kapitola 10: Diferenciální rovnice 1/14 Co je to diferenciální rovnice? Definice: Diferenciální rovnice je vztah mezi hledanou funkcí y(x), jejími derivacemi y (x), y (x), y (x),... a nezávisle proměnnou
Kapitola 10: Diferenciální rovnice 1/14 Co je to diferenciální rovnice? Definice: Diferenciální rovnice je vztah mezi hledanou funkcí y(x), jejími derivacemi y (x), y (x), y (x),... a nezávisle proměnnou
Kapitola 11: Lineární diferenciální rovnice 1/15
 Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých
 Obyčejné diferenciální rovnice Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých se vyskytují derivace neznámé funkce jedné reálné proměnné. Příklad. Bud dána funkce f : R R.
Obyčejné diferenciální rovnice Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých se vyskytují derivace neznámé funkce jedné reálné proměnné. Příklad. Bud dána funkce f : R R.
pouze u některých typů rovnic a v tomto textu se jím nebudeme až na
 Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
LDF MENDELU. Simona Fišnarová (MENDELU) LDR druhého řádu VMAT, IMT 1 / 22
 Lineární diferenciální rovnice druhého řádu Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
Lineární diferenciální rovnice druhého řádu Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
Diferenciální rovnice I
 Diferenciální rovnice I V kurzu Diferenciální rovnice I se naučíme pomocí počítačového algebraického systému Maple hledat obecná a partikulární řešení obyčejných diferenciálních rovnic 1. řádu. Pro případ,
Diferenciální rovnice I V kurzu Diferenciální rovnice I se naučíme pomocí počítačového algebraického systému Maple hledat obecná a partikulární řešení obyčejných diferenciálních rovnic 1. řádu. Pro případ,
8.3). S ohledem na jednoduchost a názornost je výhodné seznámit se s touto Základní pojmy a vztahy. Definice
 9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
Obsah Obyčejné diferenciální rovnice
 Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
diferenciální rovnice verze 1.1
 Diferenciální rovnice vyšších řádů, snižování řádu diferenciální rovnice verze 1.1 1 Úvod Následující text popisuje řešení diferenciálních rovnic, konkrétně diferenciálních rovnic vyšších řádů a snižování
Diferenciální rovnice vyšších řádů, snižování řádu diferenciální rovnice verze 1.1 1 Úvod Následující text popisuje řešení diferenciálních rovnic, konkrétně diferenciálních rovnic vyšších řádů a snižování
4. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
 FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
9.3. Úplná lineární rovnice s konstantními koeficienty
 Úplná lineární rovnice s konstantními koeficienty Cíle Nyní přejdeme k řešení úplné lineární rovnice druhého řádu. I v tomto případě si nejprve ujasníme, v jakém tvaru můžeme očekávat řešení, poté se zaměříme
Úplná lineární rovnice s konstantními koeficienty Cíle Nyní přejdeme k řešení úplné lineární rovnice druhého řádu. I v tomto případě si nejprve ujasníme, v jakém tvaru můžeme očekávat řešení, poté se zaměříme
1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu
![1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu 1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu](/thumbs/102/155926571.jpg) [M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
[M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
1 1 x 2. Jedná se o diferenciální rovnici se separovanými proměnnými, která má smysl pro x ±1 a
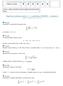
 . Řešené úlohy Příklad. (separace proměnných). Řešte počáteční úlohu y 2 + yy ( 2 ) = 0, y(0) = 2. Řešení. Rovnici přepíšeme do tvaru y 2 = yy ( 2 ) y = y2 y 2. Jedná se o diferenciální rovnici se separovanými
. Řešené úlohy Příklad. (separace proměnných). Řešte počáteční úlohu y 2 + yy ( 2 ) = 0, y(0) = 2. Řešení. Rovnici přepíšeme do tvaru y 2 = yy ( 2 ) y = y2 y 2. Jedná se o diferenciální rovnici se separovanými
Diferenciální rovnice II
 Diferenciální rovnice II Cílem tohoto kurzu je ukázat si různé příklady použití počítačového algebraického systému Maple při řešení obyčejných diferenciálních rovnic. řádu a soustav obyčejných diferenciálních
Diferenciální rovnice II Cílem tohoto kurzu je ukázat si různé příklady použití počítačového algebraického systému Maple při řešení obyčejných diferenciálních rovnic. řádu a soustav obyčejných diferenciálních
rovnic), Definice y + p(x)y = q(x), Je-li q(x) = 0 na M, nazývá se y + p(x)y =
 Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
Diferenciální rovnice
 Obyčejné diferenciální rovnice - studijní text pro cvičení v předmětu Matematika - 2. Studijní materiál byl připraven pracovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za podpory grantu IG ČVUT
Obyčejné diferenciální rovnice - studijní text pro cvičení v předmětu Matematika - 2. Studijní materiál byl připraven pracovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za podpory grantu IG ČVUT
Fakt. Každou soustavu n lineárních ODR řádů n i lze eliminací převést ekvivalentně na jednu lineární ODR
 DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
Nejdřív spočítáme jeden příklad na variaci konstant pro lineární diferenciální rovnici 2. řádu s kostantními koeficienty. y + y = 4 sin t.
 1 Variace konstanty Nejdřív spočítáme jeden příklad na variaci konstant pro lineární diferenciální rovnici 2. řádu s kostantními koeficienty. Příklad 1 Najděte obecné řešení rovnice: y + y = 4 sin t. Co
1 Variace konstanty Nejdřív spočítáme jeden příklad na variaci konstant pro lineární diferenciální rovnici 2. řádu s kostantními koeficienty. Příklad 1 Najděte obecné řešení rovnice: y + y = 4 sin t. Co
Příklady pro předmět Aplikovaná matematika (AMA) část 1
 Příklady pro předmět plikovaná matematika (M) část 1 1. Lokální extrémy funkcí dvou a tří proměnných Nalezněte lokální extrémy funkcí: (a) f 1 : f 1 (x, y) = x 3 3x + y 2 + 2y (b) f 2 : f 2 (x, y) = 1
Příklady pro předmět plikovaná matematika (M) část 1 1. Lokální extrémy funkcí dvou a tří proměnných Nalezněte lokální extrémy funkcí: (a) f 1 : f 1 (x, y) = x 3 3x + y 2 + 2y (b) f 2 : f 2 (x, y) = 1
4.1 Řešení základních typů diferenciálních rovnic 1.řádu
 4. Řešení základních tpů diferenciálních rovnic.řádu 4..4 Určete řešení z() Cauchov úloh pro rovnici + = 0 vhovující počáteční podmínce z =. Po separaci proměnných v rovnici dostaneme rovnici = d a po
4. Řešení základních tpů diferenciálních rovnic.řádu 4..4 Určete řešení z() Cauchov úloh pro rovnici + = 0 vhovující počáteční podmínce z =. Po separaci proměnných v rovnici dostaneme rovnici = d a po
MATEMATIKA III. Olga Majlingová. Učební text pro prezenční studium. Předběžná verze
 Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Obyčejné diferenciální rovnice
 1 Obyčejné diferenciální rovnice Příklad 0.1 (Motivační). Rychlost chladnutí hmotného bodu je přímo úměrná rozdílu jeho teploty minus teploty okolí. Předpokládejme teplotu bodu 30 o C v čase t = 0 a čase
1 Obyčejné diferenciální rovnice Příklad 0.1 (Motivační). Rychlost chladnutí hmotného bodu je přímo úměrná rozdílu jeho teploty minus teploty okolí. Předpokládejme teplotu bodu 30 o C v čase t = 0 a čase
Diferenciální rovnice 3
 Diferenciální rovnice 3 Lineární diferenciální rovnice n-tého řádu Lineární diferenciální rovnice (dále jen LDR) n-tého řádu je rovnice tvaru + + + + = kde = je hledaná funkce, pravá strana a koeficienty
Diferenciální rovnice 3 Lineární diferenciální rovnice n-tého řádu Lineární diferenciální rovnice (dále jen LDR) n-tého řádu je rovnice tvaru + + + + = kde = je hledaná funkce, pravá strana a koeficienty
Extrémy funkce dvou proměnných
 Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Diferenciální rovnice 1
 Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
0.1 Obyčejné diferenciální rovnice prvního řádu
 0.1 Obyčejné diferenciální rovnice prvního řádu 1 0.1 Obyčejné diferenciální rovnice prvního řádu Obyčejná diferenciální rovnice je rovnice, ve které se vyskytují derivace nebo diferenciály neznámé funkce
0.1 Obyčejné diferenciální rovnice prvního řádu 1 0.1 Obyčejné diferenciální rovnice prvního řádu Obyčejná diferenciální rovnice je rovnice, ve které se vyskytují derivace nebo diferenciály neznámé funkce
11. přednáška 10. prosince Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah
 11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
Nerovnice. Vypracovala: Ing. Stanislava Kaděrková
 Nerovnice Vypracovala: Ing. Stanislava Kaděrková Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace žáků ke studiu technických předmětů
Nerovnice Vypracovala: Ing. Stanislava Kaděrková Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace žáků ke studiu technických předmětů
Sbírka příkladů z matematické analýzy II. Petr Tomiczek
 Sbírka příkladů z matematické analýzy II Petr Tomiczek Obsah Diferenciální rovnice. řádu 3. Separace proměnných......................... 3. Přechod k separaci.......................... 4.3 Variace konstant...........................
Sbírka příkladů z matematické analýzy II Petr Tomiczek Obsah Diferenciální rovnice. řádu 3. Separace proměnných......................... 3. Přechod k separaci.......................... 4.3 Variace konstant...........................
INŽENÝRSKÁ MATEMATIKA DIFERENCIÁLNÍ ROVNICE 2
 INŽENÝRSKÁ MATEMATIKA DIFERENCIÁLNÍ ROVNICE 2 Robert Mařík 5. října 2009 c Robert Mařík, 2009 Obsah 1 LDR druhého řádu 4 2 Homogenní LDR, lineární nezávislost a wronskián 9 3 Homogenní LDR s konstantními
INŽENÝRSKÁ MATEMATIKA DIFERENCIÁLNÍ ROVNICE 2 Robert Mařík 5. října 2009 c Robert Mařík, 2009 Obsah 1 LDR druhého řádu 4 2 Homogenní LDR, lineární nezávislost a wronskián 9 3 Homogenní LDR s konstantními
Lineární diferenciální rovnice 1. řádu verze 1.1
 Úvod Lineární diferenciální rovnice. řádu verze. Následující tet popisuje řešení lineárních diferenciálních rovnic. řádu. Měl by sloužit především studentům předmětu MATEMAT2 na Univerzitě Hradec Králové
Úvod Lineární diferenciální rovnice. řádu verze. Následující tet popisuje řešení lineárních diferenciálních rovnic. řádu. Měl by sloužit především studentům předmětu MATEMAT2 na Univerzitě Hradec Králové
8.4. Shrnutí ke kapitolám 7 a 8
 8.4. Shrnutí ke kapitolám 7 a 8 Shrnutí lekce Úvodní 7. kapitola přinesla informace o druzích řešení diferenciálních rovnic prvního řádu a stručné teoretické poznatky o podmínkách existence a jednoznačnosti
8.4. Shrnutí ke kapitolám 7 a 8 Shrnutí lekce Úvodní 7. kapitola přinesla informace o druzích řešení diferenciálních rovnic prvního řádu a stručné teoretické poznatky o podmínkách existence a jednoznačnosti
Lineární rovnice prvního řádu. Máme řešit nehomogenní lineární diferenciální rovnici prvního řádu. Funkce h(t) = 2
 Cvičení Lineární rovnice prvního řádu. Najděte řešení Cauchyovy úlohy x + x tg t = cos t, které vyhovuje podmínce xπ =. Máme nehomogenní lineární diferenciální rovnici prvního řádu. Funkce ht = tg t a
Cvičení Lineární rovnice prvního řádu. Najděte řešení Cauchyovy úlohy x + x tg t = cos t, které vyhovuje podmínce xπ =. Máme nehomogenní lineární diferenciální rovnici prvního řádu. Funkce ht = tg t a
Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: =, 0 = 1 = 1. ln = +,
 Příklad Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: a) =, 0= b) =, = c) =2, = d) =2, 0= e) =, 0= f) 2 =0, = g) + =0, h) =, = 2 = i) =, 0= j) sin+cos=0,
Příklad Nalezněte obecné řešení diferenciální rovnice (pomocí separace proměnných) a řešení Cauchyho úlohy: a) =, 0= b) =, = c) =2, = d) =2, 0= e) =, 0= f) 2 =0, = g) + =0, h) =, = 2 = i) =, 0= j) sin+cos=0,
y = 1 x (y2 y), dy dx = 1 x (y2 y) dy y 2 = dx dy y 2 y y(y 4) = A y + B 5 = A(y 1) + By, tj. A = 1, B = 1. dy y 1
 ODR - řešené příkla 20 5 ANALYTICKÉ A NUMERICKÉ METODY ŘEŠENÍ ODR A. Analtické meto řešení Vzorové příkla: 5.. Příklad. Řešte diferenciální rovnici = 2. Řešení: Přepišme danou rovnici na tvar = (2 ), což
ODR - řešené příkla 20 5 ANALYTICKÉ A NUMERICKÉ METODY ŘEŠENÍ ODR A. Analtické meto řešení Vzorové příkla: 5.. Příklad. Řešte diferenciální rovnici = 2. Řešení: Přepišme danou rovnici na tvar = (2 ), což
INŽENÝRSKÁ MATEMATIKA DIFERENCIÁLNÍ ROVNICE října 2009
 INŽENÝRSKÁ MATEMATIKA DIFERENCIÁLNÍ ROVNICE 1 Robert Mařík 2. října 2009 c Robert Mařík, 2009 Obsah 1 Diferenciální rovnice úvod 4 2 DR se separovanými proměnnými 9 DR se sep. proměnnými.........................
INŽENÝRSKÁ MATEMATIKA DIFERENCIÁLNÍ ROVNICE 1 Robert Mařík 2. října 2009 c Robert Mařík, 2009 Obsah 1 Diferenciální rovnice úvod 4 2 DR se separovanými proměnnými 9 DR se sep. proměnnými.........................
LINEÁRNÍ ROVNICE S ABSOLUTNÍ HODNOTOU
 LINEÁRNÍ ROVNICE S ABSOLUTNÍ HODNOTOU LINEÁRNÍ ROVNICE S ABSOLUTNÍ HODNOTOU je lineární rovnice, ve které se vyskytuje jeden nebo více výrazů v absolutní hodnotě. ABSOLUTNÍ HODNOTA x reálného čísla x je
LINEÁRNÍ ROVNICE S ABSOLUTNÍ HODNOTOU LINEÁRNÍ ROVNICE S ABSOLUTNÍ HODNOTOU je lineární rovnice, ve které se vyskytuje jeden nebo více výrazů v absolutní hodnotě. ABSOLUTNÍ HODNOTA x reálného čísla x je
Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)
![Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6) Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)](/thumbs/96/128965676.jpg) 1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
Necht tedy máme přirozená čísla n, k pod pojmem systém lineárních rovnic rozumíme rovnice ve tvaru
 2. Systémy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic s koeficienty z pole reálných případně komplexních čísel. Uvádíme podmínku pro existenci řešení systému lineárních
2. Systémy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic s koeficienty z pole reálných případně komplexních čísel. Uvádíme podmínku pro existenci řešení systému lineárních
Lineární funkce, rovnice a nerovnice 4 lineární nerovnice
 Lineární funkce, rovnice a nerovnice 4 lineární nerovnice 4.1 ekvivalentní úpravy Při řešení lineárních nerovnic používáme ekvivalentní úpravy (tyto úpravy nijak neovlivní výsledek řešení). Jsou to především
Lineární funkce, rovnice a nerovnice 4 lineární nerovnice 4.1 ekvivalentní úpravy Při řešení lineárních nerovnic používáme ekvivalentní úpravy (tyto úpravy nijak neovlivní výsledek řešení). Jsou to především
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu (reg. č. CZ.1.07/2.2.00/28.
 Extrémy Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.ldf.mendelu.cz/cz
Extrémy Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.ldf.mendelu.cz/cz
13. Kvadratické rovnice 2 body
 13. Kvadratické rovnice 2 body 13.1. Rovnice x 2 + 2x + 2 m = 0 (s neznámou x) má dva různé reálné kořeny, které jsou oba menší než tři, právě a) m (1, 17), b) m = 2, c) m = 2 m = 5, d) m 2, 5, e) m >
13. Kvadratické rovnice 2 body 13.1. Rovnice x 2 + 2x + 2 m = 0 (s neznámou x) má dva různé reálné kořeny, které jsou oba menší než tři, právě a) m (1, 17), b) m = 2, c) m = 2 m = 5, d) m 2, 5, e) m >
Matematika I (KMI/5MAT1)
 Přednáška první aneb Úvod do algebry (opakování ze SŠ a možná i ZŠ) Seznámení s předmětem Osnova přednášky seznámení s předmětem množiny pojem množiny operace s množinami číselné obory intervaly mocniny
Přednáška první aneb Úvod do algebry (opakování ze SŠ a možná i ZŠ) Seznámení s předmětem Osnova přednášky seznámení s předmětem množiny pojem množiny operace s množinami číselné obory intervaly mocniny
metody jsou proto často jedinou možností jak danou diferenciální rovnicivyřešit.
 7. ODR počáteční úlohy Průvodce studiem Jen velmi málo diferenciálních rovnic, které se vyskytují při popisu praktických úloh, se dářešit exaktně, a i když dokážeme najít vzorce popisující analytickéřešení,
7. ODR počáteční úlohy Průvodce studiem Jen velmi málo diferenciálních rovnic, které se vyskytují při popisu praktických úloh, se dářešit exaktně, a i když dokážeme najít vzorce popisující analytickéřešení,
4. Určete definiční obor elementární funkce g, jestliže g je definována předpisem
 4 Určete definiční obor elementární funkce g jestliže g je definována předpisem a) g ( x) = x 16 + ln ( x) x 16 ( x + 4 )( x 4) Řešíme-li kvadratickou nerovnice pomocí grafu kvadratické funkce tj paraboly
4 Určete definiční obor elementární funkce g jestliže g je definována předpisem a) g ( x) = x 16 + ln ( x) x 16 ( x + 4 )( x 4) Řešíme-li kvadratickou nerovnice pomocí grafu kvadratické funkce tj paraboly
Studijní text pro obor G+K Katedra matematiky Fakulta stavební ROVNICE. Doc. RNDr. Milada Kočandrlová, CSc.
 Studijní text pro obor G+K Katedra matematiky Fakulta stavební České vysoké učení technické OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE Doc. RNDr. Milada Kočandrlová, CSc. Lektorovali: RNDr. Milan Kočandrle, CSc.,
Studijní text pro obor G+K Katedra matematiky Fakulta stavební České vysoké učení technické OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE Doc. RNDr. Milada Kočandrlová, CSc. Lektorovali: RNDr. Milan Kočandrle, CSc.,
6. Lineární ODR n-tého řádu
 6. Lineární ODR n-tého řádu A. Obecná homogenní LODRn V předcházející kapitole jsme diferenciální rovnici (libovolného řádu) nazvali lineární, je-li tato rovnice lineární vzhledem ke hledané funkci y a
6. Lineární ODR n-tého řádu A. Obecná homogenní LODRn V předcházející kapitole jsme diferenciální rovnici (libovolného řádu) nazvali lineární, je-li tato rovnice lineární vzhledem ke hledané funkci y a
9.2. Zkrácená lineární rovnice s konstantními koeficienty
 9.2. Zkrácená lineární rovnice s konstantními koeficienty Cíle Řešíme-li konkrétní aplikace, které jsou popsány diferenciálními rovnicemi, velmi často zjistíme, že fyzikální nebo další parametry (hmotnost,
9.2. Zkrácená lineární rovnice s konstantními koeficienty Cíle Řešíme-li konkrétní aplikace, které jsou popsány diferenciálními rovnicemi, velmi často zjistíme, že fyzikální nebo další parametry (hmotnost,
Funkce a lineární funkce pro studijní obory
 Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
DIFERENCIÁLNÍ ROVNICE. Jana Řezníčková. Ústav matematiky Fakulta aplikované informatiky Univerzita Tomáše Bati ve Zlíně
 DIFERENCIÁLNÍ ROVNICE Jana Řezníčková Ústav matematiky Fakulta aplikované informatiky Univerzita Tomáše Bati ve Zlíně Zlín, 2015 2 DIFERENCIÁLNÍ ROVNICE Jana Řezníčková Ústav matematiky FAI UTB ve Zlíně
DIFERENCIÁLNÍ ROVNICE Jana Řezníčková Ústav matematiky Fakulta aplikované informatiky Univerzita Tomáše Bati ve Zlíně Zlín, 2015 2 DIFERENCIÁLNÍ ROVNICE Jana Řezníčková Ústav matematiky FAI UTB ve Zlíně
Řešíme tedy soustavu dvou rovnic o dvou neznámých. 2a + b = 3, 6a + b = 27,
 Přijímací řízení 2015/16 Přírodovědecká fakulta Ostravská univerzita v Ostravě Navazující magisterské studium, obor Aplikovaná matematika (1. červen 2016) Příklad 1 Určete taková a, b R, aby funkce f()
Přijímací řízení 2015/16 Přírodovědecká fakulta Ostravská univerzita v Ostravě Navazující magisterské studium, obor Aplikovaná matematika (1. červen 2016) Příklad 1 Určete taková a, b R, aby funkce f()
7. Soustavy ODR1 Studijní text. 7. Soustavy ODR1. A. Základní poznatky o soustavách ODR1
 7 Soustavy ODR1 A Základní poznatky o soustavách ODR1 V inženýrské praxi se se soustavami diferenciálních rovnic setkáváme především v úlohách souvisejících s mechanikou Příkladem může být úloha popsat
7 Soustavy ODR1 A Základní poznatky o soustavách ODR1 V inženýrské praxi se se soustavami diferenciálních rovnic setkáváme především v úlohách souvisejících s mechanikou Příkladem může být úloha popsat
Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru. Kvadratická forma v n proměnných je tak polynom n proměnných s
 Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
INŽENÝRSKÁ MATEMATIKA DIFERENCIÁLNÍ ROVNICE
 INŽENÝRSKÁ MATEMATIKA DIFERENCIÁLNÍ ROVNICE Robert Mařík Ústav matematiky, LDF, MZLU 5. patro, budova B marik@mendelu.cz www.mendelu.cz/user/marik c Robert Mařík, 2009 Obsah 1 Diferenciální rovnice úvod
INŽENÝRSKÁ MATEMATIKA DIFERENCIÁLNÍ ROVNICE Robert Mařík Ústav matematiky, LDF, MZLU 5. patro, budova B marik@mendelu.cz www.mendelu.cz/user/marik c Robert Mařík, 2009 Obsah 1 Diferenciální rovnice úvod
Diferenciální rovnice a dynamické modely
 Diferenciální rovnice a namické modely Robert Mařík 31. srpna 2009 c Robert Mařík, 2009 G. Galilei: Velkou knihu příro mohou číst jen ti, kteří znají jazyk, jímž je tato kniha napsána. A tímto jazykem
Diferenciální rovnice a namické modely Robert Mařík 31. srpna 2009 c Robert Mařík, 2009 G. Galilei: Velkou knihu příro mohou číst jen ti, kteří znají jazyk, jímž je tato kniha napsána. A tímto jazykem
Funkce pro studijní obory
 Variace 1 Funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce Funkce je přiřazení,
Variace 1 Funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce Funkce je přiřazení,
Hledáme lokální extrémy funkce vzhledem k množině, která je popsána jednou či několika rovnicemi, vazebními podmínkami. Pokud jsou podmínky
 6. Vázané a absolutní extrémy. 01-a3b/6abs.tex Hledáme lokální extrémy funkce vzhledem k množině, která je popsána jednou či několika rovnicemi, vazebními podmínkami. Pokud jsou podmínky jednoduché, vyřešíme
6. Vázané a absolutní extrémy. 01-a3b/6abs.tex Hledáme lokální extrémy funkce vzhledem k množině, která je popsána jednou či několika rovnicemi, vazebními podmínkami. Pokud jsou podmínky jednoduché, vyřešíme
Diferenciální počet 1 1. f(x) = ln arcsin 1 + x 1 x. 1 x 1 a x 1 0. f(x) = (cos x) cosh x + 3x. x 0 je derivace funkce f(x) v bodě x0.
 Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Budeme hledat řešení y(x) okrajové úlohy pro diferenciální rovnici druhého řádu v samoadjungovaném tvaru na intervalu a, b : 2 ) y i p i+ 1
 ODR - okrajová úloha Teorie (velmi stručný výběr z přednášek) Okrajová úloha 2. řádu Budeme hledat řešení y(x) okrajové úlohy pro diferenciální rovnici druhého řádu v samoadjungovaném tvaru na intervalu
ODR - okrajová úloha Teorie (velmi stručný výběr z přednášek) Okrajová úloha 2. řádu Budeme hledat řešení y(x) okrajové úlohy pro diferenciální rovnici druhého řádu v samoadjungovaném tvaru na intervalu
5.3. Implicitní funkce a její derivace
 Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
Soustavy lineárních rovnic
 Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních diferenciálních rovnic y = a (x)y + a (x)y + + a n (x)y n + f (x) y = a (x)y + a (x)y + + a n (x)y n + f (x). y n = a
Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních diferenciálních rovnic y = a (x)y + a (x)y + + a n (x)y n + f (x) y = a (x)y + a (x)y + + a n (x)y n + f (x). y n = a
9.4. Rovnice se speciální pravou stranou
 Cíle V řadě případů lze poměrně pracný výpočet metodou variace konstant nahradit jednodušším postupem, kterému je věnována tato kapitola. Výklad Při pozorném studiu předchozího textu pozornějšího studenta
Cíle V řadě případů lze poměrně pracný výpočet metodou variace konstant nahradit jednodušším postupem, kterému je věnována tato kapitola. Výklad Při pozorném studiu předchozího textu pozornějšího studenta
1 Mnohočleny a algebraické rovnice
 1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
Q(y) dy = P(x) dx + C.
 Cíle Naše nejbližší cíle spočívají v odpovědích na základní otázky, které si klademe v souvislosti s diferenciálními rovnicemi: 1. Má rovnice řešení? 2. Kolik je řešení a jakého jsou typu? 3. Jak se tato
Cíle Naše nejbližší cíle spočívají v odpovědích na základní otázky, které si klademe v souvislosti s diferenciálními rovnicemi: 1. Má rovnice řešení? 2. Kolik je řešení a jakého jsou typu? 3. Jak se tato
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze. Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A
 Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
1. Několik základních pojmů ze středoškolské matematiky. Na začátku si připomeneme následující pojmy:
 Opakování středoškolské matematiky Slovo úvodem: Tato pomůcka je určena zejména těm studentům presenčního i kombinovaného studia na VŠFS, kteří na středních školách neprošli dostatečnou průpravou z matematiky
Opakování středoškolské matematiky Slovo úvodem: Tato pomůcka je určena zejména těm studentům presenčního i kombinovaného studia na VŠFS, kteří na středních školách neprošli dostatečnou průpravou z matematiky
Přijímací zkouška na navazující magisterské studium 2014
 Přijímací zkouška na navazující magisterské studium 4 Studijní program: Studijní obory: Příklad (5 bodů) Spočtěte Matematika MA, MMIB, MMFT, MSTR, NVM, PMSE, MDU Varianta A M xy dxdy, kde M = {(x, y) R
Přijímací zkouška na navazující magisterské studium 4 Studijní program: Studijní obory: Příklad (5 bodů) Spočtěte Matematika MA, MMIB, MMFT, MSTR, NVM, PMSE, MDU Varianta A M xy dxdy, kde M = {(x, y) R
6. dubna *********** Přednáška ***********
 KMA/MAT2 Přednáška a cvičení č. 8, Obyčejné diferenciální rovnice 2 6. dubna 2016 *********** Přednáška *********** 1 Existence a jednoznačnost řešení Cauchyovy úlohy Stále uvažujeme rovnici y = f(t, y).
KMA/MAT2 Přednáška a cvičení č. 8, Obyčejné diferenciální rovnice 2 6. dubna 2016 *********** Přednáška *********** 1 Existence a jednoznačnost řešení Cauchyovy úlohy Stále uvažujeme rovnici y = f(t, y).
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
Užití nekonečných řad při řešení obyčejných diferenciálních rovnic. Michal Ostřanský
 Užití nekonečných řad při řešení obyčejných diferenciálních rovnic Michal Ostřanský Bakalářská práce 2017 ABSTRAKT Cílem bakalářské práce je ukázat možnosti použití nekonečných řad při řešení obyčejných
Užití nekonečných řad při řešení obyčejných diferenciálních rovnic Michal Ostřanský Bakalářská práce 2017 ABSTRAKT Cílem bakalářské práce je ukázat možnosti použití nekonečných řad při řešení obyčejných
Obecná rovnice kvadratické funkce : y = ax 2 + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených funkcí je množina reálných čísel.
 5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
1. Náhodný vektor (X, Y ) má diskrétní rozdělení s pravděpodobnostní funkcí p, kde. p(x, y) = a(x + y + 1), x, y {0, 1, 2}.
 VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
Funkce jedné reálné proměnné. lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou
 Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Leden 2015 Komplexní inovace studijních programů a zvyšování kvality výuky na FEKT VUT v Brně OP VK CZ.1.07/2.2.00/28.0193
FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Leden 2015 Komplexní inovace studijních programů a zvyšování kvality výuky na FEKT VUT v Brně OP VK CZ.1.07/2.2.00/28.0193
Matematika Kvadratická rovnice. Kvadratická rovnice je matematický zápis, který můžeme (za pomoci ekvivalentních úprav) upravit na tvar
 Kvadratická rovnice Kvadratická rovnice je matematický zápis, který můžeme (za pomoci ekvivalentních úprav) upravit na tvar ax 2 + bx + c = 0. x neznámá; v kvadratické rovnici se vyskytuje umocněná na
Kvadratická rovnice Kvadratická rovnice je matematický zápis, který můžeme (za pomoci ekvivalentních úprav) upravit na tvar ax 2 + bx + c = 0. x neznámá; v kvadratické rovnici se vyskytuje umocněná na
Nerovnice v součinovém tvaru, kvadratické nerovnice
 Nerovnice v součinovém tvaru, kvadratické nerovnice Příklad: Pro která x R je součin x x 5 kladný? Řešení: Víme, že součin je kladný, mají-li oba činitelé stejné znaménko. Tedy aby platilo x x 5 0, musí
Nerovnice v součinovém tvaru, kvadratické nerovnice Příklad: Pro která x R je součin x x 5 kladný? Řešení: Víme, že součin je kladný, mají-li oba činitelé stejné znaménko. Tedy aby platilo x x 5 0, musí
INTEGRÁLY S PARAMETREM
 INTEGRÁLY S PARAMETREM b a V kapitole o integraci funkcí více proměnných byla potřeba funkce g(x) = f(x, y) dy proměnné x. Spojitost funkce g(x) = b a f(x, y) dy proměnné x znamená vlastně prohození limity
INTEGRÁLY S PARAMETREM b a V kapitole o integraci funkcí více proměnných byla potřeba funkce g(x) = f(x, y) dy proměnné x. Spojitost funkce g(x) = b a f(x, y) dy proměnné x znamená vlastně prohození limity
1 Funkce dvou a tří proměnných
 1 Funkce dvou a tří proměnných 1.1 Pojem funkce více proměnných Definice Funkce dvou proměnných je předpis, který každému bodu z R 2 (tj. z roviny) přiřazuje jediné reálné číslo. z = f(x, y), D(f) R 2
1 Funkce dvou a tří proměnných 1.1 Pojem funkce více proměnných Definice Funkce dvou proměnných je předpis, který každému bodu z R 2 (tj. z roviny) přiřazuje jediné reálné číslo. z = f(x, y), D(f) R 2
Obyčejné diferenciální rovnice
 Obyčejné diferenciální rovnice Petra Schreiberová, Petr Volný Katedra matematiky a deskriptivní geometrie, FS Katedra matematiky, FAST Vysoká škola báňská Technická Univerzita Ostrava Ostrava 2019 OBSAH
Obyčejné diferenciální rovnice Petra Schreiberová, Petr Volný Katedra matematiky a deskriptivní geometrie, FS Katedra matematiky, FAST Vysoká škola báňská Technická Univerzita Ostrava Ostrava 2019 OBSAH
Nyní využijeme slovník Laplaceovy transformace pro derivaci a přímé hodnoty a dostaneme běžnou algebraickou rovnici. ! 2 "
 ŘEŠENÉ PŘÍKLADY Z MB ČÁST Příklad Nalezněte pomocí Laplaceovy transformace řešení dané Cauchyho úlohy lineární diferenciální rovnice prvního řádu s konstantními koeficienty v intervalu 0,, které vyhovuje
ŘEŠENÉ PŘÍKLADY Z MB ČÁST Příklad Nalezněte pomocí Laplaceovy transformace řešení dané Cauchyho úlohy lineární diferenciální rovnice prvního řádu s konstantními koeficienty v intervalu 0,, které vyhovuje
Drsná matematika III 6. přednáška Obyčejné diferenciální rovnice vyšších řádů, Eulerovo přibližné řešení a poznámky o odhadech chyb
 Drsná matematika III 6. přednáška Obyčejné diferenciální rovnice vyšších řádů, Eulerovo přibližné řešení a poznámky o odhadech chyb Jan Slovák Masarykova univerzita Fakulta informatiky 23. 10. 2006 Obsah
Drsná matematika III 6. přednáška Obyčejné diferenciální rovnice vyšších řádů, Eulerovo přibližné řešení a poznámky o odhadech chyb Jan Slovák Masarykova univerzita Fakulta informatiky 23. 10. 2006 Obsah
Funkce - pro třídu 1EB
 Variace 1 Funkce - pro třídu 1EB Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv využití výukového materiálu je povoleno pouze s odkazem na www.jarjurek.cz. 1. Funkce Funkce je přiřazení, které každému
Variace 1 Funkce - pro třídu 1EB Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv využití výukového materiálu je povoleno pouze s odkazem na www.jarjurek.cz. 1. Funkce Funkce je přiřazení, které každému
Praha & EU: investujeme do vaší budoucnosti. Daniel Turzík, Miroslava Dubcová,
 E-sbírka příkladů Seminář z matematiky Evropský sociální fond Praha & EU: investujeme do vaší budoucnosti Daniel Turzík, Miroslava Dubcová, Pavla Pavlíková Obsah 1 Úpravy výrazů................................................................
E-sbírka příkladů Seminář z matematiky Evropský sociální fond Praha & EU: investujeme do vaší budoucnosti Daniel Turzík, Miroslava Dubcová, Pavla Pavlíková Obsah 1 Úpravy výrazů................................................................
Parciální derivace a diferenciál
 Parciální derivace a diferenciál Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
Parciální derivace a diferenciál Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice. študenti MFF 15. augusta 2008
 Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice študenti MFF 15. augusta 2008 1 7 Diferenciální rovnice Požadavky Soustavy lineárních diferenciálních rovnic prvního řádu lineární
Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice študenti MFF 15. augusta 2008 1 7 Diferenciální rovnice Požadavky Soustavy lineárních diferenciálních rovnic prvního řádu lineární
(4x) 5 + 7y = 14, (2y) 5 (3x) 7 = 74,
 1. V oboru celých čísel řešte soustavu rovnic (4x) 5 + 7y = 14, (2y) 5 (3x) 7 = 74, kde (n) k značí násobek čísla k nejbližší číslu n. (P. Černek) Řešení. Z první rovnice dané soustavy plyne, že číslo
1. V oboru celých čísel řešte soustavu rovnic (4x) 5 + 7y = 14, (2y) 5 (3x) 7 = 74, kde (n) k značí násobek čísla k nejbližší číslu n. (P. Černek) Řešení. Z první rovnice dané soustavy plyne, že číslo
KFC/SEM, KFC/SEMA Rovnice, nerovnice
 KFC/SEM, KFC/SEMA Rovnice, nerovnice Požadované dovednosti: Řešení lineárních rovnic a nerovnic Řešení kvadratických rovnic Řešení rovnic s odmocninou Řešení rovnic s parametrem Řešení rovnic s absolutní
KFC/SEM, KFC/SEMA Rovnice, nerovnice Požadované dovednosti: Řešení lineárních rovnic a nerovnic Řešení kvadratických rovnic Řešení rovnic s odmocninou Řešení rovnic s parametrem Řešení rovnic s absolutní
Variace. Kvadratická funkce
 Variace 1 Kvadratická funkce Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratická funkce Kvadratická
Variace 1 Kvadratická funkce Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratická funkce Kvadratická
Parciální derivace a diferenciál
 Parciální derivace a diferenciál Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
Parciální derivace a diferenciál Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
Analytická geometrie. c ÚM FSI VUT v Brně
 19. září 2007 Příklad 1. Příklad 2. Příklad 3. Příklad 1. Určete obecnou rovnici roviny, která prochází body A = [0, 1, 2], B = [ 1, 0, 3], C = [3, 1, 0]. Příklad 1. A = [0, 1, 2], B = [ 1, 0, 3], C =
19. září 2007 Příklad 1. Příklad 2. Příklad 3. Příklad 1. Určete obecnou rovnici roviny, která prochází body A = [0, 1, 2], B = [ 1, 0, 3], C = [3, 1, 0]. Příklad 1. A = [0, 1, 2], B = [ 1, 0, 3], C =
M - Kvadratické rovnice a kvadratické nerovnice
 M - Kvadratické rovnice a kvadratické nerovnice Určeno jako učební tet pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase.
M - Kvadratické rovnice a kvadratické nerovnice Určeno jako učební tet pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase.
16. Goniometrické rovnice
 @198 16. Goniometrické rovnice Definice: Goniometrická rovnice je taková rovnice, ve které proměnná (neznámá) vystupuje pouze v goniometrických funkcích. Řešit goniometrické rovnice znamená nalézt všechny
@198 16. Goniometrické rovnice Definice: Goniometrická rovnice je taková rovnice, ve které proměnná (neznámá) vystupuje pouze v goniometrických funkcích. Řešit goniometrické rovnice znamená nalézt všechny
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
M - Kvadratická funkce
 M - Kvadratická funkce Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně
M - Kvadratická funkce Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně
1.13 Klasifikace kvadrik
 5 KAPITOLA 1. KVADRIKY JAKO PLOCHY. STUPNĚ 1.13 Klasifikace kvadrik V této části provedeme klasifikaci kvadrik. Vyšetříme všechny případy, které mohou různou volbou koeficientů v rovnici kvadriky a 11
5 KAPITOLA 1. KVADRIKY JAKO PLOCHY. STUPNĚ 1.13 Klasifikace kvadrik V této části provedeme klasifikaci kvadrik. Vyšetříme všechny případy, které mohou různou volbou koeficientů v rovnici kvadriky a 11
( ) ( ) Logaritmické nerovnice II. Předpoklady: 2924
 5 Logaritmické nerovnice II Předpoklad: Pedagogická poznámka: Většina studentů spočítá pouze první tři příklad, nejlepší se dostanou až k pátému Pedagogická poznámka: U následujících dvou příkladů je opět
5 Logaritmické nerovnice II Předpoklad: Pedagogická poznámka: Většina studentů spočítá pouze první tři příklad, nejlepší se dostanou až k pátému Pedagogická poznámka: U následujících dvou příkladů je opět
Diferenciální rovnice
 Diferenciální rovnice Průvodce studiem Touto kapitolou se náplň základního kurzu bakalářské matematiky uzavírá. Je tomu tak mimo jiné proto, že jsou zde souhrnně využívány poznatky získané studiem předchozích
Diferenciální rovnice Průvodce studiem Touto kapitolou se náplň základního kurzu bakalářské matematiky uzavírá. Je tomu tak mimo jiné proto, že jsou zde souhrnně využívány poznatky získané studiem předchozích
Test M1-ZS12-2 M1-ZS12-2/1. Příklad 1 Najděte tečnu grafu funkce f x 2 x 6 3 x 2, která je kolmá na přímku p :2x y 3 0.
 Test M-ZS- M-ZS-/ Příklad Najděte tečnu grafu funkce f x x 6 3 x, která je kolmá na přímku p :x y 3 0. Zřejmě D f R. Přímka p má směrnici, tečna na ní kolmá má proto směrnici. Protože směrnice tečny ke
Test M-ZS- M-ZS-/ Příklad Najděte tečnu grafu funkce f x x 6 3 x, která je kolmá na přímku p :x y 3 0. Zřejmě D f R. Přímka p má směrnici, tečna na ní kolmá má proto směrnici. Protože směrnice tečny ke
