1.1.2 Jak se počítají známky
|
|
|
- Markéta Vítková
- před 8 lety
- Počet zobrazení:
Transkript
1 1.1.2 Jak se počítají známky Předpoklady: Pedagogická poznámka: Je naivní předpokládat, že by většinu žáků na začátku zajímala matematika nebo svět okolo nich. Známky však (bohužel) zajímají (zejména kvůli nepochopitelné české posedlosti) téměř všechny (ačkoliv příliš vypovídat nemusejí). Používám poměrně složitý známkovací systém, kterým se snažím tlačit žáky, aby dělali to, co považuji za potřebné. Nechat žáky spočítat pár zajímavostí během seznamování mě přijde docela zajímavé, jde přece o příklady z praxe, kterou budou "opravdu potřebovat". Součástí výuky na školách jsou zatím známky. Mnozí studenti je (chybně) považují za to nejdůležitější. Normální písemka Píše se přibližně jednou za týden až čtrnáct dní. Na její vypracování je určena polovina hodiny (22,5 minuty). Má čtyři příklady (každý za čtyři body) a BONUS (taky za čtyři body). Příklady jsou většinou řazeny od jednodušších ke složitějším. BONUS většinou vyžaduje schopnost překročit hranice právě probírané látky. Získané body se přepočítávají na procenta, pokud žák vypočítá správně všechny čtyři příklady (bez BONUSu), je to bráno jako zcela správně spočtená písemka hodnocená na 100%. Pokud je písemka dopředu nahlášena, není možné používat jiné než povolené pomůcky (většinou kalkulačka a oficiální soupis - vysvětleno později, používá se až od druhé pololetí prvního ročníku), pokud písemka nahlášena není, může každý používat svůj sešit (proto není vhodné při výměně sešitu starý nenosit na hodiny, dokud se nenapíše písemka). Cílem těchto písemek je udržovat žáky v obraze. Píší se poměrně často, aby se žáci museli alespoň částečně průběžně učit a neztráceli kontakt s probíranou látkou. Př. 1: Zjisti pro normální písemku: a) Kolik bodů je možné získat při vypočtení dvou celých příkladů a poloviny třetího příkladu? b) Kolik bodů odpovídá 100%? c) Kolik bodů a kolik procent může žák získat, když spočítá správně úplně všechno? d) Kolika procenty je hodnocena písemka s 9 body? e) Kolik bodů získat Petr, který z písemky dostal 31 %? a) Kolik bodů je možné získat při vypočtení dvou celých příkladů a poloviny třetího příkladu? Celý příklad: 4 body, polovina příkladu: 2 body dva a půl příkladu: = 10 bodů. b) Kolik bodů odpovídá 100%? 100% je hodnocena písemka se čtyřmi spočtenými příklady 4 4 = 1 bodů odpovídá 100%. c) Kolik bodů a kolik procent může žák získat, když spočítá správně úplně všechno? Kompletní písemka: 4 příklady a BONUS, vše po čtyřech bodech 5 4 = 20 bodů. 100%... 1 bodů x % bodů 1
2 100 Přímá úměrnost: x = x = = Žák, který spočte úplně všechno, získá za písemku 20 bodů a 125%. d) Kolika procenty je hodnocena písemka s 9 body? 100%... 1 bodů x %... 9 bodů 100 Přímá úměrnost: x = = 5, Písemka hodnocená 9 body je započtena za 5%. e) Kolik bodů získat Petr, který z písemky dostal 31 %? 100%... 1 bodů 31%... x bodů 1 Přímá úměrnost: x = 1 31 = 4, V písemce hodnocené na 31% získal Petr 5 bodů. Pedagogická poznámka: Smutné je, že se najdou žáci, kteří samostatně nevyřeší ani bod a), body d) a e) nepřekoná tak třetina třídy. V tomto okamžiku sice ukazuji řešení přes přímo úměru, ale nejslabším žákům doporučuji počítat přepočtem přes jedničku (hodiny a v učebnici pro ZŠ). K přepočtu přes jedničku se ještě vrátíme v následující hodině, pokud má i v ní někdo problémy, chci, aby si zmíněné hodiny z učebnice pro ZŠ přepočítal. Př. 2: Sestav tabulku počtů procent pro všechny možné počty bodů. Hledej co nejúspornější postup. Počty procent zaokrouhluj na jednotky Vyplnit tabulku je možné mnoha způsoby (vypisuji některé od nejpracnějšího): vypočítat jednotlivé sloupce pokaždé znovu přímo úměrou, určit počet procent, které odpovídají jednomu bodu a tento počet procent postupně načítat, napsat počty procent pro speciální počty bodů (4, 8, 12), dopočítat načítáním procenta pro počty bodů menší než 8, zbývající sloupce doplnit přičítáním 50 (do 1 bodů) a 100 (nad 1 bodů). Pedagogická poznámka: Sledovat způsob, jakým žáci tabulku vyplňují je opravdu poučné, je vidět, jak jsou sžití s početními operacemi nebo zda se naopak musí držet při zemi, protože moc neví, co kdy mají čekat. Čtvrtletka Píše se jednou za čtvrt roku, obvykle na logicky ucelenou část látky (často odpovídá dílu učebnice). Obsahuje více příkladů a píše se celou hodinu. Počty příkladů i jejich bodové hodnocení se liší. Konečný výsledek je uveden v procentech. Protože čtvrtletka se píše déle a hlavně vyžaduje naučení daleko většího množství látky, počítá se do průměru jako tři normální písemky. 2
3 Př. 3: Jarda psal tři písemky, ze kterých dostal postupně 44%, 5 %, 75 %. a) Jaká bude jeho výsledná známka, pokud dostane ze čtvrtletky 38%? b) Kolik musí ze čtvrtletky dostat, aby jeho výsledná známka byla 9%? a) Jaká bude jeho výsledná známka, pokud dostane ze čtvrtletky 38%? Spočteme průměr, do kterého započteme známku ze čtvrtletky třikrát = 48,1 48% Jardova výsledná známka bude 48%. b) Kolik musí ze čtvrtletky dostat, aby jeho výsledná známka byla 9%? Obrátíme předchozí postup. 9 jsme získali ze známek celkový součet procent musí být 9 = 414. Odečteme procenta z normálních písemek: = 239 Čtvrtletku počítáme třikrát: 239 : 3 = 79, 80% Jarda musí napsat čtvrtletku minimálně na 80%. Poznámka: Výsledky numerických výpočtů jsou udávány na pět míst (pokud obsahují periodu) a toto vyjádření je bráno jako přesné (o když není), poté jsou zaokrouhlovány na celá procenta nebo celé body. Pedagogická poznámka: Výpočet aritmetického průměru je jednou z mála dovedností, kterou zvládají v podstatě všichni žáci, proto v bodě a) stačí zopakovat, že se počítá do průměru jako tři normální písemky. V bodě b) je situace horší, snažím se co nejdéle zůstat jen u toho, že je předchozí postup nutné obrátit. Pak jej dopočítáváme na tabuli. Pedagogická poznámka: Následující příklad je vyrovnávací (aby měla chytřejší část třídy co dělat, zatímco se Ti horší trápí s předchozím příkladem). Je skoro jisté, že žáci budou spíše iterovat (postupně dosazovat zvyšující se počty normálních písemek, dopočítávat průměry a čekat než výsledek spadne pod 27%) než vyjadřovat. Př. 4: Tonda není hloupej, ale školu moc nehrotí. Jeho průměrná známka z normálních písemek je 20%, ale Tonda se pětky nebojí, protože když bude chtít, naučí se na čtvrtletku tak, aby dostal 50% a tím si známku spraví na potřebných 27%. Kolik normálních písemek může napsat, aby to byla pravda? Počet napsaných normálních písemek označíme x. Spočteme průměr (n normálních písemek x po 20% a jedna čtvrtletka 50%): = 27. x + 3 x Ze vztahu vyjádříme x: = 27 / ( x + 3) x + 3 x = 27 x + 3 ( ) x = 27x = 27x 20x 9 = 7x 3
4 9 x = = 9, ,8 7 Karel může napsat na 20% maximálně devět normálních písemek, aby dokázal známku spravit čtvrtletní písemkou hodnocenou 50 %. Opravné písemky U každé písemky (normální i čtvrtletní) je možné psát opravou písemku (opravná písemka nemusí obsahovat analogické příklady jako písemka původní, její zadání se pouze musí týkat stejné látky). Pokud je opravná písemka lepší než písemka původní, nahradí se v celkovém hodnocení původní známka novou známkou, do které se původní známka počítá jednou a nová známka dvakrát. Smyslem opravných písemek je dát žákům šanci si opravit špatný výsledek předchozí písemky tím, že se látku přece jen naučí. Vzhledem k tomu, že látka je ve většině případů ještě potřeba, považuji čas strávený nad opravnými písemkami za ospravedlnitelnou investici do toho, že žáci vyvinou vlastní iniciativu. Pokud někdo napíše vícekrát opravnou písemku stejně nebo hůře než původní (a je tedy vidět, že na to kašle pořád stejně), vyžaduji předem opravu písemky (viz. níže). Př. 5: Lenka napsala písemku na 50%. a) Jaká bude její výsledná známka, pokud napíše opravnou písemku na 84%? b) Na kolik musí napsat opravnou písemku, aby její výsledná známka byla alespoň 80%? Spočteme průměr, do kterého započteme původní známku jednou a opravenou známku dvakrát: = 72, 73% 3 b) Na kolik musí napsat opravnou písemku, aby její výsledná známka byla alespoň 80%? Obrátíme předchozí postup. 80 jsme získali ze 3 známek celkový součet procent musí být 3 80 = 240. Odečteme procenta z původní písemky: = 190 Opravnou písemku počítáme dvakrát: 190 : 2 95% Lenka musí napsat opravnou písemku minimálně na 95%, aby výsledná známka byla 80%. Pedagogická poznámka: Předchozí příklad je velmi podobný příkladu 3, pokud s ním má někdo problémy, je zřejmé, že příliš nevnímá nebo si není schopen vzít poučení. Opravy U každé písemky je možné udělat opravu. Pokud je původní písemka hodnocena na 74 a více musí být v rámci opravy vypočítán i BONUS. Písemky hodnocené na 84 % a více procent se neopravují. Uznaná oprava znamená zvýšení hodnocení o 10%. Opravu dělá žák samostatně doma (nebo ve škole s kamarády - na tom nezáleží), jeho povinností není jen napsat špatně spočtené příklady dobře do sešitu, ale donést napsanou opravu ke kontrole. Při kontrole musí prokázat, že problematickým místům opravdu rozumí. Pokud se ukáže, že jim nerozumí, může být od opravy vyhozen s tím, že se může vrátit, až si to ujasní. Cílem oprav je dotáhnout žáky na konzultaci a zkontrolovat, zda se doučili to, co bude ještě potřeba, proto jsem ochoten s žáky, kteří vypadají, že opravě nějaký čas věnovali, diskutovat (a v podstatě doučovat) docela dlouho. 4
5 Př. : Jarda psal tři písemky, ze kterých dostal postupně 44%, 5 %, 75 % a čtvrtletku na 38%. a) Jaká bude jeho výsledná známka? b) Jaká bude jeho výsledná známka, pokud si opraví všechny písemky (i čtvrletku)? c) Jaká bude jeho výsledná známka, pokud si opraví pouze čtvrletku? d) Jaká bude jeho výsledná známka, pokud si opraví dvě normální písemky? a) Jaká bude jeho výsledná známka? Spočteme průměr, do kterého započteme známku ze čtvrtletky třikrát = 48,1 48% b) Jaká bude jeho výsledná známka, pokud si opraví všechny písemky (i čtvrletku)? Pokud si opraví všechny písemky i čtvrtletku, zlepší si všechny známky v průměru a tím i výslednou známku o 10%. Kontrola dosazením: = 58,1 58%. c) Jaká bude jeho výsledná známka, pokud si opraví pouze čtvrletku? Do průměru tentokrát dosadíme za čtvrtletku 48% = 53,1 53% d) Jaká bude jeho výsledná známka, pokud si opraví dvě normální písemky? Zlepšíme známky ze dvou normálních písemek, čtvrtletku necháváme stejnou = 51, 5 52% Pedagogická poznámka: Opět je dobré sledovat, kdo si všimne, že bod a) už počítal a kdo bude otrocky počítat znovu. Při kontrole se také ptám, zda bylo potřeba počítat bod b). Kromě písemek je možné získat známky o stejné váze za mimořádné výkony (prázdný papírek Bonzáček, MO, spočtené sbírky,...). Ze všech známek se na konci pololetí spočte průměr, který ještě může být změněn znamínky. Znamínka Znamínka (plusy a mínusy) se udělují za trochaminutové testy na začátku hodin a jiné méně mimořádné výkony (za které už se nepřidělují známky navíc). Například každá nalezená a nahlášená chyba v učebnici na internetu je oceněna plusem. Trochaminutové testy na začátcích hodin slouží nejvíce k udržení kontextu v hlavách žáků a jako motivace k zvládnutí základních postupů. Písemky jsou hodnoceny +, - nebo 0 (nic). POZOR: + se uděluje většinou pouze v případě žádné nebo pouze jedné chyby. Na konci pololetí se sečtou plusy i mínusy a nechají se navzájem vyrušit (jeden plus se vyruší s jedním mínus). Pokud je mínusů víc, každý z nich znamená zmenšení hodnoty průměru ze známek o 1%. Pokud je plusů víc, procenta se naopak přidávají, ale trochu složitějším systémem tak, aby: 5
6 větší počet plusů více pomáhal žákům s horším průměrem z normálních písemek a naopak lepší žáci si nemohli pomocí plusů podstatně zlepšovat známky a museli se zaměřit i na písemky získání každého dalšího plusu znamenalo větší vylepšení průměru. Přepočet plusů je uveden v tabulce. Průměr z písemek Plusy, které se započítávají x < x < x < 9 9 x < x celé za polovinu za třetinu za čtvrtinu za pětinu 101 a víc 81 a víc 1 a víc 41 a víc 21 a víc Př. 7: Urči výsledný počet procent, pokud: a) Martin má průměr z písemek 23, 14 plusů a 20 mínusů, b) Věra má průměr z písemek 18, 1 plusů a 9 mínusů, c) Ivan má průměr z písemek 43, 14 plusů a 3 mínusy, d) Jindra má průměr z písemek 9, 12 plusů a 2 mínusy, e) Konrád má průměr z písemek 85, 24 plusů a 1 mínus. a) Martin má průměr z písemek 23, 14 plusů a 20 mínusů Znamínka: =. Procenta (první sloupec): 23 = 17. Martinův výsledný počet procent se rovná 17. b) Věra má průměr z písemek 18, 1 plusů a 9 mínusů Znamínka: 1 9 = 7. Procenta (první sloupec): = 25. Věřin výsledný počet procent se rovná 25. c) Ivan má průměr z písemek 43, 14 plusů a 3 mínusy Znamínka: = Procenta (druhý sloupec): = 52, Ivanův výsledný počet procent se rovná 53. d) Jindra má průměr z písemek 9, 12 plusů a 2 mínusy Znamínka: = Procenta (čtvrtý sloupec): = 7. 2 Jindrův výsledný počet procent se rovná 7. e) Konrád má průměr z písemek 85, 24 plusů a 1 mínus. Znamínka: = Procenta (pátý sloupec): = 93, Konrádův výsledný počet procent se rovná 93,.
7 Pedagogická poznámka: Velká většina žáků tabulku nerozluští, po chvilce napíšu (bez komentáře) na tabuli například takový příklad: Například Přemysl Otakar například ukončil pololetí takto: průměr 52%, 13 plusů, 4 mínusy. Odečtení znamínek: = + 3. Procenta (třetí sloupec): , 5 = 59, 5 0. Přemysl Otakar dosáhl konečného celkového hodnocení 0%. Po další chvilce ho okomentuji (který sloupec jsem si vybral a proč, a jak jsme rozdělil 9 na a 3) a po další chvilce napíšu na tabuli další podobné příklady. Pedagogická poznámka: Pokud zbude trochu času je dobré se zeptat, zda má v zápisu ,5 = 59,5 0 význam psát jedničku (matematicky ne, kvůli pochopení ano, je pak lépe vidět, že všechny členy za počtem procent mají tvar počet plusů koeficient ). Pedagogická poznámka: Přes polovinu třídy nezná znak a neví, do kterého sloupce přiřadit 9%. Neříkám to dopředu, ale je dobré si to uvědomovat a rychle zasáhnout. Pedagogická poznámka: Žáci mají tendenci interpretovat tabulku tak, že když jste například ve třetím sloupci a získáte sedmý plus, všechny plusy se budou započítávat za polovinu. Nechte je v popisu najít místo, které tuto možnost vylučuje ("získání každého dalšího plusu znamenalo větší vylepšení průměru"). Shrnutí: Bez matematiky si člověk nezjistí ani známku, kterou dostane na vysvědčení. 7
0.1.2 Počítání známek
 0.1.2 Počítání známek Předpoklady: 000101 Pedagogická poznámka: Hodinu samozřejmě v primě neprobereme za 45 minut celou (konec s přepočítáváním znamínek, stejně jako některé příklady s průměry jsou pro
0.1.2 Počítání známek Předpoklady: 000101 Pedagogická poznámka: Hodinu samozřejmě v primě neprobereme za 45 minut celou (konec s přepočítáváním znamínek, stejně jako některé příklady s průměry jsou pro
Procentová část
 2..2 Procentová část Předpoklady: 02024 Pedagogická poznámka: Pokud je ve třídě větší množství slabších žáků, je zřejmě výhodnější, dát příklad jen rychlejší části třídy, tu pak nechat pracovat na dalších
2..2 Procentová část Předpoklady: 02024 Pedagogická poznámka: Pokud je ve třídě větší množství slabších žáků, je zřejmě výhodnější, dát příklad jen rychlejší části třídy, tu pak nechat pracovat na dalších
Soustavy více rovnic o více neznámých I
 313 Soustavy více rovnic o více neznámých I Předpoklady: 31 Př 1: Co při řešení soustav rovnic o více neznámých představují rovnice? Co představují neznámé? Čím je určen počet řešení? Kdy je řešení právě
313 Soustavy více rovnic o více neznámých I Předpoklady: 31 Př 1: Co při řešení soustav rovnic o více neznámých představují rovnice? Co představují neznámé? Čím je určen počet řešení? Kdy je řešení právě
Soustavy více rovnic o více neznámých III
 2..15 Soustavy více rovnic o více neznámých III Předpoklady: 214 Největší problém při řešení soustav - výroba trojúhelníkového tvaru (tedy vyrábění nul). Postup v dosavadních příkladech byl rychlý - využíval
2..15 Soustavy více rovnic o více neznámých III Předpoklady: 214 Největší problém při řešení soustav - výroba trojúhelníkového tvaru (tedy vyrábění nul). Postup v dosavadních příkladech byl rychlý - využíval
Cíl a následující tabulku. t [ s ] s [ mm ]
![Cíl a následující tabulku. t [ s ] s [ mm ] Cíl a následující tabulku. t [ s ] s [ mm ]](/thumbs/61/46128935.jpg) 1.1.8 Rychlost I Předpoklady: 010107 Pomůcky: Rychlost: kolik ukazuje ručička na tachometru, jak rychle se míhá krajina za oknem, jak rychle se dostaneme z jednoho místa na druhé. Okamžitá rychlost se
1.1.8 Rychlost I Předpoklady: 010107 Pomůcky: Rychlost: kolik ukazuje ručička na tachometru, jak rychle se míhá krajina za oknem, jak rychle se dostaneme z jednoho místa na druhé. Okamžitá rychlost se
Soustavy více rovnic o více neznámých II
 2..14 Soustavy více rovnic o více neznámých II Předpoklady: 21 Největší problém při řešení soustav = výroba trojúhelníkového tvaru (tedy vyrábění nul). Postup v dosavadních příkladech byl rychlý - využíval
2..14 Soustavy více rovnic o více neznámých II Předpoklady: 21 Největší problém při řešení soustav = výroba trojúhelníkového tvaru (tedy vyrábění nul). Postup v dosavadních příkladech byl rychlý - využíval
1.1.8 Sčítání přirozených čísel
 .. Sčítání přirozených čísel Předpoklady: 000 Pedagogická poznámka: Pokud při formulaci pravidel necháváte žáky zapisovat samostatně, nedostanete se dále než k příkladu. Což využívám schválně, další hodinu
.. Sčítání přirozených čísel Předpoklady: 000 Pedagogická poznámka: Pokud při formulaci pravidel necháváte žáky zapisovat samostatně, nedostanete se dále než k příkladu. Což využívám schválně, další hodinu
( ) ( ) Rozklad mnohočlenů na součin I (vytýkání) Předpoklady:
 1.8.6 Rozklad mnohočlenů na součin I (vytýkání) Předpoklady: 010805 Pedagogická poznámka: Na začátku každé rozkládací hodiny jsou přidány příklady na opakování úprav mnohočlenů. Důvod je jediný, čtyři
1.8.6 Rozklad mnohočlenů na součin I (vytýkání) Předpoklady: 010805 Pedagogická poznámka: Na začátku každé rozkládací hodiny jsou přidány příklady na opakování úprav mnohočlenů. Důvod je jediný, čtyři
3.2.3 Podobnost trojúhelníků I
 .. Podobnost trojúhelníků I Předpoklady: 01 Shodné útvary je možné je přemístěním ztotožnit, lidově řečeno jsou stejné Co splňují útvary, které jsou podobné? Mají stejný tvar, ale různou velikost. Kdybychom
.. Podobnost trojúhelníků I Předpoklady: 01 Shodné útvary je možné je přemístěním ztotožnit, lidově řečeno jsou stejné Co splňují útvary, které jsou podobné? Mají stejný tvar, ale různou velikost. Kdybychom
[ ] ( ) ( )( ) Výrazy s proměnnou II. Předpoklady: Vypočti. a) ( ) ( ) Př. 1: = + = = = = 152
![[ ] ( ) ( )( ) Výrazy s proměnnou II. Předpoklady: Vypočti. a) ( ) ( ) Př. 1: = + = = = = 152 [ ] ( ) ( )( ) Výrazy s proměnnou II. Předpoklady: Vypočti. a) ( ) ( ) Př. 1: = + = = = = 152](/thumbs/93/112443580.jpg) 3..3 Výrazy s proměnnou II Předpoklady: 0300 Př. 1: Vypočti. { 3 + 4 7 5 + 3 + 3} ( 3) a) ( ) ( ) b) ( 5 3) 6 3 8 + 4 ( 7 10) 3 ( )( 5 7) a) { 3 4 7 ( 5 ) ( ) 3 3} ( 3) { [ 3 + 4 6] + 6} + 6 = { 5 + 6}
3..3 Výrazy s proměnnou II Předpoklady: 0300 Př. 1: Vypočti. { 3 + 4 7 5 + 3 + 3} ( 3) a) ( ) ( ) b) ( 5 3) 6 3 8 + 4 ( 7 10) 3 ( )( 5 7) a) { 3 4 7 ( 5 ) ( ) 3 3} ( 3) { [ 3 + 4 6] + 6} + 6 = { 5 + 6}
Výroková logika II. Negace. Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0).
 Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Kvadratické rovnice (dosazení do vzorce) I
 .. Kvadratické rovnice (dosazení do vzorce) I Předpoklady: 000 Rovnicí se nazývá vztah rovnosti mezi hodnotami dvou výrazů obsahujícími jednu nebo více neznámých. V této kapitole se budeme zabývat pouze
.. Kvadratické rovnice (dosazení do vzorce) I Předpoklady: 000 Rovnicí se nazývá vztah rovnosti mezi hodnotami dvou výrazů obsahujícími jednu nebo více neznámých. V této kapitole se budeme zabývat pouze
Cíl a následující tabulku: t [ s ] s [ mm ]
![Cíl a následující tabulku: t [ s ] s [ mm ] Cíl a následující tabulku: t [ s ] s [ mm ]](/thumbs/51/28654214.jpg) .. Rychlost Předpoklady: 0 Rychlost: kolik ukazuje ručička na tachometru jak rychle se míhá krajina za oknem jak rychle se dostaneme z jednoho místa na druhé Okamžitá rychlost se při jízdě autem neustále
.. Rychlost Předpoklady: 0 Rychlost: kolik ukazuje ručička na tachometru jak rychle se míhá krajina za oknem jak rychle se dostaneme z jednoho místa na druhé Okamžitá rychlost se při jízdě autem neustále
3.1.8 Hydrostatický tlak I
 18 Hydrostatický tlak I Předpoklady: 00107 Pomůcky: Pedagogická poznámka: První příklad je kontrola výsledků z minulé hodiny Počítám ho celý na tabuli, druhou půlku nechávám volnou na obecné odvození Př
18 Hydrostatický tlak I Předpoklady: 00107 Pomůcky: Pedagogická poznámka: První příklad je kontrola výsledků z minulé hodiny Počítám ho celý na tabuli, druhou půlku nechávám volnou na obecné odvození Př
3.2.3 Podobnost trojúhelníků I
 .. Podobnost trojúhelníků I Předpoklady: 01 Shodné útvary je možné je přemístěním ztotožnit, lidově řečeno jsou stejné Co splňují útvary, které jsou podobné? Mají stejný tvar, ale různou velikost. Kdybychom
.. Podobnost trojúhelníků I Předpoklady: 01 Shodné útvary je možné je přemístěním ztotožnit, lidově řečeno jsou stejné Co splňují útvary, které jsou podobné? Mají stejný tvar, ale různou velikost. Kdybychom
Soustavy více rovnic o více neznámých II
 2.3.14 Soustavy více rovnic o více neznámých II Předpoklady: 2313 Pedagogická poznámka: U odčítání rovnic je třeba se připravit na to, že slabší část třídy bude různě rozepisovat mezivýpočty, vynechávat
2.3.14 Soustavy více rovnic o více neznámých II Předpoklady: 2313 Pedagogická poznámka: U odčítání rovnic je třeba se připravit na to, že slabší část třídy bude různě rozepisovat mezivýpočty, vynechávat
4.2.3 Oblouková míra. π r2. π π. Předpoklady: Obloukovou míru známe z geometrie nebo z fyziky (kruhový pohyb) rychlé zopakování.
 .. Oblouková míra Předpoklady: 8 Obloukovou míru známe z geometrie nebo z fyziky (kruhový pohyb) rychlé zopakování. Př. : Jsou dány dvě kružnice o poloměrech r a r. Do tabulky doplň délky oblouků těchto
.. Oblouková míra Předpoklady: 8 Obloukovou míru známe z geometrie nebo z fyziky (kruhový pohyb) rychlé zopakování. Př. : Jsou dány dvě kružnice o poloměrech r a r. Do tabulky doplň délky oblouků těchto
1.5.1 Číselné soustavy
 .. Číselné soustavy Předpoklady: základní početní operace Pedagogická poznámka: Tato hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti určitě setkávají
.. Číselné soustavy Předpoklady: základní početní operace Pedagogická poznámka: Tato hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti určitě setkávají
( 2 ) ( 8) Nerovnice, úpravy nerovnic. Předpoklady: 2114, Nerovnice například 2x
 ..5 Nerovnice, úpravy nerovnic Předpoklady:, 03 Nerovnice například 3 < + 5 - zápis nerovnosti hodnot dvou výrazů. Za můžeme dosazovat různá čísla, tím měníme hodnoty obou výrazů. Hledáme takové, aby nerovnost
..5 Nerovnice, úpravy nerovnic Předpoklady:, 03 Nerovnice například 3 < + 5 - zápis nerovnosti hodnot dvou výrazů. Za můžeme dosazovat různá čísla, tím měníme hodnoty obou výrazů. Hledáme takové, aby nerovnost
součet druhé mocniny čísla zvětšeného o jedna a odmocniny z jeho trojnásobku
 .7. Zápisy pomocí výrazů I Předpoklady: 70 Pedagogická poznámka: Hodina obsahuje poměrně málo příkladů, protože se snažím, aby z ní všichni spočítali opravdové maximum. Postupujeme tedy pomalu a kontrolujeme
.7. Zápisy pomocí výrazů I Předpoklady: 70 Pedagogická poznámka: Hodina obsahuje poměrně málo příkladů, protože se snažím, aby z ní všichni spočítali opravdové maximum. Postupujeme tedy pomalu a kontrolujeme
Poměry a úměrnosti II
 1.1.12 Poměry a úměrnosti II Předpoklady: 010111 U následujících úloh je nutné poznat, zda jde o přímou nebo nepřímou úměrnost případně příklad, který není možné řešit ani jedním z obou postupů. Pedagogická
1.1.12 Poměry a úměrnosti II Předpoklady: 010111 U následujících úloh je nutné poznat, zda jde o přímou nebo nepřímou úměrnost případně příklad, který není možné řešit ani jedním z obou postupů. Pedagogická
Scénář hodiny matematiky ve 4. třídě ( )
 Scénář hodiny matematiky ve 4. třídě (20.10.2010) Vypracovaly: Zuzana Muchová + Jitka Bukvičková, Učitelství pro 1. stupeň ZŠ, 4. ročník Téma: Zlomky opakování Pomůcky: lístečky s příklady (lehčí do 100
Scénář hodiny matematiky ve 4. třídě (20.10.2010) Vypracovaly: Zuzana Muchová + Jitka Bukvičková, Učitelství pro 1. stupeň ZŠ, 4. ročník Téma: Zlomky opakování Pomůcky: lístečky s příklady (lehčí do 100
Přepočet přes jednotku - podruhé I
 1.2.25 Přepočet přes jednotku - podruhé I Předpoklady: 010224 Pedagogická poznámka: Tato a následující hodina navazují na poslední hodinu úvodní kapitoly. Jde v podstatě o stejné problémy, ale s desetinnými
1.2.25 Přepočet přes jednotku - podruhé I Předpoklady: 010224 Pedagogická poznámka: Tato a následující hodina navazují na poslední hodinu úvodní kapitoly. Jde v podstatě o stejné problémy, ale s desetinnými
1.1.1 Jak se budeme učit a proč
 1.1.1 Jak se budeme učit a proč Předpoklady: Pedagogická poznámka: Otázky v této hodině nepromítám, ale normálně pokládám. Nechávám žákům čas a chci, aby své návrhy psali do sešitu. Pedagogická poznámka:
1.1.1 Jak se budeme učit a proč Předpoklady: Pedagogická poznámka: Otázky v této hodině nepromítám, ale normálně pokládám. Nechávám žákům čas a chci, aby své návrhy psali do sešitu. Pedagogická poznámka:
PORAĎ SI SE ŠKOLOU Lucie Michálková
 PORAĎ SI SE ŠKOLOU Lucie Michálková Copyright 2015 Lucie Michálková Grafická úprava a sazba Lukáš Vik, 2015 1. vydání Lukáš Vik, 2015 ISBN epub formátu: 978-80-87749-89-0 (epub) ISBN mobi formátu: 978-80-87749-90-6
PORAĎ SI SE ŠKOLOU Lucie Michálková Copyright 2015 Lucie Michálková Grafická úprava a sazba Lukáš Vik, 2015 1. vydání Lukáš Vik, 2015 ISBN epub formátu: 978-80-87749-89-0 (epub) ISBN mobi formátu: 978-80-87749-90-6
2.3.5 Ekvivalentní úpravy
 .. Ekvivalentní úpravy Předpoklady: 000 Př. : Vyřeš rovnice. Jaký je společný rys řešení všech příkladů? a) + = 7 b) = 9 c) = d) = a) + = 7 = 7 = 9 b) = 9 = 9: = 7 c) = d) = 0 = = 7 = + = + = = 9 9 9 9
.. Ekvivalentní úpravy Předpoklady: 000 Př. : Vyřeš rovnice. Jaký je společný rys řešení všech příkladů? a) + = 7 b) = 9 c) = d) = a) + = 7 = 7 = 9 b) = 9 = 9: = 7 c) = d) = 0 = = 7 = + = + = = 9 9 9 9
( ) ( ) 9.2.10 Binomické rozdělení. Předpoklady: 9209
 9..1 Binomické rozdělení Předpoklady: 99 Př. 1: Basketbalista hází trestný hod (šestku) s pravděpodobností úspěchu,9. Urči pravděpodobnosti, že z pěti hodů: a) dá košů; b) dá alespoň jeden koš; c) dá nejdříve
9..1 Binomické rozdělení Předpoklady: 99 Př. 1: Basketbalista hází trestný hod (šestku) s pravděpodobností úspěchu,9. Urči pravděpodobnosti, že z pěti hodů: a) dá košů; b) dá alespoň jeden koš; c) dá nejdříve
P = 1;3;3; 4; Množiny. Předpoklady:
 3218 Množiny Předpoklady: 030201 Př 1: Kolik lidí může v souladu s předpisy cestovat v běžném osobním autě (například Škoda Octavia)? Hledej různé způsoby, jak odpověď vyjádřit 1 způsob: Autem může cestovat
3218 Množiny Předpoklady: 030201 Př 1: Kolik lidí může v souladu s předpisy cestovat v běžném osobním autě (například Škoda Octavia)? Hledej různé způsoby, jak odpověď vyjádřit 1 způsob: Autem může cestovat
( ) ( )( ) ( x )( ) ( )( ) Nerovnice v součinovém tvaru II. Předpoklady: Př.
 .. Nerovnice v součinovém tvaru II Předpoklady: 0 Př. 1: Řeš nerovnici x x 0. Problém: Na levé straně není součin musíme ho nejdříve vytvořit: x x x x x x x x x x + 0. ( ( ( = = + řešíme nerovnici: ( (
.. Nerovnice v součinovém tvaru II Předpoklady: 0 Př. 1: Řeš nerovnici x x 0. Problém: Na levé straně není součin musíme ho nejdříve vytvořit: x x x x x x x x x x + 0. ( ( ( = = + řešíme nerovnici: ( (
2.5.17 Dvojitá trojčlenka
 2..1 Dvojitá trojčlenka Předpoklady: 020 Př. 1: Čerpadlo o výkonu 1, kw vyčerpá ze sklepa vodu za hodiny. Za jak dlouho by vodu ze sklepa vyčerpalo čerpadlo o výkonu 2,2 kw? Čím výkonnější čerpadlo, tím
2..1 Dvojitá trojčlenka Předpoklady: 020 Př. 1: Čerpadlo o výkonu 1, kw vyčerpá ze sklepa vodu za hodiny. Za jak dlouho by vodu ze sklepa vyčerpalo čerpadlo o výkonu 2,2 kw? Čím výkonnější čerpadlo, tím
( ) ( ) ( ) Tečny kružnic I. Předpoklady: 4501, 4504
 7.5.5 Tečny kružnic I Předpoklady: 451, 454 Pedagogická poznámka: Následující dvě hodiny jsou na gymnázium asi početně nejnáročnější. Ačkoliv jsou příklady optimalizované na co nejmenší početní obtížnost,
7.5.5 Tečny kružnic I Předpoklady: 451, 454 Pedagogická poznámka: Následující dvě hodiny jsou na gymnázium asi početně nejnáročnější. Ačkoliv jsou příklady optimalizované na co nejmenší početní obtížnost,
( ) ( ) Negace složených výroků II. Předpoklady:
 1.4.7 Negace složených výroků II Předpoklady: 010405 Pedagogická poznámka: Na začátku hodiny slovně zadávám úkol najít negaci implikace. Teprve po zapsání do třídnice promítám zadání příkladů (kde je v
1.4.7 Negace složených výroků II Předpoklady: 010405 Pedagogická poznámka: Na začátku hodiny slovně zadávám úkol najít negaci implikace. Teprve po zapsání do třídnice promítám zadání příkladů (kde je v
( ) ( ) ( ) ( ) Kvadratické rovnice (dosazení do vzorce) II. Předpoklady: 1101
 Kvadratické rovnice (dosazení do vzorce) II Předpoklady: 0 Př : Vyřeš s pomocí kalkulačky na tři desetinná místa kvadratické rovnice: 3 3 = 0 5 + 4 40 = 0 a b c 3 3 = 0 = ; = 3; = 3 ( ) ( ) ( ) 3 ± 3 4
Kvadratické rovnice (dosazení do vzorce) II Předpoklady: 0 Př : Vyřeš s pomocí kalkulačky na tři desetinná místa kvadratické rovnice: 3 3 = 0 5 + 4 40 = 0 a b c 3 3 = 0 = ; = 3; = 3 ( ) ( ) ( ) 3 ± 3 4
rok počet obyvatel 27,1 30,9 34,8 38,6 43,4 49,4 56,4 62,4 68,3 74,9 82,0
 4.5.5 Trendy I Předpoklady: 040503 Pedagogická poznámka: Pokud nechcete zbytečně ztrácet čas tím, že žáci přepisují tabulku do sešitu, je lepší je vytisknout a rozdat. Pedagogická poznámka: Grafy pro příklady
4.5.5 Trendy I Předpoklady: 040503 Pedagogická poznámka: Pokud nechcete zbytečně ztrácet čas tím, že žáci přepisují tabulku do sešitu, je lepší je vytisknout a rozdat. Pedagogická poznámka: Grafy pro příklady
Projekt Vzdělávání pedagogů k realizaci kurikulární reformy (CZ.1.07/1.3.05/11.0026) Manuál č. 15
 Manuál č. 15 NÁZEV HODINY/TÉMA: OPERACE S REÁLNÝMI ČÍSLY Časová jednotka (vyuč.hod.): 1h (45min.) Vyučovací předmět: Matematika Ročník: první Obor vzdělání: 3letý Použité metody: Hra s čísly, Práce s textem,
Manuál č. 15 NÁZEV HODINY/TÉMA: OPERACE S REÁLNÝMI ČÍSLY Časová jednotka (vyuč.hod.): 1h (45min.) Vyučovací předmět: Matematika Ročník: první Obor vzdělání: 3letý Použité metody: Hra s čísly, Práce s textem,
Lineární funkce IV
 .. Lineární funkce IV Předpoklady 0 Pedagogická poznámka Říkám studentům, že cílem hodiny není naučit se něco nového, ale použít to, co už známe (a možná se také přesvědčit o tom, jak se nemůžeme obejít
.. Lineární funkce IV Předpoklady 0 Pedagogická poznámka Říkám studentům, že cílem hodiny není naučit se něco nového, ale použít to, co už známe (a možná se také přesvědčit o tom, jak se nemůžeme obejít
Pythagorova věta
 .8.19 Pythagorova věta Předpoklady: 00801 Pedagogická poznámka: Z následujícího příkladu rýsuje každý žák pouze jeden bod podle toho, v jakém sedí oddělení. Př. 1: Narýsuj pravoúhlý trojúhelník: a) ABC:
.8.19 Pythagorova věta Předpoklady: 00801 Pedagogická poznámka: Z následujícího příkladu rýsuje každý žák pouze jeden bod podle toho, v jakém sedí oddělení. Př. 1: Narýsuj pravoúhlý trojúhelník: a) ABC:
Kurzy. v 2.0. Níže popsaný návod je určen pro uživatele s rolí Administrátor, není-li uvedeno jinak. Základní popis kurzu 2
 Kurzy v 2.0 Níže popsaný návod je určen pro uživatele s rolí Administrátor, není-li uvedeno jinak. Obsah : Základní popis kurzu 2 Popis jednotlivých částí 2 Kurz 2 Trvání kurzu 4 Další parametry 4 Parametry
Kurzy v 2.0 Níže popsaný návod je určen pro uživatele s rolí Administrátor, není-li uvedeno jinak. Obsah : Základní popis kurzu 2 Popis jednotlivých částí 2 Kurz 2 Trvání kurzu 4 Další parametry 4 Parametry
{ } B =. Rozhodni, které z následujících. - je relace z A do B
 .. Binární relace Předpoklad: 0 Pedagogická poznámka: Naprostá většina studentů vřeší hodinu samostatně Ti nejrchlejší potřebují tak minut. Binární relace: Jsou dán množin A, B. Binární relace R z A do
.. Binární relace Předpoklad: 0 Pedagogická poznámka: Naprostá většina studentů vřeší hodinu samostatně Ti nejrchlejší potřebují tak minut. Binární relace: Jsou dán množin A, B. Binární relace R z A do
1.2.3 Racionální čísla I
 .2. Racionální čísla I Předpoklady: 002 Pedagogická poznámka: Hodina je trochu netypická, na jejím začátku provedu výklad (spíše opakování), který nechám na tabuli a potom až do konce řeší žáci zbytek
.2. Racionální čísla I Předpoklady: 002 Pedagogická poznámka: Hodina je trochu netypická, na jejím začátku provedu výklad (spíše opakování), který nechám na tabuli a potom až do konce řeší žáci zbytek
2.4.13 Kreslení graf obecné funkce II
 ..1 Kreslení graf obecné funkce II Předpoklady: 0, 0, 1 Stejně jako v minulé hodině budeme kreslit grafy funkcí odvozených od funkce y = f ( x), která je dána grafem na obrázku: Př. 1: Nakresli graf funkce
..1 Kreslení graf obecné funkce II Předpoklady: 0, 0, 1 Stejně jako v minulé hodině budeme kreslit grafy funkcí odvozených od funkce y = f ( x), která je dána grafem na obrázku: Př. 1: Nakresli graf funkce
vysvětlení pravidel + rozdělení žáků do skupinek (cca 5 minut)
 Didaktika matematiky s praxí II. PhDr. Eva Bomerová Cíl hodiny: Procvičení násobení a dělení z paměti hravou formou - Lovení matematických bobříků Před začátkem vyučovací hodiny si upravíme třídu tak,
Didaktika matematiky s praxí II. PhDr. Eva Bomerová Cíl hodiny: Procvičení násobení a dělení z paměti hravou formou - Lovení matematických bobříků Před začátkem vyučovací hodiny si upravíme třídu tak,
Informace k maturitní zkoušce 2017: Výpočet celkového počtu bodů hodnota předmětů
 Informace k maturitní zkoušce 2017: Výpočet celkového počtu bodů hodnota předmětů Maximálně 900 bodů 1,0 Oblast A (dílčí kvalifikace A) Oblast B (dílčí kvalifikace B) Oblast C (dílčí kvalifikace C) Maximálně
Informace k maturitní zkoušce 2017: Výpočet celkového počtu bodů hodnota předmětů Maximálně 900 bodů 1,0 Oblast A (dílčí kvalifikace A) Oblast B (dílčí kvalifikace B) Oblast C (dílčí kvalifikace C) Maximálně
1.2.9 Usměrňování zlomků
 9 Usměrňování zlomků Předpoklady: 0008 Pedagogická poznámka: Celá hodina by měla být naplňováním jediné myšlenky Při usměrňování rozšiřujeme zlomek tím, co potřebujeme Fakt, že si příklad upravíme, jak
9 Usměrňování zlomků Předpoklady: 0008 Pedagogická poznámka: Celá hodina by měla být naplňováním jediné myšlenky Při usměrňování rozšiřujeme zlomek tím, co potřebujeme Fakt, že si příklad upravíme, jak
DIGITÁLNÍ ARCHIV VZDĚLÁVACÍCH MATERIÁLŮ
 DIGITÁLNÍ ARCHIV VZDĚLÁVACÍCH MATERIÁLŮ Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast CZ.1.07/1.5.00/34.0963 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti
DIGITÁLNÍ ARCHIV VZDĚLÁVACÍCH MATERIÁLŮ Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast CZ.1.07/1.5.00/34.0963 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti
Základní provize v systému MLM ZetClub
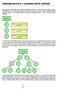 Základní provize v systému MLM ZetClub Každý prodejce může pod sebou zaregistrovat dalšího prodejce, ten zas dalšího atd. Každý prodejce, tedy může být buď zaregistrován přímo pod firmou, nebo má nad sebou
Základní provize v systému MLM ZetClub Každý prodejce může pod sebou zaregistrovat dalšího prodejce, ten zas dalšího atd. Každý prodejce, tedy může být buď zaregistrován přímo pod firmou, nebo má nad sebou
Práce s kalkulátorem
 ..8 Práce s kalkulátorem Předpoklady: 007 Ke koupi kalkulátoru: Myslím, že každý student by si kalkulačku koupit měl. V současnosti sice existují dvě možné náhrady, které buď má (mobilní telefon) nebo
..8 Práce s kalkulátorem Předpoklady: 007 Ke koupi kalkulátoru: Myslím, že každý student by si kalkulačku koupit měl. V současnosti sice existují dvě možné náhrady, které buď má (mobilní telefon) nebo
ANALÝZA VÝSLEDKŮ MAPY ŠKOLY
 ANALÝZA VÝSLEDKŮ MAPY ŠKOLY Percentilové tabulky ZŠ 2018/2019 Základní škola, Liberec, Broumovská 847/7, příspěvková organizace () Tabulky s výslednými y Jedním z výstupů dotazníkového šetření Mapa školy
ANALÝZA VÝSLEDKŮ MAPY ŠKOLY Percentilové tabulky ZŠ 2018/2019 Základní škola, Liberec, Broumovská 847/7, příspěvková organizace () Tabulky s výslednými y Jedním z výstupů dotazníkového šetření Mapa školy
0,2 0,20 0, Desetinná čísla II. Předpoklady:
 1.2.2 Desetinná čísla II Předpoklady: 010201 Pedagogická poznámka: Je třeba zahájit tak, aby se stihl ještě společný začátek příkladu 7 (pokud někdo příklad 7 začne s předstihem, nevadí to, ale jde o to,
1.2.2 Desetinná čísla II Předpoklady: 010201 Pedagogická poznámka: Je třeba zahájit tak, aby se stihl ještě společný začátek příkladu 7 (pokud někdo příklad 7 začne s předstihem, nevadí to, ale jde o to,
Bodovací systém ve fyzice základní školy. Mgr. Hana Tesařová Základní škola Edvarda Beneše Lysice
 Bodovací systém ve fyzice základní školy Mgr. Hana Tesařová Základní škola Edvarda Beneše Lysice Bodovací systém ve fyzice nižšího gymnázia Mgr. Václav Piskač Gymnázium tř.kpt.jaroše Brno Základní vlastnosti
Bodovací systém ve fyzice základní školy Mgr. Hana Tesařová Základní škola Edvarda Beneše Lysice Bodovací systém ve fyzice nižšího gymnázia Mgr. Václav Piskač Gymnázium tř.kpt.jaroše Brno Základní vlastnosti
Nepřímá úměrnost I
 .. Nepřímá úměrnost I Předpoklady: 000 Př. : Která z následujících slovních úloh popisuje nepřímou úměrnost? Zapiš nepřímou úměrnost jako funkci. a) 7 rohlíků stojí Kč. Kolik bude stát rohlíků? b) Pokud
.. Nepřímá úměrnost I Předpoklady: 000 Př. : Která z následujících slovních úloh popisuje nepřímou úměrnost? Zapiš nepřímou úměrnost jako funkci. a) 7 rohlíků stojí Kč. Kolik bude stát rohlíků? b) Pokud
2.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou
 .8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 40, 4, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli (nejlépe tak, aby se zápis mohl otočit nebo jinak schovat
.8.9 Parametrické rovnice a nerovnice s absolutní hodnotou Předpoklady: 40, 4, 806 Pedagogická poznámka: Opět si napíšeme na začátku hodiny na tabuli (nejlépe tak, aby se zápis mohl otočit nebo jinak schovat
Urči tlak, kterým působí na sníh: a) horolezec o hmotnosti 75 kg, který i s výstrojí o váží 90 kg, pokud si obul boty
 3.1.5 Pevnost v tahu Předpoklady: 030104 Pomůcky: namnožené papírky s grafem Pedagogická poznámka: Počítání s velmi malými čísly dělá žákům velké problémy. Je proto otázkou zda by nebylo lepší se vrátit
3.1.5 Pevnost v tahu Předpoklady: 030104 Pomůcky: namnožené papírky s grafem Pedagogická poznámka: Počítání s velmi malými čísly dělá žákům velké problémy. Je proto otázkou zda by nebylo lepší se vrátit
2.8.8 Výpočty s odmocninami II
 .8.8 Výpočty s odmocninami II Předpoklady: 00807 Př. : Vypočti. Odmocniny, které nejdou počítat z hlavy usměrni. 5 0 7 3 c) 5 3 5 0 = 00 = 0 7 3 = 9 3 3 = 3 3 = 9 c) 5 = 9 5 = 3 5 3 = 6 = Př. : Vypočti
.8.8 Výpočty s odmocninami II Předpoklady: 00807 Př. : Vypočti. Odmocniny, které nejdou počítat z hlavy usměrni. 5 0 7 3 c) 5 3 5 0 = 00 = 0 7 3 = 9 3 3 = 3 3 = 9 c) 5 = 9 5 = 3 5 3 = 6 = Př. : Vypočti
1.2.3 Racionální čísla I
 .2. Racionální čísla I Předpoklady: 002 Racionální jsou všechna čísla, která můžeme zapsat ve tvaru zlomku p q, kde p Z, q N. Například 2 ; ; 2 ; 6 ; umožňují počítat s částmi celků (třeba polovina dortu),
.2. Racionální čísla I Předpoklady: 002 Racionální jsou všechna čísla, která můžeme zapsat ve tvaru zlomku p q, kde p Z, q N. Například 2 ; ; 2 ; 6 ; umožňují počítat s částmi celků (třeba polovina dortu),
leváci a leváctví část č. 35 levák učitelem? aneb s čím se musí vypořádat učitel levák ivo vodička
 leváci a leváctví část č. 35 levák učitelem? aneb s čím se musí vypořádat učitel levák ivo vodička 2013 www.levactvi.cz 1 Levák učitelem? název školy: autor: anotace: klíčová slova: cílová skupina: Střední
leváci a leváctví část č. 35 levák učitelem? aneb s čím se musí vypořádat učitel levák ivo vodička 2013 www.levactvi.cz 1 Levák učitelem? název školy: autor: anotace: klíčová slova: cílová skupina: Střední
Absolutní hodnota I. π = π. Předpoklady: = 0 S nezápornými čísly absolutní hodnota nic nedělá.
 1..10 Absolutní hodnota I Předpoklady: 01005 = 0 = 0 S nezápornými čísly absolutní hodnota nic nedělá. π = π = = Záporná čísla absolutní hodnota změní na kladná (vynásobí je 1). 5 5 = Absolutní hodnota
1..10 Absolutní hodnota I Předpoklady: 01005 = 0 = 0 S nezápornými čísly absolutní hodnota nic nedělá. π = π = = Záporná čísla absolutní hodnota změní na kladná (vynásobí je 1). 5 5 = Absolutní hodnota
Rovnice s neznámou pod odmocninou I
 .7.15 Rovnice s neznámou pod odmocninou I Předpoklady: 711, 71 Pedagogická poznámka: Látka této hodiny vyžaduje tak jeden a půl vyučovací hodiny, pokud nepospícháte, můžete obětovat hodiny dvě a nechat
.7.15 Rovnice s neznámou pod odmocninou I Předpoklady: 711, 71 Pedagogická poznámka: Látka této hodiny vyžaduje tak jeden a půl vyučovací hodiny, pokud nepospícháte, můžete obětovat hodiny dvě a nechat
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Informační
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Informační
6.1.2 Operace s komplexními čísly
 6.. Operace s komplexními čísly Předpoklady: 60 Komplexním číslem nazýváme výraz ve tvaru a + bi, kde a, b jsou reálná čísla a i je číslo, pro něž platí i =. V komplexním čísle a + bi se nazývá: číslo
6.. Operace s komplexními čísly Předpoklady: 60 Komplexním číslem nazýváme výraz ve tvaru a + bi, kde a, b jsou reálná čísla a i je číslo, pro něž platí i =. V komplexním čísle a + bi se nazývá: číslo
( ) Jako základ mocnin nemusíme používat jen 10. Pokud není jasné, že číslo je uvedeno v desítkové soustavě, píšeme jej takto: ( 12054 ) 10
 .. Číselné soustavy I Předpoklady: základní početní operace Pedagogická poznámka: Tato a následující hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti
.. Číselné soustavy I Předpoklady: základní početní operace Pedagogická poznámka: Tato a následující hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti
( ) Absolutní hodnota. π = π. Předpoklady: základní početní operace. 0 = 0 S nezápornými čísly absolutní hodnota nic nedělá
 1..9 Absolutní hodnota Předpoklady: základní početní operace = 0 = 0 S nezápornými čísly absolutní hodnota nic nedělá π = π = 3 3 = Záporná čísla absolutní hodnota změní na kladná (vynásobí je 1) 5 5 3
1..9 Absolutní hodnota Předpoklady: základní početní operace = 0 = 0 S nezápornými čísly absolutní hodnota nic nedělá π = π = 3 3 = Záporná čísla absolutní hodnota změní na kladná (vynásobí je 1) 5 5 3
Rovnoměrný pohyb II
 2.2.12 Rovnoměrný pohyb II Předpoklady: 020210 Pomůcky: Př. 1: Jakou vzdálenost urazí za pět minut automobil jedoucí rychlostí 85 km/h? 5 t = 5min = h, v = 85 km/h 5 s = vt = 85 km = 7,1 km Automobil jedoucí
2.2.12 Rovnoměrný pohyb II Předpoklady: 020210 Pomůcky: Př. 1: Jakou vzdálenost urazí za pět minut automobil jedoucí rychlostí 85 km/h? 5 t = 5min = h, v = 85 km/h 5 s = vt = 85 km = 7,1 km Automobil jedoucí
1.1.4 Poměry a úměrnosti I
 1.1.4 Poměry a úměrnosti I Předpoklady: základní početní operace Poznámka: Následující látka patří mezi nejdůležitější, probírané na základní škole. Bohužel patří také mezi ty, kde je nejvíce rozšířené
1.1.4 Poměry a úměrnosti I Předpoklady: základní početní operace Poznámka: Následující látka patří mezi nejdůležitější, probírané na základní škole. Bohužel patří také mezi ty, kde je nejvíce rozšířené
Pedagogická poznámka: V následujícím příkladu nemusí všichni spočítat všechno. Pomalejší žáky je třeba přerušit, aby stihli spočítat příklad 6. Př.
 2.5.3 Rozšiřování a krácení poměru Předpoklady: 020503 Př. 1: Děti zjišťovaly poměr mezi výškou a šířkou papíru A4. Které z následujících poměrů jsou správné? Které jsou přibližně správné? Které jsou špatně?
2.5.3 Rozšiřování a krácení poměru Předpoklady: 020503 Př. 1: Děti zjišťovaly poměr mezi výškou a šířkou papíru A4. Které z následujících poměrů jsou správné? Které jsou přibližně správné? Které jsou špatně?
4.4.8 Zase nějaké... Předpoklady: ,6 l benzínu stálo 993,24 Kč. Kolik Kč by stálo 44,8 litru benzínu?
 ..8 Zase nějaké... Předpoklad: 000 Př. :, l benzínu stálo 99, Kč. Kolik Kč b stálo,8 litru benzínu? Čím více benzínu koupíme, tím více musíme zaplatit přímá úměrnost., litru 99, Kč,8 litru 99, = /,8 (cena
..8 Zase nějaké... Předpoklad: 000 Př. :, l benzínu stálo 99, Kč. Kolik Kč b stálo,8 litru benzínu? Čím více benzínu koupíme, tím více musíme zaplatit přímá úměrnost., litru 99, Kč,8 litru 99, = /,8 (cena
2.3.7 Lineární rovnice s více neznámými I
 ..7 Lineární rovnice s více neznámými I Předpoklady: 01 Pedagogická poznámka: Následující hodinu považuji za velmi důležitou hlavně kvůli pochopení soustav rovnic, které mají více než jedno řešení. Proto
..7 Lineární rovnice s více neznámými I Předpoklady: 01 Pedagogická poznámka: Následující hodinu považuji za velmi důležitou hlavně kvůli pochopení soustav rovnic, které mají více než jedno řešení. Proto
MATEMATIKA. Výrazy a rovnice 1. pracovní sešit
 MATEMATIKA Výrazy a rovnice pracovní sešit Napsali: Mgr. Michaela Jedličková; RNDr. Peter Krupka, Ph.D.; RNDr. Jana Nechvátalová Recenzentky: Mgr. Barbora Stušová; doc. RNDr. Naďa Vondrová, Ph.D. OBSAH
MATEMATIKA Výrazy a rovnice pracovní sešit Napsali: Mgr. Michaela Jedličková; RNDr. Peter Krupka, Ph.D.; RNDr. Jana Nechvátalová Recenzentky: Mgr. Barbora Stušová; doc. RNDr. Naďa Vondrová, Ph.D. OBSAH
Řešení příkladů na rovnoměrně zrychlený pohyb I
 ..9 Řešení příkladů na rovnoměrně zrychlený pohyb I Předpoklady: 8 Pedagogická poznámka: Cílem hodiny je, aby se studenti naučili samostatně řešit příklady. Aby dokázali najít vztah, který umožňuje příklad
..9 Řešení příkladů na rovnoměrně zrychlený pohyb I Předpoklady: 8 Pedagogická poznámka: Cílem hodiny je, aby se studenti naučili samostatně řešit příklady. Aby dokázali najít vztah, který umožňuje příklad
výška (cm) počet žáků
 Statistika samostatná práce 1) Ve školním roce /13 bylo v Brně 5 základních škol, ve kterých bylo celkem 5 tříd. Tyto školy navštěvovalo 1 3 žáků. Určete a) kolik tříd průměrně měla jedna ZŠ, b) kolik
Statistika samostatná práce 1) Ve školním roce /13 bylo v Brně 5 základních škol, ve kterých bylo celkem 5 tříd. Tyto školy navštěvovalo 1 3 žáků. Určete a) kolik tříd průměrně měla jedna ZŠ, b) kolik
sin(x) x lim. pomocí mocninné řady pro funkci sin(x) se středem x 0 = 0. Víme, že ( ) k=0 e x2 dx.
 Použití mocniných řad Nejprve si ukážeme dvě jednoduchá použití Taylorových řad. Příklad Spočtěte následující limitu: ( ) sin(x) lim. x x ( ) Najdeme lim sin(x) x x pomocí mocninné řady pro funkci sin(x)
Použití mocniných řad Nejprve si ukážeme dvě jednoduchá použití Taylorových řad. Příklad Spočtěte následující limitu: ( ) sin(x) lim. x x ( ) Najdeme lim sin(x) x x pomocí mocninné řady pro funkci sin(x)
Přípravný kurz - Matematika
 Přípravný kurz - Matematika Téma: Základy statistiky, kombinační úsudek v úlohách Klíčová slova: tabulky, grafy, diagramy Autor: Mlynářová 12 19 9:02 Základy statistiky Statistika je vědní obor, který
Přípravný kurz - Matematika Téma: Základy statistiky, kombinační úsudek v úlohách Klíčová slova: tabulky, grafy, diagramy Autor: Mlynářová 12 19 9:02 Základy statistiky Statistika je vědní obor, který
Svobodná chebská škola, základní škola a gymnázium s.r.o. Počítání rovnic za pomoci ekvivalentních úprav. Pravidla zacházení s rovnicemi
 METODICKÝ LIST DA61 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Rovnice I. - základ Astaloš Dušan Matematika šestý/sedmý frontální, fixační
METODICKÝ LIST DA61 Název tématu: Autor: Předmět: Ročník: Metody výuky: Formy výuky: Cíl výuky: Získané dovednosti: Stručný obsah: Rovnice I. - základ Astaloš Dušan Matematika šestý/sedmý frontální, fixační
Nový způsob práce s průběžnou klasifikací lze nastavit pouze tehdy, je-li průběžná klasifikace v evidenčním pololetí a školním roce prázdná.
 Průběžná klasifikace Nová verze modulu Klasifikace žáků přináší novinky především v práci s průběžnou klasifikací. Pro zadání průběžné klasifikace ve třídě doposud existovaly 3 funkce Průběžná klasifikace,
Průběžná klasifikace Nová verze modulu Klasifikace žáků přináší novinky především v práci s průběžnou klasifikací. Pro zadání průběžné klasifikace ve třídě doposud existovaly 3 funkce Průběžná klasifikace,
MATE MATIKA. pracovní sešit pro 2. stupeň ZŠ a víceletá gymnázia
 F MATE MATIKA pracovní sešit pro 2. stupeň ZŠ a víceletá gymnázia Milí žáci, vážení učitelé, k vašim rukám se právě dostal pracovní sešit F. Tato publikace vám nabízí velké množství inspirace, námětů a
F MATE MATIKA pracovní sešit pro 2. stupeň ZŠ a víceletá gymnázia Milí žáci, vážení učitelé, k vašim rukám se právě dostal pracovní sešit F. Tato publikace vám nabízí velké množství inspirace, námětů a
Klima školy - varianta pro žáky
 Základní škola Roztoky, okres Rakovník, příspěvková organizace Klima školy - varianta pro žáky výsledek dotazníkového šetření Název dotazníku: NEJMLADŠÍ ŽÁCI Datum: 07. 06. 2017 Graf 1: Celkový přehled
Základní škola Roztoky, okres Rakovník, příspěvková organizace Klima školy - varianta pro žáky výsledek dotazníkového šetření Název dotazníku: NEJMLADŠÍ ŽÁCI Datum: 07. 06. 2017 Graf 1: Celkový přehled
1.8.1 Méně než nula I
 1.8.1 Méně než nula I ředpoklady: Krokování se provádí na krokovacím pásu. Hráči (etr a irk na začátku stojí na prostředním startovním políčku a jsou otočení doprava. etr udělá dva kroky dopředu:. ak krok
1.8.1 Méně než nula I ředpoklady: Krokování se provádí na krokovacím pásu. Hráči (etr a irk na začátku stojí na prostředním startovním políčku a jsou otočení doprava. etr udělá dva kroky dopředu:. ak krok
Základy statistiky pro obor Kadeřník
 Variace 1 Základy statistiky pro obor Kadeřník Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz 1. Aritmetický průměr
Variace 1 Základy statistiky pro obor Kadeřník Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz 1. Aritmetický průměr
Měření složeného elektrického obvodu
 4.2.13 Měření složeného elektrického obvodu Pedagogická poznámka: Následující příklady by se za hodinu samozřejmě stihnout nedaly. Aby byla hodina využita co nejlépe, postupuji následovně. Před touto hodinou
4.2.13 Měření složeného elektrického obvodu Pedagogická poznámka: Následující příklady by se za hodinu samozřejmě stihnout nedaly. Aby byla hodina využita co nejlépe, postupuji následovně. Před touto hodinou
Jak změřit % podkožního tuku a svalovou hmotu
 FitPlan.cz/shop To nejnutnější pro rychlé hubnutí Jak změřit % podkožního tuku a svalovou hmotu VŠE CO JSTE KDY SLYŠELI O HUBNUTÍ BYLO NEJSPÍŠ ŠPATNĚ Tento podrobný návod a průvodce vám krok za krokem
FitPlan.cz/shop To nejnutnější pro rychlé hubnutí Jak změřit % podkožního tuku a svalovou hmotu VŠE CO JSTE KDY SLYŠELI O HUBNUTÍ BYLO NEJSPÍŠ ŠPATNĚ Tento podrobný návod a průvodce vám krok za krokem
Testy do hodin - souhrnný test - 6. ročník
 Kolik procent škol jste předstihli Škola: Název: Obec: BCEH ZŠ a MŠ, Slezská 316 Slavkov - 6. ročník ČESKÝ JAZYK Máte lepší výsledky než 7 % zúčastněných škol. MATEMATIKA Máte lepší výsledky než 7 % zúčastněných
Kolik procent škol jste předstihli Škola: Název: Obec: BCEH ZŠ a MŠ, Slezská 316 Slavkov - 6. ročník ČESKÝ JAZYK Máte lepší výsledky než 7 % zúčastněných škol. MATEMATIKA Máte lepší výsledky než 7 % zúčastněných
Materiál. 4 hodnotící karty 1 karta hracích kol 4 tužky. 100 křížů pokladů Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min.
 Phil Walker-Harding 100 křížů - 1000 pokladů Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min. Materiál 47 map pokladů Od každé barvy (fialová, oranžová, zelená, šedá) je k dispozici vždy 12 karet
Phil Walker-Harding 100 křížů - 1000 pokladů Počet hráčů: 2-4 Věk: od 8 let Herní doba: okolo 20 min. Materiál 47 map pokladů Od každé barvy (fialová, oranžová, zelená, šedá) je k dispozici vždy 12 karet
TEST LOGIKY. Využitelný pro měření kompetence: řešení problémů, orientace v informacích
 TEST LOGIKY Využitelný pro měření kompetence: řešení problémů, orientace v informacích Forma: papír - tužka Čas na administraci: max. 25 min. Časový limit: ano Vyhodnocení: ručně cca 10 minut jeden testovaný
TEST LOGIKY Využitelný pro měření kompetence: řešení problémů, orientace v informacích Forma: papír - tužka Čas na administraci: max. 25 min. Časový limit: ano Vyhodnocení: ručně cca 10 minut jeden testovaný
( ) ( ) Binomické rozdělení. Předpoklady: 9209
 9..1 Binomické rozdělení Předpoklady: 99 Př. 1: Basketbalista hází trestný hod (šestku) s pravděpodobností úspěchu,9. Urči pravděpodobnosti, že z pěti hodů: a) dá košů b) dá alespoň jeden koš c) dá nejdříve
9..1 Binomické rozdělení Předpoklady: 99 Př. 1: Basketbalista hází trestný hod (šestku) s pravděpodobností úspěchu,9. Urči pravděpodobnosti, že z pěti hodů: a) dá košů b) dá alespoň jeden koš c) dá nejdříve
S D Ě L E N Í 1. KRITÉRIA HODNOCENÍ ZKOUŠEK A DÍLČÍCH ZKOUŠEK SPOLEČNÉ ČÁSTI MATURITNÍ ZKOUŠKY
 V Praze dne 19. března 2013 Č. j.: MSMT-10139/2013-211 S D Ě L E N Í V souladu s 22, odst. 1 vyhlášky č. 177/2009 Sb., o bližších podmínkách ukončování vzdělávání ve středních školách maturitní zkouškou,
V Praze dne 19. března 2013 Č. j.: MSMT-10139/2013-211 S D Ě L E N Í V souladu s 22, odst. 1 vyhlášky č. 177/2009 Sb., o bližších podmínkách ukončování vzdělávání ve středních školách maturitní zkouškou,
Operace s vektory a maticemi + Funkce
 + Funkce 9. března 2010 Operátory Operátory Aritmetické: Operátory Operátory Aritmetické: maticové + (sčítání), (odčítání), (násobení), / (dělení matematicky je maticové delení násobení inverzní maticí),
+ Funkce 9. března 2010 Operátory Operátory Aritmetické: Operátory Operátory Aritmetické: maticové + (sčítání), (odčítání), (násobení), / (dělení matematicky je maticové delení násobení inverzní maticí),
Úvodní část: Představení se a úloha na zjištění kolik nám je let.
 Anežka Pekárková, Romana Bredová Výuka 12.10.2011, sudý týden Cíl: Procvičit sčítání a odčítání v různých prostředích Úvodní část: Představení se a úloha na zjištění kolik nám je let. ÚLOHA: Od čísla 100
Anežka Pekárková, Romana Bredová Výuka 12.10.2011, sudý týden Cíl: Procvičit sčítání a odčítání v různých prostředích Úvodní část: Představení se a úloha na zjištění kolik nám je let. ÚLOHA: Od čísla 100
Kritéria hodnocení žáků obor vzdělání M/02 EKONOMICKÉ LYCEUM ročník v rámci průběžné klasifikace 2017/2018 Příloha č.
 Kritéria hodnocení žáků obor vzdělání 78-42-M/02 EKONOMICKÉ LYCEUM 1. 4. ročník v rámci průběžné klasifikace 2017/2018 Příloha č. 2 školního řádu Jednotná kritéria hodnocení žáků pro předměty vyučované
Kritéria hodnocení žáků obor vzdělání 78-42-M/02 EKONOMICKÉ LYCEUM 1. 4. ročník v rámci průběžné klasifikace 2017/2018 Příloha č. 2 školního řádu Jednotná kritéria hodnocení žáků pro předměty vyučované
Umíme hodnotit žáky a studenty? Eduard Hofmann Jiří Koumar
 Umíme hodnotit žáky a studenty? Eduard Hofmann Jiří Koumar Umíme hodnotit žáky a studenty? Už jste někdy ve školním prostředí zaslechli povzdechnutí typu: Když já bych mu to býval řek, jenže jsem nerozuměl
Umíme hodnotit žáky a studenty? Eduard Hofmann Jiří Koumar Umíme hodnotit žáky a studenty? Už jste někdy ve školním prostředí zaslechli povzdechnutí typu: Když já bych mu to býval řek, jenže jsem nerozuměl
1.5.7 Znaky dělitelnosti
 1.5.7 Znaky dělitelnosti Předpoklady: 010506 Pedagogická poznámka: Příklad 1 je dořešení zadání z minulé hodiny. Je třeba se u něj nezdržovat. Př. 1: Na základní škole ses učil pravidla, podle kterých
1.5.7 Znaky dělitelnosti Předpoklady: 010506 Pedagogická poznámka: Příklad 1 je dořešení zadání z minulé hodiny. Je třeba se u něj nezdržovat. Př. 1: Na základní škole ses učil pravidla, podle kterých
Úměrnosti - opakování
 .. Úměrnosti - opakování Předpoklady: 00 Př. 1: Auto ujede za a hodin vzdálenost b km. Kolik km by ujelo za c hodin? Čím déle auto jede, tím větší vzdálenost ujede přímá úměrnost. a hodin b km c hodin
.. Úměrnosti - opakování Předpoklady: 00 Př. 1: Auto ujede za a hodin vzdálenost b km. Kolik km by ujelo za c hodin? Čím déle auto jede, tím větší vzdálenost ujede přímá úměrnost. a hodin b km c hodin
Napsali: Mgr. Michaela Jedličková; RNDr. Peter Krupka, Ph.D.; RNDr. Jana Nechvátalová Recenzenti:
 Použité symboly: Motivace k probíranému učivu na praktickém příkladu Úvahové úlohy nebo otázky poukazující na další souvislosti probírané látky s běžným životem Připomenutí učiva, na které nová látka navazuje
Použité symboly: Motivace k probíranému učivu na praktickém příkladu Úvahové úlohy nebo otázky poukazující na další souvislosti probírané látky s běžným životem Připomenutí učiva, na které nová látka navazuje
Maturita 2013_podzim Výsledky a závěrečné dokumenty
 Maturita 2013_podzim Výsledky a závěrečné dokumenty Písemné zkoušky společné části v podzimním zkušebním období maturitní zkoušky 2013 skončily. Je proto účelné připomenout důležitá pravidla předávání
Maturita 2013_podzim Výsledky a závěrečné dokumenty Písemné zkoušky společné části v podzimním zkušebním období maturitní zkoušky 2013 skončily. Je proto účelné připomenout důležitá pravidla předávání
Zase zlomky. Předpoklady: = = = = = = = = 1+ +
 ..8 Zase zlomky Předpoklady: 00 Př. : 8 b) + = = = 8 8 b) 8 = = = = = + + Př. : Myš má krk tvořený sedmi obratli. Délka krku myši je rovna /0 délky krku žirafy. Kolik obratlů tvoří krk žirafy? Matematický
..8 Zase zlomky Předpoklady: 00 Př. : 8 b) + = = = 8 8 b) 8 = = = = = + + Př. : Myš má krk tvořený sedmi obratli. Délka krku myši je rovna /0 délky krku žirafy. Kolik obratlů tvoří krk žirafy? Matematický
(Cramerovo pravidlo, determinanty, inverzní matice)
 KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
PORAĎ SI SE ŠKOLOU Lucie Michálková
 PORAĎ SI SE ŠKOLOU Lucie Michálková Copyright 2015 Lucie Michálková Grafická úprava a sazba Lukáš Vik, 2015 1. vydání Lukáš Vik, 2015 ISBN epub formátu: 978-80-87749-89-0 (epub) ISBN mobi formátu: 978-80-87749-90-6
PORAĎ SI SE ŠKOLOU Lucie Michálková Copyright 2015 Lucie Michálková Grafická úprava a sazba Lukáš Vik, 2015 1. vydání Lukáš Vik, 2015 ISBN epub formátu: 978-80-87749-89-0 (epub) ISBN mobi formátu: 978-80-87749-90-6
2. popis prostředí, nastavení pracovní plochy
 (c) mise 2013 1 2 1. úvod Tabulkový procesor program pro organizaci a správu dat pomocí tabulek určen pro zpracování dat převážně číselného charakteru Využití tabulkových procesorů přehledná prezentace
(c) mise 2013 1 2 1. úvod Tabulkový procesor program pro organizaci a správu dat pomocí tabulek určen pro zpracování dat převážně číselného charakteru Využití tabulkových procesorů přehledná prezentace
1. KRITÉRIA HODNOCENÍ ZKOUŠEK A DÍLČÍCH ZKOUŠEK SPOLEČNÉ ČÁSTI MATURITNÍ ZKOUŠKY
 V Praze dne 11. března 2015 Č. j.: MSMT-6626/2015-1 SDĚLENÍ V souladu s 22, odst. 1 vyhlášky č. 177/2009 Sb., o bližších podmínkách ukončování vzdělávání ve středních školách maturitní zkouškou, ve znění
V Praze dne 11. března 2015 Č. j.: MSMT-6626/2015-1 SDĚLENÍ V souladu s 22, odst. 1 vyhlášky č. 177/2009 Sb., o bližších podmínkách ukončování vzdělávání ve středních školách maturitní zkouškou, ve znění
( ) ( ) 9.2.7 Nezávislé jevy I. Předpoklady: 9204
 9.2.7 Nezávislé jevy I Předpoklady: 9204 Př. : Předpokládej, že pravděpodobnost narození chlapce je stejná jako pravděpodobnost narození dívky (a tedy v obou případech rovna 0,5) a není ovlivněna genetickými
9.2.7 Nezávislé jevy I Předpoklady: 9204 Př. : Předpokládej, že pravděpodobnost narození chlapce je stejná jako pravděpodobnost narození dívky (a tedy v obou případech rovna 0,5) a není ovlivněna genetickými
