Acyklické grafy, stromy a kostry
|
|
|
- Bohumír Jaroš
- před 7 lety
- Počet zobrazení:
Transkript
1 Kapitola 4 Acyklické grafy, stromy a kostry 4.1 Stromy a ich vlastnosti Definícia 4.1. Triviálny graf je taký graf G = (V, H), ktorého množina vrcholov V pozostáva z jediného vrcholu. Ak je G = (V, H) triviálny graf, potom H =. Definícia 4.2. Acyklický graf je taký graf, ktorý neobsahuje ako podgraf kružnicu. Definícia 4.3. Strom je súvislý acyklický graf. Triviálny graf je stromom. Pretože každý komponent acyklického grafu je stromom (je súvislý a neobsahuje kružnicu), možno sa na acyklický graf pozerať ako na zjednotenie stromov. Od toho je odvodený pojem les, ktorý sa používa ako synonymum pre acyklické grafy. Veta 4.1. Nech G = (V, H) je strom, ktorý má aspoň dva vrcholy. Potom V obsahuje aspoň dva vrcholy stupňa 1. Dôkaz. Nech v 1, (v 1, v 2 ), v 2,..., (v k 1, v k ), v k je cesta v strome G s najväčším počtom hrán. Ukážeme, že st(v k ) = 1. Pretože (v k 1, v k ) H, je st(v k ) aspoň 1. Keby st(v k ) > 1, musela by existovať hrana (v k, v l ), kde v l v k 1 a tiež v l v k. Keby existovalo v i = v l pre i = 1, 2,..., v k 2, mohli by sme vytvoriť kružnicu v i, (v i, v i+1 ),..., (v k 1, v k ), v k, (v k, v l ), v l = v i, čo je v spore s acykličnosťou stromu G. Je teda v l v i pre všetky i = 1, 2,..., k. Teraz už môžeme zostrojiť cestu v 1, (v 1, v 2 ), v 2,..., (v k 1, v k ), v k, (v k, v l ), ktorá obsahuje o jednu hranu viac, ako cesta (11). Z predpokladu st(v k ) > 1 sme dostali spor. Je teda st(v k ) = 1. Podobne dokážeme, že st(v 1 ) = 1. 55
2 56 KAPITOLA 4. ACYKLICKÉ GRAFY, STROMY A KOSTRY Veta 4.2. Nasledujúce tvrdenia sú ekvivalenté: a) G = (V, H) je strom. b) V grafe G = (V, H) existuje pre každé u, v V, u v jediná u-v-cesta. c) Graf G = (V, H) je súvislý a každá hrana množiny H je mostom. d) Graf G = (V, H) je súvislý a H = V 1 e) V grafe G = (V, H) platí H = V 1 a G je acyklický. Dôkaz. Dokazovanie si zjednodušíme, ak budeme dokazovať podľa schémy a) b) c) d) e) a). a) b) Dôkaz vykonáme sporom. Nech existujú dve rôzne u-v cesty. g replacements u v m 1 (u, v) m 2 (u, v) v k w k w q v p m 1 (u, v) : m 2 (u, v) : u = v 1, (v 1, v 2 ),..., (v n 1, v n ), v n = v u = w 1, (w 1, w 2 ),..., (w m 1, w m ), w m = w Obr. 4.1: Z existencie dvoch ciest vyplýva existencia cyklu Nech k je najmenšie prirodzené číslo také, že v k w k a v 1 = w 1, v 2 = w 2,..., v k 1 = w k 1. (Po vrchol v k 1 resp. w k 1 obe cesty idú cez rovnaké vrcholy a hrany, ale vo vrchole v k 1 = w k 1 sa rozchádzajú.) Označme p prvý index väčší než k, kedy je vrchol v p vrcholom cesty m 2 (u, v). Nech q prvý index väčší než k, kedy je vrchol w q vrcholom cesty m 1 (u, v). Zrejme je v p = v q. Zreťazenie ciest w k 1 = v k 1, (v k 1, v k ),..., (v p 1, v p ), v p = w q v k 1 = w k 1, (w k 1, w k ),..., (w q 1, w q ), w q = v p dáva cyklus, čo je spor s predpokladom, že G je acyklický graf. b) c) Nech v grafe G = (V, H) existuje pre každé u, v V, u v jediná u-v-cesta. Súvislosť grafu G je zrejmá z existencie u-v cesty pre každé u, v V. Ďalej pokračujeme dôkazom sporom. Nech existuje hrana (u, v) H, ktorá nie je mostom. Po odstránení hrany (u, v) graf ostáva súvislý - t.j. existuje u-v cesta m(u, v) neobsahujúca hranu (u, v), pričom cesta m(u, v) je rôzna od cesty u, (u, v), v, čo je spor s predpokladom existencie jedinej u-v cesty.
3 4.1. STROMY A ICH VLASTNOSTI 57 c) d) Nech G = (V, H) je súvislý graf a každá hrana množiny H je mostom. Chceme ukázať, že H = V 1. Budeme postupovať matematickou indukciou podľa počtu vrcholov V = n. Nech n = V = 1, potom ide o triviálny graf, ktorý je stromom a v ktorom je H = 0 a tvrdenie platí. Nech tvrdenie platí pre všetky stromy G = (V, H ), kde V < n + 1. Nech G = (V, H) je súvislý graf, v ktorom je každá hrana mostom a kde V = n + 1. Vezmime ľubovoľnú hranu h = (u, v) H. Po jej odstránení z množiny hrán sa graf G rozpadne na dva komponenty G 1 = (V 1, H 1 ), G 2 = (V 2, H 2 ) také, že u V 1, v V 2. Pretože V 1 neobsahuje vrchol v a V 2 neobsahuje vrchol u, je V 1 n, V 2 n a v oboch grafoch je každá hrana mostom. Oba teda spĺňajú požiadavky indukčného predpokladu, a preto je H 1 = V 1 1 H 2 = V 2 1 a preto H 1 + H 2 = V 1 + V 2 2 Pretože H = H 1 + H je H = V 1 + V 2 1 = V + 1 d) e) V tomto stave dôkazu už máme dokázané a) b) c) d) a teda aj a) d), čo možno formulovať ako tvrdenie: V strome G = (V, H) platí H = V 1. Toto použijem v tejto časti dôkazu Nech G = (V, H) je súvislý graf, v ktorom platí H = V 1. Chceme ukázať, že G je acyklický. Keby v grafe G existoval cyklus, odstránime z množiny hrán H jeho ľubovoľnú hranu h 1, čím neporušíme súvislosť. Položme H 1 = H {h 1 }, G 1 = (V, H 1 ). G 1 je súvislý graf. Ak G 1 neobsahuje cyklus, končíme. Inak z množiny hrán H 1 odstránime niektorú hranu cyklu h 2 a položíme H 2 = H 1 {h 2 }, G 2 = (V, H 2 ). Po odstránení konečného počtu k hrán dostaneme súvislý acyklický graf G k = (V, H k ), v ktorom je H k = H k a ktorý je stromom, takže platí súčasne: H k = H k = V 1 H = V 1 z čoho už vyplýva, že k = 0, t.j. v grafe G neexistuje ani jeden cyklus. e) a) Majme acyklický graf G = (V, H), v ktorom platí H = V 1. Stačí ukázať, že graf G je súvislý. Keby graf G nebol súvislý, rozpadol by sa na k acyklických komponentov G 1 = (V 1, H 1 ), G 2 = (V 2, H 2 ),..., G k = (V k, H k ), z ktorých každý G i je stromom, a preto preň platí H i = V i 1. Platí: V 1 = H = V = k V i H = i=1 k H i = i=1 k ( V i 1) = i=1 k H i. i=1 k V i i=1 k 1 = V k i=1
4 58 KAPITOLA 4. ACYKLICKÉ GRAFY, STROMY A KOSTRY Z posledného vzťahu vychádza k = 1 t.j. graf G má 1 komponent, t.j. je súvislý. Definícia 4.4. Koreňový strom je strom G = (V, H) s pevne vybraným vrcholom k V, ktorý nazývame koreň. Koreňový strom budeme značiť G = (V, H, k). Úroveň vrcholu u v koreňovom strome G = (V, H, k) je dĺžka (jedinej) cesty k u cesty. Výška koreňového stromu G = (V, H, k) je maximum z úrovní všetkých vrcholov koreňového stromu G. lacements úroveň 0 úroveň 1 úroveň 2 úroveň 3 úroveň 4 Obr. 4.2: Spôsoby kreslenia diagramu koreňnového stromu s koreňom 1 Diagramy koreňových stromov sa kreslia obvykle tak, že vrcholy nižšej úrovne sa umiestňujú nad vrcholy vyššej úrovne. Bežný je aj opačný spôsob vrcholy nižšej úrovne pod vrcholy vyššej úrovne. Majme strom s koreňom v 0. Nech v 0, {v 0, v 1 }, v 1,..., v n 1, {v n 1, v n }, v n je (jediná) v 0 v n cesta. Potom vrcholy v 0, v 1,..., v n 1 sa volajú predkovia vrcholu v n, vrchol v n 1 sa volá otec vrcholu v n, vrchol v n sa volá syn vrcholu v n 1. Ak je x predkom y, potom y sa volá následník alebo potomok vrcholu x. Vrchol bez následníka sa nazýva koncový vrchol. Všimnime si ešte, že po vybratí niektorého vrchola za koreň môžeme jednoznačne určiť orientácie všetkých hrán požiadavkou, aby všetky hrany boli orientované tak, že vrchol nižšej úrovne je počiatočný vrchol a vrchol vyššej úrovne je koncový vrchol ľubovoľnej hrany. Medzi koreňovými stromami majú význačné miesto tzv. binárne koreňové stromy, v ktorých má každý vrchol najviac dvoch synov. Často sa títo synovia označujú za ľavého a pravého. 4.2 Najlacnejšia a najdrahšia kostra Definícia 4.5. Definícia Kostra súvislého grafu G = (V, H) je taký jeho faktorový podgraf, ktorý je stromom. Nech G = (V, H, c) je hranovoohodnotený graf, K kostra grafu G. Cena c(k) kostry K je súčet ohodnotení jej hrán. Najlacnejšia kostra v grafe G je kostra s najmenšou cenou. Najdrahšia kostra v grafe G je kostra s najväčšou cenou. Veta 4.3. Nech K 1, K 2 sú dve kostry grafu G = (V, H). Potom pre každú hranu h 1 (K 1 K 2 ) existuje hrana h 2 (K 2 K 1 ) tak, že obe hrany h 1, h 2 ležia na (jedinom) cykle grafu K 2 {h 1 } aj na (jedinom) cykle grafu K 1 {h 2 }.
5 4.2. NAJLACNEJŠIA A NAJDRAHŠIA KOSTRA 59 PSfrag replacements a b u v h 1 h 2 G u G v w q v p Obr. 4.3: K dôkazu vety 4.3 Hrany kostry K 1 sú znázornené plnými čiarami. Cesta m 2 (u, v) = u, {u, w}, w, {w, x}, x, {x, y}, y, {y, v}, v po hranách kostry K 2 je znázornená čiarkovane. Dôkaz. Nech h = {u, v}. Graf K 1 {h 1 } má dva komponenty G u, G v, u G u, v G v. Nech m 2 (u, v) je jediná u v cesta v kostre K 2 (na obrázku čiarkovaná čiara). Táto cesta musí obsahovať aspoň jednu hranu h 2 = {x, y} takú, že x G u a y G v (lebo začína v G u a končí v G v ). Zreťazenie m 2 (u, v) (v, {v, u}, u) je cyklus v K 2 {h 1 } obsahujúci obe hrany h 1, h 2. V kostre K 1 existuje jediná x y cesta (na obrázku hrubá čiara). Pretože bolo x G u, y G v, t.j. x, y bolo v rôznych komponentoch grafu K 1 {h 1 }, musí táto cesta obsahovať hranu h 1 = {u, v}. Cyklus m 1 (x, y) (y, {y, x}, x) je jediným cyklom v K 1 {h 2 } a obsahuje obe hrany h 1, h 2. Obr. 4.4: Susedné kostry Ak ku hranám kostry K pridáme ľubovoľnú hranu h grafu G, ktorá neleží v hranovej množine kostry K (na obrázku 4.4 a) je vyznačená bodkovanou čiarou), vznikne graf K {h} obsahujúci cyklus. Vylúčením ktorejkoľvek hrany tohoto cyklu z grafu K {h} (okrem hrany h) dostaneme inú kostru K ). Definícia 4.6. Dve kostry sa nazývajú susedné, ak jednu možno získať z druhej výmenou jednej hrany. Veta 4.4. Kostra K grafu G = (V, H, c) je najlacnejšia práve vtedy, keď neexistuje lacnejšia susedná kostra.
6 60 KAPITOLA 4. ACYKLICKÉ GRAFY, STROMY A KOSTRY Dôkaz. Keď je kostra K najlacnejšia, potom nemôže existovať žiadna lacnejšia kostra. Nech K 0 je najlacnešia kostra a nech ku kostre K neexistuje žiadna lacnejšia susedná kostra. Ak by boli obe kostry totožné, bola by aj kostra K najlacnejšia. Nech teda existuje h 1 (K K 0 ). Podľa vety 4.3 existuje hrana h 2 (K 0 K) tak, že obe hrany ležia na nejakom cykle v K {h 2 } aj na nejakom cykle K 0 {h 1 }. Pretože hrana h 1 leží na cykle v grafe K {h 2 }, musí byť c(h 1 ) c(h 2 ), (4.1) ináč by nahradením hrany h 1 hranou h 2 v tomto cykle vznikla lacnejšia susedná kostra kostry K, ale kostra K podľa predpokladov nemá lacnejšiu susednú kostru. Pretože hrana h 2 leží na cykle v grafe K 0 {h 1 }, musí byť c(h 2 ) c(h 1 ), (4.2) c(h 2 ) c(h 1 ), ináč by nahradením hrany h 2 hranou h 1 v tomto cykle vznikla lacnejšia susedná kostra kostry K 0, čo je v spore s predpokladom, že K 0 je najlacnejšia kostra. Spojením (4.1), (4.2) máme c(h 1 ) = c(h 2 ). Pretože hrana h 2 kostry K 0 leží na cykle grafu K {h 2 }, jej nahradením hranou h 2 vytvoríme susednú kostru K (1) kostry K s rovnakou cenou, avšak kostra K (2) bude mať viac spoločných hrán s kostrou K 0 ako kostra K. Po konečnom počte krokov dostanem takto z kostry postupnosť kostier s rovnakou cenou K, K (1), K (2),..., K (k) = K 0, z čoho vyplýva, že c(k) = c(k 0 ) t.j. K je tiež najlacnejšia kostra. Kruskalov algoritmus na hľadanie najlacnejšej (najdrahšej) kostry súvislého hranovoohodnoteného grafu G = (V, H, c) Krok 1. Zoraď hrany podľa ich ohodnotenia vzostupne (zostupne) do postupnosti P. Krok 2. Nech prvá hrana v postupnosti P je hrana (u, v). Vylúč hranu (u, v) z postupnosti P a ak s už vybranými hranami nevytvára cyklus, zaraď ju do kostry. Krok 3. Ak je počet vybraných hrán rovný V 1, STOP. Inak GOTO krok 2. Táto formulácia algoritmu je veľmi názorná, no programátorovi by sa mohlo právom zdať, že nedostatočne formuluje, akým spôsobom skontrolovať, či pridávaná hrana nevytvára s už vybranými hranami cyklus. Túto kontrolu si môžeme značne zjednodušiť, keď vrcholom pridáme značky vyjadrujúce, v ktorom komponente lesa tvoreného zo všetkých vrcholov a doteraz vybraných hrán príslušný vrchol leží. Ak má pridávaná hrana oba koncové vrcholy v tom istom komponente, jej priadnie by znamenalo vznik cyklu. Krok 1. Zoraď hrany podľa ich ohodnotenia vzostupne (zostupne) do postupnosti P. Krok 2. Priraď každému vrcholu i V značku k(i) = 1, 2,..., n = V (každému vrcholu inú značku).
7 4.3. CESTA MAXIMÁLNEJ PRIEPUSTNOSTI 61 Krok 3. Nech prvá hrana v postupnosti P je hrana (u, v). Vylúč hranu (u, v) z postupnosti P. Ak k(u) k(v), zaraď hranu (u, v) do kostry, a i V, pre ktoré k(i) = k(v), potom polož k(i) := k(u). Krok 4. Ak je počet vybraných hrán rovný V 1, STOP. Inak GOTO krok 3. Odhadneme zložitosť Kruskalovho algoritmu. Usporiadanie m hrán grafu podľa veľkosti vyžaduje m. log m operácií. Krok 3 sa opakuje najviac m-krát. Ak sa prvá hrana postupnosti P nezaradí do (budúcej) kostry, bola s ňou urobená len jedna operácia (porovnanie značiek jej koncov). Ak hrana bola zaredná do kostry, čo nastane presne n 1 krát, bude treba preznačkovať značky vrcholov, čo vyžaduje n operácií pri jednom zaradení, n.(n 1) operácií celkom. Zložitosť Kruskalovho algoritmu v tomto tvare odhadneme teda ako O(n 2 ). V literatúre sa uvádza, že použitím vhodných dátových štruktúr možno na celý Kruskalov algoritmus vystačiť s O(m. log n) operáciami. 4.3 Cesta maximálnej priepustnosti V tejto časti sa budeme zaoberať hranovoohodnoteným grafmi G = (V, H, c), v ktorých c(h) > 0 znamená kapacitu (priepustnosť) hrany h. (Termíny kapacita a priepustnosť budeme považovať za synonymá, hoci v praxi cestného dopravného inžinierstva je medzi týmito pojmami istý rozdiel). Kapacita c(h) môže znamenať: maximálny počet vozidiel, ktoré prejdú hranou za jednotku času, únosnosť hrany maximálnu hmotnosť vozidla, ktoré prejde hranou (napr. hrana predstavuje komunikáciu na ktorej je mostík s nosnosťou 5 ton, preto najťažšie vozidlo, ktoré smie prejsť hranou môže vážiť 5 ton a v tomto prípade c(h) = 5 pre hranu, ktorá modeluje príslušnú komunikáciu), maximálnu výšku vozidla, ktoré prejde hranou maximálnu šírku vozidla, ktoré prejde hranou Iste nájdete aj ďalšie praktické príklady. V praxi priepustnosť cesty prechádzajúcej niekoľkými úsekmi je určená priepustnosťou najmenej priepustného úseku. Tým je motivovaná nasledujúca definícia. Definícia 4.7. Definícia Nech G = (V, H, c) je hranovoohodnotený graf, v ktorom cena hrany h H c(h) > 0 znamená jej priepustnosť. Priepustnosť c(m(u, v)) u v cesty (sledu, polosledu, atď.) m(u, v) definujeme ako c(m(u, v)) = min {c(h)}. h m(u,v) Veta 4.5. Nech K je najdrahšia kostra v súvislom hranovoohodnotenom grafe G = (V, H, c), nech (u, v) H je taká hrana grafu G, ktorá nepatrí k hranovej množine kostry K. Nech m(u, v) je (jediná) u-v cesta v kostre K. Potom je kapacita cesty m(u, v) väčšia alebo rovná ako kapacita hrany (u, v), t.j. c(m(u, v)) c(u, v).
8 62 KAPITOLA 4. ACYKLICKÉ GRAFY, STROMY A KOSTRY Dôkaz. Stačí dokázať, že pre ľubovoľnú hranu h m(u, v) je c(h) c(u, v). Dôkaz vykonáme sporom. Nech pre nejakú hranu h m(u, v) platí c(h) < c(u, v). Zreťazením ciest m(u, v) a u, (u, v), v dostaneme cyklus. Pridaním hrany (u, v) k množine hrán kostry K a vylúčením hrany h z cesty m(u, v) a teda aj z hranovej množiny kostry K dostaneme graf K = K {(u, v)} {h}, ktorý je súvislý a má V 1 hrán. K je teda strom kostra grafu G, ktorej cena je c(k ) = c(k) + c(u, v) c(h) > c(k). }{{} >0 Za predpokladu, že existuje hrana h m(u, v) taká, že c(h) < c(u, v), sme zostrojili kostru K, ktorej cena je väčšia než cena kostry K, čo je v spore s maximalitou K. Veta PSfrag 4.6. Nech replacements K je najdrahšia kostra v súvislom hranovoohodnotenom grafe G = (V, H, c). Potom pre ľubovoľné dva vrcholy u, v V je (jediná) (u v) cesta v K (u v) cestou maximálnej priepustnosti v G. u = v 1 v Dôkaz. v 2 v 3 v 4 v 5 v 6 v 7 v 8 v 9 Obr. 4.5: K dôkazu vety 4.6 M(u, v) = u, {u, v 2 }, v 2, {v 2, v 3 }, v 3, {v 3, v 4 }, v 4, {v 4, v}, v m(u, v 2 ) = u, {u, v 5 }, v 5, {v 5, v 6 }, v 6, hr(v 6, v 2 ), v 2, m(v 2, v 3 ) = v 2, {v 2, v 6 }, v 6, {v 6, v 3 }, v 3 m(v 3, v 4 ) = v 3, {v 3, v 7 }, v 7, {v 7, v 8 }, v 8, {v 8, v 4 }, v 4, m(v 4, v) = v 4, {v 4, v 8 }, v 8, {v 8, v 7 }, v 7, {v 7, v}, v Cesta max. priepustnosti po hranách kostry prechádza vrcholmi u, v 5, v 6, v 3, v 7, v 9, v Nech M(u, v) = v 1, (v 1, v 2 ), v 2,..., (v k 1, v k ), v k, kde v 1 = u, v k = v je u-v cesta maximálnej kapacity. Nech pre i = 1, 2,..., k 1 m(v i, v i+1 ) je v i -v i+1 cesta po hranách najdrahšej kostry K táto má podľa predchádzajúcej vety kapacitu väčšiu alebo rovnú ako c(v i, v i+1 ). Zreťazením ciest m(v i, v i+1 ) pre i = 1, 2,..., k 1 dostaneme u-v sled S po hranách kostry K, ktorého priepustnosť je väčšia alebo rovná než kapacita cesty M(u, v). Vynechaním viackrát prejdených hrán a vrcholov sledu S dostaneme u-v cestu po hranách kostry K, ktorej kapacita je väčšia alebo rovná kapacite cesty M(u, v). Keďže cesta M(u, v) bola cestou maximálnej priepustnosti, je aj u-v cesta po hranách kostry K cestou maximálnej priepustnosti. Definícia 4.8. Algoritmus na hľadanie (u v) cesty maximálnej priepustnosti v súvislom hranovohodnotenom grafe G = (V, H, c) Krok 1. V grafe G zostroj najdrahšiu kostru K.
9 4.4. APLIKÁCIE 63 Krok 2. Pre ľubovoľné dva vrcholy u, v V je (jediná) (u v) cesta v K (u v) cestou maximálnej priepustnosti v G. Uvedený algoritmus síce nájde u-v cestu maximálnej priepustnosti, no táto nemusí byť a spravidla ani nebýva optimálnou z hľadiska prejdenej vzdialenosti. Ak by sme chceli nájsť najkratšiu u-v cestu s maximálnou kapacitou, potrebujeme mať v príslušnom grafe okrem kapacitného ohodnotenia hrán aj ohodnotenie vyjadrujúce ich dĺžku. Definícia 4.9. Algoritmus na hľadanie najkratšej (u v) cesty s maximálnou priepustnosťou v súvislom hranovohodnotenom grafe G = (V, H, c, d), kde c(h) je kapacita a d(h) je dĺžka hrany h H Krok 1. V grafe G nájdeme cestu m(u, v) maximálnej priepustnosti vzhľadom na ohodnotenie hrán c. Nech C je priepustnosť cesty m(u, v). Krok 2. Vytvorme graf G = (V, H, d) kde H = {h h H, c(h) C} (H obsahuje len tie hrany pôvodného grafu, ktoré majú kapacitu väčšiu alebo rovnú než C). Krok 3. V grafe G nájdeme najkratšiu u-v cestu vzhľadom na ohodnotenie hrán d. 4.4 Aplikácie Štruktúra adresárov na disku Pevný disk počítača slúži na uloženie dát, ktoré sú usporiadané do súborov. Najmenšou logickou jednotkou, s ktorou diskový systém pracuje, je súbor. Sú média (napríklad magnetopáskové jednotky), ktoré súbory ukladajú do jednej postupnosti bez možnosti vytvárania nejakej ich štruktúry. Takáto jednoduchá organizácia dát súvisí často s tým, že takéto médium nemá priamy ale iba sekvenčný prístup ku svojim údajom. Pevný disk však má možnosť ľubovoľného prístupu k svojim dátam, čo sa dá využiť na lepšie usporiadanie súborov ako jednoduché sekvenčné usporiadanie. Na to aby sa súbory na disku dali lepšie organizovať sú súbory rozdelené do adresárov. Existuje hlavný adresár disku, ktorý nie je súčasťou žiadneho iného adresára. Každý adresár môže obsahovať súbory a ďalšie podadresáre. Takáto disková štruktúra sa modeluje koreňovým stromom, v ktorom je koreňom hlavný adresár. Synmi každého adresára sú súbory ktoré obsahuje a jeho podadresáre. Otcom každého adresára (okrem hlavného adresára) je jeho nadradený adresár. Meno súboru alebo adresára môžeme interpretovať ako značku príslušného vrchola adresárového stromu. V rámci jedného adresára žiadne dva rôzne súbory alebo podadresáre nemôžu mať rovnakú značku. Úplná špecifikácia súboru alebo adresára na pevnom disku sa získa zreťazením všetkých značiek (jedinej) cesty z koreňa do príslušného vrchola. Pretože v strome existuje jediná cesta z koreňa do ľubovoľného vrchola a pretože značky rôznych synov jedného vrchola adresárového stromu sú rôzne, úplné špecifikácie rôznych súborov sú rôzne napriek tomu, že v odlišných adresároch môžu byť súbory s rovnakým menom. Ak potrebujeme vyhľadať súbor daných vlastností v adresárovom strome, stačí nám upotrebiť niektorý z algoritmov na prehľadávanie grafov napr. Tarryho algoritmus, ktorý pri nájdení hľadaného súboru môžeme predčasne ukončiť, pri hľadaní všetkých súborov daných vlastností ho však musíme nechať dobehnúť do konca.
10 64 KAPITOLA 4. ACYKLICKÉ GRAFY, STROMY A KOSTRY Prefixové kódovanie Kódovanie je zobrazenie, ktoré každému znaku abecedy A = {a 1, a 2,..., a n } priradí slovo (t.j. konečnú postupnosť znakov) abecedy B = {b 1, b 2,..., b m }. Slová abecedy B, ktoré sú obrazom nejakého znaku abecedy A sa nazývajú kódové slová je ich práve n, ostatné slová abecedy B sú nekódové slová. Množina kódových slov sa volá kód. Účelom kódovania je prispôsobiť správu napísanú v abecede A možnostiam prenosového kanálu alebo archivačného média, skomprimovať správu, alebo vytvoriť také kódovanie, ktoré bude odolné proti chybám pri prenose. Čitateľ by sa tu mohol pozastaviť nad otázkou, prečo nepriraďujeme znakom abecedy A znaky ale slová abecedy B. Je to preto, lebo obyčajne má abeceda B menej znakov, ako abeceda A. Abecedou B je najčastejšie dvojprvková množina B = {0, 1} vtedy hovoríme o binárnom kódovaní. Príkladom binárneho kódovania je všeobecne známe priradenie znakov latinskej abecedy, cifier 0 až 9 a ďalších špeciálnych znakov 8 bitovými binárnymi číslami nazývané ASCII kód. Tu majú všetky kódové slová rovnakú dĺžku 8 znakov. V teórii kódovania sa však používajú aj také kódovania, pri ktorých nemajú kódové slová rovnakú dĺžku. Medzi nimi majú význačné postavnie tzv, prefixové kódy. Kód je prefixový, keď žiadne kódové slovo nie je začiatkom iného kódového slova. Každému prefixovému kódu prislúcha strom. Napríklad kódu {0, 101, 1100, 1101, 1101, 1111} zodpovedá strom na obrázku 4.6. PSfrag replacements Obr. 4.6: Strom prefixového kódu Strom má koreň k, vrcholy stupňa 3 vyznačené kolieskami a vrcholy stupňa 1 vyznačené štvorčekmi. Tieto zodpovedajú kódovým slovám. Na začiatku dekódovania nastavíme pomyselný ukazovateľ do vrcholu k. Podľa prijatého znaku 0 alebo 1 ideme z aktuálneho vrchola hranou označenou prijatým znakom. Keď prídeme do koncového vrchola grafu, konštatujeme, že sme prijali kódové slovo. Nastavíme ukazovateľ do vrcholu k a prijímame ďalšie znaky. Jeden vrchol stromu stupňa 1 je označený trojuholníkom a nezodpovedá žiadnemu kódovému slovu. Pri bezchybnom prenose sa do takéhoto vrcholu nemôžeme dostať. Z toho vyplýva, že kód nie je optimálny a že ho môžeme skrátiť, keď namiesto kódového slova 101 použijeme slovo 10. Dospejeme tak ku kratším zakódovaným správam. Pri komprimácii dáta a súborov sa využíva je skutočnosť, že nie všetky znaky zdrojovej abecedy A sa vyskytujú s rovnakou relatívnou početnosťou. Túto nerovnomernosť môžeme
11 4.4. APLIKÁCIE 65 využiť tak, že znaky vyskytujúce sa často zakódujeme kratším kódovým slovom, kým zriedkavým znakom pridelíme dlhšie kódové slová. Optimálne to robí konštrukcia, ktorú navrhol Huffman (čítaj hafmen) a výsledný kód sa volá Huffmanov kód Algoritmus na zostrojenie Huffmanovho kódu. Budeme postupne budovať binárny koreňový strom, ktorého všetky vrcholy stupňa 1 budú znaky zdrojovej abecedy A. Každý vrchol stromu bude mať priradenú pravdepodobnosť a každej hrane stromu priradíme a binárny znak 0 alebo 1. Krok 1: Zostrojme graf G = (V, H, p), kde V = A a kde p(v) je pravdepodobnosť znaku v. Inicializačne položme H =. Všetky vrcholy z V inicializačne prehlásime za neoznačené. Krok 2: Nájdeme dva neoznačené vrcholy u, w z množiny V s najmenšími pravdepodobnosťami p(u), p(w). Označkujme vrcholy u, v ako spracované. Množinu vrcholov V rozšírme o vrchol x, t.j. položme V := V {x} pre nejaké x / V, položme p(x) := p(u)+p(w), H := H {{x, u}, {x, v}} a nový vrchol x prehlásime za neoznačený. Hrane {x, u} priraďme značku 0, hrane {x, v} značku 1. Krok 3: Ak je graf G súvislý, prehlásime posledne pridaný vrchol x za koreň k a goto Krok 4, inak goto Krok 2. Krok 4: Teraz je graf G stromom so všetkými vrcholmi stupňa 1 zodpovedajúcimi znakom zdrojovej abecedy A. Všetky hrany stromu G sú označené binárnymi značkami 0 alebo 1. Z koreňa stromu do každého listu vedie jediná cesta, binárne značky hrán na tejto ceste určujú prefixový kód každého znaku abecedy A Riešenie zložitých elektrických obvodov Majme elektrický obvod zložený z odporov a napäťových zdrojov (zvaných tiež dvojpóly). Spoločná svorka dvoch alebo viacerých dvojpólov sa nazýva uzol, počet dvojpólov zapojených na uzol si nazveme stupeň uzla. Vetva je sériové spojenie niekoľkých dvojpólov medzi dvoma uzlami, ktoré majú apoň stupeň 3. Vyriešiť problém daného elektrického obvodu znamená určiť pre každú vetvu prúd, ktorý ňou tečie. Ku každému elektrickému obvodu O, ktorý má aspoň dva uzly vyššieho stupňa než 2, si môžeme zostrojiť graf G O = (V, H), ktorého vrcholmi budú všetky uzly príslušného obvodu so stupňom väčším ako 2 a ktorého hranami budú všetky vetvy obvodu O. Teraz už môžeme definovať slučku obvodu O ako ľubovoľný cyklus v grafe G O. Pri hľadaní prúdov vetvami používame tri fyzikálne zákony Ohmov zákon, ktorý hovorí, že ak odporom veľkosti R tečie prúd I, potom na ňom vznikne úbytok napätia U = R.I, prvý Kirchhoffov zákon hovoriaci, že algebraický súčet prúdov v uzle sa rovná nule a druhý Kirchhoffov zákon, ktorý hovorí, že algebraický súčet napätí v ľubovoľnej slučke sa rovná nule. Napätia v slučke sú dvojakého typu známe napätia zdrojov a napätia objavujúce sa na odporoch, ktoré vypočítame z prúdov tečúcich odpormi a známych veľkostiach odporov podľa Ohmovho zákona. Druhý Kirchhoffov zákon pre ľubovoľnú slučku S má tvar U i + I Rj.R j = 0, (4.3) zdroj U i leží na slučke S odpor R j leží na slučke S
12 66 KAPITOLA 4. ACYKLICKÉ GRAFY, STROMY A KOSTRY kde I Rj je prúd tečúci odporom R j. Poznamenajme, že pre všetky odpory R j v k-tej vetve je I Rj rovné vetvovému prúdu I k. Nech n je počet uzlov a m počet vetví obvodu O. Označme I 1, I 2,..., I m prúdy tečúce vetvami h 1, h 2,..., h m obvodu O. Rovnice pre prvý Kirchhoffov zákon zostavíme jednoducho {j h j H u} I j = 0 u = 1, 2,..., n (4.4) Rovníc typu (4.4) je n, ale len n 1 z nich je lineárne nezávislých. Keďže m > n, musíme ich doplniť m n + 1 rovnicami typu (4.3) vyjadrujúcimi druhý Kirchhoffov zákon. Počet slučiek v obvode O môže byť veľmi veľký, vybrať ľubovoľných (m n + 1) z nich nie je dobrá myšlienka, lebo príslušné rovnice by mohli byť lineárne závislé a riešenie výslednej sústavy by takom prípade nebolo jednoznačne určené. Stojíme teda pred problémom, ako nájsť m n + 1 lineárne nezávislých slučiek obvodu O. lacements úroveň 0 úroveň 1 úroveň 2 úroveň 3 úroveň 4 Obr. 4.7: Elektrický obvod O, k nemu príslušný graf G O a jeho kostra K Zostrojíme ľubovoľnú kostru K = (V, H K ) v grafe G. Táto kostra má podľa vety 4.2 n 1 hrán. Ostalo teda m (n 1) = m n + 1 hrán, ktoré neležia v kostre K. Ak ku hranám kostry K pridáme ľubovoľnú hranu h (H H K ), dostaneme graf K {h}, v ktorom existuje práve jeden cyklus, definujúci slučku S h v obvode O. Dá sa ukázať, že systém m n+1 slučiek {S h h (H H K )} je systém lineárne nezávislých slučiek v tom zmysle, že systém príslušných lineárnych rovníc vyjadrujúcich druhý Kirchhoffov zákon je lineárne nezávislý. Na obrázku 4.7 vidíme obvod O vľavo, vpravo k nemu príslušný graf G O, hrany jeho kostry sú vyznačené hrubými čiarami. Slučkové rovnice pre slučky (A, B, E, A), (A, E, F, H, D, A), (B, C, F, E, B), (C, G, H, F, C), (D, E, F, H, D) a (F, G, H, F ) budú lineárne nezávislé a možno ich použiť pre riešenie príslušného obvodu O. Podobne sa dá využiť kostra grafu G O na identifikáciu nezávislých slučiek pri riešení obvodov so striedavým prúdom a so všeobecnými impedanciami (odpormi, kapacitami a indukčnosťami). Na tomto príklade vidíme dva spôsoby aplikácia matematiky (v tomto prípade teórie grafov) v iných odboroch (tu konkrétne v elektrotechnike). Prvý z nich je ten, že pomáha presne definovať pojmy videli sme to na prípade definície slučky v elektrickom obvode. Druhý spôsob je, že dáva exaktný nástroj na riešenie konkrétneho problému tu zostavenia sústavy lineárne nezávislých rovníc popisujúcich elektrický obvod.
13 4.4. APLIKÁCIE Úloha o elektrifikácii Do n miest v istom regióne máme zaviesť elektrický prúd. Možné spôsoby vybudovania vedení medzi jednotlivými miestami možno modelovať hranovoohodnoteným grafom G = (V, H, c), v ktorom je V množinou všetkých miest, množinu hrán H tvoria všetky neusporiadané dvojice miest {u, v} také, že medzi miestami u a v možno viesť priame elektrické vedenie a cena hrany c({u, v}) > 0 predstavuje náklady na vybudovanie priameho vedenia medzi miestami u a v. Chceme vybudovať elektrickú sieť s najmenšími nákladmi avšak tak, aby v každom mieste bola zavedená elektrina. Na riešenie vyššie spomínanej úlohy stačí určiť, medzi ktorými vrcholmi grafu G postavíme elektrické vedenie, čo je to isté ako keď určíme, ktoré hrany grafu G vyberieme do riešenia. Nech G 1 je faktorový podgraf grafu G (t.j. podgraf obsahujúci všetky vrcholy grafu G) a práve všetky hrany vybrané pre stavbu vedenia. Ak má byť elektrina zavedená do všetkých miest, graf G 1 musí byť súvislý. Úloha o elektrifikácii sa dá teda naformulovať ako hľadanie najlacnejšieho súvislého podgrafu grafu G (najlacnejší v zmysle súčtu ocenení všetkých jeho hrán). Ak však má byť G 1 najlacnejší súvislý faktorový podgraf, nesmie obsahovať cyklus ináč by sme vylúčením ľubovoľnej hrany takéhoto cyklu dostali lacnejší súvislý faktorový podgraf grafu G. Preto G 1 musí byť kostrou grafu G. Úloha o elektrifikácii sa teda dá formulovať ako hľadanie najlacnejšej kostry v súvislom hranovoohodnotenom grafe G. Tu popísaný princíp možno bez zmeny použiť aj pri plánovaní telekomunikačných, dátových a počítačových sietí Plánovanie prepravy nadrozmerných nákladov Existujú dopravné podniky, ktoré sa špecializujú na cestnú prepravu mimoriadne veľkých nákladov ako sú riečne lode, veľké chemické reaktory, žeriavy a iné veľké konštrukcie, ktorých veľkosť, váha, výška alebo dĺžka presahujú hodnoty bežne prepravovaných predmentov. 1 Ako technické prostriedky sa na takúto prepravu používajú veľké ťahače, mnohonápravové prívesy, dlhé predmety sa prepravujú aj na dvoch prívesoch ovládaných na vpredu i vzadu. Prepravovaný náklad spravádza konvoj doprovodných vozidiel pripravených vyriešiť na mieste menšie problémy (ako odstrániť a znovu na pôvodné miesto privariť prekážajúci kovový stĺpik plota, zábradlie či dopravnú značky) i náročnejšie úlohy (zosilnenie mostíka, či dokonca naddvihnutie železničného nadjazdu nad cestou). Každá takáto mimoriadna preprava sa musí dopredu veľmi starostlivo naplánovať. Existujú počítačové modely cestnej siete, ktoré pre každý cestný úsek obsahujú jeho šírku, typ povrchu vozovky, únosnosť prípadných mostov na úseku, polomer zatáčania, svetlú výšku prípadných podjazdov, ktorými úsek prechádza, typ krajnice a mnoho ďalších údajov. Algoritmus pre hľadanie cesty maximálnej pripustnosti tu návod, ako nájsť vhodnú cestu pri zohľadnení všetkých možných požiadaviek. Bez ohľadu na to, či bolo plánovaná trasa nadmerného nákladu určená ručne alebo počítačom, krátko pred plánovanou prepravou skupina odborníkov prejde plánovaou trasou a pozorne skontroluje, či sa na nej niečo oproti evidovanému stavu nezmenilo a či je pre plánovanú prepravu skutočne vhodná. 1 Autor získal uvádzané skúsenosti pri spolupráci s podnikom Závod těžké dopravy, ČSAD, n.p. Ostrava
14 68 KAPITOLA 4. ACYKLICKÉ GRAFY, STROMY A KOSTRY 4.5 Cvičenia 1. Iným spôsobom, ako vo vete 4.2 dokážte, že v strome G = (V, H) je H = V 1. Postupujte matematickou indukciou s využitím tvrdenia vety 4.1, podľa ktorého v každom strome s aspoň dvoma vrcholmi existuje vrchol stupňa Implikácia c d z vety 4.2 sa dá dokázať aj s využitím nasledujúcej úvahy: Keďže je v G každá hrana mostom, po odobratí ľubovoľnej hrany h H bude mať graf G {h} o jeden komponent viac ako graf G. Nech H = {h 1, h 2,..., h m }, vytvorme postupnosť grafov G 1 = G {h 1 }, G 2 = G {h 1, h 2 },..., G m = G {h 1, h 2,..., h m }, v ktorej má každý graf o jeden komponent viac, ako jeho bezprostredný predchodca. Z počtu komponentov grafu G m usúďte, čomu sa rovná m. 3. Po skončení práce ľubovoľného algoritmu na hľadanie najkratšej cesty z vrcholu u do ostatných vrcholov súvislého hranovoohodnoteného grafu G = (V, H, c) dostávame v značkách x(v) vrcholov grafu G predposledný vrchol najkratšej u v cesty. Priradením x : V {u} V vlastne definujeme pre každý vrchol v V, v V predchodcu vrcholu v v nejakom koreňovom strome S s koreňom u. Strom S je faktorovým podgrafom grafu G je kostrou grafu G. Je S najlacnejšou kostrou grafu S? 4. Nech K je najlacnejšia kostra súvislého hranovoohodnoteného grafu G = (V, H, c). Pre každé u, v V je kostrou K jednoznačne určená u v cesta m K (u, v) obsahujúca len hrany kostry K. Je m K (u, v) najlacnejšou cestou v grafe G? 5. Prispôsobte Kruskalov algoritmus na hľadanie komponentov ľubovoľného grafu G. Porovnajte tento spôsob hľadania komponentov so spôsobom založeným na Tarryho algoritme. 6. Nech G = (V, H, c) je hranovoohodnotený digraf, kde c(h) > 0 je priepustnosť hrany h H. Tu nemožno použiť algoritmus na hľadanie cesty maximálnej priepustnosti založený na najdrahšej kostre. Navrhnite značkovací algoritmus pre hľadanie u v cesty maximálnej priepustnosti podobný základnému algoritmu na hľadanie najkratšej u v cesty. Značka t(v) vrcholu v nech značí priepustnosť doteraz nájdenej najpriepustnejšej u v cesty a x(v) predposledný vrchol tejto cesty. Odhadnite zložitosť navrhnutého algoritmu.
Teória grafov. Stromy a kostry 1. časť
 Teória grafov Stromy a kostry 1. časť Definícia: Graf G=(V, E) nazývame strom, ak neobsahuje kružnicu ako podgraf Definícia Strom T=(V, E T ) nazývame koreňový strom ak máme v ňom pevne vybraný vybraný
Teória grafov Stromy a kostry 1. časť Definícia: Graf G=(V, E) nazývame strom, ak neobsahuje kružnicu ako podgraf Definícia Strom T=(V, E T ) nazývame koreňový strom ak máme v ňom pevne vybraný vybraný
8. Relácia usporiadania
 8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
Obrázok Časový plán projektu, určite kritickú cestu. Obrázok Časový plán projektu, určite kritickú cestu
 Cvičenie:.. Pre každú zo sietí uvedených dole určite minimálny celkový čas, ktorý zaberie dokončenie projektu, minimálne časové ohodnotenie E(v) u jednotlivých vrcholov a kritickú cestu. (a) Obrázok..
Cvičenie:.. Pre každú zo sietí uvedených dole určite minimálny celkový čas, ktorý zaberie dokončenie projektu, minimálne časové ohodnotenie E(v) u jednotlivých vrcholov a kritickú cestu. (a) Obrázok..
Zvyškové triedy podľa modulu
 Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
PROGRAM VZDELÁVACEJ ČINNOSTI. Anotácia predmetu
 PROGRAM VZDELÁVACEJ ČINNOSTI Číslo predmetu : 32131, 2N187 Názov predmetu : Teória grafov Typ predmetu : Povinne voliteľný Študijný odbor: Biomedicinske inžinierstvo, Telekomunikácie, Aplikovaná mechanika
PROGRAM VZDELÁVACEJ ČINNOSTI Číslo predmetu : 32131, 2N187 Názov predmetu : Teória grafov Typ predmetu : Povinne voliteľný Študijný odbor: Biomedicinske inžinierstvo, Telekomunikácie, Aplikovaná mechanika
Množiny, relácie, zobrazenia
 Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Kvadratické funkcie, rovnice, 1
 Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
M úlohy (vyriešené) pre rok 2017
 M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
7. Relácia ekvivalencie a rozklad množiny
 7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
7 Relácia ekvivalencie a rozklad množiny V tejto časti sa budeme venovať špeciálnemu typu binárnych relácií na množine - reláciám ekvivalencie a ich súvisu s rozkladom množiny Relácia ekvivalencie na množine
PODPROGRAMY. Vyčlenenie podprogramu a jeho pomenovanie robíme v deklarácii programu a aktiváciu vykonáme volaním podprogramu.
 PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
ZÁKLADY TEÓRIE GRAFOV
 ZÁKLAY EÓRIE GRAFOV PRÍKLA : Minimálna kostra grafu v zadanom grafe určite minimálnu kostru grafu 9 Riešenie: Kostra grafu je taký podgraf, ktorý obsahuje všetky vrcholy pôvodného grafu a neobsahuje uzavretý
ZÁKLAY EÓRIE GRAFOV PRÍKLA : Minimálna kostra grafu v zadanom grafe určite minimálnu kostru grafu 9 Riešenie: Kostra grafu je taký podgraf, ktorý obsahuje všetky vrcholy pôvodného grafu a neobsahuje uzavretý
Metóda vetiev a hraníc (Branch and Bound Method)
 Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
Metóda vetiev a hraníc (Branch and Bound Method) na riešenie úloh celočíselného lineárneho programovania Úloha plánovania výroby s nedeliteľnosťami Podnikateľ vyrába a predáva zemiakové lupienky a hranolčeky
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P
 NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
NEVLASTNÁ VODIVOSŤ POLOVODIČOVÉHO MATERIÁLU TYPU P 1. VLASTNÉ POLOVODIČE Vlastnými polovodičmi nazývame polovodiče chemicky čisté, bez prímesí iných prvkov. V súčasnosti je najpoužívanejším polovodičovým
VECIT 2006 Tento materiál vznikol v rámci projektu, ktorý je spolufinancovaný Európskou úniou. 1/4
 Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Súmernosti. Mgr. Zuzana Blašková, "Súmernosti" 7.ročník ZŠ. 7.ročník ZŠ. Zistili sme. Zistite, či je ľudská tvár súmerná
 Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
Mgr. Zuzana Blašková, "úmernosti" 7.ročník ZŠ 1 úmernosti 7.ročník ZŠ Mgr. Zuzana Blašková 2 ZŠ taničná 13, Košice Osová súmernosť určenie základné rysovanie vlastnosti úlohy s riešeniami osovo súmerné
ČÍSELNÉ RADY. a n (1) n=1
 ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
i j, existuje práve jeden algebraický polynóm n-tého stupˇna Priamym dosadením do (2) dostávame:
 0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
Limita funkcie. Čo rozumieme pod blížiť sa? y x. 2 lim 3
 Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
KOMISNÝ PREDAJ. Obr. 1
 KOMISNÝ PREDAJ Komisný predaj sa realizuje na základe komisionárskej zmluvy, pričom ide v podstate o odložený predaj, kde práva k výrobku alebo tovaru prevedie dodávateľ (výrobca, komitent) na predajcu
KOMISNÝ PREDAJ Komisný predaj sa realizuje na základe komisionárskej zmluvy, pričom ide v podstate o odložený predaj, kde práva k výrobku alebo tovaru prevedie dodávateľ (výrobca, komitent) na predajcu
Zachovanie mentálnej mapy pri interakcií s grafom. RNDr. Jana Katreniaková PhD.
 Zachovanie mentálnej mapy pri interakcií s grafom RNDr. Jana Katreniaková PhD. Cieľ Nájsť spôsob, ako obmedziť zmeny pri kreslení hrán grafov (vizualizácia) počas používateľskej interakcie. Kreslenie grafov
Zachovanie mentálnej mapy pri interakcií s grafom RNDr. Jana Katreniaková PhD. Cieľ Nájsť spôsob, ako obmedziť zmeny pri kreslení hrán grafov (vizualizácia) počas používateľskej interakcie. Kreslenie grafov
Obsah. Reprezentácia údajov v počítači. Digitalizácia číselnej informácie. Digitalizácia znakov a textovej informácie.
 Obsah Reprezentácia údajov v počítači. Digitalizácia číselnej informácie. Digitalizácia znakov a textovej informácie. Reprezentácia údajov v počítači. Počítač je stroj, ktorý na kódovanie údajov (čísla,
Obsah Reprezentácia údajov v počítači. Digitalizácia číselnej informácie. Digitalizácia znakov a textovej informácie. Reprezentácia údajov v počítači. Počítač je stroj, ktorý na kódovanie údajov (čísla,
3 Determinanty. 3.1 Determinaty druhého stupňa a sústavy lineárnych rovníc
 3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
Skákalka. Otvoríme si program Zoner Callisto, cesta je Programy Aplikácie Grafika Zoner Callisto.
 Skákalka Otvoríme si program Zoner Callisto, cesta je Programy Aplikácie Grafika Zoner Callisto. Vyberieme si z ponuky tvarov kruh a nakreslíme ho (veľkosť podľa vlastného uváženia). Otvoríme si ponuku
Skákalka Otvoríme si program Zoner Callisto, cesta je Programy Aplikácie Grafika Zoner Callisto. Vyberieme si z ponuky tvarov kruh a nakreslíme ho (veľkosť podľa vlastného uváženia). Otvoríme si ponuku
ZÁKLADY ELEKTROTECHNICKÉHO INŽINIERSTVA
 ZÁKLADY ELEKTROTECHNICKÉHO INŽINIERSTVA Technická dokumentácia v elektrotechnike Prednáška 4 Zásady kreslenia elektrotechnických schém Pravidlá na kreslenie elektrotechnických schém sú uvedené v normách
ZÁKLADY ELEKTROTECHNICKÉHO INŽINIERSTVA Technická dokumentácia v elektrotechnike Prednáška 4 Zásady kreslenia elektrotechnických schém Pravidlá na kreslenie elektrotechnických schém sú uvedené v normách
Lineárne obvody v stacionárnom ustálenom stave 1 (Úloha A-1)
 Lineárne obvody v stacionárnom ustálenom stave 1 (Úloha ) Úloha Pomocou laboratórneho obvodového modelu experimentálne overte:.1 prvý a druhý Kirchhoffov zákon,. metódu slučkových prúdov,.3 metódu uzlových
Lineárne obvody v stacionárnom ustálenom stave 1 (Úloha ) Úloha Pomocou laboratórneho obvodového modelu experimentálne overte:.1 prvý a druhý Kirchhoffov zákon,. metódu slučkových prúdov,.3 metódu uzlových
Prevody z pointfree tvaru na pointwise tvar
 Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Základy algoritmizácie a programovania
 Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
Pozičné číselné sústavy. Dejiny. Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry).
 Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Operačný systém Úvodná prednáška
 Operačný systém Úvodná prednáška Pohľad zvonka (z vyšších úrovní) Pohľad zvnútra Pojmy správy procesov Úlohy jednotlivých častí operačného systému Autor: Peter Tomcsányi, Niektoré práva vyhradené v zmysle
Operačný systém Úvodná prednáška Pohľad zvonka (z vyšších úrovní) Pohľad zvnútra Pojmy správy procesov Úlohy jednotlivých častí operačného systému Autor: Peter Tomcsányi, Niektoré práva vyhradené v zmysle
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Cvičenie 1 Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody
Pracovné prostredie MS EXCEL 2003.
 Pracovné prostredie MS EXCEL 2003. Tabuľkové kalkulátory sú veľmi praktické aplikácie pre realizáciu výpočtov, grafických prezentácií údajov, ako aj pe prácu s rôznymi údajmi ako s bázou dát. Tieto programy
Pracovné prostredie MS EXCEL 2003. Tabuľkové kalkulátory sú veľmi praktické aplikácie pre realizáciu výpočtov, grafických prezentácií údajov, ako aj pe prácu s rôznymi údajmi ako s bázou dát. Tieto programy
Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od
 A. Právny rámec Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od 18. 4. 2016 Podľa 8 ods. 1 zákona č. 343/2015 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v znení
A. Právny rámec Osoba podľa 8 zákona finančné limity, pravidlá a postupy platné od 18. 4. 2016 Podľa 8 ods. 1 zákona č. 343/2015 Z. z. o verejnom obstarávaní a o zmene a doplnení niektorých zákonov v znení
Kreslenie vo Worde Chceme napríklad nakresliť čiaru priamku. V paneli ponúk klikneme na Vložiť a v paneli nástrojov klikneme na Tvary.
 Kreslenie vo Worde Chceme napríklad nakresliť čiaru priamku. V paneli ponúk klikneme na Vložiť a v paneli nástrojov klikneme na Tvary. V roletke klikneme na ikonku Čiara. Ukazovateľom myši, keď nim prejdeme
Kreslenie vo Worde Chceme napríklad nakresliť čiaru priamku. V paneli ponúk klikneme na Vložiť a v paneli nástrojov klikneme na Tvary. V roletke klikneme na ikonku Čiara. Ukazovateľom myši, keď nim prejdeme
Riešenie nelineárnych rovníc I
 Riešenie nelineárnych rovníc I Ako je už zo samotného názvu hodiny parné budeme sa venovať spôsobom výpočtu nelineárnych rovníc. Prečo je riešenie takýchto rovníc nevyhnutné? Nielen v samotnom chemickom
Riešenie nelineárnych rovníc I Ako je už zo samotného názvu hodiny parné budeme sa venovať spôsobom výpočtu nelineárnych rovníc. Prečo je riešenie takýchto rovníc nevyhnutné? Nielen v samotnom chemickom
CVIČENIE 1 : ZÁKLADNÉ VÝPOČTY PRAVDEPODOBNOSTI
 CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
CVIČENIE : ZÁKLDNÉ VÝOČTY RVDEODOBNOSTI. KLSICKÁ DEFINÍCI RVDEODOBNOSTI ríklad : ká je pravdepodobnosť, že pri hode kockou padne číslo resp. padne nepárne číslo? jav, kedy padne číslo B jav, že padne nepárne
Total Commander. Základné nastavenia
 je program, ktorý patrí k nadstavbovým programom OS. Jeho použitie je podobné ako u prieskumníka. Používa sa na jednoduchú prácu s adresármi (zložka, priečinok, folder) a súbormi. prezerať priečinky vyrobiť
je program, ktorý patrí k nadstavbovým programom OS. Jeho použitie je podobné ako u prieskumníka. Používa sa na jednoduchú prácu s adresármi (zložka, priečinok, folder) a súbormi. prezerať priečinky vyrobiť
Hromadná korešpondencia v programe Word Lektor: Ing. Jaroslav Mišovych
 Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
Hromadná korešpondencia v programe Word 2010 Lektor: Ing. Jaroslav Mišovych Obsah Čo je hromadná korešpondencia Spustenie hromadnej korešpondencie Nastavenie menoviek Pripojenie menoviek k zoznamu adries
1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69
 Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Typové úlohy z matematiky - PS EGJT LM - 8-ročné bilingválne štúdium Bez použitia kalkulačky 1. Otec, mama a dcéra majú spolu 69 rokov. Koľko rokov budú mať spolu o 7 rokov? a) 76 b) 90 c) 83 d) 69 2.
Blokové a prúdové šifry
 Informačná bezpečnosť 2, jar 2015 Blokové a prúdové šifry Ján Karabáš Blokové šifry a dlhé správy Bloková šifra je vhodná pre zašifrovanie iba jedného, relatívne krátkeho bloku Blok je skupina znakov (otvorenej
Informačná bezpečnosť 2, jar 2015 Blokové a prúdové šifry Ján Karabáš Blokové šifry a dlhé správy Bloková šifra je vhodná pre zašifrovanie iba jedného, relatívne krátkeho bloku Blok je skupina znakov (otvorenej
Verifikácia a falzifikácia
 Hypotézy Hypotézy - výskumný predpoklad Prečo musí mať výskum hypotézu? Hypotéza obsahuje vlastnosti, ktoré výskumná otázka nemá. Je operatívnejšia, núti výskumníka odpovedať priamo: áno, alebo nie. V
Hypotézy Hypotézy - výskumný predpoklad Prečo musí mať výskum hypotézu? Hypotéza obsahuje vlastnosti, ktoré výskumná otázka nemá. Je operatívnejšia, núti výskumníka odpovedať priamo: áno, alebo nie. V
Lineárne nerovnice, lineárna optimalizácia
 Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
PLASTOVÉ KARTY ZÁKAZNÍKOV
 PLASTOVÉ KARTY ZÁKAZNÍKOV OBSAH 1 Plastové karty základné informácie... 1 2 Distribúcia plastových kariet zákazníkom... 1 2.1 Jednorázová hromadná distribúcia kariet... 1 2.2 Pravidelná distribúcia plastových
PLASTOVÉ KARTY ZÁKAZNÍKOV OBSAH 1 Plastové karty základné informácie... 1 2 Distribúcia plastových kariet zákazníkom... 1 2.1 Jednorázová hromadná distribúcia kariet... 1 2.2 Pravidelná distribúcia plastových
Na aute vyfarbi celé predné koleso na zeleno a pneumatiku zadného kolesa vyfarbi na červeno.
 Kružnica alebo kruh Aký je rozdiel medzi kružnicou a kruhom si vysvetlíme na kolese auta. Celé koleso je z tohto pohľadu kruh. Pneumatika je obvod celého kolesa obvod kruhu a obvod kruhu nazývame inak
Kružnica alebo kruh Aký je rozdiel medzi kružnicou a kruhom si vysvetlíme na kolese auta. Celé koleso je z tohto pohľadu kruh. Pneumatika je obvod celého kolesa obvod kruhu a obvod kruhu nazývame inak
Manuál na prácu s databázou zmlúv, faktúr a objednávok Mesta Martin.
 Manuál na prácu s databázou zmlúv, faktúr a objednávok Mesta Martin. Cieľom databázy zmlúv, faktúr a objednávok Mesta Martin je zverejnenie uvedených záznamov v zmysle ustanovení zákona č. 211/2000 Z.z.
Manuál na prácu s databázou zmlúv, faktúr a objednávok Mesta Martin. Cieľom databázy zmlúv, faktúr a objednávok Mesta Martin je zverejnenie uvedených záznamov v zmysle ustanovení zákona č. 211/2000 Z.z.
To bolo ľahké. Dokážete nakresliť kúsok od prvého stromčeka rovnaký? Asi áno, veď môžete použiť tie isté príkazy.
 Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Opakuj a pomenuj Nakreslime si ovocný sad Príklad 1 Pomocou príkazového riadku skúste s korytnačkou nakresliť ovocný stromček. Vaša postupnosť príkazov sa možno podobá na nasledujúcu:? nechfp "hnedá? nechhp
Matematika pre tretiakov. Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp
 Matematika pre tretiakov Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp INFOSERVIS Prezentácia je dostupná na www.aitec.sk Otázky dávajte aj priebežne. Stíšte si, prosím,
Matematika pre tretiakov Ako reaguje séria učebných materiálov M. Belica a J. Striežovskej na zmeny v išvp INFOSERVIS Prezentácia je dostupná na www.aitec.sk Otázky dávajte aj priebežne. Stíšte si, prosím,
MANUÁL K TVORBE CVIČENÍ NA ÚLOHY S POROZUMENÍM
 MANUÁL K TVORBE CVIČENÍ NA ÚLOHY S POROZUMENÍM Cvičenia na úlohy s porozumením si vieme pre žiakov vytvoriť v programe, ktorý stiahneme zo stránky http://www.education.vic.gov.au/languagesonline/games/comprehension/index.htm.
MANUÁL K TVORBE CVIČENÍ NA ÚLOHY S POROZUMENÍM Cvičenia na úlohy s porozumením si vieme pre žiakov vytvoriť v programe, ktorý stiahneme zo stránky http://www.education.vic.gov.au/languagesonline/games/comprehension/index.htm.
Aritmetické operácie v rôznych číselných sústavách. Ľudmila MACEKOVÁ, KEMT-FEI-TUKE, sep. 2017
 111010110 Aritmetické operácie v rôznych číselných +110111001 sústavách 1110001111 Ľudmila MACEKOVÁ, KEMT-FEI-TUKE, sep. 2017 Plán Prevody medzi ČS Zobrazenie informácií v ČS: - priamy kód - inverzný kód
111010110 Aritmetické operácie v rôznych číselných +110111001 sústavách 1110001111 Ľudmila MACEKOVÁ, KEMT-FEI-TUKE, sep. 2017 Plán Prevody medzi ČS Zobrazenie informácií v ČS: - priamy kód - inverzný kód
Návrh postupu pre stanovenie počtu odborných zástupcov na prevádzkovanie verejných vodovodov a verejných kanalizácií v správe vodárenských spoločnosti
 1 Návrh postupu pre stanovenie počtu odborných zástupcov na prevádzkovanie verejných vodovodov a verejných kanalizácií v správe vodárenských spoločnosti Oprávnenie prevádzkovať verejný vodovod alebo verejnú
1 Návrh postupu pre stanovenie počtu odborných zástupcov na prevádzkovanie verejných vodovodov a verejných kanalizácií v správe vodárenských spoločnosti Oprávnenie prevádzkovať verejný vodovod alebo verejnú
Multiplexor a demultiplexor
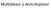 Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ. Grafy
 Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ Grafy Graf efektívne vizuálne nástroje dáta lepšie pochopiteľné graf môže odhaliť trend alebo porovnanie zobrazujú
Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ Grafy Graf efektívne vizuálne nástroje dáta lepšie pochopiteľné graf môže odhaliť trend alebo porovnanie zobrazujú
Potrebujem: plastelína, tabuľa, kriedy, papieriky veľkosti A5, pastelky, ceruzky, lepiaca páska, nožnice
 Autor: Mgr. Sláva Žilková, ZŠ s MŠ Hriňová, Školská 1575, 962 05, Hriňová Cesta na kurikulum: PREDMET ROČNÍK TEMATICKÝ CELOK Biológia 5. ročník ZŠ Vodný ekosystém Minutáž: 1 vyučovacia hodina Potrebujem:
Autor: Mgr. Sláva Žilková, ZŠ s MŠ Hriňová, Školská 1575, 962 05, Hriňová Cesta na kurikulum: PREDMET ROČNÍK TEMATICKÝ CELOK Biológia 5. ročník ZŠ Vodný ekosystém Minutáž: 1 vyučovacia hodina Potrebujem:
Formuláre PowerPoint MGR. LUCIA BUDINSKÁ,
 Formuláre PowerPoint MGR. LUCIA BUDINSKÁ, 30.11.2016 Formuláre https://docs.google.com/forms/u/0/ Online formulár Správa výsledkov Google vám sám vytvorí tabuľku s odpoveďami, alebo dokonca aj grafy Možnosť
Formuláre PowerPoint MGR. LUCIA BUDINSKÁ, 30.11.2016 Formuláre https://docs.google.com/forms/u/0/ Online formulár Správa výsledkov Google vám sám vytvorí tabuľku s odpoveďami, alebo dokonca aj grafy Možnosť
Modré obrázkové slová skladanie slov z písmen
 Modré obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Modré obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Návod na používanie súboru na vyhodnotenie testov všeobecnej pohybovej výkonnosti
 Návod na používanie súboru na vyhodnotenie testov všeobecnej pohybovej výkonnosti Na overenie trénovanosti hráčov sa o.i. vykonávajú testy všeobecnej pohybovej výkonnosti. Z hľadiska vyhodnotenia je potrebné
Návod na používanie súboru na vyhodnotenie testov všeobecnej pohybovej výkonnosti Na overenie trénovanosti hráčov sa o.i. vykonávajú testy všeobecnej pohybovej výkonnosti. Z hľadiska vyhodnotenia je potrebné
7.1 Návrhové zobrazenie dotazu
 7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
Riešenie cvičení z 3. kapitoly
 Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Import Excel Univerzál
 Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Import Excel Univerzál PRÍKLAD Ako jednoducho postupova pri importe akéhoko vek súboru z MS Excel do programu CENKROS plus, ktorý má podobu rozpo tu (napr. rozpo et vytvorený v inom programe)? RIEŠENIE
Dell S2718H/S2718HX/S2718HN/ S2718NX Dell Display Manager Návod na obsluhu
 Dell S2718H/S2718HX/S2718HN/ S2718NX Dell Display Manager Návod na obsluhu Model: S2718H/S2718HX/S2718HN/S2718NX Regulačný model: S2718Hx/S2718Nx POZNÁMKA: POZNÁMKA označuje dôležité informácie, ktoré
Dell S2718H/S2718HX/S2718HN/ S2718NX Dell Display Manager Návod na obsluhu Model: S2718H/S2718HX/S2718HN/S2718NX Regulačný model: S2718Hx/S2718Nx POZNÁMKA: POZNÁMKA označuje dôležité informácie, ktoré
OBSAH. 1. Základné pojmy informatiky 2. Digitalizácia 3. Rastrová (=bitmapová) grafika. 4. Vektorová grafika
 1. Základné pojmy informatiky 2. Digitalizácia 3. Rastrová (=bitmapová) grafika Princíp ukladania informácie Rastrové formáty obrázkov 4. Vektorová grafika OBSAH Princíp ukladania informácie Rastrové formáty
1. Základné pojmy informatiky 2. Digitalizácia 3. Rastrová (=bitmapová) grafika Princíp ukladania informácie Rastrové formáty obrázkov 4. Vektorová grafika OBSAH Princíp ukladania informácie Rastrové formáty
Informatika a jej jednotlivé oblastí
 Informatika a jej jednotlivé oblastí Vedné disciplíny, ktoré sa podieľali na vzniku informatiky Význačné udalosti vývoja informatiky do roku 1944 Abakus (počítadlo) Pascalína Kalkulačka (Leibnitz) Jcquard
Informatika a jej jednotlivé oblastí Vedné disciplíny, ktoré sa podieľali na vzniku informatiky Význačné udalosti vývoja informatiky do roku 1944 Abakus (počítadlo) Pascalína Kalkulačka (Leibnitz) Jcquard
SKLADOVÁ INVENTÚRA 1 VYTVORENIE INVENTÚRY. 1.1 Nastavenie skladovej inventúry
 SKLADOVÁ INVENTÚRA Skladové inventúry umožňujú vyrovnanie evidovaného stavu zásob so skutočným fyzicky zisteným stavom. Pri inventúre vznikajú inventúrne rozdiely medzi fyzickým a evidenčným stavom: kladné
SKLADOVÁ INVENTÚRA Skladové inventúry umožňujú vyrovnanie evidovaného stavu zásob so skutočným fyzicky zisteným stavom. Pri inventúre vznikajú inventúrne rozdiely medzi fyzickým a evidenčným stavom: kladné
Názov: Osmóza. Vek žiakov: Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút.
 Názov: Osmóza Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút Vek žiakov: 14 16 rokov Úrovne práce s materiálom: Úlohy majú rôznu úroveň náročnosti.
Názov: Osmóza Témy a kľúčové slová: osmóza, koncentrácia, zber dát a grafické znázornenie. Čas na realizáciu: 120 minút Vek žiakov: 14 16 rokov Úrovne práce s materiálom: Úlohy majú rôznu úroveň náročnosti.
Matematika Postupnosti
 Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Pracovnoprávny vzťah závislá práca
 časť 9. diel 4. kapitola 1.1 str. 1 9.4.1.1 Pracovnoprávny vzťah závislá práca Definovanie pojmu závislá práca, tak ako vyplýva z ustanovenia 1 ods. 2 a 3 ZP, ako aj všeobecne upravený pojem zamestnanca,
časť 9. diel 4. kapitola 1.1 str. 1 9.4.1.1 Pracovnoprávny vzťah závislá práca Definovanie pojmu závislá práca, tak ako vyplýva z ustanovenia 1 ods. 2 a 3 ZP, ako aj všeobecne upravený pojem zamestnanca,
Ružové obrázkové slová skladanie slov z písmen
 Ružové obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Ružové obrázkové slová skladanie slov z písmen Obrázkové slová slúžia na skladanie slov podľa začiatočných písmeniek z obrázkov. Montessori postupuje od skladania slov k ich čítaniu. Keď sa dieťa naučí
Technická univerzita v Košiciach
 Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky Katedra elektroniky a multimediálnych telekomunikácií Multiwaveletová transformácia obrazu Študijný program: IE_Ing_D, MTel_Ing_D
Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky Katedra elektroniky a multimediálnych telekomunikácií Multiwaveletová transformácia obrazu Študijný program: IE_Ing_D, MTel_Ing_D
Studentove t-testy. Metódy riešenia matematických úloh
 Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Microsoft Project CVIČENIE 6 1
 Microsoft Project CVIČENIE 6 1 Príprava na realizáciu samostatného projektu Študenti sa rozdelia do 4-členných skupín (a menej členov). Jedna skupina = jedno zadanie = jedna téma. V zápočtovom týždni (alebo
Microsoft Project CVIČENIE 6 1 Príprava na realizáciu samostatného projektu Študenti sa rozdelia do 4-členných skupín (a menej členov). Jedna skupina = jedno zadanie = jedna téma. V zápočtovom týždni (alebo
Finančný manažment, finančná matematika a účtovníctvo
 MAAG maag.euba.sk Finančný manažment, finančná matematika a účtovníctvo Finančný ný manažment ment znamená maag.euba.sk riadenie finančných ných procesov v podnikoch a inštitúciách najrôznejšieho typu.
MAAG maag.euba.sk Finančný manažment, finančná matematika a účtovníctvo Finančný ný manažment ment znamená maag.euba.sk riadenie finančných ných procesov v podnikoch a inštitúciách najrôznejšieho typu.
Riešené úlohy Testovania 9/ 2011
 Riešené úlohy Testovania 9/ 2011 01. Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11. 57x12=684 684+11=695 Skúška: 695:12=57 95 11 01. 6 9 5 02. V sude je 1,5 hektolitra dažďovej
Riešené úlohy Testovania 9/ 2011 01. Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11. 57x12=684 684+11=695 Skúška: 695:12=57 95 11 01. 6 9 5 02. V sude je 1,5 hektolitra dažďovej
CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV
 CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV Táto časť sa venuje metódam štatistického výskumu súboru, pri ktorých sa zaoberáme jednotlivými štatistickými znakmi samostatne, bez toho, žeby sme
CHARAKTERISTIKA JEDNOROZMERNÝCH ŠTATISTICKÝCH SÚBOROV Táto časť sa venuje metódam štatistického výskumu súboru, pri ktorých sa zaoberáme jednotlivými štatistickými znakmi samostatne, bez toho, žeby sme
Textový editor WORD. Práca s obrázkami a automatickými tvarmi vo Worde
 Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Textový editor WORD Práca s obrázkami a automatickými tvarmi vo Worde WordArt WordArt je objekt, pomocou ktorého vieme vytvoriť text s rôznymi efektami. Začneme na karte Vložiť, kde použijeme ikonu WordArt.
Imagine. Popis prostredia:
 Priemerný človek si zapamätá približne: - 10 % z toho, čo číta, - 20 % z toho, čo počuje, - 30 % z toho, čo vidí v podobe obrazu, - 50 % z toho, čo vidí a súčasne počuje, - 70 % z toho čo súčasne vidí,
Priemerný človek si zapamätá približne: - 10 % z toho, čo číta, - 20 % z toho, čo počuje, - 30 % z toho, čo vidí v podobe obrazu, - 50 % z toho, čo vidí a súčasne počuje, - 70 % z toho čo súčasne vidí,
Šifrovanie, kódovanie, bit a byte, digitálne informácie. Kódovanie informácií v PC binárna (dvojková) číselná sústava
 Šifrovanie, kódovanie, bit a byte, digitálne informácie Šifry šifrovanie sa používa všade tam, kde treba utajiť obsah komunikácie. Existuje veľmi veľa metód na tajné šifrovanie (a protimetód na dešifrovanie).
Šifrovanie, kódovanie, bit a byte, digitálne informácie Šifry šifrovanie sa používa všade tam, kde treba utajiť obsah komunikácie. Existuje veľmi veľa metód na tajné šifrovanie (a protimetód na dešifrovanie).
Stredná priemyselná škola Poprad. Výkonové štandardy v predmete ELEKTROTECHNIKA odbor elektrotechnika 1.ročník
 Výkonové štandardy v predmete ELEKTROTECHNIKA odbor elektrotechnika 1.ročník Žiak vie: Teória I. ÚVOD 1. Význam a úloha elektrotechniky definovať pojem elektrotechnika charakterizovať príbuzné vedné disciplíny
Výkonové štandardy v predmete ELEKTROTECHNIKA odbor elektrotechnika 1.ročník Žiak vie: Teória I. ÚVOD 1. Význam a úloha elektrotechniky definovať pojem elektrotechnika charakterizovať príbuzné vedné disciplíny
KORUNOVAČNÁ BRATISLAVA MANUÁL LOGA VER. 1/2017
 VER. 1/2017 1. Úvod Tento manuál pojednáva o základných pravidlách použitia loga Korunovačná Bratislava (ďalej KB). Logo sa smie reprodukovať iba z digitálnej predlohy, ktorá je súčasťou tohto manuálu.
VER. 1/2017 1. Úvod Tento manuál pojednáva o základných pravidlách použitia loga Korunovačná Bratislava (ďalej KB). Logo sa smie reprodukovať iba z digitálnej predlohy, ktorá je súčasťou tohto manuálu.
Základy optických systémov
 Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Základy optických systémov Norbert Tarjányi, Katedra fyziky, EF ŽU tarjanyi@fyzika.uniza.sk 1 Vlastnosti svetla - koherencia Koherencia časová, priestorová Časová koherencia: charakterizuje koreláciu optického
Iracionálne rovnice = 14 = ±
 Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Užívateľská príručka systému CEHZ. Základné zostavy Farmy podľa druhu činnosti
 Užívateľská príručka systému CEHZ Základné zostavy Farmy podľa druhu činnosti Užívateľská príručka systému CEHZ... 1 Základné zostavy Farmy podľa druhu činnosti... 1 1.1. Farmy podľa druhu činnosti...
Užívateľská príručka systému CEHZ Základné zostavy Farmy podľa druhu činnosti Užívateľská príručka systému CEHZ... 1 Základné zostavy Farmy podľa druhu činnosti... 1 1.1. Farmy podľa druhu činnosti...
Odkazy na pravidlá sú podľa aktuálnych pravidiel na stránke Slovenská verzia pravidiel sa pripravuje
 Vybavenie strelnice Odkazy na pravidlá sú podľa aktuálnych pravidiel na stránke www.worldarchery.org. Slovenská verzia pravidiel sa pripravuje Prečo sa robí kontrola strelnice? Musíme zabezpečiť aby všetky
Vybavenie strelnice Odkazy na pravidlá sú podľa aktuálnych pravidiel na stránke www.worldarchery.org. Slovenská verzia pravidiel sa pripravuje Prečo sa robí kontrola strelnice? Musíme zabezpečiť aby všetky
MEP ekonomika podniku učtovníctvo 1. časť Ekonomika podniku
 MEP ekonomika podniku učtovníctvo 1. časť Ekonomika podniku (časť: úvod do podvojného účtovníctva) - kolobeh hospodárských prostriedkov, - súvaha, výsledovka, - účtovníctvo, účet, - podvojná sústava účtovníctva,súvzťažné
MEP ekonomika podniku učtovníctvo 1. časť Ekonomika podniku (časť: úvod do podvojného účtovníctva) - kolobeh hospodárských prostriedkov, - súvaha, výsledovka, - účtovníctvo, účet, - podvojná sústava účtovníctva,súvzťažné
1. Gigabajty si hneď v prvom kroku premeníme na gigabity a postupne premieňame na bity.
 1 PRÍKLADY V INFORMATIKE: Skratky 1 : b bit B bajt kb kilobit kb kilobajt Mb megabit MB megabajt Gb gigabit GB gigabajt Tb terabit TB terabajt Tabuľka č. 1 1 B = 8 b 1 kb = 1 024 b = (1 024 : 8) B = 128
1 PRÍKLADY V INFORMATIKE: Skratky 1 : b bit B bajt kb kilobit kb kilobajt Mb megabit MB megabajt Gb gigabit GB gigabajt Tb terabit TB terabajt Tabuľka č. 1 1 B = 8 b 1 kb = 1 024 b = (1 024 : 8) B = 128
Ing. Jozef Klus KOMBINAČNÉ LOGICKÉ OBVODY
 Ing. Jozef Klus KOMBINAČNÉ LOGICKÉ OBVODY ÚVOD U týchto obvodov je výstup určený len kombináciou vstupných veličín. Hodnoty výstupných veličín nezávisia na predchádzajúcom stave logického obvodu kombinačný
Ing. Jozef Klus KOMBINAČNÉ LOGICKÉ OBVODY ÚVOD U týchto obvodov je výstup určený len kombináciou vstupných veličín. Hodnoty výstupných veličín nezávisia na predchádzajúcom stave logického obvodu kombinačný
DANE A DAŇOVÝ SYSTÉM V SR
 DANE A DAŇOVÝ SYSTÉM V SR Na tomto svete nie je nič isté, iba dane a smrť. Benjamin Franklin, 1789 DAŇ Povinná, zákonom stanovená platba, ktorú odvádza daňový subjekt, t.j. fyzická alebo právnická osoba,
DANE A DAŇOVÝ SYSTÉM V SR Na tomto svete nie je nič isté, iba dane a smrť. Benjamin Franklin, 1789 DAŇ Povinná, zákonom stanovená platba, ktorú odvádza daňový subjekt, t.j. fyzická alebo právnická osoba,
Ako započítať daňovú licenciu
 Ako započítať daňovú licenciu 1. Zápočet daňovej licencie a jej evidencia... 1 2. Započítanie DL v plnej sume... 1 3. Nárok na čiastočný zápočet DL... 2 4. Bez nároku na zápočet, daň < DL... 3 5. Bez nároku
Ako započítať daňovú licenciu 1. Zápočet daňovej licencie a jej evidencia... 1 2. Započítanie DL v plnej sume... 1 3. Nárok na čiastočný zápočet DL... 2 4. Bez nároku na zápočet, daň < DL... 3 5. Bez nároku
Štruktúra údajov pre kontajner XML údajov 1. Dátové prvky pre kontajner XML údajov
 Štruktúra údajov pre kontajner XML údajov 1. Dátové prvky pre kontajner XML údajov D.4 Kontajner XML údajov (XMLDataContainer) Skrátená forma popisu súčastí dátového prvku Kontajner XML údajov (XMLDataContainer)
Štruktúra údajov pre kontajner XML údajov 1. Dátové prvky pre kontajner XML údajov D.4 Kontajner XML údajov (XMLDataContainer) Skrátená forma popisu súčastí dátového prvku Kontajner XML údajov (XMLDataContainer)
Model epidemickej choroby (SIR model)
 Slovenská technická univerzita v Bratislave Fakulta elektrotechniky a informatiky Katedra matematiky Študentská Vedecká a Odborná Činnosť Model epidemickej choroby (SIR model) autor: konzultant: Pavol
Slovenská technická univerzita v Bratislave Fakulta elektrotechniky a informatiky Katedra matematiky Študentská Vedecká a Odborná Činnosť Model epidemickej choroby (SIR model) autor: konzultant: Pavol
Matice. Matica typu m x n je tabuľka s m riadkami a n stĺpcami amn. a ij. prvok matice, i j udáva pozíciu prvku
 Matice Matice Matica typu m x n je tabuľka s m riadkami a n stĺpcami a11 a12... a1 n a21 a22... a2n............ am1 am2... amn a ij prvok matice, i j udáva pozíciu prvku i- čísluje riadky J- čísluje stĺpce
Matice Matice Matica typu m x n je tabuľka s m riadkami a n stĺpcami a11 a12... a1 n a21 a22... a2n............ am1 am2... amn a ij prvok matice, i j udáva pozíciu prvku i- čísluje riadky J- čísluje stĺpce
Test. Ktorý valec by ste použili? A. Jednočinný valec B. Dvojčinný valec. Odpoveď:
 Test Týmto testom môžete zistiť, či sú Vaše základné znalosti o pneumatickom riadení postačujúce pre nadstavbový seminár P121, alebo je pre Vás lepšie absolvovať základný seminár EP111. Test je rýchly,
Test Týmto testom môžete zistiť, či sú Vaše základné znalosti o pneumatickom riadení postačujúce pre nadstavbový seminár P121, alebo je pre Vás lepšie absolvovať základný seminár EP111. Test je rýchly,
Zmena skupenstva látok
 1. Keď má sústava v rovnovážnom stave vo vrtkých častiach rovnaké fyzikálne a chemické vlastnosti, napr. rovnakú hustotu, štruktúru, rovnaké chemické zloženie, nazýva sa fáza. Prechod látky z jednej fázy
1. Keď má sústava v rovnovážnom stave vo vrtkých častiach rovnaké fyzikálne a chemické vlastnosti, napr. rovnakú hustotu, štruktúru, rovnaké chemické zloženie, nazýva sa fáza. Prechod látky z jednej fázy
Legislatívne zmeny týkajúce sa cyklistov od 1. novembra 2011
 Legislatívne zmeny týkajúce sa cyklistov od 1. novembra 2011 O 1. novembra vstúpili do platnosti novelizácie legislatívnych noriem 8/2009 a 9/2009 (Vyhláška Ministerstva vnútra Slovenskej republiky, ktorou
Legislatívne zmeny týkajúce sa cyklistov od 1. novembra 2011 O 1. novembra vstúpili do platnosti novelizácie legislatívnych noriem 8/2009 a 9/2009 (Vyhláška Ministerstva vnútra Slovenskej republiky, ktorou
Matematika test. Cesta trvala hodín a minút.
 GJH-Prima Test-16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 18 úloh a má 4 strany. Úlohy
GJH-Prima Test-16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Súčet Matematika test Na tento papier sa nepodpisuj. Na vypracovanie tejto skúšky máš čas 20 minút. Test obsahuje 18 úloh a má 4 strany. Úlohy
EDA Klient (príjem výsledkov z oddelení klinickej biochémie a mikrobiológie prostredníctvom internetu)
 Strana 1 z 6 EDA Klient (príjem výsledkov z oddelení klinickej biochémie a mikrobiológie prostredníctvom internetu) Prenos výsledkov z našich laboratórií k Vám lekárom je v dnešnej dobe zabezpečený nielen
Strana 1 z 6 EDA Klient (príjem výsledkov z oddelení klinickej biochémie a mikrobiológie prostredníctvom internetu) Prenos výsledkov z našich laboratórií k Vám lekárom je v dnešnej dobe zabezpečený nielen
je zmena operácie ktorou z nelineárneho systému môže spraviť lineárny. Týmto krokom sme získali signál ktorý môžeme spracovať pomocou LDKI sústavy.
 Homomorfné systémy Homomorfné systémy sú nelineárne systémy, preto pri nich neplatí princíp superpozície a proporcionality tak ako to je pri lineárnych systémoch. A vieme ich takto grafický znázorniť:
Homomorfné systémy Homomorfné systémy sú nelineárne systémy, preto pri nich neplatí princíp superpozície a proporcionality tak ako to je pri lineárnych systémoch. A vieme ich takto grafický znázorniť:
Návrh, implementácia a prevádzka informačného systému
 Návrh, implementácia a prevádzka informačného systému Návrh Výsledkom analýzy je niekoľko modelov budúceho systému. Tie popisujú, čo sa bude v IS evidovať a čo sa bude s údajmi robiť. Modely nezohľadňujú
Návrh, implementácia a prevádzka informačného systému Návrh Výsledkom analýzy je niekoľko modelov budúceho systému. Tie popisujú, čo sa bude v IS evidovať a čo sa bude s údajmi robiť. Modely nezohľadňujú
11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami
 11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami I. Úlohy na úvod 1. a) Zaokrúhlite nadol, b) zaokrúhlite nahor, c) zaokrúhlite číslo 5,47 na desatiny, číslo 483,203 na jednotky, číslo 2 996 789
11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami I. Úlohy na úvod 1. a) Zaokrúhlite nadol, b) zaokrúhlite nahor, c) zaokrúhlite číslo 5,47 na desatiny, číslo 483,203 na jednotky, číslo 2 996 789
Výstupný test projektu KEGA pre 7. roč. ZŠ. Verzia A
 Výstupný test projektu KEGA pre 7. roč. ZŠ Verzia A Meno: Problém U1 U2 Súčet 1 Zákusky pre hostí 2 Terminovaný vklad 3 Doprava po Ukrajine 4 Preprava nákladu 5 Krémy na tvár výhodne 6 Evidenčné čísla
Výstupný test projektu KEGA pre 7. roč. ZŠ Verzia A Meno: Problém U1 U2 Súčet 1 Zákusky pre hostí 2 Terminovaný vklad 3 Doprava po Ukrajine 4 Preprava nákladu 5 Krémy na tvár výhodne 6 Evidenčné čísla
