8 Dynamika soustav těles-metoda uvolňování

Transkript

1 97 8 Dynk soustv těles-etod uvolňování Vyšetřování pohybu soustv těles vázných knetcký dvojce vyšetřování dynckých slových únků působících n jednotlvá těles soustv tvoří zákld dynky stojů echnsů. Úlohy jsou v podsttě dvojího typu : V úlohách vlstní dynky vyšetřujee pohyb soustvy těles n zákldě dných kních slových únků. Ptří se vyšetřování ozběhu doběhu stojů neovnoěnost chodu stojů etody snžování neovnoěnost chodu stojů. V úlohách knetosttky se zpvdl vychází ze zdného (poždovného pohybu. Vyšetřují se kní slové únky potřebné po dosžení popř. udžení zdného pohybu ekce v knetckých vzbách vntřní slové únky potřebné po denzování. Řešení pohybu soustv těles lze řešt v zásdě zákldní způsoby: / Uvolňování jednotlvých těles ze soustvy sestvení pohybových ovnc (ť jž Newtonový nebo D Alebetový způsobe po jednotlvá těles. Vzby ez tělesy se přto zohlední poocí příslušných knetckých vzthů. / Použtí věty o zěně knetcké enege zákonů zchování enege hybnost oentu hybnost tk jk byl zňovány po soustvu hotných bodů. / Použtí etod nlytcké echnky tj. plkcí pncpu vtuální páce etodou edukce hotových slových veln obecné ovnce dynky Lgngeových ovnc. pod. 8. Sestvování pohybových ovnc po ovnné soustvy s jední stupně volnost etod uvolňování převádí řešení dynckých úloh soustvy těles n řešení dynckých úloh jednotlvých uvolněných těles. Přto se vychází buď z. Newtonov zákon nebo z d Alebetov pncpu. Pncp etody uvolňování ůžee vyjádřt následující větou : Těleso uvolněné ze soustvy těles (ve kteé je uvolněné těleso vázáno s osttní tělesy knetcký dvojce se pohybuje jko těleso volné n kteé působí vnější (kní síly vzební (ekní síly od osttních těles (vetně áu. etodu uvolňování hlvně používáe v přípdě kdy nás zjíjí hodnoty ekcí (npř. jsou-l od těchto hodnot závslé psvní odpoy. Pohyb uvolněných těles je popsán souřdnce kteé závsí n pohybu jednotlvých těles. Nejstější přípde soustv jsou ovnné soustvy s jední stupně volnost. V toto přípdě pohyb soustvy je jednoznně uen jen jednou souřdncí. N zátku řešení úlohy vybeee jednu souřdnc jko zákldní (zobecněnou ozníe j q. Následně vyjádříe všechny souřdnce x y působšť kních sl F všechn pootoení φ kních působících oentů poocí těchto souřdnce tj. nleznee vzthy x (qt y (qt φ (qt. Podevování těchto závslostí podle su ůžee vypoítt ychlost zychlení xɺ ( q qɺ t ɺɺ x ( q qɺ qɺɺ t yɺ ( q qɺ qɺɺ t ɺɺ y ( q qɺ t ϕɺ ( q qɺ t ϕɺɺ ( q qɺ t (

2 98 Jestlže do pohybových ovnc kždého uvolněného těles dosdíe z všechny ychlost všechn zychlení příslušné závslost (8. vylouíe ekní slové únky dostnee vlstní pohybovou ovnc soustvy ve tvu dfeencální ovnce duhého řádu f ( F F q qɺ qɺɺ t 0 (8. x kde F F esp. z jsou souřdnce kních sl esp. kních oentů. x y y Ze složkových pohybových ovnc psných do sěu teny k tjekto pohybu středu hotnost popř. z oentových ovnc k ose otáení je ožné přío řešt pohyb bodů popř. těles těto pohybový ovncí budee dále říkt hlvní pohybové ovnce. Aby bylo ožné tyto hlvní ovnce hned získt je nutné vhodně zvolt použtý souřdný systé (npř. přozený souřdný systé s os ovnoběžný s tenou noálovou dáhy těžště. U soustv bez psvních odpoů pk jsou hlvní pohybové ovnce záoveň ovnce vlstní tj. neobshují ekce. Z tkové soustvy vlstních pohybových ovnc je jž pk poěně sndné zjstt poocí vzthů (8. vlstní pohybovou ovnc po celou soustvu. U vzeb s psvní odpoy hlvní pohybové ovnce obshují ekce kteé uují velkost psvních odpoů (npř. hodnotu noálové složky tlku u sykového tření. V toto přípdě z hlvních pohybových ovnc dostnee ovnce vlstní pokud všechny vzební síly se v nch vyskytující vyjádříe z osttních pohybových ovnc poocí sl kních. -98-

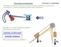
3 99 Příkld 8.. Vozdlo s příý pohone zdní hncí nápvy (ob.8. á kceleovt se zychlení. Vypoítejte hncí oent n hncí nápvě v závslost n zychlení xálně ožné zychlení př ozjezdu vozdl. Je dán hotnost kosée 900 kg hotnost nápv 50 kg oenty setvnost nápv geoetcké 5 kg velny 075 e e h 05. Psvní odpoy znedbejte. x R y T g R y R x R x R y α R y α T R x T R x N N S g h α T T P α N N e e e Ob.8.. Uvolnění vozdl s příý pohone zdní hncí nápvy. -99-

4 00 Řešení. Po tř uvolněná těles (vz. ob.8. lze plkcí d Alebetov pncpu sestvt devět podínek ovnováhy po neznáé složky vntřních ekcí R x R y R x R y v otních knetckých vzbách ez nápv koséí po složky vnějších ekcí N T N T ve vlvých knetckých vzbách hncí oent. Oezíe-l se n výpoet hncího oentu stí sestvt hlvní pohybové ovnce uvolněných těles tj. složkovou ovnc po těleso ve sěu pohybu R R ( x x 0 oentové ovnce po nápvy k pólů vlení α ( R 0 (b x ( R α 0. (c x Z zobecněnou souřdnc zvole x. Soustv á z předpokldu vlení kol (tj. po T < f0 N T < f0 N kde 0 α kol následující výz kde ϕ je úhel pootoení kol (pltí f je sountel dheze konstntní převod z něhož vyplývá po úhlové zychlení x ϕ α α (d ɺ x R x z hlvní pohybové ovnce (b poocí ( (c s ohlede n (d dostnee ɺ ϕ α. Vylouení ekce. (e Největšího ožného zychlení př ozjezdu se dosáhne př plné využtí dheze ez koly hncí nápvy vozovkou tj. př splnění podínky T f0 N Tx T (f kde f 0 je sountel dheze ez koly hncí nápvy vozovkou. Ze složkové ovnce nápvy ve sěu pohybu vozdl z ovnc ( (c vyplývá Rx. (g T Z oentové podínky ovnováhy po celou soustvu k pólu P kol (vz. ob.8. vypoítáe noálovou složku ekce g e h. (h e N Z podínky (f poto plyne výz po xální ožné zychlení vozdl -00-

5 0 x f0 g e. e e f0 h f 0 kde. Hncí oent odpovídjící touto zychlení je Po f je f0 g e. e e f0 h f 0 x x 6 s 5 N x. ( ( Příkld 8.. Vyšetřete pohyb těles uloženého n válcích jsou-l geoetcké hotnostní velny těles válců dány (ob.8.. x β T e N g T N N T R x R y g α -0- Ob.8.. Uvolnění jednotlvých těles př vyšetřování pohybu těles.

6 0 Řešení. Po tř uvolněná těles ůžee sestvt devět podínek dyncké ovnováhy po neznáé složky vntřních ekcí N T N T vnějších ekcí R x R y R x R y po zychlení posuvného pohybu těles po válcích. Složkové ovnce těles jí tv g sn β T T 0 N g cos β 0. N Složkové oentová ovnce k ose otáení válce : T g sn β R 0 x ( R y g cos β N 0 (b T N e α 0 složkové oentová ovnce ose otáení válce : T g sn β R 0 x R y g cos β N 0 (c Vzhlede k podínká oenty epového tření výzy T N e α 0. R y >> R x y R x R >> kteé pltí po lý úhel β poxujee f R 0 R ( y x f R 0 R. ( y x Soustv á konstntní převod (odvlování těles po válcích z něhož plyne (d α. (e Ze soustvy ovnc (b esp. (c vylouení složek ekcí tenou složku T esp. T vntřní ekce výz R x y R esp. R x R y plyne po T N ( e f f g ( cos β 0 sn β α (f 0 f T N ( e f f g ( cos β 0 sn β α. (g 0 f Doszení (f (g do pvní ovnce ( s uvážení vzthu (e obdžíe po zychlení těles následující výz g (( 0 f sn β ( e f cos β f g ( cos β 0 sn β ( 0 f. -0-

7 0 Řešení v uvedené tvu je spávné jen pokud je splněn podínk odvlování těles po válcích tj. pokud pltí T f0 N f0 N T kde f 0 je sountel dheze ez tělese válc. Příkld 8.. Sestvte pohybovou ovnc tyřkloubového echnsu využtí převodu devce převodu ez hnnou klkou hncí klkou (vz. ob.8.. N klku působí hncí oent n klku zátěžný oent. Hotnost těhlce znedbejte. * S. S ϕ π ϕ ϕ. ϕ ϕ ϕ L ϕ α α Ob 8.. K sestvení pohybové ovnce tyřkloubového echnsu. Řešení. Z nezávslou souřdnc zvole úhel ϕ ntoení hncí klky. Z geoetckých petů L vyplývá převod p ( ϕ devce převodu p ( ϕ α ( ( ϕ ω α p ϕ p. Úhlové zychlení hnné klky je podle (.. Př znedbání hotnost těhlce je jí přenášená osová síl S. Klky otují neovnoěně kole svých hlvních os setvnost. Hlvní pohybové ovnce uvolněných klk jí tv α S sn ( ϕ ϕ 0 sn ( ϕ ϕ α 0. S * V pohonech ůzných stojů bývá tyřkloubový echnsus vřzen ez hncí ást pohonu hnnou ást pohonu. Pokud v hnné nebo hncí ást pohonu nejsou vřzeny dlší převodové echnsy lze obě ást pohonu edukovt n příslušné klky. Znedbání hotnost těhlce je pk opodsttněné neboť oenty setvnost jsou velké. -0-

8 0 Vylouení osové síly S dostnee pohybovou ovnc echnsu ve tvu sn ( ϕ ϕ p ( ϕ α sn ( ϕ ϕ sn ( ϕ ϕ p ( ϕ ω sn ( ϕ ϕ sn ( ϕ ϕ sn ( ϕ ϕ ( ϕ přež využjee zdvhových závslostí ( ϕ ϕ ϕ tyřkloubového echnsu npř. etodou ozkldu v pólu eltvního pohybu výz p ( ϕ Pohybovou ovnc ůžee poto zpst též ve tvu sn ( ϕ ϕ sn ( ϕ ϕ. p ( ϕ ] α p ( ϕ p ( ϕ ω ( ϕ. [ p odvozených v knetce. Z knetckého řešení P vyplývá po převod p ϕ Pohybová ovnce není řeštelná v uzvřené tvu lze j řešt někteou z nueckých etod ntegce. V někteých přípdech (npř. př espektování někteých přípdů psvních odpoů nebo u soustv s poěnný převody je pohybová ovnce (8. nelneání. Její řešení je pk nutné (ž n specální přípdy povést nueckou ntegcí s uvážení příslušných poáteních podínek. Výsledke ntegce pohybové ovnce (8. jsou závslost q ( t qɺ ( t qɺ( ɺ t kteé popsují pohyb v souřdnc q. Vyšetření pohybu osttních lenů soustvy těles pk dostnee ze zdvhových závslostí x ( q y ( q ϕ ( q uvážení vzthů (8.. V úlohách kteé vedou k řešení nelneáních lgebckých ovnc s nelnetou způsobenou psvní odpoy ůžee plkovt tení etodu. Její pncp spoívá ve vyjádření psvních odpoů v pohybových ovncích ze znáých složek ekcí vypoítných v předcházející tení koku. Pvní koke je řešení př znedbání těch psvních odpoů jež vedou k nelnetě. Potože psvní odpoy jsou zpvdl eltvně lé tení etod ychle konveguje. Vzhlede k ychlé konvegenc tení etody k nepřesnéu vyjádření petů psvních odpoů v px zpvdl vyhovuje řešení v pvních dvou ž třech kocích. Vysvětlení etody uvolňování s uvážení nelneáních psvních odpoů s ukážee n následující příkldu 8.. ( -0-

9 05 Příkld 8. Zdvhcí echnsus je ozbíhán konstntní hncí oente. Převod je elzován ozubený koly s úhle ozubení β. Uvžujte tření v epech α R y α α R x N g β α N R y R x g α F F α F y 5 S 5 g S 5 g g Ob. 8.. Zdvhcí echnsus sestvení pohybových ovnc etodou uvolnění. -05-

10 06 ɺy Z nezávslou souřdnc zvole vetkální souřdnc y středu volné kldky zveďe jeho zychlení. Potože zdvhcí echnsus je echnse s konstntní převody úhlová zychlení uvolněných těles jsou typu α ( konkétně ' α α α. ( Aplkcí d Alebetov pncpu sestvíe pohybové ovnce uvolněných těles. Hotnost závěsného háku přto znedbáe. Př espektování oentů epových tření pohybové ovnce jí následující tv po těleso : R R y x N sn β 0 N cos β g 0 N cos β α 0 (b po těleso : po těleso : po těleso 5 : R N sn β 0 x R N cos β F g 0 y N cos β F α 0 ' F F S ( g ( F F α 0 0 (c (d S g 5 0 Jk je znáo ze sttky oenty epového tření jsou dány výzy (. (e f R R x y f R R x y (f f S kde f jsou sountele epových tření příslušné poloěy epů. Soustv ptnáct ovnc ( ž (f obshuje osnáct neznáých veln. Vlstní pohybová ovnce po přípd bez psvních odpoů (pvní kok řešení vyplývá z pět hlvních pohybových ovnc uvolněných těles á tv ( ' 5 ( g ' ' odkud plyne -06-

11 07 ( 5 g ' ' 5 ' '. (g Střed volné kldky se závží se tedy ozbíhá z předpokldu g > 0 > g 5 5 ' ' ovnoěně zychlený pohybe. Z výzů ( vyplývjí úhlová zychlení z pohybových ovnc (b ž (e po ekce vzeb. Př espektování oentů epového tření je soustv ovnc ( ž (f v důsledky f 0 pvních dvou ovnc v (f nelneání. Je poto nuecky výhodné vyjádřt složky ekcí v (f po výpoet oentů epového tření n zákldě řešení bez psvních odpoů z hlvních pohybových ovnc jednotlvých uvolněných těles vypoítt zychlení v duhé koku řešení g 5 ' ' ' ' 5 ' '. (h Z výzů ( vyplývjí úhlová zychlení z pohybových ovnc (b ž (e ekce vzeb v duhé koku řešení. U soustv s poěnný převode s výhodou využíváe převodových funkcí (převodů zjštěných poocí knetky p q d x d q ( esp. p d ϕ q d q ( kde x jsou souřdnce posuvného pohybu ϕ jsou úhlové výchylky otního pohybu těles. Devce podle nezávslé souřdnce q dostnee devce převodů d p ( q d x p d q d q d p ( q d q d ϕ d q ( q esp. p q (. Složky ychlostí zychlení posuvného pohybu těles esp. úhlové ychlost úhlová zychlení otního pohybu těles jsou dány vzoc v d x d q xɺ p ( q qɺ d q d t ɺ ɺɺ d p ( q d q d q ɺ d t d qɺ d t v x q p ( q p ( q q p ( q q ɺɺ ɺ (8. d x d q ɺ ϕ p ( q qɺ d q d t ω d p ( q α ɺ ω ɺɺ ϕ d q d q d t d qɺ qɺ p ( q d t p ( q qɺɺ p ( q qɺ. (8.b -07-

12 08 Knetosttcké řešení soustv v přípdě nelneáních převodů s ukážee n klkové echnsu Příkld 8.5. Uete slovou dvojc o oentu n klce po udžení konstntní úhlové ychlost ω klky výpoet ekcí ve vzbách. Předpokládejte dnou hncí sílu F ( ϕ působící n píst. Psvní odpoy tíhové síly znedbejte. e e A y x ω konst. T α C ϕ ϕ B F ( ϕ x e R Ay R Ax α R Ax R Ay - x T R By S F - y T R By R Bx R Cx F ( ϕ B R Bx - R Cy N Ob.8.5. Knetosttcké řešení klkového echnsu. -08-

13 09 Po uení setvných únků n jednotlvé leny budee zřejě potřebovt vyjádřt zychlení pístu složky zychlení x y středu hotnost ojnce její úhlové zychlení α (vzhlede k áu nebo pístu otce. Z nezávslou souřdnc zvole úhel ϕ ntoení klky z její hozontální polohy. Aplkcí vzoců z (8. po qɺ ωɺ 0 dostnee Z knetckého nlytckého řešení vyplývá tudíž po převody pltí p p p ( ϕ ω p ( ϕ ω α p ( ϕ ω p ( ϕ ω. x ϕ cosϕ cosϕ λ λ ( ϕ ( csn λ snϕ kde d ϕ λ cosϕ d ϕ ( λ snϕ d ϕ λ ( λ snϕ ( ϕ d ϕ ( ( λ snϕ ( d x d ϕ λ snϕ sn ϕ e λ ϕ ( λ snϕ p ( d x d ϕ cos ϕ λ sn cosϕ λ ( ( λ snϕ ϕ ϕ. Souřdnce středu hotnost S ojnce v souřdncové soustvě ( C x y jsou x ϕ cos e cos y ϕ ϕ sn e sn ϕ odkud po dvojí devc podle su dostnee výzy po složky zychlení středu hotnost ojnce ve tvu x ω cosϕ e ( ω cosϕ α snϕ y ω snϕ e ( ω snϕ α cosϕ. Po vyjádření setvných únků n ojnc ozložíe její obecný ovnný pohyb ve středu hotnost zákldní ozklde n unášvý posuvný pohyb eltvní otní pohyb. Poto plkcí d Alebetov pncpu sestvíe podínky ovnováhy uvolněných těles (ob.8.. Npíšee je ve tvu vhodné po příý výpoet ekcí těleso (klk : S RC x RA x F cosϕ -09-

14 0 S RC y RA y F snϕ ( R snϕ R cosϕ A x A y kde je setvná síl působící n klku je vzdálenost těžště T klky od osy otce (bod S F ω C je hotnost klky ω je úhlová ychlost otáení klky. těleso (ojnce : R R A x B x x R A y R B y y R B y R B x e snϕ e ( x snϕ e cosϕ y cosϕ α těleso (píst : R B x F ( ϕ N R B y. Z předcházejících ovnc je zřejé že ekce oent po udžení konstntní úhlové ychlost ω klky jsou závslé nejen n hncí síle F ( ϕ le explctně n úhlu ϕ pootoení klky. Algotus nueckého řešení spoívá v postupné výpotu veln ϕ p p p p ω α ϕ s jstý koke ϕ v dné ozshu ntoení klky. x y B x R ž po ůzné úhly Z hledsk zjednodušení lgotu nueckého řešení je úelné nhdt ojnc dvě hotný body v epech A B koekní oente setvnost B k (tj. oente setvnost těles složeného ze bodůvz ob. 8.5b. A F SA A R Ax R Ay k α R By R Bx B F SB Ob.8.5b Nhzení ojnce dvě hotný body koekní oente -0-

15 Setvné únky n ojnc jsou pk ekvvlentně nhzeny setvný sl působící n hotné body setvnou dvojcí příslušející koekníu oentu setvnost (vz. ob... Z podínek ovnováhy uvolněné ojnce pk vyplývá R R A x A y R F F cosϕ B x B y SB SA SA R F snϕ R B y ( R B x F SB e snϕ α e cosϕ k kde F SA A ω SB B F jsou setvné síly působící n hotné body A. Podínky ovnováhy po uvolněná těles zůstávjí nezěněné. Algotus řešení se všk zjednoduší tí že odpdne výpoet veln ω x y. 8. Použtí vět o pohybu hotných bodů V někteých pobléech řešení pohybu soustv těles je výhodné použít věty o zěně knetcké enege celkové echncké enege hybnost oentu hybnost o pohybu středu hotnost. 8.. Použtí věty o zěně echncké enege Z předpokldu působení potencálových sl byl po hotné body ntegcí pohybových ovnc odvozen zákon zchování echncké enege Podle něj pltí W E ( q ɺ E ( q E ( q ɺ E ( q (8. k p k 0 p 0 Podevování tohoto vzthu podle su ůžee tedy zse dojít k ovnc pohybové dw de k de p 0 f ( qqq ɺɺɺ (8.b dt dt dt V techncké px sto všechny pcovní síly (vetně sl potencálových všechny pcovní oenty závsí jen n polohových souřdncích. Je tou tk v přípdech kdy ůžee znedbt nebo defnovt pác psvních odpoů (v těchto přípdech působení psvních odpoů ůžee zhnout do sl pcovních. Pk je výhodná plkce věty o zěně knetcké enege. Zěnu knetcké enege běhe utého přeístění soustvy těles pk totž ůžee vyjádřt poocí páce sl slových dvojc působících n soustvu tj. pltí B B B A k k k j ϕ j A j A E E E F d d (8.5 B U soustv s jední stupně volnost zvedee zobecněnou souřdnc q jež popsuje polohu soustvy. Pk ůžee vyjádřt souřdnce všech bodů těles pootoení těles poocí závslostí x ( q y ( q ϕ ( q j vzthy ez ychlost bycho dostl podevování těchto vzthů. Vzth (8.5 pk vede obecně k dfeencální ovnc pvního řádu typu f ( F x F y j q q ɺ 0 (8.6 --

16 jejíž řešení je sndnější než řešení dfeencálních ovnc duhého řádu typu (8.. Výsledke řešení ovnce (8.6 je závslost qɺ ( q ychlost n poloze. Vyšetření ychlost osttních lenů soustvy těles pk vypoítáe poocí příslušných převodních vzthů. Zvlášť výhodná je plkce věty o zěně knetcké enege n soustvy s konstntní převody kdy tto ovnce á jednoduchý tv. Jko plkc uvedee výpoet závslost ychlost břeen (středu volné kldky n obecné souřdnc y př zdvhání břeen z kldu zdvhcí ústojí. Příkld 8.6 Uete závslost ychlost zdvíhání břeene z kldu po zdvíhcí echnsus dle ob Hncí oent př ozběhu uvžujte konstntní psvní odpoy znedbejte. α α R α y 5 G 5 g Ob.8.6. Zdvhcí echnsus plkce věty o zěně knetcké enege. --

17 -- Knetcká enege soustvy je dán výze 5 K y E ɺ ɺ ɺ ɺ ( ϕ ϕ ϕ ( kde ϕ jsou úhly ntoení jednotlvých lenů. Zdvhcí ústojí je soustvou s konstntní převody. Úhlové ychlost úhly ntoení hřídelů jsou y R v R ϕ ϕɺ y v ϕ ϕɺ y v ϕ ϕɺ. (b Vzth ( po knetckou eneg soustvy ůžee s využtí vzthů (b přepst do tvu 5 K v R E. (c Pcovní slový únky jsou oent tíh g 5 (. Podle věty o zěně knetcké enege dostnee y g v R 5 5 ( ϕ. Využtí zdvhové závslost ( y ϕ (vz. pvní ovnce ze soustvy (b v předcházející ovnc dostnee z předpokldu g R 0 g R 5 5 > > hlednou závslost ychlost břeen n obecné souřdnc y ve tvu 5 5 R y g R v (. 8.. Použtí zákonů zchování hybnost oentu hybnost Hybnost (oent hybnost k bodu nebo k ose soustvy těles je oven soutu hybností jednotlvých těles (oentů hybností k téuž bodu nebo k téže ose. Zěn hybnost (oentu hybnost k bodu nebo k ose z utou dobu je dán celkový pulse (pulsoente

18 k téuž bodu nebo k téže ose vnějších slových únků z uvedenou dobu. Aplkce vět o zěně hybnost nebo o zěně oentu hybnost je výhodná jen v přípdech kdy všechny vnější slové únky jsou funkcí su nebo jsou v utých sěech souřdných os konstntní. Výsledke řešení jsou závslost ychlostí těles n se. Věty o zěně hybnost jestlže jednotlvá těles konjí př sledovné děj posuvné pohyby věty o zěně oentu hybnost př otních pohybech lenů soustvy soustvy. Příkld 8.7. Uete závslost ozběhu pohonného ústojí s třecí spojkou (vz. ob.8.7. Předpokládejte ozběh konstntní hncí oente působící n kotou př konstntní zátěžné oentu n kotou. Poátení knetcké podínky v se t 0 n poátku sepnutí třecí spojky jsou ϕ ϕ 0 ɺ ϕ ω0 ɺ ϕ ω0 přež ω 0 > ω0. Dále uete dobu T potřebnou n vyovnání úhlových ychlostí obou kotouů spolené úhlové ychlost ω kotouů v okžku ukonení pokluzu třecí spojky ztcenou enege běhe ozběhu. TŘECÍ SPOJKA ϕ ϕ Ob.8.7. Schétcké znázonění pohonného ústojí s třecí spojkou. Po jednoduchost řešení uvžujee konstntní oent S přenášený spojkou běhe pokluzu. Předpokládeje že oenty splňují podínky > S >. Aplkcí věty o zěně oentu hybnost n uvolněné kotoue k spolené ose otce ez okžke sepnutí spojky ( t 0 ukonení pokluzu ( t T dostnee ovnce ( ω ω ( T 0 S 0 S ( ω ω ( T ( z nchž vypoítáe neznáé velny T ( ( ω0 ω0 S S S ω ω0 T ω0 T. (b Ztcenou eneg běhe ozběhu pohonného zřízení uíe z ozdílů knetckých enegí n poátku n konc děje tj. --

19 5 E ω ω 0 0 ZTR EK ω. (c Pozneneje že jednu z ovnc ( jse ohl nhdt ovncí ( ω ω ω ( T (d 0 0 kteá je vyjádření věty o zěně oentu hybnost celé soustvy. Z ovnce (d je hned zřejé že v přípdě spolená úhlová ychlost kotouů nezávsí n oentu přenášené třecí spojkou je ovn tkže ztcená enege poto je ω 0 0 ω ω E ZTR E K ω0 ω ω0 ω0 ω0 0 ω 0 ω 0 ( ω ω 0 0 ω 0. (c -5-

20 6 8.. Použtí věty o pohybu středu hotnost soustvy těles Větu o pohybu středu hotnost soustvy těles je výhodné plkovt v přípdech kdy výslednce vnějších sl v uté sěu je ovn nule. Příkld 8.8. Uete závslost pohybu neusěněného echnckého vbátou (vz. ob.8.8 volně položeného n hldkou vodoovnou desku. Poátení souřdnce celé soustvy x T je dán. V ustálené stvu předpokládejte ovnoěnou otc nevývžku úhlovou ychlostí ω. Řešení: Všechny vnější síly (tíhové g g ekce N N jí shodný vetkální sě tj. jejch složky v hozontální sěu x jsou nulové. Z defnce středu hotnost pk z předpokldu poátení kldové polohy po hozontální pohyby těžště T soustvy těles (á s otoe (otující nevývžek vyplývá x x ( x T kde x x jsou souřdnce těžště áu s otoe nevývžku. Z ob. 8.8 je zřejé že pltí x ω Po pohybu těžště desky vbátou tedy pltí kde je excentct nevývžku. x sn t. x xt snω t T T g N T N g x x T x Ob.8.8. echncký vbáto s excentcky uložený nevývžke. -6-

21 7 8. etod edukce slových hotových veln V přípdě velkého potu lenů je př etodě uvolňování velký poet sestvovných pohybových ovnc. Pokud nás nezjíjí hodnoty ekcí studovná soustv těles á jeden stupeň volnost zjíáe se jen o knetku někteého z lenů je vhodné použtí etody edukce. Pohyb soustvy s jední stupně volnost lze vyjádřt pohybe yšleného lenu kteý se pohybuje shodně se zvolený eálný lene soustvy. N tento zvolený len edukujee všechny hoty všechny pcovní slové únky. Těleso n kteé povádíe edukc ůže kont buď otní pohyb (ob.8.9 nebo posuvný pohyb (ob.8.0 příkldy konkétnáích stojních zřízení jsou n ob. 8. ob. 8.. Vycházíe přto z věty o zěně knetcké enege soustvy těles ve tvu d E d t kde P je výkon pcovních slových únků. K P P ed ed q ϕ F ed ed q x Ob.8.0. Redukce n len konjící tnslní pohyb Ob.8.9. Redukce n len konjící otní pohyb Rychlost všech těles echncké soustvy s jední stupně volnost lze vyjádřt ve tvu ɺ ( q qɺ kde q je polohová souřdnce lenu o jehož knetku se zjíáe tj. n kteý povádíe edukc. Knetcká enege soustvy těles pk ůže být vyjádřen př edukc n otující len ve tvu nebo př edukc n posouvjící len ve tvu E E ɺ ɺ k ( q q ed ( q q (8.7 ɺ ɺ k ( q q ed ( q q (8.8 kde ed ( q je edukovný oent setvnost soustvy př edukc n otující zákldní len nebo ( q edukovná hotnost soustvy př edukc n posouvjící len. Výkon všech pcovních slových únků lze př edukc n otující len vyjádřt ve tvu nebo př edukc n posouvjící len ve tvu q ed je P ( t q qɺ ( t q qɺ qɺ (8.9 P ed -7-

22 8 kde ( t q q P ( t q qɺ F ( t q qɺ qɺ (8.0 P ed ɺ je edukovný oent př edukc n otující len nebo ( t q q edukc n posouvjící len. ed F ed ɺ je edukovná síl př Potřebné edukovné velny uíe z ovnost knetckých enegí skutené edukovné soustvy [ E k ] skutená [ E k ] edukovná z ovnost výkonů skutené edukovné soustvy [ P ] [ P ] skutený (8. (8. edukovný ůžee tké použít ovnost ez vtuální pcí (vz kp. 9 skuteně působících sl vtuální páce edukovného slového únku tj. [ δ A ] [ δ A ] skutená (8.b edukovná V přípdech kdy všechny působící síly jsou konzevtvní lze ísto vzthů (8. vycházet z ovnost potencálních enegí skutené edukovné soustvy [ p ] [ E p ] skutená edukovná E. (8. Devcí knetcké enege ve tvu (8.7 esp. (8.8 dostnee esp. d E d t d E d t k k ɺɺɺ d ( q ɺ d q ed ed ( q q q q (8. ɺɺɺ d ( q ɺ d q ed ed ( q q q q. (8.5 Doszení (8.9 (8. esp. (8.0 (8.5 do ovnce (8.6 dostnee vlstní pohybovou ovnc soustvy př edukc n otující len ve tvu ed esp. př edukc n posouvjící len ve tvu ed d ed ( q ( q qɺ qɺ ed ( t q qɺ d q (8.6 d ed ( q ( q qɺ qɺ Fed ( t q qɺ d q. (8.7-8-

23 9 b F ( ϕ ed ed q ϕ x O e R S ϕ Ob.8.. Vkový echnsus ; b - edukce echnsu n otní len Pohybové ovnce (8.6 nebo (8.7 jsou nelneání dfeencální ovnce.řádu. Jsou tudíž ntegovtelné v uzvřené tvu jen ve specálních přípdech funkcí ed ed esp. F ed ed. V přípdě soustv těles s psvní odpoy jsou ez pcovní sl odpoové (třecí síly kteé jsou obecně funkcí ekcí. Příslušná pohybová ovnce by tedy nebyl vlstní pohybovou ovncí. Uvedenou potíž u soustv těles s psvní odpoy lze u někteých jednoduchých soustv odstnt jestlže se podří vyjádřt příslušnou ekc přío kní sl nebo přblžný vyjádření vlvu psvních únků npř. výkone psvních odpoů jko podílu výkonu hncích sl popř. poocí únností. K význéu zjednodušení vlstní pohybové ovnce po edukovný len dochází u soustv s konstntní převody u nchž ed esp. ed nezávsí n zobecněné souřdnc q. Pohybové ovnce (8.6 esp. (8.7 se pk zřejě zjednoduší do tvu esp. ed ed ɺɺ ϕ (8.8 ed qɺɺ F. (8.9 ed Aplkc etody edukce po přípd soustvy s konstntní převody s ukážee s ukážee n následující příkldě Příkld 8.8 Uete zychlení břeene u zdvhcího ústojí (vz. ob.8.. Řešení: Jko zákldní (edukní len s zvolíe posouvjící se břeeno

24 0 Knetcká enege soustvy je dán výze E K ɺ ɺ ɺ ϕ ɺ ϕ ϕ ( 5 y ( kde ϕ jsou úhly ntoení jednotlvých lenů. Zdvhcí ústojí je soustvou s konstntní převody. Úhlové ychlost úhly ntoení hřídelů jsou R R ϕɺ v ϕ y v y ϕɺ ϕ (b v y ϕɺ ϕ. Vzth ( po knetckou eneg soustvy ůžee s využtí vzthů (b přepst do tvu -0-

25 α α b R F ed ed qy α y 5 5 Ob.8.. Sché zdvhcího echnsu edukce n posouvjící len 5 - b R E v K 5 ed (c odkud po edukovnou hotnost ed plyne R konst.. (d ed 5 v Znedbáe-l psvní odpoy výkon pcovních slových únků ( g je dán vzthe 5 --

26 P 5 což využtí pvního výzu ze soustvy (b dává ϕɺ ( g v (e tudíž podle (8.0 pltí R P 5 ( g v (f R ( g. (g Fed 5 Doszení výzů (g (e do pohybové ovnce (8.9 dostnee pohybovou ovnc zdvhcího ústojí R R 5 ( 5 g. (h Z ní po konstntní hncí oent vyplývá konst. Rozběh zdvhcího ústojí je tedy po R ovnoěně zychlený pohybe. 5 ( 5 g > 0 > g (ch R Příkld 8.9. Vyšetřete dobu ozběhu předlohové převodovky (ob.8. kteá je poháněn konstntní hncí oente působící n vstupní hřídel z kldu n poždovné otáky n ( n. Výstupní hřídel je ztížen konstntní oente. Psvní odpoy neuvžujte. z ϕ z ϕ z z ϕ Ob.8.. Schétcké znázonění předlohové převodovky. --

27 Řešení. Z zákldní (edukní len vybeee vstupní hřídel kteý koná otní pohyb. Knetcká enege soustvy je dán výze Uvážíe-l že pltí E K ɺ ϕ ɺ ϕ ɺ ϕ. z ϕ ɺ ɺ ɺ ϕ ɺ ϕ ɺ ϕ z z z z ϕ z z z poto ůžee po knetckou eneg psát E z z z K ed z ϕ ϕ z z odkud po edukovný oent setvnost plyne ɺ z z z ed konst. z z z Znedbáe-l psvní odpoy kteé jsou závslé n ychlostních kceleních poěech echnsu je výkon pcovních slových únků (zde dvojc P P z z ɺ ϕ ɺ ϕ ɺ ϕ ɺ ed ϕ z z odkud vyplývá po edukovný oent výz z ed. z z z Potože převodové ústojí je soustvou s konstntní převody pohybová ovnce á tv (8.8. Z ní dostnee úhlové zychlení vstupního hřídele Z předpokldu z z α ɺɺ ϕ. ed z z ed z z z z z z z z > 0 > z z z z je ozběh ovnoěně zychlený potřebný s po dosžení otáek n je z z ɺ --

28 t R π n 0α π n 0 z z z z z z z z z z. Poznák. Př espektování psvních odpoů ozubených převodů vyjádřených únnost η η vyjdee z předstvy o toku výkonu. Setvné dvojce α α α působící n jednotlvé hřídele se pojevují jko vnější zátěžné dvojce. Znedbáe-l psvní odpoy ovnost výkonu přvedeného odvedeného lze zpst ve tvu ω α ω α ω ( α ω. Př espektování únností ozubených převodů je výkon hncího oentu zvětšen n α α ω ω ω α ω. ηη η Hncí oent potřebný po překonání zátěžného oentu setvných dvojc lze po vyjádření převodů zpst ve tvu z z α ηη z z η z ηη z z odkud vyplývá zpřesněný výz po úhlové zychlení α z z z ηη z z α. η z z z η η z z z z z Sestvení pohybové ovnce uvedenou etodou po přípd nekonstntního převodu s ukážee n příkldě vkového echnsu. Příkld 8.0. N vkový hřídel o oentu setvnost o k ose otce působí konstntní hncí oent o (ob.8.. Se zvedáke se posouvá těleso o celkové hotnost. Zvedák je ztížen slou F kteá závsí n úhlu pootoení hřídele. Řešení: Z zákldní (edukní len zvolíe vkový hřídel tj. povedee edukc n otní len (vz. ob.8.b. Zdvhová závslost x (ϕ ez zvedáke vkový hřídele je dán vzthe (vz. ob.8. x ( ϕ R e snϕ ( odkud po převod plyne --

29 5 d x ( ϕ p ( ϕ ecosϕ. (b d ϕ Knetcká enege soustvy je EK o ϕ x ɺ ɺ (c poto uvážíe-l že pltí d x ( ϕ d x ( ϕ d ϕ d x ( ϕ xɺ p ( ϕ ɺ ϕ eɺ ϕ cosϕ (d d t d ϕ d t d ϕ lze knetckou eneg soustvy psát ve tvu E K p ( ϕ ( ecosϕ ( ϕ ɺ ϕ O O ɺ ϕ ɺ ϕ ed ( ϕ ɺ ϕ. (e Redukovný oent setvnost (ϕ vkového echnsu tedy je ed o o ed ( ϕ p ( ϕ ( e cos ϕ. (f Znedbáe-l psvní odpoy kteé jsou závslé n ychlostních kceleních poěech echnsu výkon pcovních slových únků F ( ϕ g je P P ɺ ϕ ( g F ( ϕ xɺ (g což s využtí převodu p (ϕ dává P ( g F ( ϕ p ( ϕ ] ɺ ϕ ( ϕ ɺ ϕ (h P [ ed tkže edukovný oent ( ϕ všech pcovních slových únků tedy je ed ed ( ϕ ( g F ( ϕ p ( ϕ ( g F ( ϕ ecosϕ. (ch Doszení výzů (e (f do obecně pltné ovnce (8.6 dostnee vlstní pohybovou ovnc vkového echnsu ve tvu [ p ( ϕ ] ɺ ϕ p ( ϕ p ( ϕ ɺ ϕ ( g F ( ϕ p ( ϕ ( O kde devce převodu p ( ϕ je dán výze d p ( ϕ p ( ϕ e snϕ. (j d ϕ Řešení pohybové ovnce ( př dných poáteních podínkách t 0 ϕ ϕ0 ɺ ϕ ɺ ϕ 0 ω0 je závslost úhlu pootoení vkového hřídele n se tj. ϕ ϕ ( t. Pokud chcee vyjádřt závslost úhlové ychlost ω vkového hřídele n jeho úhlu otoení ϕ plkujee větu o zěně knetcké enege. Využjee přto vzthu (b. Dostnee -5-

30 6 ϕ ed ( ϕ ω ed ( ϕ0 ω0 ed ( ϕ d ϕ (k což po úpvě dává ϕ 0 ω ϕ ed ( ϕ0 ω0 ed ( ϕ d ϕ (l ( ϕ ( ϕ ed ed ϕ 0 k z edukovný oent ( ϕ všech pcovních slových únků dosdíe výz (e. ed Příkld 8.. Sestvte pohybovou ovnc po vku u vkového echnsu s vtnou pužnou o tuhost k (vz. ob.8.5. Předpětí S 0 pužny ve spodní úvt zvedáku hncí oent n vkové hřídel jsou dány. Vk á válcový tv o poloěu je excentcky uložen s excentctou e. Hotnost těles spojeného se zvedáke je. Psvní odpoy znedbejte. b ed ed q ϕ x O e T ϕ Ob.8.5 Vkový echnsus s pužnou - edukce echnsu n otní len -b. -6-

31 7 Řešení. Z zákldní (edukní len vybeee vkový hřídel kteý koná otní pohyb. Knetcká enege soustvy je dán výze E ( e ɺ ϕ xɺ ɺ ϕ xɺ K T O O kteý využtí zdvhové závslost x e snϕ xɺ eɺ ϕ cosϕ ( přepíšee do tvu E ( ecosϕ O K ɺ ϕ ed ( ϕ ɺ ϕ odkud po edukovný oent setvnost plyne ( ϕ ϕ ed O ( ecos. (b Výkon pcovních sl dvojc ɺ ϕ [ ( g S k e ( snϕ ] xɺ P 0 nbývá použtí zdvhové závslost tv P { [ ( g S k e ( snϕ ] ecosϕ } ϕ ɺ ϕ P odkud dostnee edukovný oent ed 0 ] 0 ɺ ed [ ( g S k e ( snϕ ecosϕ. (c Potože vkový echnsus á poěnný převod ez zvedáke vkou pohybová ovnce á tv (8.6. Doszení výzů (b (c do ovnce (8.6 dostnee pohybovou ovnc vkového echnsu ve tvu cosϕ snϕ [ ( g S 0 ɺɺ e ɺ ϕ O ( ecosϕ O ( ecosϕ ϕ k e ( snϕ ] ecosϕ. Pohybová ovnce je nelneání dfeencální ovncí duhého řádu. Její řešení v uzvřené tvu není ožné lze j řešt někteou z nueckých etod ntegce. -7-

32 8 Postup př sestvení pohybové ovnce poocí etody edukce př konstntních převodech: -Ověříe zd soustv á 0 volnost. - Do pcovního schétu zkeslíe všechny pcovní slové únky -Anlyzujee vzby není l někteá deální příslušný vzební slový únek zhnee do pcovních -Soustvou yšleně pohnee. Zkeslíe vektoy vtuálních přeístění δ j δϕ j v ístech působšť pcovních sl pcovních oentů 5- Pokud edukujee n -tý len soustvy kteý je tnslní pk jeho vtuální posunutí δ δ δ zvolíe jko zákldní. Všechn zbylá posunutí vyjádříe poocí tohoto ed zákldního tj. nleznee vzthy δ j f j (δ δϕ f ( δ j. Pokud edukujee n otní len pk jko zákldní beee pootoení tohoto lenu δϕ δϕed δϕ nleznee vzthy δ j f ( δϕ δϕ f ( δϕ j j j j. Přto používáe geoetcké souvslost ez souřdnce podínku vlení knetcké vzthy ez ychlost bodů nebo úhlový ychlost těles 6- Npíšee vzth po knetckou eneg celé soustvy (jednotlvé ychlost přto vyjádříe poocí ychlost edukovného lenu lenu edukovného. Z ovnost obou enegí tj. ze vzthu E E zjstíe hodnotu edukovné hotnost esp. edukovného oentu [ k ] skutená [ k ] edukovná setvnost 7- Npíšee vzth po vtuální všech pác všech pcovních sl pcovních oentů působících v ác dné soustvy přto se řídíe pvdly po sklání násobení vektoů sl vektoů vtuálních přeístění znázoněných n pcovní schétu. Z ovnost obou vtuálních pcí tj. ze vzthu [ δ A ] [ δ A ] skutená zjstíe edukovnou sílu esp. edukovný edukovná oent. Vzhlede k tou že u konstntních převodů jsou vzthy ez ychlost vtuální posunutí stejné ůžee edukovnou sílu esp. edukovný oent ut tké z ovnost P P výkonů tj. ze vzthu [ ] [ ] skutený edukovný 8- V přípdě edukce n tnslní len pk zjstíe zychlení lenu n kteý byl pováděn edukce ze vzthu -8-

33 9 Kontolní otázky Z eho vychází řešení soustv těles etodou uvolňování? Kdy je výhodné použtí zákon zchování enege kdy zákon zchování hybnost nebo oentu hybnost? Co je to vlstní pohybová ovnce Co je pncpe etody edukce jk zjšťujee edukovné hotnostní chktestky jk edukovné slové únky? 5 Kolk stupňů volnost usí ít soustv by bylo ožné použít etodu edukce? -9-