MASARYKOVA UNIVERZITA. Dyskalkulie a jiné specifické poruchy učení. v matematice
|
|
|
- Ludmila Konečná
- před 6 lety
- Počet zobrazení:
Transkript
1 MASARYKOVA UNIVERZITA PEDAGOGICKÁ FAKULTA Katedra Matematiky Dyskalkulie a jiné specifické poruchy učení v matematice Bakalářská práce Brno 2016 Vedoucí práce: Mgr. Lenka Pavlíčková, Ph.D Autor práce: Lucie Plodíková
2 Bibliografický záznam PLODÍKOVÁ, Lucie. Dyskalkulie a jiné specifické poruchy učení v matematice: bakalářská práce. Brno: Masarykova univerzita, Fakulta pedagogická, Katedra matematiky, 2016, 66 stran, Vedoucí bakalářské práce Lenka Pavlíčková. 2
3 Anotace Bakalářská práce Dyskalkulie a jiné specifické poruchy učení v matematice se zabývá problematikou specifických poruch učení, zejména problematikou dyskalkulie. Celá práce je rozdělena do dvou hlavních částí: teoretické a praktické. Teoretická část vychází z prostudované odborné literatury. Je zaměřena na obecné definice specifických poruch učení a dyskalkulie. Na jejich klasifikaci, diagnostiku a reedukaci. Praktická část je zaměřena na výrobu pomůcek pro žáky s dyskalkulií, popisuje funkčnost pomůcek v praxi s žáky základní školy a další možnosti využití těchto pomůcek v hodinách matematiky. Annotation Bachelor thesis Dyscalculia and other specific learning disorders in math deals with specific disorders of learning, especially with dyscalculia. The whole work is divide into two main parts: theoretical and practical. Theoretic part is based on specialized literature and focused on general definition of specific disorders of learning and dyscalculia. Practical part is focused on preparing supplies for pupils with dyscalculia and test these supplies in primary school. Klíčová slova Specifické poruchy učení, poruchy matematických schopností, vývojová dyskalkulie, diagnostika dyskalkulie, principy reedukace. Keywords Specific learning disorders, disorders in mathematical capabilities, progressional dyscalculia, diagnostic of dyscalculia, principles of re-education. 3
4 Prohlášení Prohlašuji, že jsem bakalářskou práci zpracovala samostatně, s využitím pouze citovaných literárních pramenů v souladu s Disciplinárním řádem pro studenty Pedagogické fakulty Masarykovy univerzity a se zákonem č. 121/2000 Sb., o právu autorském, o právech souvisejících s právem autorským a o změně některých zákonů (autorský zákon), ve znění pozdějších předpisů. Souhlasím, aby moje práce byla uložena na Masarykově univerzitě v knihovně Pedagogické fakulty a byla zpřístupněna ke studijním účelům. Lucie Plodíková V Brně dne
5 Poděkování Chtěla bych poděkovat Mgr. Lence Pavlíčkové, Ph.D za cenné připomínky, odbornou pomoc, ochotu, vstřícnost a trpělivost při vedení mé bakalářské práce. 5
6 Obsah 1 Úvod Specifické poruchy učení Klasifikace projevů specifických poruch učení Dyslexie Dysgrafie Dysortografie Dyskalkulie Dyspinxie Dysmúzie Dyspraxie Vývoj názorů na specifické poruchy učení Diagnostika specifických poruch učení Reedukace specifických poruch učení Poruchy matematických schopností Rozdělení poruch ovlivňující osvojování matematických dovedností Vývojová dyskalkulie Faktory ovlivňující úspěšnost žáka v matematice Klasifikace dyskalkulie Diagnostika dyskalkulie Reedukace dyskalkulie Pomůcky pro žáky s dyskalkulií Pomůcky pro 1. ročník základní školy Pomůcka k porovnávání množství (<, >, = ) Pomůcka ke sčítání Pomůcky pro 2. ročník základní školy Pomůcka k dělení
7 5.2.2 Pomůcka na násobení Domino Pomůcky pro 4. ročník základní školy Pomůcka k procvičování řady čísel Pomůcka k počítání se zlomky Pomůcka číselná osa Domino složitější Závěr Resumé Summary Seznam použité literatury Obrázková příloha
8 1 Úvod Téma bakalářské práce: Dyskalkulie a jiné specifické poruchy učení v matematice jsem si zvolila na základě zvyšujícího se počtu žáků se specifickou poruchou učení. Problematika specifických poruch učení je v současné době stále častějším tématem a je předmětem zájmu pedagogických pracovníků, širší veřejnosti i rodičů. Vzhledem k tomu, že počet žáků s těmito poruchami přibývá, je nezbytně nutné, aby se každý budoucí pedagog s touto problematikou seznámil a byl schopen tyto problémy řešit. Aby pedagog prvotní problémy žáka rozpoznal, potřebuje znalosti nejen z oblasti pedagogiky, ale také z psychologie a speciální pedagogiky. Důležitá je zejména včasná diagnostika problémů žáků a volba vhodných reedukačních a kompenzačních postupů. Bakalářská práce je rozdělena na dvě hlavní části: teoretickou a praktickou. V první části se na základě odborné literatury budu věnovat problematice specifických poruch učení, zejména dyskalkulii. Na začátku se zaměřuji na obecný popis specifických poruch učení a na jejich klasifikaci. V práci se dále zabývám poruchami matematických schopností, jejich dělením na základě osvojování matematických dovedností a faktory ovlivňujícími úspešnost žáka v matematice. V závěru teoretické části uvádím klasifikaci dyskalkulie, její diagnostiku a reedukaci. Druhá část bakalářské práce se zabývá pomůckami pro žáky s dyskalkulií. Tyto pomůcky jsem rozdělila do tří skupin. Jediným kritériem pro rozdělení pomůcek je věk žáka, pro kterého je pomůcka určena. Tyto pomůcky jsem následně na žácích vyzkoušela. U pomůcek jsem se zaměřila zejména na jejich funkční stránku, jejich nedostatky a následně na další možnosti využití v hodinách matematiky. 8
9 2 Specifické poruchy učení Problematika specifických poruch učení se i nadále řadí k aktuálním a stále více diskutovaným tématům ve školství, která jsou v podvědomí jak odborné, tak i laické veřejnosti. Týká se vysokého procenta dětské populace. Velký vliv na další vzdělávání a životní profesní dráhu jedinců se specifickou poruchou učení má včasná diagnostika. Důležité je též zajištění reedukační péče a podpory. Významnou úlohu hraje také rodina, ve které dítě vyrůstá, školní instituce a v případě osob se specifickou poruchou učení také spolupráce s poradenským pracovištěm. Specifické poruchy učení jsou dnes již jednoznačně pojmenovaným problémem. 1 Vzrůst závažností těchto poruch nepřímo souvisí s tím, že jsou svou podstatou lehkými odchylkami mentálního vývoje, jde o jevy, které se staly potížemi až s nárůstem složitosti života v hospodářsky vyspělých zemích. 2 Specifické poruchy učení postihují i oblast výkonnosti, která je výstupní branou celého vzdělávacího, intelektuálního procesu. Mezi hlavní řešená témata vzdělávání žáků se specifickými poruchami učení řadíme přístup k výuce cizích jazyků, využití mediálních prostředků se zaměřením na technologie a styl učení. Právě styl učení hraje velkou roli při terapii jedinců se specifickými poruchami učení. K tomu, aby se žáci stali úspěšnými, musí učitelé rozpoznat jejich kvality, rozumět problémům, které mají, rozpoznat různé učební a výchovné potíže, kterým žáci musí čelit, a udělat všechno pro to, aby se stali více úspěšnými. Učitelé musí rozpoznat veškeré kladné stránky žáků a identifikovat specifické obtíže, které jim stojí v cestě. 3 V případě, že by se zvolil špatný styl učení vzhledem k inteligenci a schopnostem dítěte, může se to následně odrazit v jeho negativním přístupu k terapii. 4 Je velmi obtížné vyčíslit výskyt jedinců trpících specifickou poruchou učení. U nás se uvádí přibližně 2-4%, přičemž u chlapců je výskyt asi třikrát vyšší než u dívek. 1 BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str. 6 2 BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str. 6 3 BARTOŇOVÁ, Miroslava a Marie VÍTKOVÁ. Vzdělávání žáků se speciálními vzdělávacími potřebami. 1. vyd. Brno: Paido, 2013, str BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str. 7 9
10 Problematika péče o žáky se specifickými poruchami učení je již poměrně dobře ošetřena v rámci nižšího stupně základní školy. Do popředí nyní vystupuje druhý stupeň základní školy a střední škola. Žáci se specifickými poruchami učení jsou považováni za žáky se specifickými vzdělávacími potřebami. Specifické poruchy se u jednotlivých osob projevují řadou různých příznaků, které se obtížně zobecňují. Hovoříme o tzv. symptomech (příznacích) a etiologii specifických poruch učení. Specifickým poruchám učení jsou podřazeny pojmy dyslexie, dysgrafie, dysortografie, dyskalkulie. Na řešení těchto problémů se často podílejí neurologové, psychiatři i jazykovědci. Jedná se tedy nejen o problém pedagogický ale i psychologický. 5 Definice specifických poruch učení se v dnešní době výrazně liší od dřívějších definic. Současné definice zahrnují i oblast diagnostiky. Definice expertů z USA z roku 1980 definuje specifické poruchy učení takto: Poruchy učení jsou souhrnným označením různorodé skupiny poruch, které se projevují zřetelnými obtížemi při nabývání a užívání takových dovedností, jako je mluvení, porozumění mluvené řeči, čtení, psaní, matematické usuzování nebo počítání. Tyto poruchy jsou vlastní postiženému jedinci a předpokládají dysfunkci centrálního nervového systému. I když se porucha učení může vyskytnout souběžně s jinými formami postižení (jako např. smyslové vady, mentální retardace, sociální a emocionální poruchy) nebo souběžně s jinými vlivy prostředí (např. kulturní zvláštnosti, nedostatečné nebo nevhodná výuka, psychogenní činitelé), není přímým následkem takových postižení nebo nepříznivých vlivů. 6 Důležité na této definici je, že se specifická porucha učení může vyskytnout s poruchami nespecifickými a vyjadřuje, že jde o dysfunkci centrálního nervového systému. Podstatné je si uvědomit, že žáci se specifickými poruchami učení netvoří stejnorodou skupinu a že specifické poruchy zasahují celou osobnost jedince. 5 BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str. 8 6 BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str. 9 10
11 2.1 Klasifikace projevů specifických poruch učení Na základě obecné definice můžeme rozlišovat specifické poruchy čtení (dyslexie), psaní (dysgrafie), pravopisu (dysortografie), počítání (dyskalkulie), kreslení (dyspinxie), hudebnosti (dysmúzie) a schopnosti vykonávat složité úkoly související s motorikou (dyspraxie). Jednotlivé poruchy se mohou navzájem kombinovat a mohou negativně ovlivňovat vzdělávání žáků ve všech školních předmětech. V běžné praxi se pouze v malé míře můžeme setkat s jedinci, kteří trpí pouze jednou z těchto poruch Dyslexie Dyslexie je specifická porucha čtení. V širším pojetí bývá také označována jako synonymum pro specifické poruchy učení. Je nejznámějším a nejvíce řešeným pojmem ze všech poruch učení. Začalo se o ní hovořit jako o první, protože nejnápadněji ovlivňovala úspěšnost dítěte ve škole. 8 K dyslexii bývá často přidáván přívlastek vývojová, což vystihuje její povahu. Je odvozena z latinského lexis řeč, jazyk a předpony dys, určující nedostatečnost této funkce. Na rozdíl od ostatních poruch učení má dyslexie nejvíce propracované pojmové vymezení. Projevuje se neschopností naučit se číst běžnými výukovými metodami. Dítě má problémy se zapamatováním a rozpoznáváním jednotlivých písmen, zvláště z rozlišováním tvarově podobných písmen (b-d, s-z). Problémem jsou i zvukově podobné hlásky (a-e-o, b-p). Pro dítě je složité souvislé čtení slov, spojování hlásek, související s oslabením spolupráce v oblasti mozkových hemisfér a s očními pohyby. Porucha může postihnout porozumění čtenému textu, rychlost čtení a správnost čtení. 9 Dyslexie byla definována mnoha autory. Jedna z nejnovějších definic z roku 2003, která byla publikována pracovní skupinou Mezinárodní dyslektické společnosti v Annals of Dyslexia, zní: Dyslexie je specifická porucha učení, která je neurobiologického původu. 7 BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str
12 Je charakterizovaná obtížemi se správným a/nebo plynulým rozpoznáváním slova a špatným pravopisem a dekódovacími schopnostmi. Tyto obtíže jsou typickým následkem deficitu ve fonologické složce jazyka, který je často neočekáváný ve vztahu k ostatním poznávacím schopnostem a k podmínkám efektivní výuky ve třídě. Mezi sekundární následky mohou patřit problémy s porozuměním čteného a omezené čtenářské zkušenosti, které brání růstu slovní zásoby a základních znalostí. 10 Poruchy čtení tvoří nejméně 80% všech poruch učení, čímž mezi poruchami učení jednoznačně převládají. Dyslexie velmi úzce souvisí i s matematikou. Pro dyslektika je obtížné číst zadání matematických úloh, zejména slovních úloh, a následně zadaní porozumět. Problém nastává tehdy, když je potřeba provést přepis textu do matematického jazyka. Pro některé dyslektiky je obtížné číst i symbolický matematický zápis. Existují však i děti, které symbolický zápis ovládají a to je pro ně pak záchranou v matematice Dysgrafie Dysgrafie je specifická porucha grafického projevu. Často bývá zařazována pod pojem dyslexie. 12 Postihuje hlavně celkovou úpravu písemného projevu, osvojování jednotlivých písmen, spojení hlásky s písmenem, napodobení tvarů a řazení písmen. Dítě může opět zaměňovat tvarově podobná písma jako u dyslexie. Písmo je obvykle neuspořádané, těžkopádné, neobratné. Dochází ke směšování psacího a tiskacího písma. Dítě píše pomalu, namáhavě. U těchto dětí je časté vadné držení psacího náčiní. Psaní vyžaduje více koncentrace pozornosti dítěte, není schopno se soustředit na gramatickou a obsahovou stránku projevu. 13 Žák často škrká, přepisuje písmena, má obtíže při napodobování písmen a pomalé vybavování tvarů písmen. Obtíže mohou přetrvávat i do vyšších ročníků BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení. 1. vyd. Brno: Masarykova univerzita v Brně, 2005, str
13 Dysgrafie také velmi úzce souvisí s matematikou. Dysgrafik má problém s osvojením si jednotlivých číslic a znaků, s rozlišením pojmu číslo a číslice a jejich zápisem, spojení číslo a zápis čísla pomocí číslic, zápisem čísel v řádcích a v zápisu čísel v algoritmech, kde záleží na přesnosti zápisu. Chyby mohou být způsobené pomalostí při psaní nebo neupraveností zápisu Dysortografie Dysortografie je porucha pravopisu. Velmi často se vyskytuje ve spojení s dyslexií a dysgrafií. Tato porucha nepostihuje celou oblast gramatiky jazyka, ale týká se specifických dysortografických jevů, záměn tvarově podobných písmen v písemné podobě (objevují se inverze, chyby způsobené artikulační neobratností, zkomoleniny, nesprávně umístěné nebo vynechané vyznačení délek samohlásek, chyby v měkčení), vynechávky. Tato porucha také negativně ovlivňuje aplikaci gramatického učiva. Dítě potřebuje na psaní déle času než ostatní. 16 Dysortografie také velmi úzce souvisí s matematikou. Dysortografik má problémy ve správném zaznamenávání číslic a čísel při diktátu. Dítě zaměňuje číslice nebo dochází k jejich vynechání. 17 Dochází k větší chybovosti při vlastních zápisech do sešitu nebo na tabuli. Obtíže nastávají i při písemném ověřování vědomostí Dyskalkulie Dyskalkulie je specifická porucha matematických schopností. Porucha se týká zejména základních matematických výkonů. Projevuje se obtížemi v orientaci na číselné ose, záměnami číslic, neschopností provádět matematické operace, poruchami v prostorové a pravolevé orientaci. 19 Podle charakteru potíží ji můžeme členit na: 15 BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str JUCOVIČOVÁ, Drahomíra, Hana ŽÁČKOVÁ a Hana SOVOVÁ. Specifické poruchy učení na 2. stupni základních škol: (použitelné i pro střední školství [i.e. školství]). Praha: D + H, 2007, str JUCOVIČOVÁ, Drahomíra, Hana ŽÁČKOVÁ a Hana SOVOVÁ. Specifické poruchy učení na 2. stupni základních škol: (použitelné i pro střední školství [i.e. školství]). Praha: D + H, 2007, str ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str
14 praktognostickou dyskalkulii, verbální dyskalkulii, lexickou dyskalkulii, grafickou dyskalkulii, operační dyskalkulii a ideognostickou dyskalkulii. Dyskalkulie úzce souvisí s dalšími poruchami učení, jako je dyslexie a dysgrafie Dyspinxie Dyspinxie je specifická porucha kreslení. Je charakteristická nízkou úrovní kresby. Dítě nedokáže převést svou trojrozměrnou představu do dvojrozměrného papíru. Zachází tvrdě a neobratně s tužkou, má problémy s pochopením perspektivy. 20 Tato porucha se projevuje zejména v geometrii při rýsování. Dítěti činí problém i znázornění prostorové situace v rovině a na obrázku. 21 Problémy mohou být i v orientaci v grafu a v jeho souřadnicích Dysmúzie Dysmúzie je specifická porucha schopnosti vnímat a reprodukovat hudbu. Projevuje se problémy v rozlišování tónů, dítě nedokáže rozlišit a reprodukovat rytmus, nepamatuje si melodii. Potíže se čtením a psaním not souvisí spíše s dyslexií nebo s dysgrafií. 23 Ztráta smyslu pro rytmus je problémem zejména pro matematiku. 24 Dítě má problémy při počítání po jedné, v orientaci v číselné řadě. Problémy mohou nastat i při sledování zákonitostí a závislostí BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str. 11,12 21 BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str PAVLÍČKOVÁ, Lenka. Poruchy matematických schopností žáků s dyskalkulií a jejich vliv na řešení učebních úloh ve fyzice a v matematice [online]. Brno, 2015, str BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str. 11,12 24 BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str PAVLÍČKOVÁ, Lenka. Poruchy matematických schopností žáků s dyskalkulií a jejich vliv na řešení učebních úloh ve fyzice a v matematice [online]. Brno, 2015, str
15 2.1.7 Dyspraxie Dyspraxie je specifická porucha obratnosti a schopnosti vykonávat složité úkony. Může se projevit jak při běžných denních činnostech, tak i ve vyučování. Jiným názvem specifická vývojová porucha motorické funkce (podle 10. revize Mezinárodní klasifikace nemocí). Děti s touto poruchou bývají pomalé, neupravené, nešikovné, jejich výrobky jsou nevzhledné, to často vede k nechuti k motorickým činnostem. 26 V matematice se tato porucha projevuje poruchou manipulace s konkrétními předměty a symboly, při tvoření skupin předmětů, při zápisu algoritmů operací a rýsování. Do této skupiny můžeme zařadit i problémy v grafomotorice. Dítě má problémy při psaní matematických znaků, víceciferných čísel, zápisu čísel pod sebe. Problémy můžou být i při psaní (pomalé psaní) nebo při rýsování obrazců Vývoj názorů na specifické poruchy učení V minulosti nebylo této problematice věnováno moc pozornosti. Žáci, u kterých se problémy v učení projevovaly, byli zařazeni do dvou až tří skupin, nebo byli považováni za líné nebo hloupé. Tyto problémy byly často pouze v jednom předmětu. 28 O dyslexii a následně o specifických poruchách učení se hovoří, že existují tak dlouho jako lidská vzdělanost sama. 29 První zmínky můžeme nalézt již ve starověku. K této problematice se vyjadřovali například E. Rotterdamský ve spise O včasné a svobodné výchově dětí, nebo také J. A. Komenský, který doporučoval dbát na správné metody čtení, individualitu a názornost. Specifické poruchy učení byly objeveny na přelomu 19. a 20. století, avšak teprve v padesátých letech se stávají aktuálním sociálním problémem ve všech zemích. Náhled na problematiku specifických poruch učení se rozvíjel společně s pokrokem 26 BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str PAVLÍČKOVÁ, Lenka. Poruchy matematických schopností žáků s dyskalkulií a jejich vliv na řešení učebních úloh ve fyzice a v matematice [online]. Brno, 2015, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str
16 v neurologii a příbuzných disciplínách. Neurologové se zabývali hlavně funkcí jednotlivých mozkových hemisfér. Vždy byla důležitá součinnost praktických a teoretických poznatků. V roce 1877 byl v Anglii objeven pojem slovní slepota. Jeho autorem byl německý lékař S. Kussmaul. Termín používal pro pacienty, kteří byli inteligentní, bez poškozeného zraku a i přesto nebyli schopni číst. V témže roce byl poprvé užit i termín dyslexie (nahradil původní termín slovní slepota ). Jeho autorem byl německý oční lékař R. Berling. Ke skutečnému objevu dyslexie došlo v roce Byly to angličtí lékaři P. Morgan a J. Kerr, kteří se přičinili o popsání klinických projevů a příčin poruchy. 30 Mezi zakladatele moderního směru zkoumání dyslexie můžeme zahrnout S. T. Ortona, který se zaměřoval především na poruchy řečových funkcí. Příčinu dyslexie vidí v nedokonalé dominanci jedné hemisféry, nedokonalé lateralizaci mozkových hemisfér 31, čímž je narušena jejich vzájemná souhra. Mezi naše odborníky patří psychiatr A. Heveroch, zakladatel a průkopník vhledu na problematiku specifických poruch u nás. Jako další to byl J. Langmeier, který se zabýval systematickou nápravou specifických poruch čtení v psychiatrické léčebně v Havlíčkově Brodě. Koncem padesátých let byla tato péče zásluhou O. Kučery přesunuta do Dolních Počernic. O. Kučera dělí specifické poruchy na tři skupiny: encefalopatická (LMD), hereditární a smíšená. Jako posledního odborníka bych zde chtěla uvést Z. Matějčka, který se touto problematikou zabýval více jak třicet pět roků. Jeho práce jsou vyhledávány nejen odborníky ale i rodiči. Za svoji práci získal nejvyšší ocenění. Zabýval se péčí o jedince se specifickou poruchou učení a jejich podporou Diagnostika specifických poruch učení Diagnostika je východiskem výchovně vzdělávacího procesu vůbec a reedukace především. Jejím cílem je stanovení úrovně vědomostí a dovedností, charakteristika 30 BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str
17 poznávacích procesů, sociálních vztahů, osobnostních charakteristik a dalších faktorů, které se podílejí na úspěchu či neúspěchu dítěte. 33 Diagnostická kritéria 1) Čtení IQ 90, ČQ 90 (ČQ= čtenářský kvocient), rozdíl IQ a ČQ je minimálně 20 bodů, trvale podprůměrné výsledky ve čtení, negativní nález v oblasti zraku, sluchu, nevýznamné absence ve škole, adekvátní podmínky ve škole, resistence vůči běžným pedagogickým opatřením školy. Pokud jsou všechna kritéria splněna, jedná se o dyslexii. Pokud není splněno jedno z kritérií, lze kompenzovat dvěma z následujících kritérií: prokázaná dyslexie u rodičů nebo sourozenců, LMD, poruchy v oblasti psaní, výrazně opožděný vývoj řeči, specifická porucha řeči, snížené výsledky v percepčních zkouškách (např. zrakové či sluchové vnímání). 2) Psaní trvale podprůměrné výukové výsledky v písemných projevech (nezvládání tvarů písmen, problémy v diktátech), specifické chyby ve školních pracích, IQ 90, negativní nález v oblasti zraku, sluchu, nevýznamné absence ve škole, 33 ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str
18 rezistence vůči běžným pedagogickým opatřením školy. Pokud jsou splněna všechna kritéria, jedná se o specifickou poruchu psaní. Pokud je jedno z kritérií nesplněno: lze ho kompenzovat dvěma z následujících kritérií: prokázaná dysortografie nebo dysgrafie u sourozenců nebo rodičů, LMD, poruchy v oblasti čtení, snížené výsledky v oblasti čtení, snížené výsledky v percepčních zkouškách, výrazně opožděný vývoj řeči, nápadné problémy s jemnou motorikou, vývojová dyspraxie. 3) Matematika IQ 90, výsledky v matematice se trvale pohybují pod úrovní daného ročníku, při kvalitativním hodnocení výkonu v matematice se setkáváme s problémy jako: chápání pojmu číslo, umisťování čísel na číselné ose, matematické manipulace s předměty a čísly, orientace v prostoru, pozice čísla v číslici, negativní nález v oblasti zraku, sluchu, nevýznamné absence ve škole, rezistence vůči běžným pedagogickým opatřením školy Reedukace specifických poruch učení Proces reedukace specifických poruch učení lze charakterizovat jako dlouhodobý diagnosticko-terapeutický proces, jehož cílem je odstranění nebo zmírnění obtíží dítěte a zlepšení celkového stavu psychiky dítěte. 35 Neexistuje žádná univerzální 34 BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení. 1. vyd. Brno: Masarykova univerzita v Brně, 2005, str BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str. 7 18
19 metoda. a potřeb. Každé dítě je potřeba posuzovat individuálně, na základě jeho poruchy Efektivní reedukace je týmovou spoluprací vyučujících, kteří se podílí na výchově a vzdělávání žáka. Náprava je dlouhodobá, náročná a vyžaduje značné úsilí ze strany dítěte, učitele, rodiny a dalších odborníků. Při reedukaci je důležité, aby se učitel zaměřil na celou osobnost žáka. Při reedukaci se musíme řídit určitými zásadami, aby náprava přinášela co nejlepší efekt. Mezi tyto zásady řadíme např.: diagnostický rozbor příkladu, individualitu, příznivou atmosféru, dobrý začátek, postup po malých krocích Poruchy matematických schopností Vytváření a rozvíjení početních dovedností patří v systému školní výuky nepochybně na jedno z předních míst. 37 V dnešní době se stále více setkáváme s dětmi, kterým činí osvojení početních dovedností značný problém. Pokud si dítě již od začátku školní docházky nemůže z různých důvodů budovat základní početní dovednosti, poměrně brzy jeho zájem o matematiku ustoupí. Narůstající obavy z matematiky mohou snadno přerůst v různou škálu psychosomatických obtíží. Z těchto důvodů je velmi důležité těmto nežádoucím jevům předcházet. 38 Osvojování učiva matematiky je specifický proces, při kterém se jedinec snaží naučit používat běžně užívanou soustavu kódů, operačních znaků, značek, číslic a vztahů mezi nimi, které slouží k mezilidské komunikaci. Každý jedinec má jiné předpoklady si dané dovednosti osvojit. Tímto vznikají i rozdíly mezi žáky. Tyto rozdíly mohou být malé (v rámci průměru) nebo velké (nadprůměrné, podprůměrné). Děti s nízkou dovedností v počítání mají pak viditelné obtíže v procesu výuky matematiky (fyziky), ačkoli v jiných předmětech mohou dosahovat dobrých výsledků BARTOŇOVÁ, Miroslava. Kapitoly ze specifických poruch učení I: vymezení současné problematiky. 2. vyd. Brno: Masarykova univerzita, 2010, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str
20 Poruchy matematických schopností se projevují v jejich struktuře, v úrovni a způsobech osvojování učiva matematiky. Poruchy a narušení matematických schopností je souhrnné označení pro škálu nejrůznějších obtíží, problémů a nedostatků v matematice, které zahrnuje jednak specifické vývojové poruchy učení označované předponou dys-, ale také nedostatky a obtíže nevývojového charakteru označované předponou oligo-, hypo- či příponou -asténie. 40 Matematické schopnosti jsou tvořeny jednotlivými složkami, které zasahují tyto oblasti: zrakové a sluchové vnímání, prostorové orientace, paměťové, verbální, lexické, grafické, operacionální (numerické), usuzování Rozdělení poruch ovlivňující osvojování matematických dovedností Narušení matematických dovedností má mnoho různých projevů, příčin a klasifikací. J. Novák 42 rozděluje poruchy matematických schopností následovně: Kalkulastenie Mírné narušení matematických vědomostí a dovedností podmíněné jejich nevhodnou nebo nedostatečnou stimulací ze strany školy nebo rodiny nebo sociální deprivací jedince, přičemž všeobecné rozumové schopnosti i matematické schopnosti vykazují normální úroveň i strukturu. 43 Typy kalkulastenií: 1. Kalkulastenie emocionální: selhávání v matematice je způsobeno prožíváním nevhodných reakcí okolí na vlastní počtářské obtíže; všeobecné rozumové schopnosti a matematické schopnosti jsou v normě. 40 NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str NOVÁK, Josef. Dyskalkulie: specifické poruchy počítání; metodika rozvíjení početních dovedností s přílohou Pracovní listy. Vyd. 2., v nakl. Tobiáš 1. Havlíčkův Brod: Tobiáš, 2000, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str
21 2. Kalkulastenie sociální: narušení matematických dovedností a vědomostí způsobené problematickými sociálními vlivy, nebo nevhodnou (nedostatečnou) přípravou. 3. Kalkulastenie didaktogenní: problémy v matematice jsou důsledkem výukového stylu nebo didaktických forem výuky, které neodpovídají typu utvářející se osobnosti dítěte. 44 Hypokalkulie Nespecifická porucha rozvoje základních početních dovedností podmíněná nerovnoměrnou skladbou matematických schopností a mírným snížením jejich úrovně do pásma podprůměru při celkové úrovni všeobecných rozumových schopností alespoň na dolní hranici pásma průměru. 45 Vývojová dyskalkulie Je specifická porucha počítání. Objevují se potíže s nabýváním a užíváním základních početních dovedností, které se mohou projevovat až ve vyšších ročnících základní školy. Úroveň matematických schopností je nízká a narušená ve struktuře. 46 Při dyskalkulii je jedna nebo více komponent ve struktuře výrazně retardovaná, přičemž ostatní vykazují normální úroveň. Dítě má problémy s počítáním a základními početními úkony (sečítání, odečítání, násobení a dělení). 47 Oligokalkulie Narušení rozvoje základních početních dovedností podmíněné narušením struktury matematických schopností a jejich výrazným snížením do pásma retardace při 44 NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str NOVÁK, Josef. Dyskalkulie: specifické poruchy počítání; metodika rozvíjení početních dovedností s přílohou Pracovní listy. Vyd. 2., v nakl. Tobiáš 1. Havlíčkův Brod: Tobiáš, 2000, str
22 celkové nízké úrovni všeobecných rozumových schopností. 48 Řešením takových případů je vzdělávání žáka ve zvláštní škole. 49 Akalkulie Porucha zvládání početních dovedností a početních operací, která mohla vzniknout např. na základě prožitého traumatu, přitom byly dříve dovednosti přiměřeně rozvinuty. 50 Jedná se o výrazně narušenou schopnost počítat a zvládat i nejjednodušší početní úkony. 51 R. Blažková 52 a L. Pavlíčková 53 uvádí další formy poruch ovlivňující osvojování matematických dovedností. Mezi tyto poruchy řadí: Poruchy koncentrace Dítě s poruchou koncentrace se hůře soustředí na určitou činnost, snadno se unaví, odbíhá od problému, nechává se vyrušit jakýmkoliv podmětem nesouvisejícím s prováděnou činností. Dětí trpí nedostatkem času, nestíhají, trvá jim déle, než proniknou do podstaty problému. To vše může způsobit neúspěšnost řešení v matematickém úkolu, který vyžaduje koncentraci a soustředěnost dítěte. Poruchy pravolevé orientace Preference užívání jednoho z párových orgánů způsobuje dětem problémy v matematice. Projevují se v zápisu a chápání číslic na ose, číslic jednostranně orientovaných a víceciferných čísel. Dochází ke změnám pořadí číslic v čísle. Děti píší obráceně některé číslice, mají obtíže v geometrii a při orientaci v grafu. 48 NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str NOVÁK, Josef. Dyskalkulie: specifické poruchy počítání; metodika rozvíjení početních dovedností s přílohou Pracovní listy. Vyd. 2., v nakl. Tobiáš 1. Havlíčkův Brod: Tobiáš, 2000, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str NOVÁK, Josef. Dyskalkulie: specifické poruchy počítání; metodika rozvíjení početních dovedností s přílohou Pracovní listy. Vyd. 2., v nakl. Tobiáš 1. Havlíčkův Brod: Tobiáš, 2000, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, PAVLÍČKOVÁ, Lenka. Poruchy matematických schopností žáků s dyskalkulií a jejich vliv na řešení učebních úloh ve fyzice a v matematice [online]. Brno,
23 Poruchy prostorové orientace Problémem je pochopení znázornění prostorové situace v rovině. Dítě chápe pojem krychle, avšak ve zněti čar na papíře krychli nepozná. Má obtíže při orientaci na stránce, při posunech v řazení číslic v čísle a při písemném sčítání, odčítání pod sebou. Problémy se vyskytují i v orientaci na číselné ose, odhadech vzdáleností, zápisu vzorců, řešení rovnic, při orientaci v souřadnicích a v pochopení znázornění prostorové situace v rovině. Poruchy časové orientace Dítě vnímá časové následnosti během dne. Problémem je pochopení jednotek času a převod mezi nimi, také pochopení vztahu kruhového ciferníku s lineárním plynutím času a digitálně zapsaný časový údaj. Má problémy i v orientaci v čase (v časové ose). Poruchy sluchového vnímání Dítě netrpí poruchou sluchu, avšak nevnímá, co se právě řeklo. Ptá se na to ihned po vyslovení. Ve třídě jsou i děti, které sluchově taky nevnímají a nezeptají se. Dítě nesprávně zaznamenává číslice a čísla při diktátu, zapomíná začátky a konce slov. Má problémy zapamatovat si diktovaný příklad. Poruchy reprodukce rytmu Vnímání rytmu je v matematice velmi důležité např. při počítání po jedné, při orientaci v číselné řadě, sledování závislostí a zákonitostí. Poruchy zrakového vnímání Dítě vidí dobře, avšak nevidí plně to, co by mělo vnímat jako matematické učivo. Není schopné rozlišit změny nebo orientovat se v geometrickém obrázku. Dítě má problémy při rozlišování figury a pozadí, rozlišování podobných a stranově obrácených tvarů, zaměňuje tvarově podobné číslice. Obtíže má při rozlišování geometrických tvarů a operačních znaků a matematických úkonů. 23
24 Poruchy řeči V matematice je důležitá schopnost formulovat myšlenky vlastními slovy. Přesné vyjadřování je obrazem přesného myšlení. Pokud dítě rozumí správně problému, dokáže ho správně vyjádřit. Poruchy jemné a hrubé motoriky Projevují se zejména při rýsování, v zápisu čísel a algoritmů. Dítě má problémy při tvoření skupin předmětů, při zápisu čísel a algoritmů operací, při manipulaci s konkrétními předměty nebo symboly. Poruchy chování jako důsledek poruch učení Pokud se dítěti nedaří v matematice, pak na sebe buď upoutává pozornost, nebo se 54, 55 uzavře do sebe, což je horší případ. Navázání konverzace je poté náročné. 4 Vývojová dyskalkulie V České republice se vývojová dyskalkulie vyskytuje přibližně u 3 % dětské populace. Není možné se domnívat, že se s ní někteří pedagogové ještě nesetkali. 56 I u mnohých významných osobností se setkáváme s problémy v matematice v jejich dětství, a přesto řada z nich dosáhla významných úspěchů v matematice a fyzice. Jako příklad můžeme uvést matematika N. N. Lužinu, A. Einsteina, T. A. Edisona, B. Gatese a B. Franklina. 57 Již v padesátých letech minulého století se rakouský neurolog Gertsmann zabýval neschopností dětí počítat a uvádí: Dyskalkulie je izolovaná narušená schopnost různé závažnosti, která se projevuje v neschopnosti provádět jednoduché nebo komplexní aritmetické operace a v narušení orientace v následnosti čísel a zlomků v čísle BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str PAVLÍČKOVÁ, Lenka. Poruchy matematických schopností žáků s dyskalkulií a jejich vliv na řešení učebních úloh ve fyzice a v matematice [online]. Brno, 2015, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str BLAŽKOVÁ, Růžena. Dyskalkulie. 1. vyd. Brno: Masarykova univerzita, 2012, str BLAŽKOVÁ, Růžena. Dyskalkulie. 1. vyd. Brno: Masarykova univerzita, 2012, str. 9 24
25 Podle 10. revize Mezinárodní klasifikace nemocí Duševní poruchy a poruchy chování patří dyskalkulie mezi Specifické vývojové poruchy školních dovedností kód F81.2. (1992). Tato porucha zahrnuje specifické postižení dovednosti počítat, kterou nelze vysvětlit mentální retardací ani nevhodným způsobem vyučování. Porucha se týká ovládání základních početních úkonů (sčítání, odčítání, násobení a dělení) spíše než abstraktnějších dovedností, jako je algebra, trigonometrie, nebo diferenciální počet. 59 Další definici formuloval L. Košč v roce 1985: Vývojová dyskalkulie je strukturální porucha matematických schopností, která má svůj původ v genově nebo perinatálními vlivy podmíněném narušení těch částí mozku, které jsou přímým anatomicko-fyziologickým substrátem věku přiměřeného dozrávání matematických funkcí, které však zároveň nemají za následek snížení všeobecných rozumových schopností. 60 Tuto definici rozšiřuje J. Novák a dyskalkulii definuje takto: Vývojová dyskalkulie je specifická porucha počítání projevující se zřetelnými obtížemi v nabývání a užívání základních početních dovedností, při obvyklém sociokulturním zázemí dítěte a celkové úrovni všeobecných rozumových předpokladů na dolní hranici pásma průměru nebo výše a s příznačnou vnitřní strukturou, v jejímž rámci je výrazně snížená úroveň matematických schopností a narušená jejich skladba za přítomností projevů dysfunkcí centrální nervové soustavy podmíněných vlivy dědičnými nebo vývojovými Faktory ovlivňující úspěšnost žáka v matematice Existuje mnoho faktorů ovlivňující úspěšnost žáka v matematice. Je velmi důležité tyto faktory náležitě rozlišovat alespoň do těchto tří skupin. Do první skupiny řadíme faktory, které jsou podmíněny vlivy (částečně odstranitelnými). Mezi ně patří např. způsob výuky, styl učení, motivace k učení, vhodnost přípravy na 59 BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str
26 výuku. Do druhé skupiny řadíme faktory, které jsou obtížněji odstranitelné. Do této skupiny zařazujeme dědičné vlivy nebo narušení činností těch částí mozku, které mají vliv na utváření matematických schopností. 62 Do poslední skupiny řadíme faktory, které jsou zapříčiněny nízkým nadáním pro matematiku nebo nízkým nadáním všeobecně. 63 Na úspěšnost dítěte v matematice májí vliv i další faktory. R. Blažková 64 uvádí, že problémy žáků mohou být způsobeny obsahem samotné matematiky, můžeme ji však najít i v osobnosti žáka, učitele nebo v rodičích. Tyto faktory si nyní trochu přiblížíme. Obsah učiva matematiky Matematika pracuje s abstraktními pojmy a jejich správné vytváření je pro psychiku žáka náročné. Má přesnou logickou výstavbu. Pro děti je složité přecházet od konkrétních představ k obecným. Školská matematika je předmětem, kde každý prvek nižší úrovně je nutným předpokladem k zvládnutí prvků vyšší úrovně (např. výuka algoritmů početních operací). Důležité je zvláště pochopení každého z matematických pojmů, posilování paměti a podle schopností dítěte je třeba stanovit míru vědomostí a dovedností, které je schopno vzhledem ke své poruše učení zvládnout. 65 Osobnost žáka Nemůžeme říci, že by se všechny děti rozvíjely stejně rychle. Každé dítě se rozvíjí jinou rychlostí, některé myšlenkové operace může mít vyvinuty později, přesto nemusí být snížena jeho úroveň rozumových schopností a ani nemusí trpět specifickou poruchou učení. To je i důvod, proč ke každému dítěti musíme přistupovat individuálně. Často se stává, že dítě učivo nejprve nepochopí, ale po určitém časovém úseku si ho bez problémů osvojí. Další příčiny problémů dítěte v matematice mohou souviset s jeho volními vlastnostmi. U matematiky je důležitá každodenní práce. Pokud dítě není schopno se k práci přimět, nebo není nikdo jiný, kdo by mu pomohl, nemá šanci učivo matematiky 62 BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str
27 zvládnout. S neúspěchem souvisí i nepozornost dítěte, nezájem, malé sebevědomí, úzkost, role outsidera mezi dětmi aj. Nezbytné je i sledování psychických bariér, mezi které patří např. syndrom bílého papíru (obavy z písemných prací, pětiminutovek, slovních úloh atd.). Všechny tyto problémy jsou velmi závažné a je potřeba všechny varovné signály vnímat. 66 Osobnost učitele Jedním z nejdůležitějších činitelů v práci se žáky se specifickou poruchou učení je osobnost učitele. 67 Nejčastější příčiny poruch učení dětí jsou způsobeny nedostatečnou odbornou znalostí učitele, jednak v oblasti matematiky, ale i v oblasti pedagogickopsychologické a speciálně pedagogické. Dále mohou být problémy způsobeny nevhodným stylem výuky (nemusí být vhodný, právě pro konkrétní dítě), volbou metod práce, komunikací s dětmi, nedostatečnou trpělivostí učitele, formálním přístupem k práci s dětmi, nedostatečnou motivací dětí a klasifikací. 68 Na úspěšnost práce má vliv i úroveň kompetencí učitele. Mezi tyto kompetence podle Průchy 69 patří: kompetence odborně předmětové (odborné znalosti učitele); kompetence psychodidaktické (vytváření příznivých podmínek pro učení, aktivizace myšlení, vytváření příznivého sociálního, pracovního a emocionálního klima, atd.); kompetence komunikativní (nejen ve vztahu k dětem, ale i k dospělým rodičům, nadřízeným, kolegům a jiným sociálním partnerům školy); kompetence organizační a řídící (plánování a projektování činnosti, udržování určitého řádu a systému); kompetence diagnostická a intervenční (zabývaní se tím, jak žák myslí, jedná, jaké má jeho jednání příčiny); kompetence poradenská, konzultativní; kompetence reflexe vlastní činnosti (získávání nových poznatků a zkušeností na základě analýzy své práce) BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str BLAŽKOVÁ, Růžena. Dyskalkulie. 1. vyd. Brno: Masarykova univerzita, 2010, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str PRŮCHA, Jan. Moderní pedagogika. 3., přeprac. a aktualiz. vyd. Praha: Portál, 2005, 70 PRŮCHA, Jan. Moderní pedagogika. 3., přeprac. a aktualiz. vyd. Praha: Portál, 2005, str
28 Vliv rodičů Rodiče dětí můžeme rozdělit do několika skupin podle jejich reakce na poruchy učení v matematice. 1. Do první skupiny řadíme rodiče, kteří mají pro dítě plné pochopení. Důležité je, že spolupracují s pedagogicko-psychologickou poradnou i učitelem matematiky. Snaží se dítěti pomoct. 2. Druhá skupina zahrnuje rodiče ambiciózní. Tato skupina rodičů není schopna se smířit s tím, že jejich dítě má problémy v matematice. Dítě poté nepřiměřeně zatěžují nebo odmítají. 3. Do další skupiny zahrnujeme rodiče, kteří se velmi snaží dítěti pomáhat, avšak postupem času je jejich snaha chybná a způsobí dítěti ještě větší potíže. 4. V této skupině jsou rodiče, kteří se sice o dítě zajímají, ale nehledají pro ně žádnou odbornou pomoc. 5. Poslední skupinou jsou rodiče, kteří se o dítě nestarají ani nevyhledávají odbornou pomoc Klasifikace dyskalkulie L. Košč 72 klasifikuje dyskalkulii podle základních problémů, které se u dětí vyskytují v souvislosti s vývojem a budováním matematických pojmů a vztahu, se čtením a psaním matematických výrazů. Tato vývojová období prezentuje ve své publikaci J. Novák obrázkem (obrázek 1 73 ). 71 BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str KOŠČ, Ladislav. Vývinová dyskalkulia ako porucha matematických schopností v detskom veku. Praha: Státní pedagogické nakladatelství, , 73 NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str
29 Obrázek 1: Rozdělení vývojových dyskalkulií se zřetelem na vývojová období dítěte 1. Dyskalkulie praktognostická Zasahuje rozvoj tzv. předčíselných dovedností v období 5-7 roku dítěte. V případě těžších forem se s touto poruchou můžeme setkat i v pozdějším věku. Je to porucha matematické manipulace s konkrétními předměty (např. kostkami) nebo nakreslenými symboly (např. číslice). 74 Matematická manipulace znamená poruchu tvoření skupin předmětů, řady předmětů nebo porovnávání počtu předmětů. Dítě nedospívá k pojmu přirozeného čísla. Není schopno odlišit geometrické útvary. Nemůže různě dlouhé předměty seřadit podle velikosti. Objevuje se porucha prostorového faktoru matematických schopností. Dítě má problémy s obkreslením figur, při kreslení a psaní. 2. Dyskalkulie verbální Jedná se o poměrně četnou formu poruch u dětí na začátku školní docházky. Primárně se projevuje omezenou či narušenou schopností správně a přesně rozumět významu běžného matematického pojmosloví a slovně označovat množství a počty předmětů, operační znaky a matematické úkony vůbec. 75 Když je dítě starší a má problémy s jednoduchými pojmy, je jeho porucha těžší. Dítě s touto poruchou není schopno vyjmenovat řadu čísel v určitém uspořádání (řady číslovek od nejvyšší po nejnižší a naopak). 76 Má problémy s pochopením 74 NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str
30 vysloveného čísla a jeho představy, s pochopením slovního vyjádřením matematických symbolů a znaků. 77 O projevech této dyskalkulie můžeme hovořit jen tehdy, pokud problémy u dítěte přetrvávají i nadále. Nejedná-li se tedy o aktuální nepochopení učiva. Mezi nejtěžší formy této poruchy patří senzorická verbální dyskalkulie a motorická verbální dyskalkulie Dyskalkulie lexická Jedná se o neschopnost číst matematické symboly, jako jsou čísla, číslice nebo operační symboly. 79 Při nejtěžší formě není dítě schopno přečíst izolované číslice nebo operační znaky. Při lehčí formě není schopno přečíst vícemístné číslo s nulami uprostřed, vícemístné číslo napsané svisle. 80 Nejtěžší forma lexické dyskalkulie se označuje jako tzv. slepota pro čísla. Tato forma se však vyskytuje zřídka. 81 U dětí se objevuje záměna tvarově podobných číslic, porucha pravolevé orientace a porucha orientace v prostoru Dyskalkulie grafická Jedná se o neschopnost psát matematické znaky, jako jsou číslice, čísla a další. Děti nejsou schopny psát čísla podle diktátu nebo přepisu, zapisovat čísla pod sebe (číslice téhož řádu - jednotky pod jednotky, desítky pod desítky). Mají problémy při zápisu víceciferných čísel. V geometrii mají problém při rýsování obrazců. Bývá porušena pravolevá a prostorová orientace. 5. Dyskalkulie operační Je narušena schopnost provádět matematické operace s přirozenými čísly (sčítání, odečítání, násobení, dělení). Dochází k záměně jednotlivých operací (sčítání, odečítání). Děti mají poruchy při osvojování si násobilky (dítě si může pomáhat počítáním na 77 BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str NOVÁK, Josef. Dyskalkulie: metodika rozvíjení základních početních dovedností. Vyd. 3., zcela přeprac. Havlíčkův Brod: Tobiáš, 2004, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str
31 prstech), často využívají písemného počítání i tam, kde to lze provést zpaměti. 83 Objevuje se neschopnost respektovat prioritu při provádění více operací různé parity. 84 Při manipulaci se zlomky často úplně ignorují poziční hodnotu čísel tvořících zlomek. Zaměňují čitatele za jmenovatele a opačně. V některých případech ignorují zlomkovou čáru úplně Dyskalkulie ideognostická Je porucha v oblasti pojmové činnosti, především v chápání matematických pojmů a vztahů mezi nimi. Děti mají problém řešit slovní úlohy (není schopno převést z praxe vycházející úkol do systému čísel). 86 Za nejtěžší poruchu je považována neschopnost počítat po jedné od daného čísla z hlavy. Nejlehčí stupeň se projevuje v neschopnosti chápat vztahy v matematických řadách, kdy má respondent pochopit vztahy v matematické řadě a potom v nich pokračovat (např. 5, 10, 15 ). 87 R. Blažková 88 klasifikuje dyskalkulii z hlediska oblastí učiva, ve kterých mají děti vzhledem k matematickému učivu problémy. Pochopení a zvládnutí jedné oblasti je nezbytným předpokladem k pochopení a zvládnutí oblasti další. 89 K tomuto třídění dospěla po dlouholeté práci s dětmi, kdy se ukázalo, že pokud dítě nepochopí podstatu matematického pojmu, neví jak a proč postupovat, jejich výsledky jsou vyvozovány pouze pamětně bez pochopení, je jejich náprava neefektivní. Tyto oblasti učiva dělí následovně: 1. Vytváření pojmu čísla Nejprve vytváříme pojem přirozeného čísla, poté čísla desetinného, zlomku, racionálního čísla a obecně reálného čísla. 83 ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str KOŠČ, Ladislav. Vývinová dyskalkulia ako porucha matematických schopností v detskom veku. Praha: Státní pedagogické nakladatelství, , str ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str
32 2. Čtení a zápis čísel Do této skupiny patří numerace čísel, uspořádání, zaokrouhlování přirozených čísel a desetinných čísel, porovnávání čísel. 3. Operace s čísly Nejprve operace s čísly přirozenými, poté s čísly v dalších číselných soustavách. 4. Slovní úlohy Do této oblasti patří přepis slovního vyjádření do matematického symbolického jazyka, řešení matematické úlohy a její interpretace do reality. 5. Geometrická a prostorová představivost Do této oblasti patří chápání rozmístění a vztahů předmětů v prostoru a jejich znázornění v rovině. 6. Početní geometrie Do této oblasti zahrnujeme uvědomění si velikosti útvarů, odhady, výpočty, chápání a používání vzorců. 7. Jednotky měr Do této skupiny patří pochopení každé z jednotek a převody mezi nimi Diagnostika dyskalkulie Diagnostika matematických vědomostí a dovedností je složitou činností. Je také východiskem vzdělávacího procesu a reedukace. Jejím cílem je vymezení úrovně vědomostí a dovedností, poznávacích procesů, sociálních vztahů, osobnostních charakteristik a dalších faktorů, které se podílejí na úspěchu či neúspěchu žáka. 91 Matematická schopnost je tvořena souhrnem dílčích schopností proto i diagnostika musí 90 BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str PAVLÍČKOVÁ, Lenka. Poruchy matematických schopností žáků s dyskalkulií a jejich vliv na řešení učebních úloh ve fyzice a v matematice [online]. Brno, 2015, str
33 postihnout úroveň zúčastněných psychických funkcí a dílčích dovedností, tj. rozumových schopností, řeči, percepce, pravolevé a prostorové orientace, motoriky. 92 Psychodiagnostika Brno vydala následující testy pro diagnostiku dyskalkulie: 1. Barevná kalkulie Test je určen pro děti věku 7-11 let. Obsahuje 39 úloh. Jeho administrace trvá cca 15 min. 2. Kalkulie IV Tento test nahrazuje předcházející vydání Kalkulie III. Na rozdíl od Kalkulie III je barevný a administrace trvá cca 25 min. Tento test je určen pro starší školní věk. 3. Číselný trojúhelník Tento test poskytuje doplňující informace, mezi které patří numerický, grafický a prostorový faktor. 4. Rey-Ostheriethova komplexní figura Tento test je doplněním výše zmíněných testů. 93 Na základě symptomatiky vývojové dyskalkulie byl v pedagogicko-psychologické poradně (Praha, ) sestaven a ověřován soubor úkolů, který se používá k diagnostice. Je sestaven z těchto oblastí 94 : 1. Předčíselné představy princip kvalifikace - třídění prvků podle barvy, velikosti, tvaru, princip sériace - uspořádání proužků podle velikosti, princip konzervace - porovnávání množin, které se liší prostorovým uspořádáním prvku; určování, zdali je na dvou kartičkách stejný nebo jiný počet prvků. 92 ZELINKOVÁ, Olga. Poruchy učení: dyslexie, dysgrafie, dysortografie, dyskalkulie, dyspraxie, ADHD. 10., zcela přeprac. a rozš. vyd. Praha: Portál, 2003, str ZELINKOVÁ, Olga. Poruchy učení: dyslexie, dysgrafie, dysortografie, dyskalkulie, dyspraxie, ADHD. 10., zcela přeprac. a rozš. vyd. Praha: Portál, ZELINKOVÁ, Olga. Poruchy učení: dyslexie, dysgrafie, dysortografie, dyskalkulie, dyspraxie, ADHD. 10., zcela přeprac. a rozš. vyd. Praha: Portál,
34 2. Číselné představy určování - množství prvků (stejně, méně, více), řazení karet s čísly - podle velikosti do 20, chápání smyslu číslovek, rozklady čísel. 3. Číslo, poziční hodnota číslic v čísle čti čísla - dítě čte čísla ve sloupcích i řádcích, přečti a napiš čísla - podle věku se zvyšuje obtížnost, psaní čísel podle diktátu - čísla volená podle věku dítěte, určování počtu jednotek, desítek v čísle, orientace na číselné ose. 4. Matematické operace doplňování operačních znaků, chápání smyslu operací, sčítání a odčítání čísel s přechodem i bez přechodu přes desítku zpaměti, sériové operace, písemné sčítání, odečítání, násobení, dělení. 5. Slovní matematické operace řešení slovních úloh, které odrážejí problém vyplívající z přirozené životní situace úkoly jsou předříkávány zkoušejícím, řešení obdobných úkolů jako v předchozí odrážce - dítě čte samo. 6. Pokračování číselných řad 7. Paměť sluchová paměť pro čísla, zraková paměť pro čísla. 34
35 8. Orientace v čase hodiny, dny, měsíce, roční období Další zkoušky Mohou být prováděny i během reedukace. Podávají přesnější obraz dítěte, vedou ke zkvalitnění diagnostiky a na ni navazující reedukaci. Obsahují: soubor zkoušek pro diagnostiku LMD, zkoušku vnímání a reprodukce rytmu, zkoušku zrakové a sluchové percepce, zkoušky čtení a diktát. 96 Na vyhodnocení těchto úkolů není žádná přesná vyhodnocovací stupnice, podle které by bylo možné určit, zda se jedná o dyskalkulika. Úkoly byly vytvářeny tak, aby co nejlépe zachytily úroveň funkcí, které by mohly být příčinou neúspěchu v matematice. Ne u každých problémů v matematice, je příčinou dyskalkulie. Některé děti jen potřebují delší čas na osvojení učiva Reedukace dyskalkulie Reedukační postupy se dají uvést v tzv. desateru. Je však nutné na každé dítě pohlížet individuálně a najít jeho vlastní postup reedukace. Co může pomoci jednomu dítěti, nemusí pomoct druhému. Do tohoto desatera R. Blažková 98 řadí: 1. Stanovení diagnózy Je velmi důležité stanovit správnou diagnózu, formulovat hlavní problémy dítěte v matematice. Nalézt, v které části učiva má dítě problémy. Jaké jsou příčiny těchto problémů. Podstatné je i to, jaký vztah má dítě k matematice. 2. Respektování logické výstavby matematiky a její specifičnosti Aby dítě pochopilo učivo vyšší úrovně, je nezbytné, aby pochopilo učivo nižší úrovně. Pokud dítě nepochopí nižší učivo, jsou reedukační postupy zaměřeny právě na pochopení nižšího učiva. Reedukační cvičení musí tedy začínat u toho učiva, které dítě 95 ZELINKOVÁ, Olga. Poruchy učení: dyslexie, dysgrafie, dysortografie, dyskalkulie, dyspraxie, ADHD. 10., zcela přeprac. a rozš. vyd. Praha: Portál, 2003, str ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str ZELINKOVÁ, Olga. Poruchy učení. 5. vyd. Praha: Portál, 2000, str BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita,
36 nepochopilo a přestalo zvládat. Postupy reedukace musí respektovat matematické zákonitosti a musí být použitelné i v dalším učivu. 3. Pochopení základních pojmů a operací Základní pojmy je potřeba vytvářet na konkrétních modelech. Všechny pojmy a operace s čísly je třeba odvozovat na základě vlastní manipulativní a myšlenkové činnosti dítěte. Je třeba používat různé formy práce a nové situace. 4. Navození AHA efektu K navození AHA efektu dochází, když dítě přijde samo na nějaký poznatek a přijme ho za svůj. Důležité je si uvědomit, že poznatky jsou nepřenosné. Přenosné jsou pouze informace. 5. Využití všech smyslů Významné je i zapojení všech smyslů, které se dají použít pro získávání matematických poznatků. Řadíme mezi ně zrak, sluch, hmat, pohyb. Smysly zapojujeme tak, aby to bylo dítěti příjemné a přispělo se k postupnému odbourání problémů. Velmi vhodné je i využití her. 6. Diskuze s dítětem Důležité je, aby dítě v určité situaci vidělo to stejné co učitel. Každé dítě má svoje vlastní komunikační cesty, kterými nalézá poznatky, a ty je potřeba v diskuzi s ním objevit. Neexistuje matematická slepota, každé dítě může k poznatkům nějak dojít. Dyskalkulie není omluvou pro nečinnost v matematice. 7. Pamětné zvládnutí učiva Do jaké míry je dítě schopno zapamatovat si učivo. Avšak matematické učivo nemůže být opřeno pouze o paměť bez porozumění a správného vyvození. Je důležité nalézt rovnováhu mezi vyvozováním a drilem. 8. Zvyšování nároků na samostatnost a aktivitu dítěte Je nezbytné, aby bylo dítě schopno pracovat samostatně. Tvořilo si vlastní materiály, příklady a pomůcky nebo se alespoň na tvorbě podílelo. Může si uvědomovat 36
37 své nedostatky a aktivně se podílet na jejich nápravě. Lze zde využít projektového vyučování. 9. Neustálá potřeba úspěchu Dítě potřebuje pochvalu i při sebemenším úspěchu. Také potřebuje pozitivní zážitky, pohodu, veselou, legrační cestu při nápravných cvičeních, nepřetěžování (neustálé mírné zatěžování), terapii hrou. 10. Práce podle individuálního plánu Ke každému dítěti by se mělo přistupovat individuálně. Nelze stanovit obecně platná pravidla, která by vyhovovala všem. Je nezbytné sestavení individuálního plánu pro konkrétní dítě. Individuální výuka nebo individualizovaná výuka v integrované třídě BLAŽKOVÁ, Růžena. Dyskalkulie a další specifické poruchy učení v matematice. Brno: Masarykova univerzita, 2009, str
38 5 Pomůcky pro žáky s dyskalkulií Praktická část bakalářské práce je zaměřena na výrobu pomůcek pro děti s dyskalkulií. Tyto pomůcky by měly být vhodné na procvičování a upevňování matematických dovedností. Celkově jsem vyrobila devět pomůcek, které jsem rozdělila na tři skupiny podle toho, kdy se které učivo na základní škole probírá. Pomůcky jsem následně vyzkoušela na třech různě starých dětech. Zaměřila jsem se zejména na funkční stránku pomůcek, na vylepšení nedostatků, které vyplynuly z vyzkoušení s dětmi a na využití pomůcky v matematice. 1) Do první skupiny jsem zařadila pomůcky zaměřené na: porovnávání množství (<, >, = ), sčítání. Tyto pomůcky jsou vhodné do první třídy základní školy. 2) Do druhé skupiny jsem zařadila pomůcky zaměřené na: sčítání, odčítání, násobení, dělení. Tyto pomůcky jsou vhodné do druhé třídy základní školy. 3) Do třetí skupiny jsem zařadila pomůcky zaměřené na: řady čísel, zlomky, násobení, dělení, číselnou osu. Tyto pomůcky jsou vhodné do čtvrté třídy základní školy. 38
39 5.1 Pomůcky pro 1. ročník základní školy Všechny pomůcky z této skupiny jsem vyzkoušela na Jakubovi, který navštěvuje první třídu základní školy Sokolovská ve Velkém Meziříčí. Jakubovi nebyla diagnostikována dyskalkulie, ale potíže mu činí sčítání a odečítání, které jsou nejspíše způsobeny nedostatečným procvičováním těchto matematických operací Pomůcka k porovnávání množství (<, >, = ) Obrázek 2: Pomůcka k porovnávání množství Popis pomůcky Tato pomůcka se skládá ze dvou hlavních částí. První část pomůcky tvoří barevná kolečka, která jsou vystřižena s filcového papíru. Kolečka mají různé barvy a všechna jsou stejně velká. Druhou část pomůcky tvoří kartičky s čísly (1-20) a znaky: =, <, >. Celou pomůcku můžeme vidět na obrázku 2. 39
40 Využití pomůcky Pomůcka je zaměřená na porovnávání množství. Je navržena tak, že se vždy na dvě hromádky naskládá určitý počet koleček a žák k nim přiřadí kartičku s číslem. Poté musí přiřadit správný symbol mezi tyto dvě kartičky (obrázeky 3,4) a zdůvodnit, proč zvolilo zrovna tento symbol. Tuto pomůcku lze v matematice využít nejen k porovnávání množství ale také ke sčítání, odečítání, násobení a dělení. Obrázek 3: Porovnávání množství 1 Obrázek 4: Porovnávání množství 2 Vyzkoušení pomůcky Pomůcku jsem vyzkoušela na Jakubovi. Nejprve jsme si vysvětlili, co přesně budeme dělat a co po něm budu chtít. Poté jsme si zopakovali, který znak co znamená. 40
41 Zprvu jsme pracovali jen v oboru do deseti, později jsem přidala dalších deset koleček. Po přidání více koleček začal mít Jakub trochu problémy, ale po opětovném přepočítání koleček vždy symbol umístil správně. Při větším počtu koleček se velmi osvědčilo skládat kolečka jednotlivých hromádek vedle sebe. Tímto způsobem bylo dobře vidět i bez počítání, kde je koleček více a kde méně (obrázek 5). Obrázek 5: Porovnávání množství 3 Návrhy na vylepšení pomůcky a na další využití Po vyzkoušení pomůcky jsem dospěla k názoru, že jako jedinou změnu bych navrhla použít výraznější barvičky koleček. Stávající barvičky nejsou úplně nejvhodnější, hlavně v případě, pokud se s pomůckou pracuje mimo stůl (na koberci). Kolečka se na koberci mohou trochu ztrácet. Pomůcka by se mohla rozšířit také o různé další tvary (čtverce, trojúhelníky, různě veliká kolečka, apod.). 41
42 5.1.2 Pomůcka ke sčítání Obrázek 6: Pomůcka ke sčítání Popis pomůcky Pomůcka vyrobena ze smrkového dřeva a skládá se z několika krychlí a hranolů. Každá krychle má hranu 2,5 cm a hranol má podstavu 2,5 cm x 2,5 cm a výšku v rozmezí 5-25 cm. Výška se odvíjí podle toho, kolik krychlí má hranol představovat. Pokud hranol bude představovat 4 krychle, pak má výšku 10 cm. K této pomůcce jsem přiřadila i deset kartiček od 1 do 10, které vždy nejprve ke krychlím a hranolům přiřadí (obrázek 6). Využití pomůcky Pomůcka má rozmanité využití. Může sloužit zejména ke znázornění sčítání. Tato pomůcka je navržená tak, že prvně žák přiřadí kartičky ke krychlím a hranolům tak, aby číslo znázorňovalo počet možných krychlí. Poté žakovi dáváme různé příklady na sčítání a on si pomocí krychlí ověřuje správnost výpočtu. Když žákovi 42
43 napíšu příklad 3+3 = 6 tak si tento výsledek může ověřit i na krychlích. Také si může zároveň ověřit, že 6 = nebo 6 = atd. Vyzkoušení pomůcky Pomůcku jsme si opět vyzkoušela na Jakubovi. Na začátku jsem mu vysvětlila, co přesně budeme dělat a co po něm budu požadovat. Prvně jsme si roztřídili hranoly podle velikostí a pomocí krychlí určili velikost hranolů a přiřadili k nim číslo od Poté jsem Jakubovi dávala jednoduché příklady na sčítání a on mi říkal výsledky. Tyto výsledky si i názorně zkusil na hranolech. Když jsem mu zadala příklad 2+4 odpověděl, že výsledek je 6. Poté si vzal šest krychlí a naskládal je do řady. Vedle nich poskládal hranoly velikosti dva a velikosti čtyři a nakonec hranol o velikosti šest (obrázek 7). Po vyskládání zjistil, že příklad spočítal správně. Na stejném principu jsme vyzkoušeli i dalších 20 příkladů. Obrázek 7: Sčítání Návrhy na vylepšení pomůcky a na další využití Po vyzkoušení pomůcky jsem zjistila, že by bylo na místě různě veliké hranolky odlišit i barvami, aby se lépe rozpoznávalo, které z nich jsou stejně vysoké bez opětovného zkoušení pomocí krychlí. 43
44 Pomůcka může také sloužit na určování počtu, kdy žák bude pouze přiřazovat čísla k počtům krychlí nebo k hranolům. Pomůcka se dá využít i k odečítání. 5.2 Pomůcky pro 2. ročník základní školy Všechny pomůcky z této skupiny jsem vyzkoušela na Ondrovi, který navštěvuje třetí třídu základní školy Náměšť nad Oslavou, Komenského 53. Výběr žáka 3. třídy byl záměrný, protože pomůcky jsou určeny pro učivo druhé třidy. Kdybych si vybrala žáka druhé třidy nemusel by mít toto učivo probráno. Ondra je v matematice vcelku šikovný, problém mu však dělá pamětné počítání, ve kterém občas dělá chyby Pomůcka k dělení Obrázek 8: Pomůcka k dělení Popis pomůcky Pomůcka se skládá ze dvou hlavních částí. První část pomůcky tvoří barevná kolečka, která jsou vystřižena s filcového papíru. Kolečka mají různé barvy a všechna jsou stejně velká. Druhou část pomůcky tvoří dva druhy panáčků - holčička a chlapeček (obrázek 8). 44
45 Využití pomůcky Pomůcka je zaměřená na dělení beze zbytku i se zbytkem. Je navržená tak, že prvně žakovi na papír napíšu příklad na dělení, a poté, co ho vypočítá, si tento příklad zkusí i na této pomůcce. Např. u příkladu 21:3 zjistí, že je to rovna 7. Poté mu podám 21 koleček a před něj položím tři figurky. Jeho úkolem bude rozdělit kolečka mezi figurky tak, aby měla každá figurka stejně. Takto to bude fungovat i u dělení se zbytkem, až na rozdíl, že u rozdělování koleček mezi panáčky mu pár koleček zůstane a to bude znázorňovat zbytek po dělení. Vyzkoušení pomůcky Pomůcku jsem si vyzkoušela na Ondrovi. Nejprve jsme si vysvětlili, co přesně budeme dělat a také to, co po něm budu požadovat. Začali jsme s jednoduchými příklady jako je 6:3=2. Poté, co mi Ondra řekl správný výsledek, vyzkoušeli jsme to i s panáčky a kolečky (obrázek 9). Zkusili jsme i těžší příklady a nakonec i příklady se zbytky (obrázek 10). U těchto příkladů měl Ondra trochu problém, ale po použití koleček a panáčku příklad vždy vyřešil. Obrázek 9 : Dělení 45
46 Obrázek 10: Dělení se zbytkem Návrhy na vylepšení pomůcky a na další využití Po vyzkoušení pomůcky jsem dospěla k názoru, že jako jedinou změnu bych navrhla použít výraznější barvičky koleček. Stávající barvičky nejsou úplně nejvhodnější, hlavně v případě pokud se s pomůckou pracuje mimo stůl (na koberci). Kolečka se na koberci mohou trochu ztrácet. Pomůcka se může dále využit také k určování množství, přičemž bych k panáčkům předem přiřadila množství koleček a žák by mi pak řekl, kolik koleček který panáček má, dále také, kdo jich má nejvíc a kdo nejmíň. Na závěr by mi řekl, kolik koleček mají všichni dohromady. 46
47 5.2.2 Pomůcka na násobení Obrázek 11: Pomůcka násobení- vyplněná Obrázek 12: Pomůcka na násobení Popis pomůcky Pomůcka se skládá ze dvou částí. První částí je samotná tabulka s našitou vrchní a boční lištou s čísly od 1 do 10. Druhou částí jsou výsledky násobení, které se na 47
48 tabulku lepí pomocí suchých zipů. Jednu část suchého zipu mají na sobě a druhá je trvale přišita na tabulce, takže děti přesně vidí, kam výsledek připevnit (obrázek 11). Využití pomůcky Pomůcka je zaměřena na procvičování malé násobilky. Pomůcka funguje tak, že se vždy sundají výsledky násobení a poté se dětí zeptám na násobky a oni odpovídají a zároveň připevní výsledek na to správné místo v tabulce (obrázek 12). Tento postup se opakuje, dokud nejsou všechny výsledky na správném místě. Vyzkoušení pomůcky Tuto pomůcku jsem vyzkoušela také na Ondrovi. Jako vždy jsme si nejprve vysvětili, jak pomůcka funguje, a to, co budeme dělat a co budu po Ondrovi chtít, aby udělal sám. Jako první jsme společně sundali všechny výsledky násobení a naskládali je na zem před tabulku. Poté jsem Ondrovi říkala násobky do deseti a on vždy našel správný výsledek a připevnil ho na své místo v tabulce. Po pár příkladech si všiml, že jsou vždy dva stejné výsledky u součinu dvou čísel (2*6=12 a 6*2=12) a vyplňování tabulky mu šlo mnohem rychleji. Tímto způsobem jsme vyplnili celou tabulku. Návrhy na vylepšení pomůcky a na další využití Po vyzkoušení pomůcky jsem dospěla k názoru, že jako jedinou změnu bych navrhla použít jiné barvy na vrchní a boční lištu. Tato lišta při zaplňování tabulky byla stále více podobná výsledkům a mohlo docházet k tomu, že se s nimi pletla. Pokud dítě bude stát u tabulky blízko, k záměně dojít nemůže. Pomůcka se také může použít na jednotlivé násobky čísel (obrázek 13), např. u čísla 4: 4, 8, 12, 16, 20, 24, 28, 32, 36,
49 Obrázek 13: Násobky čísla čtyři Domino Obrázek 14: Domino1 49
50 Popis pomůcky Pomůcka se skládá z 11 kartiček vyrobených z papíru. Na jedné straně je vždy číslo a na druhé straně je přiklad na sčítání nebo odečítání (obrázek 14). Využití pomůcky Pomůcka je zaměřena na procvičování sčítání a odčítání. Pomůcka funguje na principu domina. Výsledek příkladu na pravé straně musí být číslo na jiné kartičce. Například 8+2=10 proto na kartičku s příkladem 8+2 musí navazovat kartička s číslem 10, tento postup můžeme vidět na (obrázek 15). Domino je navržené tak, že při správném poskládaní kartiček za sebe, bude první kartička s poslední kartičkou opět na sebe navazovat. Obrázek 15: Přiřazování kartiček v dominu Vyzkoušení pomůcky Tuto pomůcku jsem vyzkoušela na Ondrovi. Drobným problémem bylo, že Ondra neznal domino, proto ze začátku trvalo o chvilku déle, než jsme si pomůcku vysvětlili a ukázali, jakým principem se doplňují kartičky k sobě. Ze začátku to Ondrovi moc nešlo, ale to bylo způsobeno nedostatečnou znalostí domina. Po chvilce princip domina pochopil a domino s malými zaváháními složil. 50
51 Návrhy na vylepšení pomůcky a na další využití Po vyzkoušení pomůcky jsem dospěla k názoru, že by bylo dobré domino rozšířit o další kartičky nebo udělat nová další domina, aby bylo možné sčítání a odečítání ještě více procvičit. 5.3 Pomůcky pro 4. ročník základní školy Všechny pomůcky z této skupiny jsem vyzkoušela na Martinovi, který navštěvuje pátou třídu Základní školy Sokolovská ve Velkém Meziříčí. Stejně jako u minulé skupiny pomůcek, jsem vybrala žáka páté třídy záměrně. Kdybych si vybrala žáka čtvrté třidy, nemusel by mít toto učivo probráno Pomůcka k procvičování řady čísel Obrázek 16: Pomůcka k procvičování řady čísel Popis pomůcky Pomůcka se skládá z tří hlavních částí (tři proužky s čísly a vynechávkami) a z volných lístků s čísly, které se mají doplnit do řady. Všechny tři řady jsou odlišné, první se vždy násobí dvěma předešlé číslo, u druhé se přičítá číslo dva a u třetí se přičítá číslo tři (obrázek 16). 51
52 Využití pomůcky Tato pomůcka slouží k procvičování řady čísel. Práce s pomůckou je velmi jednoduchá. Před žáka se položí jeden proužek s čísly a žák poté zkusí přijít na to, jaké budou chybějící čísla a jaký je princip číselné řady. Poté mu podám volné lístky a on je přiřadí na správné místo. Vyzkoušení pomůcky Tuto pomůcku jsem vyzkoušela na Martinovi. Ze začátku jsme si opět řekli, co přesně budeme dělat a co bude dělat on. Taky jsme si řekli, jakým způsobem se čísla v řadě mění. Tuto pomůcku Martin hned pochopil a všechny tři řady během chvilky doplnil. Návrhy na vylepšení pomůcky a na další využití Po vyzkoušení pomůcky jsem dospěla k názoru, že by bylo dobré pomůcku rozšířit i o další řady tak, aby se s touto pomůckou dalo pracovat déle (obrázek 17). Obrázek 17: Další řady čísel 52
53 5.3.2 Pomůcka k počítání se zlomky Obrázek 18: Pomůcka k počítání se zlomky Popis pomůcky Skládá se z mnoha částí. Všechny tyto části tvoří kruh a kruhové výseče. Nachází se zde celý kruh, potom 2 x 1/2, 3 x 1/3, 4 x 1/4, 5 x 1/5, 6 x 1/6, 8 x 1/8 a 16x 1/16 (obrázek 18). Všech částí je vždy tolik, aby dali dohromady celý kruh. Jednotlivé zlomky jsou barevně odlišeny, tak aby bylo lépe rozpoznatelné, který zlomek je stejný (obrázek 19). Na zadních stranách jednotlivých zlomků jsou připevněny magnety, proto se tato pomůcka hodí i na používání na tabuli, kde jsou zlomky mnohem lépe viditelné než na stole. 53
54 Obrázek 19: Barevné rozlišení zlomků Využití pomůcky Pomůcka je zaměřená na počítání se zlomky. Zejména slouží k budování pojmu zlomku, vyjádření celku, porovnávání zlomků, sčítání a odčítání zlomku. Dítě si s ní může pracovat samo nebo může s pomocí pedagoga zkoušet například že 1/3 +1/3 +1/3 = 1, když si tyto zlomky naskládá k sobě, tak mu vytvoří celý kruh (obrázek 20). Tímto způsobem mu může být vysvětleno, že pokud je kruh rozdělen na tři stejné části, každá část se nazývá jednou třetinou a dohromady dají celek. Stejně by se postupovalo i u ostatních úloh, příkladů. Obrázek 20: Sčítání zlomků 54
55 Vyzkoušení pomůcky Tuto pomůcku jsem vyzkoušela na Martinovi. Ze začátku jsme si vysvětlili (zopakovali), co to jsou zlomky, jak se jednotlivé části zlomku jmenují, a také, jak budeme s touto pomůckou pracovat. Pokaždé jsem dala Martinovi nějaký příklad a on ho pomocí zlomků spočítal, např. 1/6 + 1/6 + 1/6 = 3/6 = 1/2 (obrázek 21). Později jsme zkusili i odečítání, které mu zezačátku moc nešlo, ale po chvilce práce s pomůckou i tyto příklady zvládal dobře. Obrázek 21: Práce se zlomky Návrhy na vylepšení pomůcky a na další využití Po vyzkoušení této pomůcky jsme dospěla k názoru, že tato pomůcka plní přesně to, k čemu byla určena a bez jakýkoliv změn se dá bezproblémově používat. Pomůcka by se také dala použít při vysvětlování desetinných čísel (např. ½ = 0,5) 55
56 5.3.3 Pomůcka číselná osa Obrázek 22: Číselná osa - rozložená Obrázek 23: Číselná osa - složená Popis pomůcky Pomůcka se skládá ze 4 částí (obrázek 22). První tři části po složení (pomocí magnetek) vytvoří číselnou osu. Po složení je osa velká asi 1,3 m, proto je lepší s ní pracovat na zemi nebo na velkém stole (obrázek 23). Tato osa má rozsah od čísla -50 po číslo 100. Poslední částí jsou kartičky se samotnými čísly od -50 po
57 Využití pomůcky Pomůcka slouží ke znázornění čísel na číselné ose. Je vhodná nejen pro první stupeň základní školy ale také (kvůli rozsahu i do záporných hodnot) je možné ji využít i na druhém stupni základní školy. Pomůcka funguje tak, že si žák vybere nějaké číslo. Toto číslo poté musí na ose položit na místo, kam patří (obrázek 24). Obrázek 24: Doplňování čísel na osu Vyzkoušení pomůcky Tuto pomůcku jsem vyzkoušela na Martinovi. Zkoušela jsem pouze kladnou část číselné osy. Ze začátku jsme si jako vždy vysvětlili, jak se s pomůckou pracuje, co přesně budeme dělat a co budu po Martinovi chtít. Poté jsme si společně určili, co znázorňují jednotlivé čárky na ose a přiřadili k nim čísla 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Tyto čísla jsme přiřadili jako první, aby se Martinovi lépe orientovalo na číselné ose a zbytečně nedělal chyby. Po doplnění těchto čísel šlo už všechno velmi dobře a bez jakékoli chyby Martin čísla na osu doplnil. Návrhy na vylepšení pomůcky a na další využití Po použití pomůcky jsem dospěla k názoru, že bych na této pomůcce nic neměnila. Při používání osy ve vyšších ročnících by se mohla doplnit o další čísla v záporných hodnotách. 57
58 Dalším využitím této pomůcky by mohlo být, že si vybereme z číselné osy jen některou její (vhodnou) část a žák se bude učit orientovat v okolí zadaného čísla Domino složitější Obrázek 25: Domino 2 Popis pomůcky Pomůcka se skládá z 11 kartiček. Na obou stranách kartičky jsou příklady na počítání (obrázek 25). Využití pomůcky Pomůcka je zaměřena na procvičování sčítání, odčítání, násobení a dělení. Pomůcka funguje na principu domina. Výsledek příkladu na pravé straně jedné kartičky musí být stejný jako výsledek příkladu na levé straně druhé kartičce. Například 27:3=9 a 3*3=9 proto kartičky s 27:3 a 3*3 budou ležet vedle sebe (obrázek 26). Domino je navržené tak, že při správném poskládaní kartiček za sebe, bude první kartička s poslední kartičkou opět na sebe navazovat. 58
59 Obrázek 26: Přiřazování kartiček Vyzkoušení pomůcky Tuto pomůcku jsem vyzkoušela na Martinovi. I v tomto případě nastal drobný problém a to ten, že Martin stejně jako Ondra neznal domino, proto ze začátku trvalo o chvilku déle, než jsme si pomůcku vysvětlili a ukázali, jakým principem se doplňují kartičky k sobě. Zprvu to Martinovi moc nešlo, ale to bylo způsobeno nedostatečnou znalostí domina. Po chvilce princip domina pochopil. Ze začátku neměl v přiřazování systém, ale později si kartičky naskládal pod sebe a tím se mu rychleji hledala navazující kartička (obrázek 27). Obrázek 27: Práce s dominem 59
Specifické poruchy učení. -definice -příčiny -typy SPU
 Specifické poruchy učení -definice -příčiny -typy SPU Specifické poruchy učení jsou definovány jako neschopnost naučit se určitým dovednostem (např. čtení, psaní, počítání) pomocí běžných výukových metod
Specifické poruchy učení -definice -příčiny -typy SPU Specifické poruchy učení jsou definovány jako neschopnost naučit se určitým dovednostem (např. čtení, psaní, počítání) pomocí běžných výukových metod
Specifické poruchy učení
 Specifické poruchy učení Definice: - neschopnost naučit se číst, psát a počítat pomocí běžných výukových metod za alespoň průměrné inteligence a přiměřené sociokulturní příležitosti - nevznikají v důsledku
Specifické poruchy učení Definice: - neschopnost naučit se číst, psát a počítat pomocí běžných výukových metod za alespoň průměrné inteligence a přiměřené sociokulturní příležitosti - nevznikají v důsledku
Specifické poruchy učení
 Specifické poruchy učení pojetí, etiologie, klasifikace SPU, diagnostika SPU, charakteristika dyslexie, dysgrafie, dysortografie, dyskalkulie, legislativa SPU charakteristika Různorodá skupina poruch,
Specifické poruchy učení pojetí, etiologie, klasifikace SPU, diagnostika SPU, charakteristika dyslexie, dysgrafie, dysortografie, dyskalkulie, legislativa SPU charakteristika Různorodá skupina poruch,
Psychologické aspekty školní úspěšnosti
 Psychologické aspekty školní úspěšnosti Co ovlivňuje školní úspěšnost vnější faktory učivo učitel a vyuč. metoda celkový kontext vzdělávání vnitřní faktory motivace vědomosti vlastnosti metoda učení biolog.
Psychologické aspekty školní úspěšnosti Co ovlivňuje školní úspěšnost vnější faktory učivo učitel a vyuč. metoda celkový kontext vzdělávání vnitřní faktory motivace vědomosti vlastnosti metoda učení biolog.
SPECIFICKÉ PORUCHY UČENÍ
 SPECIFICKÉ PORUCHY UČENÍ Program: 1. Specifické poruchy učení ( SPU ) 2. Vliv SPU na psychiku mladšího školáka 3. Kineziologická cvičení 4. Individuální konzultace SPECIFICKÉ PORUCHY UČENÍ Jsou různorodé
SPECIFICKÉ PORUCHY UČENÍ Program: 1. Specifické poruchy učení ( SPU ) 2. Vliv SPU na psychiku mladšího školáka 3. Kineziologická cvičení 4. Individuální konzultace SPECIFICKÉ PORUCHY UČENÍ Jsou různorodé
Specifické poruchy učení ÚVOD. PhDr. Jarmila BUREŠOVÁ
 ÚVOD PhDr. Jarmila BUREŠOVÁ Obtíže s učením, které nejsou způsobeny celkovým snížením poznávacích schopností smyslovým nebo tělesným postižením nevhodnou metodou učení nedostatečnou příležitostí k učení
ÚVOD PhDr. Jarmila BUREŠOVÁ Obtíže s učením, které nejsou způsobeny celkovým snížením poznávacích schopností smyslovým nebo tělesným postižením nevhodnou metodou učení nedostatečnou příležitostí k učení
VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 8, S 20 DATUM VYTVOŘENÍ: 2.3. 2013
 VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 8, S 20 JMÉNO AUTORA: DATUM VYTVOŘENÍ: 2.3. 2013 PRO ROČNÍK: OBORU: VZDĚLÁVACÍ OBLAST. TEMATICKÝ OKRUH: TÉMA: Bc. Blažena Nováková 2. ročník Předškolní a mimoškolní
VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 8, S 20 JMÉNO AUTORA: DATUM VYTVOŘENÍ: 2.3. 2013 PRO ROČNÍK: OBORU: VZDĚLÁVACÍ OBLAST. TEMATICKÝ OKRUH: TÉMA: Bc. Blažena Nováková 2. ročník Předškolní a mimoškolní
Specifické poruchy učení a jejich problematika
 MASARYKOVA UNIVERZITA PEDAGOGICKÁ FAKULTA Katedra speciální pedagogiky Specifické poruchy učení a jejich problematika Bakalářská práce Brno 2006 Autor práce: Kateřina Večerková Vedoucí práce: doc. PaedDr.
MASARYKOVA UNIVERZITA PEDAGOGICKÁ FAKULTA Katedra speciální pedagogiky Specifické poruchy učení a jejich problematika Bakalářská práce Brno 2006 Autor práce: Kateřina Večerková Vedoucí práce: doc. PaedDr.
DEFINICE SPECIFICKÝCH PORUCH UČENÍ
 DEFINICE SPECIFICKÝCH PORUCH UČENÍ terminologické pojetí SPU, zákon č. 561/2004 Sb., ve znění pozdějších předpisů (dítě, žák a student se speciálními vzdělávacími potřebami), definice expertů z USA (1980)
DEFINICE SPECIFICKÝCH PORUCH UČENÍ terminologické pojetí SPU, zákon č. 561/2004 Sb., ve znění pozdějších předpisů (dítě, žák a student se speciálními vzdělávacími potřebami), definice expertů z USA (1980)
Specifické poruchy učení
 Specifické poruchy učení SPU jsou tématem, který je v českém školství neustále aktuální. Pojem poruchy učení označuje skupinu obtíží projevujících se při osvojování čtení, psaní, počítání i ostatních dovednostech.
Specifické poruchy učení SPU jsou tématem, který je v českém školství neustále aktuální. Pojem poruchy učení označuje skupinu obtíží projevujících se při osvojování čtení, psaní, počítání i ostatních dovednostech.
Práce s dětmi s poruchami učení v poradně pro percepční a motorická oslabení
 EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJEME DO VAŠÍ BUDOUCNOSTI Práce s dětmi s poruchami učení v poradně pro percepční a motorická oslabení Lenka Procházková Monika Kabátová Specifické poruchy učení
EVROPSKÝ SOCIÁLNÍ FOND PRAHA & EU: INVESTUJEME DO VAŠÍ BUDOUCNOSTI Práce s dětmi s poruchami učení v poradně pro percepční a motorická oslabení Lenka Procházková Monika Kabátová Specifické poruchy učení
11. 1. 2013. Popis využití: Výukový materiál s úkoly pro žáky s využitím dataprojektoru,
 VY_32_INOVACE_PSYPS13160ZAP Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: CZ.1.07/1.5.00/34.0883 Název projektu: Rozvoj vzdělanosti Číslo šablony: III/2 Datum vytvoření:
VY_32_INOVACE_PSYPS13160ZAP Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: CZ.1.07/1.5.00/34.0883 Název projektu: Rozvoj vzdělanosti Číslo šablony: III/2 Datum vytvoření:
VZDĚLÁVÁNÍ ŽÁKŮ SE SPECIFICKÝMI PORUCHAMI UČENÍ A CHOVÁNÍ
 VZDĚLÁVÁNÍ ŽÁKŮ SE SPECIFICKÝMI PORUCHAMI UČENÍ A CHOVÁNÍ 1. Speciální výuka 2. Podmínky pro vřazení žáka do speciální třídy 3. Charakteristika speciálních tříd 4. Vymezení pojmů SPUCH, logopedických obtíží
VZDĚLÁVÁNÍ ŽÁKŮ SE SPECIFICKÝMI PORUCHAMI UČENÍ A CHOVÁNÍ 1. Speciální výuka 2. Podmínky pro vřazení žáka do speciální třídy 3. Charakteristika speciálních tříd 4. Vymezení pojmů SPUCH, logopedických obtíží
DYSKALKULIE - porucha matematických schopností
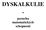 DYSKALKULIE - porucha matematických schopností Při řešení různých matematických úloh se uplatňují speciální matematické faktory: verbální (zadávání úloh, jejich řešení, odpovědi na otázky ve formě řeči
DYSKALKULIE - porucha matematických schopností Při řešení různých matematických úloh se uplatňují speciální matematické faktory: verbální (zadávání úloh, jejich řešení, odpovědi na otázky ve formě řeči
Specifické poruchy učení DYSORTOGRAFIE DYSGRAFIE. PhDr. Jarmila BUREŠOVÁ
 Specifické poruchy učení DYSORTOGRAFIE DYSGRAFIE PhDr. Jarmila BUREŠOVÁ Specifické poruchy učení Dysortografie - specifická vývojová porucha správného psaní. Projevuje se obtížemi ve správném zapsání slyšeného,
Specifické poruchy učení DYSORTOGRAFIE DYSGRAFIE PhDr. Jarmila BUREŠOVÁ Specifické poruchy učení Dysortografie - specifická vývojová porucha správného psaní. Projevuje se obtížemi ve správném zapsání slyšeného,
OVĚŘENO: Datum: třída: 2.KOP
 VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 11, S 20 JMÉNO AUTORA: DATUM VYTVOŘENÍ: 19.3. 2013 PRO ROČNÍK: OBORU: VZDĚLÁVACÍ OBLAST. TEMATICKÝ OKRUH: TÉMA: Bc. Blažena Nováková 2. ročník Předškolní a mimoškolní
VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 11, S 20 JMÉNO AUTORA: DATUM VYTVOŘENÍ: 19.3. 2013 PRO ROČNÍK: OBORU: VZDĚLÁVACÍ OBLAST. TEMATICKÝ OKRUH: TÉMA: Bc. Blažena Nováková 2. ročník Předškolní a mimoškolní
LOGOPEDICKÝ ASISTENT. Cílem kurzu je získání odborných znalostí z oblasti logopedické prevence. Mgr. Helena Vacková
 LOGOPEDICKÝ ASISTENT Cílem kurzu je získání odborných znalostí z oblasti logopedické prevence. Mgr. Helena Vacková 25.11. 2014 V LIBERCI Logopedická prevence 01 Dětský věk, zejména prvních 7 let, je dobou
LOGOPEDICKÝ ASISTENT Cílem kurzu je získání odborných znalostí z oblasti logopedické prevence. Mgr. Helena Vacková 25.11. 2014 V LIBERCI Logopedická prevence 01 Dětský věk, zejména prvních 7 let, je dobou
METODICKÉ LISTY. výstup projektu Vzdělávací středisko pro další vzdělávání pedagogických pracovníků v Chebu. reg. č. projektu: CZ.1.07/1.3.11/02.
 METODICKÉ LISTY výstup projektu Vzdělávací středisko pro další vzdělávání pedagogických pracovníků v Chebu reg. č. projektu: CZ.1.07/1.3.11/02.0007 Sada metodických listů: KABINET 1. STUPNĚ ZŠ Název metodického
METODICKÉ LISTY výstup projektu Vzdělávací středisko pro další vzdělávání pedagogických pracovníků v Chebu reg. č. projektu: CZ.1.07/1.3.11/02.0007 Sada metodických listů: KABINET 1. STUPNĚ ZŠ Název metodického
Doplnění přednášky: PEDAGOGICKO-PSYCHOLOGICKÉ PORADNY A SPECIÁLNÍ PEDAGOGICKÁ CENTRA
 TÉZE Doplnění přednášky: PEDAGOGICKO-PSYCHOLOGICKÉ PORADNY A SPECIÁLNÍ PEDAGOGICKÁ CENTRA Úkoly poradenského zařízení 1. zajišťuje pravidelnou a přímou individuální speciálně pedagogickou a psychologickou
TÉZE Doplnění přednášky: PEDAGOGICKO-PSYCHOLOGICKÉ PORADNY A SPECIÁLNÍ PEDAGOGICKÁ CENTRA Úkoly poradenského zařízení 1. zajišťuje pravidelnou a přímou individuální speciálně pedagogickou a psychologickou
Přesnost a rychlost ve vnímání množství a jejich využití při diagnostice dyskalkulie. Kateřina Pražáková Klára Špačková
 Přesnost a rychlost ve vnímání množství a jejich využití při diagnostice dyskalkulie Kateřina Pražáková Klára Špačková Dyskalkulie SPU Obtíže v matematice Intelektové schopnosti v normě Standardní podmínky
Přesnost a rychlost ve vnímání množství a jejich využití při diagnostice dyskalkulie Kateřina Pražáková Klára Špačková Dyskalkulie SPU Obtíže v matematice Intelektové schopnosti v normě Standardní podmínky
Příloha 1: Schéma levé hemisféry mozkové kůry s vyznačenými oblastmi důležitými pro čtení (obrázek)
 Seznam příloh Příloha 1: Schéma levé hemisféry mozkové kůry s vyznačenými oblastmi důležitými pro čtení (obrázek) Příloha 2: Ukázka dysgrafie (obrázek) Příloha 3: Ukázka dysortografie (obrázek) Příloha
Seznam příloh Příloha 1: Schéma levé hemisféry mozkové kůry s vyznačenými oblastmi důležitými pro čtení (obrázek) Příloha 2: Ukázka dysgrafie (obrázek) Příloha 3: Ukázka dysortografie (obrázek) Příloha
1. Pojetí speciálně pedagogické diagnostiky
 SPECIÁLNĚ PEDAGOGICKÁ DIAGNOSTIKA 1. Pojetí speciálně pedagogické diagnostiky Cílem je poznání člověka s postižením. Cílem není léčba, ale výchova a vzdělávání. Diagnostika zkoumá průběh vývoje člověka.
SPECIÁLNĚ PEDAGOGICKÁ DIAGNOSTIKA 1. Pojetí speciálně pedagogické diagnostiky Cílem je poznání člověka s postižením. Cílem není léčba, ale výchova a vzdělávání. Diagnostika zkoumá průběh vývoje člověka.
Specifické poruchy učení
 Specifické poruchy učení Vypracovala: Mgr. Jana Nováková SPECIFICKÉ PORUCHY UČENÍ Specifické poruchy učení jsou poruchy způsobující problémy v rámci vzdělávacího procesu, kdy se u takto postižených jedinců
Specifické poruchy učení Vypracovala: Mgr. Jana Nováková SPECIFICKÉ PORUCHY UČENÍ Specifické poruchy učení jsou poruchy způsobující problémy v rámci vzdělávacího procesu, kdy se u takto postižených jedinců
Obtíže žáků s učením a chováním III.
 Obtíže žáků s učením a chováním III. Obtíže žáků s učením a chováním III. (1) Vybrané skupiny žáků s obtížemi v učení a chování Příčiny školního neprospěchu - snížená úroveň rozumových schopností - nerovnoměrné
Obtíže žáků s učením a chováním III. Obtíže žáků s učením a chováním III. (1) Vybrané skupiny žáků s obtížemi v učení a chování Příčiny školního neprospěchu - snížená úroveň rozumových schopností - nerovnoměrné
Matematika a její aplikace Matematika 1. období 3. ročník
 Vzdělávací oblast : Vyučovací předmět : Období ročník : Matematika a její aplikace Matematika 1. období 3. ročník Počet hodin : 165 Učební texty : H. Staudková : Matematika č. 7 (Alter) R. Blažková : Matematika
Vzdělávací oblast : Vyučovací předmět : Období ročník : Matematika a její aplikace Matematika 1. období 3. ročník Počet hodin : 165 Učební texty : H. Staudková : Matematika č. 7 (Alter) R. Blažková : Matematika
Učební osnovy pracovní
 ZV Základní vzdělávání 5 týdně, povinný ČaPO: Sčítání a odčítání s přechodem přes desítku Žák: ČaPO: sčítá a odčítá v oboru do 20-ti s přechodem přes desítku - sčítání a odčítání v oboru přirozených čísel
ZV Základní vzdělávání 5 týdně, povinný ČaPO: Sčítání a odčítání s přechodem přes desítku Žák: ČaPO: sčítá a odčítá v oboru do 20-ti s přechodem přes desítku - sčítání a odčítání v oboru přirozených čísel
Práce speciálního pedagoga. Základní škola T. G. Masaryka Otrokovice
 Práce speciálního pedagoga Základní škola T. G. Masaryka Otrokovice Výuka předmětů speciálně pedagogické péče Pedagogická intervence Práce s nadanými a zvídavými žáky Pomoc učitelům při zpracování PLPP
Práce speciálního pedagoga Základní škola T. G. Masaryka Otrokovice Výuka předmětů speciálně pedagogické péče Pedagogická intervence Práce s nadanými a zvídavými žáky Pomoc učitelům při zpracování PLPP
Elementárních klíčových kompetencí mohou žáci dosahovat pouze za přispění a dopomoci druhé osoby.
 Rozumová výchova Charakteristika vyučovacího předmětu Vyučovací předmět Rozumová výchova je vyučován v 1. až 10.ročníku ZŠS v časové dotaci 5 hodin týdně. V každém ročníku jsou přidány 2 disponibilní hodiny.
Rozumová výchova Charakteristika vyučovacího předmětu Vyučovací předmět Rozumová výchova je vyučován v 1. až 10.ročníku ZŠS v časové dotaci 5 hodin týdně. V každém ročníku jsou přidány 2 disponibilní hodiny.
KDO, CO, PROČ A JAK? Informace pro zaměstnance o podpoře studentů se specifickými potřebami. Středisko Augustin
 KDO, CO, PROČ A JAK? Informace pro zaměstnance o podpoře studentů se specifickými potřebami Středisko Augustin STUDENT SE ZRAKOVÝM POSTIŽENÍM KDO Lehce zrakově postižený/uživatel zraku Student, jehož zraková
KDO, CO, PROČ A JAK? Informace pro zaměstnance o podpoře studentů se specifickými potřebami Středisko Augustin STUDENT SE ZRAKOVÝM POSTIŽENÍM KDO Lehce zrakově postižený/uživatel zraku Student, jehož zraková
II. MATEMATIKA A JEJÍ APLIKACE
 II. MATEMATIKA A JEJÍ APLIKACE Charakteristika vzdělávací oblasti Tato oblast je v našem vzdělávání zastoupena jedním předmětem matematikou, od 1. do 9. ročníku. Podle vývoje dětské psychiky a zejména
II. MATEMATIKA A JEJÍ APLIKACE Charakteristika vzdělávací oblasti Tato oblast je v našem vzdělávání zastoupena jedním předmětem matematikou, od 1. do 9. ročníku. Podle vývoje dětské psychiky a zejména
Záměny tvarově podobných písmen. 1
 SPECIFICKÉ PORUCHY UČENÍ Definice Poruchy učení jsou souhrnným označením různorodé skupiny poruch, které se projevují zřetelnými obtížemi při nabývání a užívání takových dovedností, jako je mluvení, porozumění
SPECIFICKÉ PORUCHY UČENÍ Definice Poruchy učení jsou souhrnným označením různorodé skupiny poruch, které se projevují zřetelnými obtížemi při nabývání a užívání takových dovedností, jako je mluvení, porozumění
PLÁN REEDUKACE PRO SPECIFICKÉ PORUCHY UČENÍ
 PLÁN REEDUKACE PRO SPECIFICKÉ PORUCHY UČENÍ DYSKALKULIE Vytvořeno v rámci realizace projektu: Reedukace specifických vývojových poruch učení a poruch řeči dětí v mikroregionu Olešnicko Vypracovali: Mgr.Noemi
PLÁN REEDUKACE PRO SPECIFICKÉ PORUCHY UČENÍ DYSKALKULIE Vytvořeno v rámci realizace projektu: Reedukace specifických vývojových poruch učení a poruch řeči dětí v mikroregionu Olešnicko Vypracovali: Mgr.Noemi
OVĚŘENO: Datum: 8.4 2013 třída: 2.KOP
 VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 9, S 20 JMÉNO AUTORA: DATUM VYTVOŘENÍ: 10.3. 2013 PRO ROČNÍK: OBORU: VZDĚLÁVACÍ OBLAST. TEMATICKÝ OKRUH: TÉMA: Bc. Blažena Nováková 2. ročník Předškolní a mimoškolní
VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 9, S 20 JMÉNO AUTORA: DATUM VYTVOŘENÍ: 10.3. 2013 PRO ROČNÍK: OBORU: VZDĚLÁVACÍ OBLAST. TEMATICKÝ OKRUH: TÉMA: Bc. Blažena Nováková 2. ročník Předškolní a mimoškolní
Metody výuky jako podpůrná opatření
 Metody výuky jako podpůrná opatření Mgr. Anna Doubková PaedDr. Karel Tomek Mgr. Anna Doubková, PaedDr. Karel Tomek www.annadoubkova.cz; www.kareltomek.cz Mgr. Anna Doubková, PaedDr. Karel Tomek www.annadoubkova.cz;
Metody výuky jako podpůrná opatření Mgr. Anna Doubková PaedDr. Karel Tomek Mgr. Anna Doubková, PaedDr. Karel Tomek www.annadoubkova.cz; www.kareltomek.cz Mgr. Anna Doubková, PaedDr. Karel Tomek www.annadoubkova.cz;
ZÁSADY A KRITÉRIA PRO POUŽÍVÁNÍ SLOVNÍHO HODNOCENÍ NEBO KOMBINACE SLOVNÍHO HODNOCENÍ A KLASIFIKACE
 PŘÍLOHA Č. 1: ZÁSADY A KRITÉRIA PRO POUŽÍVÁNÍ SLOVNÍHO HODNOCENÍ NEBO KOMBINACE SLOVNÍHO HODNOCENÍ A KLASIFIKACE Výsledky vzdělávání žáka v jednotlivých povinných předmětech stanovených školním vzdělávacím
PŘÍLOHA Č. 1: ZÁSADY A KRITÉRIA PRO POUŽÍVÁNÍ SLOVNÍHO HODNOCENÍ NEBO KOMBINACE SLOVNÍHO HODNOCENÍ A KLASIFIKACE Výsledky vzdělávání žáka v jednotlivých povinných předmětech stanovených školním vzdělávacím
Část D. 8 Vzdělávání žáků se speciálními vzdělávacími potřebami
 Část D Rámcový vzdělávací program pro základní vzdělávání VÚP Praha 2005 Část D 8 Vzdělávání žáků se speciálními vzdělávacími potřebami Za žáky se speciálními vzdělávacími potřebami jsou považováni žáci
Část D Rámcový vzdělávací program pro základní vzdělávání VÚP Praha 2005 Část D 8 Vzdělávání žáků se speciálními vzdělávacími potřebami Za žáky se speciálními vzdělávacími potřebami jsou považováni žáci
MATEMATIKA CHARAKTERISTIKA PŘEDMĚTU pro 1. až 5. ročník
 1. Obsahové, časové a organizační vymezení předmětu 1.1 Vzdělávací obsahy, ze kterých je vyučovací předmět utvořen MATEMATIKA CHARAKTERISTIKA PŘEDMĚTU pro 1. až 5. ročník Vzdělávání klade důraz na důkladné
1. Obsahové, časové a organizační vymezení předmětu 1.1 Vzdělávací obsahy, ze kterých je vyučovací předmět utvořen MATEMATIKA CHARAKTERISTIKA PŘEDMĚTU pro 1. až 5. ročník Vzdělávání klade důraz na důkladné
SPECIFICKÉ ZVLÁŠTNOSTI OSOB S MENTÁLNÍM POSTIŽENÍM
 Tento studijní materiál vznikl v rámci projektu Inovace systému odborných praxí a volitelných předmětů na VOŠ Jabok (CZ.2.17/3.1.00/36073) SPECIFICKÉ ZVLÁŠTNOSTI OSOB S MENTÁLNÍM POSTIŽENÍM Proč? Na co
Tento studijní materiál vznikl v rámci projektu Inovace systému odborných praxí a volitelných předmětů na VOŠ Jabok (CZ.2.17/3.1.00/36073) SPECIFICKÉ ZVLÁŠTNOSTI OSOB S MENTÁLNÍM POSTIŽENÍM Proč? Na co
Neubauer, K. a kol. NEUROGENNÍ PORUCHY KOMUNIKACE U DOSPĚLÝCH (Praha, Portál, r. vydání 2007).
 Neubauer, K. a kol. NEUROGENNÍ PORUCHY KOMUNIKACE U DOSPĚLÝCH (Praha, Portál, r. vydání 2007). Získané neurogenní poruchy komunikace u dospělých osob Terminologie poruchy, které mají svou lingvistickou,
Neubauer, K. a kol. NEUROGENNÍ PORUCHY KOMUNIKACE U DOSPĚLÝCH (Praha, Portál, r. vydání 2007). Získané neurogenní poruchy komunikace u dospělých osob Terminologie poruchy, které mají svou lingvistickou,
Práce s textem. PaedDr. Mgr. Hana Čechová
 Práce s textem PaedDr. Mgr. Hana Čechová Platí-li, že vzdělání je důsledek čtení, pak platí i to, že upadá-li čtenářská gramotnost, snižuje se zákonitě i celková úroveň vzdělání. J. Trávníček https://pixabay.com/cs/vzd%c4%9bl%c3%a1v%c3%a1n%c3%ad-dosp%c4%9bl%c3%bdch-kniha-knihy-2706977/
Práce s textem PaedDr. Mgr. Hana Čechová Platí-li, že vzdělání je důsledek čtení, pak platí i to, že upadá-li čtenářská gramotnost, snižuje se zákonitě i celková úroveň vzdělání. J. Trávníček https://pixabay.com/cs/vzd%c4%9bl%c3%a1v%c3%a1n%c3%ad-dosp%c4%9bl%c3%bdch-kniha-knihy-2706977/
KDO, CO, PROČ A JAK? Informace pro studenty o podpoře studentů se specifickými potřebami. Středisko Augustin
 KDO, CO, PROČ A JAK? Informace pro studenty o podpoře studentů se specifickými potřebami Středisko Augustin STUDENT SE ZRAKOVÝM POSTIŽENÍM KDO Lehce zrakově postižený/uživatel zraku Student, jehož zraková
KDO, CO, PROČ A JAK? Informace pro studenty o podpoře studentů se specifickými potřebami Středisko Augustin STUDENT SE ZRAKOVÝM POSTIŽENÍM KDO Lehce zrakově postižený/uživatel zraku Student, jehož zraková
Ukázka charakteristiky předmětu Český jazyk z pracovní verze ŠVP Základní školy logopedické, Praha 8
 Ukázka charakteristiky předmětu Český jazyk z pracovní verze ŠVP Základní školy logopedické, Praha 8 ČESKÝ JAZYK Charakteristika vyučovacího předmětu Vzdělávání v předmětu Český jazyk směřuje k: vnímání,
Ukázka charakteristiky předmětu Český jazyk z pracovní verze ŠVP Základní školy logopedické, Praha 8 ČESKÝ JAZYK Charakteristika vyučovacího předmětu Vzdělávání v předmětu Český jazyk směřuje k: vnímání,
Matematika a její aplikace Matematika
 Vzdělávací oblast : Vyučovací předmět : Období ročník : Počet hodin : 165 Učební texty : Matematika a její aplikace Matematika 1. období 2. ročník Mgr. M. Novotný, F. Novák: Matýskova matematika 4.,5.,6.díl
Vzdělávací oblast : Vyučovací předmět : Období ročník : Počet hodin : 165 Učební texty : Matematika a její aplikace Matematika 1. období 2. ročník Mgr. M. Novotný, F. Novák: Matýskova matematika 4.,5.,6.díl
Matematika na 1. stupni ZŠ pro žáky se specifickými poruchami učení
 Univerzita Hradec Králové Pedagogická fakulta Ústav primární a preprimární edukace Matematika na 1. stupni ZŠ pro žáky se specifickými poruchami učení Diplomová práce Autor: Mgr. Martina Glazarová Studijní
Univerzita Hradec Králové Pedagogická fakulta Ústav primární a preprimární edukace Matematika na 1. stupni ZŠ pro žáky se specifickými poruchami učení Diplomová práce Autor: Mgr. Martina Glazarová Studijní
SPECIÁLNĚ PEDAGOGICKÁ PÉČE. Pokaždé se něčemu přiučíme, kdykoliv otevřeme knihu
 SPECIÁLNĚ PEDAGOGICKÁ PÉČE Pokaždé se něčemu přiučíme, kdykoliv otevřeme knihu Charakteristika vzdělávacího oboru Program reedukačních skupin pro děti se specifickými poruchami učení se zaměřuje na rozvoj
SPECIÁLNĚ PEDAGOGICKÁ PÉČE Pokaždé se něčemu přiučíme, kdykoliv otevřeme knihu Charakteristika vzdělávacího oboru Program reedukačních skupin pro děti se specifickými poruchami učení se zaměřuje na rozvoj
ZMĚNY V ŠVP k :
 ZMĚNY V ŠVP k 1. 9. 2016: 1. V celém textu se používá terminologie v souladu s právními předpisy (s novelou školského zákona č. 82/2015 Sb. a vyhláškou č. 27/2016 Sb., o vzdělávání žáků se speciálními
ZMĚNY V ŠVP k 1. 9. 2016: 1. V celém textu se používá terminologie v souladu s právními předpisy (s novelou školského zákona č. 82/2015 Sb. a vyhláškou č. 27/2016 Sb., o vzdělávání žáků se speciálními
ŘEČ DĚTÍ S PORUCHAMI UČENÍ
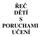 ŘEČ DĚTÍ S PORUCHAMI UČENÍ Řeč je velmi složitý psychický proces odrážející sociální vztahy, v nichž jedinec žije. Obtíže ve vývoji řeči a v jejím užívání spadají do péče foniatrů a logopedů. 1. Hodnocení
ŘEČ DĚTÍ S PORUCHAMI UČENÍ Řeč je velmi složitý psychický proces odrážející sociální vztahy, v nichž jedinec žije. Obtíže ve vývoji řeči a v jejím užívání spadají do péče foniatrů a logopedů. 1. Hodnocení
Kritéria školní zralosti
 Kritéria školní zralosti ŠKOLNÍ ZRALOST Školní zralostí rozumíme dosažení takového stupně tělesného a duševního vývoje, který umožňuje dítěti se zdarem si osvojovat školní znalosti a dovednosti. zralost
Kritéria školní zralosti ŠKOLNÍ ZRALOST Školní zralostí rozumíme dosažení takového stupně tělesného a duševního vývoje, který umožňuje dítěti se zdarem si osvojovat školní znalosti a dovednosti. zralost
Software pro procvičování dětí postižených dyskalkulií. Semestrální práce z A6M33AST. 1. část teoretický rozbor. Alisa Housková, Adam Kučera
 Software pro procvičování dětí postižených dyskalkulií Semestrální práce z A6M33AST 1. část teoretický rozbor Alisa Housková, Adam Kučera 1) Dyskalkulie Jako dyskalkulii označujeme jednu ze skupiny specifických
Software pro procvičování dětí postižených dyskalkulií Semestrální práce z A6M33AST 1. část teoretický rozbor Alisa Housková, Adam Kučera 1) Dyskalkulie Jako dyskalkulii označujeme jednu ze skupiny specifických
SPECIÁLNÍ PEDAGOGIKA
 SPECIÁLNÍ PEDAGOGIKA otázky k SZZ 1) Speciální pedagogika jako vědní obor, vymezení předmětu, vztah speciální pedagogiky k dalším vědním oborům. Vztah k pedagogice, psychologii, medicínským oborům, k sociologii.
SPECIÁLNÍ PEDAGOGIKA otázky k SZZ 1) Speciální pedagogika jako vědní obor, vymezení předmětu, vztah speciální pedagogiky k dalším vědním oborům. Vztah k pedagogice, psychologii, medicínským oborům, k sociologii.
Matematika a její aplikace Matematika
 Vzdělávací oblast : Vyučovací předmět : Období ročník : Počet hodin : 165 Matematika a její aplikace Matematika 2. období 5. ročník Učební texty : J. Justová: Alter-Matematika, Matematika 5.r.I.díl, 5.r.
Vzdělávací oblast : Vyučovací předmět : Období ročník : Počet hodin : 165 Matematika a její aplikace Matematika 2. období 5. ročník Učební texty : J. Justová: Alter-Matematika, Matematika 5.r.I.díl, 5.r.
Příloha školního řádu
 Gymnázium, Praha 10, Voděradská 2 Příloha školního řádu Pravidla pro hodnocení výsledků vzdělávání žáků Hodnocení chování O všech výchovných opatřeních musí být prokazatelnou formou informováni zákonní
Gymnázium, Praha 10, Voděradská 2 Příloha školního řádu Pravidla pro hodnocení výsledků vzdělávání žáků Hodnocení chování O všech výchovných opatřeních musí být prokazatelnou formou informováni zákonní
Specifické poruchy učení
 Specifické poruchy učení Specifické poruchy učení jsou poruchy způsobující problémy v rámci vzdělávacího procesu, kdy postižení projevují nedostatečně rozvinuté schopnosti, což jim způsobuje výukové obtíže.
Specifické poruchy učení Specifické poruchy učení jsou poruchy způsobující problémy v rámci vzdělávacího procesu, kdy postižení projevují nedostatečně rozvinuté schopnosti, což jim způsobuje výukové obtíže.
Časové a organizační vymezení
 Vzdělávací oblast Vzdělávací obor Vyučovací předmět Týdenní hodinové dotace Časové a organizační vymezení Matematika a její aplikace Matematika a její aplikace Matematika 1. stupeň 2. stupeň 1. ročník
Vzdělávací oblast Vzdělávací obor Vyučovací předmět Týdenní hodinové dotace Časové a organizační vymezení Matematika a její aplikace Matematika a její aplikace Matematika 1. stupeň 2. stupeň 1. ročník
Edukace jedinců se specifickými poruchami učení v matematice na 2. stupni základní školy
 Masarykova univerzita Pedagogická fakulta Katedra speciální pedagogiky Edukace jedinců se specifickými poruchami učení v matematice na 2. stupni základní školy Brno 2009 Vedoucí diplomové práce: Vypracovala:
Masarykova univerzita Pedagogická fakulta Katedra speciální pedagogiky Edukace jedinců se specifickými poruchami učení v matematice na 2. stupni základní školy Brno 2009 Vedoucí diplomové práce: Vypracovala:
PŘÍLOHY. Příloha č. 1 - Příloha k vyhlášce č.73/2005 Sb.
 PŘÍLOHY Příloha č. 1 - Příloha k vyhlášce č.73/2005 Sb. Minimální rozsah údajů a informací pro udělení informovaného souhlasu se zařazením žáka do některé z organizačních forem vzdělávání podle 3 této
PŘÍLOHY Příloha č. 1 - Příloha k vyhlášce č.73/2005 Sb. Minimální rozsah údajů a informací pro udělení informovaného souhlasu se zařazením žáka do některé z organizačních forem vzdělávání podle 3 této
Základní škola a Mateřská škola Olomouc, Dvorského 33. Asistent pedagoga
 Základní škola a Mateřská škola Olomouc, Dvorského 33 Asistent pedagoga Základní úkoly, fungování ve třídě a spolupráce s učiteli, zákonnými zástupci a pracovníky školního poradenského pracoviště V Olomouci
Základní škola a Mateřská škola Olomouc, Dvorského 33 Asistent pedagoga Základní úkoly, fungování ve třídě a spolupráce s učiteli, zákonnými zástupci a pracovníky školního poradenského pracoviště V Olomouci
Dodatek č. 8 k ŠVP Heřmánek
 Dodatek č. 8 k ŠVP Heřmánek Škola: Heřmánek Praha, základní škola Ředitelka školy: Mgr. Miroslava Adamcová Platnost dokumentu: od 1. 9. 2016 Dodatek k ŠVP ZV č. 1 byl projednán školskou radou dne: 29.
Dodatek č. 8 k ŠVP Heřmánek Škola: Heřmánek Praha, základní škola Ředitelka školy: Mgr. Miroslava Adamcová Platnost dokumentu: od 1. 9. 2016 Dodatek k ŠVP ZV č. 1 byl projednán školskou radou dne: 29.
Obecným obsahem poradenských služeb je tedy činnost přispívající
 A. Koncepce činnosti, aktivity, orientace B.1. Základní charakteristika zařízení Pedagogicko-psychologická poradna (PPP) zajišťuje spektrum psychologických a speciálně pedagogických služeb, které jsou
A. Koncepce činnosti, aktivity, orientace B.1. Základní charakteristika zařízení Pedagogicko-psychologická poradna (PPP) zajišťuje spektrum psychologických a speciálně pedagogických služeb, které jsou
VÝUKOVÉ METODY A FORMY V ZEMĚPISE
 VÝUKOVÉ METODY A FORMY V ZEMĚPISE Vyučování a učení činnost učitele činnost žáka učením si žáci osvojují vědomosti, dovednosti, návyky, ale i postoje a rozvíjí své schopnosti = kompetence veškerý vzdělávací
VÝUKOVÉ METODY A FORMY V ZEMĚPISE Vyučování a učení činnost učitele činnost žáka učením si žáci osvojují vědomosti, dovednosti, návyky, ale i postoje a rozvíjí své schopnosti = kompetence veškerý vzdělávací
Mgr. Alena Skotáková, Ph. D.
 Mgr. Alena Skotáková, Ph. D. POJMY Diagnostika je poznávacím procesem, jehož cílem je co nejdokonalejší poznání daného předmětu či objektu našeho zájmu, a to všech jeho důležitých znaků a charakteristik
Mgr. Alena Skotáková, Ph. D. POJMY Diagnostika je poznávacím procesem, jehož cílem je co nejdokonalejší poznání daného předmětu či objektu našeho zájmu, a to všech jeho důležitých znaků a charakteristik
Hodnocení projektu START 2017 / k datu Mgr. Dagmar Megová, speciální pedagog logoped pro MŠ
 Projekt START inkluzivního vzdělávání v Klášterci nad Ohří, s registračním číslem CZ.02.3.61/0.0/0.0/15_007/0000213, je spolufinancován v rámci Operačního programu Výzkum, Vývoj a Vzdělávání ze zdrojů
Projekt START inkluzivního vzdělávání v Klášterci nad Ohří, s registračním číslem CZ.02.3.61/0.0/0.0/15_007/0000213, je spolufinancován v rámci Operačního programu Výzkum, Vývoj a Vzdělávání ze zdrojů
Modul C Vzdělávání pracovníků v mateřinkách Středočeského kraje CZ.1.07/1.3.48/02.0045 PhDr. Ivana Šmejdová
 Modul C Vzdělávání pracovníků v mateřinkách Středočeského kraje CZ.1.07/1.3.48/02.0045 PhDr. Ivana Šmejdová Obsah kurzu: 1. Pedagogická diagnostika 2. Pedagogická diagnostika v pedagogické praxi 3. Diagnostika
Modul C Vzdělávání pracovníků v mateřinkách Středočeského kraje CZ.1.07/1.3.48/02.0045 PhDr. Ivana Šmejdová Obsah kurzu: 1. Pedagogická diagnostika 2. Pedagogická diagnostika v pedagogické praxi 3. Diagnostika
Mateřská škola a Základní škola Tábor, ČSA 925. Školní vzdělávací program Úsměv pro každého
 Název vzdělávací oblasti: Umění a kultura Charakteristika vzdělávací oblasti: Mateřská škola a Základní škola Tábor, ČSA 925 Tato oblast provází žáky po celou dobu školní docházky. Dává prostor pro uplatnění
Název vzdělávací oblasti: Umění a kultura Charakteristika vzdělávací oblasti: Mateřská škola a Základní škola Tábor, ČSA 925 Tato oblast provází žáky po celou dobu školní docházky. Dává prostor pro uplatnění
MŠ Laudova se speciálními třídami, Laudova 1030/3, 16300 Praha 6 Řepy, tel.235314514. Projekt: Předmatematická gramotnost
 MŠ Laudova se speciálními třídami, Laudova 1030/3, 16300 Praha 6 Řepy, tel.235314514 Projekt: Předmatematická gramotnost 1. Obecná východiska Rozvoj předmatematické gramotnosti je důležitý pro všestranný
MŠ Laudova se speciálními třídami, Laudova 1030/3, 16300 Praha 6 Řepy, tel.235314514 Projekt: Předmatematická gramotnost 1. Obecná východiska Rozvoj předmatematické gramotnosti je důležitý pro všestranný
Metodické doporučení č.j. 14 712/2009-61 k zabezpečení logopedické péče ve školství
 Metodické doporučení č.j. 14 712/2009-61 k zabezpečení logopedické péče ve školství Metodické doporučení se týká podmínek organizačního zabezpečení logopedické péče v resortu školství (dále jen logopedická
Metodické doporučení č.j. 14 712/2009-61 k zabezpečení logopedické péče ve školství Metodické doporučení se týká podmínek organizačního zabezpečení logopedické péče v resortu školství (dále jen logopedická
Alternativní způsoby učení dětí s mentálním postižením
 Tento dokument byl vytvořen v rámci projektu ESF OPPA č. CZ.2.17/3.1.00/36073 Inovace systému odborných praxí a volitelných předmětů na VOŠ Jabok financovaného Evropským sociálním fondem. Alternativní
Tento dokument byl vytvořen v rámci projektu ESF OPPA č. CZ.2.17/3.1.00/36073 Inovace systému odborných praxí a volitelných předmětů na VOŠ Jabok financovaného Evropským sociálním fondem. Alternativní
Předškolní a mimoškolní pedagogika Odborné předměty Výchova a vzdělávání Metody výchovy a vzdělávání
 VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 10, S 17 JMÉNO AUTORA: DATUM VYTVOŘENÍ: 9.2. 2013 PRO ROČNÍK: OBORU: VZDĚLÁVACÍ OBLAST. TEMATICKÝ OKRUH: Bc. Blažena Nováková 1. ročník Předškolní a mimoškolní pedagogika
VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 10, S 17 JMÉNO AUTORA: DATUM VYTVOŘENÍ: 9.2. 2013 PRO ROČNÍK: OBORU: VZDĚLÁVACÍ OBLAST. TEMATICKÝ OKRUH: Bc. Blažena Nováková 1. ročník Předškolní a mimoškolní pedagogika
VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 10, S 20 DATUM VYTVOŘENÍ: 19.3. 2013
 VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 10, S 20 JMÉNO AUTORA: DATUM VYTVOŘENÍ: 19.3. 2013 PRO ROČNÍK: OBORU: VZDĚLÁVACÍ OBLAST. TEMATICKÝ OKRUH: TÉMA: Bc. Blažena Nováková 2. ročník Předškolní a mimoškolní
VÝUKOVÝ MATERIÁL: VY_32_INOVACE_ DUM 10, S 20 JMÉNO AUTORA: DATUM VYTVOŘENÍ: 19.3. 2013 PRO ROČNÍK: OBORU: VZDĚLÁVACÍ OBLAST. TEMATICKÝ OKRUH: TÉMA: Bc. Blažena Nováková 2. ročník Předškolní a mimoškolní
SEMINÁŘ Z ČESKÉHO JAZYKA. Pokaždé se něčemu přiučíme, kdykoliv otevřeme knihu
 SEMINÁŘ Z ČESKÉHO JAZYKA Pokaždé se něčemu přiučíme, kdykoliv otevřeme knihu Charakteristika vzdělávacího oboru Seminář z českého jazyka Dovednost užívat češtiny jako mateřského jazyka v jeho mluvené i
SEMINÁŘ Z ČESKÉHO JAZYKA Pokaždé se něčemu přiučíme, kdykoliv otevřeme knihu Charakteristika vzdělávacího oboru Seminář z českého jazyka Dovednost užívat češtiny jako mateřského jazyka v jeho mluvené i
Práce s barevnými čtecími fóliemi pro žáky s SPU ve výuce českého, anglického a německého jazyka. Ing. Libuše Novotná
 Práce s barevnými čtecími fóliemi pro žáky s SPU ve výuce českého, anglického a německého jazyka Ing. Libuše Novotná 1 Ing. Libuše Novotná PROGRAM: 1. SPU mateřský a cizí jazyk 2. Barva jako podklad čteného
Práce s barevnými čtecími fóliemi pro žáky s SPU ve výuce českého, anglického a německého jazyka Ing. Libuše Novotná 1 Ing. Libuše Novotná PROGRAM: 1. SPU mateřský a cizí jazyk 2. Barva jako podklad čteného
I. Potřeba pedagogické diagnostiky
 I. Potřeba pedagogické diagnostiky S platností RVP ZV od roku 2007/2008 se začíná vzdělávání a výchova v základní škole realizovat prostřednictvím kurikulárního dokumentu, jehož cílem je vybavit žáka potřebnými
I. Potřeba pedagogické diagnostiky S platností RVP ZV od roku 2007/2008 se začíná vzdělávání a výchova v základní škole realizovat prostřednictvím kurikulárního dokumentu, jehož cílem je vybavit žáka potřebnými
INDIVIDUÁLNÍ PÉČE - M. Charakteristika vzdělávacího oboru
 INDIVIDUÁLNÍ PÉČE - M Charakteristika vzdělávacího oboru Individuální péče - matematika a) Obsahové vymezení: Individuální péče-matematika vychází z obsahového zaměření oboru Matematika a její aplikace
INDIVIDUÁLNÍ PÉČE - M Charakteristika vzdělávacího oboru Individuální péče - matematika a) Obsahové vymezení: Individuální péče-matematika vychází z obsahového zaměření oboru Matematika a její aplikace
Didaktika odborných předmětů. Vyučovací proces
 Didaktika odborných předmětů Vyučovací proces 1 Pojem a podstata vyučovacího procesu Vyučovací proces záměrné, cílevědomé, soustavné a racionální řízení aktivit žáků, které směřuje k dosažení stanovených
Didaktika odborných předmětů Vyučovací proces 1 Pojem a podstata vyučovacího procesu Vyučovací proces záměrné, cílevědomé, soustavné a racionální řízení aktivit žáků, které směřuje k dosažení stanovených
Integrativní speciální pedagogika Podzim 2011 DVOUOBOROVÉ STUDIUM, VÝUKA Út
 Integrativní speciální pedagogika Podzim 2011 DVOUOBOROVÉ STUDIUM, VÝUKA Út 20.9.2011 PŘEDNÁŠKY ORGANIZAČNÍ INFORMACE SAMOSTUDIUM 14. Speciálně pedagogická diagnostika (pojetí, diagnostika v raném a předškolním
Integrativní speciální pedagogika Podzim 2011 DVOUOBOROVÉ STUDIUM, VÝUKA Út 20.9.2011 PŘEDNÁŠKY ORGANIZAČNÍ INFORMACE SAMOSTUDIUM 14. Speciálně pedagogická diagnostika (pojetí, diagnostika v raném a předškolním
Katalog podpůrných opatření pro žáky s tělesným postižením a závažným onemocněním. 3 Diagnostika žáka zejména s důrazem na pedagogickou diagnostiku
 3 Diagnostika žáka zejména s důrazem na pedagogickou diagnostiku Pedagogická diagnostika je nedílnou součástí složitého výchovně-vzdělávacího procesu. Jde o proces zjišťování, rozpoznávání, klasifikování,
3 Diagnostika žáka zejména s důrazem na pedagogickou diagnostiku Pedagogická diagnostika je nedílnou součástí složitého výchovně-vzdělávacího procesu. Jde o proces zjišťování, rozpoznávání, klasifikování,
PODPORA SPU VE VÝUCE. projevy, potřeby, úpravy a metody
 PODPORA SPU VE VÝUCE projevy, potřeby, úpravy a metody Projevy Dyslexie Pomalé čtení -Namáhavé -Dvojí -Ztrácí se, vrací se -Málo chyb-opravuje -Záměny,opakuje přečtené Přepisuje velmi pomalu -Víc času
PODPORA SPU VE VÝUCE projevy, potřeby, úpravy a metody Projevy Dyslexie Pomalé čtení -Namáhavé -Dvojí -Ztrácí se, vrací se -Málo chyb-opravuje -Záměny,opakuje přečtené Přepisuje velmi pomalu -Víc času
Ukázka charakteristiky předmětu Jazyk a jazyková komunikace z pracovní verze ŠVP ZŠ pro sluchově postižené, Holečkova ul., Praha 5
 Ukázka charakteristiky předmětu Jazyk a jazyková komunikace z pracovní verze ŠVP ZŠ pro sluchově postižené, Holečkova ul., Praha 5 Jazyk a jazyková komunikace Charakteristika vyučovacího předmětu Předmět
Ukázka charakteristiky předmětu Jazyk a jazyková komunikace z pracovní verze ŠVP ZŠ pro sluchově postižené, Holečkova ul., Praha 5 Jazyk a jazyková komunikace Charakteristika vyučovacího předmětu Předmět
Dodatek ke školnímu vzdělávacímu programu č. 2/2016
 Základní škola Soběslav, tř. Dr. Edvarda Beneše 50 Tř. Dr. E. Beneše 50/II, 392 01 Soběslav IČO: 00582841 tel: 381 521 223 e-mail: skola@zs-ebeso.cz čj. ZŠ 254/2016 Dodatek ke školnímu vzdělávacímu programu
Základní škola Soběslav, tř. Dr. Edvarda Beneše 50 Tř. Dr. E. Beneše 50/II, 392 01 Soběslav IČO: 00582841 tel: 381 521 223 e-mail: skola@zs-ebeso.cz čj. ZŠ 254/2016 Dodatek ke školnímu vzdělávacímu programu
MATEMATIKA. 1. 5. ročník
 Charakteristika předmětu MATEMATIKA 1. 5. ročník Obsahové, časové a organizační vymezení Vyučovací předmět matematika má časovou dotaci 4 hodiny týdně v 1. ročníku, 5 hodin týdně ve 2. až 5. ročníku. Časová
Charakteristika předmětu MATEMATIKA 1. 5. ročník Obsahové, časové a organizační vymezení Vyučovací předmět matematika má časovou dotaci 4 hodiny týdně v 1. ročníku, 5 hodin týdně ve 2. až 5. ročníku. Časová
Výběr z nových knih 11/2016 pedagogika
 Výběr z nových knih 11/2016 pedagogika 1. Didaktické přístupy k přírodovědnému vzdělávání předškolních dětí a mladších žáků / Kateřina Jančaříková -- 1. vydání V Praze : Univerzita Karlova, Pedagogická
Výběr z nových knih 11/2016 pedagogika 1. Didaktické přístupy k přírodovědnému vzdělávání předškolních dětí a mladších žáků / Kateřina Jančaříková -- 1. vydání V Praze : Univerzita Karlova, Pedagogická
ŠKOLNÍ DOTAZNÍK K VYŠETŘENÍ ŽÁKA V SPC. Dítě je v péči dalších odborníků klinický psycholog, logoped, odborný lékař, PPP, jiné SPC
 SPECIÁLNĚ PEDAGOGICKÉ CENTRUM při Základní škole a Praktické škole Benešov Konopišťská 386, 256 01 Benešov E-mail: spcbenesov@seznam.cz mobil: 734357465 ŠKOLNÍ DOTAZNÍK K VYŠETŘENÍ ŽÁKA V SPC Vážená paní
SPECIÁLNĚ PEDAGOGICKÉ CENTRUM při Základní škole a Praktické škole Benešov Konopišťská 386, 256 01 Benešov E-mail: spcbenesov@seznam.cz mobil: 734357465 ŠKOLNÍ DOTAZNÍK K VYŠETŘENÍ ŽÁKA V SPC Vážená paní
Témata diplomových prací Katedra speciální pedagogiky studijní rok 2017/2018
 Témata diplomových prací Katedra speciální pedagogiky studijní rok 2017/2018 Mgr. Lenka Felcmanová 1. Možnosti včasné intervence u dětí ze sociálně vyloučených lokalit 2. Speciáněpedagogická podpora dětí
Témata diplomových prací Katedra speciální pedagogiky studijní rok 2017/2018 Mgr. Lenka Felcmanová 1. Možnosti včasné intervence u dětí ze sociálně vyloučených lokalit 2. Speciáněpedagogická podpora dětí
Tento výukový materiál vznikl za přispění Evropské unie, státního rozpočtu ČR a Středočeského kraje. Mgr. Monika Řezáčová
 Tento výukový materiál vznikl za přispění Evropské unie, státního rozpočtu ČR a Středočeského kraje Leden 2011 Mgr. Monika Řezáčová věda o psychické regulaci chování a jednání člověka a o jeho vlastnostech
Tento výukový materiál vznikl za přispění Evropské unie, státního rozpočtu ČR a Středočeského kraje Leden 2011 Mgr. Monika Řezáčová věda o psychické regulaci chování a jednání člověka a o jeho vlastnostech
Úvod do matematiky profesora Hejného. VISK Praha
 Úvod do matematiky profesora Hejného VISK Praha 6. 1. 2015 Metoda VOBS Schéma? Hejného metoda vyučování matematice Hejného metoda vyučování matematice Východiska Učebnice a autoři, působení Úzké spojení
Úvod do matematiky profesora Hejného VISK Praha 6. 1. 2015 Metoda VOBS Schéma? Hejného metoda vyučování matematice Hejného metoda vyučování matematice Východiska Učebnice a autoři, působení Úzké spojení
ZRAKOVÁ PERCEPCE. (zrakové vnímání)
 ZRAKOVÁ PERCEPCE (zrakové vnímání) 1. Vývoj zrakového vnímání a jeho vliv na nácvik čtení a psaní Zrakové vnímání se vyvíjí od narození dítěte. Nejdříve jsou vnímány světlo a tma, později obrysy předmětů.
ZRAKOVÁ PERCEPCE (zrakové vnímání) 1. Vývoj zrakového vnímání a jeho vliv na nácvik čtení a psaní Zrakové vnímání se vyvíjí od narození dítěte. Nejdříve jsou vnímány světlo a tma, později obrysy předmětů.
Testy do hodin - souhrnný test - 6. ročník
 Kolik procent škol jste předstihli Škola: Název: Obec: BCEH ZŠ a MŠ, Slezská 316 Slavkov - 6. ročník ČESKÝ JAZYK Máte lepší výsledky než 7 % zúčastněných škol. MATEMATIKA Máte lepší výsledky než 7 % zúčastněných
Kolik procent škol jste předstihli Škola: Název: Obec: BCEH ZŠ a MŠ, Slezská 316 Slavkov - 6. ročník ČESKÝ JAZYK Máte lepší výsledky než 7 % zúčastněných škol. MATEMATIKA Máte lepší výsledky než 7 % zúčastněných
Porozumění textu, pojem známý i neznámý Vlasta Galisová
 Porozumění textu, pojem známý i neznámý Vlasta Galisová KATEDRA ČESKÉHO JAZYKA A LITERATURY S DIDAKTIKOU, PdF OU Dovednost jedince číst, psát a počítat, v širším významu schopnost aplikovat některé specifické
Porozumění textu, pojem známý i neznámý Vlasta Galisová KATEDRA ČESKÉHO JAZYKA A LITERATURY S DIDAKTIKOU, PdF OU Dovednost jedince číst, psát a počítat, v širším významu schopnost aplikovat některé specifické
Statut školního poradenského pracoviště ZŠ a MŠ Křtiny
 Statut školního poradenského pracoviště ZŠ a MŠ Křtiny Od 3. 2. 2014 je v naší škole zřízeno školní poradenské pracoviště, které slouží k poskytování poradenských služeb pro žáky, jejich zákonné zástupce
Statut školního poradenského pracoviště ZŠ a MŠ Křtiny Od 3. 2. 2014 je v naší škole zřízeno školní poradenské pracoviště, které slouží k poskytování poradenských služeb pro žáky, jejich zákonné zástupce
Příloha č. 6 MATEMATIKA A JEJÍ APLIKACE
 Žák cvičí prostorovou představivost Žák využívá při paměťovém i písemném počítání komutativnost i asociativní sčítání a násobení Žák provádí písemné početní operace v oboru Opakování učiva 3. ročníku Písemné
Žák cvičí prostorovou představivost Žák využívá při paměťovém i písemném počítání komutativnost i asociativní sčítání a násobení Žák provádí písemné početní operace v oboru Opakování učiva 3. ročníku Písemné
Reedukace dyslexie. Dyslexie problémy rychlost čtení správnost čtení porozumění čtenému textu
 Reedukace dyslexie Dyslexie problémy rychlost čtení správnost čtení porozumění čtenému textu Projevy dyslexie problémy se zapamatováním, rozpoznáváním písmen záměny tvarově podobných písmen a sluchově
Reedukace dyslexie Dyslexie problémy rychlost čtení správnost čtení porozumění čtenému textu Projevy dyslexie problémy se zapamatováním, rozpoznáváním písmen záměny tvarově podobných písmen a sluchově
PŘEDŠKOLNÍ VĚK TESTY INTELIGENCE TESTY SPECIÁLNÍCH SCHOPNOSTÍ A ZNALOSTÍ
 PŘEDŠKOLNÍ VĚK TESTY INTELIGENCE SON - R (P. J. Tellegen, J. A. Laros, D. Heider, Testcentrum) Věkové určení: 2;5 7 let Čas potřebný k administraci: 50 60 minut Aktuálnost nástroje: Popis testu: Je to
PŘEDŠKOLNÍ VĚK TESTY INTELIGENCE SON - R (P. J. Tellegen, J. A. Laros, D. Heider, Testcentrum) Věkové určení: 2;5 7 let Čas potřebný k administraci: 50 60 minut Aktuálnost nástroje: Popis testu: Je to
český jazyk a literatura
 1 Mezipředmětové vztahy --> - 2. ročník Výchovné a vzdělávací strategie Kompetence k učení Kompetence komunikativní Kompetence k řešení problémů Kompetence sociální a personální Kompetence občanské Kompetence
1 Mezipředmětové vztahy --> - 2. ročník Výchovné a vzdělávací strategie Kompetence k učení Kompetence komunikativní Kompetence k řešení problémů Kompetence sociální a personální Kompetence občanské Kompetence
Podklady pro hodnocení profilové maturitní zkoušky
 Podklady pro hodnocení profilové maturitní zkoušky Gymnázium, Prachatice, Zlatá stezka 137 Obsah PROFILOVÁ ZKOUŠKA: Matematika... 2 PROFILOVÁ ZKOUŠKA: Německý jazyk... 3 PROFILOVÁ ZKOUŠKA: Anglický jazyk...
Podklady pro hodnocení profilové maturitní zkoušky Gymnázium, Prachatice, Zlatá stezka 137 Obsah PROFILOVÁ ZKOUŠKA: Matematika... 2 PROFILOVÁ ZKOUŠKA: Německý jazyk... 3 PROFILOVÁ ZKOUŠKA: Anglický jazyk...
Wichterlovo gymnázium, Ostrava-Poruba, příspěvková organizace. Maturitní otázky z předmětu PEDAGOGIKA A PSYCHOLOGIE
 Wichterlovo gymnázium, Ostrava-Poruba, příspěvková organizace Maturitní otázky z předmětu PEDAGOGIKA A PSYCHOLOGIE 1. Definice a předmět psychologie Základní odvětví, speciální a aplikované disciplíny,
Wichterlovo gymnázium, Ostrava-Poruba, příspěvková organizace Maturitní otázky z předmětu PEDAGOGIKA A PSYCHOLOGIE 1. Definice a předmět psychologie Základní odvětví, speciální a aplikované disciplíny,
INDIVIDUÁLNÍ PÉČE - ČJ. Pokaždé se něčemu přiučíme, kdykoliv otevřeme knihu
 INDIVIDUÁLNÍ PÉČE - ČJ Pokaždé se něčemu přiučíme, kdykoliv otevřeme knihu Charakteristika vzdělávacího oboru Individuální péče český jazyk Kvalitní osvojení a užívání mateřského jazyka v jeho mluvené
INDIVIDUÁLNÍ PÉČE - ČJ Pokaždé se něčemu přiučíme, kdykoliv otevřeme knihu Charakteristika vzdělávacího oboru Individuální péče český jazyk Kvalitní osvojení a užívání mateřského jazyka v jeho mluvené
Reálná čísla a výrazy. Početní operace s reálnými čísly. Složitější úlohy se závorkami. Slovní úlohy. Číselné výrazy. Výrazy a mnohočleny
 A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Cvičení z matematiky 3 Ročník: 9. 4 Klíčové kompetence (Dílčí kompetence) 5 Kompetence k učení učí se vybírat a využívat vhodné
A B C D E F 1 Vzdělávací oblast: Matematika a její aplikace 2 Vzdělávací obor: Cvičení z matematiky 3 Ročník: 9. 4 Klíčové kompetence (Dílčí kompetence) 5 Kompetence k učení učí se vybírat a využívat vhodné
Podpora studentů se speciálními
 Podpora studentů se speciálními potřebami při vysokoškolském studiu Inkluzivnívzdělávání, péče o handicapované studenty, RP 2011 PedFUK v Praze, PhDr. PaedDr. Anna Kucharská, Ph.D. STUDENTI SE SPECIÁLNÍMI
Podpora studentů se speciálními potřebami při vysokoškolském studiu Inkluzivnívzdělávání, péče o handicapované studenty, RP 2011 PedFUK v Praze, PhDr. PaedDr. Anna Kucharská, Ph.D. STUDENTI SE SPECIÁLNÍMI
Název materiálu: Vlohy a schopnosti Autor materiálu: PhDr. Jitka Ivanková Datum (období) vytvoření: Zařazení materiálu:
 Projekt: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Příjemce: Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Příjemce: Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
4.1.2. Vzdělávací oblast : Jazyk a jazyková komunikace Vzdělávací obor: Cizí jazyk
 4.1.2. Vzdělávací oblast : Jazyk a jazyková komunikace Vzdělávací obor: Cizí jazyk Charakteristika vyučovacího předmětu Anglický jazyk 1.Obsahové vymezení vyučovacího předmětu Cílem vzdělávání předmětu
4.1.2. Vzdělávací oblast : Jazyk a jazyková komunikace Vzdělávací obor: Cizí jazyk Charakteristika vyučovacího předmětu Anglický jazyk 1.Obsahové vymezení vyučovacího předmětu Cílem vzdělávání předmětu
