Matematyka w przyrodzie i sztuce matematyka, przyroda i sztuka w ksztaªceniu powszechnym
|
|
|
- Daniela Sedláčková
- před 8 lety
- Počet zobrazení:
Transkript
1 Pa«stwowa Wy»sza Szkoªa Zawodowa w Nowym S czu Matematyka w przyrodzie i sztuce matematyka, przyroda i sztuka w ksztaªceniu powszechnym Tom 3 Pod redakcj Adama Pªockiego Nowy S cz 2013
2 Komitet Redakcyjny doc. dr Marek Reichel przewodnicz cy; prof. dr hab. in». Jarosªaw Fr czek; prof. dr hab. Leszek Rudnicki; dr hab. n. med. Ryszard Gajdosz, prof. nadzw.; dr hab. Zdzisªawa Zacªona, prof. nadzw.; dr hab. Magdalena Sitarz, prof. nadzw.; dr hab. Wanda Pilch, prof. nadzw.; mgr Agata Witrylak-Leszy«ska Redaktor Naczelny doc. dr Marek Reichel Sekretarz Redakcji dr Tamara Bolanowska-Bobrek Redaktor wydania prof. zw. dr hab. Adam Pªocki Skªad komputerowy (LA T EX) dr Marcin Mazur Recenzenci prof. RNDr. Ji i Cihla, CSc (Univerzita Jana E. Purkyn Usti nad Labem); doc. RNDr. Roman Fri, DrSc (Katolická univerzita Ruºomberok); RNDr. Alena Kopa ková, Ph.D. (Technická univerzita Liberec); prof. zw. dr hab. Andrzej Nowicki (Uniwersytet Mikoªaja Kopernika Toru«); prof. zw. dr hab Jerzy Ombach (Uniwersytet Jagiello«ski Kraków); doc. PaedDR. Jaroslav Perný, Ph.D. (Technická univerzita Liberec); dr hab. prof. nadzw. Ewa Swoboda (Uniwersytet Rzeszowski); prof. RNDr. Pavel Tlustý, CSc (Jiho eská univerzita ƒeské Bud jovice); dr hab. prof. nadzw. Edward Tutaj (Uniwersytet Jagiello«ski Kraków) Wydano za zgod JM Rektora PWSZ w Nowym S czu prof. dra hab. in». Zbigniewa lipka Autorzy ponosz odpowiedzialno± za poprawno± j zykow tekstu c Copyright by Pa«stwowa Wy»sza Szkoªa Zawodowa w Nowym S czu Nowy S cz 2013 ISBN Adres Redakcji Nowy S cz, ul. Staszica 1 tel , briw@pwsz-ns.edu.pl Wydawca Wydawnictwo Naukowe Pa«stwowej Wy»szej Szkoªy Zawodowej w Nowym S czu Nowy S cz, ul. Staszica 1 tel , briw@pwsz-ns.edu.pl Druk EXPOL P. Rybi«ski, J. D bek Spóªka Jawna Wªocªawek, ul. Brzeska 4 tel , , sekretariat@expol.home.pl
3 Spis tre±ci Wst p 5 Kv toslav Bártek, Eva Bártková, David Nocar, Matematika v díle Albrechta Dürera 7 Eva Bártková, David Nocar, Kv toslav Bártek, Vyuºití algebraických hyperstruktur p i ur ování d di nosti krevních skupin 31 Bogumiªa Klemp-Dyczek, Mozaiki pªaszczyzny euklidesowej 41 Ivana Macha íková, Josef Molnár, roubovice v p írod a um ní 71 Marek Mokri², Príroda v úlohách z geometrie 93 Bronisªaw Pabich, Matematyka w muzyce ±wiat muzyki a matematyzacja 105 Ada Paªka, Tworzenie obrazów anamorcznych propozycja warsztatów 131 Zdzisªaw Pogoda, Matematyka szopki krakowskiej 145 Alena Prídavková, Modely pojmov teórie mnoºín s prírodovedným námetom 155 Jana P íhonská, Metody teorie graf p i e²ení problém s bludi- ²ti 167 Iveta Scholtzová, Miery v primárnej edukácii as 177 Darina Stachová, Milan Stacho, Magické ²tvorce vo výtvarnom umení 187 Radka t pánková, Pavel Tlustý, Propojení základních poznatk z genetiky a stochastiky na základní ²kole 203 Izabela Stronias, Czwarty wymiar w malarstwie i rze¹bie pocz tku XX wieku 209 Rastislav Telgársky, Mathematics without innity 223 Marián Trenkler, Kon²trukcie magických obd ºnikov 253 Vladimír Van k, Matematika a po así 261 Renata Zemanová, Radek Krpec, Lidové um ní inspirace elementární matematiky 273
4 Dzi kujemy Muzeum Historycznemu m. Krakowa za udost pnienie nam materiaªów ikonogra cznych zwi zanych z krakowskimi szopkami. Cz ± z nich prezentujemy na pustych stronach parzystych.
5 Wst p Szkolna matematyka jest od stuleci raczej izolowana od innych dziedzin wiedzy, a zwªaszcza od nauk przyrodniczych i humanistycznych. Jednym z powodów tego faktu, s obawy matematyków przed wulgaryzacj matematyki, ilekro prezentuje si j w kontek±cie realnego ±wiata. Obawy nierzadko sªuszne. Tymczasem j zyk matematyki, jej poj cia i twierdzenia wykorzystuje si w innych przedmiotach nauczania (idea wspóªrz dnych w geograi, konstrukcje przestrzenne na lekcjach wychowania technicznego), a ponadto matematyka rozwijaªa si i nadal rozwija tak»e dzi ki temu,»e jej poj cia i jej metody s narz dziami opisu realnych obiektów i towarzysz cych im stosunków ilo±ciowych i jako±ciowych (matematyzacja jako faza procesu stosowania matematyki), a przede wszystkim narz dziami rozwi zywania pozamatematycznych problemów. Zakªad Edukacji Matematyczno-Przyrodniczej PWSZ w Nowym S czu zorganizowaª w dniach 1617 maja 2013 r. trzeci mi dzynarodow konferencj Matematyka w przyrodzie i sztuce matematyka, przyroda i sztuka w kszta- ªceniu powszechnym, której tematem byªo miejsce przyrody i sztuki w matematycznej aktywizacji. Praca jest monogra, w której znalazªy si wybrane wyst pienia na tej konferencji. W dydaktyce matematyki wyró»nia si zasad integracji zewn trznej, w której chodzi o ekspansj matematycznych poj i twierdze«na inne przedmioty nauczania. Monograa dotyczy tak»e owej integracji w nauczaniu matematyki. O integracji zewn trznej mo»na mówi, gdy tworzymy matematyczny model procesu dziedziczenia cech zgodnie z prawami Mendla. W pracy analizuje si na gruncie matematyki dziedziczenie grupy krwi oraz koloru oczu w procesie panmiksji (jest to losowe kojarzenie osobników, którego rezultatem jest genotyp potomka). Cz ±ci wielu dzieª sztuki (rze¹by, obrazy) i architektury (budowle, plany miast, ogrody, czy place) s takie matematyczne obiekty, jak wielok ty, wielo±ciany (w tym bryªy plato«skie), kwadraty magiczne, zbiory, których moce s liczbami Fibonacciego, spirale Fibonacciego. W wielu tych ludzkich wytworach (zwªaszcza w architekturze) pojawiªy si geometryczne symetrie i osobliwe proporcje (zªoty podziaª odcinka). Te same obiekty odkryª czªowiek w wytworach przyrody (krysztaªy, kwiaty, drzewa, owoce, rogi zwierz t, skorupy ±limaków, proporcje czªowieka). Krzywa ±rubowa jako obiekt matematyczny pojawiªa si w ludzkich wytworach (spiralne schody, bi»uteria, spr»yny, wazony, ozdoby choinkowe, barokowe kolumny), ale ta krzywa wyst puje tak»e w przyrodzie (ukªad korzeni i gaª zi niektórych drzew, struktura molekuª DNA, mineraªy). W kontek±cie tych spiral pojawiaj si izometrie i ich rozmaite zªo»enia. O ciekawej geometrii mowa jest w kontek±cie tworzenia obrazów anamorcznych.
6 Symetria rozumiana najpierw jako przeksztaªcenie geometryczne na prostej, pªaszczy¹nie, czy w przestrzeni trójwymiarowej, pojawiªa si w malarstwie, rze¹bie, architekturze, ale tak»e w przyrodzie (krysztaªy) i w zyce. Poj ciu symetrii nadaje si dzi± szerszy, ogólniejszy sens. O symetriach mo»na mówi w muzyce. W stochastyce pojawiaj si osobliwe wnioskowania przez symetri (i nie jest to symetria geometryczna). Idea symetrii jest dzi± traktowana jako szczególne ¹ródªo interdyscyplinarnych poszukiwa«jedno±ci przyrody. Matematyka pojawia si w sztuce ludowej. W monograi opisujemy fenomen krakowskiej szopki, jej projektowanie i sklejanie zaliczaj c do aktywno±ci matematycznych. Wspominamy o ludowej architekturze, o ludowych haftach i wycinankach w Czechach. W Polsce mamy wiele regionów sªyn cych z ludowych haftów (Bobowa na S decczy¹nie, Koniaków na l sku Cieszy«skim), czy wycinanek (Kurpie, Šowicz). Symetrie w papierowej wycinance uzyskuje si poprzez odpowiednie zginanie papieru. W ten sposób ujawnia si o± symetrii lub jej ±rodek oraz ich rola w tym przeksztaªceniu. W monograi pojawiª si postulat, aby te wytwory sztuki ludowej o wyra¹nych matematycznych strukturach, wª cza do powszechnego ksztaªcenia matematycznego, ucz c przy tym pewnego lokalnego patriotyzmu (podziw dla tradycji naszych maªych ojczyzn, w których»yjemy). S to wi c tak»e wychowawcze aspekty integracji sztuki ludowej i matematyki. W monograi zebrano prace komentuj ce matematyk w przyrodzie i sztuce oraz prace dotycz ce matematyki, przyrody i sztuki w powszechnym ksztaªceniu matematycznym oraz w ksztaªceniu przez matematyk i sztuk. W tym sensie adresatem tej monograi jest tak»e nauczyciel (i to nie tylko nauczyciel matematyki). Zebrane w niej prace mog (i maj ) u±wiadomi nauczycielowi, a przede wszystkim pracownikom naukowym, którzy tych nauczycieli ksztaªc,»e wokóª nas jest sporo (nie zawsze dostrzeganej) ciekawej matematyki. Mamy tu na uwadze nowe spojrzenie na tre±ci i obiekty wykorzystywane w nauczaniu matematyki, w ksztaªceniu matematycznym, a przede wszystkim w ksztaªceniu poprzez matematyk. Prezentowane w tej monograi prace maj charakter interdyscyplinarny i potwierdzaj tez Hugona Steinhausa,»e matematyka peªni rol po±rednika mi dzy materi a duchem. Adam Pªocki Nowy S cz, w grudniu 2013 r.
7 Zeszyty Naukowe PWSZ, Nowy S cz 2013 roubovice v p írod a um ní Ivana Macha íková 1, Josef Molnár 2 1 Gymnázium Zlín Lesní tvr Lesní tvr , Zlín, ƒeská republika machacikova@gymzl.cz 2 Katedra algebry a geometrie P írodov decká fakulta Univerzita Palackého v Olomouci 17. listopadu , Olomouc, ƒeská republika josef.molnar@upol.cz Abstract The article deals with the denition of the concept of Helix and the occurrence of helixes in architecture, biology and chemistry. Abstrakt ƒlánek se zabývá denicí pojmu Helix a výskyt ²roubovic v architektu e, biologie a chemie. 1. roubovice jako trajektorie bodu V kurikulárních materiálech matematiky základních a st edních ²kol se obvykle pojem ²roubovice neobjevuje. Nalezneme ale tuto k ivku v r zných aplikacích v p írod a um ní? D íve neº odpovíme na tuto otázku, uvedeme si n kolik d leºitých pojm. roubový pohyb vzniká sloºením rovnom rného otá ivého pohybu kolem pevné p ímky o (osy ²roubového pohybu) a rovnom rného posuvného pohybu v jejím sm ru.
8 72 Ivana Macha íková, Josef Molnár roubovice je trajektorie bodu p i ²roubovém pohybu. Je to k ivka, kterou opí²e bod p i rovnom rném pohybu po kruºnici k a sou asném rovnom rném posuvu kruºnice k ve sm ru osy ²roubového pohybu, která prochází st edem kruºnice k kolmo k rovin této kruºnice k. Obr. 1 Osa ²roubového pohybu se nazývá osa ²roubovice. Obr. 2
9 roubovice v p írod a um ní 73 Pozn. 1: roubovice leºí na válcové plo²e. Za speciální p ípady ²roubovice lze povaºovat p ímku o, pop ípad téº kruºnici k. Obr. 3 Pozn. 2: P ímka, kruºnice a ²roubovice jsou jediné tzv. po sob posunovatelné k ivky. V praxi se s tímto jevem m ºeme setkat nap íklad p i zasouvání p ímého me e nebo kruhové ²avle do p ímé i kruhové pochvy. Dv po sob posunutelné ²roubovice nenalezneme v podobné situaci, nýbrº v mírumilovném ²roubu a matici. Obr. 4
10 74 Ivana Macha íková, Josef Molnár Závit ²roubovice je stopou bodu ²roubovice p i oto ení o plný úhel. Velikost odpovídajícího posunutí se nazývá vý²ka závitu. Obr. 5 roubovice je jednozna n ur ena polom rem kruºnice k, vý²kou závitu v a to ivostí (obr. 1). Na obr. 2a) je ²roubovice pravoto ivá, na obr. 2b) levoto ivá. Obr. 6
11 roubovice v p írod a um ní roubovice v innosti lov ka a v p irod Te ny ²roubovice svírají s její osou konstantní úhel, tj. ²roubovice je k ivka konstantního spádu. Obr. 7 Pr m tem ²roubovice do roviny m ºe být nap. kruºnice, sinusoida, cykloida (prodlouºená, prostá i zkrácená), spirála, p ípadn jiná k ivka, viz obr. 3 a 4. Obr. 8
12 76 Ivana Macha íková, Josef Molnár roubovice jsou sou ástí architektury a stavitelství (viz obr. 5, 6, 7), fauny (obr. 8) a ory (obr. 9), techniky (obr. 10) i nap. drhání (macramé, obr. 11). Výskytem ²roubovice v chemických slou eninách se budeme podrobn ji zabývat v následující kapitole. Obr roubovice v chemii V molekulách bílkovin se vyskytují ur ité pravideln uspo ádané úseky (tzv. sekundární struktura bílkovin). Pravidelné sekundární struktury lze popsat jako ²roubovice (helixy), li²ící se pr m rem závitu, jeho stoupáním a smyslem otá ení (mohou být pravo- nebo levoto ivé). Z daných geometrických parametr peptidové vazby a aminokyselinových zbytk m ºeme vytvo it jen omezený po et ²roubovicových konformací. V²em sterickým i energetickým poºadavk m nejlépe vyhovuje tzv. α-²roubovice (α-helix). Jeden její závit je tvo en 3,6 aminokyselinovými zbytky. V²echny skupiny CO a NH peptidových vazeb jsou v této ²roubovici orientovány zhruba rovnob ºn s její dlouhou osou a kaºdá skupina
13 roubovice v p írod a um ní 77 NH je vázána vodíkovou vazbou ke skupin CO o t i zbytky vzdálen j²í (obr. 12). Obr. 10 Sloºení bílkovin s p evahou aminokyselin s malým nebo ºádným postranním et zcem umoº ují vznik ²roubovice, jejíº skupiny NH a CO jsou orientovány kolmo na její osu. Polypeptidový et zec uspo ádaný do takové ²roubovice je v ní dále formován v druhou superponovanou ²roubovici s podstatn vy²²ím stoupáním závitu (superhelix). T i polypeptidové et zce tak vytvá ejí jediný velmi kompaktní vláknitý útvar. Tato struktura je typická pro nejroz²í en j²í ºivo i²nou bílkovinu kolagen. Základní strukturní jednotkou kolagen je tropokolagen, který se skládá ze t í vláken, z nichº kaºdé obsahuje asi aminokyselinových zbytk. Tropokolagen je trojvláknový pravoto ivý helikální prut asi 300 nm dlouhý o pr m ru 1,5 nm (obr. 13). Kaºdý ze t í et zc tvo í levoto ivá ²roubovice s NH a CO skupinami sm rovanými zhruba kolmo na její osu. Kaºdé ze t í vláken tropokolagenového superhelixu vytvá í
14 78 Ivana Macha íková, Josef Molnár vodíkové vazby mezi NH skupinami zbytk glycinu a skupinami CO v jiném vláknu. Obr. 11 Dal²ím p íkladem ²roubovice v chemii je prostorové uspo ádání DNA (sekundární struktura DNA). V roce 1953 vytvo ili J. Watson a F. Crick dnes obecn p ijímaný model molekuly DNA. Skládá se ze dvou et zc svinutých do pravoto ivých ²roubovic kolem pomyslné spole né osy za vzniku dvoj²roubovice (dihelixu, obr. 14). et zce v ní mají opa ný sm r (polaritu) a dopl kovou (komplementární) strukturu. Oba et zce jsou p i tom uspo ádány tak, ºe jejich páte e, sestávající z pentosových kruh a fosfátových zbytk, jsou vn a báze mí í dovnit dihelixu, jejich roviny jsou navzájem rovnob ºné a kolmé na osu dvoj²roubovice. Mezi dvojicemi komplementárních bází se p i tom vytvá ejí vodíkové vazby. Molekula DNA m ºe existovat ve více formách (obr. 15): B-DNA (popsaná Watsonem a Crickem) pravoto ivá, na jeden závit p ipadá 10 nukleotidových zbytk, A-DNA pravoto ivá, na jeden závit p ipadá 11 nukleotidových zbytk, dihelix má jiný pr m r, páry bází jsou posunuty od osy dihelixu a jsou k ní jinak naklon ny,
15 roubovice v p írod a um ní 79 Z-DNA levoto ivá helikální forma s 12 nukleotidovými zbytky p ipadajícími na jeden závit, páte et zce má nepravideln j²í tvar neº u forem A a B. Obr. 12. α-helix Se ²roubovicí se setkáváme i u sekundární struktury polysacharid (obr. 16). roubovice (helix) je obvykle levoto ivá, na její stabilizaci se podílejí vodíkové vazby, hydrofobní interakce i interakce s okolními látkami. S touto konformací se setkáváme u amylosy a n kterých polysacharid pojivových tkání. Po et glukosových jednotek na jeden závit m ºe být 6 aº 8. Obr. 13. Tropokolagen
16 80 Ivana Macha íková, Josef Molnár Jiný p íklad ²roubovice v chemii (p ípadn krystalograi) je ²roubová osa jako prvek prostorové symetrie (obr. 17, 18, 19, 20, 21). Operace prostorové symetrie charakterizují soum rnost struktury krystalu. Obr. 14. Model DNA Nejprve uvádíme n kolik základních pojm z krystalograe. Krystal je homogenní anizotropní diskontinuum (denice mineralogická). Obr. 15. A-DNA (pravoto ivá), B-DNA (pravoto ivá), Z-DNA (levoto ivá)
17 roubovice v p írod a um ní 81 Krystal je hmotný systém, ve kterém kaºdému m íºovému bodu náleºí stejná a stejn orientovaná báze (denice krystalogracká). Tyto denice platí pro klasické krystaly, neplatí pro tzv. kvazikrystaly (nap. tekuté krystaly). Kaºdý krystal musí mít pravidelnou vnit ní strukturu. Obr. 16. Amylosa M íº (m íºka) je mnoºina bod mající stejné okolí. Kaºdou m íº charakterizují m íºkové parametry: délky jednotlivých úse ek a, b, c, úhly α, β, γ. M íº je na rozdíl od struktury ktivní. Obr. 17. roubová osa 3 1
18 82 Ivana Macha íková, Josef Molnár Struktura je m íºka spolu s hmotnou bází, skládá se z ástic (atom, iont ). Obr. 18. roubová osa 3 2 Bu ka je elementární rovnob ºnost n s vrcholy v uzlech m íºe. Je základní stavební jednotkou kaºdé m íºe. Obr. 19. roubová osa 4 1 Zásady výb ru základní bu ky: základní bu ka musí mít stejnou soum rnost jako celá struktura,
19 roubovice v p írod a um ní 83 po et stejných hran a úhl mezi hranami musí být maximální, po et pravých úhl musí být maximální, objem základní bu ky musí být minimální. Obr. 20. roubová osa 4 2 Základní bu ky m ºeme rozd lit podle toho, kolik uzl p ipadá na jejich objem: P (R) - primitivní (prostá), A, B, C - jednodu²e (bazáln ) centrovaná, F - plo²n centrovaná, I - prostorov centrovaná. Obr. 21. roubová osa 4 3
20 84 Ivana Macha íková, Josef Molnár Primitivní bu ka obsahuje uzly pouze ve svých osmi vrcholech na objem primitivní bu ky p ipadá jeden uzel. T lesn (prostorov ) centrovaná bu ka obsahuje krom osmi uzl ve vrcholech je²t jeden uzel v pr se íku t lesových úhlop í ek na objem t lesn centrované bu ky p ipadají dva uzly. Bo n (bazáln ) centrovaná bu ka je krom osmi uzl ve vrcholech tvo ena dal²í dvojicí uzl, které leºí ve st edu dvou protilehlých st n na objem bazáln centrované bu ky p ipadají op t dva uzly. Plo²n centrovaná bu ka je tvo ena osmi uzly ve vrcholech a ²esti uzly ve st edech v²ech ²esti st n na objem plo²n centrované bu ky p ipadají ty i uzly. Existuje 14 typ strukturních m íºek, jimº odpovídá 14 základních bun k, které ozna ujeme jako Bravaisovy bu ky (obr. 22). Obr. 22. Bravaisovy bu ky (1 - trojklonná, 2 - jednoklonná, 3 - koso tvere ná, 4 - klencová, 5 - ²estere ná, 6 - tvere ná, 7 - krychlová soustava)
21 roubovice v p írod a um ní 85 Operace symetrie je taková transformace útvaru, aby nový stav (obraz) byl nerozli²itelný od p vodního (vzoru). Prvek symetrie je geometrický prvek (bod, p ímka, rovina), v i n muº provádíme p íslu²nou operaci symetrie. Prvek symetrie je invariantní vzhledem k této operaci symetrie. Mnoºina v²ech operací symetrie dané molekuly spolu s operací skládání tvo í grupu. Tuto grupu nazýváme grupa symetrie. Pokud provádíme operace symetrie s izolovanou molekulou, vºdy z stává n jaký bod beze zm ny (nepohyblivý), operace symetrie dané molekuly tvo í bodovou grupu symetrie. U bodové grupy symetrie z stává alespo jeden bod nezm n n, neuvaºuje se translace. Je vhodná pro popis geometrických t les, molekul. Prostorová grupa symetrie neponechává ºádný bod v identické poloze, uvaºuje se translace (posunutí). Je vhodná k popisu krystalových struktur. operace prvek symbol symbol (Schoenies) (Hermann-Maugin) identita identita E 1 (ponechání beze zm ny) inverze st ed symetrie i 1 rotace o 360 zrcadlení (reexe) rotace + zrcadlení rotace + inverze n n- etná rota ní osa rovina symetrie rota n reexní osa rota n inverzní osa C n σ S n n m ñ C ni n Tab. 1. P ehled operací a prvk bodové symetrie
22 86 Ivana Macha íková, Josef Molnár Prostorová symetrie obsahuje navíc translaci, takºe máme dva dal²í prvky symetrie, a to ²roubovou osu a skluznou rovinu. roubové osy symetrie jsou sloºené prvky symetrie. P íslu²né operace symetrie se skládají z: rotace o úhel α = 360, n translace podél denovaného vektoru ve sm ru této osy. Osa musí být rovnob ºná s libovolnou m íºkovou translací struktury. Sm r rotace ²roubové osy je velmi d leºitý, vychází se z pravoto ivého systému os, takºe pravoto ivá ²roubová osa ve sm ru z má transla ní vektor ve stejném sm ru vzh ru (tj. ve sm ru palce pravé ruky, kdy prsty nazna ují rota ní pohyb od osy x k y). operace prvek symbol rotace + translace ²roubová osa n k zrcadlení + translace skluzná rovina a, b, c, n, d Tab. 2. Operace a prvky prostorové symetrie Máme-li n- etnou rota ní osu symetrie, pak n oto ení o úhel α = 360 n doprovázených n translacemi τ podél ²roubové osy musí vést k transla nímu pohybu výchozího objektu (atom, molekula) o celo íselný násobek (m) m íºové translace t: nτ = mt nebo τ = m n t, kde m, n jsou celá ísla. Obecn lze vyjád it symbol ²roubové osy jako n m. Transla ní sloºky ²roubových os symetrie závisí na etnosti osy a mohou nabývat jen ur itých hodnot (hodnota v závorce ozna uje transla ní sloºku). P ehled ²roubových os (obr. 23): dvoj etná osa 2 0, 2 1 ( 1 2 ), 2 2, troj etná osa 3 0, 3 1 ( 1 3 ), 3 2 ( 2 3 ), 3 3, ty etná osa 4 0, 4 1 ( 1 4 ), 4 2 ( 2 4 ), 4 3 ( 3 4 ), 4 4, ²esti etná osa 6 0, 6 1 ( 1 6 ), 6 2 ( 2 6 ), 6 3 ( 3 6 ), 6 4 ( 4 6 ), 6 5 ( 5 6 ), 6 6.
23 roubovice v p írod a um ní 87 Dolní index zna í hodnotu m z vý²e uvedeného vztahu. Je-li m = 0, jde o istou rotaci, v p ípad, ºe je m = n, jde o istou translaci. Obr. 23. roubové osy Skluzné roviny symetrie (roviny posunutého zrcadlení) jsou prvky symetrie, kdy p íslu²nými operacemi je zrcadlení kombinované s translací podél roviny zrcadlení. Podle sm ru a velikosti translace rozli²ujeme skluzné roviny osní, diagonální a diamantové. Osní skluzné roviny (zna- íme a, b, c podle os) zrcadlení je provázeno posunutím o 1a (p íp. 2 1 b, 1 c). Úhlop í né skluzné roviny (zna ení n) zrcadlení je provázeno 2 2 posunutím o polovinu st nové úhlop í ky plo²n centrované bu ky, tedy o (p íp., ). Diamantové skluzné roviny (zna ení d) zrcadlení a+b b+c a+c 2 2 2
24 88 Ivana Macha íková, Josef Molnár je provázeno posunutím o tvrtinu st nové úhlop í ky plo²n centrované bu ky, tedy o a±b (p íp. b±c, a±c) Obr. 24. Krystalogracké soustavy tvary krystal Operace bodové symetrie a jejich moºné kombinace tvo í celkem 32 bodových grup. Bodovými grupami lze charakterizovat symetrii vn j²ího tvaru krystalu existuje 32 krystalograckých odd lení, která se rozd lují do sedmi krystalograckých soustav (obr. 24). Obr. 25. Struktura krystalu uorit CaF 2
25 roubovice v p írod a um ní 89 V roce 1890 E. S. Fedorov odvodil v²echny moºné kombinace prvk symetrie v prostoru. E. S. Fedorov, A. Schoenies, W. Barlow dokázali, ºe prostorových grup symetrie je 230. Jedná se o kombinaci v²ech moºných transformací krystalové struktury, takºe prostorová grupa charakterizuje soum rnost struktury krystalu (obr. 25 a 26). Celkový po et prostorových grup zahrnuje v²echny kombinace transla ních i beztransla ních operací symetrie, které jsou p ípustné ve 14 Bravaisových bu kách. Existuje tedy 230 moºností, jak se m ºe libovolný motiv opakovat v prostoru. Obr. 26. Struktura krystalu k emen SiO 2 4. Obecná ²roubovice roubovice leºí na rota ní válcové plo²e, tedy vzdálenost vytvá ejícího bodu ²roubovice od osy p íslu²ného rota ního pohybu je konstantní. O obecné ²roubovici mluvíme v p ípad, ºe se vzdálenost tvo-
26 90 Ivana Macha íková, Josef Molnár ícího bodu od osy p íslu²ného rota ního pohybu m ºe spojit m nit, typickým p íkladem je obecná ²roubovice leºící na rota ní kuºelové plo²e (viz obr. 27). Zajímavá ukázka obecné ²roubovice je na obrázku 28. Obr Záv r Ukázali jsme si jen malý zlomek situací, kde se m ºeme se ²roubovicí setkat. Ale i to dle na²eho názoru sta í k tomu, aby se o ²roubovicích
27 roubovice v p írod a um ní 91 a jejich uºití dov d li ºáci (zejména technických) st edních ²kol, by jen ve volitelné i nepovinné matematice nebo v deskriptivní geometrii. Obr. 28 Reference [1] B ezina F. a kol., Stereochemie a n které fyzikáln chemické metody studia anorganických látek. Vydavatelství UP, Olomouc [2] Graf U., Kabaret matematiky. Orbis, Praha 1943.
28 92 Ivana Macha íková, Josef Molnár [3] Macha íková I., Molnár J., Grupy symetrie molekul. In: Matematyka w przyrodzie i sztuce matematyka, przyroda i sztuka w ksztalceniu powszechnym. Wydawnictwo PWSZ, Nowy S cz 2012, s , ISBN [4] Urban A., Deskriptivní geometrie II. SNTL, Praha [5] Vodráºka Z., Biochemie 1. Academia, Praha 1992, ISBN [6] Vodráºka Z., Biochemie 2. Academia, Praha 1992, ISBN [7] Zimák J., Mineralogie a petrograe. Vydavatelství UP, Olomouc [8] bilko-viny_-_periodicke_motivy.html [9] [10] [11] [12] [13] symet-rie.htm [14] [15] [16] Zpracováno v rámci e²ení projektu CZ 1.07/1.1.0/ "Matematika pro v²echny".
Matematyka w przyrodzie i sztuce matematyka, przyroda i sztuka w ksztaªceniu powszechnym
 Pa«stwowa Wy»sza Szkoªa Zawodowa w Nowym S czu Matematyka w przyrodzie i sztuce matematyka, przyroda i sztuka w ksztaªceniu powszechnym Tom 3 Pod redakcj Adama Pªockiego Nowy S cz 2013 Komitet Redakcyjny
Pa«stwowa Wy»sza Szkoªa Zawodowa w Nowym S czu Matematyka w przyrodzie i sztuce matematyka, przyroda i sztuka w ksztaªceniu powszechnym Tom 3 Pod redakcj Adama Pªockiego Nowy S cz 2013 Komitet Redakcyjny
Po etní geometrie. Výpo et délky p epony: c 2 = a 2 + b 2 Výpo et délky odv sny: a 2 = c 2 b 2, b 2 = c 2 a 2
 Po etní geometrie Pythagorova v ta Obsah tverce nad p eponou je roven sou tu obsah tverc nad ob ma odv snami. Výpo et délky p epony: c = a + b Výpo et délky odv sny: a = c b, b = c a P íklad 1: Vypo t
Po etní geometrie Pythagorova v ta Obsah tverce nad p eponou je roven sou tu obsah tverc nad ob ma odv snami. Výpo et délky p epony: c = a + b Výpo et délky odv sny: a = c b, b = c a P íklad 1: Vypo t
Vektory. Vektorové veli iny
 Vektor je veli ina, která má jak velikost tak i sm r. Ob tyto vlastnosti musí být uvedeny, aby byl vektor stanoven úpln. V této ásti je návod, jak vektory zapsat, jak je s ítat a od ítat a jak je pouºívat
Vektor je veli ina, která má jak velikost tak i sm r. Ob tyto vlastnosti musí být uvedeny, aby byl vektor stanoven úpln. V této ásti je návod, jak vektory zapsat, jak je s ítat a od ítat a jak je pouºívat
Skalární sou in. Úvod. Denice skalárního sou inu
 Skalární sou in Jedním ze zp sob, jak m ºeme dva vektory kombinovat, je skalární sou in. Výsledkem skalárního sou inu dvou vektor, jak jiº název napovídá, je skalár. V tomto letáku se nau íte, jak vypo
Skalární sou in Jedním ze zp sob, jak m ºeme dva vektory kombinovat, je skalární sou in. Výsledkem skalárního sou inu dvou vektor, jak jiº název napovídá, je skalár. V tomto letáku se nau íte, jak vypo
Matematyka w przyrodzie i sztuce matematyka, przyroda i sztuka w ksztaªceniu powszechnym
 Pa«stwowa Wy»sza Szkoªa Zawodowa w Nowym S czu Matematyka w przyrodzie i sztuce matematyka, przyroda i sztuka w ksztaªceniu powszechnym Tom 3 Pod redakcj Adama Pªockiego Nowy S cz 2013 Komitet Redakcyjny
Pa«stwowa Wy»sza Szkoªa Zawodowa w Nowym S czu Matematyka w przyrodzie i sztuce matematyka, przyroda i sztuka w ksztaªceniu powszechnym Tom 3 Pod redakcj Adama Pªockiego Nowy S cz 2013 Komitet Redakcyjny
Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor, bod X se nazývá obraz.
 7. Shodná zobrazení 6. ročník 7. Shodná zobrazení 7.1. Shodnost geometrických obrazců Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor,
7. Shodná zobrazení 6. ročník 7. Shodná zobrazení 7.1. Shodnost geometrických obrazců Zobrazení v rovině je předpis, který každému bodu X roviny připisuje právě jeden bod X roviny. Bod X se nazývá vzor,
4. KRYSTALOGRAFIE A KRYSTALOCHEMIE 4.1. Geometrie krystalových mříží
 4. KRYSTALOGRAFIE A KRYSTALOCHEMIE 4.1. Geometrie krystalových mříží Základní pojmy: Struktura krystalu Konkrétní rozmístění stavebních částic (atomů, iontů) krystalických látek v prostoru nazýváme strukturou
4. KRYSTALOGRAFIE A KRYSTALOCHEMIE 4.1. Geometrie krystalových mříží Základní pojmy: Struktura krystalu Konkrétní rozmístění stavebních částic (atomů, iontů) krystalických látek v prostoru nazýváme strukturou
Mechanismy. Vazby členů v mechanismech (v rovině):
 Mechanismy Mechanismus klikový, čtyřkloubový, kulisový, západkový a vačkový jsou nejčastějšími mechanismy ve strojích (kromě převodů). Mechanismy obsahují členy (kliky, ojnice, těhlice, křižáky a další).
Mechanismy Mechanismus klikový, čtyřkloubový, kulisový, západkový a vačkový jsou nejčastějšími mechanismy ve strojích (kromě převodů). Mechanismy obsahují členy (kliky, ojnice, těhlice, křižáky a další).
Integrování jako opak derivování
 Integrování jako opak derivování V tomto dokumentu budete seznámeni s derivováním b ºných funkcí a budete mít moºnost vyzkou²et mnoho zp sob derivace. Jedním z nich je proces derivování v opa ném po adí.
Integrování jako opak derivování V tomto dokumentu budete seznámeni s derivováním b ºných funkcí a budete mít moºnost vyzkou²et mnoho zp sob derivace. Jedním z nich je proces derivování v opa ném po adí.
2. Ur íme sudost/lichost funkce a pr se íky s osami. 6. Na záv r na rtneme graf vy²et ované funkce. 8x. x 2 +4
 Pr b h funkce V této jednotce si ukáºeme jak postupovat p i vy²et ování pr b hu funkce. P edpokládáme znalost po ítání derivací a limit, které jsou dob e popsány v p edchozích letácích tohoto bloku. P
Pr b h funkce V této jednotce si ukáºeme jak postupovat p i vy²et ování pr b hu funkce. P edpokládáme znalost po ítání derivací a limit, které jsou dob e popsány v p edchozích letácích tohoto bloku. P
Pravd podobnost a statistika - cvi ení. Simona Domesová místnost: RA310 (budova CPIT) web:
 Pravd podobnost a statistika - cvi ení Simona Domesová simona.domesova@vsb.cz místnost: RA310 (budova CPIT) web: http://homel.vsb.cz/~dom0015 Cíle p edm tu vyhodnocování dat pomocí statistických metod
Pravd podobnost a statistika - cvi ení Simona Domesová simona.domesova@vsb.cz místnost: RA310 (budova CPIT) web: http://homel.vsb.cz/~dom0015 Cíle p edm tu vyhodnocování dat pomocí statistických metod
ZÁPISKY Z ANALYTICKÉ GEOMETRIE 1 SOUŘADNICE, BODY
 1 Souřadnice, body 1.1 Prostor prostor můžeme chápat jako nějaké prostředí, ve kterém můžeme mít různé věci na různých místech místo, poloha - tohle potřebujeme nějak popsat abychom mohli změřit nebo říci,
1 Souřadnice, body 1.1 Prostor prostor můžeme chápat jako nějaké prostředí, ve kterém můžeme mít různé věci na různých místech místo, poloha - tohle potřebujeme nějak popsat abychom mohli změřit nebo říci,
Kótování na strojnických výkresech 1.část
 Kótování na strojnických výkresech 1.část Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující kóty. Z tohoto důvodu je kótování jedna z nejzodpovědnějších prací na technických
Kótování na strojnických výkresech 1.část Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující kóty. Z tohoto důvodu je kótování jedna z nejzodpovědnějších prací na technických
c sin Příklad 2 : v trojúhelníku ABC platí : a = 11,6 dm, c = 9 dm, α = 65 0 30. Vypočtěte stranu b a zbývající úhly.
 9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
9. Úvod do středoškolského studia - rozšiřující učivo 9.. Další znalosti o trojúhelníku 9... Sinova věta a = sin b = sin c sin Příklad : V trojúhelníku BC platí : c = 0 cm, α = 45 0, β = 05 0. Vypočtěte
Semestrální práce z p edm tu URM (zadání), 2014/2015:
 Semestrální práce z p edm tu URM (zadání), 2014/2015: 1. Vyzna te na globusu cestu z jihu Grónska na jih Afriky, viz Obrázek 1. V po áte ní a cílové destinaci bude zapíchnutý ²pendlík sm ující do st edu
Semestrální práce z p edm tu URM (zadání), 2014/2015: 1. Vyzna te na globusu cestu z jihu Grónska na jih Afriky, viz Obrázek 1. V po áte ní a cílové destinaci bude zapíchnutý ²pendlík sm ující do st edu
Vyučovací předmět / ročník: Matematika / 5. Učivo
 Vzdělávací oblast: Matematika a její aplikace Výstupy žáka Vyučovací předmět / ročník: Matematika / 5. ČÍSLO A POČETNÍ OPERACE Zpracoval: Mgr. Dana Štěpánová orientuje se v posloupnosti přirozených čísel
Vzdělávací oblast: Matematika a její aplikace Výstupy žáka Vyučovací předmět / ročník: Matematika / 5. ČÍSLO A POČETNÍ OPERACE Zpracoval: Mgr. Dana Štěpánová orientuje se v posloupnosti přirozených čísel
Úlohy domácího kola kategorie C
 50. ročník Matematické olympiády Úlohy domácího kola kategorie 1. Najděte všechna trojmístná čísla n taková, že poslední trojčíslí čísla n 2 je shodné s číslem n. Student může při řešení úlohy postupovat
50. ročník Matematické olympiády Úlohy domácího kola kategorie 1. Najděte všechna trojmístná čísla n taková, že poslední trojčíslí čísla n 2 je shodné s číslem n. Student může při řešení úlohy postupovat
BÍLKOVINY. Autor: Mgr. Stanislava Bubíková. Datum (období) tvorby: 15. 2. 2013. Ročník: devátý
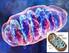 BÍLKOVINY Autor: Mgr. Stanislava Bubíková Datum (období) tvorby: 15. 2. 2013 Ročník: devátý Vzdělávací oblast: Člověk a příroda / Chemie / Organické sloučeniny 1 Anotace: Žáci se seznámí s oblastmi chemického
BÍLKOVINY Autor: Mgr. Stanislava Bubíková Datum (období) tvorby: 15. 2. 2013 Ročník: devátý Vzdělávací oblast: Člověk a příroda / Chemie / Organické sloučeniny 1 Anotace: Žáci se seznámí s oblastmi chemického
Kuželosečky a kvadriky ve škole i kolem
 Kuželosečky a kvadriky ve škole i kolem nás Bc. Aneta Mirová Kurz vznikl v rámci projektu Rozvoj systému vzdělávacích příležitostí pro nadané žáky a studenty v přírodních vědách a matematice s využitím
Kuželosečky a kvadriky ve škole i kolem nás Bc. Aneta Mirová Kurz vznikl v rámci projektu Rozvoj systému vzdělávacích příležitostí pro nadané žáky a studenty v přírodních vědách a matematice s využitím
Text m ºe být postupn upravován a dopl ován. Datum poslední úpravy najdete u odkazu na staºení souboru. Veronika Sobotíková
 Tento text není samostatným studijním materiálem. Jde jen o prezentaci promítanou na p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze na tabuli a nejsou zde obsaºeny.
Tento text není samostatným studijním materiálem. Jde jen o prezentaci promítanou na p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze na tabuli a nejsou zde obsaºeny.
nazvu obecnou PDR pro neznámou funkci
 Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
Autodesk Inventor 8 vysunutí
 Nyní je náčrt posazen rohem do počátku souřadného systému. Autodesk Inventor 8 vysunutí Následující text popisuje vznik 3D modelu pomocí příkazu Vysunout. Vyjdeme z náčrtu na obrázku 1. Obrázek 1: Náčrt
Nyní je náčrt posazen rohem do počátku souřadného systému. Autodesk Inventor 8 vysunutí Následující text popisuje vznik 3D modelu pomocí příkazu Vysunout. Vyjdeme z náčrtu na obrázku 1. Obrázek 1: Náčrt
Vektor náhodných veli in - práce s více prom nnými
 Vektor náhodných veli in - práce s více prom nnými 12. kv tna 2015 N kdy k popisu n jaké situace pot ebujeme více neº jednu náhodnou veli inu. Nap. v k, hmotnost, vý²ku. Mezi t mito veli inami mohou být
Vektor náhodných veli in - práce s více prom nnými 12. kv tna 2015 N kdy k popisu n jaké situace pot ebujeme více neº jednu náhodnou veli inu. Nap. v k, hmotnost, vý²ku. Mezi t mito veli inami mohou být
(3) Zvolíme pevné z a sledujme dráhu, kterou opisuje s postupujícím časem koncový bod vektoru E v rovině z = konst. Upravíme vztahy (2) a (3)
 Učební tet k přednášce UFY1 Předpokládejme šíření rovinné harmonické vln v kladném směru os z. = i + j kde i, j jsou jednotkové vektor ve směru os respektive a cos ( ) ω ϕ t kz = + () = cos( ωt kz+ ϕ )
Učební tet k přednášce UFY1 Předpokládejme šíření rovinné harmonické vln v kladném směru os z. = i + j kde i, j jsou jednotkové vektor ve směru os respektive a cos ( ) ω ϕ t kz = + () = cos( ωt kz+ ϕ )
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5. ROČNÍKOVÁ PRÁCE Teoretické řešení střech
 Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Teoretické řešení střech Vypracoval: Michal Drašnar Třída: 8.M Školní rok: 2015/2016 Seminář: Deskriptivní geometrie Prohlašuji, že
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Teoretické řešení střech Vypracoval: Michal Drašnar Třída: 8.M Školní rok: 2015/2016 Seminář: Deskriptivní geometrie Prohlašuji, že
Státní maturita 2010 Maturitní generálka 2010 Matematika: didaktický test - vy²²í úrove obtíºnosti MAGVD10C0T01 e²ené p íklady
 Státní maturita 00 Maturitní generálka 00 Matematika: didaktický test - vy²²í úrove obtíºnosti MAGVD0C0T0 e²ené p íklady Autor e²ení: Jitka Vachtová 6. b ezna 0 http://www.vachtova.cz/ Obsah Úloha Úloha
Státní maturita 00 Maturitní generálka 00 Matematika: didaktický test - vy²²í úrove obtíºnosti MAGVD0C0T0 e²ené p íklady Autor e²ení: Jitka Vachtová 6. b ezna 0 http://www.vachtova.cz/ Obsah Úloha Úloha
Základní prvky a všeobecná lyžařská průprava
 Základní prvky a všeobecná lyžařská průprava Základní prvky a všeobecná lyžařská průprava na běžeckých lyžích Základními prvky nazýváme prvky elementární přípravy a pohybových dovedností, jejichž zvládnutí
Základní prvky a všeobecná lyžařská průprava Základní prvky a všeobecná lyžařská průprava na běžeckých lyžích Základními prvky nazýváme prvky elementární přípravy a pohybových dovedností, jejichž zvládnutí
VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. (f(x) g(x)) dx.
 VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. Výpo et obsahu rovinných ploch a) Plocha ohrani ená k ivkami zadanými v kartézských sou adnicích. Obsah S rovinné plochy ohrani ené dv ma spojitými
VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. Výpo et obsahu rovinných ploch a) Plocha ohrani ená k ivkami zadanými v kartézských sou adnicích. Obsah S rovinné plochy ohrani ené dv ma spojitými
Limity funkcí v nevlastních bodech. Obsah
 Limity funkcí v nevlastních bodech V tomto letáku si vysv tlíme, co znamená, kdyº funkce mí í do nekone na, mínus nekone na nebo se blíºí ke konkrétnímu reálnému íslu, zatímco x jde do nekone na nebo mínus
Limity funkcí v nevlastních bodech V tomto letáku si vysv tlíme, co znamená, kdyº funkce mí í do nekone na, mínus nekone na nebo se blíºí ke konkrétnímu reálnému íslu, zatímco x jde do nekone na nebo mínus
Derivování sloºené funkce
 Derivování sloºené funkce V tomto letáku si p edstavíme speciální pravidlo pro derivování sloºené funkce (te funkci obsahující dal²í funkci). Po p e tení tohoto tetu byste m li být schopni: vysv tlit pojem
Derivování sloºené funkce V tomto letáku si p edstavíme speciální pravidlo pro derivování sloºené funkce (te funkci obsahující dal²í funkci). Po p e tení tohoto tetu byste m li být schopni: vysv tlit pojem
P íklad 1 (Náhodná veli ina)
 P íklad 1 (Náhodná veli ina) Uvaºujeme experiment: házení mincí. Výsledkem pokusu je rub nebo líc, ºe padne hrana neuvaºujeme. Pokud hovo íme o náhodné veli in, musíme p epsat výsledky pokusu do mnoºiny
P íklad 1 (Náhodná veli ina) Uvaºujeme experiment: házení mincí. Výsledkem pokusu je rub nebo líc, ºe padne hrana neuvaºujeme. Pokud hovo íme o náhodné veli in, musíme p epsat výsledky pokusu do mnoºiny
Line rn oper tory v euklidovsk ch prostorech V t to sti pou ijeme obecn v sledky o line rn ch oper torech ve vektorov ch prostorech nad komplexn mi sl
 Line rn oper tory v euklidovsk ch prostorech V t to sti pou ijeme obecn v sledky o line rn ch oper torech ve vektorov ch prostorech nad komplexn mi sly z p edchoz ch kapitol k podrobn j mu zkoum n line
Line rn oper tory v euklidovsk ch prostorech V t to sti pou ijeme obecn v sledky o line rn ch oper torech ve vektorov ch prostorech nad komplexn mi sly z p edchoz ch kapitol k podrobn j mu zkoum n line
Název školy. Moravské gymnázium Brno s.r.o. Mgr. Marie Chadimová Mgr. Věra Jeřábková. Autor. Matematika. Planimetrie. Trojúhelníky. Teorie a příklady.
 Číslo projektu Z.1.07/1.5.00/34.0743 Název školy Moravské gymnázium rno s.r.o. utor Tematická oblast Mgr. Marie hadimová Mgr. Věra Jeřábková Matematika. Planimetrie. Trojúhelníky. Teorie a příklady. Ročník
Číslo projektu Z.1.07/1.5.00/34.0743 Název školy Moravské gymnázium rno s.r.o. utor Tematická oblast Mgr. Marie hadimová Mgr. Věra Jeřábková Matematika. Planimetrie. Trojúhelníky. Teorie a příklady. Ročník
TÉMATICKÝ PLÁN OSV. čte, zapisuje a porovnává přirozená čísla do 20, užívá a zapisuje vztah rovnosti a nerovnosti
 TÉMATICKÝ PLÁN MA 1.ročník Očekávaný výstup /dle RVP/ Žák: Konkretizace výstupu, učivo, návrh realizace výstupu PT Číslo a početní operace používá přirozená čísla k modelování reálných situací, počítá
TÉMATICKÝ PLÁN MA 1.ročník Očekávaný výstup /dle RVP/ Žák: Konkretizace výstupu, učivo, návrh realizace výstupu PT Číslo a početní operace používá přirozená čísla k modelování reálných situací, počítá
e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody
 e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody V praxi se asto setkávame s p ípady, kdy je pot eba e²it více rovnic, takzvaný systém rovnic, obvykle s více jak jednou neznámou.
e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody V praxi se asto setkávame s p ípady, kdy je pot eba e²it více rovnic, takzvaný systém rovnic, obvykle s více jak jednou neznámou.
Binární operace. Úvod. Pomocný text
 Pomocný text Binární operace Úvod Milí e²itelé, binární operace je pom rn abstraktní téma, a tak bude ob as pot eba odprostit se od konkrétních p íklad a podívat se na v c s ur itým nadhledem. Nicmén e²ení
Pomocný text Binární operace Úvod Milí e²itelé, binární operace je pom rn abstraktní téma, a tak bude ob as pot eba odprostit se od konkrétních p íklad a podívat se na v c s ur itým nadhledem. Nicmén e²ení
Šroubovice a šroubové plochy
 Šroubovice a šroubové plochy Mgr. Jan Šafařík Přednáška č. 10 11 přednášková skupina P-B1VS2 učebna Z240 Literatura Základní literatura: Autorský kolektiv Ústavu matematiky a deskriptivní geometrie FaSt
Šroubovice a šroubové plochy Mgr. Jan Šafařík Přednáška č. 10 11 přednášková skupina P-B1VS2 učebna Z240 Literatura Základní literatura: Autorský kolektiv Ústavu matematiky a deskriptivní geometrie FaSt
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. NOSNÍKY NOSNÍKY
 Předmět: Ročník: Vytvořil: Datum: MECHANIKA PRVNÍ ŠČERBOVÁ M. PAVELKA V. 16. ČERVNA 2012 Název zpracovaného celku: NOSNÍKY NOSNÍKY Nosníky jsou zpravidla přímá tělesa (pruty) uloţená na podporách nebo
Předmět: Ročník: Vytvořil: Datum: MECHANIKA PRVNÍ ŠČERBOVÁ M. PAVELKA V. 16. ČERVNA 2012 Název zpracovaného celku: NOSNÍKY NOSNÍKY Nosníky jsou zpravidla přímá tělesa (pruty) uloţená na podporách nebo
5.2.1 Matematika povinný předmět
 5.2.1 Matematika povinný předmět Učební plán předmětu 1. ročník 2. ročník 3. ročník 6. ročník 7. ročník 8. ročník 9. ročník 4 4+1 4+1 4+1 4+1 4 4 3+1 4+1 Vzdělávací oblast Matematika a její aplikace v
5.2.1 Matematika povinný předmět Učební plán předmětu 1. ročník 2. ročník 3. ročník 6. ročník 7. ročník 8. ročník 9. ročník 4 4+1 4+1 4+1 4+1 4 4 3+1 4+1 Vzdělávací oblast Matematika a její aplikace v
m = V = Sv t P i tomto pohybu rozpohybuje i tekutinu, kterou má v cest. Hmotnost této tekutiny je nepochybn
 Odpor vzduchu JAKUB BENDA, MILAN ROJKO Gymnázium Jana Nerudy, Praha V kroužku experimentální fyziky jsme ov ovali vztah: F = ½ SC v (1) V tomto vztahu je F odporová aerodynamická síla p sobící na t leso
Odpor vzduchu JAKUB BENDA, MILAN ROJKO Gymnázium Jana Nerudy, Praha V kroužku experimentální fyziky jsme ov ovali vztah: F = ½ SC v (1) V tomto vztahu je F odporová aerodynamická síla p sobící na t leso
Pr b h funkce I. Obsah. Maxima a minima funkce
 Pr b h funkce I Maxima a minima funkce V této jednotce ukáºeme jak derivování m ºe být uºite né pro hledání minimálních a maximálních hodnot funkce. Po p e tení tohoto letáku nebo shlédnutí instruktáºního
Pr b h funkce I Maxima a minima funkce V této jednotce ukáºeme jak derivování m ºe být uºite né pro hledání minimálních a maximálních hodnot funkce. Po p e tení tohoto letáku nebo shlédnutí instruktáºního
Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018. 3. Reálná čísla
 Moderní technologie ve studiu aplikované fyziky CZ..07/..00/07.008 3. Reálná čísla RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny. K nejvýznamnějším patří množina reálných čísel,
Moderní technologie ve studiu aplikované fyziky CZ..07/..00/07.008 3. Reálná čísla RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny. K nejvýznamnějším patří množina reálných čísel,
Statistika pro geografy. Rozd lení etností DEPARTMENT OF GEOGRAPHY
 Statistika pro geografy Rozd lení etností DEPARTMENT OF GEOGRAPHY Faculty of Science Palacký University Olomouc t. 17. listopadu 1192/12, 771 46 Olomouc Pojmy etnost = po et prvk se stejnou hodnotou statistického
Statistika pro geografy Rozd lení etností DEPARTMENT OF GEOGRAPHY Faculty of Science Palacký University Olomouc t. 17. listopadu 1192/12, 771 46 Olomouc Pojmy etnost = po et prvk se stejnou hodnotou statistického
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 4.3 HŘÍDELOVÉ SPOJKY Spojky jsou strojní části, kterými je spojen hřídel hnacího ústrojí s hřídelem ústrojí
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 4.3 HŘÍDELOVÉ SPOJKY Spojky jsou strojní části, kterými je spojen hřídel hnacího ústrojí s hřídelem ústrojí
Integrovaná střední škola, Hlaváčkovo nám. 673, Slaný
 Označení materiálu: VY_32_INOVACE_STEIV_FYZIKA1_17 Název materiálu: Kinetická teorie látek. Tematická oblast: Fyzika 1.ročník Anotace: Prezentace slouží k výuce struktury a vlastnosti látek, složení pevných,
Označení materiálu: VY_32_INOVACE_STEIV_FYZIKA1_17 Název materiálu: Kinetická teorie látek. Tematická oblast: Fyzika 1.ročník Anotace: Prezentace slouží k výuce struktury a vlastnosti látek, složení pevných,
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ
 ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
ČÁST PÁTÁ POZEMKY V KATASTRU NEMOVITOSTÍ Pozemkem se podle 2 písm. a) katastrálního zákona rozumí část zemského povrchu, a to část taková, která je od sousedních částí zemského povrchu (sousedních pozemků)
Obsah. Pouºité zna ení 1
 Obsah Pouºité zna ení 1 1 Úvod 3 1.1 Opera ní výzkum a jeho disciplíny.......................... 3 1.2 Úlohy matematického programování......................... 3 1.3 Standardní maximaliza ní úloha lineárního
Obsah Pouºité zna ení 1 1 Úvod 3 1.1 Opera ní výzkum a jeho disciplíny.......................... 3 1.2 Úlohy matematického programování......................... 3 1.3 Standardní maximaliza ní úloha lineárního
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.5 Karosářské Know how (Vědět jak) Kapitola
Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.5 Karosářské Know how (Vědět jak) Kapitola
Č část četnost. 部 分 频 率 relativní četnost 率, 相 对 频 数
 A absolutní člen 常 量 成 员 absolutní hodnota čísla 绝 对 值 algebraický výraz 代 数 表 达 式 ar 公 亩 aritmetický průměr 算 术 均 数 aritmetika 算 术, 算 法 B boční hrana 侧 棱 boční hrany jehlanu 角 锥 的 侧 棱 boční stěny jehlanu
A absolutní člen 常 量 成 员 absolutní hodnota čísla 绝 对 值 algebraický výraz 代 数 表 达 式 ar 公 亩 aritmetický průměr 算 术 均 数 aritmetika 算 术, 算 法 B boční hrana 侧 棱 boční hrany jehlanu 角 锥 的 侧 棱 boční stěny jehlanu
doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz
 doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz Elias Tomeh / Snímek 1 Nevyváženost rotorů rotačních strojů je důsledkem změny polohy (posunutí, naklonění) hlavních os setrvačnosti rotorů vzhledem
doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz Elias Tomeh / Snímek 1 Nevyváženost rotorů rotačních strojů je důsledkem změny polohy (posunutí, naklonění) hlavních os setrvačnosti rotorů vzhledem
Nukleové kyseliny. Struktura DNA a RNA. Milada Roštejnská. Helena Klímová
 ukleové kyseliny Struktura DA a RA Milada Roštejnská elena Klímová bsah Typy nukleových kyselin DA a RA jsou tvořeny z nukleotidů Jaký je rozdíl mezi nukleotidem a nukleosidem? Fosfodiesterová vazba Komplementarita
ukleové kyseliny Struktura DA a RA Milada Roštejnská elena Klímová bsah Typy nukleových kyselin DA a RA jsou tvořeny z nukleotidů Jaký je rozdíl mezi nukleotidem a nukleosidem? Fosfodiesterová vazba Komplementarita
5. VÝROBNÍ STROJE. 5.1. Dělení výrobních strojů
 5. VÝROBNÍ STROJE Ke správnému porozumění obsahu této kapitoly je vhodné připomenout význam některých pojmů: Stroj je obecně mechanické zařízení, které má za cíl usnadnění, zrychlení a zpřesnění lidské
5. VÝROBNÍ STROJE Ke správnému porozumění obsahu této kapitoly je vhodné připomenout význam některých pojmů: Stroj je obecně mechanické zařízení, které má za cíl usnadnění, zrychlení a zpřesnění lidské
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A st eda 19. listopadu 2015, 11:2013:20 ➊ (3 body) Pro diferenciální operátor ˆL je mnoºina W q denována p edpisem W q = { y(x) Dom( ˆL) : ˆL(y(x))
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A st eda 19. listopadu 2015, 11:2013:20 ➊ (3 body) Pro diferenciální operátor ˆL je mnoºina W q denována p edpisem W q = { y(x) Dom( ˆL) : ˆL(y(x))
Plochy stavebně-inženýrské praxe
 Plochy stavebně-inženýrské praxe 9. Plochy rourové In: František Kadeřávek (author): Plochy stavebně-inženýrské praxe. (Czech). Praha: Jednota československých matematiků a fysiků, 1950. pp. 95 98. Persistent
Plochy stavebně-inženýrské praxe 9. Plochy rourové In: František Kadeřávek (author): Plochy stavebně-inženýrské praxe. (Czech). Praha: Jednota československých matematiků a fysiků, 1950. pp. 95 98. Persistent
Vlastnosti a zkoušení materiálů. Přednáška č.2 Poruchy krystalické mřížky
 Vlastnosti a zkoušení materiálů Přednáška č.2 Poruchy krystalické mřížky Opakování z minula Materiál Degradační procesy Vnitřní stavba atomy, vazby Krystalické, amorfní, semikrystalické Vlastnosti materiálů
Vlastnosti a zkoušení materiálů Přednáška č.2 Poruchy krystalické mřížky Opakování z minula Materiál Degradační procesy Vnitřní stavba atomy, vazby Krystalické, amorfní, semikrystalické Vlastnosti materiálů
stavební kostičky, z těch vše sestaví TESELACE chybí měřítko na velikosti kostiček nezáleží krystalografie na vědeckém základě
 René Hauy otec moderní krystalografie islandský živec stejné částečky (stejné úhly, plochy) 1781 prezentace pro fr. akademii věd hlubší studium i dalších krystalů: krystaly stejného složení mají stejný
René Hauy otec moderní krystalografie islandský živec stejné částečky (stejné úhly, plochy) 1781 prezentace pro fr. akademii věd hlubší studium i dalších krystalů: krystaly stejného složení mají stejný
Vazebné interakce protein s DNA
 Vazebné interakce protein s DNA Vazebné možnosti vn jší vazba atmosféra + iont kolem nabité DNA vazba ve žlábku van der Waalsovský kontakt s lé ivem ve žlábku interkalace vmeze ení planárního aromat.
Vazebné interakce protein s DNA Vazebné možnosti vn jší vazba atmosféra + iont kolem nabité DNA vazba ve žlábku van der Waalsovský kontakt s lé ivem ve žlábku interkalace vmeze ení planárního aromat.
Česká pedagogická společnost
 Česká pedagogická společnost SJEZD ČESKÉ PEDAGOGICKÉ SPOLEČNOSTI - USNESENÍ Praha, Pedagogická fakulta UK 16. 2. 2011 Sjezd České pedagogické společnosti se konal dne 16. února 2011 v Praze na Pedagogické
Česká pedagogická společnost SJEZD ČESKÉ PEDAGOGICKÉ SPOLEČNOSTI - USNESENÍ Praha, Pedagogická fakulta UK 16. 2. 2011 Sjezd České pedagogické společnosti se konal dne 16. února 2011 v Praze na Pedagogické
1.7. Mechanické kmitání
 1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
1.7. Mechanické kmitání. 1. Umět vysvětlit princip netlumeného kmitavého pohybu.. Umět srovnat periodický kmitavý pohyb s periodickým pohybem po kružnici. 3. Znát charakteristické veličiny periodického
e²ení 1. série Úvodní gulá² autor: Kolektiv org
 e²ení 1. série Úvodní gulá² autor: Kolektiv org Úloha 1.1. Bubla, Lib nka, Henry a Mat j hráli hru. Protoºe byli ty i, napsali si na tabuli ty i ty ky a jejich úkolem pak bylo vepsat mezi n t i znaménka
e²ení 1. série Úvodní gulá² autor: Kolektiv org Úloha 1.1. Bubla, Lib nka, Henry a Mat j hráli hru. Protoºe byli ty i, napsali si na tabuli ty i ty ky a jejich úkolem pak bylo vepsat mezi n t i znaménka
Státní maturita 2010 Maturitní generálka 2010 Matematika: didaktický test - základní úrove obtíºnosti MAGZD10C0T01 e²ené p íklady
 Státní maturita 00 Maturitní generálka 00 Matematika: didaktický test - základní úrove obtíºnosti MAGZD0C0T0 e²ené p íklady Autor e²ení: Jitka Vachtová 6. b ezna 0 http://www.vachtova.cz/ Obsah Úloha Úloha.
Státní maturita 00 Maturitní generálka 00 Matematika: didaktický test - základní úrove obtíºnosti MAGZD0C0T0 e²ené p íklady Autor e²ení: Jitka Vachtová 6. b ezna 0 http://www.vachtova.cz/ Obsah Úloha Úloha.
PROUDĚNÍ V SEPARÁTORU S CYLINDRICKOU GEOMETRIÍ
 PROUDĚNÍ V SEPARÁTORU S CYLINDRICKOU GEOMETRIÍ Autoři: Ing. Zdeněk CHÁRA, CSc., Ústav pro hydrodynamiku AV ČR, v. v. i., e-mail: chara@ih.cas.cz Ing. Bohuš KYSELA, Ph.D., Ústav pro hydrodynamiku AV ČR,
PROUDĚNÍ V SEPARÁTORU S CYLINDRICKOU GEOMETRIÍ Autoři: Ing. Zdeněk CHÁRA, CSc., Ústav pro hydrodynamiku AV ČR, v. v. i., e-mail: chara@ih.cas.cz Ing. Bohuš KYSELA, Ph.D., Ústav pro hydrodynamiku AV ČR,
Jméno: P íjmení: Datum: 17. ledna 2018 Nechci zápo et p i hodnocení niº²ím neº (nezávazné): vadí mi vystavení mého hodnocení na internetu.
 Jméno: P íjmení: Datum: 7. ledna 28 Nechci zápo et p i hodnocení niº²ím neº (nezávazné): vadí mi vystavení mého hodnocení na internetu. Rotující nádoba Otev ená válcová nádoba napln ná do poloviny vý²ky
Jméno: P íjmení: Datum: 7. ledna 28 Nechci zápo et p i hodnocení niº²ím neº (nezávazné): vadí mi vystavení mého hodnocení na internetu. Rotující nádoba Otev ená válcová nádoba napln ná do poloviny vý²ky
Základní škola a mateřská škola, Ostrava-Hrabůvka, Mitušova 16, příspěvková organizace Školní vzdělávací program 2. stupeň, Matematika.
 Matematika Matematika pro žáky 6. až 9. ročníku napomáhá k rozvoji paměti, logického myšlení, kritickému usuzování a srozumitelné a věcné argumentaci prostřednictvím matematických problémů. Žáci si prostřednictvím
Matematika Matematika pro žáky 6. až 9. ročníku napomáhá k rozvoji paměti, logického myšlení, kritickému usuzování a srozumitelné a věcné argumentaci prostřednictvím matematických problémů. Žáci si prostřednictvím
Seminá e. Ing. Michal Valenta PhD. Databázové systémy BI-DBS ZS 2010/11, sem. 1-13
 Seminá e Ing. Michal Valenta PhD. Katedra softwarového inºenýrství Fakulta informa ních technologií ƒeské vysoké u ení technické v Praze c Michal Valenta, 2010 Databázové systémy BI-DBS ZS 2010/11, sem.
Seminá e Ing. Michal Valenta PhD. Katedra softwarového inºenýrství Fakulta informa ních technologií ƒeské vysoké u ení technické v Praze c Michal Valenta, 2010 Databázové systémy BI-DBS ZS 2010/11, sem.
Matematika. Charakteristika vyučovacího předmětu. Výchovné a vzdělávací strategie pro rozvíjení klíčových kompetencí žáků
 Vzdělávací obor: Matematika a její aplikace Matematika Obsahové, časové a organizační vymezení Charakteristika vyučovacího předmětu 1.-2. ročník 4 hodiny týdně 3.-5. ročník 5 hodin týdně Vzdělávací obsah
Vzdělávací obor: Matematika a její aplikace Matematika Obsahové, časové a organizační vymezení Charakteristika vyučovacího předmětu 1.-2. ročník 4 hodiny týdně 3.-5. ročník 5 hodin týdně Vzdělávací obsah
KINEMATICKÉ ELEMENTY K 5 PLASTOVÉ. doc. Ing. Martin Hynek, Ph.D. a kolektiv. verze - 1.0
 Katedra konstruování stroj Fakulta strojní K 5 PLASTOVÉ KINEMATICKÉ ELEMENTY doc. Ing. Martin Hynek, Ph.D. a kolektiv verze - 1.0 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpo
Katedra konstruování stroj Fakulta strojní K 5 PLASTOVÉ KINEMATICKÉ ELEMENTY doc. Ing. Martin Hynek, Ph.D. a kolektiv verze - 1.0 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpo
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 6. prosince 2016, 13:2015:20 ➊ (8 bod ) Vy²et ete stejnom rnou konvergenci ady na mnoºin R +. n=2 x n 1 1 4n 2 + x 2 ln 2 (n) ➋ (5 bod ) Detailn
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 6. prosince 2016, 13:2015:20 ➊ (8 bod ) Vy²et ete stejnom rnou konvergenci ady na mnoºin R +. n=2 x n 1 1 4n 2 + x 2 ln 2 (n) ➋ (5 bod ) Detailn
1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací.
 1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací. Skříň rozvodovky spojena s rámem zmenšení neodpružené hmoty. Přenos točivého momentu
1 NÁPRAVA De-Dion Představuje přechod mezi tuhou nápravou a nápravou výkyvnou. Používá se (výhradně) jako náprava hnací. Skříň rozvodovky spojena s rámem zmenšení neodpružené hmoty. Přenos točivého momentu
Ergodické Markovské et zce
 1. b ezen 2013 Denice 1.1 Markovský et zec nazveme ergodickým, jestliºe z libovolného stavu m ºeme p ejít do jakéhokoliv libovolného stavu (ne nutn v jednom kroku). Denice 1.2 Markovský et zec nazveme
1. b ezen 2013 Denice 1.1 Markovský et zec nazveme ergodickým, jestliºe z libovolného stavu m ºeme p ejít do jakéhokoliv libovolného stavu (ne nutn v jednom kroku). Denice 1.2 Markovský et zec nazveme
1. (18 bod ) Náhodná veli ina X je po et rub p i 400 nezávislých hodech mincí. a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost
 (8 bod ) Náhodná veli ina X je po et rub p i nezávislých hodech mincí a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost P ( X EX < ) (9 bod ) b) Formulujte centrální limitní v tu a pomocí ní vypo
(8 bod ) Náhodná veli ina X je po et rub p i nezávislých hodech mincí a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost P ( X EX < ) (9 bod ) b) Formulujte centrální limitní v tu a pomocí ní vypo
Průniky rotačních ploch
 Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Průniky rotačních ploch Vypracoval: Vojtěch Trnka Třída: 8. M Školní rok: 2012/2013 Seminář: Deskriptivní geometrie Prohlašuji, že jsem
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Průniky rotačních ploch Vypracoval: Vojtěch Trnka Třída: 8. M Školní rok: 2012/2013 Seminář: Deskriptivní geometrie Prohlašuji, že jsem
7. Stropní chlazení, Sálavé panely a pasy - 1. část
 Základy sálavého vytápění (2162063) 7. Stropní chlazení, Sálavé panely a pasy - 1. část 30. 3. 2016 Ing. Jindřich Boháč Obsah přednášek ZSV 1. Obecný úvod o sdílení tepla 2. Tepelná pohoda 3. Velkoplošné
Základy sálavého vytápění (2162063) 7. Stropní chlazení, Sálavé panely a pasy - 1. část 30. 3. 2016 Ing. Jindřich Boháč Obsah přednášek ZSV 1. Obecný úvod o sdílení tepla 2. Tepelná pohoda 3. Velkoplošné
Státní maturita 2011 Maturitní testy a zadání jaro 2011 Matematika: didaktický test - základní úrove obtíºnosti MAMZD11C0T02 e²ené p íklady
 Státní maturita 0 Maturitní testy a zadání jaro 0 Matematika: didaktický test - základní úrove obtíºnosti MAMZDC0T0 e²ené p íklady Autor e²ení: Jitka Vachtová 0. srpna 0 http://www.vachtova.cz/ Obsah Úloha
Státní maturita 0 Maturitní testy a zadání jaro 0 Matematika: didaktický test - základní úrove obtíºnosti MAMZDC0T0 e²ené p íklady Autor e²ení: Jitka Vachtová 0. srpna 0 http://www.vachtova.cz/ Obsah Úloha
Výroba ozubených kol. Použití ozubených kol. Převody ozubenými koly a tvary ozubených kol
 Výroba ozubených kol Použití ozubených kol Ozubenými koly se přenášejí otáčivé pohyby a kroutící momenty. Přenos je zde nucený, protože zuby a zubní mezery do sebe zabírají. Kola mohou mít vnější nebo
Výroba ozubených kol Použití ozubených kol Ozubenými koly se přenášejí otáčivé pohyby a kroutící momenty. Přenos je zde nucený, protože zuby a zubní mezery do sebe zabírají. Kola mohou mít vnější nebo
Číslicová technika 3 učební texty (SPŠ Zlín) str.: - 1 -
 Číslicová technika učební texty (SPŠ Zlín) str.: - -.. ČÍTAČE Mnohá logická rozhodnutí jsou založena na vyhodnocení počtu opakujících se jevů. Takovými jevy jsou např. rychlost otáčení nebo cykly stroje,
Číslicová technika učební texty (SPŠ Zlín) str.: - -.. ČÍTAČE Mnohá logická rozhodnutí jsou založena na vyhodnocení počtu opakujících se jevů. Takovými jevy jsou např. rychlost otáčení nebo cykly stroje,
Symetrie molekul a stereochemie
 Symetrie molekul a stereochemie Symetrie molekul a stereochemie Symetrie molekul Operace symetrie Bodové grupy symetrie Optická aktivita Stereochemie izomerie Symetrie Prvky a operace symetrie výchozí
Symetrie molekul a stereochemie Symetrie molekul a stereochemie Symetrie molekul Operace symetrie Bodové grupy symetrie Optická aktivita Stereochemie izomerie Symetrie Prvky a operace symetrie výchozí
TVAROVÉ A ROZMĚROVÉ PARAMETRY V OBRAZOVÉ DOKUMENTACI. Druhy kót Části kót Hlavní zásady kótování Odkazová čára Soustavy kót
 TVAROVÉ A ROZMĚROVÉ PARAMETRY V OBRAZOVÉ DOKUMENTACI Druhy kót Části kót Hlavní zásady kótování Odkazová čára Soustavy kót KÓTOVÁNÍ Kótování jednoznačné určení rozměrů a umístění všech tvarových podrobností
TVAROVÉ A ROZMĚROVÉ PARAMETRY V OBRAZOVÉ DOKUMENTACI Druhy kót Části kót Hlavní zásady kótování Odkazová čára Soustavy kót KÓTOVÁNÍ Kótování jednoznačné určení rozměrů a umístění všech tvarových podrobností
1 Data. 2 Výsledky m ení velikostí. Statistika velikostí výtrus. Roman Ma ák
 Statistika velikostí výtrus Roman Ma ák 6.2.216 1 Data Velikost výtrus (udávaná obvykle v µm) pat í u hub k významným ur ovacím znak m, mnohdy se dva druhy makromycet li²í dokonce pouze touto veli inou.
Statistika velikostí výtrus Roman Ma ák 6.2.216 1 Data Velikost výtrus (udávaná obvykle v µm) pat í u hub k významným ur ovacím znak m, mnohdy se dva druhy makromycet li²í dokonce pouze touto veli inou.
Kelvin v kapkový generátor
 Kelvin v kapkový generátor Kry²tof Kadlec 1, Luká² Kune² 2, Luká² N me ek 3 1 Gymnázium Franti²ka Palackého, Vala²ské Mezi í í, krystoof.2@seznam.cz 2 Gymnázium, Zlatá stezka 137, Prachatice, kunamars@seznam.cz
Kelvin v kapkový generátor Kry²tof Kadlec 1, Luká² Kune² 2, Luká² N me ek 3 1 Gymnázium Franti²ka Palackého, Vala²ské Mezi í í, krystoof.2@seznam.cz 2 Gymnázium, Zlatá stezka 137, Prachatice, kunamars@seznam.cz
Teorie kategorií. Libor B hounek Verze ke dni 12. b ezna 2013.
 Teorie kategorií Studijní materiál pro kurs ALGV00051 na FF UK v LS 2012/13 Dal²í informace: www.cs.cas.cz/behounek/teaching/cat12 Libor B hounek behounek@cs.cas.cz Verze ke dni 12. b ezna 2013. Organiza
Teorie kategorií Studijní materiál pro kurs ALGV00051 na FF UK v LS 2012/13 Dal²í informace: www.cs.cas.cz/behounek/teaching/cat12 Libor B hounek behounek@cs.cas.cz Verze ke dni 12. b ezna 2013. Organiza
Zvyšování kvality výuky technických oborů
 Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.5 Karosářské Know how (Vědět jak) Kapitola
Zvyšování kvality výuky technických oborů Klíčová aktivita V.2 Inovace a zkvalitnění výuky směřující k rozvoji odborných kompetencí žáků středních škol Téma V.2.5 Karosářské Know how (Vědět jak) Kapitola
p írodní zdroje energie a surovin odpady globální problémy ochrana p írody a krajiny nástroje spole nosti na ochranu životního
 charakterizuje p sobení životního prost edí na lov ka a jeho zdraví; charakterizuje p írodní zdroje surovin a energie z hlediska jejich obnovitelnosti, posoudí vliv jejich využívání na prost edí; popíše
charakterizuje p sobení životního prost edí na lov ka a jeho zdraví; charakterizuje p írodní zdroje surovin a energie z hlediska jejich obnovitelnosti, posoudí vliv jejich využívání na prost edí; popíše
ROČNÍKOVÁ PRÁCE TEORETICKÉ ŘEŠENÍ STŘECH
 ROČNÍKOVÁ PRÁCE TEORETICKÉ ŘEŠENÍ STŘECH Vypracoval: Jan Vojtíšek Třída: 8.M Školní rok: 2011/2012 Seminář: Aplikace Deskriptivní geometrie Prohlašuji, že jsem svou ročníkovou práci napsal samostatně a
ROČNÍKOVÁ PRÁCE TEORETICKÉ ŘEŠENÍ STŘECH Vypracoval: Jan Vojtíšek Třída: 8.M Školní rok: 2011/2012 Seminář: Aplikace Deskriptivní geometrie Prohlašuji, že jsem svou ročníkovou práci napsal samostatně a
Relace. Základní pojmy.
 Relace. Základní pojmy. I kdyº pojem funkce je v matematice jeden ze základních a nejd leºit j²ích, p esto se n které vztahy mezi objekty pomocí funkce popsat nedají. Jde o situace, kdybychom cht li p
Relace. Základní pojmy. I kdyº pojem funkce je v matematice jeden ze základních a nejd leºit j²ích, p esto se n které vztahy mezi objekty pomocí funkce popsat nedají. Jde o situace, kdybychom cht li p
Symetrie molekul a stereochemie
 Symetrie molekul a stereochemie Symetrie molekul a stereochemie l Symetrie molekul Operace symetrie Bodové grupy symetrie l Optická aktivita l Stereochemie izomerie Symetrie l výchozí bod rovnovážná konfigurace
Symetrie molekul a stereochemie Symetrie molekul a stereochemie l Symetrie molekul Operace symetrie Bodové grupy symetrie l Optická aktivita l Stereochemie izomerie Symetrie l výchozí bod rovnovážná konfigurace
Výuka matematiky v 21. století na S technického typu Metodika - bude upravena po dokon ení testování modul v p ímé výuce
 Výuka matematiky v 21. století na S technického typu Metodika - bude upravena po dokon ení testování modul v p ímé výuce ƒeské Bud jovice, 2014 Obsah 1 Popis problematiky 2 1.1 Úvod..................................
Výuka matematiky v 21. století na S technického typu Metodika - bude upravena po dokon ení testování modul v p ímé výuce ƒeské Bud jovice, 2014 Obsah 1 Popis problematiky 2 1.1 Úvod..................................
Konstruk ní geometrie
 Pomocný text Konstruk ní geometrie Drazí e²itelé, V tomto povídání se, jak název napovídá, podíváme na základní konstruk ní pojmy a zkusíme si vy e²it pár jednoduchých úloh. Eukleidovské konstrukce Kdyº
Pomocný text Konstruk ní geometrie Drazí e²itelé, V tomto povídání se, jak název napovídá, podíváme na základní konstruk ní pojmy a zkusíme si vy e²it pár jednoduchých úloh. Eukleidovské konstrukce Kdyº
Bod, přímka a rovina. bezrozměrnost, jeden rozměr a dva rozměry
 Úvod Posvátná geometrie mapuje rozkrývání významu čísel v prostoru. Základní trasa vede z izolovaného bodu do přímky, následuje rozprostření do roviny, poté do třetího rozměru, ba až za jeho hranice, a
Úvod Posvátná geometrie mapuje rozkrývání významu čísel v prostoru. Základní trasa vede z izolovaného bodu do přímky, následuje rozprostření do roviny, poté do třetího rozměru, ba až za jeho hranice, a
Prezentace. Ing. Petr V elák 6. b ezna 2009
 Prezentace Ing. Petr V elák 6. b ezna 2009 1 OBSAH OBSAH Obsah 1 Úvodní slovo 3 2 P íprava prezentace 4 2.1 Jak prezentace ned lat........................ 4 2.1.1 Kontrast písma a pozadí...................
Prezentace Ing. Petr V elák 6. b ezna 2009 1 OBSAH OBSAH Obsah 1 Úvodní slovo 3 2 P íprava prezentace 4 2.1 Jak prezentace ned lat........................ 4 2.1.1 Kontrast písma a pozadí...................
Co je to tensor... Vektorový prostor
 Vektorový prostor Co je to tensor... Tato ást je tu jen pro p ipomenutí, pokud nevíte co je to vektorový prostor, tak tení tohoto textu ukon ete na konci této v ty, neb zbytek textu by pro Vás nebyl ni
Vektorový prostor Co je to tensor... Tato ást je tu jen pro p ipomenutí, pokud nevíte co je to vektorový prostor, tak tení tohoto textu ukon ete na konci této v ty, neb zbytek textu by pro Vás nebyl ni
brmiversity: Um lá inteligence a teoretická informatika
 brmiversity: Um lá inteligence a teoretická informatika P edná²ka. 6 Petr Baudi² pasky@ucw.cz brmlab 2011 Outline 1 Pravd podobnost 2 Um lá inteligence 3 Sloºitost 4 Datové struktury Pravd podobnost Pravd
brmiversity: Um lá inteligence a teoretická informatika P edná²ka. 6 Petr Baudi² pasky@ucw.cz brmlab 2011 Outline 1 Pravd podobnost 2 Um lá inteligence 3 Sloºitost 4 Datové struktury Pravd podobnost Pravd
6. Matice. Algebraické vlastnosti
 Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA I, zimní semestr 2000/2001 Michal Marvan 6 Matice Algebraické vlastnosti 1 Algebraické operace s maticemi Definice Bud te A,
Matematický ústav Slezské univerzity v Opavě Učební texty k přednášce ALGEBRA I, zimní semestr 2000/2001 Michal Marvan 6 Matice Algebraické vlastnosti 1 Algebraické operace s maticemi Definice Bud te A,
Učební osnovy Vzdělávací oblast: Matematika a její aplikace Vzdělávací obor: Volitelný předmět Matematický seminář ročník 8.
 Učební osnovy Vzdělávací oblast: Matematika a její aplikace Vzdělávací obor: Volitelný předmět Matematický seminář ročník 8. Výuka matematického semináře bude probíhat jednou týdně v dvouhodinovém bloku.
Učební osnovy Vzdělávací oblast: Matematika a její aplikace Vzdělávací obor: Volitelný předmět Matematický seminář ročník 8. Výuka matematického semináře bude probíhat jednou týdně v dvouhodinovém bloku.
ROBOTIKA. univerzální Rozdělení manipulačních zařízení podle způsobu řízení: jednoúčelové manipulátory
 ROBOTIKA je obor zabývající se teorií, konstrukcí a využitím robotů slovo robot bylo poprvé použito v roce 1920 ve hře Karla Čapka R.U.R (Rossum s Universal Robots pro umělou bytost) Robot je stroj, který
ROBOTIKA je obor zabývající se teorií, konstrukcí a využitím robotů slovo robot bylo poprvé použito v roce 1920 ve hře Karla Čapka R.U.R (Rossum s Universal Robots pro umělou bytost) Robot je stroj, který
Národní park umava. 9. kv tna Hnutí Duha
 Národní park umava 9. kv tna 2011 Hnutí Duha Hlavní cíle a metodika Hlavní cíle et ení Cílem výzkumu Factum Invenio bylo zjistit, jak ob ané R vnímají problematiku hypotetické výstavby lanovek a sjezdovek
Národní park umava 9. kv tna 2011 Hnutí Duha Hlavní cíle a metodika Hlavní cíle et ení Cílem výzkumu Factum Invenio bylo zjistit, jak ob ané R vnímají problematiku hypotetické výstavby lanovek a sjezdovek
NÁVRHOVÝ PROGRAM VÝMĚNÍKŮ TEPLA FIRMY SECESPOL CAIRO 3.5.5 PŘÍRUČKA UŽIVATELE
 NÁVRHOVÝ PROGRAM VÝMĚNÍKŮ TEPLA FIRMY SECESPOL CAIRO 3.5.5 PŘÍRUČKA UŽIVATELE 1. Přehled možností programu 1.1. Hlavní okno Hlavní okno programu se skládá ze čtyř karet : Projekt, Zadání, Výsledky a Návrhový
NÁVRHOVÝ PROGRAM VÝMĚNÍKŮ TEPLA FIRMY SECESPOL CAIRO 3.5.5 PŘÍRUČKA UŽIVATELE 1. Přehled možností programu 1.1. Hlavní okno Hlavní okno programu se skládá ze čtyř karet : Projekt, Zadání, Výsledky a Návrhový
Dynamika tuhých těles
 Dynamika tuhých těles V reálných technických aplikacích lze model bodového tělesa použít jen v omezené míře. Mnohem častější je použití modelu tuhého tělesa. Tuhé těleso je definováno jako těleso, u něhož
Dynamika tuhých těles V reálných technických aplikacích lze model bodového tělesa použít jen v omezené míře. Mnohem častější je použití modelu tuhého tělesa. Tuhé těleso je definováno jako těleso, u něhož
Zkou²ková písemná práce. 1 z p edm tu 01MAB4
 Zkou²ková písemná práce. 1 z p edm tu 01MAB4 25/05/2017, 9:00 11:00 ➊ (9 bod ) Nech je dvojrozm rná Lebesgueova míra generována vytvo ujícími funkcemi φ(x) = Θ(x)x 2 a ψ(y) = 7y. Vypo t te míru mnoºiny
Zkou²ková písemná práce. 1 z p edm tu 01MAB4 25/05/2017, 9:00 11:00 ➊ (9 bod ) Nech je dvojrozm rná Lebesgueova míra generována vytvo ujícími funkcemi φ(x) = Θ(x)x 2 a ψ(y) = 7y. Vypo t te míru mnoºiny
Výukový materiál zpracovaný v rámci projektu Výuka modern
 St ední pr myslová škola strojnická Olomouc, t. 17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka modern Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 P írodov dné
St ední pr myslová škola strojnická Olomouc, t. 17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka modern Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 P írodov dné
