GeoGebra stručný průvodce kurzem
|
|
|
- Anna Šimková
- před 8 lety
- Počet zobrazení:
Transkript
1 Beznákladové ICT pro učitele Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Úvod GeoGebra je program v oblasti dynamické geometrie (DGS), který v sobě zahrnuje i některé prvky počítačové algebry (CAS Computer Algebra System). Je průběžně lokalizován do mnoha jazyků včetně češtiny. Je přehledný, má velmi intuitivní ovládání a rychle se vyvíjí na webu ( se objevují stále nové verze (anglické, česká lokalizace se zpožděním). Program je volně dostupný pro nekomerční použití viz licenční podmínky uvedené v prostředí programu. Návody jsou přístupné na adrese Prostředí S vytvářenými objekty se dá pracovat v Grafickém okně (nákresně) nebo v okně nazývaném Algebra. Lze také spolupracovat s Tabulkou (tabulkové zobrazení a zadání dat). Příkazy je možné (kromě nástrojů v menu Grafického okna) také zadávat pomocí Příkazového řádku (vstupního pole) a přidružených pomocných polí v dolní části okna. Kterýkoliv způsob zobrazení (kromě grafického) můžeme skrýt. Nákresnu (Grafické okno) lze posouvat myší (spolu s klávesou Ctrl nebo Shift) a přibližovat/vzdalovat ji kolečkem na myši. Základní nastavení vzhledu objektů Grafického okna je ovlivněno volbami položek sady Nastavení z hlavní nabídky resp. panelu Nákresna v kontextovém menu Grafického okna. Hlavní panel nástrojů Grafické okno (nákresna) Popis nástroje/nápověda Okno Algebra Tabulka Příkazový řádek (vstupní pole) Přidružená pomocná pole V režimu výběru objektů je každý vybraný prvek zvýrazněn a to jak v grafickém, tak i v algebraickém okně. Práce v okně Algebry je mnohdy pohodlnější (např. skrývání / zobrazování objektů) než v Grafickém okně. Program podporuje ve stejné míře syntetický i algebraický přístup ke geometrickým objektům a navíc umožňuje vyhodnocování výrazů a některé algebraické úpravy, kalkulus, částečně práci s posloupnostmi a vektorový počet. 1
2 V okně Algebry je v každém okamžiku zřetelné rozdělení objektů na volné a závislé. Volné i závislé objekty je možno v jejich okně Vlastnosti (viz kontextové menu pravé tlačítko myši) předefinovat (rovněž pomocí dblciick). Lze také označit některé objekty jako pomocné. Pomocí zmíněného okna Vlastnosti lze nastavovat vlastnosti nejen pro vybraný objekt, ale pro celé třídy objektů současně (body, přímky). Způsob zobrazení v okně Algebry se dá měnit (kartézské polární souřadnice apod.) Pokud vytváříme nové objekty pomocí Příkazové řádky, klávesa F11 vyvolá nápovědu ke zvolenému příkazu. Nápověda obsahuje údaje o parametrech příkazu. Okno Tabulky poskytuje funkce obvyklé v tabulkových kalkulátorech. Navíc v jeho buňkách mohou být nejen čísla, ale libovolné objekty GeoGebry. Na obsah libovolné buňky tabulky se lze odvolávat (pomocí její adresy) nejen ve vzorcích tabulky, ale i ve výrazech zadávaných do příkazového řádku. GeoGebra dále poskytuje možnost zobrazit zápis konstrukce, vyznačit v něm tzv. body zastavení a pomocí něho konstrukci krokovat (přehrávat). Model s popisem konstrukce je možno exportovat jako html stránku, podobně jako samotný model. Vlastní model GeoGebry lze exportovat jako html stránku nejen s nastavením popisu a informativních údajů, ale zejména s volbou přístupu uživatele. Je možné nechat uživateli volný přístup k modelu, takže do něho může vkládat vlastní konstrukce. GeoGebra umožňuje také export obrázků v několika formátech a obsahuje podporu tisku obsahu grafického okna (v českém prostředí je tato volba skryta pod označením Náhled). Součástí standardní nabídky GeoGebry je možnost tvorby makrokonstrukcí tj. nových vlastních příkazů a možnost úpravy panelu nástrojů. Ovládání Výběr a kreslení myší, pohyb tažením či kurzorovými klávesami. Pokud po výběru objektu začneme psát na klávesnici, objekt se přejmenuje. Je možný výběr několika objektů: Shift, Ctrl nebo obdélníkový výběr myší v nákresně. Při pohybování pomocí kurzorových kláves: Shift zjemňuje krok, Ctrl krok zvětšuje. Chceme-li v manipulačním režimu posunout myší nákresnu, stiskneme klávesu Shift nebo Ctrl => nebudeme posouvat vybraným objektem ale celou nákresnou. Pro mazání funguje klávesa Delete nebo příkaz z kontextového menu. Grafický vstup Grafické okno umožňuje zobrazit objekty konstrukce zvoleným způsobem a se zvoleným popisem. Popis objektu nemusí být totožný s jeho (jednoznačným) názvem a může obsahovat i zobrazení hodnoty. Pomocí nástrojů umístěných v Hlavním panelu nástrojů zadáváme v grafickém okně prvky geometrických konstrukcí. K dispozici jsou následující sady nástrojů: Manipulace Bod Přímky, úsečky a vektory Konstrukce přímek Mnohoúhelníky Kružnice a oblouky Kuželosečky Měření a úhly Zobrazení Čísla a texty Servisní nástroje pro zobrazování 2
3 Manipulace Ukazovátko (výběr) také klávesa Esc Otočení kolem bodu Záznam dat do tabulky Bod Nový bod Průsečík Střed (dvojice bodů nebo úsečky) Přímky, úsečky a vektory Přímka daná dvěma body Úsečka daná dvěma body Úsečka dané délky z bodu (umožňuje otáčet koncový bod) Polopřímka určená dvěma body Vektor daný dvěma body Vektor z bodu Konstrukce přímek Kolmice Rovnoběžka Osa úsečky Osa úhlu Tečny z bodu (ke kuželosečce či grafu f-ce v jejím bodě, také tečny daného směru) Polára (bodu vzhledem ke kuželosečce či sdružený průměr) Lineární regrese Kružnice a oblouky Množina bodů (nedává analytické vyjádření, nezobrazuje se v okně Algebra) Kružnice (střed a bod) Kružnice (střed a poloměr) Kružítko Kružnice daná třemi body Polokružnice (nad průměrem) Oblouk daný středem a dvěma body Oblouk daný třemi body Kruhová výseč (střed a dva body) Mnohoúhelníky Obecný mnohoúhelník (není zvláštní nástroj pro trojúhelník) Pravidelný mnohoúhelník Kruhová výseč (tři body) 3
4 Kuželosečky Elipsa (ohniska a bod) Hyperbola (ohniska a bod) Parabola (ohnisko a řídicí přímka) Kuželosečka (daná pěti body) Měření a úhly Úhel (měří se proti směru hod. ručiček; v n-úhelníku se vyznačí všechny jeho úhly) Úhel dané velikosti (nanesení úhlu) Vzdálenost (dvou bodů, délka úsečky) Obsah (u n-úhelníků se obsah zobrazí také přímo v okně Algebra) Spád (sklon, směrnice přímky) Zobrazení Osová souměrnost Středová souměrnost Kruhová inverze (zobrazuje pouze body) Otočení Posunutí Stejnolehlost Čísla a texty Posuvník (tvorba a ovládání animací) Zaškrtávací políčko (zobrazení / skrytí skupiny vybraných objektů) Text (statický / dynamický text) Obrázek (umožní vložení obrázku) Vztah mezi objekty (zobrazí informativní textové pole, pouhý popis) Servisní nástroje pro zobrazování Posunout nákresnu (také přímo Shift či Ctrl + tažení myší) Zvětšit } obojího dosáhneme rychleji rolováním kolečka na myši; návrat k výchozímu nastavení přes kontextové menu > Standardní náhled Zmenšit Ukázat / skrýt objekt (více objektů) Ukázat / skrýt popis (více popisů) Kopírovat formát (vybereme vzorový objekt a následně všechny objekty, které mají tento formát převzít) Zrušit objekt (také klávesa Delete) 4
5 Poznámka k sadě Zobrazení: Uvedené nástroje lze zadávat i přes příkazovou řádku zápisem příslušného příkazu se všemi jeho parametry zapsanými do hranatých závorek, oddělenými čárkami. Při zápisu příkazu nutno respektovat jazykovou verzi: např. v českém prostředí Primka[A,B] zatímco ve verzi anglické Line[A,B]. Při změně nastavení jazyka se příkazy automaticky přeloží. Poznámka k sadě Čísla a texty: Posuvník obsahuje volby mezí a kroku. Posuvník se objeví v Grafickém okně automaticky také při zadání číselné proměnné pomocí Příkazového řádku následně je třeba zobrazenou číselnou hodnotu v okně Algebra nechat zviditelnit v Grafickém okně. Text statický text (řetězec) se uvádí v uvozovkách, názvy proměnných a výrazy vně uvozovek se nahrazují vyčíslenou hodnotou; části se spojují znakem +. Vzorce lze zadávat také v syntaxi. Příkazová řádka dovoluje vkládat další příkazy, které nelze zadávat v grafickém prostředí. Je to nástroj, kterým se GeoGebra přibližuje systémům CAS a není obsažen v jiných geometrických náčrtnících (Cabri, Geonext). Přikazů je velké množství podporují (a přesahují) celé středoškolské téma Funkce, Analytická geometrie a Diferenciální a integrální počet. Zadáváme-li do příkazové řádky funkci nebo logickou operaci, můžeme ji také vybrat z pomocné rozbalovací nabídky vpravo od příkazového řádku nebo alternativně zapsat pomocí klávesnice. Zápis z klávesnice odpovídá syntaxi např. JavaScriptu. Relace kolmost a rovnoběžnost je nutno zadat výběrem z pomocné nabídky. Zadání komplexního čísla např. (1 + i) * (1 i), (1 + i) / (1 i) apod. Matice se zadává po řádcích: {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}} má první řádek a první sloupec Matice lze sčítat, odčítat, násobit, transponovat, invertovat, počítat determinant. Přímý vstup Kromě zadávání předdefinovaných příkazů je možné použít příkazovou řádku pro přímý vstup zadání některých objektů. Pak je nutné respektovat několik syntaktických pravidel: Názvy příkazů zapisujeme bez diakritiky přesně tak, jak jsou uvedeny v seznamu. Zadání ukončíme klávesou Enter. Desetinná čísla se zadávají s desetinnou tečkou. Ve výrazech lze používat konstantu pi, e pouze tehdy, nejmenuje-li se již tak nějaká použitá proměnná. Obě konstanty se dají vyvolat z pomocného výběrového okna. Znak násobení * lze nahradit mezerou. Zadání bodu: A = (1.2, 4) kartézské souřadnice, B = (1; 45 ) polární souřadnice; zadání komplexního čísla: C = 2 + i ; zadání vektoru: a = (1.1, 7) jako bod, ale malým písmenem. Zadání funkce: f(x) = abs(x 1) nebo f: y = abs(x 1) (píšeme s rovnítkem). Pokud funkci nepojmenujeme, pojmenuje ji systém sám. Zadání obecné rovnice přímky a kuželosečky: h: x^2 + y^2 = 4 (uvozuje se dvojtečkou). Zadání (parametrické) přímky: napřed musíme definovat proměnnou, která bude parametrem a pak lze definovat např. p: M = ( 2, 0) + t (1, 2). Historie a použití existujících objektů Příkazy dříve zadané do příkazového řádku lze vyvolat a opětovně vložit kurzorovými klávesami. Chceme-li do aktuálně vkládaného příkazu vložit po řadě Název, Hodnotu nebo Definici existujícího objektu, označíme ho a požadované vložíme po řadě klávesami F5, F4, F3. 5
6 Příkazy dostupné z příkazové řádky Popis uvedených příkazů, jejich parametry a výstupní hodnotu lze najít v nápovědě (Index). Některé jsou intuitivní, mnohé jsou zřejmým přepisem příkazů volitelných v Grafickém okně. Následuje aktuální seznam pro českou lokalizaci programu. Asymptota BinomickyKoeficient Bod CelociselnyPodil CountIf DeliciPomer Delka DelkaHlavniOsy DelkaVedlejsiOsy Derivace Determinant DolniSoucet Dvojpomer Elipsa Excentricita Extrem FormulaText Funkce GCD Graf Histogram HlavniOsa HorniSoucet Hyperbola InflexniBod Integral InverseNormal Invert Iterace JeCelociselne JeDefinovan JednotkovyVektor JednotkovyNormVektor Jmeno Kdyz Kolmice KonstrukcniKrok KorelacniKoeficient Kovariance Krivka Krivost KrokNaOseX KrokNaOseY KruhOblouk3Body KruhObloukUhlu Kruhová VysecDanaUhlem KruhVysecDanaObloukem Kruznice Kuzelosečka LCM Maximum Mnohoclen Mnohouhelník MnozinaBodu Mod Modus NahodneBinomialne NahodneMezi NahodneNormalne NahodnePoissonovo NazevSloupce NechejJestli NormalniRozdeleni NormalovyVektor NuloveBody ObdelnikovyDiagram Objekt OblastBunek Oblouk Obratit Obsah Obvod OcIstranitNedefinovane Ohnisko OsaUhlu OsaUsecky OskulacniKruznice Osy Parabola Parametr Polara Polokruznice Polomer Poloprimka Posledni Posloupnost Posun Primka Pripojit Prumer PrumetX Prumety Prunik Prusecik Prvek Prvni Q1 Q3 Radek Regrese RegreseExponencialni RegreseLogaritmicka RegreseLogisticka RegreseMocninna RegresePolynomicka RegreseSin RegreseX RidiciPrimka RohovyBod Rotace Rozklad Rozsirit SeznamIterace SigmaXX SigmaXY SigmaYY Sjednoceni Sloupec Smazat Smernice SmerovyVektor Soucin Soumernost Spoj StandardniOdchylka Stejnolehlost Střed StredSoumernosti Suma Sxx Sxy Syy TaylorovaRada Tecna Text TextNaUnicode TextovaTabulka Teziste Transponuj TrapezodialSum Tridit Uhel UnicodeNaText UnicodeNaZnak Usecka Variance VedlejsiOsa Vektor VektorKrivosti Vlozit Vrchol Vyber Vysec Vzdalenost Vztah Zjednodusit ZlomekText ZnakNaUnicode Poznámka k příkazům: GCD = Greatest Common Divisor (or Denominator) = největší společný dělitel LCM = Least (or Lowest) Common Multiple = nejmenší společný násobek Q1, Q3 = 1. kvadrant, 3. kvadrant 6
7 Logické operace Pokud zadáváme do příkazového řádku logickou operaci, můžeme příslušný operátor vybrat z pomocného rozbalovacího menu pole voleb a nebo alternativně zapsat pomocí klávesnice (zápis z klávesnice je podobný syntaxi např. JavaScriptu). Relace kolmost a rovnoběžnost je nutno zadat výběrem z pomocné nabídky. Podporované funkce a operace +,, *, /,! (faktoriál), závorky ( ) *, mezera... skalární součin ^... mocnina x( ), y( )... x-souřadnice, y-souřadnice abs( )... absolutní hodnota sgn( )... signum x, znaménko x sqrt( )... druhá odmocnina cbrt( )... třetí odmocnina random( )... náhodné číslo v intervalu 0, 1) exp( ), e^x... exponenciální funkce ln( ), log( )... přirozený logaritmus ld( )... logaritmus o základu 2 lg( )... dekadický logaritmus round( )... zaokrouhlení sin( )... sinus cos( )... kosinus tan( )... tangens asin( )... arkus sinus acos( )... arkus kosinus atan( )... arkus tangens sinh( )... hyperbolický sinus cosh( )... hyperbolický kosinus tanh( )... hyperbolický tangens asinh( )... antihyperbolický sinus acosh( )... antihyperbolický kosinus atanh( )... antihyperbolický tangens floor( )... největší celé číslo menší n. rovné danému ceil( )... nejmenší celé číslo větší n. rovné danému Užitečné klávesové zkratky Alt + písmeno Písmena řecké abecedy (např. Alt + a... a) Alt + Shift + písmeno Velká řecká pímena (např. Alt + Shift + D... D) Alt + 2, Alt + 3 Exponent 2, exponent 3 (a další číselné exponenty) Ctrl + Alt + C Kopie hodnoty (nikoliv vzorce) Alt + + Plus-minus (±) Alt + Minus-plus ( ) Alt + = Nerovná se ( ) Alt + < Menší nebo rovno Alt + > Větší nebo rovno Ctrl + L Výběr celé vrstvy F2 Editovat objekt F3 Vložit definici objektu F4 Vložit hodnotu objektu F5 Vložit název objektu F9 Přepočítat (random) Enter Přepnutí mezi Grafickým oknem a Vstupním polem Esc Přechod do režimu výběru Shift nebo Ctrl + myš Posun nákresny Kurzorové šipky Pohyb v zápisu konstrukce, v historii Vstupního pole, zvýšení/snížení hodnoty posuvníku Ctrl + kurzorové šipky 10 zvýší rychlost pohybu Alt + kurzorové šipky 100 zvýší rychlost pohybu Zpracováno podle předlohy GeoGebra přehled a stručný tahák, Šárka Gergelitsová, Škola učitelů informatiky Lipnice nad Sázavou, srpen
GeoGebra rychlý start
 Beznákladové ICT pro učitele Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. velmi stručná příručka k programu GeoGebra GeoGebra je svobodný výukový matematický
Beznákladové ICT pro učitele Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. velmi stručná příručka k programu GeoGebra GeoGebra je svobodný výukový matematický
Maturitní okruhy z matematiky - školní rok 2007/2008
 Maturitní okruhy z matematiky - školní rok 2007/2008 1. Některé základní poznatky z elementární matematiky: Číselné obory, dělitelnost přirozených čísel, prvočísla a čísla složená, největší společný dělitel,
Maturitní okruhy z matematiky - školní rok 2007/2008 1. Některé základní poznatky z elementární matematiky: Číselné obory, dělitelnost přirozených čísel, prvočísla a čísla složená, největší společný dělitel,
MODAM Mgr. Zuzana Morávková, Ph.D.
 GeoGebra známá i neznámá (začátečníci) MODAM 2015 Mgr. Zuzana Morávková, Ph.D. MODAM 2015 GeoGebra známá i neznámá (začátečníci) Příklad 1: Kružnice opsaná trojúhelníku Zadání: Vytvořte aplikaci na sestrojení
GeoGebra známá i neznámá (začátečníci) MODAM 2015 Mgr. Zuzana Morávková, Ph.D. MODAM 2015 GeoGebra známá i neznámá (začátečníci) Příklad 1: Kružnice opsaná trojúhelníku Zadání: Vytvořte aplikaci na sestrojení
Maturitní otázky z předmětu MATEMATIKA
 Wichterlovo gymnázium, Ostrava-Poruba, příspěvková organizace Maturitní otázky z předmětu MATEMATIKA 1. Výrazy a jejich úpravy vzorce (a+b)2,(a+b)3,a2-b2,a3+b3, dělení mnohočlenů, mocniny, odmocniny, vlastnosti
Wichterlovo gymnázium, Ostrava-Poruba, příspěvková organizace Maturitní otázky z předmětu MATEMATIKA 1. Výrazy a jejich úpravy vzorce (a+b)2,(a+b)3,a2-b2,a3+b3, dělení mnohočlenů, mocniny, odmocniny, vlastnosti
Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014. 1. Obor reálných čísel
 Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014 1. Obor reálných čísel - obor přirozených, celých, racionálních a reálných čísel - vlastnosti operací (sčítání, odčítání, násobení, dělení) -
Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014 1. Obor reálných čísel - obor přirozených, celých, racionálních a reálných čísel - vlastnosti operací (sčítání, odčítání, násobení, dělení) -
GeoGebra známá i neznámá (pokročilí)
 GeoGebra známá i neznámá (pokročilí) MODAM 2017 Mgr. Zuzana Morávková, Ph.D. MODAM 2017 GeoGebra známá i neznámá (pokročilí) Příklad 1: Cykloida Zadání: Kotálením kružnice vytvoříme cykloidu. 3. 2. 1.
GeoGebra známá i neznámá (pokročilí) MODAM 2017 Mgr. Zuzana Morávková, Ph.D. MODAM 2017 GeoGebra známá i neznámá (pokročilí) Příklad 1: Cykloida Zadání: Kotálením kružnice vytvoříme cykloidu. 3. 2. 1.
MATURITNÍ TÉMATA Z MATEMATIKY
 MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
Gymnázium Česká a Olympijských nadějí, České Budějovice, Česká 64, 37021
 Maturitní témata MATEMATIKA 1. Funkce a jejich základní vlastnosti. Definice funkce, def. obor a obor hodnot funkce, funkce sudá, lichá, monotónnost funkce, funkce omezená, lokální a globální extrémy funkce,
Maturitní témata MATEMATIKA 1. Funkce a jejich základní vlastnosti. Definice funkce, def. obor a obor hodnot funkce, funkce sudá, lichá, monotónnost funkce, funkce omezená, lokální a globální extrémy funkce,
Maturitní témata od 2013
 1 Maturitní témata od 2013 1. Úvod do matematické logiky 2. Množiny a operace s nimi, číselné obory 3. Algebraické výrazy, výrazy s mocninami a odmocninami 4. Lineární rovnice a nerovnice a jejich soustavy
1 Maturitní témata od 2013 1. Úvod do matematické logiky 2. Množiny a operace s nimi, číselné obory 3. Algebraické výrazy, výrazy s mocninami a odmocninami 4. Lineární rovnice a nerovnice a jejich soustavy
MATEMATIKA STUDIJNÍ POŽADAVKY PRO JEDNOTLIVÉ ROČNÍKY STUDIA
 MATEMATIKA STUDIJNÍ POŽADAVKY PRO JEDNOTLIVÉ ROČNÍKY STUDIA Osmileté studium 1. ročník 1. Opakování a prohloubení učiva 1. 5. ročníku Číslo, číslice, množiny, přirozená čísla, desetinná čísla, číselné
MATEMATIKA STUDIJNÍ POŽADAVKY PRO JEDNOTLIVÉ ROČNÍKY STUDIA Osmileté studium 1. ročník 1. Opakování a prohloubení učiva 1. 5. ročníku Číslo, číslice, množiny, přirozená čísla, desetinná čísla, číselné
Využití programu GeoGebra v Matematické analýze
 Využití programu GeoGebra v Matematické analýze Zuzana Morávková, KMDG, VŠB-TUO 29.3.2012 Obsah přednášky všeobecné informace o programu GeoGebra vybrané problematické pojmy z Matematické analýzy - interaktivní
Využití programu GeoGebra v Matematické analýze Zuzana Morávková, KMDG, VŠB-TUO 29.3.2012 Obsah přednášky všeobecné informace o programu GeoGebra vybrané problematické pojmy z Matematické analýzy - interaktivní
CZ 1.07/1.1.32/02.0006
 PO ŠKOLE DO ŠKOLY CZ 1.07/1.1.32/02.0006 Číslo projektu: CZ.1.07/1.1.32/02.0006 Název projektu: Po škole do školy Příjemce grantu: Gymnázium, Kladno Název výstupu: Prohlubující semináře Matematika (MI
PO ŠKOLE DO ŠKOLY CZ 1.07/1.1.32/02.0006 Číslo projektu: CZ.1.07/1.1.32/02.0006 Název projektu: Po škole do školy Příjemce grantu: Gymnázium, Kladno Název výstupu: Prohlubující semináře Matematika (MI
MODAM Ing. Schreiberová Petra, Ph.D.
 GeoGebra známá i neznámá (začátečníci) MODAM 2017 RNDr. Radomír Paláček, Ph.D. Ing. Schreiberová Petra, Ph.D. MODAM 2017 GeoGebra známá i neznámá (začátečníci) Příklad 1: Kyvadlo Zadání: Vytvořte animaci
GeoGebra známá i neznámá (začátečníci) MODAM 2017 RNDr. Radomír Paláček, Ph.D. Ing. Schreiberová Petra, Ph.D. MODAM 2017 GeoGebra známá i neznámá (začátečníci) Příklad 1: Kyvadlo Zadání: Vytvořte animaci
MODAM Mgr. Zuzana Morávková, Ph.D.
 GeoGebra známá i neznámá (pokročilí) MODAM 2016 Mgr. Zuzana Morávková, Ph.D. MODAM 2016 GeoGebra známá i neznámá (pokročilí) Příklad 1: Hod kostkou Zadání: Vytvoříme simulaci hodů hrací kostkou a budeme
GeoGebra známá i neznámá (pokročilí) MODAM 2016 Mgr. Zuzana Morávková, Ph.D. MODAM 2016 GeoGebra známá i neznámá (pokročilí) Příklad 1: Hod kostkou Zadání: Vytvoříme simulaci hodů hrací kostkou a budeme
MODAM Popis okna. 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie, VŠB - TU Ostrava
 GeoGebra známá i neznámá (začátečníci) MODAM 2016 Mgr. Jana Bělohlávková. MODAM 2016 GeoGebra známá i neznámá (začátečníci) Popis okna 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie,
GeoGebra známá i neznámá (začátečníci) MODAM 2016 Mgr. Jana Bělohlávková. MODAM 2016 GeoGebra známá i neznámá (začátečníci) Popis okna 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie,
MATURITNÍ OTÁZKY Z MATEMATIKY PRO ŠKOLNÍ ROK 2010/2011
 MATURITNÍ OTÁZKY Z MATEMATIKY PRO ŠKOLNÍ ROK 2010/2011 1. Výroková logika a teorie množin Výrok, pravdivostní hodnota výroku, negace výroku; složené výroky(konjunkce, disjunkce, implikace, ekvivalence);
MATURITNÍ OTÁZKY Z MATEMATIKY PRO ŠKOLNÍ ROK 2010/2011 1. Výroková logika a teorie množin Výrok, pravdivostní hodnota výroku, negace výroku; složené výroky(konjunkce, disjunkce, implikace, ekvivalence);
MATEMATIKA Maturitní témata společná část MZ základní úroveň (vychází z Katalogu požadavků MŠMT)
 MATEMATIKA Maturitní témata společná část MZ základní úroveň (vychází z Katalogu požadavků MŠMT) 1. Číselné obory 1.1 Přirozená čísla provádět aritmetické operace s přirozenými čísly rozlišit prvočíslo
MATEMATIKA Maturitní témata společná část MZ základní úroveň (vychází z Katalogu požadavků MŠMT) 1. Číselné obory 1.1 Přirozená čísla provádět aritmetické operace s přirozenými čísly rozlišit prvočíslo
MODAM Popis okna. 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie, VŠB - TU Ostrava
 GeoGebra známá i neznámá (začátečníci) MODAM 2016 Mgr. Jana Bělohlávková. MODAM 2016 GeoGebra známá i neznámá (začátečníci) Popis okna 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie,
GeoGebra známá i neznámá (začátečníci) MODAM 2016 Mgr. Jana Bělohlávková. MODAM 2016 GeoGebra známá i neznámá (začátečníci) Popis okna 2 Jana Bělohlávková, Katedra matematiky a deskriptivní geometrie,
Úterý 8. ledna. Cabri program na rýsování. Základní rozmístění sad nástrojů na panelu nástrojů
 Úterý 8. ledna Cabri program na rýsování program umožňuje rýsování základních geometrických útvarů, měření délky úsečky, velikosti úhlu, výpočet obvodů a obsahů. Je vhodný pro rýsování geometrických míst
Úterý 8. ledna Cabri program na rýsování program umožňuje rýsování základních geometrických útvarů, měření délky úsečky, velikosti úhlu, výpočet obvodů a obsahů. Je vhodný pro rýsování geometrických míst
Nezbytnou součástí ústní zkoušky je řešení matematických příkladů, které student obdrží při zadání otázky.
 Maturitní témata Matematika Školní rok 2016/17 Nezbytnou součástí ústní zkoušky je řešení matematických příkladů, které student obdrží při zadání otázky. Příprava ke zkoušce trvá 15 minut, ústní zkouška
Maturitní témata Matematika Školní rok 2016/17 Nezbytnou součástí ústní zkoušky je řešení matematických příkladů, které student obdrží při zadání otázky. Příprava ke zkoušce trvá 15 minut, ústní zkouška
Učební plán 4. letého studia předmětu matematiky. Učební plán 6. letého studia předmětu matematiky
 Učební plán 4. letého studia předmětu matematiky Ročník I II III IV Dotace 3 3+1 2+1 2+2 Povinnost povinný povinný povinný povinný Učební plán 6. letého studia předmětu matematiky Ročník 1 2 3 4 5 6 Dotace
Učební plán 4. letého studia předmětu matematiky Ročník I II III IV Dotace 3 3+1 2+1 2+2 Povinnost povinný povinný povinný povinný Učební plán 6. letého studia předmětu matematiky Ročník 1 2 3 4 5 6 Dotace
Požadavky na konkrétní dovednosti a znalosti z jednotlivých tematických celků
 Maturitní zkouška z matematiky 2012 požadované znalosti Zkouška z matematiky ověřuje matematické základy formou didaktického testu. Test obsahuje uzavřené i otevřené úlohy. V uzavřených úlohách je vždy
Maturitní zkouška z matematiky 2012 požadované znalosti Zkouška z matematiky ověřuje matematické základy formou didaktického testu. Test obsahuje uzavřené i otevřené úlohy. V uzavřených úlohách je vždy
Maturitní témata z matematiky
 Maturitní témata z matematiky G y m n á z i u m J i h l a v a Výroky, množiny jednoduché výroky, pravdivostní hodnoty výroků, negace operace s výroky, složené výroky, tabulky pravdivostních hodnot důkazy
Maturitní témata z matematiky G y m n á z i u m J i h l a v a Výroky, množiny jednoduché výroky, pravdivostní hodnoty výroků, negace operace s výroky, složené výroky, tabulky pravdivostních hodnot důkazy
Matematika. ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání:
 Studijní obor: Aplikovaná chemie Učební osnova předmětu Matematika Zaměření: ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání: denní Celkový počet vyučovacích hodin za
Studijní obor: Aplikovaná chemie Učební osnova předmětu Matematika Zaměření: ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání: denní Celkový počet vyučovacích hodin za
MATEMATIKA 5. TŘÍDA. C) Tabulky, grafy, diagramy 1 - Tabulky, doplnění řady čísel podle závislosti 2 - Grafy, jízní řády 3 - Magické čtverce
 MATEMATIKA 5. TŘÍDA 1 - Přirozená čísla a číslo nula a číselná osa, porovnávání b zaokrouhlování c zápis čísla v desítkové soustavě d součet, rozdíl e násobek, činitel, součin f dělení, dělení se zbytkem
MATEMATIKA 5. TŘÍDA 1 - Přirozená čísla a číslo nula a číselná osa, porovnávání b zaokrouhlování c zápis čísla v desítkové soustavě d součet, rozdíl e násobek, činitel, součin f dělení, dělení se zbytkem
Požadavky k opravným zkouškám z matematiky školní rok 2013-2014
 Požadavky k opravným zkouškám z matematiky školní rok 2013-2014 1. ročník (první pololetí, druhé pololetí) 1) Množiny. Číselné obory N, Z, Q, I, R. 2) Absolutní hodnota reálného čísla, intervaly. 3) Procenta,
Požadavky k opravným zkouškám z matematiky školní rok 2013-2014 1. ročník (první pololetí, druhé pololetí) 1) Množiny. Číselné obory N, Z, Q, I, R. 2) Absolutní hodnota reálného čísla, intervaly. 3) Procenta,
MATEMATIKA Maturitní témata společná část MZ vyšší úroveň (vychází z Katalogu požadavků MŠMT)
 MATEMATIKA Maturitní témata společná část MZ vyšší úroveň (vychází z Katalogu požadavků MŠMT) 1. Číselné obory 1.1 Přirozená čísla provádět aritmetické operace s přirozenými čísly rozlišit prvočíslo a
MATEMATIKA Maturitní témata společná část MZ vyšší úroveň (vychází z Katalogu požadavků MŠMT) 1. Číselné obory 1.1 Přirozená čísla provádět aritmetické operace s přirozenými čísly rozlišit prvočíslo a
Maturitní témata z matematiky
 Maturitní témata z matematiky 1. Lineární rovnice a nerovnice a) Rovnice a nerovnice s absolutní hodnotou absolutní hodnota reálného čísla definice, geometrický význam, srovnání řešení rovnic s abs. hodnotou
Maturitní témata z matematiky 1. Lineární rovnice a nerovnice a) Rovnice a nerovnice s absolutní hodnotou absolutní hodnota reálného čísla definice, geometrický význam, srovnání řešení rovnic s abs. hodnotou
Maturitní okruhy z matematiky ve školním roce 2010/2011
 Vyučující: RNDr. Ivanka Dvořáčková Třída: 8.A Maturitní okruhy z matematiky ve školním roce 2010/2011 Otázka Okruh 1 1. Výroky a operace s nimi 2. Množiny a operace s nimi 2 3. Matematické věty a jejich
Vyučující: RNDr. Ivanka Dvořáčková Třída: 8.A Maturitní okruhy z matematiky ve školním roce 2010/2011 Otázka Okruh 1 1. Výroky a operace s nimi 2. Množiny a operace s nimi 2 3. Matematické věty a jejich
ZŠ ÚnO, Bratří Čapků 1332
 Úvodní obrazovka Menu (vlevo nahoře) Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Matematika 1 (pro 12-16 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu
Úvodní obrazovka Menu (vlevo nahoře) Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Matematika 1 (pro 12-16 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika analytická geometrie. Mgr. Pavel Liška
 Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Náplň: Cvičení z matematiky geometrie (CZMg) Systematizace a prohloubení učiva matematiky Planimetrie, Stereometrie, Analytická geometrie, Kombinatorika, Pravděpodobnost a statistika Třída: 4.
Předmět: Náplň: Cvičení z matematiky geometrie (CZMg) Systematizace a prohloubení učiva matematiky Planimetrie, Stereometrie, Analytická geometrie, Kombinatorika, Pravděpodobnost a statistika Třída: 4.
Objekty v GEONExTu, jejich vytváření, zobrazení, vlastnosti a manipulace s nimi, vztahy mezi objekty
 Objekty v GEONExTu, jejich vytváření, zobrazení, vlastnosti a manipulace s nimi, vztahy mezi objekty Typy objektů Objekty, se kterými v programu GEONExT pracujeme, mají převážně grafické znázornění. Jednak
Objekty v GEONExTu, jejich vytváření, zobrazení, vlastnosti a manipulace s nimi, vztahy mezi objekty Typy objektů Objekty, se kterými v programu GEONExT pracujeme, mají převážně grafické znázornění. Jednak
Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292
 Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292 Název předmětu: Vyrovnávací kurz z matematiky Zabezpečující ústav: Ústav
Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292 Název předmětu: Vyrovnávací kurz z matematiky Zabezpečující ústav: Ústav
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky algebra (CZMa) Systematizace a prohloubení učiva matematiky: Číselné obory, Algebraické výrazy, Rovnice, Funkce, Posloupnosti, Diferenciální
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky algebra (CZMa) Systematizace a prohloubení učiva matematiky: Číselné obory, Algebraické výrazy, Rovnice, Funkce, Posloupnosti, Diferenciální
Wolfram Alpha. v podobě html stránky, samotný výsledek je často doplněn o další informace (např. graf, jiné možné zobrazení výsledku a
 Wolfram Alpha jde o výpočetní prostředí z nejrůznějších oborů (matematika, fyzika, chemie, inženýrství... ) přístupné online: http://www.wolframalpha.com/ Jaké matematické výpočty Wolfram Alpha zvládá?
Wolfram Alpha jde o výpočetní prostředí z nejrůznějších oborů (matematika, fyzika, chemie, inženýrství... ) přístupné online: http://www.wolframalpha.com/ Jaké matematické výpočty Wolfram Alpha zvládá?
MATEMATIKA Tematické okruhy ke státní maturitní zkoušce Obor: mechanik elektronik
 MATEMATIKA Tematické okruhy ke státní maturitní zkoušce Obor: mechanik elektronik R4 1. ČÍSELNÉ VÝRAZY 1.1. Přirozená čísla počítání s přirozenými čísly, rozlišit prvočíslo a číslo složené, rozložit složené
MATEMATIKA Tematické okruhy ke státní maturitní zkoušce Obor: mechanik elektronik R4 1. ČÍSELNÉ VÝRAZY 1.1. Přirozená čísla počítání s přirozenými čísly, rozlišit prvočíslo a číslo složené, rozložit složené
Cabri pro začátečníky
 Cabri pro začátečníky učební text RNDr. Ludmila Ciglerová 1. C T 1 T 3 O 1 1 A T 2 B H T G E F S D C A B R 1 Rýsování základních geometrických útvarů a) hlavní vodorovná lišta -Soubor, Upravit,Nastavit,
Cabri pro začátečníky učební text RNDr. Ludmila Ciglerová 1. C T 1 T 3 O 1 1 A T 2 B H T G E F S D C A B R 1 Rýsování základních geometrických útvarů a) hlavní vodorovná lišta -Soubor, Upravit,Nastavit,
Maturitní témata profilová část
 Seznam témat Výroková logika, úsudky a operace s množinami Základní pojmy výrokové logiky, logické spojky a kvantifikátory, složené výroky (konjunkce, disjunkce, implikace, ekvivalence), pravdivostní tabulky,
Seznam témat Výroková logika, úsudky a operace s množinami Základní pojmy výrokové logiky, logické spojky a kvantifikátory, složené výroky (konjunkce, disjunkce, implikace, ekvivalence), pravdivostní tabulky,
Maturitní zkouška z matematiky (v profilové části) Informace o zkoušce, hodnocení zkoušky, povolené pomůcky a požadavky
 Maturitní zkouška z matematiky (v profilové části) Informace o zkoušce, hodnocení zkoušky, povolené pomůcky a požadavky A. Informace o zkoušce Písemná maturitní zkouška z matematiky v profilové části se
Maturitní zkouška z matematiky (v profilové části) Informace o zkoušce, hodnocení zkoušky, povolené pomůcky a požadavky A. Informace o zkoušce Písemná maturitní zkouška z matematiky v profilové části se
1.1 Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem
 Analytická geometrie - kružnice Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem A = ; 5 [ ] Napište středový i obecný tvar rovnice kružnice, která má střed
Analytická geometrie - kružnice Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem A = ; 5 [ ] Napište středový i obecný tvar rovnice kružnice, která má střed
ZŠ ÚnO, Bratří Čapků 1332
 Úvodní obrazovka Menu (vlevo nahoře) Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Matematika 2 (pro 12-16 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu
Úvodní obrazovka Menu (vlevo nahoře) Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Matematika 2 (pro 12-16 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu
Matematika PRŮŘEZOVÁ TÉMATA
 Matematika ročník TÉMA 1-4 Operace s čísly a - provádí aritmetické operace v množině reálných čísel - používá různé zápisy reálného čísla - používá absolutní hodnotu, zapíše a znázorní interval, provádí
Matematika ročník TÉMA 1-4 Operace s čísly a - provádí aritmetické operace v množině reálných čísel - používá různé zápisy reálného čísla - používá absolutní hodnotu, zapíše a znázorní interval, provádí
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Cvičení z matematiky Náplň: Systematizace a prohloubení učiva matematiky Třída: 4. ročník Počet hodin: 2 Pomůcky: Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné obory
Předmět: Cvičení z matematiky Náplň: Systematizace a prohloubení učiva matematiky Třída: 4. ročník Počet hodin: 2 Pomůcky: Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné obory
Základní vzorce a funkce v tabulkovém procesoru
 Základní vzorce a funkce v tabulkovém procesoru Na tabulkovém programu je asi nejzajímavější práce se vzorci a funkcemi. Když jednou nastavíte, jak se mají dané údaje zpracovávat (některé buňky sečíst,
Základní vzorce a funkce v tabulkovém procesoru Na tabulkovém programu je asi nejzajímavější práce se vzorci a funkcemi. Když jednou nastavíte, jak se mají dané údaje zpracovávat (některé buňky sečíst,
KAPITOLA 9 - POKROČILÁ PRÁCE S TABULKOVÝM PROCESOREM
 KAPITOLA 9 - POKROČILÁ PRÁCE S TABULKOVÝM PROCESOREM CÍLE KAPITOLY Využívat pokročilé možnosti formátování, jako je podmíněné formátování, používat vlastní formát čísel a umět pracovat s listy. Používat
KAPITOLA 9 - POKROČILÁ PRÁCE S TABULKOVÝM PROCESOREM CÍLE KAPITOLY Využívat pokročilé možnosti formátování, jako je podmíněné formátování, používat vlastní formát čísel a umět pracovat s listy. Používat
Systematizace a prohloubení učiva matematiky. Učebna s dataprojektorem, PC, grafický program, tabulkový procesor. Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky Systematizace a prohloubení učiva matematiky 4. ročník 2 hodiny Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky Systematizace a prohloubení učiva matematiky 4. ročník 2 hodiny Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné
Popis základního prostředí programu AutoCAD
 Popis základního prostředí programu AutoCAD Popis základního prostředí programu AutoCAD CÍL KAPITOLY: CO POTŘEBUJETE ZNÁT, NEŽ ZAČNETE PRACOVAT Vysvětlení základních pojmů: Okno programu AutoCAD Roletová
Popis základního prostředí programu AutoCAD Popis základního prostředí programu AutoCAD CÍL KAPITOLY: CO POTŘEBUJETE ZNÁT, NEŽ ZAČNETE PRACOVAT Vysvětlení základních pojmů: Okno programu AutoCAD Roletová
SBÍRKA ÚLOH I. Základní poznatky Teorie množin. Kniha Kapitola Podkapitola Opakování ze ZŠ Co se hodí si zapamatovat. Přírozená čísla.
 Opakování ze ZŠ Co se hodí si zapamatovat Přírozená čísla Číselné obory Celá čísla Racionální čísla Reálná čísla Základní poznatky Teorie množin Výroková logika Mocniny a odmocniny Množiny Vennovy diagramy
Opakování ze ZŠ Co se hodí si zapamatovat Přírozená čísla Číselné obory Celá čísla Racionální čísla Reálná čísla Základní poznatky Teorie množin Výroková logika Mocniny a odmocniny Množiny Vennovy diagramy
Bakalářská matematika I
 1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
Gymnázium Jiřího Ortena, Kutná Hora. Průřezová témata Poznámky. Téma Školní výstupy Učivo (pojmy) volné rovnoběžné promítání průmětna
 Předmět: Matematika Náplň: Stereometrie, Analytická geometrie Třída: 3. ročník a septima Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor, učebnice Stereometrie Volné rovnoběžné promítání Zobrazí
Předmět: Matematika Náplň: Stereometrie, Analytická geometrie Třída: 3. ročník a septima Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor, učebnice Stereometrie Volné rovnoběžné promítání Zobrazí
Požadavky k opravným zkouškám z matematiky školní rok 2014-2015
 Požadavky k opravným zkouškám z matematiky školní rok 2014-2015 1. ročník (první pololetí, druhé pololetí) 1) Množiny. Číselné obory N, Z, Q, I, R. 2) Absolutní hodnota reálného čísla, intervaly. 3) Procenta,
Požadavky k opravným zkouškám z matematiky školní rok 2014-2015 1. ročník (první pololetí, druhé pololetí) 1) Množiny. Číselné obory N, Z, Q, I, R. 2) Absolutní hodnota reálného čísla, intervaly. 3) Procenta,
Tematický plán Obor: Informační technologie. Vyučující: Ing. Joanna Paździorová
 Tematický plán Vyučující: Ing. Joanna Paździorová 1. r o č n í k 5 h o d i n t ý d n ě, c e l k e m 1 7 0 h o d i n Téma- Tematický celek Z á ř í 1. Opakování a prohloubení učiva základní školy 18 1.1.
Tematický plán Vyučující: Ing. Joanna Paździorová 1. r o č n í k 5 h o d i n t ý d n ě, c e l k e m 1 7 0 h o d i n Téma- Tematický celek Z á ř í 1. Opakování a prohloubení učiva základní školy 18 1.1.
Projekt IMPLEMENTACE ŠVP. pořadí početních operací, dělitelnost, společný dělitel a násobek, základní početní operace
 Střední škola umělecká a řemeslná Evropský sociální fond "Praha a EU: Investujeme do vaší budoucnosti" Projekt IMPLEMENTACE ŠVP Evaluace a aktualizace metodiky předmětu Matematika Výrazy Obory nástavbového
Střední škola umělecká a řemeslná Evropský sociální fond "Praha a EU: Investujeme do vaší budoucnosti" Projekt IMPLEMENTACE ŠVP Evaluace a aktualizace metodiky předmětu Matematika Výrazy Obory nástavbového
2. cvičení z ZI1 - Excel
 Doc.Ing. Vlastimil Jáneš... janes@fd.cvut.cz 2. cvičení z ZI1 - Excel O Excelu - organizace listů : 1 list : max. 65 536 řádků a 256 sloupců, tj. 16 777 216 buněk. Sloupce : A, B,.Z, AA, AB,. IU, IV (26
Doc.Ing. Vlastimil Jáneš... janes@fd.cvut.cz 2. cvičení z ZI1 - Excel O Excelu - organizace listů : 1 list : max. 65 536 řádků a 256 sloupců, tj. 16 777 216 buněk. Sloupce : A, B,.Z, AA, AB,. IU, IV (26
SEZNAM ANOTACÍ. CZ.1.07/1.5.00/ III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická geometrie
 SEZNAM ANOTACÍ Číslo projektu Číslo a název šablony klíčové aktivity Označení sady DUM Tematická oblast CZ.1.07/1.5.00/34.0527 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická
SEZNAM ANOTACÍ Číslo projektu Číslo a název šablony klíčové aktivity Označení sady DUM Tematická oblast CZ.1.07/1.5.00/34.0527 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická
GeoGebra známá i neznámá
 GeoGebra známá i neznámá MODAM 2018 Z. Morávková, P. Schreiberová, J. Volná, P. Volný MODAM 2018 GeoGebra známá i neznámá Příklad 1: Nejmenší společný násobek Zadání: Vytvoříme aplikaci, ve které se vygenerují
GeoGebra známá i neznámá MODAM 2018 Z. Morávková, P. Schreiberová, J. Volná, P. Volný MODAM 2018 GeoGebra známá i neznámá Příklad 1: Nejmenší společný násobek Zadání: Vytvoříme aplikaci, ve které se vygenerují
VY_32_INOVACE_In 6.,7.13 Vzorce vložení funkce
 VY_32_INOVACE_In 6.,7.13 Vzorce vložení funkce Anotace: Žák se seznámí se základními druhy funkcí a jejich vložením v programu MS Excel 2010. Pracuje na svém žákovském počítači dle pokynů v prezentaci.
VY_32_INOVACE_In 6.,7.13 Vzorce vložení funkce Anotace: Žák se seznámí se základními druhy funkcí a jejich vložením v programu MS Excel 2010. Pracuje na svém žákovském počítači dle pokynů v prezentaci.
4. Jednoduché výpočty
 7 4. Jednoduché výpočty 4. Mathcad jako lepší kalkulačka Nejprve se budeme zabývat výrazy složenými z čísel. Při psaní čísel, základních matematických operátorů a funkcí je asi nejrychlejší používat sadu
7 4. Jednoduché výpočty 4. Mathcad jako lepší kalkulačka Nejprve se budeme zabývat výrazy složenými z čísel. Při psaní čísel, základních matematických operátorů a funkcí je asi nejrychlejší používat sadu
MINISTERSTVO ŠKOLSTVÍ, MLÁDEŽE A TĚLOVÝCHOVY. Učební osnova předmětu MATEMATIKA. pro studijní obory SOŠ a SOU (8 10 hodin týdně celkem)
 MINISTERSTVO ŠKOLSTVÍ, MLÁDEŽE A TĚLOVÝCHOVY Učební osnova předmětu MATEMATIKA pro studijní obory SOŠ a SOU (8 10 hodin týdně celkem) Schválilo Ministerstvo školství, mládeže a tělovýchovy dne 14. 6. 2000,
MINISTERSTVO ŠKOLSTVÍ, MLÁDEŽE A TĚLOVÝCHOVY Učební osnova předmětu MATEMATIKA pro studijní obory SOŠ a SOU (8 10 hodin týdně celkem) Schválilo Ministerstvo školství, mládeže a tělovýchovy dne 14. 6. 2000,
Návod k programu Graph, verze 4.3
 Návod k programu Graph, verze 4.3 Obsah 1 Úvod 2 2 Popis pracovní lišty a nápovědy 2 2.1 Nastavení os...................................... 2 2.2 Nápověda....................................... 3 3 Jak
Návod k programu Graph, verze 4.3 Obsah 1 Úvod 2 2 Popis pracovní lišty a nápovědy 2 2.1 Nastavení os...................................... 2 2.2 Nápověda....................................... 3 3 Jak
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ. u. v = u v + u v. Umět ho aplikovat při
 . VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti:. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti:. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
Nápověda k používání mapové aplikace Katastrální mapy Obsah
 Nápověda k používání mapové aplikace Katastrální mapy Obsah Práce s mapou aplikací Marushka... 2 Přehledová mapa... 3 Změna měřítka... 4 Posun mapy... 5 Druhy map... 6 Doplňkové vrstvy... 7 Vyhledávání...
Nápověda k používání mapové aplikace Katastrální mapy Obsah Práce s mapou aplikací Marushka... 2 Přehledová mapa... 3 Změna měřítka... 4 Posun mapy... 5 Druhy map... 6 Doplňkové vrstvy... 7 Vyhledávání...
Prostředí Microstationu a jeho nastavení. Nastavení výkresu
 Prostředí Microstationu a jeho nastavení Nastavení výkresu 1 Pracovní plocha, panely nástrojů Seznámení s pracovním prostředím ovlivní pohodlí, rychlost, efektivitu a možná i kvalitu práce v programu Microstation.
Prostředí Microstationu a jeho nastavení Nastavení výkresu 1 Pracovní plocha, panely nástrojů Seznámení s pracovním prostředím ovlivní pohodlí, rychlost, efektivitu a možná i kvalitu práce v programu Microstation.
DUM 03 téma: Tvary - objekty
 DUM 03 téma: Tvary - objekty ze sady: 1 tematický okruh sady: Vektorová grafika ze šablony: 09 Počítačová grafika určeno pro: 2. ročník vzdělávací obor: vzdělávací oblast: číslo projektu: anotace: metodika:
DUM 03 téma: Tvary - objekty ze sady: 1 tematický okruh sady: Vektorová grafika ze šablony: 09 Počítačová grafika určeno pro: 2. ročník vzdělávací obor: vzdělávací oblast: číslo projektu: anotace: metodika:
Gymnázium Jiřího Ortena, Kutná Hora. volné rovnoběžné promítání průmětna
 Předmět: Matematika Náplň: Stereometrie, Analytická geometrie, Komplexní čísla Třída: 3. ročník Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor Volné rovnoběžné promítání Zobrazí ve volném rovnoběžném
Předmět: Matematika Náplň: Stereometrie, Analytická geometrie, Komplexní čísla Třída: 3. ročník Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor Volné rovnoběžné promítání Zobrazí ve volném rovnoběžném
Sada 2 Microsoft Word 2007
 S třední škola stavební Jihlava Sada 2 Microsoft Word 2007 18. Editor rovnic Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2 - inovace
S třední škola stavební Jihlava Sada 2 Microsoft Word 2007 18. Editor rovnic Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284 Šablona: III/2 - inovace
Práce s programem IIS Ekonom
 Práce s programem IIS Ekonom Obsah 1 Ovládání programu IIS Ekonom... 2 1.1 Ovládání přes hlavní nabídku... 2 1.2 Panel nástrojů a funkční klávesy... 2 2 Přihlašovací dialog... 4 3 Úvodní obrazovka... 4
Práce s programem IIS Ekonom Obsah 1 Ovládání programu IIS Ekonom... 2 1.1 Ovládání přes hlavní nabídku... 2 1.2 Panel nástrojů a funkční klávesy... 2 2 Přihlašovací dialog... 4 3 Úvodní obrazovka... 4
Dodatek č. 3 ke školnímu vzdělávacímu programu. Strojírenství. (platné znění k 1. 9. 2009)
 Střední průmyslová škola Jihlava tř. Legionářů 1572/3, Jihlava Dodatek č. 3 ke školnímu vzdělávacímu programu Strojírenství (platné znění k 1. 9. 09) Tento dodatek nabývá platnosti dne 1. 9. 13 (počínaje
Střední průmyslová škola Jihlava tř. Legionářů 1572/3, Jihlava Dodatek č. 3 ke školnímu vzdělávacímu programu Strojírenství (platné znění k 1. 9. 09) Tento dodatek nabývá platnosti dne 1. 9. 13 (počínaje
II. Zakresli množinu bodů, ze kterých vidíme úsečku délky 3 cm v zorném úhlu větším než 30 0 a menším než 60 0.
 Ukázky typových maturitních příkladů z matematiky..reálná čísla. 3} x R; I. Zobrazte množiny A = {x є 3} < + x R; B = {x є II. Zapište ve tvaru zlomku číslo, 486.Komplexní čísla. I. Určete a + b, a - b,
Ukázky typových maturitních příkladů z matematiky..reálná čísla. 3} x R; I. Zobrazte množiny A = {x є 3} < + x R; B = {x є II. Zapište ve tvaru zlomku číslo, 486.Komplexní čísla. I. Určete a + b, a - b,
Planimetrie 2. část, Funkce, Goniometrie. PC a dataprojektor, učebnice. Gymnázium Jiřího Ortena, Kutná Hora. Průřezová témata Poznámky
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Matematika Planimetrie 2. část, Funkce, Goniometrie 2. ročník a sexta 4 hodiny týdně PC a dataprojektor, učebnice Planimetrie II. Konstrukční úlohy Charakterizuje
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Matematika Planimetrie 2. část, Funkce, Goniometrie 2. ročník a sexta 4 hodiny týdně PC a dataprojektor, učebnice Planimetrie II. Konstrukční úlohy Charakterizuje
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ
 11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti: 1. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti: 1. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
Základy matematiky kombinované studium 714 0365/06
 Základy matematiky kombinované studium 714 0365/06 1. Některé základní pojmy: číselné množiny, intervaly, operace s intervaly (sjednocení, průnik), kvantifikátory, absolutní hodnota čísla, vzorce: 2. Algebraické
Základy matematiky kombinované studium 714 0365/06 1. Některé základní pojmy: číselné množiny, intervaly, operace s intervaly (sjednocení, průnik), kvantifikátory, absolutní hodnota čísla, vzorce: 2. Algebraické
Dodatek č. 3 ke školnímu vzdělávacímu programu. Technické lyceum. (platné znění k 1. 9. 2009)
 Střední průmyslová škola Jihlava tř. Legionářů 72/3, Jihlava Dodatek č. 3 ke školnímu vzdělávacímu programu Technické lyceum (platné znění k 1. 9. 09) Tento dodatek nabývá platnosti dne 1. 9. 13 (počínaje
Střední průmyslová škola Jihlava tř. Legionářů 72/3, Jihlava Dodatek č. 3 ke školnímu vzdělávacímu programu Technické lyceum (platné znění k 1. 9. 09) Tento dodatek nabývá platnosti dne 1. 9. 13 (počínaje
Opakování k maturitě matematika 4. roč. TAD 2 <
 8.. Otázka číslo Mocniny a odmocniny. b.) Zjednodušte: 6 b. b Opakování k maturitě matematika. roč. TAD : 6.) Zjednodušte: 6 6.) Vypočtěte: a. y : ( a. y ) =.) Usměrněte zlomek =.. Otázka číslo Lineární
8.. Otázka číslo Mocniny a odmocniny. b.) Zjednodušte: 6 b. b Opakování k maturitě matematika. roč. TAD : 6.) Zjednodušte: 6 6.) Vypočtěte: a. y : ( a. y ) =.) Usměrněte zlomek =.. Otázka číslo Lineární
3.4.1. Tabulace učebního plánu
 3.4.1. Tabulace učebního plánu Vzdělávací obsah pro vyučovací předmět: MATEMATIKA Ročník: Kvinta, 1. ročník Tématická Číselné obory Druhy čísel (N, Z, Q, R, I) - prezentuje přehled číselných oborů Mocniny
3.4.1. Tabulace učebního plánu Vzdělávací obsah pro vyučovací předmět: MATEMATIKA Ročník: Kvinta, 1. ročník Tématická Číselné obory Druhy čísel (N, Z, Q, R, I) - prezentuje přehled číselných oborů Mocniny
Změna týdenní hodinové dotace v 1. ročníku v předmětu matematika. původní dotace 3 hodiny týdně, nově 4 hodiny týdně
 Dodatek č.. Školního vzdělávacího programu Obchodní akademie Lysá nad Labem, obor -1-M/0 Obchodní akademie, platného od 1. 9. 01 - platnost dodatku je od 1. 9. 015 Změna týdenní hodinové dotace v 1. ročníku
Dodatek č.. Školního vzdělávacího programu Obchodní akademie Lysá nad Labem, obor -1-M/0 Obchodní akademie, platného od 1. 9. 01 - platnost dodatku je od 1. 9. 015 Změna týdenní hodinové dotace v 1. ročníku
Konkretizovaný výstup Konkretizované učivo Očekávané výstupy RVP. Zápis čísla v desítkové soustavě - porovnávání čísel - čtení a psaní čísel
 Ročník: I. - vytváří si názoru představu o čísle 5, 10, 20 - naučí se vidět počty prvků do 5 bez počítání po jedné - rozpozná a čte čísla 0 5 - pozná a čte čísla 0 10 - určí a čte čísla 0 20 Číselná řada
Ročník: I. - vytváří si názoru představu o čísle 5, 10, 20 - naučí se vidět počty prvků do 5 bez počítání po jedné - rozpozná a čte čísla 0 5 - pozná a čte čísla 0 10 - určí a čte čísla 0 20 Číselná řada
Nástroje v InDesignu. Panel nástrojů 1. část. Nástroje otevřeme Okna Nástroje
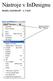 Nástroje v InDesignu Panel nástrojů 1. část Nástroje otevřeme Okna Nástroje Poklepem levé myši změníme panel nástrojů Nástroje v panelu nástrojů se používají k vybírání, úpravám a vytváření prvků stránek.
Nástroje v InDesignu Panel nástrojů 1. část Nástroje otevřeme Okna Nástroje Poklepem levé myši změníme panel nástrojů Nástroje v panelu nástrojů se používají k vybírání, úpravám a vytváření prvků stránek.
VZOROVÉ PŘÍKLADY Z MATEMATIKY A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava
 VZOROVÉ PŘÍKLADY Z MATEMATIKY A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava I Úprav algebraických výrazů zlomk, rozklad kvadratického trojčlenu,
VZOROVÉ PŘÍKLADY Z MATEMATIKY A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava I Úprav algebraických výrazů zlomk, rozklad kvadratického trojčlenu,
Cvičné texty ke státní maturitě z matematiky
 Cvičné texty ke státní maturitě z matematiky Pracovní listy s postupy řešení Brno 2010 RNDr. Rudolf Schwarz, CSc. Státní maturita z matematiky Obsah Obsah NIŽŠÍ úroveň obtížnosti 4 MAGZD10C0K01 říjen 2010..........................
Cvičné texty ke státní maturitě z matematiky Pracovní listy s postupy řešení Brno 2010 RNDr. Rudolf Schwarz, CSc. Státní maturita z matematiky Obsah Obsah NIŽŠÍ úroveň obtížnosti 4 MAGZD10C0K01 říjen 2010..........................
TEMATICKÝ PLÁN VÝUKY
 STŘEDNÍ P RŮMYSLOVÁ ŠKOLA, Praha 10, Na Třebešíně 22 TEMATICKÝ PLÁN VÝUKY Studijní 78 42 - M/01 Technické Zaměření: obor: lyceum Předmět: Matematika MAT Ročník: Počet hodin týdně: 4 3. Počet hodin celkem:
STŘEDNÍ P RŮMYSLOVÁ ŠKOLA, Praha 10, Na Třebešíně 22 TEMATICKÝ PLÁN VÝUKY Studijní 78 42 - M/01 Technické Zaměření: obor: lyceum Předmět: Matematika MAT Ročník: Počet hodin týdně: 4 3. Počet hodin celkem:
GeoGebra Prostředí programu
 GeoGebra Prostředí programu Po instalaci a spuštění programu uvidí uživatel jediné škálovatelné okno hlavní okno programu. Podle toho, zda otevíráte okno ve standardní konfiguraci (obr. 1) nebo v konfiguraci
GeoGebra Prostředí programu Po instalaci a spuštění programu uvidí uživatel jediné škálovatelné okno hlavní okno programu. Podle toho, zda otevíráte okno ve standardní konfiguraci (obr. 1) nebo v konfiguraci
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika planimetrie. Mgr. Tomáš Novotný
 Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Nový způsob práce s průběžnou klasifikací lze nastavit pouze tehdy, je-li průběžná klasifikace v evidenčním pololetí a školním roce prázdná.
 Průběžná klasifikace Nová verze modulu Klasifikace žáků přináší novinky především v práci s průběžnou klasifikací. Pro zadání průběžné klasifikace ve třídě doposud existovaly 3 funkce Průběžná klasifikace,
Průběžná klasifikace Nová verze modulu Klasifikace žáků přináší novinky především v práci s průběžnou klasifikací. Pro zadání průběžné klasifikace ve třídě doposud existovaly 3 funkce Průběžná klasifikace,
ZŠ ÚnO, Bratří Čapků 1332
 Úvodní obrazovka Menu Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Matematika 1 (pro 9-12 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu témat (horní
Úvodní obrazovka Menu Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Matematika 1 (pro 9-12 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu témat (horní
JEDNODUCHÉ LINEÁRNÍ A KVADRATICKÉ FUNKCE V GEOGEBŘE
 Obsah JEDNODUCHÉ LINEÁRNÍ A KVADRATICKÉ FUNKCE V GEOGEBŘE...2 Co je to funkce?...2 Existuje snadnější definice funkce?...2 Dobře, pořád se mi to zdá trochu moc komplikonavané. Můžeme se na základní pojmy
Obsah JEDNODUCHÉ LINEÁRNÍ A KVADRATICKÉ FUNKCE V GEOGEBŘE...2 Co je to funkce?...2 Existuje snadnější definice funkce?...2 Dobře, pořád se mi to zdá trochu moc komplikonavané. Můžeme se na základní pojmy
PRIMA Přirozená čísla Celá čísla Desetinná čísla Číselná osa Pravidla pro násobení a dělení 10, 100, 1000..a 0,1, 0,01, 0,001.. Čísla navzájem opačná
 PRIMA Přirozená čísla Celá čísla Desetinná čísla Číselná osa Pravidla pro násobení a dělení 10, 100, 1000..a 0,1, 0,01, 0,001.. Čísla navzájem opačná Racionální čísla Zlomky Rozšiřování a krácení zlomků
PRIMA Přirozená čísla Celá čísla Desetinná čísla Číselná osa Pravidla pro násobení a dělení 10, 100, 1000..a 0,1, 0,01, 0,001.. Čísla navzájem opačná Racionální čísla Zlomky Rozšiřování a krácení zlomků
Výrazy a příkazy v Maximě, jejich vkládání a vyhodnocování, vlastnosti, vztahy mezi částmi výpočtu a manipulace s nimi
 Výrazy a příkazy v Maximě, jejich vkládání a vyhodnocování, vlastnosti, vztahy mezi částmi výpočtu a manipulace s nimi Cíl této kapitoly Už jsme napsali, že Maxima je program natolik komplexní, že snažit
Výrazy a příkazy v Maximě, jejich vkládání a vyhodnocování, vlastnosti, vztahy mezi částmi výpočtu a manipulace s nimi Cíl této kapitoly Už jsme napsali, že Maxima je program natolik komplexní, že snažit
František Hudek. duben Informační a komunikační technologie MS Excel Úvod do Excelu II. Základy práce s listy a buňkami.
 VY_32_INOVACE_FH02 Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, obor, okruh, téma Anotace František Hudek duben 2012 8. ročník
VY_32_INOVACE_FH02 Jméno autora výukového materiálu Datum (období), ve kterém byl VM vytvořen Ročník, pro který je VM určen Vzdělávací oblast, obor, okruh, téma Anotace František Hudek duben 2012 8. ročník
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C)
 VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
TÉMA VÝSTUP UČIVO PRŮŘEZOVÁ TÉMATA
 Matematika ročník TÉMA G5 VÝSTUP 5.1 Teorie množin, provádí správně operace s množinami, výroková logika množiny vyžívá při řešení úloh; pracuje správně s výroky, užívá správně logické spojky a kvantifikátory;
Matematika ročník TÉMA G5 VÝSTUP 5.1 Teorie množin, provádí správně operace s množinami, výroková logika množiny vyžívá při řešení úloh; pracuje správně s výroky, užívá správně logické spojky a kvantifikátory;
TÉMA VÝSTUP UČIVO PRŮŘEZOVÁ TÉMATA
 Matematika ročník TÉMA G5 5.1 Teorie množin, provádí správně operace s množinami, výroková logika množiny vyžívá při řešení úloh; pracuje správně s výroky, užívá správně logické spojky a kvantifikátory;
Matematika ročník TÉMA G5 5.1 Teorie množin, provádí správně operace s množinami, výroková logika množiny vyžívá při řešení úloh; pracuje správně s výroky, užívá správně logické spojky a kvantifikátory;
Přehledy pro Tabulky Hlavním smyslem této nové agendy je jednoduché řazení, filtrování a seskupování dle libovolných sloupců.
 Přehledy pro Tabulky V programu CONTACT Professional 5 naleznete u firem, osob a obchodních případů záložku Tabulka. Tuto záložku lze rozmnožit, přejmenovat a sloupce je možné definovat dle vlastních požadavků
Přehledy pro Tabulky V programu CONTACT Professional 5 naleznete u firem, osob a obchodních případů záložku Tabulka. Tuto záložku lze rozmnožit, přejmenovat a sloupce je možné definovat dle vlastních požadavků
Objekty v GeoGebře, jejich vytváření, zobrazení, vlastnosti a manipulace s nimi, vztahy mezi objekty
 Objekty v GeoGebře, jejich vytváření, zobrazení, vlastnosti a manipulace s nimi, vztahy mezi objekty Typy objektů Objekty, se kterými v programu GeoGebra pracujeme, byly vytvořeny tak, aby se co nejsnáze
Objekty v GeoGebře, jejich vytváření, zobrazení, vlastnosti a manipulace s nimi, vztahy mezi objekty Typy objektů Objekty, se kterými v programu GeoGebra pracujeme, byly vytvořeny tak, aby se co nejsnáze
Gymnázium Vysoké Mýto nám. Vaňorného 163, Vysoké Mýto
 Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu / Druh CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu / Druh CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT
MANUÁL K ŘEŠENÍ TESTOVÝCH ÚLOH
 Krok za krokem k nové maturitě Maturita nanečisto 005 MA4 MANUÁL K ŘEŠENÍ TESTOVÝCH ÚLOH Matematika rozšířená úroveň Vážení vyučující! ředmětoví koordinátoři Centra pro zjišťování výsledků vzdělávání pro
Krok za krokem k nové maturitě Maturita nanečisto 005 MA4 MANUÁL K ŘEŠENÍ TESTOVÝCH ÚLOH Matematika rozšířená úroveň Vážení vyučující! ředmětoví koordinátoři Centra pro zjišťování výsledků vzdělávání pro
Matematika vzorce. Ing. Petr Šídlo. verze
 Matematika vzorce Ing. Petr Šídlo verze 0050409 Obsah Jazyk matematiky 3. Výrokový počet.......................... 3.. Logické spojky...................... 3.. Tautologie výrokového počtu...............
Matematika vzorce Ing. Petr Šídlo verze 0050409 Obsah Jazyk matematiky 3. Výrokový počet.......................... 3.. Logické spojky...................... 3.. Tautologie výrokového počtu...............
10. Analytická geometrie kuželoseček 1 bod
 10. Analytická geometrie kuželoseček 1 bod 10.1. Kružnice opsaná obdélníku ABCD, kde A[2, 3], C[8, 3], má rovnici a) x 2 10x + y 2 + 7 = 0, b) (x 3) 2 + (y 3) 2 = 36, c) x 2 + 10x + y 2 18 = 0, d) (x 10)
10. Analytická geometrie kuželoseček 1 bod 10.1. Kružnice opsaná obdélníku ABCD, kde A[2, 3], C[8, 3], má rovnici a) x 2 10x + y 2 + 7 = 0, b) (x 3) 2 + (y 3) 2 = 36, c) x 2 + 10x + y 2 18 = 0, d) (x 10)
Gymnázium Jana Pivečky a Střední odborná škola Slavičín. III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT
 Název projektu Číslo projektu Název školy Autor Název šablony Název DUMu Inovace výuky prostřednictvím šablon pro SŠ CZ.1.07/1.5.00/34.0748 Gymnázium Jana Pivečky a Střední odborná škola Slavičín Ing.
Název projektu Číslo projektu Název školy Autor Název šablony Název DUMu Inovace výuky prostřednictvím šablon pro SŠ CZ.1.07/1.5.00/34.0748 Gymnázium Jana Pivečky a Střední odborná škola Slavičín Ing.
