Studentský matematicko-fyzikální časopis
|
|
|
- Josef Němec
- před 5 lety
- Počet zobrazení:
Transkript
1 Studentský matematicko-fyzikální časopis Ročník XVIII Číslo 3 Úvodník str. 2 Zadání úloh třetí série str. 2 a 18 Téma 1: Ternární logika str. 4 Mgr Ṃ M O. Cífka: O využití operace sloučení str. 5 Téma 2: Jezero str. 7 Řesení úloh první série str. 8 Seriál o číslicových obvodech: III. díl Co jsou to číslicové obvody? str. 15 Časopis M&M a stejnojmenný korespondenční seminář je určen pro studenty středních škol, kteří se zajímají o matematiku, fyziku či informatiku. Během školního roku dostávají řešitelé zdarma čísla se zadáním úloh a témat k přemýšlení. Svá řešení odesílají k nám do redakce. My jejich příspěvky opravíme, obodujeme a pošleme zpět. Nejzajímavější řešení otiskujeme.
2 2 Milé řešitelky, milí řešitelé, přinášíme vám již třetí číslo našeho časopisu. Opět v něm najdete novou várku úloh k řešení a dozvíte se, jak se měly správně řešit úlohy z prvního čísla i jak jste obstáli se svými řešeními. Můžete si také přečíst letošní první příspěvek o ternární logice a inspirovat se pro napsání vlastního. Ať už o logice nebo o libovolném z dalších témat. Články tvoří jednu z nejdůležitějších součástí našeho semináře a podle toho jsou i bodově hodnoceny. Chtěli bychom připomenout, že článek k tématu můžete poslat kdykoli během roku. Od letoška lze navíc přemýšlet nad tématy a psát články i ve skupinách. Na začátku ledna nás čeká další kolo turnaje ve hře jezero. Těšíme se nejen na vaše programy, ale i na teoretické rozbory optimální strategie. Více informací o turnaji najdete uvnitř čísla. V minulém čísle jsme pro vás připravili bonus, který ale bohužel nikdo nevyužil. Na první stránce byl obrázek obsahující QR kód, v němž byla zakódovaná webová adresa. Stačilo adresu zadat do webového prohlížeče, vyplnit jednoduchý formulář a hned jste mohli mít bez práce jeden bod navíc. Možná, že ještě někdy něco podobného zopakujeme. Pozorně čtěte další čísla. Přejeme vám krásné prožití Vánoc. Organizátoři Zadání úloh Termín odeslání třetí série: Úloha 3.1 Hra (4b) V dávných dobách, kdy pračlověk pocítil potřebu začít se dorozumívat jinak než neartikulovanými skřeky, byl vynalezen jazyk. Jazyk, to je nad míru zajímavá věc, protože se dá třeba stočit do ruličky nebo dát na špičku nosu, a vůbec se s ním dají dělat všelijaké psí kusy. Kusy popisu staré egyptské hry, které byly nalezeny zhruba před týdnem týmem českých archeologů v okolí řeky Nilu, byly již doplněny o potřebná pravidla, takže jejich celé znění přikládáme čtenářům níže. Kámen začíná na pozici (1, 1) a pohybuje se po čtvercové síti podle následujících pravidel: 1. Z jakéhokoli místa o souřadnicích (a, b) se může přemístit na místo o souřadnicích (2a, b), nebo (a, 2b). 2. Z jakéhokoli místa o souřadnicích (a, b) se může přemístit na místo (a b, b), pokud a > b, nebo na (a, b a), pokud a < b. Na jaké pozice (n, m), kde n a m jsou přirozená čísla, je možno kámen přemístit?
3 XVIII/3 3 Úloha 3.2 Digitální hodiny (5b) Toto krátké hraní si se slůvky, bude-li okruhem čtenářů pochopeno, to bude pořádná pecka! Pecka je dutá, takže padá k zemi rychleji než kamínek, tvrdil nám tvrdohlavě Karlík, ale byla to lež. Lež, vždyť není ani šest hodin, zazívala na mne sestra, když jsem se spěšně oblékala do školy, protože na mém budíku bylo už osm. Tato úloha se bude zabývat digitálními 1 hodinami, konkrétně ve 24-hodinovém 2 formátu. Určitě jste už viděli nějaké, které měly některou ze svítících čar rozbitou (nesvítící), přičemž tento defekt často vede k situaci, že nejde poznat, kolik hodin vlastně je. Předpokládejme, že máme takové hodiny, o nichž víme, že mají právě jeden segment porouchaný, ale nevíme, který. Zkuste zjistit: a) Jakou část dne nebudeme vědět jistě, kolik je hodin? O kolik se průměrně budeme mýlit, pokud mezi možnými časy po doplnění náhodné čárky na smysluplný čas vybereme vždy náhodně (tedy při více iteracích průměr těchto časů)? b) Bylo by možné vymyslet nové číslice 0 až 9 (jako úplně libovolné kombinace segmentů) tak, aby byl displej jednoznačný i při selhání jednoho segmentu? Pokud ne, jak tyto číslice vymyslet tak, aby otázky z části a) byly řešeny optimálně? c) Jak by problém vypadal, kdybychom nevěděli, zda je nějaký segment rozbitý, nebo není? A co se dvěma nefunkčními segmenty? Nebo kdybychom vůbec nevěděli, kolik jich je rozbitých? (Nebráníme se udělování bonusových bodů.) Úloha 3.3 Stlačování plynů (4b) Jestli jste se ještě neztratili, ráda bych dodala, že dvojsmyslné slovo, které bude následovat, mne nedávno zaujalo, jelikož jeho druhý význam je od prvního (dle pořadí, v jakém je uvádím) odvozen, neboť dříve měli herci své texty napsány na svitcích papíru, jimž se také říkalo role. Role, kterou dostal ve hře Porosty českých lesů, mu příliš nevyhovovala, neboť mu při ní stále překážela koruna. Koruna mu padla přesně na jeho vysoké čelo. Čelo rozenělo své struny a nádherná melodie potěšila naše ucho. Ucho nádoby, jak praví staré české přísloví, se utrhne, když se s ní chodí pro vodu příliš dlouho. Máme nádobu a v nej zmes niekoľkých rôznych plynov (nič viac, než že sú rôzne a chemicky spolu nereagujú, o nich zatiaľ vedieť nepotrebujeme). Začnime teraz nádobu veľmi pomaly izotermicky 3 zmenšovať (napríklad do nej zasúvame piest). Asi je nám všetkým jasné, že v nádobe začne rásť tlak. Môže narásť až na 1 se sedmisegmentovým displejem 2 tedy zobrazené časy jsou 00:00 23:59 3 Tak pomaly, aby sa teplota plynu v nádobe nemenila.
4 4 takú hodnotu, že plyny postupne skvapalnejú. Ako sa bude meniť tlak v nádobe v závislosti na objeme a ako zastúpenie plynov v atmosfére? Veď keď nejaký plyn skvapalnie, tak z atmosféry skoro zmizne, alebo nie? Z nedostatku čísel v zadaní vyplýva, že tentokrát od vás nečakáme žiadne počítanie, ale čo najpodrobnejší rozbor a popis situácie a deja. Malá nápoveda: Bude sa vám hodiť vedieť, čo je to krivka nasýtenej pary a čo parciálny tlak. Úloha 3.4 Provazy (1b) Jen doufám, že tenhle bláznivý příběh nebude nakonec pořádná bota. Bota se skutálela ze schodů a ozvala se hlasitá rána. Rána jsou nejpěknější část dne, když se louka pozvolna otepluje, slunce se rodí do růžové a opodál zpívá kos. Kos celou mez, jen ne ten bez. Bez pořádného provazu není radno se slaňovat. Máme n provazů naskládaných na hromadě, ven nám tedy trčí 2n konců. Náhodně vybereme dva konce a svážeme je dohromady. To opakujeme, dokud nezbudou žádné volné konce. Jaký je průměrný počet smyček (cyklů), které tímto postupem vytvoříme? Tím se naše zvláštní, ale snad veselé povídání chýlí ke konci, protože autorce se již klíží víčka. Víčka od pivních láhví se někdy stříbrně lesknou, proto je má kamarádka nechává na zahradě pro straky doufajíc, že při jejich kradení tam někdy nějaká zanechá své vzácné pero. Pero, to je ten pravý nástroj, který byste teď měli popadnout do ruky, abyste mohli začít řešit naše nové úlohy! Řešení témat Téma 1 Ternární logika K prvnímu tématu nám přišly dva zajímvé články. Mgr Ṃ M Ondřej Cífka, jehož příspěvek níže v téměř nezměněné podobě otiskujeme, se zabývá otázkou, jak operace známé z booleovské logiky rozšířit i do logiky ternární. Nabízí k tomu docela přirozený, ale určitě ne jediný možný, přístup. Dr Ṃ M Jakub Kubečka zašel ještě dále a vytváří nové operace pro ternární logiku. Jako příklad můžeme uvést binární operaci nejistost, která nabývá jedničky, kdykoli je jedním z operandů otazník, a nuly jinak. Podobných (a užitečných) operací by určitě bylo možno vymyslet mnohem více. Přijaté články nabízí spoustu otázek k dalšímu bádání. Souhlasíte s tím, jak Mrg Ṃ M Ondřej Cífka zavedl operace pro ternární logiku? Nebo byste to udělali jinak? Můžete se také zamyslet nad dalšími smysluplnými (nejen binárními) operacemi v této logice. Jak byste převedli ternární logiku do normálního jazyka? Lze pokládat dotazy a odpovídat podobně jako v logice booleovské? Je ternární logika něco úplně nepřirozeného, nebo ji můžeme běžně využít (a třeba i využíváme, aniž
5 XVIII/3 5 si to uvědomujeme)? Případně jak by vypadala aritmetika využívající naši logiku? Mohla by být k něčemu dobrá? Kuba O využití operace sloučení Mgr Ṃ M Ondřej Cífka Od ternární logiky budeme chtít, aby byla zobecněním logiky Booleovy všechny operace Booleovy logiky tedy musejí v té ternární nad pravdou a lží fungovat tak, jak to známe. Dále si musíme rozmyslet, jaký má otazník mít vlastně význam, tedy co si slibujeme od toho, že bude vyjadřovat nejistotu. Chtěli bychom, aby se choval (dovolte mi použít ono oblíbené přirovnání) jako taková krabice se Schrödingerovou kočkou. Dokud je škatule dobře uzavřena, neexistuje způsob, jak zjistit, zda došlo k usmrcení jejího obsahu. Jakmile ji ale otevřeme, nalezneme v ní zvíře buď živé, nebo mrtvé a již není cesty zpět. Otazník ve výraze vlastně zastupuje obě logické hodnoty najednou. Je to, jako bychom se za otazník snažili dosadit nulu i jedničku zároveň kočku, která je současně mrtvá i živá. Jinak řečeno, pokud otazník ve výrazu nahradíme číslem (tj. nulou nebo jedničkou), hodnota výrazu se smí změnit z otazníku na číslo, ale nikoli z čísla na otazník nebo na jiné číslo. Nejistota se může změnit v jistotu, ale ta už je nedotknutelná. Ještě jinými slovy: Jestliže hodnota celého výrazu záleží na hodnotě otazníku (tedy při dosazení jedničky na jeho místo by výraz nabyl jiné hodnoty než při dosazení nuly), pak hodnotu výrazu nelze určit a rovná se tedy otazníku. Jestliže naopak na hodnotě otazníku nesejde, můžeme za něj dosadit libovolnou hodnotu (nulu nebo jedničku) a dostaneme jednoznačný booleovský výraz. Abychom zůstali věrni kočičí analogii, představme si například vědce, který má rovnou dvě kočky ve dvou různých krabicích a jehož úkolem je zjistit, zda jsou obě naživu. Na začátku ví, že ani o jedné, ani o druhé kočce nemůže nic říci (zapsáno logickým součinem:?? =?). Jestliže po otevření první krabice konstatuje smrt, odpoví záporně: ať už se s druhou kočkou děje cokoli, zjevně neplatí, že jsou obě živé (0? = 0). Pokud naopak najde první kočku živou, nemůže odpovědět než otazníkem (1? =?): dokud je druhá škatule zapečetěna, nelze rozhodnout. Po jejím otevření nalezne buď živou (1 1 = 1), nebo mrtvou (1 0 = 0) kočku a příslušně odpoví. Uvedená úvaha už nám vlastně dává přímočarý návod, jak převádět operace z Booleovy logiky do té ternární. Než jej vysvětlím, zavedu si binární operaci sloučení, která pro dva stejné operandy vrátí jejich hodnotu, pro dva různé otazník. x ??? y 0 1? 0 1? 0 1? sloučení 0??? 1????
6 6 Nyní kýžený postup. Nejprve si napíšeme pravdivostní tabulku dané operace jen pro nuly a jedničky (s tím, že operandy a výsledek operace píšeme do řádku). Pro každý operand nyní budeme chtít zjistit, za jakých podmínek na něm záleží výsledek operace. Vybereme tedy vždy ty dva řádky tabulky, které se liší pouze o hodnotu vybraného operandu (a případně o výsledek operace), z nich pro každé dvě hodnoty ve stejném sloupci provedeme sloučení a výsledky zapíšeme po řadě na nový řádek tabulky. Čeho tím dosáhneme? Pokud se bude pro různé hodnoty operandu lišit výsledek operace, pak na daném operandu v dané chvíli záleží a otazník od otazníku pojde. Pokud se výsledek operace v závislosti na operandu nezmění, v daném případě na něm nesejde, takže můžeme s jistotou říci, že dosadíme-li zaň otazník, výstupem bude ona neměnná hodnota. Uvedeným postupem prozkoumáme pouze ty kombinace vstupních hodnot, mezi nimiž se vyskytuje právě jeden otazník. To nám příliš nevadí, neboť operace budou většinou binární. Pokud bychom ale měli více operandů, nic nám nebrání provést tentýž postup znovu několikrát za sebou, vždy na nově přidané řádky tabulky, a získat tak i kombinace se dvěma, třemi otazníky atd. Aplikujeme-li postup na tabulku c1.2 z prvního dílu seriálu, získáme následující (uvedeny jsou pouze přidané řádky). x y 0 x y x > y x x < y y XOR x + y 0? ???? 1? 0?? 1 0?? 1? 0 0 0?? 0 0??? 1 0? 0?? 1? 1?? 0??????? x y x + y x = y ȳ y x x x y x y 1 0????? ? 0?? 1 0?? 1? 0?? 1 1?? 1 1? 1 0? 0?? 1? 1????????? 1 Dodejme, že negací otazníku je otazník. De Morganovy zákony Ternární logiku a její základní operace jsme postavili tak, aby byly jen rozšířením logiky nám dobře známé. Převedení něčeho takového jako De Morganových zákonů do ternární logiky by tedy mělo být relativně přímočaré. Nejprve si zákony napíšeme v jejich nejjednodušší formě, která jistě musí v ternární logice platit (plyne to např. z logických tabulek použitých operací): a + b = a b (1) a b = a + b (2)
7 XVIII/3 7 Pro (1): Pokud b = p + q, pak platí a b = a p + q = a p q = a + p + q. Jednoduchou indukcí pak dostaneme a 1 + a a i = a 1 a 2 a i. Analogicky tomu bude pro (2). De Morganovy zákony jsou tedy v ternární logice stejné, jako v logice Booleově. Inverzní operace Některé zběsile vypadající nápady z oblasti Booleovy logiky začnou po přenesení do logiky ternární dávat výrazně větší smysl. Jedním z nich jsou inverze standardních (binárních) operací. Například k logickému součtu můžeme mít logický rozdíl, k součinu podíl atd. Logický rozdíl definujeme tak, že a b = c, právě když a = b+c. Podobně pro logický podíl: a/b = c právě tehdy, když a = b c. Obecně budeme u inverzních operací znát výsledek výchozí operace a jeden z jejích operandů a budeme chtít zjistit ten druhý. Ternární logika se nám tu tolik hodí proto, že výsledek inverzí často nebude jednoznačný, což vyjádříme právě otazníkem. Ani tak se ovšem nevyhneme případům, kdy operace nebude pro určité hodnoty definována. x y x y x/y ?? ? 1 1?? 1 Téma 2 Jezero K tématu přišly a do prvního turnaje byly nasazeny celkem čtyři soutěžní programy, tři od Prof Ṃ M Štěpána Šimsy a jeden od Bc Ṃ M Daniela Gromady. Vítězem se stal program stepan, který dokázal vydělat za jednu hru v průměru 7 peněz, a tak si odnáší 6 bodů. Ostatní programy byly v průměru ztrátové. Druhé místo a čtyři body tak víceméně automaticky připadly programu od Bc Ṃ M Daniela Gromady a třetí místo zůstalo neuděleno. Ani jeden z řešitelů však neposlal žádný teoretický rozbor problému, ani článek o tom, jakou strategii jeho program provádí a proč tomu tak je. Pokud by byly do turnaje nasazeny i organizátorské programy, bezkonkurenčním vítězem by se stal program smart.pl od Honzy, který na jednu hru dosáhl průměrný zisk 160 peněz. Zdrojový text tohoto programu jsme vám zatím k dispozici nedali, takže můžete zkusit odhadovat
8 8 na jakém principu funguje. Honza o něm říká, že je, co do délky a složitosti, srovnatelný s veřejným economic30-70.pl. Pravidla turnaje, který se bude konat , jsou následující: Vyzkoušené a funkční programy přijímáme nejpozději v pátek Turnaj se bude skládat ze dvou menších částí. Jedna z nich budou zápasy na menší počet kol (ne více než 20) za stejných podmínek, jako je uvedeno v zadání, druhá bude turnaj za stejných podmínek jako dosud s jednou výjimkou: kontrola bude zpoplatněna částkou 5 peněz. V případě poslání kontroly tedy platí pro posílajícího hráče z = z 5 bez ohledu na to, jestli kontrola někoho chytí, nebo ne. Vítězem se stane program, který v součtu přes obě kategorie dosáhne nejvyššího průměrného zisku za jeden tah. Prémie vítězům jednotlivých kategorií předběžně nevyhlašujeme, ale udělit je můžeme. Těšíme se na vaše programy i na rozbory strategií a další příspěvky do témátka. Aktuální informace hledejte na našich stránkách, konkrétně hlavně na stránce témátka ( Honza & Jeffer Řešení úloh Úloha 1.1 Závorkový hlavolam (3b) Zadání: Soutěžící dostali proužek papíru, na němž bylo v náhodném pořadí napsáno n levých a n pravých závorek. Měli dokázat, že není-li uzávorkování správné 4, lze proužek rozstřihnout na jednom místě tak, že po vyměnění kusů dostanou správné uzávorkování. Zvládnete to vy? Řešení: Pro jednoduchost budeme v následujícím textu označovat počet levých závorek # ( a počet pravých závorek # ). Všimněme si nejdříve vlastnosti V správného uzávorkování. Procházímeli správně uzávorkovanou posloupnost zleva doprava, musí v každém místě posloupnosti platit # ( # ). Naopak, nesprávně uzávorkovaná posloupnost tuto vlastnost nemá, a tedy v ní existuje alespoň jedno takové místo, kde počet pravých závorek je ostře větší než počet levých závorek. Takových míst může být v posloupnosti i více. Rozřízneme tedy posloupnost v místě, kde # ) # ( dosahuje maxima a jednotlivé části si označíme popořadě A a B. Protože posloupnost je vyvážená (tj. obsahuje stejný počet levých a pravých závorek), musí být # ( # ) v podposloupnosti B rovno # ) # ( v podposloupnosti A. Přitom posloupnost B splňuje vlastnost V, jinak by se v ní muselo nacházet maximum # ) # ( a naše předchozí rozdělení by neplatilo. V A je jenom 4 Správné uzávorkování je takové, že každé pravé závorce předchází levá, kterou uzavírá.
9 XVIII/3 9 o tolik více ), o kolik je v B více (, a proto je i celá posloupnost BA správně uzávorkovaná. Zbývá dokázat, že vždycky najdeme maximum # ) # (. To je ale snadné, protože posunem o jedno místo v posloupnosti se změní # ) # ( právě o jedna a zároveň # ) # ( je na začátku i na konci posloupnosti 0, tedy musí existovat alespoň jedno maximum. Existuje-li jich více, zvolíme jedno libovolně. Honza Úloha 1.2 Pětiúhelník (3b) Zadání: Vězení pro geniální jedince je velmi zvláštně utvářená budova. Kupříkladu místnost, v níž nyní dlí Riki, je pětiúhelníkového tvaru. Pro tento pětiúhelník navíc platí, že tři z jeho stran (dvě sousední a jedna protější) mají stejnou délku, která také odpovídá součtu délek zbylých dvou stran. Dále je známo, že úhel, který svírá každá z kratších stran s přilehlou z dvojice sousedících dlouhých stran, je pravý. Určete obsah tohoto pětiúhelníku, je-li délka každé ze tří stejně dlouhých stran 2 m. Je dodržena minimální plocha na jednoho vězně? Řešení: Pětiúhelník označíme stejně jako na obrázku ABCDE tak, aby platilo AB = D = CD = DE = 2 m. K řešení můžeme přistupovat více způsoby. Někteří se snažili obsah nějak přímo spočítat. To dá trochu práce, ale občas to k cíli vede. My si ukážeme pěknější a trochu geometrické řešení. E Pětiúhelník si rozdělíme na trojúhelníky EAD, ABD a BCD. Dále označme A B EA = k, odtud platí BC = 2 k. Trojúhelníky EAD a BCD jsou pravoúhlé, jejich obsah tedy vyjádříme snadno. S EAD + S BCD = 2 k (2 k) 2 = 2 m 2. Nyní si všimneme, že pokud trojúhelníky EAD a BCD slepíme tak, aby se dotýkaly jejich strany ED a CD, dostaneme trojúhelník se stranami délek AD, BD a 2. Místo slepení si můžeme také představit otočení kolem bodu D o úhel CDE. Tedy nově vzniklý trojúhelník je shodný s trojúhelníkem ABD. Proto jsou jsou si rovny i jejich obsahy a platí Obsah celého pětiúhelníku potom je S ABD = S EAD + S BCD = 2 m 2. S ABCDE = S EAD + S ABD + S BCD = 4 m 2. C
10 10 Nyní máme úlohu vyřešenou a můžeme se zamyslet nad doplňující otázkou. Podle doporučení evropské Rady pro předcházení mučení (CPT) by minimální plocha pro ubytování jednoho vězně neměla být v žádném případě menší než námi dopočítané 4 m 2. Doporučená velikost cely na vězně je 6 m 2. 5 V Česku jsou za standardní plochu považovány 4 m 2 na osobu. Vzhledem k přeplněnosti věznic není ale vždy dosahováno ani této hodnoty. 6 V každém případě minimální plocha pro Rikiho celu dodržena byla. Kuba Úloha 1.3 Metahlavolam (4b) Zadání: U soudu je přítomen soudce, obhájce a žalobce. Žalobce i obhájce může být buď pravdomluvný, nebo lhář. 7 Když se žalobce a obhájce vyjadřovali o vině či nevině Rikiho, pronesli následující tvrzení: Žalobce: Riki je vinen a v minulosti spáchal i jiné zločiny. Obhájce: Riki je nevinný a žalobce je lhář. Soudce nyní položil otázku, na kterou předem znal správnou odpověď, a jeden ze dvou právníků (žalobce nebo obhájce) odpověděl. Soudce tak zjistil, zda je dotyčný pravdomluvný či lhář, a tedy je-li Riki vinen či nikoli. Zjistit, zda je Riki vinen, dáváme za úkol i vám, milí čtenáři. Jistě jste si však všimli, že zatím nemáte dostatek informací, abyste úlohu vyřešili, protože nevíte, kdo odpovídal a jak. To však vědět nepotřebujete, protože vám prozradíme ještě jednu věc: Neexistuje způsob, jak určit, zda by mohl soudce o vině či nevině Rikiho rozhodnout, kdyby na soudcovu otázku odpověděl druhý právník, než ten, který odpovídal. Nyní už můžete určit, zda je Riki vinen, či nikoli. Jak to tedy je? A víte, který ze dvou právníků na otázku odpověděl? A zda byl pravdomluvný či lhář? Řešení: Podívejme se na situaci, kdy soudce položil otázku a jeden z právníků odpověděl. Máme 4 možnosti, jak situace vypadala: 1. Odpověděl žalobce a lhal. 2. Odpověděl žalobce a mluvil pravdu. 3. Odpověděl obhájce a lhal. 4. Odpověděl obhájce a mluvil prav. Co to znamená z hlediska předchozích výroků právníků? 1. Riki být vinen může i nemusí (záleží na tom, v které části výpovědi žalobce lhal). 2. Riki je vinen. 3. Pokud obhájce lhal pouze v první části výroku, je Riki vinen, přičemž druhá část výroku skutečně může být pravdivá, protože žalobce mohl lhát jen ve druhé části svého výroku. Pokud obhájce lhal pouze ve druhé části, je žalobce pravdomluvný, tudíž je Riki vinen, jak tvrdí Každý výrok pravdomluvného je pravdivý, každý výrok lháře je nepravdivý.
11 XVIII/3 11 žalobce, ale potom nutně musela být nepravdivá i první část obhájcova výroku. V obou případech ovšem dostáváme, že Riki je vinen. 4. Riki je nevinný. (A žalobce je lhář, což je za těchto okolností pravda, protože ohledně viny Rikiho lhal.) Kterého právníka se soudce ptal? Když se podíváme na analýzu případů výše, vidíme, že pokud se soudce zeptal obhájce, tak mohl jednoznačně rozhodnout o vině Rikiho, ať tázaný lhal či nikoli. Zeptal-li se žalobce, tak nemůžeme určit, zda je Riki vinen, či nikoli. Ze zadání však víme, že to (díky poslední informaci) určit umíme. Proto se soudce ptal obhájce. Jak mu odpověděl? V případě, že je obhájce pravdomluvný, tak žalobce (dle 2. části obhájcova výroku) je lhář, tudíž bychom uměli určit, zda je Riki vinen, či není, i kdyby se soudce zeptal žalobce-lháře. Pokud obhájce lže, tak nevíme, zda je žalobce pravdommluvný, nebo lže také (stačí, že lže ve 2. části výroku), tudíž kdyby se soudce zeptal žalobce v tomto případě, tak o vině či nevině Rikiho rozhodnout nemůže. A takováto situace dle zadání přesně nastala, tudíž objájce lhal. Navíc víme, že ať už obhájce lhal či nikoli, vyplynulo z toho, že Riki je vinen. Tudíž správné řešení je, že Riki je vinen, soudce se ptal obhájce a ten lhal. Alča Úloha 1.4 Útěk po Bondovsku (4b) Zadání: Jakou zbraň by asi 10 kg vážící Riki potřeboval, aby mu tento plán (skok z okna) vyšel? Stačila by mu běžná policejní zbraň a nebo samopal na to, aby se vznášel ve vzduchu? A co kulomet? A kanón? (Nezapomeňte, že takový kanón už vzhledem k Rikimu také něco váží a musí udržet oba.) A co laserové dělo z Hvězdných válek? A co kdyby stráž připravil jen o luk a šípy? Nápadům na zbraně ani bonusovým bodům se meze (skoro) nekladou. Úplně nejlepší je ale zbraň Z s kadencí K, náboji N a střelcem S, tedy řešení obecné. Řešení: Celkom šikovne sa do úlohy pustila Markéta Vohníková, keď využila zákon zachovania hybnosti, ktorý hovorí, že hybnosť uzavretej sústavy (na ktorú nepôsobia vonkajšie sily) je nemenná. Takouto uzavretou sústavou je aj sústava Riki so zbraňou-náboj, pretože sila vystreľujúca náboj je sila vnútorná a teda hybnosť sústavy nemení. Správne namietnete, že na túto sústavu ale vonkajšia sila pôsobí. Touto silou je sila tiažová F G = mg. Zmena hybnosti sústavy je potom p = mg t, (u1.4.1) kde g predstavuje miestne tiažové zrýchlenie a t časový úsek zmena rýchlosti za čas t je v = g t. A čo sa inak deje s hybnosťou v našej uzavretej sústave? Celková hybnosť tesne pred výstrelom je v tejto sústave nulová, preto
12 12 aj hybnosť tesne po výstrele bude nulová: 0 = (m R + m z )v n = (m n )v u, (u1.4.2) kde m R je hmotnosť Rikiho, m z je hmotnosť zbrane, m n je hmotnosť náboja, v n je rýchlosť spätného nárazu a v u je úsťová rýchlosť zbrane (rýchlosť, ktorou vylieta náboj z hlavne). Ak zo vzťahu (u1.4.2) vyjadríme v n v n = m nv u m R + m z, (u1.4.3) a túto rýchlosť, ktorú Rikimu dodá jeden vystrelený náboj, vydelíme dobou medzi dvomi nábojmi T, čo je prevrátená hodnota kadencie k, takže vlastne vynásobíme kadenciou, dostaneme priemerné zrýchlenie Rikiho smerom nahor a = m nv u k. (u1.4.4) m R + m z Takže teraz vôbec nemusíme počítať s vonkajšou silou pôsobiacou na sústavu, ale stačí, aby toto zrýchlenie bolo prinajmenšom rovnaké, ako tiažové zrýchlenie a g. V takomto prípade vie Riki prinajmenšom udržiavať rýchlosť, ktorú nabral pred prvým výstrelom, v prípade a > g sa môže dokonca zahrať na raketu... Lenže, kto vysoko lieta, hlboko padá, keď mu dôjdu náboje. Opäť zaujímavé to začne byť v momente, keď zistíme, že Riki ukradol zbraň predsa len slabšiu a platí a < g. Musí sa bezpodmienečne zabiť? To záleží na rýchlosti dopadu v d a na tom, z akej výšky h Riki skáče. Pre rýchlosť dopadu z výšky h si môžeme ľahko odovodiť 8 v d = 2hg. (u1.4.5) V našom prípade dodatočné zrýchlenie znižuje pozorované tiažové zrýchlenie a tým aj rýchlosť dopadu. Takže môžeme písať v d = 2h(g a), ( v d = 2h g m ) nv u k. m R + m z (u1.4.6) Čo si po dosadení rýchlosti v n podľa (u1.4.3) môžeme prepísať na v d = 2h(g kv n ). (u1.4.7) Markéta Vohníková ďalej navrhuje stanoviť maximálnu prípustnú v d ako 50 km h 1, čo zodpovedá pádu z výšky asi desať metrov, alebo teda z výšky 8 Zo vzťahov pre dráhu a rýchlosť rovnomerne zrýchleného pohybu v závislosti na čase, alebo zo zákona zachovania (mechanickej) energie.
13 XVIII/3 13 tretieho poschodia a s týmto limitom počítať maximálnu možnú hĺbku skoku pre danú zbraň. Hurá na konkrétne prípady: Pištoľ CZ 75 veru príliš nepomôže, pridá nejakých 30 cm k bezpečnej výške. Naproti tomu samopal AK-47 zvýši bezpečnú výšku z necelých desiatich metrov na šestnásť. S československým samopalom Vz. 58 sa dostaneme už cez dvadsať metrov, ale lietať stále nemôžeme. Poobhliadneme sa teda po guľometoch a skočme rovno na tie ťažké. Tak napríklad americký Browning AN/M2 už na lietanie tesne stačí, aj keď váži cez 40 kg. A poďme ešte ďalej, známy minigun GAU-17/A tiež s Rikim nemá problémy, ťažký M61 Vulcan Rikiho spokojne odpáli snaď aj do vesmíru, aj keď sám váži cez 100 kg a napokon najťažšia váha, GAU-8 Avenger z protitankového lietadla A-10 Thunderbolt II už stráca kvôli svojej hmotnosti 1,3 t, ale stále na lietanie spoľahlivo stačí. Navrhovanému laserovému delu sa venoval len Mgr Ṃ M Jakub Šafin a celkom správne spočítal, že na lietanie by Riki potreboval laser s výkonom 30 GW. Ako na to prišiel? Jednoducho si spočítal, že každý fotón s frekvenciou ν nesie hybnosť p = hν/c, že táto hybnosť je tiež rovná p = E/c a teda, že potrebný výkon je P cgm R (celkom správne predpokladal, že až taký laser bude, bude ako každá správna futuristická zbraň veľmi ľahký). No a teraz špeciálne pre tých z vás, ktorí sa chcú niečo naučiť. Viacerí ste mimovoľne používali tvrdenie F = p/ t, čo je ale skoro prvá veta impulzová 9 F = dp dt, (u1.4.8) ktorá sa dá slovne vyjadriť tak, že časová zmena hybnosti je rovná pôsobiacej sile. Vektory si nevšímajme, budeme sa hýbať len po priamke ( voľným pádom ). Hybnosť je celkom všeobecne p = mv a pôsobiaca sila je jednak sila tiažová F G = mg, pokiaľ sa pohybujeme tak blízko povrchu Zeme, že ju môžeme považovať za konštantnú, spolu so silou spätného rázu F r = µv r, kde µ je časový úbytok hmotnosti (v prípade s nábojmi µ = m n k). Dosaďme teraz tieto hodnoty do prvej vety impulzovej (u1.4.8): µv r gm(t) = dm(t)v(t) dt, (u1.4.9) no a teraz derivujme. Celkom všeobecne sa s časom mení aj rýchlosť Rikiho, aj jeho hmotnosť ubúdajú mu náboje. Bodkou značíme, ako obvykle, časovú deriváciu. µv r gm(t) = µv(t) + m(t) v. (u1.4.10) Zaoberajme sa najprv zjednodušeným prípadom, čiže pohybom ďaleko od akéhokoľvek telesa (g = 0). Zároveň predpokladajme, že hmotnosť sa Rikimu mení 9 Druhá veta impulzová je podobná. Hovorí, že časová zmena momentu hybnosti je rovná momentu pôsobiacej sily, čiže M = dl/dt. Na praktické použitie sa pozrite do čísla XIV/5 na stranu 5.
14 14 pomaly, µ 0, takže vynecháme prvý člen na pravej strane. Dostávame µv r = m(t) v. (u1.4.11) Po predelení hmotnosťou m môžeme rovno integrovať podľa času, čo nie je nič desivé, na ľavej strane integrujeme 1/m na ln m a na pravej v na v. Dostávame tak po dosadení hornej a dolnej medze v určitom integrále (teda koncovej a počiatočnej hmotnosti): v = µv r ln m zač. m konc., (u1.4.12) čo je slávna Ciolkovského raketová rovnica, ktorá udáva, akú rýchlosť získa raketa tým, že sa postupne rýchlosťou µ zbaví hmotnosti m zač. m konc., ktorú odvrhne rýchlosťou v r. Pokiaľ teraz započítame aj konštantné gravitačné pole, skoro nič sa nezmení, len na pravú stranu riešenia pribudne člen g t. Riešenie ešte zložitejších verzií (nezanedbateľné µ) už nebudeme rozoberať. Jeffer Úloha 1.5 Booleovský výraz Zadání: Zjednodušte výraz F = (X + Y Z) + (X + Y Z) (X T + Z). (2b) Řešení: Při zjednodušování výrazu můžeme postupovat různými způsoby. Nejjednodušší je si všimnout, že výraz můžeme přepsat do tvaru F = A + A B, kde A = X + Y Z a B = X T + Z. Tento výraz můžeme přepsat na jednoduchý tvar F = A + B, neboť pokud A = 1, tak F = B = 1 a pokud A = 0, tak F = B = B, což odpovídá tomu, že F = A + B. Výraz můžeme zjednodušit F = X + Y Z + X T + Z a pak jej dále upravit F = X (1 + T ) + Z (Y + 1). Rozborem případů můžeme nahlédnout, že pro libovolné C platí C + 1 = 1. Pak X (1 + T ) = X a Z (Y + 1) = Z. Výraz tedy můžeme upravit do finální podoby F = X + Z. (R)adim
15 XVIII/3 15 Seriál o číslicových obvodech III. díl Co to jsou číslicové obvody? V předcházejících částech našeho seriálu jsme si položili jisté matematické základy pro práci s číslicovými obvody. Část z nich nyní využijeme při našem dalším putování. V tomto díle si ukážeme, co vlastně chápeme číslicovými obvody. Co to jsou číslicové obvody? Číslicovými obvody obvykle chápeme elektronické součástky, jejichž výstupy a vstupy nabývají hodnot logické nuly či logické jedničky. Tyto signály jsou realizovány jistou hodnotou elektrického napětí. Podle jednoho ze standardů můžeme mít logickou nulu definovánu jako napětí od 0 do 0,8 V a logickou jedničku jako napětí od 2 do 5 V. Napětí v intervalu od 0,8 do 2 V představuje tzv. zakázaný pás. Pokud takové napětí přivedeme na vstup číslicového obvodu, nemůžeme říct, co se bude dít a co dostaneme na výstupu. Proto se tomu raději vždy vyhneme. V katalogu s elektronickými součástkami můžeme zjistit, že se vyrábí celé řady integrovaných obvodů 10 realizující logické funkce. V jednom takovém integrovaném obvodu nalezneme obvykle několik tzv. hradel, které představují různé logické operace typu logického součtu, součinu... V případě, že sestavujeme elektrický obvod, tak jej nejdříve znázorníme pomocí tzv. schématu. Jednotlivá hradla znázorníme pomocí symbolů. Základní schematické značky pro hradla jsou znázorněna na obrázku c3.1. Použití kolečka na výstupu (resp. vstupu) znamená, že je daný výstup (resp. vstup) invertován. Z hradel můžeme skládat obvody, které rozdělíme do dvou skupin. První z nich jsou kombinační obvody. Jedná se o obvody, jejichž výstup (výstupy) závisí pouze na aktuální hodnotě vstupů. Naproti tomu máme sekvenční obvody, jejichž výstup (výstupy) závisí také na předchozím stavu obvodu. Příkladem kombinačního obvodu je například obvod, který aritmeticky sečte čísla na vstupu. Sekvenční obvody si můžeme představit například jako jednoduchou paměťovou buňku. O sekvenčních obvodech si více povíme dále. Při konstrukci zapojení s číslicovými obvody nesmíme zapomínat na několik pravidel. První je, že žádný ze vstupů nesmíme nechat nezapojený. Pokud by se tak stalo, neměli bychom na vstupu definovánu hodnotu, a tak by také výstup nebyl definován. Dále nesmíme zapomínat na napájení obvodů. To je však již spíše technický problém, který budeme řešit později. Nyní si ukážeme příklad zapojení s číslicovými obvody. Na obrázku c3.2 je znázorněno zapojení, které představuje operaci g = b c + a b d + a b d + a b c d, 10 Integrované obvody obvykle vypadají jako černé pouzdro ze kterého trčí ve dvou řadách vývody.
16 16 Logický součin AND Negovaný logický součin NAND A B A B A B A B Logický součet OR Negovaný logický součet NOR A B A + B A B A + B Vylučovací OR XOR Invertor A B A B + A B A A Obr. c3.1 Schématické značky základních typů hradel dle normy ASA. na kterém jsme si v minulém díle ukazovali použití Karnaughových map. Sekvenční obvody Jak jsme nastínili výše, tak sekvenčními obvody chápeme zapojení, kde výstup číslicového obvodu nezávisí pouze na vstupu, ale také na předchozím stavu obvodu. Příkladem nám bude tzv. R S klopný obvod. Jedná se o dvojici hradel NOR, přičemž výstup každého z nich je přiveden na vstup toho druhého. 11 R S klopný obvod má dva vstupy R (reset) a S (set). Dále má dva výstupy, výstup Q a Q, kde druhý z výstupů je pouze negací toho prvního. Obvod je znázorněn na obrázku c3.3. Pro obvod můžeme napsat jednoduché vztahy Q = R + Q, Q = S + Q. 11 V některé literatuře můžeme nalézt konstrukci R S klopného obvodu pomocí dvojice hradel NAND, které mají vstupy R a S; jedná se o ekvivalentní zapojení, což snadno uvidíme, pokud si vzpomeneme na De Morganova pravidla.
17 XVIII/3 17 a b Pozn.: g(a, b, c, d) značí nespojené vodiče značí spojené vodiče c d Obr. c3.2 Schéma zapojení realizující operaci g = b c + a b d + a b d + a b c d. Pokud je S a R ve stavu logické nuly, tak se v obvodu nic neděje, neboť se nulové signály S a R neprojeví. Dostaneme tak vztahy Q = Q a Q = Q. Zachová se nám předchozí stav na výstupu. Pokud však jeden ze signálů, řekněme že S, změníme na logickou jedničku, pak Q = 1 + Q = 0 a Q = 0 0 = 1. Změníme stav obvodu tak, že Q = 1 a Q = 0. Pokud pak opět přivedeme na S logickou nulu, tak se nám výstup nezmění. V případě, že na R přivedeme logickou jedničku, pak Q = 1 + Q = 0
18 18 a Q = 0 0 = 0, dostaneme opačný stav. Pokud bychom jak na R, tak na S přivedli logickou jedničku, tak by se nám obvod rozkmital, neboť bychom jej stále zapínali a vypínali. R Q Q S Obr. c3.3 Schéma R S klopného obvodu. Tímto ukončíme tento díl seriálu. Příště se můžete těšit na složitější, nejen sekvenční obvody. Pokud by vám něco v tomto seriálu nebylo jasné, tak se nebojte zeptat e mailem na radim@matfyz.cz. (R)adim Úloha 3.5 Černá krabička (3b) Představte si černou krabičku, která má dva vstupní bity A 0 a A 1, dva výstupní bity Y 0 a Y 1 a reset R. Na vstup můžeme přivádět signál, který představuje čísla od 0 do 3 zapsané v dvojkové soustavě. Na výstupu pak nalezneme největší číslo, které se doposud objevilo na vstupu. Resetovací signál je v klidu ve stavu logické nuly. Logická jednička na resetovacím signálu nastaví výstupní bity Y 0 a Y 1 na hodnotu logických nul. Nakreslete schéma zapojení, které by mělo stejné vlastnosti jako výše popsaná černá krabička.
19 XVIII/3 19 Výsledková listina Úlohy Poř. Jméno R. 1 r1 r2 r3 r4 t1 t2 s Dr Ṃ M J. Kubečka Mgr Ṃ M O. Cífka Bc Ṃ M D. Gromada Bc Ṃ M J. Mikel Mgr Ṃ M J. Šafin Bc Ṃ M M. Poppr Bc Ṃ M A. Šťastná Bc Ṃ M T. Bárta J. Greššák Mgr Ṃ M P. Kratochvíl Mgr Ṃ M O. Mička Mgr Ṃ M M. Töpfer Mgr Ṃ M R. Kubíček O. Benedikt J. Dolejší Mgr Ṃ M E. Gocníková M. Lieskovský Prof Ṃ M Š. Šimsa Mgr Ṃ M P. Vincena M. Vohníková Mgr Ṃ M B. Böhmová E. Harlenderová J. Kadlec M. Zmeškal M. Calábková Bc Ṃ M L. Langerová P. Turnovec T. Vysušil Sloupeček 1 je součet všech bodů získaných v našem semináři, 0 je součet bodů v aktuální sérii a Sloupeček + značí bonusové body udělované podle ročníku a součtu bodů za úlohy. Tituly uvedené v předchozím textu slouží pouze pro účely M&M.
20 20 S obsahem časopisu M&M je možné nakládat dle licence Creative Commons Attribution 3.0. Dílo smíte šířit a upravovat. Máte povinnost uvést autora. Autory textů jsou, pokud není uvedeno jinak, organizátoři M&M. Adresa redakce: M&M, OVVP, UK MFF Ke Karlovu Praha 2 Telefon: MaM@atrey.karlin.mff.cuni.cz WWW: Časopis M&M je zastřešen Oddělením pro vnější vztahy a propagaci Univerzity Karlovy, Matematicko-fyzikální fakulty a vydáván za podpory středočeské pobočky Jednoty českých matematiků a fyziků.
Výroková logika II. Negace. Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0).
 Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Seriál II.II Vektory. Výfučtení: Vektory
 Výfučtení: Vektory Abychom zcela vyjádřili veličiny jako hmotnost, teplo či náboj, stačí nám k tomu jediné číslo (s příslušnou jednotkou). Říkáme jim skalární veličiny. Běžně se však setkáváme i s veličinami,
Výfučtení: Vektory Abychom zcela vyjádřili veličiny jako hmotnost, teplo či náboj, stačí nám k tomu jediné číslo (s příslušnou jednotkou). Říkáme jim skalární veličiny. Běžně se však setkáváme i s veličinami,
Způsoby realizace této funkce:
 KOMBINAČNÍ LOGICKÉ OBVODY U těchto obvodů je výstup určen jen výhradně kombinací vstupních veličin. Hodnoty výstupních veličin nezávisejí na předcházejícím stavu logického obvodu, což znamená, že kombinační
KOMBINAČNÍ LOGICKÉ OBVODY U těchto obvodů je výstup určen jen výhradně kombinací vstupních veličin. Hodnoty výstupních veličin nezávisejí na předcházejícím stavu logického obvodu, což znamená, že kombinační
Úlohy krajského kola kategorie C
 67. ročník matematické olympiády Úlohy krajského kola kategorie C 1. Najděte nejmenší přirozené číslo končící čtyřčíslím 2018, které je násobkem čísla 2017. 2. Pro celá čísla x, y, z platí x 2 + y z =
67. ročník matematické olympiády Úlohy krajského kola kategorie C 1. Najděte nejmenší přirozené číslo končící čtyřčíslím 2018, které je násobkem čísla 2017. 2. Pro celá čísla x, y, z platí x 2 + y z =
Maticí typu (m, n), kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru:
 3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
Výpočty fyzikálních úkolů kores. sem. MFF UK pro ZŠ
 Úloha IV.C... Zákon zachování zimy 9 bodů; průměr 2,95; řešilo 39 studentů 1. Jednoho chladného pondělí sněžilo natolik, že to Tomovi zasypalo dům. Vytáhl tedy ze sklepa lopatu na sníh a pustil se do práce.
Úloha IV.C... Zákon zachování zimy 9 bodů; průměr 2,95; řešilo 39 studentů 1. Jednoho chladného pondělí sněžilo natolik, že to Tomovi zasypalo dům. Vytáhl tedy ze sklepa lopatu na sníh a pustil se do práce.
Úlohy klauzurní části školního kola kategorie B
 65. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie B 1. Kolika způsoby je možno vyplnit čtvercovou tabulku 3 3 čísly,, 3, 3, 3, 4, 4, 4, 4 tak, aby součet čísel v každém čtverci
65. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie B 1. Kolika způsoby je možno vyplnit čtvercovou tabulku 3 3 čísly,, 3, 3, 3, 4, 4, 4, 4 tak, aby součet čísel v každém čtverci
63. ročník matematické olympiády Řešení úloh krajského kola kategorie B. 1. Odečtením druhé rovnice od první a třetí od druhé dostaneme dvě rovnice
 63. ročník matematické olympiády Řešení úloh krajského kola kategorie B 1. Odečtením druhé rovnice od první a třetí od druhé dostaneme dvě rovnice (x y)(x + y 6) = 0, (y z)(y + z 6) = 0, které spolu s
63. ročník matematické olympiády Řešení úloh krajského kola kategorie B 1. Odečtením druhé rovnice od první a třetí od druhé dostaneme dvě rovnice (x y)(x + y 6) = 0, (y z)(y + z 6) = 0, které spolu s
DIGITÁLN LNÍ OBVODY A MIKROPROCESORY 1. ZÁKLADNÍ POJMY DIGITÁLNÍ TECHNIKY
 DIGITÁLN LNÍ OBVODY A MIKROPROCESORY BDOM Prof. Ing. Radimír Vrba, CSc. Doc. Ing. Pavel Legát, CSc. Ing. Radek Kuchta Ing. Břetislav Mikel Ústav mikroelektroniky FEKT VUT @feec.vutbr.cz
DIGITÁLN LNÍ OBVODY A MIKROPROCESORY BDOM Prof. Ing. Radimír Vrba, CSc. Doc. Ing. Pavel Legát, CSc. Ing. Radek Kuchta Ing. Břetislav Mikel Ústav mikroelektroniky FEKT VUT @feec.vutbr.cz
Matematický KLOKAN 2006 kategorie Junior
 Matematický KLOKAN 006 kategorie Junior Vážení přátelé, v následujících 7 minutách vás čeká stejný úkol jako mnoho vašich vrstevníků v řadě dalších evropských zemí. V níže uvedeném testu je zadáno čtyřiadvacet
Matematický KLOKAN 006 kategorie Junior Vážení přátelé, v následujících 7 minutách vás čeká stejný úkol jako mnoho vašich vrstevníků v řadě dalších evropských zemí. V níže uvedeném testu je zadáno čtyřiadvacet
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony.
 Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Přijímací zkouška na MFF UK v Praze
 Přijímací zkouška na MFF UK v Praze Studijní program Matematika, bakalářské studium Studijní program Informatika, bakalářské studium 2014, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a,
Přijímací zkouška na MFF UK v Praze Studijní program Matematika, bakalářské studium Studijní program Informatika, bakalářské studium 2014, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a,
Číselné vyjádření hodnoty. Kolik váží hrouda zlata?
 Čísla a logika Číselné vyjádření hodnoty Au Kolik váží hrouda zlata? Dekadické vážení Když přidám osmé závaží g, váha se převáží => závaží zase odeberu a začnu přidávat závaží x menší 7 závaží g 2 závaží
Čísla a logika Číselné vyjádření hodnoty Au Kolik váží hrouda zlata? Dekadické vážení Když přidám osmé závaží g, váha se převáží => závaží zase odeberu a začnu přidávat závaží x menší 7 závaží g 2 závaží
2. LOGICKÉ OBVODY. Kombinační logické obvody
 Hardware počítačů Doc.Ing. Vlastimil Jáneš, CSc, K620, FD ČVUT E-mail: janes@fd.cvut.cz Informace a materiály ke stažení na WWW: http://www.fd.cvut.cz/personal/janes/hwpocitacu/hw.html 2. LOGICKÉ OBVODY
Hardware počítačů Doc.Ing. Vlastimil Jáneš, CSc, K620, FD ČVUT E-mail: janes@fd.cvut.cz Informace a materiály ke stažení na WWW: http://www.fd.cvut.cz/personal/janes/hwpocitacu/hw.html 2. LOGICKÉ OBVODY
KOMBINAČNÍ LOGICKÉ OBVODY
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 KOMBINAČNÍ LOGICKÉ OBVODY U těchto obvodů je vstup určen jen výhradně kombinací vstupních veličin. Hodnoty
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 KOMBINAČNÍ LOGICKÉ OBVODY U těchto obvodů je vstup určen jen výhradně kombinací vstupních veličin. Hodnoty
Fyzikální korespondenční seminář MFF UK
 Úloha I.S... náhodná 10 bodů; průměr 7,04; řešilo 45 studentů a) Zkuste vlastními slovy popsat, co je to náhodná veličina a jaké má vlastnosti (postačí vlastními slovy objasnit následující pojmy: náhodná
Úloha I.S... náhodná 10 bodů; průměr 7,04; řešilo 45 studentů a) Zkuste vlastními slovy popsat, co je to náhodná veličina a jaké má vlastnosti (postačí vlastními slovy objasnit následující pojmy: náhodná
Matice přechodu. Pozorování 2. Základní úkol: Určete matici přechodu od báze M k bázi N. Každou bázi napíšeme do sloupců matice, např.
 Matice přechodu Základní úkol: Určete matici přechodu od báze M k bázi N. Každou bázi napíšeme do sloupců matice, např. u příkladu 7 (v ) dostaneme: Nyní bychom mohli postupovat jako u matice homomorfismu
Matice přechodu Základní úkol: Určete matici přechodu od báze M k bázi N. Každou bázi napíšeme do sloupců matice, např. u příkladu 7 (v ) dostaneme: Nyní bychom mohli postupovat jako u matice homomorfismu
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1. 5. Minimalizace logické funkce a implementace do cílového programovatelného obvodu CPLD
 .. Minimalizace logické funkce a implementace do cílového programovatelného obvodu Zadání. Navrhněte obvod realizující neminimalizovanou funkci (úplný term) pomocí hradel AND, OR a invertorů. Zaznamenejte
.. Minimalizace logické funkce a implementace do cílového programovatelného obvodu Zadání. Navrhněte obvod realizující neminimalizovanou funkci (úplný term) pomocí hradel AND, OR a invertorů. Zaznamenejte
12. Booleova algebra, logická funkce určitá a neurčitá, realizace logických funkcí, binární kódy pro algebraické operace.
 12. Booleova algebra, logická funkce určitá a neurčitá, realizace logických funkcí, binární kódy pro algebraické operace. Logická proměnná - proměnná nesoucí logickou hodnotu Logická funkce - funkce přiřazující
12. Booleova algebra, logická funkce určitá a neurčitá, realizace logických funkcí, binární kódy pro algebraické operace. Logická proměnná - proměnná nesoucí logickou hodnotu Logická funkce - funkce přiřazující
Úlohy krajského kola kategorie C
 6. ročník matematické olympiády Úlohy krajského kola kategorie C. Pro libovolná reálná čísla x, y, z taková, že x < y < z, dokažte nerovnost x 2 y 2 + z 2 > (x y + z) 2. 2. Honza má tři kartičky, na každé
6. ročník matematické olympiády Úlohy krajského kola kategorie C. Pro libovolná reálná čísla x, y, z taková, že x < y < z, dokažte nerovnost x 2 y 2 + z 2 > (x y + z) 2. 2. Honza má tři kartičky, na každé
Přijímací zkouška na MFF UK v Praze
 Přijímací zkouška na MFF UK v Praze pro bakalářské studijní programy fyzika, informatika a matematika 2016, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé
Přijímací zkouška na MFF UK v Praze pro bakalářské studijní programy fyzika, informatika a matematika 2016, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé
pro bakalářské studijní programy fyzika, informatika a matematika 2018, varianta A
 Přijímací zkouška na MFF UK pro bakalářské studijní programy fyzika, informatika a matematika 2018, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé úlohy
Přijímací zkouška na MFF UK pro bakalářské studijní programy fyzika, informatika a matematika 2018, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé úlohy
Báze a dimenze vektorových prostorů
 Báze a dimenze vektorových prostorů Buď (V, +, ) vektorový prostor nad tělesem (T, +, ). Nechť u 1, u 2,..., u n je konečná posloupnost vektorů z V. Existují-li prvky s 1, s 2,..., s n T, z nichž alespoň
Báze a dimenze vektorových prostorů Buď (V, +, ) vektorový prostor nad tělesem (T, +, ). Nechť u 1, u 2,..., u n je konečná posloupnost vektorů z V. Existují-li prvky s 1, s 2,..., s n T, z nichž alespoň
64. ročník matematické olympiády Řešení úloh krajského kola kategorie A
 64. ročník matematické olympiády Řešení úloh krajského kola kategorie A 1. Středy stran AC, BC označme postupně, N. Střed kružnice vepsané trojúhelníku KLC označme I. Úvodem poznamenejme, že body K, L
64. ročník matematické olympiády Řešení úloh krajského kola kategorie A 1. Středy stran AC, BC označme postupně, N. Střed kružnice vepsané trojúhelníku KLC označme I. Úvodem poznamenejme, že body K, L
P4 LOGICKÉ OBVODY. I. Kombinační Logické obvody
 P4 LOGICKÉ OBVODY I. Kombinační Logické obvody I. a) Základy logiky Zákony Booleovy algebry 1. Komutativní zákon duální forma a + b = b + a a. b = b. a 2. Asociativní zákon (a + b) + c = a + (b + c) (a.
P4 LOGICKÉ OBVODY I. Kombinační Logické obvody I. a) Základy logiky Zákony Booleovy algebry 1. Komutativní zákon duální forma a + b = b + a a. b = b. a 2. Asociativní zákon (a + b) + c = a + (b + c) (a.
Intervalové stromy. Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme. 1. Změna jednoho čísla v posloupnosti.
 Intervalové stromy Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme průběžně provádět tyto dvě operace: 1. Změna jednoho čísla v posloupnosti. 2. Zjištění součtu čísel
Intervalové stromy Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme průběžně provádět tyto dvě operace: 1. Změna jednoho čísla v posloupnosti. 2. Zjištění součtu čísel
Úlohy klauzurní části školního kola kategorie A
 62. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie A 1. V obdélníku ABCD o stranách AB = 9, BC = 8 leží vzájemně se dotýkající kružnice k 1 (S 1, r 1 ) a k 2 (S 2, r 2 ) tak,
62. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie A 1. V obdélníku ABCD o stranách AB = 9, BC = 8 leží vzájemně se dotýkající kružnice k 1 (S 1, r 1 ) a k 2 (S 2, r 2 ) tak,
CVIČNÝ TEST 51. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 51 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 V obchodě s kouzelnickými potřebami v Kocourkově
CVIČNÝ TEST 51 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 V obchodě s kouzelnickými potřebami v Kocourkově
Derivace goniometrických funkcí
 Derivace goniometrických funkcí Shrnutí Jakub Michálek, Tomáš Kučera Odvodí se základní vztahy pro derivace funkcí sinus a cosinus za pomoci věty o třech itách, odvodí se také několik typických it pomocí
Derivace goniometrických funkcí Shrnutí Jakub Michálek, Tomáš Kučera Odvodí se základní vztahy pro derivace funkcí sinus a cosinus za pomoci věty o třech itách, odvodí se také několik typických it pomocí
3.10 Rezoluční metoda ve výrokové logice
 3.10. Rezoluční metoda ve výrokové logice [070405-1102 ] 27 3.10 Rezoluční metoda ve výrokové logice Rezoluční metoda rozhoduje, zda daná množina klausulí je splnitelná nebo je nesplnitelná. Tím je také
3.10. Rezoluční metoda ve výrokové logice [070405-1102 ] 27 3.10 Rezoluční metoda ve výrokové logice Rezoluční metoda rozhoduje, zda daná množina klausulí je splnitelná nebo je nesplnitelná. Tím je také
Binární logika Osnova kurzu
 Osnova kurzu 1) Základní pojmy; algoritmizace úlohy 2) Teorie logického řízení 3) Fuzzy logika 4) Algebra blokových schémat 5) Vlastnosti členů regulačních obvodů 6) Vlastnosti regulátorů 7) Stabilita
Osnova kurzu 1) Základní pojmy; algoritmizace úlohy 2) Teorie logického řízení 3) Fuzzy logika 4) Algebra blokových schémat 5) Vlastnosti členů regulačních obvodů 6) Vlastnosti regulátorů 7) Stabilita
1.5.2 Číselné soustavy II
 .. Číselné soustavy II Předpoklady: Př. : Převeď do desítkové soustavy čísla. a) ( ) b) ( ) 4 c) ( ) 6 = + + + = 7 + 9 + = a) = 4 + 4 + 4 = 6 + 4 + = 9 b) 4 = 6 + 6 + 6 = 6 + 6 + = 6 + + = 69. c) 6 Pedagogická
.. Číselné soustavy II Předpoklady: Př. : Převeď do desítkové soustavy čísla. a) ( ) b) ( ) 4 c) ( ) 6 = + + + = 7 + 9 + = a) = 4 + 4 + 4 = 6 + 4 + = 9 b) 4 = 6 + 6 + 6 = 6 + 6 + = 6 + + = 69. c) 6 Pedagogická
CVIČNÝ TEST 37. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15
 CVIČNÝ TEST 37 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Na staré hliněné desce je namalován čtverec
CVIČNÝ TEST 37 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Na staré hliněné desce je namalován čtverec
Derivace funkcí více proměnných
 Derivace funkcí více proměnných Pro studenty FP TUL Martina Šimůnková 16. května 019 1. Derivace podle vektoru jako funkce vektoru. Pro pevně zvolenou funkci f : R d R n a bod a R d budeme zkoumat zobrazení,
Derivace funkcí více proměnných Pro studenty FP TUL Martina Šimůnková 16. května 019 1. Derivace podle vektoru jako funkce vektoru. Pro pevně zvolenou funkci f : R d R n a bod a R d budeme zkoumat zobrazení,
(Cramerovo pravidlo, determinanty, inverzní matice)
 KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
Matematická olympiáda ročník (1998/1999) Komentáře k úlohám druhého kola pro kategorie Z5 až Z7. Zadání úloh Z5 II 1
 1 of 9 20. 1. 2014 12:05 Matematická olympiáda - 48. ročník (1998/1999) Komentáře k úlohám druhého kola pro kategorie Z5 až Z7 Zadání úloh Z5 II 1 Do prostředního kroužku je možné zapsat pouze čísla 8
1 of 9 20. 1. 2014 12:05 Matematická olympiáda - 48. ročník (1998/1999) Komentáře k úlohám druhého kola pro kategorie Z5 až Z7 Zadání úloh Z5 II 1 Do prostředního kroužku je možné zapsat pouze čísla 8
Jednoduchá exponenciální rovnice
 Jednoduchá exponenciální rovnice Z běžné rovnice se exponenciální stává, pokud obsahuje proměnnou v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto: a f(x) = b g(x), kde a, b > 0. Typickým
Jednoduchá exponenciální rovnice Z běžné rovnice se exponenciální stává, pokud obsahuje proměnnou v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto: a f(x) = b g(x), kde a, b > 0. Typickým
Matematický KLOKAN 2007 kategorie Junior (A) 8 (B) 9 (C) 11 (D) 13 (E) 15 AEF? (A) 16 (B) 24 (C) 32 (D) 36 (E) 48
 Matematický KLOKAN 007 kategorie Junior Úlohy za 3 body 1. Lucka, Radek a David mají dohromady 30 míčů. Jestliže Radek dá 5 míčů Davidovi, David dá 4 míče Lucce a Lucka dá míče Radkovi, budou mít oba chlapci
Matematický KLOKAN 007 kategorie Junior Úlohy za 3 body 1. Lucka, Radek a David mají dohromady 30 míčů. Jestliže Radek dá 5 míčů Davidovi, David dá 4 míče Lucce a Lucka dá míče Radkovi, budou mít oba chlapci
CVIČNÝ TEST 49. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15
 CVIČNÝ TEST 49 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST 1 bod 1 Kolik hodnot proměnné a R existuje takových, že diference aritmetické
CVIČNÝ TEST 49 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST 1 bod 1 Kolik hodnot proměnné a R existuje takových, že diference aritmetické
CVIČNÝ TEST 15. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
Úlohy krajského kola kategorie A
 64. ročník matematické olympiády Úlohy krajského kola kategorie A 1. Je dán trojúhelník ABC s tupým úhlem při vrcholu C. Osa o 1 úsečky AC protíná stranu AB v bodě K, osa o 2 úsečky BC protíná stranu AB
64. ročník matematické olympiády Úlohy krajského kola kategorie A 1. Je dán trojúhelník ABC s tupým úhlem při vrcholu C. Osa o 1 úsečky AC protíná stranu AB v bodě K, osa o 2 úsečky BC protíná stranu AB
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Multiplexor a demultiplexor
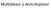 Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Logické řízení. Náplň výuky
 Logické řízení Logické řízení Náplň výuky Historie Logické funkce Booleova algebra Vyjádření Booleových funkcí Minimalizace logických funkcí Logické řídicí obvody Blokové schéma Historie Číslicová technika
Logické řízení Logické řízení Náplň výuky Historie Logické funkce Booleova algebra Vyjádření Booleových funkcí Minimalizace logických funkcí Logické řídicí obvody Blokové schéma Historie Číslicová technika
2.1 Pokyny k otevřeným úlohám. Výsledky pište čitelně do vyznačených bílých polí. 2.2 Pokyny k uzavřeným úlohám
 MATEMATIKA+ DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % 1 Základní informace k zadání zkoušky Didaktický test obsahuje 23 úloh. Časový limit pro řešení didaktického testu
MATEMATIKA+ DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % 1 Základní informace k zadání zkoušky Didaktický test obsahuje 23 úloh. Časový limit pro řešení didaktického testu
Vektory aneb když jedno číslo nestačí
 V posledním studijním textu letošního ročníku si zopakujeme několik poznatků z předchozích sérií a doplníme je novými, abychom si následně mohli spočítat základní pohyby v homogenním tíhovém poli. Vektory
V posledním studijním textu letošního ročníku si zopakujeme několik poznatků z předchozích sérií a doplníme je novými, abychom si následně mohli spočítat základní pohyby v homogenním tíhovém poli. Vektory
CVIČNÝ TEST 19. OBSAH I. Cvičný test 2. Mgr. Kateřina Nováková. II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15
 CVIČNÝ TEST 19 Mgr. Kateřina Nováková OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST 1 Určete, kolikrát je rozdíl čísel 289 a 255 větší než jejich součet.
CVIČNÝ TEST 19 Mgr. Kateřina Nováková OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 13 IV. Záznamový list 15 I. CVIČNÝ TEST 1 Určete, kolikrát je rozdíl čísel 289 a 255 větší než jejich součet.
Výběr báze. u n. a 1 u 1
 Výběr báze Mějme vektorový prostor zadán množinou generátorů. To jest V = M, kde M = {u,..., u n }. Pokud je naším úkolem najít nějakou bázi V, nejpřímočařejším postupem je napsat si vektory jako řádky
Výběr báze Mějme vektorový prostor zadán množinou generátorů. To jest V = M, kde M = {u,..., u n }. Pokud je naším úkolem najít nějakou bázi V, nejpřímočařejším postupem je napsat si vektory jako řádky
Architektura počítačů Logické obvody
 Architektura počítačů Logické obvody http://d3s.mff.cuni.cz/teaching/computer_architecture/ Lubomír Bulej bulej@d3s.mff.cuni.cz CHARLES UNIVERSITY IN PRAGUE faculty of mathematics and physics Digitální
Architektura počítačů Logické obvody http://d3s.mff.cuni.cz/teaching/computer_architecture/ Lubomír Bulej bulej@d3s.mff.cuni.cz CHARLES UNIVERSITY IN PRAGUE faculty of mathematics and physics Digitální
Přijímací zkouška na MFF UK v Praze
 Přijímací zkouška na MFF UK v Praze pro bakalářské studijní programy fyzika, informatika a matematika 017, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé
Přijímací zkouška na MFF UK v Praze pro bakalářské studijní programy fyzika, informatika a matematika 017, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
Architektura počítačů Logické obvody
 Architektura počítačů Logické obvody http://d3s.mff.cuni.cz/teaching/computer_architecture/ Lubomír Bulej bulej@d3s.mff.cuni.cz CHARLES UNIVERSITY IN PRAGUE faculty of mathematics and physics 2/36 Digitální
Architektura počítačů Logické obvody http://d3s.mff.cuni.cz/teaching/computer_architecture/ Lubomír Bulej bulej@d3s.mff.cuni.cz CHARLES UNIVERSITY IN PRAGUE faculty of mathematics and physics 2/36 Digitální
α β ) právě tehdy, když pro jednotlivé hodnoty platí β1 αn βn. Danou relaci nazýváme relace
 Monotónní a Lineární Funkce 1. Relace předcházení a to Uvažujme dva vektory hodnot proměnných α = α,, 1 αn ( ) a β = ( β β ) 1,, n x,, 1 xn. Říkáme, že vekto r hodnot α předchází vektor hodnot β (značíme
Monotónní a Lineární Funkce 1. Relace předcházení a to Uvažujme dva vektory hodnot proměnných α = α,, 1 αn ( ) a β = ( β β ) 1,, n x,, 1 xn. Říkáme, že vekto r hodnot α předchází vektor hodnot β (značíme
Úlohy domácí části I. kola kategorie C
 6. ročník Matematické olympiády Úlohy domácí části I. kola kategorie C 1. Určete všechny dvojice (x, y) reálných čísel, která vyhovují soustavě rovnic (x + )2 = y, (y )2 = x + 8. Řešení. Vzhledem k tomu,
6. ročník Matematické olympiády Úlohy domácí části I. kola kategorie C 1. Určete všechny dvojice (x, y) reálných čísel, která vyhovují soustavě rovnic (x + )2 = y, (y )2 = x + 8. Řešení. Vzhledem k tomu,
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
5. Náhodná veličina. 2. Házíme hrací kostkou dokud nepadne šestka. Náhodná veličina nabývá hodnot z posloupnosti {1, 2, 3,...}.
 5. Náhodná veličina Poznámka: Pro popis náhodného pokusu jsme zavedli pojem jevového pole S jako množiny všech možných výsledků a pravděpodobnost náhodných jevů P jako míru výskytů jednotlivých výsledků.
5. Náhodná veličina Poznámka: Pro popis náhodného pokusu jsme zavedli pojem jevového pole S jako množiny všech možných výsledků a pravděpodobnost náhodných jevů P jako míru výskytů jednotlivých výsledků.
Cvičení 5 - Inverzní matice
 Cvičení 5 - Inverzní matice Pojem Inverzní matice Buď A R n n. A je inverzní maticí k A, pokud platí, AA = A A = I n. Matice A, pokud existuje, je jednoznačná. A stačí nám jen jedna rovnost, aby platilo,
Cvičení 5 - Inverzní matice Pojem Inverzní matice Buď A R n n. A je inverzní maticí k A, pokud platí, AA = A A = I n. Matice A, pokud existuje, je jednoznačná. A stačí nám jen jedna rovnost, aby platilo,
Lingebraické kapitolky - Analytická geometrie
 Lingebraické kapitolky - Analytická geometrie Jaroslav Horáček KAM MFF UK 2013 Co je to vektor? Šipička na tabuli? Ehm? Množina orientovaných úseček majících stejný směr. Prvek vektorového prostoru. V
Lingebraické kapitolky - Analytická geometrie Jaroslav Horáček KAM MFF UK 2013 Co je to vektor? Šipička na tabuli? Ehm? Množina orientovaných úseček majících stejný směr. Prvek vektorového prostoru. V
Sekvenční logické obvody
 Sekvenční logické obvody Sekvenční logické obvody - úvod Sledujme chování jednoduchého logického obvodu se zpětnou vazbou Sekvenční obvody - paměťové členy, klopné obvody flip-flop Asynchronní klopné obvody
Sekvenční logické obvody Sekvenční logické obvody - úvod Sledujme chování jednoduchého logického obvodu se zpětnou vazbou Sekvenční obvody - paměťové členy, klopné obvody flip-flop Asynchronní klopné obvody
6 Skalární součin. u v = (u 1 v 1 ) 2 +(u 2 v 2 ) 2 +(u 3 v 3 ) 2
 6 Skalární součin Skalární součin 1 je operace, která dvěma vektorům (je to tedy binární operace) přiřazuje skalár (v našem případě jde o reálné číslo, obecně se jedná o prvek nějakého tělesa T ). Dovoluje
6 Skalární součin Skalární součin 1 je operace, která dvěma vektorům (je to tedy binární operace) přiřazuje skalár (v našem případě jde o reálné číslo, obecně se jedná o prvek nějakého tělesa T ). Dovoluje
1 Determinanty a inverzní matice
 Determinanty a inverzní matice Definice Necht A = (a ij ) je matice typu (n, n), n 2 Subdeterminantem A ij matice A příslušným pozici (i, j) nazýváme determinant matice, která vznikne z A vypuštěním i-tého
Determinanty a inverzní matice Definice Necht A = (a ij ) je matice typu (n, n), n 2 Subdeterminantem A ij matice A příslušným pozici (i, j) nazýváme determinant matice, která vznikne z A vypuštěním i-tého
2. Určete jádro KerL zobrazení L, tj. nalezněte alespoň jednu jeho bázi a určete jeho dimenzi.
 Řešené příklady z lineární algebry - část 3 Typové příklady s řešením Příklad 3.1: Zobrazení L: P 3 R 23 je zobrazení z prostoru P 3 všech polynomů do stupně 3 (včetně nulového polynomu) do prostoru R
Řešené příklady z lineární algebry - část 3 Typové příklady s řešením Příklad 3.1: Zobrazení L: P 3 R 23 je zobrazení z prostoru P 3 všech polynomů do stupně 3 (včetně nulového polynomu) do prostoru R
Úvod do řešení lineárních rovnic a jejich soustav
 Úvod do řešení lineárních rovnic a jejich soustav Rovnice je zápis rovnosti dvou výrazů, ve kterém máme najít neznámé číslo (neznámou). Po jeho dosazení do rovnice musí platit rovnost. Existuje-li takové
Úvod do řešení lineárních rovnic a jejich soustav Rovnice je zápis rovnosti dvou výrazů, ve kterém máme najít neznámé číslo (neznámou). Po jeho dosazení do rovnice musí platit rovnost. Existuje-li takové
ANALYTICKÁ GEOMETRIE V ROVINĚ
 ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ
 56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
Číselné vektory, matice, determinanty
 Číselné vektory, matice, determinanty Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny
Číselné vektory, matice, determinanty Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny
9 Kolmost vektorových podprostorů
 9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
6.1.2 Operace s komplexními čísly
 6.. Operace s komplexními čísly Předpoklady: 60 Komplexním číslem nazýváme výraz ve tvaru a + bi, kde a, b jsou reálná čísla a i je číslo, pro něž platí i =. V komplexním čísle a + bi se nazývá: číslo
6.. Operace s komplexními čísly Předpoklady: 60 Komplexním číslem nazýváme výraz ve tvaru a + bi, kde a, b jsou reálná čísla a i je číslo, pro něž platí i =. V komplexním čísle a + bi se nazývá: číslo
Figurální čísla, Pascalův trojúhelník, aritmetické posloupnost vyšších řádů
 Figurální čísla, Pascalův trojúhelník, aritmetické posloupnost vyšších řádů Jaroslav Zhouf, PedF UK, Praha Úvod Pascalův trojúhelník je schéma přirozených čísel, která má své využití např. v binomické
Figurální čísla, Pascalův trojúhelník, aritmetické posloupnost vyšších řádů Jaroslav Zhouf, PedF UK, Praha Úvod Pascalův trojúhelník je schéma přirozených čísel, která má své využití např. v binomické
Úlohy krajského kola kategorie A
 62. ročník matematické olympiády Úlohy krajského kola kategorie A 1. Je dáno 21 různých celých čísel takových, že součet libovolných jedenácti z nich je větší než součet deseti ostatních čísel. a) Dokažte,
62. ročník matematické olympiády Úlohy krajského kola kategorie A 1. Je dáno 21 různých celých čísel takových, že součet libovolných jedenácti z nich je větší než součet deseti ostatních čísel. a) Dokažte,
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
VEKTORY. Obrázek 1: Jediný vektor. Souřadnice vektoru jsou jeho průměty do souřadných os x a y u dvojrozměrného vektoru, AB = B A
 VEKTORY Vektorem se rozumí množina všech orientovaných úseček, které mají stejnou velikost, směr a orientaci, což vidíme na obr. 1. Jedna konkrétní orientovaná úsečka se nazývá umístění vektoru na obr.
VEKTORY Vektorem se rozumí množina všech orientovaných úseček, které mají stejnou velikost, směr a orientaci, což vidíme na obr. 1. Jedna konkrétní orientovaná úsečka se nazývá umístění vektoru na obr.
Těleso racionálních funkcí
 Těleso racionálních funkcí Poznámka. V minulém semestru jsme libovolnému oboru integrity sestrojili podílové těleso. Pro libovolné těleso R je okruh polynomů R[x] oborem integrity, máme tedy podílové těleso
Těleso racionálních funkcí Poznámka. V minulém semestru jsme libovolnému oboru integrity sestrojili podílové těleso. Pro libovolné těleso R je okruh polynomů R[x] oborem integrity, máme tedy podílové těleso
Diferenciální rovnice 1
 Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
Lineární algebra : Násobení matic a inverzní matice
 Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 17. března 2014, 12:42 1 2 0.1 Násobení matic Definice 1. Buďte m, n, p N, A
Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 17. března 2014, 12:42 1 2 0.1 Násobení matic Definice 1. Buďte m, n, p N, A
Matematický KLOKAN kategorie Kadet
 Matematický KLOKAN 2009 www.matematickyklokan.net kategorie Kadet Úlohy za body. Hodnota kterého z výrazů je sudé číslo? (A) 2009 (B) 2 + 0 + 0 + 9 (C) 200 9 (D) 200 9 (E) 200 + 9 2. Hvězda na obrázku
Matematický KLOKAN 2009 www.matematickyklokan.net kategorie Kadet Úlohy za body. Hodnota kterého z výrazů je sudé číslo? (A) 2009 (B) 2 + 0 + 0 + 9 (C) 200 9 (D) 200 9 (E) 200 + 9 2. Hvězda na obrázku
Návrh synchronního čítače
 Návrh synchronního čítače Zadání: Navrhněte synchronní čítač mod 7, který čítá vstupní impulsy na vstupu x. Při návrhu použijte klopné obvody typu -K a maximálně třívstupová hradla typu NAND. Řešení: Čítač
Návrh synchronního čítače Zadání: Navrhněte synchronní čítač mod 7, který čítá vstupní impulsy na vstupu x. Při návrhu použijte klopné obvody typu -K a maximálně třívstupová hradla typu NAND. Řešení: Čítač
Necht tedy máme přirozená čísla n, k pod pojmem systém lineárních rovnic rozumíme rovnice ve tvaru
 2. Systémy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic s koeficienty z pole reálných případně komplexních čísel. Uvádíme podmínku pro existenci řešení systému lineárních
2. Systémy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic s koeficienty z pole reálných případně komplexních čísel. Uvádíme podmínku pro existenci řešení systému lineárních
Lineární algebra : Násobení matic a inverzní matice
 Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Lineární algebra : Násobení matic a inverzní matice (8. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
CVIČNÝ TEST 35. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 35 Mgr. Tomáš Kotler OBSAH I. Cvičný test II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST 1 Vypočtěte [( 3 3 ) ( 1 4 5 3 0,5 ) ] : 1 6 1. 1 bod VÝCHOZÍ TEXT K ÚLOZE
CVIČNÝ TEST 35 Mgr. Tomáš Kotler OBSAH I. Cvičný test II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST 1 Vypočtěte [( 3 3 ) ( 1 4 5 3 0,5 ) ] : 1 6 1. 1 bod VÝCHOZÍ TEXT K ÚLOZE
( ) ( ) Negace složených výroků II. Předpoklady:
 1.4.7 Negace složených výroků II Předpoklady: 010405 Pedagogická poznámka: Na začátku hodiny slovně zadávám úkol najít negaci implikace. Teprve po zapsání do třídnice promítám zadání příkladů (kde je v
1.4.7 Negace složených výroků II Předpoklady: 010405 Pedagogická poznámka: Na začátku hodiny slovně zadávám úkol najít negaci implikace. Teprve po zapsání do třídnice promítám zadání příkladů (kde je v
Praha & EU: investujeme do vaší budoucnosti. Daniel Turzík, Miroslava Dubcová,
 E-sbírka příkladů Seminář z matematiky Evropský sociální fond Praha & EU: investujeme do vaší budoucnosti Daniel Turzík, Miroslava Dubcová, Pavla Pavlíková Obsah 1 Úpravy výrazů................................................................
E-sbírka příkladů Seminář z matematiky Evropský sociální fond Praha & EU: investujeme do vaší budoucnosti Daniel Turzík, Miroslava Dubcová, Pavla Pavlíková Obsah 1 Úpravy výrazů................................................................
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)
![Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6) Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)](/thumbs/96/128965676.jpg) 1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
M - Příprava na 1. zápočtový test - třída 3SA
 M - Příprava na 1. zápočtový test - třída 3SA Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento
M - Příprava na 1. zápočtový test - třída 3SA Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento
Booleova algebra. ZákonyBooleovy algebry Vyjádření logických funkcí
 Booleova algebra ZákonyBooleovy algebry Vyjádření logických funkcí pravdivostní tabulka logický výraz seznam indexů vstupních písmen mapa vícerozměrná krychle 30-1-13 O. Novák 1 Booleova algebra Booleova
Booleova algebra ZákonyBooleovy algebry Vyjádření logických funkcí pravdivostní tabulka logický výraz seznam indexů vstupních písmen mapa vícerozměrná krychle 30-1-13 O. Novák 1 Booleova algebra Booleova
Návrh čítače jako automatu
 ávrh čítače jako automatu Domovská URL dokumentu: http://dce.felk.cvut.cz/lsy/cviceni/pdf/citacavrh.pdf Obsah ÁVRH ČÍTAČE JAO AUTOMATU.... SYCHROÍ A ASYCHROÍ AUTOMAT... 2.a. Výstupy automatu mohou být
ávrh čítače jako automatu Domovská URL dokumentu: http://dce.felk.cvut.cz/lsy/cviceni/pdf/citacavrh.pdf Obsah ÁVRH ČÍTAČE JAO AUTOMATU.... SYCHROÍ A ASYCHROÍ AUTOMAT... 2.a. Výstupy automatu mohou být
Matematická analýza III.
 2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
6 Algebra blokových schémat
 6 Algebra blokových schémat Operátorovým přenosem jsme doposud popisovali chování jednotlivých dynamických členů. Nic nám však nebrání, abychom přenosem popsali dynamické vlastnosti složitějších obvodů,
6 Algebra blokových schémat Operátorovým přenosem jsme doposud popisovali chování jednotlivých dynamických členů. Nic nám však nebrání, abychom přenosem popsali dynamické vlastnosti složitějších obvodů,
Y36SAP Y36SAP-2. Logické obvody kombinační Formy popisu Příklad návrhu Sčítačka Kubátová Y36SAP-Logické obvody 1.
 Y36SAP 26.2.27 Y36SAP-2 Logické obvody kombinační Formy popisu Příklad návrhu Sčítačka 27-Kubátová Y36SAP-Logické obvody Logický obvod Vstupy a výstupy nabývají pouze hodnot nebo Kombinační obvod popsán
Y36SAP 26.2.27 Y36SAP-2 Logické obvody kombinační Formy popisu Příklad návrhu Sčítačka 27-Kubátová Y36SAP-Logické obvody Logický obvod Vstupy a výstupy nabývají pouze hodnot nebo Kombinační obvod popsán
M - Příprava na pololetní písemku č. 1
 M - Příprava na pololetní písemku č. 1 Určeno pro třídy 3SA, 3SB. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
M - Příprava na pololetní písemku č. 1 Určeno pro třídy 3SA, 3SB. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
ANTAGONISTICKE HRY 172
 5 ANTAGONISTICKÉ HRY 172 Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku, jejíž výše nezávisí
5 ANTAGONISTICKÉ HRY 172 Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku, jejíž výše nezávisí
VZOROVÝ TEST PRO 1. ROČNÍK (1. A, 3. C)
 VZOROVÝ TEST PRO. ROČNÍK (. A, 3. C) Zjednodušte daný příklad. (a 2 3 b 3 4) 2 (a 2 b 3 8) 3 max. 3 body 2 Ve které z následujících možností je uveden správný postup usměrnění daného zlomku a správný výsledek?
VZOROVÝ TEST PRO. ROČNÍK (. A, 3. C) Zjednodušte daný příklad. (a 2 3 b 3 4) 2 (a 2 b 3 8) 3 max. 3 body 2 Ve které z následujících možností je uveden správný postup usměrnění daného zlomku a správný výsledek?
Obsah. Vymezení použitých pojmů
 Obsah Vymezení použitých pojmů Základní pravidla pro svazování kvadrantů v Karnaughových mapách Základní pravidla pro tvorbu rovnic Postup při zápisu rovnice z Karnaughovy mapy Příklady řešení Vymezení
Obsah Vymezení použitých pojmů Základní pravidla pro svazování kvadrantů v Karnaughových mapách Základní pravidla pro tvorbu rovnic Postup při zápisu rovnice z Karnaughovy mapy Příklady řešení Vymezení
Dynamika vázaných soustav těles
 Dynamika vázaných soustav těles Většina strojů a strojních zařízení, s nimiž se setkáváme v praxi, lze považovat za soustavy těles. Složitost dané soustavy závisí na druhu řešeného případu. Základem pro
Dynamika vázaných soustav těles Většina strojů a strojních zařízení, s nimiž se setkáváme v praxi, lze považovat za soustavy těles. Složitost dané soustavy závisí na druhu řešeného případu. Základem pro
5.3. Implicitní funkce a její derivace
 Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu
![1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu 1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu](/thumbs/102/155926571.jpg) [M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
[M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
Spojování výroků (podmínek) logickými spojkami
 Spojování výroků (podmínek) logickými spojkami Spojování výroků logickými spojkami a) Konjunkce - spojení A B; Pravdivostní tabulka konjunkce A B A B 0 0 0 0 1 0 1 0 0 1 1 1 AND; A a současně B Konjunkce
Spojování výroků (podmínek) logickými spojkami Spojování výroků logickými spojkami a) Konjunkce - spojení A B; Pravdivostní tabulka konjunkce A B A B 0 0 0 0 1 0 1 0 0 1 1 1 AND; A a současně B Konjunkce
Řešení úloh z TSP MU SADY S 1
 Řešení úloh z TSP MU SADY S 1 projekt RESENI-TSP.CZ úlohy jsou vybírány z dříve použitých TSP MU autoři řešení jsou zkušení lektoři vzdělávací agentury Kurzy-Fido.cz Masarykova univerzita nabízí uchazečům
Řešení úloh z TSP MU SADY S 1 projekt RESENI-TSP.CZ úlohy jsou vybírány z dříve použitých TSP MU autoři řešení jsou zkušení lektoři vzdělávací agentury Kurzy-Fido.cz Masarykova univerzita nabízí uchazečům
