VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ. ING. JIŘÍ KYTÝR, CSc. ING. PETR FRANTÍK, Ph.D. STATIKA I MODUL BD03-MO1 ROZŠÍŘENÝ PRŮVODCE
|
|
|
- Vojtěch Mareš
- před 8 lety
- Počet zobrazení:
Transkript
1 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ ING. JIŘÍ KYTÝR, CSc. ING. PETR FRANTÍK, Ph.D. STATIKA I MODUL BD3-MO ROZŠÍŘENÝ PRŮVODCE STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA
2 Statika I Vážení uživateé tohoto učebního textu, předožená verze této učební pomůcky pně odpovídá původnímu záměru a uzavřené icenční smouvě na rozšířeného průvodce v rozsahu 3 stran textu. Obsahuje proto pouze zákadní partie učební átky. Během vytváření opory se ukázaa vhodnost rozšířit učební text nad rámec icenční smouvy, což si však vyžádao mnohem deší čas na zpracování. Dopňkové partie se nepodařio ve vymezeném čase dokončit a zůstay zčásti rozpracovány, což se jevio jako nekvaitní zpracování a vrhao špatné světo na ceé dío. V této nové verzi byy probematické části úpně vyřazeny a učební pomůcka je tedy bez závad. Pode časových možností se budeme snažit dopňková témata dokončit a připojit je ke stávajícímu textu, abyste měi možnost pně využívat učební pomůcku pro Vaše studium. V Brně dne Autoři Jiří Kytýr, Petr Frantík, Brno 5 - (5) -
3 Obsah OBSAH Úvod...5. Cíe...5. Požadované znaosti Doba potřebná ke studiu Kíčová sova...5 Úvod do statiky stavebních konstrukcí...7. Prutové konstrukce Výpočet přetvoření prutových soustav Virtuání veičiny a virtuání práce Virtuání práce vnějších si Virtuání práce vnitřních si Lagrangeův princip virtuáních prací Věty o vzájemnosti virtuáních prací Bettiho věta Maxweovy věty Výpočet deformací metodou jednotkových si Zjednodušení výpočtu deformací pnostěnných nosníků Vereščaginovo pravido Výpočet deformací příhradových soustav Iustrující příkad... 4 Siová metoda Stupeň statické neurčitosti Řešení rovinného rámu Obecně řešený příkad Kanonické rovnice Výpočet přetvárných součiniteů Určení vnitřních si Iustrující příkad Deformační zatížení rámu Viv změny tepoty Dané popuštění podpor rámu Řešení spojitého nosníku Deformační zatížení Obecný tvar třímomentové rovnice Oboustranně vetknutý nosník osově zatížený Příkad řešení spojitého nosníku Tabuky Studijní prameny Seznam použité iteratury Seznam dopňkové studijní iteratury Odkazy na daší studijní zdroje a prameny (5) -
4 Statika I - 4 (5) -
5 Úvod Úvod. Cíe Úkoem předmětu Statika I je zvádnout řešení prutových konstrukcí zákadní metodou, která se nazývá siová metoda. Není sice prakticky vhodná pro řešení rozsáhejších staticky neurčitých prutových konstrukcí, ae je vemi přehedná a poskytuje řešení zákadních přetvárně určitých případů (primárního i sekundárního stavu) pro anaýzu prutových konstrukcí daší metodou, a to deformační metodou, která bude obsahem předmětu Statika II. Naším cíem bude řešení nosných staticky neurčitých prutových stavebních konstrukcí a získání průběhů vnitřních si i sožek reakcí jako prostředek pro jejich dimenzování pode toho, z jakého materiáu jsou vytvořeny.. Požadované znaosti Ve Statice I se navazuje zejména na znaosti získané v předmětu Zákady stavební mechaniky (řešení průběhů vnitřních si) a v předmětu Pružnost a pevnost. Studenti by měi být obeznámeni se zákadními operacemi z integráního počtu. Z matematického aparátu využijeme zejména goniometrické funkce, vektorový a maticový počet i řešení soustav ineárních agebraických rovnic..3 Doba potřebná ke studiu Modu představuje rozšířený průvodce a obsahuje zákadní átku probíranou v průběhu téměř ceého semestru. Doba potřebná k nastudování jednotivých kapito či odstavců se iší od někoika desítek minut až po hodiny. Záeží zejména na dřívější průpravě studenta ve výše citovaných předcházejících předmětech, ae i na obtížnosti daného tématu. Potřebná doba ke studiu činí asi 4 až 5 hodin..4 Kíčová sova mechanika, statika, sía, reakce, interakce, rovnováha, poddajnost, tuhost, vektor, matice, modu pružnosti, momenty setrvačnosti, transformace, prut, prutová soustava, nosník, rám, příhradová konstrukce - 5 (5) -
6 Statika I - 6 (5) -
7 Úvod do statiky stavebních konstrukcí Úvod do statiky stavebních konstrukcí Statika stavebních konstrukcí je nauka o výpočtech stavebních konstrukcí. Každá stavební konstrukce musí bezpečně přenést veškeré zatížení, nesmí se přitom porušit, nesmí doznat nepřípustných tvarových změn a musí být stabiní. Část konstrukce, zajišťující potřebnou odonost a tuhost stavebního día, nazýváme nosnou konstrukcí. Nosná konstrukce sestává z řady různých prvků. V předmětu Statika stavebních konstrukcí se omezujeme na anaýzu pouze takových konstrukcí, jejichž statický mode ze vytvořit výhradně z prutů (obr..). Nazýváme je prutovými soustavami. V daších úvahách budeme předpokádat dokonae ineárně pružný materiá. V Zákadech stavební mechaniky jsme řešii staticky určité prutové konstrukce, k jejichž anaýze postačují statické podmínky rovnováhy. Obsahem statiky stavebních konstrukcí jsou především výpočty staticky neurčitých prutových konstrukcí. K jejich řešení už nevystačíme s podmínkami rovnováhy, ae musíme předepsat ještě přetvárné podmínky. K řešení staticky neurčitých konstrukcí se používají dvě zákadní metody, a to metoda siová (probírá se ve Statice I) a metoda deformační (je obsahem předmětu Statika II). Každá konstrukce se účinkem zatížení přetvoří. Přetvoření (deformace) se projeví posuny a pootočeními jednotivých částí stavební konstrukce. Přetvoření jsou většinou, vzhedem k rozměrům konstrukce, vemi maá. Obr..: Rovinný uzavřený rám. Prutové konstrukce Rám je prutová soustava vytvořená spojením jednotivých prutů. Ve statickém modeu ideaizujeme jak nosné prvky, tak i jejich spojení a spoupůsobení. Místo, kde se pruty spojují, nazýváme uze (styčník). Pruty bývají většinou v uzu spojeny monoiticky (tuze), anebo mohou být také připojeny koubem. Tuhé spojení (obr..a) zaručuje stejné přemístění (posunutí i pootočení) všech konců připojených prutů při deformaci a přenáší ohybové momenty. Koubové spojení (obr..b) zaručuje pouze stejné posunutí, pootočení konců připojených prutů jsou nezávisá a ohybové momenty jsou nuové. U rovinného rámu (obr..) eží v jedné rovině střednice všech prutů, zatížení, reakce a interakce a rovněž jedna z havních centráních os setrvačnosti průřezů všech prutů. Rám je typickým představiteem staticky neurčité prutové konstrukce. Jako speciání případ rámu se vyskytuje spojitý nosník (obr..3) a příhradový nosník (obr..4). - 7 (5) -
8 Statika I Obr..: Uze (styčník) rovinného rámu Rozišujeme rámy s pruty přímými (obr..5 a.7) nebo zakřivenými (obr..6), rámy pravoúhé (obr..5 a.8) či kosoúhé (obr..7), jednoduché (obr..7), sdružené (obr..6) nebo patrové (obr..5,.8 a.9), otevřené (obr..6 a.7) či uzavřené (obr..8,.9 a.), rámy s neprůběžnými pruty (obr..8 a.9) aj. Obr..3: Spojitý pnostěnný nosník Obr..4: Spojitý příhradový nosník Z termínů používaných u prutových konstrukcí uveďme nejzákadnější. Soup (stojka) je svisý prut, příče (trám) je vodorovný prut. Prut bývá nejčastěji přímý, může být i omený či zakřivený (obouk). Vnější vazby (obr..5) mohou být jednonásobné (kyvný prut, posuvná koubová podpora), dvojnásobné (neposuvný koub, posuvné vetknutí), trojnásobné (dokonaé vetknutí). Obr..5: Patrový rám Obr..6: Sdružený rám Obr..7: Jednoduchý s oboukovou příčí kosoúhý rám - 8 (5) -
9 Úvod do statiky stavebních konstrukcí Obr..8: Patrový rám Obr..9: Patrový rám Obr..: Vierendeeův s neprůběžnou příčí s neprůběžným soupem rámový nosník Otázky. Čím se zabývá statika stavebních konstrukcí?. Charakterizujte rovinnou prutovou soustavu. 3. Čím se iší rám, spojitý nosník a příhradový nosník? 4. Co zajišťuje monoitické a koubové spojení prutů ve styčníku? 5. Funkce vnitřního koubu v prutové soustavě. Shrnutí V této úvodní kapitoce jsme si vymezii obsah předmětu a naznačii rozděení rámových a ostatních prutových konstrukcí. - 9 (5) -
10 Statika I - (5) -
11 Výpočet přetvoření prutových soustav 3 Výpočet přetvoření prutových soustav Při vyšetřování nosných stavebních konstrukcí sedujeme nejen průběhy vnitřních si a napětí, ae také deformace (přetvoření). Ty je důežité posoudit jak z hediska funkčnosti konstrukce, tak i z hediska estetického, aby nedocházeo k viditeným geometrickým změnám. V některých případech postačí určit diskrétní hodnoty sožek přemístění (posuny, potočení), jindy potřebujeme znát průběh ohybové čáry ceého prutu. Obr. 3.: Deformace rovinné pnostěnné konzoy Pro řešení přetvoření staticky určitých prutových konstrukcí (obr. 3.) se používají tyto metody: apikace principu virtuáních prací, tzv. metoda jednotkových si, umožňující určit sožky přemístění v diskrétních bodech pnostěnných i příhradových nosníků; metoda je předmětem této kapitoy a její princip je využit při řešení staticky neurčitých prutových soustav siovou metodou (viz kapitoa 4), Mohrova metoda pro získání diskrétních hodnot deformací, probraná v předmětu Pružnost a pevnost, metoda integrace diferenciání rovnice ohybové čáry (popř. s Cebschovou úpravou integračního postupu) pro získání funkcí ohybové čáry nebo skonů tečen k ohybové čáře, probraná rovněž v předmětu Pružnost a pevnost, Castigianova metoda vycházející z minima přetvárné práce, přičemž při upatnění pomocné dopňkové síy se tato metoda ztotožní s metodou jednotkových si. Obr. 3.: Virtuání práce síy a momentu - (5) -
12 Statika I 3. Virtuání veičiny a virtuání práce Virtuání veičiny (označené symboem nebo později pruhem) představují virtuání přetvoření a virtuání zatížení, resp. virtuání práci. Virtuání přetvoření (s, ϕ) je vemi maé, fiktivní, myšené, ae fyzicky možné, vyvoané virtuáním zatížením (obr. 3.a). Nastává v souadu s vnějšími a vnitřními vazbami. Virtuání zatížení (F, M) je fiktivní, myšené, ae možné zatížení, neomezené veikosti (nejčastěji voené jednotkové), viz obr. 3.b. Virtuání práce síy (resp. momentu) je práce virtuání síy F (resp. virtuáního momentu M) na skutečném posunutí s (resp. pootočení ϕ) daná vztahem L = F s = Fs. (3.) Virtuání práce reáné síy F (resp. momentu M) na virtuáním posunutí s (resp. pootočení ϕ) je L = F s = Fs. (3.) Virtuání práce má kadnou hodnotu, je-i souhasný smys síy a deformace. V daším textu jsou virtuání veičiny z důvodu odišení obecné deformace (sožky přemístění) od symbou virtuáních veičin označeny pruhem, tedy F = F, s = s =, L = L = L. (3.3) Obr. 3.3: Rovinný nosník 3.. Virtuání práce vnějších si Soustava vnějších virtuáních si, tj. zatížení F i, M i či reakcí R rx, Rrz, M r (obr. 3.3), koná virtuání práci na skutečných deformacích ( i, ϕ i, u r, w r, ϕ r ) vyvoaných ibovoným skutečným siovým zatížením (F, M, q, n, m) nebo deformačním zatížením (popuštěním) od virtuáního zatížení pode vztahu L ez Fi i + = M φ, (3.4) i i - (5) -
13 Výpočet přetvoření prutových soustav od virtuáních sožek reakcí (u pružně poddajných podpor nebo u popuštění) ve tvaru Ler = ( Rrxur + Rrxwr + M rϕ r ) = Rr r, (3.5) takže ceková virtuání práce vnějších (externích) si je L e = Lez + Ler = Fi i + M iϕi + Rr r. (3.6) Obr. 3.4: Přetvoření prvku přímého nosníku - 3 (5) -
14 Statika I 3.. Virtuání práce vnitřních si Virtuání zatížení ( F i, M i) vyvoá v ibovoném průřezu x (obr. 3.4a) virtuání vnitřní síy N, V, M. Kadné sožky virtuáních vnitřních si uvažujeme pode konvence (obr. 3.4d), přičemž předpokádáme N = N, V = V, M = M. Kadné virtuání vnitřní síy N, V, M konají zápornou virtuání práci na kadných deformacích u, w, ϕ (obr. 3.4b) od skutečného zatížení (siového či deformačního), takže L = i ( N u + V w+ M ϕ ). (3.7) Přetvoření prutového eementu déky dx od vivu skutečného zatížení (vnitřních si N, V, M a změny tepoty) vyšetřujeme samostatně (obr. 3.4f h) na osové namáhání (viv normáové síy a rovnoměrné změny tepoty), příčný smyk (viv posouvající síy), ohyb (viv ohybového momentu a nerovnoměrné změny tepoty). Osové namáhání Při osovém namáhání (obr. 3.4f, c) je cekové prodoužení od tahové osové síy N a od rovnoměrného otepení t dáno výrazem N dx dx = u = un + ut = + α t tdx, (3.8) EA kde A je průřezová pocha prutu, E modu pružnosti v tahu a taku, α t součinite tepené roztažnosti, t je přírůstek tepoty pro rovnoměrnou změnu. Příčný smyk U příčného smyku patí pro vzájemné příčné posunutí od posouvající síy V (obr. 3.4g) w = γ dx, takže nakonec získáme vztah V dx w = κ, (3.9) GA kde G je modu pružnosti ve smyku, κ koeficient vivu nerovnoměrného rozděení smykového napětí po výšce průřezu (např. pro obdéník κ =, a pro kruh κ = 35/7) a A skutečná průřezová pocha prutu. Přetvoření vivem posouvající síy se často u běžných prutů zanedbává, nutno ho však respektovat u nosníků vysokých (h >> b) a smykově poddajných. Ohyb Pro viv ohybu vyšetříme vzájemné pootočení koncových průřezů od ohybového momentu M = M y (obr. 3.4h). Protože patí dx = ρ dϕ, můžeme z poměrného protažení ε x = dx/dx = z/ρ při uvažování obecného vákna ve vzdáenosti z a Hookova zákona vyjádřit přísušnou sožku od ohybového momentu. Pootočení koncových průřezů od vivu ineární nerovnoměrné změny tepoty (obr. 3.4c) při konvenci stanovení tepotního rozdíu t = t d t h poskytne druhou sožku pootočení. - 4 (5) -
15 Výpočet přetvoření prutových soustav Cekové vzájemné pootočení od vivu ohybového momentu a nerovnoměrné změny tepoty je pak M dx αt t dx dϕ = dϕ M + dϕt = +, (3.) EI h kde I y = I je moment setrvačnosti průřezu k těžištní ose y a h výška průřezu. Virtuání práci L i virtuáních vnitřních si N, V, M pode (3.7) pak získáme s využitím (3.8), (3.9) a (3.) pro přímý prut proměnného průřezu déky ve tvaru L N N VV M M i = dx + κ dx + dx + Nα t tdx + EA GA EI t Mαt h U zakřiveného prutu se zamění déka za s a dx za ds, takže můžeme napsat dx. (3.) s s s s s N N VV M M t Li = ds + κ ds + ds + Nα t tds + Mαt ds. EA GA EI h (3.) Poznamenejme, že stejnou virtuání práci konají skutečné vnitřní síy N, V, M od skutečného zatížení na virtuáních přetvořeních u, w, ϕ od virtuáního zatížení. 3. Lagrangeův princip virtuáních prací Lagrangeův princip je formuován pro virtuání přemístění (posuny). Je jedním ze zákadních zákonů mechaniky (vypývají z něho statické podmínky rovnováhy obecné prostorové soustavy si). Pro tuhé těeso ho formuova J. L. Lagrange (736 83) takto: Virtuání práce rovnovážné soustavy si působící na tuhé těeso je při ibovoném virtuáním přemístění těesa rovna nue (L = ). V 9. stoetí by tento princip rozšířen i na pružná těesa: Při ibovoném virtuáním přetvoření pružného těesa, nacházejícího se v rovnovážném stavu, je součet virtuáních prací všech vnějších a vnitřních si, působících na těeso, roven nue. Patí tedy neboi L L e + L =, (3.3) = i Le = L i. (3.4) Po dosazení (3.6) a (3.) do (3.4) obdržíme po úpravě pro zakřivený prut = F + i i M ϕ = i i s s s s s N N VV M M ds + ds ds N t tds EA κ + GA + α EI + t Mαt ds R r, r h (3.5) - 5 (5) -
16 Statika I 3.3 Věty o vzájemnosti virtuáních prací 3.3. Bettiho věta Virtuání práce jedné soustavy vnějších si F,, F i,, F n (obr. 3.5), pracujících na posunutích,, i,, n, vyvoaných druhou soustavou vnějších si F I,, F k,, F m, je rovna virtuání práci druhé soustavy si, působících na posunutích I,, k,, m, vyvoaných první soustavou si, tedy n i= m F = F. (3.6) i i k= k k Obr. 3.5: K Bettiho větě Pro virtuání práci momentů pak anaogicky patí n i= n M ϕ = M ϕ. (3.7) i i i= k k Podobné vztahy ze rovněž napsat pro spojité zatížení příčné q, osové n či momentové m Maxweovy věty Maxweovy věty představují zváštní případy Bettiho věty. První Maxweova věta se týká vzájemnosti posunutí. Uvažujme pode obr. 3.5 v rovnici (3.6) jako první soustavu F i = a druhou soustavu F k =. Pak pro vzájemná posunutí dvou ibovoných průřezů i, k patí ik = ki. (3.8) Druhá Maxweova věta pojednává o vzájemnosti pootočení. Jako první soustava se uvažuje M i = a druhá soustava M k =. Pro vzájemná pootočení dvou ibovoných průřezů i, k patí ϕ ik = ϕ ki, takže při obecném označení deformace symboem získáme vztah (3.8). Třetí Maxweova věta se týká vzájemnosti posunutí a pootočení. Jako první soustava se uvažuje F i = a druhá soustava M k =. Pro vzájemný vztah mezi posunutím a pootočením dvou ibovoných průřezů i, k pode Bettiho věty patí ik = ϕ ki, což představuje čísenou rovnost mezi posunutím ik průřezu i od M k = v průřezu k a pootočením ϕ ki průřezu k od F i = v průřezu i. Při obecném označení deformace symboem opět získáme vztah (3.8). Ze vztahu (3.8) vypývá symetrie soustavy rovnic či matice poddajnosti v siové metodě. - 6 (5) -
17 Výpočet přetvoření prutových soustav Obr. 3.6: Výpočet posunutí a pootočení průřezu rovinného pnostěnného nosníku 3.4 Výpočet deformací metodou jednotkových si Touto metodou ze vypočítat diskrétní hodnotu deformace, tj. v rovinné úoze posunutí u, w a pootočení ϕ daného průřezu nosníku (obr. 3.6). Je nutné uvažovat dva zatěžovací stavy, a to stav skutečný (způsobující přetvoření nosníku) se zatížením siovým (F, M, q, n, m) resp. deformačním (popuštění podpor či tepota) pode obr. 3.6a a stav virtuání s jednotkovou siou F m = (obr. 3.6b) působící ve směru hedaného posunutí m nebo s jednotkovým momentem M m = (obr. 3.6c) působícím ve směru hedaného pootočení ϕ m (obecně rovněž označeného m ). Z rovnice (3.5) pak po rozepsání posedního čenu pode výrazu (3.5) získáme obecně pro zakřivený prut Maxweův Mohrův vztah m = r s ( R N N ds + EA rx u r + R s rz VV κ ds + GA r s w + M r ϕ ), r M M ds + EI s Nα t ds + t s t Mαt h ds (3.9) kde m je hedané posunutí u m, w m (resp. pootočení ϕ m ), N, V, M jsou vnitřní síy od skutečného zatížení, u r, w r, ϕ r jsou dané sožky popuštění podporového průřezu r, N, V, M jsou virtuání vnitřní síy od virtuáního zatížení F = m - 7 (5) -
18 Statika I (resp. M m = ) působícího v průřezu m, R rx, Rrz, M r jsou virtuání sožky reakcí podporového průřezu r, vyvoané virtuáním zatížením F = (resp. M m = ) působícím v průřezu m, A je průřezová pocha prutu, I je moment setrvačnosti průřezu, h je jeho výška, E představuje modu pružnosti v tahu a taku, G je modu pružnosti ve smyku, t je rovnoměrné otepení průřezu, t tepotní rozdí doních a horních váken průřezu, α t součinite tepené roztažnosti a κ je koeficient vivu nerovnoměrného rozděení smykového napětí Zjednodušení výpočtu deformací pnostěnných nosníků Maxweův Mohrův vztah (3.9) zahrnuje viv všech tří sožek výsednice vnitřních si rovinného prutu od siového zatížení i obou typů deformačního zatížení (rovnoměrné a nerovnoměrné změny tepoty a nepružného popuštění podpor). Ke zjednodušení ze přihédnout v případě, je-i rovinná prutová soustava bez vivu deformačního zatížení namáhaná převážně na ohyb (nosníky, rámy), takže můžeme zanedbat virtuání práci od normáových a posouvajících si N, V. Pak z rovnice (3.9) zůstane pouze s M M m = ds. (3.) EI Je-i navíc rovinná prutová soustava sožená pouze z přímých prizmatických prutů s různými průřezovými charakteristikami (momentem setrvačnosti I j ), pak vztah (3.) přejde na tvar p j m = M Mdx j. E I (3.) j= j j Výpočet určitého integráu v (3.) ze součinu dvou funkcí M(x) od skutečného siového zatížení (F, M, q, n, m) a M (x) od virtuáního zatížení F m = (resp. M = ) ze provést těmito způsoby: m anayticky integrací z definovaných funkcí M(x), M (x), přičemž obecně ze uvažovat i ohybovou tuhost jako funkci EI(x), numerickou integrací (např. apikací Simpsonova pravida) pro pruty rovněž s obecně proměnnou ohybovou tuhostí (EI konst.), užitím tabuky 5. pro pruty konstantního průřezu (EI = konst.), apikací Vereščaginova pravida pro EI = konst. m Obr. 3.7: Vereščaginovo pravido - 8 (5) -
19 Výpočet přetvoření prutových soustav 3.4. Vereščaginovo pravido Je-i funkce M(x) ibovoná spojitá hadká funkce a M (x) ineární funkce (od F =, M = ) pode obr. 3.7, pak patí s t M Mds = AM M. (3.) Sovně to ze vyjádřit: Hodnota integráu ze součinu dvou uvedených funkcí je rovna součinu pošného obsahu momentového obrazce od ibovoné funkce a pořadnice u ineární funkce v místě těžiště obrazce s ibovonou funkcí. Vereščaginovo pravido ze apikovat i pro jiné funkce spňující výše uvedené předpokady, např. pro funkce normáových či posouvajících si. Pošné obsahy obrazců najdeme např. v tabuce 3. druhého moduu Zákadů stavební mechaniky (BD MO). Sožitější obrazce (obr. 3.8) rozkádáme na jednodušší obrazce a apikujeme princip superpozice, takže hodnota integráu je s M Mds = M M ds + M M ds + M M ds + M M ds. (3.3) s s Pro každý integrá na pravé straně rovnice (3.3) můžeme apikovat výpočet pomocí Vereščaginova pravida (3.). s s Obr. 3.8: Sožitější tvary momentových obrazců Výpočet deformací příhradových soustav Zváštností příhradových soustav (obr. 3.9) je, že u nich vyšetřujeme jen sožky posunutí u, w styčníků a v prutech vznikají pouze normáové síy N. Potom z Maxweova Mohrova vztahu (3.9) zůstane (při uvažování i deformačního zatížení) jen první a čtvrtý integrá a suma. Vzhedem ke konstantním funkcím normáových si po prutech pro sožku posunutí styčníku m (ve směru x, z) patí = m s N N EA d s + s Nα t t ds r R = r r p j= N j N j EA j j + p j= N α t j t j j r R (3.4) kde pro j =,,, p je N j osová sía prutu j od skutečného zatížení, r dané popuštění podpory, N j osová sía prutu j od virtuání síy F =, R r reakce m r r - 9 (5) -
20 Statika I vnější vazby od F m =, j déka prutu j, A j průřezová pocha prutu j, t j rovnoměrná změna tepoty prutu j a popuštění r se týká vodorovného a svisého posunu. Výsedné posunutí styčníku (obr. 3.9d) se určí z pravoúhých sožek. Obr. 3.9: Přetvoření rovinného příhradového nosníku 3.5 Iustrující příkad Jako ukázku apikace principu virtuáních prací pro řešení přetvoření pnostěnných nosníků a soustav si uvedeme případ omené konzoy. Příkad 3. Zadání Stanovte výsedné posunutí c a pootočení ϕ c průřezu c omeného konzoového nosníku (obr. 3.) s pruty konstantního obdéníkového průřezu,,3 m o dékách = 3 m, = m. Zatížení má intenzitu q = knm, modu pružnosti má hodnotu E = 3,5 GPa. Řešení Směr posunutí c průřezu c nosníku je neznámý, takže neznáme směr upatnění jednotkové virtuání síy. Proto vyjdeme z výpočtu dvou pravoúhých sožek posunutí c,v a c,h. Při řešení zanedbáme viv normáových a posouvajících si. Postačí tedy vykresit průběhy ohybových momentů, a to od zadaného spojitého rovnoměrné- - (5) -
21 Výpočet přetvoření prutových soustav ho zatížení pode obr. 3.a s průběhy v obr. 3.b a dáe samostatně tři průběhy od jednotkových si (svisé a vodorovné) a jednotkového momentu (obr. 3.c e). Vzhedem k jednoduchým průběhům sestavíme nejprve výraz pro výpočet deformace pomocí obecně označených veičin a násedně ho vyčísíme (přitom použijeme moment setrvačnosti určený ze zadaných rozměrů průřezu hodnotou I = 4,5 4 m 4 ). K řešení použijeme vztahy z tabuky 5. a Vereščaginovo pravido. Svisé posunutí c,v průřezu c Obr. 3.: Lomený konzoový nosník Použijeme momentové obrazce M (obr. 3.b) a M (obr. 3.c). Pak 3 q q q c, v = ( ) ( ) = ( + 4 ), EI 4 + 8EI 3 ( + 4 3) c, v = =,957m( ) ,5 4,5 Vodorovné posunutí c,h průřezu c S přihédnutím k momentovým obrazcům M (obr. 3.b) a M (obr. 3.d) dostaneme q EI ( ) c, h = = q, 4EI 3 c, h = =,65m( ) ,5 4,5 Výsedné posunutí c průřezu c Výsedné posunutí získáme vektorovým součtem sožek o veikosti c,v a c,h (obr. 3.f). Má veikost - (5) -
22 Statika I = + c c, h c, v a směr α c, pro nějž patí vztahy Číseně pak je c, h c, v cosα c =, sinαc =. c o ' c =,65 +,957 =,38m, α c = c Pootočení ϕ c průřezu c Využijeme momentové obrazce M (obr. 3.b) a M (obr. 3.e), takže q q q φ c = ( ) ( ) = ( + 3 ) EI 3 +, 6EI ( + 3 3) ϕ c = 6 6 3,5 4,5 4 = 5,4 3 rad, ϕ = c ' '' 74 (ve směru jednotkového momentu). Otázky. Vysvětete pojem virtuáního přetvoření, zatížení a virtuání práce.. Jak se určí virtuání práce vnějších a vnitřních si přímého prutu? 3. Princip virtuáních prací. 4. Bettiho věta o vzájemnosti virtuáních prací. 5. Maxweovy věty. 6. Maxweův Mohrův vztah pro výpočet přetvoření prutové konstrukce. 7. Jak se určí posunutí či pootočení průřezu pnostěnného nosníku? 8. Vereščaginovo pravido. 9. Jak se určí posunutí styčníku rovinného příhradového nosníku? Shrnutí Naučii jsme se určovat sožky přemístění (posunutí a pootočení) v diskrétních bodech pnostěnných i příhradových nosníků metodou jednotkových si, tj. apikací principu virtuáních prací. Proto jsme si vysvětii zákadní pojmy o virtuání práci a odvodii ji pro přímý rovinný prut. Pomocí Lagrangeova principu virtuáních prací jsme získai Maxweův Mohrův vztah pro výpočet deformací metodou jednotkových si. Uvedi jsme si zjednodušení pro pnostěnné i příhradové nosníky a pomůcku pro vyčísení integráu Vereščaginovo pravido. Získané znaosti jsme použii při řešení numerického příkadu. - (5) -
23 Siová metoda 4 Siová metoda Siová metoda je jedna ze dvou zákadních metod pro řešení staticky neurčitých prutových konstrukcí. U této metody se za neznámé voí siové veičiny (reakce, sožky výsednice vnitřních si), proto se metoda označuje jako přímá. Počet neznámých veičin a současně počet řešených rovnic určuje stupeň statické neurčitosti. Vede statických podmínek rovnováhy se navíc sestavují přetvárné (deformační) podmínky. Jako zákadní soustava se voí prutová soustava staticky určitá po odstranění přebytečných vazeb či interakcí. Siová metoda je vhodná pro řešení jednoduchých prutových soustav (s nízkým stupněm statické neurčitosti), není nevhodná k agoritmizaci, ae je nezbytná k řešení prutů zákadní přetvárně určité soustavy u deformační metody (viz předmět Statika II). Postup výpočtu prutové soustavy siovou metodou je takový, že na zákadní soustavě sestavíme deformační podmínky, čímž získáme soustavu ineárních agebraických rovnic. Jejich řešením obdržíme staticky neurčité veičiny a upatněním tří statických podmínek rovnováhy (v rovině) vyřešíme na zákadní soustavě zbývající sožky reakcí. Při všech známých sožkách reakcí běžným postupem jako u staticky určité prutové soustavy určíme průběhy vnitřních si N, V, M. Na počátku řešení staticky neurčité prutové konstrukce musí být předem zvoené (odhadnuté) rozměry průřezů všech prutů. Při dimenzování prutů na konkrétní průběhy vnitřních si se pak ukáže, zda byy zvoeny vhodně. V opačném případě se musí provést úprava průřezových poch a provést opravný výpočet. Obr. 4.: Staticky určitý, přeurčitý a neurčitý omený nosník 4. Stupeň statické neurčitosti Rovinná prutová soustava (obr. 4.) uvoněná z podporových vazeb tvoří spoečně s daným zatížením a jím vyvoanými sožkami reakcí podporových vazeb rovnovážnou rovinnou soustavu si. V rovině však můžeme sestavit pouze tři statické podmínky rovnováhy. Je-i sožek reakcí více, nestačí podmínky rovnováhy k jejich určení. Označíme-i a počet jednoduchých vnějších vazeb (event. převedených na jednoduché), je otevřená rovinná prutová soustava zevně staticky (a kinematicky) určitá, když a = 3, staticky neurčitá (a kinematicky přeurčitá), když a > 3 a staticky přeurčitá (a kinematicky neurčitá, tj. mechanismus), je-i a < (5) -
24 Statika I Obr. 4.: Vnitřní kuby Statickou neurčitost snižují vožené vnitřní kouby (obr. 4.). Jednoduchý vnitřní koub spojující dva pruty přidává jednu statickou podmínku M k =. Vnitřní koub spojující navzájem n prutů pak přidává n statických podmínek a nahrazuje n jednoduchých koubů. Obr. 4.3: Jednoduchý uzavřený rám Každá uzavřená část prutové soustavy (obr. 4.3) představuje v rovině tři neznámé sožky výsednice vnitřních si N, V, M. Rozříznutím uzavřené části a nahrazením třemi sožkami interakcí v obou řezem rozděených částech se tedy objeví tři neznámé siové veičiny. Stupeň statické neurčitosti rovinné prutové soustavy je tedy roven počtu nadbytečných staticky neurčitých veičin soustavy (podporové reakce, sožky N, V, M v ibovoném průřezu). Určíme ho obecně ze vztahu n s = (a 3) + 3u p k, (4.) kde a je počet sožek reakcí vnějších vazeb, u počet uzavřených částí, p k počet jednoduchých vnitřních koubů. Výraz a 3 představuje zevní statickou neurčitost a výraz 3u p k vnitřní statickou neurčitost. Odstraněním všech přebytečných veičin se vytvoří zákadní staticky určitá soustava. Obr. 4.4: Staticky určitá, přeurčitá a neurčitá koubová prutová soustava - 4 (5) -
25 Siová metoda Příhradová soustava (koubová prutová soustava), např. pode obr. 4.4, je jako ceek staticky (a kinematicky) určitá, když patí b = p + a (viz vztah (3.) moduu BD MO4) a současně nenastane výjimkový případ, takže determinant D. Příhradová soustava je staticky neurčitá (a kinematicky přeurčitá), patí-i b < p + a a naopak staticky přeurčitá (a kinematicky neurčitá), je-i b > p + a. Stupeň statické neurčitosti příhradové soustavy ze tedy určit ze vztahu n s = p + a b, (4.) kde p je počet prutů (vnitřních vazeb), a počet sožek reakcí vnějších vazeb, b počet styčníků. Výraz a 3 představuje zevní statickou neurčitost a p + 3 b vnitřní statickou neurčitost. Posouzení pode vztahu (4.) je rovněž možné, ae poněkud nepraktické. Ve všech případech rovinných prutových soustav však vždy musí patit a Řešení rovinného rámu Stupeň statické neurčitosti n s prutové soustavy stanovíme pode vztahu (4.). Zvoíme zákadní staticky (a kinematicky) určitou soustavu, tj. odstraníme n s vhodně zvoených jednoduchých vazeb. Přitom nesmí nastat výjimkový případ podepření (musí tedy být D ). Každou odebranou jednoduchou vazbu nahradíme odpovídající sožkou reakce či interakce X i (i =,,, n s ) s neznámou veikostí a ibovoně zvoeným smysem, které představují staticky neurčité veičiny. Zákadní staticky určitou soustavu ze vytvořit mnoha způsoby. Její tvar závisí na vobě přebytečných jednoduchých vazeb. Voíme ji vždy s ohedem na usnadnění výpočtu. Zákadní soustava je zatížena daným zatížením (siovým i deformačním) a staticky neurčitými veičinami X i. Přitom deformace musí být shodná s deformací původní staticky neurčité konstrukce. V místě odebrané jednoduché vazby předepíšeme proto deformační (přetvárné) podmínky v obecném tvaru i = d i (i =,,, n s ), (4.3) kde d i jsou předepsané hodnoty deformací (u nepoddajného podepření d i = ). Obr. 4.5: Jednoduchý staticky neurčitý rovinný rám - 5 (5) -
26 Statika I Např. u soustavy z obr. 4.5 s n s = 3 ze jako zákadní soustavu (s různými deformačními podmínkami) voit omenou konzou (obr. 4.5b), omený prostý nosník (obr. 4.5c), trojkoubový omený nosník (obr. 4.5d), soženou nosníkovou soustavu nebo po rozříznutí dvě omené konzoy (obr. 4.5e). Veičiny s čárkou (obr. 4.5d, e) představují vzájemné posunutí či pootočení průřezu po rozříznutí. Přitom nesmíme voit zákadní soustavu tak, aby vzniknu virtuání koub nebo aby tři kouby ežey v jedné přímce. Každou deformaci i zákadní soustavy ve vztahu (4.3) vyjádříme jako funkci daného zatížení a jednotivých staticky neurčitých veičin X i (s využitím principu superpozice). Díčí vyšetřované stavy pak jsou nutý stav s působícím daným zatížením a každý i tý stav s působící jedinou přísušnou staticky neurčitou veičinou X i = (s využitím principu úměrnosti) pro i =,,, n s. Obr. 4.6: Metoda jednotkových si u jednoduchého rovinného rámu 4.. Obecně řešený příkad Princip řešení rámu siovou metodou si ukážeme obecně na případu jednoduchého otevřeného rámu oboustranně vetknutého (obr. 4.6a). Pode vztahu (4.) určíme n s = 3. Zákadní soustavu zvoíme jako prostý omený nosník (obr. 4.6b) s neznámými X = M a, X = M b, X 3 = R bx. Na zákadní soustavě vyšetříme cekem n s + = 4 zatěžovací stavy, a to - 6 (5) -
27 Siová metoda nutý stav od daného zatížení (síy F), viz obr. 4.6c, jednotkové stavy až 3 pro neznámé jednotkové síy X =, X = a X 3 = (obr. 4.6d f). Pro každý z těchto zatěžovacích stavů vyšetříme průběhy ohybových momentů M i (i =,,, 3), neboť viv normáových a posouvajících si na přetvoření zanedbáme. Přetvárné (deformační) podmínky předepíšeme tak, aby deformace zákadní soustavy (s působícím zadaným zatížením a neznámými siami X i ) bya stejná jako původní staticky neurčitá soustava, tedy ϕ = =, a ϕ = =, u b b = =. 3 (4.4) Apikací principu superpozice a principu úměrnosti můžeme přetvárné podmínky rozepsat do soustavy přetvárných rovnic X,, 3, X X + X + +,, 3, X + X,3 +,3 3,3 3 X X + X 4.. Kanonické rovnice 3 3 +, + +, 3, =, =, =. (4.5) Rovnice (4.5) představují kanonické rovnice (kánon je zákon, pravido), které nezávisí na tvaru prutové soustavy. Fyzikání význam přetvárných součiniteů i,k (vzhedem k patnosti třetí Maxweovy věty) se při numerickém řešení potačuje. V úsporném tvaru pak můžeme kanonické rovnice obecně zapsat n s k = X + = ( i =,,3 n ). (4.6) i, k k i, s kde i,k je deformační součinite vyjadřující pootočení nebo posunutí průřezu i zákadní soustavy ve směru veičiny X i od k tého jednotkového stavu X k =, i, je deformační součinite vyjadřující pootočení nebo posunutí průřezu i zákadní soustavy ve směru veičiny X i od nutého zatěžovacího stavu. Index i představuje číso deformace (místo sedované deformace) a je totožné s čísem neznámé veičiny X i. Index k, resp. určuje číso zatěžovacího stavu, v němž deformace vznika. Součinitee i,i se nazývají havní deformační součinitee (neboť eží na havní diagonáe) a součinitee i,k jsou vedejší deformační součinitee (eží na vedejších diagonáách). Pode Maxweovy věty patí i,k = k,i (pro i k). (4.7) V maticové formě můžeme (bez vivu deformačního zatížení typu popuštění) zapsat kanonické rovnice ve tvaru X = (4.8) + nebo s vivem deformačního zatížení typu popuštění ve tvaru X + = d, (4.9) - 7 (5) -
28 Statika I kde je matice deformačních součiniteů,,,,...,, n s,,,,...,, ns =,... (4.) s,, s,,..., s, n s vektor staticky neurčitých veičin T { X X..., }, X =,, X ns (4.) vektor zatěžovacích čenů T {,..., }, = (4.),,, ns, event. vektor daných deformací v místech odebraných vazeb (tj. nehomogenní okrajové podmínky) T { d d..., }. d =,, d ns (4.3) 4..3 Výpočet přetvárných součiniteů Pro určení přetvárných součiniteů i,k a i, využijeme apikaci principu virtuáních prací pode kapitoy 3. Při uvažování vivu ohybových momentů, normáových i posouvajících si získáme z Maxweova Mohrova vztahu (3.9) výrazy M im NiN VV i i, = ds + ds ds, EI + EA κ (4.4) GA L L L M im k NiNk VV i k i, k = ds + ds ds, EI + EA κ (4.5) GA L L L kde k výpočtu integráů můžeme využít tabuku 5. nebo Verečšaginovo pravido (odst. 3.4.). Viv normáových a posouvajících si se u přímých prutů vemi často zanedbává. Pro určení správného znaménka přetvárného součinitee z ohybových momentů je výhodné obrazce ohybových momentů opatřit znaménky pode zvoených konvenčních váken (viz obr. 4.6). Kresíme-i důsedně pořadnice ohybových momentů na stranu skutečně tažených váken, pak patí, že jsou-i obrazce na stejné (opačné) straně, je přetvárný součinite kadný (záporný) Určení vnitřních si U každého prutu vyjmutého z rámové soustavy je nutné určit zbývající statické veičiny. Výpočet vnitřních si v průřezu x provedeme na zákadní soustavě buď pode zásad statiky, přičemž na zákadní soustavě působí dané siové zatížení a již známé síy X i, nebo pomocí superpozičních vztahů - 8 (5) -
29 Siová metoda M x = M x, + M x, X + M x, X + + M x,ns X ns, (4.6) R a = R a, + R a, X + R a, X + + R a,ns X ns. (4.7) Při uvažování vivu V, N pro výpočet přetvárných součiniteů (méně častý případ) ze anaogicky též uvažovat vztahy V x = V x, + V x, X + V x, X + + V x,ns X ns, N x = N x, + N x, X + N x, X + + N x,ns X ns. (4.8) V případě, že z výpočtu prutové soustavy určíme v koncích jednotivých prutů koncové momenty, můžeme samostatným řešením každého prutu jako prostého nosníku (obr. 4.7a) určit průběhy vnitřních si V a M z níže odvozených obecných vztahů. Dané zatížení na prutu (obr. 4.7b) a koncové momenty (obr. 4.7c) můžeme posuzovat samostatně a výsedky superponovat. Obr. 4.7: Prut ab (jako prostý nosník) vyjmutý z prutové soustavy Posouvající síu v ibovoném průřezu x prutu ab můžeme s použitím principu superpozice účinků získat ve tvaru V M M b a x = Vx, + Vx = Vx, +, (4.9) ab kde V x, je posouvající sía v průřezu x prostého nosníku ab od daného siového zatížení a V x představuje přírůstek posouvající síy od koncových momentů M a a M b, který je konstantní pro ceý prut. Nejčastěji se posouvající síy určují v koncových průřezech a nebo b. Mezipodporový moment v ibovoném průřezu x získáme ze vztahu M M x + M x a b = M + M = M +, (4.) x x, x x, ab kde M x, je ohybový moment v průřezu x prostého nosníku od daného siového zatížení, M x je přírůstek ohybového momentu v průřezu x od vivu koncových momentů. Normáové síy v prutech se určí z podmínek rovnováhy neznámých normáových si a známých posouvajících si (včetně daného siového uzového zatížení) na uvoněných uzech. - 9 (5) -
30 Statika I Kontrou rovnováhy je nutno provést jednak u jednotivých uvoněných uzů, nevyužitých pro výpočet normáových si, jednak pro ceou rámovou soustavu (upatní se v rovině tři gobání statické podmínky rovnováhy). 4.3 Iustrující příkad Jako ukázku apikace řešení rovinného rámu siovou metodou si uvedeme případ omeného nosníku oboustranně vetknutého. Příkad 4. Zadání Vyřešte daný jednoduchý otevřený rovinný rám z obr. 4.6a s pruty konstantního průřezu o dékách = v = 6 m, = v = 4 m, 3 = = 8 m, momentech setrvačnosti I =,5 m 4, I =,4 m 4, I 3 =,6 m 4, moduu pružnosti E = 7 GPa pro zatížení osaměou siou F = 8 kn ve vzdáenosti p = 6 m. Řešení Ze vztahu (4.) určíme n s = 3. Zákadní soustavu zvoíme jako prostý omený nosník (obr. 4.6b) s neznámými X = M a, X = M b, X 3 = R bx. Deformační podmínky mají tvar (4.4) a z nich pynou přetvárné rovnice (4.5). Zanedbáme-i viv normáových a posouvajících si na deformaci zákadní soustavy, můžeme přetvárné součinitee určit pode (4.5) anaogicky ke vztahu (3.) ve tvaru p j i, k = M im k dx j. E I (4.) j= j j Momentové obrazce nutého i jednotkových stavů jsou nakreseny na obr. 4.6c f. Vyčísení součiniteů i,k včetně rozměrových jednotek je: v, = v + = + = 6,9 EI EI3 3 EI 3EI3 6, = = =, = 8,3 ( knm), EI3 3 6EI3 v v v,3 = v + v = EI EI3 3 3 EI 6 4 = 3, =,65 ( kn), v 5, = + = 5,35 ( knm), EI 3EI3 v 4,3 = ( v + v) = 3, =,893 ( kn), EI 6EI 3,3 3 v = 3EI 3 v + 3EI 3 + 3EI 3 ( v + v v + v ) =,98 3 ( kn) 5 m. ( knm) EI 3 (v, + v ) = - 3 (5) -
31 Siová metoda Vyčísení součiniteů i, včetně rozměrových jednotek je:, Fpp 4 Fpp' = ( + p') =,35, p 6EI 6EI 3 ' 4 [], = ( + ) =,78 [], Fpp' 3 3, = m 6EI3 [ v ( + p') + v ( + p) ] =,43. Pro numerický výpočet byy zavedeny poměrné deformace i, = 3 E i, o veikostech ' ' ' ' ',,,3,, = 3,333kNm, ' = 4,667kNm, ' 3 = 38,667kNm i, k = 3 E i,k a = E = E,664, + = + = m E,5 3E, = E, = =,m, = E,3 = ( 6 + 4) = 7,56m, =,4444m, ' = 5,m, ' = 53,m, Soustava kanonických rovnic má čísený tvar,644x,x 7,56X +,X +,444X 5,X,3, 7,56X 5,X ,5X = 3,333, = 4,667, 3 3,3 = 38,667 a řešení X = M a =, 945kNm (po směru chodu hodinových ručiček), X = M b =, 43kNm (proti směru chodu hodinových ručiček), = R =,55kN ( X 3 bx ). Výpočet zbývajících statických veičin provedeme na zákadní soustavě. Sožky reakcí ze superpozičních vztahů jsou Rax = +,945 +,43 +,55 =,55kN( ), Raz = +,945 +,43 +,55 =,97kN( ), Rbz = +,945 +,43 +,55 = 6,9kN( ); můžeme též využít statických podmínek rovnováhy F ix =, M ib =, M ia =. Přitom patí kontroa F iz = : R R + F =. az Ohybové momenty ze superpozičních vztahů vycházejí bz 3,. 3, - 3 (5) -
32 Statika I M M M ac ca dc = M a =,945kNm, M bd = M =,43kNm, = +,945 +,43+ ( 6),55 = 3,985kNm = M = +,945 +,43 + ( 4),55 = 4,7kNm = M b 8 6 M e = M max = +,5,945 +,75,43 + 4,55 = 7,84kNm, 8 4 cd db,, Obr. 4.8: Průběhy M, V, N na jednoduchém rámu posouvající síy V V V V ac ce ce ed = V = V = V ca ec = V ce, de = R = R az ax =,55 kn, =,97 kn, M dc M cd 8 ( 4,7) ( 3,985) + = =,97 8 = 6,9 kn = R, bz =,97 kn, - 3 (5) -
33 Siová metoda V bd a normáové síy N ac = Vdb = Rbx =,55 kn = N ca = R az =,97kN( tak), N cd = N dc = R ax =,55kN( tak), N bd = N db = R bz = 6,9kN( tak). Průběhy vnitřních si jsou vyneseny na obr Deformační zatížení rámu 4.4. Viv změny tepoty Změna tepoty tvoří samostatný zatěžovací stav, přičemž i,k jsou stejná jako u siového zatížení (obvyke pouze s vivem M) a i, je nutno určit pro přísušný nutý stav. Tepotní účinek ze rozožit na rovnoměrnou změnu tepoty ( t ), způsobující prodoužení či zkrácení prutu, a na nerovnoměrnou změnu tepoty ( t ) ineárně se měnící po výšce průřezu, způsobující ohyb. Pro obdéníkový průřez patí t = ( td + t h ), t = t d t h. (4.) Pode Maxweova Mohrova vztahu (3.9) patí obecně p j p j t i, = Niα t tdx j + M iα t dx j, ( i =,,..., ns ) (4.3) h j= j= a při t = konst., t /h = konst. je p j p j t i, = αt ( t) j Ni dx j + M i dx j. (4.4) j= j= h j Pro i tý jednotkový stav nutno určit nejen M i, ae i N i. Zváštní případ nastane, jedná-i se o viv rovnoměrné změny tepoty při t = konst. a uspořádání vnějších vazeb nebrání tepené deformaci (obr. 4.9). Pak toto zatížení nevyvoá R a N, V, M. Obr. 4.9: Rovnoměrné otepení otevřeného (a) a uzavřeného (b) rovinného rámu - 33 (5) -
34 Statika I 4.4. Dané popuštění podpor rámu Dané nepružné popuštění rámu tvoří samostatný zatěžovací stav, přičemž i,k je stejné jako u siového zatížení a i, nutno určit pro přísušný nutý stav. Pode zvoené zákadní soustavy se viv popuštění projeví u odebraných jednonásobných vazeb, kde se hodnota popuštění d i (i té vazby s neznámou staticky neurčitou veičinou X i ) objeví na pravé straně přetvárné rovnice (znaménka pode smysů d i a X i ); deformace v místě původního podepření není nuová, ae je rovna danému popuštění (tj. nehomogenní okrajová podmínka), u ponechaných jednonásobných vazeb, kde se viv popuštění r (konkrétně u r, w r, ϕ r ) projeví pomocí nutého zatěžovacího stavu; absoutní přetvárné součinitee i,,p pak určíme pode Maxweova Mohrova vztahu ve tvaru p v v = Rr, i r = ( R p u + R w + M ϕ ), ( i =,.., n ),(4.5) i,, p rx, i r rz, i r r, i r s r= r= kde R r,i jsou sožky reakcí v ponechaných vazbách r zákadní soustavy v i tém stavu, r je hodnota daného popuštění vazby r ve směru reakce R r,i (znaménko pode smysu reakce), p v je počet ponechaných vazeb zákadní soustavy (obvyke 3). Přetvárné rovnice (pro obě varianty zadávání daného popuštění) jsou ns k = a po úpravě ns k = X + = d, ( i =,,..., n ) (4.6) i, k k i,, p i s p v i, k X k = i,, p + di = Rr, i r + di, ( i =,,..., ns ). (4.7) r = 4.5 Řešení spojitého nosníku Spojitý pnostěnný nosník (obr. 4.) je přímý nosník uožený na více než dvou podporách. Aespoň jedna podpora je pevná (vetknutí nebo neposuvný koub), ostatní podpory jsou posuvné. Neuvažují se vožené vnitřní kouby v poích. Nad vnitřními podporami probíhá nosník spojitě (nejsou tam vnitřní kouby). Poe je část spojitého nosníku mezi sousedními podporami, rozpětí je déka poe (obr. 4.), průřez spojitého nosníku může být konstantní po ceé déce, konstantní v jednotivých poích nebo se jedná o pruty s náběhy u podpor. Obr. 4.: Spojitý nosník o třech poích - 34 (5) -
35 Siová metoda Stupeň statické neurčitosti se stanoví zjednodušením vztahu (4.) n s = a 3, takže jednoduše patí pro spojitý nosník s pevným koubem (obr. 4.a), že n s je rovno počtu vnitřních podpor, pro spojitý nosník s vetknutím (obr. 4.b) patí, že n s je roven počtu všech jednoduchých posuvných podpor. Obr. 4.: Zákadní staticky určitá soustava spojitého nosníku K řešení spojitého nosníku se dá výhodně použít metoda třímomentových rovnic. Je to v podstatě metoda siová se zváštní vobou zákadní staticky určité soustavy. Zákadní soustava se vytvoří vožením koubů do podpor, takže vznikne soustava prostých nosníků pode obr. 4.c (v počtu všech poí), která je z hediska apikace siové metody nejvýhodnější. Za neznámé se voí podporové momenty M i (i =,,, n s ) ve vetknutí a nad vnitřními podporami. Za kadné podporové momenty (obr. 4.c) se považují momenty natahující spodní (konvenční) vákna nosníku. Deformační podmínka pak zajišťuje, že u vnitřní podpory (např. podpory b nosníku z obr. 4.b) nesmí nastat zom, tj. zůstává stejný skon tečen - 35 (5) -
36 Statika I k ohybové čáře spojitého nosníku zeva i zprava. Přitom je přijata konvence, že kadné pootočení působí směrem doů (viz obr. 4.d g). Pak patí Φ ba = Φ bc. (4.8) Ve vetknutí nenastane pootočení, takže je Φ ab =. (4.9) Skony tečen k ohybové čáře u vnitřní podpory b rozepíšeme pode obr. 4.d f Φ ba = M a β ba + M b α ba + ϕ ba, (4.3) Φ bc = M b α bc + M c β bc + ϕ bc. (4.3) Z podmínky spojitosti (4.8) získáme dosazením výrazů (4.3) a (4.3) po úpravě pro dvě sousední poe třímomentovou rovnici (Capeyronovu rovnici) pro podporu b s vivem siového zatížení M a β ba + M b (α ba + α bc ) + M c β bc + ϕ ba + ϕ bc = (4.3) s neznámými podporovými momenty M a, M b, M c. Pro daší podpory vyjádříme třímomentovou rovnici cykickou záměnou indexů. Obr. 4.: Vetknutý konec a spojitého nosníku Pro vetknutý konec a (obr. 4.a) ze uvažovat dvě varianty odvození. Buď rozepíšeme přímo podmínku (4.9) Φ ab = pomocí výrazu (4.3), v němž provedeme cykickou záměnu indexů b a, c b, takže rovnice pro podporu a má jednodušší tvar M a α ab + M b β ab + ϕ ab =. (4.33) V druhém případě přepíšeme třímomentovou rovnici (4.3) s cykickou záměnu indexů a o, b a, c b na tvar M o β ao + M a (α ao + α ab ) + M b β ab + ϕ ao + ϕ ab = (4.34) a zjednodušíme ji pomocí tzv. tuhého nuového poe oa (obr. 4.b), pro které uvažujeme oa a dosazujeme M o =, α ao = β ao = ϕ ao =. Viv svisého zatížení převisého konce se upatní vyjádřením známého podporového momentu. Např. pro podporu d v obr. 4.6 patí M d = F sinα de při respektování konvence z obr. 4.c (5) -
37 Siová metoda 4.5. Deformační zatížení Deformační zatížení spojitého nosníku zahrnuje dané nepružné popuštění podpor a viv nerovnoměrné změny tepoty. Rovnoměrná změna vede na prodoužení nosníku bez vzniku V, M a neupatní se u spojitých nosníků s jedinou vazbou proti vodorovnému posunu. Při daném popuštění podpor se střednice prostých nosníků ab, bc zákadní soustavy (obr. 4.g) pootočí o úhy ϕ ϕ ba, p bc, p tgϕ tgϕ ba, p bc, p wa w = ab wc w = ac b b., (4.35) Ve vetknutí (obr. 4.c) pokesne o stejnou hodnotu ceé nuové poe oa, takže w o = w a a tím ϕ oa,p =. Obr. 4.3: Nerovnoměrná ineární změna tepoty nosníku Při nerovnoměrné změně tepoty uvažujeme ineární změnu tepoty po výšce průřezu. Přitom se tepota doních váken se změní o hodnotu (přírůstek) t d a tepota horních váken se změní o hodnotu t h. Podporové průřezy prostých nosníků zákadní soustavy u podpory b (obr. 4.3) se pootočí pode Maxweova Mohrova vztahu (3.9) o úhy ϕ ϕ ba, t bc, t = = ab bc t( x) M ( x) αt dx = h( x) t( x) αt M ( x) αt dx = h( x) ab bc x t( x) αt αt dx = h( x) ab bc ( bc ab t( x) x) dx, h( x) ab t( x) x dx, h( x) (4.36) kde pode (4.) patí t (x) = t d t h a h(x) je výška průřezu. U nosníku s konstantním průřezem ze pootočení vyjádřit jednoduššími vztahy αt tabab αt tbcbc ϕ ba, t =, ϕbc, t =, (4.37) h h ab kde tepotní rozdíy jsou pak t ab = t ab,d t ab,h, t bc = t bc,d t bc,h. bc - 37 (5) -
38 Statika I 4.5. Obecný tvar třímomentové rovnice S přihédnutím ke vztahům (4.3), (4.36) a (4.35) pak můžeme pro podporu b spojitého nosníku při uvažování siového i deformačního zatížení napsat obecný tvar třímomentové rovnice M β + M ( α + α ) + M β + ϕ + ϕ + a ba wa w + ab b b ba wc w + ac b bc αt + bc ab bc c bc ba bc t( x) αt x dx + h( x) bc ( bc t( x) (4.38) x) dx =. h( x) U prutů s konstantním průřezem v jednotivých poích jsou deformační úhy dány vztahy α α ab = αba = α =, β = = (4.39) 3EI 6EI a úhy ϕ určíme pomocí Maxweova Mohrova vztahu (3.9) nebo z tabuky 5.. Integráy vyjadřující pootočení od vivu nerovnoměrné změny tepoty ze vyjádřit jednoduchými vztahy (4.37). Průběhy vnitřních si u spojitého nosníku určíme násedovně. Momentový obrazec ze vynést hned po vyřešení soustavy třímomentových rovnic tak, že z pořadnic podporových momentů získáme v každém poi posunutou zákadní čáru a od ní pak vynášíme obrazce ohybových momentů pode typu zatížení jako na prostém nosníku. Zbývající statické veičiny spojitého nosníku ze výhodně určit z vypočtených podporových momentů, které představují koncové momenty na jednotivých prutech. Pro posouvající síu v ibovoném průřezu x patí výraz (4.9) a pro mezipodporový moment rovnice (4.). Obr. 4.4: Uvoněný nosníkový eement s reakcí R b Podporovou reakci posuvného koubu stanovíme z rovnováhy svisých si působících na uvoněný nosníkový eement nad podporou b (obr. 4.4) a získáme takže F iz = : R b V b, + V b,p =, (4.4) R b = V b, + V b,p = V ba + V bc. (4.4) Vodorovná sožka reakce spojitého nosníku s jedinou vazbou proti vodorovnému posunu (pevný koub nebo dokonaé vetknutí) je staticky určitá veičina a určí se z podmínky rovnováhy všech vodorovných si F ix = pro ceý spojitý nosník. Nosník se dvěma vazbami proti vodorovnému posunutí (obr. 4.5) je pro osové siové zatížení řešen v násedujícím odstavci (5) -
39 Siová metoda Oboustranně vetknutý nosník osově zatížený Nosník se dvěma vazbami proti vodorovnému posunutí (obr. 4.5) je jedenkrát staticky neurčitý pro osové siové zatížení a řeší se s uvažováním vivu normáových si, tj. pomocí prvního integráu vztahu (3.9). Při uvoněné pravé podpoře b je neznámá X = R bx. Přetvárnou podmínku u b = ze rozepsat do tvaru X + =, (4.4) kde představuje osovou poddajnost a pro posun konce b od X = při N(x) = a N ( x) = u prutu konstantního průřezu patí = dx =. (4.43) EA EA Zatěžovací sía vyvoá deformaci uvoněného konce b o veikosti, takže při N(x) = F v intervau, p a N ( x) = získáme p F = dx = Fp. (4.44) EA EA Pak neznámá vodorovná sožka reakce vyjde z (4.4) ve tvaru Fp X R EA = bx = = = F EA p (4.45) a z podmínky rovnováhy do vodorovné osy dořešíme R ax (obr. 4.5). Řešení staticky neurčitého nosníku zatíženého osovým zatížením vede na anaogii s výpočtem posouvajících si prostého nosníku příčně zatíženého (obr. 4.5i). Obr. 4.5: Oboustranně vetknutý nosník s osovým zatížením - 39 (5) -
40 Statika I Příkad řešení spojitého nosníku Příkad 4. Zadání Vyřešte spojitý nosník konstantního průřezu po ceé déce z obr. 4.6a pro zatížení F = 3 kn, α = 3º, q = knm. Řešení Postup řešení naeznete v učebnici [] na str. 6 až 8. Výsedné průběhy vnitřních si jsou na obr. 4.6c e. Obr. 4.6: Spojitý nosník o třech poích s převisým koncem - 4 (5) -
41 Siová metoda Otázky. Stupeň statické neurčitosti rovinné prutové soustavy.. Voba staticky neurčitých veičin rámu. 3. Podstata řešení rovinného rámu siovou metodou. 4. Výpočet přetvárných součiniteů. 5. Vysvětete pojem rovinný spojitý pnostěnný nosník. 6. Voba staticky neurčitých veičin spojitého nosníku. 7. Jakou deformační podmínku vyjadřuje třímomentová rovnice? 8. Viv převisého konce u spojitého nosníku. 9. Výpočet podporových reakcí spojitého nosníku.. Viv změny tepoty rovinného rámu.. Viv daného popuštění rovinného rámu. Shrnutí V této kapitoe jsme si objasnii princip řešení staticky neurčitých prutových soustav siovou metodou. Nejprve jsme si ukázai řešení rovinného rámu a násedně řešení spojitého nosníku pomocí speciání voby zákadní soustavy, vedoucí na odvození třímomentové rovnice. Zabývai jsme se rovněž vivem deformačního zatížení při řešení rovinných rámů a spojitých nosníků. - 4 (5) -
Přednáška 10, modely podloží
 Statika stavebních konstrukcí II.,.ročník kaářského studia Přednáška, modey podoží Úvod Winkerův mode podoží Pasternakův mode podoží Nosník na pružném Winkerově podoží, řešení OD atedra stavební mechaniky
Statika stavebních konstrukcí II.,.ročník kaářského studia Přednáška, modey podoží Úvod Winkerův mode podoží Pasternakův mode podoží Nosník na pružném Winkerově podoží, řešení OD atedra stavební mechaniky
Statika 2. Vetknuté nosníky. Miroslav Vokáč 2. listopadu ČVUT v Praze, Fakulta architektury. Statika 2. M.
 3. přednáška Průhybová čára Mirosav Vokáč mirosav.vokac@kok.cvut.cz ČVUT v Praze, Fakuta architektury 2. istopadu 2016 Průhybová čára ohýbaného nosníku Znaménková konvence veičin M z x +q +w +ϕ + q...
3. přednáška Průhybová čára Mirosav Vokáč mirosav.vokac@kok.cvut.cz ČVUT v Praze, Fakuta architektury 2. istopadu 2016 Průhybová čára ohýbaného nosníku Znaménková konvence veičin M z x +q +w +ϕ + q...
Přednáška 12 Obecná deformační metoda, nelineární úlohy u prutových soustav
 Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Téma 4 Výpočet přímého nosníku
 Stavební statika, 1.ročník bakaářského studia Téma 4 Výpočet přímého nosníku Výpočet nosníku v osové úoze Výpočet nosníku v příčné úoze ve svisé a vodorovné havní rovině Výpočet nosníku v krutové úoze
Stavební statika, 1.ročník bakaářského studia Téma 4 Výpočet přímého nosníku Výpočet nosníku v osové úoze Výpočet nosníku v příčné úoze ve svisé a vodorovné havní rovině Výpočet nosníku v krutové úoze
Linearní teplotní gradient
 Poznámky k semináři z předmětu Pružnost pevnost na K68 D ČVUT v Praze (pracovní verze). Tento materiá má pouze pracovní charakter a ude v průěhu semestru postupně dopňován. utor: Jan Vyčich E mai: vycich@fd.cvut.cz
Poznámky k semináři z předmětu Pružnost pevnost na K68 D ČVUT v Praze (pracovní verze). Tento materiá má pouze pracovní charakter a ude v průěhu semestru postupně dopňován. utor: Jan Vyčich E mai: vycich@fd.cvut.cz
Téma 4 Normálové napětí a přetvoření prutu namáhaného tahem (prostým tlakem)
 Pružnost a pasticita, 2.ročník bakaářského studia Téma 4 ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného prutu
Pružnost a pasticita, 2.ročník bakaářského studia Téma 4 ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného prutu
Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím
 Stavební mechanika, 2.ročník bakalářského studia AST Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita Ostrava Osnova přednášky
Stavební mechanika, 2.ročník bakalářského studia AST Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita Ostrava Osnova přednášky
4.1 Shrnutí základních poznatků
 4.1 Shrnutí zákadních poznatků V případech příčných deformací přímých prutů- nosníků se zabýváme deformací jejich střednice, tj. spojnice těžiště příčných průřezů. Tuto deformovanou křivku nazýváme průhybová
4.1 Shrnutí zákadních poznatků V případech příčných deformací přímých prutů- nosníků se zabýváme deformací jejich střednice, tj. spojnice těžiště příčných průřezů. Tuto deformovanou křivku nazýváme průhybová
Inovace předmětů studijních programů strojního inženýrství v oblasti teplotního namáhání
 Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Řešení úloh 1. kola 60. ročníku fyzikální olympiády. Kategorie B Autoři úloh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6)
 Řešení úoh 1. koa 60. ročníku fyzikání oympiády. Kategorie B Autoři úoh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6) h 1.a) Protože vzdáenost bodů K a O je cos α, je doba etu kuičky z bodu K do bodu
Řešení úoh 1. koa 60. ročníku fyzikání oympiády. Kategorie B Autoři úoh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6) h 1.a) Protože vzdáenost bodů K a O je cos α, je doba etu kuičky z bodu K do bodu
STATIKA STAVEBNÍCH KONSTRUKCÍ I
 VŠB Technická univerzita Ostrava Fakulta stavební, Ludvíka Podéště 1875, 708 33 Ostrava Ivan Kološ, Martin Krejsa, Stanislav Pospíšil, Oldřich Sucharda STATIKA STAVEBNÍCH KONSTRUKCÍ I Vzdělávací pomůcka
VŠB Technická univerzita Ostrava Fakulta stavební, Ludvíka Podéště 1875, 708 33 Ostrava Ivan Kološ, Martin Krejsa, Stanislav Pospíšil, Oldřich Sucharda STATIKA STAVEBNÍCH KONSTRUKCÍ I Vzdělávací pomůcka
Přednáška 1 Obecná deformační metoda, podstata DM
 Statika stavebních konstrukcí II., 3.ročník bakalářského studia Přednáška 1 Obecná deformační metoda, podstata DM Základní informace o výuce předmětu SSK II Metody řešení staticky neurčitých konstrukcí
Statika stavebních konstrukcí II., 3.ročník bakalářského studia Přednáška 1 Obecná deformační metoda, podstata DM Základní informace o výuce předmětu SSK II Metody řešení staticky neurčitých konstrukcí
FAKULTA STAVEBNÍ. Stavební statika. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Vnitřní síly na nosnících Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW:
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Vnitřní síly na nosnících Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW:
Normálové napětí a přetvoření prutu namáhaného tahem (prostým tlakem) - staticky určité úlohy
 Pružnost a pasticita, 2.ročník bakaářského studia ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) - staticky určité úohy Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného
Pružnost a pasticita, 2.ročník bakaářského studia ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) - staticky určité úohy Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného
FAKULTA STAVEBNÍ. Stavební statika. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Přednáška 2 pro kombinované studium Jiří Brožovský Kancelář: LP C 303/1 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Přednáška 2 pro kombinované studium Jiří Brožovský Kancelář: LP C 303/1 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
1. Stanovení modulu pružnosti v tahu přímou metodou
 . Stanovení moduu pružnost v tahu přímou metodou.. Zadání úohy. Určte modu pružnost v tahu přímou metodou pro dva vzorky různých materáů a výsedky porovnejte s tabukovým hodnotam.. Z naměřených hodnot
. Stanovení moduu pružnost v tahu přímou metodou.. Zadání úohy. Určte modu pružnost v tahu přímou metodou pro dva vzorky různých materáů a výsedky porovnejte s tabukovým hodnotam.. Z naměřených hodnot
Kapitola 4. Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena. Každý prut v rovině má 3 volnosti (kap.1).
 Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
1 ROZMĚRY STĚN. 1.1 Délka vnější stěny. 1.2 Výška vnější stěny
 1 ROZMĚRY STĚN Důežitými kritérii pro zhotovení cihených stěn o větších rozměrech (déce a výšce) je rozděení stěn na diatační ceky z hediska zatížení tepotou a statického posouzení stěny na zatížení větrem.
1 ROZMĚRY STĚN Důežitými kritérii pro zhotovení cihených stěn o větších rozměrech (déce a výšce) je rozděení stěn na diatační ceky z hediska zatížení tepotou a statického posouzení stěny na zatížení větrem.
Téma 2 Deformace staticky určitých prutových konstrukcí
 Statika stavebních konstrukcí I.,.ročník bakaářského studia Téma Deformace staticky určitých prutových konstrukcí Katedra stavební mechaniky Fakuta stavební, VŠB - Technická univerzita Ostrava Osnova přednášky
Statika stavebních konstrukcí I.,.ročník bakaářského studia Téma Deformace staticky určitých prutových konstrukcí Katedra stavební mechaniky Fakuta stavební, VŠB - Technická univerzita Ostrava Osnova přednášky
Statika soustavy těles.
 Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
I Stabil. Lepený kombinovaný nosník se stojnou z desky z orientovaných plochých třísek - OSB. Navrhování nosníků na účinky zatížení podle ČSN 73 1701
 I Stabi Lepený kombinovaný nosník se stojnou z desky z orientovaných pochých třísek - OSB Navrhování nosníků na účinky zatížení pode ČSN 73 1701 Část A Část B Část C Část D Výchozí předpokady, statické
I Stabi Lepený kombinovaný nosník se stojnou z desky z orientovaných pochých třísek - OSB Navrhování nosníků na účinky zatížení pode ČSN 73 1701 Část A Část B Část C Část D Výchozí předpokady, statické
1. výpočet reakcí R x, R az a R bz - dle kapitoly 3, q = q cosα (5.1) kolmých (P ). iz = P iz sinα (5.2) iz = P iz cosα (5.3) ix = P ix cosα (5.
 Kapitola 5 Vnitřní síly přímého šikmého nosníku Pojem šikmý nosník je používán dle publikace [1] pro nosník ležící v souřadnicové rovině xz, který je vůči vodorovné ose x pootočen o úhel α. Pro šikmou
Kapitola 5 Vnitřní síly přímého šikmého nosníku Pojem šikmý nosník je používán dle publikace [1] pro nosník ležící v souřadnicové rovině xz, který je vůči vodorovné ose x pootočen o úhel α. Pro šikmou
Podpora digitalizace a využití ICT na SPŠ CZ.1.07/1.5.00/34.0632 1
 Střední průmysová škoa a Vyšší odborná škoa technická Brno, Sokoská 1 Šabona: Inovace a zkvaitnění výuky prostřednictvím ICT Název: Téma: Autor: Číso: Anotace: echanika, pružnost pevnost Nosníky stejné
Střední průmysová škoa a Vyšší odborná škoa technická Brno, Sokoská 1 Šabona: Inovace a zkvaitnění výuky prostřednictvím ICT Název: Téma: Autor: Číso: Anotace: echanika, pružnost pevnost Nosníky stejné
Betonové konstrukce (S) Přednáška 3
 Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
A x A y. α = 30. B y. A x =... kn A y =... kn B y =... kn. Vykreslení N, V, M. q = 2kN/m M = 5kNm. F = 10 kn A c a b d ,5 2,5 L = 10
 Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Mechanické vlastnosti materiálů.
 Mechancké vastnost materáů. Obsah přednášky : tahová zkouška, zákadní mechancké vastnost materáu, prodoužení př tahu nebo taku, potencání energe, řešení statcky neurčtých úoh Doba studa : as hodna Cí přednášky
Mechancké vastnost materáů. Obsah přednášky : tahová zkouška, zákadní mechancké vastnost materáu, prodoužení př tahu nebo taku, potencání energe, řešení statcky neurčtých úoh Doba studa : as hodna Cí přednášky
Zjednodušená deformační metoda (2):
 Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
NOVÁ METODA NÁVRHU PRŮMYSLOVÝCH PODLAH Z VLÁKNOBETONU
 NOVÁ METODA NÁVRHU PRŮMYSLOVÝCH PODLAH Z VLÁKNOBETONU Jan Loško, Lukáš Vrábík, Jaromír Jaroš Úvod Nejrozšířenějším příkadem využití váknobetonu v současné době jsou zřejmě podahové a zákadové desky. Při
NOVÁ METODA NÁVRHU PRŮMYSLOVÝCH PODLAH Z VLÁKNOBETONU Jan Loško, Lukáš Vrábík, Jaromír Jaroš Úvod Nejrozšířenějším příkadem využití váknobetonu v současné době jsou zřejmě podahové a zákadové desky. Při
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici)
![Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici) Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici)](/thumbs/61/45546970.jpg) Kapitola 8 Vnitřní síly rovinně zakřiveného prutu V této kapitole bude na příkladech vysvětleno řešení vnitřních sil rovinně zakřivených nosníků, jejichž střednici tvoří oblouk ve tvaru kvadratické paraboly[1].
Kapitola 8 Vnitřní síly rovinně zakřiveného prutu V této kapitole bude na příkladech vysvětleno řešení vnitřních sil rovinně zakřivených nosníků, jejichž střednici tvoří oblouk ve tvaru kvadratické paraboly[1].
PŘÍČNÉ LISOVANÉ ZTUŽIDLO VE STŘEŠNÍ ROVINĚ KONSTRUKCÍ Z DŘEVĚNÝCH
 PŘÍČNÉ LISOVANÉ ZTUŽIDLO VE STŘEŠNÍ ROVINĚ KONSTRUKCÍ Z DŘEVĚNÝCH VAZNÍKŮ S KOVOVÝMI DESKAMI S PROLISOVANÝMI TRNY Petr Kukík 1, Micha Grec 2, Aeš Tajbr 3 Abstrakt Timber trusses with punched meta pate
PŘÍČNÉ LISOVANÉ ZTUŽIDLO VE STŘEŠNÍ ROVINĚ KONSTRUKCÍ Z DŘEVĚNÝCH VAZNÍKŮ S KOVOVÝMI DESKAMI S PROLISOVANÝMI TRNY Petr Kukík 1, Micha Grec 2, Aeš Tajbr 3 Abstrakt Timber trusses with punched meta pate
Téma 12, modely podloží
 Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Statika 1. Reakce na rovinných staticky určitých konstrukcích. Miroslav Vokáč ČVUT v Praze, Fakulta architektury.
 reálných 3. přednáška Reakce na rovinných staticky určitých konstrukcích Miroslav Vokáč miroslav.vokac@cvut.cz ČVUT v Praze, Fakulta architektury 21. března 2016 Dřevěný trámový strop - Anežský klášter
reálných 3. přednáška Reakce na rovinných staticky určitých konstrukcích Miroslav Vokáč miroslav.vokac@cvut.cz ČVUT v Praze, Fakulta architektury 21. března 2016 Dřevěný trámový strop - Anežský klášter
Příhradové konstrukce
 Příhradové konstrukce Základní předpoklady konstrukce je vytvořena z přímých prutů pruty jsou navzájem pospojovány v bodech =>styčnících vzájemné spojení prutů se ve všech styčnících se předpokládá kloubové
Příhradové konstrukce Základní předpoklady konstrukce je vytvořena z přímých prutů pruty jsou navzájem pospojovány v bodech =>styčnících vzájemné spojení prutů se ve všech styčnících se předpokládá kloubové
NOSNÍK NA PRUŽNÉM PODLOŽÍ (WINKLEROVSKÉM)
 NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
Kmitavý pohyb trochu jinak
 Kmitavý pohyb trochu jinak JIŘÍ ESAŘ, PER BAROŠ Katedra fyziky, Pedaoická fakuta, JU České Budějovice Kmitavý pohyb patří mezi zákadní fyzikání děje. Většinou se tato část fyziky redukuje na matematický
Kmitavý pohyb trochu jinak JIŘÍ ESAŘ, PER BAROŠ Katedra fyziky, Pedaoická fakuta, JU České Budějovice Kmitavý pohyb patří mezi zákadní fyzikání děje. Většinou se tato část fyziky redukuje na matematický
Postup při výpočtu prutové konstrukce obecnou deformační metodou
 Vysoké učení technické v Brně Fakulta stavební Ústav stavební mechaniky Postup při výpočtu prutové konstrukce obecnou deformační metodou Petr Frantík Obsah 1 Vytvoření modelu 2 2 Styčníkové vektory modelu
Vysoké učení technické v Brně Fakulta stavební Ústav stavební mechaniky Postup při výpočtu prutové konstrukce obecnou deformační metodou Petr Frantík Obsah 1 Vytvoření modelu 2 2 Styčníkové vektory modelu
PRUŽNOST A PLASTICITA I
 Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Téma 2 Úvod ke staticky neurčitým prutovým konstrukcím
 Stvební mechnik,.ročník bkářského studi AST Tém Úvod ke stticky neurčitým prutovým konstrukcím Ktedr stvební mechniky Fkut stvební, VŠB - Technická univerzit Ostrv Osnov přednášky Stticky neurčité konstrukce,
Stvební mechnik,.ročník bkářského studi AST Tém Úvod ke stticky neurčitým prutovým konstrukcím Ktedr stvební mechniky Fkut stvební, VŠB - Technická univerzit Ostrv Osnov přednášky Stticky neurčité konstrukce,
α = 210 A x =... kn A y =... kn A M =... knm
 Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
Pružnost a plasticita II
 Pružnost a pasticita II 3. ročník bakaářského studia doc. Ing. artin Krejsa, Ph.D. Katedra stavební echaniky Neineární chování ateriáů, podínky pasticity, ezní pastická únosnost Úvod, zákadní pojy Teorie
Pružnost a pasticita II 3. ročník bakaářského studia doc. Ing. artin Krejsa, Ph.D. Katedra stavební echaniky Neineární chování ateriáů, podínky pasticity, ezní pastická únosnost Úvod, zákadní pojy Teorie
BETONOVÉ KONSTRUKCE B03C +B03K ŠTÍHLÉ BETONOVÉ KONSTRUKCE. Betonové konstrukce B03C + B03K. Betonové konstrukce B03C +6B03K
 BETONOVÉ KONSTRUKCE B03C +B03K ŠTÍHLÉ BETONOVÉ KONSTRUKCE Betonové konstrukce B03C +4B03K Betonové konstrukce B03C +5B03K Betonové konstrukce B03C +6B03K prvky namáhané kombinací [M+N] N M tak (tah) s
BETONOVÉ KONSTRUKCE B03C +B03K ŠTÍHLÉ BETONOVÉ KONSTRUKCE Betonové konstrukce B03C +4B03K Betonové konstrukce B03C +5B03K Betonové konstrukce B03C +6B03K prvky namáhané kombinací [M+N] N M tak (tah) s
Stav napjatosti materiálu.
 tav napjatosti materiáu. Zákad mechanik, 9. přednáška Obsah přednášk : jednoosý a dvojosý stav napjatosti, stav napjatosti ohýbaného nosníku, deformace ohýbaného nosníku, řešení statick neurčitých úoh
tav napjatosti materiáu. Zákad mechanik, 9. přednáška Obsah přednášk : jednoosý a dvojosý stav napjatosti, stav napjatosti ohýbaného nosníku, deformace ohýbaného nosníku, řešení statick neurčitých úoh
Zakřivený nosník. Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly. Stavební statika, 1.ročník bakalářského studia
 Stavební statika, 1.ročník bakalářského studia Zakřivený nosník Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita
Stavební statika, 1.ročník bakalářského studia Zakřivený nosník Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí
 Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
3. kapitola. Průběhy vnitřních sil na lomeném nosníku. Janek Faltýnek SI J (43) Teoretická část: Příkladová část: Stavební mechanika 2
 3. kapitola Stavební mechanika Janek Faltýnek SI J (43) Průběhy vnitřních sil na lomeném nosníku Teoretická část: Naším úkolem je v tomto příkladu vyšetřit průběh vnitřních sil na lomeném rovinném nosníku
3. kapitola Stavební mechanika Janek Faltýnek SI J (43) Průběhy vnitřních sil na lomeném nosníku Teoretická část: Naším úkolem je v tomto příkladu vyšetřit průběh vnitřních sil na lomeném rovinném nosníku
4.6.3 Příhradové konstrukce
 4.6.3 Příhradové konstrukce Forth Bridge (1890) 2529 m Akashi Kaikyō Bridge (1998) 3911 m "Forth rail bridge head-on-panorama josh-von-staudach" by Josh von Staudach - Own work. "The Forth Bridge seen
4.6.3 Příhradové konstrukce Forth Bridge (1890) 2529 m Akashi Kaikyō Bridge (1998) 3911 m "Forth rail bridge head-on-panorama josh-von-staudach" by Josh von Staudach - Own work. "The Forth Bridge seen
Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím
 Sttik stvebních konstrukcí I.,.ročník bkářského studi Tém 3 Úvod ke stticky neurčitým prutovým konstrukcím Ktedr stvební mechniky Fkut stvební, VŠB - Technická univerzit Ostrv Osnov přednášky Stticky neurčité
Sttik stvebních konstrukcí I.,.ročník bkářského studi Tém 3 Úvod ke stticky neurčitým prutovým konstrukcím Ktedr stvební mechniky Fkut stvební, VŠB - Technická univerzit Ostrv Osnov přednášky Stticky neurčité
Mezní napětí v soudržnosti
 Mení napětí v soudržnosti Pro žebírkovou výtuž e stanovit návrhovou hodnotu meního napětí v soudržnosti vtahu: = η η ctd kde je η součinite ávisý na kvaitě podmínek v soudržnosti a pooe prutu během betonáže
Mení napětí v soudržnosti Pro žebírkovou výtuž e stanovit návrhovou hodnotu meního napětí v soudržnosti vtahu: = η η ctd kde je η součinite ávisý na kvaitě podmínek v soudržnosti a pooe prutu během betonáže
Výpočet přetvoření a dimenzování pilotové skupiny
 Inženýrský manuál č. 18 Aktualizace: 08/2018 Výpočet přetvoření a dimenzování pilotové skupiny Program: Soubor: Skupina pilot Demo_manual_18.gsp Cílem tohoto inženýrského manuálu je vysvětlit použití programu
Inženýrský manuál č. 18 Aktualizace: 08/2018 Výpočet přetvoření a dimenzování pilotové skupiny Program: Soubor: Skupina pilot Demo_manual_18.gsp Cílem tohoto inženýrského manuálu je vysvětlit použití programu
Autor: Vladimír Švehla
 Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
trojkloubový nosník bez táhla a s
 Kapitola 10 Rovinné nosníkové soustavy: trojkloubový nosník bez táhla a s táhlem 10.1 Trojkloubový rám Trojkloubový rám se skládá ze dvou rovinně lomených nosníků v rovinné úloze s kloubovým spojením a
Kapitola 10 Rovinné nosníkové soustavy: trojkloubový nosník bez táhla a s táhlem 10.1 Trojkloubový rám Trojkloubový rám se skládá ze dvou rovinně lomených nosníků v rovinné úloze s kloubovým spojením a
Elastické deformace těles
 Eastické eformace těes 15 Na oceový rát ék L 15 m a průměru 1 mm zavěsíme závaží o hmotnosti m 110 kg přičemž Youngův mou pružnosti ocei v tahu E 16 GPa a mez pružnosti ocei σ P 0 Pa Určete reativní prooužení
Eastické eformace těes 15 Na oceový rát ék L 15 m a průměru 1 mm zavěsíme závaží o hmotnosti m 110 kg přičemž Youngův mou pružnosti ocei v tahu E 16 GPa a mez pružnosti ocei σ P 0 Pa Určete reativní prooužení
Stavební mechanika přednáška, 10. dubna 2017
 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Obecná deformační metoda 8) poznámky k využití symetrie 9) využití výpočetních programů 10) kontrola
Stavební mechanika 3 7. přednáška, 10. dubna 2017 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Obecná deformační metoda 8) poznámky k využití symetrie 9) využití výpočetních programů 10) kontrola
FAKULTA STAVEBNÍ. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
OHYB (Napjatost) M A M + qc a + b + c ) M A = 2M qc a + b + c )
 3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
Modelování kmitavých soustav s jedním stupněm volnosti
 Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
Téma 8 Příčně zatížený rám a rošt
 Statika stavebních konstrukcí I.,.ročník bakalářského studia Téma 8 Příčně zatížený rám a rošt Základní vlastnosti příčně zatíženého rámu Jednoduchý příčně zatížený otevřený rám Základní vlastnosti roštu
Statika stavebních konstrukcí I.,.ročník bakalářského studia Téma 8 Příčně zatížený rám a rošt Základní vlastnosti příčně zatíženého rámu Jednoduchý příčně zatížený otevřený rám Základní vlastnosti roštu
Statika 1. Vnitřní síly na prutech. Miroslav Vokáč 11. dubna ČVUT v Praze, Fakulta architektury. Statika 1. M.
 Definování 4. přednáška prutech iroslav okáč miroslav.vokac@cvut.cz ČUT v Praze, Fakulta architektury 11. dubna 2016 prutech nitřní síly síly působící uvnitř tělesa (desky, prutu), které vznikají působením
Definování 4. přednáška prutech iroslav okáč miroslav.vokac@cvut.cz ČUT v Praze, Fakulta architektury 11. dubna 2016 prutech nitřní síly síly působící uvnitř tělesa (desky, prutu), které vznikají působením
ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ
 7. cvičení ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ V této kapitole se probírají výpočty únosnosti průřezů (neboli posouzení prvků na prostou pevnost). K porušení materiálu v tlačených částech průřezu dochází: mezní
7. cvičení ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ V této kapitole se probírají výpočty únosnosti průřezů (neboli posouzení prvků na prostou pevnost). K porušení materiálu v tlačených částech průřezu dochází: mezní
ZDM RÁMOVÉ KONSTRUKCE
 ioš Hüttner SR D rámové onstruce cvičení 0 adání D RÁOVÉ KONSTRUKCE Příad č. Vyresete průběhy vnitřních si na onstruci zobrazené na Obr.. Příad převzat z atedrové wiipedie (originá e stažení zde http://mech.fsv.cvut.cz/wii/images/d/de/dm_.pdf).
ioš Hüttner SR D rámové onstruce cvičení 0 adání D RÁOVÉ KONSTRUKCE Příad č. Vyresete průběhy vnitřních si na onstruci zobrazené na Obr.. Příad převzat z atedrové wiipedie (originá e stažení zde http://mech.fsv.cvut.cz/wii/images/d/de/dm_.pdf).
STATIKA. Vyšetřování reakcí soustav. Úloha jednoduchá. Ústav mechaniky a materiálů K618
 STATIKA Vyšetřování reakcí soustav Úloha jednoduchá Ústav mechaniky a materiálů K618 1 Zadání Posuďte statickou určitost a vyšetřete reakce rovinné soustavy zadané dle obrázku: q 0 M Dáno: L = 2 m M =
STATIKA Vyšetřování reakcí soustav Úloha jednoduchá Ústav mechaniky a materiálů K618 1 Zadání Posuďte statickou určitost a vyšetřete reakce rovinné soustavy zadané dle obrázku: q 0 M Dáno: L = 2 m M =
Řešení úloh 1. kola 49. ročníku fyzikální olympiády. Kategorie D. Dosazením do rovnice(1) a úpravou dostaneme délku vlaku
 Řešení úoh koa 49 ročníku fyzikání oympiády Kategorie D Autořiúoh:JJírů(,3,4,5,6,),TDenkstein(), a) Všechny uvažované časy jsou měřené od začátku rovnoměrně zrychené pohybu vaku a spňují rovnice = at,
Řešení úoh koa 49 ročníku fyzikání oympiády Kategorie D Autořiúoh:JJírů(,3,4,5,6,),TDenkstein(), a) Všechny uvažované časy jsou měřené od začátku rovnoměrně zrychené pohybu vaku a spňují rovnice = at,
Reakce. K618 FD ČVUT v Praze (pracovní verze). Tento materiál má pouze pracovní charakter a bude v průbehu semestru
 Poznámky ke cvičení z předmětu Pružnost pevnost na K618 D ČVU v Praze (pracovní verze). ento materiá má pouze pracovní charakter a bude v průbehu semestru postupně dopňován. Autor: Jan Vyčich E mai: vycich@fd.cvut.cz
Poznámky ke cvičení z předmětu Pružnost pevnost na K618 D ČVU v Praze (pracovní verze). ento materiá má pouze pracovní charakter a bude v průbehu semestru postupně dopňován. Autor: Jan Vyčich E mai: vycich@fd.cvut.cz
ZDM PŘÍMÉ NOSNÍKY. Příklad č. 1. Miloš Hüttner SMR2 ZDM přímé nosníky cvičení 09. Zadání
 iloš Hüttner SR D přímé nosníky cvičení 09 adání D PŘÍÉ NOSNÍKY Příklad č. 1 Vykreslete průběhy vnitřních sil na konstrukci zobrazené na Obr. 1. Příklad převzat z katedrové wikipedie (originál ke stažení
iloš Hüttner SR D přímé nosníky cvičení 09 adání D PŘÍÉ NOSNÍKY Příklad č. 1 Vykreslete průběhy vnitřních sil na konstrukci zobrazené na Obr. 1. Příklad převzat z katedrové wikipedie (originál ke stažení
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady. Část 1 - Test
 Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
6. Statika rovnováha vázaného tělesa
 6. Statika rovnováha vázaného tělesa 6.1 Rovnováha vázaného tělesa Těleso je vystaveno působení vnějších sil akčních, kterými mohou být osamělé síly, spojité zatížení a momenty silových dvojic. Akční síly
6. Statika rovnováha vázaného tělesa 6.1 Rovnováha vázaného tělesa Těleso je vystaveno působení vnějších sil akčních, kterými mohou být osamělé síly, spojité zatížení a momenty silových dvojic. Akční síly
Zde je uveden abecední seznam důležitých pojmů interaktivního učebního textu
 index 1 Rejstřík Zde je uveden abecední seznam důležitých pojmů interaktivního učebního textu Pružnost a pevnost. U každého termínu je uvedeno označení kapitoly a čísla obrazovek, na nichž lze pojem nalézt.
index 1 Rejstřík Zde je uveden abecední seznam důležitých pojmů interaktivního učebního textu Pružnost a pevnost. U každého termínu je uvedeno označení kapitoly a čísla obrazovek, na nichž lze pojem nalézt.
Kapitola 2. o a paprsek sil lze ztotožnit s osou x (obr.2.1). sil a velikost rovnou algebraickému součtu sil podle vztahu R = F i, (2.
 Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL
 Předmět: Ročník: Vytvoři: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 9. ČERVNA 2013 Název zpracovaného ceku: NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL ÚLOHA 1
Předmět: Ročník: Vytvoři: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 9. ČERVNA 2013 Název zpracovaného ceku: NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL ÚLOHA 1
7 Mezní stavy použitelnosti
 7 Mezní stavy použitenosti Cekové užitné vastnosti konstrukcí mají spňovat dva zákadní požadavky. Prvním požadavkem je bezpečnost, která je zpravida vyjádřena únosností. Druhým požadavkem je použitenost,
7 Mezní stavy použitenosti Cekové užitné vastnosti konstrukcí mají spňovat dva zákadní požadavky. Prvním požadavkem je bezpečnost, která je zpravida vyjádřena únosností. Druhým požadavkem je použitenost,
* Modelování (zjednodušení a popis) tvaru konstrukce. pruty
 2. VNITŘNÍ SÍLY PRUTU 2.1 Úvod * Jak konstrukce přenáší atížení do vaeb/podpor? Jak jsou prvky konstrukce namáhány? * Modelování (jednodušení a popis) tvaru konstrukce. pruty 1 Prut: konstrukční prvek,
2. VNITŘNÍ SÍLY PRUTU 2.1 Úvod * Jak konstrukce přenáší atížení do vaeb/podpor? Jak jsou prvky konstrukce namáhány? * Modelování (jednodušení a popis) tvaru konstrukce. pruty 1 Prut: konstrukční prvek,
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
Couloumbuv zákon stejne jako vetsina zakonu elektrostatiky jsou velmi podobna zakonum gravitacniho pole.
 1) Eektrostaticke poe, Cooumbuv zákon, Permitivita kazde dve teesa nabite eektrickym nabojem Q na sebe pusobi vzajemnou siou. Ta je vysise pomoci Couombovyho zákona: F = 1 4 Q Q 1 2 r r 2 0 kde první cast
1) Eektrostaticke poe, Cooumbuv zákon, Permitivita kazde dve teesa nabite eektrickym nabojem Q na sebe pusobi vzajemnou siou. Ta je vysise pomoci Couombovyho zákona: F = 1 4 Q Q 1 2 r r 2 0 kde první cast
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady.
 Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění )
 1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
Úlohy rovnováhy staticky určitých konstrukcí
 Úohy rovnováhy staticky určitých konstrukcí Úoha: Posoudit statickou určitost či navrhnout podepření konstrukce Určit síy v reakcích a ve vnitřních vazbách Předpokady: Konstrukce je ideaizována soustavou
Úohy rovnováhy staticky určitých konstrukcí Úoha: Posoudit statickou určitost či navrhnout podepření konstrukce Určit síy v reakcích a ve vnitřních vazbách Předpokady: Konstrukce je ideaizována soustavou
ZÁKLADY STAVEBNÍ MECHANIKY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ ING. JIŘÍ KYTÝR, CSc. ING. ZBYNĚK KERŠNER, CSc. ING. ROSTISLAV ZÍDEK ING. ZBYNĚK VLK ZÁKLADY STAVEBNÍ MECHANIKY MODUL BD01-MO3 STATICKY URČITÉ PRUTOVÉ KONSTRUKCE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ ING. JIŘÍ KYTÝR, CSc. ING. ZBYNĚK KERŠNER, CSc. ING. ROSTISLAV ZÍDEK ING. ZBYNĚK VLK ZÁKLADY STAVEBNÍ MECHANIKY MODUL BD01-MO3 STATICKY URČITÉ PRUTOVÉ KONSTRUKCE
Téma 8 Přetvoření nosníků namáhaných ohybem I.
 Pružnost psticit, ročník kářského studi Tém 8 Přetvoření nosníků nmáhných ohem Zákdní vzth předpokd řešení Přetvoření nosníků od nerovnoměrného otepení etod přímé integrce diferenciání rovnice ohové čár
Pružnost psticit, ročník kářského studi Tém 8 Přetvoření nosníků nmáhných ohem Zákdní vzth předpokd řešení Přetvoření nosníků od nerovnoměrného otepení etod přímé integrce diferenciání rovnice ohové čár
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Složené soustavy. Úloha: Sestavení statického schématu, tj. modelu pro statický výpočet (např.výpočet reakcí)
 Složené soustavy Vznikají spojením jednotlivých konstrukčních prvků Úloha: Sestavení statického schématu, tj. modelu pro statický výpočet (např.výpočet reakcí) Metoda: Konstrukci idealizujeme jako soustavu
Složené soustavy Vznikají spojením jednotlivých konstrukčních prvků Úloha: Sestavení statického schématu, tj. modelu pro statický výpočet (např.výpočet reakcí) Metoda: Konstrukci idealizujeme jako soustavu
Pružnost a pevnost. zimní semestr 2013/14
 Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Jev elektromagnetické indukce
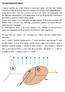 Jev eektromagnetické indukce V minuých kapitoách jsme si jistě uvědomii, že pojmy kid a pohyb, které byy vemi významné u mechanických dějů, při zkoumání eektrických a magnetických jevů nabyy přímo zásadní
Jev eektromagnetické indukce V minuých kapitoách jsme si jistě uvědomii, že pojmy kid a pohyb, které byy vemi významné u mechanických dějů, při zkoumání eektrických a magnetických jevů nabyy přímo zásadní
Pružnost a plasticita II CD03
 Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Stavební mechanika 2 (K132SM02)
 Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D2034 e-mail: matej.leps@fsv.cvut.cz konzultační hodiny budou upřesněny později https://mech.fsv.cvut.cz/student/
Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D2034 e-mail: matej.leps@fsv.cvut.cz konzultační hodiny budou upřesněny později https://mech.fsv.cvut.cz/student/
K výsečovým souřadnicím
 3. cvičení K výsečovým souřadnicím Jak již bylo řečeno, výsečové souřadnice přiřazujeme bodům na střednici otevřeného průřezu, jejich soustava je dána pólem B a výsečovým počátkem M 0. Velikost výsečové
3. cvičení K výsečovým souřadnicím Jak již bylo řečeno, výsečové souřadnice přiřazujeme bodům na střednici otevřeného průřezu, jejich soustava je dána pólem B a výsečovým počátkem M 0. Velikost výsečové
UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ. katedra fyziky ZÁKLADY FYZIKY II. Pro obory DMML, TŘD a AID prezenčního studia DFJP
 UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ katedra fyziky ZÁKLADY FYZIKY II Pro obory DMML, TŘD a AID prezenčního studia DFJP RNDr Jan Z a j í c, CSc, 005 4 MAGNETICKÉ JEVY 4 NESTACIONÁRNÍ ELEKTROMAGNETICKÉ
UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ katedra fyziky ZÁKLADY FYZIKY II Pro obory DMML, TŘD a AID prezenčního studia DFJP RNDr Jan Z a j í c, CSc, 005 4 MAGNETICKÉ JEVY 4 NESTACIONÁRNÍ ELEKTROMAGNETICKÉ
Pružnost a pevnost. 2. přednáška, 10. října 2016
 Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady
 Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
Téma 1 Deformace staticky určitých prutových konstrukcí
 Stavební mechanka, 2.ročník bakaářského studa AST Téma 1 Deformace statck určtých prutových konstrukcí Katedra stavební mechank Fakuta stavební, VŠB - Techncká unverzta Ostrava Stavební statka - přednášející
Stavební mechanka, 2.ročník bakaářského studa AST Téma 1 Deformace statck určtých prutových konstrukcí Katedra stavební mechank Fakuta stavební, VŠB - Techncká unverzta Ostrava Stavební statka - přednášející
Přetvořené ose nosníku říkáme ohybová čára. Je to rovinná křivka.
 OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
5. Statika poloha střediska sil
 5. Statika poloha střediska sil 5.1 Rovnoběžné sily a jejich střed Uvažujeme soustavu vzájemně rovnoběžných sil v prostoru s pevnými působišti. Každá síla má působiště dané polohovým vektorem. Všechny
5. Statika poloha střediska sil 5.1 Rovnoběžné sily a jejich střed Uvažujeme soustavu vzájemně rovnoběžných sil v prostoru s pevnými působišti. Každá síla má působiště dané polohovým vektorem. Všechny
Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr.
 . cvičení Klopení nosníků Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr. Ilustrace klopení Obr. Ohýbaný prut a tvar jeho ztráty
. cvičení Klopení nosníků Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr. Ilustrace klopení Obr. Ohýbaný prut a tvar jeho ztráty
2.2 Mezní stav pružnosti Mezní stav deformační stability Mezní stav porušení Prvek tělesa a napětí v řezu... p03 3.
 obsah 1 Obsah Zde je uveden přehled jednotlivých kapitol a podkapitol interaktivního učebního textu Pružnost a pevnost. Na tomto CD jsou kapitoly uloženy v samostatných souborech, jejichž název je v rámečku
obsah 1 Obsah Zde je uveden přehled jednotlivých kapitol a podkapitol interaktivního učebního textu Pružnost a pevnost. Na tomto CD jsou kapitoly uloženy v samostatných souborech, jejichž název je v rámečku
-R x,a. Příklad 2. na nejbližší vyšší celý mm) 4) Výpočet skutečné plochy A skut 5) Výpočet maximálního napětíσ max 6) Porovnání napětí. Výsl.
 Zákdy dimenzování prutu nmáhného prostým tkem them Th prostý tk-zákdy dimenzování Už známe:, 3 -, i i 3 3 ormáové npětí [P] konst. po výšce průřezu Deformce [m] ii E ově zákdní vzthy: Průřezová chrkteristik
Zákdy dimenzování prutu nmáhného prostým tkem them Th prostý tk-zákdy dimenzování Už známe:, 3 -, i i 3 3 ormáové npětí [P] konst. po výšce průřezu Deformce [m] ii E ově zákdní vzthy: Průřezová chrkteristik
ZÁKLADY STAVEBNÍ MECHANIKY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ ING. JIŘÍ KYTÝR, CSc. ING. ZBYNĚK KERŠNER, CSc. ING. ROSTISLAV ZÍDEK ING. ZBYNĚK VLK ZÁKLADY STAVEBNÍ MECHANIKY MODUL BD01-MO4 STATICKY URČITÉ PRUTOVÉ KONSTRUKCE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ ING. JIŘÍ KYTÝR, CSc. ING. ZBYNĚK KERŠNER, CSc. ING. ROSTISLAV ZÍDEK ING. ZBYNĚK VLK ZÁKLADY STAVEBNÍ MECHANIKY MODUL BD01-MO4 STATICKY URČITÉ PRUTOVÉ KONSTRUKCE
Jsou to konstrukce vytvořené z jednotlivých prutů, které jsou na koncích vzájemně spojeny a označujeme je jako příhradové konstrukce nosníky.
 7. Prutové soustavy Jsou to konstrukce vytvořené z jednotlivých prutů, které jsou na koncích vzájemně spojeny a označujeme je jako příhradové konstrukce nosníky. s styčník (ruší 2 stupně volnosti) každý
7. Prutové soustavy Jsou to konstrukce vytvořené z jednotlivých prutů, které jsou na koncích vzájemně spojeny a označujeme je jako příhradové konstrukce nosníky. s styčník (ruší 2 stupně volnosti) každý
Podmínky k získání zápočtu
 Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
Stěnové nosníky. Obr. 1 Stěnové nosníky - průběh σ x podle teorie lineární pružnosti.
 Stěnové nosníky Stěnový nosník je plošný rovinný prvek uložený na podporách tak, že prvek je namáhán v jeho rovině. Porovnáme-li chování nosníků o výškách h = 0,25 l a h = l, při uvažování lineárně pružného
Stěnové nosníky Stěnový nosník je plošný rovinný prvek uložený na podporách tak, že prvek je namáhán v jeho rovině. Porovnáme-li chování nosníků o výškách h = 0,25 l a h = l, při uvažování lineárně pružného
