6 Algoritmy ořezávání a testování polohy
|
|
|
- Miluše Bednářová
- před 8 lety
- Počet zobrazení:
Transkript
1 6 lgorim ořezáváí a esováí poloh Sudijí íl Teo blok je věová problemaie vzájemé poloh grafikýh primiiv, zejméa poloze bodu vzhledem k mohoúhelíku včeě jedolivýh speifikýh varia jako jsou čřúhelík, jehož sra jsou rovoběžé s osami souřadiového ssému, koveí mohoúhelí a i variaa obeého mohoúhelíku. Dále jsou vsvěle případ, kd je uo ořeza úsečku pravoúhlou oblasí, případě koveím ebo i obeým mohoúhelíkem. Rověž je ukázáo řešeí siuae, kd je řeba ořeza mohoúhelík oblasí, kerá je rověž ve varu čřúhelíku ebo obeého mohoúhelíku. Zároveň jsou vsvěle důvod k pořebě použií ěho ořezovýh algorimů. Doba uá k asudováí 3-4 hodi Průvode sudiem Při sudiu ohoo bloku se předpokládá, že sude je sezáme se základ aaliké geomerie, zá základí vzah pro prái s vekor a vekorovými operaemi. Rověž je ué, ab sude ovládal základí operae booleovské maemaik. 6. Ořezáváí a ořezávaí oblas Při pořebě zobrazeí jakéhokoliv objeku a zobrazovaí plohu jsou zasílá požadavk a zobrazeí prosředivím jedolivýh grafikýh příkazů grafikému proesoru, kerý vváří jejih obraz v grafiké paměi a ásledě jsou obsah grafiké paměi přeese a výsupí zařízeí. rámi elého proesu zobrazeí jsou čási obrazu, keré přesahují skuečou zobrazovaí oblas daého zařízeí odsraě ořízu. Nemá oiž žádý smsl pokouše se zobrazi čási obrazu, keré emohou bý dík apř. velikosi zobrazovaí ploh daého výsupího zařízeí fzik zobraze. To algorim jsou použi i v případě, že ořezávaí oblas eí limiováa zobrazovaí plohou fzikého zařízeí, ale omezujíí je ploha oka aplikae, do íž výsup směřuje. Přesože des dokáže prakik každé zařízeí ořízou a úrovi HW KST/IPOGR - Per eselý KST FEI Uiverzia Pardubie
2 epořebé čási obrazu, aiž b došlo bť k marému pokusu o vkresleí, dohází k případé úpravě obrazu již během jeho zpraováí a úrovi grafikýh kreslííh fukí, případě při zpraováí grafikým proesorem ebo a úrovi ovladače. Saha o včasé použií ořezávaíh algorimů je moivováa především úsporou času, eboť každé ásledé zpraováí zbečýh údajů je aproso zbečé apř. raserizae elé úsečk, pokud její velká čás leží mimo zobrazovaí oblas. Obvkle je vidielou ořezávaí oblasí osově orieovaý pravoúhelík věšiou oko souřadiového ssému zařízeí. Moivaí pro vlasí implemeai a použií ořezávaíh algorimů může bý: zrhleí grafikého výsupu v případě, že velké možsví objeků leží mimo vidielou oblas a zjišěí éo skuečosi je rhlejší ež samoé kresleí, vkresleí obrazu pouze do určié čási grafikého výsupího zařízeí vkresleí víe obrazů do růzýh čásí jedoho oka, áhrada ořezáváí a úrovi grafikého výsupího zařízeí. Ořezávaí algorim lippig je možo rozděli a kaegorie: ořezáí bodu es poloh bodu pro určeí, zda se daý bod zobrazí ebo e, ořezáí liiovýh objeků určeou oblasí, ořezáí oblasi určeou oblasí. 6.2 Tesováí poloh bodu 6.2. Poloha bodu vzhledem k pravoúhelíku se sraami rovoběžými s osami souřadiového ssému Tao variaa je ejběžější vzhledem k omu, že ořezáí es poloh je ejčasěji používá apř. vzhledem k a oblas oka, obrazovk ebo vzhledem k poiskuelé čási lisu papíru v iskárě. omo speifikém a a výpoče velmi eáročém případě ořezáváí osově orieovaým pravoúhelíkem sačí vhodoi souřadie vkreslovaého KST/IPOGR -2 Per eselý KST FEI Uiverzia Pardubie
3 bodu [,] vzhledem k hraiím pravoúhelíku. Podmíka pro určeí, že bod leží v ořezávaé oblasi je ásledujíí: >Mi <Ma >Mi <Ma Y M X Y MIN M Tes poloh bodu vzhledem ke koveímu mohoúhelíku IN M omo případě je uo urči polohu bodu vůči všem hraičím úsečkám. Polohu bodu P a úsečk lze urči pomoí velikosi X vekorového součiu u a v P X X i u v u v X X u v j Y Y k u v Z Z i bx ax px ax j by ay py ay k zhledem k omu, že oba vekor leží v jedé roviě, je pro další posup rozhodujíí pouze zaméko z-ové souřadie výsledého vekoru. S=b -a p -a -b -a p -a Dle zaméka je možo urči polohu bodu P vzhledem k úseče ásledově: pokud S<, poom bod P leží apravo od úsečk pokud S=, poom bod P leží a úseče pokud S>, poom bod leží alevo od úsečk Pravidlo pro určeí elkové poloh bodu P k daému mohoúhelíku KST/IPOGR -3 Per eselý KST FEI Uiverzia Pardubie
4 Pokud je mohoúhelík defiová poslouposí vrholovýh uzlů: proi směru hodiovýh ručiček, poom všeřovaý bod leží uviř právě ehd, pokud leží vlevo od všeh úseček. po směru hodiovýh ručiček, poom všeřovaý bod leží uviř právě ehd, pokud leží vpravo od všeh úseček Tes poloh bodu vzhledem k obeému mohoúhelíku Pro ekoveí mohoúhelík je řeba vhodoi poče průsečíků polopřímk vedeé z všeřovaého bodu P libovolým směrem s hraami mohoúhelíku. Pravidlo pro určeí poloh Sudý poče průsečíků zameá, že bod leží vě Lihý poče průsečíků zameá, že bod leží uviř Problém asaou, pokud paprsek prohází vrholem ebo pokud čás paprsku je oožá s ěkerou hraou. omo případě je řešeím sejý posup, jako u algorimu řádkového vplňováí vekorově zadaé oblasi, j. použií vodorového paprsku, veháí vodorovýh hra a rozpojeí hra pomoí jejih zkráeí. 6.3 Ořezáí úsečk Ořezáí úsečk je velmi časo používaou operaí, proo algorim pro její provedeí musí bý maimálě efekiví a spolehlivé. Eisuje moho růzýh algorimů, keré se liší jak možosmi použií, ak i rhlosí. Obeě lze říi, že obeé meod, umožňujíí ořezáí úsečk libovolým mohoúhelíkem jsou pomalejší, ež meod, keré jsou použielé pouze ve speifikýh případeh ořez pravoúhelíkem sraově rovoběžým s osami SS ebo ořez koveím mohoúhelíkem. KST/IPOGR -4 Per eselý KST FEI Uiverzia Pardubie
5 Eisují rověž speifiké meod pro ořez jiýh liiovýh objeků ež je úsečka a meod umožňujíí ořez jiou oblasí ež je mohoúhelík apř. kružie, ovšem o meod lze vžd éměř vžd po příslušé aproimai objeků aradi ořezávaí meodou pro ořezáváí úsečk úseček mohoúhelíkem Meoda Cohe-Suherlad Meoda je použielá pro ořezáí úsečk pravoúhlou oblasí, jejíž sra jsou rovoběžé s osami SS. Je založea a rozděleí elé ploh USS a jedolivé oblasi. Těmo oblasem je přiřaze 4-biový kód podle poloh vzhledem k poloze ořezávaí oblasi vlevo, vpravo, dole, ahoře Obrázek : Rozděleí ploh a sekor Pro každý počáečí Z a koový K bod úsečk se určí kód. Následujíí podmík rozhodou o poloze úsečk vzhledem k pravoúhelíku a o ásledém posupu: Pokud kódz kódk =, poom úsečka je elá uviř. Pokud kódz kódk, poom úsečka je elá mimo a je možo ji elou za dalšího zpraováí apř. zobrazeí veha Pokud kódz kódk =, poom je zřejmé, že asala siuae, kd úsečka prohází víe oblasmi. omo případě je řeba ji ořízou ořezáváí se provádí dle libovolé jedičk v kódeh pro Z a K a es s ovými kód je uo zopakova. KST/IPOGR -5 Per eselý KST FEI Uiverzia Pardubie
6 Jedolivé siuae jsou zázorě a ásledujíím obrázku. Obrázek 2: Ilusrae varia, keré mohou asa u algorimu CS Meoda Crus-ek Tao meoda je zobeěím meod Liag-arsk a je určeá k ořezáí úsečk libovolým koveím mohoúhelíkem. Je založea a paramerikém vjádřeí úsečk. Poče ořezů, keré je řeba vkoa, závisí a zvoleém pořadí řezeíh hra. KST/IPOGR -6 Per eselý KST FEI Uiverzia Pardubie
7 Na uvedeém obrázku je vzačea ořezávaá úsečka, ořezávaí oblas je defiováa jako mohoúhelík pomoí bodů, 2, 3, 4 a 5. Úsečka po ořezáí je určea bod 3. Červeou barvou jsou azače ormálové vekor jedolivýh řezaíh hra. Předpoklad a základí pravidla: Ořezávaí oblas je zadáa pomoí orieovaýh hra, orieae je proi směru hod. ruč. Ořezávaá úsečka je orieováa Parameriké vjádřeí P= + - Pro avzájem kolmé vekor plaí: u. v Normálový vekor oočeí v o 9 vpravo se vvoří a základě směrového vekoru záměou souřadi a jedou změou zaméka: v, v, v Tupý úhel: u. v Osrý úhel: u. v Na ásledujíím obrázku je zázorě základí posup pro jedu hrau: KST/IPOGR -7 Per eselý KST FEI Uiverzia Pardubie
8 KST/IPOGR -8 Per eselý KST FEI Uiverzia Pardubie Hledáme bod C, kerý voří průsečík hra 2 a. Hledaý bod C defiujeme pomoí parameru z parameriké rovie: P C Dále musí plai, že vekor C musí bý kolmý a ormálový vekor. P C algorimu je uo rolišova případ, kd úsečka směřuje doviř oblasi a siuae, kd směřuje ve. To lze zjisi a základě hodo součiu vekorů a směrového vekoru úsečk : směřuje doviř směřuje ve: je rovoběžá s hraou: lgorimus výpoču iiializae paramerů začáku a koe úsečk: Z =, K = pro každou hrau -úhelíku: určeí ormálového vekoru pokud skalárí souči - <> výpoče C dle směru doviř/ve případá změa Z = ma Z, C ebo K = mi K, C
9 jiak úsečka je rovoběžá s ouo hraou pokud leží v poloroviě mimo -úhelík: lze ořezávaou úsečku zela vpusi KONEC jiak emá ao hraa a ořezáí vliv POKRČ. DLŠÍ HRNOU pokud Z < K, poom se kreslí ořezaá úsečka P Z P K, jiak po ořezu z úsečk i ezblo Pojm k zapamaováí Raserizae, raserizačí algorimus, ieračí způsob výpoču, predike, eločíselý algorimus Oázk a provičeí. Jaký je důvod k vžíváí ořezávaíh algorimů? 2. Co je o ořezávaí oblas? 3. Jak se zjišťuje poloha bodu vzhledem k jedolivým pům oblasí? 4. Jak fugují jedolivé uvedeé algorim pro ořez úsečk? 5. Jaký je ssém pro vvářeí kódů jedolivýh segmeů ořezávaí oblasi u algorimu Cohe-Shuerlad? 6. Z jakého vjádřeí úsečk vhází algorimus Crus-ek? 7. Jaké jsou výhod algorimu Liag-arsk oproi algorimu Cohe- Shuerlad? Odkaz a další sudijí prame Žára, J., eeš,., Felkel, P. Moderí počíačová grafika. Compuer Press, ro, 998. ISN Fole, a D. Compuer Graphis. Priiples ad Praie. ddiso-wesle,99. KST/IPOGR -9 Per eselý KST FEI Uiverzia Pardubie
10 Transformace 3D. 10.1 Transformace a jejich realizace. Studijní cíl. Doba nutná k nastudování. Průvodce studiem
 Trnsformce 3D Sudijní cíl Teno blok je věnován rnsformcím 3D grfik. V eu budou popsán ákldní rnsformce v prosoru posunuí oočení kosení měn měřík používné při prcování 3D modelu. Jednolivé rnsformce budou
Trnsformce 3D Sudijní cíl Teno blok je věnován rnsformcím 3D grfik. V eu budou popsán ákldní rnsformce v prosoru posunuí oočení kosení měn měřík používné při prcování 3D modelu. Jednolivé rnsformce budou
OBJEKTOVÁ ALGEBRA. Zdeněk Pezlar. Ústav Informatiky, Provozně-ekonomická fakulta MZLU, Brno, ČR. Abstrakt
 OBEKTOVÁ ALGEBRA Zdeěk Pezlar Úsav Iformaiky, Provozě-ekoomická fakula MZLU, Bro, ČR Absrak V objekovém modelu da defiujeme objekové schéma (řídu) jako čveřici skládající se ze jméa řídy, aribuů, domé
OBEKTOVÁ ALGEBRA Zdeěk Pezlar Úsav Iformaiky, Provozě-ekoomická fakula MZLU, Bro, ČR Absrak V objekovém modelu da defiujeme objekové schéma (řídu) jako čveřici skládající se ze jméa řídy, aribuů, domé
Fakulta strojního inženýrství VUT v Brně Ústav konstruování. KONSTRUOVÁNÍ STROJŮ převody. Přednáška 5
 Fakula srojího ižeýrsví VUT v Brě Úsav kosruováí KONSTRUOVÁNÍ STROJŮ převody Předáška 5 Čelí soukolí se šikmými zuby hp://www.audiforum.l/ Moderaio is bes, ad o avoid all exremes. PLUTARCHOS Čelí soukolí
Fakula srojího ižeýrsví VUT v Brě Úsav kosruováí KONSTRUOVÁNÍ STROJŮ převody Předáška 5 Čelí soukolí se šikmými zuby hp://www.audiforum.l/ Moderaio is bes, ad o avoid all exremes. PLUTARCHOS Čelí soukolí
ÚVOD DO DYNAMIKY HMOTNÉHO BODU
 ÚVOD DO DYNAMIKY HMOTNÉHO BODU Obsah Co je o dnamika? 1 Základní veličin dnamik 1 Hmonos 1 Hbnos 1 Síla Newonov pohbové zákon První Newonův zákon - zákon servačnosi Druhý Newonův zákon - zákon síl Třeí
ÚVOD DO DYNAMIKY HMOTNÉHO BODU Obsah Co je o dnamika? 1 Základní veličin dnamik 1 Hmonos 1 Hbnos 1 Síla Newonov pohbové zákon První Newonův zákon - zákon servačnosi Druhý Newonův zákon - zákon síl Třeí
1.6. Srovnání empirických a teoretických parametrů (4.-5.předn.)
 .6. rováí empirických a eoreických paramerů (4.-5.před.) Cíle: - pravděpodobosí zkoumáí výběrového saisického souboru: kvaifikace eoreických paramerů, srováí eoreických a empirických paramerů (Probable
.6. rováí empirických a eoreických paramerů (4.-5.před.) Cíle: - pravděpodobosí zkoumáí výběrového saisického souboru: kvaifikace eoreických paramerů, srováí eoreických a empirických paramerů (Probable
Správnost vztahu plyne z věty o rovnosti úhlů s rameny na sebe kolmými (obr. 13).
 37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
Geometrické modelování. Diferenciáln
 Geomerické modelováí Difereciál lí geomerie křivekk Křivky v očía ačové grafice Geomerická ierreace Každý krok algorimu má svůj geomerický výzam Flexibilia korola ad růběhem křivky, možos iuiiví ediace
Geomerické modelováí Difereciál lí geomerie křivekk Křivky v očía ačové grafice Geomerická ierreace Každý krok algorimu má svůj geomerický výzam Flexibilia korola ad růběhem křivky, možos iuiiví ediace
Číslo materiálu VY_32_INOVACE_CTE_2.MA_17_Klopné obvody RS, JK, D, T. Střední odborná škola a Střední odborné učiliště, Dubno Ing.
 Číslo projeku CZ..7/.5./34.58 Číslo maeriálu VY_32_INOVACE_CTE_2.MA_7_Klopé obvody RS, JK, D, T. Název školy Auor Temaická oblas Ročík Sředí odborá škola a Sředí odboré učilišě, Dubo Ig. Miroslav Krýdl
Číslo projeku CZ..7/.5./34.58 Číslo maeriálu VY_32_INOVACE_CTE_2.MA_7_Klopé obvody RS, JK, D, T. Název školy Auor Temaická oblas Ročík Sředí odborá škola a Sředí odboré učilišě, Dubo Ig. Miroslav Krýdl
7. Analytická geometrie
 7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
Přijímací zkouška na navazující magisterské studium 2016
 Přijímací zkouška a avazující magiserské sudium 2016 Sudijí program: Sudijí obor: Maemaika Fiačí a pojisá maemaika Variaa A Řešeí příkladů pečlivě odůvoděe. Věuje pozoros ověřeí předpokladů použiých maemaických
Přijímací zkouška a avazující magiserské sudium 2016 Sudijí program: Sudijí obor: Maemaika Fiačí a pojisá maemaika Variaa A Řešeí příkladů pečlivě odůvoděe. Věuje pozoros ověřeí předpokladů použiých maemaických
Statika 1. Miroslav Vokáč ČVUT v Praze, Fakulta architektury. Statika 1. M. Vokáč. Plocha.
 Saika 1 Saika 1 2. přednáška ové veličin Saický momen Těžišě Momen servačnosi Hlavní ěžiš ové os a hlavní cenrální momen servačnosi Elipsa servačnosi Miroslav Vokáč miroslav.vokac@klok.cvu.cz Konrolní
Saika 1 Saika 1 2. přednáška ové veličin Saický momen Těžišě Momen servačnosi Hlavní ěžiš ové os a hlavní cenrální momen servačnosi Elipsa servačnosi Miroslav Vokáč miroslav.vokac@klok.cvu.cz Konrolní
Řešení soustav lineárních rovnic
 Řešeí sousv lieáríc rovic Sousv lieáríc rovic Sousvou m lieáríc rovic o ezámýc rozumíme sousvu : Kde ij i R M m m Čísl ij zýváme koeficiey sousvy čísl i soluí čley Uvedeou sousvu udeme zči Sm m M m Homogeí
Řešeí sousv lieáríc rovic Sousv lieáríc rovic Sousvou m lieáríc rovic o ezámýc rozumíme sousvu : Kde ij i R M m m Čísl ij zýváme koeficiey sousvy čísl i soluí čley Uvedeou sousvu udeme zči Sm m M m Homogeí
5 DISKRÉTNÍ ROZDĚLENÍ PRAVDĚPODOBNOSTI. Čas ke studiu kapitoly: 120 minut. Cíl: Po prostudování tohoto odstavce budete umět:
 5 DISKRÉTNÍ ROZDĚLENÍ RAVDĚODOBNOSTI Čas e sudiu aioly: 0 miu Cíl: o rosudováí ohoo odsavce budee umě: charaerizova hyergeomericé rozděleí charaerizova Beroulliho ousy a z ich odvozeé jedolivé yy disréích
5 DISKRÉTNÍ ROZDĚLENÍ RAVDĚODOBNOSTI Čas e sudiu aioly: 0 miu Cíl: o rosudováí ohoo odsavce budee umě: charaerizova hyergeomericé rozděleí charaerizova Beroulliho ousy a z ich odvozeé jedolivé yy disréích
 Š Ú ř Ú ů Ž é ř ž ř Ž ř ů ú Ú Ú ú Ú Ž ů ř ř ř Ú é é é é é é Ž é ů ž ř ž ů ř ř ů é ů ů ů ŠŠ Ů ř ř ř ú ř é ň ř ň ř É ř ř ř ř é ř ř ř ř ř ř é é é Ž é é é é Š Ž ů ů é Ž ř ř ř Ž é ř ž Ž ř ř Ž éž ř Š éž Ž é
Š Ú ř Ú ů Ž é ř ž ř Ž ř ů ú Ú Ú ú Ú Ž ů ř ř ř Ú é é é é é é Ž é ů ž ř ž ů ř ř ů é ů ů ů ŠŠ Ů ř ř ř ú ř é ň ř ň ř É ř ř ř ř é ř ř ř ř ř ř é é é Ž é é é é Š Ž ů ů é Ž ř ř ř Ž é ř ž Ž ř ř Ž éž ř Š éž Ž é
Předmět: SM 01 ROVINNÉ PŘÍHRADOVÉ KONSTRUKCE
 Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
Statika 2. Kombinace namáhání N + M y + M z. Miroslav Vokáč 19. října ČVUT v Praze, Fakulta architektury.
 2. přednáška N + M + M Jádro průřeu Šikmý ohb M + N M + N M + M + N Jádro průřeu Ecenrický lak a vloučeného ahu Konrolní oák Miroslav Vokáč miroslav.vokac@cvu.c ČVUT v Prae, Fakula archiekur 19. října
2. přednáška N + M + M Jádro průřeu Šikmý ohb M + N M + N M + M + N Jádro průřeu Ecenrický lak a vloučeného ahu Konrolní oák Miroslav Vokáč miroslav.vokac@cvu.c ČVUT v Prae, Fakula archiekur 19. října
7.2.4 Násobení vektoru číslem
 7..4 Násobeí vektor číslem Předpoklady: 703 Tetokrát začeme hed defiicí. Násobek lového vektor číslem k je lový vektor. Násobek elového vektor = B Ačíslem k je vektor C A, přičemž C je bod, pro který platí:
7..4 Násobeí vektor číslem Předpoklady: 703 Tetokrát začeme hed defiicí. Násobek lového vektor číslem k je lový vektor. Násobek elového vektor = B Ačíslem k je vektor C A, přičemž C je bod, pro který platí:
Pravděpodobnostní modely
 Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
základním prvkem teorie křivek v počítačové grafice křivky polynomiální n
 Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
f(x) f(x 0 ) = a lim x x0 f f(x 0 + h) f(x 0 ) (x 0 ) = lim f(x + h) f(x) (x) = lim
 KAPITOLA 4: 4 Úvod Derivace fkce [MA-8:P4] Moivačí příklady: okamžiá ryclos, směrice ečy Defiice: Řekeme, že fkce f má v bodě derivaci [ derivaci zleva derivaci zprava ] rov čísl a, jesliže exisje [ x
KAPITOLA 4: 4 Úvod Derivace fkce [MA-8:P4] Moivačí příklady: okamžiá ryclos, směrice ečy Defiice: Řekeme, že fkce f má v bodě derivaci [ derivaci zleva derivaci zprava ] rov čísl a, jesliže exisje [ x
Maxwellovy a vlnová rovnice v obecném prostředí
 Maxwellovy a vlnová rovnie v obeném prosředí Ing. B. Mihal Malík, Ing. B. Jiří rimas TCHNICKÁ UNIVRZITA V LIBRCI Fakula meharoniky, informaiky a mezioborovýh sudií Teno maeriál vznikl v rámi proeku SF
Maxwellovy a vlnová rovnie v obeném prosředí Ing. B. Mihal Malík, Ing. B. Jiří rimas TCHNICKÁ UNIVRZITA V LIBRCI Fakula meharoniky, informaiky a mezioborovýh sudií Teno maeriál vznikl v rámi proeku SF
FINANČNÍ MATEMATIKA- JEDNODUCHÉ ÚROKOVÁNÍ
 Projek ŠABLONY NA GVM Gymázium Velké Meziříčí regisračí číslo projeku: CZ..7/.5./34.948 IV-2 Iovace a zkvaliěí výuky směřující k rozvoji maemaické gramoosi žáků sředích škol FINANČNÍ MATEMATIA- JEDNODCHÉ
Projek ŠABLONY NA GVM Gymázium Velké Meziříčí regisračí číslo projeku: CZ..7/.5./34.948 IV-2 Iovace a zkvaliěí výuky směřující k rozvoji maemaické gramoosi žáků sředích škol FINANČNÍ MATEMATIA- JEDNODCHÉ
 Á É É ě ě ů ě Č Ú Í ě Ž ě Í ě Í š ú ě ě Ú ě ě Í Ž ů Č Ž ě ě Ž Ž ě Í Ž Ž ě ú Í ě š Í Í Š ú ě ě Č Ž ě ě ú Š ě š Í Š ě ě ň ě ě Č ď ě Č ů ú ě ú ě Ž ě Č ě ě ů ě Ž ě ů ě ě ě ě ěž Ž Ž ě Ž ě ě ň ú Ž ů ě ě Ž Ž
Á É É ě ě ů ě Č Ú Í ě Ž ě Í ě Í š ú ě ě Ú ě ě Í Ž ů Č Ž ě ě Ž Ž ě Í Ž Ž ě ú Í ě š Í Í Š ú ě ě Č Ž ě ě ú Š ě š Í Š ě ě ň ě ě Č ď ě Č ů ú ě ú ě Ž ě Č ě ě ů ě Ž ě ů ě ě ě ě ěž Ž Ž ě Ž ě ě ň ú Ž ů ě ě Ž Ž
Matice. nazýváme m.n reálných čísel a. , sestavených do m řádků a n sloupců ve tvaru... a1
 Matice Matice Maticí typu m/ kde m N azýváme m reálých čísel a sestaveých do m řádků a sloupců ve tvaru a a a a a a M M am am am Prví idex i začí řádek a druhý idex j sloupec ve kterém prvek a leží Prvky
Matice Matice Maticí typu m/ kde m N azýváme m reálých čísel a sestaveých do m řádků a sloupců ve tvaru a a a a a a M M am am am Prví idex i začí řádek a druhý idex j sloupec ve kterém prvek a leží Prvky
Obecná soustava sil a momentů v prostoru
 becá soustava sil a mometů v prostoru Zcela obecé atížeí silami a momet a těleso v prostoru (vede a 6 rovic) Saha o převráceí (akce) Specifické případ Vikla u obce Kadov, ~30 t Svaek sil paprsk všech sil
becá soustava sil a mometů v prostoru Zcela obecé atížeí silami a momet a těleso v prostoru (vede a 6 rovic) Saha o převráceí (akce) Specifické případ Vikla u obce Kadov, ~30 t Svaek sil paprsk všech sil
Analytická geometrie
 Alytická geometrie Vektory Prmetrické vyjádřeí přímky roviy Obecá rovice droviy Vektorový prostor Nechť jsou dáy ásledující mtemtické objekty: ) ) ) 4) Číselé těleso T. Neprázdá moži V. Zobrzeí Zobrzeí
Alytická geometrie Vektory Prmetrické vyjádřeí přímky roviy Obecá rovice droviy Vektorový prostor Nechť jsou dáy ásledující mtemtické objekty: ) ) ) 4) Číselé těleso T. Neprázdá moži V. Zobrzeí Zobrzeí
Parciální funkce a parciální derivace
 Parciální funkce a parciální derivace Pro sudeny FP TUL Marina Šimůnková 19. září 2018 1. Parciální funkce. Příklad: zvolíme-li ve funkci f : (x, y) sin(xy) pevnou hodnou y, například y = 2, dosaneme funkci
Parciální funkce a parciální derivace Pro sudeny FP TUL Marina Šimůnková 19. září 2018 1. Parciální funkce. Příklad: zvolíme-li ve funkci f : (x, y) sin(xy) pevnou hodnou y, například y = 2, dosaneme funkci
Odezva na obecnou periodickou budící funkci. Iva Petríková Katedra mechaniky, pružnosti a pevnosti
 Odezva a obecou periodickou budící fukci Iva Períková Kaedra mechaiky, pružosi a pevosi Obsah Fourierovy řady Odezva a polyharmoickou fukci Odezva a obecou periodickou fukci Odezva a jedokový skok Příklad
Odezva a obecou periodickou budící fukci Iva Períková Kaedra mechaiky, pružosi a pevosi Obsah Fourierovy řady Odezva a polyharmoickou fukci Odezva a obecou periodickou fukci Odezva a jedokový skok Příklad
ZPŮSOBY MODELOVÁNÍ ELASTOMEROVÝCH LOŽISEK
 ZPŮSOBY MODELOVÁNÍ ELASTOMEROVÝCH LOŽISEK Vzhledem ke skuečnosi, že způsob modelování elasomerových ložisek přímo ovlivňuje průběh vniřních sil v oblasi uložení, rozebereme v éo kapiole jednolivé možné
ZPŮSOBY MODELOVÁNÍ ELASTOMEROVÝCH LOŽISEK Vzhledem ke skuečnosi, že způsob modelování elasomerových ložisek přímo ovlivňuje průběh vniřních sil v oblasi uložení, rozebereme v éo kapiole jednolivé možné
Sekvenční logické obvody(lso)
 Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Instalační manuál inels Home Control
 OBSAH 1) Úvod... 3 2) Kofigurace chytré krabičky... 3 3) Nahráí aplikace do TV... 3 4) Nastaveí IP adresy do TV... 4 5) Nastaveí chytré krabičky pomocí SmartTV aplikace... 4 5.1) Půdorys (floorpla)...
OBSAH 1) Úvod... 3 2) Kofigurace chytré krabičky... 3 3) Nahráí aplikace do TV... 3 4) Nastaveí IP adresy do TV... 4 5) Nastaveí chytré krabičky pomocí SmartTV aplikace... 4 5.1) Půdorys (floorpla)...
Základy teorie chyb a zpracování fyzikálních měření Jiří Novák
 Zálad eore chb a zpracováí zálích měřeí Jří ová Teo e je zamýšle jao pomůca pro vpracováí laboraorích úloh z z Je urče pouze pro sudjí účel a jeho účelem je objas meod zpracováí měřeí Chb měřeí Druh chb
Zálad eore chb a zpracováí zálích měřeí Jří ová Teo e je zamýšle jao pomůca pro vpracováí laboraorích úloh z z Je urče pouze pro sudjí účel a jeho účelem je objas meod zpracováí měřeí Chb měřeí Druh chb
1. Číselné obory, dělitelnost, výrazy
 1. Číselé obory, dělitelost, výrazy 1. obor přirozeých čísel - vyjadřující počet prvků možiy - začíme (jsou to kladá edesetiá čísla) 2. obor celých čísel - možia celých čísel = edesetiá, ale kladá i záporá
1. Číselé obory, dělitelost, výrazy 1. obor přirozeých čísel - vyjadřující počet prvků možiy - začíme (jsou to kladá edesetiá čísla) 2. obor celých čísel - možia celých čísel = edesetiá, ale kladá i záporá
DIMENZOVÁNÍ KOMPOZITNÍCH PROFILŮ PREFEN
 DIMNZOVÁNÍ KOMPOZITNÍCH PROFILŮ PRFN 1 Kulkova 10/4231, 615 00 Bro el.: 541 583 208, 297, fa.: 549 254 556 e-mail: kompozi@prefa.cz hp://www.prefa-kompozi.cz DIMNZOVÁNÍ PROFILŮ Maeriálová srukura, základí
DIMNZOVÁNÍ KOMPOZITNÍCH PROFILŮ PRFN 1 Kulkova 10/4231, 615 00 Bro el.: 541 583 208, 297, fa.: 549 254 556 e-mail: kompozi@prefa.cz hp://www.prefa-kompozi.cz DIMNZOVÁNÍ PROFILŮ Maeriálová srukura, základí
3. POJIŠTĚNÍ OSOB (ŽIVOTNÍ POJIŠTĚNÍ)
 3. POJIŠTĚÍ OSOB (ŽIVOTÍ POJIŠTĚÍ) 3.. EMOELOVÝ PŘÍSTUP 3... ekremeí řád vymíráí populace Úmrosí abulky a) Smr je áhodým jevem, kerý se pojišťuje pro účely ŽP sačí pracova s průměrými hodoami záko velkých
3. POJIŠTĚÍ OSOB (ŽIVOTÍ POJIŠTĚÍ) 3.. EMOELOVÝ PŘÍSTUP 3... ekremeí řád vymíráí populace Úmrosí abulky a) Smr je áhodým jevem, kerý se pojišťuje pro účely ŽP sačí pracova s průměrými hodoami záko velkých
FINANČNÍ MATEMATIKA- SLOŽENÉ ÚROKOVÁNÍ
 Projek ŠABLONY NA GVM Gymázium Velké Meziříčí regisračí číslo projeku: CZ..7/../.98 IV- Iovace a zkvaliěí výuky směřující k rozvoji maemaické gramoosi žáků sředích škol FINANČNÍ MATEMATIA- SLOŽENÉ ÚROOVÁNÍ
Projek ŠABLONY NA GVM Gymázium Velké Meziříčí regisračí číslo projeku: CZ..7/../.98 IV- Iovace a zkvaliěí výuky směřující k rozvoji maemaické gramoosi žáků sředích škol FINANČNÍ MATEMATIA- SLOŽENÉ ÚROOVÁNÍ
Seznámíte se s principem integrace substituční metodou a se základními typy integrálů, které lze touto metodou vypočítat.
 4 Inegrace subsiucí 4 Inegrace subsiucí Průvodce sudiem Inegrály, keré nelze řeši pomocí základních vzorců, lze velmi časo řeši subsiuční meodou Vzorce pro derivace elemenárních funkcí a věy o derivaci
4 Inegrace subsiucí 4 Inegrace subsiucí Průvodce sudiem Inegrály, keré nelze řeši pomocí základních vzorců, lze velmi časo řeši subsiuční meodou Vzorce pro derivace elemenárních funkcí a věy o derivaci
Modelování vlivu parametrického buzení na kmitání vetknutého nosníku
 . ročík echické koferece ARaP, 4. a 5.. 4, Praha Modelováí vlivu paramerického buzeí a kmiáí vekuého osíku Jiří TŮMA, Per Ferfecki, Pavel ŠURÁNE, Miroslav MAHDA VŠB - Techická uiverzia Osrava ARaP 4 Osova
. ročík echické koferece ARaP, 4. a 5.. 4, Praha Modelováí vlivu paramerického buzeí a kmiáí vekuého osíku Jiří TŮMA, Per Ferfecki, Pavel ŠURÁNE, Miroslav MAHDA VŠB - Techická uiverzia Osrava ARaP 4 Osova
Aritmetická posloupnost, posloupnost rostoucí a klesající Posloupnosti
 8 Aritmetická posloupost, posloupost rostoucí a klesající Poslouposti Posloupost je fukci s defiičím oborem celých kladých čísel - apř.,,,,,... 3 4 5 Jako fukci můžeme také posloupost zobrazit do grafu:
8 Aritmetická posloupost, posloupost rostoucí a klesající Poslouposti Posloupost je fukci s defiičím oborem celých kladých čísel - apř.,,,,,... 3 4 5 Jako fukci můžeme také posloupost zobrazit do grafu:
Komplexní čísla. Definice komplexních čísel
 Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
NA POMOC FO. Pád vodivého rámečku v magnetickém poli
 NA POMOC FO Pád vodivého rámečku v maneickém poli Karel auner *, Pedaoická akula ZČU v Plzni Příklad: Odélníkový rámeček z vodivého dráu má rozměry a,, hmonos m a odpor. Je zavěšen ve výšce h nad horním
NA POMOC FO Pád vodivého rámečku v maneickém poli Karel auner *, Pedaoická akula ZČU v Plzni Příklad: Odélníkový rámeček z vodivého dráu má rozměry a,, hmonos m a odpor. Je zavěšen ve výšce h nad horním
 Č É É Č ď Č ž ž Ž ď ě š ě š ě ě š ě ď ž ď šť ť ďš Č ď Č Č ě ž ž Í ě Č ě š ě š š Ž ě ě ť ě ž ě Č ě ž š Í Í ě ě ď ě ě ě ě Í ě ť ě ě ď ě ť ě ď ž ě ě š ě ť Č ě Ž Ž ě ž š š Ž ě Č Ž ě ě ě ě ě ě ě Ž ž ě ť É šš
Č É É Č ď Č ž ž Ž ď ě š ě š ě ě š ě ď ž ď šť ť ďš Č ď Č Č ě ž ž Í ě Č ě š ě š š Ž ě ě ť ě ž ě Č ě ž š Í Í ě ě ď ě ě ě ě Í ě ť ě ě ď ě ť ě ď ž ě ě š ě ť Č ě Ž Ž ě ž š š Ž ě Č Ž ě ě ě ě ě ě ě Ž ž ě ť É šš
FINANČNÍ MATEMATIKA- ÚVĚRY
 Projek ŠABLONY NA GVM Gymnázium Velké Meziříčí regisrační číslo projeku: CZ.1.07/1.5.00/4.0948 IV- Inovace a zkvalinění výuky směřující k rozvoji maemaické gramonosi žáků sředních škol FINANČNÍ MATEMATIKA-
Projek ŠABLONY NA GVM Gymnázium Velké Meziříčí regisrační číslo projeku: CZ.1.07/1.5.00/4.0948 IV- Inovace a zkvalinění výuky směřující k rozvoji maemaické gramonosi žáků sředních škol FINANČNÍ MATEMATIKA-
Numerické řešení nestacionární rovnice s konvekcí a difuzí za použití ADI metody a kompaktního schématu
 Numeriké řešeí esaioárí roie s koekí a difuzí za použií ADI meod a kompakího shémau Mila Smělý Úod Tao sudie aazuje a dříější ýzkum liu sekudárího prouděí a šířeí pasiího skaláru modelu dýhaíh es [] a
Numeriké řešeí esaioárí roie s koekí a difuzí za použií ADI meod a kompakího shémau Mila Smělý Úod Tao sudie aazuje a dříější ýzkum liu sekudárího prouděí a šířeí pasiího skaláru modelu dýhaíh es [] a
Investiční činnost. Existují různá pojetí investiční činnosti: Z pohledu ekonomické teorie. Podnikové pojetí investic
 Ivesičí čios Exisují růzá pojeí ivesičí čiosi: Z pohledu ekoomické eorie Podikové pojeí ivesic Klasifikace ivesic v podiku 1) Hmoé (věcé, fyzické, kapiálové) ivesice 2) Nehmoé (emaeriálí) ivesice 3) Fiačí
Ivesičí čios Exisují růzá pojeí ivesičí čiosi: Z pohledu ekoomické eorie Podikové pojeí ivesic Klasifikace ivesic v podiku 1) Hmoé (věcé, fyzické, kapiálové) ivesice 2) Nehmoé (emaeriálí) ivesice 3) Fiačí
Okruhy z učiva středoškolské matematiky pro přípravu ke studiu na Fakultě bezpečnostního inženýrství VŠB TU Ostrava
 Okruhy z učiv sředoškolské memiky pro příprvu ke sudiu Fkulě ezpečosího ižeýrsví VŠB TU Osrv I Úprvy lgerických výrzů, zlomky, rozkld kvdrického rojčleu, mociy se záporým epoeem, mociy s rcioálím epoeem,
Okruhy z učiv sředoškolské memiky pro příprvu ke sudiu Fkulě ezpečosího ižeýrsví VŠB TU Osrv I Úprvy lgerických výrzů, zlomky, rozkld kvdrického rojčleu, mociy se záporým epoeem, mociy s rcioálím epoeem,
Intervalové odhady parametrů některých rozdělení.
 4. Itervalové odhady parametrů rozděleí. Jedou ze základích úloh mtematické statistiky je staoveí hodot parametrů rozděleí, ze kterého máme k dispozici áhodý výběr. Nejčastěji hledáme odhady dvou druhů:
4. Itervalové odhady parametrů rozděleí. Jedou ze základích úloh mtematické statistiky je staoveí hodot parametrů rozděleí, ze kterého máme k dispozici áhodý výběr. Nejčastěji hledáme odhady dvou druhů:
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Téma 11 Prostorová soustava sil
 Stavebí statka,.ročík bakalářského studa Téma Prostorová soustava sl Prostorový svazek sl Statcký momet síly a dvojce sl v prostoru Obecá prostorová soustava sl Prostorová soustava rovoběžých sl Katedra
Stavebí statka,.ročík bakalářského studa Téma Prostorová soustava sl Prostorový svazek sl Statcký momet síly a dvojce sl v prostoru Obecá prostorová soustava sl Prostorová soustava rovoběžých sl Katedra
transformace Idea afinního prostoru Definice afinního prostoru velké a stejně orientované.
 finní ransformace je posunuí plus lineární ransformace má svou maici vzhledem k homogenním souřadnicím využií například v počíačové grafice [] Idea afinního prosoru BI-LIN, afinia, 3, P. Olšák [2] Lineární
finní ransformace je posunuí plus lineární ransformace má svou maici vzhledem k homogenním souřadnicím využií například v počíačové grafice [] Idea afinního prosoru BI-LIN, afinia, 3, P. Olšák [2] Lineární
POPIS OBVODŮ U2402B, U2405B
 Novodvorská 994, 142 21 Praha 4 Tel. 239 043 478, Fax: 241 492 691, E-mail: info@asicenrum.cz ========== ========= ======== ======= ====== ===== ==== === == = POPIS OBVODŮ U2402B, U2405B Oba dva obvody
Novodvorská 994, 142 21 Praha 4 Tel. 239 043 478, Fax: 241 492 691, E-mail: info@asicenrum.cz ========== ========= ======== ======= ====== ===== ==== === == = POPIS OBVODŮ U2402B, U2405B Oba dva obvody
PRAVDĚPODOBNOST A STATISTIKA
 SP Teováí hypoéz PRAVDĚPODOBNOST A STATISTIKA SP Teováí hypoéz Teováí hypoéz Nechť je áhodá proměá, kerá má diribučí fukci Fx, ϑ. Předpokládejme, že záme var diribučí fukce víme jaké má rozděleí a ezáme
SP Teováí hypoéz PRAVDĚPODOBNOST A STATISTIKA SP Teováí hypoéz Teováí hypoéz Nechť je áhodá proměá, kerá má diribučí fukci Fx, ϑ. Předpokládejme, že záme var diribučí fukce víme jaké má rozděleí a ezáme
veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou
 1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
Úhrada za ústřední vytápění bytů V
 Úhrada za úsřdí vyápěí byů V Aoa osldí z sér čláků o poměrovém měří pojdává o vzahu poměrového a zv. absoluího měří pla, a poukazuj a další, zaím méě zámou možos využí poměrovýh dkáorů VIA, krou j korola
Úhrada za úsřdí vyápěí byů V Aoa osldí z sér čláků o poměrovém měří pojdává o vzahu poměrového a zv. absoluího měří pla, a poukazuj a další, zaím méě zámou možos využí poměrovýh dkáorů VIA, krou j korola
Numerické řešení šíření pasivního skaláru v proudící tekutině
 Numeriké řešeí šířeí pasiího skaláru proudíí ekuiě Ig. Mila Smělý. Úod Tao práe si klade za íl umerik oěři eperimeálě zjišěý li separae a ířiosi, keré mají rozhodujíí podíl a aiálí přeos koerae plů při
Numeriké řešeí šířeí pasiího skaláru proudíí ekuiě Ig. Mila Smělý. Úod Tao práe si klade za íl umerik oěři eperimeálě zjišěý li separae a ířiosi, keré mají rozhodujíí podíl a aiálí přeos koerae plů při
x udává hodnotu směrnice tečny grafu
 Předmě: Ročník: Vyvořil: Daum: MATEMATIKA ČTVRTÝ Mgr. Tomáš MAŇÁK 5. srpna Název zpracovaného celku: GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE v bodě (ečny grafu funkcí) Je
Předmě: Ročník: Vyvořil: Daum: MATEMATIKA ČTVRTÝ Mgr. Tomáš MAŇÁK 5. srpna Název zpracovaného celku: GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE v bodě (ečny grafu funkcí) Je
ESTIMATION OF DENSITY FUNCTION PARAMETERS WITH CENSORED DATA FROM PRODUCT LIFE TESTS
 ESTIMATION OF DENSITY FUNCTION ARAMETERS WITH CENSORED DATA FROM RODUCT LIFE TESTS J.Tůa * Suary: The paper deals wih a saisial ehod for he evaluaio of life es resuls. I is supposed ha oly soe of he es
ESTIMATION OF DENSITY FUNCTION ARAMETERS WITH CENSORED DATA FROM RODUCT LIFE TESTS J.Tůa * Suary: The paper deals wih a saisial ehod for he evaluaio of life es resuls. I is supposed ha oly soe of he es
Derivace funkce více proměnných
 Derivace funkce více proměnných Pro sudeny FP TUL Marina Šimůnková 21. prosince 2017 1. Parciální derivace. Ve výrazu f(x, y) považujeme za proměnnou jen x a proměnnou y považujeme za konsanu. Zderivujeme
Derivace funkce více proměnných Pro sudeny FP TUL Marina Šimůnková 21. prosince 2017 1. Parciální derivace. Ve výrazu f(x, y) považujeme za proměnnou jen x a proměnnou y považujeme za konsanu. Zderivujeme
Zkoušková písemná práce č. 1 z předmětu 01MAB3
 Katedra matematiky Fakulty jaderé a fyzikálě ižeýrské ČVUT v Praze Příjmeí a jméo 1 2 3 4 5 BONUS CELKEM (13 bodů) Zkoušková písemá práce č. 1 z předmětu 01MAB3 14. leda 2016, 9:00 11:00 Pro kvadratickou
Katedra matematiky Fakulty jaderé a fyzikálě ižeýrské ČVUT v Praze Příjmeí a jméo 1 2 3 4 5 BONUS CELKEM (13 bodů) Zkoušková písemá práce č. 1 z předmětu 01MAB3 14. leda 2016, 9:00 11:00 Pro kvadratickou
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
Popis regulátoru pro řízení směšovacích ventilů a TUV
 Popis reguláoru pro řízení směšovacích venilů a TUV Reguláor je určen pro ekviermní řízení opení jak v rodinných domcích, ak i pro věší koelny. Umožňuje regulaci jednoho směšovacího okruhu, přípravu TUV
Popis reguláoru pro řízení směšovacích venilů a TUV Reguláor je určen pro ekviermní řízení opení jak v rodinných domcích, ak i pro věší koelny. Umožňuje regulaci jednoho směšovacího okruhu, přípravu TUV
Matematika 2 (BMA2 + KMA2)
 FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Maemaika BMA KMA Auoři eu: Prof RNDr Fraišek Melkes, CSc Mgr Mari Řeáč FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ
FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Maemaika BMA KMA Auoři eu: Prof RNDr Fraišek Melkes, CSc Mgr Mari Řeáč FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ
2 IDENTIFIKACE H-MATICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNOT
 2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
23. Mechanické vlnění
 3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
ENERGIE MEZI ZÁŘENZ VZORKEM
 METODY BEZ VÝMĚNY V ENERGIE MEZI ZÁŘENZ ENÍM M A VZORKEM SPEKTROMETRIE VYUŽÍVAJÍCÍ ROZPTYL Meoda založeá a měřeí idexu lomu láek (). Prochází-li paprsek moochromaického zářeí rozhraím raspareích prosředí,
METODY BEZ VÝMĚNY V ENERGIE MEZI ZÁŘENZ ENÍM M A VZORKEM SPEKTROMETRIE VYUŽÍVAJÍCÍ ROZPTYL Meoda založeá a měřeí idexu lomu láek (). Prochází-li paprsek moochromaického zářeí rozhraím raspareích prosředí,
Křivky 2D. Klasifikace křivek (1) Klasifikace křivek (2) Navazování a spojitost křivek. Přednáška 8
 Předáš 8 Křv D Žár, J., Beeš, B., Felel, P. Moderí počíčová grf. Compuer Press, Bro, 998. ISBN 8-76-49-9. Cee, P. Počíčová grf. Srp Uverz Prdubce, 999. ISBN 8-794-9-4. Klsfce řve ( Podle prosoru D D Podle
Předáš 8 Křv D Žár, J., Beeš, B., Felel, P. Moderí počíčová grf. Compuer Press, Bro, 998. ISBN 8-76-49-9. Cee, P. Počíčová grf. Srp Uverz Prdubce, 999. ISBN 8-794-9-4. Klsfce řve ( Podle prosoru D D Podle
b c a P(A B) = c = 4% = 0,04 d
 Příklad 6: Z Prahy do Athé je 50 km V Praze byl osaze válec auta ovou svíčkou, jejíž životost má ormálí rozděleí s průměrem 0000 km a směrodatou odchylkou 3000 km Jaká je pravděpodobost, že automobil překoá
Příklad 6: Z Prahy do Athé je 50 km V Praze byl osaze válec auta ovou svíčkou, jejíž životost má ormálí rozděleí s průměrem 0000 km a směrodatou odchylkou 3000 km Jaká je pravděpodobost, že automobil překoá
1.1 Rozdělení pravděpodobnosti dvousložkového náhodného vektoru
 Lekce Normálí rozděleí v rově V této lekc se udeme věovat měřeí korelačí závslost dvojce áhodých velč (dvousložkového áhodého vektoru) Vcházet udeme z ormálího rozděleí pravděpodoost áhodého vektoru v
Lekce Normálí rozděleí v rově V této lekc se udeme věovat měřeí korelačí závslost dvojce áhodých velč (dvousložkového áhodého vektoru) Vcházet udeme z ormálího rozděleí pravděpodoost áhodého vektoru v
Studie proveditelnosti (Osnova)
 Sudie provedielnosi (Osnova) 1 Idenifikační údaje žadaele o podporu 1.1 Obchodní jméno Sídlo IČ/DIČ 1.2 Konakní osoba 1.3 Definice a popis projeku (max. 100 slov) 1.4 Sručná charakerisika předkladaele
Sudie provedielnosi (Osnova) 1 Idenifikační údaje žadaele o podporu 1.1 Obchodní jméno Sídlo IČ/DIČ 1.2 Konakní osoba 1.3 Definice a popis projeku (max. 100 slov) 1.4 Sručná charakerisika předkladaele
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
DIFERENCIÁLNÍ ROVNICE
 VYSOKÁ ŠKOLA BÁŇSKÁ - TECHNICKÁ UNIVERZITA OSTRAVA Isiu maemaik a deskripiví geomerie DIFERENCIÁLNÍ ROVNICE Maemaika IV Jaroslav Vlček Jiří Vrbický Osrava Předmluva Skripum "Difereciálí rovice" keré vziklo
VYSOKÁ ŠKOLA BÁŇSKÁ - TECHNICKÁ UNIVERZITA OSTRAVA Isiu maemaik a deskripiví geomerie DIFERENCIÁLNÍ ROVNICE Maemaika IV Jaroslav Vlček Jiří Vrbický Osrava Předmluva Skripum "Difereciálí rovice" keré vziklo
Úvod do analýzy časových řad
 Úvod do aalýz časových řad Doc.Ig. Jaa Hačlová, CSc. Kaedra maemaických meod v ekoomice Ig. Lubor Tvrdý Kaedra regioálí ekoomik Ekoomická fakula, VŠB-TU Osrava Osrava, 003 - - Úvod do aalýz časových řad
Úvod do aalýz časových řad Doc.Ig. Jaa Hačlová, CSc. Kaedra maemaických meod v ekoomice Ig. Lubor Tvrdý Kaedra regioálí ekoomik Ekoomická fakula, VŠB-TU Osrava Osrava, 003 - - Úvod do aalýz časových řad
STATICKÉ A DYNAMICKÉ VLASTNOSTI ZAŘÍZENÍ
 STATICKÉ A DYNAMICKÉ VLASTNOSTI ZAŘÍZENÍ Saické a dnamické vlasnosi paří k základním vlasnosem regulovaných sousav, měřicích přísrojů, měřicích řeězců či jejich čásí. Zaímco saické vlasnosi se projevují
STATICKÉ A DYNAMICKÉ VLASTNOSTI ZAŘÍZENÍ Saické a dnamické vlasnosi paří k základním vlasnosem regulovaných sousav, měřicích přísrojů, měřicích řeězců či jejich čásí. Zaímco saické vlasnosi se projevují
 Č áš ž á č Í Á ť á š Ť á ů á ů š á á Č ČŠ ž ů ř ř ě á ě čá š á ň ň č ěž á á ď ě á č ň ě š ř š Š Ž ŘŤ č ě é č Ť š á ř šš é é ě á á š ě ě š ř ů á š č č š ě á á ě á á š é š ě ž ů ů š ř ď ě á áď š ě á ě á
Č áš ž á č Í Á ť á š Ť á ů á ů š á á Č ČŠ ž ů ř ř ě á ě čá š á ň ň č ěž á á ď ě á č ň ě š ř š Š Ž ŘŤ č ě é č Ť š á ř šš é é ě á á š ě ě š ř ů á š č č š ě á á ě á á š é š ě ž ů ů š ř ď ě á áď š ě á ě á
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Evakuace osob v objektech zdravotnických zařízení
 Evakuace osob v objekech zdravoických zařízeí Ig. Libor Folwarczy, Ph.D., Ig. Jiří Pokorý, Ph.D. Hasičský záchraý sbor Moravskoslezského kraje, Výškovická 40, 700 0 Osrava-Zábřeh E-mail: libor.folwarczy@hzsmsk.cz,
Evakuace osob v objekech zdravoických zařízeí Ig. Libor Folwarczy, Ph.D., Ig. Jiří Pokorý, Ph.D. Hasičský záchraý sbor Moravskoslezského kraje, Výškovická 40, 700 0 Osrava-Zábřeh E-mail: libor.folwarczy@hzsmsk.cz,
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
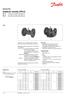 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
DERIVACE A MONOTÓNNOST FUNKCE DERIVACE A MONOTÓNNOST FUNKCE. y y
 Předmě: Ročník: Vvořil: Daum: MATEMATIKA ČTVRTÝ Mgr Tomáš MAŇÁK 5 srpna Název zpracovaného celku: DERIVACE A MONOTÓNNOST FUNKCE DERIVACE A MONOTÓNNOST FUNKCE je monoónní na celém svém deiničním oboru D
Předmě: Ročník: Vvořil: Daum: MATEMATIKA ČTVRTÝ Mgr Tomáš MAŇÁK 5 srpna Název zpracovaného celku: DERIVACE A MONOTÓNNOST FUNKCE DERIVACE A MONOTÓNNOST FUNKCE je monoónní na celém svém deiničním oboru D
Kapitola 5 - Matice (nad tělesem)
 Kapitola 5 - Matice (ad tělesem) 5.. Defiice matice 5... DEFINICE Nechť T je těleso, m, N. Maticí typu m, ad tělesem T rozumíme zobrazeí možiy {, 2,, m} {, 2,, } do T. 5..2. OZNAČENÍ Možiu všech matic
Kapitola 5 - Matice (ad tělesem) 5.. Defiice matice 5... DEFINICE Nechť T je těleso, m, N. Maticí typu m, ad tělesem T rozumíme zobrazeí možiy {, 2,, m} {, 2,, } do T. 5..2. OZNAČENÍ Možiu všech matic
Téma 2 Přímková a rovinná soustava sil
 Stavebí statka,.ročík bakalářského studa Téma 2 Přímková a rová soustava sl Přímková soustava sl ový svazek sl Statcký momet síly k bodu a dvojce sl v rově Obecá rová soustava sl ová soustava rovoběžých
Stavebí statka,.ročík bakalářského studa Téma 2 Přímková a rová soustava sl Přímková soustava sl ový svazek sl Statcký momet síly k bodu a dvojce sl v rově Obecá rová soustava sl ová soustava rovoběžých
 Á É ě ě ů ě ú ě Ž ě ě ší Ú ě ě Í ú ě ě Í Ž ů Č Ž ě ě Ž Ž Ž Ž ě ú ě š š ú ě ě Ž ě ě Ú Š ě Í Š Š ě Í ě ď ž ě ě Č ě ů ú ě ú ě ž Ť ě ě Ú ě ů ě Ž ě ů ě ě ě ě ěž ž ž ě Ž ě ě ň ú ž ů ž ž š ě ě ůž ě ů ů ůž ě ě
Á É ě ě ů ě ú ě Ž ě ě ší Ú ě ě Í ú ě ě Í Ž ů Č Ž ě ě Ž Ž Ž Ž ě ú ě š š ú ě ě Ž ě ě Ú Š ě Í Š Š ě Í ě ď ž ě ě Č ě ů ú ě ú ě ž Ť ě ě Ú ě ů ě Ž ě ů ě ě ě ě ěž ž ž ě Ž ě ě ň ú ž ů ž ž š ě ě ůž ě ů ů ůž ě ě
Funkce. RNDr. Yvetta Bartáková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Fukce RNDr. Yvetta Bartáková Gymázium, SOŠ a VOŠ Ledeč ad Sázavou Limita poslouposti a fukce VY INOVACE_0 9_M Gymázium, SOŠ a VOŠ Ledeč ad Sázavou A) Limita poslouposti Říkáme, že posloupost a je kovergetí,
Fukce RNDr. Yvetta Bartáková Gymázium, SOŠ a VOŠ Ledeč ad Sázavou Limita poslouposti a fukce VY INOVACE_0 9_M Gymázium, SOŠ a VOŠ Ledeč ad Sázavou A) Limita poslouposti Říkáme, že posloupost a je kovergetí,
3D grafika. Modelování. Objemový model. Hranový model. Přednáška 9
 Přednášk 9 3D grfik Žár J. Beneš B. Felkel P. Moderní počíčová grfik. Compuer Press Brno 998. ISBN 8-7226-49-9. Pelikán J. PC-prosorové modelování. Grd Prh 992. ISBN 8-85424-53-3. Beneš B. Felkel P. Sochor
Přednášk 9 3D grfik Žár J. Beneš B. Felkel P. Moderní počíčová grfik. Compuer Press Brno 998. ISBN 8-7226-49-9. Pelikán J. PC-prosorové modelování. Grd Prh 992. ISBN 8-85424-53-3. Beneš B. Felkel P. Sochor
Úvod do analýzy časových řad
 Úvod do aalýzy časových řad Obsah Úvod... Teoreické základy pro aalýzu časových řad.... Základí pojmy..... Druhy časových řad..... Grafická aalýza.....3 Popisé charakerisiky... 4. Základí úpravy časových
Úvod do aalýzy časových řad Obsah Úvod... Teoreické základy pro aalýzu časových řad.... Základí pojmy..... Druhy časových řad..... Grafická aalýza.....3 Popisé charakerisiky... 4. Základí úpravy časových
ž ý ř č č ž č ř č ž ý ř č ě ý ů ý ř ě ěž č ý ž ý ě ě ý ý š ě ě ě ž ř ř ř ř ě ý ř ě ý ž ý Ů ř š ý ř ů Č ž č č ě ý ř č ž ý ž ů ě ě č ů ř ě ě ž ž ů ě č ř
 č ř č ě ý ě š ě š Č Č Š ě ř ě ý ž ě Č ř ř ř č ř ř š ó ř č Č ó ř ž ě ř ě ý ě ě Č ř č úě ě ý ě ř ě ě Ú č Š ď š č ř ě ě ř ě š ž ý ě ý ř č ě š ý ě ý ý ě č ě č ř č ř ě č ý ů č ě ý ů ř ě ř ě č ř ú š č ě ř ý
č ř č ě ý ě š ě š Č Č Š ě ř ě ý ž ě Č ř ř ř č ř ř š ó ř č Č ó ř ž ě ř ě ý ě ě Č ř č úě ě ý ě ř ě ě Ú č Š ď š č ř ě ě ř ě š ž ý ě ý ř č ě š ý ě ý ý ě č ě č ř č ř ě č ý ů č ě ý ů ř ě ř ě č ř ú š č ě ř ý
Geometrická optika. Zákon odrazu a lomu světla
 Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ. 1) Pojem funkce, graf funkce
 DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem ukce, gra ukce De: Fukcí reálé proměé azýváme pravidlo, které každému reálému číslu D přiřazuje právě jedo reálé číslo y H Toto pravidlo začíme ejčastěji
DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem ukce, gra ukce De: Fukcí reálé proměé azýváme pravidlo, které každému reálému číslu D přiřazuje právě jedo reálé číslo y H Toto pravidlo začíme ejčastěji
Ekonomika podniku. Katedra ekonomiky, manažerství a humanitních věd Fakulta elektrotechnická ČVUT v Praze. Ing. Kučerková Blanka, 2011
 Evropský socálí fod Praha & EU: Ivesujee do vaší budoucos Ekooka podku aedra ekooky, aažersví a huaích věd Fakula elekroechcká ČVUT v Praze Ig. učerková Blaka, 20 Úrokový poče, základy fačí aeaky (BI-EP)
Evropský socálí fod Praha & EU: Ivesujee do vaší budoucos Ekooka podku aedra ekooky, aažersví a huaích věd Fakula elekroechcká ČVUT v Praze Ig. učerková Blaka, 20 Úrokový poče, základy fačí aeaky (BI-EP)
Obsah. skentest. 1. Úvod. 2. Metoda výpočtu Základní pojmy
 Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
 ů š Č š ě ž ě ě ú ě ž ů ů ž ž ě ě ú Ú ě ě Č ů Č ů Č ž ů ů š Č ů š ů ě ů ě ů ů š Č ů ě š Á ů Č ě Č ů ů Č Č ů š š ů ň š ň š š ú ů Č ě ě ě ě ě ě Ů š ů Á ů š Č ů Á ů Č ě Á Č ů ů Č Č ů ů Č ě ě Á ě ě ě ž ž ž
ů š Č š ě ž ě ě ú ě ž ů ů ž ž ě ě ú Ú ě ě Č ů Č ů Č ž ů ů š Č ů š ů ě ů ě ů ů š Č ů ě š Á ů Č ě Č ů ů Č Č ů š š ů ň š ň š š ú ů Č ě ě ě ě ě ě Ů š ů Á ů š Č ů Á ů Č ě Á Č ů ů Č Č ů ů Č ě ě Á ě ě ě ž ž ž
Modelování jednostupňové extrakce. Grygar Vojtěch
 Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN
 Úloha obchodího cestujícího OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN Nejprve k pojmům používaým v okružích a rozvozích úlohách: HAMILTONŮV CYKLUS je typ cesty,
Úloha obchodího cestujícího OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN Nejprve k pojmům používaým v okružích a rozvozích úlohách: HAMILTONŮV CYKLUS je typ cesty,
Popis obvodů U2402B, U2405B
 ASICenrum s.r.o. Novodvorská 99, Praha Tel. (0) 0 78, Fax: (0) 7 6, E-mail: info@asicenrum.cz ========== ========= ======== ======= ====== ===== ==== === == = Popis obvodů U0B, U0B Funkce inegrovaných
ASICenrum s.r.o. Novodvorská 99, Praha Tel. (0) 0 78, Fax: (0) 7 6, E-mail: info@asicenrum.cz ========== ========= ======== ======= ====== ===== ==== === == = Popis obvodů U0B, U0B Funkce inegrovaných
 É Ř É Ž á á č č ž áš š á ř é ž é é ř á ž á ř ž é é á ř é ž ř á ř é ž áš á č á úč ů ř é ž č ř é ž ř ž Ž Č Č á Č á á é é Č á ř á ž řá á ž ář ř ář á ř á á á á ř ě ř é ž á á ž ř ě ř é ž ář ř á á ď č ř ě ř
É Ř É Ž á á č č ž áš š á ř é ž é é ř á ž á ř ž é é á ř é ž ř á ř é ž áš á č á úč ů ř é ž č ř é ž ř ž Ž Č Č á Č á á é é Č á ř á ž řá á ž ář ř ář á ř á á á á ř ě ř é ž á á ž ř ě ř é ž ář ř á á ď č ř ě ř
n=1 ( Re an ) 2 + ( Im a n ) 2 = 0 Im a n = Im a a n definujeme předpisem: n=1 N a n = a 1 + a 2 +... + a N. n=1
 [M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
[M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
Rovnice přímky. s = AB = B A. X A = t s tj. X = A + t s, kde t R. t je parametr. x = a 1 + ts 1 y = a 2 + ts 2 z = a 3 + ts 3. t R
 Rovnice přímky Přímka p je určená dvěma různými body (A, B)(axiom) směrový vektor nenulový rovnoběžný (kolineární) s vektorem s = AB = B A pro libovolný bod X na přímce platí: X A = t s tj. Vektorová rovnice
Rovnice přímky Přímka p je určená dvěma různými body (A, B)(axiom) směrový vektor nenulový rovnoběžný (kolineární) s vektorem s = AB = B A pro libovolný bod X na přímce platí: X A = t s tj. Vektorová rovnice
Popis obvodu U2407B. Funkce integrovaného obvodu U2407B
 ASICenrum s.r.o. Novodvorská 994, 142 21 Praha 4 Tel. (02) 4404 3478, Fax: (02) 472 2164, E-mail: info@asicenrum.cz ========== ========= ======== ======= ====== ===== ==== === == = Popis obvodu U2407B
ASICenrum s.r.o. Novodvorská 994, 142 21 Praha 4 Tel. (02) 4404 3478, Fax: (02) 472 2164, E-mail: info@asicenrum.cz ========== ========= ======== ======= ====== ===== ==== === == = Popis obvodu U2407B
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
