Pokroky matematiky, fyziky a astronomie
|
|
|
- Bohumila Burešová
- před 8 lety
- Počet zobrazení:
Transkript
1 Pokroky matematiky, fyziky a astronomie B. Onderlička Některé problémy výzkumu metagalaxie Pokroky matematiky, fyziky a astronomie, Vol. 4 (1959), No. 5, Persistent URL: Terms of use: Jednota českých matematiků a fyziků, 1959 Institute of Mathematics of the Academy of Sciences of the Czech Republic provides access to digitized documents strictly for personal use. Each copy of any part of this document must contain these Terms of use. This paper has been digitized, optimized for electronic delivery and stamped with digital signature within the project DML-CZ: The Czech Digital Mathematics Library
2 Pokroky matematiky, fysiky a astronomie, ročník IV, čfsio 5 ASTRONOMIE- NĚKTERÉ PROBLÉMY VÝZKUMU METAGALAXIE B. ONDERUČKA Již v^roce 1734 vystoupil švédský filosof E. Swedenborg 9 myšlenkou, že v prostoru existuje mnoho hvězdných soustav podobných naší soustavě Mléčné dráhy. Aókoli Swedenborgovy úvahy byly ryze spekulativní, obsahovaly zdravé jádro, neboť vykládaly svět tak, že hmota je stejná ve všech částech vesmíru a jen forma hmoty se mění. Pozorovací astronomie po vynalezení dalekohledu zprvu jen zvolna rozšiřovala naše obzory za hranice sluneční soustavy. Jeden z prvních katalogu mlhovin, pořízený Messierem v r. 1784, obsahoval 107 objektů, z nichž některé, jak se později ukázalo, byly více nebo méně kompaktní skupiny hvězd. Již o rok později vydal průkopník stelární astronomie Herschel katalog 1000 mlhovin a hvězdokup. Trvalo však značně dlouho, než pozprovací technika bezpečně zjistila, že mnohé z těchto mlhovin jsou hvězdnými soustavami, které jsou od nás v obrovských vzdálenostech. Ještě v r Bohlin uveřejnil podrobná měření, která dávala pro trigonometrickou paralaxu galaxie M31 hodnotu 0,171", což odpovídá vzdálenosti pouhých 6 ps! O čtyři roky později porovnáním jasnosti supernovy, která se objevila v M31 v r. 1885, s jasností novy v Perseovi z r. 1901, odvodil Věry (za předpokladu stejné absolutní jasnosti obou objektů) pro M31 vzdálenost 500 ps. Obdobné srovnání provedl v r Curtis pro supernovy ve čtyřech blízkých galaxiích a dospěl naopak k přeceněné vzdálenosti 6. 10* ps, neboť přepokládal pro galaktické novy průměrnou vzdálenost příliš velkou ( ps). Velmi důležitý indikátor velkých vzdáleností poskytl výzkum Magalhaensových oblaků na< jižní obloze: V r objevila Leavittová korelaci mezi periodou a zdánlivou jasností u cefeid v těchto dvou soustavách. V r a 1918 určili Hertzsprung a Shapley statistickou metodou absolutní jasnosti cefeid a provedli tak kalibraci vztahu objeveného Leavittovou. Tak sice bylo ukázáno, že Magalhaensova oblaka leží mimo naši Galaxii, avšak pokud jde o spirální mlhoviny, ještě v r se rozcházela mínění astronomů o tom, jde-li o hvězdné soustavy mimo naši Galaxii nebo o objekty patřící k naší Galaxii. Definitivní rozřešení této otázky přinesl rok 1924, kdy Hubble pomocí 2,5 m dalekohledu rozložil ramena nejbližších spirálních mlhovin na hvězdy, mezi nimiž zjistil také cefeidy. Tím byl dán základ pro výzkum našim pozorovacím prostředkům dostupné oblasti vesmíru metagalaxie: Klasifikace galaxií Studium jakéhokoli komplexu objektů vyžaduje především roztřídění, klasifikaci do skupin podle charakteristických společných znaků. "Úkolem teorie je pak hledat a vykládat zákonitosti a vztahy v takto roztříděném materiálu. Klasifikace hvězd podle spekter a roztřídění hvězd na oblasti v diagramu 584
3 Hertzsprungově-Rus8ellově byly -podkladencz něhož vycházely teorie atmosfér, nitra a posléze vývoje hvězd. Při klasifikaci galaxii je předevsím nasnadě -zaměřit se na celkový tvar a strukturu. Již v minulém století bylo zavedeno rozdělení na spirály (Rosse 1845) a eliptické galaxie (.Alexander 1852); později byly přidány spirály s příčkou (Curtis 1918). Hubble na základě obsáhlého materiálu dospěl ke své známé klasifikaci galaxii, klané ve schématu T?n T?n/ SO-Sa-Sb-Sc x r ^-^XSBO-SBa-SBb-SBc/^ U eliptických galaxií (E) je Číslicemi 0 7 dán stupeň zplošťění od kulových (0) až po velmi zploštělé (7). Spirály jsou rozděleny do dvou paralelních větví normální (S) a s příčkou (SB), při čemž a značí velmi kompaktní tvar, c velmi rozevřená ramena; S0, SBO jsou přechodné tvary mezi eliptickými a spirálnimi tvary. Konečně třídu prb sebe tvoří nepravidelné útvary (I). Zjemnění Hubbleovy klasifikace spirál zavedl v posledních letech de Vaucouleurs na základě několikaletého výzkumu jižních galaxií. Pokud jde o stupeň rozvinutí, nahrazuje přechodný stupeň 0 třemi stupni 0~, 0, 0+ a za otevřenými spirálami přidává ještě stupeň d (velmi pozdní) a m (tvar Magalhaensových oblaků). Kromě zcela nepravidelných útvarů I zavádí ještě typ Im (tvar Magalhaensových oblaků, avšak bez zbytkové spirální struktury). Spirály rozděluje de Vaucouleurs opět do dvou rodin: normální (A) a s příčkou (B), zavádí však navíc smíšený typ (AB). Kromě toho zavádí další hledisko třídění: spirály prstencové (r) a tvaru S" (s), mezi nimiž je opět přechodný typ (rs). Jinou cestu při klasifikaci galaxií nastoupil Morgan, který vyšel z integrálního spektra soustavy. Ukázal, že existuje těsná závislost mezi integrálním spektrálním typem, který charakterisuje převládající populaci v dané hvězdné soustavě, a mezi tvarem této soustavy. Nepravidelné soustavy typu Magalhaensových oblaků a spirály s nepatrnou centrální koncentrací jsou charakterisovány integrálním spektrem typu A; druhý extrém, obří eliptické galaxie a spirály ja^o M31, kde je světlo silně koncentrováno ke středu, je charakterisován integrálním spektrem gk. Soustavy se střední koncentrací pvítivosti jsou charakterisovány integrálním spektrem mezi těmito extrémy. Vzhledem ke zmíněné těsné závislosti je možno podle stupně světelné koncentrace charakterisovat převládající populaci ve hvězdné soustavě. Morgan zavádí pro minimální koncentraci symbol a, pro maximální symbol k; mezistupně jsou af, f, fg, g, gk. Jako druhý klasifikační parametr slouží tvar: S označuje spirály, B spirály s příčkou, E eliptické galaxie, I nepravidelné soustavy, Ep eliptické s prachovou absorpcí, D soustavy s rotační symetrií bez výrazné eliptické nebo spirální struktury, L soustavy s nízkou povrchovou jasností, N soustavy s malým svítícím jádrem na mnohem slabším podkladě. K těmto dvěma klasifikačním parametrům se připojují číslice 1 7, udávající polohu hlavní roviny soustavy v prostoru; značí: 1 rovina kolmá k zornému paprsku, 7 rovina jdoucí zorným paprskem. Morgan klasifikoval dosud přes 600 galaxií v novém systému: např. M31 je typu ks5, její průvodce NGC keb, M33... / 3, M51... fsí, její průvodce... Ip Ep. Morgan zjistil, že různé typy galaxií nejsou rovnoměrně rozloženy v prostoru. Např. v oblasti rektascense 10* 12 h a deklinace + 30 (- 60 je nápadně velký počet soustav a" mezi blízkými galaxiemi. Metoda integrálnich spekter je teprve v začátcích. Přesná klasifikace však 585
4 slibuje zajímavé výsledky: např. v M31 převládající populaci tvoří normální obři, nikoli obři se slabými čarami, jak je tomu v populaci II v naší galaxii. Na obr. 1 je z ingrálních spekter vyznačen hypotetický Hertzsprungův- Bussellův diagram pro převládající populaci ve spirále M 31 a v nepravidelné galaxii NGC 4449 (typ al). U eliptických galaxií byla zjištěna korelace mezi svítivostí a šířkou spektrálních čar, kterou bude možno využit k určení spektroskopických paralax vzdálenějších objektů, pokud bude možno získat dosti zřetelná spektra. Vzdálenosti galaxii Hlavním kritériem pro určování vzdáleností blízkých galaxií byl áž* dosud vztah perioda-svítivost pro cefeidy. Avšak přesná fotoelektrická měřeni Arpova ukázala, že pro cefeidy v kulových hvězdokupách tento yztah není jednoznačný, nýbrž vykazuje při určité peri- ^1 r i 1 'i odě rozptyl více než jedné magnitudy. Sandage vyšel ze vztahu PTQ = Q (P = perioda, Q = střední hustota, Q = konstanta) a odvodil za použití některých empirických vztahů pro cefeidy populace I závislost perioda-svítivost, v níž však vystupuje jako třetí parametr ještě barevný index. Tato závislost je poněkud jiná pro cefeidy Egge- Obr.l. HypothetwkýHertzspnmgův-Ruasel. nova typu A, B, než pro typ C (viz lův diagram pro galaxiingc 4449 (vodorovné. obr. 2). Při určité periodě je rozptyl čárkování) a M 31 (svislé čárkování), odvoze- absolutních jasností podle Sandage 1,2". ný z integrálního spektra. J e z a i í m a v é ) ž e že Vakin ^ 8Vé-teorie Hvězdné proměnnosti odvozuje zcela stejný rozptyl. Nepřekvapuje tedy, že několik cefeid, o nichž bylo v poslední době zjištěno, že patří k některým otevřeným hvězdokupám o známé vzdálenosti, dává různé hodnoty pro kalibraci vztahu perioda-svítivost. To vše ovšem nevylučuje použití cefeid k přesnému určení extragalaktických vzdáleností za předpokladu, že nějaký vhodný parametr jako třeba tvar světelné křivky, nebo ještě lépe podle Ževakina fázový rozdíl mezi křivkou radiálních rychlostí a křivkou světelnou určí místo dotyčného objektu v rozptylovém pásmu perioda-svítivost. Cefeid lze při dnešních pozorovacích prostředcích použít do vzdálenosti 4Mps, tj. v místní skupině galaxii, ve skupině M 81 a M 101. Palomarským dalekohledem byly zjištěny cefeidy v téměř 30 galaxiích (oproti sedmi, které měl k disposici Hubble s 2,5 m dalekohledem). Ovšem, chceme-li např. zjistit závislost rudého posuvu na vzdálenosti, musíme jít do vzdálenosti aspoň Mps, aby systematické rychlosti převládly nad rozptylovými. Hubble k tomu použil nejjasnějších hvězd v galaxiích. Jak ukázal Sandage, identifikoval však Hubble myln& jako nejjasnější hvězdy též některé svítící oblasti HII (které jsou asi o 2 m jasnější). Dnešní technika fotografie v červeném světle umožní snadno vodíkové oblasti rozpoznat. Obtížnější je vyčlenit skutečně jednotlivé nadobry, neboť jak je známo, vyskytují se tyto hvězdy ve skupinách. V blízké galaxii M33 je možno na fotografii 5m dalekohledem zřetelně 586
5 rozeznat asociace nadobrů, obdobné kupám h -+- % Per; úhlový rozměr těchto asociací je asi 16". V desetinásobné vzdálenosti by odlišení podobné asociace od jednotlivé hvězdy bylo možně jen s největšími obtížemi, neboť zdánlivý rozměr asociace by se blížil rozměrům hvězd na desce. Systematické chyby byly též vneseny do HubbleoVých vzdáleností při určování jasnosti velmi slabých objektů. V současné době probíhá nové určování extragalaktických, vzdáleností. Podnět k tomu byl dán v r Baadeovým zjištěním, že nulový bod ve vztahu perioda-svítivost pro cefeidy je třeba posunout asi o \Jfr* (což odpovídá zdvojnásobení vzdálenosti). Předběžná kalibrace nových vzdá- Obr. 2. Vztah periodar-barva-evítivost pro cefeidy I. populace podle Sandage. Periody ve dnech jsou vyznačeny zvlášť pro typy A, B a pro typ C leností, kterou provádí Sandage, se opírá o-normální povy, zjištěné v okolních soustavách. Pro galaxii M 100 (nejjasnější objekt v kupě galaxií v ranně) vychází vzdálenost asi 14 Mps. Je však možné, že nové vzdálenosti budou vyžadovat ještě určité korekce o mezigálaktickou absorpci. Místní skupina galaxií Nejbližšími sousedy naší Galaxie jsou Velký a Malý mrak Magalhaensův, které jsou od nás ve vzdálenosti asi 55 kps a tvoří vlastně souputníky naši soustavy. Obě soustavy jsou nepravidelnými galaxiemi. Dále následuji dvě trpasličí eliptické galaxie v Sochaři (80 kps) a v Peci (200 kps)* nepravidelná galaxie NGC 6822 (280 kps) a dvě velmi slabé trpasličí eliptické galaxie ve Lvu (300 kps). V přibližně stejné vzdálenosti (500 kps) jsou známé spirály v Troj- 687
6 úhelníku (M 33) a v Andromedě (M 31). Posledně jmenovaná soustava má čtyři souputníky, vesměs trpasličí eliptické galaxie: M 32, NGC 205, NGC 185, NGC 147. Rovněž ve vzdálenosti asi 500 kps je nepravidelná galaxie IC Konečně nepravidelná galaxie Wolfova-Lundmarkova ve Velrybě je ve vzdálenosti asi 600 kps. K místní skupině pravděpodobně patří též velké spirály. *?!»*. Obr. 3. Schematické znázornění místní a sousední supergalaxie. Poloha naší Galaxie je vyznačena písmenem G. NGC 6946, IC 10 a IC 342, které však leží poměrně blízko roviny Mléčné dráhy, takže značná absorpce světla ztěžuje správné určení jejich vzdáleností. Totéž platí o pekuliární galaxii NGC 5128, která je silným radiovým zdrojem. Místní supergalaxie a rozložení galaxií v prostoru Naše místní skupina však není samostatnou jednotkou, nýbrž je součástí větší soustavy galaxií, tzv. místní supergalaxie. Již před lety poukázali někteří badatelé, např. Holmberg a Reiz, na to, že velká většina jasnějších galaxií 588
7 leží v poměrně úzkém pásu okolo galaktických poledníků o délkách 100 a 280. De Vaucouleurs zkoumal podrobně rozložení jasnějších i slabších galaxií a dospěl k závěru, že naše galaxie i s místní skupinou leží ve velké soustavě, jejíž střed je přibližně v kupě galaxií v Panně ve vzdálenosti 10 14Mps. Tato supergalaxie je značně zploštělá (1:5). Na jižní polokouli zjistil de Vaucouleurs existenci podobné poněkud menší supergalaxie, jejíž střed je ve vzdálenosti jen o něco větší než střed naší supergalaxie, a to ve směru sou- Obr. 4. Isofoty rozložení galaxií do 18.5 m v oblasti Had-Pastýř-Panna podle Neymana, Scottové a Shanea. hvězdí Pece a Eridana; je tvořen kompaktní skupinou galaxií NGC Obě supergalaxie jsou znázorněny na obr. 3. Studiem radiálních rychlostí galaxií v naší supergalaxii dospěl de Vaucouleurs k názoru, že celá soustava se otáčí (perioda v oblasti naší místní skupiny činí asi let) a současně rozpíná. Počet galaxií v místní supergalaxii je asi Je třeba se zmínit o tom, že již před několika lety Cooper-Rubinová a Ogorodnikov odvodili z tehdy známých radiálních rychlostí galaxií rotační pohyb jakési vyšší soustavy. Nicméně neprovedli vyšetření prostorového rozložení galaxií, jejichž rychlosti zkoumali. Jejich výsledky se značně rozcházejí s výsledky de Vaucouleursovými a nelze je připsat nějaké místní vyšší soustavě. V dřívějších letech převládal názor, že většina galaxií je více méně rovnoměrně rozptýlena v prostoru a shluky galaxií jsou nepříliš častým zjevem. Teprve systematické studie pomocí širokoúhlých komor jako 50 cm dvojitý astrograf Lickovj^ observatoře, a 120 cm Schmidtova komora namt. Palomaru ukázaly, že naprostá většina galaxií patří kupám. Ne vždy jsou ovšem tyto kupy patrné na první pohled. Jednak se může překrývat několik kup, které leží v různých vzdálenostech, a jednak se kupy mohou také přímo prostupovat. 589
8 Je tedy ostrovní charakter rozložení hmoty v těchto velkých měřítcích odlišný od rozložení hvězd (vzájemné vzdálenosti jsou 10 7 x větší než rozměry hvězd) nebo i galaxií (vzájemné vzdálenosti jsou 10 X větší než rozměry galaxií). Statistickým studiem rozložení galaxií se zabývali Neyman, Scottová a Shane. Obr. 5. Kupa galaxií v Severní koruně. Snímek 5m dalekohledem. Dospěli k závěru, že všechny galaxie jsou uspořádány do kup a centra zhuštění jsou rozložena v prostoru v prvním přiblížení nahodile. Nicméně předběžné výsledky jejich dosud neuzavřené podrobnější studie svědčí o možnosti, že i kupy jsou opět uspořádány ve vyšší celky. Na obr. 4 je isofotami vyznačeno 590
9 rozloženi galaxii v části souhvězdí Hada, Pastýře a Panny podle výzkumu Neymanna, Scottové a Shanea. Čísla u isofot udávají počet galaxií jasnějších než 18,5 m na čtvereční stupeň. Shluk galaxií v levém horním rohu má 1200 členů na dvaceti čtverečních stupních, v koncent^acidole uprostřed bylo napočítáno asi 2800 galaxií, které patří asi Šesti překrývajícím se kupám. Vzdálenost obou zmíněných shluků je asi 35 Mps. Vzhledem k tomu, že kupy, o nichž uvažují Neyman, Scotťová a Shane, jsou někdy velmi řídké a obsahují jen malý počet členů, je možno mluvit o jakémsi všeobecném poli galaxii" a vedle toho o bohatých a poměrně hustých kupách. Známější bohaté kupy jsou např.. v Panně (vzdálenpst asi 14 Mps), v Rybách (46 Mps), V Perseovi (55 Mps), ve Vlasech Bereniky (70 Mps) a v Herkulovi (100 Mps). Ze vzdálenějších je možno jmenovat zejména velmi bohatou kupu v Severní koruně (220 Mps), viz obr. 5. Podle F. Zwickyho, který připravuje obsáhlý katalog galaxií do 15,5 m a bohatých kup galaxií do cteminace 30, připadá v průměru na 2 čtvereční stupně jedna bohatá kupa a tři galaxie jasnější než 15,5*. Připravovaný katalog bude obsahovat zhruba kup a galaxií. Abell studoval rozložení více než 2700 bohatých kup galaxií na palomarsjtém fotografickém atlasu oblohy. Dospěl k těmto závěrům: a) četnost kup rychle klesá s rostoucím počtem galaxií v kupě, b) dosavadní materiál nesvědčí o žádné změně prostprové hijstoty kup se vzdáleností, c) existují reálné shluky kup galaxií. Zwicky si položil otázku, zda kupy galaxií jsou největšími organizovanými celky hmoty ve vesmíru, nebo zda existují celky ještě větší. Za předpokladu, že gravitační působení se šíří konečnou rychlostí, dospěl k sávěru, že organisované celky hmoty nemohou být neomezeně velké. Jestliže se gravitační působeni šíří nanejvýše rychlostí světla, vychází maximální rozměr Oj^anisované kupy asi 6 ^Ips. Shluky kup galaxií (a také např. místní supergalaxje) by tedy za uve4eného předpokladu nemohly být organisovanými celky (tj. gravitačně stabilní). A priori nelze ovšem také vyloučit možnost, že rozmístění a pohyby hmoty v tak velkých prostorácji je.řízeno jinými zákony než gravitací, stejně jako je tomu naopak ve světě mikročástic. Hmota v mezigalaktickém prostoru Zwicky se podrobně zabýval studiem dvojitých a vícenásobných galaxií, které se vyskytují velmi často. Zjistil u značného počtu takových soustav, že jednotlivé galaxie jsou spojeny svítícími filamentý, které jéou někdy i na nejlepších snímcích na hranici viditelnosti. Výrazný příklad vidíme na obr- 6, kde z dolní spirály vybíhá ještě též filameňt ve směru do druhé galaxie. Je to poměrně častý případ. Vyobrazená dvojice je ve vzdálenosti asi 70 Mps, takže jejich úhlová vzájemná vzdálenost odpovídá téměř 200 kpa, tj. */, vadálenosti mlhoviny v Andromeclě. Je zajímavé, že horní spirála ukazuje výrazné emisní čáry vodíku a zakázanou kyslíkovou čáru (A 3727 A), zatím co dolní spirála má neostré spektrum bez jakýchkoli emisních čar. Pokusy získat spektra slabých filamentů byly delší dobu neúspěšné. Z toho bylo možno odvodit závěr, že většinou půjde o spektra absorpční', tj. filamentý jsou složeny z hvězd, neboť emisní Čáry by se projevily Ve spektru mnohem snáze. Teprve v loňském roce se Zwickymu podařilo vyfotografovat v primárním ohnisku 5m dalekohledu se šestihodinovými exposicemi dvě spektra filamentů. Jeden z nich, spojující dvě galaxie, vzdálené asi 60 Mps, ukaztrje4ypické absorpční spektrum, 591
10 odpovídající hvězdné populaci. U jedné z obou galaxií vystupuje zřetelně zakázaná cárá 3727 A v emisi a její sklon svědčí o rychlé rotaci této galaxie. Ve druhém případě jde o dvojici galaxií ve vzdálenosti 85Mps; jedna galaxie je spirála s příčkou, z drulié, eliptické, vybíhá opačným směrem zřetelný filament modrého zabarvení. V absorpčním spektru obou galaxií je emisní čára 3727 A,'která dominuje ve spektru filamentu a její intensita je tam téměř stejná jako ve zmíněné eliptické galaxii, která je v integrálním světle mnohem svítivější než filament. Zwicky zdůrazňuje, že tento druhý případ (filament s emisním spektrem) je výjimkou. Z mnoha dalších zajímavých násobnýehgalaxií s filamenty se zmiňme alespoň o soustavě IC 3481, První z obou galaxií má menšího souputníka, který má, stejně jako IC 3481, radiální rychlost 7300 km/s. Naproti tomu třetí galaxie IC 3483, která je s oběma prvními spojena filamentem, má radiální rychlost pouze 100 km/s. Vytvoření filamentu při tak obrovské relativní rychlosti galaxií lze stěží vysvětlit gravitačním slapovým působením. Carpenter studoval osm těsných dvojic galaxií spojených zcela krátkými filamenty (na rozdíl od filamentu velkých rozměrů, které Obr. 6. Dvojice galaxií (oc =23 h 39 ra 16 8, ó == 3 49', zkoumal Zwicky). V pěti ep ) s filamenty mezigalaktické hmoty. případech u filamentu byla Snímek 5m dalekohledem. zjištěna emise 3727 A, v ostatních nikoli. Je zajímavé, že právě dvě ze tří dvojic bez emise jsou rádiovými zdroji. Bude třeba ještě mnoho soustavného studia násobných galaxií, filamentu a rádiového záření, než se objasní jejich vzájemný vztah. Šklovskij soudí, že rádiové záření galaxií je především brzdným zářením relativistických elektronů. Zwicky se domnívá, že i v metagalaktickém prostoru, zejména v bohatých kupách galaxií, je dosti rozptýlené difusní hmoty. Burbidge ukázal, že alespoň část energie brzdného rádiového záření z mezigalaktického prostoru v kupách galaxií je přeměněná vnitřní kinetická energie těchto kup. Rudý posuv Lineární závislost rudého posuvu ve spektrech galaxií na jejich vzdálenosti objevil Hubble v r Pozdější Hubbleovy výzkumy vedly k hodnotě pro konstantu rudého posuvu H = 530 km/s/mps. Revise extragalaktických vzdáleností vedla v r Humasona, Mayalla a Sandage též k revisi konstanty H. Tito autoři zpracovali více než 800 radiálních rychlostí (až do hodnoty 1 / 5 rychlosti světla) galaxií a kup galaxií a dospěli k provisorní hodnotě H = 180km/s/Mps. Novější data, zejména přesnější vzdálenost kupy galaxií v Panně, vedou k ještě nižší hodnotě H. Podle Sandage je H v rozmezí 50 až 592
11 100 km/s/mps a bude třeba dalších přesných určeni vzdálenosti, aby bylo možno definitivně hodnotu H upřesnit. Otázka, zda rudý posuv je možno skutečně interpretovat dopplerovsky jako expánsivní pohyb, byla mnohokrát diskutována. Prozatím nebyly vypracovány konkrétní podklady pro jiný výkla<jl Vé prospěch dopplerovského výkladu mluví objev rudého posuvu v rádiovém zářeni vzdálené galaxie v Labuti, který plně odpovídá radiální rychlosti odvozené z posuvu ve viditelném záření téže galaxie; vlnové délky viditelného světla a rádiového záření jsou v tomto případě v poměru 1 : Z kosmologického hlediska je závažná odchylka od linearity v závislosti rudého posuvu na vzdálenosti, kterou zjistili Humaaon, líayall a Sandage pro rychlqsti řádově 0,2 rychlosti světla. Tato jak se zdá reálná odchylka by nasvědčovala zpomalení expanse. K spolehlivému určeni zmíněné odchylky bude třeba provést ještě přesná měřeni rozdělení energie ve spektrech vzdálených galaxií a také vyšetřit změnu absolutní jasnosti galaxie s čaéem na základě teorie, vývoje hvězd. Je možno očekávat, že v blízké budoucnosti díky rádiovým metodám bude možno měřit ještě podstatně větší rudé posuvy než dosud, což jistě přispěje k rozhodnuti o tom, který kosmologický model nejlépe charakterisuje rozložení a pohyb hmot v metagalaxíi dostupné pozorování. Výtoj galaxií Otázka vývoje galaxií byla až dosud příliš obtížná pro konkrétní formulaci. Byly propracovány některé dí^čí problémy, jako např. vývoj spirální struktury. Stále rostoucí faktický materiál, zejména s přihlédnutím k rádiovým pozorováním, vyžaduje vytyčení tvůrčích hypothes, jejichž ověřování by usměrnilo další pozorovatelskou činnost. V tomto smyslu je třeba uvítat nedávnou práci Ambarcumjanovu, která je logickým pokračováním tvůrčích myšlenek téhož autora v oblasti vývoje hvězd. Ambarcumjan vychází především z existence násobných galaxií, z tendence galaxii ke shlukování. Studium pohybových vlastností skupin galaxii vede především k závěru, že v současných podmínkách se takové skupiny mohou bud udržovat nebo rozpadat, nemohou však se obohacovat o galaxie, které by vznikly mimo tyto skupiny. Velký počet pozorovaných násobných jgalaxií ^ede k závěru, že složky těchto soustav v naprosté většině případů měly společný vznik. Na rozdíl od násobných hvězjd mezi násobnými galaxiemi zcela převládají konfigurace typu Lichoběžníka (tj. konfigurace, v nichž lze nalézt alespoň tři galaxie takové, že jejich vzájemné vzdálenosti jsou téhož řádu). Ambarcumjan si všímá dále relativních radiálních rychlostí násobných galaxií a vyvozuje, že existují soustavy, v nichž jedna nebo více složek mají rychlosti větší neí únikové. Rovněž disperse rychlostí v některých velkých kupách galaxií je tak velká, že tyto soustavy se nutně rozpadají. Současný vznik a tendence expanse u galaxii vedou Ambaroumjana k hypothese, že prvotní jádro galaxie se může z dosud neznámých příčin rozdělit na části, které dávají vznik samostatným gajlaxiím, tvořícím pak skupiny. Je možno si představit, že při dělení jádra dochází k bouřlivým nestacionárním dějům, které se projevují intensivním rádiovým zářením, jako např. u zdrojů Perseus A (= NGrC 1275) a Cygnus A. Ambarcumjan tedy proti domněnce, že jde o srážky galaxií, staví domněnku, zcela opačnou: jde o proces dělení jádra galaxie. Obří radiogalaxie Virgo A(= M 87) se vyznačuje tím, že zdroje rádiového záření jsou rozloženy spojitě, zatím co opticky vidíme řadu filamentů, vysílajících polarisované zářeni. Ambarcumjan soudí, že jde o poměrně menší hmoty vy- 593
12 vržené z jádra galaxie, které se v poměrně krátké době přeměňuji v nestacionární hvězdy, mezihvězdný plyn a v oblaka částic vysoké energie. Podobné výrony hmoty, nápadně modře zbarvené, pozorujeme též u jiných eliptických galaxií. Jde vesměs o nestacionární mladé konglomeráty hmoty. Dále si Ambarcumjan všímá filamentů mezi násobnými galaxiemi. Tyto filamenty, jak možno ukázat, nelze ve většině případů vyložit slapovým působením. Ve světle hy-. pothesy o dělení jader je možno pohlížet na filamenty jako na útvary vznikající při e:spansi dvou nebo více galaxií, které vznikly z téhož jádra. TJ galaupe M 51 a podobně u gřtlaxie NGC 7752 pozorujeme v zakončení jednoho spirál-, ního ramene vedlejší galaxii. Ambarcumjan soudí, že tento jev svědčí o vztahu mezi dělením prvotního jádra a vznikem spirálních větví. Ambarcumjan tedy pokládá jádra galaxií za zdroje vznikajících galaxií. Je zajímavé, že u spirály. v Andromedě bylo zjištěno jádro vysoké svítivosti neobyčejně malých rozměru j (několik ps). Podle Ambarcumjana takové jádro obsahuje značné množství předhvězdné látky o vysoké hustotě; nelze si totiž představit djělení jader, která by se skládala z normální hvězdné populace. Ambarcumjanova obsáhlá studie obsahuje mnoho zajímavých úvah, které jsou velmi podnětné pro další pozorovatelské i teoretické výzkumy metagalaxie. FYSIKÁLNÍ P b ODMÍNKT. EXISTENCE ŽIVOjTA VE VESMÍRU*) G. M. IDLIS Tlyod Astronomie má velký vyznám pro vědecký světový názor. Utváří vědeckými poznatky podloženou předstayu o. obklopujícím nás světě, o jeho stavbě a vývoji. Ale většinou se tak děje pouze jednostranně. Z faktických dat o struktuře astronomií poznaného vesmíru se vědečtí pracovníci snaží vyvodit historii jeho vývoje, zákonitosti vzniku galaxií* hvězd, sluneční soustavy, Země a nakonec i života až do nejvýše organisovaných živých bytostí, schopných myslet a poznávat přírodu. Zajímavé a zásadně důležité je položit proti obvyklému postupu otázku naopak: proč je námi pozorovaná část vesmíru rozpínající se soustavou galaxií, v nichž nalézáme hvězdy, kolem kterých obíhají planety, na jedné z nichž, žijeme my? Nebylo by možno řešit tuto otázku již ze samého faktu naší existence? Jinými slovy nejsou základní rysy astronomií pozorovaného vesmíru prostým důsledkem toho, že před námi není libovolná část vesmíru, nekonečného ve své mnohotvárnosti, ale právě ta jeho konkrétní, konečná oblast, ve které měl život možnost vzniknout a existovat i v současné době? Cílem této práce je pokus postupně řešit tento problém: proč je*svět, který nás obklopuje, takový, jaký je? Filosofický význam této otázce odpovídajících závěrů spočívá ve zdůvodnění a zdůraznění toho, že některé pozorované záko-* nitoati přírody (např. diferenciace hmoty na kosmické objekty typu naší Galaxie, na hvězdy a planety, dále rudý posuv galaxií apod.) jsou typické pro ty oblasti -^psmíru, ve kterých existuje život (typické v prostoru i v čafce), zatím co pro celý nekonečný vesmír typickými být nemusí. *) Г. М. И дли с, Основные черты наблюдаемой астрономической вселенной как характерные свойства обитаемой космической системы, 1ют. Авйговпёевкодо шиам* А.СТ КахвЙВ, 8Т. VII (1968), шът
Galaxie Vesmír velkých měřítek GALAXIE. Základy astronomie Galaxie 1/47
 GALAXIE Základy astronomie 2 16.4.2014 Galaxie 1/47 Galaxie 2/47 Galaxie 3/47 Hubbleův systém klasifikace 1936 1924 Hubble rozlišil okraje blízkých galaxií, identifikoval v nich hvězdy klasifikace zároveň
GALAXIE Základy astronomie 2 16.4.2014 Galaxie 1/47 Galaxie 2/47 Galaxie 3/47 Hubbleův systém klasifikace 1936 1924 Hubble rozlišil okraje blízkých galaxií, identifikoval v nich hvězdy klasifikace zároveň
Hvězdy se rodí z mezihvězdné látky gravitačním smrštěním. Vlastní gravitací je mezihvězdný oblak stažen do poměrně malého a hustého objektu
 Hvězdy se rodí z mezihvězdné látky gravitačním smrštěním. Vlastní gravitací je mezihvězdný oblak stažen do poměrně malého a hustého objektu kulovitého tvaru. Tento objekt je nazýván protohvězda. V nitru
Hvězdy se rodí z mezihvězdné látky gravitačním smrštěním. Vlastní gravitací je mezihvězdný oblak stažen do poměrně malého a hustého objektu kulovitého tvaru. Tento objekt je nazýván protohvězda. V nitru
Úvod do neeukleidovské geometrie
 Úvod do neeukleidovské geometrie Obsah In: Václav Hlavatý (author): Úvod do neeukleidovské geometrie. (Czech). Praha: Jednota československých matematiků a fysiků, 1926. pp. 209 [212]. Persistent URL:
Úvod do neeukleidovské geometrie Obsah In: Václav Hlavatý (author): Úvod do neeukleidovské geometrie. (Czech). Praha: Jednota československých matematiků a fysiků, 1926. pp. 209 [212]. Persistent URL:
Časopis pro pěstování mathematiky a fysiky
 Časopis pro pěstování mathematiky a fysiky František Kaňka Důsledky akusticko-dynamického principu. [V.] Časopis pro pěstování mathematiky a fysiky, Vol. 47 (1918), No. 2-3, 158--163 Persistent URL: http://dml.cz/dmlcz/122325
Časopis pro pěstování mathematiky a fysiky František Kaňka Důsledky akusticko-dynamického principu. [V.] Časopis pro pěstování mathematiky a fysiky, Vol. 47 (1918), No. 2-3, 158--163 Persistent URL: http://dml.cz/dmlcz/122325
Vzdálenosti ve vesmíru
 Vzdálenosti ve vesmíru Proč je dobré, abychom je znali? Protože nám udávají : Výchozí bod pro astrofyziku: Vzdálenosti jakéhokoli objektu ve vesmíru je rozhodující parametr k pochopení mechanizmu tvorby
Vzdálenosti ve vesmíru Proč je dobré, abychom je znali? Protože nám udávají : Výchozí bod pro astrofyziku: Vzdálenosti jakéhokoli objektu ve vesmíru je rozhodující parametr k pochopení mechanizmu tvorby
VY_32_INOVACE_FY.19 VESMÍR
 VY_32_INOVACE_FY.19 VESMÍR Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Vesmír je souhrnné označení veškeré hmoty, energie
VY_32_INOVACE_FY.19 VESMÍR Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Vesmír je souhrnné označení veškeré hmoty, energie
NO Severní obloha podzimní souhvězdí
 NO Severní obloha podzimní souhvězdí v-h. v. vzd. dekl. objekt souh. pol. [mag] [mag/(1 ) 2 ] ú. r. tvar typ tř. [ly] rekt. [ ] 2,6 M 2,5 M 2,5 M 2,8 M 2 500 1 300 27 M je satelitní galaxií M 31, trochu
NO Severní obloha podzimní souhvězdí v-h. v. vzd. dekl. objekt souh. pol. [mag] [mag/(1 ) 2 ] ú. r. tvar typ tř. [ly] rekt. [ ] 2,6 M 2,5 M 2,5 M 2,8 M 2 500 1 300 27 M je satelitní galaxií M 31, trochu
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Antonín Bohun Elektronová emise, luminiscence a zbarvení iontových krystalů Pokroky matematiky, fyziky a astronomie, Vol. 6 (1961), No. 3, 150--153 Persistent URL:
Pokroky matematiky, fyziky a astronomie Antonín Bohun Elektronová emise, luminiscence a zbarvení iontových krystalů Pokroky matematiky, fyziky a astronomie, Vol. 6 (1961), No. 3, 150--153 Persistent URL:
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěstování matematiky a fysiky Jaroslav Šafránek Některé fysikální pokusy s katodovou trubicí Časopis pro pěstování matematiky a fysiky, Vol. 66 (1937), No. 4, D285--D289 Persistent URL: http://dml.cz/dmlcz/123398
Časopis pro pěstování matematiky a fysiky Jaroslav Šafránek Některé fysikální pokusy s katodovou trubicí Časopis pro pěstování matematiky a fysiky, Vol. 66 (1937), No. 4, D285--D289 Persistent URL: http://dml.cz/dmlcz/123398
Extragalaktické novy a jejich sledování
 Extragalaktické novy a jejich sledování Novy těsné dvojhvězdy v pokročilém stadiu vývoje přenos hmoty velikost bílého trpaslíka Spektrum klasické novy Objevy nov v ČR 1936 - Záviš Bochníček objevuje ve
Extragalaktické novy a jejich sledování Novy těsné dvojhvězdy v pokročilém stadiu vývoje přenos hmoty velikost bílého trpaslíka Spektrum klasické novy Objevy nov v ČR 1936 - Záviš Bochníček objevuje ve
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Vladimír Štefl Viriálová věta v astrofyzice Pokroky matematiky, fyziky a astronomie, Vol 25 (1980), No 6, 348--351 Persistent URL: http://dmlcz/dmlcz/138182 Terms
Pokroky matematiky, fyziky a astronomie Vladimír Štefl Viriálová věta v astrofyzice Pokroky matematiky, fyziky a astronomie, Vol 25 (1980), No 6, 348--351 Persistent URL: http://dmlcz/dmlcz/138182 Terms
Historie objevu Hubbleova zákona Vladimír Štefl, ÚTFA, PřF MU
 Historie objevu Hubbleova zákona Vladimír Štefl, ÚTFA, PřF MU Již od dob Williama Herschela (1732 1822) byly na obloze pozorovány a studovány,,mlhoviny. K objasnění jejich podstaty byla vyzdvižena řada
Historie objevu Hubbleova zákona Vladimír Štefl, ÚTFA, PřF MU Již od dob Williama Herschela (1732 1822) byly na obloze pozorovány a studovány,,mlhoviny. K objasnění jejich podstaty byla vyzdvižena řada
Konvexní útvary. Kapitola 4. Opěrné roviny konvexního útvaru v prostoru
 Konvexní útvary Kapitola 4. Opěrné roviny konvexního útvaru v prostoru In: Jan Vyšín (author): Konvexní útvary. (Czech). Praha: Mladá fronta, 1964. pp. 49 55. Persistent URL: http://dml.cz/dmlcz/403505
Konvexní útvary Kapitola 4. Opěrné roviny konvexního útvaru v prostoru In: Jan Vyšín (author): Konvexní útvary. (Czech). Praha: Mladá fronta, 1964. pp. 49 55. Persistent URL: http://dml.cz/dmlcz/403505
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Josef B. Slavík; B. Klimeš Hluk jako methodická pomůcka při zjišťování příčin chvění v technické praxi Pokroky matematiky, fyziky a astronomie, Vol. 2 (957), No.
Pokroky matematiky, fyziky a astronomie Josef B. Slavík; B. Klimeš Hluk jako methodická pomůcka při zjišťování příčin chvění v technické praxi Pokroky matematiky, fyziky a astronomie, Vol. 2 (957), No.
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Vladimír Kořínek Poznámky k postgraduálnímu studiu matematiky učitelů škol 2. cyklu Pokroky matematiky, fyziky a astronomie, Vol. 12 (1967), No. 6, 363--366 Persistent
Pokroky matematiky, fyziky a astronomie Vladimír Kořínek Poznámky k postgraduálnímu studiu matematiky učitelů škol 2. cyklu Pokroky matematiky, fyziky a astronomie, Vol. 12 (1967), No. 6, 363--366 Persistent
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěstování matematiky a fysiky Jindřich Procházka Pokusy o interferenci a odrazu zvuku Časopis pro pěstování matematiky a fysiky, Vol. 67 (1938), No. Suppl., D197--D200 Persistent URL: http://dml.cz/dmlcz/120811
Časopis pro pěstování matematiky a fysiky Jindřich Procházka Pokusy o interferenci a odrazu zvuku Časopis pro pěstování matematiky a fysiky, Vol. 67 (1938), No. Suppl., D197--D200 Persistent URL: http://dml.cz/dmlcz/120811
Několik úloh z geometrie jednoduchých těles
 Několik úloh z geometrie jednoduchých těles Úlohy ke cvičení In: F. Hradecký (author); Milan Koman (author); Jan Vyšín (author): Několik úloh z geometrie jednoduchých těles. (Czech). Praha: Mladá fronta,
Několik úloh z geometrie jednoduchých těles Úlohy ke cvičení In: F. Hradecký (author); Milan Koman (author); Jan Vyšín (author): Několik úloh z geometrie jednoduchých těles. (Czech). Praha: Mladá fronta,
Identifikace vzdělávacího materiálu VY_52_INOVACE_F.9.A.35 EU OP VK. Fyzika Orientace na obloze
 Identifikace vzdělávacího materiálu VY_52_INOVACE_F.9.A.35 EU OP VK Škola, adresa Autor ZŠ Smetanova 1509, Přelouč Mgr. Ladislav Hejný Období tvorby VM Červen 2012 Ročník 9. Předmět Fyzika Orientace na
Identifikace vzdělávacího materiálu VY_52_INOVACE_F.9.A.35 EU OP VK Škola, adresa Autor ZŠ Smetanova 1509, Přelouč Mgr. Ladislav Hejný Období tvorby VM Červen 2012 Ročník 9. Předmět Fyzika Orientace na
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Zdeněk Češpíro Výbojový vakuoměr bez magnetického pole Pokroky matematiky, fyziky a astronomie, Vol. 3 (1958), No. 3, 299--302 Persistent URL: http://dml.cz/dmlcz/137111
Pokroky matematiky, fyziky a astronomie Zdeněk Češpíro Výbojový vakuoměr bez magnetického pole Pokroky matematiky, fyziky a astronomie, Vol. 3 (1958), No. 3, 299--302 Persistent URL: http://dml.cz/dmlcz/137111
Determinanty a matice v theorii a praxi
 Determinanty a matice v theorii a praxi 1. Lineární závislost číselných soustav In: Václav Vodička (author): Determinanty a matice v theorii a praxi. Část druhá. (Czech). Praha: Jednota československých
Determinanty a matice v theorii a praxi 1. Lineární závislost číselných soustav In: Václav Vodička (author): Determinanty a matice v theorii a praxi. Část druhá. (Czech). Praha: Jednota československých
O nerovnostech a nerovnicích
 O nerovnostech a nerovnicích Kapitola 3. Množiny In: František Veselý (author); Jan Vyšín (other); Jiří Veselý (other): O nerovnostech a nerovnicích. (Czech). Praha: Mladá fronta, 1982. pp. 19 22. Persistent
O nerovnostech a nerovnicích Kapitola 3. Množiny In: František Veselý (author); Jan Vyšín (other); Jiří Veselý (other): O nerovnostech a nerovnicích. (Czech). Praha: Mladá fronta, 1982. pp. 19 22. Persistent
VY_12_INOVACE_115 HVĚZDY
 VY_12_INOVACE_115 HVĚZDY Pro žáky 6. ročníku Člověk a příroda Zeměpis - Vesmír Září 2012 Mgr. Regina Kokešová Slouží k probírání nového učiva formou - prezentace - práce s textem - doplnění úkolů. Rozvíjí
VY_12_INOVACE_115 HVĚZDY Pro žáky 6. ročníku Člověk a příroda Zeměpis - Vesmír Září 2012 Mgr. Regina Kokešová Slouží k probírání nového učiva formou - prezentace - práce s textem - doplnění úkolů. Rozvíjí
Neurčité rovnice. In: Jan Vyšín (author): Neurčité rovnice. (Czech). Praha: Jednota československých matematiků a fyziků, 1949. pp. 21--24.
 Neurčité rovnice 4. Nejjednodušší rovnice neurčité 2. stupně In: Jan Vyšín (author): Neurčité rovnice. (Czech). Praha: Jednota československých matematiků a fyziků, 1949. pp. 21--24. Persistent URL: http://dml.cz/dmlcz/402869
Neurčité rovnice 4. Nejjednodušší rovnice neurčité 2. stupně In: Jan Vyšín (author): Neurčité rovnice. (Czech). Praha: Jednota československých matematiků a fyziků, 1949. pp. 21--24. Persistent URL: http://dml.cz/dmlcz/402869
Časopis pro pěstování mathematiky a fysiky
 Časopis pro pěstování mathematiky a fysiky František Kaňka Důsledky akusticko-dynamického principu. [IV.] Časopis pro pěstování mathematiky a fysiky, Vol. 47 (1918), No. 1, 25--31 Persistent URL: http://dml.cz/dmlcz/124004
Časopis pro pěstování mathematiky a fysiky František Kaňka Důsledky akusticko-dynamického principu. [IV.] Časopis pro pěstování mathematiky a fysiky, Vol. 47 (1918), No. 1, 25--31 Persistent URL: http://dml.cz/dmlcz/124004
O dělitelnosti čísel celých
 O dělitelnosti čísel celých 9. kapitola. Malá věta Fermatova In: František Veselý (author): O dělitelnosti čísel celých. (Czech). Praha: Mladá fronta, 1966. pp. 98 105. Persistent URL: http://dml.cz/dmlcz/403572
O dělitelnosti čísel celých 9. kapitola. Malá věta Fermatova In: František Veselý (author): O dělitelnosti čísel celých. (Czech). Praha: Mladá fronta, 1966. pp. 98 105. Persistent URL: http://dml.cz/dmlcz/403572
Astronomie. Astronomie má nejužší vztah s fyzikou.
 Astronomie Je věda, která se zabývá jevy za hranicemi zemské atmosféry. Zvláště tedy výzkumem vesmírných těles, jejich soustav, různých dějů ve vesmíru i vesmírem jako celkem. Astronom, česky hvězdář,
Astronomie Je věda, která se zabývá jevy za hranicemi zemské atmosféry. Zvláště tedy výzkumem vesmírných těles, jejich soustav, různých dějů ve vesmíru i vesmírem jako celkem. Astronom, česky hvězdář,
Časopis pro pěstování mathematiky a fysiky
 Časopis pro pěstování mathematiky a fysiky Jan Sommer Pokus vysvětliti Machův klam optický Časopis pro pěstování mathematiky a fysiky, Vol. 20 (1891), No. 2, 101--105 Persistent URL: http://dml.cz/dmlcz/109224
Časopis pro pěstování mathematiky a fysiky Jan Sommer Pokus vysvětliti Machův klam optický Časopis pro pěstování mathematiky a fysiky, Vol. 20 (1891), No. 2, 101--105 Persistent URL: http://dml.cz/dmlcz/109224
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Emil Calda; Oldřich Odvárko Speciální třídy na SVVŠ v Praze pro žáky nadané v matematice a fyzice Pokroky matematiky, fyziky a astronomie, Vol. 13 (1968), No. 5,
Pokroky matematiky, fyziky a astronomie Emil Calda; Oldřich Odvárko Speciální třídy na SVVŠ v Praze pro žáky nadané v matematice a fyzice Pokroky matematiky, fyziky a astronomie, Vol. 13 (1968), No. 5,
Jubilejní almanach Jednoty čs. matematiků a fyziků 1862 1987
 Jubilejní almanach Jednoty čs. matematiků a fyziků 1862 1987 Zdeněk Horský Písemnosti z pozůstalosti prof. dr. A. Seydlera In: Libor Pátý (editor): Jubilejní almanach Jednoty čs. matematiků a fyziků 1862
Jubilejní almanach Jednoty čs. matematiků a fyziků 1862 1987 Zdeněk Horský Písemnosti z pozůstalosti prof. dr. A. Seydlera In: Libor Pátý (editor): Jubilejní almanach Jednoty čs. matematiků a fyziků 1862
O dělitelnosti čísel celých
 O dělitelnosti čísel celých 6. kapitola. Nejmenší společný násobek In: František Veselý (author): O dělitelnosti čísel celých. (Czech). Praha: Mladá fronta, 1966. pp. 73 79. Persistent URL: http://dml.cz/dmlcz/403569
O dělitelnosti čísel celých 6. kapitola. Nejmenší společný násobek In: František Veselý (author): O dělitelnosti čísel celých. (Czech). Praha: Mladá fronta, 1966. pp. 73 79. Persistent URL: http://dml.cz/dmlcz/403569
Hvězdný diagram. statistika nuda je, má však cenné údaje. obdobně i ve světě hvězd! náhodný vzorek skupina osob. sportovci na ZOH 2018
 Hvězdný diagram statistika nuda je, má však cenné údaje náhodný vzorek skupina osob sportovci na ZOH 2018 obdobně i ve světě hvězd! Trocha historie 1889 Carl Vilhelm Ludvig Charlier první tabulka Plejády
Hvězdný diagram statistika nuda je, má však cenné údaje náhodný vzorek skupina osob sportovci na ZOH 2018 obdobně i ve světě hvězd! Trocha historie 1889 Carl Vilhelm Ludvig Charlier první tabulka Plejády
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěstování matematiky a fysiky M. Jahoda; Ivan Šimon Užití sodíkového světla pro Ramanův zjev Časopis pro pěstování matematiky a fysiky, Vol. 69 (1940), No. 3-4, 187--190 Persistent URL: http://dml.cz/dmlcz/123324
Časopis pro pěstování matematiky a fysiky M. Jahoda; Ivan Šimon Užití sodíkového světla pro Ramanův zjev Časopis pro pěstování matematiky a fysiky, Vol. 69 (1940), No. 3-4, 187--190 Persistent URL: http://dml.cz/dmlcz/123324
Základy teorie matic
 Základy teorie matic 7. Vektory a lineární transformace In: Otakar Borůvka (author): Základy teorie matic. (Czech). Praha: Academia, 1971. pp. 43--47. Persistent URL: http://dml.cz/dmlcz/401335 Terms of
Základy teorie matic 7. Vektory a lineární transformace In: Otakar Borůvka (author): Základy teorie matic. (Czech). Praha: Academia, 1971. pp. 43--47. Persistent URL: http://dml.cz/dmlcz/401335 Terms of
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Jiří Švestka Nobelova cena za fyziku za objev reliktního záření Pokroky matematiky, fyziky a astronomie, Vol. 24 (1979), No. 4, 202--205 Persistent URL: http://dml.cz/dmlcz/137797
Pokroky matematiky, fyziky a astronomie Jiří Švestka Nobelova cena za fyziku za objev reliktního záření Pokroky matematiky, fyziky a astronomie, Vol. 24 (1979), No. 4, 202--205 Persistent URL: http://dml.cz/dmlcz/137797
Časopis pro pěstování mathematiky a fysiky
 Časopis pro pěstování mathematiky a fysiky Josef Janoušek O nepravidelném rozkladu světla Časopis pro pěstování mathematiky a fysiky, Vol. 1 (1872), No. 5, 256--261 Persistent URL: http://dml.cz/dmlcz/122691
Časopis pro pěstování mathematiky a fysiky Josef Janoušek O nepravidelném rozkladu světla Časopis pro pěstování mathematiky a fysiky, Vol. 1 (1872), No. 5, 256--261 Persistent URL: http://dml.cz/dmlcz/122691
- mezihvězdná látka - složení: plyny a prach - dělení: 1) Jasné září vlastním nebo rozptýleným světlem emisní reflexní planetární 2) Temné pohlcují
 Mgr. Veronika Kuncová, 2013 - mezihvězdná látka - složení: plyny a prach - dělení: 1) Jasné září vlastním nebo rozptýleným světlem emisní reflexní planetární 2) Temné pohlcují světlo z blízkých zdrojů
Mgr. Veronika Kuncová, 2013 - mezihvězdná látka - složení: plyny a prach - dělení: 1) Jasné září vlastním nebo rozptýleným světlem emisní reflexní planetární 2) Temné pohlcují světlo z blízkých zdrojů
Vzdálenost středu Galaxie
 praktikum Vzdálenost středu Galaxie Připomínám každému, kdo bude měřit hvězdný vesmír, že hvězdné kupy jsou signální světla. Ukazují cestu do centra Galaxie i na její okraje... Kulové hvězdokupy jsou svého
praktikum Vzdálenost středu Galaxie Připomínám každému, kdo bude měřit hvězdný vesmír, že hvězdné kupy jsou signální světla. Ukazují cestu do centra Galaxie i na její okraje... Kulové hvězdokupy jsou svého
Funkcionální rovnice
 Funkcionální rovnice Úlohy k procvičení In: Ljubomir Davidov (author); Zlata Kufnerová (translator); Alois Kufner (translator): Funkcionální rovnice. (Czech). Praha: Mladá fronta, 1984. pp. 88 92. Persistent
Funkcionální rovnice Úlohy k procvičení In: Ljubomir Davidov (author); Zlata Kufnerová (translator); Alois Kufner (translator): Funkcionální rovnice. (Czech). Praha: Mladá fronta, 1984. pp. 88 92. Persistent
DUM č. 20 v sadě. 12. Fy-3 Průvodce učitele fyziky pro 4. ročník
 projekt GML Brno Docens DUM č. 20 v sadě 12. Fy-3 Průvodce učitele fyziky pro 4. ročník Autor: Miroslav Kubera Datum: 21.06.2014 Ročník: 4B Anotace DUMu: Prezentace je zaměřena na základní popis a charakteristiky
projekt GML Brno Docens DUM č. 20 v sadě 12. Fy-3 Průvodce učitele fyziky pro 4. ročník Autor: Miroslav Kubera Datum: 21.06.2014 Ročník: 4B Anotace DUMu: Prezentace je zaměřena na základní popis a charakteristiky
Aritmetické hry a zábavy
 Aritmetické hry a zábavy 1. Doplnění naznačených výkonů In: Karel Čupr (author): Aritmetické hry a zábavy. (Czech). Praha: Jednota českých matematiků a fysiků, 1942. pp. 5 9. Persistent URL: http://dml.cz/dmlcz/4329
Aritmetické hry a zábavy 1. Doplnění naznačených výkonů In: Karel Čupr (author): Aritmetické hry a zábavy. (Czech). Praha: Jednota českých matematiků a fysiků, 1942. pp. 5 9. Persistent URL: http://dml.cz/dmlcz/4329
Plochy stavebně-inženýrské praxe
 Plochy stavebně-inženýrské praxe 10. Plochy šroubové In: František Kadeřávek (author): Plochy stavebně-inženýrské praxe. (Czech). Praha: Jednota československých matematiků a fysiků, 1950. pp. 99 106.
Plochy stavebně-inženýrské praxe 10. Plochy šroubové In: František Kadeřávek (author): Plochy stavebně-inženýrské praxe. (Czech). Praha: Jednota československých matematiků a fysiků, 1950. pp. 99 106.
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost
 Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence
Hvězdný diagram. statistika nuda je, má však cenné údaje. náhodný vzorek skupina osob. obdobně i ve světě hvězd!
 Hvězdný diagram statistika nuda je, má však cenné údaje náhodný vzorek skupina osob obdobně i ve světě hvězd! Trocha historie 1889 Carl Vilhelm Ludvig Charlier první tabulka Plejády 1910 Hans Oswald Rosenberg
Hvězdný diagram statistika nuda je, má však cenné údaje náhodný vzorek skupina osob obdobně i ve světě hvězd! Trocha historie 1889 Carl Vilhelm Ludvig Charlier první tabulka Plejády 1910 Hans Oswald Rosenberg
Staroegyptská matematika. Hieratické matematické texty
 Staroegyptská matematika. Hieratické matematické texty Počítání se zlomky In: Hana Vymazalová (author): Staroegyptská matematika. Hieratické matematické texty. (Czech). Praha: Český egyptologický ústav
Staroegyptská matematika. Hieratické matematické texty Počítání se zlomky In: Hana Vymazalová (author): Staroegyptská matematika. Hieratické matematické texty. (Czech). Praha: Český egyptologický ústav
Plochy stavebně-inženýrské praxe
 Plochy stavebně-inženýrské praxe 9. Plochy rourové In: František Kadeřávek (author): Plochy stavebně-inženýrské praxe. (Czech). Praha: Jednota československých matematiků a fysiků, 1950. pp. 95 98. Persistent
Plochy stavebně-inženýrské praxe 9. Plochy rourové In: František Kadeřávek (author): Plochy stavebně-inženýrské praxe. (Czech). Praha: Jednota československých matematiků a fysiků, 1950. pp. 95 98. Persistent
O dynamickém programování
 O dynamickém programování 9. kapitola. Cauchy-Lagrangeova nerovnost In: Jaroslav Morávek (author): O dynamickém programování. (Czech). Praha: Mladá fronta, 1973. pp. 65 70. Persistent URL: http://dml.cz/dmlcz/403801
O dynamickém programování 9. kapitola. Cauchy-Lagrangeova nerovnost In: Jaroslav Morávek (author): O dynamickém programování. (Czech). Praha: Mladá fronta, 1973. pp. 65 70. Persistent URL: http://dml.cz/dmlcz/403801
Úvod do filosofie matematiky
 Úvod do filosofie matematiky Axiom nekonečna In: Otakar Zich (author): Úvod do filosofie matematiky. (Czech). Praha: Jednota československých matematiků a fysiků, 1947. pp. 114 117. Persistent URL: http://dml.cz/dmlcz/403163
Úvod do filosofie matematiky Axiom nekonečna In: Otakar Zich (author): Úvod do filosofie matematiky. (Czech). Praha: Jednota československých matematiků a fysiků, 1947. pp. 114 117. Persistent URL: http://dml.cz/dmlcz/403163
Naše Galaxie dávná historie poznávání
 Mléčná dráha Naše Galaxie dávná historie poznávání galaxie = gravitačně vázaný strukturovaný a organizovaný systém z řeckého γαλαξίας Galaxie x Mléčná dráha Mléčná dráha antika: Anaxagoras (cca 500 428
Mléčná dráha Naše Galaxie dávná historie poznávání galaxie = gravitačně vázaný strukturovaný a organizovaný systém z řeckého γαλαξίας Galaxie x Mléčná dráha Mléčná dráha antika: Anaxagoras (cca 500 428
Jan Sobotka (1862 1931)
 Jan Sobotka (1862 1931) Martina Kašparová Vysokoškolská studia Jana Sobotky In: Martina Kašparová (author); Zbyněk Nádeník (author): Jan Sobotka (1862 1931). (Czech). Praha: Matfyzpress, 2010. pp. 231--234.
Jan Sobotka (1862 1931) Martina Kašparová Vysokoškolská studia Jana Sobotky In: Martina Kašparová (author); Zbyněk Nádeník (author): Jan Sobotka (1862 1931). (Czech). Praha: Matfyzpress, 2010. pp. 231--234.
Všechny galaxie vysílají určité množství elektromagnetického záření. Některé vyzařují velké množství záření a nazývají se aktivní.
 VESMÍR Model velkého třesku předpovídá, že vesmír vznikl explozí před asi 15 miliardami let. To, co dnes pozorujeme, bylo na začátku koncentrováno ve velmi malém objemu, naplněném hmotou o vysoké hustotě
VESMÍR Model velkého třesku předpovídá, že vesmír vznikl explozí před asi 15 miliardami let. To, co dnes pozorujeme, bylo na začátku koncentrováno ve velmi malém objemu, naplněném hmotou o vysoké hustotě
Virtual Universe Future of Astrophysics?
 Future of Astrophysics? Robert Klement a Pet oš 8. Listopadu 2009 1 Virtuální Observatoře: Co to je a k čemu jsou? 2 Pár slov k 3 Jak se s pracuje 4 5 6 Vlastní článek Vědecké metody Proč VO? Každé tři
Future of Astrophysics? Robert Klement a Pet oš 8. Listopadu 2009 1 Virtuální Observatoře: Co to je a k čemu jsou? 2 Pár slov k 3 Jak se s pracuje 4 5 6 Vlastní článek Vědecké metody Proč VO? Každé tři
Rozhledy matematicko-fyzikální
 Rozhledy matematicko-fyzikální Rudolf Klepáček; Martin Macháček Chemická analýza pomocí optických vláken Rozhledy matematicko-fyzikální, Vol. 80 (2005), No. 2, 21 24 Persistent URL: http://dml.cz/dmlcz/146100
Rozhledy matematicko-fyzikální Rudolf Klepáček; Martin Macháček Chemická analýza pomocí optických vláken Rozhledy matematicko-fyzikální, Vol. 80 (2005), No. 2, 21 24 Persistent URL: http://dml.cz/dmlcz/146100
Fyzikální vzdělávání. 1. ročník. Učební obor: Kuchař číšník Kadeřník. Implementace ICT do výuky č. CZ.1.07/1.1.02/ GG OP VK
 Fyzikální vzdělávání 1. ročník Učební obor: Kuchař číšník Kadeřník 1 6.1Slunce, planety a jejich pohyb, komety Vesmír - Slunce - planety a jejich pohyb, - komety, hvězdy a galaxie 2 Vesmír či kosmos (z
Fyzikální vzdělávání 1. ročník Učební obor: Kuchař číšník Kadeřník 1 6.1Slunce, planety a jejich pohyb, komety Vesmír - Slunce - planety a jejich pohyb, - komety, hvězdy a galaxie 2 Vesmír či kosmos (z
O dynamickém programování
 O dynamickém programování 7. kapitola. O jednom přiřazovacím problému In: Jaroslav Morávek (author): O dynamickém programování. (Czech). Praha: Mladá fronta, 1973. pp. 55 59. Persistent URL: http://dml.cz/dmlcz/403799
O dynamickém programování 7. kapitola. O jednom přiřazovacím problému In: Jaroslav Morávek (author): O dynamickém programování. (Czech). Praha: Mladá fronta, 1973. pp. 55 59. Persistent URL: http://dml.cz/dmlcz/403799
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Jan Šlégr Předpověď a pozorování radiových emisí z planety Jupiter Pokroky matematiky, fyziky a astronomie, Vol. 55 (2010), No. 4, 297--301 Persistent URL: http://dml.cz/dmlcz/141973
Pokroky matematiky, fyziky a astronomie Jan Šlégr Předpověď a pozorování radiových emisí z planety Jupiter Pokroky matematiky, fyziky a astronomie, Vol. 55 (2010), No. 4, 297--301 Persistent URL: http://dml.cz/dmlcz/141973
Hvězdný diagram. statistika nuda je, má však cenné údaje. náhodný vzorek skupina osob. obdobně i ve světě hvězd!
 Hvězdný diagram statistika nuda je, má však cenné údaje náhodný vzorek skupina osob obdobně i ve světě hvězd! Trocha historie Plejády 1889 Carl Vilhelm Ludvig Charlier první tabulka 1910 Hans Oswald Rosenberg
Hvězdný diagram statistika nuda je, má však cenné údaje náhodný vzorek skupina osob obdobně i ve světě hvězd! Trocha historie Plejády 1889 Carl Vilhelm Ludvig Charlier první tabulka 1910 Hans Oswald Rosenberg
B. Hvězdy s větší hmotností spalují termojaderné palivo pomaleji,
 HVĚZDY 1. Většina hvězd se při pozorování v průběhu noci pohybuje od A. Západu k východu, B. Východu k západu, C. Severu k jihu, D. Jihu k severu. 2. Ve většině hvězd se energie uvolňuje A. Prudkou rotací
HVĚZDY 1. Většina hvězd se při pozorování v průběhu noci pohybuje od A. Západu k východu, B. Východu k západu, C. Severu k jihu, D. Jihu k severu. 2. Ve většině hvězd se energie uvolňuje A. Prudkou rotací
Neurčité rovnice. In: Jan Vyšín (author): Neurčité rovnice. (Czech). Praha: Jednota československých matematiků a fyziků, pp
 Neurčité rovnice 2. Lineární rovnice o dvou neznámých In: Jan Vyšín (author): Neurčité rovnice. (Czech). Praha: Jednota československých matematiků a fyziků, 1949. pp. 10 14. Persistent URL: http://dml.cz/dmlcz/402867
Neurčité rovnice 2. Lineární rovnice o dvou neznámých In: Jan Vyšín (author): Neurčité rovnice. (Czech). Praha: Jednota československých matematiků a fyziků, 1949. pp. 10 14. Persistent URL: http://dml.cz/dmlcz/402867
Co víme o přirozených číslech
 Co víme o přirozených číslech 4. Největší společný dělitel a nejmenší společný násobek In: Jiří Sedláček (author): Co víme o přirozených číslech. (Czech). Praha: Mladá fronta, 1961. pp. 24 31. Persistent
Co víme o přirozených číslech 4. Největší společný dělitel a nejmenší společný násobek In: Jiří Sedláček (author): Co víme o přirozených číslech. (Czech). Praha: Mladá fronta, 1961. pp. 24 31. Persistent
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěstování matematiky a fysiky Jan Novák Aritmetika v primě a sekundě Časopis pro pěstování matematiky a fysiky, Vol. 67 (1938), No. Suppl., D254--D257 Persistent URL: http://dml.cz/dmlcz/120798
Časopis pro pěstování matematiky a fysiky Jan Novák Aritmetika v primě a sekundě Časopis pro pěstování matematiky a fysiky, Vol. 67 (1938), No. Suppl., D254--D257 Persistent URL: http://dml.cz/dmlcz/120798
Aneb galaxie pod pláštíkem temnoty. Filip Hroch
 Mrtvé oázy vesmíru Aneb galaxie pod pláštíkem temnoty. Filip Hroch ASTRO@BRNO.2006 Spirální galaxie NGC 1309 Eri, 2 2 Hubble Heritage Spirální galaxie s příčkou NGC 1300, Eri, 7 4 Hubble Heritage Nepravidelná
Mrtvé oázy vesmíru Aneb galaxie pod pláštíkem temnoty. Filip Hroch ASTRO@BRNO.2006 Spirální galaxie NGC 1309 Eri, 2 2 Hubble Heritage Spirální galaxie s příčkou NGC 1300, Eri, 7 4 Hubble Heritage Nepravidelná
Acta Universitatis Palackianae Olomucensis. Facultas Rerum Naturalium. Mathematica-Physica-Chemica
 Acta Universitatis Palackianae Olomucensis. Facultas Rerum Naturalium. Mathematica-Physica-Chemica Cyril Dočkal Automatické elektromagnetické váhy Acta Universitatis Palackianae Olomucensis. Facultas Rerum
Acta Universitatis Palackianae Olomucensis. Facultas Rerum Naturalium. Mathematica-Physica-Chemica Cyril Dočkal Automatické elektromagnetické váhy Acta Universitatis Palackianae Olomucensis. Facultas Rerum
Kombinatorika. In: Antonín Vrba (author): Kombinatorika. (Czech). Praha: Mladá fronta, pp. 3 [6].
![Kombinatorika. In: Antonín Vrba (author): Kombinatorika. (Czech). Praha: Mladá fronta, pp. 3 [6]. Kombinatorika. In: Antonín Vrba (author): Kombinatorika. (Czech). Praha: Mladá fronta, pp. 3 [6].](/thumbs/94/118357644.jpg) Kombinatorika Předmluva In: Antonín Vrba (author): Kombinatorika. (Czech). Praha: Mladá fronta, 1980. pp. 3 [6]. Persistent URL: http://dml.cz/dmlcz/403963 Terms of use: Antonín Vrba, 1080 Institute of
Kombinatorika Předmluva In: Antonín Vrba (author): Kombinatorika. (Czech). Praha: Mladá fronta, 1980. pp. 3 [6]. Persistent URL: http://dml.cz/dmlcz/403963 Terms of use: Antonín Vrba, 1080 Institute of
Základy teorie matic
 Základy teorie matic 23. Klasifikace regulárních párů matic In: Otakar Borůvka (author): Základy teorie matic. (Czech). Praha: Academia, 1971. pp. 162--168. Persistent URL: http://dml.cz/dmlcz/401352 Terms
Základy teorie matic 23. Klasifikace regulárních párů matic In: Otakar Borůvka (author): Základy teorie matic. (Czech). Praha: Academia, 1971. pp. 162--168. Persistent URL: http://dml.cz/dmlcz/401352 Terms
Kongruence. 1. kapitola. Opakování základních pojmů o dělitelnosti
 Kongruence 1. kapitola. Opakování základních pojmů o dělitelnosti In: Alois Apfelbeck (author): Kongruence. (Czech). Praha: Mladá fronta, 1968. pp. 3 9. Persistent URL: http://dml.cz/dmlcz/403653 Terms
Kongruence 1. kapitola. Opakování základních pojmů o dělitelnosti In: Alois Apfelbeck (author): Kongruence. (Czech). Praha: Mladá fronta, 1968. pp. 3 9. Persistent URL: http://dml.cz/dmlcz/403653 Terms
Základy teorie grupoidů a grup
 Základy teorie grupoidů a grup 13. Homomorfní zobrazení (deformace) grupoidů In: Otakar Borůvka (author): Základy teorie grupoidů a grup. (Czech). Praha: Nakladatelství Československé akademie věd, 1962.
Základy teorie grupoidů a grup 13. Homomorfní zobrazení (deformace) grupoidů In: Otakar Borůvka (author): Základy teorie grupoidů a grup. (Czech). Praha: Nakladatelství Československé akademie věd, 1962.
Extragalaktická astrofyzika
 Extragalaktická astrofyzika Jan Schee Ústav fyziky, Filozoficko-přírodovědecká fakulta, Slezská univerzita v Opavě 1 2 RZ = 6378 km MZ= 5,9742 1024 kg 3 4 RS = 6.955 105 km MS= 1.9891 1030kg 5 6 RG = 15
Extragalaktická astrofyzika Jan Schee Ústav fyziky, Filozoficko-přírodovědecká fakulta, Slezská univerzita v Opavě 1 2 RZ = 6378 km MZ= 5,9742 1024 kg 3 4 RS = 6.955 105 km MS= 1.9891 1030kg 5 6 RG = 15
Časopis pro pěstování mathematiky a fysiky
 Časopis pro pěstování mathematiky a fysiky Astronomická zpráva na květen a červen 1909 Časopis pro pěstování mathematiky a fysiky, Vol. 38 (1909), No. 4, 525--528 Persistent URL: http://dml.cz/dmlcz/121459
Časopis pro pěstování mathematiky a fysiky Astronomická zpráva na květen a červen 1909 Časopis pro pěstování mathematiky a fysiky, Vol. 38 (1909), No. 4, 525--528 Persistent URL: http://dml.cz/dmlcz/121459
VY_32_INOVACE_FY.20 VESMÍR II.
 VY_32_INOVACE_FY.20 VESMÍR II. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Galaxie Mléčná dráha je galaxie, v níž se nachází
VY_32_INOVACE_FY.20 VESMÍR II. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 Galaxie Mléčná dráha je galaxie, v níž se nachází
Neurčité rovnice. In: Jan Vyšín (author): Neurčité rovnice. (Czech). Praha: Jednota československých matematiků a fyziků, pp
 Neurčité rovnice 3. Neurčité rovnice 1. stupně o 3 neznámých In: Jan Vyšín (author): Neurčité rovnice. (Czech). Praha: Jednota československých matematiků a fyziků, 1949. pp. 15 20. Persistent URL: http:dml.czdmlcz402868
Neurčité rovnice 3. Neurčité rovnice 1. stupně o 3 neznámých In: Jan Vyšín (author): Neurčité rovnice. (Czech). Praha: Jednota československých matematiků a fyziků, 1949. pp. 15 20. Persistent URL: http:dml.czdmlcz402868
Faktoriály a kombinační čísla
 Faktoriály a kombinační čísla 5. kapitola. Několik otázek z matematické statistiky In: Jiří Sedláček (author): Faktoriály a kombinační čísla. (Czech). Praha: Mladá fronta, 964. pp. 50 59. Persistent URL:
Faktoriály a kombinační čísla 5. kapitola. Několik otázek z matematické statistiky In: Jiří Sedláček (author): Faktoriály a kombinační čísla. (Czech). Praha: Mladá fronta, 964. pp. 50 59. Persistent URL:
Základy teorie grupoidů a grup
 Základy teorie grupoidů a grup 27. Cyklické grupy In: Otakar Borůvka (author): Základy teorie grupoidů a grup. (Czech). Praha: Nakladatelství Československé akademie věd, 1962. pp. 198--202. Persistent
Základy teorie grupoidů a grup 27. Cyklické grupy In: Otakar Borůvka (author): Základy teorie grupoidů a grup. (Czech). Praha: Nakladatelství Československé akademie věd, 1962. pp. 198--202. Persistent
Staroegyptská matematika. Hieratické matematické texty
 Staroegyptská matematika. Hieratické matematické texty Staroegyptská matematika In: Hana Vymazalová (author): Staroegyptská matematika. Hieratické matematické texty. (Czech). Praha: Český egyptologický
Staroegyptská matematika. Hieratické matematické texty Staroegyptská matematika In: Hana Vymazalová (author): Staroegyptská matematika. Hieratické matematické texty. (Czech). Praha: Český egyptologický
Časopis pro pěstování mathematiky a fysiky
 Časopis pro pěstování mathematiky a fysiky Ferdinand Pietsch O pokroku v osvětlování elektřinou. [IV.] Časopis pro pěstování mathematiky a fysiky, Vol. 39 (1910), No. 5, 529--533 Persistent URL: http://dml.cz/dmlcz/123804
Časopis pro pěstování mathematiky a fysiky Ferdinand Pietsch O pokroku v osvětlování elektřinou. [IV.] Časopis pro pěstování mathematiky a fysiky, Vol. 39 (1910), No. 5, 529--533 Persistent URL: http://dml.cz/dmlcz/123804
O tom, co skrývají centra galaxíı. F. Hroch. 26. březen 2015
 Kroužíme kolem černé díry? O tom, co skrývají centra galaxíı F. Hroch ÚTFA MU, Brno 26. březen 2015 Kroužíme kolem černé díry? Jak zkoumat neviditelné objekty? Specifika černých děr Objekty trůnící v centrech
Kroužíme kolem černé díry? O tom, co skrývají centra galaxíı F. Hroch ÚTFA MU, Brno 26. březen 2015 Kroužíme kolem černé díry? Jak zkoumat neviditelné objekty? Specifika černých děr Objekty trůnící v centrech
VESMÍR, SLUNEČNÍ SOUSTAVA
 VESMÍR, SLUNEČNÍ SOUSTAVA Anotace: Materiál je určen k výuce přírodovědy v 5. ročníku ZŠ. Seznamuje žáky se základními informacemi o vesmíru a sluneční soustavě a jejich zkoumání. Vesmír také se mu říká
VESMÍR, SLUNEČNÍ SOUSTAVA Anotace: Materiál je určen k výuce přírodovědy v 5. ročníku ZŠ. Seznamuje žáky se základními informacemi o vesmíru a sluneční soustavě a jejich zkoumání. Vesmír také se mu říká
v01.00 Messierův v katalog Ing. Neliba Vlastimil AK Kladno, 2004
 v01.00 Messierův v katalog Ing. Neliba Vlastimil AK Kladno, 2004 Messierův v katalog První katalog mlhavých objektů, které by pozorovatel mohl zaměnit za kometu Katalog sestavil v roce 1784 francouzský
v01.00 Messierův v katalog Ing. Neliba Vlastimil AK Kladno, 2004 Messierův v katalog První katalog mlhavých objektů, které by pozorovatel mohl zaměnit za kometu Katalog sestavil v roce 1784 francouzský
Jednota českých matematiků a fyziků ve 150. roce aktivního života
 Jednota českých matematiků a fyziků ve 150. roce aktivního života Organizace JČMF In: Jiří Dolejší (editor); Jiří Rákosník (editor): Jednota českých matematiků a fyziků ve 150. roce aktivního života. (Czech).
Jednota českých matematiků a fyziků ve 150. roce aktivního života Organizace JČMF In: Jiří Dolejší (editor); Jiří Rákosník (editor): Jednota českých matematiků a fyziků ve 150. roce aktivního života. (Czech).
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěstování matematiky a fysiky Ferdinand Pietsch Výpočet cívky pro demonstraci magnetoindukce s optimálním využitím mědi v daném prostoru Časopis pro pěstování matematiky a fysiky, Vol. 62 (1933),
Časopis pro pěstování matematiky a fysiky Ferdinand Pietsch Výpočet cívky pro demonstraci magnetoindukce s optimálním využitím mědi v daném prostoru Časopis pro pěstování matematiky a fysiky, Vol. 62 (1933),
Determinanty a matice v theorii a praxi
 Determinanty a matice v theorii a praxi Rejstřík In: Václav Vodička (author): Determinanty a matice v theorii a praxi. Část druhá. (Czech). Praha: Jednota československých matematiků a fysiků, 1950. pp.
Determinanty a matice v theorii a praxi Rejstřík In: Václav Vodička (author): Determinanty a matice v theorii a praxi. Část druhá. (Czech). Praha: Jednota československých matematiků a fysiků, 1950. pp.
Booleova algebra. 1. kapitola. Množiny a Vennovy diagramy
 Booleova algebra 1. kapitola. Množiny a Vennovy diagramy In: Oldřich Odvárko (author): Booleova algebra. (Czech). Praha: Mladá fronta, 1973. pp. 5 14. Persistent URL: http://dml.cz/dmlcz/403767 Terms of
Booleova algebra 1. kapitola. Množiny a Vennovy diagramy In: Oldřich Odvárko (author): Booleova algebra. (Czech). Praha: Mladá fronta, 1973. pp. 5 14. Persistent URL: http://dml.cz/dmlcz/403767 Terms of
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Aleš Fořt Několik poznámek o dosavadním vývoji palivových článků Pokroky matematiky, fyziky a astronomie, Vol. 5 (1960), No. 6, 697--700 Persistent URL: http://dml.cz/dmlcz/138258
Pokroky matematiky, fyziky a astronomie Aleš Fořt Několik poznámek o dosavadním vývoji palivových článků Pokroky matematiky, fyziky a astronomie, Vol. 5 (1960), No. 6, 697--700 Persistent URL: http://dml.cz/dmlcz/138258
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Jan Vlachý Zaměstnání, kvalifikace a věková struktura pracovníků matematicko-fyzikálních věd Pokroky matematiky, fyziky a astronomie, Vol. 15 (1970), No. 5, 230--233
Pokroky matematiky, fyziky a astronomie Jan Vlachý Zaměstnání, kvalifikace a věková struktura pracovníků matematicko-fyzikálních věd Pokroky matematiky, fyziky a astronomie, Vol. 15 (1970), No. 5, 230--233
Výfučtení: Vzdálenosti ve vesmíru
 Výfučtení: Vzdálenosti ve vesmíru Není jednotka jako jednotka Na měření rozměrů nebo vzdáleností různých objektů je nutné zavést nějakou jednotku vzdálenosti. Jednou ze základních jednotek soustavy SI
Výfučtení: Vzdálenosti ve vesmíru Není jednotka jako jednotka Na měření rozměrů nebo vzdáleností různých objektů je nutné zavést nějakou jednotku vzdálenosti. Jednou ze základních jednotek soustavy SI
Základy teorie grupoidů a grup
 Základy teorie grupoidů a grup 12. Základní pojmy o grupoidech In: Otakar Borůvka (author): Základy teorie grupoidů a grup. (Czech). Praha: Nakladatelství Československé akademie věd, 1962. pp. 94--100.
Základy teorie grupoidů a grup 12. Základní pojmy o grupoidech In: Otakar Borůvka (author): Základy teorie grupoidů a grup. (Czech). Praha: Nakladatelství Československé akademie věd, 1962. pp. 94--100.
Malý výlet do moderní matematiky
 Malý výlet do moderní matematiky Úvod [též symboly] In: Milan Koman (author); Jan Vyšín (author): Malý výlet do moderní matematiky. (Czech). Praha: Mladá fronta, 1972. pp. 3 6. Persistent URL: http://dml.cz/dmlcz/403755
Malý výlet do moderní matematiky Úvod [též symboly] In: Milan Koman (author); Jan Vyšín (author): Malý výlet do moderní matematiky. (Czech). Praha: Mladá fronta, 1972. pp. 3 6. Persistent URL: http://dml.cz/dmlcz/403755
Přírodopis 9. Naše Země ve vesmíru. Mgr. Jan Souček. 2. hodina
 Přírodopis 9 2. hodina Naše Země ve vesmíru Mgr. Jan Souček VESMÍR je soubor všech fyzikálně na sebe působících objektů, který je současná astronomie a kosmologie schopna obsáhnout experimentálně observační
Přírodopis 9 2. hodina Naše Země ve vesmíru Mgr. Jan Souček VESMÍR je soubor všech fyzikálně na sebe působících objektů, který je současná astronomie a kosmologie schopna obsáhnout experimentálně observační
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěstování matematiky a fysiky F. Císař Kinematografie při vyučování matematice. [II.] Časopis pro pěstování matematiky a fysiky, Vol. 60 (1931), No. 3, D39--D43 Persistent URL: http://dml.cz/dmlcz/123948
Časopis pro pěstování matematiky a fysiky F. Císař Kinematografie při vyučování matematice. [II.] Časopis pro pěstování matematiky a fysiky, Vol. 60 (1931), No. 3, D39--D43 Persistent URL: http://dml.cz/dmlcz/123948
Reliktní záření a jeho polarizace. Ústav teoretické fyziky a astrofyziky
 Reliktní záření a jeho polarizace Jiří Krtička Ústav teoretické fyziky a astrofyziky Proč je obloha temná? v hlubohém lese bychom v každém směru měli vidět kmen stromu. Proč je obloha temná? pokud jsou
Reliktní záření a jeho polarizace Jiří Krtička Ústav teoretické fyziky a astrofyziky Proč je obloha temná? v hlubohém lese bychom v každém směru měli vidět kmen stromu. Proč je obloha temná? pokud jsou
Eta Carinae. Eta Carinae. Mlhovina koňské hlavy. Vypracoval student Petr Hofmann 8.3.2004 z GChD jako seminární práci z astron. semináře.
 Eta Carinae Vzdálenost od Země: 9000 ly V centru je stejnojmenná hvězda 150-krát větší a 4-milionkrát jasnější než Slunce. Do poloviny 19. století byla druhou nejjasnější hvězdou na obloze. Roku 1841 uvolnila
Eta Carinae Vzdálenost od Země: 9000 ly V centru je stejnojmenná hvězda 150-krát větší a 4-milionkrát jasnější než Slunce. Do poloviny 19. století byla druhou nejjasnější hvězdou na obloze. Roku 1841 uvolnila
Zlatý řez nejen v matematice
 Zlatý řez nejen v matematice Zlaté číslo a jeho vlastnosti In: Vlasta Chmelíková author): Zlatý řez nejen v matematice Czech) Praha: Katedra didaktiky matematiky MFF UK, 009 pp 7 Persistent URL: http://dmlcz/dmlcz/40079
Zlatý řez nejen v matematice Zlaté číslo a jeho vlastnosti In: Vlasta Chmelíková author): Zlatý řez nejen v matematice Czech) Praha: Katedra didaktiky matematiky MFF UK, 009 pp 7 Persistent URL: http://dmlcz/dmlcz/40079
PANM 16. List of participants. http://project.dml.cz. Terms of use:
 PANM 16 List of participants In: Jan Chleboun and Karel Segeth and Jakub Šístek and Tomáš Vejchodský (eds.): Programs and Algorithms of Numerical Mathematics, Proceedings of Seminar. Dolní Maxov, June
PANM 16 List of participants In: Jan Chleboun and Karel Segeth and Jakub Šístek and Tomáš Vejchodský (eds.): Programs and Algorithms of Numerical Mathematics, Proceedings of Seminar. Dolní Maxov, June
Objev gama záření z galaxie NGC 253
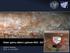 Objev gama záření z galaxie NGC 253 Dalibor Nedbal ÚČJF, Kosmické záření (KZ) Otázky Jak vzniká? Kde vzniká? Jak se šíří? Vysvětlení spektra? Paradigma KZ ze supernov (SN) Pokud platí, lze očekávat velké
Objev gama záření z galaxie NGC 253 Dalibor Nedbal ÚČJF, Kosmické záření (KZ) Otázky Jak vzniká? Kde vzniká? Jak se šíří? Vysvětlení spektra? Paradigma KZ ze supernov (SN) Pokud platí, lze očekávat velké
O mnohoúhelnících a mnohostěnech
 O mnohoúhelnících a mnohostěnech I. Úhly a mnohoúhelníky v rovině In: Bohuslav Hostinský (author): O mnohoúhelnících a mnohostěnech. (Czech). Praha: Jednota československých matematiků a fysiků, 1947.
O mnohoúhelnících a mnohostěnech I. Úhly a mnohoúhelníky v rovině In: Bohuslav Hostinský (author): O mnohoúhelnících a mnohostěnech. (Czech). Praha: Jednota československých matematiků a fysiků, 1947.
O rovnicích s parametry
 O rovnicích s parametry 3. kapitola. Kvadratické rovnice In: Jiří Váňa (author): O rovnicích s parametry. (Czech). Praha: Mladá fronta, 1964. pp. 45 [63]. Persistent URL: http://dml.cz/dmlcz/403496 Terms
O rovnicích s parametry 3. kapitola. Kvadratické rovnice In: Jiří Váňa (author): O rovnicích s parametry. (Czech). Praha: Mladá fronta, 1964. pp. 45 [63]. Persistent URL: http://dml.cz/dmlcz/403496 Terms
Jak se měří vesmír? RNDr. Jan May, Ph.D
 Jak se měří vesmír? RNDr. Jan May, Ph.D 1. Měření vzdáleností hvězd pomocí paralaxy První vědecký pokus zmapovat a změřit vesmír proběhl již před 2150 lety. Řecký astronom Hipparchus narozený v Nicei v
Jak se měří vesmír? RNDr. Jan May, Ph.D 1. Měření vzdáleností hvězd pomocí paralaxy První vědecký pokus zmapovat a změřit vesmír proběhl již před 2150 lety. Řecký astronom Hipparchus narozený v Nicei v
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Jan Vlachý Postavení fyziky, věd o Zemi a astronomie, v rozpočtech amerických federálních ministerstev a agentur Pokroky matematiky, fyziky a astronomie, Vol. 13
Pokroky matematiky, fyziky a astronomie Jan Vlachý Postavení fyziky, věd o Zemi a astronomie, v rozpočtech amerických federálních ministerstev a agentur Pokroky matematiky, fyziky a astronomie, Vol. 13
Jak vytváří statistika obrazy světa a života. II. díl
 Jak vytváří statistika obrazy světa a života. II. díl Předmluva In: Jaroslav Janko (author): Jak vytváří statistika obrazy světa a života. II. díl. (Czech). Praha: Jednota českých matematiků a fysiků,
Jak vytváří statistika obrazy světa a života. II. díl Předmluva In: Jaroslav Janko (author): Jak vytváří statistika obrazy světa a života. II. díl. (Czech). Praha: Jednota českých matematiků a fysiků,
Časopis pro pěstování mathematiky a fysiky
 Časopis pro pěstování mathematiky a fysiky Josef Kounovský O projektivnosti involutorní Časopis pro pěstování mathematiky a fysiky, Vol. 43 (1914), No. 3-4, 433--439 Persistent URL: http://dml.cz/dmlcz/109245
Časopis pro pěstování mathematiky a fysiky Josef Kounovský O projektivnosti involutorní Časopis pro pěstování mathematiky a fysiky, Vol. 43 (1914), No. 3-4, 433--439 Persistent URL: http://dml.cz/dmlcz/109245
VESMÍR Hvězdy. Životní cyklus hvězdy
 VESMÍR Hvězdy Pracovní list HEUREKA! aneb podpora badatelských aktivit žáků ZŠ v přírodovědných předmětech ASTRONOMIE Úloha 1. Ze života hvězdy. Úloha 1a. Očísluj jednotlivé fáze vývoje hvězdy. Následně
VESMÍR Hvězdy Pracovní list HEUREKA! aneb podpora badatelských aktivit žáků ZŠ v přírodovědných předmětech ASTRONOMIE Úloha 1. Ze života hvězdy. Úloha 1a. Očísluj jednotlivé fáze vývoje hvězdy. Následně
