Perkolace a kvantové procházky Percolations and quantum walks
|
|
|
- Irena Bláhová
- před 5 lety
- Počet zobrazení:
Transkript
1 Czech Tchnical University in Prague Faculty of Nuclear Sciences and Physical Engineering Department of Physics Perkolace a kvantové procházky Percolations and quantum walks RESEARCH WORK Author: Bc. Jan Mare² Supervisor: prof. Ing. Igor Jex, DrSc. Consultant: Ing. Jaroslav Novotný, Ph.D. Year: 2013
2 Prohlá²ení Prohla²uji, ºe jsem sv j výzkumný úkol vypracoval samostatn a pouºil jsem pouze podklady uvedené v p iloºeném seznamu. Nemám závaºný d vod proti uºití ²kolního díla ve smyslu Ÿ60 Zákona 212/2000 Sb., o právu autorském, o právech souvisejících s právem autorským a o zm n n kterých zákon (autorský zákon). Declaration I declare, I wrote my Research Project independently and exclusively with the use of cited bibliography. I agree with the usage of this thesis in the purport of the Ÿ60 Act 121/2000 (Copyright Act). V Praze dne Bc. Jan Mare²
3 Acknowledgments I would like to thank my supervisor, especially for a very interesting subject of the work in a currently developing area of research. I am also grateful for various corrections and recommendations during writing the work. Bc. Jan Mare²
4 Contents Introduction 6 1 Percolation What is percolation Classical percolation results Dynamic percolation Quantum walks Classical random walk Quantum walk on a line Quantum walk on a 2D lattice Percolation in QW - Numerical approach Percolated QW on a line Dynamic gaps Quantum tunnelling Percolation in QW on 2D lattice Percolation in QW - Asymptotic dynamics QW on a general percolated graph The attractor subspace p-attractors Attractors for QW General attractors Method summary The step condition
5 5 Fluctuating space D graph example Settings Perfect graph Percolated graph Results D graph example Perfect graph Percolated graph Conclusion 36 Literature 37 5
6 Introduction This work deals with percolation in coined quantum walks. Quantum walks are a quantum counterpart of classical random walks. There is quite a big interest in quantum walks recently as they can be used for example to simulate other physical quantum systems or even be utilised for quantum computing. Great part of the research is done on imperfections in quantum walks. It is important to know, how is the evolution inuenced by various external eects. Here we use the model of percolation known from classical physics as an example of a disturbance in quantum walks. In particular we are interested in asymptotic behaviour. First we summarize some published results mainly about spreading of a quantum walk on an innite percolated graph. The main part of this work is than nding possible asymptotic states for a partially percolated quantum walk on two particular nite graphs. 6
7 Chapter 1 Percolation 1.1 What is percolation In this chapter we will introduce the concept of a classical percolation. Percolation is a very simple model of disordered media. To illustrate the concept of percolation on a physical model, one can think of a big block of some porous material submerged in water. Such material contains narrow channels through which water can leak into the block. We assume, that (compared to the size of channels), the block can be considered "innitely" large. Now we ask, what is the probability of the center of the block getting wet given a microscopic structure of the material. This is actually how the problem of percolation was originally stated. In modern terms, percolation takes place on some graph G = (V, E), where V is set of vertices and E set of edges. This graph is connected (there is a path between any two vertices) and for simplicity undirected. Standard terminology in percolation theory is using sites instead of vertices and bonds instead of edges. (In this work we will sometimes use these terms interchangeably.) In a percolation model we basically create a new graph form G by removing some of it's sites or bonds. Therefore we have two types of percolation: site percolation and bond percolation if we remove sites or bonds respectively. In both cases there is a given p (0 p 1) and each site/bond is independently maintained with the probability p or removed with the probability 1 p. It is said, that remaining sites/bonds are open and removed sites/bonds are closed. The value p is sometimes called percolation probability. We can now ask about the properties of the resulting graph as a function of p. In particular an important question is whether there exists an innite cluster of connected sites. This takes us back to our motivation example with the block of porous material. The existence of such innite open cluster containing the centre of the block is equivalent to the center being reached by the water coming from outside. For a given graph there is a particular critical probability p c. For p < p c, the probability of the existence of an innite open cluster is zero and for p > p c there surely 7
8 is exactly one such cluster. Except for several special cases, nding exact values of p c for dierent graphs is a very dicult problem. Nevertheless much progress has been done in answering another questions about percolation. In particular, so called power laws have been discovered. Those are formulas describing distributions of open clusters in percolated graphs with p close to p c, which hold for large classes of graphs. 1.2 Classical percolation results We will use the symbol θ(p) for the probability of the existence of an open path from the origin to innity. This θ(p) is often called percolation probability, which we have also used for p. Hopefully, there will be no misunderstanding due to this. We can now dene the critical probability as p c = sup{p θ(p) = 0}. Further we denote the open cluster containing the vertex x by C(x) and specically the open cluster containing the origin as C(0). If p < p c, all open clusters are nite. On the other hand p > p c means, that C(0) is innite with strictly positive probability. If we have a lattice (or another homogeneous graph), the probability of C(x) being innite is the same for all x. By using Kolmogorov's zero-one law, we obtain the result that there is some innite cluster with probability 1. It can also be seen intuitively. If C(0) is nite, we just pick some vertex not belonging to C(0) and try again, so we have innitely many "attempts" with non-zero chance of success. Exact values of p c were found just for several types of graphs. For example p c = 1 2 for bond percolation on a square 2D lattice and site percolation on a triangular 2D lattice. Some other values of p c where foud numerically with good precision. For example, for site percolation on a 2D square lattice it is p c = ± [8]. We will now just very briey describe, what those earlier mentioned power laws are. Although it has been proven only for some special 2D lattices and higher dimensional graphs (about d > 19), it is believed that some functions of p are given by universal formulas independently of a specic graph structure. (Possibility of getting results for high dimensional graphs is given by their similarity with regular trees.) For example the expected number of vertices in C(0) behaves like (p c p) γ for some γ as p grows towards p c. Further θ(p) behaves like (p p c ) β as we go down to p c. These critical exponents (γ, β,...) are believed to depend only on dimensionality of the graph. So for example all 2D lattices should have the same γ. 1.3 Dynamic percolation So far we have been discussing only cases when the percolation graph is given at the beginning and undergoes no change during the process. When we model our system with some discrete time process like e.g. random walks or coined quantum 8
9 walks, we can naturally consider some changes in the graph structure during the process. If these changes are still much slower than the characteristic time step of the process, we call it static uctuations (may lead to Anderson localisation). On the other hand if the typical time of the graph change in comparable to the step time we have dynamic uctuations (may lead to diusion). An obvious example of the later case is when we generate a new percolated graph in every time step of the process. 9
10 Chapter 2 Quantum walks Here we introduce the concept of a classical random walk and than focus on quantum walks. Even though a quantum walk (QW) is a quantum counterpart of a classical random walk, the dierence is signicant. While perfect quantum walks rely heavily on coherence and can exhibit specic wave properties, classical random walks are incoherent processes. Nevertheless, when we introduce some disturbance in a QW (partial measurements, classical randomness like percolation,...) the dierence may be suppressed or even vanish. 2.1 Classical random walk Let us rst very briey introduce a classical random walk. Random walk is a discrete stochastic process on a graph. In the simplest scenario, we have an innite line of discrete uniformly distributed points and a walker with a coin. In discrete time steps, the walker ips a coin and makes one step to the left or to the right according to the coin ip. Now we can ask, what is the probability of the walker being at a given position x (relative to his starting point) after n steps. In other words, we want to nd the probability distribution of his position. Let us assume, that the coin is unbiased (the same probability for heads and tails) and so we get a balanced random walk. It is easy to see, that the walker's position mean is his starting point (for all n). Actually in our case his position follows a binomial distribution (Figure 2.1) and therefore the standard deviation is n. 2.2 Quantum walk on a line In the quantum version we will also begin with a walk on a line. The underlying graph is the same (line of nodes with edges between nearest neighbours), but now the vertices represent orthonormal states in the position Hilbert space of the quantum walker (denoted H x ). The walker has a coin as well. (As in the classical version, we 10
11 Figure 2.1: The probability distribution of a classical random walk with unbiased coin after 20 steps. If we consider only even positions (odd positions are unoccupied in even steps and vice versa), we get a binomial distribution. will consider only discrete time quantum walk - a continuous time walk has no coin in either case.) Here the coin is some two level quantum system (spin, polarisation,...) with the coin Hilbert space (denoted H c ). Let us use the symbols 1 and +1 for orthonormal bases states in H c. The entire state of a quantum walker is a vector from the tensor product of the position Hilbert space and the coin space H x H c. In contrast to classical random walk, the state of a walker can be now an arbitrary superposition of all position and coin states. The time evolution of a quantum walk is given by the unitary operator U = SC. Here C = (1 x C c ) is the coin operator. C c acting only on H c is extended by unity on position space H x. S stands for the step operator governing the walker's motion on the lattice. The resulting state of the walker starting in the state ψ in after t steps is therefore: ψ t = U t ψ in = (SC) t ψ in. In the case of a quantum walk on a line, the operator C is represented by an unitary 2 2 matrix in each vertex. In general it can be written in the form: [ C c (gen) = cos(ξ) e iφ sin(ξ) e iθ sin(ξ) e i(θ+φ) cos(ξ) ], (2.1) where 0 θ π, 0 φ π and 0 ξ 2π. A commonly used example is the Hadamard coin: C (Hadamard) c = [ ] = 1 2 [ ]. The step operator can be written as: 11
12 S = x x + 1, +1 x, +1 + x 1, 1 x, 1. Here we are using notation X x C c X, C and the order of symbols is the same for dual bra vectors. So the action of the step operator on bases states is: S x, +1 = x + 1, +1, (2.2) S x, 1 = x 1, 1. It shifts the position of the walker according to state of the coin and leaves the coin part of the system unchanged. Note, that the action of this operator is the same for all x. The walker is at the beginning in some state ψ in, which is typically chosen in the form: ψ in = 0 (α 1 + β +1 ). The walker starts at the origin with the coin in some superposition. The evolution "spreads" the walker from the origin by creating superposition of still more distant vertex states. There are numerous dierences between classical random walks and quantum walks. A typical quantum feature is interference, which in a quantum walk fundamentally inuences the resulting probability distribution. Figure 2.2 shows the probability distribution of the walker's position (summed over coin states) for a quantum walk on line with the Hadamard coin and the initial state ψ in = ( 1 + i +1 ) after 100 steps. This setting produces a symmetric position distribution of the quantum walker. As can be seen from the gure, a quantum walk (here we are still talking just about 1D walk) spreads much faster than a classical random walk. It's standard deviation grows linearly with the number of steps. (That is a quadratic speed-up over classical.) This property is not inuenced by changing the initial state or the coin operator. An illustration of this is presented on gures 2.3 and 2.4. The gure 2.3 shows the probability distribution of quantum walks with dierent initial states and 2.4 for various coins. The ballistic spread is obvious in all cases, even if the scaling prefactor depends on the coin choise. 2.3 Quantum walk on a 2D lattice Let us consider a square two dimensional regular lattice of vertices. (Nearest neighbours are connected with edges.) In the classical case, the walker would need a four sided "coin" (rather a dice) to toss at each step. The same holds for a quantum walk, where this coin is some four level quantum system with basis states 12
13 Figure 2.2: Position probability distribution (summed over coin states) for a quantum walk on line with the Hadamard coin and the initial state ψ in = ( 1 + i +1 ) after 100 steps. Only even positions are displayed since the probability at odd positions is zero in even time steps. Figure 2.3: Position distribution (summed over coin states) for quantum walk on line with Hadamard coin and the initial states: a) ψ a = ( 1 + i +1 ) b) ψ b = 0 (i +1 ) and c) ψ a = 0 1 after 100 steps. Only even positions are displayed since the probability at odd positions is zero in even time steps. 13
14 Figure 2.4: Position distribution (summed over coin states) for quantum walk on line with the initial state ψ a = ( 1 + i +1 ) and the coin 2.1 with a) ξ = π/4 (Hadamard), b)ξ = π/6 and c) ξ = π/8 after 100 steps. Even though the speed of the spread diers for dierent choices of ξ, it is still ballistic (proportional to the number of steps). Only even positions are displayed since the probability at odd positions is zero in even time steps. L, R, D, U. In contrast to a 1D walk, the choice of the coin inuences significantly the behaviour of a quantum walk. For illustration of a 2D quantum walk, we will use for example so called Grover's coin. In the matrix representation it is written as: C c (Grover) = (2.3) The advantage of the Grover's coin is it's symmetry. (Although is is not the only coin allowing for a symmetric QW.) It treats all directions equally except from a sign ip performed on the direction the walker came from. This choice also requires a modication of the step operator (to preserve unitarity [4]) - it inverts coin states: S 4 x, y, L = x 1, y, R, (2.4) S 4 x, y, R = x + 1, y, L, S 4 x, y, D = x, y 1, U, S 4 x, y, U = x, y + 1, D. A quantum walk on a 2D grid is signicantly dierent from the one dimensional version. While ballistic spread is a robust eect (not dependent on the initial state 14
15 nor the coin) in a walk on a line, it is not so here. There is one speci c initial state exhibiting spread like 1D walk, but for most initial states, there is a central peak of probability in the origin. Nevertheless the spread is still faster than for a classical random walk. The situation is illustrated on gures 2.5(a) and 2.5(b). Figure 2.5(a) shows the walk with the special initial state mentioned above, speci cally ψin i = 21 0, 0i ( Li + Ri + Di + U i). On the gure 2.5(b) there is probability distribution averaged over 500 walks with randomly chosen initial states. From this we see, that in 2D quantum walk, it matters which initial state we choose. Therefore in further investigation, we will be careful to indicate whether we use the fast spreading initial state presented above or some other one or possibly some averaging over more initial states. (a) Random states (b) Random phases Figure 2.5: Figure 2.5(a) shows a probability distribution of 2D quantum walk with 20 steps, Grover's coin and special initial state ψin i = 21 0, 0i ( Li + Ri + Di + U i). Figure 2.5(b) shows an average probability distribution for 500 2D quantum walks with 20 steps, Grover's coin and randomly chosen initial states. The random initial states are of the form 0, 0i (rand(-1,1) Li + rand(-1,1) Ri + rand(-1,1) Di + rand(-1,1) U i) after normalisation. 15
16 Chapter 3 Percolation in QW - Numerical approach In this chapter we will summarize results by Leung et al [4] to introduce some basic phenomena which can occur in percolated quantum walks on innite graphs. 3.1 Percolated QW on a line First let us consider a walk on a line. In the scope of percolation, there is an obvious problem. For any percolation probability p < 1, there will certainly be some broken edge both on the left and on the right of the origin. The walker can not pass through those broken links and the walk becomes just a quantum walk on a nite line. Two approaches solving this problem are suggested in [4] - dynamic gaps and quantum tunnelling. For purposes of this summary, we will stick to the notation of the paper and use slightly dierently (but equivalently) parametrized form of a general coin operator: [ ] η e C c (gen) iθ 1 η = e iφ 1 η e i(θ+φ), η where 0 θ π, 0 φ π and 0 η Dynamic gaps Here we use the concept of dynamic percolation mentioned earlier. We generate a new percolation lattice at every time step. This ensures, that broken sites/edges do not block the walker permanently. We modify the step operator by making it position and time dependent. If the edge in a given direction is present we use operator (2.2). If the edge in plus or minus direction is absent, we use a transformation 16
17 x, +1 x, 1, (3.1) x, 1 x, +1, respectively. The walker is reected on a missing edge. While using the Hadamard coin, this type of disruption of a quantum walk leads after some number of steps (scaling as 1/(1 p)) to a classical spreading of the walk. It has an eect similar to nonunitary evolution caused by random measurements. The speed of such a quantum walk is proportional to t (with a higher prefactor than for a classical random walk) Quantum tunnelling This model considers the well known phenomenon on quantum particles - tunnelling through potential barriers. The quantum walker can now pass broken links, but here we use a biased coin (3.1) with η < 0, 5 on both sides of the gap. This corresponds to a slower spreading over broken links. Figure 3.1 shows numerical results for a quantum walk with 100, 1000 and steps with η = 0, 25 and dierent percolation probabilities. We can see that quantum coherence remains for some time (100 steps), but asymptotically the walk with 0 < p < 1 spreads like a classical random walk on an unpercolated line. (The scaling prefactor is again higher for a quantum walk.) Long-term quantum coherence lasts only for extreme cases of all edges present or pure tunnelling. 3.2 Percolation in QW on 2D lattice On percolated lattice we have vertices of dierent degree, so we must dene appropriate coin operators to keep the evolution unitary. In [4] generalized Grover's coin is used which for dimension d has elements (Cd Grover ) ij = 2/d δ ij. (Matrix lled with the number 2/d and the diagonal reduced by 1.) The coin for particular conguration is a matrix with one-dimensional blocks -1 for broken edges and the rest constructed from corresponding Grover's matrix. Simulations were done for three settings. For two pure initial states states: ψ max = 1 0, 0 ( L + R + D + U ), (3.2) 2 ψ min = 1 0, 0 ( L R + D + U ), 2 with maximal respectively minimal spreading and also for walk averaged over random choices of sign. 17
18 Figure 3.1: Quantum walk with tunnelling (η = 0.25) with various setting: 100 (top), 1000 (middle) and (bottom) steps with percolation probability p = 1 (black), 0.75 (red), 0.5 (green), 0.25 (blue) and 0 (orange). Only even positions are displayed, since probability at odd positions is zero in even time steps. [4]. As a measure of spreading, the mean distance from the origin: r = x,y x2 + y 2 p(x, y) is used, where p(x, y) is probability of the walker being measured at vertex (x, y) (summed over coin states). Figure 3.2 shows results for the setting with random states. With very small p, the walker has basically nowhere to go. Than r starts growing (before classical percolation probability for bond and 0.59 for site percolation). At some point the growth slows down, when the size of a typical open cluster outgrows the area covered by the walk with given number of steps. At p close to 1 both bond and site percolated walks behave equally. Due to restoring lattice symmetry, the spread grows to perfect-lattice walk values. We can further study the scaling of r with growing t for given p. Figure 3.3 shows log-log plot. We can see, that after over-going initial nite-size eects we get straight lines (neglecting four-steps periodic zig-zag behaviour). It means, that r scales as t α. For p around 0.9, the coecient α reaches the value 0.5 (spreading for classical random walk on perfect lattice) and than rises fast to α = 1 for perfect quantum walk. Examining similar data for ψ max shows, that spreading in this case has higher α than averaged walks [4], so spreading scales dierently. 18
19 Figure 3.2: Value r of 2D quantum walk as a function of percolation probability p for dierent numbers of steps using initial states with random phases (both, bond and site percolation). [4]. Figure 3.3: Value r of 2D quantum walk as a function number of steps t for various percolation probabilities p using initial states with random phases. [4]. 19
20 Chapter 4 Percolation in QW - Asymptotic dynamics Applying the results by Novotný et al on asymptotic dynamic of random unitary operations [5], Kollár et al [6, 7] describes asymptotic dynamics of coined quantum walks on nite percolated graphs. We will now introduce these ideas and use them in the next chapter. 4.1 QW on a general percolated graph First we need to describe quantum walk on an arbitrary bond-percolated graph. Let the graph be G = (V, E), where V is the set o vertices (sites) and E the set of edges (bonds). As in previous cases the walk is driven by an evolution operator U K. Here K E stands for a subset of edges which remained open, thus (V, K) is a graph given by particular realisation of the percolation process. We can describe U K as: U K = S K C, (4.1) where C is an operator acting on the coin space and S K is a step operator given by: S K = a V,d (a,a d) K a d, d a, d + a V,d (a,a d)/ K R a a, d a, d. (4.2) Here d goes over all directions possible at the vertex a, a d denotes the nearest neighbouring vertex of a in the direction d and R a is the reection operator in the vertex a. The operator S K moves the walker to an appropriate neighbouring site if the edge needed is present in K and leaves him at the current position if this edge is missing. In the case of a missing edge the reection operator R a acting on the coin state is applied, which ensures unitarity of S K. 20
21 In the case of a d-regular graph, we may use the same coin operator (C c ) in all vertices and than the resulting coin operator can be written as C = I x C c, where again I x is the identity operator acting on the position space. It is important, that even if the coin in every vertex is dierent, the evolution operator U K decomposes into subsequent application of two other unitary operators C and S K. Now the problem of investigation is to obtain analytical results about the behaviour of a dynamical percolation on nite graphs. Due to the presence of a classical uncertainty in generating a new percolation graph in every step, we need to describe our walker by a density operator. The initial state is now some ρ 0 and the evolution is given by a superoperator Φ derived from U K as ρ(n + 1) = Φ(ρ(n)) = K π K (p)u K ρ(n)u K, (4.3) where π K (p) is the probability that the percolation process leads to the conguration K if the percolation probability is p. 4.2 The attractor subspace Equation (4.3) for Φ exactly corresponds with the denition of random unitary operator investigated in [5], therefore we can use methods described there to nd the asymptotic dynamics of our quantum walk. First we need to nd so called attractors. Those are special operators forming a subspace of the possible asymptotic states of the walker. (They are not necessarily valid density operators.) All other components of the initial state are suppressed after a sucient number of iterations. Attractors are all possible solutions X λ,i of the equation: U K X λ,i U K = λx λ,i, where λ = 1, for K. (4.4) The index i distinguishes dierent orthogonal "eigenvectors" (operators solving the equation) of a given eigenvalue λ. We will denote the set of all eigenvalues λ as σ. By K we either mean K E or a subset of 2 E containing all possible congurations, when we consider only partial percolation on some edges. (Therefore some congurations are not allowed by denition of the problem.) The asymptotic state is given by: ρ(n) = Φ n (ρ 0 ) n λ σ,i λ n Tr(X λ,i ρ 0)X λ,i. (4.5) From there we can observe, that the asymptotic behaviour is independent of values π K (p) and therefore independent of p as long as 0 < p < 1. These probabilities 21
22 only determine the speed of convergence of the actual state towards our predicted asymptotic behaviour. If there is just one attractor, it is the only possible asymptotic state. On the other hand, if there are attractors corresponding to eigenvalues λ 1, there can be asymptotic cycles in the walker state p-attractors The article [7] gives a method, how to nd some attractors more easily by using common eigenvectors of all operators U K. Let us denote the basis of those common eigenvectors { φ α,iα }. Therefore these states full the equation U K φ α,iα = α φ α,iα, for K. (4.6) Now we can simply construct attractors corresponding to λ from matrices of the type φ α,iα φ β,iβ as: Y λ,i = αβ =λ,i α,i β A α,iα β,i β φ α,iα φ β,iβ. (4.7) We will call these attractors p-attractors. It is important to know, that p-attractors are not the only attractors of the system. It is easy to see, that p-attractors satisfy the condition Y λ U K = λu K Y λ,i, where λ = 1 for K, K, (4.8) In fact this relation is equivalent to Y λ,i being an p-attractor [7]. 4.3 Attractors for QW General attractors If we use the specic form of U K given by (4.1), we can rewrite equation (4.4) into the form CX λ,i C = λs K X λ,is K for K. (4.9) The left hand side of the equation is independent of chosen K E and therefore: 22
23 We can therefore separately solve S K X λ,i S K = S K X λ,i S K for K, K. (4.10) CX λ,i C = λs K X λ,is K (4.11) for one particular choice of K and than constrain the result by the step conditions In comparison to solving fully percolated walk (where all edges undergo percolation), in our case we have a problem. For partial percolation (where some edges are always present) we can not use the convenient conguration with all edges missing (resulting to local conditions). It means, that we really have to solve the equation in the whole Hilbert space (with dimension of the number of all possible directions in all vertices combined). Hypothetically we could use a brute-force method. In fact the equation 4.12 is equivalent to (SC) (SC) x = λx, (4.12) where x is dened by a, b x = a X b. This is just the task of nding eigenstates of an unitary operator, but the problem is it's size. For example for our rather small 4-regular graph with 3 6 sites the dimension of the space on which SC acts is 72 and therefore (SC) (SC) is a matrix. Finding eigenstates for such a matrix has signicant demands on computation resources. (It is not reasonably feasible on a 2,6 GHz processor, 6 GB RAM computer using the function Eigensystem[] in Wolfram Mathematica software.) To overcome the diculty described above we can use p-attractors. We can use the fact, that p-attractors can be constructed from common eigenstates of the evolution operator. The general attractor equation can be understood as being the p-attractor equation CX λ,i C = λs K X λ,is K (4.13) CX λ,i C = λs L X λ,is L (4.14) where we have just chosen both L and L to be K. This will allow us tu nd the solution of one conguration (on which we will subsequently apply the step condition 4.10) using pure states requiring just a fraction of computer resources compared to the straightforward approach. 23
24 4.3.2 Method summary The method we will use is the following: Let the dimension of the full Hilbert space be N. First, we nd all N eigenstates { φ α,iα } of one chosen operator U K = S K C (not common eigenstates). From those we can construct N N operators Those all solve the equation Z α,iα,β,i β = φ α,iα φ β,iβ. (4.15) S K CZ α,iα,β,i β S K C = αβ Z α,iα,β,i β. (4.16) On the other hand we want to solve the equation CX λ,i C = λs K X λ,is K, S K CX λ,i (S K C) = λx λ,i. (4.17) Note, that all Z α,iα,β,iβ are solutions of 4.17 with λ = αβ. As we cannot nd more than N N mutually orthogonal solutions, we have them all. The next step is to nd restrictions given by the step condition. We do not want to loose any attractors and therefore instead of using the condition for pure states we will instead be follow S K φ α,i α = S K φ α,iα, for K, K, (4.18) (4.19) S K X λ,i S K = S K X λ,i S K for K, K. (4.20) It is important that we do not only test Z α,iα,β,iβ on fullling the step condition. We must consider all linear combinations within each eigenvalue subspace and nd all that t The step condition Here we will present some general ndings about the step condition 4.10 for partially percolated graphs. Let us have have two operators S K1 and S K2. (This can be obviously generalised for comparing more operators.) Let us use the notation 24
25 Figure 4.1: Illustration of the notation in solving the step condition. K = K 1 K 2 (edges present in both sets), L 1 = K 1 \ K (edges present just in K 1 ), L 2 = K 2 \ K (edges present just in K 2 ) and M = E \ (L 1 K L2) (edges missing in both sets). (See gure 4.1.) Now we can write: S K1 = S K2 = (a,a d) K + (a,a d) M (a,a d) K + (a,a d) M a d, d a, d + (a,a d) L 1 a d, d a, d + R a a, d a, d A + B 1 + C 1 + D, a d, d a, d + (a,a d) L 1 R a a, d a, d + R a a, d a, d A + B 2 + C 2 + D, (a,a d) L 2 R a a, d a, d + (a,a d) L 2 a d, d a, d + where A, B 1, B 2, C 1, C 2 and D are just a shorthand for corresponding terms. Now the equation is S K1 XS K 1 = S K2 XS K 2, (A + B 1 + C 1 + D)X(A + B 1 + C 1 + D) = (A + B 2 + C 2 + D)X(A + B 2 + C 2 + D). After removing terms that are the same on both sides we have (A + D)X(B 1 + C 1 ) + (B 1 + C 1 )X(B 1 + C 1 ) + (B 1 + C 1 )X(A + D) = = (A + D)X(B 2 + C 2 ) + (B 2 + C 2 )X(B 2 + C 2 ) + (B 2 + C 2 )X(A + D). The operator X can be in general written as X = s 1,c 1,s 2,c 2 X s 1,c 1 s 2,c 2 s 1, c 1 s 2, c 2. After plugging this form into the above equation we can perform scalar products and we are left with just particular coecients X s 1,c 1 s 2,c 2 given by the "bra part" of S and operators given by the "ket part" of S. Now we should note, that these "ket parts" are the resulting states after applying the step operator with the given conguration. There are two ways how the walker can get into a particular state (position and orientation) - by passing the edge or by reection. For one given edge conguration only one of those eects may happen 25
26 for every initial state (before the application of the step operator). It is often the case, that each state can be reached only from one initial state by applying the step operator. (A typical example is a regular square lattice with the reection operator that just ips direction.) In such a situation it can not happen, that two terms on one side of the equation would contain the same ket. Let us now "dene" the reection operator. Let R be such that it does not aect the walker's position and if the walker faces some edge and it happens to be closed, he is reected to the direction he would have been facing if he had reached the vertex by traversing that edge. In particular we have two cases in mind here. The rst one is again the square lattice with the reection operator that ips directions. The other is a "reversed" situation. Here the reection operator does nothing (identity operator), but the normal step turns the walker to return. We will use both these settings later. Let us use the notation that c is the state after reection if the original state was c, therefore R s, c = s, c. Using our assumptions and because the states are mutually orthogonal, the condition splits into equality of individual terms. The only restriction is that we have to hold together terms associated with each edge, because those swap due to percolation. Let us for example rst examine: AX(B 1 ) = AX(B 2 ), which is explicitly written as (a,a d) K = ( ) a d, d a, d Xs s1,c1 2,c 2 s 1, c 1 s 2, c 2 b b, e b, e = s 1,c 1,s 2,c 2 (b,b e) L 1 ( ) a d, d a, d Xs s1,c1 2,c 2 s 1, c 1 s 2, c 2 b, ẽ b, e. s 1,c 1,s 2,c 2 (b,b e) L 1 (a,a d) K After performing scalar products we have: a d, d X (a,a d) K (b,b e) L 1 a,d b,e b b, e = a d, d X (a,a d) K (b,b e) L 1 a,d b,e b, ẽ. Now we can make a step similar to the substitution but it really is just renaming the summing index. Let us exchange b for b e and e for ẽ on the right hand side. Now the equation is: 26
27 a d, d X (a,a d) K (b,b e) L 1 a,d b,e b b, e = a d, d X (a,a d) K (b e,b) L 1 a,d b e,ẽ b e, e. Finally we just have to realise, that the graph is undirected and therefore (b, b e) L 1 (b e, b) L 1, so the conditions in sums are identical. Finally we can compare individual terms in the sum and get the condition X a,d b,e = Xa,d b e,ẽ for all (a, a d) K and (b, b e) L 1. By using the other equations with just one "indexed term" (B 1, B 2, C 1 or C 2 ), we have the overall conditions X a,d b,e = Xa,d b e,ẽ and X b,e a,d = Xb e,ẽ a,d for all (a, a d) K M and (b, b e) L 1 L 2. Let us now have a look at the equation B 1 X(B 1 ) = B 2 X(B 2 ). Again the explicit expression is ( ) a d, d a, d Xs s1,c1 2,c 2 s 1, c 1 s 2, c 2 b b, e b, e = (a,a d) L 1 s 1,c 1,s 2,c 2 (b,b e) L 1 = ( ) a, d a, d Xs s1,c1 2,c 2 s 1, c 1 s 2, c 2 b, ẽ b, e. s 1,c 1,s 2,c 2 (b,b e) L 1 (a,a d) L 1 After performing scalar products we have: a d, d X (a,a d) L 1 (b,b e) L 1 a,d b,e b e, e = and nally using the same trick as before we have (a,a d) L 1 (b,b e) L 1 a, d X a,d b,e b, ẽ 27
28 a d, d X (a,a d) L 1 (b,b e) L 1 a,d b,e b e, e = a d, d X (a,a d) L 1 (b,b e) L 1 a d, d b e,ẽ b e, e. Together with the three remaining equations the resulting conditions are X a,d b,e = Xa d,d b e,ẽ for all (a, a d) L 1 and (b, b e) L 1 or (a, a d) L 2 and (b, b e) L 2 and further X a,d b e,ẽ = Xa d,d b,e for all (a, a d) L 1 and (b, b e) L 2 or (a, a d) L 2 and (b, b e) L 1. We will use these results in the next chapter to solve some simple particular cases. 28
29 Chapter 5 Fluctuating space In this chapter we will examine QWs on some specic partially percolated (some edges will always remain present) nite graphs. The rst graph (gure 5.1) can be thought as representing two 1D systems weakly coupled to each other. This can be for instance two molecules forming a weakly bond system. The other possibility is to understand this literally as two coupled one dimensional spaces. The second graph (gure 5.3) may represent two 2D spaces with a connection that changes it's dimensionality. A one-dimensional connection is still present and the other two connecting edges only open randomly in some time steps. We want to examine the inuence of this dimensionality change D graph example Settings Our rst graph consists of two 4-loops connected by one edge, see gure (5.1). Only this connecting edge (dashed line) undergoes percolation, all others are still present. This scheme also shows the coin state notation. The vertices with just two neighbours have the coin states in clockwise direction labelled "+" and in counterclockwise direction labelled "-". Connecting vertices have one additional direction labelled "0". In analogy to any other discrete quantum walk on a graph, the evolution of our system is given by the unitary operator U, which consists of the coin operator C and the step operator S. We have one uctuating edge and therefore two dierent unitary operators U 1 = CS 1 for the graph with the connection and U 2 = CS 2 for the graph without the connecting edge. Let us now specify the exact behaviour of our step operator. In vertices {1, 2, 3, 6, 7, 8} we just follow the denition given by 4.2, where the second part with the reection operator is not even needed. In connecting vertices 4 and 5, we will also use this 29
30 Figure 5.1: The diagram of the investigated graph. The dashed line represents the only percolated edge. denition with the identity operator as the reection operator. This choice implies the following behaviour: If the walker comes through the connecting edge, he will face to return. If he faces the connecting edge and it is closed, he just does nothing. In loops the walker circulates unless his direction is changed by the coin operator. As the coin operator, we will use the Hadamard coin C 2 in vertices of degree 2 and the Grover coin C 3 at vertices of degree 3. In the matrix representation it is: C 2 = 1 2 [ ], C 3 = The whole coin operator C is therefore a direct sum: C = C 2 C 2 C 2 C 3 C 3 C 2 C 2 C Perfect graph Let us rst solve the behaviour of the QW on the perfect graph (with the connecting edge present). We will use this result when investigating the percolated version. Here we only need to nd eigenstates of the unitary evolution operator U 1 = CS 1. It is very straightforward to do, but U 1 is represented by matrix. I have done the calculation using Wolfram Mathematica software, see appendix space_1.nb Percolated graph Now we want to restrict our asymptotic states with the step condition to those, that remain even with the percolation of the connecting edge. Here we can use the result from the previous chapter because it is not possible that the reection would send the walker to a state that he could also reach through some other edge. We still use the notation S K1 for the step operator for the perfect graph and S K2 for the step operator for the graph with the connecting edge missing. Therefore 30
31 S K1 = E and S K2 = E \ (4, 5). To t the notation to what we used in the previous chapter we have: K = E \ (4, 5), L 1 = (4, 5), L 2 =, M =. Let us remind the previous result that we will now use. The attractors must full: X a,d b,e = Xa,d b e,ẽ and X b,e a,d = Xb e,ẽ a,d for all (a, a d) K M and (b, b e) L 1 L 2 and further X a,d b,e = Xa d,d b e,ẽ for all (a, a d) L 1 and (b, b e) L 1 or (a, a d) L 2 and (b, b e) L 2 and X a,d b e,ẽ = Xa d,d b,e for all (a, a d) L 1 and (b, b e) L 2 or (a, a d) L 2 and (b, b e) L 1. In our particular case that is for all (a, a d) K and X a,d 4,0 = X a,d 5,0 and X 4,0 a,d = X5,0 a,d, X 4,0 4,0 = X 5,0 5,0, X 4,0 5,0 = X 5,0 4, Results All calculations are to be found in the appendix space_1.nb. The evolution operator for the perfect graph (with the connecting edge) has 18 non-degenerate eigenvalues, so each eigenstate represents a whole subspace. Those give rise to the total number of 82 "operator eigenvalues". The degeneracy of the eigenvalue 1 is 18. The subspace of states corresponding to the eigenvalue 1 is the only one where density matrices can be found. After introducing the percolation only 41 dierent eigenvalues remain corresponding in total to 82 attractors. 10 of those attractors are in the subspace of the eigenvalue 1 and can be made density operators. They give 10 dierent full-state distributions and 6 dierent distributions summed over coin states. Nevertheless all these distributions follow the symmetry of the graph. It is important to note, that these distributions are not asymptotic states of some simple initial states (like a state starting at one vertex). It would be very dicult to produce such states and therefore this should be understood just as a visualisation of some building blocks that make up the asymptotic state. 31
32 Figure 5.2: Dierent asymptotic probability distributions of 1D walk that remain after introducing percolation. Figure 5.3: Schema of the second investigated graph. Symbols A and B just denote edges (3, 3 3, 4) and (1, 3 1, 4) D graph example Perfect graph Our second graph consists of two small two-dimensional square grids connected by three edges (5.3). Two of those edges uctuate between being simultaneously open and closed. This changes locally the dimensionality of the connection. In our investigation let us rst solve a QW on an unpercolated graph with only the middle connecting edge present. There are no step conditions, we just have to nd eigenstates of the evolution operator. We will use the same coin C c at all vertices and the reecting boundaries settings. It corresponds to a situation, where there are permanently closed edges pointing out of the graph. Due to the fact, that the graph we are examining is not homogeneous, there is no obvious simplication for nding eigenstates of the evolution operator U. As the graph has 18 vertices each corresponding to a 4-dimensional subspace, we have in total the operator U acting on a 64-dimensional Hilbert space. Our QW is fully dened when we choose the coin. Let us follow [7] and examine the Hadamard coin (C H ), the Grover coin(c G ) and the Fourier (C F ) coin: 32
33 C H = 1 2 C F = i 1 i i 1 i, C G = When we investigate the eigenstates the symmetry of the graph and the whole walk should be conserved. It is obvious in cases of one-dimensional subspaces of eigenstates corresponding to one eigenvalue. Showing this for example for eigenvalue λ = 1 (large degeneracy for all three coins) would require nding convenient bases instead of the one given by the numerical solution. That appears to be rather dicult because of possible sign ips in both directions associated with the symmetrical reection. We will not discuss this question further in this work., Percolated graph Let us now examine the QW on the graph shown in the gure 5.3 with the two percolated edges (dashed lines). We have two edges determining the step conditions. In particular the interesting directions are φ 1,3,R with φ 1,4,L and φ 3,3,R with φ 3,4,L. We will use the setting where both these edges are closed or open simultaneously. Therefore we again have just two step operators to examine. Here again in the notation of the preceding chapter we have: K = E \ {(1, 3 1, 4), (3, 3 3, 4)}, L 1 = {(1, 3 1, 4), (3, 3 3, 4)}, L 2 =, M =. Let us once more repeat the general result for the step condition. The attractors must full: X a,d b,e = Xa,d b e,ẽ and X b,e a,d = Xb e,ẽ a,d for all (a, a d) K M and (b, b e) L 1 L 2 and further X a,d b,e = Xa d,d b e,ẽ for all (a, a d) L 1 and (b, b e) L 1 or (a, a d) L 2 and (b, b e) L 2 and X a,d b e,ẽ = Xa d,d b,e for all (a, a d) L 1 and (b, b e) L 2 or (a, a d) L 2 and (b, b e) L 1. 33
34 Figure 5.4: Some example probability distributions for 2D percolated walk with the Hadamard coin. In our particular case that is X a,d 1,3,R = Xa,d 1,4,L, X a,d 3,3,R = Xa,d 3,4,L, X1,3,R a,d X3,3,R a,d = X 1,4,L a,d, = X 3,4,L a,d for all (a, a d) K and further X 1,3,R 1,3,R = X1,4,L 1,4,L, X 3,3,R 3,3,R = X3,4,L 3,4,L, X 1,3,R 3,3,R = X1,4,L 3,4,L, X 3,3,R 1,3,R = X3,4,L 1,4,L, X1,3,R 1,4,L = X1,4,L 1,3,R, X3,3,R 3,4,L = X3,4,L 3,3,R, X1,3,R 3,4,L = X1,4,L 3,3,R, X3,3,R 1,4,L = X3,4,L 1,3,R. Due to the fact that here we have more than one-dimensional subspaces, we cannot apply conditions directly on found states and we have to consider linear combinations within particular eigenvalue subspaces. Hadamard coin If we use the Hadamard coin, there are in total 36 dierent eigenvalues of the evolution operator U, and 544 "attractor eigenvalues" for the walk on the perfect graph. For the perfect walk the total degeneracy of the eigenvalue 1 is 280. After introducing the percolation only 96 eigenvalues remain corresponding in total to 1602 attractors. The most of them correspond to eigenvalue 1 and therefore are candidates for proper density operators. All 150 attractors corresponding to 1 can be made density operators (Hermitian, trace equal to one, attractor) and give rise to a lot of non-uniform non-symmetrical distributions (even when summed in vertices). 34
35 Grover coin If we use the Grover coin, there are in total 22 dierent eigenvalues of the evolution operator U (signicantly bigger degeneracy of eigenvalue 1 than in the case of the Hadamard coin), and 222 "attractor eigenvalues" for the walk on the perfect graph. For the perfect walk the total degeneracy of the eigenvalue 1 is 996. After introducing the percolation only 52 eigenvalues remain corresponding in total to 2116 attractors. The most of them correspond to eigenvalue 1 and therefore are candidates for proper density operators. Unfortunately I was not able to construct proper density matrices from those states. The conditions for hermicity produces too large system of equations due to 808 states in the linear combination (about 3 million equations for 808 variables). The combination of my method and my computer was not capable of such a computation. Nevertheless it can be presumed that there will again be states with non-uniform probability distributions. Maybe better method or longer computation time will solve this in the future. Fourier coin If we use the Fourier coin, all 72 eigenvalues of the evolution operator U are dierent (no degeneracy), and there are in total 4464 "attractor eigenvalues" for the walk on the perfect graph. For the perfect walk the total degeneracy of the eigenvalue 1 is just 72 (minimum constructed as λλ for all 72 eigenvalues of U). After introducing the percolation only the eigenvalue 1 remains corresponding to just 2 attractors. Those can be both made proper density matrices both giving a uniform (full state - not summed in vertices) probability distribution. The only dierence is in anti-diagonal terms. 35
36 Conclusion This work has two goals. One is to give some introduction to the elds of random and quantum walks and percolation and also present some previous work on spreading of a percolated quantum walk on an innite lattice. The other part deals with asymptotic evolution of quantum walks on nite percolated graphs. Here I have examined two particular nite graphs representing 1D and 2D walks. I have calculated possible asymptotic states for perfect graphs and for partially percolated graphs (graphs consist of two parts connected by percolated edges). In order to do these calculations I had to examine the step condition for those problems. I consider the general result for the step condition for comparing two step operators to be the main analytical result of my work. It can now be easily used for investigation of various similar graphs. The two specic example graphs presented here were chosen to represent 1D and 2D walks and in particular the exact form of the percolation of the later graph is supposed to represent a dimensionality change of the connection. This work is just a rst step in investigating this phenomenon. For now we only have asymptotic states (the simplest problem we may address) for a few choices of coins in two particular graphs. It is apparent that the coin choice has a fundamental inuence on the possible asymptotic states, therefore it is necessary to explore more coins and nd some general behaviour that is independent of their choice. If we really want to focus on the dimensionality changes, we should also vary the graphs and percolation settings. Further it would be desirable to solve larger graphs to eliminate the inuence of the boundary conditions. I must admit that using my current methods without further optimization I am not able to solve much larger walks than is the 2D case presented here. Nevertheless some modication can surely be done especially if one would be interested in just some particular property of the asymptotic evolution and some general analytical results and uses of some symmetry or homogeneity may help. 36
37 Literature [1] KESTEN, H. What is percolation. Notices of the AMS. May 2006, 53/5, s [2] KIRKPATRICK, S. Percolation and Conduction. Reviews of Modern Physics. (1973), 45, s [3] BOLLOBÁS, B. and RIORDAN, O. Percolation. Cambridge University Press, New York, [4] LEUNG, G., KNOTT, P., BAILEY, J. and KENDON, V. Coined quantum walks on percolation graphs. New Journal of Physics. (2010), [5] NOVOTNÝ, J., ALBER, G., and JEX, I. Asymptotic evolution of Random Unitary Operations Central Euro. J. Phys. (2010) [6] KOLLÁR, B., KISS, T., NOVOTNÝ, J. and JEX, I. Asymptotic dynamics of coined quantum walks on percolation graphs. Physical Review Letters. (2012), [7] KOLLÁR, B., KISS, T., NOVOTNÝ, J. and JEX, I. Percolation induced symmetry breaking in 2D quantum walks: exact asymptotic solutions Unpublished. [8] GEBELE, T. Site percolation threshold for square lattice. Journal of Physics A. (1984),
Gymnázium, Brno, Slovanské nám. 7 WORKBOOK. Mathematics. Teacher: Student:
 WORKBOOK Subject: Teacher: Student: Mathematics.... School year:../ Conic section The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.
WORKBOOK Subject: Teacher: Student: Mathematics.... School year:../ Conic section The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
WORKSHEET 1: LINEAR EQUATION 1
 WORKSHEET 1: LINEAR EQUATION 1 1. Write down the arithmetical problem according the dictation: 2. Translate the English words, you can use a dictionary: equations to solve solve inverse operation variable
WORKSHEET 1: LINEAR EQUATION 1 1. Write down the arithmetical problem according the dictation: 2. Translate the English words, you can use a dictionary: equations to solve solve inverse operation variable
Transportation Problem
 Transportation Problem ١ C H A P T E R 7 Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply s i ) to n
Transportation Problem ١ C H A P T E R 7 Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply s i ) to n
VY_32_INOVACE_06_Předpřítomný čas_03. Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace
 VY_32_INOVACE_06_Předpřítomný čas_03 Autor: Růžena Krupičková Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu: Zkvalitnění ICT ve slušovské škole Číslo projektu: CZ.1.07/1.4.00/21.2400
VY_32_INOVACE_06_Předpřítomný čas_03 Autor: Růžena Krupičková Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu: Zkvalitnění ICT ve slušovské škole Číslo projektu: CZ.1.07/1.4.00/21.2400
Compression of a Dictionary
 Compression of a Dictionary Jan Lánský, Michal Žemlička zizelevak@matfyz.cz michal.zemlicka@mff.cuni.cz Dept. of Software Engineering Faculty of Mathematics and Physics Charles University Synopsis Introduction
Compression of a Dictionary Jan Lánský, Michal Žemlička zizelevak@matfyz.cz michal.zemlicka@mff.cuni.cz Dept. of Software Engineering Faculty of Mathematics and Physics Charles University Synopsis Introduction
DC circuits with a single source
 Název projektu: utomatizace výrobních procesů ve strojírenství a řemeslech egistrační číslo: Z..07/..0/0.008 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 09 Tento projekt je spolufinancován
Název projektu: utomatizace výrobních procesů ve strojírenství a řemeslech egistrační číslo: Z..07/..0/0.008 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 09 Tento projekt je spolufinancován
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA
 GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
Litosil - application
 Litosil - application The series of Litosil is primarily determined for cut polished floors. The cut polished floors are supplied by some specialized firms which are fitted with the appropriate technical
Litosil - application The series of Litosil is primarily determined for cut polished floors. The cut polished floors are supplied by some specialized firms which are fitted with the appropriate technical
FIRE INVESTIGATION. Střední průmyslová škola Hranice. Mgr. Radka Vorlová. 19_Fire investigation CZ.1.07/1.5.00/
 FIRE INVESTIGATION Střední průmyslová škola Hranice Mgr. Radka Vorlová 19_Fire investigation CZ.1.07/1.5.00/34.0608 Výukový materiál Číslo projektu: CZ.1.07/1.5.00/21.34.0608 Šablona: III/2 Inovace a zkvalitnění
FIRE INVESTIGATION Střední průmyslová škola Hranice Mgr. Radka Vorlová 19_Fire investigation CZ.1.07/1.5.00/34.0608 Výukový materiál Číslo projektu: CZ.1.07/1.5.00/21.34.0608 Šablona: III/2 Inovace a zkvalitnění
EU peníze středním školám digitální učební materiál
 EU peníze středním školám digitální učební materiál Číslo projektu: Číslo a název šablony klíčové aktivity: Tematická oblast, název DUMu: Autor: CZ.1.07/1.5.00/34.0515 III/2 Inovace a zkvalitnění výuky
EU peníze středním školám digitální učební materiál Číslo projektu: Číslo a název šablony klíčové aktivity: Tematická oblast, název DUMu: Autor: CZ.1.07/1.5.00/34.0515 III/2 Inovace a zkvalitnění výuky
USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING
 USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING Eva Minaříková Institute for Research in School Education, Faculty of Education, Masaryk University Structure of the presentation What can we as teachers
USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING Eva Minaříková Institute for Research in School Education, Faculty of Education, Masaryk University Structure of the presentation What can we as teachers
Gymnázium, Brno, Slovanské nám. 7, SCHEME OF WORK Mathematics SCHEME OF WORK. cz
 SCHEME OF WORK Subject: Mathematics Year: first grade, 1.X School year:../ List of topisc # Topics Time period Introduction, repetition September 1. Number sets October 2. Rigtht-angled triangle October,
SCHEME OF WORK Subject: Mathematics Year: first grade, 1.X School year:../ List of topisc # Topics Time period Introduction, repetition September 1. Number sets October 2. Rigtht-angled triangle October,
CZ.1.07/1.5.00/
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Aplikace matematiky. Dana Lauerová A note to the theory of periodic solutions of a parabolic equation
 Aplikace matematiky Dana Lauerová A note to the theory of periodic solutions of a parabolic equation Aplikace matematiky, Vol. 25 (1980), No. 6, 457--460 Persistent URL: http://dml.cz/dmlcz/103885 Terms
Aplikace matematiky Dana Lauerová A note to the theory of periodic solutions of a parabolic equation Aplikace matematiky, Vol. 25 (1980), No. 6, 457--460 Persistent URL: http://dml.cz/dmlcz/103885 Terms
Základy teorie front III
 Základy teorie front III Aplikace Poissonova procesu v teorii front II Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta
Základy teorie front III Aplikace Poissonova procesu v teorii front II Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Využití hybridní metody vícekriteriálního rozhodování za nejistoty. Michal Koláček, Markéta Matulová
 Využití hybridní metody vícekriteriálního rozhodování za nejistoty Michal Koláček, Markéta Matulová Outline Multiple criteria decision making Classification of MCDM methods TOPSIS method Fuzzy extension
Využití hybridní metody vícekriteriálního rozhodování za nejistoty Michal Koláček, Markéta Matulová Outline Multiple criteria decision making Classification of MCDM methods TOPSIS method Fuzzy extension
Search and state transfer by means of quantum walk. Vyhledávání a přenos stavu pomocí kvantové procházky
 Czech Technical University in Prague Faculty of uclear Sciences and Physical Engineering Search and state transfer by means of quantum walk Vyhledávání a přenos stavu pomocí kvantové procházky Master s
Czech Technical University in Prague Faculty of uclear Sciences and Physical Engineering Search and state transfer by means of quantum walk Vyhledávání a přenos stavu pomocí kvantové procházky Master s
Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost
 Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost Registrační číslo: CZ.1.07/1. 5.00/34.0084 Šablona: II/2 Inovace a zkvalitnění výuky cizích jazyků na středních
Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost Registrační číslo: CZ.1.07/1. 5.00/34.0084 Šablona: II/2 Inovace a zkvalitnění výuky cizích jazyků na středních
Czech Republic. EDUCAnet. Střední odborná škola Pardubice, s.r.o.
 Czech Republic EDUCAnet Střední odborná škola Pardubice, s.r.o. ACCESS TO MODERN TECHNOLOGIES Do modern technologies influence our behavior? Of course in positive and negative way as well Modern technologies
Czech Republic EDUCAnet Střední odborná škola Pardubice, s.r.o. ACCESS TO MODERN TECHNOLOGIES Do modern technologies influence our behavior? Of course in positive and negative way as well Modern technologies
Projekt: ŠKOLA RADOSTI, ŠKOLA KVALITY Registrační číslo projektu: CZ.1.07/1.4.00/21.3688 EU PENÍZE ŠKOLÁM
 ZÁKLADNÍ ŠKOLA OLOMOUC příspěvková organizace MOZARTOVA 48, 779 00 OLOMOUC tel.: 585 427 142, 775 116 442; fax: 585 422 713 email: kundrum@centrum.cz; www.zs-mozartova.cz Projekt: ŠKOLA RADOSTI, ŠKOLA
ZÁKLADNÍ ŠKOLA OLOMOUC příspěvková organizace MOZARTOVA 48, 779 00 OLOMOUC tel.: 585 427 142, 775 116 442; fax: 585 422 713 email: kundrum@centrum.cz; www.zs-mozartova.cz Projekt: ŠKOLA RADOSTI, ŠKOLA
The Over-Head Cam (OHC) Valve Train Computer Model
 The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
Introduction to MS Dynamics NAV
 Introduction to MS Dynamics NAV (Item Charges) Ing.J.Skorkovský,CSc. MASARYK UNIVERSITY BRNO, Czech Republic Faculty of economics and business administration Department of corporate economy Item Charges
Introduction to MS Dynamics NAV (Item Charges) Ing.J.Skorkovský,CSc. MASARYK UNIVERSITY BRNO, Czech Republic Faculty of economics and business administration Department of corporate economy Item Charges
STUDY EDITS FOR BETTER TRANSPORT IN THE CENTRE OF NÁCHOD
 CZECH TECHNICAL UNIVERSITY IN PRAGUE Faculty of transportation sciences Title of project STUDY EDITS FOR BETTER TRANSPORT IN THE CENTRE OF NÁCHOD 2006 Petr Kumpošt Basic information about town Náchod Náchod
CZECH TECHNICAL UNIVERSITY IN PRAGUE Faculty of transportation sciences Title of project STUDY EDITS FOR BETTER TRANSPORT IN THE CENTRE OF NÁCHOD 2006 Petr Kumpošt Basic information about town Náchod Náchod
Database systems. Normal forms
 Database systems Normal forms An example of a bad model SSN Surnam OfficeNo City Street No ZIP Region President_of_ Region 1001 Novák 238 Liteň Hlavní 10 26727 Středočeský Rath 1001 Novák 238 Bystřice
Database systems Normal forms An example of a bad model SSN Surnam OfficeNo City Street No ZIP Region President_of_ Region 1001 Novák 238 Liteň Hlavní 10 26727 Středočeský Rath 1001 Novák 238 Bystřice
Instrukce: Cvičný test má celkem 3 části, čas určený pro tyto části je 20 minut. 1. Reading = 6 bodů 2. Use of English = 14 bodů 3.
 Vážení studenti, na následujících stranách si můžete otestovat svou znalost angličtiny a orientačně zjistit, kolik bodů za jazykové kompetence byste získali v přijímacím řízení. Maximální počet bodů je
Vážení studenti, na následujících stranách si můžete otestovat svou znalost angličtiny a orientačně zjistit, kolik bodů za jazykové kompetence byste získali v přijímacím řízení. Maximální počet bodů je
AIC ČESKÁ REPUBLIKA CZECH REPUBLIC
 ČESKÁ REPUBLIKA CZECH REPUBLIC ŘÍZENÍ LETOVÉHO PROVOZU ČR, s.p. Letecká informační služba AIR NAVIGATION SERVICES OF THE C.R. Aeronautical Information Service Navigační 787 252 61 Jeneč A 1/14 20 FEB +420
ČESKÁ REPUBLIKA CZECH REPUBLIC ŘÍZENÍ LETOVÉHO PROVOZU ČR, s.p. Letecká informační služba AIR NAVIGATION SERVICES OF THE C.R. Aeronautical Information Service Navigační 787 252 61 Jeneč A 1/14 20 FEB +420
Just write down your most recent and important education. Remember that sometimes less is more some people may be considered overqualified.
 CURRICULUM VITAE - EDUCATION Jindřich Bláha Výukový materiál zpracován v rámci projektu EU peníze školám Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Bc. Jindřich Bláha. Dostupné z Metodického
CURRICULUM VITAE - EDUCATION Jindřich Bláha Výukový materiál zpracován v rámci projektu EU peníze školám Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Bc. Jindřich Bláha. Dostupné z Metodického
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku
 Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
CZ.1.07/1.5.00/ Zefektivnění výuky prostřednictvím ICT technologií III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT
 Autor: Sylva Máčalová Tematický celek : Gramatika Cílová skupina : mírně pokročilý - pokročilý Anotace Materiál má podobu pracovního listu, který obsahuje cvičení, pomocí nichž si žáci procvičí rozdíly
Autor: Sylva Máčalová Tematický celek : Gramatika Cílová skupina : mírně pokročilý - pokročilý Anotace Materiál má podobu pracovního listu, který obsahuje cvičení, pomocí nichž si žáci procvičí rozdíly
Informace o písemných přijímacích zkouškách. Doktorské studijní programy Matematika
 Informace o písemných přijímacích zkouškách (úplné zadání zkušebních otázek či příkladů, které jsou součástí přijímací zkoušky nebo její části, a u otázek s výběrem odpovědi správné řešení) Doktorské studijní
Informace o písemných přijímacích zkouškách (úplné zadání zkušebních otázek či příkladů, které jsou součástí přijímací zkoušky nebo její části, a u otázek s výběrem odpovědi správné řešení) Doktorské studijní
PC/104, PC/104-Plus. 196 ept GmbH I Tel. +49 (0) / I Fax +49 (0) / I I
 E L E C T R O N I C C O N N E C T O R S 196 ept GmbH I Tel. +49 (0) 88 61 / 25 01 0 I Fax +49 (0) 88 61 / 55 07 I E-Mail sales@ept.de I www.ept.de Contents Introduction 198 Overview 199 The Standard 200
E L E C T R O N I C C O N N E C T O R S 196 ept GmbH I Tel. +49 (0) 88 61 / 25 01 0 I Fax +49 (0) 88 61 / 55 07 I E-Mail sales@ept.de I www.ept.de Contents Introduction 198 Overview 199 The Standard 200
Project 3 Unit 7B Kelly s problem
 VY_32_INOVACE_94 Project 3 Unit 7B Kelly s problem Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 8. P3 U7B důvod náladový nepřátelský rada někomu zavolat bazar
VY_32_INOVACE_94 Project 3 Unit 7B Kelly s problem Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 8. P3 U7B důvod náladový nepřátelský rada někomu zavolat bazar
Škola: Střední škola obchodní, České Budějovice, Husova 9. Inovace a zkvalitnění výuky prostřednictvím ICT
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
SPECIAL THEORY OF RELATIVITY
 SPECIAL THEORY OF RELATIVITY 1. Basi information author Albert Einstein phenomena obsered when TWO frames of referene moe relatie to eah other with speed lose to the speed of light 1905 - speial theory
SPECIAL THEORY OF RELATIVITY 1. Basi information author Albert Einstein phenomena obsered when TWO frames of referene moe relatie to eah other with speed lose to the speed of light 1905 - speial theory
Angličtina v matematických softwarech 2 Vypracovala: Mgr. Bronislava Kreuzingerová
 Angličtina v matematických softwarech 2 Vypracovala: Mgr. Bronislava Kreuzingerová Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace
Angličtina v matematických softwarech 2 Vypracovala: Mgr. Bronislava Kreuzingerová Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace
CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA
 CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA &KDSWHUSUHVHQWVWKHGHVLJQDQGIDEULFDW LRQRIPRGLILHG0LQNRZVNLIUDFWDODQWHQQD IRUZLUHOHVVFRPPXQLFDWLRQ7KHVLPXODWHG DQGPHDVXUHGUHVXOWVRIWKLVDQWHQQDDUH DOVRSUHVHQWHG
CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA &KDSWHUSUHVHQWVWKHGHVLJQDQGIDEULFDW LRQRIPRGLILHG0LQNRZVNLIUDFWDODQWHQQD IRUZLUHOHVVFRPPXQLFDWLRQ7KHVLPXODWHG DQGPHDVXUHGUHVXOWVRIWKLVDQWHQQDDUH DOVRSUHVHQWHG
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky
 Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: Education Označení materiálu: VY_32_INOVACE_MAT27 Datum vytvoření: 10.10.2013
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: Education Označení materiálu: VY_32_INOVACE_MAT27 Datum vytvoření: 10.10.2013
PITSTOP VY_22_INOVACE_26
 PITSTOP VY_22_INOVACE_26 Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 9. PITSTOP 1/ Try to complete the missing words. Then listen and check your ideas. Eight
PITSTOP VY_22_INOVACE_26 Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 9. PITSTOP 1/ Try to complete the missing words. Then listen and check your ideas. Eight
Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční
 Příloha I Seznam tabulek Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční odměny pro rozhodčí platný od roku
Příloha I Seznam tabulek Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční odměny pro rozhodčí platný od roku
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Výukový materiál zpracovaný v rámci projektu EU peníze do škol. illness, a text
 Výukový materiál zpracovaný v rámci projektu EU peníze do škol ZŠ Litoměřice, Ladova Ladova 5 412 01 Litoměřice www.zsladovaltm.cz vedeni@zsladovaltm.cz Pořadové číslo projektu: CZ.1.07/1.4.00/21.0948
Výukový materiál zpracovaný v rámci projektu EU peníze do škol ZŠ Litoměřice, Ladova Ladova 5 412 01 Litoměřice www.zsladovaltm.cz vedeni@zsladovaltm.cz Pořadové číslo projektu: CZ.1.07/1.4.00/21.0948
Vánoční sety Christmas sets
 Energy news 7 Inovace Innovations 1 Vánoční sety Christmas sets Na jaře tohoto roku jste byli informováni o připravované akci pro předvánoční období sety Pentagramu koncentrátů a Pentagramu krémů ve speciálních
Energy news 7 Inovace Innovations 1 Vánoční sety Christmas sets Na jaře tohoto roku jste byli informováni o připravované akci pro předvánoční období sety Pentagramu koncentrátů a Pentagramu krémů ve speciálních
CZ.1.07/1.5.00/34.0527
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
ROLZ-2. Portable AV/Conference Center. Assembly Instructions
 1 ROLZ-2 Portable AV/Conference Center Assembly Instructions Rolz-2 Portable AV/Conference Center Part Drawing Description Qty Part Drawing Description Qty Hardware List A 1 ½ Flat Head Screw 2 EA P-1
1 ROLZ-2 Portable AV/Conference Center Assembly Instructions Rolz-2 Portable AV/Conference Center Part Drawing Description Qty Part Drawing Description Qty Hardware List A 1 ½ Flat Head Screw 2 EA P-1
Theme 6. Money Grammar: word order; questions
 Theme 6 Money Grammar: word order; questions Čas potřebný k prostudování učiva lekce: 8 vyučujících hodin Čas potřebný k ověření učiva lekce: 45 minut KLÍNSKÝ P., MÜNCH O., CHROMÁ D., Ekonomika, EDUKO
Theme 6 Money Grammar: word order; questions Čas potřebný k prostudování učiva lekce: 8 vyučujících hodin Čas potřebný k ověření učiva lekce: 45 minut KLÍNSKÝ P., MÜNCH O., CHROMÁ D., Ekonomika, EDUKO
CHAIN TRANSMISSIONS AND WHEELS
 Second School Year CHAIN TRANSMISSIONS AND WHEELS A. Chain transmissions We can use chain transmissions for the transfer and change of rotation motion and the torsional moment. They transfer forces from
Second School Year CHAIN TRANSMISSIONS AND WHEELS A. Chain transmissions We can use chain transmissions for the transfer and change of rotation motion and the torsional moment. They transfer forces from
User manual SŘHV Online WEB interface for CUSTOMERS June 2017 version 14 VÍTKOVICE STEEL, a.s. vitkovicesteel.com
 1/ 11 User manual SŘHV Online WEB interface for CUSTOMERS June 2017 version 14 2/ 11 Contents 1. MINIMUM SYSTEM REQUIREMENTS... 3 2. SŘHV ON-LINE WEB INTERFACE... 4 3. LOGGING INTO SŘHV... 4 4. CONTRACT
1/ 11 User manual SŘHV Online WEB interface for CUSTOMERS June 2017 version 14 2/ 11 Contents 1. MINIMUM SYSTEM REQUIREMENTS... 3 2. SŘHV ON-LINE WEB INTERFACE... 4 3. LOGGING INTO SŘHV... 4 4. CONTRACT
VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O.
 VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O. Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová práce 2013 Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová
VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O. Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová práce 2013 Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová
By David Cameron VE7LTD
 By David Cameron VE7LTD Introduction to Speaker RF Cavity Filter Types Why Does a Repeater Need a Duplexer Types of Duplexers Hybrid Pass/Reject Duplexer Detail Finding a Duplexer for Ham Use Questions?
By David Cameron VE7LTD Introduction to Speaker RF Cavity Filter Types Why Does a Repeater Need a Duplexer Types of Duplexers Hybrid Pass/Reject Duplexer Detail Finding a Duplexer for Ham Use Questions?
Chapter 7: Process Synchronization
 Chapter 7: Process Synchronization Background The Critical-Section Problem Synchronization Hardware Semaphores Classical Problems of Synchronization Critical Regions Monitors Synchronization in Solaris
Chapter 7: Process Synchronization Background The Critical-Section Problem Synchronization Hardware Semaphores Classical Problems of Synchronization Critical Regions Monitors Synchronization in Solaris
Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám
 VY_22_INOVACE_AJOP40764ČER Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: Název projektu: Číslo šablony: CZ.1.07/1.5.00/34.0883 Rozvoj vzdělanosti II/2 Datum vytvoření:
VY_22_INOVACE_AJOP40764ČER Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: Název projektu: Číslo šablony: CZ.1.07/1.5.00/34.0883 Rozvoj vzdělanosti II/2 Datum vytvoření:
On large rigid sets of monounary algebras. D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia
 On large rigid sets of monounary algebras D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia coauthor G. Czédli, University of Szeged, Hungary The 54st Summer School on General Algebra
On large rigid sets of monounary algebras D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia coauthor G. Czédli, University of Szeged, Hungary The 54st Summer School on General Algebra
EXACT DS OFFICE. The best lens for office work
 EXACT DS The best lens for office work EXACT DS When Your Glasses Are Not Enough Lenses with only a reading area provide clear vision of objects located close up, while progressive lenses only provide
EXACT DS The best lens for office work EXACT DS When Your Glasses Are Not Enough Lenses with only a reading area provide clear vision of objects located close up, while progressive lenses only provide
Klepnutím lze upravit styl předlohy. nadpisů. nadpisů.
 1/ 13 Klepnutím lze upravit styl předlohy Klepnutím lze upravit styl předlohy www.splab.cz Soft biometric traits in de identification process Hair Jiri Prinosil Jiri Mekyska Zdenek Smekal 2/ 13 Klepnutím
1/ 13 Klepnutím lze upravit styl předlohy Klepnutím lze upravit styl předlohy www.splab.cz Soft biometric traits in de identification process Hair Jiri Prinosil Jiri Mekyska Zdenek Smekal 2/ 13 Klepnutím
Jméno autora: Mgr. Alena Chrastinová Datum vytvoření: Číslo DUMu: VY_32_INOVACE_O7_AJ
 Jméno autora: Mgr. Alena Chrastinová Datum vytvoření: 24.07.2012 Číslo DUMu: VY_32_INOVACE_O7_AJ Ročník: IV. Anglický jazyk Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: cizí jazyk anglický
Jméno autora: Mgr. Alena Chrastinová Datum vytvoření: 24.07.2012 Číslo DUMu: VY_32_INOVACE_O7_AJ Ročník: IV. Anglický jazyk Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: cizí jazyk anglický
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Čtvrtý Pentagram The fourth Pentagram
 Energy News 4 1 Čtvrtý Pentagram The fourth Pentagram Na jaře příštího roku nabídneme našim zákazníkům již čtvrtý Pentagram a to Pentagram šamponů. K zavedení tohoto Pentagramu jsme se rozhodli na základě
Energy News 4 1 Čtvrtý Pentagram The fourth Pentagram Na jaře příštího roku nabídneme našim zákazníkům již čtvrtý Pentagram a to Pentagram šamponů. K zavedení tohoto Pentagramu jsme se rozhodli na základě
Aktivita CLIL Chemie III.
 Aktivita CLIL Chemie III. Škola: Gymnázium Bystřice nad Pernštejnem Jméno vyučujícího: Mgr. Marie Dřínovská Název aktivity: Balancing equations vyčíslování chemických rovnic Předmět: Chemie Ročník, třída:
Aktivita CLIL Chemie III. Škola: Gymnázium Bystřice nad Pernštejnem Jméno vyučujícího: Mgr. Marie Dřínovská Název aktivity: Balancing equations vyčíslování chemických rovnic Předmět: Chemie Ročník, třída:
PAINTING SCHEMES CATALOGUE 2012
 Evektor-Aerotechnik a.s., Letecká č.p. 84, 686 04 Kunovice, Czech Republic Phone: +40 57 57 Fax: +40 57 57 90 E-mail: sales@evektor.cz Web site: www.evektoraircraft.com PAINTING SCHEMES CATALOGUE 0 Painting
Evektor-Aerotechnik a.s., Letecká č.p. 84, 686 04 Kunovice, Czech Republic Phone: +40 57 57 Fax: +40 57 57 90 E-mail: sales@evektor.cz Web site: www.evektoraircraft.com PAINTING SCHEMES CATALOGUE 0 Painting
Dynamic Signals. Ananda V. Mysore SJSU
 Dynamic Signals Ananda V. Mysore SJSU Static vs. Dynamic Signals In principle, all signals are dynamic; they do not have a perfectly constant value over time. Static signals are those for which changes
Dynamic Signals Ananda V. Mysore SJSU Static vs. Dynamic Signals In principle, all signals are dynamic; they do not have a perfectly constant value over time. Static signals are those for which changes
Číslo materiálu: VY 32 INOVACE 29/18. Číslo projektu: CZ.1.07/1.4.00/
 Číslo materiálu: Název materiálu: Ironic Číslo projektu: CZ.1.07/1.4.00/21.1486 Zpracoval: Mgr. Petra Březinová IRONIC 1. Listen to the song Ironic from the singer Alanis Morissette. For the first time
Číslo materiálu: Název materiálu: Ironic Číslo projektu: CZ.1.07/1.4.00/21.1486 Zpracoval: Mgr. Petra Březinová IRONIC 1. Listen to the song Ironic from the singer Alanis Morissette. For the first time
DATA SHEET. BC516 PNP Darlington transistor. technický list DISCRETE SEMICONDUCTORS Apr 23. Product specification Supersedes data of 1997 Apr 16
 zákaznická linka: 840 50 60 70 DISCRETE SEMICONDUCTORS DATA SHEET book, halfpage M3D186 Supersedes data of 1997 Apr 16 1999 Apr 23 str 1 Dodavatel: GM electronic, spol. s r.o., Křižíkova 77, 186 00 Praha
zákaznická linka: 840 50 60 70 DISCRETE SEMICONDUCTORS DATA SHEET book, halfpage M3D186 Supersedes data of 1997 Apr 16 1999 Apr 23 str 1 Dodavatel: GM electronic, spol. s r.o., Křižíkova 77, 186 00 Praha
VY_22_INOVACE_číslo přílohy 1_AJ_6A_29. Úvodní část seznámení s cílem hodiny pohádka The Ugly Ducklings
 VY_22_INOVACE_číslo přílohy 1_AJ_6A_29 Úvodní část seznámení s cílem hodiny pohádka The Ugly Ducklings Hlavní část žák čte text s porozuměním, s textem pracuje, odpovídá na otázky, které se k textu vztahují,
VY_22_INOVACE_číslo přílohy 1_AJ_6A_29 Úvodní část seznámení s cílem hodiny pohádka The Ugly Ducklings Hlavní část žák čte text s porozuměním, s textem pracuje, odpovídá na otázky, které se k textu vztahují,
Byznys a obchodní záležitosti
 - Úvod Dear Mr. President, Dear Mr. President, Velmi formální, příjemce má speciální titul či status, který musí být použit v místě jejich jména Dear Sir, Formální, příjemce muž, jméno neznámé Dear Madam,
- Úvod Dear Mr. President, Dear Mr. President, Velmi formální, příjemce má speciální titul či status, který musí být použit v místě jejich jména Dear Sir, Formální, příjemce muž, jméno neznámé Dear Madam,
A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients
 KYBERNETIKA VOLUME 8 (1972), NUMBER 6 A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients JAROSLAV KRAL In many applications (for example if the effect
KYBERNETIKA VOLUME 8 (1972), NUMBER 6 A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients JAROSLAV KRAL In many applications (for example if the effect
Configuration vs. Conformation. Configuration: Covalent bonds must be broken. Two kinds of isomers to consider
 Stereochemistry onfiguration vs. onformation onfiguration: ovalent bonds must be broken onformation: hanges do NT require breaking of covalent bonds onfiguration Two kinds of isomers to consider is/trans:
Stereochemistry onfiguration vs. onformation onfiguration: ovalent bonds must be broken onformation: hanges do NT require breaking of covalent bonds onfiguration Two kinds of isomers to consider is/trans:
SPECIFICATION FOR ALDER LED
 SPECIFICATION FOR ALDER LED MODEL:AS-D75xxyy-C2LZ-H1-E 1 / 13 Absolute Maximum Ratings (Ta = 25 C) Parameter Symbol Absolute maximum Rating Unit Peak Forward Current I FP 500 ma Forward Current(DC) IF
SPECIFICATION FOR ALDER LED MODEL:AS-D75xxyy-C2LZ-H1-E 1 / 13 Absolute Maximum Ratings (Ta = 25 C) Parameter Symbol Absolute maximum Rating Unit Peak Forward Current I FP 500 ma Forward Current(DC) IF
CZ.1.07/1.5.00/
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Mikrokvadrotor: Návrh,
 KONTAKT 2011 Mikrokvadrotor: Návrh, Modelování,, Identifikace a Řízení Autor: Jaromír r Dvořák k (md( md@unicode.cz) Vedoucí: : Zdeněk Hurák (hurak@fel.cvut.cz) Katedra řídicí techniky FEL ČVUT Praha 26.5.2011
KONTAKT 2011 Mikrokvadrotor: Návrh, Modelování,, Identifikace a Řízení Autor: Jaromír r Dvořák k (md( md@unicode.cz) Vedoucí: : Zdeněk Hurák (hurak@fel.cvut.cz) Katedra řídicí techniky FEL ČVUT Praha 26.5.2011
Číslo projektu: CZ.1.07/1.5.00/ Název projektu: Inovace a individualizace výuky
 Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: European Union Označení materiálu: VY_32_INOVACE_MAT 22 Datum vytvoření:
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: European Union Označení materiálu: VY_32_INOVACE_MAT 22 Datum vytvoření:
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Zelené potraviny v nových obalech Green foods in a new packaging
 Energy News1 1 Zelené potraviny v nových obalech Green foods in a new packaging Již v minulém roce jsme Vás informovali, že dojde k přebalení všech tří zelených potravin do nových papírových obalů, které
Energy News1 1 Zelené potraviny v nových obalech Green foods in a new packaging Již v minulém roce jsme Vás informovali, že dojde k přebalení všech tří zelených potravin do nových papírových obalů, které
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Škola: Střední škola obchodní, České Budějovice, Husova 9. Inovace a zkvalitnění výuky prostřednictvím ICT
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products
 Energy news2 1 Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products Doposud jste Energy znali jako výrobce a dodavatele humánních přírodních doplňků stravy a kosmetiky.
Energy news2 1 Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products Doposud jste Energy znali jako výrobce a dodavatele humánních přírodních doplňků stravy a kosmetiky.
Dynamic programming. Optimal binary search tree
 The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamic programming Optimal binary search tree Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The complexity
The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamic programming Optimal binary search tree Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The complexity
Next line show use of paragraf symbol. It should be kept with the following number. Jak může státní zástupce věc odložit zmiňuje 159a.
 1 Bad line breaks The follwing text has prepostions O and k at end of line which is incorrect according to Czech language typography standards: Mezi oblíbené dětské pohádky patří pohádky O Palečkovi, Alenka
1 Bad line breaks The follwing text has prepostions O and k at end of line which is incorrect according to Czech language typography standards: Mezi oblíbené dětské pohádky patří pohádky O Palečkovi, Alenka
http://www.zlinskedumy.cz
 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Výklad a cvičení z větné stavby, vy_32_inovace_ma_33_01
Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Výklad a cvičení z větné stavby, vy_32_inovace_ma_33_01
ENGLISH FOR ACADEMIC PURPOSES
 Slezská univerzita v Opavě Fakulta veřejných politik v Opavě ENGLISH FOR ACADEMIC PURPOSES Distanční studijní opora Veronika Portešová Opava 2012 Projekt č. CZ.1.07/2.2.00/15.0178 Inovace studijního programu
Slezská univerzita v Opavě Fakulta veřejných politik v Opavě ENGLISH FOR ACADEMIC PURPOSES Distanční studijní opora Veronika Portešová Opava 2012 Projekt č. CZ.1.07/2.2.00/15.0178 Inovace studijního programu
7.VY_32_INOVACE_AJ_UMB7, Tázací dovětky.notebook. September 08, 2013
 1 2 3 SPECIAL CASES: 1. After Let s... the question tag is... shall we? 2. After the imperative (Do.../Don t... the tag is usually... will you? 3. Note that we say... aren t I? (=am I not?) instead of
1 2 3 SPECIAL CASES: 1. After Let s... the question tag is... shall we? 2. After the imperative (Do.../Don t... the tag is usually... will you? 3. Note that we say... aren t I? (=am I not?) instead of
Zubní pasty v pozměněném složení a novém designu
 Energy news4 Energy News 04/2010 Inovace 1 Zubní pasty v pozměněném složení a novém designu Od října tohoto roku se začnete setkávat s našimi zubními pastami v pozměněném složení a ve zcela novém designu.
Energy news4 Energy News 04/2010 Inovace 1 Zubní pasty v pozměněném složení a novém designu Od října tohoto roku se začnete setkávat s našimi zubními pastami v pozměněném složení a ve zcela novém designu.
SEZNAM PŘÍLOH. Příloha 1 Dotazník Tartu, Estonsko (anglická verze) Příloha 2 Dotazník Praha, ČR (česká verze)... 91
 SEZNAM PŘÍLOH Příloha 1 Dotazník Tartu, Estonsko (anglická verze)... 90 Příloha 2 Dotazník Praha, ČR (česká verze)... 91 Příloha 3 Emailové dotazy, vedení fakult TÜ... 92 Příloha 4 Emailové dotazy na vedení
SEZNAM PŘÍLOH Příloha 1 Dotazník Tartu, Estonsko (anglická verze)... 90 Příloha 2 Dotazník Praha, ČR (česká verze)... 91 Příloha 3 Emailové dotazy, vedení fakult TÜ... 92 Příloha 4 Emailové dotazy na vedení
18.VY_32_INOVACE_AJ_UMB18, Frázová slovesa.notebook. September 09, 2013
 1 (Click on the text to move to the section) Worksheet Methodology Sources 2 Decide which words are considered prepositions (předložky) and which are particles (částice) Source: SWAN, Michael a Catharine
1 (Click on the text to move to the section) Worksheet Methodology Sources 2 Decide which words are considered prepositions (předložky) and which are particles (částice) Source: SWAN, Michael a Catharine
ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ
 ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ MGR. VLADIMÍR BRADÁČ ROZVOJ KOMPETENCÍ MANAGEMENTU A PRACOVNÍKŮ VŠ MSK (S PODPOROU ICT) PROJEKT OP VK 2.2: CZ.1.07/2.2.00/15.0176 OSTRAVA 2012 Tento projekt je
ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ MGR. VLADIMÍR BRADÁČ ROZVOJ KOMPETENCÍ MANAGEMENTU A PRACOVNÍKŮ VŠ MSK (S PODPOROU ICT) PROJEKT OP VK 2.2: CZ.1.07/2.2.00/15.0176 OSTRAVA 2012 Tento projekt je
CZ.1.07/1.5.00/34.0527
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
VY_22_INOVACE_60 MODAL VERBS CAN, MUST
 VY_22_INOVACE_60 MODAL VERBS CAN, MUST Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 9. MODAL VERBS CAN, MUST, SHOULD 1/ Connect the verbs to their future forms.
VY_22_INOVACE_60 MODAL VERBS CAN, MUST Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 9. MODAL VERBS CAN, MUST, SHOULD 1/ Connect the verbs to their future forms.
11/ Podmínkové věty. ( 1st Conditional) VY_32_INOVACE_AJ_UMA11,Podmínkové věty (1st Conditional).notebook. January 28, 2014
 Úroveň jazyka Pre-Intermediate 11/ Podmínkové věty ( 1st Conditional) Citace a zdroje Zpracovala: Mgr.Alena Závorová 1 Podmínkové věty typu 1 ( First Conditional ) Vedlejší věty podmínkové vyjadřují podmínku,
Úroveň jazyka Pre-Intermediate 11/ Podmínkové věty ( 1st Conditional) Citace a zdroje Zpracovala: Mgr.Alena Závorová 1 Podmínkové věty typu 1 ( First Conditional ) Vedlejší věty podmínkové vyjadřují podmínku,
POSLECH. M e t o d i c k é p o z n á m k y k z á k l a d o v é m u t e x t u :
 POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Mgr. Martin Zicháček aj9-kap-zic-pos-07 Z á k l a d o v ý t e x t : Margaret: Hi Eric. Eric: Oh, hi Margaret. How are you doing? Margaret:
POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Mgr. Martin Zicháček aj9-kap-zic-pos-07 Z á k l a d o v ý t e x t : Margaret: Hi Eric. Eric: Oh, hi Margaret. How are you doing? Margaret:
6.867 Machine Learning
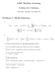 . Machine Learning Problem Set Solutions Due date: Monday November Problem : Model Selection. P (y,..., y n x,..., x n, PST) = = K [ [,] K [ K p n+ i i ( p i ) n i dpi ] = p n+ i i K ( p i ) n i n + i!
. Machine Learning Problem Set Solutions Due date: Monday November Problem : Model Selection. P (y,..., y n x,..., x n, PST) = = K [ [,] K [ K p n+ i i ( p i ) n i dpi ] = p n+ i i K ( p i ) n i n + i!
VŠEOBECNÁ TÉMATA PRO SOU Mgr. Dita Hejlová
 VŠEOBECNÁ TÉMATA PRO SOU Mgr. Dita Hejlová VZDĚLÁVÁNÍ V ČR VY_32_INOVACE_AH_3_03 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět
VŠEOBECNÁ TÉMATA PRO SOU Mgr. Dita Hejlová VZDĚLÁVÁNÍ V ČR VY_32_INOVACE_AH_3_03 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět
The Czech education system, school
 The Czech education system, school Pracovní list Číslo projektu Číslo materiálu Autor Tematický celek CZ.1.07/1.5.00/34.0266 VY_32_INOVACE_ZeE_AJ_4OA,E,L_10 Mgr. Eva Zemanová Anglický jazyk využívání on-line
The Czech education system, school Pracovní list Číslo projektu Číslo materiálu Autor Tematický celek CZ.1.07/1.5.00/34.0266 VY_32_INOVACE_ZeE_AJ_4OA,E,L_10 Mgr. Eva Zemanová Anglický jazyk využívání on-line
2 Axiomatic Definition of Object 2. 3 UML Unified Modelling Language Classes in UML Tools for System Design in UML 5
 Contents Contents 1 Semestrální práce 1 2 Axiomatic Definition of Object 2 3 UML Unified Modelling Language 2 3.1 Classes in UML............................ 3 4 Tools for System Design in UML 5 5 Student
Contents Contents 1 Semestrální práce 1 2 Axiomatic Definition of Object 2 3 UML Unified Modelling Language 2 3.1 Classes in UML............................ 3 4 Tools for System Design in UML 5 5 Student
Mechanika Teplice, výrobní družstvo, závod Děčín TACHOGRAFY. Číslo Servisní Informace Mechanika: 5-2013
 Mechanika Teplice, výrobní družstvo, závod Děčín TACHOGRAFY Servisní Informace Datum vydání: 20.2.2013 Určeno pro : AMS, registrované subj.pro montáž st.měř. Na základě SI VDO č./datum: Není Mechanika
Mechanika Teplice, výrobní družstvo, závod Děčín TACHOGRAFY Servisní Informace Datum vydání: 20.2.2013 Určeno pro : AMS, registrované subj.pro montáž st.měř. Na základě SI VDO č./datum: Není Mechanika
SSOS_AJ_2.14_ Podmínkové věty (Zero/First conditional)
 Číslo a název projektu Číslo a název šablony DUM číslo a název CZ.1.07/1.5.00/34.0378 Zefektivnění výuky prostřednictvím ICT technologií III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT SSOS_AJ_2.14_
Číslo a název projektu Číslo a název šablony DUM číslo a název CZ.1.07/1.5.00/34.0378 Zefektivnění výuky prostřednictvím ICT technologií III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT SSOS_AJ_2.14_
Budějovice Název materiálu: Reported Speech. Datum (období) vytvoření: Srpen 2013. Autor materiálu: PhDr. Dalibor Vácha PhD. Zařazení materiálu:
 Projekt: Příjemce: Budějovice Název materiálu: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova
Projekt: Příjemce: Budějovice Název materiálu: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova
Digitální učební materiál
 Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/34.0802 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/2 Inovace a zkvalitnění výuky prostřednictvím
7 Distribution of advertisement
 Legal regulation relating to the text message advertisement: There are different conditions regarding the SMS advertisement for two groups of recipients. The first group consists of recipients who are
Legal regulation relating to the text message advertisement: There are different conditions regarding the SMS advertisement for two groups of recipients. The first group consists of recipients who are
Fytomineral. Inovace Innovations. Energy News 04/2008
 Energy News 4 Inovace Innovations 1 Fytomineral Tímto Vám sdělujeme, že již byly vybrány a objednány nové lahve a uzávěry na produkt Fytomineral, které by měly předejít únikům tekutiny při přepravě. První
Energy News 4 Inovace Innovations 1 Fytomineral Tímto Vám sdělujeme, že již byly vybrány a objednány nové lahve a uzávěry na produkt Fytomineral, které by měly předejít únikům tekutiny při přepravě. První
