Katolická univerzita v Ružomberku. Pedagogická fakulta Katedra informatiky POČÍTAČOVÁ GRAFIKA. Doc. Ing. Rudolf Volner, Ph.D.
|
|
|
- Andrea Doležalová
- před 8 lety
- Počet zobrazení:
Transkript
1 Katolická univerzita v Ružomberku Pedagogická fakulta Katedra informatiky POČÍTAČOVÁ GRAFIKA Doc. Ing. Rudolf Volner, Ph.D. Ružomberok, 2010
2 Obsah 1. Úvod 3 2. Barevné modely Pixely a souřadnice Palety Formáty pro ukládání grafické informace Grafické editory Obrázky v pohybu animace 95 Príloha A. - Algoritmy počítačové grafiky 102 Autotest 106 Literatura 109 Klíč k autotestu 109 2
3 1. Úvod Grafika je jedním z druhů výtvarného umění. Vymezení pojmu je poměrně složité. Obecně můžeme říci, že grafikou nazýváme umělecké dílo, kdy umělec použije jednu z grafických technik a dílo rozmnoží ručním řemeslným postupem na předem stanovený počet exemplářů. Počet exemplářů tvoří náklad, za který umělec odpovídá, a proto jej také podepisuje. Každý z exemplářů je považovanán za originál, nikoliv za kopii. První grafické tisky se objevily v Číně v 6. století. Používanou technikou byl dřevořez, pomocí něhož se tiskly náboženské amulety. První dochovanou knihou, která se tiskla pomocí dřevořezu je z roku 868. Ve 13. století se dřevěné štočky používaly k tisku na plátno. Postupem času již technika dřevořezu či později dřevorytu přestala vyhovovat a umělci hledali techniku a materiál, který by byl schopen přenést jemnější práci. Odkud pramení vynález tisku z hloubky - kdy umělec vyryje námět do ocelové či měděné destičky. Do grafiky nepatří plakáty, pohlednice, knižní ilustrace ap. V některých případech je velmi těžké rozpoznat rozdíl mezi původní grafikou a reprodukcí. Ve většině případů pomůže důkladné prozkoumání pomocí lupy, kdy po zvětšení objevíme na reprodukci rastr (síťovou mřížku). Dalším vodítkem může být porovnání díla s listy v depozitáři galerií. Grafiku můžeme řadit dle mnoha hledisek. Vymezení jednotlivých kategorií je vždy sporné a mnohé skupiny se velmi často překrývají. Za základní rozdělení je možno považovat dělení dle oborů a to na grafiku volnou, užitou, reprodukční a dekorativní: Volná grafika - (též grafika umělecká) je grafikou, která je zcela duševním majetkem svého tvůrce. Umělec tvoří dílo dle vlastní volné představy, jeho je námět, myšlenka i provedení. Díla mají nejblíže k obrazům. Do volné grafiky patří nejhodnotnější díla, jelikož vznikají bez vnějších vlivů, Užitá grafika - Jde o grafiku k praktickým účelům. Patří sem novoročenky, ex libris, pozvánky, svatební oznámení, ale i plakáty, knižní obaly ap. Jelikož všechny tyto obory existují nejen jako původní grafika, je zde třeba rozlišovat mezi díly, která vznikla grafickými technikami a obyčejnými tisky z tiskárny, Reprodukční grafika - Je grafikou dle cizí předlohy. Ve starší literatuře je možné zaznamenat názor, že tato skupina grafiky je méně hodnotná a v principu není hodna pozornosti. Tento názor již není zastáván a neodpovídá obrovskému významu, který měla reprodukční grafika v dobách před vynalezením fotografie pro vývoj a hlavně popularizaci 3
4 umění. Nejlepší malíři si vždy vážili oněch řemeslníků, kterým svěřovali svá díla k rozšíření v grafickém přepisu, Dekorativní grafika - Tento vžitý název je vlastně nesprávný. Dnes bychom tuto skupinu grafik mohli pojmenovat ilustrace. Jedná se o díla, která byla původní součástí nějakého knižního díla a doprovázela text. Patří sem např. grafika květin, ptáků, pohledy na města (jimž se říká veduty), výjevy z venkovského života a mnohé jiné. Grafické techniky se řadí do tří skupin: tisk z výšky (např. dřevoryt), tisk z hloubky (např. lept, suchá jehla), tisk z plochy (litografie). Dále existují techniky mino tyto skupiny jako sítotisk (serigrafie), monotyp, papírotisk ap. U soudobé grafiky dochází často ke kombinaci několika technik, nebo k soutiskům z několika desek. Dochází také k celé řadě experimentů (např. tisk z igelitu, tisk z koláže ap.). Grafické sounáležitosti: Papír - Drtivá většina grafických listů je tištěna na papír. Existuje jen několik málo výjimek (tisk na hedvábí, plátno, sklo ap.) které se dají považovat spíše za kuriozity. Nejstarším papírem je papír ruční. Strojový papír vznikl až na začátku 19. století a od poloviny tohoto století je používán i na tisk grafik. Přesto je i dnes většina kvalitních grafických listů tištěna na papír ruční a to zejména pro vhodnější vlastnosti při tisku, Tisk - V počátcích grafiky byl umělec autorem námětu, rytcem i tiskařem. Dnes je poměrně časté, že si umělci nechávají své grafiky tisknout v tiskařských dílnách. Zejména to platí pro litografii, kde je k tisku třeba speciálního vybavení. Většina grafiků, pokud si listy netiskne sama, používá jen jednoho tiskaře, jelikož používané techniky bývají často velmi odlišné a způsob tisku vyžaduje značnou dávku zkušeností, Stavy - Někdy se můžeme v literatuře, či u označení listu setkat s popisem 2. stav. Jedná se o situaci, kdy grafik vyryje destičku a natiskne z ní náklad. Pak se mu může zdát, že něco na grafice přebývá nebo naopak schází. Vrátí se znovu k destičce a vyryje nebo zaretušuje některé součásti a znovu tiskne. Tak vnikají různé stavy. Ve výjimečných případech měla grafika i několik stavů. U současné grafiky se stavy vyskytují jen zřídka, Autorské tisky - Autorským tiskem (též tisk zkusmý) se rozumí výtisk mimo náklad. Tento výtisk je podepsán autorem a označen E.A., A.T., aut. tisk ap. Počet autorských tisků by nikdy neměl přesáhnout 5-10% číslovaného nákladu. Jedná se o tisky, při nichž autor 4
5 zkouší různé barevné tóny či stav desky. Často si také autor pořídí několik málo autorských tisků pro svůj archiv v případě, že byl celý náklad objednán sběratelem či institucí. U některých důležitějších děl je číslován i náklad autorských tisků. Na rozdíl od běžného číslovaní, kde se používají arabské číslice, se autorské tisky číslují římsky. Označení E.A. VIII/XX pak znamená tisk č. 8 z nákladu 20 autorských tisků, Tiskařská značka - Je důkazem, že grafiku tiskl sám autor. Většinou bývá umístěna vlevo hned pod okraj tiskové plochy. Tiskařské značky se vyskytují výhradně na moderní grafice. Je jich poměrně málo - jestliže list nemá tiskařskou značku, tak to neznamená, že jej autor netiskl sám. Někdy autoři vedle podpisu či na zadní stranu připisují vytiskl autor ap. Jestliže byl list vytištěn některým ze známých tiskařů, může mít i pečeť, slepotisk či tiskařskou značku tiskaře nebo tiskařské dílny a nikoliv autora grafiky, Podpis - Celou rozlehlou oblast grafiky by bylo možno dělit jinak, a to na listy umělcem podepsané a nepodepsané. Podpis má být jakousi zárukou pravosti. Zvyk podepisovat grafiky se ujal až v druhé polovině 19. století. Listy se podepisují zásadně tužkou. U moderní grafiky můžeme říci, že listy jsou až na výjimky signovány, Monografisté - Nejstarší grafika byla anonymní. Kolem 16. století se ujal zvyk opatřovat grafiky autorským monogramem. Nemusí to být monogramy v dnešním slova smyslu (tj. počáteční písmena umělcova jména). Někdy to býval heraldický znak, jindy obrazový symbol jména ap. Monogramů jsou tisíce a jejich rozboru je věnováno mnoho knih. S monogramem se můžeme setkat i u současné grafiky. Obyčejně se jedná o zkratku autorova jména v obrazové části. Většina listů je poté ještě signována tužkou. Pokud má současná grafika monogram a není signována, tak se list označuje jako signováno v tisku, signováno na kameni nebo signováno v desce, Náklad - Nákladem se rozumí celkový počet listů vytištěných z jedné desky. U staré grafiky je velmi těžké náklad stanovit. U starých listů záleželo spíše na poptávce než na technických možnostech. Jinak je tomu u moderní grafiky. Zde je většina děl nejen signováno, ale i číslována. Ve většině případů nepřesahuje náklad 100 tisků. Při tisku dochází k postupnému opotřebování desky a některé techniky (např. suchá jehla, mezzotinta) poskytnou jen zhruba kvalitních tisků. Počítače slouží ke zpracování informací. Tradiční oblastí je zpracování číselných informací, později se začalo uplatňovat i zpracování textových informací. S příchodem levných grafických výstupních zařízení, které se staly standardní součástí počítačových 5
6 systémů, se značně rozšířilo i zpracování informací grafických. Grafická zařízení se v počítačových systémech používají od šedesátých let, jednalo se však o ojedinělé aplikace s využitím drahých kreslicích stolů anebo vektorových obrazovek pro výstup grafických informací. V současné době jsou standardem personální počítače, které mají vysoký výpočetní výkon, rozsáhlou paměť a výstup všech informací pro uživatele (alfanumerických i grafických) se realizuje na grafické obrazovce. Vzhledem ke snadné dostupnosti těchto výkonných prostředků můžeme využívat prostředků počítačové grafiky prakticky ve všech oblastech zpracování informací, v informačních a řídících systémech i jiných aplikacích. Počítačová grafika a grafické schopnosti počítače se využívají v řadě oblastí. Jednou z nejjednodušších ale zároveň asi nejpoužívanějších aplikací je prezentační grafika, která umožňuje grafické zobrazení funkčních závislostí (např. stav a trendy růstu nebo poklesu hospodářských ukazatelů). Jinou aplikační oblastí jsou geografické informační systémy, které mohou sloužit ve státní správě pro údržbu a zobrazování informací v registru katastrů. Geografické informační systémy mohou také obsahovat informace o technické infrastruktuře jako jsou rozvodové sítě, silniční nebo železniční komunikace apod. Pomocí těchto údajů potom můžeme provádět potřebné analýzy, optimalizovat a simulovat dopravní a logistické procesy, navrhovat optimální plány rozvoje územních celků a používat takový systém pro podporu rozhodování ve státní správě. Počítačovou grafiku používáme i v řadě dalších oblastí: při tvorbě výkresové dokumentace, návrhu a technických výpočtech konstrukcí v různých průmyslových odvětvích, tvorbě nástřihových plánů v oděvním a obuvnickém průmyslu, ale také při programování počítačových her anebo pro animaci při tvorbě trikových filmů. Když jsme krátce ukázali možnosti uplatnění počítačové grafiky, můžeme se vrátit k vlastní definici počítačové grafiky. Podle normy ISO je počítačová grafika definována takto: Počítačovou grafikou rozumíme metody a postupy pro převod údajů na grafické zobrazení a naopak pomocí počítače. Definice používá tři důležité pojmy, které ukazují na tři základní prvky počítačové grafiky. Jsou to údaje, počítač a grafické zobrazení. V systémech počítačové grafiky tedy musíme mít k dispozici počítač, grafické zobrazovací zařízení a údaje, se kterými budeme pracovat. Všechny tyto prvky jsou běžně dostupné v současných personálních počítačích. Hlavní důvod rychlého rozšíření aplikací počítačové grafiky však můžeme hledat v následujícím tvrzení: 6
7 Vizuální grafická informace je nejsrozumitelnějším a nejvýkonnějším prostředkem komunikace mezi počítačem a operátorem. O této skutečnosti už asi dnes není třeba nikoho přesvědčovat. Grafické uživatelské rozhraní je standardním prostředkem komunikace v prostředí WINDOWS a každý už jistě ocenil výhody tohoto prostředí ve srovnání s komunikací pomocí alfanumerických příkazů zadávaných z klávesnice. Přednosti grafického zobrazení ukážeme ještě na jednom příkladu. Počítače jsou výkonným prostředkem pro zpracování informací a limitujícím prvkem v systému zpracování údajů je často podsystém vstupu a výstupu. Současné počítače běžně pracují nejen s číselnými, ale i s alfanumerickými údaji a výsledkem výpočtů je obvykle množství bezvadně zpracovaných tabulek. Tabulky sice obsahují přesné hodnoty, ale jsou málo přehledné a nejsou proto vhodné pro většinu běžných aplikací, ve kterých vyžadujeme především rychlou orientaci a rozhodnutí na základě zobrazených výsledků. Pro takové aplikace je vhodné zobrazení výsledků ve tvaru grafů nebo jiného grafického výstupu. Porovnání přehlednosti grafického a alfanumerického zobrazení informací je ukázáno na obr. 1.1 a v tab Tabulka obsahuje údaje časového průběhu naměřených hodnot určité veličiny a na obrázku jsou tyto údaje zobrazeny v grafické formě. Předpokládejme nyní, že máme za úkol posoudit stabilitu chování sledovaného systému anebo určit, zda naměřené hodnoty rostou anebo klesají. Je zřejmé, že při použití tabulky bychom museli velmi podrobně studovat všechny údaje a přesto bychom jen obtížně mohli určit trendy vývoje sledované závislosti. Naproti tomu u grafického zobrazení můžeme uvažované otázky zodpovědět snadno a rychle, vyšší přesnost číselných údajů v tabulce je pro zodpovězení našich otázek nepotřebná. X Y X Y 0,17 0,4543 2,72 0,9842 0,39 0,1765 2,91 0,9105 0,56 0,0291 3,18 0,8856 0,76 0,2817 3,35 0,9311 0,93 0,5867 3,50 0,9832 1,10 0,8503 3,71 1,0271 1,37 0,9313 3,90 1,0181 1,59 0,7776 4,18 0,9659 1,75 0,6898 4,30 0,9538 1,90 0,6918 4,59 0,9716 2,19 0,8828 4,70 0,9891 7
8 X Y X Y 2,33 0,9779 4,95 1,0167 2,51 1,0296 5,15 1,0128 y 1,0 Tab.1.1 Tabulka naměřených hodnot 0,8 0,6 0,4 0,2 0, x Obr.1.1 Graf funkční závislosti zadané v tab. 1.1 Uvedený příklad by mohl být ukázkou výhod grafického výstupu v oblasti systémů pro podporu rozhodování. Zodpovědný pracovník se může na základě grafického zobrazení rychle informovat o trendu vývoje a vydat příslušné řídicí rozhodnutí. Vrátíme-li se k definici počítačové grafiky, můžeme uvažovat o převodu údajů na grafické zobrazení i naopak a údaje můžeme zřejmě v počítači i modifikovat. Můžeme potom rozlišit následující oblasti počítačové grafiky: generativní počítačová grafika, která provádí převod údajů na grafické zobrazení, generovaný obraz je přitom určen programem a údaji v počítači, skládá se z obrazových prvků, jako jsou úsečky, oblouky, kružnice, plochy, textové řetězce apod., obraz můžeme dělit na části (segmenty) a jednotlivé části obrazu transformovat, analýza obrazů, která zpracovává vstupní grafické informace zadané digitalizací obrazu z papírové nebo jiné předlohy, vybírá z nich informace o jednotlivých objektech, vztazích mezi objekty a převádí je na údaje v počítači, zpracování údajů, mezi které můžeme zahrnout transformace pro změnu polohy objektů na scéně, změny způsobu promítání anebo velmi atraktivní animaci obrazu (scény), při které se generovaný obraz mění v čase tak, aby znázorňoval pohyb objektů na scéně (např. pohyb vozidel nebo osob). V dalších částech se budeme věnovat především problémům generativní grafiky, která může být pasivní anebo interaktivní. 8
9 Pasivní grafika se používá pro generování výstupní grafické informace. Vytvoření obrazu přitom řídíme programem anebo zadáním potřebných údajů a jejich zpracováním v počítači. Interaktivní grafika dovoluje vytvoření požadovaného obrazu v přímé spolupráci operátora s grafickými vstupními a výstupními zařízeními. Operátor zadává vstupní údaje prostřednictvím vhodného grafického vstupního zařízení a zároveň kontroluje správnost zadání na grafické zobrazovací jednotce (obvykle obrazovce), kde se mění obraz podle zadávaných vstupních údajů. Celá komunikace operátora s grafickým systémem probíhá často s minimálními nároky na znalosti operátora z oblasti programování a výpočetní techniky. Příkladem interaktivní práce na počítači je práce pod operačním systémem WINDOWS. História počítačovej grafiky Počítačová grafika je jednou z generačných premien vo výpočtovej technike. Od drahých zariadení určených pre vojenské a špičkové priemyselné aplikácie sa počas necelých tridsiatich rokov rozšírila až do škôl a domácností ako výhodné informačné médium a prostriedok poučenia i zábavy. V 4. tisícročí pred n. l. vzniklo prvé ucelené obrázkové písmo v Mezopotámii. O tisíc rokov neskôr, obchodníci féničania zostrojili abakus (mechanické počítadlo). O niekoľko desaťročí nato, sa objavili prvé súvislé znakové sady, do tohto obdobia sa datuje aj vznik abecedy. Zhruba v roku 1580, bol založený odbor analytickej geometrie FraCoisom Viteom a následne René Descartes v období vymedzil algebru, ktorá je základným nástrojom nie len počítačovej grafiky. Od roku 1952 Ben F. Laposky sa venoval tvorbe grafík na analógových počítačoch. O rok neskôr Ben F. Laposky vystavil analógovú počítačovú grafiku v Sanford Museum Cherokee v USA. V roku 1960 pracovníci firmy Boeing zaviedli pojem počítačová grafika a konala sa výstava skupiny analógovej grafiky. V roku 1961 Edward E. Zajac vytvoril prvý film animovaný počítačom s názvom Two-Gyro Gravity Gradient Attitude Control System, ktorý trval 4 minúty. Rok 1962 priniesol jednu zaujímavosť. V rámci svojej dizertačnej práce na univerzite v Massachussets vyvinul Ivan Sutherland interaktívny grafický program Sketchpad ovládaný svetelným perom s výstupom na grafickú obrazovku. V roku 1963 bol vyrobený prvý plotter. Rok 1964 predstavil ďalší významný medzník. Douglas Engelbart zo Stanfordského výskumného inštitútu v Kalifornii vymyslel x-y coordinate 9
10 indicator for graphics systems, čo je dnes dobre známa myš. Rok 1968 v Československu bol rokom kedy sa usporadúvali prvé výstavy počítačového umenia s medzinárodnou účasťou u nás. Našu tvorbu zastupovali Miroslav Klivar a Ľubomír Sochor. V roku 1969 sa objavil prvý stolný počítač FLEX, ktorý používal grafiku, okienka a myš. V roku 1971 svetlo sveta uzrela kniha Computer Grafik Computer Kunst od Herberta W. Frankeho, ktorého dnes pokladajú za otca počítačového umenia. Rok 1972 je rokom, kedy bol pre počítačovú grafiku definovaný nový pojem CAD (Computer Aided Design), obsah ktorého sa stal výraznou časťou počítačovej grafiky a prispel k nemalému rozvoju interaktívnych grafických editorov. Pre Slovensko je výrazným medzníkom rok 1973, kedy Jozef Jankovič a Imrich Bertók vytvorili prvé slovenské počítačové grafiky. V bývalom Československu sa v roku 1982 konala v Prahe prvá celoštátna výstava počítačového umenia a pre Slovensko bol tento rok opäť medzníkom: Daniel Fischer a Igor Kolčanský vytvorili prvý slovenský film animovaný počítačom. Ďalej si spomenieme ešte niektoré firmy a pojmy, ktoré prispeli k rozvoju počítačovej grafiky. Firma Autodesk dokázala svojím AutoCADom, že CAD sa stal nástrojom naozaj pre všetkých. Ďalším adeptom je firma ATARI, ktorá priniesla počítačové hry. Firma COREL dokázala svojím CORELDRAW, že kresliť pomocou počítača môže naozaj každý. Podobne firmy Adobe (Ilustrator, Photoshop) a Aldus (Freehand) priniesli pre používateľov ďalšie netušené možnosti grafických editorov. Záverom úvodu sa teda vráťme k slovám, ktoré povedal zakladateľ počítačového umenia Herbert W. Franke o úlohe počítača ako ďalšieho prostriedku k vytváraniu obrazov: Je obraz vytvorený počítačom umelecké dielo? To by sme sa tiež mohli opýtať: Sú tóny hrané na husle hudba? V obidvoch prípadoch sa jedná o nástroje, o pomôcky tvorby. Vstupné grafické zariadenia: Myš, Trackball (polohovacie zariadenie, ktoré sa vyskytuje najmä u prenosných PC), Touchpad (vyskytuje sa v notebookoch namiesto Trackballov), Joystick, Tablet, Scanner, Optické pero (umožňuje interaktívne zasahovať do obrazu na displeji). Výstupné grafické zariadenia: 10
11 Tlačiareň, Ploter, Monitor. 11
12 2. Barevné modely Světlo lze z fyzikálního hlediska chápat jako vlnění v oblasti 10 8 MHz. Každá barva odpovídá určité frekvenci. Rozsah člověkem vnímatelných barev je od červené (4, MHz) až po fialovou (7, MHz). Nižší hodnoty odpovídají infračervenému světlu, vyšší ultrafialovému záření. V rámci viditelné části spektra je člověk schopen rozlišit víc než různých barev a jejich odstínu. Existují tzv. komplementární barvy, jejichž složením vznikne bílé světlo. Barevné modely určují, ze kterých základních barev se budou ostatní skládat, jaký bude poměr jednotlivých základních barev a jakým způsobem se budou základní barvy míchat. Svetlo je charakterizované niekoľkými svojimi atribútmi: farba, je základným atribútom svetla a závisí od už spomínanej frekvencie (resp. vlnovej dĺžky), jas odpovedá vlastne intenzite svetla. Jasnosť zdroja svetla je v priamej úmere s intenzitou, sýtosť farby uvádza jej čistotu. Čím vyššia je sýtosť, tým užšie je spektrum frekvencií obsiahnutých vo svetle, svetlosť je vlastne veľkosť achromatickej zložky vo svetle s určitou dominantnou frekvenciou. Hlavným ľudským orgánom prijímania obrazových informácií je oko. Obraz je vytváraný na sietnici oka, kde je aj najviac nervových ukončení. Na sietnici sa nachádzajú dva druhy receptorov. Prvý druh sa nachádza v strede sietnice a je citlivý na farby. Senzitívnosť tohto druhu receptorov je možné rozdeliť ešte do dvoch skupín, ktoré rozlišujú farebný rozdiel spektra červená-zelená a modrá-žltá. Druhý druh rovnomerne pokrýva celú sietnicu a umožňuje vnímať všeobecné obrazové informácie ako obrysy prípadne jas. Obr. 2.1 Relatívna citlivosť ľudského oka 12
13 Aditivní barevný model pracuje na principu přidávání barev do černé. Můžeme si jej představit jako tri barevné žárovičky blízko sebe, které se rozsvěcují v různé intenzitě. Pokud jsou dostatečně blízko sebe, vnímá lidské oko jen výslednou složenou barvu. Typický aditivní model je RGB Red, Green, Blue (červená, zelená, modrá), Barvy jsou vytvářeny přidáváním (přičítáním) barvy do černé, Čím více barev se přidá, tím více se blíží bílé, Aditivní barevné prostředí nepotřebuje vnější světlo (např. barvy na monitoru). Obr. 2.2 Model RGB Barevný model RGB Jako užitečná myšlenka se ukazuje, chápat množinu spektrálních funkcí jako vektorový prostor. Vzato striktně matematicky je množina všech funkcí na intervalu vektorový prostor s nekonečnou dimenzí. Nemůže tedy existovat žádná konečná báze prostoru, žádná konečná množina spektrálních funkcí, a tedy žádná konečná množina základních barev, ze kterých by se všechny ostatní barvy dály složit. Vzhledem k nedokonalým rozlišovacím schopnostem lidského oka se však ukazuje, že naprostá většina rozlišitelných barevných odstínů se dá nakombinovat ze tří základních barev a že tedy vektorový prostor spektrálních funkcí představujících lidským okem rozlišitelné barevné odstíny má dimenzi 3. Je tedy možné zvolit tři základní barvy a všechny ostatní barevné odstíny získat jako jejich lineární kombinace. Z hlediska vektorové algebry je jedno jaké tři základní barvy budou zvoleny jako báze vektorového prostoru (pokud nebudou tyto tři barvy lineárně závislé, např. červená, žlutá a oranžová by bázi vektorového prostoru barev netvořily). Z historických a také z technických důvodů se jako báze vektorového prostoru barev nejčastěji používají barvy červená (Red, R), zelená (Green, G) a modrá (Blue, B). 13
14 Barevný model založený na této bázi vektorového prostoru, tedy na těchto třech základních barvách, se nazývá podle počátečních písmen barev - model RGB. Barevný model RGB se nazývá také model aditivní (sčítací). Toto označení souvisí se způsobem, jakým jsou ve vektorovém prostoru barev jednotlivé barvy kombinovány. U aditivního modelu se barvy A a B kombinují tak, že se sečtou jejich spektrální funkce, tedy tak, že se dají dohromady energie v jednotlivých frekvencích pro obě dvě barvy A a B. Laicky řečeno, nerozlišitelně blízko o d sebe se rozsvítí žárovičky v barvách A a B. Výsledný vjem pak bude odpovídat barvě vzniklé jako kombinace barev A a B. Tímto způsobem vznikne jako kombinace barvy červené a zelené barva žlutá (Yellow, Y), jako kombinace červené a modré barva fialová (Magenta, M) a jako kombinace zelené a modré barva azurová (Cyan, C). Jako kombinace všech tří základních barev červené, modré a zelené pak vzniká barva bílá (White, W). Barvy R,G,B,Y,M,C a W tvoří sedm z osmi vrcholů jednotkové krychle v barevném prostoru RGB. Poslední vrchol odpovídá lineární kombinaci základních barev s koeficienty (0, 0, 0), tedy barvě se spektrální funkcí rovnou konstantní nule. To je barva černá (black, K). Všechny ostatní barvy pak odpovídají jednotlivým bodům uvnitř jednotkové krychle RGB, tedy trojicím čísel (r, g, b) z intervalu (0, 1). Jelikož interval reálných čísel (0, 1) obsahuje nekonečně mnoho hodnot, je možno v modelu RGB teoreticky zakódovat nekonečně mnoho barevných odstínů. Je vhodné si uvědomit, že přesto se nemusí jednat o všechny odstíny, které je lidské oko schopno rozeznat. Dopustili jsme se totiž podstatného zjednodušení situace, když jsme prostor všech barev, který má ve skutečnosti nekonečnou dimenzi, prohlásili za prostor třírozměrný. Zkušenosti ale ukazují, že naprostá většina barevných odstínů, které se v běžném světě vyskytují, se dá v modelu RGB zakódovat, nebo alespoň dobře aproximovat. Při reálném používání modelu RGB není vhodné povolit pro hodnoty souřadnic v jednotkové krychli libovolnou hodnotu z intervalu (0, 1). Ve skutečnosti je vhodné se omezit jen na nějaký předem omezený počet hodnot souřadnic. Podle toho, kolik různých hodnot souřadnic povolíme v osách r, g, b, tolik různých barevných odstínů budeme schopni zakódovat. Nejjednodušší variantou modelu RGB je situace, kdy jako hodnoty souřadnic jsou povolena jen čísla 0 a 1. V tom případě jsme schopni zakódovat jen osm vrcholů jednotkové krychle a tedy 8 základních barev, které jim odpovídají (červená, zelená, modrá, žlutá fialová, azurová, bílá, černá). Na zakódování barvy nám stačí 3 bity. Pro reálné zachyceni světa je 14
15 pochopitelně 8 barev velmi málo, v některých případech však může mít takovýto zjednodušený model opodstatnění. Jiná, občas používaná stupnice, povoluje 8 různých hodnot v ose r, 8 různých hodnot v ose g a 4 různé hodnoty v ose b. Diskriminace odstínů modré barvy má fyziologický důvod, běžné lidské oko totiž rozpoznává odstíny modré opravdu přibližně dvakrát hůře, než odstíny červené a zelené. Takováto stupnice vede na možnost zakódovat 8.8.4= 256 různých barev. Pro zakódování jedné barvy pak potřebujeme =8 bitů, tedy 1 byte. Nejčastěji používanou variantou modelu RGB je varianta zvaná někdy (poněkud nadneseně) True Color. U ní může barevná stupnice v každé z os obsahovat 256 různých stupňů. Celkem je tedy k dispozici = barevných odstínů. Pro zakódování jednoho odstínu je potřeba 3.8=24 bitů, tedy 3 byte. Teoreticky by pochopitelně bylo možné stupnici na jednotlivých osách dále zjemňovat, získat tím ještě větší počet barevných odstínů za cenu ještě většího prostoru nutného pro jejich ukládání. Reálný význam však takové snahy nemají, neboť počet barevných odstínů zakódovatelných v modelu True Color i tak více než 100 krát přesahuje počet barevných odstínů, které rozezná člověk s velmi dobrým barvocitem. Reálný smysl naopak mají snahy rozšířit model RGB o další souřadnici a tedy chápat prostor barev jako více než trojrozměrný. Tím způsobem je totiž možné se dostat k barvám, které v reálném světě existují, ale které leží mimo jednotkovou krychli RGB. Obr. 2.3 Spektrální funkce barevných složek světla 15
16 Obr. 2.4 Model RGB Obr. 2.5 Barevný model RGB Obr. 2.6 Aditivní skládání barev Obr. 2.7 Barevný model RGB, paleta 3x3x2 16
17 Subtraktivní barevný model Základní barvy jsou odečítány od bílého světla, čím více odečtu, tím více se blížím černé. (Každá barva vlastně pohltí část spektra černá je absolutní pohlcovač světla, bílá všechno světlo odrazí.) Typický subtraktivní model je CMY Cyan, Magenta, Yellow (tyrkysová, fialová, žlutá). Subtraktivní prostředí je prostředí, které odráží světlo, a proto potřebuje vnější zdroj světla. Jakákoliv předloha zobrazená na papíře je příkladem subtraktivního modelu. Používá se v tiskárnách, plotrech, ve fotografii. Obr. 2.8 Model CMY Další možnou variantou je model CMY (K), kde je přidána ještě černá barva. Důvodem je šetření barevných kazet například u tiskáren. Modely CMY, CMYK Dalším z často používaných barevných modelů je model CMY. Pojmenovaný je podle svých tří základních barev modrozelené (Kyan, C), fialové (Agenta, M) a žluté (Yellow, Y). Jak jste si jistě povšimli, jedná se o tři doplňkové barvy k základním barvám RGB. Model CMY tedy popisuje tu samou základní krychli barev jako model RGB, jen počátek souřadnic se nachází v jiném vrcholu a osy souřadnic mají jiný směr. Model CMY je model odečítací subtraktivní. Složení dvou barev x a y získáme tak, že vezmeme doplňky ke spektrálním funkcím f x, a f y, tyto doplňky sečteme a výsledkem bude opět doplněk k tomuto součtu. (2.1) Uvedený způsob subtraktivního skládání barev odpovídá běžnému skládání barev při kreslení na bílý papír. Bílý papír je hmota, která odráží (téměř) všechny světelné paprsky. Namalujeme-li na bílý papír žluté kolo, nanášíme na něj hmotu, která odráží pouze paprsky 17
18 žluté barvy a ostatní pohlcuje. V třírozměrném barevném prostoru se paprsky žluté barvy získají jako kombinace paprsků červených a zelených. Paprsky těchto barev tedy žlutý povrch odrazí, paprsky modré pohltí. Přes žlutou skvrnu nakreslíme ještě skvrnu fialovou. Fialová skvrna naopak pohlcuje paprsky zelené a odráží paprsky červené a modré. Výsledný efekt tedy bude pohlcení modrých i zelených paprsků a odražení pouze paprsků červených. Barva skvrny bude červená. Počátkem souřadného systému pro barevný model CMY je barva složená ze všech paprsků spektra, tedy barva bílá (W). Protilehlým bodem barevné krychle je barva, která odpovídá povrchu pohlcujícímu všechny paprsky, tedy barva černá (K), Z výše uvedeného výkladu je zřejmé, že model CMY se využije především v situacích, kdy zobrazení rastrového obrázku probíhá pomocí nanášení barev na bílý papír, tedy při tisku na barevné tiskárně, inkoustové i laserové. Pokud máme obrázek uložený jak bývá zvykem, pomocí modelu RGB, je potřeba jej před tiskem na tiskárně převést do subtraktivního modelu CMY. Převod mezi modely RGB a CMY je jednoduchý. Barva modrozelená (C) vznikne jako aditivní složení barev modré (B) a zelené (G). Jedná se tedy o doplněk ke třetí základní barvě, barvě červené (R) do barvy bílé (W) Podobně odvodíme i další dva převody (2.2) a také vztahy pro převod opačným směrem (2.3) (2.4) Barevné tiskárny tedy obvykle obsahují tři kartuše, či tonery s inkoustem, či práškem, ve třech barvách C, M a Y. Podle vypočtených hodnot po převodu do modelu CMY bude na papír naneseno příslušném množství hmoty v těchto základních barvách. Nebude-li na papír naneseno nic, což odpovídá barvě o CMY souřadnicích (0,0,0) zůstane papír bílý. Nanesením plného množství všech tří barev bychom měli dostat barvu o CMY souřadnicích (1,1,1), tedy barvu černou. Takový postup by však nebyl vhodný. Jednak je obtížné technicky dosáhnout správného poměru všech tří základních barev. Barva, kterou dostaneme směsí barev C, M a Y v plném poměru tedy nebude skutečně černá, ale jen velmi tmavá šedohnědá. Ostatně ani barva s CMY souřadnicemi (0, 1, 1), což by měla být barva červená, nebude přesnou červenou 18
19 z modelu RGB. V tomto případě to ovšem tolik nevadí. Lidské oko je totiž daleko více vycvičené na rozeznání přesného odstínu černé barvy, než na rozeznání přesných odstínů ostatních barev. Navíc se ve většině tištěných dokumentů černá barva objevuje ze všech barev nejvíce. Její míchání ze tři základních barev C, M a Y by bylo neekonomické. Barvy jsou v provozních nákladech barevných tiskáren nejdůležitější složkou. Při výše uvedeném postupu bychom pro nejčastější barvu v dokumentech potřebovali největší množství základních barev, výslednou barvu bychom navíc nedokázali namíchat přesně. Řešením je zavedení další souřadnice do barevného modelu. Tato souřadnice odpovídá barvě černé. Model CMY se tím mění na model CMYK. Osy souřadnic C, M, Y a K netvoři bázi vektorového prostoru barev, neboť hodnoty C, M, Y a K jsou na sobě lineárně závislé. Ze znalostí tří hodnot lze čtvrtou dopočítat. Pro tisk na papíře je ovšem takovéto vyjádření barev vhodnější. Obr.2.9 Barevný model CMY Obr Model CMY Barevný model HSV, HLS Všechny výše popsané modely popisují tu samou množinu barev jako model RGB pouze používají jiné souřadné systémy. Neodstraňují však jednu z nevýhod modelu RGB, totiž redukci dimenze prostoru barev z nekonečné dimenze na dimenzi 3. Díky tomu nelze v modelu RGB a ani v modelech z něj odvozených vyjádřit úplně všechny barvy, které je 19
20 schopno lidské oko vnímat. Tento nedostatek se pokouší odstranit modely nazývané HSV a HLS. Model HSV skládá barvu ze tří složek - barevného tónu (Hue), sytosti barvy (Saturation) a jejího jasu (Value). Barevný tón Hue se udává v úhlech a popisuje bod na obvodu pravidelného šestiúhelníka. V jeho vrcholech se nachází tři základní barvy červená (0 stupňů), zelená (120 stupňů) a modrá (240 stupňů) a dále doplňkové barvy žlutá (60 stupňů), azurová (180 stupňů) a fialová (300 stupňů). Odstínem se rozumí základní spektrální barva. Její hodnota se většinou vybírá tak, jak jdou barvy duhy za sebou. Pro 3 bytové barvy (TrueColor) je tudíž vybráno 256 základních spektrálních barev. Někdy se při zadávání používá zobrazení barev do kruhu a barva se potom udává ve stupních od 0 0 do a program si ji vnitřně přepočítá na číselné hodnoty (0 255). Sytost barvy vyjadřuje množství příměsí jiných barev k základní barvě. V popisovaném šestiúhelníku leží barvy s maximální sytostí na jeho obvodu, směrem ke středu šestiúhelník sytost barev klesá. Ve středu šestiúhelníka je barva bílá, barva s minimální sytostí. Sytost udává množství bílé barvy, přičemž úplně sytá barva neobsahuje ani trochu bílé. Částečně sytá barva je světlejší právě díky přidání bílé (červená barva s 50% sytostí je růžová). Třetí souřadnice, jas barvy, se geometricky vyjadřuje jako hloubka ve směru pod tento základní šestiúhelník. Všechny barvy v modelu HSV tedy vyplňují pravidelný šestiboký jehlan s hlavním vrcholem obráceným směrem dolů. V tomto hlavním vrcholu je umístěna barva s minimálním jasem, tedy barva černá (K). Sbíhání hran jehlanu směrem k vrcholu K vyjadřuje skutečnost, že s klesajícím jasem je pro lidské oko obtížnější rozeznat jednotlivé barevné odstíny. Je jedním z modelu orientovaných na uživatele, které používají intuitivní fyzikální veličiny. Mění se počet barevných úrovní, pomocí nichž se vytvářejí nové barvy. Intenzita (jas) je stupen zářivosti barvy, tj. kolik světla odráží. Barva s malou intenzitou je tmavá. Změnu jasu si můžeme představit tak, že do základní spektrální barvy přidáváme černou. Model HSV se tak nejvíce přibližuje systému používanému malíři a jinými umělci, neboť ti vytvářejí nové odstíny barev přidáváním bílé a černé do jiných barev, aby vytvořili jejich nádechy. 20
21 Obr Vybírání barvy v programu Corel Draw Obr Model HSV Obr Barevný model HSV Ve většině programu můžete zadávat barvy několika způsoby (viz obr. B. 3), protože existují převodní algoritmy mezi jednotlivými systémy. Do souboru se ale barvy nejčastěji ukládají v modelu RGB. 21
22 Model HSV má některé nedostatky, které se pokouší odstranit jeho variace nazývaná HLS, tedy barevný tón (Hue), světlost (Light) a sytost (Saturation). V modelu HLS vyplňují barvy dvojitý kužel. Na obvodu jeho podstavy jsou opět základní barvy RGB a doplňkové barvy CMY pod stejnými úhly jako u modelu HSV. Sytost barvy opět vyjadřuje vzdálenost od středu podstavy. Ve středu podstavy je barva s nulovou sytostí a průměrným jasem. Podle modelu HLS je to barva šedá (G, Grey). Směrem ke spodnímu vrcholu kužele klesá jas barev. Ve spodním vrcholu kužele je barva s minimálním jasem, tedy barva černá. Směrem k hornímu vrcholu kužele jas barev stoupá až k barvě s maximálním jasem, barvě bílé. Se zvyšujícím se jasem též klesá schopnost lidského oka rozeznat jednotlivé barevné odstíny, podobně jako v případě snížení jasu. Obr Barevný model HLS Obr Model HLS Převod mezi modely HSV či HLS a standardním modelem RGB nelze vyjádřit jedním vzorcem. Tento převod má charakter algoritmu. Zobrazení definované tímto algoritmem navíc není prosté. Existují různé barvy v modelu HSV, které po převodu do modelu RGB budou vyjádřeny stejně. Kromě toho, že modely HSV a HLS umožňují zachycení většího počtu barevných odstínů, než model RGB, mohou být i příjemnější pro uživatele, který chce 22
23 jednoduše upravovat některé barevné charakteristiky pixelů. Po převodu do modelu HLS lze např. jednoduše upravit sytost barev. Po úpravě může být výsledná barva opět převedena a uložena ve standardním barevném modelu RGB. Tab. 2.1 Hodnoty barev pro různé barevné modely Obidva posledne definované modely umožňujú meniť jednotlivé farebné charakteristiky pri zachovaní ostatných typických vlastností farieb. Model YC b C r, Model YC b C r, se používá pro přenos televizních signálů v normě SECAM. Své využití má i při kódování rastrových obrázků pomocí ztrátové komprese, konkrétně v kompresním algoritmu JPEG. Hodnota Y v tomto souřadném systému znamená jas každé jednotlivé barvy. Lidské oko vnímá každou ze tři základních barev jako jinak jasnou. Nejjasněji vnímá barvu zelenou, o něco méně jasněji barvu červenou. Barva modrá je vnímána jako barva s nejmenším jasem. Z průměrného poměru lidského vnímání jasu základních barev byla sestavena rovnice definující pojem jas barvy (2.5) Zbývající dvě souřadnice C b a C r, v prostoru YC b C r, pak vyjadřují barevný posun od šedivé barvy směrem k barvě modré (C b ) a červené (C r ). Tyto barevné posuny se dají vyjádřit jako 23
24 (2.6) Takto vypočtené hodnoty souřadnic C b a C r, se nacházejí v intervalu < -0,5, 0,5 >. Podobným způsobem by se pochopitelně dal odvodit i doplněk do barvy zelené C g. Tím bychom ovšem získali čtvrtou souřadnici, která by byla lineárně závislá na souřadnicích Y, C b a C r a její použití by tedy bylo nadbytečné. Televizní norma PAL používá pro přenos signálu příbuzný model nazývaný YUV. Hodnota Y vyjadřuje opět jas barvy spočítaný podle rovnice (2.7) Zbývající dvě souřadnice nesou opět informace o velikosti barevných složek. Spočítají se podle následujících vztahů (2.8) 24
25 3. Pixely a souřadnice Pixel (picture element) je jeden ze základních pojmu počítačové grafiky. V počítačové grafice jsou pozice dat uloženy jako matematické souřadnice; zobrazovací plocha výstupního zařízení je však fyzický objekt. Proto je nutné si uvědomit rozdíly mezi pixely (body) fyzickými a logickými. Fyzické pixely jsou body, které používá k zobrazování výstupní zařízení. Tyto prvky jsou přímo ovládány hardwarem výstupního zařízení. V praxi obrazové zařízení překrývá nebo skládá vedle sebe několik menších bodu tak, aby vytvořily jeden barevný bod: obrazovka několik malých bodu vysvítí jeden pixel, inkoustová tiskárna velikost pixelu odpovídá velikosti kapičky barvy, laserová tiskárna velikost bodu odpovídá několika zrnkům toneru. Logické pixely jsou matematické body, které specifikují polohu. Kromě informace o poloze nesou s sebou informaci o své barvě. Jsou to vlastně nejmenší částečky obrazu. Je třeba programově zajistit mapování mezi logickými a fyzickými pixely. Hloubka pixelu a displeje Počet bitů, které reprezentují daný pixel, určuje počet barev, kterých muže pixel nabýt. Čím vetší počet bitu, tím vetší i možný počet barev. Hloubkou pixelu se většinou rozumí právě počet bitu nutných pro reprezentaci jeho barvy tab Někdy se jako hloubka pixelu (bodu) přímo uvažuje tento počet barev. Více bitu na jeden pixel také znamená vetší paměťovou náročnost uložení grafické informace. Tab. 3.1 Hloubka pixelu Většina moderních zobrazovacích zařízení dokáže zobrazit více než 16,8 miliónu barev, což odpovídá 24 bitům na barvu jednoho pixelu. O těchto zařízeních se říká, že jsou schopné zobrazovat tzv. pravé barvy (True Color). True Color je nejdokonalejší z popisovaných režimu a obrázky mohou být reprezentovány v jedné ze dvou variant. TrueColor RGB pracuje se třemi bajty pro každý 25
26 pixel. TrueColor RGBA má k dispozici čtyři bajty, přičemž čtvrtá složka (A neboli α) nese informaci o průhlednosti pixelu a nevztahuje se přímo k barvě. Někdy se skutečný počet barev na pixel, které jsou uloženy v grafickém souboru, liší od těch, které mohou být zobrazeny na daném výstupním zařízení. Zejména pokud je v souboru více barev, než je schopné výstupní zařízení zobrazit, muže docházet ke ztrátě barev, a tím i kvality. Počet bodů obrázku o rozlišení Nejdůležitějším parametrem rastrového obrázku je počet bodů, ze kterých se skládá. Čím více bodů, tím lépe, ale na druhou stranu tím více místa zabere obrázek při práci v paměti počítače a také tím více místa zabere na disku po svém uložení. Takže ideální je, pokud je bodů přiměřeně. S tímto pojmem by si možná poradil nějaký filosof, ale grafici používají přesnější (a hlavně jasně definovaný) pojem rozlišení obrázku. Rozlišení (DPl) Rozlišení je počet obrazových bodů na jednotku vzdálenosti. Je totiž zřejmé, že samotný počet bodů pro určení kvality nestačí. Kvalita obrázku (jak hladké, jemné má detaily) závisí také na jeho plošné velikosti. Rozlišení se udává v počtu bodů na palec - v DPI (Dots Per Inch). Jeden palec je cca 2,54 cm, pro jednoduchost stačí uvažovat, že jeden palec = 2,5 cm. Takže obrázek, který by byl 2,5 cm (tj. jeden palec) široký a obsahoval by na šířku 100 bodů, by měl rozlišení 100 DPI. Na obr. 3.1 vidíte ukázky obrázku v malém a přiměřeném, rozlišení. Pokud je rozlišení příliš malé, vidíte zřetelně bodovou strukturu obrázku, obrázek je zrnitý. Obr. 3.1 Rozdíl v hodnotě DPI, levý 50, pravý
27 Obrazovka a tiskárna Potřebné rozlišení závisí na účelu obrázku, přesněji na jeho využití. Pokud obrázek bude součástí webové stránky, stačí rozlišení menší, než jaké potřebujeme u obrázku, který chceme pěkně vytisknout. Proč? Protože obrazovka (monitor) má hrubší rastr, obsahuje méně bodů než obrázek vytisknutý na tiskárně: U monitorů se jejich, rozlišení udává v počtu bodů (pixelů), které jsou na obrazovce. Dnes nejobvyklejší rozlišení, používané u 17palcoých (17') monitorů, je 1024 x 768 bodů. Pokud si změníte jeho rozměry, převedete na palce a vydělíte, dojdete k výsledku, že monitor má rozlišení asi 90 DPI, Běžná tiskárna pak tiskne obrázky v rozlišení DPI. Potřebuje tedy na jednotku vzdálenosti více bodů než monitor, z toho plyne, že obrázky vložené do textu musíte pouze zmenšovat, aby se zvýšilo jejich rozlišení, Monitory počítačů se vyvíjejí a mění a bohužel nezobrazují všechny stejný počet bodů. Starší 15palcové monitory zobrazovali většinou 800 x 600bodů, 17 palcové 1024 x 768, LCD panely 1240 x 1024 bodů. Ale tento počet bodů je možné nastavit i na 15 palcovém monitoru a na 17 palcovém třeba i 1600 x 1200 bodů, Digitální fotoaparáty produkují obrázky podle počtu bodů jejich snímače, např. fotoaparát s 3 megapixelovým (3 Mpx) snímačem obrázky x bodů, 4 Mpx x bodů, 7 Mpx x bodů. Je to tedy (mnohem) více, než je potřeba pro jejich zobrazení na monitoru, velký počet bodů využijeme pouze při tisku ve velkém formátu. Obr. 3.2 Zobrazení obrázku 1024 x 768 na monitoru a při tlačení 27
28 Obr. 3.3 Zobrazení obrázku o rozměru 800 x 600 na různych typech monitorů Obr. 3.4 Různy počet DPI pro jeden obrázek Barevná hloubka Již víte, že bodů musí mít obrázek tolik, aby při požadované velikosti měl rozlišení potřebné ke kvalitnímu tisku, tj. zhruba 300 DPI. S počtem barev je to podobné. Opět jich musí být přiměřeně. Každý z jednotlivých bodů barevného obrázku může nabývat jednu z barev zvolené barevné palety. Nejčastěji se dnes používá paleta RGB barev, která obsahuje 16,7 milionů barev a paleta 256 stupňů šedi, která se používá pro černobílé fotografie. Na webu se pak setkáme s paletou 256 barev, která se používá pro tlačítka, linky apod., prostě pro pomocnou grafiku, nikoliv pro fotografie. Černobílá fotografie pak není jen černobílá, obsahuje, jak již bylo řečeno, 256 odstínů šedi, tj. od světloučce šedé až po šedočernou - obr Obr. 3.5 Paleta šedi 28
29 4. Palety Obrazová data, která mají hloubku více než jeden bit na pixel, se často ukládají pomocí palety. Paleta (mapa barev, indexová mapa, tabulka barev) je jednorozměrné pole hodnot barev. Grafický soubor s paletou potom obsahuje nejprve popis palety a potom teprve vlastní data, kde jsou barvy určeny indexem do palety obr V některých případech je lepší ukládat data jako indexy do palety, v jiných je lepší ukládat hodnotu barvy přímo. Pro obrazové předlohy, které obsahují nejvýše 256 barev (grafy, schémata, ale i některé obrazové předlohy), je vhodnější ukládání pres paletu, protože se tím výrazně zmenší velikost souboru. Pro pravé barvy se paleta neužívá. Obr. 4.1 Použití palety na zobrazení barev Typy palet Paleta univerzální paleta (256 barev). Barvy se skládají kombinací z 8 odstínu červené (3 bity), 8 odstínu zelené (3 bity) a 4 odstínu modré (2 bity). Na obr. 4.2 je vidět část paletových barev. Obr. 4.2 Paleta pro model RGB 29
30 Paleta (252 barev) zohledňuje různou citlivost oka na barevné složky základní barvy jsou: 7 odstínu červené, 12 odstínu zelené, 3 odstíny modré. Adaptovaná paleta je paleta optimalizovaná na jeden konkrétní obrázek. Paleta se určuje podle barev, které se v obrázku vyskytují. Výpočet palety bývá časově náročný, ale výsledek muže výrazně snížit velikost souboru, protože není třeba ukládat v pravých barvách. Možností, jak vybrat v barvách obrázku množství barev potřebné do palety (nejčastěji 256), je mnoho. Základní metody konstrukce palety jsou dvě: shora dolu vybíráme z množiny použitých barev tak dlouho, až dostaneme požadovaný počet barev (třeba podle četnosti jednotlivých odstínu), zdola nahoru sdružují se příbuzné barvy do skupin, dokud nemáme požadovaný počet skupin. Poznámka: Velikost výsledného souboru při ukládání obrázku muže být opravdu velmi podstatná. Např. při vytváření obrázku do webových stránek byste měli na tuto skutečnost myslet. Čím je vetší velikost souboru s obrázkem, tím je pomalejší jeho zobrazování ve stránce a navíc mnohdy zbytečně zatěžuje sít. Dokladem toho, jak tvůrci stránek tuto skutečnost podceňují, jsou často stránky, na kterých je větší množství obrázku v náhledové velikosti". Teprve po kliknutí na náhled se otvírá obrázek ve skutečné velikosti. Správně by v této situaci mely být nachystány obrázky dva jeden malý (velikostí i počtem barev) pro náhled a druhý vetší a kvalitnější pro případné následné zobrazení. Pokud tvůrci stránek neuvažují a malý obrázek dostanou tak, že jen zmenší obrázek až ve webové stránce, tak zcela zbytečně stahujete množství dat navíc. V tab. 4.1 je ukázka rozdílu ve velikosti souboru při uložení nascanované fotografie. Jednou bylo scanováno s rozlišením 100 dpi, podruhé s rozlišením 200 dpi. Tab. 4.1 Ilustrativní údaje o paměťové náročnosti Ukázky na obr. 4.3 předvádějí, jak budou vypadat výsledky ukládání s různými nastaveními palet. Rozdíl mezi uložením v pravých barvách a v adaptované palete je minimální. Z toho je vidět, že pro předlohy, které neobsahují celou škálu barev, lze adaptovanou paletu s úspěchem použít. 30
31 Obr. 4.3 Použití adaptované palety při ukládání souboru 31
32 5. Formáty pro ukládání grafické informace Formáty pro ukládání grafické informace rozumíme formáty souboru, které obsahují grafická data, stejně jako textové soubory obsahují texty. Grafických formátu je celá rada, liší se podle původu a účelu, ke kterému mají sloužit. Znalost grafických formátu a s tím související znalost programu, které s těmito formáty pracují, nám ušetří mnohé zklamání při práci s grafickými daty. Např. už z podstaty vektorového formátu je nemožné, aby se ve vektorovém editoru dalo efektivně pracovat na úpravách fotografií (měnit jim ostrost, odstíny barev apod.). Stejně tak je ale nemožné v programu, určeném na zpracování rastrové grafiky, kreslit přesné plány budov. Prostě každá oblast grafiky chce svoje. Grafické formáty můžeme rozdělit na následující skupiny: Rastrové (bitmapové) obsahují data jako matici barevných bodu, Vektorové obsahují data jako popis grafických prvku, Metaformáty obsahují rastrové i vektorové části, Scénové, animační a multimediální formáty. V následujícím textu se budeme stručně věnovat rastrovým a vektorovým formátům a základním rozdílům mezi nimi. Zájemce o práci s multimediálními formáty je třeba odkázat na odbornou literaturu. Rastrový obrázek - Rastrové (bitmapové) formáty Rastry (také bitmapy) představují nejčastěji fotografie a také namalované obrázky (např. v programu Malování. Hlavním rysem rastru je, že se skládá z jednotlivých obrazových bodů, tzv. pixelů. Těchto bodů je hodně, jsou velmi malé, v nejlepším případě pro nás neviditelné. Mohou mít různou barvu a výsledkem je pěkná fotografie nebo malba. Fotografie je také taková malba, jen ji nevytváříte vy, ale fotoaparát, opět se skládá z množství barevných bodů, které tvoří výslednou fotografii. Obr. 5.1 Změna přiblížení rastrového obrázku 32
33 Obr. 5.2 Příklad rastrového obrázku (přehnaně zvětšeno) Rastrové formáty ukládají obraz jako posloupnost grafických elementu, bodu, pixelu. Každý pixel má jako svůj atribut barvu. Pro tyto formáty se také často používá název bitmapové (bitmap - bitová mapa). Navíc jeden ze základních rastrových formátu má koncovku.bmp. Podle počtu možných barev rozlišujeme formáty: monochromatické (postihují jen dvě různé barvy), ve stupnici šedi, barevné. Popis každého formátu se skládá z hlavičky, palety (mapy barev) a vlastních rastrových grafických dat. Hlavička muže obsahovat: identifikaci a verzi grafického formátu, informaci o uloženém obrazu, informace určující velikost obrázku jako jsou: rozměry, poměr stran, počet řádku v předloze, počet pixelu na řádku apod., počet bitu pro uložení barevné hodnoty pixelu (tj. počet možných barev), způsob uložení grafických dat například do vzorkovacího řádku (u každého pixelu okamžitě všechny barvy) nebo planární data (nejdřív pro všechny body hodnoty červené, potom zelené ), informace o případné kompresní metodě. Paleta (mapa barev) slouží k zajištění nezávislosti grafického formátu na technickém vybavení. Popisuje, jakým způsobem se má hodnota abstraktní barvy (popsané číslem) zobrazit na konkrétním zařízení. O paletách viz výše. 33
34 Rastrová data - Zde jsou uloženy informace o barvě jednotlivých pixelu obrazu (nejčastěji v modelu RGB). Způsob uložení dat se podle jednotlivých formátu liší. K tomu, aby byla data správně interpretována, jsou potřebné údaje z hlavičky. Každý bit popisuje stav jednoho pixelu, např. tak, že hodnota 0 znamená černou barvu a hodnota 1 barvu bílou. Tímto způsobem lze naprosto obecně popsat libovolný rastrový černobílý obrázek, Podobně utvořenou bitmapu lze použit i pro jiné účely např. pro popis tvaru rovinného obrazce. Hodnota 0 v tomto případě znamená, že daný pixel leží vně obrazce, hodnota 1 znamená, že pixel leží uvnitř obrazce. Opět lze takovým způsobem naprosto obecně vyjádřit libovolný rovinný obrazec, pochopitelně s přesností danou velikostí jednoho pixelu. V obecnějším případě může bitmapa u každého pixelu obsahovat více informaci, než jen jeden bit. Typicky může být u každého pixelu popsána jeho barva. Pro popis barvy pixelu můžeme použít výše popsaný model RGB s barevným rozlišením 256 stupňů v každé z os barevného modelu, tedy tzv. True Color. Tím pádem potřebujeme pro popis každého pixelu 3 byty, říkáme, že obrázek má barevnou hloubku 3 byty či 24 bitů. Každý pixel může mít jednu z barev. Takovýto způsob popisu rastrového obrázku spolu s jistou pevně danou a nepříliš velkou hlavičkou souboru, používá rastrový grafický formát BMP využívaný hlavně v operačním systému Windows. Výhodou takového formátu je nesporně jeho jednoduchost. Nevýhodou je často velký objem dat potřebný i pro popis velmi jednoduchého obrázku. Rastrový způsob generování obrazu je určen pro grafická zařízení, která mají kreslicí plochu rozdělenou na pevnou síť bodů a pro každý bod můžeme určit jeho jas a barvu. Obraz se tiskne nebo zobrazuje po řádcích a kvalita kresby je určována velikostí kroku zvolené sítě. Typická výstupní grafická zařízení, která pracují na rastrovém principu, jsou obrazovky personálních počítačů (svou technologií podobné obrazovkám televizním) anebo běžně používané tiskárny. Interpolace úsečky při rastrovém způsobu generování obrazu je ukázána na obr
35 A 2 (x 2, y 2 ) A 1 (x 1, y 1 ) Obr. 5.3 Rastrový způsob generování úsečky (lineární interpolace) Postup lineární interpolace pro rastrový způsob generování obrazu můžeme ukázat na jednoduchém algoritmu. Máme interpolovat úsečku z bodu A 1 (x 1, y 1 ) do bodu A 2 (x 2, y 2 ). Při interpolaci budeme počítat body ležící na interpolované úsečce (nakreslené tečkovaně v obr.4) podle rovnice přímky y = y 1 + k.(x 2 - x 1 ) (5.1) kde směrnici k vypočteme podle vztahu k y x y x (5.2) a vyhledávat takové průsečíky sítě, které leží co nejblíže ideální interpolované úsečce. Popsaný postup můžeme realizovat tak, že budeme nastavovat po krocích sítě tu souřadnici, pro kterou je větší vzdálenost mezi počáteční a koncovou hodnotou (pro obrázek 4 je to souřadnice x, protože x 2 -x 1 > y 2 -y 1 ). Druhou souřadnici potom nastavíme tak, aby bod ležel co nejblíže ideální poloze interpolované úsečky (ponecháme ji jako v předchozím kroku anebo ji také změníme o jeden krok sítě). Uvedený postup můžeme popsat následovným algoritmem: Krok 0 - Zadej hodnoty souřadnic počátečního bodu (x 1, y 1 ) a koncového bodu (x 2, y 2 ). Vypočti diference Dx = x 2 - x 1 a Dy = y 2 - y 1 a hodnotu L = max( Dx, Dy ), která udává počet kroků interpolace, Krok 1 - Vypočti přírůstky na jeden krok Kx = Dx/L a Ky = Dy/L a nastav počáteční hodnoty souřadnic x = x1 a y = y, Krok 2 - Nakresli bod o souřadnicích (round(x), round(y)), kde round(x) znamená zaokrouhlení hodnoty x na nejbližší celé číslo. Zvětši hodnoty x = x+dx a y = y+dy, zmenši počet kroků L = L-1, Krok 3 - Opakuj Krok 2 pokud L 0, jinak interpolaci ukonči. Pro interpolace úseček existuje řada algoritmů, které mohou být realizovány programovými nebo technickými prostředky počítače. V obou případech požadujeme rychlost
36 a efektivnost práce interpolačního algoritmu, protože je velmi často používán a závisí na něm proto i celková rychlost kreslení. Proto se používají algoritmy, které co nejméně používají operace náročné na čas (jako je násobení, dělení, odmocňování, výpočet hodnot trigonometrických funkcí) a spokojí se s jednoduchými a rychlými operacemi jako je sčítání, odečítaní anebo aritmetický posuv. Výše uvedený algoritmus takové požadavky splňuje. Pro zajímavost můžeme uvést, že i kvadratickou interpolaci je možné realizovat podobně pouze použitím operace sčítání, odečítání a logického posuvu bez potřeby použití trigonometrických funkcí, mocnění anebo odmocňování. Na obr. 5.4 je ukázka naprosto vymyšleného formátu, který by mel názorně ukázat, jak se do rastrového souboru uloží obrázek, na kterém je kružnice. Současně by z příkladu mělo být vidět použití palety (čtyřbarevné) k uložení dat. Obr. 5.4 Rastrový formát Z toho, jak rastrová data vypadají, vyplývají výhody, ale také omezení těchto grafických formátu. Klady Jsou speciálně určeny pro ukládání předloh z reálného světa (skenované obrázky, digitální fotografie). Rastrové soubory mohou být snadno vytvářeny z existujících pixelových dat uložených v poli někde v paměti. 36
37 Rastrové hodnoty mohou být modifikovány individuálně nebo po větších množstvích, na těchto modifikacích se muže podílet i paleta. Např. není problém v obrázku najednou vyměnit jednu barvu za jinou. Mohou být snadno přenášeny na rastrová výstupní zařízení. Obrazovka i většina tiskáren pracuje na rastrovém principu. Zápory Jsou většinou velmi rozsáhlé a to zejména tehdy, když je v předloze množství barev. Datová komprese sice muže objem barevných dat zmenšit, ale před dalším použitím musí být data dekomprimována, což snižuje rychlost čtecího a zobrazovacího procesu. Většinou jsou problémy s výraznější změnou jejich velikosti: zmenšení mizí tenké cáry, zvetšení snížení kvality. Při výrazném zvetšení můžeme dostat buďto rozmazané obrázky, nebo zubaté" okraje a cáry. Záleží na tom, jak se při zvetšení dopočítají chybějící pixely. Průhlednost Kromě barvy lze přiřadit jednotlivým pixelům v rastrovém obrázku i další hodnoty. Jednou z nejčastěji používaných hodnot je průhlednost pixelu vyjádřená pomocí veličiny nazývané -kanál. V jednoduchém případě mohou hodnoty být rovné 0, nebo 1. Pixel tedy může být buď zcela průhledný, nebo zcela neprůhledný. Mluvíme pak též o masce průhlednosti. Jednobitová průhlednost se využívá ve variantě RGB modelu nazývané High Color. V této variantě je rezervováno pro každou ze tři barevných složek R, G a B 5 bitů. Existuje tedy 32 stupňů pro každou z těchto tří základních barev. Celkem je k dispozici 32 3 = barev. Pro zakódování těchto barev je zapotřebí 15 bitů. Poslední 16-tý bit pro doplnění do zaokrouhleného počtu 2 bytů je využíván pro hodnotu -kanálu, tedy pro hodnotu průhlednosti pixelu. Jinou, v dnešní době častěji využívanou variantou použití -kanálu, je model nazývaný RGBA. V tomto modelu jsou pro zakódování každého pixelu vyhrazeny 4 byty, tedy 32 bitů. První 3 byty, tedy 24 bitů zachycují jednotlivé barevné složky R, G a B v běžně používaném režimu True Color. Posledních 8 bitů umožňuje uložit 256 stupňů průhlednosti 37
38 pixelů. Pokud na sebe položíme dva obrázky A a B s částečně průhlednými pixely, bude výsledně zobrazená barva spočítána podle vzorce (5.3) kde A a B - hodnoty -kanálů, tedy hodnoty průhlednosti u obrázků A a B, C A a C B - hodnoty barev pixelů v těchto dvou obrázcích, tedy vektory o třech složkách R, G a B. Komprese dat Uvědomme si, že běžný nepříliš kvalitní digitální fotoaparát má rozlišení v řádu jednotek Megapixeiů. Takový fotoaparát produkuje rastrové obrázky s pixelů. Pokud by na zakódování barvy každého pixelu byly potřeba 3 byty, musel by mít výsledný soubor velikost přibližně 24 Megabytů. Pokud bychom obrázek opravdu uložili ve formátu BMP, k podobnému číslu bychom se dostali. Pro běžnou nepříliš kvalitní digitální fotografii je to však příliš velké množství dat. Množství dat potřebných pro uložení rastrového obrázku lze obvykle dost výrazně snížit pomocí algoritmů pro kompresi dat. V zásadě existují dva typy kompresních algoritmů: Bezztrátové kompresní algoritmy se pokouší zmenšit velikost souboru potřebného pro uložení dat, aniž by došlo ke ztrátě informace o obrázku. Původní obrázek tedy lze zcela přesně zrekonstruovat i ze zkomprimovaného souboru. Bezztrátové kompresní algoritmy se obvykle pokouší objevit v souboru jisté pravidelnosti a ty využit pro zmenšení množství dat. Pokud se pravidelnosti objevit nepodaří, může se stát, že bezztrátový kompresní algoritmus selže a velikost souboru vůbec nezmenší. V extrémním případě se může dokonce i zvětšit, neboť kompresní algoritmus požaduje uložení jistých režijních informací v hlavičce souboru, Ztrátové kompresní algoritmy počítají s tím, že se část informací o obrázku při kompresi ztratí, Ze zkomprimovaného souboru tedy už nepůjde obrázek v původní podobě rekonstruovat. Pokud však bude ztrátový kompresní algoritmus použit rozumným způsobem, může se stát, že změny, ke kterým v obrázku došlo, nebudou lidským okem vůbec postřehnutelné, nebo budou postřehnutelné jen s velkými obtížemi. Na druhou 38
39 stranu ztrátové kompresní algoritmy jsou schopny zaručit zmenšení velikosti souboru v každém případě, tedy pro jakýkoliv obrázek. Nejjednodušším a historicky nejstarším algoritmem bezztrátové komprese dat je metoda Run Length (RLM - Run Length Method, RLE - Run Length Encoding). Tato metoda je založena na prohledávání obrázku, tedy souboru pixeíů, po řádcích. Pokud bude nalezeno za sebou dva nebo více pixelů stejné barvy, nebude informace o této barvě pokaždé znovu opakována. Bude pouze poznamenáno, na kolika pixelech se barva opakuje a pak bude pouze jednou tato barva uvedena. Kompresní metoda RLM je v dnešní době již překonána a nepoužívá ji žádný ze současných běžných formátů rastrové počítačové grafiky. Z historických formátů, které metodu RLM používaly, je nejznámější formát PCX (Picture Exchange Format) používaný např. programem Paint Brush. Kompresní metoda RLM zafunguje dobře pouze v případě obrázků, které po řádcích obsahují dlouhé jednobarevné posloupnosti pixelů. Typickými představiteli takových obrázků jsou obrázky s málo barvami, např. černobílé perokresby, nebo nascanované stránky textu. Převedeme-li takovýto obrázek z formátu BMP do formátu PCX, velikost souboru se může někdy i velmi podstatně zmenšit. Naproti tomu je metoda RLM nevhodná pro obrázky, které obsahují velké množství barevných odstínů a spojité přechody mezi nimi. Typickým příkladem takového obrázku je digitální fotografie, zvláště pak fotografie exteriéru. Při převodu takového obrázku z formátu BMP do formátu PCX se velikost souboru obvykle nezmenší' naopak se může i zvětšit, neboť kompresní algoritmus RLM vyžaduje jistou režii, která se projeví ve zvětšení hlavičky souboru. Vyšším a v současnosti častěji používaným způsobem bezztrátové komprese dat jsou komprese slovníkové. Tyto kompresní algoritmy vyhledávají v souboru opakující se vzory, v případě rastrového obrázku tedy opakující se posloupnosti střídání barev. V závislosti na konkrétním algoritmu je možné takové vzory hledat po řádcích, podobně jako v případě metody RLM, po sloupcích obrázku, nebo ještě jinými kombinovanými způsoby. Pokud je nějaký opakující se vzor nalezen, je uložen do slovníku a při jeho dalším výskytu je použit místo nového kompletního popisu vzoru pouze odkaz do tohoto slovníku. Na obr. 1.9 je na jednoduchém školním příkladě vidět zápis černobílé bitmapy bez použití kompresního algoritmu, při použití komprese RLM a při použití jednoduché varianty slovníkové komprese. Slovníkové komprese se běžně používají i pro komprimování jiných souborů, než rastrových obrázků. Mezi nejznámější konkrétní algoritmy slovníkových kompresí patří algoritmus LZW 39
40 (pojmenovaný podle jeho tvůrců Lempel, Zip, Welch) a jeho varianty, např. LZ77. Z dalších složitějších a modernějších algoritmů slovníkových kompresí lze jmenovat Huffmannovo kódování, nebo aritmetické kódování. Z kompresních programů a formátů mimo oblast počítačové grafiky, které používají různé varianty slovníkové komprese, lze jmenovat např. formáty ZIP, ARJ, či RAR. Obr. 5.5 Kompresní metody Úpravy rastrových obrázků Programy pro úpravu rastrových obrázků umožňují obvykle velké množství jejich úprav. Úpravy lze rozdělit na geometrické a na úpravy barev pixelů. Při geometrických úpravách se nemění barevné hodnoty jednotlivých pixelů, pouze se mění jejich uspořádání. Geometrické úpravy Nejjednoduššími geometrickými úpravami je otočení, či překlopení obrázku. U těchto úprav nedochází k žádné změně obsahu jednotlivých pixelů, dojde pouze k jejich přeuspořádání. V případě rozsáhlých obrázků, obsahujících několik milionů pixelů může ovšem takovéto jejich přeuspořádáni být časově poměrně dost náročné. Při přeuspořádání pixelů za účelem otočení obrázku se nesmí zapomenout na změnu rozměrů obrázku. Rozměry obrázku bývají umístěny v jeho hlavičce. Další jednoduchou geometrickou úpravou je ořezání obrázku do tvaru obdélníka, popřípadě podle nějakého složitějšího tvaru. Při ořezaní do tvaru obdélníka dojde opět ke změně rozměrů obrázku a následně k vypuštění pixelů, které leží mimo hranice ořezávací oblasti. Ořezání pomocí složitějších tvarů obvykle není možné řešit přímo. Naprostá většina formátů rastrové grafiky totiž umožňuje ukládat pouze obrázky 40
41 obdélníkového tvaru. Při ořezání pomocí složitějšího tvaru je nutné obrázek doplnit do opsaného trojúhelníka pomocí pixelů v barvě pozadí, tedy obvykle pomocí pixelů bílých. Pokud používáme -kanál pro zachycení průhlednosti lze tyto okrajové pixely též u]ožit jako zcela průhledné. Obr. 5.6 Otočení obrázku o 90 stupňů Zvétšování a zmenšování Zvětšování a zmenšování rastrového obrázku je další častou úpravou. Algoritmicky je jednodušší řešit zmenšování obrázku. Pokud zmenšíme rozměr obrázku např. na polovinu, zobrazí se vždy 4 pixely původního obrázku do jednoho pixelu výsledného obrázku. Barvu tohoto výsledného pixelu lze spočítat jako aritmetický průměr barev čtyř původních pixelů. Při zvětšování obrázku je naopak jeden pixel původního obrázku nahrazen maticí pixelů v novém obrázku. Jednoduchý postup by radil, aby všechny tyto nové pixelu měly stejnou barvu. Tím by ovšem vznikl v obrázku nežádoucí jev nazývaný alias. Alias se projevuje např. vznikem zubatých okrajů původně rovných okrajů ploch. Metody nazývané antialiasing se pokouší tento jev odstranit. Důsledkem antialisingu je rozmazání takto vzniklých zubatých okrajů. Při antialisingu se do barvy výsledných pixelů promítá nejen barva pixelu původního, jehož zvětšením nové pixely vznikly, ale v určitém poměru i barvy pixelů okolních. Poměry vlivu jednotlivých pixelů na barvu výsledku jsou odvozeny z Fourierovy transformace. Praktický výpočet spočívá v přenásobení vzniklého obrazu vhodnou filtrační maticí, která způsobí rozmazání obrazu. 41
42 Obr. 5.7 Princip zmenšování obrázku na 10% Obr. 5.8 Původní obrázek Obr. 5.9 Detail zvětšeného obrázku Obr Detail zvětšeného obrázku při použití antialiasingu 42
43 Warping a morphing Warping a morphing jsou zajímavé úpravy rastrových obrázků, které vedou ke vzniku různých efektů. Warping je ve své podstatě úprava geometrická. Jednotlivé pixely se v něm přesouvají na nová místa. Tento přesun ovšem není jednoduše popsatelný jako např. v případě otáčení obrázků. Warping obrázku bývá popsán pomocí soustavy čar nazývané síť Warpingu. Body na síti warpingu v původním obrázku mají svůj obraz v bodech na síti warpingu v obrázku výsledném. Ostatní body jsou přemístěny pomocí bilineární aproximace podle jejich polohy. Obvykle se jako jedna ze síti warpingu volí pravidelná čtvercová síť. Warping lze použít globálně pro celý obrázek. Tím dojde k jeho zajímavému pokroucení, jako by byl obrázek zobrazen v křivém zrcadle. Warping lze též použít pouze na malou část obrázku, např. pro úpravu portrétu osoby. Morphing znamená obecně přeměnu jednoho objektu v druhý. V rastrové počítačové grafice je pojmem morphing míněna postupná přeměna jednoho obrázku v druhý. Morphing lze popsat pomocí parametrické rovnice (5.4) kde C A - barva určitého pixelu v původním obrázku, C B - barva pixelu ve výsledném obrázku, C(t) - barva tohoto pixelu v morphingovém obrázku pro hodnotu parametru t. Při morphingu je obvykle vygenerována posloupnost obrázků pro určité vzorky hodnot parametru t rostoucí po jistém pevně daném kroku. Např. pro krok 0,25 budou kromě dvou okrajových obrázků vygenerovány 3 přechodové morphingové obrázky. Obr Využití warpingu pro úpravu fotografie 43
44 Obr Použití Morphingu t=0 Obr Použití Morphingu t=0,25 Obr Použití Morphingu t=0,5 44
45 Obr Použití Morphingu t=0,75 Obr Použití Morphingu t=1 Obr Původní obrázek Histogram jasu a barevného rozložení Mnoho úprav rastrových obrázků a speciálně digitálních fotografií nemění polohu samotných pixelů ale pracuje pouze s jejich barevností. Smyslem takovýchto úprav je jisté 45
46 vylepšení fotografie, jejíž výsledný dojem byl pokažen např. špatnou expozicí. Odvěkým sporem, který se potáhne i do budoucnosti, je otázka, zda se mají u fotografií takovéto úpravy vůbec dělat. Tento spor je však spíše sporem uměleckým, než technickým. Každopádně technické metody pro úpravu barevnosti pixelů existují a naprostá většina programů pro úpravu rastrových obrázků tyto metody nabízí. Výchozí informací pro zhodnocení dojmu, který na člověka obrázek dělá, může být histogram barevného rozložení jeho pixelů. Má-li obrázek řádově miliony pixelů, nelze zkoumat každý pixel samostatně. Je však možné zkoumat histogram výskytu některých hodnot v obrázku a na jeho základě se rozhodnout pro jisté úpravy. Nejjednoduššími histogramy jsou histogramy výskytu jednotlivých barevných složek R, G a B. Pokud používáme režim True Color, může každá z těchto barevných složek nabývat 256-ti různých hodnot. Počet pixelů, které nabývají konkrétní hodnotu v nějakém pixelu obrázku je v histogramu zachycen výškou příslušného sloupce. Lidské oko vnímá jako nejpříjemnější obrázky s relativně stejnou hustotou výskytu všech barevných složek. Přidáním některé barevné složky na úkor jiné lze dosáhnout jistých psychologických efektů. Např. modrá barva je chápána jako barva studená, smutná a naopak barva červená jako barva jasná, žívá. Je na místě poznamenat, že se v těchto případech nejedná jen o fyziologický vjem, ale i o kulturní kontext, ve kterém se nachází člověk, který obrázek vnímá. Význam barev pro vyznavače jiných náboženství, než křesťanství, je často oproti jejich běžně chápanému významu v západním světě posunut. Změny jasu K zásadnějším rozhodnutím a úpravám obvykle vede vyhodnocení a případné změny jasu pixelu. Jas pixelu je definován již výše uvedenou rovnicí (5.5) Pokud používáme model True Color, tedy pokud hodnoty R, G a B leží v intervalu <0, 255>, budou i výsledné hodnoty jasu v intervalu <0, 255>. Lidské oko opět nejpříjemněji vnímá obrázky, u kterých jsou relativně stejně zastoupené všechny odstíny jasu. U mnoha nepovedených digitálních fotografii dochází především z důvodů špatné expozice k převaze jasových tónů v jedné části histogramu. Lidské oko navíc špatně rozeznává barevné odstíny u příliš tmavých, nebo u příliš světlých barev. Situace, kdy se v obrázku vyskytuje mnoho jasových odstínů v krajních částech jasového intervalu má za důsledek i fakt, že lidské oko 46
47 nerozezná v těchto částech fotografie tolik detailů. V některých případech lze takovéto obrázky upravit, či vylepšit změnou hodnoty jasu jednotlivých pixelů. Změna hodnoty jasu se dá provádět podle různých funkcí. Nejjednodušší je prosté přidání či ubrání jasu pomocí přičtení dané konstanty. Na obrázcích jsou vidět jasové grafy takovýchto úprav. Na vodorovné ose je původní jas pixelu v rozsahu od 0 do 255, na svislé ose pak výsledný jas pixelu v témže intervalu. Vidíme, že při prostém zvětšení jasu z obrázku zcela zmizí nejméně jasné tóny. Výsledný obrázek tedy neobsahuje vůbec černou barvu ani barvy k ní blízké. Naopak některé odstíny barev blízkých barvě bílé budou zaokrouhleny přímo na bílou barvu. Ve většině případů není prostá změna jasu vhodnou metodou pro úpravu obrázku. Další, někdy vhodnější a často používanou metodou je zvětšení kontrastu obrázku. Při zvětšení kontrastu s pevným bodem 1/2 budou všechny pixely s jasem menším než 1/2 (respektive 128) ztmaveny a všechny pixely s jasem větším zesvětleny. V šedivém obrázku s nejasnými hranicemi objektů tak tyto hranice lépe vyniknou. Naopak při snižování kontrastu budou tmavé pixely zesvětleny a světlé ztmaveny. Snížení kontrastu je vhodné použít, pokud je v histogramu jasu mnoho hodnot v krajních částech intervalu <0, 255> a málo hodnot poblíž jeho středu. Pro zesvětlení či ztmaveni obrázku je často vhodné namísto prostého zvětšení či zmenšení hodnot jasu použít úpravu nazývanou -korekce. Při -torekci je jas pixelu upraven pomocí tak zvané funkce. Její nejjednodušší vyjádření je 1 / Y Y (5.6) Symbol Y označuje původní jas pixelu vyjádřený jako hodnota z intervalu <0, 1), / Y je výsledný jas pixelu vyjádřený jako hodnota z téhož intervalu. Pokud je původní jas vyjádřen jako hodnota z intervalu < 0,255), je třeba jej nejprve podělit hodnotou 255 a po převedení pomocí funkce opět tuto hodnotou vynásobit. Pro hodnoty > 1 dojde k zesvětlení obrázku, pro hodnoty < 1 k jeho ztmavení. Přitom pro jasovou hodnotu Y =0 dostaneme / Y =0. Černá barva bude tedy i po korekci zachována. Podobně zůstane zachována i barva bílá. Nejvíce zesvětleny nebo ztmaveny budou barvy se středním odstínem jasu. U mnoha poexponovaných či přeexponovaných fotografií je korekce úprava, která jejich výsledný dojem vylepší, nebo alespoň trochu napraví. 47
48 Obr Histogram jasu pro původní obrázek Obr Graf pro ubírání jasu Obr Graf pro přidávaní jasu Obr Obrázek po prostém přidání jasu Obr Histogram po prostém přidání jasu Obr Graf pro přidání kontrastu 48
49 Obr Graf pro ubrání kontrastu Obr Obrázek po přidání kontrastu Obr Histogram po přidání kontrastu Obr Graf pro korekci s parametrem 2,5 Obr Obrázek po zesvětlení pomocí -korekce Obr Histogram po zesvětlení pomocí -korekce 49
50 Redukce počtu barev Častou praktickou úlohou v rastrové počítačové grafice je redukování počtu barev, pomocí nichž je obrázek vytvořen. Důvodem pro takovou redukci mohou být např. požadavky formátu, do kterého chceme obrázek uložit. Typickým příkladem je formát GIF, který umožňuje použití pouze 256 barev podle adaptivní barevné palety. Jiným důvodem pro redukci počtu barev v obrázku mohou být možnosti výstupního zařízeni, na kterém chceme obrázek zobrazit. Typický může být převod barevného obrázku na černobílý (pixely mohou mít jen dvě hodnoty 0=černá, 1=bílá) při jeho tisku na černobílé tiskárně. Své opodstatnění má i převod obrázku do stupní šedi - obvyk e 256 barev, stupňů šedi, ležících na tělesové úhlopříčce krychle RGB - nebo převod obrázku do pevné barevné palety 3bity x 3bity x2bity, tedy do 256 předem pevně daných barev. Převod do stupňů šedi Převod do stupňů šedi je algoritmicky poměrně jednoduchá úloha. Obrázek lze zpracovávat bezkontextově. To znamená, že výsledná barva (stupeň šedi) pixelu závisí pouze na původní barvě tohoto pixelu a ne na dalších okolnostech, např. na barvách jeho sousedů. Pokud používáme běžnou True Color paletu, tedy 8 bitů x 8bitů x 8bitů = 256 x 256 x 256 barev = barev, je logické, aby po převodu do odstínů šedi obrázek obsahoval 256 odstínů šedi. Hodnotou, podle které se rozhodneme o stupni šedi daného konkrétního pixelu, je jeho jas. Nejjednodušší b y bylo definovat jas jako průměr hodnot jednotlivých barevných složek R, G, B. V tom případě by černá barva měla minimální jas 0, bílá barva maximální jas 255, jednotlivé tři základní barvy R, G, B by měly jas 255/3 =85, odvozené barvy C, M, Y by měly jas 2/3 x 256 = 170. Ukazuje se, že tento přístup není příliš vhodný, jelikož lidské oko je různě citlivé na jas jednotlivých barevných složek. Vnímání jasu jednotlivých barevných složek je sice mírně subjektivní záležitost, ale běžné lidské oko vnímá zelenou barvu jako nejsvětlejší a modrou jako nejtmavší. Je tedy vhodné jas barvy nechápat jako pouhý součet hodnot jednotlivých barevných složek, ale jako jejich vážený součet, ve kterém bude mít barva zelená váhu největší a barva modrá váhu nejmenší. Podle expertní skupiny John Photopgraph Expert Group (JPEG) při mezinárodní standardizační organizaci ISO je vhodnou definicí jasu barvy vzorec (5.7) 50
51 Pokud budeme hodnoty jednotlivých barevných složek chápat jako hodnoty z intervalu <0, 255> a hodnoty výsledného jasu barvy, tedy stupně šedi též jako hodnoty z intervalu <0, 255), dostaneme pro základní barvy tyto stupně šedi tab Tab. 5.2 Stupně šědi Převod na černobílý obrázek Nejjednodušším způsobem, jak převést obrázek barevný, anebo obrázek ve stupních šedi, na obrázek černobílý je metoda prostého zaokrouhlení jasu. Pokud se jedná o barevný obrázek, bude nejprve postupem popsaným v předcházející části převeden na obrázek ve stupních šedi. Po té bude provedeno prosté zaokrouhlení, tedy rozhodnutí podle prvního bitu vyjádření stupně šedi. Pro hodnoty jasu menší než 128 bude pixelu přiřazena barva černá, pro hodnoty jasu větší nebo rovné 128 mu bude přiřazena barva bílá. Tento výpočet je velmi rychlý. Ve většině případů však výsledky nejsou příliš dobré. Lidské oko totiž nevnímá jas každého pixelu samostatně, ale vnímá vždy určitou skupinu pixelů v jistém okolí společně a podle průměrného jasu této skupiny si utváří svůj vjem. Výše popsaná metoda tuto schopnost lidského oka nebere do úvahy. Jak je vidět na obrázku, výsledek převodu na černobílý obrázek pomocí prostého zaokrouhlení hodnot jasu, může být a často bývá katastrofální. Jedinými typy obrázků, kde lze podobnou metodu doporučit, jsou obrázky s velkým jasovým kontrastem, tedy např. perokresby, nebo nascanovaný text. Z výše uvedeného příkladu vyplývá, že pro převod barevného obrázku na černobílý je vhodné použít složitější metody, než pouhé zaokrouhlení hodnot jasu. První krok, převod na obrázek ve stupních šedi,je u většiny používaných metod společný. Metoda polotónování (Half Tonning), někdy též nazývaná metoda maticového rozptylování, používá základní myšlenku, podle které bude jeden pixel v obrázku ve stupních šedi nahrazen maticí více 51
52 pixelů v černobílém obrázku. V této matici pak bude bíle vybarven takový počet pixelů, kolik odpovídá stupni šedi pixelu původního. Nejjednodušším případem polotónování je nahrazeni každého pixelu obrázku ve stupních šedi maticí 16x16 pixelů v černobílém obrázku. Taková matice obsahuje 256 hodnot a je tedy možné každý jednotlivý stupeň šedi vyjádřit jinou maticí. Nevýhodou je, že velikost obrázku se v každé z os souřadnic zvětší 16krát. Respektive, pokud trváme na zachování výsledné velikosti obrázku, což je obvyklá situace, musíme přistoupit na 16-ti násobné snížení jeho rozlišení. Kompromisem může být použití matic velikost 8x8, které umožní vyjádřit 64 stupňů šedi, matic velikosti 4x4, které umožní vyjádřit 16 stupňů šedi, či matic velikosti 2x2, které umožní vyjádřit 4 stupně šedi. Polotónovací matice nám popisuje, které z pixelů vložené matice máme vybarvit černě při použití příslušného stupně šedi. Např. následující matice velikosti 4x4 popisuje, jak vyplnit vzor v případě, že chci aproximovat pomocí černobílé matice stupně jasu z intervalu <0,16>. Příslušný stupeň šedi udává, kolik pixelů zůstane bílých a kolik jich bude vybarveno černě. V případě jasu 0 budou černě vybarveny všechny pixelu, v případě jasu 16 zůstanou všechny pixely bílé. V případě jasu x 0, 16 vybarvím černě 16 - x pixelů. Budou to ty pixely, které mají v polotónovací matici hodnoty menší než 16 - x. Tak např. pro jas rovný 7 bude vybarveno černě 9 pixelů a výsledná matice, kterou bude jeden pixel původního obrázku nahrazen, bude vypadat takto Poznamenejme, že tvorba vhodných polotónovacích matic není jednoduchou záležitostí. Je totiž třeba zamezit různým nežádoucím optickým efektům, jako je vznik vodorovného, svislého, či úhlopříčného šrafování. Též se ukazuje, že pro různé typy výstupních zařízení je vhodné použít jiné polotónovací matice. Výše uvedená matice je vhodná pro použití na černobílých (či jinak dvoubarevných) monitorech počítačů. Vytváří totiž vzory podobné šachovnici, což je pro uživatele podobných zařízení vhodný vzor. Naopak při tisku na tiskárně by takovýto vzor působil rušivě, a proto by bylo vhodné použít jinou 52
53 polotónovací matici. Mnohé polotónovací matice jsou též předmětem patentů, či součástí firemních tajemství. Obr.5.30 Obrázek po prostém zaokrouhlení na černou a bílou barvu Obr Polotónování Rozptylování Rozptylování (distribuce chyby, dithering) je další metodou pro převod obrázku ve stupních šedi do obrázku černobílého. Odstraňuje základní nevýhodu polotónování, totiž nárůst velikosti obrázku, respektive snížení jeho rozlišení. Jedná se o metodu kontextovou. Pro výpočet výsledné barvy pixelu použijeme nejen jeho původní barvu (jas), ale i informace o barvě (jasu) některých jeho sousedů. Základní myšlenka je podobná jako při metodě prostého zaokrouhlování jasu. Při zaokrouhlení jasu na hodnotu 0, nebo 255 dojde k chybě (s výnimkou extrémních případů, kdy již původní jas měl jednu z hodnot 0, nebo 255). Při metodě prostého zaokrouhlování jasu se tato chyba zapomenula a dále se s ní nepracovalo. Při práci s metodou rozptylování se tato chyba použije pro úpravu jasu některých sousedáních pixelů. Pokud zpracováváme pixely sekvenčně po řádcích, je vhodné, aby se zaokrouhlovací chyba distribuovala mezi pixely, které ještě nebyly zpracovány. Tedy mezi pixely ležící ve stejném řádku napravo od zpracovávaného pixelu a mezi pixely na řádku, či řádcích následujících. 53
54 Jedním z často používaných rozptylovacích algoritmů je algoritmus Floyd- Steinbergův. Podle něj bude 7/16 zaokrouhlovací chyby přičteno k pixelu, který. následuje za zpracovávaným pixelem na stejném řádku (východní soused), 1/16 k sousedu na následujícím řádku o jeden sloupec vlevo (jihozápadní soused), 5 /16 k sousedu o řádek niž ve stejném sloupci (jižní soused) a konečně zbývající 3/16 chyby k sousedu v následujícím řádku o sloupec vpravo (jihovýchodní soused). Pokud při distribuci chyby narazíme na okraj obrázku, chyba se zapomíná podobně jako při metodě prostého zaokrouhlení jasu. Na následujícím příkladě je předveden postup Floyd-Steinbergova rozptylování na oblast uprostřed obrázku. Předpokládáme, že obrázek je již předveden do stupňů šedi a jas jednotlivých pixelů je následující Předpokládejme, že levý pixel v prvním ze zpracovávaných řádků (vyznačený kurzívou) byl již zpracován. Nyní zpracováváme druhý pixel v prvním řádku (vyznačený tučné). Jeho jasová hodnota je 135, tedy více než 128. Pixel bude zaokrouhlen na hodnotu 255, tedy na bílou barvu. Chyba, kterou bude třeba distribuovat je rovna = -120 Podle výše popsaného pravidla bude 7/16 chyby distribuováno k východnímu sousedovi. Ten tedy nabude hodnoty 120-7/16.120=68 Jihozápadní soused bude mít hodnotu 15-1/16.120=8 jižní soused hodnotu 123-5/16.120=86 Konečně jihovýchodní soused by měl mít hodnotu 14-3/16.120=-8 Jelikož ale jas může nabývat hodnot jen z intervalu <0, 255>, bude tomuto pixelu přiřazena jasová hodnota 0, tedy barva černá. Tomuto principu se říká princip zarážky. Po zpracování uvedeného pixelu bude popisovaná část obrázku vypadat následovně 54
55 Obr Floyd-Steinbergovo rozptylování Převod barev do pevné palety Zobecněním situace při převodu barevného obrázku na černobílý je redukce počtu barev obrázku s větším počtem barev do pevné palety s menším počtem barev. Typická situace je např. převod obrázku z režimu True Color, kdy je k dispozici = do palety nazývané 3x3x2. Tato paleta umožňuje uložení 256-ti barev, přičemž v červené a zelené ose je povoleno 8 stupňů a v modré 4 stupně. Pro uložení 1 pixelu pak potřebujeme 8 bitů, tedy 1 byte. Převod lze opět provést prostým zaokrouhlením. Pokud je tedy hodnota barvy původního pixelu v červené ose r, potom výsledná hodnota pixelu bude rovna r int (5.8) 32 / r ose bude platit Tato hodnota se bude pohybovat v intervalu 0, 7. Podobně pro souřadnici v zelené g int (5.9) 32 / g Pro modrou souřadnici pak b int (5.10) 64 / r a hodnota b' se bude pohybovat v intervalu <0,3>. Převod do menší barevné palety prostým zaokrouhlením obvykle nedopadne tak tragicky, jako převod na černobílý obrázek (tedy vlastně do dvouhodnotové palety). Přesto je 55
56 možné a často i užitečné použít při převodu metody podobné jako bylo rozptylování popsané v předchozí části. Např. Floyd-Steinbergův algoritmus lze použít téměř bez úprav i v tomto případě. Jediným rozdílem bude to, že se budou distribuovat tři typy chyb, chyba v souřadnici R, chyba v souřadnici G a chyba v souřadnici B. Obr Obrázek po převodu pomocí F-S algoritmu Vytváření adaptivní barevné palety Použití pevné barevné palety o daném počtu barev má tu nevýhodu, že některé barvy se v obrázku mohou vyskytovat jen velmi zřídka, popřípadě vůbec. Např. fotografie západu slunce na mořské pláži obsahuje mnoho odstínů modré, též nějaké odstíny červené, ale zelená barva se na ni v podstatě nevyskytuje. Přesto je při použití palety 3x3x2 rezervováno pro odstíny zelené dvakrát více místa než pro odstíny modré. V případě této konkrétní fotografie je to plýtvání. Pokud by byla paleta vytvořena adaptivně tak, aby obsahovala více odstínů modré na úkor odstínů zelené, byl by obrázek při použití stejného počtu barev (256) a stejného místa v paměti (1 byte na pixel) uložen mnohem kvalitněji. U obrázků s adaptivní barevnou paletou je v hlavičce souboru popsána právě tato paleta. Na 256-ti řádcích je popsáno 256 (nebo jiný počet) odstínů použitých v paletě způsobem obvyklým v režimu RGB. V těle souboru pak již nebude popsána samotná barva, ale bude zde uveden pouze odkaz do této palety. Paleta může být adaptivní, vytváří se tedy pro každý konkrétní obrázek zvlášť, podle toho, jak obrázek vypadá. Tímto způsobem funguje např. oblíbený formát GIF. Každý konkrétní obrázek obsahuje jenom 256 barev. Tyto barvy však nejsou předem dány, je možné je vybírat z celkového počtu barev obvyklých v obrázcích v režimu True Color. Adaptivní barevná paleta se dá vytvářet různými způsoby'. Obvyklý postup je takový, že se nejprve spočítá histogram výskytu barev. Tedy pro každou barvu použitou v obrázku se 56
57 spočítá četnost jejího výskytu, poté se krychle RGB rozdělí na daný počet (256) kvádrů tak, aby každý kvádr obsahoval přibližně stejný počet pixelů s barvami, které do něj padnou. Pro toto rozdělení se dají použít techniky podobné B-stromům. Krychle se bude dělit vždy podle té barevné osy, ve které je největší rozsah hodnot. Rozdělení bude provedeno podle takové roviny, aby nalevo i napravo od ní byl stejný počet pixelů, popřípadě, aby se tento počet lišit maximálně o 1. Toto dělení se bude rekurzivně opakovat do té doby, než bude krychle RGB rozdělena na předem daný počet oblastí (256). Na závěr zbývá zvolit v každé oblasti jednoho zástupce. Tedy barvu, na kterou se budou všechny ostatní barvy z oblasti zaokrouhlovat. Jako tuto barvu lze volit buď nejčastěji se vyskytující odstín v oblasti, nebo nějakou vypočtenou hodnotu, např. těžiště všech bodů v oblasti. V druhém případě se může stát, že při redukci počtu barev na 256 se v obrázku paradoxně objeví barvy, které se v původním obrázku nevyskytovaly. Po vytvoření adaptivní barevné palety následuje převod všech barev do této palety. Podobně jako v předchozích případech je tento převod možno provést buď prostým zaokrouhlením nebo pomocí rozptylování. Pokud bude použito rozptylování je třeba myslet na to, že při kumulaci chyb může dojít k situaci, kdy dojde k posunu barvy na krajní hodnotu 0, nebo 255. Proto je vhodné při vytváření adaptivní barevné palety do ní napevno vložit 8 vrcholů krychle RGB, tedy barvy W, K, R, G, B, C, M a Y. Výše popsaným způsobem se pak adaptivně vytvoří pouze zbývajících 248 barev palety. Obr Dělení roviny pomocí B-stromu Příklady rastrových formátu: BMP (Microsoft Windows Bitmap) mono, 4, 8, 24 bity; vytvořen pro Microsoft Windows, chybí mu dobré kompresní schéma, nehodí se pro ukládání dat s velkou barevnou 57
58 hloubkou a pestrostí (je velký), GIF (Graphics Interchange Format) univerzální, hojně využíván v internetu, barevné obrázky, rychlý, snadno citelný, umí průhlednou" barvu, lze vytvářet animované obrázky, JPEG, JPG (Joint Photographic experts Group) metoda pro přenos grafických údajů a současně i název formátu, zejména pro programy manipulující s grafikou, užívaný v internetu pro předlohy z reálného světa (fotografie), má ztrátovou komprimační metodu, Obr Sekvenční postup JPEG komprese PCX není univerzální, rozšířený v DOS-ovském" světe. Nemá příliš dobrou kompresi, TIFF se užívá převážně v typografii, příliš nezávisí na platformě, generují ho skenery, rozmanitý formát někdy přináší problémy (mnoho různých verzí). Okno rastrového programu Rastrový program zpravidla obsahuje panel nástrojů (toolbox), na kterém najdete vše, co k malování potřebujete. Vše je asi hodně nepřesné slovo, protože nabídky programů se poměrně hodně liší, ale základní nástroje najdete stejné ve většině programů. A protože malování obrázků je vlastně umění, je to s ním stejné jako u většiny uměleckých činností: někomu stačí pár nástrojů k pěkným obrázkům, jinému ani sebedokonalejší program k výbornému výsledku nepomůže. Obr ukazuje nástroje programu Malování, který najdete 58
59 v příslušenství systémů Windows Start/Programy/Příslušenství/Malování. Vpravo je pak okno nástrojů pokročilého grafického proglamu Gimp, který bývá součástí distribucí systému Linux. Postup při vytváření obrázku: Přípravné práce o Načrtněte si celý obrázek na papír, o Rozmyslete si potřebnou velikost plátna, o Nastavte velikost plátna s obrázkem a barevnost obrázku. Rozměry zvolte malé, pro zkušební účely stačí cca 800 X 600 bodů, o Uložte dokument na disk na zvolené místo pod (dobře) zvoleným názvem. V průběhu další práce pravidelně ukládejte obrázek na dlsk, o Pomocí uvedených nástrojů programu namalujte obrázek, Použití nástrojů programu (Malování), pracujte tak, že: o vyberte (myší) nástroj, o nastavte vlastnosti tohoto nástroje (např. šířku stopy) na panelu vlastností, o vyberte barvu nástroje, o malujte, případně použijte lupu k přiblížení obrázku při malování. Program Malování nedisponuje příliš velkým počtem nástrojů. Chybí mu také širší možnosti nastavení vlastností nástrojů. Pokud to myslíte s vytvářením vlastních maleb vážně, je třeba sáhnout po jiném programu. A jestliže si chcete opravdu vyhrát je nutné zakoupit tablet, což je elektronické pero s podložkou, které umožňuje kreslit mnohem lépe než myš. S tabletem pak většinou získáte i několik programů určených na malování obrázků. Obr Okno rastrového programu, levý W-M, pravý - Gimp 59
60 Obr Příklad použití tabletu Vektorové formáty -Vektorový obrázek O vektorové počítačové grafice hovoříme tehdy, pokud nezachycujeme výsledný vzhled dvourozměrného obrázku, ale pouze způsob, jakým obrázek vznikl. Základním pojmem ve vektorové počítačové grafice je entita. Jednoduché entity mohou být geometrické úsečka, kružnice, složitější křivka,.... Ve složitějších případech může být entitou pro vektorový obrázek i poměrně komplikovaný objekt. Např. v profesním systému pro podporu projektování ve stavebnictví, což je v zásadě též program vektorové počítačové grafiky, mohou být entitou celé vstupní dveře objektu včetně svého způsobu provedení, svých rozměrů, ceny, tepelně izolačních vlastností a mnoha dalších parametrů. Vektorové objekty nejsou tvořeny jednotlivými body, ale křivkami. Je proto možné je téměř libovolně zvětšovat a zmenšovat. Rastr je ve vektorové kresbě pouze jedním z použitelných objektů. Obr Vektorový obrázek 60
61 Jednoduché entity Nejjednodušší a zároveň jedinou bezrozměrnou entitou vektorové počítačové grafiky je bod. Pro zadání bodu v rovině je třeba zadat jeho dvě souřadnice (x, y). O bodech říkáme, že nemají topologii. Nemohou totiž být spolu v žádné jiné souvislosti, než jaká vyplývá bezprostředně z jejich souřadnic. Dva body mohou být od sebe daleko nebo blízko nemohou však spolu např. sousedit nebo na sebe navazovat. Základní a pravděpodobně nejčastější vektorovou entitou je úsečka. Její nejjednodušší zadání je pomocí dvou krajních bodů, tedy pomocí čtyř souřadnic (x 1, y 1 ) a (x 2, y 2 ). Úsečku lze však zadávat i jinými způsoby. Např. pomocí počátečního bodu (x 1, y 1 ) a pomocí rozdílu souřadnic x, y kde x x 2 x 1 a y y 2 y1 (5.11) nebo pomocí počátečního bodu (x 1, y 1 ), délky úsečky a azimutu úsečky, tedy úhlu který sečka svírá s kladným směrem osy y (směrem na sever). Matematicky lze úsečku vyjádřit parametrickým způsobem (5.12) kde t - parametr z intervalu Obr Způsoby zadání úsečky 61
62 Obr Vznik elipsy jako průsečíku roviny a plášte dvoukužele Při vyjádření implicitní rovnicí (5.13) vektor (a, b) představuje vektor kolmý k úsečce (může tedy být např. a, b ). y x Směrnicové vyjádření úsečky zní (5.14) kde y k - směrnice úsečky, tady tangenta úhlu sevřeného úsečkou a kladnou x poloosou osy x. Směrnicovým tvarem nelze vyjádřit úsečky rovnoběžné s osou y. Ve většině vektorových kreslících programů jsou dále s dispozici různé typy křivek nazývaných kuželosečky. Kuželosečky mohou vzniknout jako průsečík pláště dvojitého kužele a roviny. Jejich obecná implicitní rovnice je kvadratická, tedy kuželoseček. (5.15) V závislosti na vzájemném vztahu koeficientů a, b, c, d, e a f dostaneme různé typy Nejjednodušší kuželosečkou je kružnice. Kružnice je obvykle zadána pomocí svého středu x 0, y 0 a poloměru r. Její implicitní rovnice pak zní (5.16) Po rozepsání tohoto vztahu je patrné, že se jedná o specielní případ obecné rovnice kuželosečky. Pro kružnici se středem v počátku souřadnic (0,0) se rovnice zjednoduší na 62
63 (5.17) a pro jednotkovou kružnici s poloměrem 1 pak na (5.18) Parametricky lze obecnou kružnici vyjádřit pomocí goniometrických funkcí (5.19) Kreslící programy umožňují uživatelům obvykle i jiné metody zadání kružnice Pomocí středu a průmeru kružnice, Pomocí dvou protilehlých bodů na obvodě kružnice, Pomocí tří libovolných bodů na obvodu kružnice, tedy pomocí vepsaného trojúhelníka, Pomocí tří tečen kružnice, tedy pomocí opsaného trojúhelníka. Z kružnice odvozenou entitou je kruhový oblouk. U kruhového oblouku je potřeba kromě parametrů kružnice (tedy středu a poloměru) zadat ještě počáteční a koncový úhel oblouku, tedy počáteční 1 a koncovou 2 hodnotu parametru v parametrickém vyjádření kružnice. Úhel sevřený kruhovým obloukem je pak roven 2 1. Zobecněním kružnice je elipsa. Implicitní rovnice elipsy je (5.20) Pro a=b dostaneme rovnici kružnice, která je tedy speciálním případem elipsy. Hodnoty a a b představují délky poloos elipsy. Elipsu obvykle zadáváme právě pomocí jejího středu x 0, y 0 a pomocí délek jejich poloos. Podobně jako z kružnice lze odvodit kruhový oblouk, lze z elipsy odvodit eliptický oblouk. Dalšími kuželosečkami, které získáme při vhodně nastavených parametrech v obecné rovnici kuželosečky jsou parabola a hyperbola. Ty se však v programech pro vektorové kreslení používají mnohem méně často než elipsa. Další metodou pro získání složitějších jednorozměrných vektorových entit je spojování jednoduchých na sebe navazujících jednorozměrných entit (úseček, popřípadě kruhových či eliptických oblouků) do řetězců. Takto vzniklá entita se nazývá polyline 63
64 (polylajna). V české verzi programu AutoCAD je pro ni použito poněkud nepřesné označeni křivka. Pod pojmem multiline (multilajna, multičára) se obvykle rozumí soustava několika jednoduchých entit, nejčastěji úseček které jsou navzájem rovnoběžné a jsou v nějaké předem dané vzdálenosti od sebe. Pomocí multičar je možné snadno kreslit takové objekty jako např. silnice na mapě nebo zdi ve stavebním výkresu. Obr Parametrické vyjádření kružnice Obr.5.42 Kruhový oblouk Obr Elipsa Obr.5.44 Polylajna 64
65 Obr Multilajna Interpolační a aproximační křivky Velmi často se ve vektorové počítačové grafice objevuje situace, kdy je průběh nějaké křivky zadán pomocí množiny bodů, kterými má křivka procházet, či má jejich rozložení alespoň přibližně kopírovat. Příkladem může být např. zadání průběhu silnice terénem pomocí množiny pravidelně rozložených trasovacích bodů. Pokud se pokoušíme o matematické vyjádření křivky, která přesně prochází všemi body zadané množiny, mluvíme o interpolační křivce. Pokud netrváme důsledně na tom, že křivka bude procházet všemi zadanými body, ale požadujeme pouze, aby v určitém smyslu kopírovala jejich rozložení, mluvíme o křivce aproximační. Obr Interpolace a aproximace Vektorový způsob generování obrazu se používá u zařízení, která mohou nastavovat polohu pisátka do libovolné požadované polohy a pohyb pisátka z počáteční do koncové polohy je přitom přímočarý (po úsečce) anebo po oblouku. Pod pisátkem si přitom můžeme představit technické pero na kreslicím stole anebo paprsek na stínítku obrazovky. Příkladem grafických zařízení, která pracují vektorovým způsobem, může být souřadnicový zapisovač anebo obrazovka osciloskopu. U obou zařízení se přivádí na vstup analogový signál (např. napětí), který určuje polohu pisátka ve směru každé ze souřadných os x a y. Dalším ovládacím 65
66 signálem je logický signál, který určuje stav pisátka (zdvihnuté nebo spuštěné technické pero na zapisovači, zhasnutý nebo rozsvícený paprsek na obrazovce). Běžně používaná zařízení používají dva druhy interpolací: lineární interpolace, pomocí které můžeme libovolné dva body na kreslicí ploše spojit úsečkou, kvadratická interpolace, která dovoluje generování kvadratických křivek (kružnic, kruhových oblouků a elips). Lineární interpolace vyžaduje pro generování úsečky z bodu A 1 (x 1, y 1 ) do bodu A 2 (x 2, y 2 ) pouze zajistit rovnoměrnou změnu souřadnice x z hodnoty x 1 na hodnotu x 2 a souřadnice y z hodnoty y 1 na hodnotu y 2 za stejný časový interval T. Máme-li vykreslit úsečku, bude signál řízení pisátka nastaven na hodnotu spuštěno. Časové diagramy jednotlivých signálů jsou ukázány na obr x x 2 Časové diagramy Generovaná úsečka y x 1 A 2 (x 2, y 2 ) y t 0 t 0 +T t A 1 (x 1, y 1 ) x y 2 y 1 t 0 t 0 +T t stav pisátka spuštěno zdvihnuto t 0 +T t 0 Obr Časový průběh řídicích signálů při generování úsečky t 66
67 Průběh signálů podle obr je poněkud idealizovaný, protože u reálných zobrazovacích systémů je třeba vzít do úvahy setrvačnosti hmot mechanického kreslicího zařízení anebo setrvačnosti vychylovacího systému obrazovky. Kvadratická interpolace generuje kvadratické křivky podobným způsobem jako byl generován vektor při lineární interpolaci. Průběh změn souřadnic při lineární interpolaci můžeme vyjádřit rovnicemi x = (1-t). x 1 + t. x 2 y = (1-t). y 1 + t. y 2 (5.21) kde parametr t se mění z hodnoty 0 na 1 pro časový interval <0, T >. Podobně můžeme změny souřadnic při kvadratické interpolaci pro kružnici o středu S (x s, y s ) a poloměru R vyjádřit rovnicemi x = x s + R.cos (.t) y = y s + R.sin (.t) (5.22) což jsou parametrické rovnice kružnice, podle kterých by interpolátor pro interval hodnot t<0,1> vygeneroval půlkružnici. Kreslení složitějších prvků obrazu, jako jsou například alfanumerické znaky, používá některý z výše uvedených způsobů interpolace a motiv kresby se potom může skládat z elementárních úseček, kruhových oblouků a kružnic. Obr Interpolace parabolou 67
68 Obr Kvadratická interpolace přímkou rovnoběžnou s osou x Obr nterpolace polynomem 5 stupně Obr Interpolace polynomem 5 stupně detail Spline křivky Základní myšlenkou interpolace pomocí spline (splajn) křivek je pokus vyjádřit křivku, jejíž matematický popis by byl jinak příliš komplikovaný, tak, že se pomocí jednodušších funkcí vyjádří její části a tyto části se pak v přechodových místech vhodně navážou, aby byly splněny nějaké požadované podmínky. V případě interpolace množiny bodů pomocí polynomických spline křivek lze postupovat takto: 68
69 Zvolí se stupeň interpolační spline křivky n, Zadaná množina bodů se rozdělí podle x-ových souřadnic na úsekv déikv n + 1 bodů, Každý takový úsek bude interpolován polynomickou křivkou n-tého stupně, podobně, jako to bylo popsáno v předchozí části, V hraničních bodech jednotlivých úseků se vyjádření funkcí vhodně upraví tak, aby byla zaručena spojitost všech derivací vzniklé funkce až po (n - 1). Nejjednodušším případem polynomické spline interpolace je interpolace křivkou po částech prvního stupně. V takovém případě se množina vstupních bodů rozdělí na úseky po dvou bodech. Každý takový úsek bude interpolován funkcí prvního stupně, tedy úsečkou. V hraničních bodech pak budou úsečky na sebe navazovat tak. že bude zaručeno spojitost nulté derivace, tedy spojitost samotné funkce. Interpolace spline křivkou prvního stupně se obvykle nazývá interpolace lomenou čarou a takto vzniklou křivku nebývá zvykem ani řadit mezi spline křivky. V případě interpolace spline křivkou druhého stupně se vstupní množina bodů rozdělí na úseky po třech bodech. Tyto úseky budou interpolovány funkcemi druhého stupně, tedy parabolami. V hraničních bodech pak bude zaručeno takové navázání parabol, které bude mít spojitou první derivaci. Výsledná funkce bude tedy hladká, což je schopen lidský mozek poměrně snadno rozeznat. Zároveň je však výpočet parametrů takové funkce i samotné vyjádření hodnot funkce dostatečně jednoduché. Z těchto důvodů je kvadratická spline funkce nejčastěji používaným typem spline interpolace. Mnoho uživatelských programů pro zjednodušení nazývá podobné křivky prostě spline křivky a přívlastek kvadratický vynechává. Obr Spline křivka 1 stupně lomená čára 69
70 Obr Spline křivka 2 stupně Aproximace V případě aproximace zadané množiny bodů nepožadujeme, aby aproximační křivka procházela body ze zadané množiny. Požadujeme pouze, aby tvar této množiny bodů přibližně kopírovala. Tato definice je ovšem jen velmi měkká, z matematického hlediska lze za aproximační křivku považovat zcela libovolnou křivku. Pro praktické použití požadujeme u aproximační křivky především dvě vlastnosti: Aby její vyjádření bylo dostatečně jednoduché a tím pádem výpočty potřebné při dosazování do její rovnice byly dostatečně efektivní, Aby výsledná křivka dostatečně dobře realizovala smyslový dojem, který má lidský mozek ze zadaného rozložení bodů. Ve statistice je oblíbenou interpolační metodou interpolace metodou nejmenších čtverců. Pro zadanou množinu n bodů x y, x, y,...,,, x y n n se nejprve zvolí typ funkce, pomocí které budeme body aproximovat'. Nejčastěji se jedná o aproximaci polynomickou funkcí m-tého stupně, kde m n 1, a proto není možné zajistit interpolaci. Výsledná polynomická funkce m-tého stupně x y f má tu vlastnost, že ze všech funkcí dané třídy (polynomických funkcí m-tého stupně) dává nejmenší součet čtverců odchylek od skutečné hodnoty. Tedy, aby hodnota n yi f x i i1 2 (5.23) 70
71 byla minimální. Na obrázku je ukázka lineární aproximace množiny pěti bodů metodou nejmenších čtverců. Pro zadaných pět bodů byla vypočítána přímka, která má mezi všemi přímkami tu vlastnost, že součet ploch vyšrafovaných čtverců je minimální. Metodu nejmenších čtverců lze zobecnit na použití jiné než druhé mocniny v exponentu. V takovém případě mluvíme o aproximaci metodou minimalizace -tých momentů a příslušný výraz, který se bude minimalizovat n i1 y f i x i (5.24) Obecně vede aproximace při minimalizaci -tého momentu k jiným funkcím, než při minimalizaci 2. momentu, tedy při použití metody nejmenších čtverců. Ve statistice se podobné metody často používají. Jejich význam pro počítačovou grafiku však není příliš velký. Intuitivně je totiž jen obtížně pochopitelné, jak se změní tvar aproximační křivky při změně polohy jednoho ze zadaných řídících bodů. Bézierova aproximace Tento zádrhel, malou intuitivnost statistických aproximací, odstraňuje metoda navržená francouským inženýrem a konštruktérem Piérem Bézierem. Metoda se nazývá Bézierova aproximace a vzniklá křivka Bézierova křivka. Bézierova křivka n-tého stupně je polynomická křivka n-tého stupně a je zadána pomocí n+1 řídících bodů P,..., 0, P1 Pn. Povšimněme si tedy, že počet zadaných, řídících bodů,je stejný, jako u polynomické interpolace. Podmínky, které musí splňovat Bézierova křivka, jsou však odlišné: Bézierova křivka prochází dvěma krajními řídícími body P 0, P n, Tečný vektor k Bézierově křivce v bodě P 0 je roven vektoru P 0 P 1, Tečný vektor k Bézierově křivce v bodě P n je roven vektoru P n,p n-1, Celá Bézierova křivka leží v konvexním obalu množiny bodů P,..., 0, P1 Pn. takto Podle výzkumů Piera Béziera splňuje tyto vlastnosti křivka vyjádřená parametricky (5.25) 71
72 Výraz (5.26) se někdy nazývá, i-tý Bersteinův polynom n-tého stupně a značí se symbolem t B n i. Vyjádření Bézierovy křivky se pak zjednoduší na: (5.27) Obr Bézierova parabola Obr Bézierova parabola po změne prostředního řídícího bodu 72
73 Obr Bézierova křivka 5 stupně I pro větší počty řídících bodů lze podle výše uvedeného vzorce vytvořit křivku, která bude splňovat vlastnosti Bézierovy křivky. Jak již bylo uvedeno, je-li k dispozici n-1 řídících bodů, je příslušná Bézierova křivka polynomickou křivkou n-tého stupně. Se vzrůstajícím počtem řídících bodů tedy stoupá obtížnost vyjádření křivky i všech výpočtů spojených s její konstrukcí. Často se tedy využívá podobný trik, jaký jsme viděli při konstrukci interpolačních spline křivek. Množina řídících bodů se rozdělí na úseky, každý z nich se pak aproximuje samostatnou Bézierovou křivkou. Vhodnou úpravou parametrů křivek se pak dosáhne jejich hladkého navázání v přechodových bodech. Křivky vzniklé tímto postupem se obecně nazývají Bézierovy spline křivky (B-spline) a mají řadu variant. K nejoblíbenějším patří např. tzv. NURBS křivky. Podrobný popis postupů, které vedou k jejich konstrukci, přesahuje rámec těchto skript. Rasterizace Při práci s vektorovými entitami je nutné velmi často provádět jejich převod do rastrové podoby. Naprostá většina výstupních zařízení dnešních počítačů jsou totiž zařízeni rastrová. Týká se to především monitoru počítače a také naprosté většiny typů tiskáren. Při tvorbě vektorového výkresu uživatel pochopitelně požaduje, aby výsledek své práce okamžitě viděl na monitoru počítače. Po vytvoření entity je tedy nutné okamžitě provést její pasterizaci tedy převod do rastrové podoby za účelem jejího zobrazeni na monitoru počítače. Je zřejmé, že algoritmy pro rasterizaci vektorových entit musí pracovat velmi rychle. Často totiž nastane situace, kdy uživatel změní jedním příkazem způsob pohledu na výkres, 73
74 který může obsahovat i velké množství entit. Uživatel může např. požadovat rychlé přiblížení či oddálení výkresu, v případě třírozměrného modelu pak rychlou změnu směru pohledu na něj. Pro rasterizaci jednoduchých entit, především pak úsečky bylo vyvinuto mnoho velmi rychlých algoritmů. Rasterizace složitějších objektů, např. parametricky zadaných křivek by však mohla být časově dosti náročná. Obvykle tedy rasterizace složitějších objektů probíhá ve dvou fázích. V první fází nazývané regenerace, je složitější objekt aproximován soustavou úseček, tedy lomenou čarou. V případě, že uživatel požaduje pouze malou změnu způsobu pohledu na výkres, např. pouze jeho malé přiblížení, neprovádí se tato regenerace znovu, ale použije se stejná aproximace složitějšího objektu pomocí lomené čáry jako v případě předchozího pohledu. V druhé fázi se pak provádí samotná rasterizace úseček. Při popisu algoritmů pro rasterizaci úsečky budeme předpokládat, že úsečka je zadána svými dvěma krajními body x, y 1 1 a x, y 2 2. Na základě těchto dvou krajních bodů můžeme spočítat směrový vektor úsečky ( x, y ), kde x x 2 x1 a y y 2 y1, Pokud x 0, můžeme dále spočítat směrnici úsečky y k x. Všechny tyto údaje je vhodné spočítat jednorázově předem v okamžiku, kdy uživatel vektorového kreslícího programu úsečku vytvoří. Většina algoritmů pro rasterizaci úsečky má několik variant v závislosti na poloze úsečky. Dnes nejčastěji používaný algoritmus pro rasterizaci úsečky se jmenuje Bressenhamův. Obr variant Bressenhamova algoritmu 74
75 Obr Bressenhamův algoritmus Obr Příklad rasterizace úšečky Vektorizace Vektorizace je opačnou úlohou k rasterizaci. Úkolem vektorizace je převod rastrového obrázku do vektorové podoby. Na základě výsledné podoby obrázku tedy máme určit, jakým způsobem, z jakých vektorových entit obrázek vznikl. Je patrné, že již ze samotného svého principu je algoritmické řešení úlohy vektorizace podstatně obtížnější než řešení úlohy rasterizace. Rastrový obrázek totiž obsahuje pouze informace o jenom z možných pohledů na entity, neobsahuje informace o entitách samotných. Obsahuje tedy mnohem méně informací, tyto informace je při vektorizaci potřeba nějakým způsobem dodat, nebo automaticky vygenerovat. Na druhou stranu není potřeba vektorizační úlohy řešit zdaleka tak často,jako úlohy pasterizační. V případě vektorizace se jedná obvykle o jednorázové řešení, u kterého doba výpočtu sice hraje roli, ale tak zásadní jako v případě pasterizace. Vektorizace se obvykle neprovádí v reálném čase (on-line) a ani to z hlediska složitosti úlohy není rozumné požadovat. Zcela automaticky prováděné vektorizační algoritmy jsou sice myslitelné, ale vyžadují poměrně dosti složitou analýzu za oženou mnohdy na obtížně definovatelných měkkých matematických metodách. Mnoho z těchto algoritmů využívá principy tak zvané 75
76 umělé inteligence. I tak se ale nevyhnou chybám a jejich úspěšnost není nikdy zdaleka stoprocentní. Druhým extrémem je provádění vektorizace ručně, pouze za podpory nějakého programu. Jednoduché vektorízační programy např. umožňují promítnout rastrový obrázek na pozadí monitoru počítače a pomocí polohovacího zařízení (myši) zadávat souřadnice jednotlivých entit vektorového výkresu. Rozumným kompromisem bývá poloautomatická vektorizace s různým stupněm automatizace. Některé jednoduché výpočty, jako je např. sledování jasné jednobarevné linie v rastrovém obrázku, může provádět program automaticky bez zásahu uživatele. V případě nejasností o dalším pokračování pak program požádá uživatele o podporu. Poloautomatická vektorizace je rychlejší než vektorizace ruční, na druhou stranu při ní vzniká méně chyb, než při vektorizaci automatické. Za speciální případ vektorizace je možné považovat optické rozpoznávání textů (optical Character Recognize, OCR). Vstup pro tuto úlohu je opět rastrový obrázek obsahující nascanovaný text. Je vhodné, aby barva textu a barva jeho pozadí byty ve velkém kontrastu, tedy, aby vzdálenost těchto dvou barev v barevném prostoru RGB byla co možná největší. Výstupem je textový soubor obsahující zpracovávaný text. Při OCR postupech se opět často použijí metody nazývané umělá inteligence, zvláště pro odstraňování šumu v rastrovém obrázku. Pro rozpoznávání daných vzorů (zadaných tvarů písmen) lze někdy využít neuronové sítě. Počítačem podporované kreslení Nejjednodušší programy pro tvorbu vektorových výkresů se nazývají programy pro počítačem podporované kreslení (Computer Aided Drafting). Počítačem podporované vektorové kreslení je základním stavebním kamenem i pro mnoho jiných složitějších programů, např. pro programy počítačem podporovaného projektování (Computer Aided Design) včetně nejrozšířenějšího z nich - programu AutoCAD. Klady vektorové grafiky Paměťové nároky v zásadě odpovídají složitosti obrázku (počtu objektu) a jsou v praxi většinou nižší než u rastrových obrázku obdobného obsahu, 76
77 Vektorový popis obrázku lze snadno editovat (upravovat). Změna objektu se provede změnou některé jeho vlastnosti. Např. pro zvetšení kružnice stačí zvětšit její poloměr, Při zobrazování a tisku je využíváno rozlišení daného zařízení. Kvalita závisí pouze na tom, jak kvalitní se např. tiskárna použije. Protože většina výstupních zařízení pracuje na rastrovém principu, je nutné vektorový obrázek převést do rastrové podoby (tzv. rasterizace). Dělá se to až těsně před tiskem a v takovém rozlišení, jaké je potřeba, proto není problém se změnou velikosti obrázku při tisku. Zápory vektorové grafiky Omezená oblast použití, těžko lze převést do vektorové podoby třeba fotografii. Velká škála formátu, z nichž mnohé nejsou mezi sebou převoditelné. Příklady vektorových formátu: DXF (Data exchange Format) světový standard pro výměnu mezi CAD systémy. Většinou v tomto formátu lze vyměňovat data ve všech vektorových grafických programech, VML (Vector Markup Language) navrhovaný formát pro vektorovou a čárovou grafiku, který by mel být zahrnut v internetových prohlížecích, PLT(HPGL) informace pro výstupní zařízení komunikující v jazyce HP-GL (Hewlet Packard Graphic Language). Tento formát je převážně určen pro plotry a tiskárny. Jednotlivé programy mají své vlastní vektorové formáty, například: AutoCAD (DWG), CorelDraw (CDR) Příklady metaformátu, které obsahují současně vektorová a rastrová data. Princip je takový, že co jde, je zadáno ve vektorové podobě a jen menší část (např. textury) je zadána jako rastrová data: WMF (Windows Meta File) používají ho všechny aplikace pod Microsoft Windows, EPS (Encapsulated PostScript) je určen pro tiskové soubory pro tiskárny, osvitové jednotky apod., které umí interpretovat jazyk PostScript. Mnohé aplikace jej umí vytvářet, ale neumí jej číst. Používá se zejména v DTP. Skládáni vektorových kreseb Vektorový program dává téměř nekonečné možností skládání kompozice 77
78 z geometrických objektů (čar, obdélníků, elips a mnohoúhelníků), textů a fotografií, které můžete libovolně kombinovat, uspořádat a dávat jim snad nekonečně mnoho vlastností. Na rozdíl od rastrů, probíraných v předchozích kapitolách, jsou objekty popsány křivkami, je proto možné libovolně je zvětšovat nebo zmenšovat. Rastrový obrázek (fotografie) je ve vektorovém programu jeden z využitelných objektů v dokumentu. Obr Příklad jednoduché skládačky - vizitka Okno vektorového programu Ukázky v předkládaném textu jsou z programů Corel Draw, Zoner Callisto a openoffice.org Draw. Protože všechny vektorové (kreslicí) programy vycházejí ze stejých principů práce, najdete v nich také stejné základní prvky: standardní panel pro práci se soubory (otevření, uložení apod.), panel kreslicích nástrojů, panel vlastností, panel barev, stavoý řádek. Obr Příklad zobrazení okna programu Corel Draw Podobně jako v rastrovém programu, i zde je základní pomůckou lupa. Často také můžete volit kvalitu a způsob zobrazení kresby: 78
79 Nástroj Lupa umožňuje přiblížení, vzdálení, zobrazeni celé stránky, zobrazení všech objektů apod., vždy je k dispozici náhled kresby, často volba kvality zobrazení od čárového modelu (jen obrysy) po nejlepší zobrazení s vyhlazováním hran písem, Pro manipulací s objekty používáme nástroj Výběr. Obr Lupa Po výběru příslušného kreslicího nástroje vytváříte základní objekty. Některá klávesa (Ctrl nebo Shift) vnáší do kreslení pravidelnost, umožňuje tedy vytvářet čtverce, kružnice apod. Výběr více objektů Již víte, že pro manipulaci s objekty používáme nástroj výběr. Často je potřeba vybrat více obiektů: požadované objekty orámujete (celé) nástrojem výběr, nebo držíte klávesu Shift a postupně na ně klepnete. Změna polohy a velikosti, duplikát, rotace a mazání objektů Změna polohy objektu - objekt uchopíte nástrojem výběr a přemístíte ho na zvolené místo, Změna velikosti objektu - objekt označíte výběrovým nástrojem a za úchopové body ho zvětšíte nebo zmenšíte. Pokud objekt nechcete deformovat, musíte ho zvětšovat nebo zmenšovat vždy za rohy ne za boky, někdy je třeba držet klávesu (Shift), Rotace a zkosení objektů se provádí tak, že na již označený objekt znovu klepnete myší, objeví se okolo něho šipky, za které můžete objekt otočit nebo zkosit, otáčíte za 79
80 šipky v rozích, zkosíte za šipky na bocích. Případně je k dispozici příkaz Rotovat v nabídce Nástroje, objekty je možné duplikovat, tato volba je většinou v nabídce Úpravy, označený objekt smažete klávesou Delete. Obr Základní objekty Obr Úpravy obrazců V kreslicím programu jsou k dispozici základní tvary (obdélník, elipsa, čára...). Ty je možné jakkoli transformovat, natáčet apod., ale není je možné dále tvarovat. Dalším typem objektů jsou tzv. Bezierovy křivky, které je možné libovolně tvarovat pomocí uzlových bodů a směrnic tečen v těchto bodech. Křivka vznikne např. kreslením čáry od ruky. Druhou, častěji používanou možností je převod libovolného objektu na křivku. Jestliže tedy chcete např. dále tvarovat obdélník, je potřeba ho nejdříve převést na křivku (tato volba je obvykle v nabídce Změnit). Tvarování objektů se provádí pomocí tvarovacího nástroje. Můžete s ním libovolně měnit polohu jednotlivých uzlů a také tvar křivky v těchto uzlech. Uzly je možné přidávat i mazat, křivku v nich rozpojovat i spojovat atd. Vzhled objektů určují dvě zásadní vlastností obrys objektu a jeho výplň. Díky nim můžete dosáhnout téměř libovolného vzhledu každého objektu. U obrysu se nastavuje barva, šířka a druh čáry, u neuzavřených tvarů i zakončení (šipky apod.), U výplně se určuje, zda vůbec bude mít objekt výplň, pak samozřejmě barva výplně, dále různé přechody, vzorky, šrafování, textury (vzory). Výplní objektu může být i (rastrový) obrázek načtený z disku. 80
81 Obr Základní lišta Pro přesné umístění objektů na stránce a další operace s nimi poskytuje kreslicí program několik důležitých nástrojů: Zařazení objektu dopředu nebo dozadu - Jakmile začnete umisťovat objekty přes sebe, okamžitě vyvstane otázka: Který objekt je nahoře a který pod ním? Vybraný objekt můžete zařadit dozadu (bude pode všemi objekty) nebo dopředu (objeví se úplně nahoře na ostatních objektech), případně pod stanovený objekt nebo nad něj, Zarovnání objektů vůči sobě i pomocí vodicích linek o Zarovnat dva nebo více objektů můžete tak, že označíte (ten, vůči kterému se bude zarovnávat) obvykle první nebo poslední a poté na panelu nástrojů (nebo v galerii Zarovnání objektu) určíte způsob jejich zarovnání, o Vodicí linky si vytáhnete z pravítek nahoře a vlevo v okně programu. Můžete k nim umístit objekty ručně, nebo je můžete nastavit jako magnetické a nechat k nim objekty přichytit, Seskupení objektů a jejich oddělení - Při kreslení často nastane situace, kdy je potřeba pracovat s několika objekty tak, jako by to byl objekt jeden. Např. máte hotový detail obrázku a ještě s ním chcete manipulovat, potřebujete zarovnat část obrázku sestávající z několika objektů vůči jinému objektu nebo stránce apod. V takovém případě jednoduše označíte více objektů najednou (všechny je orámujete výběrovým nástrojem, nebo na ně klepete a přitom držíte klávesu Shift). Na panelu nástrojů nebo v nabídce pak vyberete jejích seskupení, od té chvíle se budou chovat jako jeden objekt. Pokud chcete manipulovat jen s některým objektem ze skupiny, musíte objekty od sebe zase oddělit, zrušit skupinu objektů, Oříznutí a průnik objektů, s loučení objektů - Tyto tři operace (někdy se označují jako logické operace s objekty) se většinou nacházejí v jedné nabídce (galerií nástrojů), všechny se provádějí s dvěma objekty a výsledkem je nový zajímavý objekt, 81
82 S efekty raději opatrně - Použití efektů na objekty je velmi oblíbené, doporučuje se však používat je opatrně, a to ze dvou důvodů: o Výpočty efektů (hlavně stíny a průhlednost) velmi zatíží procesor počítače a hlavně při tisku dokumentu mohou způsobit problémy, o Efekty poskytují nemalou šanci vyrobit nevkusný obrázek. Stín a průhlednost jsou v současné době velmi moderní efekty. Stínovaný nadpis vypadá zajímavě a průhlednost umožňuje působivé kresby. Obr Zarovnávání Obr.5.68 Seskupování Obr Průhlednost I fotografie může být objektem - Již víte, že fotografie (obecně rastrové neboli bitmapové obrázky) upravujeme v rastrovém editoru, kterému byla věnována celá kapitola. Ve vektorovém programu je rastr jedním z objektů. Vloží se do vytvářené kresby většinou příkazem Soubor/Importovat, případně přetažením z okna složky, ve které se nachází soubor s obrázkem. I když je rastr (bitmapa) jakoby cizí prvek v kreslicím programu mají moderní vektorové programy řadu nástrojů pro jeho úpravy. Barevné korekce, úpravu jasu a kontrastu, a dokonce i množství filtrů - to vše najdete v nabídce Rastry nebo Bitmapy. Pozor na rozlišení. Zcela zásadní je počet bodů vloženého rastrového obrázku vzhledem k jeho velikosti ve výsledném dokumentu, tj. jeho rozlišení. Z teorie víte, že pro zobrazení na obrazovce stačí 100 DPI, pro kvalitní 82
83 tisk DPI, ovšem obrázek z 5 megapixelového fotoaparátu, vložený do kresby a zmenšený tažením za roh na velikost cca 6 x 4 cm má klidně rozlišení DPI! Stále má totiž plný počet bodů a je v barevné hloubce 16,7 milionu barev, zabere tedy cca 15 MB paměti. Tažením za roh se počet bodů rastrů nemění, mění se však jeho velikost, tudíž i jeho rozlišení. Pokud takových obrázků do kresby vložíte více, výsledkem bude soubor, se kterým bude počítač nápadně pomalu pracovat a který i po uložení na disk bude mít velikost desítky megabajtů. To vše zcela zbytečně, stačilo před vložením převzorkovat kopie použitých obrázků na výrazně menší počet bodů nebo takový velký obrázek převzorkovat až po vložení do vektorového programu, pokud tuto volbu program nabízí, Kliparty, jejich použití a úpravy - Kliparty jsou vektorové obrázky, které získáte s většinou kreslicích programů. Některé jsou také volně dostupné na Internetu, zde je třeba dávat si pozor na reklamu často zasílanou po nezbytné registraci. Kliparty můžete vkládat (importovat) do svých kreseb podobně jako rastrové obrázky. Většinou se vloží jako skupina objektů, kterou můžete zrušit a části klipartu změnit. Obr Zmena rastru a vlyv na rozlíšení Obr Kliparty 83
84 Text ve vektorovém programu se vyžívá velmi často, protože V rastrovém programu můžete Sice vytvořit text s nekonečně mnoha efekty, ale po sloučení vrstev se stane součástí rastru, tj. množinou bodů - je proto dále neupravitelný a také s kvalitou jeho tisku mohou nastat potíže. Zato text ve vektorovém programu zůstává dá e upravitelným textem i s nejrůznějšími efekty a tvařováním. Vektorový program navíc mívá výrazně více typografických funkcí pro formátování textu. Proto je k nezaplacení všude tam, kde potřebujete kombinovat text s grafikou a s rastrovými obrázky - a to je skoro všude. Co jiného jsou vizitky, pozvánky, diplomy, letáky, strany časopisů než kombinace textu, rastrů a grafiky? Ve vektorovém programu můžete použít dva druhy textů: První z nich, text řetězcový, se vytvoří nástrojem Text a klepnutím do místa, kde má být text umístěn. Chová se jako libovolný objekt, může mít obrys a výplň a můžete ho libovolně upravovat. Výborně se dá použít pro krátké nápisy, Jinak se pracuje s textem odstavcovým, který vytvoříte také nástrojem Text a vymezením obdélníka, do kterého pak text píšete a který se chová podobně jako textové pole v textovém editoru. Jestliže má dokument obsahovat delší blok souvislého textu, využijete text odstavcový. Text může většinou přetékat z jednoho rámečku do druhého a libovolný objekt může být textem v rámečku také obtékán. U obou druhů textů je možné měnit písmo, velikost a styl textu a podle kvality programu nastavovat další vlastnosti textu známé z textového editoru. Zajímavou možností je umístit řetězcový text na libovolnou křivku. Již z názvu funkce Text na křivce plyne, jak asi budete postupovat - nakreslíte křivku, napíšete text a tento text na tuto křivku umístíte. A protože už víte, že operace se aplikují na označený objekt, tušíte, že jak text, tak křivku musíte vybrat (označit). Pak již stačí vybrat příslušnou volbu v nabídce Text (Přizpůsobit text osnově, Umístit na křivku apod.) a vyhrát si s nastaveními. 84
85 6. Grafické editory Grafické editory jsou programy určené primárně pro práci s grafikou, i když v mnohých z nich lze například připravovat i jednoduché publikace včetně textu. Jejich škála je velmi široká od volně šiřitelných až po drahé softwary určené pro grafická studia či ateliéry. Můžeme je zhruba rozdělit podle toho, pro jaké druhy grafických dat jsou určeny a k jakému účelu mají sloužit. Rozdělení grafických editoru ukazuje obr Oblasti použití grafických programu se ve skutečnosti pochopitelně překrývají. Například některé CAD systémy velmi dobře zvládají i tvorbu 3Dobjektu, v některých vektorových editorech určených primárně pro volné kreslení můžete nakreslit a okótovat jednoduchý plánek. Obr. 6.1 Rozdělení grafických editoru Obr. 6.2 Časti editora Editor pozostáva z týchto častí: Editovacia časť: prepisovanie, vkladanie, vymazávanie, nahradzovanie, kopírovanie a posúvanie v rámci P, prekopírovanie externých súborov do pamäte P, 85
86 Prechodová časť: mení aktuálne pozície spracovania v Z a E a obnovuje tomu zodpovedajúce obsahy Z a E. Typickými operáciami sú: prechod na ďalší riadok, prechod na novú pozíciu alebo ďalšiu stranu, atď., Zobrazovacia časť: Zobrazuje aktuálnu časť pamäte P a riadi výstup dát na výstupné zariadenie (napr. tlačiareň). Rozlišujeme textové, grafické a integrované editory. Toto rozdelenie odzrkadľuje historický vývoj editorov. Delenie grafických editorov je možné rozdeliť podľa rôznych hľadísk: podľa typov spracovávaných objektov a spôsobu práce: o vektorové, o rastrové, podľa rozmeru spracovávanej grafickej informácie na: o 2D (2-dimensional, rovinné, plošné) grafické editory, o 3D (3-dimensional, priestorové) grafické editory, podľa typu spracovania grafickej informácie na: o kresliace, o upravovacie, podľa oblasti použitia na: o technické grafické editory (najčastejšie v CAD systémoch), o grafické editory pre voľnú tvorbu (napr. na maľovanie), podľa rozsahu oblastí, v ktorých sa grafický editor používa na: o všeobecné editory, o špecializované editory. Racionální využívání technických prostředků počítačové grafiky vyžaduje i odpovídající programové vybavení a znalost základních algoritmů pro práci s grafickými informacemi. V předchozí kapitole jsme ukázali, že vygenerování jedné úsečky nebo kružnice vyžaduje poměrně složitý interpolační algoritmus. Samozřejmě je nemyslitelné, aby každý uživatel programoval základní ovládací funkce výstupních zařízení a proto je ovládání výstupních zařízení částí standardního programového vybavení počítače. Podobně jako z pohledu technického byl základem grafického systému počítač, bude základním programovým vybavením operační systém počítače. U současných personálních počítačů to bude asi nejčastěji systém WINDOWS, který poskytuje rozsáhlé grafické funkce. 86
87 Na úrovni grafického výstupního zařízení potřebujeme ovladač, což je program, který řídí práci zařízení např. tím, že dovoluje zapisovat jas a barvu bodů obrazu do videopaměti, ze které se potom motiv zobrazuje na obrazovce. Příslušný ovladač je dodáván s technickým zařízením. Například podle obrazovky a grafické karty používáme ovladače pro EGA, VGA anebo SuperVGA grafiku. Všechny uvedené systémy dovolují zobrazování barevných grafických informací. Starší systém EGA (Enhanced Graphical Adapter) dovoloval rozlišení 640x340 bodů a použití 16 barev. Systém VGA používá rozlišení 640x480 bodů, takže každé políčko na obrazovce je zhruba čtvercové, a dovoluje použití až 256 barev. Současné počítače používají nejčastěji systémy SuperVGA, které dovolují vyšší rozlišení (až 1600x1280 bodů) a věrné zobrazení barev (true color), což znamená více než 16 milionů barevných odstínů. Grafický ovladač řídí práci výstupního zařízení při každém grafickém výstupu. Pro uživatelskou práci však potřebujeme příkazy, které použijeme pro sestavování uživatelských programů. Takové příkazy jsou částí programovacích jazyků a jsou obsaženy v knihovnách grafických funkcí jazyka. Používáním těchto příkazů je zajištěna určitá jednotnost uživatelských programů alespoň v rámci jednoho programovacího jazyka (a jednoho typu překladače). Samozřejmě by bylo vhodné používat standardní grafické příkazy pokud možno ve všech aplikacích a zajistit tak přenositelnost programů mezi různými výpočetními systémy. Takovým standardním systémem je norma GKS. Standardní programové prostředí - norma GKS Norma GKS (Graphical Kernel System - Základní grafický systém) byla pokusem o sjednocení grafických aplikačních programů a byla přijata mezinárodní normalizační společností ISO. Jejímu praktickému rozšíření zabránil poměrně velký rozsah definovaných funkcí a z toho plynoucí náročnost na interpretaci programů napsaných podle této normy. Překlad příkazů podle normy GKS se řešil opět připojením knihoven procedur GKS k překladači programovacího jazyka. Normalizovaná rozhraní (syntaxe příkazů) byla definována pro jazyk FORTRAN, jazyk C a Pascal. Systém grafických funkcí je velmi důmyslně definován a může sloužit jako vzor při tvorbě uživatelských grafických programů. Proto alespoň některé základní vlastnosti normy GKS ukážeme. Norma GKS je určena pro dvourozměrnou grafiku (v rovině) i pro trojrozměrnou grafiku (v prostoru). Programové vybavení grafického systému při použití normy GKS je uspořádáno do několika úrovní: 87
88 technické prostředky počítače a grafická periferní zařízení jako jsou obrazovka, tiskárna, zapisovač, představují pracovní stanice, s kterými bude grafický systém komunikovat, operační systém počítače zabezpečuje ovládání jednotlivých zařízení (pracovních stanic), základní grafický systém GKS realizuje základní grafické činnosti, jako jsou výstup (vykreslování) a vstup grafických prvků, nastavování měřítka, segmentace obrazu, transformace kresby apod., jazykově závislá úroveň definuje vazbu grafických příkazů systému GKS na programovací jazyk, ve kterém je programována aplikace, aplikační program. Vstupní činnosti jsou rozděleny na úrovně: a - bez grafického vstupu, b - vstup jen v režimu REQUEST, tzn. vstup na požádání, c - plný vstup, režimy vstupu REQUEST, SAMPLE a EVENT. Úroveň implementace 1b tedy znamená plné možnosti výstupu s použitím segmentů a vstup pouze v režimu REQUEST. Každý uživatel si může zvolit implementaci, která odpovídá nejlépe jeho potřebám. Grafické výstupní prvky jako jsou lomená čára, sled značek nebo text mají definováno množství atributů (vlastností), které blíže určují způsob vykreslení prvku. Například u lomené čáry můžeme zadat typ čáry (plnou, čárkovanou, tečkovanou) a tloušťku čáry, u textu můžeme zadat typ a kvalitu písma, výšku písma a směr vykreslení. Vlastnosti kresby můžeme dělit na geometrické atributy, které určují geometrické vlastnosti grafického prvku (jako jsou výška písma, orientace znaku, směr vykreslení, umístění textu vůči vztažnému bodu); geometrické atributy podléhají změnám při transformaci kresby a jsou platné pro vykreslení obrazu na všech pracovních stanicích, obecné atributy nepodléhají změnám při transformaci kresby a mohou být stanoveny buď s platností pro všechny pracovní stanice anebo jsou určovány podle tabulek atributů pro jednotlivé pracovní stanice. Norma GKS definuje následující výstupní grafické prvky a jejich atributy: POLYLINE - lomená čára spojující body o souřadnicích zadaných v poli PoleBodů, POLYMARKER - sled značek v bodech o souřadnicích zadaných v poli PoleBodů, TEXT - výpis textového řetězce umístěný na souřadnicích Poloha, 88
89 CELL ARRAY - pole buněk dovoluje definovat obdélníkovou plochu a motiv jejího vyplnění různobarevnými body, Volání procedury GCellArray. FILL AREA - mnohoúhelník s vyplněním, hranice mnohoúhelníka jsou zadány v PoleBodů, GENERALIZED DRAWING PRIMITIVE - zobecněný výstupní prvek může být definován podle potřeb a podle možností konkrétní implementace např. pro kružnice, kruhové oblouky, elipsy apod. Přehled výstupních prvků je velmi stručný a má pouze naznačit možnosti systému GKS a ukázat parametry, které je třeba zadávat při použití jednotlivých prvků. Vstupní grafické prvky poskytují vstupy potřebné pro vytvoření kresby. Proto musí dovolovat zadání rozmanitých informací od zadání souřadnic a číselných informací až po informace alfanumerické a informace vztahující se k dané kresbě. Opět uvedeme pouze velmi stručný přehled vstupních prvků. LOCATOR - zadává polohu bodu ve světových souřadnicích a je základní vstupní informací při tvorbě kresby, VALUATOR - zadává číselnou hodnotu vstupem z klávesnice anebo nastavením v grafickém režimu pomocí různých potenciometrů nebo jiných zobrazených analogových prvků, STRING - je znakový řetězec, který se obvykle zadává vstupem z klávesnice, CHOICE - se používá pro volbu z několika pevně určených možností např. pro volbu činnosti z menu, PICK - je výběr obrazového prvku nebo segmentu. Abychom umožnili případnou paralelní práci počítače, používáme různé režimy vstupních činností: REQUEST - je režim podobný použití vstupu z klávesnice v jazyku PASCAL. Počítač žádá o zadání vstupní hodnoty, předá řízení plně vstupnímu zařízení a pozastaví další zpracování programu až do ukončení vstupu operátorem, SAMPLE - je režim vzorkování, při kterém počítač automaticky ve stanovených časových intervalech odečítá hodnoty nastavené na vstupním zařízení, EVENT - je nejsložitějším režimem řízení vstupních činností. Při tomto režimu zadává operátor vstupní údaje v podstatě nezávisle na práci počítače a zadané vstupní údaje jsou zařazovány do fronty vstupních požadavků. 89
90 V systému GKS můžeme použít každý z uvedených režimů (pokud je implementován) pro zadání každého z uvedených vstupních prvků. Rastrové (bitmapové) editory Zástupci: Paint, Adobe PhotoShop, Corel PhotoPaint, Image Composer, Photo Styler Základem práce je zpracování rastrového obrazu, tj. kreslení i úpravy ve výsledku znamenají změny barvy bodu. Primárně jsou určeny pro zpracování fotografií či vytváření uměleckých" obrázku. Základní vlastnosti: napodobují ruční kreslení tužka, guma, sprej, různé typy štětců, obsahují nástroje na vytvoření základních geometrických tvaru, umožňují manipulace s obrazem, např. výřezy, převracení apod., obsahují barevné výplně různých typu, tyto výplně lze modifikovat a vytvářet vlastní, úpravy obrázku = změny barevných tónu, jasu, kontrastu, změny palety široká škála rastrových efektu retušovací nástroje, rozmazávání, zostřování... Obr. 6.3 Rastrové efekty Vektorové editory Zástupci: CorelDraw, Adobe Ilustrator, Aldus FreeHand, Zoner Callisto Základem je zpracování vektorového obrazu. Kreslení znamená vytváření nových objektu a úpravy znamenají změny vlastností těchto objektu. Primárně jsou určeny pro tvorbu grafiky z předdefinovaného prvku, které můžeme nejrůznějším způsobem upravovat a doplňovat. Lze do nich vkládat rastrové obrázky, ale možnost jejich úprav je většinou omezená. Základní vlastnosti: 90
91 základní geometrické objekty úsečky, křivky, geometrické tvary (kružnice, mnohoúhelníky), písmo. výběr objektu a manipulace s nimi posun, kopie, zvětšování (i neproporční), otáčení, zkosení. perspektiva, transformace jednoho objektu ve druhý, editace křivek. rozsáhlé možnosti práce s textem,. Obr. 6.4 Práce s textem ve vektorovém editoru Obr. 6.5 Rez CAD systémy Zástupci: AutoCAD, MicroStation, Spirit, ArchiCAD, TurboCAD CAD (Computer Aided Design) - počítačová podpora projektování, navrhování pomocí počítače. Většina CAD systému umožňuje kromě efektivního vytváření výkresové dokumentace v rovině i prostorové kreslení. Existují buďto obecné systémy nebo specializované programy pro jednotlivé profese. Tyto specializované programy často fungují jako nadstavby na obecné systémy, proto je výhodnější se nejprve naučit některý z obecných 91
Volná grafika, základní druhy a techniky
 Volná grafika, základní druhy a techniky Grafika ve smyslu umělecké grafiky je jedním z druhů výtvarného umění. Obecně můžeme říci, že grafikou nazýváme umělecké dílo, kdy umělec použije jednu z grafických
Volná grafika, základní druhy a techniky Grafika ve smyslu umělecké grafiky je jedním z druhů výtvarného umění. Obecně můžeme říci, že grafikou nazýváme umělecké dílo, kdy umělec použije jednu z grafických
Práce na počítači. Bc. Veronika Tomsová
 Práce na počítači Bc. Veronika Tomsová Barvy Barvy v počítačové grafice I. nejčastější reprezentace barev: 1-bitová informace rozlišující černou a bílou barvu 0... bílá, 1... černá 8-bitové číslo určující
Práce na počítači Bc. Veronika Tomsová Barvy Barvy v počítačové grafice I. nejčastější reprezentace barev: 1-bitová informace rozlišující černou a bílou barvu 0... bílá, 1... černá 8-bitové číslo určující
Barvy a barevné modely. Počítačová grafika
 Barvy a barevné modely Počítačová grafika Barvy Barva základní atribut pro definici obrazu u každého bodu, křivky či výplně se definuje barva v rastrové i vektorové grafice všechny barvy, se kterými počítač
Barvy a barevné modely Počítačová grafika Barvy Barva základní atribut pro definici obrazu u každého bodu, křivky či výplně se definuje barva v rastrové i vektorové grafice všechny barvy, se kterými počítač
Úvod do počítačové grafiky
 Úvod do počítačové grafiky elmag. záření s určitou vlnovou délkou dopadající na sítnici našeho oka vnímáme jako barvu v rámci viditelné části spektra je člověk schopen rozlišit přibližně 10 milionů barev
Úvod do počítačové grafiky elmag. záření s určitou vlnovou délkou dopadající na sítnici našeho oka vnímáme jako barvu v rámci viditelné části spektra je člověk schopen rozlišit přibližně 10 milionů barev
IVT. 8. ročník. listopad, prosinec 2013. Autor: Mgr. Dana Kaprálová
 IVT Počítačová grafika - úvod 8. ročník listopad, prosinec 2013 Autor: Mgr. Dana Kaprálová Zpracováno v rámci projektu Krok za krokem na ZŠ Želatovská ve 21. století registrační číslo projektu: CZ.1.07/1.4.00/21.3443
IVT Počítačová grafika - úvod 8. ročník listopad, prosinec 2013 Autor: Mgr. Dana Kaprálová Zpracováno v rámci projektu Krok za krokem na ZŠ Želatovská ve 21. století registrační číslo projektu: CZ.1.07/1.4.00/21.3443
Počítačová grafika SZŠ A VOŠZ MERHAUTOVA 15, BRNO
 Počítačová grafika SZŠ A VOŠZ MERHAUTOVA 15, BRNO 1 Základní dělení 3D grafika 2D grafika vektorová rastrová grafika 2/29 Vektorová grafika Jednotlivé objekty jsou tvořeny křivkami Využití: tvorba diagramů,
Počítačová grafika SZŠ A VOŠZ MERHAUTOVA 15, BRNO 1 Základní dělení 3D grafika 2D grafika vektorová rastrová grafika 2/29 Vektorová grafika Jednotlivé objekty jsou tvořeny křivkami Využití: tvorba diagramů,
Světlo, které vnímáme, představuje viditelnou část elektromagnetického spektra. V
 Kapitola 2 Barvy, barvy, barvičky 2.1 Vnímání barev Světlo, které vnímáme, představuje viditelnou část elektromagnetického spektra. V něm se vyskytují všechny známé druhy záření, např. gama záření či infračervené
Kapitola 2 Barvy, barvy, barvičky 2.1 Vnímání barev Světlo, které vnímáme, představuje viditelnou část elektromagnetického spektra. V něm se vyskytují všechny známé druhy záření, např. gama záření či infračervené
VY_32_INOVACE_INF.10. Grafika v IT
 VY_32_INOVACE_INF.10 Grafika v IT Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 GRAFIKA Grafika ve smyslu umělecké grafiky
VY_32_INOVACE_INF.10 Grafika v IT Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 GRAFIKA Grafika ve smyslu umělecké grafiky
Počítačová grafika. OBSAH Grafické formy: Vektorová grafika Bitmapová (rastrová grafika) Barevné modely
 Počítačová grafika OBSAH Grafické formy: Vektorová grafika Bitmapová (rastrová grafika) Barevné modely Vektorová grafika Vektorová grafika Příklad vektorové grafiky Zpět na Obsah Vektorová grafika Vektorový
Počítačová grafika OBSAH Grafické formy: Vektorová grafika Bitmapová (rastrová grafika) Barevné modely Vektorová grafika Vektorová grafika Příklad vektorové grafiky Zpět na Obsah Vektorová grafika Vektorový
Kde se používá počítačová grafika
 POČÍTAČOVÁ GRAFIKA Kde se používá počítačová grafika Tiskoviny Reklama Média, televize, film Multimédia Internetové stránky 3D grafika Virtuální realita CAD / CAM projektování Hry Základní pojmy Rastrová
POČÍTAČOVÁ GRAFIKA Kde se používá počítačová grafika Tiskoviny Reklama Média, televize, film Multimédia Internetové stránky 3D grafika Virtuální realita CAD / CAM projektování Hry Základní pojmy Rastrová
Úvod do počítačové grafiky
 Úvod do počíta tačové grafiky Počíta tačová grafika zobrazování popis objektů obraz modelování (model světa) rekostrukce zpracování obrazu Popis obrazu rastrový neboli bitmapový obraz = matice bodů vektorový
Úvod do počíta tačové grafiky Počíta tačová grafika zobrazování popis objektů obraz modelování (model světa) rekostrukce zpracování obrazu Popis obrazu rastrový neboli bitmapový obraz = matice bodů vektorový
VYUŽITÍ POČÍTAČOVÉ GRAFIKY
 POČÍTAČOVÁ GRAFIKA VYUŽITÍ POČÍTAČOVÉ GRAFIKY ÚPRAVA FOTOGRAFIÍ NAFOCENÉ FOTOGRAFIE Z DIGITÁLNÍHO FOTOAPARÁTU MŮŽEME NEJEN PROHLÍŽET, ALE TAKÉ UPRAVOVAT JAS KONTRAST BAREVNOST OŘÍZNUTÍ ODSTRANĚNÍ ČERVENÝCH
POČÍTAČOVÁ GRAFIKA VYUŽITÍ POČÍTAČOVÉ GRAFIKY ÚPRAVA FOTOGRAFIÍ NAFOCENÉ FOTOGRAFIE Z DIGITÁLNÍHO FOTOAPARÁTU MŮŽEME NEJEN PROHLÍŽET, ALE TAKÉ UPRAVOVAT JAS KONTRAST BAREVNOST OŘÍZNUTÍ ODSTRANĚNÍ ČERVENÝCH
Počítačová grafika. Studijní text. Karel Novotný
 Počítačová grafika Studijní text Karel Novotný P 1 Počítačová grafika očítačová grafika je z technického hlediska obor informatiky 1, který používá počítače k tvorbě umělých grafických objektů a dále také
Počítačová grafika Studijní text Karel Novotný P 1 Počítačová grafika očítačová grafika je z technického hlediska obor informatiky 1, který používá počítače k tvorbě umělých grafických objektů a dále také
Počítačová grafika - úvod
 Autor: Mgr. Dana Kaprálová Počítačová grafika - úvod Datum (období) tvorby: listopad, prosinec 2013 Ročník: osmý Vzdělávací oblast: IVT 1 Anotace: Žáci se seznámí se základními pojmy počítačové grafiky,
Autor: Mgr. Dana Kaprálová Počítačová grafika - úvod Datum (období) tvorby: listopad, prosinec 2013 Ročník: osmý Vzdělávací oblast: IVT 1 Anotace: Žáci se seznámí se základními pojmy počítačové grafiky,
Rozšíření bakalářské práce
 Rozšíření bakalářské práce Vojtěch Vlkovský 2011 1 Obsah Seznam obrázků... 3 1 Barevné modely... 4 1.1 RGB barevný model... 4 1.2 Barevný model CMY(K)... 4 1.3 Další barevné modely... 4 1.3.1 Model CIE
Rozšíření bakalářské práce Vojtěch Vlkovský 2011 1 Obsah Seznam obrázků... 3 1 Barevné modely... 4 1.1 RGB barevný model... 4 1.2 Barevný model CMY(K)... 4 1.3 Další barevné modely... 4 1.3.1 Model CIE
Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Přednáška kurzu MPOV. Barevné modely
 Přednáška kurzu MPOV Barevné modely Ing. P. Petyovský (email: petyovsky@feec.vutbr.cz), kancelář E512, tel. 1194, Integrovaný objekt - 1/11 - Barvy v počítačové grafice Barevné modely Aditivní modely RGB,
Přednáška kurzu MPOV Barevné modely Ing. P. Petyovský (email: petyovsky@feec.vutbr.cz), kancelář E512, tel. 1194, Integrovaný objekt - 1/11 - Barvy v počítačové grafice Barevné modely Aditivní modely RGB,
Grafické systémy. Obrázek 1. Znázornění elektromagnetického spektra.
 1. 1.5 Světlo a vnímání barev Pro vnímání barev je nezbytné světlo. Viditelné světlo je elektromagnetické záření o vlnové délce 400 750 nm. Různé frekvence světla vidíme jako barvy, od červeného světla
1. 1.5 Světlo a vnímání barev Pro vnímání barev je nezbytné světlo. Viditelné světlo je elektromagnetické záření o vlnové délce 400 750 nm. Různé frekvence světla vidíme jako barvy, od červeného světla
Rastrová grafika. Grafický objekt je zaznamenán jednotlivými souřadnicemi bodů v mřížce. pixel ( picture element ) s definovanou barvou
 Rastrová grafika Grafický objekt je zaznamenán jednotlivými souřadnicemi bodů v mřížce. pixel ( picture element ) s definovanou barvou Kvalita je určena rozlišením mřížky a barevnou hloubkou (počet bitů
Rastrová grafika Grafický objekt je zaznamenán jednotlivými souřadnicemi bodů v mřížce. pixel ( picture element ) s definovanou barvou Kvalita je určena rozlišením mřížky a barevnou hloubkou (počet bitů
POČÍTAČOVÁ GRAFIKA. Lenka Bednaříková
 POČÍTAČOVÁ GRAFIKA Lenka Bednaříková POČÍTAČOVÁ GRAFIKA - OBSAH Barevné modely Základní dělení počítačové grafiky Vektorová grafika Rastrová (bitmapová) grafika Rozlišení Barevná hloubka Komprese, komprimace
POČÍTAČOVÁ GRAFIKA Lenka Bednaříková POČÍTAČOVÁ GRAFIKA - OBSAH Barevné modely Základní dělení počítačové grafiky Vektorová grafika Rastrová (bitmapová) grafika Rozlišení Barevná hloubka Komprese, komprimace
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost
 Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence schopnost, který je spolufinancován
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence schopnost, který je spolufinancován
Světlo. Podstata světla. Elektromagnetické záření Korpuskulární charakter. Rychlost světla. Vlnová délka. Vlnění, foton. c = 1 079 252 848,8 km/h
 Světlo Světlo Podstata světla Elektromagnetické záření Korpuskulární charakter Vlnění, foton Rychlost světla c = 1 079 252 848,8 km/h Vlnová délka Elektromagnetické spektrum Rádiové vlny Mikrovlny Infračervené
Světlo Světlo Podstata světla Elektromagnetické záření Korpuskulární charakter Vlnění, foton Rychlost světla c = 1 079 252 848,8 km/h Vlnová délka Elektromagnetické spektrum Rádiové vlny Mikrovlny Infračervené
B_PPG PRINCIPY POČÍTAČOVÉ GRAFIKY
 B_PPG PRINCIPY POČÍTAČOVÉ GRAFIKY RNDr. Jana Štanclová, Ph.D. jana.stanclova@ruk.cuni.cz ZS 2/0 Z Obrázky (popř. slajdy) převzaty od RNDr. Josef Pelikán, CSc., KSVI MFF UK Obsah seminářů 03.10.2011 [1]
B_PPG PRINCIPY POČÍTAČOVÉ GRAFIKY RNDr. Jana Štanclová, Ph.D. jana.stanclova@ruk.cuni.cz ZS 2/0 Z Obrázky (popř. slajdy) převzaty od RNDr. Josef Pelikán, CSc., KSVI MFF UK Obsah seminářů 03.10.2011 [1]
Co je počítačová grafika
 Počítačová grafika Co je počítačová grafika Počítačovou grafikou rozumíme vše, co zpracovává počítač a co lze sledovat očima Využití počítačové grafiky Tiskoviny - časopisy, noviny, knihy, letáky Reklama
Počítačová grafika Co je počítačová grafika Počítačovou grafikou rozumíme vše, co zpracovává počítač a co lze sledovat očima Využití počítačové grafiky Tiskoviny - časopisy, noviny, knihy, letáky Reklama
Zobrazování barev. 1995-2015 Josef Pelikán CGG MFF UK Praha. pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/
 Zobrazování barev 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ ColorRep 2015 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 18 Barevné schopnosti HW True-color
Zobrazování barev 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ ColorRep 2015 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 18 Barevné schopnosti HW True-color
Barvy v počítačové grafice
 arvy v počítačové grafice 2. přednáška předmětu Zpracování obrazů Martina Mudrová 2004 arvy v počítačové grafice Co je barva? světlo = elmg. vlnění v rozsahu 4,3.10 14-7,5.10 14 Hz rentgenové zář ení zář
arvy v počítačové grafice 2. přednáška předmětu Zpracování obrazů Martina Mudrová 2004 arvy v počítačové grafice Co je barva? světlo = elmg. vlnění v rozsahu 4,3.10 14-7,5.10 14 Hz rentgenové zář ení zář
Základy informatiky. 10 Počítačová grafika
 Základy informatiky 10 Počítačová grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Reprezentace barev v PC Způsoby míchání barev Barevné modely Bitová hloubka Rastrová grafika
Základy informatiky 10 Počítačová grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Reprezentace barev v PC Způsoby míchání barev Barevné modely Bitová hloubka Rastrová grafika
Multimediální systémy. 02 Reprezentace barev v počítači
 Multimediální systémy 02 Reprezentace barev v počítači Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Reprezentace barev v PC Způsoby míchání barev Barevné modely Bitová hloubka Barvy
Multimediální systémy 02 Reprezentace barev v počítači Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Reprezentace barev v PC Způsoby míchání barev Barevné modely Bitová hloubka Barvy
Barvy na počítači a grafické formáty
 Barvy na počítači a grafické formáty Hlavním atributem, který se používá při práci s obrazem či s grafickými formáty, je barva. Při práci s barvami je důležité určit základní množinu barev, se kterou budeme
Barvy na počítači a grafické formáty Hlavním atributem, který se používá při práci s obrazem či s grafickými formáty, je barva. Při práci s barvami je důležité určit základní množinu barev, se kterou budeme
Pavel Roubal Výukový modul projektu: Nové formy výuky ve školách kraje Vysočina
 Pavel Roubal 2009 Výukový modul projektu: Nové formy výuky ve školách kraje Vysočina Projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky Pavel Roubal 2009 1. Výukový
Pavel Roubal 2009 Výukový modul projektu: Nové formy výuky ve školách kraje Vysočina Projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky Pavel Roubal 2009 1. Výukový
1. Polotóny, tisk šedých úrovní
 1. Polotóny, tisk šedých úrovní Studijní cíl Tento blok kurzu je věnován problematice principu tisku polotónů a šedých úrovní v oblasti počítačové grafiky. Doba nutná k nastudování 2 hodiny 1.1 Základní
1. Polotóny, tisk šedých úrovní Studijní cíl Tento blok kurzu je věnován problematice principu tisku polotónů a šedých úrovní v oblasti počítačové grafiky. Doba nutná k nastudování 2 hodiny 1.1 Základní
Digitální učební materiál
 Střední hotelová škola, s.r.o. Floriánské náměstí 350, 272 01 Kladno Digitální učební materiál Číslo projektu Název projektu Název školy Předmět Tematický okruh Téma CZ.1.07/1.5.00/34.0112 Moderní škola
Střední hotelová škola, s.r.o. Floriánské náměstí 350, 272 01 Kladno Digitální učební materiál Číslo projektu Název projektu Název školy Předmět Tematický okruh Téma CZ.1.07/1.5.00/34.0112 Moderní škola
Digitální fotografie. Mgr. Milana Soukupová Gymnázium Česká Třebová
 Digitální fotografie Mgr. Milana Soukupová Gymnázium Česká Třebová Téma sady didaktických materiálů Digitální fotografie I. Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu
Digitální fotografie Mgr. Milana Soukupová Gymnázium Česká Třebová Téma sady didaktických materiálů Digitální fotografie I. Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu
Barva. v počítačové grafice. Poznámky k přednášce předmětu Počítačová grafika
 Barva v počítačové grafice Poznámky k přednášce předmětu Počítačová grafika Martina Mudrová 2007 Barvy v počítačové grafice Co je barva? světlo = elmg. vlnění v rozsahu 4,3.10 14-7,5.10 14 Hz rentgenové
Barva v počítačové grafice Poznámky k přednášce předmětu Počítačová grafika Martina Mudrová 2007 Barvy v počítačové grafice Co je barva? světlo = elmg. vlnění v rozsahu 4,3.10 14-7,5.10 14 Hz rentgenové
Barvy v počítačové grafice
 Barvy v počítačové grafice KAPITOLA 4 V této kapitole: Reprezentace barev v počítači Barevné prostory Barvy na periferiích počítače Barvy a design webových stránek Počítačová grafika je velmi široký pojem
Barvy v počítačové grafice KAPITOLA 4 V této kapitole: Reprezentace barev v počítači Barevné prostory Barvy na periferiích počítače Barvy a design webových stránek Počítačová grafika je velmi široký pojem
5.3.1 Disperze světla, barvy
 5.3.1 Disperze světla, barvy Předpoklady: 5103 Svítíme paprskem bílého světla ze žárovky na skleněný hranol. Světlo se láme podle zákona lomu na zdi vznikne osvětlená stopa Stopa vznikla, ale není bílá,
5.3.1 Disperze světla, barvy Předpoklady: 5103 Svítíme paprskem bílého světla ze žárovky na skleněný hranol. Světlo se láme podle zákona lomu na zdi vznikne osvětlená stopa Stopa vznikla, ale není bílá,
Barvy a barevné systémy Formáty obrázků pro WWW
 Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
DUM 01 téma: Úvod do počítačové grafiky
 DUM 01 téma: Úvod do počítačové grafiky ze sady: 02 tematický okruh sady: Bitmapová grafika ze šablony: 09 Počítačová grafika určeno pro: 2. ročník vzdělávací obor: vzdělávací oblast: číslo projektu: anotace:
DUM 01 téma: Úvod do počítačové grafiky ze sady: 02 tematický okruh sady: Bitmapová grafika ze šablony: 09 Počítačová grafika určeno pro: 2. ročník vzdělávací obor: vzdělávací oblast: číslo projektu: anotace:
Informační a komunikační technologie. Základy informatiky. 5 vyučovacích hodin. Osobní počítače, soubory s fotografiemi
 Výstupový indikátor 06.43.19 Název Autor: Vzdělávací oblast: Vzdělávací obory: Ročník: Časový rozsah: Pomůcky: Projekt Integrovaný vzdělávací systém města Jáchymov - Mosty Digitální fotografie Petr Hepner,
Výstupový indikátor 06.43.19 Název Autor: Vzdělávací oblast: Vzdělávací obory: Ročník: Časový rozsah: Pomůcky: Projekt Integrovaný vzdělávací systém města Jáchymov - Mosty Digitální fotografie Petr Hepner,
Informatika Počítačová grafika Mgr. Jan Jílek (v.11/12) Počítačová grafika
 Počítačová grafika - obor informatiky zabývající se zpracováním grafické informace (př. obrázky, videa, fotografie, informační plakáty, reklamy, konstrukční plány, návrhy, virtuální světy, hry aj.) První
Počítačová grafika - obor informatiky zabývající se zpracováním grafické informace (př. obrázky, videa, fotografie, informační plakáty, reklamy, konstrukční plány, návrhy, virtuální světy, hry aj.) První
On-line škola mladých autorů , pořadatel: ČVUT FEL. Jak na obrázky? Martin Žáček
 On-line škola mladých autorů 20. 2. 18. 4. 2013, pořadatel: ČVUT FEL Jak na obrázky? Martin Žáček zacekm@fel.cvut.cz http://www.aldebaran.cz/onlineskola/ Jak na obrázky? Osnova 1. Co je to vůbec obrázek,
On-line škola mladých autorů 20. 2. 18. 4. 2013, pořadatel: ČVUT FEL Jak na obrázky? Martin Žáček zacekm@fel.cvut.cz http://www.aldebaran.cz/onlineskola/ Jak na obrázky? Osnova 1. Co je to vůbec obrázek,
Barvy a barevné systémy Formáty obrázků pro WWW
 Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
Barevné modely, práce s barvou. Martin Klíma
 Barevné modely, práce s barvou Martin Klíma Proč je barva důležitá Důležitý vizuální atribut Různá zařízení, aplikace, média Monitor Tiskárna Video Televize Světlo a barvy Elektromagnetické vlnění Viditelná
Barevné modely, práce s barvou Martin Klíma Proč je barva důležitá Důležitý vizuální atribut Různá zařízení, aplikace, média Monitor Tiskárna Video Televize Světlo a barvy Elektromagnetické vlnění Viditelná
Webové stránky. 6. Grafické formáty pro web. Datum vytvoření: 11. 10. 2012. str ánk y. Vytvořil: Petr Lerch. www.isspolygr.cz
 Webové stránky 6. Vytvořil: Petr Lerch www.isspolygr.cz Datum vytvoření: 11. 10. 2012 Webové Strana: 1/6 Škola Ročník Název projektu Číslo projektu Číslo a název šablony Autor Tématická oblast Název DUM
Webové stránky 6. Vytvořil: Petr Lerch www.isspolygr.cz Datum vytvoření: 11. 10. 2012 Webové Strana: 1/6 Škola Ročník Název projektu Číslo projektu Číslo a název šablony Autor Tématická oblast Název DUM
Rastová a vektorová grafika
 Rastová a vektorová grafika Ke zlepšení vzhledu dokumentů aplikace Microsoft Word můžete použít dva základní typy grafiky: vektorovou (Nakreslený objekt: Libovolná nakreslená nebo vložená grafika, kterou
Rastová a vektorová grafika Ke zlepšení vzhledu dokumentů aplikace Microsoft Word můžete použít dva základní typy grafiky: vektorovou (Nakreslený objekt: Libovolná nakreslená nebo vložená grafika, kterou
Barvy v počítačové grafice
 arvy v počítačové grafice 2. přednáška předmětu Zpracování obrazů Martina Mudrová 24 arvy v počítačové grafice o je barva? světlo = elmg. vlnění v rozsahu 4,3. 4-7,5. 4 Hz viditelná č ást spektra rentgenové
arvy v počítačové grafice 2. přednáška předmětu Zpracování obrazů Martina Mudrová 24 arvy v počítačové grafice o je barva? světlo = elmg. vlnění v rozsahu 4,3. 4-7,5. 4 Hz viditelná č ást spektra rentgenové
Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám
 Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: CZ.1.07/1.5.00/34.0883 Název projektu: Rozvoj vzdělanosti Číslo šablony: III/2 Datum vytvoření: 17. 1. 2013 Autor: MgA.
Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: CZ.1.07/1.5.00/34.0883 Název projektu: Rozvoj vzdělanosti Číslo šablony: III/2 Datum vytvoření: 17. 1. 2013 Autor: MgA.
DATOVÉ FORMÁTY GRAFIKY, JEJICH SPECIFIKA A MOŽNOSTI VYUŽITÍ
 DATOVÉ FORMÁTY GRAFIKY, JEJICH SPECIFIKA A MOŽNOSTI VYUŽITÍ UMT Tomáš Zajíc, David Svoboda Typy počítačové grafiky Rastrová Vektorová Rastrová grafika Pixely Rozlišení Barevná hloubka Monitor 72 PPI Tiskárna
DATOVÉ FORMÁTY GRAFIKY, JEJICH SPECIFIKA A MOŽNOSTI VYUŽITÍ UMT Tomáš Zajíc, David Svoboda Typy počítačové grafiky Rastrová Vektorová Rastrová grafika Pixely Rozlišení Barevná hloubka Monitor 72 PPI Tiskárna
VY_32_INOVACE_INF4_12. Počítačová grafika. Úvod
 VY_32_INOVACE_INF4_12 Počítačová grafika Úvod Základní rozdělení grafických formátů Rastrová grafika (bitmapová) Vektorová grafika Základním prvkem je bod (pixel). Vhodná pro zpracování digitální fotografie.
VY_32_INOVACE_INF4_12 Počítačová grafika Úvod Základní rozdělení grafických formátů Rastrová grafika (bitmapová) Vektorová grafika Základním prvkem je bod (pixel). Vhodná pro zpracování digitální fotografie.
Téma: Barevné modely, formáty souborů
 Téma: Barevné modely, formáty souborů Vypracoval/a: Ing. Jana Wasserbauerová TE NTO PR OJ E KT J E S POLUFINANC OVÁN EVR OPS KÝ M S OC IÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Barevné modely
Téma: Barevné modely, formáty souborů Vypracoval/a: Ing. Jana Wasserbauerová TE NTO PR OJ E KT J E S POLUFINANC OVÁN EVR OPS KÝ M S OC IÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Barevné modely
Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115
 Číslo projektu: Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo šablony: 8 Název materiálu: Ročník: Identifikace materiálu: Jméno autora: Předmět: Tématický celek: Anotace: CZ.1.07/1.5.00/34.0410
Číslo projektu: Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo šablony: 8 Název materiálu: Ročník: Identifikace materiálu: Jméno autora: Předmět: Tématický celek: Anotace: CZ.1.07/1.5.00/34.0410
VOLBA BAREVNÝCH SEPARACÍ
 VOLBA BAREVNÝCH SEPARACÍ SOURAL Ivo Fakulta chemická, Ústav fyzikální a spotřební chemie Vysoké učení technické v Brně, Purkyňova 118, 612 00 Brno E-mail : Pavouk.P@centrum.cz K tomu aby byly pochopitelné
VOLBA BAREVNÝCH SEPARACÍ SOURAL Ivo Fakulta chemická, Ústav fyzikální a spotřební chemie Vysoké učení technické v Brně, Purkyňova 118, 612 00 Brno E-mail : Pavouk.P@centrum.cz K tomu aby byly pochopitelné
Základy práce v programovém balíku Corel
 Základy práce v programovém balíku Corel Mgr. Tomáš Pešina Výukový text vytvořený v rámci projektu DOPLNIT První jazyková základní škola v Praze 4, Horáčkova 1100, 140 00 Praha 4 - Krč Základy počítačové
Základy práce v programovém balíku Corel Mgr. Tomáš Pešina Výukový text vytvořený v rámci projektu DOPLNIT První jazyková základní škola v Praze 4, Horáčkova 1100, 140 00 Praha 4 - Krč Základy počítačové
IVT. Rastrová grafika. 8. ročník
 IVT Rastrová grafika 8. ročník listopad, prosinec 2013 Autor: Mgr. Dana Kaprálová Zpracováno v rámci projektu Krok za krokem na ZŠ Želatovská ve 21. století registrační číslo projektu: CZ.1.07/1.4.00/21.3443
IVT Rastrová grafika 8. ročník listopad, prosinec 2013 Autor: Mgr. Dana Kaprálová Zpracováno v rámci projektu Krok za krokem na ZŠ Želatovská ve 21. století registrační číslo projektu: CZ.1.07/1.4.00/21.3443
III/ 2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Metodický list k didaktickému materiálu Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu Autor Téma sady didaktických materiálů Téma didaktického materiálu Vyučovací předmět
Metodický list k didaktickému materiálu Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu Autor Téma sady didaktických materiálů Téma didaktického materiálu Vyučovací předmět
(15) Výstupní zařízení
 (15) Výstupní zařízení Osnova 1. Panely LCD, plasmová zobrazovače, projektory 1. Připojení 2. LCD monitory 3. Plasmový displej 4. Dataprojektor 2. Tiskárny 1. Kvalita tisku, rozlišení (DPI), připojení
(15) Výstupní zařízení Osnova 1. Panely LCD, plasmová zobrazovače, projektory 1. Připojení 2. LCD monitory 3. Plasmový displej 4. Dataprojektor 2. Tiskárny 1. Kvalita tisku, rozlišení (DPI), připojení
stručně popsat historii grafiky a grafického designu definovat základní pojmy z oblasti grafiky
 1 ÚVOD Grafika je jedním z druhů výtvarného umění. Vymezení pojmu je poměrně složité. Obecně můžeme říci, že grafikou nazýváme umělecké dílo, kdy umělec použije jednu z grafických technik a dílo rozmnoží
1 ÚVOD Grafika je jedním z druhů výtvarného umění. Vymezení pojmu je poměrně složité. Obecně můžeme říci, že grafikou nazýváme umělecké dílo, kdy umělec použije jednu z grafických technik a dílo rozmnoží
zdroj světla). Z metod transformace obrázku uvedeme warping a morfing, které se
 Kapitola 3 Úpravy obrazu V následující kapitole se seznámíme se základními typy úpravy obrazu. První z nich je transformace barev pro výstupní zařízení, dále práce s barvami a expozicí pomocí histogramu
Kapitola 3 Úpravy obrazu V následující kapitole se seznámíme se základními typy úpravy obrazu. První z nich je transformace barev pro výstupní zařízení, dále práce s barvami a expozicí pomocí histogramu
Přednáška kurzu BZVS. Barevné modely
 Přednáška kurzu BZVS Barevné modely Ing. P. Petyovský (email: petyovsky@feec.vutbr.cz), kancelář SD3.152, tel. 6434, Technická 12, VUT v Brně - 1/16 - Barvy v počítačové grafice Barevné modely Aditivní
Přednáška kurzu BZVS Barevné modely Ing. P. Petyovský (email: petyovsky@feec.vutbr.cz), kancelář SD3.152, tel. 6434, Technická 12, VUT v Brně - 1/16 - Barvy v počítačové grafice Barevné modely Aditivní
Rastrové počítačové obrazy (poněkud sporně často označované jako bitmapové) jsou pravděpodobně nejběžnější variantou obrazů v počítači.
 Ot 2. Rastrová počítačová grafika 1.1.1 Rastrové obrazy Rastrové počítačové obrazy (poněkud sporně často označované jako bitmapové) jsou pravděpodobně nejběžnější variantou obrazů v počítači. Rastrový
Ot 2. Rastrová počítačová grafika 1.1.1 Rastrové obrazy Rastrové počítačové obrazy (poněkud sporně často označované jako bitmapové) jsou pravděpodobně nejběžnější variantou obrazů v počítači. Rastrový
1. Nastavení dokumentu
 Obsah as a asta 2. Okno / více dokumentů otevírání, zavírání, vytváření nového, přepínání, ukládání 3. Barevný režim dokumentu 4. Zobrazení, vlastní pohledy 5. Objekty vkládání 1. Nastavení dokumentu Uprostřed
Obsah as a asta 2. Okno / více dokumentů otevírání, zavírání, vytváření nového, přepínání, ukládání 3. Barevný režim dokumentu 4. Zobrazení, vlastní pohledy 5. Objekty vkládání 1. Nastavení dokumentu Uprostřed
Kde se používá počítačová grafika (PG)?
 Počítačová grafika Kde se používá počítačová grafika (PG)? Tiskoviny - časopisy, noviny, letáky Reklama billboardy, propagační mat., reklamní spoty Média, televize, film titulky, efekty, triky Multimédia
Počítačová grafika Kde se používá počítačová grafika (PG)? Tiskoviny - časopisy, noviny, letáky Reklama billboardy, propagační mat., reklamní spoty Média, televize, film titulky, efekty, triky Multimédia
Grafika na počítači. Bc. Veronika Tomsová
 Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Barvy. Radek Fiala. Podpořeno z projektu FRVŠ 584/2011
 fialar@kma.zcu.cz Podpořeno z projektu FRVŠ 584/2011 Kde se berou barvy? Co je barva Světlo jako elmg. záření nemá barvu. Jednou z vlastností světla je tzv. spektrální rozdělení (Spectral Power Distribution,
fialar@kma.zcu.cz Podpořeno z projektu FRVŠ 584/2011 Kde se berou barvy? Co je barva Světlo jako elmg. záření nemá barvu. Jednou z vlastností světla je tzv. spektrální rozdělení (Spectral Power Distribution,
Reprezentace bodu, zobrazení
 Reprezentace bodu, zobrazení Ing. Jan Buriánek VOŠ a SŠSE P9 Jan.Burianek@gmail.com Obsah Témata Základní dělení grafických elementů Rastrový vs. vektorový obraz Rozlišení Interpolace Aliasing, moiré Zdroje
Reprezentace bodu, zobrazení Ing. Jan Buriánek VOŠ a SŠSE P9 Jan.Burianek@gmail.com Obsah Témata Základní dělení grafických elementů Rastrový vs. vektorový obraz Rozlišení Interpolace Aliasing, moiré Zdroje
Ing. Jan Buriánek. Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické v Praze Jan Buriánek, 2010
 Ing. Jan Buriánek (ČVUT FIT) Reprezentace bodu a zobrazení BI-MGA, 2010, Přednáška 2 1/33 Ing. Jan Buriánek Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické
Ing. Jan Buriánek (ČVUT FIT) Reprezentace bodu a zobrazení BI-MGA, 2010, Přednáška 2 1/33 Ing. Jan Buriánek Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické
Teorie barev. 1. Barvený model. 2. Gamut. 3. Barevný prostor. Barevný prostor různých zařízení
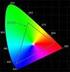 Teorie barev 1. Barvený model Barevný model představuje metodu (obvykle číselnou) popisu barev. Různé barevné modely popisují barvy, které vidíme a se kterými pracujeme v digitálních obrazech a při jejich
Teorie barev 1. Barvený model Barevný model představuje metodu (obvykle číselnou) popisu barev. Různé barevné modely popisují barvy, které vidíme a se kterými pracujeme v digitálních obrazech a při jejich
Počítačová grafika 1. Úvod do grafiky, základní pojmy. Rastrová grafika.
 Počítačová grafika 1 Úvod do grafiky, základní pojmy. Rastrová grafika. Proč vůbec grafika? Zmrzlinový pohár s převažující červenou barvou. Základem je jahodová zmrzlina, která se nachází ve spodní části
Počítačová grafika 1 Úvod do grafiky, základní pojmy. Rastrová grafika. Proč vůbec grafika? Zmrzlinový pohár s převažující červenou barvou. Základem je jahodová zmrzlina, která se nachází ve spodní části
13 Barvy a úpravy rastrového
 13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
Průvodce kvalitou barev
 Stránka 1 z 5 Průvodce kvalitou barev Tento průvodce se snaží uživatelům vysvětlit operace, které jsou na tiskárně k dispozici a mohou být užity pro úpravu a přizpůsobení barevného výstupu. nabídka Kvalita
Stránka 1 z 5 Průvodce kvalitou barev Tento průvodce se snaží uživatelům vysvětlit operace, které jsou na tiskárně k dispozici a mohou být užity pro úpravu a přizpůsobení barevného výstupu. nabídka Kvalita
Škola: Gymnázium, Brno, Slovanské náměstí 7 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Název projektu: Inovace výuky na GSN
 Škola: Gymnázium, Brno, Slovanské náměstí 7 Šablona: III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Název projektu: Inovace výuky na GSN prostřednictvím ICT Číslo projektu: CZ.1.07/1.5.00/34.0940
Škola: Gymnázium, Brno, Slovanské náměstí 7 Šablona: III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Název projektu: Inovace výuky na GSN prostřednictvím ICT Číslo projektu: CZ.1.07/1.5.00/34.0940
Barevné systémy 1995-2015 Josef Pelikán CGG MFF UK Praha
 Barevné systémy 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Colors 2015 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 21 Rozklad spektrálních barev
Barevné systémy 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Colors 2015 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 21 Rozklad spektrálních barev
Metodické listy pro kombinované studium předmětu. B_PPG Principy počítačové grafiky
 Metodické listy pro kombinované studium předmětu B_PPG Principy počítačové grafiky Metodický list č. l Název tématického celku: BARVY V POČÍTAČOVÉ GRAFICE Cíl: Základním cílem tohoto tematického celku
Metodické listy pro kombinované studium předmětu B_PPG Principy počítačové grafiky Metodický list č. l Název tématického celku: BARVY V POČÍTAČOVÉ GRAFICE Cíl: Základním cílem tohoto tematického celku
2.12 Vstupní zařízení II.
 Název školy Číslo projektu Autor Název šablony Název DUMu Tematická oblast Předmět Druh učebního materiálu Anotace Vybavení, pomůcky Ověřeno ve výuce dne, třída Střední průmyslová škola strojnická Vsetín
Název školy Číslo projektu Autor Název šablony Název DUMu Tematická oblast Předmět Druh učebního materiálu Anotace Vybavení, pomůcky Ověřeno ve výuce dne, třída Střední průmyslová škola strojnická Vsetín
POČÍTAČOVÁ GRAFIKA. Počítačová grafika 1
 Počítačová grafika 1 POČÍTAČOVÁ GRAFIKA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro nižší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky
Počítačová grafika 1 POČÍTAČOVÁ GRAFIKA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro nižší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky
12 Metody snižování barevného prostoru
 12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
Zobrazovací jednotky a monitory
 Zobrazovací jednotky a monitory Zobrazovací jednotka - karta, která se zasunuje do jednoho z konektorů na sběrnici uvnitř počítače. Dva režimy činnosti: Textový režim - zobrazuje znaky uvedené v tabulce
Zobrazovací jednotky a monitory Zobrazovací jednotka - karta, která se zasunuje do jednoho z konektorů na sběrnici uvnitř počítače. Dva režimy činnosti: Textový režim - zobrazuje znaky uvedené v tabulce
Úvod do problematiky. Význam počítačové grafiky. Trochu z historie. Využití počítačové grafiky
 Přednáška 1 Úvod do problematiky Význam počítačové grafiky Obrovský přínos masovému rozšíření počítačů ovládání počítače vizualizace výsledků rozšíření možnosti využívání počítačů Bouřlivý rozvoj v oblasti
Přednáška 1 Úvod do problematiky Význam počítačové grafiky Obrovský přínos masovému rozšíření počítačů ovládání počítače vizualizace výsledků rozšíření možnosti využívání počítačů Bouřlivý rozvoj v oblasti
INFORMATIKA. Grafické studio ve škole
 INFORMATIKA Grafické studio ve škole LUKÁŠ RACHŮNEK Přírodovědecká fakulta UP, Olomouc V současné době školy všech typů často potřebují grafické práce. Jedná se například o prezentaci školy ve formě brožur,
INFORMATIKA Grafické studio ve škole LUKÁŠ RACHŮNEK Přírodovědecká fakulta UP, Olomouc V současné době školy všech typů často potřebují grafické práce. Jedná se například o prezentaci školy ve formě brožur,
ODRAZ A LOM SVĚTLA. Mgr. Jan Ptáčník - GJVJ - Septima - Fyzika - Optika
 ODRAZ A LOM SVĚTLA Mgr. Jan Ptáčník - GJVJ - Septima - Fyzika - Optika Odraz světla Vychází z Huygensova principu Zákon odrazu: Úhel odrazu vlnění je roven úhlu dopadu. Obvykle provádíme konstrukci pomocí
ODRAZ A LOM SVĚTLA Mgr. Jan Ptáčník - GJVJ - Septima - Fyzika - Optika Odraz světla Vychází z Huygensova principu Zákon odrazu: Úhel odrazu vlnění je roven úhlu dopadu. Obvykle provádíme konstrukci pomocí
Tvorba posterů prakticky
 Tvorba posterů prakticky Ivo Šnábl Web studio Institut biostatistiky a analýz MU snabl@iba.muni.cz Operační program Vzdělávání pro konkurenceschopnost Projekt Zvyšování IT gramotnosti zaměstnanců vybraných
Tvorba posterů prakticky Ivo Šnábl Web studio Institut biostatistiky a analýz MU snabl@iba.muni.cz Operační program Vzdělávání pro konkurenceschopnost Projekt Zvyšování IT gramotnosti zaměstnanců vybraných
Inovace výuky prostřednictvím ICT v SPŠ Zlín, CZ.1.07/1.5.00/34.0333 Vzdělávání v informačních a komunikačních technologií
 VY_32_INOVACE_31_13 Škola Název projektu, reg. č. Vzdělávací oblast Vzdělávací obor Tematický okruh Téma Tematická oblast Název Autor Vytvořeno, pro obor, ročník Anotace Přínos/cílové kompetence Střední
VY_32_INOVACE_31_13 Škola Název projektu, reg. č. Vzdělávací oblast Vzdělávací obor Tematický okruh Téma Tematická oblast Název Autor Vytvořeno, pro obor, ročník Anotace Přínos/cílové kompetence Střední
Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na. x 2 x 1
 Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
Bitmapová grafika: Vrstvy - interakce (režimy prolnutí)
 VY_32_INOVACE_PG3108 ; Mgr. Pavel Hauer ; 5/2012; 1.ročník; bitmapová grafika, Počítačová grafika; názorná pomůcka pro výuku, opakování, doplnění látky Bitmapová grafika: Vrstvy - interakce (režimy prolnutí)
VY_32_INOVACE_PG3108 ; Mgr. Pavel Hauer ; 5/2012; 1.ročník; bitmapová grafika, Počítačová grafika; názorná pomůcka pro výuku, opakování, doplnění látky Bitmapová grafika: Vrstvy - interakce (režimy prolnutí)
Práce s obrazovým materiálem CENTRUM MEDIÁLNÍHO VZDĚLÁVÁNÍ. Akreditované středisko dalšího vzdělávání pedagogických pracovníků
 Práce s obrazovým materiálem CENTRUM MEDIÁLNÍHO VZDĚLÁVÁNÍ Akreditované středisko dalšího vzdělávání pedagogických pracovníků Obrazový materiál příjemná součást prezentace lépe zapamatovatelný často nahrazení
Práce s obrazovým materiálem CENTRUM MEDIÁLNÍHO VZDĚLÁVÁNÍ Akreditované středisko dalšího vzdělávání pedagogických pracovníků Obrazový materiál příjemná součást prezentace lépe zapamatovatelný často nahrazení
Fungování předmětu. 12 vyučovacích hodin ve 3 blocích Evidence docházky Zápočtový test Aktuální informace a materiály na smetana.filmovka.
 Fungování předmětu 12 vyučovacích hodin ve 3 blocích Evidence docházky Zápočtový test Aktuální informace a materiály na smetana.filmovka.cz Počítačová grafika, základy počítačového zobrazení 2 Cíle předmětu
Fungování předmětu 12 vyučovacích hodin ve 3 blocích Evidence docházky Zápočtový test Aktuální informace a materiály na smetana.filmovka.cz Počítačová grafika, základy počítačového zobrazení 2 Cíle předmětu
Barvy a barevné systémy. Ivo Peterka
 Barvy a barevné systémy Ivo Peterka Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konktrétním světle zastoupeny složky všech vlnových délek, vnímáme toto světlo
Barvy a barevné systémy Ivo Peterka Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konktrétním světle zastoupeny složky všech vlnových délek, vnímáme toto světlo
Úloha 1. Text úlohy. Vyberte jednu z nabízených možností: NEPRAVDA. PRAVDA Úloha 2. Text úlohy
 Úloha 1 Úloha 2 Otázka se týká předchozího kódu. Určete pravdivost následujícího tvrzení: "Pro každý bod vytvoří úsečku mezi ním a středem panelu." Úloha 3 Otázka se týká předchozího kódu. Určete pravdivost
Úloha 1 Úloha 2 Otázka se týká předchozího kódu. Určete pravdivost následujícího tvrzení: "Pro každý bod vytvoří úsečku mezi ním a středem panelu." Úloha 3 Otázka se týká předchozího kódu. Určete pravdivost
Úvod do počítačové grafiky
 Úvod do počítačové grafiky Zpracoval: ing. Jaroslav Chlubný Počítačová grafika Počítačová grafika a digitální fotografie zaujímá v současnosti stále významnější místo v našem životě. Uveďme si jen několik
Úvod do počítačové grafiky Zpracoval: ing. Jaroslav Chlubný Počítačová grafika Počítačová grafika a digitální fotografie zaujímá v současnosti stále významnější místo v našem životě. Uveďme si jen několik
StatSoft Jak vyzrát na datum
 StatSoft Jak vyzrát na datum Tento článek se věnuje podrobně možnostem práce s proměnnými, které jsou ve formě datumu. A že jich není málo. Pokud potřebujete pracovat s datumem, pak se Vám bude tento článek
StatSoft Jak vyzrát na datum Tento článek se věnuje podrobně možnostem práce s proměnnými, které jsou ve formě datumu. A že jich není málo. Pokud potřebujete pracovat s datumem, pak se Vám bude tento článek
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost
 Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence
Barevné prostory. RGB, CMYK, HSV a Lab gamut
 J. Vrzal, 1.0 Barevné prostory RGB, CMYK, HSV a Lab gamut rozsah všech barev, které jsou dosažitelné v určitém barevném prostoru barvy mimo oblast gamutu jsou reprodukovány nejbližší dostupnou barvou z
J. Vrzal, 1.0 Barevné prostory RGB, CMYK, HSV a Lab gamut rozsah všech barev, které jsou dosažitelné v určitém barevném prostoru barvy mimo oblast gamutu jsou reprodukovány nejbližší dostupnou barvou z
Úvod do Adobe Illustrator CS 5
 Úvod do Adobe Illustrator CS 5 Ivo Šnábl Web studio Institut biostatistiky a analýz MU snabl@iba.muni.cz Operační program Vzdělávání pro konkurenceschopnost Projekt Zvyšování IT gramotnosti zaměstnanců
Úvod do Adobe Illustrator CS 5 Ivo Šnábl Web studio Institut biostatistiky a analýz MU snabl@iba.muni.cz Operační program Vzdělávání pro konkurenceschopnost Projekt Zvyšování IT gramotnosti zaměstnanců
Průvodce kvalitou barev
 Stránka 1 z 6 Průvodce kvalitou barev Průvodce kvalitou barev pomáhá uživatelům vysvětlit operace, které jsou na tiskárně k dispozici a mohou být užity pro úpravu a přizpůsobení barevného výstupu. Nabídka
Stránka 1 z 6 Průvodce kvalitou barev Průvodce kvalitou barev pomáhá uživatelům vysvětlit operace, které jsou na tiskárně k dispozici a mohou být užity pro úpravu a přizpůsobení barevného výstupu. Nabídka
SOU Valašské Klobouky. VY_32_INOVACE_3_01 IKT Pc grafika základní pojmy Mgr. Radomír Soural. Zkvalitnění výuky prostřednictvím ICT
 SOU Valašské Klobouky VY_32_INOVACE_3_01 IKT Pc grafika základní pojmy Mgr. Radomír Soural Zkvalitnění výuky prostřednictvím ICT Název a číslo projektu CZ.1.07/1.5.00/34.0459 Název školy SOU Valašské Klobouky,
SOU Valašské Klobouky VY_32_INOVACE_3_01 IKT Pc grafika základní pojmy Mgr. Radomír Soural Zkvalitnění výuky prostřednictvím ICT Název a číslo projektu CZ.1.07/1.5.00/34.0459 Název školy SOU Valašské Klobouky,
INFORMATIKA VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ HELENA NOVOTNÁ MODUL 5 POČÍTAČOVÁ GRAFIKA
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ HELENA NOVOTNÁ INFORMATIKA MODUL 5 POČÍTAČOVÁ GRAFIKA STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA c Helena Novotná, Brno 2004 Obsah
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ HELENA NOVOTNÁ INFORMATIKA MODUL 5 POČÍTAČOVÁ GRAFIKA STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA c Helena Novotná, Brno 2004 Obsah
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
Základy počítačové grafiky
 Gymnázium Petra Bezruče, příspěvková organizace Vrchlického, Frýdek-Místek Projekt Využití ICT ve výuce na gymnáziích, registrační číslo projektu CZ.1.07/1.1.07/02.0030 Základy počítačové grafiky Metodický
Gymnázium Petra Bezruče, příspěvková organizace Vrchlického, Frýdek-Místek Projekt Využití ICT ve výuce na gymnáziích, registrační číslo projektu CZ.1.07/1.1.07/02.0030 Základy počítačové grafiky Metodický
DIGITÁLNÍ FOTOGRAFIE
 DIGITÁLNÍ FOTOGRAFIE Petr Vaněček, katedra informatiky a výpočetní techniky Fakulta aplikovaných věd, Západočeská univerzita v Plzni 19. listopadu 2009 1888, Geroge Eastman You press the button, we do
DIGITÁLNÍ FOTOGRAFIE Petr Vaněček, katedra informatiky a výpočetní techniky Fakulta aplikovaných věd, Západočeská univerzita v Plzni 19. listopadu 2009 1888, Geroge Eastman You press the button, we do
Barvy v digitální fotografii. Jaroslav Svoboda
 Barvy v digitální fotografii Jaroslav Svoboda Co je fotografie? Stroj času Trošku víc fyzikálně a bez sci-fi Záznam odrazu světla v určitém časovém intervalu Můžeme zaznamenat nejen intenzitu, ale i vlnovou
Barvy v digitální fotografii Jaroslav Svoboda Co je fotografie? Stroj času Trošku víc fyzikálně a bez sci-fi Záznam odrazu světla v určitém časovém intervalu Můžeme zaznamenat nejen intenzitu, ale i vlnovou
