protony) se mohou chovat jako vlnění (tedy mohou interferovat) i jako částice (lze
|
|
|
- Kryštof Blažek
- před 6 lety
- Počet zobrazení:
Transkript
1 1 Chování fotonu na děliči svazků Co je to vlastně foton? Pojmem foton myslíme kvantum elektromagnetického záření. Pokud budeme zmenšovat energii elektromagnetického záření (světla), potom někde na hodnotě J zjistíme, že už se tato energie záření nebude měnit spojitě, ale po jednotlivých skocích, po kvantech, kterým říkáme fotony. Fotony a stejně i další mikročástice (elektrony, protony) se mohou chovat jako vlnění (tedy mohou interferovat) i jako částice (lze je jednotlivě spočítat). Tomuto dvojakému chování se říká dualismus. 1.1 Chování fotonu Fotony jako elementární částice světla jsou nehmotné a pohybují se rychlostí světla v daném prostředí (cca m/s ve vakuu). Fotony i světlo jsou charakterizovány vlnovou délkou, tedy vzdáleností, na kterou se zreprodukuje sinusový kmit vektoru elektrické intenzity. S touto vlnovou délkou souvisí frekvence ν = c/λ, tedy kolik maxim za sekundu dosáhne vektor elektrické intenzity v daném místě. Pro popis světla se může použít i úhlová frekvence ω = 2πν. Klasická intenzita světla se popisuje jako kvadrát amplitudy vektoru elektrické intenzity. U jednotlivých fotonů roli intenzity přebírá četnost, tedy počet fotonů za sekundu. Energii jednotlivých fotonů lze spočítat podle vztahu E = hν = hω = hc/λ, kde h = Js resp. h = Js značí Planckovu resp. redukovanou Planckovu konstantu. Pro popis energie mikročástic se často používá jednotka elektronvolt [ev], značí kinetickou energii, kterou získá elektron urychlením napětím jednoho voltu, 1 ev = J. Energie fotonu s vlnovou délkou 555 nm (zelená oblast) je přibližně 2.2 ev. Rozdíl v chování klasické intenzity světla a jednoho fotonu lze demonstrovat pomocí polopropustného zrcátka. To způsobí částečný odraz dopadajícího záření, polovina intenzity projde, polovina se odrazí. Foton je ale nedělitelný, musí se rozhodnout, jestli projde nebo se odrazí. Tato volba je zcela náhodná, dopředu dokážeme akorát říct, že v polovině případů foton projde a v polovině případů se foton odrazí, viz obr mw T=R=1/2 2 mw 1 mw 50 % T=R=1/2 50 % Obrázek 1: Chování klasické intenzity světla (vlevo) a jednotlivých fotonů (vpravo) na polopropustném zrcátku. Tohoto efektu lze využít při generaci vyvážené sekvence náhodných dat. Na oba výstupy děliče zařadíme detektor schopný registrovat jednotlivé fotony (obr. 2). Detekce na detektoru na průchod bude třeba znamenat logickou 0 a detekce odraženého fotonu potom logickou 1. V reálném zařízení ale nebudou tato data vyvážená, nuly nebo jedničky 1
2 budou častější. Tuto nerovnováhu může mít na svědomí nevyvážený dělící poměr polopropustného zrcátka, kdy odrazivost R bude odlišná od propustnosti T. Jelikož reálné fotonové detektory nemají stoprocentní účinnost registrace fotonu, musíme počítat i s případem, kdy kvantové účinnosti použitých detektorů budou odlišné. Nicméně lze tato nevyvážená data upravit tak, aby byla četnost nul a jedniček stejná, ovšem za cenu ztráty 3/4 čísel. Metoda je znázorněna v následující tabulce, pokud budou dvě čísla za sebou shodná, tak se vyškrtnou, kombinace 01 se nahradí vyváženou nulou, pár 10 potom vyváženou jedničkou. D 1 T=R=1/2 D 0 hrubá data vyvážená data 0 1 Obrázek 2: Princip generátoru náhodných čísel a vyvážení generovaných dat. Chování fotonu v interferometru je také trochu rozdílné než v případě klasických intenzit. Na obrázku je Machův-Zehnderův (MZ) interferometr, který je tvořen dvěma polopropustnými a dvěma úplně odraznými zrcadly. Je-li na vstupu takového interferometru světlo s klasickou intenzitou, tak na prvním polopropustném zrcátku (děliči) se rozdělí intenzita na dvě poloviny, tyto dva oddělené svazky se odrazí od zrcátek a opět se sejdou na druhém děliči, kde se amplitudově sečtou. To značí, že výstupní amplituda bude dána součtem obou amplitud. Musíme si ale uvědomit, že amplituda, tj. poloha vektoru elektrické intenzity v rámci sinusového průběhu, může být i záporná. Pokud je vzdálenost obou ramen interferometru stejná nebo se liší o celý násobek vlnové délky, potom se amplitudy sejdou ve fázi. V tomto případě oba svazky konstruktivně interferují a všechna intenzita ze vstupu opustí interferometr vodorovným výstupem a druhý výstup bude temný. Naopak, bude-li jeden svazek v interferometru zpožděn posunem zrcadla a amplitudy se na výstupním děliči sejdou s opačnou fází, potom budou destruktivně interferovat a vodorovný výstup bude temný. Všechna intenzita vyjde druhým výstupem. V případě obecného zpoždění dojde k částečné interferenci, na jednotlivých výstupech budeme pozorovat část světla (v součtu vstupní intenzitu), v závislosti na dráhovém zpoždění v interferometru. Intenzita na výstupech bude mít opět sinusový průběh, přičemž rozposunutím jednoho ramene o vlnovou délku použitého záření se intenzita na jednom výstupu změní z maxima přes tmu opět do maxima. Kvalitu interferometru nebo to, jak jsou světelné svazky v ramenech nerozlišitelné, lze poměřovat pomocí vizibility, V = I max I min I max + I min, (1) kde I max a I min značí maximální a minimální intenzitu v závislosti na dráhovém rozdílu. Maximální hodnota vizibility (kontrastu) je jedna, svazky jsou absolutně nerozlišitelné. Minimální hodnota je potom nula, intenzita na výstupu interferometru se nemění. 2
3 Chování fotonu v interferometru nebude stejné, ale podobné. Roli intenzity světla převezme pravděpodobnost výskytu fotonu. Za prvním děličem je situace stejná jako u generátoru náhodných čísel. V polovině případů foton projde, v polovině se odrazí. Pokud ale sledujeme pravděpodobnost detekce na výstupu interferometru, zjistíme, že nemáme na obou výstupech pravděpodobnost detekce jedna polovina, tedy ne vždy. Ta pravděpodobnost detekce se bude měnit v závislosti na dráhovém rozdílu stejně jako v případě klasické intenzity světla. Opět bude docházet ke konstruktivní a destruktivní interferenci. Obecně se dá říci, že k interferenci fotonu sama se sebou dochází kdykoliv, kdy se foton může šířit více drahami tak, že nedokážeme přesně určit, v kterém rameni se nachází. Pokud bude nějaká možnost zjistit, jestli se foton nachází v určitém rameni, tak tím interferenci zrušíme a na výstupech budeme mít pravděpodobnost detekce fotonu 1/2. Obrázek 3: Jeden foton na vstupu Machova-Zehnderova interferometru. Průběh interferenčních proužků vzniklých sledováním detekcí fotonů na jednom výstupu interferometru v závislosti na dráhovém rozposunutí MZ interferometru je na této sérii obrázků. Na vstup interferometru dopadal zeslabený klasický (koherentní) signál s určitou statistikou počtu fotonů v pulzu. V tomto případě byla intenzita utlumena tak, že ve většině případů nebyl v pulzu žádný foton, v části případů byl v pulzu právě jeden foton a v zanedbatelných případech bylo v pulzu dva a více fotonů. Interferenční proužek tedy nebude patrný hned, ale po určité době, kdy detektor zaznamená dostatečný počet fotonových detekcí. 1.2 Vláknový interferometr Pokud chceme sestrojit nějaký interferometr, musíme dokázat trasovat světlo, tedy donutit světlo šířit se námi definovaným směrem. Bud se to dá provést ve volném prostoru pomocí zrcadel. Nebo můžeme světlo navázat do optického vlákna, ve kterém se šíří na základě totálního odrazu na rozhraní dvou prostředí s rozdílným indexem lomu. Pomocí vláknových komponent můžeme sestrojit i interferometr, odpadne nám nutnost použití zrcadel, protože dráha svazku je lokalizovaná ve vlákně. Polopropustná zrcátka mohou nahradit vláknové děliče svazků. Interferometry sestrojené pomocí vláken mají svoje výhody a nevýhody. Při interferenci obecně je potřeba, aby interferující svazky 3
4 Obra zek 4: C asovy vy voj za znamu jednofotonove interference. byly od sebe co nejme ne odlis itelne vc etne pr ı c ne ho profilu. Jednomodova vla kna fungujı jako filtr pr ı c ne ho profilu (prostorove ho mo du). Jednomodovy m vla knem se mu z e s ı r it pouze za kladnı TEM00 mo d, proto je nerozlis itelnost svazku v tomto ohledu splne na vz dy. Vla knova implementace mu z e by t te z kompaktne js ı nez ta ve volne m prostoru. Interferometr s de lkou ramen 1 km ve volne m prostoru na jednom laboratornı m stole sestrojit prakticky nelze, v porovna nı se dve ma s pulkami opticke ho vla kna. Navı c vla knove komponenty jsou kompatibilnı s vlnovodny mi strukturami, lze tedy integrovat sloz ite js ı zar ı zenı na opticky c ip. Nevy hodou vla knove konstrukce je obecne ve ts ı u tlum jednotlivy ch komponent. V klasicky ch cirkula rnı ch vla knech se take musı kompenzovat zme na polarizac nı ho stavu (pr ı c ny pohyb vektoru elektricke intenzity), interferujı cı svazky musı by t nerozlis itelne i s ohledem na polarizaci. K zamezenı nechte ne polarizac nı zme ny lze pouz ı t specia lnı vla kna zachova vajı cı polarizaci (PM vla kna). U opticky ch vla ken je take nutne dba t na teplotnı stabilizaci, jelikoz i u opticky ch vla ken se me nı de lka s teplotou, tedy i dra hovy rozdı l mezi dve ma vla kny tvor ı cı ramena interferometru se me nı s gradientem teploty. Teplotnı roztaz nost je sice mala, ale v interferometru se pome r uje vlnovou de lkou pouz ite ho za r enı (zlomky µm). Nicme ne na chylnosti vla knove ho interferometru na zme nu teploty nebo na rotaci lze vyuz ı t pro detekci takove zme ny. Na obra zku je zna zorne n teplotnı drift, tedy posun fa ze (polohy minima prouz ku) v c ase zpu sobeny teplotnı zme nou dra hove ho rozdı lu ramen interferometru. Ze zac a tku je posun velmi rychly, postupne se zpomaluje, jak se v interferometr hermeticky uzavr e a teplota v obou ramenech interferometru se vyrovna va. Nynı bude uveden vy c et komponent, ze ktery ch se da sloz it vla knovy interferometr. Klı c ove souc a stky jsou vla knove de lic e. Tu mohou mı t fixnı de lı cı pome r (FC), nebo lze jejich de lı cı pome r me nit pomocı mikrometricke ho s roubu c i piezoelektricke ho posuvu (VRC). Pokud jsou na vy stupnı m de lic i skla dajı rozdı lne intenzity sve tla z obou ramen interferometru, sniz uje to vizibilitu interferenc nı ch prouz ku. V tom pr ı pade je 4
5 Obrázek 5: Stabilita vláknového interferometru - časový vývoj fázové nuly. potřeba ztráty vyvážit pomocí zeslabovače (atenuátoru, A). Stejně tak je potřeba zajistit, aby na výstupním děliči měly svazky stejnou polarizaci, polarizaci lze ve vlákně upravit pomocí vláknového rotátoru (kontroleru, PC). Jednotlivá vlákna, ze kterých je interferometr složen, mají určitou délku. Aby obě ramena měla stejnou délku s přesností na vlnovou délku nelze prakticky dosáhnout jinak, než použít vzduchovou mezeru (AG). Tou lze měnit dráhový rozdíl ve velkém rozsahu, řádově milimetry až centimetry, ale s obvykle používaným krokovým motorem nelze touto vzduchovou mezerou udělat krok rovný zlomku vlnové délky. Toto rozlišení je potřeba pro naměření více bodů v rámci jednoho interferenčního proužku. K tomuto účelu se používá fázový modulátor (PM). Obrázek 6: Schéma vláknového interferometru. Principy funkce jednotlivých komponent: FC smotaná vlákna spečená dohromady nebo dva vlnovody v těsné blízkosti tak, aby mohlo elektromagnetické pole přecházet z jedné dráhy do druhé, dělící poměr je úměrný interakční vzdálenosti VRC dvě vlákna v imerzní kapalině v blízké vzdálenosti, která se může měnit mikroposuvem 5
6 A signál pomocí čočky vyvázán z vlákna do volného prostoru a opět navázán do vlákna, v mezeře je clona, která se zasouvá do dráhy svazku, narušený prostorový mód je po krátkém šíření ve vlákně obnoven PC soustava vláknových smyček, poloměr smyčky je vypočítán tak, aby se realizovala čtvrtvlnná destička, otáčení smyčky funguje potom podobně jako rotace fázové destičky, PC je sestaven ze tří nezávislých dílů, které tvoří jedna, dvě a jedna smyčka (pomocí kombinace čtvrt, půl a čtvrtvlnné destičky lze libovolnou polarizaci transformovat na jinou polarizaci) AG vyvázání signálu z vlákna do volného prostoru pomocí asférické čočky a následné navázání pomocí stejné čočky zpět do vlákna PM fázový modulátor na bázi lineárního elektrooptického jevu - v krystalu se díky přiloženému napětí změní index lomu a tedy i doba průchodu signálu, vláknový napínač - pomocí piezoposuvů se může vlákno napnout prodloužit 1.3 Měření spektra pomocí interferometru Jedno z možných využití interferometru je měření spektra záření a i jednotlivých fotonů. Záření můžeme rozdělit na monochromatické a polychromatické. S polychromatickým světlem se setkáváme dnes a denně, jakékoliv tepelné záření (sluneční, žárovka, světlo ohně) je směsí mnoha vlnových délek. Monochromatické záření produkují lasery s kontinuálním výkonem. Hranice mezi mono a polychromatickým zářením záleží na okolnostech, obecně každý zdroj má nějakou šířku čáry, tedy rozmezí vlnových délek, na kterých svítí. Šířka spektra má také vliv na interferenci. Například pokud budeme měnit dráhový rozdíl ramen interferometru výrazněji než jen o několik vlnových délek, tak se bude vizilita interferenčního obrazce zmenšovat. Pro velké rozposunutí už potom nebude vizibilita pozorována vůbec. Oblast pozorování interference se nazývá koherenční délka. Obecně platí, že pokud má zdroj světla užší spektru, potom má toto světlo větší koherenční délku. Naopak, jedná-li se o tzv. bílé světlo (směs mnoha vlnových délek v rozsahu přes celou viditelnou oblast), potom je oblast interference jen několik málo vlnových délek. Pokud tedy změříme závislost vizibility, popř. i průběh interferenčních proužků, světla z daného zdroje v interferometru pro velký rozsah dráhového zpoždění (je relevantní jen oblast s interferencí), můžeme získat informaci o spektrálním složení tohoto zdroje. Křivka závislosti vizibility na dráhovém rozdílu (autokorelační křivka) nemusí mít jednoduchý tvar. V ideálním případě má tvar gaussovský. Spektrum záření se potom vypočítá podle Wienerova-Chinčinova teorému jako Fourierova transformace průběhu intenzity na výstupu interferometru, v jednodušším přiblížení stačí i autokorelační křivka. S(ν) = 2 I(τ) cos (2πντ)dτ. (2) 0 Příklad autokorelační křivky a vypočítaného spektrálního průběhu jsou na obrázku 7. 6
7 Obrázek 7: Naměřená autokorelační křivka laserové diody (vlevo), vypočítaný průběh spektra (vpravo). 7
protony) se mohou chovat jako vlnění (tedy mohou interferovat) i jako částice (lze
 1 Chování fotonu na děliči svazků Co je to vlastně foton? Pojmem foton myslíme kvantum elektromagnetického záření. Pokud budeme zmenšovat energii elektromagnetického záření (světla), potom někde na hodnotě
1 Chování fotonu na děliči svazků Co je to vlastně foton? Pojmem foton myslíme kvantum elektromagnetického záření. Pokud budeme zmenšovat energii elektromagnetického záření (světla), potom někde na hodnotě
Charakteristiky optického záření
 Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
VLNOVÁ OPTIKA. Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník
 VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
Laboratorní práce č. 3: Měření vlnové délky světla
 Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Laboratorní práce č. 3: Měření vlnové délky světla G Gymnázium Hranice Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Gymnázium G Hranice Test
Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Laboratorní práce č. 3: Měření vlnové délky světla G Gymnázium Hranice Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Gymnázium G Hranice Test
1 Rezonátorová optika
 1 Rezonátorová optika Optické rezonátory jsou zařízení, ve kterých lze akumulovat optickou energii. Mohou také působit jako frekvenční filtr. Obojího se využívá v laseru, kde je aktivní prostředí, které
1 Rezonátorová optika Optické rezonátory jsou zařízení, ve kterých lze akumulovat optickou energii. Mohou také působit jako frekvenční filtr. Obojího se využívá v laseru, kde je aktivní prostředí, které
Laboratorní úloha č. 7 Difrakce na mikro-objektech
 Laboratorní úloha č. 7 Difrakce na mikro-objektech Úkoly měření: 1. Odhad rozměrů mikro-objektů z informací uváděných výrobcem. 2. Záznam difrakčních obrazců (difraktogramů) vzniklých interakcí laserového
Laboratorní úloha č. 7 Difrakce na mikro-objektech Úkoly měření: 1. Odhad rozměrů mikro-objektů z informací uváděných výrobcem. 2. Záznam difrakčních obrazců (difraktogramů) vzniklých interakcí laserového
CZ.1.07/2.2.00/ AČ (RCPTM) Spektroskopie 1 / 24
 MĚŘENÍ SPEKTRA SVĚTLA Antonín Černoch Regionální centrum pokročilých technologií a materiálů CZ.1.07/2.2.00/15.0147 AČ (RCPTM) Spektroskopie 1 / 24 Úvod Obsah 1 Úvod 2 Zobrazovací spektrometry Disperzní
MĚŘENÍ SPEKTRA SVĚTLA Antonín Černoch Regionální centrum pokročilých technologií a materiálů CZ.1.07/2.2.00/15.0147 AČ (RCPTM) Spektroskopie 1 / 24 Úvod Obsah 1 Úvod 2 Zobrazovací spektrometry Disperzní
Světlo jako elektromagnetické záření
 Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Fyzika 2 - rámcové příklady vlnová optika, úvod do kvantové fyziky
 Fyzika 2 - rámcové příklady vlnová optika, úvod do kvantové fyziky 1. Vysvětlete pojmy kulová a rovinná vlnoplocha. 2. Pomocí Hyugensova principu vysvětlete konstrukci tvaru vlnoplochy v libovolném budoucím
Fyzika 2 - rámcové příklady vlnová optika, úvod do kvantové fyziky 1. Vysvětlete pojmy kulová a rovinná vlnoplocha. 2. Pomocí Hyugensova principu vysvětlete konstrukci tvaru vlnoplochy v libovolném budoucím
Vznik a šíření elektromagnetických vln
 Vznik a šíření elektromagnetických vln Hlavní body Rozšířený Coulombův zákon lektromagnetická vlna ve vakuu Zdroje elektromagnetických vln Přehled elektromagnetických vln Foton vlna nebo částice Fermatův
Vznik a šíření elektromagnetických vln Hlavní body Rozšířený Coulombův zákon lektromagnetická vlna ve vakuu Zdroje elektromagnetických vln Přehled elektromagnetických vln Foton vlna nebo částice Fermatův
ZÁKLADNÍ ČÁSTI SPEKTRÁLNÍCH PŘÍSTROJŮ
 ZÁKLADNÍ ČÁSTI SPEKTRÁLNÍCH PŘÍSTROJŮ (c) -2008, ACH/IM BLOKOVÉ SCHÉMA: (a) emisní metody (b) absorpční metody (c) luminiscenční metody U (b) monochromátor často umístěn před kyvetou se vzorkem. Části
ZÁKLADNÍ ČÁSTI SPEKTRÁLNÍCH PŘÍSTROJŮ (c) -2008, ACH/IM BLOKOVÉ SCHÉMA: (a) emisní metody (b) absorpční metody (c) luminiscenční metody U (b) monochromátor často umístěn před kyvetou se vzorkem. Části
Optika pro mikroskopii materiálů I
 Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Optika pro mikroskopii materiálů I Jan.Machacek@vscht.cz Ústav skla a keramiky VŠCHT Praha +42-0- 22044-4151 Osnova přednášky Základní pojmy optiky Odraz a lom světla Interference, ohyb a rozlišení optických
Laserové technologie v praxi I. Přednáška č.1. Fyzikální princip činnosti laserů. Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011
 Laserové technologie v praxi I. Přednáška č. Fyzikální princip činnosti laserů Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 0 LASER kvantový generátor světla Fyzikální princip činnosti laserů LASER zkratka
Laserové technologie v praxi I. Přednáška č. Fyzikální princip činnosti laserů Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 0 LASER kvantový generátor světla Fyzikální princip činnosti laserů LASER zkratka
λ, (20.1) 3.10-6 infračervené záření ultrafialové γ a kosmické mikrovlny
 Elektromagnetické vlny Optika, část fyziky zabývající se světlem, patří spolu s mechanikou k nejstarším fyzikálním oborům. Podle jedné ze starověkých teorií je světlo vyzařováno z oka a oko si jím ohmatává
Elektromagnetické vlny Optika, část fyziky zabývající se světlem, patří spolu s mechanikou k nejstarším fyzikálním oborům. Podle jedné ze starověkých teorií je světlo vyzařováno z oka a oko si jím ohmatává
Digitální učební materiál
 Číslo projektu Název projektu Číslo a název šablony klíčové aktivity Digitální učební materiál CZ.1.07/1.5.00/3.080 Zkvalitnění výuky prostřednictvím ICT III/ Inovace a zkvalitnění výuky prostřednictvím
Číslo projektu Název projektu Číslo a název šablony klíčové aktivity Digitální učební materiál CZ.1.07/1.5.00/3.080 Zkvalitnění výuky prostřednictvím ICT III/ Inovace a zkvalitnění výuky prostřednictvím
7 FYZIKÁLNÍ OPTIKA. Interference Ohyb Polarizace. Co je to ohyb? 27.2 Ohyb
 1 7 FYZIKÁLNÍ OPTIKA Interference Ohyb Polarizace Co je to ohyb? 27.2 Ohyb Ohyb vln je jev charakterizovaný odchylkou od přímočarého šíření vlnění v témže prostředí. Ve skutečnosti se nejedná o nový jev
1 7 FYZIKÁLNÍ OPTIKA Interference Ohyb Polarizace Co je to ohyb? 27.2 Ohyb Ohyb vln je jev charakterizovaný odchylkou od přímočarého šíření vlnění v témže prostředí. Ve skutečnosti se nejedná o nový jev
27. Vlnové vlastnosti světla
 27. Vlnové vlastnosti světla Základní vlastnosti světla (rychlost světla, šíření světla v různých prostředích, barva tělesa) Jevy potvrzující vlnovou povahu světla Ohyb a polarizace světla (ohyb světla
27. Vlnové vlastnosti světla Základní vlastnosti světla (rychlost světla, šíření světla v různých prostředích, barva tělesa) Jevy potvrzující vlnovou povahu světla Ohyb a polarizace světla (ohyb světla
Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako
![Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako Podle studijních textů k úloze [1] se divergence laserového svaku definuje jako](/thumbs/55/36333813.jpg) Úkoly 1. Změřte divergenci laserového svazku. 2. Z optické stavebnice sestavte Michelsonův interferometr. K rozšíření svazku sestavte Galileův teleskop. Ze známých ohniskových délek použitých čoček spočtěte,
Úkoly 1. Změřte divergenci laserového svazku. 2. Z optické stavebnice sestavte Michelsonův interferometr. K rozšíření svazku sestavte Galileův teleskop. Ze známých ohniskových délek použitých čoček spočtěte,
Nástin formální stavby kvantové mechaniky
 Nástin formální stavby kvantové mechaniky Karel Smolek Ústav technické a experimentální fyziky, ČVUT Komplexní čísla Pro každé reálné číslo platí, že jeho druhá mocnina je nezáporné číslo. Např. 3 2 =
Nástin formální stavby kvantové mechaniky Karel Smolek Ústav technické a experimentální fyziky, ČVUT Komplexní čísla Pro každé reálné číslo platí, že jeho druhá mocnina je nezáporné číslo. Např. 3 2 =
Fyzika II. Marek Procházka Vlnová optika II
 Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Vlnově částicová dualita
 Vlnově částicová dualita Karel Smolek Ústav technické a experimentální fyziky, ČVUT Vlnění Vlněním rozumíme šíření změny nějaké veličiny prostorem. Příklady: Vlny na moři šíření změny výšky hladiny Zvukové
Vlnově částicová dualita Karel Smolek Ústav technické a experimentální fyziky, ČVUT Vlnění Vlněním rozumíme šíření změny nějaké veličiny prostorem. Příklady: Vlny na moři šíření změny výšky hladiny Zvukové
Optické spektroskopie 1 LS 2014/15
 Optické spektroskopie 1 LS 2014/15 Martin Kubala 585634179 mkubala@prfnw.upol.cz 1.Úvod Velikosti objektů v přírodě Dítě ~ 1 m (10 0 m) Prst ~ 2 cm (10-2 m) Vlas ~ 0.1 mm (10-4 m) Buňka ~ 20 m (10-5 m)
Optické spektroskopie 1 LS 2014/15 Martin Kubala 585634179 mkubala@prfnw.upol.cz 1.Úvod Velikosti objektů v přírodě Dítě ~ 1 m (10 0 m) Prst ~ 2 cm (10-2 m) Vlas ~ 0.1 mm (10-4 m) Buňka ~ 20 m (10-5 m)
Zvuk. 1. základní kmitání. 2. šíření zvuku
 Zvuk 1. základní kmitání - vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin - podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění elastického
Zvuk 1. základní kmitání - vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin - podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění elastického
Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením.
 Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením. Na čem závisí účinnost vedení? účinnost vedení závisí na činiteli útlumu β a na činiteli odrazu
Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením. Na čem závisí účinnost vedení? účinnost vedení závisí na činiteli útlumu β a na činiteli odrazu
4. Z modové struktury emisního spektra laseru určete délku aktivní oblasti rezonátoru. Diskutujte,
 1 Pracovní úkol 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřené závislosti zpracujte graficky. Stanovte prahový proud i 0. 2. Pomocí Hg výbojky okalibrujte
1 Pracovní úkol 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřené závislosti zpracujte graficky. Stanovte prahový proud i 0. 2. Pomocí Hg výbojky okalibrujte
rychlostí šíření světla v tomto prostředí ku vakuu, n = c/v. Pro vzduch je index lomu přibližně 1, voda má 1.33, sklo od 1.5 do 1.9.
 1 Transport světla Pro popis šíření světla se může použít více metod v závislosti na okolnostech. Pokud je vlnová délka zanedbatelně malá nebo překážky, které klademe světlu do cesty, jsou mnohem větší
1 Transport světla Pro popis šíření světla se může použít více metod v závislosti na okolnostech. Pokud je vlnová délka zanedbatelně malá nebo překážky, které klademe světlu do cesty, jsou mnohem větší
Optická spektroskopie
 Univerzita Palackého v Olomouci Přírodovědecká fakulta Optická spektroskopie Antonín Černoch, Radek Machulka, Jan Soubusta Olomouc 2012 Oponenti: Mgr. Karel Lemr, Ph.D. RNDr. Dagmar Chvostová Publikace
Univerzita Palackého v Olomouci Přírodovědecká fakulta Optická spektroskopie Antonín Černoch, Radek Machulka, Jan Soubusta Olomouc 2012 Oponenti: Mgr. Karel Lemr, Ph.D. RNDr. Dagmar Chvostová Publikace
Řešení: Nejdříve musíme určit sílu, kterou působí kladka proti směru pohybu padajícího vědra a napíná tak lano. Moment síly otáčení kladky je:
 Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
PRAKTIKUM III. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III. úlohač.20 Název: Stavba Michelsonova interferometru a ověření jeho funkce Pracoval: Lukáš Ledvina stud.skup.14 dne:3.3.2010
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III. úlohač.20 Název: Stavba Michelsonova interferometru a ověření jeho funkce Pracoval: Lukáš Ledvina stud.skup.14 dne:3.3.2010
28 NELINEÁRNÍ OPTIKA. Nelineární optické jevy Holografie a optoelektronika
 336 28 NELINEÁRNÍ OPTIKA Nelineární optické jevy Holografie a optoelektronika Světelná vlna (jako každá jiná vlna) vyjádřená ve tvaru y=y o sin (út - ) je charakterizována základními charakteristikami:
336 28 NELINEÁRNÍ OPTIKA Nelineární optické jevy Holografie a optoelektronika Světelná vlna (jako každá jiná vlna) vyjádřená ve tvaru y=y o sin (út - ) je charakterizována základními charakteristikami:
Fabry Perotův interferometr
 Fabry Perotův interferometr Princip Dvě zrcadla jsou sestavena tak aby tvořila tzv. Fabry Perotův interferometr, s jehož pomocí je vyšetřován svazek paprsků vycházejících z laseru. Při experimentu se pohybuje
Fabry Perotův interferometr Princip Dvě zrcadla jsou sestavena tak aby tvořila tzv. Fabry Perotův interferometr, s jehož pomocí je vyšetřován svazek paprsků vycházejících z laseru. Při experimentu se pohybuje
Paradoxy kvantové mechaniky
 Paradoxy kvantové mechaniky Karel molek Ústav technické a experimentální fyziky, ČVUT Bezinterakční měření Mějme bombu, která je aktivována velmi citlivým mechanismem v podobě zrcátka, které je propojeno
Paradoxy kvantové mechaniky Karel molek Ústav technické a experimentální fyziky, ČVUT Bezinterakční měření Mějme bombu, která je aktivována velmi citlivým mechanismem v podobě zrcátka, které je propojeno
Kvantová informatika pro komunikace v budoucnosti
 Kvantová informatika pro komunikace v budoucnosti Antonín Černoch Regionální centrum pokročilých technologií a materiálů Společná laboratoř optiky University Palackého a Fyzikálního ústavu Akademie věd
Kvantová informatika pro komunikace v budoucnosti Antonín Černoch Regionální centrum pokročilých technologií a materiálů Společná laboratoř optiky University Palackého a Fyzikálního ústavu Akademie věd
Spektrometrické metody. Reflexní a fotoakustická spektroskopie
 Spektrometrické metody Reflexní a fotoakustická spektroskopie odraz elektromagnetického záření - souvislost absorpce a reflexe Kubelka-Munk funkce fotoakustická spektroskopie Měření odrazivosti elmg záření
Spektrometrické metody Reflexní a fotoakustická spektroskopie odraz elektromagnetického záření - souvislost absorpce a reflexe Kubelka-Munk funkce fotoakustická spektroskopie Měření odrazivosti elmg záření
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Název: Stavba Michelsonova interferometru a ověření jeho funkce
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III. Úloha č. 20 Název: Stavba Michelsonova interferometru a ověření jeho funkce Pracoval: Lukáš Vejmelka obor (kruh) FMUZV
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III. Úloha č. 20 Název: Stavba Michelsonova interferometru a ověření jeho funkce Pracoval: Lukáš Vejmelka obor (kruh) FMUZV
Dualismus vln a částic
 Dualismus vln a částic Filip Horák 1, Jan Pecina 2, Jiří Bárdoš 3 1 Mendelovo gymnázium, Opava, Horaksro@seznam.cz 2 Gymnázium Jeseník, pecinajan.jes@mail.com 3 Gymnázium Teplice, jiri.bardos@post.gymtce.cz
Dualismus vln a částic Filip Horák 1, Jan Pecina 2, Jiří Bárdoš 3 1 Mendelovo gymnázium, Opava, Horaksro@seznam.cz 2 Gymnázium Jeseník, pecinajan.jes@mail.com 3 Gymnázium Teplice, jiri.bardos@post.gymtce.cz
Otázka č. 14 Světlovodné přenosové cesty
 Fresnelův odraz: Otázka č. 4 Světlovodné přenosové cesty Princip šíření světla v optickém vlákně Odraz a lom světla: β α lom ke kolmici n n β α lom od kolmice n n Zákon lomu n sinα = n sin β Definice indexu
Fresnelův odraz: Otázka č. 4 Světlovodné přenosové cesty Princip šíření světla v optickém vlákně Odraz a lom světla: β α lom ke kolmici n n β α lom od kolmice n n Zákon lomu n sinα = n sin β Definice indexu
MODERNÍ METODY CHEMICKÉ FYZIKY I lasery a jejich použití v chemické fyzice Přednáška 5
 MODERNÍ METODY CHEMICKÉ FYZIKY I lasery a jejich použití v chemické fyzice Přednáška 5 Ondřej Votava J. Heyrovský Institute of Physical Chemistry AS ČR Opakování z minula Light Amplifier by Stimulated
MODERNÍ METODY CHEMICKÉ FYZIKY I lasery a jejich použití v chemické fyzice Přednáška 5 Ondřej Votava J. Heyrovský Institute of Physical Chemistry AS ČR Opakování z minula Light Amplifier by Stimulated
FTTX - Měření v optických sítích. František Tejkl 17.9.2014
 FTTX - Měření v optických sítích František Tejkl 17.9.2014 Náplň prezentace Co lze měřit v optických sítích Vizuální kontrola povrchu ferule konektoru Vizuální hledání chyb Optický rozpočet Přímá metoda
FTTX - Měření v optických sítích František Tejkl 17.9.2014 Náplň prezentace Co lze měřit v optických sítích Vizuální kontrola povrchu ferule konektoru Vizuální hledání chyb Optický rozpočet Přímá metoda
PRAKTIKUM III. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009.
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
??): Radiová oblast vlnové délky od kilometrů po 0.1 m, záření se generuje a detekuje pomocí
 Měření spektra světla Spektroskopie označuje metody určení frekvence ν resp. vlnové délky λ = c/ν elektromagnetického záření. Celé elektromagnetické spektrum lze rozdělit do podoblastí (viz obr.??): Radiová
Měření spektra světla Spektroskopie označuje metody určení frekvence ν resp. vlnové délky λ = c/ν elektromagnetického záření. Celé elektromagnetické spektrum lze rozdělit do podoblastí (viz obr.??): Radiová
Úloha č.3 Interferometry a vlastnosti laserového záření
 Úloha č.3 Interferometry a vlastnosti ového záření Optické interferometry jsou přístroje pro velmi přesná měření, jejiž princip je založen na interferenci světla. Interferometry se dnes používají k měření
Úloha č.3 Interferometry a vlastnosti ového záření Optické interferometry jsou přístroje pro velmi přesná měření, jejiž princip je založen na interferenci světla. Interferometry se dnes používají k měření
Jaký obraz vytvoří rovinné zrcadlo? Zdánlivý, vzpřímený, stejně velký. Jaký obraz vytvoří vypuklé zrcadlo? Zdánlivý, vzpřímený, zmenšený
 Jan Olbrecht Jaký obraz vytvoří rovinné zrcadlo? Zdánlivý, vzpřímený, stejně velký Jaký obraz vytvoří vypuklé zrcadlo? Zdánlivý, vzpřímený, zmenšený Jaký typ lomu nastane při průchodu světla z opticky
Jan Olbrecht Jaký obraz vytvoří rovinné zrcadlo? Zdánlivý, vzpřímený, stejně velký Jaký obraz vytvoří vypuklé zrcadlo? Zdánlivý, vzpřímený, zmenšený Jaký typ lomu nastane při průchodu světla z opticky
Konstrukce interferometru
 PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI Katedra optiky Konstrukce interferometru pro měření kvantového šumu světla DIPLOMOVÁ PRÁCE Petra Doležalová 2007 PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY
PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO V OLOMOUCI Katedra optiky Konstrukce interferometru pro měření kvantového šumu světla DIPLOMOVÁ PRÁCE Petra Doležalová 2007 PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY
Měření charakteristik pevnolátkového infračerveného Er:Yag laseru
 Měření charakteristik pevnolátkového infračerveného Er:Yag laseru Ondřej Ticháček, PORG, ondrejtichacek@gmail.com Abstrakt: Úkolem bylo proměření základních charakteristik záření pevnolátkového infračerveného
Měření charakteristik pevnolátkového infračerveného Er:Yag laseru Ondřej Ticháček, PORG, ondrejtichacek@gmail.com Abstrakt: Úkolem bylo proměření základních charakteristik záření pevnolátkového infračerveného
Fyzika II, FMMI. 1. Elektrostatické pole
 Fyzika II, FMMI 1. Elektrostatické pole 1.1 Jaká je velikost celkového náboje (kladného i záporného), který je obsažen v 5 kg železa? Předpokládejme, že by se tento náboj rovnoměrně rozmístil do dvou malých
Fyzika II, FMMI 1. Elektrostatické pole 1.1 Jaká je velikost celkového náboje (kladného i záporného), který je obsažen v 5 kg železa? Předpokládejme, že by se tento náboj rovnoměrně rozmístil do dvou malých
Infračervená spektroskopie
 Infračervená spektroskopie 1 Teoretické základy Podstatou infračervené spektroskopie je interakce infračerveného záření se studovanou hmotou, kdy v případě pohlcení fotonu studovanou hmotou mluvíme o absorpční
Infračervená spektroskopie 1 Teoretické základy Podstatou infračervené spektroskopie je interakce infračerveného záření se studovanou hmotou, kdy v případě pohlcení fotonu studovanou hmotou mluvíme o absorpční
ABSORPČNÍ A EMISNÍ SPEKTRÁLNÍ METODY
 ABSORPČNÍ A EMISNÍ SPEKTRÁLNÍ METODY 1 Fyzikální základy spektrálních metod Monochromatický zářivý tok 0 (W, rozměr m 2.kg.s -3 ): Absorbován ABS Propuštěn Odražen zpět r Rozptýlen s Bilance toků 0 = +
ABSORPČNÍ A EMISNÍ SPEKTRÁLNÍ METODY 1 Fyzikální základy spektrálních metod Monochromatický zářivý tok 0 (W, rozměr m 2.kg.s -3 ): Absorbován ABS Propuštěn Odražen zpět r Rozptýlen s Bilance toků 0 = +
MĚŘENÍ ABSOLUTNÍ VLHKOSTI VZDUCHU NA ZÁKLADĚ SPEKTRÁLNÍ ANALÝZY Measurement of Absolute Humidity on the Basis of Spectral Analysis
 MĚŘENÍ ABSOLUTNÍ VLHKOSTI VZDUCHU NA ZÁKLADĚ SPEKTRÁLNÍ ANALÝZY Measurement of Absolute Humidity on the Basis of Spectral Analysis Ivana Krestýnová, Josef Zicha Abstrakt: Absolutní vlhkost je hmotnost
MĚŘENÍ ABSOLUTNÍ VLHKOSTI VZDUCHU NA ZÁKLADĚ SPEKTRÁLNÍ ANALÝZY Measurement of Absolute Humidity on the Basis of Spectral Analysis Ivana Krestýnová, Josef Zicha Abstrakt: Absolutní vlhkost je hmotnost
Katedra fyzikální elektroniky. Jakub Kákona
 České vysoké učení technické v Praze Fakulta jaderná a fyzikálně inženýrská Katedra fyzikální elektroniky Bakalářská práce Jakub Kákona Praha 2012 Vzor titulní strany na pevných deskách Jméno autora a
České vysoké učení technické v Praze Fakulta jaderná a fyzikálně inženýrská Katedra fyzikální elektroniky Bakalářská práce Jakub Kákona Praha 2012 Vzor titulní strany na pevných deskách Jméno autora a
Úvod, optické záření. Podkladový materiál k přednáškám A0M38OSE Obrazové senzory ČVUT- FEL, katedra měření, Jan Fischer, 2014
 Úvod, optické záření Podkladový materiál k přednáškám A0M38OSE Obrazové senzory ČVUT- FEL, katedra měření, Jan Fischer, 2014 Materiál je pouze grafickým podkladem k přednášce a nenahrazuje výklad na vlastní
Úvod, optické záření Podkladový materiál k přednáškám A0M38OSE Obrazové senzory ČVUT- FEL, katedra měření, Jan Fischer, 2014 Materiál je pouze grafickým podkladem k přednášce a nenahrazuje výklad na vlastní
PSK1-14. Optické zdroje a detektory. Bohrův model atomu. Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 Ing. Marek Nožka.
 PSK1-14 Název školy: Autor: Anotace: Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 Ing. Marek Nožka Optické zdroje a detektory Vzdělávací oblast: Informační a komunikační technologie Předmět:
PSK1-14 Název školy: Autor: Anotace: Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 Ing. Marek Nožka Optické zdroje a detektory Vzdělávací oblast: Informační a komunikační technologie Předmět:
Fotonické sítě jako médium pro distribuci stabilních signálů z optických normálů frekvence a času
 Fotonické sítě jako médium pro distribuci stabilních signálů z optických normálů frekvence a času Ondřej Číp, Šimon Řeřucha, Radek Šmíd, Martin Čížek, Břetislav Mikel (ÚPT AV ČR) Josef Vojtěch a Vladimír
Fotonické sítě jako médium pro distribuci stabilních signálů z optických normálů frekvence a času Ondřej Číp, Šimon Řeřucha, Radek Šmíd, Martin Čížek, Břetislav Mikel (ÚPT AV ČR) Josef Vojtěch a Vladimír
Lasery optické rezonátory
 Lasery optické rezonátory Optické rezonátory Optickým rezonátorem se rozumí dutina obklopená odrazovými plochami, v níž je pasivní dielektrické prostředí. Rezonátor je nezbytnou součástí laseru, protože
Lasery optické rezonátory Optické rezonátory Optickým rezonátorem se rozumí dutina obklopená odrazovými plochami, v níž je pasivní dielektrické prostředí. Rezonátor je nezbytnou součástí laseru, protože
5.3.5 Ohyb světla na překážkách
 5.3.5 Ohyb světla na překážkách Předpoklady: 3xxx Světlo i zvuk jsou vlnění, ale přesto jsou mezi nimi obrovské rozdíly. Slyšíme i to, co se děje za rohem x Co se děje za rohem nevidíme. Proč? Vlnění se
5.3.5 Ohyb světla na překážkách Předpoklady: 3xxx Světlo i zvuk jsou vlnění, ale přesto jsou mezi nimi obrovské rozdíly. Slyšíme i to, co se děje za rohem x Co se děje za rohem nevidíme. Proč? Vlnění se
- Ideálně koherentním světelným svazkem se rozumí elektromagnetické vlnění o stejné frekvenci, stejném směru kmitání a stejné fázi.
 P7: Optické metody - V klasické optice jsou interferenční a difrakční jevy popisovány prostřednictvím ideálně koherentních, ideálně nekoherentních, později také částečně koherentních světelných svazků
P7: Optické metody - V klasické optice jsou interferenční a difrakční jevy popisovány prostřednictvím ideálně koherentních, ideálně nekoherentních, později také částečně koherentních světelných svazků
2. Vyhodnoťte získané tloušťky a diskutujte, zda je vrstva v rámci chyby nepřímého měření na obou místech stejně silná.
 1 Pracovní úkoly 1. Změřte tloušťku tenké vrstvy ve dvou různých místech. 2. Vyhodnoťte získané tloušťky a diskutujte, zda je vrstva v rámci chyby nepřímého měření na obou místech stejně silná. 3. Okalibrujte
1 Pracovní úkoly 1. Změřte tloušťku tenké vrstvy ve dvou různých místech. 2. Vyhodnoťte získané tloušťky a diskutujte, zda je vrstva v rámci chyby nepřímého měření na obou místech stejně silná. 3. Okalibrujte
Lom světla na kapce, lom 1., 2. a 3. řádu Lom světla na kapce, jenž je reprezentována kulovou plochou rozhraní, je složitý mechanismus rozptylu dopada
 Fázový Dopplerův analyzátor (PDA) Základy geometrické optiky Index lomu látky pro světlo o vlnové délce λ je definován jako poměr rychlosti světla ve vakuu k rychlosti světla v látce. cv n = [-] (1) c
Fázový Dopplerův analyzátor (PDA) Základy geometrické optiky Index lomu látky pro světlo o vlnové délce λ je definován jako poměr rychlosti světla ve vakuu k rychlosti světla v látce. cv n = [-] (1) c
Signál v čase a jeho spektrum
 Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
knové senzory v geotechnice a stavebnictví
 Optovláknov knové senzory v geotechnice a stavebnictví Safibra, s.r.o. 1 Obsah Proč monitorovat? Co lze optovlákny monitorovat. FBG technologie Raman OTDR Brillouin OTDR Úloha firmy Safibra 2 Proč monitorovat?
Optovláknov knové senzory v geotechnice a stavebnictví Safibra, s.r.o. 1 Obsah Proč monitorovat? Co lze optovlákny monitorovat. FBG technologie Raman OTDR Brillouin OTDR Úloha firmy Safibra 2 Proč monitorovat?
Úvod do laserové techniky
 Úvod do laserové techniky Světlo jako elektromagnetické záření II. část Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze jan.sulc@fjfi.cvut.cz 6. října 016 Kontakty Ing. Jan
Úvod do laserové techniky Světlo jako elektromagnetické záření II. část Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze jan.sulc@fjfi.cvut.cz 6. října 016 Kontakty Ing. Jan
Úloha 15: Studium polovodičového GaAs/GaAlAs laseru
 Petra Suková, 2.ročník, F-14 1 Úloha 15: Studium polovodičového GaAs/GaAlAs laseru 1 Zadání 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřenézávislostizpracujtegraficky.Stanovteprahovýproud
Petra Suková, 2.ročník, F-14 1 Úloha 15: Studium polovodičového GaAs/GaAlAs laseru 1 Zadání 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřenézávislostizpracujtegraficky.Stanovteprahovýproud
Refraktometrie, interferometrie, polarimetrie, nefelometrie, turbidimetrie
 Refraktometrie, interferometrie, polarimetrie, nefelometrie, turbidimetrie Refraktometrie Metoda založená na měření indexu lomu Při dopadu paprsku světla na fázové rozhraní mohou nastat dva jevy: Reflexe
Refraktometrie, interferometrie, polarimetrie, nefelometrie, turbidimetrie Refraktometrie Metoda založená na měření indexu lomu Při dopadu paprsku světla na fázové rozhraní mohou nastat dva jevy: Reflexe
- studium jevů pozorovaných při průchodu světla prostředím: - absorpce - rozptyl (difúze) - rozklad světla
 VLNOVÁ OPTIKA - studium jevů založených na vlnové povaze světla: - interference (jev podmíněný skládáním vlnění) - polarizace - difrakce (ohyb) - disperze (jev související se závislostí n n ) - studium
VLNOVÁ OPTIKA - studium jevů založených na vlnové povaze světla: - interference (jev podmíněný skládáním vlnění) - polarizace - difrakce (ohyb) - disperze (jev související se závislostí n n ) - studium
Úloha č.3 Interferometry a vlastnosti laserového záření
 Úloha č.3 Interferometry a vlastnosti ového záření 1 Teoretický úvod Vyskytují-li se ve stejném prostoru a čase současně dvě (nebo více) optických vln, dochází k interferenci světla, kdy je výsledná vlnová
Úloha č.3 Interferometry a vlastnosti ového záření 1 Teoretický úvod Vyskytují-li se ve stejném prostoru a čase současně dvě (nebo více) optických vln, dochází k interferenci světla, kdy je výsledná vlnová
4. V jednom krychlovém metru (1 m 3 ) plynu je 2, molekul. Ve dvou krychlových milimetrech (2 mm 3 ) plynu je molekul
 Fyzika 20 Otázky za 2 body. Celsiova teplota t a termodynamická teplota T spolu souvisejí známým vztahem. Vyberte dvojici, která tento vztah vyjadřuje (zaokrouhleno na celá čísla) a) T = 253 K ; t = 20
Fyzika 20 Otázky za 2 body. Celsiova teplota t a termodynamická teplota T spolu souvisejí známým vztahem. Vyberte dvojici, která tento vztah vyjadřuje (zaokrouhleno na celá čísla) a) T = 253 K ; t = 20
Na základě toho vysvětlil Eisnstein vnější fotoefekt, kterým byla platnost tohoto vztahu povrzena.
 Vlnově-korpuskulární dualismus, fotony, fotoelektrický jev vnější a vnitřní. Elmg. teorie záření vysvětluje dobře mnohé jevy v optice interference, difrakci, polarizaci. Nelze jí ale vysvětlit např. fotoelektrický
Vlnově-korpuskulární dualismus, fotony, fotoelektrický jev vnější a vnitřní. Elmg. teorie záření vysvětluje dobře mnohé jevy v optice interference, difrakci, polarizaci. Nelze jí ale vysvětlit např. fotoelektrický
Optické měřicí 3D metody
 Univerzita Palackého v Olomouci Přírodovědecká fakulta Optické měřicí 3D metod Michal Pochmon Olomouc 212 Oponent: RNDr. Tomáš Rössler Ph.D. Publikace bla připravena v rámci projektu Investice do rozvoje
Univerzita Palackého v Olomouci Přírodovědecká fakulta Optické měřicí 3D metod Michal Pochmon Olomouc 212 Oponent: RNDr. Tomáš Rössler Ph.D. Publikace bla připravena v rámci projektu Investice do rozvoje
Aplikovaná optika. Optika. Vlnová optika. Geometrická optika. Kvantová optika. - pracuje s čistě geometrickými představami
 Aplikovaná optika Optika Geometrická optika Vlnová optika Kvantová optika - pracuje s čistě geometrickými představami - zanedbává vlnovou a kvantovou povahu světla - elektromagnetická teorie světla -světlo
Aplikovaná optika Optika Geometrická optika Vlnová optika Kvantová optika - pracuje s čistě geometrickými představami - zanedbává vlnovou a kvantovou povahu světla - elektromagnetická teorie světla -světlo
Úvod do laserové techniky KFE FJFI ČVUT Praha Michal Němec, 2014. Plynové lasery. Plynové lasery většinou pracují v kontinuálním režimu.
 Aktivní prostředí v plynné fázi. Plynové lasery Inverze populace hladin je vytvářena mezi energetickými hladinami některé ze složek plynu - atomy, ionty nebo molekuly atomární, iontové, molekulární lasery.
Aktivní prostředí v plynné fázi. Plynové lasery Inverze populace hladin je vytvářena mezi energetickými hladinami některé ze složek plynu - atomy, ionty nebo molekuly atomární, iontové, molekulární lasery.
Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky
 Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky Úkol : 1. Určete mřížkovou konstantu d optické mřížky a porovnejte s hodnotou udávanou výrobcem. 2. Určete vlnovou délku λ jednotlivých
Měření vlnové délky spektrálních čar rtuťové výbojky pomocí optické mřížky Úkol : 1. Určete mřížkovou konstantu d optické mřížky a porovnejte s hodnotou udávanou výrobcem. 2. Určete vlnovou délku λ jednotlivých
λ hc Optoelektronické součástky Fotorezistor, Laserová dioda
 Optoelektronické součástky Fotorezistor, Laserová dioda Úvod Optoelektronické součástky jsou založeny na interakci optického záření s elektricky nabitými částicemi v polovodičích. Vztah mezi energií fotonů
Optoelektronické součástky Fotorezistor, Laserová dioda Úvod Optoelektronické součástky jsou založeny na interakci optického záření s elektricky nabitými částicemi v polovodičích. Vztah mezi energií fotonů
FYZIKA II. Marek Procházka 1. Přednáška
 FYZIKA II Marek Procházka 1. Přednáška Historie Dělení optiky Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení
FYZIKA II Marek Procházka 1. Přednáška Historie Dělení optiky Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení
5.3.1 Disperze světla, barvy
 5.3.1 Disperze světla, barvy Předpoklady: 5103 Svítíme paprskem bílého světla ze žárovky na skleněný hranol. Světlo se láme podle zákona lomu na zdi vznikne osvětlená stopa Stopa vznikla, ale není bílá,
5.3.1 Disperze světla, barvy Předpoklady: 5103 Svítíme paprskem bílého světla ze žárovky na skleněný hranol. Světlo se láme podle zákona lomu na zdi vznikne osvětlená stopa Stopa vznikla, ale není bílá,
Karel Lemr. web: Karel Lemr Fotonové páry 1 / 26
 Kvantové zpracování informace s fotonovými páry Karel Lemr Společná laboratoř optiky UP Olomouc a FzÚ AVČR web: http://jointlab.upol.cz/lemr email: lemr@jointlab.upol.cz Karel Lemr Fotonové páry 1 / 26
Kvantové zpracování informace s fotonovými páry Karel Lemr Společná laboratoř optiky UP Olomouc a FzÚ AVČR web: http://jointlab.upol.cz/lemr email: lemr@jointlab.upol.cz Karel Lemr Fotonové páry 1 / 26
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV RADIOELEKTRONIKY. OPTICKÝ SPOJ LR-830/1550 Technický popis
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV RADIOELEKTRONIKY OPTICKÝ SPOJ LR-830/1550 Technický popis BRNO, 2009 1 Návrh a konstrukce dálkového spoje 1.1 Optická
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV RADIOELEKTRONIKY OPTICKÝ SPOJ LR-830/1550 Technický popis BRNO, 2009 1 Návrh a konstrukce dálkového spoje 1.1 Optická
P5: Optické metody I
 P5: Optické metody I - V klasické optice jsou interferenční a difrakční jevy popisovány prostřednictvím ideálně koherentních, ideálně nekoherentních, později také částečně koherentních světelných svazků
P5: Optické metody I - V klasické optice jsou interferenční a difrakční jevy popisovány prostřednictvím ideálně koherentních, ideálně nekoherentních, později také částečně koherentních světelných svazků
Stručný úvod do spektroskopie
 Vzdělávací soustředění studentů projekt KOSOAP Slunce, projevy sluneční aktivity a využití spektroskopie v astrofyzikálním výzkumu Stručný úvod do spektroskopie Ing. Libor Lenža, Hvězdárna Valašské Meziříčí,
Vzdělávací soustředění studentů projekt KOSOAP Slunce, projevy sluneční aktivity a využití spektroskopie v astrofyzikálním výzkumu Stručný úvod do spektroskopie Ing. Libor Lenža, Hvězdárna Valašské Meziříčí,
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Příklady použití tenkých vrstev Jaromír Křepelka
 Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
Příklady použití tenkých vrstev Jaromír Křepelka Příklad 01 Spočtěte odrazivost prostého rozhraní dvou izotropních homogenních materiálů s indexy lomu n 0 = 1 a n 1 = 1,52 v závislosti na úhlu dopadu pro
3. Optoelektronický generátor náhodných čísel
 3 Optoelektronický generátor náhodných čísel Fyzikální generátor náhodných čísel může být založen na nejrůznějších fyzikálních procesech Jde přitom o to, aby proces samotný byl náhodný ve smyslu nepředpověditelnosti
3 Optoelektronický generátor náhodných čísel Fyzikální generátor náhodných čísel může být založen na nejrůznějších fyzikálních procesech Jde přitom o to, aby proces samotný byl náhodný ve smyslu nepředpověditelnosti
Měření optických vlastností materiálů
 E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
2. Zdroje a detektory světla
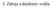 2. Zdroje a detektory světla transmitance (%) Spektrální rozsah Krátkovlné limity: Absorpce vzduchu (O 2,N 2,vodní pára) - 190 nm Propustnost optiky Spektrální rozsah zdroje vlnová délka (nm) http://www.hellma-analytics.com/text/283/en/material-and-technical-information.html
2. Zdroje a detektory světla transmitance (%) Spektrální rozsah Krátkovlné limity: Absorpce vzduchu (O 2,N 2,vodní pára) - 190 nm Propustnost optiky Spektrální rozsah zdroje vlnová délka (nm) http://www.hellma-analytics.com/text/283/en/material-and-technical-information.html
Úloha 10: Interference a ohyb světla
 Úloha 10: Interference a ohyb světla FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 29.3.2010 Jméno: František Batysta Pracovní skupina: 5 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovník: Štěpán
Úloha 10: Interference a ohyb světla FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 29.3.2010 Jméno: František Batysta Pracovní skupina: 5 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovník: Štěpán
c) vysvětlení jednotlivých veličin ve vztahu pro okamžitou výchylku, jejich jednotky
 Harmonický kmitavý pohyb a) vysvětlení harmonického kmitavého pohybu b) zápis vztahu pro okamžitou výchylku c) vysvětlení jednotlivých veličin ve vztahu pro okamžitou výchylku, jejich jednotky d) perioda
Harmonický kmitavý pohyb a) vysvětlení harmonického kmitavého pohybu b) zápis vztahu pro okamžitou výchylku c) vysvětlení jednotlivých veličin ve vztahu pro okamžitou výchylku, jejich jednotky d) perioda
VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ
 VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ P. Novák, J. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán výukový software pro
VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ P. Novák, J. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán výukový software pro
 Interference světla Vlnovou podstatu světla prokázal až roku 1801 Thomas Young, když pozoroval jeho interferenci (tj. skládání). Youngův experiment interference světla na dvou štěrbinách (animace) http://micro.magnet.fsu.edu
Interference světla Vlnovou podstatu světla prokázal až roku 1801 Thomas Young, když pozoroval jeho interferenci (tj. skládání). Youngův experiment interference světla na dvou štěrbinách (animace) http://micro.magnet.fsu.edu
Neživá příroda I. Optické vlastnosti minerálů
 Neživá příroda I Optické vlastnosti minerálů 1 Charakter světla Světelný paprsek definuje: vlnová délka (λ): vzdálenost mezi následnými vrcholy vln, amplituda: výchylka na obě strany od rovnovážné polohy,
Neživá příroda I Optické vlastnosti minerálů 1 Charakter světla Světelný paprsek definuje: vlnová délka (λ): vzdálenost mezi následnými vrcholy vln, amplituda: výchylka na obě strany od rovnovážné polohy,
Fotoelektrické snímače
 Fotoelektrické snímače Úloha je zaměřena na měření světelných charakteristik fotoelektrických prvků (součástek). Pro měření se využívají fotorezistor, fototranzistor a fotodioda. Zadání 1. Seznamte se
Fotoelektrické snímače Úloha je zaměřena na měření světelných charakteristik fotoelektrických prvků (součástek). Pro měření se využívají fotorezistor, fototranzistor a fotodioda. Zadání 1. Seznamte se
Fyzika pro chemiky II
 Fyzika pro chemiky II P. Klang, J. Novák, R. Štoudek, Ústav fyziky kondenzovaných látek, PřF MU Brno 18. února 2004 1 Optika 1. Rovinná elektromagnetická vlna o frekvenci f = 5.45 10 14 Hz polarizovaná
Fyzika pro chemiky II P. Klang, J. Novák, R. Štoudek, Ústav fyziky kondenzovaných látek, PřF MU Brno 18. února 2004 1 Optika 1. Rovinná elektromagnetická vlna o frekvenci f = 5.45 10 14 Hz polarizovaná
Zadání. Pracovní úkol. Pomůcky
 Pracovní úkol Zadání 1. Najděte směr snadného průchodu polarizátoru užívaného v aparatuře. 2. Ověřte, že zdroj světla je polarizován kolmo k vodorovné rovině. 3. Na přiložených vzorcích proměřte závislost
Pracovní úkol Zadání 1. Najděte směr snadného průchodu polarizátoru užívaného v aparatuře. 2. Ověřte, že zdroj světla je polarizován kolmo k vodorovné rovině. 3. Na přiložených vzorcích proměřte závislost
Klasické a inovované měření rychlosti zvuku
 Klasické a inovované měření rychlosti zvuku Jiří Tesař katedra fyziky, Pedagogická fakulta JU Klíčová slova: Rychlost zvuku, vlnová délka, frekvence, interference vlnění, stojaté vlnění, kmitny, uzly,
Klasické a inovované měření rychlosti zvuku Jiří Tesař katedra fyziky, Pedagogická fakulta JU Klíčová slova: Rychlost zvuku, vlnová délka, frekvence, interference vlnění, stojaté vlnění, kmitny, uzly,
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 18.4.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Měření s polarizovaným světlem Abstrakt V
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 18.4.2012 Jméno: Jakub Kákona Pracovní skupina: 2 Hodina: Po 7:30 Spolupracovníci: Viktor Polák Hodnocení: Měření s polarizovaným světlem Abstrakt V
MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM
 MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM Difrakce (ohyb) světla je jedním z několika projevů vlnových vlastností světla. Z těchto důvodů světlo při setkání s překážkou nepostupuje dále vždy
MĚŘENÍ VLNOVÝCH DÉLEK SVĚTLA MŘÍŽKOVÝM SPEKTROMETREM Difrakce (ohyb) světla je jedním z několika projevů vlnových vlastností světla. Z těchto důvodů světlo při setkání s překážkou nepostupuje dále vždy
Geometrická optika. předmětu. Obrazový prostor prostor za optickou soustavou (většinou vpravo), v němž může ležet obraz - - - 1 -
 Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Úvod do spektrálních metod pro analýzu léčiv
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Úvod do spektrálních metod pro analýzu léčiv Pavel Matějka, Vadym Prokopec pavel.matejka@vscht.cz pavel.matejka@gmail.com Vadym.Prokopec@vscht.cz
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Úvod do spektrálních metod pro analýzu léčiv Pavel Matějka, Vadym Prokopec pavel.matejka@vscht.cz pavel.matejka@gmail.com Vadym.Prokopec@vscht.cz
Základním praktikum z laserové techniky
 Úloha: Základním praktikum z laserové techniky FJFI ČVUT v Praze #6 Nelineární transmise saturovatelných absorbérů Jméno: Ondřej Finke Datum měření: 30.3.016 Spolupracoval: Obor / Skupina: 1. Úvod Alexandr
Úloha: Základním praktikum z laserové techniky FJFI ČVUT v Praze #6 Nelineární transmise saturovatelných absorbérů Jméno: Ondřej Finke Datum měření: 30.3.016 Spolupracoval: Obor / Skupina: 1. Úvod Alexandr
Zdroje optického záření
 Metody optické spektroskopie v biofyzice Zdroje optického záření / 1 Zdroje optického záření tepelné výbojky polovodičové lasery synchrotronové záření Obvykle se charakterizují zářivostí (zářivý výkon
Metody optické spektroskopie v biofyzice Zdroje optického záření / 1 Zdroje optického záření tepelné výbojky polovodičové lasery synchrotronové záření Obvykle se charakterizují zářivostí (zářivý výkon
CZ.1.07/2.2.00/ AČ (SLO/RCPTM) Detekce a zpracování optického signálu 1 / 30
 DETEKCE A ZPRACOVÁNÍ OPTICKÉHO SIGNÁLU Antonín Černoch Společná laboratoř optiky UP a FZÚ AV ČR Regionální centrum pokročilých technologií a materiálů CZ107/2200/070018 AČ (SLO/RCPTM) Detekce a zpracování
DETEKCE A ZPRACOVÁNÍ OPTICKÉHO SIGNÁLU Antonín Černoch Společná laboratoř optiky UP a FZÚ AV ČR Regionální centrum pokročilých technologií a materiálů CZ107/2200/070018 AČ (SLO/RCPTM) Detekce a zpracování
2. Pomocí Hg výbojky okalibrujte stupnici monochromátoru SPM 2.
 1 Pracovní úkoly 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřené závislosti zpracujte graficky. Stanovte prahový proud i 0. 2. Pomocí Hg výbojky okalibrujte
1 Pracovní úkoly 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřené závislosti zpracujte graficky. Stanovte prahový proud i 0. 2. Pomocí Hg výbojky okalibrujte
2. Elektrotechnické materiály
 . Elektrotechnické materiály Předpokladem vhodného využití elektrotechnických materiálů v konstrukci elektrotechnických součástek a zařízení je znalost jejich vlastností. Elektrické vlastnosti materiálů
. Elektrotechnické materiály Předpokladem vhodného využití elektrotechnických materiálů v konstrukci elektrotechnických součástek a zařízení je znalost jejich vlastností. Elektrické vlastnosti materiálů
