Search and state transfer by means of quantum walk. Vyhledávání a přenos stavu pomocí kvantové procházky
|
|
|
- Romana Čechová
- před 6 lety
- Počet zobrazení:
Transkript
1 Czech Technical University in Prague Faculty of uclear Sciences and Physical Engineering Search and state transfer by means of quantum walk Vyhledávání a přenos stavu pomocí kvantové procházky Master s Thesis Author: Supervisor: Stanislav Skoupý Ing. Martin Štefaňák, Ph.D. Academic year: 06/07
2
3 - Zadání práce -
4 - Zadání práce (zadní strana -
5 Acknowledgment: I would like to express my honest gratitude to Ing. Martin Štefaňák, Ph.D. for supervising my work on this master s thesis.
6 Prohlášení Prohlašuji, že jsem svou diplomovou práci vypracoval samostatně a použil jsem pouze podklady (literaturu, software, atd.... uvedené v přiloženém seznamu. emám závažný důvod proti použití tohoto školního díla ve smyslu 60 Zákona č. /000 Sb., o právu autorském, o právech souvisejících s právem autorským a o změně některých zákonů (autorský zákon. V Praze dne Stanislav Skoupý
7 ázev práce: Vyhledávání a přenos stavu pomocí kvantové procházky Autor: Stanislav Skoupý Obor: Matematická fyzika Druh práce: Diplomová práce Vedoucí práce: Ing. Martin Štefaňák, Ph.D., České vysoké učení technické v Praze, Fakulta jaderná a fyzikálně inženýrská, Katedra fyziky Abstrakt: V této práci studujeme vyhledávací algoritmus a algoritmus pro přenos stavu docílený kvantovou procházkou. Je představeno obecné schéma vyhledávacího algoritmu a algoritmu pro přenos stavu. Je ukázáno, že úplného přenosu stavu pomocí kvantové procházky v diskrétním čase s mincí je docíleno na grafu hvězda, úplném bipartitním grafu a úplné grafu s jednou smyčkou na každém vrcholu v O ( krocích. Úplný přenos stavu se také objeví na úplném grafu použitím Szegedyho kvantové procházky a kvantové procházky ve spojitém času. akonec dokážeme podmínku optimality vyhledávacího algoritmu pomocí Szegedyho kvantové procházky na regulárním grafu s využitím spektrálních vlastností příslušné stochastické matice. Klíčová slova: kvantová procházka, vyhledávací algoritmus, přenos stavu Title: Search and state transfer by means of quantum walk Author: Stanislav Skoupý Abstract: In this thesis we study the search algorithm and the state transfer algorithm by means of quantum walk. The general scheme of the search algorithm and the state transfer algorithm is introduced. It is shown that perfect state transfer is achieved for the star graph, the complete bipartite graph and the complete graph with self loop at each vertex using discrete time quantum walk with coins in O ( steps. The perfect state transfer also occurs on the complete graph using the Szegedy s quantum walk and the continuous time quantum walk. At last the we prove the condition of optimality for the Szegedy s quantum walk search algorithm on the regular graphs using the spectral properties of the associated stochastic matrix. Key words: quantum walk, search algorithm, state transfer
8 Contents Introduction 9 Grover search algorithm 0 Quantum walk search and state transfer 4. Discrete quantum walk with coins Szegedy s walk Continuous time quantum walk Perfect state transfer 9 3. Star graph Complete bipartite graph Complete graph with self loop Szegedy s quantum walk on the complete graph Continuous time quantum walk on complete graph with self loops Quantum search on regular graphs 3 4. Continuous time quantum walk on random graphs Szegedy s quantum walk search on regular graphs Conclusion 39 8
9 Introduction In this thesis we study the search algorithm and state transfer algorithm by means of quantum. Quantum walks are important part of quantum computer science because it has been shown that they can be used as universal tool to implement quantum algorithms. We focus on the quantum walk search algorithm which can be used to speed up the search in unsorted database. Classic search algorithm need O ( steps in comparison to the quantum search O ( steps. The state transfer algorithm can be use to communication across the quantum network. In the first Chapter we study the Grover search algorithm and the Grover state transfer algorithm. The Grover search algorithm is not based on the quantum walk but the calculation of the success probability and the number of steps are very similar to the calculation used in the quantum walk search algorithm. In the second Chapter we describe the general scheme of the search algorithm and the state transfer algorithm by means of discrete time quantum walk with coins, Szegedy s discrete time quantum walk and continuous time quantum walk. In the third Chapter we present the graph where the perfect state transfer is achieved in the sense that fidelity of the transfer goes to one. Using the discrete time quantum walk we show that the perfect state occurs at the star graph, the complete bipartite graph and the complete graph with self loop at each vertex. We obtain the perfect state transfer on the complete graph also using the Szegedy s walk state transfer algorithm and the continuous time quantum walk state transfer algorithm. In the last Chapter we study the search algorithm on a random graphs. We review the work of Chakraborty et al. for the continuous time quantum walk on the random graph. They proved that the search algorithm is optimal for almost all graphs. In the second part of this Chapter we show that the Szegedy s quantum walk search algorithm is optimal for d-random regular graphs with the high probability. 9
10 Chapter Grover search algorithm In the first part of this chapter we describe the Grover search algorithm which was introduce in [] by L. Grover. In the second part we modify the algorithm to achieve state transfer. This modification is general in a sense that we use the same modification in quantum walk search algorithm in both discrete and continuous time. The Grover s algorithm is quantum algorithm designed to search in unsorted database. The algorithm operate on quantum register of qubits. Let us describe the Hilbert space of the quantum register and evolution operator of the algorithm. The basis of qubit register of length n is spanned states A A... A n where A k {0, }. The dimension of the register Hilbert space is = n. To simplify the notation we label the states A A... A n as j where A A... A n is binary representation of j, i.e. j = n k= A k k +. Then the Hilbert space is spanned by orthonormal basis { j, j {,,..., }}. The fact that algorithm works on quantum register is important for the physical implementation but it does not effect calculation of success probability. Hence, we suppose for following calculation in this chapter that is any natural number and not just n for some n. The evolution operator of the search algorithm is composed of two operators which are Grover operator and quantum query. The Grover operator reads where ψ is equal superposition of all basis states Ĝ = Î + ψ ψ, (. ψ = j. (. For a purpose of the search algorithm we suppose that there is a set of marked basis states which we want to find using the algorithm. Let us label the set and its elements as M = {m, m,..., m M }, where M is the size of M. At each step of the algorithm we apply phase shift by π at the marked states and then the Grover operator. We implement the phase shift by π as quantum query which has a following form ˆQ = Î m i m i. (.3 m i M ow we write the evolution operator of the algorithm as follows Û = Ĝ ˆQ. (.4 After describing the Hilbert space and the evolution operator of the algorithm we give exact steps of the Grover search algorithm: 0
11 . Initialize the system in equal superposition of basis states. Apply the evolution operator Û given by (.4 T-times. 3. Measure the system. init = ψ. (.5 We have to calculate the number of steps and the probability of success to complete the full definition of the algorithm. We start the calculation by defining two orthonormal states which read ψ m = m i M ψ = m i M M j M. (.6 j It is easy to see that these two states span invariant subspace of evolution operator Û Û ψ m = M Û ψ = M( M ψ m M( M ψ m + M ψ ψ. (.7 The initial state of the algorithm also lies in this subspace M M init = ψ m + ψ. (.8 Hence, we analyse the evolution of the system only in this subspace which reduce the dimension and simplify the calculation. We introduce the effective evolution operator that is in the orthonormal basis (.6 given by matrix of the following form U e f f = M M( M M( M M Let us now calculate the spectrum of (.9. Û e f f has two conjugate eigenvalues where eigenphase ω reads Corresponding eigenvectors are given by The initial state in the eigenbasis has a following form. (.9 λ ± = e ±iω, (.0 ( M ω = arccos. (. λ ± = ( ψ m ± i ψ. (. init = M + i M λ + + M i M λ. (.3
12 ow we calculate the state of the system after T steps as follows φ(t = Û T init = = M + i M e iωt λ + + M cos (ωt + M sin (ωt ψ m + M + i M e iωt λ From (.4 we calculate the probability of success which is given by p(t = m i M The expression has the highest value for condition. (.4 M cos (ωt M sin (ωt ψ M cos (ωt + M sin (ωt m i φ(t =. (.5 ωt = arccos M. (.6 Hence the number of steps is the closest integer to the number given by ( M arccos T arccos ( M π M ( + O (.7 where we use the Taylor expansion for large. For T given by (.7 the success probability (.5 goes to as follows ( p = O. (.8 Let us now modify the Grover search algorithm to achieve state transfer between two marked basis states, let us call them sender and receiver. We label the state corresponding to the sender as s and the state corresponding to the receiver as r. We use the same evolution operator (.4 with query ˆQ = Î s s r r. (.9 Difference between the search algorithm and the state transfer algorithm is the initial state. In the case of the state transfer algorithm we start with initial state s. Thus the state transfer algorithm has a following steps:. Initialize the system in the state. Apply the evolution operator Û given by (.4 T-times. 3. Measure the system. init = s. (.0 We calculate the number of steps T to achieve the maximum fidelity of the state transfer to the target state r. We start again by finding invariant subspace of the algorithm. It is easy to see that the invariant
13 subspace is spanned by the initial and target state and state ψ given by (.6 for M =. The effective evolution operator in basis { s, r, ψ } is given by 3 3 matrix of the following form U e f f = 4. (. We diagonalize the effective evolution operator to calculate the number of steps T. One eigenvalue λ 0 is equal to and corresponding eigenvector is The other two conjugate eigenvalues are given by λ 0 = ( s r. (. λ ± = e ±iω, (.3 where ω has a following form Eigenvalues λ ± have eigenvectors ( 4 ω = arccos. (.4 λ ± = ( s + r ± i ψ. (.5 The sender and the receiver states have in the eigenbasis of Û e f f the form The state of the system after T steps reads s = λ 0 + ( λ + + λ r = λ 0 +. (.6 ( λ + + λ φ (T = Û T init = λ 0 + eiωt ( λ+ + e iωt λ (.7 We see that (.7 rotate for ωt = π to the state r. Hence, we achieve the perfect state transfer if we set the number of steps T as the closest integer to π ω. Using Taylor expansion we estimate T as follows T π arccos ( 4 π ( + O. (.8 We also calculate the fidelity after T of steps of the state transfer. It reads ( ωt F (T = r φ (T = sin 4. (.9 ow if we substitute T = π and (.4 in (.9 and we use Taylor expansion, we get the estimation of the maximum fidelity as follows ( ( 4 π F max ( = sin arccos 4 4 O. (.30 Hence, the perfect state transfer using modified Grover s algorithm is achieved. 3
14 Chapter Quantum walk search and state transfer In this Chapter we describe the three search algorithm on a graph which are based on different quantum walks. We start with discrete time quantum walk with coins, then we present Szegedy s walk algorithms and as the last type of walk we introduce continuous time quantum walk. Furthermore, we present how the quantum walk search algorithm is used for state transfer across the graph for all three cases.. Discrete quantum walk with coins Our introduction of discrete time quantum walk algorithms is based on articles [],[3],[4] and [5]. Before anything else we need to construct Hilbert space H G of the graph and the evolution operator Û of one step of the walk. Let G = (V, E be a graph, where V is the set of vertices and E is the set of edges. At first we assign to every vertex v V the position state v p. If the system is in the state v p then the particle is located at the vertex v. For implementation of the discrete time quantum walk we have to add to every vertex so called coin space which directs the evolution of the walk. The basis of the coin space of the vertex v is spanned by states w c for all w where w is the neighbouring vertex of v in the graph, i.e. {v, w} E. Hence, the basis states of the walk Hilbert space have the form and the whole basis reads Then we implement so called shift operator as follows v, w := v p w c (. { v, w v, w V : {v, w} E}. (. Ŝ v, w := w, v. (.3 ow we can say that if the system of the walk is in the state v, w then the particle is located at the vertex v and it will move to vertex w after application of the shift operator Ŝ. The evolution of the system is trivial if we use only the shift operator Ŝ. The evolution operator Û of the search algorithm consist of two operators, of the shift operator Ŝ and so called coin operator Ĉ Û := Ŝ Ĉ. (.4 The main idea of the walk search algorithm is that we use different coin operators on the marked vertex coin space and on the coin spaces of other vertices. In the following chapters we use so called Grover 4
15 coin Ĝ on the vertices which are not marked and on the marked vertices we use only a phase shift by π or the Grover coin and the phase shift by π. The Grover coin reads Ĝ v = Î + ψ v ψ v (.5 where ψ v is equal superposition of all directions of the coin space at the vertex v given by ψ v = d (v w {v,w} E v, w, (.6 where d (v is the degree of the vertex v. The Grover coin is derived from the Grover operator (.. Let us have a set of marked vertices M. The coin operator Ĉ has the form Ĉ = Gˆ v ˆP v + (Ĉm Ĝ m ˆP m (.7 v V m M where Ĉ m is the coin operator at the marked vertex m and ˆP v is projector on the coin subspace at the vertex v. The projector ˆP v reads ˆP v = v, w v, w. (.8 w {v,w} E We can now finally describe the general form of the discrete time quantum walk search algorithm. It is composed of following steps:. Initialize the system in the superposition of basis states init = E v V w {v,w} E. Apply the evolution operator Û given by (.4 T-times. 3. Measure the system. v, w. (.9 The complexity of algorithm T and the probability of succes p depend on the structure and the size of the graph. It was proved that the general quantum search algorithm cannot perform better then Ω (, where = V is the size of the graph [6]. Hence, we call the search algorithm on the graph G optimal if T = O ( holds true. The state transfer algorithm can be obtain from the search algorithm by simple modification. We have now two marked vertices, let us called them the sender and the receiver and we label these vertices by s and r respectively. Because we have two marked vertices we have to modify the coin operator, it is given by Ĉ = Gˆ v ˆP v + ( Ĉ s Ĝ s ˆP s + ( Ĉ r Ĝ r ˆP r. (.0 v V Then state transfer algorithm has the following steps:. Initialize the system in the superposition of all directions at the sender vertex init = d (s 5 w {s,w} E s, w. (.
16 . Apply the evolution operator Û given by (.4 T-times. 3. Measure the system. The particle moves from the sender to the receiver with fidelity F. The complexity of algorithm T and the fidelity F depend again on the structure and the size of the graph. We say that the algorithm achieves the perfect state transfer if the fidelity is close to, i.e. the particle moves from the sender to the receiver.. Szegedy s walk In this chapter we present different model of the quantum walks, so called Szegedy s walk. This model is a coinless discrete time quantum walk where the evolution operator is composed of reflection operators on the bipartite graph. We present two models of Szegedy s search algorithm. The first was introduced in [7] by Szegedy and it is based on modification of stochastic matrix P associated with graph G which also modifies the reflection operators. The second was presented in [8] by Santos who adds quantum quarry to the unperturbed Szegedy s walk. We describe at first the Hilbert space of the walk and the reflection operators and then we present the evolution operator for both cases. Let us have the graph G = (V, E where we label the vertices from to, i.e. V = {... }. We construct the new bipartite graph G with vertices from the original G by copying the original graph G, removing all edges in both graphs and adding new edges so that vertex v from original graph is connected to the vertex w in the copy only if in the original graph vertices v and w were connected. The Hilbert space of Szegedy s walk is a tensor product of two -dimensional Hilbert spaces and its basis is spanned by vectors of the following form j, k = j k, j, k {... } (. for j, k {... } where j denotes the position in the original graph and k denotes position in the copy. The reflection operators that compose the evolution operator are reflection around subspaces spanned by states Φ j and Ψ k. These operators read ˆR A = Φ j Φ j I ˆR B = Ψ k Ψ k I k= (.3 where Φ j and Ψ k are given by Φ j = j P jk k k=. (.4 Ψ k = Pk j j k The numbers P jk are elements of stochastic matrix associated to the graph G. The unperturbed evolution operator has the form U = ˆR B ˆR A. (.5 6
17 The search algorithm used in [7] uses reflection operators with modified stochastic matrix P which elements are given by P jk = { P jk δ jk j M j M (.6 where P jk are elements of the original stochastic matrix of graph G, δ jk is Kronecker delta and M is the set of marked vertices. The evolution operator Û of the search algorithm uses the reflection operator ˆR A and ˆR B around states Φ j and Ψ j where we use P instead of P. Second approach uses operator composed of quantum quarries which reads ˆR M = Î m m Î (.7 m M and it is applyed before every step of unpertube walk. Thus we get the evolution operator Û according to [8] reads which reads The Szegedy algorithms has the following steps: Û = ˆR B ˆR A ˆR M. (.8. Initialize the system in the superposition of all basis states corresponding to edges of the graph init = j,k=. Apply the evolution operator Û (or Û in the second case T-times. 3. Measure the system. P j,k j, k. (.9 The number of steps T and the probability of success depend on the structure and the size of the graph and also on the choice of the evolution operator. Moving on to the state transfer algorithm, we have as before the sender and the receiver vertex. The algorithm goes as follows:. Initialize the system in the state corresponding to the sender vertex init = Φ s (or Φ s in the second case.. Apply the evolution operator Û (or Û in the second case T-times. 3. Measure the system. The number of steps T and the probability of success depend again on the structure and the size of the graph and also on the choice of the evolution operator..3 Continuous time quantum walk Last but not least, we describe the continuous time quantum walk search and state transfer algorithm. This section is based on articles [] and [9]. The Hilbert space is simpler than for discrete time quantum 7
18 walks. The Hilbert space of graph G is spanned by states { v, v V} which form the orthonormal basis. The evolution of the system is driven by the Schrödinger equation i t φ (t = Ĥ φ (t, (.0 where Ĥ is Hamiltonian of the system. Since we use the Hamiltonian which is time independent we can express the evolution operator as follows Û(t = e iĥt (. where we set = from now on. In the case of the search algorithm the Hamiltonian reads Ĥ = γâ G m m (. m M where M is the set of the marked vertices, Â G is given by adjacency matrix A G of the graph G and γ is a real number. The continuous time quantum walk search algorithm has the following steps:. Initialize the system in the superposition of basis states. Let the system evolve with Hamiltonian (. for time T. 3. Measure the system. init = v. (.3 V The probability of success p and the time T depend on the structure and the size of the graph G. In the case of the state transfer algorithm the Hamiltonian reads v V Ĥ = γâ G s s r r (.4 where s is the sender vertex and r is the sender vertex. The state transfer algorithm has the following steps:. Initialize the system in the state init = s.. Let the system evolve with Hamiltonian (.4 for time T. 3. Measure the system. The fidelity of the state transfer F and the time T depend on the structure and the size of the graph G. 8
19 Chapter 3 Perfect state transfer In this Chapter we present some examples of graphs where the perfect state transfer is achieved. We start with discrete time quantum walk state tranfer on the star graph, complete bipartite graph and complete graph with one additional self-loop at each vertex. Then we calculate the state transfer with Szegedy s walk on complete graph. The last expample is the continuous time quantum walk state transfer on the complete graph with self loops. We find subspace in the Hilbert space which is invariant with respect to the quantum walk and contains the initial and the target state. This helps us highly reduce the dimension of the problem. The results for the discrete time quantum walk state tranfer on the star graph and on the complete graph with one self loop and Szegedy s walk state transfer for complete graph are published in paper [0]. The result for complete bipartite graph is published in paper []. 3. Star graph At first we introduce the star graph and its Hilbert space, then we present invariant subspace and effective evolution operator and at last we show that the perfect state transfer is reached. The star graph consists of one central vertex and other vertices which are connected to the central vertex but not to each other. We label the central vertex as 0 and the vertices around from to. Hence, the corresponding position vectors are j p where j goes form 0 to. Because the outer vertices have only one neighbour their coin space is one dimensional, i.e. it is spanned by 0 c. The central vertex has -dimensional coin space spanned by states j c for j running from to. The general Hilbert space of the star graph is spanned by states 0, j and j, 0 for j {... }. The shift operator (.3 can be written in this basis as Ŝ = ( 0, j j, 0 + j, 0 0, j. (3. Let the sender and the receiver be outer vertices marked by vectors s, 0 and r, 0. Then the coin operator (.0 reads Ĉ = Ĝ 0 ˆP 0 + Î ˆP 0 ˆP s ˆP r, (3. where the Ĝ 0 is the Grover coin (.5 at the central vertex. The evolution operator has the form (.4. Because the star graph is bipartite graph, the amplitude on the receiver vertex is non-zero only after even number of steps. To simplify our calculations we can use Û instead of Û, i.e. we made steps at once. 9
20 If we define now the following orthonormal states as s := s, 0 r := r, 0 ψ := j, 0 j s,r (3.3 we see that they form invariant subspace with respect to Û Û s = s r ψ Û r = s + r ψ Û ψ = s + r + 4 ψ. (3.4 We introduce the effective evolution operator of the transfer algorithm with initial state s and denote it as Û e f f. Û e f f is in the basis { s, r, z } given by the following 3 3 matrix U e f f = 4. (3.5 This is the same effective evolution operator as in the Grover state transfer algorithm (.. Because in the case of the star graph effective evolution operator correspond to two steps of the walk the number of steps is twice the number of steps of the Grover state transfer algorithm (.8. Hence the number of steps is the closest even integer to the number T π ( + O. (3.6 After (3.6 number of steps we reach the same fidelity as in the Grovers state transfer algorithm (.30 and perfect state transfer is achieved on the star graph with discrete time quantum walk. 3. Complete bipartite graph In the case of the complete bipartite we apply the same methods as in the star graph. The set of vertices of complete bipartite graph consists of subsets, they are usually called parts of the graph. The vertices in one part are not connected between each other but they are connected to all vertices of the other part. Let us denote these parts as V and V, where the part V is the part that contains the sender vertex. The size of V we denote by and the size of V by M. The position space of V is spanned by states j p where j goes from to and the position space of V is spanned by states β p where β goes from to M. The coin space of vertices in V is spanned by vectors β c for β {... M} and the coin space of vertices in V is spanned by vectors j c for j {... }. The shift operator (.3 reads Ŝ = M ( β, j j, β + j, β β, j. (3.7 β= 0
21 There are two cases of positions of the marked vertices. The first case is that both the sender and the receiver are in the part V. The coin in this case is given by Ĉ = M Ĝ j ˆP j ˆP s ˆP r + Ĝ α ˆP α. (3.8 j s,r where Ĝ j and Ĝ α are the Grover coins (.5 and on the sender and receiver we use the phase shift by π. We again use U instead of evolution operator U. If we set the invariant subspace of Û to be spanned by the following basis states α= s := M s, β M β= r := M r, β M ψ := β= (M( j s,r M j, β β= (3.9 we find out that the effective evolution operator has exactly the same form as the effective evolution operator of the star graph (3.5. Thus perfect state transfer is achieved after (3.6 steps in the case where both the sender and the receiver are in the same part. In the second case, where the receiver is in the part V, the coin operator reads Ĉ = M Ĝ j ˆP j ˆP s + Ĝ α ˆP α ˆP r. (3.0 j s To simplify the problem we find the invariant subspace in V with respect to Û and we move the initial state of the algorithm from part V to V by one application of Û. We can do that because the amplitude on receiver state is non-zero only after odd number of steps. ow we start with new initial state and we use Û and define the effective evolution operator. The orthogonal vectors that span the invariant subspace have the form α := r, s α := α 3 := α 4 := α= α s r, j j s M β, s M β= β r M (M ( β= β r β, j j s. (3.
22 The new initial state is given by init M = Û s, β M = M β, s = M α M M M α 3 (3. β= We also need to express the target state in the basis of invariant subspace. It reads r = M β= r, j = α + α. (3.3 The effective evolution operator in basis (3. is given by the following 4 4 matrix M M 4 (M ( M U e f f = M M (M M M ( M (M ( M. (3.4 One eigenvector corresponding to eigenvalue λ 0, = can be seen right away, it is the vector α. There is a second eigenvector with eigenvalue λ 0, = and it has the following form λ 0 = M M + α + M + α M + α 4. (3.5 The conjugate eigenvalues have the form of λ ± = e ±iω where eigenphase ω is given by ( M M + ω = arccos. (3.6 M The corresponding eigenvectors can be written as λ ± = M i (M ( (M + (M (M + (M + α + + M M + M+ ( α 3 + i (M ( (M + M + (M + α 4 (3.7 If we express the receiver and the initial states in the eigenbasis of (3.4 we can calculate the general fidelity of the state transfer after t application of (3.4. The expression of the receiver and the initial state in eigenbasis of Û e f f are rather long and they are only useful to calculate the fidelity. We write just the fidelity after t + number of steps. It reads F (t + = r (Ûe t f f init = M (M ( cos(ωt + (M ( (M + sin(ωt. (3.8 = M(M + We find that (3.8 reach the maximum for (M ( ωt = arccos M. (3.9
23 We calculate the number of steps of the walk from (3.9 and from (3.6 as follows ( (M ( arccos M T = t + arccos ( + (3.0 M M + M More precisely we chose the odd integer which is the closet to the number (3.0. If we substitute the condition (3.9 in (3.8 we get the expression for the maximum fidelity as follows F max (, M = M + ( (M + M. (3. From that we see that the perfect state transfer is achieved only if = M. Substituting this condition in (3.0 and with help of Taylor expansion we get the same number of steps as in the star graph T π ( + O. (3. In this case we can estimate the maximum fidelity again with help of Taylor expansion from (3.8 as follows ( F max ( O. (3.3 The perfect state transfer with the sender and the receiver in different parts of bipartite graph occurs after T = π steps when both parts have the same size. In figure 3. we see how the maximum fidelity depends on the size of both parts. The time evolution of fidelity is displayed in figure 3. for the bipartite graph where the both parts have 00 vertices. F Figure 3.: The maximum of fidelity F max depending on the size of V given by (3.. The part with the receiver vertex V has 00 vertices. The perfect state transfer is reached for V = 00. 3
24 F step Figure 3.: The time evolution of the fidelity F of the state transfer from the sender vertex to the receiver vertex during 00 steps on the bipartite graph with 00 vertices in each part. The dots correspond to the numerical simulation and the line is given by (3.8. The fidelity is plotted only at the odd positions, because it is zero at the even positions. The maximum is reached after 30 steps which agrees with ( Complete graph with self loop We consider the state transfer on the complete graph with one self loop because it was shown in [] that the search algorithm on the same graph finds the marked vertex with probability close to. Additional self loops slow down the search and also lower the probability of success. We start again with description of the graph and its Hilbert space before we show that the perfect state transfer works. We label the vertices of the complete graph from to. Then the position space is spanned by vectors j p where j goes from to. The coin space at each vertex is spanned by j c where j runs from to. In this case the Hilbert space can be written as a tensor product of the position space and the coin space We use the same shift operator (.3. It can be now rewritten as H G = H p H c. (3.4 Ŝ = j, k k, j. (3.5 j,k= But the coin operator of the marked vertices is now different from the coin operator of the star graph and the complete bipartite graph. ow we use at the marked vertices the Grover coin with additional phase shift by π instead of just phase shift alone. The coin operator reads Ĉ = Ĝ j ˆP j Ĝ s ˆP s Ĝ r ˆP r. (3.6 The evolution operator is given by (.4. Because it was proven in [] that two steps of the walk are equivalent to one step of the Grover algorithm we use again Û instead of the evolution operator 4
25 to simplify the calculation. Let us now have subspace spanned by following orthonormal vectors s := s, k k= r := r, k k= ψ := ( ψ := j,k= j,k s,r ψ 3 := ( ψ 4 := ( ( j, s + j, r j s,r j, k s, k ( s, s + s, r ( r, k ( r, s + r, r ( k= k= (3.7 where we see that s is the initial state of the walk and r is the receiver state. This subspace is invariant with respect to the Û, but can be further reduce to dimension 5. Because the invariant subspace contains one eigenvector ϕ of Û which is orthogonal to the sender and the receiver state, the orthogonal complement in this subspace is also invariant subspace of Û and it contains the sender and the receiver. We set this orthogonal complement as our new invariant subspace. The eigenvector ϕ is given by ϕ = ψ + ψ + ψ 3 + ψ 4. (3.8 The basis of reduced invariant subspace is spanned by s, r and three other vectors which have the form ψ = ψ ψ = ψ = ψ 3 ψ 4 = ( ( j, s + j, r ( j s,r ( s, k r, k + 4 k= k s,r ψ 3 = ψ + ψ ψ 3 ψ 4 = + ( 8 j,k= j,k s,r j, k + ( j, s + j, r j s,r ( r, r + r, s + s, r + s, s 5 ( s, k + r, k k= k s,r j,k= j,k s,r j, k ( r, r + r, s s, r s, s (3.9.
26 The effective evolution operator in this basis is given by following 5 5 matrix U e f f = ( ( 4 ( 4 4 ( ( 4 ( 4 ( ( 4 4 ( ( 4 4 ( 4 ( ( ( ( 4 4 ( ( 4. (3.30 The spectrum of Û e f f is composed of λ 0 = and two pairs of conjugate eigenvalues of the following form λ,± = e ±iω λ,± = e ±iω (3.3 where the eigenphase ω is given by (.4. The corresponding eigenvectors reads λ 0 = s + r + ψ λ,± = s r i ψ. (3.3 λ,± = s + r ψ ± i ψ 3 The sender and the receiver states can be rewritten in eigenbasis of Û e f f as s = λ 0 + ( λ,+ + λ, + ( λ,+ + λ, r = λ 0 ( λ,+ + ϕ, + (3.33 (. λ,+ + λ, The state of the walk after t steps can be now expressed as Û t s = ( t Û e f f s = λ 0 + eiωt ( λ,+ + e iωt λ, + eiωt ( λ,+ + e 4iωt λ,. (3.34 We see that for ωt = π the state of the walk (3.34 is equal to r. We get the same condition for the number of steps as for the star graph. The number of steps T is the same as for the star graph (3.6. The evolution of fidelity is given by F (T = t = r t ( ωt (Ûe f f s = cos (ωt sin 4 (3.35 and the maximum fidelity after T = π has the same form as (.30. Hence, the perfect state transfer is reached. 3.4 Szegedy s quantum walk on the complete graph In this section we examine the state transfer algorithm on the complete graph using Santos model of Szegedy s quantum walk. For G to be complete graph the elements of the stochastic matrix has the following form p jk = δ jk. (3.36 6
27 The vectors (.4 now read Φ j = Ψ k = j, k k= k j. (3.37 j, k j k We show using evolution operator (.8 that it takes O ( steps for the large size graph to transfer the initial state s = Φ s = s, k (3.38 k= k s to the final state r = Φ r = r, k (3.39 k= k r with high probability. We find that the invariant subspace is spanned by the states s and r and further five orthonormal states which have the following form ψ = ψ = ψ 3 = ψ 4 = ψ 5 = ( ( 3 ( ( ( ( j, s j s,r j, r j s,r j,k= j,k s,r j k j, k s, k k= k s,r r, k k= k s,r s, r r, s. (3.40 7
28 The effective evolution operator in this basis has the form of following 7 7 matrix U e f f = 3 ( ( ( ( 3 ( 3 ( 3 3/ 0 ( ( 5/ 3 ( 0 ( ( 3 3/ 0 ( 5/ ( ( ( 3 ( 5 3 ( 3 ( ( 3/ (+ 3 3 ( 5/ 3 ( 5/ ( ( 3 ( 5/ ( 3 4( 3/ ( 5/ ( 5/ 4( 3/ ( ( 5/ 3 ( 3/ 0 (+ 3 ( 0 ( 3 3/ 0 ( ( 3 ( ( 3/ ( 3 0 ( 3 3/ ( ( ( 3/ 0 4 ( 3( 5 ( 3( 5 ( ( 3 ( 5/ ( 5/ ( 3 4 ( 5/ ( 3 ( ( 3 ( ( 5/ ( 3 ( ( 3 ( The spectrum of (3.4 is composed of one eigenvalues λ 0 = and 3 pairs of conjugate eigenvalues given by (3.4. λ,± = e ±iω λ,± = e ±iω λ,± = e ±iω 3 (3.4 where eigephases read with of the following form = ( 4 + ω = arccos ( ( 4 ω = arccos ( ( (4 5 ω 3 = arccos ( ( (3.44 The calculation of eigenvectors is quite difficult and we present only eigenvectors that are important for the estimation of the number of steps. The eigenvector corresponding to λ 0 reads ( 3 + λ 0 = ( s r + (( (( ( ψ 4 ψ 5 (. (3.45 ( s r + O We see that λ 0 gets for large close to the form of eigenvector of the Grover state transfer algorithm (.. Another two important eigenvectors are λ,± which correspond to eigenvalues λ,±. The vectors λ,± for large have the form λ,± = ( s + r ± ( ψ + O. (3.46 The rest of the eigenstates can be neglected because their overlaps with the initial and the final state goes to zero as O(. The eigenvectors λ,± also resemble the eigenstates of the Grover state transfer 8
29 algorithm (3.7. Hence, we see for that evolution of Szegedy s walk is close to effective evolution of the Grover state transfer algorithm. The eigenphase ω is different then the eigenphase (.4 in the Grover state transfer algorithm but the condition Tω = π for the limit of large is sufficient for the perfect state transfer. The number of steps T is the closest integer to π/ω, i.e. we get the estimation of the following form π T arccos ( π 4 + ( + O (. (3.47 We estimate the fidelity with the same precision as follows F (t = r t ( (Ûe f f s sin 4 tω. (3.48 π We show that the Szegedy s walk performs the perfect state transfer for sufficiently large after steps. The time evolution of the fidelity is presented in figure 3.3 for the complete graph with 40 vertices. F step Figure 3.3: The time evolution of the fidelity F of the state transfer in Szegedy s quantum walk model during 0 steps. The corresponding complete graph has 40 vertices. The dots correspond to the numerical simulation and the line is given by (3.48. The maximum is reached after 7 steps which agrees with ( Continuous time quantum walk on complete graph with self loops Since we calculate the state transfer on the complete graph with two different types of discrete time quantum walk we do the same same for continuous time walk. The Hilbert space is spanned by vector { j ; j {,,..., }}. We consider the complete graph with L self loops at each vertex. The adjacency matrix, which defines the Hamiltonian of the system (.4, reads L L A,L =..... = L L L (3.49
30 where the dimension of the matrices are and L is the number of self loops at each vertex. Because the Hamiltonians Ĥ and Ĥ + αî generate the same evolution for any real α it follows from (3.49 that number of loops does not matter. We set the graph to have one self loop at each vertex. We also set γ = in (.4. It is easy to see that subspace spanned by states s, r and ψ = j j s,r (3.50 is invariant with respect to the Hamiltonian (.4. Since the initial and the target states lies in this subspace we find the invariant subspace of the state transfer algorithm. We introduce the effective Hamiltonian which is given in basis { s, r, ψ } by 3 3 matrix + H e f f = +. (3.5 Let us now calculate the running time of the algorithm by diagonalizing the effective Hamiltonian. Spectrum of Ĥ e f f is composed of three eigenvalues which are given by Their corresponding eigenvectors reads λ = λ = λ 3 = +. (3.5 λ = ( s r λ = + 4 ( s + r + 4 ψ. (3.53 λ 3 = 4 ( s + r + 4 ψ The initial state and the target state have in the eigenbasis of Ĥ e f f the following form s = + λ + λ + λ 3 4 r = λ + 4 F (T = r e iĥt s = + λ + 4 ow we calculate the evolution of fidelity as follows ( cos ( T 30. (3.54 λ sin ( T. (3.55
31 For T = π fidelity (3.55 reaches the maximum and goes to. Hence the perfect state transfer is achieved for time T = π. 3
32 Chapter 4 Quantum search on regular graphs In first part of this Chapter we review the results from S. Chakraborty et al. [9] for continuous time quantum walk search. They found a sufficient condition for the search algorithm to be optimal and they used it to show that the search algorithm is optimal for almost all graphs. We use their results as motivation, because in the second part of this Chapter we focus on the Szegedy s search algorithm on the regular graph. We find the condition for the Szegedy s search algorithm on the regular graph to find marked vertex after O ( steps with probability σ 4 O ( where σ is the gap between the largest and the second largest eigenvalue of the associated stochastic matrix. 4. Continuous time quantum walk on random graphs In this section we describe the results of [9] in further detail. We start by presenting condition for the continuous time quantum walk search to achieve optimality, i.e. to find the marked vertex in O ( time. Then we show with the help of this condition that the optimal search is reached for almost all graphs. Using the Hamiltonian (. and initial state init = ψ = j Chakraborty et al. proved the following condition for optimality of the search: Lemma. Let Ĥ be a Hamiltonian with eigenvalues λ λ... λ k (satisfying λ = and λ i c < for all i > and eigenvectors v = ψ, v,..., v k and let Ĥ = m m with m ψ = ɛ. For an appropriate choice of r = O(, applying the Hamiltonian ( + rĥ + Ĥ to the starting state v = ψ for time Θ ( ɛ search is achieved when λa λ A results in a state f with m f c +c O(. Let λ A λa... λa be eigenvalues of the adjacency matrix A G. Then the first Hamiltonian Ĥ in Lemma corresponds to the adjacency matrix Ĥ = γâ G where γ is chosen to be. The optimal λ A c < and when ψ is eigenvector of  G, since m ψ = implies that the search time is Θ (. Since equal superposition of all basis states ψ is an eigenvector of all d-regular graph with largest eigenvalue d they directly fulfil one condition of the Lemma. It has been shown in [3] that the second largest eigenvalue of d-random regular graph is O ( d 3 4 for d 3 with high probability where d-random regular graph is a graph uniformly picked up from the set of all d-regular graphs. Hence d-random graphs fulfil λa = O ( d λ A 4 < with high probability and the optimal search is achieved according to Lemma. Another model of random graphs is Erdös-Renyi random graph which is a graph G(, P with vertices where every edge between any two vertices has probability P to be in this graph. Some property 3
33 of the graph holds for almost all graphs if the probability for graph G(, P having this property goes to for going to infinity. Chakraborty et al. found using results in [4] and [5] that as long as the probability is higher than log3/4 ( there is a spectral gap between the largest and the second largest eigenvalue of the adjacency matrix and λa is bounded by a constant. They also found that the equal λ A superposition of all basis states converges to the eigenvector of the largest eigenvalue for P log3/ (. Thus the optimal search is achieved according to the Lemma for almost all graphs. 4. Szegedy s quantum walk search on regular graphs In this section we consider the Szegedy s quantum walk search algorithm on the regular graph using the evolution operator Û. At first we write the results for the regular graph which were already proven by Szegedy in [7]. He found relation between the spectrum of the symmetric stochastic matrix and the spectrum of the evolution operator of the walk and the relation between spectral gap of the symmetric stochastic matrix and the upper bound of the number of steps of the search algorithm. Since this theorem does not give the exact number of steps of the algorithm we later prove theorem for regular graphs which gives better estimations on the number of steps and a different estimation of the probability of success. At first let us look on the theorem proved by Szegedy. The theorem reads for one marked vertex Theorem. Let P be a symmetric stochastic matrix of graph G with[ one marked vertex. Let σ be the eigenvalue gap of P. Then after randomly picked number of steps T, 000 ] σ the probability to find the marked vertex is at least 000. The inconveniences of this theorem are that the number of steps is picked randomly from the large interval and the lower bound of success probability is quite low. Also the only graph that is connected and has a symmetric stochastic matrix is the regular graph, so the theorem only holds for regular graphs. The limitation of the regular graphs comes from the fact that we can calculate directly the spectrum of the evolution operator only from the spectrum of the symmetric stochastic matrix. Before we write the spectrum of the evolution operator we introduce concept of idle and busy subspaces also used by Szegedy. Lets have two subspaces A and B of the Hilbert space of the walk which are spanned by the states { Φ,..., Φ } and { Ψ,..., Ψ } respectively. We call the subspace A B idle subspace since the evolution operator (.5 acts as identity on this subspace. The busy subspace is the orthogonal complement of the idle subspace, i.e ( A B. Since the spectrum of the evolution operator is trivial in the idle subspace we are only interested in the spectrum in the busy space. ow we describe the spectrum of the evolution operator. The spectrum was already found by Szegedy in [7]. The spectrum of the evolution operator (.5 on the busy space is derived from the spectrum P jk P T jk = of matrix D which is given by D = P P T where is the element-wise product, i.e. D jk = P jk P k j. All states that lies in the subspace A B are eigenvectors of the evolution operator with eigenvalue. To describe the rest of the spectrum we define two linear mapping L A, L B which map C onto the subspace A and B respectively and read ( L x A = x j Φ j. (4. ( L x B = x k Ψ k k= 33
34 The eigenvectors of the evolution operator which correspond to eigenvalue are given by u ( 0 A = L u 0 A and u 0 B = L ( u 0 B where u 0 is the eigenvector of the matrix D with eigenvalue 0. We get two conjugate eigenvalues λ ν ± of the evolution operator for every eigenvalue ν of the matrix D for which > ν > 0 holds true. The eigenvalues λ ν ± are given by λ ν ± = ν ± iν ν. (4. The eigenphase ω ν which corresponds to eigenvalues λ ν ± = e ±iων is given by ω ν = arccos ( ν. The eigenvectors of λ ν ± have the following form λ ν ± = ( ( u νa + ν i ν u ν ν B (4.3 where u ν is the eigenvector of D with eigenvalue ν, u ν A = L ( u ν A and u ν B = L ( u ν B. We are focusing on the regular graphs because the stochastic matrix is symmetric and hence D = P, i.e. we get direct connection between the spectrum of the stochastic matrix and the evolution operator. Also it holds for regular graph that P = d A G where d is degree of vertices and A G is the adjacency matrix of the graph. Thus we obtain the eigenvalues of the stochastic matrix of the d-regular graph just by dividing the eigenvalues of the adjacency matrix by d. Let us now look at the matrix D derived from the modified stochastic matrix P for the search algorithm. For the symmetric stochastic matrix P which has the form P = P P P T (4.4 0 we get the matrix P which reads P = ( P P 0 (4.5 where we consider only one marked vertex in the graph and we arrange the marked vertex at the last position without lost of generality. Then the matrix D reads ( D P 0 =. (4.6 0 The largest eigenvalue of the matrix D is, the second largest eigenvalue µ of D is the largest eigenvalue of P which is ( ( symmetric matrix. The following Lemma proven by Szegedy in [7] gives an estimation of the size of µ. The lemma reads: Lemma 3. The largest eigenvalue µ of P lies in the interval [, ] σ where σ is the gap between the first and the second largest eigenvalue of the original stochastic matrix P. We use Lemma 3 further in the text to prove estimation of the probability of the success, so we repeat briefly the proof given by Szegedy. The lower bound on the largest eigenvalue comes from the fact that for symmetric matrix with nonnegative elements the largest eigenvalue is equal to the norm of the matrix. We get µ = P = sup { P x : x C x = } P y = 34 (4.7
35 where is y is normalized equal superposition of all basis vectors in dimension. Finding the upper bound of µ is more difficult. The eigenvector of the largest eigenvalue of the symmetric matrix with non-negative elements has also non-negative coordinates. Let us denote this eigenvector of P as a, i.e. P a = µ a. We define dimensional expansion vector of a and label it as a. The first coordinates of a are the coordinates of a and last one is zero. We rewrite the vector a in the eigenbasis of the original stochastic matrix P as follows a = α y + α k u k k= where y is normalized equal superposition of all basis vectors in dimension and also P y = y, u k are other normalized eigenvectors of P. Since a = holds true we have α + k α k =. We estimate the size of α as follows α = ( a y = ( a y where ( is the scalar product in C and C. From (4.9 we get k= α k = α. Suppose ν k is the eigenvalue associated with u k then we get P a = α y + k= α k ν k u k. Since ν k σ we have the following estimation P a = α + α k ν k α + ( σ α k ν k k k α + ( σ α k ν k α + α k ν k σ α k ν k σ. (4.0 At last from k k k (4.8 (4.9 P a D a = P a = µ (4. and from (4.0 we receive the upper bound µ σ µ σ. Having proven the Lemma 3 we move on to the search algorithm itself and we summarize our results in the following theorem: Theorem 4. Let P be a symmetric stochastic matrix of the d-regular graph G with one[ marked vertex. Let σ be the eigenvalue gap of P that fulfils σ. Then after number of steps T ] π 8, π 8 σ the probability to find the marked vertex is at least σ 4 O (. We prove the Theorem 4 by showing that it is possible to approximate the evolution of the walk in the busy subspace by evolution only in the two dimensional subspace spanned by states λ µ ±. The two eigenstates λ µ ± of the evolution operator Û have the form ( ( λ µ ± = a A + µ i µ a B (4. µ and they correspond to the eigenvector a with the eigenvalue µ that is defines in the proof of the Lemma ( 3. The state a A and a B in (4. are constructed using linear map (4. because we have L a A = ( L A a ( and LB a ( = LB a thanks to a = 0. The initial and the target states are given by init = Φ i. (4.3 target = Φ 35
36 ow we calculate the scalar product between the states (4. and the initial and the target state. At first we calculate c := a A init = a B init = a A target = a j P jk P jk = j,k= a Pk P k = 0 k= a j k= ( f := a B target = a j P j P j = a j P j = a P P jk = a j = ( a y (4.4 where y is the normalized equal superposition of all basis vectors in C. Using the fact that P y = y we rewrite f as follows ( a ( y = y ( a = y P ( a = y D ( a + a P = µ ( y ( a + a P ( f = a P = ( µ ( a. (4.5 y Then we get ( c ± := λ µ c ± init = µ i µ µ (. (4.6 f ± := λ µ f ± target = µ i µ µ ow we rewrite the initial and the target states init = c + λ µ + + c λ µ + k r target = f + λ µ + + f λ µ + k r (4.7 where the states r j are orthogonal to λ µ ± and normalized to. From init = and target = we get the conditions for k and k that read k = c ± = ( a ( µ y µ = + µ ( a y + µ k = ( a ( µ y + µ (4.8 The accuracy of the approximation of the evolution with the initial state init in the subspace spanned by λ µ ± is growing with k getting smaller. We show by finding the lower bound of the scalar product ( a y that k. We use the perturbation theory on the vector a to find the lower bound of ( a y. Suppose that a is expressed as follows a = y + ε j z j (4.9 j 36
Gymnázium, Brno, Slovanské nám. 7 WORKBOOK. Mathematics. Teacher: Student:
 WORKBOOK Subject: Teacher: Student: Mathematics.... School year:../ Conic section The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.
WORKBOOK Subject: Teacher: Student: Mathematics.... School year:../ Conic section The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.
VY_32_INOVACE_06_Předpřítomný čas_03. Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace
 VY_32_INOVACE_06_Předpřítomný čas_03 Autor: Růžena Krupičková Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu: Zkvalitnění ICT ve slušovské škole Číslo projektu: CZ.1.07/1.4.00/21.2400
VY_32_INOVACE_06_Předpřítomný čas_03 Autor: Růžena Krupičková Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu: Zkvalitnění ICT ve slušovské škole Číslo projektu: CZ.1.07/1.4.00/21.2400
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
WORKSHEET 1: LINEAR EQUATION 1
 WORKSHEET 1: LINEAR EQUATION 1 1. Write down the arithmetical problem according the dictation: 2. Translate the English words, you can use a dictionary: equations to solve solve inverse operation variable
WORKSHEET 1: LINEAR EQUATION 1 1. Write down the arithmetical problem according the dictation: 2. Translate the English words, you can use a dictionary: equations to solve solve inverse operation variable
Transportation Problem
 Transportation Problem ١ C H A P T E R 7 Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply s i ) to n
Transportation Problem ١ C H A P T E R 7 Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply s i ) to n
Základy teorie front III
 Základy teorie front III Aplikace Poissonova procesu v teorii front II Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta
Základy teorie front III Aplikace Poissonova procesu v teorii front II Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta
DC circuits with a single source
 Název projektu: utomatizace výrobních procesů ve strojírenství a řemeslech egistrační číslo: Z..07/..0/0.008 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 09 Tento projekt je spolufinancován
Název projektu: utomatizace výrobních procesů ve strojírenství a řemeslech egistrační číslo: Z..07/..0/0.008 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 09 Tento projekt je spolufinancován
On large rigid sets of monounary algebras. D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia
 On large rigid sets of monounary algebras D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia coauthor G. Czédli, University of Szeged, Hungary The 54st Summer School on General Algebra
On large rigid sets of monounary algebras D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia coauthor G. Czédli, University of Szeged, Hungary The 54st Summer School on General Algebra
Quantum walks, search algorithm and state transfer. Kvantové procházky, vyhledávací algoritmus
 Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering Quantu walks, search algorith and state transfer Kvantové procházky, vyhledávací algoritus a přenos stavu Bachelor
Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering Quantu walks, search algorith and state transfer Kvantové procházky, vyhledávací algoritus a přenos stavu Bachelor
Gymnázium, Brno, Slovanské nám. 7, SCHEME OF WORK Mathematics SCHEME OF WORK. cz
 SCHEME OF WORK Subject: Mathematics Year: first grade, 1.X School year:../ List of topisc # Topics Time period Introduction, repetition September 1. Number sets October 2. Rigtht-angled triangle October,
SCHEME OF WORK Subject: Mathematics Year: first grade, 1.X School year:../ List of topisc # Topics Time period Introduction, repetition September 1. Number sets October 2. Rigtht-angled triangle October,
Compression of a Dictionary
 Compression of a Dictionary Jan Lánský, Michal Žemlička zizelevak@matfyz.cz michal.zemlicka@mff.cuni.cz Dept. of Software Engineering Faculty of Mathematics and Physics Charles University Synopsis Introduction
Compression of a Dictionary Jan Lánský, Michal Žemlička zizelevak@matfyz.cz michal.zemlicka@mff.cuni.cz Dept. of Software Engineering Faculty of Mathematics and Physics Charles University Synopsis Introduction
Czech Technical University in Prague DOCTORAL THESIS
 Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering DOCTORAL THESIS CERN-THESIS-2015-137 15/10/2015 Search for B! µ + µ Decays with the Full Run I Data of The ATLAS
Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering DOCTORAL THESIS CERN-THESIS-2015-137 15/10/2015 Search for B! µ + µ Decays with the Full Run I Data of The ATLAS
USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING
 USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING Eva Minaříková Institute for Research in School Education, Faculty of Education, Masaryk University Structure of the presentation What can we as teachers
USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING Eva Minaříková Institute for Research in School Education, Faculty of Education, Masaryk University Structure of the presentation What can we as teachers
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA
 GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
Využití hybridní metody vícekriteriálního rozhodování za nejistoty. Michal Koláček, Markéta Matulová
 Využití hybridní metody vícekriteriálního rozhodování za nejistoty Michal Koláček, Markéta Matulová Outline Multiple criteria decision making Classification of MCDM methods TOPSIS method Fuzzy extension
Využití hybridní metody vícekriteriálního rozhodování za nejistoty Michal Koláček, Markéta Matulová Outline Multiple criteria decision making Classification of MCDM methods TOPSIS method Fuzzy extension
Angličtina v matematických softwarech 2 Vypracovala: Mgr. Bronislava Kreuzingerová
 Angličtina v matematických softwarech 2 Vypracovala: Mgr. Bronislava Kreuzingerová Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace
Angličtina v matematických softwarech 2 Vypracovala: Mgr. Bronislava Kreuzingerová Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace
6.867 Machine Learning
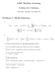 . Machine Learning Problem Set Solutions Due date: Monday November Problem : Model Selection. P (y,..., y n x,..., x n, PST) = = K [ [,] K [ K p n+ i i ( p i ) n i dpi ] = p n+ i i K ( p i ) n i n + i!
. Machine Learning Problem Set Solutions Due date: Monday November Problem : Model Selection. P (y,..., y n x,..., x n, PST) = = K [ [,] K [ K p n+ i i ( p i ) n i dpi ] = p n+ i i K ( p i ) n i n + i!
Database systems. Normal forms
 Database systems Normal forms An example of a bad model SSN Surnam OfficeNo City Street No ZIP Region President_of_ Region 1001 Novák 238 Liteň Hlavní 10 26727 Středočeský Rath 1001 Novák 238 Bystřice
Database systems Normal forms An example of a bad model SSN Surnam OfficeNo City Street No ZIP Region President_of_ Region 1001 Novák 238 Liteň Hlavní 10 26727 Středočeský Rath 1001 Novák 238 Bystřice
2. Entity, Architecture, Process
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Praktika návrhu číslicových obvodů Dr.-Ing. Martin Novotný Katedra číslicového návrhu Fakulta informačních technologií ČVUT v Praze Miloš
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Praktika návrhu číslicových obvodů Dr.-Ing. Martin Novotný Katedra číslicového návrhu Fakulta informačních technologií ČVUT v Praze Miloš
Návrh a implementace algoritmů pro adaptivní řízení průmyslových robotů
 Návrh a implementace algoritmů pro adaptivní řízení průmyslových robotů Design and implementation of algorithms for adaptive control of stationary robots Marcel Vytečka 1, Karel Zídek 2 Abstrakt Článek
Návrh a implementace algoritmů pro adaptivní řízení průmyslových robotů Design and implementation of algorithms for adaptive control of stationary robots Marcel Vytečka 1, Karel Zídek 2 Abstrakt Článek
Just write down your most recent and important education. Remember that sometimes less is more some people may be considered overqualified.
 CURRICULUM VITAE - EDUCATION Jindřich Bláha Výukový materiál zpracován v rámci projektu EU peníze školám Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Bc. Jindřich Bláha. Dostupné z Metodického
CURRICULUM VITAE - EDUCATION Jindřich Bláha Výukový materiál zpracován v rámci projektu EU peníze školám Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Bc. Jindřich Bláha. Dostupné z Metodického
Aplikace matematiky. Dana Lauerová A note to the theory of periodic solutions of a parabolic equation
 Aplikace matematiky Dana Lauerová A note to the theory of periodic solutions of a parabolic equation Aplikace matematiky, Vol. 25 (1980), No. 6, 457--460 Persistent URL: http://dml.cz/dmlcz/103885 Terms
Aplikace matematiky Dana Lauerová A note to the theory of periodic solutions of a parabolic equation Aplikace matematiky, Vol. 25 (1980), No. 6, 457--460 Persistent URL: http://dml.cz/dmlcz/103885 Terms
CZ.1.07/1.5.00/ Zefektivnění výuky prostřednictvím ICT technologií III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT
 Autor: Sylva Máčalová Tematický celek : Gramatika Cílová skupina : mírně pokročilý - pokročilý Anotace Materiál má podobu pracovního listu, který obsahuje cvičení, pomocí nichž si žáci procvičí rozdíly
Autor: Sylva Máčalová Tematický celek : Gramatika Cílová skupina : mírně pokročilý - pokročilý Anotace Materiál má podobu pracovního listu, který obsahuje cvičení, pomocí nichž si žáci procvičí rozdíly
Introduction to MS Dynamics NAV
 Introduction to MS Dynamics NAV (Item Charges) Ing.J.Skorkovský,CSc. MASARYK UNIVERSITY BRNO, Czech Republic Faculty of economics and business administration Department of corporate economy Item Charges
Introduction to MS Dynamics NAV (Item Charges) Ing.J.Skorkovský,CSc. MASARYK UNIVERSITY BRNO, Czech Republic Faculty of economics and business administration Department of corporate economy Item Charges
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Litosil - application
 Litosil - application The series of Litosil is primarily determined for cut polished floors. The cut polished floors are supplied by some specialized firms which are fitted with the appropriate technical
Litosil - application The series of Litosil is primarily determined for cut polished floors. The cut polished floors are supplied by some specialized firms which are fitted with the appropriate technical
VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O.
 VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O. Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová práce 2013 Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová
VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O. Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová práce 2013 Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová
Radiova meteoricka detekc nı stanice RMDS01A
 Radiova meteoricka detekc nı stanice RMDS01A Jakub Ka kona, kaklik@mlab.cz 15. u nora 2014 Abstrakt Konstrukce za kladnı ho softwarove definovane ho pr ijı macı ho syste mu pro detekci meteoru. 1 Obsah
Radiova meteoricka detekc nı stanice RMDS01A Jakub Ka kona, kaklik@mlab.cz 15. u nora 2014 Abstrakt Konstrukce za kladnı ho softwarove definovane ho pr ijı macı ho syste mu pro detekci meteoru. 1 Obsah
Gymnázium, Brno, Slovanské nám. 7 WORKBOOK. Mathematics. Student: Draw: Convex angle Non-convex angle
 WORKBOOK http://agb.gymnaslo.cz Subject: Student: Mathematics.. School year:../ Topic: Trigonometry Angle orientation Types of angles 90 right angle - pravý less than 90 acute angles ("acute" meaning "sharp")-
WORKBOOK http://agb.gymnaslo.cz Subject: Student: Mathematics.. School year:../ Topic: Trigonometry Angle orientation Types of angles 90 right angle - pravý less than 90 acute angles ("acute" meaning "sharp")-
Chapter 7: Process Synchronization
 Chapter 7: Process Synchronization Background The Critical-Section Problem Synchronization Hardware Semaphores Classical Problems of Synchronization Critical Regions Monitors Synchronization in Solaris
Chapter 7: Process Synchronization Background The Critical-Section Problem Synchronization Hardware Semaphores Classical Problems of Synchronization Critical Regions Monitors Synchronization in Solaris
Present Perfect x Past Simple Předpřítomný čas x Minulý čas Pracovní list
 VY_32_INOVACE_AJ_133 Present Perfect x Past Simple Předpřítomný čas x Minulý čas Pracovní list PhDr. Zuzana Žantovská Období vytvoření: květen 2013 Ročník: 1. 4. ročník SŠ Tematická oblast: Gramatika slovesa
VY_32_INOVACE_AJ_133 Present Perfect x Past Simple Předpřítomný čas x Minulý čas Pracovní list PhDr. Zuzana Žantovská Období vytvoření: květen 2013 Ročník: 1. 4. ročník SŠ Tematická oblast: Gramatika slovesa
CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA
 CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA &KDSWHUSUHVHQWVWKHGHVLJQDQGIDEULFDW LRQRIPRGLILHG0LQNRZVNLIUDFWDODQWHQQD IRUZLUHOHVVFRPPXQLFDWLRQ7KHVLPXODWHG DQGPHDVXUHGUHVXOWVRIWKLVDQWHQQDDUH DOVRSUHVHQWHG
CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA &KDSWHUSUHVHQWVWKHGHVLJQDQGIDEULFDW LRQRIPRGLILHG0LQNRZVNLIUDFWDODQWHQQD IRUZLUHOHVVFRPPXQLFDWLRQ7KHVLPXODWHG DQGPHDVXUHGUHVXOWVRIWKLVDQWHQQDDUH DOVRSUHVHQWHG
PC/104, PC/104-Plus. 196 ept GmbH I Tel. +49 (0) / I Fax +49 (0) / I I
 E L E C T R O N I C C O N N E C T O R S 196 ept GmbH I Tel. +49 (0) 88 61 / 25 01 0 I Fax +49 (0) 88 61 / 55 07 I E-Mail sales@ept.de I www.ept.de Contents Introduction 198 Overview 199 The Standard 200
E L E C T R O N I C C O N N E C T O R S 196 ept GmbH I Tel. +49 (0) 88 61 / 25 01 0 I Fax +49 (0) 88 61 / 55 07 I E-Mail sales@ept.de I www.ept.de Contents Introduction 198 Overview 199 The Standard 200
Czech Republic. EDUCAnet. Střední odborná škola Pardubice, s.r.o.
 Czech Republic EDUCAnet Střední odborná škola Pardubice, s.r.o. ACCESS TO MODERN TECHNOLOGIES Do modern technologies influence our behavior? Of course in positive and negative way as well Modern technologies
Czech Republic EDUCAnet Střední odborná škola Pardubice, s.r.o. ACCESS TO MODERN TECHNOLOGIES Do modern technologies influence our behavior? Of course in positive and negative way as well Modern technologies
PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL
 PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL Ing. Jan HAVLÍK, MPA tajemník Městského úřadu Žďár nad Sázavou Chief Executive Municipality of Žďár nad Sázavou CO
PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL Ing. Jan HAVLÍK, MPA tajemník Městského úřadu Žďár nad Sázavou Chief Executive Municipality of Žďár nad Sázavou CO
EU peníze středním školám digitální učební materiál
 EU peníze středním školám digitální učební materiál Číslo projektu: Číslo a název šablony klíčové aktivity: Tematická oblast, název DUMu: Autor: CZ.1.07/1.5.00/34.0515 III/2 Inovace a zkvalitnění výuky
EU peníze středním školám digitální učební materiál Číslo projektu: Číslo a název šablony klíčové aktivity: Tematická oblast, název DUMu: Autor: CZ.1.07/1.5.00/34.0515 III/2 Inovace a zkvalitnění výuky
Dynamic Signals. Ananda V. Mysore SJSU
 Dynamic Signals Ananda V. Mysore SJSU Static vs. Dynamic Signals In principle, all signals are dynamic; they do not have a perfectly constant value over time. Static signals are those for which changes
Dynamic Signals Ananda V. Mysore SJSU Static vs. Dynamic Signals In principle, all signals are dynamic; they do not have a perfectly constant value over time. Static signals are those for which changes
Department of Mathematical Analysis and Applications of Mathematics Faculty of Science, Palacký University Olomouc Czech Republic
 ROBUST 13. září 2016 regression regresních modelů Categorical Continuous - explanatory, Eva Fišerová Department of Mathematical Analysis and Applications of Mathematics Faculty of Science, Palacký University
ROBUST 13. září 2016 regression regresních modelů Categorical Continuous - explanatory, Eva Fišerová Department of Mathematical Analysis and Applications of Mathematics Faculty of Science, Palacký University
Vánoční sety Christmas sets
 Energy news 7 Inovace Innovations 1 Vánoční sety Christmas sets Na jaře tohoto roku jste byli informováni o připravované akci pro předvánoční období sety Pentagramu koncentrátů a Pentagramu krémů ve speciálních
Energy news 7 Inovace Innovations 1 Vánoční sety Christmas sets Na jaře tohoto roku jste byli informováni o připravované akci pro předvánoční období sety Pentagramu koncentrátů a Pentagramu krémů ve speciálních
Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční
 Příloha I Seznam tabulek Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční odměny pro rozhodčí platný od roku
Příloha I Seznam tabulek Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční odměny pro rozhodčí platný od roku
Zelené potraviny v nových obalech Green foods in a new packaging
 Energy News1 1 Zelené potraviny v nových obalech Green foods in a new packaging Již v minulém roce jsme Vás informovali, že dojde k přebalení všech tří zelených potravin do nových papírových obalů, které
Energy News1 1 Zelené potraviny v nových obalech Green foods in a new packaging Již v minulém roce jsme Vás informovali, že dojde k přebalení všech tří zelených potravin do nových papírových obalů, které
SPECIAL THEORY OF RELATIVITY
 SPECIAL THEORY OF RELATIVITY 1. Basi information author Albert Einstein phenomena obsered when TWO frames of referene moe relatie to eah other with speed lose to the speed of light 1905 - speial theory
SPECIAL THEORY OF RELATIVITY 1. Basi information author Albert Einstein phenomena obsered when TWO frames of referene moe relatie to eah other with speed lose to the speed of light 1905 - speial theory
Uni- and multi-dimensional parametric tests for comparison of sample results
 Uni- and multi-dimensional parametric tests for comparison of sample results Jedno- a více-rozměrné parametrické testy k porovnání výsledků Prof. RNDr. Milan Meloun, DrSc. Katedra analytické chemie, Universita
Uni- and multi-dimensional parametric tests for comparison of sample results Jedno- a více-rozměrné parametrické testy k porovnání výsledků Prof. RNDr. Milan Meloun, DrSc. Katedra analytické chemie, Universita
Stojan pro vrtačku plošných spojů
 Střední škola průmyslová a hotelová Uherské Hradiště Kollárova 617, Uherské Hradiště Stojan pro vrtačku plošných spojů Závěrečný projekt Autor práce: Koutný Radim Lukáš Martin Janoštík Václav Vedoucí projektu:
Střední škola průmyslová a hotelová Uherské Hradiště Kollárova 617, Uherské Hradiště Stojan pro vrtačku plošných spojů Závěrečný projekt Autor práce: Koutný Radim Lukáš Martin Janoštík Václav Vedoucí projektu:
Next line show use of paragraf symbol. It should be kept with the following number. Jak může státní zástupce věc odložit zmiňuje 159a.
 1 Bad line breaks The follwing text has prepostions O and k at end of line which is incorrect according to Czech language typography standards: Mezi oblíbené dětské pohádky patří pohádky O Palečkovi, Alenka
1 Bad line breaks The follwing text has prepostions O and k at end of line which is incorrect according to Czech language typography standards: Mezi oblíbené dětské pohádky patří pohádky O Palečkovi, Alenka
POPIS TUN TAP. Vysvetlivky: Modre - překlad Cervene - nejasnosti Zelene -poznamky. (Chci si ujasnit o kterem bloku z toho schematu se mluvi.
 Vysvetlivky: Modre - překlad Cervene - nejasnosti Zelene -poznamky POPIS TUN TAP (Chci si ujasnit o kterem bloku z toho schematu se mluvi.) VAS MODEL OpenVPN MUJ MODEL funkce virtuálního sítového rozhrani
Vysvetlivky: Modre - překlad Cervene - nejasnosti Zelene -poznamky POPIS TUN TAP (Chci si ujasnit o kterem bloku z toho schematu se mluvi.) VAS MODEL OpenVPN MUJ MODEL funkce virtuálního sítového rozhrani
Goal: to construct some general-purpose algorithms for solving systems of linear Equations
 Chapter IV Solving Systems of Linear Equations Goal: to construct some general-purpose algorithms for solving systems of linear Equations S4.4 Norms and the Analysis of Errors S4.4 Norms and the Analysis
Chapter IV Solving Systems of Linear Equations Goal: to construct some general-purpose algorithms for solving systems of linear Equations S4.4 Norms and the Analysis of Errors S4.4 Norms and the Analysis
Obrábění robotem se zpětnovazební tuhostí
 Obrábění robotem se zpětnovazební tuhostí Odbor mechaniky a mechatroniky ČVUT v Praze, Fakulta strojní Student: Yaron Sela Vedoucí: Prof. Ing. Michael Valášek, DrSc Úvod Motivace Obráběcí stroj a důležitost
Obrábění robotem se zpětnovazební tuhostí Odbor mechaniky a mechatroniky ČVUT v Praze, Fakulta strojní Student: Yaron Sela Vedoucí: Prof. Ing. Michael Valášek, DrSc Úvod Motivace Obráběcí stroj a důležitost
STUDY EDITS FOR BETTER TRANSPORT IN THE CENTRE OF NÁCHOD
 CZECH TECHNICAL UNIVERSITY IN PRAGUE Faculty of transportation sciences Title of project STUDY EDITS FOR BETTER TRANSPORT IN THE CENTRE OF NÁCHOD 2006 Petr Kumpošt Basic information about town Náchod Náchod
CZECH TECHNICAL UNIVERSITY IN PRAGUE Faculty of transportation sciences Title of project STUDY EDITS FOR BETTER TRANSPORT IN THE CENTRE OF NÁCHOD 2006 Petr Kumpošt Basic information about town Náchod Náchod
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
RNDr. Jakub Lokoč, Ph.D. RNDr. Michal Kopecký, Ph.D. Katedra softwarového inženýrství Matematicko-Fyzikální fakulta Univerzita Karlova v Praze
 RNDr. Jakub Lokoč, Ph.D. RNDr. Michal Kopecký, Ph.D. Katedra softwarového inženýrství Matematicko-Fyzikální fakulta Univerzita Karlova v Praze 1 Relační algebra / Relational Algebra 2 Kino(Jmeno, Mesto,
RNDr. Jakub Lokoč, Ph.D. RNDr. Michal Kopecký, Ph.D. Katedra softwarového inženýrství Matematicko-Fyzikální fakulta Univerzita Karlova v Praze 1 Relační algebra / Relational Algebra 2 Kino(Jmeno, Mesto,
Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products
 Energy news2 1 Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products Doposud jste Energy znali jako výrobce a dodavatele humánních přírodních doplňků stravy a kosmetiky.
Energy news2 1 Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products Doposud jste Energy znali jako výrobce a dodavatele humánních přírodních doplňků stravy a kosmetiky.
Čtvrtý Pentagram The fourth Pentagram
 Energy News 4 1 Čtvrtý Pentagram The fourth Pentagram Na jaře příštího roku nabídneme našim zákazníkům již čtvrtý Pentagram a to Pentagram šamponů. K zavedení tohoto Pentagramu jsme se rozhodli na základě
Energy News 4 1 Čtvrtý Pentagram The fourth Pentagram Na jaře příštího roku nabídneme našim zákazníkům již čtvrtý Pentagram a to Pentagram šamponů. K zavedení tohoto Pentagramu jsme se rozhodli na základě
POSLECH. Cinema or TV tonight (a dialogue between Susan and David about their plans for tonight)
 POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Zora Smolková aj9-jes-smo-pos-01 Z á k l a d o v ý t e x t : Cinema or TV tonight (a dialogue between Susan and David about their plans
POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Zora Smolková aj9-jes-smo-pos-01 Z á k l a d o v ý t e x t : Cinema or TV tonight (a dialogue between Susan and David about their plans
VŠEOBECNÁ TÉMATA PRO SOU Mgr. Dita Hejlová
 VŠEOBECNÁ TÉMATA PRO SOU Mgr. Dita Hejlová VZDĚLÁVÁNÍ V ČR VY_32_INOVACE_AH_3_03 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět
VŠEOBECNÁ TÉMATA PRO SOU Mgr. Dita Hejlová VZDĚLÁVÁNÍ V ČR VY_32_INOVACE_AH_3_03 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Informace o písemných přijímacích zkouškách. Doktorské studijní programy Matematika
 Informace o písemných přijímacích zkouškách (úplné zadání zkušebních otázek či příkladů, které jsou součástí přijímací zkoušky nebo její části, a u otázek s výběrem odpovědi správné řešení) Doktorské studijní
Informace o písemných přijímacích zkouškách (úplné zadání zkušebních otázek či příkladů, které jsou součástí přijímací zkoušky nebo její části, a u otázek s výběrem odpovědi správné řešení) Doktorské studijní
Immigration Studying. Studying - University. Stating that you want to enroll. Stating that you want to apply for a course.
 - University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
- University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
Immigration Studying. Studying - University. Stating that you want to enroll. Stating that you want to apply for a course.
 - University Rád/a bych se zapsal/a na vysoké škole. Stating that you want to enroll Rád/a bych se zapsal/a na. Stating that you want to apply for a course bakalářské studium postgraduální studium doktorské
- University Rád/a bych se zapsal/a na vysoké škole. Stating that you want to enroll Rád/a bych se zapsal/a na. Stating that you want to apply for a course bakalářské studium postgraduální studium doktorské
LOGBOOK. Blahopřejeme, našli jste to! Nezapomeňte. Prosím vyvarujte se downtrade
 název cache GC kód Blahopřejeme, našli jste to! LOGBOOK Prosím vyvarujte se downtrade Downtrade (z GeoWiki) Je to jednání, kterého byste se při výměnách předmětů v keších měli vyvarovat! Jedná se o snížení
název cache GC kód Blahopřejeme, našli jste to! LOGBOOK Prosím vyvarujte se downtrade Downtrade (z GeoWiki) Je to jednání, kterého byste se při výměnách předmětů v keších měli vyvarovat! Jedná se o snížení
TKGA3. Pera a klíny. Projekt "Podpora výuky v cizích jazycích na SPŠT"
 Projekt "Podpora výuky v cizích jazycích na SPŠT" Pera a klíny TKGA3 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem ČR Pera a klíny Pera a klíny slouží k vytvoření rozbíratelného
Projekt "Podpora výuky v cizích jazycích na SPŠT" Pera a klíny TKGA3 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem ČR Pera a klíny Pera a klíny slouží k vytvoření rozbíratelného
http://www.zlinskedumy.cz
 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Výklad a cvičení z větné stavby, vy_32_inovace_ma_33_01
Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Výklad a cvičení z větné stavby, vy_32_inovace_ma_33_01
A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients
 KYBERNETIKA VOLUME 8 (1972), NUMBER 6 A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients JAROSLAV KRAL In many applications (for example if the effect
KYBERNETIKA VOLUME 8 (1972), NUMBER 6 A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients JAROSLAV KRAL In many applications (for example if the effect
Enabling Intelligent Buildings via Smart Sensor Network & Smart Lighting
 Enabling Intelligent Buildings via Smart Sensor Network & Smart Lighting Petr Macháček PETALIT s.r.o. 1 What is Redwood. Sensor Network Motion Detection Space Utilization Real Estate Management 2 Building
Enabling Intelligent Buildings via Smart Sensor Network & Smart Lighting Petr Macháček PETALIT s.r.o. 1 What is Redwood. Sensor Network Motion Detection Space Utilization Real Estate Management 2 Building
CHAIN TRANSMISSIONS AND WHEELS
 Second School Year CHAIN TRANSMISSIONS AND WHEELS A. Chain transmissions We can use chain transmissions for the transfer and change of rotation motion and the torsional moment. They transfer forces from
Second School Year CHAIN TRANSMISSIONS AND WHEELS A. Chain transmissions We can use chain transmissions for the transfer and change of rotation motion and the torsional moment. They transfer forces from
kupi.cz Michal Mikuš
 kupi.cz Michal Mikuš redisgn website kupi.cz, reduce the visual noise. ADVERT ADVERT The first impression from the website was that i dint knew where to start. It was such a mess, adverts, eyes, products,
kupi.cz Michal Mikuš redisgn website kupi.cz, reduce the visual noise. ADVERT ADVERT The first impression from the website was that i dint knew where to start. It was such a mess, adverts, eyes, products,
ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ
 ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ MGR. VLADIMÍR BRADÁČ ROZVOJ KOMPETENCÍ MANAGEMENTU A PRACOVNÍKŮ VŠ MSK (S PODPOROU ICT) PROJEKT OP VK 2.2: CZ.1.07/2.2.00/15.0176 OSTRAVA 2012 Tento projekt je
ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ MGR. VLADIMÍR BRADÁČ ROZVOJ KOMPETENCÍ MANAGEMENTU A PRACOVNÍKŮ VŠ MSK (S PODPOROU ICT) PROJEKT OP VK 2.2: CZ.1.07/2.2.00/15.0176 OSTRAVA 2012 Tento projekt je
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky
 Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: Education Označení materiálu: VY_32_INOVACE_MAT27 Datum vytvoření: 10.10.2013
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: Education Označení materiálu: VY_32_INOVACE_MAT27 Datum vytvoření: 10.10.2013
Klepnutím lze upravit styl předlohy. nadpisů. nadpisů.
 1/ 13 Klepnutím lze upravit styl předlohy Klepnutím lze upravit styl předlohy www.splab.cz Soft biometric traits in de identification process Hair Jiri Prinosil Jiri Mekyska Zdenek Smekal 2/ 13 Klepnutím
1/ 13 Klepnutím lze upravit styl předlohy Klepnutím lze upravit styl předlohy www.splab.cz Soft biometric traits in de identification process Hair Jiri Prinosil Jiri Mekyska Zdenek Smekal 2/ 13 Klepnutím
User manual SŘHV Online WEB interface for CUSTOMERS June 2017 version 14 VÍTKOVICE STEEL, a.s. vitkovicesteel.com
 1/ 11 User manual SŘHV Online WEB interface for CUSTOMERS June 2017 version 14 2/ 11 Contents 1. MINIMUM SYSTEM REQUIREMENTS... 3 2. SŘHV ON-LINE WEB INTERFACE... 4 3. LOGGING INTO SŘHV... 4 4. CONTRACT
1/ 11 User manual SŘHV Online WEB interface for CUSTOMERS June 2017 version 14 2/ 11 Contents 1. MINIMUM SYSTEM REQUIREMENTS... 3 2. SŘHV ON-LINE WEB INTERFACE... 4 3. LOGGING INTO SŘHV... 4 4. CONTRACT
Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost
 Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost Registrační číslo: CZ.1.07/1. 5.00/34.0084 Šablona: II/2 Inovace a zkvalitnění výuky cizích jazyků na středních
Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost Registrační číslo: CZ.1.07/1. 5.00/34.0084 Šablona: II/2 Inovace a zkvalitnění výuky cizích jazyků na středních
Friction drives have constant or variable drives (it means variators). Friction drives are used for the transfer of smaller outputs.
 Third School Year FRICTION DRIVES 1. Introduction In friction drives the peripheral force between pressed wheels is transferred by friction. To reach peripheral forces we need both a pressed force and
Third School Year FRICTION DRIVES 1. Introduction In friction drives the peripheral force between pressed wheels is transferred by friction. To reach peripheral forces we need both a pressed force and
Střední škola obchodní, České Budějovice, Husova 9, VY_INOVACE_ANJ_741. Škola: Střední škola obchodní, České Budějovice, Husova 9
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
PITSTOP VY_22_INOVACE_26
 PITSTOP VY_22_INOVACE_26 Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 9. PITSTOP 1/ Try to complete the missing words. Then listen and check your ideas. Eight
PITSTOP VY_22_INOVACE_26 Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 9. PITSTOP 1/ Try to complete the missing words. Then listen and check your ideas. Eight
Instrukce: Cvičný test má celkem 3 části, čas určený pro tyto části je 20 minut. 1. Reading = 6 bodů 2. Use of English = 14 bodů 3.
 Vážení studenti, na následujících stranách si můžete otestovat svou znalost angličtiny a orientačně zjistit, kolik bodů za jazykové kompetence byste získali v přijímacím řízení. Maximální počet bodů je
Vážení studenti, na následujících stranách si můžete otestovat svou znalost angličtiny a orientačně zjistit, kolik bodů za jazykové kompetence byste získali v přijímacím řízení. Maximální počet bodů je
Aktivita CLIL Fyzika 2
 Škola: Gymnázium Bystřice nad Pernštejnem Jméno vyučujícího: Mgr. Monika Stará Aktivita CLIL Fyzika 2 Název aktivity: Fáze měsíce a fyzikální výpočty Předmět: Fyzika Ročník, třída: kvarta Jazyk a jazyková
Škola: Gymnázium Bystřice nad Pernštejnem Jméno vyučujícího: Mgr. Monika Stará Aktivita CLIL Fyzika 2 Název aktivity: Fáze měsíce a fyzikální výpočty Předmět: Fyzika Ročník, třída: kvarta Jazyk a jazyková
The Czech education system, school
 The Czech education system, school Pracovní list Číslo projektu Číslo materiálu Autor Tematický celek CZ.1.07/1.5.00/34.0266 VY_32_INOVACE_ZeE_AJ_4OA,E,L_10 Mgr. Eva Zemanová Anglický jazyk využívání on-line
The Czech education system, school Pracovní list Číslo projektu Číslo materiálu Autor Tematický celek CZ.1.07/1.5.00/34.0266 VY_32_INOVACE_ZeE_AJ_4OA,E,L_10 Mgr. Eva Zemanová Anglický jazyk využívání on-line
II_ _Listening Pracovní list č. 2.doc II_ _Listening Pracovní list č. 3.doc II_ _Listening Řešení 1,2.doc
 Název školy: ZŠ Brno, Měšťanská 21, Brno -Tuřany Název práce: Listening Pořadové číslo: II_2-01-06 Předmět: Anglický jazyk Třída: 9. AC Téma hodiny: Problémy Vyučující: Mgr. Milena Polášková Cíl hodiny:
Název školy: ZŠ Brno, Měšťanská 21, Brno -Tuřany Název práce: Listening Pořadové číslo: II_2-01-06 Předmět: Anglický jazyk Třída: 9. AC Téma hodiny: Problémy Vyučující: Mgr. Milena Polášková Cíl hodiny:
Škola: Střední škola obchodní, České Budějovice, Husova 9. Inovace a zkvalitnění výuky prostřednictvím ICT
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9. Inovace a zkvalitnění výuky prostřednictvím ICT
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ, Česká Lípa, 28. října 2707, příspěvková organizace
 Název školy STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ, Česká Lípa, 28. října 2707, příspěvková organizace Číslo a název projektu: CZ.1.07/1.5.00/34.0880 Digitální učební materiály www.skolalipa.cz
Název školy STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ, Česká Lípa, 28. října 2707, příspěvková organizace Číslo a název projektu: CZ.1.07/1.5.00/34.0880 Digitální učební materiály www.skolalipa.cz
Výukový materiál zpracovaný v rámci projektu EU peníze do škol. illness, a text
 Výukový materiál zpracovaný v rámci projektu EU peníze do škol ZŠ Litoměřice, Ladova Ladova 5 412 01 Litoměřice www.zsladovaltm.cz vedeni@zsladovaltm.cz Pořadové číslo projektu: CZ.1.07/1.4.00/21.0948
Výukový materiál zpracovaný v rámci projektu EU peníze do škol ZŠ Litoměřice, Ladova Ladova 5 412 01 Litoměřice www.zsladovaltm.cz vedeni@zsladovaltm.cz Pořadové číslo projektu: CZ.1.07/1.4.00/21.0948
Výuka odborného předmětu z elektrotechniky na SPŠ Strojní a Elektrotechnické
 Jihočeská univerzita v Českých Budějovicích Pedagogická fakulta Oddělení celoživotního vzdělávání Závěrečná práce Výuka odborného předmětu z elektrotechniky na SPŠ Strojní a Elektrotechnické Vypracoval:
Jihočeská univerzita v Českých Budějovicích Pedagogická fakulta Oddělení celoživotního vzdělávání Závěrečná práce Výuka odborného předmětu z elektrotechniky na SPŠ Strojní a Elektrotechnické Vypracoval:
Název projektu: Multimédia na Ukrajinské
 Základní škola, Ostrava Poruba, Ukrajinská 1533, příspěvková organizace Operační program Vzdělávání pro konkurenceschopnost Název projektu: Multimédia na Ukrajinské číslo projektu: CZ1.07/1.4.00/21.3759
Základní škola, Ostrava Poruba, Ukrajinská 1533, příspěvková organizace Operační program Vzdělávání pro konkurenceschopnost Název projektu: Multimédia na Ukrajinské číslo projektu: CZ1.07/1.4.00/21.3759
POSLECH. M e t o d i c k é p o z n á m k y k z á k l a d o v é m u t e x t u :
 POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Mgr. Martin Zicháček aj9-kap-zic-pos-07 Z á k l a d o v ý t e x t : Margaret: Hi Eric. Eric: Oh, hi Margaret. How are you doing? Margaret:
POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Mgr. Martin Zicháček aj9-kap-zic-pos-07 Z á k l a d o v ý t e x t : Margaret: Hi Eric. Eric: Oh, hi Margaret. How are you doing? Margaret:
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku
 Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
The Over-Head Cam (OHC) Valve Train Computer Model
 The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
18.VY_32_INOVACE_AJ_UMB18, Frázová slovesa.notebook. September 09, 2013
 1 (Click on the text to move to the section) Worksheet Methodology Sources 2 Decide which words are considered prepositions (předložky) and which are particles (částice) Source: SWAN, Michael a Catharine
1 (Click on the text to move to the section) Worksheet Methodology Sources 2 Decide which words are considered prepositions (předložky) and which are particles (částice) Source: SWAN, Michael a Catharine
Počítačové kognitivní technologie ve výuce geometrie
 Počítačové kognitivní technologie ve výuce geometrie Jiří Vaníček Univerzita Karlova v Praze - Pedagogická fakulta 2009 Počítačové kognitivní technologie ve výuce geometrie Abstrakt Kniha se zabývá využíváním
Počítačové kognitivní technologie ve výuce geometrie Jiří Vaníček Univerzita Karlova v Praze - Pedagogická fakulta 2009 Počítačové kognitivní technologie ve výuce geometrie Abstrakt Kniha se zabývá využíváním
Jednoduché polookruhy. Katedra algebry
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Vítězslav Kala Jednoduché polookruhy Katedra algebry Vedoucí bakalářské práce: Prof. RNDr. Tomáš Kepka, DrSc. Studijní program:
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Vítězslav Kala Jednoduché polookruhy Katedra algebry Vedoucí bakalářské práce: Prof. RNDr. Tomáš Kepka, DrSc. Studijní program:
Automatika na dávkování chemie automatic dosing
 Automatika na dávkování chemie automatic dosing Swimmingpool Technology Autodos 700 Automatické dávkování Autodos Autodos automatic dosing Autodos 700 je jedno-kanálové zaøízení, pro mìøení a dávkování.
Automatika na dávkování chemie automatic dosing Swimmingpool Technology Autodos 700 Automatické dávkování Autodos Autodos automatic dosing Autodos 700 je jedno-kanálové zaøízení, pro mìøení a dávkování.
Project Life-Cycle Data Management
 Project Life-Cycle Data Management 1 Contend UJV Introduction Problem definition Input condition Proposed solution Reference Conclusion 2 UJV introduction Research, design and engineering company 1000
Project Life-Cycle Data Management 1 Contend UJV Introduction Problem definition Input condition Proposed solution Reference Conclusion 2 UJV introduction Research, design and engineering company 1000
Výukový materiál zpracován v rámci projektu EU peníze školám
 Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.4.00/21.3149 Šablona: III/2 č. materiálu: VY_32_INOVACE_140 Jméno autora: Marina Hozmanová Třída/ročník:
Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.4.00/21.3149 Šablona: III/2 č. materiálu: VY_32_INOVACE_140 Jméno autora: Marina Hozmanová Třída/ročník:
AIC ČESKÁ REPUBLIKA CZECH REPUBLIC
 ČESKÁ REPUBLIKA CZECH REPUBLIC ŘÍZENÍ LETOVÉHO PROVOZU ČR, s.p. Letecká informační služba AIR NAVIGATION SERVICES OF THE C.R. Aeronautical Information Service Navigační 787 252 61 Jeneč A 1/14 20 FEB +420
ČESKÁ REPUBLIKA CZECH REPUBLIC ŘÍZENÍ LETOVÉHO PROVOZU ČR, s.p. Letecká informační služba AIR NAVIGATION SERVICES OF THE C.R. Aeronautical Information Service Navigační 787 252 61 Jeneč A 1/14 20 FEB +420
Dynamic programming. Optimal binary search tree
 The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamic programming Optimal binary search tree Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The complexity
The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamic programming Optimal binary search tree Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The complexity
Právní formy podnikání v ČR
 Bankovní institut vysoká škola Praha Právní formy podnikání v ČR Bakalářská práce Prokeš Václav Leden, 2009 Bankovní institut vysoká škola Praha Katedra Bankovnictví Právní formy podnikání v ČR Bakalářská
Bankovní institut vysoká škola Praha Právní formy podnikání v ČR Bakalářská práce Prokeš Václav Leden, 2009 Bankovní institut vysoká škola Praha Katedra Bankovnictví Právní formy podnikání v ČR Bakalářská
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Let s(x) denote the sum of the digits in the decimal expansion of x. Find all positive integers n such that 1 s(n!) = 9.
 Integers 4 th autumn series Date due: 8 th January 2018 Pozor, u této série přijímáme pouze řešení napsaná anglicky! Problem 1. Consider a pair of integers with the following properties: (3 points) (i)
Integers 4 th autumn series Date due: 8 th January 2018 Pozor, u této série přijímáme pouze řešení napsaná anglicky! Problem 1. Consider a pair of integers with the following properties: (3 points) (i)
Configuration vs. Conformation. Configuration: Covalent bonds must be broken. Two kinds of isomers to consider
 Stereochemistry onfiguration vs. onformation onfiguration: ovalent bonds must be broken onformation: hanges do NT require breaking of covalent bonds onfiguration Two kinds of isomers to consider is/trans:
Stereochemistry onfiguration vs. onformation onfiguration: ovalent bonds must be broken onformation: hanges do NT require breaking of covalent bonds onfiguration Two kinds of isomers to consider is/trans:
