Quantum walks, search algorithm and state transfer. Kvantové procházky, vyhledávací algoritmus
|
|
|
- Vratislav Štěpánek
- před 6 lety
- Počet zobrazení:
Transkript
1 Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering Quantu walks, search algorith and state transfer Kvantové procházky, vyhledávací algoritus a přenos stavu Bachelor s Degree Project Author: Supervisor: Stanislav Skopuý Ing. Martin Štefaňák, Ph.D. Acadeic year: 014/015
2
3 - Zadání práce -
4 - Zadání práce (zadní strana) -
5 Acknowledgent: I would like to express y honest gratitude to Ing. Martin Štefaňák, Ph.D. for supervising y work on this bachelor s degree project.
6 Prohlášení Prohlašuji, že jse svou bakalářskou práci vypracoval saostatně a použil jse pouze podklady (literaturu, software, atd.... ) uvedené v přiložené seznau. Neá závažný důvod proti použití tohoto školního díla ve syslu 60 Zákona č. 11/000 Sb., o právu autorské, o právech souvisejících s práve autorský a o zěně některých zákonů (autorský zákon). V Praze dne Stanislav Skoupý
7 Název práce: Kvantové procházky, vyhledávací algoritus a přenos stavu Autor: Stanislav Skoupý Obor: Mateatické inženýrství Zaěření: Mateatická fyzika Druh práce: Bakalářská práce Vedoucí práce: Ing. Martin Štefaňák, Ph.D., České vysoké učení technické v Praze, Fakulta jaderná a fyzikálně inženýrská, Katedra fyziky Abstrakt: V této práci se zaěříe na téa kvantových procházek a jejich využití. Představíe základ diskrétní kvantové procházky a zíníe kontinuální kvantovou procházku. Poté popíšee Groverův algoritus a odhadnee jeho složitost. Také stanovíe dolní hranici počtu kroků potřebných k nalezení označeného stavu. Definujee vyhledávací algoritus založený na kvantové procházce a opět ukážee jeho složitost. Provedee srovnání obou typů algoritu. Předvedee jiný způsob odhadu počtu kroků algoritu založeného na kvantové procházce poocí vlastností spektra zobecněného evolučního operátoru. Na závěr se zaěříe na uplatnění kvantových procházek při přenosu stavu a kounikaci na řížce. Klíčová slova: kvantová procházka, přenos stavu, vyhledávací algoritus Title: Quantu walks, search algorith and state transfer Author: Stanislav Skoupý Abstract: In this text we focus on the topic of quantu walks and their usage. We introduce basic of the discrete tie quantu walks and ention the continuous tie quantu walk. We describe the Grover s search algorith and estiate its coplexity. We also prove the lower bound of nuber of steps necessary to find the arked state. We define quantu walk search algorith and again show its coplexity. We present the difference between both kind of algorith. We show the different ethod of approxiating the nuber of steps of walk search algorith using the properties of spectru of the generalised evolution operator. At the end we focus on use of quantu walks in the state transfer and counication on the regular lattice. Key words: quantu walks, search algoriths, state transfer
8 Contents Introduction 9 1 Matheatical foralis Quantu Mechanics Asyptotic notation Quantu walk 1.1 Discrete tie quantu walk Continuous tie quantu walk Search algorith Grover s algorith Quantu walk search algorith on a hypercube Quantu walk search algorith on regular lattice Different look on the walk search algorith Search on the hypercube Search on the regular lattice State transfer State transfer as the discrete tie quantu walk An aplitude transfer across regular lattice Conclusion 36 8
9 Introduction In this bachelor s degree project I study the topic of quantu walks and their application in quantu algorith. The quantu walks are fast developing topic because there are any ways how to physically ipleent the and test their properties in experients. I focus on search algorith and briefly on state transfer. In the first chapters of this text we introduce the atheatical foralis of the quantu physic that we use and the basic concept of the quantu walks. Then we describe the quantu walk search algorith and Grover s algorith, which is not based on quantu walks, and copare their properties. In Chapter 4 we discuss the quantu walk search algorith again to estiate their coplexity fro different point of view. Last chapter presents use of discrete tie quantu walk for the transfer of the state and counications across the grid thanks to quantu walk search algorith. 9
10 Chapter 1 Matheatical foralis 1.1 Quantu Mechanics Basic axios of Quantu echanic settle that every quantu syste can be described with Hilbert space H, which is often called state space, and every state of this syste is described by one-diensional subspace of H. Vector fro H is denoted ψ. Sybol ψ represent eleent fro dual space and is assigned to vector ψ by Riesz s lea. Scalar product of ψ and ϕ is written in for ϕ ψ. Because one state of the syste is represented by vectors fro one diensional subspace, we can choose vector, which nor is equal 1. This will enable us to write siple for of any following expressions. If Hilbert space has countable orthogonal basis, we can write decoposition of state in the basis ψ = i ψ i. (1.1) i=1 In case of finite diension spaces su is also finite. One of the ost iportant thing for physics is how we can predict results of easureent. If the state of syste is ψ, then the probability to easure syste in the state i is equal to ψ i. However quantu syste can change trough tie, so we have to know how to calculate the tie evolution. Evolution of state is deterined by the Schödinger equation ψ (t) i = Ĥ ψ (t), (1.) t where Ĥ is the Hailtonian operator of the syste. Now we take scalar product of solutions fro equation (1.) and execute its tie derivative. ( ) ( ) d ϕ (t) ψ (t) ϕ (t) ψ (t) = ψ (t) + ϕ (t) = dt t t (1.3) = i ϕ (t) Ĥ ψ (t) i ϕ (t) Ĥ ψ (t) = 0 Fro (1.3) follows that the operator of tie evolution directed by (1.) ust be unitary to guarantee invariance of scalar product. We want to preserve this property, when we consider discrete tie instead of continuous. So every discrete tie step will be also perfored by unitary operator. 1. Asyptotic notation Another thing we will often use is following standard coputer science notation. Let us say f (n) = O(g(n)) if there are positive constants c and k such that 0 f (n) cg(n) for n k. 10
11 Siilarly we say f (n) = Ω(g(n)) if there are c, k 0 and 0 cg(n) f (n) for n k. If function f coply f (n) = O(g(n)) and f (n) = Ω(g(n)) we say f (n) = Θ(g(n)). 11
12 Chapter Quantu walk In this Chapter we present the basic of quantu walks. First in Section.1 we introduce discrete tie quantu walk and then in Section. we briefly describe continuous tie quantu walk..1 Discrete tie quantu walk To introduce discrete quantu walks gently we will at first briefly describe classical rando walk on discrete line, then we ove to the discrete tie quantu walk on discrete line and later we introduce quantu walk on general type of graph. Classic rando walk on discrete line is a process, where we have one walker on discrete line with grid-length 1. Moveent of the walker is rando, but we know at each step probabilities for walker to go right and left, let us denote the p + for right and p for left. Walker starts at position 0 and we are interested in the probability that he is in certain position after the fixed nuber of steps. Distribution of probability with rising nuber of steps will approxiate to Gauss distribution. Walk is said to be unbiased, if the probabilities are p + = p = 1. For introducing quantu walk we have to construct underlying Hilbert space. Let { i : i Z} be the basis that span position Hilbert space H p. To use advantages of quantu world we want walker to travel siultaneously in both neighbouring position in each step. But it is easy to see that (.1) is not unitary transforation. Position space need to be augented with soething, which will direct the ove of every step. We set another auxiliary space H c with basis {, }. This space is often called coin-space. Final state space is H = H c H p. Unitary transition operator, which will shift position depending on the state of coin-space, has the for Ŝ = i + 1 i + i 1 i. (.) i Tie evolution only under (.) is quit trivial. State with defined orientation, i.e. or, will siply shift in one direction. To obtain non-trivial evolution we will first conduct rotation on the coin-space, let us call it coin-flip. Then one step of the walk will consist of coin-flip and application of shift operator Û = Ŝ (Ĉ Î). Let us start the walk in the initial state 0, take one step and execute easureent on coin-space, after this we would like to get probability distribution of classical unbiased walk. Balanced coin, that is often used to anage this [1], is the so called Hadaard coin C = 1 ( ) 1 1. (.3) i
13 If we easure coin-space after every step, we will get the sae probability distribution as for classical unbiased walk. To get proper quantu walk we conduct easureent at the end of the walk. Quantu properties starts to eerge since third step due to interference. As an exaple of quantu walk we consider 3 step walk with initial state 0 ( 1 ψ 3 = Û 3 ( 0 ) = Û ) 1 = ( 1 = Û + 1 ( + ) 0 1 ) = (.4) = ( + ) Probability distribution is no longer approaching Gauss distribution. The highest probabilities are not in the centre but on the edges. Walk in this case is also not syetric, because chosen coin treats states and differently [1]. See figure p position Figure.1: The probability distribution of the discrete quantu walk after 100 steps with the initial state 0. Only the probability on the even points is plotted. The highest probability is shifted to the right because initial state of the coin is unsyetrical. Now we introduce generalization of quantu walks for general graph G. Degree d v of vertex v of graph G is nuber of edges outgoing fro the vertex. We restrict us on so called regular graph, i.e. all vertices have sae degree d. We also label edges outgoing fro each vertex fro 1 to d. Then underlying Hilbert space of is spanned by orthogonal basis { i v : v G, i 1... d}. Shift operator is defined as Ŝ i v = i w, where vertices v and w are connected by edge arked with i on v s side. Every vertex can have generally different coin. One step of walk now has the for Û = Ŝ Ĉ v v v. v G. Continuous tie quantu walk We introduce continuous tie quantu walk on regular graph. It take place only on position space H p with orthogonal basis { v : v G}. Tie evolution of the state is deterined by (1.). 13
14 We express Hailtonian of the syste in basis v Ĥ w = α v w, v and w are connected 0 v w, v and w are not connected dα v = w. (.5) In classical approxiation α can be seen as probability to ove fro one vertex to another connected vertex [1]. The Hailtonian (.5) is tie-independent, so fro (1.) we can calculate the tie evolution operator Û(t) = e iĥt (.6) where we set = 1. 14
15 Chapter 3 Search algorith In this Chapter we introduce the quantu search algorith. We estiate the nuber of steps they need to succeed and describe their properties. We start with Grover s algorith in Section 3.1 and then in Section 3. introduce quantu walk algorith on hypercube. At the end in Section 3.3 we shortly present quantu walk algorith on regular lattice. 3.1 Grover s algorith Grover s algorith is quantu search algorith over unsorted data. Before we begin with algorith, we need to describe the basic quantu unit of inforation so called qubit and quantu eory register. Classical coputer operate with two state systes called bits. Qubits are bits quantu equivalent. Qubit can be in superposition of both states at the sae tie instead of bit which can be in only one of the two states at the tie. For description of qubit state we will use Hilbert space of C. Quantu eory register is coposed of qubits and underlying Hilbert space is tensor product of particular qubit s spaces. For siplicity of notation we will write i j = i j. Now we describe the proble for the Grover s algorith. Let us have quantu register with n qubits. Orthogonal basis { i 1 i... i n ; i k {0, 1}} have N = n eleents. We label these eleents S 1, S,..., S N. Let there be a unique state fro basis, labelled S, that satisfies the condition C( S ) = 1, where for all other basis states C( S i ) = 0, i. We assue that condition C( S i ) can be evaluated in unit tie. Now we use Grover s algorith to find state S. Algorith is coposed of following steps: 1. Initialize the syste in the superposition of basis states i.e. there is the sae aplitude to be in each of the N states.. Repeat following unitary operation O( N) ties N i=1 1 N S i, (3.1) (a) Rotate the phase of basis state S if C( S ) = 1 by π. If C( S ) = 0, leave the syste unaltered. (b) Apply the diffusion transfor ˆD which is defined by atrix D = (D i j ) as follows: i ˆD j = D i j = N if i j and i ˆD i = D ii = 1 + N (3.) 15
16 3. Measure the the resulting state. This will be state S with probability of at least 0,5. [] Let us show that the algorith works. It is easy to see fro the definition of the atrix D that it can be written in the for D = I + P, where P i j = 1 N for all i, j. (3.3) Aplitudes of vector ˆP x are equal to the average of aplitudes of vector x. When we let ˆD act on arbitrary vector x ˆD x = ( Î + ˆP) x = x + ˆP x (3.4) and label the average of aplitudes as A, we can express i th aplitude of vector ˆD x i ˆD x = i x + A = (A + (A i x )). (3.5) Expression (3.5) shows that ˆD is acting like inversion about the average []. Let us apply ˆD on vector which have one aplitude equal to 1 C and rest aplitudes equal to C N, where C is a real nuber lying between 1 and 1. The average A is approxiately equal to C N and hence aplitudes C N do not change significantly after applying ˆD. Marked state aplitude becoes positive and increases by C N. Thus every iteration in the second step of the algorith increases aplitude in the arked state by C N. As long as the aplitude 1 C is less then 1 the increent is grater then 1 N. This eans that there exist a nuber T less then N and eeting the condition, that after we repeat T-ties second step, we will easure the arked state with probability grater then 1. So the algorith can find the result with O( N) steps. In figure 3.1 we can see exaple of the evolution of the probability to easure the arked state. p step Figure 3.1: The evolution of the probability p to find the arked state during 100 steps. We use the Grover s algorith and search within 104 eleents. On the other hand we prove that quantu search algorith cannot perfor better then Ω( N). In general the quantu search algorith step is coposed fro the application of the so called oracle operator Ô = Î, which changes the phase of the arked state by π, 16
17 and the application of the evolution operator Û n in n th step. the following states At beginning of the prove we define ϕ n = Û n... Û Û 1 ϕ 0 ϕ n = Û n Ô Û n 1... Û Ô Û 1 Ô ϕ 0. (3.6) We show the lower bound of the nuber of steps by bounding quantity A n defined as follows A n = ϕ n ϕ n (3.7) For sipler notation we denote the vectors fro the Hilbert space x = x. At first we show that the upper bound of (3.7) is 4n. We prove this by atheatical induction. For n = 0 it holds true because A 0 = 0. Now we ove to the inductive step A n+1. Using x + y x + x y + y we write A n+1 = Ô ϕ n ϕ n = Ô (ϕ n ϕ n ) + (Ô Î)ϕ n (. (3.8) ϕ n ϕ n + 4 ϕ n ϕ n ϕ n + 4 ϕ n ) Now we use Cauchy-Schwarz inequality 1 N N a i b i a i N b i i=1 i=1 i=1 1 (3.9) and the fact that ϕ n = ϕ = 1 (3.10) to bound A n+1 as follows 1 1 A n+1 A n + 4 ϕ n ϕ n ϕ n + 4 A n + 4 (3.11) A n + 4 4n + 8n + 4 = 4(n + 1) which eans that A n 4n holds true. To find the lower bound of A n we suppose that ϕ n 1 which eans that we find the arked state with probability higher than 1. We can also suppose without lost of generality that ϕ n = ϕ n. We can now estiate the following expression ϕ n = ϕ n. (3.1) Another useful inequality holds true for any noralized state x x ( ) R x N x N N (3.13) 17
18 where we use the following estiation 1 x x 1 1 N. (3.14) Using (3.9),(3.1),(3.13) and x y x x y + y we can calculate the lower boundary of A n A n = ( ϕ n ) (ϕ n ) ϕ n ϕ n ϕ n + ϕ n 1 1 ϕ n ϕ n ϕ n + ϕ n. (3.15) 1 1 ϕ n ϕ n [ (N ) 1 N ( N N ) ] 1 Fro this and A n 4n follows that n ( N N ) 1 ( N N ) 1. (3.16) So the nuber of steps of search has lower bound c N where c is approxiately equal to. Hence any quantu search algorith ust have at least Ω ( ) N steps. One thing that should be entioned before we ove to another algorith is that atrix D can be represented as product of three atrices D = WRW [], where R is the phase rotation atrix and W is so called Walsh-Hadaard Transfor Matrix, which are defined as follows R i j = 0 if i j, R ii = 1 if i 0, R 00 = 1 W i j = n ( 1) i j. (3.17) Here i and j are binary representation of nubers i and j, which are lying in {0, 1,..., N 1}, i j is a bitwise product []. This expression of D is iportant for the ipleentation of the Grover s algorith in quantu coputers. 3. Quantu walk search algorith on a hypercube Quantu walk search algorith on a hypercube is based on a discrete tie quantu walk. Before we introduce the algorith itself, we at first describe hypercube as a graph, its Hilbert space and unperturbed quantu walk. The hypercube is n-diensional cube with edge-length 1. It has N = n vertices, which we label with an n-bit binary strings corresponding to their coordinates. Two vertices a and b of hypercube are connected, if their bit strings a and b differ only by a single bit flip. Hence, every vertex have degree equal to n. Hilbert space of a quantu walk on a hypercube is H = H n H n. We denote the states fro this Hilbert space as d, a, where a is a bit string of underlying vertex 18
19 and d labels the direction on a hypercube. We define the operator Ŝ to shift the state d, a to the state d, a d, where a d is bit string a with bit flip on d th place Ŝ = n d, a d d, a. (3.18) d=1 a For unperturbed walk we need to denote also the coin operator Ĉ 0 on the coin space. We choose so called Grover diffusion operator Ĉ 0 = Ĝ = Î + s C s C, where s C = 1 n d. (3.19) n Then the evolution operator of the walk is Û = Ŝ ( Cˆ 0 Î). However, in the quantu walk search algorith we have soe arked state that we need to treat differently than others to produce higher aplitude of probability in the state at the final easureent. At each step we will use different coin on the arked state, denoted by Ĉ, and Ĉ 0 will used on the other states. Coin Ĉ can be chosen siply equal to Î. Thanks to high syetry of the hypercube we can assue that the arked state is 0, where 0 is a string consisting only fro zeros [4]. Coin operator acting on the whole space have the for Ĉ = Ĉ 0 Î + ( Ĉ Ĉ 0 ) 0 0 = Ĉ0 Î s C s C 0 0. (3.0) Shift operator is the sae as in the unperturbed walk, so the perturbed operator Û is defined as follows Û = Ŝ Ĉ = Ŝ (Ĉ 0 Î) Ŝ ( s C s C 0 0 ) = Û Ŝ ( s C s C 0 0 ). (3.1) Algorith itself is coposed of the following steps: 1. Initialize the syste in the superposition of basis states ϕ 0 = where a is binary representation of a. n n 1 d=1 a=0. Apply unitary operator Û t f = π n ties. 3. Measure the resulting state [4]. d=1 1 d, a, (3.) n n We will show that the arked state have probability 1 O ( 1 n) to be easured at the end of the algorith. To siplify the proble we first show that the perturbed walk on the hypercube can be collapsed to the walk on the line. Then we introduce two approxiate eigenvectors of Û, initial state ϕ 0 and ϕ 1, which both have high overlap with subspace of two eigenvalues of Û. We denote these eigenvalues by e iω and the state e iω and their eigenvectors by ω and ω. We approxiate these vectors by linear cobination of ϕ 0 and ϕ 1. After that we show that application of Û is approxiation of rotation in subspace spanned by ϕ 0 and ϕ 1 with rotation angle 1 approxiately equal to. Since we show that the state ϕ n 1 1 is well approxiation of the arked state, the algorith will finish after π n steps. 19
20 Let us define the perutation operator ˆP i j as follows ˆP i j d, (a 1, a,..., a i,..., a j,..., a n ) = d P, (a 1, a,..., a j,..., a i,..., a n ) where d P = d for d {i, j}, d P = i for d = j, d P = j for d = i. (3.3) Because the unperturbed evolution operator Û treats all directions in the sae way the operator ˆP i j coutes with Û. It is easy to show that ˆP i j also coutes with perturbed evolution operator Û [4]. Fro the expression (3.) of the initial state we see that ϕ 0 is an eigenvector of ˆP i j with eigenvalue 1. Fro this it follows that ϕ t = (Û ) t ϕ 0 is also an eigenvector of ˆP i j with eigenvalue 1 for any t N i.e. (Û ) t preserves the syetry of initial state with respect to bit swaps. Because of that all interediate states of algorith are placed in subspace spanned by eigenvectors of eigenvalue 1 of ˆP i j. Before we define new basis, we will define function called Haing weight which assigns to every bit string nuber of ones in the string. Haing weight of string a is denoted by a. This function will siplify subsequent notation. Now we define subspace basis { R, 0, L, 1, R, 1,..., R, n 1, L, n } as follows L, a = 1 a ( ) d, a (3.4) n a a =a a d =1 R, a = 1 (n a) ( ) d, a. (3.5) n a a =a a d =0 Using these states we can reduce the quantu walk on the hypercube to the quantu walk on the line [4]. Marked state corresponds to R, 0. Shift operator has the for n 1 Ŝ = R, a L, a L, a + 1 R, a (3.6) a=0 and the unperturbed coin has the for Ĉ = n a=0 ( ) cos (ωa ) sin (ω a ) a a, (3.7) sin (ω a ) cos (ω a ) where cos (ω a ) = 1 a n and sin (ω a) = n a(n a) and where first part acts on the space spanned by { R, L } and second part acts on position space { 0, 1,..., n } [4]. The unperturbed evolution operator Û on subspace acts as n 1 Û = R, a ( cos (ω a+1 ) L, a sin (ω a+1 ) R, a + 1 )+ a=0 n L, a (sin (ω a 1 ) L, a 1 + cos (ω a 1 ) R, a 1 ) a=1 (3.8) and perturbed operator Û acts as Û = Û + Û = Û L, 1 R, 0. (3.9) 0
21 The initial state ϕ 0 expressed in the new basis have the for (n 1 ) ϕ 0 = 1 1 n 1 R, 0 + L, n + a R, a + n n n a=1 (n 1 a 1 ) L, a n. (3.30) Let us defined arc A of coplex nubers with absolute value 1 as follows A = {z Re(z) > 1 3n }, z = 1. (3.31) It can be shown that on this arc lie exactly two eigenvalues of Û [4]. They ust be a coplex conjugate pair. Let us denote the by e iω and e iω. Corresponding eigenvectors ω and ω coply ω = ω. Let us define the state ϕ 1 as follows ϕ 1 = 1 n 1 1 c a=0 ( ) R, a 1 n 1 a ( ) L, a + 1 (3.3) n 1 a where c is a noralization constant c = n 1 a=0 1 ). (3.33) If the syste is in the state ϕ 1 we will easure with high probability p the state R, 0 which we identify with the arked state. Because for sufficiently large n hold c 1 + n we can estiate the probability p p = R, 0 ϕ 0 = 1 c 1 ( ) 1 + = 1 ( ) 1 O. (3.34) n n It can be shown that states ϕ 0 and ϕ 1 are approxiately eigenvectors of Û with eigenvalue 1 [4]. Furtherore, it can be proven that eigenvectors ω and ω can be written as a linear cobination of states ϕ 0 and ϕ 1 as follows ( n 1 a ω = p 0 ϕ 0 + p 1 e iη ϕ p 0 p 1 r 0 ω = p 0 ϕ 0 + p 1 e iη ϕ p 0 p 1 r 0 (3.35) where r 0 is noralized vector orthogonal to ϕ 0 and ϕ 1. Also p 0 and p 1 obey 1 p 0 1 3n and ( ) n+1 1 p 1 1 3n 8c ( n 1 n/) and eiη n = i +, where = O [4]. Fro (3.35) we express initial state as ( n 1 n/) ϕ 0 = p 0 ( ω + ω ) + δ r. (3.36) where δ = 1 p 0 = O( n n ) a and r is a noralized vector orthogonal to ω and ω. Now we apply t ties step operator Û on the initial state (Û ) t ϕ 0 = p 0 (e iωt ω + e iωt ω ) + δ r = = p 0 cos ωt ϕ 0 p 0 p 1 (sin ωt + Re(e iωt )) ϕ p 0 p 1 (e iωt r 0 + e iωt r 0 ) + δ r = ( ) n 3/4 = cos ωt ϕ 0 sin ωt ϕ 1 + O r n 1 (3.37)
22 where r is soe noralized residual vector [4]. Fro (3.37) it can be seen that after applying operator Û t f = π ω ties the state of the syste will approxiately rotate fro ϕ 0 to ϕ 1. Thanks to (3.34) we see that we find the arked state with probability 1 O ( 1 n). To estiate tie in relation to diension of hypercube n we need to estiate ω. It can be shown [4] that ω + 1 c n 1 O n 3 n. (3.38) Fro (3.38) we can approxiate tie t f = ( π n O ( 1 n)). So after nuber of steps equal to the closest integer to t f = π n 1 we will easure the arked state with probability p = 1 O ( 1 n). We see the exaple of evolution of the probability to easure the arked state in figure p step Figure 3.: The evolution of the probability p to find the arked state during 60 steps. We use the quantu walk algorith on the hypercube with diension 7. Now it is interesting to copare the properties of quantu walk algorith with the Grover s search algorith. They have soe siilarities. They both start with initial state equal to superposition of all states and both change in every step the phase of the arked state by π. Quantu walk algorith takes O ( n 1) steps and n = N is nuber of vertices, so both algorith have the sae running tie of O ( ) N. There are also soe differences. First of the is that the Grover s algorith can be presented as rotation in two diensional subspace instead of quantu walk where it is just an approxiation of rotation [4]. Also the two diensional subspace in the Grover s algorith is spanned by initial state and arked state whereas in the walk algorith the second state has just a large overlap with arked state. Another difference is in the use of the diffusion operator (coin in the case of the walk algorith). In the case of the Grover s algorith it is used on the whole n diensional space. Quantu walk algorith uses diffusion operator only on n diensional space. This property can have soe practical use in certain physical ipleentations of quantu coputer [4]. 3.3 Quantu walk search algorith on regular lattice Quantu walk search algorith on regular lattice is siilar to the walk algorith on the hypercube. Hence we will just briefly describe the algorith. We will introduce the regular lattice as the graph and
23 the siilar operators we have introduced in search on the hypercube. Then we define the algorith and entioned its properties. The regular lattice is an n-diensional grid with diension n and N vertices arranged as n N n N... n N. We can identify each vertex with vector a 1, a,..., a n where a i {1,,..., n N}. We add the coin space spanned by n directions in the regular lattice H n. Then the final Hilbert space of the walk is H = H n H N. We use the sae unperturbed coin operator Ĉ 0 as in (3.19). Let us denote the arked vertex by. Then coin operator of the perturbed walk has a for siilar to (3.0) except there is projector instead of 0 0. Now we define two shift operators Ŝ f f and Ŝ in the case of two diensional lattice. Let us assue that there is an orthogonal basis of the coin space {,,, } which describe the directions. Then Ŝ f f is defined as follows Ŝ f f x, y = x + 1, y Ŝ f f x, y = x 1, y, (3.39) Ŝ f f x, y = x, y + 1 Ŝ f f x, y = x, y 1 where x, y {1,..., n N}. We assue that periodic boundary conditions hold true, i.e. if any x or y is equal to n N and after application of the shift operator it can exceed n N, the corresponding coordinate will be shifted to 1 instead, for x or y equal to 1 and shift down it will be shifted to n N. We call (3.39) "flip-flop" shift operator, because after the shift the coin changes the direction. The "flip-flop" operator can be defined also in higher diension obeying the sae flipping rule as in two diension. Operator Ŝ is defined to not change the directions as follows Ŝ x, y = x + 1, y Ŝ x, y = x 1, y. (3.40) Ŝ x, y = x, y + 1 Ŝ x, y = x, y 1 Ŝ is a classical shift operator and it can be also expanded to any diension of regular lattice. Now we define the unperturbed step operator Û = Ŝ f f (Ĉ0 Î ) and the perturbed step operator Û as follows Û = Ŝ f f Ĉ = Û Ŝ f f ( s C s C ). (3.41) Then the algorith is consisting of the following steps: 1. Initialize the syste in the superposition of the states where a label vertices.. Apply unitary operator Û T-ties. 3. Measure the resulting state. ϕ 0 = n N d=1 a=1 3 1 nn d, a, (3.4)
24 If the diension of the lattice is equal or higher then three the nuber of steps T is required O ( ) N. Then the probability to easure the arked state is Θ (1), i.e. it is constant [5]. In case of two diensional lattice after T = O ( ) ( ) N log (N) probability p to easure the arked state is p = O 1 [5]. log(n) See exaple of the search on the two diensional lattice in figure 3.3. We can use aplitude aplification to increase the probability of success, then the algorith with coplexity O ( N log (N) ) will find the arked state with constant probability [5]. It can be also shown that if we use Ŝ instead of Ŝ f f algorith will take at least Ω (N) steps [5]. 0.0 p step Figure 3.3: The evolution of the probability p to find the arked state during 00 steps. We use the quantu walk algorith without aplitude aplification on the two diensional regular lattice with 30 ties 30 vertices. To show that the algorith works we repeat the sae process as in the search on the hypercube. It can be shown that there are two eigenvectors of Û, denoted by ω and ω, with eigenvalues e iω and e iω. Then the initial state and the arked state can be approxiately written as linear cobinations of ω and ω. Application of Û is approxiately rotation in the subspace spanned by the initial state and the arked state. The nuber of steps is derived fro the angle of rotation which depends on the diension of the lattice [5]. Before we ove to another chapter there is interesting property of regular lattice worth entioning. In case of the two diensional lattice there can be used only two diensional coin instead of four diensional. Let { 0, 1 } be the standard qubit basis. Then we can choose directions of the coin = 0, = 1, = and = If there is no arked state, Û acts like this If there is a arked state, Û has for Û x, y = x + 1, y Û x, y = x 1, y. (3.43) Û x, y = x, y + 1 Û x, y = x, y 1 Û = Û ( Î s, s, ) (3.44) 4
25 where s = It can be shown that the algorith based on this choice needs the sae nuber of steps T = O ( N log (N) ) to succeed [5]. 5
26 Chapter 4 Different look on the walk search algorith In this Chapter we return to the quantu walk search algorith and estiate the nuber of steps to succeed fro the different perspective. In Section 4.1 we do so for the search algorith on the hypercube and in Section 4. for the search on the regular lattice. 4.1 Search on the hypercube In this chapter we exaine different approach to estiating the nuber of steps in the search algorith. We introduce the walk operator Û λ and show how the nuber of steps can be derived fro the properties of the spectru of Û λ. We use the definition (3.18) and (3.19). Let us now introduce the relevant eigenvalues of Û = Ŝ (Ĉ 0 Î). There are following eigenvalues v ± k = e±iϕ k = 1 k n ± i n in the spectru of Û with corresponding eigenvectors v ± k = β k ( 1) k a n n α ± k a d d, a d=1 where α ± 1 if k d = 1 k d = k i if k d = 0 n k k(n k) (4.1) (4.) { if k = 0 or k = n and β k = 1 else. Other eigenvectors of Û correspond to eigenvalues ±1 and they are not affected by the perturbation, hence they have no influence on the properties of the algorith. We denote the arked vertex by. Fro the fact that the coin state s C is eigenvector of Ĉ 0 with eigenvalue 1, i.e. Ĉ 0 s C = s C, we can express Û fro (3.1) in the for Û = Û Ŝ ( s s ) = Û Ŝ Ĉ ( s s ) = = Û ( Î s s ). We write s C = s for sipler notation. Now let us define a faily of operators Û λ as follows (4.3) Û λ = Û [ Î + ( e iλπ 1 ) s s ]. (4.4) 6
27 Fro (4.4) it is easy to see that Û 0 = Û and Û 1 = Û. Operator Û λ is also periodic with period. If we apply Û λ on (4.) we see that the eigenstates orthogonal to s do not change. Hence we can restrict us only to eigenstates not orthogonal to s and fro each degenerate eigenspace we choose only one vector. After noralization this vector has the for ϕ ± k = 1 ( n k ) ( 1) j v ± j. (4.5) j =k Selection of these eigenstate depends on the position of the arked state. Because it can be shown that Û λ coutes with (3.3)[6], i.e. it preserves high syetry of the hypercube, we can again choose that the arked state is 0. Then (4.5) has the sipler for ϕ ± k = 1 ( n k ) j =k v ± j. (4.6) These states span the n diensional subspace H. The arked state s is in H and the Hilbert space H also coplies Û λ (H ) = H. Again to siplify notation we change index k and ± for new index l such that l { n + 1,..., n} and {k, ±} = { l, sgn(l)}. Now we write e ±iϕ k = e iϕ l and ϕ ± k = ϕ l. Thus we can restrict us on Hilbert space H with basis { ϕ l l { n + 1,, n}}. Let us describe the properties of the spectru of Û λ. The eigenphases ϕ l of the unperturbed walk fro (4.1) stay largely unchanged with changing λ. Moreover, there are eigenstates ρ λ with eigenphase approxiately parallel to the line πλ [6]. An avoided crossing can be found at points where eigenphase related to ϕ l get near to the eigenphase of ρ λ. See figure 4.1 for exaple of eigenphase of Û λ as a function of λ. It can be shown that the application of Û λ on H near the avoided crossing can be approxiately described as evolution in two diensional subspace, i.e. the other states in H are far less influenced. One of the vectors that span the syste at l th -crossing is ϕ l. It is easy to show that the state ϕ l is approxiate eigenvector of (4.4). Let us apply operator (4.4) on the state ϕ l and we get Û λ ϕ l = e iϕ l ϕ l + n+1 ( e iλπ 1 ) (n ) β l e iψ l Û s, (4.7) l where e iψ l = e ±iψ k = k± n k n and β l is given in (4.). We see that if l is close to 0 or n ϕ l is an approxiate eigenstate of Û λ with exponentially sall reinder. Now let us define function g(λ) as a eigenphase of ρ λ, i.e. e ig(λ) is eigenvalue of (4.4). We write ρ λ as linear cobination of basis states ρ λ = n+ n l= n+1 (n ) β l e iψ l a l ϕ l (4.8) l where coefficients a l need to be specified yet. We can calculate the scalar product s ρ λ = n 3 b [6] where b is defined as follows n ( ) n b = β l a l. (4.9) l l= n+1 7
28 φ/π λ Figure 4.1: The eigenphase of the operator Û λ as a function of λ for the 7-diensional hypercube. Now we choose the coefficients a l to accoplish Û λ ρ λ = e ig(λ) ρ λ. To do so we apply (4.4) on (4.8) and get Û λ ρ λ =Û ρ λ + ( e iλπ 1 ) Û s s ρ λ n (n ) =e ig(λ) ρ λ + n+1 β l e iψ l ϕ l l l= n+1 [( ) e ig(λ) + e iϕ l al + ( e iλπ 1 ) n 1 e iϕ l b ]. (4.10) We see that if we set a l = ( e iλπ 1 ) n 1 e iϕ l b e ig(λ) + e iϕ l (4.11) the second ter in (4.10) disappears and the state ρ λ is eigenstate of Û λ. However constant b also depends on coefficients a l thus (4.11) and (4.9) represent a set of linear equations. We can express the condition for the equations to have solution by inserting (4.11) in (4.9). We get the expression 1 = n l= n+1 β l ( ) ( n e iλπ 1 ) n 1 e iϕ l l e iϕ l e ig(λ) (4.1) which iplicitly define g(λ). Now we construct the second vector µ l in the two diensional subspace at the l th -crossing by taking fro ρ λl only the part which is orthogonal to ϕ l. So µ l coplies µ l = ρ λl ϕ l ρ λl ϕ l where we denote λ at l th -crossing by λ l. Fro construction of µ l it follows that µ l is orthogonal to the state ϕ l. The state µ l expressed in basis { ϕ l } n l= n+1 has the for µ l = b 3n+1 ( 1 e iλ l π ) n k= n+1 k l 8 ( ) n e i(ϕ k +ψ k ) β k k e iϕ k e ig(λ l ) ϕ k (4.13)
29 where b is noralization constant. It can be shown [6] that b is equal to g b = (λ) n+1. (4.14) π It is easy to see fro (4.13) and (4.14) that the ter which µ l differs fro ρ λl is exponentially sall and thus µ l is approxiately eigenvector of Û λl. It can be shown that the two diensional space spanned by the states ϕ l and µ l has high overlap with true eigenstates ω ± l of Û λl at the avoided crossing. ( Hence we can write ϕ l 1 ω + l + ω l ) ( and µ l i ω + l ω l ) [6]. Then we apply Û λl on ϕ l for t ties and we get the following expression (Û λl ) t ϕ l 1 ) (e it(ϕ l+ 1 l) ω + l + e it(ϕ l 1 l) ω l (4.15) where l is gap between two eigenphases at the l th avoided crossing. We see that if we choose the nuber of steps T l to coply e it 1 l l = i we rotate the state ϕ l in the state µ l. In different words after T l = ) π Tl l steps we get (Ûλl ϕ l ie it lϕ l µ l. The gap between two eigenphases can be calculated for sall differences as the gap between two eigenvalues. To estiate the spectral gap we express Û λl in the two diensional subspace as atrix W as follows ( ) A B W = where C D A = µ l U λl µ l = e ig(λ l) = e iϕ l ) g (λ l ) B = ϕ l U λl µ l = n 1 ( e iλ lπ 1 ) e i(ϕ l+ψ l ) β l (n l π ) g (λ l ). (4.16) C = µ l U λl ϕ l = ( n 1 e iλlπ 1 ) (n e i(ϕ l ψ l ) β l l [ D = ϕ l U λl ϕ l = e iϕ l 1 + ( e iλlπ 1 ) ( )] n n 1 β l l π In (4.16) we use the fact that at the l th -crossing we can set g(λ l ) = ϕ l with fulfilling the condition (4.1) up to exponentially sall reinder [6]. The spectral gap of W coplies ( l ) = (D A) + 4BC (4.17) and after inserting (4.16) in (4.17) we obtain following approxiation of l l = e iλ l π 1 ( ) n n g ( ( )) (λ l ) n βl + O n. (4.18) l π l Entering (4.18) in T l = π l the nuber of step that is necessary to rotate the state ϕl in the state µ l is The probability to easure the arked state after T l steps is π n π g (λ l ) T l = e iλlπ 1 ( n ) βl. (4.19) l µ l s n 3 b g (λ ). (4.0) π 9
30 The search algorith on the hypercube constructed in previous chapter corresponds to the avoided crossing at λ = 1 and ϕ 0 = 0, so called 0 th -crossing. It can be shown that g(0) = 1 and g (1) = π ( 1 + γ n n+1) Using this we can estiate the nuber of steps in the algorith π n π g (1) T = where γ n 1 n for large n [6]. (4.1) ( π 4 N n ) + n+1 π 4 N (4.) and the probability to easure the arked state is approxiately equal to 1. This atches our results in previous chapter. Fro the relation between the nuber of steps and the eigenphase gap follows that the nuber of steps declines with the rising gap. So algorith based on higher avoided crossing will be faster. But it was shown that after crossing particular l the algorith fails because the probability to easure the arked state falls. Also the initial state of the algorith at the 0 th -crossing ϕ 0 does not depend on choice of the arked state but on the other crossings the initial state depend on the position of the arked state. So before we start the algorith based on the other crossings we need to find the initial state and there is no suitable ethod to do so that still preserve the iproveent of the higher crossing. 4. Search on the regular lattice We can perfor the sae process for estiation of the nuber of steps on regular lattice search as we did with the search on the hypercube. We define Û λ by (4.4) and restrict us on the subspace spanned by the spatial eigenvectors of Û that are not orthogonal to the arked state. Again the avoided crossings in the spectru of Û λ is found. The dynaic at the avoided crossing can be describe as rotation in two diensional subspace spanned by two approxiate eigenvectors. The nuber of steps is inversely proportional to the gap between the eigenphases at the avoided crossing T = π. We focus only on 0 th -crossing. It can be shown that the eigenphase gap is equal to = 4b ( ) 1 + O (4.3) N N where b is defined as s µ 0 = b. The constant b is chosen to noralized the state µ 0. The value of b depends on the diension as follows ( ) 1 ( ) = Θ 1 b π ln(n)+ 8 π ( K)+ π ln 8 ln(n) for d = +O( π N 1 ) (4.4) Θ(1) for d 3 where K 0, 916 is Catalan s constant and d is the diension of the regular lattice. Then after T nuber of steps π N T = 4 π ln (N) + 8 ( K) + π π ln ( ) 8 = O ( ) π N ln (N) for d = O( (4.5) N) for d 3 30
31 we easure the arked state with probability p = s µ 0 = b p = ( Θ ) 1 ln(n) for d = Θ(1) for d 3. (4.6) In the case of the two diensional lattice it is necessary to use aplitude aplification so the algorith will find the arked state with probability Θ(1). By doing so as we discuss in previous chapter algorith need O ( N ln (N) ) steps. φ/π λ Figure 4.: The eigenphase of the operator Û λ as a function of λ for the two diensional regular lattice with 10 ties 10 vertices. 31
32 Chapter 5 State transfer In Section.1 we show how quantu discrete walk can be used for the state transfer. In Section. we use the properties of the quantu search on the regular lattice to counicate across the grid. 5.1 State transfer as the discrete tie quantu walk One of the any use of quantu walks is a state transfer, in particular we focus on the discrete quantu walk realization of the state transfer on a spin chain with position dependent couplings. First we describe in general the syste we use and the quantu walk. Then we introduce connection between properties of walk and physical properties of the syste. Finally we describe the way the transfer works. In general the syste is a network with every vertex corresponding to spin 1. If there is an interaction between vertex i and j we say that these vertices are connected. We consider an XX odel od spin-spin interaction with Hailtonian of the network ( Ĥ = J i j ˆσ i x ˆσ x j + ˆσ i y ˆσ y j ) (5.1) {i, j} E where E denotes the set of edges, σ i x is Pauli X atrix for the i th spin and J i j is strength of spin interaction between i and j, J i j is often called spin coupling paraeter [8]. Because (5.1) conserves the total spin nuber along Z axis i σ z i we can restrict us to subspace with fixed nuber of excitation where by excitation it is eant a spin pointing up along the Z axis. In particular we focus on cases with zero or one excitation. The first case is invariant under the evolution generated by (5.1) and the second case can be consider as walking particle on an underlying network [8]. On the network we arked the two spins as a sender and a receiver. We prepare the sender spin in state α + β and rest of the network has spin down. The state of the network can be written in the for (α + β ) s... net r. (5.) We want to use the evolution generated by (5.1) to transfer the state of sender to receiver. So the final state of the syste will have the for s... net (α + β ) r. (5.3) We use as the network the spin chain so the interaction occurs only between neighbouring spins. 3
33 In the transfer of the state we use the one diensional discrete tie quantu walk. The evolution operator Û = Ŝ Ĉ has in general the for Û x, = cos (θ) x + 1, sin (θ) x 1, Û x, = sin (θ) x + 1, + cos (θ) x 1, (5.4) where θ denotes the coin flip rate. The equivalent notation of Û is Û = e i ˆP ˆσ z e i ˆσ yθ (5.5) where ˆP is the oentu operator and ˆσ j are Pauli atrices acting on the coin space [8]. We can use (5.5) to build the analogy between properties of the walk and physical properties of the syste of relativistic particle in one diension. We write the operator Û in the for Û = Û(t) = e i ˆP ˆσ z vt e i ˆσ yωt (5.6) where vt = 1 and ωt = θ. We can identify v with the velocity and ω with the angular frequency. Then if we take the infinitesial steps and apply the Trotter theore we get ( t )) n li (Û = e i( ˆP ˆσ z v+ ˆσ y ω)t [8]. (5.7) n n This operator is generated by Hailtonian, which has the for of one diensional Dirac Hailtonian Ĥ = c ˆP ˆσ z + c ˆσ y (5.8) where we identify v with speed of light and ω with the ass of particle. The Dirac Hailtonian describe the relativistic particle in one diension. Because we take t = 1 we see that the ass of the particle correspond to the coin flip rate [8]. The operator (5.5) does not differentiate between θ and θ + π and in case of + the flip rate of the coin corresponds to θ π. Hence we can choose the relation = tg (θ). Another analogy can be constructed using (5.1) to obtain relation between ass and the spin coupling paraeter J = 1 [8]. Now let us introduce the state transfer itself. We work with the finite chains of spins so at the end of the chain we use reversing coin, i.e. coin with flip rate equal to θ = π. For the transfer we use the engineered couplings protocol. This protocol is based on the properly chosen couplings paraeter between each spins. The protocol sets the coupling paraeter between spin n and n + 1 to be J n = λ n (N n) where λ is real positive paraeter coon for all couplings [8]. Then the ass for the transfer between n and n + 1 position is The evolution operator have for n = 1 J n = 1 λ n(n n). (5.9) U(n) = e i ˆP ˆσ z e i ˆσ yθ n (5.10) where θ n depends on position. In the case of one diensional discrete quantu walk interference appears only between positions separated by the distance of two, hence we can study two independent walks on even and on odd positions [8]. We can treat even positions as edges and odd as vertices and use for the evolution operator Û instead of Û. So we use N positions to siulated the chain with N spins. Coins associated with edges positions correspond to ass and at the vertex position we can set the coin 33
34 flip rate θ k 1 = 0, i. e. coin is the identity operator. It can be shown that different choice of the coin on vertex positions produces the siilar results [8]. On the edges positions the coin flip rate is derived fro its relation with ass and has the for 1 θ l = arctan λ k ( N k) (5.11) where k {1,,..., N 1}. It was shown in [8] that the transfer strongly depends on the paraeter λ. At first the transfer is perfect for sall values of λ. This case is called large ass liit. Around λ = π N the transfer starts to fall and it is restored for λ = O (1) and higher [8], this is called sall ass liit. It can be shown that in case of the large ass liit Û is generated by Heritian operator whose action is the sae as the action of the Hailtonian introduce by Christandl [8]. So it can be shown that the state of the sender is fully transfered to the receiver. In the case of sall ass liit it follows that cos (θ k ) 1 and sin (θ k ) 0. (5.1) Thus the double step operator Û is approxiately equal to e i ˆP ˆσ z. The transfer take the N steps. The initial state of the sender is α 1, + β 1,. The first part oves left and it is reflected at position 0, then it oves to position N 1, so it results in α N 1,. β 1, first oves to the position N where is reflected and also its phase is changed by π, then it oves to the position N 1 and results in β N 1,. After application of operator ˆσ y the state of the receiver is α N 1, + β N 1, and so we reach the full state transfer [8]. This shows how discrete tie quantu walk can be used to transfer the state across one diensional chain. The continuous tie quantu walk can be also used to transfer the state. However the discrete walk has the additional degree of freedo, the coin, which gives us ore possibilities to control the walk [8]. 5. An aplitude transfer across regular lattice The process used in the search algorith on the regular lattice can be used to transfer aplitude across regular lattice. In this section we describe how we can achieve the transfer and its basic properties. First we need to expand the search algorith for ore arked states. Suppose we have l arked states 1,..., l for l N. We define a faily of operators analogous to (odkaz na U-labda) with set of paraeters λ = (λ 1,..., λ l ) as follows l Û λ = Û 1 + ( e iπλ j 1 ) s j s j. (5.13) j=1 At λ = (1,..., 1) around the eigenphase equal to 0 we can find l 1 degenerate eigenvalues and two further values foring and avoided crossing with degenerate subset [9]. The subspace spanned by corresponding vectors have high overlap with space spanned by initial state ϕ 0 and approxiate eigenvectors ρ 1 λ=1,..., ρl λ=1. We denote ρ j λ=1 = ρ j for sipler notation. The states ρ j are orthogonal to ϕ 0 and they coply ρ j ρ k δ jk. As in the previous chapter the search algorith can be construct on the avoided crossing. It can be shown [9] that the nuber of steps necessary to find one of the arked 34
35 states is inversely proportional to the gap between non-degenerate levels at the avoided crossing. This gap is equal to = ɛ l where ɛ = s j ρ j ( ) 1 + O (5.14) N N In (5.14) s j ρ j does not depend on j. Finally (5.14) and T π iply that the nuber of steps π N of the search algorith with ore arked states is T = for diension higher then 3 and T = for diension equal to. π N ln(n) Now we describe the transfer itself. Let us first assue that there exists Hailtonian Ĥ which coplies Û λ=1 = e iĥ. In the basis { ϕ 0, ρ 1, ρ,..., ρ l } the Hailtonian Ĥ can be expressed as (l + 1) (l + 1) atrix as follows 0 iɛ... iɛ iɛ H (l+1) (l+1) = iɛ (5.15) where ɛ is defined by (5.14). eigenvectors H (l+1) (l+1) has eigenvalues 0 with l 1 eigenvectors and ±ɛ l with ν ± = i l i l ϕ 0 + l ρ j. (5.16) j=1 We start the transfer of the aplitude with the syste in the state where ν 0 = ρ 1 = i l ( ν+ ν + i (l 1) ν 0 ) 1 l (l 1) (1 l) ρ1 + l (5.17) ρ j. We see that ν 0 is orthogonal to ν ± so it is eigenstate of (5.15) with eigenvalues 0. Hence it applies that Û 1 ν 0 = ν 0. Now we use the operator Û 1 on the state ρ 1 T t ties where T t = = T Û T t 1 ρ1 = i ( e iɛ lt t ν + e iɛ lt t ν + i ) (l 1) ν 0 = l j= = i ( ν+ + ν + i (l 1) ν 0 ) = l ( = 1 ) l ρ 1 l l ρ j j= π ɛ l. (5.18) So we transfer the aplitude to other states. If we set l = we get full transfer. This process can be used for counication between sender and receiver across the regular lattice without the knowledge of their exact position. It can be shown that this process can also track oving receiver though the speed of the receiver is liited by the transfer tie T t N (T t N ln (N) for diension equal to ) [9]. 35
36 Conclusion In this text we study the quantu walks and their use in search algorith and state transfer protocol. We introduce the concept of the discrete tie quantu walks and ention difference between quantu walks and classic rando walks. In Chapter 3 we described the Grover s search algorith and showed that it needs O ( N ) steps. We also proved the lower bound for quantu search algorith in general and hence there can not be faster algorith than Ω ( N ). We also presented the quantu search algorith on the hypercube and on regular lattice and shown that it also takes O ( N ) steps to succeed except the two diensional lattice which need O ( N ) ln (N) steps. We copared the properties of the Grover s algorith and the walk search algorith and recognised their advantages and disadvantages. In Chapter 4 we again estiated the nuber of steps of the walk search algorith fro perspective of the avoided crossing of eigenphases of the operator Û λ. In the last chapter we focused on use of discrete quantu walk to accoplish the transfer of state and counication across the grid thanks to echanis of the quantu walk search on the regular lattice. We notice that the counication can be achieved without knowledge of position of sender and receiver and that it is possible even with oving receiver. 36
Search and state transfer by means of quantum walk. Vyhledávání a přenos stavu pomocí kvantové procházky
 Czech Technical University in Prague Faculty of uclear Sciences and Physical Engineering Search and state transfer by means of quantum walk Vyhledávání a přenos stavu pomocí kvantové procházky Master s
Czech Technical University in Prague Faculty of uclear Sciences and Physical Engineering Search and state transfer by means of quantum walk Vyhledávání a přenos stavu pomocí kvantové procházky Master s
Gymnázium, Brno, Slovanské nám. 7 WORKBOOK. Mathematics. Teacher: Student:
 WORKBOOK Subject: Teacher: Student: Mathematics.... School year:../ Conic section The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.
WORKBOOK Subject: Teacher: Student: Mathematics.... School year:../ Conic section The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.
WORKSHEET 1: LINEAR EQUATION 1
 WORKSHEET 1: LINEAR EQUATION 1 1. Write down the arithmetical problem according the dictation: 2. Translate the English words, you can use a dictionary: equations to solve solve inverse operation variable
WORKSHEET 1: LINEAR EQUATION 1 1. Write down the arithmetical problem according the dictation: 2. Translate the English words, you can use a dictionary: equations to solve solve inverse operation variable
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
VY_32_INOVACE_06_Předpřítomný čas_03. Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace
 VY_32_INOVACE_06_Předpřítomný čas_03 Autor: Růžena Krupičková Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu: Zkvalitnění ICT ve slušovské škole Číslo projektu: CZ.1.07/1.4.00/21.2400
VY_32_INOVACE_06_Předpřítomný čas_03 Autor: Růžena Krupičková Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu: Zkvalitnění ICT ve slušovské škole Číslo projektu: CZ.1.07/1.4.00/21.2400
Základy teorie front III
 Základy teorie front III Aplikace Poissonova procesu v teorii front II Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta
Základy teorie front III Aplikace Poissonova procesu v teorii front II Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta
Aplikace matematiky. Dana Lauerová A note to the theory of periodic solutions of a parabolic equation
 Aplikace matematiky Dana Lauerová A note to the theory of periodic solutions of a parabolic equation Aplikace matematiky, Vol. 25 (1980), No. 6, 457--460 Persistent URL: http://dml.cz/dmlcz/103885 Terms
Aplikace matematiky Dana Lauerová A note to the theory of periodic solutions of a parabolic equation Aplikace matematiky, Vol. 25 (1980), No. 6, 457--460 Persistent URL: http://dml.cz/dmlcz/103885 Terms
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA
 GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
Gymnázium, Brno, Slovanské nám. 7, SCHEME OF WORK Mathematics SCHEME OF WORK. cz
 SCHEME OF WORK Subject: Mathematics Year: first grade, 1.X School year:../ List of topisc # Topics Time period Introduction, repetition September 1. Number sets October 2. Rigtht-angled triangle October,
SCHEME OF WORK Subject: Mathematics Year: first grade, 1.X School year:../ List of topisc # Topics Time period Introduction, repetition September 1. Number sets October 2. Rigtht-angled triangle October,
Compression of a Dictionary
 Compression of a Dictionary Jan Lánský, Michal Žemlička zizelevak@matfyz.cz michal.zemlicka@mff.cuni.cz Dept. of Software Engineering Faculty of Mathematics and Physics Charles University Synopsis Introduction
Compression of a Dictionary Jan Lánský, Michal Žemlička zizelevak@matfyz.cz michal.zemlicka@mff.cuni.cz Dept. of Software Engineering Faculty of Mathematics and Physics Charles University Synopsis Introduction
USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING
 USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING Eva Minaříková Institute for Research in School Education, Faculty of Education, Masaryk University Structure of the presentation What can we as teachers
USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING Eva Minaříková Institute for Research in School Education, Faculty of Education, Masaryk University Structure of the presentation What can we as teachers
Database systems. Normal forms
 Database systems Normal forms An example of a bad model SSN Surnam OfficeNo City Street No ZIP Region President_of_ Region 1001 Novák 238 Liteň Hlavní 10 26727 Středočeský Rath 1001 Novák 238 Bystřice
Database systems Normal forms An example of a bad model SSN Surnam OfficeNo City Street No ZIP Region President_of_ Region 1001 Novák 238 Liteň Hlavní 10 26727 Středočeský Rath 1001 Novák 238 Bystřice
CHAIN TRANSMISSIONS AND WHEELS
 Second School Year CHAIN TRANSMISSIONS AND WHEELS A. Chain transmissions We can use chain transmissions for the transfer and change of rotation motion and the torsional moment. They transfer forces from
Second School Year CHAIN TRANSMISSIONS AND WHEELS A. Chain transmissions We can use chain transmissions for the transfer and change of rotation motion and the torsional moment. They transfer forces from
Litosil - application
 Litosil - application The series of Litosil is primarily determined for cut polished floors. The cut polished floors are supplied by some specialized firms which are fitted with the appropriate technical
Litosil - application The series of Litosil is primarily determined for cut polished floors. The cut polished floors are supplied by some specialized firms which are fitted with the appropriate technical
Transportation Problem
 Transportation Problem ١ C H A P T E R 7 Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply s i ) to n
Transportation Problem ١ C H A P T E R 7 Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply s i ) to n
Využití hybridní metody vícekriteriálního rozhodování za nejistoty. Michal Koláček, Markéta Matulová
 Využití hybridní metody vícekriteriálního rozhodování za nejistoty Michal Koláček, Markéta Matulová Outline Multiple criteria decision making Classification of MCDM methods TOPSIS method Fuzzy extension
Využití hybridní metody vícekriteriálního rozhodování za nejistoty Michal Koláček, Markéta Matulová Outline Multiple criteria decision making Classification of MCDM methods TOPSIS method Fuzzy extension
Introduction to MS Dynamics NAV
 Introduction to MS Dynamics NAV (Item Charges) Ing.J.Skorkovský,CSc. MASARYK UNIVERSITY BRNO, Czech Republic Faculty of economics and business administration Department of corporate economy Item Charges
Introduction to MS Dynamics NAV (Item Charges) Ing.J.Skorkovský,CSc. MASARYK UNIVERSITY BRNO, Czech Republic Faculty of economics and business administration Department of corporate economy Item Charges
DC circuits with a single source
 Název projektu: utomatizace výrobních procesů ve strojírenství a řemeslech egistrační číslo: Z..07/..0/0.008 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 09 Tento projekt je spolufinancován
Název projektu: utomatizace výrobních procesů ve strojírenství a řemeslech egistrační číslo: Z..07/..0/0.008 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 09 Tento projekt je spolufinancován
On large rigid sets of monounary algebras. D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia
 On large rigid sets of monounary algebras D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia coauthor G. Czédli, University of Szeged, Hungary The 54st Summer School on General Algebra
On large rigid sets of monounary algebras D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia coauthor G. Czédli, University of Szeged, Hungary The 54st Summer School on General Algebra
Gymnázium, Brno, Slovanské nám. 7 WORKBOOK. Mathematics. Student: Draw: Convex angle Non-convex angle
 WORKBOOK http://agb.gymnaslo.cz Subject: Student: Mathematics.. School year:../ Topic: Trigonometry Angle orientation Types of angles 90 right angle - pravý less than 90 acute angles ("acute" meaning "sharp")-
WORKBOOK http://agb.gymnaslo.cz Subject: Student: Mathematics.. School year:../ Topic: Trigonometry Angle orientation Types of angles 90 right angle - pravý less than 90 acute angles ("acute" meaning "sharp")-
Dynamic Signals. Ananda V. Mysore SJSU
 Dynamic Signals Ananda V. Mysore SJSU Static vs. Dynamic Signals In principle, all signals are dynamic; they do not have a perfectly constant value over time. Static signals are those for which changes
Dynamic Signals Ananda V. Mysore SJSU Static vs. Dynamic Signals In principle, all signals are dynamic; they do not have a perfectly constant value over time. Static signals are those for which changes
6.867 Machine Learning
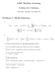 . Machine Learning Problem Set Solutions Due date: Monday November Problem : Model Selection. P (y,..., y n x,..., x n, PST) = = K [ [,] K [ K p n+ i i ( p i ) n i dpi ] = p n+ i i K ( p i ) n i n + i!
. Machine Learning Problem Set Solutions Due date: Monday November Problem : Model Selection. P (y,..., y n x,..., x n, PST) = = K [ [,] K [ K p n+ i i ( p i ) n i dpi ] = p n+ i i K ( p i ) n i n + i!
CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA
 CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA &KDSWHUSUHVHQWVWKHGHVLJQDQGIDEULFDW LRQRIPRGLILHG0LQNRZVNLIUDFWDODQWHQQD IRUZLUHOHVVFRPPXQLFDWLRQ7KHVLPXODWHG DQGPHDVXUHGUHVXOWVRIWKLVDQWHQQDDUH DOVRSUHVHQWHG
CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA &KDSWHUSUHVHQWVWKHGHVLJQDQGIDEULFDW LRQRIPRGLILHG0LQNRZVNLIUDFWDODQWHQQD IRUZLUHOHVVFRPPXQLFDWLRQ7KHVLPXODWHG DQGPHDVXUHGUHVXOWVRIWKLVDQWHQQDDUH DOVRSUHVHQWHG
2. Entity, Architecture, Process
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Praktika návrhu číslicových obvodů Dr.-Ing. Martin Novotný Katedra číslicového návrhu Fakulta informačních technologií ČVUT v Praze Miloš
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Praktika návrhu číslicových obvodů Dr.-Ing. Martin Novotný Katedra číslicového návrhu Fakulta informačních technologií ČVUT v Praze Miloš
Next line show use of paragraf symbol. It should be kept with the following number. Jak může státní zástupce věc odložit zmiňuje 159a.
 1 Bad line breaks The follwing text has prepostions O and k at end of line which is incorrect according to Czech language typography standards: Mezi oblíbené dětské pohádky patří pohádky O Palečkovi, Alenka
1 Bad line breaks The follwing text has prepostions O and k at end of line which is incorrect according to Czech language typography standards: Mezi oblíbené dětské pohádky patří pohádky O Palečkovi, Alenka
Dynamic programming. Optimal binary search tree
 The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamic programming Optimal binary search tree Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The complexity
The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamic programming Optimal binary search tree Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The complexity
SPECIAL THEORY OF RELATIVITY
 SPECIAL THEORY OF RELATIVITY 1. Basi information author Albert Einstein phenomena obsered when TWO frames of referene moe relatie to eah other with speed lose to the speed of light 1905 - speial theory
SPECIAL THEORY OF RELATIVITY 1. Basi information author Albert Einstein phenomena obsered when TWO frames of referene moe relatie to eah other with speed lose to the speed of light 1905 - speial theory
MIKROPROCESORY PRO VÝKONOVÉ SYSTÉMY. Stručný úvod do programování v jazyce C 2.díl. České vysoké učení technické Fakulta elektrotechnická
 MIKROPROCESORY PRO VÝKONOVÉ SYSTÉMY Stručný úvod do programování v jazyce C 2.díl České vysoké učení technické Fakulta elektrotechnická A1B14MIS Mikroprocesory pro výkonové systémy 07 Ver.1.10 J. Zděnek,
MIKROPROCESORY PRO VÝKONOVÉ SYSTÉMY Stručný úvod do programování v jazyce C 2.díl České vysoké učení technické Fakulta elektrotechnická A1B14MIS Mikroprocesory pro výkonové systémy 07 Ver.1.10 J. Zděnek,
CZ.1.07/1.5.00/
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Czech Republic. EDUCAnet. Střední odborná škola Pardubice, s.r.o.
 Czech Republic EDUCAnet Střední odborná škola Pardubice, s.r.o. ACCESS TO MODERN TECHNOLOGIES Do modern technologies influence our behavior? Of course in positive and negative way as well Modern technologies
Czech Republic EDUCAnet Střední odborná škola Pardubice, s.r.o. ACCESS TO MODERN TECHNOLOGIES Do modern technologies influence our behavior? Of course in positive and negative way as well Modern technologies
Angličtina v matematických softwarech 2 Vypracovala: Mgr. Bronislava Kreuzingerová
 Angličtina v matematických softwarech 2 Vypracovala: Mgr. Bronislava Kreuzingerová Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace
Angličtina v matematických softwarech 2 Vypracovala: Mgr. Bronislava Kreuzingerová Název školy Název a číslo projektu Název modulu Obchodní akademie a Střední odborné učiliště, Veselí nad Moravou Motivace
ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ
 ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ MGR. VLADIMÍR BRADÁČ ROZVOJ KOMPETENCÍ MANAGEMENTU A PRACOVNÍKŮ VŠ MSK (S PODPOROU ICT) PROJEKT OP VK 2.2: CZ.1.07/2.2.00/15.0176 OSTRAVA 2012 Tento projekt je
ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ MGR. VLADIMÍR BRADÁČ ROZVOJ KOMPETENCÍ MANAGEMENTU A PRACOVNÍKŮ VŠ MSK (S PODPOROU ICT) PROJEKT OP VK 2.2: CZ.1.07/2.2.00/15.0176 OSTRAVA 2012 Tento projekt je
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku
 Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
Vánoční sety Christmas sets
 Energy news 7 Inovace Innovations 1 Vánoční sety Christmas sets Na jaře tohoto roku jste byli informováni o připravované akci pro předvánoční období sety Pentagramu koncentrátů a Pentagramu krémů ve speciálních
Energy news 7 Inovace Innovations 1 Vánoční sety Christmas sets Na jaře tohoto roku jste byli informováni o připravované akci pro předvánoční období sety Pentagramu koncentrátů a Pentagramu krémů ve speciálních
STUDY EDITS FOR BETTER TRANSPORT IN THE CENTRE OF NÁCHOD
 CZECH TECHNICAL UNIVERSITY IN PRAGUE Faculty of transportation sciences Title of project STUDY EDITS FOR BETTER TRANSPORT IN THE CENTRE OF NÁCHOD 2006 Petr Kumpošt Basic information about town Náchod Náchod
CZECH TECHNICAL UNIVERSITY IN PRAGUE Faculty of transportation sciences Title of project STUDY EDITS FOR BETTER TRANSPORT IN THE CENTRE OF NÁCHOD 2006 Petr Kumpošt Basic information about town Náchod Náchod
PC/104, PC/104-Plus. 196 ept GmbH I Tel. +49 (0) / I Fax +49 (0) / I I
 E L E C T R O N I C C O N N E C T O R S 196 ept GmbH I Tel. +49 (0) 88 61 / 25 01 0 I Fax +49 (0) 88 61 / 55 07 I E-Mail sales@ept.de I www.ept.de Contents Introduction 198 Overview 199 The Standard 200
E L E C T R O N I C C O N N E C T O R S 196 ept GmbH I Tel. +49 (0) 88 61 / 25 01 0 I Fax +49 (0) 88 61 / 55 07 I E-Mail sales@ept.de I www.ept.de Contents Introduction 198 Overview 199 The Standard 200
Enabling Intelligent Buildings via Smart Sensor Network & Smart Lighting
 Enabling Intelligent Buildings via Smart Sensor Network & Smart Lighting Petr Macháček PETALIT s.r.o. 1 What is Redwood. Sensor Network Motion Detection Space Utilization Real Estate Management 2 Building
Enabling Intelligent Buildings via Smart Sensor Network & Smart Lighting Petr Macháček PETALIT s.r.o. 1 What is Redwood. Sensor Network Motion Detection Space Utilization Real Estate Management 2 Building
Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost
 Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost Registrační číslo: CZ.1.07/1. 5.00/34.0084 Šablona: II/2 Inovace a zkvalitnění výuky cizích jazyků na středních
Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost Registrační číslo: CZ.1.07/1. 5.00/34.0084 Šablona: II/2 Inovace a zkvalitnění výuky cizích jazyků na středních
A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients
 KYBERNETIKA VOLUME 8 (1972), NUMBER 6 A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients JAROSLAV KRAL In many applications (for example if the effect
KYBERNETIKA VOLUME 8 (1972), NUMBER 6 A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients JAROSLAV KRAL In many applications (for example if the effect
Návrh a implementace algoritmů pro adaptivní řízení průmyslových robotů
 Návrh a implementace algoritmů pro adaptivní řízení průmyslových robotů Design and implementation of algorithms for adaptive control of stationary robots Marcel Vytečka 1, Karel Zídek 2 Abstrakt Článek
Návrh a implementace algoritmů pro adaptivní řízení průmyslových robotů Design and implementation of algorithms for adaptive control of stationary robots Marcel Vytečka 1, Karel Zídek 2 Abstrakt Článek
UPM3 Hybrid Návod na ovládání Čerpadlo UPM3 Hybrid 2-5 Instruction Manual UPM3 Hybrid Circulation Pump 6-9
 www.regulus.cz UPM3 Hybrid Návod na ovládání Čerpadlo UPM3 Hybrid 2-5 Instruction Manual UPM3 Hybrid Circulation Pump 6-9 CZ EN UPM3 Hybrid 1. Úvod V továrním nastavení čerpadla UPM3 Hybrid je profil PWM
www.regulus.cz UPM3 Hybrid Návod na ovládání Čerpadlo UPM3 Hybrid 2-5 Instruction Manual UPM3 Hybrid Circulation Pump 6-9 CZ EN UPM3 Hybrid 1. Úvod V továrním nastavení čerpadla UPM3 Hybrid je profil PWM
EU peníze středním školám digitální učební materiál
 EU peníze středním školám digitální učební materiál Číslo projektu: Číslo a název šablony klíčové aktivity: Tematická oblast, název DUMu: Autor: CZ.1.07/1.5.00/34.0515 III/2 Inovace a zkvalitnění výuky
EU peníze středním školám digitální učební materiál Číslo projektu: Číslo a název šablony klíčové aktivity: Tematická oblast, název DUMu: Autor: CZ.1.07/1.5.00/34.0515 III/2 Inovace a zkvalitnění výuky
CZ.1.07/1.5.00/ Zefektivnění výuky prostřednictvím ICT technologií III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT
 Autor: Sylva Máčalová Tematický celek : Gramatika Cílová skupina : mírně pokročilý - pokročilý Anotace Materiál má podobu pracovního listu, který obsahuje cvičení, pomocí nichž si žáci procvičí rozdíly
Autor: Sylva Máčalová Tematický celek : Gramatika Cílová skupina : mírně pokročilý - pokročilý Anotace Materiál má podobu pracovního listu, který obsahuje cvičení, pomocí nichž si žáci procvičí rozdíly
a rhomboid, a side, an angle,a vertex, a height, a perimeter, an area an acute angle, an obtuse angle, opposite sides, parallel sides
 Autor: Ing. Milada Kyselovská Škola: ZŠ a MŠ Klíč s.r.o. Česká Lípa440 RHOMBOID Mezipředmětové vztahy: Matematika, zeměpis, dějepis Časová dotace: 45minut Ročník: 7 Cíle: Matematika : procvičit výpočet
Autor: Ing. Milada Kyselovská Škola: ZŠ a MŠ Klíč s.r.o. Česká Lípa440 RHOMBOID Mezipředmětové vztahy: Matematika, zeměpis, dějepis Časová dotace: 45minut Ročník: 7 Cíle: Matematika : procvičit výpočet
Configuration vs. Conformation. Configuration: Covalent bonds must be broken. Two kinds of isomers to consider
 Stereochemistry onfiguration vs. onformation onfiguration: ovalent bonds must be broken onformation: hanges do NT require breaking of covalent bonds onfiguration Two kinds of isomers to consider is/trans:
Stereochemistry onfiguration vs. onformation onfiguration: ovalent bonds must be broken onformation: hanges do NT require breaking of covalent bonds onfiguration Two kinds of isomers to consider is/trans:
18.VY_32_INOVACE_AJ_UMB18, Frázová slovesa.notebook. September 09, 2013
 1 (Click on the text to move to the section) Worksheet Methodology Sources 2 Decide which words are considered prepositions (předložky) and which are particles (částice) Source: SWAN, Michael a Catharine
1 (Click on the text to move to the section) Worksheet Methodology Sources 2 Decide which words are considered prepositions (předložky) and which are particles (částice) Source: SWAN, Michael a Catharine
Czech Technical University in Prague DOCTORAL THESIS
 Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering DOCTORAL THESIS CERN-THESIS-2015-137 15/10/2015 Search for B! µ + µ Decays with the Full Run I Data of The ATLAS
Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering DOCTORAL THESIS CERN-THESIS-2015-137 15/10/2015 Search for B! µ + µ Decays with the Full Run I Data of The ATLAS
VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O.
 VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O. Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová práce 2013 Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová
VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O. Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová práce 2013 Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová
Radiova meteoricka detekc nı stanice RMDS01A
 Radiova meteoricka detekc nı stanice RMDS01A Jakub Ka kona, kaklik@mlab.cz 15. u nora 2014 Abstrakt Konstrukce za kladnı ho softwarove definovane ho pr ijı macı ho syste mu pro detekci meteoru. 1 Obsah
Radiova meteoricka detekc nı stanice RMDS01A Jakub Ka kona, kaklik@mlab.cz 15. u nora 2014 Abstrakt Konstrukce za kladnı ho softwarove definovane ho pr ijı macı ho syste mu pro detekci meteoru. 1 Obsah
LOGBOOK. Blahopřejeme, našli jste to! Nezapomeňte. Prosím vyvarujte se downtrade
 název cache GC kód Blahopřejeme, našli jste to! LOGBOOK Prosím vyvarujte se downtrade Downtrade (z GeoWiki) Je to jednání, kterého byste se při výměnách předmětů v keších měli vyvarovat! Jedná se o snížení
název cache GC kód Blahopřejeme, našli jste to! LOGBOOK Prosím vyvarujte se downtrade Downtrade (z GeoWiki) Je to jednání, kterého byste se při výměnách předmětů v keších měli vyvarovat! Jedná se o snížení
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky
 Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: Education Označení materiálu: VY_32_INOVACE_MAT27 Datum vytvoření: 10.10.2013
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: Education Označení materiálu: VY_32_INOVACE_MAT27 Datum vytvoření: 10.10.2013
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL
 PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL Ing. Jan HAVLÍK, MPA tajemník Městského úřadu Žďár nad Sázavou Chief Executive Municipality of Žďár nad Sázavou CO
PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL Ing. Jan HAVLÍK, MPA tajemník Městského úřadu Žďár nad Sázavou Chief Executive Municipality of Žďár nad Sázavou CO
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
A constitutive model for non-reacting binary mixtures
 A constitutive model for non-reacting binary mixtures Ondřej Souček ondrej.soucek@mff.cuni.cz Joint work with Vít Průša Mathematical Institute Charles University 31 March 2012 Ondřej Souček Charles University)
A constitutive model for non-reacting binary mixtures Ondřej Souček ondrej.soucek@mff.cuni.cz Joint work with Vít Průša Mathematical Institute Charles University 31 March 2012 Ondřej Souček Charles University)
Just write down your most recent and important education. Remember that sometimes less is more some people may be considered overqualified.
 CURRICULUM VITAE - EDUCATION Jindřich Bláha Výukový materiál zpracován v rámci projektu EU peníze školám Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Bc. Jindřich Bláha. Dostupné z Metodického
CURRICULUM VITAE - EDUCATION Jindřich Bláha Výukový materiál zpracován v rámci projektu EU peníze školám Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Bc. Jindřich Bláha. Dostupné z Metodického
Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční
 Příloha I Seznam tabulek Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční odměny pro rozhodčí platný od roku
Příloha I Seznam tabulek Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční odměny pro rozhodčí platný od roku
Immigration Studying. Studying - University. Stating that you want to enroll. Stating that you want to apply for a course.
 - University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
- University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
Immigration Studying. Studying - University. Stating that you want to enroll. Stating that you want to apply for a course.
 - University Rád/a bych se zapsal/a na vysoké škole. Stating that you want to enroll Rád/a bych se zapsal/a na. Stating that you want to apply for a course bakalářské studium postgraduální studium doktorské
- University Rád/a bych se zapsal/a na vysoké škole. Stating that you want to enroll Rád/a bych se zapsal/a na. Stating that you want to apply for a course bakalářské studium postgraduální studium doktorské
CZ.1.07/1.5.00/
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Dynamic Development of Vocabulary Richness of Text. Miroslav Kubát & Radek Čech University of Ostrava Czech Republic
 Dynamic Development of Vocabulary Richness of Text Miroslav Kubát & Radek Čech University of Ostrava Czech Republic Aim To analyze a dynamic development of vocabulary richness from a methodological point
Dynamic Development of Vocabulary Richness of Text Miroslav Kubát & Radek Čech University of Ostrava Czech Republic Aim To analyze a dynamic development of vocabulary richness from a methodological point
Entrance test from mathematics for PhD (with answers)
 Entrance test from mathematics for PhD (with answers) 0 0 3 0 Problem 3x dx x + 5x +. 3 ln 3 ln 4. (4x + 9) dx x 5x 3. 3 ln 4 ln 3. (5 x) dx 3x + 5x. 7 ln. 3 (x 4) dx 6x + x. ln 4 ln 3 ln 5. 3 (x 3) dx
Entrance test from mathematics for PhD (with answers) 0 0 3 0 Problem 3x dx x + 5x +. 3 ln 3 ln 4. (4x + 9) dx x 5x 3. 3 ln 4 ln 3. (5 x) dx 3x + 5x. 7 ln. 3 (x 4) dx 6x + x. ln 4 ln 3 ln 5. 3 (x 3) dx
Číslo projektu: CZ.1.07/1.5.00/ Název projektu: Inovace a individualizace výuky
 Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: European Union Označení materiálu: VY_32_INOVACE_MAT 22 Datum vytvoření:
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: European Union Označení materiálu: VY_32_INOVACE_MAT 22 Datum vytvoření:
Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products
 Energy news2 1 Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products Doposud jste Energy znali jako výrobce a dodavatele humánních přírodních doplňků stravy a kosmetiky.
Energy news2 1 Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products Doposud jste Energy znali jako výrobce a dodavatele humánních přírodních doplňků stravy a kosmetiky.
Třída: VI. A6 Mgr. Pavla Hamříková VI. B6 RNDr. Karel Pohaněl Schváleno předmětovou komisí dne: Podpis: Šárka Richterková v. r.
 MATURITNÍ TÉMATA Školní rok: 2016/2017 Ředitel školy: PhDr. Karel Goš Předmětová komise: Matematika a deskriptivní geometrie Předseda předmětové komise: Mgr. Šárka Richterková Předmět: Matematika Třída:
MATURITNÍ TÉMATA Školní rok: 2016/2017 Ředitel školy: PhDr. Karel Goš Předmětová komise: Matematika a deskriptivní geometrie Předseda předmětové komise: Mgr. Šárka Richterková Předmět: Matematika Třída:
Informace o písemných přijímacích zkouškách. Doktorské studijní programy Matematika
 Informace o písemných přijímacích zkouškách (úplné zadání zkušebních otázek či příkladů, které jsou součástí přijímací zkoušky nebo její části, a u otázek s výběrem odpovědi správné řešení) Doktorské studijní
Informace o písemných přijímacích zkouškách (úplné zadání zkušebních otázek či příkladů, které jsou součástí přijímací zkoušky nebo její části, a u otázek s výběrem odpovědi správné řešení) Doktorské studijní
PITSTOP VY_22_INOVACE_26
 PITSTOP VY_22_INOVACE_26 Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 9. PITSTOP 1/ Try to complete the missing words. Then listen and check your ideas. Eight
PITSTOP VY_22_INOVACE_26 Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 9. PITSTOP 1/ Try to complete the missing words. Then listen and check your ideas. Eight
Stojan pro vrtačku plošných spojů
 Střední škola průmyslová a hotelová Uherské Hradiště Kollárova 617, Uherské Hradiště Stojan pro vrtačku plošných spojů Závěrečný projekt Autor práce: Koutný Radim Lukáš Martin Janoštík Václav Vedoucí projektu:
Střední škola průmyslová a hotelová Uherské Hradiště Kollárova 617, Uherské Hradiště Stojan pro vrtačku plošných spojů Závěrečný projekt Autor práce: Koutný Radim Lukáš Martin Janoštík Václav Vedoucí projektu:
Travel information. 1. from Prague to Ostrava
 1. from Prague to Ostrava Travel information Ostrava, as a city with more than 330 thousands inhabitants, has a regular flight connection with Prague, usually arranged by the Czech Airlines, which is a
1. from Prague to Ostrava Travel information Ostrava, as a city with more than 330 thousands inhabitants, has a regular flight connection with Prague, usually arranged by the Czech Airlines, which is a
Friction drives have constant or variable drives (it means variators). Friction drives are used for the transfer of smaller outputs.
 Third School Year FRICTION DRIVES 1. Introduction In friction drives the peripheral force between pressed wheels is transferred by friction. To reach peripheral forces we need both a pressed force and
Third School Year FRICTION DRIVES 1. Introduction In friction drives the peripheral force between pressed wheels is transferred by friction. To reach peripheral forces we need both a pressed force and
Fytomineral. Inovace Innovations. Energy News 04/2008
 Energy News 4 Inovace Innovations 1 Fytomineral Tímto Vám sdělujeme, že již byly vybrány a objednány nové lahve a uzávěry na produkt Fytomineral, které by měly předejít únikům tekutiny při přepravě. První
Energy News 4 Inovace Innovations 1 Fytomineral Tímto Vám sdělujeme, že již byly vybrány a objednány nové lahve a uzávěry na produkt Fytomineral, které by měly předejít únikům tekutiny při přepravě. První
Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise
 Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise ROZHODNUTÍ KOMISE ze dne 27. června 1997 o postupu prokazování shody stavebních výrobků ve smyslu čl. 20 odst. 2
Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise ROZHODNUTÍ KOMISE ze dne 27. června 1997 o postupu prokazování shody stavebních výrobků ve smyslu čl. 20 odst. 2
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
CZ.1.07/1.5.00/
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
User manual SŘHV Online WEB interface for CUSTOMERS June 2017 version 14 VÍTKOVICE STEEL, a.s. vitkovicesteel.com
 1/ 11 User manual SŘHV Online WEB interface for CUSTOMERS June 2017 version 14 2/ 11 Contents 1. MINIMUM SYSTEM REQUIREMENTS... 3 2. SŘHV ON-LINE WEB INTERFACE... 4 3. LOGGING INTO SŘHV... 4 4. CONTRACT
1/ 11 User manual SŘHV Online WEB interface for CUSTOMERS June 2017 version 14 2/ 11 Contents 1. MINIMUM SYSTEM REQUIREMENTS... 3 2. SŘHV ON-LINE WEB INTERFACE... 4 3. LOGGING INTO SŘHV... 4 4. CONTRACT
Právní formy podnikání v ČR
 Bankovní institut vysoká škola Praha Právní formy podnikání v ČR Bakalářská práce Prokeš Václav Leden, 2009 Bankovní institut vysoká škola Praha Katedra Bankovnictví Právní formy podnikání v ČR Bakalářská
Bankovní institut vysoká škola Praha Právní formy podnikání v ČR Bakalářská práce Prokeš Václav Leden, 2009 Bankovní institut vysoká škola Praha Katedra Bankovnictví Právní formy podnikání v ČR Bakalářská
GENERAL INFORMATION RUČNÍ POHON MANUAL DRIVE MECHANISM
 KATALOG CATALOGUE RUČNÍ POHONY PRO VENKOVNÍ PŘÍSTROJE, MONTÁŽ NA BETONOVÉ SLOUPY MANUAL DRIVE MECHANISM FOR THE ACTUATION OF OUTDOOR TYPE SWITCHING DEVICES MOUNTED ON THE CONCRETE POLES TYP RPV ISO 9001:2009
KATALOG CATALOGUE RUČNÍ POHONY PRO VENKOVNÍ PŘÍSTROJE, MONTÁŽ NA BETONOVÉ SLOUPY MANUAL DRIVE MECHANISM FOR THE ACTUATION OF OUTDOOR TYPE SWITCHING DEVICES MOUNTED ON THE CONCRETE POLES TYP RPV ISO 9001:2009
2N Voice Alarm Station
 2N Voice Alarm Station 2N Lift1 Installation Manual Version 1.0.0 www.2n.cz EN Voice Alarm Station Description The 2N Voice Alarm Station extends the 2N Lift1/ 2N SingleTalk with an audio unit installed
2N Voice Alarm Station 2N Lift1 Installation Manual Version 1.0.0 www.2n.cz EN Voice Alarm Station Description The 2N Voice Alarm Station extends the 2N Lift1/ 2N SingleTalk with an audio unit installed
Aktivita CLIL Fyzika 2
 Škola: Gymnázium Bystřice nad Pernštejnem Jméno vyučujícího: Mgr. Monika Stará Aktivita CLIL Fyzika 2 Název aktivity: Fáze měsíce a fyzikální výpočty Předmět: Fyzika Ročník, třída: kvarta Jazyk a jazyková
Škola: Gymnázium Bystřice nad Pernštejnem Jméno vyučujícího: Mgr. Monika Stará Aktivita CLIL Fyzika 2 Název aktivity: Fáze měsíce a fyzikální výpočty Předmět: Fyzika Ročník, třída: kvarta Jazyk a jazyková
STLAČITELNOST. σ σ. během zatížení
 STLAČITELNOST Princip: Naneseme-li zatížení na zeminu, dojde k porušení rovnováhy a dochází ke stlačování zeminy (přemístňují se částice). Stlačení je ukončeno jakmile nastane rovnováha mezi působícím
STLAČITELNOST Princip: Naneseme-li zatížení na zeminu, dojde k porušení rovnováhy a dochází ke stlačování zeminy (přemístňují se částice). Stlačení je ukončeno jakmile nastane rovnováha mezi působícím
1, Žáci dostanou 5 klíčových slov a snaží se na jejich základě odhadnout, o čem bude následující cvičení.
 Moje hlavní město Londýn řešení: 1, Žáci dostanou 5 klíčových slov a snaží se na jejich základě odhadnout, o čem bude následující cvičení. Klíčová slova: capital, double decker bus, the River Thames, driving
Moje hlavní město Londýn řešení: 1, Žáci dostanou 5 klíčových slov a snaží se na jejich základě odhadnout, o čem bude následující cvičení. Klíčová slova: capital, double decker bus, the River Thames, driving
Present Perfect x Past Simple Předpřítomný čas x Minulý čas Pracovní list
 VY_32_INOVACE_AJ_133 Present Perfect x Past Simple Předpřítomný čas x Minulý čas Pracovní list PhDr. Zuzana Žantovská Období vytvoření: květen 2013 Ročník: 1. 4. ročník SŠ Tematická oblast: Gramatika slovesa
VY_32_INOVACE_AJ_133 Present Perfect x Past Simple Předpřítomný čas x Minulý čas Pracovní list PhDr. Zuzana Žantovská Období vytvoření: květen 2013 Ročník: 1. 4. ročník SŠ Tematická oblast: Gramatika slovesa
Chapter 7: Process Synchronization
 Chapter 7: Process Synchronization Background The Critical-Section Problem Synchronization Hardware Semaphores Classical Problems of Synchronization Critical Regions Monitors Synchronization in Solaris
Chapter 7: Process Synchronization Background The Critical-Section Problem Synchronization Hardware Semaphores Classical Problems of Synchronization Critical Regions Monitors Synchronization in Solaris
Škola: Střední škola obchodní, České Budějovice, Husova 9. Inovace a zkvalitnění výuky prostřednictvím ICT
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
POSLECH. M e t o d i c k é p o z n á m k y k z á k l a d o v é m u t e x t u :
 POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Mgr. Martin Zicháček aj9-kap-zic-pos-07 Z á k l a d o v ý t e x t : Margaret: Hi Eric. Eric: Oh, hi Margaret. How are you doing? Margaret:
POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Mgr. Martin Zicháček aj9-kap-zic-pos-07 Z á k l a d o v ý t e x t : Margaret: Hi Eric. Eric: Oh, hi Margaret. How are you doing? Margaret:
POSLECH. Cinema or TV tonight (a dialogue between Susan and David about their plans for tonight)
 POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Zora Smolková aj9-jes-smo-pos-01 Z á k l a d o v ý t e x t : Cinema or TV tonight (a dialogue between Susan and David about their plans
POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Zora Smolková aj9-jes-smo-pos-01 Z á k l a d o v ý t e x t : Cinema or TV tonight (a dialogue between Susan and David about their plans
VŠEOBECNÁ TÉMATA PRO SOU Mgr. Dita Hejlová
 VŠEOBECNÁ TÉMATA PRO SOU Mgr. Dita Hejlová VZDĚLÁVÁNÍ V ČR VY_32_INOVACE_AH_3_03 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět
VŠEOBECNÁ TÉMATA PRO SOU Mgr. Dita Hejlová VZDĚLÁVÁNÍ V ČR VY_32_INOVACE_AH_3_03 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti Název školy Název šablony Předmět
The Over-Head Cam (OHC) Valve Train Computer Model
 The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise
 Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise ROZHODNUTÍ KOMISE ze dne 17. února 1997 o postupu prokazování shody stavebních výrobků ve smyslu čl. 20 odst. 2
Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise ROZHODNUTÍ KOMISE ze dne 17. února 1997 o postupu prokazování shody stavebních výrobků ve smyslu čl. 20 odst. 2
Execrices. Mathematics FRDIS
 Eecrices Mathematics FRDIS Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.
Eecrices Mathematics FRDIS Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.
Název projektu: Multimédia na Ukrajinské
 Základní škola, Ostrava Poruba, Ukrajinská 1533, příspěvková organizace Operační program Vzdělávání pro konkurenceschopnost Název projektu: Multimédia na Ukrajinské číslo projektu: CZ1.07/1.4.00/21.3759
Základní škola, Ostrava Poruba, Ukrajinská 1533, příspěvková organizace Operační program Vzdělávání pro konkurenceschopnost Název projektu: Multimédia na Ukrajinské číslo projektu: CZ1.07/1.4.00/21.3759
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
RNDr. Jakub Lokoč, Ph.D. RNDr. Michal Kopecký, Ph.D. Katedra softwarového inženýrství Matematicko-Fyzikální fakulta Univerzita Karlova v Praze
 RNDr. Jakub Lokoč, Ph.D. RNDr. Michal Kopecký, Ph.D. Katedra softwarového inženýrství Matematicko-Fyzikální fakulta Univerzita Karlova v Praze 1 Relační algebra / Relational Algebra 2 Kino(Jmeno, Mesto,
RNDr. Jakub Lokoč, Ph.D. RNDr. Michal Kopecký, Ph.D. Katedra softwarového inženýrství Matematicko-Fyzikální fakulta Univerzita Karlova v Praze 1 Relační algebra / Relational Algebra 2 Kino(Jmeno, Mesto,
Univerzita Pardubice Fakulta filozofická. Franz Kafka: Pojetí systému v Proměně. Lukáš Vavrečka
 Univerzita Pardubice Fakulta filozofická Franz Kafka: Pojetí systému v Proměně Lukáš Vavrečka Bakalářská práce 2009 University of Pardubice Faculty of Arts and Philosophy Franz Kafka: The Conception of
Univerzita Pardubice Fakulta filozofická Franz Kafka: Pojetí systému v Proměně Lukáš Vavrečka Bakalářská práce 2009 University of Pardubice Faculty of Arts and Philosophy Franz Kafka: The Conception of
STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ, Česká Lípa, 28. října 2707, příspěvková organizace
 Název školy STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ, Česká Lípa, 28. října 2707, příspěvková organizace Číslo a název projektu: CZ.1.07/1.5.00/34.0880 Digitální učební materiály www.skolalipa.cz
Název školy STŘEDNÍ ODBORNÁ ŠKOLA a STŘEDNÍ ODBORNÉ UČILIŠTĚ, Česká Lípa, 28. října 2707, příspěvková organizace Číslo a název projektu: CZ.1.07/1.5.00/34.0880 Digitální učební materiály www.skolalipa.cz
Střední škola obchodní, České Budějovice, Husova 9, VY_INOVACE_ANJ_741. Škola: Střední škola obchodní, České Budějovice, Husova 9
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Rozvoj vzdělávání žáků karvinských základních škol v oblasti cizích jazyků Registrační číslo projektu: CZ.1.07/1.1.07/02.0162
 Rozvoj vzdělávání žáků karvinských základních škol v oblasti cizích jazyků Registrační číslo projektu: CZ.1.07/1.1.07/02.0162 Určeno pro Sekce Předmět Téma / kapitola Zpracoval (tým 1) žáky 2. stupně ZŠ
Rozvoj vzdělávání žáků karvinských základních škol v oblasti cizích jazyků Registrační číslo projektu: CZ.1.07/1.1.07/02.0162 Určeno pro Sekce Předmět Téma / kapitola Zpracoval (tým 1) žáky 2. stupně ZŠ
AJ 3_16_Prague.notebook. December 20, 2013. 1.úvodní strana
 1.úvodní strana 1 PRAGUE AJ 3 Konverzační témata DUM č. 16 oktáva osmiletého gymnázia Mgr. Jitka Freundová Gymnázium Sušice Tento materiál byl vytvořen v rámci projektu Gymnázium Sušice Brána vzdělávání
1.úvodní strana 1 PRAGUE AJ 3 Konverzační témata DUM č. 16 oktáva osmiletého gymnázia Mgr. Jitka Freundová Gymnázium Sušice Tento materiál byl vytvořen v rámci projektu Gymnázium Sušice Brána vzdělávání
FIRE INVESTIGATION. Střední průmyslová škola Hranice. Mgr. Radka Vorlová. 19_Fire investigation CZ.1.07/1.5.00/
 FIRE INVESTIGATION Střední průmyslová škola Hranice Mgr. Radka Vorlová 19_Fire investigation CZ.1.07/1.5.00/34.0608 Výukový materiál Číslo projektu: CZ.1.07/1.5.00/21.34.0608 Šablona: III/2 Inovace a zkvalitnění
FIRE INVESTIGATION Střední průmyslová škola Hranice Mgr. Radka Vorlová 19_Fire investigation CZ.1.07/1.5.00/34.0608 Výukový materiál Číslo projektu: CZ.1.07/1.5.00/21.34.0608 Šablona: III/2 Inovace a zkvalitnění
Název projektu: Multimédia na Ukrajinské
 Základní škola, Ostrava Poruba, Ukrajinská 1533, příspěvková organizace Operační program Vzdělávání pro konkurenceschopnost Název projektu: Multimédia na Ukrajinské číslo projektu: CZ1.07/1.4.00/21.3759
Základní škola, Ostrava Poruba, Ukrajinská 1533, příspěvková organizace Operační program Vzdělávání pro konkurenceschopnost Název projektu: Multimédia na Ukrajinské číslo projektu: CZ1.07/1.4.00/21.3759
