Moderní metody stegoanalýzy
|
|
|
- Alexandra Valentová
- před 8 lety
- Počet zobrazení:
Transkript
1 Mendelova zemědělská a lesnická univerzita v Brně Provozně ekonomická fakulta Moderní metody stegoanalýzy Diplomová práce Vedoucí práce: Ing. Jan Přichystal, Ph.D. Bc. Jan Prudil Brno 2009
2 Je mou milou povinností poděkovat na tomto místě Ing. Janu Přichystalovi, Ph.D., za poskytnutí cenných konzultací během tvorby této práce, bez nichž by mnoho faktů zůstalo opomenuto. Také bych rád poděkoval své rodině a přítelkyni Romaně, kteří mi dokázali vytvořit velmi důležité zázemí pro napsání této práce.
3 Prohlašuji, že jsem tuto diplomovou práci vypracoval samostatně a veškeré zdroje uvádím v seznamu použité literatury. V Brně dne
4 4 Abstract Prudil, J. Modern Methods of Steganalysis. Diploma thesis. Brno, 2009 Steganalysis is the opposite discipline to steganography a science and an art of information hiding. Steganography deals with embedding of secret messages to different types of media. The most commonly used cover media in modern steganography are image files. In this work we create on the basis of available resources an overview of current issues of steganography and steganalysis. We also describe the practical implementation of two steganalysis techniques extraction and detection attack. This implementation represents the design of the BMPdetect tool, which can be applicated to the BMP format images with color depth 24-bit per pixel. Abstrakt Prudil, J. Moderní metody stegoanalýzy. Diplomová práce. Brno, 2009 Stegoanalýza je opoziční disciplínou steganografie, vědy a současně dovednosti, která se zabývá ukrýváním tajných zpráv do různých druhů nosičů. Moderní steganografie jako nosič nejčastěji využívá obrázkové soubory. Tato práce na základě dostupných zdrojů vytváří přehled aktuální problematiky digitální steganografie a stegoanalýzy a popisuje praktickou implementaci dvou technik stegoanalýzy extrakčního a detekčního útoku. Tuto implementaci představuje navržení programu BMPdetect, stegoanalytického nástroje s použitelností na obrázky formátu BMP s barevnou hloubkou 24 bitů na pixel.
5 OBSAH 5 Obsah 1 Úvod a cíl práce Úvod Cíl práce Teoretický přehled problematiky Vymezení pojmu steganografie Stručná historie Moderní steganografické metody Principy steganografických systémů Oblasti moderní steganografie Obrázkové soubory a jejich využití ve steganografii Barevný prostor RGB Barevný prostor YC B C R Ostatní barevné prostory Formáty obrázkových souborů Struktura formátu BMP Metody vkládání dat do obrázkových souborů Steganografické metody v obrázkových souborech Maskování a filtrování Oblast obrazová a transformační Obrazová oblast (image domain) Nejméně významný bit (LSB) LSB a obrázky s barevnou paletou Transformační oblast (transform domain) Komprese formátu JPEG Steganografie soubory ve formátu JPEG Metody oblasti obrazové i transformační Srovnání steganografických technik Nástroje pro ukrývání zpráv EzStego Steghide Steganografický on-line systém Matěje Zapletala (M. Z.) OutGuess Algoritmus F Steganografie dílčí shrnutí Stegoanalýza Vězňův problém Definice stegoanalýzy Techniky stegoanalýzy Možnosti útoků na steganografické systémy Vizuální útok
6 OBSAH Statistické útoky Útok testem χ Útok analýzou RQP Útok RS analýzou Další typy statistických útoků Vlastní práce Metodika a návrh řešení Steganografie pomocí aplikace M. Z Steganografie pomocí aplikace Steghide Načtení obrázku formátu BMP Implementace útoku analýzou RQP Výpočet ukazatelů U a P Modifikace souboru skrytím testovací zprávy Funkce porovnání poměrů R a R Výsledky Útok extrahováním LSB Funkce čtení LSB Extrahování LSB ze steganografického obrázku vytvořeného aplikací M. Z Extrahování LSB ze steganografického obrázku vytvořeného aplikací Steghide Dokumentace programu BMPdetect Použití Třída Bod Třída Picture Třída Stat Třída LSBReader Třída Modifikator Zdrojový kód programu BMPdetect Hodnocení 70 5 Závěr 71 6 Literatura 72
7 1 ÚVOD A CÍL PRÁCE 7 1 Úvod a cíl práce 1.1 Úvod Stegoanalýza je vědní disciplínou, podle některých autorů současně i dovedností, která se zabývá odhalováním a případným odstraňováním skrytých informací. Nabízí se otázka, co je možné si představit pod velmi obecným pojmem skrytá informace. Skrývání informací je předmětem opoziční vědní disciplíny s podobným názvem steganografie. Steganografie v moderním pojetí umožňuje skrývat informace do nejrůznějších druhů digitálních formátů např. do textových souborů, obrázků či zvuku. Ovšem steganografie v klasickém pojetí je disciplína stará téměř jako sama evropská civilizace. První zmínky o použití steganografie z doby 400 let před naším letopočtem najdeme v díle starořeckého historika Hérodota (Johnson, 1995). Tehdejší techniky by pro dnešního člověka byly jistě nepoužitelné, ovšem základní myšlenka přetrvala až do současnosti: chci s někým komunikovat, ale nechci, aby o této komunikaci věděl někdo jiný. Rozdíl mezi steganografií a šifrováním spočívá ve schopnosti budit či nebudit podezření (Cummins et al., 2004). Komunikujeme-li s někým pomocí šifrovaných zpráv, nikdo další jim sice neporozumí, avšak tato komunikace vzbudí podezření. Komunikace pomocí steganografie by naproti tomu měla zůstat tajnou a tudíž žádné podezření nebudit. Jako klasický příklad využití steganografie bývá uváděna komunikace mezi teroristy z organizace al-káida. Provos a Honeyman v článku (Provos a Honeyman, 2003) popisují svůj výzkum, kdy ověřovali hypotézu, zda za tímto účelem nejsou využívány obrázky na elektronické aukční síni ebay. Steganografie však poskytuje i některé velmi užitečné a komerčně důležité funkce v digitálním světě, zejména jde o digitální vodotisk. Jeho aplikace umožňuje autorovi vložit do svého elektronického díla skrytý podpis, který dokazuje jeho intelektuální vlastnictví nebo ověřuje celistvost díla (Kessler, 2004). Stegoanalýza tedy informace skryté v nejrůznějších médiích pomocí steganografie odhaluje, extrahuje a případně ničí. Její techniky jsou dnes převážně statistické povahy a jejich úspěšnost závisí na mnoha faktorech. V dokumentu (Fridrich a Goljan, 2002) je uvedeno, že techniky, které spolehlivě detekují přítomnost skryté zprávy v obrázcích, se stávají stále důležitější. V obrázcích může být ukryto velké množství škodlivého kódu, detekce skrytých informací v obrázkových souborech by proto měla být implementována v každém antivirovém programu. Stegoanalýza by bez steganografie zcela jistě nemohla existovat, ale zároveň je velmi pravděpodobné, že steganografie by bez stegoanalýzy nikdy nenabídla tak důmyslné techniky, jako je tomu v současnosti.
8 1.2 Cíl práce Cíl práce Za dílčí cíl této práce lze považovat vymezení technik a nástrojů, které tvoří základ moderní digitální steganografie a její opoziční disciplíny stegoanalýzy. Sestavení co možná nejkomplexnějšího obrazu novodobého pojetí těchto klasických kryptologických disciplín by mělo umožnit realizaci praktické implementace některé z metod stegoanalýzy. Na základě teoretických východisek bude sestavena metodika vlastního řešení této implementace. Práce bude zaměřena na ty oblasti digitální steganografie a stegoanalýzy, které se zabývají ukrýváním zpráv do obrázkových nosičů. Cílem práce pak bude navržení praktického postupu stegoanalýzy, v němž bude využita některá z teoreticky popsaných technik. Postup bude využívat za tímto účelem navržený program, jehož funkčnost umožní vybranou techniku provést. Sestavený program bude implementovat dva různé druhy útoků proti zvoleným steganografickým nástrojům a vybranému formátu obrázku v roli steganografického média.
9 2 TEORETICKÝ PŘEHLED PROBLEMATIKY 9 2 Teoretický přehled problematiky 2.1 Vymezení pojmu steganografie Označení steganografie je původem z řečtiny, kde vzniklo spojením slov steganós (ukrytý) a gráphien (psát). Dle definice Cachina (Cachin, 1998) steganografií rozumíme umění komunikace a současně vědu o komunikaci, během níž nesmí být odhalena přítomnost určité zprávy. Jednoduché techniky steganografie se používaly po staletí, ovšem se vzrůstajícím využitím souborů v elektronické podobě je možné aplikovat zcela nové metody ukrývání zpráv, což je fakt, který předchází naprosté většině aktuálních pojednání o této problematice, např. (Kessler, 2004), (Cachin, 1998), (Johnson et al., 2000). Gary C. Kessler (Kessler, 2001) uvádí, že steganografie je věda o skrývání informace. Dále poznamenává, že je-li cílem kryptografie učinit data pro třetí stranu nečitelná, cílem steganografie je data před třetí stranou ukrýt. Steganografie je srovnávána s kryptografií i v publikaci (Johnson et al., 2000): Steganografie je umění utajit přítomnost informace ve zdánlivě neškodně vyhlížejícím nosiči. Lze na ni pohlížet jako na disciplínu velmi blízkou kryptografii, protože obě byly během známých dějin používány k ochraně informace. Jejich techniky se mohou zdát velmi podobné, ovšem odlišnost nacházíme v jejich cíli. Kryptografické techniky zprávu modifikují takovým způsobem, že v případě jejího zachycení jí nesmí být porozuměno. Steganografie ve své podstatě zprávu skryje a činí ji prakticky neviditelnou, potlačuje tedy skutečnost, že určitá zpráva byla vůbec poslána. Zpráva zašifrovaná pomocí kryptografie může být podezřelá, kdežto zpráva ukrytá pomocí steganografie nikoliv. F. L. Bauer v článku (Bauer, 2002) uvádí, že účelem steganografie je utajit komunikaci, a tak skrýt zprávu před třetí stranou. To ji odlišuje od kryptografie, jejíž účel není tajit samotnou komunikaci, ale zprávu učinit pro třetí stranu nečitelnou. Ačkoliv jsou steganografie a kryptografie disciplíny odlišné, existuje mezi nimi množství pojítek a někteří autoři steganografii klasifikují jako formu kryptografie. Srovnání různých technik zabezpečené komunikace lze vidět v tabulce 1, převzata z dokumentu (Cummins et al., 2004), kde je též uvedeno: Šifrování (kryptografie) umožňuje zabezpečenou komunikaci vyžadující k porozumění informace klíč. Útočník nemůže šifrování odstranit, ale může poměrně jednoduše modifikovat zprávu a učinit ji tak pro zamýšleného příjemce nečitelnou. Digitální podpis 1 je využíván k nepopiratelnosti autorství zprávy, protože podpis sice lze snadno odstranit, ale jakákoliv změna v jednou podepsané zprávě učiní digitální podpis neplatným je tak zaručena integrita zprávy. Steganografie představuje nástroj zabezpečené komunikace, kdy zprávu nelze odstranit bez viditelné modifikace dat, v nichž je vložena. Skrytá zpráva zůstává důvěrná, dokud útočník nezjistí, jakým způsobem ji detekovat. 1 V Evropě označovaný jako elektronický podpis. Problematiku terminologie komentuje např. J. Petreka na
10 2.2 Stručná historie 10 Tab. 1: Různé techniky zabezpečené komunikace. Tabulka převzata z Steganography And Digital Watermarking (Cummins et al., 2004). Důvěrnost Integrita Neodstranitelnost Šifrování ano ne ano Digitální podpis ne ano ne Steganografie ano/ne ano/ne ano Dle dokumentu (Cummins et al., 2004) svébytnou oblast steganografie představuje vkládání ochranných značek do dokumentů, takzvaný watermarking, kdy je podstatné, aby vložená značka nemohla být jednoduše odstraněna. Pojem se do českého jazyka překládá jako digitální vodotisk. Dle téhož autora lze do problematiky steganografie řadit i takzvané vkládání digitálních otisků (fingerprinting), což je technika podobná vodotisku, ovšem označující každý dokument jedinečnou značkou. Vše je znázorněno na obrázku 1. Obr. 1: Typy steganografie. Převzato z Steganography And Digital Watermarking (Cummins et al., 2004). V dokumentu (Kessler, 2004) je uvedeno následující: Steganografie umožňuje ukrýt určitou zprávu, ale nikoliv skutečnost, že mezi dvěma stranami probíhá komunikace. Proces steganografie znamená skrytí tajné zprávy v přenosovém médiu zvaném nosič. Použitím steganografického klíče lze dosáhnout zašifrování skryté zprávy nebo vložení náhodné složky do procesu ukrytí. Zpráva vložená v nosiči představuje steganografické médium. Lze tedy psát: steganografické médium = skrytá zpráva + nosič + steganografický klíč 2.2 Stručná historie Neil F. Johnson v dokumentu (Johnson, 1995) uvádí asi nejstarší zaznamenaný případ použití steganografie, kdy odkazuje na dílo Dějiny starověkého historika Hérodota. V antickém Řecku se používaly k přenosu zpráv dřevěné destičky zalité voskem, do kterého bylo vyryto písmo. Hérodotos popisuje vyrytí zprávy přímo do dřevěné destičky, která byla následně zalita voskem a vypadala jako nepopsaná. Řek Demeratus takto varoval Spartu před chystanou Perskou invazí do Řecka.
11 2.3 Moderní steganografické metody 11 Jinou důmyslnou starověkou metodou bylo oholení poslovy hlavy a vytetování zprávy přímo na její kůži. Poté, co vlasy opět dorostly, byla zpráva skryta až do chvíle, než byla poslova hlava opět oholena (Johnson, 1995). Jako další příklad ukrývání tajných zpráv se uvádí použití neviditelného inkoustu během druhé světové války. Nevinně vyhlížející dopis mohl obsahovat velmi odlišnou zprávu zapsanou například mezi řádky (Zim, 1948). Na začátku druhé světové války steganografické techniky sestávaly téměř výhradně z použití neviditelného inkoustu, jenž byl tvořen mlékem, octem, ovocnými šťávami nebo močí všechny tyto látky po zahřátí tmavnou (Kahn, 1967). Cummins, Diskin, Lau a Parlett v dokumentu (Cummins et al., 2004) uvádí jiný příklad z druhé světové války, kdy zajatci využívali pro tajnou komunikaci v dopisech morseovu abecedu. Konkrétně využili teček a čárek nad písmeny i, j, f a t. Nesporně zajímavou technikou ukrývání tajné informace v období druhé světové války byly takzvané mikrotečky. Kahn k tomu v knize (Kahn, 1967) uvádí: Se zlepšováním odhalování zpráv byly vyvíjeny nové postupy, jak předat větší množství informace a současně ji učinit hůře zjistitelnou. Němci vyvinutá technika mikroteček byla označena ředitelem FBI Hooverem za protivníkovo mistrovské špionážní dílo. Mikrotečka vznikla vyfotografováním standardní zprávy napsané na psacím stroji a jejím následným zmenšením na velikost tečky na konci věty v dokumentu. Zpráva nebyla skryta ani zašifrována. Mikrotečka byla zkrátka tak malá, že nebudila pozornost (určitou dobu). Avšak bez ohledu na velikost, mikrotečky umožňovaly přenášení velkého množství dat včetně kreseb a fotografií. V dokumentu (Johnson, 1995) je uveden i příklad takzvaného algoritmu posunu slov (word-shifting) publikovaný roku Postup je možné použít u značkovacího jazyka HTML a jeho princip spočívá v označení slov v dokumentu, která tvoří tajnou zprávu pomocí mezer různé velikosti (dosaženo starším způsobem díky atributu font). Parser poté příslušně pozměněné mezery nahradí za tagy <b> nebo </b> a v dokumentu takto dojde k vyznačení tajné zprávy. 2.3 Moderní steganografické metody Principy steganografických systémů Niels Provos a Peter Honeyman v článku (Provos a Honeyman, 2003) definují tři aspekty hodnocení systémů pro ukrývání informace: kapacita, bezpečnost, robustnost. Kapacitou rozumíme množství informace, kterou lze do nosiče ukrýt, bezpečnost představuje nemožnost narušitele odhalit tajnou zprávu a robustnost vyjadřuje schopnost nosiče uchovat skrytá data i po jeho případné modifikaci.
12 2.3 Moderní steganografické metody 12 Johnson a Jajodia v článku (Johnson a Jajodia, Feb. 1998) zmiňují problematiku bezpečnosti steganografických systémů: Bezpečnost klasického steganografického systému závisí na utajení metody ukrývání zprávy. Například již zmíněný postup tetování tajné zprávy na oholenou hlavu posla, čekání, až vlasy opět dorostou, a následné vyslání posla. Provos a Honeyman k tomu v článku (Provos a Honeyman, 2003) dodávají, že ačkoliv takový systém může určitý čas fungovat, ve chvíli, kdy dojde k prozrazení této metody, není složité zavést kontrolu spočívající v oholení všech procházejících lidí a tím steganografický systém diskreditovat. Moderní steganografie usiluje o to, aby byla detekovatelná pouze ve chvíli, kdy je odhalena nějaká tajná informace například sdílený klíč (Peticolas et al., 1999). To je podobné Kerckhoffsovu principu v kryptografii, kdy bezpečnost komunikace nezávisí na použitém algoritmu, nýbrž na utajení klíče (Kerckhoffs, 1883). V článku (Provos a Honeyman, 2003) je také uvedeno, že ve steganografii je velmi důležité udržet v tajnosti i originální médium použité jako nosič pro ukrytí zprávy, neboť v případě jeho odhalení by při porovnání nosiče a steganografického média byly ihned identifikovány změny. Teorie informace umožňuje blíže specifikovat stav, kdy je systém dokonale bezpečný. Christian Cachin v dokumentu (Cachin, 1998) předkládá teoretický informační model pro steganografii, jenž uvažuje bezpečnost steganografického systému ve vztahu k pasivnímu narušiteli 2. Základní předpoklad v tomto modelu říká, že protivník má úplnou znalost ukrývajícího systému, ale nezná tajný klíč. Protivníkova úloha spočívá v navržení takového modelu rozdělení pravděpodobnosti P c pro všechna média použitelná jako nosiče a rozdělení pravděpodobnosti P s pro všechna možná steganografická média (nosič + zpráva). Protivník pak může využít teorii detekce, která mu umožní rozhodnout mezi hypotézou C (zpráva neobsahuje skrytou informaci) a hypotézou S (zpráva obsahuje skrytou informaci). Systém je pak dokonale bezpečný, pokud neexistuje pravidlo, podle něhož lze rozhodnout lépe než pomocí náhodných pokusů. Provos a Honeyman v článku (Provos a Honeyman, 2003) shrnují podstatu moderní steganografické komunikace v modelu, kde jsou využity archetypální postavy Alice (komunikující strana A odesílatel) a Bob (komunikující strana B příjemce): Alice a Bob se dohodou na použitém steganografickém systému a tajném klíči. Alice vytvoří či jinak získá potřebný nosič (např. fotografie, zvuk, video, text). Nosič, zprávu a tajný klíč Alice použije jako vstupy steganografického systému. Systém dle tajného klíče určí, jak budou bity zprávy zakódovány do redundantních bitů nosiče. Výstupem systému je steganografické médium, které Alice pošle nezabezpečeným kanálem Bobovi. Když Bob steganografické médium obdrží, použije dohodnutý steganografický systém a tajný klíč. Získá tak ukrytou zprávu. 2 Pasivní narušitel nemá možnost médium modifikovat, může jej pouze číst (podrobněji v kapitole ).
13 2.3 Moderní steganografické metody 13 Výše popsaný proces je znázorněn na obrázku 2. V tomto případě (ukrývání do redundantních dat) je přítomnost skryté zprávy možné odhalit statistickou analýzou (Provos a Honeyman, 2003). Obr. 2: Moderní steganografická komunikace. Obrázek převzat z článku Hide and Seek: An Introduction to Steganography (Provos a Honeyman, 2003) Oblasti moderní steganografie Ke členění technik moderní steganografie lze přistoupit z mnoha pohledů. V nejobecnější rovině je možné setkat se v literatuře s rozlišením na ukrývání tajných zpráv a na vkládání elektronických otisků, například digitálních vodotisků, do elektronických médií. V dokumentu (Cummins et al., 2004) je uvedeno, že steganografii lze rozlišit na dva druhy křehkou steganografii a robustní steganografii. Křehká steganografie umožňuje takové vložení informace do souboru, že tato informace je při nepatrné modifikaci souboru zničena nebo poškozena. Křehká steganografie není dle dokumentu (Cummins et al., 2004) vhodná ke vkládání značek chránících autorství souboru, neboť taková ochrana by mohla být velmi snadno odstraněna. Je ovšem uplatnitelná v situacích, kdy je nutné prokázat, že se souborem bylo manipulováno například pokud je soubor použit jako důkaz u soudu a má-li být dokázáno, že nějakým zásahem byl odstraněn ochranný vodotisk. Naproti tomu robustní steganografie umožňuje takové vkládání informace do souboru, které není možné jednoduše odstranit. V dokumentu (Cummins et al., 2004) je uvedeno, že ačkoliv žádná takto vložená značka nikdy nebude skutečně nezničitelná, je možné považovat systém za robustní, pokud změny vyžadované k odstranění značky učiní soubor neužitečným. Proto by značka měla být skrývána do takové části souboru, kde by její odstranění bylo vnímáno nejsnáze. Robustní značkování dělíme dle dokumentu (Cummins et al., 2004) do dvou skupin:
14 2.3 Moderní steganografické metody 14 Digitální otisk (fingerprinting) skrytí jedinečného identifikátoru do souboru pro každého, kdo získá právo s tímto souborem disponovat (např. na základě licence). Digitální vodotisk (watermarking) identifikuje vlastníka autorského práva k souboru. Na rozdíl od jedinečných digitálních otisků, digitální vodotisk nepomáhá odhalit ty, kteří poruší licenční smlouvu, ale ty, kteří vlastní nelegální kopii souboru. Vodotisk je zpravidla skryt proto, aby se zabránilo jeho detekci či odstranění (označováno jako neviditelný vodotisk). Někdy se však používá viditelný vodotisk, kupříkladu při vkládání vizuálního ochranného vzoru přes obrázek. Rozdělení steganografických metod lze učinit i jiným, poněkud obecnějším způsobem, například jako v dokumentu (Kessler, 2004). Kessler zde definuje šest skupin metod: Technická steganografie používá k ukrytí zpráv vědecké metody, například neviditelný inkoust, mikrotečky či podobné techniky zmenšování. Lingvistická steganografie je dělena na semagramy a otevřené šifry. Semagramy ukrývají informaci za použití symbolů či značek. Vizuální semagramy tajnou zprávu ukryjí pomocí objektů, se kterými se každodenně setkáváme např. různé malůvky, rozmístění předmětů na psacím stole či uspořádání prvků na webové stránce. Textové semagramy zprávu skryjí pomocí modifikace textu např. drobnými změnami ve fontu písma, přidáním bílých znaků, případně zdobnými prvky u ručně psaného textu. Otevřené šifry ukryjí zprávu tak, že nosič má dvě podoby pro zasvěceného a nezasvěceného pozorovatele. Jsou členěny na slang a otevřené ukrývání. Slang jazyky či nářečí, kterým rozumí určitá skupina lidí a ostatním nedávají smysl, například: žargon podsvětí, warchalking 3 či obyčejně se tvářící konverzace, jejíž speciální významovou rovinu chápou pouze hovořící. Otevřené ukrývání (cover ciphers) techniky, jež vloží do nosiče zprávu otevřeně, tzn. kdokoli zná princip ukrytí, přečte zprávu velmi jednoduše. Tyto metody představuje například běžně vyhlížející dopis, z něhož tajnou zprávu získáme například čtením každého třetího slova nebo každého druhého písmene. Speciálním druhem ukrývání v nosiči jsou tzv. mřížkové šifry, které jsou realizovány pomocí děrované šablony, jež po přiložení na textový nosič odhalí pouze slova či písmena tajné zprávy. Dále je tamtéž uvedeno: Se vzrůstajícím objemem dat uložených v počítačích a přenášených sítěmi není překvapující, že steganografie vstoupila do digitálního věku. Aplikace steganografie na elektronická média umožňuje skrývat jakýkoliv binární soubor v jakémkoliv jiném binárním souboru. Nejběžnějšími nosiči jsou však v dnešní době obrázkové a zvukové soubory. 3 symboly označující přítomnost a druh pokrytí bezdrátovou sítí
15 2.4 Obrázkové soubory a jejich využití ve steganografii 15 Autoři dokumentu (Cummins et al., 2004) podávají ucelený přehled technik moderní digitální steganografie, kdy vychází z formátu potenciálních nosičů a ze speciálního přístupu ke každému z nich: techniky skrývání dat v binárních souborech např. pořadí zaměnitelných instrukcí jednoznačně identifikuje majitele licence programu techniky skrývání dat v textu využití bílých znaků vhodné modifikace vlastního obsahu techniky skrývání dat v obrázcích techniky skrývání dat ve zvuku techniky skrývání dat ve videu. V literatuře se můžeme setkat i s definicí toho, co steganografií není. Například Andrew Ker v dokumentu (Ker, 2008) tvrdí, že za steganografii nelze být považováno: ukrývání dat do pseudonáhodných proudů, například TrueCrypt 4, což Ker charakterizuje jako příliš jednoduché, ukrývání dat v nevyužitých částech hlaviček paketů či souborů různých formátů, což Ker označuje za málo bezpečné. 2.4 Obrázkové soubory a jejich využití ve steganografii Barevný prostor RGB Žára a kol. v publikaci (Žára et al., 2004) uvádějí: Různé barvy, které se používají při vytváření obrazu, jsou tvořeny kombinací několika základních barev z barevného spektra. Na barevné obrazovce například vidíme barvu jako výsledek složení tří složek červené (R, red), zelené (G, green) a modré (B, blue). Barvy lze vyjádřit trojicí (barevným vektorem), jejíž složky nabývají hodnot z intervalu 0, 1. Bývají uváděny i v celočíselném rozsahu 0 255, což odpovídá kódování každé ze složek RGB v jednom bajtu. Hodnota 0 znamená, že složka není zastoupena, maximální hodnota indikuje, že složka nabývá své největší intenzity. Vyjádření barevných složek pomocí tří bajtů je v současnosti nejběžnější. Popis barvy třemi složkami R, G, B není jedinou možností. Uvedená volba základních barev je dána technickými vlastnostmi monitorů. Říká se, že barva je vyjádřena v barevném prostoru RGB. Jeho základní vlastností je součtové, aditivní skládání barev čím více barev složíme (sečteme), tím světlejší je výsledek. 4
16 2.4 Obrázkové soubory a jejich využití ve steganografii Barevný prostor YC B C R V publikaci (Žára et al., 2004) je také uvedeno, že v počítačové grafice se při zápisu rastrových obrázků ve formátu JPEG setkáváme s barevným prostorem YC B C R. Protože se v této práci budeme formátem JPEG zabývat, uveďme několik poznámek k tomuto barevnému prostoru převzatých z publikace (Žára et al., 2004). Podle standardu CCIR 601 má hodnota Y být v intervalu 0.0, 1.0 a hodnoty C B, C R v intervalu 0.5, 0.5. Pokud chceme složky C B a C R při počítačovém zpracování ukládat jako celá čísla v rozsahu 0 255, musíme je nejprve posunout do kladné poloosy přičtením konstanty. Y C B C R = Zkráceně lze definovat hodnoty C B a C R jako Ostatní barevné prostory C B = (B Y ) C R = (R Y ) Vzhledem k tomu, že v následujících kapitolách budeme pracovat výhradně s prostorem RGB, neboť ten je, jak uvádí publikace (Žára et al., 2004), technicky orientovaný prostor, vhodný pro displeje, od definice ostatních barevných prostorů upustíme. Jen pro úplnost uveďme, že existuje např. barevný prostor pro tisk (CMY, CMYK), barvený prostor pro televizní techniku a videotechniku (YUV) nebo chromatický diagram CIE pro vyjádření barev bez ohledu na subjektivitu lidského vnímání Formáty obrázkových souborů G. Kessler v dokumentu (Kessler, 2001) pojednává o problematice obrázkových souborů a jejich využití ve steganografii: Předtím než bude zmíněno, jakým způsobem lze data ukrývat do obrázkových souborů, proberme nejprve, jak jsou obrázkové soubory ukládány. Obrázkový soubor je v podstatě souborem binárním, který obsahuje binární reprezentaci barevné či jasové intenzity pro každý bod obrázku (pixel), přičemž matice pixelů vytváří výsledný obraz. Pro obrázky se většinou využívají buď 8bitová nebo 24bitová barevná schémata. V případě použití 8bitového schématu může pixel nabývat až 256 různých barev. V případě použití 24bitového schématu se použitelná množina barev značně rozšíří každý pixel je reprezentován třemi bajty, kdy každý bajt nese informaci o intenzitě třech základních barev (červené, zelené a modré). Velikost obrázkového souboru je poté přímo úměrná množství pixelů a barevnému schématu. Například obrázek o rozměru pixelů s barevnou paletou čítající 256 barev bude vyžadovat k uložení prostor 307 kb, zatímco obrázek o rozměru pixelů s 24bitovým barevným schématem zabere při uložení paměť velikosti 2,36 MB. R G B
17 2.4 Obrázkové soubory a jejich využití ve steganografii 17 Aby se předešlo ukládání obrázkových souborů do těchto enormních velikostí, bylo vyvinuto množství kompresních schémat. Jmenujme například soubory formátu: Graphic Interchange Format (GIF), Joint Photographic Experts Group (JPEG), Portable Network Graphic (PNG). O rozšířenosti obrázků v současném digitálním světě se můžeme poměrně snadno informovat pomocí internetového vyhledávače Google 5, který dokáže po zadání dotazu ve tvaru filetype:xyz v sekci Images vyhledat v internetu pouze obrázky formátu XYZ. Pro nás zajímavou funkcí je vypsání přibližného počtu všech nálezů. Na základě možností exportu v grafickém programu Corel PHOTO-PAINT X4 lze sestavit seznam formátů souborů, jejichž četnost v internetu budeme chtít zjistit JPG, GIF, PNG, BMP, TIF, PCX, TGA, WI, PP5. Výsledek jednotlivých dotazů je znázorněn v tabulce 2. Tab. 2: Výsledky vyhledávání obrázků dle jejich formátu pomocí vyhledávače Google. Za nejrozšířenější formáty obrázků lze považovat JPG, GIF a PNG. Zdroj: Dotaz Počet výsledků filetype:jpg filetype:gif filetype:png filetype:bmp filetype:tif filetype:pcx 236 filetype:tga 78 filetype:wi 3 filetype:pp5 0 V dokumentu (Kessler, 2001) je dále uvedeno: Nicméně ne všechny zmíněné formáty jsou pro účely steganografie stejně vhodné. Soubory formátu GIF a 8bitové BMP využívají postupu, který umožňuje programům přesně rekonstruovat původní nekomprimovaný obraz to bývá označováno jako neztrátová komprese. Naproti tomu formát JPEG používá kompresi ztrátovou, což znamená, že komprimovaný obraz je tomu původnímu sice velmi podobný, ale není jeho přesnou kopií. Neztrátová komprese je mnohem více vhodná pro aplikace požadující zachování integrity originální informace. Mezi tyto aplikace patří i steganografie. Formát JPEG lze sice pro účely steganografie využít, mnohem běžnější je však ukrývat data v souborech formátu GIF nebo BMP. Avšak z důvodu značného rozšíření obrázků ve formátu JPEG na internetu byly vyvinuty steganografické metody i pro ukrývání dat do tohoto formátu, což bude přiblíženo v dalším textu. 5
18 2.4 Obrázkové soubory a jejich využití ve steganografii 18 V literatuře věnované steganografickým metodám bývá na základě údajů v tabulce 2 neprávem opomíjen formát PNG. Protože se s tímto formátem v dalších kapitolách již nesetkáme, považujeme za důležité nastínit zde, jakým způsobem jej lze využít ve steganografii. Dle článku (Tišnovský, 2006) lze PNG považovat za neztrátový formát, kdy způsoby uložení obrazových dat mohou být následující: Obrázky uložené ve stupních šedi. Pro tento typ obrázků platí, že hodnota každého pixelu vyjadřuje procentuální světlost mezi 0 % (zcela černá) a 100 % (čistě bílá). Obrázky v pravých barvách. Každému pixelu je možné přiřadit prakticky libovolnou barvu. Vzhledem k tomu, že PNG je založeno na barevném modelu RGB, je každá barva specifikována pomocí tří koeficientů podílů základních barev R, G a B. Obrázky s barevnou paletou, ve kterých není každému pixelu uloženému v rastru přiřazena barva, ale index do barevné palety. Teprve tato paleta obsahuje seznam všech barev, ze kterých se obrázek může skládat. Protože se dle výše uvedeného jedná o neztrátový formát s velmi podobnými možnostmi uložení dat jako v případě formátu BMP (viz dále), můžeme se domnívat, že i steganografické techniky aplikovatelné na formát BMP budou aplikovatelné i na formát PNG. Tuto domněnku potvrzuje například existence webové aplikace Steganography Encode 6 nebo dokumentu An Image Steganography Algorithm for 24-bit Color Images Using Edge-Detection Filter 7. V obou případech je jedna steganografická metoda použita pro skrývání dat v obrázcích formátu BMP i PNG Struktura formátu BMP Se strukturou formátu BMP se lze seznámit například na webových stránkách (fileformat.info, 2009). Je zde uvedeno, že typický BMP soubor obsahuje následující bloky dat: Hlavička BMP souboru uloženy obecné informace o souboru. Informace o bitmapě tzv. hlavička DIB (Device Independent Bitmaps). Uloženy podrobné informace o souboru. Barevná paleta uloženy definice barev pro soubory využívající barevnou paletu. Bitmapa uložen vlastní obraz, pixel po pixelu. Struktury hlavička BMP souboru je detailně znázorněna v tabulce 3. Struktura hlavičky DIB je uvedena v tabulce 4. Na webových stránkách (fileformat.info, 2009) je dále uvedeno, že pixely jsou ve vlastní bitmapě uloženy v pořadí, kdy se začíná pixelem z dolního levého rohu, 6 Encode pdf
19 2.4 Obrázkové soubory a jejich využití ve steganografii 19 Tab. 3: Struktura hlavičky souboru formátu BMP. Zdroj: Pozice Velikost Účel 0000h 2 B magická hodnota identifikující soubor BMP 0002h 4 B velikost souboru (v bajtech) 0006h 2 B vyhrazeno pro záznamy aplikace 0008h 2 B vyhrazeno pro záznamy aplikace 000Ah 4 B pozice bajtu, kde začíná výpis pixelů Tab. 4: Struktura informací o souboru formátu BMP (hlavička DIB). Zdroj: Pozice Velikost Účel Eh 4 B velikost této hlavičky 12h 4 B šířka bitmapy v pixelech 16h 4 B výška bitmapy v pixelech 1Ah 2 B počet barevných rovin (musí být 1) 1Ch 2 B počet bitů na pixel barevná hloubka 1Eh 4 B použitá metoda komprese 22h 4 B velikost obrazových dat 26h 4 B horizontální rozlišení 2Ah 4 B vertikální rozlišení 2Eh 4 B počet barev v paletě nebo 0 32h 4 B počet důležitých barev nebo 0 poté se pokračuje zleva doprava po všech řadách až k pravému hornímu pixelu. Každá řada bývá zakončena oddělovači, což bývá zpravidla různý počet nulových hodnot. Bitmapa může být uložena v různých barevných hloubkách: jeden bit na pixel (dvě barvy), čtyři bity na pixel (16 barev, indexy do barevné palety), osm bitů na pixel (256 barev, indexy do barevné palety), 24 bitů na pixel (barevný prostor RGB). Výhodou formátu BMP je jeho jednoduchost, rozšířenost v systémech Windows, absence patentu a dobrá dokumentace. To jej činí vhodným formátem pro použití v nejrůznějších operačních systémech. Nevýhodou je naopak velikost, což lze obejít např. neztrátovou kompresí ZIP (až na 0,1 % původní velikosti) Metody vkládání dat do obrázkových souborů V dokumentu (Cummins et al., 2004) jsou uvedeny následující techniky vkládání dat do obrázkových souborů:
20 2.4 Obrázkové soubory a jejich využití ve steganografii 20 Digitální vodotisk vloží určitý vzor přes existující obrázek. Většinou tímto vzorem rozumíme opět obrázek logo nebo podobné, jež překryje původní obrázek. Na obrázku 3 je znázorněn velmi jednoduchý příklad digitálního vodotisku. Obr. 3: Jednoduchý příklad viditelného digitálního vodotisku. Lze jej realizovat v běžném grafickém editoru. Převzato z Steganography And Digital Watermarking (Cummins et al., 2004). Skrývání do nejméně významného bitu (LSB) Least Significant Bit hiding, tato metoda je pravděpodobně nejjednodušší způsob skrytí dat do obrázku a je překvapivě efektivní. Metoda funguje tak, že do nejnižších bitů hodnot pixelů obrázku vkládá bity ukrývaných dat. Následující příklad demonstruje postup vkládání obrázku do obrázku, přičemž nejvyšší bity obrázku skrývaného vkládá do nejnižších bitů nosiče (počet bitů ovlivňuje výslednou kvalitu, jak ilustruje obrázek 4): načti obrázek-nosič a vkládaný obrázek; zvol počet nejméně významných bitů v bajtech nosiče, do nichž budou vkládány nejvíce významné bity tajného obrázku (čím více bitů zvolíme, tím více zachováme kvalitu vkládaného obrázku, ovšem tím více zhoršíme kvalitu nosiče); vytvoř nový obrázek kombinující pixely nosiče a vkládaných dat; pro získání vložené informace zpět z nosiče je třeba znát počet bitů, do nichž bylo vkládáno poté vezmi tento počet nejméně významných bitů každého pixelu nosiče a použij je jako nejvýznamnější bity rekonstruované informace. Nejčastěji je možné setkat se s přepisováním nejnižšího (nejméně významného) bitu. Tato metoda bude vzhledem ke své významnosti pro tuto práci probrána velmi podrobně v dalším textu. Využití komprese JPEG formát JPEG využívá pro kompresi algoritmus podrobně popsaný v kapitole Podstatou je rozdělení vstupního obrazu na velmi malé bloky (např. 8 8 pixelů), nad nimiž je provedena diskrétní kosinová transformace. Takto dostaneme matice koeficientů, které jsou nejprve kvantovány a poté kódovány zpravidla pomocí Huffmanova kódování. Jedna z implementací skrývá data během kroku kvantování koeficientů. Je-li nutné zakódovat bit hodnoty 0 do určitého čtverce 8 8 pixelů, je třeba nejprve zajistit, aby všechny hodnoty v něm byly sudé (např. vhodnou úpravou). Bit hodnoty 1 naopak zakódujeme pomocí úpravy, jež zajistí, že všechny hodnoty
21 2.5 Steganografické metody v obrázkových souborech 21 ve čtverci budou liché. Pokud jsou ve velkém obrázku tímto způsobem skryta data, je velmi obtížné je detekovat v porovnávání s metodou LSB. Skrytá data jsou takto více rozprostřena, a proto je tato metoda robustnější. Existují však i další implementace, které jsou ještě více robustní a současně mnohem složitější než implementace popsaná. Vlnková transformace je integrální transformace umožňující získat časově frekvenční popis signálu. Uplatňuje se například při odstranění šumu, detekci příznaků nebo kompresi signálů 8. Komprese obrázků pomocí vlnkové transformace představuje vylepšení oproti DCT pro vysoce komprimovaná data. Vkládání dat do takto komprimovaných obrázků je zajištěno pomocí vhodné modifikace tzv. vlnkových koeficientů. Obr. 4: Ukázka vkládání dat do nejméně významného bitu (LSB). Počet použitých bitů určí, kolik nejvyšších bitů dat skrývaného obrázku (levý) je vloženo do kolika nejnižších bitů dat nosiče (pravý). Je možné pozorovat změny v kvalitě obou médií. Převzato z Steganography And Digital Watermarking (Cummins et al., 2004). 2.5 Steganografické metody v obrázkových souborech Rodriguez, Agaian a Collins ve své práci (Rodriguez et al., 2003) klasifikují metody vkládání dat do obrázkových souborů do čtyř skupin: vkládání textu, vkládání obrázku, vkládání komprimovaných dat, náhodné vkládání dat s klíčem. 8 Více o teorii vlnkové transformace např. na -intro-html.html
22 2.5 Steganografické metody v obrázkových souborech 22 V článku (Johnson a Jajodia, Feb. 1998) autoři uvádějí, že informace mohou být skryty v digitálních obrázcích mnoha různými způsoby. Bity tajné zprávy mohou být sekvenčně zakódovány do načítaných dat obrázku, nebo mohou být nejprve vybrány oblasti obrázku s větším šumem (oblasti s velkým rozptylem přirozených barev), do nichž budou bity tajné zprávy následně ukryty. Bity tajné zprávy mohou být také pomocí kódování náhodných vzorů rozprostřeny po celém obrázku. Existuje množství postupů, jak ukrýt informaci do digitálního obrazu. Běžně používané metody zahrnují: vkládání do nejméně významného bitu, maskování a filtrování, algoritmy a transformace. Každá z těchto technik může být aplikována na různé obrázkové soubory s různou úspěšností. Relativně samostatnou skupinu tvoří metody vkládání digitálních otisků, které bychom mohli zařadit pod maskování a filtrování. Nejprve tedy stručně pojednáme o nich, v dalším textu pak podrobně rozebereme metody implementující digitální steganografii v pravém slova smyslu, tedy ukrývání dat do elektronických médií. Zde budeme hovořit o dvou fundamentálních přístupech, a to sice o ukrývání dat v oblasti obrazové a v oblasti transformační Maskování a filtrování Techniky maskovací a filtrovací ukrývají informaci poznačením obrazu podobně jako vodotisk v papírové podobě. Obvykle jsou tyto techniky omezeny na použití v 24bitových obrázcích a obrázcích v odstínech šedé. V dokumentu (Johnson a Jajodia, Feb. 1998) je uvedeno: Mezi tyto techniky lze zařadit digitální vodotisk, jehož důležitou vlastností je velká míra integrace do obrázku. Z tohoto důvodu odolává vodotisk například ztrátové kompresi. Viditelné digitální vodotisky nejsou steganografií dle jejich nejčastějších definic, avšak tato odlišnost je záměrná. Tradiční steganografie ukrývá informaci, kdežto digitální vodotisk informaci zdůrazňuje a stává se vlastností obrázku. Digitální vodotisk může vkládat informaci o autorských právech, vlastnictví či licenci. Ve steganografii je předmětem komunikace zpráva ukrytá v obrázku. V digitálním vodotisku je předmětem komunikace obrázek samotný Oblast obrazová a transformační Silman v dokumentu (Silman, 2001) uvádí, že steganografické techniky lze rozdělit do dvou skupin: ty z oblasti obrazové (image domain) a ty z oblasti transformační (transform domain). Lee a Chen k tomu v (Lee a Chen, 2000) dodávají, že techniky obrazové oblasti vkládají tajné zprávy přímo do hodnot pixelů, zatímco techniky transformační (někdy frekvenční) oblasti vkládají tajné zprávy do dat obrázků, nad nimž proběhla určitá transformace. (Například DCT koeficienty při kompresi
23 2.6 Obrazová oblast (image domain) 23 ve formátu JPEG.) V dokumentu (Venkatraman et al., 2004) je uvedeno, že nejvhodnějšími obrázkovými formáty pro steganografii z obrazové oblasti jsou ty, které podporují neztrátovou kompresi. Přičemž použitelná steganografická technika závisí na konkrétním formátu souboru. Johnson a Jajodia v (Johnson a Jajodia, Apr. 1998) upřesňují, že techniky steganografie z transformační oblasti vyžadují i implementaci konkrétních algoritmů provádějících danou transformaci obrázkových dat. Wang a Wang uvádějí, že tyto metody skrývají tajné zprávy ve význačnějších oblastech obrázku-nosiče, proto je takové ukrytí více robustní (Wang a Wang, 2004). V dokumentu (Venkatraman et al., 2004) je zmíněno, že mnoho steganografických metod z transformační oblasti je nezávislých na formátu obrázku a vložená zpráva může přežít i konverzi mezi ztrátovou a neztrátovou kompresí. Rozdělení steganografie dle dokumentu (Morkel et al., 2005) je prezentováno na obrázku 5. Obr. 5: Rozdělení steganografických metod. Zvláštní důraz je kladen na členění technik obrázkové steganografie. Převzato z An Overview of Image Steganography (Morkel et al., 2005). 2.6 Obrazová oblast (image domain) Nejméně významný bit (LSB) Kessler v dokumentu (Kessler, 2004) uvádí, že nejběžnější steganografické metody pro obrázkové a zvukové soubory využívají nějaký druh substituce či přepisu nejméně významných bitů. Pojem nejméně významný bit vychází z numerické významnosti bitů v rámci bajtu. Nejvyšší nebo nejvíce významný bit je ten, který nese
24 2.6 Obrazová oblast (image domain) 24 nejvyšší aritmetickou hodnotou (např. 2 7 = 128), zatímco nejnižší nebo nejméně významný bit je ten, který nese nejnižší aritmetickou hodnotu (např. 2 0 = 1). V článku (Johnson a Jajodia, Feb. 1998) je uvedeno, že vkládání tajné zprávy metodou nejméně významného bitu (LSB) je nejběžnější a nejjednodušší technika, jak ukrýt informaci do obrázku-nosiče. Krenn v dokumentu (Krenn, 2004) upřesňuje: Ačkoliv metoda LSB trpí značnými nedostatky, je relativně nejjednodušší na implementaci, což ji činí tak populární. Aby bylo možné ukrýt do obrázku tajnou zprávu, je nutné použít čistý obrázkový soubor, jenž bude sloužit jako přenosové médium. Protože tato metoda využívá bity každého pixelu obrázku, je také nutné použít formát obrázku neumožňující ztrátovou kompresi. V opačném případě dojde ke ztrátě vložených dat v důsledku aplikace algoritmu ztrátové komprese. Použijeme-li k ukrytí zprávy obrázek s barevnou hloubkou 24 bitů na pixel, je možné pro uložení tajné zprávy využít informaci o všech barevných složkách (červená, zelená, modrá) každého pixelu. Barevná složka je v tomto případě definována jedním bajtem, z něhož lze využít jeden (nejméně významný) bit. Máme-li tedy obrázek o rozměrech pixelů, je možné do něj vložit až bitů ( bajtů) skrytých dat. Princip LSB demonstrujme na následujícím příkladu. Mějme posloupnost tří pixelů (každý definovaný třemi bajty), jež zabírá celkem 9 B paměti: ( ) ( ) ( ) Chtějme nyní do této posloupnosti pixelů ukrýt znak a, jehož binární reprezentace je (hodnota 97 dle ASCII tabulky). Výše uvedená posloupnost pixelů bude poté vypadat takto: ( ) ( ) ( ) V tomto případě bylo nutno reálně změnit hodnotu pěti bitů, aby byl znak úspěšně vložen. V průměru je při použití této metody měněna polovina bitů, pokud je kapacita nosiče využita maximálně. Výsledné změny v obrázku jsou lidským okem nepostřehnutelné. V případě použití nosiče o barevné hloubce pouze 8 bitů je nutné volit opatrnější postup. Je to z důvodu, že pixel obrázku s barevnou hloubkou 24 bitů je určen třemi bajty, kdežto u obrázku s barevnou hloubkou 8 bitů je každý pixel určen pouze jedním bajtem. Je tedy zřejmé, že změna tohoto bajtu může vyústit ve viditelnou změnu obrázku-nosiče, neboť barevná paleta je méně rozsáhlá. Je tedy nutné klást větší důraz na výběr nosiče ideální je použít obrázek v odstínech šedé, neboť takto lze lidské oko nejlépe oklamat. Wang a Wang v práci (Wang a Wang, 2004) uvádějí, že v případě, kdy je pro ukrytí zprávy využita nepřerušená posloupnost bajtů od začátku do konce souboru (jako v příkladu výše), je toto vložení tajných dat nejsnáze detekovatelné. Anderson a Peticolas v dokumentu (Anderson a Petitcolas, 1998) dodávají, že bezpečnější
25 2.6 Obrazová oblast (image domain) 25 formou LSB je sdílení tajného klíče mezi odesílatelem a příjemcem. Pomocí tajného klíče je specifikováno, v jakých konkrétních pixelech jsou tajná data ukryta, což potenciálnímu útočníkovi ztíží detekci tajných dat i v případě, že je známo použití metody LSB. Krenn se v dokumentu (Krenn, 2004) zabývá i využitelností metody LSB: Metoda LSB ve své nejjednodušší podobě vyžaduje použití obrázků ve formátu BMP, neboť ten podporuje pouze neztrátovou kompresi. Hlavní nevýhodu tohoto použití představuje skutečnost, že pro ukrytí tajné zprávy do obrázku ve formátu BMP je třeba značně velký nosič. A v dnešní době se na internetu s obrázky ve formátu BMP o rozměrech pixelů příliš nesetkáme. Autoři dokumentu (Morkel et al., 2005) uvádějí, že z tohoto důvodu byla steganografická metoda LSB upravena i pro použití v jiných formátech obrázků LSB a obrázky s barevnou paletou V dokumentu (Morkel et al., 2005) je uvedeno, že formát GIF je dalším oblíbeným formátem pro prezentování obrázků na internetu. V referenční příručce (devx.com, 2009) jsou o tomto formátu uvedeny následující informace: Z definice formátu GIF nemohou obrázky disponovat větší barevnou hloubkou než osm bitů, z čehož plyne maximální zobrazitelný počet barev při použití tohoto formátu 256. Obrázky uložené v tomto formátu jsou tzv. indexované, což znamená, že barvy použité v konkrétním obrázku jsou uloženy v jeho záhlaví ve formě barevné palety (někdy uváděné jako vyhledávací tabulka barev) a hodnoty pixelů představují odkazy (indexy) do této palety. Johnson a Jajodia v článku (Johnson a Jajodia, Apr. 1998) uvádějí, že barvy popsané v barevné paletě jsou obvykle řazeny od nejčastěji se vyskytující barvy obrázku k nejméně často se vyskytující barvě, aby se takto zkrátil čas potřebný k vyhledání konkrétní barvy. Johnson a Jajodia se zabývají v článku (Johnson a Jajodia, Apr. 1998) i využitím formátu GIF ve steganografii: Obrázky ve formátu GIF lze ve steganografii použít, ovšem za dodržení určitých zásad. Hlavní omezení souvisí s metodou použití barevné palety, kdy i malá změna v hodnotě pixelu způsobená technikou nejméně významného bitu může vyústit ve zobrazení zcela odlišné barvy, protože je změněn index do barevné palety. V případě, že sousední položky barevné palety jsou podobné, zmíněná změna nepovede ke vnímatelnému rozdílu, ovšem pokud sousední položky podobné nejsou, je zřejmé, že změna bude evidentní. Morkel, Eloff a Olivier poukazují na některá řešení popsaného problému: Setřídění barevné palety takovým způsobem, aby byly minimalizovány rozdíly mezi sousedními barvami v paletě (Chandramouli et al., 2003). Přidání nových barev do palety, přičemž tyto barvy budou pro lidské oko velmi podobné těm již v barevné paletě existujícím. Toto řešení vyžaduje, aby původní obrázek (nosič) obsahoval méně jedinečných barev, než je maximální množství barev vycházející z barevné hloubky obrázku (Morkel et al., 2005).
26 2.7 Transformační oblast (transform domain) 26 Dle autorů (Morkel et al., 2005) je nejlepším řešením použít jako nosiče obrázky ve stupních šedé. V 8bitovém obrázku formátu GIF ve stupních šedé nalezneme 256 různých odstínů šedé, přičemž přechody mezi barvami jsou velmi plynulé, což ztěžuje detekci změny nejnižších bitů indexů. 2.7 Transformační oblast (transform domain) Komprese formátu JPEG Pro pochopení steganografických technik pracujících s formátem obrázků JPEG je nutné nejprve se seznámit s jeho strukturou a s principy, jak jsou obrázková data v tomto formátu uložena. Kolektiv autorů v publikaci (Žára et al., 2004) uvádí, že metoda řízená ztrátové komprese využívající diskrétní kosinové transformace byla vyvinuta skupinou JPEG 9 v rámci mezinárodní standardizační organizace ISO v roce Je vhodná pro kódování fotografií, u nichž mají sousední pixely sice odlišné, ale přesto blízké barvy. Naopak není vhodná pro obrazy s nižším barevným rozlišením (na velkých barevných plochách vytváří artefakty v podobě čtverců či pruhů). Zcela nepoužitelná je pro černobílé obrázky, které rozmazává. Optimálním vstupem je obraz ve 24 bitech na pixel. Dále je tamtéž pojednáno o diskrétní kosinové transformaci (DCT): jde o formu diskrétní Fourierovy transformace, přičemž obrazová data jsou považována za vzorky spojitých funkcí naměřených v diskrétní síti pixelů. Výsledkem kosinové transformace je nalezení sady parametrů kosinových funkcí, jejichž složením lze rekonstruovat původní obraz. Pro kódování obrazu ve formátu JPEG se používá dopředná transformace (FDCT), při dekódování zpětná transformace (IDCT). Postup při kompresi JPEG se sestává z pěti kroků, při dekompresi jsou tyto kroky prováděny analogicky v obráceném pořadí (Žára et al., 2004): 1. Transformace barev Provede se převod do barevného prostoru YC B C R. V další fázi jsou jasové složky Y a barevné složky C B a C R zpracovány odděleně. 2. Redukce barev Sníží se objem dat zprůměrováním barevných složek několika sousedních pixelů a nahrazením jedinou hodnotou. Používají se dvě varianty: 2h1v: průměrování sousedních dvojic 2h2v: průměrování sousedních čtveřic Tento krok nezpůsobí zásadní zhoršení obrazu. Jasové složky Y všech pixelů zůstávají zachovány. 3. Dopředná diskrétní kosinová transformace Obrazová data jsou rozdělena do čtverců 8 8. Každý čtverec je podroben diskrétní kosinové transformaci. Výsledkem je matice 8 8 tzv. DCT koeficientů 9 Joint Photographic Expert Group
27 2.7 Transformační oblast (transform domain) 27 (F (u, v)) získaných výpočtem z hodnot pixelů f(x, y) podle vzorce: F (u, v) = C(u)C(v) cos x=0 y=0 (2x + 1)uπ cos 16 C(u), C(v) = 1 2 pro u, v = 0, resp. 1 jinde. Zpětná (inverzní) transformace má tvar: f(x, y) = 1 [ 7 7 C(u)C(v)F (u, v)cos 4 u=0 v=0 (2x + 1)uπ cos 16 (2y + 1)vπ 16 ] (2y + 1)vπ 16 Hodnoty získané dopřednou transformací nejsou celočíselné a jsou zaokrouhleny až v další fázi zpracování. 4. Kvantování koeficientů DCT V této fázi je určena úroveň komprese. Rozsah DCT koeficientů F (u, v) je snižován vydělením určitým kvantizačním činitelem. Posléze jsou koeficienty zaokrouhleny. DCT koeficient F (0, 0) v levém horním rohu matice je nazýván DC člen a má největší celkový vliv na veškerá obsažená data v matici. Ostatní koeficienty se nazývají AC členy a ovlivňují vyšší frekvence, tedy změny mezi jednotlivými pixely. Čím větší je jejich index (vzdálenost od DC členu, tím menší mají vliv). Kvantizační tabulky byly stanoveny komisí JPEG a jsou obsaženy v různých tabulkách pro složky YC B a C R. Každý koeficient ve zpracovávané matici je dělen jednou odpovídající hodnotou z kvantizační tabulky. Kvantizační tabulky jsou stejné pro celý obrázek a jsou ukládány do výstupního obrazu kvůli rekonstrukci obrazu. 5. Kódování Výsledkem předchozích kroků jsou numerické úpravy čtvercové podoblasti vstupního obrazu, které zjednodušily tvar až do podoby řídké matice s dominantním levým horním rohem. Tato matice je nyní kódována a zapisována do výstupního souboru, přičemž je využito toho, že většina koeficientů v okolí pravého dolního rohu má nulovou hodnotu. Matice čísel je převedena na posloupnost tak, jak ukazuje obr. 6 a tato posloupnost je zakódována Huffmanovým nebo aritmetickým kódováním. Členy DC se zapisují samostatně. Nejprve se sdruží DC členy z celého obrázku a poté jsou kódovány jejich rozdílové hodnoty Steganografie soubory ve formátu JPEG V dokumentu (Morkel et al., 2005) autoři podávají stručný úvod k problematice ukrývání tajných zpráv do souborů formátu JPEG: Původně se předpokládalo, že soubory ve formátu JPEG nebudou ke steganografii vhodné z důvodu použití
28 2.7 Transformační oblast (transform domain) 28 Obr. 6: Sekvence postupného čtení hodnot kvantovaných koeficientů z matice. Převzato z Programujeme JPEG: Kvantizace DCT koeficientů (Tišnovský, 2007). ztrátové komprese, jež způsobuje určitou modifikaci dat obrázku. Jedna z hlavních charakteristik steganografie totiž spočívá v ukrývání tajných informací do redundantních dat obrázkového nosiče, ovšem formát JPEG tyto redundantní data odstraňuje (což souvisí se ztrátovou kompresí). Existovalo tedy důvodné podezření, že ukrývaná zpráva bude ztrátovou kompresí nevratně poškozena. A i v případě, že by se podařilo skrytou zprávu udržet neporušenou, bylo by složité zprávu vložit do nosiče tak, aby změny v nosiči byly nevnímatelné z důvodu aplikace hrubé komprese. Vlastnosti kompresního algoritmu však byly využity za účelem vyvinutí steganografického algoritmu i pro soubory ve formátu JPEG. Konkrétně využití jedné z vlastností formátu JPEG popisují Johnson a Jajodia v článku (Johnson a Jajodia, Feb. 1998): Během fáze Kvantování koeficientů DCT kompresního algoritmu se vyskytují zaokrouhlovací chyby u koeficientů, přičemž toto není ve výsledku nijak patrné. Ačkoliv kvůli této vlastnosti je kompresní algoritmus formátu JPEG klasifikován jako ztrátový, je možné využít ji i ke skrývání dat do obrázkového nosiče (Morkel et al., 2005). Autoři dokumentu (Morkel et al., 2005) popisují princip využití steganografie v souborech formátu JPEG: Důležitým aspektem je rozlišení kompresního algoritmu na ztrátovou a neztrátovou část. Fáze transformace DCT a kvantizace koeficientů považujeme za část ztrátovou zatímco fázi aplikace Huffmanova kódování považujeme za část neztrátovou. Steganografie své místo nalezne mezi těmito částmi. Metoda vkládání do nejméně významného bitu může být použita pro vložení bitů tajné zprávy do nejméně významných bitů kvantizovaných DCT koeficientů před aplikací Huffmanova kódování. Vložením tajné informace v této části (během transformace odtud transformační oblast) docílíme toho, že vloženou informaci bude velmi složité detekovat, neboť k modifikaci nedochází v oblasti vizuální. Jinými slovy změna v nejméně významném bitu neovlivní jeden pixel, ale bude rozložena na celou skupinu sousedních pixelů. Příkladem aplikací pracujících v oblasti transformační mohou být steganografické nástroje Jsteg 10 a OutGuess 11. Oba nástroje ukrývají data do DCT koeficientů paul/crypto/jsteg/ 11
29 2.8 Metody oblasti obrazové i transformační Metody oblasti obrazové i transformační Jak je zřejmé z obrázku 5, některé steganografické algoritmy jsou zařaditelné do obou oblastí. Morkel, Eloff a Olivier k tomu v dokumentu (Morkel et al., 2005) uvádějí, že tato kategorizace záleží na konkrétní implementaci daného algoritmu. Tamtéž je uvedeno, že mezi tyto algoritmy řadíme následující techniky: Patchwork lze přeložit jako slepovací nebo spojovací metoda. Johnson a Jajodia v článku (Johnson a Jajodia, Apr. 1998) uvádějí, že algoritmus této metody nejprve přidá redundanci k ukrývaným datům a poté je rozptýlí po celém obrázkovém nosiči. Bender, Gruhl a Morimoto v článku (Bender et al., 1996) upřesňují: Za použití pseudonáhodného generátoru jsou zvoleny dvě oblasti obrázku patch A a patch B. Všechny pixely v patchi A jsou poté zesvětleny, zatímco v patchi B jsou ztmaveny (intenzity pixelů jsou buď zvýšeny nebo sníženy o konstantní hodnotu). Kontrastní změny mezi oběma podmnožinami poté kódují jeden bit skrývané zprávy, uvádí Johnson a Jajodia v článku (Johnson a Jajodia, Apr. 1998). Stejní autoři dodávají, že průměrný jas obrázkového nosiče není použitím této techniky změněn. Rozprostřené spektrum techniky rozprostřeného spektra tajná data ukrývají rozprostřena v celém nosiči, aby se takto maximálně ztížila jejich detekce (Wang a Wang, 2004). V článku (Marvel et al., 1999) je uvedeno: Steganografie využívající rozprostřené spektrum vkládá tajnou zprávu do šumu, který je poté sloučený s obrázkovým nosičem, čímž je vytvořeno steganografické médium. 2.9 Srovnání steganografických technik Autoři dokumentu (Morkel et al., 2005) podávají zevrubné srovnání steganografických technik popsaných výše. Konkrétně srovnávají metodu LSB (Least Significant Bit) ve formátu BMP, LSB ve formátu GIF, kompresi JPEG, patchwork a rozprostřené spektrum z následujících hledisek: neviditelnost (steganografický algoritmus musí zajistit neviditelnost vkládané zprávy), kapacita nosiče (jak velkou informaci lze do nosiče ukrýt), odolnost proti statistickým útokům (vložená data nesmí způsobit v obrázkovém nosiči statisticky významné změny), odolnost proti manipulaci s nosičem (vložená zpráva by měla odolat ořezávání či rotaci obrázkového nosiče), nezávislost na formátu nosiče, nenápadnost (steganografický algoritmus nesmí vzbudit podezření, že obrázkový nosič je použit pro přenos zprávy je nutné se vyvarovat např. netypické velikosti souboru). Stejní autoři dospěli k výsledku, jenž je zachycen v tabulce 5. Úrovně, v nichž jednotlivé algoritmy vyhovují požadavkům uvedeným výše, jsou určeny jako vysoká,
30 2.9 Srovnání steganografických technik 30 střední a nízká. Vysoká úroveň znamená, že algoritmus plně vyhovuje danému požadavku, a naopak nízká úroveň indikuje skutečnost, že algoritmus má v daném požadavku slabiny. Střední úroveň vypovídá o tom, že splnění požadavku závisí na dalších okolnostech, např. na volbě nosiče (LSB ve formátu GIF může ukrýt velké množství informace, ovšem za podmínky použití vhodného nosiče). Tab. 5: Srovnání algoritmů obrázkové steganografie. Tabulka převzata z An Overview of Image Steganography (Morkel et al., 2005). LSB v BMP LSB v GIF JPEG komprese Patchwork Rozprostřené spektrum Neviditelnost vysoká střední vysoká vysoká vysoká Kapacita nosiče vysoká střední střední nízká střední Odolnost proti statistickým útokům nízká nízká střední vysoká vysoká Odolnost proti manipulaci s nosičem nízká nízká střední vysoká střední Nezávislost na formátu nosiče nízká nízká nízká vysoká vysoká Nenápadnost nízká nízká vysoká vysoká vysoká Výsledek své práce stejní autoři shrnují v přehledu, jenž je možné chápat jako manuál pro výběr konkrétní steganografické metody: LSB v souborech BMP Pokud pro ukrývání dat použijeme hrubý obrázek, jenž není nijak modifikován kompresí, je nutné uvažovat souvislost mezi neviditelností skryté zprávy a množstvím skrývaných dat. Do obrázků formátu BMP je teoreticky možné ukrýt velké množství dat, ovšem čím více bitů je tímto změněno, tím více vzroste riziko odhalení pouhým okem. Hlavní nevýhodu aplikace LSB na obrázky formátu BMP představuje velikost BMP souborů. Přenos neobvykle velkých obrázků formátu BMP může vzbudit podezření, protože používání tohoto formátu není příliš rozšířeno. Doporučené použití: V aplikacích, kde je nejdůležitější objem přenesené informace a již méně je důležitá její utajitelnost. LSB v souborech GIF Vlastnosti podobné LSB v souborech BMP ovšem s tím rozdílem, že obrázky formátu GIF disponují pouze 8bitovou barevnou hloubkou, takže množství potenciálně ukryté informace je menší než v případě BMP. Soubory GIF jsou velmi citlivé na statistický i vizuální útok. Síla metody LSB v těchto souborech je závislá na barevnosti použitého obrázkového nosiče. Doporučené použití: V aplikacích, které ukrývají přiměřené množství dat do obrázků v odstínech šedé. JPEG komprese Proces vložení tajné informace do nosiče během JPEG komprese vede k vytvoření steganografického média s vysokou mírou neviditelnosti, protože vkládání se děje v oblasti transformační. JPEG je pro svou malou velikost velmi rozšířeným formátem obrázků na internetu, díky čemuž budí jeho
31 2.10 Nástroje pro ukrývání zpráv 31 přenos minimální podezření. Nicméně proces komprese představuje velmi složitý matematický postup, což činí tuto metodu složitější na implementaci. Doporučené použití: V aplikacích, kdy jsou obrázky přenášeny otevřeným kanálem, což je například internet. Patchwork Nevýhodou je velmi malé množství potenciálně ukryté informace. Naopak výhodou této metody je její robustnost, kdy skrytá data odolávají i operacím ořezu či rotace. Doporučené použití: V aplikacích přenášející velmi malý objem velmi citlivé informace. Rozprostřené spektrum Velmi robustní metoda odolávající statistickým útokům, neboť ukrytá data jsou roztroušena po celém obrázkovém nosiči, což vede k neměnnosti statistických vlastností obrázku před a po vložení zprávy. Doporučené použití: Ve většině steganografických aplikací. Implementaci může ztížit komplikovanost a matematická náročnost metody Nástroje pro ukrývání zpráv EzStego Aplikace vyvinutá Romanou Machlado 12 ukrývá zprávy do obrázků formátu GIF. V dokumentu (Westfeld a Pfitzmann, 1999) je uvedeno, že aplikace data ukrývá pomocí hodnot pixelů (indexů do barevné palety), přičemž barevná paleta zůstává beze změny. Steganografický algoritmus vytvoří kopii barevné palety utříděnou takovým způsobem, aby rozdíly mezi sousedními barvami byly minimální. Vkládací funkce čte sekvenčně od začátku hodnoty jednotlivých pixelů a porovnává jejich steganografickou hodnotu (hodnotu nejméně významného bitu) s hodnotou bitu, který je třeba vložit. Pokud například potřebujeme skrýt hodnotu 0 a hodnota pixelu (indexu) je například 4 (binárně 100), neprovádí se žádná úprava. Pokud bychom potřebovali ukrýt hodnotu 1, index bude modifikován tak, aby ukazoval na sousední barvu v utříděné paletě. Z indexu 4 se pak stane index 5 (binárně 101). V principu jde tedy o jednoduchou implementaci metody LSB, ovšem za předpokladu vhodně utříděné barevné palety, což je v souborech formátu GIF podstatné. Postup ilustruje obrázek 7. V dokumentu (Westfeld a Pfitzmann, 1999) je také poznámka, že bity potenciálně ukryté zprávy lze extrahovat velmi snadno. Pokud bychom například chtěli skrytá data vykreslit jako černobílý obrázek, můžeme pro steganografickou hodnotu přečteného pixelu 0 vykreslit černou a pro hodnotu 1 bílou barvu. 12
32 2.10 Nástroje pro ukrývání zpráv 32 Obr. 7: Princip algoritmu nástroje EzStego. Původní paleta vytvořena dle četnosti barev v obrázku formátu GIF. Převzato z Attacks on Steganographic Systems (Westfeld a Pfitzmann, 1999) Steghide Autorem tohoto steganografického programu je Stefan Hetzl a domovská stránka aplikace se nachází na adrese Následující popis je sestaven na základě oficiálního manuálu programu. Steghide je schopen skrývat data v různých obrázkových a zvukových souborech. Metoda skrytí je odolná proti statistickým testům prvního řádu, neboť četnosti barev v obrázku nejsou výrazně měněny. Mezi jeho funkčnosti patří i komprese a šifrování skrývaných dat nebo vkládání kontrolního součtu. Formáty podporovaných nosičů jsou JPEG, BMP, WAV a AU. Steghide používá při skrývání dat poznatky z teorie grafů. Algoritmus vložení dat funguje zhruba takto: 1. Tajná data jsou nejprve zkomprimována a zašifrována. 2. Je získána posloupnost pozic pixelů pomocí generátoru pseudonáhodných čísel, který je inicializován hodnotou hesla (do těchto pixelů budou ukryta tajná data). 3. Pixely, které není třeba nijak modifikovat, neboť již obsahují požadovanou hodnotu, jsou odstraněny ze seznamu pozic. 4. Zbývající pozice se stanou vstupem algoritmu párování v bipartitním grafu, který hledá takové páry pixelů, v nichž by výměna hodnot měla stejný efekt jako vložení odpovídající části tajných dat. Jakmile žádný další pár nelze nalézt, je výměna hodnot provedena. Tyto pixely jsou ze seznamu pozic také odstraněny. 5. Na zbývajících pixelech se provede modifikace, aby obsahovaly odpovídající část tajných dat (tato modifikace již způsobuje přepis hodnot pixelů). Díky skutečnosti, že většina pixelů je pouze zaměněna, a nikoliv přepsána, je algoritmus odolný proti statistikám prvního řádu.
33 2.10 Nástroje pro ukrývání zpráv Steganografický on-line systém Matěje Zapletala (M. Z.) Jde o jednoduchou webovou aplikaci vytvořenou Matějem Zapletalem 13. Aplikace je dostupná na xzaplet8/kas/. Aplikace zprávy zapsané v textovém poli ukrývá do 24bitových obrázků formátu BMP. Její algoritmus vkládá data tajných zpráv do LSB sekvenčně od začátku souboru. Kromě toho lze skrývaná data i zašifrovat pomocí algoritmu TripleDES. Pro testovací účely aplikace umožňuje zprávy skrývat i do nejvyššího bitu, což opticky zvýrazní pixely, do nichž jsou bity zprávy vkládány OutGuess Outguess 14 je program, jehož autor, Niels Provos, chtěl vyvinout nástroj pro skrývání zpráv v obrázcích formátu JPEG, který by odolával statistickým útokům prvního řádu. Jeho algoritmus je zveřejněný ve článku (Provos a Honeyman, 2003): Vstup: zpráva, klíč, nosič Výstup: steganografický obrázek inicializuj generátor pseudonáhodných čísel pomocí klíče; dokud (jsou data k~vložení) dělej získej pseudonáhodný DCT koeficient z~nosiče; když (DCT!= 0) a~(dct!= 1) pak získej hodnotu dalšího LSB ze zprávy; přepiš LSB DCT koeficientu LSB získaným ze zprávy; konec když; vlož DCT do steganografického obrázku; konec dokud; Algoritmus F5 V literatuře (Provos a Honeyman, 2003), (Kessler, 2004) je označován za jeden z nejobtížněji detekovatelných steganografických algoritmů. Byl vyvinut Andreasem Westfeldem, spoluautorem dokumentu (Westfeld a Pfitzmann, 1999). Ve článku (Provos a Honeyman, 2003) je uvedeno, že algoritmus nenahrazuje nejméně významné bity DCT koeficientů bity vkládané zprávy, ale snižuje jejich absolutní hodnotu procesem zvaným matrix encoding. Tamtéž je také popsán jeho netriviální algoritmus
34 2.11 Steganografie dílčí shrnutí Steganografie dílčí shrnutí Na základě doposud uvedeného je zřejmé, že předmětem steganografie je ukrývání zpráv do různých objektů, které nazýváme nosiči. Nosič obsahující skrytou zprávu je pak nazýván steganografické médium. Nosičem pak může být prakticky jakýkoliv objekt reálného světa, do něhož jsme schopni pomocí nějakého postupu, steganografického algoritmu, skrýt tajnou zprávu. Nezasvěcený účastník komunikace vnímá steganografické médium v jeho původním významu, kdežto zasvěcený účastník jej chápe jako obálku pro očekávanou zprávu. Předmětem této práce je steganografie digitální, která jako nosič nejčastěji využívá obrázkové soubory, např. formátu BMP, PNG, GIF či JPEG. Metody ukrývání do těchto nosičů mohou být různé, obvykle se podřizují charakteristikám jednotlivých formátů. Mezi nejjednodušší techniky ukrývání zpráv patří metoda vkládání do nejméně významného bitu (LSB), která může být vylepšena selekcí pozic pomocí generátoru pseudonáhodných čísel inicializovaným tajným heslem. Jsou možné i další obměny této metody, které sofistikovaněji vybírají oblasti obrázku, jejichž nejméně významné bity využijí. Tato metoda je vhodná především pro obrázky formátu BMP, PNG či obrázky formátu GIF v odstínech šedé. Jiný přístup vyžaduje ukrývání zpráv do obrázků formátu JPEG, kde nelze modifikovat přímo obrazová data (ta bývají upravena ztrátovou kompresí), ale ukrývaná data se zpravidla zapisují do DCT koeficientů. Vzhledem ke skutečnosti, že takto je ovlivněn celý blok pixelů o rozměrech 8 8, je výsledné ukrytí robustnější než v případě LSB. I v tomto přístupu lze využít generátoru pseudonáhodných čísel. Postupně se objevují i další dokonalejší a složitější steganografické algoritmy, například algoritmus F5, patchwork či rozprostřené spektrum. Jejich lepší schopnosti jsou vykoupeny poměrně složitější implementací, než jaká je u základních technik Stegoanalýza Vězňův problém Takzvaný Vězňův problém publikovaný Simmonsem v článku (Simmons, 1983) je často využíván k popisu steganografie, ačkoliv byl původně určen k popisu kryptografického scénáře. V dokumentech (Chandramouli, 2002) a (Fridrich et al., 2003) je problém ve steganografickém významu popsán: Obsahem problému jsou dva vězni, Alice a Bob, kteří jsou zamčeni v oddělených celách a kteří spolu potřebují komunikovat za účelem dohodnutí plánu na útěk. Alice a Bob jsou schopni posílat si zprávy, ovšem dozorce William může všechny tyto zprávy číst. Alice a Bob vědí, že William jejich komunikaci v případě odhalení tajného komunikačního kanálu okamžitě ukončí. Dozorce William může jednat buď v pasivním režimu nebo v aktivním režimu. V modelu pasivního dozorce William kontroluje každou zprávu a na základě své schopnosti detekovat skrytou komunikaci rozhoduje, zda zprávu pustí dále či
35 2.12 Stegoanalýza 35 nikoliv. V modelu aktivního dozorce může William kontrolované zprávy navíc libovolně modifikovat. Podezíravý dozorce může modifikovat všechny zprávy za účelem zničení potenciálního skrytého komunikačního kanálu, a v tomto případě musí Alice a Bob použít velmi robustní steganografickou metodu. Obtížnost dozorcovy úlohy závisí převážně na složitosti steganografického algoritmu a na počáteční Willamově znalosti. Kessler v dokumentu (Kessler, 2004) k tomu dodává, že můžeme rozlišovat čistý steganografický model a steganografický model s tajným klíčem: Čistý steganografický model je založen na předpokladu, že William neví nic o steganografické metodě, jakou Alice a Bob používají. Ve skutečném světě však předpoklad nastává výjimečně, v oblasti kryptografie prakticky vůbec. Steganografický model s tajným klíčem naopak předpokládá, že William zná steganografický algoritmus, avšak nezná tajný steganografický (kryptografický) klíč používaný Alicí a Bobem. Tato situace v praxi nastává spíše Definice stegoanalýzy Stegoanalýza je ve své podstatě opakem steganografie. Pokouší-li se steganograf vyvinout a implementovat nové metody pro skrývání zpráv do různých médií, stegoanalytik se snaží skrytý obsah v potenciálním nosiči odhalovat. Chandramouli v dokumentu (Chandramouli, 2002) uvádí, že stegoanalýzou rozumíme detekci steganografie třetí stranou. Dle stejného autora jde o relativně mladou vědní disciplínu, v důsledku čehož se před rokem 1990 nesetkáme s velkým množstvím publikovaných článků. Stegoanalýza je vědou i dovedností, která se zabývá detekcí nebo odhadem skryté informace a spočívá v průzkumu libovolného datového transferu bez předpokladů o steganografickém algoritmu (Chandramouli, 2002). Autoři dokumentu (Jackson et al., 2002) navíc dodávají, že pouhá detekce skrytých dat nemusí být dostatečná. Stegoanalytik může také chtít skrytou zprávu extrahovat, zneplatnit (aby ji původní příjemce nemohl přečíst), nebo pozměnit (aby byl původní příjemce oklamán). Andrew Ker z Oxfordské univerzity v jedné ze svých přednášek (Ker, 2008) uvádí několik aspektů, dle nichž může být na stegoanalýzu pohlíženo: Cíl: Detekovat, zda objekt obsahuje skrytý obsah. Stegoanalýza může být cílená na konkrétní steganografický algoritmus (nejčastější), slepá potenciálně odhalí i doposud neznámou metodu (vzácná, obvykle slabá). Výstup stegoanalýzy může být binární ano/ne (obsažena skrytá data?), kvantitativní (odhad délky skrytých dat). Metodologie stegoanalýzy:
36 2.12 Stegoanalýza 36 kombinatorická analýza operace skrytí dat (musí být cílená), aplikace technik strojového učení. U metodologií Ker popisuje jejich výhody a nevýhody. Kombinatorická analýza operace skrytí dat je obvykle vysoce citlivá a aplikovatelná na mnoho typů nosičů. Naopak bývá velmi složité navrhnout detekční algoritmus. Aplikace technik strojového učení vyniká v tom, že může využít standardních technik a postup vkládání dat nemusí být přesně znám. Naopak bývá výpočetně náročná a různé typy nosičů vyžadují odlišný trénink Techniky stegoanalýzy K rozdělení technik stegoanalýzy lze přistoupit mnoha způsoby. V literatuře se nejčastěji setkáme s rozlišením podle typu útoku nebo podle dostupnosti informací. S druhým uvedeným členěním se můžeme setkat například v dokumentu (Curran a Bailey, 2003) nebo v dokumentu (Johnson a Jajodia, Apr. 1998), kdy autoři tvrdí, že techniky stegoanalýzy lze klasifikovat podobným způsobem jako techniky kryptoanalýzy, tedy podle množství informace, kterou má stegoanalytik k dispozici: Steganography-only attack: steganografické médium je jediná položka dostupná pro analýzu. Known-carrier attack: Pro analýzu je dostupné steganografické médium a originální nosič. Known-message attack: Je známa skrytá zpráva. Chosen-steganography attack: Dostupné je steganografické médium a steganografický algoritmus. Chosen-message attack: Je známa skrývaná zpráva a steganografický algoritmus, pomocí nichž lze vytvořit steganografické médium pro budoucí analýzu a porovnání. Known-steganography attack: Je dostupný původní nosič a současně i steganografické médium a steganografický algoritmus. Již konkrétnější pohled na techniky stegoanalýzy nabízí základní členění podle typu útoku. Westfeld a Pfiltzmann ve svém výzkumu (Westfeld a Pfitzmann, 1999) uvažují klasifikaci technik na: vizuální útoky, statistické útoky. Toto členění vychází z činnosti steganografických algoritmů v obrazové nebo transformační oblasti popsané v kapitole Není však možné tvrdit, že tam, kde použijeme vizuální útok, nemá smysl používat útok statistický a naopak. Metody jednotlivých útoků budou uvedeny dále. Další možné rozdělení technik stegoanalýzy předkládají autoři dokumentu (Phan a Ling, 2004) nebo (Jackson et al., 2002), kde je opět použit princip klasifikace dle typu útoku:
37 2.13 Možnosti útoků na steganografické systémy 37 Detekční útoky: RQP útok, RS útok, known-carrier attack. Extrakční útoky: extrakce nejméně významného bitu (LSB), permutace bitů i zprávy na bity y i steganografického média. Zneplatňující útoky: destrukční útok, přepisovací útok. Je zřejmé, že toto rozdělení vychází z teoretických poznatků zmíněných v kapitole , kdy je jako výstup stegoanalýzy samostatně zmiňována detekce, extrakce a zneplatnění skryté zprávy. Dle výzkumu, který byl prováděn na Binghamtonské univerzitě (Fridrich et al., 2003), lze techniky stegoanalýzy klasifikovat již velmi podrobně dle konkrétních typů obrázkových nosičů, jež mohou být použity. Stegoanalýza pak může být zaměřena na: obrázky formátu JPEG, nekomprimované hrubé (raw) obrázky, obrázky s barevnou paletou. Digitální vodotisk, ač součást steganografie, vyžaduje ve smyslu stegoanalýzy speciální přístup. Útoky na digitální vodotisk tedy můžeme považovat za zvláštní druh stegoanalýzy. Andrew Ker v dokumentu (Ker, 2008) uvádí, že těmito útoky chápeme opačnou disciplínu ke vkládání digitálních vodotisků, přičemž cílem je zničit skrytá data (protivník chce odstranit digitální vodotisk, aniž by zničil označené médium nosič). Ker útoky na digitální vodotisk klasifikuje takto: noise attack (přidání šumu do označeného obrázku sníží spolehlivost vodotisku), collusion attack (zprůměrování kopií jednoho nosiče poznačeného odlišnými vodotisky), desynchronization attack (narušení prostorovosti poznačeného obrázku, např. odebráním sloupce pixelů, což učiní vodotisk nedetekovatelný), watermark estimation (pokusit se porovnáním objektů se shodným vodotiskem či prostým pokusem odhadnout strukturu vodotisku a poté jej vyjmout) Možnosti útoků na steganografické systémy Nyní přistupme k popisu útoků, se kterými se v dostupné literatuře můžeme nejčastěji setkat. Dle základních charakteristik jednotlivých útoků rozdělme popisované do dvou částí: vizuální útok a statistické útoky.
38 2.13 Možnosti útoků na steganografické systémy Vizuální útok Autoři dokumentu (Westfeld a Pfitzmann, 1999) uvádějí, že většina steganografických algoritmů ukládá bity zprávy modifikací pečlivě vybíraných bitů nosiče. Strojově pak bývá velmi obtížné rozlišit náhodná data v obrázku a data tvořící vlastní obrázek, ještě obtížnější je pak odlišení nejméně významných bitů od náhodných bitů. Velmi složité je také formálně definovat přípustný obsah obrázku. Zde pak může pomoci lidská představivost, neboť lidské smysly jsou trénovány rozlišovat známé věci. Podstatou vizuálního útoku je odstranění všech částí obrázku zakrývající data tajné zprávy. Lidské oko poté může rozlišit, zda tento rozdíl odpovídá stále původnímu obrázku, či zda se jedná o potenciálně ukrytou zprávu. Proces filtrování závisí na domnělém steganografickém algoritmu a jeho struktura je znázorněna na obrázku 8. (Westfeld a Pfitzmann, 1999) Obr. 8: Proces filtrování krycích částí obrázku. Převzato z Attacks on Steganographic Systems (Westfeld a Pfitzmann, 1999). V kapitole byl popsán steganografický systém EzStego, na němž Westfeld a Pfitzmann princip vizuálního útoku demonstrují. EzStego využívá barev pixelů, definovaných v barevné paletě, pro vyjádření ukrývaných bitů zprávy. Westfeld a Pfitzmann uvádějí, že filtrace krycích částí obrázku spočívá v nahrazení původní barevné palety černobílou paletou. Tvorba černobílé palety vychází z toho, zda v utříděné paletě (programem EzStego) má barva lichý či sudý index (tato skutečnost souvisí s ukrytím binární jedničky či nuly). Tvorbu filtru ilustruje obrázek 9, přičemž navazuje na setříděnou barevnou paletu programem EzStego popsanou v kapitole Westfeld a Pfitzmann dále provedli experiment (Westfeld a Pfitzmann, 1999), kde vizuálnímu útoku podrobili steganografická média třech různých formátů a vytvořených steganografickými nástroji EzStego, S-Tools, Steganos a Jsteg. Výsledek experimentu lze shrnout do následujících bodů: EzStego program vkládá bity zprávy sekvenčně od začátku nosiče. Skrytá data jsou velmi snadno pomocí vizuálního útoku detekovatelná, pokud je použit nosič s malým rozptylem barev (obr. 10). Pokud je jako nosič použit obrázek s vyšším rozptylem barev či s minimem souvislých ploch, stává se vizuální útok nepoužitelný (viz obr. 11, v němž žádná skrytá data nejsou). S-Tools nástroj vkládá bity zprávy rozprostřené po celém nosiči. Z toho důvodu ve filtrovaném obrázku nenarazíme na jasnou hranici skrytých dat jako
39 2.13 Možnosti útoků na steganografické systémy 39 Obr. 9: Tvorba filtru pro vizuální útok na program EzStego. Převzato z Attacks on Steganographic Systems (Westfeld a Pfitzmann, 1999). v případě programu EzStego. Na obrázku 12 je ilustrováno filtrování steganografického média se skrytou zprávou obsazující 50 % steganografické kapacity. Neznáme-li filtrovanou podobu originálního nosiče, pak je bez porovnání identifikace tajných dat prakticky nemožná. Steganos program vkládá bity zprávy sekvenčně od začátku, jejich objem vždy doplní na objem maximální steganografické kapacity nosiče. To má za důsledek, že i v případě, kdy bychom do nosiče chtěli ukrýt pouze jediný bit, bude situace stejná, jako při vkládání nejdelší možné zprávy. Vizuální útok odhalí zvýšený šum po celém obrázku, což v případě větších barevných ploch může být podezřelé. Příklad ukrytí jediného bitu znázorněn na obrázku 13. Jsteg nástroj skrývá zprávy pouze do obrázků formátu JPEG. Protože tajná data se ukrývají v oblasti transformační do DCT koeficientů, není možné použít vizuální útok. Jeden steganografický bit totiž ovlivní až 256 pixelů. Obr. 10: Ideální případ vizuálního útoku. Tajná zpráva ukryta pomocí nástroje EzStego sekvenčně do nosiče (nalevo jeho filtrovaná podoba) s nízkým rozptylem barev. Napravo filtrovaná podoba steganografického obrázku. Převzato z Attacks on Steganographic Systems (Westfeld a Pfitzmann, 1999). Autoři dokumentu (Fridrich a Goljan, 2002) uvádějí, že tento útok je aplikovatelný obzvláště na obrázky využívající barevnou paletu, kdy metoda LSB modifikuje odkazy (indexy) do palety. Pokud je zpráva ukryta sekvenčně, je možné odhalit pomocí vizuálního útoku přítomnost tajné zprávy a získat pro to dostatečný důkaz.
40 2.13 Možnosti útoků na steganografické systémy 40 Obr. 11: Kvůli složitému obrazu není možné vizuální útok použít (obrázek nalevo neobsahuje skrytá data). Převzato z Attacks on Steganographic Systems (Westfeld a Pfitzmann, 1999). Obr. 12: Skrytá data rozprostřena po celé délce nosiče (nalevo) nástrojem S-Tools. Převzato z Attacks on Steganographic Systems (Westfeld a Pfitzmann, 1999). Vizuální útok selhává, pokud je aplikován na obrázky obsahující šum či na složitě strukturované obrázky. Ačkoliv je vizuální útok ve své podstatě jednoduchý, je těžké jej automatizovat a jeho spolehlivost je také diskutabilní Statistické útoky V dokumentu (Kessler, 2004) je uvedeno, že druhý přístup ke stegoanalýze spočívá v hledání strukturálních odchylek, které by napověděly, že došlo k manipulaci s nosičem. Technika vkládání do nejméně významného bitu často způsobí vytvoření velkého počtu téměř duplicitních nových barev, které se od barev originálního nosiče liší pouze v nejméně významném bitu. Autoři dokumentu (Jackson et al., 2002) dodávají, že steganografické programy, které ukrývají informaci pomocí manipulace s pořadím barev v barevné paletě, také způsobují strukturální změny. Strukturální změny často vytvářejí charakteristický podpis, který identifikuje použitý steganografický algoritmus. Například dle článku (Fridrich a Goljan, 2002) steganografické techniky obecně mění statistiky nosiče, přičemž dlouhá skrytá zpráva pozmění nosič více než zpráva krátká.
41 2.13 Možnosti útoků na steganografické systémy 41 Obr. 13: Program Steganos vždy doplní délku skrývané zprávy na nejdelší možnou. Do obrázku nalevo byl vložen jeden bit skrytých dat. Napravo jeho filtrovaná podoba. Převzato z Attacks on Steganographic Systems (Westfeld a Pfitzmann, 1999). V dokumentu (Jackson et al., 2002) je uvedeno, že statistická analýza je obvykle využívána k detekci skrytých zpráv pokud analytik pracuje naslepo (tj. Stego-only attack). Statistická analýza obrázkových nebo hudebních souborů může ukázat, zda se jejich statistické vlastnosti odlišují od očekávané normy (Provos a Honeyman, 2003). Petr Wayner k tomu v publikaci (Wayner, 2002) dodává, že takzvané statistiky prvního řádu průměry, rozptyly, chi-kvadrát (χ 2 ) testy mohou měřit množství redundantní informace nebo narušení v médiu. Ačkoliv tato měření mohou podat informaci o modifikaci obsahu či alespoň označit obsah za podezřelý, nejsou definitivní. Provos a Honeyman v článku (Provos a Honeyman, 2003) upřesňují, že se statistická analýza realizuje složitě, neboť mnoho steganografických algoritmů disponuje schopností statistikám prvního řádu odolávat, což tento typ detekce komplikuje. Tamtéž je dále uvedeno, že zašifrování ukrývané zprávy tento typ detekce činí též složitější, neboť zašifrovaná data vykazují obecně vyšší stupeň náhodnosti, takže binární jedničky a nuly se vyskytují v takových datech se stejnou pravděpodobností. Je zřejmé, že statistické útoky jsou díky určité přenositelnosti ve srovnání s vizuálními více použitelné. Popisu vybraných statistických útoků se věnují následující kapitoly, v nichž zmíníme: útok testem χ 2, útok analýzou RQP, útok RS analýzou, Couple detector, klasifikátory Útok testem χ 2 Westfeld a Pfitzmann předkládají v dokumentu (Westfeld a Pfitzmann, 1999) ideu útoku na steganografické systémy, který je založen na analýze histogramu obrázku
42 2.13 Možnosti útoků na steganografické systémy 42 a následném použití χ 2 testu pro stanovení pravděpodobnosti přítomnosti skrytých dat. Základní principy pro pochopení útoku autoři podávají na příkladu nástroje EzStego (kapitola ): Ukrývající funkce aplikace EzStego přepisuje nejméně významné bity hodnot jednotlivých pixelů (indexy barevné palety). Přepis nejméně významných bitů transformuje jednu hodnotu do druhé tak, že se liší pouze nejméně významným bitem. Tyto hodnoty (lišící se pouze nejméně významným bitem) označíme jako pairs of values (PoV), tedy páry hodnot. Pokud jsou bity, kterými přepisujeme nejméně významné bity pixelů (tedy bity zprávy) rozděleny se stejnou pravděpodobností, potom i četnosti obou hodnot v každém PoV budou stejné. Na obrázku 14 je vidět, jak se změní četnosti barev, pokud je obrázek modifikován vložením dat, jejichž bity vykazují stejnou pravděpodobnost výskytu jedniček a nul. Myšlenka tohoto útoku je založena na porovnání teoreticky očekávaného rozdělení četností ve steganografickém médiu s rozdělením pozorovaným ve vzorku potenciálně modifikovaného nosiče (Westfeld a Pfitzmann, 1999). Jinými slovy: Teoreticky očekávané rozdělení představuje rozdělení četností hodnot (např. hodnot indexů do barevné palety), pokud by analyzovaný obrázek byl steganografickým médiem. Pozorovaná rozdělení četností odpovídá analyzovanému obrázku. Pokud jsou rozdělení podobná, což se ověří statistickým testem, pak analyzovaný obrázek obsahuje skrytá data. Obr. 14: Histogram rozdělení barev před a po vložení zprávy nástrojem EzStego. Převzato z Attacks on Steganographic Systems (Westfeld a Pfitzmann, 1999). Westfeld a Pfitzmann dále uvádějí, že kritickým bodem je stanovení teoreticky očekávané četnosti rozdělení (tj. četnost výskytu hodnot, jež budeme očekávat po aplikaci steganografických změn). Tato četnost nesmí být odvozena od náhodného vzorku analyzovaného obrázku, neboť ten by mohl být již pozměněn steganografic-
43 2.13 Možnosti útoků na steganografické systémy 43 kým algoritmem. Ve většině případů však originální nosič nemáme pro porovnání k dispozici. Pak teoreticky očekávané četnosti stanovíme jako aritmetický průměr dvou četností v PoV. Čárkovaná linka na obr. 14 spojuje právě tyto průměry. Protože vkládací algoritmus přepisuje nejméně významné bity, nezmění se součet četností dvou hodnot v PoV. Četnost liché hodnoty PoV je přenášena do četnosti sudé hodnoty PoV a naopak. Díky tomu, že součet zůstává konstatují, je aritmetický průměr hodnot PoV stejný pro originální nosič i pro nosič obsahující tajná data. Z tohoto důvodu můžeme teoreticky očekávané četnosti odvodit od náhodného vzorku a nepotřebujeme originální nosič. Stupeň podobnosti je dle Westfelda a Pfitzmanna určen pomocí chi-kvadrát testu. Jednotlivé kroky testu jsou popsány v následujících bodech: 1. Předpokládáme k kategorií, v nichž budeme pořizovat náhodný vzorek pro výpočet očekávaných četností. Každé pozorování proběhne právě v jedné kategorii. Kategorie představují například indexy barevné palety. Z důvodu, že vyšetřujeme páry hodnot, omezíme kategorie pouze na sudé položky palety. 2. Pro i-tou kategorii spočteme teoreticky očekávané četnosti jako n i = {barva utridenyindex(barva) {2i, 2i + 1}} 2 3. Pozorovaná četnost výskytu v našem náhodném vzorku bude n i = {barva utridenyindex(barva) = 2i} 4. χ 2 statistika je daná jako χ 2 k 1 = k (n i n i )2 i=1 s k 1 stupni volnosti. n i 5. p je pravděpodobnost naší statistiky za podmínky, že rozdělení n i a n i jsou stejná. Vypočteme jako integraci funkce hustoty pravděpodobnosti: p = k 1 2 Γ( k 1 2 ) χ 2 k 1 kde Γ představuje Eulerovu funkci Gamma. 0 e x 2 x k dx Westfeld a Pfitzmann provedli experiment (Westfeld a Pfitzmann, 1999), ve kterém zhodnotili sílu útoku testem χ 2, když jej testovali na steganografických médiích vytvořených nástroji EzStego, S-Tools, Steganos a Jsteg. Lze konstatovat, že útok testem χ 2 vykazuje velmi dobré výsledky při sekvenčním přepisování nejméně významných bitů. Například na obrázku 15 vidíme, že útok testem χ 2 poměrně přesvědčivě odhalí zprávu, která byla vložena pomocí programu EzStego, a to i v případě obrázku, kdy by byl vizuální útok bezradný. Důležitá vlastnost útoku χ 2 je ta, že jej lze použít na více formátů obrázků. Například Provos a Honeyman jeho implementaci využili ve svém projektu (Provos a Honeyman, 2003) a potvrdili hypotézu, že pro sekvenčně skrytá data vykazuje test výborné výsledky i v případě analýzy obrázku formátu JPEG. V případě tohoto
44 2.13 Možnosti útoků na steganografické systémy 44 Obr. 15: Nalevo je steganografické médium, do jehož 50 % byla ukryta zpráva nástrojem EzStego. Graf napravo ilustruje úspěšně provedený útok χ 2. Je možné odhadnout i délku skryté zprávy. Převzato z Attacks on Steganographic Systems (Westfeld a Pfitzmann, 1999). formátu se však porovnávaly četnosti nikoliv indexů barevné palety, ale DCT koeficientů. Sekvenčně skrývá data do DCT koeficientů například nástroj Jsteg, který je tímto útokem také dobře odhalitelný, jak je uvedeno nejen v dokumentu (Westfeld a Pfitzmann, 1999), ale i v článku (Provos a Honeyman, 2003). Skutečnost, že se jedná o relativně jednoduchý statistický útok, prokazují nepřesvědčivé výsledky útoku na steganografické médium, do něhož byla data tajné zprávy vložena pomocí pseudonáhodného generátoru. Nejméně významné bity nosiče nejsou v tomto případě modifikovány sekvenčně od začátku, ale v pseudonáhodných intervalech v rámci celého nosiče. Provos a Honeyman útok použili na obrázek, do něhož byla tajná data vložena pomocí nástroje OutGuess. Útok χ 2 ve své nejjednodušší podobě nepodal přesvědčivý důkaz o existenci tajné zprávy, ačkoliv jisté podezření vzbudit může, což je vidět na obrázku 16. Obr. 16: Výsledek útoku χ 2 na steganografické médium vytvořené nástrojem OutGuess. Převzato z Hide and Seek: An Introduction to Steganography (Provos a Honeyman, 2003). Provos a Honeyman v článku (Provos a Honeyman, 2003) nabízejí řešení, v jehož rámci předkládají rozšířený útok χ 2, kdy tento útok není aplikován na obrázek jako celek, ale postupně na jeho dílčí části. Při stanovení šířky této dílčí části jeho autoři
45 2.13 Možnosti útoků na steganografické systémy 45 vychází z výpočtu aritmetického průměru dvou nesouvisejících četností koeficientů (n 2i 1 a n 2i ). Následně se pomocí binárního vyhledávání najde hodnota, pro níž rozšířený χ 2 test nevykazuje korelaci s očekávanou četností odvozenou z nesouvisejících koeficientů (Provos a Honeyman, 2003) Útok analýzou RQP Jessica Fridrich se svými kolegy (Fridrich a Goljan, 2002) vyvinula metodu detekce vložení dat do nejméně významného bitu (LSB) pro obrázky s 24bitovou barevnou hloubkou. Nazvali ji metoda RQP (Raw Quick Pairs). Metoda je založena na analýze párů blízkých barev, které jsou vytvářeny při vkládání dat do LSB. Barvy jsou v obrázcích s 24bitovou barevnou hloubkou reprezentovány hodnotami barevných složek R, G a B. Každá z těchto hodnot je uložena v jednom bajtu. Nechť počet jedinečných barev v obrázku je U. Dále prohlašme o dvou barvách (R 1, G 1, B 1 ) a (R 2, G 2, B 2 ), že tvoří pár blízkých barev, pokud platí R 1 R 2 1 a G 1 G 2 1 a B 1 B 2 1 Uvažujeme-li pouze jedinečné barvy, pak je počet všech párů barev vyjádřitelný kombinačním číslem ( ) U P 2 kde P je počet párů blízkých barev v barevné paletě obrázku. Stanovme poměr R mezi počtem párů blízkých barev a počtem všech párů barev jako R = P ( U 2) kdy poměr R vyjadřuje relativní počet párů blízkých barev v obrázku. Detekční algoritmus je pak následující: 1. V analyzovaném obrázku vyjádříme počet jedinečných barev a v nich počet párů blízkých barev. 2. Vyjádříme poměr R pomocí rovnice uvedené výše. 3. Náhodně vybereme pixely obrázku a vložíme do nejméně významných bitů jejich hodnot bity testovací zprávy. Testovací zpráva by neměla být příliš dlouhá, což by mělo vyloučit případné chyby ve výpočtech pravděpodobnosti. Optimální délka může být určena experimentem na jiných obrázcích. 4. V takto pozměněném obrázku vyjádříme počet jedinečných barev a počet párů blízkých barev. Označme je U a P. Poté vyjádříme poměr R podle stejné rovnice.
46 2.13 Možnosti útoků na steganografické systémy 46 Poměrný počet párů blízkých barev ve vztahu k počtu všech možných párů barev bude nižší v obrázku obsahujícím ukrytou zprávu než v obrázku, jenž skrytou zprávu neobsahuje. Důležitou roli hraje pozorování provedené na pokusném obrázku. Pokud obrázek zprávu již obsahuje, změna v poměrech před a po vložení testovací zprávy nebude výrazná. Tedy R R. Naopak pokud obrázek zprávu neobsahuje, poměr vypočtený před vložením testovací zprávy bude menší než poměr vypočtený poté. Tedy R > R. Jako první krok analýzy by měla být sestavena obsáhlá tréninková databáze obrázků, dle níž bychom stanovili mezní hodnotu pro R. Tato mezní hodnota by R umožnila rozlišit čistý obrázek a steganografický obrázek. Mezní hodnotu autoři navrhují stanovit např. dle vzorce T h = µσ(s) + µ(s)σ σ + σ(s) kde µ, σ jsou průměrná a směrodatná odchylka poměrů R v sadě čistých obrázků. R µ(s), σ(s) jsou průměrná a směrodatná odchylka poměrů R v sadě steganografických R obrázků. Autoři metody v dokumentu (Fridrich a Goljan, 2002) tvrdí, že analýza RQP funguje obstojně, pokud počet jedinečných barev v obrázku (nosiči) nepřesáhne 30 % počtu pixelů. Metoda provádí pouze hrubý odhad velikosti skryté zprávy. Výsledky se stanou vysoce nespolehlivé, pokud počet jedinečných barev přesáhne 50 % počtu pixelů. To často nastává v případě skenovaných obrazů či obrázků vytvořených digitálním fotoaparátem uložených v nekomprimovaných formátech. Další nevýhodou metody RQP je nemožnost její aplikace na obrázky v odstínech šedé Útok RS analýzou Dalším typem statistického útoku představeným v dokumentu (Fridrich et al., 2003) je takzvaná RS analýza. Metoda je použitelná pro nekomprimované hrubé formáty obrázků. Její autoři uvádějí, že vkládání do LSB vytváří nerovnováhu mezi sousedními hodnotami pixelů během vkládání bývají hodnoty 2i a 2i + 1 vzájemně zaměněny, ale nikdy nejsou vzájemně zaměněny s hodnotami 2i 1 nebo 2i+2. Vycházeje ze svého dalšího výzkumu autoři definovali vztah mezi rovinou LSB a rovinou zbývajících sedmi bitů, kdy neztrátová kapacita má být funkcí počtu regulárních a singulárních skupin pixelů. Rozdíl mezi těmito dvěma počty byl stanoven jako rozlišovací statistika. V následujícím textu principy analýzy popíšeme. Předpokládejme, že máme nosič v podobě obrázku o rozměrech M N pixelů, kdy každému pixelu přiřadíme hodnotu z množiny P = {0,...,255 }. Zavedeme diskriminační funkci f, která přiřadí reálné číslo f(x 1,..., x n ) R skupině pixelů G = (x 1,..., x n ). Nechť je funkce f definována jako:
47 2.13 Možnosti útoků na steganografické systémy 47 f(x 1, x 2,..., x n ) = n 1 i=1 x i+1 x i Funkce f měří hladkost skupiny G čím je ve skupině G větší šum, tím vyšší hodnoty nabývá funkce f. Vkládání do LSB zvyšuje šum v obrázku, takže je očekáváno, že hodnota funkce f poté vzroste. Definujme zaměňující funkci F 1 jako následující permutaci na množině P : 0 1, 2 3,..., Změna LSB na x představujícím odstíny šedé je totéž, co aplikace F 1 na x. Definujme také duální koncept nazvaný posunutá záměna LSB F 1 jako: 1 0, 1 2, 3 4,..., , nebo F 1 (x) = F 1 (x + 1) 1, x P Pro úplnost ještě definujme F 0 jako identickou permutaci F (x) = x, x P. Diskriminační funkce f a operace záměny definují tři skupiny pixelů: skupina G je regulární (R), pokud platí f(f (G) > f(g), skupina G je singulární (S), pokud platí f(f (G) < f(g), skupina G je neměnná (U), pokud platí f(f (G) = f(g). F (G) znamená aplikaci záměnné funkce F na členy vektoru G = (x 1,..., x n ). Pokud aplikujeme rozdílnou záměnu na rozdílné pixely skupiny G, zachytíme přiřazení záměny pixelů maskou M, což je n-tice s hodnotami 1, 0 a 1. Zaměňovaná skupina F (G) je definována jako (F M(1) (x 1 ), F M(2) (x 2 ),..., F M(n) (x n )). Záměna v typických obrázcích častěji vede k růstu diskriminační funkce f než k jejímu poklesu. Celkový počet regulárních skupin bude pak vyšší než celkový počet singulárních skupin. Označme relativní počet regulárních skupin s nikoliv negativní maskou M jako R M (v procentech všech skupin) a označme S M relativní počet singulárních skupin. Máme tedy R M + S M 1 a R M + S M 1. Důležitou hypotézou této stegoanalytické metody pro typický obrázkový nosič je předpoklad, že hodnota R M je přibližně rovna hodnotě R M. Totéž pro S M a S M : R M R M a S M S M Dle autorů je zjištěno, že tato rovnice velmi přesně odpovídá obrázkům vytvořeným digitálním fotoaparátem a uložených ve formátu JPEG i v nekomprimovaných formátech. Vztahy v rovnici jsou narušeny náhodností, která vznikne vkládáním do LSB. Náhodnost v LSB způsobí, že se rozdíl mezi R M a S M zmenšuje se zvyšující se délkou ukrývané zprávy. Rozdíl mezi R M a S M se tím naopak zvětší. Graf znázorňující R M, S M, R M a S M jako funkci počtu pixelů se změněným LSB je znázorněn na obr. 17 (RS diagram). Diagram znázorňuje očekávané hodnoty R M a S M celého statistického vzorku pro všechny možné (náhodné) podoby LSB. Vysvětlení rozdílu mezi R M a S M autoři provedli za použitím masky M = [010], přičemž podobně lze údajně argumentovat i pro jiné masky. Definujme množiny C i =
48 2.13 Možnosti útoků na steganografické systémy 48 Obr. 17: RS diagram obrázku pořízeného digitálním fotoaparátem. Osa x představuje procento pixelů se záměnou LSB, osa y představuje relativní počet regulárních a singulárních skupin s maskou M a M, M = [0110]. Převzato z Quantitative steganalysis of digital images: Estimating the secret message length (Fridrich et al., 2003). {i, 2i + 1}, i = 0, , a nadskupiny C rst = {G C C r C s C t }. Dostaneme tak nadskupin (clique), každá nadskupina se skládá z osmi skupin (trojic). Čím větší náhodnost LSB, tím více jsou si nadskupiny blízké. Za účelem analýzy autoři rozlišují čtyři typy nadskupin. Tab. 6: Čtyři typy nadskupin (clique). Tabulka převzata z Quantitative steganalysis of digital images: Estimating the secret message length (Fridrich et al., 2003). Typ nadskupiny Záměna F 1 Záměna F 1 r = s = t 2R, 2S, 4U 8R r = s > t 2R, 2S, 4U 4R, 4U r < s > t 4R, 4S 4R, 4S r = s = t 8U 8U V tabulce 6 jsou uvedeny tyto čtyři typy nadskupin a počty skupin R, S a U jako výstup funkcí F 1 a F 1 poté, co bylo provedeno znáhodnění LSB. Z tabulky lze vyčíst, že zatímco znáhodnění nejnižších bitů (LSB) má tendenci vyrovnat počty skupin R a S v každé nadskupině, kde byla použita funkce F 1, v nadskupinách, kde byla aplikována funkce F 1, se počet skupin R zvyšuje a počet skupin S snižuje. Dalším krokem analýzy je odhad délky skryté zprávy, jehož netriviální postup je taktéž uveden v dokumentu (Fridrich et al., 2003). Pouze uvedeme, že dle autorů mají vliv na přesnost odhadu skryté zprávy tři faktory: charakter nosiče, úroveň šumu a umístění zprávy.
49 2.13 Možnosti útoků na steganografické systémy Další typy statistických útoků V literatuře jsou popsány ještě složitější metody statistických útoků, které spočívají v definování efektivní diskriminační funkce, jež je schopna na základě tréninkových množin čistých a steganografických obrázků detekovat skrytá data. Například Ker v dokumentu (Ker, 2008) představuje takzvaný Couple detector. Metoda porovnává změny v hodnotách sousedních párů pixelů způsobené operací vkládání do LSB. Rozlišuje následující typy párů pixelů: P m všechny hodnoty sousedních pixelů (x, y), C m páry pixelů (x, y) odpovídající hodnotě x 2 y 2 = m, E m páry s hodnotami ve tvaru (2k, 2k + m), O m páry s hodnotami ve tvaru (2k + 1, 2k m). Ker uvádí příklad: Pokud jsou hodnoty sousedních pixelů 66 a 72, pak tento pár bude považován za typy P, C 3 a E 6. Typy párů poté vytvoří takzvané trasovací množiny a trasovací podmnožiny (viz obrázek 18). Obr. 18: Trasovací množiny a podmnožiny v metodě Couple detector. Převzato z Information Hiding and Covert Communication (Ker, 2008). V dalším postupu poté Ker vychází z předpokladu, že vkládání do LSB přemisťuje páry v rámci trasovacích podmnožin, ale páry v trasovacích množinách neovlivní. Mějme tedy index m. Poté zjišťujeme, jak jsou ovlivněny trasovací podmnožiny trasovací množiny C m. Ker zkonstruoval pomocí porovnání párů před a po vložení do LSB estimátor e m, který odpovídá počtu párů v množině E m před vložením do LSB a estimátor o m, který odpovídá počtu párů v množině O m po vložení do LSB. Ker dále odvodil, že pro přirozené obrázky platí: e m o m Pokročilou oblast stegoanalytických metod představují takzvané klasifikátory (classification engines). Klasifikátory mají za cíl rozlišit, zda analyzovaný obrázek patří do třídy steganografických obrázků či do třídy normálních obrázků (Provos a Honeyman, 2003). Tamtéž je dále uvedeno, že statistiky odvozené z obrázků v tréninkové množině určují vlastnosti diskriminační funkce, která rozděluje obrázky do tříd. Soubor těchto statistik nazýváme vektor charakteristik. Dle Kera se lze setkat s následujícími klasifikátory (Ker, 2008):
50 2.13 Možnosti útoků na steganografické systémy 50 Fisherův lineární diskriminátor, vícevrstvé neuronové sítě, algoritmus podpůrných vektorů, algoritmus k nejbližších sousedů. Všechny zmíněné metody představují algoritmy strojového učení. Jejich podrobný popis již přesahuje rozsah této práce, neboť se jedná o značně netriviální nástroje. Důležitá je jejich správná aplikace na problém stegoanalýzy. Provos a Honeyman v článku (Provos a Honeyman, 2003) popisují principy implementace algoritmu podpůrných vektorů. Podstatou je konstrukce diskriminační funkce statistik obrázku, která rozlišuje mezi dvěmi třídami. Pomocí Neyman- -Pearsnova kritéria se ověřuje platnost hypotéz H 0 (obrázek neobsahuje steganografický obsah) a H 1 (obrázek obsahuje steganografický obsah).
51 3 VLASTNÍ PRÁCE 51 3 Vlastní práce 3.1 Metodika a návrh řešení Pro praktickou realizaci některé z technik stegoanalýzy bylo bylo nutné sestavit na základě literatury určitá teoretická východiska. V kapitole 2 je podán přehled technik moderní digitální steganografie a stegoanalýzy, z něhož je možné dále čerpat. Vzhledem ke skutečnosti, že stegoanalýza je poměrně mladou vědní disciplínou (Chandramouli, 2002), je velmi složité vycházet z odborné literatury, která by byla v podobě tištěných publikací. Naprostou většina článků o problematice steganografie a stegoanalýzy nalezneme v elektronické podobě. V některých případech se lze setkat i s tištěnou podobou těchto článků v odborných vědeckých časopisech. Zcela jednoznačná je absence odborných článků v českém jazyce. Velmi důležitou roli hrál tedy při sestavování teoretických východisek překlad z anglického jazyka. Zvláště v případě odborného názvosloví bylo nutno vyhnout se zavádění opisných neologismů, které by sice vystihovaly podstatu pojmu, ale z čistě formálního hlediska by se jednalo o nesmysly komplikující orientaci v problematice (např. stego-only attack). Z množství analyzovatelných formátů steganografických nosičů byl pro účel této práce vybrán formát BMP s barevnou hloubkou 24 bitů na pixel. Jedná se o nevhodné rozhodnutí vzhledem k současné nepopularitě formátu BMP na internetu, ovšem rozhodujícím faktorem byla možnost velmi jednoduchého přístupu k datům nesoucím skrytou informaci. Autor této práce je přesvědčen o zobecnitelnosti podstaty implementovaných technik i na jiné obrázkové či mediální formáty. Protože cílem práce je implementovat techniky stegoanalýzy konkrétně na steganografický nástroj Steghide a on-line steganografický systém Matěje Zapletala (M. Z.), bylo nutné seznámit se s jejich strukturou a vyhodnotit způsob, jakým ukrývají zprávy do obrázkových nosičů formátu BMP. Za tímto účelem byl navrhnut algoritmus vypisující obrazová data ve formátované podobě. Výsledky tohoto pozorování byly použity pro definici algoritmu extrahování skryté zprávy. K nástrojům Steghide a M. Z. byl zvolen odlišný přístup, neboť technické rozdíly mezi nimi jsou velmi podstatné. M. Z. představuje velmi jednoduchý steganografický nástroj, naopak Steghide představuje velmi složitě detekovatelnou aplikaci. Pro analýzu činnosti programu Steghide byly stanoveny zjednodušující předpoklady: Steghide je použit ve svém nejjednodušším (tzn. i nejméně bezpečném) módu není využito šifrování, komprese zprávy, ani nejsou vkládány doplňující informace jako kontrolní součet či název souboru se zprávou. Šifrování nebylo využito ani u aplikace M. Z. V případě obou programů uvažujeme pouze práci se soubory formátu BMP. V případě nástroje M. Z. jsme se zaměřili na implementaci extrakčního útoku, v případě Steghide na implementaci statistického útoku analýzou RQP. Stanovili jsme, že řešením bude navržení programu s názvem BMPdetect. Požadavky na jeho funkčnost byly definovány následovně:
52 3.2 Steganografie pomocí aplikace M. Z. 52 spustitelnost v režimech čtení obrázku, analýza obrázku, extrakce tajné zprávy z LSB, přeložitelnost pod operačním systémem Windows i Unix, v režimu analýza obrázku bude výstupem informace o přítomnosti či nepřítomnosti skryté zprávy, v režimu extrakce tajné zprávy z LSB bude výstupem smysluplná zpráva získaná z nejnižších bitů obrázku (pokud zpráva nebude smysluplná, zobrazí se informace, že nosič zprávu neobsahuje). Součástí řešení byl i praktický test funkčnosti navrženého programu. Bylo stanoveno za jakých podmínek lze toto řešení úspěšně použít a za jakých již nikoliv. Jako implementační nástroj byl zvolen programovací jazyk C++, který odpovídá požadavku na přenositelnost, je nízkoúrovňový a disponuje předdefinovanými datovými kontejnery, které usnadní práci s obrazovými daty. Díky tomu, že se jedná o objektově orientovaný jazyk, bylo možné snadno využít všech výhod spojených s objektovým návrhem programu. 3.2 Steganografie pomocí aplikace M. Z. Funkci aplikace s námi stanoveným pracovním názvem M. Z. demonstrujeme na skrytí pokusné zprávy do obrázku formátu BMP o rozměru 5 5 pixelů. Obrázek je tvořen jednolitou barvou s hodnotami jednotlivých barevných složek (R = 0, G = 0, B = 0), což odpovídá černé. Na obrázku 19 vidíme vytvořený obrázek v měřítku 16 : 1, přičemž obrázek byl vytvořen v programu Corel PHOTO-PAINT X4. Na stejném obrázku můžeme vidět i výstup programu BMPdetect, který představuje praktický výstup této práce. Program byl spuštěn v režimu formátovaného výpisu všech pixelů po pěticích. Jak již bylo uvedeno, jednotlivé barevné složky všech pixelů jsou rovny nule. Nyní proveďme skrytí tajné zprávy do nosiče, kterým bude pokusný obrázek, pomocí webové aplikace M. Z. Tajnou zprávou bude znak a, jehož decimální reprezentace dle ASCII tabulky je 97, binárně Ponecháme implicitní nastavení aplikace, tedy operace: skrýt, použít šifrování TripleDES: ne, metoda uložení zprávy: do nejnižšího bitu. Jako obrázek zadáme námi vytvořená pokusný obrázek black 5x5.bmp. Po odeslání formuláře se na webové stránce zobrazí steganografický obrázek obsahující námi zadanou zprávu i obrázek původní. Steganografický obrázek s názvem black 5x5 copy.bmp opět otevřeme v grafickém programu a zadáme měřítko 16 : 1. Zároveň necháme vypsat obsah steganografického obrázku programem BMPdetect. Výsledek operace je znázorněn na obrázku 20. Z výpisu obsahu steganografického obrázku je patrné, že čteme-li nejméně významné bity sekvenčně od začátku, dostáváme binární posloupnost (Bajty představující barevné složky R, G a B jsou v datech formátu BMP uvedeny naopak, tedy B, G, R. Z toho vyplývá, že i nejméně významné bity musíme číst v tomto pořadí, tedy B G R B G R... )
53 3.2 Steganografie pomocí aplikace M. Z. 53 Obr. 19: Pokusný obrázek formátu BMP o rozměrech 5 5 pixelů. Nalevo poté výpis jeho bitmapy programem BMPdetect. Zdroj: vlastní práce. Neobvyklá situace nastává, porovnáme-li oddělovače konců řádků původního a steganografického obrázku. Ve výpisu na obrázku 19 je možné vidět, že za počtem pixelů odpovídající šířce obrázku, je zapsán bajt hodnoty 0, který slouží jako oddělovač řádků. Ovšem ve výpisu na obrázku 19 je možné si všimnout, že oddělovač za prvním řádkem byl změněn následkem vkládání do LSB na 1. Aplikace M. Z. tedy pro vkládání do nejméně významných bitů používá i hodnoty oddělovačů řádků. To je velmi důležitý poznatek, který bude muset být zohledněn při implementaci detekce skryté zprávy, případně při jejím extrahování. Je například možné tvrdit, že narazíme-li při analýze obrázku na modifikovaný oddělovač konce řádku, pak se téměř jistě bude jednat o steganografické médium vytvořené aplikací M.. Z. Je tedy ověřeno, že aplikace M. Z. vkládá data tajné zprávy do obrázku sek- Obr. 20: Pokusný obrázek se zprávou a skrytou aplikací M. Z. Vpravo jeho výpis programem BMPdetect. Zdroj: vlastní práce.
54 3.3 Steganografie pomocí aplikace Steghide 54 venčně od začátku. Dále je ověřeno, že zpráva je ukončena binární posloupností , což odpovídá hodnotě 255 dekadicky. Při extrahování zprávy zohledníme i tuto skutečnost. Z uvedeného je možné odvodit obecný vztah pro výpočet kapacity nosiče v závislosti na počtu pixelů. Každý pixel je představován třemi bajty, do nichž lze skrýt tři bity zprávy. Nechť P ix představuje počet pixelů nosiče. Pak počet bitů zprávy, jenž lze ukrýt, bude 3P ix 8 (odečtení osmi odráží vložení ukončovací sekvence o rozsahu osmi bitů). Víme-li, že osm bitů tvoří jeden bajt, pak maximální počet vkládaných bajtů h max bude: (3P ix 8) h max = 8 Pokud bychom chtěli být naprosto přesní, zohledníme i vkládání bitů do oddělovačů, kdy by byl čitatel ve tvaru (3P ix 8) + P O, kde P O představuje počet všech oddělovačů řádků v obrázku. 3.3 Steganografie pomocí aplikace Steghide Základní principy ukrývání zpráv do obrázků (i audio souborů) byly popsány v kapitole Základní odlišnost od programu M. Z. spočívá v implementaci pseudonáhodného výběru pixelů pro vložení dat zprávy. Modifikace LSB se tedy nedějí sekvenčně od začátku, ale jsou realizovány v rámci celého nosiče. Základní předpoklady útoku na tento pokročilý nástroj byl uveden v metodice konstantní inicializační heslo, nevyužití komprese, šifrování, kontrolního součtu a neukládání názvu souboru se zprávou. Předpoklady budou splněny, pokud program bude spuštěn s přepínači -Z (nekomprimovat zprávu), -K (nevkládat kontrolní součet), -N (nevkládat jméno souboru) a -e none (nešifrovat zprávu). Při výzvě k zadání hesla bude zadán prázdný řetězec. Stejně jako v příkladu v předchozí kapitole, připravme testovací zprávu v rozsahu jednoho znaku a, kterou zapíšeme do textového souboru. Pokud se pokusíme zprávu vložit do obrázku black 5x5.bmp zmíněného v předchozí kapitole, setkáme se s varovným hlášením: steghide: the cover file is too short to embed the data. Je tedy zřejmé, že nosič o rozměrech 5 5 pixelů (75 bajtů) je pro ukrytí zprávy o rozsahu jeden bajt příliš malý. Vytvoříme-li pokusný nosič o rozměrech pixelů, pak již skrytí zprávy proběhne úspěšně. Je třeba stanovit, jaká je minimální délka nosiče pro ukrytí zprávy o rozsahu 1 B. Byla tedy provedena série experimentů s obrázkem o původních rozměrech 26 1 pixel, kdy se průběžně měnila jeho velikost a sledovalo se, zda Steghide povolí vložení jednobajtové zprávy. Výsledkem experimentu jsou tato zjištění: na skrytí zprávy rozsahu 1 B je třeba alespoň 84 pixelů, na skrytí každého dalšího bajtu zprávy je třeba obrázek rozšířit o 8 pixelů.
55 3.3 Steganografie pomocí aplikace Steghide 55 Pro skrývání zpráv pomocí Steghide do obrázků formátu BMP s barevnou hloubkou 24 bajtů na pixel je možné popsat vztah mezi velikostí vkládané zprávy (v bajtech) a minimálním počtem pixelů obrázku pomocí vzorce: P ix min = h mes kde P ix min je nutný minimální počet pixelů nosiče a h mes je velikost zprávy v bajtech. Z uvedeného vztahu lze odvodit obecný vzorec pro maximální kapacitu nosiče, pokud je do něj skryta zpráva nástrojem Steghide: P ix 76 h max = 8 kde h max je maximální velikost zprávy v bajtech a P ix je počet pixelů nosiče. Tento vztah budeme používat pro stanovení velikosti zprávy, která zabere např. 50 % kapacity nosiče. Vytvořme tedy obrázek o rozměrech 7 12 pixelů jednolité barvy (R = 0, G = 0, B = 0), do něhož pomocí nástroje Steghide ukryjeme zprávu a. Situaci před a po vložení ilustrují obr. 21 a 22. Obr. 21: Vpravo část výpisu pokusného obrázku o rozměrech 7 12 pixelů, vlevo zvětšený obrázek. Všechny barevné složky jsou nulové. Zdroj: vlastní práce. Obr. 23 ilustruje pozici pozměněných pixelů následkem vložení do LSB. Ačkoliv se nejedná o všechny použité pixely, je patrná náhodnost jejich výběru a rozprostření po celém obsahu nosiče. Porovnáme-li výpis programu BMPdetect na obr. 22 s uměle vyznačenými pozicemi změněných pixelů na obr. 23, dospějeme k závěru, že bitmapy jsou zrcadlově otočeny kolem pomyslné horizontální osy vedoucí středem bitmapy. Je tomu tak proto, že BMPdetect načítá obrazová data opačným způsobem než Steghide. Při implementaci extrahování dat bude tento poznatek vhodné zohlednit.
56 3.4 Načtení obrázku formátu BMP 56 Obr. 22: Steganografický obrázek o rozměrech 7 12 pixelů se skrytou zprávou. Nalevo část výpisu, přičemž pixely, kde došlo ke změně jsou označeny. Zdroj: vlastní práce. Obr. 23: Steganografický obrázek se zprávou a. Bíle označeny pozměněné pixely. Zdroj: vlastní práce. Jako zásadní úkol při implementaci extrahování LSB ve steganografických médiích vytvořených aplikací Steghide se jeví simulace činnosti generátoru pseudonáhodných čísel, na jehož základě jsou vybírány pixely určeny pro obsažení bitů tajné zprávy. Vycházet lze i ze znalosti, že vkládací algoritmus Steghide tento generátor inicializuje pomocí hashe MD5 získaného ze zadaného hesla. V našem případě bude tato hodnota konstantní a bude odpovídat hashi MD5 prázdného řetězce. 3.4 Načtení obrázku formátu BMP Fundamentální úkol pro zajištění funkce programu pro analýzu digitálního obrázku je načtení obrazových dat do paměti. Jelikož byl pro realizaci programu BMPdetect zvolen jazyk C++, bude vhodné využívat datový kontejner vector. Jedná se o šablonu, jež očekává jako parametr definici datového typu, jehož budou položky vektoru (pole). Zásadní výhodou použití datového kontejneru je ovšem jeho dynamická velikost, neboť při počáteční deklaraci může být jeho velikost nulová. Nyní odpovězme na otázku, co bude do dynamického pole představující konkrétní obrázek ukládáno. Předmětem stegoanalýzy budou hodnoty obrazových bodů
57 3.4 Načtení obrázku formátu BMP 57 pixelů. Hodnota každého pixelu je v obrázcích formátu BMP s barevnou hloubkou 24 bitů na pixel představována třemi bajty, které nesou informaci o barevných složkách R, G a B. Položky vektoru nechť tedy představují jednotlivé pixely. Každý pixel nechť obsahuje tři celočíselné proměnné malého rozsahu odpovídající barevným složkám. Budeme-li chtít zachovat přirozenou strukturu obrázku ve smyslu šířka výška, použijeme pro uchování hodnot pixelů nikoliv jednorozměrné dynamické pole, ale vícerozměrné. Implementace v jazyku C++ umožňuje jako parametr datového kontejneru vector dosadit datový typ jiného vektoru. Popsaný princip ilustruje obr. 24 Obr. 24: Uložení obrazových dat pomocí datového kontejneru vector. Pixely uchovávány v podobě matice. Zdroj: vlastní práce. Vektor obsahující odkazy na vektory obrazových bodů bude mít rozměr odpovídající výšce obrázku a jednotlivé vektory obrazových bodů budou mít rozměr odpovídající šířce obrázku (v pixelech). Tímto způsobem docílíme efektivnějšího procházení obrázku. Protože samotné pixely jsou tvořeny dalšími třemi hodnotami, bude vhodné každý pixel považovat za samostatný objekt. Vektor obrazových bodů bude moci poté obsahovat pouze ukazatele na jednotlivé body. Definujme tedy třídu Bod, jež bude tvořena třemi soukromými atributy popisujícími barevné složky pixelu. Jednotlivé definice zmíněné výše tedy shrňme: class Bod { public: unsigned short r; unsigned short g; unsigned short b; }; vector< vector<bod*> > obrazek; // odkazy na řádky vector<bod*> line; // řádek obrázku
58 3.5 Implementace útoku analýzou RQP 58 Protože pro stegoanalýzu médií vytvořených aplikací M. Z. je nutné uchovávat i hodnoty oddělovačů řádků, za tímto účelem ještě definujme vektor vektorů uchovávající datový typ short. Oddělovačů může být blíže nespecifikovaný počet, z toho důvodu je vhodné pro ukládání konkrétních hodnot využít dynamické pole. Všechny operace s obrázkovými daty shrňme do samostatnou třídy Picture. Pro případnou komunikaci s jinými objekty v třídě definujme důležitou veřejnou metodu, která bude vracet odkaz na vektor obsahující obrázkové body a metodu vracející odkaz na vektor oddělovačů. 3.5 Implementace útoku analýzou RQP Výpočet ukazatelů U a P Vycházejme z teoretických poznatků uvedených v kapitole Základ algoritmu RQP analýzy vyžaduje vyčíslení proměnných U (počet jedinečných barev analyzovaného obrázku) a P (počet párů blízkých barev v barevné paletě, tedy mezi jedinečnými barvami). Abychom oddělili logiku zpracování obrazových dat a výpočtů statistik, zavedeme třídu Stat, která bude zajišťovat provedení RQP analýzy. Konstruktor převezme odkaz na vektor obrazových dat a následně z nich vytvoří vlastní barevnou paletu obrázku. Barevná paleta může být opět realizována jako datový kontejner vector obsahující odkazy na instance (objekty) třídy Bod. Tento vektor pojmenujme barevnapaleta. Za účelem naplnění barevné palety bude nutné projít všechny uložené pixely obrázku a při pokusu přidat je do palety bude nutné zase kontrolovat, zda se neshoduje s nějakým z již přidaných pixelů. Pokud nikoliv, jedná se o jedinečnou barvu (resp. hodnoty R, G, B) a pixel, který ji reprezentuje, může být přidán do palety. Algoritmus ilustruje obr. 25. Obr. 25: Algoritmus přidávání barev do barevné palety obrázku. Zdroj: vlastní práce.
59 3.5 Implementace útoku analýzou RQP 59 Je-li barevná paleta připravena, pak lze vyčíslit atributy U a P. Jednodušší je vyčíslení počtu jedinečných barev, neboť toto odpovídá velikosti (počtu položek) barevné palety. Třída vector disponuje metodou size(), jež vrací počet položek v datovém kontejneru. Atribut U tedy vyčíslíme jako U = barevnapaleta.size(); Vyčíslení atributu P vyžaduje podobný postup, jako byl popsán pro vkládání nové barvy do barevné palety. V kapitole je uvedeno, že dvě barvy v pojetí naší implementace to jsou současně objekty představující obrazové body (R 1, G 1, B 1 ) a (R 2, G 2, B 2 ) tvoří pár blízkých barev, je-li splněna podmínka ( R 1 R 2 1 a současně G 1 G 2 1 a současně B 1 B 2 1). To lze přepsat jako (R 1 R 2 ) 2 + (G 1 G 2 ) 2 + (B 1 B 2 ) 2 3 Definujme soukromou metodu umocnina2(int zaklad), jež bude vracet výsledek operace druhé mocniny celého čísla předaného v parametru. Atribut P na počátku nastavme na nulu. Pro stanovení počtu párů blízkých barev bude nutné každý pixel v barevné paletě porovnat se všemi ostatními pixely v barevné paletě, přičemž bude proveden součet druhých mocnin rozdílů atributů r, g a b. V případě, že součet bude menší nebo roven třem, zvýšíme počítadlo P o jedna. Na konci průchodu bude atribut P roven počtu párů blízkých barev. Algoritmus ilustruje obr. 26. Obr. 26: Algoritmus vyčíslení počtu párů blízkých barev. Zdroj: vlastní práce. Je zřejmě efektivnější porovnávat pixel na i-té pozici palety pouze s pixely na pozici nulté až i 1 než se všemi pixely palety, neboť i takto dojde k otestování všech možných dvojic.
60 3.5 Implementace útoku analýzou RQP 60 Kvůli výpočtu poměru R je nutné definovat metodu faktorial(int cislo), jež rekurzivním způsobem vypočítá faktoriál celého čísla předaného v parametru. S pomocí této funkce vyčíslíme kombinační číslo ( ) U 2 podle vztahu pro výpočet ( ) n k = n! pro n k 0. Pro náš specifický případ, kdy chceme zjistit počet k!(n k)! všech možných dvojic, je možné vztah upravit na ( ) U = U! 2 2(U 2)!. Vlastní výpočet poměru R = ( P je pak již triviální záležitostí. Poměr takto U 2) získaný je třeba následně vložit do kontextu vlastností analyzovaného obrázku. Za tímto účelem by měla být sestavena tréninková databáze vlastností obrázků, z níž by bylo možné odvodit, zda se jedná o steganografické médium či nikoliv Modifikace souboru skrytím testovací zprávy Podstatou analýzy RQP je, jak bylo uvedeno v kap , porovnání poměrů počtu párů jedinečných barev ku počtu všech možných párů jedinečných barev analyzovaného obrázku a analyzovaného obrázku modifikovaného vložením krátké testovací zprávy. Za tímto účelem tedy definujme třídu Modifikator, která do kopie matice pixelů analyzovaného obrázku vloží testovací zprávu. Je zřejmé, že délka testovací zprávy bude různá pro různé velikosti analyzovaných obrázků. Protože budeme chtít proces vkládání automatizovat, zavedeme pro nárůst velikosti testovací zprávy krok 50 B. Soubory s testovacími zprávami pojmenujeme dle vzoru velikost v bajtech.txt. Vytvoříme tedy testovací zprávy v souborech 20.txt, 50.txt, 100.txt, 150.txt, 200.txt, 250.txt,..., 950.txt, 1000.txt. Na základě několika pokusů byla optimální velikost testovací zprávy stanovena jako 20 % maximální steganografické kapacity analyzovaného média. Např. pro program Steghide je výpočet této kapacity uveden v kapitole 3.3. Nechť konstruktor třídy Modifikator převezme ukazatel na objekt třídy Picture. Načte ukazatel na vzorovou matici pixelů a získá výšku a šířku obrázku v pixelech. Na základě těchto údajů stanoví 20 % maximální kapacity (požadovaná velikost testovací zprávy více v kapitole 3.5.4) a toto číslo zaokrouhlí na padesátku nahoru. Požadovaná velikost bude převedena na řetězec a tento řetězec bude konkatenován s řetězcem ".txt". Výsledný řetězec představuje název souboru s potřebnou testovací zprávou. Tímto postupem automatizujeme výběr testovací zprávy. Konstruktor dále vytvoří kopii vzorové matice pixelů pro účely modifikace. Soubor s testovací zprávou načteme v binárním režimu. Budeme z něj číst bloky o rozsahu jeden bajt. Každý načtený bajt převedeme na osm bitů, které vložíme do pole bitů (datový kontejner vector obsahující buď čísla jedna nebo nula). Převod načteného bajtu na bity ilustruje obrázek 27. Bity testovací zprávy z vektoru bitpole vložíme do kopie matice pixelů pomocí náhodného výběru hostitelských pixelů. Náhodný výběr umožní použití generátoru náhodných čísel, který se inicializuje systémovým časem. Vygenerované náhodné číslo bude udávat vzdálenost od naposledy použitého hostitelského pixelu (pixelu, do něhož vkládáme 3 bity testovací zprávy).
61 3.5 Implementace útoku analýzou RQP 61 Obr. 27: Schématické znázornění algoritmu převádějícího hodnoty bajtů na pole bitů. Zdroj: vlastní práce. Generování náhodného čísla musí probíhat v intervalu 1, max, kde horní hranici max vypočteme jako 3P ix max = h mess kde P ix je počet pixelů a h mess je délka testovací zprávy v bitech. Výpočet vychází z úvahy, že do každého pixelu vložíme tři bity zprávy. Vydělením trojnásobku počtu pixelů počtem bitů zprávy zjistíme kolikrát se bity zprávy vejdou do bitů pixelů. Pokud jednou, maximální vzdálenost hostitelských pixelů bude 1. Pokud označíme pixel za hostitelský, přepíšeme LSB jeho atributů r, g a b tak, aby odpovídaly třem bitům skrývané testovací zprávy uložených ve vektoru bitpole. Učiníme tak podle pravidla 0 1, 2 3,..., Jinými slovy je-li třeba změnit LSB bajtu o hodnotě 255, změň ji na 254 a naopak. Skrytou testovací zprávu sice nebudeme schopni zpětně přečíst (generování náhodných čísel nejsme schopni inicializovat stejnou hodnotou systémového času), což ale nepředstavuje žádnou komplikaci. Smyslem této modifikace je pouze pozměnit kopii pixelů analyzovaného obrázku vložením testovací zprávy do LSB. Veřejná metoda vratpixely() vrátí ukazatel na modifikovanou matici pixelů, což je důležité pro to, aby tato matice mohla být využita objektem třídy Stat za účelem porovnání poměrů R a R Funkce porovnání poměrů R a R Jak bylo zmíněno v kapitole , důležitou úlohu při stanovení, zda se jedná či nejedná o steganografické médium představuje porovnání dvou poměrů R (získa-
62 3.5 Implementace útoku analýzou RQP 62 ného z analyzovaného obrázku) a R (získaného ze stejného obrázku, ale do něhož byla vložena krátká testovací zpráva). Poté by mělo platit: Pokud analyzovaný obrázek obsahuje skrytou zprávu, bude R R. Tzn. R 1. R Pokud analyzovaný obrázek neobsahuje skrytou zprávu, bude R > R, tedy R > 1. R Definujme veřejnou metodu třídy Stat, která ponese název porovnej2r(). Metoda převezme jako parametry dvě hodnoty R a R. Na základě výše popsaného vypočte poměr R R. Zásadní otázkou je, jak stanovit toleranci pro vztah R 1. Hodnoty 1,0 výsledný poměr dosahuje jen ve velmi speciálním případě, kdy by byla testovací zpráva R totožná se zprávou ukrytou v analyzovaném obrázku a kdy by navíc byla ukryta ve stejných bitech. V kapitole je popsán postup stanovení fixní tolerance 10 % Výsledky Experimentálně bylo použito několika obrázků formátu BMP, které se vyznačovaly podobným počtem pixelů, a to přibližně Obrázky nebyly velkých rozměrů především z důvodu rychlejšího výpočtu statistik. Lze je rozdělit na skupiny, zejména dle poměru počtu jedinečných barev ku počtu pixelů. Jak bylo uvedeno v kapitole , analýza RQP je nejúčinnější pokud počet jedinečných barev nepřesáhne 30 % počtu pixelů. Cílem bylo odhalování přítomnosti zpráv skrytých pomocí aplikace Steghide. Za pomoci programu BMPdetect spuštěného v režimu Analýza souboru byly postupně vyčísleny hodnoty R a R pro obrázky čisté i steganografické. Následně byl stanoven fixní limit pro poměr R, jenž by ve většině případů rozlišoval, zda je analyzovaný R obrázek steganografický či nikoliv. Má-li u steganografických obrázků platit R 1, R pak ve většině námi zjištěných případů (kdy měla analýza RQP smysl) byla vhodná tolerance 10 %. Důležitým prvkem analýzy RQP je porovnání analyzovaného obrázku s jeho kopií, do níž byla vložena krátká testovací zpráva. Jako délka testovací zprávy se nám osvědčilo 20 % kapacity analyzovaného obrázku v bajtech. Tato hodnota byla zohledněna při nastavení ve třídě Modifikator. Analýzu obrázku sample.bmp je možné provést spuštěním programu BMPdetect s následujícími parametry: BMPdetect -a sample.bmp. Program vypočítá a porovná hodnoty R, R a pokud bude jejich rozdíl činit maximálně 10 %, o souboru sample.bmp bude prohlášeno, že pravděpodobně obsahuje skrytou zprávu, neboť platí R R. Pokud bude poměr jedinečných barev ku počtu pixelů souboru sample.bmp větší než 30 %, program zobrazí upozornění na nespolehlivost analýzy. Pokus jsme provedli na pěti obrázcích z kategorií: textura, barevný přechod, jednoduchá ilustrace, ilustrace v pravých barvách, jednoduchá fotografie, fotografie v pravých barvách. Přívlastkem jednoduchá je myšleno neobsahující více než 255 jedinečných barev. Zástupce jednotlivých kategorií ilustruje obrázek 28.
63 3.5 Implementace útoku analýzou RQP 63 Obr. 28: Kategorie obrázků použitých v experimentu: fotografie v pravých barvách (fototrue.bmp), jednoduchá fotografie (fotolow.bmp), jednoduchá ilustrace (ilustlow.bmp), ilustrace v pravých barvách (ilusttrue.bmp), barevný přechod (prechod.bmp) a textura. Zdroj: vlastní práce. Výsledky analýzy jsou uvedeny v tabulce 7. Do obrázků byla vkládána zpráva pomocí programu Steghide o rozsahu 50 % jejich steganografické kapacity. Velmi zajímavé a zároveň důležité je zjištění, že z důvodu použití generátoru náhodných čísel při vkládání testovací zprávy se výsledky R provedeného v rámci R jednoho obrázku liší případ od případu (vždy je vkládáno do jiných pixelů). Rozptyl výsledků sice není velký, ovšem z tohoto zjištění plyne doporučení, aby byla analýza spuštěna vícekrát (my jsme ji u jednoho souboru spouštěli pětkrát). Pokud se status kvůli výskytu hodnoty poměru na hranici tolerance liší, je vhodné k výsledkům analýzy přistupovat opatrně. Poměry R představují aritmetický průměr z pěti provedených analýz daného R souboru. Tab. 7: Výsledky útoku analýzou RQP. Sloupec Průměrné R R představuje aritmetický průměr z pěti výsledků. Zdroj: vlastní práce. Soubor Skrytá zpráva Průměrné R R textura.bmp ne 1,3861 ne ( U = 0, 02) ano 1,0015 ano P ix prechod.bmp ne 86,9493 ne ( U = 0, 02) ano 0,9821 ano P ix ilustlow.bmp ne 115,0094 ne ( U = 0, 02) ano 1,0968 ano P ix ilusttrue.bmp ne 1,0972 ano ( U = 0, 28) ano 1,0797 ano P ix fotolow.bmp ne 41,5207 ne ( U = 0, 03) ano 1,0281 ne P ix fototrue.bmp ne 0,9926 ano = 0, 88) ano 1,0012 ano ( U P ix Status BMPdetect V tabulce 7 jsou tučně vyznačeny případy, kdy došlo k chybné detekci. Poprvé to bylo v případě ilustrace v pravých barvách, kde poměr jedinečných barev ku počtu pixelů byl 0,28. To se velmi blíží kritické hranici 30 %, kdy analýza není spolehlivá.
Počítačová grafika SZŠ A VOŠZ MERHAUTOVA 15, BRNO
 Počítačová grafika SZŠ A VOŠZ MERHAUTOVA 15, BRNO 1 Základní dělení 3D grafika 2D grafika vektorová rastrová grafika 2/29 Vektorová grafika Jednotlivé objekty jsou tvořeny křivkami Využití: tvorba diagramů,
Počítačová grafika SZŠ A VOŠZ MERHAUTOVA 15, BRNO 1 Základní dělení 3D grafika 2D grafika vektorová rastrová grafika 2/29 Vektorová grafika Jednotlivé objekty jsou tvořeny křivkami Využití: tvorba diagramů,
VYUŽITÍ POČÍTAČOVÉ GRAFIKY
 POČÍTAČOVÁ GRAFIKA VYUŽITÍ POČÍTAČOVÉ GRAFIKY ÚPRAVA FOTOGRAFIÍ NAFOCENÉ FOTOGRAFIE Z DIGITÁLNÍHO FOTOAPARÁTU MŮŽEME NEJEN PROHLÍŽET, ALE TAKÉ UPRAVOVAT JAS KONTRAST BAREVNOST OŘÍZNUTÍ ODSTRANĚNÍ ČERVENÝCH
POČÍTAČOVÁ GRAFIKA VYUŽITÍ POČÍTAČOVÉ GRAFIKY ÚPRAVA FOTOGRAFIÍ NAFOCENÉ FOTOGRAFIE Z DIGITÁLNÍHO FOTOAPARÁTU MŮŽEME NEJEN PROHLÍŽET, ALE TAKÉ UPRAVOVAT JAS KONTRAST BAREVNOST OŘÍZNUTÍ ODSTRANĚNÍ ČERVENÝCH
Konverze grafických rastrových formátů
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA MAPOVÁNÍ A KARTOGRAFIE Konverze grafických rastrových formátů semestrální práce Jakub Hořejší Ondřej Šalanda V
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA MAPOVÁNÍ A KARTOGRAFIE Konverze grafických rastrových formátů semestrální práce Jakub Hořejší Ondřej Šalanda V
Škola: Gymnázium, Brno, Slovanské náměstí 7 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Název projektu: Inovace výuky na GSN
 Škola: Gymnázium, Brno, Slovanské náměstí 7 Šablona: III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Název projektu: Inovace výuky na GSN prostřednictvím ICT Číslo projektu: CZ.1.07/1.5.00/34.0940
Škola: Gymnázium, Brno, Slovanské náměstí 7 Šablona: III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Název projektu: Inovace výuky na GSN prostřednictvím ICT Číslo projektu: CZ.1.07/1.5.00/34.0940
III/ 2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Metodický list k didaktickému materiálu Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu Autor Téma sady didaktických materiálů Téma didaktického materiálu Vyučovací předmět
Metodický list k didaktickému materiálu Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu Autor Téma sady didaktických materiálů Téma didaktického materiálu Vyučovací předmět
12 Metody snižování barevného prostoru
 12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
Využití ICT techniky především v uměleckém vzdělávání. Akademie - VOŠ, Gymn. a SOŠUP Světlá nad Sázavou
 Datum: 1. 12. 2013 Projekt: Registrační číslo: Číslo DUM: Škola: Jméno autora: Název sady: Název práce: Předmět: Ročník: Obor: Časová dotace: Vzdělávací cíl: Pomůcky: Využití ICT techniky především v uměleckém
Datum: 1. 12. 2013 Projekt: Registrační číslo: Číslo DUM: Škola: Jméno autora: Název sady: Název práce: Předmět: Ročník: Obor: Časová dotace: Vzdělávací cíl: Pomůcky: Využití ICT techniky především v uměleckém
13 Barvy a úpravy rastrového
 13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
Vodoznačení video obsahu
 Vodoznačení video obsahu Bc. Jiří Hošek Email: hosek.j@seznam.cz Ústav Telekomunikací, FEKT, VUT v Brně Tento článek je zaměřen na problematiku vodoznačení a zejména pak na techniky vkládání vodoznaku
Vodoznačení video obsahu Bc. Jiří Hošek Email: hosek.j@seznam.cz Ústav Telekomunikací, FEKT, VUT v Brně Tento článek je zaměřen na problematiku vodoznačení a zejména pak na techniky vkládání vodoznaku
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Úlohy nad rastrovými daty Daniela
Systémy digitálního vodotisku. Digital Watermarking Systems
 Systémy digitálního vodotisku Digital Watermarking Systems Simona PEJSAROVÁ Česká zemědělská univerzita v Praze, Provozně ekonomická fakulta Katedra informačních technologií Kamýcká 129, Praha 6, Česká
Systémy digitálního vodotisku Digital Watermarking Systems Simona PEJSAROVÁ Česká zemědělská univerzita v Praze, Provozně ekonomická fakulta Katedra informačních technologií Kamýcká 129, Praha 6, Česká
Co je počítačová grafika
 Počítačová grafika Co je počítačová grafika Počítačovou grafikou rozumíme vše, co zpracovává počítač a co lze sledovat očima Využití počítačové grafiky Tiskoviny - časopisy, noviny, knihy, letáky Reklama
Počítačová grafika Co je počítačová grafika Počítačovou grafikou rozumíme vše, co zpracovává počítač a co lze sledovat očima Využití počítačové grafiky Tiskoviny - časopisy, noviny, knihy, letáky Reklama
Komprese dat Obsah. Komprese videa. Radim Farana. Podklady pro výuku. Komprese videa a zvuku. Komprese MPEG. Komprese MP3.
 Komprese dat Radim Farana Podklady pro výuku Obsah Komprese videa a zvuku. Komprese MPEG. Komprese MP3. Komprese videa Velký objem přenášených dat Typický televizní signál - běžná evropská norma pracuje
Komprese dat Radim Farana Podklady pro výuku Obsah Komprese videa a zvuku. Komprese MPEG. Komprese MP3. Komprese videa Velký objem přenášených dat Typický televizní signál - běžná evropská norma pracuje
Rastrová grafika. Grafický objekt je zaznamenán jednotlivými souřadnicemi bodů v mřížce. pixel ( picture element ) s definovanou barvou
 Rastrová grafika Grafický objekt je zaznamenán jednotlivými souřadnicemi bodů v mřížce. pixel ( picture element ) s definovanou barvou Kvalita je určena rozlišením mřížky a barevnou hloubkou (počet bitů
Rastrová grafika Grafický objekt je zaznamenán jednotlivými souřadnicemi bodů v mřížce. pixel ( picture element ) s definovanou barvou Kvalita je určena rozlišením mřížky a barevnou hloubkou (počet bitů
POČÍTAČOVÁ GRAFIKA. Počítačová grafika 1
 Počítačová grafika 1 POČÍTAČOVÁ GRAFIKA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro nižší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky
Počítačová grafika 1 POČÍTAČOVÁ GRAFIKA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro nižší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky
KOMPRIMACE. aneb Aby to zabralo méně místa
 KOMPRIMACE aneb Aby to zabralo méně místa Komprimace nebo také komprese je jednoduše řečeno sbalení či spakování dat na mnohem menší velikost. Ve skutečnosti se jedná o vypuštění nadbytečné informace takovým
KOMPRIMACE aneb Aby to zabralo méně místa Komprimace nebo také komprese je jednoduše řečeno sbalení či spakování dat na mnohem menší velikost. Ve skutečnosti se jedná o vypuštění nadbytečné informace takovým
STEGANOGRAFICKÁ ANALÝZA
 STEGANOGRAFICKÁ ANALÝZA Steganographical analysis Ing. Bc. Marek Čandík, Ph.D. Abstrakt Steganografie představuje označení pro metody a techniky tajné komunikace, jejíž hlavním účelem je skrýt výskyt komunikace
STEGANOGRAFICKÁ ANALÝZA Steganographical analysis Ing. Bc. Marek Čandík, Ph.D. Abstrakt Steganografie představuje označení pro metody a techniky tajné komunikace, jejíž hlavním účelem je skrýt výskyt komunikace
Úvod do počítačové grafiky
 Úvod do počítačové grafiky elmag. záření s určitou vlnovou délkou dopadající na sítnici našeho oka vnímáme jako barvu v rámci viditelné části spektra je člověk schopen rozlišit přibližně 10 milionů barev
Úvod do počítačové grafiky elmag. záření s určitou vlnovou délkou dopadající na sítnici našeho oka vnímáme jako barvu v rámci viditelné části spektra je člověk schopen rozlišit přibližně 10 milionů barev
Počítačová grafika. OBSAH Grafické formy: Vektorová grafika Bitmapová (rastrová grafika) Barevné modely
 Počítačová grafika OBSAH Grafické formy: Vektorová grafika Bitmapová (rastrová grafika) Barevné modely Vektorová grafika Vektorová grafika Příklad vektorové grafiky Zpět na Obsah Vektorová grafika Vektorový
Počítačová grafika OBSAH Grafické formy: Vektorová grafika Bitmapová (rastrová grafika) Barevné modely Vektorová grafika Vektorová grafika Příklad vektorové grafiky Zpět na Obsah Vektorová grafika Vektorový
Barvy a barevné modely. Počítačová grafika
 Barvy a barevné modely Počítačová grafika Barvy Barva základní atribut pro definici obrazu u každého bodu, křivky či výplně se definuje barva v rastrové i vektorové grafice všechny barvy, se kterými počítač
Barvy a barevné modely Počítačová grafika Barvy Barva základní atribut pro definici obrazu u každého bodu, křivky či výplně se definuje barva v rastrové i vektorové grafice všechny barvy, se kterými počítač
Digitální učební materiál
 Střední hotelová škola, s.r.o. Floriánské náměstí 350, 272 01 Kladno Digitální učební materiál Číslo projektu Název projektu Název školy Předmět Tematický okruh Téma CZ.1.07/1.5.00/34.0112 Moderní škola
Střední hotelová škola, s.r.o. Floriánské náměstí 350, 272 01 Kladno Digitální učební materiál Číslo projektu Název projektu Název školy Předmět Tematický okruh Téma CZ.1.07/1.5.00/34.0112 Moderní škola
Práce na počítači. Bc. Veronika Tomsová
 Práce na počítači Bc. Veronika Tomsová Barvy Barvy v počítačové grafice I. nejčastější reprezentace barev: 1-bitová informace rozlišující černou a bílou barvu 0... bílá, 1... černá 8-bitové číslo určující
Práce na počítači Bc. Veronika Tomsová Barvy Barvy v počítačové grafice I. nejčastější reprezentace barev: 1-bitová informace rozlišující černou a bílou barvu 0... bílá, 1... černá 8-bitové číslo určující
Webové stránky. 6. Grafické formáty pro web. Datum vytvoření: 11. 10. 2012. str ánk y. Vytvořil: Petr Lerch. www.isspolygr.cz
 Webové stránky 6. Vytvořil: Petr Lerch www.isspolygr.cz Datum vytvoření: 11. 10. 2012 Webové Strana: 1/6 Škola Ročník Název projektu Číslo projektu Číslo a název šablony Autor Tématická oblast Název DUM
Webové stránky 6. Vytvořil: Petr Lerch www.isspolygr.cz Datum vytvoření: 11. 10. 2012 Webové Strana: 1/6 Škola Ročník Název projektu Číslo projektu Číslo a název šablony Autor Tématická oblast Název DUM
Zdroj: http://www.root.cz/clanky/pravda-a-myty-o-gifu/
 Zdroj: http://www.root.cz/clanky/pravda-a-myty-o-gifu/ Bitmapový formát (rastrový obrázek) Většina z používaných grafických formátů (JPEG, PNG, TGA, BMP) obsahuje popis rastrového obrázku jako celku ukládají
Zdroj: http://www.root.cz/clanky/pravda-a-myty-o-gifu/ Bitmapový formát (rastrový obrázek) Většina z používaných grafických formátů (JPEG, PNG, TGA, BMP) obsahuje popis rastrového obrázku jako celku ukládají
Obraz jako data. Biofyzikální ústav Lékařské fakulty Masarykovy univerzity Brno. prezentace je součástí projektu FRVŠ č.2487/2011
 Získávání a analýza obrazové informace Obraz jako data Biofyzikální ústav Lékařské fakulty Masarykovy univerzity Brno prezentace je součástí projektu FRVŠ č.2487/2011 Osnova 1 Datové formáty obrazu 2 Datové
Získávání a analýza obrazové informace Obraz jako data Biofyzikální ústav Lékařské fakulty Masarykovy univerzity Brno prezentace je součástí projektu FRVŠ č.2487/2011 Osnova 1 Datové formáty obrazu 2 Datové
POČÍTAČOVÁ GRAFIKA. Lenka Bednaříková
 POČÍTAČOVÁ GRAFIKA Lenka Bednaříková POČÍTAČOVÁ GRAFIKA - OBSAH Barevné modely Základní dělení počítačové grafiky Vektorová grafika Rastrová (bitmapová) grafika Rozlišení Barevná hloubka Komprese, komprimace
POČÍTAČOVÁ GRAFIKA Lenka Bednaříková POČÍTAČOVÁ GRAFIKA - OBSAH Barevné modely Základní dělení počítačové grafiky Vektorová grafika Rastrová (bitmapová) grafika Rozlišení Barevná hloubka Komprese, komprimace
Kosinová transformace 36ACS
 Kosinová transformace 36ACS 10. listopadu 2006 Martin BruXy Bruchanov bruxy@regnet.cz Uplatnění diskrétní kosinové transformace Úkolem transformačního kódování je převést hodnoty vzájemně závislých vzorků
Kosinová transformace 36ACS 10. listopadu 2006 Martin BruXy Bruchanov bruxy@regnet.cz Uplatnění diskrétní kosinové transformace Úkolem transformačního kódování je převést hodnoty vzájemně závislých vzorků
Rastrový obraz, grafické formáty
 Rastrový obraz, grafické formáty 1995-2010 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ RasterFormats Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 35 Snímání
Rastrový obraz, grafické formáty 1995-2010 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ RasterFormats Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 35 Snímání
Základy informatiky. 10 Počítačová grafika
 Základy informatiky 10 Počítačová grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Reprezentace barev v PC Způsoby míchání barev Barevné modely Bitová hloubka Rastrová grafika
Základy informatiky 10 Počítačová grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Reprezentace barev v PC Způsoby míchání barev Barevné modely Bitová hloubka Rastrová grafika
Barvy na počítači a grafické formáty
 Barvy na počítači a grafické formáty Hlavním atributem, který se používá při práci s obrazem či s grafickými formáty, je barva. Při práci s barvami je důležité určit základní množinu barev, se kterou budeme
Barvy na počítači a grafické formáty Hlavním atributem, který se používá při práci s obrazem či s grafickými formáty, je barva. Při práci s barvami je důležité určit základní množinu barev, se kterou budeme
IVT. Rastrová grafika. 8. ročník
 IVT Rastrová grafika 8. ročník listopad, prosinec 2013 Autor: Mgr. Dana Kaprálová Zpracováno v rámci projektu Krok za krokem na ZŠ Želatovská ve 21. století registrační číslo projektu: CZ.1.07/1.4.00/21.3443
IVT Rastrová grafika 8. ročník listopad, prosinec 2013 Autor: Mgr. Dana Kaprálová Zpracováno v rámci projektu Krok za krokem na ZŠ Želatovská ve 21. století registrační číslo projektu: CZ.1.07/1.4.00/21.3443
Kódy a kódování dat. Binární (dvojkové) kódy. Kód Aikenův
 Kódy a kódování dat Kódování je proces, při kterém se každému znaku nebo postupnosti znaků daného souboru znaků jednoznačně přiřadí znak nebo postupnost znaků z jiného souboru znaků. Kódování je tedy transformace
Kódy a kódování dat Kódování je proces, při kterém se každému znaku nebo postupnosti znaků daného souboru znaků jednoznačně přiřadí znak nebo postupnost znaků z jiného souboru znaků. Kódování je tedy transformace
BPC2E_C09 Model komunikačního systému v Matlabu
 BPCE_C9 Model komunikačního systému v Matlabu Cílem cvičení je vyzkoušet si sestavit skripty v Matlabu pro model jednoduchého komunikačního systému pro přenos obrázků. Úloha A. Sestavte model komunikačního
BPCE_C9 Model komunikačního systému v Matlabu Cílem cvičení je vyzkoušet si sestavit skripty v Matlabu pro model jednoduchého komunikačního systému pro přenos obrázků. Úloha A. Sestavte model komunikačního
Kapitola 1. Signály a systémy. 1.1 Klasifikace signálů
 Kapitola 1 Signály a systémy 1.1 Klasifikace signálů Signál představuje fyzikální vyjádření informace, obvykle ve formě okamžitých hodnot určité fyzikální veličiny, která je funkcí jedné nebo více nezávisle
Kapitola 1 Signály a systémy 1.1 Klasifikace signálů Signál představuje fyzikální vyjádření informace, obvykle ve formě okamžitých hodnot určité fyzikální veličiny, která je funkcí jedné nebo více nezávisle
Adobe Photoshop 18. Ukládání dokumentu formáty
 Adobe Photoshop 18. Ukládání dokumentu formáty www.isspolygr.cz Vytvořila: Bc. Blažena Kondelíková Vytvořila dne: 20. 11. 2012 Strana: 1/5 Škola Ročník 4. ročník (SOŠ, SOU) Název projektu Interaktivní
Adobe Photoshop 18. Ukládání dokumentu formáty www.isspolygr.cz Vytvořila: Bc. Blažena Kondelíková Vytvořila dne: 20. 11. 2012 Strana: 1/5 Škola Ročník 4. ročník (SOŠ, SOU) Název projektu Interaktivní
Práce s obrazovým materiálem CENTRUM MEDIÁLNÍHO VZDĚLÁVÁNÍ. Akreditované středisko dalšího vzdělávání pedagogických pracovníků
 Práce s obrazovým materiálem CENTRUM MEDIÁLNÍHO VZDĚLÁVÁNÍ Akreditované středisko dalšího vzdělávání pedagogických pracovníků Obrazový materiál příjemná součást prezentace lépe zapamatovatelný často nahrazení
Práce s obrazovým materiálem CENTRUM MEDIÁLNÍHO VZDĚLÁVÁNÍ Akreditované středisko dalšího vzdělávání pedagogických pracovníků Obrazový materiál příjemná součást prezentace lépe zapamatovatelný často nahrazení
Kompresní algoritmy grafiky. Jan Janoušek F11125
 Kompresní algoritmy grafiky Jan Janoušek F11125 K čemu je komprese dobrá? Pokud je třeba skladovat datově náročné soubory. Např. pro záznam obrazu, hudby a hlavně videa je třeba skladovat překvapivě mnoho
Kompresní algoritmy grafiky Jan Janoušek F11125 K čemu je komprese dobrá? Pokud je třeba skladovat datově náročné soubory. Např. pro záznam obrazu, hudby a hlavně videa je třeba skladovat překvapivě mnoho
1. ZÁKLADNÍ POJMY POČÍTAČOVÉ GRAFIKY
 1. ZÁKLADNÍ POJMY POČÍTAČOVÉ GRAFIKY Pixel: je zkratka anglického PICture Element, tedy obrazový bod. Velikost obrázku: na monitoru v obrazových bodech - počet obrazových bodů, ze kterých je obrázek sestaven
1. ZÁKLADNÍ POJMY POČÍTAČOVÉ GRAFIKY Pixel: je zkratka anglického PICture Element, tedy obrazový bod. Velikost obrázku: na monitoru v obrazových bodech - počet obrazových bodů, ze kterých je obrázek sestaven
Cvičení 1. Úpravy obrázků programem IrfanView. Zpracoval: Ing. Vladimír Solnický SPŠ stavební, Opava, příspěvková organizace
 Cvičení 1 Úpravy obrázků programem IrfanView. Zpracoval: Ing. Vladimír Solnický SPŠ stavební, Opava, příspěvková organizace Uvedená práce (dílo) podléhá licenci Creative Commons Uveďte autora-nevyužívejte
Cvičení 1 Úpravy obrázků programem IrfanView. Zpracoval: Ing. Vladimír Solnický SPŠ stavební, Opava, příspěvková organizace Uvedená práce (dílo) podléhá licenci Creative Commons Uveďte autora-nevyužívejte
1 Strukturované programování
 Projekt OP VK Inovace studijních oborů zajišťovaných katedrami PřF UHK Registrační číslo: CZ.1.07/2.2.00/28.0118 1 Cíl Seznámení s principy strukturovaného programování, s blokovou strukturou programů,
Projekt OP VK Inovace studijních oborů zajišťovaných katedrami PřF UHK Registrační číslo: CZ.1.07/2.2.00/28.0118 1 Cíl Seznámení s principy strukturovaného programování, s blokovou strukturou programů,
VY_32_INOVACE_INF.10. Grafika v IT
 VY_32_INOVACE_INF.10 Grafika v IT Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 GRAFIKA Grafika ve smyslu umělecké grafiky
VY_32_INOVACE_INF.10 Grafika v IT Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 GRAFIKA Grafika ve smyslu umělecké grafiky
SOU Valašské Klobouky. VY_32_INOVACE_3_01 IKT Pc grafika základní pojmy Mgr. Radomír Soural. Zkvalitnění výuky prostřednictvím ICT
 SOU Valašské Klobouky VY_32_INOVACE_3_01 IKT Pc grafika základní pojmy Mgr. Radomír Soural Zkvalitnění výuky prostřednictvím ICT Název a číslo projektu CZ.1.07/1.5.00/34.0459 Název školy SOU Valašské Klobouky,
SOU Valašské Klobouky VY_32_INOVACE_3_01 IKT Pc grafika základní pojmy Mgr. Radomír Soural Zkvalitnění výuky prostřednictvím ICT Název a číslo projektu CZ.1.07/1.5.00/34.0459 Název školy SOU Valašské Klobouky,
Multimediální systémy. 03 Počítačová 2d grafika
 Multimediální systémy 03 Počítačová 2d grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Rastrová počítačová grafika Metody komprese obrazu Rastrové formáty Vektorová grafika Křivky
Multimediální systémy 03 Počítačová 2d grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Rastrová počítačová grafika Metody komprese obrazu Rastrové formáty Vektorová grafika Křivky
KRY. Projekt č. 2. Kamil Dudka xdudka00
 KRY Projekt č. 2 Kamil Dudka xdudka00 1 Úvod Úkolem bylo vytvořit program, který do určeného obrázku umí schovat text a tento text z obrázku později vytáhnout. Schovaný text měl být zabezpečený pomocí
KRY Projekt č. 2 Kamil Dudka xdudka00 1 Úvod Úkolem bylo vytvořit program, který do určeného obrázku umí schovat text a tento text z obrázku později vytáhnout. Schovaný text měl být zabezpečený pomocí
aneb jak se to tam všechno vejde?
 768 576 KOMPRIMACE aneb jak se to tam všechno vejde? Položme si hned na začátku zdánlivě nepodstatnou otázku: Kolik místa zabere dvouhodinový film na CD nebo DVD? Uvažujme následující příklad: rozlišení
768 576 KOMPRIMACE aneb jak se to tam všechno vejde? Položme si hned na začátku zdánlivě nepodstatnou otázku: Kolik místa zabere dvouhodinový film na CD nebo DVD? Uvažujme následující příklad: rozlišení
Informatika Počítačová grafika Mgr. Jan Jílek (v.11/12) Počítačová grafika
 Počítačová grafika - obor informatiky zabývající se zpracováním grafické informace (př. obrázky, videa, fotografie, informační plakáty, reklamy, konstrukční plány, návrhy, virtuální světy, hry aj.) První
Počítačová grafika - obor informatiky zabývající se zpracováním grafické informace (př. obrázky, videa, fotografie, informační plakáty, reklamy, konstrukční plány, návrhy, virtuální světy, hry aj.) První
On-line škola mladých autorů , pořadatel: ČVUT FEL. Jak na obrázky? Martin Žáček
 On-line škola mladých autorů 20. 2. 18. 4. 2013, pořadatel: ČVUT FEL Jak na obrázky? Martin Žáček zacekm@fel.cvut.cz http://www.aldebaran.cz/onlineskola/ Jak na obrázky? Osnova 1. Co je to vůbec obrázek,
On-line škola mladých autorů 20. 2. 18. 4. 2013, pořadatel: ČVUT FEL Jak na obrázky? Martin Žáček zacekm@fel.cvut.cz http://www.aldebaran.cz/onlineskola/ Jak na obrázky? Osnova 1. Co je to vůbec obrázek,
Webové stránky. 16. Obrázky na webových stránkách, optimalizace GIF. Datum vytvoření: 12. 1. 2013. str ánk y. Vytvořil: Petr Lerch. www.isspolygr.
 Webové stránky 16. Vytvořil: Petr Lerch www.isspolygr.cz Datum vytvoření: 12. 1. 2013 Webové Strana: 1/6 Škola Ročník Název projektu Číslo projektu Číslo a název šablony Autor Tématická oblast Název DUM
Webové stránky 16. Vytvořil: Petr Lerch www.isspolygr.cz Datum vytvoření: 12. 1. 2013 Webové Strana: 1/6 Škola Ročník Název projektu Číslo projektu Číslo a název šablony Autor Tématická oblast Název DUM
Vodoznaky. Jozef Mlích Pavel Zemčík Michal Španěl
 Vodoznaky Jozef Mlích Pavel Zemčík Michal Španěl Department of Computer Graphics and Multimedia Brno University of Technology, Faculty of Information Technology Božetěchova 2, 612 66 Brno, Czech Republic
Vodoznaky Jozef Mlích Pavel Zemčík Michal Španěl Department of Computer Graphics and Multimedia Brno University of Technology, Faculty of Information Technology Božetěchova 2, 612 66 Brno, Czech Republic
Rastrové počítačové obrazy (poněkud sporně často označované jako bitmapové) jsou pravděpodobně nejběžnější variantou obrazů v počítači.
 Ot 2. Rastrová počítačová grafika 1.1.1 Rastrové obrazy Rastrové počítačové obrazy (poněkud sporně často označované jako bitmapové) jsou pravděpodobně nejběžnější variantou obrazů v počítači. Rastrový
Ot 2. Rastrová počítačová grafika 1.1.1 Rastrové obrazy Rastrové počítačové obrazy (poněkud sporně často označované jako bitmapové) jsou pravděpodobně nejběžnější variantou obrazů v počítači. Rastrový
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost
 Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence
Kde se používá počítačová grafika
 POČÍTAČOVÁ GRAFIKA Kde se používá počítačová grafika Tiskoviny Reklama Média, televize, film Multimédia Internetové stránky 3D grafika Virtuální realita CAD / CAM projektování Hry Základní pojmy Rastrová
POČÍTAČOVÁ GRAFIKA Kde se používá počítačová grafika Tiskoviny Reklama Média, televize, film Multimédia Internetové stránky 3D grafika Virtuální realita CAD / CAM projektování Hry Základní pojmy Rastrová
Programátorská dokumentace
 Programátorská dokumentace Požadavky Cílem tohoto programu bylo představit barevné systémy, zejména převody mezi nejpoužívanějšími z nich. Zároveň bylo úkolem naprogramovat jejich demonstraci. Pro realizaci
Programátorská dokumentace Požadavky Cílem tohoto programu bylo představit barevné systémy, zejména převody mezi nejpoužívanějšími z nich. Zároveň bylo úkolem naprogramovat jejich demonstraci. Pro realizaci
Pohled do nitra mikroprocesoru Josef Horálek
 Pohled do nitra mikroprocesoru Josef Horálek Z čeho vycházíme = Vycházíme z Von Neumannovy architektury = Celý počítač se tak skládá z pěti koncepčních bloků: = Operační paměť = Programový řadič = Aritmeticko-logická
Pohled do nitra mikroprocesoru Josef Horálek Z čeho vycházíme = Vycházíme z Von Neumannovy architektury = Celý počítač se tak skládá z pěti koncepčních bloků: = Operační paměť = Programový řadič = Aritmeticko-logická
Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115
 Číslo projektu: Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo šablony: 8 Název materiálu: Ročník: Identifikace materiálu: Jméno autora: Předmět: Tématický celek: Anotace: CZ.1.07/1.5.00/34.0410
Číslo projektu: Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo šablony: 8 Název materiálu: Ročník: Identifikace materiálu: Jméno autora: Předmět: Tématický celek: Anotace: CZ.1.07/1.5.00/34.0410
III/ 2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Metodický list k didaktickému materiálu Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu Autor Téma sady didaktických materiálů Téma didaktického materiálu Vyučovací předmět
Metodický list k didaktickému materiálu Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu Autor Téma sady didaktických materiálů Téma didaktického materiálu Vyučovací předmět
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost
 Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence
Téma: Barevné modely, formáty souborů
 Téma: Barevné modely, formáty souborů Vypracoval/a: Ing. Jana Wasserbauerová TE NTO PR OJ E KT J E S POLUFINANC OVÁN EVR OPS KÝ M S OC IÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Barevné modely
Téma: Barevné modely, formáty souborů Vypracoval/a: Ing. Jana Wasserbauerová TE NTO PR OJ E KT J E S POLUFINANC OVÁN EVR OPS KÝ M S OC IÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY. Barevné modely
STRUKTURA RASTROVÝCH DAT
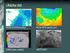 STRUKTURA RASTROVÝCH DAT dva typy rastrové vrstvy v GIS 1) Digitální obraz TV, počítač, mobil - obrazovka obraz z bodů mapa - mřížka s barevnými plochami 2) Rastrová data data pro analýzu a) binární -
STRUKTURA RASTROVÝCH DAT dva typy rastrové vrstvy v GIS 1) Digitální obraz TV, počítač, mobil - obrazovka obraz z bodů mapa - mřížka s barevnými plochami 2) Rastrová data data pro analýzu a) binární -
Číslo DUM: VY_32_INOVACE_04_01 Autor: Mgr. Ivana Matyášková Datum vytvoření: březen 2013 Ročník: prima Vzdělávací obor: informační technologie
 Číslo DUM: VY_32_INOVACE_04_01 Autor: Mgr. Ivana Matyášková Datum vytvoření: březen 2013 Ročník: prima Vzdělávací obor: informační technologie Tematický celek: počítačová grafika Název projektu: Zvyšování
Číslo DUM: VY_32_INOVACE_04_01 Autor: Mgr. Ivana Matyášková Datum vytvoření: březen 2013 Ročník: prima Vzdělávací obor: informační technologie Tematický celek: počítačová grafika Název projektu: Zvyšování
Úvod do počítačové grafiky
 Úvod do počítačové grafiky Zpracoval: ing. Jaroslav Chlubný Počítačová grafika Počítačová grafika a digitální fotografie zaujímá v současnosti stále významnější místo v našem životě. Uveďme si jen několik
Úvod do počítačové grafiky Zpracoval: ing. Jaroslav Chlubný Počítačová grafika Počítačová grafika a digitální fotografie zaujímá v současnosti stále významnější místo v našem životě. Uveďme si jen několik
DATOVÉ FORMÁTY GRAFIKY, JEJICH SPECIFIKA A MOŽNOSTI VYUŽITÍ
 DATOVÉ FORMÁTY GRAFIKY, JEJICH SPECIFIKA A MOŽNOSTI VYUŽITÍ UMT Tomáš Zajíc, David Svoboda Typy počítačové grafiky Rastrová Vektorová Rastrová grafika Pixely Rozlišení Barevná hloubka Monitor 72 PPI Tiskárna
DATOVÉ FORMÁTY GRAFIKY, JEJICH SPECIFIKA A MOŽNOSTI VYUŽITÍ UMT Tomáš Zajíc, David Svoboda Typy počítačové grafiky Rastrová Vektorová Rastrová grafika Pixely Rozlišení Barevná hloubka Monitor 72 PPI Tiskárna
Kódováni dat. Kódy používané pro strojové operace
 Kódováni dat Před zpracováním dat například v počítači je třeba znaky převést do tvaru, kterému počítač rozumí, tj. přiřadit jim určité kombinace bitů. Tomuto převodu se říká kódování. Kód je předpis pro
Kódováni dat Před zpracováním dat například v počítači je třeba znaky převést do tvaru, kterému počítač rozumí, tj. přiřadit jim určité kombinace bitů. Tomuto převodu se říká kódování. Kód je předpis pro
základní informace o kurzu základní pojmy literatura ukončení, požadavky, podmiňující předměty,
 základní informace o kurzu ukončení, požadavky, podmiňující předměty, základní pojmy kód x šifra kryptologie x steganografie kryptografie x kryptoanalyza literatura klasická x moderní kryptologie základní,
základní informace o kurzu ukončení, požadavky, podmiňující předměty, základní pojmy kód x šifra kryptologie x steganografie kryptografie x kryptoanalyza literatura klasická x moderní kryptologie základní,
CAD II přednáška č. 5. Grafické formáty PCX GIF TIFF BMP
 PCX GIF TIFF BMP PCX vyvinuto firmou ZSoft bezztrátová komprese každý obrázek obsahuje 128 bitovou hlavičku,následují komprimovaná data nabízítři druhy komprimace podle počtu barev (16-barev, 256-barev
PCX GIF TIFF BMP PCX vyvinuto firmou ZSoft bezztrátová komprese každý obrázek obsahuje 128 bitovou hlavičku,následují komprimovaná data nabízítři druhy komprimace podle počtu barev (16-barev, 256-barev
Vzdělávací obsah vyučovacího předmětu
 V.9.3. Vzdělávací obsah vyučovacího předmětu Vzdělávací oblast: Inormatika a informační a komunikační technologie Vyučovací předmět: Informatika Ročník: 1. ročník + kvinta chápe a používá základní termíny
V.9.3. Vzdělávací obsah vyučovacího předmětu Vzdělávací oblast: Inormatika a informační a komunikační technologie Vyučovací předmět: Informatika Ročník: 1. ročník + kvinta chápe a používá základní termíny
Reprodukce obrazových předloh
 fialar@kma.zcu.cz Podpořeno z projektu FRVŠ 584/2011 Historie Reprodukční fotografie V reprodukční fotografii se používají různé postupy pro reprodukci pérovek (pouze černá a bílá) jednoduché (viz přednáška
fialar@kma.zcu.cz Podpořeno z projektu FRVŠ 584/2011 Historie Reprodukční fotografie V reprodukční fotografii se používají různé postupy pro reprodukci pérovek (pouze černá a bílá) jednoduché (viz přednáška
Barvy a barevné systémy Formáty obrázků pro WWW
 Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
Bitmapová grafika: Vrstvy - interakce (režimy prolnutí)
 VY_32_INOVACE_PG3108 ; Mgr. Pavel Hauer ; 5/2012; 1.ročník; bitmapová grafika, Počítačová grafika; názorná pomůcka pro výuku, opakování, doplnění látky Bitmapová grafika: Vrstvy - interakce (režimy prolnutí)
VY_32_INOVACE_PG3108 ; Mgr. Pavel Hauer ; 5/2012; 1.ročník; bitmapová grafika, Počítačová grafika; názorná pomůcka pro výuku, opakování, doplnění látky Bitmapová grafika: Vrstvy - interakce (režimy prolnutí)
Úvod do teorie informace
 PEF MZLU v Brně 24. září 2007 Úvod Výměna informací s okolím nám umožňuje udržovat vlastní existenci. Proces zpracování informací je trvalý, nepřetržitý, ale ovlivnitelný. Zabezpečení informací je spojeno
PEF MZLU v Brně 24. září 2007 Úvod Výměna informací s okolím nám umožňuje udržovat vlastní existenci. Proces zpracování informací je trvalý, nepřetržitý, ale ovlivnitelný. Zabezpečení informací je spojeno
Volba zobrazení (Direct Current, Scaling) - FFT 1D, FFT 2D
 Volba zobrazení (Direct Current, Scaling) - FFT 1D, FFT 2D Jiří Stančík Fakulta chemická, Vysoké učení technické v Brně Purkyňova 118, 61200 Brno e-mail: HTUxcstancik@fch.vutbr.czUTH Úkolem této práce
Volba zobrazení (Direct Current, Scaling) - FFT 1D, FFT 2D Jiří Stančík Fakulta chemická, Vysoké učení technické v Brně Purkyňova 118, 61200 Brno e-mail: HTUxcstancik@fch.vutbr.czUTH Úkolem této práce
FORMÁTY UKLÁDÁNÍ OBRAZOVÝCH INFORMACÍ VÝMĚNA DAT MEZI CAD SYSTÉMY
 FORMÁTY UKLÁDÁNÍ OBRAZOVÝCH INFORMACÍ VÝMĚNA DAT MEZI CAD SYSTÉMY FORMÁTY UKLÁDÁNÍ OBRAZOVÝCH INFORMACÍ VEKTOROVÁ GRAFIKA Obraz reprezentován pomocí geometrických objektů (body, přímky, křivky, polygony).
FORMÁTY UKLÁDÁNÍ OBRAZOVÝCH INFORMACÍ VÝMĚNA DAT MEZI CAD SYSTÉMY FORMÁTY UKLÁDÁNÍ OBRAZOVÝCH INFORMACÍ VEKTOROVÁ GRAFIKA Obraz reprezentován pomocí geometrických objektů (body, přímky, křivky, polygony).
1. Základy teorie přenosu informací
 1. Základy teorie přenosu informací Úvodem citát o pojmu informace Informace je název pro obsah toho, co se vymění s vnějším světem, když se mu přizpůsobujeme a působíme na něj svým přizpůsobováním. N.
1. Základy teorie přenosu informací Úvodem citát o pojmu informace Informace je název pro obsah toho, co se vymění s vnějším světem, když se mu přizpůsobujeme a působíme na něj svým přizpůsobováním. N.
Barvy v počítačové grafice
 Barvy v počítačové grafice KAPITOLA 4 V této kapitole: Reprezentace barev v počítači Barevné prostory Barvy na periferiích počítače Barvy a design webových stránek Počítačová grafika je velmi široký pojem
Barvy v počítačové grafice KAPITOLA 4 V této kapitole: Reprezentace barev v počítači Barevné prostory Barvy na periferiích počítače Barvy a design webových stránek Počítačová grafika je velmi široký pojem
Digitální podepisování pomocí asymetrické kryptografie
 Digitální podepisování pomocí asymetrické kryptografie 11. dubna 2011 Trocha historie Asymetrické metody Historie Historie Vlastnosti Asymetrické šifrování 1976 Whitfield Diffie a Martin Hellman první
Digitální podepisování pomocí asymetrické kryptografie 11. dubna 2011 Trocha historie Asymetrické metody Historie Historie Vlastnosti Asymetrické šifrování 1976 Whitfield Diffie a Martin Hellman první
Principy moderní digitální steganografie a stegoanalýzy
 Principy moderní digitální steganografie a stegoanalýzy The principles of modern digital steganography and stegoanalysis Ing. Bc. Marek Čandík, PhD. Abstrakt Steganografie se používá k vkládání skrytých
Principy moderní digitální steganografie a stegoanalýzy The principles of modern digital steganography and stegoanalysis Ing. Bc. Marek Čandík, PhD. Abstrakt Steganografie se používá k vkládání skrytých
KOMPRESE OBRAZŮ. Václav Hlaváč, Jan Kybic. Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání.
 1/25 KOMPRESE OBRAZŮ Václav Hlaváč, Jan Kybic Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz http://cmp.felk.cvut.cz/ hlavac KOMPRESE OBRAZŮ, ÚVOD
1/25 KOMPRESE OBRAZŮ Václav Hlaváč, Jan Kybic Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz http://cmp.felk.cvut.cz/ hlavac KOMPRESE OBRAZŮ, ÚVOD
Počítačová grafika a vizualizace I
 Počítačová grafika a vizualizace I KOMPRESE, GRAFICKÉ FORMÁTY Mgr. David Frýbert david.frybert@gmail.com OSNOVA Barva pro TV Datový tok Bitmapové formáty (JPEG, TIFF, PNG, PPM, ) Formáty videa MPEG-1,2,4,7,21
Počítačová grafika a vizualizace I KOMPRESE, GRAFICKÉ FORMÁTY Mgr. David Frýbert david.frybert@gmail.com OSNOVA Barva pro TV Datový tok Bitmapové formáty (JPEG, TIFF, PNG, PPM, ) Formáty videa MPEG-1,2,4,7,21
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného)
 Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Vyhodnocení 2D rychlostního pole metodou PIV programem Matlab (zpracoval Jan Kolínský, dle programu ing. Jana Novotného) 1 Obecný popis metody Particle Image Velocimetry, nebo-li zkráceně PIV, je měřící
Výukový materiál zpracován v rámci projektu EU peníze školám
 Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ. 1.07/1.5.00/34.0233 Šablona III/2 Název VY_32_INOVACE_197_Grafika Název školy Hotelová škola Bohemia s.r.o.
Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ. 1.07/1.5.00/34.0233 Šablona III/2 Název VY_32_INOVACE_197_Grafika Název školy Hotelová škola Bohemia s.r.o.
Úvod do zpracování signálů
 1 / 25 Úvod do zpracování signálů Karel Horák Rozvrh přednášky: 1. Spojitý a diskrétní signál. 2. Spektrum signálu. 3. Vzorkovací věta. 4. Konvoluce signálů. 5. Korelace signálů. 2 / 25 Úvod do zpracování
1 / 25 Úvod do zpracování signálů Karel Horák Rozvrh přednášky: 1. Spojitý a diskrétní signál. 2. Spektrum signálu. 3. Vzorkovací věta. 4. Konvoluce signálů. 5. Korelace signálů. 2 / 25 Úvod do zpracování
Úloha 1. Úloha 2. Úloha 3. Text úlohy. Text úlohy. Text úlohy
 Úloha 1 Zkratka ERP jako celopodniková transakční aplikace znamená: a. Enterprise Route Planning b. Enterprise Resource Planning c. Enterprise Re-implementation Planning d. Enterprise Resource Processing
Úloha 1 Zkratka ERP jako celopodniková transakční aplikace znamená: a. Enterprise Route Planning b. Enterprise Resource Planning c. Enterprise Re-implementation Planning d. Enterprise Resource Processing
Základy práce v programovém balíku Corel
 Základy práce v programovém balíku Corel Mgr. Tomáš Pešina Výukový text vytvořený v rámci projektu DOPLNIT První jazyková základní škola v Praze 4, Horáčkova 1100, 140 00 Praha 4 - Krč Základy počítačové
Základy práce v programovém balíku Corel Mgr. Tomáš Pešina Výukový text vytvořený v rámci projektu DOPLNIT První jazyková základní škola v Praze 4, Horáčkova 1100, 140 00 Praha 4 - Krč Základy počítačové
Grafika na počítači. Bc. Veronika Tomsová
 Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Barvy a barevné systémy Formáty obrázků pro WWW
 Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
ZPRACOVÁNÍ OBRAZU přednáška 4
 ZPRACOVÁNÍ OBRAZU přednáška 4 Vít Lédl vit.ledl@tul.cz TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.07/2.2.00/07.0247,
ZPRACOVÁNÍ OBRAZU přednáška 4 Vít Lédl vit.ledl@tul.cz TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií Tento materiál vznikl v rámci projektu ESF CZ.1.07/2.2.00/07.0247,
Přednáška kurzu MPOV. Barevné modely
 Přednáška kurzu MPOV Barevné modely Ing. P. Petyovský (email: petyovsky@feec.vutbr.cz), kancelář E512, tel. 1194, Integrovaný objekt - 1/11 - Barvy v počítačové grafice Barevné modely Aditivní modely RGB,
Přednáška kurzu MPOV Barevné modely Ing. P. Petyovský (email: petyovsky@feec.vutbr.cz), kancelář E512, tel. 1194, Integrovaný objekt - 1/11 - Barvy v počítačové grafice Barevné modely Aditivní modely RGB,
Zobrazovací jednotky a monitory
 Zobrazovací jednotky a monitory Zobrazovací jednotka - karta, která se zasunuje do jednoho z konektorů na sběrnici uvnitř počítače. Dva režimy činnosti: Textový režim - zobrazuje znaky uvedené v tabulce
Zobrazovací jednotky a monitory Zobrazovací jednotka - karta, která se zasunuje do jednoho z konektorů na sběrnici uvnitř počítače. Dva režimy činnosti: Textový režim - zobrazuje znaky uvedené v tabulce
Počítačová grafika. Studijní text. Karel Novotný
 Počítačová grafika Studijní text Karel Novotný P 1 Počítačová grafika očítačová grafika je z technického hlediska obor informatiky 1, který používá počítače k tvorbě umělých grafických objektů a dále také
Počítačová grafika Studijní text Karel Novotný P 1 Počítačová grafika očítačová grafika je z technického hlediska obor informatiky 1, který používá počítače k tvorbě umělých grafických objektů a dále také
Rozšíření bakalářské práce
 Rozšíření bakalářské práce Vojtěch Vlkovský 2011 1 Obsah Seznam obrázků... 3 1 Barevné modely... 4 1.1 RGB barevný model... 4 1.2 Barevný model CMY(K)... 4 1.3 Další barevné modely... 4 1.3.1 Model CIE
Rozšíření bakalářské práce Vojtěch Vlkovský 2011 1 Obsah Seznam obrázků... 3 1 Barevné modely... 4 1.1 RGB barevný model... 4 1.2 Barevný model CMY(K)... 4 1.3 Další barevné modely... 4 1.3.1 Model CIE
Elektromagnetické záření. Zdroj: http://www.fotografovani.cz/images3/rom_svetlo_1_02.gif
 Počítačová grafika Elektromagnetické záření Zdroj: http://www.fotografovani.cz/images3/rom_svetlo_1_02.gif Jak vidíme Naše oči vnímají elektromagnetické záření Jsou citlivé na vlnové délky 390 až 800 nm
Počítačová grafika Elektromagnetické záření Zdroj: http://www.fotografovani.cz/images3/rom_svetlo_1_02.gif Jak vidíme Naše oči vnímají elektromagnetické záření Jsou citlivé na vlnové délky 390 až 800 nm
Kurz digitální fotografie. blok 1 data/úpravy fotografií
 Kurz digitální fotografie blok 1 data/úpravy fotografií Grafické soubory Grafické soubory Obsahují grafická (obrazová) data, která mohou být uložena různými způsoby, tedy formou různých grafických formátů.
Kurz digitální fotografie blok 1 data/úpravy fotografií Grafické soubory Grafické soubory Obsahují grafická (obrazová) data, která mohou být uložena různými způsoby, tedy formou různých grafických formátů.
Postupy práce se šablonami IS MPP
 Postupy práce se šablonami IS MPP Modul plánování a přezkoumávání, verze 1.20 vypracovala společnost ASD Software, s.r.o. dokument ze dne 27. 3. 2013, verze 1.01 Postupy práce se šablonami IS MPP Modul
Postupy práce se šablonami IS MPP Modul plánování a přezkoumávání, verze 1.20 vypracovala společnost ASD Software, s.r.o. dokument ze dne 27. 3. 2013, verze 1.01 Postupy práce se šablonami IS MPP Modul
VY_32_INOVACE_INF4_12. Počítačová grafika. Úvod
 VY_32_INOVACE_INF4_12 Počítačová grafika Úvod Základní rozdělení grafických formátů Rastrová grafika (bitmapová) Vektorová grafika Základním prvkem je bod (pixel). Vhodná pro zpracování digitální fotografie.
VY_32_INOVACE_INF4_12 Počítačová grafika Úvod Základní rozdělení grafických formátů Rastrová grafika (bitmapová) Vektorová grafika Základním prvkem je bod (pixel). Vhodná pro zpracování digitální fotografie.
Základní práce v souborovém manažeru
 Základní práce v souborovém manažeru 18-20-M/01 Informační technologie Základní pojmy a prostředky pro programování webových stránek Zvládnutí nástrojů typických pro programování webových aplikací Základní
Základní práce v souborovém manažeru 18-20-M/01 Informační technologie Základní pojmy a prostředky pro programování webových stránek Zvládnutí nástrojů typických pro programování webových aplikací Základní
Grafické editory. Ing. Jan Steringa 2008
 Grafické editory Ing. Jan Steringa 2008 Grafický editor aplikace určená pro tvorbu nebo úpravu grafických dat (obrázky, výkresy) rozdělení grafických editorů vektorové rastrové jednoúčelové komplexní pro
Grafické editory Ing. Jan Steringa 2008 Grafický editor aplikace určená pro tvorbu nebo úpravu grafických dat (obrázky, výkresy) rozdělení grafických editorů vektorové rastrové jednoúčelové komplexní pro
Obsah. Úvod... 9. Barevná kompozice... 16 Světlo... 18 Chromatická teplota světla... 19 Vyvážení bílé barvy... 20
 Obsah Úvod.............................................................................................. 9 Historie grafického designu a tisku..................................... 10 Od zadání k návrhu..............................................................
Obsah Úvod.............................................................................................. 9 Historie grafického designu a tisku..................................... 10 Od zadání k návrhu..............................................................
Základy šifrování a kódování
 Materiál byl vytvořen v rámci projektu Nové výzvy, nové příležitosti, nová škola Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky Základy šifrování a kódování
Materiál byl vytvořen v rámci projektu Nové výzvy, nové příležitosti, nová škola Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky Základy šifrování a kódování
1 Základní funkce pro zpracování obrazových dat
 1 Základní funkce pro zpracování obrazových dat 1.1 Teoretický rozbor 1.1.1 Úvod do zpracování obrazu v MATLABu MATLAB je primárně určen pro zpracování a analýzu numerických dat. Pro analýzu obrazových
1 Základní funkce pro zpracování obrazových dat 1.1 Teoretický rozbor 1.1.1 Úvod do zpracování obrazu v MATLABu MATLAB je primárně určen pro zpracování a analýzu numerických dat. Pro analýzu obrazových
Informatika / bezpečnost
 Informatika / bezpečnost Bezpečnost, šifry, elektronický podpis ZS 2015 KIT.PEF.CZU Bezpečnost IS pojmy aktiva IS hardware software data citlivá data hlavně ta chceme chránit autorizace subjekt má právo
Informatika / bezpečnost Bezpečnost, šifry, elektronický podpis ZS 2015 KIT.PEF.CZU Bezpečnost IS pojmy aktiva IS hardware software data citlivá data hlavně ta chceme chránit autorizace subjekt má právo
