Rozptylovací tabulky
|
|
|
- Václav Kopecký
- před 6 lety
- Počet zobrazení:
Transkript
1 Rozptylovací tabulky Hash tables Jan Kybic / 31
2 Rozptylovací tabulka Hash table Rozptylovací tabulka = implementace množiny / asociativního pole + velmi rychlé vkládání i hledání, O(1) neudržuje uspořádání (hledání maxima/minima) méně efektivní využití paměti Co je to hash? hash rozemlít, rozsekat, sekané maso, haše,... hašiš hash function rozptylovací/transformační/hašovací/hešovací/ funkce: objekt celé číslo hash / fingerprint haš/heš, otisk 2 / 31
3 Rozptylovací tabulka (Hash table) Základní myšlenky a vlastnosti pole m přihrádek (slots) pro ukládání položek. položka (item) = klíč (key) + hodnota (value) klíč je unikátní rozptylovací funkce (hash function) : ϕ: klíč číslo přihrádky 0... m 1 více položek v jedné přihrádce = kolize (collision/clash) operace jsou rychlé, protože víme, v které přihrádce hledat v každé přihrádce je jen omezený počet položek 3 / 31
4 Relativní naplnění tabulky (load factor) Průměrný počet položek na přihrádku load factor λ = počet položek n počet přihrádek m velké λ hodně kolizí zpomalení operací malé λ hodně prázdných položek nevyužitá paměť 4 / 31
5 Příklad m = 11 přihrádek, rozptylovací funkce ϕ(x) = x mod m = x % m Vložíme čísla Vznikne tabulka x ϕ(x) Relativní naplnění λ = 6/ / 31
6 Rozptylovací funkce Hash function Nutné vlastnosti Stejné klíče musí mít stejný otisk x = y ϕ(x) = ϕ(y) Neměnnost / nenáhodnost / konstantnost / opakovatelnost Požadované vlastnosti Rychlost výpočtu Různé klíče mají mít pokud možno různý otisk x y velká P [ ϕ(x) ϕ(y) ] každý klíč jiný otisk = perfect hashing rovnoměrné využití všech přihrádek pravděpodobnost zvolení konkrétní přihrádky 1/m (i pro strukturované vstupy) malé množství kolizí Kvalitu lze ověřit experimentálně. Souvislost s kryptografií a náhodnými čísly. 6 / 31
7 Rozptylovací funkce Pro celá čísla ϕ(x) = x mod m = x % m Pro znaky ord(c) % m Pro k-tice ϕ ( (x 1, x 2,..., x k ) ) k = x i p i 1 mod m kde p je vhodné prvočíslo dostatečně velké a nesoudělné s m. i=1 7 / 31
8 Rozptylovací funkce Pro celá čísla ϕ(x) = x mod m = x % m Pro znaky ord(c) % m Pro k-tice ϕ ( (x 1, x 2,..., x k ) ) k = x i p i 1 mod m kde p je vhodné prvočíslo dostatečně velké a nesoudělné s m. i=1 def hash_string(x,m): h=0 for c in x: h=((h*67)+ord(c)) % m return h Soubor hashing.py. 7 / 31
9 Rozptylovací funkce v Pythonu Funkce hash pro neměnné hodnoty (immutable): čísla, řetězce, n-tice, logické hodnoty, funkce, neměnné množiny (frozenset), objekty... nikoliv pro pole, množiny (set) Vrací (velké) celé číslo. print(hash(34)) 34 print(hash("les")) print(hash((7,"pes"))) / 31
10 Rozptylovací funkce v Pythonu Funkce hash pro neměnné hodnoty (immutable): čísla, řetězce, n-tice, logické hodnoty, funkce, neměnné množiny (frozenset), objekty... nikoliv pro pole, množiny (set) Vrací (velké) celé číslo. print(hash(34)) 34 print(hash("les")) print(hash((7,"pes"))) Používáme hash(x) % m. V Pythonu y % m 0 pokud m > 0. 8 / 31
11 Další použití rozptylovacích funkcí Rychlé ověřené rovnosti velkých objektů (DNA řetězce, otisky prstů, obrázky,... ): Předpočítej otisk každého objektu v databázi Pokud hash(x)=hash(y), pokračuj úplným porovnáním x a y 9 / 31
12 Velikost rozptylovací tabulky Vhodná velikost je prvočíselná např. 11, 103, Jinak riziko kolizí pokud ϕ(x) {k, 2k, 3k,... } Dynamická realokace: pokud se tabulka naplní (λ > λmax ) vytvoříme větší tabulku (m 2m) pokud se tabulka vyprázdní (λ < λ min ) vytvoříme menší tabulku (m m/2) Možné hodnoty m 0 = 11, λ max = 0.75, λ min = / 31
13 Nalezení prvočíselné velikosti Najde první prvočíslo větší než n. Pokud takové není, vrátí n a vypíše varování. primes=prvocisla_eratosthenes(100000) def find_prime_size(n): for i in range(len(primes)): if primes[i]>n: return n print("pozor, tabulka prvočísel je příliš krátká.") return n Zrychlování Tabulku (vybraných) prvočísel lze předpočítat. Vyhledávání lze zrychlit binárním půlením. Prvočísla nejsou potřeba všechna. Soubor hashing.py. 11 / 31
14 Řešení kolizí Co když dvě položky mají stejný otisk? Zřetězení (chaining) Každá přihrádka je seznam (nebo pole). Zaplnění λ může být > / 31
15 Řešení kolizí Co když dvě položky mají stejný otisk? Zřetězení (chaining) Každá přihrádka je seznam (nebo pole). Zaplnění λ může být > 1. Otevřené adresování (open addressing) Kapacita přihrádky je 1. Pokud je přihrádka m 0 = ϕ(x) obsazená, zkusíme jinou (m 1, m 2,... ) Lineární zkoušení (linear probing) zkusíme mi = m 0 + i. 12 / 31
16 Řešení kolizí Co když dvě položky mají stejný otisk? Zřetězení (chaining) Každá přihrádka je seznam (nebo pole). Zaplnění λ může být > 1. Otevřené adresování (open addressing) Kapacita přihrádky je 1. Pokud je přihrádka m 0 = ϕ(x) obsazená, zkusíme jinou (m 1, m 2,... ) Lineární zkoušení (linear probing) zkusíme mi = m 0 + i. Kvadratické zkoušení (quadratic probing) zkusíme m i = m 0 + ai 2 + bi, např. a = 1, b = 0. Dvojité rozptylování (double hashing) zkusíme m i = m 0 + iψ(x). 12 / 31
17 Řešení kolizí Co když dvě položky mají stejný otisk? Zřetězení (chaining) Každá přihrádka je seznam (nebo pole). Zaplnění λ může být > 1. Otevřené adresování (open addressing) Kapacita přihrádky je 1. Pokud je přihrádka m 0 = ϕ(x) obsazená, zkusíme jinou (m 1, m 2,... ) Lineární zkoušení (linear probing) zkusíme mi = m 0 + i. Kvadratické zkoušení (quadratic probing) zkusíme m i = m 0 + ai 2 + bi, např. a = 1, b = 0. Dvojité rozptylování (double hashing) zkusíme m i = m 0 + iψ(x). Menší režie než zřetězení. Zaplnění λ nesmí být velké ( 0.7). Rozptylovací funkce nesmí vytvářet shluky. 12 / 31
18 Počet porovnání při hledání úspěšné neúspěšné zřetězení 1 + λ 2 λ ( ) ( ( ) ) 2 1 otevřené adresování λ λ Počet přístupů do paměti je větší o 1 + režie přihrádek (např. 2 přístupy na porovnání u spojového seznamu). 13 / 31
19 Otevřené adresování příklad m = 11 přihrádek, rozptylovací funkce ϕ(x) = x mod m Vložíme čísla x ϕ(x) Po vložení 31: / 31
20 Otevřené adresování příklad m = 11 přihrádek, rozptylovací funkce ϕ(x) = x mod m Vložíme čísla x ϕ(x) Po vložení 44: / 31
21 Otevřené adresování příklad m = 11 přihrádek, rozptylovací funkce ϕ(x) = x mod m Vložíme čísla x ϕ(x) Po vložení 55: / 31
22 Otevřené adresování příklad m = 11 přihrádek, rozptylovací funkce ϕ(x) = x mod m Vložíme čísla x ϕ(x) Po vložení 20: / 31
23 Otevřené adresování příklad m = 11 přihrádek, rozptylovací funkce ϕ(x) = x mod m Vložíme čísla x ϕ(x) Po vložení 20: Prázdné položky = speciální hodnota. Implementace např. Problem Solving with Algorithms and Data Structures 14 / 31
24 Mazání položek Zřetězení smažeme ze seznamu přihrádky. 15 / 31
25 Mazání položek Zřetězení smažeme ze seznamu přihrádky. Otevřené adresování smazané položky označíme speciální hodnotou přeskoč. Mazání často není potřeba 15 / 31
26 Implementace rozptylové tabulky Asociativní mapa, kolizní strategie zřetězení. Podobné rozhraní jako BinarySearchTree a dict: h=hashtable(n) vytvoření h=put(h,key,value) vložení položky get(h,key) value nalezení/vyzvednutí hodnoty items(h) seznam dvojic (klíč,hodnota) class Hashtable: def init (self,n=13): # n je doporučená velikost self.size=find_prime_size(n) self.keys =[ [] for i in range(self.size) ] self.values=[ [] for i in range(self.size) ] self.count=0 Soubor hashing.py. 16 / 31
27 Nalezení položky def get(h,key): """ Vrátí value prvku s klíčem key, jinak None """ m=hash(key) % h.size # číslo příhrádky i=find_index(h.keys[m],key) # je tam? if i is None: # není return None return h.values[m][i] def find_index(l,x): """ Vrátí index i aby l[i]==x nebo None pokud x není v l """ for i,v in enumerate(l): # dvojice index, hodnota if v==x: return i return None V pythonu existuje metoda pole index, používá výjimky. Soubor hashing.py. 17 / 31
28 Vložení položky def put(h,key,value): """ Vloží pár key -> value do tabulky a vrátí odkaz na aktualizovanou """ m=hash(key) % h.size # číslo přihrádky i=find_index(h.keys[m],key) # je tam? if i is not None: # klíč v tabulce už je h.values[m][i]=value return h h.keys[m].append(key) # klíč v tabulce není h.values[m].append(value) h.count+=1 if h.count>h.size*0.75: # je tabulka moc plná? return grow_table(h) return h 18 / 31
29 Zvětšení tabulky def grow_table(h): """ Vytvoří větší tabulku, překopíruje tam obsah a vrátí ji """ hnew=hashtable(2*h.size) for i in range(h.size): # okopíruj vše do hnew keys=h.keys[i] values=h.values[i] for j in range(len(keys)): put(hnew,keys[j],values[j]) return hnew 19 / 31
30 Získání obsahu tabulky def items(h): """ Vrátí seznam dvojic klíč,hodnota """ r=[] for i in range(h.size): r+=zip(h.keys[i],h.values[i]) return list(r) 20 / 31
31 Získání obsahu tabulky def items(h): """ Vrátí seznam dvojic klíč,hodnota """ r=[] for i in range(h.size): r+=zip(h.keys[i],h.values[i]) return list(r) Další možná rozhraní iter, reduce, iterátor... list dělá z posloupnosti (lazy/on-demand) seznam volíme dle aplikace 20 / 31
32 Příklad from hashing import * t=hashtable() t=put(t, pi, ) t=put(t, e, ) t=put(t, sqrt2, ) t=put(t, golden, ) print(get(t, pi )) print(get(t, e )) print(get(t, gamma )) None 21 / 31
33 Příklad: Počítání frekvence slov Zjistěte relativní frekvence slov v daném textu (souboru) Načtení souboru, rozdělení na slova. Spočítání frekvence slov Seřazení a vytisknutí def word_frequencies(filename): w=read_words(filename) # seznam slov c=word_counts_dictionary(w) # seznam dvojic (slovo,počet) print_frequencies(c) Soubor word_frequencies.py. 22 / 31
34 Načtení slov word_pattern=re.compile(r [A-Za-z]+ ) def read_words(filename): words=[] with open(filename, rt ) as f: # otevři textový soubor for line in f.readlines(): # čti řádku po řádce line_words=word_pattern.findall(line) line_words=map(lambda x: x.lower(),line_words) words+=line_words return words 23 / 31
35 Spočítání slov (1) dict Asociativní mapa count uchovává počet výskytů, klíčem je slovo. def word_counts_dictionary(words): """ Vrátí seznam dvojic slov a jejich frekvencí """ counts={} # slovník for w in words: if w in counts: counts[w]+=1 else: counts[w]=1 return list(counts.items()) 24 / 31
36 Spočítání slov (2) Rozptylovací tabulka import hashing def word_counts_hashtable(words): """ Vrátí seznam dvojic slov a jejich frekvencí """ counts=hashing.hashtable() for w in words: value=hashing.get(counts,w) if value is None: counts=hashing.put(counts,w,1) else: counts=hashing.put(counts,w,value+1) return hashing.items(counts) 25 / 31
37 Spočítání slov (3) Vyhledávací strom import binary_search_tree as bst # implementace pomocí vyhledávacího stromu def word_counts_bst(words): """ Vrátí seznam dvojic slov a jejich frekvencí """ counts=none for w in words: value=bst.get(counts,w) if value is None: counts=bst.put(counts,w,1) else: counts=bst.put(counts,w,value+1) return bst.items(counts) 26 / 31
38 Setřídění a tisk def print_frequencies(counts,n=10): """ Vytiskne n nečastěji použitých slov dle seznamu dvojic (slovo,frekvence) counts """ # setřiď od nejčastějšího counts.sort(key=lambda x: x[1],reverse=true) # celkový počet slov nwords=functools.reduce(lambda acc,x: x[1]+acc,counts,0) for i in range(min(n,len(counts))): print("%10s %6.3f%%" % (counts[i][0],counts[i][1]/nwords*100.)) 27 / 31
39 Frekvence slov příklad Terminal> python3 word_frequencies.py poe.txt the 7.653% of 4.589% and 2.605% to 2.484% a 2.282% in 2.096% i 1.371% it 1.233% that 1.121% was 1.103% is 0.912% with 0.844% at 0.812% as 0.761% this 0.732% 28 / 31
40 Porovnání rychlosti Četnost slov word_counts_dictionary word_counts_hashtable word_counts_bst time [s] N 29 / 31
41 Rozptylovací tabulky shrnutí Implementace asociativní mapy nebo množiny. Velmi rychlé operace vkládání a vyhledávání (v průměru O(1), nejhorší případ O(n)). Citlivé na volbu rozptylovací funkce a velikost tabulky. Potřebuje rozptylovací funkci a test na rovnost. Nepotřebuje/neumí porovnávat velikost. 30 / 31
42 Náměty na domácí práci Implementujte otevřenou adresaci. Najděte závislost času na zaplnění tabulky. Implementujte mazání. Implementujte zcela stejné rozhraní jako dict Implementujte počítání frekvence slov bez asociativní mapy, například na základě třídění. Porovnejte efektivitu. 31 / 31
Datové struktury 2: Rozptylovací tabulky
 Datové struktury 2: Rozptylovací tabulky prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy
Datové struktury 2: Rozptylovací tabulky prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy
Návrh designu: Radek Mařík
 Návrh designu: Radek Mařík 1. Hashovací (=rozptylovací) funkce a) převádí adresu daného prvku na jemu příslušný klíč b) vrací pro každý klíč jedinečnou hodnotu c) pro daný klíč vypočte adresu d) vrací
Návrh designu: Radek Mařík 1. Hashovací (=rozptylovací) funkce a) převádí adresu daného prvku na jemu příslušný klíč b) vrací pro každý klíč jedinečnou hodnotu c) pro daný klíč vypočte adresu d) vrací
Adresní vyhledávání (přímý přístup, zřetězené a otevřené rozptylování, rozptylovací funkce)
 13. Metody vyhledávání. Adresní vyhledávání (přímý přístup, zřetězené a otevřené rozptylování, rozptylovací funkce). Asociativní vyhledávání (sekvenční, binárním půlením, interpolační, binární vyhledávací
13. Metody vyhledávání. Adresní vyhledávání (přímý přístup, zřetězené a otevřené rozptylování, rozptylovací funkce). Asociativní vyhledávání (sekvenční, binárním půlením, interpolační, binární vyhledávací
HASHING GENERAL Hashovací (=rozptylovací) funkce
 Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Spojový seznam. Jan Kybic.
 Spojový seznam Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2017 1 / 25 Složitost operací u lineárních datových struktur v Pythonu operace zásob. fronta pole pole řetězce přidej na začátek
Spojový seznam Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2017 1 / 25 Složitost operací u lineárních datových struktur v Pythonu operace zásob. fronta pole pole řetězce přidej na začátek
Vyhledávání, zejména rozptylování
 Datové struktury a algoritmy Část 11 Vyhledávání, zejména rozptylování Petr Felkel 16.5.2016 Topics Vyhledávání Rozptylování (hashing) Rozptylovací funkce Řešení kolizí Zřetězené rozptylování Otevřené
Datové struktury a algoritmy Část 11 Vyhledávání, zejména rozptylování Petr Felkel 16.5.2016 Topics Vyhledávání Rozptylování (hashing) Rozptylovací funkce Řešení kolizí Zřetězené rozptylování Otevřené
Stromy. Jan Kybic.
 Stromy Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 1 / 44 Stromy Binární vyhledávací stromy Množiny a mapy 2 / 44 Strom (Tree) Strom skládá se s uzlů (nodes) spojených hranami (edges).
Stromy Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 1 / 44 Stromy Binární vyhledávací stromy Množiny a mapy 2 / 44 Strom (Tree) Strom skládá se s uzlů (nodes) spojených hranami (edges).
Prioritní fronta, halda
 Prioritní fronta, halda Priority queue, heap Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2018 1 / 26 Prioritní fronta Halda Heap sort 2 / 26 Prioritní fronta (priority queue) Podporuje
Prioritní fronta, halda Priority queue, heap Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2018 1 / 26 Prioritní fronta Halda Heap sort 2 / 26 Prioritní fronta (priority queue) Podporuje
Základy algoritmizace. Hašování
 Základy algoritmizace Hašování Problematika hašování Hašování - nástroj na jednoduchý způsob "zakódování vstupních dat. Vstupní data jsou zpracována hašovací funkcí jsou jistým způsobem komprimována. Relativně
Základy algoritmizace Hašování Problematika hašování Hašování - nástroj na jednoduchý způsob "zakódování vstupních dat. Vstupní data jsou zpracována hašovací funkcí jsou jistým způsobem komprimována. Relativně
Úvod. Úvod do programování. Úvod. Hashovací tabulky
 do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava do programování, 2004/2005 Mnohé aplikace nepotřebují ke svému provozu celou škálu operací podporovaných
do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava do programování, 2004/2005 Mnohé aplikace nepotřebují ke svému provozu celou škálu operací podporovaných
Třetí skupina zadání projektů do předmětu Algoritmy II, letní semestr 2017/2018
 Třetí skupina zadání projektů do předmětu Algoritmy II, letní semestr 2017/2018 doc. Mgr. Jiří Dvorský, Ph.D. 24. dubna 2018 Verze zadání 24. dubna 2018 První verze 1 1 Hašovací tabulka V tomto zadání
Třetí skupina zadání projektů do předmětu Algoritmy II, letní semestr 2017/2018 doc. Mgr. Jiří Dvorský, Ph.D. 24. dubna 2018 Verze zadání 24. dubna 2018 První verze 1 1 Hašovací tabulka V tomto zadání
POZOR klíč NENÍ index (adresa), ale podle klíče se hodnoty ukládají na indexy (adresy).
 Hashovací tabulka = Hash table Hashovací tabulka (hash table, rozptýlená tabulka, hešovací tabulka) je datová struktura, která slouží k ukládání dvojic klíč-hodnota. kombinuje výhody vyhledávání pomocí
Hashovací tabulka = Hash table Hashovací tabulka (hash table, rozptýlená tabulka, hešovací tabulka) je datová struktura, která slouží k ukládání dvojic klíč-hodnota. kombinuje výhody vyhledávání pomocí
vyhledávací stromové struktury
 0.05.0 vyhledávací algoritmy Brute Force, Binary Search, Interpolation Search indexové soubory Dense index, Sparse index, Multilevel index transformační funkce Perfect Hash Close Hash Table Open Hash Table
0.05.0 vyhledávací algoritmy Brute Force, Binary Search, Interpolation Search indexové soubory Dense index, Sparse index, Multilevel index transformační funkce Perfect Hash Close Hash Table Open Hash Table
B3B33ALP - Algoritmy a programování - Zkouška z předmětu B3B33ALP. Marek Boháč bohacm11
 333LP - lgoritmy a programování - Zkouška z předmětu 333LP Jméno Příjmení Už. jméno Marek oháč bohacm11 Zkouškový test Otázka 1 Jaká je hodnota proměnné count po vykonání následujícího kódu: data=[4,4,5,5,6,6,6,7,7,7,7,8,8]
333LP - lgoritmy a programování - Zkouška z předmětu 333LP Jméno Příjmení Už. jméno Marek oháč bohacm11 Zkouškový test Otázka 1 Jaká je hodnota proměnné count po vykonání následujícího kódu: data=[4,4,5,5,6,6,6,7,7,7,7,8,8]
B3B33ALP - Algoritmy a programování - Zkouška z předmětu B3B33ALP. Marek Boháč bohacm11
 Jméno Příjmení Už. jméno Marek oháč bohacm11 Zkouškový test Otázka 1 Jaká je hodnota proměnné count po vykonání následujícího kódu: data=[4,4,5,5,6,6,6,7,7,7,7,8,8] count=0 for i in range(1,len(data)):
Jméno Příjmení Už. jméno Marek oháč bohacm11 Zkouškový test Otázka 1 Jaká je hodnota proměnné count po vykonání následujícího kódu: data=[4,4,5,5,6,6,6,7,7,7,7,8,8] count=0 for i in range(1,len(data)):
HASHING GENERAL Hashovací (=rozptylovací) funkce
 Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Níže uvedené úlohy představují přehled otázek, které se vyskytly v tomto nebo v minulých semestrech ve cvičení nebo v minulých semestrech u zkoušky. Mezi otázkami semestrovými a zkouškovými není žádný
Třídění a vyhledávání Searching and sorting
 Třídění a vyhledávání Searching and sorting Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 1 / 33 Vyhledávání Třídění Třídící algoritmy 2 / 33 Vyhledávání Searching Mějme posloupnost (pole)
Třídění a vyhledávání Searching and sorting Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 1 / 33 Vyhledávání Třídění Třídící algoritmy 2 / 33 Vyhledávání Searching Mějme posloupnost (pole)
vyhledávací stromové struktury
 vyhledávací algoritmy Brute Force Binary Search Interpolation Search indexové soubory Dense index, Sparse index transformační funkce Perfect Hash, Close Hash Table, Open Hash Table vyhledávací stromové
vyhledávací algoritmy Brute Force Binary Search Interpolation Search indexové soubory Dense index, Sparse index transformační funkce Perfect Hash, Close Hash Table, Open Hash Table vyhledávací stromové
SPJA, cvičení 1. ipython, python, skripty. základy syntaxe: základní datové typy, řetězce. podmínky: if-elif-else, vyhodnocení logických výrazů
 SPJA, cvičení 1 ipython, python, skripty základy syntaxe: základní datové typy, řetězce podmínky: if-elif-else, vyhodnocení logických výrazů cykly: for, while kolekce: seznam, n-tice, slovník funkce, list
SPJA, cvičení 1 ipython, python, skripty základy syntaxe: základní datové typy, řetězce podmínky: if-elif-else, vyhodnocení logických výrazů cykly: for, while kolekce: seznam, n-tice, slovník funkce, list
Algoritmy a datové struktury
 Algoritmy a datové struktury Stromy 1 / 32 Obsah přednášky Pole a seznamy Stromy Procházení stromů Binární stromy Procházení BS Binární vyhledávací stromy 2 / 32 Pole Hledání v poli metodou půlení intervalu
Algoritmy a datové struktury Stromy 1 / 32 Obsah přednášky Pole a seznamy Stromy Procházení stromů Binární stromy Procházení BS Binární vyhledávací stromy 2 / 32 Pole Hledání v poli metodou půlení intervalu
Jazyk C++ II. STL knihovna kontejnery část 2
 Jazyk C++ II STL knihovna kontejnery část 2 AR 2013/2014 Jazyk C++ II Asociativní kontejnery Slovníky u kterých pořadí dat nemá smysl. Kontejner si sám určuje, kam který údaj uloží. Údaje mají tvar klíč/hodnota.
Jazyk C++ II STL knihovna kontejnery část 2 AR 2013/2014 Jazyk C++ II Asociativní kontejnery Slovníky u kterých pořadí dat nemá smysl. Kontejner si sám určuje, kam který údaj uloží. Údaje mají tvar klíč/hodnota.
boolean hasnext() Object next() void remove() Kolekce
 11. Kontejnery Kontejnery Kontejnery jako základní dynamické struktury v Javě Kolekce, iterátory (Collection, Iterator) Seznamy (rozhraní List, třídy ArrayList, LinkedList) Množiny (rozhraní Set, třída
11. Kontejnery Kontejnery Kontejnery jako základní dynamické struktury v Javě Kolekce, iterátory (Collection, Iterator) Seznamy (rozhraní List, třídy ArrayList, LinkedList) Množiny (rozhraní Set, třída
Konečný automat. Jan Kybic.
 Konečný automat Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2017 1 / 33 Konečný automat finite state machine Konečný automat = výpočetní model, primitivní počítač Řídící jednotka s
Konečný automat Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2017 1 / 33 Konečný automat finite state machine Konečný automat = výpočetní model, primitivní počítač Řídící jednotka s
Semestrální práce 2 znakový strom
 Semestrální práce 2 znakový strom Ondřej Petržilka Datový model BlockFileRecord Bázová abstraktní třída pro záznam ukládaný do blokového souboru RhymeRecord Konkrétní třída záznamu ukládaného do blokového
Semestrální práce 2 znakový strom Ondřej Petržilka Datový model BlockFileRecord Bázová abstraktní třída pro záznam ukládaný do blokového souboru RhymeRecord Konkrétní třída záznamu ukládaného do blokového
IB111 Úvod do programování skrze Python
 Vyhledávání, řazení, složitost IB111 Úvod do programování skrze Python 2012 Otrávené studny 8 studen, jedna z nich je otrávená laboratorní rozbor dokáže rozpoznat přítomnost jedu ve vodě je drahý (je časově
Vyhledávání, řazení, složitost IB111 Úvod do programování skrze Python 2012 Otrávené studny 8 studen, jedna z nich je otrávená laboratorní rozbor dokáže rozpoznat přítomnost jedu ve vodě je drahý (je časově
Algoritmizace Dynamické programování. Jiří Vyskočil, Marko Genyg-Berezovskyj 2010
 Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
Algoritmizace Hashing II. Jiří Vyskočil, Marko Genyg-Berezovskyj 2010
 Hashing II Jiří Vyskočil, Marko Genyg-Berezovskyj 010 Srůstající hashování (coalesced hashing) Znám předem počet prvků (odhad) Z důvodů efektivity nechci ukazatele (mezi prvky). Na jednu pozici tabulky
Hashing II Jiří Vyskočil, Marko Genyg-Berezovskyj 010 Srůstající hashování (coalesced hashing) Znám předem počet prvků (odhad) Z důvodů efektivity nechci ukazatele (mezi prvky). Na jednu pozici tabulky
NPRG030 Programování I, 2018/19 1 / :03:07
 NPRG030 Programování I, 2018/19 1 / 20 3. 12. 2018 09:03:07 Vnitřní třídění Zadání: Uspořádejte pole délky N podle hodnot prvků Měřítko efektivity: * počet porovnání * počet přesunů NPRG030 Programování
NPRG030 Programování I, 2018/19 1 / 20 3. 12. 2018 09:03:07 Vnitřní třídění Zadání: Uspořádejte pole délky N podle hodnot prvků Měřítko efektivity: * počet porovnání * počet přesunů NPRG030 Programování
Časová složitost / Time complexity
 Časová složitost / Time complexity Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2018 1 / 24 Složitost algoritmů Algorithm complexity Časová a paměťová složitost Trvání výpočtu v závislosti
Časová složitost / Time complexity Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2018 1 / 24 Složitost algoritmů Algorithm complexity Časová a paměťová složitost Trvání výpočtu v závislosti
Vestavěné nástroje Pythonu
 Vestavěné nástroje Pythonu Petr Pošík Katedra kybernetiky, FEL ČVUT v Praze OI, B4B33RPH Řešení problémů a hry, 2016 Credits David Beazley (http://www.dabeaz.com/): Builtin Superheros! PyData Chicago,
Vestavěné nástroje Pythonu Petr Pošík Katedra kybernetiky, FEL ČVUT v Praze OI, B4B33RPH Řešení problémů a hry, 2016 Credits David Beazley (http://www.dabeaz.com/): Builtin Superheros! PyData Chicago,
Tabulka. Často jde nejenom o dynamickou množinu, ale i statickou množinu. Matematické tabulky statická množina
 Tabulka Často jde nejenom o dynamickou množinu, ale i statickou množinu Matematické tabulky statická množina x cos x 0,0 1,000 0,1 0,995 0,2 0,980 0,3 0,955 0,4 0,921 0,5 0,878 0,6 0,825 0,7 0,765 0,8
Tabulka Často jde nejenom o dynamickou množinu, ale i statickou množinu Matematické tabulky statická množina x cos x 0,0 1,000 0,1 0,995 0,2 0,980 0,3 0,955 0,4 0,921 0,5 0,878 0,6 0,825 0,7 0,765 0,8
Programování v Pythonu
 ƒeské vysoké u ení technické v Praze FIT Programování v Pythonu Ji í Znamená ek P íprava studijního programu Informatika je podporována projektem nancovaným z Evropského sociálního fondu a rozpo tu hlavního
ƒeské vysoké u ení technické v Praze FIT Programování v Pythonu Ji í Znamená ek P íprava studijního programu Informatika je podporována projektem nancovaným z Evropského sociálního fondu a rozpo tu hlavního
5. Vyhledávání a řazení 1
 Jiří Vokřínek, 2016 B6B36ZAL - Přednáška 5 1 Základy algoritmizace 5. Vyhledávání a řazení 1 doc. Ing. Jiří Vokřínek, Ph.D. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze
Jiří Vokřínek, 2016 B6B36ZAL - Přednáška 5 1 Základy algoritmizace 5. Vyhledávání a řazení 1 doc. Ing. Jiří Vokřínek, Ph.D. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze
Da D to t v o é v ty t py IB111: Datové typy
 Datové typy IB111: Datové typy Data a algoritmizace jaká data potřebuji pro vyřešení problému? jak budu data reprezentovat? jaké operaci s nimi potřebuji provádět? Navržení práce s daty je velice důležité
Datové typy IB111: Datové typy Data a algoritmizace jaká data potřebuji pro vyřešení problému? jak budu data reprezentovat? jaké operaci s nimi potřebuji provádět? Navržení práce s daty je velice důležité
Základní informace o předmětu Otázka:
 Základní informace o předmětu Otázka: Proč vůbec porovnávat algoritmy? Vlastnosti algoritmů přirozenost a stabilita algoritmu časová náročnost algoritmu asymetrická a asymptotická časová náročnost algoritmů
Základní informace o předmětu Otázka: Proč vůbec porovnávat algoritmy? Vlastnosti algoritmů přirozenost a stabilita algoritmu časová náročnost algoritmu asymetrická a asymptotická časová náročnost algoritmů
Dynamické datové struktury IV.
 Dynamické datové struktury IV. Prioritní fronta. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra
Dynamické datové struktury IV. Prioritní fronta. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra
Algoritmy výpočetní geometrie
 Algoritmy výpočetní geometrie prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Algoritmy výpočetní geometrie prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Topics. Vyhledávání, zejména rozptylování. Slovník - Dictionary. Vyhledávání. Rozptylování - Hashing. Rozptylování - Hashing
 8..007 Datové struktury a algoritmy Vyhlednávání Topics ást Vyhledávání, zejména rozptylování Petr Felkel Rozptylování (hashing) Rozptylovací funkce ešení kolizí Z et zené rozptylování Otev ené rozptylování
8..007 Datové struktury a algoritmy Vyhlednávání Topics ást Vyhledávání, zejména rozptylování Petr Felkel Rozptylování (hashing) Rozptylovací funkce ešení kolizí Z et zené rozptylování Otev ené rozptylování
Algoritmy I, složitost
 A0B36PRI - PROGRAMOVÁNÍ Algoritmy I, složitost České vysoké učení technické Fakulta elektrotechnická v 1.01 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená??
A0B36PRI - PROGRAMOVÁNÍ Algoritmy I, složitost České vysoké učení technické Fakulta elektrotechnická v 1.01 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená??
Lekce 4. Kolekce. Kolekce - seznamy, N-tice a slovníky. C2184 Úvod do programování v Pythonu podzim 2016
 Lekce 4 - seznamy, N-tice a slovníky. C2184 Úvod do programování v Pythonu podzim 2016 Národní centrum pro výzkum biomolekul Masarykova univerzita 4.1 seznam (list) N-tice (tuple) slovník (dictonary, dict)
Lekce 4 - seznamy, N-tice a slovníky. C2184 Úvod do programování v Pythonu podzim 2016 Národní centrum pro výzkum biomolekul Masarykova univerzita 4.1 seznam (list) N-tice (tuple) slovník (dictonary, dict)
Programování v Pythonu
 ƒeské vysoké u ení technické v Praze FIT Programování v Pythonu Ji í Znamená ek P íprava studijního programu Informatika je podporována projektem nancovaným z Evropského sociálního fondu a rozpo tu hlavního
ƒeské vysoké u ení technické v Praze FIT Programování v Pythonu Ji í Znamená ek P íprava studijního programu Informatika je podporována projektem nancovaným z Evropského sociálního fondu a rozpo tu hlavního
Náplň. v.0.03 16.02.2014. - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění
 Náplň v.0.03 16.02.2014 - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění Spojení dvou samostatně setříděných polí void Spoj(double apole1[], int adelka1, double
Náplň v.0.03 16.02.2014 - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění Spojení dvou samostatně setříděných polí void Spoj(double apole1[], int adelka1, double
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 21.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Množina v C++ (set, multiset).
 Množina v C++ (set, multiset). Množina je datová struktura, ve které jsou uloženy nějaké prvky. V množině nesmí být dva stejné prvky. Naopak multimnožina může obsahovat i stejné prvky. Nad množinou lze
Množina v C++ (set, multiset). Množina je datová struktura, ve které jsou uloženy nějaké prvky. V množině nesmí být dva stejné prvky. Naopak multimnožina může obsahovat i stejné prvky. Nad množinou lze
Rekurze a rychlé třídění
 Rekurze a rychlé třídění Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2017 1 / 54 Rekurze Rychlé třídění 2 / 54 Rekurze Recursion Rekurze = odkaz na sama sebe, definice za pomoci sebe
Rekurze a rychlé třídění Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 2017 1 / 54 Rekurze Rychlé třídění 2 / 54 Rekurze Recursion Rekurze = odkaz na sama sebe, definice za pomoci sebe
Hašování (Vyhledávání metodou transformace klíče)
 Hašování (Vyhledávání metodou transformace klíče) Velmi účinnou vyhledávací metodou je hašování. Pro její anglický název hashing se poměrně obtížně hledá vhodný překlad do českého jazyka, proto zůstaneme
Hašování (Vyhledávání metodou transformace klíče) Velmi účinnou vyhledávací metodou je hašování. Pro její anglický název hashing se poměrně obtížně hledá vhodný překlad do českého jazyka, proto zůstaneme
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 12.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Stromy. Jan Hnilica Počítačové modelování 14
 Stromy Jan Hnilica Počítačové modelování 14 1 Základní pojmy strom = dynamická datová struktura, složená z vrcholů (uzlů, prvků) propojených hranami hrany chápeme jako orientované, tzn. vedou z uzlu A
Stromy Jan Hnilica Počítačové modelování 14 1 Základní pojmy strom = dynamická datová struktura, složená z vrcholů (uzlů, prvků) propojených hranami hrany chápeme jako orientované, tzn. vedou z uzlu A
Programování: základní konstrukce, příklady, aplikace. IB111 Programování a algoritmizace
 Programování: základní konstrukce, příklady, aplikace IB111 Programování a algoritmizace 2011 Připomenutí z minule, ze cvičení proměnné, výrazy, operace řízení výpočtu: if, for, while funkce příklady:
Programování: základní konstrukce, příklady, aplikace IB111 Programování a algoritmizace 2011 Připomenutí z minule, ze cvičení proměnné, výrazy, operace řízení výpočtu: if, for, while funkce příklady:
Šablony, kontejnery a iterátory
 7. října 2010, Brno Připravil: David Procházka Šablony, kontejnery a iterátory Programovací jazyk C++ Šablony Strana 2 / 21 Šablona funkce/metody Šablona je obecný popis (třídy, funkce) bez toho, že by
7. října 2010, Brno Připravil: David Procházka Šablony, kontejnery a iterátory Programovací jazyk C++ Šablony Strana 2 / 21 Šablona funkce/metody Šablona je obecný popis (třídy, funkce) bez toho, že by
Databázové systémy Cvičení 5.2
 Databázové systémy Cvičení 5.2 SQL jako jazyk pro definici dat Detaily zápisu integritních omezení tabulek Integritní omezení tabulek kromě integritních omezení sloupců lze zadat integritní omezení jako
Databázové systémy Cvičení 5.2 SQL jako jazyk pro definici dat Detaily zápisu integritních omezení tabulek Integritní omezení tabulek kromě integritních omezení sloupců lze zadat integritní omezení jako
1. Databázové systémy (MP leden 2010)
 1. Databázové systémy (MP leden 2010) Fyzickáimplementace zadáníaněkterářešení 1 1.Zkolikaajakýchčástíseskládáčasprovstupněvýstupníoperaci? Ze tří částí: Seektime ječas,nežsehlavadiskudostanenadsprávnou
1. Databázové systémy (MP leden 2010) Fyzickáimplementace zadáníaněkterářešení 1 1.Zkolikaajakýchčástíseskládáčasprovstupněvýstupníoperaci? Ze tří částí: Seektime ječas,nežsehlavadiskudostanenadsprávnou
Seznamy a iterátory. Kolekce obecně. Rozhraní kolekce. Procházení kolekcí
 Kolekce obecně Seznamy a iterátory doc. Ing. Miroslav Beneš, Ph.D. katedra informatiky FEI VŠB-TUO A-1007 / 597 324 213 http://www.cs.vsb.cz/benes Miroslav.Benes@vsb.cz Kolekce ::= homogenní sada prvků
Kolekce obecně Seznamy a iterátory doc. Ing. Miroslav Beneš, Ph.D. katedra informatiky FEI VŠB-TUO A-1007 / 597 324 213 http://www.cs.vsb.cz/benes Miroslav.Benes@vsb.cz Kolekce ::= homogenní sada prvků
Kombinatorika, výpočty
 Kombinatorika, výpočty Radek Pelánek IV122 Styl jednoduché výpočty s čísly vesměs spíše opakování + pár dílčích zajímavostí užitečný trénink programování Kombinace, permutace, variace Daná množina M s
Kombinatorika, výpočty Radek Pelánek IV122 Styl jednoduché výpočty s čísly vesměs spíše opakování + pár dílčích zajímavostí užitečný trénink programování Kombinace, permutace, variace Daná množina M s
Spojová implementace lineárních datových struktur
 Spojová implementace lineárních datových struktur doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB
Spojová implementace lineárních datových struktur doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB
1 2 3 4 5 6 součet cvičení celkem. známka. Úloha č.: max. bodů: skut. bodů:
 Úloha č.: max. bodů: skut. bodů: 1 2 3 4 5 6 součet cvičení celkem 20 12 20 20 14 14 100 známka UPOZORNĚNÍ : a) Písemná zkouška obsahuje 6 úloh, jejichž řešení musí být vepsáno do připraveného formuláře.
Úloha č.: max. bodů: skut. bodů: 1 2 3 4 5 6 součet cvičení celkem 20 12 20 20 14 14 100 známka UPOZORNĚNÍ : a) Písemná zkouška obsahuje 6 úloh, jejichž řešení musí být vepsáno do připraveného formuláře.
Dynamické datové struktury III.
 Dynamické datové struktury III. Halda. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra aplikované
Dynamické datové struktury III. Halda. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz (Katedra aplikované
Dynamicky vázané metody. Pozdní vazba, virtuální metody
 Dynamicky vázané metody Pozdní vazba, virtuální metody Motivace... class TBod protected: float x,y; public: int vrat_pocet_bodu() return 1; ; od třídy TBod odvodíme: class TUsecka: public TBod protected:
Dynamicky vázané metody Pozdní vazba, virtuální metody Motivace... class TBod protected: float x,y; public: int vrat_pocet_bodu() return 1; ; od třídy TBod odvodíme: class TUsecka: public TBod protected:
Časová a prostorová složitost algoritmů
 .. Časová a prostorová složitost algoritmů Programovací techniky doc. Ing. Jiří Rybička, Dr. ústav informatiky PEF MENDELU v Brně rybicka@mendelu.cz Hodnocení algoritmů Programovací techniky Časová a prostorová
.. Časová a prostorová složitost algoritmů Programovací techniky doc. Ing. Jiří Rybička, Dr. ústav informatiky PEF MENDELU v Brně rybicka@mendelu.cz Hodnocení algoritmů Programovací techniky Časová a prostorová
Programování v C++, 2. cvičení
 Programování v C++, 2. cvičení 1 1 Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Zimní semestr 2018/2019 Přehled 1 Operátory new a delete 2 3 Operátory new a delete minule
Programování v C++, 2. cvičení 1 1 Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Zimní semestr 2018/2019 Přehled 1 Operátory new a delete 2 3 Operátory new a delete minule
AVL stromy. pro každý uzel u stromu platí, že rozdíl mezi výškou jeho levého a pravého podstromu je nejvýše 1 stromy jsou samovyvažující
 Stromy 2 AVL AVL stromy jména tvůrců stromů: dva Rusové Adelson-Velskii, Landis vyvážené binární stromy pro každý uzel u stromu platí, že rozdíl mezi výškou jeho levého a pravého podstromu je nejvýše 1
Stromy 2 AVL AVL stromy jména tvůrců stromů: dva Rusové Adelson-Velskii, Landis vyvážené binární stromy pro každý uzel u stromu platí, že rozdíl mezi výškou jeho levého a pravého podstromu je nejvýše 1
Databáze I. 5. přednáška. Helena Palovská
 Databáze I 5. přednáška Helena Palovská palovska@vse.cz SQL jazyk definice dat - - DDL (data definition language) Základní databáze, schemata, tabulky, indexy, constraints, views DATA Databáze/schéma
Databáze I 5. přednáška Helena Palovská palovska@vse.cz SQL jazyk definice dat - - DDL (data definition language) Základní databáze, schemata, tabulky, indexy, constraints, views DATA Databáze/schéma
Využití OOP v praxi -- Knihovna PHP -- Interval.cz
 Page 1 of 6 Knihovna PHP Využití OOP v praxi Po dlouhé teorii přichází na řadu praxe. V následujícím textu si vysvětlíme možnosti přístupu k databázi pomocí různých vzorů objektově orientovaného programování
Page 1 of 6 Knihovna PHP Využití OOP v praxi Po dlouhé teorii přichází na řadu praxe. V následujícím textu si vysvětlíme možnosti přístupu k databázi pomocí různých vzorů objektově orientovaného programování
Základní datové struktury
 Základní datové struktury Martin Trnečka Katedra informatiky, Přírodovědecká fakulta Univerzita Palackého v Olomouci 4. listopadu 2013 Martin Trnečka (UPOL) Algoritmická matematika 1 4. listopadu 2013
Základní datové struktury Martin Trnečka Katedra informatiky, Přírodovědecká fakulta Univerzita Palackého v Olomouci 4. listopadu 2013 Martin Trnečka (UPOL) Algoritmická matematika 1 4. listopadu 2013
map, multimap - Asociativní pole v C++.
 map, multimap - Asociativní pole v C++. Jedná se o asociativní pole. V asociativním poli jsou uloženy hodnoty ve tvaru (klíč,hodnota), kde klíč je vlastně "index" prvku. Klíčem může být libovolný objekt,
map, multimap - Asociativní pole v C++. Jedná se o asociativní pole. V asociativním poli jsou uloženy hodnoty ve tvaru (klíč,hodnota), kde klíč je vlastně "index" prvku. Klíčem může být libovolný objekt,
Zpracování deklarací a přidělování paměti
 Zpracování deklarací a přidělování paměti Účel deklarací -pojmenování objektů -umístění objektů v paměti Tabulka symbolů -uchovává informace o objektech -umožňuje kontextové kontroly -umožňuje operace
Zpracování deklarací a přidělování paměti Účel deklarací -pojmenování objektů -umístění objektů v paměti Tabulka symbolů -uchovává informace o objektech -umožňuje kontextové kontroly -umožňuje operace
Standardní algoritmy vyhledávací.
 Standardní algoritmy vyhledávací. Vyhledávací algoritmy v C++ nám umožňují vyhledávat prvky v datových kontejnerech podle různých kritérií. Také se podíváme na vyhledávání metodou půlením intervalu (binární
Standardní algoritmy vyhledávací. Vyhledávací algoritmy v C++ nám umožňují vyhledávat prvky v datových kontejnerech podle různých kritérií. Také se podíváme na vyhledávání metodou půlením intervalu (binární
ALS1 Přednáška 1. Pravěpodobnost, náhodná proměnná, očekávaná hodnota náhodné proměnné, harmonická čísla
 ALS Přednáška Pravěpodobnost, náhodná proměnná, očekávaná hodnota náhodné proměnné, harmonická čísla Prostor elementárních jevů S je množina, jejíž prvky se nazývají elementární jev. Jev je podmnožina
ALS Přednáška Pravěpodobnost, náhodná proměnná, očekávaná hodnota náhodné proměnné, harmonická čísla Prostor elementárních jevů S je množina, jejíž prvky se nazývají elementární jev. Jev je podmnožina
Binární vyhledávací stromy pokročilé partie
 Binární vyhledávací stromy pokročilé partie KMI/ALS lekce Jan Konečný 30.9.204 Literatura Cormen Thomas H., Introduction to Algorithms, 2nd edition MIT Press, 200. ISBN 0-262-5396-8 6, 3, A Knuth Donald
Binární vyhledávací stromy pokročilé partie KMI/ALS lekce Jan Konečný 30.9.204 Literatura Cormen Thomas H., Introduction to Algorithms, 2nd edition MIT Press, 200. ISBN 0-262-5396-8 6, 3, A Knuth Donald
Zadání k 2. programovacímu testu
 Zadání k 2. programovacímu testu Úvod do programovacích jazyků (Java) 4.12.2008 00:08 Michal Krátký Katedra informatiky Technická univerzita Ostrava Historie změn, příklady: 21 Poznámka: Pokud není řečeno
Zadání k 2. programovacímu testu Úvod do programovacích jazyků (Java) 4.12.2008 00:08 Michal Krátký Katedra informatiky Technická univerzita Ostrava Historie změn, příklady: 21 Poznámka: Pokud není řečeno
SQL tříhodnotová logika
 SQL tříhodnotová logika Jmeno Prijmeni Student Jaroslav Novák true Josef Novotný false Jiří Brabenec SELECT * FROM OSOBA WHERE Student!= true Jaký bude výsledek? SQL tříhodnotová logika Jmeno Prijmeni
SQL tříhodnotová logika Jmeno Prijmeni Student Jaroslav Novák true Josef Novotný false Jiří Brabenec SELECT * FROM OSOBA WHERE Student!= true Jaký bude výsledek? SQL tříhodnotová logika Jmeno Prijmeni
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Třídění, vyhledávání Daniela Szturcová
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Třídění, vyhledávání Daniela Szturcová
Algoritmizace a programování
 Algoritmizace a programování Vyhledávání, vkládání, odstraňování Vyhledání hodnoty v nesetříděném poli Vyhledání hodnoty v setříděném poli Odstranění hodnoty z pole Vkládání hodnoty do pole Verze pro akademický
Algoritmizace a programování Vyhledávání, vkládání, odstraňování Vyhledání hodnoty v nesetříděném poli Vyhledání hodnoty v setříděném poli Odstranění hodnoty z pole Vkládání hodnoty do pole Verze pro akademický
Michal Krátký. Úvod do programování. Cíl kurzu. Podmínky získání zápočtu III/III
 Michal Krátký Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 tel.: +420 596 993 239 místnost: A1004 mail: michal.kratky@vsb.cz
Michal Krátký Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 tel.: +420 596 993 239 místnost: A1004 mail: michal.kratky@vsb.cz
Abstraktní datové typy II.
 Datové struktury a algoritmy Abstraktní datové typy II. Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol., 2012 Datové struktury a algoritmy,
Datové struktury a algoritmy Abstraktní datové typy II. Karel Richta a kol. Katedra počítačů Fakulta elektrotechnická České vysoké učení technické v Praze Karel Richta a kol., 2012 Datové struktury a algoritmy,
TGH07 - Chytré stromové datové struktury
 TGH07 - Chytré stromové datové struktury Jan Březina Technical University of Liberec 1. dubna 2014 Prioritní fronta Datová struktura s operacemi: Odeber Minum (AccessMin, DeleteMin) - vrat prvek s minimálním
TGH07 - Chytré stromové datové struktury Jan Březina Technical University of Liberec 1. dubna 2014 Prioritní fronta Datová struktura s operacemi: Odeber Minum (AccessMin, DeleteMin) - vrat prvek s minimálním
Potřebovali bychom tedy umět do heše přidávat nové hodnoty, najít hodnotu pro
 Hešování (V literatuře se také často setkáme s jinými přepisy tohoto anglicko-českého patvaru (hashování), či více či méně zdařilými pokusy se tomuto slovu zcela vyhnout a místo heš používat například
Hešování (V literatuře se také často setkáme s jinými přepisy tohoto anglicko-českého patvaru (hashování), či více či méně zdařilými pokusy se tomuto slovu zcela vyhnout a místo heš používat například
Dynamické datové struktury I.
 Dynamické datové struktury I. Seznam. Fronta. Zásobník. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Dynamické datové struktury I. Seznam. Fronta. Zásobník. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Robert Haken [MVP ASP.NET/IIS, MCT] software architect, HAVIT, Základní algoritmy v praxi
![Robert Haken [MVP ASP.NET/IIS, MCT] software architect, HAVIT, Základní algoritmy v praxi Robert Haken [MVP ASP.NET/IIS, MCT] software architect, HAVIT, Základní algoritmy v praxi](/thumbs/80/81246411.jpg) Robert Haken [MVP ASP.NET/IIS, MCT] software architect, HAVIT, s.r.o. haken@havit.cz, @RobertHaken Základní algoritmy v praxi Agenda Intro Řazení Vyhledávání Datové struktury LINQ to Objects Intro Asymptotická
Robert Haken [MVP ASP.NET/IIS, MCT] software architect, HAVIT, s.r.o. haken@havit.cz, @RobertHaken Základní algoritmy v praxi Agenda Intro Řazení Vyhledávání Datové struktury LINQ to Objects Intro Asymptotická
Algoritmizace prostorových úloh
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Datové struktury Daniela Szturcová
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Datové struktury Daniela Szturcová
Pole a kolekce. v C#, Javě a C++
 Pole a kolekce v C#, Javě a C++ C# Deklarace pole typ_prvku_pole[] jmeno_pole; Vytvoření pole jmeno_pole = new typ_prvku_pole[pocet_prvku_pole]; Inicializace pole double[] poled = 4.8, 8.2, 7.3, 8.0; Java
Pole a kolekce v C#, Javě a C++ C# Deklarace pole typ_prvku_pole[] jmeno_pole; Vytvoření pole jmeno_pole = new typ_prvku_pole[pocet_prvku_pole]; Inicializace pole double[] poled = 4.8, 8.2, 7.3, 8.0; Java
Dynamické programování
 Dynamické programování Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 1 / 26 Memoizace Dynamické programování 2 / 26 Memoizace (Memoization/caching) Pro dlouhotrvající funkce f (x) Jednou
Dynamické programování Jan Kybic http://cmp.felk.cvut.cz/~kybic kybic@fel.cvut.cz 2016 1 / 26 Memoizace Dynamické programování 2 / 26 Memoizace (Memoization/caching) Pro dlouhotrvající funkce f (x) Jednou
Složitost algoritmů. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava
 Složitost algoritmů doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 27. prosince 2015 Jiří Dvorský (VŠB TUO) Složitost algoritmů
Složitost algoritmů doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 27. prosince 2015 Jiří Dvorský (VŠB TUO) Složitost algoritmů
IB111 Úvod do programování skrze Python Přednáška 7
 IB111 Úvod do programování skrze Python Přednáška 7 Správa paměti (proměnné podrobněji) Práce se soubory Nikola Beneš 2. listopad 2016 IB111 přednáška 7: správa paměti, práce se soubory 2. listopad 2016
IB111 Úvod do programování skrze Python Přednáška 7 Správa paměti (proměnné podrobněji) Práce se soubory Nikola Beneš 2. listopad 2016 IB111 přednáška 7: správa paměti, práce se soubory 2. listopad 2016
PB161 Programování v jazyce C++ Přednáška 3
 PB161 Programování v jazyce C++ Přednáška 3 Kontejnery Iterátory Algoritmy Nikola Beneš 4. října 2016 PB161 přednáška 3: kontejnery, iterátory, algoritmy 4. října 2016 1 / 25 Standardní knihovna C++ Už
PB161 Programování v jazyce C++ Přednáška 3 Kontejnery Iterátory Algoritmy Nikola Beneš 4. října 2016 PB161 přednáška 3: kontejnery, iterátory, algoritmy 4. října 2016 1 / 25 Standardní knihovna C++ Už
Organizace a zpracování dat I
 DBI007 Organizace a zpracování dat I Index-sekvenční a indexovaný soubor 4. přednáška RNDr. Michal Žemlička, Ph.D. Index-sekvenční soubor Přístup k záznamům je možný jak sekvenčně, tak i přímo Části: primární
DBI007 Organizace a zpracování dat I Index-sekvenční a indexovaný soubor 4. přednáška RNDr. Michal Žemlička, Ph.D. Index-sekvenční soubor Přístup k záznamům je možný jak sekvenčně, tak i přímo Části: primární
George J. Klir Vilem Vychodil (Palacky University, Olomouc) State University of New York (SUNY) Binghamton, New York 13902, USA
 A Tutorial Indexing structures in RDBMs George J Klir Vilem Vychodil (Palacky University, Olomouc) State University of New York (SUNY) Binghamton, New York 1390, USA gklir@binghamtonedu Palacky University,
A Tutorial Indexing structures in RDBMs George J Klir Vilem Vychodil (Palacky University, Olomouc) State University of New York (SUNY) Binghamton, New York 1390, USA gklir@binghamtonedu Palacky University,
IAJCE Přednáška č. 9. int[] pole = new int[pocet] int max = pole[0]; int id; for(int i =1; i< pole.length; i++) { // nikoli 0 if (Pole[i] > max) {
![IAJCE Přednáška č. 9. int[] pole = new int[pocet] int max = pole[0]; int id; for(int i =1; i< pole.length; i++) { // nikoli 0 if (Pole[i] > max) { IAJCE Přednáška č. 9. int[] pole = new int[pocet] int max = pole[0]; int id; for(int i =1; i< pole.length; i++) { // nikoli 0 if (Pole[i] > max) {](/thumbs/57/40266838.jpg) Vyhledání extrému v poli použito v algoritmech řazení hledání maxima int[] pole = new int[pocet] int max = pole[0]; int id; for(int i =1; i< pole.length; i++) // nikoli 0 if (Pole[i] > max) max = pole[i];
Vyhledání extrému v poli použito v algoritmech řazení hledání maxima int[] pole = new int[pocet] int max = pole[0]; int id; for(int i =1; i< pole.length; i++) // nikoli 0 if (Pole[i] > max) max = pole[i];
IAJCE Přednáška č. 8. double tprumer = (t1 + t2 + t3 + t4 + t5 + t6 + t7) / 7; Console.Write("\nPrumerna teplota je {0}", tprumer);
 Pole (array) Motivace Častá úloha práce s větším množstvím dat stejného typu o Př.: průměrná teplota za týden a odchylka od průměru v jednotlivých dnech Console.Write("Zadej T pro.den: "); double t = Double.Parse(Console.ReadLine());
Pole (array) Motivace Častá úloha práce s větším množstvím dat stejného typu o Př.: průměrná teplota za týden a odchylka od průměru v jednotlivých dnech Console.Write("Zadej T pro.den: "); double t = Double.Parse(Console.ReadLine());
Základy algoritmizace. Pattern matching
 Základy algoritmizace Pattern matching 1 Pattern matching Úloha nalézt v nějakém textu výskyty zadaných textových vzorků patří v počítačové praxi k nejfrekventovanějším. Algoritmy, které ji řeší se používají
Základy algoritmizace Pattern matching 1 Pattern matching Úloha nalézt v nějakém textu výskyty zadaných textových vzorků patří v počítačové praxi k nejfrekventovanějším. Algoritmy, které ji řeší se používají
Tabulka. Datová struktura, která umožňuje vkládat a později vybírat informace podle identifikačního klíče. Mohou být:
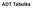 ADT Tabulka Datová struktura, která umožňuje vkládat a později vybírat informace podle identifikačního klíče. Mohou být: pevně definované (LUT Look Up Table) s proměnným počtem položek Konvence: Tabulka
ADT Tabulka Datová struktura, která umožňuje vkládat a později vybírat informace podle identifikačního klíče. Mohou být: pevně definované (LUT Look Up Table) s proměnným počtem položek Konvence: Tabulka
Fronta (Queue) Úvod do programování. Fronta implementace. Fronta implementace pomocí pole 1/4. Fronta implementace pomocí pole 3/4
 Fronta (Queue) Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 Fronta uplatňuje mechanismus přístupu FIFO first
Fronta (Queue) Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 Fronta uplatňuje mechanismus přístupu FIFO first
Datové struktury. alg12 1
 Datové struktury Jedna z klasických knih o programování (autor prof. Wirth) má název Algorithms + Data structures = Programs Datová struktura je množina dat (prvků, složek, datových objektů), pro kterou
Datové struktury Jedna z klasických knih o programování (autor prof. Wirth) má název Algorithms + Data structures = Programs Datová struktura je množina dat (prvků, složek, datových objektů), pro kterou
Šablony, kontejnery a iterátory
 11. března 2015, Brno Připravil: David Procházka Šablony, kontejnery a iterátory Programovací jazyk C++ Šablony Strana 2 / 31 Obsah přednášky 1 Šablony 2 Abstraktní datové struktury 3 Iterátory 4 Array
11. března 2015, Brno Připravil: David Procházka Šablony, kontejnery a iterátory Programovací jazyk C++ Šablony Strana 2 / 31 Obsah přednášky 1 Šablony 2 Abstraktní datové struktury 3 Iterátory 4 Array
Pokročilá algoritmizace amortizovaná složitost, Fibonacciho halda, počítačová aritmetika
 amortizovaná složitost, Fibonacciho halda, počítačová aritmetika Jiří Vyskočil, Marko Genyg-Berezovskyj 2009 Amortizovaná složitost Asymptotická složitost často dostatečně nevypovídá o složitosti algoritmů,
amortizovaná složitost, Fibonacciho halda, počítačová aritmetika Jiří Vyskočil, Marko Genyg-Berezovskyj 2009 Amortizovaná složitost Asymptotická složitost často dostatečně nevypovídá o složitosti algoritmů,
Algoritmy II. Otázky k průběžnému testu znalostí
 Algoritmy II Otázky k průběžnému testu znalostí Revize ze dne 19. února 2018 2 Lineární datové struktury 1 1. Vysvětlete co znamená, že zásobník představuje paměť typu LIFO. 2. Co je to vrchol zásobníku?
Algoritmy II Otázky k průběžnému testu znalostí Revize ze dne 19. února 2018 2 Lineární datové struktury 1 1. Vysvětlete co znamená, že zásobník představuje paměť typu LIFO. 2. Co je to vrchol zásobníku?
Různé algoritmy mají různou složitost
 / 1 Různé algoritmy mají různou složitost 1/ 1 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená?? 2/ 1 Asymptotická složitost y y x x Každému algoritmu
/ 1 Různé algoritmy mají různou složitost 1/ 1 Rychlost... Jeden algoritmus (program, postup, metoda ) je rychlejší než druhý. Co ta věta znamená?? 2/ 1 Asymptotická složitost y y x x Každému algoritmu
2 Datové struktury. Pole Seznam Zásobník Fronty FIFO Haldy a prioritní fronty Stromy Hash tabulky Slovníky
 Pole Seznam Zásobník Fronty FIFO Haldy a prioritní fronty Stromy Hash tabulky Slovníky 25 Pole Datová struktura kolekce elementů (hodnot či proměnných), identifikovaných jedním nebo více indexy, ze kterých
Pole Seznam Zásobník Fronty FIFO Haldy a prioritní fronty Stromy Hash tabulky Slovníky 25 Pole Datová struktura kolekce elementů (hodnot či proměnných), identifikovaných jedním nebo více indexy, ze kterých
Python profesionálně: dynamické parametry, generátory, lambda funkce... with. Dynamické parametry
 1 z 9 09.11.2015 10:02 Python profesionálně: dynamické parametry, generátory, lambda funkce a with Články - Michal Hořejšek (https://www.zdrojak.cz/autori/michal-horejsek/) - Různé (https://www.zdrojak.cz/ruzne/)
1 z 9 09.11.2015 10:02 Python profesionálně: dynamické parametry, generátory, lambda funkce a with Články - Michal Hořejšek (https://www.zdrojak.cz/autori/michal-horejsek/) - Různé (https://www.zdrojak.cz/ruzne/)
IB111 Základy programování Radek Pelánek
 Proměnné, paměť, soubory IB111 Základy programování Radek Pelánek 2017 1 / 54 Rozcvička I a = [3, 1, 7] print(sorted(a)) print(a) b = [4, 3, 1] print(b.sort()) print(b) 2 / 54 Rozcvička II a = ["magic"]
Proměnné, paměť, soubory IB111 Základy programování Radek Pelánek 2017 1 / 54 Rozcvička I a = [3, 1, 7] print(sorted(a)) print(a) b = [4, 3, 1] print(b.sort()) print(b) 2 / 54 Rozcvička II a = ["magic"]
