Mikrorezonátory v integrované fotonice
|
|
|
- Pavel Matějka
- před 9 lety
- Počet zobrazení:
Transkript
1 Mikrorezonátory v integrované fotonice Vlnovodné struktury s mikrorezonátory ( 99, B. E. Little et al., MIT, Cambridge, USA) in through V rezonanci out in through Mimo rezonanci mikrorezonátor out
2 Spektrální vlastnosti mikrorezonátoru in drop through Rezonanční vln. délka 3 pnd = qlq, q celé číslo ( - ) Dl FSR I drop Vzdálenost mezi rezonancemi FSR» l /( pn D) Jemnost F = FSR/ Dl q g intenzita I throuh I in Činitel jakosti Q = qf Vlnová délka nebo fáze Žebrový vlnovod, nebo mikrodisk? in out through Žebrový vlnovod: technologicky náročnější, jednodušší návrh a modelování Mikrodisk: technologicky jednodušší, velmi náročný návrh a modelování ( whispering gallery modes ) in out through
3 Mikrorezonátor jako stavební prvek integrovaných fotonických struktur in Pasivní mikrorezonátor spektrální filtr, add drop de/multiplexor Syntéza tvaru spektrálních charakteristik kaskádní řazení mikrorezonátorů Elektroopticky/termoopticky laditelný mikrorezonátor modulátor, přepínač (Δf GHz) křížový přepínač princip kaskádního filtru 3. řádu in out out Technologické aspekty Laterální vazba mezi mikrorezonátorem a vlnovodem je velmi kritická: MIT, Cambridge, Al,5 Ga,5 As GaAs systém šířka vlnovodů,4,6 µm šířka štěrbin,8,3 µm hloubka leptání µm Alternativa: vertikální vazba 3
4 Laterální a vertikální vazba mezi µr a vlnovodem Laterální vazba Jednostupňová litografie kritická vazební štěrbina menší flexibilita 3D vektorové modelování zádoucí vazební štěrbina prstenec vlnovod substrát Vertikální vazba dvoustupňová litografie lepší reprodukovatelnost větší flexibilita 3D vektorové modelování nezbytné vazební štěrbina prstenec substrát vlnovod Vlnovodné filtry na bázi mikrorezonátorů Příklad : Termoopticky laděný filtr vyšších řádů Filtry. až. řádu, ø 7 µm SiO /Hydex (n s =,45, n g =,7), Ø 5 µm ztráty na čipu,5 db Little Optics, Inc., PTL, Sept. 4 (nyní Infinera) Termoopticky laděné spektrální charakteristiky filtru 5. řádu, Δf = 5 GHz 4
5 Demonstrátor projektu NAIS Rekonfigurovatelný demultiplexor s termoopticky laděnými mikrorezonátory (Realizace: University of Twente, NL, systémové testy: Nortel, UK) Využití nelineárních optických efektů ve fotonických strukturách s mikrorezonátory 5
6 ain a Nelineární šíření optického záření v mikrorezonátoru: Kerrovská nelinearita automodulace fáze t k a a out ifl a = abe e ifnl ( ) /( ln ) f =-g a -b b NL nelineární změna fáze (automodulace)..8 Round-trip phase.75 æaout ö æt kö æain ö a = k t a ç ç ç è ø è ø è ø a- ta ain =, k a = ta + ka out in Output intensity Input intensity (a.u., ~ W/µm ) Jednoduchý model optického spínání v mikrorezonátoru Vertikální čerpání: jednoduché, rychlé, vhodné pro základní experiment Thru Vlnovodné čerpání: rezonanční zesílení; pomalejší, ale vhodné pro aplikace Thru Pump Signal in Drop Pump Signal in Drop 6
7 Spínač využívající křížovou fázovou modulaci v mikrorezonátoru pump signal thru drop Parametry: Interakce je popsaná dvojicí vázaných nelineárních rovnic pro dva (spektrálně se nepřekrývající) impulsy: Materiál: Křemík na SiO Průměr mikrorezonátoru: µm Rozměry vlnovodů: 3 4 nm Nosná vln.délka signálu: 545 nm Vlnová délka čerpací ho ipulsu: 577 nm Vstupní impuls: gaussovský, t s 5 ps Čerpací impuls: gaussovský, t p 5 ps Špičkový čerpací výkon: P p.5 W u (,) z t u b u b u z t t 6 t ( ) 3 s s, s s 3, s s - ib, sus + b, s + i - + = ig 3, sus us + up u (,) z t u b u b u ( ) 3 p p, p p 3, p p - ib, pup + b, p + i - + = ig 3, pup us + up z t t 6 t signál čerpání Nelineární optické přepínání: časová závislost...8 input.8 input signal Power (W).6.4 drop Power (W).6.4 thru. thru. drop time (ps) time (ps) pump Power (W) Parameters: g = W m ring radius 5 µm l s = nm l p = nm Signal peak power. W Gauss, FWHM 5 ps Pump peak power.5 W Gauss, FWHM 5 ps delay.6 ps time (ps) Power (W) input thru drop time (ps) 7
8 Výhody a nevýhody vlnovodných struktur s mikrorezonátory Výhody: Relativně velká variabilita realizovatelných funkcí spektrální filtr, modulátor, přepínač, laser(?),... Technologická homogenita prvků s různými funkcemi Malé rozměry stavebních bloků (řádu µm) Nevýhody: Vysoká technologická náročnost Návrh a modelování vyžaduje nové metody (3D, všesměrové šíření) Obtížnost účinné vazby na vláknové vlnovody Omezené technické parametry (šířka pásma filtru, mezní frekvence modulátoru,...) Dnes patrně nejperspektivnější technologie pro large scale photonic integration Měření parametrů fotonických vlnovodných struktur 8
9 Metody měření základních parametrů vlnovodů. Vidová spektroskopie planárních vlnovodů metody určování profilu indexu lomu dvouhranolová, jednohranolová metoda měření s pomocí vazební mřížky. Měření útlumu vlnovodů útlum planárních vlnovodů útlum kanálkových vlnovodů rezonátorová metoda měření grupového indexu lomu 3. Měření spektrálních vlastností vlnovodých struktur měření spektrálních charakteristik 4. Měření dynamických vlastností vlnovodných struktur měření parametrů EO modulátorů měření vlastností AO vlnovodů Vidová spektroskopie planárních vlnovodů j m n p j y s c n p J N = n n p p cos c sin s = sin j c + s + ( p - J) = p, c = J-s N = n cos c = n cos Jcos s + n sin Jsin s p p p n cos s = n - n sin s = n -sin j p p p p N = n - sin jcos J + sin Jsin j p N = n - sin j sin y + cos ysinj m p m m 9
10 Experimentální uspořádání: metoda dvou hranolů Laser clonka pro nastavení zpětného odrazu j m y Fotodetektor Vlnovod je umístěn na otočném stolku (goniometru). Nastavíme kolmý odraz od vlnovodu. Nastavíme kolmý odraz od hranolu 3. Nastavujeme synchronní úhly φ m 4. Vypočteme N m Nm = np - sin jm sin y + cos ysinjm Často lze současně měřit i index lomu podložky Jednohranolová metoda ( tmavá vidová spektroskopie) vlnovod substrát přítlačný hrot substrát m = Pokud synchronní úhly všech vidů leží uvnitř vstupního kužele, vybudí se všechny vidy současně. Na stínítku vznikne světlý kruh s tmavými čarami v místech odpovídajících výstupním úhlům vidů, poněvadž vybuzené vidy odvedou energii z místa dopadu optického svazku. Stínítko lze okalibrovat přímo v hodnotách ef. indexů lomu, nebo je možno smímat rozložení pole CCD kamerou a ze zpracování obrazu vyhodnotit hodnoty ef. indexů lomu
11 Určení profilu indexu lomu planárního vlnovodu ze spektra vedených vidů é n n æ n ö ù é g Nm n n ù - æ ö s g Nm -ns kd ng - Nm = arctan arctan mp n + + s ng Nm n ê çè ø - ú ê çè sø ng -Nm ë û ë úû U vrstvového vlnovodu stačí v principu znát hodnotu ef. indexů vidů, poněvadž neznáme parametry tloušťku a index lomu vlnovodné vrstvy. Pokud je vidů víc, hledáme minimum výrazu d M- M- d = å( ) d m - d, d = å m M - d m= M - m= ì n n ï æn ö g N n m -n æ ö s g Nm -ns m íarctan arctan k n ng N çè m s ø ng -N ç m èn ï sø ng -Nm s é ù é ù ü = + + mpï ý - ê ú ê ú ïî ë û ë û ïþ jako funkci indexu lomu vrstvy n g. Nejpravděpodobnější hodnota tloušťky je pak d. Určení profilu indexu lomu difúzního vlnovodu ze spektra vedených vidů xo n () ( ) arctan ê n Nm -na ò m ( ) êçè na ø n - Nm ë p», pokud n ( ) -Nm Nm-na ( m) = x( N m ) 3. ò ( )- ( + 4 )..8 N n s x o (N ) WKB aproximace: fn k n x N dx m p Předpokládejme profil indexu lomu ve tvaru po částech lineární funkce s vrcholy v bodech ( x, N ). éæ ö ù æ ö k n x - N = ê + m + p ç çè 4 ú ø û Integrál je pak možno spočítat analyticky; získáme rekurentní vzorec m m ( ) rel. hloubka x / x d -/ xm = xm-+ Nm-- Nm (White a Heidrich. 976) ì m- 3 æ ö xk - xk- é 3/ 3/ ùü ï í l m- -- ( Nk- Nm) ( Nk N ï ê m) úý 4 ç çè 4 ø å ïî k= Nk- - N k ë ûïþ pro určení bodů obratu (hloubek vlnovodu, ve kterých je hodnota indexu lomu vlnovodu rovna efektivnímu inxexu lomu daného vidu). Kritické je určení hodnoty n() na povrchu vlnovodu. n (x) n s.6.4. N n s N n s... x o (N ) x o (N )...
12 Určení profilu indexu lomu gradientního vlnovodu: dvouparametrický profil Parametry obecného dvouparametrického profilu (gaussovského, parabolického, lineárního ap. lze určovat podobně: nechť ì n é ( ) ( / ),, s n n ù + ê - s úf x xd x ³ n ( x) = ï ë û í ï na, x < ïî f ( x) je monotónně klesající funkce, < f ( x) <. Neznáme povrchovou hodnotu indexu lomu n ( ) a difúzní hloubku. Pak můžeme použít postup jako u vrstvy: kx = dm, x ( N m)/ x d ò 3 ( m + ) 4 p n( x/ x )- N d( x/ x ) d m d x s d d = x M - å x d M - d, m m= M - = å - M - m= ( dm d). Měření útlumu planárních vlnovodů Dvouhranolová metoda: I I L L log( Iout, / Iout, ) b = ( L - L ) Tříhranolová metoda: Měníme polohu středního hranolu bez změny vazby vstupního a výstupního hranolu (!!!) [db/cm] Problém: vzorek musí mít dostatečně velké rozměry Přesnost metody typicky řádu db/cm Problém: neměnit účinnost (výstupní) vazby L L I I I I I I
13 Měření útlumu planárních vlnovodů Metoda snímání rozptýleného záření PC C CCD kamera Příklad sejmuté stopy v GaN vlnovodu na safíru Laser j m d q m d n g Detektor = 78 nm n s Rozptýlený výkon (log.j.) TE.8 db/cm TE 4.6 db/cm TE 5dB/cm TE 3 5.8dB/cm TE 5.5 db/cm Útlum roste s vidovým indexem, což je typická vlastnost vlnovodů, u nichž je dominantním mechanismem ztrát rozptyl na rozhraních mezi vlnovodnou vrstvou a okolními prostředími Podélná poloha ve vlnovodu (mm) Měření s fázovým kontrastem a heterodynní detekcí 3
14 Měření útlumu kanálkových vlnovodů Metoda Fabryových-Perotových rezonancí detektor Uspořádání měřícího pracoviště Kanálkový vlnovod se chová jako FP rezonátor v důsledku odrazů od leštěných čel vlnovodu Modální transmitance ( -R ) exp( -al) T = + R exp( - al) exp( ik NL) R je modální reflektance, a činitel útlumu, L délka, Z poměru max. a min. transmitance vyjádříme měrný útlum (db/cm) 434. æ + max ln K ln N + ö b = -, K = T. L ç K N è - - ø T min Záznam měření Ti:LiNbO 3 vlnovodu. Měření útlumu kanálkových vlnovodů Transmitance Transmitance nm 55nm 6nm měrný útlum.365 db/cm.55 db/cm.44 db/cm Vlnová délka (nm) Sklo #4A, =55nm 6.sada.kanálek-ztráty.35 db/cm 5.sada 4.kanálek-ztráty.4 db/cm Loss [db/cm] Spektrální závislost útlumu vlnovodů vytvořených iontovými výměnami Ag + Na + a K + Na + ve skle dopovaném Er "K" "Ag" Wavelength [nm] Vlnová délka (nm) 4
15 Měření grupového indexu lomu kanálkových vlnovodů Rezonanční podmínka FP rezonátoru je dána vztahem pn c q N( n ) L = pq, q je celé číslo æ dn ö c Pro vzdálenost sousedních rezonancí (FSR) platí D [ nn ( n) ] = ç N + n dn = Ng D n = çè dn ø L, c c l D n =, neboli Ng = = grupový index lomu NL DnL DlL g q Ti:LiNbO 3 vlnovod Si 3 N 4 /SiO vlnovod Grupový eff. index Spektrální perioda (pm) Grupový ef. index [-] Vlnová délka (nm) Vlnová délka [nm] Charakterizace mikrorezonátorů (F. Ondráček, FEL ČVUT a ÚFE) Si 3 N 4 /SiO prstencový µr, R = 5 µm technologie: Uni Twente, NL Si 3 N 4 g PECVD SiO air, Through port Drop port PECVD SiO buffer layer Thermal SiO Transmission [a.u.],8,6,4,, Wavelength [nm] 5
16 Si 3 N 4 /SiO µr (vzorek Uni Twente), FSR 9 nm Drop transmission [a.u.],8,6,4, F = Wavelength [nm] Měření blízkého pole skanovacím optickým mikroskopem 6
17 Interferometrické měření s fázovým kontrastem Šíření femtosekundového impulsu v mikrorezonátoru Experiment: interferenční mikroskopie blízkého pole, Uni Twente, NL, 3 Délka impulsu ~ 8 fs, vlnová délka ~ 8 nm (Ti:safírový laser) 7
Mikrorezonátory v integrované fotonice
 Mikrorezonátory v integrované fotonice Vlnovodné struktury s mikrorezonátory ( 990, B. E. Little et al., MIT, Cambridge, USA) in through V rezonanci out in through Mimo rezonanci mikrorezonátor out Spektrální
Mikrorezonátory v integrované fotonice Vlnovodné struktury s mikrorezonátory ( 990, B. E. Little et al., MIT, Cambridge, USA) in through V rezonanci out in through Mimo rezonanci mikrorezonátor out Spektrální
Integrovaná fotonika POČÁTKY INTEGROVANÉ OPTIKY
 Integrovaná fotonika POČÁTKY INTEGROVANÉ OPTIKY ZÁKLADNÍ SOUČÁSTKY 3 4 Základy technologie fotonických vlnovodných struktur 5 Některé významnější technologie Ti:LiNbO 3, APE LiNbO 3 (annealed proton exchange)
Integrovaná fotonika POČÁTKY INTEGROVANÉ OPTIKY ZÁKLADNÍ SOUČÁSTKY 3 4 Základy technologie fotonických vlnovodných struktur 5 Některé významnější technologie Ti:LiNbO 3, APE LiNbO 3 (annealed proton exchange)
Fyzika II. Marek Procházka Vlnová optika II
 Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Fyzika II Marek Procházka Vlnová optika II Základní pojmy Reflexe (odraz) Refrakce (lom) jevy na rozhraní dvou prostředí o různém indexu lomu. Disperze (rozklad) prostorové oddělení složek vlnění s různou
Glass temperature history
 Glass Glass temperature history Crystallization and nucleation Nucleation on temperature Crystallization on temperature New Applications of Glass Anorganické nanomateriály se skelnou matricí Martin Míka
Glass Glass temperature history Crystallization and nucleation Nucleation on temperature Crystallization on temperature New Applications of Glass Anorganické nanomateriály se skelnou matricí Martin Míka
Světlo jako elektromagnetické záření
 Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Integrovaná fotonika POČÁTKY INTEGROVANÉ OPTIKY
 Integrovaná fotonika POČÁTKY INTEGROVANÉ OPTIKY ZÁKLADNÍ SOUČÁSTKY 3 4 Základy technologie fotonických vlnovodných struktur 5 Některé významnější technologie Ti:LiNbO 3, APE LiNbO 3 (annealed proton exchange)
Integrovaná fotonika POČÁTKY INTEGROVANÉ OPTIKY ZÁKLADNÍ SOUČÁSTKY 3 4 Základy technologie fotonických vlnovodných struktur 5 Některé významnější technologie Ti:LiNbO 3, APE LiNbO 3 (annealed proton exchange)
CZ.1.07/2.2.00/ AČ (RCPTM) Spektroskopie 1 / 24
 MĚŘENÍ SPEKTRA SVĚTLA Antonín Černoch Regionální centrum pokročilých technologií a materiálů CZ.1.07/2.2.00/15.0147 AČ (RCPTM) Spektroskopie 1 / 24 Úvod Obsah 1 Úvod 2 Zobrazovací spektrometry Disperzní
MĚŘENÍ SPEKTRA SVĚTLA Antonín Černoch Regionální centrum pokročilých technologií a materiálů CZ.1.07/2.2.00/15.0147 AČ (RCPTM) Spektroskopie 1 / 24 Úvod Obsah 1 Úvod 2 Zobrazovací spektrometry Disperzní
Fotonické nanostruktury (nanofotonika)
 Základy nanotechnologií KEF/ZANAN Fotonické nanostruktury (nanofotonika) Jan Soubusta 4.11. 2015 Obsah 1. ÚVOD 2. POHLED DO MIKROSVĚTA 3. OD ELEKTRONIKY K FOTONICE 4. FYZIKA PRO NANOFOTONIKU 5. PERIODICKÉ
Základy nanotechnologií KEF/ZANAN Fotonické nanostruktury (nanofotonika) Jan Soubusta 4.11. 2015 Obsah 1. ÚVOD 2. POHLED DO MIKROSVĚTA 3. OD ELEKTRONIKY K FOTONICE 4. FYZIKA PRO NANOFOTONIKU 5. PERIODICKÉ
Akustooptický modulátor s postupnou a stojatou akustickou vlnou
 Úloha č. 8 pro laserová praktika (ZPLT) KFE, FJFI, ČVUT, Praha v. 2017/2018 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské
Úloha č. 8 pro laserová praktika (ZPLT) KFE, FJFI, ČVUT, Praha v. 2017/2018 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské
Fotonické nanostruktury (alias nanofotonika)
 Základy nanotechnologií KEF/ZANAN Fotonické nanostruktury (alias nanofotonika) Jan Soubusta 27.10. 2017 Obsah 1. ÚVOD 2. POHLED DO MIKROSVĚTA 3. OD ELEKTRONIKY K FOTONICE 4. FYZIKA PRO NANOFOTONIKU 5.
Základy nanotechnologií KEF/ZANAN Fotonické nanostruktury (alias nanofotonika) Jan Soubusta 27.10. 2017 Obsah 1. ÚVOD 2. POHLED DO MIKROSVĚTA 3. OD ELEKTRONIKY K FOTONICE 4. FYZIKA PRO NANOFOTONIKU 5.
1. Pevnolátkový Nd:YAG laser v režimu volné generace a v režimu Q-spínání. 2. Zesilování laserového záření a generace druhé harmonické
 Úloha č. 1 pro laserová praktika KFE, FJFI, ČVUT v Praze, verze 2010/1 1. Pevnolátkový Nd:YAG laser v režimu volné generace a v režimu Q-spínání. 2. Zesilování laserového záření a generace druhé harmonické
Úloha č. 1 pro laserová praktika KFE, FJFI, ČVUT v Praze, verze 2010/1 1. Pevnolátkový Nd:YAG laser v režimu volné generace a v režimu Q-spínání. 2. Zesilování laserového záření a generace druhé harmonické
Akustooptický modulátor s postupnou a stojatou akustickou vlnou
 Úloha č. 8 pro laserová praktika KFE, FJFI, ČVUT v Praze, verze 2010/1 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské cely,
Úloha č. 8 pro laserová praktika KFE, FJFI, ČVUT v Praze, verze 2010/1 Akustooptický modulátor s postupnou a stojatou akustickou vlnou Akustooptické modulátory (AOM), někdy též nazývané Braggovské cely,
SPEKTROMETRIE. aneb co jsem se dozvěděla. autor: Zdeňka Baxová
 SPEKTROMETRIE aneb co jsem se dozvěděla autor: Zdeňka Baxová FTIR spektrometrie analytická metoda identifikace látek (organických i anorganických) všech skupenství měříme pohlcení IČ záření (o různé vlnové
SPEKTROMETRIE aneb co jsem se dozvěděla autor: Zdeňka Baxová FTIR spektrometrie analytická metoda identifikace látek (organických i anorganických) všech skupenství měříme pohlcení IČ záření (o různé vlnové
elektrické filtry Jiří Petržela filtry založené na jiných fyzikálních principech
 Jiří Petržela filtry založené na jiných fyzikálních principech piezoelektrický jev při mechanickém namáhání krystalu ve správném směru na něm vzniká elektrické napětí po přiložení elektrického napětí se
Jiří Petržela filtry založené na jiných fyzikálních principech piezoelektrický jev při mechanickém namáhání krystalu ve správném směru na něm vzniká elektrické napětí po přiložení elektrického napětí se
Integrovaná fotonika
 Integrovaná fotonika Doc. Ing. Jiří Čtyroký, DrSc. Ústav radiotechniky a elektroniky Akademie věd ČR HTTctyroky@ure.cas.czTTH Úvod V r. 1969 vyšlo v časopise Bellových laboratoří v USA několik článků poukazujících
Integrovaná fotonika Doc. Ing. Jiří Čtyroký, DrSc. Ústav radiotechniky a elektroniky Akademie věd ČR HTTctyroky@ure.cas.czTTH Úvod V r. 1969 vyšlo v časopise Bellových laboratoří v USA několik článků poukazujících
Otázka č. 14 Světlovodné přenosové cesty
 Fresnelův odraz: Otázka č. 4 Světlovodné přenosové cesty Princip šíření světla v optickém vlákně Odraz a lom světla: β α lom ke kolmici n n β α lom od kolmice n n Zákon lomu n sinα = n sin β Definice indexu
Fresnelův odraz: Otázka č. 4 Světlovodné přenosové cesty Princip šíření světla v optickém vlákně Odraz a lom světla: β α lom ke kolmici n n β α lom od kolmice n n Zákon lomu n sinα = n sin β Definice indexu
Komplexní soubor měření optických tras při nasazování vysokorychlostních systémů xwdm
 Komplexní soubor měření optických tras při nasazování vysokorychlostních systémů xwdm Miroslav Švrček, Martin Hájek MIKROKOM, s.r.o. Nové nároky vysokorychlostních DWDM a CWDM systémů na optickou trasu
Komplexní soubor měření optických tras při nasazování vysokorychlostních systémů xwdm Miroslav Švrček, Martin Hájek MIKROKOM, s.r.o. Nové nároky vysokorychlostních DWDM a CWDM systémů na optickou trasu
PRAKTIKUM III. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009.
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III Úloha č. XXVI Název: Vláknová optika Pracoval: Jan Polášek stud. skup. 11 dne 23.4.2009 Odevzdal dne: Možný počet bodů
Modelování světla v mikro- či nanostrukturách
 Modelování světla v mikro- či nanostrukturách Jiří Beran, Miroslav Hanzelka, David Roesel VOŠ a SPŠE Olomouc, Gymnázium Česká Lípa, PORG Libeň mr.beba@gmail.com, mirdahanzelka@seznam.cz, roesel@gmail.com
Modelování světla v mikro- či nanostrukturách Jiří Beran, Miroslav Hanzelka, David Roesel VOŠ a SPŠE Olomouc, Gymnázium Česká Lípa, PORG Libeň mr.beba@gmail.com, mirdahanzelka@seznam.cz, roesel@gmail.com
Úloha č.9 Měření optických kabelů metodou OTDR (Optical Time Domain Reflectometry)
 Úloha č.9 Měření optických kabelů metodou OTDR (Optical Time Domain Reflectometry) 1 Teoretický úvod Měření parametrů optických vláken metodou zpětného rozptylu představuje v současnosti velmi důležitý
Úloha č.9 Měření optických kabelů metodou OTDR (Optical Time Domain Reflectometry) 1 Teoretický úvod Měření parametrů optických vláken metodou zpětného rozptylu představuje v současnosti velmi důležitý
ZÁKLADNÍ ČÁSTI SPEKTRÁLNÍCH PŘÍSTROJŮ
 ZÁKLADNÍ ČÁSTI SPEKTRÁLNÍCH PŘÍSTROJŮ (c) -2008, ACH/IM BLOKOVÉ SCHÉMA: (a) emisní metody (b) absorpční metody (c) luminiscenční metody U (b) monochromátor často umístěn před kyvetou se vzorkem. Části
ZÁKLADNÍ ČÁSTI SPEKTRÁLNÍCH PŘÍSTROJŮ (c) -2008, ACH/IM BLOKOVÉ SCHÉMA: (a) emisní metody (b) absorpční metody (c) luminiscenční metody U (b) monochromátor často umístěn před kyvetou se vzorkem. Části
Podpora rozvoje praktické výchovy ve fyzice a chemii
 VLNOVÁ DÉLKA A FREKVENCE SVĚTLA 1) Vypočítejte frekvenci fialového světla, je-li jeho vlnová délka 390 nm. Rychlost světla ve vakuu je 3 10 8 m s 1. = 390 nm = 390 10 9 m c = 3 10 8 m s 1 f=? (Hz) Pro
VLNOVÁ DÉLKA A FREKVENCE SVĚTLA 1) Vypočítejte frekvenci fialového světla, je-li jeho vlnová délka 390 nm. Rychlost světla ve vakuu je 3 10 8 m s 1. = 390 nm = 390 10 9 m c = 3 10 8 m s 1 f=? (Hz) Pro
Charakteristiky laseru vytvářejícího světelné impulsy o délce několika pikosekund
 Charakteristiky laseru vytvářejícího světelné impulsy o délce několika pikosekund H. Picmausová, J. Povolný, T. Pokorný Gymnázium, Česká Lípa, Žitavská 2969; Gymnázium, Brno, tř. Kpt. Jaroše 14; Gymnázium,
Charakteristiky laseru vytvářejícího světelné impulsy o délce několika pikosekund H. Picmausová, J. Povolný, T. Pokorný Gymnázium, Česká Lípa, Žitavská 2969; Gymnázium, Brno, tř. Kpt. Jaroše 14; Gymnázium,
FTTX - pasivní infrastruktura. František Tejkl 17.09.2014
 FTTX - pasivní infrastruktura František Tejkl 17.09.2014 Náplň prezentace Optické vlákno - teorie, struktura a druhy vláken (SM,MM), šíření světla vláknem, přenos opt. signálů Vložný útlum a zpětný odraz
FTTX - pasivní infrastruktura František Tejkl 17.09.2014 Náplň prezentace Optické vlákno - teorie, struktura a druhy vláken (SM,MM), šíření světla vláknem, přenos opt. signálů Vložný útlum a zpětný odraz
Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením.
 Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením. Na čem závisí účinnost vedení? účinnost vedení závisí na činiteli útlumu β a na činiteli odrazu
Jaký význam má kritický kmitočet vedení? - nejnižší kmitočet vlny, při kterém se vlna začíná šířit vedením. Na čem závisí účinnost vedení? účinnost vedení závisí na činiteli útlumu β a na činiteli odrazu
Projekt FRVŠ č: 389/2007
 Závěrečné oponentní řízení 7.2.2007 Projekt FRVŠ č: 389/2007 Název: Řešitel: Spoluřešitelé: Pracoviště: TO: Laboratoř infračervené spektrometrie Doc. Ing. Milan Honner, Ph.D. Ing. Petra Vacíková, Ing.
Závěrečné oponentní řízení 7.2.2007 Projekt FRVŠ č: 389/2007 Název: Řešitel: Spoluřešitelé: Pracoviště: TO: Laboratoř infračervené spektrometrie Doc. Ing. Milan Honner, Ph.D. Ing. Petra Vacíková, Ing.
VLNOVÁ OPTIKA. Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník
 VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
VLNOVÁ OPTIKA Mgr. Jan Ptáčník - GJVJ - Fyzika - Optika - 3. ročník Vlnová optika Světlo lze chápat také jako elektromagnetické vlnění. Průkopníkem této teorie byl Christian Huyghens. Některé jevy se dají
Optická mikroskopie a spektroskopie nanoobjektů. Nanoindentace. Pavel Matějka
 Optická mikroskopie a spektroskopie nanoobjektů Nanoindentace Pavel Matějka Optická mikroskopie a spektroskopie nanoobjektů 1. Optická mikroskopie blízkého pole 1. Princip metody 2. Instrumentace 2. Optická
Optická mikroskopie a spektroskopie nanoobjektů Nanoindentace Pavel Matějka Optická mikroskopie a spektroskopie nanoobjektů 1. Optická mikroskopie blízkého pole 1. Princip metody 2. Instrumentace 2. Optická
Fyzika laserů. 4. dubna Katedra fyzikální elektroniky.
 Fyzika laserů Přitahováni frekvencí. Spektrum laserového záření. Modelocking Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 4. dubna 2013 Program přednášek 1.
Fyzika laserů Přitahováni frekvencí. Spektrum laserového záření. Modelocking Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 4. dubna 2013 Program přednášek 1.
13. Spektroskopie základní pojmy
 základní pojmy Spektroskopicky významné OPTICKÉ JEVY absorpce absorpční spektrometrie emise emisní spektrometrie rozptyl rozptylové metody Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
základní pojmy Spektroskopicky významné OPTICKÉ JEVY absorpce absorpční spektrometrie emise emisní spektrometrie rozptyl rozptylové metody Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Historie vláknové optiky
 Historie vláknové optiky datuje se zpět 200 let, kde postupně: 1790 - franc. inženýr Claude Chappe vynalezl optický telegraf 1840 - Daniel Collodon a Jacque Babinet prokázali, že světlo může být vedeno
Historie vláknové optiky datuje se zpět 200 let, kde postupně: 1790 - franc. inženýr Claude Chappe vynalezl optický telegraf 1840 - Daniel Collodon a Jacque Babinet prokázali, že světlo může být vedeno
Slide 1. užívanými ke stanovení hodnoty indexu lomu vzduchu. interferometrie. Nepostradatelným parametrem pro stanovení takto měřené
 FS004 Státní závěřečná zkouška Bc Průvodní text k obhajobě Petr Šafařík Slide 1 Vážení členové komise, vážení přátelé; dovolte mi, abych se zde v krátkosti pokusil prezentovat svou bakalářskou práci Metody
FS004 Státní závěřečná zkouška Bc Průvodní text k obhajobě Petr Šafařík Slide 1 Vážení členové komise, vážení přátelé; dovolte mi, abych se zde v krátkosti pokusil prezentovat svou bakalářskou práci Metody
Spektrální charakteristiky
 Spektrální charakteristiky Cíl cvičení: Měření spektrálních charakteristik filtrů a zdrojů osvětlení 1 Teoretický úvod Interakcí elektromagnetického vlnění s libovolnou látkou vzniká optický jev, který
Spektrální charakteristiky Cíl cvičení: Měření spektrálních charakteristik filtrů a zdrojů osvětlení 1 Teoretický úvod Interakcí elektromagnetického vlnění s libovolnou látkou vzniká optický jev, který
VIBRAČNÍ SPEKTROMETRIE
 VIBRAČNÍ SPEKTROMETRIE (c) -2012 RAMANOVA SPEKTROMETRIE 1 PRINCIP METODY Měří se rozptýlené záření, které vzniká interakcí monochromatického záření z viditelné oblasti s molekulami vzorku za současné změny
VIBRAČNÍ SPEKTROMETRIE (c) -2012 RAMANOVA SPEKTROMETRIE 1 PRINCIP METODY Měří se rozptýlené záření, které vzniká interakcí monochromatického záření z viditelné oblasti s molekulami vzorku za současné změny
optické vlastnosti polymerů
 optické vlastnosti polymerů V.Švorčík, vaclav.svorcik@vscht.cz Definice světelného paprsku světlo se šíří ze zdroje podél přímek (paprsky) Maxwell: světlo se šířív módech (videch) = = jediná možná cesta
optické vlastnosti polymerů V.Švorčík, vaclav.svorcik@vscht.cz Definice světelného paprsku světlo se šíří ze zdroje podél přímek (paprsky) Maxwell: světlo se šířív módech (videch) = = jediná možná cesta
F7030 Rentgenový rozptyl na tenkých vrstvách
 F7030 Rentgenový rozptyl na tenkých vrstvách O. Caha PřF MU Prezentace k přednášce Numerické simulace Příklady experimentů Vybrané vztahy Sylabus Elementární popis vlnového pole: Rtg vlna ve vakuu; Greenova
F7030 Rentgenový rozptyl na tenkých vrstvách O. Caha PřF MU Prezentace k přednášce Numerické simulace Příklady experimentů Vybrané vztahy Sylabus Elementární popis vlnového pole: Rtg vlna ve vakuu; Greenova
Úloha č. 7 - Disperze v optických vláknech
 Úloha č. 7 - Disperze v optických vláknech 1 Teoretický úvod Optické vláknové vlnovody jsou důležitou komponentou optických komunikačních sítí. Jejich nejvýznamnějšími parametry jsou měrný útlum a přenosová
Úloha č. 7 - Disperze v optických vláknech 1 Teoretický úvod Optické vláknové vlnovody jsou důležitou komponentou optických komunikačních sítí. Jejich nejvýznamnějšími parametry jsou měrný útlum a přenosová
Fabry Perotův interferometr
 Fabry Perotův interferometr Princip Dvě zrcadla jsou sestavena tak aby tvořila tzv. Fabry Perotův interferometr, s jehož pomocí je vyšetřován svazek paprsků vycházejících z laseru. Při experimentu se pohybuje
Fabry Perotův interferometr Princip Dvě zrcadla jsou sestavena tak aby tvořila tzv. Fabry Perotův interferometr, s jehož pomocí je vyšetřován svazek paprsků vycházejících z laseru. Při experimentu se pohybuje
Úvod do spektrálních metod pro analýzu léčiv
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Úvod do spektrálních metod pro analýzu léčiv Pavel Matějka, Vadym Prokopec pavel.matejka@vscht.cz pavel.matejka@gmail.com Vadym.Prokopec@vscht.cz
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Úvod do spektrálních metod pro analýzu léčiv Pavel Matějka, Vadym Prokopec pavel.matejka@vscht.cz pavel.matejka@gmail.com Vadym.Prokopec@vscht.cz
Fotoelektronová spektroskopie Instrumentace. Katedra materiálů TU Liberec
 Fotoelektronová spektroskopie Instrumentace RNDr. Věra V Vodičkov ková,, PhD. Katedra materiálů TU Liberec Obecné schéma metody Dopad rtg záření emitovaného ze zdroje na vzorek průnik fotonů několik µm
Fotoelektronová spektroskopie Instrumentace RNDr. Věra V Vodičkov ková,, PhD. Katedra materiálů TU Liberec Obecné schéma metody Dopad rtg záření emitovaného ze zdroje na vzorek průnik fotonů několik µm
Rovinná harmonická elektromagnetická vlna
 Rovinná harmonická elektromagnetická vlna ---- 1. příklad -------------------------------- 2 GHz prochází prostředím s parametry: r 5, r 1, 0.005 S / m. Amplituda intenzity magnetického pole je H m 0.25
Rovinná harmonická elektromagnetická vlna ---- 1. příklad -------------------------------- 2 GHz prochází prostředím s parametry: r 5, r 1, 0.005 S / m. Amplituda intenzity magnetického pole je H m 0.25
MODERNÍ METODY CHEMICKÉ FYZIKY I lasery a jejich použití v chemické fyzice Přednáška 5
 MODERNÍ METODY CHEMICKÉ FYZIKY I lasery a jejich použití v chemické fyzice Přednáška 5 Ondřej Votava J. Heyrovský Institute of Physical Chemistry AS ČR Opakování z minula Light Amplifier by Stimulated
MODERNÍ METODY CHEMICKÉ FYZIKY I lasery a jejich použití v chemické fyzice Přednáška 5 Ondřej Votava J. Heyrovský Institute of Physical Chemistry AS ČR Opakování z minula Light Amplifier by Stimulated
4. Z modové struktury emisního spektra laseru určete délku aktivní oblasti rezonátoru. Diskutujte,
 1 Pracovní úkol 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřené závislosti zpracujte graficky. Stanovte prahový proud i 0. 2. Pomocí Hg výbojky okalibrujte
1 Pracovní úkol 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřené závislosti zpracujte graficky. Stanovte prahový proud i 0. 2. Pomocí Hg výbojky okalibrujte
SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH
 SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH MECHANIKA MOLEKULOVÁ FYZIKA A TERMIKA ELEKTŘINA A MAGNETISMUS KMITÁNÍ A VLNĚNÍ OPTIKA FYZIKA MIKROSVĚTA ODRAZ A LOM SVĚTLA 1) Index lomu vody je 1,33. Jakou rychlost má
SBÍRKA ŘEŠENÝCH FYZIKÁLNÍCH ÚLOH MECHANIKA MOLEKULOVÁ FYZIKA A TERMIKA ELEKTŘINA A MAGNETISMUS KMITÁNÍ A VLNĚNÍ OPTIKA FYZIKA MIKROSVĚTA ODRAZ A LOM SVĚTLA 1) Index lomu vody je 1,33. Jakou rychlost má
Digitální učební materiál
 Číslo projektu Název projektu Číslo a název šablony klíčové aktivity Digitální učební materiál CZ.1.07/1.5.00/3.080 Zkvalitnění výuky prostřednictvím ICT III/ Inovace a zkvalitnění výuky prostřednictvím
Číslo projektu Název projektu Číslo a název šablony klíčové aktivity Digitální učební materiál CZ.1.07/1.5.00/3.080 Zkvalitnění výuky prostřednictvím ICT III/ Inovace a zkvalitnění výuky prostřednictvím
NÁVODY PRO LABORATOŘE OBORU ANORGANICKÁ CHEMIE. Planární optické vlnovody
 NÁVODY PRO LABORATOŘE OBORU ANORGANICKÁ CHEMIE LABORATOŘ F05 Planární optické vlnovody Pavla Nekvindová a kol. 2007 Na publikaci se podílel kolektiv autorů, jmenovitě: Ing. Pavla Nekvindová Ph.D. RNDr.
NÁVODY PRO LABORATOŘE OBORU ANORGANICKÁ CHEMIE LABORATOŘ F05 Planární optické vlnovody Pavla Nekvindová a kol. 2007 Na publikaci se podílel kolektiv autorů, jmenovitě: Ing. Pavla Nekvindová Ph.D. RNDr.
Optoelektronika. Katedra fyzikální elektroniky FJFI ČVUT
 Optoelektronika Katedra fyzikální elektroniky FJFI ČVUT Letní semestr 2017-2018, 26. února - 18. května 2018, 2 (z+zk), pro bakalářské obory FE, LASE a magisterský obor 2IT Pondělí 11.0 1.15 přednášky:
Optoelektronika Katedra fyzikální elektroniky FJFI ČVUT Letní semestr 2017-2018, 26. února - 18. května 2018, 2 (z+zk), pro bakalářské obory FE, LASE a magisterský obor 2IT Pondělí 11.0 1.15 přednášky:
Zdroje optického záření
 Metody optické spektroskopie v biofyzice Zdroje optického záření / 1 Zdroje optického záření tepelné výbojky polovodičové lasery synchrotronové záření Obvykle se charakterizují zářivostí (zářivý výkon
Metody optické spektroskopie v biofyzice Zdroje optického záření / 1 Zdroje optického záření tepelné výbojky polovodičové lasery synchrotronové záření Obvykle se charakterizují zářivostí (zářivý výkon
Fotonické sítě jako médium pro distribuci stabilních signálů z optických normálů frekvence a času
 Fotonické sítě jako médium pro distribuci stabilních signálů z optických normálů frekvence a času Ondřej Číp, Šimon Řeřucha, Radek Šmíd, Martin Čížek, Břetislav Mikel (ÚPT AV ČR) Josef Vojtěch a Vladimír
Fotonické sítě jako médium pro distribuci stabilních signálů z optických normálů frekvence a času Ondřej Číp, Šimon Řeřucha, Radek Šmíd, Martin Čížek, Břetislav Mikel (ÚPT AV ČR) Josef Vojtěch a Vladimír
Využití fotonických služeb e-infrastruktury pro přenos ultrastabilních optických frekvencí
 Využití fotonických služeb e-infrastruktury pro přenos ultrastabilních optických frekvencí Ondřej Číp, Martin Čížek, Lenka Pravdová, Jan Hrabina, Václav Hucl a Šimon Řeřucha (ÚPT AV ČR) Josef Vojtěch a
Využití fotonických služeb e-infrastruktury pro přenos ultrastabilních optických frekvencí Ondřej Číp, Martin Čížek, Lenka Pravdová, Jan Hrabina, Václav Hucl a Šimon Řeřucha (ÚPT AV ČR) Josef Vojtěch a
Modulace vlnoplochy. SLM vytváří prostorově modulovaný koherentní optický signál
 OPT/OZI L06 Modulace vlnoplochy prostorové modulátory světla (SLM) SLM vytváří prostorově modulovaný koherentní optický signál řízení elektronicky adresovaný SLM opticky adresovaný SLM technologie fotografická
OPT/OZI L06 Modulace vlnoplochy prostorové modulátory světla (SLM) SLM vytváří prostorově modulovaný koherentní optický signál řízení elektronicky adresovaný SLM opticky adresovaný SLM technologie fotografická
Vlnové vlastnosti světla. Člověk a příroda Fyzika
 Název vzdělávacího materiálu: Číslo vzdělávacího materiálu: Autor vzdělávací materiálu: Období, ve kterém byl vzdělávací materiál vytvořen: Vzdělávací oblast: Vzdělávací obor: Vzdělávací předmět: Tematická
Název vzdělávacího materiálu: Číslo vzdělávacího materiálu: Autor vzdělávací materiálu: Období, ve kterém byl vzdělávací materiál vytvořen: Vzdělávací oblast: Vzdělávací obor: Vzdělávací předmět: Tematická
Úloha č.6 Dvouvlnové směšování ve fotorefraktivním materiálu a fázová
 Úloha č.6 Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace 1 Teoretický úvod Dvouvlnové směšování neboli dvouvlnová interference ve fotorefraktivním (FRV) materiálu je proces, který
Úloha č.6 Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace 1 Teoretický úvod Dvouvlnové směšování neboli dvouvlnová interference ve fotorefraktivním (FRV) materiálu je proces, který
Laserové technologie v praxi I. Přednáška č.4. Pevnolátkové lasery. Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011
 Laserové technologie v praxi I. Přednáška č.4 Pevnolátkové lasery Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011 Dělení pevnolátkových laserů podle druhu matrice a dopantu Matrice (nosič): Dopant: Alexandrit
Laserové technologie v praxi I. Přednáška č.4 Pevnolátkové lasery Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011 Dělení pevnolátkových laserů podle druhu matrice a dopantu Matrice (nosič): Dopant: Alexandrit
4.7 Planární širokopásmové antény
 4.7 Planární širokopásmové antény Základní teorie Širokopásmová technologie Systémy s extrémní šířkou pásma patří k perspektivním systémům moderní rádiové vysokokapacitní komunikace. Původně byla tato
4.7 Planární širokopásmové antény Základní teorie Širokopásmová technologie Systémy s extrémní šířkou pásma patří k perspektivním systémům moderní rádiové vysokokapacitní komunikace. Původně byla tato
2. Zdroje a detektory světla
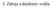 2. Zdroje a detektory světla transmitance (%) Spektrální rozsah Krátkovlné limity: Absorpce vzduchu (O 2,N 2,vodní pára) - 190 nm Propustnost optiky Spektrální rozsah zdroje vlnová délka (nm) http://www.hellma-analytics.com/text/283/en/material-and-technical-information.html
2. Zdroje a detektory světla transmitance (%) Spektrální rozsah Krátkovlné limity: Absorpce vzduchu (O 2,N 2,vodní pára) - 190 nm Propustnost optiky Spektrální rozsah zdroje vlnová délka (nm) http://www.hellma-analytics.com/text/283/en/material-and-technical-information.html
Nová koncepční a konstrukční řešení pro zobrazení s PMS
 Nová koncepční a konstrukční řešení pro zobrazení s PMS P. Bouchal (FSI VUT Brno) a Z. Bouchal (KO PřF UP Olomouc) PB 4 Zobrazování s podporou technologie PMS Garant: R. Chmelík Program PB4: Metody a systémy
Nová koncepční a konstrukční řešení pro zobrazení s PMS P. Bouchal (FSI VUT Brno) a Z. Bouchal (KO PřF UP Olomouc) PB 4 Zobrazování s podporou technologie PMS Garant: R. Chmelík Program PB4: Metody a systémy
2. Pomocí Hg výbojky okalibrujte stupnici monochromátoru SPM 2.
 1 Pracovní úkoly 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřené závislosti zpracujte graficky. Stanovte prahový proud i 0. 2. Pomocí Hg výbojky okalibrujte
1 Pracovní úkoly 1. Změřte současně světelnou i voltampérovou charakteristiku polovodičového laseru. Naměřené závislosti zpracujte graficky. Stanovte prahový proud i 0. 2. Pomocí Hg výbojky okalibrujte
= , = (1) (2)
 Název a číslo úlohy Nelineární jevy v ultrarychlé optice úloha č. 9 Datum měření 30. 11. 2015 Měření provedli Jan Fait, Marek Vlk Vypracoval Jan Fait Datum 4. 12. 2015 Hodnocení Během úlohy jsme se seznámili
Název a číslo úlohy Nelineární jevy v ultrarychlé optice úloha č. 9 Datum měření 30. 11. 2015 Měření provedli Jan Fait, Marek Vlk Vypracoval Jan Fait Datum 4. 12. 2015 Hodnocení Během úlohy jsme se seznámili
PB169 Operační systémy a sítě
 PB169 Operační systémy a sítě Přenos dat v počítačových sítích Marek Kumpošt, Zdeněk Říha Způsob propojení sítí opak. Drátové sítě TP (twisted pair) kroucená dvoulinka 100Mbit, 1Gbit Koaxiální kabel vyšší
PB169 Operační systémy a sítě Přenos dat v počítačových sítích Marek Kumpošt, Zdeněk Říha Způsob propojení sítí opak. Drátové sítě TP (twisted pair) kroucená dvoulinka 100Mbit, 1Gbit Koaxiální kabel vyšší
Spektrometrické metody. Reflexní a fotoakustická spektroskopie
 Spektrometrické metody Reflexní a fotoakustická spektroskopie odraz elektromagnetického záření - souvislost absorpce a reflexe Kubelka-Munk funkce fotoakustická spektroskopie Měření odrazivosti elmg záření
Spektrometrické metody Reflexní a fotoakustická spektroskopie odraz elektromagnetického záření - souvislost absorpce a reflexe Kubelka-Munk funkce fotoakustická spektroskopie Měření odrazivosti elmg záření
Úvod do laserové techniky KFE FJFI ČVUT Praha Michal Němec, 2014. Plynové lasery. Plynové lasery většinou pracují v kontinuálním režimu.
 Aktivní prostředí v plynné fázi. Plynové lasery Inverze populace hladin je vytvářena mezi energetickými hladinami některé ze složek plynu - atomy, ionty nebo molekuly atomární, iontové, molekulární lasery.
Aktivní prostředí v plynné fázi. Plynové lasery Inverze populace hladin je vytvářena mezi energetickými hladinami některé ze složek plynu - atomy, ionty nebo molekuly atomární, iontové, molekulární lasery.
Měření optických vlastností materiálů
 E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
Krátká teorie. Monochromatická elektromagnetická vlna Intenzita světla Superpozice elektrických polí. Intenzita interferenčního obrazce.
 Interference 1 Krátká teorie Monochromatická elektromagnetická vlna Intenzita světla Superpozice elektrických polí Intenzita interferenčního obrazce 2 ), ( ), ( t r E t r I 2 E r E p I r p r p E E E E
Interference 1 Krátká teorie Monochromatická elektromagnetická vlna Intenzita světla Superpozice elektrických polí Intenzita interferenčního obrazce 2 ), ( ), ( t r E t r I 2 E r E p I r p r p E E E E
Plazmová depozice tenkých vrstev oxidu zinečnatého
 Plazmová depozice tenkých vrstev oxidu zinečnatého Bariérový pochodňový výboj za atmosférického tlaku Štěpán Kment Doc. Dr. Ing. Petr Klusoň Mgr. Zdeněk Hubička Ph.D. Obsah prezentace Úvod do problematiky
Plazmová depozice tenkých vrstev oxidu zinečnatého Bariérový pochodňový výboj za atmosférického tlaku Štěpán Kment Doc. Dr. Ing. Petr Klusoň Mgr. Zdeněk Hubička Ph.D. Obsah prezentace Úvod do problematiky
INTERAKCE IONTŮ S POVRCHY II.
 Úvod do fyziky tenkých vrstev a povrchů INTERAKCE IONTŮ S POVRCHY II. Metody IBA (Ion Beam Analysis): pružný rozptyl nabitých částic (RBS), detekce odražených atomů (ERDA), metoda PIXE, Spektroskopie rozptýlených
Úvod do fyziky tenkých vrstev a povrchů INTERAKCE IONTŮ S POVRCHY II. Metody IBA (Ion Beam Analysis): pružný rozptyl nabitých částic (RBS), detekce odražených atomů (ERDA), metoda PIXE, Spektroskopie rozptýlených
??): Radiová oblast vlnové délky od kilometrů po 0.1 m, záření se generuje a detekuje pomocí
 Měření spektra světla Spektroskopie označuje metody určení frekvence ν resp. vlnové délky λ = c/ν elektromagnetického záření. Celé elektromagnetické spektrum lze rozdělit do podoblastí (viz obr.??): Radiová
Měření spektra světla Spektroskopie označuje metody určení frekvence ν resp. vlnové délky λ = c/ν elektromagnetického záření. Celé elektromagnetické spektrum lze rozdělit do podoblastí (viz obr.??): Radiová
Optika. Nobelovy ceny za fyziku 2005 a 2009. Petr Malý Katedra chemické fyziky a optiky Matematicko fyzikální fakulta UK
 Optika Nobelovy ceny za fyziku 2005 a 2009 Petr Malý Katedra chemické fyziky a optiky Matematicko fyzikální fakulta UK Optika zobrazování aplikace základní fyzikální otázky např. test kvantové teorie
Optika Nobelovy ceny za fyziku 2005 a 2009 Petr Malý Katedra chemické fyziky a optiky Matematicko fyzikální fakulta UK Optika zobrazování aplikace základní fyzikální otázky např. test kvantové teorie
Spektrometr pro měření Ramanovy optické aktivity: proč a jak. Optická sestava a využití motorizovaných jednotek.
 Spektrometr pro měření Ramanovy optické aktivity: proč a jak. Optická sestava a využití motorizovaných jednotek. Josef Kapitán Centrum digitální optiky Digitální Ramanova spektroskopie a Ramanova optická
Spektrometr pro měření Ramanovy optické aktivity: proč a jak. Optická sestava a využití motorizovaných jednotek. Josef Kapitán Centrum digitální optiky Digitální Ramanova spektroskopie a Ramanova optická
Elektronová mikroskopie SEM, TEM, AFM
 Elektronová mikroskopie SEM, TEM, AFM Historie 1931 E. Ruska a M. Knoll sestrojili první elektronový prozařovací mikroskop 1939 první vyrobený elektronový mikroskop firma Siemens rozlišení 10 nm 1965 první
Elektronová mikroskopie SEM, TEM, AFM Historie 1931 E. Ruska a M. Knoll sestrojili první elektronový prozařovací mikroskop 1939 první vyrobený elektronový mikroskop firma Siemens rozlišení 10 nm 1965 první
Měření optických vlastností materiálů
 E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
E Měření optických vlastností materiálů Úkoly : 1. Určete spektrální propustnost vybraných materiálů různých typů stavebních skel a optických filtrů pomocí spektrofotometru 2. Určete spektrální odrazivost
Charakteristiky optického záření
 Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
Fyzika III - Optika Charakteristiky optického záření / 1 Charakteristiky optického záření 1. Spektrální charakteristika vychází se z rovinné harmonické vlny jako elementu elektromagnetického pole : primární
Lasery optické rezonátory
 Lasery optické rezonátory Optické rezonátory Optickým rezonátorem se rozumí dutina obklopená odrazovými plochami, v níž je pasivní dielektrické prostředí. Rezonátor je nezbytnou součástí laseru, protože
Lasery optické rezonátory Optické rezonátory Optickým rezonátorem se rozumí dutina obklopená odrazovými plochami, v níž je pasivní dielektrické prostředí. Rezonátor je nezbytnou součástí laseru, protože
1 Zadání. 2 Úvod. Název a číslo úlohy 9 - Nelineární jevy v ultrarychlé optice. Měření provedli Jan Fait, Marek Vlk Vypracoval
 Název a číslo úlohy 9 - Nelineární jevy v ultrarychlé optice Datum měření 30.11.2015 Měření provedli Jan Fait, Marek Vlk Vypracoval Marek Vlk Datum 19.12.2015 Hodnocení 1 Zadání 1. Naladění systému; Naved
Název a číslo úlohy 9 - Nelineární jevy v ultrarychlé optice Datum měření 30.11.2015 Měření provedli Jan Fait, Marek Vlk Vypracoval Marek Vlk Datum 19.12.2015 Hodnocení 1 Zadání 1. Naladění systému; Naved
nano.tul.cz Inovace a rozvoj studia nanomateriálů na TUL
 Inovace a rozvoj studia nanomateriálů na TUL nano.tul.cz Tyto materiály byly vytvořeny v rámci projektu ESF OP VK: Inovace a rozvoj studia nanomateriálů na Technické univerzitě v Liberci Experimentální
Inovace a rozvoj studia nanomateriálů na TUL nano.tul.cz Tyto materiály byly vytvořeny v rámci projektu ESF OP VK: Inovace a rozvoj studia nanomateriálů na Technické univerzitě v Liberci Experimentální
Laserová technika 1. Rychlostní rovnice pro Q-spínaný laser. 22. prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Rychlostní rovnice pro Q-spínaný laser Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program přednášek
Laserová technika 1 Aktivní prostředí Rychlostní rovnice pro Q-spínaný laser Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program přednášek
Vlnovodn{ optika. 2 Vlnovodn{ optika. 2.1 Úvod. 2.2 Princip přenosu v optickém vl{kně
 Vlnovodn{ optika Cíl kapitoly Cílem kapitoly je sezn{mit se s principem vedení optikého sign{lu v optických kan{lech, jejich buzení a detekci. Poskytuje podklady pro studenty umožňující objasnění těchto
Vlnovodn{ optika Cíl kapitoly Cílem kapitoly je sezn{mit se s principem vedení optikého sign{lu v optických kan{lech, jejich buzení a detekci. Poskytuje podklady pro studenty umožňující objasnění těchto
Laserové technologie v praxi I. Přednáška č.2. Základní konstrukční součásti laserů. Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011
 Laserové technologie v praxi I. Přednáška č.2 Základní konstrukční součásti laserů Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011 Konstrukce laseru 1 - Aktivní prostředí 2 - Čerpací zařízení 3 - Optický
Laserové technologie v praxi I. Přednáška č.2 Základní konstrukční součásti laserů Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011 Konstrukce laseru 1 - Aktivní prostředí 2 - Čerpací zařízení 3 - Optický
Vysoké frekvence a mikrovlny
 Vysoké frekvence a mikrovlny Osnova Úvod Maxwellovy rovnice Typy mikrovlnného vedení Použití ve fyzice plazmatu Úvod Mikrovlny jsou elektromagnetické vlny o vlnové délce větší než 1mm a menší než 1m, což
Vysoké frekvence a mikrovlny Osnova Úvod Maxwellovy rovnice Typy mikrovlnného vedení Použití ve fyzice plazmatu Úvod Mikrovlny jsou elektromagnetické vlny o vlnové délce větší než 1mm a menší než 1m, což
Základním praktikum z optiky
 Úloha: Základním praktikum z optiky FJFI ČVUT v Praze #6 - Zdroje optického záření a jejich vlastnosti Jméno: Ondřej Finke Datum měření: 7.4.2016 Spolupracoval: Obor / Skupina: 1. Úvod Alexandr Špaček
Úloha: Základním praktikum z optiky FJFI ČVUT v Praze #6 - Zdroje optického záření a jejich vlastnosti Jméno: Ondřej Finke Datum měření: 7.4.2016 Spolupracoval: Obor / Skupina: 1. Úvod Alexandr Špaček
PRAKTIKUM III. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Název: Studium ohybových jevů v laserovém svazku
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III. Úloha č. 6 Název: Studium ohybových jevů v laserovém svazku Pracoval: Lukáš Vejmelka obor (kruh) FMUZV (73) dne 10.3.2014
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM III. Úloha č. 6 Název: Studium ohybových jevů v laserovém svazku Pracoval: Lukáš Vejmelka obor (kruh) FMUZV (73) dne 10.3.2014
Úloha č. 8 Vlastnosti optických vláken a optické senzory
 Úloha č. 8 Vlastnosti optických vláken a optické senzory Optické vlákna patří k nejmodernějším přenosovým médiím. Jejich vysoká přenosová kapacita a nízký útlum jsou hlavní výhody, které je staví před
Úloha č. 8 Vlastnosti optických vláken a optické senzory Optické vlákna patří k nejmodernějším přenosovým médiím. Jejich vysoká přenosová kapacita a nízký útlum jsou hlavní výhody, které je staví před
Řešení: Nejdříve musíme určit sílu, kterou působí kladka proti směru pohybu padajícího vědra a napíná tak lano. Moment síly otáčení kladky je:
 Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Úvod, optické záření. Podkladový materiál k přednáškám A0M38OSE Obrazové senzory ČVUT- FEL, katedra měření, Jan Fischer, 2014
 Úvod, optické záření Podkladový materiál k přednáškám A0M38OSE Obrazové senzory ČVUT- FEL, katedra měření, Jan Fischer, 2014 Materiál je pouze grafickým podkladem k přednášce a nenahrazuje výklad na vlastní
Úvod, optické záření Podkladový materiál k přednáškám A0M38OSE Obrazové senzory ČVUT- FEL, katedra měření, Jan Fischer, 2014 Materiál je pouze grafickým podkladem k přednášce a nenahrazuje výklad na vlastní
1 Rezonátorová optika
 1 Rezonátorová optika Optické rezonátory jsou zařízení, ve kterých lze akumulovat optickou energii. Mohou také působit jako frekvenční filtr. Obojího se využívá v laseru, kde je aktivní prostředí, které
1 Rezonátorová optika Optické rezonátory jsou zařízení, ve kterých lze akumulovat optickou energii. Mohou také působit jako frekvenční filtr. Obojího se využívá v laseru, kde je aktivní prostředí, které
Laserové technologie v praxi I. Přednáška č.8. Laserové zpracování materiálu. Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011
 Laserové technologie v praxi I. Přednáška č.8 Laserové zpracování materiálu Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011 Lasery pro průmyslové zpracování materiálu E (ev) 0,12 1,17 1,17 1,2 1,5 4,17
Laserové technologie v praxi I. Přednáška č.8 Laserové zpracování materiálu Hana Chmelíčková, SLO UP a FZÚ AVČR Olomouc, 2011 Lasery pro průmyslové zpracování materiálu E (ev) 0,12 1,17 1,17 1,2 1,5 4,17
Laboratorní práce č. 3: Měření vlnové délky světla
 Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Laboratorní práce č. 3: Měření vlnové délky světla G Gymnázium Hranice Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Gymnázium G Hranice Test
Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Laboratorní práce č. 3: Měření vlnové délky světla G Gymnázium Hranice Přírodní vědy moderně a interaktivně SEMINÁŘ FYZIKY Gymnázium G Hranice Test
11. Polovodičové diody
 11. Polovodičové diody Polovodičové diody jsou součástky, které využívají fyzikálních vlastností přechodu PN nebo přechodu kov - polovodič (MS). Nelinearita VA charakteristiky, zjednodušeně chápaná jako
11. Polovodičové diody Polovodičové diody jsou součástky, které využívají fyzikálních vlastností přechodu PN nebo přechodu kov - polovodič (MS). Nelinearita VA charakteristiky, zjednodušeně chápaná jako
Úloha 10: Interference a ohyb světla
 Úloha 10: Interference a ohyb světla FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 29.3.2010 Jméno: František Batysta Pracovní skupina: 5 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovník: Štěpán
Úloha 10: Interference a ohyb světla FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 29.3.2010 Jméno: František Batysta Pracovní skupina: 5 Ročník a kroužek: 2. ročník, pond. odp. Spolupracovník: Štěpán
Měření a analýza mechanických vlastností materiálů a konstrukcí. 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály
 FP 1 Měření a analýza mechanických vlastností materiálů a konstrukcí Úkoly : 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály 2. Určete moduly pružnosti vzorků nepřímo pomocí měření rychlosti
FP 1 Měření a analýza mechanických vlastností materiálů a konstrukcí Úkoly : 1. Určete moduly pružnosti E z ohybu tyče pro 4 různé materiály 2. Určete moduly pružnosti vzorků nepřímo pomocí měření rychlosti
Mikroskopie se vzorkovací sondou. Pavel Matějka
 Mikroskopie se vzorkovací sondou Pavel Matějka Mikroskopie se vzorkovací sondou 1. STM 1. Princip metody 2. Instrumentace a příklady využití 2. AFM 1. Princip metody 2. Instrumentace a příklady využití
Mikroskopie se vzorkovací sondou Pavel Matějka Mikroskopie se vzorkovací sondou 1. STM 1. Princip metody 2. Instrumentace a příklady využití 2. AFM 1. Princip metody 2. Instrumentace a příklady využití
MĚŘENÍ ÚHLOVÝCH KMITŮ ZA ROTACE
 26. mezinárodní konference DIAGO 27 TECHNICKÁ DIAGNOSTIKA STROJŮ A VÝROBNÍCH ZAŘÍZENÍ MĚŘENÍ ÚHLOVÝCH KMITŮ ZA ROTACE Jiří TŮMA VŠB Technická Univerzita Ostrava Osnova Motivace Kalibrace měření Princip
26. mezinárodní konference DIAGO 27 TECHNICKÁ DIAGNOSTIKA STROJŮ A VÝROBNÍCH ZAŘÍZENÍ MĚŘENÍ ÚHLOVÝCH KMITŮ ZA ROTACE Jiří TŮMA VŠB Technická Univerzita Ostrava Osnova Motivace Kalibrace měření Princip
Jak vyrobit monochromatické Slunce
 Jak vyrobit monochromatické Slunce Spektroskopie (nejen) ve sluneční fyzice LS 011/01 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Pozorování Slunce ve spektrální čáře Spektroheliogram
Jak vyrobit monochromatické Slunce Spektroskopie (nejen) ve sluneční fyzice LS 011/01 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Pozorování Slunce ve spektrální čáře Spektroheliogram
Optická konfokální mikroskopie a mikrospektroskopie. Pavel Matějka
 Optická konfokální mikroskopie a Pavel Matějka 1. Konfokální mikroskopie 1. Princip metody - konfokalita 2. Instrumentace metody zobrazování 3. Analýza obrazu 2. Konfokální 1. Luminiscenční 2. Ramanova
Optická konfokální mikroskopie a Pavel Matějka 1. Konfokální mikroskopie 1. Princip metody - konfokalita 2. Instrumentace metody zobrazování 3. Analýza obrazu 2. Konfokální 1. Luminiscenční 2. Ramanova
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK FYZIKÁLNÍ PRAKTIKUM III Úloha číslo: 16 Název: Měření indexu lomu Fraunhoferovou metodou Vypracoval: Ondřej Hlaváč stud. skup.: F dne:
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK FYZIKÁLNÍ PRAKTIKUM III Úloha číslo: 16 Název: Měření indexu lomu Fraunhoferovou metodou Vypracoval: Ondřej Hlaváč stud. skup.: F dne:
Otázka 22(42) Přístroje pro měření signálů, metody pro měření v časové a frekvenční doméně. Přístroje
 Otázka 22(42) Přístroje pro měření signálů, metody pro měření v časové a frekvenční doméně Rozmanitost signálů v komunikační technice způsobuje, že rozdělení měřicích metod není jednoduché a jednoznačné.
Otázka 22(42) Přístroje pro měření signálů, metody pro měření v časové a frekvenční doméně Rozmanitost signálů v komunikační technice způsobuje, že rozdělení měřicích metod není jednoduché a jednoznačné.
Molekulová spektroskopie 1. Chemická vazba, UV/VIS
 Molekulová spektroskopie 1 Chemická vazba, UV/VIS 1 Chemická vazba Silová interakce mezi dvěma atomy. Chemické vazby jsou soudržné síly působící mezi jednotlivými atomy nebo ionty v molekulách. Chemická
Molekulová spektroskopie 1 Chemická vazba, UV/VIS 1 Chemická vazba Silová interakce mezi dvěma atomy. Chemické vazby jsou soudržné síly působící mezi jednotlivými atomy nebo ionty v molekulách. Chemická
Ideální pedagogická koncepce výuky mikrovlnných planárních obvodů
 Ideální pedagogická koncepce výuky mikrovlnných planárních obvodů Jiří Svačina Ústav radioelektroniky FEKT VUT v Brně svacina @ feec.vutbr.cz 1 Ideální koncepce výuky Co je to? 2 Ideální koncepce výuky
Ideální pedagogická koncepce výuky mikrovlnných planárních obvodů Jiří Svačina Ústav radioelektroniky FEKT VUT v Brně svacina @ feec.vutbr.cz 1 Ideální koncepce výuky Co je to? 2 Ideální koncepce výuky
Jan Fait, Filip Grepl Jan Fait Datum Hodnocení
 Název a číslo úlohy Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace úloha č. 6 Datum měření 16. 10. 2015 Měření provedli Vypracoval Jan Fait, Filip Grepl Jan Fait Datum 22. 10. 2015
Název a číslo úlohy Dvouvlnové směšování ve fotorefraktivním materiálu a fázová konjugace úloha č. 6 Datum měření 16. 10. 2015 Měření provedli Vypracoval Jan Fait, Filip Grepl Jan Fait Datum 22. 10. 2015
Proč elektronový mikroskop?
 Elektronová mikroskopie Historie 1931 E. Ruska a M. Knoll sestrojili první elektronový prozařovací mikroskop,, 1 1939 první vyrobený elektronový mikroskop firma Siemens rozlišení 10 nm 1965 první komerční
Elektronová mikroskopie Historie 1931 E. Ruska a M. Knoll sestrojili první elektronový prozařovací mikroskop,, 1 1939 první vyrobený elektronový mikroskop firma Siemens rozlišení 10 nm 1965 první komerční
