Parametrizace rozdělení škod v
|
|
|
- Marek Veselý
- před 6 lety
- Počet zobrazení:
Transkript
1 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Mária Špaková Parametrizace rozdělení škod v neživotním pojištení Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: RNDr. Michal Pešta, Ph.D. Studijní program: Matematika Studijní obor: Finanční a pojistná matematika Praha 2013
2 Charles University in Prague Faculty of Mathematics and Physics MASTER THESIS Mária Špaková Parameterization of claims distribution in non-life insurance Department of Probability and Mathematical Statistics Supervisor of the master thesis: RNDr. Michal Pešta, Ph.D. Study programme: Mathematics Specialization: Financial and Insurance Mathematics Prague 2013
3 First of all, I would like to express gratitude to my supervisor, RNDr. Michal Pešta, Ph.D., for his help, valuable advice, ideas and time he has devoted to me. Furthermore, I would like to thank my boyfriend for his technical help, language corrections and all provided support and care. Last but not least, I would like to send my thanks to my beloved parents and three younger sisters for the moral support not only during the time of writing but also during my whole studies.
4 I declare that I carried out this master thesis independently, and only with the cited sources, literature and other professional sources. I understand that my work relates to the rights and obligations under the Act No. 121/2000 Coll., the Copyright Act, as amended, in particular the fact that the Charles University in Prague has the right to conclude a license agreement on the use of this work as a school work pursuant to Section 60 paragraph 1 of the Copyright Act. In Prague Mária Špaková
5 Název práce: Parametrizace rozdělení škod v neživotním pojištení Autor: Bc. Mária Špaková Katedra: Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: RNDr. Michal Pešta, Ph.D., MFF UK Abstrakt: Předložená práce se zabývá parametrizací rozdělení škod v neživotním pojištění. Skláda se z teoretické a aplikační části. V první části se zabýváme obvyklými rozděleními škod a jejich vlastnostmi, přičemž jedna sekce je věnována rozdělení extrémních hodnot. Následně zmíníme nejznámější metody pro odhad parametrů metodu maximální věrohodnosti, metodu momentů a metodu vážených momentů. Poslední teoretická kapitola je zaměřena na některé validační techniky a goodness-of-fit testy. V praktické části aplikujeme některé z diskutovaných přístupů na reálná data. Soustředíme se však zejména na modelování velkých škod nejprve zvolíme přiměřenou prahovou hodnotu pro naše data a pak odhadujeme škody zobecněnou Paretovou distribucí a všemi představenými postupy parametrizace. Na základě výsledků použitých validačních metod zvolíme vhodné modely pro největší škody. Klíčová slova: parametrizace, neživotní pojištení, distribuce škod. Title: Parameterization of claims distribution in non-life insurance Author: Bc. Mária Špaková Department: Department of Probability and Mathematical Statistics Supervisor: RNDr. Michal Pešta Ph.D., MFF UK Abstract: This paper deals with the parameterization of claim size distributions in non-life insurance. It consists of the theoretical and the practical part. In the first part we discuss the usual distributions of claims and their properties. One section is devoted to extreme values distributions. Consequently, we mention the most known methods for parameter estimation the maximum likelihood method, the method of moments and the method of weighted moments. The last theoretical chapter is focused on some validation techniques and goodness-of-fit tests. In the practical part we apply some of the discussed approaches on real data. However, we concentrate mainly on the large claims modeling firstly, we select a reasonable threshold for our data and then we fit the claims by the generalized Pareto distribution together with the introduced parameterization procedures. Based on the results of the applied validation methods we will choose appropriate models for the biggest claims. Keywords: parametrization, non-life insurance, claims distribution.
6 Contents List of Abbreviations 2 1 Introduction 3 2 Theoretical background for claims distribution Individual and collective risk model Overview of claim size distributions Exponential distribution Log-normal distribution Pareto distribution Burr distribution Weibull distribution Gamma distribution Mixing of models Parametric models of extreme values Generalized extreme value distribution Generalized Pareto distribution Methods for fitting parameters of claim distributions Maximum likelihood Method of moments Method of weighted moments Back diagnostics and validation techniques χ 2 goodness-of-fit statistic Kolmogorov-Smirnov statistic Cramer-von Mises family Mean excess function Limited expected value function Threshold selection Threshold choice plot Mean excess plot L-moments plot Dispersion index plot Application on the real data Description of the data Parameterization of the medical claims Threshold selection Big claims modeling Discussion Conclusion 47 Bibliography 49 1
7 List of Abbreviations EM - Expectation-Maximization GEV - Generalized extreme value distribution GPD - Generalized Pareto distribution MDA - Maximum domain of attraction ML - Maximum likelihood MM - Method of moments MWM - Method of weighted moments POT - Peaks over threshold 2
8 1. Introduction The modeling of claims and searching for a satisfying parameterization of the distributions that can describe them appropriately, is one of the key problems in non-life insurance. In order to predict the future claims, and accordingly adjust some characteristics of the existing products or prepare new ones, a company needs to know how the claims behave in particular types of insurance, groups of clients, regions, periods. Concerning the claims distributions, we can model either the claim sizes or the number of claims. However, in addition to the modeling these two properties individually we can model the claims complexly and take both the size and the number into account. The topic of this thesis is finding a good parameterization of the claim size distributions first on a theoretical basis and later practically by an application on the real claim size data. A motivation for writing this thesis has been to create a graspable handbook for young non-life actuaries. It should theoretically summarize some essential methods for claim size parameterization and validation techniques connected with this topic as well as show some of them in practice. Obviously, our intention has not been to include everything an actuary should know about the claim size modeling this task would greatly exceed the scope of a master thesis. In the first chapter of the thesis Theoretical background for claim distributions we deal with the basic theoretical knowledge about the claim size distributions. We briefly introduce the model of individual and collective risk. Further, we describe the most known and used distributions for modeling the claim size namely the exponential, log-normal, Weibull, gamma, Pareto and Burr distribution. In the next short section, we mention the idea of mixing more distributions. A very important part of this chapter is devoted to the modeling of big or extreme values. The second chapter is called Methods of fitting parameters of claim distributions. As the name already says, we discuss some widespread methods for estimation of parameters figuring in the claim size distributions. We focus mainly on the maximum likelihood estimation and the method of moments. In addition, we introduce the method of weighted moments as well. After finding a reasonable claim size distribution with appropriate parameter estimates, there is a need to measure the quality of the fit. For this purpose we use different goodness-of-fit methods. In the third chapter Back diagnostics and validation techniques we talk about the tests based on the difference between the empirical and theoretical distribution function, such as Kolmogorov-Smirnov, Anderson-Darling and Cramer-von Mises. We also mention the χ 2 statistic. Moreover, two sections of this chapter deal with the special methods used by some actuaries the mean excess function and the limited expected value function. At the end of the chapter we discuss the methods for threshold selection, that could be also perceived as a type of validation techniques. 3
9 The theoretical part of the thesis consisting of the three above introduced chapters serves as a basis for the application part named Application on the real data. In this chapter we work with the real claim size data from the US medical claims database and we have three claim years 1997, 1998 and 1999 at disposal. Since our aim is not to apply all methods mentioned in the theoretical part of the thesis, we choose only the biggest claims and model them by the method Peaks over threshold in detail firstly we try to find a reasonable threshold for them and after that we fit the large claims. Nevertheless, in the application part we do not devote to the usual claims as the process of the parameterization is analogical, except of the threshold selection, and in line with the methods discussed in the first parts of the thesis. 4
10 2. Theoretical background for claims distribution The selection of an appropriate statistical model is an essential task in claims modeling in non-life insurance. However, before estimation of parameters we need to know possible statistical distributions which may approximate our observed data. In this chapter, we explore the theoretical background for these distributions. Firstly, we introduce the individual and the collective model in non-life insurance. Consequently, we discuss some well-known distributions potentially describing the behavior of claims size, such as the exponential, log-normal, Pareto, Burr, Weibull and gamma distribution. For each of these distributions, we state their characteristics and properties. We also mention more complex distributions created by utilizing two or more distributions or compounding. In the last part of the chapter we shortly present distributions of extreme values the generalized extreme value distribution and the generalized Pareto distribution. 2.1 Individual and collective risk model One of the most important problems for an insurance company is modeling the total amount of damage occurring in a given time period for all the insurance contracts of a certain type. This set of insurance contracts is called insurance portfolio [17]. Let S be a random variable representing a sum of claims for a fixed period of length T. Individual risk model operates with risks associated with individual policies in the insurance portfolio. Let the insurance portfolio contain ν policies and for i = 1,..., ν let Y i be a claim belonging to a separate policy in the considered period. For the sum of damage S = we assume independent random variables Y i, i = 1,...ν. ν Y i (2.1) i=1 Collective risk model is based on an assumption that in a sufficiently homogeneous insurance portfolio we can consider the claims belonging to the individual policies as equally distributed random variables. The sum of damages is then expressed by the relation S = N X i, (2.2) i=1 where a random variable N represents a number of all claims in the considered period and X i, i = 1, 2,... is a sequence of claims regardless to the policy they are related to. If X i, i = 1, 2,... is the sequence of independent and equally distributed 5
11 random variables and the random variable N does not depend on X i, i = 1, 2,..., the sum of damages S has a compound distribution. 2.2 Overview of claim size distributions We will discuss several well-known claims modeling distributions in this paragraph. While choosing an appropriate distribution we should stay aware of the non-negativity of claims, as well as the significant skewness typical for claims in many insurance segments (i.e. higher frequency of smaller damages). These are the reasons why the normal distribution is not an appropriate model, although it is the main model in other parts of mathematical statistics. In claims modeling, the exponential distribution is the dominant model [17], followed by other typical candidates for claim size distributions log-normal, Pareto, Burr, Weibull, and gamma distributions [3] Exponential distribution The distribution and density functions of exponential distribution can be characterized as F (x) = 1 e βx, x 0; β > 0; (2.3) General formula for the k-th raw moment is The expectation and variance are equal to f(x) = βe βx, x 0; β > 0. (2.4) m k = k! β k. (2.5) EX = 1 β, (2.6) Coefficient of skewness is γ 1 = VarX = 1 β 2. (2.7) E(X EX)3 (VarX) 3/2 = 2. (2.8) According to [3], the maximum likelihood estimator equal to the the method of moments estimator for β is given by ˆβ = 1ˆm 1, (2.9) where is the sample k-th raw moment. ˆm k = 1 n n x k i (2.10) i=1 6
12 Exponential distribution is not always suitable for describing a distribution of claims, unless the sample data suggests there is a high probability of a high damage event (e.g. fire insurance or liability insurance). In that case, the convergence of the function 1 F (x) to zero as x is too fast and therefore the model with exponential distribution may underestimate the probability of the occurrence of high damage Log-normal distribution Consider a random variable X with the normal distribution and the density f N (x) = 1 exp{ 1 (x µ) 2 }, x R (2.11) 2πσ 2 σ 2 Let Y = e X so that X = log Y. Then the probability density function of Y is given by the formula f(y) = f N (log y) 1 y = 1 exp{ 1 (log y µ) 2 }, y > 0, (2.12) 2πσy 2 σ 2 where σ > 0 is the scale and µ R is the location parameter. The log-normal distribution function is given by ( ) log y µ F (y) = Φ, y > 0, (2.13) σ where Φ is the standard normal distribution function with the mean equal to 0 and the variance equal to 1. The k-th raw moment for log-normal distribution can be derived using results for normal random variables [3] m k = E(Y k ) = E(e kx ) = exp {µk + σ2 k 2 }. (2.14) 2 The mean and the variance of log-normal distribution are EX = exp{µ + σ2 }, (2.15) 2 VarX = ( exp{σ 2 } 1 ) exp{2µ + σ 2 }. (2.16) For standard parameter estimation techniques (see the chapter 3) the estimators are known in a closed form. The maximum likelihood estimators are given by ˆσ 2 = 1 n ˆµ = 1 n n log (x i ), (2.17) i=1 n {log (x i ) ˆµ} 2, (2.18) i=1 and using the methods of moments we get ( ) ( 1 n ˆµ = 2 log x i 1 n n log 1 n i=1 7 n i=1 x 2 i ), (2.19)
13 ˆσ 2 = log ( 1 n n i=1 x 2 i ) 2 log ( 1 n n x i ). (2.20) The log-normal distribution is very useful in claims modeling. It is right-skewed, it has a heavy tail and fits many situations well. For a small σ it resembles the normal distribution, although this is not always desirable. It is infinitely divisible and closed under scale and power transformations. However, it has also some drawbacks the most significant one is the lack of a moment generating function [3] Pareto distribution Pareto distribution is the most frequently used distribution for an analytical description of high claims. Its distribution function is ( ) α x + λ F (x) = 1, x > 0; α > 0, λ > 0. (2.21) λ We can derive this distribution as logarithmic-exponential : if ξ is a random variable with an exponential distribution i=1 the random variable F (ξ > x) = e αx, α > 0, (2.22) X = λe ξ, λ > 0, (2.23) has the Pareto distribution with parameters α and λ. For X holds ( ) α x + λ P(X > x+λ) = P(ξ+log λ > log(x+λ)) = e α(log(x+λ) log λ) =, x 0. λ (2.24) A density of the Pareto distribution is given by this formula f(x) = αλ α (x + λ) α 1, x 0; (2.25) and in comparison with the exponential distribution, it converges to zero rather slowly for x. This fact is shown in its expectation which is finite only for α > 1, and its variance finite only for α > 2. If both expectation and variance of the Pareto distribution are finite, they are expressed by the relationships EX = λ α 1, (2.26) VarX = λ 2 α (α 1) 2 (α 2). (2.27) We can alleviate the problem of non-existence of moments in case the damage will not exceed certain finite upper bound C, we can use a distribution function of the censored Pareto distribution 8
14 F C (x) = F (x), λ x < C. (2.28) F (C) It is the distribution function of the conditional distribution P(X x X C) for λ x < C. The moments of the censored Pareto distribution are always finite. For the Pareto distribution the method of moments estimators are given by ˆα = 2 ˆm 2 ˆm 2 1, (2.29) ˆm 2 2 ˆm 2 1 ˆα = ˆm 1 ˆm 2, (2.30) ˆm 2 2 ˆm 2 1 where ˆm k is the sample k-th raw moment as above (2.10) Burr distribution Experience has shown that the Pareto distribution is often an appropriate model for the claim distribution, particularly when exceptionally large claims may occur. However, sometimes we need to use heavy tailed distributions offering greater flexibility. Such flexibility is provided by the Burr distribution and its additional shape parameter τ > 0 [3]. If Y has the Pareto distribution, then X = Y 1 τ has the Burr distribution. Its density and distribution function are given by x τ 1 f(x) = ταλ α, x > 0, (λ + x τ ) α+1 (2.31) ( ) α λ F (x) = 1, x > 0. λ + x τ (2.32) The k-th raw moment m k = 1 ( Γ(α) λk/τ Γ 1 + k ) ( Γ α k ), (2.33) τ τ exists only for k < τα. Since the distribution is derived from Pareto distribution, it also has no moment generating function. As mentioned in the article [3] the maximum likelihood and method of moments estimators for the Burr distributions can be only evaluated numerically Weibull distribution If V is a variable with exponential distribution, then the distribution of X = V 1/τ, τ > 0, is called Weibull 1 distribution. Its density and distribution function are given by formulas f(x) = ταx τ 1 e αxτ, x > 0, (2.34) F (x) = 1 e αxτ, x > 0. (2.35) 1 the name Frechet distribution is also used in some literature 9
15 The Weibull distribution is roughly symmetrical for the shape parameter τ 3, 6. When τ is smaller the distribution is right-skewed and in reverse, when τ is larger, it is left-skewed [3]. The k-th raw moment is m k = α k/τ Γ ( 1 + k τ ). (2.36) Similarly to the Burr distribution, the maximum likelihood and method of moments estimators can only be evaluated numerically [3] Gamma distribution The following distribution, which can serve for claims modeling, is Gamma distribution with the distribution function and density f(x) = F (x) = x 0 α 1 e βs β(βs) ds, x > 0, (2.37) Γ(α) βα Γ(α) xα 1 e βx, x 0; α > 0, β > 0. (2.38) For integer-valued α, relation (2.38) is the density of sum of α mutually independent random variables with the same exponential distribution and the density αe αx. Therefore following holds true x 0 x βe β(x y) f(y)dy = βα+1 Γ(α) e βx 0 y α 1 dy = βα+1 Γ(α + 1) xα e βx. (2.39) If the shape parameter α = 1, we can calculate the density of the exponential distribution from (2.38); if β = 1/2 and α = ν/2, the distribution is called χ 2 distribution with ν degrees of freedom [3]. The k-th raw moment can be calculated from the formula m k = Γ(α + k) Γ(α)β k. (2.40) The mean and the variance of the gamma distribution with the density (2.38) are EX = α β, (2.41) VarX = α β 2. (2.42) The method of moments estimators for the gamma distribution can be expressed as listed below; nevertheless, maximum likelihood estimators can be evaluated only numerically [3]. ˆα = ˆm 2 1, (2.43) ˆm 2 ˆm
16 ˆβ = ˆm 1. (2.44) ˆm 2 ˆm 2 1 One of the properties of the gamma distribution is that a sum of independent gamma variates with the parameter β gives the gamma distribution with the same parameter β. Therefore the distribution is infinitely divisible. What is more, as mentioned in [3], it is right-skewed and approaches a normal distribution in the limit as α. The gamma distribution is one of the most vital distributions for modeling because of its attributes, however, it is rarely a reasonable model for insurance claims. 2.3 Mixing of models According to [12], one way in which long-tailed and/or skewed distributions arise naturally is through a mixture of models. It can occasionally happen while observing independent variables with a certain distribution, that due to some defect in the process, we observe a random variable which has another distribution. The idea of mixing can be extended to a mixture of more than two distributions. Suppose that we have k distributions with probability density functions f 1 (x), f 2 (x),..., f k (x), means µ 1, µ 2,..., µ k and variances σ1, 2 σ2, 2..., σk 2 with positive mixing probabilities p 1, p 2,...p k, where the sum of these probabilities gives 1. Then the density of the mixture is p 1 f 1 (x) + p 2 f 2 (x) p k f k (x) = Mean and variance of such distribution are as follows: EX = k p i xf i (x)dx = i=1 VarX = k p i σi 2 + i=1 k p i f i (x). (2.45) i=1 k p i µ i = µ, (2.46) i=1 k p i (µ i µ) 2. (2.47) The mixture of distributions is sometimes called compounding. In the article [11] there are two particular compound distributions used for the claims modeling gamma + log-gamma and gamma + log-normal. Authors of the article suggested to choose these types of distributions when a sample of observed losses contained some claims that involved litigation and others that did not. In situations like this a single distribution may not fit the data as well as a combination of two or more distributions mixed together. The most known compound distributions include the negative binomial and the generalized Pareto distribution. Although the negative binomial distribution is not used for the claim size modeling, we discuss both of them in next paragraphs. i=1 11
17 Let X be a Poisson-distributed variable with the parameter θ. We would like to mix an infinite number of Poisson distributions with different values of θ. Let the weighting function be the density of the gamma distributions of the variable θ with parameters α and λ. Thus, the compound distribution is 0 [ ] [ ] λ α θ Γ(α) θα 1 e λθ x e θ dθ = λα x! Γ(α)x! 0 θ α+x 1 e θ(1+λ) dθ. (2.48) If we compare this integrand to the gamma probability density function with parameters α + x and λ + 1, the density is equal to Γ(α + x)λ α, x = 0, 1, 2,... (2.49) Γ(α)x!(1 + λ) α+x If α = r, where r is a positive integer, and λ = p/(1 p), 0 < p < 1, then acoording to [12] the expression (2.49) becomes (r + x 1)! p r (1 p) x, x = 0, 1, 2,... (2.50) (r 1)!x! It means that X has a distribution corresponding to the distribution of the number of excess trials needed to obtain r successes in a sequence of independent trials with the probability of success p. This distribution is called the negative binomial distribution and has been used as a model for number of accidents for motorists [12]. Now we are going to develop a heavy-tailed skewed distribution which is very important to actuaries for modeling the size of loss distributions. Let X be a variable with conditional gamma density and parameters k and θ. The weighting function for θ will be a gamma density with parameters α and λ. Hence, the unconditional density of the variable X is f(x) = 0 λ α x k 1 θ α+k 1 e (λ+x)θ dθ. (2.51) Γ(α)Γ(k) Comparing this integrand to the gamma probability density function with parameters α + k and λ + x we get f(x) = Γ(α + k)λα x k 1, 0 < x <, (2.52) Γ(α)Γ(k)(λ + x) α+k what is the density of the generalized Pareto distribution. When k = 1, the density f(x) = αλ α, 0 < x < (2.53) (λ + x) α+1 represents the density of the Pareto distribution discussed in the previous section. Both of these compound distributions have thicker tails than the original gamma distribution. According to [12] the mean and the variance of the generalized Pareto distribution can be found by comparing the integrals representing EX and EX 2 with the 12
18 density of that distribution when k is k + 1 and k + 2. We present only the simplified formulas for the mean and the variance. 2 and µ = EX = kλ α 1, α > 1 (2.54) EX 2 = thus for α > 2 the variance is σ 2 = (k + 1)kλ2, α > 2, (2.55) (α 1)(α 2) k(α + k 1)λ2 (α 1) 2 (α 2). (2.56) From the Pareto distribution we can create another useful compound long-tailed distribution by letting X = Y τ, 0 < τ. It is the Burr distribution with the distribution function (2.32) and the density (2.31). 2.4 Parametric models of extreme values In non-life insurance we sometimes deal with the claims which are extremely high. This may be the case of floods and earthquakes, large traffic accidents etc. Size of claims resulting from these extreme events can be modeled by parametric distributions discussed in this section based mainly on the article [18]. We need to model the claim size parametrically because we are interested in values which occur with small probabilities and rarely in the observed data. There are two main data adjustment methods which allow us to apply the models on these extreme values: The block maxima approach The data X 1, X 2,... are divided into m blocks with the size n and consequently the maximal values for each block M n1,..., M nm are obtained. Peaks over threshold (POT) Only the observations exceeding a set threshold are used for modeling. We briefly deal with the distribution of the data adjusted by these two methods in the following subsections. However, more detailed information as well as the proofs of the theorems presented later in this section can be found in [18] or [9]. 2 The whole derivation of the mean and the variance of the generalized Pareto distribution can be found in [12]. 13
19 2.4.1 Generalized extreme value distribution The parametric models used for the analysis of the block maxima are called the extreme value distributions. They are limit distributions for the sequences of appropriately standardized maxima M n from n independent identically distributed variables as n. Here are distribution functions of extreme value distributions: Gumbel distribution: Frechet distribution: Weibull distribution: G 0 (x) = exp ( e x ), x R (2.57) G 1,α (x) = exp ( x α ), x 0, α > 0 (2.58) G 2,α (x) = exp ( ( x) α ), x 0, α < 0 (2.59) After adding the parameters µ (location), σ (scale) and γ (shape) these three distributions can be merged into a single parametric family: the generalized extreme value distribution (GEV) [20]. The GEV has a distribution function defined by [ ( G(x) = exp 1 + γ x µ ) ] 1/γ (2.60) σ The Frechet case is obtained when γ > 0 and the negative Weibull when γ < 0. When γ 0, we get the Gumbel distribution. Let X 1, X 2,... be a sequence of independent and identically distributed random variables with a distribution function F. Then M n = max(x 1,..., X n ) has a distribution function F n. The limit behavior of normalized maxima is characterized by the following Fischer-Tippet theorem. Theorem 2.1. Suppose there exist normalizing constants c n > 0 and d n R such that: ( ) lim P Mn d n x = lim F n (c n x + d n ) = G(x) (2.61) n c n n for a non-degenerate distribution function G. Then G is the distribution function of the GEV distribution. If the assumption for the Fischer-Tippet theorem is met, we can say the distribution function F belongs to the maximum domain of attraction (MDA) of a distribution with a distribution function G, F M DA(G). MDA of extreme values is characterized by the following theorem, where F (x) = 1 F (x) 14
20 Theorem 2.2. Distribution function F belongs to the MDA of the extreme values distribution with the distribution function G and normalizing constants c n > 0, d n R, if and only if lim n F (c n x + d n ) = ln G(x), x R. 3 (2.62) n Generalized Pareto distribution For the analysis of the data by the POT method the generalized Pareto distributions (GPD) are of a great importance. 4 They have the following distribution functions: Exponential distribution: Pareto distribution: Beta distribution: W 0 (x) = 1 e x, x 0 (2.63) W 1,α (x) = 1 x α, x 1 (2.64) W 2,α (x) = 1 ( x) α, 1 x 0 (2.65) As was the case with GEV, we can introduce a single form of the distribution function dependent on the newly chosen parameter of shape γ for the description of above mentioned distribution function with appropriately chosen parameters of location µ and scale σ. Hence, we get the distribution function of GPD ( W (x) = γ x µ ) 1/γ, (2.66) σ where the Pareto distribution matches the choice of γ > 0 and x 0 and the beta distribution correspond to (2.66) as γ < 0 and 0 x 1/ γ. Moreover, if γ 0, (2.66) converges to the distribution function of the exponential distribution. Now we can discuss the distribution function of the values which exceed the set threshold u among the observations with the distribution function F. Let us denote this function by F [u]. It has the expression F [u] F (x) F (u) (x) = P(X x X > u) =, x u. (2.67) 1 F (u) For the distribution function of the excesses over the threshold u holds F (u) (x) = P(X u x X > u) = F (x + u) F (u). (2.68) 1 F (u) The parametric modeling of the distribution function F [u] for high values of u by the GPD is based on the following theorem, where b u and a u are constants and x F stands for the maximal possible value of the threshold 3 For G(x) = 0 we interpret the limit as +. 4 We have derived the GPD in the previous section dealing with compound distributions. 15
21 Theorem 2.3. If F [u] (b u + a u x) has a continuous limit distribution function for u x F, then lim F [u] (x) W (x) = 0. (2.69) u x F We can use the convergence of the excesses to the GPD for the characterization of the maximum domain of attraction of the GEV distribution. Consider the distribution functions of the GEV and GPD in the forms G γ (x) = exp ( (1 + γx) 1/γ ), γ 0, (2.70) W γ,µ,σ = 1 Then the following theorem holds: ( 1 + γ x µ ) 1/γ. (2.71) σ Theorem 2.4. Distribution function F belongs to the MDA(G γ ) if and only if there exists a positive function β(u) so that lim u x F sup F (u) (x) W γ,0,β(u) (x) = 0. (2.72) 0<x<x F u In other words, the distributions for which the normalized maxima converge to the GEV create a set where corresponding distributions of excesses converge to the GPD with an increasing boundary x F. Moreover, the parameter defining a shape of the limit distribution of excesses is the same as a parameter of the limit distribution of the maxima. If we consider the distribution functions (2.63), (2.64) and (2.65), according to [18] we can see that the GPD always belongs to the maximum domain of attraction of the GEV with the same parameter α and the distribution functions (2.57), (2.58) and (2.59) since lim W 0 n (x + ln n) = G 0 (x), (2.73) n lim W 1,α(n n 1/α x) = G 1,α (x), (2.74) n lim W 2,α(n n 1/α x) = G 2,α (x). (2.75) n 16
22 3. Methods for fitting parameters of claim distributions Suppose we have a random sample X 1, X 2,..., X n from a distribution represented by the density function f(x; θ) and we want to find an estimator u(x 1, X 2,..., X n ) of θ. After sample items have been observed to be equal to X 1 = x 1, X 2 = x 2,..., X n = x n, we wish the estimate u(x 1, x 2,..., x n ) to be close to the true parameter θ [12]. Any estimation method should satisfy certain criteria. According to [19], if we try to estimate a parameter θ from a model which has been selected, we would generally select an estimator ˆθ which is a function of the data and thus a random variable. It is desirable that Eˆθ = θ and any estimator satisfying this criteria is said to be unbiased. Nevertheless, many good estimators are biased, and consequently a better criterion in most situations is the the consistency, which means ˆθ θ in probability. Incidentally, consistent estimators are asymptotically unbiased, i.e. Eˆθ θ as n. The next vital property of good estimators is their efficiency. It other words, out of two estimators ˆθ 1 and ˆθ 2, if all else is equal, we choose ˆθ 1 if it has a smaller variance (varˆθ 1 < varˆθ 2 ). There are many procedures for finding the appropriate estimators. To the most important methods belongs the maximum likelihood estimation which we discuss in the first section of this chapter. The second section is devoted to the next frequently used method the method of moments; and the third part of this chapter deals with one of its modification the method of weighted moments. Obviously, there is a great number of other methods used by statisticians or actuaries for fitting the parameters of distributions, such as the Bayesian estimation [2], minimum χ 2 estimation [12], the method of the least squares [12], L-moments, transformation moments or mixed-moments estimation [15]. Unfortunately, we do not have enough space to discuss them in detail. 3.1 Maximum likelihood According to [10], maximum likelihood (ML) is the best known, most widely used and most important method of parameter estimation of a statistical model. Let X = (X 1,..., X n ) be a random vector with the density f(x, Θ) relative to σ-finite measure ν. We consider only cases when Θ = θ is an one-dimensional parameter belonging to a non-empty interval Ω. The density f(x, θ) represents the function of the variable x fixed at the value θ. However, f(x, θ) can be understood as a function of the variable θ for each fixed x. For this function we will use a label L(x, Ω) and a name likelihood function [1]. Obviously, L(x, Ω) is equal to f(x, Ω) for any pairs (x, Ω). If there is a point θ Ω that for each θ Ω holds 17
23 L(X, θ) L(X, θ ), (3.1) then we say θ is an estimate of the parameter θ obtained by ML. If L(x, θ) is a sufficiently smooth function of the parameter θ for each x (e.g., if for each x the derivative L(X, θ)/ θ exists), then θ has to be a solution of the following equation L(X, θ) = 0. (3.2) θ If we suppose ln 0 =, then the inequality (3.1) holds if and only if the following relationship is met for each θ Ω: lnl(x, θ) lnl(x, θ ). (3.3) Instead of (3.2), we can write θ has to be a root of the equation lnl(x, θ) = 0 (3.4) θ in a case, when L is a smooth function. The formula (3.4) is called likelihood equation in mathematical statistics. The assumption about openness of the interval Ω is essential here; if there was at least one extreme point belonging to the interval Ω, it could happen that the estimation θ satisfying the condition (3.1) is equal to this extreme point. In this case the estimation θ might not be a root of the likelihood equation. We consider the case when X 1,..., X n is a random sample from a distribution with the density f(x, θ) relative to σ-finite measure µ. Then the vector X = (X 1,..., X n ) has the joint density f(x, θ) = f(x 1, θ)...f(x n, θ) (3.5) relative to ν = µ... µ. In this case, the likelihood function (3.4) has the form n i=1 lnf(x i, θ) θ = 0. (3.6) Popularity of ML estimators, denoted by ˆθ n (X), is according to [24] mainly based on their properties for large sample sizes. We summarize the most essential properties, described also in [16], below. Consistency The ML estimation ˆθ n = ˆθ(X 1, X 2,..., X n ) is consistent when ɛ > 0 lim P[ ˆθ n θ ɛ] = 0. n This feature refers to the low probability of a big error if the range of the sample increases sufficiently. 18
24 Asymptotic normality The ML estimation ˆθ n = ˆθ(X 1, X 2,..., X n ) is asymptotic normal when ˆθ n N (0, V ), where n and V is a positively definite matrix. Asymptotic efficiency The ML estimation ˆθ n = ˆθ(X 1, X 2,..., X n ) is asymptotic efficient when n(ˆθn θ) d N (0, V ), where V is a positively definite matrix and d represents the convergence in a distribution. Concerning a computation of ML, it is not always easy to find the equations whose solution give the ML estimators. Such equations may not have explicit solutions and therefore iterative methods are needed to solve them. To the general optimization methods which have been found most useful in computing ML estimations belong the Newton-Raphson technique, the Fisher s method of scoring, the simplex method and the Expectation-Maximization (EM) algorithm. All of them are described in [10]. 3.2 Method of moments Another widely spread method for estimating parameters of a statistical model is the method of moments (MM). Since this method is based on the Law of Large Numbers, we introduce this law first. Theorem 3.1. Let M 1, M 2,... be independent and identically distributed random variables having a common distribution possessing a mean µ M. Then the sample means converge to the distributional mean as the number of observations increase. M n = 1 n n M i µ M, n (3.7) i=1 We assume X 1,..., X n is a random sample from a distribution depending on a parameter Θ = (θ 1,..., θ m ). We will also assume existence of the general moments µ k = EX k i, k = 1,..., m (3.8) for each Θ Ω. These moments generally depend on Θ, so we are supposed to write µ k (Θ) explicitly instead of µ k. Sample general moments are given by the formula 19
25 M k = 1 n n Xi k, k = 1, 2,... (3.9) i=1 The idea of the method of moments for estimating the parameter Θ takes the result of finding roots Θ of equation µ k (Θ) = M k, k = 1, 2,... (3.10) Sometimes m equations (3.10) are not enough for an unambiguous determination of Θ. Then next equations µ k (Θ) = M k, k = m + 1, m + 2 etc. are added until a sufficient number is obtained. Obviously, the relevant moments µ k have to exist. If µ k exists, then according to the Law of large numbers (3.7) M k µ k in probability. We describe the procedure of finding the estimation by MM in several steps [10]: Step 1 Denote µ m = EX m = k m (θ). If the model has d parameters, we compute the function k m for the first d moments µ 1 = k 1 (θ 1, θ 2,..., θ d ),..., θ d ),..., µ d = k d (θ 1, θ 2,..., θ d ) obtaining d equations with d variables. Step 2 We then solve for the d parameters as a function g of the moments. θ 1 = g 1 (µ 1, µ 2,..., µ d ),..., θ d = g d (µ 1, µ 2,..., µ d ) Step 3 Based on the data x = (x 1, x 2,..., x n ) we compute the first d sample moments M 1, M 2,..., M d. Using the Law of large numbers (3.7) we have µ m M m. Step 4 We replace the distributional moments µ m by the sample moments M m, then the solution (Step 2) gives us formulas for the method of moments estimators (ˆθ 1, ˆθ 2,..., ˆθ d ). For the data x these estimates are ˆθ 1 (x) = g 1 (M 1, M 2,..., M d ),..., ˆθ d (x) = g d (M 1, M 2,..., M d ). The method of moments is used in cases when other estimation procedures are numerically only difficult handled. On the other hand, this method may produce the estimations of low efficiency and it is generally usable only if the random variables are independent and identically distributed. Moreover, it is not possible to use this method for distributions without finite moments. Sometimes the estimations obtained by the method of moments can be treated like an initial approximation for solving the likelihood equations if there is a need to solve them by iteration [1]. 20
26 3.3 Method of weighted moments In order to estimate unknown parameters in a probability function we can use a method of weighted moments. This method extends the traditional and previously mentioned method of moments and what is more, it provides us with robustness [15] since it is not sensitive to extreme observations. Let X 1, X 2,..., X n be a sample with the probability function f(x; θ 1, θ 2,..., θ k ) where unknown parameters (θ 1, θ 2,..., θ k ) Θ and Θ R k. For a positive integer j the j-th weighted moment of the sample is defined as X j w = n w i X j i, (3.11) i=1 where w i [0, 1] and n i=1 w i = 1. In a case w i = n 1 the relation (3.11) characterizes the usual sample moments [15]. Let the first k sample moments exist as explicit functions v j (θ 1,.., θ k ), j = 1,..., k, of the unknown parameters. The method of weighted moments consists of an equation of the realized values X j w in the sample and the hypothetical moments stated below as v j (θ 1, θ 2,..., θ k ) = X j w, j = 1, 2,..., k (3.12) and its solution for θ 1, θ 2,..., θ k. It is given by the following formula ˆθ w,j = ˆθ w,j (X 1, X 2,..., X n ), j = 1, 2,..., k, (3.13) where ˆθ w,j is called the weighted moments estimator [15]. We should remember that X w j is an unbiased estimator of EX j. Moreover, it converges in probability to EX j. The weighted moments estimators of the mean EX and the variance varx < of the sample X 1, X 2,..., X n obtained by the weighted method of moments are as follows ÊX = X w = varx = X 2 w ( X w ) 2 = n w i X i (3.14) i=1 n w i (X i X w ) 2 = s 2 w,n (3.15) i=1 We can summarize the most crucial properties of Xw and s 2 w,n in the following theorems. We do not include their proofs as these they can be found in [15]. Theorem 3.2. Let X 1, X 2,..., X n be a random sample from the probability function f(x; θ 1, θ 2,..., θ k ) with EX = µ and varx = σ 2 <. Then E X w = µ (3.16) 21
27 var X n w = σ 2 wi 2. (3.17) i=1 Furthermore, if v k = EX k and µ k = E(X v 1 ) k, k = 1, 2, 3, 4 exists, then ) n E(s 2 w,n) = µ 2 (1 i=1 w 2 i (3.18) var(s 2 w,n) = µ 4 and ( n n wi 2 (1 w i ) 2 +µ 2 2 w i w j (1 2w i +3w i w j ) µ i=1 i,j=1,i j n i=1 w 2 i ) 2 (3.19) cov( X n w, s 2 w,n) = µ 3 wi 2 (1 w i ) (3.20) i=1 The following theorem describes the distribution of the weighted moment estimate of the mean. Theorem 3.3. Let X 1, X 2,..., X n be a random sample from the normal distribution N(µ, σ 2 ). Then X w N (µ, σ 2 n i=1 w2 i ). 22
28 4. Back diagnostics and validation techniques To get the best statistical model for our data we have to choose a distribution and an unique parameter estimate. After the selection of the distribution class and the estimation of the parameters by using one of the available methods the goodness-of-fit has to be tested. The most natural approach is based on measuring the distance between the empirical and the fitted analytical distribution function. Possible statistics and tests solving this task are discussed in first three sections of this chapter. Namely, we discuss χ 2 statistic, Kolmogorov-Smirnov test and statistics belonging to the Cramer-von Mises family. In the next two parts we deal with two ad hoc tests used by actuaries [12]. The type of an appropriate distribution for our data can be easily selected thanks to the first one by comparing the shapes of the empirical and theoretical mean excess function, which is based on conditioning a random variable exceeding a certain level. The second test is the so-called limited expected value function and tries to solve the problem of comparing a discontinuous step function with a continuous curve. The last part of this chapter is dedicated to some graphical techniques of threshold selection when approximating the data by GPD. The following methods are introduced: the threshold choice plot, the mean residual life plot, the L-moments plot as well as the dispersion index plot. 4.1 χ 2 goodness-of-fit statistic To test, whether our model is adequate we could compare the fitted model with the model of the actual data [19]. A very natural statistic to use with claim frequency data is the goodness-of-fit statistic obtained as follows. For the random sample X 1, X 2,..., X n we divide the real line into k intervals [a 0, a 1 ),..., [a k 1, ). Let us denote the number of X i falling into the (i + 1)-st interval by O i ; and the probability under the fitted model that an observation falls into the (i + 1)-st interval by p i. Then, according to [19], the statistic D = k (O i np i ) 2 i=0 np i (4.1) can be used to judge a fit of the model. If we have used the data to estimate r parameters, then for large n the statistic D has an approximate χ 2 distribution with (k r 1) degrees of freedom. Generally, the quality of the fit increases with the decreasing value of D. The fit is acceptable if D > D 0 where D 0 is a selected percentile of the distribution, 23
29 P[χ 2 (k r 1) D 0 ] = 1 α. (4.2) Usually, the value of α is chosen to be 0,05 or 0,1 and D 0 can be obtained from tables or from the series expansion for the incomplete gamma function. This test becomes more discriminating as the sample size become larger. In any event, it is sensitive to deviations in the tails and provides a good relative measure for comparing models with the same number of parameters. A second measure of fit, useful for grouped and discrete data, is the likelihood ratio statistic in the form k 1 ( ) Oi 2 O i log. (4.3) np i i=0 Similarly to the goodness-of fit statistic (4.1), the likelihood ratio statistic (4.3) has an approximate χ 2 distribution with (k r 1) degrees of freedom. 4.2 Kolmogorov-Smirnov statistic According to [7], statistics measuring the difference between the empirical F n (x) and the fitted F (x) distribution function (so-called edf statistic) is based on the vertical difference between the distributions. The distance is usually measured by a supremum norm or a quadratic norm. The most popular supremum statistic is known as Kolmogorov-Smirnov statistic: It can be written as two supremum statistics D = sup F n (x) F (x). (4.4) x R D + = sup{f n (x) F (x)}, (4.5) x D = sup{f (x) F n (x)}; (4.6) x where the formula (4.5) represents the largest vertical difference when F n (x) > F (x) and the second one (4.6) is the largest difference in the case F n (x) < F (x). The Kolmogorov-Smirnov statistic is then calculated as D = max (D +, D ). A closely related statistic mentioned in the article [3] is a sum of two differences: V = D + + D. From the formula (4.4) it is obvious that to find the supremum we have to test 2n values, although many of these can be ruled out immediately, particularly if F n (x) and F (x) are graphed. According to [12], under H 0, D has a distribution that is not well known, but it has been tabled in many books on statistics, for instance [13]. In addition, if we want to know a critical value c such that P[D > c; H 0 ] = α, approximate values of c can be found by the table below (4.1). However, these approximations are good provided n
30 Table 4.1: Kolmogorov-Smirnov statistic - critical values α 0,20 0,10 0,05 0,01 c 1, 07/ n 1, 22/ n 1, 36/ n 1, 63/ n An advantage of Kolmogorov-Smirnov statistic compared with the goodness-of-fit statistic introduced in the previous section is the fact that it avoids the selection of the value k and the endpoints a 0, a 1,...a k of the intervals [12]. 4.3 Cramer-von Mises family The second class of test statistics for measuring a discrepancy is represented by the Cramer-von Mises family given by the formula Q = n {F n (x) F (x)} 2 ψ(x)df (x); (4.7) where ψ(x) is a suitable weighting function for the squared difference {F n (x) F (x)} 2. There are following well-known values of ψ(x): ψ(x) = 1 obtaining the Cramer-von Mises W 2 statistic and ψ(x) = [F (x){1 F (x)}] 1 giving the Anderson and Darling A 2 statistic. Suitable computing formulas from the definitions of statistics discussed above can be found by utilizing the transformation Z = F (X). When F (x) is the distribution function of the variable X, the random variable Z is uniformly distributed on the unit interval [3]. Considering a sample x 1,..., x n assigning values z i = F (x i ), i = 1,..., n we can show that for values z and x the corresponding vertical differences between the empirical and the fitted distribution functions in the edf diagrams for variables X and Z are equal. If we compare the edf statistics calculated from the empirical distribution function of z i, i = 1,..., n compared with the uniform distribution; and edf statistics calculated from the empirical distribution function of x i, i = 1,..., n compared with F (x), they will have the same values [4]. This fact leads to the following formulas in terms of the order statistics z (1) < z (2) <... < z (n) : { i D + = max 1 i n D = max 1 i n n z (i) { z (i) i 1 n }, (4.8) }, (4.9) D = max (D +, D ), (4.10) V = D + + D, (4.11) 25
31 W 2 = n i=1 { z (i) 2i 1 } n 12n, (4.12) A 2 = n 1 n n {(2i 1) log z (i) + (2n + 1 2i) log(1 z (i) )}. (4.13) i=1 In order to interpret the results of the applied tests we have to compare the calculated values of their test statistics with the corresponding critical values C α for the same significance level α. If the value of the test is smaller than the corresponding critical value C α, we can accept the fit as adequate. In other words, we have to construct a test of fit with the null hypothesis saying a specific distribution is acceptable and the alternative saying that it is not: H 0 : F n (x) = F (x; φ), H 1 : F n (x) F (x; φ), (4.14) where φ is a vector of the known parameters. Small values of a test statistic T are an evidence in favor of H 0 whereas its large values indicate the invalidity of H 0. P -value shows how unlikely such large result would be if H 0 was true. We reject the null hypothesis when a small p-value is obtained. However, we want to test the hypothesis saying the sample has a common distribution function F (x; θ) with an unknown parameter φ. Firstly, we need to estimate the parameters. If the value of the test statistic T is d, then the p-value is overestimated by P U (T d), when P U indicates that the probability is computed under the assumptions of an uniformly distributed sample [3]. Thus, if P U (T d) is small, then the p-value will be small as well and the hypothesis will be rejected. If it is large we have to obtain a more accurate estimate of the p-value. Monte Carlo simulations can be used in this context as well [21]. Firstly the estimate ˆθ of a vector parameter is found and the edf statistic is calculated assuming that the sample is distributed according to F (x; ˆθ). This calculation returns a value of d. Consequently, a sample of n variates with the distribution F (x; ˆθ) is generated. For this simulated sample the parameter vector ˆθ 1 is estimated and the pdf statistics is calculated under an assumption that the sample has the distribution F (x; ˆθ 1 ). The simulation is repeated as many times as required to achieve a certain level of accuracy. The estimate of the p-value is obtained as a proportion of the number of cases when the test quantity was equal or larger than d [3]. Stephens [22] proposed an alternative solution to the problem of unknown parameters known as the half-sample approach. In is based on using only half the data to estimate the parameters. Nevertheless, to conduct the test the entire data set has to be used. This method is faster than the Monte Carlo approach but, on the other hand, it is not invariant depending on the selection of the half-samples different test values are obtained. 26
Gymnázium, Brno, Slovanské nám. 7 WORKBOOK. Mathematics. Teacher: Student:
 WORKBOOK Subject: Teacher: Student: Mathematics.... School year:../ Conic section The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.
WORKBOOK Subject: Teacher: Student: Mathematics.... School year:../ Conic section The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.
Základy teorie front III
 Základy teorie front III Aplikace Poissonova procesu v teorii front II Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta
Základy teorie front III Aplikace Poissonova procesu v teorii front II Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta
Department of Mathematical Analysis and Applications of Mathematics Faculty of Science, Palacký University Olomouc Czech Republic
 ROBUST 13. září 2016 regression regresních modelů Categorical Continuous - explanatory, Eva Fišerová Department of Mathematical Analysis and Applications of Mathematics Faculty of Science, Palacký University
ROBUST 13. září 2016 regression regresních modelů Categorical Continuous - explanatory, Eva Fišerová Department of Mathematical Analysis and Applications of Mathematics Faculty of Science, Palacký University
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Využití hybridní metody vícekriteriálního rozhodování za nejistoty. Michal Koláček, Markéta Matulová
 Využití hybridní metody vícekriteriálního rozhodování za nejistoty Michal Koláček, Markéta Matulová Outline Multiple criteria decision making Classification of MCDM methods TOPSIS method Fuzzy extension
Využití hybridní metody vícekriteriálního rozhodování za nejistoty Michal Koláček, Markéta Matulová Outline Multiple criteria decision making Classification of MCDM methods TOPSIS method Fuzzy extension
Transportation Problem
 Transportation Problem ١ C H A P T E R 7 Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply s i ) to n
Transportation Problem ١ C H A P T E R 7 Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply s i ) to n
Gymnázium, Brno, Slovanské nám. 7, SCHEME OF WORK Mathematics SCHEME OF WORK. cz
 SCHEME OF WORK Subject: Mathematics Year: first grade, 1.X School year:../ List of topisc # Topics Time period Introduction, repetition September 1. Number sets October 2. Rigtht-angled triangle October,
SCHEME OF WORK Subject: Mathematics Year: first grade, 1.X School year:../ List of topisc # Topics Time period Introduction, repetition September 1. Number sets October 2. Rigtht-angled triangle October,
Compression of a Dictionary
 Compression of a Dictionary Jan Lánský, Michal Žemlička zizelevak@matfyz.cz michal.zemlicka@mff.cuni.cz Dept. of Software Engineering Faculty of Mathematics and Physics Charles University Synopsis Introduction
Compression of a Dictionary Jan Lánský, Michal Žemlička zizelevak@matfyz.cz michal.zemlicka@mff.cuni.cz Dept. of Software Engineering Faculty of Mathematics and Physics Charles University Synopsis Introduction
Litosil - application
 Litosil - application The series of Litosil is primarily determined for cut polished floors. The cut polished floors are supplied by some specialized firms which are fitted with the appropriate technical
Litosil - application The series of Litosil is primarily determined for cut polished floors. The cut polished floors are supplied by some specialized firms which are fitted with the appropriate technical
USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING
 USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING Eva Minaříková Institute for Research in School Education, Faculty of Education, Masaryk University Structure of the presentation What can we as teachers
USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING Eva Minaříková Institute for Research in School Education, Faculty of Education, Masaryk University Structure of the presentation What can we as teachers
CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA
 CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA &KDSWHUSUHVHQWVWKHGHVLJQDQGIDEULFDW LRQRIPRGLILHG0LQNRZVNLIUDFWDODQWHQQD IRUZLUHOHVVFRPPXQLFDWLRQ7KHVLPXODWHG DQGPHDVXUHGUHVXOWVRIWKLVDQWHQQDDUH DOVRSUHVHQWHG
CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA &KDSWHUSUHVHQWVWKHGHVLJQDQGIDEULFDW LRQRIPRGLILHG0LQNRZVNLIUDFWDODQWHQQD IRUZLUHOHVVFRPPXQLFDWLRQ7KHVLPXODWHG DQGPHDVXUHGUHVXOWVRIWKLVDQWHQQDDUH DOVRSUHVHQWHG
Uni- and multi-dimensional parametric tests for comparison of sample results
 Uni- and multi-dimensional parametric tests for comparison of sample results Jedno- a více-rozměrné parametrické testy k porovnání výsledků Prof. RNDr. Milan Meloun, DrSc. Katedra analytické chemie, Universita
Uni- and multi-dimensional parametric tests for comparison of sample results Jedno- a více-rozměrné parametrické testy k porovnání výsledků Prof. RNDr. Milan Meloun, DrSc. Katedra analytické chemie, Universita
WORKSHEET 1: LINEAR EQUATION 1
 WORKSHEET 1: LINEAR EQUATION 1 1. Write down the arithmetical problem according the dictation: 2. Translate the English words, you can use a dictionary: equations to solve solve inverse operation variable
WORKSHEET 1: LINEAR EQUATION 1 1. Write down the arithmetical problem according the dictation: 2. Translate the English words, you can use a dictionary: equations to solve solve inverse operation variable
Introduction to MS Dynamics NAV
 Introduction to MS Dynamics NAV (Item Charges) Ing.J.Skorkovský,CSc. MASARYK UNIVERSITY BRNO, Czech Republic Faculty of economics and business administration Department of corporate economy Item Charges
Introduction to MS Dynamics NAV (Item Charges) Ing.J.Skorkovský,CSc. MASARYK UNIVERSITY BRNO, Czech Republic Faculty of economics and business administration Department of corporate economy Item Charges
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA
 GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
Aplikace matematiky. Dana Lauerová A note to the theory of periodic solutions of a parabolic equation
 Aplikace matematiky Dana Lauerová A note to the theory of periodic solutions of a parabolic equation Aplikace matematiky, Vol. 25 (1980), No. 6, 457--460 Persistent URL: http://dml.cz/dmlcz/103885 Terms
Aplikace matematiky Dana Lauerová A note to the theory of periodic solutions of a parabolic equation Aplikace matematiky, Vol. 25 (1980), No. 6, 457--460 Persistent URL: http://dml.cz/dmlcz/103885 Terms
EXACT DS OFFICE. The best lens for office work
 EXACT DS The best lens for office work EXACT DS When Your Glasses Are Not Enough Lenses with only a reading area provide clear vision of objects located close up, while progressive lenses only provide
EXACT DS The best lens for office work EXACT DS When Your Glasses Are Not Enough Lenses with only a reading area provide clear vision of objects located close up, while progressive lenses only provide
VY_32_INOVACE_06_Předpřítomný čas_03. Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace
 VY_32_INOVACE_06_Předpřítomný čas_03 Autor: Růžena Krupičková Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu: Zkvalitnění ICT ve slušovské škole Číslo projektu: CZ.1.07/1.4.00/21.2400
VY_32_INOVACE_06_Předpřítomný čas_03 Autor: Růžena Krupičková Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu: Zkvalitnění ICT ve slušovské škole Číslo projektu: CZ.1.07/1.4.00/21.2400
A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients
 KYBERNETIKA VOLUME 8 (1972), NUMBER 6 A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients JAROSLAV KRAL In many applications (for example if the effect
KYBERNETIKA VOLUME 8 (1972), NUMBER 6 A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients JAROSLAV KRAL In many applications (for example if the effect
DC circuits with a single source
 Název projektu: utomatizace výrobních procesů ve strojírenství a řemeslech egistrační číslo: Z..07/..0/0.008 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 09 Tento projekt je spolufinancován
Název projektu: utomatizace výrobních procesů ve strojírenství a řemeslech egistrační číslo: Z..07/..0/0.008 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 09 Tento projekt je spolufinancován
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Database systems. Normal forms
 Database systems Normal forms An example of a bad model SSN Surnam OfficeNo City Street No ZIP Region President_of_ Region 1001 Novák 238 Liteň Hlavní 10 26727 Středočeský Rath 1001 Novák 238 Bystřice
Database systems Normal forms An example of a bad model SSN Surnam OfficeNo City Street No ZIP Region President_of_ Region 1001 Novák 238 Liteň Hlavní 10 26727 Středočeský Rath 1001 Novák 238 Bystřice
Dynamic Development of Vocabulary Richness of Text. Miroslav Kubát & Radek Čech University of Ostrava Czech Republic
 Dynamic Development of Vocabulary Richness of Text Miroslav Kubát & Radek Čech University of Ostrava Czech Republic Aim To analyze a dynamic development of vocabulary richness from a methodological point
Dynamic Development of Vocabulary Richness of Text Miroslav Kubát & Radek Čech University of Ostrava Czech Republic Aim To analyze a dynamic development of vocabulary richness from a methodological point
Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products
 Energy news2 1 Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products Doposud jste Energy znali jako výrobce a dodavatele humánních přírodních doplňků stravy a kosmetiky.
Energy news2 1 Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products Doposud jste Energy znali jako výrobce a dodavatele humánních přírodních doplňků stravy a kosmetiky.
Czech Technical University in Prague DOCTORAL THESIS
 Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering DOCTORAL THESIS CERN-THESIS-2015-137 15/10/2015 Search for B! µ + µ Decays with the Full Run I Data of The ATLAS
Czech Technical University in Prague Faculty of Nuclear Sciences and Physical Engineering DOCTORAL THESIS CERN-THESIS-2015-137 15/10/2015 Search for B! µ + µ Decays with the Full Run I Data of The ATLAS
2. Entity, Architecture, Process
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Praktika návrhu číslicových obvodů Dr.-Ing. Martin Novotný Katedra číslicového návrhu Fakulta informačních technologií ČVUT v Praze Miloš
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Praktika návrhu číslicových obvodů Dr.-Ing. Martin Novotný Katedra číslicového návrhu Fakulta informačních technologií ČVUT v Praze Miloš
Extrakce nezávislé komponenty
 Extrakce nezávislé komponenty Zbyněk Koldovský Acoustic Signal Analysis and Processing Group, Faculty of Mechatronics, Informatics, and Interdisciplinary Studies, Technical University in Liberec, https://asap.ite.tul.cz
Extrakce nezávislé komponenty Zbyněk Koldovský Acoustic Signal Analysis and Processing Group, Faculty of Mechatronics, Informatics, and Interdisciplinary Studies, Technical University in Liberec, https://asap.ite.tul.cz
VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O.
 VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O. Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová práce 2013 Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová
VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O. Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová práce 2013 Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová
AIC ČESKÁ REPUBLIKA CZECH REPUBLIC
 ČESKÁ REPUBLIKA CZECH REPUBLIC ŘÍZENÍ LETOVÉHO PROVOZU ČR, s.p. Letecká informační služba AIR NAVIGATION SERVICES OF THE C.R. Aeronautical Information Service Navigační 787 252 61 Jeneč A 1/14 20 FEB +420
ČESKÁ REPUBLIKA CZECH REPUBLIC ŘÍZENÍ LETOVÉHO PROVOZU ČR, s.p. Letecká informační služba AIR NAVIGATION SERVICES OF THE C.R. Aeronautical Information Service Navigační 787 252 61 Jeneč A 1/14 20 FEB +420
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku
 Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
FIRE INVESTIGATION. Střední průmyslová škola Hranice. Mgr. Radka Vorlová. 19_Fire investigation CZ.1.07/1.5.00/
 FIRE INVESTIGATION Střední průmyslová škola Hranice Mgr. Radka Vorlová 19_Fire investigation CZ.1.07/1.5.00/34.0608 Výukový materiál Číslo projektu: CZ.1.07/1.5.00/21.34.0608 Šablona: III/2 Inovace a zkvalitnění
FIRE INVESTIGATION Střední průmyslová škola Hranice Mgr. Radka Vorlová 19_Fire investigation CZ.1.07/1.5.00/34.0608 Výukový materiál Číslo projektu: CZ.1.07/1.5.00/21.34.0608 Šablona: III/2 Inovace a zkvalitnění
Kvantifikace operačního rizika v rámci Přistupu distribuce ztrát
 Kvantifikace operačního rizika v rámci Přistupu distribuce ztrát Jiří Havlický 1 Abstrakt Článek je zaměřen na stanovení a zhodnocení citlivosti výše očekávané a neočekávané ztráty plynoucí z podstupovaného
Kvantifikace operačního rizika v rámci Přistupu distribuce ztrát Jiří Havlický 1 Abstrakt Článek je zaměřen na stanovení a zhodnocení citlivosti výše očekávané a neočekávané ztráty plynoucí z podstupovaného
B1 MORE THAN THE CITY
 B1 MORE THAN THE CITY INTRODUCTION ÚVOD B1 Budova B1 je součástí moderního kancelářského projektu CITY WEST a nově budované městské čtvrti Západní město, Praha 5 - Stodůlky. Tato lokalita kromě vynikající
B1 MORE THAN THE CITY INTRODUCTION ÚVOD B1 Budova B1 je součástí moderního kancelářského projektu CITY WEST a nově budované městské čtvrti Západní město, Praha 5 - Stodůlky. Tato lokalita kromě vynikající
Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční
 Příloha I Seznam tabulek Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční odměny pro rozhodčí platný od roku
Příloha I Seznam tabulek Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční odměny pro rozhodčí platný od roku
Social Media a firemní komunikace
 Social Media a firemní komunikace TYINTERNETY / FALANXIA YOUR WORLD ENGAGED UČTE SE OD STARTUPŮ ANALYSIS -> PARALYSIS POUŽIJTE TO, CO ZNÁ KAŽDÝ POUŽIJTE TO, CO ZNÁ KAŽDÝ POUŽIJTE TO, CO ZNÁ KAŽDÝ POUŽIJTE
Social Media a firemní komunikace TYINTERNETY / FALANXIA YOUR WORLD ENGAGED UČTE SE OD STARTUPŮ ANALYSIS -> PARALYSIS POUŽIJTE TO, CO ZNÁ KAŽDÝ POUŽIJTE TO, CO ZNÁ KAŽDÝ POUŽIJTE TO, CO ZNÁ KAŽDÝ POUŽIJTE
Dynamic programming. Optimal binary search tree
 The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamic programming Optimal binary search tree Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The complexity
The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamic programming Optimal binary search tree Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The complexity
Chapter 7: Process Synchronization
 Chapter 7: Process Synchronization Background The Critical-Section Problem Synchronization Hardware Semaphores Classical Problems of Synchronization Critical Regions Monitors Synchronization in Solaris
Chapter 7: Process Synchronization Background The Critical-Section Problem Synchronization Hardware Semaphores Classical Problems of Synchronization Critical Regions Monitors Synchronization in Solaris
Informace o písemných přijímacích zkouškách. Doktorské studijní programy Matematika
 Informace o písemných přijímacích zkouškách (úplné zadání zkušebních otázek či příkladů, které jsou součástí přijímací zkoušky nebo její části, a u otázek s výběrem odpovědi správné řešení) Doktorské studijní
Informace o písemných přijímacích zkouškách (úplné zadání zkušebních otázek či příkladů, které jsou součástí přijímací zkoušky nebo její části, a u otázek s výběrem odpovědi správné řešení) Doktorské studijní
6.867 Machine Learning
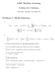 . Machine Learning Problem Set Solutions Due date: Monday November Problem : Model Selection. P (y,..., y n x,..., x n, PST) = = K [ [,] K [ K p n+ i i ( p i ) n i dpi ] = p n+ i i K ( p i ) n i n + i!
. Machine Learning Problem Set Solutions Due date: Monday November Problem : Model Selection. P (y,..., y n x,..., x n, PST) = = K [ [,] K [ K p n+ i i ( p i ) n i dpi ] = p n+ i i K ( p i ) n i n + i!
Právní formy podnikání v ČR
 Bankovní institut vysoká škola Praha Právní formy podnikání v ČR Bakalářská práce Prokeš Václav Leden, 2009 Bankovní institut vysoká škola Praha Katedra Bankovnictví Právní formy podnikání v ČR Bakalářská
Bankovní institut vysoká škola Praha Právní formy podnikání v ČR Bakalářská práce Prokeš Václav Leden, 2009 Bankovní institut vysoká škola Praha Katedra Bankovnictví Právní formy podnikání v ČR Bakalářská
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Just write down your most recent and important education. Remember that sometimes less is more some people may be considered overqualified.
 CURRICULUM VITAE - EDUCATION Jindřich Bláha Výukový materiál zpracován v rámci projektu EU peníze školám Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Bc. Jindřich Bláha. Dostupné z Metodického
CURRICULUM VITAE - EDUCATION Jindřich Bláha Výukový materiál zpracován v rámci projektu EU peníze školám Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Bc. Jindřich Bláha. Dostupné z Metodického
Czech Republic. EDUCAnet. Střední odborná škola Pardubice, s.r.o.
 Czech Republic EDUCAnet Střední odborná škola Pardubice, s.r.o. ACCESS TO MODERN TECHNOLOGIES Do modern technologies influence our behavior? Of course in positive and negative way as well Modern technologies
Czech Republic EDUCAnet Střední odborná škola Pardubice, s.r.o. ACCESS TO MODERN TECHNOLOGIES Do modern technologies influence our behavior? Of course in positive and negative way as well Modern technologies
The Over-Head Cam (OHC) Valve Train Computer Model
 The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
Karta předmětu prezenční studium
 Karta předmětu prezenční studium Název předmětu: Číslo předmětu: 545-0250 Garantující institut: Garant předmětu: Ekonomická statistika Institut ekonomiky a systémů řízení RNDr. Radmila Sousedíková, Ph.D.
Karta předmětu prezenční studium Název předmětu: Číslo předmětu: 545-0250 Garantující institut: Garant předmětu: Ekonomická statistika Institut ekonomiky a systémů řízení RNDr. Radmila Sousedíková, Ph.D.
Třída: VI. A6 Mgr. Pavla Hamříková VI. B6 RNDr. Karel Pohaněl Schváleno předmětovou komisí dne: Podpis: Šárka Richterková v. r.
 MATURITNÍ TÉMATA Školní rok: 2016/2017 Ředitel školy: PhDr. Karel Goš Předmětová komise: Matematika a deskriptivní geometrie Předseda předmětové komise: Mgr. Šárka Richterková Předmět: Matematika Třída:
MATURITNÍ TÉMATA Školní rok: 2016/2017 Ředitel školy: PhDr. Karel Goš Předmětová komise: Matematika a deskriptivní geometrie Předseda předmětové komise: Mgr. Šárka Richterková Předmět: Matematika Třída:
Škola: Střední škola obchodní, České Budějovice, Husova 9. Inovace a zkvalitnění výuky prostřednictvím ICT
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Výuka odborného předmětu z elektrotechniky na SPŠ Strojní a Elektrotechnické
 Jihočeská univerzita v Českých Budějovicích Pedagogická fakulta Oddělení celoživotního vzdělávání Závěrečná práce Výuka odborného předmětu z elektrotechniky na SPŠ Strojní a Elektrotechnické Vypracoval:
Jihočeská univerzita v Českých Budějovicích Pedagogická fakulta Oddělení celoživotního vzdělávání Závěrečná práce Výuka odborného předmětu z elektrotechniky na SPŠ Strojní a Elektrotechnické Vypracoval:
DATA SHEET. BC516 PNP Darlington transistor. technický list DISCRETE SEMICONDUCTORS Apr 23. Product specification Supersedes data of 1997 Apr 16
 zákaznická linka: 840 50 60 70 DISCRETE SEMICONDUCTORS DATA SHEET book, halfpage M3D186 Supersedes data of 1997 Apr 16 1999 Apr 23 str 1 Dodavatel: GM electronic, spol. s r.o., Křižíkova 77, 186 00 Praha
zákaznická linka: 840 50 60 70 DISCRETE SEMICONDUCTORS DATA SHEET book, halfpage M3D186 Supersedes data of 1997 Apr 16 1999 Apr 23 str 1 Dodavatel: GM electronic, spol. s r.o., Křižíkova 77, 186 00 Praha
EU peníze středním školám digitální učební materiál
 EU peníze středním školám digitální učební materiál Číslo projektu: Číslo a název šablony klíčové aktivity: Tematická oblast, název DUMu: Autor: CZ.1.07/1.5.00/34.0515 III/2 Inovace a zkvalitnění výuky
EU peníze středním školám digitální učební materiál Číslo projektu: Číslo a název šablony klíčové aktivity: Tematická oblast, název DUMu: Autor: CZ.1.07/1.5.00/34.0515 III/2 Inovace a zkvalitnění výuky
PC/104, PC/104-Plus. 196 ept GmbH I Tel. +49 (0) / I Fax +49 (0) / I I
 E L E C T R O N I C C O N N E C T O R S 196 ept GmbH I Tel. +49 (0) 88 61 / 25 01 0 I Fax +49 (0) 88 61 / 55 07 I E-Mail sales@ept.de I www.ept.de Contents Introduction 198 Overview 199 The Standard 200
E L E C T R O N I C C O N N E C T O R S 196 ept GmbH I Tel. +49 (0) 88 61 / 25 01 0 I Fax +49 (0) 88 61 / 55 07 I E-Mail sales@ept.de I www.ept.de Contents Introduction 198 Overview 199 The Standard 200
Caroline Glendinning Jenni Brooks Kate Gridley. Social Policy Research Unit University of York
 Caroline Glendinning Jenni Brooks Kate Gridley Social Policy Research Unit University of York Growing numbers of people with complex and severe disabilities Henwood and Hudson (2009) for CSCI: are the
Caroline Glendinning Jenni Brooks Kate Gridley Social Policy Research Unit University of York Growing numbers of people with complex and severe disabilities Henwood and Hudson (2009) for CSCI: are the
Klepnutím lze upravit styl předlohy. nadpisů. nadpisů.
 1/ 13 Klepnutím lze upravit styl předlohy Klepnutím lze upravit styl předlohy www.splab.cz Soft biometric traits in de identification process Hair Jiri Prinosil Jiri Mekyska Zdenek Smekal 2/ 13 Klepnutím
1/ 13 Klepnutím lze upravit styl předlohy Klepnutím lze upravit styl předlohy www.splab.cz Soft biometric traits in de identification process Hair Jiri Prinosil Jiri Mekyska Zdenek Smekal 2/ 13 Klepnutím
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky
 Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: Education Označení materiálu: VY_32_INOVACE_MAT27 Datum vytvoření: 10.10.2013
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: Education Označení materiálu: VY_32_INOVACE_MAT27 Datum vytvoření: 10.10.2013
Probability density estimation Parametric methods
 Probability density estimation Parametric methods Václav Hlaváč Czech Technical University in Prague Czech Institute of Informatics, Robotics and Cybernetics 166 36 Prague 6, Jugoslávských partyzánů 1580/3,
Probability density estimation Parametric methods Václav Hlaváč Czech Technical University in Prague Czech Institute of Informatics, Robotics and Cybernetics 166 36 Prague 6, Jugoslávských partyzánů 1580/3,
Dynamic Signals. Ananda V. Mysore SJSU
 Dynamic Signals Ananda V. Mysore SJSU Static vs. Dynamic Signals In principle, all signals are dynamic; they do not have a perfectly constant value over time. Static signals are those for which changes
Dynamic Signals Ananda V. Mysore SJSU Static vs. Dynamic Signals In principle, all signals are dynamic; they do not have a perfectly constant value over time. Static signals are those for which changes
SEZNAM PŘÍLOH. Příloha 1 Dotazník Tartu, Estonsko (anglická verze) Příloha 2 Dotazník Praha, ČR (česká verze)... 91
 SEZNAM PŘÍLOH Příloha 1 Dotazník Tartu, Estonsko (anglická verze)... 90 Příloha 2 Dotazník Praha, ČR (česká verze)... 91 Příloha 3 Emailové dotazy, vedení fakult TÜ... 92 Příloha 4 Emailové dotazy na vedení
SEZNAM PŘÍLOH Příloha 1 Dotazník Tartu, Estonsko (anglická verze)... 90 Příloha 2 Dotazník Praha, ČR (česká verze)... 91 Příloha 3 Emailové dotazy, vedení fakult TÜ... 92 Příloha 4 Emailové dotazy na vedení
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Research infrastructure in the rhythm of BLUES. More time and money for entrepreneurs
 Research infrastructure in the rhythm of BLUES More time and money for entrepreneurs 1 I. What is it? II. How does it work? III. References Where to find out more? IV. What is it good for? 2 I. What is
Research infrastructure in the rhythm of BLUES More time and money for entrepreneurs 1 I. What is it? II. How does it work? III. References Where to find out more? IV. What is it good for? 2 I. What is
Risk management in the rhythm of BLUES. Více času a peněz pro podnikatele
 Risk management in the rhythm of BLUES Více času a peněz pro podnikatele 1 I. What is it? II. How does it work? III. How to find out more? IV. What is it good for? 2 I. What is it? BLUES Brain Logistics
Risk management in the rhythm of BLUES Více času a peněz pro podnikatele 1 I. What is it? II. How does it work? III. How to find out more? IV. What is it good for? 2 I. What is it? BLUES Brain Logistics
CZ.1.07/1.5.00/
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Gymnázium, Brno, Slovanské nám. 7 WORKBOOK. Mathematics. Student: Draw: Convex angle Non-convex angle
 WORKBOOK http://agb.gymnaslo.cz Subject: Student: Mathematics.. School year:../ Topic: Trigonometry Angle orientation Types of angles 90 right angle - pravý less than 90 acute angles ("acute" meaning "sharp")-
WORKBOOK http://agb.gymnaslo.cz Subject: Student: Mathematics.. School year:../ Topic: Trigonometry Angle orientation Types of angles 90 right angle - pravý less than 90 acute angles ("acute" meaning "sharp")-
On large rigid sets of monounary algebras. D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia
 On large rigid sets of monounary algebras D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia coauthor G. Czédli, University of Szeged, Hungary The 54st Summer School on General Algebra
On large rigid sets of monounary algebras D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia coauthor G. Czédli, University of Szeged, Hungary The 54st Summer School on General Algebra
Úvod do datového a procesního modelování pomocí CASE Erwin a BPwin
 Úvod do datového a procesního modelování pomocí CASE Erwin a BPwin (nově AllFusion Data Modeller a Process Modeller ) Doc. Ing. B. Miniberger,CSc. BIVŠ Praha 2009 Tvorba datového modelu Identifikace entit
Úvod do datového a procesního modelování pomocí CASE Erwin a BPwin (nově AllFusion Data Modeller a Process Modeller ) Doc. Ing. B. Miniberger,CSc. BIVŠ Praha 2009 Tvorba datového modelu Identifikace entit
CZ.1.07/1.5.00/34.0527
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL
 PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL Ing. Jan HAVLÍK, MPA tajemník Městského úřadu Žďár nad Sázavou Chief Executive Municipality of Žďár nad Sázavou CO
PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL Ing. Jan HAVLÍK, MPA tajemník Městského úřadu Žďár nad Sázavou Chief Executive Municipality of Žďár nad Sázavou CO
STLAČITELNOST. σ σ. během zatížení
 STLAČITELNOST Princip: Naneseme-li zatížení na zeminu, dojde k porušení rovnováhy a dochází ke stlačování zeminy (přemístňují se částice). Stlačení je ukončeno jakmile nastane rovnováha mezi působícím
STLAČITELNOST Princip: Naneseme-li zatížení na zeminu, dojde k porušení rovnováhy a dochází ke stlačování zeminy (přemístňují se částice). Stlačení je ukončeno jakmile nastane rovnováha mezi působícím
Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise
 Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise ROZHODNUTÍ KOMISE ze dne 27. června 1997 o postupu prokazování shody stavebních výrobků ve smyslu čl. 20 odst. 2
Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise ROZHODNUTÍ KOMISE ze dne 27. června 1997 o postupu prokazování shody stavebních výrobků ve smyslu čl. 20 odst. 2
CZ.1.07/1.5.00/
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Obrábění robotem se zpětnovazební tuhostí
 Obrábění robotem se zpětnovazební tuhostí Odbor mechaniky a mechatroniky ČVUT v Praze, Fakulta strojní Student: Yaron Sela Vedoucí: Prof. Ing. Michael Valášek, DrSc Úvod Motivace Obráběcí stroj a důležitost
Obrábění robotem se zpětnovazební tuhostí Odbor mechaniky a mechatroniky ČVUT v Praze, Fakulta strojní Student: Yaron Sela Vedoucí: Prof. Ing. Michael Valášek, DrSc Úvod Motivace Obráběcí stroj a důležitost
By David Cameron VE7LTD
 By David Cameron VE7LTD Introduction to Speaker RF Cavity Filter Types Why Does a Repeater Need a Duplexer Types of Duplexers Hybrid Pass/Reject Duplexer Detail Finding a Duplexer for Ham Use Questions?
By David Cameron VE7LTD Introduction to Speaker RF Cavity Filter Types Why Does a Repeater Need a Duplexer Types of Duplexers Hybrid Pass/Reject Duplexer Detail Finding a Duplexer for Ham Use Questions?
Škola: Střední škola obchodní, České Budějovice, Husova 9. Inovace a zkvalitnění výuky prostřednictvím ICT
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
SPECIAL THEORY OF RELATIVITY
 SPECIAL THEORY OF RELATIVITY 1. Basi information author Albert Einstein phenomena obsered when TWO frames of referene moe relatie to eah other with speed lose to the speed of light 1905 - speial theory
SPECIAL THEORY OF RELATIVITY 1. Basi information author Albert Einstein phenomena obsered when TWO frames of referene moe relatie to eah other with speed lose to the speed of light 1905 - speial theory
Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise
 Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise ROZHODNUTÍ KOMISE ze dne 17. února 1997 o postupu prokazování shody stavebních výrobků ve smyslu čl. 20 odst. 2
Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise ROZHODNUTÍ KOMISE ze dne 17. února 1997 o postupu prokazování shody stavebních výrobků ve smyslu čl. 20 odst. 2
Immigration Studying. Studying - University. Stating that you want to enroll. Stating that you want to apply for a course.
 - University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
- University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
Immigration Studying. Studying - University. Stating that you want to enroll. Stating that you want to apply for a course.
 - University Rád/a bych se zapsal/a na vysoké škole. Stating that you want to enroll Rád/a bych se zapsal/a na. Stating that you want to apply for a course bakalářské studium postgraduální studium doktorské
- University Rád/a bych se zapsal/a na vysoké škole. Stating that you want to enroll Rád/a bych se zapsal/a na. Stating that you want to apply for a course bakalářské studium postgraduální studium doktorské
Číslo materiálu: VY 32 INOVACE 29/18. Číslo projektu: CZ.1.07/1.4.00/
 Číslo materiálu: Název materiálu: Ironic Číslo projektu: CZ.1.07/1.4.00/21.1486 Zpracoval: Mgr. Petra Březinová IRONIC 1. Listen to the song Ironic from the singer Alanis Morissette. For the first time
Číslo materiálu: Název materiálu: Ironic Číslo projektu: CZ.1.07/1.4.00/21.1486 Zpracoval: Mgr. Petra Březinová IRONIC 1. Listen to the song Ironic from the singer Alanis Morissette. For the first time
DOPLNĚK K FACEBOOK RETRO EDICI STRÁNEK MAVO JAZYKOVÉ ŠKOLY MONCHHICHI
 MONCHHICHI The Monchhichi franchise is Japanese and held by the Sekiguchi Corporation, a famous doll company, located in Tokyo, Japan. Monchhichi was created by Koichi Sekiguchi on January 25, 1974. Sekiguchi
MONCHHICHI The Monchhichi franchise is Japanese and held by the Sekiguchi Corporation, a famous doll company, located in Tokyo, Japan. Monchhichi was created by Koichi Sekiguchi on January 25, 1974. Sekiguchi
Odhady polohy mzdového rozdělení pomocí vybraných robustních odhadových funkcí
 Odhady polohy mzdového rozdělení pomocí vybraných robustních odhadových funkcí 1. Úvod Odhady polohy rozdělení náhodné proměnné patří k základním statistickým otázkám. Aritmetický v mnoha případech není
Odhady polohy mzdového rozdělení pomocí vybraných robustních odhadových funkcí 1. Úvod Odhady polohy rozdělení náhodné proměnné patří k základním statistickým otázkám. Aritmetický v mnoha případech není
Geometry of image formation
 eometry of image formation Tomáš Svoboda, svoboda@cmp.felk.cvut.cz Czech Technical University in Prague, Center for Machine Perception http://cmp.felk.cvut.cz Last update: July 4, 2008 Talk Outline Pinhole
eometry of image formation Tomáš Svoboda, svoboda@cmp.felk.cvut.cz Czech Technical University in Prague, Center for Machine Perception http://cmp.felk.cvut.cz Last update: July 4, 2008 Talk Outline Pinhole
Klasifikace a rozpoznávání. Bayesovská rozhodovací teorie
 Klasifikace a rozpoznávání Bayesovská rozhodovací teorie Extrakce příznaků 3 25 2 Granáty Jablka Četnost 15 1 5 2 3 4 5 6 7 8 Váha [dkg] Pravděpodobnosti - diskrétní příznaky Uvažujme diskrétní příznaky
Klasifikace a rozpoznávání Bayesovská rozhodovací teorie Extrakce příznaků 3 25 2 Granáty Jablka Četnost 15 1 5 2 3 4 5 6 7 8 Váha [dkg] Pravděpodobnosti - diskrétní příznaky Uvažujme diskrétní příznaky
Theme 6. Money Grammar: word order; questions
 Theme 6 Money Grammar: word order; questions Čas potřebný k prostudování učiva lekce: 8 vyučujících hodin Čas potřebný k ověření učiva lekce: 45 minut KLÍNSKÝ P., MÜNCH O., CHROMÁ D., Ekonomika, EDUKO
Theme 6 Money Grammar: word order; questions Čas potřebný k prostudování učiva lekce: 8 vyučujících hodin Čas potřebný k ověření učiva lekce: 45 minut KLÍNSKÝ P., MÜNCH O., CHROMÁ D., Ekonomika, EDUKO
TechoLED H A N D B O O K
 TechoLED HANDBOOK Světelné panely TechoLED Úvod TechoLED LED světelné zdroje jsou moderním a perspektivním zdrojem světla se širokými možnostmi použití. Umožňují plnohodnotnou náhradu žárovek, zářivkových
TechoLED HANDBOOK Světelné panely TechoLED Úvod TechoLED LED světelné zdroje jsou moderním a perspektivním zdrojem světla se širokými možnostmi použití. Umožňují plnohodnotnou náhradu žárovek, zářivkových
ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ
 ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ MGR. VLADIMÍR BRADÁČ ROZVOJ KOMPETENCÍ MANAGEMENTU A PRACOVNÍKŮ VŠ MSK (S PODPOROU ICT) PROJEKT OP VK 2.2: CZ.1.07/2.2.00/15.0176 OSTRAVA 2012 Tento projekt je
ANGLICKÁ KONVERZACE PRO STŘEDNĚ POKROČILÉ MGR. VLADIMÍR BRADÁČ ROZVOJ KOMPETENCÍ MANAGEMENTU A PRACOVNÍKŮ VŠ MSK (S PODPOROU ICT) PROJEKT OP VK 2.2: CZ.1.07/2.2.00/15.0176 OSTRAVA 2012 Tento projekt je
ENGLISH FOR ACADEMIC PURPOSES
 Slezská univerzita v Opavě Fakulta veřejných politik v Opavě ENGLISH FOR ACADEMIC PURPOSES Distanční studijní opora Veronika Portešová Opava 2012 Projekt č. CZ.1.07/2.2.00/15.0178 Inovace studijního programu
Slezská univerzita v Opavě Fakulta veřejných politik v Opavě ENGLISH FOR ACADEMIC PURPOSES Distanční studijní opora Veronika Portešová Opava 2012 Projekt č. CZ.1.07/2.2.00/15.0178 Inovace studijního programu
Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise
 Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise ROZHODNUTÍ KOMISE ze dne 17. února 1997 o postupu prokazování shody stavebních výrobků ve smyslu čl. 20 odst. 2
Příručka ke směrnici 89/106/EHS o stavebních výrobcích / Příloha III - Rozhodnutí Komise ROZHODNUTÍ KOMISE ze dne 17. února 1997 o postupu prokazování shody stavebních výrobků ve smyslu čl. 20 odst. 2
ODHADY NÁVRATOVÝCH HODNOT
 ODHADY NÁVRATOVÝCH HODNOT KLIMATOLOGICKÝCH DAT Katedra aplikované matematiky Fakulta přírodovědně-humanitní a pedagogická Technická univerzita v Liberci Robust 2018 ÚVOD Velká pozornost v analýze extrémních
ODHADY NÁVRATOVÝCH HODNOT KLIMATOLOGICKÝCH DAT Katedra aplikované matematiky Fakulta přírodovědně-humanitní a pedagogická Technická univerzita v Liberci Robust 2018 ÚVOD Velká pozornost v analýze extrémních
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
SMES-EU D&H-5P Workshop 1. Prague November 2003 V Praze listopadu 2003
 SMES-EU D&H-5P Workshop 1 Prague November 2003 V Praze listopadu 2003 SMES-EU D&H-5P Workshop 1 The presentation includes comments and observations made during the Czech Republic Workshop of November 2003.
SMES-EU D&H-5P Workshop 1 Prague November 2003 V Praze listopadu 2003 SMES-EU D&H-5P Workshop 1 The presentation includes comments and observations made during the Czech Republic Workshop of November 2003.
PART 2 - SPECIAL WHOLESALE OFFER OF PLANTS SPRING 2016 NEWS MAY 2016 SUCCULENT SPECIAL WHOLESALE ASSORTMENT
 PART 2 - SPECIAL WHOLESALE OFFER OF PLANTS SPRING 2016 NEWS MAY 2016 SUCCULENT SPECIAL WHOLESALE ASSORTMENT Dear Friends We will now be able to buy from us succulent plants at very good wholesale price.
PART 2 - SPECIAL WHOLESALE OFFER OF PLANTS SPRING 2016 NEWS MAY 2016 SUCCULENT SPECIAL WHOLESALE ASSORTMENT Dear Friends We will now be able to buy from us succulent plants at very good wholesale price.
Vánoční sety Christmas sets
 Energy news 7 Inovace Innovations 1 Vánoční sety Christmas sets Na jaře tohoto roku jste byli informováni o připravované akci pro předvánoční období sety Pentagramu koncentrátů a Pentagramu krémů ve speciálních
Energy news 7 Inovace Innovations 1 Vánoční sety Christmas sets Na jaře tohoto roku jste byli informováni o připravované akci pro předvánoční období sety Pentagramu koncentrátů a Pentagramu krémů ve speciálních
Instrukce: Cvičný test má celkem 3 části, čas určený pro tyto části je 20 minut. 1. Reading = 6 bodů 2. Use of English = 14 bodů 3.
 Vážení studenti, na následujících stranách si můžete otestovat svou znalost angličtiny a orientačně zjistit, kolik bodů za jazykové kompetence byste získali v přijímacím řízení. Maximální počet bodů je
Vážení studenti, na následujících stranách si můžete otestovat svou znalost angličtiny a orientačně zjistit, kolik bodů za jazykové kompetence byste získali v přijímacím řízení. Maximální počet bodů je
ξ σ DANIELA JARUŠKOVÁ 1), MARTIN HANEK 2)
 J. Hydrol. Hydromech., 54, 2006, 4, 309 319 PEAKS OVER THRESHOLD METHOD IN COMPARISON WITH BLOCK-MAXIMA METHOD FOR ESTIMATING HIGH RETURN LEVELS OF SEVERAL NORTHERN MORAVIA PRECIPITATION AND DISCHARGES
J. Hydrol. Hydromech., 54, 2006, 4, 309 319 PEAKS OVER THRESHOLD METHOD IN COMPARISON WITH BLOCK-MAXIMA METHOD FOR ESTIMATING HIGH RETURN LEVELS OF SEVERAL NORTHERN MORAVIA PRECIPITATION AND DISCHARGES
Why PRIME? 20 years of Erasmus Programme Over 2 million students in total Annually
 What is PRIME? Problems of Recognition In Making Erasmus European-wide research project Conducted by ESN with the support of the European Commission Two editions: 1 st in 2009 Follow-up in 2010 Why PRIME?
What is PRIME? Problems of Recognition In Making Erasmus European-wide research project Conducted by ESN with the support of the European Commission Two editions: 1 st in 2009 Follow-up in 2010 Why PRIME?
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
MODELOVÁNÍ CHVOSTŮ TEORIE EXTRÉMNÍCH ODHADY PARETOVA INDEXU. Jan Dienstbier HODNOT. contact:
 MODELOVÁNÍ CHVOSTŮ TEORIE EXTRÉMNÍCH HODNOT ODHADY PARETOVA INDEXU Jan Dienstbier contact: dienstbi@karlin.mff.cuni.cz Univerzita Karlova MFF UK - KPMS Praha KPMS, 31.10. 2007 MODELOVÁNÍ CHVOSTŮ JAK TO
MODELOVÁNÍ CHVOSTŮ TEORIE EXTRÉMNÍCH HODNOT ODHADY PARETOVA INDEXU Jan Dienstbier contact: dienstbi@karlin.mff.cuni.cz Univerzita Karlova MFF UK - KPMS Praha KPMS, 31.10. 2007 MODELOVÁNÍ CHVOSTŮ JAK TO
Radiova meteoricka detekc nı stanice RMDS01A
 Radiova meteoricka detekc nı stanice RMDS01A Jakub Ka kona, kaklik@mlab.cz 15. u nora 2014 Abstrakt Konstrukce za kladnı ho softwarove definovane ho pr ijı macı ho syste mu pro detekci meteoru. 1 Obsah
Radiova meteoricka detekc nı stanice RMDS01A Jakub Ka kona, kaklik@mlab.cz 15. u nora 2014 Abstrakt Konstrukce za kladnı ho softwarove definovane ho pr ijı macı ho syste mu pro detekci meteoru. 1 Obsah
POSLECH. M e t o d i c k é p o z n á m k y k z á k l a d o v é m u t e x t u :
 POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Mgr. Martin Zicháček aj9-kap-zic-pos-07 Z á k l a d o v ý t e x t : Margaret: Hi Eric. Eric: Oh, hi Margaret. How are you doing? Margaret:
POSLECH Jazyk Úroveň Autor Kód materiálu Anglický jazyk 9. třída Mgr. Martin Zicháček aj9-kap-zic-pos-07 Z á k l a d o v ý t e x t : Margaret: Hi Eric. Eric: Oh, hi Margaret. How are you doing? Margaret:
Čtvrtý Pentagram The fourth Pentagram
 Energy News 4 1 Čtvrtý Pentagram The fourth Pentagram Na jaře příštího roku nabídneme našim zákazníkům již čtvrtý Pentagram a to Pentagram šamponů. K zavedení tohoto Pentagramu jsme se rozhodli na základě
Energy News 4 1 Čtvrtý Pentagram The fourth Pentagram Na jaře příštího roku nabídneme našim zákazníkům již čtvrtý Pentagram a to Pentagram šamponů. K zavedení tohoto Pentagramu jsme se rozhodli na základě
http://www.zlinskedumy.cz
 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Výklad a cvičení z větné stavby, vy_32_inovace_ma_33_01
Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Výklad a cvičení z větné stavby, vy_32_inovace_ma_33_01
