Probability density estimation Parametric methods
|
|
|
- Milada Marková
- před 6 lety
- Počet zobrazení:
Transkript
1 Probability density estimation Parametric methods Václav Hlaváč Czech Technical University in Prague Czech Institute of Informatics, Robotics and Cybernetics Prague 6, Jugoslávských partyzánů 1580/3, Czech Republic also Center for Machine Perception, Courtesy: V. Franc, R. Gutierrez-Osuna. Outline of the talk: Three taxonomies. Maximum likelihood (ML) estimation. Examples: Gaussian, discrete distribution. ML for pattern rec., a coin example. Logistic regression. Bayesian estimate, a coin example.
2 What if the statistical model is unknown? 2/38 Bayesian and non-bayesian methods allow designing the optimal classifier provided we have a statistical model describing the observation x X and the hidden state y Y. Bayesian methods require posterior probability p(y x). Non-Bayesian methods require the conditional probability p(x y). In most practical situations, the statistical model is unknown and must be estimated from the training multiset of examples { (x1, y 1 ),..., (x m, y m ) } ˆp(x, y). The estimated ˆp(x, y) replaces the true distribution p(x, y). Note: Estimation (in statistics) is also called learning (in pattern recognition and machine learning).
3 Taxonomy 1: according to the statistical model Parametric nonparametric 3/38 Parametric: A particular form of the density function (e.g. Gaussian) is assumed to be known and only its parameters θ Θ need to be estimated (e.g. the mean, the covariance). Sought: p(x, θ); Performed: {x 1,..., x n } ˆθ. Nonparametric: No assumption on the form of the distribution. However, many more training examples are required in comparison with parametric methods. Sought: p(x); Performed: {x 1,..., x n } ˆp(x).
4 Taxonomy 2: according to the input information Supervised, unsupervised & semi-supervised 4/38 The goal is to estimate the probability density p(x, y) or p(x). The probability density estimation methods can be categorized according to the information available in the training multiset. Supervised methods: Completely labeled examples are available. Sought: p(x, y; θ); Performed: {(x 1, y 1 )..., (x n, y n )} ˆθ. Unsupervised methods: Unlabeled examples of observations, used, e.g. for clustering. Sought: p(x; θ); Performed: {x 1,..., x n } ˆθ. Semi-supervised methods: Both n labeled and m n unlabeled examples. Sought: p(x, y; θ); Performed: {(x 1, y 1 ),..., (x n, y n ), x n+1,..., x n+m } ˆθ.
5 Taxonomy 3: according to the estimation principle Maximum-Likelihood estimation: Sought: p(x, y; θ), where θ is fixed but unknown. Performed: ˆθ = argmax p(dataset θ) θ In words: The ML solution seeks the solution, which is the best explanation of the dataset X X using the likelihood function. Bayesian estimation: Sought: p(x, y; θ). θ is a random variable with the known prior p(θ). In words: Bayesian method estimates the optimal parameter Θ of the given probability density, which maximizes the posterior probability density p(θ X). Minimax estimation: (suggested by M.I. Schlesinger, not explicated here) Sought: p(x, y; θ) Performed: ˆθ = arg max θ min p(x i, θ),...,m 5/38
6 This lecture: supervised methods 6/38 This lecture covers the supervised methods estimating a known probability distribution, i.e. parametric methods. There will be a separate lecture in this course on non-parametric metods (as histogram-based; kernel density estimation; Parzen window estimation, k-nearest Neighbors estimation); unsupervised methods (as K-means clustering; EM-algorithm).
7 Assumptions Maximum likelihood estimation 7/38 The density function p(x; θ) is known up to a parameter θ Θ. The column vector of parameters θ = [θ 1,..., θ d ] R d. i.i.d. assumption: A measured data (set of examples) D={x1,..., xn} independently drawn from the identical distribution p(x; θ ) is available. The true parameter θ Θ is unknown but it is fixed. The probability p(x; θ) assumes that n examples D were generated (measured) for a given Θ is called the likelihood function p(d; θ) = n p(x i ; θ). Maximum likelihood estimation ˆθ ML = argmax ˆθ ML, which best explains the examples D. θ Θ p(d; θ) seeks for the parameter
8 Log-likelihood function L(θ) 8/38 It is convenient to maximize the log-likelihood function L(θ) = log p(d; θ) = log n p(x i ; θ) = log p(x i ; θ) Because the logarithm is monotonically increasing, it holds ˆθ ML = argmax θ Θ p(d; θ) = argmax θ Θ log p(x i ; θ) } {{} L(θ) = argmax θ Θ L(θ) Maximizing a sum of terms is always an easier task than maximizing a product; cf. the difficulty of expressing derivative of a long product of terms. In particular, the logarithm of a Gaussian is very easy.
9 ML estimate of the log-likelihood function 9/38 The (maximally likely) ML estimate can be often obtained by finding the stationary point of the log-likelihood function L(θ) θ j = θ L = 0. L(θ) = θ j θ j = = log p(x i ; θ) θ j log p(x i ; θ) 1 p(x i ; θ) p(x i ; θ) θ j = 0 Provided L(θ) is convex, the found solution is the ML estimate ˆθ ML.
10 Example: Normal distribution, ML estimate (1) 10/38 Input D = {x1, x2,..., xn} Rn ( ) p(x; θ = (µ, σ)) = 1 σ exp (x µ) 2 2π 2σ θ = {(µ, σ) µ R, σ R+}. 0 x x x x x x x μ Likelihood function p(d; θ) and its logarithm, i.e. log-likelihood function L(θ) σ 5 5 x x x x x x x x x x p(d; θ) = n p(x i ; θ) = n 1 σ 2π exp ( ) (x µ) 2 2σ L(θ) = log p(d; θ) = ( log σ log 2π (x i µ) 2 ) 2σ 2
11 Example: Normal distribution, ML estimate (2) To compute ˆθ ML = argmax θ L(θ), we will solve θ L = L(θ) θ = 0. L(θ) = log p(d; θ) = ( log σ log 2π (x i µ) 2 ) 2σ 2 11/38 Mean value ˆµML: n L µ = ( ) 2(xi µ) 2σ 2 = 0 ˆµ ML = 1 n x i Variance ˆσ2ML: L σ = n ( 1 σ (x i µ) 2 2 ( )) 2 σ 3 = 0 σ 3 ( σ 2 + (x i µ) 2) = 0 ˆσ 2 ML = 1 n (x i µ) 2
12 Properties of the estimates (1) 12/38 ˆθ is a random variable. Consequently, we can talk about its mean value (the most probable value) and its variance. Bias Tells how close is the estimate to the true value. ) Unbiased estimate: E (ˆθ = θ. Variance How much does the estimate change for different runs, e.g. for different datasets? Bias-variance tradeoff: In most cases: One can only decrease either the bias or the variance at the expense of the other.
13 Properties of the estimates (2) 13/38 ) Efficiency of the estimate: var (ˆθ = E (ˆθ θ ) 2. The best estimate has the minimal dispersion. ) Consistent estimate E (ˆθ ) = θ for n ; var (ˆθ = 0 for n. The growing amount of samples induces that statistical characteristics converge to the true value. (The consequence of the rule of large numbers.)
14 2D illustration of the estimate bias and efficiency 14/38
15 ML estimate of the m-variate Gaussian 15/38 One data sample xi X = (x1, x2,..., xm). It can be derived similarly that the Maximum Likelihood parameter estimate yields the sample mean vector and the sample covariance matrix. Sample mean vector Sample covariance matrix ˆµ ML = 1 n x i ˆΣ = 1 n (x i ˆµ)(x i ˆµ)
16 Example: Discrete distribution, ML estimate (1) D = {x1, x2,..., xn} Discrete range (quantization levels) x X = {1, 2,..., m} p(x; θ) = p(x = 1) = θ 1 p(x = 2) = θ 2. p(x = m) = θ m 16/38 Likelihood function; δ is Dirac function p(x 1,..., x n ; θ) = n p(x i ) = n p(x) δ(x i = x) x X = x X p(x) n(x) Logarithm of the likelihood function L(θ) = log p(x 1,..., x n ; θ) = x X n(x) log p(x)
17 Example: Discrete distribution, ML estimate (2) 17/38 Logarithm of the likelihood function L(θ) = x X n(x) log p(x) is minimized under the condition p(x) = 1, p(x) 0 x X Lagrange multipliers method is used F (θ) = x X n(x) log p(x) + λ ( x X p(x) 1 ) F (θ) p(x) = n(x) p(x) + λ = 0, for x
18 Example: Discrete distribution, ML estimate (3) 18/38 Rewritten from the previous slide: F (θ) p(x) = n(x) p(x) + λ = 0, for x n(x) = λ p(x) p(x) = n(x) λ It follows from the constraint: x X p(x) = 1 = x X n(x) λ = 1 λ λ = n x X n(x) = n λ p(x) = n(x) λ = n(x) n
19 Maximum likelihood estimate if there is no analytical solution 19/38 If the analytical solution to ˆθ ML = argmax θ L(θ) does not exist then the ML estimation task can be solved numerically: 1. Using standard optimization techniques like gradient methods or Newton methods. 2. Using the Expectation-Maximization algorithm when p(x; θ) = h H p(x, h; θ) For example, in the case of the mixture models p(x; θ) = H p(x h; θ) p(h; θ) h=1
20 Pros: Properties of the ML estimate ML has favorable statistical properties. It is asymptotically (i.e. for n ) unbiased, it has the smallest dispersion, and it is consistent. ML leads to simple analytical solution for many simple distributions as was demonstrated in the Gaussian example. Cons: There can be several solutions with the same quality. There is a single global solution (the value of the quality). However, it is difficult to find it. There is no analytical solution for the mixture of Gaussians. In this case, EM algorithm is used often (and mentioned in this lecture later). Note: The ML estimate has often mentioned properties. In general, however, these properties cannot be guaranteed because the estimate values need not be real numbers. Thus we cannot claim what their distribution was. 20/38
21 ML estimation in pattern recognition (1) 21/38 D = {(x1, y1), (x2, y2)..., (xn, yn)} (X Y)n x X... discrete (a finite set) or continuous (an infinite set), typically X R m y Y... discrete (a finite set) p(x, y; θ) = p(x y; θy) p(y; θa) θ = θ 1 θ 2. θ Y θ A The likelihood function p(d; θ) reads p (D; θ) = n p(x j, y j ; θ y ) = n p(x j y j ; θ yj ) p(y j ; θ A ) j=1 j=1
22 ML estimation in pattern recognition (2) 22/38 L(θ) = log p (D; θ) = log p(x j y j ; θ yj ) + log p(y j ; θ A ) = y Y j=1 log p(x j y; θ y ) + j {i y i =y} j=1 j=1 log p(y j ; θ A ) The original maximization task decomposes into Y + 1 simpler independent tasks: ˆθ y = argmax log p(x j y; θ y ), y Y θ y j {i y i =y} ˆθ A = argmax p(y j θ A ) θ A j=1
23 Example: Is the coin fair? (ML case 1) 23/38 Assume a coin flipping experiment with the training set D = {head, head, tail, head,..., tail}. Let n be the length of the experiment (number of tosses) and k the number of heads observed in experiments. The probabilistic model of the unknown coin is: p(x = head θ) = θ and p(x = tail θ) = 1 θ. The likelihood of θ Θ = [0, 1] is given by Bernoulli distribution, p(d θ) = n p(x j θ) = θ k (1 θ) n k j=1
24 Example: Is the coin fair? (ML case 2) 24/38 Repeated from previous slide: p(d θ) = n j=1 p(x j θ) = θ k (1 θ) n k ML estimate ˆθ = argmax θ p(d θ) = k n. The optimal value is illustrated as the red dot. Example: What if only m = 2 samples are available? p(d θ) 0.5 p(d θ) 0.5 p(d θ) θ θ θ p ( m=2 k=2 θ) = θ 2 p ( m=2 k=0 θ) = (1 θ) 2 p ( m=2 k=1 θ) = θ(1 θ)
25 Use of ML in unsupervised learning (1) D X = {x1, x2,..., xn}... only observable states. p(x, y; θ) = p(x y; θy) p(y, θa)... the statistical model considers an unknown hidden state y. 25/38 p(d x ; θ) = = n j=1 n j=1 n p(x j ; θ) = p(x j, y; θ) j=1 y Y p(x j y; θ) p(y; θ A ) y Y L(θ) = log p(d; θ) = = log j=1 y Y log p(x j y; θ) p(y; θ A ) y Y j=1 p(x j y; θ) p(y; θ A )
26 Use of ML in unsupervised learning (2) 26/38 The quality of the solution is copied from the previous page, L(θ) = log j=1 y Y p(x j y; θ) p(y; θ A ) (1) θ L(θ) = 0 does not have the analytical solution! Expectation-Maximization (EM) algorithm is often used for this unsupervised learning task. It is an iterative method, which can be used to find the ML estimate of Equation (1). It can be used if we are able to perform ML estimate from DX. One lecture is dedicated to EM algorithm later in this course.
27 Logistic regression (1) Given examples D = {(x1, y1),..., (xn, yn)} (Rn {+1, 1})n. Assuming the examples were i.i.d. drawn. The goal is to find the posterior model p(y x) needed for the classification. Let assume that the logarithm of the likelihood ratio is a linear function 27/38 log p(y = +1 x) p(y = 1 x) = x, w + b Under this assumption, we get that the p(y = 1 x) is the logical function (i.e. yielding the value TRUE or FALSE) p(y x; w) = exp ( y( x, w + b) ) The likelihood of the parameters θ = (w, b) given the examples D reads p(d; w, b) = n p(x i, y i ; w, b) = n p(y i x i ; w, b) p(x i )
28 Logistic regression (2) Bayes classifier does not require the model of p(x) and hence 28/38 (ŵ, ˆb) = argmax w,b = argmax w,b = argmax w,b n p(y i x i ; w, b) p(x) ( n log p(y i x i ; w, b) + log p(y i x i ; w, b) log p(x i ) ) The maximization task is concave in variables w, b. However, the task does not have the analytical solution. Bayes classifier minimizing the classification error leads to the linear rule log p(y = +1 x) p(y = 1 x) = x, w + b q(x) = { +1 if x, w + b 0 1 if x, w + b < 0
29 Bayesian estimate, the introduction Our uncertainty about the parameters Θ is represented by the probability distribution in the Bayesian approach. Before we observe the data, the parameters are described by a prior density p(θ), which is typically very broad reflecting the fact that we know little about its true value. Once we obtain data, we use the Bayes theorem to find the posterior p(θ X). Ideally, we want the data to sharpen the posterior p(θ X). Said differently, we want to reduce our uncertainty about the parameters. 29/38 However, it has be kept in mind that our goal is to estimate the density p(x) or, more precisely, the density p(x X), the density given the evidence provided by the dataset X.
30 Bayesian estimate of the probability density parameters (1) 30/38 D = {x1, x2,..., xn}... observed data. p(d, θ)... joint probability distribution of D and θ. θ Θ... is understood as a realization of the random variable (in the contrast to ML estimate) with the known prior distribution p(x θ). The likelihood function p(d θ) = n j=1 p(x j θ). Bayesian estimation seeks the posterior distribution of the parameter θ best explaining the observed data D. It is obtained by Bayes formula: p(d θ) = n p(x j θ). j=1
31 Use of Bayesian estimation 31/38 What is the posterior distribution p(θ D) = p(d θ) p(θ) p(d) good for? 1. Marginalize over the parameter θ (numerically expensive) p(x D) = θ Θ p(x, θ D) dθ = θ Θ p(x θ) p(θ D) dθ 2. Compute the point estimate by minimizing the expected risk ˆθ = argmin θ θ Θ W (θ, θ) p(θ, D) dθ, where W : Θ Θ R is a penalty function penalizing incorrectly estimated parameters.
32 Bayesian estimation: Examples of loss functions 32/38 Zero-one penalty function W (θ, θ) = { 0 if θ = θ 1 if θ θ leads to the Maximum Aposteriori (MAP) estimate ˆθ = argmax p(θ D). θ Note: ML estimate ˆθ = argmax p(d θ) can be seen as the MAP estimate with an uninformative prior p(θ). θ Quadratic penalty function W (θ, θ) = (θ θ)2 leads to the estimate of the expected value of the parameter ˆθ = θ Θ θ p(θ D) dθ
33 Bayesian estimate of the probability density parameters (2) 33/38 The estimate ˆθ = Ψ(D) is formulated as in Bayesian decision with the penalty function W : Θ Θ R. Bayesian risk R(Ψ) = D The optimal decision function (stragegy, drule) Ψ (D) = argmin Ψ θ R(Ψ) = argmin ψ p(d, θ) W (θ, Ψ(D)) θ p(d, θ) W (θ, Ψ(D))
34 Bayesian estimate for the W (θ, Ψ(D)) = (θ ψ(d)) 2 34/38 After the substitution Ψ (D) = argmin the minimal loss Ψ Ψ θ ( ) p(d, θ) (θ Ψ) 2 = 0 θ p(d, θ) (θ Ψ) 2, it must hold for Ψ θ p(d, θ) = θ θ p(d, θ) Ψ (D) = θ θ p(d, θ) p(d) = θ θ p(θ D) p(d) p(d) = p(d) θ θ p(θ D) p(d) Ψ (D) = θ θ p(θ D)
35 Example: Is the coin fair? (Bayesian case 1) 35/38 (The same slide as in the ML case. The slide No. 23 is repeated here.) Assume a coin flipping experiment with the training set D = {head, head, tail, head,..., tail}. Let n be the length of the experiment (number of tosses) and k the number of heads observed in experiments. The probabilistic model of the unknown coin is: p(x = head θ) = θ and p(x = tail θ) = 1 θ. The likelihood of θ Θ = [0, 1] is given by Bernoulli distribution, p(d θ) = n p(x j θ) = θ k (1 θ) n k j=1
36 Example: Is the coin fair? (Bayesian case 2) 36/38 Assume the uniform prior p(θ) = { 1 for θ [0, 1], 0 otherwise. ˆθ B = p(x = head D) = Ψ θ p(d θ) p(θ) dθ (D) = p(d) 1 0 = θk+1 (1 θ) n k dθ 1 0 θk (1 θ) n k dθ = k + 1 n + 2. Note 1: ˆθML = kn. Note 2: For n, it also holds ˆΘB ˆΘML. 1 0
37 Example: Is the coin fair? (Bayesian case 3) 37/38 ML estimate ˆθ ML = k n (red dot) versus Bayesian estimate ˆθ B = k+1 n+2 (black dot). Example: What if only m = 2 samples are available? p(d θ) 0.5 p(d θ) 0.5 p(d θ) θ θ θ p ( m=2 k=2 θ) = θ 2 p ( m=2 k=0 θ) = (1 θ) 2 p ( m=2 k=1 θ) = θ(1 θ)
38 Relationship between the Maximal likelihood and Bayesian estimation 38/38 By definition, p(x Θ) peaks at the ML estimate. If this peak is relatively sharp and the prior is broad, then the outcome will be dominated by the region around the ML estimate. Thus, the Bayesian estimate will approximate the ML solution. When the number of available data increases, the posterior p(θ X) tends to sharpen. Therefore, the Bayesian estimate of p(x) will approach the ML estimate for number of samples N. In practice, when we have a limited number of observations will the two approaches yield different results.
Department of Mathematical Analysis and Applications of Mathematics Faculty of Science, Palacký University Olomouc Czech Republic
 ROBUST 13. září 2016 regression regresních modelů Categorical Continuous - explanatory, Eva Fišerová Department of Mathematical Analysis and Applications of Mathematics Faculty of Science, Palacký University
ROBUST 13. září 2016 regression regresních modelů Categorical Continuous - explanatory, Eva Fišerová Department of Mathematical Analysis and Applications of Mathematics Faculty of Science, Palacký University
Vapnik-Chervonenkis learning theory
 Vapnik-Chervonenkis learning theory Václav Hlaváč Czech Technical University in Prague Czech Institute of Informatics, Robotics and Cybernetics 160 00 Prague 6, Jugoslávských partyzánu 1580/3, Czech Republic
Vapnik-Chervonenkis learning theory Václav Hlaváč Czech Technical University in Prague Czech Institute of Informatics, Robotics and Cybernetics 160 00 Prague 6, Jugoslávských partyzánu 1580/3, Czech Republic
Gymnázium, Brno, Slovanské nám. 7 WORKBOOK. Mathematics. Teacher: Student:
 WORKBOOK Subject: Teacher: Student: Mathematics.... School year:../ Conic section The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.
WORKBOOK Subject: Teacher: Student: Mathematics.... School year:../ Conic section The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost.
 Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Tento materiál byl vytvořen v rámci projektu Operačního programu Vzdělávání pro konkurenceschopnost. Projekt MŠMT ČR Číslo projektu Název projektu školy Klíčová aktivita III/2 EU PENÍZE ŠKOLÁM CZ.1.07/1.4.00/21.2146
Transportation Problem
 Transportation Problem ١ C H A P T E R 7 Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply s i ) to n
Transportation Problem ١ C H A P T E R 7 Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply s i ) to n
Klasifikace a rozpoznávání. Bayesovská rozhodovací teorie
 Klasifikace a rozpoznávání Bayesovská rozhodovací teorie Extrakce příznaků 3 25 2 Granáty Jablka Četnost 15 1 5 2 3 4 5 6 7 8 Váha [dkg] Pravděpodobnosti - diskrétní příznaky Uvažujme diskrétní příznaky
Klasifikace a rozpoznávání Bayesovská rozhodovací teorie Extrakce příznaků 3 25 2 Granáty Jablka Četnost 15 1 5 2 3 4 5 6 7 8 Váha [dkg] Pravděpodobnosti - diskrétní příznaky Uvažujme diskrétní příznaky
Využití hybridní metody vícekriteriálního rozhodování za nejistoty. Michal Koláček, Markéta Matulová
 Využití hybridní metody vícekriteriálního rozhodování za nejistoty Michal Koláček, Markéta Matulová Outline Multiple criteria decision making Classification of MCDM methods TOPSIS method Fuzzy extension
Využití hybridní metody vícekriteriálního rozhodování za nejistoty Michal Koláček, Markéta Matulová Outline Multiple criteria decision making Classification of MCDM methods TOPSIS method Fuzzy extension
WORKSHEET 1: LINEAR EQUATION 1
 WORKSHEET 1: LINEAR EQUATION 1 1. Write down the arithmetical problem according the dictation: 2. Translate the English words, you can use a dictionary: equations to solve solve inverse operation variable
WORKSHEET 1: LINEAR EQUATION 1 1. Write down the arithmetical problem according the dictation: 2. Translate the English words, you can use a dictionary: equations to solve solve inverse operation variable
Extrakce nezávislé komponenty
 Extrakce nezávislé komponenty Zbyněk Koldovský Acoustic Signal Analysis and Processing Group, Faculty of Mechatronics, Informatics, and Interdisciplinary Studies, Technical University in Liberec, https://asap.ite.tul.cz
Extrakce nezávislé komponenty Zbyněk Koldovský Acoustic Signal Analysis and Processing Group, Faculty of Mechatronics, Informatics, and Interdisciplinary Studies, Technical University in Liberec, https://asap.ite.tul.cz
Základy teorie front III
 Základy teorie front III Aplikace Poissonova procesu v teorii front II Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta
Základy teorie front III Aplikace Poissonova procesu v teorii front II Mgr. Rudolf B. Blažek, Ph.D. prof. RNDr. Roman Kotecký, DrSc. Katedra počítačových systémů Katedra teoretické informatiky Fakulta
Gymnázium, Brno, Slovanské nám. 7, SCHEME OF WORK Mathematics SCHEME OF WORK. cz
 SCHEME OF WORK Subject: Mathematics Year: first grade, 1.X School year:../ List of topisc # Topics Time period Introduction, repetition September 1. Number sets October 2. Rigtht-angled triangle October,
SCHEME OF WORK Subject: Mathematics Year: first grade, 1.X School year:../ List of topisc # Topics Time period Introduction, repetition September 1. Number sets October 2. Rigtht-angled triangle October,
Aplikace matematiky. Dana Lauerová A note to the theory of periodic solutions of a parabolic equation
 Aplikace matematiky Dana Lauerová A note to the theory of periodic solutions of a parabolic equation Aplikace matematiky, Vol. 25 (1980), No. 6, 457--460 Persistent URL: http://dml.cz/dmlcz/103885 Terms
Aplikace matematiky Dana Lauerová A note to the theory of periodic solutions of a parabolic equation Aplikace matematiky, Vol. 25 (1980), No. 6, 457--460 Persistent URL: http://dml.cz/dmlcz/103885 Terms
Litosil - application
 Litosil - application The series of Litosil is primarily determined for cut polished floors. The cut polished floors are supplied by some specialized firms which are fitted with the appropriate technical
Litosil - application The series of Litosil is primarily determined for cut polished floors. The cut polished floors are supplied by some specialized firms which are fitted with the appropriate technical
A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients
 KYBERNETIKA VOLUME 8 (1972), NUMBER 6 A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients JAROSLAV KRAL In many applications (for example if the effect
KYBERNETIKA VOLUME 8 (1972), NUMBER 6 A Note on Generation of Sequences of Pseudorandom Numbers with Prescribed Autocorrelation Coefficients JAROSLAV KRAL In many applications (for example if the effect
Compression of a Dictionary
 Compression of a Dictionary Jan Lánský, Michal Žemlička zizelevak@matfyz.cz michal.zemlicka@mff.cuni.cz Dept. of Software Engineering Faculty of Mathematics and Physics Charles University Synopsis Introduction
Compression of a Dictionary Jan Lánský, Michal Žemlička zizelevak@matfyz.cz michal.zemlicka@mff.cuni.cz Dept. of Software Engineering Faculty of Mathematics and Physics Charles University Synopsis Introduction
Database systems. Normal forms
 Database systems Normal forms An example of a bad model SSN Surnam OfficeNo City Street No ZIP Region President_of_ Region 1001 Novák 238 Liteň Hlavní 10 26727 Středočeský Rath 1001 Novák 238 Bystřice
Database systems Normal forms An example of a bad model SSN Surnam OfficeNo City Street No ZIP Region President_of_ Region 1001 Novák 238 Liteň Hlavní 10 26727 Středočeský Rath 1001 Novák 238 Bystřice
EXACT DS OFFICE. The best lens for office work
 EXACT DS The best lens for office work EXACT DS When Your Glasses Are Not Enough Lenses with only a reading area provide clear vision of objects located close up, while progressive lenses only provide
EXACT DS The best lens for office work EXACT DS When Your Glasses Are Not Enough Lenses with only a reading area provide clear vision of objects located close up, while progressive lenses only provide
Vánoční sety Christmas sets
 Energy news 7 Inovace Innovations 1 Vánoční sety Christmas sets Na jaře tohoto roku jste byli informováni o připravované akci pro předvánoční období sety Pentagramu koncentrátů a Pentagramu krémů ve speciálních
Energy news 7 Inovace Innovations 1 Vánoční sety Christmas sets Na jaře tohoto roku jste byli informováni o připravované akci pro předvánoční období sety Pentagramu koncentrátů a Pentagramu krémů ve speciálních
Klepnutím lze upravit styl předlohy. nadpisů. nadpisů.
 1/ 13 Klepnutím lze upravit styl předlohy Klepnutím lze upravit styl předlohy www.splab.cz Soft biometric traits in de identification process Hair Jiri Prinosil Jiri Mekyska Zdenek Smekal 2/ 13 Klepnutím
1/ 13 Klepnutím lze upravit styl předlohy Klepnutím lze upravit styl předlohy www.splab.cz Soft biometric traits in de identification process Hair Jiri Prinosil Jiri Mekyska Zdenek Smekal 2/ 13 Klepnutím
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA
 GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
GUIDELINES FOR CONNECTION TO FTP SERVER TO TRANSFER PRINTING DATA What is an FTP client and how to use it? FTP (File transport protocol) - A protocol used to transfer your printing data files to the MAFRAPRINT
Introduction to MS Dynamics NAV
 Introduction to MS Dynamics NAV (Item Charges) Ing.J.Skorkovský,CSc. MASARYK UNIVERSITY BRNO, Czech Republic Faculty of economics and business administration Department of corporate economy Item Charges
Introduction to MS Dynamics NAV (Item Charges) Ing.J.Skorkovský,CSc. MASARYK UNIVERSITY BRNO, Czech Republic Faculty of economics and business administration Department of corporate economy Item Charges
USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING
 USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING Eva Minaříková Institute for Research in School Education, Faculty of Education, Masaryk University Structure of the presentation What can we as teachers
USING VIDEO IN PRE-SET AND IN-SET TEACHER TRAINING Eva Minaříková Institute for Research in School Education, Faculty of Education, Masaryk University Structure of the presentation What can we as teachers
Czech Republic. EDUCAnet. Střední odborná škola Pardubice, s.r.o.
 Czech Republic EDUCAnet Střední odborná škola Pardubice, s.r.o. ACCESS TO MODERN TECHNOLOGIES Do modern technologies influence our behavior? Of course in positive and negative way as well Modern technologies
Czech Republic EDUCAnet Střední odborná škola Pardubice, s.r.o. ACCESS TO MODERN TECHNOLOGIES Do modern technologies influence our behavior? Of course in positive and negative way as well Modern technologies
Uni- and multi-dimensional parametric tests for comparison of sample results
 Uni- and multi-dimensional parametric tests for comparison of sample results Jedno- a více-rozměrné parametrické testy k porovnání výsledků Prof. RNDr. Milan Meloun, DrSc. Katedra analytické chemie, Universita
Uni- and multi-dimensional parametric tests for comparison of sample results Jedno- a více-rozměrné parametrické testy k porovnání výsledků Prof. RNDr. Milan Meloun, DrSc. Katedra analytické chemie, Universita
Bioinformatika a výpočetní biologie. KFC/BIN VII. Fylogenetická analýza
 ioinformatika a výpočetní biologie KF/IN VII. Fylogenetická analýza RNr. Karel erka, Ph.. Univerzita Palackého v Olomouci Fylogeneze Vznik a vývoj jednotlivých linií organismů Vývoj člověka phylogenetic
ioinformatika a výpočetní biologie KF/IN VII. Fylogenetická analýza RNr. Karel erka, Ph.. Univerzita Palackého v Olomouci Fylogeneze Vznik a vývoj jednotlivých linií organismů Vývoj člověka phylogenetic
VY_32_INOVACE_06_Předpřítomný čas_03. Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace
 VY_32_INOVACE_06_Předpřítomný čas_03 Autor: Růžena Krupičková Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu: Zkvalitnění ICT ve slušovské škole Číslo projektu: CZ.1.07/1.4.00/21.2400
VY_32_INOVACE_06_Předpřítomný čas_03 Autor: Růžena Krupičková Škola: Základní škola Slušovice, okres Zlín, příspěvková organizace Název projektu: Zkvalitnění ICT ve slušovské škole Číslo projektu: CZ.1.07/1.4.00/21.2400
Geometry of image formation
 eometry of image formation Tomáš Svoboda, svoboda@cmp.felk.cvut.cz Czech Technical University in Prague, Center for Machine Perception http://cmp.felk.cvut.cz Last update: July 4, 2008 Talk Outline Pinhole
eometry of image formation Tomáš Svoboda, svoboda@cmp.felk.cvut.cz Czech Technical University in Prague, Center for Machine Perception http://cmp.felk.cvut.cz Last update: July 4, 2008 Talk Outline Pinhole
Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční
 Příloha I Seznam tabulek Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční odměny pro rozhodčí platný od roku
Příloha I Seznam tabulek Tabulka 1 Stav členské základny SK Praga Vysočany k roku 2015 Tabulka 2 Výše členských příspěvků v SK Praga Vysočany Tabulka 3 Přehled finanční odměny pro rozhodčí platný od roku
Jak importovat profily do Cura (Windows a
 Jak importovat profily do Cura (Windows a macos) Written By: Jakub Dolezal 2019 manual.prusa3d.com/ Page 1 of 10 Step 1 Stažení Cura profilů V tomto návodu se dozvíte, jak importovat a aktivovat nastavení
Jak importovat profily do Cura (Windows a macos) Written By: Jakub Dolezal 2019 manual.prusa3d.com/ Page 1 of 10 Step 1 Stažení Cura profilů V tomto návodu se dozvíte, jak importovat a aktivovat nastavení
6.867 Machine Learning
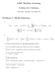 . Machine Learning Problem Set Solutions Due date: Monday November Problem : Model Selection. P (y,..., y n x,..., x n, PST) = = K [ [,] K [ K p n+ i i ( p i ) n i dpi ] = p n+ i i K ( p i ) n i n + i!
. Machine Learning Problem Set Solutions Due date: Monday November Problem : Model Selection. P (y,..., y n x,..., x n, PST) = = K [ [,] K [ K p n+ i i ( p i ) n i dpi ] = p n+ i i K ( p i ) n i n + i!
PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL
 PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL Ing. Jan HAVLÍK, MPA tajemník Městského úřadu Žďár nad Sázavou Chief Executive Municipality of Žďár nad Sázavou CO
PRODEJNÍ EAUKCE A JEJICH ROSTOUCÍ SEX-APPEAL SELLING EAUCTIONS AND THEIR GROWING APPEAL Ing. Jan HAVLÍK, MPA tajemník Městského úřadu Žďár nad Sázavou Chief Executive Municipality of Žďár nad Sázavou CO
ÚVOD DO ROZPOZNÁVÁNÍ
 ÚVOD DO ROZPOZNÁVÁNÍ 1/29 Václav Hlaváč Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz, http://cmp.felk.cvut.cz/ hlavac Osnova přednášky Modelování
ÚVOD DO ROZPOZNÁVÁNÍ 1/29 Václav Hlaváč Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz, http://cmp.felk.cvut.cz/ hlavac Osnova přednášky Modelování
Dynamic programming. Optimal binary search tree
 The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamic programming Optimal binary search tree Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The complexity
The complexity of different algorithms varies: O(n), Ω(n ), Θ(n log (n)), Dynamic programming Optimal binary search tree Různé algoritmy mají různou složitost: O(n), Ω(n ), Θ(n log (n)), The complexity
STLAČITELNOST. σ σ. během zatížení
 STLAČITELNOST Princip: Naneseme-li zatížení na zeminu, dojde k porušení rovnováhy a dochází ke stlačování zeminy (přemístňují se částice). Stlačení je ukončeno jakmile nastane rovnováha mezi působícím
STLAČITELNOST Princip: Naneseme-li zatížení na zeminu, dojde k porušení rovnováhy a dochází ke stlačování zeminy (přemístňují se částice). Stlačení je ukončeno jakmile nastane rovnováha mezi působícím
Production: The Case of One Producer
 Production: The Case of One Producer Economics II: Microeconomics VŠE Praha November 2009 Aslanyan (VŠE Praha) Monopoly 11/09 1 / 27 Microeconomics Consumers: Firms: People. Households. Optimisation Now
Production: The Case of One Producer Economics II: Microeconomics VŠE Praha November 2009 Aslanyan (VŠE Praha) Monopoly 11/09 1 / 27 Microeconomics Consumers: Firms: People. Households. Optimisation Now
Radiova meteoricka detekc nı stanice RMDS01A
 Radiova meteoricka detekc nı stanice RMDS01A Jakub Ka kona, kaklik@mlab.cz 15. u nora 2014 Abstrakt Konstrukce za kladnı ho softwarove definovane ho pr ijı macı ho syste mu pro detekci meteoru. 1 Obsah
Radiova meteoricka detekc nı stanice RMDS01A Jakub Ka kona, kaklik@mlab.cz 15. u nora 2014 Abstrakt Konstrukce za kladnı ho softwarove definovane ho pr ijı macı ho syste mu pro detekci meteoru. 1 Obsah
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky
 Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: Education Označení materiálu: VY_32_INOVACE_MAT27 Datum vytvoření: 10.10.2013
Číslo projektu: CZ.1.07/1.5.00/34.0036 Název projektu: Inovace a individualizace výuky Autor: Mgr. Libuše Matulová Název materiálu: Education Označení materiálu: VY_32_INOVACE_MAT27 Datum vytvoření: 10.10.2013
Mechanika Teplice, výrobní družstvo, závod Děčín TACHOGRAFY. Číslo Servisní Informace Mechanika: 5-2013
 Mechanika Teplice, výrobní družstvo, závod Děčín TACHOGRAFY Servisní Informace Datum vydání: 20.2.2013 Určeno pro : AMS, registrované subj.pro montáž st.měř. Na základě SI VDO č./datum: Není Mechanika
Mechanika Teplice, výrobní družstvo, závod Děčín TACHOGRAFY Servisní Informace Datum vydání: 20.2.2013 Určeno pro : AMS, registrované subj.pro montáž st.měř. Na základě SI VDO č./datum: Není Mechanika
Dynamic Signals. Ananda V. Mysore SJSU
 Dynamic Signals Ananda V. Mysore SJSU Static vs. Dynamic Signals In principle, all signals are dynamic; they do not have a perfectly constant value over time. Static signals are those for which changes
Dynamic Signals Ananda V. Mysore SJSU Static vs. Dynamic Signals In principle, all signals are dynamic; they do not have a perfectly constant value over time. Static signals are those for which changes
Karta předmětu prezenční studium
 Karta předmětu prezenční studium Název předmětu: Číslo předmětu: 545-0250 Garantující institut: Garant předmětu: Ekonomická statistika Institut ekonomiky a systémů řízení RNDr. Radmila Sousedíková, Ph.D.
Karta předmětu prezenční studium Název předmětu: Číslo předmětu: 545-0250 Garantující institut: Garant předmětu: Ekonomická statistika Institut ekonomiky a systémů řízení RNDr. Radmila Sousedíková, Ph.D.
Neparametrické odhady hustoty pravděpodobnosti
 Neparametrické odhady hustoty pravděpodobnosti Václav Hlaváč Elektrotechnická fakulta ČVUT Katedra kybernetiky Centrum strojového vnímání 121 35 Praha 2, Karlovo nám. 13 hlavac@fel.cvut.cz Statistické
Neparametrické odhady hustoty pravděpodobnosti Václav Hlaváč Elektrotechnická fakulta ČVUT Katedra kybernetiky Centrum strojového vnímání 121 35 Praha 2, Karlovo nám. 13 hlavac@fel.cvut.cz Statistické
Invitation to ON-ARRIVAL TRAINING COURSE for EVS volunteers
 Invitation to ON-ARRIVAL TRAINING COURSE for EVS volunteers (český text pro hostitelské organizace následuje na str. 3) 6.11. 11.11. 2015 Hotel Kaskáda, Ledeč nad Sázavou Husovo nám. 17, 584 01 Ledeč nad
Invitation to ON-ARRIVAL TRAINING COURSE for EVS volunteers (český text pro hostitelské organizace následuje na str. 3) 6.11. 11.11. 2015 Hotel Kaskáda, Ledeč nad Sázavou Husovo nám. 17, 584 01 Ledeč nad
DC circuits with a single source
 Název projektu: utomatizace výrobních procesů ve strojírenství a řemeslech egistrační číslo: Z..07/..0/0.008 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 09 Tento projekt je spolufinancován
Název projektu: utomatizace výrobních procesů ve strojírenství a řemeslech egistrační číslo: Z..07/..0/0.008 Příjemce: SPŠ strojnická a SOŠ profesora Švejcara Plzeň, Klatovská 09 Tento projekt je spolufinancován
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku
 Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
Vliv metody vyšetřování tvaru brusného kotouče na výslednou přesnost obrobku Aneta Milsimerová Fakulta strojní, Západočeská univerzita Plzeň, 306 14 Plzeň. Česká republika. E-mail: anetam@kto.zcu.cz Hlavním
Immigration Studying. Studying - University. Stating that you want to enroll. Stating that you want to apply for a course.
 - University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
- University I would like to enroll at a university. Stating that you want to enroll I want to apply for course. Stating that you want to apply for a course an undergraduate a postgraduate a PhD a full-time
Immigration Studying. Studying - University. Stating that you want to enroll. Stating that you want to apply for a course.
 - University Rád/a bych se zapsal/a na vysoké škole. Stating that you want to enroll Rád/a bych se zapsal/a na. Stating that you want to apply for a course bakalářské studium postgraduální studium doktorské
- University Rád/a bych se zapsal/a na vysoké škole. Stating that you want to enroll Rád/a bych se zapsal/a na. Stating that you want to apply for a course bakalářské studium postgraduální studium doktorské
On large rigid sets of monounary algebras. D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia
 On large rigid sets of monounary algebras D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia coauthor G. Czédli, University of Szeged, Hungary The 54st Summer School on General Algebra
On large rigid sets of monounary algebras D. Jakubíková-Studenovská P. J. Šafárik University, Košice, Slovakia coauthor G. Czédli, University of Szeged, Hungary The 54st Summer School on General Algebra
1, Žáci dostanou 5 klíčových slov a snaží se na jejich základě odhadnout, o čem bude následující cvičení.
 Moje hlavní město Londýn řešení: 1, Žáci dostanou 5 klíčových slov a snaží se na jejich základě odhadnout, o čem bude následující cvičení. Klíčová slova: capital, double decker bus, the River Thames, driving
Moje hlavní město Londýn řešení: 1, Žáci dostanou 5 klíčových slov a snaží se na jejich základě odhadnout, o čem bude následující cvičení. Klíčová slova: capital, double decker bus, the River Thames, driving
CZ.1.07/1.5.00/
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
By David Cameron VE7LTD
 By David Cameron VE7LTD Introduction to Speaker RF Cavity Filter Types Why Does a Repeater Need a Duplexer Types of Duplexers Hybrid Pass/Reject Duplexer Detail Finding a Duplexer for Ham Use Questions?
By David Cameron VE7LTD Introduction to Speaker RF Cavity Filter Types Why Does a Repeater Need a Duplexer Types of Duplexers Hybrid Pass/Reject Duplexer Detail Finding a Duplexer for Ham Use Questions?
SSOS_AJ_3.18 British education
 Číslo a název projektu Číslo a název šablony DUM číslo a název CZ.1.07/1.5.00/34.0378 Zefektivnění výuky prostřednictvím ICT technologií III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT SSOS_AJ_3.18
Číslo a název projektu Číslo a název šablony DUM číslo a název CZ.1.07/1.5.00/34.0378 Zefektivnění výuky prostřednictvím ICT technologií III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT SSOS_AJ_3.18
LOGBOOK. Blahopřejeme, našli jste to! Nezapomeňte. Prosím vyvarujte se downtrade
 název cache GC kód Blahopřejeme, našli jste to! LOGBOOK Prosím vyvarujte se downtrade Downtrade (z GeoWiki) Je to jednání, kterého byste se při výměnách předmětů v keších měli vyvarovat! Jedná se o snížení
název cache GC kód Blahopřejeme, našli jste to! LOGBOOK Prosím vyvarujte se downtrade Downtrade (z GeoWiki) Je to jednání, kterého byste se při výměnách předmětů v keších měli vyvarovat! Jedná se o snížení
CZ.1.07/1.5.00/
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
2. Entity, Architecture, Process
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Praktika návrhu číslicových obvodů Dr.-Ing. Martin Novotný Katedra číslicového návrhu Fakulta informačních technologií ČVUT v Praze Miloš
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Praktika návrhu číslicových obvodů Dr.-Ing. Martin Novotný Katedra číslicového návrhu Fakulta informačních technologií ČVUT v Praze Miloš
SPECIAL THEORY OF RELATIVITY
 SPECIAL THEORY OF RELATIVITY 1. Basi information author Albert Einstein phenomena obsered when TWO frames of referene moe relatie to eah other with speed lose to the speed of light 1905 - speial theory
SPECIAL THEORY OF RELATIVITY 1. Basi information author Albert Einstein phenomena obsered when TWO frames of referene moe relatie to eah other with speed lose to the speed of light 1905 - speial theory
Dynamic Development of Vocabulary Richness of Text. Miroslav Kubát & Radek Čech University of Ostrava Czech Republic
 Dynamic Development of Vocabulary Richness of Text Miroslav Kubát & Radek Čech University of Ostrava Czech Republic Aim To analyze a dynamic development of vocabulary richness from a methodological point
Dynamic Development of Vocabulary Richness of Text Miroslav Kubát & Radek Čech University of Ostrava Czech Republic Aim To analyze a dynamic development of vocabulary richness from a methodological point
Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products
 Energy news2 1 Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products Doposud jste Energy znali jako výrobce a dodavatele humánních přírodních doplňků stravy a kosmetiky.
Energy news2 1 Energy vstupuje na trh veterinárních produktů Energy enters the market of veterinary products Doposud jste Energy znali jako výrobce a dodavatele humánních přírodních doplňků stravy a kosmetiky.
DATA SHEET. BC516 PNP Darlington transistor. technický list DISCRETE SEMICONDUCTORS Apr 23. Product specification Supersedes data of 1997 Apr 16
 zákaznická linka: 840 50 60 70 DISCRETE SEMICONDUCTORS DATA SHEET book, halfpage M3D186 Supersedes data of 1997 Apr 16 1999 Apr 23 str 1 Dodavatel: GM electronic, spol. s r.o., Křižíkova 77, 186 00 Praha
zákaznická linka: 840 50 60 70 DISCRETE SEMICONDUCTORS DATA SHEET book, halfpage M3D186 Supersedes data of 1997 Apr 16 1999 Apr 23 str 1 Dodavatel: GM electronic, spol. s r.o., Křižíkova 77, 186 00 Praha
Image Analysis and MATLAB. Jiří Militky
 Image Analysis and MATLAB Jiří Militky Basic Matlab commands 0.5 0.8 IMREAD Read image from graphics file IMHIST Display histogram of image data. 0.694 GRAYTHRESH Compute global image threshold using Otsu's
Image Analysis and MATLAB Jiří Militky Basic Matlab commands 0.5 0.8 IMREAD Read image from graphics file IMHIST Display histogram of image data. 0.694 GRAYTHRESH Compute global image threshold using Otsu's
Enabling Intelligent Buildings via Smart Sensor Network & Smart Lighting
 Enabling Intelligent Buildings via Smart Sensor Network & Smart Lighting Petr Macháček PETALIT s.r.o. 1 What is Redwood. Sensor Network Motion Detection Space Utilization Real Estate Management 2 Building
Enabling Intelligent Buildings via Smart Sensor Network & Smart Lighting Petr Macháček PETALIT s.r.o. 1 What is Redwood. Sensor Network Motion Detection Space Utilization Real Estate Management 2 Building
USER'S MANUAL FAN MOTOR DRIVER FMD-02
 USER'S MANUAL FAN MOTOR DRIVER FMD-02 IMPORTANT NOTE: Read this manual carefully before installing or operating your new air conditioning unit. Make sure to save this manual for future reference. FMD Module
USER'S MANUAL FAN MOTOR DRIVER FMD-02 IMPORTANT NOTE: Read this manual carefully before installing or operating your new air conditioning unit. Make sure to save this manual for future reference. FMD Module
Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám
 VY_22_INOVACE_AJOP40764ČER Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: Název projektu: Číslo šablony: CZ.1.07/1.5.00/34.0883 Rozvoj vzdělanosti II/2 Datum vytvoření:
VY_22_INOVACE_AJOP40764ČER Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: Název projektu: Číslo šablony: CZ.1.07/1.5.00/34.0883 Rozvoj vzdělanosti II/2 Datum vytvoření:
Configuration vs. Conformation. Configuration: Covalent bonds must be broken. Two kinds of isomers to consider
 Stereochemistry onfiguration vs. onformation onfiguration: ovalent bonds must be broken onformation: hanges do NT require breaking of covalent bonds onfiguration Two kinds of isomers to consider is/trans:
Stereochemistry onfiguration vs. onformation onfiguration: ovalent bonds must be broken onformation: hanges do NT require breaking of covalent bonds onfiguration Two kinds of isomers to consider is/trans:
Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost
 Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost Registrační číslo: CZ.1.07/1. 5.00/34.0084 Šablona: II/2 Inovace a zkvalitnění výuky cizích jazyků na středních
Výukový materiál zpracovaný v rámci operačního programu Vzdělávání pro konkurenceschopnost Registrační číslo: CZ.1.07/1. 5.00/34.0084 Šablona: II/2 Inovace a zkvalitnění výuky cizích jazyků na středních
CHAIN TRANSMISSIONS AND WHEELS
 Second School Year CHAIN TRANSMISSIONS AND WHEELS A. Chain transmissions We can use chain transmissions for the transfer and change of rotation motion and the torsional moment. They transfer forces from
Second School Year CHAIN TRANSMISSIONS AND WHEELS A. Chain transmissions We can use chain transmissions for the transfer and change of rotation motion and the torsional moment. They transfer forces from
Just write down your most recent and important education. Remember that sometimes less is more some people may be considered overqualified.
 CURRICULUM VITAE - EDUCATION Jindřich Bláha Výukový materiál zpracován v rámci projektu EU peníze školám Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Bc. Jindřich Bláha. Dostupné z Metodického
CURRICULUM VITAE - EDUCATION Jindřich Bláha Výukový materiál zpracován v rámci projektu EU peníze školám Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Bc. Jindřich Bláha. Dostupné z Metodického
Pravděpodobnost a statistika; Opakování pro rozpoznávání
 Pravděpodobnost a statistika; Opakování pro rozpoznávání Václav Hlaváč České vysoké učení technické v Praze Centrum strojového vnímání (přemosťuje skupiny z) Český institut informatiky, robotiky a kybernetiky
Pravděpodobnost a statistika; Opakování pro rozpoznávání Václav Hlaváč České vysoké učení technické v Praze Centrum strojového vnímání (přemosťuje skupiny z) Český institut informatiky, robotiky a kybernetiky
Parametrizace rozdělení škod v
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Mária Špaková Parametrizace rozdělení škod v neživotním pojištení Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Mária Špaková Parametrizace rozdělení škod v neživotním pojištení Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové
VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O.
 VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O. Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová práce 2013 Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová
VYSOKÁ ŠKOLA HOTELOVÁ V PRAZE 8, SPOL. S R. O. Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová práce 2013 Návrh konceptu konkurenceschopného hotelu v době ekonomické krize Diplomová
The Over-Head Cam (OHC) Valve Train Computer Model
 The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
The Over-Head Cam (OHC) Valve Train Computer Model Radek Tichanek, David Fremut Robert Cihak Josef Bozek Research Center of Engine and Content Introduction Work Objectives Model Description Cam Design
Výukový materiál zpracovaný v rámci projektu EU peníze do škol. illness, a text
 Výukový materiál zpracovaný v rámci projektu EU peníze do škol ZŠ Litoměřice, Ladova Ladova 5 412 01 Litoměřice www.zsladovaltm.cz vedeni@zsladovaltm.cz Pořadové číslo projektu: CZ.1.07/1.4.00/21.0948
Výukový materiál zpracovaný v rámci projektu EU peníze do škol ZŠ Litoměřice, Ladova Ladova 5 412 01 Litoměřice www.zsladovaltm.cz vedeni@zsladovaltm.cz Pořadové číslo projektu: CZ.1.07/1.4.00/21.0948
Algebraic methods in Computer Vision Zuzana Kukelova, Tomas Pajdla, Martin Bujnak
 Algebraic methods in Computer Vision Zuzana Kukelova, Tomas Pajdla, Martin Bujnak Center for Machine Perception Department of Cybernetics, Faculty of Electrical Engineering Czech Technical University in
Algebraic methods in Computer Vision Zuzana Kukelova, Tomas Pajdla, Martin Bujnak Center for Machine Perception Department of Cybernetics, Faculty of Electrical Engineering Czech Technical University in
http://www.zlinskedumy.cz
 Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Výklad a cvičení z větné stavby, vy_32_inovace_ma_33_01
Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast Autor CZ.1.07/1.5.00/34.0514 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Výklad a cvičení z větné stavby, vy_32_inovace_ma_33_01
Informace o písemných přijímacích zkouškách. Doktorské studijní programy Matematika
 Informace o písemných přijímacích zkouškách (úplné zadání zkušebních otázek či příkladů, které jsou součástí přijímací zkoušky nebo její části, a u otázek s výběrem odpovědi správné řešení) Doktorské studijní
Informace o písemných přijímacích zkouškách (úplné zadání zkušebních otázek či příkladů, které jsou součástí přijímací zkoušky nebo její části, a u otázek s výběrem odpovědi správné řešení) Doktorské studijní
GENERAL INFORMATION MATCH: ALSA PRO ARENA MASTERS DATE: TIME SCHEDULE:
 GENERAL INFORMATION MATCH: ALSA PRO ARENA MASTERS DATE: 22.9. - 23.9.2018 TIME SCHEDULE: Mainmatch 1 - Saturday 22.9. registration: 22.9.2018-9.00h first shot: 22.9.2018-10.00h Mainmatch 2 - Sunday 23.9.
GENERAL INFORMATION MATCH: ALSA PRO ARENA MASTERS DATE: 22.9. - 23.9.2018 TIME SCHEDULE: Mainmatch 1 - Saturday 22.9. registration: 22.9.2018-9.00h first shot: 22.9.2018-10.00h Mainmatch 2 - Sunday 23.9.
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49
 Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
Střední průmyslová škola strojnická Olomouc, tř.17. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205 Šablona: III/2 Anglický jazyk
LOGOMANUÁL / LOGOMANUAL
 LOGOMANUÁL / LOGOMANUAL OBSAH / CONTENTS 1 LOGOTYP 1.1 základní provedení logotypu s claimem 1.2 základní provedení logotypu bez claimu 1.3 zjednodušené provedení logotypu 1.4 jednobarevné a inverzní provedení
LOGOMANUÁL / LOGOMANUAL OBSAH / CONTENTS 1 LOGOTYP 1.1 základní provedení logotypu s claimem 1.2 základní provedení logotypu bez claimu 1.3 zjednodušené provedení logotypu 1.4 jednobarevné a inverzní provedení
VY_22_INOVACE_84. P3 U3 Revision
 VY_22_INOVACE_84 P3 U3 Revision Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 7. 1. Complete with will/won t have travel drive solve need be (2x) My dad thinks
VY_22_INOVACE_84 P3 U3 Revision Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 7. 1. Complete with will/won t have travel drive solve need be (2x) My dad thinks
Chapter 7: Process Synchronization
 Chapter 7: Process Synchronization Background The Critical-Section Problem Synchronization Hardware Semaphores Classical Problems of Synchronization Critical Regions Monitors Synchronization in Solaris
Chapter 7: Process Synchronization Background The Critical-Section Problem Synchronization Hardware Semaphores Classical Problems of Synchronization Critical Regions Monitors Synchronization in Solaris
Čtvrtý Pentagram The fourth Pentagram
 Energy News 4 1 Čtvrtý Pentagram The fourth Pentagram Na jaře příštího roku nabídneme našim zákazníkům již čtvrtý Pentagram a to Pentagram šamponů. K zavedení tohoto Pentagramu jsme se rozhodli na základě
Energy News 4 1 Čtvrtý Pentagram The fourth Pentagram Na jaře příštího roku nabídneme našim zákazníkům již čtvrtý Pentagram a to Pentagram šamponů. K zavedení tohoto Pentagramu jsme se rozhodli na základě
Why PRIME? 20 years of Erasmus Programme Over 2 million students in total Annually
 What is PRIME? Problems of Recognition In Making Erasmus European-wide research project Conducted by ESN with the support of the European Commission Two editions: 1 st in 2009 Follow-up in 2010 Why PRIME?
What is PRIME? Problems of Recognition In Making Erasmus European-wide research project Conducted by ESN with the support of the European Commission Two editions: 1 st in 2009 Follow-up in 2010 Why PRIME?
kupi.cz Michal Mikuš
 kupi.cz Michal Mikuš redisgn website kupi.cz, reduce the visual noise. ADVERT ADVERT The first impression from the website was that i dint knew where to start. It was such a mess, adverts, eyes, products,
kupi.cz Michal Mikuš redisgn website kupi.cz, reduce the visual noise. ADVERT ADVERT The first impression from the website was that i dint knew where to start. It was such a mess, adverts, eyes, products,
A constitutive model for non-reacting binary mixtures
 A constitutive model for non-reacting binary mixtures Ondřej Souček ondrej.soucek@mff.cuni.cz Joint work with Vít Průša Mathematical Institute Charles University 31 March 2012 Ondřej Souček Charles University)
A constitutive model for non-reacting binary mixtures Ondřej Souček ondrej.soucek@mff.cuni.cz Joint work with Vít Průša Mathematical Institute Charles University 31 March 2012 Ondřej Souček Charles University)
Mut goes shopping VY_22_INOVACE_27. Vzdělávací oblast: Jazyk a jazyková komunikace. Vzdělávací obor: Anglický jazyk. Ročník: 6
 Mut goes shopping VY_22_INOVACE_27 Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 6 1.Find the hidden words in the word search and write their meaning: A O U P T
Mut goes shopping VY_22_INOVACE_27 Vzdělávací oblast: Jazyk a jazyková komunikace Vzdělávací obor: Anglický jazyk Ročník: 6 1.Find the hidden words in the word search and write their meaning: A O U P T
Škola: Střední škola obchodní, České Budějovice, Husova 9. Inovace a zkvalitnění výuky prostřednictvím ICT
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Britské společenství národů. Historie Spojeného království Velké Británie a Severního Irska ročník gymnázia (vyšší stupeň)
 Název vzdělávacího materiálu: Číslo vzdělávacího materiálu: Autor vzdělávací materiálu: Období, ve kterém byl vzdělávací materiál vytvořen: Vzdělávací oblast: Vzdělávací obor: Vzdělávací předmět: Tematická
Název vzdělávacího materiálu: Číslo vzdělávacího materiálu: Autor vzdělávací materiálu: Období, ve kterém byl vzdělávací materiál vytvořen: Vzdělávací oblast: Vzdělávací obor: Vzdělávací předmět: Tematická
ISS Numerické cvičení / Numerical exercise 6 Honza Černocký, FIT VUT Brno, December 14, 2016
 ISS Numerické cvičení / Numerical exercise Honza Černocký, FIT VUT Brno, December 14, 01 Číslicové filtry / Digital filters Číslicový filtr je zadaný následujícím schématem / A digital filter is given
ISS Numerické cvičení / Numerical exercise Honza Černocký, FIT VUT Brno, December 14, 01 Číslicové filtry / Digital filters Číslicový filtr je zadaný následujícím schématem / A digital filter is given
Verb + -ing or infinitive
 Verb + -ing or infinitive Verb + -ing or infinitive There are 3 groups of verbs: 1. Verbs followed by ing form 2. Verbs followed by infinitive 3. Verbs that can have ing form or infinitive, but the meaning
Verb + -ing or infinitive Verb + -ing or infinitive There are 3 groups of verbs: 1. Verbs followed by ing form 2. Verbs followed by infinitive 3. Verbs that can have ing form or infinitive, but the meaning
CZ.1.07/1.5.00/
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
PRAVIDLA ZPRACOVÁNÍ STANDARDNÍCH ELEKTRONICKÝCH ZAHRANIČNÍCH PLATEBNÍCH PŘÍKAZŮ STANDARD ELECTRONIC FOREIGN PAYMENT ORDERS PROCESSING RULES
 PRAVIDLA ZPRACOVÁNÍ STANDARDNÍCH ELEKTRONICKÝCH ZAHRANIČNÍCH PLATEBNÍCH PŘÍKAZŮ STANDARD ELECTRONIC FOREIGN PAYMENT ORDERS PROCESSING RULES Použité pojmy Platební systém Elektronický platební příkaz Účetní
PRAVIDLA ZPRACOVÁNÍ STANDARDNÍCH ELEKTRONICKÝCH ZAHRANIČNÍCH PLATEBNÍCH PŘÍKAZŮ STANDARD ELECTRONIC FOREIGN PAYMENT ORDERS PROCESSING RULES Použité pojmy Platební systém Elektronický platební příkaz Účetní
WYSIWYG EDITOR PRO XML FORM
 WYSIWYG EDITOR PRO XML FORM Ing. Tran Thanh Huan, Ing. Nguyen Ba Nghien, Doc. Ing. Josef Kokeš, CSc Abstract: In this paper, we introduce the WYSIWYG editor pro XML Form. We also show how to create a form
WYSIWYG EDITOR PRO XML FORM Ing. Tran Thanh Huan, Ing. Nguyen Ba Nghien, Doc. Ing. Josef Kokeš, CSc Abstract: In this paper, we introduce the WYSIWYG editor pro XML Form. We also show how to create a form
CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA
 CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA &KDSWHUSUHVHQWVWKHGHVLJQDQGIDEULFDW LRQRIPRGLILHG0LQNRZVNLIUDFWDODQWHQQD IRUZLUHOHVVFRPPXQLFDWLRQ7KHVLPXODWHG DQGPHDVXUHGUHVXOWVRIWKLVDQWHQQDDUH DOVRSUHVHQWHG
CHAPTER 5 MODIFIED MINKOWSKI FRACTAL ANTENNA &KDSWHUSUHVHQWVWKHGHVLJQDQGIDEULFDW LRQRIPRGLILHG0LQNRZVNLIUDFWDODQWHQQD IRUZLUHOHVVFRPPXQLFDWLRQ7KHVLPXODWHG DQGPHDVXUHGUHVXOWVRIWKLVDQWHQQDDUH DOVRSUHVHQWHG
Obrábění robotem se zpětnovazební tuhostí
 Obrábění robotem se zpětnovazební tuhostí Odbor mechaniky a mechatroniky ČVUT v Praze, Fakulta strojní Student: Yaron Sela Vedoucí: Prof. Ing. Michael Valášek, DrSc Úvod Motivace Obráběcí stroj a důležitost
Obrábění robotem se zpětnovazební tuhostí Odbor mechaniky a mechatroniky ČVUT v Praze, Fakulta strojní Student: Yaron Sela Vedoucí: Prof. Ing. Michael Valášek, DrSc Úvod Motivace Obráběcí stroj a důležitost
Jan Černocký ÚPGM FIT VUT Brno, FIT VUT Brno
 SRE 2 - Statistické rozpoznávání vzorů Jan Černocký ÚPGM FIT VUT Brno, cernocky@fit.vutbr.cz FIT VUT Brno SRE 2 - Statistické rozpoznávání vzorů Jan Černocký, ÚPGM FIT VUT Brno, 25/6 1/6 Plán... SRE 2
SRE 2 - Statistické rozpoznávání vzorů Jan Černocký ÚPGM FIT VUT Brno, cernocky@fit.vutbr.cz FIT VUT Brno SRE 2 - Statistické rozpoznávání vzorů Jan Černocký, ÚPGM FIT VUT Brno, 25/6 1/6 Plán... SRE 2
Next line show use of paragraf symbol. It should be kept with the following number. Jak může státní zástupce věc odložit zmiňuje 159a.
 1 Bad line breaks The follwing text has prepostions O and k at end of line which is incorrect according to Czech language typography standards: Mezi oblíbené dětské pohádky patří pohádky O Palečkovi, Alenka
1 Bad line breaks The follwing text has prepostions O and k at end of line which is incorrect according to Czech language typography standards: Mezi oblíbené dětské pohádky patří pohádky O Palečkovi, Alenka
Perception Motivated Hybrid Approach to Tone Mapping
 Perception Motivated Hybrid Approach to Tone Mapping Martin Čadík Czech Technical University in Prague, Czech Republic Content HDR tone mapping Hybrid Approach Perceptually plausible approach Cognitive
Perception Motivated Hybrid Approach to Tone Mapping Martin Čadík Czech Technical University in Prague, Czech Republic Content HDR tone mapping Hybrid Approach Perceptually plausible approach Cognitive
Škola: Střední škola obchodní, České Budějovice, Husova 9. Inovace a zkvalitnění výuky prostřednictvím ICT
 Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Škola: Střední škola obchodní, České Budějovice, Husova 9 Projekt MŠMT ČR: EU PENÍZE ŠKOLÁM Číslo projektu: CZ.1.07/1.5.00/34.0536 Název projektu školy: Výuka s ICT na SŠ obchodní České Budějovice Šablona
Effect of temperature. transport properties J. FOŘT, Z. PAVLÍK, J. ŽUMÁR,, M. PAVLÍKOVA & R. ČERNÝ Č CTU PRAGUE, CZECH REPUBLIC
 Effect of temperature on water vapour transport properties J. FOŘT, Z. PAVLÍK, J. ŽUMÁR,, M. PAVLÍKOVA & R. ČERNÝ Č CTU PRAGUE, CZECH REPUBLIC Outline Introduction motivation, water vapour transport Experimental
Effect of temperature on water vapour transport properties J. FOŘT, Z. PAVLÍK, J. ŽUMÁR,, M. PAVLÍKOVA & R. ČERNÝ Č CTU PRAGUE, CZECH REPUBLIC Outline Introduction motivation, water vapour transport Experimental
SPECIFICATION FOR ALDER LED
 SPECIFICATION FOR ALDER LED MODEL:AS-D75xxyy-C2LZ-H1-E 1 / 13 Absolute Maximum Ratings (Ta = 25 C) Parameter Symbol Absolute maximum Rating Unit Peak Forward Current I FP 500 ma Forward Current(DC) IF
SPECIFICATION FOR ALDER LED MODEL:AS-D75xxyy-C2LZ-H1-E 1 / 13 Absolute Maximum Ratings (Ta = 25 C) Parameter Symbol Absolute maximum Rating Unit Peak Forward Current I FP 500 ma Forward Current(DC) IF
