Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO
|
|
|
- Václav Ovčačík
- před 8 lety
- Počet zobrazení:
Transkript
1 FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO Garant předmětu: doc. Ing. Václav Zeman, Ph.D. Autoři textu: doc. Ing. Václav Zeman, Ph.D. BRNO 2014 Vznik těchto skript byl podpořen projektem č. CZ.1.07/2.2.00/ Evropského sociálního fondu a státním rozpočtem České republiky.
2
3 2 FEKT Vysokého učení technického v Brně Autoři doc. Ing. Václav Zeman, Ph.D., Název Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO Vydavatel Vysoké učení technické v Brně Fakulta elektrotechniky a komunikačních technologií Ústav telekomunikací Technická 12, Brno Vydání první Rok vydání 2014 Náklad elektronicky ISBN Tato publikace neprošla redakční ani jazykovou úpravou.
4 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 3 Obsah 1 Úvod 7 2 Postranní kanály v kryptografii Časový postranní kanál Proudový postranní kanál Statická výkonová spotřeba Dynamická výkonová spotřeba Hazardní stavy v CMOS obvodech Elektromagnetický postranní kanál Akustický postranní kanál Optický postranní kanál Chybový postranní kanál Proudová analýza Jednoduchá proudová analýza SPA Přímé interpretování proudové spotřeby Útoky pomocí šablon Diferenciální proudová analýza DPA Útok založený na korelačním koeficientu Útok založený na rozdílu středních hodnot Útok založený na vzdálenosti středních hodnot Útok pomocí šablon Modely proudové spotřeby Metody protiopatření Skrývání Ovlivnění časové oblasti proudové spotřeby Ovlivnění okamžité velikosti proudové spotřeby Maskování Způsoby implementace protiopatření
5 4 FEKT Vysokého učení technického v Brně Softwarové implementace Hardwarové implementace Reference 88 5 Příloha Šifrovací algoritmus AES Matematický úvod Princip algoritmu AES Substituční tabulka S-box Neuronové sítě v kryptografii Útok DPAContest Příklad DPA útoku
6 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 5 SEZNAM OBRÁZKŮ 1.1 Model útoku využívající postranní kanály Algoritmus verifikace hesla Ukázka jednoduché časové analýzy, druhý krok útoku Obecné schéma proudové spotřeby CMOS obvodu Model invertoru a) nabíjení b) vybíjení parazitní kapacity Výsledky simulací nabíjení a vybíjení parazitní kapacity [91] Jednoduchý kombinační obvod u kterého může nastat hazardní stav Proudová spotřeba kryptografického modulu PIC16f84a Princip přímé emise magnetického a elektrického pole IO Průběh šifrovaní algoritmem AES naměřený EM sondou EM otisky pro jednotlivé instrukce kryptografického modulu Spektra různých operací mikroprocesoru [100] a)zařízení OPTICA b)příklad naměřených dat pomocí PICA [37] Princip chybového postranního kanálu na operační mód CBC Proudová spotřeba algoritmu square and multiply [49] Algoritmus square and multiply Detail první rundy AES Proudový průběh instrukce MOV nese informaci o HW šifrovacího klíče Část implementace operace AddRoundKey Proudová spotřeba instrukce MOV pro různé HW Blokový diagram znázorňující kroky 3 až 5 DPA útoku Průběh proudové spotřeby operací AddRoundKey a SubBytes Proudové vzory spotřeby pro všechny hodnoty klíče Detail proudové spotřeby pro všechny hodnoty klíče Struktura vytvořené neuronové sítě Grafické znázornění kompletních výsledků klasifikace V cel Výsledky klasifikace pro 5 náhodně vybraných klíčů Maximální hodnoty pravděpodobnosti a určené odhady klíče Výstupní vektor chybně klasifikovaného odhadu klíče
7 6 FEKT Vysokého učení technického v Brně 3.16 Blokový diagram znázorňující kroky 3 až 5 DPA útoku Proudová spotřeba korespondující s první rundou AES Průběh jednotlivých kroků DPA Výsledky korelační matice Proudový průběh z DPA Contest V Blokový diagram popisující funkci nástroje AttackWrapper Útok na maskovaný šifrovací algoritmus s využitím ANN Korelace mezi offsetem a proudovým průběhem maskovaného AES Výpis terminálu při spuštěném útoku Pole bajtů stav, výstupní a vstupní pole bajtů Struktura šifrování a dešifrování algoritmem AES Expanze klíče Formální neuron Neuronová síť Obecná struktura třívrstvé neuronové síě
8 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 7 1 ÚVOD Učební text popisuje zajištění důvěrnosti přenášených dat symetrickým šifrovacím algoritmem AES (Advanced Encryption Standard), který je v dnešní době často využíván v kryptografických zařízení a protokolech (Transport Layer Security (TLS), Wi-Fi Protected Access (WPA2) atd. ). Důvod použití je prokazatelná bezpečnost tohoto šifrovacího algoritmu. Se stále zrychlujícím se vývojem moderních komunikačních a počítačových systémů se objevila řada nových typů útoků na kryptografické systémy. Útočníci neodposlouchávají pasivně přenosový kanál, ale využívají stále sofistikovanějších metod kryptoanalýzy k prolomení těchto bezpečných šifrovacích algoritmů. Popis nových metod kryptoanalýz cílených na algoritmu AES je hlavním obsahem tohoto učebního textu. Hlavním úkolem pro kryptografické systémy je zajištění bezpečnosti. V současnosti používané kryptografické prostředky v informačních systémech poskytují k zajištění bezpečnosti tyto služby: důvěrnost (confidentiality) - utajení informace před neoprávněnými uživateli, autentičnost (authentication) - příjemce je schopen ověřit autora zprávy, integritu dat (integrity) - příjemce dokáže jednoznačně rozpoznat, zda byla zpráva během přenosu modifikována, nepopíratelnost (non-repuditation) - odesílatel nemůže popřít, že danou zprávu odeslal. Tyto kryptografické služby v celém systému zajišťuje kryptografický modul, který bývá součástí bezpečnostního subsystému (obr.1.1). Tento modul je v podstatě fyzickou implementací konkrétního kryptografického algoritmu popř. protokolu. Realizace kryptografického modulu může být hardwarová, softwarová nebo kombinovaná. Během činnosti kryptografického modulu probíhají uvnitř procesy, které jsou spojeny s šifrováním, dešifrováním, ověřením, autentizací atd. Během těchto činností pracuje modul se senzitivními daty (např. tajný klíč), které bývají uloženy v paměti modulu. Z toho plyne, že praktická realizace kryptografického modulu, která v sobě obsahuje všechny pravidla, klíče a další senzitivní materiál, do značné míry ovlivňuje bezpečnost celého systému. Dosavadní konvenční způsoby kryptoanalýzy (viz obr.1.1, zelená čerchovaná čára) se soustředily na objevení slabiny v matematické podstatě kryptografických algoritmů. Proti
9 8 FEKT Vysokého učení technického v Brně Útočník Informační systém Bezpečnostní subsystém Nežádoucí komunikace Vstupy Kryptografický modul Výstupy Konveční způsoby útoku Senzitivní informace Útoky postranními kanály Obrázek 1.1: Model útoku využívající postranní kanály. v současnosti používaným šifrovacím algoritmům je tento způsob neefektivní a časově prakticky nerealizovatelný. Nový způsob kryptoanalýzy, využívající postranní kanály, se soustředí na konkrétní implementace algoritmů a protokolů. Při konstrukci modulu se předpokládá jediná možná komunikace modulu s okolím a to jen prostřednictvím přesně definované vstupů a výstupů. V reálném prostředí modul během své činnosti komunikuje se svým okolím i jiným, nežádoucím způsobem. Modul může vyzařovat do svého okolí např. tepelné nebo elektromagnetické záření, každý reálný modul při své činnosti odebírá určitý proud ze zdroje, každá jeho operace způsobuje různé časové zpoždění, na konkrétní situaci reaguje modul stavovým nebo chybovým hlášením, klávesnice modulu může být mechanicky opotřebená atd. Všechny tyto projevy modulu jsou neodmyslitelně spojeny s jeho činností, při které mohou být vyneseny některé ze senzitivních informací. Každý nežádoucí způsob výměny informace mezi kryptografickým modulem a jeho okolím se nazývá postranním kanálem.
10 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 9 Analýzou postranního kanálu (Side Channels analysis) je označován postup, při kterém je možné získat užitečné informace, které lze odvodit ze signálu přicházejícím po tomto kanálu. Útok vedený pomocí postranního kanálu je založen na využití takto získané informace k napadení daného kryptografického modulu a získání tak senzitivních informací. Blokové schéma kryptoanalýzy využívající postranní kanály je zobrazeno na obr. 1.1 červenou čárkovanou čárou. Koncept útoku postranními kanály, tak jak je chápán v dnešní době, zadefinoval a popsal Kocher v práci [57] v roce Princip útoku byl proveden na algoritmus Data Encryption Standard metodou založenou na rozdílu středních hodnot. Postranní kanály se prakticky využívaly dříve, kdy se definice postranních kanálů nepoužívala. Akustický postranní kanál patří k nejstarším používaným postranním kanálům, např. v roce 1956 Britové získávají informace z egyptského šifrátoru odposlechem zvuků klávesnice a v roce 1961 Američané provádějí akustický odposlech prostřednictvím ústředního topení. Elektromagnetický postranní kanál byl ve své historii také nejdříve využíván v armádě a tajných službách. Tyto organizace se odborně zabývaly studiem problematiky parazitních emisí, která označovaly termínem TEMPEST. Hlavním zájmem vojenských organizací bylo zamezení nežádoucích emisí a naopak využití tohoto vyzařování k špionážní činnosti. Pojem TEMPEST vznikl na přelomu 60. a 70.let dvacátého století a označuje i skupinu vojenských standardů, ve kterých jsou stanoveny maximální povolené limity elektromagnetického záření v různých elektronických systémech. Postranní kanály zcela mění celkový pohled na bezpečnost systému. Již nestačí zvolit kvalitní šifru, ale je nezbytné velkou pozornost věnovat i její implementaci. Návrháři a konstruktéři kryptografického modulu často neví a ani nemohou vědět o existenci všech nežádoucích postranních kanálů. Existují ovšem některé postranní kanály, které jsou schopni minimalizovat. V současné době neexistuje žádný konkrétní návod pro návrh zcela imunního kryptografického modulu vůči postranním kanálům, ale existují testy které otestují navrhovaný modul na některé konkrétní typy postranních kanálů a na množství unikající informace.
11 10 FEKT Vysokého učení technického v Brně
12 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 11 2 POSTRANNÍ KANÁLY V KRYPTOGRAFII Cílem kapitoly je uvést základní přehled postranních kanálů a definovat další používané odborné pojmy, které jsou nutné k pochopení problematiky. Úvod kapitoly vysvětluje pomocí časového postranního kanálu základní princip útoku postranním kanálem a následně je pozornost věnována detailnímu popisu proudového postranního kanálu, protože lze využít téměř u všech moderní kryptografických modulů, které musí být během své činnosti napájeny ze zdroje. Ostatní typy postranních kanálů jsou uvedeny pro úplnost a přehlednost problematiky stručnějším popisem. Každý typ postranního kanálu je založen na konkrétní měřitelné informaci a často mívají tyto informace podobu fyzikální veličiny, kterou je schopen potencionální útočník změřit. Základní dělení postranních kanálů vychází z fyzikální veličiny nebo typu informace unikající prostřednictvím postranního kanálu. Kryptoanalytici považují v současné době za hlavní druhy postranních kanálů následující typy (pro lepší orientaci s odbornou literaturou je v závorce uveden anglický název): časový (timing), proudový (power), elektromagnetický (electromagnetic), chybový (fault), optický (optical), ostatní typy postranních kanálů. Prostřednictvím postranního kanálu unikají informace obsahující senzitivní údaje z kryptografického modulu, které musí útočník v rámci útoku zpracovat a vyhodnotit. Zpracování a vyhodnocení informací je v kryptografii souhrnně nazýváno analýzou kanálu. Existují dvě základní analýzy: jednoduchá (Simple Analysis, SA), diferenciální (Differential Analysis, DA). Jednoduchá analýza představuje základní způsob zpracování výsledků. Informace získané z postranního kanálu jsou útočníkem přímo pozorovány a vyhodnoceny. Diferenciální analýza vyžaduje použití matematického aparátu. Často však umožňuje nalézt citlivé informace i z postranních kanálů, kde jejich přítomnost není zřejmá. Na každý typ postranního
13 12 FEKT Vysokého učení technického v Brně kanálu můžeme aplikovat oba způsoby analýz např. pro proudový postranní kanál je to jednoduchá proudová analýza (Simple power analysis, SPA) nebo diferenciální proudová analýza (Diferent power analysis, DPA). Útok postranním kanálem lze chápat jako proces využití informace získané postranním kanálem k napadení kryptografického modulu. Následující text bude obsahovat podrobnější popis konkrétních typů postranních kanálů a principu jejich vzniku. Do kategorie ostatní typy postranních kanálů spadají ty jejichž existence byla prokázána, ale na využití ještě nebyla soustředěna dostatečná pozornost a tudíž se zatím nedostaly do popředí. Patří sem například postranní kanál frekvenční [106] nebo využívající viditelné světlo [58]. V následujícím textu jsou jednotlivé postranní kanály vysvětlovány na konkrétních příkladech implementací kryptografických algoritmů. Ve většině případů se jedná o symetrický šifrovací algoritmus AES. Z tohoto důvodu je nejprve vhodné, nastudovat princip fungování šifrovacího algoritmu AES v příloze Časový postranní kanál Časový postranní kanál je prvním publikovaným a typickým příkladem postranního kanálu. Základní myšlenka útoku byla publikována na vědecké konferenci již v roce 1996 [57]. S existencí možnosti vedení útoku na kryptografický modul přišel známý americký kryptolog Paul Carl Kocher. Časový útok (Timing Analysis, TA) je založen na měření času, který je potřebný k vykonání určitých operací ve sledovaném modulu. Pod pojmem určité operace uvnitř kryptografického modulu chápeme například procesorové instrukce (násobení, dělení, sčítání, rotace...), větvení programu (tj. vykonání podmíněných příkazů), operace čtení a zápisu dat do paměti atd. Jedná se v podstatě o provádění kryptografického algoritmu, kde prováděné operace mají různou délku trvání v závislosti na vstupních datech a tajném šifrovacím klíči. Z uvedeného vyplývá, že útok časovým postranním kanálem je použitelný k napadení každého kryptografického modulu, ve kterém existuje přímá souvislost mezi hodnotou klíče a dobou výpočtu. Konkrétní realizace útoků využívají různé operace příslušného kryptografického modulu a různé sofistikované statistické nástroje pro vyhodnocování naměřených časových údajů. Ve většině odborných publikací bývá TA vy-
14 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 13 Input: PU =(P[0],..., P[7]), PS =(P[0],...,P[7]), Output: true or false 1: for j = 0 to 7, j++ 2: if (PU[j] ~= PS[j]) 3: return false 4: end 5: return true Obrázek 2.1: Algoritmus verifikace hesla. světlována na implementaci algoritmu RSA (iniciály autorů Rivest, Shamir, Adleman) 1 [57]. V tomto učebním textu je pro změnu představena jednoduchá časová analýza na implementaci algoritmu verifikace hesla [34]. Tento příklad jednoduché analýzy je uveden z důvodu vysvětlení a snadného pochopení principu útoku postranními kanály. Útok na verifikaci hesla Některé aplikace vyžadují po uživateli při procesu autentizace heslo, aby umožnily přístup k informacím nebo datům jen pro oprávněné uživatele (proces autorizace). Například soubor vyžaduje po uživateli heslo pro otevření obsahu nebo na webovém rozhraní se musí uživatel přihlásit zadáním jména a hesla. Má-li heslo délku 8 bajtů, útok hrubou silou 2 by vyžadoval realizovat = 2 64 pokusů. Osobní počítač s procesorem o frekvenci jádra 3GHz by na útok hrubou silou potřeboval cca dní a to odpovídá 195 rokům. Pro běžného uživatele je tato výpočetně prokazatelná bezpečnost dostatečná. Verifikace hesla bývá v praxi implementována algoritmem, který je zobrazen na obr. 2.1, kde PU představuje osmi bajtové heslo zadané uživatelem a PS značí správné heslo [53]. Princip algoritmu je na první pohled zřejmý, jednoduchý podmíněný cyklus vrací true v případě, že heslo bylo zadáno korektně a v opačném případě vrací hodnotu false. Útočník může měřit čas potřebný k vykonání algoritmu a z průběhu algoritmu plyne, že doba vykonání algoritmu bude delší při zadání správného hesla, ve srovnání s dobou, kdy se heslo bude lišit např. hned ve druhém bajtu. Na této skutečnosti je založen následující 1 Algoritmus RSA je založen na matematické operaci modulární mocniny, na implementaci výpočtu se často používá tzv. algoritmus square and multiply, který je založen na postupném zpracování jednotlivých bitů soukromého klíče, doba výpočtu je závislá na hodnotě klíče. 2 Při útoku hrubou silou útočník zkouší postupně všechny možné kombinace tajného klíče dokud nenalezne správnou kombinaci.
15 14 FEKT Vysokého učení technického v Brně útok využívající jednoduchou časovou analýzu: 1. útočník si nejprve vytvoří sadu 256-ti hesel délky 8-mi bajtů následujícím způsobem: P U = {n, 0, 0, 0, 0, 0, 0, 0}, kde 0 n 256 představuje hodnotu prvního bajtu hesla. Útočník měří odpovídající čas vykonání algoritmu τ[n] pro všechny vytvořené hesla. 2. Následně vybere maximální naměřenou hodnotu: τ[n 0 ] := max τ[n], (2.1) 0 n 256 a tím získá první hodnotu bajtu hesla P U[0], která odpovídá n Hodnota prvního bajtu je odtajněna a útočník pokračuje stejným způsobem pro druhý bajt hesla P U = {P [0], n, 0, 0, 0, 0, 0, 0}. Tento postup opakuje dokud nezíská hodnoty všech bajtů hesla. Praktická ukázka druhého kroku útoku pro první bajt uloženého hesla 3 P U = {25, 186, 254, 4, 98, 84, 67, 2} je zobrazena na obr Útok výše popsaným způsobem je velice efektivní, pro získání hesla potřebujeme maximálně = 2048 realizací verifikačního algoritmu. Útočník je schopen otestovat jednu realizaci algoritmu na běžně dostupném počítači během 1s, z toho plyne, že celý útok může trvat cca. 30 minut. I pro běžného uživatele je tato výpočetně prokazatelná bezpečnost zcela nedostatečná. Z porovnání časů potřebných na prolomení hesla, kdy útočník použije metodu hrubé síly a TA je vidět vysoká efektivita a síla postranních kanálů. Jako nejjednodušší protiopatření proti TA můžeme použít vložení náhodného zpoždění před návratovou hodnotu algoritmu. To však nezabrání útočníkovi v podobném útoku. Útok v tomto případě bude probíhat úplně stejným způsobem, jen v prvním kroku útočník zkouší heslo P U = {n, 0, 0, 0, 0, 0, 0, 0} t-krát a měří odpovídající průměrné časy τ[n] pro 0 n 256. Obtížnost útoku se zvýšila o faktor t. Jediným správným protiopatřením TA je realizace konstantní časové implementace algoritmu bez závislosti vstupních dat. 3 V praxi se hesla neukládají přímo, ale pouze jejich haše (otisky). Haše nijak neodhalují hesla (díky jednocestnosti hašovacích funkcí), z nichž jsou vypočteny, ale přitom umožňují kontrolu jejich správnosti při přihlašování uživatelů. Aby se vyloučil slovníkový útok, kdy si útočník předvypočítá haše pro často používaná slova a výrazy, používá se tzv. metoda solení. Při ní se vždy při ukládání otisku hesla vygeneruje i náhodný řetězec (tzv. sůl), který se poté hašuje dohromady s vlastním heslem. Do databáze hašů se pak ukládá dvojice (sůl, hash(heslo, sůl)).
16 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 15 Obrázek 2.2: Ukázka jednoduché časové analýzy, druhý krok útoku. Příklady útoků diferenciální časovou analýzou využívající vyrovnávací paměť procesorů, které nejsou učebním textem probírány, jsou uvedeny například v pracích [15, 92, 87, 85]. 2.2 Proudový postranní kanál Proudová analýza (Power analysis, PA) studuje proudovou spotřebu kryptografického zařízení v závislosti na jeho činnosti, byla představena v roce 1999 panem Kocherem [57]. Průběh proudové spotřeby elektronického zařízení (kryptografického modulu) není s časem konstantní a na první pohled připomíná nahodilý šum. Většina moderních kryptografických zařízení bývá založena na technologii CMOS (Complementary Metal Oxide Semiconductor). Celková proudová spotřeba CMOS obvodu je dána součtem proudových spotřeb jednotlivých buněk, z kterých se skládá obvod. Z tohoto důvodu proudová spotřeba závisí na počtu logických buněk v obvodu, na spojení mezi nimi a na tom jak jsou buňky tvořeny. Obvody CMOS jsou většinou napájeny konstantním napájecím napětím U DD, jak ukazuje obr. 2.3, při práci obvodu logické buňky zpracovávají vstupní data a odebírají proud ze zdroje napětí. Celkový okamžitý proud označíme i DD (t) a okamžitou výkonovou spotřebu
17 16 FEKT Vysokého učení technického v Brně I DD Vstup Buňky pro logické operace Výstup U DD.. CMOS obvod.. Obrázek 2.3: Obecné schéma proudové spotřeby CMOS obvodu. p obv (t). Potom průměrná výkonová spotřeba P obv obvodu za čas T může být vypočítána podle vztahu: P obv = 1 T T 0 p obv (t)dt = U DD T T 0 i DD (t)dt. (2.2) Základním stavebním logickým prvkem (buňkou) založeným na CMOS technologii je invertující člen (obr. 2.4). Pomocí invertoru bude podrobně vysvětlen princip odebírání proudu ze zdroje, tento princip platí i pro všechny složitější buňky. Invertor obsahuje jen dva tranzistory řízené napětím s opačným typem vodivosti. Složitější buňky pracují na stejném principu, ale obsahují více těchto tranzistorů. Branami CMOS tranzistorů u invertoru protékají tři různé druhy proudů [91], první se nazývá svodový proud (direct path current), druhý proud nabíjející/vybíjecí (charge/discharge current) parazitní kapacity a třetí se nazývá zbytkový proud (leakage current). Vznik jednotlivých proudů a popis činnosti invertoru je podrobněji popsán v následujícím textu. Obecně lze celkovou výkonovou spotřebu invertoru rozdělit do dvou základních částí. První částí je statická výkonová spotřeba P stat, která je odebírána invertorem ve stabilních stavech. Druhou částí spotřeby je dynamická spotřeba P dyn, která nastane dojde-li k přepnutí stavu na vstupu nebo výstupu invertoru. Celková spotřeba invertoru je následně dána součtem P stat a P dyn. Pro krátký časový úsek a výstup invertoru můžeme obecně
18 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 17 U DD = 5V T1 T1 I C I svod U IN = 0V U IN = 5V T2 I D C U OUT = 5V U OUT = 0V T2 U IN = 0V 5V U IN = 0V I zbytk C U OUT = 0V U OUT = 5V a) b) Obrázek 2.4: Model invertoru a) nabíjení b) vybíjení parazitní kapacity. definovat čtyři přechody viz tab Pro dva přechody 0 0 a 1 1 je výkonová spotřeba dána statickou spotřebou a pro zbylé přechody 0 1 a 1 0 je celková výkonová spotřeba dána součtem statistické a dynamické výkonové spotřeby. Obecně platí P 00 P 11 P 01, P 10 a z toho plyne, že dynamická spotřeba invertoru je závislá na právě zpracovávaných datech. Tabulka 2.1: Přechody výstupu invertoru a odpovídající výkonová spotřeba. Přechod Výkonová spotřeba Typ výkonové spotřeby 0 0 P 00 statická 0 1 P 01 statická + dynamická 1 0 P 10 statická + dynamická 1 1 P 11 statická Statická výkonová spotřeba Invertor obsahuje dva tranzistory T1 (PMOS) a T2 (NMOS) řízené napětím s opačným typem vodivosti (viz obr.2.4). Invertor pracuje následovně: je-li vstupní napětí (U IN ) v logické úrovni 1, je otevřen tranzistor T2 a T1 je uzavřen, je-li vstupní napětí (U IN ) v logické úrovni 0, je otevřen tranzistor T1 a T2 je uzavřen. V obou těchto stabilních stavech je výkonová spotřeba minimální. Například při vstupní hodnotě napětí U IN menší než hodnota prahového napětí tranzistoru je tranzistor T2
19 18 FEKT Vysokého učení technického v Brně (NMOS) uzavřen (cutoff region). Invertorem neprotéká prakticky žádný proud. Přesněji řečeno invertorem protéká velmi malý zbytkový proud odpovídající podprahovému proudu NMOS tranzistoru a závěrným proudům P-N přechodů oblastí emitoru a kolektoru. Označme zbytkový proud I zbytk, potom statická spotřeba P stat může být spočítána dle vztahu: P stat = I zbytk U DD. (2.3) Zbytkový proud pro MOS tranzistor je typicky v rozsahu A, tato hodnota se neustále zvyšuje pro moderní výrobní technologie. Zbytkový proud pro samostatný tranzistor NMOS je dán vztahem: I zbytk,nmos = I 0 W L e U TH/nkT/q, (2.4) kde U TH je prahové napětí transistoru, I 0 a n jsou parametry závislé na technologii, W/L je poměr tranzistoru (W - šířka kanálu a L - délka kanálu), T je teplota, k Boltzmanova konstanta a q náboj elektronu. Analogický vztah platí pro PMOS tranzistor. Velikost zbytkového proudu (rovnice 2.4) je silně závislá na teplotě a velikosti prahového napětí U TH. Zbytkový proud CMOS invertoru odpovídá zbytkovému proudu transistoru NMOS nebo PMOS (rovnice 2.4) v závislosti na tom, který z nich je právě uzavřen. Jak je popsáno výše, je-li vstupní napětí (U IN ) v logické úrovni 1, je otevřen tranzistor T2 (NMOS) a T1 (PMOS) je uzavřen a je-li vstupní napětí v logické úrovni 0, je otevřen tranzistor T1 a T2 je uzavřen. Velikost prahového napětí u reálné CMOS technologie je rozdílná pro NMOS a PMOS tranzistor tedy i odpovídající zbytkové proudy jsou rozdílné (rovnice 2.4). Z předchozích tvrzení vyplývá, že velikost zbytkového proudu silně závisí na vstupu digitálního obvodu [3]. Útočník může dát do souvislosti vstupní otevřený text a průběhy zbytkových proudů a zjistí tímto informace o tajném klíči. Zbytkový proud může být měřen obdobným způsobem jako proud u dynamické výkonové spotřeby v tradiční proudové analýze. Označení statické proudové analýzy je LPA (Leakage Power Analysis) a vychází tedy z existence zbytkového proudu. Obecná existence zbytkových a závěrných proudů byla poprvé publikována v článku [43], z této publikace vychází práce [62], která se zabývá simulacemi zbytkových proudů a na výsledky aplikuje znalosti z klasické proudové analýzy. Tyto publikace nerozebírají teoretické základy LPA a konkrétní reálný útok. LPA
20 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 19 byla poprvé analyzována systematickým způsobem v r a to z pohledu teoretického i experimentálního panem Aliotem [9]. Práce se opírá o fakt, že pro nové výrobní technologie čipů již není dynamický výkon hlavní částí z celkového výkonu čipu, ale mnohem rychleji vzrůstá výše zmiňovaný statický výkon [9]. Například u výrobní technologie 65nm je statický výkon polovina celkové výkonové spotřeby čipu a plánuje se další zvyšování v následujících generacích Dynamická výkonová spotřeba Dynamická výkonová spotřeba nastává vždy, když je změněn vnitřní stav nebo výstupní stav invertoru, obecně buňky obvodu. Proudová spotřeba odpovídající přepnutí vnitřních stavů buňky se zpravidla zanedbává, protože je daleko nižší ve srovnání s proudovou spotřebou pro přepnutí výstupního stavu buňky. Existují dvě příčiny pro dynamickou výkonovou spotřebu. První příčina nastává při přepnutí stavu invertoru, kdy po krátký čas jsou otevřeny oba tranzistory (T1, T2) a napájení je přes ně zkratováno k zemi (svodový proud). Velikost proudové špičky je úměrná počtu právě přepínaných tranzistorů v celém integrovaném obvodu. Průměrná výkonová spotřeba P svod která je způsobena svodovým proudem během časového okamžiku T může být vypočítána dle následujícího vztahu: P svod = 1 T T 0 p svod (t)dt = P 0 1 f U DD I svod t svod, (2.5) kde p svod (t) je okamžitá výkonová spotřeba invertoru během krátkého časového úseku T, I svod je svodový proud a t svod je doba po kterou jsou otevřeny oba transistory. Druhá příčina je nabíjení parazitní kapacity proudem I C a vybíjení parazitní kapacity proudem I D (vybíjecí/nabíjecí proud), což je dominantní zdroj výkonové spotřeby. Tato parazitní kapacita představuje kapacity řídicích elektrod následujících tranzistorů a spoje mezi buňkami. Její velikost záleží na fyzikálních vlastnostech použitého materiálu, výrobní technologii, délkách spojů atd. Velikost parazitní kapacity se pohybuje typicky mezi 10 3 až 1 pf. Dynamická výkonová spotřeba invertoru způsobena nabíjením parazitní kapacity lze vyjádřit vztahem [91]: P dyn = 1 T T 0 p nab (t)dt = P 0 1 f C U 2 DD, (2.6)
21 20 FEKT Vysokého učení technického v Brně x 10-4 x 10-4 I(A) I(A) a) t(s) x 10 8 b) t(s) x 10 8 Obrázek 2.5: Výsledky simulací nabíjení a vybíjení parazitní kapacity [91]. kde p nab (t) je okamžitá výkonová spotřeba invertoru během nabíjení parazitní kapacity za čas T, C je parazitní kapacita, P 0 1 je pravděpodobnost přechodu mezi stavy 0 1, f je kmitočet spínání a U DD je napájecí napětí. Pokud měříme výkonovou spotřebu (na zemnící nebo napájecí svorce invertoru) bude největší špička během nabíjení parazitní kapacity, protože během vybíjení můžeme měřit jen svodový proud. Výsledky simulací invertoru zobrazeného na obr. 2.4 znázorňují grafy na obr. 2.5, které potvrzují předchozí tvrzení. Vstupní signál (U IN ) představoval sled pulsů. Obr. 2.5 a) zobrazuje velikost proudu transistorem NMOS (modrá barva) a proud parazitní kapacitou (červená barva). Obr. 2.5 b) zachycuje proud procházející svorkou U DD nebo GND, hodnoty proudu odpovídají součtu předchozích průběhů. Důsledkem výše popsaných příčin výkonových změn je, že výkonová spotřeba kryptografického modulu je přímo závislá na zpracovávaných datech a probíhajících operacích Hazardní stavy v CMOS obvodech V CMOS obvodech je typicky spojeno více logických kombinačních buněk za sebou, tzn. že výstup jedné kombinační buňky je vstupem druhé kombinační buňky. Výstup druhé je použit jako vstup třetí kombinační buňky atd. To je nazýváno jako vícestupňový logicky kombinační obvod. Na obr. 2.6 je zobrazen jednoduchý vícestupňový logicky kombinační obvod, pro který může nastat situace, že jednotlivé vstupní hodnoty kombinačních buněk
22 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 21 a b INV 1 c NAND & d Obrázek 2.6: Jednoduchý kombinační obvod u kterého může nastat hazardní stav. nemusí vždy přijít ve stejný časový okamžik. Tato situace je způsobena nenulovým šířením signálu na propojovacích vodičích při šíření signálu z výstupu první buňky na vstup druhé buňky. Určitou dobu trvá také přepnutí výstupního stavu buňky při změně vstupního stavu buňky. Různé časy příchodu vstupních signálů způsobí dočasný výstupní stav buňky. Tato dočasná výstupní hodnota (výstupní stav) kombinační buňky je nazývána hazardním stavem kombinačního obvodu (glitches) a způsobuje změny ve výstupech logických buněk v celém obvodu [94, 105]. Počet takto vzniklých hazardních stavů v integrovaném obvodu roste s počtem stupňů kombinačního obvodu a vzniklé dočasné stavy se zde šíří jako lavina. Pokud například nastane dočasný stav buňky v prvním stupni kombinačního obvodu, tak tato jednoduchá chyba vede k chybám na výstupech všech integrovaných obvodů, které jsou na tuto buňku napojeny. Ve složitějších CMOS obvodech se tyto chyby mohou stát dominantním prvkem proudové spotřeby. Z principu vzniku hazardních stavů plyne závislost na zpracovávaných datech a použití v proudové analýze [101]. Za dobu své existence útoky jednoduchou a diferenční proudovou analýzou jsou obsáhle publikovány, například útok na algoritmus DES (Data Encryption Standard) [57, 112, 49, 7, 103, 102], RSA [53, 49, 78, 2] a AES [104, 11, 10, 108, 69, 89, 90]. Tato četnost vychází z faktu, že zařízení na měření výkonové spotřeby je cenově dostupné prakticky komukoli, útočník nemusí mít k dispozici žádné drahé speciální zařízení, ale postačí měřicí karta do počítače nebo osciloskop. Pro shrnutí, v klasické PA se zkoumá závislost dynamické výkonové spotřeby (viz rovnice 2.6) v závislosti na vstupním otevřeném textu, který je šifrován kryptografickým
23 22 FEKT Vysokého učení technického v Brně Obrázek 2.7: Proudová spotřeba kryptografického modulu PIC16f84a. modulem za pomoci tajného klíče. Hodnoty okamžité proudové spotřeby jsou zaznamenávány měřicím zařízením v průběhu šifrování pro jednotlivé otevřené texty. Z naměřených proudových průběhů pak následně útočník odečte senzitivní informace přímo (SPA) nebo je následně analyzuje matematickým aparátem pomocí DPA. Podrobný popis konkrétních analýz včetně příkladů je předmětem následujícího textu (kapitola 3). Pro ilustraci závislosti proudové spotřeby na implementovaném šifrovacím algoritmu uvádí obr. 2.7 proudovou spotřebu kryptografického modulu (mikrokontroler PIC16F84A), na kterém je implementovaný algoritmus AES. Na průběhu jsou zřetelně viditelné jednotlivé rundy šifrovacího algoritmu (viz příloha 5.1.2). 2.3 Elektromagnetický postranní kanál V předchozí kapitole jsou pomocí invertujícího členu logiky CMOS (obr. 2.4) popsány zdroje změn výkonové spotřeby. Tento popis je vhodný i pro vysvětlení příčin vzniku elektromagnetického postranního kanálu. Následkem nabíjení a vybíjení parazitní kapa-
24 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 23 city C, vzniká v obvodu skoková změna proudu, projevující se emitací elektromagnetického pole v blízkém okolí invertoru. Dnešní integrované obvody jsou složeny z milionů tranzistorů a spojů, ve kterých protékají proudy, které jsou závislé na přenášených datech. Tyto proudy generují proměnné elektromagnetické (EM) pole, které může být v okolí měřeno pomocí sond. Způsoby, jakými se projevuje EM záření emitované integrovanými obvody, jsou následující: Vodivá emise - projevuje se na pinech integrovaného obvodu, respektive v cestách na ně připojených, kdy se vlivem skokové změny proudu tyto cesty mohou chovat jako antény emitující rušení. Elektrická a magnetická emise v blízkém poli - EM pole je generováno vlivem proudových smyček v integrovaném obvodu. Magnetická složka pole lze rozdělit na dvě části H1 a H2, viz obr Pole H1 se uzavírá kolem zemnícího kontaktu tištěného spoje, pole H2 je generováno proudy ve vnitřních kondenzátorech a uzavírá se v oblasti nad povrchem IO v dosahu přibližně do 10 mm. Magnetické pole H2 je výrazně větší než pole H1. Elektrické pole se nachází v okolí součástí pod napětím. V IO jsou zdrojem elektrického pole vnitřní vodivé spoje. Na obr. 2.8 je zobrazena emise elektrickým polem E způsobená hodinovým signálem. Většina toku se uzavírá do země, ale část toku je vyzářena do okolí. Vyjdeme-li z předpokladu, že integrovaný obvod generuje elektromagnetické pole, pak je možné charakterizovat elektromagnetickou emisi obvodu, pomocí měření těchto polí. Tato měření se realizují pomocí elektrických a magnetických sond [91, 41, 66, 97, 84]. Měření pomocí rozměrově malé magnetické sondy slouží k zjištění velikosti magnetické složky blízkého EM pole. Výhodou těchto sond je, že mohou být umístěny co nejblíže ke zdroji záření a zvyšují tak přesnost měření. Pokud se sonda umístí do větší vzdálenosti, pak bývá zachycen u mikroprocesorů hodinový signál CLK. Důvodem je, že CLK signály jsou v uvedených zařízeních dominantní a jejich úroveň významně převyšuje úroveň ostatních signálů. Pokud sondu umístíme do blízkosti některého zařízení, je možné pozorovat emisi konkrétního části zařízení (např. CPU, sběrnice, paměti apod.). Užitečné EM signály, které jsou závislé na zpracovávaných datech lze zachytit v oblastech procesoru a pamětí kryptosystému [91, 86]. K zachování věrnosti měření by měla veškerá měření probíhat v blízké zóně, tedy ve vzdálenosti do maximálně délky vlny od zdroje. V této zóně všechny
25 24 FEKT Vysokého učení technického v Brně H2 E U DD GND C Blok I IO Čip H1 Obrázek 2.8: Princip přímé emise magnetického a elektrického pole IO. signály mohou být považovány za kvazistatické. Proto lze definovat Biot-Savartův zákon popisující magnetickou indukci pole B: d B= μi dl ^r 4π r 2, (2.7) kde μ je permeabilita prostředí, I je proud, dl je vektor jehož rozměr určuje délku diferenciálního elementu a jeho směr určuje směr konvenčního proudu a r je vektor specifikující vzdálenost mezi zdrojem záření a bodem měření, pro ^r platí (^r = r / r ). Pomocí Faradayova zákona lze vyjádřit hodnotu magnetomotorického napětí, které se bude v sondě indukovat: U emf = N dφ dt, (2.8) dφ = surface B ds, (2.9) kde U emf je magnetomotorické napětí, N je počet závitů sondy (cívky) a dφ vyjadřuje změnu magnetického toku za dobu dt. Z výše uvedeného vyplývá, že bude potřeba volit kompromis v počtu závitů cívky měřicí sondy, jelikož velikost magnetomotorického napětí
26 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO Runda 2. Runda 3. Runda 4. Runda 5. Runda 6. Runda 7. Runda 8. Runda 9. Runda 10. Runda Obrázek 2.9: Průběh šifrovaní algoritmem AES naměřený EM sondou. je přímo úměrná počtu závitů cívky. Na druhou stranu z teorie snímání EM pole vyplývá požadavek na co nejkratší měřicí cívku. Elektromagnetický postranní kanál byl ve své historii nejdříve využíván v armádě a tajných službách. Tyto organizace se odborně zabývaly studiem problematiky parazitních emisí, které označovaly termínem TEMPEST 4. Hlavním zájmem vojenských organizací bylo zamezení nežádoucích emisí a naopak využití tohoto vyzařování k špionážní činnosti. Pojem TEMPEST vznikl na přelomu 60. a 70.let dvacátého století a označuje i skupinu vojenských standardů, ve kterých jsou stanoveny maximální povolené limity elektromagnetického záření v různých elektronických systémech. Ve veřejném sektoru se o významný posuv na poli elektromagnetických útoků zasloužil nizozemský vědec van Eck [35], který jako první dokázal, že je možné zachytit a změřit velikost elektromagnetického pole počítačových monitorů a z naměřených průběhů extrahovat snímaný obraz. Obranu proti tomuto útoku vynalezli vědci Kuhn a Anderson [59], jednalo se o speciální stínící fólii, která snižovala elektromagnetické záření monitoru. První veřejně publikovanou prací na téma EM analýzy integrovaných obvodů a výpočetních jednotek provádějících kryptografické operace, byla v roce 2001 práce Electomagnetic Analysis: Concrete Results autorů Gandolfiho, Mourtela, Oliviera [40]. Útok prováděli pomocí několika antén umístěných v blízkosti výpočetních integrovaných obvodů čipové karty. Tento útok byl invazivní, což znamená, že vyžadoval porušení pouzdra čipové karty, tak aby bylo možné umístit an- 4 Termín TEMPEST je krycím jménem vytvořeno NSA v 60. letech pro operace snažící se zabezpečit elektronická komunikující zařízení proti odposlechu, vláda USA uvedla že tato zkratka nemá žádný význam i když několik bylo navrhováno př. Transmitted Electro-Magnetic Pulse / Energy Standards & Testing.
27 26 FEKT Vysokého učení technického v Brně Obrázek 2.10: EM otisky pro jednotlivé instrukce kryptografického modulu. tény co nejblíže pasivační vrstvě. Na tuto práci následně navázali o rok později Agrawal, Archambeault, Rao a Rohatgi [4], kteří ve své práci The EM-Side-Channels: Attacks and Assessment Methodologies využili odtajněných materiálů z projektu TEMPEST a ukázali, že útoky EM postranním kanálem na kryptografická zařízení jsou prakticky realizovatelné a zároveň, že některé informace unikající prostřednictvím EM kanálu, bylo možné získat z proudového postranního kanálu pouze velmi obtížně. Pro porovnání obr. 2.9 znázorňuje změřený průběh šifrování algoritmem AES EM sondou (kryptografický modul byl opět mikrokontroler PIC16F84A, porovnej s obr. 2.7). Pro ilustraci obr zobrazuje EM otisk pro jednotlivé instrukce mikrokontroleru.
28 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 27 Obrázek 2.11: Spektra různých operací mikroprocesoru [100]. 2.4 Akustický postranní kanál Akustický postranní kanál patří k nejstarším postranním kanálům. Byl používán již v době, kdy se definice postranních kanálů ještě nepoužívala, např. v roce 1956 Britové získávali informace z egyptského šifrátoru odposlechem zvuků klávesnice a v roce 1961 Američané provádějí akustický odposlech prostřednictvím ústředního topení. Další akustické útoky byly prováděny na klávesy psacího stroje a jehličkové tiskárny. Nyní se tento postranní kanál zaměřuje na zvuky vydávané počítačovými klávesnicemi [114]. V jednotlivých akustických útocích na klávesnice byly použity různé metody zpětného převodu naměřeného akustického signálu na psaný text. Např. v práci Dictionary Attacks Using Keyboard Acoustic Emanations se pro zpětnou analýzu využíval anglický slovník a neuronová síť [114]. V práci [38] byly počítány rozdíly v době příchodu zvukové vlny na dva mikrofony a ke klasifikaci byly použity neuronové sítě. Vypočítané spektrogramy pro jednotlivá tlačítka byly použity v pracích [70] a [64], kde pro klasifikaci byla použita také neuronová síť. Zajímavostí je, že žádná z metod není schopna rekonstruovat stisk více kláves najednou. Akustický postranní kanál se dá využít také na vnitřní komponenty PC (mikroprocesor, koprocesor...) [100]. Obr zachycuje výsledky experimentu, který se snaží rozlišit spektra různých operací mikroprocesoru.
29 28 FEKT Vysokého učení technického v Brně OPTICA Synchronizace PIC16F84A Vdd Vss OSC1 OSC2 a) 7V 6MHz b) Obrázek 2.12: a)zařízení OPTICA b)příklad naměřených dat pomocí PICA [37]. 2.5 Optický postranní kanál Optický postranní kanál byl poprvé představen v práci [58], kde na základě sledování rozptýleného odrazu světla na překážce, jehož zdrojem je CRT zobrazovací jednotka, byl rekonstruován původní obraz. V práci je poukázáno na možnost použití stejné techniky i pro rekonstrukci obrazu z LED zobrazovacích jednotek. Optický postranní kanál v moderním pojetí byl poprvé představen v roce 2008 dvojicí autorů Ferrignem a českým spoluautorem Hlaváčem [37]. Základní myšlenka optického postranního kanálu je přímo geniálně prostá a účinná, a proto se předpokládá, že bude mít určitě ještě v kryptoanalýze pokračování. Integrované obvody se skládají z tranzistorů, jejichž stavy reprezentují hodnotu 0 nebo 1. Pokaždé, když tranzistor v integrovaném obvodu změní svůj stav, vyzáří několik fotonů. Jedna z možných technik, která je schopna detekovat polohu a čas vyzářených fotonů se nazývá pikosekundová zobrazovací obvodová analýza (picosecond imaging circuit analysis, PICA [107]). Máme-li důkladně provedenou synchronizaci s algoritmem, který je prováděn na pozorovaném zařízení (mikrokontroléru), je PICA schopna identifikovat přepínající se transistory v paměti. Zařízení OPTICA, využívající výše popsanou měřící techniku, měli autoři k dispozici v laboratoři CNES. Blokové schéma měřicího zařízení představuje obr.2.12 add a). Pro sledování informací prosakujících prostřednictvím
30 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 29 optického postranního kanálu byla použita jednoduchá implementace části zdrojového kódu algoritmu AES (část AddRoundKey), běžící na PIC16F84A mikrokontroléru. Tyto mikrokontroléry nemají žádné protiopatření proti prosakování informací prostřednictvím postranních kanálů a taktovací frekvence není nijak modifikována, což je nutné k snadné synchronizaci s měřicím zařízením OPTICA. Ve fázi AddRoundKey jsou bajty otevřeného textu xorovány s bajty prvního rundovního klíče. Obsah paměťové buňky (tranzistoru) reprezentující bit otevřeného textu se změní, pokud příslušný bit klíče je 1. Pokud je bit klíče 0, operace XOR (Exclusive OR) ponechá bit otevřeného textu nezměněn. Když tranzistory pozorujete speciálním zařízením v době, kdy dochází k této operaci tranzistory na nás zablikají nebo nezablikají v závislosti na tom zda byl bit klíče 1 nebo 0. Prostřednictvím optického postranního kanálu tedy tranzistory tajný klíč AES přímo útočníkovi vyblikají (obr.2.12 add b) bajt tajného klíče ). Opakované spouštění kódu mikrokontroléru se stejnými vstupními daty vedlo k identickým (optickým) výsledkům získaných pomocí optického postranního kanálu. Výsledky experimentu ukázaly, že oba přechody tranzistorů, jak přechod z 1 0 tak přechod 0 1, jsou detekovatelné. Můžeme také předpokládat, že výsledky budou podobné pro další instrukce (addwf, andwf, iorwf, subwf). Tato možnost rozšíří eventuální použití optického postranního kanálu k útoku na další šifrovací algoritmy. Nevýhodou postranního kanálu je, že zařízení určené pro snímání fotonů (př. OPTICA) není tak snadno dostupné, jako zařízení pro získávání informací z jiných postranních kanálů. Cena tohoto zařízení se pohybuje v řádu desítek milionů českých korun. K realizaci útoku je nutná přesná synchronizace. Protiopatření implementovaná v nových čipech např. náhodné provádění instrukcí znesnadní realizaci útoku. Dalším problémem realizace je, že za účelem pozorování vyzářeného světla z přístroje potřebujeme zeslabit vrstvu silikonu na zadní straně čipu minimálně na 100 μm [37]. Po zeslabení je nutné vrstvu vyčistit speciálním leštícím systémem. Ztenčení a leštění vrstev silikonu dovolí IR světlu proniknout zadní stranou čipu, a tak může být provedena detekce záření. Výše popsané aspekty činní optický kanál atraktivní pro případné útočníky a vědce, ale také realizovatelný zatím jen v precizních laboratorních podmínkách.
31 30 FEKT Vysokého učení technického v Brně 2.6 Chybový postranní kanál Vznik výše popsaných postranních kanálů je založen na určité fyzikální vlastnosti kryptografického modulu, ale existují i postranní kanály, které využívají jiný typ komunikace. Příkladem je právě chybový postranní kanál, podstatou chybového postranního kanálu [32, 56] je existence komunikace kryptografického modulu s okolím při vzniku chyby. Několik let se všichni kryptologové plně věnovali bezpečnosti kryptografických algoritmů a považovali chybová hlášení jako vedlejší činnost systému, která nemůže mít vliv na bezpečnost a pro případného útočníka nemá význam. Přesto se chybová hlášení stávají dalším postranním kanálem a umožňují napadení kryptografických modulů. Typickým příkladem útoku založeném na zdánlivě neškodném chybovém hlášení je útok na implementace blokových šifrovacích algoritmů pracujících v operačním módu CBC (Cipher Block Chaining), který je zobrazen na obr Při implementaci algoritmu v CBC režimu, je nutné vyřešit šifrování posledního bloku dat (popřípadě neúplného bloku dat). Možné řešení popisuje například norma PKCS#5 [51], kde je použito techniky doplnění (padding) na předepsanou délku bloku. Doplnění chybějících bajtů o počtu i je provedeno bajty o stejné hodnotě i. Například jsou doplněny 2 bajty s hodnotou 2 nebo 3 bajty s hodnotou 3 atd. Při dešifrování pak systém na základě hodnoty posledního bajtu zjistí počet doplněných bajtů. Pokud mají stejnou hodnotu, doplněk je odstraněn a vzniklý otevřený text je předán dále. Pokud je hodnota jiná, systém vyhodnotí chybu přenosového kanálu a o jejím výskytu informuje odesílatele. Právě toto, na první pohled korektní a neškodné chybové hlášení, vytváří postranní kanál, jehož důsledné využití vede až k získání celého otevřeného textu. Útočník k realizaci tohoto útoku nepotřebuje žádné speciální technické zařízení, dostačuje osobní počítač připojený k síti, ve které probíhá šifrovaná komunikace o kterou má zájem (například komunikace mezi uživatelem a serverem pomocí protokolu TLS). Útočník nejprve zachytí šifrovaná data, poté serveru posílá svá podvržená data s využitím fragmentu původních dat, která jsou doplněna o vhodně volené doplňky. Vyhodnocením chybových hlášení serveru je útočník schopen získat otevřený text. Data o n bajtech lze takovýmto způsobem zjistit přibližně po 128 n dotazech. Složitost útoku tedy není velká. Tento způsob prolomení je v současnosti učebnicovým příkladem aktivního útoku postranním kanálem a vznikla proti němu řada protiopatření.
32 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 31 Dešifrovací Zařízení Server Šifrovaný text Otevřený text Klient Otevřený text! Chybové hlášení Útočník Obrázek 2.13: Princip chybového postranního kanálu na operační mód CBC. Jako nejlepší je známo ABYT-PAD (Arbitrary Tail-padding) pro bajtově orientovaný typ dat a ABIT-PAD pro bitově orientovaný typ dat. Bohužel i toto protiopatření obsahuje chyby umožňující útok. Podobný typ útoku využívající chybový postranní kanál lze použít i na implementace asymetrických algoritmů, mezi které patří zejména algoritmy RSA, DSA [76, 17]. Podstata útoku spočívá v napadení operace dešifrování, která využívá k výpočtu čínskou větu o zbytcích. S další možností využití chybového postranního kanálu přišel v roce 1998 švédský kryptolog Daniel Bleichenbacher [18]. Princip tohoto útoku spočívá v úpravě formátu dané šifrované zprávy do takové podoby, kdy dešifrovací zařízení reaguje na tento stav chybovým hlášením, ze kterého je útočník schopen určit žádané informace. Pro integritní kontrolu platnosti zformátované zprávy se využívá speciálního kódování, jehož činnost umožňuje útočníkovi získat konkrétní části původního nešifrovaného textu. Z důvodu možnosti realizace Bleichenbacherova útoku byla navržena nová dokonalejší formátovací metoda OAEP, která do celé zprávy určitým způsobem vnáší náhodné prvky a tím zabraňuje realizaci útoku švédského kryptologa. Na možné chyby formátovací metody OAEP upozornil v roce 2001 kryptolog Manger. Manger dokázal existenci postranního kanálu využívající nedokonalosti implementace metody OAEP [68].
33 32 FEKT Vysokého učení technického v Brně
34 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 33 3 PROUDOVÁ ANALÝZA Cílem kapitoly je detailně popsat jednoduchou a diferenciální proudovou analýzu používanou při útoku na kryptografické zařízení. Na obdobných principech jsou založeny všechny jednoduché a diferenciální analýzy postranním kanálem (př. elektromagnetickým, časovým, frekvenčním atd.). Další část kapitoly popisuje techniky protiopatření vedoucí k znesnadnění a nebo plnému znemožnění útoku proudovým postranním kanálem. 3.1 Jednoduchá proudová analýza SPA V této kapitole bude vysvětlen princip jednoduché proudové analýzy a následně budou popsány různé typy SPA. Jednoduchá proudová analýza byla definována Kocherem [57] následovně: jednoduchá proudová analýza je technika, která představuje přímé interpretování proudové spotřeby měřené během provozu kryptografického zařízení. Jinými slovy se útočník snaží určit tajný klíč přímo ze změřených průběhů proudové spotřeby. To činí SPA pro potencionální útočníky atraktivní technikou, ale ti většinou potřebují detailní znalost implementovaného algoritmu a kryptografického zařízení. SPA můžeme rozdělit do dvou základních skupin a to na analýzu jen jednoho proudového průběhu (single-shot SPA) a analýzu několika proudových průběhů (multiple-shot). Analýza jednoho proudového průběhu představuje extrémní případ, kdy útočník zaznamenal a zkoumá jen jeden průběh proudové spotřeby odpovídající jednomu vstupnímu textu. Ve většině případů je nutné použít statistických metod k extrakci užitečného signálu. Při jednoduché analýze několika proudových průběhů má útočník k dispozici více naměřených proudových průběhů, a to pro stejný nebo různý vstupní text, které použije k redukci šumu v naměřených datech. Pro oba typy útoku SPA je nutné, aby v kryptografickém zařízení, na které je prováděn útok, existovala výrazná (přímá nebo nepřímá) závislost proudové spotřeby na hodnotě šifrovacího klíče Přímé interpretování proudové spotřeby Přímé interpetování proudové spotřeby (Visual Inspections) je založeno na následujících skutečnostech. Všechny algoritmy, které běží na kryptografickém zařízení jsou vykonávány
35 34 FEKT Vysokého učení technického v Brně Obrázek 3.1: Proudová spotřeba algoritmu square and multiply [49]. postupně v přesně definovaném pořadí. Kryptografický algoritmus se ve většině případů skládá z několika dílčích funkcí (operací), které jsou následně po implementaci přeloženy do podporovaných instrukcí zařízení. Například algoritmus AES může být popsán funkcemi podrobně rozebranými v kapitole (expanze klíče, přičtení klíče, nelineární bajtová substituce, rotace řádků a násobení maticí). Algoritmus AES může být implementován do mikroprocesoru, kde jsou jednotlivé funkce implementovány pomocí instrukcí podporovaných mikroprocesorem. Mikroprocesory mají instrukční sadu, která obsahuje aritmetické instrukce (sčítání), logické instrukce (XOR), instrukce práce s daty (uložení, přesun) a instrukce větvení programu (skok nebo podmínka). Každá instrukce pracuje s různým počtem bitů popřípadě bajtů a používá k tomu různé části obvodu, například aritmeticko-logickou jednotku, čtení popřípadě zápis do interní nebo externí paměti, vstupní a výstupní porty. Tyto komponenty mikroprocesoru jsou fyzicky odděleny a liší se funkčností a realizací. Z tohoto důvodu mají charakteristickou proudovou spotřebu, která vede k charakteristickému proudovému vzoru (otisku) v proudové spotřebě. Možnost rozlišit jednotlivé instrukce v proudové spotřebě vede k vážné bezpečnostní hrozbě pokud posloupnost instrukcí závisí přímo na hodnotě šifrovacího klíče. Pokud v průběhu zpracování algoritmu je určitá instrukce zpracovávána v případě, že bit klíče je 1 a odlišná instrukce je zpracovávána pokud bit klíče je 0, pak je možné určit šifrovací klíč přímo analýzou naměřeného průběhu na základě posloupnosti vykonávaných instrukcí. Tato skutečnost je demonstrována následujícím příkladem.
36 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 35 Přímé interpretování proudové spotřeby - příklad útoku na RSA Typickým příkladem tohoto typu SPA je implementace asymetrického kryptosystému RSA [53, 49, 39]. Asymetrický algoritmus RSA je založen na matematické operaci modulární mocniny. Pro výpočet modulární mocniny existuje více metod, ale pro implementaci v kryptografických modulech se často používá tzv. algoritmus square and multiply, který je založen na postupném zpracování jednotlivých bitů soukromého klíče k. Princip algoritmu je zobrazen na následujícím obrázku (viz obr. 3.2), kde b představuje počet bitů soukromého klíče k, n modul algoritmu RSA a k(i) = k 0... k b 1 reprezentaci soukromého klíče. Algoritmus square and multiply 1.R = m 2.for i = 0:(b - 1) { 3. R = (R*R)mod(n) 4. if (k(i)==1) { 5. R=(R*m)mod(n) } 6. } 7. return R představuje binární Obrázek 3.2: Algoritmus square and multiply. Z naměřené proudové spotřeby prováděného algoritmu square and multiply může útočník určit sekvenci prováděných instrukcí, tedy v kterém kroku byl prováděn řádek 5 v závislosti na hodnotě soukromého klíče. Přímá interpretace proudové spotřeby algoritmu square and multiply na hodnotu soukromého klíče je zobrazena na obr Přímé interpretování proudové spotřeby - příklad algoritmus AES Vizuální inspekce neboli přímé pozorování proudové spotřeby lze využít i u symetrických šifrovacích algoritmů. V tomto případě neexistuje přímá závislost proudové spotřeby na hodnotě tajného klíče (tak jako v předchozím útoku na implementaci RSA), proto útočník není schopen šifrovací klíč odhalit. Touto jednoduchou analýzou je schopen útočník určit např. implementovaný algoritmus, lokalizovat prováděné operace nebo zajímavé body pro následnou DPA analýzu atd. Příklad vizuální inspekce proudového odběru algoritmu AES uvádí následující text.
37 36 FEKT Vysokého učení technického v Brně 8 6 x 10-3 Přičtení klíče 166μs Expanze klíče 151μs Transpozice 173μs Násobení maticí 236μs 4 2 U[V] A I t[n] x 10 5 Obrázek 3.3: Detail první rundy AES. Obrázek 2.7 ukazuje proudovou spotřebu kryptografického modulu, na kterém je implementovaný algoritmus AES. Na průběhu jsou zřetelně viditelné jednotlivé rundy šifrovacího algoritmu a to konkrétně 9 normálních rund a poslední desátá runda, u které je vynechána operace násobení maticí (MixColumns). Pro útočníka je tedy jednoduché identifikovat jednotlivé rundy a zaměřit se na analýzu konkrétní rundy. U algoritmu AES je přirozenou volbou první runda, protože při operaci přičtení šifrovacího klíče (operace AddRoundKey) pracuje kryptografické zařízení přímo s šifrovacím klíčem, ze kterého jsou pak následně vypočítány všechny rundovní klíče (viz příloha 5.1.2, operace expanze klíče) používané během celého procesu šifrování. Detail proudové spotřeby první rundy je zobrazen na obr. 3.3, jedná se o přiblížený průběh obr Hrubé obrysy jednotlivých operací algoritmu AES jsou vidět i pouhým okem. Algoritmus začíná počáteční fázi, kde dochází operací AddRoundKey k přičtení šifrovacího klíče a tato fáze zabere mikroprocesoru 166μs. Následuje operace expanze klíče (KeyExpansion) s délkou 151μs, která je kvůli nedostatku paměťového místa na mikroprocesoru prováděna v každém cyklu a nedochází tak k výpočtu všech rundovních subklíčů před začátkem šifrování. Následují transpoziční operace nelineární bajtové substituce (SubBytes) a rotace řádků (ShiftRows), které modul vykoná během 151μs. Poslední operací je násobení maticí (MixColumns), které je poměrně
38 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 37 Obrázek 3.4: Proudový průběh instrukce MOV nese informaci o HW šifrovacího klíče. časově náročné a zabere mikroprocesoru 236μs. Celková doba trvání jedné rundy této konkrétní implementace šifrovacího algoritmu AES-128 je 726μs. Poznamenejme, že implementace algoritmu AES ve své původní podobě pracuje s bloky dat o délce 128 bitů tedy matice 4x4 bajty. Detail výše zmiňované operace AddRoundKey prováděné v první rundě šifrovacího algoritmu je zobrazen na obr Během této operace je šifrovací klíč (označme K) v počáteční fázi procesu šifrování přičten operací XOR k poli Stav (označme S). Výsledek operace je uložen opět do registru Stav S. Rovnici přičtení rundovního klíče 5.24 můžeme pro jednoduchost vyjádřit v maticové podobě: S = S K, (3.1) S = s 1 s 2 s 3 s 4 s 5 s 6 s 7 s 8 s 9 s 10 s 11 s 12 k 1 k 2 k 3 k 4 k 5 k 6 k 7 k 8 k 9 k 10 k 11 k 12. (3.2) s 13 s 14 s 15 s 16 k 13 k 14 k 15 k 16
39 38 FEKT Vysokého učení technického v Brně ;Operation AddRoundKey bsf Sync movf k1,w xorwf s1,f movf k2,w xorwf s2,f... bcf Sync goto SubByte Obrázek 3.5: Část implementace operace AddRoundKey. kde S = [s 1, s 2,, s 16 ] a K = [k 1, k 2,, k 16 ]. Implementace této operace v jazyku symbolických adres obsahuje v podstatě jen dvě instrukce, první z nich je instrukce MOVF, která načte bajt šifrovacího klíče k i do pracovního registru a následně druhá instrukce XORWF, která provede přičtení pracovního registru s registrem stavu s i. Část implementovaného kódu uvádí obr V průběhu našeho experimentálního měření, byla matice otevřeného textu S naplněna hodnotami FFh. Matice šifrovacího klíče K byla naplněna prvky s hodnotami od 01h do FFh tak, že každý prvek v matici měl Hammingovu váhu o jedno vyšší. Například první prvek k 1 byl roven 01h (B ), tudíž hodnota Hammingovy váhy je w(k 1 ) = 1. Následující prvek matice měl nastavenou hodnotu 03h (B ), tedy Hammingova váha je rovna w(k 1 ) = 2 a tak dále. Poslední prvek matice k 16 měl hodnotu FFh (B ), kde w(k 16 ) = 8. Matice šifrovacího klíče, který byl uložen v kryptografickém modulu je uvedena následující rovnicí (hexadecimální zápis): K = F 1F 3F 7F FF F 1F 3F 7F FF (3.3) Podívejme se nyní zpět na obr Na obrázku jsou patrné proudové špičky odpovídající práci s daty. Důležitá je viditelnost závislosti právě zpracovávaných dat na proudovou spotřebu, která odpovídá Hammingově váze šifrovacího klíče načítaného instrukcí MOV do pracovního registru. Tento důležitý fakt je využíván v diferenčních proudových analýzách.
40 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO Útoky pomocí šablon Útok postranním kanálem využívající šablony (Template Based Attacks) je typickým příkladem profilujícího útoku (Profiling attack), který obsahuje vždy dvě fáze: profilující fázi a fázi útoku [23, 67, 24]. Při tomto typu útoku předpokládáme, že útočník disponuje stejným zařízením, na které hodlá provádět útok (př. stejný typ čipové karty, mikrokontroleru atd.). Jinými slovy útočník má fyzický přístup k dvojici zařízení, které jsou označovány jako profilující zařízení (profiling device) a cílené zařízení (target device). V první profilující fázi útoku, útočník charakterizuje profilující zařízení a ve fázi útoku použije vytvořené charakteristiky z profilující fáze k útoku na cílené zařízení. Naproti tomu, neprofilujicí útoky (non-profiled attacks) postranním kanálem provádějí útok přímo na cílené zařízení. Typickým příkladem je útok využívající korelační koeficient, který je popsán v následující kapitole [20]. Profilující fáze - Obecně mohou být naměřené proudové průběhy kryptografického modulu charakterizovány vícerozměrným normálním rozdělením, které je plně definováno vektorem středních hodnot a kovarianční maticí (m, C) [67]. Tuto dvojici (m, C) označíme šablonou. Útočník předpokládá, že může profilující zařízení charakterizovat pomocí těchto šablon pro jednotlivé instrukce (posloupnost instrukcí), které pracují nebo jsou spojeny s cílenou hodnotou (předkládejme nyní, že cíl útoku je uložený šifrovací klíč). Na tomto zařízení spustí sekvence instrukcí pro různá vstupní data d i a různý šifrovací klíč k j a zaznamená si proudové průběhy. Následně seskupí odpovídající průběhy (d i, k j ) a vypočte vektor středních hodnot a kovarianční matici vícerozměrného normálního rozdělení. Výsledkem získá šablony pro všechny dvojce dat a klíčů (d i, k j ) : h di,k j = (m, C) di,k j. Fáze útoku - Ve fázi útoku, útočník použije připravené šablony a naměřenou proudovou spotřebu cíleného zařízení (označme t) k určení uloženého šifrovacího klíče. Útočník vypočte pravděpodobnosti pro změřenou proudovou spotřebu t pro všechny šablony dle následujícího vztahu: p(t; (m, C) di,k j ) = exp( 1 (t 2 m) C 1 (t m)). (3.4) (2 π) T det(c) Pravděpodobnosti ukazují jak dobře šablona odpovídá změřenému průběhu. Intuitivně by nejvýší pravděpodobnost měla odpovídat správné šabloně, protože každá šablona je
41 40 FEKT Vysokého učení technického v Brně asociována s tajným klíčem, určí tímto způsobem útočník hodnotu tajného klíče. Tato metoda vychází z metody maximální věrohodnosti (maximum-likelihood, ML) a z teorie popsané v [52]. Metoda předpokládá, že všechny hodnoty klíče mají stejnou pravděpodobnost, potom rozhodovací pravidlo minimalizující pravděpodobnost pro špatný odhad klíče je pospáno následujícím vztahem: p(t; h di,k j ) > p(t; h di,k l ) l j. (3.5) Při praktické realizaci útoku využívající šablony je možné narazit na různé problémy spojené s kovarianční maticí. Prvním z nich je fakt, že velikost kovarianční matice roste s druhou mocninou počtu bodů proudového průběhu. Z tohoto důvodu zaměřujeme obě fáze útoku pouze na zajímavé body, které nesou informaci o cílené instrukci (například HW instrukce MOV zpracovávaných dat). Počet zajímavých bodů budeme označovat N P. Metoda volby zajímavých bodů představuje kritickou část těchto typů útoků [67, 12, 13, 24]. Druhým problémem je výpočet inverzní matice ve vztahu 3.4 (singularita kovariančí matice). Další výpočetní problémy mohou vzniknout z důvodu malých hodnot v exponentu. Za účelem odstranění mocnění bývá rovnice 3.4 pro praktické výpočty logaritmována. Správný klíč poté bude odpovídat šabloně s nejmenší absolutní hodnotou logaritmu pravděpodobnosti: ln p(t; (m, C)) = 1 2 (ln ((2 π)np det C) + (t m) C 1 (t m)). (3.6) ln p(t; h di,k j ) < ln p(t; h di,k l ) l j. (3.7) Pro eliminaci problému s inverzí kovarianční matice, můžeme prohlásit kovarianční matice rovny matici jednotkové. To v podstatě znamená, že nebereme v potaz vzájemnou kovarianci mezi body proudové spotřeby. Takto vytvořené šablony obsahují jen vektor středních hodnot a útok veden pomocí nich bývá označován jako redukovaný útok využívající šablony (reduced template attack). Nahrazením kovarianční matice maticí jednotkouvou dojde ke zjednodušení výpočtu pravděpodobnosti vícerozměrného normálního
42 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 41 Obrázek 3.6: Proudová spotřeba instrukce MOV pro různé HW. rozdělení následujícím způsobem: p(t; m) = 1 exp ( 1 (2 π) N IP 2 (t m) (t m)). (3.8) Pro odstranění problémů s umocňováním bývá opět v praxi výpočet rovnice 3.8 logaritmován: ln p(t; m) = 1 2 (ln (2 π)n IP + (t m) (t m)). (3.9) Útok pomocí šablon - příklad MOV instrukce V předchozích kapitolách již bylo zmíněno, že jednotlivé instrukce, které jsou prováděny kryptografickým zařízením, vedou k různým proudovým vzorům (viz kapitola 2.2 a 2.3). Jinými slovy lze říct, že tvar proudového průběhu závisí na vykonávané instrukci. Dále byl v předchozí kapitole představen útok využívající šablony, který zkoumá závislost právě zpracovávaných dat na proudovou spotřebu. V tomto jednoduchém příkladě využijeme předchozí znalosti a realizujeme útok využívající šablony na odhalení HW zpracovávaných dat.
43 42 FEKT Vysokého učení technického v Brně Obrázek 3.7: Blokový diagram znázorňující kroky 3 až 5 DPA útoku. Opět byl do kryptografického modulu PIC16F84A implementován algoritmus AES pomocí jazyku symbolických adres. Následně byly naměřeny proudové průběhy odpovídající operaci AddRoundKey, která je implementována pomocí instrukcí MOV a XOR (viz předchozí kapitola 3.1.1). Obrázek 3.6 zobrazuje 9 naměřených proudových spotřeb vykonávané instrukce MOV pro různá data. Z obrázku je patrné, že největší rozdíly mezi průběhy jsou okolo času t = V ostatních místech se proudové průběhy takřka přesně překrývají. Detail proudové špičky pro t = 4100 zobrazuje obr. 3.7, kde legenda přiřazuje proudové průběhy Hammingovým vahám. Z průběhu jdou vyvodit následující fakta: jednotlivé proudové průběhy mohou být mezi sebou jasně rozlišitelné, vzdálenosti mezi jednotlivými průběhy jsou si rovny, zpracování bajtu s Hammingovou váhou 0 způsobí největší proudovou spotřebu, naopak zpracování bajtu s Hammingovou váhou 8 vykazuje nejmenší proudovou spotřebu (způsobeno typem datové sběrnice, precharged bus). Lze odvodit závěr, že výška několika bodů z naměřeného průběhu je nepřímo úměrná Hammingově váze zpracovávaných dat. V důsledku toho je možné vytvořit šablony, které
44 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 43 nám dovolí klasifikovat MOV instrukce podle Hammingovy váhy. V průběhu útoku lze použít šablony k určení HW zpracovávaných dat kryptografickým modulem. Celkem je možných devět HW, připravíme devět šablon. Připomeňme, že šablona je tvořena vektorem středních hodnot a kovarianční maticí. Velikost kovarianční matice roste kvadraticky s počtem bodů proudové spotřeby, proto se zaměřujeme jen na zajímavé body, které nesou informaci například o HW zpracovávaných dat. Zajímavé body můžeme jednoduše určit přímo z obr. 3.7 tak, že vybereme body, ve kterých se proudové průběhy významně liší. Například vybereme celkem 4 body pro vytvoření šablon t = (4091, 4105, 4119, 4134). První vytvořená šablona h 0 = (m 0, C 0 ) pro instrukci MOV zpracovávající data s Hammingovou váhou 0 je dána následovně: C 0 = m 0 = 2, 94 1, 45 0, 61 0, 14 1, 45 1, 02 0, 65 0, , (3.10) 0, 61 0, 65 1, 07 0, 34 0, 14 0, 23 0, 34 0, 28 ( ) 0, 47 0, 32 0, 17 0, 18 (3.11) Nyní vyzkoušíme jak dobře vytvořené šablony odpovídají naměřeným proudovým průběhům, které naměříme během fáze útoku. Následující matice T obsahuje zajímavé body devíti proudových průběhů vykonávané instrukce MOV: T = 0, 48 0, 33 0, 18 0, 19 0, 73 0, 41 0, 23 0, 24 0, 95 0, 54 0, 30 0, 31 1, 14 0, 66 0, 37 0, 36 1, 36 0, 72 0, 41 0, 39 1, 54 0, 82 0, 47 0, 43 1, 72 0, 92 0, 50 0, 45 1, 91 1, 00 0, 59 0, 50 2, 05 1, 11 0, 65 0, 55. (3.12)
45 44 FEKT Vysokého učení technického v Brně První proudový průběh odpovídá t 1 uložený v prvním řádku matice T a koresponduje s vykonáním instrukce MOV s Hammingovou váhou 0, druhý proudový průběh t 2 odpovídá zpracovávaným datům s Hammingovou váhou 1 atd. Nyní můžeme vypočítat pravděpodobnost jak naměřené průběhy odpovídají připraveným šablonám dle rovnice 3.6. ln p(t 1 ; h 0 ) = 15, 05 (3.13) ln p(t 1 ; h 1 ) = 28, 36 (3.14) ln p(t 1 ; h 2 ) = 93, 40 (3.15) ln p(t 1 ; h 3 ) = 166, 37 (3.16) ln p(t 1 ; h 4 ) = 291, 90 (3.17) ln p(t 1 ; h 5 ) = 543, 02 (3.18) ln p(t 1 ; h 6 ) = 953, 24 (3.19) ln p(t 1 ; h 7 ) = 2, (3.20) ln p(t 1 ; h 8 ) = 2, (3.21) Dle výsledků šablona h 0 odpovídá nejlépe naměřenému průběhu t 1, protože vede k nejmenší absolutní hodnotě viz rovnice 3.7. Z toho plyne, že t 1 byla naměřena když kryptografický modul zpracovával data s Hammingovou váhou 0. Útok pomocí neuronových sítí - příklad AES Stejně tak jak charakterizujeme proudové průběhy pomocí šablon (kovarianční matice a vektorem středních hodnot), můžeme využít neuronové sítě. Neuronové sítě byly poprvé použity při klasifikaci informací unikajících prostřednictvím akustického postranního kanálu např. [38, 64, 114]. Při analýze proudovým postranním kanálem byla možnost využití neuronových sítí poprvé publikována v práci [93]. Následně na tuto práci navazovali další autoři např. [60], kteří se zabývali klasifikací proudových otisků, tedy přiřazením specifických proudových otisků jednotlivým prováděným instrukcím kryptografického modulu. Jednalo se v podstatě o metody zpětného inženýrství využívající proudovou spotřebu
46 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 45 k určení vykonávaného kryptografického algoritmu. Použití neuronových sítí při analýze proudovým postranním kanálem a při klasifikaci konkrétní hodnoty bajtu tajného klíče bylo doposud velice málo publikováno a testováno. Práce zabývající se touto problematikou jsou založeny na algoritmech podpůrných vektorů (Support vector machines (SVM) [48, 14] a nevyužívají klasické vícevrstvé neuronové sítě s algoritmy učení. Základní teoretické informace o neuronových sítích jsou uvedeny v příloze 5.2. Proudová analýza využívající NN pracuje per partes, stejně jako většina diferenciálních analýz postranním kanálem, tedy cílem je určení tajného klíče po jednotlivých bajtech, kde tajný klíč je vyjádřený bajtově K = {k 1, k 2, k 3, k 4, k 5, k 6, k 7, k 8 } pro 0 k i 255 a pro kroky metody označené i = 0 až 8. Metoda tedy v prvním cyklu určí hodnotu prvního bajtu k 1 v dalším cyklu druhého k 2 a v posledním kroku hodnotu posledního bajtu tajného klíče k 8. Rozdíl mezi jednotlivými kroky bude v rozdělení naměřené proudové spotřeby na části odpovídající jednotlivým bajtům tajného klíče. Na obr. 3.8 je zobrazen naměřený proudový průběh odpovídající operacím AddRoudnKey a SubBytes, kdy došlo ke změně pouze v prvním bajtu tajného klíče k 1 a to z hodnoty 1 na hodnotu 255. Na průběhu jsou jasně patrny úseky, na které má vliv první bajt. Čísla označují jednotlivé části, které odpovídají jednotlivým krokům metody. V následujícím textu bude pojmem tajný klíč (K taj ) označen klíč uložený v kryptografickém modulu (první bajt k 1 ), na který je prováděn útok. Pojmem odhad klíče (K odh ) bude myšlena hodnota odhadu tajného klíče, kterou klasifikuje metoda využívající NN (NNA). Cílem metody je, aby si na konci analýzy hodnota tajného klíče a odhadu klíče byla rovna. Metoda využívající neuronové sítě je opět typickým příkladem profilujícího útoku a obsahuje fázi profilující a fázi útoku: profilující fáze obsahuje přípravu vzorů pro tajné klíče k i a vytvoření a trénování neuronové sítě vytvořenými vzory, fáze útoku, určení odhadu klíče. Provedení těchto fází umožní útočníkovi realizovat jeden krok analýzy, tedy určení jednoho bajtu tajného klíče k i. V první fázi si útočník připraví trénovací množinu dat, kterými bude následně učit neuronovou síť. Útočník musí znát typ kryptografického modulu, na který hodlá útočit a musí stejný typ modulu mít zcela pod kontrolou (například plánuje-li
47 I [A] 46 FEKT Vysokého učení technického v Brně AddRoundKey SubBytes Klíč 1 Klíč t [n] x 10 4 Obrázek 3.8: Průběh proudové spotřeby operací AddRoundKey a SubBytes. útoky na čipovou kartu obsahující mikrokontrolér PIC16F84 musí tuto kartu vlastnit, viz předchozí kapitola popisující útok pomocí šablon). Na kryptografický modul implementuje požadovaný kryptografický algoritmus a zaznamená proudové průběhy pro operace AddRoundKey a SubBytes pro všechny varianty tajného klíče k i (256 možných variant). Naměřené průběhy proudové spotřeby odpovídající práci s bajtem k i použije útočník k natrénování neuronové sítě, která bude dané průběhy přiřazovat k hodnotám tajného klíče. Po úspěšném natrénování neuronové sítě může útočník pokračovat fází útoku, kdy využije natrénovanou neuronovou síť k napadení kryptografického modulu. V poslední fázi útoku útočník naměří proudovou spotřebu kryptografického modulu, na který útočí a přivede ji na vstup naučené neuronové sítě. Neuronová síť následně přiřadí proudovou spotřebu k odhadům tajného klíče a odhad klíče s největší pravděpodobností bude odpovídat hodnotě tajného klíče a tím dojde k určení hodnoty k i. Profilující fáze - Cílem této fáze je získat trénovací vzory proudové spotřeby pro operaci AddRoundKey a SubBytes pro všechny varianty tajného klíče k 1 (256 možných variant). Měření proudových průběhů bylo prováděno pomocí metody měření založené na proudové sondě CT-6. Do kryptografického modulu byl implementován algoritmus AES
48 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 47 Obrázek 3.9: Proudové vzory spotřeby pro všechny hodnoty klíče. a synchronizace byla provedena jen na operace AddRoundKey a SubBytes. Program pracoval ve smyčce a před započetím každé smyčky byla načtena data klíče k i do paměti tak, aby smyčka vždy pracovala se stejnými vstupními proměnnými. Program umožňoval inkrementovat nebo dekrementovat hodnotu klíče a indikovat tuto operaci odesláním aktuální hodnoty klíče pomocí sériové linky do počítače. Obrázek 3.8 zobrazuje proudové průběhy pro operace AddRoundKey a SubBytes pro hodnoty klíče 1 a 255. Proudové průběhy jsou si takřka identické s vyjímkou začátku průběhu, který odpovídá načtení registru a operaci XOR otevřeného textu s hodnotou tajného klíče a části pro čas t = 35000, který odpovídá operacím prováděným během substituce. Je zřejmé, že je zbytečné a značně neefektivní učit neuronovou síť na celé průběhy a proto byly všechny průběhy redukovány na místa práce s prvním bajtem tajného klíče. Takto redukované a připravené proudové průběhy pro všechny hodnoty tajného klíče určených pro neuronovou síť zobrazuje obrázek 3.9. Detail první proudové špičky je zobrazen na obrázku 3.10 a je patrné, že proudové průběhy jsou rozděleny do několika skupin, které logicky odpovídají Hammingově vzdálenosti právě zpracovávaných dat.
49 I [A] 48 FEKT Vysokého učení technického v Brně Klíč 0 Klíč 1 Klíč 2 Klíč t [n] Obrázek 3.10: Detail proudové spotřeby pro všechny hodnoty klíče Naměřené průběhy byly uloženy a importovány do matice K data v programu MATLAB pro následné zpracování. Celkem bylo naměřeno 2560 proudových průběhů, kde pro každou hodnotu tajného klíče bylo naměřeno 10 proudových průběhů. Pro implementaci neuronové sítě byl použit toolbox Netlab Neural Network v prostředí MATLAB. Autory tohoto toolboxu jsou Ian Nabney a Christopher Bishop z Aston University v Birminghamu a toolbox je volně ke stažení [82]. Vytvořená neuronová síť byla typická třívrstvá neuronová síť viz obr Vstupní vrstva musí mít stejný počet neuronů jako je počet vzorků v průběhu tedy Stejně tak jak u útoku využívající šablony je vhodnější vybrat pouze zajímavé body, ale výpočetní a paměťová náročnost neroste exponenciálně jak u TA. Tento jednoduchý příklad bere jako vstup celý proudový průběh odpovídající operacím AddRoundKey a SubBytes (v praxi je doporučováno redukovat na zajímavé body). Výstupní vrstva klasifikuje vstup na jednotlivé hodnoty klíče k 1, tedy musí obsahovat 256 neuronů pro všechny kombinace 0 až 255. Skrytá vrstva může mít libovolný počet neuronů v závislosti na složitosti řešeného problému. V implementaci bylo možné počet neuronů konfigurovat od 128 do 256. S těmito počty bylo provedeno
50 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 49 Skrytá vrstva Výstupní vrstva Vstupní vrstva X1 Y1 Z1 X12000 Y100 Z256 Obrázek 3.11: Struktura vytvořené neuronové sítě. testování a dosahovalo se nejlepších výsledků. Typ aktivační funkce byl zvolen na logistic, což odpovídá standardní sigmoidě. Za metodu učení byl zvolen algoritmus využívající zpětné šíření chyby (Backpropagation), která patří k nejpoužívanějším principům učení neuronových sítí. Tato metoda je popsána následujícími kroky. Krok 1: Počáteční inicializace vah w ij a prahů θ i jednotlivých neuronů. Krok 2: Přivedení vstupního vektoru X = [x 1,..., x N ] T výstupní odezvy D = [d 1,..., d M ] T. Krok 3: Výpočet aktuálního výstupu podle následujících vztahů: a definice požadováné y l (t) = N 2 f s ( w kl(t)x k(t) θ l ), 1 l M, výstupní vrstva, (3.22) k=1 x k(t) = N 1 f s ( w jk(t)x j(t) θ k), 1 k N 2, skrytá vrstva, (3.23) x j(t) = f s ( j=1 N i=1 Výpočet platí pro třívrstvou neuronovou síť. w ij (t)x i (t) θ j ), 1 j N 1, vstupní vrstva. (3.24) Krok 4: Adaptace vah a prahů dle následujících vtahů: w ij (t + 1) = w ij (t) + ηδ j x i, popř. (3.25) w ij (t + 1) = w ij (t) + ηδ j x i + α(w ij (t) w ij (t 1)). (3.26)
51 50 FEKT Vysokého učení technického v Brně Nastavení vah začíná u výstupních neuronů a postupuje rekurzivně směrem ke vstupním neuronům. V uvedených vztazích jsou w ij váhy mezi i-tým skrytým neuronem popřípadě vstupním a uzlem j-tým v čase t. Výstup i-tého neuronu je označen x i, η je koeficient učení, α je tzv. momentový koeficient a δ j je chyba, pro kterou platí následující vztahy: δ j = y j (1 y j )(d j y j ), pro výstupní neurony, (3.27) δ j = x j(1 x j)( δ k w jk ), pro skryté neurony, (3.28) kde k se mění přes všechny neurony vrstvy, které následují za uzlem j. Krok 5: Opakování kroků 3 až 5, dokud chyba není menší než předem stanovená hodnota. Fáze útoku - Pro ověření funkčnosti proudové analýzy využívající NN byla použita 10-fold křížová validace vytvořené neuronové sítě. Křížová validace je ve strojovém učení a při vytěžování dat typickou metodou ověření funkčnosti modelu. Při 10-fold křížové validaci je vstupní sada dat rozdělena na 10 podmnožin této sady, kde jedna podmnožina slouží vždy jako testovací a zbylé podmnožiny slouží jako trénovací. Neuronová síť se naučí na trénovací sadě a pomocí testovací sady se testuje přesnost a výkonnost sítě (obecně modelu). Tento proces se 10 krát opakuje, pokaždé s jinou podmnožinou tvořící Tabulka 3.1: Výsledky křížové validace. Pořadí validace err chyby klasifikace err[ ] ,7 trénovací a testovací sadu. Výsledkem validace může být průměrná hodnota přesnosti modelu získaná z jednotlivých kroků validace. Během naší realizace byla vstupní sadou dat vytvořená matice K data obsahující 2560 proudových průběhů, vždy 10 pro hodnotu tajného klíče 0 až 255. Proudové průběhy korespondující se stejnou hodnotou tajného klíče byly uloženy v řádcích pod sebou, tedy matice obsahovala 256 submatic o velikosti Křížová validace dělila sadu dat (všechny submatice) postupně po řádcích, tzn. v prvním kroku byl první proudový průběh testovací a zbylých 9 (2-10) trénovací, v druhém kroku byl druhý proudový průběh testovací a zbylé průběhy (1, 3 až 10) trénovací atd.
52 K odh Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO K taj Obrázek 3.12: Grafické znázornění kompletních výsledků klasifikace V cel. Tabulka 3.1 zobrazuje výsledky křížové validace, tedy počet chybně určených hodnot klíčů. Metoda průměrně klasifikovala chybně 11, 7 odhadů, což odpovídá úspěšnosti 95, 71%. Pro podrobnější analýzu výsledků klasifikace budou popsány výsledky devátého kroku validace. Výsledkem analýzy testovací sady korespondující se všemi hodnotami tajného klíče byla matice V cel o rozměrech Hodnota indexu řádku odpovídala hodnotě tajného klíče, pro který byla měřena proudová spotřeba a index sloupce představoval odhad klíče přiřazeného neuronovou sítí. Neuronová síť přiřadila každému průběhu proudové spotřeby vektor obsahují pravděpodobnosti pro jednotlivé odhady klíče (řádek matice V cel ). Celkové výsledky klasifikace jsou graficky znázorněny na obr a pro lepší představu je část výsledné matice číselně zapsána do tabulky 3.2. Z tabulky je patrno, že neuronová síť klasifikovala například proudovou spotřebu pro tajný klíč s hodnotou 0 s pravděpodobností 91, 42% pro odhad klíče 0 a pro proudový průběh odpovídající hodnotě tajného klíče 1 klasifikovala odhad klíče 1 s pravděpodobností 89, 15%. Pro získaní lepší představy o výsledcích klasifikace neuronové sítě a rozložení pravděpodobnosti odhadů klíčů jsou na obr zobrazeny výsledky klasifikace pro 5 náhodně vybraných proudových průběhů korespondující s pěti hodnotami tajných klíčů. Na ose x
53 Pravděpodobnost [%] 52 FEKT Vysokého učení technického v Brně Tabulka 3.2: Výsledky analýzy - část matice V cel. Ktaj Pravděpodobnost odhadu klíče K odh ,00% 0,00% 0,00% 5,02% 0,00% 83,57% 0,00% 4 0,00% 0,00% 18,77% 0,00% 52,62% 0,00% 0,00% 3 0,00% 0,00% 0,00% 51,35% 0,00% 0,00% 0,00% 2 0,00% 0,00% 20,80% 0,00% 7,20% 0,00% 0,00% 1 0,00% 89,15% 0,00% 0,00% 0,00% 0,00% 0,00% 0 91,42% 0,00% 0,00% 0,00% 0,00% 0,00% 0,00% jsou zobrazeny odhady klíče, tzn. výstup neuronové sítě a osa y udává s jakou pravděpodobností se odhad klíče rovná tajnému klíči. Barevně jsou vyznačeny jednotlivé průběhy odpovídající tajnému klíči, tedy byly vybrány proudové průběhy pro hodnoty tajného klíče 5, 41, 81, 129 a 248 (dekadický zápis). Z obr je patrno, že pravděpodobnost odhadu klíče 5 pro proudový průběh s hodnotu tajného klíče 5 byla 83% a ostatní pravděpodobnosti určené neuronovou sítí byly: 5% pro odhad klíče 3, 9% pro odhad klíče 33 a 38% pro odhad klíče 75. Analogicky lze vyčíst rozložení pravděpodobností pro ostatní K 5 taj K taj 41 K 81 taj K 129 taj K 248 taj K odh Obrázek 3.13: Výsledky klasifikace pro 5 náhodně vybraných klíčů.
54 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 53 vybrané hodnoty tajného klíče. Zobrazené hodnoty korespondují s maticí výsledků V cel a tabulkou 3.2. Pro náhodně vybrané hodnoty tajného klíče největší pravděpodobnost odhadu klíče odpovídala vždy hodnotě tajného klíče. Vybrané maximální hodnoty pravděpodobností odhadu klíče pro všechny jednotlivé hodnoty tajného klíče jsou zobrazeny na obr Graf ukazuje jaký odhad klíče byl klasifikován neuronovou sítí s největší pravděpodobností pro konkrétní proudový průběh korespondující s hodnotou tajného klíče. Graf je zobrazen se dvěma osami y a to pro lepší přehlednost a názornost. Osa x představuje odhady klíčů a modrá osa y příslušné maximální pravděpodobnosti. Červená osa y koresponduje s hodnotou tajného klíče. Z požadavků metody je zřejmé, aby odhad klíče byl roven tajnému klíči, tedy v ideálním případě platí funkce K odh = K taj. Průběh funkce K odh = K taj je markantní na první pohled. Hladký průběh funkce ruší body, které indikují chyby klasifikace. Jedná se o odhady klíče, které byly chybně klasifikovány, tedy kdy vybraný odhad klíče s největší pravděpodobností nekorespondoval s hodnotou tajného klíče v kryptografickém modulu (K odh K taj ). Seznam všech chybně klasifikovaných tajných klíčů je zapsán do tab Tabulka 3.3: Chybně určené odhady klíčů. K taj [dec] K odh [dec] P max [%] 40,22 7,85 25,41 18,93 19,83 21,61 14,64 P spr [%] 39,89 6,07 23,37 7,94 13,82 20,02 11,8 ΔP [%] 0,33 1,78 2,04 10,99 6,01 1,59 2,84 Z testovacího souboru, který byl určen pro ověření metody, neuronová síť přiřadila sedmkrát špatný odhad klíče. V tabulce je uvedena dekadická hodnota tajného klíče, chybného odhadu klíče, klasifikovaná maximální pravděpodobnost P max, pravděpodobnost správného odhadu klíče P spr a rozdíl těchto pravděpodobností ΔP = P max P spr. Zajímavým poznatkem je, že hodnota ΔP byla malá pro všechny chybně klasifikované klíče. Ve skutečnosti pravděpodobnost správného odhadu klíče byla vždy druhá nejvyšší u všech chybně klasifikovaných hodnot. Graficky znázorněný výstupní vektor pravděpodobností korespondující s hodnotou tajného klíče 21 ukazuje obr Tuto vhodnou vlastnost může využít útočník během útoku k redukci všech možných variant tajného klíče pokud by byl celý klíč chybně klasifikován. Předpokládejme, že útočník provádí na-
55 P[%] 54 FEKT Vysokého učení technického v Brně Maximální pravděpodobnost Odhad klíče K taj K odh Obrázek 3.14: Maximální hodnoty pravděpodobnosti a určené odhady klíče. vrhovanou proudovou analýzu na algoritmus AES s délkou tajného klíče 128 bitů tedy 16 bajtů. Na konci analýzy dešifruje kryptogram a zjistí chybně určený tajný klíč, tedy výstupem operace dešifrování je nesmyslný text. Útočník nyní využije výsledky klasifikace a vyzkouší všechny varianty klíče pro dvě nejvyšší hodnoty pravděpodobností. Prostor všech možných variant klíčů je redukován z na 2 16, což odpovídá redukci o 34 řádů. Jednoduchá proudová analýza - shrnutí Kocher [57] byl první, který představil proudovou analýzu kryptografických algoritmů a také poukázal na závislost proudové spotřeby na prováděných instrukcích. Jako příklad byla uvedena analýza algoritmu RSA a DES. V práci [75] byla diskutována SPA na algoritmus DES, který byl implementován na 8 bitový mikrokontrolér. Útok byl zaměřen na určení Hammingovy váhy šifrovacího klíče, který redukoval prostor potřebný na útok hrubou silou. Podobný útok SPA založený na určení Hammingovy váhy z proudového průběhu instrukce MOV je uveden v práci [72]. V práci [16] byl nastíněn útok na implementaci
56 Pravděpodobnost [%] Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO Nejvyšší hodnota pravděpodobnosti, chybný odhad hodnoty klíče K taj Druhá nevyšší hodnota pravděpodobnosti, správný odhad hodnoty klíče K taj K taj K odh Obrázek 3.15: Výstupní vektor chybně klasifikovaného odhadu klíče 21. algoritmu AES, který využíval analýzu proudového průběhu, který byl naměřen během vykonávání operací substituce při přístupu do vyrovnávací paměti. Mangard v práci [65] diskutoval SPA analýzu algoritmu AES, která je zaměřena na operaci expanze klíče. Útoky využívající šablony byly definovány a představeny poprvé v práci [23]. Praktické aspekty těchto útoků byly rozebrány v [96, 5, 46, 88]. 3.2 Diferenciální proudová analýza DPA Cílem útoků DPA je získat šifrovací klíč kryptografického zařízení na základě znalosti velkého počtu proudových spotřeb, které byly zaznamenány útočníkem během provádění operace šifrování nebo dešifrování pro různá vstupní data. Hlavní výhodou diferenciální proudové analýzy ve srovnání s SPA je, že útočník nepotřebuje detailní znalost kryptografického zařízení a šifrovacího algoritmu. Dalším důležitým rozdílem mezi těmito analýzami je způsob zpracování naměřených dat. V SPA jsou proudové průběhy zpracovávány většinou v časové ose. Útočník se zde pokouší v jednom proudovém průběhu najít vzor, známý
57 56 FEKT Vysokého učení technického v Brně d 1 d 2 Otevřený text nebo zašifrovaný text d D k 1 k 2 k K Předpokládané hodnoty proudové spotřeby h 1,1 h 2,1 h 1,2 h 2,2 h 1,K h 2,K Změřené průběhy proudové spotřeby t 1,1 t 1,2 t 1,T t 2,1 t 2,2 t 2,T Odhady klíče h D,1 h D,2 h D,K t D,1 t D,2 t D,T Šifrovací algoritmus v 1,1 v 2,1 v 1,2 v 2,2 Matice hypotéz mezivýsledků v 1,K v 2,K v D,1 v D,2 v D,K Statistická analýza r 1,1 r 1,2 r 1,T r 2,1 r 2,2 r 2,T r K,1 r K,2 r K,T Model spotřeby Výsledky porovnání přepokládané a změřené proudové spotřeby Obrázek 3.16: Blokový diagram znázorňující kroky 3 až 5 DPA útoku. otisk instrukce nebo šablonu. Naproti tomu, tvar proudového průběhu v časové oblasti není v DPA důležitý. DPA analyzuje závislost proudové spotřeby v určitý konstantní časový okamžik na právě zpracovávaných datech. V následujícím textu bude popsán detailněji postup získání šifrovacího klíče metodou DPA. Všechny DPA útoky využívají prakticky stejného postupu, který se skládá z pěti kroků. Toto obecné schéma je názorně zobrazeno na obr První krok: Volba mezivýsledku algoritmu Prvním krokem DPA je volba mezivýsledku kryptografického algoritmu, který je vykonáván zařízením. Mezivýsledek musí být funkcí f(d, k), kde d jsou známá nekonstantní data a k je malá část šifrovacího klíče (např. první bajt). Ve většině případů DPA útoku d představuje otevřený text nebo šifrovaný text. Takto definovaný mezivýsledek může být
58 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 57 použit k určení části šifrovacího klíče k. Druhý krok: Měření proudové spotřeby Druhým krokem DPA útoku je měření proudové spotřeby kryptografického zařízení při šifrování nebo dešifrování různých bloků dat D. Pro všechny operace šifrování či dešifrovaní potřebuje útočník znát hodnoty zpracovávaných dat d, které se podílí na výpočtu mezivýsledku zvoleného v prvním kroku. Hodnoty známých dat tvoří vektor d = (d 1,..., d D ), kde d i označuje hodnotu i-tého kroku šifrování nebo dešifrování. V průběhu každého tohoto kroku si útočník zaznamenává proudovou spotřebu. Průběhy proudové spotřeby, korespondující s bloky dat d i, označíme t i = (t i,1,..., T i,t ), kde T označuje délku naměřené proudové spotřeby. Útočník měří proudovou spotřebu pro každý blok dat D, a proto naměřené průběhy mohou být zapsány do matice T o velikosti D T. Pro DPA útok je klíčové, aby naměřené proudové průběhy byly přesně zarovnané. To znamená, že hodnoty pro jednotlivé sloupce t j matice T musí odpovídat stejné operaci. K získání takto zarovnaných dat je nutná správná synchronizace s měřicím zařízením, nebo je zapotřebí zarovnat data softwarově pomocí nalezení několika markantů (otisků v proudovém průběhu). Třetí krok: Výpočet hypotetických mezivýsledků Dalším krokem útoku je výpočet hypotetických mezivýsledků pro všechny možné hodnoty šifrovacího klíče k. Všechny možnosti klíče lze zapsat jako vektor k = (k 1,..., k K ), kde K označuje celkový počet možných klíčů. V DPA jsou jednotlivé prvky vektoru k označovány za hypotézy klíče nebo odhady klíče. Z vektoru známých dat d a vektoru hypotéz všech klíčů může útočník jednoduše vypočítat hodnotu mezivýsledku f(d, k) pro všechny šifrovací operace D a pro všechny hypotézy klíče K. Výsledkem výpočtu je matice V o rozměrech D K vypočtená dle následujícího vztahu: v i,j = f(d i, k j ) i = 1,..., D j = 1,..., K (3.29) Sloupec j matice V obsahuje mezivýsledky, které byly vypočítány dle hypotéz klíče k j. Je zřejmé, že jeden sloupec matice V obsahuje takové mezivýsledky, které byly vypočítány v zařízení během šifrování a dešifrování. Jinými slovy, jednotlivé sloupce matice V
59 58 FEKT Vysokého učení technického v Brně obsahují mezivýsledky pro všechny klíče, tedy i pro klíč který byl použit v zařízení. Tento index bude označen ck, tedy k ck označuje hledaný tajný klíč. Cílem DPA je nalezení odpovídajícího sloupce, který byl zpracováván při operacích šifrování a dešifrování v zařízení a tedy nalezení k ck. Čtvrtý krok: Mapování hypotetických mezivýsledků na hodnoty proudové spotřeby Čtvrtým krokem DPA útoku je namapování matice hypotetických mezivýsledků V na matici H reprezentující předpokládané hodnoty proudové spotřeby. V tomto bodě se využívá simulace proudové spotřeby kryptografického zařízení. Použitý model spotřeby přiřadí každému hypotetickému mezivýsledku v i,j předpokládanou hodnotu proudové spotřeby h i,j. Správnost výsledků simulace silně závisí na útočníkových znalostech o zařízení a činní DPA efektivnější. Mezi často používané modely přiřazení hodnot V na H patří model Hammingovy vzdálenosti a Hammingovy váhy (viz kapitola 3.2.5). Pátý krok: Porovnání hypotetických hodnot s naměřenými průběhy proudové spotřeby V posledním kroku útočník porovná předpokládané hodnoty proudové spotřeby závislé na odhadu klíče (hodnoty ve sloupci h i matice H) se změřenými průběhy proudové spotřeby (hodnoty ve sloupci t j matice T). Výsledkem je matice R o velikosti K T, kde každý element r i,j představuje výsledek porovnání sloupců h i a t j. Samotné porovnání je realizováno různými metodami, které jsou detailněji popsány v následujícím textu (kapitoly 3.2.1, a 3.2.3). Společná vlastnost všech postupů je, že hodnota r i,j je větší pro lepší shodu sloupců h i a t j. Určení tajného klíče využívá následujících skutečností. Proudové průběhy odpovídají proudové spotřebě zařízení během provádění algoritmu šifrování nebo dešifrování pro různá vstupní data. Mezivýsledek, který byl vybrán v prvním kroku, je částí tohoto algoritmu. Z těchto důvodu počítá zařízení hodnotu mezivýsledku v ck v průběhu šifrování nebo dešifrování pro různá vstupní data. V důsledku toho jsou naměřené průběhy v určitých časových okamžicích závislé na hodnotě mezivýsledku. Označíme toto místo naměřených průběhů jako ct (to znamená, že sloupec t ct obsahuje hodnoty proudové spotřeby, které
60 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 59 závisí na hodnotě mezivýsledku v ck ). Hypotetické hodnoty proudové spotřeby h ck byly simulovány útočníkem na základě hodnot v ck. Proto jsou sloupce h ck a t ct na sobě silně závislé. Ve skutečnosti tyto dva sloupce vedou k největší hodnotě v R, to znamená, že největší hodnota matice R je hodnota r ck,ct. Další prvky matice R mají malou hodnotu, protože ostatní sloupce H a T nejsou na sobě silně závislé. Útočník tak může určit index pro správný klíč ck a časový okamžik ct jednoduše a to nalezením největší hodnoty v matici R. Příslušné indexy této hodnoty jsou pak výsledkem DPA útoku. V praxi se může stát, že všechny hodnoty z R si budou prakticky rovny. V tomto případě útočník nezměřil dostatečné množství proudových průběhů k ustanovení vztahu mezi řádky H a T. Čím více průběhů útočník změří, tím více elementů budou mít sloupce H a T a tím lépe může útočník určit vztah mezi sloupci Útok založený na korelačním koeficientu Korelační koeficient (Correlation coefficient) patří k nejznámější metodě k určení lineární závislosti mezi dvěma náhodnými proměnnými. Proto je to také vhodná metoda pro provedení DPA útoku. Existuje velmi dobře definovaná teorie pro korelační koeficient, který může být použit k modelování statických vlastností DPA útoků. Korelační koeficient je definován pro veličiny X a Y pomocí kovariance vztahem: ρ(x, Y ) = Cov(X, Y ) σ 2 (X) σ 2 (Y ), (3.30) kde Cov(X, Y ) označuje kovarianci tedy střední hodnotu součinu odchylek obou náhodných veličin X, Y od jejich středních hodnot a σ 2 (X) a σ 2 (Y ) označují rozptyl těchto veličin. Veličina ρ je bezrozměrná a může nabývat hodnot 1 ρ 1. Hodnota 1 korelačního koeficientu značí nepřímou závislost (změna v jedné skupině je provázena opačnou změnou ve skupině druhé). Hodnota 0 korelačního koeficientu značí, že mezi hodnotami obou skupin neexistuje žádná statisticky zjistitelná lineární závislost. Při nulovém korelačním koeficientu na sobě veličiny mohou záviset, ale tento vztah nelze vyjádřit lineární funkcí. Jestliže korelační koeficient je roven 1, značí to přímou závislost, dokonalou korelaci mezi hodnotami obou skupin. Výpočet ρ se liší podle typu zkoumaných statistických proměnných. V případě, že náhodné veličiny X a Y jsou kvantitativní náhodné veličiny
61 60 FEKT Vysokého učení technického v Brně se společným dvourozměrným normálním rozdělením, je pro konkrétní hodnoty (x 1, y 1 ), (x 2, y 2 ),..., (x n, y n ) výběrový korelační koeficient dán vztahem: r = ni=1 (x i x) (y i y) ni=1 (x i x) 2 n i=1 (y i y) 2. (3.31) V DPA je korelační koeficient použit k určení lineární závislosti mezi sloupci h i a t j pro i = 1,..., K a j = 1,..., T. Výsledkem je matice R obsahujicí korelační koeficienty. Označíme každou hodnotu jako r i,j na základě elementů D ze sloupců h i a t j. Použijeme-li předchozí definici korelačního koeficientu, můžeme vztah 3.31 vyjádřit: r i,j = Dd=1 (h d,i h i ) (t d,j t j ) Dd=1 (h d,i h i ) 2 D d=1 (t d,j t j ) 2, (3.32) kde h i a t j označují průměrné hodnoty sloupců h i a t j Útok založený na rozdílu středních hodnot Základem statistické metody založené na rozdílu středních hodnot (Difference of mean) je srovnání dvou skupin naměřených hodnot (distribucí) výpočtem rozdílu středních hodnot těchto skupin. Systematický popis metody je uveden v práci [106]. Tato metoda používá jiný způsob k určení závislosti mezi sloupci matice H a T. Útočník vytvoří binární matici H, která rozdělí naměřené proudové průběhy do dvou skupin. Posloupnost nul a jedniček v každém sloupci H je funkcí vstupních dat d a odhadů klíče k i. Za účelem ověření zda odhad klíče k i je správný, útočník může rozdělit matici T na dva soubory řádků (tzn. dvě sady proudových spotřeb podle h i ). První soubor obsahuje ty řádky matice T, kde index odpovídá pozici nul ve vektoru h i. Druhý soubor obsahuje zbylé řádky T. Následně útočník vypočítá průměr řádků. Vektor m 0i značí průměr řádků prvního souboru a m 1i označuje průměr druhého souboru. Odhad klíče k i je správný pokud existuje výrazný rozdíl mezi m 0i a m 1i. Rozdíl mezi m 0i a m 1i indikuje vztah mezi h ck a některým ze sloupců T. Stejně tak jako v předchozím případě tato diference označuje časový okamžik kdy jsou mezivýsledky odpovídající h ck zpracovávány. V jiných okamžicích je diference mezi vektory rovna nule. Výsledkem útoku je tedy matice R, kde každý řádek odpovídá
62 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 61 rozdílu mezi vektory m 0i a m 1i pro jeden odhad klíče. Rovnice výpočtu R je dána vztahem: n h l,i t l,j, (3.33) l=1 n (1 h l,i ) t l,j, (3.34) l=1 n 1,i = n h l,i, (3.35) l=1 n 0i = n (1 h l,i ), (3.36) l=1 R = M 1 M 0, (3.37) m 1i,j = 1 n 1i m 0i,j = 1 n 0i kde n značí počet řádků matice H (tzn. počet naměřených proudových spotřeb) Útok založený na vzdálenosti středních hodnot Tato metoda založená na vzdálenosti středních hodnot (Distance of Means) je vylepšení předchozí metody, protože bere v úvahu směrodatné odchylky. Metoda je založena na běžně používaném testu k porovnání rovnosti středních hodnot dvou různých rozdělení. Útok rozdělí matici T na dvě skupiny řádků pro každý odhad klíče stejně jak bylo popsáno v předchozí kapitole Rozdíl od předchozí metody spočívá v tom, že střední hodnoty jsou porovnány podle testu vzdálenosti středních hodnot. Prvky matice R jsou vypočítány dle následujícího vztahu: kde s i,j je směrodatná odchylka pro rozdělení dvou skupin. r i,j = m 1i,j m 0i,j s i,j, (3.38) Útok pomocí šablon Útoky popsané v předchozích kapitolách 3.2.1, a předpokládaly, že útočník má jen velmi omezené znalosti o proudové spotřebě kryptografického zařízení, na které provádí útok. Ve většině případů bývají používány jednoduché modely proudové spotřeby a to model Hammingovy váhy a model Hammingovy vzdálenosti (podrobněji popisuje následující kapitola 3.2.5). Je zřejmé, že čím lépe bude odpovídat model skutečnosti, tím se útok stává efektivnějším. Při útoku DPA využívající šablony útočník popisuje
63 62 FEKT Vysokého učení technického v Brně proudovou spotřebu pomocí šablon (Template Based Attack). Tento typ útoku DPA byl poprvé představen v práci [4], kde jsou v podstatě rozšířeny šablony z SPA útoků. Pro vysvětlení útoku bude pozornost zaměřena nejprve na jeden proudový průběh tzn. t i z matice T. V tomto případě útočníka zajímá odpověď na otázku: jaká je pravděpodobnost toho, že klíč v zařízení se rovná k j pro j = 1,..., K s ohledem na naměřený průběh t i. Tato podmíněná pravděpodobnost p(k j t i) může být spočtena dle Bayesova teorému [52]. Bayesova věta umožní spočítat pravděpodobnost p(k j t i) v závislosti na pravděpodobnosti a priori p(k l ) a pravděpodobnosti p(t i k l ) pro l = 1,..., K vztahem: p(k j t i) = p(t i k j ) p(k j ) Kl=1 (p(t i k l ) p(k l )). (3.39) Pravděpodobnosti a priori jsou pravděpodobnosti pro různé klíče bez ohledu na průběh t i. Bayesův teorém pak může být vnímán jako funkce, kde vstupem jsou pravděpodobnosti a priori p(k l ) bez ohledu na průběh t i a výstupem jsou pravděpodobnosti a posteriori p(k j t i) s ohledem na t i. Pro jediný proudový průběh t i platí, že správný odhad klíče je klíč k j s nejvyšší pravděpodobností p(k j t i). Útoky založené jen na jednom proudovém průběhu nemohou být vždy úspěšné, protože v jednom průběhu nemusí být dostatek informací k nalezení klíče. Z tohoto důvodu rozšíříme tento přístup pro více naměřených proudových průběhů a to na určení pravděpodobnosti p(k j T). Rozšíření p(k j t i) na p(k j T) není složité, protože proudové průběhy jsou statisticky nezávislé a tak můžeme pravděpodobnosti pro odpovídající průběhy násobit a rovnici 3.39 přepsat následujícím vztahem: p(k j T) = ( Di=1 p(t i k j ) ) p(k j ) Kl=1 ( ( Di=1 p(t i k l ) ) p(k l ) ). (3.40) Rovnice 3.40 představuje podstatu útoku a výsledkem jsou pravděpodobnosti p(k j T) pro j = 1,..., K, které jsou použity k určení tajného klíče. Důležitou otázkou zůstává jak útočník může určit všechny pravděpodobnosti p(k j ) a p(t i k j ) potřebné k určení p(k j T). Nalezení pravděpodobností a priori p(k j ) je většinou snadné a útočník stanoví, že všechny klíče mají stejnou pravděpodobnost p(k j ) = 1/K. Určení pravděpodobnosti p(t i k j ) je mnohem složitější záležitostí a jsou zde používány šablony. Útočník může použít v podstatě stejné šablony jak při SPA útoku, viz kapitola
64 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 63 Obrázek 3.17: Proudová spotřeba korespondující s první rundou AES. Útok diferenciální proudovou analýzou - příklad algoritmus AES Následující kapitola popisuje realizovaný útok DPA využívající korelační koeficient. Jsou postupně popsány jednotlivé kroky s ohledem na obecné schéma útoku. Do kryptografického modulu (opět 8-bitový mikroprocesor) byl implementován algoritmus AES. Tento program byl upraven dle potřeb měření, byl vložen synchronizační signál pro konkrétní operace a zdrojový kód byl doplněn o komunikaci přes port RS-232. Přes rozhraní RS- 232 probíhala veškerá komunikace s kryptografickým modulem, zaslání otevřeného textu a přijmutí zašifrovaného textu. Následující text popisuje jednotlivé kroky útoku. Realizovaný útok odpovídal obecnému schématu popsanému v kapitole 3.2 a podrobněji jsou jednotlivé kroky a výpočty znázorněny na obr V prvním kroku DPA útoku byla nejprve zvolena vnitřní hodnota algoritmu AES. Tato hodnota musí být závislá na známých datech a části klíče. Vnitřní hodnotou byl zvolen první výstupní bajt operace SubBytes v první rundě AES. Tedy první bajt otevřeného textu je nejprve přičten operací XOR ke klíči a následně je hodnota substituována substituční tabulkou.
65 256 klíčů (0 až 255) Hledaná hodnota klíče 200 průběhů 200 bloků dat 64 FEKT Vysokého učení technického v Brně T = (t i,j ) 200, vzorků V = (v i,j ) 200,256 v i,j = S (d i XOR k j ) H = (h i,j ) 200,256 h i,j = HW(v i,j ) 256 klíčů (0 až 255) Čas, ve kterém kryptografický modul zpracovává námi zvolené hodnoty Správný odhad klíče, který je hledán Korelace R = corr(t,h) R = (r i,j ) 256, vzorků Čas, ve kterém kryptografický modul zpracovává námi zvolené hodnoty Obrázek 3.18: Průběh jednotlivých kroků DPA. V druhém kroku byly naměřeny průběhy proudové spotřeby šifrovacího algoritmu a synchronizační signál byl vložen na první rundu algoritmu. Celkem bylo naměřeno 200 proudových průběhů pro šifrování 200 náhodných bloků otevřeného textu. Příklad namě-
66 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 65 řené proudové spotřeby korespondující s první rundou je zobrazen na obr Naměřené a redukované průběhy proudové spotřeby byly uloženy do matice T znázorněnou na obr a příslušné vstupy do proměnné inputs. Třetí krok DPA útoku spočíval v stanovení hypotéz vnitřních hodnot algoritmu AES. Tyto hodnoty jsou určeny pro 200 bloků známého otevřeného textu a všechny hodnoty tajného klíče (0 až 255). Výsledkem byla matice V. Pro její prvky platí v i,j = S(d i k j ), kde d 1,..., d 200 je první bajt z každého bloku otevřeného textu a k j = j 1 pro j = 1,..., 256. Matice V obsahuje celkově hypotéz vnitřních hodnot. V prostředí MATLAB byla tato operace implementována následovně: [m,n] = size(t); key = [0:255]; V = zeros(m,256); for i=1:m V(i,:) = SubBytes(bitxor(inputs(i),key)+1); end, kde SubBytes odpovídá vektoru dekadických hodnot ze substituční tabulky (99, 124, 119, 123, 242,... ). Ve čtvrtém kroku je každé hypotetické vnitřní hodnotě v i,j z matice V přiřazena hypotetická hodnota proudové spotřeby h i,j. K tomu je nutné vytvořit simulaci proudové spotřeby kryptografického zařízení, tzv.model spotřeby (viz kapitola 3.2.5). Zpravidla má útočník jen omezené množství informací o napadeném zařízení, a proto se snaží využít, co možná nejjednodušší model HW nebo HD. V uvedeném příkladě je použit model Hammingovy váhy. Jeho aplikací na matici V hypotetických vnitřních hodnot vznikne matice H pro hypotézy proudové spotřeby. Implementace uvedených modelů byla provedena následovně: H = HW(V+1); % model HW for i=1:m %model HD H(i,:) = HW(bitxor(inputs(i),V(i,:))+1); end,
67 66 FEKT Vysokého učení technického v Brně Obrázek 3.19: Výsledky korelační matice. kde HW odpovídá vektoru dekadických hodnot Hammingových vah pro všechny hodnoty bajtu 0 až 255 (0, 1, 1, 2, 1, ). Pátý krok DPA útoku slouží k vyhodnocení míry lineární závislosti (korelace) hypotéz proudové spotřeby pro všechny odhady klíče (hodnoty ve sloupci h i matice H) a změřených průběhů (hodnoty ve sloupci t j matice T). K vyhodnocení míry lineární závislosti mezi sloupci h i a t j, kde i = 1,..., K a j = 1,..., T, se využívá různých metod viz kapitola 3.2.1, a Ze zmíněných metod je nejčastěji používán korelační koeficient. Výsledkem této metody je matice R korelačních koeficientů. Každá hodnota korelačního koeficientu r i,j je určena následovně: r i,j = Dd=1 (h d,i h i ) (t d,j t j ) Dd=1 (h d,i h i ) 2 D d=1 (t d,j t j ) 2, (3.41) kde hodnoty h i a t j označují průměrné hodnoty prvků ve sloupcích h i a t j. D udává počet těchto prvků. Matici R lze zobrazit jako množinu grafů. Každý graf znázorňuje jeden
68 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 67 řádek matice R, tedy jednu hypotézu (odhad) klíče. Na obr jsou zachyceny grafické průběhy pro hypotézy klíče 117 až 120 právě provedeného útoku. V průběhu pro hypotézu klíče 120 lze pozorovat velké špičky. Tyto špičky jsou ve skutečnosti nejvyšší v celé matici R. Všechny ostatní hodnoty matice R jsou výrazně menší. Tato skutečnost poskytuje útočníkovi informaci, že první bajt tajného klíče má hodnotu 120. Z počtu špiček daného průběhu dále vyplývá, že mikrokontrolér s touto vnitřní hodnotou pracuje v několika instrukcích. To je zpravidla obvyklé pro softwarovou implementaci šifrovacího algoritmu, kdy při práci s hledanou vnitřní hodnotou dochází k přesunu této hodnoty mezi pamětí a registrem mikrokontroléru a obráceně. Kompletní zdrojový kód útoků DPA založených na DOM a korelačním koeficientu je uveden v příloze 5.4. Diferenciální proudová analýza - shrnutí Koncept útoku DPA byl poprvé popsán v práci [57]. Útok byl proveden na algoritmus DES metodou založenou na rozdílu středních hodnot. Následně pak byly diskutovány možné aplikovatelné statistické testy v [28]. Proudové modely byly poprvé definovány v práci [21] a v [6] byly základní proudové modely analyzovány v kontextu čipových karet. Simulační modely jsou stále modifikovány k zvýšení efektivity PA [91, 79, 36]. V [20] je popsáno použití korelačního koeficientu jako statistické metody. Ve vědecké literatuře se stalo populárním zavádět nové názvy pro DPA útoky, které jsou drobnou variací obecného schématu (viz kapitola 3.2), např. používají jen jiný statistický test (Korelační analýza [20, 26]). V kontextu DPA je důležité si uvědomit, že pojem DPA útok je nezávislý na použitém statistickém testu nebo použitém mezivýsledku. Pokročilé metody DPA jsou uvedeny v práci [110]. V práci [98] byla představena koncepce stochastických modelů. Útoky vyššího řádu (Higher-order DPA) kombinují DPA útoky pro několik zvolených mezivýsledků algoritmu. Tato myšlenka byla zmíněna již v prvním článku o DPA [57], ale až práce [74] popisuje konkrétní implementaci. Navazující práce [8, 109] popisují metody maskování a útoky vyššího řádu umožňující získat senzitivní data. Důležitá otázka vlivu předzpracování naměřených dat na efektivitu DPA byla prezentována v pracích [50, 47].
69 68 FEKT Vysokého učení technického v Brně Modely proudové spotřeby V diferenciální proudové analýze je nutné mapování mezivýsledků na hodnoty proudové spotřeby (viz kapitola 3.2, čtvrtý krok útoku). Jedná se v podstatě o simulaci proudové spotřeby zařízení. Tyto simulace jsou typicky jednoduché a to z toho důvodu, že útočník většinou nedisponuje podrobnějšími znalostmi o zařízení, na které útočí. Model Hammingovy váhy Model Hammingovy váhy (HW, Hamming weight) je nejjednodušším modelem a je obvykle použit pokud útočník nemá žádné znalosti o vnitřní struktuře zařízení nebo nezná právě zpracovávaná data. Při použití HW modelu útočník předpokládá, že proudová spotřeba je přímo úměrná počtu právě nastavených nenulových bitů ve zpracovávaných datech. Datové hodnoty, které byly zpracovávány před nebo následně po této hodnotě jsou ignorovány. Z tohoto důvodu tento model není teoreticky vhodný pro popis CMOS obvodů, ale experimentální výsledky z praxe však ukazují, že HW zpracovávaných dat je závislá na proudové spotřebě CMOS obvodů a můžeme tento model použít. Model Hammingovy vzdálenosti Při použití modelu Hammingovy vzdálenosti (HD, Hamming Distance) útočník předpokládá, že proudová spotřeba je úměrná počtu změněných míst ve zpracovávaných datech. Podrobněji je v těchto simulacích model Hammingovy vzdálenosti použit k mapování přechodů, které nastávají na výstupu buněk vnitřního zapojení, na hodnoty proudové spotřeby. Útočník nemá většinou přístup k vnitřnímu zapojení, a tak nemůže provést kompletní simulaci. V praxi má útočník většinou některé informace o částech vnitřního zapojení a může tak provést simulace těchto částí. Například je-li kryptografické zařízení mikroprocesor, je velice pravděpodobné, že mikroprocesor je vyroben podobným způsobem jako veřejně známe mikroprocesory. Bude tak obsahovat registry, datové sběrnice, aritmeticko logickou jednotku a nějaké komunikační rozhraní atd. Tyto komponenty obvodu mají své typické vlastnosti, např. datová sběrnice je dlouhá a připojena k mnoha dalším částem obvodu. Proto je kapacitní zátěž této sběrnice velká a významně přispívá k celkové proudové spotřebě mikroprocesoru. Na datové sběrnici nenastávají chyby způ-
70 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 69 sobené vícestupňovou strukturou (viz kapitola 2.2.3). Lze také předpokládat, že kapacitní zátěž všech jednotlivých vodičů datové sběrnice si je rovna. Na základě těchto tvrzení je zřejmé, že model HD se velmi dobře hodí k popsání proudové spotřeby datových sběrnic. Útočník tak může mapovat data, která jsou přenášena datovou sběrnicí na hodnoty proudové spotřeby bez znalosti vnitřního zařízení. Proudová spotřeba, která je způsobena změnou datové sběrnice z hodnoty v 0 na hodnotu v 1, je úměrná HD(v 0, v 1 ) = HW (v 0 v 1 ). Podobně toto tvrzení může být aplikováno na další sběrnice, např. adresní a také na popis proudové spotřeby registrů. Registry jsou řízeny hodinovým signálem, a proto mění hodnotu jen jednou v průběhu hodinového cyklu. Útočník tak může simulovat proudovou spotřebu registrů počítáním HD dat, které jsou uleženy v registrech pro po sobě jdoucí hodinové cykly. Obecně lze tedy HD model použít k simulaci proudové spotřeby části zařízení dle vnitřního zapojení pokud útočník zná zpracovávána data. Pro případ kombinačních buněk, kde útočník neví hodnoty zpracovávaných dat z důvodu vícestupňové struktury, je tento přístup nevhodný. Model HD je proto hlavně používán k simulaci registrů a sběrnic.
71 70 FEKT Vysokého učení technického v Brně
72 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 71 4 METODY PROTIOPATŘENÍ Cílem kapitoly je popsat techniky protiopatření (countermeasure methods) vedoucí k znesnadnění a nebo plnému znemožnění útoku proudovým postranním kanálem. Zpravidla není nezbytné odstranit kanál samotný, ale postačuje zajistit, aby kanálem neunikaly z modulu citlivé informace nebo útočníkovy znesnadnit následnou analýzu naměřených dat. Přesto je odstranění kanálu samotného také žádoucí, neboť hrozí nalezení nové techniky a opětovného využití kanálu k útoku. Hlavním cílem protiopatření je zajistit, aby proudová spotřeba byla nezávislá na hodnotě mezivýsledku a operacích právě zpracovávaných kryptografickým modulem. Metody a techniky, kterými lze tuto nezávislost více či méně docílit jsou detailněji popsány v následující kapitole. Obecně lze techniky protiopatření kryptografického modulu proti útoku postranním kanálem rozdělit do dvou velkých skupin a to techniky skrývání (hiding) a maskování (masking). Tyto dvě skupiny se následně dělí do dvou podskupin dle implementace na hardwarová a softwarová protiopatření. 4.1 Skrývání Cílem skrývání je zajistit, aby proudová spotřeba byla nezávislá na hodnotě mezivýsledků, operacích právě zpracovávaných kryptografickým modulem a hodnotě dat. V podstatě existují dva způsoby jak docílit této požadované nezávislosti. První způsob je vyrobit zařízení takovým způsobem, aby proudová spotřeba byla náhodná. To znamená, že v každém hodinovém taktu bude proudová spotřeba různá i pro stejné instrukce. Druhý způsob je vyrobit zařízení takovým způsobem, že proudová spotřeba bude konstantní pro všechny operace a všechny datové hodnoty, tzn. proudová spotřeba bude v každém hodinovém cyklu stejná. Ideálním cílem skrývání, kterého však v praxi nelze dosáhnout, je realizace takového zařízení. Existuje několik návrhů a řešení jak se k tomuto ideálnímu stavu proudové spotřeby alespoň přiblížit. Tyto řešení můžeme rozdělit do dvou skupin. První skupina návrhů znáhodní proudovou spotřebu provedením operací kryptografického algoritmu v různých časových okamžicích při každém spuštění algoritmu. Tyto návrhy mají vliv na časovou oblast proudové spotřeby. Druhá skupina návrhů si klade za cíl učinit
73 72 FEKT Vysokého učení technického v Brně proudovou spotřebu náhodnou nebo konstantní a to přímo změnou charakteristické proudové spotřeby prováděných operací. Z tohoto důvodu mají tyto návrhy vliv na okamžitou velikost proudové spotřeby Ovlivnění časové oblasti proudové spotřeby V kapitole 3.2 byl uveden důležitý požadavek DPA a to že naměřené proudové průběhy musí být správně zasynchronizovány. To znamená, že otisky pro jednotlivé instrukce by se měly nacházet vždy na stejné pozici v proudovém průběhu. Pokud tento požadavek není splněn, útočník k DPA útoku potřebuje podstatně více naměřených průběhů. Tento podmět je motivací k vytvoření kryptografického zařízení, které provádí instrukce algoritmu v náhodném pořadí. Výsledkem tohoto opatření je, že proudová spotřeba se jeví náhodná. Čím více je provádění jednotlivých instrukcí v čase náhodné, tím více je obtížné provést útok na zařízení. Nejpoužívanějšími technikami k znáhodnění prováděných instrukcí je náhodné vkládání prázdných operací (dummy operations) nebo přesouvání operací (shuffling of operations). Technika vkládání prázdných operací spočívá v náhodném vkládání prázdných instrukcí do kryptografického algoritmu. Pokaždé když je algoritmus spuštěn jsou vygenerovány náhodná čísla, která slouží k určení pozic vložení prázdných instrukcí. Je důležité, aby celkový počet vložených prázdných instrukcí byl vždy stejný. V tomto případě útočník nemůže zjistit žádnou informaci o počtu vložených instrukcí opětovným měřením času vykonání celého algoritmu. V implementaci chráněnou touto technikou je pozice každé instrukce závislá na počtu vložených prázdných operací. Čím více je tato pozice proměnná, tím více je celková proudová spotřeba náhodná. Tedy znáhodnění proudové spotřeby přímo závisí na počtu vložených prázdných instrukcí. Je také zřejmé, že čím více je vloženo prázdných instrukcí, tím klesá rychlost provádění algoritmu (degraduje se optimalizace algoritmu). V praxi je proto optimální volit kompromis mezi rychlostí a znáhodněním proudové spotřeby pro každou konkrétní implementaci algoritmu. Alternativní technikou k vkládání prázdných operacích je technika přesouvání operací popřípadě instrukcí kryptografického algoritmu. Základní myšlenkou techniky je znáhodnění provádění instrukcí algoritmu, u kterého lze instrukce a operace provádět v libovolném pořadí. Například u algoritmu AES při operaci SubByte je prováděna substituce dle sub-
74 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 73 stituční tabulky (viz příloha 5.1.2). Těchto 16 substitucí je na sobě nezávislých a mohou být provedeny v libovolném pořadí. Při použití techniky přesouvání operací jsou vygenerována náhodná čísla při každém spuštění algoritmu, které jsou použity k určení pořadí provádění 16 substitucí. Přesouvání operací znáhodní proudovou spotřebu jednoduchým způsobem tak jako vkládání prázdných operací. Přesouvání operací nemá vliv na výkon algoritmu, tedy nedegraduje rychlost provádění algoritmu, ale nejde použít na všechny operace algoritmu a počet operací je tak omezen. Tento počet se odvíjí od použitého kryptografického algoritmu a konkrétní implementace. V praxi se tyto dvě techniky často používají současně Ovlivnění okamžité velikosti proudové spotřeby Tato technika na rozdíl od předchozích přímo mění charakteristické proudové otisky prováděných instrukcí a operací. Základní myšlenkou je snížit množství unikající informace prostřednictvím postranního kanálu snížením odstupu signálu od šumu prováděných operací. Optimálním výsledkem této metody je hodnota SNR (Signal-to-noise ratio) rovna 0. Toho může být teoreticky docíleno buď snížením užitečného signálu na nulu nebo zvýšením šumu v měřeném signálu na nekonečno. V praxi tyto předpoklady můžeme realizovat jen do určité míry. Nejjednodušším způsobem jak zvýšit šum jednotlivých instrukcí je provádět několik nezávislých operací paralelně. Proto jsou vhodnější hardwarové architektury kryptografických algoritmů s širokou strukturou datových cest. Například je daleko složitější provést útok na jeden bit proudové spotřeby AES v 128 bitové architektuře než v 32 bitové architektuře. Druhým způsobem zvýšení šumu je použití speciálních šumových rušiček. Tyto rušičky provádějí náhodné přepínání aktivních a paralelních operací. Naopak snížení užitečného signálu na nulu docílíme pokud bude proudová spotřeba stejná pro všechny instrukce a všechny datové hodnoty. Na první pohled se může zdát úkol zkonstruovat zařízení s konstantní proudovou spotřebou pro všechny instrukce a data snadno realizovatelný. Pokud se však tento úkol prostuduje podrobněji je jasné, že splnění není triviální. Existují dva způsoby jak se tomuto cíli přiblížit. Nejpoužívanější metodou je použití specializovaných logických buněk. Celková proudová spotřeba zařízení je součtem proudové spotřeby všech buněk logické struktury. Pokud budou všechny buňky vytvo-
75 74 FEKT Vysokého učení technického v Brně řeny tak, že jejich proudová spotřeba bude konstantní, potom bude výsledná proudová spotřeba také konstantní. Druhým způsobem snížení užitečného signálu je filtrování proudové spotřeby. Základní myšlenkou této metody je odstranit datovou závislost a závislost na operacích používaných komponent z proudové spotřeby za použití filtrů. 4.2 Maskování Cílem všech opatření je, aby proudová spotřeba byla nezávislá na hodnotě mezivýsledku a operacích právě zpracovávaných kryptografickým modulem. Maskování přistupuje k tomuto problému znáhodněním mezivýsledku zpracovávaným kryptografickým modulem. Výhodou této metody je, že může být implementována na úrovni algoritmu bez nutnosti změn charakteristické proudové spotřeby zařízení. Jinými slovy, maskování umožní vytvořit proudovou spotřebu nezávislou na mezivýsledcích a to i v případě, že zařízení má proudovou spotřebu závislou na zpracovávaných datech. Při maskování je každý mezivýsledek v zamaskován náhodnou hodnotou m, kterou nazýváme maska v m = v * m. Maska m je generována interně v kryptografickém modulu a pro každé spuštění má jinou hodnotu, proto její hodnotu útočník nezná. Operace * je typicky definovaná dle operací, které jsou použity algoritmem. Tato operace je většinou v kryptografickém modulu realizována exklusivním součtem XOR značeným symbolem (aditivní maskování) nebo násobením značeným symbolem (multiplikativní maskování). Ve většině případů jsou masky používány přímo na otevřený text nebo tajný klíč. Při použití maskování musí být implementace algoritmu mírně modifikována s ohledem na maskované mezivýsledky. Výsledkem kryptografického algoritmu je také maska, kterou je nutno odstranit k získání kryptogramu. Typické maskovací schéma popisuje jak jsou všechny mezivýsledky maskovány a jak se masky mění v algoritmu a následně konečné odstranění masek. Následující text uvede základní typy maskování, detailnější přehled technik maskování a implementace maskování je uveden v [67, 19, 89]. Rozlišujeme mezi booleanovským a aritmetickým maskováním. Při použití boolean maskování je mezivýsledek skryt exklusivním součtem s maskou v m = v m. Při implementaci aritmetického maskování je mezivýsledek skryt aritmetickou operací sčítáním nebo násobením často v modulu n, v m = v + m( mod n). Některé algoritmy jsou založeny na
76 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 75 boolean a aritmetických operacích, a proto je nutné použít oba typy maskování. To je problematické, protože přechod mezi maskováními vyžaduje značné množství přídavných operací [27, 44]. Kryptografické algoritmy využívají lineární a nelineární funkce. Lineární funkce je například pro boolean maskování vyjádřena předpisem f(x m) = f(x) f(m). Z toho plyne, že lineární operace jsou snadno maskovány s booleanovským maskováním. Příklad nelineární operace je AES S-box S(x m) S(x) S(m). V tomto případě se maska mění daleko složitějším způsobem, a proto není snadné používat boolean maskování na nelineární operace. Substituce S-box je založena na výpočtu multiplikativního inverzního prvku f(x) = x 1 (viz příloha 5.1.2) a to je vhodné pro multiplikativní maskování f(x m) = (x m) 1 = f(x) f(m). Efektivní schéma pro přechod mezi multiplikativními a booleanovskými maskamy je uvedeno např. [7]. Velkou nevýhodou multiplikativního maskování je nemožnost maskování mezivýsledku s nulovou hodnotou. V předchozím textu bylo uvedeno, že při maskování je každý mezivýsledek v zamaskován náhodnou hodnotou m, kterou nazýváme maska, např. při použití booleanovského maskování v m = v m. Hodnota mezivýsledku v může být vypočtena za pomoci v m a m. Jinými slovy hodnota mezivýsledku v je reprezentována dvěma parametry (v m, m). Znalost jednoho parametru nevede k žádné informaci o v, útočník potřebuje znát oba parametry k určení v (maskování sdílením tajemství ). Následně maskování založené na sdílením tajemství používá tyto dva sdílené parametry. Sdílení tajemství s několika maskami je základní metoda maskování, tzn. že několik masek je použito pro jednu hodnotu mezivýsledku [22]. U asymetrických algoritmů je aditivní maskování nebo multiplikativní maskování velice efektivní. Aplikace aritmetického maskování je v kontextu asymetrické kryptografie nazýváno oslepení. Například u algoritmu RSA u procesu dešifrování je aplikovatelné multiplikativní maskování na vstupní zprávu v : v m = v m e. Výsledek v d může být jednoduše získán na konci algoritmu protože platí: (v m ) d (v d mod n). Tato technika se nazývá oslepení zpráv (message blinding).
77 76 FEKT Vysokého učení technického v Brně 4.3 Způsoby implementace protiopatření Podle toho na které úrovni architektury je implementováno protiopatření, rozlišujeme softwarové a hardwarové implementace. Je zřejmé, že ekonomicky výhodnější jsou softwarová protiopatření, a to z důvodu jejich snadné implementace do stávajících kryptografických zařízení. Mnohem nákladnější hardwarová protiopatření, ale přináší zpravidla vyšší úroveň bezpečnosti Softwarové implementace Možnosti jak měnit průběh proudové spotřeby pomocí softwarové implementace jsou značně omezené. Charakteristické proudové spotřeby jednotlivých instrukcí jsou definovány hardwarem na nižší úrovni architektury. Nejpoužívanějším protiopatřením je výše popsané skrývání v časové oblasti, jedná se o vkládání prázdných instrukcí a přesouvání instrukcí popřípadě celých operací. Tyto protiopatření jsou snadno implementovatelné v programu, avšak potřebují ke své činnosti generátor náhodných čísel, který musí být implementován v zařízení. Obecně lze konstatovat, že vkládání prázdných instrukcí a přesouvání operací nepřináší velký stupeň ochrany proti útokům proudovým postranním kanálem. Softwarově lze měnit i okamžitá velikost proudové spotřeby. Charakteristické proudové spotřeby jednotlivých instrukcí jsou definovány hardwarem na nižší úrovni architektury, ale je to program, který určuje konkrétní instrukce k implementaci algoritmu. Výběrem instrukcí, které jsou použity k implementaci algoritmu, lze přímo ovlivňovat okamžitou velikost proudové spotřeby. Toto řešení zabrání útokům SPA při přímé interpretaci proudové spotřeby, ale není většinou dostatečné k zamezení provedení DPA útoku Hardwarové implementace Na úrovni hardwaru existuje podstatně více možností k ochraně kryptografického zařízení pomocí skrývání. V časové oblasti navíc existují dvě skupiny protiopatření, které náhodně mění časový okamžik provádění instrukcí. První skupina je stejná jako při softwarové implementaci, tj. vkládání prázdných instrukcí a přesouvání operací. Tyto implementace jsou provedeny stejně tak jak na softwarové úrovni. Druhá skupina protiopatření ovlivňuje
78 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 77 hodinový signál. Tyto protiopatření náhodně mění hodinový signál tak, aby znesnadnili synchronizaci proudové spotřeby. Mezi nejčastěji používané techniky k změně hodinového signálu patří: vynechání hodinového pulzu, náhodná změna frekvence hodinového signálu, existence více zdrojů hodinového signálu a přepínaní mezi nimi. Okamžitá velikost proudové spotřeby může být ovlivněna na hardwarové úrovni snadněji než na softwarové úrovni. Proudová spotřeba může být rovna pro všechny operace a hodnoty dat filtrováním nebo může být zvyšována hodnota šumu vytvořenými šumovými rušičkami. V praxi je filtrování proudové spotřeby provedeno spínacími kapacitory, zdroji konstantního proudu a dalšími prvky obvodu, které regulují proudovou spotřebu. Rušičky bývají vytvořeny na základě generátoru náhodných čísel. S cílem získat co největší vliv na proudovou spotřebu bývají generátory připojeny k síti velkých kapacitorů. Náhodné nabíjení a vybíjení této sítě vede k zvýšení šumu v proudové spotřebě, která činí útok PA obtížnější. Při hardwarové implementaci je důležité si uvědomit, že SNR nezávisí jen na kryptografickém zařízení, ale také na měřicím pracovišti a metodě, které jsou použity k analýze proudové spotřeby. Pokud protiopatření sníží SNR pro jednu konfiguraci měřicího pracoviště, nesnižuje tím SNR pro všechny ostatní konfigurace měřicích pracovišť. Například metoda filtrování proudové spotřeby značně ztíží měření proudové spotřeby při použití proudového bočníku. Pokud by útočník měřil prosakující informaci prostřednictvím elektromagnetického postranního kanálu, nemělo by toto protiopatření výrazný efekt. Ze stejného důvodu by rušičky měly být rozprostřeny rovnoměrně v celém obvodu a neměly by být umístěny na jednom místě. Protiopatření proti proudové analýze - příklad AES Pro ukázku útoku na maskovací schéma algoritmu AES využijeme soutěž DPA Cotest. V roce 2008 výzkumná skupina 1 z francouzské technické univerzity Telecom ParisTech vytvořila první verzi soutěže DPA Contest. Jejich cílem bylo poskytnout odborné veřejnosti objektivní způsob pro porovnání různých metod proudové analýzy, především DPA útoku. 1 Webová stránka výzkumné skupiny
79 78 FEKT Vysokého učení technického v Brně Nezávislé porovnání těchto metod je velice problematické z několika důvodů. Např. kvůli použití jiných měřicích zařízení, odlišné implementace šifrovacího algoritmu, různým podmínkám okolního prostředí, atd. DPA Contest se snaží tyto faktory, ovlivňující porovnání, odstranit. K tomu veřejně poskytuje proudové průběhy z kryptografického modulu, které jsou měřeny za předem stanovených podmínek. Pro všechny průběhy jsou také poskytnuty použité otevřené texty, tajné klíče a odpovídající šifrované texty. Dále poskytuje testovací framework pro detailní vyhodnocení vytvořeného útoku. Tím umožňuje nezávislým výzkumníkům možnost vyvíjet vlastní útoky a porovnávat je s ostatními. V současné době probíhá již čtvrtá verze této soutěže (rok 2014), která tvoří základ následující ukázky. Použitý kryptografický modul (čipová karta Atmel ATMega-163) pro DPA Contest V4 má v sobě implementován maskovaný algoritmus AES-256. Pro maskování AES je použita metoda RSM (Rotating Sbox Masking). Podle [83] se tato metoda maskování vyznačuje jednoduchou implementací a nízkou výpočetní náročností, avšak odolnou vůči některým útokům postranními kanály. Cílem útoku je získat prvních 128 bitů tajného klíče. Vzhledem k tomu, že první runda AES-128 je stejná i pro variantu AES-256, lze se dále zaměřit pouze na AES-128. Maskování RSM algoritmu AES používané v DPA Contest V4 využívá 16 masek v = {v 0, v 1,..., v 15 }, které jsou veřejně dostupné. Na začátku každého šifrování se vygeneruje náhodná hodnota od 0 do 15, tzv.offset, která je tajná. Poté na každý i-tý bajt otevřeného textu a masku v i+offset je aplikována operace XOR: m 0... m 12 v 0+offset... v 12+offset s 0... s 12 m 1... m 13 v 1+offset... v 13+offset s 1... s 13 = = Stav, (4.1) m 2... m 14 v 2+offset... v 14+offset s 2... s 14 m 3... m 15 v 3+offset... v 15+offset s 3... s 15 kde hodnota i + offset je spočítána operací modulo 16. Původní substituce SubBytes se nahradí šestnácti maskovanými MaskedSubBytes i (s j ) = SubBytes(s j v i ) v i+1, kde i {1, 2,..., 16}. Po lineární části AES následuje dodatečná operace, která zajistí, aby Stav vstupující do další rundy byl roven: s 0 v 0+offset+r O0 r... v 0+offset+r+1... v 12+offset+r+1 s 1 v 0+offset+r O1 r... v MC SR SBox 1+offset+r+1... v 13+offset+r+1 s 2 v 0+offset+r O2 r, (4.2)... v 2+offset+r+1... v 14+offset+r+1 s 3 v 0+offset+r O3 r... v 3+offset+r+1... v 15+offset+r+1
80 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 79 kde r {1,..., 9} (pro AES-128) je číslo rundy a Oi r je (i + 1) bajt r-tého subklíče. SR a MC reprezentují popořadě transformace ShiftRow a MixColumns. Maskování pro poslední rundu (r = 10 pro AES-128) zajistí, že na jejím výstupu bude: s 0 v 0+offset+r O0 r... v 0+offset+r+1... v 12+offset+r+1 s 1 v 0+offset+r O1 r... v SR SBox 1+offset+r+1... v 13+offset+r+1 s 2 v 0+offset+r O2 r. (4.3)... v 2+offset+r+1... v 14+offset+r+1 s 3 v 0+offset+r O3 r... v 3+offset+r+1... v 15+offset+r+1 Poslední maska je odstraněna operací XOR. Další informace o použitém způsobu maskování v článku [83] a na webové stránce [45]. Princip fungování maskovaného algoritmu AES lze popsat pomocí algoritmu 1. Přičemž jeho původní nechráněnou verzi lze získat odstraněním řádků zvýrazněných modrou barvou a záměnou operace MaskedSubBytes za operaci Subbytes. Algoritmus 1 Maskování algoritmu AES-256 v DPA Contest V4 [83]. Vstup: Otevřený text X; 16 bajtů X i, kde i 0, 15, Expanze klíče; bitových konstant RoundKey[r], kde r 0, 14 Výstup: Šifrovaný text X; 16 bajtů X i, kde i 0, 15, 1: Náhodně generovaný offset 0, 15 s rovnoměrným rozdělením. 2: X = X Mask offset 3: // Maskování otevřeného textu 4: // Všechny rundy kromě poslední 5: for r 0, 12 do 6: X = X RoundKey[r] 7: // AddRoundKey 8: for i 0, 15 do 9: X i = MaskedSubBytes offset+i+r (X i ) 10: end for 11: X = ShiftRows(X) 12: X = MixColumns(X) 13: X = X MaskCompensation offset+1+r 14: end for 15: // Poslední runda 16: X = X RoundKey[13] 17: for i 0, 15 do 18: X i = MaskedSubBytes offset+13+r (X i ) 19: end for 20: X = ShiftRows(X) 21: X = X RoundKey[14] 22: // Odmaskování šifrovaného textu 23: X = X MaskCompensationLastRound offset+14
81 80 FEKT Vysokého učení technického v Brně Proudové průběhy pro použitý kryptografický modul byly měřeny v laboratořích Digital Electronic Systems výzkumné skupiny Telecom ParisTech za stanovených podmínek následujícími přístroji: elektromagnetickou sondou Langer RF-U 5-2, předzesilovačem Langer PA303, digitálním osciloskopem Lecroy Waverunner 6100A, regulovatelným zdrojem Agilent E3631A. Pro soutěž DPA Contest V4 je veřejně zpřístupněno průběhů. Všechny průběhy odpovídají operaci šifrování pro stejný tajný klíč a zobrazují pouze první rundu algoritmu AES (viz obr. 4.1). K testování vytvořeného útoku je nutné, kromě změřených průběhů, stáhnout z webových stránek soutěže indexový soubor obsahující potřebné informace pro každý průběh. Jeden řádek souboru odpovídá jednomu průběhu a informace v něm jsou odděleny mezerou takto: 1. sloupec: klíč AES-256 (256 bitů reprezentováno 64 hexadecimálními čísly), 2. sloupec: otevřený text (128 bitů reprezentováno 32 hexadecimálními čísly), 3. sloupec: šifrovaný text (128 bitů reprezentováno 32 hexadecimálními čísly), 4. sloupec: offset (dekadická hodnota 0 15 reprezentována 1 hexadecimálním číslem), 5. sloupec: název adresáře s uloženými průběhy, 6. sloupec: název průběhu. Pro zjednodušení práce jsou proudové průběhy rozděleny do 10 samostatných komprimovaných archivů. Každý archiv obsahuje průběhů. Autoři soutěže DPA Contest nabízí ke stažení softwarové nástroje pro implementaci vlastního útoku. Jedním z nich je AttackWrapper představující softwarové jádro, které umožňuje přistupovat k databázi průběhů a k souborovému systému, spouštět vytvořený útok a na závěr předat výsledky k vyhodnocení nástroji ComputeResults. ComputeResults z výsledků vyhodnotí úspěšnost vytvořeného útoku. Blokový diagram na obr. 4.2 znázorňuje operace prováděné nástrojem AttackWrapper. AttackWrapper je nástroj určený ke spouštění útoku a k jeho vyhodnocení. Může být nainstalován na jakýkoli operační systém unixového typu (Linux, Mac OS X, atd. )
82 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO I [ma] vzorky [-] Obrázek 4.1: Proudový průběh z DPA Contest V4. Útok Uživatelské parametry AttackWrapper Databáze průběhů ComputeResults Vyhodnocení útoku Obrázek 4.2: Blokový diagram popisující funkci nástroje AttackWrapper.
83 82 FEKT Vysokého učení technického v Brně nebo Windows. K implementaci útoku lze použít libovolný programovací jazyk (C, C ++, Python, Perl) nebo Matlab. Společně s tímto nástrojem jsou také dodávány nástroje ComputeResults a Traces2Text. První zmíněný slouží k analýze uložených výsledků z AttackWrapperu a druhý umožňuje převést proudový průběh do čitelného textového souboru. Protože k implementaci útoku bylo zvoleno prostředí Matlab běžící na operačním systému Ubuntu , bude další popis užívaní nástroje AttackWrapper omezen na tento operační systém. K instalaci nástroje je zapotřebí mít k dispozici: počítačovou platformu x86 nebo x86-64, kompilátor C ++ (např. g ++ ), knihovnu libbz2. Instalace nástroje se provádí v terminálu operačního systému pomocí následujících příkazů. 1 $ tar xzf attack_wrapper 2.0.tar.gz $ cd attack_wrapper $./configure $ make Pokud instalace proběhne v pořádku, tak se v adresáři src objeví tři spustitelné soubory (attack_wrapper, compute_results a traces2text). Ovládání nástroje AttackWrapper probíhá přes příkazovou řádku. Následující příkaz slouží k zobrazení dostupných parametrů. $ attack_wrapper help Tyto parametry jsou povinné: -e edice: verze soutěže (v4_rsm), -d adresář: umístění složky s proudovými průběhy, -x soubor: umístění indexového souboru. Ostatní jsou volitelné:
84 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 83 -i iterace: počet použitých průběhů k analýze (ve výchozím stavu použity všechny průběhy), -o soubor: název souboru s výsledky (ve výchozím stavu results), -t: přepsání souboru s výsledky (ve výchozím stavu nepřepisuje), -f: režim FIFO (bude popsán později). Po spuštění útoku a jeho vykonání lze výsledný soubor předat nástroji ComputeResults, viz následující příkaz. 1 $ attack_wrapper f d DPA_contestv4_rsm x dpav4_rsm_index e v4_rsm fifo $ compute_results results Útok vytvořený v prostředí Matlab komunikuje s nástrojem AttackWrapper prostřednictvím režimu FIFO (First In First Out). Tento režim využívá dva speciální soubory (tzv. roury). Nejprve je spuštěn AttackWrapper, který vytvoří soubory xxx_from_wrapper v režimu pouze pro čtení a xxx_to_wrapper v režimu pouze pro zápis. Poté se manuálně spustí útok v Matlabu, který tyto soubory otevře a využívá je pro čtení nebo zápis dat. Písmena xxx jsou nahrazena posledním argumentem příkazu pro spuštění AttackWrapperu. Útok na maskovaný šifrovací algoritmus AES tvoří dvě části. V první části je extrahována hodnota masky. K tomuto účelu je aplikována naučená neuronová síť (alternativou může být útok využívající šablony). Po odmaskování následuje druhá část útoku, která využívá diferenciální proudovou analýzu DPA s korelačním koeficientem pro odhalení tajného klíče. K naučení neuronové sítě je nutné pro kontrolovaný kryptografický modul naměřit sadu proudových průběhů T. Následně vybrat p bodů t 1, t 2, t p, které jsou výrazně korelovány se známými hodnotami masky. Tyto body slouží pro učení neuronové sítě, která pro daný proudový průběh T v čase t 1, t 2, t p vrací d hodnot masky. Obr. 4.3 rekapituluje celý postup. Nejprve je provedena implementace maskovaného šifrovacího algoritmu do kryptografického modulu. Po změření proudových průběhů následuje další fáze, a to redukce počtu bodů každého průběhu na ty, které poskytují největší
85 84 FEKT Vysokého učení technického v Brně 1. Příprava 2. Analýza dat a učení ANN Kryptografický modul Změření proudových průběhů Předzpracování naměřených dat Učení ANN 4. Vyhodnocení útoku 3. Útok Určení úrovně zabezpečení DPA analýza Hodnota masky Klasifikace pomocí ANN Obrázek 4.3: Útok na maskovaný šifrovací algoritmus s využitím ANN. množství informace o použité masce a jsou vhodné pro učení neuronové sítě. Třetí fáze tvoří samotný útok s cílem získat hodnotu tajného klíče. Tato fáze poté umožňuje při vyhodnocení určit odolnost kryptografického modulu tedy jeho úroveň zabezpečení, např. na základě počtu průběhů potřebných k odhalení klíče. Úspěšnost navrženého útoku odhalit korektní hodnotu klíče přímo souvisí se schopností neuronové sítě určit správnou hodnotu masky. Tedy čím menší chyba mezi správnými a vyhodnocenými hodnotami masky, tím větší bude korelace mezi změřenými průběhy a hypotetickou proudovou spotřebou pro správný klíč. V případě, kdy neuronová síť dokáže určit hodnoty masky s pravděpodobností 100 %, tak DPA analýza odhalí klíč se stejným počtem průběhů jako v případě nemaskovaného šifrovacího algoritmu. Před vytvářením a učením neuronové sítě bylo třeba nalézt v proudových průbězích body, které jsou výrazně korelovány s tajnou hodnotou offsetu. Na obr. 4.4 lze pozorovat, že zejména první tři čtvrtiny zachyceného proudového průběhu obsahují velké množství informace o hodnotě offsetu. Je tedy možné předpokládat, že neuronová síť určí správný offset s vysokou pravděpodobností. Vytvořená neuronová síť má klasickou třívrstvou strukturu a pro její učení byl zvolen algoritmus Backpropagation. Učící množinu tvořilo proudových průběhů. Během předzpracování se z každého průběhu vybralo 48 bodů, které vykazovaly nejvyšší korelaci s hodnotou offsetu. Testovací množina se skládala také z proudových průběhů. Na testovací množině byla ověřena úspěšnost klasifikace offsetu. Procentuální úspěšnost dosahovala 99,7 %. Po vytvoření funkční neuronové sítě byl implementován DPA útok založený na korelač-
86 Ochrana informací šifrováním pro integrovanou výuku VUT a VŠB-TUO 85 Obrázek 4.4: Korelace mezi offsetem a proudovým průběhem maskovaného AES. ním koeficientu, který útočí na výstup operace SubBytes. Vytvořený útok na maskovaný šifrovací algoritmus AES odhalil šifrovací klíč při 20 proudových průbězích. Na obr. 4.5 je zobrazen výpis terminálového okna při spuštěném útoku. Řádek zvýrazněný červenou barvou udává, že již při analýze 20 proudových průběhů byl nalezen šifrovací klíč maskovaného algoritmu AES. Průměrná doba zpracování jednoho průběhu činila 585 ms. Výsledek ukazuje, že maskovací schéma implementované v DPA Contest V4 může být v praxi prolomeno využitím neuronových sítí v kombinaci s diferenciální proudovou analýzou. Důvodem je vyzařující operace bělení otevřeného textu, z kterého lze určit masky a následně se útočí jak na nemaskované schéma algoritmu AES. Zdrojový kód útoku je uveden v příloze 5.3.
Postranními kanály k tajemství čipových karet
 SIX Research Centre Vysoké učení technické v Brně martinasek@feec.vutbr.cz crypto.utko.feec.vutbr.cz Kryptoanaly za postrannı mi kana ly Proudova analy za Pr edstavenı U vod Crypto Research Group, Vysoke
SIX Research Centre Vysoké učení technické v Brně martinasek@feec.vutbr.cz crypto.utko.feec.vutbr.cz Kryptoanaly za postrannı mi kana ly Proudova analy za Pr edstavenı U vod Crypto Research Group, Vysoke
KRYPTOANALÝZA POSTRANNÍMI KANÁLY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
J.Breier, M.Vančo, J.Ďaďo, M.Klement, J.Michelfeit, Masarykova univerzita Fakulta informatiky
 Analýza postranních kanálů (kryptoanalýza hardvérových zařízení) J.Breier, M.Vančo, J.Ďaďo, M.Klement, J.Michelfeit, M.Moráček, J.Kusák, J.Hreško Masarykova univerzita Fakulta informatiky 6.5.2010 Klasifikace
Analýza postranních kanálů (kryptoanalýza hardvérových zařízení) J.Breier, M.Vančo, J.Ďaďo, M.Klement, J.Michelfeit, M.Moráček, J.Kusák, J.Hreško Masarykova univerzita Fakulta informatiky 6.5.2010 Klasifikace
Protiopatření eliminující proudovou analýzu
 SIX Research Centre Vysoké učení technické v Brně martinasek@feec.vutbr.cz crypto.utko.feec.vutbr.cz Proudová analýza (PA) V dnešní době představuje efektivní a úspěšný způsob útoku cílený na bezpečné
SIX Research Centre Vysoké učení technické v Brně martinasek@feec.vutbr.cz crypto.utko.feec.vutbr.cz Proudová analýza (PA) V dnešní době představuje efektivní a úspěšný způsob útoku cílený na bezpečné
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKACNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKACNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
PA159 - Bezpečnostní aspekty
 PA159 - Bezpečnostní aspekty 19. 10. 2007 Formulace oblasti Kryptografie (v moderním slova smyslu) se snaží minimalizovat škodu, kterou může způsobit nečestný účastník Oblast bezpečnosti počítačových sítí
PA159 - Bezpečnostní aspekty 19. 10. 2007 Formulace oblasti Kryptografie (v moderním slova smyslu) se snaží minimalizovat škodu, kterou může způsobit nečestný účastník Oblast bezpečnosti počítačových sítí
Bezpečnostní mechanismy
 Hardwarové prostředky kontroly přístupu osob Bezpečnostní mechanismy Identifikační karty informace umožňující identifikaci uživatele PIN Personal Identification Number úroveň oprávnění informace o povolených
Hardwarové prostředky kontroly přístupu osob Bezpečnostní mechanismy Identifikační karty informace umožňující identifikaci uživatele PIN Personal Identification Number úroveň oprávnění informace o povolených
Sběrnicová struktura PC Procesory PC funkce, vlastnosti Interní počítačové paměti PC
 Informační systémy 2 Obsah: Sběrnicová struktura PC Procesory PC funkce, vlastnosti Interní počítačové paměti PC ROM RAM Paměti typu CACHE IS2-4 1 Dnešní info: Informační systémy 2 03 Informační systémy
Informační systémy 2 Obsah: Sběrnicová struktura PC Procesory PC funkce, vlastnosti Interní počítačové paměti PC ROM RAM Paměti typu CACHE IS2-4 1 Dnešní info: Informační systémy 2 03 Informační systémy
Moderní metody substitučního šifrování
 PEF MZLU v Brně 11. listopadu 2010 Úvod V současné době se pro bezpečnou komunikaci používají elektronická média. Zprávy se před šifrováním převádí do tvaru zpracovatelného technickým vybavením, do binární
PEF MZLU v Brně 11. listopadu 2010 Úvod V současné době se pro bezpečnou komunikaci používají elektronická média. Zprávy se před šifrováním převádí do tvaru zpracovatelného technickým vybavením, do binární
Procesor. Hardware - komponenty počítačů Procesory
 Procesor Jedna z nejdůležitějších součástek počítače = mozek počítače, bez něhož není počítač schopen vykonávat žádné operace. Procesor v počítači plní funkci centrální jednotky (CPU - Central Processing
Procesor Jedna z nejdůležitějších součástek počítače = mozek počítače, bez něhož není počítač schopen vykonávat žádné operace. Procesor v počítači plní funkci centrální jednotky (CPU - Central Processing
Informatika / bezpečnost
 Informatika / bezpečnost Bezpečnost, šifry, elektronický podpis ZS 2015 KIT.PEF.CZU Bezpečnost IS pojmy aktiva IS hardware software data citlivá data hlavně ta chceme chránit autorizace subjekt má právo
Informatika / bezpečnost Bezpečnost, šifry, elektronický podpis ZS 2015 KIT.PEF.CZU Bezpečnost IS pojmy aktiva IS hardware software data citlivá data hlavně ta chceme chránit autorizace subjekt má právo
U Úvod do modelování a simulace systémů
 U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
Parametry ovlivňující proudovou analýzu mikroprocesoru vykonávajícího funkci AddRoundKey
 Rok / Year: Svazek / Volume: Číslo / Number: 211 13 5 Parametry ovlivňující proudovou analýzu mikroprocesoru vykonávajícího funkci AddRoundKey Parameters affecting the current analysis of the microprocessor
Rok / Year: Svazek / Volume: Číslo / Number: 211 13 5 Parametry ovlivňující proudovou analýzu mikroprocesoru vykonávajícího funkci AddRoundKey Parameters affecting the current analysis of the microprocessor
PSK2-16. Šifrování a elektronický podpis I
 PSK2-16 Název školy: Autor: Anotace: Vzdělávací oblast: Předmět: Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 Ing. Marek Nožka Jak funguje asymetrická šifra a elektronický podpis Informační
PSK2-16 Název školy: Autor: Anotace: Vzdělávací oblast: Předmět: Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 Ing. Marek Nožka Jak funguje asymetrická šifra a elektronický podpis Informační
 Šifrování Kafková Petra Kryptografie Věda o tvorbě šifer (z řečtiny: kryptós = skrytý, gráphein = psát) Kryptoanalýza Věda o prolamování/luštění šifer Kryptologie Věda o šifrování obecné označení pro kryptografii
Šifrování Kafková Petra Kryptografie Věda o tvorbě šifer (z řečtiny: kryptós = skrytý, gráphein = psát) Kryptoanalýza Věda o prolamování/luštění šifer Kryptologie Věda o šifrování obecné označení pro kryptografii
Témata profilové maturitní zkoušky
 Obor: 18-20-M/01 Informační technologie Předmět: Databázové systémy Forma: praktická 1. Datový model. 2. Dotazovací jazyk SQL. 3. Aplikační logika v PL/SQL. 4. Webová aplikace. Obor vzdělání: 18-20-M/01
Obor: 18-20-M/01 Informační technologie Předmět: Databázové systémy Forma: praktická 1. Datový model. 2. Dotazovací jazyk SQL. 3. Aplikační logika v PL/SQL. 4. Webová aplikace. Obor vzdělání: 18-20-M/01
CO JE KRYPTOGRAFIE Šifrovací algoritmy Kódovací algoritmus Prolomení algoritmu
 KRYPTOGRAFIE CO JE KRYPTOGRAFIE Kryptografie je matematický vědní obor, který se zabývá šifrovacími a kódovacími algoritmy. Dělí se na dvě skupiny návrh kryptografických algoritmů a kryptoanalýzu, která
KRYPTOGRAFIE CO JE KRYPTOGRAFIE Kryptografie je matematický vědní obor, který se zabývá šifrovacími a kódovacími algoritmy. Dělí se na dvě skupiny návrh kryptografických algoritmů a kryptoanalýzu, která
2.8 Procesory. Střední průmyslová škola strojnická Vsetín. Ing. Martin Baričák. Název šablony Název DUMu. Předmět Druh učebního materiálu
 Název školy Číslo projektu Autor Název šablony Název DUMu Tematická oblast Předmět Druh učebního materiálu Anotace Vybavení, pomůcky Ověřeno ve výuce dne, třída Střední průmyslová škola strojnická Vsetín
Název školy Číslo projektu Autor Název šablony Název DUMu Tematická oblast Předmět Druh učebního materiálu Anotace Vybavení, pomůcky Ověřeno ve výuce dne, třída Střední průmyslová škola strojnická Vsetín
Gymnázium Vysoké Mýto nám. Vaňorného 163, Vysoké Mýto
 Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Petr
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Petr
Středoškolská technika SCI-Lab
 Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT SCI-Lab Kamil Mudruňka Gymnázium Dašická 1083 Dašická 1083, Pardubice O projektu SCI-Lab je program napsaný v jazyce
Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT SCI-Lab Kamil Mudruňka Gymnázium Dašická 1083 Dašická 1083, Pardubice O projektu SCI-Lab je program napsaný v jazyce
Šifrová ochrana informací věk počítačů PS5-2
 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací věk počítačů PS5-2 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
VŠFS; Aplikovaná informatika; SW systémy 2005/2006 1 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací věk počítačů PS5-2 VŠFS; Aplikovaná informatika; SW systémy 2005/2006 2 Osnova
AGP - Accelerated Graphics Port
 AGP - Accelerated Graphics Port Grafiku 3D a video bylo možné v jisté vývojové etapě techniky pracovních stanic provozovat pouze na kvalitních pracovních stanicích (cena 20 000 USD a více) - AGP představuje
AGP - Accelerated Graphics Port Grafiku 3D a video bylo možné v jisté vývojové etapě techniky pracovních stanic provozovat pouze na kvalitních pracovních stanicích (cena 20 000 USD a více) - AGP představuje
UKRY - Symetrické blokové šifry
 UKRY - Symetrické blokové šifry Martin Franěk (frankiesek@gmail.com) Fakulta jaderná a fyzikálně inženýrská, ČVUT Praha 18. 3. 2013 Obsah 1 Typy šifer Typy šifer 2 Operační mody Operační mody 3 Přiklady
UKRY - Symetrické blokové šifry Martin Franěk (frankiesek@gmail.com) Fakulta jaderná a fyzikálně inženýrská, ČVUT Praha 18. 3. 2013 Obsah 1 Typy šifer Typy šifer 2 Operační mody Operační mody 3 Přiklady
INFORMAČNÍ A KOMUNIKAČNÍ TECHNOLOGIE
 Název školy: Střední odborná škola stavební Karlovy Vary Sabinovo náměstí 16, 360 09 Karlovy Vary Autor: Ing. Hana Šmídová Název materiálu: VY_32_INOVACE_13_HARDWARE_S1 Číslo projektu: CZ 1.07/1.5.00/34.1077
Název školy: Střední odborná škola stavební Karlovy Vary Sabinovo náměstí 16, 360 09 Karlovy Vary Autor: Ing. Hana Šmídová Název materiálu: VY_32_INOVACE_13_HARDWARE_S1 Číslo projektu: CZ 1.07/1.5.00/34.1077
I/O modul VersaPoint. Analogový výstupní modul, 16 bitový, napětí, 1 kanál IC220ALG321. Specifikace modulu. Spotřeba. Vlastnosti. Údaje pro objednávku
 Analogový výstupní modul, 16 bitový, napětí, 1 kanál Modul slouží pro výstup analogových napěťových signálů. Tyto signály jsou k dispozici v 16 bitovém rozlišení. Specifikace modulu Rozměry pouzdra (šířka
Analogový výstupní modul, 16 bitový, napětí, 1 kanál Modul slouží pro výstup analogových napěťových signálů. Tyto signály jsou k dispozici v 16 bitovém rozlišení. Specifikace modulu Rozměry pouzdra (šířka
Symetrické šifry, DES
 Symetrické šifry, DES Jiří Vejrosta Fakulta jaderná a fyzikálně inženýrská, ČVUT Jiří Vejrosta (FJFI) UKRY 1 / 20 Klíče Symetrická šifra tajný klíč klíč stejný u odesilatele i příjemce Asymetrická šifra
Symetrické šifry, DES Jiří Vejrosta Fakulta jaderná a fyzikálně inženýrská, ČVUT Jiří Vejrosta (FJFI) UKRY 1 / 20 Klíče Symetrická šifra tajný klíč klíč stejný u odesilatele i příjemce Asymetrická šifra
ELT1 - Přednáška č. 6
 ELT1 - Přednáška č. 6 Elektrotechnická terminologie a odborné výrazy, měřicí jednotky a činitelé, které je ovlivňují. Rozdíl potenciálů, elektromotorická síla, napětí, el. napětí, proud, odpor, vodivost,
ELT1 - Přednáška č. 6 Elektrotechnická terminologie a odborné výrazy, měřicí jednotky a činitelé, které je ovlivňují. Rozdíl potenciálů, elektromotorická síla, napětí, el. napětí, proud, odpor, vodivost,
Šifrová ochrana informací věk počítačů PS5-2
 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací věk počítačů PS5-2 1 Osnova šifrová ochrana využívající výpočetní techniku např. Feistelova šifra; symetrické a asymetrické šifry;
Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací věk počítačů PS5-2 1 Osnova šifrová ochrana využívající výpočetní techniku např. Feistelova šifra; symetrické a asymetrické šifry;
Profilová část maturitní zkoušky 2013/2014
 Střední průmyslová škola, Přerov, Havlíčkova 2 751 52 Přerov Profilová část maturitní zkoušky 2013/2014 TEMATICKÉ OKRUHY A HODNOTÍCÍ KRITÉRIA Studijní obor: 78-42-M/01 Technické lyceum Předmět: TECHNIKA
Střední průmyslová škola, Přerov, Havlíčkova 2 751 52 Přerov Profilová část maturitní zkoušky 2013/2014 TEMATICKÉ OKRUHY A HODNOTÍCÍ KRITÉRIA Studijní obor: 78-42-M/01 Technické lyceum Předmět: TECHNIKA
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto
 Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Jana Kubcová Název
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Jana Kubcová Název
Základní pojmy. Program: Algoritmus zapsaný v programovacím jazyce, který řeší nějaký konkrétní úkol. Jedná se o posloupnost instrukcí.
 Základní pojmy IT, číselné soustavy, logické funkce Základní pojmy Počítač: Stroj na zpracování informací Informace: 1. data, která se strojově zpracovávají 2. vše co nám nebo něčemu podává (popř. předává)
Základní pojmy IT, číselné soustavy, logické funkce Základní pojmy Počítač: Stroj na zpracování informací Informace: 1. data, která se strojově zpracovávají 2. vše co nám nebo něčemu podává (popř. předává)
Pohled do nitra mikroprocesoru Josef Horálek
 Pohled do nitra mikroprocesoru Josef Horálek Z čeho vycházíme = Vycházíme z Von Neumannovy architektury = Celý počítač se tak skládá z pěti koncepčních bloků: = Operační paměť = Programový řadič = Aritmeticko-logická
Pohled do nitra mikroprocesoru Josef Horálek Z čeho vycházíme = Vycházíme z Von Neumannovy architektury = Celý počítač se tak skládá z pěti koncepčních bloků: = Operační paměť = Programový řadič = Aritmeticko-logická
Charakteristiky optoelektronických součástek
 FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Spolupracoval Jan Floryček Jméno a příjmení Jakub Dvořák Ročník 1 Měřeno dne Předn.sk.-Obor BIA 27.2.2007 Stud.skup. 13 Odevzdáno dne Příprava Opravy Učitel
FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Spolupracoval Jan Floryček Jméno a příjmení Jakub Dvořák Ročník 1 Měřeno dne Předn.sk.-Obor BIA 27.2.2007 Stud.skup. 13 Odevzdáno dne Příprava Opravy Učitel
Algoritmizace diskrétních. Ing. Michal Dorda, Ph.D.
 Algoritmizace diskrétních simulačních modelů Ing. Michal Dorda, Ph.D. 1 Úvodní poznámky Při programování simulačních modelů lze hlavní dílčí problémy shrnout do následujících bodů: 1) Zachycení statických
Algoritmizace diskrétních simulačních modelů Ing. Michal Dorda, Ph.D. 1 Úvodní poznámky Při programování simulačních modelů lze hlavní dílčí problémy shrnout do následujících bodů: 1) Zachycení statických
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ MODERNÍ KRYPTOANALÝZA DIPLOMOVÁ PRÁCE FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
3. Maturitní otázka PC komponenty 1. Počítačová skříň 2. Základní deska
 3. Maturitní otázka Počítač, jeho komponenty a periferní zařízení (principy fungování, digitální záznam informací, propojení počítače s dalšími (digitálními) zařízeními) Počítač je elektronické zařízení,
3. Maturitní otázka Počítač, jeho komponenty a periferní zařízení (principy fungování, digitální záznam informací, propojení počítače s dalšími (digitálními) zařízeními) Počítač je elektronické zařízení,
5. Umělé neuronové sítě. Neuronové sítě
 Neuronové sítě Přesný algoritmus práce přírodních neuronových systémů není doposud znám. Přesto experimentální výsledky na modelech těchto systémů dávají dnes velmi slibné výsledky. Tyto systémy, včetně
Neuronové sítě Přesný algoritmus práce přírodních neuronových systémů není doposud znám. Přesto experimentální výsledky na modelech těchto systémů dávají dnes velmi slibné výsledky. Tyto systémy, včetně
Paměti Josef Horálek
 Paměti Josef Horálek Paměť = Paměť je pro počítač životní nutností = mikroprocesor z ní čte programy, kterými je řízen a také do ní ukládá výsledky své práce = Paměti v zásadě můžeme rozdělit na: = Primární
Paměti Josef Horálek Paměť = Paměť je pro počítač životní nutností = mikroprocesor z ní čte programy, kterými je řízen a také do ní ukládá výsledky své práce = Paměti v zásadě můžeme rozdělit na: = Primární
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
Kryptografie, elektronický podpis. Ing. Miloslav Hub, Ph.D. 27. listopadu 2007
 Kryptografie, elektronický podpis Ing. Miloslav Hub, Ph.D. 27. listopadu 2007 Kryptologie Kryptologie věda o šifrování, dělí se: Kryptografie nauka o metodách utajování smyslu zpráv převodem do podoby,
Kryptografie, elektronický podpis Ing. Miloslav Hub, Ph.D. 27. listopadu 2007 Kryptologie Kryptologie věda o šifrování, dělí se: Kryptografie nauka o metodách utajování smyslu zpráv převodem do podoby,
Obvodové prvky a jejich
 Obvodové prvky a jejich parametry Ing. Martin Černík, Ph.D. Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace. Elektrický obvod Uspořádaný systém elektrických prvků a vodičů sloužící
Obvodové prvky a jejich parametry Ing. Martin Černík, Ph.D. Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace. Elektrický obvod Uspořádaný systém elektrických prvků a vodičů sloužící
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ Ing. Zdeněk Martinásek KRYPTOANALÝZA POSTRANNÍMI KANÁLY SIDE CHANNEL CRYPTANALYSIS ZKRÁCENÁ VERZE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ Ing. Zdeněk Martinásek KRYPTOANALÝZA POSTRANNÍMI KANÁLY SIDE CHANNEL CRYPTANALYSIS ZKRÁCENÁ VERZE
Odolnost kryptografického HW s ohledem na nasazení
 Odolnost kryptografického HW s ohledem na nasazení Vašek Lorenc, Vašek Matyáš XVIII. konference EurOpen Fakulta informatiky Masarykova univerzita Brno Vašek Lorenc, Vašek Matyáš (FIMU) Odolnost kryptografického
Odolnost kryptografického HW s ohledem na nasazení Vašek Lorenc, Vašek Matyáš XVIII. konference EurOpen Fakulta informatiky Masarykova univerzita Brno Vašek Lorenc, Vašek Matyáš (FIMU) Odolnost kryptografického
Princip funkce počítače
 Princip funkce počítače Princip funkce počítače prvotní úlohou počítačů bylo zrychlit provádění matematických výpočtů první počítače kopírovaly obvyklý postup manuálního provádění výpočtů pokyny pro zpracování
Princip funkce počítače Princip funkce počítače prvotní úlohou počítačů bylo zrychlit provádění matematických výpočtů první počítače kopírovaly obvyklý postup manuálního provádění výpočtů pokyny pro zpracování
Základní pojmy informačních technologií
 Základní pojmy informačních technologií Informační technologie (IT): technologie sloužící k práci s daty a informacemi počítače, programy, počítač. sítě Hardware (HW): jednoduše to, na co si můžeme sáhnout.
Základní pojmy informačních technologií Informační technologie (IT): technologie sloužící k práci s daty a informacemi počítače, programy, počítač. sítě Hardware (HW): jednoduše to, na co si můžeme sáhnout.
GFK-2004-CZ Listopad Rozměry pouzdra (šířka x výška x hloubka) Připojení. Skladovací teplota -25 C až +85 C.
 Modul slouží pro výstup digitálních signálů 24 Vss. Specifikace modulu Rozměry pouzdra (šířka x výška x hloubka) Připojení 48,8 mm x 120 mm x 71,5 mm dvou-, tří- a čtyřdrátové Provozní teplota -25 C až
Modul slouží pro výstup digitálních signálů 24 Vss. Specifikace modulu Rozměry pouzdra (šířka x výška x hloubka) Připojení 48,8 mm x 120 mm x 71,5 mm dvou-, tří- a čtyřdrátové Provozní teplota -25 C až
Memristor. Úvod. Základní struktura mertistorů
 Memristor Úvod Vědcům společnosti HP (Hewlett-Packard) se skoro náhodou povedlo nanotechnologií prakticky realizovat nový typ součástky s vlastnostmi již dříve předvídaného prvku pojmenovaného jako memristor
Memristor Úvod Vědcům společnosti HP (Hewlett-Packard) se skoro náhodou povedlo nanotechnologií prakticky realizovat nový typ součástky s vlastnostmi již dříve předvídaného prvku pojmenovaného jako memristor
Témata profilové maturitní zkoušky
 Obor vzdělání: 18-20-M/01 informační technologie Předmět: programování 1. Příkazy jazyka C# 2. Datové konstrukce 3. Objektově orientované programování 4. Tvorba vlastních funkcí Obor vzdělání: 18-20-M/01
Obor vzdělání: 18-20-M/01 informační technologie Předmět: programování 1. Příkazy jazyka C# 2. Datové konstrukce 3. Objektově orientované programování 4. Tvorba vlastních funkcí Obor vzdělání: 18-20-M/01
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ PROUDOVÝ POSTRANNÍ KANÁL BAKALÁŘSKÁ PRÁCE FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TELEKOMUNIKACÍ FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF TELECOMMUNICATIONS
ISMS. Autentizace ve WiFi sítích. V Brně dne 5. a 12. prosince 2013
 ISMS Případová studie Autentizace ve WiFi sítích V Brně dne 5. a 12. prosince 2013 Pojmy Podnikové WiFi sítě Autentizace uživatelů dle standardu 802.1X Hlavní výhodou nasazení tohoto standardu je pohodlná
ISMS Případová studie Autentizace ve WiFi sítích V Brně dne 5. a 12. prosince 2013 Pojmy Podnikové WiFi sítě Autentizace uživatelů dle standardu 802.1X Hlavní výhodou nasazení tohoto standardu je pohodlná
Abychom se vyhnuli užití diferenčních sumátorů, je vhodné soustavu rovnic(5.77) upravit následujícím způsobem
 Abychom se vyhnuli užití diferenčních sumátorů, je vhodné soustavu rovnic(5.77) upravit následujícím způsobem I 1 = 1 + pl 1 (U 1 +( )), = 1 pc 2 ( I 1+( I 3 )), I 3 = pl 3 (U 3 +( )), 1 U 3 = (pc 4 +1/
Abychom se vyhnuli užití diferenčních sumátorů, je vhodné soustavu rovnic(5.77) upravit následujícím způsobem I 1 = 1 + pl 1 (U 1 +( )), = 1 pc 2 ( I 1+( I 3 )), I 3 = pl 3 (U 3 +( )), 1 U 3 = (pc 4 +1/
Rozšiřující desce s dalšími paralelními porty Rozšiřující desce s motorkem Elektrickém zapojení Principu činnosti Způsobu programování
 8. Rozšiřující deska Evb_IO a Evb_Motor Čas ke studiu: 2-3 hodiny Cíl Po prostudování tohoto odstavce budete něco vědět o Výklad Rozšiřující desce s dalšími paralelními porty Rozšiřující desce s motorkem
8. Rozšiřující deska Evb_IO a Evb_Motor Čas ke studiu: 2-3 hodiny Cíl Po prostudování tohoto odstavce budete něco vědět o Výklad Rozšiřující desce s dalšími paralelními porty Rozšiřující desce s motorkem
I/O modul VersaPoint. Analogový výstupní modul, 16 bitový, napětí/proud, 1 kanál IC220ALG320. Specifikace modulu. Spotřeba. Údaje pro objednávku
 Analogový výstupní modul, 16 bitový, napětí/proud, 1 kanál Modul slouží pro výstup analogových napěťových nebo proudových signálů. Tyto signály jsou k dispozici v 16 bitovém rozlišení. Specifikace modulu
Analogový výstupní modul, 16 bitový, napětí/proud, 1 kanál Modul slouží pro výstup analogových napěťových nebo proudových signálů. Tyto signály jsou k dispozici v 16 bitovém rozlišení. Specifikace modulu
Laboratorní úloha č. 5 Faradayovy zákony, tíhové zrychlení
 Laboratorní úloha č. 5 Faradayovy zákony, tíhové zrychlení Úkoly měření: 1. Měření na digitálním osciloskopu a přenosném dataloggeru LabQuest 2. 2. Ověřte Faradayovy zákony pomocí pádu magnetu skrz trubici
Laboratorní úloha č. 5 Faradayovy zákony, tíhové zrychlení Úkoly měření: 1. Měření na digitálním osciloskopu a přenosném dataloggeru LabQuest 2. 2. Ověřte Faradayovy zákony pomocí pádu magnetu skrz trubici
Profilová část maturitní zkoušky 2017/2018
 Střední průmyslová škola, Přerov, Havlíčkova 2 751 52 Přerov Profilová část maturitní zkoušky 2017/2018 TEMATICKÉ OKRUHY A HODNOTÍCÍ KRITÉRIA Studijní obor: 78-42-M/01 Technické lyceum Předmět: TECHNIKA
Střední průmyslová škola, Přerov, Havlíčkova 2 751 52 Přerov Profilová část maturitní zkoušky 2017/2018 TEMATICKÉ OKRUHY A HODNOTÍCÍ KRITÉRIA Studijní obor: 78-42-M/01 Technické lyceum Předmět: TECHNIKA
I. Současná analogová technika
 IAS 2010/11 1 I. Současná analogová technika Analogové obvody v moderních komunikačních systémech. Vývoj informatických technologií v poslední dekádě minulého století digitalizace, zvýšení objemu přenášených
IAS 2010/11 1 I. Současná analogová technika Analogové obvody v moderních komunikačních systémech. Vývoj informatických technologií v poslední dekádě minulého století digitalizace, zvýšení objemu přenášených
LABORATORNÍ PROTOKOL Z PŘEDMĚTU SILNOPROUDÁ ELEKTROTECHNIKA
 LABORATORNÍ PROTOKOL Z PŘEDMĚTU SILNOPROUDÁ ELEKTROTECHNIKA Transformátor Měření zatěžovací a převodní charakteristiky. Zadání. Změřte zatěžovací charakteristiku transformátoru a graficky znázorněte závislost
LABORATORNÍ PROTOKOL Z PŘEDMĚTU SILNOPROUDÁ ELEKTROTECHNIKA Transformátor Měření zatěžovací a převodní charakteristiky. Zadání. Změřte zatěžovací charakteristiku transformátoru a graficky znázorněte závislost
Magnetické vlastnosti látek (magnetik) jsou důsledkem orbitálního a rotačního pohybu elektronů. Obíhající elektrony představují elementární proudové
 MAGNETICKÉ POLE V LÁTCE, MAXWELLOVY ROVNICE MAGNETICKÉ VLASTNOSTI LÁTEK Magnetické vlastnosti látek (magnetik) jsou důsledkem orbitálního a rotačního pohybu elektronů. Obíhající elektrony představují elementární
MAGNETICKÉ POLE V LÁTCE, MAXWELLOVY ROVNICE MAGNETICKÉ VLASTNOSTI LÁTEK Magnetické vlastnosti látek (magnetik) jsou důsledkem orbitálního a rotačního pohybu elektronů. Obíhající elektrony představují elementární
(2) Zásady bezpečnostní politiky jsou rozpracovány v návrhu bezpečnosti informačního systému
 Strana 5882 Sbírka zákonů č. 453 / 2011 Částka 155 453 VYHLÁŠKA ze dne 21. prosince 2011, kterou se mění vyhláška č. 523/2005 Sb., o bezpečnosti informačních a komunikačních systémů a dalších elektronických
Strana 5882 Sbírka zákonů č. 453 / 2011 Částka 155 453 VYHLÁŠKA ze dne 21. prosince 2011, kterou se mění vyhláška č. 523/2005 Sb., o bezpečnosti informačních a komunikačních systémů a dalších elektronických
OPS Paralelní systémy, seznam pojmů, klasifikace
 Moorův zákon (polovina 60. let) : Výpočetní výkon a počet tranzistorů na jeden CPU chip integrovaného obvodu mikroprocesoru se každý jeden až dva roky zdvojnásobí; cena se zmenší na polovinu. Paralelismus
Moorův zákon (polovina 60. let) : Výpočetní výkon a počet tranzistorů na jeden CPU chip integrovaného obvodu mikroprocesoru se každý jeden až dva roky zdvojnásobí; cena se zmenší na polovinu. Paralelismus
VÝUKOVÝ MATERIÁL. 3. ročník učebního oboru Elektrikář Přílohy. bez příloh. Identifikační údaje školy
 VÝUKOVÝ MATERIÁL Identifikační údaje školy Číslo projektu Název projektu Číslo a název šablony Autor Tematická oblast Číslo a název materiálu Anotace Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková
VÝUKOVÝ MATERIÁL Identifikační údaje školy Číslo projektu Název projektu Číslo a název šablony Autor Tematická oblast Číslo a název materiálu Anotace Vyšší odborná škola a Střední škola, Varnsdorf, příspěvková
Přípravek pro demonstraci řízení pohonu MAXON prostřednictvím
 Přípravek pro demonstraci řízení pohonu MAXON prostřednictvím karty Humusoft MF624. (Jan Babjak) Popis přípravku Pro potřeby výuky na katedře robototechniky byl vyvinut přípravek umožňující řízení pohonu
Přípravek pro demonstraci řízení pohonu MAXON prostřednictvím karty Humusoft MF624. (Jan Babjak) Popis přípravku Pro potřeby výuky na katedře robototechniky byl vyvinut přípravek umožňující řízení pohonu
Měřená veličina. Rušení vyzařováním: magnetická složka (9kHz 150kHz), magnetická a elektrická složka (150kHz 30MHz) Rušivé elektromagnetické pole
 13. VYSOKOFREKVENČNÍ RUŠENÍ 13.1. Klasifikace vysokofrekvenčního rušení Definice vysokofrekvenčního rušení: od 10 khz do 400 GHz Zdroje: prakticky všechny zdroje rušení Rozdělení: rušení šířené vedením
13. VYSOKOFREKVENČNÍ RUŠENÍ 13.1. Klasifikace vysokofrekvenčního rušení Definice vysokofrekvenčního rušení: od 10 khz do 400 GHz Zdroje: prakticky všechny zdroje rušení Rozdělení: rušení šířené vedením
Přenos signálů, výstupy snímačů
 Přenos signálů, výstupy snímačů Topologie zařízení, typy průmyslových sběrnic, výstupní signály snímačů Přenosy signálů informací Topologie Dle rozmístění ŘS Distribuované řízení Většinou velká zařízení
Přenos signálů, výstupy snímačů Topologie zařízení, typy průmyslových sběrnic, výstupní signály snímačů Přenosy signálů informací Topologie Dle rozmístění ŘS Distribuované řízení Většinou velká zařízení
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 1. Základní informace o této fyzikální veličině Symbol vlastní indukčnosti je L, základní jednotka henry, symbol
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 1. Základní informace o této fyzikální veličině Symbol vlastní indukčnosti je L, základní jednotka henry, symbol
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto
 Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Petr
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Petr
GFK-1913-CZ Prosinec 2001. Rozměry pouzdra (šířka x výška x hloubka) Připojení. Skladovací teplota -25 C až +85 C.
 Modul slouží pro výstup digitálních signálů 24 Vss. Specifikace modulu Rozměry pouzdra (šířka x výška x hloubka) Připojení 48,8 mm x 120 mm x 71,5 mm dvou- a třídrátové Provozní teplota -25 C až +55 C
Modul slouží pro výstup digitálních signálů 24 Vss. Specifikace modulu Rozměry pouzdra (šířka x výška x hloubka) Připojení 48,8 mm x 120 mm x 71,5 mm dvou- a třídrátové Provozní teplota -25 C až +55 C
Popis obvodu U2403B. Funkce integrovaného obvodu U2403B
 ASICentrum s.r.o. Novodvorská 994, 142 21 Praha 4 Tel. (02) 4404 3478, Fax: (02) 472 2164, E-mail: info@asicentrum.cz ========== ========= ======== ======= ====== ===== ==== === == = Popis obvodu U2403B
ASICentrum s.r.o. Novodvorská 994, 142 21 Praha 4 Tel. (02) 4404 3478, Fax: (02) 472 2164, E-mail: info@asicentrum.cz ========== ========= ======== ======= ====== ===== ==== === == = Popis obvodu U2403B
8. RSA, kryptografie s veřejným klíčem. doc. Ing. Róbert Lórencz, CSc.
 Bezpečnost 8. RSA, kryptografie s veřejným klíčem doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních programů
Bezpečnost 8. RSA, kryptografie s veřejným klíčem doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních programů
Integrovaná střední škola, Sokolnice 496
 Integrovaná střední škola, Sokolnice 496 Název projektu: Moderní škola Registrační číslo: CZ.1.07/1.5.00/34.0467 Název klíčové aktivity: III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT Kód výstupu:
Integrovaná střední škola, Sokolnice 496 Název projektu: Moderní škola Registrační číslo: CZ.1.07/1.5.00/34.0467 Název klíčové aktivity: III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT Kód výstupu:
Kerchhoffův princip Utajení šifrovacího algoritmu nesmí sloužit jako opatření nahrazující nebo garantující kvalitu šifrovacího systému
 Základní cíle informační bezpečnosti Autentikace Autorizace Nepopiratelnost Integrita Utajení Shannonův model kryptosystému Kerchhoffův princip Utajení šifrovacího algoritmu nesmí sloužit jako opatření
Základní cíle informační bezpečnosti Autentikace Autorizace Nepopiratelnost Integrita Utajení Shannonův model kryptosystému Kerchhoffův princip Utajení šifrovacího algoritmu nesmí sloužit jako opatření
Základy elektrotechniky
 Základy elektrotechniky Přednáška Tranzistory 1 BIPOLÁRNÍ TRANZISTOR - třívrstvá struktura NPN se třemi vývody (elektrodami): e - emitor k - kolektor b - báze Struktura, náhradní schéma a schematická značka
Základy elektrotechniky Přednáška Tranzistory 1 BIPOLÁRNÍ TRANZISTOR - třívrstvá struktura NPN se třemi vývody (elektrodami): e - emitor k - kolektor b - báze Struktura, náhradní schéma a schematická značka
Teorie měření a regulace
 Ústav technologie, mechanizace a řízení staveb CW01 Teorie měření a regulace Praxe názvy 1. ZS 2015/2016 2015 - Ing. Václav Rada, CSc. OBECNÝ ÚVOD - praxe Elektrotechnická měření mohou probíhat pouze při
Ústav technologie, mechanizace a řízení staveb CW01 Teorie měření a regulace Praxe názvy 1. ZS 2015/2016 2015 - Ing. Václav Rada, CSc. OBECNÝ ÚVOD - praxe Elektrotechnická měření mohou probíhat pouze při
GFK-2005-CZ Prosinec Rozměry pouzdra (šířka x výška x hloubka) Připojení. Provozní teplota -25 C až +55 C. Skladovací teplota -25 C až +85 C
 Výstup 24 Vss, negativní logika, 0,5 A, 2 body Modul slouží pro výstup digitálních signálů 24 Vss. Specifikace modulu Rozměry pouzdra (šířka x výška x hloubka) Připojení 12,2 mm x 120 mm x 71,5 mm dvou-,
Výstup 24 Vss, negativní logika, 0,5 A, 2 body Modul slouží pro výstup digitálních signálů 24 Vss. Specifikace modulu Rozměry pouzdra (šířka x výška x hloubka) Připojení 12,2 mm x 120 mm x 71,5 mm dvou-,
Nelineární obvody. V nelineárních obvodech však platí Kirchhoffovy zákony.
 Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
O čem byl CHES a FDTC? Jan Krhovják Fakulta informatiky Masarykova univerzita v Brně
 O čem byl CHES a FDTC? Jan Krhovják Fakulta informatiky Masarykova univerzita v Brně Hlavní témata workshopů Cryptographic Hardware and Embedded Systems Speciální hardware Efektivní hardware Nedostatek
O čem byl CHES a FDTC? Jan Krhovják Fakulta informatiky Masarykova univerzita v Brně Hlavní témata workshopů Cryptographic Hardware and Embedded Systems Speciální hardware Efektivní hardware Nedostatek
Struktura a architektura počítačů (BI-SAP) 10
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Struktura a architektura počítačů (BI-SAP) 10 doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta informačních technologii
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Struktura a architektura počítačů (BI-SAP) 10 doc. Ing. Hana Kubátová, CSc. Katedra číslicového návrhu Fakulta informačních technologii
T-DIDACTIC. Motorová skupina Funkční generátor Modul Simatic S7-200 Modul Simatic S7-300 Třífázová soustava
 Popis produktu Systém T-DIDACTIC představuje vysoce sofistikovaný systém pro výuku elektroniky, automatizace, číslicové a měřící techniky, popř. dalších elektrotechnických oborů na středních a vysokých
Popis produktu Systém T-DIDACTIC představuje vysoce sofistikovaný systém pro výuku elektroniky, automatizace, číslicové a měřící techniky, popř. dalších elektrotechnických oborů na středních a vysokých
Úvod do modelování a simulace. Ing. Michal Dorda, Ph.D.
 Úvod do modelování a simulace systémů Ing. Michal Dorda, Ph.D. 1 Základní pojmy Systém systémem rozumíme množinu prvků (příznaků) a vazeb (relací) mezi nimi, která jako celek má určité vlastnosti. Množinu
Úvod do modelování a simulace systémů Ing. Michal Dorda, Ph.D. 1 Základní pojmy Systém systémem rozumíme množinu prvků (příznaků) a vazeb (relací) mezi nimi, která jako celek má určité vlastnosti. Množinu
AD4RS. měřící převodník. 4x vstup pro měření unifikovaného signálu 0 10 V, 0 20 ma, 4 20 ma. komunikace linkami RS232 nebo RS485
 měřící převodník 4x vstup pro měření unifikovaného signálu 0 10 V, 0 20 ma, 4 20 ma komunikace linkami RS232 nebo RS485. Katalogový list Vytvořen: 4.5.2007 Poslední aktualizace: 15.6 2009 09:58 Počet stran:
měřící převodník 4x vstup pro měření unifikovaného signálu 0 10 V, 0 20 ma, 4 20 ma komunikace linkami RS232 nebo RS485. Katalogový list Vytvořen: 4.5.2007 Poslední aktualizace: 15.6 2009 09:58 Počet stran:
popsat princip činnosti základních zapojení čidel napětí a proudu samostatně změřit zadanou úlohu
 9. Čidla napětí a proudu Čas ke studiu: 15 minut Cíl Po prostudování tohoto odstavce budete umět popsat princip činnosti základních zapojení čidel napětí a proudu samostatně změřit zadanou úlohu Výklad
9. Čidla napětí a proudu Čas ke studiu: 15 minut Cíl Po prostudování tohoto odstavce budete umět popsat princip činnosti základních zapojení čidel napětí a proudu samostatně změřit zadanou úlohu Výklad
u = = B. l = B. l. v [V; T, m, m. s -1 ]
![u = = B. l = B. l. v [V; T, m, m. s -1 ] u = = B. l = B. l. v [V; T, m, m. s -1 ]](/thumbs/51/28180013.jpg) 5. Elektromagnetická indukce je děj, kdy ve vodiči, který se pohybuje v magnetickém poli a protíná magnetické, indukční čáry, vzniká elektrické napětí. Vodič se stává zdrojem a je to nejrozšířenější způsob
5. Elektromagnetická indukce je děj, kdy ve vodiči, který se pohybuje v magnetickém poli a protíná magnetické, indukční čáry, vzniká elektrické napětí. Vodič se stává zdrojem a je to nejrozšířenější způsob
11. Logické analyzátory. 12. Metodika měření s logickým analyzátorem
 +P12 11. Logické analyzátory Základní srovnání logického analyzátoru a číslicového osciloskopu Logický analyzátor blokové schéma, princip funkce Časová analýza, glitch mód a transitional timing, chyba
+P12 11. Logické analyzátory Základní srovnání logického analyzátoru a číslicového osciloskopu Logický analyzátor blokové schéma, princip funkce Časová analýza, glitch mód a transitional timing, chyba
Protokol TELNET. Schéma funkčních modulů komunikace protokolem TELNET. Telnet klient. login shell. Telnet server TCP/IP TCP/IP.
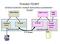 Protokol TELNET Schéma funkčních modulů komunikace protokolem TELNET Telnet klient Telnet server login shell terminal driver Operační systém TCP/IP TCP spojení TCP/IP Pseudo terminal driver Operační systém
Protokol TELNET Schéma funkčních modulů komunikace protokolem TELNET Telnet klient Telnet server login shell terminal driver Operační systém TCP/IP TCP spojení TCP/IP Pseudo terminal driver Operační systém
Software pro vzdálenou laboratoř
 Software pro vzdálenou laboratoř Autor: Vladimír Hamada, Petr Sadovský Typ: Software Rok: 2012 Samostatnou část vzdálených laboratoří tvoří programové vybavené, které je oživuje HW část vzdáleného experimentu
Software pro vzdálenou laboratoř Autor: Vladimír Hamada, Petr Sadovský Typ: Software Rok: 2012 Samostatnou část vzdálených laboratoří tvoří programové vybavené, které je oživuje HW část vzdáleného experimentu
Číselné vyjádření hodnoty. Kolik váží hrouda zlata?
 Čísla a logika Číselné vyjádření hodnoty Au Kolik váží hrouda zlata? Dekadické vážení Když přidám osmé závaží g, váha se převáží => závaží zase odeberu a začnu přidávat závaží x menší 7 závaží g 2 závaží
Čísla a logika Číselné vyjádření hodnoty Au Kolik váží hrouda zlata? Dekadické vážení Když přidám osmé závaží g, váha se převáží => závaží zase odeberu a začnu přidávat závaží x menší 7 závaží g 2 závaží
Voltmetr SC5-IA1. Obr. 1 Voltmetr SC5-IA1
 SC5-IA1 Stručná charakteristika: SC5-IA1 patří do kategorie PERUSB periferií systému SensorFor. Tyto moduly se vyznačují širokou variabilitou použití a to zejména díky své kompatibilitě s nejrůznějšími
SC5-IA1 Stručná charakteristika: SC5-IA1 patří do kategorie PERUSB periferií systému SensorFor. Tyto moduly se vyznačují širokou variabilitou použití a to zejména díky své kompatibilitě s nejrůznějšími
SIM karty a bezpečnost v mobilních sítích
 Spojujeme software, technologie a služby SIM karty a bezpečnost v mobilních sítích Václav Lín programátor 19.5.2009 1 Osnova SIM karty Role SIM karet v telekomunikacích Hardwarové charakteristiky Bezpečnost
Spojujeme software, technologie a služby SIM karty a bezpečnost v mobilních sítích Václav Lín programátor 19.5.2009 1 Osnova SIM karty Role SIM karet v telekomunikacích Hardwarové charakteristiky Bezpečnost
FVZ K13138-TACR-V004-G-TRIGGER_BOX
 TriggerBox Souhrn hlavních funkcí Synchronizace přes Ethernetový protokol IEEE 1588 v2 PTP Automatické určení možnosti, zda SyncCore zastává roli PTP master nebo PTP slave dle mechanizmů standardu PTP
TriggerBox Souhrn hlavních funkcí Synchronizace přes Ethernetový protokol IEEE 1588 v2 PTP Automatické určení možnosti, zda SyncCore zastává roli PTP master nebo PTP slave dle mechanizmů standardu PTP
MĚŘENÍ HRADLA 1. ZADÁNÍ: 2. POPIS MĚŘENÉHO PŘEDMĚTU: 3. TEORETICKÝ ROZBOR. Poslední změna
 MĚŘENÍ HRADLA Poslední změna 23.10.2016 1. ZADÁNÍ: a) Vykompenzujte sondy potřebné pro připojení k osciloskopu b) Odpojte vstupy hradla 1 na přípravku a nastavte potřebný vstupní signál (Umax, Umin, offset,
MĚŘENÍ HRADLA Poslední změna 23.10.2016 1. ZADÁNÍ: a) Vykompenzujte sondy potřebné pro připojení k osciloskopu b) Odpojte vstupy hradla 1 na přípravku a nastavte potřebný vstupní signál (Umax, Umin, offset,
Kvantová informatika pro komunikace v budoucnosti
 Kvantová informatika pro komunikace v budoucnosti Antonín Černoch Regionální centrum pokročilých technologií a materiálů Společná laboratoř optiky University Palackého a Fyzikálního ústavu Akademie věd
Kvantová informatika pro komunikace v budoucnosti Antonín Černoch Regionální centrum pokročilých technologií a materiálů Společná laboratoř optiky University Palackého a Fyzikálního ústavu Akademie věd
Vrstvy periferních rozhraní
 Vrstvy periferních rozhraní Cíl přednášky Prezentovat, jak postupovat při analýze konkrétního rozhraní. Vysvětlit pojem vrstvy periferních rozhraní. Ukázat způsob využití tohoto pojmu na rozhraní RS 232.
Vrstvy periferních rozhraní Cíl přednášky Prezentovat, jak postupovat při analýze konkrétního rozhraní. Vysvětlit pojem vrstvy periferních rozhraní. Ukázat způsob využití tohoto pojmu na rozhraní RS 232.
Řízení IO přenosů DMA řadičem
 Řízení IO přenosů DMA řadičem Doplňující text pro POT K. D. 2001 DMA řadič Při přímém řízení IO operací procesorem i při použití přerušovacího systému je rychlost přenosu dat mezi IO řadičem a pamětí limitována
Řízení IO přenosů DMA řadičem Doplňující text pro POT K. D. 2001 DMA řadič Při přímém řízení IO operací procesorem i při použití přerušovacího systému je rychlost přenosu dat mezi IO řadičem a pamětí limitována
Základy šifrování a kódování
 Materiál byl vytvořen v rámci projektu Nové výzvy, nové příležitosti, nová škola Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky Základy šifrování a kódování
Materiál byl vytvořen v rámci projektu Nové výzvy, nové příležitosti, nová škola Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky Základy šifrování a kódování
Historie počítačů. 0.generace. (prototypy)
 Historie počítačů Historie počítačů se dělí do tzv. generací, kde každá generace je charakteristická svou konfigurací, rychlostí počítače a základním stavebním prvkem. Generace počítačů: Generace Rok Konfigurace
Historie počítačů Historie počítačů se dělí do tzv. generací, kde každá generace je charakteristická svou konfigurací, rychlostí počítače a základním stavebním prvkem. Generace počítačů: Generace Rok Konfigurace
1 Strukturované programování
 Projekt OP VK Inovace studijních oborů zajišťovaných katedrami PřF UHK Registrační číslo: CZ.1.07/2.2.00/28.0118 1 Cíl Seznámení s principy strukturovaného programování, s blokovou strukturou programů,
Projekt OP VK Inovace studijních oborů zajišťovaných katedrami PřF UHK Registrační číslo: CZ.1.07/2.2.00/28.0118 1 Cíl Seznámení s principy strukturovaného programování, s blokovou strukturou programů,
Šifrová ochrana informací věk počítačů PS5-1
 Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací věk počítačů PS5-1 1 Osnova šifrová ochrana využívající výpočetní techniku např. Feistelova šifra; symetrické a asymetrické šifry;
Bezpečnost informací BI Ing. Jindřich Kodl, CSc. Šifrová ochrana informací věk počítačů PS5-1 1 Osnova šifrová ochrana využívající výpočetní techniku např. Feistelova šifra; symetrické a asymetrické šifry;
I N V E S T I C E D O R O Z V O J E V Z D Ě L Á V Á N Í. výstup
 ELEKTONIKA I N V E S T I C E D O O Z V O J E V Z D Ě L Á V Á N Í 1. Usměrňování a vyhlazování střídavého a. jednocestné usměrnění Do obvodu střídavého proudu sériově připojíme diodu. Prochází jí proud
ELEKTONIKA I N V E S T I C E D O O Z V O J E V Z D Ě L Á V Á N Í 1. Usměrňování a vyhlazování střídavého a. jednocestné usměrnění Do obvodu střídavého proudu sériově připojíme diodu. Prochází jí proud
T- MaR. Ústav technologie, mechanizace a řízení staveb. Teorie měření a regulace. Podmínky názvy. 1.c-pod. ZS 2015/ Ing. Václav Rada, CSc.
 Ústav technologie, mechanizace a řízení staveb Teorie měření a regulace Podmínky názvy 1.c-pod. ZS 2015/2016 2015 - Ing. Václav Rada, CSc. MĚŘENÍ praktická část OBECNÝ ÚVOD Veškerá měření mohou probíhat
Ústav technologie, mechanizace a řízení staveb Teorie měření a regulace Podmínky názvy 1.c-pod. ZS 2015/2016 2015 - Ing. Václav Rada, CSc. MĚŘENÍ praktická část OBECNÝ ÚVOD Veškerá měření mohou probíhat
Účinky elektrického proudu. vzorová úloha (SŠ)
 Účinky elektrického proudu vzorová úloha (SŠ) Jméno Třída.. Datum.. 1. Teoretický úvod Elektrický proud jako jev je tvořen uspořádaným pohybem volných částic s elektrickým nábojem. Elektrický proud jako
Účinky elektrického proudu vzorová úloha (SŠ) Jméno Třída.. Datum.. 1. Teoretický úvod Elektrický proud jako jev je tvořen uspořádaným pohybem volných částic s elektrickým nábojem. Elektrický proud jako
