Klauzulární logika. úvod. Šárka Vavrečková. 20. října Ústav informatiky Filozoficko-Přírodovědecká fakulta Slezské univerzity, Opava
|
|
|
- Dagmar Lišková
- před 8 lety
- Počet zobrazení:
Transkript
1 Klauzulární logika úvod Šárka Vavrečková Ústav informatiky Filozoficko-Přírodovědecká fakulta Slezské univerzity, Opava 20. října 2008
2 Klauzulární logika Hlavní vlastnosti pracujeme s klauzulemi, které získáváme z klauzulí predikátové logiky klauzule klauzulární logiky: 1 ekvivalentními operacemi předsuneme postupně všechny kvantifikátory na začátek klauzule 2 takto vytvořený prefix z kvantifikátorů odstraníme (ale při případných úpravách bereme v úvahu kvantifikaci jednotlivých proměnných a pořadí kvantifikátorů) 3 jádro formule bez kvantifikátorů upravíme do klauzulární formy používáme pouze jedinou logickou spojku implikaci (žádnou jinou, ani negaci!), specifické vlastnosti nevyjádřitelné implikací reprezentujeme jinak
3 Klauzulární logika Hlavní vlastnosti pracujeme s klauzulemi, které získáváme z klauzulí predikátové logiky klauzule klauzulární logiky: 1 ekvivalentními operacemi předsuneme postupně všechny kvantifikátory na začátek klauzule 2 takto vytvořený prefix z kvantifikátorů odstraníme (ale při případných úpravách bereme v úvahu kvantifikaci jednotlivých proměnných a pořadí kvantifikátorů) 3 jádro formule bez kvantifikátorů upravíme do klauzulární formy používáme pouze jedinou logickou spojku implikaci (žádnou jinou, ani negaci!), specifické vlastnosti nevyjádřitelné implikací reprezentujeme jinak
4 Klauzulární logika Hlavní vlastnosti pracujeme s klauzulemi, které získáváme z klauzulí predikátové logiky klauzule klauzulární logiky: 1 ekvivalentními operacemi předsuneme postupně všechny kvantifikátory na začátek klauzule 2 takto vytvořený prefix z kvantifikátorů odstraníme (ale při případných úpravách bereme v úvahu kvantifikaci jednotlivých proměnných a pořadí kvantifikátorů) 3 jádro formule bez kvantifikátorů upravíme do klauzulární formy používáme pouze jedinou logickou spojku implikaci (žádnou jinou, ani negaci!), specifické vlastnosti nevyjádřitelné implikací reprezentujeme jinak
5 Klauzulární logika Hlavní vlastnosti pracujeme s klauzulemi, které získáváme z klauzulí predikátové logiky klauzule klauzulární logiky: 1 ekvivalentními operacemi předsuneme postupně všechny kvantifikátory na začátek klauzule 2 takto vytvořený prefix z kvantifikátorů odstraníme (ale při případných úpravách bereme v úvahu kvantifikaci jednotlivých proměnných a pořadí kvantifikátorů) 3 jádro formule bez kvantifikátorů upravíme do klauzulární formy používáme pouze jedinou logickou spojku implikaci (žádnou jinou, ani negaci!), specifické vlastnosti nevyjádřitelné implikací reprezentujeme jinak
6 Klauzulární logika Hlavní vlastnosti pracujeme s klauzulemi, které získáváme z klauzulí predikátové logiky klauzule klauzulární logiky: 1 ekvivalentními operacemi předsuneme postupně všechny kvantifikátory na začátek klauzule 2 takto vytvořený prefix z kvantifikátorů odstraníme (ale při případných úpravách bereme v úvahu kvantifikaci jednotlivých proměnných a pořadí kvantifikátorů) 3 jádro formule bez kvantifikátorů upravíme do klauzulární formy používáme pouze jedinou logickou spojku implikaci (žádnou jinou, ani negaci!), specifické vlastnosti nevyjádřitelné implikací reprezentujeme jinak
7 Klauzulární logika Hlavní vlastnosti pracujeme s klauzulemi, které získáváme z klauzulí predikátové logiky klauzule klauzulární logiky: 1 ekvivalentními operacemi předsuneme postupně všechny kvantifikátory na začátek klauzule 2 takto vytvořený prefix z kvantifikátorů odstraníme (ale při případných úpravách bereme v úvahu kvantifikaci jednotlivých proměnných a pořadí kvantifikátorů) 3 jádro formule bez kvantifikátorů upravíme do klauzulární formy používáme pouze jedinou logickou spojku implikaci (žádnou jinou, ani negaci!), specifické vlastnosti nevyjádřitelné implikací reprezentujeme jinak
8 Definice (Klauzule) Definice klauzulí Báze: Literály predikátů jsou klauzule. Indukce: Jestliže A a B jsou klauzule, pak A B je také klauzule. Zobecnění: Všechny formule, které jsou utvořeny použitím konečného počtu pravidel v bázi a indukci, jsou klauzule, žádná jiná formule není klauzule.
9 Definice (Hornovy klauzule) Definice klauzulí jsou klauzule s nejvýše jedním pozitivním literálem (tj. literálem bez negace). Můžeme je psát v následujících tvarech: Definice ((Obecné) klauzule) A 1 A 2... A n B (A 1, A 2,..., A n ) B A 1 A 2... A n B 1 B 2 B m (A 1 &A 2 &... &A n ) (B 1 B 2... B m )
10 Definice (Hornovy klauzule) Definice klauzulí jsou klauzule s nejvýše jedním pozitivním literálem (tj. literálem bez negace). Můžeme je psát v následujících tvarech: Definice ((Obecné) klauzule) A 1 A 2... A n B (A 1, A 2,..., A n ) B A 1 A 2... A n B 1 B 2 B m (A 1 &A 2 &... &A n ) (B 1 B 2... B m )
11 1 proměnné (X, Prom,... ) Abeceda 2 individuové konstanty (28, 3.4, jaguár,... ) 3 logické konstanty (true, false T, F) 4 existenční (Skolemovy) konstanty ) 5 funkční symboly (funktory) mají přiřazenu aritu = přirozené číslo (vč. nuly) = počet argumentů 6 existenční (Skolemovy) funktory (@f,... ) mají aritu 7 predikátové symboly začínají písmenem, mají aritu 8 pomocné symboly čárky, závorky 9 logická spojka implikace
12 Term: proměnná Syntaktické prvky konstanta (individuová, logická) existenční konstanta funktor, jehož argumenty jsou termy existenční funktor, jehož argumenty jsou termy Atom: predikátový symbol, jehož argumenty jsou termy logická konstanta
13 Term: proměnná Syntaktické prvky konstanta (individuová, logická) existenční konstanta funktor, jehož argumenty jsou termy existenční funktor, jehož argumenty jsou termy Atom: predikátový symbol, jehož argumenty jsou termy logická konstanta
14 Klauzule: kde p i, q j jsou atomy. Význam: p 1, p 2,..., p n antecedent(a) konjunkce Syntaktické prvky q 1, q 2,..., q m konsekvent(k) disjunkce (p 1 &p 2 &... &p n ) (q 1 q 2... q m ) (p 1 &p 2 &... &p n ) (q 1 q 2... q m ) p 1 p 2... p n q 1 q 2... q m
15 Klauzule: kde p i, q j jsou atomy. Význam: p 1, p 2,..., p n antecedent(a) konjunkce Syntaktické prvky q 1, q 2,..., q m konsekvent(k) disjunkce (p 1 &p 2 &... &p n ) (q 1 q 2... q m ) (p 1 &p 2 &... &p n ) (q 1 q 2... q m ) p 1 p 2... p n q 1 q 2... q m
16 Syntaxe Formy klauzulí p 1, p 2,... p n q 1, q 2,... q m (1) q 1, q 2,... q m (2) p 1, p 2,... p n (3) Význam 1 žádná z množin A, K není prázdná (základní forma), 2 A = je FAKT, 3 K = NEPLATNÉ tvrzení.
17 Odvození vzorce: Rezoluce v klauzulární logice p X, X q p q p X, X q p q substituce [A p], [B q] A X, X B A B
18 Odvození vzorce: Rezoluce v klauzulární logice p X, X q p q p X, X q p q substituce [A p], [B q] A X, X B A B
19 Odvození vzorce: Rezoluce v klauzulární logice p X, X q p q p X, X q p q substituce [A p], [B q] A X, X B A B
20 Tvrzení jsou Typy tvrzení univerzální (tvrzení platí obecně pro vše, co je dosazeno), může obsahovat pouze univerzálně vázané proměnné (X, P rom, N ekdo, apod.), konstanty. existenční (existuje hodnota taková, že po dosazení bude formule splněna), může obsahovat vše z předchozího bodu, existenční konstanty, existenční funktory.
21 Tvrzení jsou Typy tvrzení univerzální (tvrzení platí obecně pro vše, co je dosazeno), může obsahovat pouze univerzálně vázané proměnné (X, P rom, N ekdo, apod.), konstanty. existenční (existuje hodnota taková, že po dosazení bude formule splněna), může obsahovat vše z předchozího bodu, existenční konstanty, existenční funktory.
22 Příklad Slovně V létě mají všichni školáci prázdniny. Predikátová logika v klauzulárním tvaru (chceme, aby každá proměnná byla vázaná obecným kvantifikátorem): x rocni obd(leto) skolak(x)) ma(x, prazdniny) Klauzulární logika: rocni obd(leto), skolak(x) ma(x, prazdniny)
23 Příklad Slovně V létě mají všichni školáci prázdniny. Predikátová logika v klauzulárním tvaru (chceme, aby každá proměnná byla vázaná obecným kvantifikátorem): x rocni obd(leto) skolak(x)) ma(x, prazdniny) Klauzulární logika: rocni obd(leto), skolak(x) ma(x, prazdniny)
24 Příklad Slovně V létě mají všichni školáci prázdniny. Predikátová logika v klauzulárním tvaru (chceme, aby každá proměnná byla vázaná obecným kvantifikátorem): x rocni obd(leto) skolak(x)) ma(x, prazdniny) Klauzulární logika: rocni obd(leto), skolak(x) ma(x, prazdniny)
25 Příklad Slovně Psi štěkají (všichni psi štěkají, každý pes štěká). Predikátová logika v klauzulárním tvaru x pes(x) steka(x) Klauzulární logika: pes(x) steka(x)
26 Příklad Slovně Psi štěkají (všichni psi štěkají, každý pes štěká). Predikátová logika v klauzulárním tvaru x pes(x) steka(x) Klauzulární logika: pes(x) steka(x)
27 Příklad Slovně Psi štěkají (všichni psi štěkají, každý pes štěká). Predikátová logika v klauzulárním tvaru x pes(x) steka(x) Klauzulární logika: pes(x) steka(x)
28 Příklad Slovně V létě má listí zelenou barvu, zatímco na podzim má listí žlutou nebo červenou barvu. Predikátová logika v klauzulárním tvaru x rocni obd(leto) & listi(x) barva(x, zelena) & rocni obd(podzim) & listi(x) barva(x, zluta) barva(x, cervena) Klauzulární logika: rocni obd(leto), listi(x) barva(x, zelena) rocni obd(podzim), listi(x) barva(x, zluta), barva(x, cervena)
29 Příklad Slovně V létě má listí zelenou barvu, zatímco na podzim má listí žlutou nebo červenou barvu. Predikátová logika v klauzulárním tvaru x rocni obd(leto) & listi(x) barva(x, zelena) & rocni obd(podzim) & listi(x) barva(x, zluta) barva(x, cervena) Klauzulární logika: rocni obd(leto), listi(x) barva(x, zelena) rocni obd(podzim), listi(x) barva(x, zluta), barva(x, cervena)
30 Příklad Slovně V létě má listí zelenou barvu, zatímco na podzim má listí žlutou nebo červenou barvu. Predikátová logika v klauzulárním tvaru x rocni obd(leto) & listi(x) barva(x, zelena) & rocni obd(podzim) & listi(x) barva(x, zluta) barva(x, cervena) Klauzulární logika: rocni obd(leto), listi(x) barva(x, zelena) rocni obd(podzim), listi(x) barva(x, zluta), barva(x, cervena)
31 Slovně Stůl je tvrdý. Příklad Predikátová logika v klauzulárním tvaru X stul(x) tvrdy(x) Klauzulární logika: nebo stul(x) tvrdy(x) tvrdy(stul)
32 Slovně Stůl je tvrdý. Příklad Predikátová logika v klauzulárním tvaru X stul(x) tvrdy(x) Klauzulární logika: nebo stul(x) tvrdy(x) tvrdy(stul)
33 Slovně Stůl je tvrdý. Příklad Predikátová logika v klauzulárním tvaru X stul(x) tvrdy(x) Klauzulární logika: nebo stul(x) tvrdy(x) tvrdy(stul)
34 Příklad Slovně Když je hezké počasí, děti jdou na procházku. Predikátová logika v klauzulárním tvaru X pocasi(hezke) & dite(x) jde(x, prochazka) Klauzulární logika: pocasi(hezke), dite(x) jde(x, prochazka)
35 Příklad Slovně Když je hezké počasí, děti jdou na procházku. Predikátová logika v klauzulárním tvaru X pocasi(hezke) & dite(x) jde(x, prochazka) Klauzulární logika: pocasi(hezke), dite(x) jde(x, prochazka)
36 Příklad Slovně Když je hezké počasí, děti jdou na procházku. Predikátová logika v klauzulárním tvaru X pocasi(hezke) & dite(x) jde(x, prochazka) Klauzulární logika: pocasi(hezke), dite(x) jde(x, prochazka)
37 Příklad Slovně Musím do školy, protože píšu písemku. Predikátová logika v klauzulárním tvaru Klauzulární logika: pise(ja, pisemka) musi do(ja, skola) pise(ja, pisemka) musi do(ja, skola) nebo ja(x), pise(x, pisemka) musi do(x, skola)
38 Příklad Slovně Musím do školy, protože píšu písemku. Predikátová logika v klauzulárním tvaru Klauzulární logika: pise(ja, pisemka) musi do(ja, skola) pise(ja, pisemka) musi do(ja, skola) nebo ja(x), pise(x, pisemka) musi do(x, skola)
39 Příklad Slovně Musím do školy, protože píšu písemku. Predikátová logika v klauzulárním tvaru Klauzulární logika: pise(ja, pisemka) musi do(ja, skola) pise(ja, pisemka) musi do(ja, skola) nebo ja(x), pise(x, pisemka) musi do(x, skola)
40 Příklad Slovně Děti mladší 10 let půjdou po zelené značce, děti starší půjdou po stejné značce jako dospělí. Predikátová logika v klauzulárním tvaru X X Y Z dite(x) & vek(x) < 10 jde po(x, zelena) dite(x) & vek(x) = 10 & & dospely(y ), jde po(y, Z) jde po(x, Z) Klauzulární logika: dite(x), vek(x) < 10 jde po(x, zelena) dite(x), vek(x) = 10, dospely(y ), jde po(y, Z) jde po(x, Z)
41 Příklad Slovně Děti mladší 10 let půjdou po zelené značce, děti starší půjdou po stejné značce jako dospělí. Predikátová logika v klauzulárním tvaru X X Y Z dite(x) & vek(x) < 10 jde po(x, zelena) dite(x) & vek(x) = 10 & & dospely(y ), jde po(y, Z) jde po(x, Z) Klauzulární logika: dite(x), vek(x) < 10 jde po(x, zelena) dite(x), vek(x) = 10, dospely(y ), jde po(y, Z) jde po(x, Z)
42 Příklad Slovně Děti mladší 10 let půjdou po zelené značce, děti starší půjdou po stejné značce jako dospělí. Predikátová logika v klauzulárním tvaru X X Y Z dite(x) & vek(x) < 10 jde po(x, zelena) dite(x) & vek(x) = 10 & & dospely(y ), jde po(y, Z) jde po(x, Z) Klauzulární logika: dite(x), vek(x) < 10 jde po(x, zelena) dite(x), vek(x) = 10, dospely(y ), jde po(y, Z) jde po(x, Z)
43 Převod z predikátové logiky x y z A(x,y,z) x y z A(x,y,z) A(@X, Y, Z) (X), Z) x y z A(x,y,z) A(X, Y ))
44 Převod z predikátové logiky Existenční vazba Existenční vazba x y z A(x,y,z) x y z A(x,y,z) Univerzální vazby A(@X, Y, Z) Univerzální vazby (X), Z) Existenční vazba x y z A(x,y,z) Univerzální vazby A(X, Y ))
45 Převod z predikátové logiky Existenční vazba Existenční vazba x y z A(x,y,z) x y z A(x,y,z) Univerzální vazby A(@X, Y, Z) Univerzální vazby (X), Z) Existenční vazba x y z A(x,y,z) Univerzální vazby A(X, Y ))
46 Existenční konstanty Příklady 1 Jana něco vlastní (existuje něco, co vlastní Jana). 2 Někdo jde lesem. jde kudy(@nekdo, les) 3 Existuje někdo, koho baví logika (někoho baví logika). bavi(@nekdo, logika) 4 Vidím něco modrého. modre(@c)
47 Existenční konstanty Příklady 1 Jana něco vlastní (existuje něco, co vlastní Jana). 2 Někdo jde lesem. jde kudy(@nekdo, les) 3 Existuje někdo, koho baví logika (někoho baví logika). bavi(@nekdo, logika) 4 Vidím něco modrého. modre(@c)
48 Existenční konstanty Příklady 1 Jana něco vlastní (existuje něco, co vlastní Jana). 2 Někdo jde lesem. jde kudy(@nekdo, les) 3 Existuje někdo, koho baví logika (někoho baví logika). bavi(@nekdo, logika) 4 Vidím něco modrého. modre(@c)
49 Existenční konstanty Příklady 1 Jana něco vlastní (existuje něco, co vlastní Jana). 2 Někdo jde lesem. jde kudy(@nekdo, les) 3 Existuje někdo, koho baví logika (někoho baví logika). bavi(@nekdo, logika) 4 Vidím něco modrého. modre(@c)
50 Existenční konstanty Příklady 1 Jana něco vlastní (existuje něco, co vlastní Jana). 2 Někdo jde lesem. jde kudy(@nekdo, les) 3 Existuje někdo, koho baví logika (někoho baví logika). bavi(@nekdo, logika) 4 Vidím něco modrého. modre(@c)
51 Kdy použít existenční funktor Existenční funktory Každý zaměstnanec má svého nadřízeného.
52 Existenční funktory Kdy použít existenční funktor Každý zaměstnanec má svého nadřízeného. Špatně: zamestnanec(x) nadrizeny(y, X) (1) zamestnanec(x) X) (2)
53 Kdy použít existenční funktor Existenční funktory Každý zaměstnanec má svého nadřízeného. Špatně: zamestnanec(x) nadrizeny(y, X) (1) zamestnanec(x) X) (2) Ve skutečnosti znamená: 1 Každý zaměstnanec má nadřízeného, který je v proměnné Y (tj. všichni jsou nadřízenými všech zaměstnanců). 2 Existuje nadřízený společný všem zaměstnancům.
54 Kdy použít existenční funktor Existenční funktory Každý zaměstnanec má svého nadřízeného. Dobře: zamestnanec(x) X) Každého nadřízeného vážeme vždy na konkrétního zaměstnance, existenční je interpretován tabulkou.
Logika a logické programování
 Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
Klauzulární logika. Znalostní báze. Šárka Vavrečková
 Klauzulární logika Znalostní báze Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 26. listopadu 2007 (Znalostní báze) Klauzulární
Klauzulární logika Znalostní báze Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 26. listopadu 2007 (Znalostní báze) Klauzulární
Negace bázového atomu Negace atomu s existenčním termem Negace klauzule Negace množiny klauzulí Predikát rovnosti. Klauzulární logika
 Vlastnosti klauzulí, negace Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 27. října 2008 Věta o transferu bázového atomu
Vlastnosti klauzulí, negace Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 27. října 2008 Věta o transferu bázového atomu
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
Hilbertovský axiomatický systém
 Hilbertovský axiomatický systém Predikátová logika H 1 Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 24. října 2008 Specifikace H 1 Jazyk L H1 přejímáme jazyk predikátové logiky
Hilbertovský axiomatický systém Predikátová logika H 1 Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 24. října 2008 Specifikace H 1 Jazyk L H1 přejímáme jazyk predikátové logiky
Predikátová logika Individua a termy Predikáty
 Predikátová logika Predikátová logika je rozšířením logiky výrokové o kvantifikační výrazy jako každý, všichni, někteří či žádný. Nejmenší jazykovou jednotkou, kterou byla výroková logika schopna identifikovat,
Predikátová logika Predikátová logika je rozšířením logiky výrokové o kvantifikační výrazy jako každý, všichni, někteří či žádný. Nejmenší jazykovou jednotkou, kterou byla výroková logika schopna identifikovat,
6. Logika a logické systémy. Základy logiky. Lucie Koloušková, Václav Matoušek / KIV. Umělá inteligence a rozpoznávání, LS
 Základy logiky Umělá inteligence a rozpoznávání, LS 2012 6-1 Logika je naukou, která se zabývá studiem lidského uvažování. Mezi základní úlohy logiky patří nalézání metod správného usuzování, tedy postupů,
Základy logiky Umělá inteligence a rozpoznávání, LS 2012 6-1 Logika je naukou, která se zabývá studiem lidského uvažování. Mezi základní úlohy logiky patří nalézání metod správného usuzování, tedy postupů,
Predikátová logika. prvního řádu
 Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
7 Jemný úvod do Logiky
 7 Jemný úvod do Logiky Základem přesného matematického vyjadřování je správné používání (matematické) logiky a logických úsudků. Logika jako filozofická discipĺına se intenzivně vyvíjí už od dob antiky,
7 Jemný úvod do Logiky Základem přesného matematického vyjadřování je správné používání (matematické) logiky a logických úsudků. Logika jako filozofická discipĺına se intenzivně vyvíjí už od dob antiky,
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
Výroková logika. Sémantika výrokové logiky
 Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
λογος - LOGOS slovo, smysluplná řeč )
 MATA P1: Výroky, množiny a operace s nimi Matematická logika (z řeckého slova λογος - LOGOS slovo, smysluplná řeč ) Výrok primitivní pojem matematické logiky. Tvrzení, pro které má smysl otázka o jeho
MATA P1: Výroky, množiny a operace s nimi Matematická logika (z řeckého slova λογος - LOGOS slovo, smysluplná řeč ) Výrok primitivní pojem matematické logiky. Tvrzení, pro které má smysl otázka o jeho
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Stefan Ratschan. Fakulta informačních technologíı. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Logika. 2. Výroková logika. RNDr. Luděk Cienciala, Ph. D.
 Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Základy logiky Logika a logické systémy. Umělá inteligence a rozpoznávání, LS
 Základy logiky 22. 4. 2015 Umělá inteligence a rozpoznávání, LS 2015 6-1 Logika je naukou, která se zabývá studiem lidského uvažování. Mezi základní úlohy logiky patří nalézání metod správného usuzování,
Základy logiky 22. 4. 2015 Umělá inteligence a rozpoznávání, LS 2015 6-1 Logika je naukou, která se zabývá studiem lidského uvažování. Mezi základní úlohy logiky patří nalézání metod správného usuzování,
Programovací jazyk Prolog
 Programovací jazyk Prolog Logické programování Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 1. prosince 2008 Prolog Co je
Programovací jazyk Prolog Logické programování Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 1. prosince 2008 Prolog Co je
Přednáška 2: Formalizace v jazyce logiky.
 Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
LOGIKA VÝROKOVÁ LOGIKA
 LOGIKA Popisuje pravidla odvozování jedněch tvrzení z druhých. Je to myšlenková cesta ke správným závěrům. Vznikla jako součást filosofie. Zakladatelem byl Aristoteles. VÝROKOVÁ LOGIKA Obsahuje syntaktická,
LOGIKA Popisuje pravidla odvozování jedněch tvrzení z druhých. Je to myšlenková cesta ke správným závěrům. Vznikla jako součást filosofie. Zakladatelem byl Aristoteles. VÝROKOVÁ LOGIKA Obsahuje syntaktická,
Logika. 5. Rezoluční princip. RNDr. Luděk Cienciala, Ph. D.
 Logika 5. Rezoluční princip RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Logika 5. Rezoluční princip RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Interpretace klauzule Atomy v klauzulích Prázdný antecedent/konsekvent Konjunkce/disjunkce atomů. Klauzulární logika. Interpretace klauzule
 Klauzulární logika Interpretace klauzule Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 27. října 2008 Jak na klauzuli p 1,
Klauzulární logika Interpretace klauzule Šárka Vavrečková Ústav informatiky, Filozoficko-přírodovědecká fakulta Slezské univerzity v Opavě sarka.vavreckova@fpf.slu.cz 27. října 2008 Jak na klauzuli p 1,
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Rezoluční kalkulus pro logiku prvního řádu
 AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
Skolemizace. x(x + f(x) = 0). Interpretace f unární funkce, která pro daný
 Skolemizace převod formulí na formule bez existenčních kvantifikátorů v jazyce, který je rozšířen o tzv. Skolemovy funkce; zachovává splnitelnost idea převodu: formuli x 1... x n yp (x 1,..., x n, y) transformujeme
Skolemizace převod formulí na formule bez existenčních kvantifikátorů v jazyce, který je rozšířen o tzv. Skolemovy funkce; zachovává splnitelnost idea převodu: formuli x 1... x n yp (x 1,..., x n, y) transformujeme
M - Výroková logika VARIACE
 M - Výroková logika Autor: Mgr. Jaromír Juřek Kopírování a další šíření povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu
M - Výroková logika Autor: Mgr. Jaromír Juřek Kopírování a další šíření povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu
Predikátová logika. Teoretická informatika Tomáš Foltýnek
 Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Výroková logika - opakování
 - opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
- opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
KMA/MDS Matematické důkazy a jejich struktura
 Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
2.5 Rezoluční metoda v predikátové logice
 2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
teorie logických spojek chápaných jako pravdivostní funkce
 Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
SINGULÁRNÍ VÝROKY: Jednoduchý singulární výrok vznikne spojením singulárního termínu s termínem obecným pomocí spony=slova je.
 Studijní text Co je singulární výrok SINGULÁRNÍ VÝROKY: PETR Petr je veselý. Jednoduchý singulární výrok vznikne spojením singulárního termínu s termínem obecným pomocí spony=slova je. Příklad: Pavel je
Studijní text Co je singulární výrok SINGULÁRNÍ VÝROKY: PETR Petr je veselý. Jednoduchý singulární výrok vznikne spojením singulárního termínu s termínem obecným pomocí spony=slova je. Příklad: Pavel je
Databázové systémy. * relační kalkuly. Tomáš Skopal. - relační model
 Databázové systémy Tomáš Skopal - relační model * relační kalkuly Osnova přednášky relační kalkuly doménový n-ticový Relační kalkuly využití aparátu predikátové logiky 1. řádu pro dotazování rozšíření
Databázové systémy Tomáš Skopal - relační model * relační kalkuly Osnova přednášky relační kalkuly doménový n-ticový Relační kalkuly využití aparátu predikátové logiky 1. řádu pro dotazování rozšíření
1 Výroková logika 1. 2 Predikátová logika 3. 3 Důkazy matematických vět 4. 4 Doporučená literatura 7
 1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
Predikátová logika [Predicate logic]
![Predikátová logika [Predicate logic] Predikátová logika [Predicate logic]](/thumbs/74/70612837.jpg) Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Prolog PROgramming in LOGic část predikátové logiky prvního řádu rozvoj začíná po roce 1970 Robert Kowalski teoretické základy Alain Colmerauer, David
 Úvod do Prologu Prolog PROgramming in LOGic část predikátové logiky prvního řádu rozvoj začíná po roce 1970 Robert Kowalski teoretické základy Alain Colmerauer, David Warren (Warren Abstract Machine) implementace
Úvod do Prologu Prolog PROgramming in LOGic část predikátové logiky prvního řádu rozvoj začíná po roce 1970 Robert Kowalski teoretické základy Alain Colmerauer, David Warren (Warren Abstract Machine) implementace
0. ÚVOD - matematické symboly, značení,
 0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
Logika. 8. Automatické dokazování v predikátové logice (obecná rezoluční metoda)
 Logika 8. Automatické dokazování v predikátové logice (obecná rezoluční metoda) RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním
Logika 8. Automatické dokazování v predikátové logice (obecná rezoluční metoda) RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním
VÝROKOVÁ LOGIKA. Výrok srozumitelná oznamovací věta (výraz, sdělení), která může být buď jen pravdivá nebo jen nepravdivá..
 VÝROKOVÁ LOGIKA Teorie: Logika je vědní obor zabývající se studiem různých forem vyjadřování a pravidel správného posuzování. (Matematická logika je součástí tohoto vědního oboru a ve velké míře užívá
VÝROKOVÁ LOGIKA Teorie: Logika je vědní obor zabývající se studiem různých forem vyjadřování a pravidel správného posuzování. (Matematická logika je součástí tohoto vědního oboru a ve velké míře užívá
výrok-každésdělení,uněhožmásmyslseptát,zdaječinenípravdivé, aproněžprávějednaztěchtodvoumožnostínastává.
 1 Základní pojmy matematické logiky Výrokový počet... syntaktické hledisko Predikátový počet... sémantické hledisko 1.1 VÝROKOVÝ POČET výrok-každésdělení,uněhožmásmyslseptát,zdaječinenípravdivé, aproněžprávějednaztěchtodvoumožnostínastává.
1 Základní pojmy matematické logiky Výrokový počet... syntaktické hledisko Predikátový počet... sémantické hledisko 1.1 VÝROKOVÝ POČET výrok-každésdělení,uněhožmásmyslseptát,zdaječinenípravdivé, aproněžprávějednaztěchtodvoumožnostínastává.
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Výroková a predikátová logika - V
 Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Sémantika predikátové logiky
 Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Logika. Akademie managementu a komunikace, Praha PhDr. Peter Jan Kosmály, PhD.
 Akademie managementu a komunikace, Praha PhDr. Peter Jan Kosmály, PhD. Tematické okruhy: 1. Stručné dějiny logiky a její postavění ve vědě 2. Analýza složených výroků pomocí pravdivostní tabulky 3. Subjekt-predikátová
Akademie managementu a komunikace, Praha PhDr. Peter Jan Kosmály, PhD. Tematické okruhy: 1. Stručné dějiny logiky a její postavění ve vědě 2. Analýza složených výroků pomocí pravdivostní tabulky 3. Subjekt-predikátová
Predikátová logika (logika predikátů)
 Predikátová logika (logika predikátů) Ve výrokové logice pracujeme s jednoduchými či složenými výroky, aniž nás zajímá jejich struktura. Příklad. Jestliže Karel je studentem, pak je (Karel) chytřejší než
Predikátová logika (logika predikátů) Ve výrokové logice pracujeme s jednoduchými či složenými výroky, aniž nás zajímá jejich struktura. Příklad. Jestliže Karel je studentem, pak je (Karel) chytřejší než
Programovací jazyk Prolog
 Programovací jazyk Prolog doc. Ing. Miroslav Beneš, Ph.D. katedra informatiky FEI VŠB-TUO A-1007 / 597 324 213 http://www.cs.vsb.cz/benes Miroslav.Benes@vsb.cz Obsah Logický program Fakt, dotaz, pravidlo
Programovací jazyk Prolog doc. Ing. Miroslav Beneš, Ph.D. katedra informatiky FEI VŠB-TUO A-1007 / 597 324 213 http://www.cs.vsb.cz/benes Miroslav.Benes@vsb.cz Obsah Logický program Fakt, dotaz, pravidlo
Převyprávění Gödelova důkazu nutné existence Boha
 Převyprávění Gödelova důkazu nutné existence Boha Technické podrobnosti Důkaz: Konečná posloupnost výrokůkorektně utvořených formulí nějakého logického kalkulu), z nichž každý jelogickým) axiomem, postulátemteorie),
Převyprávění Gödelova důkazu nutné existence Boha Technické podrobnosti Důkaz: Konečná posloupnost výrokůkorektně utvořených formulí nějakého logického kalkulu), z nichž každý jelogickým) axiomem, postulátemteorie),
Predik atov a logika - pˇredn aˇska () Predik atov a logika - pˇredn aˇska / 16
 Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Cvičení 4. negace konjunkce disjunkce implikace ekvivalence. a) Najděte UDNF, UKNF a stanovte log. důsledky. 1) [p (p q)] [( p q) (q p)]
![Cvičení 4. negace konjunkce disjunkce implikace ekvivalence. a) Najděte UDNF, UKNF a stanovte log. důsledky. 1) [p (p q)] [( p q) (q p)] Cvičení 4. negace konjunkce disjunkce implikace ekvivalence. a) Najděte UDNF, UKNF a stanovte log. důsledky. 1) [p (p q)] [( p q) (q p)]](/thumbs/92/108888591.jpg) Cvičení 4 negace konjunkce disjunkce implikace ekvivalence a) Najděte UDNF, UKNF a stanovte log. důsledky 1) [p (p q)] [( p q) (q p)] p q p q p q q p p A B C D E UEK UED A B C D E F 0 0 1 1 0 0 0 1 p q
Cvičení 4 negace konjunkce disjunkce implikace ekvivalence a) Najděte UDNF, UKNF a stanovte log. důsledky 1) [p (p q)] [( p q) (q p)] p q p q p q q p p A B C D E UEK UED A B C D E F 0 0 1 1 0 0 0 1 p q
Umělá inteligence I. Roman Barták, KTIML.
 Umělá inteligence I Roman Barták, KTIML roman.bartak@mff.cuni.cz http://ktiml.mff.cuni.cz/~bartak Už umíme používat výrokovou logiku pro reprezentaci znalostí a odvozování důsledků. Dnes Dnes zopakujeme
Umělá inteligence I Roman Barták, KTIML roman.bartak@mff.cuni.cz http://ktiml.mff.cuni.cz/~bartak Už umíme používat výrokovou logiku pro reprezentaci znalostí a odvozování důsledků. Dnes Dnes zopakujeme
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Matematika pro informatiky KMA/MATA
 Matematika pro informatiky KMA/MATA Informace k předmětu Mgr. Přemysl Rosa rosapr00@pf.jcu.cz, J349 Konzultační hodiny v ZS: úterý 10-11, čtvrtek 15-16 nebo individuálně po předchozí domluvě aktivní účast
Matematika pro informatiky KMA/MATA Informace k předmětu Mgr. Přemysl Rosa rosapr00@pf.jcu.cz, J349 Konzultační hodiny v ZS: úterý 10-11, čtvrtek 15-16 nebo individuálně po předchozí domluvě aktivní účast
Logické programování
 Logické programování Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 1 1 Prolog a Logické programování Prolog vznikl jako programovací jazyk v Marseille 1970, jeho autorem
Logické programování Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 1 1 Prolog a Logické programování Prolog vznikl jako programovací jazyk v Marseille 1970, jeho autorem
Úvod do predikátové logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
 Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Základní pojmy matematické logiky
 KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
Místo pojmu výroková formule budeme používat zkráceně jen formule. Při jejich zápisu
 VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
Systém přirozené dedukce výrokové logiky
 Systém přirozené dedukce výrokové logiky Korektnost, úplnost a bezespornost Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 6. října 2008 Věta o korektnosti Věta (O korektnosti Systému
Systém přirozené dedukce výrokové logiky Korektnost, úplnost a bezespornost Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 6. října 2008 Věta o korektnosti Věta (O korektnosti Systému
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
1. Matematická logika
 Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018 1. Matematická logika Základem každé vědy (tedy i matematiky i fyziky) je soubor jistých znalostí. To, co z těchto izolovaných poznatků
Moderní technologie ve studiu aplikované fyziky CZ.1.07/2.2.00/07.0018 1. Matematická logika Základem každé vědy (tedy i matematiky i fyziky) je soubor jistých znalostí. To, co z těchto izolovaných poznatků
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
přednáška 2 Marie Duží
 Logika v praxi přednáška 2 Marie Duží marie.duzi@vsb.cz 1 1 Výroková logika Analyzuje způsoby skládání jednoduchých výroků do výroků složených pomocí logických spojek. Co je to výrok? Výrok je tvrzení,
Logika v praxi přednáška 2 Marie Duží marie.duzi@vsb.cz 1 1 Výroková logika Analyzuje způsoby skládání jednoduchých výroků do výroků složených pomocí logických spojek. Co je to výrok? Výrok je tvrzení,
Klasická predikátová logika
 Klasická predikátová logika Matematická logika, LS 2012/13, závěrečná přednáška Libor Běhounek www.cs.cas.cz/behounek/teaching/malog12 PřF OU, 6. 5. 2013 Symboly klasické predikátové logiky Poznámky Motivace
Klasická predikátová logika Matematická logika, LS 2012/13, závěrečná přednáška Libor Běhounek www.cs.cas.cz/behounek/teaching/malog12 PřF OU, 6. 5. 2013 Symboly klasické predikátové logiky Poznámky Motivace
Logické programy Deklarativní interpretace
 Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logika. 1. Úvod, Výroková logika
 Logika 1. Úvod, Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Logika 1. Úvod, Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Spojování výroků (podmínek) logickými spojkami
 Spojování výroků (podmínek) logickými spojkami Spojování výroků logickými spojkami a) Konjunkce - spojení A B; Pravdivostní tabulka konjunkce A B A B 0 0 0 0 1 0 1 0 0 1 1 1 AND; A a současně B Konjunkce
Spojování výroků (podmínek) logickými spojkami Spojování výroků logickými spojkami a) Konjunkce - spojení A B; Pravdivostní tabulka konjunkce A B A B 0 0 0 0 1 0 1 0 0 1 1 1 AND; A a současně B Konjunkce
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Další (neklasické) logiky. Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20
 Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Výroková a predikátová logika - XII
 Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Částečná korektnost. Petr Štěpánek. S využitím materialu Krysztofa R. Apta
 Částečná korektnost Petr Štěpánek S využitím materialu Krysztofa R. Apta 2007 Logické programování 14 1 Částečná korektnost je vlastností programu a znamená, že program vydává korektní výsledky pro dané
Částečná korektnost Petr Štěpánek S využitím materialu Krysztofa R. Apta 2007 Logické programování 14 1 Částečná korektnost je vlastností programu a znamená, že program vydává korektní výsledky pro dané
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony.
 Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška třetí Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška třetí Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Tableaux metody. Jiří Vyskočil 2011
 Tableaux metody Jiří Vyskočil 2011 Tableau [tabló] metoda Tableau metoda je další oblíbená metoda užívaná pro automatické dokazování vět v predikátové logice, ale i v dalších (modálních, temporálních,
Tableaux metody Jiří Vyskočil 2011 Tableau [tabló] metoda Tableau metoda je další oblíbená metoda užívaná pro automatické dokazování vět v predikátové logice, ale i v dalších (modálních, temporálních,
Rezoluce v predikátové logice
 Rezoluce v predikátové logice Jiří Velebil: X01DML 15. října 2010: Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná
Rezoluce v predikátové logice Jiří Velebil: X01DML 15. října 2010: Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná
1 REZOLUČNÍ FORMÁLNÍ DŮKAZY
 Vážená kolegyně / vážený kolego, součástí Vašeho rozšiřujícího studia informatiky je absolvování předmětu Logika pro učitele 2, jehož cílem je v návaznosti na předmět Logika pro učitele 1 seznámení se
Vážená kolegyně / vážený kolego, součástí Vašeho rozšiřujícího studia informatiky je absolvování předmětu Logika pro učitele 2, jehož cílem je v návaznosti na předmět Logika pro učitele 1 seznámení se
Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Formální systém výrokové logiky
 Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Matematická indukce, sumy a produkty, matematická logika
 Matematická indukce, sumy a produkty, matematická logika 8.9. -.0.009 Matematická indukce Jde o následující vlastnost přirozených čísel: Předpokládejme:. Nějaké tvrzení platí pro.. Platí-li tvrzení pro
Matematická indukce, sumy a produkty, matematická logika 8.9. -.0.009 Matematická indukce Jde o následující vlastnost přirozených čísel: Předpokládejme:. Nějaké tvrzení platí pro.. Platí-li tvrzení pro
Rezoluce v predikátové logice
 Rezoluce v predikátové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná iff X =
Rezoluce v predikátové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná iff X =
Seminární práce z Teorie ICT
 ČESKÁ ZEMĚDĚLSKÁ UNIVERZITA V PRAZE Provozně ekonomická fakulta Seminární práce z Teorie ICT Implementace logické hádanky v Prologu Autor : Petr Pechek 1 Popis zvoleného problému Mým úkolem bylo vyřešit
ČESKÁ ZEMĚDĚLSKÁ UNIVERZITA V PRAZE Provozně ekonomická fakulta Seminární práce z Teorie ICT Implementace logické hádanky v Prologu Autor : Petr Pechek 1 Popis zvoleného problému Mým úkolem bylo vyřešit
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Logika Libor Barto. Výroková logika
 Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Logika. Dana Nejedlová Katedra informatiky Ekonomická fakulta Technická univerzita v Liberci
 Logika Dana Nejedlová Katedra informatiky Ekonomická fakulta Technická univerzita v Liberci 1 Úloha logiky v umělé inteligenci převést fakta na formalizované výroky, se kterými se dá automatizovaně operovat
Logika Dana Nejedlová Katedra informatiky Ekonomická fakulta Technická univerzita v Liberci 1 Úloha logiky v umělé inteligenci převést fakta na formalizované výroky, se kterými se dá automatizovaně operovat
Výroková a predikátová logika - VI
 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
vhodná pro strojové dokazování (Prolog) metoda založená na vyvracení: dokazuje se nesplnitelnost formulí
 Rezoluce: další formální systém vhodná pro strojové dokazování (Prolog) metoda založená na vyvracení: dokazuje se nesplnitelnost formulí pracujeme s formulemi v nkf (též klauzulárním tvaru), ale používáme
Rezoluce: další formální systém vhodná pro strojové dokazování (Prolog) metoda založená na vyvracení: dokazuje se nesplnitelnost formulí pracujeme s formulemi v nkf (též klauzulárním tvaru), ale používáme
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
ZÁKLADY LOGIKY A METODOLOGIE
 ZÁKLADY LOGIKY A METODOLOGIE Metodický list č. 1 Téma: Předmět logiky a metodologie, základy logiky a formalizace. Toto téma lze rozdělit do tří základních tématických oblastí: 1) Předmět logiky a metodologie
ZÁKLADY LOGIKY A METODOLOGIE Metodický list č. 1 Téma: Předmět logiky a metodologie, základy logiky a formalizace. Toto téma lze rozdělit do tří základních tématických oblastí: 1) Předmět logiky a metodologie
1. MATEMATICKÁ LOGIKA A MNOŽINY
 . MATEMATICKÁ LOGIKA A MNOŽINY Průvodce studiem V následující kapitole si připomeneme některé význačné poznatky z matematické logiky a teorie množin, tvořící základ množinově logického aparátu. S celou
. MATEMATICKÁ LOGIKA A MNOŽINY Průvodce studiem V následující kapitole si připomeneme některé význačné poznatky z matematické logiky a teorie množin, tvořící základ množinově logického aparátu. S celou
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
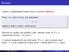 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Logické programování I
 Logické programování I PROLOG Program popisuje "svět" Prologu = databáze faktů a pravidel (tzv. klauzulí). fakta: predikát(arg1, arg2,...argn). cíle:?- predikát(arg1, arg2,...argn). pravidla: hlava :-
Logické programování I PROLOG Program popisuje "svět" Prologu = databáze faktů a pravidel (tzv. klauzulí). fakta: predikát(arg1, arg2,...argn). cíle:?- predikát(arg1, arg2,...argn). pravidla: hlava :-
Rezoluční kalkulus pro výrokovou logiku
 AD4M33AU Automatické uvažování Rezoluční kalkulus pro výrokovou logiku Petr Pudlák Výroková logika Výhody Jednoduchý jazyk. Rozhodnutelnost dokazatelnosti i nedokazatelnosti. Rychlejší algoritmy. Nevýhody
AD4M33AU Automatické uvažování Rezoluční kalkulus pro výrokovou logiku Petr Pudlák Výroková logika Výhody Jednoduchý jazyk. Rozhodnutelnost dokazatelnosti i nedokazatelnosti. Rychlejší algoritmy. Nevýhody
Úvod do výrokové a predikátové logiky
 Úvod do výrokové a predikátové logiky Eva Ondráčková Na této přednášce se seznámíte se základy výrokové a predikátové logiky. Zjistíte, že podstatou logiky není vyplňování pravdivostních tabulek ani negování
Úvod do výrokové a predikátové logiky Eva Ondráčková Na této přednášce se seznámíte se základy výrokové a predikátové logiky. Zjistíte, že podstatou logiky není vyplňování pravdivostních tabulek ani negování
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce
 Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
