Výroková a predikátová logika - VI
|
|
|
- Luboš Tobiška
- před 7 lety
- Počet zobrazení:
Transkript
1 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
2 Predikátová logika Úvod Predikátová logika Zabývá se tvrzeními o individuích, jejich vlastnostech a vztazích. Je inteligentní a její otec zná pana rektora. I(x) Z(o(x), r) x je proměnná, reprezentuje individuum, r je konstantní symbol, reprezentuje konkrétní individuum, o je funkční symbol, reprezentuje funkci, I, Z jsou relační (predikátové) symboly, reprezentují relace (vlastnost být inteligentní a vztah znát ). Funkce f je na (surjektivní). ( x)( y)(f (y) = x) ( x) je všeobecný (univerzální) kvantifikátor proměnné x, ( y) je existenční kvantifikátor proměnné y, = je (binární) relační symbol, reprezentuje identickou relaci. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
3 Jazyk Jazyk Jazyk 1. řádu obsahuje proměnné x, y, z,..., x 0, x 1,... (spočetně mnoho), množinu všech proměnných značíme Var, funkční symboly f, g, h,..., včetně konstantních symbolů c, d,..., což jsou nulární funkční symboly, relační (predikátové) symboly P, Q, R,..., případně symbol = (rovnost) jako speciální relační symbol, kvantifikátory ( x), ( x) pro každou proměnnou x Var, logické spojky,,,, závorky (, ) Každý funkční i relační symbol S má danou aritu (četnost) ar(s) N. Poznámka Oproti výrokové logice nemáme (explicitně) výrokové proměnné, lze je zavést jako nulární relační symboly. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
4 Jazyk Signatura jazyka Proměnné, kvantifikátory, logické spojky a závorky jsou logické symboly, zatímco funkční a relační symboly (kromě případné rovnosti) jsou mimologické symboly. Rovnost (obvykle) uvažujeme zvlášt. Signatura je dvojice R, F disjunktních množin relačních a funkčních symbolů s danými aritami, přičemž žádný z nich není rovnost. Signatura tedy určuje všechny mimologické symboly. Jazyk je dán signaturou L = R, F a uvedením, zda jde o jazyk s rovností či bez rovnosti. Jazyk musí obsahovat alespoň jeden relační symbol (mimologický nebo rovnost). Poznámka Význam symbolů není v jazyce určen, např. symbol + nemusí reprezentovat standardní sčítání. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
5 Jazyk Příklady jazyků Jazyk obvykle uvádíme výčtem mimologických symbolů s případným upřesněním, zda jde o funkční či relační symboly a jakou mají aritu. Následující příklady jazyků jsou všechny s rovností. L = je jazyk čisté rovnosti, L = c i i N je jazyk spočetně mnoha konstant, L = je jazyk uspořádání, L = E je jazyk teorie grafů, L = +,, 0 je jazyk teorie grup, L = +,,, 0, 1 je jazyk teorie těles, L =,,, 0, 1 je jazyk Booleových algeber, L = S, +,, 0, je jazyk aritmetiky, kde c i, 0, 1 jsou konstantní symboly, S, jsou unární funkční symboly, +,,, jsou binární funkční symboly, E, jsou binární relační symboly. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
6 Termy Termy Jsou výrazy reprezentující hodnoty (složených) funkcí. Termy jazyka L jsou dány induktivním předpisem (i) každá proměnná nebo konstantní symbol je term, (ii) je-li f funkční symbol jazyka L s aritou n > 0 a t 0,..., t n 1 jsou termy, pak je i výraz f (t 0,..., t n 1 ) term, (iii) každý term vznikne konečným užitím pravidel (i), (ii). Konstantní (ground) term je term bez proměnných, např. f (0) + 1. Množinu všech termů jazyka L značíme Term L. Termu, jenž je součástí jiného termu t, říkáme podterm termu t. Strukturu termu můžeme reprezentovat jeho vytvořujícím stromem. U binárních funkčních symbolů často používáme infixního zápisu, např. píšeme (x + y) namísto +(x, y). Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
7 Termy Příklady termů (S(0) + x) y (x y) S(0) + x y (x y) S(0) x x y a) 0 b) x y a) Vytvořující strom termu (S(0) + x) y jazyka aritmetiky. b) Výrokové formule se spojkami,,, případně s konstantami, lze chápat jako termy jazyka Booleových algeber. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
8 Formule Atomické formule Jsou nejjednodušší formule. Atomická formule jazyka L je výraz R(t 0,..., t n 1 ), kde R je n-ární relační symbol jazyka L a t 0,..., t n 1 jsou termy jazyka L. Množinu všech atomických formulí jazyka L značíme AFm L. Strukturu atomické formule můžeme reprezentovat vytvořujícím stromem z vytvořujících podstromů jejích termů. U binárních relačních symbolů často používáme infixního zápisu, např. t 1 = t 2 namísto =(t 1, t 2 ) či t 1 t 2 namísto (t 1, t 2 ). Příklady atomických formulí Z(o(x), r), x y (S(0) + x) y, (x y) =. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
9 Formule Formule Formule jazyka L jsou výrazy dané induktivním předpisem (i) každá atomická formule jazyka L je formule, (ii) jsou-li ϕ, ψ formule, pak i následující výrazy jsou formule ( ϕ), (ϕ ψ), (ϕ ψ), (ϕ ψ), (ϕ ψ), (iii) je-li ϕ formule a x proměnná, jsou výrazy (( x)ϕ) a (( x)ϕ) formule. (iv) každá formule vznikne konečným užitím pravidel (i), (ii), (iii). Množinu všech formulí jazyka L značíme Fm L. Formuli, jež je součástí jiné formule ϕ, nazveme podformule formule ϕ. Strukturu formule můžeme reprezentovat jejím vytvořujícím stromem. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
10 Formule Konvence zápisu Zavedení priorit binárních funkčních symbolů např. +, umožňuje při infixním zápisu vypouštět závorky okolo podtermu vzniklého symbolem vyšší priority, např. x y + z reprezentuje term (x y) + z. Zavedení priorit logických spojek a kvantifikátorů umožňuje vypouštět závorky okolo podformule vzniklé spojkou s vyšší prioritou. (1), (2), (3), ( x), ( x) Okolo podformulí vzniklých, ( x), ( x) lze závorky vypustit vždy. Můžeme vypustit závorky i okolo ( x) a ( x) pro každé x Var. Rovněž vnější závorky můžeme vynechat. ((( (( x)r(x))) (( y)p(y))) ( ((( x)r(x)) ( (( y)p(y)))))) ( x)r(x) ( y)p(y) (( x)r(x) ( y)p(y)) Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
11 Formule Příklad formule ( x)(x y (S(0) + x) y) x y (S(0) + x) y x y (S(0) + x) y x y S(0) + x y S(0) x 0 Vytvořující strom formule ( x)(x y (S(0) + x) y). Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
12 Otevřené a uzavřené formule Výskyt proměnné Necht ϕ je formule a x je proměnná. Výskyt proměnné x ve ϕ je list vytvořujícího stromu ϕ označený x. Výskyt x ve ϕ je vázaný, je-li součástí nějaké podformule ψ začínající kvantifikátorem ( x) nebo ( x). Není-li výskyt vázaný, je volný. Proměnná x je volná ve ϕ, pokud má volný výskyt ve ϕ. Je vázaná ve ϕ, pokud má vázaný výskyt ve ϕ. Proměnná x může být zároveň volná i vázaná ve ϕ. Např. ve formuli ( x)( y)(x y) x z. Zápis ϕ(x 1,..., x n ) značí, že x 1,..., x n jsou všechny volné proměnné ve formuli ϕ. Poznámka Uvidíme, že pravdivostní hodnota formule (při dané interpretaci symbolů) závisí pouze na ohodnocení volných proměnných. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
13 Otevřené a uzavřené formule Otevřené a uzavřené formule Formule je otevřená, neobsahuje-li žádný kvantifikátor. Pro množinu OFm L všech otevřených formulí jazyka L platí AFm L OFm L Fm L. Formule je uzavřená (sentence), pokud nemá žádnou volnou proměnnou, tj. všechny výskyty proměnných jsou vázané. Formule může být otevřená i uzavřená zároveň, pak všechny její termy jsou konstantní. x + y 0 otevřená, ϕ(x, y) ( x)( y)(x + y 0) uzavřená (sentence), ( x)(x + y 0) ani otevřená, ani uzavřená, ϕ(y) otevřená i uzavřená Poznámka Uvidíme, že sentence má při dané interpretaci symbolů pevný význam, tj. její pravdivostní hodnota nezávisí na ohodnocení proměnných. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
14 Instance a varianty Instance Když do formule za volnou proměnnou x dosadíme term t, požadujeme, aby vzniklá formule říkala (nově) o termu t totéž, co předtím říkala o proměnné x. ϕ(x) ( y)(x + y = 1) existuje prvek 1 x pro t = 1 lze ϕ(x/t) ( y)(1 + y = 1) existuje prvek 1 1 pro t = y nelze ( y)(y + y = 1) 1 je dělitelné 2 Term t je substituovatelný za proměnnou x ve formuli ϕ, pokud po současném nahrazení všech volných výskytů x za t nevznikne ve ϕ žádný vázaný výskyt proměnné z t. Pak vzniklou formuli značíme ϕ(x/t) a zveme ji instance formule ϕ vzniklá substitucí termu t za proměnnou x do ϕ. t není substituovatelný za x do ϕ, právě když x má volný výskyt v nějaké podformuli ϕ začínající ( y) nebo ( y) pro nějakou proměnnou y z t. Konstantní termy jsou substituovatelné vždy. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
15 Instance a varianty Varianty Kvantifikované proměnné lze (za určitých podmínek) přejmenovat tak, že vznikne ekvivalentní formule. Necht (Qx)ψ je podformule ve ϕ, kde Q značí či, a y je proměnná, tž. 1) y je substituovatelná za x do ψ, a 2) y nemá volný výskyt v ψ. Nahrazením podformule (Qx)ψ za (Qy)ψ(x/y) vznikne varianta formule ϕ v podformuli (Qx)ψ. Postupnou variací jedné či více podformulí ve ϕ vznikne varianta formule ϕ. Např. ( x)( y)(x y) je formule ϕ, ( u)( v)(u v) je varianta ϕ, ( y)( y)(y y) není varianta ϕ, neplatí 1), ( x)( x)(x x) není varianta ϕ, neplatí 2). Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
16 Základní sémantika PL Struktury Struktury - příklady S = S, uspořádaná množina, kde je reflexivní, antisymetrická, tranzitivní binární relace na S, G = V, E neorientovaný graf bez smyček, kde V je množina vrcholů, E je ireflexivní, symetrická binární relace na V (sousednost), Z p = Z p, +,, 0 grupa sčítání celých čísel modulo p, Q = Q, +,,, 0, 1 těleso racionálních čísel. P(X ) = P(X ),,,,, X potenční algebra nad množinou X, N = N, S, +,, 0, standardní model aritmetiky (přirozených čísel), konečné automaty a další modely výpočtu, relační databáze,... Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
17 Základní sémantika PL Struktury Struktura pro jazyk Necht L = R, F je jazyk a A je neprázdná množina. Realizace (interpretace) relačního symbolu R R na A je libovolná relace R A A ar(r). Realizace rovnosti na A je relace Id A (identita). Realizace (interpretace) funkčního symbolu f F na A je libovolná funkce f A : A ar(f ) A. Realizace konstantního symbolu je tedy prvek z A. Struktura pro jazyk L (L-struktura) je trojice A = A, R A, F A, kde A je neprázdná množina, zvaná doména (univerzum) struktury A, R A = R A R R je soubor realizací relačních symbolů (relací), F A = f A f F je soubor realizací funkčních symbolů (funkcí). Strukturu pro jazyk L nazýváme také model jazyka L. Třída všech modelů jazyka L se značí M(L). Např. struktury pro jazyk L = jsou N,, Q, >, X, E pokud X, P(X ),. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
18 Základní sémantika PL Pravdivostní hodnota Hodnota termu Necht t je term jazyka L = R, F a A = A, R A, F A je struktura pro L. Ohodnocení proměnných v množině A je funkce e : Var A. Hodnota t A [e] termu t ve struktuře A při ohodnocení e je dána induktivním předpisem x A [e] = e(x) pro každé x Var, (f (t 0,..., t n 1 )) A [e] = f A (t0 A [e],..., tn 1[e]) A pro každé f F. Speciálně, pro konstantní symbol c je c A [e] = c A. Je-li t konstantní term, jeho hodnota v A nezávisí na ohodnocení e. Hodnota termu v A závisí pouze na ohodnocení jeho proměnných. Např. hodnota termu x + 1 ve struktuře N = N,, 3 při ohodnocení e, pro které e(x) = 2, je (x + 1) N [e] = 6. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
19 Základní sémantika PL Pravdivostní hodnota Hodnota atomické formule Necht ϕ je atomická formule tvaru R(t 0,..., t n 1 ) jazyka L = R, F a A = A, R A, F A je struktura pro L. Hodnota Hat A (ϕ)[e] formule ϕ ve struktuře A při ohodnocení e je { Hat A 1 pokud (t0 A (R(t 0,..., t n 1 ))[e] = [e],..., t n 1 A [e]) RA, 0 jinak. přičemž = A je Id A, tj. Hat A (t 0 = t 1 )[e] = 1 pokud t0 A[e] = t 1 A [e], jinak 0. Je-li ϕ sentence, tj. všechny její termy jsou konstantní, její hodnota v A nezávisí na ohodnocení e. Hodnota ϕ v A závisí pouze na ohodnocení jejích (volných) proměnných. Např. hodnota formule ϕ tvaru x ve struktuře N = N, +, 1, při ohodnocení e je H N at (ϕ)[e] = 1 právě když e(x) = 0. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
20 Základní sémantika PL Pravdivostní hodnota Hodnota formule Hodnota H A (ϕ)[e] formule ϕ ve struktuře A při ohodnocení e je H A (ϕ)[e] = H A at (ϕ)[e] pokud ϕ je atomická, H A ( ϕ)[e] = 1 (H A (ϕ)[e]) H A (ϕ ψ)[e] = 1 (H A (ϕ)[e], H A (ψ)[e]) H A (ϕ ψ)[e] = 1 (H A (ϕ)[e], H A (ψ)[e]) H A (ϕ ψ)[e] = 1 (H A (ϕ)[e], H A (ψ)[e]) H A (ϕ ψ)[e] = 1 (H A (ϕ)[e], H A (ψ)[e]) H A (( x)ϕ)[e] = min a A (H A (ϕ)[e(x/a)]) H A (( x)ϕ)[e] = max a A (H A (ϕ)[e(x/a)]) kde 1, 1, 1, 1, 1 jsou Booleovské funkce dané tabulkami a e(x/a) pro a A značí ohodnocení získané z e nastavením e(x) = a. Pozorování H A (ϕ)[e] závisí pouze na ohodnocení volných proměnných ve ϕ. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
21 Základní sémantika PL Platnost (pravdivost) Platnost při ohodnocení Formule ϕ je pravdivá (platí) ve struktuře A při ohodnocení e, pokud H A (ϕ)[e] = 1. Pak píšeme A = ϕ[e], v opačném případě A = ϕ[e]. Platí A = ϕ[e] A = ϕ[e] A = (ϕ ψ)[e] A = ϕ[e] a A = ψ[e] A = (ϕ ψ)[e] A = ϕ[e] nebo A = ψ[e] A = (ϕ ψ)[e] jestliže A = ϕ[e], pak A = ψ[e] A = (ϕ ψ)[e] A = ϕ[e] právě když A = ψ[e] A = ( x)ϕ[e] A = ϕ[e(x/a)] pro každé a A A = ( x)ϕ[e] A = ϕ[e(x/a)] pro nějaké a A Pozorování Necht term t je substituovatelný za proměnnou x do formule ϕ a formule ψ je varianta ϕ. Pak pro každou strukturu A a ohodnocení e platí 1) A = ϕ(x/t)[e] právě když A = ϕ[e(x/a)] pro a = t A [e], 2) A = ϕ[e] právě když A = ψ[e]. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
22 Základní sémantika PL Platnost (pravdivost) Platnost ve struktuře Necht ϕ je formule jazyka L a A je struktura pro L. ϕ je pravdivá (platí) ve struktuře A, značeno A = ϕ, pokud A = ϕ[e] pro každé ohodnocení e : Var A. V opačném případě píšeme A = ϕ. ϕ je lživá v A, pokud A = ϕ, tj. A = ϕ[e] pro každé e : Var A. Pro každé formule ϕ, ψ, proměnnou x a strukturu A platí (1) A = ϕ A = ϕ (2) A = ϕ ψ A = ϕ a A = ψ (3) A = ϕ ψ A = ϕ nebo A = ψ (4) A = ϕ A = ( x)ϕ Je-li ϕ sentence, je ϕ pravdivá v A či lživá v A a tedy implikace (1) platí i obráceně. Je-li ϕ nebo ψ sentence, implikace (3) platí i obráceně. Z (4) plyne, že A = ϕ právě když A = ψ, kde ψ je generální uzávěr ϕ, tj. formule ( x 1 ) ( x n )ϕ, v níž x 1,..., x n jsou všechny volné proměnné ϕ. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
23 Základní sémantika PL Teorie - sémantika Platnost v teorii a logická platnost Teorie jazyka L je libovolná množina T formulí jazyka L (tzv. axiomů). Model teorie T je L-struktura A taková, že A = ϕ pro každé ϕ T, značíme A = T. Třída modelů teorie T je M(T ) = {A M(L) A = T }. Formule ϕ je pravdivá v T (platí v T ), značíme T = ϕ, pokud A = ϕ pro každý model A teorie T. V opačném případě píšeme T = ϕ. Formule ϕ je lživá v T, pokud T = ϕ, tj. je lživá v každém modelu T. Formule ϕ je nezávislá v T, pokud není pravdivá v T ani lživá v T. Je-li T =, je M(T ) = M(L) a teorii T vynecháváme, případně říkáme v logice. Pak = ϕ značí, že ϕ je pravdivá ((logicky) platí, tautologie). Důsledek T je množina θ L (T ) všech sentencí jazyka L pravdivých v T, tj. θ L (T ) = {ϕ Fm L T = ϕ a ϕ je sentence}. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
24 Základní sémantika PL Teorie - sémantika Příklad teorie Teorie uspořádání T jazyka L = s rovností má axiomy x x (reflexivita) x y y x x = y (antisymetrie) x y y z x z (tranzitivita) Modely T jsou L-struktury S, S, tzv. uspořádané množiny, ve kterých platí axiomy T, např. A = N, nebo B = P(X ), pro X = {0, 1, 2}. Formule ϕ ve tvaru x y y x platí v A, ale neplatí v B, nebot např. B = ϕ[e] při ohodnocení e(x) = {0}, e(y) = {1}, je tedy nezávislá v T. Sentence ψ ve tvaru ( x)( y)(y x) je pravdivá v B a lživá v A, je tedy rovněž nezávislá v T. Píšeme B = ψ, A = ψ. Formule χ ve tvaru (x y y z z x) (x = y y = z) je pravdivá v T, píšeme T = χ, totéž platí pro její generální uzávěr. Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/ / 24
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Výroková a predikátová logika - XI
 Výroková a predikátová logika - XI Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XI ZS 2014/2015 1 / 21 Další dokazovací systémy PL Hilbertovský kalkul
Výroková a predikátová logika - XI Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XI ZS 2014/2015 1 / 21 Další dokazovací systémy PL Hilbertovský kalkul
Predikátová logika. Teoretická informatika Tomáš Foltýnek
 Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
Výroková a predikátová logika - XII
 Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Predikátová logika. prvního řádu
 Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Výroková a predikátová logika - XIII
 Výroková a predikátová logika - XIII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIII ZS 2013/2014 1 / 13 Úvod Algoritmická (ne)rozhodnutelnost Které
Výroková a predikátová logika - XIII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIII ZS 2013/2014 1 / 13 Úvod Algoritmická (ne)rozhodnutelnost Které
Výroková a predikátová logika Výpisky z cvičení Martina Piláta
 Výroková a predikátová logika Výpisky z cvičení Martina Piláta Jan Štětina 1. prosince 2009 Cviˇcení 29.9.2009 Pojem: Sekvence je konečná posloupnost, značíme ji predikátem seq(x). lh(x) je délka sekvence
Výroková a predikátová logika Výpisky z cvičení Martina Piláta Jan Štětina 1. prosince 2009 Cviˇcení 29.9.2009 Pojem: Sekvence je konečná posloupnost, značíme ji predikátem seq(x). lh(x) je délka sekvence
Základy matematické logiky
 OBSAH 1 Základy matematické logiky Obsah 1 Úvod 2 1.1 Předmět matematiky.......................... 2 1.2 Nástin historie.............................. 2 1.3 Axiomatická výstavba matematických teorií.............
OBSAH 1 Základy matematické logiky Obsah 1 Úvod 2 1.1 Předmět matematiky.......................... 2 1.2 Nástin historie.............................. 2 1.3 Axiomatická výstavba matematických teorií.............
Výroková a predikátová logika - V
 Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Výroková a predikátová logika - V Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - V ZS 2015/2016 1 / 21 Dokazovací systémy VL Hilbertovský kalkul Hilbertovský
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2017/2018 1 / 16 2-SAT 2-SAT Výrok je v k-cnf, je-li v CNF a
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Výroková a predikátová logika - XII
 Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2015/2016 1 / 15 Algebraické teorie Základní algebraické teorie
Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2015/2016 1 / 15 Algebraické teorie Základní algebraické teorie
Pro každé formule α, β, γ, δ platí: Pro každé formule α, β, γ platí: Poznámka: Platí právě tehdy, když je tautologie.
 Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Úvod do predikátové logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
 Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Základy logiky a teorie množin
 Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Logika Libor Barto. Výroková logika
 Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
1 Pravdivost formulí v interpretaci a daném ohodnocení
 1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
Predikátová logika. Z minula: 1. jazyk logiky 1. řádu. 2. term a formule. 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy
 1 Predikátová logika Z minula: 1. jazyk logiky 1. řádu 2. term a formule 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy 5. vázané a volné výskyty proměnných ve formuli 6. otevřené
1 Predikátová logika Z minula: 1. jazyk logiky 1. řádu 2. term a formule 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy 5. vázané a volné výskyty proměnných ve formuli 6. otevřené
Další (neklasické) logiky. Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20
 Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Výroková a predikátová logika - IV
 Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Řešení: Ano. Řešení: Ne.
 1 ÚLOHY Z PREDIKÁTOVÉ LOGIKY Instance, varianty. UF.1.1. Substituovatelnost. 1. Buď ϕ formule ( z)(x=z)&y < x a dále x, y, z různé proměnné, F unární funkční symbol, c konstantní symbol. Uveďte, zda je
1 ÚLOHY Z PREDIKÁTOVÉ LOGIKY Instance, varianty. UF.1.1. Substituovatelnost. 1. Buď ϕ formule ( z)(x=z)&y < x a dále x, y, z různé proměnné, F unární funkční symbol, c konstantní symbol. Uveďte, zda je
Sémantika predikátové logiky
 Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Predikátová logika dokončení
 Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Matematická analýza 1
 Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Matematická analýza 1 ZS 2019-20 Miroslav Zelený 1. Logika, množiny a základní číselné obory 2. Limita posloupnosti 3. Limita a spojitost funkce 4. Elementární funkce 5. Derivace 6. Taylorův polynom Návod
Formální systém výrokové logiky
 Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
2.2 Sémantika predikátové logiky
 14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
Výroková logika - opakování
 - opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
- opakování ormální zavedení Výroková formule: Máme neprázdnou nejvýše spočetnou množinu A výrokových proměnných. 1. Každá proměnná je výroková formule 2. Když α, β jsou formule, potom ( α), (α β), (α
Rezoluční kalkulus pro logiku prvního řádu
 AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
Základy logiky a teorie množin
 1 Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz URL (slajdy): http://pajas.matfyz.cz/vyuka 2 Proč studovat matematickou logiku a teorii množin objasnění vztahu jazyka a významu (syntaxe a sémantiky)
1 Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz URL (slajdy): http://pajas.matfyz.cz/vyuka 2 Proč studovat matematickou logiku a teorii množin objasnění vztahu jazyka a významu (syntaxe a sémantiky)
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce
 Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Základy logiky a teorie množin
 1 2 Proč studovat matematickou logiku a teorii množin Základy logiky a teorie množin objasnění vztahu jazyka a významu (syntaxe a sémantiky) precizace klíčových matematických pojmů: axiom, teorie, důkaz,
1 2 Proč studovat matematickou logiku a teorii množin Základy logiky a teorie množin objasnění vztahu jazyka a významu (syntaxe a sémantiky) precizace klíčových matematických pojmů: axiom, teorie, důkaz,
Logické programy Deklarativní interpretace
 Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Predik atov a logika - pˇredn aˇska () Predik atov a logika - pˇredn aˇska / 16
 Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Predikátová logika [Predicate logic]
![Predikátová logika [Predicate logic] Predikátová logika [Predicate logic]](/thumbs/74/70612837.jpg) Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Výroková a predikátová logika - I
 Výroková a predikátová logika - I Petr Gregor KTIML MFF UK ZS 2019/2020 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - I ZS 2019/2020 1 / 19 K čemu je logika? Pro matematiky: matematika o matematice.
Výroková a predikátová logika - I Petr Gregor KTIML MFF UK ZS 2019/2020 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - I ZS 2019/2020 1 / 19 K čemu je logika? Pro matematiky: matematika o matematice.
Sémantika výrokové logiky. Alena Gollová Výroková logika 1/23
 Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Úvod do výrokové a predikátové logiky
 Úvod do výrokové a predikátové logiky Eva Ondráčková Na této přednášce se seznámíte se základy výrokové a predikátové logiky. Zjistíte, že podstatou logiky není vyplňování pravdivostních tabulek ani negování
Úvod do výrokové a predikátové logiky Eva Ondráčková Na této přednášce se seznámíte se základy výrokové a predikátové logiky. Zjistíte, že podstatou logiky není vyplňování pravdivostních tabulek ani negování
1 Výroková logika 1. 2 Predikátová logika 3. 3 Důkazy matematických vět 4. 4 Doporučená literatura 7
 1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1 Predikátová logika. 1.1 Syntax. jaký mohou mít formule význam (sémantiku). 1. Logických symbolů: 2. Speciálních (mimologických) symbolů:
 1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
Matematická logika. Rostislav Horčík. horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Predikátová logika Motivace Výroková
Výroková a predikátová logika - XIV
 Výroková a predikátová logika - XIV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIV ZS 2018/2019 1 / 20 Nerozhodnutelnost Úvod Rekurzivní a rekurzivně
Výroková a predikátová logika - XIV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIV ZS 2018/2019 1 / 20 Nerozhodnutelnost Úvod Rekurzivní a rekurzivně
Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka
 Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Základní pojmy matematické logiky
 KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
Místo pojmu výroková formule budeme používat zkráceně jen formule. Při jejich zápisu
 VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
0. ÚVOD - matematické symboly, značení,
 0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
0. ÚVOD - matematické symboly, značení, číselné množiny Výroky Výrok je každé sdělení, u kterého lze jednoznačně rozhodnout, zda je či není pravdivé. Každému výroku lze proto přiřadit jedinou pravdivostní
teorie logických spojek chápaných jako pravdivostní funkce
 Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková logika teorie logických spojek chápaných jako pravdivostní funkce zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků používá specifický jazyk složený z výrokových
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2015/2016 1 / 22 Herbrandova věta Úvod Redukce nesplnitelnosti na
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2015/2016 1 / 22 Herbrandova věta Úvod Redukce nesplnitelnosti na
Cvičení ke kursu Klasická logika II
 Cvičení ke kursu Klasická logika II (12. května 2017) 1. Nechť P a Q jsou unární a R binární predikát. Dokažte, že následující formule jsou logicky platné, ale obrátíme-li (vnější) implikaci, ve všech
Cvičení ke kursu Klasická logika II (12. května 2017) 1. Nechť P a Q jsou unární a R binární predikát. Dokažte, že následující formule jsou logicky platné, ale obrátíme-li (vnější) implikaci, ve všech
prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. BI-ZMA ZS 2009/2010
 Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Základní pojmy prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Výroková logika syntaxe a sémantika
 syntaxe a sémantika Jiří Velebil: AD0B01LGR 2015 Handout 01: & sémantika VL 1/16 1 Proč formální jazyk? 1 Přirozené jazyky jsou složité a často nejednoznačné. 2 Komunikace s formálními nástroji musí být
syntaxe a sémantika Jiří Velebil: AD0B01LGR 2015 Handout 01: & sémantika VL 1/16 1 Proč formální jazyk? 1 Přirozené jazyky jsou složité a často nejednoznačné. 2 Komunikace s formálními nástroji musí být
Modely Herbrandovské interpretace
 Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
Modely Herbrandovské interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 8 1 Uvedli jsme termové interpretace a termové modely pro logické programy a také nejmenší
verze 29/9/09 textu o logice, aritmetice a M. Bizzarrimu.
 1 verze 29/9/09 Toto je prozatím definitivní verze provizorního textu o logice, aritmetice a množinách. věnováno Laskavým čtenářům a čtenářkám, kteří navštěvovali tyto přednášky. poděkování Za upozornění
1 verze 29/9/09 Toto je prozatím definitivní verze provizorního textu o logice, aritmetice a množinách. věnováno Laskavým čtenářům a čtenářkám, kteří navštěvovali tyto přednášky. poděkování Za upozornění
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
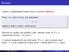 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Přednáška 2: Formalizace v jazyce logiky.
 Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
UDL 2004/2005 Cvičení č.6 řešení Strana 1/5
 UDL 2004/2005 Cvičení č.6 řešení Strana 1/5 Opakování pojmů relace a funkce Relace R nad množinami A, B je podmnožina kartézského součinu: R A B Kartézský součin množin A = {a 1, a 2,, a 4 }, B = {b 1,
UDL 2004/2005 Cvičení č.6 řešení Strana 1/5 Opakování pojmů relace a funkce Relace R nad množinami A, B je podmnožina kartézského součinu: R A B Kartézský součin množin A = {a 1, a 2,, a 4 }, B = {b 1,
(zkráceně jen formule), jestliže vznikla podle následujících pravidel:
 1 Kapitola 1 Výroková logika 1.1 Výroky 1.1.1 Výroky. Máme danou neprázdnou množinu A tzv. elementárních výroků (též jim říkáme logické nebo výrokové proměnné). Konečnou posloupnost prvků z množiny A,
1 Kapitola 1 Výroková logika 1.1 Výroky 1.1.1 Výroky. Máme danou neprázdnou množinu A tzv. elementárních výroků (též jim říkáme logické nebo výrokové proměnné). Konečnou posloupnost prvků z množiny A,
2.5 Rezoluční metoda v predikátové logice
 2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
Predikátová logika: Axiomatizace, sémantické stromy, identita. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 13
 Predikátová logika: Axiomatizace, sémantické stromy, identita (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 13 Axiomatizace predikátové logiky Axiomatizace predikátové logiky Definice Hilbertovský
Predikátová logika: Axiomatizace, sémantické stromy, identita (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 13 Axiomatizace predikátové logiky Axiomatizace predikátové logiky Definice Hilbertovský
Stefan Ratschan. Fakulta informačních technologíı. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Klasická predikátová logika
 Klasická predikátová logika Matematická logika, LS 2012/13, závěrečná přednáška Libor Běhounek www.cs.cas.cz/behounek/teaching/malog12 PřF OU, 6. 5. 2013 Symboly klasické predikátové logiky Poznámky Motivace
Klasická predikátová logika Matematická logika, LS 2012/13, závěrečná přednáška Libor Běhounek www.cs.cas.cz/behounek/teaching/malog12 PřF OU, 6. 5. 2013 Symboly klasické predikátové logiky Poznámky Motivace
KMA/MDS Matematické důkazy a jejich struktura
 Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Úvod do logiky (PL): sémantika predikátové logiky
 Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sémantika predikátové logiky doc. PhDr. Jiří
Logika: systémový rámec rozvoje oboru v ČR a koncepce logických propedeutik pro mezioborová studia (reg. č. CZ.1.07/2.2.00/28.0216, OPVK) Úvod do logiky (PL): sémantika predikátové logiky doc. PhDr. Jiří
Teorie množin. Čekají nás základní množinové operace kartézské součiny, relace zobrazení, operace. Teoretické základy informatiky.
 Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
Teorie množin V matematice je všechno množina I čísla jsou definována pomocí množin Informatika stojí na matematice Znalosti Teorie množin využijeme v databázových systémech v informačních systémech při
Logika. 2. Výroková logika. RNDr. Luděk Cienciala, Ph. D.
 Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Logika 2. Výroková logika RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216, Logika:
Přijímací zkouška - matematika
 Přijímací zkouška - matematika Jméno a příjmení pište do okénka Číslo přihlášky Číslo zadání 1 Grafy 1 Pro který z následujících problémů není znám žádný algoritmus s polynomiální časovou složitostí? Problém,
Přijímací zkouška - matematika Jméno a příjmení pište do okénka Číslo přihlášky Číslo zadání 1 Grafy 1 Pro který z následujících problémů není znám žádný algoritmus s polynomiální časovou složitostí? Problém,
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška pátá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Úvod do informatiky přednáška pátá Miroslav Kolařík Zpracováno dle učebního textu R. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008 a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 15 Sémantická věta o dedukci Věta Pro
LOGIKA VÝROKOVÁ LOGIKA
 LOGIKA Popisuje pravidla odvozování jedněch tvrzení z druhých. Je to myšlenková cesta ke správným závěrům. Vznikla jako součást filosofie. Zakladatelem byl Aristoteles. VÝROKOVÁ LOGIKA Obsahuje syntaktická,
LOGIKA Popisuje pravidla odvozování jedněch tvrzení z druhých. Je to myšlenková cesta ke správným závěrům. Vznikla jako součást filosofie. Zakladatelem byl Aristoteles. VÝROKOVÁ LOGIKA Obsahuje syntaktická,
Aplikovaná matematika I, NMAF071
 M. Rokyta, MFF UK: Aplikovaná matematika I kap. 1: Úvod, čísla, zobrazení, posloupnosti 1 Aplikovaná matematika I, NMAF071 M. Rokyta, KMA MFF UK ZS 2013/14 Sylabus = obsah (plán) přednášky [a orientační
M. Rokyta, MFF UK: Aplikovaná matematika I kap. 1: Úvod, čísla, zobrazení, posloupnosti 1 Aplikovaná matematika I, NMAF071 M. Rokyta, KMA MFF UK ZS 2013/14 Sylabus = obsah (plán) přednášky [a orientační
Databázové systémy. * relační kalkuly. Tomáš Skopal. - relační model
 Databázové systémy Tomáš Skopal - relační model * relační kalkuly Osnova přednášky relační kalkuly doménový n-ticový Relační kalkuly využití aparátu predikátové logiky 1. řádu pro dotazování rozšíření
Databázové systémy Tomáš Skopal - relační model * relační kalkuly Osnova přednášky relační kalkuly doménový n-ticový Relační kalkuly využití aparátu predikátové logiky 1. řádu pro dotazování rozšíření
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška desátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. Obsah 1 Úvod do modální logiky 2 Logické programování a Prolog 3
Matematická logika přednáška desátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. Obsah 1 Úvod do modální logiky 2 Logické programování a Prolog 3
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony.
 Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Booleovská algebra. Booleovské binární a unární funkce. Základní zákony. Tomáš Bayer bayertom@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta UK. Tomáš Bayer bayertom@natur.cuni.cz
Výroková logika. Sémantika výrokové logiky
 Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
Výroková logika Výroková logika se zabývá vztahy mezi dále neanalyzovanými elementárními výroky. Nezabývá se smyslem těchto elementárních výroků, zkoumá pouze vztahy mezi nimi. Elementární výrok je takový
MATEMATICKÁ LOGIKA. Petr Hájek a Vítězslav Švejdar. Praha, listopad (povrchní typografická revize v červnu 99)
 MATEMATICKÁ LOGIKA Předběžný studijní text Petr Hájek a Vítězslav Švejdar Praha, listopad 1994 (povrchní typografická revize v červnu 99) 2 OBSAH Obsah Úvod 3 1 Výroková a predikátová logika 5 1.1 Formule
MATEMATICKÁ LOGIKA Předběžný studijní text Petr Hájek a Vítězslav Švejdar Praha, listopad 1994 (povrchní typografická revize v červnu 99) 2 OBSAH Obsah Úvod 3 1 Výroková a predikátová logika 5 1.1 Formule
B i n á r n í r e l a c e. Patrik Kavecký, Radomír Hamřík
 B i n á r n í r e l a c e Patrik Kavecký, Radomír Hamřík Obsah 1 Kartézský součin dvou množin... 3 2 Binární relace... 6 3 Inverzní relace... 8 4 Klasifikace binární relací... 9 5 Ekvivalence... 12 2 1
B i n á r n í r e l a c e Patrik Kavecký, Radomír Hamřík Obsah 1 Kartézský součin dvou množin... 3 2 Binární relace... 6 3 Inverzní relace... 8 4 Klasifikace binární relací... 9 5 Ekvivalence... 12 2 1
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 2017
 Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 207 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od jara 207 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Úvod do teoretické informatiky(2017/2018) cvičení 6 1
 Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Logika. Materiály ke kurzu MA007. Poslední modifikace: prosinec zkoumá způsob vyvozování. Lidské uvažování
 Výroková úplnosti Materiály ke kurzu MA007 Poslední modifikace: prosinec 2018 http://www.fi.muni.cz/usr/kucera/teaching.html 2. věta o dokazování prosinec 2018 1/171 Logika. Výroková úplnosti 2. věta o
Výroková úplnosti Materiály ke kurzu MA007 Poslední modifikace: prosinec 2018 http://www.fi.muni.cz/usr/kucera/teaching.html 2. věta o dokazování prosinec 2018 1/171 Logika. Výroková úplnosti 2. věta o
