Monopol, Teorie her, Oligopol
|
|
|
- Antonín Vaněk
- před 7 lety
- Počet zobrazení:
Transkript
1 December 7, 2012
2 Denice monopolu Monopol struktura odv tví s jedinou rmou na trhu. Ale jaký je relevantní trh? Monopoly mohou vzniknout z n kolika d vod : exkluzivní vlastnictví vstupu, licence patenty p irozený monopol (velký MES)
3 Maximalizace zisku monopolu p(y) ozna uje inverzní trºní poptávku, r(y) = p(y)y p íjmovou funkci a c(y) nákladovou funkci. Podmínka prvního ádu je max r(y) c(y) p i omezení y 0. y MR(y) MC(y) = 0 MR(y) = MC(y). A podmínka druhého ádu je MR (y) MC (y) 0 MC (y) MR (y). Monopol maximalizuje zisk, kdyº si zvolí takový výstup y, p i kterém se mezní p íjmy rovnají mezním náklad m, je sklon k ivky MC(y) v t²í neº sklon k ivky MR(y).
4 Monopol a elasticita Dosazením r(y) = p(y)y do podmínky prvního ádu získáme MR(y) = p(y) + p (y)y = MC(y). (1) Zvý²ení výstupu má dva efekty na p íjmy monopolu. P íjmy vzrostou o p(y), protoºe vzroste prodané mnoºství, klesnou o p (y)y, protoºe klesne cena. Rovnici m ºeme upravit tak, ºe získáme [ ] MR(y) = p(y) 1 + p (y) y = MC(y) p(y) [ ] MR(y) = p(y) 1 1 = MC(y). (2) ɛ(y)
5 Neefektivnost monopolu Dokonalá konkurence: p c = MC(y c ) Monopol: MR(y m ) = MC(y m ) Monopolní cena p m > p c a monopolní mnoºství y m < y c.
6 P íklad 1 Renomovaný ekonom dopsal u ebnici mikroekonomie. Poptávka po této u ebnici bude Q = P, kde P je cena u ebnice. P íprava této u ebnice na tisk stojí K, honorá autora je K a náklady na jeden výtisk jsou 200 K. 1 Jakou cenu nakladatel nastaví a kolik knih prodá? Jaký bude jeho zisk po tomto vydání? Nakreslete situaci monopolu do grafu. 2 U ebnice dob e prodává, takºe se nakladatel rozhodne vydat tuto u ebnici podruhé. Poptávka po druhém vydání je Q = P. Za jakou cenu nakladatelství knihu nabídne a kolik výtisk prodá? 3 Jak spolu souvisí cenová elasticita poptávky a p iráºka nad mezní náklady (p/mc )?
7 P íklad 3 Inverzní poptávková k ivka monopolu je p(y) = 16 y a nákladová funkce je c(y) = y 2. Odpov na následující otázky odvo te ze ziskové funkce monopolu. 1 Jak velké mnoºství produktu bude monopol prodávat? 2 Jak velké mnoºství produktu bude monopol prodávat, kdyº na n j stát uvalí mnoºstevní da ve vý²i 4? 3 Stát zru²í mnoºstevní da a uvalí na monopol da ze zisku ve vý²i 50 %. Jak velký produkt bude monopol prodávat nyní?
8 P íklad 4 Monopol elí klesající poptávkové k ivce s konstantní elasticitou poptávky ve vý²i 4. Cena produktu je Jaké jsou jeho mezní náklady na této úrovni výstupu? 2 M ºeme íct, co by se stalo s cenou monopolu, kdyby se elasticita poptávky zm nila na 3? M ºeme íct, co by se stalo s jeho p iráºkou nad mezní náklady? Vysv tlete.
9 P íklad 5 Monopol elí inverzní poptávkové funkci p(q) = 100 2q. Jeho nákladová funkce má tvar c(q) = q. 1 Jedná se o p irozený monopol? Vysv tlete. 2 Vláda poºaduje, aby tento monopol vyráb l kladné mnoºství produktu a m l nulový zisk. Jak velké mnoºství produktu bude vyráb t? 3 Tuto situaci nakreslete. V grafu vyzna te také MC. Budou MC vy²²í neº AC?
10 Cenová diskriminace prvního stupn Kaºdá jednotka je prodána spot ebiteli, který si jí nejvíc cení, za maximální cenu, kterou je ochotný zaplatit. Monopol bude nabízet kaºdému spot ebiteli dokonale konkuren ní mnoºství x 0 1 a x 0 2, pro které p(x 0 1 ) = MC(x 0 1 ) a p(x 0 2 ) = MC(x 0 2 ). Nevzniká ztráta mrtvé váhy. Stejné, jako kdyby monopol prodal kaºdému spot ebiteli 1 mnoºství x1 0 za cenu A + MCx 1 0 a spot ebiteli 2 mnoºství x 2 0 za cenu B + MCx2 0.
11 Cenová diskriminace druhého stupn Cenová diskriminace druhého stupn cena závisí na mnoºství, které spot ebitel nakoupí (také nonlinear pricing). Problém: Monopol chce provád t cenovou diskriminaci, ale neumí poznat spot ebitele s vysokou ochotou platit. e²ení: Monopol nabídne takové kombinace mnoºství a ceny balení, ºe se spot ebitelé s vysokou ochotu platit prozradí sami. Nabídne spot ebitel m s nízkou ochotou platit tak nízké mnoºství (kvalitu), ºe si ostatní rad²i p iplatí za vy²²í mnoºství (kvalitu).
12 P íklad 1 asopis nabízí p edplatné lánk na internetu dv ma skupinám tená : manaºer m a student m ekonomie. Ob skupiny mají 100 osob. Kaºdý manaºer má inverzní poptávkovou funkci po láncích p M (x) = 100 x a kaºdý student p S (x) = 60 x, kde x je po et lánk za rok a ceny p jsou v eurocentech. Náklady na zve ejn ní lánku dal²ímu tená i jsou nulové. 1 ƒasopis pozná, jestli p edplatné poptávají manaºe i nebo studenti, a provádí dokonalou cenovou diskriminaci. 2 ƒasopis není schopný rozpoznat, kdo je manaºer a kdo je student. Jaké ceny bude ú tovat manaºer m, kdyº nechá cenu a po et lánk u studentského p edplatného stejné? 3 P i jakých po tech lánk v p edplatném a jakých cenách p edplatného pro manaºery a studenty by v novém roce asopis maximalizoval zisk?
13 Cenová diskriminace t etího stupn Cenová diskriminace t etího stupn monopol prodává za r zné ceny lidem v r zných skupinách (podmínka: nemoºnost arbitráºe) Inverzní poptávka na trzích 1 a 2: p 1 (y 1 ) a p 2 (y 2 ) Nákladová funkce monopolu: c(y 1 + y 2 ) Monopol maximalizuje zisk Podmínky prvního ádu jsou max p 1 (y 1 )y 1 + p 2 (y 2 )y 2 c(y 1 + y 2 ) y 1,y 2 MR 1 (y 1 ) = MC 1 (y 1 + y 2 ) MR 2 (y 2 ) = MC 1 (y 1 + y 2 ).
14 P íklad 2 Americká farmaceutická rma vynalezla nový lék proti malárii. Tento lék prodává do dvou afrických zemí. Relativn bohatá zem A má ro ní poptávku po tomto léku Q A = P A a relativn chudá zem B má ro ní poptávku po tomto léku Q B = P B. Ro ní podíl xních náklad je dolar. Náklady na výrobu a dopravu jednoho balení jsou 4 dolary.
15 P íklad 5 Do jediného zábavního parku ²iroko daleko chodí kaºdý den 100 náv²t vník s poptávkou po jízdách x = 25 0, 5p. Mezní náklady parku na jízdu jsou 0. Jaký je maximální denní zisk zábavního parku, který pouºívá dvousloºkový tarif?
16 Oligopol Oligopol struktura odv tví s n kolika rmami na trhu. Firmy v oligopolu v í, ºe jejich chování (volba mnoºství nebo ceny) ovlivní chování ostatních rem na trhu. Dochází ke strategickým interakcím. P íklady oligopolních odv tví: procesory (Intel vs. AMD) kolové nápoje (Coke vs. Pepsi) mobilní telefony automobily
17 Teorie her Teorie her slouºí ke zkoumání strategických interakcí Hra obsahuje hrá e, moºné akce a preference hrá. Výsledkem hry je tzv. prol akcí. Budeme zabývat dv ma typy her: simultánní hra hrá i se rozhodují zárove, sekven ní hra hrá i se rozhodují v daném po adí.
18 P íklad simultánní hry Máme simultánní hru, která obsahuje hrá e A a B mnoºinu akcí pro hrá e A (nahoru T, dol B) a hrá e B (doleva L, doprava R) preference hrá dané výplatami pro v²echny proly akcí, kde hrá A má preference BL TL BR TR, hrá B má preference TL BL TR BR. L R T 1,2 0,1 B 2,1 1,0
19 Rovnováha Dominantní strategie je akce, která je pro hrá e optimální p i jakékoliv akci jiných hrá. Pokud má kaºdý hrá dominatní strategii, pak mluvíme o rovnováze v dominantních strategiích. Nashova rovnováha je prol akcí, ve kterém kaºdý hrá hraje optimální akci, p i akcích ostatních hrá. Jak najít Nashovu rovnováhu? Pomocí reak ních funkcí (ukazuje optimální akci pro v²echny kombinace kací ostatních hrá ) Ov it, ºe se ºádný hrá nechce z prolu akcí jednostrann odchýlit
20 P íklad 1 Dva hrá i na za átku hry dostanou 100 K, které si mohou nechat nebo je vloºit do ve ejného fondu. Peníze vloºené do ve ejného fondu se vynásobí 1,5krát a rozd lí se rovným dílem mezi hrá e. 1 Nakreslete výplatní matici této hry. Mají hrá i v této h e dominantní strategii? Pokud ano, jakou? 2 Má tato hra rovnováhu v dominantních strategiích? Pokud ano, jakou? 3 Má tato hra n jaké Nashovy rovnováhy? Pokud ano, jaké?
21 Nashova rovnováha: poznámky V²imn te si, ºe: V Nashov rovnováze mají hrá i správná o ekávání o otm, co budou d lat ostatní hrá i Pokud je n co rovnováha v dominantních strategiích, pak je to i Nashova rovnováha Hra m ºe mít více Nashových rovnováh, a naopak n kdy nemusí v istých strategiích Nashova rovnováha v bec existovat Ne e²íme otázku, jak se hrá i do Nashovy rovnováhy dostanou
22 Cournot v model Cournot v model je simultánní hra, ve které hrá i jsou rmy, akce jsou mnoºství, které rmy vyrábí, preference hrá jsou dané zisky rem. Nashova (Cournotova) rovnováha je kombinace mnoºství produkce rem, p i které kaºdá rma reaguje optimáln na produkci ostatních rem. Kaºdá rma volí mnoºství produkce, které maximalizuje její zisk p i daných mnoºstvích ostatních rem. Nashovu rovnováhu najdeme pomocí reak ních funkcí.
23 P íklad 1 Saki a Kiku jsou jediní dva farmá i, kte í odlehlém hornatém regionu p stují dýni Hokaido. Trºní poptávka je q = p. Saki má polí ko na jiºní stran hory. Jeho náklady na vyp stování kaºdé dal²í dýn jsou 1 yen. Kiku má polí ko na západní stran hory a jeho náklady na výp stování kaºdé dal²í dýn jsou 4 yeny. Ani jeden nemá dal²í náklady související s p stováním dýní. Saki a Kiku se rozhodují ve stejný okamºik, kolik zasadí a vyp stují dýní. 1 Jaké budou reak ní funkce obou farmá? 2 Jaká bude Nashova rovnováha této hry? Jaká bude trºní cena? Jaké budou zisky t chto farmá?
24 Cournotova rovnováha s n rmami Celkový výstup odv tví je Y = y y n, kde n je po et rem v odv tví. Firma i e²í maximaliza ní problém max y i π i = p(y )y i c(y i ). Podmínka prvního ádu je p(y )+ dp(y ) dy y i = MC(y i ) p(y )[1+ dp(y ) ] Y y i = MC(y i ) dy p(y ) Y
25 Cournotova rovnováha s n rmami (pokra ování) Kdyº pouºijeme denici elasticity agregátní poptávkové k ivky ɛ(y ) a dosadíme s i = y i /Y, získáme ) p(y )(1 s i = MC(y i ). ɛ(y ) Tento výraz m ºeme napsat také jako [ ] 1 p(y ) 1 = MC(y i ). ɛ(y ) /s i Výraz ɛ(y ) /s i m ºeme chápat jako elasticitu poptávky po produkci rmy i. Kdyº je na trhu 1 rma, máme monopol, který elí trºní poptávce, mnoho rem, poptávka po produkci jedné rmy je velmi elastická a situace na trhu se blíºí dokonalé konkurenci s p(y ) = MC(y i ).
26 P íklad 4 P edpokládejte, ºe cenová elasticita poptávky po leteckých sluºbách mezi dv ma dv ma m sty je -2. Máme v odv tví 4 letecké spole nosti v Cournotov rovnováze. V²echny tyto spole nosti mají stejné náklady. Jaký bude pom r mezi cenou a mezními náklady jedné rmy?
27 Bertrand v model Bertrand v model je simultánní hra, ve které hrá i jsou rmy, akce jsou ceny produkce, preference hrá jsou dané zisky rem. Firmy maximalizující zisk si zárove volí ceny produkce. Nashova (Bertrandova) rovnováha je taková kombinace cen rem, p i které kaºdá rma reaguje optimáln na ceny ostatních rem.
28 Bertrandova rovnováha se 2 rmami Základní verze Bertrandova modelu: stejné konstantní mezní náklady MC 1 (y 1 ) = MC 2 (y 2 ) = c, identický produkt inverzní trºní poptávka p = a b(y 1 + y 2 ). Poptávka po produkci rmy je 0 kdyº p i > p j, a p y i = i kdyº p 2b i = p j, a p i kdyº p b i < p j, Nashova (Bertrandova) rovnováha je (p 1, p 2 ), kde p 1 = p 2 = c. Kdyby p i cen rmy j p j = c rma i zvý²ila cenu, neprodala by nic (nepolep²í si), sníºila cenu, byla by ve ztrát (pohor²í si).
29 Sekven ní hry Máme sekven ní hru, která obsahuje hrá e A a B, mnoºinu kone ných historií (TL, TR, BL, BR), hrá skou funkci: první na tahu je hrá A, pak hrá B, preference hrá jsou dané výplatami pro v²echny historie:
30 Dokonalá rovnováha vzhledem k podhrám Tato hra má dv Nashovy rovnováhy TL a BR, pouze BR je dokonalá rovnováha vzhledem k podhrám (SPE). SPE (Subgame Perfect Equilibrium) je prol akcí, ve kterém kaºdý hrá v kaºdé podh e (t.j. v kaºdém okamºiku, kdy je na tahu) hraje optimální akci p i akcích ostatních hrá. Hru e²íme zp tnou indukcí: Hrá B volí podle své reak ní funkce: f B (T ) = L, R a f B (B) = R. Hrá A si zvolí B, protoºe BR TL TR.
31 P íklad 3 Dva loupeºníci, Lotrando a Vincek, jsou domluvení, ºe Vincek p jde na rozcestí a p esv d í pocestného, aby se vydal do m sta zkratkou p es les. Lotrando si pak na pocestného po ká pod dubem a oloupí ho a kaºdý získá 5 dukát. Problém je v tom, ºe oba loupeºníci rádi spí. Kdyº se rozhodnou prospat den, je to pro n stejn dobré jako 3 dukáty. Kdyº ale kterýkoli z nich usne, pocestného se jim nepoda í oloupit. 1 Nakreslete výplatní matici této hry. Má tato hra n jaké Nashovy rovnováhy? 2 Jaká bude rovnováha této hry, kdyº víme, ºe Lotrando, kdyº vyleze na dub, vidí hned ráno, jestli Vincek eká na rozcestí na pocestného nebo spí?
32 P íklad 4 P edpokládejte, ºe se AMD rozhoduje, jestli vstoupí nebo nevstoupí na trh s nejnov j²ím ipem od Intelu. Kdyº vstoupí na trh, Intel m ºe bojovat, zvý²í výstup a sníºí ceny, nebo nebojovat a rozd lí se s AMD o trh. Diskontované zisky z tohoto trhu v miliardách dolar jsou dané výplatní maticí bojovat nebojovat vstoupit -2,10 10,14 nevstoupit 0,20 0,24 Za kaºdé 2 miliardy dolar, které Intel zainvestuje do p ebyte ných výrobních kapacit, vzroste jeho zisk v p ípad boje o 1 miliardu. Bude Intel ochotný investovat do výrobních kapacit? Pokud ano, kolik miliard?
33 Stackelberg v model Stackelberg v model (mnoºstevní v dcovství) je sekven ní hra, kde hrá i jsou rmy v dce a následovník, v dce si volí mnoºství produkce první a následovník druhý, preference hrá jsou dané zisky rem.
34 P íklad 2 Situace Sakiho a Kika je stejná jako v p edchozím p íklad s jedním rozdílem. Na Sakiho polí ku sleze sníh o n kolik dní d ív neº na Kikov polí ku. Saki tak m ºe zasadit dýn d ív neº Kiku, takºe Kiku jasn vidí, kolik dýní Saki plánuje vyp stovat. 1 Jakému modelu odpovídá tato trºní situace? 2 Jaká bude u této hry dokonalá rovnováha vzhledem k podhrám? Jaká bude trºní cena? Jaké budou zisky t chto farmá?
35 Cenové v dcovství Cenové v dcovství je sekven ní hra, ve které nejd ív si volí cenu v dce a pak následovník, preference hrá jsou dané zisky rem. Základní verze modelu dále p edpokládá: v dce má konstantní mezní náklady c a následovník má rostoucí funkci mezních náklad, identický produkt Zp tná indukce: Následovník bude prodávat za cenu v dce p 2 = p 1 a bude chtít nabízet takové mnoºství produkce, aby maximalizoval sv j zisk. Chová se jako v dokonalé konkurenci. V dce si zvolí cenu produkce, která maximalizuje jeho zisk p i známém nabízeném mnoºství produkce následovníka.
36 P íklad 9 V odv tví je 20 malých rem, které se chovají dokonale konkuren n a mají kaºdá nákladovou funkci c(y) = y 2 /2. Dále je zde jeden cenový v dce s nulovými náklady. Trºní poptávková funkce je D(p) = p. 1 Jaká je celková nabídka dokonale konkuren ních rem? 2 Jaké mnoºství a za jaké ceny bude nabízet cenový v dce? 3 Jaké mnoºství budou nabízet dokonale konkuren ní rmy?
37 Záv r Dotazy?
Mezi firmami v oligopolu dochází ke strategickým interakcím. Při zkoumání strategických interakcí používáme teorii her.
 Teorie her a oligopol Varian: Mikroekonomie: moderní přístup, oddíly 26.1-9, 27.1-3 a 27.7-8 Varian: Intermediate Microeconomics, Sections 27.1-9, 28.1-3, 28.7-8 () 1 / 36 Obsah přednášky V této přednášce
Teorie her a oligopol Varian: Mikroekonomie: moderní přístup, oddíly 26.1-9, 27.1-3 a 27.7-8 Varian: Intermediate Microeconomics, Sections 27.1-9, 28.1-3, 28.7-8 () 1 / 36 Obsah přednášky V této přednášce
Teorie rmy, Dokonalá konkurence
 November 15, 2012 Teorie rmy Ukáºmeme si Jak popsat technologii rmy Jak se rma rozhoduje Jak se odvozuje nabídka rmy a poptávka po výrobních faktorech Jak vypadá nabídka v prost edí dokonalé konkurence
November 15, 2012 Teorie rmy Ukáºmeme si Jak popsat technologii rmy Jak se rma rozhoduje Jak se odvozuje nabídka rmy a poptávka po výrobních faktorech Jak vypadá nabídka v prost edí dokonalé konkurence
Monopol a monopolní chování Varian: Mikroekonomie: moderní přístup, kapitoly 23 a 24 Varian: Intermediate Microeconomics, 8e, Chapters 24 and 25
 Monopol a monopolní chování Varian: Mikroekonomie: moderní přístup, kapitoly 23 a 24 Varian: Intermediate Microeconomics, 8e, Chapters 24 and 25 () 1 / 43 Na této přednášce se dozvíte jak si monopol volí
Monopol a monopolní chování Varian: Mikroekonomie: moderní přístup, kapitoly 23 a 24 Varian: Intermediate Microeconomics, 8e, Chapters 24 and 25 () 1 / 43 Na této přednášce se dozvíte jak si monopol volí
Dokonalá konkurence. Mikroekonomie. Opakování. Řešení. Příklad. Příklad. Řešení Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU
 Opakování Mikroekonomie Dokonalá konkurence Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU U firmy v rámci dokonalé konkurence jsou výrobní náklady dány vztahem: TC = 20000 + 2 a) Jestliže tržní cena
Opakování Mikroekonomie Dokonalá konkurence Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU U firmy v rámci dokonalé konkurence jsou výrobní náklady dány vztahem: TC = 20000 + 2 a) Jestliže tržní cena
Limity funkcí v nevlastních bodech. Obsah
 Limity funkcí v nevlastních bodech V tomto letáku si vysv tlíme, co znamená, kdyº funkce mí í do nekone na, mínus nekone na nebo se blíºí ke konkrétnímu reálnému íslu, zatímco x jde do nekone na nebo mínus
Limity funkcí v nevlastních bodech V tomto letáku si vysv tlíme, co znamená, kdyº funkce mí í do nekone na, mínus nekone na nebo se blíºí ke konkrétnímu reálnému íslu, zatímco x jde do nekone na nebo mínus
Teorie her a ekonomické rozhodování. 9. Modely nedokonalých trhů
 Teorie her a ekonomické rozhodování 9. Modely nedokonalých trhů 9.1 Dokonalý trh Dokonalý trh Dokonalá informovanost kupujících Dokonalá informovanost prodávajících Nulové náklady na změnu dodavatele Homogenní
Teorie her a ekonomické rozhodování 9. Modely nedokonalých trhů 9.1 Dokonalý trh Dokonalý trh Dokonalá informovanost kupujících Dokonalá informovanost prodávajících Nulové náklady na změnu dodavatele Homogenní
Poptávka, Slutského rovnice, P ebytek spot ebitele, Rovnováha
 Poptávka, Slutského rovnice, P ebytek spot ebitele, Rovnováha October 25, 2012 Individuální poptávka Poptávková funkce je vztah mezi optimálním mnoºstvím a cenami a p íjmem: x 1 = x 1 (p 1, p 2, m) x 2
Poptávka, Slutského rovnice, P ebytek spot ebitele, Rovnováha October 25, 2012 Individuální poptávka Poptávková funkce je vztah mezi optimálním mnoºstvím a cenami a p íjmem: x 1 = x 1 (p 1, p 2, m) x 2
Nejistota, Asymetrické informace, V²eobecná rovnováha
 Nejistota, Asymetrické informace, V²eobecná rovnováha December 10, 2012 Nejistota Výsledné stavy jsou r zné výsledky ur ité náhodné události. Kaºdý výsledný stav nastane s danou pravd podobností. Situaci,
Nejistota, Asymetrické informace, V²eobecná rovnováha December 10, 2012 Nejistota Výsledné stavy jsou r zné výsledky ur ité náhodné události. Kaºdý výsledný stav nastane s danou pravd podobností. Situaci,
JEB007 Mikroekonomie I
 JEB007 Mikroekonomie I Seminá 2 Petr Polák Institute of Economic Studies Faculty of Social Sciences Charles University 26. února 2014 Petr Polák (IES) JEB007 Mikroekonomie I 26. února 2014 1 / 12 Rekapitulace
JEB007 Mikroekonomie I Seminá 2 Petr Polák Institute of Economic Studies Faculty of Social Sciences Charles University 26. února 2014 Petr Polák (IES) JEB007 Mikroekonomie I 26. února 2014 1 / 12 Rekapitulace
MODELY OLIGOPOLU COURNOTŮV MODEL, STACKELBERGŮV MODEL
 MODELY OLIGOPOLU COURNOTŮV MODEL, STACKELBERGŮV MODEL DOKONALÁ KONKURENCE Trh dokonalé konkurence je charakterizován velkým počtem prodávajících, kteří vyrábějí homogenní produkt a nemohou ovlivnit tržní
MODELY OLIGOPOLU COURNOTŮV MODEL, STACKELBERGŮV MODEL DOKONALÁ KONKURENCE Trh dokonalé konkurence je charakterizován velkým počtem prodávajících, kteří vyrábějí homogenní produkt a nemohou ovlivnit tržní
1 Technologie. 2 Maximalizace zisku
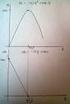 1 Technologie 1. Spo ítejte technickou míru substituce (TRS) u následujících produk ních funkcí. Je mezní produkt faktor x a y konstantní, klesající nebo rostoucí? a) f(x, y) = x + y b) f(x, y) = x 2 +
1 Technologie 1. Spo ítejte technickou míru substituce (TRS) u následujících produk ních funkcí. Je mezní produkt faktor x a y konstantní, klesající nebo rostoucí? a) f(x, y) = x + y b) f(x, y) = x 2 +
Skalární sou in. Úvod. Denice skalárního sou inu
 Skalární sou in Jedním ze zp sob, jak m ºeme dva vektory kombinovat, je skalární sou in. Výsledkem skalárního sou inu dvou vektor, jak jiº název napovídá, je skalár. V tomto letáku se nau íte, jak vypo
Skalární sou in Jedním ze zp sob, jak m ºeme dva vektory kombinovat, je skalární sou in. Výsledkem skalárního sou inu dvou vektor, jak jiº název napovídá, je skalár. V tomto letáku se nau íte, jak vypo
e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody
 e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody V praxi se asto setkávame s p ípady, kdy je pot eba e²it více rovnic, takzvaný systém rovnic, obvykle s více jak jednou neznámou.
e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody V praxi se asto setkávame s p ípady, kdy je pot eba e²it více rovnic, takzvaný systém rovnic, obvykle s více jak jednou neznámou.
OP3BK_FEK. Ekonomika. Jaro / 13:55 15:35 / učebna č.20
 OP3BK_FEK Ekonomika Jaro 2013 16.03.2013 / 13:55 15:35 / učebna č.20 Přehled témat (osnova): 1. Úvod do ekonomie Základní pojmy Vývoj ekonomie Aktuální problémy 2. Mikroekonomie Tržní struktury Dokonalá
OP3BK_FEK Ekonomika Jaro 2013 16.03.2013 / 13:55 15:35 / učebna č.20 Přehled témat (osnova): 1. Úvod do ekonomie Základní pojmy Vývoj ekonomie Aktuální problémy 2. Mikroekonomie Tržní struktury Dokonalá
Charakteristika oligopolu
 Oligopol Charakteristika oligopolu Oligopol v ekonomice převažuje - základní rysy: malý počet firem - činnost několika firem v odvětví vyráběný produkt může být homogenní (čistý oligopol) nebo heterogenní
Oligopol Charakteristika oligopolu Oligopol v ekonomice převažuje - základní rysy: malý počet firem - činnost několika firem v odvětví vyráběný produkt může být homogenní (čistý oligopol) nebo heterogenní
Binární operace. Úvod. Pomocný text
 Pomocný text Binární operace Úvod Milí e²itelé, binární operace je pom rn abstraktní téma, a tak bude ob as pot eba odprostit se od konkrétních p íklad a podívat se na v c s ur itým nadhledem. Nicmén e²ení
Pomocný text Binární operace Úvod Milí e²itelé, binární operace je pom rn abstraktní téma, a tak bude ob as pot eba odprostit se od konkrétních p íklad a podívat se na v c s ur itým nadhledem. Nicmén e²ení
Integrování jako opak derivování
 Integrování jako opak derivování V tomto dokumentu budete seznámeni s derivováním b ºných funkcí a budete mít moºnost vyzkou²et mnoho zp sob derivace. Jedním z nich je proces derivování v opa ném po adí.
Integrování jako opak derivování V tomto dokumentu budete seznámeni s derivováním b ºných funkcí a budete mít moºnost vyzkou²et mnoho zp sob derivace. Jedním z nich je proces derivování v opa ném po adí.
5.7 Kooperativní hry 5.7.1 Kooperativní hra 2 hráčů 5.7.2 Kooperativní hra N hráčů 5.8 Modely oligopolu 5.9 Teorie redistribučních systémů 5.
 Mikroekonomie bakalářský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2010 Téma 6 Teorie her, volby teorie redistribučních systémů a teorie veřejné Obsah 5.7 Kooperativní hry 5.7.1
Mikroekonomie bakalářský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2010 Téma 6 Teorie her, volby teorie redistribučních systémů a teorie veřejné Obsah 5.7 Kooperativní hry 5.7.1
MONOPOL.
 MONOPOL Nedokonalá konkurence představuje situaci, kdy je na trhu alespoň jeden prodávající nebo kupující, který může ovlivnit tržní cenu V nedokonalé konkurenci na straně nabídky rozlišujeme -monopolní
MONOPOL Nedokonalá konkurence představuje situaci, kdy je na trhu alespoň jeden prodávající nebo kupující, který může ovlivnit tržní cenu V nedokonalé konkurenci na straně nabídky rozlišujeme -monopolní
Pr b h funkce I. Obsah. Maxima a minima funkce
 Pr b h funkce I Maxima a minima funkce V této jednotce ukáºeme jak derivování m ºe být uºite né pro hledání minimálních a maximálních hodnot funkce. Po p e tení tohoto letáku nebo shlédnutí instruktáºního
Pr b h funkce I Maxima a minima funkce V této jednotce ukáºeme jak derivování m ºe být uºite né pro hledání minimálních a maximálních hodnot funkce. Po p e tení tohoto letáku nebo shlédnutí instruktáºního
1 Individuální poptávka
 1 Individuální poptávka 1. Petr má uºitkovou funkci U = x B x R, kde x B je po et balon a x R je po et branká ských rukavic. Jeho rozpo tové omezení je p B x B + p R x R = m, kde p B je cena balonu a p
1 Individuální poptávka 1. Petr má uºitkovou funkci U = x B x R, kde x B je po et balon a x R je po et branká ských rukavic. Jeho rozpo tové omezení je p B x B + p R x R = m, kde p B je cena balonu a p
OLIGOPOL.
 OLIGOPOL CHARAKTERISTICKÉ RYSY OLIGOPOLU Malý počet firem a vysoký stupeň vzájemné závislosti při rozhodování (ceně, množství, kvalitě atd.) Firma musí předvídat reakci svých konkurentů na svá vlastní
OLIGOPOL CHARAKTERISTICKÉ RYSY OLIGOPOLU Malý počet firem a vysoký stupeň vzájemné závislosti při rozhodování (ceně, množství, kvalitě atd.) Firma musí předvídat reakci svých konkurentů na svá vlastní
Motivace. Dnes se zaměříme na monopoly.
 Monopol Motivace V reálném světě není dokonalá konkurence příliš častá. Obvyklejší jsou různé formy nedokonalé konkurence: monopoly oligopoly monopolistická konkurence Dnes se zaměříme na monopoly. Co
Monopol Motivace V reálném světě není dokonalá konkurence příliš častá. Obvyklejší jsou různé formy nedokonalé konkurence: monopoly oligopoly monopolistická konkurence Dnes se zaměříme na monopoly. Co
Vektor náhodných veli in - práce s více prom nnými
 Vektor náhodných veli in - práce s více prom nnými 12. kv tna 2015 N kdy k popisu n jaké situace pot ebujeme více neº jednu náhodnou veli inu. Nap. v k, hmotnost, vý²ku. Mezi t mito veli inami mohou být
Vektor náhodných veli in - práce s více prom nnými 12. kv tna 2015 N kdy k popisu n jaké situace pot ebujeme více neº jednu náhodnou veli inu. Nap. v k, hmotnost, vý²ku. Mezi t mito veli inami mohou být
Rovnice a nerovnice. Posloupnosti.
 .. Veronika Sobotíková katedra matematiky, FEL ƒvut v Praze, http://math.feld.cvut.cz/ 30. srpna 2018.. 1/75 (v reálném oboru) Rovnicí resp. nerovnicí v reálném oboru rozumíme zápis L(x) P(x), kde zna
.. Veronika Sobotíková katedra matematiky, FEL ƒvut v Praze, http://math.feld.cvut.cz/ 30. srpna 2018.. 1/75 (v reálném oboru) Rovnicí resp. nerovnicí v reálném oboru rozumíme zápis L(x) P(x), kde zna
charakteristika oligopolu kartel Cournotův model duopolu oligopol s dominantní firmou Sweezyho model (se zalomenou křivkou poptávky) Nashova
 charakteristika oligopolu kartel Cournotův model duopolu oligopol s dominantní firmou Sweezyho model (se zalomenou křivkou poptávky) Nashova rovnováha Soukupová et al.: Mikroekonomie. Kapitola 11, str.
charakteristika oligopolu kartel Cournotův model duopolu oligopol s dominantní firmou Sweezyho model (se zalomenou křivkou poptávky) Nashova rovnováha Soukupová et al.: Mikroekonomie. Kapitola 11, str.
NEDOKONALÁ KONKURENCE
 NEDOKONALÁ KONKURENCE OBECNÁ CHARAKTERISTIKA NEDOKONALÉ KONKURENCE Trh, na kterém alespoň jeden prodávající (kupující) je schopen ovlivnit tržní cenu Cenový tvůrce Diferencovaný produkt-kvalita, vzhled,
NEDOKONALÁ KONKURENCE OBECNÁ CHARAKTERISTIKA NEDOKONALÉ KONKURENCE Trh, na kterém alespoň jeden prodávající (kupující) je schopen ovlivnit tržní cenu Cenový tvůrce Diferencovaný produkt-kvalita, vzhled,
Dokonale konkurenční odvětví
 Dokonale konkurenční odvětví Východiska určení výstupu pro maximalizaci zisku ekonomický zisk - je rozdíl mezi příjmy a ekonomickými náklady (alternativními náklady) účetní zisk - je rozdíl mezi příjmy
Dokonale konkurenční odvětví Východiska určení výstupu pro maximalizaci zisku ekonomický zisk - je rozdíl mezi příjmy a ekonomickými náklady (alternativními náklady) účetní zisk - je rozdíl mezi příjmy
Elasticita a její aplikace
 Elasticita a její aplikace Motivace Firmu zajímá, jak ovlivní její tržby tyto změny: firmě rostou náklady, proto chce zdražit svou produkci konkurenční firma vyrábějící podobný výrobek zlevnila očekává
Elasticita a její aplikace Motivace Firmu zajímá, jak ovlivní její tržby tyto změny: firmě rostou náklady, proto chce zdražit svou produkci konkurenční firma vyrábějící podobný výrobek zlevnila očekává
Přijímací řízení ak. r. 2010/11 Kompletní znění testových otázek mikroekonomie. Správná odpověď je označena tučně
 řijímací řízení ak. r. 2010/11 Kompletní znění testových otázek mikroekonomie Správná odpověď je označena tučně 1. řebytek spotřebitele je rozdíl mezi a... a) cenou, mezními náklady b) cenou, celkovými
řijímací řízení ak. r. 2010/11 Kompletní znění testových otázek mikroekonomie Správná odpověď je označena tučně 1. řebytek spotřebitele je rozdíl mezi a... a) cenou, mezními náklady b) cenou, celkovými
Modely oligopolu. I. Dokonalý trh II. Nedokonalý trh 1. Modely oligopolu. Dokonalý trh. Nedokonalý trh
 Modely oligopolu Obsah kapitoly Studijní cíle I. Dokonalý trh II. Nedokonalý trh 1. Modely oligopolu Student získá komplexní přehled teorií oligopolu, které lze úspěšně aplikovat v realitě. Doba potřebná
Modely oligopolu Obsah kapitoly Studijní cíle I. Dokonalý trh II. Nedokonalý trh 1. Modely oligopolu Student získá komplexní přehled teorií oligopolu, které lze úspěšně aplikovat v realitě. Doba potřebná
Nabídka firmy a nabídka odvětví Varian: Mikroekonomie: moderní přístup, kapitoly 21 a 22 Varian: Intermediate Microeconomics, 8e, Chapters 22 and 23
 Nabídka firmy a nabídka odvětví Varian: Mikroekonomie: moderní přístup, kapitoly 21 a 22 Varian: Intermediate Microeconomics, 8e, Chapters 22 and 23 () 1 / 39 Na této přednášce se dozvíte jaká jsou omezení
Nabídka firmy a nabídka odvětví Varian: Mikroekonomie: moderní přístup, kapitoly 21 a 22 Varian: Intermediate Microeconomics, 8e, Chapters 22 and 23 () 1 / 39 Na této přednášce se dozvíte jaká jsou omezení
T i hlavní v ty pravd podobnosti
 T i hlavní v ty pravd podobnosti 15. kv tna 2015 První p íklad P edstavme si, ºe máme atomy typu A, které se samovolným radioaktivním rozpadem rozpadají na atomy typu B. Pr m rná doba rozpadu je 3 hodiny.
T i hlavní v ty pravd podobnosti 15. kv tna 2015 První p íklad P edstavme si, ºe máme atomy typu A, které se samovolným radioaktivním rozpadem rozpadají na atomy typu B. Pr m rná doba rozpadu je 3 hodiny.
Minimalizace nákladů. Varian: Mikroekonomie: moderní přístup, kapitoly 19 a 20 Varian: Intermediate Microeconomics, 8e, Chapters 20 and 21 () 1 / 34
 Minimalizace nákladů a nákladové křivky Varian: Mikroekonomie: moderní přístup, kapitoly 19 a 20 Varian: Intermediate Microeconomics, 8e, Chapters 20 and 21 () 1 / 34 Na této přednášce se dozvíte co je
Minimalizace nákladů a nákladové křivky Varian: Mikroekonomie: moderní přístup, kapitoly 19 a 20 Varian: Intermediate Microeconomics, 8e, Chapters 20 and 21 () 1 / 34 Na této přednášce se dozvíte co je
2. Ur íme sudost/lichost funkce a pr se íky s osami. 6. Na záv r na rtneme graf vy²et ované funkce. 8x. x 2 +4
 Pr b h funkce V této jednotce si ukáºeme jak postupovat p i vy²et ování pr b hu funkce. P edpokládáme znalost po ítání derivací a limit, které jsou dob e popsány v p edchozích letácích tohoto bloku. P
Pr b h funkce V této jednotce si ukáºeme jak postupovat p i vy²et ování pr b hu funkce. P edpokládáme znalost po ítání derivací a limit, které jsou dob e popsány v p edchozích letácích tohoto bloku. P
Mikroekonomie. Příklad - zadání. Příklad - řešení. Příklad. k opakování firma. Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU.
 Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Tržní struktury Téma: 4 Trh výrobních faktorů y k opakování firma - zadání Q FC VC TC AC AVC AFC MC 0 X X X X X X X 1 5 5 X X X X X 2 X 9
Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Tržní struktury Téma: 4 Trh výrobních faktorů y k opakování firma - zadání Q FC VC TC AC AVC AFC MC 0 X X X X X X X 1 5 5 X X X X X 2 X 9
Mikroekonomie I: Monopol
 1 3Ѓ0 0ЁЄЃ0Ќ0iny vzniku monopolu hr. raha, VЃ0 7FS, 22.11.2010 1 3Co je monopol? Ѓ0 0ЁЄЃ0Ќ0iny vzniku monopolu Monopol = nejsilnё jѓ0 8ЁЄ forma nedokonalё konkurence na trhu existuje jedinѓ0 5 nabёєzejёєcёє,
1 3Ѓ0 0ЁЄЃ0Ќ0iny vzniku monopolu hr. raha, VЃ0 7FS, 22.11.2010 1 3Co je monopol? Ѓ0 0ЁЄЃ0Ќ0iny vzniku monopolu Monopol = nejsilnё jѓ0 8ЁЄ forma nedokonalё konkurence na trhu existuje jedinѓ0 5 nabёєzejёєcёє,
4. Křivka nabídky monopolní firmy je totožná s částí křivky mezních nákladů.
 Firma v nedokonalé konkurenci 1. Zdroji nedokonalé konkurence jsou: - jednak nákladové podmínky podnikání, - jednak. 2. Zapište vzorec Lernerova indexu. K čemu slouží? 3. Zakreslete celkový příjem monopolní
Firma v nedokonalé konkurenci 1. Zdroji nedokonalé konkurence jsou: - jednak nákladové podmínky podnikání, - jednak. 2. Zapište vzorec Lernerova indexu. K čemu slouží? 3. Zakreslete celkový příjem monopolní
Vektory. Vektorové veli iny
 Vektor je veli ina, která má jak velikost tak i sm r. Ob tyto vlastnosti musí být uvedeny, aby byl vektor stanoven úpln. V této ásti je návod, jak vektory zapsat, jak je s ítat a od ítat a jak je pouºívat
Vektor je veli ina, která má jak velikost tak i sm r. Ob tyto vlastnosti musí být uvedeny, aby byl vektor stanoven úpln. V této ásti je návod, jak vektory zapsat, jak je s ítat a od ítat a jak je pouºívat
Studijní opora. Téma: Rozhodování firmy v podmínkách dokonalé konkurence.
 Studijní opora Název předmětu: Ekonomie I Zpracoval: Ing. Lenka Brizgalová, Ph.D. Téma: Rozhodování firmy v podmínkách dokonalé konkurence. Vzdělávací cíl: Téma Rozhodování firmy v podmínkách dokonalé
Studijní opora Název předmětu: Ekonomie I Zpracoval: Ing. Lenka Brizgalová, Ph.D. Téma: Rozhodování firmy v podmínkách dokonalé konkurence. Vzdělávací cíl: Téma Rozhodování firmy v podmínkách dokonalé
DOKONALÁ KONKURENCE.
 DOKONALÁ KONKURENCE www.ekofun.cz ZÁKLADNÍ POJMY PLATNÉ PRO DOKONALOU I NEDOKONALOU KONKURENCI Cíl firmy je maximalizace zisku -největší(kladné) rozpětí mezi TR a TC Maximalizujeme zisk s ohlédnutím na
DOKONALÁ KONKURENCE www.ekofun.cz ZÁKLADNÍ POJMY PLATNÉ PRO DOKONALOU I NEDOKONALOU KONKURENCI Cíl firmy je maximalizace zisku -největší(kladné) rozpětí mezi TR a TC Maximalizujeme zisk s ohlédnutím na
( x ) 2 ( ) 2.5.4 Další úlohy s kvadratickými funkcemi. Předpoklady: 2501, 2502
 .5. Další úlohy s kvadratickými funkcemi Předpoklady: 50, 50 Pedagogická poznámka: Tato hodina patří mezi ty méně organizované. Společně řešíme příklad, při dalším počítání se třída rozpadá. Já řeším příklady
.5. Další úlohy s kvadratickými funkcemi Předpoklady: 50, 50 Pedagogická poznámka: Tato hodina patří mezi ty méně organizované. Společně řešíme příklad, při dalším počítání se třída rozpadá. Já řeším příklady
Monopol a monopolistická konkurence
 Monopol a monopolistická konkurence Vznik nedokonalé konkurence Příčiny vzniku Nákladové podmínky vedou ke vzniku nedokonalé konkurence v podobě úspor z rozsahu. Průměrné náklady s růstem výroby klesají
Monopol a monopolistická konkurence Vznik nedokonalé konkurence Příčiny vzniku Nákladové podmínky vedou ke vzniku nedokonalé konkurence v podobě úspor z rozsahu. Průměrné náklady s růstem výroby klesají
P íklady k prvnímu testu - Pravd podobnost
 P íklady k prvnímu testu - Pravd podobnost 28. února 204 Instrukce: Projd te si v²echny p íklady. Kaºdý p íklad se snaºte pochopit. Pak vymyslete a vy- e²te p íklad podobný. Tím se ujistíte, ºe p íkladu
P íklady k prvnímu testu - Pravd podobnost 28. února 204 Instrukce: Projd te si v²echny p íklady. Kaºdý p íklad se snaºte pochopit. Pak vymyslete a vy- e²te p íklad podobný. Tím se ujistíte, ºe p íkladu
 Mikroekonomie magisterský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2013 Téma 4 Teorie her pro manažery Obsah 5.7 Kooperativní hry 5.7.1 Kooperativní hra 2 hráčů 5.7.2 Kooperativní
Mikroekonomie magisterský kurz - VŠFS Jiří Mihola, jiri.mihola@quick.cz, www.median-os.cz, 2013 Téma 4 Teorie her pro manažery Obsah 5.7 Kooperativní hry 5.7.1 Kooperativní hra 2 hráčů 5.7.2 Kooperativní
Pravd podobnost a statistika - cvi ení. Simona Domesová místnost: RA310 (budova CPIT) web:
 Pravd podobnost a statistika - cvi ení Simona Domesová simona.domesova@vsb.cz místnost: RA310 (budova CPIT) web: http://homel.vsb.cz/~dom0015 Cíle p edm tu vyhodnocování dat pomocí statistických metod
Pravd podobnost a statistika - cvi ení Simona Domesová simona.domesova@vsb.cz místnost: RA310 (budova CPIT) web: http://homel.vsb.cz/~dom0015 Cíle p edm tu vyhodnocování dat pomocí statistických metod
1. (18 bod ) Náhodná veli ina X je po et rub p i 400 nezávislých hodech mincí. a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost
 (8 bod ) Náhodná veli ina X je po et rub p i nezávislých hodech mincí a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost P ( X EX < ) (9 bod ) b) Formulujte centrální limitní v tu a pomocí ní vypo
(8 bod ) Náhodná veli ina X je po et rub p i nezávislých hodech mincí a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost P ( X EX < ) (9 bod ) b) Formulujte centrální limitní v tu a pomocí ní vypo
11. Trhy výrobních faktorů Průvodce studiem: 11.1 Základní charakteristika trhu výrobních faktorů Poptávka po VF Nabídka výrobního faktoru
 11. Trhy výrobních faktorů V předchozích kapitolách jsme zkoumali způsob rozhodování firmy o výstupu a ceně v rámci různých tržních struktur (dokonalá a nedokonalá konkurence). Ačkoli se fungování firem
11. Trhy výrobních faktorů V předchozích kapitolách jsme zkoumali způsob rozhodování firmy o výstupu a ceně v rámci různých tržních struktur (dokonalá a nedokonalá konkurence). Ačkoli se fungování firem
P íklad 1 (Náhodná veli ina)
 P íklad 1 (Náhodná veli ina) Uvaºujeme experiment: házení mincí. Výsledkem pokusu je rub nebo líc, ºe padne hrana neuvaºujeme. Pokud hovo íme o náhodné veli in, musíme p epsat výsledky pokusu do mnoºiny
P íklad 1 (Náhodná veli ina) Uvaºujeme experiment: házení mincí. Výsledkem pokusu je rub nebo líc, ºe padne hrana neuvaºujeme. Pokud hovo íme o náhodné veli in, musíme p epsat výsledky pokusu do mnoºiny
Ergodické Markovské et zce
 1. b ezen 2013 Denice 1.1 Markovský et zec nazveme ergodickým, jestliºe z libovolného stavu m ºeme p ejít do jakéhokoliv libovolného stavu (ne nutn v jednom kroku). Denice 1.2 Markovský et zec nazveme
1. b ezen 2013 Denice 1.1 Markovský et zec nazveme ergodickým, jestliºe z libovolného stavu m ºeme p ejít do jakéhokoliv libovolného stavu (ne nutn v jednom kroku). Denice 1.2 Markovský et zec nazveme
DK cena odvozená z trhu
 Dokonalá konkurence DK cena odvozená z trhu π (Kč) TR STC ZISK ZTRÁTA Q 1 Q 2 Q (ks) MR, MC (Kč/ks) MC MR Q 1 Q 2 Q (ks) ZiskfirmyvDK Nulový zisk v DK normální zisk Ztráta firmy v DK Křivka nabídky firmy
Dokonalá konkurence DK cena odvozená z trhu π (Kč) TR STC ZISK ZTRÁTA Q 1 Q 2 Q (ks) MR, MC (Kč/ks) MC MR Q 1 Q 2 Q (ks) ZiskfirmyvDK Nulový zisk v DK normální zisk Ztráta firmy v DK Křivka nabídky firmy
Derivování sloºené funkce
 Derivování sloºené funkce V tomto letáku si p edstavíme speciální pravidlo pro derivování sloºené funkce (te funkci obsahující dal²í funkci). Po p e tení tohoto tetu byste m li být schopni: vysv tlit pojem
Derivování sloºené funkce V tomto letáku si p edstavíme speciální pravidlo pro derivování sloºené funkce (te funkci obsahující dal²í funkci). Po p e tení tohoto tetu byste m li být schopni: vysv tlit pojem
Dokonalá konkurence. Téma cvičení. Mikroekonomie Q FC VC Příklad řešení. Bod uzavření firmy
 opakování zjistěte zbývající údaje Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Q FC VC 0 20 1 10 2 18 3 24 4 36 Co lze zjistit? FC - pro Q = 1, 2, 3, 4 TC AC AVC AFC řešení opakování
opakování zjistěte zbývající údaje Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Q FC VC 0 20 1 10 2 18 3 24 4 36 Co lze zjistit? FC - pro Q = 1, 2, 3, 4 TC AC AVC AFC řešení opakování
FAKULTA EKONOMICKÁ ZČU PLZEŇ. Katedra ekonomie a financí. Mikroekonomie cvičení 8
 FAKULTA EKONOMICKÁ ZČU PLZEŇ Katedra ekonomie a financí Mikroekonomie cvičení 8 8. FIRMA V DOKONALÉ A NEDOKONALÉ KONKURENCI PŘÍKLAD Č. 1 Definujte rovnováhu spotřebitele, rovnováhu firmy a tržní rovnováhu
FAKULTA EKONOMICKÁ ZČU PLZEŇ Katedra ekonomie a financí Mikroekonomie cvičení 8 8. FIRMA V DOKONALÉ A NEDOKONALÉ KONKURENCI PŘÍKLAD Č. 1 Definujte rovnováhu spotřebitele, rovnováhu firmy a tržní rovnováhu
Obsah charakteristika volba výstupu firmy v SR a LR Chamberlinův model efektivnost monopolistické konkurence
 8. Monopolistická konkurence Obsah charakteristika volba výstupu firmy v SR a LR Chamberlinův model efektivnost monopolistické konkurence Literatura Soukupová et al.: Mikroekonomie. Kapitola 10, str. 291
8. Monopolistická konkurence Obsah charakteristika volba výstupu firmy v SR a LR Chamberlinův model efektivnost monopolistické konkurence Literatura Soukupová et al.: Mikroekonomie. Kapitola 10, str. 291
Přednáška #8. Základy mikroekonomie TEORIE HER
 Přednáška #8 Základy mikroekonomie TEORIE HER 14.11.2012 V minulé přednášce jsme si vysvětlili, co je to oligopolistické tržní uspořádání Oligopol jako tržní uspořádání stojí mezi monopolem a režimem dokonalé
Přednáška #8 Základy mikroekonomie TEORIE HER 14.11.2012 V minulé přednášce jsme si vysvětlili, co je to oligopolistické tržní uspořádání Oligopol jako tržní uspořádání stojí mezi monopolem a režimem dokonalé
Kvízové otázky Obecná ekonomie I. Teorie firmy
 1. Firmy působí: a) na trhu výrobních faktorů b) na trhu statků a služeb c) na žádném z těchto trhů d) na obou těchto trzích Kvízové otázky Obecná ekonomie I. Teorie firmy 2. Firma na trhu statků a služeb
1. Firmy působí: a) na trhu výrobních faktorů b) na trhu statků a služeb c) na žádném z těchto trhů d) na obou těchto trzích Kvízové otázky Obecná ekonomie I. Teorie firmy 2. Firma na trhu statků a služeb
MONOPOLISTICKÁ KONKURENCE
 MONOPOLISTICKÁ KONKURENCE CHARAKTERISTIKY MONOPOLISTICKÉ KONKURENCE www.ekofun.cz Velký počet výrobců, jejichž výrobky jsou velmi blízké substituty produkt je však diferencovaný Velký počet firem způsobuje,
MONOPOLISTICKÁ KONKURENCE CHARAKTERISTIKY MONOPOLISTICKÉ KONKURENCE www.ekofun.cz Velký počet výrobců, jejichž výrobky jsou velmi blízké substituty produkt je však diferencovaný Velký počet firem způsobuje,
Bod uzavření firmy. Bod zvratu. Mikroekonomie. Důležité FC, VC, TC (graf) Náklady firmy - důležité. Průběh funkcí nákladů - grafy
 Důležité FC, VC, TC (graf) Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Náklady firmy - důležité Průběh funkcí nákladů - grafy TC = FC + VC AC = AFC + AVC AFC = FC/Q AVC = VC/Q MC =
Důležité FC, VC, TC (graf) Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Náklady firmy - důležité Průběh funkcí nákladů - grafy TC = FC + VC AC = AFC + AVC AFC = FC/Q AVC = VC/Q MC =
Firmy na dokonale konkurenčních trzích
 Firmy na dokonale konkurenčních trzích Motivace Každá firma musí učinit následující rozhodnutí: kolik vyrábět jakou cenu si účtovat s jakými výrobními faktory (kolik práce a kolik kapitálu) Tato rozhodnutí
Firmy na dokonale konkurenčních trzích Motivace Každá firma musí učinit následující rozhodnutí: kolik vyrábět jakou cenu si účtovat s jakými výrobními faktory (kolik práce a kolik kapitálu) Tato rozhodnutí
Vysoká škola technická a ekonomická v Českých Budějovicích
 Firma a odvětví. Koncentrace odvětví. Vztah firmy ke konkurentům a oligopol. Limitní cena. Kvantitativní modely duopolu. Cenové modely duopolu. Možnosti využití teorie her. Teorie firmy Firma a odvětví
Firma a odvětví. Koncentrace odvětví. Vztah firmy ke konkurentům a oligopol. Limitní cena. Kvantitativní modely duopolu. Cenové modely duopolu. Možnosti využití teorie her. Teorie firmy Firma a odvětví
Produkční analýza. a) Co je to produkční funkce? Vyjadřuje max. objem produkce, jež je možno vyrobit danou kombinací VF při dané úrovni technologie.
 MIKROEKONOMIE 1 cvičení 9-12 [1] Produkční analýza a) Co je to produkční funkce? Vyjadřuje max. objem produkce, jež je možno vyrobit danou kombinací VF při dané úrovni technologie. b) Vysvětlete zákon
MIKROEKONOMIE 1 cvičení 9-12 [1] Produkční analýza a) Co je to produkční funkce? Vyjadřuje max. objem produkce, jež je možno vyrobit danou kombinací VF při dané úrovni technologie. b) Vysvětlete zákon
Jevy, nezávislost, Bayesova v ta
 Jevy, nezávislost, Bayesova v ta 17. b ezna 2015 Instrukce: Projd te si v²echny p íklady. Kaºdý p íklad se snaºte pochopit. Pak vymyslete a vy- e²te p íklad podobný. Tím se ujistíte, ºe p íkladu rozumíte.
Jevy, nezávislost, Bayesova v ta 17. b ezna 2015 Instrukce: Projd te si v²echny p íklady. Kaºdý p íklad se snaºte pochopit. Pak vymyslete a vy- e²te p íklad podobný. Tím se ujistíte, ºe p íkladu rozumíte.
Produkční analýza. a) Co je to produkční funkce? Vyjadřuje max. objem produkce, jež je možno vyrobit danou kombinací VF při dané úrovni technologie.
 MIKROEKONOMIE 1 cvičení 9-13 [1] Produkční analýza a) Co je to produkční funkce? Vyjadřuje max. objem produkce, jež je možno vyrobit danou kombinací VF při dané úrovni technologie. b) Vysvětlete zákon
MIKROEKONOMIE 1 cvičení 9-13 [1] Produkční analýza a) Co je to produkční funkce? Vyjadřuje max. objem produkce, jež je možno vyrobit danou kombinací VF při dané úrovni technologie. b) Vysvětlete zákon
Přednáška #6. Základy mikroekonomie MONOPOL
 Přednáška #6 Základy mikroekonomie MONOPOL 31.10.2012 V minulých přednáškách jsme analyzovali režim dokonalé konkurence V režimu dokonalé konkurence jsou firmy cenovými příjemci a volí optimální produkci
Přednáška #6 Základy mikroekonomie MONOPOL 31.10.2012 V minulých přednáškách jsme analyzovali režim dokonalé konkurence V režimu dokonalé konkurence jsou firmy cenovými příjemci a volí optimální produkci
RŮZNÉ TYPY TRŽNÍ STRUKTURY dokonalá konkurence, nedokonalá konkurence, monopol
 RŮZNÉ TYPY TRŽNÍ STRUKTURY dokonalá konkurence, nedokonalá konkurence, monopol CHARAKTERISTIKA DK Jak byste charakterizovali DK z hlediska (ceny, vstupu do odvětví, informací, produktu, počet prodávajících
RŮZNÉ TYPY TRŽNÍ STRUKTURY dokonalá konkurence, nedokonalá konkurence, monopol CHARAKTERISTIKA DK Jak byste charakterizovali DK z hlediska (ceny, vstupu do odvětví, informací, produktu, počet prodávajících
Teorie her. Klasikace. Pomocný text
 Pomocný text Teorie her Milí e²itelé, první ty i úlohy kaºdé série spojuje jisté téma a vám bude poskytnut text, který vás tímto tématem mírn provede a pom ºe vám p i e²ení t chto úloh. Teorie her, jiº
Pomocný text Teorie her Milí e²itelé, první ty i úlohy kaºdé série spojuje jisté téma a vám bude poskytnut text, který vás tímto tématem mírn provede a pom ºe vám p i e²ení t chto úloh. Teorie her, jiº
CZ.1.07/1.5.00/34.0218 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu Šablona CZ.1.07/1.5.00/34.0218 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Zim10 Vypracoval(a),
Název školy Gymnázium, Šternberk, Horní nám. 5 Číslo projektu Šablona CZ.1.07/1.5.00/34.0218 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Označení materiálu VY_32_INOVACE_Zim10 Vypracoval(a),
Teorie nákladů. Rozlišení zisku. Mikroekonomie. Účetní zisk. Ekonomický zisk. Normální zisk. Zisk firmy. Důležité. Účetní, ekonomický a normální zisk
 Zisk firmy Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Zisk (π) je rozdíl mezi celkovými příjmy a celkovými náklady. Π = TR - TC Je také vynásobený objem produkce rozdílem průměrného
Zisk firmy Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Zisk (π) je rozdíl mezi celkovými příjmy a celkovými náklady. Π = TR - TC Je také vynásobený objem produkce rozdílem průměrného
ízení Tvorba kritéria 2. prosince 2014
 ízení. prosince 014 Spousta lidí má pocit, ºe by m la n co ídit. A n kdy to bývá pravda. Kdyº uº nás my²lenky na ízení napadají, m li bychom si poloºit následující t i otázky: ídit? Obrovskou zku²eností
ízení. prosince 014 Spousta lidí má pocit, ºe by m la n co ídit. A n kdy to bývá pravda. Kdyº uº nás my²lenky na ízení napadají, m li bychom si poloºit následující t i otázky: ídit? Obrovskou zku²eností
Motivace. Dnes se zaměříme na monopoly.
 Monopol Motivace V reálném světě není dokonalá konkurence příliš častá. Obvyklejší jsou různé formy nedokonalé konkurence: monopoly oligopoly monopolistická konkurence Dnes se zaměříme na monopoly. Co
Monopol Motivace V reálném světě není dokonalá konkurence příliš častá. Obvyklejší jsou různé formy nedokonalé konkurence: monopoly oligopoly monopolistická konkurence Dnes se zaměříme na monopoly. Co
a) Do produkční funkce firmy dosadíme počet jednotek práce, pro něž máme určit dosazený objem produkce
 Řešené příklady 1. Firma Karkulka, s.r.o šije červené čepečky. Produkční funkce firmy má tvar Q = 41. + 20. 2 (1/3). 3. Kde jsou hodiny práce za den. a) Určete, kolik firma ušije denně čepečků, pokud najme
Řešené příklady 1. Firma Karkulka, s.r.o šije červené čepečky. Produkční funkce firmy má tvar Q = 41. + 20. 2 (1/3). 3. Kde jsou hodiny práce za den. a) Určete, kolik firma ušije denně čepečků, pokud najme
Text m ºe být postupn upravován a dopl ován. Datum poslední úpravy najdete u odkazu na staºení souboru. Veronika Sobotíková
 Tento text není samostatným studijním materiálem. Jde jen o prezentaci promítanou na p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze na tabuli a nejsou zde obsaºeny.
Tento text není samostatným studijním materiálem. Jde jen o prezentaci promítanou na p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze na tabuli a nejsou zde obsaºeny.
1.1.11 Poměry a úměrnosti I
 1.1.11 Poměry a úměrnosti I Předpoklady: základní početní operace, 010110 Poznámka: Následující látka bohužel patří mezi ty, kde je nejvíce rozšířené používání samospasitelných postupů, které umožňují
1.1.11 Poměry a úměrnosti I Předpoklady: základní početní operace, 010110 Poznámka: Následující látka bohužel patří mezi ty, kde je nejvíce rozšířené používání samospasitelných postupů, které umožňují
ALTERNATIVNÍ CÍLE FIRMY
 ALTERNATIVNÍ CÍLE FIRMY Příčiny vzniku alternativních teorií firmy My známe maximalizace zisku jako cíl firmy Stakeholders rozdílné cíle ( a person, group, organization, member or system who affects or
ALTERNATIVNÍ CÍLE FIRMY Příčiny vzniku alternativních teorií firmy My známe maximalizace zisku jako cíl firmy Stakeholders rozdílné cíle ( a person, group, organization, member or system who affects or
Nyní položíme mezní náklady rovny ceně a hledáme optimální výstup (q): 17-6q + q 2 = 50 q 2-6q - 33 = 0 hledáme kořeny kvadratické rovnice
 Řešené příklady 1. Firma Datel a syn je drobným výrobcem děrovaček. Na trhu stejné děrovačky vyrábí dalších 100 větších či menších firem. Jeho nákladová funkce je dána rovnicí TC = 30 + 17q 3q 2 + 1/3q
Řešené příklady 1. Firma Datel a syn je drobným výrobcem děrovaček. Na trhu stejné děrovačky vyrábí dalších 100 větších či menších firem. Jeho nákladová funkce je dána rovnicí TC = 30 + 17q 3q 2 + 1/3q
29. mezní a průměrná produktivita práce MC a AC při 15 hodinách práce? AC = w = 4,5 Kč při 15 hodinách práce MC = w + L pro L = 15
 29. mezní a průměrná produktivita práce MC a AC při 15 hodinách práce? AC = w = 4,5 Kč při 15 hodinách práce MC = w + L pro L = 15 1 30. Optimum při nájmu výrobního faktoru Nabídka vstupu Z je dána rovnicí
29. mezní a průměrná produktivita práce MC a AC při 15 hodinách práce? AC = w = 4,5 Kč při 15 hodinách práce MC = w + L pro L = 15 1 30. Optimum při nájmu výrobního faktoru Nabídka vstupu Z je dána rovnicí
Mikroekonomie I. Přednáška 3. Trh výrobních faktorů ekonomický koloběh. Podstatné z minulé přednášky. Křivka nabídky (S) Zákon rostoucí nabídky
 Přednáška 3. Mikroekonomie I 3. přednáška Poptávka substituční a důchodový efekt, konkurence, elasticita poptávky Poptávka substituční a důchodový efekt, konkurence, elasticita poptávky Podstatné z minulé
Přednáška 3. Mikroekonomie I 3. přednáška Poptávka substituční a důchodový efekt, konkurence, elasticita poptávky Poptávka substituční a důchodový efekt, konkurence, elasticita poptávky Podstatné z minulé
 TISKOVÁ ZPRÁVA Centrum pro výzkum veřejného mínění Sociologický ústav AV ČR, v.v.i. Jilská 1, Praha 1 Tel./fax: 286 80 129 E-mail: paulina.tabery@soc.cas.cz Názory obyvatel na zadlužení a přijatelnost
TISKOVÁ ZPRÁVA Centrum pro výzkum veřejného mínění Sociologický ústav AV ČR, v.v.i. Jilská 1, Praha 1 Tel./fax: 286 80 129 E-mail: paulina.tabery@soc.cas.cz Názory obyvatel na zadlužení a přijatelnost
8. Dokonalá konkurence
 8. Dokonalá konkurence Kompletní text ke kapitole viz. KRAFT, J., BEDNÁŘOVÁ, P, KOCOUREK, A. Ekonomie I. TUL Liberec, 2010. ISBN 978-80-7372-652-2; str.64-75 Dokonale konkurenční tržní prostředí lze charakterizovat
8. Dokonalá konkurence Kompletní text ke kapitole viz. KRAFT, J., BEDNÁŘOVÁ, P, KOCOUREK, A. Ekonomie I. TUL Liberec, 2010. ISBN 978-80-7372-652-2; str.64-75 Dokonale konkurenční tržní prostředí lze charakterizovat
Příjmy firmy můžeme rozdělit na celkové, průměrné a mezní.
 7 Příjmy firmy Příjmy firmy představují sumu peněžních prostředků, které firmě plynou z realizace její produkce, proto někteří autoři používají analogický pojem tržby. Jestliže vycházíme z cíle formy v
7 Příjmy firmy Příjmy firmy představují sumu peněžních prostředků, které firmě plynou z realizace její produkce, proto někteří autoři používají analogický pojem tržby. Jestliže vycházíme z cíle formy v
Technologie a maximalizace zisku Varian: Mikroekonomie: moderní přístup, kapitoly 17 a 18 Varian: Intermediate Microeconomics, 8e, Chapters 18 and 19
 Technologie a maximalizace zisku Varian: Mikroekonomie: moderní přístup, kapitoly 17 a 18 Varian: Intermediate Microeconomics, 8e, Chapters 18 and 19 () 1 / 40 Teorie firmy a tržní struktury Firmy maximalizují
Technologie a maximalizace zisku Varian: Mikroekonomie: moderní přístup, kapitoly 17 a 18 Varian: Intermediate Microeconomics, 8e, Chapters 18 and 19 () 1 / 40 Teorie firmy a tržní struktury Firmy maximalizují
www.thunova.cz MIES SBZ - Okruh č. 4
 8. Nedokonalá konkurence na trhu výrobků a služeb - charakteristika, příčiny vzniku Shodné a rozdílné rysy DK a NDK ( rozdílné rysy: tvar individuální křivky poptávky, příjmy, vztah mezních nákladů a ceny
8. Nedokonalá konkurence na trhu výrobků a služeb - charakteristika, příčiny vzniku Shodné a rozdílné rysy DK a NDK ( rozdílné rysy: tvar individuální křivky poptávky, příjmy, vztah mezních nákladů a ceny
Plánování výroby elekt iny a ízení rizik na liberalizovaném trhu
 Plánování výroby elekt iny a ízení rizik na liberalizovaném trhu 23. listopadu 2011 prezentace k lánku Power Generation Planning and Risk Managment in a Liberalised Market Thor Bjorkvoll, Stein-Erik Fleten,
Plánování výroby elekt iny a ízení rizik na liberalizovaném trhu 23. listopadu 2011 prezentace k lánku Power Generation Planning and Risk Managment in a Liberalised Market Thor Bjorkvoll, Stein-Erik Fleten,
Mikroekonomie I: Trh a tržní rovnováha
 PhDr. Praha, VŠFS, 1.11.2010 Trh Trh je svobodná neomezovaná směna statků. Na trhu se střetává nabídka s poptávkou. Trh se neustále vyvíjí. Trh není dokonalý, existují statky, které nelze směňovat na trhu
PhDr. Praha, VŠFS, 1.11.2010 Trh Trh je svobodná neomezovaná směna statků. Na trhu se střetává nabídka s poptávkou. Trh se neustále vyvíjí. Trh není dokonalý, existují statky, které nelze směňovat na trhu
Mikroekonomie Q FC VC Příklad řešení. Kontrolní otázky Příklad opakování zjistěte zbývající údaje
 Příklad opakování zjistěte zbývající údaje Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Q FC VC 0 20 1 10 2 18 3 24 4 36 Co lze zjistit? FC - pro Q = 1, 2, 3, 4 TC AC AVC AFC Příklad
Příklad opakování zjistěte zbývající údaje Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Q FC VC 0 20 1 10 2 18 3 24 4 36 Co lze zjistit? FC - pro Q = 1, 2, 3, 4 TC AC AVC AFC Příklad
Vedoucí autorského kolektivu: Ing. Jana Soukupová, CSc. Tato publikace vychází s laskavým přispěním společnosti RWE Transgas, a. s.
 Autoři kapitol: Doc. Ing. Bronislava Hořejší, CSc. (kapitoly 1, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15, 16) Doc. PhDr. Libuše Macáková, CSc. (kapitoly 4, 17.6, 18, 19) Prof. Ing. Jindřich Soukup, CSc. (kapitoly
Autoři kapitol: Doc. Ing. Bronislava Hořejší, CSc. (kapitoly 1, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15, 16) Doc. PhDr. Libuše Macáková, CSc. (kapitoly 4, 17.6, 18, 19) Prof. Ing. Jindřich Soukup, CSc. (kapitoly
křivka MFC L roste dvakrát rychleji než AFC L
 10. Nedokonale konkurenční trh práce, nabídka práce Struktura charakteristika NedoKo.. trhu práce optimální množství práce v SR optimální množství práce v LR mzdová diskriminace monopsonu individuální
10. Nedokonale konkurenční trh práce, nabídka práce Struktura charakteristika NedoKo.. trhu práce optimální množství práce v SR optimální množství práce v LR mzdová diskriminace monopsonu individuální
co je vězňovo dilema, jak funguje kartel a kdy je kartel stabilní.
 Kartel a asymetrické informace Varian: Mikroekonomie: moderní přístup, kapitoly 26.10-11, 27.4-6, 34 Varian: Intermediate Microeconomics, Chapters 27.10-11, 28.4-6, 37 () 1 / 42 Na této přednášce se dozvíte
Kartel a asymetrické informace Varian: Mikroekonomie: moderní přístup, kapitoly 26.10-11, 27.4-6, 34 Varian: Intermediate Microeconomics, Chapters 27.10-11, 28.4-6, 37 () 1 / 42 Na této přednášce se dozvíte
Kelvin v kapkový generátor
 Kelvin v kapkový generátor Kry²tof Kadlec 1, Luká² Kune² 2, Luká² N me ek 3 1 Gymnázium Franti²ka Palackého, Vala²ské Mezi í í, krystoof.2@seznam.cz 2 Gymnázium, Zlatá stezka 137, Prachatice, kunamars@seznam.cz
Kelvin v kapkový generátor Kry²tof Kadlec 1, Luká² Kune² 2, Luká² N me ek 3 1 Gymnázium Franti²ka Palackého, Vala²ské Mezi í í, krystoof.2@seznam.cz 2 Gymnázium, Zlatá stezka 137, Prachatice, kunamars@seznam.cz
Rozlišení zisku. Mikroekonomie. Účetní zisk = Ekonomický zisk. Normální zisk. Zisk firmy. Co je důležité pro členění zisku
 Zisk firmy Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Zisk (π) je rozdíl mezi celkovými příjmy a celkovými náklady. Π = TR - TC Je také vynásobený objem produkce rozdílem průměrného
Zisk firmy Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Zisk (π) je rozdíl mezi celkovými příjmy a celkovými náklady. Π = TR - TC Je také vynásobený objem produkce rozdílem průměrného
Národní hospodářství poptávka a nabídka
 Národní hospodářství poptávka a nabídka Chování spotřebitele a poptávka Užitek a spotřebitelův přebytek Jedním ze základních problémů, které spotřebitel řeší, je, kolik určitého statku má kupovat a jak
Národní hospodářství poptávka a nabídka Chování spotřebitele a poptávka Užitek a spotřebitelův přebytek Jedním ze základních problémů, které spotřebitel řeší, je, kolik určitého statku má kupovat a jak
NEDOKONALÁ KONKURENCE
 NEDOKONALÁ KONKURENCE CHARAKTERISTIKA NK Jak byste charakterizovali NK? (z hlediska ceny) Jaké jsou další charakteristiky ceny? (uvádějte příklady) Produkt Náklady na změnu dodavatele Informace Počet producentů
NEDOKONALÁ KONKURENCE CHARAKTERISTIKA NK Jak byste charakterizovali NK? (z hlediska ceny) Jaké jsou další charakteristiky ceny? (uvádějte příklady) Produkt Náklady na změnu dodavatele Informace Počet producentů
Sazba zdrojových kód. Jakub Kadl ík 20. 03. 2014
 Sazba zdrojových kód Jakub Kadl ík 20. 03. 2014 1 Obsah 1 Základní prost edí verbatim 3 2 Balí ek listings 3 3 Sazba kódu z externího souboru 5 4 Téma Solarized 5 4.1 Solarized light.............................
Sazba zdrojových kód Jakub Kadl ík 20. 03. 2014 1 Obsah 1 Základní prost edí verbatim 3 2 Balí ek listings 3 3 Sazba kódu z externího souboru 5 4 Téma Solarized 5 4.1 Solarized light.............................
Obsah. Předmluva autora... VII. Oddíl A Metoda a předmět ekonomie
 Obsah Předmluva autora... VII Oddíl A Metoda a předmět ekonomie 1. Jaká věda je ekonomie?... 3 1.1 Pozitivní věda... 3 1.2 Vize a model v ekonomii... 5 1.3 Ekonomie věda o lidském jednání... 7 1.4 Racionalita
Obsah Předmluva autora... VII Oddíl A Metoda a předmět ekonomie 1. Jaká věda je ekonomie?... 3 1.1 Pozitivní věda... 3 1.2 Vize a model v ekonomii... 5 1.3 Ekonomie věda o lidském jednání... 7 1.4 Racionalita
VOLBA VÝSTUPU DOKONALE KONKURENČNÍ FIRMOU
 VOLBA VÝSTUPU DOKONALE KONKURENČNÍ FIRMOU URČENÍ VÝSTUPU, PŘI NĚMŽ FIRMA MAXIMALIZUJE ZISK Ekonomický zisk- Π =TR-TC Π= P.Q-w.L-r.K Π=P.f(K,L)-w.L-r.K Nulový ekonomický zisk-vstupy svým fungováním přinášejí
VOLBA VÝSTUPU DOKONALE KONKURENČNÍ FIRMOU URČENÍ VÝSTUPU, PŘI NĚMŽ FIRMA MAXIMALIZUJE ZISK Ekonomický zisk- Π =TR-TC Π= P.Q-w.L-r.K Π=P.f(K,L)-w.L-r.K Nulový ekonomický zisk-vstupy svým fungováním přinášejí
8. Firmy na dokonale konkurenčních trzích
 8. Firmy na dokonale konkurenčních trzích Motivace Každá firma musí učinit následující rozhodnutí: kolik vyrábět jakou cenu si účtovat s jakými výrobními faktory (kolik práce a kolik kapitálu) Tato rozhodnutí
8. Firmy na dokonale konkurenčních trzích Motivace Každá firma musí učinit následující rozhodnutí: kolik vyrábět jakou cenu si účtovat s jakými výrobními faktory (kolik práce a kolik kapitálu) Tato rozhodnutí
Inovace (praxe) 1 Úvod, p edstavení rmy, omezení práce. 16. listopadu 2010, Organizace a informace. Karel Kohout
 Inovace (praxe) 1 Úvod, p edstavení rmy, omezení práce V rámci seminární práce jsou rozebrány t i inovace, realizované záºitkovou agenturou FAN MOTION 1. Dv z nich jsou spí²e technického rázu (sb r údaj
Inovace (praxe) 1 Úvod, p edstavení rmy, omezení práce V rámci seminární práce jsou rozebrány t i inovace, realizované záºitkovou agenturou FAN MOTION 1. Dv z nich jsou spí²e technického rázu (sb r údaj
Charakteristika monopolu
 Monopol charakteristika monopolu příčiny jeho vzniku volba rovnovážného výstupu stanovení ceny monopolem křivka nabídky monopolu cenová diskriminace alokační a výrobní efektivnost monopolu regulace monopolu
Monopol charakteristika monopolu příčiny jeho vzniku volba rovnovážného výstupu stanovení ceny monopolem křivka nabídky monopolu cenová diskriminace alokační a výrobní efektivnost monopolu regulace monopolu
Frikce pracovního trhu
 12. listopadu 2010 Literatura Mandelman, F. S. - Zanetti F.: Technical Handbook - No. 1.: Estimating general equilibrium models: an application with labour market frictions Centre for Central Banking Studies,
12. listopadu 2010 Literatura Mandelman, F. S. - Zanetti F.: Technical Handbook - No. 1.: Estimating general equilibrium models: an application with labour market frictions Centre for Central Banking Studies,
