}w!"#$%&'()+,-./012345<ya
|
|
|
- Jan Kadlec
- před 7 lety
- Počet zobrazení:
Transkript
1 MASARYKOVA UNIVERZITA FAKULTA INFORMATIKY }w!"#$%&'()+,-./012345<ya Vývoj algoritmu pro detekci kapes v proteinech DIPLOMOVÁ PRÁCE Bc. Andrej Kuročenko Brno, podzim 2014
2 Prohlášení Prohlašuji, že tato diplomová práce je mým původním autorským dílem, které jsem vypracoval samostatně. Všechny zdroje, prameny a literaturu, které jsem při vypracování používal nebo z nich čerpal, v práci řádně cituji s uvedením úplného odkazu na příslušný zdroj. Bc. Andrej Kuročenko Vedoucí práce: RNDR. Barbora Kozlíková, Ph.D. ii
3 Poděkování Tímto děkují RNDr. Barboře Kozlíkové, Ph.D. za vedení této diplomové práce. Také za čas věnovaný konzultacím, trpělivost, vstřícnost a cenné rady. iii
4 Shrnutí Analýza struktur molekul proteinů je v poslední době jedním z hlavních témat v biochemickém výzkumu. Vznikly nástroje pro detailní snímání těchto struktur a ukládaní jejich reprezentací do obsáhlých databází. Na základě těchto dat bylo vyvinuto mnoho nástrojů pro vizualizaci molekul proteinů a jejich struktur. Také vznikly nástroje pro analýzu a následnou vizualizaci různých útvarů a speciálních vazebních míst molekul proteinů. V této diplomové práci je čtenář seznámen s proteiny a jejich strukturami. Dále jsou představeny útvary, jež taková struktura může obsahovat a jsou zajímavé z hlediska interakcí molekul proteinů s jinými malými molekulami ligandy. Diplomová práce se pak zaměřuje na kapsy na povrchu molekul proteinů, analyzuje existující přístupy k detekci kapes. Hlavně pak se zaměřuje na přístupy využívající Voroného diagram a Delaunayho triangulaci. Cílem diplomové práce je navrhnout vlastní řešení detekce kapes na povrchu molekul proteinů vycházející z Voroného diagramu. Následně tento algoritmus implementovat do programu CAVER Analyst. iv
5 Klíčová slova Protein, kapsa, molekula, aktivní místo, Java, CAVER, CAVER Analyst. v
6 Obsah 1 Úvod Proteiny a jejich struktura Co je to protein Funkce proteinu Povrch proteinu Struktura proteinu Aktivní místo Analýza volného prostoru v proteinech Póry Tunely Asymetrické tunely Kanály Dutiny Kapsy Detekce kapes v molekulách proteinů Úvod Technické pojmy α koule Delaunayho triangulace Voroného diagram Obecné přístupy k detekci kapes Detekce kapes za pomocí sondy ve tvaru koule Detekce kapes pomocí 3D mřížky Detekce kapes porovnáváním Detekce pomocí α koulí, Voroného diagramu a Delaunayho triangulace Vlastní řešení detekce kapes v molekulách proteinů CAVER Analyst Voroného diagram v CAVER Analyst Vnější uzly Voroného diagramu Teoretické předpoklady Analýza cesty
7 4.2.2 Detekce kapes Popis algoritmu Analýza Voroného diagramu, sestavení cest Krok 1: Filtrace sousedních uzlů Krok 2: Evoluce postupu Krok 3: Vlastnosti uzlů cest Analýza cest, detekce kapes Vizualizace kapes v molekule proteinu Implementace algoritmu Zakomponování algoritmu do aplikace CAVER Analyst Srovnání s existujícím algoritmem Srovnání výsledků detekce kapes Příklad 1: molekula 1ACJ Příklad 2: molekula 1QIF Příklad 3: molekula 1ESA Příklad 4: molekula 2P3B Srovnání rychlosti Závěr Plány do budoucna
8 Kapitola 1 Úvod Molekuly proteinů jsou všudypřítomné v buňce živých organismů a vykonávají různé funkce nezbytné pro život. Většina těchto funkcí probíhá v interakci s jinými molekulami tzv. ligandy. Tyto interakce jsou zprostředkovány specifickými aminokyselinami nacházejícími se na určitých pozicích (v tzv. aktivních místech, více v sekci 2.3.1) v molekulách proteinů. Lokace těchto pozic a zkoumání struktury proteinů je nezbytná k lepšímu pochopení funkcionality různých typů proteinů a také k pochopení, jak a s jakými ligandy tyto interakce probíhají. Zkoumání aktivních míst pomůže odpovědět na otázky, zda aktivní místa interagující s podobnými ligandy mají rovněž podobnou strukturu a zda pomocí této struktury lze předpovědět funkce celého proteinu. Snaha o pochopení fungování proteinů a jejích interakcí je důsledkem pokroku v určování proteinových struktur pomocí rentgenové krystalografie [26] a nukleární magnetické rezonance [16]. Desítky tisíc proteinových struktur a malých molekul ligandů bylo nasnímáno výše zmíněnými metodami a uloženo do proteinové data banky PDB [9]. Díky tomu existuje rozmanitá kolekce struktur, které lze zkoumat algoritmicky za využití různých geometrických přístupů. Tyto algoritmy poskytují možností analýzy prostorové konfigurace těchto struktur, která je zásadní z pohledu reaktivity dané struktury. V důsledku toho lze předpovědět různé vlastnosti a chování daných struktur v kombinaci s různými ligandy. Navíc při použití moderních grafických karet lze dosáhnout významného zdokonalení a zrychlení použitých geometrických algoritmů. Jednou ze základních zkoumaných částí molekul proteinů, která má významný vliv na reaktivitu daného proteinu, jsou aktivní místa. Jedná se o volný prostor se schopností navázat na sebe malou molekulu ligandu. Aktivní místa se mohou nacházet hluboko uvnitř proteinu, ale i na jeho povrchu 2.2. Právě problémem detekce aktivních míst nacházejících se na povrchu proteinů se zabývá tato diplomová práce. Cílem práce je detekovat tzv. kapsy 2.4.6, což jsou prohlubně konkávního tvaru dostupné z povrchu proteinu. Právě v některých kapsách je možné následně detekovat přítomnost aktivního místa. K této znalosti je však zapotřebí dalších biochemic- 3
9 1. ÚVOD kých znalostí tykajících se aminokyselin v okolí detekovaných kapes. Za uplynulá léta bylo představeno velké množství způsobů, jakými lze výše zmíněné kapsy detekovat. Mezi nejčastější metody detekce patří analýza povrchu molekuly za použití sond (popsána v sekci 3.3.1), dělení do 3D mřížky (sekce 3.3.2) nebo využití pseudo-struktur jako jsou Delaunayho triangulace a Voroného diagram (sekce 3.3.4). Po popisu již existujících řešení je součástí této diplomové práce návrh a implementace vlastního přístupu k detekci kapes v molekulách proteinů. Tento přístup je vychází z Voroného diagramu následně je zaintegrován do programu CAVER Analyst [2], který se zabývá analýzou a vizualizaci proteinových struktur. Poslední část diplomové práce se věnuje porovnání výsledků detekce kapes pomocí vlastního přístupu s jedním z existujících a nejčastěji používaným řešením. 4
10 Kapitola 2 Proteiny a jejich struktura 2.1 Co je to protein Proteiny jsou jedním ze základních stavebních prvků buněk všech živých organismů. Mají na starost téměř každý úkol, který daná buňka musí vykonat, určují její tvar a vnitřní uspořádání, vyrábí potřebné látky a zbavují se nepotřebných. Pomocí proteinů může buňka komunikovat s okolím přijímáním různých signálů a odesíláním odpovědí. Soubor proteinů v buňce určuje její zdravotní stav a funkci Funkce proteinu Proteiny jsou makromolekuly složeny z různých aminokyselinových řetězců, které vznikají pomocí syntézy z informace uložené v genech (DNA). Veškeré známé proteiny jsou tvořeny různými kombinacemi pouze dvaceti aminokyselin. Každá molekula proteinu může obsahovat jeden či více takovýchto řetězců, jejichž unikátní uspořádání a typ určuje funkci molekuly, jako například: Metabolická funkce některé typy proteinů jsou specifické tím, že dokáží vytvářet určitý typ látky pomocí biochemické reakce (katalýza). Tyto proteiny se nazývají enzymy a mají na svém povrchu nebo uvnitř sebe tzv. aktivní místa (viz 2.3.1) umožňující již zmíněnou reakci. Strukturální funkce typ proteinů, který se stará o tvar buněk, slouží jako spojovací materiál či tvoří základ kostí, mimo jiné rovněž nehtů, vlasů, srsti, atd. Komunikační funkce další skupina proteinů slouží jako komunikační média, mohou měnit tvar i aktivitu v závislosti na metabolických signálech či zprávách z okolních buněk. 5
11 2. PROTEINY A JEJICH STRUKTURA 2.2 Povrch proteinu Povrch proteinové molekuly je důležitý z hlediska zkoumání jejích vlastností. Obsahuje totiž různé útvary (viz 2.4), jež definují funkcionalitu proteinu. Povrch proteinu se nejčastěji popisuje následujícími třemi typy (viz Obrázek 2.1): 1. Van der Waalsův povrch každý atom je reprezentován koulí, jejíž poloměr odpovídá Wan der Waalsovu poloměru daného atomu. Tento typ povrchu slouží ke znázornění prostoru, který daná molekula proteinu zabírá [10]. Wan der Waalsův povrch je pak definován jako vnější povrch sjednocení všech koulí těchto atomů každý atom je reprezentován jako koule o velikosti Van der Waalsova poloměru. 2. Solvent accessible surface (SAS) tento typ povrchu, který definovali Lee a Richards [3] je rozšířením Van der Waalsova povrchu. Jeho cílem je zobrazit všechny oblasti molekuly, které jsou dostupné pro malou molekulu solventu (např. vody). Tvar a velikost molekuly solventu jsou aproximovány koulí, která se nazývá sonda. SAS tedy odpovídá Van der Waalsovu povrchu, který je zvětšen o poloměr sondy. Vznik SAS si lze představit jako valení koule (sondy) po Van der Waalsově povrchu, kdy výsledný SAS je tvořen pozicemi středu sondy. 3. Solvent excluded surface (SES) tento typ povrchu [10] je konstruován podobným způsobem jako SAS. Místo trasování středu sondy valící se po atomech se bere v úvahu vnější obálka sondy. Jiná definice popisuje SES jako topologickou hranici sjednocení všech možných pozic sondy, ve kterých sonda neprochází skrz žádný atom. SES povrch je složen ze tří možných typů vzorků, které může sonda vytvořit. Jedná se o konvexní sférické vzorky, které vznikají když se sonda dotýká právě jednoho atomu. Dalším typem jsou toroidní vzorky vzniklé při dotyku sondy s právě dvěma atomy. Třetí typ je tvořen konkávními sférickými vzorky, které vznikají, když sonda leží ve fixní pozici a dotýká se právě tří atomů. 2.3 Struktura proteinu Pro práci s proteinovými strukturami v počítačovém programu je nejdříve potřeba vytvořit virtuální reprezentaci prostorového uspořádání molekuly. Toho lze docílit rentgenovou krystalografií či nukleární magnetickou rezonancí. Metody umožňují nasnímat pozice atomů v daném čase a převést je 6
12 2. PROTEINY A JEJICH STRUKTURA r SAS SES Van der Waals Sonda Obrázek 2.1: Typy povrchů molekul do standardizovaného formátu. Jedním z nejběžnějších a nejčastěji používaných formátů je formát PDB [9]. Strukturu proteinu lze členit do čtyř základních kategorií podle úrovně abstrakce (viz Obrázek 2.2): Primární struktura znázorňuje celé aminokyselinové řetězce a jejich pořadí s polypeptidovými vazbami. Tato unikátní struktura proteinu určuje jeho funkci. Sekundární struktura jedná se o abstrahované zobrazení opakujících se částí aminokyselinového řetězce spojených vodíkovými vazbami. Terciární struktura oproti sekundární struktuře se jedná o prostorové zobrazení celé molekuly. Kvartérní struktura tento typ abstrakce lze použít u proteinů skládajících se z více domén (polypeptidových řetězců). Tyto domény jsou vzájemně prostorově uspořádány. Obrázek 2.2: Ukázka proteinových struktur. Zleva primární, sekundární, terciální a kvartérní struktura. (Převzato z cn/book/biochemistry/chapt07/sim1.htm) 7
13 2. PROTEINY A JEJICH STRUKTURA Aktivní místo Proteinové molekuly enzymy obsahují specifická místa na svém povrchu nebo ve vnitřních dutinách, která dokáží na sebe vázat jiné volné molekuly (ligandy, substráty, molekuly solventu, molekuly vody, atd.). Tyto volné molekuly se pohybují v okolí proteinů a za určitých podmínek může proběhnout katalytická reakce mezi nimi a daným proteinem. Tím lze volnou molekulu transformovat na jinou. Výše zmíněná specifická místa se nazývají vazebná neboli aktivní místa. U již dobře strukturně popsaných proteinů je pozice aktivního místa známa, avšak u nově vzniklých syntetických proteinů je potřeba jej vyhledat. Neexistuje univerzální technika či algoritmus se 100% úspěšností vyhledávání. Většina existujících algoritmů a nástrojů se soustředí na nalezení pozice aktivního místa u specifické skupiny proteinů a u ostatních skupin nemá často tak vysokou úspěšnost. Hledání aktivního místa má velký význam při výrobě nových léků nebo jiných chemických látek (například látek pro rozklad toxinů). Při kontaktu aktivního místa proteinu s ligandem dojde bud k modifikaci proteinu nebo ligandu samotného. Tohoto jevu lze využít k modifikaci vlastností proteinů nebo při výrobě nové látky z nějaké jiné. 2.4 Analýza volného prostoru v proteinech Každá proteinová molekula má poměrně komplikovanou jak povrchovou, tak i vnitřní strukturu. Obsahuje různé výběžky, rýhy, vnitřní dutiny a prohlubně. Tyto útvary jsou zajímavé z hlediska samotného fungování proteinu a jejich studium je důležité za účelem hledání a vytváření nových katalyzátorů a léků. Pro odlišení již zmíněných útvarů se používají pojmy jako póry, kapsy, tunely, kanály, vnitřní dutiny. Aby nedocházelo k chybné interpretaci textu, budou v následujícím textu popsány tyto útvary s jejich vizualizací a existující programy pro jejich vyhledávání Póry Póry jsou speciálním typem kanálů. Zprostředkovávají přesun iontů či jiných molekul přes biologické membrány. Nejčastějším nástrojem pro jejich vyhledávání je PoreWalker4 [22]. Ukázku póru lze vidět na obrázku
14 2. PROTEINY A JEJICH STRUKTURA Obrázek 2.3: Příklad póru v proteinu, vytvořeno v programu CAVER Analyst [2] Tunely Tunely jsou v podstatě cesty spojující vnitřní dutinu proteinové molekuly (aktivní místo) s okolním soventem, v němž se molekula nachází. Pro jejich vyhledávání se používají programy CAVER 3.0 [15], MOLE 2.01 [23] a MolAxis2 [36]. Ukázku tunelu lze vidět na obrázku Asymetrické tunely Asymetrický tunel se od klasického tunelu liší tvarem svého povrchu. Asymetrický tunel lépe kopíruje jeho skutečný tvar a lépe tak vystihuje i biochemickou podstatu tunelu. Biochemické vlastnosti (hydrofobicitu či parciální náboj) okolí tunelu lze rovněž promítnout na povrch tunelu pomocí barevné škály. Uživatel má tak možnost okamžitě zhodnotit kompatibilitu fyziko-chemikálních vlastností tunelu s vlastnostmi ligandu, pro který byl tunel spočten. Ukázku asymetrického tunelu lze vidět na obrázku
15 2. P ROTEINY A JEJICH STRUKTURA Obrázek 2.4: Pr íklad tunelu v proteinu. Vlevo asymetrický, vpravo symetrický tunel. Vytvor eno v programu CAVER Analyst [2] Kanály Kanály jsou cesty procházející skrz proteinovou molekulu, pr ic emž oba konce spojují okolní solvent, v ne mž se molekula nachází. Ukázku kanálu lze vide t na obrázku 2.5. Obrázek 2.5: Pr íklad kanálu v proteinu, vytvor eno v programu CAVER Analyst [2]. 10
16 2. PROTEINY A JEJICH STRUKTURA Dutiny Jako dutina je označováno prázdné místo uvnitř molekuly, které není přímo dostupné z povrchové části proteinu. Dutiny představují z biochemického hlediska velmi významné útvary, protože se v nich může nacházet aktivní místo proteinu. Právě přítomnost a dostupnost aktivního místa má zásadní vliv na reaktivitu daného proteinu. Ukázku dutin v molekule proteinu lze vidět na obrázku 2.6. Obrázek 2.6: Příklad dutiny v proteinu. Aktivním místo se nachází v největší dutině. Vytvořeno v programu CAVER Analyst [2] Kapsy Jako kapsu označujeme prohlubeň na povrchu proteinové molekuly, která může rovněž obsahovat aktivní místo. Účelem této diplomové práce je návrh vlastního přístupu k detekci kapes na povrchu proteinu a následná 11
17 2. P ROTEINY A JEJICH STRUKTURA implementace a integrace do aplikace CAVER Analyst [2]. Ukázku kapes v molekule proteinu lze vide t na obrázku 2.7. Obrázek 2.7: Pr íklad kapes na povrchu proteinu. Detekováno programem Fpocket [28], vizualizováno v programu PyMOL [25] 12
18 Kapitola 3 Detekce kapes v molekulách proteinů 3.1 Úvod Povrch proteinových molekul často obsahuje aktivní místa, která na sebe vážou ligandy ze svého okolí a interagují s nimi. Taková aktivní místa jsou nejčastěji umístěna v takzvaných kapsách (viz 2.4.6), jež mají konkávní tvar. Jelikož povrch proteinu je hrbolatý, je potřeba rozlišovat, kdy se jedná o kapsu a kdy pouze o menší prohlubeň. Pokud je kapsa rozsáhlejší, je třeba určit, zda jde o jednu velkou kapsu nebo o více propojených kapes. 3.2 Technické pojmy V této podkapitole jsou definovány technické pojmy a pomocné struktury použity k popisu existujících i nového vlastního přístupu k detekci kapes v proteinových molekulách α koule Pojem α koule je při zkoumání vlastností molekuly použit pro popsání prostoru mezi čtyřmi atomy, přičemž všechny čtyři atomy se dotýkají okraje α koule jsou ve stejné vzdálenosti od jejího středu (viz Obrázek 3.1). Poloměr α koule je dán pozicí čtveřice atomů. Pokud například atomy budou uspořádány za sebou, poloměr bude nekonečně velký. Obecně platí, že α koule ve vnitřní struktuře molekuly mají menší poloměr než na povrchu. Pojem α koule vychází z definice α shape [8] Delaunayho triangulace Delaunayho triangulace [1] je speciální případ triangulace na množině bodů P, kdy sousední body tvoří vrcholy trojúhelníků takových, že žádný bod p P neleží uvnitř kružnice opsané danému trojúhelníku. Výsledný diagram je úzce spojen s Voroného diagramem [30], protože středy opsaných 13
19 3. DETEKCE KAPES V MOLEKULÁCH PROTEINŮ r atomy -koule Obrázek 3.1: α koule s poloměrem r ležící mezi čtyřmi atomy kružnic tvoří vrcholy polygonů Voroného diagramu. Graf vzniklý Delaunayho triangulací je duálním grafem k Voroného diagramu (viz Obrázek 3.2) Voroného diagram Voroného diagram vznikne rozdělením uzlů p P grafu G do oblastí ve tvaru konvexních polygonů, kdy v každé oblasti je pouze jeden uzel p a všechny body v dané oblasti jsou blíže k danému uzlu než k ostatním bodům z P (viz Obrázek 3.2). Obrázek 3.2: Delaunayho triangulace na bodech množiny P (černě) se zobrazenými opsanými kružnicemi (šedě) a duální Voroného diagram (červeně) 14
20 3.3 Obecné přístupy k detekci kapes 3. DETEKCE KAPES V MOLEKULÁCH PROTEINŮ Existuje velké množství různých algoritmů, které se snaží co nejlépe a nejpřesněji najít kapsy s aktivním místem na povrchu proteinové molekuly. Některé algoritmy využívají poznatku, že kapsa má konkávní tvar a snaží se ji detekovat analýzou geometrické struktury molekuly. Jiné algoritmy se pokoušejí najít podobnost okolí již detekovaných kapes s místy na povrchu jiných molekul, které mají podobnou strukturu. Další algoritmy používají tzv. pseudo-struktury. Následuje podrobný popis existujících přístupů k detekci kapes a programů, které je využívají Detekce kapes za pomocí sondy ve tvaru koule Jeden z nejjednodušších přístupů k detekci kapes v proteinové molekule je za použití sond ve tvaru koule. Postup je podobný tomu pro získání povrchu molekul (viz 2.2). Vychází z 3D struktury molekuly. Podle typu proteinu se zvolí velikosti pro velkou a malou sondu [17]. Tyto sondy se postupně valí po molekule a zaznamenávají povrch. Jako kapsy jsou následně označeny ty prohlubně, do kterých se vešla malá sonda, ale velká už nikoliv (viz Obrázek 3.3). Tento algoritmus je použit v programech POCASA [33] a PASS [11]. Obrázek 3.3: Detekce kapes v molekule proteinu pomocí malé (vlevo) a velké (vpravo) sondy. Atomy, které tvoří povrch molekuly, jsou zvýrazněny šedou barvou. 15
21 3.3.2 Detekce kapes pomocí 3D mřížky 3. DETEKCE KAPES V MOLEKULÁCH PROTEINŮ Molekulární struktura se rozdělí do husté 3D mřížky, která je sestrojena z kostek a každá kostka má vlastní souřadnici [x, y, z] (viz Obrázek 3.4). U těchto bodů se následně zjistí, zda reprezentují volné prostranství, či nikoliv (v jejich vnitřním prostoru se nacházejí atomy). Poté se hledají shluky bodů s volným prostranstvím kapsy jež jsou dostupné okolnímu solventu. Nevýhodou této metody je neúspěšnost hledání kapes, které jsou orientovány ve 45 vůči ortogonálním osám. Tento nedostatek se řeší přidáním čtvrté, kubické [13], osy. Mezi programy využívající tuto metody patří např. POCKET [6], LIGSITE [20], PocketPicker [31] nebo PocketDepth [35]. Obrázek 3.4: Detekovaná kapsa v molekule proteinu pomocí mřížky ve zjednodušeném 2D modelu. Červeně je znázorněna neprázdná část mřížky s atomy, modře pak volné prostranství vyznačující kapsu Detekce kapes porovnáváním V této metodě se vychází z předpokladu, že molekulární funkce proteinu závisí na struktuře molekuly. Algoritmy používající tento způsob detekce porovnávají okolní strukturu kapes s aktivními místy dobře známých molekul se strukturou novějších či méně prozkoumaných molekul a podle shody u nich predikují aktivní místa, či doporučují ligandy, které by mohly s daným místem reagovat. Porovnávací algoritmus se dělí na dvě části. První částí je hodnotící funkce, která podle předem definovaných kritérií převádí strukturu molekuly na interní reprezentaci. Druhou část tvoří databáze známých aktivních míst, která obsahuje již ohodnocené kapsy s aktivními místy. Detekce kapes 16
22 3. DETEKCE KAPES V MOLEKULÁCH PROTEINŮ pak probíhá ohodnocením nových struktur hodnotící funkcí a porovnáním oproti databázi již známých aktivních míst. Algoritmy se liší podle toho, s jakou strukturou pracují. Například Con- Cavity [4], Apoc [19] a PocketAlign [34] používají okolní aminokyseliny kapes a jejich chemické vlastnosti. PARIS [14] používá soubor všech okolních atomů, DoGSiteScorer [29] pouze určitých typů atomů Detekce pomocí α koulí, Voroného diagramu a Delaunayho triangulace Algoritmus vyvinutý v rámci této diplomové práce je založen na znalosti Voroného diagramu (viz 3.2.3), proto jednotlivé, již existující přístupy používající stejné nástroje, budou popsány podrobněji než ostatní. Fpocket k detekci kapes na povrchu proteinových molekul využívá algoritmus [28] pomocných struktur Voroného diagram a α koule. Proces detekce kapes je rozdělen do tří kroků: Vypočítají se α koule pro celou strukturu proteinové molekuly za použití Voroného diagramu. Z těchto koulí se vyfiltrují příliš malé či naopak příliš velké podle parametru minimálních a maximálních povolených rozměrů koulí. Odstraní se tak prostor nedostupný okolnímu solventu nebo naopak vnější prostor molekuly. Ke každé ze získaných koulí se poznamená, jakých typů atomů se dotýkají. Prochází se výsledky prvního kroku a rozdělují se do shluků, nejdříve podle jejich pozice. Všechny shluky obsahující jednu α kouli se odstraní, pro ostatní se spočítá jejich molekulární hmotnost. Tyto shluky se dále spojují, pokud jejich těžiště jsou blízko sebe nebo pokud shluky sdílí určitý počet α koulí. Potenciální kapsy se ohodnotí v závislosti na výskytu určitých atomů v jejich okolí (ty, jež se dotýkají α koulí) za účelem zjištění typů ligandů, které by se mohly vázat na potenciální aktivní místo. CAST algoritmus [18], stejně jako předchozí, používá Voroného diagram a Delaunayho triangulaci pro detekci kapes a dutin v proteinové molekule. Výstup algoritmu navíc obsahuje informaci o velikosti kapsy, její hloubce, obvodu a ploše dostupné solventu. Tento algoritmus byl následovně rozšířen o webovou databázi a klienta CASTp [7]. Pomocí něj si může kdokoliv zadáním kódu molekuly v PDB [9] formátu nechat vypočítat kapsy a dutiny. Výsledky jsou zaslány zájemci na ovou adresu. Více podrobné výsledky jsou pak k vidění na webových stránkách. 17
23 3. DETEKCE KAPES V MOLEKULÁCH PROTEINŮ SplitPocket program [27] detekuje potencionální kapsy na povrchu proteinové molekuly pomocí Delaunayho triangulace a algoritmu pro diskrétní tok [12]. Predikce kapes je pro každou strukturu prováděna dvakrát. Poprvé se analyzuje struktura včetně ligandů, následně struktura bez nich. V dalším kroku se porovnává struktura detekovaných kapes s ligandem a bez něho. Změna struktury téže kapsy indikuje interaktivitu částí molekuly v kapse a ligandu. Program je rovněž vystaven na webovém serveru, kde lze vizualizovat kapsy na zvolených molekulách proteinů pomocí PDB [9] formátu. 18
24 Kapitola 4 Vlastní řešení detekce kapes v molekulách proteinů Cílem této diplomové práce je navrhnout vlastní řešení k detekci kapes v molekulách proteinů a implementovat navržený algoritmus do programu CAVER Analyst [2]. V této kapitole je čtenář obeznámen s programem CA- VER Analyst (viz 4.1) a s teorií (viz 4.2), z níž vychází návrh vlastního algoritmu (sekce 4.3) a jeho implementace (viz 4.4). Nakonec jsou výsledky porovnány s jedním z existujících programů pro detekci kapes v molekulách proteinů (sekce 4.6). 4.1 CAVER Analyst Program CAVER Analyst [2] vznikl jako grafické rozhraní pro program CA- VER [15], což je softwarový nástroj pro výpočet transportních cest, tunelů a kanálů ve statických i dynamických makromolekulárních strukturách. CA- VER je konzolový program, který vrací výstupy v textové podobě. Tento přístup je vhodný pro spouštění v dávkovém režimu na velmi výkonných počítačích. Analýza výstupu programu CAVER není však uživatelsky přívětivá, vizuální analýza zcela chybí. Za tímto účelem vznikl nástroj CA- VER Analyst (dříve CAVER Viewer), který v jádru využívá již zmíněný nástroj CAVER. CAVER Analyst přináší pohodlné grafické rozhraní (viz Obrázek 4.1) pro vizualizaci molekul proteinů, jejich povrchu a struktur. Dále slouží k intuitivnímu nastavení výpočtů tunelů, kanálů, atd., a vizualizaci těchto výpočtů. To vše lze provést jak pro statické, tak i pro dynamické struktury molekul proteinů. CAVER Analyst je multiplatformní program napsaný v jazyce Java za použití Netbeans platformy [5]. V současné době využívá programu CA- VER ve verzi Vlastní řešení algoritmu pro detekci kapes v molekulách proteinů je založeno na Voroného diagramu. Nejdříve je tedy nutné popsat, jakým způsobem je Voroného diagram reprezentován v programu CAVER Analyst. 19
25 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ Voroného diagram v CAVER Analyst CAVER Analyst má zabudovanou podporu pro výpočet Voroného diagramu pro libovolnou molekulu proteinu díky tomu, že v jádru využívá program CAVER, který tuto funkcionalitu podporuje. Voroného diagram je reprezentován uzly a hranami. Uzly Voroného diagramu leží ve středu kružnic Delaunayho triangulace (viz Obrázek 3.2). Hrany reprezentují spojení mezi sousedními uzly. Každý uzel je identifikován unikátním číslem a nese s sebou dodatečné informace souřadnice udávající jeho pozici v 3D struktuře molekuly, poloměr α koule vyplňující prostor mezi okolními atomy, identifikační čísla sousedních Voroného uzlů (každý uzel má maximálně čtyři sousedy) a další, pro tuto práci nepodstatné informace Vnější uzly Voroného diagramu Některé z Voroného uzlů slouží pouze k uchycení hrany, která rozděluje dva atomy na okraji struktury molekuly (viz Obrázek 3.2). Takové uzly se nacházejí v nekonečnu (v programu reprezentováno velkou vzdáleností cca Å od povrchu molekuly proteinu) a mají nastaven speciální příznak. Dále v textu jsou tyto uzly označeny jako vnější Voroného uzly. Obrázek 4.1: Ukázka programu CAVER Analyst, konkrétně vizualizace molekuly 1DMP, jejího povrchu a vypočítaných tunelů. 20
26 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ 4.2 Teoretické předpoklady V této sekci jsou popsány teoretické předpoklady, na základě kterých je navržen a implementován vlastní algoritmus sloužící k detekci kapes na povrchu molekul proteinů Analýza cesty Navržený algoritmus vychází ze znalostí, že kapsy mají konkávní tvar, nacházejí se na povrchu molekuly, a že sít Voroného vrcholů a hran je dostatečně hustá, aby pokryla celý povrch molekuly. Budeme-li postupovat po Voroného hranách z vnějšího Voroného uzlu směrem dovnitř molekuly, pak se šířka Voroného hrany (poloměr α koule v místě jejího počátku) bude postupně snižovat, jak se bude přibližovat povrchu molekuly. Znatelné zúžení nastane při vstupu hrany dovnitř molekuly proteinu, jelikož mezi atomy je mnohem méně místa než na povrchu. Další rozvoj šířek Voroného hrany závisí na vnitřní struktuře proteinové molekuly. Bude-li hrana procházet např. středem tunelu, bude šířka větší oproti případu, kdy by hrana procházela mezi blízkými atomy (viz Obrázek 4.2). Obrázek 4.2: Zjednodušená ukázka cesty sestavené z Voroného hran (modře) uvnitř tunelu (červeně) s odbočkami (zeleně) mezi okolní atomy (černě). Na obrázku lze vidět, že šířka cesty v tunelu je větší, než šířka cest mimo tunel Detekce kapes Budeme-li vycházet z povrchu molekuly proteinu vytvořeného velkou koulí (viz Obrázek 3.3), pak se šířka cesty sestavené z Voroného hran v případě kapsy nesníží významně ihned po vstupu hrany pod povrch molekuly pro- 21
27 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ teinu, ale až v následujících krocích. Průměr koule pro vytvoření povrchu u enzymů je odhadován na cca 3 Å (je to dáno běžnými rozměry enzymů, velikostí jejich vnitřních útvarů a vzdáleností mezi jejich atomy). Tento jev je zobrazen na obrázku 4.3. Šířka cest je následně analyzována pomocí grafů na obrázku 4.4. Jedná se však o velmi zjednodušený model. Přesné modely budou reprezentovány na skutečných datech dále v textu Obrázek 4.3: Ukázka dvou Voroného vnějších uzlů (s číslem 0), a analya šířky Voroného hran (zobrazeno červenými kruhy) směřujících dovnitř molekuly. Skutečný povrch molekuly je zobrazen světlé modrou čárou, povrch vytvořený koulí o velkém průměru (viz Obrázek 3.3) je zobrazen černou barvou. Atomy jsou reprezentovány šedými kruhy. Pravá cesta prochází kapsou a její šířka se nemění tak rychle jako šířka levé cesty. Obrázek 4.4: Grafy s logaritmickou osou y zobrazující šířky Voroného hran z obrázku 4.3. Na pravém grafu lze detekovat kapsu tím, že po proniknutí pod povrch molekuly se šířka hrany téměř nemění narozdíl od levého grafu. 22
28 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ 4.3 Popis algoritmu Vlastní algoritmus je kvůli lepšímu popisu a jednodušší implementaci rozdělen na tři části: 1. analýza Voroného diagramu a sestavení cest (4.3.1), 2. analýza cest a detekce kapes (4.3.2), 3. vizualizace detekovaných kapes (4.3.3). Tyto části jsou dále samostatně popsány Analýza Voroného diagramu, sestavení cest První část algoritmu má za úkol z Voroného diagramu na vstupu vytvořit seznam cest vedoucích z vnějšku molekuly proteinu dovnitř skrz povrch. Níže je popsán způsob, jakým se filtrují Voroného uzly a sestavují do cest, datové struktury reprezentující uzly na sestavených cestách a řešení nedostatků původního návrhu. Krok 1: Filtrace sousedních uzlů Vstupem této části algoritmu je Voroného diagram vypočítaný nad danou strukturou molekuly proteinu, výstupem jsou cesty reprezentovány uzly a pomyslnými hranami mezi nimi. Analýza Voroného diagramu začíná na jeho vnějších uzlech Pro každý vnější uzel se v paměti vytváří vlastní cesta přidáváním sousedů. Soused může být přidán do cesty pouze za splnění následujících podmínek: 1. Sousední uzel není doposud použit v žádné jiné cestě. 2. Sousední uzel leží blíže ke středu dané struktury molekuly proteinu než aktuálně analyzovaný uzel. 3. Vektor hrany mezi aktuálním uzlem a jeho sousedem má odchylku maximálně 90 s vektorem hrany mezi vnějším uzlem dané cesty a jeho bezprostředním sousedem (první a druhý uzel na cestě). První podmínka zajistí jedinečnost každé cesty, druhá a třetí podmínka udržuje potřebný směr, filtruje irelevantní hrany a vybírá pouze ty, jež prochází povrchem molekuly. 23
29 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ Krok 2: Evoluce postupu Původní verze algoritmu se spokojila s prvním sousedním uzlem splňujícím výše uvedené podmínky, avšak tento způsob mohl zvýhodnit kratší (slepé) cesty a přeskočit lepší (delší) cesty, které navíc procházejí kapsou. Proto byl algoritmus upraven, aby kontroloval již zmíněné podmínky pro každého ze čtyř sousedů aktuálně analyzovaného uzlu. Pokud podmínky jsou splněny více než jedním sousedem, z aktuální analyzované cesty se vytvoří kopie a její analýza probíhá zvlášt. Analýza cesty končí, pokud podmínkám nevyhoví žádný ze sousedů aktuálního uzlu. Krok 3: Vlastnosti uzlů cest Pro každý uzel z analyzovaných cest se poznamená šířka cesty v daném bodě (poloměr α koule) a pořadí uzlu. Pokud se uzel nachází v bezprostřední blízkosti povrchu molekuly vytvořeného velkou koulí, tato skutečnost se poznačí nastavením příznaku. Příznak se nastaví, pokud šířka cesty klesne pod hodnotu 3 Å (viz 4.2.2). Vizualizovaný výstup algoritmu lze vidět na obrázku 4.5. Obrázek 4.5: Ukázka výstupu prvního kroku algoritmu pro detekci kapes v molekulách proteinů. Na obrázku jsou vidět cesty vedoucí po Voroného hranách z vnějšího prostoru skrz povrch dovnitř molekuly. Červenými kuličkami jsou znázorněny uzly s příznakem, že se nachází blízko povrchu molekuly (viz 4.3.1). 24
30 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ Sestavení cest lze vidět na pseudokódu první části algoritmu 4.1, který vrací stromovou strukturu (les) cest. Pro následující krok algoritmu je potřeba tento les převést do lineární podoby do množiny samostatných cest. Algoritmus 4.1 Analýza Voroného diagramu, sestavení cest visited {} outerp athn odes convert (voronoi.outern odes) tov isit {outerp athnodes} while tov isit do actual tov isit.pop () visited actual for all n c actual.neighbours do Filtrace nevhodných sousedů if closert ocenter (n, actual) = n & deviation (actual, n) < 90 then pathnode convert (n) Provázání předchůdců actual.children {pathn ode} pathn ode.parent actual Nastavení příznaků if actual.radius > 3 Å & n.radius < 3 Å then pathn ode.nearsurf ace true end if tov isit {pathnode} end if end for end while return outerp athn odes Analýza cest, detekce kapes Druhá část algoritmu má za úkol detekovat cesty, které vedou kapsou na povrchu molekuly proteinu. Vstupem algoritmu jsou všechny cesty z prvního kroku V aktuálně zpracovávané cestě se nejprve dohledá uzel A s příznakem, který označuje, že uzel je v těsné blízkosti povrchu molekuly. Poté se postupně analyzují uzly na cestě, které leží za uzlem A. Pokud jejich šířka je v intervalu 50%; +25% vzhledem k šířce uzlu A, nastaví se jim příznak, že se nacházejí v kapse. Jakmile šířka aktuálního uzlu vyjde z hranic intervalu, analýza cesty končí. Nakonec se cesty s detekovanými kapsami filtrují podle délky 25
31 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ kapsy (počet uzlů s příznakem, že leží v kapse). Je-li délka kapsy menší než minimální povolená délka, pak se cesty zahazují. Minimální povolenou délku lze nastavit parametrem algoritmu a výchozí hodnota je 5. Pro lepší pochopení druhého kroku je přiložen pseudokód 4.2. Také jsou k dispozici ukázky analyzovaných dat na obrázku 4.6. Obrázek 4.6: Ukázka dat analyzovaných v druhém kroku algoritmu. Na grafech jsou vyobrazeny šířky cest (v Å). Horní graf reprezentuje cestu procházející kapsou (šířka cesty po průniku povrchem téměř neklesá). Spodní graf reprezentuje cestu, která kapsou neprochází (šířka hrany se významně mění po průniku povrchem molekuly). 26
32 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ Algoritmus 4.2 Detekce kapsy na cestě z Voroného uzlů result {} for all path paths do surfacenode getnearsurfacenode (path) Ignorují se cesty neprocházející povrchem if surfacenode then minr surfacenode.radius 0.5 maxr surfacenode.radius 1.25 node surf acen ode.next c 0 Detekce uzlů v kapse while node & node.radius minr; maxr do c c + 1 node node.next end while Příliš mělké kapsy se ignorují if c MIN_P OCKET _LENGT H then node surf acen ode.next while c 0 do node.inp osket true node node.next end while result path end if end if end for return result Vizualizace kapes v molekule proteinu Poslední krok algoritmu má za úkol vizualizovat nalezené kapsy v grafickém rozhraní programu CAVER Analyst. Vstupem tohoto kroku jsou cesty obsahující uzly, které se nacházejí v kapse proteinové molekuly. Tato skutečnost je reprezentována příznakem u daných uzlů. Kapsa je vizualizována výplní jejího prostoru koulemi. Tyto koule se kreslí na pozicích uzlů s výše zmíněným příznakem (nastavovaný v druhém kroku algoritmu 4.3.2) s poloměrem α koule v daném místě. Aby výplň kapsy byla souvislá, mezi jednotlivými koulemi se vykreslí dalších x překrývajících se koulí, což vytváří požadovaný vizuální efekt. Hod- 27
33 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ notu x lze měnit parametrem algoritmu. Příklad vizualizace lze vidět na obrázku 4.7. Obrázek 4.7: Ukázka výstupu třetího kroku algoritmu pro detekci kapes v molekulách proteinů. Na obrázku jsou vidět detekované kapsy, jejichž prázdný prostor je vyplněný koulemi červené barvy. 4.4 Implementace algoritmu Algoritmus, stejně jako aplikace CAVER Analyst, je implementován v programovacím jazyce Java a je přímo zakomponován do programu. Samotná implementace je rozdělena do tří kroků odpovídajících výše popsanému algoritmu 4.3. Při vývoji byl kladen důraz na čistotu a malou invazivnost do již stávajícího kódu. Implementace obsahuje jednu datovou strukturu PathNode, která reprezentuje samostatný uzel na cestě Cesta je opět reprezentována prvním uzlem cesty PathNode, který nemá odkaz na předky (atribut parent), ale odkazuje na další uzel cesty (atribut children). Jedná se o spojovaný seznam [21]. Do stávajícího programu byly přidány tři nové komponenty (viz Obrázek 4.8): 1. PathAnalyzingService analyzuje Voroného diagram a vytváří cesty. Odpovídá prvnímu kroku algoritmu PocketFindingAlgorithm v cestách na vstupu vyhledává ty, jež 28
34 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ prochází kapsami a dává je na výstup. Tato komponenta poskytuje funkcionalitu popsanou ve druhém kroku algoritmu PocketVizualizer vizualizuje nalezené kapsy. Poskytuje funkcionalitu popsanou v třetím kroku algoritmu Vstupním bodem celého algoritmu je komponenta grafického rozhraní MoreSitesPoreDetectionTopComponent. Komponenta se ovládá pomocí interakce s uživatelem (např. kliknutím na tlačítko), pomocí ní lze pohodlně zadávat konfigurace a spouštět samotný algoritmus. Obrázek 4.8: Diagram tříd zobrazující strukturu implementace navrženého algoritmu k detekci kapes v molekulach proteinů. Žlutou barvou jsou vyobrazeny třídy již existující v programu CAVER Analyst, zelenou barvou jsou zobrazeny třídy přidané za účelem této diplomové práce. 4.5 Zakomponování algoritmu do aplikace CAVER Analyst Jedním z požadavků v zadání této diplomové práce bylo zakomponování vyvinutého algoritmu do aplikace CAVER Analyst. Úloha spočívá v navázání vstupů algoritmu na grafické prvky (tlačítka pro spuštění, formulář pro úpravu parametrů). Dalším z nutných kroků je grafická interpretace výsledků. 29
35 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ Grafické rozhraní programu CAVER Analyst je strukturováno podle komponent, které mají rozdělené funkce počítání tunelů, interakce se strukturou molekuly atd. Detekce kapes je jednou z takovýchto funkcionalit a zaslouží si vlastní komponentu. Tento krok bude proveden následovně v další verzi programu CAVER Analyst. Prozatím pro vývoj algoritmu k detekci kapes bylo vymezeno místo v komponentě k detekci pórů. Integraci lze vidět na obrázku 4.9. Dalším z prvků přidaných do ovládání je možnost uložení cest do souborů na disk ve formátu CSV [24] pro další zpracování. Například zobrazení grafů šířek cest (viz Obrázek 4.6) pomocí programu GNUPlot [32]. Data se ukládají do pracovního adresáře programu CAVER Analyst do složky pockets. Obrázek 4.9: Ukázka integrace ovládání algoritmu k detekci kapes v molekulách proteinů do programu CAVER Analyst (v hnědém obdélníku). Pomocí grafických prvků lze měnit parametry algoritmu minimální délku kapes (viz 4.3.2) a granularitu výplně pro vizualizaci kapsy (viz 4.3.3). Vizualizace výsledků (detekovaných kapes) se provádí do speciálního renderovaciho okna programu CAVER Analyst určeného k těmto účelům. Možný výstup lze vidět na obrázku 4.7. Obsáhlejší popis, jak vizualizace funguje, se nachází v kapitole
36 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ 4.6 Srovnání s existujícím algoritmem V této části kapitoly je vlastní algoritmus porovnáván s jíž existujícím řešením pro detekci kapes v molekulách proteinů Fpocket Nejdříve je porovnán vizuální výstup a detekované kapsy. Dále je srovnána rychlost a nedostatky obou algoritmů Srovnání výsledků detekce kapes Při hodnocení výsledků je třeba brát v potaz rozdílný přístup k detekci kapes oběma algoritmy. Program Fpocket detekuje kapsy podle shluků α koulí v blízkosti povrchu molekuly a tyto shluky dále filtruje podle typu okolních atomů. Algoritmus vytvořený v rámci této diplomové práce naopak vyhledává všechny prohlubně na povrchu molekuly proteinu, které odpovídají určitým parametrům a nijak je dále nefiltruje. Dalším faktorem je rozdílná vizualizace výsledků. Kapsy detekovány programem Fpocket jsou vizualizovány obarvením okolního povrchu podle výskytu α koulí. Výstup vlastního algoritmu se vizualizuje jako výplň kapes. Z níže uvedených výsledků lze soudit, že způsob použitý v programu CAVER Analyst přesněji znázorňuje lokaci kapsy oproti programu Fpocket. Žádný z algoritmů není schopen detekovat kapsy se 100% přesností. Vlastní algoritmus detekuje i prohlubně bez aktivních míst. Zatímco program Fpocket občas dokáže špatně vyhodnotit shluky α koulí a detekuje kapsy uvnitř molekul nebo naopak ve výběžcích povrchu namísto prohlubní. Za účelem srovnání výsledků byly vybrány čtyři molekuly proteinů s PDB ID: 1ACJ, 1QIF, 1ESA a 2P3B. První dvě molekuly jsou lehčí (molekulární hmotnost okolo u), zbyle dvě jsou těžší (cca u). V příkladech uvedených níže jsou znázorněny velikosti molekul a počet atomů v jednotlivých molekulách. Dále je uveden počet detekovaných kapes jednotlivými algoritmy s odůvodněním těchto výsledků. Na vstupu vlastního algoritmu byl parametr minimální délky kapsy nastaven na hodnotu 7 (počet uzlů na cestě). Příklad 1: molekula 1ACJ Podle PDB databáze je molekula složena z 4107 atomů a její molekulární hmotnost je 60991, 47 u. Z tabulky 4.1 lze vidět, že oba algoritmy detekovaly téměř stejný počet kapes, které se navíc překrývají (viz Obrázek 4.10). Lze tedy soudit, že 31
37 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ detekce proběhla správně. Použitý algoritmus CAVER Analyst Fpocket Počet detekovaných kapes Tabulka 4.1: Počet detekovaných kapes programy CAVER Analyst a Fpocket na molekule 1ACJ. Obrázek 4.10: Ukázka detekovaných kapes na molekule 1ACJ. Oranžovými skvrnami na povrchu jsou zobrazeny kapsy detekovány programem Fpocket. Červeně pak kapsy detekovány vlastním algoritmem. Příklad 2: molekula 1QIF Podle PDB databáze molekula je složena z 4247 atomů a její molekulární hmotnost je 60737, 20 u. Podobně jako v prvním případě algoritmy detekovaly podobný počet kapes (viz Tabulka 4.2). V tomto případě je však počet kapes detekovaný programem Fpocket větší. Je to dáno tím, že program detekoval některé kapsy špatně, uvnitř molekuly. Většina detekovaných kapes oběma algo- 32
38 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ ritmy, nacházejících se skutečně na povrchu proteinu, se opět překrývá (viz Obrázek 4.11). Použitý algoritmus CAVER Analyst Fpocket Počet detekovaných kapes Tabulka 4.2: Počet detekovaných kapes programy CAVER Analyst a Fpocket na molekule 1QIF. Obrázek 4.11: Ukázka detekovaných kapes na molekule 1QIF. Oranžovými skvrnami na povrchu jsou zobrazeny kapsy detekovány programem Fpocket. Červeně pak kapsy detekovány vlastním algoritmem. Příklad 3: molekula 1ESA Podle PDB databáze molekula je složena z 1832 atomů a její molekulární hmotnost je 26160, 40 u. V tomto případě se analýza počtu detekovaných kapes (viz Tabulka 4.3) a vizuálního výstupu (viz Obrázek 4.12) téměř neliší od předchozí molekuly. 33
39 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ Použitý algoritmus CAVER Analyst Fpocket Počet detekovaných kapes 9 10 Tabulka 4.3: Počet detekovaných kapes programy CAVER Analyst a Fpocket na molekule 1ESA. Obrázek 4.12: Ukázka detekovaných kapes na molekule 1ESA. Oranžovými skvrnami na povrchu jsou zobrazeny kapsy detekovány programem Fpocket. Červeně pak kapsy detekovány vlastním algoritmem. Příklad 4: molekula 2P3B Podle PDB databáze molekula je složena z 1602 atomů a její molekulární hmotnost je 22594, 99 u. V poslední analyzované molekule je velký rozdíl v počtu detekovaných kapes oběma algoritmy (viz Tabulka 4.4). Tyto výsledky ovlivňují dva faktory. Prvním faktorem je skutečnost, že kapsy detekovány programem Fpo- 34
40 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ cket jsou velmi rozsáhlé a zasahují najednou do několika prohlubní (viz Obrázek 4.13). Zatímco kapsy detekovány vlastním algoritmem jsou lokalizovány do jednotlivých prohlubní. Druhým faktorem je neschopnost vlastního algoritmu filtrovat kapsy podle typu okolních atomů. Obrázek 4.13: Ukázka detekovaných kapes na molekule 2P3B. Oranžovými skvrnami na povrchu jsou zobrazeny kapsy detekovány programem Fpocket. Červeně pak kapsy detekovány vlastním algoritmem. Použitý algoritmus CAVER Analyst Fpocket Počet detekovaných kapes 17 5 Tabulka 4.4: Počet detekovaných kapes programy CAVER Analyst a Fpocket na molekule 2P3B. Z výše uvedených výsledků lze soudit, že vlastní algoritmus je schopen detekovat většinu kapes podobně jako program Fpocket a je tedy úspěšný. Navíc kapsy detekované vlastním algoritmem jsou lépe lokalizovatelné na vizuálním výstupu. 35
41 4. VLASTNÍ ŘEŠENÍ DETEKCE KAPES V MOLEKULÁCH PROTEINŮ Srovnání rychlosti Táto část kapitoly se zabývá srovnáním rychlosti detekce kapes obou algoritmů. Měření rychlostí je provedeno na stejném vzorku molekul jako při porovnávání výsledků (sekce 4.6.1). Oba algoritmy jsou testovány na počítači s procesorem Intel Core i5 (3 GHz) a 8 GB operační paměti. U vlastního algoritmu je měřená rychlost jeho jednotlivých částí (sestavení cest, detekce kapsy a vizualizace). Zatímco u programu Fpocket je měřen celkový čas a to pomocí příkazu time v linuxové konzoli. Výsledky měření jsou uvedeny v tabulce 4.5. CAVER Analyst Fpocket 1ACJ (4.2 p f v) 4.2 s 2.5 s 1QIF (6.4 p f v) 6.4 s 3.1 s 1ESA (1.1 p f v) 0.9 s 0.8 s 2P3B (0.8 p f v) 0.8 s 0.7 s Tabulka 4.5: Měření rychlosti detekce kapes (v sekundách) v molekulách proteinu programy CAVER Analyst a Fpocket. Čas detekce vlastního algoritmu je rozdělen na jednotlivé části: p sestavení cest, f detekce kapes, v vizualizace. Z výše uvedených výsledků lze vidět, že program Fpocket je rychlejší, než vlastní algoritmus. Zejména pak na větších molekulách. Je nutno ovšem podotknout, že vlastní algoritmus byl implementován intuitivně bez ohledu na výkon. Zrychlení by se dalo vyřešit optimalizováním procesu vytváření cest (např. paralelizací). 36
42 Kapitola 5 Závěr Táto práce poskytuje lehký úvod do problematiky zkoumání molekul proteinů a hledání aktivního místa. Popisuje různé typy struktur a útvarů v proteinech a přináší přehled existujících přístupů k detekci kapes v molekulách proteinů. Dále představuje vlastní řešení detekce kapes v molekulách proteinů za pomocí Voroného diagramu a vysvětluje implementaci řešení do programu CAVER Analyst. Na konci jsou prezentovány výsledky práce a srovnání s jiným úspěšným řešením. 5.1 Plány do budoucna Zde jsou uvedeny nápady pro budoucí práci a zlepšení vlastního algoritmu: Nastavení parametrů algoritmu podle typu molekul v současné verzi je většina parametrů (např. poloměr koule pro vytvoření povrchu) algoritmu zabudována do kódu, nebo manuálně nastavitelná pomocí uživatelského rozhraní aplikace CAVER Analyst. Do budoucna by bylo dobré prozkoumat rozsáhlou databázi již detekovaných kapes u různých typů molekul proteinů a sestavit ideální parametry pro tyto typy molekul. Zkoumání biochemických vlastností v současné době algoritmus vyhledává jakékoliv prohlubně na povrchu proteinových molekul. Dalším krokem by mohla být biochemická analýza okolí struktur nalezených kapes, což pomůže více zpřesnit výsledky. Optimalizace výkonu naměřené výsledky rychlosti detekce kapes (sekce 4.6.2) ukázaly náročnost vlastního algoritmu na výpočetní čas, kterou však lze dále optimalizovat. 37
43 Bibliografie [1] Okabe A, Boots B a Sugihara K. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. In: New York: Wiley, 1992, s [2] Kozlikova B et al. CAVER Analyst 1.0: graphic tool for interactive visualization and analysis of tunnels and channels in protein structures. In: Bioinformatics 30 (2014), s [3] Lee B a Richards FM. The interpretation of protein structures: estimation of static accessibility. In: Journal of Molecular Biology 55 (1971), s [4] John A. Capra et al. Predicting Protein Ligand Binding Sites by Combining Evolutionary Sequence Conservation and 3D Structure. In: BMC Bioinformatics 5(12) (2009). [5] Oracle Corporation. The NetBeans Platform. URL: org/features/platform/ (cit ). [6] Levitt DG a Banaszak LJ. POCKET: A computer graphics method for identifying and displaying protein cavities and their sur-rounding amino acids. In: J Mol Graph 10 (1992), s [7] Joe Dundas et al. CASTp: computed atas of surface topography of proteins with structural and topographical mapping of functionally annotated residues. In: Nucl. Acids Res. 34 (2006), W116 W118. [8] H. Edelsbrunner, D. G. Kirkpatrick a R. Seidel. On the shape of a set of points in the plane. In: IEEE Trans. Inform. Theory IT29 (1983), s [9] F.C.Bernstein et al. The Protein Data Bank: A Computer-based Archival File For Macromolecular Structures. In: J. of. Mol. Biol. 112 (1977), s [10] Richards FM. Areas, volumes, packing and protein structure. In: Annu Rev Biophys Bioeng 1977 (1977), s
Geometrické algoritmy pro počítačovou grafiku
 České vysoké učení technické v Praze Fakulta jaderná a fyzikálně inženýrská Katedra fyzikální elektroniky Informatická fyzika Geometrické algoritmy pro počítačovou grafiku Semestrální práce Autor práce:
České vysoké učení technické v Praze Fakulta jaderná a fyzikálně inženýrská Katedra fyzikální elektroniky Informatická fyzika Geometrické algoritmy pro počítačovou grafiku Semestrální práce Autor práce:
Voronoiův diagram. RNDr. Petra Surynková, Ph.D. Univerzita Karlova v Praze Matematicko-fyzikální fakulta
 12 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info Definice V( P) nad množinou bodů P { p v rovině 1,
12 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info Definice V( P) nad množinou bodů P { p v rovině 1,
TÉMATICKÝ OKRUH Softwarové inženýrství
 TÉMATICKÝ OKRUH Softwarové inženýrství Číslo otázky : 24. Otázka : Implementační fáze. Postupy při specifikaci organizace softwarových komponent pomocí UML. Mapování modelů na struktury programovacího
TÉMATICKÝ OKRUH Softwarové inženýrství Číslo otázky : 24. Otázka : Implementační fáze. Postupy při specifikaci organizace softwarových komponent pomocí UML. Mapování modelů na struktury programovacího
9. přednáška z předmětu GIS1 Digitální model reliéfu a odvozené povrchy. Vyučující: Ing. Jan Pacina, Ph.D.
 9. přednáška z předmětu GIS1 Digitální model reliéfu a odvozené povrchy Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Lehký úvod Digitální modely terénu jsou dnes v geoinformačních systémech
9. přednáška z předmětu GIS1 Digitální model reliéfu a odvozené povrchy Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Lehký úvod Digitální modely terénu jsou dnes v geoinformačních systémech
Algoritmizace prostorových úloh
 Algoritmizace prostorových úloh Vektorová data Daniela Szturcová Prostorová data Geoobjekt entita definovaná v prostoru. Znalost jeho identifikace, lokalizace umístění v prostoru, vlastností vlastních
Algoritmizace prostorových úloh Vektorová data Daniela Szturcová Prostorová data Geoobjekt entita definovaná v prostoru. Znalost jeho identifikace, lokalizace umístění v prostoru, vlastností vlastních
P ro te i n o vé d a ta b á ze
 Proteinové databáze Osnova Základní stavební jednotky proteinů Hierarchie proteinové struktury Stanovení proteinové struktury Důležitost proteinové struktury Proteinové strukturní databáze Proteinové klasifikační
Proteinové databáze Osnova Základní stavební jednotky proteinů Hierarchie proteinové struktury Stanovení proteinové struktury Důležitost proteinové struktury Proteinové strukturní databáze Proteinové klasifikační
MBI - technologická realizace modelu
 MBI - technologická realizace modelu 22.1.2015 MBI, Management byznys informatiky Snímek 1 Agenda Technická realizace portálu MBI. Cíle a principy technického řešení. 1.Obsah portálu - objekty v hierarchiích,
MBI - technologická realizace modelu 22.1.2015 MBI, Management byznys informatiky Snímek 1 Agenda Technická realizace portálu MBI. Cíle a principy technického řešení. 1.Obsah portálu - objekty v hierarchiích,
13 Barvy a úpravy rastrového
 13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
Zpráva o zhotoveném plnění
 Zpráva o zhotoveném plnění Aplikace byla vytvořena v souladu se Smlouvou a na základě průběžných konzultací s pověřenými pracovníky referátu Manuscriptorium. Toto je zpráva o zhotoveném plnění. Autor:
Zpráva o zhotoveném plnění Aplikace byla vytvořena v souladu se Smlouvou a na základě průběžných konzultací s pověřenými pracovníky referátu Manuscriptorium. Toto je zpráva o zhotoveném plnění. Autor:
Základy informatiky. Teorie grafů. Zpracoval: Pavel Děrgel Úprava: Daniela Szturcová
 Základy informatiky Teorie grafů Zpracoval: Pavel Děrgel Úprava: Daniela Szturcová Obsah přednášky Barvení mapy Teorie grafů Definice Uzly a hrany Typy grafů Cesty, cykly, souvislost grafů Barvení mapy
Základy informatiky Teorie grafů Zpracoval: Pavel Děrgel Úprava: Daniela Szturcová Obsah přednášky Barvení mapy Teorie grafů Definice Uzly a hrany Typy grafů Cesty, cykly, souvislost grafů Barvení mapy
Programátorská dokumentace
 Programátorská dokumentace Požadavky Cílem tohoto programu bylo představit barevné systémy, zejména převody mezi nejpoužívanějšími z nich. Zároveň bylo úkolem naprogramovat jejich demonstraci. Pro realizaci
Programátorská dokumentace Požadavky Cílem tohoto programu bylo představit barevné systémy, zejména převody mezi nejpoužívanějšími z nich. Zároveň bylo úkolem naprogramovat jejich demonstraci. Pro realizaci
xrays optimalizační nástroj
 xrays optimalizační nástroj Optimalizační nástroj xoptimizer je součástí webového spedičního systému a využívá mnoho z jeho stavebních bloků. xoptimizer lze nicméně provozovat i samostatně. Cílem tohoto
xrays optimalizační nástroj Optimalizační nástroj xoptimizer je součástí webového spedičního systému a využívá mnoho z jeho stavebních bloků. xoptimizer lze nicméně provozovat i samostatně. Cílem tohoto
Triangulace. Význam triangulace. trojúhelník je základní grafický element aproximace ploch předzpracování pro jiné algoritmy. příklad triangulace
 Význam triangulace trojúhelník je základní grafický element aproximace ploch předzpracování pro jiné algoritmy příklad triangulace Definice Triangulace nad množinou bodů v rovině představuje takové planární
Význam triangulace trojúhelník je základní grafický element aproximace ploch předzpracování pro jiné algoritmy příklad triangulace Definice Triangulace nad množinou bodů v rovině představuje takové planární
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
Typy molekul, látek a jejich vazeb v organismech
 Typy molekul, látek a jejich vazeb v organismech Typy molekul, látek a jejich vazeb v organismech Organismy se skládají z molekul rozličných látek Jednotlivé látky si organismus vytváří sám z jiných látek,
Typy molekul, látek a jejich vazeb v organismech Typy molekul, látek a jejich vazeb v organismech Organismy se skládají z molekul rozličných látek Jednotlivé látky si organismus vytváří sám z jiných látek,
2. přednáška z předmětu GIS1 Data a datové modely
 2. přednáška z předmětu GIS1 Data a datové modely Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky z www.gis.zcu.cz Předmět KMA/UGI, autor Ing. K.
2. přednáška z předmětu GIS1 Data a datové modely Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky z www.gis.zcu.cz Předmět KMA/UGI, autor Ing. K.
2. úkol MI-PAA. Jan Jůna (junajan) 3.11.2013
 2. úkol MI-PAA Jan Jůna (junajan) 3.11.2013 Specifikaci úlohy Problém batohu je jedním z nejjednodušších NP-těžkých problémů. V literatuře najdeme množství jeho variant, které mají obecně různé nároky
2. úkol MI-PAA Jan Jůna (junajan) 3.11.2013 Specifikaci úlohy Problém batohu je jedním z nejjednodušších NP-těžkých problémů. V literatuře najdeme množství jeho variant, které mají obecně různé nároky
Manuál k programu IDP 1.0
 Příloha B Manuál k programu IDP 1.0 Toto je manuál k programu IDP - Interakční diagram průřezu 1.0, který byl vytvořen v rámci této diplomové práce za podpory grantu Studentské grantové soutěže ČVUT v
Příloha B Manuál k programu IDP 1.0 Toto je manuál k programu IDP - Interakční diagram průřezu 1.0, který byl vytvořen v rámci této diplomové práce za podpory grantu Studentské grantové soutěže ČVUT v
Pohled do nitra mikroprocesoru Josef Horálek
 Pohled do nitra mikroprocesoru Josef Horálek Z čeho vycházíme = Vycházíme z Von Neumannovy architektury = Celý počítač se tak skládá z pěti koncepčních bloků: = Operační paměť = Programový řadič = Aritmeticko-logická
Pohled do nitra mikroprocesoru Josef Horálek Z čeho vycházíme = Vycházíme z Von Neumannovy architektury = Celý počítač se tak skládá z pěti koncepčních bloků: = Operační paměť = Programový řadič = Aritmeticko-logická
Využití metod strojového učení v bioinformatice David Hoksza
 Využití metod strojového učení v bioinformatice David Hoksza SIRET Research Group Katedra softwarového inženýrství, Matematicko-fyzikální fakulta Karlova Univerzita v Praze Bioinformatika Biologické inspirace
Využití metod strojového učení v bioinformatice David Hoksza SIRET Research Group Katedra softwarového inženýrství, Matematicko-fyzikální fakulta Karlova Univerzita v Praze Bioinformatika Biologické inspirace
Hemoglobin a jemu podobní... Studijní materiál. Jan Komárek
 Hemoglobin a jemu podobní... Studijní materiál Jan Komárek Bioinformatika Bioinformatika je vědní disciplína, která se zabývá metodami pro shromážďování, analýzu a vizualizaci rozsáhlých souborů biologických
Hemoglobin a jemu podobní... Studijní materiál Jan Komárek Bioinformatika Bioinformatika je vědní disciplína, která se zabývá metodami pro shromážďování, analýzu a vizualizaci rozsáhlých souborů biologických
Meo S-H: software pro kompletní diagnostiku intenzity a vlnoplochy
 Centrum Digitální Optiky Meo S-H: software pro kompletní diagnostiku intenzity a vlnoplochy Výzkumná zpráva projektu Identifikační čí slo výstupu: TE01020229DV003 Pracovní balíček: Zpracování dat S-H senzoru
Centrum Digitální Optiky Meo S-H: software pro kompletní diagnostiku intenzity a vlnoplochy Výzkumná zpráva projektu Identifikační čí slo výstupu: TE01020229DV003 Pracovní balíček: Zpracování dat S-H senzoru
1. Dědičnost a polymorfismus
 1. Dědičnost a polymorfismus Cíl látky Cílem této kapitoly je představit klíčové pojmy dědičnosti a polymorfismu. Předtím však je nutné se seznámit se základními pojmy zobecnění neboli generalizace. Komentář
1. Dědičnost a polymorfismus Cíl látky Cílem této kapitoly je představit klíčové pojmy dědičnosti a polymorfismu. Předtím však je nutné se seznámit se základními pojmy zobecnění neboli generalizace. Komentář
Sítě SFN Systém pro analýzu a vizualizaci pokrytí a rušení vysílacích sítí
 Sítě SFN Systém pro analýzu a vizualizaci pokrytí a rušení vysílacích sítí Sítě SFN ver. 7 je výpočetní systém pro analýzu pokrytí a rušení vysílacích sítí pro služby FM, TV, DVB- T a T-DAB a analýzu a
Sítě SFN Systém pro analýzu a vizualizaci pokrytí a rušení vysílacích sítí Sítě SFN ver. 7 je výpočetní systém pro analýzu pokrytí a rušení vysílacích sítí pro služby FM, TV, DVB- T a T-DAB a analýzu a
Kontingenční tabulky v MS Excel 2010
 Kontingenční tabulky v MS Excel 2010 Autor: RNDr. Milan Myšák e-mail: milan.mysak@konero.cz Obsah 1 Vytvoření KT... 3 1.1 Data pro KT... 3 1.2 Tvorba KT... 3 2 Tvorba KT z dalších zdrojů dat... 5 2.1 Data
Kontingenční tabulky v MS Excel 2010 Autor: RNDr. Milan Myšák e-mail: milan.mysak@konero.cz Obsah 1 Vytvoření KT... 3 1.1 Data pro KT... 3 1.2 Tvorba KT... 3 2 Tvorba KT z dalších zdrojů dat... 5 2.1 Data
Experimentální systém pro WEB IR
 Experimentální systém pro WEB IR Jiří Vraný Školitel: Doc. RNDr. Pavel Satrapa PhD. Problematika disertační práce velmi stručný úvod WEB IR information retrieval from WWW, vyhledávání na webu Vzhledem
Experimentální systém pro WEB IR Jiří Vraný Školitel: Doc. RNDr. Pavel Satrapa PhD. Problematika disertační práce velmi stručný úvod WEB IR information retrieval from WWW, vyhledávání na webu Vzhledem
Tabulkový procesor. Základní rysy
 Tabulkový procesor Tabulkový procesor je počítačový program zpracovávající data uložená v buňkách tabulky. Program umožňuje použití vzorců pro práci s daty a zobrazuje výsledné hodnoty podle vstupních
Tabulkový procesor Tabulkový procesor je počítačový program zpracovávající data uložená v buňkách tabulky. Program umožňuje použití vzorců pro práci s daty a zobrazuje výsledné hodnoty podle vstupních
Využití tabulkového procesoru MS Excel
 Semestrální práce Licenční studium Galileo srpen, 2015 Využití tabulkového procesoru MS Excel Ing Marek Bilko Třinecké železárny, a.s. Stránka 1 z 10 OBSAH 1. ÚVOD... 2 2. DATOVÝ SOUBOR... 2 3. APLIKACE...
Semestrální práce Licenční studium Galileo srpen, 2015 Využití tabulkového procesoru MS Excel Ing Marek Bilko Třinecké železárny, a.s. Stránka 1 z 10 OBSAH 1. ÚVOD... 2 2. DATOVÝ SOUBOR... 2 3. APLIKACE...
Automatická detekce anomálií při geofyzikálním průzkumu. Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011
 Automatická detekce anomálií při geofyzikálním průzkumu Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011 Cíle doktorandské práce Seminář 10. 11. 2010 Najít, implementovat, ověřit a do praxe
Automatická detekce anomálií při geofyzikálním průzkumu Lenka Kosková Třísková NTI TUL Doktorandský seminář, 8. 6. 2011 Cíle doktorandské práce Seminář 10. 11. 2010 Najít, implementovat, ověřit a do praxe
Grafy. RNDr. Petra Surynková, Ph.D. Univerzita Karlova v Praze Matematicko-fyzikální fakulta.
 6 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info množina vrcholů a množina hran hrana vždy spojuje
6 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info množina vrcholů a množina hran hrana vždy spojuje
Buněčné automaty a mřížkové buněčné automaty pro plyny. Larysa Ocheretna
 Buněčné automaty a mřížkové buněčné automaty pro plyny Larysa Ocheretna Obsah Buněčný automat: princip modelu, vymezení pojmů Mřížkový buněčný automat pro plyny Příklady aplikace principů mřížkových buněčných
Buněčné automaty a mřížkové buněčné automaty pro plyny Larysa Ocheretna Obsah Buněčný automat: princip modelu, vymezení pojmů Mřížkový buněčný automat pro plyny Příklady aplikace principů mřížkových buněčných
Novinky ve FlowMon 6.x/FlowMon ADS 6.x
 Novinky ve FlowMon 6.x/FlowMon ADS 6.x FlowMon je kompletní řešení pro monitorování a bezpečnost počítačových sítí, které je založeno na technologii sledování IP toků (NetFlow/IPFIX/sFlow) a analýze chování
Novinky ve FlowMon 6.x/FlowMon ADS 6.x FlowMon je kompletní řešení pro monitorování a bezpečnost počítačových sítí, které je založeno na technologii sledování IP toků (NetFlow/IPFIX/sFlow) a analýze chování
3. úloha - problém batohu metodami branch & bound, dynamické programování, heuristika s testem
 ČVUT FEL X36PAA - Problémy a algoritmy 3. úloha - problém batohu metodami branch & bound, dynamické programování, heuristika s testem Jméno: Marek Handl Datum: 1. 1. 2009 Cvičení: Pondělí 9:00 Zadání Naprogramujte
ČVUT FEL X36PAA - Problémy a algoritmy 3. úloha - problém batohu metodami branch & bound, dynamické programování, heuristika s testem Jméno: Marek Handl Datum: 1. 1. 2009 Cvičení: Pondělí 9:00 Zadání Naprogramujte
Uživatelská příručka. 06/2018 Technické změny vyhrazeny.
 Uživatelská příručka 1 OBSAH 1 ÚVOD... 3 1.1 Merbon SCADA... 3 1.1.1 K čemu program slouží...3 2 Přihlášení a odhlášení z programu... 4 3 Projekty... 5 3.1 Výběr zobrazení... 5 3.2 Schémata... 6 3.3 Grafy...
Uživatelská příručka 1 OBSAH 1 ÚVOD... 3 1.1 Merbon SCADA... 3 1.1.1 K čemu program slouží...3 2 Přihlášení a odhlášení z programu... 4 3 Projekty... 5 3.1 Výběr zobrazení... 5 3.2 Schémata... 6 3.3 Grafy...
Algoritmy pro shlukování prostorových dat
 Algoritmy pro shlukování prostorových dat Marta Žambochová Katedra matematiky a informatiky Fakulta sociálně ekonomická Univerzita J. E. Purkyně v Ústí nad Labem ROBUST 21. 26. leden 2018 Rybník - Hostouň
Algoritmy pro shlukování prostorových dat Marta Žambochová Katedra matematiky a informatiky Fakulta sociálně ekonomická Univerzita J. E. Purkyně v Ústí nad Labem ROBUST 21. 26. leden 2018 Rybník - Hostouň
Zápočtová úloha z předmětu KIV/ZSWI DOKUMENT SPECIFIKACE POŽADAVKŮ
 Zápočtová úloha z předmětu KIV/ZSWI DOKUMENT SPECIFIKACE POŽADAVKŮ 10. 5. 2011 Tým: Simplesoft Členové: Zdeněk Malík Jan Rada Ladislav Račák Václav Král Marta Pechová malikz@students.zcu.cz jrada1@students.zcu.cz
Zápočtová úloha z předmětu KIV/ZSWI DOKUMENT SPECIFIKACE POŽADAVKŮ 10. 5. 2011 Tým: Simplesoft Členové: Zdeněk Malík Jan Rada Ladislav Račák Václav Král Marta Pechová malikz@students.zcu.cz jrada1@students.zcu.cz
Vzdálenost uzlů v neorientovaném grafu
 Vzdálenosti a grafy Vzdálenost uzlů v neorientovaném grafu Je dán neorientovaný neohodnocený graf G = (V,E,I) vzdálenost uzlů u a v v neorientovaném souvislém grafu G je délka nejkratší cesty spojující
Vzdálenosti a grafy Vzdálenost uzlů v neorientovaném grafu Je dán neorientovaný neohodnocený graf G = (V,E,I) vzdálenost uzlů u a v v neorientovaném souvislém grafu G je délka nejkratší cesty spojující
Reranking založený na metadatech
 České vysoké učení technické v Praze Fakulta informačních technologií Katedra softwarového inženýrství Reranking založený na metadatech MI-VMW Projekt IV - 1 Pavel Homolka Ladislav Kubeš 6. 12. 2011 1
České vysoké učení technické v Praze Fakulta informačních technologií Katedra softwarového inženýrství Reranking založený na metadatech MI-VMW Projekt IV - 1 Pavel Homolka Ladislav Kubeš 6. 12. 2011 1
ÚLOHY S POLYGONEM. Polygon řetězec úseček, poslední bod je totožný s prvním. 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU
 ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
ÚLOHY S POLYGONEM Polygon řetězec úseček, poslední bod je totožný s prvním 6 bodů: X1, Y1 až X6,Y6 Y1=X6, Y1=Y6 STANOVENÍ PLOCHY JEDNOHO POLYGONU 3 úsečky (segmenty) v horní části 2 úsečky ve spodní části
9 Prostorová grafika a modelování těles
 9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
8. přednáška z předmětu GIS1 Rastrový datový model a mapová algebra
 8. přednáška z předmětu GIS1 Rastrový datový model a mapová algebra Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky z www.gis.zcu.cz Předmět KMA/UGI,
8. přednáška z předmětu GIS1 Rastrový datový model a mapová algebra Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Pro přednášku byly použity texty a obrázky z www.gis.zcu.cz Předmět KMA/UGI,
Genomické databáze. Shlukování proteinových sekvencí. Ivana Rudolfová. školitel: doc. Ing. Jaroslav Zendulka, CSc.
 Genomické databáze Shlukování proteinových sekvencí Ivana Rudolfová školitel: doc. Ing. Jaroslav Zendulka, CSc. Obsah Proteiny Zdroje dat Predikce struktury proteinů Cíle disertační práce Vstupní data
Genomické databáze Shlukování proteinových sekvencí Ivana Rudolfová školitel: doc. Ing. Jaroslav Zendulka, CSc. Obsah Proteiny Zdroje dat Predikce struktury proteinů Cíle disertační práce Vstupní data
Jádrem systému je modul GSFrameWork, který je poskytovatelem zejména těchto služeb:
 Technologie Marushka Základním konceptem technologie Marushka je použití jádra, které poskytuje přístup a jednotnou grafickou prezentaci geografických dat. Jádro je vyvíjeno na komponentním objektovém
Technologie Marushka Základním konceptem technologie Marushka je použití jádra, které poskytuje přístup a jednotnou grafickou prezentaci geografických dat. Jádro je vyvíjeno na komponentním objektovém
Grafy. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 13.
 Grafy doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Grafy 104 / 309 Osnova přednášky Grafy
Grafy doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 13. března 2017 Jiří Dvorský (VŠB TUO) Grafy 104 / 309 Osnova přednášky Grafy
Rozvoj tepla v betonových konstrukcích
 Úvod do problematiky K novinkám v požární odolnosti nosných konstrukcí Praha, 11. září 2012 Ing. Radek Štefan prof. Ing. Jaroslav Procházka, CSc. Znalost rozložení teploty v betonové konstrukci nebo její
Úvod do problematiky K novinkám v požární odolnosti nosných konstrukcí Praha, 11. září 2012 Ing. Radek Štefan prof. Ing. Jaroslav Procházka, CSc. Znalost rozložení teploty v betonové konstrukci nebo její
12 Metody snižování barevného prostoru
 12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
Zobrazování těles. problematika geometrického modelování. základní typy modelů. datové reprezentace modelů základní metody geometrického modelování
 problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
Jana Dannhoferová Ústav informatiky, PEF MZLU
 Počítačová grafika 1. Definice oblasti souvisí: a) s definováním množiny všech bodů, které náleží do hranice a zároveň do jejího vnitřku b) s popisem její hranice c) s definováním množiny všech bodů, které
Počítačová grafika 1. Definice oblasti souvisí: a) s definováním množiny všech bodů, které náleží do hranice a zároveň do jejího vnitřku b) s popisem její hranice c) s definováním množiny všech bodů, které
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA
 INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Vektorová data Michal Kačmařík, Daniela
INOVACE BAKALÁŘSKÝCH A MAGISTERSKÝCH STUDIJNÍCH OBORŮ NA HORNICKO-GEOLOGICKÉ FAKULTĚ VYSOKÉ ŠKOLY BÁŇSKÉ - TECHNICKÉ UNIVERZITY OSTRAVA Algoritmizace prostorových úloh Vektorová data Michal Kačmařík, Daniela
Reliance 3 design OBSAH
 Reliance 3 design Obsah OBSAH 1. První kroky... 3 1.1 Úvod... 3 1.2 Založení nového projektu... 4 1.3 Tvorba projektu... 6 1.3.1 Správce stanic definice stanic, proměnných, stavových hlášení a komunikačních
Reliance 3 design Obsah OBSAH 1. První kroky... 3 1.1 Úvod... 3 1.2 Založení nového projektu... 4 1.3 Tvorba projektu... 6 1.3.1 Správce stanic definice stanic, proměnných, stavových hlášení a komunikačních
Algoritmy výpočetní geometrie
 Algoritmy výpočetní geometrie prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Algoritmy výpočetní geometrie prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Metodika analýzy. Příloha č. 1
 Metodika analýzy Příloha č. 1 Příloha č. 1 1 Účel dokumentu Dokument popisuje závaznou metodiku systémové analýzy, je upraven na míru pro prostředí Podniku. Dokument je provázán s Podnikovou analýzou,
Metodika analýzy Příloha č. 1 Příloha č. 1 1 Účel dokumentu Dokument popisuje závaznou metodiku systémové analýzy, je upraven na míru pro prostředí Podniku. Dokument je provázán s Podnikovou analýzou,
OSTRAVSKÁ UNIVERZITA V OSTRAVĚ PŘÍRODOVĚDECKÁ FAKULTA
 OSTRAVSKÁ UNIVERZITA V OSTRAVĚ PŘÍRODOVĚDECKÁ FAKULTA BAKALÁŘSKÁ PRÁCE 2002 SEDLÁK MARIAN - 1 - OSTRAVSKÁ UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA KATEDRA INFORMATIKY A POČÍTAČŮ Vizualizace principů výpočtu konečného
OSTRAVSKÁ UNIVERZITA V OSTRAVĚ PŘÍRODOVĚDECKÁ FAKULTA BAKALÁŘSKÁ PRÁCE 2002 SEDLÁK MARIAN - 1 - OSTRAVSKÁ UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA KATEDRA INFORMATIKY A POČÍTAČŮ Vizualizace principů výpočtu konečného
Základní pojmy teorie grafů [Graph theory]
![Základní pojmy teorie grafů [Graph theory] Základní pojmy teorie grafů [Graph theory]](/thumbs/25/4817299.jpg) Část I Základní pojmy teorie grafů [Graph theory] V matematice grafem obvykle rozumíme grafické znázornění funkční závislosti. Pro tento předmět je však podstatnější pohled jiný. V teorii grafů rozumíme
Část I Základní pojmy teorie grafů [Graph theory] V matematice grafem obvykle rozumíme grafické znázornění funkční závislosti. Pro tento předmět je však podstatnější pohled jiný. V teorii grafů rozumíme
U Úvod do modelování a simulace systémů
 U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
Dynamicky vázané metody. Pozdní vazba, virtuální metody
 Dynamicky vázané metody Pozdní vazba, virtuální metody Motivace... class TBod protected: float x,y; public: int vrat_pocet_bodu() return 1; ; od třídy TBod odvodíme: class TUsecka: public TBod protected:
Dynamicky vázané metody Pozdní vazba, virtuální metody Motivace... class TBod protected: float x,y; public: int vrat_pocet_bodu() return 1; ; od třídy TBod odvodíme: class TUsecka: public TBod protected:
Záznam dat Úvod Záznam dat zahrnuje tři základní funkce: Záznam dat v prostředí třídy Záznam dat s MINDSTORMS NXT
 Úvod Záznam dat umožňuje sběr, ukládání a analýzu údajů ze senzorů. Záznamem dat monitorujeme události a procesy po dobu práce se senzory připojenými k počítači prostřednictvím zařízení jakým je NXT kostka.
Úvod Záznam dat umožňuje sběr, ukládání a analýzu údajů ze senzorů. Záznamem dat monitorujeme události a procesy po dobu práce se senzory připojenými k počítači prostřednictvím zařízení jakým je NXT kostka.
Studie webů automobilek
 Studie webů automobilek červen 2006 [manažerské shrnutí] Obsah Obsah... 1 Manažerské shrnutí... 2 Kvalita obsahu a použitelnost webu... 3 Základní nedostatky negativně ovlivňují použitelnost většiny webů...
Studie webů automobilek červen 2006 [manažerské shrnutí] Obsah Obsah... 1 Manažerské shrnutí... 2 Kvalita obsahu a použitelnost webu... 3 Základní nedostatky negativně ovlivňují použitelnost většiny webů...
Bioinformatika a výpočetní biologie KFC/BIN. I. Přehled
 Bioinformatika a výpočetní biologie KFC/BIN I. Přehled RNDr. Karel Berka, Ph.D. Univerzita Palackého v Olomouci Definice bioinformatiky (Molecular) bio informatics: bioinformatics is conceptualising biology
Bioinformatika a výpočetní biologie KFC/BIN I. Přehled RNDr. Karel Berka, Ph.D. Univerzita Palackého v Olomouci Definice bioinformatiky (Molecular) bio informatics: bioinformatics is conceptualising biology
5 Orientované grafy, Toky v sítích
 Petr Hliněný, FI MU Brno, 205 / 9 FI: IB000: Toky v sítích 5 Orientované grafy, Toky v sítích Nyní se budeme zabývat typem sít ových úloh, ve kterých není podstatná délka hran a spojení, nýbž jejich propustnost
Petr Hliněný, FI MU Brno, 205 / 9 FI: IB000: Toky v sítích 5 Orientované grafy, Toky v sítích Nyní se budeme zabývat typem sít ových úloh, ve kterých není podstatná délka hran a spojení, nýbž jejich propustnost
Typy geometrie v. Rhinu. Body
 Typy geometrie v 16 Rhinu Rhino rozeznává pět základních typů geometrie: body (points), křivky (curves), plochy (surfaces) a spojené plochy (polysurfaces). Navíc jsou plochy nebo spojené plochy, které
Typy geometrie v 16 Rhinu Rhino rozeznává pět základních typů geometrie: body (points), křivky (curves), plochy (surfaces) a spojené plochy (polysurfaces). Navíc jsou plochy nebo spojené plochy, které
FUNKCE 3. Autor: Mgr. Dana Kaprálová. Datum (období) tvorby: září, říjen 2013. Ročník: sedmý. Vzdělávací oblast: Informatika a výpočetní technika
 FUNKCE 3 Autor: Mgr. Dana Kaprálová Datum (období) tvorby: září, říjen 2013 Ročník: sedmý Vzdělávací oblast: Informatika a výpočetní technika 1 Anotace: Žáci se seznámí se základní obsluhou tabulkového
FUNKCE 3 Autor: Mgr. Dana Kaprálová Datum (období) tvorby: září, říjen 2013 Ročník: sedmý Vzdělávací oblast: Informatika a výpočetní technika 1 Anotace: Žáci se seznámí se základní obsluhou tabulkového
Rastrová reprezentace geoprvků model polí Porovnání rastrové a vektorové reprezentace geoprvků Digitální model terénu GIS 1 153GS01 / 153GIS1
 GIS 1 153GS01 / 153GIS1 Martin Landa Katedra geomatiky ČVUT v Praze, Fakulta stavební 14.11.2013 Copyright c 2013 Martin Landa Permission is granted to copy, distribute and/or modify this document under
GIS 1 153GS01 / 153GIS1 Martin Landa Katedra geomatiky ČVUT v Praze, Fakulta stavební 14.11.2013 Copyright c 2013 Martin Landa Permission is granted to copy, distribute and/or modify this document under
Opakování
 Slabé vazebné interakce Opakování Co je to atom? Opakování Opakování Co je to atom? Atom je nejmenší částice hmoty, chemicky dále nedělitelná. Skládá se z atomového jádra obsahujícího protony a neutrony
Slabé vazebné interakce Opakování Co je to atom? Opakování Opakování Co je to atom? Atom je nejmenší částice hmoty, chemicky dále nedělitelná. Skládá se z atomového jádra obsahujícího protony a neutrony
PRODUKTY. Tovek Tools
 jsou desktopovou aplikací určenou k vyhledávání informací, tvorbě různých typů analýz a vytváření přehledů a rešerší. Jsou vhodné pro práci i s velkým objemem textových dat z různorodých informačních zdrojů.
jsou desktopovou aplikací určenou k vyhledávání informací, tvorbě různých typů analýz a vytváření přehledů a rešerší. Jsou vhodné pro práci i s velkým objemem textových dat z různorodých informačních zdrojů.
Grafové algoritmy. Programovací techniky
 Grafové algoritmy Programovací techniky Grafy Úvod - Terminologie Graf je datová struktura, skládá se z množiny vrcholů V a množiny hran mezi vrcholy E Počet vrcholů a hran musí být konečný a nesmí být
Grafové algoritmy Programovací techniky Grafy Úvod - Terminologie Graf je datová struktura, skládá se z množiny vrcholů V a množiny hran mezi vrcholy E Počet vrcholů a hran musí být konečný a nesmí být
7. Geografické informační systémy.
 7. Geografické informační systémy. 154GEY2 Geodézie 2 7.1 Definice 7.2 Komponenty GIS 7.3 Možnosti GIS 7.4 Datové modely GIS 7.5 Přístup k prostorovým datům 7.6 Topologie 7.7 Vektorové datové modely 7.8
7. Geografické informační systémy. 154GEY2 Geodézie 2 7.1 Definice 7.2 Komponenty GIS 7.3 Možnosti GIS 7.4 Datové modely GIS 7.5 Přístup k prostorovým datům 7.6 Topologie 7.7 Vektorové datové modely 7.8
Novinky v Solid Edge ST7
 Novinky v Solid Edge ST7 Primitiva Nově lze vytvořit základní geometrii pomocí jednoho příkazu Funkce primitiv je dostupná pouze v synchronním prostředí Těleso vytvoříme ve dvou navazujících krocích, kde
Novinky v Solid Edge ST7 Primitiva Nově lze vytvořit základní geometrii pomocí jednoho příkazu Funkce primitiv je dostupná pouze v synchronním prostředí Těleso vytvoříme ve dvou navazujících krocích, kde
FORTANNS. havlicekv@fzp.czu.cz 22. února 2010
 FORTANNS manuál Vojtěch Havlíček havlicekv@fzp.czu.cz 22. února 2010 1 Úvod Program FORTANNS je software určený k modelování časových řad. Kód programu má 1800 řádek a je napsán v programovacím jazyku
FORTANNS manuál Vojtěch Havlíček havlicekv@fzp.czu.cz 22. února 2010 1 Úvod Program FORTANNS je software určený k modelování časových řad. Kód programu má 1800 řádek a je napsán v programovacím jazyku
Architektura počítačů
 Architektura počítačů Studijní materiál pro předmět Architektury počítačů Ing. Petr Olivka katedra informatiky FEI VŠB-TU Ostrava email: petr.olivka@vsb.cz Ostrava, 2010 1 1 Architektura počítačů Pojem
Architektura počítačů Studijní materiál pro předmět Architektury počítačů Ing. Petr Olivka katedra informatiky FEI VŠB-TU Ostrava email: petr.olivka@vsb.cz Ostrava, 2010 1 1 Architektura počítačů Pojem
Vzdělávací obsah vyučovacího předmětu
 V.9.3. Vzdělávací obsah vyučovacího předmětu Vzdělávací oblast: Inormatika a informační a komunikační technologie Vyučovací předmět: Informatika Ročník: 1. ročník + kvinta chápe a používá základní termíny
V.9.3. Vzdělávací obsah vyučovacího předmětu Vzdělávací oblast: Inormatika a informační a komunikační technologie Vyučovací předmět: Informatika Ročník: 1. ročník + kvinta chápe a používá základní termíny
1 Strukturované programování
 Projekt OP VK Inovace studijních oborů zajišťovaných katedrami PřF UHK Registrační číslo: CZ.1.07/2.2.00/28.0118 1 Cíl Seznámení s principy strukturovaného programování, s blokovou strukturou programů,
Projekt OP VK Inovace studijních oborů zajišťovaných katedrami PřF UHK Registrační číslo: CZ.1.07/2.2.00/28.0118 1 Cíl Seznámení s principy strukturovaného programování, s blokovou strukturou programů,
PRODUKTY. Tovek Tools
 Analyst Pack je desktopovou aplikací určenou k vyhledávání informací, tvorbě různých typů analýz a vytváření přehledů a rešerší. Jsou vhodné pro práci i s velkým objemem textových dat z různorodých informačních
Analyst Pack je desktopovou aplikací určenou k vyhledávání informací, tvorbě různých typů analýz a vytváření přehledů a rešerší. Jsou vhodné pro práci i s velkým objemem textových dat z různorodých informačních
Návod na základní používání Helpdesku AGEL
 Návod na základní používání Helpdesku AGEL Úvod Přihlášení Nástěnka Vyhledání a otevření úlohy Otevření úlohy Seznam úloh Vyhledávání úloh Vytvoření nové úlohy Práce s úlohami Editace úlohy Změna stavu
Návod na základní používání Helpdesku AGEL Úvod Přihlášení Nástěnka Vyhledání a otevření úlohy Otevření úlohy Seznam úloh Vyhledávání úloh Vytvoření nové úlohy Práce s úlohami Editace úlohy Změna stavu
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika planimetrie. Mgr. Tomáš Novotný
 Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
PQ-stromy a rozpoznávání intervalových grafů v lineárním čase
 -stromy a rozpoznávání intervalových grafů v lineárním čase ermutace s předepsanými intervaly Označme [n] množinu {1, 2,..., n}. Mějme permutaci π = π 1, π 2,..., π n množiny [n]. Řekneme, že množina S
-stromy a rozpoznávání intervalových grafů v lineárním čase ermutace s předepsanými intervaly Označme [n] množinu {1, 2,..., n}. Mějme permutaci π = π 1, π 2,..., π n množiny [n]. Řekneme, že množina S
Obsah. Zpracoval:
 Zpracoval: houzvjir@fel.cvut.cz 03. Modelem řízený vývoj. Doménový (business), konceptuální (analytický) a logický (návrhový) model. Vize projektu. (A7B36SIN) Obsah Modelem řízený vývoj... 2 Cíl MDD, proč
Zpracoval: houzvjir@fel.cvut.cz 03. Modelem řízený vývoj. Doménový (business), konceptuální (analytický) a logický (návrhový) model. Vize projektu. (A7B36SIN) Obsah Modelem řízený vývoj... 2 Cíl MDD, proč
Matematická morfologie
 / 35 Matematická morfologie Karel Horák Rozvrh přednášky:. Úvod. 2. Dilatace. 3. Eroze. 4. Uzavření. 5. Otevření. 6. Skelet. 7. Tref či miň. 8. Ztenčování. 9. Zesilování..Golayova abeceda. 2 / 35 Matematická
/ 35 Matematická morfologie Karel Horák Rozvrh přednášky:. Úvod. 2. Dilatace. 3. Eroze. 4. Uzavření. 5. Otevření. 6. Skelet. 7. Tref či miň. 8. Ztenčování. 9. Zesilování..Golayova abeceda. 2 / 35 Matematická
Rastrová reprezentace
 Rastrová reprezentace Zaměřuje se na lokalitu jako na celek Používá se pro reprezentaci jevů, které plošně pokrývají celou oblast, případně se i spojitě mění. Používá se i pro rasterizované vektorové vrstvy,
Rastrová reprezentace Zaměřuje se na lokalitu jako na celek Používá se pro reprezentaci jevů, které plošně pokrývají celou oblast, případně se i spojitě mění. Používá se i pro rasterizované vektorové vrstvy,
Ovládání Open Office.org Calc Ukládání dokumentu : Levým tlačítkem myši kliknete v menu na Soubor a pak na Uložit jako.
 Ukládání dokumentu : Levým tlačítkem myši kliknete v menu na Soubor a pak na Uložit jako. Otevře se tabulka, v které si najdete místo adresář, pomocí malé šedočerné šipky (jako na obrázku), do kterého
Ukládání dokumentu : Levým tlačítkem myši kliknete v menu na Soubor a pak na Uložit jako. Otevře se tabulka, v které si najdete místo adresář, pomocí malé šedočerné šipky (jako na obrázku), do kterého
Aplikovaná bioinformatika
 Aplikovaná bioinformatika Číslo aktivity: 2.V Název klíčové aktivity: Na realizaci se podílí: Implementace nových předmětů do daného studijního programu doc. RNDr. Michaela Wimmerová, Ph.D., Mgr. Josef
Aplikovaná bioinformatika Číslo aktivity: 2.V Název klíčové aktivity: Na realizaci se podílí: Implementace nových předmětů do daného studijního programu doc. RNDr. Michaela Wimmerová, Ph.D., Mgr. Josef
Autodesk AutoCAD Civil 3D
 Novinky 2018 Autodesk AutoCAD Civil 3D www.graitec.cz www.cadnet.cz, helpdesk.graitec.cz, www.graitec.com Obsah: 1. Vyřešení překrytí koridorů (motýlkování)... 3 2. Relativní návrhové linie... 4 3. Dynamické
Novinky 2018 Autodesk AutoCAD Civil 3D www.graitec.cz www.cadnet.cz, helpdesk.graitec.cz, www.graitec.com Obsah: 1. Vyřešení překrytí koridorů (motýlkování)... 3 2. Relativní návrhové linie... 4 3. Dynamické
SRSW4IT Inventarizační SW. Prezentace aplikace. Vedoucí DP: ing. Lukáš Macura Autor: Bc. Petr Mrůzek
 Prezentace aplikace Vedoucí DP: ing. Lukáš Macura Autor: Bc. Petr Mrůzek Osnova Úvod Programovací jazyk - PHP Etapy vývoje Funkce aplikace Co SW umí Na čem se pracuje Vize do budoucna Úvod Úvod Inspirováno
Prezentace aplikace Vedoucí DP: ing. Lukáš Macura Autor: Bc. Petr Mrůzek Osnova Úvod Programovací jazyk - PHP Etapy vývoje Funkce aplikace Co SW umí Na čem se pracuje Vize do budoucna Úvod Úvod Inspirováno
Digitální model reliéfu (terénu) a analýzy modelů terénu
 Digitální model reliéfu (terénu) a analýzy modelů terénu Digitální modely terénu jsou dnes v geoinformačních systémech hojně využívány pro různé účely. Naměřená terénní data jsou často zpracována do podoby
Digitální model reliéfu (terénu) a analýzy modelů terénu Digitální modely terénu jsou dnes v geoinformačních systémech hojně využívány pro různé účely. Naměřená terénní data jsou často zpracována do podoby
Počítačová chemie: Laboratoř za monitorem
 T-Report Počítačová chemie: Laboratoř za monitorem Lektorka: Zora Střelcová Vypracovala: Eva Vojáčková Tématem T-Exkurze, kterou jsme absolvovala, byla počítačová/výpočetní chemie. Tento obor stojí na
T-Report Počítačová chemie: Laboratoř za monitorem Lektorka: Zora Střelcová Vypracovala: Eva Vojáčková Tématem T-Exkurze, kterou jsme absolvovala, byla počítačová/výpočetní chemie. Tento obor stojí na
Tvorba kurzu v LMS Moodle
 Tvorba kurzu v LMS Moodle Před počátkem práce na tvorbě základního kurzu znovu připomínám, že pro vytvoření kurzu musí být profil uživatele nastaven administrátorem systému minimálně na hodnotu tvůrce
Tvorba kurzu v LMS Moodle Před počátkem práce na tvorbě základního kurzu znovu připomínám, že pro vytvoření kurzu musí být profil uživatele nastaven administrátorem systému minimálně na hodnotu tvůrce
Dijkstrův algoritmus
 Dijkstrův algoritmus Hledání nejkratší cesty v nezáporně hranově ohodnoceném grafu Necht je dán orientovaný graf G = (V, H) a funkce, která každé hraně h = (u, v) H přiřadí nezáporné reálné číslo označované
Dijkstrův algoritmus Hledání nejkratší cesty v nezáporně hranově ohodnoceném grafu Necht je dán orientovaný graf G = (V, H) a funkce, která každé hraně h = (u, v) H přiřadí nezáporné reálné číslo označované
IS pro podporu BOZP na FIT ČVUT
 IS pro podporu BOZP na FIT ČVUT Závěrečná zpráva pro 2. iteraci 21. dubna 2011 Zadavatel: Ing. Jiří Chludil Řešitelský tým: Jiří Kopecký Jan Kratochvíl Milan Matějček Štefan Pinďák Kristýna Streitová Úvod
IS pro podporu BOZP na FIT ČVUT Závěrečná zpráva pro 2. iteraci 21. dubna 2011 Zadavatel: Ing. Jiří Chludil Řešitelský tým: Jiří Kopecký Jan Kratochvíl Milan Matějček Štefan Pinďák Kristýna Streitová Úvod
Reporting. Ukazatele je možno definovat nad libovolnou tabulkou Helios Orange, která je zapsána v nadstavbě firmy SAPERTA v souboru tabulek:
 Finanční analýza Pojem finanční analýza Finanční analýza umožňuje načítat data podle dimenzí a tyto součty dlouhodobě vyhodnocovat. Pojem finanční analýza není nejpřesnější, protože ukazatele mohou být
Finanční analýza Pojem finanční analýza Finanční analýza umožňuje načítat data podle dimenzí a tyto součty dlouhodobě vyhodnocovat. Pojem finanční analýza není nejpřesnější, protože ukazatele mohou být
PROGRAM RP56 Odvodnění pláně Příručka uživatele Základní verze 2014
 PROGRAM RP56 Odvodnění pláně Příručka uživatele Základní verze 2014 Pragoprojekt a.s. 2014 1 Program RP-56 Program RP-56... 2 Funkce programu a zásady použité při jejich řešení... 2 56-1. Zadávací okno
PROGRAM RP56 Odvodnění pláně Příručka uživatele Základní verze 2014 Pragoprojekt a.s. 2014 1 Program RP-56 Program RP-56... 2 Funkce programu a zásady použité při jejich řešení... 2 56-1. Zadávací okno
Popis funkcí tlačítek jednotlivých modulů programu OGAMA
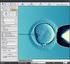 Nevázaná příloha bakalářské práce VYUŽITÍ OPEN-SOURCE NÁSTROJŮ PRO PŘÍPRAVU, PRŮBĚH A VYHODNOCENÍ EYE-TRACKING EXPERIMENTŮ Popis funkcí tlačítek jednotlivých modulů programu OGAMA Michal KUČERA, 2014 Replay
Nevázaná příloha bakalářské práce VYUŽITÍ OPEN-SOURCE NÁSTROJŮ PRO PŘÍPRAVU, PRŮBĚH A VYHODNOCENÍ EYE-TRACKING EXPERIMENTŮ Popis funkcí tlačítek jednotlivých modulů programu OGAMA Michal KUČERA, 2014 Replay
Microsoft Visio 2013 vypadá jinak než ve starších verzích, proto jsme vytvořili tuto příručku, která vám pomůže se s ním rychle seznámit.
 Úvodní příručka Microsoft Visio 2013 vypadá jinak než ve starších verzích, proto jsme vytvořili tuto příručku, která vám pomůže se s ním rychle seznámit. Aktualizované šablony Šablony vám pomáhají při
Úvodní příručka Microsoft Visio 2013 vypadá jinak než ve starších verzích, proto jsme vytvořili tuto příručku, která vám pomůže se s ním rychle seznámit. Aktualizované šablony Šablony vám pomáhají při
Základy informatiky. 07 Teorie grafů. Kačmařík/Szturcová/Děrgel/Rapant
 Základy informatiky 07 Teorie grafů Kačmařík/Szturcová/Děrgel/Rapant Obsah přednášky barvení mapy teorie grafů definice uzly a hrany typy grafů cesty, cykly, souvislost grafů Barvení mapy Kolik barev je
Základy informatiky 07 Teorie grafů Kačmařík/Szturcová/Děrgel/Rapant Obsah přednášky barvení mapy teorie grafů definice uzly a hrany typy grafů cesty, cykly, souvislost grafů Barvení mapy Kolik barev je
Operační výzkum. Síťová analýza. Metoda CPM.
 Operační výzkum Síťová analýza. Metoda CPM. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo
Operační výzkum Síťová analýza. Metoda CPM. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo
BALISTICKÝ MĚŘICÍ SYSTÉM
 BALISTICKÝ MĚŘICÍ SYSTÉM UŽIVATELSKÁ PŘÍRUČKA Verze 2.3 2007 OBSAH 1. ÚVOD... 5 2. HLAVNÍ OKNO... 6 3. MENU... 7 3.1 Soubor... 7 3.2 Měření...11 3.3 Zařízení...16 3.4 Graf...17 3.5 Pohled...17 1. ÚVOD
BALISTICKÝ MĚŘICÍ SYSTÉM UŽIVATELSKÁ PŘÍRUČKA Verze 2.3 2007 OBSAH 1. ÚVOD... 5 2. HLAVNÍ OKNO... 6 3. MENU... 7 3.1 Soubor... 7 3.2 Měření...11 3.3 Zařízení...16 3.4 Graf...17 3.5 Pohled...17 1. ÚVOD
Specializovaná mapa s odborným obsahem
 Program bezpečnostního výzkumu České republiky na léta 2016-2021 Specializovaná mapa s odborným obsahem VH 20162017003 Vliv reklamních zařízení na bezpečnost silničního provozu České vysoké učení technické
Program bezpečnostního výzkumu České republiky na léta 2016-2021 Specializovaná mapa s odborným obsahem VH 20162017003 Vliv reklamních zařízení na bezpečnost silničního provozu České vysoké učení technické
