Predikátová logika 1. řádu shrnutí
|
|
|
- Bohuslav Vacek
- před 8 lety
- Počet zobrazení:
Transkript
1 Predikátová logika 1. řádu shrnutí Symboly: Syntaxe: Logické symboly: proměnné:x Var,kdeVar = {x 0,x 1,x 2,...} logickéspojky:,,,, kvantifikátory:, závorky: ), ( symbol pro rovnost: = Mimologickésymboly dánysignaturous = (P,F,C,arity): predikátové symboly: P P funkčnísymboly:f F konstantní symboly: c C t ::= x c f(t,t,...,t) ϕ ::= P(t,t,...,t) t =t ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ xϕ xϕ Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
2 Predikátová logika 1. řádu shrnutí Sémantika: Hodnotatermupři I = (A,v): prox Var: I(x) =v(x) proc C: I(c) =c A prof F(kdearity(f) =n)atermyt 1,t 2,...,t n : I(f(t 1,t 2,...,t n )) =f A (I(t 1 ),I(t 2 ),...,I(t n )) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
3 Predikátová logika 1. řádu shrnutí Pravdivostformulepři I = (A,a): ProP P,kdearity(P) =n,aprotermyt 1,t 2,...,t nplatí I =P(t 1,t 2,...,t n) právětehdy,když (I(t 1),I(t 2),...,I(t n)) P A Protermyt 1,t 2platí I =t 1 =t 2právětehdy,když I(t 1) = I(t 2) I = neplatínikdy,tj.vždyplatí I = I = platívždy I = ϕplatíprávětehdy,když I = ϕ I = ϕ ψplatíprávětehdy,když I = ϕai = ψ I = ϕ ψplatíprávětehdy,když I = ϕnebo I = ψ I = ϕ ψplatíprávětehdy,když I = ϕnebo I = ψ I = ϕ ψplatíprávětehdy,když I = ϕai = ψ,nebokdyž I = ϕai = ψ I = xϕplatíprávětehdy,kdyžprokaždéa Aplatí I[x a] = ϕ I = xϕplatíprávětehdy,kdyžexistujenějakéa Atakové,že I[x a] = ϕ Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
4 Volné a vázané výskyty proměnných Každývýskytproměnnéxvevpodformulitvaru xϕnebo xϕjevázaný. Výskyt proměnné, který není vázaný, je volný. free(t) množina proměnných, které se vyskytují jako volné proměnné vtermut: free(x) = {x}prox Var free(c) = proc C free(f(t 1,t 2,...,t n)) =free(t 1) free(t 2)... free(t n)prof F free(ϕ) množina proměnných, které se vyskytují jako volné proměnné ve formuli ϕ: free(p(t 1,t 2,...,t n)) =free(t 1) free(t 2) free(t n)prop P free(t 1 =t 2) =free(t 1) free(t 2) free( ) =free( ) = free( ϕ) = free(ϕ) free(ϕ ψ) =free(ϕ) free(ψ)pro {,,, } free(qxϕ) =free(ϕ) {x}proq {, }ax Var Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
5 Volné a vázané výskyty proměnných Pravdivostformule ϕpři I = (A,v)závisípouzena Aahodnotách,které v přiřazuje proměnným z množiny free(ϕ). Speciálněvpřípadě,kdyfree(ϕ) =,takpravdivost ϕpři I = (A,v) závisí pouze na interpretaci A. Proformule ϕ,kdefree(ϕ) =,můžemepsát A = ϕ nebo A = ϕ Formule ϕ, kde free(ϕ) =, se nazývá uzavřená formule neboli sentence. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
6 Substituce ϕ formule, x proměnná, t term Formule, kterou dostaneme, když dosadíme term t za volné výskyty proměnnéxveformuli ϕ: ϕ[t/x] Příklad: ϕ := x(p(x) R(f(x,z),y)), t :=g(f(y,w)) Formule ϕ[t/z]: x(p(x) R(f(x,g(f(y,w))),y)) Poznámka:Jetřebadátpozornato,abysevolnývýskytproměnné v termu t nestal po dosazení vázaným. V takovém případě je potřeba vázanou proměnnou přejmenovat. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
7 Dedukční systém pro predikátovou logiku 1. řádu Dedukční systém obsahující stejná pravidla jako systém pro výrokovou logiku. Navíc několik pravidel pro práci s kvantifikátory a s rovností. e: Γ xa Γ A[t/x] Příklad: x(p(x) Q(x)),P(c) Q(c) Γ := x(p(x) Q(x)),P(c) 1. Γ x(p(x) Q(x)) (Assm) 2. Γ P(c) Q(c) ( e1) 3. Γ P(c) (Assm) 4. Γ Q(c) ( e2,3) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
8 Univerzální kvantifikátor i: Γ A[y/x] Γ xa (y free(γ, xa)) Speciální případ: Γ A Γ xa (x free(γ)) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
9 Univerzální kvantifikátor Příklad: x(p(x) Q(x)), x(q(x) R(x)) x(p(x) R(x)) 1. Γ x(p(x) Q(x)) (Assm) 2. Γ P(x) Q(x) ( e1) 3. Γ,P(x) P(x) (Assm) 4. Γ,P(x) P(x) R(x) ( i 1 3) 5. Γ,Q(x) x(q(x) R(x)) (Assm) 6. Γ,Q(x) Q(x) R(x) ( e5) 7. Γ,Q(x) Q(x) (Assm) 8. Γ,Q(x) R(x) ( e6,7) 9. Γ,Q(x) P(x) R(x) ( i 2 8) 10. Γ P(x) R(x) ( e2,4,9) 11. Γ x(p(x) R(x)) ( i10) Γ := x(p(x) Q(x)), x(q(x) R(x)) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
10 Existenční kvantifikátor i: Γ A[t/x] Γ xa e: Γ xa Γ,A[y/x] B Γ B (y free(γ, xa,b)) Speciální případ: Γ xa Γ,A B Γ B (x free(γ,b)) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
11 Rovnost =e: =i: t =t Γ t =t Γ A[t/x] Γ A[t /x] Příklad: Γ t 1 =t 2 Γ t 2 =t 1 1. Γ t 1 =t 2 (premisa) 2. t 1 =t 1 (=i) 3. Γ t 1 =t 1 (Ant2) 4. Γ (x =t 1 )[t 1 /x] (rep.3,x free(t 1 )) 5. Γ (x =t 1 )[t 2 /x] (=e1,4) 6. Γ t 2 =t 1 (rep.5) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
12 Některé důležité ekvivalence Poznámka: Všechny následující ekvivalence jsou i dokazatelné( ) Pokudx free(ψ): xϕ x ϕ xϕ x ϕ ( xϕ) ψ x(ϕ ψ) ( xϕ) ψ x(ϕ ψ) ( xϕ) ψ x(ϕ ψ) ( xϕ) ψ x(ϕ ψ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
13 Některé důležité ekvivalence Pokudy free(ϕ): Pokudx free(ϕ): ( xϕ) ( xψ) x(ϕ ψ) ( xϕ) ( xψ) x(ϕ ψ) x yϕ y xϕ x yϕ y xϕ xϕ y(ϕ[y/x]) xϕ y(ϕ[y/x]) xϕ ϕ xϕ ϕ Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
14 Existuje právě jeden Předpokládejme, že: ϕjeformule proměnnáyjerůznáodproměnnéx y free(ϕ) Tvrzení proprávějedenprvekxplatí ϕ sedázapsatformulí x(ϕ y(ϕ[y/x] x =y)) Označuje se také: =1 xϕ Poznámka:Vestejnémvýznamujako =1 sepoužívajínapříkladsymboly 1, =1,!. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
15 Přirozená čísla Signatura ({<},{σ,+, },{0},arity),kdearity(<) =2,arity(σ) =1, arity(+) =2,arity( ) =2 Příklady formulí: x y(x <y) kekaždémupřirozenémučísluexistujevětšípřirozené číslo σ(0)+σ(0) = σ(σ(0)) platí,že1+1 =2 σ(0) <x y z(σ(0) <y σ(0) <z y z =x) formule s volnou proměnnou x reprezentující tvrzení, že x je prvočíslo Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
16 Přirozená čísla Robinsonova a Peanova aritmetika Axiomy: x(σ(x) 0) x y(σ(x) = σ(y) x =y) x(x =0 y(σ(y) =x)) x(x +0 =x) x y(x +σ(y) = σ(x +y)) x(x 0 =0) x y(x σ(y) = (x y)+x) x y(x <y z(σ(z)+x =y)) Schéma axiomů indukce: y 1 y n (ϕ[0/x] x(ϕ ϕ[σ(x)/x]) xϕ) ϕjelibovolnáformule,kdefree(ϕ) {x,y 1,...,y n } Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
17 Definice Předpokládejme, že je dána množina axiomů Γ. Definice predikátového symbolu P, kde arity(p) = n: x 1 x n (P(x 1,...,x n ) ϕ) kdefree(ϕ) {x 1,...,x n } Definicefunkčníhosymboluf,kdearity(f) =n: x 1 x n y (f(x 1,...,x n ) =y ϕ) kdefree(ϕ) {x 1,...,x n,y},přičemž Γ x 1 x n =1 y(ϕ) Definice konstantního symbolu c: ϕ[c/x] kdefree(ϕ) {x},přičemž Γ =1 x(ϕ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
18 Teorie grup Signatura (,{ },{e},arity),kdearity( ) =2 Axiomy: x y z((x y) z =x (y z)) x(x e =x) x y(x y =e) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
19 Teorie množin Signatura ({ },,,arity),kdearity( ) =2 Příklady některých axiomů teorie množin: Axiom extenzionality: x y( z(z x z y) x =y) Schéma axiomů vydělení: y z x(x z (x y ϕ)) kde ϕjelibovolnáformule,kdez free(ϕ) Množinatvořenátěmiprvkyxmnožinyy,prokteréplatí ϕ: {x y ϕ} Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
20 Často používané zkratky Tvrzení existujexzmnožinyatakové,žeproxplatí ϕ : x(x A ϕ) Zkrácený zápis: ( x A)(ϕ) Tvrzení prokaždéxzmnožinyaplatí ϕ : x(x A ϕ) Zkrácený zápis: ( x A)(ϕ) Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
21 Formální jazyky Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
22 Abeceda a slovo Definice Abeceda je libovolná neprázdná konečná množina symbolů(znaků). Poznámka: Abeceda se často označuje řeckým písmenem Σ(velké sigma). Definice Slovo v dané abecedě je libovolná konečná posloupnost symbolů z této abecedy. Příklad 1: Σ = {A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} Slova v abecedě Σ: AHOJ ABRACADABRA ERROR Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
23 Abeceda a slovo Příklad 2: Σ 2 = {A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z, } Slovovabecedě Σ 2 : HELLO WORLD Příklad 3: Σ 3 = {0,1,2,3,4,5,6,7,8,9} Slovavabecedě Σ 3 : 0, ,65536 Příklad 4: Slovavabecedě Σ 4 = {0,1}: ,111, Příklad 5: Slovavabecedě Σ 5 = {a,b}:aababb,abbabbba,aaab Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
24 Abeceda a slovo Příklad 6: Abeceda Σ 6 jemnožinavšechasciiznaků. Příklad slova: class HelloWorld { public static void main(string[] args) { System.out.println("Hello, world!"); } } class HelloWorld { public static void main(str Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
25 Teorie formálních jazyků motivace Jazyk množina(některých) slov tvořených symboly z dané abecedy Příklady typů problémů, při jejichž řešení se využívá poznatků z teorie formálních jazyků: Tvorba překladačů: lexikální analýza syntaktická analýza Vyhledávání v textu: hledání zadaného vzorku hledání textu zadaného regulárním výrazem Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
26 Práce s formálními jazyky Když chceme nějaký jazyk popsat, máme několik možností: Můžeme vyjmenovat všechna jeho slova(což je ale použitelné jen pro malé konečné jazyky). Příklad: L = {aab, babba, aaaaaa} Můžeme specifikovat nějakou vlastnost, kterou mají právě ta slova, která do tohoto jazyka patří: Příklad: Jazyk nad abecedou {0, 1}, obsahující všechna slova, ve kterých je počet výskytů symbolu 1 sudý. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
27 Práce s formálními jazyky V teorii formálních jazyků se používají především následující dva přístupy: Popsat(idealizovaný) stroj, zařízení, algoritmus, který rozpozná slova patřící do daného jazyka vede k použití tzv. automatů. Popsat nějaký mechanismus umožňující generovat všechna možná slovapatřícídodanéhojazyka vedektzv.gramatikáma regulárním výrazům. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 14. března / 27
Formální jazyky. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 2. března / 32
 Formální jazyky Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 2. března 2017 1/ 32 Abeceda a slovo Definice Abeceda je libovolná neprázdná konečná množina symbolů(znaků). Poznámka: Abeceda se často
Formální jazyky Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 2. března 2017 1/ 32 Abeceda a slovo Definice Abeceda je libovolná neprázdná konečná množina symbolů(znaků). Poznámka: Abeceda se často
Formální jazyky. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března / 50
 Formální jazyky Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března 2013 1/ 50 Abeceda a slovo Definice Abeceda je libovolná neprázdná konečná množina symbolů(znaků). Poznámka: Abeceda se často
Formální jazyky Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 21. března 2013 1/ 50 Abeceda a slovo Definice Abeceda je libovolná neprázdná konečná množina symbolů(znaků). Poznámka: Abeceda se často
Rovnost lze vyjádřit jako predikát, např. můžeme zvolit, že P(x, y) reprezentujetvrzení xjerovnoy.
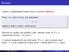 Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Rovnost Jedním z nejdůležitějších druhů relací je rovnost(identita). Prvkyxayjsousirovny,cožzapisujeme x =y, jestližesejednáojedenatentýžprvek. Rovnost lze vyjádřit jako predikát, např. můžeme zvolit,
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Příklad Necht L je jazyk obsahující
Matematická logika. Rostislav Horčík. horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 20 Predikátová logika Motivace Výroková
Výroková a predikátová logika - VI
 Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Výroková a predikátová logika - VI Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VI ZS 2017/2018 1 / 24 Predikátová logika Úvod Predikátová logika Zabývá
Predikátová logika. Teoretická informatika Tomáš Foltýnek
 Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
Predikátová logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz strana 2 Opakování z minulé přednášky Z čeho se skládá jazyk výrokové logiky? Jaká jsou schémata pro axiomy VL? Formulujte
4.2 Syntaxe predikátové logiky
 36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
36 [070507-1501 ] 4.2 Syntaxe predikátové logiky V tomto oddíle zavedeme syntaxi predikátové logiky, tj. uvedeme pravidla, podle nichž se tvoří syntakticky správné formule predikátové logiky. Význam a
1 Pravdivost formulí v interpretaci a daném ohodnocení
 1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
1 Pravdivost formulí v interpretaci a daném ohodnocení Než uvedeme konkrétní příklady, zopakujme si definici interpretace, ohodnocení a pravdivosti. Necht L je nějaký jazyk. Interpretaci U, jazyka L tvoří
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2013/2014 1 / 15 Korektnost a úplnost Důsledky Vlastnosti teorií
platné nejsou Sokrates je smrtelný. (r) 1/??
 Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Predikátová logika plně přejímá výsledky výrokové logiky zabývá se navíc strukturou jednotlivých jednoduchých výroků na základě této analýzy lze odvodit platnost některých výroků, které ve výrokové logice
Výroková a predikátová logika - XI
 Výroková a predikátová logika - XI Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XI ZS 2014/2015 1 / 21 Další dokazovací systémy PL Hilbertovský kalkul
Výroková a predikátová logika - XI Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XI ZS 2014/2015 1 / 21 Další dokazovací systémy PL Hilbertovský kalkul
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2018/2019 1 / 16 Rozšiřování teorií Extenze o definice Rozšiřování
Predikátová logika. prvního řádu
 Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Predikátová logika prvního řádu 2 Predikát Predikát je n-ární relace - vyjadřuje vlastnosti objektů a vztahy mezi objekty - z jednoduchého výroku vznikne vypuštěním alespoň jednoho jména objektu (individua)
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2013/2014 1 / 21 Sémantika PL Teorie Vlastnosti teorií Teorie
Výroková a predikátová logika - XII
 Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2018/2019 1 / 15 Rezoluční metoda v PL Rezoluční důkaz Obecné
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2015/2016 1 / 16 Tablo metoda v PL Důsledky úplnosti Vlastnosti
Logika Libor Barto. Výroková logika
 Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Logika Libor Barto Výroková logika Definice.(Jazyk výrokové logiky) Ve výrokové logice používáme tyto symboly: (1) Výrokové proměnné: velká písmena, případně opatřená indexy. (2) Výrokovéspojky:,,&,,,....
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška pátá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Predikátová logika: Axiomatizace, sémantické stromy, identita. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 13
 Predikátová logika: Axiomatizace, sémantické stromy, identita (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 13 Axiomatizace predikátové logiky Axiomatizace predikátové logiky Definice Hilbertovský
Predikátová logika: Axiomatizace, sémantické stromy, identita (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 13 Axiomatizace predikátové logiky Axiomatizace predikátové logiky Definice Hilbertovský
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2017/2018 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - XIII
 Výroková a predikátová logika - XIII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIII ZS 2013/2014 1 / 13 Úvod Algoritmická (ne)rozhodnutelnost Které
Výroková a predikátová logika - XIII Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIII ZS 2013/2014 1 / 13 Úvod Algoritmická (ne)rozhodnutelnost Které
Další (neklasické) logiky. Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20
 Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Predikátová logika Jiří Velebil: AD0B01LGR 2015 Predikátová logika 1/20 Jazyk predikátové logiky Má dvě sorty: 1 Termy: to jsou objekty, o jejichž vlastnostech chceme hovořit. Mohou být proměnné. 2 Formule:
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz
 Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Úvod do TI - logika Predikátová logika 1.řádu (4.přednáška) Marie Duží marie.duzi@vsb.cz Jednoduché úsudky, kde VL nestačí Všechny opice mají rády banány Judy je opice Judy má ráda banány Z hlediska VL
Převyprávění Gödelova důkazu nutné existence Boha
 Převyprávění Gödelova důkazu nutné existence Boha Technické podrobnosti Důkaz: Konečná posloupnost výrokůkorektně utvořených formulí nějakého logického kalkulu), z nichž každý jelogickým) axiomem, postulátemteorie),
Převyprávění Gödelova důkazu nutné existence Boha Technické podrobnosti Důkaz: Konečná posloupnost výrokůkorektně utvořených formulí nějakého logického kalkulu), z nichž každý jelogickým) axiomem, postulátemteorie),
Výroková a predikátová logika - VIII
 Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VIII Petr Gregor KTIML MFF UK ZS 2016/2017 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VIII ZS 2016/2017 1 / 21 Tablo Tablo metoda v PL - rozdíly Formule
Výroková a predikátová logika - VII
 Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Výroková a predikátová logika - VII Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - VII ZS 2018/2019 1 / 15 Platnost (pravdivost) Platnost ve struktuře
Cvičení ke kursu Klasická logika II
 Cvičení ke kursu Klasická logika II (12. května 2017) 1. Nechť P a Q jsou unární a R binární predikát. Dokažte, že následující formule jsou logicky platné, ale obrátíme-li (vnější) implikaci, ve všech
Cvičení ke kursu Klasická logika II (12. května 2017) 1. Nechť P a Q jsou unární a R binární predikát. Dokažte, že následující formule jsou logicky platné, ale obrátíme-li (vnější) implikaci, ve všech
Predikátová logika dokončení
 Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Predikátová logika dokončení Jiří Velebil: X01DML 1. října 2010: Predikátová logika dokončení 1/18 Syntaktická analýza Jako ve výrokové logice (syntaktické stromy). Každý list úspěšného stromu je obsazen
Okruh č.3: Sémantický výklad predikátové logiky
 Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Okruh č.3: Sémantický výklad predikátové logiky Predikátová logika 1.řádu formalizuje úsudky o vlastnostech předmětů a vztazích mezi předměty pevně dané předmětné oblasti (univerza). Nebudeme se zabývat
Rezoluční kalkulus pro logiku prvního řádu
 AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
AD4M33AU Automatické uvažování Rezoluční kalkulus pro logiku prvního řádu Petr Pudlák Logika prvního řádu (Někdy nepřesně nazývaná predikátová logika.) Výhody Vyšší vyjadřovací schopnost jazyka, V podstatě
Úvod do teoretické informatiky
 Úvod do teoretické informatiky Zdeněk Sawa Katedra informatiky, FEI, Vysoká škola báňská Technická universita Ostrava 17. listopadu 15, Ostrava-Poruba 708 33 Česká republika 11. února 2018 Z. Sawa (VŠB-TUO)
Úvod do teoretické informatiky Zdeněk Sawa Katedra informatiky, FEI, Vysoká škola báňská Technická universita Ostrava 17. listopadu 15, Ostrava-Poruba 708 33 Česká republika 11. února 2018 Z. Sawa (VŠB-TUO)
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška šestá Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
2.2 Sémantika predikátové logiky
 14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
14 [101105-1155] 2.2 Sémantika predikátové logiky Nyní se budeme zabývat sémantikou formulí, tj. jejich významem a pravdivostí. 2.2.1 Interpretace jazyka predikátové logiky. Interpretace predikátové logiky
Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika XI. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Řešení: Ano. Řešení: Ne.
 1 ÚLOHY Z PREDIKÁTOVÉ LOGIKY Instance, varianty. UF.1.1. Substituovatelnost. 1. Buď ϕ formule ( z)(x=z)&y < x a dále x, y, z různé proměnné, F unární funkční symbol, c konstantní symbol. Uveďte, zda je
1 ÚLOHY Z PREDIKÁTOVÉ LOGIKY Instance, varianty. UF.1.1. Substituovatelnost. 1. Buď ϕ formule ( z)(x=z)&y < x a dále x, y, z různé proměnné, F unární funkční symbol, c konstantní symbol. Uveďte, zda je
Predik atov a logika - pˇredn aˇska () Predik atov a logika - pˇredn aˇska / 16
 Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Predikátová logika - přednáška 3 6. 1. 2015 () Predikátová logika - přednáška 3 6. 1. 2015 1 / 16 Věta (o dedukci) Bud L jazyk, T teorie pro L, ϕ L-sentence a ψ L-formule. Pak Věta (o kompaktnosti) T ϕ
Úvod do teoretické informatiky(2017/2018) cvičení 6 1
 Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Úvod do teoretické informatiky(2017/2018) cvičení 6 1 Cvičení 6 Příklad 1: Pro každou z následujících sekvencí symbolů rozhodněte, zda se jedná o a) term, b) formuli predikátové logiky(používejte běžné
Sémantika predikátové logiky
 Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Sémantika predikátové logiky pro analýzu sémantiky potřebujeme nejprve specifikaci jazyka (doména, konstanty, funkční a predikátové symboly) příklad: formální jazyk s jediným binárním predikátovým symbolem
Základy matematické logiky
 OBSAH 1 Základy matematické logiky Obsah 1 Úvod 2 1.1 Předmět matematiky.......................... 2 1.2 Nástin historie.............................. 2 1.3 Axiomatická výstavba matematických teorií.............
OBSAH 1 Základy matematické logiky Obsah 1 Úvod 2 1.1 Předmět matematiky.......................... 2 1.2 Nástin historie.............................. 2 1.3 Axiomatická výstavba matematických teorií.............
Výroková a predikátová logika - X
 Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2015/2016 1 / 22 Herbrandova věta Úvod Redukce nesplnitelnosti na
Výroková a predikátová logika - X Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - X ZS 2015/2016 1 / 22 Herbrandova věta Úvod Redukce nesplnitelnosti na
Unární je také spojka negace. pro je operace binární - příkladem může být funkce se signaturou. Binární je velká většina logických spojek
 Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Otázka 06 - Y01MLO Zadání Predikátová logika, formule predikátové logiky, sentence, interpretace jazyka predikátové logiky, splnitelné sentence, tautologie, kontradikce, tautologicky ekvivalentní formule.
Úvod do predikátové logiky. (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/ / 1
 Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Úvod do predikátové logiky (FLÚ AV ČR) Logika: CZ.1.07/2.2.00/28.0216 2013 1 / 1 Relace Neuspořádaná vs. uspořádaná dvojice {m, n} je neuspořádaná dvojice. m, n je uspořádaná dvojice. (FLÚ AV ČR) Logika:
Stefan Ratschan. Fakulta informačních technologíı. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Logika pro každodenní přežití Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Základní pojmy matematické logiky
 KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
KAPITOLA 1 Základní pojmy matematické logiky Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. 1. Výroková logika Co je
Místo pojmu výroková formule budeme používat zkráceně jen formule. Při jejich zápisu
 VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
VÝROKOVÁ LOGIKA Matematická logika se zabývá studiem výroků, jejich vytváření a jejich pravdivostí. Základním kamenem výrokové logiky jsou výroky. Co je výrok nedefinujejme, pouze si řekneme, co si pod
Každé formuli výrokového počtu přiřadíme hodnotu 0, půjde-li o formuli nepravdivou, a hodnotu 1, půjde-li. α neplatí. β je nutná podmínka pro α
 1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
1. JAZYK ATEATIKY 1.1 nožiny nožina je souhrn objektů určitých vlastností, které chápeme jako celek. ZNAČENÍ. x A x A θ A = { { a, b a A = B A B 0, 1 2 a, a,..., a n x patří do množiny A x nepatří do množiny
Predikátová logika. Z minula: 1. jazyk logiky 1. řádu. 2. term a formule. 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy
 1 Predikátová logika Z minula: 1. jazyk logiky 1. řádu 2. term a formule 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy 5. vázané a volné výskyty proměnných ve formuli 6. otevřené
1 Predikátová logika Z minula: 1. jazyk logiky 1. řádu 2. term a formule 3. interpretace jazyka (relační struktura) 4. Tarského definice pravdy 5. vázané a volné výskyty proměnných ve formuli 6. otevřené
Výroková a predikátová logika - IX
 Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Výroková a predikátová logika - IX Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IX ZS 2018/2019 1 / 13 Dokončené tablo Chceme, aby dokončená bezesporná
Klasická predikátová logika
 Klasická predikátová logika Matematická logika, LS 2012/13, závěrečná přednáška Libor Běhounek www.cs.cas.cz/behounek/teaching/malog12 PřF OU, 6. 5. 2013 Symboly klasické predikátové logiky Poznámky Motivace
Klasická predikátová logika Matematická logika, LS 2012/13, závěrečná přednáška Libor Běhounek www.cs.cas.cz/behounek/teaching/malog12 PřF OU, 6. 5. 2013 Symboly klasické predikátové logiky Poznámky Motivace
2.5 Rezoluční metoda v predikátové logice
 2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
2.5. Rezoluční metoda v predikátové logice [101104-1520] 19 2.5 Rezoluční metoda v predikátové logice Rezoluční metoda v predikátové logice je obdobná stejnojmenné metodě ve výrokové logice. Ovšem vzhledem
Výroková a predikátová logika - XIV
 Výroková a predikátová logika - XIV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIV ZS 2018/2019 1 / 20 Nerozhodnutelnost Úvod Rekurzivní a rekurzivně
Výroková a predikátová logika - XIV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XIV ZS 2018/2019 1 / 20 Nerozhodnutelnost Úvod Rekurzivní a rekurzivně
1 Predikátová logika. 1.1 Syntax. jaký mohou mít formule význam (sémantiku). 1. Logických symbolů: 2. Speciálních (mimologických) symbolů:
 1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
1 Predikátová logika 1.1 Syntax Podobně jako ve výrokové logice začneme nejprve se syntaxí predikátové logiky, která nám říká, co jsou správně utvořené formule predikátové logiky. V další části tohoto
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce
 Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Úvod do logiky (presentace 2) Naivní teorie množin, relace a funkce Marie Duží marie.duzi@vsb.cz 1 Úvod do teoretické informatiky (logika) Naivní teorie množin Co je to množina? Množina je soubor prvků
Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka
 Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Celkové hodnocení BI-MLO (nevyplňujte!) Semestr Zkouška Cvičení Aktivita 1. část 2. část 3. část Ústní Celkem Známka BI-MLO Písemná zkouška 9. února 2016 Matematická logika FIT ČVUT v Praze Varianta B
Logické programy Deklarativní interpretace
 Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Logické programy Deklarativní interpretace Petr Štěpánek S využitím materialu Krysztofa R. Apta 2006 Logické programování 7 1 Algebry. (Interpretace termů) Algebra J pro jazyk termů L obsahuje Neprázdnou
Cvičení ke kursu Logika II, část III
 Cvičení ke kursu Logika II, část III (30. listopadu 2008) Osnova přednášky přednáška je určena studentům, kteří absolvovali úvodní kursy logiky a teorie rekurzívních funkcí. Předpokládané znalosti: syntax
Cvičení ke kursu Logika II, část III (30. listopadu 2008) Osnova přednášky přednáška je určena studentům, kteří absolvovali úvodní kursy logiky a teorie rekurzívních funkcí. Předpokládané znalosti: syntax
Výroková logika. Teoretická informatika Tomáš Foltýnek
 Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Výroková logika Teoretická informatika Tomáš Foltýnek foltynek@pef.mendelu.cz Teoretická informatika strana 2 Opakování z minulé přednášky Co je to formalismus a co je jeho cílem? Formulujte Russelův paradox
Přednáška 2: Formalizace v jazyce logiky.
 Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Přednáška 2: Formalizace v jazyce logiky. Marie Duží marie.duzi@vsb.cz Úvod do teoretické informatiky (logika) Dva základní logické systémy: Výroková logika a predikátová logika. řádu. Výroková logika
Rezoluce v predikátové logice
 Rezoluce v predikátové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná iff X =
Rezoluce v predikátové logice Jiří Velebil: AD0B01LGR 2015 Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná iff X =
Rezoluce v predikátové logice
 Rezoluce v predikátové logice Jiří Velebil: X01DML 15. října 2010: Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná
Rezoluce v predikátové logice Jiří Velebil: X01DML 15. října 2010: Rezoluce v PL 1/16 Základní myšlenky 1 M = ϕ iff X = M { ϕ} nesplnitelná. (M musí být množina sentencí, ϕ sentence.) 2 X nesplnitelná
Matematická logika. Rostislav Horčík. horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik
 Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Predikátová logika Motivace Výroková
Matematická logika Rostislav Horčík horcik@math.feld.cvut.cz horcik@cs.cas.cz www.cs.cas.cz/ horcik Rostislav Horčík (ČVUT FEL) Y01MLO Letní semestr 2007/2008 1 / 18 Predikátová logika Motivace Výroková
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2017/2018 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2017/2018 1 / 17 Předběžnosti Základní pojmy n-ární relace a funkce
Výroková logika syntaxe a sémantika
 syntaxe a sémantika Jiří Velebil: AD0B01LGR 2015 Handout 01: & sémantika VL 1/16 1 Proč formální jazyk? 1 Přirozené jazyky jsou složité a často nejednoznačné. 2 Komunikace s formálními nástroji musí být
syntaxe a sémantika Jiří Velebil: AD0B01LGR 2015 Handout 01: & sémantika VL 1/16 1 Proč formální jazyk? 1 Přirozené jazyky jsou složité a často nejednoznačné. 2 Komunikace s formálními nástroji musí být
Formální jazyky. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 7. března / 46
 Formální jzyky Z. Sw (VŠB-TUO) Úvod do teoretické informtiky 7. řezn 2012 1/ 46 Teorie formálních jzyků motivce Příkldy typů prolémů, při jejichž řešení se využívá pozntků z teorie formálních jzyků: Tvor
Formální jzyky Z. Sw (VŠB-TUO) Úvod do teoretické informtiky 7. řezn 2012 1/ 46 Teorie formálních jzyků motivce Příkldy typů prolémů, při jejichž řešení se využívá pozntků z teorie formálních jzyků: Tvor
Predikátová logika [Predicate logic]
![Predikátová logika [Predicate logic] Predikátová logika [Predicate logic]](/thumbs/74/70612837.jpg) Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Predikátová logika [Predicate logic] Přesněji predikátová logika prvého řádu. Formalizuje výroky o vlastnostech předmětů (entit) a vztazích mezi předměty, které patří do dané předmětné oblasti univerza.
Klauzulární logika. úvod. Šárka Vavrečková. 20. října Ústav informatiky Filozoficko-Přírodovědecká fakulta Slezské univerzity, Opava
 Klauzulární logika úvod Šárka Vavrečková Ústav informatiky Filozoficko-Přírodovědecká fakulta Slezské univerzity, Opava 20. října 2008 Klauzulární logika Hlavní vlastnosti pracujeme s klauzulemi, které
Klauzulární logika úvod Šárka Vavrečková Ústav informatiky Filozoficko-Přírodovědecká fakulta Slezské univerzity, Opava 20. října 2008 Klauzulární logika Hlavní vlastnosti pracujeme s klauzulemi, které
Úvod do výrokové a predikátové logiky
 Úvod do výrokové a predikátové logiky Eva Ondráčková Na této přednášce se seznámíte se základy výrokové a predikátové logiky. Zjistíte, že podstatou logiky není vyplňování pravdivostních tabulek ani negování
Úvod do výrokové a predikátové logiky Eva Ondráčková Na této přednášce se seznámíte se základy výrokové a predikátové logiky. Zjistíte, že podstatou logiky není vyplňování pravdivostních tabulek ani negování
1 Výroková logika 1. 2 Predikátová logika 3. 3 Důkazy matematických vět 4. 4 Doporučená literatura 7
 1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
1 Výroková logika 1 Výroková logika 1 2 Predikátová logika 3 3 Důkazy matematických vět 4 4 Doporučená literatura 7 Definice 1.1 Výrokem rozumíme každé sdělení, o kterém má smysl uvažovat, zda je, či není
Matematická logika. Lekce 1: Motivace a seznámení s klasickou výrokovou logikou. Petr Cintula. Ústav informatiky Akademie věd České republiky
 Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Matematická logika Lekce 1: Motivace a seznámení s klasickou výrokovou logikou Petr Cintula Ústav informatiky Akademie věd České republiky www.cs.cas.cz/cintula/mal Petr Cintula (ÚI AV ČR) Matematická
Základy logiky a teorie množin
 Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
Pracovní text k přednášce Logika a teorie množin (I/2007) 1 1 Struktura přednášky Matematická logika 2 Výroková logika Základy logiky a teorie množin Petr Pajas pajas@matfyz.cz Predikátová logika 1. řádu
pouze u některých typů rovnic a v tomto textu se jím nebudeme až na
 Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Úvod do informatiky. Miroslav Kolařík
 Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Úvod do informatiky přednáška první Miroslav Kolařík Zpracováno dle učebního textu prof. Bělohlávka: Úvod do informatiky, KMI UPOL, Olomouc 2008. Obsah 1 Co a k čemu je logika? 2 Výroky a logické spojky
Formální systém výrokové logiky
 Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
Formální systém výrokové logiky 1.Jazyk výrokové logiky Nechť P = {p,q,r, } je neprázdná množina symbolů, které nazýváme prvotní formule. Symboly jazyka L P výrokové logiky jsou : a) prvky množiny P, b)
6. Logika a logické systémy. Základy logiky. Lucie Koloušková, Václav Matoušek / KIV. Umělá inteligence a rozpoznávání, LS
 Základy logiky Umělá inteligence a rozpoznávání, LS 2012 6-1 Logika je naukou, která se zabývá studiem lidského uvažování. Mezi základní úlohy logiky patří nalézání metod správného usuzování, tedy postupů,
Základy logiky Umělá inteligence a rozpoznávání, LS 2012 6-1 Logika je naukou, která se zabývá studiem lidského uvažování. Mezi základní úlohy logiky patří nalézání metod správného usuzování, tedy postupů,
doplněk, zřetězení, Kleeneho operaci a reverzi. Ukážeme ještě další operace s jazyky, na které je
 28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
28 [181105-1236 ] 2.7 Další uzávěrové vlastnosti třídy regulárních jazyků Z předchozích přednášek víme, že třída regulárních jazyků je uzavřena na sjednocení, průnik, doplněk, zřetězení, Kleeneho operaci
Matematické důkazy Struktura matematiky a typy důkazů
 Matematické důkazy Struktura matematiky a typy důkazů Petr Liška Masarykova univerzita 18.9.2014 Motto: Matematika je tvořena z 50 procent formulemi, z 50 procent důkazy a z 50 procent představivostí.
Matematické důkazy Struktura matematiky a typy důkazů Petr Liška Masarykova univerzita 18.9.2014 Motto: Matematika je tvořena z 50 procent formulemi, z 50 procent důkazy a z 50 procent představivostí.
Výroková a predikátová logika - XII
 Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2015/2016 1 / 15 Algebraické teorie Základní algebraické teorie
Výroková a predikátová logika - XII Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - XII ZS 2015/2016 1 / 15 Algebraické teorie Základní algebraické teorie
Skolemizace. x(x + f(x) = 0). Interpretace f unární funkce, která pro daný
 Skolemizace převod formulí na formule bez existenčních kvantifikátorů v jazyce, který je rozšířen o tzv. Skolemovy funkce; zachovává splnitelnost idea převodu: formuli x 1... x n yp (x 1,..., x n, y) transformujeme
Skolemizace převod formulí na formule bez existenčních kvantifikátorů v jazyce, který je rozšířen o tzv. Skolemovy funkce; zachovává splnitelnost idea převodu: formuli x 1... x n yp (x 1,..., x n, y) transformujeme
Systém přirozené dedukce výrokové logiky
 Systém přirozené dedukce výrokové logiky Korektnost, úplnost a bezespornost Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 6. října 2008 Věta o korektnosti Věta (O korektnosti Systému
Systém přirozené dedukce výrokové logiky Korektnost, úplnost a bezespornost Šárka Vavrečková Ústav informatiky, FPF SU Opava Poslední aktualizace: 6. října 2008 Věta o korektnosti Věta (O korektnosti Systému
KMA/MDS Matematické důkazy a jejich struktura
 Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.0141 KMA/MDS Matematické důkazy a jejich struktura Seminář 3 Predikátový počet Uvažujme následující úsudek.
Formální jazyky a gramatiky Teorie programovacích jazyků
 Formální jazyky a gramatiky Teorie programovacích jazyků doc. Ing. Jiří Rybička, Dr. ústav informatiky PEF MENDELU v Brně rybicka@mendelu.cz Připomenutí základních pojmů ABECEDA jazyk je libovolná podmnožina
Formální jazyky a gramatiky Teorie programovacích jazyků doc. Ing. Jiří Rybička, Dr. ústav informatiky PEF MENDELU v Brně rybicka@mendelu.cz Připomenutí základních pojmů ABECEDA jazyk je libovolná podmnožina
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2013/2014 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2013/2014 1 / 20 Základní syntax Jazyk Výroková logika je logikou
Výroková logika dokazatelnost
 Výroková logika dokazatelnost Ke zjištění, zda formule sémanticky plyne z dané teorie (množiny formulí), máme k dispozici tabulkovou metodu. Velikost tabulky však roste exponenciálně vzhledem k počtu výrokových
Výroková logika dokazatelnost Ke zjištění, zda formule sémanticky plyne z dané teorie (množiny formulí), máme k dispozici tabulkovou metodu. Velikost tabulky však roste exponenciálně vzhledem k počtu výrokových
Výroková a predikátová logika - III
 Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Výroková a predikátová logika - III Petr Gregor KTIML MFF UK ZS 2014/2015 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - III ZS 2014/2015 1 / 21 Výroková logika Horn-SAT Horn-SAT Jednotková
Logika, Gödel, neúplnost
 Logika, Gödel, neúplnost Vítězslav Švejdar Karlova Univerzita v Praze, http://www.cuni.cz/~svejdar/ Český klub skeptiků, 23. únor 2018 Vítězslav Švejdar, FF UK Praha Logika, Gödel, neúplnost 1/13 Obsah
Logika, Gödel, neúplnost Vítězslav Švejdar Karlova Univerzita v Praze, http://www.cuni.cz/~svejdar/ Český klub skeptiků, 23. únor 2018 Vítězslav Švejdar, FF UK Praha Logika, Gödel, neúplnost 1/13 Obsah
Pro každé formule α, β, γ, δ platí: Pro každé formule α, β, γ platí: Poznámka: Platí právě tehdy, když je tautologie.
 Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Zpracoval: hypspave@fel.cvut.cz 5. Výroková logika, formule výrokové logiky a jejich pravdivostní ohodnocení, splnitelné formule, tautologie, kontradikce, sémantický důsledek, tautologicky ekvivalentní
Logika a logické programování
 Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
Logika a logické programování témata ke zkoušce Poslední aktualizace: 16. prosince 2009 Zkouška je písemná, skládá se obvykle ze sedmi otázek (může být více nebo méně, podle náročnosti otázek), z toho
Výroková a predikátová logika Výpisky z cvičení Martina Piláta
 Výroková a predikátová logika Výpisky z cvičení Martina Piláta Jan Štětina 1. prosince 2009 Cviˇcení 29.9.2009 Pojem: Sekvence je konečná posloupnost, značíme ji predikátem seq(x). lh(x) je délka sekvence
Výroková a predikátová logika Výpisky z cvičení Martina Piláta Jan Štětina 1. prosince 2009 Cviˇcení 29.9.2009 Pojem: Sekvence je konečná posloupnost, značíme ji predikátem seq(x). lh(x) je délka sekvence
Sémantika výrokové logiky. Alena Gollová Výroková logika 1/23
 Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
Výroková logika Alena Gollová Výroková logika 1/23 Obsah 1 Formule výrokové logiky 2 Alena Gollová Výroková logika 2/23 Formule výrokové logiky Výrok je oznamovací věta, o jejíž pravdivosti lze rozhodnout.
(zkráceně jen formule), jestliže vznikla podle následujících pravidel:
 1 Kapitola 1 Výroková logika 1.1 Výroky 1.1.1 Výroky. Máme danou neprázdnou množinu A tzv. elementárních výroků (též jim říkáme logické nebo výrokové proměnné). Konečnou posloupnost prvků z množiny A,
1 Kapitola 1 Výroková logika 1.1 Výroky 1.1.1 Výroky. Máme danou neprázdnou množinu A tzv. elementárních výroků (též jim říkáme logické nebo výrokové proměnné). Konečnou posloupnost prvků z množiny A,
Výroková a predikátová logika - IV
 Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
Výroková a predikátová logika - IV Petr Gregor KTIML MFF UK ZS 2018/2019 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - IV ZS 2018/2019 1 / 17 Tablo metoda Tablo Tablo - příklady F (((p q)
verze 29/9/09 textu o logice, aritmetice a M. Bizzarrimu.
 1 verze 29/9/09 Toto je prozatím definitivní verze provizorního textu o logice, aritmetice a množinách. věnováno Laskavým čtenářům a čtenářkám, kteří navštěvovali tyto přednášky. poděkování Za upozornění
1 verze 29/9/09 Toto je prozatím definitivní verze provizorního textu o logice, aritmetice a množinách. věnováno Laskavým čtenářům a čtenářkám, kteří navštěvovali tyto přednášky. poděkování Za upozornění
Matematická logika. Miroslav Kolařík
 Matematická logika přednáška třetí Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Matematická logika přednáška třetí Miroslav Kolařík Zpracováno dle textu R. Bělohlávka: Matematická logika poznámky k přednáškám, 2004. a dle učebního textu R. Bělohlávka a V. Vychodila: Diskrétní matematika
Logika. 6. Axiomatický systém výrokové logiky
 Logika 6. Axiomatický systém výrokové logiky RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Logika 6. Axiomatický systém výrokové logiky RNDr. Luděk Cienciala, Ph. D. Tato inovace předmětu Úvod do logiky je spolufinancována Evropským sociálním fondem a Státním rozpočtem ČR, projekt č. CZ. 1.07/2.2.00/28.0216,
Matematická indukce, sumy a produkty, matematická logika
 Matematická indukce, sumy a produkty, matematická logika 8.9. -.0.009 Matematická indukce Jde o následující vlastnost přirozených čísel: Předpokládejme:. Nějaké tvrzení platí pro.. Platí-li tvrzení pro
Matematická indukce, sumy a produkty, matematická logika 8.9. -.0.009 Matematická indukce Jde o následující vlastnost přirozených čísel: Předpokládejme:. Nějaké tvrzení platí pro.. Platí-li tvrzení pro
Algoritmizace a programování
 Algoritmizace a programování Řídicí struktury jazyka Java Struktura programu Příkazy jazyka Blok příkazů Logické příkazy Ternární logický operátor Verze pro akademický rok 2012/2013 1 Struktura programu
Algoritmizace a programování Řídicí struktury jazyka Java Struktura programu Příkazy jazyka Blok příkazů Logické příkazy Ternární logický operátor Verze pro akademický rok 2012/2013 1 Struktura programu
Výroková a predikátová logika - II
 Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
Výroková a predikátová logika - II Petr Gregor KTIML MFF UK ZS 2015/2016 Petr Gregor (KTIML MFF UK) Výroková a predikátová logika - II ZS 2015/2016 1 / 18 Základní syntax Jazyk Výroková logika je logikou
2.1 Formule predikátové logiky. větám. Použijte k tomu predikátových symbolu uvedených v textu.
 6 Kapitola 2 Příklady z predikátové logiky 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolu uvedených
6 Kapitola 2 Příklady z predikátové logiky 2.1 Formule predikátové logiky 2.1.1 Příklad. Napište formule predikátové logiky odpovídající následujícím větám. Použijte k tomu predikátových symbolu uvedených
postaveny výhradně na syntaktické bázi: jazyk logiky neinterpretujeme, provádíme s ním pouze syntaktické manipulace důkazy
 Formální systémy (výrokové) logiky postaveny výhradně na syntaktické bázi: jazyk logiky neinterpretujeme, provádíme s ním pouze syntaktické manipulace důkazy cíl: získat formální teorii jako souhrn dokazatelných
Formální systémy (výrokové) logiky postaveny výhradně na syntaktické bázi: jazyk logiky neinterpretujeme, provádíme s ním pouze syntaktické manipulace důkazy cíl: získat formální teorii jako souhrn dokazatelných
