1 Grafická data Vektorová data Rastrová data Typy rastrových obrázků Kontrolní otázky... 25
|
|
|
- Milena Matějková
- před 9 lety
- Počet zobrazení:
Transkript
1 Základy počítačové grafiky Jana Procházková, Vojtěch Vitásek
2 c Mgr. Jana Procházková, Ph.D., Ing. Vojtěch Vitásek 2007
3 Obsah 1 Grafická data Vektorová data Rastrová data Typy rastrových obrázků Kontrolní otázky Literatura Barvy, barvy, barvičky Vnímání barev Jak funguje lidské oko Barevné modely Kontrolní otázky Literatura Úpravy obrazu Transformace barev Warping a morfing Warping Morfing Obrazy s vysokým dynamickým rozsahem (High Dynamic Range HDR) Histogram Kontrolní otázky Literatura Rasterizace objektů Úsečka a lomenná čára Algoritmus DDA Bresenhamův algoritmus pro kresbu úsečky Kresba silné a přerušované čáry Kružnice a elipsa Kontrolní otázky Literatura
4 4 OBSAH 5 Řešení viditelnosti Pamět hloubky z-buffer Malířův algoritmus Painter s algorithm Malířův algoritmus se stromem BSP Metoda vržení paprsku Kontrolní otázky Literatura Objektově orientované programování Koncepce Ukázkový příklad Definice třídy Vytvoření objektu Vlastnosti objektu Metody objektu Konstruktor a destruktor objektu Dědičnost Kontrolní otázky Literatura Křivky a plochy technické praxe Základní princip Základní typy křivek a ploch technické praxe Fergusonovy křivky a plochy Bézierovy křivky a plochy Coonsovy křivky a plochy B-spline křivky a plochy NURBS křivky a plochy T-spline Kontrolní otázky Literatura Transformace v rovině Transformace v rovině Transformace v prostoru Kontrolní otázky Literatura
5 Kapitola 1 Grafická data Grafická data se obvykle dělí na data vektorová a rastrová. Základní rozdíl je v způsobu popisu daného objektu. V případě vektorové grafiky jsou objekty popsány pomocí geometrických parametrů. U rastrových dat je objekt popsán jako shluk bodů. Úsečka popsaná rastrem je množina bodů o různých souřadnicích, které zobrazené dohromady tvoří obraz úsečky. Úsečka ve vektorovém zápisu bude obsahovat pouze počáteční a koncový bod a informaci o barvě a tloušt ce. 1.1 Vektorová data Vektorový grafický soubor obsahuje informace o objektech složených z křivek a jednoduchých těles, které umožňují jejich geometrickou konstrukci. Je-li takto uložena např. kružnice, soubor neobsahuje informace o všech jednotlivých bodech, které na ní leží. Informuje o tom, že se jedná o kružnici, dále obsahuje souřadnice jejího středu, jednoho bodu, který na ní leží a poslední bod určuje rovinu její konstrukce. Připojeny jsou rovněž informace o barvě objektu a tloušt ce čáry, kterou má být sestrojen. Program, pro který jsou tato data určena, musí být schopen tyto informace správně přečíst a musí obsahovat algoritmus, který na základě těchto informací kružnici sestrojí. Vektorová data jsou typická např. pro technické výkresy. Z grafických softwaru je používá např. CorelDraw, Adobe Illustrator. Obrázek 1.1: Obrázek je popsán pomocí vektorových dat jako soustava křivek 5
6 6 KAPITOLA 1. GRAFICKÁ DATA Výhody změnou měřítka nedochází ke ztrátě informace, výstupní soubory jsou poměrně malé, vhodné na tvorbu log, map apod., tedy obrázků, které se používají v různých rozměrech, jednoduché kreslení, výstupní soubory:.eps,.pdf,.pict (Mac) Nevýhody některé čáry mohou zmizet při velmi velkém změnšení při velkém zvětšení jsou vidět chyby v kresbě 1.2 Rastrová data Rastrová data dohromady tvoří obrázek. Ten se skládá z matice jednotlivých teček (pixelů). Každý má svoji vlastní barvu. Někdy bývají uloženy i informace o způsobu případné komprese a kódování barev. Rastrově jsou ukládány bud informace, které již nebudou dále upravovány systémem, kterým byly vytvořeny (např. žánrový pohled na strojní součást), nebo obrazy, které nebyly pořízeny počítačem (např. fotografie). Na rastrovém principu funguje většina zobrazovacích zařízení (monitory, jehličkové, inkoustové i laserové tiskárny, televize apod.). Na obr. 1.2 je ukázka rastrového obrázku. V detailu je vidět složení obrázku ze čtverců s danou barvou. Lidské oko nedokáže rozlišit jednotlivé čtverce, proto na nás výsledek působí spojitě. Počet pixelů záleží na daném obrázku, v jaké velikosti jej chceme tisknout či prezentovat. Aby se dalo porovnávat rozlišení obrázků, byla zavedena jednotka DPI - Dots Per Inch (počet bodů na palec). Rozlišení 800x600 může poskytovat vysoce kvalitní (malý) obraz na čtrnáctipalcovém monitoru a díky omezené rozlišovací schopnosti lidského oka zde již nemá smysl použít rozlišení větší. Totéž rozlišení však bude asi nedostatečné na monitoru jednadvacetipalcovém Typy rastrových obrázků Rastrové obrázky mohou obsahovat libovolný počet barev, ale rozlišujeme čtyři základní kategorie. 1. Line-art. Tyto obrázky obsahují pouze dvě barvy, obvykle černou a bílou. Každý pixel je definová pouze jedním bitem (on=černá, off=bílá).
7 1.2. RASTROVÁ DATA 7 Obrázek 1.2: Rastrový obrázek 2. Odstíny šedi. Obsahuje paletu stínů šedé, také čistou černou či bílou. 3. Tónované. Tento obrázek obsahuje odstíny dvou či více barev. Nejoblíbenější je použití dvou barev, které se obvykle skládá z černé a druhé barvy. 4. Plně barevné. Barevná informace může být popsána užitím množství barevných prostorů: RGB, CMYK, atp. Více o nich budeme mluvit v kapitole 2. Obrázek 1.3: 1. Line-art 2. Odstíny šedi 3. Tónované 4. Plně barevné Výhody jednoduché pro výstup, pokud má tiskárna dostatečnou pamět výstupní soubory:.eps,.gif,.jpg,.tiff,.pict (Mac).
8 8 KAPITOLA 1. GRAFICKÁ DATA Nevýhody velká pamět ová náročnost (A4 formát střední kvality bez komprese má 40 MB), nelze libovolně zvětšovat dochází ke čtvercování, při zmenšení ztrácí ostrost. 1.3 Kontrolní otázky 1. Jaký je základní rozdíl vektorovými a rastrovými daty? 2. Jaká je hlavní výhoda užití vektorových dat? 3. Na jaký typ kreseb jsou vhodná vektorová data? 4. Jaké jsou typy rastrových obrázků? 5. Popište způsob uložení rastrových dat. 6. Jaké jsou nevýhody užití rastrových dat? 7. Co znamená zkratka DPI? 1.4 Literatura popis bmp obrázků
9 Kapitola 2 Barvy, barvy, barvičky 2.1 Vnímání barev Světlo, které vnímáme, představuje viditelnou část elektromagnetického spektra. V něm se vyskytují všechny známé druhy záření, např. gama záření či infračervené záření. Lidské oko vnímá pouze oblast vlnových délek 380 až 720 nm. Uvnitř této oblasti vnímáme záření s určitou vlnovou délkou jako barvu. Jak tedy vnímáme barvy? Tak například, když bílé světlo dopadne na červený objekt, tento objekt absorbuje (pohltí) všechny složky bílého světla kromě červené. Objekt pak odráží záření v červené části spektra. Jak již v minulém století zjistil pan Heimholz, lidské oko má buňky (receptory), které jsou citlivé na červenou, zelenou a modrou barvu, tyto barvy jsou též základními složkami bílého světla. Kombinací různých úrovní těchto tří základních barev je lidský mozek schopen vnímat tisíce jemnějších barevných odstínů. Elektromagnetické záření s kratšími vlnovými délkami nese více energie. V oblasti paprsků x nese záření dostatečnou energii, která umožňuje prostoupit větším objemem hmoty (např. lidské tělo). Toho se využívá v lékařství. Také gama paprsky mají význam v lékařství. Obrazy získané pomocí gama záření se používají pro odhalení funkcí. Infračervené záření vydávají zahřáté objekty. Toho využívají moderní přístroje pro noční vidění. Za světelný zdroj nejčastěji bereme Slunce, ale je jím i žárovka. Světelný zdroj vysílá paprsky všech frekvencí, které se skládají ve výsledné bílé světlo. Toto světlo se nazývá achromatické. Paprsky světla dopadají na objekty, některé frekvence se odrazí, jiné jsou pohlceny. Odražené světlo přijímá naše oko a mozek zpracovává a rozpozná výslednou barvu. Pro popis světla se kromě frekvence používá ještě jas, sytost a světlost. Jas odpovídá intenzitě světla, sytost určuje čistotu barvy a světlost určuje velikost achromatické složky ve světle s určitou dominantní frekvencí (např. světle nebo tmavě modrá). 9
10 10 KAPITOLA 2. BARVY, BARVY, BARVIČKY Jak funguje lidské oko Obrázek 2.1: Barevné spektrum Lidské oko je velmi složitý orgán. Příchozí obraz je promítán na sítnici. Tato fotocitlivá vrstva pokrývá dvě třetiny vnitřního povrchu oka. Obsahuje dva druhy receptorů: tyčinky a čípky. Tyčinek je více ( ) a zajišt ují noční vidění. Jsou také více citlivé. Čípky (8 106 ) nám zprostředkovávají barevné vidění. Tyčinky a čípky nejsou pravidelně rozmístěny po celé sítnici. Každý čípek je připojen k nervovému zakončení. Oproti tomu je vždy několik tyčinek propojeno pouze k jednomu nervu. Všechny signály z čípků a tyčinek jsou pomocí zrakového nervu předávány do mozku. Zajímavostí je, že po cestě informace do mozku dojde k rekombinaci informací. Z původních tří hodnot červená, zelená a modrá dojde do mozku informace o poměru červená-zelená, žlutá-modrá, zelená-červená. 2.2 Barevné modely Při tisku nebo zobrazení obrázku jsou vytvářeny jeho barvy většinou pomocí tři složek - červená (red), zelená (green), modrá (blue), které nabývají většinou hodnot od 0 do 255. (V některých systémech může být rozmezí jiné, např. 0,1) To odpovídá kódování každé ze složek RGB v jednom bytu. Hodnota nula znamená, že daná barva není ve výsledné vůbec zastoupena, hodnota 255 znamená, že daná složka má největší intenzitu. Máme tedy tři barvy (R,G,B) a jejich hodnotami můžeme určit = barev. Lidské oko dokáže rozpoznat asi deset milionů barev, proto je tento počet dostatečný. Tyto barvy označujeme jako true color. V minulosti byla termínem
11 2.2. BAREVNÉ MODELY 11 true color označována i zařízení o 15 resp 16 bitech na pixel (32768 resp barev). Pro reprodukci, tj. zobrazení barev se používají dvě metody: subtraktivní a aditivní míchání barev. 1. Aditivní metoda Když použijeme červené, zelené a modré světlo (RGB) používáme aditivní míchání barev. Termín aditivní doplňkové znamená, že začneme s černým pozadím a přidáváme jednotlivé barevné RGB složky pro vytvoření konkrétního barevného odstínu. Kombinací všech tří RGB barev vznikne bílá barva. Barevná televize, počítačový monitor, scanner a jevištní osvětlovací technika pracuje tímto způsobem. Složením (kombinací) tří základních barev vzniknou další barvy. 2.Subtraktivní metoda Subtraktivní míchání barev je opačný k aditivnímu. Začínáme s bílým pozadím a přidáváme barvy Cyan, Magenta a Yellow (zkratka CMY), abychom jejich překrytím vytvořili černou barvu. Subtraktivní metoda se používá v tiskovém průmyslu, kde se obvykle tiskne na bílý papír. CMY pigmenty absorbují (odečítají) konkrétní vlnové délky dopadajícího světla a naopak dovolují ostatním, aby se od potištěného papíru odrazily. Tak tedy Cyan absorbuje (pohltí - odečte) červenou část dopadajícího světla. Magenta absorbuje zelené světlo a Yellow absorbuje modré světlo. Když sloučíme subtraktivní barvy získáme opět základní aditivní barvy. Černá barva, která vzniká smísením všech složek CMY však není čistě černá, jedná se spíše o tmavě hnědou. Z tohoto důvodu se k složkám CMY přidává samostatná černá barva K (black). Vzniká tak prostor CMYK. Obrázek 2.2: Citlivost lidského oka na barvy
12 12 KAPITOLA 2. BARVY, BARVY, BARVIČKY Obrázek 2.3: Barevný systém RGB Uživatelsky však zadávání barev pomocí prostorů RGB nebo CMY není snadné. Odhadnout, které barvy a v jakém poměru smíchat k výslednému odstínu není vůbec intuitivní, proto se zavedly další barevné modely pro snažší práci s barvami (využívají se v grafických softwarech). Modely HSV, HLS Barva je definována opět trojicí složek. Nejsou to ale barvy jako u RGB či CMYK. Hlavní využití je v grafických programech pro snadnější míchání barev. Jsou to ty lišty při návrhu barvy, kde lze jednoduše změnit světlost či sytost barvy. HSV - Hue (barevný tón)+saturation(sytost)+value(jas) HLS - Hue (barevný tón)+lightness(světlost)+saturation(sytost) Modely CIE, YUV, YIQ Každou barvu vnímá každý člověk jinak. Záleží na únavě očí, světle okolí. Přesné rozlišování barev trápilo v době před nástupem počítačů zejména výrobce barev pro tiskárny a textilky, a tak se v roce 1931 sešli odbornící na barvy v organizaci CIE (Commission Internationale de l Eclairage) a vytvořili hypotetického standardního pozorovatele a jemu odpovídající barevný prostor, nezávislý na použité technologii. Tento prostor, dnes nazývaný CIE-XYZ, umožňuje popsat jakoukoliv barvu (dokonce i takovou, kterou nelze namíchat ze třech základních), či přesněji vjem z této barvy, pouze dvěma hodnotami (velmi zjednodušeně je lze nazvat poměrná červenost a poměrná modrost). Třetí hodnotou je pak světlost barvy. Po nástupu počítačů vznikla potřeba přizpůsobit prostor CIE-XYZ tak, aby bylo možné co nejomezenějším počtem bitů, které budou každé složce přiděleny, pokrýt co nejlépe možnosti barevného rozlišení oka. A tak vznikly barevné prostory CIE
13 2.3. KONTROLNÍ OTÁZKY 13 Obrázek 2.4: Barevné modely HSV, HLS Obrázek 2.5: Barevný model CIE L*u*v* a CIE L*a*b*, oba značně výpočetně náročné. To sice nevadí při přípravě pro tisk, ale při zobrazování v reálném čase ano. S dalšími podobnými prostory přišli tvůrci norem pro barevné televizní vysílání (YUV, YIQ). 2.3 Kontrolní otázky 1. Jakou funkci mají tyčinky a čípky?
14 14 KAPITOLA 2. BARVY, BARVY, BARVIČKY 2. Popište aditivní metodu mísení barev. 3. Popište subtraktivní metodu mísení barev. 4. Co znamená RGB? 5. Jaká barva vznikne smísením červené a zelené? 6. Proč se zavedly barevné modely HSV a HLS? 7. Co to je CIE? 2.4 Literatura Žára, Beneš, Sochor, Felkel - Moderní počítačová grafika
15 Kapitola 3 Úpravy obrazu V následující kapitole se seznámíme se základními typy úpravy obrazu. První z nich je transformace barev pro výstupní zařízení, dále práce s barvami a expozicí pomocí histogramu a úpravy obrázků s vysokým dynanickým rozlišením (obrázky obsahující zdroj světla). Z metod transformace obrázku uvedeme warping a morfing, které se využívají v grafickém designu. 3.1 Transformace barev Úprava barvy, například zesvětlení či ztmavení, přidání konstrastu atd., se velice často používají při úpravě fotografií. Práce s barvami je ale potřebná i při tisku. Obraz je upraven s ohledem na technologii barevného tisku a sníží se celkový počet použitých barev. Pokud omezíme počet barev, dochází automaticky ke ztrátě informace. Současné algoritmy se snaží, aby oko člověka tyto změny nedokázalo poznat. Metody, které se používají, se nazývají polotónování (halftoning) a rozptylování (dithering). Obě metody vychází z toho, že naše oko dokáže mít vjem jednoho odstínu barvy jako kombinace několika barevných bodů blízko u sebe. Podle obr. 3.1 vidíme. Na předmět, který obsahuje fialovou a žlutou dopadá světlo. Vyruší se a výsledná barva, kterou oko přijímá a mozek interpretuje, je červená. Takže, když se díváte na knihu s červeným přebalem, tak pod mikroskopem byste viděli sít fialových a žlutých bodů. Analogicky je to na obrázku pro ostatní barvy. Obrázek 3.1: Odraz a vstřebávání paprsků světla 15
16 16 KAPITOLA 3. ÚPRAVY OBRAZU 3.2 Warping a morfing Hlavní využití obou transformací je v oblasti počítačové animace. Filmový průmysl pracuje s měnícími se objekty a scény nejsou reálné, pouze se generují na výkonných počítačích. Objekty se mohou různě pohybovat, vzájemně ovlivňovat a v některých případech i měnit svůj tvar. Pokud chceme tento jev zachytit i v počítačové animaci, používáme animační techniku známou jako morphing. Morphing samozřejmě nemá uplatnění pouze v animaci přírodních jevů (růstové simulace), ale používá se zejména pro tvorbu nejrůznějších speciálních efektů. Warping se spíše užívá v oblasti designu, kdy nepotřebujeme vidět průběh transformace, ale pouze výsledek. Warping = metoda, která z jednoho obrázků vykreslí zmodifikovaný jiný (zkřivený, deformavaný). Změnu určí uživatel sám na původním obrázku. Morfing = posloupnost, která zobrazuje přechod od jednoho k druhému obrázku. Jako vstup jsou potřeba dva obrázky původní a ten, ke kterému chceme přejít Warping Warping lze podle způsobu provedení rozdělit do dvou tříd. První třída pouze předepsanou transformací upraví vložený obrázek, například udělá vlnu či spirálu. Druhá třída obsahuje obecné metody, které umožňují libovolnou transformaci. Lze použít sít ový či úsečkový warping. Sít ový pokryje obrázek sítí křivek (většinou bezierovách kubik či spline křivek) a těmi uživatel pohybuje. Ty ovlivní pixely obrázku a podle algoritmu jej přepočítají. Úsečkový warping se používá při lokálních změnách obrazu. Na obr. 3.2 jsou v prvním okně vyznačeny části, které se budou měnit. Ve druhém okně je potom výsledná proměna. Obrázek 3.2: Příklad úsečkového warpingu
17 3.3. OBRAZY S VYSOKÝM DYNAMICKÝM ROZSAHEM(HIGH DYNAMIC RANGE HDR) Morfing Úlohu morphingu lze formalizovat následovně. Máme dány dva zdrojové objekty výchozí a cílový. Úkolem je nalézt transformaci mezi výchozím a cílovým objektem. Takových transformací existuje jistě velké množství, ale pro nás je důležitá ta třída transformací, která působí reálným dojmem. Obrázek 3.3: Morfing 3.3 Obrazy s vysokým dynamickým rozsahem (High Dynamic Range HDR) Ve svém okolí můžeme vnímat různé rozsahy intenzity světla. V tmavém lese vidíme stíny s jasem v řádu 10 5 cd m 2, ale písek na pláži v poledne může mít jas až Dynamický rozsah obrázku se vyjadřuje jako poměr nejvyššího k nejnižšímu jasu. Obyčejná scéna z výletu má dynamický rozsah kolem 15:1, ale stůl s rozsvícenou lampou může mít i rozsah :1. Pokud sami děláte fotografie, není možné na jedno nastavení expozice zachytit nejtmavější a nejsvětlejší části scény. Obrázky s HDR (High Dynamic Range) se získávají např. kombinací různých snímků s různou expozicí nebo jsou k dispozici speciální snímače. Monitory mají dynamický rozsah asi 100:1, tiskárny kolem 30:1. Obrázek se tedy musí transformovat (mapovat) na daný rozsah. Tomuto úkolu se říká mapování tónů (tone mapping). Tato metoda má za úkol ze získaného HDR snímku udělat obrázek na výstupní zařízení, který bude odpovídat scéně, jak ji viděl člověk, který snímek vytvořil. Existuje několik metod k mapování tónů globální či lokální, které dokáží s různou přesností zrekonstruovat a zobrazit původní scénu. Zajímavé a v praxi užitečné (například ve filmu) jsou časově závislé metody, které berou v úvahu časovou asiaci oka. Ve tmě se oko přizpůsobí a po nějaké době slabě vnímá okolní předměty.
18 18 KAPITOLA 3. ÚPRAVY OBRAZU 3.4 Histogram Histogram je graf, který vám dá přehled o tom, kolik pixelů je na vašem snímku obsaženo ve škále od nejtemnější do největšího jasu; bývá ve výbavě lepších editorů a velmi dobrých fotoaparátů. Jeho hlavní využití je při kontrole expozice dané fotografie a její další úpravě v počítači. Na malém display digitálního fotoaparátu je těžko rozeznatelná správná či špatná expozice, proto se v lepších fotoaparátech zobrazuje histogram. Pokud tuto funkci ve fotoaparátu nemáte, nabízí se možnost zpětné úpravy histogramu ve vhodném počítačovém programu (např. Photoshop, Gimp free software). Jak tedy rozpoznat správně exponovanou fotografii? Musí obsahovat všechny úrovně jasu. Je však nutné si dát pozor na snímky, které jsou tmavší a obsahují pouze malé množství světlých pixelů (viz obr. 3.4). Obrázek 3.4: Tmavý obrázek pokoje a jeho histogram Špatně naexponované snímky mají silně zastoupeny pouze některé z krajních hodnot (bílá vpravo nebo černá vlevo v grafu) jak je vidět na obr Pro barevné fotografie jsou většinou ukázány tři histogramy pro každou z barevných složek RGB. Výsledný jasový diagram celé fotografie se vypočítá podle vztahu Jas = 0.3 R G B U barevných fotografií si je nutné dávat pozor na přeexponování pouze jedné barvy, která ve výsledném jasovém diagramu nemusí být poznat, nebot ve výpočtu jasu má jen 30-ti procentní vliv. Obrázek 3.5: RGB histogram
19 3.5. KONTROLNÍ OTÁZKY 19 Obrázek 3.6: Histogram špatně naexponovaného obrázku podexponovaný a přeexponovaný obrázek Shrnutí Histogram je graf, který zobrazuje počet jednotlivých jasových stupňů v obrázku. Pokud máte fotoaparát se zobrazením histogramu, snažte se, aby pro vaše fotky vypadal podobně jako na obr. Když tuto funkci nemáte, zkontrolujte si histogram fotografií v programu v počítači a upravte jej na ideální tvar. Obrázek 3.7: Histogram ideální expozice 3.5 Kontrolní otázky 1. Co je to warping? 2. Popište princip morfingu. 3. Co znamená zkratka HDR? 4. Kdy vznikají obrázky s HDR? 5. Co je to histogram? 6. Jak se dá histogram využít při úpravě fotografií?
20 20 KAPITOLA 3. ÚPRAVY OBRAZU 3.6 Literatura Úprava barev Warping a morphing (česky) (demo ukázky) (morfing fraktálů) Práce s obrázky s HDR Histogram
21 Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní zařízení potřebujeme zajistit co nejvěrnější podobnost reálného a zobrazovaného modelu. Omezíme se v tomto textu na rastrové výstupní zařízení, jehož nejjednodušším grafickým prvkem je bod. Protože složitější objekty jsou jen skládankou jednodušších objektů, potřebujeme mít k dispozici algoritmy na výpočet polohy bodů jednoduchých objektů jako úsečky, kružnice, elipsy, oblouků, atd... Ukážeme si některé algoritmy pro výpočet bodů úsečky a kružnice. 4.1 Úsečka a lomenná čára Úsečka je nejjednodušším grafickým prvkem. Jejich skládáním se dají vytvářet lomené čáry a další křivočaré útvary. Vykreslení úsečky by mělo být co nejefektivnější a nejrychlejší. Úsečka lze zapsat dvěma způsoby: 1. souřadnicemi počátečního a koncového bodu [x 1, y 1 ], [x 2, y 2 ], 2. pomocí počátečního bodu [x 1, y 1 ] a směrového vektoru m = x y = y 2 y 1 x 2 x 1 Podle velikost směrnice m se určí, vzhledem ke které ose se bude vzorkovat. Pro m < 1 je úsečka blíž k ose x a tedy bude vzorkována vzhledem k ní. Pro m > 1 je úsečka vzorkována na ose y a pro m = 1 může být řídící osa libovolná. Rozlišujeme dva typy posloupnosti pixelů (obr. 4.1): 1. osmispojitá (8-connected) - každý pixel má osm sousedů čtyři ve vodorovném a svislém směru a čtyři úhlopříčně 21
22 22 KAPITOLA 4. RASTERIZACE OBJEKTŮ 2. čtyřspojitá (4-connected) - používá se zřídka, každý pixel má jen čtyři sousedy ve vodorovném s svislém směru. Obrázek 4.1: 4-spojitý a 8-spojitý pixel Vzhledem ke zvolenému typu pixelů se objekty vykreslují vybarvováním pixelů, které co nejvíce vystihují úsečku. Pro určení, které pixely budou vykresleny existuje několik algoritmů. My si ukážeme algoritmus DDA a Bresenhamův algoritmus pro kresbu úsečky Algoritmus DDA Jedná se o přírůstkový algoritmus pro výpočet bodů úsečky. Postup spočívá v tom, že postupně zvedáme o jeden pixel hodnoty na x-ové souřadné ose a dopočítáváme odpovídající bod y. Jelikož jsou souřadnice pixelů vždy celá čísla, provede s zaokrouhlení hodnoty a pixel se vykreslí. Algoritmus je jednoduchý, ale relativně pomalý, protože pracuje v oboru reálných čísel. Alogitmus pro rasterizaci ve směru osy x. Pro m > 1 je prováděna rasterizace ve směru osy y a v algoritmu se zamění operace s x a y. 1. Z koncových bodů [x 1, y 1 ], [x 2, y 2 ] urči směrnici m podle vzorce výše. 2. Inicializuj bod [x, y] hodnotou [x 1, y 1 ]. 3. Dokud je x x 2 opakuj: (a) Vykresli bod [x, zaokrouhlené (y)] (b) x = x + 1 (c) y = y + m
23 4.1. ÚSEČKA A LOMENNÁ ČÁRA 23 Obrázek 4.2: Vykreslení úsečky algoritmem DDA (rasterizace ve směru osy x) Bresenhamův algoritmus pro kresbu úsečky Tento algoritmus byl objeven v šedesátých letech minulého století panem Bresenhamem. Jeho výhoda je v tom, že pracuje pouze s celými čísly. Víme, že od daného pixelu [x, y] můžeme umístit další pixel (při rasterizace po ose x) pouze na dvou pozicích [x+1, y] nebo [x+1, y +1]. Rozdíly mezi souřadnicí y středů uvedených pixelů a skutečnou souřadnicí y označíme d 1, d 2 a můžeme je celočíselně vypočítat z parametrické rovnice kreslené úsečky. Jejich rozdíl potom vyhodnotíme. Pokud je kladný, je d 1 > d 2 a bližším pixelem je ten ve vzdálenosti d 2. Postup je názorně předveden na obr Obrázek 4.3: Princip Bresenhamova algoritmu Na obr. 4.4 je ukázka rasterizace obecné úsečky a obdélníka Kresba silné a přerušované čáry Silnou čáru můžeme kreslit pomocí dvou typů algoritmů. Jednoduchý postup je rychlý, ale dochází v něm k nepřesnostem. Jedná se o Bresenhamův algoritmus, kdy se v každém kroku vykresluje několik pixelů nad sebou či vedle sebe. Má však
24 24 KAPITOLA 4. RASTERIZACE OBJEKTŮ Obrázek 4.4: dd nevýhody. První z nich je, že se tloušt ka čáry liší podle jejího sklonu (vzhledem k metrice rastru) a druhou nevýhodou je zakončení čar, které je rovnoběžné s některou souřadnou osou. Přesný postup je však početně náročnější. Pracuje na principu vyplňování plochy, která určuje silnou čáru. Jako nejjednodušší tvar se používá obdélník, u něj je problém při napojování lomené čáry. Vhodnější je kresba pomocí obdélníků se zakulacenými rohy. Pro kresbu přerušované čáry opět uvedeme dva algoritmy. První je založen na známém Bresenhamově algoritmu, kdy přidáme informaci o tom, zda jsme v úseku, který má být zobrazen či ne. Nevýhodou je opět metrika na rastrovém poli. Při různých sklonech úsečky budou dělící dílky nestejně dlouhé, což opticky působí nepřirozeně. V praxi se většinou používá přesnější postup, založený na výpočtu délek dělících úseček. Potom se teprve použije známý algoritmus pro každý dílek samostatně. V závislosti na kvalitě programu je možné pozorovat různé zobrazení koncových dílku. Některé algritmy umí rozdělit úsečku tak, aby poslední dílek byl vždy viditelný. 4.2 Kružnice a elipsa Kružnice se klasicky definuje středem a poloměrem. Elipsa je zase dána středem a velikostí hlavní a vedlejší poloosy. Otočením ji lze umístit do libovolné polohy. Při kresbě eliptických či kružnicových oblouků je navíc nutné definovat počáteční a koncový bod oblouku. Při výpočtu bodů na kružnici stačí nalézt souřadnice oblouku 45 stupňů (obr. 4.6 vlevo), nebot všechny další body dostaneme záměnou souřadnic a změnou znamének.
25 4.3. KONTROLNÍ OTÁZKY 25 Obrázek 4.5: Kresba silné čáry v rastru Princip je opět na bázi Bresenhamova algoritmu pro úsečky. Jsme ve výchozím pixelu a ptáme se, kam ted můžu jít a testujeme, která pozice je blíž vykreslované kružnici (obr. 4.6 vpravo). Výhodu tohoto postupu je opět rychlost, nebot vždy pracujeme pouze s celými čísly. Obrázek 4.6: Rasterizace kružnice Elipsa se na rozdíl od kružnice musí vygenerovat pro celý kvadrant, tj. devadesát stupňů. Opět se použije Bresenhamův algortimus pouze s celočíselnou aritmetikou. Jediný rozdíl je ve tvaru testovací funkce, který z možných kandidátů na další bod leží blíž elipse. 4.3 Kontrolní otázky 1. Popište Bresenhamův algoritmus kreslení úsečky. 2. Co je algoritmus DDA?
26 26 KAPITOLA 4. RASTERIZACE OBJEKTŮ 3. Jaký je rozdíl mezi 8-spojitým a 4-spojitým pixelem. 4. Jaký je princip kreslení přerušované čáry? 5. Jaký je princip kreslení tlusté čáry? 6. Popište myšlenku kreslení kružnice. 4.4 Literatura Bresenham algoritmus (česky s Javou) GraphicsNotes/Bresenhams-Algorithm/Bresenhams-Algorithm.html s_line_algorithm Kresba tlusté čáry a kružnice 3_CoordinateSpace.html // algoritmus pro kružnici
27 Kapitola 5 Řešení viditelnosti Řešit viditelnost ve scéně umí většina grafických programů. Cílem je určit ty objekty, resp. jejich části, které jsou viditelné z určitého místa. Tyto algoritmy jsou vždy svázány s určitou reprezentací objektů ve scéně. Podle toho, v jakém tvaru jsou výstupní data, rozdělujeme algoritmy do dvou skupin: 1. Vektorové algoritmy jejich výstupem je soubor geometrických prvků, např. úseček, které představují viditelné části zobrazovaných objektů. Používá se především v technických aplikacích. Bez změny viditelnosti lze plynuje úsečky zvětšovat. Nevýhodou je, že při numerické chybě je špatně celá úsečka, což výrazně mění celý pohled. 2. Rastrové algoritmy pracují pouze v rastru. Výsledek je obraz, jehož jednotlivé pixely obsahují barvu odpovídajících viditelných ploch.nevýhodou je pevný rozměr obrázku. Většina metod patří do této skupiny. Mezi rastrové algoritmy patří z-buffer, malířův algoritmus či algoritmus plovoucího horizontu. 5.1 Pamět hloubky z-buffer Tato metoda patří k nejznámějším a nejefektivnějším. Základem je použití paměti hloubky z-bufferu. Ta tvoří dvojrozměrné pole, jehož rozměry odpovídají velikosti obrazu. Každá položka paměti hloubky obsahuje souřadnici z toho bodu, který leží nejblíže pozorovateli a jehož průmět leží v odpovídajícím pixelu v rastru. Na obr. vidíme scénu a odpovídající z-buffer. Čím blíže je předmět k pozorovateli, tím světlejší má odstín. Výhody metody: není třeba třídit, umí správně vykreslit nestandardní situace (např. průseky), rychlost, jednoduchost výpočtu. 27
28 28 KAPITOLA 5. ŘEŠENÍ VIDITELNOSTI Obrázek 5.1: Z-buffer Nevýhody metody: větší pamět ová náročnost, některé pixely se vícekrát překreslují. Algoritmus Pro každý pixel ukládáme jeho barvu a vzdálenost od pozorovatele (z-buffer). V inicializační části nastavíme barvu pro všechny pixely na barvu pozadí, pamět hloubky vypníme hodnotou minus nekonečno. 1. Každou plochu rozlož na pixely a pro každý její pixel [x i, y i ] stanov hloubku z i 2. Má-li z i větší hodnotu než položka [x i, y i ] v z-bufferu pak: a. obarvi pixel[x i, y i ] v obrazové paměti barvou této plochy b. položku [x i, y i ] v z-bufferu aktualizuj hodnotou z i Obrázek 5.2: Princip fungování algoritmu z-buffer
29 5.2. MALÍŘŮV ALGORITMUS PAINTER S ALGORITHM Malířův algoritmus Painter s algorithm Algoritmus je založen na myšlence vykreslování všech ploch postupně odzadu dopředu - přes objekty v pozadí se kreslí objekty v popředí. Inspirováno představou práce malíře který na podkladovou barevnou vrstvu nanáší další vrstvy (viz obrázek 5.3). Obrázek 5.3: Princip malířova algoritmu Algoritmus Nejprve nalezneme pro každou plochu její nejmenší z-ovou souřadnici. a podle ní plochy uspořádáme. První plocha v seznamu je označena jako aktivní a je podrobena několika testům překrývání s ostatními plochami a pokud lze po nich rozhodnout, že leží za všemi ostatními je vykreslena a vyřazena ze seznamu. V opačném případě dojde v seznamu k výměně aktivní plochy s plochou u které dopadly všechny testy negativně. Malířův algoritmus není vhodný pro všechny případy. Některé pozice (protínání) zobrazovaných objektů mohou vést ke špatnému zobrazení. Pokud se objekty navzájem překrývají může to vést až k zacyklení algoritmu. Takový případ nastane například při situaci na obrázku 5.4. Obrázek 5.4: Problémový případ pro malířův algoritmus Setřid objekty podle hloubky. Vstup: plošky, které se neprotínají for všechny objekty v určeném pořadí do { for každý pixel[x][y] pokrytý objektem do{ Obarvi pixel[x][y] barvou objektu. } }
30 30 KAPITOLA 5. ŘEŠENÍ VIDITELNOSTI 5.3 Malířův algoritmus se stromem BSP BSP (Binary Space Partitioning trees) jsou datové struktury, které popisují danou scénu s jejími vazbami. Pomáhají urychlit řadu algoritmů, ale jsou vhodné pouze pro statické scény. Popisují složení objektů a jejich vzájemné vazby. Při zobrazování procházíme strom BSP od kořene a v každém uzlu určujeme, který poloprostor je vůči poyorovateli vzdálenější a který bližší. Nejprve vykreslíme vzdálenější část prostoru, poté obsah aktuálního uzlu a nakonec oblast bližší pozorovateli. Obrázek 5.5: BSP strom 5.4 Metoda vržení paprsku Tato metoda spočívá ve vysílání paprsku od pozorovatele a následné hledání průsečíků s objekty ve scéně a určení toho, který je pozorovateli nejblíže. Pokud paprsek protíná pouze jeden objekt, je situace jednoduchá. Jestliže protíná průnik více těles, je nutné užít množinové operace. for každý pixel[x][y] obrazu do { /* Nejbližší objekt zasažený promítacím paprskem */ for každý objekt ve scéně do if existuje průsečík paprsku s objektem { Porovnej hloubku z a vyber bližší objekt }. if nalezen objekt { Obarvi pixel[x][y] barvou objektu } else { Obarvi pixel[x][y] barvou pozadí } }
31 5.5. KONTROLNÍ OTÁZKY Kontrolní otázky 1. Na jaké druhy rozdělujeme algoritmy viditelnosti podle typu výstupu? 2. Jaké jsou výhody a nevýhody z-bufferu? 3. Popište princip z-buffer určování viditelnosti. 4. Popište princip malířova algoritmu. 5. Jaké jsou nevýhody malířova algoritmu? 6. Co je to BSP strom? 7. Popište základní myšlenku metody vržení paprsku. 5.6 Literatura Z-buffer =view&id=8721&itemid=44&limit=1&limitstart=3 Malířův algoritmus s_algorithm Žára, Beneš, Sochor, Felkel - Moderní počítačová grafika BSP stromy
32 32 KAPITOLA 5. ŘEŠENÍ VIDITELNOSTI
33 Kapitola 6 Objektově orientované programování Objektově orientované programování (zkracováno na OOP, z anglického Object oriented programming) je metodika vývoje softwaru, založená na těchto myšlenkách, koncepci: 6.1 Koncepce Objekty jednotlivé prvky modelované reality (jak data, tak související funkčnost) jsou v programu seskupeny do entit, nazývaných objekty. Objekty si pamatují svůj stav a navenek poskytují operace (přístupné jako metody pro volání). Abstrakce programátor, potažmo program, který vytváří, může abstrahovat od některých detailů práce jednotlivých objektů. Každý objekt pracuje jako černá skříňka, která dokáže provádět určené činnosti a komunikovat s okolím, aniž by vyžadovala znalost způsobu, kterým vnitřně pracuje. Zapouzdření zaručuje, že objekt nemůže přímo přistupovat k vnitřním parametrům jiných objektů, což by mohlo vést k nekonzistenci. Každý objekt navenek zpřístupňuje rozhraní, pomocí kterého (a nijak jinak) se s objektem pracuje. Skládání objekt může využívat služeb jiných objektů tak, že je požádá o provedení operace. Dědičnost objekty jsou organizovány stromovým způsobem, kdy objekty nějakého druhu mohou dědit z jiného druhu objektů, čímž přebírají jejich schopnosti, ke kterým pouze přidávají svoje vlastní rozšíření. Tato myšlenka se obvykle implementuje pomocí rozdělení objektů do tříd, přičemž každý objekt je instancí nějaké třídy. Každá třída pak může dědit od jiné třídy (v některých programovacích jazycích i z několika jiných tříd). 33
34 34 KAPITOLA 6. OBJEKTOVĚ ORIENTOVANÉ PROGRAMOVÁNÍ Polymorfismus odkazovaný objekt se chová podle toho, jaký je jeho skutečný typ. Pokud několik objektů poskytuje stejné rozhraní, pracuje se s nimi stejným způsobem, ale jejich konkrétní chování se liší. V praxi se tato vlastnost projevuje např. tak, že na místo, kde je očekávána instance nějaké třídy, můžeme dosadit i instanci libovolné její podtřídy (třídy, která přímo či nepřímo z této třídy dědí), která se může chovat jinak, než by se chovala instance rodičovské třídy, ovšem v rámci mantinelů, daných popisem rozhraní. Pokud předchozí koncepci již rozumíme, bude pro nás pochopení objektově orientovaného programování jednoduché. Pokud však nerozumíme, což se předpokládá, nevadí. K dalšímu vysvětlení nám vřele pomůže ukázkový příklad. 6.2 Ukázkový příklad Nejprve si představme, že celý svět se skládá z objektů. Objektem můžeme rozumět města, ulice, domy, stromy, auta, silnice, atd. Aby se nám tyto objekty nepletli, rozdělíme si je na různé druhy, resp. různé třídy. V programování bývá nejčastějším ukázkovým příkladem tříd třída aut. Představme si auto (objekt). Každé auto, pokud neuvažujeme některé speciální případy, je přesně určeno státní poznávací značkou, respektive písmeny a číslicemi na SPZ. Můžeme tedy říci, že SPZ je charakteristická vlastnost auta, neboli vlastnost objektu. Pochopitelně má každé auto mnohem více vlastností, jako je například značka, barva, typ, objem motoru, atd. 6.3 Definice třídy Nadefinujme si tedy třídu aut, tak aby obsahovala tyto vlastnosti: spz, typ, objem Motoru. Třídu aut, jak je v Delphi zvykem, nazveme TAuto. V této třídě budeme uvažovat spz a typ jako řetězce a objemmotoru jako celočíselnou hodnotu. Syntaxe této třídy je následující: type TAuto = class spz, typ: String; objemmotoru: Integer; end; Tuto definici nové třídy TAuto umístíme v Delphi do oblasti, kde definujeme nové typy, tedy za příkaz type. Každá nová třída se zadává stejným způsobem: jmenotridy = class, kde class nám udává, že se jedná o třídu. Po výčtu vlastností třídy, ukončíme definici příkazem end;, jak je vidět výše.
35 6.4. VYTVOŘENÍ OBJEKTU Vytvoření objektu Nyní máme nadefinovanou třídu TAuto, ale zatím nemáme žádný objekt. Představme si, že vlastníme dva automobily (objekty): služební a soukromý. Aby jsme mohli tyto objekty vytvořit, musíme si je nejdříve deklarovat. Objekty budeme deklarovat stejně jako proměnné v části programu určené k deklaraci (tedy za klíčovým slovem var) a tyto objekty budou typu TAuto. var sluzebniauto, soukromeauto: TAuto; Abychom mohli s objekty pracovat, je zapotřebí je nejdříve vytvořit. Vytvoření se provede pomocí konstruktoru (konstruktor bude vysvětlen později) tímto způsobem: sluzebniauto := TAuto.Create; soukromeauto := TAuto.Create; Takto byli vytvořeny dva objekty sluzebniauto a soukromeauto. Přesněji řečeno, jsme si uvolnily v paměti počítače místo pro tyto objekty a nyní s nimi můžeme pracovat. V objektově orientovaném programování je zapotřebí stále pamatovat na to, že objekty musíme nejdříve vytvořit a až pak s nimi můžeme pracovat. Jestliže už objekt k práci nepotřebujeme, je zapotřebí objekt zrušit, přesněji uvolnit zabrané místo v paměti počítače. To se provede příkazem Free následovně: sluzebniauto.free; soukromeauto.free; Po tomto příkazu již naše objekty neexistují, nemůžeme tedy s nimi pracovat. 6.5 Vlastnosti objektu Vrat me se nyní trochu zpět a předpokládejme, že máme vytvořeny objekty sluzebni Auto a soukromeauto. Tyto objekty jsou typu TAuto a tudíž obsahují vlastnosti spz, typ a objemmotoru. Pokud chceme přistupovat k vlastnostem objektu, budeme k nim přistupovat pomocí tečky. Pokud tedy chceme zadat vlastnosti našich aut, uděláme to takto: sluzebniauto.spz := 1B ; sluzebniauto.typ := Škoda ; sluzebniauto.objemmotoru := 1600; soukromeauto.spz := 2B ; soukromeauto.typ := Porshe ; soukromeauto.objemmotoru := 3200;
36 36 KAPITOLA 6. OBJEKTOVĚ ORIENTOVANÉ PROGRAMOVÁNÍ Naopak, pokud budeme chtít vypsat do dialogového okna typ našeho služebního auta, napíšeme tento příkaz: MessageDlg( Typ mého soukromého auta je: + soukromeauto.typ, mtinformation, [mbok], 0); 6.6 Metody objektu Dosud jsme si vysvětlili, že každý objekt může obsahovat různé vlastnosti a my k nim pak jednoduše pomocí tečky přistupujeme. Nabízí se otázka: K čemu je to dobré?, když stejně tak funguje v Delphi záznam, neboli record. Vysvětlení je jednoduché. Objekty nám nabízejí mnohem více možností a jednou z nich jsou metody, neboli funkce či procedury uvnitř objektu. Vrat me se zpět k našim autům a chtějme sledovat stav benzínu v nádrži pomocí vlastnosti palivo. Dále budeme předpokládat, že množství paliva ubývá, pokud ujedeme nějakou vzdálenost v závislosti na spotřebě (spotreba) a přibývá, pokud tankujeme na čerpací stanici. Tyto dva poznatky nám zaručí procedury Ujed a Tankuj. Deklarace třídy TAuto bude vypadat následovně: type TAuto = class spz, typ: String; objemmotoru: Integer; palivo, spotreba: Double; procedure Ujed(vzdalenost: Double); procedure Tankuj(mnozstviPaliva: Double); end; Dále je zapotřebí vytvořit těla našich nových dvou procedur. To provedeme kdekoliv v části zdrojového textu, tedy za příkazem implementation, jak jsme zvyklí. Procedury budou vypadat následovně: procedure TAuto.Ujed(vzdalenost: Double); begin palivo := palivo - vzdalenost * (spotreba / 100); end; procedure TAuto.Tankuj(mnozstviPaliva: Double); begin palivo := palivo + mnozstvipaliva; end;
37 6.7. KONSTRUKTOR A DESTRUKTOR OBJEKTU 37 Nyní si všimněme, že při definici nových procedur jsme jako název uvedli TAuto. Ujed, resp. TAuto.Tankuj místo pouhého Ujed, resp. Tankuj. Důvod je velmi jednoduchý. Pokud bychom v programu měli více tříd, které by obsahovaly proceduru Ujed a přitom v každé třídě by procedura měla jinou definici, nastal by při překladu zdrojového textu zmatek. Další důležitý poznatek je v proměnné palivo. Všimněme si, že neuvádíme např. soukromeauto.palivo, ale pouze palivo. Jak tedy program pozná jaké palivo má změnit? Jednoduše. Změní palivo toho objektu, na kterém byla daná procedura volána. Tedy pokud voláme nad objektem soukromého auta (soukromeauto. Ujed(50)), odečte požadovanou hodnotu z paliva tohoto objektu, tedy z soukromeauto. palivo. 6.7 Konstruktor a destruktor objektu Už dříve jsme se zmínili o konstruktoru. Používá se k tomu, aby nám vytvořil objekt, resp. aby alokoval místo v paměti pro tento náš objekt. Často je však velmi vhodné, když už při vytváření objektu specifikujeme některé vlastnosti, v našem případě spz, typ, objemmotoru, palivo a spotreba. Docílíme toho tak, že předefinujeme klasický konstruktor Delphi. Do definice třídy TAuto přidáme zmínku o tom, že budeme konstruktor vytvářet vlastní. Definice třídy pak bude vypadat: type TAuto = class spz, typ: String; objemmotoru: Integer; palivo, spotreba: Double; constructor Create(sspz, ttyp: String; oobjemmotoru: Integer; sspotreba: Double); procedure Ujed(vzdalenost: Double); procedure Tankuj(mnozstviPaliva: Double); end; Konstruktor je uveden klíčovým slovem constructor a název může být jakýkoliv, avšak je vhodné název ponechat tak, jak je zvykem, tedy Create. Definice samotného konstruktoru se opět provádí v části implementace a může vypadat takto: constructor TAuto.Create(sspz, ttyp: String; oobjemmotoru: Integer; sspotreba: Double); begin inherited Create;
38 38 KAPITOLA 6. OBJEKTOVĚ ORIENTOVANÉ PROGRAMOVÁNÍ spz := sspz; typ := ttyp; objemmotoru := oobjemmotoru; palivo := 0; spotreba := sspotreba; end; Příkaz inheroted Create nám slouží k vlastnímu vytvoření objektu, další příkazy jsou snad zřejmé a jednoduché. Pokud tedy budeme chtít vytvořit opět služební a soukromý vůz, budeme postupovat takto: sluzebniauto := TAuto.Create( 1B , Škoda, 1600, 7.8); soukromeauto := TAuto.Create( 2B , Porshe, 3200, 11.4); Někdy je zapotřebí něco provést, než se objekt zruší. Třeba uložit důležitá data do souboru. K tomu nám hravě poslouží předefinování destruktoru. Je to stejné jako v případě konstruktoru, pouze klíčové slovo je destructor a je běžné používání názvu Destroy. Destruktor pak může vypadat takto: destructor TAuto.Destroy; begin UlozeniDat; inherited Destroy; end; Pozorný čtenář si všimne, že výše jsme k zrušení objektu použili příkazu Free, nikoliv Destroy. Bylo to z důvodu, že procedura Free nejdříve zjistí zda daný objekt existuje a pokud existuje, tak pak teprve volá destruktor třídy Destroy. 6.8 Dědičnost Dědičnost je další důležitou vlastností při objektově orientovaném programování. Představme si, že máme již vytvořenou třídu TAuto, které splňuje požadavky pro veškerá auta. Nyní však budeme chtít vytvořit třídy pro auta osobní a nákladní, které budou mít stejné vlastnosti jako třída TAuto. Navíc u třídy TOsobniAuto budeme požadovat vlastnost pocetmist a u třídy TNakladniAuto budeme požadovat vlastnost nosnost. Díky dědičnosti v OOP je definice těchto tříd velmi jednoduchá: type TOsobniAuto = class(tauto) pocetmist: Integer; end; TNakladniAuto = class(tauto) nosnost: Integer; end;
39 6.9. KONTROLNÍ OTÁZKY 39 Jak je vidět, syntaxe nových tříd je velmi jednoduchá, stačí pouze do závorky za příkaz class napsat jméno třídy, po které bude nová třída dědit vlastnosti a metody. Znamená to tedy, že např. nová třída TOsobniAuto obsahuje vlastnosti spz, typ, objemmotoru, palivo, spotreba a pocetmist a metody Ujed a Tankuj. Pokud chceme aby vlastnost pocetmist byla zadávána již při vytváření objektu osobního auta, musíme změnit konstruktor třídy TOsobniAuto. To uděláme obdobně, jako jsme to dělali ve třídě TAuto. 6.9 Kontrolní otázky 6.10 Literatura
40 40 KAPITOLA 6. OBJEKTOVĚ ORIENTOVANÉ PROGRAMOVÁNÍ
41 Kapitola 7 Křivky a plochy technické praxe V technické praxi se setkáváme s tím, že potřebujeme křivky a plochy, které se dají libovolně upravovat a zároveň je jejich matematické vyjádření jednoduché. V šedesátých letech minulého století se objevily Fergusonovy, později Bézierovy a Coonsovy křivky a plochy. Na ně navázaly splajny a v současné době se v moderních CAD systémech používají NURBS křivky a plochy. V roce 2003 se ve studiu Maya objevily plochy T-spline. 7.1 Základní princip Základem všech výše uvedených ploch a křivek jsou řídicí body. Křivka či plocha jimi obecně neprochází, jedná se tedy o aproximační křivky a plochy. K těmto bodů jsou podle typu vybrány řídicí bázové funkce - bersteinovy polynomy pro bézierovy křivky a plochy, B-spline funkce pro splajny a NURBS. Výsledný bod na křivce či ploše je dán jako lineární kombinace řídicího bodu s funkci k němu patřící. Vysvětlíme si to na Bézierově křivce. Máme dány čtyři řídicí body P 0, P 1, P 2, P 3 a bázové bersteinovy polynomy: B 0 (t) = (1 t) 3 B 1 (t) = 3t (1 t) 2 (7.1) B 2 (t) = 3t 2 (1 t) B 3 (t) = t 3 Parametr t probíhá v intervalu od nuly do jedné a pro každou hodnotu určí jeden bod na výsledné křivce. Vezmeme pevně parametr t roven 0, 25 a vypočítáme výsledný bod jako kombinaci C(0, 25) = P 0 B 0 (0, 25) + P 1 B 1 (0, 25) + P 2 B 2 (0, 25) + P 3 B 3 (0, 25) 41
42 42 KAPITOLA 7. KŘIVKY A PLOCHY TECHNICKÉ PRAXE Vypočítáme hodnoty bersteinových polynomů a pak postupně vezmeme x, y, z- ovou souřadnici jednotlivých bodů a dostaneme tři čísla, která udávají výsledný bod na křivce. Matematický zápise je: Q(t) = 3 P i B i (t), t 0, 1 (7.2) i=0 Pro plochy je výpočet obtížnější. Jako vstup máme sít řídicích bodů a tedy každý bod má dva indexy řádkový a sloupcový. Při výpočtu přiřadíme každému bodu dvě bázové funkce, které odpovídají indexům daného bodu, tzn. bod P 31 bude násoben bersteinovými polynomy B 3 a B 1. Jak víme plocha je dána dvěma parametry, proto první funkce bude vyčíslena s prvním parametrem a druhá s druhým parametrem. Matematicky můžeme všechny tyto kombinace zapsat jako: S(r, s) = 3 3 P ij B i (r)b j (s), (7.3) i=0 j=0 Tento princip funguje i pro další typy křivek a ploch jen s různými tvary bázových polynomů. 7.2 Základní typy křivek a ploch technické praxe Fergusonovy křivky a plochy Základní oblouk je určen čtyřmi body P 0, P 1, P 2, P 3. Křivka má krajní body P 0, P 3. Tečné vektory v těchto bodech jsou P 0 P 1, P 3 P 2. Velikost těchto vektorů ovlivňuje tvar křivky čím je vektor větší, tím více se křivka k vektoru přibližuje. Křivka je definována parametrickými rovnicemi: Q(t) = 3 P i F i (t), t 0, 1 (7.4) i=0 F 0 (t) = t 3 t 2 t + 1 F 1 (t) = t 3 2t 2 + t (7.5) F 2 (t) = 3t 3 + 4t 2 F 3 (t) = t 3 t 2 Dvojrozměrným zobecněním Fergusonových křivek dostaneme Fergusonovy plochy. Jsou dány sítí reálných bodů P ij a jejich rovnice je:
43 7.2. ZÁKLADNÍ TYPY KŘIVEK A PLOCH TECHNICKÉ PRAXE 43 Obrázek 7.1: Fergusonova plocha. 3 3 Q(r, s) = P ij F i (r)f j (s), (7.6) i=0 j=0 kde F i jsou polynomy definované v rovnici (7.5) a (r, s) 0, 1 0, Bézierovy křivky a plochy Bézierovy křivky a plochy jsou velmi často používány v technické praxi. Za jejich zakladatele je považován P. E. Bézier a nezávisle na něm také P. de Casteljau. Křivka je určena čtyřmi body a prochází prvním a posledním z nich. Vektory P 0 P 1, P 3 P 2 určují tečny v krajních bodech. Jejich směrnice jsou rovny třetině délky těchto úseček. Křivka je definována parametrickými rovnicemi: Q(t) = 3 P i B i (t), t 0, 1 (7.7) i=0 B 0 (t) = (1 t) 3 B 1 (t) = 3t (1 t) 2 (7.8) B 2 (t) = 3t 2 (1 t) B 3 (t) = t 3
44 44 KAPITOLA 7. KŘIVKY A PLOCHY TECHNICKÉ PRAXE. Obrázek 7.2: Bézierova křivka a plocha Obecná Bézierova křivka vznikne zobecněním předchozího případu. Bázové polynomy tvoří binomický rozvoj. Mějme dáno n + 1 řídicích bodů, potom je Bézierova křivka tvaru: Q(t) = n P i Bi n (t), t 0, 1, (7.9) i=0 B n i (t) = ( ) n t i (1 t) n i. i Dvojrozměrným zobecněním Bézierových křivek dostaneme Bézierovy plochy. Jsou dány sítí reálných bodů P ij a rovnice plochy je: Q(r, s) = 3 i=0 3 P ij B i (r)b j (s), (7.10) kde B i jsou polynomy definované v rovnici (7.8) a (r, s) 0, 1 0, 1. j= Coonsovy křivky a plochy Podobné Fergusonovým křivkám jsou Coonsovy křivky, pojmenované po S. A. Coonsovi. Jediným rozdílem je tvar bázových polynomů. Základní oblouk je opět určen čtyřmi body P 0, P 1, P 2, P 3. Křivka však nezačíná ani nekončí v žádném z těchto bodů. Počáteční a koncový bod leží v antitěžištích trojúhelníků P 0 P 1 P 2 a P 1 P 2 P 3. Křivka je definována parametrickými rovnicemi:
45 7.2. ZÁKLADNÍ TYPY KŘIVEK A PLOCH TECHNICKÉ PRAXE 45 Q(t) = P i C i (t), t 0, 1 (7.11) i=0 C 0 (t) = (1 t) 3 C 1 (t) = 3t 3 6t (7.12) C 2 (t) = 3t 3 + 3t 2 + 3t + 1 C 3 (t) = t 3 Jednotlivé Coonsovy kubiky je možné hladce napojit. Pokud má navazující oblouk první tři body shodné s posledními třemi předchozího oblouku, dostáváme po částech polynomiální křivku, která se nazývá Coonsův kubický B-spline. Dvojrozměrným zobecněním Coonsových křivek dostaneme Coonsovy plochy. Jsou dány sítí reálných bodů P ij a rovnice plochy je: Q(r, s) = 3 3 P ij C i (r)c j (s), (7.13) i=0 j=0 kde C i jsou polynomy definované v rovnici (7.12) a (r, s) 0, 1 0, B-spline křivky a plochy Ve všech předchozích případech probíhal parametr t interval od nuly do jedné a záleželo pouze na tvaru bázových funkcí. Přidejme nyní k bázových funkcím posloupnost reálných čísel, podle které se budou počítat jednotlivé hodnoty funkcí. Tyto bázové funkce se nazývají B-spline funkce a posloupnosti se říká uzlový vektor. Na uzlový vektor jsou kladena další omezení je neklesající, uzly se mohou opakovat jen tolikrát, kolik je stupeň křivky a většinou bývá v intervalu od nuly do jedné, ale obecně nemusí. B-spline funkce je definována rekurentně následujícím předpisem: Necht t = (t 0, t 1,... t n ) je uzlový vektor. B-spline funkce je definována jako: N k i (t) = N 0 i (t) = { 1 pro t t i, t i+1 ) 0 jinak t t i N k 1 i (t) + t i+k+1 t N k 1 i+1 t i+k t i t i+k+1 t i+1 (t), (7.14) kde 0 i n k 1, 1 k n 1, 0 := 0. 0
46 46 KAPITOLA 7. KŘIVKY A PLOCHY TECHNICKÉ PRAXE Obrázek 7.3: Ukázka B-spline funkcí - ekvidistantní a neekvidistantní B-spline křivka je dána klasicky jako kombinace bodů s hodnotou příslušné bázové funkce. Výpočet je však náročnější a používá se k němu deboorův algoritmus, který je založen na určitých vlastnostech B-spline funkcí. Mějme dáno m+1 řídicích (kontrolních) bodů P 0, P 1,..., P m, kde P i R d, uzlový vektor t = (t 0, t 1,... t m+n+1 ). B-spline křivka stupně n pro řídicí body P i a uzlový vektor t je definována jako: C(t) = m P i Ni n (t), (7.15) i=0 kde N n i jsou bázové B-spline funkce. Plocha je definována nad sítí bodů se dvěma stupni, dvěma uzlovými vektory pro řádky a sloupce. S(r, s) = k l P ij N i (r)n j (s), (7.16) i=0 j= NURBS křivky a plochy Zkratka NURBS bývá vtipně vysvětlována jako Nobody Understand Rational B- Spline. Ve skutečnosti však znamená neuniformní racionální B-spline. Kromě slova racionální jsme se již se všemi ostatními pojmy setkali. B-spline funkce a tedy i křivky a plochy byly probrány v předchozí části. Jsou to aproximační křivky a plochy dané řídicími body a spjaté s B-spline funkcemi. Tyto funkce jsou zadány rekurentně a jejich tvar závisí na uzlovém vektoru. Neuniformní znamená, že rozdíl sousedních čísel v uzlovém vektoru není konstantní. Tj. průběh křivkou není plynulý, což dává větší možnosti při úpravě tvaru.
47 7.2. ZÁKLADNÍ TYPY KŘIVEK A PLOCH TECHNICKÉ PRAXE 47 Obrázek 7.4: Vliv váhy na tvar křivky Pojem racionální vznikl přidáním vah k bodům. Každému bodu je přiřazeno obvykle kladné číslo, které udává, jakou silou se bude křivka k danému bodu přitahovat. Pokud je v intervalu 0,1, znamená to, že vliv je malý a křivka jde od bodu dál. Pokud je větší než jedna, zvyšuje se síla tohoto bodu a ten si křivku přitáhne. Geometricky je výpočet plochy s váhami řešen rozšířením prostoru o dimenzi výše. Za čtvrtou souřadnici bodu se bere váha a počítá se s ní stejně jako s ostatními souřadnicemi. Na konci výpočtu se vahou první tři vypočtené hodnoty vydělí. Matematicky to lze zapsat jako: C (t) = m i=0 w ip i Ni n (t) m i=0 w ini n (t), (7.17) NURBS křivky a plochy se používají v CAD systémech pro jejich velmi dobré modelační schopnosti. Změnou polohy bodu, velikosti váhy či tvarem uzlového vektoru se může měnit lokálně tvar křivky či plochy. Oproti předchozím typům křivek dovedou NURBS jako jediné přesně vyjádřit kuželosečky a tedy s nimi jdou konstruovat základní tělesa (kužel, válec, anuloid, atd.). Obecná NURBS plocha vypadá matematicky již poměrně složitě: C (u, v) = r j=0 w ijp ij Ni m (u) Nj n (v) q r i=0 j=0 N i m (u) Nj n (v), (7.18) q i= T-spline Následovníkem NURBS se staly T-spline plochy. Jsou ve všem podobné NURBS plochám řídicí body, bázové B-spline funkce, váhy ALE NEPOTŘEBUJÍ PRA- VIDELNOU SÍŤ. Jejich uspořádání je libovolné a jsou propojeny pouze pomocí lokálních uzlových vektorů, které popisují jejich vztah k ostatním bodům v okolí. Nepravidelné navazování je nazýváno T-junctions, což je místo, kde v síti bodů leží jeden krajní bod hrany uprostřed hrany jiné. Výhodou používání T-spline je omezení počtu kontrolních bodů. Každý NURBS plocha je zároveň i T-spline. Pomocí algoritmu nazvaného T-spline simplification lze omezit počet řídicích bodů původní NURBS plochy na polovinu až třetinu. Dále se zbavíme tzv. superflous(nadbytečných) bodů, které jsou v NURBS síti pouze pro doplnění její pravidelnosti.
48 48 KAPITOLA 7. KŘIVKY A PLOCHY TECHNICKÉ PRAXE Obrázek 7.5: NURBS plocha a její řídicí sít Další předností T-spline je velmi dobré napojování libovolně velkých ploch. Pro grafiky je také velmi výhodná funkce přidávání nových bodů pomocí algoritmu T- spline refinement bez změny tvaru výsledné plochy a bez přidávání celého sloupce a řádku do sítě. Pravidla pro tvorbu T-mesh sítí a T-spline ploch jsou náročnější, ale zájemci je naleznou v odkazech. 1 s t Obrázek 7.6: Obecná T-mesh 7.3 Kontrolní otázky 1. Co jsou to matematické křivky a plochy?
49 7.4. LITERATURA 49 Obrázek 7.7: Obecná T-spline plocha (z = 0, z obecné) 2. Jaké znáte matematické křivky? 3. Vysvětlete základní princip tvorby mat. křivek. 4. Prochází bézierova křivka krajními body a proč? 5. Jaký je rozdíl mezi bézierovými a B-spline křivkami a plochami? 6. Co znamená zkratka NURBS? 7. Jaký je hlavní rozdíl mezi NURBS a T-spline? 8. Co dělají algoritmy T-spline simplification a T-spline refinement? 7.4 Literatura Procházková, J. - Disertační práce Martišek, D. - Matematické principy grafických systémů
zdroj světla). Z metod transformace obrázku uvedeme warping a morfing, které se
 Kapitola 3 Úpravy obrazu V následující kapitole se seznámíme se základními typy úpravy obrazu. První z nich je transformace barev pro výstupní zařízení, dále práce s barvami a expozicí pomocí histogramu
Kapitola 3 Úpravy obrazu V následující kapitole se seznámíme se základními typy úpravy obrazu. První z nich je transformace barev pro výstupní zařízení, dále práce s barvami a expozicí pomocí histogramu
Světlo, které vnímáme, představuje viditelnou část elektromagnetického spektra. V
 Kapitola 2 Barvy, barvy, barvičky 2.1 Vnímání barev Světlo, které vnímáme, představuje viditelnou část elektromagnetického spektra. V něm se vyskytují všechny známé druhy záření, např. gama záření či infračervené
Kapitola 2 Barvy, barvy, barvičky 2.1 Vnímání barev Světlo, které vnímáme, představuje viditelnou část elektromagnetického spektra. V něm se vyskytují všechny známé druhy záření, např. gama záření či infračervené
Delphi - objektově orientované
 Kapitola 6 Delphi - objektově orientované programování Objektově orientované programování (zkracováno na OOP, z anglického Object oriented programming) je metodika vývoje softwaru, založená na těchto myšlenkách,
Kapitola 6 Delphi - objektově orientované programování Objektově orientované programování (zkracováno na OOP, z anglického Object oriented programming) je metodika vývoje softwaru, založená na těchto myšlenkách,
Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na. x 2 x 1
 Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
1. Vektorové algoritmy jejich výstupem je soubor geometrických prvků, např.
 Kapitola 5 Řešení viditelnosti Řešit viditelnost ve scéně umí většina grafických programů. Cílem je určit ty objekty, resp. jejich části, které jsou viditelné z určitého místa. Tyto algoritmy jsou vždy
Kapitola 5 Řešení viditelnosti Řešit viditelnost ve scéně umí většina grafických programů. Cílem je určit ty objekty, resp. jejich části, které jsou viditelné z určitého místa. Tyto algoritmy jsou vždy
Křivky a plochy technické praxe
 Kapitola 7 Křivky a plochy technické praxe V technické praxi se setkáváme s tím, že potřebujeme křivky a plochy, které se dají libovolně upravovat a zároveň je jejich matematické vyjádření jednoduché.
Kapitola 7 Křivky a plochy technické praxe V technické praxi se setkáváme s tím, že potřebujeme křivky a plochy, které se dají libovolně upravovat a zároveň je jejich matematické vyjádření jednoduché.
Práce na počítači. Bc. Veronika Tomsová
 Práce na počítači Bc. Veronika Tomsová Barvy Barvy v počítačové grafice I. nejčastější reprezentace barev: 1-bitová informace rozlišující černou a bílou barvu 0... bílá, 1... černá 8-bitové číslo určující
Práce na počítači Bc. Veronika Tomsová Barvy Barvy v počítačové grafice I. nejčastější reprezentace barev: 1-bitová informace rozlišující černou a bílou barvu 0... bílá, 1... černá 8-bitové číslo určující
Rozšíření bakalářské práce
 Rozšíření bakalářské práce Vojtěch Vlkovský 2011 1 Obsah Seznam obrázků... 3 1 Barevné modely... 4 1.1 RGB barevný model... 4 1.2 Barevný model CMY(K)... 4 1.3 Další barevné modely... 4 1.3.1 Model CIE
Rozšíření bakalářské práce Vojtěch Vlkovský 2011 1 Obsah Seznam obrázků... 3 1 Barevné modely... 4 1.1 RGB barevný model... 4 1.2 Barevný model CMY(K)... 4 1.3 Další barevné modely... 4 1.3.1 Model CIE
Barvy a barevné modely. Počítačová grafika
 Barvy a barevné modely Počítačová grafika Barvy Barva základní atribut pro definici obrazu u každého bodu, křivky či výplně se definuje barva v rastrové i vektorové grafice všechny barvy, se kterými počítač
Barvy a barevné modely Počítačová grafika Barvy Barva základní atribut pro definici obrazu u každého bodu, křivky či výplně se definuje barva v rastrové i vektorové grafice všechny barvy, se kterými počítač
Úvod do počítačové grafiky
 Úvod do počítačové grafiky elmag. záření s určitou vlnovou délkou dopadající na sítnici našeho oka vnímáme jako barvu v rámci viditelné části spektra je člověk schopen rozlišit přibližně 10 milionů barev
Úvod do počítačové grafiky elmag. záření s určitou vlnovou délkou dopadající na sítnici našeho oka vnímáme jako barvu v rámci viditelné části spektra je člověk schopen rozlišit přibližně 10 milionů barev
MRBT M8. VIDITELNOST OBJEKTŮ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ. Bc. MARTIN MAŠTERA
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV AUTOMATIZACE A MĚŘICÍ TECHNIKY MRBT M8. VIDITELNOST OBJEKTŮ AUTOŘI PRÁCE Bc. JAKUB BERÁNEK Bc. MARTIN MAŠTERA VEDOUCÍ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV AUTOMATIZACE A MĚŘICÍ TECHNIKY MRBT M8. VIDITELNOST OBJEKTŮ AUTOŘI PRÁCE Bc. JAKUB BERÁNEK Bc. MARTIN MAŠTERA VEDOUCÍ
Grafické systémy. Obrázek 1. Znázornění elektromagnetického spektra.
 1. 1.5 Světlo a vnímání barev Pro vnímání barev je nezbytné světlo. Viditelné světlo je elektromagnetické záření o vlnové délce 400 750 nm. Různé frekvence světla vidíme jako barvy, od červeného světla
1. 1.5 Světlo a vnímání barev Pro vnímání barev je nezbytné světlo. Viditelné světlo je elektromagnetické záření o vlnové délce 400 750 nm. Různé frekvence světla vidíme jako barvy, od červeného světla
VYUŽITÍ POČÍTAČOVÉ GRAFIKY
 POČÍTAČOVÁ GRAFIKA VYUŽITÍ POČÍTAČOVÉ GRAFIKY ÚPRAVA FOTOGRAFIÍ NAFOCENÉ FOTOGRAFIE Z DIGITÁLNÍHO FOTOAPARÁTU MŮŽEME NEJEN PROHLÍŽET, ALE TAKÉ UPRAVOVAT JAS KONTRAST BAREVNOST OŘÍZNUTÍ ODSTRANĚNÍ ČERVENÝCH
POČÍTAČOVÁ GRAFIKA VYUŽITÍ POČÍTAČOVÉ GRAFIKY ÚPRAVA FOTOGRAFIÍ NAFOCENÉ FOTOGRAFIE Z DIGITÁLNÍHO FOTOAPARÁTU MŮŽEME NEJEN PROHLÍŽET, ALE TAKÉ UPRAVOVAT JAS KONTRAST BAREVNOST OŘÍZNUTÍ ODSTRANĚNÍ ČERVENÝCH
Počítačová grafika. OBSAH Grafické formy: Vektorová grafika Bitmapová (rastrová grafika) Barevné modely
 Počítačová grafika OBSAH Grafické formy: Vektorová grafika Bitmapová (rastrová grafika) Barevné modely Vektorová grafika Vektorová grafika Příklad vektorové grafiky Zpět na Obsah Vektorová grafika Vektorový
Počítačová grafika OBSAH Grafické formy: Vektorová grafika Bitmapová (rastrová grafika) Barevné modely Vektorová grafika Vektorová grafika Příklad vektorové grafiky Zpět na Obsah Vektorová grafika Vektorový
Barevné modely, práce s barvou. Martin Klíma
 Barevné modely, práce s barvou Martin Klíma Proč je barva důležitá Důležitý vizuální atribut Různá zařízení, aplikace, média Monitor Tiskárna Video Televize Světlo a barvy Elektromagnetické vlnění Viditelná
Barevné modely, práce s barvou Martin Klíma Proč je barva důležitá Důležitý vizuální atribut Různá zařízení, aplikace, média Monitor Tiskárna Video Televize Světlo a barvy Elektromagnetické vlnění Viditelná
Počítačová grafika. Studijní text. Karel Novotný
 Počítačová grafika Studijní text Karel Novotný P 1 Počítačová grafika očítačová grafika je z technického hlediska obor informatiky 1, který používá počítače k tvorbě umělých grafických objektů a dále také
Počítačová grafika Studijní text Karel Novotný P 1 Počítačová grafika očítačová grafika je z technického hlediska obor informatiky 1, který používá počítače k tvorbě umělých grafických objektů a dále také
Kde se používá počítačová grafika
 POČÍTAČOVÁ GRAFIKA Kde se používá počítačová grafika Tiskoviny Reklama Média, televize, film Multimédia Internetové stránky 3D grafika Virtuální realita CAD / CAM projektování Hry Základní pojmy Rastrová
POČÍTAČOVÁ GRAFIKA Kde se používá počítačová grafika Tiskoviny Reklama Média, televize, film Multimédia Internetové stránky 3D grafika Virtuální realita CAD / CAM projektování Hry Základní pojmy Rastrová
Přednáška kurzu MPOV. Barevné modely
 Přednáška kurzu MPOV Barevné modely Ing. P. Petyovský (email: petyovsky@feec.vutbr.cz), kancelář E512, tel. 1194, Integrovaný objekt - 1/11 - Barvy v počítačové grafice Barevné modely Aditivní modely RGB,
Přednáška kurzu MPOV Barevné modely Ing. P. Petyovský (email: petyovsky@feec.vutbr.cz), kancelář E512, tel. 1194, Integrovaný objekt - 1/11 - Barvy v počítačové grafice Barevné modely Aditivní modely RGB,
Metodické listy pro kombinované studium předmětu. B_PPG Principy počítačové grafiky
 Metodické listy pro kombinované studium předmětu B_PPG Principy počítačové grafiky Metodický list č. l Název tématického celku: BARVY V POČÍTAČOVÉ GRAFICE Cíl: Základním cílem tohoto tematického celku
Metodické listy pro kombinované studium předmětu B_PPG Principy počítačové grafiky Metodický list č. l Název tématického celku: BARVY V POČÍTAČOVÉ GRAFICE Cíl: Základním cílem tohoto tematického celku
B_PPG PRINCIPY POČÍTAČOVÉ GRAFIKY
 B_PPG PRINCIPY POČÍTAČOVÉ GRAFIKY RNDr. Jana Štanclová, Ph.D. jana.stanclova@ruk.cuni.cz ZS 2/0 Z Obrázky (popř. slajdy) převzaty od RNDr. Josef Pelikán, CSc., KSVI MFF UK Obsah seminářů 03.10.2011 [1]
B_PPG PRINCIPY POČÍTAČOVÉ GRAFIKY RNDr. Jana Štanclová, Ph.D. jana.stanclova@ruk.cuni.cz ZS 2/0 Z Obrázky (popř. slajdy) převzaty od RNDr. Josef Pelikán, CSc., KSVI MFF UK Obsah seminářů 03.10.2011 [1]
Barvy. Radek Fiala. Podpořeno z projektu FRVŠ 584/2011
 fialar@kma.zcu.cz Podpořeno z projektu FRVŠ 584/2011 Kde se berou barvy? Co je barva Světlo jako elmg. záření nemá barvu. Jednou z vlastností světla je tzv. spektrální rozdělení (Spectral Power Distribution,
fialar@kma.zcu.cz Podpořeno z projektu FRVŠ 584/2011 Kde se berou barvy? Co je barva Světlo jako elmg. záření nemá barvu. Jednou z vlastností světla je tzv. spektrální rozdělení (Spectral Power Distribution,
Barvy v počítačové grafice
 arvy v počítačové grafice 2. přednáška předmětu Zpracování obrazů Martina Mudrová 2004 arvy v počítačové grafice Co je barva? světlo = elmg. vlnění v rozsahu 4,3.10 14-7,5.10 14 Hz rentgenové zář ení zář
arvy v počítačové grafice 2. přednáška předmětu Zpracování obrazů Martina Mudrová 2004 arvy v počítačové grafice Co je barva? světlo = elmg. vlnění v rozsahu 4,3.10 14-7,5.10 14 Hz rentgenové zář ení zář
Co je počítačová grafika
 Počítačová grafika Co je počítačová grafika Počítačovou grafikou rozumíme vše, co zpracovává počítač a co lze sledovat očima Využití počítačové grafiky Tiskoviny - časopisy, noviny, knihy, letáky Reklama
Počítačová grafika Co je počítačová grafika Počítačovou grafikou rozumíme vše, co zpracovává počítač a co lze sledovat očima Využití počítačové grafiky Tiskoviny - časopisy, noviny, knihy, letáky Reklama
13 Barvy a úpravy rastrového
 13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
13 Barvy a úpravy rastrového Studijní cíl Tento blok je věnován základním metodám pro úpravu rastrového obrazu, jako je např. otočení, horizontální a vertikální překlopení. Dále budo vysvětleny různé metody
Barva. v počítačové grafice. Poznámky k přednášce předmětu Počítačová grafika
 Barva v počítačové grafice Poznámky k přednášce předmětu Počítačová grafika Martina Mudrová 2007 Barvy v počítačové grafice Co je barva? světlo = elmg. vlnění v rozsahu 4,3.10 14-7,5.10 14 Hz rentgenové
Barva v počítačové grafice Poznámky k přednášce předmětu Počítačová grafika Martina Mudrová 2007 Barvy v počítačové grafice Co je barva? světlo = elmg. vlnění v rozsahu 4,3.10 14-7,5.10 14 Hz rentgenové
Počítačová grafika SZŠ A VOŠZ MERHAUTOVA 15, BRNO
 Počítačová grafika SZŠ A VOŠZ MERHAUTOVA 15, BRNO 1 Základní dělení 3D grafika 2D grafika vektorová rastrová grafika 2/29 Vektorová grafika Jednotlivé objekty jsou tvořeny křivkami Využití: tvorba diagramů,
Počítačová grafika SZŠ A VOŠZ MERHAUTOVA 15, BRNO 1 Základní dělení 3D grafika 2D grafika vektorová rastrová grafika 2/29 Vektorová grafika Jednotlivé objekty jsou tvořeny křivkami Využití: tvorba diagramů,
Světlo. Podstata světla. Elektromagnetické záření Korpuskulární charakter. Rychlost světla. Vlnová délka. Vlnění, foton. c = 1 079 252 848,8 km/h
 Světlo Světlo Podstata světla Elektromagnetické záření Korpuskulární charakter Vlnění, foton Rychlost světla c = 1 079 252 848,8 km/h Vlnová délka Elektromagnetické spektrum Rádiové vlny Mikrovlny Infračervené
Světlo Světlo Podstata světla Elektromagnetické záření Korpuskulární charakter Vlnění, foton Rychlost světla c = 1 079 252 848,8 km/h Vlnová délka Elektromagnetické spektrum Rádiové vlny Mikrovlny Infračervené
Geometrická optika. Vnímání a měření barev. světlo určitého spektrálního složení vyvolá po dopadu na sítnici oka v mozku subjektivní barevný vjem
 Vnímání a měření barev světlo určitého spektrálního složení vyvolá po dopadu na sítnici oka v mozku subjektivní barevný vjem fyzikální charakteristika subjektivní vjem světelný tok subjektivní jas vlnová
Vnímání a měření barev světlo určitého spektrálního složení vyvolá po dopadu na sítnici oka v mozku subjektivní barevný vjem fyzikální charakteristika subjektivní vjem světelný tok subjektivní jas vlnová
Digitální fotografie. Mgr. Milana Soukupová Gymnázium Česká Třebová
 Digitální fotografie Mgr. Milana Soukupová Gymnázium Česká Třebová Téma sady didaktických materiálů Digitální fotografie I. Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu
Digitální fotografie Mgr. Milana Soukupová Gymnázium Česká Třebová Téma sady didaktických materiálů Digitální fotografie I. Číslo a název šablony Číslo didaktického materiálu Druh didaktického materiálu
Barvy v počítačové grafice
 arvy v počítačové grafice 2. přednáška předmětu Zpracování obrazů Martina Mudrová 24 arvy v počítačové grafice o je barva? světlo = elmg. vlnění v rozsahu 4,3. 4-7,5. 4 Hz viditelná č ást spektra rentgenové
arvy v počítačové grafice 2. přednáška předmětu Zpracování obrazů Martina Mudrová 24 arvy v počítačové grafice o je barva? světlo = elmg. vlnění v rozsahu 4,3. 4-7,5. 4 Hz viditelná č ást spektra rentgenové
IVT. 8. ročník. listopad, prosinec 2013. Autor: Mgr. Dana Kaprálová
 IVT Počítačová grafika - úvod 8. ročník listopad, prosinec 2013 Autor: Mgr. Dana Kaprálová Zpracováno v rámci projektu Krok za krokem na ZŠ Želatovská ve 21. století registrační číslo projektu: CZ.1.07/1.4.00/21.3443
IVT Počítačová grafika - úvod 8. ročník listopad, prosinec 2013 Autor: Mgr. Dana Kaprálová Zpracováno v rámci projektu Krok za krokem na ZŠ Želatovská ve 21. století registrační číslo projektu: CZ.1.07/1.4.00/21.3443
Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám
 Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: CZ.1.07/1.5.00/34.0883 Název projektu: Rozvoj vzdělanosti Číslo šablony: III/2 Datum vytvoření: 17. 1. 2013 Autor: MgA.
Výukový materiál v rámci projektu OPVK 1.5 Peníze středním školám Číslo projektu: CZ.1.07/1.5.00/34.0883 Název projektu: Rozvoj vzdělanosti Číslo šablony: III/2 Datum vytvoření: 17. 1. 2013 Autor: MgA.
Počítačová grafika - úvod
 Autor: Mgr. Dana Kaprálová Počítačová grafika - úvod Datum (období) tvorby: listopad, prosinec 2013 Ročník: osmý Vzdělávací oblast: IVT 1 Anotace: Žáci se seznámí se základními pojmy počítačové grafiky,
Autor: Mgr. Dana Kaprálová Počítačová grafika - úvod Datum (období) tvorby: listopad, prosinec 2013 Ročník: osmý Vzdělávací oblast: IVT 1 Anotace: Žáci se seznámí se základními pojmy počítačové grafiky,
Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527
 Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Projekt: Příjemce: Digitální učební materiály ve škole, registrační číslo projektu CZ.1.07/1.5.00/34.0527 Střední zdravotnická škola a Vyšší odborná škola zdravotnická, Husova 3, 371 60 České Budějovice
Omezení barevného prostoru
 Úpravy obrazu Omezení barevného prostoru Omezení počtu barev v obraze při zachování obrazového vjemu z obrazu Vytváření barevné palety v některých souborových formátech Různé filtry v grafických programech
Úpravy obrazu Omezení barevného prostoru Omezení počtu barev v obraze při zachování obrazového vjemu z obrazu Vytváření barevné palety v některých souborových formátech Různé filtry v grafických programech
Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Grafická data jsou u 2D vektorové grafiky uložena ve voxelech."
 Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Grafická data jsou u 2D vektorové grafiky uložena ve voxelech." Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Na
Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Grafická data jsou u 2D vektorové grafiky uložena ve voxelech." Téma: Vektorová grafika. Určete pravdivost následujícího tvrzení: "Na
Text úlohy. Která barva nepatří do základních barev prostoru RGB? Vyberte jednu z nabízených možností: a. Černá b. Červená c. Modrá d.
 Úloha 1 Která barva nepatří do základních barev prostoru RGB? a. Černá b. Červená c. Modrá d. Zelená Úloha 2 V rovině je dán NEKONVEXNÍ n-úhelník a bod A. Pokud paprsek (polopřímka) vedený z tohoto bodu
Úloha 1 Která barva nepatří do základních barev prostoru RGB? a. Černá b. Červená c. Modrá d. Zelená Úloha 2 V rovině je dán NEKONVEXNÍ n-úhelník a bod A. Pokud paprsek (polopřímka) vedený z tohoto bodu
DATOVÉ FORMÁTY GRAFIKY, JEJICH SPECIFIKA A MOŽNOSTI VYUŽITÍ
 DATOVÉ FORMÁTY GRAFIKY, JEJICH SPECIFIKA A MOŽNOSTI VYUŽITÍ UMT Tomáš Zajíc, David Svoboda Typy počítačové grafiky Rastrová Vektorová Rastrová grafika Pixely Rozlišení Barevná hloubka Monitor 72 PPI Tiskárna
DATOVÉ FORMÁTY GRAFIKY, JEJICH SPECIFIKA A MOŽNOSTI VYUŽITÍ UMT Tomáš Zajíc, David Svoboda Typy počítačové grafiky Rastrová Vektorová Rastrová grafika Pixely Rozlišení Barevná hloubka Monitor 72 PPI Tiskárna
POČÍTAČOVÁ GRAFIKA. Počítačová grafika 1
 Počítačová grafika 1 POČÍTAČOVÁ GRAFIKA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro nižší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky
Počítačová grafika 1 POČÍTAČOVÁ GRAFIKA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro nižší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky
Barevné systémy 1995-2015 Josef Pelikán CGG MFF UK Praha
 Barevné systémy 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Colors 2015 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 21 Rozklad spektrálních barev
Barevné systémy 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Colors 2015 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 21 Rozklad spektrálních barev
ODRAZ A LOM SVĚTLA. Mgr. Jan Ptáčník - GJVJ - Septima - Fyzika - Optika
 ODRAZ A LOM SVĚTLA Mgr. Jan Ptáčník - GJVJ - Septima - Fyzika - Optika Odraz světla Vychází z Huygensova principu Zákon odrazu: Úhel odrazu vlnění je roven úhlu dopadu. Obvykle provádíme konstrukci pomocí
ODRAZ A LOM SVĚTLA Mgr. Jan Ptáčník - GJVJ - Septima - Fyzika - Optika Odraz světla Vychází z Huygensova principu Zákon odrazu: Úhel odrazu vlnění je roven úhlu dopadu. Obvykle provádíme konstrukci pomocí
VY_32_INOVACE_INF4_12. Počítačová grafika. Úvod
 VY_32_INOVACE_INF4_12 Počítačová grafika Úvod Základní rozdělení grafických formátů Rastrová grafika (bitmapová) Vektorová grafika Základním prvkem je bod (pixel). Vhodná pro zpracování digitální fotografie.
VY_32_INOVACE_INF4_12 Počítačová grafika Úvod Základní rozdělení grafických formátů Rastrová grafika (bitmapová) Vektorová grafika Základním prvkem je bod (pixel). Vhodná pro zpracování digitální fotografie.
VY_32_INOVACE_INF.10. Grafika v IT
 VY_32_INOVACE_INF.10 Grafika v IT Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 GRAFIKA Grafika ve smyslu umělecké grafiky
VY_32_INOVACE_INF.10 Grafika v IT Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Jiří Kalous Základní a mateřská škola Bělá nad Radbuzou, 2011 GRAFIKA Grafika ve smyslu umělecké grafiky
Digitální učební materiál
 Střední hotelová škola, s.r.o. Floriánské náměstí 350, 272 01 Kladno Digitální učební materiál Číslo projektu Název projektu Název školy Předmět Tematický okruh Téma CZ.1.07/1.5.00/34.0112 Moderní škola
Střední hotelová škola, s.r.o. Floriánské náměstí 350, 272 01 Kladno Digitální učební materiál Číslo projektu Název projektu Název školy Předmět Tematický okruh Téma CZ.1.07/1.5.00/34.0112 Moderní škola
Úloha 1. Text úlohy. Vyberte jednu z nabízených možností: NEPRAVDA. PRAVDA Úloha 2. Text úlohy
 Úloha 1 Úloha 2 Otázka se týká předchozího kódu. Určete pravdivost následujícího tvrzení: "Pro každý bod vytvoří úsečku mezi ním a středem panelu." Úloha 3 Otázka se týká předchozího kódu. Určete pravdivost
Úloha 1 Úloha 2 Otázka se týká předchozího kódu. Určete pravdivost následujícího tvrzení: "Pro každý bod vytvoří úsečku mezi ním a středem panelu." Úloha 3 Otázka se týká předchozího kódu. Určete pravdivost
Barvy na počítači a grafické formáty
 Barvy na počítači a grafické formáty Hlavním atributem, který se používá při práci s obrazem či s grafickými formáty, je barva. Při práci s barvami je důležité určit základní množinu barev, se kterou budeme
Barvy na počítači a grafické formáty Hlavním atributem, který se používá při práci s obrazem či s grafickými formáty, je barva. Při práci s barvami je důležité určit základní množinu barev, se kterou budeme
DUM 01 téma: Úvod do počítačové grafiky
 DUM 01 téma: Úvod do počítačové grafiky ze sady: 02 tematický okruh sady: Bitmapová grafika ze šablony: 09 Počítačová grafika určeno pro: 2. ročník vzdělávací obor: vzdělávací oblast: číslo projektu: anotace:
DUM 01 téma: Úvod do počítačové grafiky ze sady: 02 tematický okruh sady: Bitmapová grafika ze šablony: 09 Počítačová grafika určeno pro: 2. ročník vzdělávací obor: vzdělávací oblast: číslo projektu: anotace:
Jana Dannhoferová Ústav informatiky, PEF MZLU
 Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115
 Číslo projektu: Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo šablony: 8 Název materiálu: Ročník: Identifikace materiálu: Jméno autora: Předmět: Tématický celek: Anotace: CZ.1.07/1.5.00/34.0410
Číslo projektu: Gymnázium a Střední odborná škola, Rokycany, Mládežníků 1115 Číslo šablony: 8 Název materiálu: Ročník: Identifikace materiálu: Jméno autora: Předmět: Tématický celek: Anotace: CZ.1.07/1.5.00/34.0410
Zobrazování barev. 1995-2015 Josef Pelikán CGG MFF UK Praha. pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/
 Zobrazování barev 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ ColorRep 2015 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 18 Barevné schopnosti HW True-color
Zobrazování barev 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ ColorRep 2015 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 18 Barevné schopnosti HW True-color
Grafická data jsou u 2D vektorové grafiky uložena ve voxelech NEPRAVDA Grafická data jsou u rastrové grafiky uložena v pixelech PRAVDA Grafická data
 Grafická data jsou u 2D vektorové grafiky uložena ve voxelech Grafická data jsou u rastrové grafiky uložena v pixelech Grafická data jsou u vektorové grafiky uložena v pixelech Na rozdíl od rastrové grafiky
Grafická data jsou u 2D vektorové grafiky uložena ve voxelech Grafická data jsou u rastrové grafiky uložena v pixelech Grafická data jsou u vektorové grafiky uložena v pixelech Na rozdíl od rastrové grafiky
Barvy a barevné systémy Formáty obrázků pro WWW
 Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
Rastrová grafika. Grafický objekt je zaznamenán jednotlivými souřadnicemi bodů v mřížce. pixel ( picture element ) s definovanou barvou
 Rastrová grafika Grafický objekt je zaznamenán jednotlivými souřadnicemi bodů v mřížce. pixel ( picture element ) s definovanou barvou Kvalita je určena rozlišením mřížky a barevnou hloubkou (počet bitů
Rastrová grafika Grafický objekt je zaznamenán jednotlivými souřadnicemi bodů v mřížce. pixel ( picture element ) s definovanou barvou Kvalita je určena rozlišením mřížky a barevnou hloubkou (počet bitů
Přednáška kurzu BZVS. Barevné modely
 Přednáška kurzu BZVS Barevné modely Ing. P. Petyovský (email: petyovsky@feec.vutbr.cz), kancelář SD3.152, tel. 6434, Technická 12, VUT v Brně - 1/16 - Barvy v počítačové grafice Barevné modely Aditivní
Přednáška kurzu BZVS Barevné modely Ing. P. Petyovský (email: petyovsky@feec.vutbr.cz), kancelář SD3.152, tel. 6434, Technická 12, VUT v Brně - 1/16 - Barvy v počítačové grafice Barevné modely Aditivní
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C)
 VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
Kristýna Bémová. 13. prosince 2007
 Křivky v počítačové grafice Kristýna Bémová Univerzita Karlova v Praze 13. prosince 2007 Kristýna Bémová (MFF UK) Křivky v počítačové grafice 13. prosince 2007 1 / 36 Pojmy - křivky a jejich parametrické
Křivky v počítačové grafice Kristýna Bémová Univerzita Karlova v Praze 13. prosince 2007 Kristýna Bémová (MFF UK) Křivky v počítačové grafice 13. prosince 2007 1 / 36 Pojmy - křivky a jejich parametrické
Reprezentace bodu, zobrazení
 Reprezentace bodu, zobrazení Ing. Jan Buriánek VOŠ a SŠSE P9 Jan.Burianek@gmail.com Obsah Témata Základní dělení grafických elementů Rastrový vs. vektorový obraz Rozlišení Interpolace Aliasing, moiré Zdroje
Reprezentace bodu, zobrazení Ing. Jan Buriánek VOŠ a SŠSE P9 Jan.Burianek@gmail.com Obsah Témata Základní dělení grafických elementů Rastrový vs. vektorový obraz Rozlišení Interpolace Aliasing, moiré Zdroje
PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII
 PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII V úvodu analytické geometrie jsme vysvětlili, že její hlavní snahou je popsat geometrické útvary (body, vektory, přímky, kružnice,...) pomocí čísel nebo proměnných.
PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII V úvodu analytické geometrie jsme vysvětlili, že její hlavní snahou je popsat geometrické útvary (body, vektory, přímky, kružnice,...) pomocí čísel nebo proměnných.
Barvy a barevné systémy Formáty obrázků pro WWW
 Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
Barvy a barevné systémy Formáty obrázků pro WWW Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konkrétním světle zastoupeny složky všech vlnových délek, vnímáme
Vývoj počítačové grafiky. Tomáš Pastuch Pavel Skrbek 15.3. 2010
 Vývoj počítačové grafiky Tomáš Pastuch Pavel Skrbek 15.3. 2010 Počítačová grafika obor informatiky, který používá počítače k tvorbě umělých grafických objektů nebo pro úpravu již nasnímaných grafických
Vývoj počítačové grafiky Tomáš Pastuch Pavel Skrbek 15.3. 2010 Počítačová grafika obor informatiky, který používá počítače k tvorbě umělých grafických objektů nebo pro úpravu již nasnímaných grafických
Úvod do počítačové grafiky
 Úvod do počíta tačové grafiky Počíta tačová grafika zobrazování popis objektů obraz modelování (model světa) rekostrukce zpracování obrazu Popis obrazu rastrový neboli bitmapový obraz = matice bodů vektorový
Úvod do počíta tačové grafiky Počíta tačová grafika zobrazování popis objektů obraz modelování (model světa) rekostrukce zpracování obrazu Popis obrazu rastrový neboli bitmapový obraz = matice bodů vektorový
Ing. Jan Buriánek. Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické v Praze Jan Buriánek, 2010
 Ing. Jan Buriánek (ČVUT FIT) Reprezentace bodu a zobrazení BI-MGA, 2010, Přednáška 2 1/33 Ing. Jan Buriánek Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické
Ing. Jan Buriánek (ČVUT FIT) Reprezentace bodu a zobrazení BI-MGA, 2010, Přednáška 2 1/33 Ing. Jan Buriánek Katedra softwarového inženýrství Fakulta informačních technologií České vysoké učení technické
1. Polotóny, tisk šedých úrovní
 1. Polotóny, tisk šedých úrovní Studijní cíl Tento blok kurzu je věnován problematice principu tisku polotónů a šedých úrovní v oblasti počítačové grafiky. Doba nutná k nastudování 2 hodiny 1.1 Základní
1. Polotóny, tisk šedých úrovní Studijní cíl Tento blok kurzu je věnován problematice principu tisku polotónů a šedých úrovní v oblasti počítačové grafiky. Doba nutná k nastudování 2 hodiny 1.1 Základní
11 Zobrazování objektů 3D grafiky
 11 Zobrazování objektů 3D grafiky Studijní cíl Tento blok je věnován základním algoritmům zobrazení 3D grafiky. Postupně budou probrány základní metody projekce kolmé promítání, rovnoběžné promítání a
11 Zobrazování objektů 3D grafiky Studijní cíl Tento blok je věnován základním algoritmům zobrazení 3D grafiky. Postupně budou probrány základní metody projekce kolmé promítání, rovnoběžné promítání a
VEKTOR. Vymyslete alespoň tři příklady vektorových a skalárních fyzikálních veličin. vektorové: 1. skalární
 VEKTOR Úvod Vektor je abstraktní pojem sloužící k vyjádření jistého směru a velikosti. S vektorovými veličinami se setkáváme například ve fyzice. Jde o veličiny, u nichž je rozhodující nejen velikost,
VEKTOR Úvod Vektor je abstraktní pojem sloužící k vyjádření jistého směru a velikosti. S vektorovými veličinami se setkáváme například ve fyzice. Jde o veličiny, u nichž je rozhodující nejen velikost,
VOLBA BAREVNÝCH SEPARACÍ
 VOLBA BAREVNÝCH SEPARACÍ SOURAL Ivo Fakulta chemická, Ústav fyzikální a spotřební chemie Vysoké učení technické v Brně, Purkyňova 118, 612 00 Brno E-mail : Pavouk.P@centrum.cz K tomu aby byly pochopitelné
VOLBA BAREVNÝCH SEPARACÍ SOURAL Ivo Fakulta chemická, Ústav fyzikální a spotřební chemie Vysoké učení technické v Brně, Purkyňova 118, 612 00 Brno E-mail : Pavouk.P@centrum.cz K tomu aby byly pochopitelné
5.3.1 Disperze světla, barvy
 5.3.1 Disperze světla, barvy Předpoklady: 5103 Svítíme paprskem bílého světla ze žárovky na skleněný hranol. Světlo se láme podle zákona lomu na zdi vznikne osvětlená stopa Stopa vznikla, ale není bílá,
5.3.1 Disperze světla, barvy Předpoklady: 5103 Svítíme paprskem bílého světla ze žárovky na skleněný hranol. Světlo se láme podle zákona lomu na zdi vznikne osvětlená stopa Stopa vznikla, ale není bílá,
POPIS PROSTŘEDÍ PROGRAMU GIMP 2. Barvy 2. Okno obrázku 4 ZÁKLADNÍ ÚPRAVA FOTOGRAFIÍ V GRAFICKÉM EDITORU 6. Změna velikosti fotografie 6
 Obsah POPIS PROSTŘEDÍ PROGRAMU GIMP 2 Barvy 2 Okno obrázku 4 ZÁKLADNÍ ÚPRAVA FOTOGRAFIÍ V GRAFICKÉM EDITORU 6 Změna velikosti fotografie 6 Ořezání obrázku 7 TRANSFORMACE 9 Rotace 9 Překlopení 11 Perspektiva
Obsah POPIS PROSTŘEDÍ PROGRAMU GIMP 2 Barvy 2 Okno obrázku 4 ZÁKLADNÍ ÚPRAVA FOTOGRAFIÍ V GRAFICKÉM EDITORU 6 Změna velikosti fotografie 6 Ořezání obrázku 7 TRANSFORMACE 9 Rotace 9 Překlopení 11 Perspektiva
Fergusnova kubika, která je definována pomocí bodu P1, vektoru P1P2, bodu P3 a vektoru P3P4
 Která barva nepatří do základních barev prostoru RGB? a. Černá b. Zelená c. Modrá d. Červená Úloha 2 Jakým minimálním počtem bodů je jednoznačně určena interpolační křivka 5. řádu? a. 6 b. 3 c. 5 d. 7
Která barva nepatří do základních barev prostoru RGB? a. Černá b. Zelená c. Modrá d. Červená Úloha 2 Jakým minimálním počtem bodů je jednoznačně určena interpolační křivka 5. řádu? a. 6 b. 3 c. 5 d. 7
POČÍTAČOVÁ GRAFIKA. Lenka Bednaříková
 POČÍTAČOVÁ GRAFIKA Lenka Bednaříková POČÍTAČOVÁ GRAFIKA - OBSAH Barevné modely Základní dělení počítačové grafiky Vektorová grafika Rastrová (bitmapová) grafika Rozlišení Barevná hloubka Komprese, komprimace
POČÍTAČOVÁ GRAFIKA Lenka Bednaříková POČÍTAČOVÁ GRAFIKA - OBSAH Barevné modely Základní dělení počítačové grafiky Vektorová grafika Rastrová (bitmapová) grafika Rozlišení Barevná hloubka Komprese, komprimace
Informační a komunikační technologie. Základy informatiky. 5 vyučovacích hodin. Osobní počítače, soubory s fotografiemi
 Výstupový indikátor 06.43.19 Název Autor: Vzdělávací oblast: Vzdělávací obory: Ročník: Časový rozsah: Pomůcky: Projekt Integrovaný vzdělávací systém města Jáchymov - Mosty Digitální fotografie Petr Hepner,
Výstupový indikátor 06.43.19 Název Autor: Vzdělávací oblast: Vzdělávací obory: Ročník: Časový rozsah: Pomůcky: Projekt Integrovaný vzdělávací systém města Jáchymov - Mosty Digitální fotografie Petr Hepner,
Geometrická optika. předmětu. Obrazový prostor prostor za optickou soustavou (většinou vpravo), v němž může ležet obraz - - - 1 -
 Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Geometrická optika Optika je část fyziky, která zkoumá podstatu světla a zákonitosti světelných jevů, které vznikají při šíření světla a při vzájemném působení světla a látky. Světlo je elektromagnetické
Multimediální systémy. 02 Reprezentace barev v počítači
 Multimediální systémy 02 Reprezentace barev v počítači Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Reprezentace barev v PC Způsoby míchání barev Barevné modely Bitová hloubka Barvy
Multimediální systémy 02 Reprezentace barev v počítači Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Reprezentace barev v PC Způsoby míchání barev Barevné modely Bitová hloubka Barvy
Základy informatiky. 10 Počítačová grafika
 Základy informatiky 10 Počítačová grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Reprezentace barev v PC Způsoby míchání barev Barevné modely Bitová hloubka Rastrová grafika
Základy informatiky 10 Počítačová grafika Michal Kačmařík Institut geoinformatiky, VŠB-TUO Osnova přednášky Reprezentace barev v PC Způsoby míchání barev Barevné modely Bitová hloubka Rastrová grafika
Barevné prostory. RGB, CMYK, HSV a Lab gamut
 J. Vrzal, 1.0 Barevné prostory RGB, CMYK, HSV a Lab gamut rozsah všech barev, které jsou dosažitelné v určitém barevném prostoru barvy mimo oblast gamutu jsou reprodukovány nejbližší dostupnou barvou z
J. Vrzal, 1.0 Barevné prostory RGB, CMYK, HSV a Lab gamut rozsah všech barev, které jsou dosažitelné v určitém barevném prostoru barvy mimo oblast gamutu jsou reprodukovány nejbližší dostupnou barvou z
Zobrazování těles. problematika geometrického modelování. základní typy modelů. datové reprezentace modelů základní metody geometrického modelování
 problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
Barvy a barevné systémy. Ivo Peterka
 Barvy a barevné systémy Ivo Peterka Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konktrétním světle zastoupeny složky všech vlnových délek, vnímáme toto světlo
Barvy a barevné systémy Ivo Peterka Viditelné světlo. Elektromagnetické záření o vlnové délce 390 760 nanometrů. Jsou-li v konktrétním světle zastoupeny složky všech vlnových délek, vnímáme toto světlo
GEOMETRICKÁ OPTIKA. Znáš pojmy A. 1. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci.
 Znáš pojmy A. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci. Tenká spojka při zobrazování stačí k popisu zavést pouze ohniskovou vzdálenost a její střed. Znaménková
Znáš pojmy A. Znázorni chod význačných paprsků pro spojku. Čočku popiš a uveď pro ni znaménkovou konvenci. Tenká spojka při zobrazování stačí k popisu zavést pouze ohniskovou vzdálenost a její střed. Znaménková
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
Řízení robota pomocí senzoru barev. Tematický celek: Světlo. Úkol:
 Název: Řízení robota pomocí senzoru barev. Tematický celek: Světlo. Úkol: Zopakuj si, čím je daná barva předmětu a jak se míchají barvy ve fyzice a výpočetní technice. Zjisti, jak pracuje senzor barev.
Název: Řízení robota pomocí senzoru barev. Tematický celek: Světlo. Úkol: Zopakuj si, čím je daná barva předmětu a jak se míchají barvy ve fyzice a výpočetní technice. Zjisti, jak pracuje senzor barev.
Grafika na počítači. Bc. Veronika Tomsová
 Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Grafika na počítači Bc. Veronika Tomsová Proces zpracování obrazu Proces zpracování obrazu 1. Snímání obrazu 2. Digitalizace obrazu převod spojitého signálu na matici čísel reprezentující obraz 3. Předzpracování
Aproximační křivky. Trocha historie. geometrické modelování veliký pokrok v oblasti letectví 1944 Roy Liming
 Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
Trocha historie geometrické modelování veliký pokrok v oblasti letectví 944 Roy Liming analytik, North American Aviation (výrobce letadel) společně s konstruktérem a designérem Edgardem Schmuedem matematizace
Viditelné elektromagnetické záření
 Aj to bude masakr 1 Viditelné elektromagnetické záření Vlnová délka 1 až 1 000 000 000 nm Světlo se chová jako vlnění nebo proud fotonů (záleží na okolnostech) 2 Optické záření 1645 Korpuskulární teorie
Aj to bude masakr 1 Viditelné elektromagnetické záření Vlnová délka 1 až 1 000 000 000 nm Světlo se chová jako vlnění nebo proud fotonů (záleží na okolnostech) 2 Optické záření 1645 Korpuskulární teorie
Kde se používá počítačová grafika (PG)?
 Počítačová grafika Kde se používá počítačová grafika (PG)? Tiskoviny - časopisy, noviny, letáky Reklama billboardy, propagační mat., reklamní spoty Média, televize, film titulky, efekty, triky Multimédia
Počítačová grafika Kde se používá počítačová grafika (PG)? Tiskoviny - časopisy, noviny, letáky Reklama billboardy, propagační mat., reklamní spoty Média, televize, film titulky, efekty, triky Multimédia
Světlo je elektromagnetické vlnění, které má ve vakuu vlnové délky od 390 nm do 770 nm.
 1. Podstata světla Světlo je elektromagnetické vlnění, které má ve vakuu vlnové délky od 390 nm do 770 nm. Vznik elektromagnetických vln (záření): 1. při pohybu elektricky nabitých částic s nenulovým zrychlením
1. Podstata světla Světlo je elektromagnetické vlnění, které má ve vakuu vlnové délky od 390 nm do 770 nm. Vznik elektromagnetických vln (záření): 1. při pohybu elektricky nabitých částic s nenulovým zrychlením
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Základy parametrického modelování Skicovací nástroje
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Název: Téma: Autor: Inovace a zkvalitnění výuky prostřednictvím ICT Základy parametrického modelování Skicovací nástroje
Monochromatické zobrazování
 Monochromatické zobrazování 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Mono 2015 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 27 Vnímání šedých odstínů
Monochromatické zobrazování 1995-2015 Josef Pelikán CGG MFF UK Praha pepca@cgg.mff.cuni.cz http://cgg.mff.cuni.cz/~pepca/ Mono 2015 Josef Pelikán, http://cgg.mff.cuni.cz/~pepca 1 / 27 Vnímání šedých odstínů
12 Metody snižování barevného prostoru
 12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
12 Metody snižování barevného prostoru Studijní cíl Tento blok je věnován základním metodám pro snižování barevného rozsahu pro rastrové obrázky. Postupně zde jsou vysvětleny důvody k použití těchto algoritmů
Základy počítačové grafiky
 Gymnázium Petra Bezruče, příspěvková organizace Vrchlického, Frýdek-Místek Projekt Využití ICT ve výuce na gymnáziích, registrační číslo projektu CZ.1.07/1.1.07/02.0030 Základy počítačové grafiky Metodický
Gymnázium Petra Bezruče, příspěvková organizace Vrchlického, Frýdek-Místek Projekt Využití ICT ve výuce na gymnáziích, registrační číslo projektu CZ.1.07/1.1.07/02.0030 Základy počítačové grafiky Metodický
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 Elektronická podpora zkvalitnění výuky CZ.1.07 Vzděláním pro konkurenceschopnost
 Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence schopnost, který je spolufinancován
Registrační číslo projektu: CZ.1.07/1.5.00/34.0553 CZ.1.07 Vzděláním pro konkurenceschopnost Projekt je realizován v rámci Operačního programu Vzdělávání pro konkurence schopnost, který je spolufinancován
(15) Výstupní zařízení
 (15) Výstupní zařízení Osnova 1. Panely LCD, plasmová zobrazovače, projektory 1. Připojení 2. LCD monitory 3. Plasmový displej 4. Dataprojektor 2. Tiskárny 1. Kvalita tisku, rozlišení (DPI), připojení
(15) Výstupní zařízení Osnova 1. Panely LCD, plasmová zobrazovače, projektory 1. Připojení 2. LCD monitory 3. Plasmový displej 4. Dataprojektor 2. Tiskárny 1. Kvalita tisku, rozlišení (DPI), připojení
Teorie barev. 1. Barvený model. 2. Gamut. 3. Barevný prostor. Barevný prostor různých zařízení
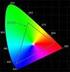 Teorie barev 1. Barvený model Barevný model představuje metodu (obvykle číselnou) popisu barev. Různé barevné modely popisují barvy, které vidíme a se kterými pracujeme v digitálních obrazech a při jejich
Teorie barev 1. Barvený model Barevný model představuje metodu (obvykle číselnou) popisu barev. Různé barevné modely popisují barvy, které vidíme a se kterými pracujeme v digitálních obrazech a při jejich
PROGRAMY PRO GIS. Formovat/formulovat problém pro aplikaci v počítači. Fungování GIS programů na základní úrovni - "uvažovat" jako počítač
 PROGRAMY PRO GIS Formovat/formulovat problém pro aplikaci v počítači Fungování GIS programů na základní úrovni - "uvažovat" jako počítač Jak počítače řeší problémy procesor central processing unit - CPU
PROGRAMY PRO GIS Formovat/formulovat problém pro aplikaci v počítači Fungování GIS programů na základní úrovni - "uvažovat" jako počítač Jak počítače řeší problémy procesor central processing unit - CPU
Programování v jazyku LOGO - úvod
 Programování v jazyku LOGO - úvod Programovací jazyk LOGO je určen pro výuku algoritmizace především pro děti školou povinné. Programovací jazyk pracuje v grafickém prostředí, přičemž jednou z jeho podstatných
Programování v jazyku LOGO - úvod Programovací jazyk LOGO je určen pro výuku algoritmizace především pro děti školou povinné. Programovací jazyk pracuje v grafickém prostředí, přičemž jednou z jeho podstatných
9 Prostorová grafika a modelování těles
 9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
9 Prostorová grafika a modelování těles Studijní cíl Tento blok je věnován základům 3D grafiky. Jedná se především o vysvětlení principů vytváření modelů 3D objektů, jejich reprezentace v paměti počítače.
Programátorská dokumentace
 Programátorská dokumentace Požadavky Cílem tohoto programu bylo představit barevné systémy, zejména převody mezi nejpoužívanějšími z nich. Zároveň bylo úkolem naprogramovat jejich demonstraci. Pro realizaci
Programátorská dokumentace Požadavky Cílem tohoto programu bylo představit barevné systémy, zejména převody mezi nejpoužívanějšími z nich. Zároveň bylo úkolem naprogramovat jejich demonstraci. Pro realizaci
Čtvrtek 8. prosince. Pascal - opakování základů. Struktura programu:
 Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
2D grafika. Jak pracuje grafik s 2D daty Fotografie Statické záběry Záběry s pohybem kamery PC animace. Počítačová grafika, 2D grafika 2
 2D grafika Jak pracuje grafik s 2D daty Fotografie Statické záběry Záběry s pohybem kamery PC animace Počítačová grafika, 2D grafika 2 2D grafika PC pracuje s daným počtem pixelů s 3 (4) kanály barev (RGB
2D grafika Jak pracuje grafik s 2D daty Fotografie Statické záběry Záběry s pohybem kamery PC animace Počítačová grafika, 2D grafika 2 2D grafika PC pracuje s daným počtem pixelů s 3 (4) kanály barev (RGB
GIS Geografické informační systémy
 GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
GIS Geografické informační systémy Obsah přednášky Prostorové vektorové modely Špagetový model Topologický model Převody geometrií Vektorový model Reprezentuje reálný svět po jednotlivých složkách popisu
Bitmapová grafika: Vrstvy - interakce (režimy prolnutí)
 VY_32_INOVACE_PG3108 ; Mgr. Pavel Hauer ; 5/2012; 1.ročník; bitmapová grafika, Počítačová grafika; názorná pomůcka pro výuku, opakování, doplnění látky Bitmapová grafika: Vrstvy - interakce (režimy prolnutí)
VY_32_INOVACE_PG3108 ; Mgr. Pavel Hauer ; 5/2012; 1.ročník; bitmapová grafika, Počítačová grafika; názorná pomůcka pro výuku, opakování, doplnění látky Bitmapová grafika: Vrstvy - interakce (režimy prolnutí)
